同济大学数据库作业lab9

合集下载

file_5174fb699d910同济大学高等数学英语版

9) If F ( x) is an antiderivative of f ( x) , C is any constant, then _B___ is correct. A. F ( x) = C ∫ f ( x)dx C. F '( x) = f ( x) +C B. F ( x) = ∫ f ( x)dx
If f ( x) = e x , then
∫
f '(ln x) dx = _|x|+C___________. x
d2 f 1 −2sin x = − + f ( x) ln(cos x) + tan x , then 7) = 2 2 dx cos x cos3 x
If F ( x), f ( x), g ( x), h( x) are continuous in (−∞, ∞) . g ( x) ≤ f ( x) ≤ h( x) with
Increasing intervals: ( 5)
3 + 33 −3 + 33 , 0 ), ( , +∞) 4 4
= we have: a)
dy dt
(3 marks) Write out the concave up and concave down intervals of f ( x)
∫ f ( x)dx∫ g ( x)dx < 0
∫
b
a
f ( x)dx ∫ g ( x)dx < 0
a
b
2008-2009 学年第一学期《高等数学 D（英语）》期末考试试卷（A 卷）--2
2. Fill in the blanks (10 marks)
1)

同济大学数据库作业lab7,8

同济大学《数据库技术及应用》实验报告实验报告题目：建立与数据库的链接和基于绑定的数据库访问姓名：学号：年级：专业：指导教师：日期： 2014 年 11 月 16 日一．实验目的1.掌握数据库访问模型的主要对象和功能2.掌握SQL和数据库的链接方法3.学习绑定对象的操作方法二．实验内容（实验题目+运行界面截图+实现代码）1.掌握前台和SqlServer后台的链接方法Imports Class Form1Private Sub Form1_Load(sender As Object, e As EventArgs) HandlesDim myconn As New SqlConnection("database=university;data source=jd43\SQLEXPRESS; integrated security=true")Dim mysql As String = "select * from student"Dim myadapter As New SqlDataAdapter(mysql, myconn)Dim mydataset As New DataSet(mydataset, "student")= (0)End SubEnd Class2.在university上用完成如下界面Imports Class Form2Private Sub Form2_Load(sender As Object, e As EventArgs) HandlesDim myconn As New SqlConnection("database=university;data source=jd43\SQLEXPRESS; integrated security=true")Dim mysql As String = "select as '学号',sname as '姓名',count(secnum) as '选修课程门数',avg(score) as '平均成绩',sum(1-score/60) as '不及格门数' from student,sc where = group by ,sname"Dim myadapter As New SqlDataAdapter(mysql, myconn)Dim mydataset As New DataSet(mydataset, "student")= (0)End SubEnd Class3.建立university和student的浏览界面Imports Class Form1Dim mybind As New BindingSourceDim mysql As String = "select * from student"Dim myconn As New SqlConnection("database=university;data source=jd43\SQLEXPRESS;integrated security=true")Dim myadapter As New SqlDataAdapter(mysql, myconn)Dim mydataset As New DataSetPrivate Sub退出系统ToolStripMenuItem_Click(sender As Object, e As EventArgs) Handles退出系统EndEnd SubPrivate Sub Form1_Load(sender As Object, e As EventArgs) Handles(mydataset, "student")= mydataset= "student"Binding("text", mybind, "snum", True))Binding("text", mybind, "sname", True))Binding("text", mybind, "sex", True))Binding("text", mybind, "dept", True))Binding("text", mybind, "birthday", True))End SubPrivate Sub Button4_Click(sender As Object, e As EventArgs) Handles ()End SubPrivate Sub Button5_Click(sender As Object, e As EventArgs) Handles ()End SubPrivate Sub Button6_Click(sender As Object, e As EventArgs) Handles ()End SubPrivate Sub Button7_Click(sender As Object, e As EventArgs) Handles ()End SubPrivate Sub Button1_Click(sender As Object, e As EventArgs) Handles ()End SubPrivate Sub Button2_Click(sender As Object, e As EventArgs) Handles ()End SubPrivate Sub Button3_Click(sender As Object, e As EventArgs) Handles ()()Dim cm As New SqlCommandBuilder(myadapter)(0))End SubEnd Class4.完成学生成绩浏览功能的设计Imports Class Form2Dim mybind As New BindingSourceDim mysql As String = "select * from shiyan8"Dim myconn As New SqlConnection("database=university;data source=jd43\SQLEXPRESS;integrated security=true")Dim myadapter As New SqlDataAdapter(mysql, myconn)Dim mydataset As New DataSetPrivate Sub Form2_Load(sender As Object, e As EventArgs) Handles(mydataset, "shiyan8")= mydataset= "shiyan8"Binding("text", mybind, "snum", True))Binding("text", mybind, "sname", True))Binding("text", mybind, "cname", True))Binding("text", mybind, "score", True))End SubPrivate Sub Button1_Click(sender As Object, e As EventArgs) Handles()End SubPrivate Sub Button2_Click(sender As Object, e As EventArgs) Handles()End SubPrivate Sub Button3_Click(sender As Object, e As EventArgs) Handles()End SubPrivate Sub Button4_Click(sender As Object, e As EventArgs) Handles()End SubEnd Class三．实验体会或收获（有感而发，没有体会也可以不写）在用代码进行数据库的链接时发现data source后不能加（local），否则总是显示无法访问。

同济大学数据库-实验一答案

同济⼤学数据库-实验⼀答案实验⼀讲解By Zhu Jing12主窗体MainForm 运⾏界⾯0.主窗体项⽬解决⽅案资源管理器主窗体主要属性设置：IsMdiContainer为True（设置主窗体为多⽂档界⾯容器）；WindowState为Maximized(运⾏时最⼤化)3主窗体代码：Public Class MainFormApplication.Exit()End SubPrivate Sub 实验1ToolStripMenuItem_Click(…) …Dim f1 As New shiyan1()f1.MdiParent = Mef1.Show()End SubPrivate Sub 实验2ToolStripMenuItem_Click(…) …Dim f2 As New shiyan2()f2.MdiParent = Mef2.Show()End Sub4Private Sub 实验3ToolStripMenuItem_Click(…)…Dim f3 As New shiyan3()f3.MdiParent = Mef3.Show()End SubPrivate Sub 实验4ToolStripMenuItem_Click(…) …Dim f4 As New shiyan4()f4.MdiParent = Mef4.Show()End SubPrivate Sub 实验5ToolStripMenuItem_Click(...) …Dim f5 As New shiyan5()f5.MdiParent = Mef5.Show()End Sub.5Private Sub 实验6ToolStripMenuItem_Click(…) …Dim f6 As New shiyan6()f6.MdiParent = Mef6.Show()End SubDim f7_1As New shiyan7_1()f7_1.Show()End SubPrivate Sub 实验8ToolStripMenuItem_Click(…) …Dim f8 As New shiyan8()f8.MdiParent = Mef8.Show()End SubEnd Class61. 实验1：⽂本框练习7实验1代码：Public Class shiyan1Private Sub Button1_Click(…) …'⾪书按钮TextBox1.Font = New Font("⾪书", 25, FontStyle.Bold Or FontStyle.Italic) End Sub Private Sub Button2_Click(…) …'幼圆按钮TextBox1.Font = New Font("幼圆", 18, FontStyle.Italic Or FontStyle.Underline) End Sub 8Private Sub Button3_Click(…) …'复制按钮TextBox2.Text = TextBox1.SelectedTextTextBox2.Font = TextBox1.FontEnd SubEnd Class92. 实验2：求鸡和兔的个数10实验2代码：Public Class shiyan2Private Sub TextBox2_KeyDown(…) …If e.KeyCode = Keys.Enter ThenDim x, y As Integer 'x--鸡数，y--兔数If Not IsNumeric(TextBox1.Text.Trim) ThenMessageBox.Show("'头数'必须输⼊数字", "警告")TextBox1.Text = ""TextBox3.Text = ""Exit SubEnd If11If Not IsNumeric(TextBox2.Text.Trim) Then MessageBox.Show("'脚数'必须输⼊数字", "警告") Me.TextBox2.Text = "" Me.TextBox3.Text = ""Exit SubEnd IfIf Val(TextBox2.Text.trim) Mod 2 <> 0 Then MessageBox.Show("脚必须是双数", "警告")TextBox2.Focus()Exit SubEnd If12x = Val(4 * TextBox1.Text -TextBox2.Text) / 2y = Val(TextBox2.Text -2 * TextBox1.Text) / 2If x < 0 Or y < 0 Then '若头数是负数MsgBox("荒唐解，请重新输⼊！")Me.TextBox3.Text = ""ElseTextBox3.Text = x & " " & yEnd IfEnd IfEnd SubEnd Class13143. 实验3：求解1元2次⽅程的根实验3运⾏界⾯实验3代码：Imports System.MathPublic Class shiyan3Dim a, b, c, disc, realpart, imagpart As DoublePrivate Sub Button1_Click(…) …'计算按钮If String.IsNullOrEmpty(TextBox1.Text.Trim()) And String.IsNullOrEmpty(TextBox2.Text.Trim()) Then MsgBox("请为a,b赋值")Exit SubEnd IfIf TextBox1.Text.Trim() = "" ThenTextBox1.Text = 0End If15If TextBox2.Text.Trim() = "" ThenTextBox2.Text = 0End IfIf TextBox3.Text.Trim() = "" ThenTextBox3.Text = 0End Ifa = TextBox1.Text.Trimb = TextBox2.Text.Trimc = TextBox3.Text.TrimIf a = 0 Then 'a为0时If b<> 0 Then 'a为0,b不为0时TextBox4.Text = Round(-c / b, 2)TextBox5.Text = ""GroupBox1.Text = "不是2次⽅程,只有⼀个根" Else 'a,b都为0时MsgBox("a,b不能同时为0")End If16Elsedisc = b * b -4 * a * cIf disc = 0 Then ' disc为0时GroupBox1.Text = "有两个相同的实根" TextBox4.Text = Round(-b / (2 * a), 2) TextBox5.Text = Round(-b / (2 * a), 2) ElseIf disc > 0 Then ' disc ⼤于0时GroupBox1.Text = "有两个不同的实根" TextBox4.Text =Round((-b + Sqrt(disc)) / (2 * a), 2) TextBox5.Text =Round((-b -Sqrt(disc)) / (2 * a), 2)Else ' disc⼩于0时GroupBox1.Text = "有两个不同的虚根" realpart = Round(-b / (2 * a), 2)imagpart = Round(Sqrt(-disc) / (2 * a), 2)17TextBox4.Text = realpart & "+" & imagpart & "i" TextBox5.Text = realpart & "-" & imagpart & "i" End IfEnd IfEnd SubPrivate Sub Button2_Click(…) …'结束按钮Me.Close()End SubEnd Class18194. 实验4：⽣成随机数实验4运⾏界⾯。

同济大学案例分析样题及答案

gist数据要素构成要素类别要素名称描述网络要素路网道路路段道路网络中心线及其属性节点路段交叉点小区连接点等拓扑关系路段的连接路口转向车道转向等公交公交站点公交车站点公交线路线路信息动态分段映射分段映射及换乘信息交通小区小区连接线连接小区质心和路段的线小区多边形为交通分析而划分的多边形区域点要素检测点检测车道流量scats数据检测进口道流量及交叉口相位非路边停车场位于路边的动态停车点泊位景点著名风景点出租车扬招点路段上出租车搭载乘客的服务点重要地标省政府及市政府等行政机构自行车服务点路段上提供公共自行车的服务点生活服务poi售票点航空火车和汽车加油站和大型超市线要素铁路铁路网络中心线面要素行政区域按行政管理划分的界线公园绿地水系河流湖泊等重大基础设施地标公共机构医院商厦等2数据关系该数据库主要包括路网数据集公交数据集小区数据集和兴趣点数据集
1) 地理地图（基础地理信息数据）：境界、水系、交通路网、居民地、地形、植被、地貌、工业设施。测绘部门，再编辑加工 2) 遥感影像：购买。纠正、再编辑加工 3) 专题数据：绿地、旅游景点、宾馆酒店等企事业单位的基本信息以及居民区、街巷、高层建筑、行政区划、社区、居委会、有地名意义的单位等机关、企事业单位的信息。规划管理部门、野外调查。编辑加工。 4) 辅助数据：道路名称、地名。民政、规划和土地管理部门。
6) 扩展事件类专门用于对未包括在上述大类中而又确需分类管理的事件的扩充。 3、技术指标按照建设部相关的技术规范，分类调查城市部件，调查应覆盖规定范围内的所有城市部件，提交的数据成果文件格式应为常用的空间数据格式。城市部件的基本属性信息内容应符合规范，能说明部件的基本特性；对于详细属性（附加属性）可向相关市政部门收集资料。地理编码库中的信息根据普查的对象确定，并要求能唯一标识普查对象，地理编码信息应完整规范。 a) 部件定位精度要求对不同类别的部件，给出不同的精度指标，保证所有部件定位精度符合建库的要求。每平方公里内位置误差超出允许范围的个数与该范围内部件总数之比应不超过 3%，超过为不合格。 b) 部件普查遗漏允许指标每平方公里内遗漏个数不得超出总数的 3%，否则为不合格。 c) 部件普查属性错误允许指标部件属性中有一个属性项错误即认为该部件的属性错误，每平方公里内部件属性错误个数不得超出部件总数的 3%，否则为不合格。 d) 地理编码普查错误允许指标地理编码普查中所属街道和小区属性错误每平方公里不得超出总数的 3%，门牌号错误不等超出 3%，超出任何一项指标均为不合格。 e) 地理编码普查遗漏允许指标每平方公里内遗漏个数不得超出总数的 3%，否则为不合格。（3）简述基础数据处理与建库的内容和主要技术流程。答： 1) 数据处理：数据格式统一、数据编码统一、数据编码统一、数据内容编辑修改 2) 数据建库：数据整理、数据处理、数据质量检查、数据预入库、数据最终入库、数据库更新、数据历史数据库建立、数据库元数据表达

工程数学线性代数(同济大学第六版)课后习题答案(全)

第一章行列式1? 利用对角线法则计算下列三阶行列式?(1)381141102---?解 381141102---解解 (4)y x y x x y x y yx y x +++?解 yx y x x y x y yx y x +++?x (x ?y )y ?yx (x ?y )?(x ?y )yx ?y 3?(x ?y )3?x 3 ?3xy (x ?y )?y 3?3x 2 y ?x 3?y 3?x 3 ??2(x 3?y 3)?2?按自然数从小到大为标准次序?求下列各排列的逆序数?(1)1 2 3 4?解逆序数为0(2)4 1 3 2?解逆序数为4? 41? 43? 42? 32?(3)3 4 2 1?解逆序数为5? 3 2? 3 1? 4 2? 4 1, 2 1?解解解4 2(1个)6 2? 6 4(2个)??????(2n)2? (2n)4? (2n)6????? (2n)(2n?2) (n?1个) 3?写出四阶行列式中含有因子a11a23的项?解含因子a11a23的项的一般形式为(?1)t a11a23a3r a4s?其中rs 是2和4构成的排列? 这种排列共有两个? 即24和42? 所以含因子a 11a 23的项分别是(?1)t a 11a 23a 32a 44?(?1)1a 11a 23a 32a 44??a 11a 23a 32a 44? (?1)t a 11a 23a 34a 42?(?1)2a 11a 23a 34a 42?a 11a 23a 34a 42? 4? 计算下列各行列式?(1)71100251020214214? 解解解 ef cf bf de cd bd ae ac ab ---e c b e c b ec b adf ---=abcdef adfbce 4111111111=---=?(4)dc b a 100110011001---?解 d c b a 100110011001---dc b aab ar r 10011001101021---++=====cdad ab +-+--=+111)1)(1(23?abcd ?ab ?cd ?ad ?1? 5? 证明:(1)1112222b b a a b ab a +?(a ?b )3;5232125232125232125232122222++++++++++++=d d d d c c c c b b b b a a a a (c 4?c 3? c 3?c 2得) 022122212221222122222=++++=d d c c b b a a ?(4)444422221111d c b a d c b a d c b a ?(a ?b )(a ?c )(a ?d )(b ?c )(b ?d )(c ?d )(a ?b ?c ?d ); 证明=(a ?b )(a ?c )(a ?d )(b ?c )(b ?d )(c ?d )(a ?b ?c ?d )?当则D n 6?翻转? D 1证明D 1 证明因为D ?det(a ij )? 所以 D D n n n n 2)1()1()2( 21)1()1(--+-+⋅⋅⋅++-=-=?同理可证 nnn n n n a a a a D ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-=- )1(11112)1(2D D n n T n n 2)1(2)1()1()1(---=-=? D D D D D n n n n n n n n =-=--=-=----)1(2)1(2)1(22)1(3)1()1()1()1(?7? 计算下列各行列式(D k 为k 阶行列式)?(1)aaD n 11⋅⋅⋅=, 其中对角线上元素都是a ? 未写出的元素都是0?解D n=( 解 (3)111 1 )( )1()( )1(1111⋅⋅⋅-⋅⋅⋅⋅⋅⋅⋅⋅⋅-⋅⋅⋅⋅⋅⋅-⋅⋅⋅--⋅⋅⋅-=---+n a a a n a a a n a a a D n n n n n n n ; 解根据第6题结果? 有此行列式为范德蒙德行列式? ∏≥>≥+-=11)(j i n j i ?(4)n nnnn d c d c b a b a D ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=11112;解于是而所以 (5) D ?det(a ij )? 其中a ij ?|i ?j |; 解 a ij ?|i ?j |??(?1)n ?1(n ?1)2n ?2?(6)nn a a a D +⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅+⋅⋅⋅+=1 11 1 1111121, 其中a 1a 2 ? ? ? a n?0?解)11)((121∑=+=ni in a a a a ? 8? 用克莱姆法则解下列方程组?(1)⎪⎩⎪⎨⎧=+++-=----=+-+=+++01123253224254321432143214321x x x x x x x x x x x x x x x x ?解因为所以解 150751001651000651000650000611==D ? 114551010651000650000601000152-==D ?70351100650000601000051001653==D ? 39551000601000051000651010654-==D ? 2121105100065100651100655==D ? 所以9? 解令于是? 10 解 ?(1??)3?2(1??)2???3? 令D ?0? 得??0? ??2或??3?于是? 当??0? ??2或??3时? 该齐次线性方程组有非零解?第二章矩阵及其运算1? 已知线性变换?⎪⎩⎪⎨⎧++=++=++=3213321232113235322y y y x y y y x y y y x ? 求从变量x 1? x 2? x 3到变量y 1? y 2? y 3的线性变换? 解由已知?⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛221321323513122y y y x x x ?故 2? 求从z 1 3? 设⎪⎪⎭⎫ ⎝⎛--=111111111A ? ⎪⎪⎭⎫⎝⎛--=150421321B ? 求3AB ?2A 及A T B ?解 ⎪⎪⎭⎫⎝⎛---⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛--=-1111111112150421321111111111323A AB⎪⎪⎭⎫⎝⎛----=⎪⎪⎭⎫ ⎝⎛---⎪⎪⎭⎫ ⎝⎛-=2294201722213211111111120926508503?⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛--=092650850150421321111111111B A T ? 4? 计算下列乘积?(1)⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-127075321134? 解 ⎪⎫ ⎛⎪⎫ ⎛-27321134⎪⎫ ⎛⨯+⨯-+⨯⨯+⨯+⨯=132)2(71112374⎪⎫ ⎛=635? ⎭⎝-204 (5)⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛321332313232212131211321)(x x x a a a a a a a a a x x x ? 解?(a 11x 1?a 12x 2?a 13x 3 a 12x 1?a 22x 2?a 23x 3 a 13x 1?a 23x 2?a 33x 3)⎪⎪⎭⎫ ⎝⎛321x x x322331132112233322222111222x x a x x a x x a x a x a x a +++++=?5? 设⎪⎭⎫ ⎝⎛=3121A ? ⎪⎭⎫ ⎝⎛=2101B ? 问? (1)AB ?BA 吗?解 AB ?BA ?因为⎪⎭⎫ ⎝⎛=6443AB ? ⎪⎭⎫ ⎝⎛=8321BA ? 所以AB ?BA ? 222但所以(A 而故(A ?B )(A ?B )?A 2?B 2? 6? 举反列说明下列命题是错误的?(1)若A 2?0? 则A ?0?解取⎪⎭⎫ ⎝⎛=0010A ? 则A 2?0? 但A ?0? (2)若A 2?A ? 则A ?0或A ?E ?解取⎪⎭⎫ ⎝⎛=0011A ? 则A 2?A ? 但A ?0且A ?E ? (3)若AX ?AY ? 且A ?0? 则X ?Y ?解取 ⎪⎭⎫ ⎝⎛=0001A ? ⎪⎭⎫ ⎝⎛-=1111X ? ⎪⎭⎫ ⎝⎛=1011Y ? 则AX ?AY ? 且A ?0? 但X ?Y ?7? 8? ⎪⎪⎭⎫ ⎝⎛=⋅=43423434004064λλλλλλA A A ? ⎪⎪⎭⎫ ⎝⎛=⋅=545345450050105λλλλλλA A A ? ? ? ? ? ? ??⎝⎛=k A k k k k k k k k k k λλλλλλ0002)1(121----⎪⎪⎪⎭⎫ ? 用数学归纳法证明?当k ?2时? 显然成立?假设k 时成立，则k ?1时，⎫⎛++--+111)1()1(k k k k k k λλλ 9?? 从而B AB ?BA (AB )T ?(BA )T ?A T B T ?AB ?即AB 是对称矩阵?必要性? 因为A T ?A ? B T ?B ? 且(AB )T ?AB ? 所以AB ?(AB )T ?B T A T ?BA ?11? 求下列矩阵的逆矩阵?(1)⎪⎭⎫ ⎝⎛5221?解 ⎪⎭⎫ ⎝⎛=5221A ? |A |?1? 故A ?1存在? 因为 ⎪⎭⎫ ⎝⎛--=⎪⎭⎫ ⎝⎛=1225*22122111A A A A A ? 故 *||11A A A =-⎪⎭⎫ ⎝⎛--=1225? (2)⎪⎭⎫ ⎝⎛-θθθθcos sin sin cos ?所以所以 (4)⎪⎪⎪⎭⎫ ⎝⎛n a a a 0021(a 1a 2? ? ?a n ?0) ?解 ⎪⎪⎪⎭⎫ ⎝⎛=n a a a A 0021? 由对角矩阵的性质知⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=-n a a a A 10011211 ? 12? 解下列矩阵方程?(1)⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛12643152X ?(4)⎪⎪⎭⎝--=⎪⎪⎭ ⎝⎪⎪⎭ ⎝021102010100100001X ? 解 11010100001021102341100001010--⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛---⎪⎪⎭⎫ ⎝⎛=X ⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛---⎪⎪⎭⎫ ⎝⎛=010100001021102341100001010⎪⎪⎭⎫ ⎝⎛---=201431012? 13? 利用逆矩阵解下列线性方程组?(1)⎪⎩⎪⎨⎧=++=++=++3532522132321321321x x x x x x x x x ? 解方程组可表示为⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛321153522321321x x x ? 故 ⎪⎫ ⎛⎪⎫ ⎛⎪⎫ ⎛⎪⎫ ⎛-1132111x 故故有证明因为A k ?O ? 所以E ?A k ?E ? 又因为E ?A k ?(E ?A )(E ?A ?A 2?? ? ??A k ?1)?所以 (E ?A )(E ?A ?A 2?? ? ??A k ?1)?E ?由定理2推论知(E ?A )可逆? 且(E ?A )?1?E ?A ?A 2?? ? ??A k ?1?证明一方面? 有E ?(E ?A )?1(E ?A )?另一方面? 由A k ?O ? 有E ?(E ?A )?(A ?A 2)?A 2?? ? ??A k ?1?(A k ?1?A k )?(E ?A ?A 2?? ? ??A k ?1)(E ?A )?故 (E ?A )?1(E ?A )?(E ?A ?A 2?? ? ??A k ?1)(E ?A )?两端同时右乘(E ?A )?1? 就有(E ?A )?1(E ?A )?E ?A ?A 2?? ? ??A k ?1?15? 设方阵A 满足A 2?A ?2E ?O ? 证明A 及A ?2E 都可逆? 并求A ?1及(A ?2E )或或即故 |A |?0?所以A 可逆? 而A ?2E ?A 2? |A ?2E |?|A 2|?|A |2?0? 故A ?2E 也可逆?由 A 2?A ?2E ?O ?A (A ?E )?2E?A ?1A (A ?E )?2A ?1E ?)(211E A A -=-? 又由 A 2?A ?2E ?O ?(A ?2E )A ?3(A ?2E )??4E? (A ?2E )(A ?3E )??4 E ?所以 (A ?2E )?1(A ?2E )(A ?3E )??4(A ?2 E )?1?)3(41)2(1A E E A -=+-? 16? 设A 为3阶矩阵? 21||=A ? 求|(2A )?1?5A *|? 解因为*||11A A A =-? 所以 ?|?2A ?1|?(?2)3|A ?1|??8|A |?1??8?2??16??1?1从而又A 所以A *?O ? 这与|A *|?0矛盾，故当|A |?0时? 有|A *|?0?(2)由于*||11A A A =-? 则AA *?|A |E ? 取行列式得到 |A ||A *|?|A |n ?若|A |?0? 则|A *|?|A |n ?1?若|A |?0? 由(1)知|A *|?0? 此时命题也成立?因此|A *|?|A |n ?1?19? 设⎪⎪⎭⎫ ⎝⎛-=321011330A ? AB ?A ?2B ? 求B ? 解由AB ?A ?2E 可得(A ?2E )B ?A ? 故⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛---=-=--321011330121011332)2(11A E A B ⎪⎪⎭⎫ ⎝⎛-=011321330? 20? 设⎪⎫ ⎛=020101A ? 且AB ?E ?A 2?B ? 求B ? 即 ??8(?2E ?2A )?1?4(E ?A )?1?4[diag(2? ?1? 2)]?1?2diag(1? ?2? 1)?22? 已知矩阵A 的伴随阵⎪⎪⎪⎭⎫ ⎝⎛-=8030010100100001*A ?且ABA ?1?BA ?1?3E ? 求B ?解由|A *|?|A |3?8? 得|A |?2?由ABA ?1?BA ?1?3E 得AB ?B ?3A ?B ?3(A ?E )?1A ?3[A (E ?A ?1)]?1A⎪⎪⎫ ⎛=⎪⎪⎫ ⎛-=-06060060000601010010000161? 而故求?(A ) ?diag(1?1?58)[diag(5?5?5)?diag(?6?6?30)?diag(1?1?25)]?diag(1?1?58)diag(12?0?0)?12diag(1?0?0)??(A )?P ?(?)P ?1⎪⎪⎭⎫ ⎝⎛=1111111114? 25? 设矩阵A 、B 及A ?B 都可逆? 证明A ?1?B ?1也可逆? 并求其逆阵? 证明因为A ?1(A ?B )B ?1?B ?1?A ?1?A ?1?B ?1?而A ?1(A ?B )B ?1是三个可逆矩阵的乘积? 所以A ?1(A ?B )B ?1可逆? 即A ?1?B ?1可逆? (A ?1?B ?1)?1?[A ?1(A ?B )B ?1]?1?B (A ?B )?1A ?26? 计算⎪⎪⎪⎭⎫ ⎝⎛---⎪⎪⎪⎭⎫ ⎝⎛30003200121013013000120010100121? 解设⎪⎭⎫ ⎝⎛=10211A ? ⎪⎭⎫ ⎝⎛=30122A ? ⎪⎭⎫ ⎝⎛-=12131B ? ⎪⎭⎫ ⎝⎛--=30322B ? 则而所以即而 01111|||||||| ==D C B A ? 故 |||||||| D C B A D C B A ≠? 28? 设⎪⎪⎪⎭⎫ ⎝⎛-=22023443O O A ? 求|A 8|及A 4?解令⎪⎭⎫ ⎝⎛-=34431A ? ⎪⎭⎫ ⎝⎛=22022A ? 则 ⎪⎭⎫ ⎝⎛=21A O O A A ? 故 8218⎪⎭⎫ ⎝⎛=A O O A A ⎪⎭⎫ ⎝⎛=8281A O O A ? 1682818281810||||||||||===A A A A A ? ⎫⎛405 所以解设⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛-43211D D D D B C O A ? 则 ⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛++=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛s n E O O E BD CD BD CD AD AD D D D D B C O A 4231214321? 由此得 ⎪⎩⎪⎨⎧=+=+==s n E BD CD O BD CD O AD E AD 423121?⎪⎩⎪⎨⎧=-===----14113211B D CA B D O D A D ?所以 ⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-----11111B CA B O A BC O A ? 30? 求下列矩阵的逆阵?(1)⎪⎪⎪⎭⎫ ⎝⎛2500380000120025? 解设⎪⎭⎫ ⎝⎛=1225A ? ⎪⎭⎫ ⎝⎛=2538B ? 则于是 1? 把下列矩阵化为行最简形矩阵?(1)⎪⎪⎭⎫ ⎝⎛--340313021201? 解 ⎪⎪⎭⎫ ⎝⎛--340313021201(下一步? r 2?(?2)r 1? r 3?(?3)r 1? )~⎪⎪⎭⎫ ⎝⎛---020*********(下一步? r 2?(?1)? r 3?(?2)? ) ~⎪⎪⎭⎫ ⎝⎛--010*********(下一步? r 3?r 2? ) ~⎪⎪⎭⎫ ⎝⎛--300031001201(下一步? r 3?3? ) ~⎪⎪⎭⎫ ⎝⎛000031005010? (3)⎪⎪⎪⎭⎫ ⎝⎛---------12433023221453334311?解 ⎪⎪⎪⎭⎫ ⎝⎛---------12433023221453334311(下一步? r 2?3r 1? r 3?2r 1? r 4?3r 1? ) ~⎪⎪⎪⎭⎫ ⎝⎛--------1010500663008840034311(下一步? r 2?(?4)? r 3?(?3) ? r 4?(?5)? ) ⎪⎫ ⎛---2210034311 ⎭⎝41000 ~⎪⎪⎪⎭⎫ ⎝⎛----00000410001111020201(下一步? r 2?r 3? ) ~⎪⎪⎪⎭⎫ ⎝⎛--00000410003011020201?2? 设⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛987654321100010101100001010A ? 求A ? 解 ⎪⎪⎭⎫ ⎝⎛100001010是初等矩阵E (1? 2)? 其逆矩阵就是其本身? ⎪⎪⎭⎫ ⎝⎛100010101是初等矩阵E (1? 2(1))? 其逆矩阵是 3? 故逆矩阵为⎪⎪⎪⎪⎭⎫ ⎝⎛----21021211233267? (2)⎪⎪⎪⎭⎫ ⎝⎛-----1210232112201023?解 ⎪⎪⎪⎭⎫ ⎝⎛-----10000100001000011210232112201023 ~⎪⎪⎪⎭⎫ ⎝⎛----00100301100001001220594012102321 ⎪⎫ ⎛---01002321 4?⎪⎭ ⎝-113⎪⎭⎝-13 解因为⎪⎪⎭⎫ ⎝⎛----=132231 113122214) ,(B A ⎪⎪⎭⎫ ⎝⎛--412315210 100010001 ~r ? 所以 ⎪⎪⎭⎫ ⎝⎛--==-4123152101B A X ?(2)设⎪⎪⎭⎫ ⎝⎛---=433312120A ? ⎪⎭⎫ ⎝⎛-=132321B ? 求X 使XA ?B ? 解考虑A T X T ?B T ? 因为⎪⎪⎭⎫ ⎝⎛----=134313*********) ,(T T B A ⎪⎪⎭⎫ ⎝⎛---411007101042001 ~r ? 所以 ⎪⎫ ⎛--==-7142)(1TT T B A X ? 从而 5? 所以 6?r 阶子式?0的r 例如? ⎪⎪⎭⎫ ⎝⎛=010*********A ? R (A )?3? 0000是等于0的2阶子式? 010001000是等于0的3阶子式? 7? 从矩阵A 中划去一行得到矩阵B ? 问A ? B 的秩的关系怎样? 解 R (A )?R (B )?这是因为B 的非零子式必是A 的非零子式? 故A 的秩不会小于B 的秩? 8? 求作一个秩是4的方阵? 它的两个行向量是(1? 0? 1? 0? 0)? (1? ?1? 0? 0? 0)?解用已知向量容易构成一个有4个非零行的5阶下三角矩阵?⎪⎪⎪⎪⎫ ⎛-01000001010001100001? 9? (2)⎪⎪⎭⎫ ⎝⎛-------815073*********? 解 ⎪⎪⎭⎫ ⎝⎛-------815073*********(下一步? r 1?r 2? r 2?2r 1? r 3?7r 1? ) ~⎪⎭⎫ ⎝⎛------15273321059117014431(下一步? r 3?3r 2? )~⎪⎭⎫ ⎝⎛----0000059117014431? 矩阵的秩是2? 71223-=-是一个最高阶非零子式? (3)⎪⎪⎪⎭⎫ ⎝⎛---02301085235703273812?10? 设A 、B 都是m ?n 矩阵? 证明A ~B 的充分必要条件是R (A )?R (B )? 证明根据定理3? 必要性是成立的?充分性? 设R (A )?R (B )? 则A 与B 的标准形是相同的? 设A 与B 的标准形为D ? 则有A ~D ? D ~B ?由等价关系的传递性? 有A ~B ?11? 设⎪⎪⎭⎫ ⎝⎛----=32321321k k k A ? 问k 为何值? 可使 (1)R (A )?1? (2)R (A )?2? (3)R (A )?3?解 ⎪⎪⎭⎫ ⎝⎛----=32321321k k k A ⎪⎪⎭⎫ ⎝⎛+-----)2)(1(0011011 ~k k k k k r ?于是 ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎭⎫ ⎝⎛1343344321k x x x x (k 为任意常数)? (2)⎪⎩⎪⎨⎧=-++=--+=-++05105036302432143214321x x x x x x x x x x x x ? 解对系数矩阵A 进行初等行变换? 有A ?⎪⎪⎭⎫ ⎝⎛----5110531631121~⎪⎪⎭⎫ ⎝⎛-000001001021? 于是 ⎪⎩⎪⎨⎧===+-=4432242102x x x x x x x x ? 故方程组的解为⎫⎛⎫⎛-⎫⎛121x 于是 ⎪⎩==0043x x (4)⎪⎩⎪⎨⎧=++-=+-+=-+-=+-+03270161311402332075434321432143214321x x x x x x x x x x x x x x x x ? 解对系数矩阵A 进行初等行变换? 有A ?⎪⎪⎪⎭⎫ ⎝⎛-----3127161311423327543~⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--000000001720171910171317301?于是⎪⎪⎪⎨⎧=-=-=33432431172017191713173x x x x x x x x ? 于是R (2)⎪⎩⎪⎨-=+-=-+-=+-69413283542z y x z y x z y x ? 解对增广矩阵B 进行初等行变换? 有B ?⎪⎪⎪⎭⎫ ⎝⎛-----69141328354214132~⎪⎪⎪⎭⎫ ⎝⎛--0000000021101201?于是 ⎪⎩⎪⎨⎧=+=--=zz z y z x 212? 即 ⎪⎪⎭⎫ ⎝⎛-+⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛021112k z y x (k 为任意常数)? (3)⎪⎩⎪⎨⎧=--+=+-+=+-+12222412w z y x w z y x w z y x ?于是即 ⎪⎭ ⎝--25341⎭⎝00000于是 ⎪⎪⎩⎪⎪⎨⎧==--=++=w w z z w z y w z x 757975767171?即 ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-+⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-+⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛00757610797101757121k k w z y x (k 1? k 2为任意常数)? 14? 写出一个以为通解的齐次线性方程组?解根据已知? 可得或或 ⎩321 (1)有唯一解? (2)无解? (3)有无穷多个解?解 ⎪⎪⎭⎫ ⎝⎛=21111111λλλλλB ⎪⎭⎫ ⎝⎛+-+----22)1)(1()2)(1(00)1(11011 ~λλλλλλλλλλr? (1)要使方程组有唯一解? 必须R (A )?3? 因此当??1且???2时方程组有唯一解.(2)要使方程组无解? 必须R (A )?R (B )? 故(1??)(2??)?0? (1??)(??1)2?0?因此???2时? 方程组无解?(3)要使方程组有有无穷多个解? 必须R (A )?R (B )?3? 故(1??)(2??)?0? (1??)(??1)2?0?因此当??1时? 方程组有无穷多个解.当? 即 ⎭⎝⎭⎝⎭⎝013x 当???2时?⎪⎪⎭⎫ ⎝⎛-----=421121212112B ~⎪⎪⎭⎫ ⎝⎛--000021102101? 方程组解为⎩⎨⎧+=+=223231x x x x 或⎪⎩⎪⎨⎧=+=+=33323122x x x x x x ? 即 ⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛022111321k x x x (k 为任意常数)? 17? 设⎪⎩⎪⎨⎧--=-+--=--+=-+-1)5(4224)5(2122)2(321321321λλλλx x x x x x x x x ? 问??所以当??1时? 方程组有无穷多解?此时，增广矩阵为B ~⎪⎪⎭⎫ ⎝⎛-000000001221? 方程组的解为⎪⎩⎪⎨⎧==++-=3322321 1x x x x x x x ?或 ⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛00110201221321k k x x x (k 1? k 2为任意常数)? 18? 证明R (A )?1的充分必要条件是存在非零列向量a 及非零行向量b T ? 使A ?ab T ?证明必要性? 由R (A )?1知A 的标准形为)0 , ,0 ,1(01000001⋅⋅⋅⎪⎪⎫ ⎛=⎪⎪⎫ ⎛⋅⋅⋅⋅⋅⋅? ? 且A ? A )?1? 所以R (1)方程AX ?E m 有解的充分必要条件是R (A )?m ?证明由定理7? 方程AX ?E m 有解的充分必要条件是R (A )?R (A ? E m )?而| E m |是矩阵(A ? E m )的最高阶非零子式? 故R (A )?R (A ? E m )?m ? 因此? 方程AX ?E m 有解的充分必要条件是R (A )?m ?(2)方程YA ?E n 有解的充分必要条件是R (A )?n ?证明注意? 方程YA ?E n 有解的充分必要条件是A T Y T ?E n 有解? 由(1)A T Y T?E n有解的充分必要条件是R(A T)?n?因此，方程YA?E n有解的充分必要条件是R(A)?R(A T)?n?20?设A为m?n矩阵?证明?若AX?AY?且R(A)?n?则X?Y?证明由AX?AY?得A(X?Y)?O?因为R(A)?n?由定理9?方程A(X?Y)?O只有零解?即X?Y?O?也就是X?Y?第四章向量组的线性相关性1?T T T2?a2?(103?证明B知R(A)?R(A?B)?3?所以B组能由A组线性表示?由知R(B)?2?因为R(B)?R(B?A)?所以A组不能由B组线性表示?4?已知向量组A?a1?(0? 1? 1)T?a2?(1? 1? 0)T?B?b1?(?1? 0? 1)T?b2?(1? 2? 1)T? b3?(3? 2??1)T?证明A 组与B 组等价? 证明由⎪⎪⎭⎫⎝⎛-⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛--=000001122010311112201122010311011111122010311) ,(~~r r A B ?知R (B )?R (B ? A )?2? 显然在A 中有二阶非零子式? 故R (A )?2? 又R (A )?R (B ? A )?2? 所以R (A )?2? 从而R (A )?R (B )?R (A ? B )? 因此A 组与B 组等价? 5? ? 又由R (a 故a 4能由a a 2? a 3 6? 所以R (A )?2小于向量的个数? 从而所给向量组线性相关? (2)以所给向量为列向量的矩阵记为B ? 因为022200043012||≠=-=B ?所以R (B )?3等于向量的个数? 从而所给向量组线性相无关? 7? 问a 取什么值时下列向量组线性相关？ a 1?(a ? 1? 1)T ? a 2?(1? a ? ?1)T ? a 3?(1? ?1? a )T ?解以所给向量为列向量的矩阵记为A ? 由知? 当a ??1、0、1时? R (A )?3? 此时向量组线性相关?8? 设a 1? a 2线性无关? a 1?b ? a 2?b 线性相关? 求向量b 用a 1? a 2线性表示的表示式?解因为a 1?b ? a 2?b 线性相关? 故存在不全为零的数?1? ?2使 ?1(a 1?b )??2(a 2?b )?0? 1121λλλλλλλλλλλλ设=c 9 而a 1? 示?m 线性相关? 但a 1不能由a 2? ? ? ?? a m 线性表示? (2)若有不全为0的数?1? ?2? ? ? ?? ?m 使?1a 1? ? ? ? ??m a m ??1b 1? ? ? ? ??m b m ?0成立? 则a 1? a 2? ? ? ?? a m 线性相关, b 1? b 2? ? ? ?? b m 亦线性相关? 解有不全为零的数?1? ?2? ? ? ?? ?m 使?1a 1? ? ? ? ??m a m ??1b 1? ? ? ? ??m b m ?0?原式可化为?1(a1?b1)??????m(a m?b m)?0?取a1?e1??b1?a2?e2??b2?????a m?e m??b m?其中e1?e2?????e m为单位坐标向量?则上式成立?而a1?a2?????a m和b1?b2?????b m均线性无关?(3)若只有当?1??2??????m全为0时?等式?1a1??????m a m??1b1??????m b m?0才能成立?则a1?a2?????a m线性无关, b1?b2?????b m亦线性无关?解由于只有当?1??2??????m全为0时?等式成立?成立??但a1?0的数???1??2?11?设b1?a1?a2?b2?a2?a3? b3?a3?a4? b4?a4?a1?证明向量组b1?b2?b3?b4线性相关?证明由已知条件得a1?b1?a2?a2?b2?a3? a3?b3?a4? a4?b4?a1?于是a1 ?b1?b2?a3?b1?b2?b3?a4?b1?b2?b3?b4?a1?从而 b 1?b 2?b 3?b 4?0?这说明向量组b 1? b 2? b 3? b 4线性相关?12? 设b 1?a 1? b 2?a 1?a 2? ? ? ?? b r ?a 1?a 2? ? ? ? ?a r ? 且向量组a 1? a 2? ? ? ? ? a r 线性无关? 证明向量组b 1? b 2? ? ? ? ? b r 线性无关? 证明已知的r 个等式可以写成⎪⎪⎫⎛⋅⋅⋅⋅⋅⋅⋅⋅⋅=⋅⋅⋅110111) , , ,() , , ,(2121r r a a a b b b ? ? b 2? ?? ? ? b r 知R (a 1 所以a 1? a 2 ⎪⎪⎭⎝⎪⎪⎭ ⎝----⎪⎪⎭⎝----=00000010180590763451) , ,(321a a a ? 知R (a 1T ? a 2T ? a 3T )?R (a 1? a 2? a 3)?2? 因为向量a 1T 与a 2T 的分量不成比例? 故a 1T ? a 2T 线性无关? 所以a 1T ? a 2T 是一个最大无关组?14? 利用初等行变换求下列矩阵的列向量组的一个最大无关组?(1)⎪⎪⎪⎭⎫⎝⎛4820322513454947513253947543173125? 解因为⎪⎪⎪⎭⎫ ⎝⎛482032251345494751325394754317312513121433~r r r r r r ---⎪⎪⎪⎭⎫ ⎝⎛531053103210431731253423~r r r r --⎪⎪⎪⎭⎫ ⎝⎛00003100321043173125? ⎪⎭⎝----⎪⎭ ⎝---⎪⎭ ⎝=52001110611011103111332) , , ,(2143b a a b a b a a a a ?而R (a 1? a 2? a 3? a 4)?2? 所以a ?2? b ?5?16? 设a 1? a 2? ? ? ?? a n 是一组n 维向量? 已知n 维单位坐标向量e 1? e 2?? ? ?? e n 能由它们线性表示? 证明a 1? a 2? ? ? ?? a n 线性无关?证法一记A ?(a 1? a 2? ? ? ?? a n )? E ?(e 1? e 2?? ? ?? e n )? 由已知条件知? 存在矩阵K ? 使E?AK?两边取行列式?得|E|?|A||K|?可见|A|?0?所以R(A)?n?从而a1?a2?????a n线性无关?证法二因为e1?e2?????e n能由a1?a2?????a n线性表示?所以R(e1?e2?????e n)?R(a1?a2?????a n)?而R(e1?e2?????e n)?n?R(a1?a2?????a n)?n?所以R(a1?a2?????a n)?n?从而?a2?a是??而a1?a2?????a n即R(aa k (2?k?m???? ?m?使?1a1??2a2??????m a m?0?而且?2??3??????m不全为零?这是因为?如若不然?则?1a1?0?由a1?0知?1?0?矛盾?因此存在k(2?k?m)?使?k?0??k?1??k?2??????m?0?于是?1a1??2a2??????k a k?0?a k??(1/?k)(?1a1??2a2??????k?1a k?1)?即a k 能由a 1? a 2? ? ? ?? a k ?1线性表示?19? 设向量组B ? b 1? ? ? ?? b r 能由向量组A ? a 1? ? ? ?? a s 线性表示为 (b 1? ? ? ?? b r )?(a 1? ? ? ?? a s )K ? 其中K 为s ?r 矩阵? 且A 组线性无关? 证明B 组线性无关的充分必要条件是矩阵K 的秩R (K )?r ?证明令B ?(b 1? ? ? ?? b r )? A ?(a 1? ? ? ?? a s )? 则有B ?AK ? 必要性? 设向量组B 线性无关?及因此R ?于是r 线性无关? 证明将已知关系写成⎪⎪⎪⎪⎭⎫ ⎝⎛⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=⋅⋅⋅0111101111011110) , , ,() , , ,(2121n n αααβββ? 将上式记为B ?AK ? 因为0)1()1(0111101111011110||1≠--=⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=-n K n ? 所以K 可逆? 故有A ?BK ?1? 由B ?AK 和A ?BK ?1可知向量组?1? ?2? ? ? ?? ?n 与向量组?1? ?2? ? ? ?? ?n 可相互线性表示? 因此向量组?1? ?2? ? ? ?? ?n 与向量组?1??2? ? ? ?? ?n 等价?32? A x ? A 2x 所以B ? 故3x ?A x 22? 求下列齐次线性方程组的基础解系? (1)⎪⎩⎪⎨⎧=-++=-++=++-02683054202108432143214321x x x x x x x x x x x x ?解对系数矩阵进行初等行变换? 有⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛---=00004/14/3100401 2683154221081~r A ?于是得⎩⎨⎧+=-=43231)4/1()4/3(4x x x x x ?取(x 3? x 4)T ?(4? 0)T ? 得(x 1? x 2)T ?(?16? 3)T ? 取(x 3? x 4)T ?(0? 4)T ? 得(x 1? x 2)T ?(0? 1)T ? 因此方程组的基础解系为?1?(?16? 3? 4? 0)T ? ?2?(0? 1? 0? 4)T ? x n ??nx 1?(n ?1)x 2? ? ? ? ?2x n ?1?取x 1?1? x 2?x 3? ? ? ? ?x n ?1?0? 得x n ??n ?取x 2?1? x 1?x 3?x 4? ? ? ? ?x n ?1?0? 得x n ??(n ?1)??n ?1? ? ? ? ?取x n ?1?1? x 1?x 2? ? ? ? ?x n ?2?0? 得x n ??2? 因此方程组的基础解系为 ?1?(1? 0? 0? ? ? ?? 0? ?n )T ??2?(0? 1? 0? ? ? ?? 0? ?n ?1)T ? ? ? ???n ?1?(0? 0? 0? ? ? ?? 1? ?2)T ?23? 设⎪⎭⎫ ⎝⎛--=82593122A , 求一个4?2矩阵B , 使AB ?0, 且 R (B )?2.解显然B 的两个列向量应是方程组AB ?0的两个线性无关的解? 因为 r⎪⎪⎪⎭ ⎝+⎪⎪⎪⎭⎝=⎪⎪⎪⎭ ⎝012321214321k k x x x , 即⎪⎩⎪⎨=+=+=1421321221322k x k k x k k x ? (k 1? k 2?R )? 消去k 1? k 2得⎩⎨⎧=+-=+-023032431421x x x x x x ? 此即所求的齐次线性方程组. 25? 设四元齐次线性方程组。

数据库课堂练习全（答案全）

数据库课堂练习全（答案全）⼀．以下涉及的教学数据库含有4个关系，⽅便起见，其名称简化为T、S、C和SC 教师关系T(Tno,Tname,Title)学⽣关系S(Sno,Sname,Age,Sex)课程关系C(Cno,Cname,Tno)选课关系SC(Sno,Cno,Score)1.查询选修了课程号为C2课程的学⽣学号和姓名2.查询⾄少选修了钟教授所教课程中⼀门课程的学⽣学号和姓名。

3.查询不选修C2课程的学⽣姓名和年龄。

4.查询选修了全部课程的学⽣姓名。

5.查询⾄少有学号为S2和S4学⽣选修的课程的课程号。

解：1.ΠSno,Sname(6Cno=’C2’(S SC))2.ΠSno,Sname(6Tname=’钟’(S SC T C))3.ΠSname,Age(S)——ΠSname,Age(6Cno=’C2’(S SC))4.ΠSname(S(ΠSno,Cno(SC)))——ΠCno(C))5.ΠCno(61.Sno=’S2’∧2.Sno=’S4’∧(SC*SC))⼆、以下涉及的教学数据库含有4个关系，⽅便起见，其名称简化为T、S、C和SC教师关系T(Tno,Tname,Title)学⽣关系S(Sno,Sname,Age,Sex)课程关系C(Cno,Cname,Tno)选课关系SC(Sno,Cno,Score)要求检索⼥同学选修课程的课程名和任课教师名。

1.试写出该查询的关系代数表达式Πcname,Tname(sex='⼥'(S SC C T))2.画出查询表达式的语法树3.使⽤启发式优化算法，对语法树进⾏优化，并画出优化后的语法树三、⽤SQL完成下⾯的查询和操作1.查询不选修C2课程的学⽣姓名和年龄。

2.查询⾄少选修课程号C2和C4的学⽣学号。

3.求每⼀教师每门课程的学⽣选修⼈数（超过30⼈），要求显⽰教师⼯号、课程号和学⽣⼈数。

查询结果按⼈数升序排列，⼈数相同按⼯号升序、课程号按降序排列。

matlab数学实验习题全部答案(胡良剑)

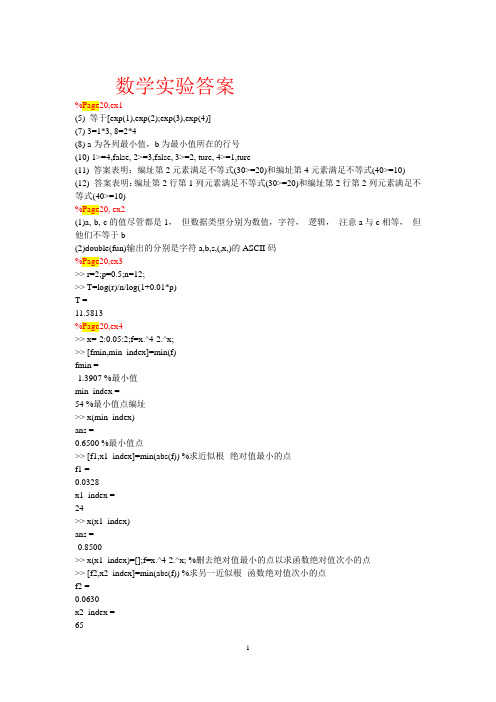
数学实验答案%Page20,ex1(5) 等于[exp(1),exp(2);exp(3),exp(4)](7) 3=1*3, 8=2*4(8) a为各列最小值，b为最小值所在的行号(10) 1>=4,false, 2>=3,false, 3>=2, ture, 4>=1,ture(11) 答案表明：编址第2元素满足不等式(30>=20)和编址第4元素满足不等式(40>=10)(12) 答案表明：编址第2行第1列元素满足不等式(30>=20)和编址第2行第2列元素满足不等式(40>=10)%Page20, ex2(1)a, b, c的值尽管都是1，但数据类型分别为数值，字符，逻辑，注意a与c相等，但他们不等于b(2)double(fun)输出的分别是字符a,b,s,(,x,)的ASCII码%Page20,ex3>> r=2;p=0.5;n=12;>> T=log(r)/n/log(1+0.01*p)T =11.5813%Page20,ex4>> x=-2:0.05:2;f=x.^4-2.^x;>> [fmin,min_index]=min(f)fmin =-1.3907 %最小值min_index =54 %最小值点编址>> x(min_index)ans =0.6500 %最小值点>> [f1,x1_index]=min(abs(f)) %求近似根--绝对值最小的点f1 =0.0328x1_index =24>> x(x1_index)ans =-0.8500>> x(x1_index)=[];f=x.^4-2.^x; %删去绝对值最小的点以求函数绝对值次小的点>> [f2,x2_index]=min(abs(f)) %求另一近似根--函数绝对值次小的点f2 =0.0630x2_index =65>> x(x2_index)ans =1.2500%Page20,ex5>> z=magic(10)z =92 99 1 8 15 67 74 51 58 4098 80 7 14 16 73 55 57 64 414 81 88 20 22 54 56 63 70 4785 87 19 21 3 60 62 69 71 2886 93 25 2 9 61 68 75 52 3417 24 76 83 90 42 49 26 33 6523 5 82 89 91 48 30 32 39 6679 6 13 95 97 29 31 38 45 7210 12 94 96 78 35 37 44 46 5311 18 100 77 84 36 43 50 27 59>> sum(z)ans =505 505 505 505 505 505 505 505 505 505 >> sum(diag(z))ans =505>> z(:,2)/sqrt(3)ans =57.157746.188046.765450.229553.693613.85642.88683.46416.928210.3923>> z(8,:)=z(8,:)+z(3,:)z =92 99 1 8 15 67 74 51 58 4098 80 7 14 16 73 55 57 64 414 81 88 20 22 54 56 63 70 4785 87 19 21 3 60 62 69 71 2886 93 25 2 9 61 68 75 52 3417 24 76 83 90 42 49 26 33 6523 5 82 89 91 48 30 32 39 6683 87 101 115 119 83 87 101 115 11910 12 94 96 78 35 37 44 46 5311 18 100 77 84 36 43 50 27 59%Page 40 ex1先在编辑器窗口写下列M函数，保存为eg2_1.m function [xbar,s]=ex2_1(x)n=length(x);xbar=sum(x)/n;s=sqrt((sum(x.^2)-n*xbar^2)/(n-1));例如>>x=[81 70 65 51 76 66 90 87 61 77];>>[xbar,s]=ex2_1(x)xbar =72.4000s =12.1124%Page 40 ex2s=log(1);n=0;while s<=100n=n+1;s=s+log(1+n);endm=n计算结果m=37%Page 40 ex3clear;F(1)=1;F(2)=1;k=2;x=0;e=1e-8; a=(1+sqrt(5))/2;while abs(x-a)>ek=k+1;F(k)=F(k-1)+F(k-2); x=F(k)/F(k-1);enda,x,k计算至k=21可满足精度%Page 40 ex4clear;tic;s=0;for i=1:1000000s=s+sqrt(3)/2^i;ends,toctic;s=0;i=1;while i<=1000000s=s+sqrt(3)/2^i;i=i+1;ends,toctic;s=0;i=1:1000000;s=sqrt(3)*sum(1./2.^i);s,toc%Page 40 ex5t=0:24;c=[15 14 14 14 14 15 16 18 20 22 23 25 28 ...31 32 31 29 27 25 24 22 20 18 17 16];plot(t,c)%Page 40 ex6%(1)x=-2:0.1:2;y=x.^2.*sin(x.^2-x-2);plot(x,y)y=inline('x^2*sin(x^2-x-2)');fplot(y,[-2 2])%(2)参数方法t=linspace(0,2*pi,100);x=2*cos(t);y=3*sin(t); plot(x,y)%(3)x=-3:0.1:3;y=x;[x,y]=meshgrid(x,y);z=x.^2+y.^2;surf(x,y,z)%(4)x=-3:0.1:3;y=-3:0.1:13;[x,y]=meshgrid(x,y);z=x.^4+3*x.^2+y.^2-2*x-2*y-2*x.^2.*y+6;surf(x,y,z)%(5)t=0:0.01:2*pi;x=sin(t);y=cos(t);z=cos(2*t);plot3(x,y,z)%(6)theta=linspace(0,2*pi,50);fai=linspace(0,pi/2,20); [theta,fai]=meshgrid(theta,fai);x=2*sin(fai).*cos(theta);y=2*sin(fai).*sin(theta);z=2*cos(fai);surf(x,y,z)%(7)x=linspace(0,pi,100);y1=sin(x);y2=sin(x).*sin(10*x);y3=-sin(x);plot(x,y1,x,y2,x,y3)%page41, ex7x=-1.5:0.05:1.5;y=1.1*(x>1.1)+x.*(x<=1.1).*(x>=-1.1)-1.1*(x<-1.1);plot(x,y)%page41,ex8分别使用which trapz, type trapz, dir C:\MA TLAB7\toolbox\matlab\datafun\ %page41,ex9clear;close;x=-2:0.1:2;y=x;[x,y]=meshgrid(x,y);a=0.5457;b=0.7575;p=a*exp(-0.75*y.^2-3.75*x.^2-1.5*x).*(x+y>1);p=p+b*exp(-y.^2-6*x.^2).*(x+y>-1).*(x+y<=1);p=p+a*exp(-0.75*y.^2-3.75*x.^2+1.5*x).*(x+y<=-1);mesh(x,y,p)%page41, ex10lookfor lyapunovhelp lyap>> A=[1 2 3;4 5 6;7 8 0];C=[2 -5 -22;-5 -24 -56;-22 -56 -16];>> X=lyap(A,C)X =1.0000 -1.0000 -0.0000-1.0000 2.0000 1.0000-0.0000 1.0000 7.0000%Chapter 3%Exercise 1>> a=[1,2,3];b=[2,4,3];a./b,a.\b,a/b,a\bans =0.5000 0.5000 1.0000ans =2 2 1ans =0.6552 %一元方程组x[2,4,3]=[1,2,3]的近似解ans =0 0 00 0 00.6667 1.3333 1.0000%矩阵方程[1,2,3][x11,x12,x13;x21,x22,x23;x31,x32,x33]=[2,4,3]的特解%Exercise 2(1)>> A=[4 1 -1;3 2 -6;1 -5 3];b=[9;-2;1];>> rank(A), rank([A,b]) %[A,b]为增广矩阵ans =3ans =3 %可见方程组唯一解>> x=A\bx =2.38301.48942.0213%Exercise 2(2)>> A=[4 -3 3;3 2 -6;1 -5 3];b=[-1;-2;1];>> rank(A), rank([A,b])ans =3ans =3 %可见方程组唯一解>> x=A\bx =-0.4706-0.2941%Exercise 2(3)>> A=[4 1;3 2;1 -5];b=[1;1;1];>> rank(A), rank([A,b])ans =2ans =3 %可见方程组无解>> x=A\bx =0.3311-0.1219 %最小二乘近似解%Exercise 2(4)>> a=[2,1,-1,1;1,2,1,-1;1,1,2,1];b=[1 2 3]';%注意b的写法>> rank(a),rank([a,b])ans =3ans =3 %rank(a)==rank([a,b])<4说明有无穷多解>> a\bans =110 %一个特解%Exercise 3>> a=[2,1,-1,1;1,2,1,-1;1,1,2,1];b=[1,2,3]';>> x=null(a),x0=a\bx =-0.62550.6255-0.20850.4170x0 =11%通解kx+x0%Exercise 4>> x0=[0.2 0.8]';a=[0.99 0.05;0.01 0.95];>> x1=a*x, x2=a^2*x, x10=a^10*x>> x=x0;for i=1:1000,x=a*x;end,xx =0.83330.1667>> x0=[0.8 0.2]';>> x=x0;for i=1:1000,x=a*x;end,xx =0.83330.1667>> [v,e]=eig(a)v =0.9806 -0.70710.1961 0.7071e =1.0000 00 0.9400>> v(:,1)./xans =1.17671.1767 %成比例，说明x是最大特征值对应的特征向量%Exercise 5%用到公式(3.11)(3.12)>> B=[6,2,1;2.25,1,0.2;3,0.2,1.8];x=[25 5 20]';>> C=B/diag(x)C =0.2400 0.4000 0.05000.0900 0.2000 0.01000.1200 0.0400 0.0900>> A=eye(3,3)-CA =0.7600 -0.4000 -0.0500-0.0900 0.8000 -0.0100-0.1200 -0.0400 0.9100>> D=[17 17 17]';x=A\Dx =37.569625.786224.7690%Exercise 6(1)>> a=[4 1 -1;3 2 -6;1 -5 3];det(a),inv(a),[v,d]=eig(a) ans =-94ans =0.2553 -0.0213 0.04260.1596 -0.1383 -0.22340.1809 -0.2234 -0.0532v =0.0185 -0.9009 -0.3066-0.7693 -0.1240 -0.7248-0.6386 -0.4158 0.6170d =-3.0527 0 00 3.6760 00 0 8.3766%Exercise 6(2)>> a=[1 1 -1;0 2 -1;-1 2 0];det(a),inv(a),[v,d]=eig(a) ans =1ans =2.0000 -2.0000 1.00001.0000 -1.0000 1.00002.0000 -3.0000 2.0000v =-0.5773 0.5774 + 0.0000i 0.5774 - 0.0000i-0.5773 0.5774 0.5774-0.5774 0.5773 - 0.0000i 0.5773 + 0.0000id =1.0000 0 00 1.0000 + 0.0000i 00 0 1.0000 - 0.0000i%Exercise 6(3)>> A=[5 7 6 5;7 10 8 7;6 8 10 9;5 7 9 10]A =5 76 57 10 8 76 8 10 95 7 9 10>> det(A),inv(A), [v,d]=eig(A)ans =1ans =68.0000 -41.0000 -17.0000 10.0000-41.0000 25.0000 10.0000 -6.0000-17.0000 10.0000 5.0000 -3.000010.0000 -6.0000 -3.0000 2.0000v =0.8304 0.0933 0.3963 0.3803-0.5016 -0.3017 0.6149 0.5286-0.2086 0.7603 -0.2716 0.55200.1237 -0.5676 -0.6254 0.5209d =0.0102 0 0 00 0.8431 0 00 0 3.8581 00 0 0 30.2887%Exercise 6(4)(以n=5为例)%关键是矩阵的定义%方法一（三个for）n=5;for i=1:n, a(i,i)=5;endfor i=1:(n-1),a(i,i+1)=6;endfor i=1:(n-1),a(i+1,i)=1;enda%方法二（一个for）n=5;a=zeros(n,n);a(1,1:2)=[5 6];for i=2:(n-1),a(i,[i-1,i,i+1])=[1 5 6];enda(n,[n-1 n])=[1 5];a%方法三（不用for）n=5;a=diag(5*ones(n,1));b=diag(6*ones(n-1,1));c=diag(ones(n-1,1));a=a+[zeros(n-1,1),b;zeros(1,n)]+[zeros(1,n);c,zeros(n-1,1)] %下列计算>> det(a)ans =665>> inv(a)ans =0.3173 -0.5865 1.0286 -1.6241 1.9489-0.0977 0.4887 -0.8571 1.3534 -1.62410.0286 -0.1429 0.5429 -0.8571 1.0286-0.0075 0.0376 -0.1429 0.4887 -0.58650.0015 -0.0075 0.0286 -0.0977 0.3173>> [v,d]=eig(a)v =-0.7843 -0.7843 -0.9237 0.9860 -0.92370.5546 -0.5546 -0.3771 -0.0000 0.3771-0.2614 -0.2614 0.0000 -0.1643 0.00000.0924 -0.0924 0.0628 -0.0000 -0.0628-0.0218 -0.0218 0.0257 0.0274 0.0257d =0.7574 0 0 0 00 9.2426 0 0 00 0 7.4495 0 00 0 0 5.0000 00 0 0 0 2.5505%Exercise 7(1)>> a=[4 1 -1;3 2 -6;1 -5 3];[v,d]=eig(a)v =0.0185 -0.9009 -0.3066-0.7693 -0.1240 -0.7248-0.6386 -0.4158 0.6170d =-3.0527 0 00 3.6760 00 0 8.3766>> det(v)ans =-0.9255 %v行列式正常, 特征向量线性相关，可对角化>> inv(v)*a*v %验算ans =-3.0527 0.0000 -0.00000.0000 3.6760 -0.0000-0.0000 -0.0000 8.3766>> [v2,d2]=jordan(a) %也可用jordanv2 =0.0798 0.0076 0.91270.1886 -0.3141 0.1256-0.1605 -0.2607 0.4213 %特征向量不同d2 =8.3766 0 00 -3.0527 - 0.0000i 00 0 3.6760 + 0.0000i>> v2\a*v2ans =8.3766 0 0.00000.0000 -3.0527 0.00000.0000 0.0000 3.6760>> v(:,1)./v2(:,2) %对应相同特征值的特征向量成比例ans =2.44912.44912.4491%Exercise 7(2)>> a=[1 1 -1;0 2 -1;-1 2 0];[v,d]=eig(a)v =-0.5773 0.5774 + 0.0000i 0.5774 - 0.0000i-0.5773 0.5774 0.5774-0.5774 0.5773 - 0.0000i 0.5773 + 0.0000id =1.0000 0 00 1.0000 + 0.0000i 00 0 1.0000 - 0.0000i>> det(v)ans =-5.0566e-028 -5.1918e-017i %v的行列式接近0, 特征向量线性相关，不可对角化>> [v,d]=jordan(a)v =1 0 11 0 01 -1 0d =1 1 00 1 10 0 1 %jordan标准形不是对角的，所以不可对角化%Exercise 7(3)>> A=[5 7 6 5;7 10 8 7;6 8 10 9;5 7 9 10]A =5 76 57 10 8 76 8 10 95 7 9 10>> [v,d]=eig(A)v =0.8304 0.0933 0.3963 0.3803-0.5016 -0.3017 0.6149 0.5286-0.2086 0.7603 -0.2716 0.55200.1237 -0.5676 -0.6254 0.5209d =0.0102 0 0 00 0.8431 0 00 0 3.8581 00 0 0 30.2887>> inv(v)*A*vans =0.0102 0.0000 -0.0000 0.00000.0000 0.8431 -0.0000 -0.0000-0.0000 0.0000 3.8581 -0.0000-0.0000 -0.0000 0 30.2887%本题用jordan不行, 原因未知%Exercise 7(4)参考6(4)和7(1), 略%Exercise 8 只有(3)对称, 且特征值全部大于零, 所以是正定矩阵. %Exercise 9(1)>> a=[4 -3 1 3;2 -1 3 5;1 -1 -1 -1;3 -2 3 4;7 -6 -7 0]>> rank(a)ans =3>> rank(a(1:3,:))ans =2>> rank(a([1 2 4],:)) %1,2,4行为最大无关组ans =3>> b=a([1 2 4],:)';c=a([3 5],:)';>> b\c %线性表示的系数ans =0.5000 5.0000-0.5000 1.00000 -5.0000%Exercise 10>> a=[1 -2 2;-2 -2 4;2 4 -2]>> [v,d]=eig(a)v =0.3333 0.9339 -0.12930.6667 -0.3304 -0.6681-0.6667 0.1365 -0.7327d =-7.0000 0 00 2.0000 00 0 2.0000>> v'*vans =1.0000 0.0000 0.00000.0000 1.0000 00.0000 0 1.0000 %v确实是正交矩阵%Exercise 11%设经过6个电阻的电流分别为i1, ..., i6. 列方程组如下%20-2i1=a; 5-3i2=c; a-3i3=c; a-4i4=b; c-5i5=b; b-3i6=0;%i1=i3+i4;i5=i2+i3;i6=i4+i5;%计算如下>> A=[1 0 0 2 0 0 0 0 0;0 0 1 0 3 0 0 0 0;1 0 -1 0 0 -3 0 0 0; 1 -1 0 0 0 0 -4 0 0;0 -1 1 0 0 0 0 -5 0;0 1 0 0 0 0 0 0 -3; 0 0 0 1 0 -1 -1 0 0;0 0 0 0 -1 -1 0 1 0;0 0 0 0 0 0 -1 -1 1];>>b=[20 5 0 0 0 0 0 0 0]'; A\bans =13.34536.44018.54203.3274-1.18071.60111.72630.42042.1467%Exercise 12>> A=[1 2 3;4 5 6;7 8 0];>> left=sum(eig(A)), right=sum(trace(A))left =6.0000right =6>> left=prod(eig(A)), right=det(A) %原题有错, (-1)^n应删去left =27.0000right =27>> fA=(A-p(1)*eye(3,3))*(A-p(2)*eye(3,3))*(A-p(3)*eye(3,3)) fA =1.0e-012 *0.0853 0.1421 0.02840.1421 0.1421 0-0.0568 -0.1137 0.1705>> norm(fA) %f(A)范数接近0ans =2.9536e-013%Exercise 1(1)roots([1 1 1])%Exercise 1(2)roots([3 0 -4 0 2 -1])%Exercise 1(3)p=zeros(1,24);p([1 17 18 22])=[5 -6 8 -5];roots(p)%Exercise 1(4)p1=[2 3];p2=conv(p1, p1);p3=conv(p1, p2);p3(end)=p3(end)-4; %原p3最后一个分量-4roots(p3)%Exercise 2fun=inline('x*log(sqrt(x^2-1)+x)-sqrt(x^2-1)-0.5*x');fzero(fun,2)%Exercise 3fun=inline('x^4-2^x');fplot(fun,[-2 2]);grid on;fzero(fun,-1),fzero(fun,1),fminbnd(fun,0.5,1.5)%Exercise 4fun=inline('x*sin(1/x)','x');fplot(fun, [-0.1 0.1]);x=zeros(1,10);for i=1:10, x(i)=fzero(fun,(i-0.5)*0.01);end;x=[x,-x]%Exercise 5fun=inline('[9*x(1)^2+36*x(2)^2+4*x(3)^2-36;x(1)^2-2*x(2)^2-20*x(3);16*x(1)-x(1)^3-2*x(2)^ 2-16*x(3)^2]','x');[a,b,c]=fsolve(fun,[0 0 0])%Exercise 6fun=@(x)[x(1)-0.7*sin(x(1))-0.2*cos(x(2)),x(2)-0.7*cos(x(1))+0.2*sin(x(2))];[a,b,c]=fsolve(fun,[0.5 0.5])%Exercise 7clear; close; t=0:pi/100:2*pi;x1=2+sqrt(5)*cos(t); y1=3-2*x1+sqrt(5)*sin(t);x2=3+sqrt(2)*cos(t); y2=6*sin(t);plot(x1,y1,x2,y2); grid on; %作图发现4个解的大致位置，然后分别求解y1=fsolve('[(x(1)-2)^2+(x(2)-3+2*x(1))^2-5,2*(x(1)-3)^2+(x(2)/3)^2-4]',[1.5,2])y2=fsolve('[(x(1)-2)^2+(x(2)-3+2*x(1))^2-5,2*(x(1)-3)^2+(x(2)/3)^2-4]',[1.8,-2])y3=fsolve('[(x(1)-2)^2+(x(2)-3+2*x(1))^2-5,2*(x(1)-3)^2+(x(2)/3)^2-4]',[3.5,-5])y4=fsolve('[(x(1)-2)^2+(x(2)-3+2*x(1))^2-5,2*(x(1)-3)^2+(x(2)/3)^2-4]',[4,-4])%Exercise 8(1)clear;fun=inline('x.^2.*sin(x.^2-x-2)');fplot(fun,[-2 2]);grid on; %作图观察x(1)=-2;x(3)=fminbnd(fun,-1,-0.5);x(5)=fminbnd(fun,1,2);fun2=inline('-x.^2.*sin(x.^2-x-2)');x(2)=fminbnd(fun2,-2,-1);x(4)=fminbnd(fun2,-0.5,0.5);x(6)=2feval(fun,x)%答案: 以上x(1)(3)(5)是局部极小，x(2)(4)(6)是局部极大，从最后一句知道x(1)全局最小，x(2)最大。

2022年同济大学软件工程专业《操作系统》科目期末试卷A(有答案)

2022年同济大学软件工程专业《操作系统》科目期末试卷A（有答案）一、选择题1、列选项中，不可能在用户态发生的事件是（）。

A.系统调用B.外部中断C.进程切换D.缺页2、下列观点中，不是描述操作系统的典型观点的是（）。

A.操作系统是众多软件的集合B.操作系统是用户和计算机之间的接口C.操作系统是资源的管理者D.操作系统是虚拟机3、银行家算法在解决死锁问题中用于（）。

A.预防死锁B.死锁避免C.检测死锁D.解除死锁4、下面所列进程的3种基本状态之间的转换不正确的是（）A.就绪状态→执行状态B.执行状态→就绪状态C.执行状态→阻塞状态D.就绪状态→阻塞状态5、若系统S1采用死锁避免方法，S2采用死锁检测方法。

下列叙述中，正确的是（）。

I.S1会限制用户申请资源的顺序，而S2不会II.S1需要进程运行所需资源总最信息，而S2不需要III.SI不会给可能导致死锁的进程分配资源，而S2会A.仅I、IIB.仅II、IIIC. 仅I、IID. I、II、III6、缓存技术的缓冲池在（）中。

A.内存B.外存C.ROMD.寄存器7、在采用SPOOLing技术的系统中，用户暂时未能打印的数据首先会被送到（）存储起来。

A.磁盘固定区域B.内存固定区域C.终端D.打印机8、位示图可用于（）A.实现文件的保护和保密B.文件目录的查找C.磁盘空间的管理D.主存空间的共享9、下列文件物理结构中，适合随机访问且易于文件扩展的是（）。

A.连续结构B.索引结构C.链式结构且磁盘块定长D.链式结构且磁盘块变长10、在下述存储管理方案中，（）管理方式要求作业占用连续的存储空间。

A.分区B.分页C.分段D.段页式11、下面关于虚拟存储器的论述中，正确的是（）。

A.在段页式系统中以段为单位管理用户的逻辑地址空间，以页为单位管理内存的物理地址空间，有了虚拟存储器才允许用户使用比内存更大的地址空间B.为了提高请求分页系统中内存的利用率，允许用户使用不同大小的页面C.为了能让更多的作业同时运行，通常只装入10%~30%的作业即启动运行D.最佳置换算法是实现虚拟存储器的常用算法12、采用分段存储管理的系统中，若段地址用24位表示，其中8位表示段号，则允许每段的最大长度是（）。

同济大学Matlab实验报告(matlab应用实例)

实验报告班级机械三班学号姓名- 1 -- 2 -画出衰减振荡曲线t ey t 3sin 3-=及其它的包络线30t e y -=，31t e y --=。

t 值的范围是');- 3 -4．通过M 脚本文件，画出下列分段函数所表示的曲面，用冷色调。

⎪⎪⎩⎪⎪⎨⎧-≤+≤+<->+=+-------15457.0117575.015457.0),(215.175.375.0216215.175.375.02112122212212122x x e x x ex x e x x p x x x x x x x x [X1,X2]=meshgrid(-1.5:0.1:1.5,-2:0.1:2);P=0.5457*exp(-0.75*X2.^2-3.75*X1.^2-1.5*X1).*(X1+X2>1)... + 0.7575*exp(-X2.^2-6*X1.^2).*(X1+X2>-1&X1+X2<=1)... + 0.5457*exp(-0.75*X2.^2-3.75*X1.^2+1.5*X1).*(X1+X2<=-1); surf(X1,X2,P);colormap(cool);colorbar('horiz'); shading flat;实验体会与总结通过此次实验，把课堂所学的理论知识运用到了实际中，了解了Matlab 的基本功能和用途。

经过4个实验基，本上掌握了Matlab 绘制曲线、曲面和构造分段函数的方法，相信此次实验会为以后Matlab 的学习奠定坚实的基础。

- 1 -实验报告班级机械三班学号姓名的值，输出一元二次方程2ax bx c ++=root方程形式:a*x^2+b*x+c=0 请输入各项系数: a=1 b=1 c=-1ans =-1.6180 0.6180exchange 请输入x ：1 请输入y ：0 x=0, y=1- 2 -',num2str(discount*100),'%']) 请输入商品价格：100折扣： 0%实际价格：100请输入商品价格：300 折扣： 3% 实际价格：291请输入商品价格：700 折扣： 5% 实际价格：665 请输入商品价格：1500 折扣： 8% 实际价格：1380请输入商品价格：3000折扣： 10% 实际价格：2700 请输入商品价格：6000 折扣： 14% 实际价格：5160- 3 -4．在.m 文件中编写程序实现，在同一坐标内，分别用不同线型和颜色绘制曲线0.510.2cos(4)y e x x π-=和0.522cos()y e x x π-=，标记两曲线交叉点，给出每条曲线的图注。

机器学习智慧树知到课后章节答案2023年下同济大学

机器学习智慧树知到课后章节答案2023年下同济大学第一章测试1.回归和分类都是有监督学习问题。

（）A:对 B:错答案:对2.输出变量为有限个离散变量的预测问题是回归问题；输出变量为连续变量的预测问题是分类问题。

（）A:错 B:对答案:错3.关于“回归（Regression）”和“相关（Correlation）”，下列说法正确的是？注意：x 是自变量，y 是因变量。

（）A:回归和相关在 x 和 y 之间都是互为对称的B:回归在 x 和 y 之间是对称的，相关在 x 和 y 之间是非对称的C:回归和相关在 x 和 y 之间都是非对称的D:回归在 x 和 y 之间是非对称的，相关在 x 和 y 之间是互为对称的答案:回归在 x 和 y 之间是非对称的，相关在 x 和 y 之间是互为对称的4.如果一个经过训练的机器学习模型在测试集上达到 100% 的准确率，这就意味着该模型将在另外一个新的测试集上也能得到 100% 的准确率。

（）A:错 B:对答案:错5.机器学习学得的模型适用于新样本的能力，称为"泛化"能力，这是针对分类和回归等监督学习任务而言的，与聚类这样的无监督学习任务无关。

（）A:错 B:对答案:错6.机器学习时，我们通常假设样本空间中的全体样本都服从某个未知"分布"，并且我们获得的每个样本都是独立地从这个分布上采样获得的。

（）A:对 B:错答案:对7.从归纳偏好一般性原则的角度看，"奥卡姆剃刀" (Occam's razor)准则与“大道至简”说的是相同的道理。

（）A:错 B:对答案:对8.以下方法或系统属于"符号主义" (symbolism)学习技术的是（）A:"概念学习系统"B:支持向量机C:"结构学习系统"D:"基于逻辑的归纳学习系统“答案:"概念学习系统";"结构学习系统";"基于逻辑的归纳学习系统“9.以下方法或技术属于统计学习范畴的是（）A:核方法B:Hopfield神经网络C:支持向量机D:感知机答案:核方法;支持向量机10.归纳学习相当于"从样例中学习"，即从训练样例中归纳出学习结果。

考研数据库9套题及答案

考研数据库9套题及答案随着考研的日益普及，数据库这门专业课程也备受关注。

对于考研学子来说，熟悉并掌握数据库相关知识是非常重要的。

为了帮助广大考研学子更好地备考数据库，本文将为大家提供9套考研数据库题目及答案，希望能够帮助大家更好地了解和应对考试。

第一套题：1.请简要解释什么是数据库事务（Transaction）？答：数据库事务是数据库管理系统中的一个重要概念，指的是由一个或多个操作组成的一个逻辑工作单位。

事务是数据库中数据处理的基本单位，具有原子性、一致性、隔离性和持久性四个特征。

2.什么是数据库索引（Index）？请列举一些索引的优点。

答：数据库索引是一种用于提高数据库检索速度的数据结构。

它通过创建特定的索引字段，将数据按照一定的顺序进行存储和组织，以便于快速查询和检索。

索引的优点包括：加快数据检索速度、减少数据存储空间、提高数据的唯一性和完整性、加速排序和分组操作。

3.请简要介绍数据库范式（Normalization）的概念及其作用。

答：数据库范式是一种用于设计关系型数据库的规范化方法。

它通过消除数据冗余，并将数据按照一定的标准进行分解和组织，以提高数据库的数据存储和查询效率，保证数据的一致性和完整性。

第二套题：1.请简要解释什么是数据库视图（View）？答：数据库视图是一种虚拟表，它是基于一个或多个实际表的查询结果所创建的。

视图可以像表一样进行查询操作，但它并不实际存储数据，只是保存了查询的逻辑表示。

2.什么是数据库连接池（Connection Pool）？请列举一些使用连接池的好处。

答：数据库连接池是一种用于管理数据库连接的技术，它通过预先创建多个数据库连接对象并保存在连接池中，以便于重复使用。

使用连接池的好处包括：减少数据库连接和断开的开销、提高连接的重用性、优化数据库资源的利用、增加系统的并发性能。

3.请简要介绍数据库备份（Backup）的概念及其重要性。

答：数据库备份是一种用于将数据库中的数据和结构拷贝到其他介质上的操作。

同济大学数据库大作业

┊┊┊┊┊┊┊┊┊┊┊┊┊装┊┊┊┊┊订┊┊┊┊┊线┊┊┊┊┊┊┊┊┊┊┊┊┊同济大学《数据库技术及应用》项目报告项目名称：医院一体化系统小组成员：1350871 倪荫豪1350870 李天扬年级：大二专业：土木工程指导教师：王睿智日期：2014 年12 月30 日┊ ┊ ┊ ┊ ┊ ┊ ┊ ┊ ┊ ┊ ┊ ┊ ┊ 装 ┊ ┊ ┊ ┊ ┊ 订 ┊ ┊ ┊ ┊ ┊ 线 ┊ ┊ ┊ ┊ ┊ ┊ ┊ ┊ ┊ ┊ ┊ ┊ ┊目录一、系统概述 (3)1.系统简介..................................................................3 2.功能特色 (3)二、需求分析 (3)1.系统功能需求分析......................................................3 2.数据库需求分析 (4)三、数据库设计 (4)1.概念模式设计............................................................4 2.逻辑模式设计............................................................6 3.物理数据库设计.........................................................6 4.触发器设计...............................................................11 5.存储过程设计 (13)四、系统设计和实现 (14)1.窗体类和功能类统计表................................................14 2.界面设计及其代码实现 (15)五、系统测试 (41)1.触发器测试用例.........................................................41 2.存储过程测试用例......................................................41 3.功能测试用例 (41)六、总结 (52)┊ ┊ ┊ ┊ ┊ ┊ ┊ ┊ ┊ ┊ ┊ ┊ ┊ 装 ┊ ┊ ┊ ┊ ┊ 订 ┊ ┊ ┊ ┊ ┊ 线 ┊ ┊ ┊ ┊ ┊ ┊ ┊ ┊ ┊ ┊ ┊ ┊ ┊一. 系统概述1.1系统简介当前医患关系、医院挂号等一直是社会热点问题。

同济大学数据库作业答案及讲解

共享事件
打开文件对话框的使用
根据输入查找
利用inputBox函数的输入值
保存文件对话框
39
本章目录
添加新数据
单击 “添加数据”菜单项
全局变量
• 在标准模块(Module)中声明的，其可访问性为公有的(public )变量，它的作用域为整个程序集，可被该程序的所有过程访问。如，声明一个全局变量x，并赋初值0 Module commonvariable Public x% = 0 End Module
三个按钮的单击事件过程
代码
实验一(2)
知识点：变量声明，表达式，数据类型转换、 if语
句、IsNumeric函数、MsgBox的使用
题目：编程求解鸡兔同笼问题
光标从TextBox2 中移出（失焦）
编写TextBox2的LostFocus事件过程
代码
变量声明
• 局部变量声明的语法 Dim 变量名 [As 类型] [=初值] 如, Dim a As Integer 或 Dim a% 常见类型 Integer(%) Long(&) Single(!) Double(#) String($) Char Date Boolean
例 Dim x(,) As Integer = {{1,2,3,4}, {5,6,7,8}}
数组x
1 5
2 6
3 7
4 8
21
本章目录
Rnd 随机函数
形式： Rnd() 作用：产生[0，1) 双精度随机数。
产生某范围的整数值，其通用表达式为：
Int(Rnd() * (上界-下界+1) +下界)
要产生1～100 整数：Int(Rnd()*100+1)

同济数据库实验四

1．列出不及格成绩的学生名单。

SELECT s.snum, sname FROM student s JOIN Sc ON s.snum=Sc.snum WHERE score < 60 运行结果：2．列出选修了计算机系课程的学生姓名和年龄。

SELECT DISTINCT sname as姓名,year(getdate())-year(birthday)as年龄FROM student s JOIN Sc JOIN Sections JOIN CourseON um=umON Sections.secnum=Sc.secnumON Sc.snum=s.snumWHERE Course.dept='计算机系'运行结果：3．检索选修了数据库技术课程的学生姓名和系别。

SELECT DISTINCT sname as姓名, s.dept as系别FROM student s JOIN Sc JOIN Sections JOIN CourseON um=umON Sections.secnum=Sc.secnumON Sc.snum=s.snumWHERE ame='数据库技术'运行结果：4．列出选修了所有课程的学生名单。

SELECT s.snum as学号, sname as姓名FROM student s JOIN Sc JOIN Sections JOIN CourseON um=umON Sections.secnum=Sc.secnumON Sc.snum=s.snumGROUP BY s.snum,snameHA VING COUNT(Sc.secnum)=(SELECT COUNT(*)FROM Course)或--列出选修了所有课程的学生名单。

SELECT snum A S学号,sname AS姓名FROM student sWHERE NOT EXISTS(SELECT cnum FROM courseWHERE cnum NOT IN(SELECT um FROM sc JOIN sections JOIN courseON um=umON sc.secnum=sections.secnum WHERE sc.snum=s.snum))运行结果：5．补充题：列出选修了’s007’学生所有课程的学生名单。

同济大学数据库技术与应用考试代码 (1)

1.select student.snum ,student.sname ,ame ,sc.scorefrom student inner join sc on student.snum=sc.snum inner join sections on sections.secnum=sc.secnum inner join course on um=umwhere sc.score < 602.select distinct student.sname,YEAR(GETDATE())-YEAR(student.bithday) As agefrom student inner join sc on student.snum=sc.snum inner join sections on sections.secnum=sc.secnum inner join course on um=umwhere course.dept like '计算机系'3.select distinct student.sname,student.deptfrom student inner join sc on student.snum=sc.snum inner join sections on sections.secnum=sc.secnum inner join course on um=umwhere ame='数据库技术'4.select snum,sname from studentwhere snum in( select snum from sc group by snum having count(*)>=(select count(*) from course ))5.select snum,sname from studentwhere snum in (select snum from sc group by snum having MIN(score)>=80)6.select snum , sname from student where snum in (select snum from sc group by snum having min(score)>=80 and avg(score)>=90)7.select student.sname,student.snum,sc.scorefrom student inner join sc on student.snum=sc.snum inner join sections on sections.secnum=sc.secnum inner join course on um=umwhere ame='大学英语' order by sc.score desc8.select um , COUNT(*) AS 人数from student inner join sc on student.snum=sc.snum inner join sections on sections.secnum=sc.secnum inner join course on um=umgroup by um9.Select student.sname,student.deptFrom studentWhere snum in(select sc.snum from sc inner join sections on sections.secnum=sc.secnum inner join course on um=um where ame=’数据库技术’)And snum not in(select sc.snum from sc inner join sections on sections.secnum=sc.secnum inner join course on um=um where ame=’高等数学’)10.select cname from coursewhere textbook like '%高等教育出版社%'11.Select um as 课程号, max(sc.score) as 最高分,min(sc.score) as 最低分,avg(sc.score) as 平均分From sc inner join sections on sc.secnum=sections.secnumGroup by cnum12.Select um As 课程名称, count(*) As 总人数, count(case when sc.score <60 then 1 else 0 end) As 不及格人数From course inner join sections on um=um inner join sc on sc.secnum=sections.secnumGroup by um13.Select sname,snum from studentWhere dept='土木工程' or dept='交通工程' or dept='城市规划'14.(select student.snum from student,course,sc,sections where student.snum=sc.snum and sc.secnum=sections.secnum and um=um and ame='数据库技术')union(select student.snum from student,course,sc,sections where student.snum=sc.snum and sc.secnum=sections.secnum and um=um and ame='多媒体技术')15.(select student.snum,sname,sex,student.dept,birthday,telephone from student where student.dept='计算机') intersect (select student.snum,sname,sex,student.dept,birthday,telephone from student where (year(GETDATE())-year(birthday)<=19))16.(select student.snum,sname,sex,student.dept,birthday,telephone from student where student.dept='计算机') except (select student.snum,sname,sex,student.dept,birthday,telephone from student where (year(GETDATE())-year(birthday)<=19))。

同济大学信息检索与利用试卷

同济大学信息检索与利用试卷（A）专业________ 姓名_________ 学号__________一. 名词解释（10分）1.一次文献：即原始文献。

它是作者以生产或科研为依据而创作的原始文献。

如专著、期刊论文、学位论文等。

2. 技术档案：指生产、设计、建设、科研等专业部门，在科技活动中形成的文件、图书、照片、数据等原始记录文献，包括项目规划、设计、实施方案、任务说明书、协议书、技术指标、实验计划等，具有保密性和内部使用的特点。

3.目录：是图书、期刊或其他单位出版物外表特征的揭示与报道。

它是以一本书、一种刊物为著录的基本单位，记录图书、期刊、资料等的名称、著者、出版项与馆藏项等内容，并按照一定的编排体例进行编制，但不涉及书中的章节或期刊中具体的文章。

4.检索语言：又称为情报语言、情报存储和检索语言、信息组织语言等。

它是根据检索的需要而创作的人工语言，把信息的存储和检索联系起来，把标引人员与检索人员联系起来，以便取得共同理解、实现交流的语言。

5. 追溯法：以已获文献后面所附参考文献为线索进行追溯查找，又称为参考文献法。

二. 判断题（对的打“√”，错的打“×”）（14分）1.通过BA、ISTP、Kluwer online、Springer Link 数据库都能检索到外文期刊论文全文。

（×）2.在重庆维普数据库检索系统中能查到企业名录。

（×）3.利用某个图书馆的书刊目录查询系统（OPAC），可以了解该图书馆收藏有哪些印刷型图书和期刊。

（∨）4.截词检索相当于用逻辑“或”扩展检索的范围，可以提高检索的查全率。

（∨）5.联合目录可以帮助读者确定其所需要的文献收藏在那个情报机构。

（∨）6.综述因附有大量参考文献，所以是二次文献。

（×）7.通过“万方数据资源系统”可以查找标准文献的全文。

（∨）三. 填空题(30分)1．按文献载体形式划分，文献可分为___书写型、印刷型、缩微型、视听型、和数字型。