数学七年级下册《实数课件》.ppt
合集下载
人教版《实数》优秀课件初中数学ppt

品比赛,小红很高兴,他 想裁出一块面积为25dm2 的正方形画布,画上自己 的得意之作参加比赛,这 块正方形画布的边长应取 多少?你能帮小明算一算 吗?
二、推进新课
填表1
正方形的边长 1 正方形的面积 1
3 0.1 9 0.01
思考:你能从表格中发现什么共同点吗?
已知一个正数,求这个正数的平方, 这就是平方运算。
一、创设情境,导入新课 一、创设情境,导入新课 算数平方根的数学符号表示 会用根号表示一个数的算术平方根(重点); 一个正数有两个算术平方根,且互为相反数。 问题:学校要举行美术作品比赛,小红很高兴,他想裁出一块面积为25dm2的正方形画布,画上自己的得意之作参加比赛,这块正方 形画布的边长应取多少?你能帮小明算一算吗? 第1课时 算术平方根 了解算术平方根的概念; 思考:你从表2中能发现什么? 算术平方根具有双重非负性 算数平方根的数学符号表示 已知一个数的平方,求这个数的运算叫做开平方。 会用根号表示一个数的算术平方根(重点); 了解算术平方根的概念; 问题:学校要举行美术作品比赛,小红很高兴,他想裁出一块面积为25dm2的正方形画布,画上自己的得意之作参加比赛,这块正方 形画布的边长应取多少?你能帮小明算一算吗? 一个正数有两个算术平方根,且互为相反数。 用大小完全相同的250块正方形地板砖,铺一间面积为160 m2的地面,每块地板砖的边长是多少? 第1课时 算术平方根 会用根号表示一个数的算术平方根(重点); 已知一个正数,求这个正数的平方,这就是平方运算。
已知一个数的平方,求这个数的运算叫做开平方。
算数平方根的数学符号表示
所以m+n=2
了解算术平方根的概念;
算术平方根具有双重非负性
问题:学校要举行美术作品比赛,小红很高兴,他想裁出一块面积为25dm2的正方形画布,画上自己的得意之作参加比赛,这块正方
二、推进新课
填表1
正方形的边长 1 正方形的面积 1
3 0.1 9 0.01
思考:你能从表格中发现什么共同点吗?
已知一个正数,求这个正数的平方, 这就是平方运算。
一、创设情境,导入新课 一、创设情境,导入新课 算数平方根的数学符号表示 会用根号表示一个数的算术平方根(重点); 一个正数有两个算术平方根,且互为相反数。 问题:学校要举行美术作品比赛,小红很高兴,他想裁出一块面积为25dm2的正方形画布,画上自己的得意之作参加比赛,这块正方 形画布的边长应取多少?你能帮小明算一算吗? 第1课时 算术平方根 了解算术平方根的概念; 思考:你从表2中能发现什么? 算术平方根具有双重非负性 算数平方根的数学符号表示 已知一个数的平方,求这个数的运算叫做开平方。 会用根号表示一个数的算术平方根(重点); 了解算术平方根的概念; 问题:学校要举行美术作品比赛,小红很高兴,他想裁出一块面积为25dm2的正方形画布,画上自己的得意之作参加比赛,这块正方 形画布的边长应取多少?你能帮小明算一算吗? 一个正数有两个算术平方根,且互为相反数。 用大小完全相同的250块正方形地板砖,铺一间面积为160 m2的地面,每块地板砖的边长是多少? 第1课时 算术平方根 会用根号表示一个数的算术平方根(重点); 已知一个正数,求这个正数的平方,这就是平方运算。
已知一个数的平方,求这个数的运算叫做开平方。
算数平方根的数学符号表示
所以m+n=2
了解算术平方根的概念;
算术平方根具有双重非负性
问题:学校要举行美术作品比赛,小红很高兴,他想裁出一块面积为25dm2的正方形画布,画上自己的得意之作参加比赛,这块正方
人教版七年级数学下7.1.1有序实数对课件(共42张PPT)

(3)甲地距我市29km
如图,写出表示下列各点的有序数对:
如图,写出表示下列各点的有序数对:
或者老师说一个数对,请代表相应位置的人站起来。
如图,写出表示下列各点的有序数对:
下列关于有序数对的说法正确的是( )
5排8号 5排6号 在数轴上,确定一个点的位置需要几个数据呢?
问题⑴: 新学期开始,老师要重新调整学生的座位,老师如何描述才能让学生准确地找到自己的新座位呢?
的方式表示出图中“怪兽”经过的其他几个位置吗?
排5
(4,5) (5,5)
4
(5,4)
(7,4)
3
(3,3)
(4,3)
在生活中,确定物体的位置,还有
其他方法吗2? (1,2)(3,2)(7,3) (8,3)
1 (1,1)
列
1
2
3
4
5
6
7
8
如图( 1 , 3 )表示 第一列第三排,请用 彩笔把以下位置的五 角星涂上颜色。
(4 ,6)
(3 ,4)
(5 ,4)
设计图案
排 7 6
5
4
3
(2 ,2)
2
(4 ,2)
1
(6 ,2)
12
34
5
6
7列
神州飞船的发 射和回收都那么成 功 ,圆了几代中国 人的梦想,让全中 国人为之骄傲和自 豪!但是,同学们知 道我们的科学家是 怎样迅速地找到返 回舱着陆的位置的 吗?
神州飞船
这全依赖于 “GPS——卫星全球定位系统”
A.(7,4)
B.(4,7)
C.(7,5)
D.(7,6)
例1. 如图,点A表示3街与5大道的十字路口,点B 表示5街与3大道的十字路口,如果用(3,5)→(4,5) →(5,5)→(5,4)→(5,3)表示由A到B的一条路径,那么 你能用同样的方法写出由A到B的其他几条路径吗?
人教版七年级下册数学第六章实数课件:6.3 实数

正有理数
正实数
实数
正无理数
0 负实数
负有理数
负无理数
4.实数与数轴上的点是一一对应的.
教学课件 七年级数学下册(RJ)
第六章 实数
6.3 实根(2)
课前预习
带着问题自学课本P54“思考”
1.无理数也有相反数吗?怎么表示? 2.有绝对值吗?怎么表示? 3.有倒数吗?怎么表示?
探究新知
(1) 2的相反数是 ____2___ -π的相反数是____π_____ 0的相反数是____0_____
无理数的概念
所有的数都可以写成有限小数和无限循 环小数的形式吗?
2 =1.41421356237309504880168… 3 5 =1.70997594667669698935310…
π=3.1415926535897932384626…
1.01001000100001…(两个1之间依次多一个0)
解:- 的相反数是 π -3.14的相反数是3.14-π
(2)指出 - 5 ,1- 3 3 分别是什么数的相反数;
(2)- 是 的相反数; 1- 是 -1 的相反数;
例题讲解
(3)求 3 64 的绝对值;
|
|=|-4|=4.
(4)已知一个数的绝对值是 3 ,求这个数。
绝对值为 的数是 或-
实数的运算
35
9
3 4
0.6
(6)实数集合: 9 3 5
0.6
3 4
3 9 3 0.13
64
0.6
3
3
4
0.13
3 9
64 3
3 9
人教版七年级下册数学《平方根》实数PPT教学课件

想一想
1. 121的平方根是什么? 11
2. 0的平方根是什么?
0
3.
16 49
的平方根是什么?
4 7
4. -9有没有平方根?为什么?
问题:(1)正数有几个平方根? (2)0有几个平方根? (3)负数呢?
没有,因为一个数的平方不可能是负数.
归纳总结
正数有2个平方根,它们互为相反数; 0的平方根是0; 负数没有平方根。
方根是平方根的一种. 2.只有非负数才有平方根和算术平方根. 3. 0的平方根是0,算术平方根也是0. 区别:1.个数不同:一个正数有两个平方根,但只有
一个算术平方根.
2.表示法不同:平方根表示为 a ,而算术平
方根表示为 a .
随堂练习
1.“± a ”的意义是( C ) A.a的平方根 B.a的算术平方根 C.当a≥0时,± a 是a的平方根 D.以上均不正确
开平方及相关运算
例 a的一个平方根是3,则另一个平方根是 -3 , a= 9 。
练一练
1.分别求下列各数的平方根:
(1)36 ; (2)295 ;
(3)1.21 .
2. 若一个数的平方等于5,则这个数等于 ___5___.
3.下列说法正确的是__①__④__⑤___ ① -3是9的平方根; ②25的平方根是5; ③ -36的平方根是-6; ④平方根等于0的数是0; ⑤64的算术平方根是8.
4.下列说法不正确的是___B___ A.0的平方根是0 B. 22 的平方根是2 C.非负数的平方根互为相反数 D.一个正数的算术平方根一定大于这个数的相反数
1.a的一个平方根是3,则另一个平方根是 -3 ,a= 9 . 2.81的平方根是___9_, 81 的算术平方根是__3__ . 3.3a-2和2a-3是一个正数的两个平方根,则这两个平方根 是__1_和_-_1_,这个数是_1__.
人教版七年级数学下册全册第六章《实数》PPT课件

… 0.25 0.790 6 2.5 7.906 25 79.06 250 …
规律:被开方数的小数点向右每移动 2 位,它的 算术平方根的小数点就向右移动 1 位;被开方数 的小数点向左每移动 2 位,它的算术平方根的小 数点就向左移动 1 位.
(2)用计算器计算 3(精确到0.001),并利用你在(1) 中发现的规律说出 0.03, 300, 30 000 的近似值,你 能根据 3 的值说出 30 是多少吗?
2.会求非负数的算术平方根,掌握算术平方根的非负 性.(重点、难点)
导入新课
历史感悟
毕达哥拉斯(公元前570年~公元前500年) 公元前500多年古希腊的哲学家、数学家、天文学家。
导入新课
万物皆数
导入新课
情境引入 学校要举行美术作品比赛,小明很高兴,他想
裁出一块面积为25dm2的正方形画布,画上自己的得 意之作参加比赛,这块正方形画布的边长应取多少? 你能帮小明算一算吗?
所以这个数是3或-3. 会不会是巧合呢?
解:设每块地板砖的边长为x m.由题意得
240x2 60, x2 1 . 4
x 1 1 0.5 42
故每块地板砖的边长是0.5 m.
拓展提升
已知:|x+2y|+ 3x 7 (5y z)2 0
求x-3y+4z的值. 解:由题意得:
3x 7 0, x 2y 0,5y z 0,
所以正数 t 4 2 (秒). 即铁球到达地面需要2秒.
当堂练习
1.填空:(看谁算得又对又快) (1) 一个数的算术平方根是3,则这个数是 9 . (2) 一个自然数的算术平方根为a,则这个自然数 是_a_2_;和这个自然数相邻的下一个自然数是 a2+1 .
规律:被开方数的小数点向右每移动 2 位,它的 算术平方根的小数点就向右移动 1 位;被开方数 的小数点向左每移动 2 位,它的算术平方根的小 数点就向左移动 1 位.
(2)用计算器计算 3(精确到0.001),并利用你在(1) 中发现的规律说出 0.03, 300, 30 000 的近似值,你 能根据 3 的值说出 30 是多少吗?
2.会求非负数的算术平方根,掌握算术平方根的非负 性.(重点、难点)
导入新课
历史感悟
毕达哥拉斯(公元前570年~公元前500年) 公元前500多年古希腊的哲学家、数学家、天文学家。
导入新课
万物皆数
导入新课
情境引入 学校要举行美术作品比赛,小明很高兴,他想
裁出一块面积为25dm2的正方形画布,画上自己的得 意之作参加比赛,这块正方形画布的边长应取多少? 你能帮小明算一算吗?
所以这个数是3或-3. 会不会是巧合呢?
解:设每块地板砖的边长为x m.由题意得
240x2 60, x2 1 . 4
x 1 1 0.5 42
故每块地板砖的边长是0.5 m.
拓展提升
已知:|x+2y|+ 3x 7 (5y z)2 0
求x-3y+4z的值. 解:由题意得:
3x 7 0, x 2y 0,5y z 0,
所以正数 t 4 2 (秒). 即铁球到达地面需要2秒.
当堂练习
1.填空:(看谁算得又对又快) (1) 一个数的算术平方根是3,则这个数是 9 . (2) 一个自然数的算术平方根为a,则这个自然数 是_a_2_;和这个自然数相邻的下一个自然数是 a2+1 .
6.3实数(课件)七年级数学下册(人教版)

●
●
●
●
●
●
●
-2
-1
●
●●
0
π
1
2
●
●
●
3
4
从图中可以看出,OO’的长是这个圆的周长π,所以点O’对应的数是π.
这样,无理数π可以用数轴上的点表示出来.
探究新知
人教版数学七年级下册
数轴上的点可以表示有理数,那它可以表示无理数吗,
你能在数轴上画出表示 的点吗?
2
-2
2-1
0
1
2
2
当数的范围从有理数扩充到实数后,实数与数轴上的点是一一对应
例1 (1)分别写出− 和π-3.14的相反数;
(2)指出− , −
��分别是什么数的相反数;
(3)求 −的绝对值;
(4)已知一个数的绝对值是 ,求这个数.
解:(1)因为
( 6) 6 ,-(π-3.14)=3.14-π,
所以, 6 ,π-3.14的相反数分别为 6 ,3.14-π.
人教版数学七年级下册
人教版数学七年级下册
第6.3 实数
学习目标
人教版数学七年级下册
1.理解无理数和实数的概念.
2.对实数进行分类,判断一个数是有理数还是无理数.
3.理解实数和数轴上的点一一对应.
4.掌握实数的运算法则及运算律.
情境引入
人教版数学七年级下册
探究
我们知道有理数包括整数和分数,请把下列分数写成
例题讲解
例2
人教版数学七年级下册
计算下列各式的值:
(1)( 3
2)
2; (2)3 3 2 3
解:
(1)( 3 2) 2
●
●
●
●
●
●
-2
-1
●
●●
0
π
1
2
●
●
●
3
4
从图中可以看出,OO’的长是这个圆的周长π,所以点O’对应的数是π.
这样,无理数π可以用数轴上的点表示出来.
探究新知
人教版数学七年级下册
数轴上的点可以表示有理数,那它可以表示无理数吗,
你能在数轴上画出表示 的点吗?
2
-2
2-1
0
1
2
2
当数的范围从有理数扩充到实数后,实数与数轴上的点是一一对应
例1 (1)分别写出− 和π-3.14的相反数;
(2)指出− , −
��分别是什么数的相反数;
(3)求 −的绝对值;
(4)已知一个数的绝对值是 ,求这个数.
解:(1)因为
( 6) 6 ,-(π-3.14)=3.14-π,
所以, 6 ,π-3.14的相反数分别为 6 ,3.14-π.
人教版数学七年级下册
人教版数学七年级下册
第6.3 实数
学习目标
人教版数学七年级下册
1.理解无理数和实数的概念.
2.对实数进行分类,判断一个数是有理数还是无理数.
3.理解实数和数轴上的点一一对应.
4.掌握实数的运算法则及运算律.
情境引入
人教版数学七年级下册
探究
我们知道有理数包括整数和分数,请把下列分数写成
例题讲解
例2
人教版数学七年级下册
计算下列各式的值:
(1)( 3
2)
2; (2)3 3 2 3
解:
(1)( 3 2) 2
人教版七年级数学课件《实数的相关概念及分类》

3.14-π.
3
3
3
3
(2)因为-(- 5)= 5,-( 3-1)=1- 3,所以,- 5,1- 3分别是 5, 3-1的相反数.
3
3
3
(3)因为 −64=- 64 =-4,所以| −64|=|-4|=4.
(4)因为| 3|= 3,|- 3|= 3,所以绝对值是 3的数是 3或- 3.
针对练习
人教版数学七年级下册
± 11
右
12.数轴上表示-3.14的点在表示-π的点的______侧.
13.若将三个数- 3, 7, 11表示在数轴上,其中能被如图所示
7
的墨迹覆盖的数是______.
达标检测
人教版数学七年级下册
14.请将图中数轴上标有字母的各点与下列实数对应起来:
3
解:A:-3,B:-2.5,C: 3,D:2 2,E: 15.
正实数
实数
正无理数
0
负有理数
负实数
负无理数
小结梳理
人教版数学七年级下册
事实上,每一个无理数都可以用数轴上的一个点表示出来.
当数的范围从有理数扩充到实数以后,实数与数轴上的点是一一对应的,
即每一个实数都可以用数轴上的一个点来表示;反过来,数轴上的每一个
点都表示一个实数.
与规定有理数的大小一样,对于数轴上的任意两个点,右边的点所表示的
圆上的一点由原点到达点O',点O'对应的数是多少?
OO'的长是这个圆的周长π,所以点O'的坐标为π.
无理数π可以用数轴上的点来表示出.
知识精讲
人教版数学七年级下册
如图,以单位长度为边长画一个正方形,以原点为圆心,
正方形对角线为半径画弧,与正半轴的交点就表示 2,与负半轴
3
3
3
3
(2)因为-(- 5)= 5,-( 3-1)=1- 3,所以,- 5,1- 3分别是 5, 3-1的相反数.
3
3
3
(3)因为 −64=- 64 =-4,所以| −64|=|-4|=4.
(4)因为| 3|= 3,|- 3|= 3,所以绝对值是 3的数是 3或- 3.
针对练习
人教版数学七年级下册
± 11
右
12.数轴上表示-3.14的点在表示-π的点的______侧.
13.若将三个数- 3, 7, 11表示在数轴上,其中能被如图所示
7
的墨迹覆盖的数是______.
达标检测
人教版数学七年级下册
14.请将图中数轴上标有字母的各点与下列实数对应起来:
3
解:A:-3,B:-2.5,C: 3,D:2 2,E: 15.
正实数
实数
正无理数
0
负有理数
负实数
负无理数
小结梳理
人教版数学七年级下册
事实上,每一个无理数都可以用数轴上的一个点表示出来.
当数的范围从有理数扩充到实数以后,实数与数轴上的点是一一对应的,
即每一个实数都可以用数轴上的一个点来表示;反过来,数轴上的每一个
点都表示一个实数.
与规定有理数的大小一样,对于数轴上的任意两个点,右边的点所表示的
圆上的一点由原点到达点O',点O'对应的数是多少?
OO'的长是这个圆的周长π,所以点O'的坐标为π.
无理数π可以用数轴上的点来表示出.
知识精讲
人教版数学七年级下册
如图,以单位长度为边长画一个正方形,以原点为圆心,
正方形对角线为半径画弧,与正半轴的交点就表示 2,与负半轴
《实数》ppt课件

指数运算法则可以用于简化复杂的数 学表达式。
03
CATALOGUE
实数的分类
有理数和无理数
有理数
可以表示为两个整数之比的数, 包括整数、有限小数和无限循环 小数。
无理数
无法表示为两个整数之比的数, 常见于无限不循环小数,如π和 √2。
正数、负数和零
01
02
03
正数
大于零的实数,包括正整 数、正小数和正无理数。
其结果仍为实数。
详细描述
实数的加法运算与整数、有理 数类似,遵循交换律和结合律 ,即a+b=b+a, (a+b)+c=a+(b+c)。
总结词
正数与负数相加,结果的符号 取决于绝对值较大的数。
详细描述
如果a>0,b<0,则a+b=a-(b);如果a<0,b>0,则 a+b=b-(-a)。
减法运算
总结词
《实数》PPT课件
目 录
• 实数的基本概念 • 实数的运算 • 实数的分类 • 实数在生活实数的基本概念
实数的定义
实数的定义
实数是包括有理数和无理数在内的所有数的集合,即实数集。实数集可以用实数轴来表 示,实数轴上的每一个点都对应一个实数,每一个实数都可以在实数轴上找到一个点来
乘法运算
总结词
乘法运算在实数范围内具有封闭性, 即任何两个实数相乘,其结果仍为实 数。
详细描述
实数的乘法运算遵循交换律和结合律 ,即ab=ba,(ab)c=a(bc)。
总结词
正数与负数相乘得负数,负数与负数 相乘得正数。
详细描述
正数乘以正数得正数,如2*3=6;正 数乘以负数得负数,如2*(-3)=-6; 负数乘以负数得正数,如(-2)*(3)=6。
人教版七年级下册 第六章 实数 6.3 实数 课件(共16张PPT)

3 1.7320
3 5 1.710
5 2.2360 3 7 1.913
3.14159265
无限不循环小数
无限不循环小数叫无理数
我们把这类无限不循环的小数叫做无理数。
☆无理数的特征:
1.圆周率及一些含有 的数 2 1
2.开方开不尽数 2、3 5
注意:带根号 的数不一定 是无理数
3
2
0.5050050005 (每两个5之间依次增加一个 0)
正有理数: 9 , __________________;
正无理数:_0_.5_0_5_0_0_5_0_0_0_5___,_3_3__, ;
3
1
负有理数: 8 , ____________3______;
,
正无理数: 5 2 __________________;
2 ___2___ ______ 0 _0___
a是一个实数,它的相反数为 -a
一个正实数的绝对值是它本身; 一个负实数的绝对值是它的相反数; 0的绝对值是0
1、正实数的绝对值是 它本身 ,0的绝对值是 0 , 负实数的绝对值是它的相反数 .
2、 3 的相反数是 3 ,绝对值是
3、一个数的绝对值是 p ,则这个数是 2
4、比较大小:-7 大于 50
3.
p 2
.
5、绝对值等于 5 的数是 5 。
(1)( 3 2) 2; (2)3 3 2 3
解:(1)( 3 2) 2 3 2 2 3
(2)3 3 2 3 (3 2) 3 5 3
解:由题知,a010 a
2 实数: __5_, _9_,_3__8,__13_,_0._•_,_0_,_2__,0_.5_0_5_0_050005 , 3 3
2020人教版七年级数学下册第六章6.3实数(1)实数的概念课件(共32张PPT)

6,
••
, 1. 2 3,
22 , 36
2
7
1.232232223 (两个3之间依次多一个 2)
有理数是:1.
•
2
•
3
22
,7
36
无理数是: 6
,,
2
1.232232223 ,(两个3之间依次多一个 2)
思考:无理数一般有哪些形式?
(1)像 7, 3, 12 的开不尽方的数是无理数。
020
002
000
02…是无
理数吗?
1.57079632679...
2
它们都是无限 不循环小数,
2.02002000200002…
是无理数
常见的一些无理数:
(1)含 π 的一些数;
(2)含开不尽方的数; (3)有规律但不循环的小数,如1.01001000100001…
例:判断下列数哪些是有理数?哪些是无理数?
人教版七年级数学 下册
6.3 实 数 第1课时 实数的概念
1.了解实数的意义,并能将实数按要求进 行准确的分类;
2.熟练掌握实数大小的比较方法;(重点) 3.了解实数和数轴上的点一一对应,能用 数轴上的点 表示无理数.(难点)
认真阅读课本中6.3 实数的 内容,完成下面练习并体验知 识点的形成过程。
• 这个矛盾说明, 2 不能写成分数的形式, 即 2 不是有理数。
• 实际上, 2 是无限不循环小数。
实数的概念:
在前面的学习中,我们知道,许多数的平方根和 立方根都是无限不循环小数,它们不能化成分数.我 们给无限不循环小数起个名字,叫“无理数”.有理 数和无理数统称为实数.
思考:
七年级数学下册教学课件《实数的概念》
2. 求下列各数的相反数与绝对值:
【教材P56 练习 第2题】
相反数: 绝对值:
2.5 , 7 , π , 3 2 , 0 2
π
-2.5
7
2
2 3 0
π
2.5
7
2
2 3 0
3. 求下列各式中的实数x:
(1)x 2; 3
x2 3
(3)x 10;
x 10
【教材P56 练习 第3题】
(2)x 0;
∴ 5,1 3 3分别是 5,3 3 1的相反数
例1 (3)求 3 64 的绝对值;
∵3 64 3 64 4 ∴ 3 64 4 4
【教材P55 例1】
(4)已知一个数的绝对值是 3 ,求这个数.
∵ 3 3
3 3
∴绝对值是 3的数是 3或 3
随堂训练
1. 下列说法正确的是( B ) A.带根号的数和分数统称实数 B.正实数包括正有理数和正无理数 C.实数包括正实数和负实数 D.无理数包括正无理数、负无理数和0
9 3,是有理数
2.将下列各数分别填入下列相应的括号内:
3 9 ,1 ,7 ,π,- 16 , 5 , 8 , 4 ,0 ,
4
9
25 ,0.525225……
无理数:
3 9 ,7 ,π, 5 ,0.525225……
有理数: 正实数: 负实数:
1 ,- 16 , 8 ,4 ,0 ,25
4
9
3 9 ,1 ,7 ,π,4 ,0 ,25 ,0.525225……
不能写成分数的形式 以看成分母是1的分数)
有
理 数
实数
和
无
分数
理
有理数
数
无理数
6.3.1实数-人教版七年级数学下册课件

你能求出下列各数的相反数、倒数和绝对值吗?
限 47 限 设点C表示的实数为x,则点A到点C的距离为-1-x,
5 . 8 7 5 2.会在实数范围内求一个数的相反数、倒数、绝对值.
小 8 循 思考: 是无理数吗?2.
反过来,数轴上的每一点都表示一个实数,即实数和数轴上的点是一一对应的。
数 环 ⑤无理数一定都带根号.
(√) (√) (√) (× ) (× ) (√) (× ) (√)
2、把下列各数分别填在相应的集合里
22 , 3.1415926, 7, 8, 3 2 , 0.6, 0,
7 36 ,
,
3
..
1.652,
0.3131131113
有理数集合
无理数集合
4. 下列说法不正确的是 A.|3-π|= 3-π C.2的相反数是-2
|-π|=___π_____,|3-π|=__π_-__3___.
2.我们在有理数范围内学过的运算法则和运算律是 否在实数范围内还能继续用呢?
在实数范围内,相反数、倒数、绝对值的意义和有理 数范围内的相反数、倒数、绝对值的意义完全一样。
学以致用 知行并进
你能求出下列各数的相反数、 倒数和绝对值吗?
7.如图所示,数轴上A,B两点表示的数分别为-1 和 3 ,点B关于点A的对称点为C,求点C所表示的 实数.
解:∵数轴上A,B两点表示的数分别为-1和 3 , ∴点B到点A的距离为1+ 3 ,则点C到点A的距离为 1+ 3 , 设点C表示的实数为x,则点A到点C的距离为-1-x, ∴-1-x=1+ 3 , ∴x=-2- 3
02002000200002… 有理数和无理数统称为实数
它们都是无限不循环小数,是无理数
6.3 实数 课件1(数学人教版七年级下册)

9
3 0. 6 4 3 0 . 6 64 4
3
9 3 0.13 3 0.13
64
3
3
9
9
3 4
3
9
3 4
0. 6
3
0.13
3 0. 6 4
3
5
64
9 3 0.13
随堂练习
一、判断:
1.实数不是有理数就是无理数。( 2.无理数都是无限不循环小数。(
、 2 这样的无理数的
点吗?
探究 问题1.无理数能在数轴上表示出来吗?
如图,直径为1个单位长度的圆从原点沿数轴向右 动一周,圆上一点从原点到达A点,则点A的坐标为多
倍 速 课 时 学
-4
-3
-2
-1
0
1
2
3A
4
无理数 可以用数轴上的点来表示.
探究
问题2.你能在数轴上表示出 2 吗
2
- 2
倍 速 课 时 学 -2 -1 0 1 8, 0Fra bibliotek无理数有
,
3
2
3
实数有22 , 1 , , 7 3
2 , 0. 3,
9,
3
8, 0
通过今天的学习, 用你自己的话说说你的收获和体会.
倍 速 课 时 学
11 5 , 90 9 47 5.875, 8 5 0. 5 9
无限不循环的小数 ---------- 叫做无理数.
(1) 你能举出一些无理数吗? (2)每个有理数都可以用数轴上的点表示,那么无理数 倍 速 课 时 学 是否也可以用数轴上的点来表示呢? (3) 你能在数轴上找到表示
人教版七年级数学下册《平方根》实数PPT优质课件

第六章 实数
平方根
第1课时
学习目标
1.了解算术平方根的概念,会用根号表示正数的算术平方根,并了解算术平
方根的非负性;
2.了解开方与乘方互为逆运算,会求某些非负数的算术平方根;
新课导入
学校要举行美术作品比赛,小明很高兴,他想裁出一块面积为
25 dm2的正方形画布,画上自己的得意之作参加比赛,这块正
是0.002,即 0.000004 0.002.
随堂练习
6.用大小完全相同的240块正方形地板砖,铺一间面积为60 m2的会
议室的地面,每块地板砖的边长是多少?
解:设每块地板砖的边长为x m.由题意得
1
240 x 2 60, x 2 .
4
1 1
x
0.5
4 2
故每块地板砖的边长是0.5 m.
方形画布的边长应取多少?你能帮小明算一算吗?
5 dm
因为 52=25
合作探究
新知一
什么是算术平方根
完成表1:
正方形的边长/dm
正方形的面积/dm2
1
1
3
9
6
2
5
36
4
25
4
16
你能从表1中各运算发现什么共同点吗
已知一个正数,求这个正数的平方
合作探究
完成表2:
正方形的面积/dm2
正方形的边长/dm
➢ 用计算器求解:
一般情况下按键顺序:
a
=
课堂总结
例1 估算 19 的值 ( D )
A.在1和2之间
B.在2和3之间
C.在3和4之间
D.在4和5之间
解析:因为42<19<52,所以4< 19 <5.
平方根
第1课时
学习目标
1.了解算术平方根的概念,会用根号表示正数的算术平方根,并了解算术平
方根的非负性;
2.了解开方与乘方互为逆运算,会求某些非负数的算术平方根;
新课导入
学校要举行美术作品比赛,小明很高兴,他想裁出一块面积为
25 dm2的正方形画布,画上自己的得意之作参加比赛,这块正
是0.002,即 0.000004 0.002.
随堂练习
6.用大小完全相同的240块正方形地板砖,铺一间面积为60 m2的会
议室的地面,每块地板砖的边长是多少?
解:设每块地板砖的边长为x m.由题意得
1
240 x 2 60, x 2 .
4
1 1
x
0.5
4 2
故每块地板砖的边长是0.5 m.
方形画布的边长应取多少?你能帮小明算一算吗?
5 dm
因为 52=25
合作探究
新知一
什么是算术平方根
完成表1:
正方形的边长/dm
正方形的面积/dm2
1
1
3
9
6
2
5
36
4
25
4
16
你能从表1中各运算发现什么共同点吗
已知一个正数,求这个正数的平方
合作探究
完成表2:
正方形的面积/dm2
正方形的边长/dm
➢ 用计算器求解:
一般情况下按键顺序:
a
=
课堂总结
例1 估算 19 的值 ( D )
A.在1和2之间
B.在2和3之间
C.在3和4之间
D.在4和5之间
解析:因为42<19<52,所以4< 19 <5.
《初中数学实数》课件

总结词
理解实数减法在数学中的重要性和应用,能够运用实数减 法解决实际问题。
详细描述
实数减法在数学中有广泛的应用,如计算差值、速度、加 速度等。通过掌握实数减法的运算法则和性质,可以更好 地解决实际问题。
实数的乘法运算
总结词
理解实数乘法的意义和性质,掌握实数乘法的运算法则 。
详细描述
实数的乘法运算与普通乘法运算类似,但需要考虑正负 数相乘的情况。实数乘法的意义是表示两个数在数轴上 的倍数关系,具有结合律和交换律。
实数的开方运算
04
平方根的定义和性质
平方根的定义
如果一个数的平方等于a,那么这个数就是a的平方根。例如,4的平方根是±2 。
平方根的性质
一个正数的平方根有两个值,一个正数和一个负数;0的平方根是0;负数没有 实数平方根。
立方根的定义和性质
立方根的定义
如果一个数的立方等于a,那么这个 数就是a的立方根。例如,8的立方 根是2。
无限性也是数学和物理学中许 多重要概念的基础,如无穷大 、无穷小等。
实数的运算
03
实数的加法运算
总结词
理解实数加法的意义和性质,掌握实数加法的运算法则 。
详细描述
实数的加法运算与普通加法运算类似,但需要考虑正负 数相加的情况。实数加法的意义是表示两个数在数轴上 的位移,具有结合律和交换律。
总结词
01
02
03
长度测量
实数可以用来表示物体的 长度,例如身高、体重等 。
时间计算
用实数表示时间,例如秒 、分、小时等。
货ห้องสมุดไป่ตู้计算
用实数表示货币,例如元 、角、分等。
实数在数学中的运用
代数运算
实数可以用于代数运算, 例如加、减、乘、除等。
理解实数减法在数学中的重要性和应用,能够运用实数减 法解决实际问题。
详细描述
实数减法在数学中有广泛的应用,如计算差值、速度、加 速度等。通过掌握实数减法的运算法则和性质,可以更好 地解决实际问题。
实数的乘法运算
总结词
理解实数乘法的意义和性质,掌握实数乘法的运算法则 。
详细描述
实数的乘法运算与普通乘法运算类似,但需要考虑正负 数相乘的情况。实数乘法的意义是表示两个数在数轴上 的倍数关系,具有结合律和交换律。
实数的开方运算
04
平方根的定义和性质
平方根的定义
如果一个数的平方等于a,那么这个数就是a的平方根。例如,4的平方根是±2 。
平方根的性质
一个正数的平方根有两个值,一个正数和一个负数;0的平方根是0;负数没有 实数平方根。
立方根的定义和性质
立方根的定义
如果一个数的立方等于a,那么这个 数就是a的立方根。例如,8的立方 根是2。
无限性也是数学和物理学中许 多重要概念的基础,如无穷大 、无穷小等。
实数的运算
03
实数的加法运算
总结词
理解实数加法的意义和性质,掌握实数加法的运算法则 。
详细描述
实数的加法运算与普通加法运算类似,但需要考虑正负 数相加的情况。实数加法的意义是表示两个数在数轴上 的位移,具有结合律和交换律。
总结词
01
02
03
长度测量
实数可以用来表示物体的 长度,例如身高、体重等 。
时间计算
用实数表示时间,例如秒 、分、小时等。
货ห้องสมุดไป่ตู้计算
用实数表示货币,例如元 、角、分等。
实数在数学中的运用
代数运算
实数可以用于代数运算, 例如加、减、乘、除等。
【新】人教版七年级数学下册第六章《 实 数》公开课课件.ppt

famous sights. If I'd gone alone, I couldn't have seen nearly as much, because I wouldn't have known my way about. 。2020年12月15日星期二2020/12/152020/12/152020/12/15
【预习导学】
②用一张硬纸片前一个半径为1cm的小圆,计算圆的周长,周长是有理 数还是无理数?如何在数轴上表示圆的周长呢?
归纳总结:实数与数轴上的点是 一一对应的 ,即任何一个都可以用数轴上的一 个点来表示;反过来,数轴上的每一个点都表示一个实数。数轴上的任意两个 点,右边的点表示的数总比左边的点表示的数 大 。
1、有理数的运算法则及运算律同样适用于实数的运算;当 遇到无理数并需要求出结果的近似值时,应按照要求的精 确度用相应的近似有限小数去代替无理数,再进行计算。
9、春去春又回,新桃换旧符。在那桃花盛开的地方,在这醉人芬芳的季节,愿你生活像春天一样阳光,心情像桃花一样美丽,日子像桃子一样甜蜜。 2020/12/152020/12/15Tuesday, December 15, 2020
【预习导学】
一、自学指导 1、自学1:自学课本P53-54页,完成54页“探究”,掌握实数的相关概念,理解实数与
数轴上的点的对应关系,完成下列填空。5分钟 归纳总结: 有理数 和 无理数 统称实数。 实数按正负分可分为 正实数 、 0 、 负实数 。
点拨精讲:带根号的不一定都是无理数;所有的无限循环小数都可以化成分数。
解:没有最大的实数,没有最小的实数,绝对值最小的实数是0. 2、设a是最小的自然数,b是最大的负整数,c是绝对值最小的实数,求
【预习导学】
②用一张硬纸片前一个半径为1cm的小圆,计算圆的周长,周长是有理 数还是无理数?如何在数轴上表示圆的周长呢?
归纳总结:实数与数轴上的点是 一一对应的 ,即任何一个都可以用数轴上的一 个点来表示;反过来,数轴上的每一个点都表示一个实数。数轴上的任意两个 点,右边的点表示的数总比左边的点表示的数 大 。
1、有理数的运算法则及运算律同样适用于实数的运算;当 遇到无理数并需要求出结果的近似值时,应按照要求的精 确度用相应的近似有限小数去代替无理数,再进行计算。
9、春去春又回,新桃换旧符。在那桃花盛开的地方,在这醉人芬芳的季节,愿你生活像春天一样阳光,心情像桃花一样美丽,日子像桃子一样甜蜜。 2020/12/152020/12/15Tuesday, December 15, 2020
【预习导学】
一、自学指导 1、自学1:自学课本P53-54页,完成54页“探究”,掌握实数的相关概念,理解实数与
数轴上的点的对应关系,完成下列填空。5分钟 归纳总结: 有理数 和 无理数 统称实数。 实数按正负分可分为 正实数 、 0 、 负实数 。
点拨精讲:带根号的不一定都是无理数;所有的无限循环小数都可以化成分数。
解:没有最大的实数,没有最小的实数,绝对值最小的实数是0. 2、设a是最小的自然数,b是最大的负整数,c是绝对值最小的实数,求
《实数的概念》课件

实数在生活中的应用
温度计上的实数
温度计上的数字表示实际温 度
温度计在生活中的应用:测 量体温、监测天气等
温度计的种类:水银温度计、 电子温度计等
温度计的准确性和使用注意 事项
身高体重指数(BMI)中的实数
身高体重指数(BMI)的定义 BMI中的实数计算 BMI指数在健康生活中的应用 如何根据BMI指数调整生活方式
课堂互动环节设计
案例分析:通过分析具体案例,让 学生更好地理解实数的概念和应用
添加标题
添加标题
添加标题
添加标题
分组讨论:将学生分成小组,让他 们讨论相关问题,提高合作能力
课堂测验:通过小测验或练习题, 检验学生对实数概念的理解和掌握 情况
练习题与答案解析
● 题目1:什么是实数? 答案1:实数包括有理数和无理数,有理数包括整数、分数、小数等,无理数包括无限不循 环小数等。
添加标题 添加标题 添加标题 添加标题
地图上的经纬度
经纬度定义:经度和纬度是地图上的两个基本坐标系统,用于确定地球上 任何位置的坐标。
实数与经纬度的关系:经度和纬度都是实数,可以用小数或度数表示。
经纬度在地图上的应用:通过经纬度可以确定地球上任何位置的精确位置, 从而进行导航、定位和地理信息系统的应用。
添加标题
添加标题
实数与其他数学概念的关系
总结与回顾
本节课的重点与难点总结
重点:实数的概 念、分类和性质
难点:实数的运 算规则和实际应 用
解决方法:通过 例题讲解和练习 巩固,加深对实 数概念的理解和 掌握
总结:回顾本节 课所学内容,强 调容
数
无理数与有理 数的区别:定 义、性质、运 算规则等方面
的差异
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
...
无理数集合
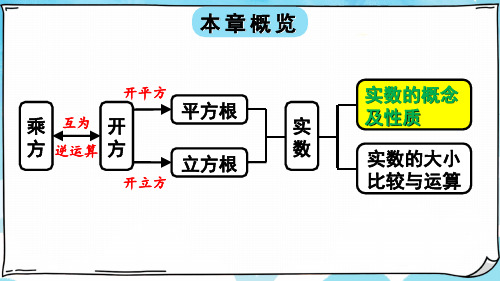
实数的分类
有理数和无理数统称实数
有理数 初中阶段对数的认识范围扩充为
新加入
无理数
实数
思考:实数如何分类?
实数的分类
(一)按定义分类
有 无实理数数
有限循小环数小分整或数数数无限
无限不循环小数
实数的分类
(二)按性质符号分类
正负实实实0数数数
正正有无理理数数
负无有理数
实数的分类
有理数和无理数统称实数.
4
4
A. 2 个
B.3个
C.4个
D.1个
热身运动(二)
判断正误 (1) -2是负数 (2) π是正数 (3) 1-π是正数
(4) 5 是正数
(5) 6是负数
( √) (√ ) ( ×)
(√ )
(√ )
热身运动(三)
1. 3的相反数是 -3
.
2. 3 的相反数是 3 .
1
3. 2 的倒数是 2 . 4. 3 2 的绝对值 是32 .
实数的运算顺序
先算乘方和开方,再算乘除,最后算 加减。如果遇到括号, 则先进行括号里 的运算
例1:求下列各式的值。
(1)( 3 2) 2
(2) 3 3 2 3
解: (1)
( 3 2) 2 3 ( 2 2) 30 3
(2) 3 3 2 3
(3 2) 3
5 3
(加法结合律 ) (分配律)
确度要比预定的精确度多取一位
练习:
1. 2 3 3 2 5 3 3 2 3 3
2. 3 2 3 1 1
3.
2 3
(4)2 2
4 3 ___________
.
热身运动(一)
1.下列各数不是有理数的是( B )
gg
A.3.14
B.-π C. 0.21 D. 102
2.在 1 , 7, 3 5 ,9,中是无理数的有( A )
2 • • 22 7
有理数是:1.23 , 7 , 36
无理数是:
6, 2
,
3.232232223
实学数以的致定用义
把下列各数分别填入相应的集合内:
有理数和无理数统称实数 22 , 7
3,
3
8,
0.101, ,
3
3
9,
64
20 , 3
•
2.1 21,
9 1,
16
0.3737737773
...
有理数集合
(1)a是一个实数,它的相反数为 a ,
绝对值为 a ;
1
(2)如果a 0,那么它的倒数为 a .
在实数范围内,相反数、绝对值的意义和有理数范围内 的相反数、绝对值的意义完全一样。
a是一个实数,实数a的相反数为 -a 。 一个正实数的绝对值是它本身; 一个负实数的绝对值是它的相反数; 0的绝对值是0
实数与数轴上的点是一一对应的。
练习
1.(1)请将数轴上是各点与下列实数对应起来:
22 1 1..55 55 33
A
B C DE
-3 -2 -1 0 1 2 3 4
(2)比较它们的大小(用“<”号连接)
-1.5< < 5 < 3 <
在数轴上表示的两个实数, 右边的数总比左边的数大。
课堂小结
我们主要学习了
义务教育课程标准实验教科书
知识回顾 有理数包括哪些数?有数整数正有理数 有理数 零
像 5,
分数
负有理数
2 5
,
287,
161,
1930,
8 9
.
探究1
试一试,把下列有理数写成小数的形式,有限你小数 有什么发现?
像事5实,上,25任,何一287个,有理161数,都1可930以无,限写循89成环.小数 156也有1 =都限=反5是0小.0过.5有数.4来.理或,1259任数无30=何=.限_有0循0_..1限_4环4_.小_小289_8数7数_=或的=0无_.形38_..限3式_7_循.5__环__小_数__
5.|-5|= 5 ,| 13 | 13 .| 21 |= 21 .
6.|-π|=
, | 3 17 |= 3 17 .
(3)求 3 64的绝对值 (4)已知一个数的绝对值是 3
求这个数.
填空 实力神枪手——看谁百发百中
1、正实数的绝对值是 它本身 ,0的绝对值是 0 , 负实数的绝对值是 它的相反数 .
2、 3 的相反数是 3 ,绝对值是 3 .
3.π-3.14的相反数是 ___3._14_-π 绝对值是 π-3.14
0.12345678910111213 …〔小数部分由相继的正整数组成〕…
无理数的分类
无限不循环小数叫做无理数.
无理数也有正负之分,例如:
正无理数: , 2 , 3 …
负无理数:— , — 2 , — 3 …
练习:判断下列数哪些是有理数?哪些是无理数?
6,
,
••
1. 2 3,
22 , 36 3.232232223
2、绝对值性质及应用
1)一个正数的绝对值是_它__本_身__,
一个负数的绝对值是它__的__相__反_数__,
零的绝对值是__零__。
a
a 0
a0 a0
a a 0
2) 对任何实数a,总有︱a︱_≥___0.
例题
(1)分别写出- 6 , 3.14 的相反数; (2)指出 5,1 3各是什么数的相反数
新无知理数的概念
所有的数都可以写成有限小数和无限循环 小数的形式吗?
2 =1.41421356237309504880168…
3 5 =1.70997594667669698935310…
π=3.1415926535897932384626…
1.01001000100001…(两个1之间依次多一个0)
4、比较大小:-7
50
5、绝对值等于 5 的数是 5 。
合作学习
请同学们总结有理数的运算律和运算法则
1.交换律 : 加法 a+b=b+a 乘法a×b=b×a
2.结合律: 加法(a+b)+c=a+(b+c) 乘法(a×b)×c=a×(b×c)
3.分配律: a× (b+c)= a×b+ a×c 注:有理数的运算律和运算法则在实数范围内同样适用
例2:计算
(1)
5 (精确到0.01);
( 2)
3 2 (结果保留3个有效数字)
解: (在1实)数5运算π中,2当.2遇36到无3.理14数2并且5.需38要;
求 确出度(结用2)果 相的 应3近 的 似 近2值似时有1,限.7可小32以数按去1.4照代1所替4 要无2求理.4的数5精,.
再进行计算。 在中间运算中 ,为了使结果更精确,精
无理数 可以用数轴上的点来表示.
探究2 把两个边长为1的小正方形通过剪、拼,得到一个大
正方形,大正方形的边长为 2 从而说明边长为1的小正方形的对角线为 2 。
21
1
2
问题2.你能在数轴上表示出 2和 吗?2
(1)如下图,以一个单位长度为边长画一个正方形,以原
点为圆心,正方形对角线为半径画弧,与正、负半轴的交点
(5)无理数都是无限小数。( )
•
(6)无限小数都是无理数。如 0(.3就×是)有理
探究2
问题1.你能在数轴上表示出π吗?
如图,直径为1个单位长度的圆从原点沿数轴向右滚动
一周,圆上一点从原点o到达A点,则点A的坐标为多少?
直径为1的圆的周长是 多少?
-4 -3 -2 -1 0 1 2 3A 4
OA= π A的坐标是 π
分别为点A和点B,数轴上A点和B点对应的数是什么?
(2事)实如上果将,所每有一有个理无数理都数标到都数可轴以上用,数那轴么上数轴的一填满个吗点? 来表示出来。
数轴上的点有些 C 表示有理数,有
21
些表示无理数.
B
1
A
-2 2-1
O
1 22
每一个实数都可以用数轴上的一个点来表示;
反过来,数轴上的每一点都表示一个实数。
通1.无过理这数的节概课念的无学理数习是,无限你不学循环习的了小数什. 么
2新.实的数的知概识念?有谈理谈数和你无理有数哪统称些为收实数获. ?
3.实数的分类
整数 有理数
实数
分数
无理数
有限小数和无限循环小数 无限不循环小数
正有理数
实数
正实数 正无理数
0 负实数
负有理数
负无理数
4.实数与数轴上的点是一一对应的.
无限不循环小数叫做无理数.
无理数的特征
无理数有三类:
1.圆周率 及一些含有 的数; ,
,
2 1 …
2
2.开不尽方的数; 注意:带根号的数
3,
37
12 …
不一定是无理数 如 4,3 8
3.有一定的规律,但不循环的无限小数.
0.1010010001…〔两个1之间依次多一个0〕
—168.3232232223…〔两个3之间依次多一个2〕
整数
有理数
实数
分数
有限小数和无限循环小数
无理数
无限不循环小数
正实数 实数 0
负实数
正有理数
正无理数 负有理数 负无理数
练一练
1.判断下列说法是否正确
(1)实数不是有理数就是无理数。( )
(2)无理数都是无限不循环小数。(
(3)带根号的数都是无理数。如(×9是)有理数
(4)无理数一定都带根号。如 ( 就×没有)根
带着问题自学课本54页“思考”
1.无理数也有相反数吗?怎么表示? 2.有绝对值吗?怎么表示? 3.有倒数吗?怎么表示?
