大学物理课件光的量子性
哈工大大学物理课件(马文蔚教材)-第19章-1量子物理

量子物理的前沿研究与未来发展
目前,量子物理领域的研究重点 包括量子纠缠、量子相干性、量
子计算复杂度等。
未来,随着实验技术的不断进步 和理论研究的深入,量子物理有 望在多个领域取得突破性进展。
例如,利用量子力学原理开发新 型传感器、探测器、加速器等设 备,以及探索宇宙中的量子现象
量子物理
目录
• 量子物理概述 • 光的量子性 • 量子力学的诞生 • 原子结构与量子力学 • 量子力学的数学基础 • 量子力学的应用与展望
01 量子物理概述
量子物理的发展历程
1900年
普朗克提出能量子假说,认为 能量是离散的,而不是连续的。
1925年
海森堡和薛定谔分别提出量子 力学的矩阵力学和波动力学两 种数学描述方式。
测量误差
由于不确定性原理的存在,我们无法同时精确测 量一个量子粒子பைடு நூலகம்位置和动量,测量结果会存在 误差。
互补性
互补性是量子力学中的另一个重要概念,它表明 某些物理量在测量时具有相互排斥的特性,无法 同时精确测量。
06 量子力学的应用与展望
量子计算与量子计算机
量子计算机利用量子比特(qubit)作为信息的 基本单位,相比传统计算机的经典比特(bit), 量子比特具有叠加和纠缠的特性,能够在理论 上大幅度提升计算速度。
薛定谔方程是描述量子粒子运动的偏微分方程, 它决定了波函数的演化。
时间演化
薛定谔方程描述了量子态随时间演化的过程,时 间演化由系统的哈密顿量决定。
空间演化
薛定谔方程的空间部分描述了波函数在空间中的 传播,与粒子的动量和位置有关。
海森堡不确定性原理
大学物理课件8光的量子性.ppt

激光 , 日光灯发光不是热辐射
dW
限于平衡热辐射的讨论。
(λ λ d λ)
T
2. 辐射度量
[1]光谱辐出度
单位面积
单位时间
(spectral radiant excitance)
单位时间内,从物体单位表面发出波长在λ附近
单位波长间隔内的电磁波的能量 ,称为光谱辐射
出射度用Mλ(λ,T)表示.。
蓝
紫
1885年,观测到的氢原子光谱线已有14条
▲巴耳末(J.J.Balmer)公式(可见光波段)
波数
~
1
41 B ( 22
1 n2
)
,
n 3,4,5,
B = 3645.6Å(经验常数) Å=10-10m
▲里德伯(J.R.Rydberg)公式(全波段)
~
R(
1 m2
1 n2
2.实验规律 装置:如图所示 规律:观察现象得出
光照射阴极 K,光电子从阴极 表面逸出。向阳极 A 运动,形 成光电流。
(1)饱和光电流Im 入射光一定,两极电压达到一
定数值后,光电流的稳定值。
饱和光电流与阴极逸出电子 I
数N之间有如下关系
Im2
I2
Im Ne
Im1
I1
——与入射光强度成正比。 Ua (2)截止电压Ua
康普顿 (A. pton) 美国人(1892-1962)
18.4 原子光谱和玻尔原子理论
一、原子光谱
原子光谱是原子发射光的强度随波长的分布, 是研究原子结构的基本方法。
1(85A3.J年.A。瑞ng典st人r‥o埃m)格斯特朗
测。得氢可见光光谱谱线, A即由此得来。
大学物理课件8光的量子性

[2]辐出度(radiant exc单ita位nc时e间) 内,从物体单位表面发出所有波长
的电磁波的能量 ,称为辐出度,用M(T)表示。 M(T ) M (,T )d 单位:W/m2 0
[3]吸收比与反射比
物体单位表面吸收或反射能量与入射能量比 值称为吸收比(λ,T)或反射比(λ,T).
(,T ) (,T ) 1
1o光子与束缚很紧的电子发生碰撞
相当于光子和整个原子碰撞,原子质量大; 散射光子的能量(波长)几乎不改变
2o可见光光子能量不够大,原子内电子不能视 为自由,不能产生康普顿效应。
康普顿 (A. pton) 美国人(1892-1962)
18.4 原子光谱和玻尔原子理论
一、原子光谱
原子光谱是原子发射光的强度随波长的分布, 是研究原子结构的基本方法。
“
普朗克:提出量子概念
发 爱因斯坦:提出光子学说
展 史
玻尔:建立量子论,解释原子光谱
德布罗意:建立波粒二象性概念
主要内容: 波粒二象性 激光
18.1 热辐射和普朗克能量子学说
一、 热辐射(heat radiation )1. 基本概念
物体在一定时间内辐射能量多少和辐射能按 波长分布与温度相关的电磁辐射称为热辐射。
o
510
nm
,
定出:
T表面 = 5700K C.斯特藩-玻耳兹曼定律
M0(T)=T 4
= 5.6710-8 W/m2K4
斯特藩—玻耳兹曼常量
1879年斯特藩从实验上总结而得
1884年玻耳兹曼从理论上证明
三、黑体辐射理论
1.经典物理学遇到的困难
问题:如何从理论上找到符合实验的函数式?
著名公式之一: 维恩公式(1896年)
2. 2. 光的量子性
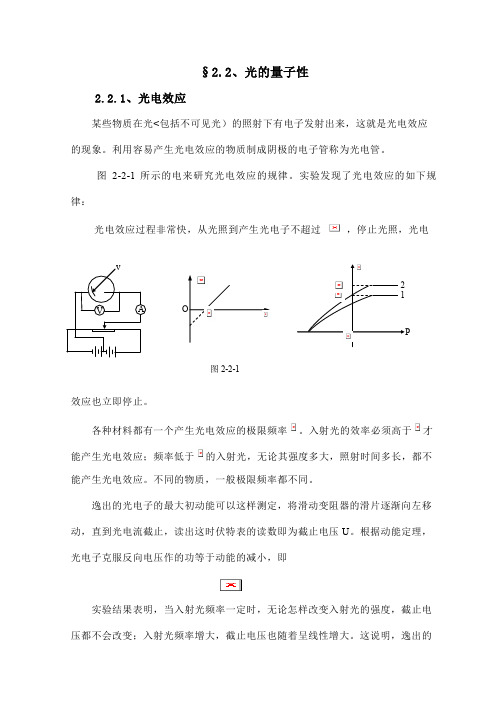
§2.2、光的量子性2.2.1、光电效应某些物质在光<包括不可见光)的照射下有电子发射出来,这就是光电效应的现象。
利用容易产生光电效应的物质制成阴极的电子管称为光电管。
图2-2-1所示的电来研究光电效应的规律。
实验发现了光电效应的如下规律:光电效应过程非常快,从光照到产生光电子不超过,停止光照,光电效应也立即停止。
各种材料都有一个产生光电效应的极限频率。
入射光的效率必须高于才能产生光电效应;频率低于的入射光,无论其强度多大,照射时间多长,都不能产生光电效应。
不同的物质,一般极限频率都不同。
逸出的光电子的最大初动能可以这样测定,将滑动变阻器的滑片逐渐向左移动,直到光电流截止,读出这时伏特表的读数即为截止电压U 。
根据动能定理,光电子克服反向电压作的功等于动能的减小,即实验结果表明,当入射光频率一定时,无论怎样改变入射光的强度,截止电压都不会改变;入射光频率增大,截止电压也随着呈线性增大。
这说明,逸出的图2-2-1光电子的最大初动能只能随入射光频率增大而增大,与入射光强度无关。
最大初动能与入射光频率的关系如图2-2-1所示。
在入射光频率一定条件下,向右移动变阻器的滑动片,光电流的强度随着逐渐增大,但当正向电压增大到某一值后继续再增大时,光电流维持一个固定图2-3值不变,此时光电流达到饱和。
增大入射光的强度P,饱和光电流也随着成正比地增大。
如图2-2-1所示。
2.2.2、光子说光电效应的四个特点中,只有第四个特点够用电磁来解释,其他特点都与电磁场理论推出的结果相矛盾。
爱因斯坦于1905年提出的光子说,完美地解释了这一现象。
光子说指出:空间传播的光<以及其他电磁波)都是不连续的,是一份一份的,每一份叫做一个光子。
光子的能量跟它的频率成正比即E=hv式中h为普朗克恒量。
光子也是物质,它具有质量,其质量等于光子也具有动量,其动量等于根据能量守恒定律得出:上式称为爱因斯坦光电效应方程。
式中W称为材料的逸出功,表示电子从物而中逸出所需要的最小能量。
《光的量子性与激光》PPT课件

M T
1 4.9651
hc k
b
19
普朗克辐射公式的讨论:
普朗克在推导过程中仍然使用了经典的波尔兹 曼分布,且最小能量为零;实际上振子在最低的
能量状态,也还有能量h/2 。 玻色和爱因斯坦
应用量子统计,重新导出了普朗克辐射公式,并 消除了波尔兹曼分布的在推导过程中的存在。
普朗克获得1918年诺贝尔物理学奖。
获得1923年诺贝尔物理学奖
2020年11月29日
29
§6 康普顿效应(1922~1923)
2020年11月29日
30
1.X射线在石墨上的 散射实验结果:
I
康普顿散射
=0o
准直系统
入射光0
散射光
石墨
散射体
探测器
I
=45o
(1) 散射的射线中有与 入射波长 相同的射线,也有波长
的射线.
0
0
。
2020年11月29日热辐射的光谱是连续光谱。
3
基尔霍夫定律:
定义辐射体在其波长附近的单位波长间隔
内的辐出度为单色辐出度:
(,T ) dM 0 d
物体在其波长附近的单位波长间隔内的吸收率,
称为单色吸收率: (,T ) dA d
基尔霍夫定律:处于平衡辐射中的任何物体
,其单色辐出度和单色吸收率之比是温度和波
由波尔兹曼分布,热平衡下,能量为的几率
正比于e-/kT:
e kTd
( ,T )
0
e kTd
kT
0
这个结果对应的,正是瑞利――金斯公式。
普朗克意识到,失败的原因就是引用了“谐振
子的能量是连续变化的”这个概念;他考虑谐振
光的量子性

产生光电子数目越多,光电流越大.( 0 时)
光子射至金属表面,一个光子携带的能量 h 将一 次性被一个电子吸收,若 0 ,电子立即逸出,
无需时间积累(瞬时性).
12 – 1 光的量子性
第十二章 量子物理基础
例1 波长为200nm的紫外线射到某种金属的表
解 (1)
E
h
hc
4.42 10 19 J
2.76eV
p
h
E c
1.47
10 27 kg
m s1
2.76eV /
c
(2) Ek E W (2.76 2.29)eV 0.47eV
(3)
hc E
5.18 10 7 m
518 nm
12 – 1 光的量子性
第十二章 量子物理基础
光电效应在近代技术中的应用
2πhc2
5
hc
e kT
* **
**
* *
* *
* 维恩曲线
* *
** *
* *
** *
O
这个公式在长波段与实验曲线相差较大!
12 – 1 光的量子性
第十二章 量子物理基础
瑞利 - 金斯公式(1900-1905年)
M 0 (T )
瑞利 - 金斯曲线
实验曲线
瑞利 - 金斯公式
M 0 (T )
2 π kcT
对同一种金属,W 一定,Ek ,与光强无关
几种金属的逸出功
金属
钠 铝 锌 钨 银铂
W / eV 2.28 4.08 3.34 4.54 4.73 6.35
12 – 1 光的量子性
第十二章 量子物理基础
《光学》光的量子性71√

光学课件目录
30
1 2 mv eU a 2 U a U 0
(1)
(2)
1 2 mv e eU 0 2
结论:光电子初动能和入射光频率成正比,与入射光 光强无关。 3、存在截止频率(红限) 对于给定的金属, 当照射光频率 0 小于某一数值 (称为红限)时, 无论照射光多强都不会产生光电效应。
2019/3/10
济南大学物理学院
光学课件目录
15
§7.1.3 黑体辐射的实验规律 一、绝对黑体 如果一个物体能全部吸收投射在它上面的辐射而 无反射,这种物体称为绝对黑体,简称黑体。
a0 ( , t ) 1.
基尔霍夫定律中的普适函数就是黑体的光谱辐出度
e( , t ) r0 ( , t ).
2019/3/10
济南大学物理学院
光学课件目录
31
因为初动能大于零,因而产生光电效应的条件是:
U0 0 . k
0 红限频率(截止频率)
U 0 / k。
4 . 光电效应瞬时响应性质
实验发现,无论光强如何微弱,从光照射到光电
子出现只需要 109 s 的时间。
结论:光电效应的产生几乎无需时间的累积。
(n为正整数)
2019/3/10
济南大学物理学院
光学课件目录
Hale Waihona Puke 23对于频率为 的谐振子最小能量为
h
h ——称为普朗克常数。
h 6.63 1034 J s
振子在辐射或吸收能量时,从一个状态跃迁到另 一个状态。 在能量子假说基础上,普朗克给出了黑体辐射 公式。 二、普朗克公式
r0 ( , T ) 2hc
e0 ( , T )
大学物理,量子物理基础2102光的量子性光电效应

第21章 量子物理基础
光电效应的实验规律是经典理论不能解释的。
按照光的电磁理论,光是电磁波。
当光照到金属上时,金属中的电子受到入 射光波中电场的作用而受迫振动,吸收光波的 能量,从而逸出金属表面。
光的强度和光振动的振幅有关,而且,光 的能量是连续分布在光场中的。
11
21.2 光的量子性
第21章 量子物理基础
研究光电效应主要是要解决以下问题:
1) 当光照射到金属表面时,从金属表面逸出 的光电子数和什么因素有关;
2) 光电子的初动能由什么因素决定;
3) 产生光电效应的条件是什么;
4) 如何从理论上解释光电效应。
3
21.2 光的量子性
第21章 量子物理基础
一、光电效应实验的规律
W 石英窗
光线经石英窗照在光
他用两套放电电极做实验,一套产生振荡, 发出电磁波;另一套充当接收器。电极之间存在 火花放电的缝隙。他发现当紫外光照在负电极上 时,放电就比较容易发生。
2
21.2 光的量子性
第21章 量子物理基础
外光电效应: 由于金属表面的电子吸收外界的 光子, 克服金属的束缚而逸出金属表面的现象。
内光电效应: 一些晶体或半导体在受到光照时, 其内部的原子释放的光电子仍留在材料内部,使材 料的导电性增强。
入射光强(光的能流密度), 等于单位时间垂直通过单位横截 面积的光能,就是单位时间垂直 通过单位横截面积的光子数与每
一光子能量 h 的乘积。
即为:I=Nh 。光强正比于单位时间通过
单位面积的光子数。光强越大,光子数越多。
因此,对单个光子,能量取决于频率;对一束
光来说,能量既与频率有关,又与光子数有关。
光吸收一个光子后,就获得 h 的能量,
大学高等物理课件大学高等物理课件A12_光的量子效应及光子理论

单元十二 光的量子效应及光子理论一 选择题01. 金属的光电效应的红限依赖于: 【 C 】(A) 入射光的频率; (B) 入射光的强度;(C) 金属的逸出功; (D) 入射光的频率和金属的逸出功。
根据爱因斯坦光电方程:2max 12v A h m W ν=+ —— A W 是金属的逸出功 红限频率:0A h W ν= —— 只和金属的逸出功有关。
正确答案(C)02. 已知某单色光照射到一金属表面产生了光电效应,若此金属的逸出电势是0U (使电子从金属逸出需做功0eU ),则此单色光的波长λ必须满足: 【 A 】(A)0hc eU λ≤; (B) 0hc eU λ≥; (C) 0eU hc λ≤; (D) 0eU hcλ≥。
产生光电效应光的最低频率:00A h W eU ν≥=−−→00eU hν≥ 将其上式代入00cλν=得到:0hceU λ≤—— 正确答案(A) 03. 在均匀磁场B内放置一簿板的金属片,其红限波长为0λ。
今用单色光照射,发现有电子放出,放出的电子(质量为m ,电量的绝对值为e )在垂直于磁场的平面内作半径为R 的圆周运动,那么此照射光光子的能量是: 【 B 】(A) 0hc λ; (B) 20()2hceRB m λ+; (C) 0hc eRB mλ+; (D) 02hceRB λ+。
根据红限波长得到金属的逸出功:00A cW h hνλ==光电效应产生的电子在磁场中作圆周运动的动能:212v k E m =电子作圆周运动满足:2v v m eB R =−−→2()2k eRB E m=照射光子的能量:2max 12v A h m W ν=+−−→20()2eRB ch h mνλ=+ —— 正确答案(B)04. 用强度为I ,波长为λ的X 射线分别照射锂(3)Z =和铁(26)Z =,若在同一散射角下测得康普顿散射的X 射线波长分别为Li λ和Fe λ(,)Li Fe λλλ>,它们对应的强度分别为Li I 和Fe I ,则【 C 】(A),Li Fe Li Fe I I λλ><; (B) ,Li Fe Li Fe I I λλ==;(C),Li Fe Li Fe I I λλ=>; (D) ,Li Fe Li Fe I I λλ<>。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2.物质波对玻尔理论解释 2020/6/6
电子轨道周长与德布罗意波长有如下关系
2020/6/6
[2]辐出度(radiant excitance) 单位时间内,从物体单位表面发出所有波长
的电磁波的能量 ,称为辐出度,用M(T)表示。 M(T) M(,T)d 单位:W/m2 0
[3]吸收比与反射比
物体单位表面吸收或反射能量与入射能量比 值称为吸收比(λ,T)或反射比(λ,T).
测。得氢可见光光谱谱线, A即由此得来。
6562.8Å
红
4861.3Å 4340.5Å
蓝
紫
1885年,观测到的氢原子光谱线已有14条
▲巴耳末(J.J.Balmer)公式(可见光波段)
波数 2020/6/6
~1B 4(2 1 2n 1 2), n33. 康普顿散射实验的意义
支持了“光量子”概念,进一步证实 e = h 。
了 首次实验证实了爱因斯坦提出的“光量子具有 动 量”的假设
P = E/c = h/c = h/
证实了在微观的单个碰撞事件中,动量和能量 守恒定律仍然是成立的
1o光子与束缚很紧的电子发生碰撞
相当于光子和整个原子碰撞,原子质量大; 散射光子的能量(波长)几乎不改变
e0( ,T)C 15e C T 2 C1 ,C2 为常数
——从热力学理论及实验数据的分析而得。
著名公式之二: 瑞利-金斯公式(1900年)
kT e0(λ,T)2πC λ4
k1.3 8 1 2 0 J 3K 1
——从经典电动力学和统计物理学理论推
2020/6/6
导而得。
♠ 由经典理论导出的 M (T)~ 公式都与实验结
▲里德伯(J.R.Rydberg)公式(全波段)
~R(m12
1 n2
)
m1,2,3, n m 1 ,m 2 ,m 3 ,
R4/B——里德伯常数
R=1.0967758107m-1(现代值)
m=1,2,3,4,5的谱系分别称为赖曼系、巴耳末
系、帕邢系、布喇开系和普芳德系。
10 原子光谱是分立的线状光谱;
问题: 电子作圆周运动要辐
射能量, 原子不稳定。
(2)普朗克、爱因斯坦量子化 eh
2. 玻尔氢原子理论的基础 ▲ 定态假设:E1< E2< E3 …
▲ 量子跃迁假设: En Em
h
▲ 量子化假设:
Lnhn n1,2, 量子数
2020/6/6
2π
3.对氢原子的计算
vn
氢原子所服从的方程
e2
4 e0r2
2020/6/6
12mm 2 eUa
截止电压 Ua 与 入射光 频率ν 呈线性关系
Ua KU0
其中: K 是一个普适常数, Uo 与材料有关。
——光电子初动能与入射光强无关。
(3)截止频率νo
对于给定材料,存在一个极限频率νo, ν < νo时, 无论入射光多强,不产生光电效应。
(4)响应时间很短
T
2. 辐射度量
[1]光谱辐出度
单位面积
单位时间
(spectral radiant excitance)
单位时间内,从物体单位表面发出波长在λ附近
单位波长间隔内的电磁波的能量 ,称为光谱辐射
出射度用Mλ(λ,T)表示.。
M(,T)dW d(T)
相关因素:T、λ 物质种类 表面情况
不同温度下辐射能按波长分布。由Mλ(λ,T) 分布可确定物体的温度。
20 谱线间相关,构成线系,可用经验公式表示;
30 谱线的波数可以用两个光谱项之差表示:
ν ~ T (m ) T (n ) —— 并合原则
2020/6/6
n
连续
5 4 3
2
帕邢系 巴耳末系
1赖曼系
2020/6/6
1 .36
3.39 1.51 0.85 0.54
eV
二、玻尔的原子理论
1. 玻尔氢原子理论的基础 (1)卢瑟福原子核式模型
2020/6/6
二、经典理论的困难
光的波动学说不能解释光电效应。
三、爱因斯坦的光子理论
1.光子(photon) 光不仅在吸收、辐射时是以能量子的微粒形式
出现,而且在传播中也是以光速运动的微粒,称
为光量子,简称光子。光子的物理量为
Eh mh/c2 ph/
2.光电效应方程(photoelectric effect equation)
“
普朗克:提出量子概念
发 爱因斯坦:提出光子学说
展 史
玻尔:建立量子论,解释原子光谱
德布罗意:建立波粒二象性概念
主要内容: 波粒二象性 激光
2020/6/6
18.1 热辐射和普朗克能量子学说
一、 热辐射(heat radiation)
1. 基本概念 物体在一定时间内辐射能量多少和辐射能按
波长分布与温度相关的电磁辐射称为热辐射。
果不符合!
M0( , T )
维恩公式
—— 长波部分出现偏差。
瑞利 — 金斯公式
—— 短波部分完全不符
1646 K
“紫外灾难”
物理学晴朗天空中的一朵乌云! 2. 普朗克量子假说
( 10 -6 m )
辐射物质中具有带电的线性谐振子,每个
谐振子只能吸收或发射不连续的一份一份的能量 2020/6/6
这个能量正比于振子频率 ,并且只能是最小能 量单元e 0 h(能量子)的整数倍。
2o可见光光子能量不够大,原子内电子不能视 为自由,不能产生康普顿效应。
2020/6/6
康普顿 (A. pton) 美国人(1892-1962)
2020/6/6
18.4 原子光谱和玻尔原子理论
一、原子光谱
原子光谱是原子发射光的强度随波长的分布, 是研究原子结构的基本方法。
1(85A3.J年.A。瑞ng典st人r‥o埃m)格斯特朗
(,T )(,T )1
二、黑体及辐射规律
1.黑体(Black-body ) 完全吸收各种波长电磁波而无反射的物体
2020/6/6
M0(λ,T)最大, 且只与温度有关而和材料及 表面状态无关。
M ((,T ,T))M0(,T)
——基尔霍夫辐射定律
♠ 维恩设计的黑体——空腔开口面
2.黑体辐射的基本规律 A.黑体辐射谱
碰撞 光子把部分能
量传给电子 光子的
能量 散射X射线的
频率,波长 2020/6/6
定量分析: 能量守恒:
P0
h0
c
nˆ0
e
P
h
nˆ
jc
动h量0守m 恒0:c2h h 0 hm c2cojsm c m0 osmv
0chcsij nm sin
c
利用 mm0
1c22
c
0
c
0
λc2020/6/6m hoC0 0.0m 2h 0C4(1310 10cm—oj—s)称康为普康顿普散顿射波公长式
M0(,T)
170K0
实验规律!(如图) 曲线与横轴围的面积就 是Mo(T)
2020/6/6
150K0 110K0
o
B.维恩位移定律(Wien displacement law)
Tm b
M0(,T)
170K0
b2 .89 18 3 0 m K
1893年由理论推导而得,
150K0 110K0
若19视11太年阳获为得黑诺体贝,尔测物得理学m奖51on0m, 定出:
温度 发射的能量 电磁波的短波成分
—— 低温物体发出的是红外光; —— 炽热物体发出的是可见光; —— 高温物体发出的是紫外光; 注 当物体辐射能量等于它同时间内吸收的辐射能 意 时,物体温度保持不变,称为平衡热辐射。
2020/6/6
激光 , 日光灯发光不是热辐射
dW
限于平衡热辐射的讨论。
(λλdλ)
1
hc
令:
C1
2hc2,C2
hc k
ekT
e0(,T)C15eCT2
维恩公式
当波长很长,温度较高时
hc/(kT ) 1
e0(λ,T)2πh2 C λ5
1
hc
eλkT 1
eh kc T1h kcT 1 2(h kcT )2
M 0(,T)2ck 4T 金斯公式
2o对Mo(λ,T)求导和积分,可以给出维恩位移定 律和玻尔兹曼定律。
主量子数 n
Enl 6 5
-0.85eV 4 -1.81eV 3
1 布喇开系 En n2 E1
帕邢系
13.6 n2 eV
-3.39eV 2 -13.6eV 1
巴耳末系(可见区)
赖曼系(紫外区)
由能级算出 的光谱线频 率和实验结 果完全一致
2020/6/6
氢原子能级图
18.5 实物粒子的波动性
me4
n28e2h2
分立能级
0
n 1时 E113 .6eV——基态能级
n 2时 En
光子频率:
13.6n12
eV——激发态能级
E n hE m4(4 m 0 4)e2e 3[m 12n 12] En
●
~c4(4m 04)e2 e3c[m 12n 12] Em
e R 2020/4 6/6 (4 m0 4)e231.097 317 70m 311符实合验
随散射角j 增加而
0 j
0
探 测
石墨体 (散射物质)
器
X 射线
谱仪
1927年获诺
增加,与散射物质无关。
贝尔奖。
变线的强度随原子序数增加而减小。
2020/6/6
二、康普顿效应的理论解释
1.经典理论 按经典理论,原子中电子受照射光作用,做
