运筹学最短路径实验word精品
最短路径问题(珍藏版)_201710261614551 (1)

【问题概述】最短路径问题是图论研究中的一个经典算法问题,旨在寻找图(由结点和路径组成的)中两结点之间的最短路径.算法具体的形式包括:①确定起点的最短路径问题 - 即已知起始结点,求最短路径的问题.②确定终点的最短路径问题 - 与确定起点的问题相反,该问题是已知终结结点,求最短路径的问题.③确定起点终点的最短路径问题 - 即已知起点和终点,求两结点之间的最短路径.④全局最短路径问题 - 求图中所有的最短路径.【问题原型】“将军饮马”,“造桥选址”,“费马点”.【涉及知识】“两点之间线段最短”,“垂线段最短”,“三角形三边关系”,“轴对称”,“平移”.【出题背景】角、三角形、菱形、矩形、正方形、梯形、圆、坐标轴、抛物线等.【解题思路】找对称点实现“折”转“直”,近两年出现“三折线”转“直”等变式问题考查.【十二个基本问题】【问题1】作法图形原理连AB,与l交点即为P.两点之间线段最短.PA+PB 最小值为 AB.在直线l上求一点P,使PA+PB 值最小.【问题2】“将军饮马”作法图形原理作B关于l的对称点B'两点之间线段最短.连A B',与l交点即为P.PA+PB 最小值为 A B'.在直线l上求一点P,使PA+PB 值最小.【问题3】作法图形原理分别作点P关于两直线的两点之间线段最短.对称点P'和P',连P'P',PM+MN+PN 的最小值为在直线l1、l2上分别求点与两直线交点即为M,N.线段P'P''的长.M、N,使△PMN 的周长最小.【问题4】作法图形原理分别作点Q、P关于直线两点之间线段最短.l1、 l2的对称点Q'和P'四边形PQMN周长的最小连Q'P',与两直线交点即值为线段P'P''的长.在直线l1、l2上分别求点为M,N.M 、N ,使四边形 PQMN的周长最小.- 1 -【问题5】“造桥选址”作法图形原理将点A向下平移MN的长两点之间线段最短.度单位得A',连A'B,交nAM+MN+BN 的最小值为于点N,过N作NM⊥ m于直线m∥ n,在m、n,A'B+MN.M.上分别求点M、N,使MN⊥ m,且AM+MN+BN的值最小.【问题6】作法图形原理将点A向右平移a个长度单位得A',作A'关于l 两点之间线段最短.的对称点A'',连A''B,交AM+MN+BN 的最小值为在直线l上求两点M、N(M 直线l于点N,将N点向A''B+MN.在左),使MN=a,并使左平移a个单位得M.AM+MN+NB 的值最小.【问题7】作法图形原理作点P关于l1的对称点点到直线,垂线段最短.2于B,交PA+AB PP',作 P'B⊥l 的最小值为线段'在l1上求点A,在l2上求l2于A.B的长.点B,使PA+AB值最小.【问题8】作法图形原理作点A关于l2的对称点两点之间线段最短.A',作点 B 关于l1的对AM+MN+NB 的最小值为A 为l1上一定点,B 为l2上称点B',连A'B'交l2于线段A'B'的长.一定点,在l2上求点M,M,交l1于 N.在l1上求点N,使AM+MN+NB 的值最小.【问题9】作法图形原理垂直平分上的点到线段两连AB,作AB的中垂线与端点的距离相等.在直线l上求一点P,使直线l的交点即为P.PA - PB =0.PA - PB 的值最小.、【问题10】作法图形原理三角形任意两边之差小于作直线AB,与直线l的交第三边.PA - PB ≤AB.在直线l上求一点P,使点即为P.PA - PB 的最大值=AB.PA - PB 的值最大.【问题11】作法图形原理三角形任意两边之差小于作B关于l的对称点B'第三边.PA - PB ≤AB'.作直线A B',与l交点即在直线l上求一点P,使为P.PA - PB 最大值=AB'.PA - PB 的值最大.【问题12】“费马点”作法图形原理所求点为“费马点”,即满足∠APB=∠BPC=∠APC=120°.以 AB、AC 两点之间线段最短.为边向外作等边△ABD、PA+PB+PC 最小值=CD.△ABC中每一内角都小于△ACE,连CD、BE相交120°,在△ABC内求一点于P,点P即为所求.P,使 PA+PB+PC 值最小.【精品练习】1.如图所示,正方形ABCD的面积为12,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为()A D A.2 3 B.2 6 C.3D. 6 PEB C2.如图,在边长为 2 的菱形ABCD中,∠ABC=60°,若将△ACD绕点A旋转,当AC′、AD′分别与BC、CD 交于点E、F,则△CEF的周长的最小值为()A.2 B.2 3C.2+ 3 D.4- 3 -3.四边形 ABCD 中,∠B =∠D =90°,∠C =70°,在 BC 、CD 上分别找一点 M 、N ,使△AMN 的周长最小时, ∠AMN +∠ANM 的度数为( )A .120°B .130°C .110°D .140°4.如图,在锐角△ABC 中,AB =4 2 ,∠BAC =45°,∠BAC 的平分线交 BC 于点 D ,M 、N 分别是 AD 和 AB上的动点,则 BM +MN 的最小值是.5.如图,Rt △ABC 中,∠C =90°,∠B =30°,AB =6,点 E 在 AB 边上,点 D 在 BC 边上(不与点 B 、C 重合),且 ED =AE ,则线段 AE 的取值范围是 .6.如图,∠AOB =30°,点 M 、N 分别在边 OA 、OB 上,且 OM =1,ON =3,点 P 、Q 分别在边 OB 、OA 上,则 MP +PQ +QN 的最小值是_________.(注“勾股定理”:直角三角形中两直角边的平方和等于斜边的平方,即 Rt △ABC 中,∠C =90°,则有 AC 2 + BC 2 = AB 2)7.如图,三角形△ABC 中,∠OAB =∠AOB =15°,点 B 在 x 轴的正半轴,坐标为 B ( 6 3 ,0).OC 平分∠AOB ,点 M 在 OC 的延长线上,点 N 为边 OA 上的点,则 MA +MN 的最小值是______.- 4 -8.已知A(2,4)、B(4,2).C在y轴上,D在x轴上,则四边形ABCD的周长最小值为,此时C、D两点的坐标分别为.9.已知A(1,1)、B(4,2).(1)P为x轴上一动点,求PA+PB的最小值和此时P点的坐标;(2)P为x轴上一动点,求PA PB的值最大时P点的坐标;(3)CD为x轴上一条动线段,D在C点右边且CD=1,求当AC+CD+DB的最小值和此时C点的坐标;10.点C为∠AOB内一点.(1)在OA求作点D,OB上求作点E,使△CDE的周长最小,请画出图形;(2)在(1)的条件下,若∠AOB=30°,OC=10,求△CDE周长的最小值和此时∠DCE的度数.- 5 -。
最短路径的实验报告

最短路径的实验报告最短路径的实验报告引言:最短路径问题是图论中一个经典的问题,涉及到在一个带有权重的图中找到两个顶点之间的最短路径。
本实验旨在通过实际操作和算法分析,深入探讨最短路径算法的性能和应用。
实验设计:本次实验使用了Dijkstra算法和Floyd-Warshall算法来解决最短路径问题。
首先,我们使用Python编程语言实现了这两个算法,并对它们进行了性能测试。
然后,我们选择了几个不同规模的图进行实验,以比较这两种算法的时间复杂度和空间复杂度。
最后,我们还在实际应用中使用了最短路径算法,以验证其实用性。
实验过程:1. 实现Dijkstra算法Dijkstra算法是一种贪心算法,用于求解单源最短路径问题。
我们首先实现了该算法,并对其进行了性能测试。
在测试中,我们使用了一个包含1000个顶点和5000条边的图,记录了算法的运行时间。
结果显示,Dijkstra算法的时间复杂度为O(V^2),其中V表示图中的顶点数。
2. 实现Floyd-Warshall算法Floyd-Warshall算法是一种动态规划算法,用于求解所有顶点对之间的最短路径。
我们在Python中实现了该算法,并对其进行了性能测试。
在测试中,我们使用了一个包含100个顶点和5000条边的图,记录了算法的运行时间。
结果显示,Floyd-Warshall算法的时间复杂度为O(V^3),其中V表示图中的顶点数。
3. 比较两种算法通过对Dijkstra算法和Floyd-Warshall算法的性能测试,我们可以看到,Dijkstra算法在处理较大规模的图时性能更好,而Floyd-Warshall算法在处理较小规模的图时性能更好。
因此,在实际应用中,我们可以根据图的规模选择合适的算法。
4. 应用实例为了验证最短路径算法的实际应用性,我们选择了一个城市交通网络图进行实验。
我们使用了Dijkstra算法来计算两个城市之间的最短路径,并将结果与实际的驾车时间进行比较。
最短路径实验报告

最短路径实验报告最短路径实验报告引言:最短路径算法是计算机科学中的一个经典问题,它在许多领域中都有广泛的应用,如交通规划、电路设计、网络通信等。
本实验旨在通过实践探索最短路径算法的实际应用,并对其性能进行评估。
一、问题描述:我们将研究一个城市的交通网络,其中包含多个节点和连接这些节点的道路。
每条道路都有一个权重,表示通过该道路所需的时间或距离。
我们的目标是找到两个节点之间的最短路径,即使得路径上各个道路权重之和最小的路径。
二、算法选择:为了解决这个问题,我们选择了Dijkstra算法和Floyd-Warshall算法作为比较对象。
Dijkstra算法是一种单源最短路径算法,它通过不断选择当前最短路径的节点来逐步扩展最短路径树。
Floyd-Warshall算法则是一种多源最短路径算法,它通过动态规划的方式计算任意两个节点之间的最短路径。
三、实验设计:我们首先构建了一个包含10个节点和15条道路的交通网络,每条道路的权重随机生成。
然后,我们分别使用Dijkstra算法和Floyd-Warshall算法计算两个节点之间的最短路径,并记录计算时间。
四、实验结果:经过实验,我们发现Dijkstra算法在计算单源最短路径时表现出色,但是在计算多源最短路径时效率较低。
而Floyd-Warshall算法在计算多源最短路径时表现出色,但是对于大型网络的单源最短路径计算则需要较长的时间。
五、性能评估:为了评估算法的性能,我们对不同规模的交通网络进行了测试,并记录了算法的计算时间。
实验结果显示,随着交通网络规模的增大,Dijkstra算法的计算时间呈指数级增长,而Floyd-Warshall算法的计算时间则呈多项式级增长。
因此,在处理大型网络时,Floyd-Warshall算法具有一定的优势。
六、实际应用:最短路径算法在实际应用中有着广泛的用途。
例如,在交通规划中,最短路径算法可以帮助我们找到最优的行车路线,减少交通拥堵。
最短路径实验报告
云南财经大学信息学院学生综合性与设计性实验报告(2013—2014 学年第 2 学期)一、实验内容与目的1.内容查看“最短路径.swf”,选择熟悉的程序设计语言定义有向图,根据动画演示求取从有向图任一结点到其他结点的最短路径。
2.实验目的了解最短路径的概论,掌握求最短路径的方法。
二、实验原理或技术路线(可使用流程图描述)实验原理:(李燕妮负责设计,周丽琼负责编程)图是由结点的有穷集合V和边的集合E组成,求最短路径用迪杰斯特拉算法:1)适用条件&范围:a) 单源最短路径(从源点s到其它所有顶点v);b) 有向图&无向图(无向图可以看作(u,v),(v,u)同属于边集E的有向图)c) 所有边权非负(任取(i,j)∈E都有Wij≥0);2)算法描述:a)初始化:dis[v]=maxint(v∈V,v≠s); dis[s]=0; pre[s]=s; S={s};b)For i:=1 to n1.取V-S中的一顶点u使得dis[u]=min{dis[v]|v∈V-S}2.S=S+{u}3.For V-S中每个顶点v do Relax(u,v,Wu,v)c)算法结束:dis[i]为s到i的最短距离;pre[i]为i的前驱节点三、实验环境条件(使用的软件环境)Microsoft Visual C++6.0四、实验方法、步骤(列出程序代码或操作过程)/*本程序的功能是求图中任意两点间的最短路径*/#include<stdio.h>#include<stdlib.h>#include<conio.h>#include<string.h>#define ING 9999typedef struct ArcCell{int adj;/*顶点关系类型,用1表示相邻,0表示不相邻*/}ArcCell,**AdjMatrix;/*邻接矩阵*/typedef struct type{char data[3];/*顶点值*/}VertexType;typedef struct{VertexType *vexs; /*顶点向量*/AdjMatrix arcs; /*邻接矩阵*/int vexnum,arcnum; /*图的顶点数和边数*/}MGraph;/*初始图*/void InitGraph(MGraph *G){int i,nu,mu;printf("\n输入顶点的个数和(边)弧的个数:");scanf("%d %d",&nu,&mu);G->arcs=(ArcCell **)malloc(nu*sizeof(ArcCell *));for(i=0;i<nu;i++)/*分配邻接矩阵空间*/G->arcs[i]=(ArcCell *)malloc(nu*sizeof(ArcCell));G->vexs=(VertexType *)malloc(nu*sizeof(VertexType)); /*分配顶点空间*/ G->vexnum=nu;G->arcnum=mu; /*图的顶点数和边数*/}void InsertGraph(MGraph *G,int i,VertexType e){if(i<0||i>G->vexnum) return;strcpy(G->vexs[i].data,e.data);}/*确定v1在图顶点中的位置*/int Locate(MGraph G,VertexType v1){int i;for(i=0;i<G.vexnum;i++)if(strcmp(v1.data,G.vexs[i].data)==0) return i;return -1;}/*采用数组(邻接矩阵)和邻接表表示无向图*/void CreateUND(MGraph *G){int i,j,k,*p,w;VertexType v1,v2;p=(int *)malloc(G->vexnum*sizeof(int));for(i=0;i<10;i++) p[i]=0;for(i=0;i<G->vexnum;++i) /*初始邻接表*/{for(j=0;j<G->vexnum;++j)G->arcs[i][j].adj=ING;}for(k=0;k<G->arcnum;++k){printf("\n输入第%d 条(边)弧相对的两个顶点值:\n",k+1);scanf("%s %s",v1.data,v2.data);/*输入相邻的两个点值*/printf("输入它们的权值: ");scanf("%d",&w);i=Locate(*G,v1);j=Locate(*G,v2); /*用i 和j来确定它们的位置*/G->arcs[i][j].adj=w;}}/*输出邻接矩阵*/void Pint(MGraph G){int i,j;for(i=0;i<G.vexnum;i++){for(j=0;j<G.vexnum;j++){if(G.arcs[i][j].adj!=ING)printf("\t%d",G.arcs[i][j].adj);else{if(i==j)printf("\t0");else printf("\t∞");}}printf("\n");}}/*对顶点V0到其余顶点v的最短路径p[v]及其带权长度D[v]若p[v][w]为1,则w是从V0到W当前求得最短路径上的顶点, final[v]为1,当且仅当v属于S,即已经求得从v0到v的最短路*/void ShortestPath(MGraph G,int v0,int **p,int *D){int v,u,i,w,min;int *final;final=(int *)malloc(G.vexnum*sizeof(int));/*分配空间*/for(v=0;v<G.vexnum;++v){final[v]=0;D[v]=G.arcs[v0][v].adj;/*初始化*/for(w=0;w<G.vexnum;++w) p[v][w]=0;/*设空路径*/if(D[v]<ING){p[v][v0]=1;p[v][v]=1;}/*v到v0有路径*/}D[v0]=0;final[v0]=1;/*初始化,V0顶点属于S集*/for(i=1;i<G.vexnum;i++){/*其余G.vexnum-1个顶点*/min=ING;for(w=0;w<G.vexnum;++w) /*求出矩阵这一行的最小值*/ if(!final[w]) /*W顶点属于V-S中*/if(D[w]<min){v=w;min=D[w];}final[v]=1;/*离V0顶点最近的V加入S集*/for(w=0;w<G.vexnum;++w) /*更新当前最短路径及距离*/ if(!final[w]&&(min+G.arcs[v][w].adj<D[w])){ /*不是最小的,修改D[w],P[w]*/D[w]=min+G.arcs[v][w].adj;for(u=0;u<G.vexnum;u++)p[w][u]=p[v][u];p[w][w]=1;}}free(final);}void main(){MGraph G;VertexType e;int i,j;int **p;int *D;InitGraph(&G);p=(int **)malloc(G.vexnum*sizeof(int *));for(i=0;i<G.vexnum;i++)p[i]=(int *)malloc(G.vexnum*sizeof(int));D=(int *)malloc(G.vexnum*sizeof(int));printf("顶点值:\n");for(i=0;i<G.vexnum;++i)/*给图顶点向量付值*/{scanf("%s",e.data);InsertGraph(&G,i,e);}CreateUND(&G);/*构造图结构*/printf("邻接矩阵为:\n");Pint(G);for(i=0;i<G.vexnum;i++) /*输出邻接矩阵*/{ShortestPath(G,i,p,D); /*调用最短函数*/for(j=0;j<G.vexnum;j++)if(i!=j) printf(" %s 到%s 的最短路径为%d \n",G.vexs[i].data,G.vexs[j].data,D[j]);printf("\n\n");}getch();}五、实验过程原始记录( 测试数据、图表)请给出各个操作步骤的截图和说明,要求有对时间复杂度和空间复杂度的说明。
最短路径问题的求解PPT精选文档

.
3
最短路径问题的求解
三、等代价搜索法 等代价搜索法也是在宽度优先搜索的基础上进行了部分优化的一种算法,它与
启发式搜索的相似之处都是每次只展开某一个结点(不是展开所有结点),不同之 处在于:它不需要去另找专门的估价函数,而是以该结点到A点的距离作为估价值, 也就是说,等代价搜索法是启发式搜索的一种简化版本。它的大体思路是:
.
2
最短路径问题的求解
二、 启发式搜索 在宽度优先搜索算法的基础上,每次并不是把所有可展开的结点展开,
而是对所有没有展开的结点,利用一个自己确定的估价函数对所有没展开 的结点进行估价,从而找出最应该被展开的结点(也就是说我们要找的答 案最有可能是从该结点展开),而把该结点展开,直到找到目标结点为止。
.
12
最短路径问题的求解
八、Dijkstra算法(从一个顶点到其余各顶点的最短路径,单源最短路径) 例3、如下图,假设C1,C2,C3,C4,C5,C6是六座城市,他们之间的连线表示两 城市间有道路相通,连线旁的数字表示路程。请编写一程序,找出C1到Ci 的最短路径(2≤i≤6),输出路径序列及最短路径的路程长度。
3、由数轴可见,A与A'点相比,A点离原点近,因而保留A点,删除A'点,相应的,B、B'点保留B点, D、D'保留D',E、E'保留E',得到下图:
.
11
最短路径问题的求解
4、此时再以离原点最近的未展开的点B联接的所有点,处理后,再展开离原点最近未展开的D点, 处理后得到如下图的最终结果:
运筹学-最短路问题

V1 0 V2 2 V3 5 D = V4 − V5 − V6 − V7 −
பைடு நூலகம்
v2
2 0 2 4 6 − −
v3
5 2 0 1 − 3 −
v4
− 4 1 0 4 1 4
v5
− 6 − 4 0 − 1
v6
− − 3 1 − 0 2
v7
− − − 4 1 2 0
二、最短路算法: 最短路算法:
1. D氏标号法(Dijkstra) 氏标号法(Dijkstra) (1)求解思路 求解思路——从始点出发,逐步顺序 从始点出发, 从始点出发 逐步顺序 地向外探寻,每向外延伸一步都要求是最 地向外探寻,每向外延伸一步都要求是最 短的。 短的。 (2)使用条件 使用条件——网络中所有的弧权均 网络中所有的弧权 网络中所有的弧权均 非负, 非负,即 wij ≥ 0 。
(4) 计算步骤及例:
第三步:若网络图中已无T标号点 标号点, 第三步:若网络图中已无 标号点,停止 计算。否则 令 计算。否则,令 二步。 二步。 此时,要注意将第二步中的 此时,
T ( v j0 ) =
min {T ( v )}
v j ∈s j
,
然后将 标号改成P 然后将 v j0 的T 标号改成 标号 ,转入第
步骤 考察点 T标号点集 标号点集 v1 0
标 v2
标号) 号( 表P标号) 标号 v3 v4 v5 v6 v7
1 2 3 4 5 6
v1 v2 v3 v4 v6 v5
{v2,…,v7} , {v3,…,v7} , {v4,…,v7} , {v5,v6,v7} {v5,v7} {v7}
2
5 2+2 4
实验报告6-最短路径问题

HUNAN UNIVERSITY 课程实习报告题目最短路径问题学生姓名学生学号专业年级指导老师完成日期一、需求分析本实验是求最短路径的问题,从文件中读入有向网中顶点的数量和顶点间的票价的矩阵,以用户指定的起点,在文件中输出到其余各顶点的最短路径及花费。
(1)输入:输入的形式:(文件)5-1 10 3 20 -1-1 -1 -1 5 -1-1 2 -1 -1 15-1 -1 -1 -1 11-1 -1 -1 -1 -1(用户)输入起点:0输入值的范围:文件输入中,顶点数和矩阵中顶点间的票价均为整型int,用户输入中,起点数为整型int。
(2)输出的形式:(文件)源点0到顶点1的最小花费为:5路径为:0——>2——>1源点0到顶点2的最小花费为:3路径为:0——>2源点0到顶点3的最小花费为:10路径为:0——>2——>1——>3源点0到顶点4的最小花费为:18路径为:0——>2——>4(3)程序所达到的功能:在文件中给出有向网的顶点个数和顶点间的票价的矩阵,以用户指定的起点,在文件中输出起点到其余各顶点的最短路径及花费。
(4)测试数据:a.输入:(文件)5-1 10 3 20 -1-1 -1 -1 5 -1-1 2 -1 -1 15-1 -1 -1 -1 11-1 -1 -1 -1 -1(用户)输入起点:0输出:(文件)源点0到顶点1的最小花费为:5路径为:0——>2——>1源点0到顶点2的最小花费为:3路径为:0——>2源点0到顶点3的最小花费为:10路径为:0——>2——>1——>3源点0到顶点4的最小花费为:18路径为:0——>2——>4b.输入:(文件)5-1 10 3 20 -1-1 -1 -1 5 -1-1 2 -1 -1 15-1 -1 -1 -1 11-1 -1 -1 -1 -1(用户)输入起点:2输出:(文件)源点2到顶点0:没有连通路径源点2到顶点1的最小花费为:2路径为:2——>1源点2到顶点3的最小花费为:7路径为:2——>1——>3源点2到顶点4的最小花费为:15路径为:2——>4c.输入:(文件)618 10 3 20 -1 915 -1 -1 5 -1 -1-1 20 16 -1 -1 15-1 -1 30 -1 6 32 9 -1 20 -1 -1-1 8 12 -1 -1 5(用户)输入起点:5输出:(文件)源点5到顶点0的最小花费为:21路径为:5——>1——>3——>4——>0源点5到顶点1的最小花费为:8路径为:5——>1源点5到顶点2的最小花费为:12路径为:5——>2源点5到顶点3的最小花费为:13路径为:5——>1——>3源点5到顶点4的最小花费为:19路径为:5——>1——>3——>4d.输入:(文件)618 10 3 20 -1 915 -1 -1 5 -1 -1-1 20 16 -1 -1 15-1 -1 30 -1 6 32 9 -1 20 -1 -1-1 8 12 -1 -1 5(用户)输入起点:3输出:(文件)源点3到顶点0的最小花费为:8路径为:3——>4——>0源点3到顶点1的最小花费为:11路径为:3——>5——>1源点3到顶点2的最小花费为:11路径为:3——>4——>0——>2源点3到顶点4的最小花费为:6路径为:3——>4源点3到顶点5的最小花费为:3路径为:3——>5e.输入:(文件)3-1 -1 -1-1 -1 -1-1 -1 -1(用户)输入起点:1输出:(文件)源点1到顶点0:没有连通路径源点1到顶点2:没有连通路径f.输入:(文件)3-1 -1 -1-1 -1 -1-1 -1 -1(用户)输入起点:3输出:(文件)源点3到顶点0的最小花费为:-572562307路径为:3——>1——>0源点3到顶点1的最小花费为:-572662307路径为:3——>1源点3到顶点2的最小花费为:-572662307路径为:3——>2二、概要设计(1)所有抽象数据类型的定义:const int MaxNum=100000;//利用邻接矩阵存储图:class Graph{private:int *Adj;//保存邻接矩阵的一维数组j和k之间权值存储在Adj[j*Num+k]中int Num;public:Graph();~Graph();void Floyd(int start);};(2)算法的基本思想:采用邻接矩阵为图的存储结构,保存邻接矩阵的一维数组j和k之间权值存储Adj[j*Num+k]中,以用户指定的起点,进行弗洛伊德算法,先初始化最短路径,对角线元素设置为0,其他元素设置为边的权值,没有有向边设置为MaxNum,依次插入中间点k,判断是否检查Dis(i,k) + Dis(k,j) < Dis(i,j)是否成立,若不成立则路径不改变,若成立则更新最短路径,设置Dis(i,j) = Dis(i,k) + Dis(k,j),直至循环结束,更新后的最短路径入栈,在文件中输出到其余各顶点的最短路径及花费。
(完整word版)最短路径算法附应用

最短路径算法及应用乘汽车旅行的人总希望找出到目的地的尽可能的短的行程。
如果有一张地图并在图上标出每对十字路口之间的距离,如何找出这一最短行程?一种可能的方法就是枚举出所有路径,并计算出每条路径的长度,然后选择最短的一条。
那么我们很容易看到,即使不考虑包含回路的路径,依然存在数以百万计的行车路线,而其中绝大多数是不值得考虑的。
在这一章中,我们将阐明如何有效地解决这类问题。
在最短路径问题中,给出的是一有向加权图G=(V,E,W),其中V为顶点集,E为有向边集,W为边上的权集。
最短路径问题研究的问题主要有:单源最短路径问题、与所有顶点对之间的最短路径问题。
一、单源最短路径问题所谓单源最短路径问题是指:已知图G=(V,E),我们希望找出从某给定的源结点S∈V 到V中的每个结点的最短路径。
首先,我们可以发现有这样一个事实:如果P是G中从vs到vj的最短路,vi是P中的一个点,那么,从vs沿P到vi的路是从vs到vi的最短路。
(一)Dijkstra算法对于图G,如果所有Wij≥0的情形下,目前公认的最好的方法是由Dijkstra于1959年提出来的。
例1 已知如下图所示的单行线交通网,每弧旁的数字表示通过这条单行线所需要的费用,现在某人要从v1出发,通过这个交通网到v8去,求使总费用最小的旅行路线。
Dijkstra方法的基本思想是从vs出发,逐步地向外探寻最短路。
执行过程中,与每个点对应,记录下一个数(称为这个点的标号),它或者表示从vs到该点的最短路的权(称为P 标号)、或者是从vs到该点的最短路的权的上界(称为T标号),方法的每一步是去修改T标号,并且把某一个具T标号的改变为具P标号的点,从而使G中具P标号的顶点数多一个,这样至多经过n-1(n为图G的顶点数)步,就可以求出从vs到各点的最短路。
在叙述Dijkstra方法的具体步骤之前,以例1为例说明一下这个方法的基本思想。
例1中,s=1。
因为所有Wij≥0,故有d(v1, v1)=0。
最短路径实验报告

D[w] = min+mgraph.arcs[v][w].adj; //更新D[w]
for(j = 0;j<mgraph.vexnum;j++)
//修改P[w],v0到w经过的顶点包括v0到v经过的顶点再加上顶点w
{
P[w][j] = P[v][j];
}
P[w][w] = true;
}
}
}
}
3、运行与测试
for(w = 0;w<mgraph.vexnum;w++)
{
D[v][w] = mgraph.arcs[v][w].adj;//顶点v到顶点w的直接距离
for(u = 0;u<mgraph.vexnum;u++)
{
P[v][w][u] = false;//路径矩阵初值
}
if(D[v][w]<infinity)
//根据新并入的顶点,更新不在S集的顶点到v0的距离和路径数组
{
if(!final[w]&&min<infinity&&mgraph.arcs[v][w].adj<infinity&&
(min+mgraph.arcs[v][w].adj<D[w]))
// w不属于S集且v0→v→w的距离<目前v0→w的距离
程序运行如图所示。
Step1:运行程序,屏幕显示菜单。
Step2:运行功能选择。
Case1:输入“1”,选择菜单项1,进入图的创建操作。
1.1根据屏幕提示,创建有向网。
1.2屏幕显示网信息。
Case2:输入“2”,选择菜单项2,进入求源点到其他各点的距离操作。
(完整word版)《数据结构课程设计》最短路径问题实验报告要点

一、概述 (1)二、....................... 系统分析1三、....................... 概要设计2四、....................... 详细设计54.1建立图的存储结构 (5)4.2单源最短路径 (6)4.3任意一对顶点之间的最短路径 (7)五、运行与测试 (8)参考文献 (11)附录12交通咨询系统设计(最短路径问题)一、概述在交通网络日益发达的今天,针对人们关心的各种问题,利用计算机建立一个交通咨询系统。
在系统中采用图来构造各个城市之间的联系,图中顶点表示城市,边表示各个城市之间的交通关系,所带权值为两个城市间的耗费。
这个交通咨询系统可以回答旅客提出的各种问题,例如:如何选择一条路径使得从A城到B城途中中转次数最少;如何选择一条路径使得从A城到B城里程最短;如何选择一条路径使得从A城到B城花费最低等等的一系列问题。
二、系统分析设计一个交通咨询系统,能咨询从任何一个城市顶点到另一城市顶点之间的最短路径(里程)、最低花费或是最少时间等问题。
对于不同的咨询要求,可输入城市间的路程、所需时间或是所需费用等信息。
针对最短路径问题,在本系统中采用图的相关知识,以解决在实际情况中的最短路径问题,本系统中包括了建立图的存储结构、单源最短问题、对任意一对顶点间最短路径问题三个问题,这对以上几个问题采用了迪杰斯特拉算法和弗洛伊德算法。
并未本系统设置一人性化的系统提示菜单,方便使用者的使用。
二、概要设计可以将该系统大致分为三个部分:①建立交通网络图的存储结构;②解决单源最短路径问题;③实现两个城市顶点之间的最短路径问题。
交通咨询系统迪杰斯特拉算法(单源最短路径)费洛依德算法(任意顶点对间最短路迪杰斯特拉算法流图:弗洛伊德算法流图:四、详细设计4.1建立图的存储结构定义交通图的存储结构。
邻接矩阵是表示图形中顶点之间相邻关系的矩阵。
设G=(V,E)是具有n个顶点的图,贝S G的邻接矩阵是具有如下定义的n阶方阵。
word完整版最短路径问题归纳总结推荐文档

八年级数学最短路径问题【问题概述1 最短路径问题是图论研究中的一个经典算法问题, 点之间的最短路径.算法具体的形式包括:①确定起点的最短路径问题②确定终点的最短路径问题③确定起点终点的最短路径问题④全局最短路径问题【问题原型1【涉及知识1【出题背景1【解题思路1旨在寻找图(由结点和路径组成的)中两结即已知起始结点,求最短路径的问题.与确定起点的问题相反,该问题是已知终结结点,求最短路径的问题.-即已知起点和终点,求两结点之间的最短路径.求图中所有的最短路径.“将军饮马”,“造桥选址”,“费马点”.“两点之间线段最短”,“垂线段最短”,“三角形三边关系”,“轴对称”,“平移”.角、三角形、菱形、矩形、正方形、梯形、圆、坐标轴、抛物线等.找对称点实现“折”转“直”,近两年岀现“三折线”转“直”等变式问题考查.【十二个基本问题1【问题11作法图形原理-------------- I•B在直线I上求一点P,使PA+PB值最小.【问题21 “将军饮马”连AB,与l交点即为P.AP在直线I上求一点P, PA+PB值最小.【问题31I1两点之间线段最短.FA + PB最小值为AB.作法图形原理作B关于I的对称点B /连A B /,与I交点即为P . P七IB'两点之间线段最短.FA+PB最小值为A B/.作法图形原理•Pl2在直线I1、12上分别求点M、^使^ PMN的周长最小.【问题41分别作点P关于两直线的对称点P/和P〃,连P' P 〃,与两直线交点即为M , N .两点之间线段最短.l lI2PM+MN + PN的最小值为线段P P,的长.P"作法图形原理・Q•PI2在直线I1、12上分别求点M、N,使四边形PQMN 的周长最小.【问题51 “造桥选址”分别作点Q、P关于直线l i、I2的对称点Q,和P/ 连QP,与两直线交点即为M ,N.作法I1QPN*P'Q.图形l2两点之间线段最短. 四边形PQMN周长的最小值为线段PP,的长.原理在11上求点A,在I2上求点B,使PA+AB值最小.作点P关于I i的对称点P/,作P^BX I2 于B,交I2于A.点到直线,垂线段最短.PA+AB的最小值为线段PB的长.A为I i上一定点,B为12上一定点,在12上求点M, 在I i上求点N ,使AM + MN + NB的值最小.作点A关于I2的对称点A/,作点B关于I1的对称点B,连A,B,交|2于M, 交I i于N .AnM m•B直线m // n,在m、n , 上分别求点M、N,使MN 丄m , 且AM + MN + BN 的值最小.【问题6】在直线I上求两点M、(M 在左),使MN a,并使AM + MN + NB的值最小.【问题7】将点A向下平移MN的长度单位得A,,连A/B,交n 于点N,过N作NM丄m于M .作法将点A向右平移a个长度单位得对称点A ,作A /关于I的A〃,连A〃B,交直线N,将N点向左平I于点移a个单位得M .作法AA'V\M>B图形I图形两点之间线段最短.AM+MN + BN的最小值为A B+MN.原理两点之间线段最短.AM +MN + BN的最小值为A〃B+MN .原理【问题8】作法图形原理【问题9】作法图形原理A.*B 1 在直线I上求一点P, |PA PB|的值最小.【问题10】连AB,作AB的中垂线与直线I的交点即为P. I垂直平分上的点到线段两端点的距离相等.PA PBI = 0 .作法图形原理I2两点之间线段最短.AM +MN + NB 的最小值为线段A,B,的长.BA|PA PB|的值最大.【精品练习】1•如图所示,正方形 ABCD 的面积为12,^ ABE 是等边三角形,点 E 在正方形ABCD 内,在对角线 AC 上有 一点P ,使PD+ PE的和最小,则这个最小值为()A . 2 亦B . 2 恵C . 3D .762•如图,在边长为 2的菱形 ABCD 中,/ ABC = 60 °若将△ ACD 绕点A 旋转,当 交于点E 、F ,则△ CEF 的周长的最小值为( )B . 2^33•四边形 ABCD 中,/ B = Z D = 90 ° / C = 70 °在 BC 、CD 上分别找一点 M 、N ,在直线丨上求一点P ,使 作直线AB , 与直线I 的交点即为P .pA PB |的值最大. 【问题11】 作法 ---- I*B 在直线I 上求一点P ,作B 关于I 的对称点B / 作直线A B/,与I 交点即为P .图形 I三角形任意两边之差小于第三边.IPA PB < AB .|PA PB 的最大值 =AB .原理三角形任意两边之差小于第三边.PA PB < AB /.PA PB 最大值=AB /.【问题12】“费马点”作法图形 原理所求点为“费马点”,即满 足/ APB = / BPC = /△ ABC 中每一内角都小于120 °,在^ ABC 内求一点 P ,使FA+PB + PC 值最小.APC = 120 ° .以 AB 、AC为边向外作等边^ ABD 、△ ACE ,连 CD 、BE 相交 于P ,点P 即为所求.两点之间线段最短.PA+PB+PC 最小值=CD .AC'、AD '分别与 BC 、CD 使^ AMN 的周长最小时,DAB = 4、区,/ BAC = 45 °, / BAC 的平分线交 BC 于点D ,M 、N 分别是 AD 和AB上的动点,贝y BM+MN 的最小值是/ AMN+ / ANM 的度数为( A . 120 °B . 130°)C .110 °D . 140°5. 且 如图,Rt △ ABC 中,/ C = 90 °, / B = 30 °, AB = 6,点 E 在 AB 边上,点 D 在 BC 边上 ED = AE ,则线段AE 的取值范围是 (不与点 B 、C 重合),如图,/ AOB = 30。
实训十二 图论(三)——最短路径
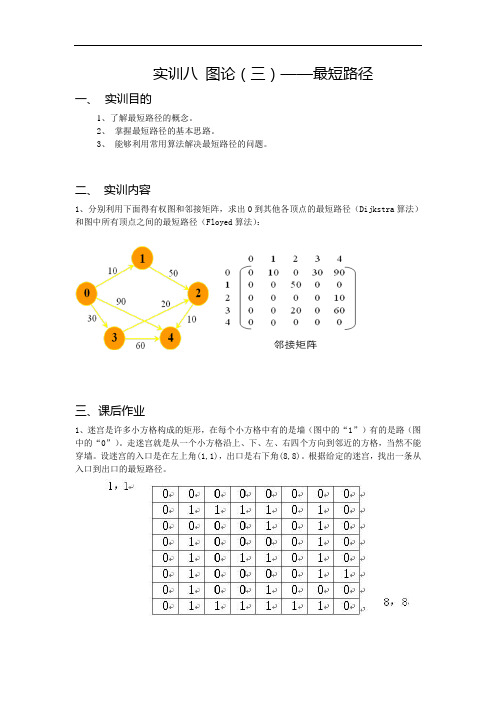
实训八图论(三)——最短路径
一、实训目的
1、了解最短路径的概念。
2、掌握最短路径的基本思路。
3、能够利用常用算法解决最短路径的问题。
二、实训内容
1、分别利用下面得有权图和邻接矩阵,求出0到其他各顶点的最短路径(Dijkstra算法)和图中所有顶点之间的最短路径(Floyed算法):
三、课后作业
1、迷宫是许多小方格构成的矩形,在每个小方格中有的是墙(图中的“1”)有的是路(图中的“0”)。
走迷宫就是从一个小方格沿上、下、左、右四个方向到邻近的方格,当然不能穿墙。
设迷宫的入口是在左上角(1,1),出口是右下角(8,8)。
根据给定的迷宫,找出一条从入口到出口的最短路径。
运筹学最短路问题实验报告

运筹学最短路问题实验报告
姓名:雷超敏
学号:
班级:安全101
指导教师:冯树虎
一、实验目的:
1、学会独立建模能力,并用模型解决相关现实问题。
2、通过实验,把所学的运筹学理论知识与实践相结合,从而强化相关理论知识。
3、进一步加强对现实问题的认识,提高独立运用理论知识解决现实问题。
4、通过上机实验检验运筹学理论,发现相关理论知识的适用范围及不足。
二、实验任务:
1、提出一个有关运筹学的实际问题;
2、建立模型;
3、运用软件进行求解;
4、撰写分析报告。
三、实验软件
Excel2003。
最短路径实验报告

一、实验目的学习掌握图的存储结构利用最短路径算法,通过java编程实现最短路径输出。
二、实验环境Eclipse平台三、实验过程最短路径算法问题是计算机科学、运筹学、地理信息系统和交通诱导、导航系统等领域研究的一个热点。
传统的最短路径算法主要有Floyd算法和Dijkstra算法。
Floyd算法用于计算所有结点之间的最短路径。
Dijkstra算法则用于计算一个结点到其他所有结点的最短路径。
本程序利用Dijkstra算法用java语言实现最短路径的可视化。
流程: 画无向邻接矩阵邻接矩阵初始化求取最短路径Java文件如下M ain.java 文件:import java.awt.BorderLayout;import java.awt.Color;import java.awt.FlowLayout;import java.awt.event.ActionEvent;import java.awt.event.ActionListener;import java.awt.event.ItemEvent;import java.awt.event.ItemListener;import java.util.StringTokenizer;import javax.swing.JButton;import javax.swing.JComboBox;import javax.swing.JFrame;import javax.swing.JLabel;import javax.swing.JPanel;import javax.swing.border.TitledBorder;public class Main {public static void main(String args[]) {new UI("最短路径");}}@SuppressWarnings("serial")class UI extends JFrame implements ActionListener, ItemListener { JFrame frame;JButton button;JLabel label1, label2, label3;JComboBox list1, list2;JPanel panel1, panel2;ShortCanvas canvas;ShortInit inits;SetFont f;String circlename[];String circle1, circle2;String path[];int circlenum;int list2_index;int D[];int renum[];int num = 0;UI(String s) {super(s);canvas = new ShortCanvas();add(canvas,BorderLayout.CENTER);f=new SetFont();inits = new ShortInit();circlename = inits.getcirclename();circlenum =inits.getcirclenum();circle1 = circlename[0];circle2 = circlename[0];panel2 = new JPanel();panel2.setBorder(new TitledBorder("最短路径"));panel2.setBackground(Color.white);panel2.setLayout(new FlowLayout(FlowLayout.LEADING, 5, 5));label1 = new JLabel("起点", JLabel.LEFT);label1.setFont(f.setSysFontAndFace());panel2.add(label1);list1 = new JComboBox();list1.addItemListener(this);list1.setMaximumRowCount(5);// 设置 JComboBox 显示的最大行数panel2.add(list1);label2 = new JLabel("终点");label2.setFont(f.setSysFontAndFace());panel2.add(label2);list2 = new JComboBox();list2.addItemListener(this);panel2.add(list2);list2.setMaximumRowCount(5);// 设置 JComboBox 显示的最大行数for (int i = 0; i < circlenum; i++) {list1.addItem(circlename[i]);list2.addItem(circlename[i]);}button = new JButton("确定");button.addActionListener(this);button.setFont(f.setSysFontAndFace());panel2.add(button);label3 = new JLabel("");label3.setFont(f.setSysFontAndFace());panel2.add(label3);add(panel2,BorderLayout.SOUTH);setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE);setBounds(100, 100, 530, 547);setVisible(true);validate();}public void itemStateChanged(ItemEvent e) {if (e.getSource() == list1)circle1 = (String) list1.getSelectedItem();if (e.getSource() == list2) {circle2 = (String) list2.getSelectedItem();list2_index = list2.getSelectedIndex();}}public void actionPerformed(ActionEvent e) {if (e.getSource() == button) {ShortPath sp = new ShortPath(circle1, circle2);path = sp.getpath();D = sp.getD();label3.setText("最短路径为:" + D[list2_index]);renum = new int[circlenum];StringTokenizer fenxi = newStringTokenizer(path[list2_index], "->");num = 0;while (fenxi.hasMoreTokens()) {String str = fenxi.nextToken();for (int i = 0; i < circlenum; i++) {if (str.equals(circlename[i])) {renum[num] = i;num++;}}}canvas.flag = 1;canvas.resultroad = renum;canvas.num = num;canvas.repaint();}}}SetFont.java文件import java.awt.Font;import javax.swing.JFrame;import javax.swing.UIManager;import javax.swing.UnsupportedLookAndFeelException;//系统外观处理@SuppressWarnings("serial")public class SetFont extends JFrame {public Font setSysFontAndFace() {try {// 根据类名称设置外观UIManager.setLookAndFeel("com.sun.java.swing.plaf.windows.WindowsLookAndFeel" );} catch (UnsupportedLookAndFeelException ex) {} catch (IllegalAccessException ex) {} catch (InstantiationException ex) {} catch (ClassNotFoundException ex) {}Font font = new Font("新宋体", Font.ITALIC + Font.BOLD, 17);return font;}}ShortCanvas.java文件://画无向邻接矩阵import java.awt.Canvas;import java.awt.Color;import java.awt.Graphics;@SuppressWarnings("serial")public class ShortCanvas extends Canvas {SetFont f;ShortInit init;String circlename[];int roadlength[];int arcs[][]; // 带权邻接矩阵int circlenum;int roadnum;int location[][]; // 各点坐标int flag = 0;int num;int resultroad[];// 结果线路ShortCanvas() {f = new SetFont();init = new ShortInit();circlename = init.getcirclename();roadlength = init.getroadlength();circlenum = init.getcirclenum();roadnum = init.getroadnum();arcs = new int[circlenum][circlenum];location = new int[circlenum][2];for (int i = 0; i < circlenum; i++)for (int j = 0; j < circlenum; j++)arcs[i][j] = 10000;set();}public void paint(Graphics g) {g.setFont(f.setSysFontAndFace());g.drawOval(60, 60, 25, 25); // ag.drawString(circlename[0], 70, 75);g.drawString(String.valueOf(roadlength[0]), 135, 135);g.drawOval(200, 180, 25, 25); // bg.drawString(circlename[1], 210, 195);g.drawLine(70, 85, 200, 192); // a--bg.drawOval(100, 300, 25, 25); // cg.drawString(circlename[2], 110, 315);g.drawString(String.valueOf(roadlength[1]), 90, 195);g.drawLine(70, 85, 112, 300); // a--cg.drawString(String.valueOf(roadlength[2]), 165, 250);g.drawLine(200, 192, 112, 300); // b--cg.drawOval(350, 180, 25, 25); // dg.drawString(circlename[3], 360, 195);g.drawString(String.valueOf(roadlength[3]), 285, 190);g.drawLine(225, 192, 350, 192); // b--dg.drawOval(250, 360, 25, 25); // gg.drawString(circlename[4], 260, 375);g.drawString(String.valueOf(roadlength[4]), 185, 345);g.drawLine(125, 315, 250, 375); // c--gg.drawString(String.valueOf(roadlength[5]), 305, 270);g.drawLine(275, 372, 350, 192); // g--dg.drawOval(450, 80, 25, 25); // eg.drawString(circlename[5], 460, 95);g.drawString(String.valueOf(roadlength[6]), 420, 150);g.drawLine(375, 192, 462, 105); // d--eg.drawOval(480, 300, 25, 25); // fg.drawString(circlename[6], 490, 315);g.drawString(String.valueOf(roadlength[7]), 465, 205);g.drawLine(462, 105, 492, 300); // e--fg.drawString(String.valueOf(roadlength[8]), 420, 280);g.drawLine(375, 192, 480, 312); // d--fg.drawString(String.valueOf(roadlength[9]), 370, 330);g.drawLine(275, 372, 480, 312); // g--fg.drawString(String.valueOf(roadlength[10]), 260, 85);g.drawLine(70, 85, 450, 92); // a--eint i, j;if (flag == 1) {g.setColor(Color.red);for (i = 0; i < num - 1; i++) {j = i + 1;g.drawLine(location[resultroad[i]][0] + 12,location[resultroad[i]][1] + 12,location[resultroad[j]][0] + 12,location[resultroad[j]][1] + 12);}}}public void set() {location[0][0] = 60;location[0][1] = 60;location[1][0] = 200;location[1][1] = 180;location[2][0] = 100;location[2][1] = 300;location[3][0] = 350;location[3][1] = 180;location[4][0] = 250;location[4][1] = 360;location[5][0] = 450;location[5][1] = 80;location[6][0] = 480;location[6][1] = 300;arcs[0][1] = arcs[1][0] = roadlength[0];arcs[0][2] = arcs[2][0] = roadlength[1];arcs[1][2] = arcs[2][1] = roadlength[2];arcs[1][3] = arcs[3][1] = roadlength[3];arcs[2][4] = arcs[4][2] = roadlength[4];arcs[4][3] = arcs[3][4] = roadlength[5];arcs[3][5] = arcs[5][3] = roadlength[6];arcs[5][6] = arcs[6][5] = roadlength[7];arcs[3][6] = arcs[6][3] = roadlength[8];arcs[4][6] = arcs[6][4] = roadlength[9];arcs[0][5] = arcs[5][0] = roadlength[10];}public int[][] getarcs() {return arcs;}}ShortInit.java文件:public class ShortInit {int circlenum=7;int roadnum=9;int num[];String circlename[];int roadlength[];ShortInit (){circlename=new String[10];roadlength=new int[15];circlename[0]="a";circlename[1]="b";circlename[2]="c";circlename[3]="d";circlename[4]="g";circlename[5]="e";circlename[6]="f";roadlength[0]=7;roadlength[1]=6;roadlength[2]=3;roadlength[3]=20;roadlength[4]=5;roadlength[5]=3;roadlength[6]=9;roadlength[7]=6;roadlength[8]=8;roadlength[9]=11;roadlength[10]=8;}public String[] getcirclename(){return circlename;}public int[] getroadlength(){return roadlength;}public int getcirclenum(){return circlenum;}public int getroadnum(){return roadnum;}}Shortpath.java 文件//求取最短路径public class ShortPath {int maxlength = 10000;int maxcirclenum = 30;ShortInit init;ShortCanvas canvas;String circlename[];String start, end;String path[];int arcs[][];int circlenum;int roadnum;int v0;int D[];ShortPath(String s1, String s2) {init = new ShortInit();canvas = new ShortCanvas();circlename = init.getcirclename();circlenum = init.getcirclenum();roadnum = init.getroadnum();start = s1;end = s2;arcs = canvas.getarcs();path = new String[circlenum];for (int p = 0; p < circlenum; p++)path[p] = start;for (int k = 0; k < circlenum; k++) {if (start.equals(circlename[k])) {v0 = k;}}shortestpath(v0);}public void shortestpath(int v0) {int v, i, w;int min;boolean finald[] = new boolean[maxcirclenum];D = new int[maxcirclenum];boolean p[][] = new boolean[maxcirclenum][maxcirclenum];for (v = 0; v < circlenum; v++) {finald[v] = false;D[v] = arcs[v0][v];for (w = 0; w < circlenum; ++w)p[v][w] = false;if (D[v] < maxlength) {p[v][v0] = true;p[v][v] = true;}}D[v0] = 0;finald[v0] = true;for (i = 1; i < circlenum; i++) {min = maxlength;for (w = 0; w < circlenum; w++)if (!finald[w])if (D[w] < min) {v = w;min = D[w];}finald[v] = true;path[v] = path[v] + "->" + circlename[v];for (w = 0; w < circlenum; w++) {if (!finald[w] && (min + arcs[v][w] < D[w])) {D[w] = min + arcs[v][w];path[w] = path[v];p[w][w] = true;}}}for (int j = 0; j < circlenum; ++j) {System.out.println(path[j] + ": "+ String.valueOf(D[j]) + "km");}}public String[] getpath() {return path;}public int[] getD() {return D;}}四、实验结果五、实验体会通过这次实验,懂得了如何通过邻接矩阵存储图,然后利用迪杰斯特拉算法算出最短路径。
运筹学最短路问题及程序

运筹学最短路问题----------关于旅游路线最短及程序摘要:随着社会的发展,人民的生活水平的提高,旅游逐渐成为一种时尚,越来越多的人喜欢旅游。
而如何才能最经济的旅游也成为人民考虑的一项重要环节,是选择旅游时间最短,旅游花费最少还是旅游路线最短等问题随之出现,如何决策成为一道难题。
然而,如果运用运筹学方法来解决这一系列的问题,那么这些问题就能迎刃而解。
本文以旅游路线最短问题为列,给出问题的解法,确定最短路线,实现优化问题。
关键词:最短路 0-1规划约束条件提出问题:从重庆乘飞机到北京、杭州、桂林、哈尔滨、昆明五个城市做旅游,每个城市去且仅去一次,再回到重庆,问如何安排旅游线路,使总旅程最短。
各城市之间的航线距离如下表:重庆北京杭州桂林哈尔滨昆明重庆0 1640 1500 662 2650 649北京1640 0 1200 1887 1010 2266杭州1500 1200 0 1230 2091 2089桂林662 1887 1230 0 2822 859哈尔滨2650 1010 2091 2822 0 3494昆明649 2266 2089 859 3494 0问题分析:1.这是一个求路线最短的问题,题目给出了两两城市之间的距离,而在最短路线中,这些城市有的两个城市是直接相连接的(即紧接着先后到达的关系),有些城市之间就可能没有这种关系,所以给出的两两城市距离中有些在最后的最短路线距离计算中使用到了,有些则没有用。
这是一个0-1规划的问题,也是一个线性规划的问题。
2.由于每个城市去且仅去一次,最终肯定是形成一个圈的结构,这就导致了这六个城市其中有的两个城市是直接相连的,另外也有两个城市是不连接的。
这就可以考虑设0-1变量,如果两个城市紧接着去旅游的则为1,否则为0。
就如同下图3. 因为每个城市只去一次,所以其中任何一个城市的必有且仅有一条进入路线和一条出去的路线。
解法:为了方便解题,给上面六个城市进行编号,如下表(因为重庆是起点,将其标为1)重庆北京杭州桂林哈尔滨昆明123456假设:设变量x11。
最短路径问题举例
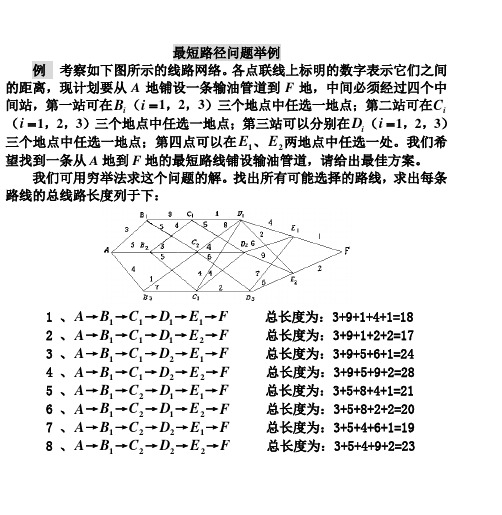
最短路径问题举例例 考察如下图所示的线路网络。
各点联线上标明的数字表示它们之间的距离,现计划要从A 地铺设一条输油管道到F 地,中间必须经过四个中间站,第一站可在i B (=i 1,2,3)三个地点中任选一地点;第二站可在i C (=i 1,2,3)三个地点中任选一地点;第三站可以分别在i D (=i 1,2,3)三个地点中任选一地点;第四点可以在1E 、2E 两地点中任选一处。
我们希望找到一条从A 地到F 地的最短路线铺设输油管道,请给出最佳方案。
我们可用穷举法求这个问题的解。
找出所有可能选择的路线,求出每条路线的总线路长度列于下:1 、A →1B →1C →1D →1E →F 总长度为:3+9+1+4+1=182 、A →1B →1C →1D →2E →F 总长度为:3+9+1+2+2=173 、A →1B →1C →2D →1E →F 总长度为:3+9+5+6+1=24 4 、A →1B →1C →2D →2E →F 总长度为:3+9+5+9+2=285 、A →1B →2C →1D →1E →F 总长度为:3+5+8+4+1=216 、A →1B →2C →1D →2E →F 总长度为:3+5+8+2+2=207 、A →1B →2C →2D →1E →F 总长度为:3+5+4+6+1=198 、A →1B →2C →2D →2E →F 总长度为:3+5+4+9+2=23123110、A →1B →2C →3D →2E →F 总长度为:3+5+6+5+2=21 11、A →2B →1C →1D →1E →F 总长度为:5+4+1+4+1=15 12、A →2B →1C →1D →2E →F 总长度为:5+4+1+2+2=14 13、A →2B →1C →2D →1E →F 总长度为:5+4+5+6+1=21 14、A →2B →1C →2D →2E →F 总长度为:5+4+5+9+2=25 15、A →2B →2C →1D →1E →F 总长度为:5+3+8+4+1=21 16、A →2B →2C →1D →2E →F 总长度为:5+3+8+2+2=20 17、A →2B →2C →2D →1E →F 总长度为:5+3+4+6+1=19 18、A →2B →2C →2D →2E →F 总长度为: 5+3+4+9+2=23 19、A →2B →2C →3D →1E →F 总长度为:5+3+6+7+1=22 20、A →2B →2C →3D →2E →F 总长度为: 5+3+6+5+2=21 21、A →2B →3C →1D →1E →F 总长度为:5+5+4+4+1=19 22、A →2B →3C →1D →2E →F 总长度为:5+5+4+2+2=18 23、A →2B →3C →2D →1E →F 总长度为: 5+5+4+6+l=21 24、A →2B →3C →2D →2E →F 总长度为:5+5+4+9+2=25 25、A →2B →3C →3D →1E →F 总长度为:5+5+2+7+1=20 26、A →2B →3C →3D →2E →F 总长度为:5+5+2+5+2=19 27、A →3B →2C →1D →1E →F 总长度为:4+1+8+4+1=18 28、A →3B →2C →1D →2E →F 总长度为: 4+1+8+2+2=17 29、A →3B →2C →2D →1E →F 总长度为:4+1+4+6+1=16 30、A →3B →2C →2D →2E →F 总长度为:4+1+4+9+2=20 31、A →3B →2C →3D →1E →F 总长度为:4+1+6+7+1=19323233、A →3B →3C →1D →1E →F 总长度为:4+7+4+4+1=20 34、A →3B →3C →1D →2E →F 总长度为:4+7+4+2+2=19 35、A →3B →3C →2D →1E →F 总长度为: 4+7+4+6+1=22 36、A →3B →3C →2D →2E →F 总长度为:4+7+4+9+2=26 37、A →3B →3C →3D →1E →F 总长度为: 4+7+2+7+1=2l 38、A →3B →3C →3D →2E →F 总长度为:4+7+2+5+2=20 比较上面38条不同路线的结果可知最短路线是标号为“12、”的那条路线,即A →2B →1C →1D →2E →F ,最短路线的长度14。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验学时:4
实验日期:2012年11月30日
实验要求:案例模型分析
实验内容:用最短路径模型解决具体问题
刖言
运输是物流过程的主要职能之一,也是物流过程各项业务的中心活动。物流过程中 的其它各项活动,如包装、装卸搬运、物流信息等,都是围绕着运输而进行的。可以说, 在科学技术不断进步、生产的社会化和专业化程度不断提高的今天,一切物质产品的生 产和消费都离不开运输。物流合理化,在很大程度上取决于运输合理化。所以,在物流 过程的各项业务活动中,运输是关键,起着举足轻重的作用。而有效的缩减路径可以使 得运输费用降低。本文运用Dijkstra算法求出最短路径,以最大限度地节约运输费用 降低物流成本,Dijkstra算法用于求解最短路径问题最常用的方法之一。
(2)比较所有T标号,「TV7,T V8 ?,T V7=14最小,给V7以P标号,令
7为刚得到P标号的点,考察V7,V8
T V8=minTy,PV7I7J = min 17,14 1〕=15
(2)比较所有T标号,T V8=15最小,给V8以P标号,令PV8=15,记录路 径V7,V8
(2)比较所有T标号,汀V4,T V6,TV I,T V4=9最小,给V以P标号,令PV4]=9,记录路径V2,V4
6.(1)V4为刚得到P标号的点,考察V4,V6,V4,V7
T V6二minTV6FV4 J =min 13,9 +9】=13 T V7二mi nTV7,PV4n 14,9 7 L14
T VU-minT V5,PV2I25=min〔::,4 4=8
(2)比较所有T标号,^TV3,TV4,TV5\ T V3=6最小,给V以P标号,令
PV3=6,记录路径V1,V3
4.(1)V3为刚得到P标号的点,考察V3,V4,V3,V5
T V4二mi nTV4,PV3l3J-mi n9,64〕=9
至此可以得到最短路径为—V2rV5rV7rV8,最短行程为15
实验总结
科学合理的运输路线对物流的成本的大小影响很大。Dijkstra算法就是通过一
种方法,使运输路线最短,运费最少,尽可能的降低物流成本,提高产品的竞争力,Dijkstra,根据距V从近到远的顺序,依次求得V1到V各顶点的最短路径和距离,直至V8,算法结束。根据记录的最后路径逆推至V5,V7,V2,V5,VV,总结出路
(2)比较所有T标号,汀V6,T V7 1,T V6=13最小,给V以P标号,令PV6=13,记录路径V5,V6
7.(1)V为刚得到P标号的点,考察V6,V7,V6,V8
T V7=min T V7,P V6 I6J=min 14,13 41 = 14 T Vs二min T V8, P V6b丄min〔,13 4丨-17
Dijkstra
(1)给起点V!以P标号PV!二0,其余各点均给以T标号,TV=o
(2)若Vi点为刚得到的P标号的点,考虑这样的点为Vj,考虑Vi,Vj这条边,且Vj为T标号,对Vj的T标号进行如下更改
TVj二minTvj,PViI」
(3)比较所有具有T标号的点,把最小者改为P标号,即PV二mi门匕】,当存 在两个以上最小者时,可同时改为P标号,若全部点均为P标号,则停止,否则v:代Vi改为第二步重做。
T V5二mi nTV5,PV3l3J-mi n 8,67 I-8
(2)比较所有T标号,<TV4,T V5 \T V5 =8最小,给V以P标号,令
PV5=8,记录路径V2M
5.(1)V为刚得到P标号的点,考察WWW
T V6]=minT V6,P乂l5J- min〔::,8 51-13
T%i=minT V7,P V5I57=minI::,8 6=14
径为Vi>V2>V5>V7,所以最短距离为15.
T V3=minTV3,Pyl1J-min〔::,06丨-6
(2)比较所有T标号^T V2,T V3\,TV^-4最小,所以给V2以P标号,令
PV2=4,记录路径V1,V2
3.(1)V2为刚得到P标号的点,考察边V2,V4,V2,V5
T V4i;=min T V4,P V2l2J- mi n〔::,45丨-9
案例分析
下图所示是某地区交通运输的示意图,试问从v1出发,经哪条路线达到v8才能使总
行程最短?使用Dijkstra求解。
步骤:
1.首先给vi以P标号,PVi=0,给其余所有的点以T标号,T乂i=1,2,…,8
2.(1)考察点Vi,边MN,Vi,V3
TV2AminTv2,P« l12=min〔::,04=4
