姚端正《数学物理方法》(第三版)部分勘误表
数学物理方法姚端正CH作业解答.doc

数理方法CH3 作业解答P51习题3.21. 确定下列级数的收敛半径:∞kk(2)∑kz=12k∞(4)∑(k =0k + a )k z kk z k∞kk解:(2)∑kz k=12a k k +1 2k收敛半径为:R lim | | lim | /( ) | lim 2k= = = =k k+1→a 2 2 k +1→∞k ∞k →k ∞ k+1 ∞(4)∑(kk= 0 + a ) k z kk z kka k + ak解:收敛半径为:R lim | | lim | |若|a |≤1,则= = k+1k →a (k +1) + a∞k→∞k +1kk a+lim |→k∞+k (k 1) a+|1=+1若| a |> 1,则k k 1 k - 2-罗比塔法则k a 1 ka k(k 1)a 1罗比塔法则+ + -lim | | lim | | lim | |= =k =k k→∞k +1 k k ka k - 1 a(k 1) a 1 (k 1)a ( 1) |→∞+ + ++→∞+|∞k2.∑akz 的收敛半径为R (0 ≤R < ∞) ,确定下列级数的收敛半径:k=1∞(1)∑kk= 0 n a zkknk a k a k ak n k n k解:) | lim | |收敛半径为:lim | ) |= lim | ( ) | ?| |= lim | ( ?nk (k 1) a k +1 a k 1 a+ + k →∞k k →∞→∞k →∞k+1 k +1 +1kn 而lim |( ) |=1k k +1→∞limk→∞|akak+1|= R所以,所求收敛半径为RP55习题3.311.将下列函数在 z = 0 点展开成幂级数,并指出其收敛范围:(1)(1- 1 z)2解 : 解法之一 : 利用多项式的乘法 :1∞k已知 ∑= z1- z 0k=| z |< 1,(1 1 - 2 z)=∞ ∞kz k(∑0) ?∑z (k = k =0)= 1+ 2z +2 + 3+ + + k+ 3z 4z ... (k 1)z...=∞(∑k= 0k k+1)z解法之二:逐项求导: (1 1 1 = ( )' 2 z - z) 1- 1 则 = 2(1- z)( ∞ ∞ k kz k- 12+ 3 + + k - 1 +z )' 1 2 3 4 ... ...= ∑ = = + z + z z kz∑k =0 k =1由于(1- 1 2 z)在复平面内有唯一的奇点 z =1 ,它与展开中心的距离为1,故该级 数的收敛范围为| z |< 1 (2) 1 az+b k1 a1 1 ∞a ∞ k k k z k解: ∑ ∑= = (- 1) ( z) = (- 1)a k +1 az +b b b 0 b b(1+ z) bk =0 k =a 收敛范围:|z|<1bb 即|z|<||a(5)1+1z+ 2z解:1+11-z1z==-213133 z+z1-z-z-z令1∞3t=z,则∑=t1-t0k=k,故211 ∞3k= z∑3- z 0k =z31- z= ∞3kz∑k= 0+11∞∞3k 3k+1所以,= z ∑- z 收敛范围为| z|<11+ + zz ∑2k =0 k =02. 将下列函数按(z- 1) 的幂展开,并指明其收敛范围:(1)cosz解:cosz = cos[(z - 1) +1] = cos(z - 1) cos1 - sin(z - 1) sin 1=k 2k k 2k∞(- 1) (z - 1) ∞- z 1)( 1) ( -cos1 - sin1∑∑= (2k )! (2k + 1)!k 0 k =0+1收敛范围:| z- 1 |< ∞3.应用泰勒级数求下列积分:sinz (3)=∫Siz0 z zdz解:利用正弦函数的泰勒展开式:sink 2k +1∞(- 1) zz = ,得到∑(2k + 1)!k =0sinzz=k 2k∞(- 1) z∑= (2k + 1)!k 0则k 2k k 2k k 2k +1sin z (- 1) z (- 1) z (- 1) z∞∞∞z z zdz = dz= dz=∫∫∑∑∫∑0 z )! (2 1)!(2 1)0 = ( + 1)! ( k k + k +2k 0 2 +1k 0 k =0 k= 04.函数α(1+ z) 在α不等于整数时是多值函数,试证明普遍的二项式定理:(1( - 1) ( )( 2)2 + - 1 - +αααααααα3+ z) =1 [1+ z+ z z1! 2! 3!...]式中,α为任意复数;αe iαkπ21 =解:(1 + z)α= α( 1+Ln 1 eα[ln( + + e e+ = 1 z 2kπ] = ?z ) i α) iα2 ln(kπez)下面将α在z < 1中作泰勒展开:ln(1+ z)e∞α+z = a z ,其中,ln( 1 ) k记∑f (z) = ekk= 0 ak=f (k ) (0)k!f '(z) = αα+ αln(1 z) f ze = ( )1+ z 1+ z①? f ' (0) = α同时由①式有:(1+ z) f '(z) = αf (z) ②将②式两边再对z求导:(1+ z) f ''( z) + f '( z) = αf ' (z) 得到(1+ z) f ''(z) = (α- 1) f '( z) ③3得f '' (0) = α(α- 1)将③式两边再对z求导得:(1 ( z f z f z ( z f z3) 3)+ z) f ( ) + ''( ) = (α- 1) ''( ) 得到(1+ z) f ( ) = (α- 2) ''( )( 3 = αα- α-)得(0) ( 1) ( 2)f( k =αα- α- α- k +)以此类推,得(0) ( 1)( 2)...( 1)f( k)f (0) 1= = ( - 1) ( - 2)...( - k +1)则akααααk! k!所以∞∞∞1ln( z a z a z1 ) k kα+ = = ke ∑∑( 1) ( 2)...( k 1)z= ∑αα- α- α- + k k k!k 0 k 0 k =0= =∞则kαiα2kπ1+ ∑= αααα(1 z) e ( - 1)( - 2)...( - k +1)zk!k=0( - 1) ( 1)( 2)2 + - - + αααααα3αz <1 = 1 [1+ z+ z z ...]1! 2! 3!5.将Ln(1+ z)在z = 0 的邻域内展开为泰勒级数。
姚端正《数学物理方法》(第三版)部分勘误表

姚端正《数理方法》(第三版)勘误表(部分)P9,“(3)若()f x 在闭区域……”应更正为“(3)若()f z 在闭区域……”P33,中部“任意一条分段光滑的曲线”应更正为“任意一条分段光滑的封闭曲线” P66,习题3.5第2(2)题:“0||z b R <-<”应更正为“||z b R -<”P85,倒数第6行、第7行“1res ()n k f z =∑”应更正为“1res ()nkk f z =∑” P86,例3的计算过程中“||1a <”应更正为“01a <<”,但计算结果仍然对“||1a <”范围成立,即该例题的讨论过程不够完整。
P87,第10行“d[(π)]θ--”应更正为“d(π)θ-”P88,第4行“如图5.4”应更正为“如图5.4(b )”;第4题需补充条件:01x <<;第5题:“适当围道计算”应更正为“适当围道(图5.4(a ))计算”。
P107,第3行“稳定状态”应更正为“稳恒状态”;“则热量将停止流动”应去掉这段文字。
倒数第3行“F 为单位长度……”应更正为“F 为单位体积……”P108,第6行“通过介面”应更正为“单位时间通过介面”P111,第6行“k h E =”应更正为“k h EA =” P120,第1行“//at x a cat x a c ++--⎰ ”应准确写为“()/()()/()at x a c at x a c ++--⎰ ”P121,第4-5行“则在τ∆这段时间内”应更正为“则在τ∆这段时间以后”;第6行“t τττ<<+∆”应更正为“t τ<”P124,第4大题中“()x ψ”应更正为“(,)x y ψ”;“()x ϕ”应更正为“(,)x y ϕ”;解的表达式应更正为()01(,,)2π1 d 2πM M at at M a t t u x y t a t a τσσστ-⎡⎤∂=+⎢∂⎢⎣⎡⎤+⎢⎢⎣⎰⎰⎰⎰⎰⎰⎰P146,第2行“I 2I u xx u a u =”应更正为“I 2I tt xx u a u =” P271,第1行“2(2)(1)lim lim 1(1)(1)k k k k c k k R c l l k k →∞→∞+++===+-+”应更正为“1k k R ===” P274,习题14.1第2题“0y xy ''-=”应更正为“0y xy ''-=” P280,习题14.2第6题“介电常数为ε”应更正为“相对介电常数为ε”P286,习题14.3第3题(1)”部分习题答案勘误第一篇习题 3.22 (3)k R 应更正为n R ;第二篇习题 6.36 两端受压:“00(2)0t t t u l x u ε==⎧=-⎪⎨=⎪⎩”应更正为“0020t t t u x u ε==⎧=-⎪⎨=⎪⎩” 习题 7.22(3)2132at axt +应更正为2132t xt +; 习题 8.13(3)“…224(21)πek -+…”应更正为“…224(21)πe k t -+…”; 4 1π()sin n n n x a T t l ∞=∑应更正为1π()sin n n n n x a T t l ∞=∑; 10 “...4616πAb ...”应更正为“ (4)664πAb …” 习题 8.23(1)另一形式的答案:32223212(1)ππ()cos sin 6(π)n n A Al n at n x u x l x a n a l l ∞=-=-+∑。
王成优_“数学物理方法”(第4版)勘误表
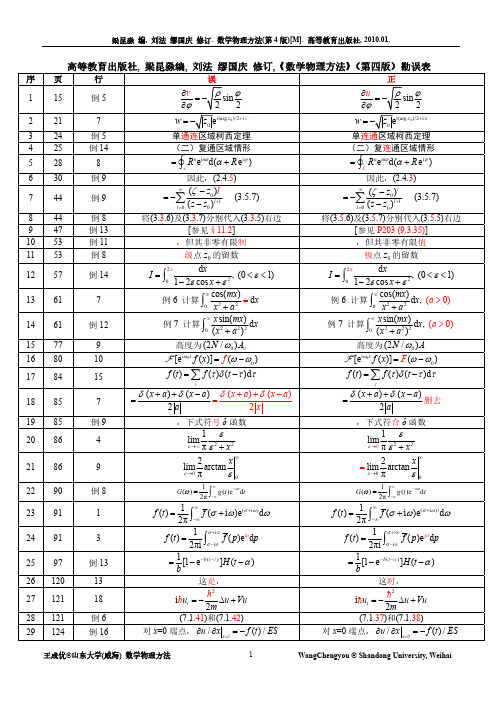
1 d d 1 dx d d (sin ) ( sin 2 ) sin d d sin d dx dx d d (1 x 2 ) dx dx
d m2 2 d (1 x ) [ l ( l 1) ] 0 dx d 1 x2
2π
[ei x f ( x)] f ( 0 )
0
f (t ) f ( ) (t )d
r
[ei x f ( x)] F ( 0 )
0
f (t ) f ( ) (t )d
( x a) ( x a)
2a
( x a) ( x a)
2x
( x a) ( x a)
2a
删去
,下式符号 δ 函数 1 lim π 2 x 2
,下式符合 δ 函数 1 lim 0 π 2 x 2
2 x lim arctan 0 π 0
G ( )
(1 2rx r 2 ) lr l 1Pl ( x)
l 0
(1 2rx r 2 ) lr l 1Pl ( x)
王成优©山东大学(威海) 数学物理方法
2
WangChengyou © Shandong University, Weihai
梁昆淼 编, 刘法 缪国庆 修订. 数学物理方法(第 4 版)[M]. 高等教育出版社, 2010.01.
F ( )
1
2
[ xJ1 ( x) x] 0
F ( )
1
2
[ xJ1 ( x)] 0
渐进
渐近
a k cos a, b k sin a eikp cos( a )
数学物理方法教学大纲(可编辑修改word版)

《数学物理方法》课程教学大纲(72 学时)(理论课程)一课程说明(一)课程概况课程中文名称:《数学物理方法》课程英文名称:Mathematics physics method课程编码:3910252114开课学院:理学院适用专业/开课学期:物理学/第 4 学期学分/周学时:4 学分/周4 学时《数学物理方法》是物理学本科专业的必修专业主干课,通过该课程的学习,使学生掌握复变函数、数学物理方程和特殊函数的基本理论、建模方法和计算方法,培养学生用数学方法和物理规律解决各类物理实际问题的能力,为后续课程的学习打下良好的基础。
本课程是前期课程《高等数学》的延伸,为后继开设的《电动力学》、《量子力学》等课程提供必需的数学理论知识和计算工具。
本课程在本科物理学专业中占有重要的地位,本专业学生必须掌握它们的基本内容,否则对后继课的学习将会带来很大困难。
(二)课程目标通过本课程的学习,使学生掌握处理物理问题的一些基本数学方法,为进一步学习后继课程提供必要的数学基础。
要求学生熟悉复变函数(特别是解析函数)的一些基本概念,掌握泰勒级数及洛朗级数的展开方法,利用留数定理来计算回路积分和三类实变函数的定积分;掌握傅立叶变换和拉普拉斯变换的概念及性质,并能运用拉普拉斯变换方法求解积分、微分方程。
了解三种类型的数学物理方程的导出过程,能熟练写出定解问题;掌握用行波法求解一维无界及半无界波动方程,利用分离变量法求解各类齐次及非齐次方程;了解特殊函数的常微分方程,掌握用级数解法求解二阶常微分方程,了解施图姆-刘维尔本征值问题及性质;掌握勒让德多项式、贝塞尔函数及性质,并能利用勒让德多项式求解三维轴对称拉普拉斯方程。
(三)学时分配二教学方法和手段1.本课程课堂讲授约需 72 课时。
2.学生在学习过程中应注重各专题所要求内容的全貌,以掌握基本思想和基本方法为主,培养创新精神。
3.在学习过程中,应以推荐教材为主,适当参考所列出的或其它的参考书,要适应各种不同的教材的编排体系和书写符号等。
数学物理方法第三版答案

数学物理方法第三版答案【篇一:数学物理方法试卷答案】xt>一、选择题(每题4分,共20分) 1.柯西问题指的是( b ) a.微分方程和边界条件. b. 微分方程和初始条件. c.微分方程和初始边界条件. d. 以上都不正确. 2.定解问题的适定性指定解问题的解具有( d)a.存在性和唯一性. b. 唯一性和稳定性. c. 存在性和稳定性. d. 存在性、唯一性和稳定性.??2u?0,?3.牛曼内问题 ??u 有解的必要条件是( c)??n?f??a.f?0.b.u??0.c.?fds?0. d.?uds?0.???x(x)??x(x)?0,0?x?l4.用分离变量法求解偏微分方程中,特征值问题??x(0)?x(l)?0的解是( b )n?n??n???n??x ).b.( ?x ). a.( ??,cos?,sinllll????(2n?1)?(2n?1)??(2n?1)???(2n?1)??x ).d.( ?x ). c.( ??,cos?,sin2l2l2l2l????22225.指出下列微分方程哪个是双曲型的( d )a.uxx?4uxy?5uyy?ux?2uy?0. b.uxx?4uxy?4uyy?0.c.x2uxx?2xyuxy?y2uyy?xyux?y2uy?0. d.uxx?3uxy?2uyy?0.二、填空题(每题4分,共20分)??2u?2u?2?2?0, 0?x??, t?0?t?x??1.求定解问题?ux?0?2sint, ux????2sint, t?0的解是(2sintcosx).??ut?0?0, utt?0?2cosx, 0?x????2.对于如下的二阶线性偏微分方程a(x,y)uxx?2b(x,y)uxy?c(x,y)uyy?dux?euy?fu?0其特征方程为( a(x,y)(dy)2?2b(x,y)dxdy?c(x,y)(dx)2?0). 3.二阶常微分方程y(x)?或0).4.二维拉普拉斯方程的基本解为( ln1().r1 ),三维拉普拉斯方程的基本解为r113y(x)?(?2)y(x)?0的任一特解y?( jx44x1(x) 3225.已知j1(x)?222sinx, j1(x)?cosx,利用bessel函数递推公式求??x?x23j3(x)?(221221dsinx(sinx?cosx)??x()()). ?xx?xdxx三、(15分)用分离变量法求解如下定解问题2??2u2?u??t2?a?x2?0, 0?x?l, t?0??u??u?0, ?0, t?0 ??xx?l??xx?0?u?x, utt?0?0, 0?x?l.?t?0?解:第一步:分离变量(4分) 设u(x,t)?x(x)t(t),代入方程可得x(x)t(x)x(x)t(t)?ax(x)t(t)??2x(x)at(x)2此式中,左端是关于x的函数,右端是关于t的函数。
数学物理方法(第三版)

展望
研究前沿
随着科技的发展,数学物理方法 在各个领域的应用越来越广泛, 如量子力学、金融数学、生物信
息学等。
未来趋势
未来,数学物理方法将继续发展, 与其他学科交叉融合,产生新的理 论和方法。
对读者的建议
读者应保持对数学物理方法发展的 关注,不断学习和探索新的理论和 应用。
THANKS
泛函分析方法
总结词
泛函分析是研究函数空间和算子的数学分支,通 过引入抽象的函数空间和算子,泛函分析为解决 复杂的数学问题提供了有力的工具。
总结词
泛函分析方法的应用不仅限于物理学,还涉及到 其他数学领域如微分方程、实变函数、复变函数 等。通过泛函分析的方法,可以更好地揭示数学 问题本质,推动数学的发展。
感谢观看
详细描述
在物理学中,泛函分析方法被广泛应用于量子力 学、统计物理等领域。通过将物理问题转化为泛 函分析问题,可以更好地理解和求解复杂的物理 现象。
详细描述
为了更好地应用泛函分析方法,需要深入理解其 基本概念和性质,如函数空间、算子、谱理论等 。同时,也需要与其他数学方法结合使用,以解 决各种复杂的数学问题。
积分方程方法的应用案例
积分方程在统计学中的应用
01
积分方程被用来描述概率分布,解决统计学中的各种问题,如
参数估计和假设检验。
积分方程在工程学中的应用
02
在解决结构优化、控制系统设计和信号处理等问题时,积分方
程是重要的数学工具。
积分方程在金融学中的应用
03
积分方程被用来描述金融市场的价格变动,评估投资组合的风
都非常重要。
03
促进学科交叉
数学物理方法是一门跨学科的学科,它促进了数学和物理学之间的交叉
数学物理方法姚端正CH7作业解答

uΙ =
1 x+t sin αdα = sin x sin t 2 ∫x − t 1 t 2 ∫0
t 0
由无界纯强迫振动解的公式,得
u ΙΙ =
∫
x + ( t −τ )
x − ( t −τ )
τ sin αdαdτ =
1 t {cos[ x − (t − τ )] − cos[ x + (t − τ )]}τdτ 2 ∫0
t 0
= ∫ sin x sin( t − τ )τdτ = sin x ∫ sin( t − τ )τdτ = t sin x − sin x sin t
(上式最后一步用了分部积分法) 则 u = u + u = t sin x
Ι ΙΙ
3
utt − a 2u xx = x (3) u ( x,0) = 0 u ( x,0) = 3 t
① ② ③
① 即 f1 ( x) − f 2 ( x) = −ϕ ( x) ②
解:方程 utt = u xx 的通解为: u ( x, t ) = f1 ( x + t ) + f 2 ( x − t ) 将④式代入定解条件②得: f1 (0) + f 2 (2 x) = ϕ ( x )
④
⑤
1
将④式代入定解条件③得:
2
u xx − u yy = 8 (2) u ( x,0) = 0 u ( x,0) = 0 y 解:由冲量原理,原定解问题可转化为以下定解问题: v yy − vxx = 0 v( x,τ ) = 0 v ( x,τ ) = −8 y 由 D ' Alembert 公式,该问题的解为: v( x, y;τ ) = 1 x + a ( y −τ ) − 8dα =8τ − 8 y 2 ∫x − a ( y −τ )
数学物理方法-复变函数与解析函数

2
数学物理方法 课程说明
数学物理方法为2013学年第二学期理工学院12级光信息专业所 开设, 72学时。 本课程在高等数学(一元和多元微积分、幂级数和Fourier级数、 微分方程、线性代数和概率论)和普通物理(力学、热学、电学和 光学)的基础上,以讲授古典数学物理中的常用方法为主,适当 介绍近年来的新发展,为光信息专业后继的基础课程和专业课 程研究有关的数学物理问题作准备,也为今后工作学习中遇到 的数学物理问题的求解提供基础。
R 0 0 0
第一章 复变函数和解析函数
21
y
(z )
z1
z2
o
x
第一章 复变函数和解析函数
22
第一章 复变函数和解析函数
23
例1:用复数方程表示: (1)过两点 z j = x j + i y j (j = 1 , 2 )的直线; (2)中心在点( 0 , - 1 ) 点的表示:z = x + i y <=> 复平面上的点 P ( x , y )
第一章 复变函数和解析函数
19
向量表示法
第一章 复变函数和解析函数
20
计算 arg z (z ≠ 0) 的公式
y arctan x 0, y x π x 0, y argz 2 y arctan π x 0, y x π x 0, y
2
G : w 4, 0 argw π
函数 w = z2(D) 的几何表示
第一章 复变函数和解析函数
34
常见的复变函数
w = z 2 ; u = x 2- y 2, v = 2 x y
第一章 复变函数和解析函数
数学物理方法姚端正CH3 作业解答

= ∑ ak z k , 其中, ak =
k =0
∞
f ( k ) (0) k!
① ②
f '( z) =
α α ln(1+ z ) α e = f ( z) 1+ z 1+ z
⇒
f ' (0) = α
同时由①式有: (1 + z ) f ' ( z ) = αf ( z ) 将②式两边再对 z 求导: (1 + z ) f ' ' ( z ) + f ' ( z ) = αf ' ( z )
∞ 1 ∞ 1 1 1 1 1 1 = = ⋅( = )= ∑ ∑ k k +1 z ( z + 1) − 1 z + 1 1 − 1 z + 1 k = 0 ( z + 1) k = 0 ( z + 1) z +1
其中,
1 1 1 1 1 ∞ ( z + 1)k ∞ ( z + 1) k = = ⋅ = ⋅∑ = ∑ k +1 1 − z 2 − ( z + 1) 2 1 − z + 1 2 k = 0 2 k k =0 2 2 f ( z) =
k →∞
lim |
k + ak |= 1 ( k + 1) + a k +1
若 | a |> 1 ,则
lim |
罗比塔法则 k + ak k ( k − 1) a k − 2 1 + ka k −1 罗比塔法则 1 = = | lim | | lim | |= k +1 k k −1 → ∞ → ∞ k k ( k + 1) + a 1 + (k + 1)a ( k + 1) ka |a|
数学物理方法姚端正CH3 作业解答

k →∞
k →∞
所以,所求收敛半径为 R
P55 习题 3.3
1
1.将下列函数在 z = 0 点展开成幂级数,并指出其收敛范围: (1) 1 (1 − z ) 2
解:解法之一:利用多项式的乘法: 已知
∞ 1 = ∑ zk 1 − z k =0
| z |< 1 ,
∞ ∞ 1 k = ( z ) ⋅ ( zk ) ∑ ∑ 2 (1 − z ) k =0 k =0
k →∞
lim |
k + ak |= 1 ( k + 1) + a k +1
若 | a |> 1 ,则
lim |
罗比塔法则 k + ak k ( k − 1) a k − 2 1 + ka k −1 罗比塔法则 1 = = | lim | | lim | |= k +1 k k −1 → ∞ → ∞ k k ( k + 1) + a 1 + (k + 1)a ( k + 1) ka |a|
收敛范围: | (5)
a z |< 1 b
即 | z |<|
b | a
1 1 + z + z2 1 1− z 1 z 解: = − = 2 3 3 1+ z + z 1− z 1 − z 1 − z3 令 t = z 3 ,则
∞ 1 = ∑t k , 1 − t k =0
故
2
∞ 1 = ∑ z 3k 1 − z3 k =0
数理方法 CH3 作业解答 P51 习题 3.2
1. 确定下列级数的收敛半径: (2) ∑ k k z k k =1 2 k k z k k =1 2 ak k k +1 2k |= lim | k /( k +1 ) |= lim =2 k →∞ k + 1 a k +1 k → ∞ 2 2
代数学方法(第一卷)勘误表
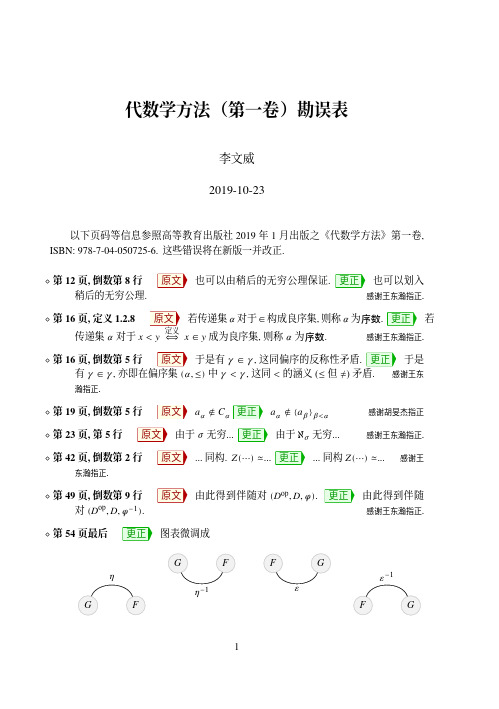
代数学方法(第一卷)勘误表李文威2019-10-23以下页码等信息参照高等教育出版社2019年1月出版之《代数学方法》第一卷, ISBN:978-7-04-050725-6.这些错误将在新版一并改正.⋄第12页,倒数第8行原文也可以由稍后的无穷公理保证.更正也可以划入稍后的无穷公理.感谢王东瀚指正.⋄第16页,定义1.2.8原文若传递集α对于∈构成良序集,则称α为序数.更正若传递集α对于x<y定义⟺x∈y成为良序集,则称α为序数.感谢王东瀚指正.⋄第16页,倒数第5行原文于是有γ∈γ,这同偏序的反称性矛盾.更正于是有γ∈γ,亦即在偏序集(α,≤)中γ<γ,这同<的涵义(≤但≠)矛盾.感谢王东瀚指正.⋄第19页,倒数第5行原文aα∉Cα更正aα∉{aβ}β<α感谢胡旻杰指正⋄第23页,第5行原文由于σ无穷...更正由于ℵσ无穷...感谢王东瀚指正.⋄第42页,倒数第2行原文...同构.Z(⋯)≃...更正...同构Z(⋯)≃...感谢王东瀚指正.⋄第49页,倒数第9行原文由此得到伴随对(D op,D,φ).更正由此得到伴随对(D op,D,φ−1).感谢王东瀚指正.⋄第54页最后更正图表微调成兴许更易懂.感谢熊锐提供意见.⋄第94页,习题5倒数第2行原文Yang–Baxter方程.更正杨–Baxter方程.⋄第116页,第5行原文H⊆N G(H)更正H⊊N G(H)⋄第126页,第6行原文(⋯)n i=0更正(⋯)n−1i=0⋄第141页,第11行原文另外约定S′n={1}更正另外约定S′1={1}⋄第149页,第3行CRing表交换环范畴.另外此行应缩进.⋄第165页,5.3.11之上两行原文∃s∈R更正∃s∈S⋄第205页,第7行原文M作为R/ann(M)-模自动是无挠的.更正M作为R/ann(M)-模的零化子自动是{0}.感谢戴懿韡指正.⋄第220页本页出现的Bil(•×•;•)都应该改成Bil(•,•;•),以和216页的符号保持一致.⋄第228页,倒数第4行原文∑y∈R更正∑y∈Y⋄第230页,第13行原文萃取处更正萃取出⋄第235页底部图表中的垂直箭头f i,f i−1应改为ϕi,ϕi−1.⋄第237页,命题6.8.5证明最后两行原文故(v)⟹(i);更正故(iv)⟹(i);⋄第238页,第8行原文Y′→Y→Y正合更正Y′→Y→Y″正合⋄第246頁,第16行原文u i f i更正u iαi感谢陆睿远指正.⋄第247頁,第6—7行原文其长度记为n+1.更正其长度定为n.⋄第264頁,第14行原文如果ann(M)={0}更正如果ann(N)={0}⋄第311页,命题8.3.2证明第4行更正分别取......和F′|E′.⋄第315页,倒数第2行原文deg f(X p)=pf(X)更正deg f(X p)=p deg f(X)感谢杨历指正.⋄第317页,倒数第13行(出现两次)原文∏n i=1⋯更正∏n m=1⋯⋄第359页,倒数第2行原文∈A F更正∈A E感谢杨历指正.⋄第360页,证明将所有χ(⋯)=1改成χ(⋯)=0,以确保与之前的惯例一致.感谢杨历指正.⋄第417页,最后一行它被刻画为对...。
武汉大学姚端正报告——浅谈数学物理方法的学习共54页

Wuhan University
一、本课程的内容和特点
对物理问题的处理,通常需要三个步骤: ➢ 利用物理定律将物理问题翻译成数学问题; ➢ 解该数学问题,其中解数学物理方程占有很 大的比重,有多种解法; ➢ 将所得的数学结果翻译成物理,即讨论所得 结果的物理意义。
Wuhan University
二、数学物理方法在物理学中的地位
1.数理方法是物理学科的重要基础课 2.数理方法是进行基础研究的重要工具 3.数理方法是培养学生逻辑思维能力和 创造思维能力的重要课程
“金钱如粪土,朋友值千金” “朋友如粪土”
Wuhan University
二、数学物理方法在物理学中的地位
3.数理方法是培养学生逻辑思维能力和 创造思维能力的重要课程
1.数理方法是物理学科的重要基础课
数理方法是普通物理与四大力学的“粘合剂”
力学
热学
电学
原子物理
理力
热统
Wuhan University
电动
量子力学
二、数学物理方法在物理学中的地位
1.数理方法是物理学科的重要基础课
数理方法是普通物理与四大力学的“粘合剂”
力学
热学
电学 原子物理
数学物理方法
理力
热统
数理方法是普通物理与四大力学的“粘合剂” 数理方法是学习专业课的奠基石
材料物理: 热处理 热传导方程 光学、电子科技: 电磁波传播 波动方程
理论物理: 稳恒场 泊松方程
基础课与专业课的关系:
“这好比一把斧头,基础是斧背,专业是斧刃。 斧背要厚,斧刃要尖,这样的斧头才会锋利无比”。
数学物理方法第三版答案

数学物理方法第三版答案【篇一:数学物理方法试卷答案】xt>一、选择题(每题4分,共20分) 1.柯西问题指的是( b ) a.微分方程和边界条件. b. 微分方程和初始条件. c.微分方程和初始边界条件. d. 以上都不正确. 2.定解问题的适定性指定解问题的解具有( d)a.存在性和唯一性. b. 唯一性和稳定性. c. 存在性和稳定性. d. 存在性、唯一性和稳定性.??2u?0,?3.牛曼内问题 ??u 有解的必要条件是( c)??n?f??a.f?0.b.u??0.c.?fds?0. d.?uds?0.???x(x)??x(x)?0,0?x?l4.用分离变量法求解偏微分方程中,特征值问题??x(0)?x(l)?0的解是( b )n?n??n???n??x ).b.( ?x ). a.( ??,cos?,sinllll????(2n?1)?(2n?1)??(2n?1)???(2n?1)??x ).d.( ?x ). c.( ??,cos?,sin2l2l2l2l????22225.指出下列微分方程哪个是双曲型的( d )a.uxx?4uxy?5uyy?ux?2uy?0. b.uxx?4uxy?4uyy?0.c.x2uxx?2xyuxy?y2uyy?xyux?y2uy?0. d.uxx?3uxy?2uyy?0.二、填空题(每题4分,共20分)??2u?2u?2?2?0, 0?x??, t?0?t?x??1.求定解问题?ux?0?2sint, ux????2sint, t?0的解是(2sintcosx).??ut?0?0, utt?0?2cosx, 0?x????2.对于如下的二阶线性偏微分方程a(x,y)uxx?2b(x,y)uxy?c(x,y)uyy?dux?euy?fu?0其特征方程为( a(x,y)(dy)2?2b(x,y)dxdy?c(x,y)(dx)2?0). 3.二阶常微分方程y(x)?或0).4.二维拉普拉斯方程的基本解为( ln1().r1 ),三维拉普拉斯方程的基本解为r113y(x)?(?2)y(x)?0的任一特解y?( jx44x1(x) 3225.已知j1(x)?222sinx, j1(x)?cosx,利用bessel函数递推公式求??x?x23j3(x)?(221221dsinx(sinx?cosx)??x()()). ?xx?xdxx三、(15分)用分离变量法求解如下定解问题2??2u2?u??t2?a?x2?0, 0?x?l, t?0??u??u?0, ?0, t?0 ??xx?l??xx?0?u?x, utt?0?0, 0?x?l.?t?0?解:第一步:分离变量(4分) 设u(x,t)?x(x)t(t),代入方程可得x(x)t(x)x(x)t(t)?ax(x)t(t)??2x(x)at(x)2此式中,左端是关于x的函数,右端是关于t的函数。
武汉大学姚端正报告——浅谈数学物理方法的学习

四大力学
理论力学 热 统
数理方法
数理方程 分离变量法 正交曲线坐标 格林函数法 (电象法) 傅里叶变换法 δ函数 特殊函数 变分原理
电动力学
量子力学
Wuhan University
二、数学物理方法在物理学中的地位
1.数理方法是物理学科的重要基础课
数理方法是普通物理与四大力学的‚粘合剂‛ 理论力学: 用拉格朗日方程
---牛顿
xi xi (t ), t
“只要能解微分方程,我就能预测宇宙的过去 和将来‛ -Laplace
Wuhan University
二、数学物理方法在物理学中的地位
1.数理方法是物理学科的重要基础课 2.数理方法是进行基础研究的重要工具 3.数理方法是培养学生逻辑思维能力和 创造思维能力的重要课程
数理方法是普通物理与四大力学的‚粘合剂‛ 力学 热学 电学 原子物理
理力
Wuhan University
热统
电动
量子力学
二、数学物理方法在物理学中的地位
1.数理方法是物理学科的重要基础课
数理方法是普通物理与四大力学的‚粘合剂‛
力学 热学 电学 原子物理
数学物理方法
理力
Wuhan University
1.数理方法是物理学科的重要基础课
数理方法是普通物理与四大力学的‚粘合剂‛ 统计物理:用波尔兹曼输运方程
f f F f f v ( )c t r m v t
得到非平衡态的速度分布函数 量子力学:用 Nhomakorabea定谔方程
2 2 Zes2 ( ) E 2
Wuhan University
数学物理方法 复变函数 第一章 解析函数

7
复数的表示
三角表示
指数表示
z =r (cosφ + i sinφ)
r = |z|(模), φ= Arg(z)(辐角)
z =r exp(iφ)
exp(iφ) = cosφ + i sinφ
代数表示
z = x + iy
x = Re(z), y = Im (z)
8
共轭复数
实部相同而虚部绝对值相等符号相反的两个复数称 为共轭复数.
18
复平面上的点集
z z0 z0 定义 由不等式 (δ为任意的正数)所确定的复平面点集(以后平面点 集均简称点集),就是以z0为中心的δ邻域或邻域。而 称由不等式 0 zz
0
δ
所确定的点集为z0的去心δ邻域或去心邻域。
19
内点,外点,边界点 开集 定义 设D为点集,z0为D中的一点。如果存在z0的 一个邻域,该邻域内的所有点都属于D,则称z0为D的 内点;点z0的某一个邻域内的点都不属于D ,则称 点z0为D的外点。若在点z0的任意一个邻域内,既有属 于D的点,也有不属于D的点,则称点z0为D的边界点, 点集D的全部边界点称为D的边界。
z1 z 2 z1 z 2
- z2
复数加减法满足 平行四边形法则
z1 +(- z2)
13
乘法运算
z1 z2 ( x1 x2 y1 y2 ) i( x1 y2 x2 y1 ) 1 2 exp[i(1 2 )] 1 2 cos(1 2 ) i sin(1 2 )
除法运算
z1 x1 x2 y1 y2 x1 y2 x2 y1 i 2 2 2 z2 x2 y2 x2 y22
数学物理方法姚端正CH9作业解答

则 1~2 式化为 ~(ω , t ) du ~ (ω , t ) = 0..................3 + a 2ω 2u dt ~ ~ u (ω ,0) = ϕ (ω )....................................4 满足初始条件 4 式的方程 3 的解为:
2 2
1 2π
∫
∞
−∞
e − a ω t eiωx dω =
2
2
1 ∞ − a 2 tω 2 e cos ωxdω π ∫0
b2
由教材 P91 积分公式
∫
∞
0
e
− ax 2
1 − π cos bxdx = e 4 a ,上式积分结果为: 2 a
2
F [e
−1
− a 2ω 2 t
1 1 − 4a 2t ]= e π 2
e
−
ξ2 4 a 2t
(sin x cos ξ − cos x sin ξ )dξ 1 2a πt e
− ax 2
=
−∞
e
−
ξ2 4a t
2
sin x cos ξdξ =
sin x ∫ e
−∞
∞
−
ξ2 4 a 2t
cos ξdξ
b2
再一次应用教材 P91 积分公式
∫
∞
0
π 1 − cos bxdx = e 4 a ,上式积分结果为: 2 a
F [sin ηx 2 ] = −
数学物理方法姚端正答案

数学物理方法姚端正答案【篇一:2014年省培在线课程列表】培在线学习先是选课环节,每位老师可以选2门课程,请把课程对应的序号私聊发到我qq上,我汇总后激活课程,学习流程于8月4号-6号发至群共享,请届时查看并自行开展在线学习。
【篇二:2013年下半年集中培训课程】ass=txt>2附件2 在线培训课程45【篇三:大学物理专业毕业去向分析_3】t>三、本专业去向分析(一)毕业去向分析1.直接就业,去中学任教,传授物理学知识。
2.继续深造考研。
考研主要专业研究方向有:理论物理、凝聚态物理、光学、原子分子物理、粒子物理核物理、声学、等离子体物理、半导体物理以及天体物理等。
最近几年,也有为数不少的物理系学生,考取了计算机类、经济管理类等专业的硕士研究生。
考研选择的主要院校有国内外科研院所和有关高校。
据不完全统计,北京某著名高校物理系在过去20年中,三分之一以上的的学生出国了,仅在美国的就有500多人。
根据研究方向的不同,考研的学生毕业后,一般去高校或科研院所工作或继续攻读博士学位。
也有一小部分去了企业或公司从事开发工作。
3.去企事业单位从事与物理学普及有关的管理、推广工作。
(二)毕业去向统计分析安徽某著名大学2007接参加工作的比例会高一些。
所以,上表中的统计数据,仅仅具有参考意义。
四、本专业与相关专业的比较与物理学专业相关的本科专业有:应用物理学、光信息科学与技术、材料物理、微电子学、电子科学与技术、材料物理学等。
下面,我们通过这几个相关专业的主要课程和培养目标来看他们与物理学专业的比较。
(一)物理学专业骨干课程:力学、热学、电磁学、光学、原子物理、理论力学、电动力学、量子力学、热力学与统计物理、数学物理方法、高等数学、电子技术与实验、普通物理实验、近代物理实验、固体物理等。
培养目标:本专业培养掌握物理学的基本理论与方法,具有良好的数学基础和实验技能,能在物理学或相关的科学技术领域中从事科研、教学、技术和相关的管理工作的高级专门人才。
数学物理方法姚端正CH1作业解答

数学物理方法CH1作业题解答P6习题1.11. 用复变量表示:(1)上半平面; (2)左半平面解:(1)上半平面为:0Im >z(2)左半平面为0Re <z4. 求下列复数的实部、虚部、模与辐角主值(3)3)3(−+i 解:先将i z +=3记为指数形式,i z +=3=)26(2ππk i e+ 则i e e e z i k i k i 81818122)62()26(333−====−+−+−−−πππππ 其实部为0,虚部为81−,模为81,辐角主值为2π− 6. 计算下列数值:(2)5)3(i − 解:先将i z −=3记为指数形式,i z −=3=)26(2ππk i e+−,则 )3(16)]65sin()65[cos(323232265)1065()26(555i i e e e z i k i k i +−=−+−====−+−+−πππππππ 7.求解方程(1)013=−z解:13=z ,则 −−=+−======i e i e e e e z i i k i k i 23212321113432032323ππππ 分别对应 ===210k k k 8.设流体在点i z 21+=的流速为ii v −+=23,求其大小和方向. 解:即求其模及辐角主值:i i i i i i v +=+=++=−+=15555)2)(3(23,其模为2,其辐角主值为4arg π=v P9习题1.22. 画出下列关系所表示的z 点的轨迹的图形并确定它是不是区域。
(1)1Im >z 且2||<z如图示阴影部分,不含边界线。
满足区域的两个条件:(1)全由内点组成;(2)点集中任意两点可用全在点集中的折线连接;所以是区域。
P15习题1.32. 讨论下列函数的可微性和解析性(1)2z w =解:记iy x z +=,),(),(y x iv y x u w +=;则xy i y x z w 2)(222+−==w 的实部22y x u −=,虚部xy v 2=x x u 2=∂∂, y y u 2−=∂∂, y xv 2=∂∂, x y v 2=∂∂ 可见,w 的实部和虚部有连续的一阶偏微商,且满足C-R 条件,所以,2z w =在复平面可微,从而在复平面是解析的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
姚端正《数理方法》(第三版)勘误表(部分)
P9,“(3)若()f x 在闭区域……”应更正为“(3)若()f z 在闭区域……”
P33,中部“任意一条分段光滑的曲线”应更正为“任意一条分段光滑的封闭曲线” P66,习题3.5第2(2)题:“0||z b R <-<”应更正为“||z b R -<”
P85,倒数第6行、第7行“1res ()n k f z =∑”应更正为“1res ()n
k
k f z =∑” P86,例3的计算过程中“||1a <”应更正为“01a <<”,但计算结果仍然对“||1a <”范围成立,即该例题的讨论过程不够完整。
P87,第10行“d[(π)]θ--”应更正为“d(π)θ-”
P88,第4行“如图5.4”应更正为“如图5.4(b )”;第4题需补充条件:01x <<;
第5题:“适当围道计算”应更正为“适当围道(图5.4(a ))计算”。
P107,第3行“稳定状态”应更正为“稳恒状态”;“则热量将停止流动”应去掉这段文字。
倒数第3行“F 为单位长度……”应更正为“F 为单位体积……”
P108,第6行“通过介面”应更正为“单位时间通过介面”
P111,第6行“k h E =”应更正为“k h EA =” P120,第1行“//at x a c
at x a c ++--⎰ ”应准确写为“()/()()/()at x a c at x a c ++--⎰ ”
P121,第4-5行“则在τ∆这段时间内”应更正为“则在τ∆这段时间以后”;
第6行“t τττ<<+∆”应更正为“t τ<”
P124,第4大题中“()x ψ”应更正为“(,)x y ψ”;“()x ϕ”应更正为“(,)x y ϕ”;
解的表达式应更正为
()01(,,)2π1 d 2πM M at at M a t t u x y t a t a τσσστ-⎡⎤∂=+⎢∂⎢⎣⎡⎤+⎢⎢⎣⎰⎰⎰⎰⎰⎰⎰
P146,第2行“I 2I u xx u a u =”应更正为“I 2I tt xx u a u =” P271,第1行“2(2)(1)lim lim 1(1)(1)
k k k k c k k R c l l k k →∞→∞+++===+-+”应更正为
“1k k R ===” P274,习题14.1第2题“0y xy ''-=”应更正为“0y xy ''-=” P280,习题14.2第6题“介电常数为ε”应更正为“相对介电常数为ε”
P286,习题14.3第3题(1)
”
部分习题答案勘误
第一篇
习题 3.2
2 (3)k R 应更正为n R ;
第二篇
习题 6.3
6 两端受压:“00(2)0t t t u l x u ε==⎧=-⎪⎨
=⎪⎩”应更正为“0020t t t u x u ε==⎧=-⎪⎨=⎪⎩” 习题 7.2
2(3)2132at axt +应更正为2132t xt +; 习题 8.1
3(3)“…224(21)πe
k -+…”应更正为“…224(21)πe k t -+…”; 4 1
π()sin n n n x a T t l ∞=∑应更正为1π()sin n n n n x a T t l ∞=∑; 10 “...4616πAb ...”应更正为“ (4)
664π
Ab …” 习题 8.2
3(1)另一形式的答案:3222321
2(1)ππ()cos sin 6(π)n n A Al n at n x u x l x a n a l l ∞=-=-+∑。
习题 8.5 10 2221212cos sin π2()π(2)(14)
n n n q q q n H k Ha a kn Ha n ρϕϕ∞-=++++-∑应更正为 221212cos 2sin π2()π(2)(14)
n n n q q q n H k Ha a kn Ha n ρρϕϕ∞-=++++-∑; 习题 9.1
10 (2)正确答案为12i ()i ()021112212
e e 1()[]()()t t x t
f ωτωτωωωωωωωω++=+---; (3)正确答案为1212i ()i ()i ()i ()
0121221121221e e e e ()[]()()()()t t t t x t f ωτωτωτωτωωωωωωωωωωωω+--+=+------; 第三篇
习题 14.1 2 311134673(31)n n x y x n n -∞
==+⋅⋅⋅⋅⋅⋅+∑应更正为31
1134673(31)n n x y x n n +∞==+⋅⋅⋅⋅⋅⋅+∑; 习题 14.2
6 印刷有误,“……1(cos )P θ”应更正为“……(cos )l P θ”
; 12 印刷有误,“...6451(cos )16a P r θ...” 应更正为“ (6)
45
1(cos )16a P r θ-…”;
习题 14.3
1 (21,11,12,12,1(,)(,)](,)(,)]Y Y Y Y θϕθϕθϕθϕ----。
