有限元大作业matlab课程设计例子

合集下载

有限元法MATLAB作业

例题：如图所示的受力均匀分布载荷作用的薄平板结构，将平板离散成两个线性三角元，如图所示，假定2210,0.3,0.025,3000/m E GPa v t m w KN ====。

求（1）该结构的整体刚度矩阵。

（2）节点2和节点3的水平位移和垂直位移。

（3）节点1和节点4的支反力。

（4）每个单元的应力。

（5）每个单元的主应力和主应力方向角。

图2. 用双线性三角元离散化的薄木板解：（1）离散化域我们将平板分为两个单元，4个节点，如图2所示，分布载荷的总作用力平均分给节点2和节点3，由于结构是薄平板，所以假定其属于平面应力情况。

MATLAB 中采用的计算单位是KN 和m 。

表1给出了该题的单元连通性。

（2）单元刚度矩阵通过调用MATLAB 的LinearTriangleElementStiffness 函数，得到两个单元矩阵k 1和k 2，每个矩阵都是66⨯的。

k1=gangdujuzhen(@LinearTriangleElementStiffness, 210000000, 0.3, 0.025, 0, 0, 0.5, 0.25, 0, 0.25, 1)的源程序：function k1= gangdujuzhen( f,E,NU,t,xi,yi,xj,yj,xm,ym,p ) %UNTITLED4 此处显示有关此函数的摘要% 此处显示详细说明k1=gangdujuzhen(@LinearTriangleElementStiffness, 210000000, 0.3, 0.025, 0, 0, 0.5, 0.25, 0, 0.25, 1)图1. 薄平板结构k1= f(E,NU,t,xi,yi,xj,yj,xm,ym,p);>>k1=gangdujuzhen(@LinearTriangleElementStiffness, 210000000, 0.3, 0.025, 0, 0, 0.5, 0.25, 0, 0.25, 1)k1 =1.0e+06 *2.0192 0 0 -1.0096 -2.0192 1.00960 5.7692 -0.8654 0 0.8654 -5.76920 -0.8654 1.4423 0 -1.4423 0.8654-1.0096 0 0 0.5048 1.0096 -0.5048-2.0192 0.8654 -1.4423 1.0096 3.4615 -1.87501.0096 -5.7692 0.8654 -0.5048 -1.8750 6.2740k2=gangdujuzhen2(@LinearTriangleElementStiffness, 210000000, 0.3, 0.025, 0, 0, 0.5, 0, 0.5, 0.25, 1)的源程序：function k2= gangdujuzhen2( f,E,NU,t,xi,yi,xj,yj,xm,ym,p )%UNTITLED3 此处显示有关此函数的摘要% 此处显示详细说明k2=gangdujuzhen2(@LinearTriangleElementStiffness, 210000000, 0.3, 0.025, 0, 0, 0.5, 0, 0.5, 0.25, 1)k2= f(E,NU,t,xi,yi,xj,yj,xm,ym,p);>>k2=gangdujuzhen2(@LinearTriangleElementStiffness, 210000000, 0.3, 0.025, 0, 0, 0.5, 0, 0.5, 0.25, 1)k2 =1.0e+06 *1.4423 0 -1.4423 0.8654 0 -0.86540 0.5048 1.0096 -0.5048 -1.0096 0-1.4423 1.0096 3.4615 -1.8750 -2.0192 0.86540.8654 -0.5048 -1.8750 6.2740 1.0096 -5.76920 -1.0096 -2.0192 1.0096 2.0192 0-0.8654 0 0.8654 -5.7692 0 5.7692（3）集成整体刚度矩阵⨯的，因此为了得到整体刚度矩阵K，我们由于结构有4个节点，所以刚度矩阵是88⨯的零矩阵。

有限元平面矩形单元MATLAB程序设计【范本模板】

有限元平面矩形单元MATLAB程序设计摘要本论文主要研究内容是有限元平面矩形单元的基本原理和MATLAB软件的图形用户界面及函数编程的基本知识，并根据有限元平面矩形单元的计算单元刚度矩阵,结点位移等原理和方法，运用MATLAB 语言编写弹性力学平面矩形单元的计算程序，使得程序能够完成对不同荷载类型，不同结构单元的计算，同时设计了图形用户界面(GUI),使得程序能够在图形用户界面（GUI)上对应的输入框内输入相应数据,并能够计算出单元刚度矩阵，等效结点荷载，有限元上结点位移和单元应力;最后将集中荷载和均布荷载情况下的实例进行对MATLAB计算得出的位移和单元结点应力与ANSYS计算值比较分析，验证其正确性和通用性,并总结了MATLAB软件在有限元的运用.关键词MATLAB程序设计;有限元；矩形单元；刚度矩阵;单元应力The Rectangle Unit Plane of Finite Element of theMATLAB ProgrammingAbstractThis dissertation mainly studies the radical principle of the rectangle unit plane of the finite element and the basic knowledge of the Graphical User Interface and the function programming of the MATLAB software 。

And make use of MATLAB language to make up the GUI and the computation program of MATLAB according to the theory and method of the rectangle unit plane of the finite element to compute the element stiffness matrix , nodes’displacement and so on about different types of loads and different elements 。

有限元matlab仿真

有限元matlab仿真最近写有有限元作业，用matlab实现了整个的过程，顺便熟悉一下有限元的整体解题思路，感觉这确实是一种很好方法。

下面对书上的一道题做仿真吧，最后结果如下。

题目：如图所示薄板忽略自重，在力F的作用下，求各节点位移和各单元应力，已知假定该问题为平面应力问题。

这是一个正方形的薄板，上面两个顶点处被吊起来，在中心处受到一个向下的力。

现分成四个单元（下面的两个顶点编号为1,2，上面个两个为3,4，中间的5）执行程序得到如下结果1节点的位移:（u，v） = （-1.42857e-006, -7.14286e-006）2节点的位移:（u，v） = （1.42857e-006, -7.14286e-006）3节点的位移:（u，v） = （0, 0）4节点的位移:（u，v） = （0, 0）5节点的位移:（u，v） = （0, -8.57143e-006）第1单元:应力为（750000，3.75e+006，-2.25e+006）应变为（3.57143e-006，1.78571e-005，-2.14286e-005）第2单元:应力为（1.5e+006，-1.5e+006，6.98492e-010）应变为（7.14286e-006，-7.14286e-006，1.01644e-020）第3单元:应力为（750000，3.75e+006，2.25e+006）应变为（3.57143e-006，1.78571e-005，2.14286e-005）第4单元:应力为（0，9e+006，0）应变为（0，4.28571e-005，0）还可以实现各顶点移动的动画图，本来想做个gif，但发现getframe截不了屏，郁闷只能在这贴几张图了这个是不是就是ANSYS的有限元分析啊！代码部分如下，显示动画的代码麻烦点，就不贴了，从代码也可以看到，好的数据结构的重要性：main.m文件：clcclear allclose all% 数据choise = 1;switch choisecase 1% 作业第3题verts = [0 0;2 0;2 2;0 2;1 1;]*0.2;eleindex = [1 5 4;2 5 1;3 5 2;4 5 3];vertdisind = [1 1 1 1 0 0 0 0 0 1]'; R = [0 0 0 0 0 0 0 0 0 -30000]'; case 2% 书上例题verts = [0 2;0 1;1 1;0 0;1 0;2 0];eleindex = [5 2 4;6 3 5;2 5 3;3 1 2];endfigurepatch('Faces', eleindex, 'Vertices', verts, 'FaceColor', 'r'); % 绘制数据axis equalaxis off% 构造FEMhFEM.vertcount = size(verts, 1);hFEM.verts = verts;hFEM.elecount = size(eleindex, 1);hFEM.eleindex = eleindex;hFEM.mu = 0;hFEM.E = 210e9;hFEM.t = 0.01;hFEM = FEM(hFEM);% 求解有限元方程得各节点位移hFEM = FEMSolve(hFEM, vertdisind, R);for k = 1:hFEM.vertcountfprintf('%d节点的位移:（u，v）= （%g, %g）\n', k, hFEM.vertdis([2*k-1, 2*k]));end% 求各单元应力、应变for k = 1:hFEM.elecountind(1:2:5) = 2*hFEM.eleindex(k, :)-1;ind(2:2:6) = 2*hFEM.eleindex(k, :);stress = hFEM.eletruct(k).S * hFEM.vertdis(ind);strain = hFEM.eletruct(k).B * hFEM.vertdis(ind);fprintf('第%d单元:\n应力为（%g，%g，%g）\n', k, stress);fprintf('应变为（%g，%g，%g）\n', strain);endFEM.m文件：% 计算FEM分析的各种矩阵function hFEM = FEM(hFEM)% 处理每个单元for i = 1:hFEM.elecounthFEM.eletruct(i) = FEMele(hFEM, i);end% 计算合成刚度矩阵hFEM.K = FEMCalcCombiningK(hFEM);endfunction hFEMele = FEMele(hFEM, ind) hFEMele.ele = hFEM.verts(hFEM.eleindex(ind, :), :); hFEMele.B = FEMCalcB(hFEMele);hFEMele.D = FEMCalcD(hFEM);hFEMele.S = FEMCalcS(hFEMele);hFEMele.K = FEMCalcK(hFEM, hFEMele);end% 计算几何矩阵function B = FEMCalcB(hFEMele)ele = hFEMele.ele;A(:, 2:3) = ele;A(:, 1) = 1;invA = inv(A);B(1, 1:2:5) = invA(2, :);B(2, 2:2:6) = invA(3, :);B(3, 1:2:5) = invA(3, :);B(3, 2:2:6) = invA(2, :);end% 计算应力矩阵function D = FEMCalcD(hFEM)mu = hFEM.mu;E = hFEM.E;D = [1 mu 0;mu 1 0;0 0 (1-mu)/2]*E/(1-mu^2);end% 计算应力变换矩阵function S = FEMCalcS(hFEMele)S = hFEMele.D*hFEMele.B;end% 计算单元刚度矩阵function K = FEMCalcK(hFEM, hFEMele)triarea = CalcTriangleArea(hFEMele.ele);K = hFEM.t*triarea*hFEMele.B'*hFEMele.D*hFEMele.B; end% 计算三角形面积function area = CalcTriangleArea(ele)A(:, 2:3) = ele;A(:, 1) = 1;area = 0.5*det(A);end% 计算合成矩阵function K = FEMCalcCombiningK(hFEM) vertcount = hFEM.vertcount;elecount = hFEM.elecount;eleindex = hFEM.eleindex;eleK = zeros(6, 6, elecount);for k = 1:elecounteleK(:, :, k) = hFEM.eletruct(k).K;endK = zeros(vertcount*2);for i = 1:vertcountfor j = 1:vertcountfor k = 1:elecountindi = find(eleindex(k, :)==i);indj = find(eleindex(k, :)==j);if ~isempty(indi) && ~isempty(indj)K(2*i-1:2*i, 2*j-1:2*j) = K(2*i-1:2*i, 2*j-1:2*j) + eleK(2*indi-1:2*indi, 2*indj-1:2*indj, k);endendendendendFEMSolve.m文件：% 求解有限元方程function hFEM = FEMSolve(hFEM, vertdisind, R)K = hFEM.K;hFEM.vertdis = SolveFEM(vertdisind, R, K);for i = 1:hFEM.elecounthFEM.eletruct(i).vertdis(1:2:5) = hFEM.vertdis(2*hFEM.eleindex(i, :) - 1); % uhFEM.eletruct(i).vertdis(2:2:6) = hFEM.vertdis(2*hFEM.eleindex(i, :)); % vendendfunction vertdis = SolveFEM(vertdisind, R, K)vertdis = vertdisind;ind = find(vertdisind ~= 0);Krule = K(ind, ind); Rrule = R(ind);vertdis(ind) = Krule\Rrule; end。

《有限元分析》课程作业

《有限元分析》课程作业任课教师：徐亚兰学生姓名：陈新杰学号：班级：1304012时间：2016-01-05一、问题描述及分析问题：如图1所示，有一矩形平板，在右侧受到P=10KN/m 的分布力，材料常数为：弹性模量Pa E 7101⨯=；泊松比3/1=μ；板的厚度为t=；试按平面应力问题利用三角形与矩形单元分别计算各个节点位移及支座反力。

图1 平面矩形结构的有限元分析分析：使用两种方案：一、基于3节点三角形单元的有限元建模，将矩形划分为两个3节点三角形单元；二、基于4节点矩形单元的有限元建模，使用一个4节点矩形单元。

利用MATLAB 软件计算出各要求量，再将两种方案的计算结果进行比较、分析、得出结论。

二、有限元建模及分析1、基于3节点三角形单元的有限元建模及分析（1）结构的离散化与编号如图2所示，将平面矩形结构分为两个3节点三角形单P=10KN/m1m1m元。

单元①三个节点的编号为1，2，4，单元②三个节点的编号为3，4，2，各个节点的位置坐标为(),,1,2,3,4i i x y i =，各个节点的位移（分别沿x 方向和y 方向）为(),,1,2,3,4i i u v i =。

图2 方案一：使用两个3节点三角形单元（2）各单元的刚度矩阵及刚度方程 a.单元的几何和节点描述单元①有6个节点位移自由度（DOF ）。

将所有节点上的位移组成一个列阵，记作(1)q ；同样，将所有节点上的各个力也组成一个列阵，记作(1)F ，则有(1)112244,,,,,)q u v u v u v =（(1)112244(,,,,,)x y x y x y F F F F F F F =同理，对于单元②，有(2)334422,,,,,)q u v u v u v =（1234X y ①②(2)334422(,,,,,)x y x y x y F F F F F F F =b.单元的位移场描述对于单元①，设位移函数012012(,)(,)u x y a a x a y v x y b b x b y ⎫=++⎪⎬=++⎪⎭(1-1)由节点条件，在,i i x x y y ==处，有(,)(,)i i i i i i u x y u v x y v =⎫⎬=⎭1,2,4i = (1-2) 将式(1-1)代入节点条件式(1-2)中，可求出式（1-1）中待定系数，即011122211223444411()22u x y a u x y a u a u a u AAu x y ==++ (1-3) 11122112234441111()221u y a u y b u b u b u AAu y ==++ (1-4) 21122112234441111()221x u a x u c u c u c u AAx u ==++ (1-5) 01122341()2b a v a v a v A =++(1-6) 11122341()2b b v b v b v A =++(1-7) 21122341()2b c v c v c v A =++(1-8)在式(1-3)~式(1-8)中1122123441111()221x y A x y a a a x y ==++ (1-9)2212442442124421244(1,2,3)1111x y a x y x y x y y b y y y x c x x x ⎫==-⎪⎪⎪⎪=-=-⎬⎪⎪⎪==-+⎪⎭ (1-10) 上式中的符号(1,2,3)表示下标轮换，如12,23,31→→→同时更换。

(完整版)有限元大作业matlab---课程设计例子

有限元大作业程序设计学校：天津大学院系：建筑工程与力学学院专业：01级工程力学姓名：刘秀学号：\\\\\\\\\\\指导老师：连续体平面问题的有限元程序分析[题目]：如图所示的正方形薄板四周受均匀载荷的作用，该结构在边界上受正向分布压力，m kNp 1=，同时在沿对角线y 轴上受一对集中压力，载荷为2KN ，若取板厚1=t ，泊松比0=v 。

[分析过程]：由于连续平板的对称性，只需要取其在第一象限的四分之一部分参加分析，然后人为作出一些辅助线将平板“分割”成若干部分，再为每个部分选择分析单元。

采用将此模型化分为4个全等的直角三角型单元。

利用其对称性，四分之一部分的边界约束，载荷可等效如图所示。

[程序原理及实现]：用FORTRAN程序的实现。

由节点信息文件NODE.IN和单元信息文件ELEMENT.IN，经过计算分析后输出一个一般性的文件DATA.OUT。

模型基本信息由文件为BASIC.IN生成。

该程序的特点如下：问题类型：可用于计算弹性力学平面问题和平面应变问题单元类型：采用常应变三角形单元位移模式：用用线性位移模式载荷类型：节点载荷，非节点载荷应先换算为等效节点载荷材料性质：弹性体由单一的均匀材料组成约束方式：为“0”位移固定约束，为保证无刚体位移，弹性体至少应有对三个自由度的独立约束方程求解：针对半带宽刚度方程的Gauss消元法输入文件：由手工生成节点信息文件NODE.IN，和单元信息文件ELEMENT.IN结果文件：输出一般的结果文件DATA.OUT程序的原理如框图：（1）主要变量：ID：问题类型码，ID＝1时为平面应力问题，ID=2时为平面应变问题N_NODE：节点个数N_LOAD：节点载荷个数N_DOF：自由度，N_DOF=N_NODE*2（平面问题）N_ELE：单元个数N_BAND：矩阵半带宽N_BC：有约束的节点个数PE：弹性模量PR：泊松比PT：厚度LJK_ELE(I,3)：单元节点编号数组，LJK_ELE(I,1)，LJK_ELE(I,2)，LJK_ELE(I,3)分别放单元I的三个节点的整体编号X(N_NODE), Y(N_NODE)：节点坐标数组，X(I),Y(I)分别存放节点I的x，y 坐标值P_LJK(N_BC,3)：节点载荷数组，P_LJK(I,1)表示第I个作用有节点载荷的节点的编号，P_LJK(I,2)，P_LJK(I,3)分别为该节点沿x,y方向的节点载荷数值AK(N_DOF,N_BAND)：整体刚度矩阵AKE(6,6)：单元刚度矩阵BB(3,6)：位移……应变转换矩阵（三节点单元的几何矩阵）DD(3,3)：弹性矩阵SS(3,6)；应力矩阵RESULT_N(N_NOF)：节点载荷数组，存放节点载荷向量，解方程后该矩阵存放节点位移DISP_E(6):：单元的节点位移向量STS_ELE(N_ELE,3)：单元的应力分量STS_ND(N_NODE,3)：节点的应力分量（2）子程序说明：READ_IN：读入数据BAND_K：形成半带宽的整体刚度矩阵FORM_KE：计算单元刚度矩阵FORM_P：计算节点载荷CAL_AREA：计算单元面积DO_BC：处理边界条件CLA_DD：计算单元弹性矩阵SOLVE：计算节点位移CLA_BB：计算单元位移……应变关系矩阵CAL_STS：计算单元和节点应力（3）文件管理：源程序文件：chengxu.for程序需读入的数据文件：BASIC.IN，NODE.IN，ELEMENT.IN（需要手工生成）程序输出的数据文件：DATA.OUT（4）数据文件格式：需读入的模型基本信息文件BASIC.IN的格式如下表需读入的节点信息文件NODE.IN的格式如下表需读入的单元信息文件ELEMENT.IN的格式如下表输出结果文件DATA.OUT格式如下表[算例原始数据和程序分析]：（1）模型基本信息文件BASIC.IN的数据为1,4,6,5,31.,0.,1.1,1,0,2,1,0,4,1,1,5,0,1,6,0,11,-0.5,-1.5,3.,-1.,-1,6,-0.5,-0.5（2）手工准备的节点信息文件NODE.IN的数据为1 0.0 2.02 0.0 1.03 1.0 1.04 0. 0.5 1.0 0.6 2.0 0.（3）手工准备的单元信息文件ELEMENT.IN的数据为1 2 3 3 0 0 0 0 1 1 1 1 0 12 4 5 5 0 0 0 0 1 1 1 1 0 25 3 2 2 0 0 0 0 1 1 1 1 0 33 5 6 6 0 0 0 0 1 1 1 1 04 （4）源程序文件chengxu.for为：PROGRAM FEM2DDIMENSION IJK_ELE(500,3),X(500),Y(500),IJK_U(50,3),P_IJK(50,3),&RESULT_N(500),AK(500,100)D IMENSION STS_ELE(500,3),STS_ND(500,3)OPEN(4,FILE='BASIC.IN')OPEN(5,FILE='NODE.IN')OPEN(6,FILE='ELEMENT.IN')OPEN(8,FILE='DATA.OUT')OPEN(9,FILE='FOR_POST.DAT')READ(4,*)ID,N_ELE,N_NODE,N_BC,N_LOADIF(ID.EQ.1)WRITE(8,20)IF(ID.EQ.2)WRITE(8,25)20 FORMAT(/5X,'=========PLANE STRESS PROBLEM========')25 FORMAT(/5X,'=========PLANE STRAIN PROBLEM========')CALL READ_IN(ID,N_ELE,N_NODE,N_BC,N_BAND,N_LOAD,PE,PR,PT, & IJK_ELE,X,Y,IJK_U,P_IJK)CALL BAND_K(N_DOF,N_BAND,N_ELE,IE,N_NODE,& IJK_ELE,X,Y,PE,PR,PT,AK)CALL FORM_P(N_ELE,N_NODE,N_LOAD,N_DOF,IJK_ELE,X,Y,P_IJK, & RESULT_N)CALL DO_BC(N_BC,N_BAND,N_DOF,IJK_U,AK,RESULT_N)CALL SOLVE(N_NODE,N_DOF,N_BAND,AK,RESULT_N)CALL CAL_STS(N_ELE,N_NODE,N_DOF,PE,PR,IJK_ELE,X,Y,RESULT_N, & STS_ELE,STS_ND)c to putout a data fileWRITE(9,70)REAL(N_NODE),REAL(N_ELE)70 FORMAT(2f9.4)WRITE(9,71)(X(I),Y(I),RESULT_N(2*I-1),RESULT_N(2*I),& STS_ND(I,1),STS_ND(I,2),STS_ND(I,3),I=1,N_NODE)71 FORMA T(7F9.4)WRITE(9,72)(REAL(IJK_ELE(I,1)),REAL(IJK_ELE(I,2)),&REAL(IJK_ELE(I,3)),REAL(IJK_ELE(I,3)),&STS_ELE(I,1),STS_ELE(I,2),STS_ELE(I,3),I=1, N_ELE)72 FORMAT(7f9.4)cCLOSE(4)CLOSE(5)CLOSE(6)CLOSE(8)CLOSE(9)E NDcc to get the original data in order to model the problemSUBROUTINE READ_IN(ID,N_ELE,N_NODE,N_BC,N_BAND,N_LOAD,PE,PR, &PT,IJK_ELE,X,Y,IJK_U,P_IJK)DIMENSION IJK_ELE(500,3),X(N_NODE),Y(N_NODE),IJK_U(N_BC,3), & P_IJK(N_LOAD,3),NE_ANSYS(N_ELE,14)REAL ND_ANSYS(N_NODE,3)READ(4,*)PE,PR,PTREAD(4,*)((IJK_U(I,J),J=1,3),I=1,N_BC)READ(4,*)((P_IJK(I,J),J=1,3),I=1,N_LOAD)READ(5,*)((ND_ANSYS(I,J),J=1,3),I=1,N_NODE)READ(6,*)((NE_ANSYS(I,J),J=1,14),I=1,N_ELE)DO 10 I=1,N_NODEX(I)=ND_ANSYS(I,2)Y(I)=ND_ANSYS(I,3)10 CONTINUEDO 11 I=1,N_ELEDO 11 J=1,3IJK_ELE(I,J)=NE_ANSYS(I,J)11 CONTINUEN_BAND=0DO 20 IE=1,N_ELEDO 20 I=1,3DO 20 J=1,3IW=IABS(IJK_ELE(IE,I)-IJK_ELE(IE,J))IF(N_BAND.LT.IW)N_BAND=IW20 CONTINUEN_BAND=(N_BAND+1)*2IF(ID.EQ.1) THENELSEPE=PE/(1.0-PR*PR)PR=PR/(1.0-PR)END IFR ETURNENDcC to form the stiffness matrix of elementSUBROUTINE FORM_KE(IE,N_NODE,N_ELE,IJK_ELE,X,Y,PE,PR,PT,AKE) DIMENSION IJK_ELE(500,3),X(N_NODE),Y(N_NODE),BB(3,6),DD(3,3), & AKE(6,6), SS(6,6)CALL CAL_DD(PE,PR,DD)CALL CAL_BB(IE,N_NODE,N_ELE,IJK_ELE,X,Y,AE,BB)DO 10 I=1,3DO 10 J=1,6SS(I,J)=0.0DO 10 K=1,310 SS(I,J)=SS(I,J)+DD(I,K)*BB(K,J)DO 20 I=1,6DO 20 J=1,6AKE(I,J)=0.0DO 20 K=1,320 AKE(I,J)=AKE(I,J)+SS(K,I)*BB(K,J)*AE*PTRETURNENDcc to form banded global stiffness matrixSUBROUTINE BAND_K(N_DOF,N_BAND,N_ELE,IE,N_NODE,IJK_ELE,X,Y,PE, & PR,PT,AK)DIMENSIONIJK_ELE(500,3),X(N_NODE),Y(N_NODE),AKE(6,6),AK(500,100)N_DOF=2*N_NODEDO 40 I=1,N_DOFDO 40 J=1,N_BAND40 AK(I,J)=0DO 50 IE=1,N_ELECALL FORM_KE(IE,N_NODE,N_ELE,IJK_ELE,X,Y,PE,PR,PT,AKE)DO 50 I=1,3DO 50 II=1,2IH=2*(I-1)+IIIDH=2*(IJK_ELE(IE,I)-1)+IIDO 50 J=1,3DO 50 JJ=1,2IL=2*(J-1)+JJIZL=2*(IJK_ELE(IE,J)-1)+JJIDL=IZL-IDH+1IF(IDL.LE.0) THENELSEAK(IDH,IDL)=AK(IDH,IDL)+AKE(IH,IL)END IF50 CONTINUERETURNENDcc to calculate the area of elementSUBROUTINE CAL_AREA(IE,N_NODE,IJK_ELE,X,Y,AE)DIMENSION IJK_ELE(500,3),X(N_NODE),Y(N_NODE)I=IJK_ELE(IE,1)J=IJK_ELE(IE,2)K=IJK_ELE(IE,3)XIJ=X(J)-X(I)YIJ=Y(J)-Y(I)XIK=X(K)-X(I)YIK=Y(K)-Y(I)AE=(XIJ*YIK-XIK*YIJ)/2.0RETURNENDcc to calculate the elastic matrix of elementSUBROUTINE CAL_DD(PE,PR,DD)DIMENSION DD(3,3)DO 10 I=1,3DO 10 J=1,310 DD(I,J)=0.0DD(1,1)=PE/(1.0-PR*PR)DD(1,2)=PE*PR/(1.0-PR*PR)DD(2,1)=DD(1,2)DD(2,2)=DD(1,1)DD(3,3)=PE/((1.0+PR)*2.0)RETURNENDcc to calculate the strain-displacement matrix of elementSUBROUTINE CAL_BB(IE,N_NODE,N_ELE,IJK_ELE,X,Y,AE,BB) DIMENSION IJK_ELE(500,3),X(N_NODE),Y(N_NODE),BB(3,6)I=IJK_ELE(IE,1)J=IJK_ELE(IE,2)K=IJK_ELE(IE,3)DO 10 II=1,3DO 10 JJ=1,310 BB(II,JJ)=0.0BB(1,1)=Y(J)-Y(K)BB(1,3)=Y(K)-Y(I)BB(1,5)=Y(I)-Y(J)BB(2,2)=X(K)-X(J)BB(2,4)=X(I)-X(K)BB(2,6)=X(J)-X(I)BB(3,1)=BB(2,2)BB(3,2)=BB(1,1)BB(3,3)=BB(2,4)BB(3,4)=BB(1,3)BB(3,5)=BB(2,6)BB(3,6)=BB(1,5)CALL CAL_AREA(IE,N_NODE,IJK_ELE,X,Y,AE)DO 20 I1=1,3DO 20 J1=1,620 BB(I1,J1)=BB(I1,J1)/(2.0*AE)RETURNENDcc to form the global load matrixSUBROUTINE FORM_P(N_ELE,N_NODE,N_LOAD,N_DOF,IJK_ELE,X,Y,P_IJK, & RESULT_N)DIMENSION IJK_ELE(500,3),X(N_NODE),Y(N_NODE),P_IJK(N_LOAD,3), & RESULT_N(N_DOF)DO 10 I=1,N_DOF10 RESULT_N(I)=0.0DO 20 I=1,N_LOADII=P_IJK(I,1)RESULT_N(2*II-1)=P_IJK(I,2)20 RESULT_N(2*II)=P_IJK(I,3)RETURNENDcc to deal with BC(u) (here only for fixed displacement) using "1-0" method SUBROUTINE DO_BC(N_BC,N_BAND,N_DOF,IJK_U,AK,RESULT_N) DIMENSION RESULT_N(N_DOF),IJK_U(N_BC,3),AK(500,100)DO 30 I=1,N_BCIR=IJK_U(I,1)DO 30 J=2,3IF(IJK_U(I,J).EQ.0)THENELSEII=2*IR+J-3AK(II,1)=1.0RESULT_N(II)=0.0DO 10 JJ=2,N_BAND10 AK(II,JJ)=0.0DO 20 JJ=2,II20 AK(II-JJ+1,JJ)=0.0END IF30 CONTINUERETURNENDcc to solve the banded FEM equation by GAUSS eliminationSUBROUTINE SOLVE(N_NODE,N_DOF,N_BAND,AK,RESULT_N) DIMENSION RESULT_N(N_DOF),AK(500,100)DO 20 K=1,N_DOF-1IF(N_DOF.GT.K+N_BAND-1)IM=K+N_BAND-1IF(N_DOF.LE.K+N_BAND-1)IM=N_DOFDO 20 I=K+1,IML=I-K+1C=AK(K,L)/AK(K,1)IW=N_BAND-L+1DO 10 J=1,IWM=J+I-K10 AK(I,J)=AK(I,J)-C*AK(K,M)20 RESULT_N(I)=RESULT_N(I)-C*RESULT_N(K)RESULT_N(N_DOF)=RESULT_N(N_DOF)/AK(N_DOF,1)DO 40 I1=1,N_DOF-1I=N_DOF-I1IF(N_BAND.GT.N_DOF-I-1)JQ=N_DOF-I+1IF(N_BAND.LE.N_DOF-I-1)JQ=N_BANDDO 30 J=2,JQK=J+I-130 RESULT_N(I)=RESULT_N(I)-AK(I,J)*RESULT_N(K)40 RESULT_N(I)=RESULT_N(I)/AK(I,1)WRITE(8,50)50 FORMAT(/12X,'* * * * * RESULTS BY FEM2D * * * * *',//8X,&'--DISPLACEMENT OF NODE--'//5X,'NODE NO',8X,'X-DISP',8X,'Y-DISP') DO 60 I=1,N_NODE60 WRITE(8,70) I,RESULT_N(2*I-1),RESULT_N(2*I)70 FORMAT(8X,I5,7X,2E15.6)RETURNENDcc calculate the stress components of element and nodeSUBROUTINECAL_STS(N_ELE,N_NODE,N_DOF,PE,PR,IJK_ELE,X,Y,RESULT_N, &STS_ELE,STS_ND)DIMENSION IJK_ELE(500,3),X(N_NODE),Y(N_NODE),DD(3,3),BB(3,6), &SS(3,6),RESULT_N(N_DOF),DISP_E(6)DIMENSION STS_ELE(500,3),STS_ND(500,3)WRITE(8,10)10 FORMAT(//8X,'--STRESSES OF ELEMENT--')CALL CAL_DD(PE,PR,DD)DO 50 IE=1,N_ELECALL CAL_BB(IE,N_NODE,N_ELE,IJK_ELE,X,Y,AE,BB)DO 20 I=1,3DO 20 J=1,6SS(I,J)=0.0DO 20 K=1,320 SS(I,J)=SS(I,J)+DD(I,K)*BB(K,J)DO 30 I=1,3DO 30 J=1,2IH=2*(I-1)+JIW=2*(IJK_ELE(IE,I)-1)+J30 DISP_E(IH)=RESULT_N(IW)STX=0STY=0TXY=0DO 40 J=1,6STX=STX+SS(1,J)*DISP_E(J)STY=STY+SS(2,J)*DISP_E(J)40 TXY=TXY+SS(3,J)*DISP_E(J)STS_ELE(IE,1)=STXSTS_ELE(IE,2)=STYSTS_ELE(IE,3)=TXY50 WRITE(8,60)IE,STX,STY,TXY60 FORMAT(1X,'ELEMENT NO.=',I5/18X,'STX=',E12.6,5X,'STY=',&E12.6,2X,'TXY=',E12.6)c the following part is to calculate stress components of nodeWRITE(8,55)55 FORMAT(//8X,'--STRESSES OF NODE--')DO 90 I=1,N_NODEA=0.B=0.C=0.II=0DO 70 K=1,N_ELEDO 70 J=1,3IF(IJK_ELE(K,J).EQ.I) THENII=II+1A=A+STS_ELE(K,1)B=B+STS_ELE(K,2)C=C+STS_ELE(K,3)END IF70 CONTINUESTS_ND(I,1)=A/IISTS_ND(I,2)=B/IISTS_ND(I,3)=C/IIWRITE(8,75)I,STS_ND(I,1),STS_ND(I,2),STS_ND(I,3)75 FORMAT(1X,'NODE NO.=',I5/18X,'STX=',E12.6,5X,'STY=',&E12.6,2X,'TXY=',E12.6)90 CONTINUERETURNENDc FEM2D programm end[算例结果]：chengxu.for所输出的数据文件DATA.OUT数据内容如下：=========PLANE STRESS PROBLEM========* * * * * RESULTS BY FEM2D * * * * *--DISPLACEMENT OF NODE--NODE NO X-DISP Y-DISP1 .000000E+00 -.525275E+012 .000000E+00 -.225275E+013 -.108791E+01 -.137363E+014 .000000E+00 .000000E+005 -.824176E+00 .000000E+006 -.182418E+01 .000000E+00--STRESSES OF ELEMENT--ELEMENT NO.= 1STX=-.108791E+01 STY=-.300000E+01 TXY= .439560E+00ELEMENT NO.= 2STX=-.824176E+00 STY=-.225275E+01 TXY= .000000E+00ELEMENT NO.= 3STX=-.108791E+01 STY=-.137363E+01 TXY= .307692E+00ELEMENT NO.= 4STX=-.100000E+01 STY=-.137363E+01 TXY=-.131868E+00--STRESSES OF NODE--NODE NO.= 1STX=-.108791E+01 STY=-.300000E+01 TXY= .439560E+00NODE NO.= 2STX=-.100000E+01 STY=-.220879E+01 TXY= .249084E+00NODE NO.= 3STX=-.105861E+01 STY=-.191575E+01 TXY= .205128E+00NODE NO.= 4STX=-.824176E+00 STY=-.225275E+01 TXY= .000000E+00NODE NO.= 5STX=-.970696E+00 STY=-.166667E+01 TXY= .586081E-01NODE NO.= 6STX=-.100000E+01 STY=-.137363E+01 TXY=-.131868E+00[结论与体会]:通过本次的课程设计，我对有限元的概念有了更加深刻的理解，同时也弥补了平时学习是疏忽的地方，充实了有限元知识。

有限元平面问题MATLAB程序

计算力学(有限元方法部分) 程序设计程序说明书程序1：平面问题的有限元分析文件名：h01.m算例文本：h01.txt输出文本：result1.txt使用前请先将h01.txt放入默认的文本读取路径（我的要求与m文件在同一文件夹内）！文本输入顺序：材料信息（编号、弹性模量、泊松比）注意：材料编号须按1、2、3、4……的顺序排列节点信息（编号、x坐标、y坐标）注意：节点编号须按1、2、3、4……的顺序排列约束信息（约束节点号、x方向有无约束、y方向有无约束、x方向位移、y 方向位移）有约束处填一正数，无约束处填0。

无约束处请勿输入位移。

单元信息（厚度、材料编号、节点编号，若为3节点单元，则第四个编号填0）注意：单元编号须按1、2、3、4……的顺序排列集中力（作用节点号、x方向力、y方向力）线荷载（作用边上的两个节点号、x方向分布力、y方向分布力）面荷载（作用单元号、x方向分布力、y方向分布力）程序可调部分：4-6行中可以指定输出哪些图像（按顺序依次为节点、单元图像，x、y方向位移图像，xx、yy、xy方向应力图像），第7行中可以指定输入的.txt文本名称。

文本输出内容：结点位移信息（节点号、x方向位移、y方向位移）单元形心处的应变信息（单元号、x方向正应变、y方向正应变、xy方向工程切应变）单元形心处的应力信息（单元号、x方向正应力、y方向正应力、xy方向切应力）本程序附有三角形单元自动加密前处理部分h01auto.m，其算例文本：h01coarse.txt，输出文本：h01new.txt。

它可以适用于本题的要求，在已给定本题所需全部信息的情况下将已有的单元加密为三角形单元。

其输出文本可直接作为上面程序的输入文本。

h01.m h01.txt h01auto.m h01coarse.txt欢迎交流与提问！附上邮箱：***************。

祝力学学习顺利！。

MATLAB电磁场有限元计算

电磁场实验报告实验二 MATLAB电磁场有限元计算学院：电气工程与自动化班级：电气1003班学号：1010430317姓名：张洋一、两根载流长直导线的磁场问题描述: 两根载流长直导线,相距为0.8,导线直径为0.2, 求电流引起的磁场. 从麦克斯韦(Maxwell)方程组出发,其磁场强度B和磁感应强度H的关系为: μB H=磁场势A 与B 有如下关系: =∇⨯B A故可简化为椭圆方程:2μA J∇=-画出大小为2* 2的矩形R1,两导线用直径为0. 2、相距0. 8 的两个圆表示.矩形的边界条件是Di richlet边界条件,取h= 1, r= 0。

这种做法是模拟远处的磁场势为零.在设置方程类型时, 选取应用模式为Mangetostatics.故在选择方程时选取Elliptic(椭圆)方程, 对于矩形其它部分系数取μ=1、J=0.在表示导线的圆内,取μ= 1, J=1.两根载流长直导线的磁场势和磁力线如下图所示,磁力线用箭头表示.二、静电场中的导体问题描述: 在电场强度为 E 的静电场中放置一根无限长的导体,研究截面上的电势分布。

首先画一个2*2的矩形R1,然后在中心原点画半径为0. 3的圆E1.然后将Set formula对话框中的公式改为R1-E1,表示求解区域为二者之差.矩形所有的边界条件是Dirichlet边界条件, 取h=1, r= y.而在圆的边界取h=1, r=0.由于求解域没有电荷,因此在选择方程时选取Elliptic(椭圆)方程,系数为c=1, a=0, f=0.其电势分布如下图所示,电力线用箭头表示.三、静电场仿真两点电荷的电场：两等值异号点电荷单位, 两者间距为1,求其电势分布.整个求解域取中心为原点,半径为 2 的圆,两空间电荷点位置为(-0.5,0)和( 0.5,0),作为一种近似,画一个尽量小的圆,取半径为0.05.大圆的边界条件是Di richlet边界条件,取h= 1, r= 0,这种做法是模拟远处的电势为零.由于大圆与小圆之间的区域没有电荷, 满足Laplace 方程, 因此在选择方程时选取Elliptic(椭圆)方程,其方程类型为:取系数为c= 1, a= 0, f= 0.在表示点电荷的小圆内, 我们认为电荷是均匀分布的, 满足 Poisson 方程, 在选择方程时也取Elliptic方程, 取系数为c= 1, a= 0, f= 0. 2.其两点电荷电势分布上图所示,电力线用箭头表示.。

弹力有限元作业

6-4对下图所示的离散结构，试求结点1，2的位移及铰支座3，4，5的反力（按平面应力问题计算）采用MATLAB进行运算程序：一、计算弹性模量E、泊松比NU、厚度t、节点坐标为（xi,yi）、(xj,yj)、(xm,ym)的单元刚度矩阵。

p=1表明函数用于平面应力情况。

p=2表明函数用于平面应变情况。

function y=LinearTriangleElementStiffness(E,NU,t,xi,yi,xj,yj,xm,ym,p) A=(xi*(yj-ym)+xj*(ym-yi)+xm*(yi-yj))/2;betai=yj-ym;betaj=ym-yi;betam=yi-yj;gammai=xm-xj;gammaj=xi-xm;gammam=xj-xi;B=[betai 0 betaj 0 betam 0;0 gammai 0 gammaj 0 gammam;gammai betai gammaj betaj gammam betam]/(2*A);if p==1D=(E/(1-NU*NU))*[1 NU 0;NU 1 0; 0 0 (1-NU)/2];elseif p==2D=(E/(1+NU)/(1-2*NU))*[1-NU NU 0; NU 1-NU 0;0 0 (1-2*NU)/2]; endy=t*A*B'*D*B;二、计算整体刚度矩阵K。

function y=LinearTriangleAssemble(K,k,i,j,m)K(2*i-1,2*i-1)=K(2*i-1,2*i-1)+k(1,1);K(2*i-1,2*i)=K(2*i-1,2*i)+k(1,2);K(2*i-1,2*j-1)=K(2*i-1,2*j-1)+k(1,3);K(2*i-1,2*j)=K(2*i-1,2*j)+k(1,4);K(2*i-1,2*m-1)=K(2*i-1,2*m-1)+k(1,5);K(2*i-1,2*m)=K(2*i-1,2*m)+k(1,6);K(2*i,2*i-1)=K(2*i,2*i-1)+k(2,1);K(2*i,2*i)=K(2*i,2*i)+k(2,2);K(2*i,2*j-1)=K(2*i,2*j-1)+k(2,3);K(2*i,2*j)=K(2*i,2*j)+k(2,4);K(2*i,2*m-1)=K(2*i,2*m-1)+k(2,5);K(2*i,2*m)=K(2*i,2*m)+k(2,6);K(2*j-1,2*i-1)=K(2*j-1,2*i-1)+k(3,1); K(2*j-1,2*i)=K(2*j-1,2*i)+k(3,2);K(2*j-1,2*j-1)=K(2*j-1,2*j-1)+k(3,3); K(2*j-1,2*j)=K(2*j-1,2*j)+k(3,4);K(2*j-1,2*m-1)=K(2*j-1,2*m-1)+k(3,5); K(2*j-1,2*m)=K(2*j-1,2*m)+k(3,6);K(2*j,2*i-1)=K(2*j,2*i-1)+k(4,1);K(2*j,2*i)=K(2*j,2*i)+k(4,2);K(2*j,2*j-1)=K(2*j,2*j-1)+k(4,3);K(2*j,2*j)=K(2*j,2*j)+k(4,4);K(2*j,2*m-1)=K(2*j,2*m-1)+k(4,5);K(2*j,2*m)=K(2*j,2*m)+k(4,6);K(2*m-1,2*i-1)=K(2*m-1,2*i-1)+k(5,1); K(2*m-1,2*i)=K(2*m-1,2*i)+k(5,2);K(2*m-1,2*j-1)=K(2*m-1,2*j-1)+k(5,3); K(2*m-1,2*j)=K(2*m-1,2*j)+k(5,4);K(2*m-1,2*m-1)=K(2*m-1,2*m-1)+k(5,5); K(2*m-1,2*m)=K(2*m-1,2*m)+k(5,6);K(2*m,2*i-1)=K(2*m,2*i-1)+k(6,1);K(2*m,2*i)=K(2*m,2*i)+k(6,2);K(2*m,2*j-1)=K(2*m,2*j-1)+k(6,3);K(2*m,2*j)=K(2*m,2*j)+k(6,4);K(2*m,2*m-1)=K(2*m,2*m-1)+k(6,5);K(2*m,2*m)=K(2*m,2*m)+k(6,6);y=K;三、计算单元位移矢量为u时的单元应力。

有限元钢架结构分析~手算+matlab+ansys模拟

有限元大作业——钢架结构分析选题人：日期：2016年6月2日目录：第一章：问题重述 (1)一、题目容： (1)二、题目要求： (1)第二章：有限元法手工求解 (2)一、平面两单元离散化 (2)二、单元分析 (2)三、单元组装 (5)四、边界条件引入及组装总体方程 (5)五、求解整体刚度方程，计算节点2的位移和转角 (6)六、求节点1、3支撑反力 (6)七、设定数据，求解结果 (7)八、绘制轴力图、弯矩图、剪力图 (8)第三章、matlab编程求解： (9)一、总体流程图绘制： (9)二、输入数据： (9)三、计算单元刚度矩阵： (10)四、建立总体刚度矩阵： (10)五、计算未约束点位移： (10)六、计算支反力： (10)七、输出数据： (10)八、编程： (10)第四章有限元求解 (11)一、预处理 (11)二、模型建立： (12)二、分析计算 (14)三、求解结果 (15)四、绘制图像 (16)第五章结果比较 (19)第六章心得体会 (19)一、王小灿： (19)二、明哲： (20)三、国威 (20)第七章附录 (22)一、matlab程序 (22)第一章：问题重述一、题目容：图示平面钢架结构图1.1 题目容二、题目要求：（1）采用平面梁单元进行有限元法手工求解，要求写出完整的求解步骤，包括：a）离散化：单元编号、节点编号；b）单元分析：单元刚度矩阵，单元节点等效载荷向量；c）单元组长：总体刚度矩阵，总体位移向量，总体节点等效载荷；d）边界条件的引入及总体刚度方程的求解；e）B点的位移，A、C处支撑反力，并绘制该结构的弯矩图、剪力图和轴力图。

（2）编制通用平面钢架分析有限元Matlab程序，并计算盖提，与手工结果进行比较；（3）利用Ansys求解，表格列出B点的位移，A、C处支反力，绘制弯矩图、剪力图和轴力图，并与手算和Matlab程序计算结果比较。

（4）攥写报告，利用A4纸打印；（5）心得体会，并简要说明各成员主要负责完成的工作。

matlab大作业例子

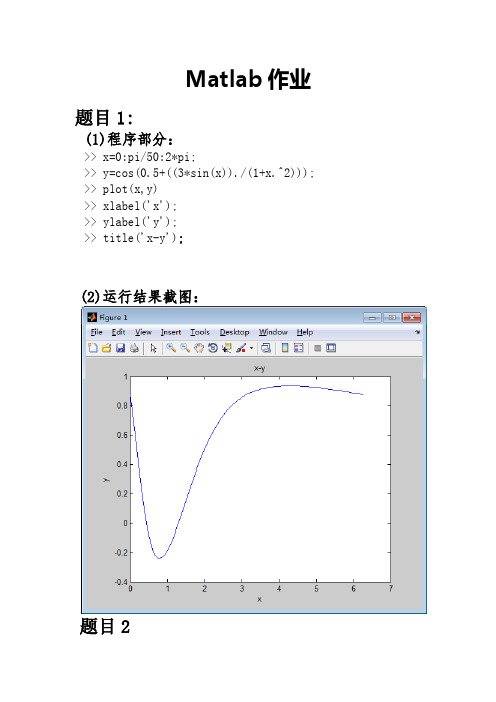
Matlab作业题目1:(1)程序部分：>> x=0:pi/50:2*pi;>> y=cos(0.5+((3*sin(x))./(1+x.^2))); >> plot(x,y)>> xlabel('x');>> ylabel('y');>> title('x-y');(2)运行结果截图：（1）程序部分：>> clear>> clc>> x=0:pi/100:4*pi;>> y1=sin(x);>> y2=cos(x);>> plot(x,y1,'r-',x,y2,'g:') >> hold on>> y3=x(find(abs(y1-y2)<0.001)); >> plot(y3,sin(y3),'*')（2）运行结果截图：（1）程序部分：>> t=(0:2*pi/100:2*pi)'; >> y1=sin(t)*[1,-1]; >> y2=sin(t).*sin(9*t); >> subplot(2,1,1);>> plot(t,[y1,y2]);>> subplot(2,1,2);>> plot(t,[y1,y2]) （2）运行结果截图：题目4（1）程序部分：>> t=0:pi/50:4*pi;>> y=exp(-t/3);>> y0=exp(-t/3).*sin(3*t); >> plot(t,y,'r-',t,y0,'b:') >> xlabel('\bf\it t')>> ylabel('\bf\it y')>> grid on;（2）运行结果截图：题目5（1）程序部分：>> n=0;>> sum=0;>> while sum<2000n=n+1;sum=sum+n;end>> n（2）运行结果截图：题目6（1）程序部分：for j=1:3n=input('n='); sum=0;for i=1:na=1/(i.^2);sum=sum+a;endPI=sqrt(6*sum) end（2）运行结果截图：题目7（1）程序部分：n0=0;y0=0;while 3*y0<5n0=n0+1;y0=y0+1/(2*n0-1);y=y0-1/(2*n0-1);n=n0-1;endn（2）运行结果截图：题目8（1）程序部分：for i=1:7x=input('put x:');if x<0&x~-3y=x^2+x-6;elseif x>=0&x<5&x~=3&x~=2 y=x*x-5*x+6;elsey=x*x-x-1;endend（2）运行结果截图：题目9①switch语句（1）程序部分：>> score=input('请输入成绩'); switch fix(score/10)case {9,10}disp('A');case {8}disp('B');case {7}disp('C');case {6}disp('D');case {0,5}disp('E');otherwisedisp('error');end（2）运行结果截图：如右图②if语句（1）程序部分：score=input('请输入成绩:') n=score/10;if n>=9&n<10disp Aelseif n>=8&n<9disp Belseif n>=7&n<8disp Celseif n>=6&n<7disp Delseif n>=0&n<6disp Eelsedisp errorend（2）运行结果截图：题目10（1）程序部分：t=input('员工的工作时间:')if t<60m=84*t-700;elseif t>120m=84*(t-120)*1.15+84*120;elsem=84*t;endm2）运行结果截图：题目11（1）程序部分：a=round(20*rand(5,6))n=input('请输入n的值:') tryb=a(n,:);catchb=a(5,:);endblasterr（2）运行结果截图：。

有限元课程设计matlab

有限元课程设计matlab一、课程目标知识目标：1. 学生能理解有限元分析的基本原理，掌握运用MATLAB进行有限元建模和求解的基本步骤。

2. 学生能够运用MATLAB软件进行简单物理场的有限元模拟，并解释模拟结果。

3. 学生掌握如何将实际问题抽象为有限元模型，并能够运用MATLAB进行模型参数的设定和调整。

技能目标：1. 学生能够独立操作MATLAB软件，进行有限元模型的构建和求解。

2. 学生能够通过MATLAB编程实现有限元模型的自动化处理，包括前处理、求解和后处理。

3. 学生通过解决实际问题，提高数值分析能力和计算机应用能力。

情感态度价值观目标：1. 学生培养对科学研究的兴趣，特别是在工程计算和仿真领域。

2. 学生通过解决实际问题，体会数学和工程结合的美，增强对工程问题的探究欲望。

3. 学生通过团队合作解决问题，培养协作精神和解决问题的能力。

本课程针对高年级本科生或研究生，他们具备一定的数学基础和编程能力。

课程性质偏重实践，旨在通过MATLAB这一工具将有限元理论应用于具体问题的求解。

课程目标旨在使学生不仅掌握理论知识，而且能够实际操作，将理论知识转化为解决实际问题的技能。

通过课程学习，学生应能够将所学知识应用于未来的学术研究或工程实践中。

二、教学内容1. 有限元方法基本原理回顾：包括有限元离散化、单元划分、形函数、刚度矩阵和载荷向量等概念。

- 教材章节：第二章有限元方法基础2. MATLAB编程基础：介绍MATLAB的基本操作、数据结构、流程控制、函数编写等。

- 教材章节：第三章 MATLAB编程基础3. MATLAB中的有限元工具箱使用：学习如何使用MATLAB内置的有限元工具箱进行建模和求解。

- 教材章节：第四章 MATLAB有限元工具箱介绍4. 有限元模型构建与求解：结合实际问题，学习如何构建有限元模型，并进行求解。

- 教材章节：第五章有限元模型构建与求解5. 实例分析与上机操作：通过案例分析，让学生实际操作MATLAB软件，解决具体的有限元问题。

计算力学(有限元)matlab编程大作业(空间网架)

逐一输入第 i 个节点和其他节点的连接情况,若连接,输入 1,否则输入 0,令和自身连接情况为 0：1 逐一输入第 i 个节点和其他节点的连接情况,若连接,输入 1,否则输入 0,令和自身连接情况为 0：1 逐一输入第 i 个节点和其他节点的连接情况,若连接,输入 1,否则输入 0,令和自身连接情况为 0：1 逐一输入第 i 个节点和其他节点的连接情况,若连接,输入 1,否则输入 0,令和自身连接情况为 0：1 逐一输入第 i 个节点和其他节点的连接情况,若连接,输入 1,否则输入 0,令和自身连接情况为 0：1 逐一输入第 i 个节点和其他节点的连接情况,若连接,输入 1,否则输入 0,令和自身连接情况为 0：0 逐一输入第 i 个节点和其他节点的连接情况,若连接,输入 1,否则输入 0,令和自身连接情况为 0：1 逐一输入第 i 个节点和其他节点的连接情况,若连接,输入 1,否则输入 0,令和自身连接情况为 0：0 逐一输入第 i 个节点和其他节点的连接情况,若连接,输入 1,否则输入 0,令和自身连接情况为 0：1 逐一输入第 i 个节点和其他节点的连接情况,若连接,输入 1,否则输入 0,令和自身连接情况为 0：1 逐一输入第 i 个节点和其他节点的连接情况,若连接,输入 1,否则输入 0,令和自身连接情况为 0：1 逐一输入第 i 个节点和其他节点的连接情况,若连接,输入 1,否则输入 0,令和自身连接情况为 0：0 输入结构约束总数：11 按照编号逐一输入结构约束编号（先输入节点号））：1 输入约束节点对应的位移号（输入范围：1~3））：1 按照编号逐一输入结构约束编号（先输入节点号））：1 输入约束节点对应的位移号（输入范围：1~3））：2 按照编号逐一输入结构约束编号（先输入节点号））：1 输入约束节点对应的位移号（输入范围：1~3））：3 按照编号逐一输入结构约束编号（先输入节点号））：3 输入约束节点对应的位移号（输入范围：1~3））：1 按照编号逐一输入结构约束编号（先输入节点号））：3 输入约束节点对应的位移号（输入范围：1~3））：2 按照编号逐一输入结构约束编号（先输入节点号））：3 输入约束节点对应的位移号（输入范围：1~3））：3 按照编号逐一输入结构约束编号（先输入节点号））：4 输入约束节点对应的位移号（输入范围：1~3））：1 按照编号逐一输入结构约束编号（先输入节点号））：4 输入约束节点对应的位移号（输入范围：1~3））：2 按照编号逐一输入结构约束编号（先输入节点号））：5 输入约束节点对应的位移号（输入范围：1~3））：1 按照编号逐一输入结构约束编号（先输入节点号））：5 输入约束节点对应的位移号（输入范围：1~3））：2 按照编号逐一输入结构约束编号（先输入节点号））：5 输入约束节点对应的位移号（输入范围：1~3））：3 输入施加在结构上的总的力的个数：3 按照编号逐一输入力作用节点编号（先输入节点号））：2 逐一输入力对应的向量中的坐标值：0 逐一输入力对应的向量中的坐标值：0 逐一输入力对应的向量中的坐标值：-1 输入力的大小：1000 按照编号逐一输入力作用节点编号（先输入节点号））：2 逐一输入力对应的向量中的坐标值：0 逐一输入力对应的向量中的坐标值：1

2012年-有限元作业-matlab编程实现有限元求解简单结构位移及应力

2012年有限元作业对于三角形单元有： 1、形函数⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎣⎡⎥⎦⎤=⎩⎨⎧⎭⎬⎫k k j j i i k jik j i k j i k j ik j ik j i v u v u v u c c c b b b a a a c c c b b b a a a y x y x A v u 00000000000000001000000121 其中：j m m i m m j j i y x y x y x y x a -==m j mji y y y y b -=-=11j m m j i x x x x c -==11 kkj ji iy x y x y x A 1112=相乘后得：()])()()[(21,k k k k j j j j i i i i u y c x b a u y c x b a u y c x b a A y x u ++++++++=()])()()[(21,k k k k j j j j i i i i v y c x b a v y c x b a v y c x b a Ay x v ++++++++=也可写成：()()kk j j i i k k j j i i v N v N v N y x v u N u N u N y x u ++=++=,,简写为：][}{q N v u =⎩⎨⎧⎭⎬⎫其中}}{{Tk kj j i iv u v u v uq =Ay c x b a N A y c x b a N A y c x b a N k k k i j j j i i i i i 2/)(2/)(2/)(++=++=++= 2、应变有弹性力学知道：xvy u y v x u xy y x ∂∂+∂∂=∂∂=∂∂==γεε,,，可得 }{}{}{q B v u v u v u c b c b c b c c c b b b A u b u b u b v c v c v c v c v c v c u b u b u b A v u x yy xy v x u y v x u k k j j i i k kjjiik j i k j ik k j j i i k k j j i i k k j j i i k k j j i i =⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤=⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤+++++++++=⎩⎨⎧⎭⎬⎫⎪⎪⎪⎩⎪⎪⎪⎨⎧⎪⎪⎪⎭⎪⎪⎪⎬⎫∂∂∂∂∂∂∂∂=⎪⎪⎪⎩⎪⎪⎪⎨⎧⎪⎪⎪⎪⎪⎪⎪⎭⎫∂∂+∂∂∂∂∂∂=000000212100ε3、应力}{][}{[][]{}q B D D ==εσ[]⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--=2100010112μμμμE D 4、刚度矩阵[]()⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-+-+-+-+-=s r s r sr s r s r s r s r s r rs b b c c cb bc b c b b c c b b A Et K 21212121142μμμμμμμ 题目：如图所示是一平面梁。

有限元的matlab编程

考虑几何非线性。本程序采用荷载分级加载的方式考虑网架的几何非线性。将总荷载分成1000份分步施加，求解各荷载步下的节点位移，修改网架相应节点坐标以及刚度矩阵，依次迭代求出网架的总位移。
本程序的网架位移求解函数附在主程序后面，主程序运行时调用该函数。
完整ppt
14
几何建模定义荷载
用自定义输入
加下划线的为单元编号
完整ppt
5
形成等效荷载列阵
f=[0;0;0;a;0;0;0;a;0;0;0;a;0;0;0;a;0;0;0;a];%每个节点两个自由度，a 为之前输入的节点力
集成总刚：
获取单元两端节点坐标
xi = Node( Element( ie, 1 ), 1 ) ;%ie为单元号，以下相同 yi = Node( Element( ie, 1 ), 2 ) ; xj = Node( Element( ie, 2 ), 1 ) ; yj = Node( Element( ie, 2 ), 2 ) ;
节点号：',num2str(Element(ie,2)),' 轴力:',num2str(nodef(1))] ) ;
完整ppt
12
end
例二：网架
完整ppt
13
思路分析
几点说明
网架是由多根杆件按照一定的网格形式通过节点连结而成的空间结构。构成网架的基本单元有三角锥，三棱体，正方体，截头四角锥等。鉴于网架的形式较多，本程序提供一种通用的网架输入方法，但录入较为繁琐，同时提供一种正放四角锥网架的简易输入方法作为典型。
有限元编程示例
完整ppt
1
例一：桁架
题目描述:
如下图所示的平面桁架，杆件长度、弹性模量、截面积以及所受节点力P的大小可以自行定义。求节点位移及杆件轴力。

matlab有限元分析实例

为了使用matlab进行有限元分析，我们必须首先学习MATLAB 的基本操作以及使用MATLAB进行有限元分析的基本操作。

复习：最后一课分析弹簧系统，得出系统刚度矩阵matlab有限元分析20140226 matlab有限元分析20140226为了使用matlab进行有限元分析，我们首先必须学习MATLAB的基本操作，还要学习使用matlab进行有限元分析的基本操作。

1.回顾：最后一堂课分析了弹簧系统并推导出系统刚度矩阵。

2.为了使用matlab进行有限元分析，我们应该首先学习MATLAB的基本操作，然后再学习使用MATLAB进行有限元分析的基本操作。

Matlab有限元分析20140226为了使用Matlab进行有限元分析，首先必须学习MATLAB的基本操作以及使用MATLAB进行有限元分析的基本操作。

1.回顾：在上一课中对弹簧系统进行了分析，并得出了系统刚度矩阵。

2. MATLAB有限元分析的基本运算单位划分（选择哪个单位和划分多少个元素）分为两部分：单位选择和单位数回顾：最后一课分析了运算的基础MATLAB弹簧系统有限元分析matlab有限元分析20140226为了使用matlab进行有限元分析，我们首先应该学习MATLAB的基本操作，也要学会使用matlab进行有限元分析的基本操作。

1.回顾：最后一堂课分析了弹簧系统并推导出系统刚度矩阵。

2. Matlab导出系统刚度矩阵。

Matlab有限元分析的操作基础Matlab有限元分析20140226为了使用MATLAB进行有限元分析，首先必须学习MATLAB的基本操作，还必须学会使用Matlab 进行有限元分析的基本操作。

matlab 有限元编程

MATLAB 是一种高级编程语言和交互式环境，常用于数值计算、数据分析、算法开发、数据可视化以及应用开发等。

在有限元分析（FEA）中，MATLAB 可以用来编写和运行有限元程序。

以下是一个简单的 MATLAB 有限元分析编程示例：这个例子假设你正在解决一个一维拉普拉斯方程，其形式为 -d^2u/dx^2 = f，在区间 [0, 1] 上。

```matlab% 参数定义L = 1; % 长度h = 0.01; % 步长N = L/h; % 元素数量x = linspace(0, L, N+1); % x 向量% 创建有限元网格nodes = x(1:N+1);elements = [nodes(2:end-1) nodes(1:end-1) nodes(2:end)]; % 定义载荷向量 ff = sin(pi*x);% 定义刚度矩阵 A 和载荷向量 FA = zeros(N, N);F = zeros(N, 1);for i = 1:Nfor j = 1:i-1A(i, j) = A(j, i) = h^2/(6*(x(i)-x(j))^2);endF(i) = -f(i)*h/2;end% 使用 MATLAB 的线性方程求解器u = A\F;% 绘制结果plot(x, u);xlabel('x');ylabel('u');title('有限元解');```这个代码首先定义了问题的参数，然后创建了一个有限元网格。

然后，它定义了刚度矩阵 A 和载荷向量 F。

最后，它使用 MATLAB 的线性方程求解器来求解方程，并绘制结果。

请注意，这只是一个非常简单的例子。

在实际的有限元分析中，问题可能会更复杂，并且需要更多的编程工作。