固体物理学理论第二章晶体的结合和弹性
固体物理 课后习题解答(黄昆版)第二章

黄昆 固体物理 习题解答第二章 晶体的结合2.1 证明两种一价离子组成的一维晶格的马德隆常数为α = 2 2n解:设想一个由正负两种离子相间排列的无限长的离子键,取任一负离子作参考离子(这样马德隆常数中的正负号可以这样取,即遇正离子取正号,遇负离子取负号),用 r 表示相邻离子间的距离,于是有α= ∑ ′ ( 1)=2[1 1 1 1 −+−+ ...]r jr ijr 2r 3r 4r前边的因子 2 是因为存在着两个相等距离 的离子,一个在参考离子左面,一个在其右面,i1 1 1故对一边求和后要乘 2,马德隆常数为234α = 2[1− + − + ...] 2 3 4xx xQl n(1 + x ) = −x + − + ... 当 x=1 时,有12 3 4 1 1 1...− + − + = l n2∴ =α 2 2n2 3 42.2 讨论使离子电荷加倍所引起的对 Nacl 晶格常数及结合能的影响(排斥势看作不变)α2e C解: u r ( )= −α2+rrnα2nC1du e nCenC 由| =−= 0 解得=+r e−1 r2n +12n 1( ) (=2)ndrrrrr 0nC11α e于是当 e 变为 2e 时,有 r−1= 4 −1 r e( )(2 ) (=2)nn= − α214α e结合能为 u r( )e (1−) 当 e 变为 2e 时,有4α e 2r0 1nnu e(2 )= −r (2 ) (1 −) = u e( ) 4 −n 1nu r( )= − α+βm n 2.3 若一晶体两个离子之间的相互作用能可以表示为计算: 1) 平衡间距r0解答(初稿)作者季正华- 1 -r r黄昆固体物理习题解答2) 结合能W(单个原子的)3) 体弹性模量4) 若取m = 2, n = 10, r= 0.3 , = 4 eV计算αβ, 的值解:1) 平衡间距r0的计算NαβdU= mαnβU r ( ) = (−+m n) dr0 −r m+1 + r n+1 = 0晶体内能nβ 12 r r平衡条件r r0 即0 0r0= ( )n m所以mα2) 单个原子的结合能W = −1u( )r u r( ) (0= −α+βm n) r nβ 1r r0=( ) n m2 0β−m r r0 αmW = 1 α(1−)( )m n n m2 n mα3)体弹性模量K = ∂2U(2)V⋅V0∂V0晶体的体积V = NAr3—— A 为常数,N 为原胞数目NαβU r ( ) = (−+m n)晶体内能∂=α2nβr rU∂U r∂N m− 1∂V ∂∂r V= 2 ( r m+1 r n+1 ) NAr23∂2 = ∂∂mαnβU N r[( −) 1 ]∂V 2 2 ∂∂V r rm+1 r n+1 3 N Ar2∂2U∂2UN1[2αmn2βmαnβK = (2)V⋅V0 ∂V2= 2 9V2−r m+ r n−r m+ r n]体弹性模量由平衡条件∂U∂V=N mα−V Vnβ 1= 00 0 0 0∂V 2 ( r m+1 r n+1 ) 3NAr2V V0解答(初稿)作者季正华0 0 0- 2 -α=n β∂2UN黄昆 固体物理 习题解答m 2αn 2βm r 0mr 0n ∂V 2V V=1[− 2 9V 02r 0m + r 0n ]体弹性模量 K= ∂2U(2)V⋅V 0∂2U=mn(−U )∂ V∂ V2 V V 9V 2mn K = U 0V 904)若取 m =β12, n = 10, r 0=0.3 ,= 4 eVβ−m计算 α β,的值r = n( ) −n mW = 1 α (1− )( )m n n mαm2 αn mβ =Wr 10α = r 2β+W 2[r 102 ]β =1.2 ×10-95eV ⋅m 103α =−7.5 ×1019eV ⋅ m 22.4 经过 sp 杂化后形成的共价键,其方向沿着立方体的四条对角线 的方向,求共价键之间的夹角。
固体物理:第二章 晶体的结合

晶体为什么形成这么有序的结构?
7
原子结合成晶体时,原子的外层电子要作重新
分布
不同分布产生了不同类型的结合
力
不同类型的结合力,导致了晶体结合
的不同类型。
+ = 原子
原子核+ 芯电子(稳定、满壳层)
价电子
原子外层的芯电子层对相互作用贡献不大,价电子的
相互作用
决定了原子间的相互作用后的性质。
同一种原子,不同的结合类型中具有不同的电子云分布,因此呈现出
10
我们讲到:
原子外层的芯电子层对相互作用贡献不大,价电子相互
作用
决定了原子间相互作用的性质。
原来中性的原子能够结合成晶体,除了外界的压力和温度 等条件的作用外,主要取决于原子最外层电子的作用。没 有一种晶体结合类型,不是与原子的电性有关的。
下面我们来系统学习一下:18
各壳层容纳的电子数
19
能量最低原理 “电子优先占据最低能态”
20
21
22
原子捕获电子的能力(电性)
一、电离能
定义:使原子失去一个电子所需要的能量称为原子的电离能。 从原子中移去第一个电子所需要的能量为第一电离能,从正1 价离子中再移去一个电子所需要的能量为第二电离能。
Na + 5.14 eV Na+ + e
23
电离能的大小可以用来度量原子对价电子的束缚强弱。 电离能越大,越难失去电子;电离能越小,越易失去电 子,金属性越强。 在一个周期内,从左到右,电离能不断增加。
24
二、电子亲和能
定义:一个中性原子获得一个电子成为负离子所释放出的能 量称为电子亲和能,亲和过程不能看成是电离过程的逆过程。 电子亲和能越大,那么得到电子的能力越大。 电子亲和能一般随原子半径的减小而增大。因为原子半径小, 核电荷对电子的吸引力较强,对应较大的互作用势。
《固体物理学》房晓勇-思考题02第二章 晶体的结合和弹性

第二章 晶体的结合和弹性2.1 是否有库仑力无关的晶体结合类型?解答:(参考王矜奉2.1.1,中南大学2.1.1)共价结合中,电子虽然不能脱离电负性大的原子,但靠近的两个电负性大的原子可以各出一个电子,形成电子共享的形式,即这一对电子的主要活动范围处于两个原子之间,通过库仑力,把两个原子连接起来。
离子晶体中,正离子与负离子的吸引力就是库仑力。
金属结合中,原子实依靠原子实与电子云之间的库仑力紧紧地吸引着。
分子结合中,是电偶极矩把原本分离的原子结合成了晶体。
电偶极矩的作用力实际就是库仑力。
氢键结合中,氢先与电负性大的原子形成共价结合后,氢核与负电中心不在重合,迫使它通过库仑力再与另一个电负性大的原子结合。
可见,所有晶体结合类型都与库仑力有关。
2.2 如何理解库仑力是原子结合的动力?解答:(参考王矜奉2.1.2,中南大学2.1.2)晶体结合中, 原子间的排斥力是短程力, 在原子吸引靠近的过程中, 把原本分离的原子拉近的动力只能是长程力, 这个长程吸引力就是库仑力. 所以, 库仑力是原子结合的动力.2.3 为什么组成晶体的粒子(分子、原子或离子)间的相互作用力除吸引力还要有排斥力?排斥力的来源是什么?解答:(参考王矜奉2.1.4,中南大学2.1.4)邻的原子靠得很近, 以至于它们内层闭合壳层的电子云发生重叠时, 相邻的原子间便产生巨大排斥力. 也就是说, 原子间的排斥作用来自相邻原子内层闭合壳层电子云的重叠.2.4 晶体的结合能、内能、以及原子间的相互作用势能有何区别?解答:(参考王矜奉2.1.3,中南大学2.1.3)自由粒子结合成晶体过程中释放出的能量, 或者把晶体拆散成一个个自由粒子所需要的能量, 称为晶体的结合能.原子的动能与原子间的相互作用势能之和为晶体的内能.在0K 时, 原子还存在零点振动能. 但零点振动能与原子间的相互作用势能的绝对值相比小得多. 所以, 在0K 时原子间的相互作用势能的绝对值近似等于晶体的结合能.2.5 试述范德瓦耳斯力的起源和特点。
《固体物理学》第二章_晶体的结合和弹性

二、原子晶体(共价晶体)
第Ⅳ族、第Ⅴ族、第Ⅵ族、第Ⅶ族元素都可以形成原子晶
体。典型的原子晶体: 金刚石、硅、锗等晶 体。
结合力: 共价键。
共价键的特点
饱和性 原子晶体的配位数较低。 方向性
共价键:共价晶体中,相邻原子各出一个价电子形成自旋 相反的共用电子对,这样的原子键合,称为共价键.
饱和性:一个原子只能形成一定数目的共价键.
晶体体积的函数 U(v)
若取EN=0,则晶体的结合能: E b = E N − E 0 = − E 0 = −U ( r0 )
三、压缩系数和体积弹性模量(体积压缩模量)
U (r) =
N 2
ui
=
N 2
N
∑ 'u ( rij )
j=1
在三维晶体中,假设晶体的体积为V,包含N个原胞,每个
原胞的体积为v,每个原胞的势能为u (r),U为N个原胞的总的
j=1
则由N个原子组成的晶体的总的相互作用势能
为:
∑ ∑∑ u(r) =
1 2
N
ui
i =1
=
1 2
N i =1
N
u(rij )
j =1
因为晶体中原子数很多,因此晶体表面原子与晶体内部原 子的差别可以忽略,上式近似为:
U (r) =
N 2
ui
=
N 2
Nபைடு நூலகம்
∑ 'u ( rij )
j=1
原子数目 U(r) 原子间距
一、原子间的相互作用 吸引力
原子间的相互作用力 排斥力
库仑引力 库仑斥力 泡利原理引起
假设相距无穷远的两个自由原子间的相互作用能为零,相
互作用力为零。
固体物理学_答案(黄昆)

《固体物理学》习题解答黄昆原著韩汝琦改编 (陈志远解答,仅供参考)第一章晶体结构1.1、解:实验表明,很多元素的原子或离子都具有或接近于球形对称结构。
因此,可以把这些原子或离子构成的晶体看作是很多刚性球紧密堆积而成。
这样,一个单原子的晶体原胞就可以看作是相同的小球按点阵排列堆积起来的。
它的空间利用率就是这个晶体原胞所包含的点的数目n 和小球体积V 所得到的小球总体积nV 与晶体原胞体积Vc 之比,即:晶体原胞的空间利用率,VcnV x =(1)对于简立方结构:(见教材P2图1-1) a=2r ,V=3r 34π,Vc=a 3,n=1 ∴52.06r8r34ar 34x 3333=π=π=π=(2)对于体心立方:晶胞的体对角线BG=x 334a r 4a 3=⇒=n=2, Vc=a 3∴68.083)r 334(r 342ar342x 3333≈π=π⨯=π⨯=(3)对于面心立方:晶胞面对角线BC=r 22a ,r 4a 2=⇒= n=4,Vc=a 374.062)r 22(r344ar344x 3333≈π=π⨯=π⨯=(4)对于六角密排:a=2r 晶胞面积:S=6260sin a a 6S ABO ⨯⨯=⨯∆=2a 233晶胞的体积:V=332r 224a23a 38a 233C S ==⨯=⨯n=1232126112+⨯+⨯=6个74.062r224r 346x 33≈π=π⨯=(5)对于金刚石结构,晶胞的体对角线BG=3r 8a r 24a 3=⇒⨯= n=8, Vc=a 334.063r338r 348ar348x 33333≈π=π⨯=π⨯=1.2、试证:六方密排堆积结构中633.1)38(a c2/1≈= 证明:在六角密堆积结构中,第一层硬球A 、B 、O 的中心联线形成一个边长a=2r 的正三角形,第二层硬球N 位于球ABO 所围间隙的正上方并与这三个球相切,于是: NA=NB=NO=a=2R.即图中NABO 构成一个正四面体。
《固体物理学》房晓勇主编教材-习题解答参考02第二章 晶体的结合和弹性

2
)
12
+
( 4 / 3)
6
6
(
6 1 +0 +0
2 2 2
)
12
+
( 4 / 3)
2
6
(
12 12 + 12 + 02
)
12
+ = =
( 4 / 3)
(
24
(3 / 2)
2
+ (1/ 2 ) + (1/ 2 )
2
)
12
( 4 / 3)
6
(
8 12 + 12 + 12
)
12
+
( 4 / 3)
mi
1
2 2 n12 + n2 + n3
) (
=
mi
2 2 n12 + n2 + n3
)
12
雷纳德-琼斯参数
A6 = ∑ A6,i = ∑
i =1 i =1 N N
N
N
( (
mi
2 2 + n3 n12 + n2
)
A12 = ∑ A12,i = ∑
i =1 i =1
mi
2 2 + n3 n12 + n2
mn mn −U 0 = U 0 2 9V0 9V0
(2)惰性分子晶体原子之间的相互作用势可以下式描述
σ ⎤ ⎡σ u (r ) = 4ε ⎢( )12 − 2( )6 ⎥ r ⎦ ⎣ r
……(7)
A2 ⎛B⎞ 此时 m=12,n=6,式中 σ = ⎜ ⎟ , ε ≡ ,称为雷纳德-琼斯参数。 4B ⎝ A⎠
固体物理第二章复习

式中
B
1
6
;
A2
A
4B
'N 1
A12
j
a12 j
A6 , A12 是仅与晶体结构有关的常数。
'N 1
A6
j
a6 j
3.原子晶体、金属晶体和氢键晶体
(1)原子晶体
结构:第Ⅳ族、第Ⅴ族、第Ⅵ族、第Ⅶ族元素都可以形成
原子晶体。
结合力: 共价键 (2)金属晶体
饱和性 方向性
层一共有 8 个量子态, 最多能接纳(8- N)个电子, 形成(8- N)个共价键. 这就 是共价结合的 “饱和性”.
共价键的形成只在特定的方向上, 这些方向是配对电子波函数的对称轴方向, 在这个方向上交迭的电子云密度最大. 这就是共价结合的 “方向性”.
10. 为什么许多金属为密积结构? 金属结合中, 受到最小能量原理的约束, 要求原子实与共有电子电子云间的
(2)结合力: 范德瓦尔斯力。
(3)配位数: 通常取密堆积,配位数为12。
(4)互作用势能:
u(r )
4
12
6
r r
U ( R)
2 N
A12
R
12
A6
R
6
雷纳德-琼斯势
r1 rA a, a1 1, r2 rB 2a, a2 2, r3 rC 3a, a3 3,
2( 1 1 1 1 ) ln( 1 x ) x x2 x3 x4
固体物理第二章答案

第21. 有一晶体,平衡时体积为 0V , 原子间相互作用势为0.如果相距为 r 的两原子互作用势为 ()n m r r a r u β+-= 证明(1) 体积弹性模量为 K=.90V mnU (2) 求出体心立方结构惰性分子的体积弹性模量.[解答]设晶体共含有 N 个原子,则总能量为U(r)=()∑∑i jij r u '21. 由于晶体表面层的原子数目与晶体内原子数目相比小得多,因此可忽略它们之间的基异,于是上式简化为 U=().2'∑jijr u N设最近邻原子间的距离为R 则有j ij a r =R再令 A ,1'∑=j m j m a A ,1'∑=jn j n a 得到 U=.200⎪⎪⎭⎫ ⎝⎛+-n n m m R A R A N βα 平衡时R=R 0,则由已知条件U(R 0) = 0U 得0002U R A R A N n n m m =⎪⎪⎭⎫⎝⎛+-βα 由平衡条件 0)(0=R dRR dU得021010=⎪⎪⎭⎫⎝⎛-++n nm m R A n R A m N βα. 由(1),(2)两式可解得.)(2,)(20000n n m m nR n m N U A nR n m N U A -=-=βα利用体积弹性模量公式[参见《固体物理教程》(2.14)式]K=0220209R R U V R ⎪⎪⎭⎫ ⎝⎛∂∂得K= ⎥⎦⎤⎢⎣⎡+++-n n m m R A n n R A m m N V 000)1()1(291βα = ⎥⎦⎤⎢⎣⎡-++-+-)(2)1()(2)1(2910000000n m N mR U R n n n m N nR U R m m N V nnm m = .900V mn U - 由于,00<U 因此,00U U -= 于是 K= .90V mnU (1) 由《固体物理教程》(2.18)式可知,一对惰性气体分子的互作用能为.)(126r B r A r u +-=若令 61,42⎪⎭⎫⎝⎛==A B B A σε,则N 个惰性气体分子的互作用势能可表示为⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛=6612122)(R A R A N r U σσε.由平衡条件0)(0=R dRR dU 可得 R .2616120⎪⎪⎭⎫ ⎝⎛=A A σ进一步得 .2)(122600A A N R U U ε-==代入K=.900V mn U 并取 m =6,n =12,V 300334R N =得 K=5126123233⎪⎪⎭⎫⎝⎛A A A σε.对体心立方晶体有 A .11.9,25.12126==A 于是.1.703σε=K 2. 一维原子链,正负离子间距为a ,试证:马德隆常数为2=μ1n2. [解答] 相距ij r 的两个离子间的互作用势能可表示成.4)(2n ijij ij r br q r u +=πμ设最近邻原子间的距离为R 则有 R a r j ij =, 则总的离子间的互作用势能 U=()∑∑∑-⎪⎪⎭⎫ ⎝⎛±-=jn jn j j j ij a bRa R q N r u N ''0'114[22πε. 基中 jja 1'±=∑μ 为离子晶格的马德隆常数,式中+;- 号分别对应于与参考离子相异和相同的离子.任选一正离子作为参考离子,在求和中对负离子到正号,对正离子取负号,考虑到对一维离子两边的离子是正负对称分布的,则有.413121112)1('⎥⎦⎤⎢⎣⎡+-+-=±=∑Λj ja μ利用正面的展开式 1n(1+x ),432432Λ+-+-x x x x 并令 1=x 得Λ+-+-41312111=1n(1+1)=1n2.于是,一维离子链的马德常数为2=μ1n23. 计算面心立方面简单格子的6A 和12A(1) 只计最近邻; (2) 计算到次近邻; (3) 计算到次近邻.[解答]图2.26示出了面心立方简单格子的一个晶胞.角顶O 原子周围有8个这样的晶胞,标号为1的原子是原子O 的最近邻标号为2的原子是O 原子的最近邻,标号为3的原子是O 原子的次次近邻.由此得到,面心立方简单格子任一原子有12个最近邻,6个次近邻及24个次次近邻.以最近邻距离度量,其距离分别为:.3,2,1===j j j a a a 由 .1,112'126'6⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛=∑∑jj j j a A a A图2.6 面心立方晶胞得(1) 只计最近邻时1211*12)1(66=⎪⎭⎫⎝⎛=A , 1211*12)1(1212\=⎪⎭⎫⎝⎛=A .(2) 计算到次近邻时.094.1221*611*12)2(,750.1221*611*12)2(121212666=⎪⎭⎫ ⎝⎛+⎪⎭⎫⎝⎛==⎪⎭⎫ ⎝⎛+⎪⎭⎫⎝⎛=A A(3) 计算到次次近邻时.127.12033.0094.1231*2421*611*12)3(,639.13899.0750.1231*2421*611*12)3(121212126666=+=⎪⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+⎪⎭⎫⎝⎛==+=⎪⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+⎪⎭⎫⎝⎛=A A 由以上可以看出,由于12A中的幂指数较大,12A 收敛得很快,而6A 中的幂指数较小,因此 6A 收敛得较慢,通常所采用的面心立方简单格子的 6A 和 12A 的数值分别是14.45与12.13.4. 用埃夫琴方法计算二维正方离子(正负两种)格子的马德隆常数. [解答]马德隆常数的定义式为 jja 1'±=∑μ,式中+、-号分别对应于与参考离子相异和相同的离子,二维正方离子(正负两种)格子,实际是一个面心正方格子,图 2.7示出了一个埃夫琴晶胞.设参考离子O 为正离子,位于边棱中点的离子为负离子,它们对晶胞的贡献为4*(1/2).对参考离子库仑能的贡献为图2.7二维正方离子晶格.121*4顶角上的离子为正离子,它们对晶胞的贡献为4*(1/4), 对参考离子库仑能的贡献为 .241*4-因此通过一个埃夫琴晶胞算出的马德隆常数为 .293.1241*4121*4=-=ν再选取422=个埃夫琴晶胞作为考虑对象,这时离子O 的最的邻,次近邻均在所考虑的范围内,它们对库仑能的贡献为,2414-而边棱上的离子对库仑能的贡献为 ,521*8221*4+- 顶角上的离子对为库仑能的贡献为 ,841*4-这时算出的马德隆常数为图 2.8 4个埃夫琴晶胞同理对932=个埃夫琴晶胞进行计算,所得结果为611.11841*41321*81021*8321*48458242414=⎪⎪⎪⎪⎭⎫ ⎝⎛-+-+⎪⎪⎭⎫ ⎝⎛-+-+⎪⎭⎫ ⎝⎛-=μ 对 1642=个埃夫琴晶胞进行计算,所得结果为614.13241*42521*81721*81021*8421*4184138108348458242414=⎪⎪⎪⎪⎭⎫ ⎝⎛-+-+-+⎪⎪⎭⎫ ⎝⎛-+-+⎪⎪⎭⎫ ⎝⎛-+-+⎪⎭⎫ ⎝⎛-=μ当选取 n 2个埃夫琴晶胞来计算二维正方离子(正负两种)格子的马德隆常数,其计算公式(参见刘策军,二维NaC1 晶体马德隆常数计算,《大学物理》,Vo1.14,No.12,1995.)为 [][].1,8411>+++=--n D C B A n n n n μ其中 ,21)1(,1)1(11111nB t A n n n t t n +-=+--=-=∑,1)1(1)1()2()1(1)1()1(2112212221112122122222222221⎪⎪⎪⎪⎪⎭⎫⎝⎛+--+--+-+-+--++⎪⎪⎭⎫⎝⎛+++-+⎪⎪⎭⎫ ⎝⎛+---n n n n n C n n ΛΛ.121)1()1(2181222222+-+-++++-=n n n n n D n n Λ5. 用埃夫琴方法计算CsCl 型离子晶体的马德隆常数(1) 只计最近邻 (2) 取八个晶胞 [解答](1) 图2.29是CsCl 晶胸结构,即只计及最近邻的最小埃夫琴晶胞,图2.29()a 是将Cs +双在体心位置的结构,图2.9(a)是将 Cl -取在体心位置的结构,容易求得在只计及最近邻情况下,马德隆常数为1.图2.29 (a )Cs 取为体心的CsC1晶胞,(b) C1取为体心的CsC1晶胞(2)图2.10是由8个CsCl 晶胞构成的埃夫琴晶胞,8个最近邻在埃夫琴晶胞内,每个离子对晶胞的贡献为1,它们与参考离子异号,所以这8个离子对马德隆常数的贡献为8埃夫琴晶胞6个面上的离子与参考离子同号,它们对埃夫琴晶胞的贡献是21,它们与参考离子的距离为32R 它们对马德隆常数的贡献为-()3/2*621图 2.10 8个CsCl 晶胞构成的一个埃夫琴晶胞埃夫琴晶胞楞上的12个离子,与参考离子同号,它们对埃夫琴晶胞的贡献是41它们与参考离子的距离为322R 它们对马德隆常数的贡献为-()3224/1*12埃夫琴晶胞角顶上的 8个离子,与参考离子同号,它们对埃夫琴晶胞的贡献是81它们与参考离子的距离为2R 它们对马德隆常数的贡献为 -()281*8,由8个CsCl 晶胞构成的埃夫琴晶胞计算的马德隆常数.064806.32)8/1(*8322)4/1(*123/2)2/1(*68=---=μ 为了进一步找到马德常数的规律,我们以计算了由27个CsCl 晶胞构成的埃夫琴晶胞的马德隆常数,结果发现,由27个CsCl 晶胞构成的埃夫琴晶胞的马德隆常数是0.439665.马德隆常数的不收敛,说明CsCl 晶胞的结构的马德隆常数不能用传统的埃夫琴方法计算.为了找出合理的计算方法,必须首先找出采用单个埃夫琴晶胞时马德隆常数不收敛的原因.为了便于计算,通常取参考离子处于埃夫琴晶胞的中心.如果以Cs +作参考离子,由于埃夫琴晶胞是电中性的要求,则边长为pa 2(p 是大于或等于1的整数)的埃夫琴晶胞是由(2p )3个CsCl 晶胞所构成,埃夫琴晶胞最外层的离子与参考离子同号,而边长为(2p +1)的埃夫琴晶胞是由(2p +1)3 个 CsCl 晶胞所构成,但埃夫琴晶胞的最外层离子与参考离子异号,如果以C1-作参考离子也有同样的规律,设参考离子处于坐标原点O ,沿与晶胞垂直的方向(分别取为x,y,z 图2.11示出了z 轴)看去,与参考郭同号的离子都分布在距O 点ia 的层面上,其中i 是大于等于 1的整数,与 O 点离子异号的离子都分布在距O 点(i -0.5)a 的层面上,图 2.11(a) 示出了同号离子层,图2.11(b)示出了异号离子层.图2.11 离子层示意图(a)表示同号离子层, O 离子所在层与 O '离子所在层相距ia(b)表示异号离子层, O 离子所在层和O ' 离子所在层相距(i -0.5)a当 CsCl 埃夫琴晶胞边长很大时,晶胞最外层的任一个离子对参考离子的库仑能都变得很小,但它们对参考离子总的库仑能不能忽略.对于由(2p )3个CsCl 晶胞所构成的埃夫琴晶胞来说,最外层有6*(2p )2个与参考离子同号的离子,它们与参考离子的距离为(1/2)pa ~(23)pa ,它们与参考离子的库仑能为a pe 024πε量级,这是一个相对大的正值.对于由(2p +1)3个CsCl 晶胞所构成的埃夫琴晶胞来说,离外层有6*(2p +1)2个与参考离子异号的离子,它们与参考离子的库仑能为a pe 024πε-量级,这是一个绝对值相对大的负值,因此,由(2p )3个CsCl 晶胞构成的埃夫琴晶胞所计算的库仑能,与由(2p +1)3个CsCl 晶胞构成的埃夫琴晶胞所计算的库仑能会有较大的差异.即每一情况计算的库仑能都不能代表CsCl 晶体离子间相互作用的库仑能.因此这两种情况所计算的马德隆常数也必定有较大的差异,由1个CsCl 晶胞、8个CsCl 晶胞和27个CsCl 晶胞构成的埃夫琴晶胞的计算可知, CsCl 埃夫琴晶胞体积不大时,这种现象已经存在.为了克服埃夫琴方法在计算马德隆常数时的局限性,可采取以下方法,令由 (2p )3个CsCl 晶胞构成的埃夫琴晶胞计算的库仑能为1U ,由(2p +1)3个CsCl 晶胞构成的埃夫琴晶胞所计算的库仑能为1U ,则CsCl 晶体离子间相互作用的库仑能可近似取作 )(2121U U U +=(1) 因子1/2 的引入是考虑除了(2p +1)3个CsCl 晶胞构成的埃夫琴晶胞最外层离子外,其他离子间的库仑能都累计了两偏,计算1U 和2U 时要选取体积足够大的埃夫琴晶胞,此时埃夫琴晶胞最外层离子数与晶胞内的离子数相比是个很小的数,相应的马德隆常数应为 )(2121μμμ+=(2) 其中:=1μ⎪⎪⎭⎫ ⎝⎛±∑i ja 1'是由(2p )3个CsC1晶胞构成的埃夫琴晶胞计算的值; =1μ⎪⎪⎭⎫ ⎝⎛±∑i ja 1'由 (2p +1)3 个CsC1晶胞构成的埃夫琴晶胞所计算成本的值.为简化计算,特选取晶胞边长a 为计算单位,由于,32a R =所以,23'μμ= ⎪⎪⎭⎫ ⎝⎛±=∑'''1i i a μ (3) 其中'i a 是某一离子到参点的距离与a 的比值.考虑到对称性,对选定的埃夫琴晶胞,把晶胞的离子看成分布在一个个以参考离子为对称心的正六面体的六个面上,体积不同的正六面六个面上的离子分别计算.由(2p )3个CsC1晶胞构成埃夫琴晶胞时,由分析整理可得,231111⎪⎪⎭⎫ ⎝⎛++=∑∑=-=p pi i p i i C B A μ (4) 由(2p +1)3个 CsC1 晶胸构成埃夫琴晶胞时,,231112⎪⎪⎭⎫ ⎝⎛++=∑∑=-=p pi i p i i D B A μ (5)其中:),1(''''22'2'p i i y x k A i x iy y x i <≤++-=∑∑(6)i A 表示与 O 点距离为ia 的6个面上所有的离子对马德隆常数的面贡献,因为这些离子与参考离子同号,故到负号.'x 、'y 是离子在平面 '''y x o 上的坐标, ''y x k 代表 6个面上等价离子的个数,其取值规则为:(1) 在角上(如E 点),即'x =i 且 'y = i. 时, ''y x k =8;(2) 在棱与坐标轴的交点(如 F 点),'x =i 且'y = 0或 'x =0且'y = 0时, ''y x k =6 (3) 在棱上的其他点(如H 、I 点)即不满足上述条件,且'x =i 或'y = i.时, ''y x k =12 (4) 在'O 点,即'x =0且'y = 0时, ''y x k =6(5) 在除'O 点外的面上的点(如J 点),即不满足上述条件时,''y x k =24.),1()5.0(5.05.05.05.022'2''''''p i i y x k B i x i y yx i ≤≤-++=∑∑-=-=(7)i B 代表距O 点距离为(i -0.5)a 的6个面上的离子对马德隆常数的贡献,因为这种些离子与参考离子异号,故取正号. 'x ,'y 是离子在平面'''y x o 上的坐标, '''y x k 代表这6个面上等价离子的个数,其取值规则为:(1) 在角上(如K 点),即'x =i 且 'y = i.时, '''y x k =8;(2) 在棱下(如L 、M 点),即不满足不述条件,且'x =i 或'y = i 时,'''y x k =12; (3) 在面上(如N 点)好不满足上述条件时, '''y x k =24.),(0022'2'"''''p i i y x k C i x iy i yx =++-=∑∑==i C 表示在边长为2pa 的晶胞最外层,即与参考离子相距pa 的6个面上的离子对马德隆常数的贡献,应取负号,与iA 的不同在于"''y x k的取值: (1) 在角上, "''y x k =''y x k /8; (2) 在棱上, "''y x k =''y x k /4; (3) 在面上, "''y x k=''y x k /2.),()5.0(5.05.05.05.022'2''''''''p i i y x k D i x i y yx i =-++=∑∑-=-=i D 表示在边长为2a p )1(+的晶胞最外层,即与参考离子相距(p +0.5)a 的离子层对马德隆常数的贡献,应取正号,与i B 的不同在于'''''yx k 的取值: (1) 在角上, '''''y x k ='''y x k /8; (2) 在棱上, '''''y x k ='''y x k /4; (3) 在面上, '''''y x k ='''y x k /2.表2.1给出了计算结果,给出的μ是由分别对应2p 和2p+1的1μ和2μ求得的,实际上, 1μ和2μ只需对应边长相近的埃夫琴晶胞即可,如取对应2p 和2p-1的埃夫琴晶胞也可得到一样的收敛结果,由以上数据可见,马德隆常数μ随晶胞边长的增大而迅速收敛.该方法适用于NaC1结构以外离子晶体马德隆常数的计算.6.只计及最近邻间的排斥作用时,一离子晶体离子间的互作用势为⎪⎪⎩⎪⎪⎨⎧±-=-)2(,)1(,)(22r e R e e r u R ρλ(1)最近邻(2)最近邻以外 式中ρλ,是常数,R 是最近邻距离,求晶体平衡时,原子间总的互作用势.[解 答]设离子数目为2N,以j ij a r =R 表示第j 个离子到参考离子i 的距离,忽略表面效应,则总的相互作用能可表示为U =N ⎥⎥⎦⎤⎢⎢⎣⎡+⎪⎪⎭⎫ ⎝⎛±-∑∑-ρλR j j e R a e 2' (∑表示最近邻)=N ,2⎥⎦⎤⎢⎣⎡+--ρλμR e Z R e其中⎪⎪⎭⎫⎝⎛±=∑j ia 1'μ 为马德隆常数,+号对应于异号离子,-号对应于同号离子;Z 为任一离子的最近邻数目,设平衡时R=R 0 ,由平衡条件,02020=⎥⎦⎤⎢⎣⎡+=-ρρλμR R e Z R e N dRdU 得.0202ρλμρR e Z R e -=平衡时的总相互作用为.1)(0020200⎪⎪⎭⎫⎝⎛-=⎥⎦⎤⎢⎣⎡+-=-R R e N e Z R e N R U R ρμλμρ 7. 设离子晶体中,离子间的互作用势为⎪⎪⎩⎪⎪⎨⎧±+-=最近邻以外最近邻,,)(22re R b R e r u m(1) 求晶体平衡时,离子间总的相互作用势能)(0R U (2) 证明: )(0R U 11-⎪⎪⎭⎫⎝⎛∝m mZ μ其中μ是马德隆常数,Z 是晶体配位数 [解答](1)设离子数目为2N , 以j ij a r =R 表示第j 个离子到参考离子i 的距离,忽略表面效应,则总的相互作用能可表示U =N ⎥⎥⎦⎤⎢⎢⎣⎡+⎪⎪⎭⎫ ⎝⎛±-∑∑m j j R b R a e 2'(∑表示最近邻) =N ,2⎥⎦⎤⎢⎣⎡+-m R b Z Re μ其中⎪⎪⎭⎫ ⎝⎛±=∑j i a 1'μ,为马德隆常数,+号对应于异号离子,-号对应于同号离子.Z 为任一离子的最近邻数目,设平衡时R=R 0由平衡条件,0102020=⎥⎦⎤⎢⎣⎡-=+m R R Zmb R e N drdUμ得10-m R Zmb=2e μ即1120-⎪⎪⎭⎫ ⎝⎛=m e Zmb R μ.于是,晶体平衡时离子间总的相互作用势能0U =).1(000--=⎥⎦⎤⎢⎣⎡+-m R NZbR b Z R Zmb N m m m(2)晶体平衡时离子间的相互作用势能可进一步化为0U =.)()()1()1(1111121211--------=⎪⎪⎭⎫ ⎝⎛--m m m m mm m m m m mb Ze Nbm e Zmb ZNbm μμ由上式可知 .110-⎪⎪⎭⎫⎝⎛∝m mZ U μ8.一维离子链,其上等间距载有正负2N 个离子,设离子间的泡利排斥只出现在最近邻离子之间,且为b/R n,b,n 是常R 是两最近邻离子的间距,设离子电荷为q ,(1) 试证明平衡间距下 )(0R U =;114212002⎪⎭⎫⎝⎛--n R n Nq πε(2) 令晶体被压缩,使0R )1(0δ-→R , 试证明在晶体被压缩单位长度的过程中外力作功的主项为c 2δ其中c=;21)1(02R n q n -(3) 求原子链被压缩了2)1(0<<e e NR δδ时的外力[解答](1) 因为离子间是等间距的,且都等于R ,所以认定离子与第j 个离子的距离j r 总可表示成为R a r j j =ja 是一整数,于是离子间总的互作用势能⎥⎥⎦⎤⎢⎢⎣⎡-⎪⎪⎭⎫ ⎝⎛±-=⎥⎥⎦⎤⎢⎢⎣⎡+=∑∑n i in j j j R b a R q N r b r q N R U 214242)('202'0πεπεμ,其中+、-分别对应相异离子和相同离子的相互作用.一维离子晶格的马德隆常数(参见本章习题2)为=⎪⎪⎭⎫ ⎝⎛±∑i ia 1'21n2. 利用平衡条件0)(0=R dRR dU得到b=nq 01-n 0241n2R πε,)(R U =⎪⎪⎭⎫ ⎝⎛---n n nR R R Nq 102141n22πε. 在平衡间距下⎪⎭⎫⎝⎛--n R Nq R U 1141n22)(0020πε.(2) 将互作用势能在平衡间距附近展成级数Λ+-⎪⎪⎭⎫ ⎝⎛+-⎪⎭⎫⎝⎛+=202200)(21)()()(0R R dR U d R R dR dU R U R U R R 由外力作的功等于晶体内能的增量,可得外力作功的主项为W=20220)(21)()(0R R dR U d R U R U R-⎪⎪⎭⎫ ⎝⎛=-, 其中利用平衡条件,将R=R )1(0δ- ,代入上式,得到W=δδπε)2(421)1(2102002NR R n q n ⎥⎥⎦⎤⎢⎢⎣⎡-. 晶体被压缩单位长度的过程中,外力作的功的主项δ02W NR =δπε⎥⎥⎦⎤⎢⎢⎣⎡-2002421)1(21R n q n 令c=202421)1(R n q n πε-(CGS)得到在晶体被压缩单位长度的过程中,外力作的功的主项为2δc . (3)设e δδ=时外力为F e ,由于在弹性范围内,外力与晶格的形变成正比,所以 F= )2(0δαNR , F e = )2(0e NR δα,其中α为比例系数离子链被压缩e NR δ02过程中外力作的功W e =δδαδδd NR NR Fdx e eNR e 020002)]2([0⎰⎰== e e e F NR NR δδα022022121)2(=.由于 W e =)2(20e eNR c δδ,所以离子链被压缩了e NR δ02时的外力为F e =202)1(21R n n q c ee δδ-=.9.设泡利排斥项的形式不变,讨论电荷加倍对NaC1晶格常数,体积弹性模量以及结合能的影响。
固体物理 第二章 晶体的结合

资料范本本资料为word版本,可以直接编辑和打印,感谢您的下载固体物理第二章晶体的结合地点:__________________时间:__________________说明:本资料适用于约定双方经过谈判,协商而共同承认,共同遵守的责任与义务,仅供参考,文档可直接下载或修改,不需要的部分可直接删除,使用时请详细阅读内容第二章晶体的结合填空体1. 晶体的结合类型为:共价结合、离子结合、分子结合、金属结合和氢键结合。
2. 共价结合的特点方向性和饱和性。
3. 晶体中原子的相互作用力可分为两类吸引力和排斥力。
4. 一般固体的结合可概括为范德瓦耳斯结合、金属结合、离子结合和共价结合四种基本类型。
5. 金属具有延展性的微观根源是金属原子容易相对滑动。
6. 石墨晶体的结合涉及到的结合类型有共价结合、氢键结合和金属结合。
7. GaAs晶体的结合涉及到的结合类型有共价结合和离子结合。
二、基本概念1. 电离能始原子失去一个电子所需要的能量。
2.电子的亲和能电子的亲和能:一个中性原子获得一个电子成为负离子所释放出的能量。
3.电负性描述化合物分子中组成原子吸引电子倾向强弱的物理量。
4.共价键原子间通过共享电子所形成的化学键。
5.离子键两个电负性相差很大的元素结合形成晶体时,电负性小的原子失去电子形成正离子,电负性大的得到电子形成负离子,这种靠正、负离子之间库仑吸引的结合成为离子键。
6. 范德瓦尔斯力答:分子晶体的粒子间偶极矩相互作用以及瞬时偶极矩相互诱生作用力称为范德瓦耳斯力。
7.氢键答:氢原子处于两个电负性很强的原子(如氟、氧、氮、氯等)之间时,可同时受两个原子的吸引而与它们结合,这种结合作用称为氢键。
8.金属键答:在金属中,组成金属的原子的价电子已脱离母原子而成为自由电子,自由电子为整个晶体共有,而剩下的离子实就好像沉浸在自由电子的海洋中。
自由电子与离子实间的互相吸引作用具有负的势能,使势能降低形成稳定结构。
这种公有化的价电子(自由电子)与离子实间的互作用称为金属键。
固体物理--晶体结合与弹性常量共价晶体
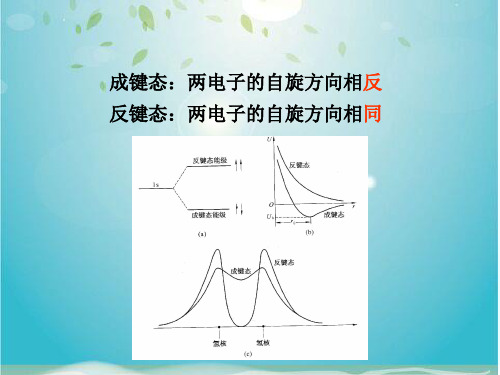
例子 氮原子有7个电子:1s2, 2s2, 2p3 两 px 轨道交叠后的电子对称分布在 yz 平面的两侧,这样的共价键常称为 p 键; 反键态:两电子的自旋方向相同
3. 共价晶体
共价键的饱和性,决定了共价晶体的配位数 只能等于原子的共价键数,而具体的晶体结构又 决定于共价键的方向性
饱和性是指一个原子只能形成一定数目的 共价键
例子 氮原子有7个电子:1s pz) 电子 自旋未配对,它们可以与 其它原子形成3个共价键
当两个氮原子沿着 z 轴方向靠近时,两个 pz 电子相 互交叠,交叠后的原子对称地分布在两氮原子连线的周围,
形成的共价键常称为 s 键
碳原子与4个氢原子形成加 CH4,碳原子 的3个 2p 轨道成相互垂直的哑铃状,而 2s 轨道 和氢原子的 1s 轨道则是球状
因此3个 2p 电子与氢的 1s 电子形成的价键 应相互垂直,而 2s 电子与氢的 1s 电子的价键 则可以在任何方位;但实验指出 CH4 的4个共 价键呈对称分布,为何?
理论上认为,4个未配对电子 2s, 2px, 2py, 2pz 轨道相互混合,重新组合成4个新的未配对 的 sp3 杂化轨道
方向性是指原子只在特定的方向上形成共 价键,一个原子在价电子波函数最大的方向上 形成共价键
例如 p 电子的波函数具有哑铃的形状, 便是在对称轴方向上形成共价键
由于共价键的方向 性,原子在形成共价键 时可以发生轨道杂化
轨道杂化
1s 2s 2p
碳原子有6个电子:1s2, 2s2, 2p2 ,共有2个未配 对电子,但碳原子在与其它原子结合的过程中,1 个 2s 电子常被激发到 2p 轨道,形成如下激发态
成键态:两电子的自旋方向相反 反键态:两电子的自旋方向相同
固体物理学第二章 固体的结合

(2) 结构特点 总趋向于密堆积模型—立方密排(Cu, Ag, Au)和六角密排 (Mg, Zn, Cd)或稍低于密堆积的情况: 体心立方(碱金属Na,K…) (3) 物性特点 A :存在自由电子,导热、导电性良好; B: 结构上无特殊要求,因此易产生缺陷、具有范性,易于加 工成丝、带、片等形状; C:价电子非定域, 完全为晶体共有,键即无方向性也无饱和性 要求,易于形成合金,与溶质、溶剂的关系差不多,其合 金又称固溶体,材料具有一定硬度。
2-3 金属性结合 (1)一般特点 原子外层电子全部丢掉(不是转移、也不是共有), 这时,晶体 变为: 原子实(内层电子+原子核)+近自由电子气系统。 吸引力是库仑引力——原子实与自由电子气之间的作用 排斥力来源于: (A)体积压缩时电子气密度增加,系统动能升 高(E~ρ2/3),电子间排斥力增加,等效于排斥作用。 (B)进一步压缩,电子云交叠, 也会有不相容确定的排斥作用增大 原子实之间的斥力也加大。 泡利(Pauli) 不相容原理!
A r u吸 6 P P P P r 相互作用势: r r6 B 排斥是重叠效应:u斥 12 (与惰性气体相符) r 两原子的相互作用势为: (r ) A B ,A、B为参数 u r 6 r 12
1 2 3
1 2
习惯上原子相互作用势写为:
/4ε
称Lennard-Jones(勒纳—琼斯)势其中ε、ζ r0 rm 是参数,4 εζ6=A, 4 εζ12=B.这种表示的方便 σ/ 处在于,用这两个参数给出的势是归一化的。 对于惰性气体元素,N个原子组成的晶体,其晶体势能可选一个 原子作为出发点: 1 12 6 ' u1 ( r ) 4 [( ) ( ) ] r a r
固体物理学讲义2.1

第二章 固体的结合晶体中粒子的相互作用力可以分为两大类,即吸引力和排斥力,前者在远距离是主要的,后者在近距离是主要的;在某一适当的距离,两者平衡,使晶格处于稳定状态。
吸引作用来自于异性电荷的库仑作用;排斥作用源于:一、同种电荷之间的库仑作用,二、泡利原理所引起的作用。
固体的结合根据结合力的性质分为四种基本形式:⎪⎪⎩⎪⎪⎨⎧范德瓦尔结合金属性结合共价性结合离子性结合 实际结合可能是兼有几种结合形式或者具有两种结合之间的过渡性质。
§2-1 离子性结合离子性结合的基本特点是以离子而不是以原子为结合的单位,结合的平衡依靠较强的静电库仑力,要求离子间相间排列。
其结构比较稳定,结合能为800千焦耳/摩尔数量级。
结合的稳定性导致导电性能差、熔点高、硬度高和膨胀系数小等特点。
以N a Cl 晶体为例,由于N a +和 Cl -离子满壳层的结构,具有球对称结构,可以看成点电荷,若令r 表示相邻离子的距离,则一个正离子的平均库仑能为:∑++-++321321,,2122322222102)(4)1(21n n n n n n r n r n r n q πε这里n 1,n 2,n 3为整数且不能同时为零。
一个元胞的库仑能为:απεπεr q n n n r q n n n n n n 02,,21232221024)()1(4321321-≡∑++-++上式中α为无量纲量,称为马德隆常数。
当邻近离子的电子云显著重叠时,将出现排斥,其能量可以由下式描述:n r rr bbe 或者0-因此含N 个元胞的晶体的系统内能可以表示为:)(nr B r A N U +-= 其和体积或者晶格常数的关系如下图(1) 晶格常数结合最稳定时的原子间距即为晶格常数,由下式决定0)(0=∂∂=r r r r U(2) 压缩系数压缩系数定义为单位体积的改变随单位压强的变化的负值,即:T pV V )(1∂∂-=κ 由热力学第一定律有:pdV dU -=(这里忽略了热效应),则压缩系数为:TV UV )(122∂∂=κ 体弹性模量为:κ1=K(3) 抗张强度晶体能够承受的最大张力,叫抗张强度。
固体物理学 第二章 第一节

06/16
正离子的平均库仑能 同样一个负离子的平均库仑能 同样一个负离子的平均库仑能
—— 整数 一个原胞有两个离子, 一个原胞有两个离子,其原胞的能量
ห้องสมุดไป่ตู้
02_01_固体的结合——离子性结合
07/16
令
(−1) −α = ∑ ' 2 2 2 1/ 2 n1, n2 , n3 (n + n2 + n3 ) 1
n1+n2 +n3
— α 马德隆常数 取决于晶体的结构
几种常见的晶体晶格的马德隆常数 离子晶体 马德隆常数 NaCl 1.748 CsCl 1.763 ZnS 1.638
08/16
02_01_固体的结合——离子性结合
相邻两个离子因电子云有显著重叠时的排斥能
NaCl —— 计近邻离子排斥作用,每个原胞平均排斥能 计近邻离子排斥作用 排斥作用, 晶体中有N个原胞, 晶体中有 个原胞,系统的内能 个原胞
02_01_固体的结合——离子性结合
10/16
不考虑热效应, 不考虑热效应,外界作功等于系统内能增量
一般条件下, 晶体只受大气压的作用, 一般条件下 晶体只受大气压的作用,对晶体体积的影响很小
dU − = p0 ≈ 0 dV
—— 如果已知晶体的内能, 如果已知晶体的内能, 根据极值条件来确定晶体平 衡时的体积和晶格常数
离子晶体的特征
一种离子的最近邻离子为异性离子 离子晶体的配位数最多只能是8(例如 晶体) 离子晶体的配位数最多只能是 (例如CsCl晶体) 晶体 导电性能差、熔点高、 离子晶体结合的稳定性 —— 导电性能差、熔点高、 硬度高和膨胀系数小
02_01_固体的结合——离子性结合
固体物理第二章

§2.1 晶体结合的基本类型
一、离子晶体
正负离子的电子壳层饱和,电子云分布基本上球对称,
满足球密堆积原则。 结合能 ~ 150 kcal/mol 典型晶体:NaCl、LiF等
二、共价晶体 共价结合的特征是具有方向性和饱和性。电子云分 布不是球对称的,不满足球密堆积原则。 共价结合的键合能力相当强,共价晶体一般硬度高, 熔点高。 结合能:~150 kcal/mol 典型晶体:金刚石、SiC等
任意两离子间的相互作用能为
q2 b u( r ) n 4 0 r r
q:一个离子所带的电量,异号: =+1 ;同号: =-1 设晶体中有N个正离子和N个负离子,
j q2 1 b U (2 N ) 4 r r n 2 j 0 0 j j
令
rj jr ,r为最近邻两离子间的距离,有
N q2 B U (r) n 4 0 r r
j0
j
j
—— Madelung常数,只与晶体结构有关
b B N n j0 j
待定
u实验(10-18J/pair) u理论(10-18J/pair) NaCl NaBr KCl KBr RbCl RbBr -1.27 -1.21 -1.15 -1.10 -1.11 -1.06 -1.25 -1.18 -1.13 -1.08 -1.10 -1.05
C2 C2 fi = 2 2 = 2 E h + C Eg
Zn
Se
2. 电离度 a. Coulson标度
2 PA - PB 1-λ fi = = 2 PA + PB 1+λ
PA、PB: 在A原子和B原子上找到电子的概率
第2章 晶体结合

《固体物理学》 微电子与固体电子学院
15
2.1 晶体结合的普遍特征
结论:同一周期元素自左至右电负性逐渐增大,同一族元素 自上而下电负性逐渐减小,过渡族元素的电负性比较接近。
电负性定性判断晶体类型:
(1)当两个成键原子的电负性差值较大时,晶体结合往往采
取离子键; (2)同种原子之间的成键,主要是共价键或金属键; (3)电负性差值小的原子之间成键主要是共价键。
4
2.1 晶体结合的普遍特征
(3)排斥作用起源于:(a) 同性电荷之间的库仑力;(b) 由于Pauli不相容原理的限制所 引起的排斥作用。
O
U(r)
r0 rm
r
b 排斥势可表示为: u R ( r ) rn
b是晶格参量,n是玻恩指数, 都是实验确定的常数
O
f(r)
r
《固体物理学》 微电子与固体电子学院
12
2.1 晶体结合的普遍特征
3. 体弹性模量
(1)晶体受外力时体积的变化。即∆P与-∆V/V之比。
P U 2U K V V ( ) V V V V V 2
2U T=0时,K V0 2 V V0
弹性模量可由实验测定。
《固体物理学》 微电子与固体电子学院
N 2 2
《固体物理学》 微电子与固体电子学院
20
2.2 离子键与离子晶体
设 rij ij R ,R是最近邻间距:
N U U ( R) 2 2e 2 ' 1 1 ' b ( ) n ( n ) ij R ij 40 R
19
2.2 离子键与离子晶体
第 i 个离子与其它N-1个个离子间的互作用势:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
电离能
Байду номын сангаас
(单位:eV)
元素 Na
Mg
Al
Si
P
S
Cl
Ar
电离能 5.138 7.644 5.984 8.149 10.55 10.357 13.01 15.755
元素 K
Ca
Ga
Ge
As
Se
Br
Kr
电离能 4.339 6.111 6.00 7.88 9.87 9.75 11.84 13.996
三、电子亲和能
原子的电负性
一个中性原子获得一个电子成为负离子所释放出的能量, 叫电子的亲和能。
电子亲和能随原子半径的减小而增大,原子半径小,获得 一个电子将释放出较大的能量。
原子的电负性 四、电负性
电离能和电子亲和能从不同的角度表征了原子驾驭电子的 能力。为了综合表征原子得失电子的能力,定义电负性的 概念。
穆力肯 (R. S. Mulliken)
金属键使金属原子结合形成晶体,称为金属晶体。
晶体的结合类型
金属键及金属晶体的特点 1、金属键强度低于离子键强度; 2、金属键对原子排列的具体形式没有特殊要求,原子排 列越紧密,库仑势能越低。晶体体积越小,负电子云密 度越高,库仑相互作用势能越低,晶体结合越稳定(体 积效应);
固体物理学理论
第二章 晶体的结合和弹性
第二章 晶体的结合和弹性
2.1
原子的电负性
2.2
晶体的结合类型
2.3
结合力的一般性质
2.4
非极性分子晶体的结合能
2.5
离子晶体结合能
2.6
原子晶体的结合
2.7
原子的电负性
第一节 原子的电负性
原子的电负性
原子结合成晶体时,其外层电子要做重新分布,不同的分布 产生了不同类型的结合力。不同类型的结合力导致了晶体结 合的不同类型:共价结合、离子结合、金属结合、分子结合 和氢键结合。
电负性表征原子束缚价电子能力的强弱。 同一主族不同原子的性质相近,不同主族中的原子失电子难 易程度不同。
一、原子的电子分布
原子的电负性
电子组态 泡利不相容原理 洪特规则 能量最低原理
电子组态
原子的电负性
定义:给定原子所有电子的主量子数n和轨道量子 数l的组合。 主量子数n=1、2、3、 … 轨道量子数l=0、1、2、3、 …(n-1)
A、NaCl结构:
晶体的结合类型
结合成晶体时,Na原子的价电子转移到Cl原子上,形成Na+和 Cl-(都具有满壳层电子结构)。Na+和Cl-各自构成面心立方布拉 菲晶格,沿晶胞基矢方向相互移动半个晶格常数套构形成氯化钠 结构。Na+和Cl-相间排列,以异号离子为邻。
B、氯化铯结构
晶体的结合类型
结合成晶体时,Cs原子的价电子转移到Cl原子上, 形成Cs+和Cl-(都具有满壳层电子结构)。Cs+和Cl各自构成简单立方布拉菲晶格,沿体对角线方向相互 移动1/2对角线长度套构形成氯化铯结构。Cs和Cl-相 间排列,以异号离子为邻。
电子占据轨道的顺序
原子的电负性
泡利不相容原理
原子的电负性
定义:包括自旋,不可能存在量子态全同的两个 电子。
洪特规则
原子的电负性
电子依能量由低到高依次进入轨道并先单一 自旋平行地占据尽量多的等价轨道。
能量最低原理
原子的电负性
任何稳定体系,其能量最低。
原子的电负性 二、电离能
使原子失去一个电子所需的能量,称为电离能。
晶体的结合类型
金刚石结构 金刚石结构中,每个碳原子与4个邻近碳原子以共价键结
合,共价键之间的夹角为109o28/,形成正四面体结构。
晶体的结合类型
三、金属晶体 当金属原子结合形成晶体时,价电子不再束缚在
原子上,而在整个晶体中运动,形成共有化运动负电 子云和固定在格点上的正离子,正离子与负电子云之 间的库仑吸引力称为金属键。
晶体的结合类型
3、如果价电子壳层中的电子数目不到半满,形成共价键的 数目与价电子数相等。如果价电子壳层中的电子数目超过半 满,形成共价键的数目等于未填充的量子态数(共价键的饱 和性); 4、原子只能在特定方向上形成共价键(共价键的方性); 5、共价的强弱决定于形成共价键的两个电子波函数的交叠 程度; 6、共价晶体结构稳定,熔点高,硬度大,导电性差,范性 差;
库仑吸引力是原子结合成晶体的动力,是长程力;晶体原子
间还存在排斥力,是短程力。一块晶体处于稳定平衡态时,
其总能量E0比组成这晶体N个原子在自由时的总能量低,二者
之差:
Eb=EN-E0
称为结合能。
原子的电负性
中性原子结合成晶体,除了外界的压力和温度等条件的作用 外,主要取决于原子最外层电子的作用。所有晶体的结合类 型都与原子的电负性有关。
选取系数0.18是为了使Li的电负性为1.
原子的电负性
自左至右电负性依次增大
由
元素周期表
上
向
下
电
负
性
依
次
减
小
电负性小的是金属性元素,电负性大的是非金属性元素。
第二节 晶体的结合类型
晶体的结合类型
周期表上同一族的元素具有相似的属性,因此,可以预期 原子结合成晶体时,会出现一些比较典型的结合类型,根 据结合力的性质把晶体分为五个典型的结合类型,分别为: 原子晶体、离子晶体、金属晶体、分子晶体、氢键晶体。
晶体的结合类型
二、原子晶体 元素周期表中第Ⅳ族元素C、Si、Ge、Sn的晶体是典型代 表,其主要依靠具有饱和性和方向性的共价键结合。 典型的有:金刚石、Si、InSb和半导体。
晶体的结合类型
共价键及原子晶体的特点 1、以原子作为结合的基本单元; 2、在结合过程中,自旋相反的两个电子配对,在两个原 子核之间的区域形成较大电子云密度,与原子核形成较 强吸引力,并使两个原子形成满壳层电子结构。
晶体的结合类型
一、离子晶体 依靠正负离子的库仑吸引力结合形成的晶体称为离子 晶体。由元素周期表中第Ⅰ族碱金属元素与第Ⅶ族的 卤族元素化合而成。碱金属元素Li、Na、K、Rb、Cs 和卤族元素F、Cl、Br、I之间形成的化合物,典型的 离子晶体有NaCl型和CsCl型。
晶体的结合类型
离子晶体的特点 1、以离子作为结合的基本单元; 2、正负离子相间排列,当离子间距大于平衡间距时,库仑 作用总效果呈吸引性,当离子间距小于平衡间距时,离子之 间产生强烈排斥。当吸引和排斥作用达到平衡时,形成稳定 晶体结构; 3、正、负离子都具有满壳层电子结构离子,电子分布为球 对称分布; 4、离子晶体结构稳定,熔点较高,硬度较大,导电性差。
