【专题培优】2018年九年级数学上册二次函数压轴题培优专题(含答案)

合集下载

2018年九年级数学中考专题压轴题培优(含答案)

2018年九年级数学中考专题压轴题培优
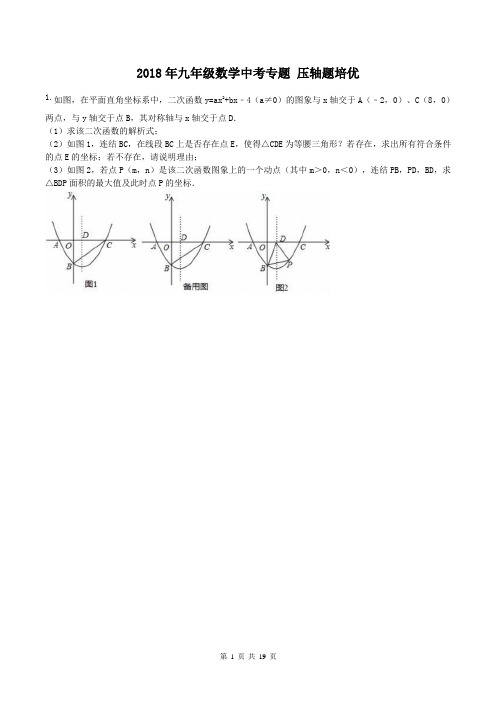
1.如图，在平面直角坐标系中，二次函数y=ax2+bx﹣4（a≠0）的图象与x轴交于A（﹣2，0）、C（8，0）
两点，与y轴交于点B，其对称轴与x轴交于点D．
（1）求该二次函数的解析式；
（2）如图1，连结BC，在线段BC上是否存在点E，使得△CDE为等腰三角形？若存在，求出所有符合条件的点E的坐标；若不存在，请说明理由；
（3）如图2，若点P（m，n）是该二次函数图象上的一个动点（其中m＞0，n＜0），连结PB，PD，BD，求△BDP面积的最大值及此时点P的坐标．
2.如图,在平面直角坐标系中,抛物线与x轴的交点为点A与y轴的交点为点B,过点B作x轴的
平行线BC,交抛物线于点C,连结AC.现有两动点P，Q分别从O,C两点同时出发,点P以每秒4个单位的速度沿OA 向终点A移动,点Q以每秒1个单位的速度沿CB向点B移动,点P停止运动时,点Q也同时停止运动，线段OC,PQ相交于点D,过点D作DE∥OA,交CA于点E,射线QE交x轴于点F.设动点P,Q移动的时间为t（单位:秒）
（1）求A，B，C三点的坐标和抛物线的顶点的坐标；
（2）当t为何值时，四边形PQCA为平行四边形?请写出计算过程；
（3）当0<t<4.5时，△PQF的面积是否总为定值?若是，求出此定值，若不是，请说明理由；
（4）当t为何值时，△PQF为等腰三角形?请写出解答过程．。

2018年中考数学二次函数压轴题汇编(含答案)

2018年中考数学二次函数压轴题汇编1．如图，直线y=﹣x+c与x轴交于点A（3，0），与y轴交于点B，抛物线y=﹣x2+bx+c经过点A，B．（1）求点B的坐标和抛物线的解析式；（2）M（m，0）为x轴上一动点，过点M且垂直于x轴的直线与直线AB 及抛物线分别交于点P，N．①点M在线段OA上运动，若以B，P，N为顶点的三角形与△APM相似，求点M的坐标；②点M在x轴上自由运动，若三个点M，P，N中恰有一点是其它两点所连线段的中点（三点重合除外），则称M，P，N三点为“共谐点”．请直接写出使得M，P，N三点成为“共谐点”的m的值．2．如图1，在平面直角坐标系xOy中，抛物线C：y=ax2+bx+c与x轴相交于A，B两点，顶点为D（0，4），AB=4，设点F（m，0）是x轴的正半轴上一点，将抛物线C绕点F旋转180°，得到新的抛物线C′．（1）求抛物线C的函数表达式；（2）若抛物线C′与抛物线C在y轴的右侧有两个不同的公共点，求m的取值范围．（3）如图2，P是第一象限内抛物线C上一点，它到两坐标轴的距离相等，点P在抛物线C′上的对应点P′，设M是C上的动点，N是C′上的动点，试探究四边形PMP′N能否成为正方形？若能，求出m的值；若不能，请说明理由．3．在平面直角坐标系xOy中的点P和图形M，给出如下的定义：若在图形M上存在一点Q，使得P、Q两点间的距离小于或等于1，则称P为图形M 的关联点．（1）当⊙O的半径为2时，①在点P1（，0），P2（，），P3（，0）中，⊙O的关联点是．②点P在直线y=﹣x上，若P为⊙O的关联点，求点P的横坐标的取值范围．（2）⊙C的圆心在x轴上，半径为2，直线y=﹣x+1与x轴、y轴交于点A、B．若线段AB上的所有点都是⊙C的关联点，直接写出圆心C的横坐标的取值范围．4．如图，在平面直角坐标系中，抛物线y=﹣x2+ax+b交x轴于A（1，0），B （3，0）两点，点P是抛物线上在第一象限内的一点，直线BP与y轴相交于点C．（1）求抛物线y=﹣x2+ax+b的解析式；（2）当点P是线段BC的中点时，求点P的坐标；（3）在（2）的条件下，求sin∠OCB的值．5．如图，抛物线y=﹣x2+bx+c与x轴交于点A和点B，与y轴交于点C，点B坐标为（6，0），点C坐标为（0，6），点D是抛物线的顶点，过点D作x 轴的垂线，垂足为E，连接BD．（1）求抛物线的解析式及点D的坐标；（2）点F是抛物线上的动点，当∠FBA=∠BDE时，求点F的坐标；（3）若点M是抛物线上的动点，过点M作MN∥x轴与抛物线交于点N，点P在x轴上，点Q在坐标平面内，以线段MN为对角线作正方形MPNQ，请写出点Q的坐标．6．已知抛物线y=x2+bx﹣3（b是常数）经过点A（﹣1，0）．（1）求该抛物线的解析式和顶点坐标；（2）P（m，t）为抛物线上的一个动点，P关于原点的对称点为P'．①当点P'落在该抛物线上时，求m的值；②当点P'落在第二象限内，P'A2取得最小值时，求m的值．7．在同一直角坐标系中，抛物线C1：y=ax2﹣2x﹣3与抛物线C2：y=x2+mx+n 关于y轴对称，C2与x轴交于A、B两点，其中点A在点B的左侧．（1）求抛物线C1，C2的函数表达式；（2）求A、B两点的坐标；（3）在抛物线C1上是否存在一点P，在抛物线C2上是否存在一点Q，使得以AB为边，且以A、B、P、Q四点为顶点的四边形是平行四边形？若存在，求出P、Q两点的坐标；若不存在，请说明理由．8．已知函数y=﹣x2+（m﹣1）x+m（m为常数）．（1）该函数的图象与x轴公共点的个数是．A.0B.1C.2D.1或2（2）求证：不论m为何值，该函数的图象的顶点都在函数y=（x+1）2的图象上．（3）当﹣2≤m≤3时，求该函数的图象的顶点纵坐标的取值范围．9．已知直线y=2x+m与抛物线y=ax2+ax+b有一个公共点M（1，0），且a＜b．（Ⅰ）求抛物线顶点Q的坐标（用含a的代数式表示）；（Ⅱ）说明直线与抛物线有两个交点；（Ⅲ）直线与抛物线的另一个交点记为N．（ⅰ）若﹣1≤a≤﹣，求线段MN长度的取值范围；（ⅱ）求△QMN面积的最小值．10．在平面直角坐标系中，设二次函数y1=（x+a）（x﹣a﹣1），其中a≠0．（1）若函数y1的图象经过点（1，﹣2），求函数y1的表达式；（2）若一次函数y2=ax+b的图象与y1的图象经过x轴上同一点，探究实数a，b满足的关系式；（3）已知点P（x0，m）和Q（1，n）在函数y1的图象上，若m＜n，求x0的取值范围．11．定义：如图1，抛物线y=ax2+bx+c（a≠0）与x轴交于A，B两点，点P 在该抛物线上（P点与A、B两点不重合），如果△ABP的三边满足AP2+BP2=AB2，则称点P为抛物线y=ax2+bx+c（a≠0）的勾股点．（1）直接写出抛物线y=﹣x2+1的勾股点的坐标．（2）如图2，已知抛物线C：y=ax2+bx（a≠0）与x轴交于A，B两点，点P （1，）是抛物线C的勾股点，求抛物线C的函数表达式．（3）在（2）的条件下，点Q在抛物线C上，求满足条件S=S△ABP的Q△ABQ点（异于点P）的坐标．12．如图，二次函数y=x2+bx+c的图象与x轴交于A、B两点，与y轴交于点C，OB=OC．点D在函数图象上，CD∥x轴，且CD=2，直线l是抛物线的对称轴，E是抛物线的顶点．（1）求b、c的值；（2）如图①，连接BE，线段OC上的点F关于直线l的对称点F'恰好在线段BE上，求点F的坐标；（3）如图②，动点P在线段OB上，过点P作x轴的垂线分别与BC交于点M，与抛物线交于点N．试问：抛物线上是否存在点Q，使得△PQN与△APM 的面积相等，且线段NQ的长度最小？如果存在，求出点Q的坐标；如果不存在，说明理由．13．如图，在平面直角坐标系中，抛物线y=x2﹣x﹣与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C，对称轴与x轴交于点D，点E（4，n）在抛物线上．（1）求直线AE的解析式；（2）点P为直线CE下方抛物线上的一点，连接PC，PE．当△PCE的面积最大时，连接CD，CB，点K是线段CB的中点，点M是CP上的一点，点N是CD上的一点，求KM+MN+NK的最小值；（3）点G是线段CE的中点，将抛物线y=x2﹣x﹣沿x轴正方向平移得到新抛物线y′，y′经过点D，y′的顶点为点F．在新抛物线y′的对称轴上，是否存在点Q，使得△FGQ为等腰三角形？若存在，直接写出点Q的坐标；若不存在，请说明理由．14．如图，抛物线y=ax2+bx+2经过点A（﹣1，0），B（4，0），交y轴于点C；（1）求抛物线的解析式（用一般式表示）；=S△ABD？若存在（2）点D为y轴右侧抛物线上一点，是否存在点D使S△ABC请直接给出点D坐标；若不存在请说明理由；（3）将直线BC绕点B顺时针旋转45°，与抛物线交于另一点E，求BE的长．15．如图，直线y=kx+b（k、b为常数）分别与x轴、y轴交于点A（﹣4，0）、B（0，3），抛物线y=﹣x2+2x+1与y轴交于点C．（1）求直线y=kx+b的函数解析式；（2）若点P（x，y）是抛物线y=﹣x2+2x+1上的任意一点，设点P到直线AB 的距离为d，求d关于x的函数解析式，并求d取最小值时点P的坐标；（3）若点E在抛物线y=﹣x2+2x+1的对称轴上移动，点F在直线AB上移动，求CE+EF的最小值．16．如图，已知二次函数y=x2﹣4的图象与x轴交于A，B两点，与y轴交于点C，⊙C的半径为，P为⊙C上一动点．（1）点B，C的坐标分别为B（），C（）；（2）是否存在点P，使得△PBC为直角三角形？若存在，求出点P的坐标；若不存在，请说明理由；（3）连接PB，若E为PB的中点，连接OE，则OE的最大值=．17．已知点A（﹣1，1）、B（4，6）在抛物线y=ax2+bx上（1）求抛物线的解析式；（2）如图1，点F的坐标为（0，m）（m＞2），直线AF交抛物线于另一点G，过点G作x轴的垂线，垂足为H．设抛物线与x轴的正半轴交于点E，连接FH、AE，求证：FH∥AE；（3）如图2，直线AB分别交x轴、y轴于C、D两点．点P从点C出发，沿射线CD方向匀速运动，速度为每秒个单位长度；同时点Q从原点O出发，沿x轴正方向匀速运动，速度为每秒1个单位长度．点M是直线PQ与抛物线的一个交点，当运动到t秒时，QM=2PM，直接写出t的值．18．已知直线y=kx+b与抛物线y=ax2（a＞0）相交于A、B两点（点A在点B 的左侧），与y轴正半轴相交于点C，过点A作AD⊥x轴，垂足为D．（1）若∠AOB=60°，AB∥x轴，AB=2，求a的值；（2）若∠AOB=90°，点A的横坐标为﹣4，AC=4BC，求点B的坐标；（3）延长AD、BO相交于点E，求证：DE=CO．19．如图，抛物线y=mx2﹣16mx+48m（m＞0）与x轴交于A，B两点（点B 在点A左侧），与y轴交于点C，点D是抛物线上的一个动点，且位于第四象限，连接OD、BD、AC、AD，延长AD交y轴于点E．（1）若△OAC为等腰直角三角形，求m的值；（2）若对任意m＞0，C、E两点总关于原点对称，求点D的坐标（用含m 的式子表示）；（3）当点D运动到某一位置时，恰好使得∠ODB=∠OAD，且点D为线段AE 的中点，此时对于该抛物线上任意一点P（x0，y0）总有n+≥﹣4my02﹣12y0﹣50成立，求实数n的最小值．20．如图，在平面直角坐标系中，直线y=x+2与x轴交于点A，与y轴交于点C，抛物线y=﹣x2+bx+c经过A、C两点，与x轴的另一交点为点B．（1）求抛物线的函数表达式；（2）点D为直线AC上方抛物线上一动点，①连接BC、CD，设直线BD交线段AC于点E，△CDE的面积为S1，△BCE的面积为S2，求的最大值；②过点D作DF⊥AC，垂足为点F，连接CD，是否存在点D，使得△CDF中的某个角恰好等于∠BAC的2倍？若存在，求点D的横坐标；若不存在，请说明理由．21．在平面直角坐标系xOy中，抛物线y=ax2+bx+c的开口向上，且经过点A （0，）（1）若此抛物线经过点B（2，﹣），且与x轴相交于点E，F．①填空：b=（用含a的代数式表示）；②当EF2的值最小时，求抛物线的解析式；（2）若a=，当0≤x≤1，抛物线上的点到x轴距离的最大值为3时，求b 的值．22．如图，在平面直角坐标系中，抛物线y=ax2+bx+1交y轴于点A，交x轴正半轴于点B（4，0），与过A点的直线相交于另一点D（3，），过点D作DC⊥x轴，垂足为C．（1）求抛物线的表达式；（2）点P在线段OC上（不与点O、C重合），过P作PN⊥x轴，交直线AD 于M，交抛物线于点N，连接CM，求△PCM面积的最大值；（3）若P是x轴正半轴上的一动点，设OP的长为t，是否存在t，使以点M、C、D、N为顶点的四边形是平行四边形？若存在，求出t的值；若不存在，请说明理由．23．如图，抛物线y=ax2+bx﹣3经过点A（2，﹣3），与x轴负半轴交于点B，与y轴交于点C，且OC=3OB．（1）求抛物线的解析式；（2）点D在y轴上，且∠BDO=∠BAC，求点D的坐标；（3）点M在抛物线上，点N在抛物线的对称轴上，是否存在以点A，B，M，N为顶点的四边形是平行四边形？若存在，求出所有符合条件的点M的坐标；若不存在，请说明理由．24．已知函数y=mx2﹣（2m﹣5）x+m﹣2的图象与x轴有两个公共点．（1）求m的取值范围，并写出当m取范围内最大整数时函数的解析式；（2）题（1）中求得的函数记为C1．①当n≤x≤﹣1时，y的取值范围是1≤y≤﹣3n，求n的值；②函数C2：y=m（x﹣h）2+k的图象由函数C1的图象平移得到，其顶点P落在以原点为圆心，半径为的圆内或圆上．设函数C1的图象顶点为M，求点P与点M距离最大时函数C2的解析式．25．如图，抛物线y=x2+x+c与x轴的负半轴交于点A，与y轴交于点B，连结AB，点C（6，）在抛物线上，直线AC与y轴交于点D．（1）求c的值及直线AC的函数表达式；（2）点P在x轴正半轴上，点Q在y轴正半轴上，连结PQ与直线AC交于点M，连结MO并延长交AB于点N，若M为PQ的中点．①求证：△APM∽△AON；②设点M的横坐标为m，求AN的长（用含m的代数式表示）．26．如图，过抛物线y=x2﹣2x上一点A作x轴的平行线，交抛物线于另一点B，交y轴于点C，已知点A的横坐标为﹣2．（1）求抛物线的对称轴和点B的坐标；（2）在AB上任取一点P，连结OP，作点C关于直线OP的对称点D；①连结BD，求BD的最小值；②当点D落在抛物线的对称轴上，且在x轴上方时，求直线PD的函数表达式．27．如图，已知抛物线y=ax2+bx+c（a≠0）的图象的顶点坐标是（2，1），并且经过点（4，2），直线y=x+1与抛物线交于B，D两点，以BD为直径作圆，圆心为点C，圆C与直线m交于对称轴右侧的点M（t，1），直线m上每一点的纵坐标都等于1．（1）求抛物线的解析式；（2）证明：圆C与x轴相切；（3）过点B作BE⊥m，垂足为E，再过点D作DF⊥m，垂足为F，求BE：MF的值．28．平面直角坐标系xOy中，点A、B的横坐标分别为a、a+2，二次函数y=﹣x2+（m﹣2）x+2m的图象经过点A、B，且a、m满足2a﹣m=d（d为常数）．（1）若一次函数y1=kx+b的图象经过A、B两点．①当a=1、d=﹣1时，求k的值；②若y1随x的增大而减小，求d的取值范围；（2）当d=﹣4且a≠﹣2、a≠﹣4时，判断直线AB与x轴的位置关系，并说明理由；（3）点A、B的位置随着a的变化而变化，设点A、B运动的路线与y轴分别相交于点C、D，线段CD的长度会发生变化吗？如果不变，求出CD的长；如果变化，请说明理由．29．如图，抛物线y=﹣x2+x+3与x轴交于A、B两点（点A在点B 的左侧），与y轴交于点C，连接AC、BC．点P沿AC以每秒1个单位长度的速度由点A向点C运动，同时，点Q沿BO以每秒2个单位长度的速度由点B向点O运动，当一个点停止运动时，另一个点也随之停止运动，连接PQ．过点Q作QD⊥x轴，与抛物线交于点D，与BC交于点E，连接PD，与BC交于点F．设点P的运动时间为t秒（t＞0）．（1）求直线BC的函数表达式；（2）①直接写出P，D两点的坐标（用含t的代数式表示，结果需化简）②在点P、Q运动的过程中，当PQ=PD时，求t的值；（3）试探究在点P，Q运动的过程中，是否存在某一时刻，使得点F为PD 的中点？若存在，请直接写出此时t的值与点F的坐标；若不存在，请说明理由．30．如图，在平面直角坐标系xOy中，抛物线y=x2﹣2x﹣3交x轴于A，B两点（点A在点B的左侧），将该抛物线位于x轴上方曲线记作M，将该抛物线位于x轴下方部分沿x轴翻折，翻折后所得曲线记作N，曲线N交y轴于点C，连接AC、BC．（1）求曲线N所在抛物线相应的函数表达式；（2）求△ABC外接圆的半径；（3）点P为曲线M或曲线N上的一动点，点Q为x轴上的一个动点，若以点B，C，P，Q为顶点的四边形是平行四边形，求点Q的坐标．31．如图，是将抛物线y=﹣x2平移后得到的抛物线，其对称轴为x=1，与x 轴的一个交点为A（﹣1，0），另一个交点为B，与y轴的交点为C．（1）求抛物线的函数表达式；（2）若点N为抛物线上一点，且BC⊥NC，求点N的坐标；（3）点P是抛物线上一点，点Q是一次函数y=x+的图象上一点，若四边形OAPQ为平行四边形，这样的点P、Q是否存在？若存在，分别求出点P、Q的坐标；若不存在，说明理由．32．如图，已知二次函数y=ax2+bx+3（a≠0）的图象经过点A（3，0），B（4，1），且与y轴交于点C，连接AB、AC、BC．（1）求此二次函数的关系式；（2）判断△ABC的形状；若△ABC的外接圆记为⊙M，请直接写出圆心M的坐标；（3）若将抛物线沿射线BA方向平移，平移后点A、B、C的对应点分别记为点A1、B1、C1，△A1B1C1的外接圆记为⊙M1，是否存在某个位置，使⊙M1经过原点？若存在，求出此时抛物线的关系式；若不存在，请说明理由．33．抛物线y=4x2﹣2ax+b与x轴相交于A（x1，0），B（x2，0）（0＜x1＜x2）两点，与y轴交于点C．（1）设AB=2，tan∠ABC=4，求该抛物线的解析式；（2）在（1）中，若点D为直线BC下方抛物线上一动点，当△BCD的面积最大时，求点D的坐标；（3）是否存在整数a，b使得1＜x1＜2和1＜x2＜2同时成立，请证明你的结论．34．如图，已知二次函数y=ax2+bx+c（a≠0）的图象经过A（﹣1，0）、B（4，0）、C（0，2）三点．（1）求该二次函数的解析式；（2）点D是该二次函数图象上的一点，且满足∠DBA=∠CAO（O是坐标原点），求点D的坐标；（3）点P是该二次函数图象上位于第一象限上的一动点，连接PA分别交BC、y轴于点E、F，若△PEB、△CEF的面积分别为S1、S2，求S1﹣S2的最大值．35．如图1，抛物线y=ax2+bx+c经过平行四边形ABCD的顶点A（0，3）、B （﹣1，0）、D（2，3），抛物线与x轴的另一交点为E．经过点E的直线l将平行四边形ABCD分割为面积相等的两部分，与抛物线交于另一点F．点P 为直线l上方抛物线上一动点，设点P的横坐标为t．（1）求抛物线的解析式；（2）当t何值时，△PFE的面积最大？并求最大值的立方根；（3）是否存在点P使△PAE为直角三角形？若存在，求出t的值；若不存在，说明理由．36．如图，某日的钱塘江观潮信息如图：按上述信息，小红将“交叉潮”形成后潮头与乙地之间的距离s（千米）与时间t（分钟）的函数关系用图3表示，其中：“11：40时甲地‘交叉潮’的潮头离乙地12千米”记为点A（0，12），点B坐标为（m，0），曲线BC可用二次函数s=t2+bt+c（b，c是常数）刻画．（1）求m的值，并求出潮头从甲地到乙地的速度；（2）11：59时，小红骑单车从乙地出发，沿江边公路以0.48千米/分的速度往甲地方向去看潮，问她几分钟后与潮头相遇？（3）相遇后，小红立即调转车头，沿江边公路按潮头速度与潮头并行，但潮头过乙地后均匀加速，而单车最高速度为0.48千米/分，小红逐渐落后．问小红与潮头相遇到落后潮头 1.8千米共需多长时间？（潮水加速阶段速度v=v0+（t﹣30），v0是加速前的速度）．37．如图1，抛物线y=ax2+bx+2与x轴交于A，B两点，与y轴交于点C，AB=4，矩形OBDC的边CD=1，延长DC交抛物线于点E．（1）求抛物线的解析式；（2）如图2，点P是直线EO上方抛物线上的一个动点，过点P作y轴的平行线交直线EO于点G，作PH⊥EO，垂足为H．设PH的长为l，点P的横坐标为m，求l与m的函数关系式（不必写出m的取值范围），并求出l的最大值；（3）如果点N是抛物线对称轴上的一点，抛物线上是否存在点M，使得以M，A，C，N为顶点的四边形是平行四边形？若存在，直接写出所有满足条件的点M的坐标；若不存在，请说明理由．38．如图，抛物线y=﹣x2+bx+c与直线AB交于A（﹣4，﹣4），B（0，4）两点，直线AC：y=﹣x﹣6交y轴于点C．点E是直线AB上的动点，过点E 作EF⊥x轴交AC于点F，交抛物线于点G．（1）求抛物线y=﹣x2+bx+c的表达式；（2）连接GB，EO，当四边形GEOB是平行四边形时，求点G的坐标；（3）①在y轴上存在一点H，连接EH，HF，当点E运动到什么位置时，以A，E，F，H为顶点的四边形是矩形？求出此时点E，H的坐标；②在①的前提下，以点E为圆心，EH长为半径作圆，点M为⊙E上一动点，求AM+CM它的最小值．39．抛物线y=ax2+bx+3经过点A（1，0）和点B（5，0）．（1）求该抛物线所对应的函数解析式；（2）该抛物线与直线y=x+3相交于C、D两点，点P是抛物线上的动点且位于x轴下方，直线PM∥y轴，分别与x轴和直线CD交于点M、N．①连结PC、PD，如图1，在点P运动过程中，△PCD的面积是否存在最大值？若存在，求出这个最大值；若不存在，说明理由；②连结PB，过点C作CQ⊥PM，垂足为点Q，如图2，是否存在点P，使得△CNQ与△PBM相似？若存在，求出满足条件的点P的坐标；若不存在，说明理由．40．《函数的图象与性质》拓展学习片段展示：【问题】如图①，在平面直角坐标系中，抛物线y=a（x﹣2）2﹣经过原点O，与x轴的另一个交点为A，则a=．【操作】将图①中抛物线在x轴下方的部分沿x轴折叠到x轴上方，将这部分图象与原抛物线剩余部分的图象组成的新图象记为G，如图②．直接写出图象G对应的函数解析式．【探究】在图②中，过点B（0，1）作直线l平行于x轴，与图象G的交点从左至右依次为点C，D，E，F，如图③．求图象G在直线l上方的部分对应的函数y随x增大而增大时x的取值范围．【应用】P是图③中图象G上一点，其横坐标为m，连接PD，PE．直接写出△PDE的面积不小于1时m的取值范围．1．如图1，经过原点O的抛物线y=ax2+bx（a≠0）与x轴交于另一点A（，0），在第一象限内与直线y=x交于点B（2，t）．（1）求这条抛物线的表达式；（2）在第四象限内的抛物线上有一点C，满足以B，O，C为顶点的三角形的面积为2，求点C的坐标；（3）如图2，若点M在这条抛物线上，且∠MBO=∠ABO，在（2）的条件下，是否存在点P，使得△POC∽△MOB？若存在，求出点P的坐标；若不存在，请说明理由．2．如图①，在平面直角坐标系中，二次函数y=﹣x2+bx+c的图象与坐标轴交于A，B，C三点，其中点A的坐标为（﹣3，0），点B的坐标为（4，0），连接AC，BC．动点P从点A出发，在线段AC上以每秒1个单位长度的速度向点C作匀速运动；同时，动点Q从点O出发，在线段OB上以每秒1个单位长度的速度向点B作匀速运动，当其中一点到达终点时，另一点随之停止运动，设运动时间为t秒．连接PQ．（1）填空：b=，c=；（2）在点P，Q运动过程中，△APQ可能是直角三角形吗？请说明理由；（3）在x轴下方，该二次函数的图象上是否存在点M，使△PQM是以点P 为直角顶点的等腰直角三角形？若存在，请求出运动时间t；若不存在，请说明理由；（4）如图②，点N的坐标为（﹣，0），线段PQ的中点为H，连接NH，当点Q关于直线NH的对称点Q′恰好落在线段BC上时，请直接写出点Q′的坐标．3．定义：对于给定的两个函数，任取自变量x的一个值，当x＜0时，它们对应的函数值互为相反数；当x≥0时，它们对应的函数值相等，我们称这样的两个函数互为相关函数．例如：一次函数y=x﹣1，它的相关函数为y=．（1）已知点A（﹣5，8）在一次函数y=ax﹣3的相关函数的图象上，求a的值；（2）已知二次函数y=﹣x2+4x﹣．①当点B（m，）在这个函数的相关函数的图象上时，求m的值；②当﹣3≤x≤3时，求函数y=﹣x2+4x﹣的相关函数的最大值和最小值；（3）在平面直角坐标系中，点M，N的坐标分别为（﹣，1），（，1），连结MN．直接写出线段MN与二次函数y=﹣x2+4x+n的相关函数的图象有两个公共点时n的取值范围．4．如图，在平面直角坐标系xOy中，已知A，B两点的坐标分别为（﹣4，0），（4，0），C（m，0）是线段A B上一点（与A，B点不重合），抛物线L1：y=ax2+b1x+c1（a＜0）经过点A，C，顶点为D，抛物线L2：y=ax2+b2x+c2（a＜0）经过点C，B，顶点为E，AD，BE的延长线相交于点F．（1）若a=﹣，m=﹣1，求抛物线L1，L2的解析式；（2）若a=﹣1，AF⊥BF，求m的值；（3）是否存在这样的实数a（a＜0），无论m取何值，直线AF与BF都不可能互相垂直？若存在，请直接写出a的两个不同的值；若不存在，请说明理由．5．如图，已知抛物线y=ax2﹣2ax﹣9a与坐标轴交于A，B，C三点，其中C（0，3），∠BAC的平分线AE交y轴于点D，交BC于点E，过点D的直线l与射线AC，AB分别交于点M，N．（1）直接写出a的值、点A的坐标及抛物线的对称轴；（2）点P为抛物线的对称轴上一动点，若△PAD为等腰三角形，求出点P 的坐标；（3）证明：当直线l绕点D旋转时，+均为定值，并求出该定值．6．如图1，矩形OABC的顶点A，C的坐标分别为（4，0），（0，6），直线AD交B C于点D，tan∠OAD=2，抛物线M1：y=ax2+bx（a≠0）过A，D两点．（1）求点D的坐标和抛物线M1的表达式；（2）点P是抛物线M1对称轴上一动点，当∠CPA=90°时，求所有符合条件的点P的坐标；（3）如图2，点E（0，4），连接AE，将抛物线M1的图象向下平移m（m＞0）个单位得到抛物线M2．①设点D平移后的对应点为点D′，当点D′恰好在直线AE上时，求m的值；②当1≤x≤m（m＞1）时，若抛物线M2与直线AE有两个交点，求m的取值范围．7．如图，已知抛物线y=ax2+2x+c与y轴交于点A（0，6），与x轴交于点B （6，0），点P是线段AB上方抛物线上的一个动点．（1）求这条抛物线的表达式及其顶点坐标；（2）当点P移动到抛物线的什么位置时，使得∠PAB=75°，求出此时点P的坐标；（3）当点P从A点出发沿线段AB上方的抛物线向终点B移动，在移动中，点P的横坐标以每秒1个单位长度的速度变动；与此同时点M以每秒1个单位长度的速度沿AO向终点O移动，点P，M移动到各自终点时停止．当两个动点移动t秒时，求四边形PAMB的面积S关于t的函数表达式，并求t 为何值时，S有最大值，最大值是多少？8．如图，直线y=﹣x+分别与x轴、y轴交于B、C两点，点A在x轴上，∠ACB=90°，抛物线y=ax2+bx+经过A，B两点．（1）求A、B两点的坐标；（2）求抛物线的解析式；（3）点M是直线BC上方抛物线上的一点，过点M作MH⊥BC于点H，作MD∥y轴交BC于点D，求△DMH周长的最大值．9．如图，抛物线y=ax2+bx﹣2的对称轴是直线x=1，与x轴交于A，B两点，与y轴交于点C，点A的坐标为（﹣2，0），点P为抛物线上的一个动点，过点P作PD⊥x轴于点D，交直线BC于点E．（1）求抛物线解析式；（2）若点P在第一象限内，当OD=4PE时，求四边形POBE的面积；（3）在（2）的条件下，若点M为直线BC上一点，点N为平面直角坐标系内一点，是否存在这样的点M和点N，使得以点B，D，M，N为顶点的四边形是菱形？若存在，直接写出点N的坐标；若不存在，请说明理由．【温馨提示：考生可以根据题意，在备用图中补充图形，以便探究】10．如图，抛物线y=﹣x2+bx+c与x轴分别交于A（﹣1，0），B（5，0）两点．（1）求抛物线的解析式；（2）在第二象限内取一点C，作CD垂直X轴于点D，链接AC，且AD=5，CD=8，将Rt△ACD沿x轴向右平移m个单位，当点C落在抛物线上时，求m 的值；（3）在（2）的条件下，当点C第一次落在抛物线上记为点E，点P是抛物线对称轴上一点．试探究：在抛物线上是否存在点Q，使以点B、E、P、Q 为顶点的四边形是平行四边形？若存在，请出点Q的坐标；若不存在，请说明理由．11．如图，已知抛物线y=ax2+bx+c过点A（﹣1，0），B（3，0），C（0，3），点M、N为抛物线上的动点，过点M作MD∥y轴，交直线BC于点D，交x 轴于点E．（1）求二次函数y=ax2+bx+c的表达式；（2）过点N作NF⊥x轴，垂足为点F，若四边形MNFE为正方形（此处限定点M在对称轴的右侧），求该正方形的面积；（3）若∠DMN=90°，MD=MN，求点M的横坐标．12．如图1，已知二次函数y=ax2+bx+c（a、b、c为常数，a≠0）的图象过点O（0，0）和点A（4，0），函数图象最低点M的纵坐标为﹣，直线l的解析式为y=x．（1）求二次函数的解析式；（2）直线l沿x轴向右平移，得直线l′，l′与线段OA相交于点B，与x轴下方的抛物线相交于点C，过点C作CE⊥x轴于点E，把△BCE沿直线l′折叠，当点E恰好落在抛物线上点E′时（图2），求直线l′的解析式；（3）在（2）的条件下，l′与y轴交于点N，把△BON绕点O逆时针旋转135°得到△B′ON′，P为l′上的动点，当△PB′N′为等腰三角形时，求符合条件的点P的坐标．13．如图，矩形OABC的两边在坐标轴上，点A的坐标为（10，0），抛物线y=ax2+bx+4过点B，C两点，且与x轴的一个交点为D（﹣2，0），点P是线段CB上的动点，设CP=t（0＜t＜10）．（1）请直接写出B、C两点的坐标及抛物线的解析式；（2）过点P作PE⊥BC，交抛物线于点E，连接BE，当t为何值时，∠PBE=∠OCD？（3）点Q是x轴上的动点，过点P作PM∥BQ，交CQ于点M，作PN∥CQ，交BQ于点N，当四边形PMQN为正方形时，请求出t的值．14．如图所示，在平面直角坐标系中，⊙C经过坐标原点O，且与x轴，y 轴分别相交于M（4，0），N（0，3）两点．已知抛物线开口向上，与⊙C交于N，H，P三点，P为抛物线的顶点，抛物线的对称轴经过点C且垂直x轴于点D．（1）求线段CD的长及顶点P的坐标；（2）求抛物线的函数表达式；（3）设抛物线交x轴于A，B两点，在抛物线上是否存在点Q，使得S四边形=8S△QAB，且△QAB∽△OBN成立？若存在，请求出Q点的坐标；若不存OPMN在，请说明理由．15．如图，在平面直角坐标系中，抛物线y=ax2+bx+c（a≠0）与y轴交与点C（0，3），与x轴交于A、B两点，点B坐标为（4，0），抛物线的对称轴方程为x=1．（1）求抛物线的解析式；（2）点M从A点出发，在线段AB上以每秒3个单位长度的速度向B点运动，同时点N从B点出发，在线段BC上以每秒1个单位长度的速度向C点运动，其中一个点到达终点时，另一个点也停止运动，设△MBN的面积为S，点M运动时间为t，试求S与t的函数关系，并求S的最大值；（3）在点M运动过程中，是否存在某一时刻t，使△MBN为直角三角形？若存在，求出t值；若不存在，请说明理由．16．已知抛物线y=ax2+bx+c，其中2a=b＞0＞c，且a+b+c=0．（1）直接写出关于x的一元二次方程ax2+bx+c=0的一个根；（2）证明：抛物线y=ax2+bx+c的顶点A在第三象限；（3）直线y=x+m与x，y轴分别相交于B，C两点，与抛物线y=ax2+bx+c相。

初三数学二次函数的专项培优练习题(含答案)含详细答案

初三数学二次函数的专项培优练习题(含答案)含详细答案一、二次函数1．某厂家生产一种新型电子产品，制造时每件的成本为40元，通过试销发现，销售量(y 万件)与销售单价(x 元)之间符合一次函数关系，其图象如图所示．()1求y 与x 的函数关系式；()2物价部门规定：这种电子产品销售单价不得超过每件80元，那么，当销售单价x 定为每件多少元时，厂家每月获得的利润()w 最大？最大利润是多少？【答案】（1）2280y x =-+；（2）当销售单价x 定为每件80元时，厂家每月获得的利润()w 最大，最大利润是4800元．【解析】【分析】()1根据函数图象经过点()40,200和点()60,160，利用待定系数法即可求出y 与x 的函数关系式；()2先根据利润=销售数量(⨯销售单价-成本)，由试销期间销售单价不低于成本单价，也不高于每千克80元，结合电子产品的成本价即可得出x 的取值范围，根据二次函数的增减性可得最值．【详解】解：()1设y 与x 的函数关系式为()0y kx b k =+≠，Q 函数图象经过点()40,200和点()60,160，{4020060160k b k b +=∴+=，解得：{2280k b =-=， y ∴与x 的函数关系式为2280y x =-+．()2由题意得：()()224022802360112002(90)5000w x x x x x =--+=-+-=--+． Q 试销期间销售单价不低于成本单价，也不高于每千克80元，且电子产品的成本为每千克40元，∴自变量x 的取值范围是4080x ≤≤．20-<Q ，∴当90x <时，w 随x 的增大而增大，80x ∴=时，w 有最大值，当80x =时，4800w =，答：当销售单价x 定为每件80元时，厂家每月获得的利润()w 最大，最大利润是4800元．【点睛】本题考查了一次函数和二次函数的应用，根据点的坐标利用待定系数法求出函数关系式是解题的关键，并注意最值的求法．2．抛物线y ＝ax 2+bx ﹣3（a≠0）与直线y ＝kx+c （k≠0）相交于A （﹣1，0）、B （2，﹣3）两点，且抛物线与y 轴交于点C ．（1）求抛物线的解析式；（2）求出C 、D 两点的坐标（3）在第四象限抛物线上有一点P ，若△PCD 是以CD 为底边的等腰三角形，求出点P 的坐标．【答案】（1）y ＝x 2﹣2x ﹣3;（2）C （0，﹣3）,D （0，﹣1）;（3）P （2，﹣2）.【解析】【分析】（1）把A （﹣1，0）、B （2，﹣3）两点坐标代入y ＝ax 2+bx ﹣3可得抛物线解析式．（2）当x ＝0时可求C 点坐标，求出直线AB 解析式，当x ＝0可求D 点坐标．（3）由题意可知P 点纵坐标为﹣2，代入抛物线解析式可求P 点横坐标．【详解】解：（1）把A （﹣1，0）、B （2，﹣3）两点坐标代入y ＝ax 2+bx ﹣3可得 304233a b a b --=⎧⎨+-=-⎩ 解得12a b =⎧⎨=-⎩∴y ＝x 2﹣2x ﹣3（2）把x ＝0代入y ＝x 2﹣2x ﹣3中可得y ＝﹣3∴C （0，﹣3）设y ＝kx+b ，把A （﹣1，0）、B （2，﹣3）两点坐标代入023k b k b -+=⎧⎨+=-⎩解得11 kb=-⎧⎨=-⎩∴y＝﹣x﹣1∴D（0，﹣1）（3）由C（0，﹣3），D（0，﹣1）可知CD的垂直平分线经过（0，﹣2）∴P点纵坐标为﹣2，∴x2﹣2x﹣3＝﹣2解得：x＝1±2，∵x＞0∴x＝1+2．∴P（1+2，﹣2）【点睛】本题是二次函数综合题，用待定系数法求二次函数的解析式，把x＝0代入二次函数解析式和一次函数解析式可求图象与y轴交点坐标，知道点P纵坐标带入抛物线解析式可求点P 的横坐标．3．如图，抛物线y＝x2+bx+c与x轴交于A、B两点，B点坐标为（3，0），与y轴交于点C（0，3）．（1）求抛物线y＝x2+bx+c的表达式；（2）点D为抛物线对称轴上一点，当△BCD是以BC为直角边的直角三角形时，求点D的坐标；（3）点P在x轴下方的抛物线上，过点P的直线y＝x+m与直线BC交于点E，与y轴交于点F，求PE+EF的最大值．【答案】（1）y=x2﹣4x+3；（2）（2，﹣1）；（3）42【解析】试题分析：（1）利用待定系数法求抛物线解析式；（2）如图1，设D（2，y），利用两点间的距离公式得到BC2=32+32=18，DC2=4+（y﹣3）2，BD2=（3﹣2）2+y2=1+y2，然后讨论：当BD为斜边时得到18+4+（y﹣3）2=1+y2；当CD 为斜边时得到4+（y﹣3）2=1+y2+18，再分别解方程即可得到对应D的坐标；（3）先证明∠CEF=90°得到△ECF为等腰直角三角形，作PH⊥y轴于H，PG∥y轴交BC于G，如图2，△EPG、△PHF都为等腰直角三角形，则PE 2，PF2，设P（t，t2﹣4t+3）（1＜t＜3），则G（t，﹣t+3），接着利用t表示PF、PE，这样PE+EF=2PE+PF=﹣2t2+42t，然后利用二次函数的性质解决问题．试题解析：解：（1）把B（3，0），C（0，3）代入y=x2+bx+c得：9303b cc++=⎧⎨=⎩，解得：43bc=-⎧⎨=⎩，∴抛物线y=x2+bx+c的表达式为y=x2﹣4x+3；（2）如图1，抛物线的对称轴为直线x=﹣42-=2，设D（2，y），B（3，0），C（0，3），∴BC2=32+32=18，DC2=4+（y﹣3）2，BD2=（3﹣2）2+y2=1+y2，当△BCD是以BC为直角边，BD为斜边的直角三角形时，BC2+DC2=BD2，即18+4+（y﹣3）2=1+y2，解得：y=5，此时D点坐标为（2，5）；当△BCD是以BC为直角边，CD为斜边的直角三角形时，BC2+DB2=DC2，即4+（y﹣3）2=1+y2+18，解得：y=﹣1，此时D点坐标为（2，﹣1）；（3）易得BC的解析式为y=﹣x+3．∵直线y=x+m与直线y=x平行，∴直线y=﹣x+3与直线y=x+m垂直，∴∠CEF=90°，∴△ECF为等腰直角三角形，作PH⊥y轴于H，PG∥y轴交BC于G，如图2，△EPG、△PHF都为等腰直角三角形，PE=22PG，PF=2PH，设P（t，t2﹣4t+3）（1＜t＜3），则G（t，﹣t+3），∴PF=2PH=2t，PG=﹣t+3﹣（t2﹣4t+3）=﹣t2+3t，∴PE=22PG=﹣22t2+322t，∴PE+EF=PE+PE+PF=2PE+PF=﹣2t2+32t+2t=﹣2t2+42t=﹣2（t﹣2）2+42，当t=2时，PE+EF的最大值为42．点睛：本题考查了二次函数的综合题．熟练掌握等腰直角三角形的性质、二次函数图象上点的坐标特征和二次函数的性质；会利用待定系数法求二次函数解析式；理解坐标与图形性质，记住两点间的距离公式．4．如图1，已知抛物线y＝ax2+bx+3(a≠0)与x轴交于点A(1，0)和点B(﹣3，0)，与y轴交于点C．(1)求抛物线的解析式；(2)设抛物线的对称轴与x轴交于点M，问在对称轴上是否存在点P，使△CMP为等腰三角形？若存在，请直接写出所有符合条件的点P的坐标；若不存在，请说明理由．(3)在(1)中抛物线的对称轴上是否存在点Q，使得△QAC的周长最小？若存在，求出Q点的坐标；若不存在，请说明理由．(4)如图2，若点E为第二象限抛物线上一动点，连接BE、CE，求四边形BOCE面积的最大值，并求此时E点的坐标．【答案】（1）y＝﹣x2﹣2x+3；（2）存在符合条件的点P，其坐标为P（﹣1，10）或P（﹣1，﹣10）或P（﹣1，6）或P（﹣1，53）；（3）存在，Q（﹣1，2）；（4）63 8，315,24E⎛⎫-⎪⎝⎭.【解析】【分析】（1）已知抛物线过A、B两点，可将两点的坐标代入抛物线的解析式中，用待定系数法即可求出二次函数的解析式；（2）可根据（1）的函数解析式得出抛物线的对称轴，也就得出了M点的坐标，由于C是抛物线与y轴的交点，因此C的坐标为（0，3），根据M、C的坐标可求出CM的距离．然后分三种情况进行讨论：①当CP＝PM时，P位于CM的垂直平分线上．求P点坐标关键是求P的纵坐标，过P作PQ⊥y轴于Q，如果设PM＝CP＝x，那么直角三角形CPQ中CP＝x，OM的长，可根据M 的坐标得出，CQ＝3﹣x，因此可根据勾股定理求出x的值，P点的横坐标与M的横坐标相同，纵坐标为x，由此可得出P的坐标．②当CM＝MP时，根据CM的长即可求出P的纵坐标，也就得出了P的坐标（要注意分上下两点）．③当CM＝C P时，因为C的坐标为（0，3），那么直线y＝3必垂直平分PM，因此P的纵坐标是6，由此可得出P的坐标；（3）根据轴对称﹣最短路径问题解答；（4）由于四边形BOCE不是规则的四边形，因此可将四边形BOCE分割成规则的图形进行计算，过E作EF⊥x轴于F，S四边形BOCE＝S△BFE+S梯形FOCE．直角梯形FOCE中，FO为E的横坐标的绝对值，EF为E的纵坐标，已知C的纵坐标，就知道了OC的长．在△BFE中，BF＝BO﹣OF，因此可用E的横坐标表示出BF的长．如果根据抛物线设出E的坐标，然后代入上面的线段中，即可得出关于四边形BOCE的面积与E的横坐标的函数关系式，根据函数的性质即可求得四边形BOCE的最大值及对应的E的横坐标的值．即可求出此时E的坐标．【详解】（1）∵抛物线y ＝ax 2+bx+3（a≠0）与x 轴交于点A （1，0）和点B （﹣3，0）， ∴309330a b a b ++=⎧⎨-+=⎩，解得：12a b =-⎧⎨=-⎩． ∴所求抛物线解析式为：y ＝﹣x 2﹣2x+3；（2）如答图1，∵抛物线解析式为：y ＝﹣x 2﹣2x+3，∴其对称轴为x ＝22-＝﹣1， ∴设P 点坐标为（﹣1，a ），当x ＝0时，y ＝3，∴C （0，3），M （﹣1，0）∴当CP ＝PM 时，（﹣1）2+（3﹣a ）2＝a 2，解得a ＝53， ∴P 点坐标为：P 1（﹣1，53）； ∴当CM ＝PM 时，（﹣1）2+32＝a 2，解得a ＝±10，∴P 点坐标为：P 2（﹣1，10）或P 3（﹣1，﹣10）；∴当CM ＝CP 时，由勾股定理得：（﹣1）2+32＝（﹣1）2+（3﹣a ）2，解得a ＝6， ∴P 点坐标为：P 4（﹣1，6）．综上所述存在符合条件的点P ，其坐标为P （﹣1，10）或P （﹣1，﹣10）或P （﹣1，6）或P （﹣1，53）；（3）存在，Q （﹣1，2），理由如下：如答图2，点C （0，3）关于对称轴x ＝﹣1的对称点C′的坐标是（﹣2，3），连接AC′，直线AC′与对称轴的交点即为点Q ．设直线AC′函数关系式为：y＝kx+t（k≠0）．将点A（1，0），C′（﹣2，3）代入，得23 k tk t+=⎧⎨-+=⎩，解得11kt=-⎧⎨=⎩，所以，直线AC′函数关系式为：y＝﹣x+1．将x＝﹣1代入，得y＝2，即：Q（﹣1，2）；（4）过点E作EF⊥x轴于点F，设E（a，﹣a2﹣2a+3）（﹣3＜a＜0）∴EF＝﹣a2﹣2a+3，BF＝a+3，OF＝﹣a∴S四边形BOCE＝12BF•EF+12（OC+EF）•OF＝12（a+3）•（﹣a2﹣2a+3）+12（﹣a2﹣2a+6）•（﹣a）＝﹣32a2﹣92a+92＝﹣32（a+32）2+638，∴当a＝﹣32时，S四边形BOCE最大，且最大值为638．此时，点E坐标为（﹣32，154）．【点睛】本题主要考查了二次函数的综合知识，要注意的是（2）中，不确定等腰三角形哪条边是底边的情况下，要分类进行求解，不要漏解．5．如图，已知直线y＝﹣2x+4分别交x轴、y轴于点A、B．抛物线过A、B两点，点P是线段AB上一动点，过点P作PC⊥x轴于点C，交抛物线于点D．（1）如图1，设抛物线顶点为M，且M的坐标是（12，92），对称轴交AB于点N．①求抛物线的解析式；②是否存在点P，使四边形MNPD为菱形？并说明理由；（2）是否存在这样的点D，使得四边形BOAD的面积最大？若存在，求出此时点D的坐标；若不存在，请说明理由．【答案】（1）①y＝﹣2x2+2x+4；；②不存在点P，使四边形MNPD为菱形；；（2）存在，点D的坐标是（1，4）．【解析】【分析】（1）①由一次函数图象上点的坐标特征求得点B的坐标，设抛物线解析式为y＝a21922x⎛⎫-+⎪⎝⎭，把点B的坐标代入求得a的值即可；②不存在点P，使四边形MNPD为菱形．设点P的坐标是（m，﹣2m+4），则D（m，﹣2m2+2m+4），根据题意知PD∥MN，所以当PD＝MN时，四边形MNPD为平行四边形，根据该等量关系列出方程﹣2m2+4m＝32，通过解方程求得m的值，易得点N、P的坐标，然后推知PN＝MN是否成立即可；（2）设点D的坐标是（n，﹣2n2+2n+4），P（n，﹣2n+4）．根据S四边形BOAD＝S△BOA+S△ABD ＝4+S△ABD，则当S△ABD取最大值时，S四边形BOAD最大．根据三角形的面积公式得到函数S△ABD＝﹣2（n﹣1）2+2．由二次函数的性质求得最值．【详解】解：①如图1，∵顶点M的坐标是19,22⎛⎫ ⎪⎝⎭，∴设抛物线解析式为y＝21922a x⎛⎫-+⎪⎝⎭（a≠0）．∵直线y＝﹣2x+4交y轴于点B，∴点B的坐标是（0，4）．又∵点B在该抛物线上，∴21922a⎛⎫-+⎪⎝⎭＝4，解得a＝﹣2．故该抛物线的解析式为：y＝219222x⎛⎫--+⎪⎝⎭＝﹣2x2+2x+4；②不存在．理由如下：∵抛物线y＝219222x⎛⎫--+⎪⎝⎭的对称轴是直线x＝12，且该直线与直线AB交于点N，∴点N的坐标是1,32⎛⎫ ⎪⎝⎭．∴93322MN=-=．设点P的坐标是（m，﹣2m+4），则D（m，﹣2m2+2m+4），∴PD＝（﹣2m2+2m+4）﹣（﹣2m+4）＝﹣2m2+4m．∵PD∥MN．当PD＝MN时，四边形MNPD是平行四边形，即﹣2m2+4m＝32．解得 m1＝12（舍去），m2＝32．此时P（32，1）．∵PN∴PN≠MN，∴平行四边形MNPD不是菱形．∴不存在点P，使四边形MNPD为菱形；（2）存在，理由如下：设点D的坐标是（n，﹣2n2+2n+4），∵点P在线段AB上且直线PD⊥x轴，∴P（n，﹣2n+4）．由图可知S四边形BOAD＝S△BOA+S△ABD．其中S△BOA＝12OB•OA＝12×4×2＝4．则当S△ABD取最大值时，S四边形BOAD最大．S△ABD＝12（y D﹣y P）（x A﹣x B）＝y D﹣y P＝﹣2n2+2n+4﹣（﹣2n+4）＝﹣2n2+4n＝﹣2（n﹣1）2+2．当n＝1时，S△ABD取得最大值2，S四边形BOAD有最大值．此时点D的坐标是（1，4）．【点睛】主要考查了二次函数的解析式的求法和与几何图形结合的综合能力的培养．要会利用数形结合的思想把代数和几何图形结合起来，利用点的坐标的意义表示线段的长度，从而求出线段之间的关系．6．（10分）（2015•佛山）如图，一小球从斜坡O点处抛出，球的抛出路线可以用二次函数y=﹣x2+4x刻画，斜坡可以用一次函数y=x刻画．（1）请用配方法求二次函数图象的最高点P的坐标；（2）小球的落点是A，求点A的坐标；（3）连接抛物线的最高点P与点O、A得△POA，求△POA的面积；（4）在OA上方的抛物线上存在一点M（M与P不重合），△MOA的面积等于△POA的面积．请直接写出点M的坐标．【答案】（1）（2，4）；（2）（，）；（3）；（4）（，）．【解析】试题分析：（1）利用配方法抛物线的一般式化为顶点式，即可求出二次函数图象的最高点P的坐标；（2）联立两解析式，可求出交点A的坐标；（3）作PQ⊥x轴于点Q，AB⊥x轴于点B．根据S△POA=S△POQ+S△梯形PQBA﹣S△BOA，代入数值计算即可求解；（4）过P作OA的平行线，交抛物线于点M，连结OM、AM，由于两平行线之间的距离相等，根据同底等高的两个三角形面积相等，可得△MOA的面积等于△POA的面积．设直线PM的解析式为y=x+b，将P（2，4）代入，求出直线PM的解析式为y=x+3．再与抛物线的解析式联立，得到方程组，解方程组即可求出点M的坐标．试题解析：（1）由题意得，y=﹣x2+4x=﹣（x﹣2）2+4，故二次函数图象的最高点P的坐标为（2，4）；（2）联立两解析式可得：，解得：，或．故可得点A的坐标为（，）；（3）如图，作PQ⊥x轴于点Q，AB⊥x轴于点B．S△POA=S△POQ+S△梯形PQBA﹣S△BOA=×2×4+×（+4）×（﹣2）﹣××=4+﹣=；（4）过P作OA的平行线，交抛物线于点M，连结OM、AM，则△MOA的面积等于△POA的面积．设直线PM的解析式为y=x+b，∵P的坐标为（2，4），∴4=×2+b，解得b=3，∴直线PM的解析式为y=x+3．由，解得，，∴点M的坐标为（，）．考点：二次函数的综合题7．已知二次函数的图象以A（﹣1，4）为顶点，且过点B（2，﹣5）（1）求该函数的关系式；（2）求该函数图象与坐标轴的交点坐标；（3）将该函数图象向右平移，当图象经过原点时，A、B两点随图象移至A′、B′，求△O A′B′的面积．【答案】（1）y=﹣x2﹣2x+3；（2）抛物线与x轴的交点为：（﹣3，0），（1，0）（3）15.【解析】【分析】（1）已知了抛物线的顶点坐标，可用顶点式设该二次函数的解析式，然后将B 点坐标代入，即可求出二次函数的解析式；（2）根据函数解析式，令x=0，可求得抛物线与y轴的交点坐标；令y=0，可求得抛物线与x轴交点坐标；（3）由（2）可知：抛物线与x轴的交点分别在原点两侧，由此可求出当抛物线与x轴负半轴的交点平移到原点时，抛物线平移的单位，由此可求出A′、B′的坐标．由于△OA′B′不规则，可用面积割补法求出△OA′B′的面积．【详解】（1）设抛物线顶点式y=a（x+1）2+4，将B（2，﹣5）代入得：a=﹣1，∴该函数的解析式为：y=﹣（x+1）2+4=﹣x2﹣2x+3；（2）令x=0，得y=3，因此抛物线与y轴的交点为：（0，3），令y=0，﹣x2﹣2x+3=0，解得：x1=﹣3，x2=1，即抛物线与x轴的交点为：（﹣3，0），（1，0）；（3）设抛物线与x轴的交点为M、N（M在N的左侧），由（2）知：M（﹣3，0），N（1，0），当函数图象向右平移经过原点时，M与O重合，因此抛物线向右平移了3个单位，故A'（2，4），B'（5，﹣5），∴S△OA′B′=12×（2+5）×9﹣12×2×4﹣12×5×5=15．【点睛】本题考查了用待定系数法求抛物线解析式、函数图象与坐标轴交点、图形面积的求法等知识．熟练掌握待定系数法、函数图象与坐标轴的交点的求解方法、不规则图形的面积的求解方法等是解题的关键.8．在平面直角坐标系xOy中（如图）．已知抛物线y=﹣12x2+bx+c经过点A（﹣1，0）和点B（0，52），顶点为C，点D在其对称轴上且位于点C下方，将线段DC绕点D按顺时针方向旋转90°，点C落在抛物线上的点P处．（1）求这条抛物线的表达式；（2）求线段CD的长；（3）将抛物线平移，使其顶点C移到原点O的位置，这时点P落在点E的位置，如果点M在y轴上，且以O、D、E、M为顶点的四边形面积为8，求点M的坐标．【答案】（1）抛物线解析式为y=﹣12x 2+2x+52；（2）线段CD 的长为2；（3）M 点的坐标为（0，72）或（0，﹣72）．【解析】【分析】（1）利用待定系数法求抛物线解析式；（2）利用配方法得到y=﹣12（x ﹣2）2+92，则根据二次函数的性质得到C 点坐标和抛物线的对称轴为直线x=2，如图，设CD=t ，则D （2，92﹣t ），根据旋转性质得∠PDC=90°，DP=DC=t ，则P （2+t ，92﹣t ），然后把P （2+t ，92﹣t ）代入y=﹣12x 2+2x+52得到关于t的方程，从而解方程可得到CD 的长；（3）P 点坐标为（4，92），D 点坐标为（2，52），利用抛物线的平移规律确定E 点坐标为（2，﹣2），设M （0，m ），当m ＞0时，利用梯形面积公式得到12•（m+52+2）•2=8当m ＜0时，利用梯形面积公式得到12•（﹣m+52+2）•2=8，然后分别解方程求出m 即可得到对应的M 点坐标．【详解】（1）把A （﹣1，0）和点B （0，52）代入y=﹣12x 2+bx+c 得 10252b c c ⎧--+=⎪⎪⎨⎪=⎪⎩，解得252b c =⎧⎪⎨=⎪⎩，∴抛物线解析式为y=﹣12x 2+2x+52；（2）∵y=﹣12（x ﹣2）2+92， ∴C （2，92），抛物线的对称轴为直线x=2，如图，设CD=t ，则D （2，92﹣t ），∵线段DC 绕点D 按顺时针方向旋转90°，点C 落在抛物线上的点P 处， ∴∠PDC=90°，DP=DC=t ， ∴P （2+t ，92﹣t ），把P （2+t ，92﹣t ）代入y=﹣12x 2+2x+52得﹣12（2+t ）2+2（2+t ）+52=92﹣t ，整理得t 2﹣2t=0，解得t 1=0（舍去），t 2=2， ∴线段CD 的长为2；（3）P 点坐标为（4，92），D 点坐标为（2，52）， ∵抛物线平移，使其顶点C （2，92）移到原点O 的位置， ∴抛物线向左平移2个单位，向下平移92个单位，而P 点（4，92）向左平移2个单位，向下平移92个单位得到点E ， ∴E 点坐标为（2，﹣2），设M （0，m ），当m ＞0时，12•（m+52+2）•2=8，解得m=72，此时M 点坐标为（0，72）；当m ＜0时，12•（﹣m+52+2）•2=8，解得m=﹣72，此时M 点坐标为（0，﹣72）；综上所述，M 点的坐标为（0，72）或（0，﹣72）．【点睛】本题考查了二次函数的综合题，涉及到待定系数法、抛物线上点的坐标、旋转的性质、抛物线的平移等知识，综合性较强，正确添加辅助线、运用数形结合思想熟练相关知识是解题的关键.9．如图，抛物线25(0)y ax bx a =+-≠经过x 轴上的点A （1，0）和点B 及y 轴上的点C ，经过B 、C 两点的直线为y x n =+． ①求抛物线的解析式．②点P 从A 出发，在线段AB 上以每秒1个单位的速度向B 运动，同时点E 从B 出发，在线段BC 上以每秒2个单位的速度向C 运动．当其中一个点到达终点时，另一点也停止运动．设运动时间为t 秒，求t 为何值时，△PBE 的面积最大并求出最大值．③过点A 作AM BC ⊥于点M ，过抛物线上一动点N （不与点B 、C 重合）作直线AM 的平行线交直线BC 于点Q ．若点A 、M 、N 、Q 为顶点的四边形是平行四边形，求点N 的横坐标．【答案】①265y x x =-+-；②当2t =时，△PBE 的面积最大，最大值为22③点N 的横坐标为：4或5412+或5412．【解析】【分析】①点B 、C 在直线为y x n =+上，则B （﹣n ，0）、C （0，n ），点A （1，0）在抛物线上，所以250505a b an bn n +-=⎧⎪+-=⎨⎪=-⎩，解得1a =-，6b =，因此抛物线解析式：265y x x =-+-；②先求出点P 到BC 的高h 为2sin 45(4)2BP t ︒=-，于是21122)22)2222PBE S BE h t t t ∆=⋅=-⨯=-+2t =时，△PBE 的面积最大，最大值为22③由①知，BC 所在直线为：5y x =-，所以点A 到直线BC 的距离22d =N 作x 轴的垂线交直线BC 于点P ，交x 轴于点H ．设()2,65N m m m -+-，则(,0)H m 、(,5)P m m -，易证△PQN 为等腰直角三角形，即22NQ PQ ==4PN =，Ⅰ．4NH HP +=，所以265(5)4m m m -+---=解得11m =（舍去），24m =，Ⅱ．4NH HP +=，()25654m m m ---+-=解得1541m +=，2541m -=去），Ⅲ．4NH HP -=，()265[(5)]4m m m --+----=，解得15412m =（舍去），252m =．【详解】解：①∵点B 、C 在直线为y x n =+上， ∴B （﹣n ，0）、C （0，n ）， ∵点A （1，0）在抛物线上，∴250505a b an bn n +-=⎧⎪+-=⎨⎪=-⎩， ∴1a =-，6b =，∴抛物线解析式：265y x x =-+-； ②由题意，得，4PB t =-，2BE t =，由①知，45OBC ︒∠=， ∴点P 到BC 的高h为sin 45)BP t ︒=-，∴211)22)22PBE S BE h t t t ∆=⋅=-⨯=-+ 当2t =时，△PBE的面积最大，最大值为 ③由①知，BC 所在直线为：5y x =-， ∴点A 到直线BC的距离d =过点N 作x 轴的垂线交直线BC 于点P ，交x 轴于点H ．设()2,65N m m m -+-，则(,0)H m 、(,5)P m m -，易证△PQN为等腰直角三角形，即NQ PQ == ∴4PN =， Ⅰ．4NH HP +=， ∴265(5)4m m m -+---= 解得11m =，24m =，∵点A 、M 、N 、Q 为顶点的四边形是平行四边形， ∴4m =；Ⅱ．4NH HP +=， ∴()25654m m m ---+-=解得1m =，2m =∵点A 、M 、N 、Q 为顶点的四边形是平行四边形，5m >，∴541m +=， Ⅲ．4NH HP -=，∴()265[(5)]4m m m --+----=，解得15412m +=，25412m -=，∵点A 、M 、N 、Q 为顶点的四边形是平行四边形，0m <，∴5412m -=，综上所述，若点A 、M 、N 、Q 为顶点的四边形是平行四边形，点N 的横坐标为：4或541+或541-．【点睛】本题考查了二次函数，熟练掌握二次函数的性质、平行四边形的判定与性质是解题的关键．10．已知抛物线C 1：y=ax 2﹣4ax ﹣5（a ＞0）．（1）当a=1时，求抛物线与x 轴的交点坐标及对称轴；（2）①试说明无论a 为何值，抛物线C 1一定经过两个定点，并求出这两个定点的坐标； ②将抛物线C 1沿这两个定点所在直线翻折，得到抛物线C 2，直接写出C 2的表达式；（3）若（2）中抛物线C 2的顶点到x 轴的距离为2，求a 的值．【答案】（1）（﹣1，0）或（5，0）（2）①（0，﹣5），（4，﹣5）②y=﹣ax 2+4ax ﹣5（3）a=或【解析】试题分析：（1）将a=1代入解析式，即可求得抛物线与x轴交点；（2）①化简抛物线解析式，即可求得两个点定点的横坐标，即可解题；②根据抛物线翻折理论即可解题；（3）根据（2）中抛物线C2解析式，分类讨论y=2或﹣2，即可解题试题解析：（1）当a=1时，抛物线解析式为y=x2﹣4x﹣5=（x﹣2）2﹣9，∴对称轴为y=2；∴当y=0时，x﹣2=3或﹣3，即x=﹣1或5；∴抛物线与x轴的交点坐标为（﹣1，0）或（5，0）；（2）①抛物线C1解析式为：y=ax2﹣4ax﹣5，整理得：y=ax（x﹣4）﹣5；∵当ax（x﹣4）=0时，y恒定为﹣5；∴抛物线C1一定经过两个定点（0，﹣5），（4，﹣5）；②这两个点连线为y=﹣5；将抛物线C1沿y=﹣5翻折，得到抛物线C2，开口方向变了，但是对称轴没变；∴抛物线C2解析式为：y=﹣ax2+4ax﹣5，（3）抛物线C2的顶点到x轴的距离为2，则x=2时，y=2或者﹣2；当y=2时，2=﹣4a+8a﹣5，解得，a=；当y=﹣2时，﹣2=﹣4a+8a﹣5，解得，a=；∴a=或；考点：1、抛物线与x轴的交点；2、二次函数图象与几何变换11．（本小题满分12分）如图，在平面直角坐标系xOy中，抛物线（）与x轴交于A，B两点（点A在点B的左侧），经过点A的直线l：与y轴负半轴交于点C，与抛物线的另一个交点为D，且CD=4AC．（1）直接写出点A的坐标，并求直线l的函数表达式（其中k，b用含a的式子表示）；（2）点E是直线l上方的抛物线上的动点，若△ACE的面积的最大值为，求a的值；（3）设P是抛物线的对称轴上的一点，点Q在抛物线上，以点A，D，P，Q为顶点的四边形能否成为矩形？若能，求出点P的坐标；若不能，请说明理由．【答案】（1）A（－1，0），；（2）；（3）P的坐标为（1，）或（1，－4）．【解析】试题分析：（1）在中，令y=0，得到，，得到A（－1，0），B（3，0），由直线l经过点A，得到，故，令，即，由于CD＝4AC，故点D的横坐标为4，即有，得到，从而得出直线l的函数表达式；（2）过点E作EF∥y轴，交直线l于点F，设E（，），则F（，），EF＝=，S△ACE＝S△AFE－S△CFE＝＝，故△ACE的面积的最大值为，而△ACE的面积的最大值为，所以，解得；（3）令，即，解得，，得到D （4，5a），因为抛物线的对称轴为，设P（1，m），然后分两种情况讨论：①若AD是矩形的一条边，②若AD是矩形的一条对角线．试题解析：（1）∵=，令y=0，得到，，∴A（－1，0），B（3，0），∵直线l经过点A，∴，，∴，令，即，∵CD＝4AC，∴点D的横坐标为4，∴，∴，∴直线l的函数表达式为；（2）过点E作EF∥y轴，交直线l于点F，设E（，），则F（，），EF＝=，S△ACE＝S△AFE－S△CFE＝＝＝，∴△ACE的面积的最大值为，∵△ACE的面积的最大值为，∴，解得；（3）令，即，解得，，∴D（4，5a），∵，∴抛物线的对称轴为，设P（1，m），①若AD是矩形的一条边，则Q（－4，21a），m＝21a＋5a＝26a，则P（1，26a），∵四边形ADPQ为矩形，∴∠ADP＝90°，∴，∴，即，∵，∴，∴P1（1，）；②若AD 是矩形的一条对角线，则线段AD 的中点坐标为（，），Q （2，），m ＝，则P （1，8a ），∵四边形APDQ 为矩形，∴∠APD ＝90°，∴，∴，即，∵，∴，∴P 2（1，－4）．综上所述，以点A 、D 、P 、Q 为顶点的四边形能成为矩形，点P 的坐标为（1，）或（1，－4）．考点：二次函数综合题．12．如图，已知抛物线2(0)y ax bx a =+≠过点3,-3) 和3,0)，过点A 作直线AC//x 轴，交y 轴与点C ．（1）求抛物线的解析式；（2）在抛物线上取一点P ，过点P 作直线AC 的垂线，垂足为D ，连接OA ，使得以A ，D ，P 为顶点的三角形与△AOC 相似，求出对应点P 的坐标；（3）抛物线上是否存在点Q ，使得13AOC AOQ S S ∆∆=?若存在，求出点Q 的坐标；若不存在，请说明理由.【答案】（1）21332y x x =-；（2）P 点坐标为（383,- 43）；（3）Q 点坐标（30）或（315）【解析】【分析】（1）把A 与B 坐标代入抛物线解析式求出a 与b 的值，即可确定出解析式；（2）设P 坐标为2133,22x x x ⎛⎫- ⎪ ⎪⎝⎭，表示出AD 与PD ，由相似分两种情况得比例求出x 的值，即可确定出P 坐标；（3）存在，求出已知三角形AOC 边OA 上的高h ，过O 作OM ⊥OA ，截取OM=h,与y 轴交于点N ，分别确定出M 与N 坐标，利用待定系数法求出直线MN 解析式，与抛物线解析式联立求出Q 坐标即可．【详解】（1）把3A 3)-和点(33B 0)代入抛物线得：33327330a b a b ⎧+=-⎪⎨+=⎪⎩，解得：12a =，332b =-，则抛物线解析式为213322y x x =-；（2）当P 在直线AD 上方时，设P 坐标为2133,2x x x ⎛⎫ ⎪ ⎪⎝⎭，则有3AD x =213332PD x x =+，当OCA ADP ∆∆∽时，OC CA AD DP =2331333x x x =--+，整理得：239318236x x x -+=-，即23113240x x -+=，解得：6x =，即3x =或x =此时P 4)3-；当OCA PDA ∆∆∽时，OC CA PD AD =22=，296x x -+=-2120x -+=，解得：x =x =此时P 6)；当点()0,0P 时，也满足OCA PDA ∆∆∽；当P 在直线AD 下方时，同理可得：P的坐标为10)3-，综上，P的坐标为，4)3-或6)或10)3-或()0,0；（3）在Rt AOC ∆中，3OC =，AC =根据勾股定理得：OA =Q 11··22OC AC OA h =， 32h ∴=，132AOC AOQ S S ∆∆==Q ， AOQ ∴∆边OA 上的高为92，过O 作OM OA ⊥，截取92OM =，过M 作//MN OA ，交y 轴于点N ，如图所示：在Rt OMN ∆中，29ON OM ==，即()0,9N ，过M 作MH x ⊥轴，在Rt OMH ∆中，1924MH OM ==，393OH ==，即93(M ，9)4，设直线MN 解析式为9y kx =+，把M 坐标代入得：99394=+，即3k =39y x =+，联立得：23913322y x y x x ⎧=-+⎪⎨=-⎪⎩，解得：330x y ⎧=⎪⎨=⎪⎩315x y ⎧=-⎪⎨=⎪⎩(33Q 0)或(23-，15)，则抛物线上存在点Q ，使得13AOC AOQ S S ∆∆=，此时点Q 的坐标为(330)或(23-15)．【点睛】二次函数综合题，涉及的知识有：待定系数法求函数解析式，相似三角形的判定与性质，点到直线的距离公式，熟练掌握待定系数法是解本题的关键．13．如图1，抛物线y=ax 2+2x+c 与x 轴交于A （﹣4，0），B （1，0）两点，过点B 的直线y=kx+23分别与y 轴及抛物线交于点C ，D ．（1）求直线和抛物线的表达式；（2）动点P 从点O 出发，在x 轴的负半轴上以每秒1个单位长度的速度向左匀速运动，设运动时间为t 秒，当t 为何值时，△PDC 为直角三角形？请直接写出所有满足条件的t 的值；（3）如图2，将直线BD 沿y 轴向下平移4个单位后，与x 轴，y 轴分别交于E ，F 两点，在抛物线的对称轴上是否存在点M ，在直线EF 上是否存在点N ，使DM+MN 的值最小？若存在，求出其最小值及点M ，N 的坐标；若不存在，请说明理由．【答案】（1）抛物线解析式为：y=228233x x +-，BD 解析式为y=﹣2233x +；（2）t 的值为4915129±、233．（3）N 点坐标为（﹣2，﹣2），M 点坐标为（﹣32，﹣54），213 【解析】分析：（1）利用待定系数法求解可得；（2）先求得点D 的坐标，过点D 分别作DE ⊥x 轴、DF ⊥y 轴，分P 1D ⊥P 1C 、P 2D ⊥DC 、P 3C ⊥DC 三种情况，利用相似三角形的性质逐一求解可得；（3）通过作对称点，将折线转化成两点间距离，应用两点之间线段最短．详解：（1）把A （﹣4，0），B （1，0）代入y=ax 2+2x+c ，得168020a c a c -+=⎧⎨++=⎩，解得：2383a c ⎧=⎪⎪⎨⎪=-⎪⎩，∴抛物线解析式为：y=228233x x +-， ∵过点B 的直线y=kx+23， ∴代入（1，0），得：k=﹣23， ∴BD 解析式为y=﹣2233x +；（2）由2282332233y x xy x﹣⎧=+-⎪⎪⎨⎪=+⎪⎩得交点坐标为D（﹣5，4），如图1，过D作DE⊥x轴于点E，作DF⊥y轴于点F，当P1D⊥P1C时，△P1DC为直角三角形，则△DEP1∽△P1OC，∴DEPO=PEOC，即4t=523t-，解得t=151296±，当P2D⊥DC于点D时，△P2DC为直角三角形由△P2DB∽△DEB得DBEB=2P BDB，5252，解得：t=233；当P3C⊥DC时，△DFC∽△COP3，∴DFOC=3CFP O，即523=103t，解得：t=49，∴t的值为49、151296、233．（3）由已知直线EF解析式为：y=﹣23x﹣103，在抛物线上取点D的对称点D′，过点D′作D′N⊥EF于点N，交抛物线对称轴于点M过点N 作NH ⊥DD′于点H ，此时，DM+MN=D′N 最小．则△EOF ∽△NHD′ 设点N 坐标为（a ，﹣21033a -）， ∴OE NH =OF HD '，即52104()33a ---=1032a -，解得：a=﹣2，则N 点坐标为（﹣2，﹣2），求得直线ND′的解析式为y=32x+1，当x=﹣32时，y=﹣54， ∴M 点坐标为（﹣32，﹣54），此时，DM+MN 的值最小为22D H NH '+=2246+=213．点睛：本题是二次函数和几何问题综合题，应用了二次函数性质以及转化的数学思想、分类讨论思想．解题时注意数形结合．14．如图，已知抛物线2y ax bx c =++（a≠0）经过A （﹣1，0）、B （3，0）、C （0，﹣3）三点，直线l 是抛物线的对称轴．（1）求抛物线的函数关系式；（2）设点P 是直线l 上的一个动点，当点P 到点A 、点B 的距离之和最短时，求点P 的坐标；（3）点M 也是直线l 上的动点，且△MAC 为等腰三角形，请直接写出所有符合条件的点M 的坐标．【答案】（1）223y x x =--；（2）P （1，0）；（3）．【解析】试题分析：（1）直接将A 、B 、C 三点坐标代入抛物线的解析式中求出待定系数即可；（2）由图知：A ．B 点关于抛物线的对称轴对称，那么根据抛物线的对称性以及两点之间线段最短可知，直线l 与x 轴的交点，即为符合条件的P 点；（3）由于△MAC 的腰和底没有明确，因此要分三种情况来讨论：①MA=AC 、②MA=MC 、③AC=MC ；可先设出M 点的坐标，然后用M 点纵坐标表示△MAC 的三边长，再按上面的三种情况列式求解．试题解析：（1）将A （﹣1，0）、B （3，0）、C （0，﹣3）代入抛物线2y ax bx c=++中，得：0{9303a b c a b c c -+=++==-，解得：1{23a b c ==-=-，故抛物线的解析式：223y x x =--．（2）当P 点在x 轴上，P ，A ，B 三点在一条直线上时，点P 到点A 、点B 的距离之和最短，此时x=2ba-=1，故P （1，0）；（3）如图所示：抛物线的对称轴为：x=2ba-=1，设M （1，m ），已知A （﹣1，0）、C （0，﹣3），则：2MA =24m +，2MC =2(3)1m ++=2610m m ++，2AC =10；①若MA=MC ，则22MA MC =，得：24m +=2610m m ++，解得：m=﹣1； ②若MA=AC ，则22MA AC =，得：24m +=10，得：m=6±；③若MC=AC ，则22MC AC =，得：2610m m ++=10，得：10m =，26m =-；当m=﹣6时，M 、A 、C 三点共线，构不成三角形，不合题意，故舍去；综上可知，符合条件的M 点，且坐标为 M （1，6）（1，6-）（1，﹣1）（1，0）．考点：二次函数综合题；分类讨论；综合题；动点型．15．如图1，四边形OABC 是矩形，点A 的坐标为(3,0)，点c 的坐标为(0,6).点P 从点O 出发，沿OA 以每秒1个单位长度的速度向点A 运动，同时点Q 从点A 出发，沿AB 以每秒2个单位长度的速度向点B 运动，当点P 与点A 重合时运动停止.设运动时间为t 秒.（1）当2t =时，线段PQ 的中点坐标为________；（2）当CBQ ∆与PAQ ∆相似时，求t 的值；（3）当1t =时，抛物线2y x bx c =++经过P 、Q 两点，与y 轴交于点M ，抛物线的顶点为K ，如图2所示.问该抛物线上是否存在点D ，使12MQD MKQ ∠=∠，若存在，求出所有满足条件的D 点坐标；若不存在，说明理由. 【答案】（1）PQ 的中点坐标是(2.5,2)；（2）9352t -=或3t 4=；（3）124(,)39D ，2240(,)39D -. 【解析】分析：（1）先根据时间t=2，和速度可得动点P 和Q 的路程OP 和AQ 的长，再根据中点坐标公式可得结论；（2）根据矩形的性质得：∠B=∠PAQ=90°，所以当△CBQ 与△PAQ 相似时，存在两种情况：①当△PAQ ∽△QBC 时，PA QB AQ BC ＝，②当△PAQ ∽△CBQ 时，PA BC AQ QB＝，分别列方程可得t 的值；（3）根据t=1求抛物线的解析式，根据Q （3，2），M （0，2），可得MQ ∥x 轴，∴KM=KQ ，KE ⊥MQ ，画出符合条件的点D ，证明△KEQ ∽△QMH ，列比例式可得点D 的坐标，同理根据对称可得另一个点D ．详解：（1）如图1，∵点A 的坐标为（3，0）， ∴OA=3，当t=2时，OP=t=2，AQ=2t=4， ∴P （2，0），Q （3，4），。

初三数学二次函数的专项培优练习题含详细答案

初三数学二次函数的专项培优练习题含详细答案一、二次函数1．已知：如图，抛物线y=ax2+bx+c与坐标轴分别交于点A（0，6），B（6，0），C（﹣2，0），点P是线段AB上方抛物线上的一个动点．（1）求抛物线的解析式；（2）当点P运动到什么位置时，△PAB的面积有最大值？（3）过点P作x轴的垂线，交线段AB于点D，再过点P做PE∥x轴交抛物线于点E，连结DE，请问是否存在点P使△PDE为等腰直角三角形？若存在，求出点P的坐标；若不存在，说明理由．【答案】（1）抛物线解析式为y=﹣12x2+2x+6；（2）当t=3时，△PAB的面积有最大值；（3）点P（4，6）．【解析】【分析】（1）利用待定系数法进行求解即可得；（2）作PM⊥OB与点M，交AB于点N，作AG⊥PM，先求出直线AB解析式为y=﹣x+6，设P（t，﹣12t2+2t+6），则N（t，﹣t+6），由S△PAB=S△PAN+S△PBN=12PN•AG+12PN•BM=12PN•OB列出关于t的函数表达式，利用二次函数的性质求解可得；（3）由PH⊥OB知DH∥AO，据此由OA=OB=6得∠BDH=∠BAO=45°，结合∠DPE=90°知若△PDE为等腰直角三角形，则∠EDP=45°，从而得出点E与点A重合，求出y=6时x的值即可得出答案．【详解】（1）∵抛物线过点B（6，0）、C（﹣2，0），∴设抛物线解析式为y=a（x﹣6）（x+2），将点A（0，6）代入，得：﹣12a=6，解得：a=﹣12，所以抛物线解析式为y=﹣12（x﹣6）（x+2）=﹣12x2+2x+6；（2）如图1，过点P作PM⊥OB与点M，交AB于点N，作AG⊥PM于点G，设直线AB 解析式为y=kx+b ，将点A （0，6）、B （6，0）代入，得：660b k b =⎧⎨+=⎩，解得：16k b =-⎧⎨=⎩，则直线AB 解析式为y=﹣x+6，设P （t ，﹣12t 2+2t+6）其中0＜t ＜6，则N （t ，﹣t+6）， ∴PN=PM ﹣MN=﹣12t 2+2t+6﹣（﹣t+6）=﹣12t 2+2t+6+t ﹣6=﹣12t 2+3t ， ∴S △PAB =S △PAN +S △PBN=12PN•AG+12PN•BM =12PN•（AG+BM ） =12PN•OB =12×（﹣12t 2+3t ）×6 =﹣32t 2+9t =﹣32（t ﹣3）2+272， ∴当t=3时，△PAB 的面积有最大值；（3）如图2，∵PH ⊥OB 于H ，∴∠DHB=∠AOB=90°，∴DH ∥AO ，∵OA=OB=6，∴∠BDH=∠BAO=45°，∵PE ∥x 轴、PD ⊥x 轴，∴∠DPE=90°，若△PDE 为等腰直角三角形，则∠EDP=45°，∴∠EDP 与∠BDH 互为对顶角，即点E 与点A 重合，则当y=6时，﹣12x 2+2x+6=6，解得：x=0（舍）或x=4，即点P （4，6）．【点睛】本题考查了二次函数的综合问题，涉及到待定系数法、二次函数的最值、等腰直角三角形的判定与性质等，熟练掌握和灵活运用待定系数法求函数解析式、二次函数的性质、等腰直角三角形的判定与性质等是解题的关键.2．新春佳节，电子鞭炮因其安全、无污染开始走俏．某商店经销一种电子鞭炮，已知这种电子鞭炮的成本价为每盒80元，市场调查发现，该种电子鞭炮每天的销售量y （盒）与销售单价x （元）有如下关系：y=﹣2x+320（80≤x≤160）．设这种电子鞭炮每天的销售利润为w 元．（1）求w 与x 之间的函数关系式；（2）该种电子鞭炮销售单价定为多少元时，每天的销售利润最大？最大利润是多少元？（3）该商店销售这种电子鞭炮要想每天获得2400元的销售利润，又想卖得快．那么销售单价应定为多少元？【答案】（1）w=﹣2x 2+480x ﹣25600；（2）销售单价定为120元时，每天销售利润最大，最大销售利润3200元（3）销售单价应定为100元【解析】【分析】（1）用每件的利润()80x -乘以销售量即可得到每天的销售利润，即()()()80802320w x y x x =-=--+，然后化为一般式即可；（2）把（1）中的解析式进行配方得到顶点式()221203200w x =--+，然后根据二次函数的最值问题求解；（3）求2400w =所对应的自变量的值，即解方程()2212032002400x --+=．然后检验即可.【详解】（1）()()()80802320w x y x x =-=--+，2248025600x x =-+-，w 与x 的函数关系式为：2248025600w x x =-+-；（2）()2224802560021203200w x x x =-+-=--+，2080160x -<≤≤Q ，，∴当120x =时，w 有最大值．w 最大值为3200．答：销售单价定为120元时，每天销售利润最大，最大销售利润3200元．（3）当2400w =时，()2212032002400x --+=．解得：12100140x x ，．== ∵想卖得快， 2140x ∴=不符合题意，应舍去．答：销售单价应定为100元．3．如图，抛物线y ＝﹣x 2﹣2x+3的图象与x 轴交于A 、B 两点(点A 在点B 的左边)，与y 轴交于点C ，点D 为抛物线的顶点．(1)求点A 、B 、C 的坐标；(2)点M(m ，0)为线段AB 上一点(点M 不与点A 、B 重合)，过点M 作x 轴的垂线，与直线AC 交于点E ，与抛物线交于点P ，过点P 作PQ ∥AB 交抛物线于点Q ，过点Q 作QN ⊥x 轴于点N ，可得矩形PQNM ．如图，点P 在点Q 左边，试用含m 的式子表示矩形PQNM 的周长；(3)当矩形PQNM 的周长最大时，m 的值是多少？并求出此时的△AEM 的面积；(4)在(3)的条件下，当矩形PMNQ 的周长最大时，连接DQ ，过抛物线上一点F 作y 轴的平行线，与直线AC 交于点G(点G 在点F 的上方)．若FG ＝22DQ ，求点F 的坐标．【答案】(1)A(﹣3，0)，B(1，0)；C(0，3) ；(2)矩形PMNQ 的周长＝﹣2m 2﹣8m+2；(3) m ＝﹣2；S ＝12；(4)F(﹣4，﹣5)或(1，0)．【解析】【分析】（1）利用函数图象与坐标轴的交点的求法，求出点A ，B ，C 的坐标；（2）先确定出抛物线对称轴，用m表示出PM，MN即可；（3）由（2）得到的结论判断出矩形周长最大时，确定出m，进而求出直线AC解析式，即可；（4）在（3）的基础上，判断出N应与原点重合，Q点与C点重合，求出DQ＝DC＝，再建立方程（n+3）﹣（﹣n2﹣2n+3）＝4即可．【详解】(1)由抛物线y＝﹣x2﹣2x+3可知，C(0，3)．令y＝0，则0＝﹣x2﹣2x+3，解得，x＝﹣3或x＝l，∴A(﹣3，0)，B(1，0)．(2)由抛物线y＝﹣x2﹣2x+3可知，对称轴为x＝﹣1．∵M(m，0)，∴PM＝﹣m2﹣2m+3，MN＝(﹣m﹣1)×2＝﹣2m﹣2，∴矩形PMNQ的周长＝2(PM+MN)＝(﹣m2﹣2m+3﹣2m﹣2)×2＝﹣2m2﹣8m+2．(3)∵﹣2m2﹣8m+2＝﹣2(m+2)2+10，∴矩形的周长最大时，m＝﹣2．∵A(﹣3，0)，C(0，3)，设直线AC的解析式y＝kx+b，∴303k bb-+=⎧⎨=⎩解得k＝l，b＝3，∴解析式y＝x+3，令x＝﹣2，则y＝1，∴E(﹣2，1)，∴EM＝1，AM＝1，∴S＝12AM×EM＝12．(4)∵M(﹣2，0)，抛物线的对称轴为x＝﹣l，∴N应与原点重合，Q点与C点重合，∴DQ＝DC，把x＝﹣1代入y＝﹣x2﹣2x+3，解得y＝4，∴D(﹣1，4)，∴DQ＝DC∵FG＝，∴FG＝4．设F(n，﹣n2﹣2n+3)，则G(n，n+3)，∵点G在点F的上方且FG＝4，∴(n+3)﹣(﹣n2﹣2n+3)＝4．解得n ＝﹣4或n ＝1，∴F(﹣4，﹣5)或(1，0)．【点睛】此题是二次函数综合题，主要考查了函数图象与坐标轴的交点的求法，待定系数法求函数解析式，函数极值的确定，解本题的关键是用m 表示出矩形PMNQ 的周长．4．如图，抛物线y=ax 2+bx+c 与x 轴交于点A 和点B （1，0），与y 轴交于点C （0，3），其对称轴l 为x=﹣1．（1）求抛物线的解析式并写出其顶点坐标；（2）若动点P 在第二象限内的抛物线上，动点N 在对称轴l 上．①当PA ⊥NA ，且PA=NA 时，求此时点P 的坐标；②当四边形PABC 的面积最大时，求四边形PABC 面积的最大值及此时点P 的坐标．【答案】（1）y=﹣（x+1）2+4，顶点坐标为（﹣1，4）；（2）①点P 2﹣1，2）；②P （﹣32，154）【解析】试题分析：（1）将B 、C 的坐标代入已知的抛物线的解析式，由对称轴为1x =-即可得到抛物线的解析式；（2）①首先求得抛物线与x 轴的交点坐标，然后根据已知条件得到PD=OA ，从而得到方程求得x 的值即可求得点P 的坐标；②ΔOBC ΔAPD ABCP C =PDO S S S S ++四边形梯形，表示出来得到二次函数，求得最值即可．试题解析：（1）∵抛物线2y ax bx c =++与x 轴交于点A 和点B （1，0），与y 轴交于点C （0，3），其对称轴l 为1x =-，∴0{312a b c c b a++==-=-，解得：1{23a b c =-=-=，∴二次函数的解析式为223y x x =--+=2(1)4x -++，∴顶点坐标为（﹣1，4）；（2）令2230y x x =--+=，解得3x =-或1x =，∴点A （﹣3，0），B （1，0），作PD ⊥x 轴于点D ，∵点P 在223y x x =--+上，∴设点P （x ，223x x --+），①∵PA ⊥NA ，且PA=NA ，∴△PAD ≌△AND ，∴OA=PD ，即2232y x x =--+=，解得x=21-（舍去）或x=21--，∴点P （21--，2）；②设P(x ，y)，则223y x x =--+，∵ΔOBC ΔAPD ABCP C =PDO S S S S ++四边形梯形=12OB•OC+12AD•PD+12(PD+OC)•OD=11131+(3)(3)()222x y y x ⨯⨯⨯+++-=333222x y -+ =2333(23)222x x x -+--+=239622x x --+=23375()228x -++， ∴当x=32-时，ABCP S 四边形最大值=758，当x=32-时，223y x x =--+=154，此时P （32-，154）．考点：1．二次函数综合题；2．二次函数的最值；3．最值问题；4．压轴题．5．如图，直线l ：y ＝﹣3x +3与x 轴、y 轴分别相交于A 、B 两点，抛物线y ＝ax 2﹣2ax +a +4（a ＜0）经过点B ，交x 轴正半轴于点C ．（1）求该抛物线的函数表达式；（2）已知点M 是抛物线上的一个动点，并且点M 在第一象限内，连接AM 、BM ，设点M 的横坐标为m ，△ABM 的面积为S ，求S 与m 的函数表达式，并求出S 的最大值及此时动点M 的坐标；（3）将点A 绕原点旋转得点A ′，连接CA ′、BA ′，在旋转过程中，一动点M 从点B 出发，沿线段BA ′以每秒3个单位的速度运动到A ′，再沿线段A ′C 以每秒1个单位长度的速度运动到C 后停止，求点M 在整个运动过程中用时最少是多少？【答案】（1）y＝﹣x2+2x+3；（2）S与m的函数表达式是S＝252m m--，S的最大值是25 8，此时动点M的坐标是（52，74）；（3）点M82秒．【解析】【分析】（1）首先求出B点的坐标，根据B点的坐标即可计算出二次函数的a值，进而即可计算出二次函数的解析式;（2）计算出C点的坐标，设出M点的坐标，再根据△ABM的面积为S＝S四边形OAMB﹣S△AOB ＝S△BOM+S△OAM﹣S△AOB，化简成二次函数，再根据二次函数求解最大值即可.（3）首先证明△OHA′∽△OA′B，再结合A′H+A′C≥HC即可计算出t的最小值.【详解】（1）将x＝0代入y＝﹣3x+3，得y＝3，∴点B的坐标为（0，3），∵抛物线y＝ax2﹣2ax+a+4（a＜0）经过点B，∴3＝a+4，得a＝﹣1，∴抛物线的解析式为：y＝﹣x2+2x+3；（2）将y＝0代入y＝﹣x2+2x+3，得x1＝﹣1，x2＝3，∴点C的坐标为（3，0），∵点M是抛物线上的一个动点，并且点M在第一象限内，点M的横坐标为m，∴0＜m＜3，点M的坐标为（m，﹣m2+2m+3），将y＝0代入y＝﹣3x+3，得x＝1，∴点A的坐标（1，0），∵△ABM的面积为S，∴S＝S四边形OAMB﹣S△AOB＝S△BOM+S△OAM﹣S△AOB＝()2123313 222m mm⨯-++⨯⨯+-，化简，得S＝252m m--＝21525228m⎛⎫--+⎪⎝⎭，∴当m ＝52时，S 取得最大值，此时S ＝258，此时点M 的坐标为（52，74），即S 与m 的函数表达式是S ＝252m m --，S 的最大值是258，此时动点M 的坐标是（52，74）；（3）如右图所示，取点H 的坐标为（0，13），连接HA ′、OA ′， ∵∠HOA ′＝∠A ′OB ，13OH OA '=，13OA OB '=， ∴△OHA ′∽△OA ′B ，∴3BA A H''=，即3BA A H ''=， ∵A ′H +A ′C ≥HC ＝2218233⎛⎫+= ⎪⎝⎭， ∴t ≥82，即点M 在整个运动过程中用时最少是82秒．【点睛】本题主要考查抛物线的性质，关键在于设元，还有就是（3）中利用代替法计算t 的取值范围，难度系数较大，是中考的压轴题.6．对于某一函数给出如下定义：若存在实数m ，当其自变量的值为m 时，其函数值等于﹣m ，则称﹣m 为这个函数的反向值．在函数存在反向值时，该函数的最大反向值与最小反向值之差n 称为这个函数的反向距离．特别地，当函数只有一个反向值时，其反向距离n 为零．例如，图中的函数有4，﹣1两个反向值，其反向距离n 等于5．（1）分别判断函数y＝﹣x+1，y＝1x-，y＝x2有没有反向值？如果有，直接写出其反向距离；（2）对于函数y＝x2﹣b2x，①若其反向距离为零，求b的值；②若﹣1≤b≤3，求其反向距离n的取值范围；（3）若函数y＝223()3()x x x mx x x m⎧-≥⎨--<⎩请直接写出这个函数的反向距离的所有可能值，并写出相应m的取值范围．【答案】（1）y＝−1x有反向值，反向距离为2；y＝x2有反向值，反向距离是1；（2）①b＝±1；②0≤n≤8；（3）当m＞2或m≤﹣2时，n＝2，当﹣2＜m≤2时，n＝4．【解析】【分析】(1)根据题目中的新定义可以分别计算出各个函数是否有方向值，有反向值的可以求出相应的反向距离；(2)①根据题意可以求得相应的b的值；②根据题意和b的取值范围可以求得相应的n的取值范围；(3)根据题目中的函数解析式和题意可以解答本题．【详解】(1)由题意可得，当﹣m＝﹣m+1时，该方程无解，故函数y＝﹣x+1没有反向值，当﹣m＝1m-时，m＝±1，∴n＝1﹣(﹣1)＝2，故y＝1x-有反向值，反向距离为2，当﹣m＝m2，得m＝0或m＝﹣1，∴n＝0﹣(﹣1)＝1，故y＝x2有反向值，反向距离是1；(2)①令﹣m＝m2﹣b2m，解得，m＝0或m＝b2﹣1，∵反向距离为零，∴|b2﹣1﹣0|＝0，解得，b＝±1；②令﹣m＝m2﹣b2m，解得，m＝0或m＝b2﹣1，∴n＝|b2﹣1﹣0|＝|b2﹣1|，∵﹣1≤b ≤3，∴0≤n ≤8；(3)∵y ＝223()3()x x x m x x x m ⎧-≥⎨--<⎩， ∴当x ≥m 时，﹣m ＝m 2﹣3m ，得m ＝0或m ＝2，∴n ＝2﹣0＝2，∴m ＞2或m ≤﹣2；当x ＜m 时，﹣m ＝﹣m 2﹣3m ，解得，m ＝0或m ＝﹣4，∴n ＝0﹣(﹣4)＝4，∴﹣2＜m ≤2，由上可得，当m ＞2或m ≤﹣2时，n ＝2，当﹣2＜m ≤2时，n ＝4．【点睛】本题是一道二次函数综合题，解答本题的关键是明确题目中的新定义，找出所求问题需要的条件，利用新定义解答相关问题．7．如图，抛物线2y ax bx c =++的图象过点(10)(30)(03)A B C ﹣，、，、，.（1）求抛物线的解析式；（2）在抛物线的对称轴上是否存在一点P ，使得△PAC 的周长最小，若存在，请求出点P 的坐标及△PAC 的周长；若不存在，请说明理由；（3）在（2）的条件下，在x 轴上方的抛物线上是否存在点M （不与C 点重合），使得PAM PAC S S ∆∆＝？若存在，请求出点M 的坐标；若不存在，请说明理由．【答案】（1）223y x x =++-；（2）存在，点(12)P ，1032；（3）存在，点M 坐标为(14)，【解析】【分析】（1）由于条件给出抛物线与x 轴的交点1030A B （﹣，）、（，），故可设交点式13y a x x +＝（）（﹣），把点C 代入即求得a 的值，减小计算量．（2）由于点A 、B 关于对称轴：直线1x ＝对称，故有PA PB ＝，则PAC C AC PC PA AC PC PB ∆++++＝＝，所以当C 、P 、B 在同一直线上时，PAC C AC CB ∆+＝最小．利用点A 、B 、C 的坐标求AC 、CB 的长，求直线BC 解析式，把1x ＝代入即求得点P 纵坐标．（3）由PAM PAC S S ∆∆＝可得，当两三角形以PA 为底时，高相等，即点C 和点M 到直线PA 距离相等．又因为M 在x 轴上方，故有//CM PA ．由点A 、P 坐标求直线AP 解析式，即得到直线CM 解析式．把直线CM 解析式与抛物线解析式联立方程组即求得点M 坐标．【详解】解：（1）∵抛物线与x 轴交于点1030A B （﹣，）、（，）∴可设交点式13y a x x +＝（）（﹣）把点03C （，）代入得：33a ﹣＝1a ∴＝﹣21323y x x x x ∴+++＝-（）（﹣）＝﹣∴抛物线解析式为223y x x ++＝-（2）在抛物线的对称轴上存在一点P ，使得PAC ∆的周长最小．如图1，连接PB 、BC∵点P 在抛物线对称轴直线1x ＝上，点A 、B 关于对称轴对称PA PB ∴＝PAC C AC PC PA AC PC PB ∆∴++++＝＝∵当C 、P 、B 在同一直线上时，PC PB CB +＝最小103003A B C Q （﹣，）、（，）、（，）AC BC ∴===PAC C AC CB ∆∴+＝设直线BC 解析式为3y kx +＝把点B 代入得：330k +＝，解得：1k ＝﹣∴直线BC ：3y x +＝﹣132P y ∴+＝﹣＝∴点12P （，）使PAC ∆．（3）存在满足条件的点M ，使得PAM PAC S S ∆∆＝．∵PAM PAC S S ∆∆＝S △PAM ＝S △PAC∴当以PA 为底时，两三角形等高∴点C 和点M 到直线PA 距离相等∵M 在x 轴上方//CM PA ∴1012A P Q （﹣，），（，），设直线AP 解析式为y px d +＝ 02p d p d -+=⎧∴⎨+=⎩ 解得：p 1d 1=⎧⎨=⎩ ∴直线1AP y x +：＝∴直线CM 解析式为：3y x +＝2323y x y x x =+⎧⎨=-++⎩Q 解得：1103x y =⎧⎨=⎩（即点C ），2214x y =⎧⎨=⎩ ∴点M 坐标为14（，）【点睛】考查了待定系数法求二次函数解析式、一次函数解析式，轴对称的最短路径问题，勾股定理，平行线间距离处处相等，一元二次方程的解法．其中第（3）题条件给出点M 在x 轴上方，无需分类讨论，解法较常规而简单．8．如图，抛物线y ＝ax 2+bx+c 经过A （﹣3，0），B （1，0），C （0，3）三点．（1）求抛物线的函数表达式；（2）如图1，P 为抛物线上在第二象限内的一点，若△PAC 面积为3，求点P 的坐标；（3）如图2，D 为抛物线的顶点，在线段AD 上是否存在点M ，使得以M ，A ，O 为顶点的三角形与△ABC 相似？若存在，求点M 的坐标；若不存在，请说明理由．【答案】（1）y ＝﹣x 2﹣2x+3；（2）点P 的坐标为（﹣1，4）或（﹣2，3）；（3）存在，（3 2 -，32）或（34-，94），见解析.【解析】【分析】（1）利用待定系数法，然后将A、B、C的坐标代入解析式即可求得二次函数的解析式；（2））过P点作PQ垂直x轴，交AC于Q，把△APC分成两个△APQ与△CPQ，把PQ作为两个三角形的底，通过点A，C的横坐标表示出两个三角形的高即可求得三角形的面积．（3）通过三角形函数计算可得∠DAO=∠ACB，使得以M，A，O为顶点的三角形与△ABC 相似，则有两种情况，∠AOM=∠CAB=45°，即OM为y=-x，若∠AOM=∠CBA，则OM为y=-3x+3，然后由直线解析式可求OM与AD的交点M．【详解】（1）把A（﹣3，0），B（1，0），C（0，3）代入抛物线解析式y＝ax2+bx+c得9303a b ca b cc-+=⎧⎪++=⎨⎪=⎩，解得123abc=-⎧⎪=-⎨⎪=⎩，所以抛物线的函数表达式为y＝﹣x2﹣2x+3．（2）如解（2）图1，过P点作PQ平行y轴，交AC于Q点，∵A（﹣3，0），C（0，3），∴直线AC解析式为y＝x+3，设P点坐标为（x，﹣x2﹣2x+3．），则Q点坐标为（x，x+3），∴PQ＝﹣x2﹣2x+3﹣（x+3）＝﹣x2﹣3x．∴S△PAC＝1PQ A2O⋅，∴()213332x x --⋅=，解得：x 1＝﹣1，x 2＝﹣2．当x ＝﹣1时，P 点坐标为（﹣1，4），当x ＝﹣2时，P 点坐标为（﹣2，3），综上所述：若△PAC 面积为3，点P 的坐标为（﹣1，4）或（﹣2，3），（3）如解（3）图1，过D 点作DF 垂直x 轴于F 点，过A 点作AE 垂直BC 于E 点，∵D 为抛物线y ＝﹣x 2﹣2x+3的顶点，∴D 点坐标为（﹣1，4），又∵A （﹣3，0），∴直线AC 为y ＝2x+4，AF ＝2，DF ＝4，tan ∠PAB ＝2，∵B （1，0），C （0，3）∴tan ∠ABC ＝3，BC 10，sin ∠ABC 310BC 解析式为y ＝﹣3x+3． ∵AC ＝4，∴AE ＝AC•sin ∠ABC ＝310410⨯＝6105，BE ＝105， ∴CE 310， ∴tan ∠ACB ＝2AE CE =， ∴tan ∠ACB ＝tan ∠PAB ＝2，∴∠ACB ＝∠PAB ，∴使得以M ，A ，O 为顶点的三角形与△ABC 相似，则有两种情况，如解（3）图2Ⅰ．当∠AOM ＝∠CAB ＝45°时，△ABC ∽△OMA ，即OM 为y ＝﹣x ，设OM 与AD 的交点M （x ，y ）依题意得：3y x y x =-⎧⎨=+⎩，解得3232x y ⎧=-⎪⎪⎨⎪=⎪⎩，即M 点为（32-，32）． Ⅱ．若∠AOM ＝∠CBA ，即OM ∥BC ，∵直线BC 解析式为y ＝﹣3x+3．∴直线OM 为y ＝﹣3x ，设直线OM 与AD 的交点M （x ，y ）．则依题意得：33y x y x =-⎧⎨=+⎩，解得3494x y ⎧=-⎪⎪⎨⎪=⎪⎩，即M 点为（34-，94），综上所述：存在使得以M ，A ，O 为顶点的三角形与△ABC 相似的点M ，其坐标为（32-，32）或（34-，94）．【点睛】本题结合三角形的性质考查二次函数的综合应用，函数和几何图形的综合题目，要会利用数形结合的思想把代数和几何图形结合起来，利用点的坐标的意义表示线段的长度，从而求出线段之间的关系．9．在平面直角坐标系中，抛物线223y x x =--+与x 轴交于A ，B 两点（A 在B 的左侧），与y 轴交于点C ，顶点为D ．（1）请直接写出点A ，C ，D 的坐标；（2）如图（1），在x 轴上找一点E ，使得△CDE 的周长最小，求点E 的坐标；（3）如图（2），F 为直线AC 上的动点，在抛物线上是否存在点P ，使得△AFP 为等腰直角三角形？若存在，求出点P 的坐标，若不存在，请说明理由．【答案】（1）A （﹣3，0），C （0，3），D （﹣1，4）；（2）E （37-，0）；（3）P （2，﹣5）或（1，0）．【解析】试题分析：（1）令抛物线解析式中y=0，解关于x 的一元二次方程即可得出点A 、B 的坐标，再令抛物线解析式中x=0求出y 值即可得出点C 坐标，利用配方法将抛物线解析式配方即可找出顶点D 的坐标；（2）作点C 关于x 轴对称的点C′，连接C′D 交x 轴于点E ，此时△CDE 的周长最小，由点C 的坐标可找出点C′的坐标，根据点C′、D 的坐标利用待定系数法即可求出直线C′D 的解析式，令其y=0求出x 值，即可得出点E 的坐标；（3）根据点A 、C 的坐标利用待定系数法求出直线AC 的解析式，假设存在，设点F （m ，m+3），分∠PAF=90°、∠AFP=90°和∠APF=90°三种情况考虑．根据等腰直角三角形的性质结合点A 、F 点的坐标找出点P 的坐标，将其代入抛物线解析式中即可得出关于m 的一元二次方程，解方程求出m 值，再代入点P 坐标中即可得出结论．试题解析：（1）当223y x x =--+中y=0时，有2230x x --+=，解得：1x =﹣3，2x =1，∵A 在B 的左侧，∴A （﹣3，0），B （1，0）．当223y x x =--+中x=0时，则y=3，∴C （0，3）．∵223y x x =--+=2(1)4x -++，∴顶点D （﹣1，4）．（2）作点C 关于x 轴对称的点C′，连接C′D 交x 轴于点E ，此时△CDE 的周长最小，如图1所示．∵C （0，3），∴C′（0，﹣3）．设直线C′D 的解析式为y=kx+b ，则有：3{4b k b =--+=，解得：7{3k b =-=-，∴直线C′D 的解析式为y=﹣7x ﹣3，当y=﹣7x ﹣3中y=0时，x=37-，∴当△CDE 的周长最小，点E 的坐标为（37-，0）．（3）设直线AC 的解析式为y=ax+c ，则有：3{30c a c =-+=，解得：1{3a c ==，∴直线AC 的解析式为y=x+3．假设存在，设点F （m ，m+3），△AFP 为等腰直角三角形分三种情况（如图2所示）： ①当∠PAF=90°时，P （m ，﹣m ﹣3），∵点P 在抛物线223y x x =--+上，∴2323m m m --=--+，解得：m 1=﹣3（舍去），m 2=2，此时点P 的坐标为（2，﹣5）；②当∠AFP=90°时，P （2m+3，0）∵点P 在抛物线223y x x =--+上，∴20(23)2(23)3m m =-+-++，解得：m 3=﹣3（舍去），m 4=﹣1，此时点P 的坐标为（1，0）；③当∠APF=90°时，P （m ，0），∵点P 在抛物线223y x x =--+上，∴2023m m =--+，解得：m 5=﹣3（舍去），m 6=1，此时点P 的坐标为（1，0）．综上可知：在抛物线上存在点P ，使得△AFP 为等腰直角三角形，点P 的坐标为（2，﹣5）或（1，0）．考点：二次函数综合题；最值问题；存在型；分类讨论；综合题．10．如图，在平面直角坐标系中，抛物线y=ax 2+2x+c 与x 轴交于A （﹣1，0）B （3，0）两点，与y 轴交于点C ，点D 是该抛物线的顶点．（1）求抛物线的解析式和直线AC的解析式；（2）请在y轴上找一点M，使△BDM的周长最小，求出点M的坐标；（3）试探究：在拋物线上是否存在点P，使以点A，P，C为顶点，AC为直角边的三角形是直角三角形？若存在，请求出符合条件的点P的坐标；若不存在，请说明理由．【答案】（1）抛物线解析式为y=﹣x2+2x+3；直线AC的解析式为y=3x+3；（2）点M的坐标为（0，3）；（3）符合条件的点P的坐标为（73，209）或（103，﹣139），【解析】分析：（1）设交点式y=a（x+1）（x-3），展开得到-2a=2，然后求出a即可得到抛物线解析式；再确定C（0，3），然后利用待定系数法求直线AC的解析式；（2）利用二次函数的性质确定D的坐标为（1，4），作B点关于y轴的对称点B′，连接DB′交y轴于M，如图1，则B′（-3，0），利用两点之间线段最短可判断此时MB+MD的值最小，则此时△BDM的周长最小，然后求出直线DB′的解析式即可得到点M的坐标；（3）过点C作AC的垂线交抛物线于另一点P，如图2，利用两直线垂直一次项系数互为负倒数设直线PC的解析式为y=-13x+b，把C点坐标代入求出b得到直线PC的解析式为y=-13x+3，再解方程组223133y x xy x⎧-++⎪⎨-+⎪⎩＝＝得此时P点坐标；当过点A作AC的垂线交抛物线于另一点P时，利用同样的方法可求出此时P点坐标．详解：（1）设抛物线解析式为y=a（x+1）（x﹣3），即y=ax2﹣2ax﹣3a，∴﹣2a=2，解得a=﹣1，∴抛物线解析式为y=﹣x2+2x+3；当x=0时，y=﹣x2+2x+3=3，则C（0，3），设直线AC的解析式为y=px+q，把A（﹣1，0），C（0，3）代入得3p qq-+=⎧⎨=⎩，解得33pq=⎧⎨=⎩，∴直线AC的解析式为y=3x+3；（2）∵y=﹣x2+2x+3=﹣（x﹣1）2+4，∴顶点D的坐标为（1，4），作B点关于y轴的对称点B′，连接DB′交y轴于M，如图1，则B′（﹣3，0），∵MB=MB′，∴MB+MD=MB′+MD=DB′，此时MB+MD的值最小，而BD的值不变，∴此时△BDM的周长最小，易得直线DB′的解析式为y=x+3，当x=0时，y=x+3=3，∴点M的坐标为（0，3）；（3）存在．过点C作AC的垂线交抛物线于另一点P，如图2，∵直线AC的解析式为y=3x+3，∴直线PC的解析式可设为y=﹣13x+b，把C（0，3）代入得b=3，∴直线PC的解析式为y=﹣13x+3，解方程组223133y x xy x⎧-++⎪⎨-+⎪⎩＝＝，解得3xy=⎧⎨=⎩或73209xy⎧=⎪⎪⎨⎪=⎪⎩，则此时P点坐标为（73，209）；过点A作AC的垂线交抛物线于另一点P，直线PC的解析式可设为y=﹣x+b，把A（﹣1，0）代入得13+b=0，解得b=﹣13，∴直线PC的解析式为y=﹣13x﹣13，解方程组2231133y x xy x⎧-++⎪⎨--⎪⎩＝＝，解得1xy=-⎧⎨=⎩或103139xy⎧=⎪⎪⎨⎪=-⎪⎩，则此时P点坐标为（103，﹣139）.综上所述，符合条件的点P的坐标为（73，209）或（103，﹣139）.点睛：本题考查了二次函数的综合题：熟练掌握二次函数图象上点的坐标特征和二次函数的性质；会利用待定系数法求函数解析式，理解两直线垂直时一次项系数的关系，通过解方程组求把两函数的交点坐标；理解坐标与图形性质，会运用两点之间线段最短解决最短路径问题；会运用分类讨论的思想解决数学问题．11．已知矩形ABCD中，AB=5cm，点P为对角线AC上的一点，且AP=25cm.如图①，动点M从点A出发，在矩形边上沿着A B C→→的方向匀速运动(不包含点C).设动点M的运动时间为t(s)，APM∆的面积为S(cm²)，S与t的函数关系如图②所示：(1)直接写出动点M的运动速度为/cm s，BC的长度为cm;(2)如图③，动点M重新从点A出发，在矩形边上，按原来的速度和方向匀速运动.同时，另一个动点N从点D出发，在矩形边上沿着D C B→→的方向匀速运动，设动点N的运动速度为()/v cm s.已知两动点M、N经过时间()x s在线段BC上相遇(不包含点C)，动点M、N相遇后立即停止运动，记此时APM DPN∆∆与的面积为()()2212,S cm S cm.①求动点N运动速度()/v cm s的取值范围;②试探究12S S⋅是否存在最大值.若存在，求出12S S⋅的最大值并确定运动速度时间x的值；若不存在，请说明理由.【答案】(1)2，10；(2)①2/6/3cm s v cm s≤＜；②当154x=时，12S S⋅取最大值2254.【解析】【分析】（1）由题意可知图像中0~2.5s时，M在AB上运动，求出速度，2.5~7.5s时，M在BC上运动，求出BC长度；（2）①分别求出在C点相遇和在B点相遇时的速度，取中间速度，注意C点相遇时的速度不能取等于；②过M点做MH⊥AC，则125 MH CM==得到S1，同时利用12()PAD CDM ABM NABCDS S S S S S∆∆∆+=---（N）矩形=15，得到S2，再得到12S S⋅关于x的二次函数，利用二次函数性质求得最大值【详解】(1)5÷2.5=2/cm s；（7.5-2.5）×2=10cm(2)①解：在C点相遇得到方程57.5v=在B点相遇得到方程152.5v=∴5=7.515=2.5vv⎧⎪⎪⎨⎪⎪⎩解得23=5vv⎧=⎪⎨⎪⎩∵在边BC上相遇，且不包含C点∴2/6/3cm s v cm s≤＜②如下图12()PAD CDM ABM NABCDS S S S S S∆∆∆+=---（N）矩形()()5152525751022x x⨯-⨯-=---=15过M点做MH⊥AC，则125MH CM==∴112152S MH AP x =⋅=-+ ∴22S x =()122152S S x x ⋅=-+⋅ =2430x x -+ =215225444x ⎛⎫--+ ⎪⎝⎭因为152.57.54＜＜，所以当154x =时，12S S ⋅取最大值2254. 【点睛】本题重点考查动点问题，二次函数的应用，求不规则图形的面积等知识点，第一问关键能够从图像中得到信息，第二问第一小问关键在理清楚运动过程，第二小问关键在能够用x 表示出S 1和S 212．如图，已知直线AB 与抛物线C ：2y ax 2x c =++ 相交于()1,0A -和点()B 2,3两点.⑴求抛物线C 的函数表达式；⑵若点M 是位于直线AB 上方抛物线上的一动点，以MA MB 、为相邻两边作平行四边形MANB ,当平行四边形MANB 的面积最大时，求此时四边形MANB 的面积S 及点M 的坐标；⑶在抛物线C 的对称轴上是否存在定点F ,使抛物线C 上任意一点P 到点F 的距离等于到直线17y 4=的距离，若存在，求出定点F 的坐标；若不存在，请说明理由. 【答案】⑴2y x 2x 3=-++；⑵当12a =，S □MANB =2S △ABM =274，此时115M ,24⎛⎫ ⎪⎝⎭；⑶存在. 当15F 1,4⎛⎫⎪⎝⎭时，无论x 取任何实数，均有PG PF =. 理由见解析.【解析】【分析】（1）利用待定系数法，将A ，B 的坐标代入y=ax 2+2x+c 即可求得二次函数的解析式；（2）过点M作MH⊥x轴于H，交直线AB于K，求出直线AB的解析式，设点M（a，-a2+2a+3），则K（a，a+1），利用函数思想求出MK的最大值，再求出△AMB面积的最大值，可推出此时平行四边形MANB的面积S及点M的坐标；（3）如图2，分别过点B，C作直线y=174的垂线，垂足为N，H，设抛物线对称轴上存在点F，使抛物线C上任意一点P到点F的距离等于到直线y=174的距离，其中F（1，a），连接BF，CF，则可根据BF=BN，CF=CN两组等量关系列出关于a的方程组，解方程组即可．【详解】（1）由题意把点（-1，0）、（2，3）代入y=ax2+2x+c，得，20 443 a ca c-+=⎧⎨++=⎩，解得a=-1，c=3，∴此抛物线C函数表达式为：y=-x2+2x+3；（2）如图1，过点M作MH⊥x轴于H，交直线AB于K，将点（-1，0）、（2，3）代入y=kx+b中，得，0 23k bk b-+⎧⎨+⎩＝＝，解得，k=1，b=1，∴y AB=x+1，设点M（a，-a2+2a+3），则K（a，a+1），则MK=-a2+2a+3-（a+1）=-（a-12）2+94，根据二次函数的性质可知，当a=12时，MK有最大长度94，∴S△AMB最大=S△AMK+S△BMK=12MK•AH+12MK•（x B-x H）=12MK•（x B-x A）=12×94×3=278，∴以MA、MB为相邻的两边作平行四边形MANB，当平行四边形MANB的面积最大时，S最大=2S△AMB最大=2×278=274，M（12，154）；（3）存在点F，∵y=-x2+2x+3=-（x-1）2+4，∴对称轴为直线x=1，当y=0时，x1=-1，x2=3，∴抛物线与点x轴正半轴交于点C（3，0），如图2，分别过点B，C作直线y=174的垂线，垂足为N，H，抛物线对称轴上存在点F，使抛物线C上任意一点P到点F的距离等于到直线y=174的距离，设F（1，a），连接BF，CF，则BF=BN=174-3=54，CF=CH=174，由题意可列：2222225(21)(3)417(31)4aa⎧⎛⎫-+-=⎪ ⎪⎪⎝⎭⎨⎛⎫⎪-+= ⎪⎪⎝⎭⎩，解得，a=154，∴F（1，154）．【点睛】此题考查了待定系数法求解析式，还考查了用函数思想求极值等，解题关键是能够判断出当平行四边形MANB的面积最大时，△ABM的面积最大，且此时线段MK的长度也最大．13．抛物线y=x2+bx+c与x轴交于A（1，0），B（m，0），与y轴交于C．（1）若m=﹣3，求抛物线的解析式，并写出抛物线的对称轴；（2）如图1，在（1）的条件下，设抛物线的对称轴交x轴于D，在对称轴左侧的抛物线上有一点E，使S△ACE=S△ACD，求点E的坐标；（3）如图2，设F（﹣1，﹣4），FG⊥y于G，在线段OG上是否存在点P，使∠OBP=∠FPG？若存在，求m的取值范围；若不存在，请说明理由．【答案】（1）抛物线的解析式为：y=x2+2x﹣3=（x+1）2﹣4；对称轴是：直线x=﹣1；（2）点E的坐标为E（﹣4，5）（3）当﹣4≤m＜0或m=3时，在线段OG上存在点P，使∠OBP=∠FPG.【解析】试题分析：（1）利用待定系数法求二次函数的解析式，并配方求对称轴；（2）如图1，设E（m，m2+2m﹣3），先根据已知条件求S△ACE=10，根据不规则三角形面积等于铅直高度与水平宽度的积列式可求得m的值，并根据在对称轴左侧的抛物线上有一点E，则点E 的横坐标小于﹣1，对m的值进行取舍，得到E的坐标；（3）分两种情况：①当B在原点的左侧时，构建辅助圆，根据直径所对的圆周角是直角，只要满足∠BPF=90°就可以构成∠OBP=∠FPG，如图2，求出圆E与y轴有一个交点时的m值，则可得取值范围；②当B在原点的右侧时，只有△OBP是等腰直角三角形，△FPG也是等腰直角三角形时满足条件，直接计算即可．试题解析：（1）当m=﹣3时，B（﹣3，0），把A（1，0），B（﹣3，0）代入到抛物线y=x2+bx+c中得：，解得，∴抛物线的解析式为：y=x2+2x﹣3=（x+1）2﹣4；对称轴是：直线x=﹣1；（2）如图1，设E（m，m2+2m﹣3），由题意得：AD=1+1=2，OC=3，S△ACE=S△ACD=×ADOC=×2×3=10，设直线AE的解析式为：y=kx+b，把A（1，0）和E（m，m2+2m﹣3）代入得，，解得：，∴直线AE的解析式为：y=（m+3）x﹣m﹣3，∴F（0，﹣m﹣3），∵C（0，﹣3），∴FC=﹣m﹣3+3=﹣m，∴S△ACE=FC（1﹣m）=10，﹣m（1﹣m）=20，m2﹣m﹣20=0，（m+4）（m﹣5）=0，m1=﹣4，m2=5（舍），∴E（﹣4，5）；（3）如图2，当B在原点的左侧时，连接BF，以BF为直径作圆E，当⊙E与y轴相切时，设切点为P，∴∠BPF=90°，∴∠FPG+∠OPB=90°，∵∠OPB+∠OBP=90°，∴∠OBP=∠FPG，连接EP，则EP⊥OG，∵BE=EF，∴EP是梯形的中位线，∴OP=PG=2，∵FG=1，tan∠FPG=tan∠OBP=，∴，∴m=﹣4，∴当﹣4≤m＜0时，在线段OG上存在点P，使∠OBP=∠FPG；如图3，当B在原点的右侧时，要想满足∠OBP=∠FPG，则∠OBP=∠OPB=∠FPG，∴OB=OP，∴△OBP是等腰直角三角形，△FPG也是等腰直角三角形，∴FG=PG=1，∴OB=OP=3，∴m=3，综上所述，当﹣4≤m＜0或m=3时，在线段OG上存在点P，使∠OBP=∠FPG．考点：二次函数的综合题.14．一次函数y＝x的图象如图所示，它与二次函数y＝ax2－4ax＋c的图象交于A、B两点（其中点A在点B的左侧），与这个二次函数图象的对称轴交于点C．（1）求点C的坐标；（2）设二次函数图象的顶点为D．①若点D与点C关于x轴对称，且△ACD的面积等于3，求此二次函数的关系式；②若CD＝AC，且△ACD的面积等于10，求此二次函数的关系式．【答案】（1）点C（2，）；（2）①y＝x2－x；②y＝－x2＋2x＋．【解析】试题分析：（1）求得二次函数y＝ax2－4ax＋c对称轴为直线x＝2，把x＝2代入y＝x求得y=，即可得点C的坐标；（2）①根据点D与点C关于x轴对称即可得点D的坐标，并且求得CD的长，设A（m，m），根据S△ACD＝3即可求得m的值，即求得点A的坐标，把A.D的坐标代入y＝ax2－4ax＋c得方程组，解得a、c的值即可得二次函数的表达式.②设A（m，m）（m<2），过点A作AE⊥CD于E，则AE＝2－m，CE＝－m，根据勾股定理用m表示出AC的长，根据△ACD的面积等于10可求得m的值，即可得A 点的坐标，分两种情况：第一种情况，若a＞0，则点D在点C下方，求点D的坐标；第二种情况，若a＜0，则点D在点C上方，求点D的坐标，分别把A、D的坐标代入y＝ax2－4ax＋c即可求得函数表达式.试题解析：（1）y＝ax2－4ax＋c＝a（x－2）2－4a＋c．∴二次函数图像的对称轴为直线x ＝2．当x＝2时，y＝x＝，∴C（2，）．（2）①∵点D与点C关于x轴对称，∴D（2，－），∴CD＝3.设A（m，m）（m<2），由S△ACD＝3，得×3×（2－m）＝3，解得m＝0，∴A（0，0）.由A（0，0）、 D（2，－）得解得a＝，c＝0.∴y＝x2－x.②设A（m，m）（m<2），过点A作AE⊥CD于E，则AE＝2－m，CE＝－m，。

人教版数学九年级上册第二十二章《二次函数》压轴题综合培优训练(含答案)

《二次函数》压轴题综合培优训练1．如图1，在平面直角坐标系中，抛物线y ＝与x 轴交于A 、B 两点（点A 在点B 的左侧），与y 轴交于点C ．（1）判断△ABC 的形状；（2）过点C 的直线y ＝交x 轴于点H ，若点P 是第四象限内抛物线上的一个动点，且在对称轴的右侧，过点P 作PQ ∥y 轴交直线CH 于点Q ，作PN ∥x 轴交对称轴于点N ，以PQ 、PN 为邻边作矩形PQMN ，当矩形PQMN 的周长最大时，在y 轴上有一动点K ，x轴上有一动点T ，一动点G 从线段CP 的中点R 出发以每秒1个单位的速度沿R →K →T 的路径运动到点T ，再沿线段TB 以每秒2个单位的速度运动到B 点处停止运动，求动点G 运动的最少时间及此时点T 的坐标；（3）如图2，将△ABC 绕点B 顺时针旋转至△A ′BC ′的位置，点A 、C 的对应点分别为A ′、C ′，且点C ′恰好落在抛物线的对称轴上，连接AC ′．点E 是y 轴上的一个动点，连接AE 、C ′E ，将△AC ′E 沿直线C ′E 翻折为△A ″C ′E ，是否存在点A ′，使得△BAA ″为等腰三角形？若存在，请求出点E 的坐标；若不存在，请说明理由．解：（1）△ABC 是以AC 为底的等腰三角形．理由如下：由题意知抛物线y ＝与x 轴交于A 、B 两点（点A 在点B 的左侧），与y轴交于点C ，∴令x ＝0，解得y ＝；令x ＝0，解得：x 1＝，x 2＝4；∴A （，0），，；∴AC2＝AM2+MC2＝＝30，BC2＝OB2+OC2＝＝75，AB2＝（OA+OB）2＝＝75∴AB＝BC∴△ABC是以AC为底的等腰三角形．（2）如图1中，过点C的直线y＝交x轴于点H，令y＝0，解得x＝，∴设P（m，﹣﹣3），则Q（m，﹣3），∵y＝＝﹣∴抛物线对称轴为：直线x＝，∴QP＝（﹣3）﹣（﹣﹣3）＝﹣+，NP＝m﹣，＝2（QP+NP）＝2（﹣+﹣）＝∴矩形PQMN的周长C矩形PQMN+∵﹣＜0，开口向下，∴当m＝3时，C最小，此时，P（3，﹣3），矩形PQMN∵R为线段CP的中点，∴R （，﹣3），作点R 关于y 轴对称点R ′（﹣，﹣3），此时R 与N 重合，由题意知：动点G 运动的最少时间t ＝RK +KT +TB ，在y 轴正半轴上取点S （0，4），连接直线BS ，则直线BS 解析式为y ＝﹣x +4，过点R ′作R ′J ⊥BS 于J ，交y 轴于K ，交x 轴于T ，则R ′J 即为所求，∵tan ∠SBO ＝＝＝，∴∠SBO ＝30°，∴TJ ＝TB 即t ＝R ′K +KT +TJ ，∵RR ′＝3，∠RR ′J ＝∠BTJ ＝60°，∴△KRR ′为等边三角形，∠RKR ′＝∠KRR ′＝60° ∴∠KRM ＝∠KHR ＝30°∴R ′J ＝2RR ′＝6即动点G 运动的最少时间t ＝6（秒）；∵△JMT ∽△JRR ′∴＝，即＝∴TM ＝3﹣3 ∴T （，0）；（3）①当AA ''＝A ''B 时，如图2中，此时，A''在对称轴上对称性可知∠AC′E＝∠A''C′E又∠HEC′＝∠A''C′E∴∠AC′E＝∠HEC′∴HE＝HC'＝5∴OE＝HE﹣HO＝∴②当AA''＝AB时，如图3中，设A″C′交y轴于J．此时AA''＝AB＝BC'＝A''C'∴四边形A''ABC'为菱形由对称性可知∠AC'E＝∠A''C'E＝30°∴JE＝∴OE＝OJ﹣JE＝6∴E（0，6）③当AA''＝A''B时，如图4中，设AC′交y轴于M．此时，A''在对称轴上∠MC'E＝75°又∠AMO＝∠EMC'＝30°∴∠MEC'＝75°∴ME＝MC'∴MC'＝∴OE＝∴E（）④当A''B＝AB时，如图5中，此时AC'＝A''C'＝A''B＝AB∴四边形AC'A''B为菱形由对称性可知，C''，E，B共线∴OE＝，∴E（0，12）．综上所述，满足条件的点E坐标为（0，3﹣）或（0，6）或（0，3+）或（0，12）．2．如图，已知抛物线y ＝ax 2+bx +5与x 轴交于A （﹣1，0），B （5，0）两点（点A 在点B 的左侧），与y 轴交于点C ．（1）求抛物线的解析式；（2）点D 是第一象限内抛物线上的一个动点（与点C ，B 不重合），过点D 作DF ⊥x 轴于点F ，交直线BC 于点E ，连接BD ，直线BC 能否把△BDF 分成面积之比为2：3的两部分？若能，请求出点D 的坐标；若不能，请说明理由．（3）若M 为抛物线对称轴上一动点，使得△MBC 为直角三角形，请直接写出点M 的坐标．解：（1）将A （﹣1，0），B （5，0）代入y ＝ax 2+bx +5，得：，解得，则抛物线解析式为y ＝﹣x 2+4x +5；（2）能．设直线BC 的解析式为y ＝kx +b ，把C （0，5），B （5，0）代入得，解得，所以直线BC 的解析式为y ＝﹣x +5，设D （x ，﹣x 2+4x +5），则E （x ，﹣x +5），F （x ，0），（0＜x ＜5）， ∴DE ＝﹣x 2+4x +5﹣（﹣x +5）＝﹣x 2+5x ，EF ＝﹣x +5，当DE ：EF ＝2：3时，S △BDE ：S △BEF ＝2：3，即（﹣x 2+5x ）：（﹣x +5）＝2：3，整理得3x 2﹣17x +10＝0，解得x 1＝，x 2＝5（舍去），此时D 点坐标为（，）；当DE ：EF ＝3：2时，S △BDE ：S △BEF ＝3：2，即（﹣x 2+5x ）：（﹣x +5）＝3：2，整理得2x 2﹣13x +15＝0，解得x 1＝，x 2＝5（舍去），此时D 点坐标为（，）；综上所述，当点D 的坐标为（，）或（，）时，直线BC 把△BDF 分成面积之比为2：3的两部分；（3）抛物线的对称轴为直线x ＝2，如图，设M （2，t ），∵B （5，0），C （0，5），∴BC 2＝52+52＝50，MC 2＝22+（t ﹣5）2＝t 2﹣10t +29，MB 2＝（2﹣5）2+t 2＝t 2+9，当BC 2+MC 2＝MB 2时，△BCM 为直角三角形，∠BCM ＝90°，即50+t 2﹣10t +29＝t 2+9，解得t ＝7，此时M 点的坐标为（2，7）；当BC 2+MB 2＝MC 2时，△BCM 为直角三角形，∠CBM ＝90°，即50+t 2+9＝t 2﹣10t +29，解得t ＝﹣3，此时M 点的坐标为（2，﹣3）；当MC 2+MB 2＝BC 2时，△BCM 为直角三角形，∠CMB ＝90°，即t 2﹣10t +29+t 2+9＝50，解得t 1＝6，t 2＝﹣1，此时M 点的坐标为（2，6）或（2，﹣1），综上所述，满足条件的M 点的坐标为（2，7），（2，﹣3），（2，6），（2，﹣1）．3．如图，在平面直角坐标系中，已知抛物线y＝ax2+bx+c（a＜0）经过点A（﹣1，0）、B（4，0）与y轴交于点C，tan∠ABC＝．（1）求抛物线的解析式；（2）点M在第一象限的抛物线上，ME平行y轴交直线BC于点E，连接AC、CE，当ME 取值最大值时，求△ACE的面积．（3）在y轴负半轴上取点D（0，﹣1），连接BD，在抛物线上是否存在点N，使∠BAN＝∠ACO﹣∠OBD？若存在，请求出点N的坐标；若不存在，请说明理由．解：（1）∵B（4，0），∴OB＝4，∵tan∠ABC＝＝＝，∴OC＝2，∴C（0，2），设y＝a（x﹣1）（x﹣4），把C（0，2）代入求得a＝﹣，∴抛物线的解析式为y＝﹣（x﹣1）（x﹣4）＝﹣x2+x+2；（2）设直线BC的解析式为y＝kx+2，把B（4，0）代入求得k＝﹣，∴直线BC解析式为y＝﹣x+2，设M（m，﹣m2+m+2），则E （m ，﹣m +2），∴ME ＝﹣m 2+2m ，∴当m ＝2时，ME 取得最大值2， ∴E （2，1），∴S △ACE ＝S △ABC ﹣S △ABE ＝×5×（2﹣1）＝；（3）作C ′（0，﹣2）与 C 关于x 轴对称，连接BC ′，过点D 作DE ⊥BC ′于点E ，∴∠ABC ＝∠ABC ′，∵＝，∠AOC ＝∠BOC ＝90°，∴△AOC ∽△COB ， ∴∠ABC ＝∠ACO ， ∴∠ABC ′＝∠ACO ，即∠BAN ＝∠ACO ﹣∠OBD ＝∠DBC ′，由题意得DC ′＝1、DB ＝，BC ′＝2，∵S △DBC ′＝＝，∴DE ＝，∴BE ＝，∴tan ∠DBC ′＝tan ∠BAN ＝，设N （n ，﹣n 2+n +2），且n ＞0，∴tan ∠BAN ＝＝＝，①当2n +2＝9×（﹣n 2+n +2）时，n 1＝，n 2＝﹣1（舍去）；②当2n +2＝﹣9×（﹣n 2+n +2）时，n 1＝，n 2＝﹣1（舍去）；∴N 点的坐标为（，）或（，﹣）．4．抛物线y ＝x 2+（m +2）x +4的顶点C 在x 轴正半轴上，直线y ＝x +2与抛物线交于A ，B 两点（点A 在点B 的左侧）．（1）求抛物线的函数表达式；（2）点P 是抛物线上一点，若S △PAB ＝2S △ABC ，求点P 的坐标；（3）将直线AB 上下平移，平移后的直线y ＝x +t 与抛物线交于A '，B '两点（A '在B '的左侧），当以点A '，B '和（2）中第二象限的点P 为顶点的三角形是直角三角形时，求t 的值．解：（1）∵抛物线y ＝x 2+（m +2）x +4的顶点C 在x 轴正半轴上，∴．解得m ＝﹣6．∴抛物线的函数表达式是y ＝x 2﹣4x +4；（2）如图1，过点C 作CE ∥AB 交y 轴于点E ，设直线AB 交y 轴于点H ．由直线AB ：y ＝x +2，得点H （0，2）．设直线CE ：y ＝x +b ．∵y ＝x 2﹣4x +4＝（x ﹣2）2，∴C （2，0）．∴2+b ＝0，则b ＝﹣2．∴HE ＝4、由S △PAB ＝2S △ABC ，可在y 轴上且点H 上方取一点F ，使FH ＝2HE ，则F （0，10）．过点F 作FP ∥AB 交抛物线于点P 1、P 2．此时满足S △PAB ＝2S △ABC ，设直线P 1、P 2的函数解析式为：y ＝x +k ．∵F （0，10）在直线P 1、P 2上，∴k ＝10．∴直线P 1、P 2的函数解析式为：y ＝x +10．联立．解得，，综上，满足条件的点P 的坐标是P 1（﹣1，9），P 2（6，16）；（3）设A ′（x 1，y 1），B ′（x 2，y 2），显然，∠PA ′B ′≠90°．（i ）如图2，当∠A ′B ′P ＝90°时，过点B ′作直线MN ∥y 轴，A ′M ⊥MN 于M ，PN ⊥MN 于N ．∵直线A ′B ′的解析式是y ＝x +t ，∴∠B ′AM ＝45°．进一步可得到△A ′B ′M ，△PB ′N 都是等腰直角三角形．∴PN ＝NB ′，∴x 2+1＝9﹣y 2，即x 2+y 2＝8 ①又y 2＝x 2+t ，②联立①②解得．将点（4﹣t ，4+）代入二次函数解析式，得4+＝（4﹣﹣2）2．解得 t 1＝0，t 2＝10（此时点A ′与点P 重合，舍去）；②如图3，当∠A ′PB ′＝90°时，过点P 作EF ∥y 轴，A ′E ⊥EF 于E ，B ′F ⊥EF 于F ．则△A ′EP ∽△PFB ′．∴＝．∴＝，∴x 1x 2+（x 1+x 2）+1＝9（y 1+y 2）﹣y 1y 2﹣81．令x 2﹣4x +4＝x +t ，则x 2﹣5x +4﹣t ＝0．则x 1+x 2＝5，x 1x 2＝4﹣t ．y 1+y 2＝（x 1+t ）+（x 2+t ）＝x 1+x 2+2t ＝5+2t ．y 1y 2＝（x 1+t ）（x 2+t ）＝x 1x 2+t （x 1+x 2）+t 2＝t 2+4t +4．∴（4﹣t ）+5+1＝9（5+2t ）﹣（t 2+4t +4）﹣81．整理，得t 2﹣15t ﹣50＝0．解得 t 1＝20，t 2＝﹣5（舍去）．综上所述，t 的值是0或20．5．在平面直角坐标系中，矩形OABC 的顶点B 的坐标为（2，4），抛物线y ＝﹣2x 2+bx +c 经过A 、C 两点，与x 轴的另一个交点为点D ．（1）如图1，求抛物线的函数表达式；（2）如图2，连接AC、AD，将△ABC沿AC折叠后与AD、y轴分别交于点交于E、G，求OG的长度；（3）如图3，将抛物线在AC上方的图象沿AC折叠后与y轴交与点F，求点F的坐标．解：（1）如图1，∵四边形OABC是矩形，B（2，4），∴A（0，4），C（2，0），∵抛物线y＝﹣2x2+bx+c经过A、C两点，∴，∴，∴抛物线的函数表达式为：y＝﹣2x2+2x+4；（2）如图2，由题意得：△ABC≌△AB′C．∴∠BCA＝∠B′CA．∵AO∥BC，∴∠BCA＝∠B′CA，∠BCA＝∠OAC，∴∠B′CA＝∠OAC．∴AG＝CG．设OG＝x，则AG＝CG＝4﹣x．在Rt△OGC中，22+x2＝（4﹣x）2，得，∴；（3）如图3，在AC上方的抛物线图象取点F的对称点F′，过点F′作y轴的平行线交直线AC于点G．由题意得：∠FAC＝∠F′AC，F′A＝FA．∵AO∥F′G，∴∠FAC＝∠AGF′．∵∠FAC＝∠F′AC，∠FAC＝∠AGF′．∴∠F′AC＝∠AGF′，∴F′A＝F′G．易得直线AC的解析式为：y＝﹣2x+4．设点F（n，﹣2n2+2n+4），则G（n，﹣2n+4）．∴F′G＝﹣2n2+4n，F′A2＝n2+（﹣2n2+2n）2．∵F′A＝F′G．∴F′A2＝F′G2．即：n2+（﹣2n2+4n）2＝（﹣2n2+2n）2，解得：n＝0（舍去），．1∴．∴F′A＝F′G＝FA＝，∴F（0，）．6．如图，已知抛物线y＝x2+bx+c与x轴交于A、B两点（点A在点B左），与y轴交于点C （0，﹣3），对称轴是直线x＝1，直线BC与抛物线的对称轴交于点D．（1）求抛物线的函数表达式；（2）求直线BC的函数表达式；（3）点E为y轴上一动点，CE的垂直平分线交CE于点F，交抛物线于P、Q两点，且点P在第三象限．①当线段时，求tan∠CED的值；②当以C、D、E为顶点的三角形是直角三角形时，请求出点P的坐标．解：（1）∵抛物线的对称轴为直线x＝1，∴﹣＝﹣＝1，∴b＝﹣2∵抛物线与y轴交于点C（0，﹣3），∴c＝﹣3，∴抛物线的函数表达式为y＝x2﹣2x﹣3；（2）∵抛物线与x轴交于A、B两点，当y＝0时，x2﹣2x﹣3＝0．∴x1＝﹣1，x2＝3．∵A点在B点左侧，∴A（﹣1，0），B（3，0）设过点B（3，0）、C（0，﹣3）的直线的函数表达式为y＝kx+m，则，∴∴直线BC的函数表达式为y＝x﹣3；（3）①∵AB＝4，PQ＝AB，∴PQ＝3∵PQ⊥y轴∴PQ∥x轴，则由抛物线的对称性可得PM＝，∵对称轴是直线x＝1，∴P到y轴的距离是，∴点P的横坐标为﹣，∴P（﹣，﹣），∴F（0，﹣），∴FC＝3﹣OF＝3﹣＝，∵PQ垂直平分CE于点F，∴CE＝2FC＝，∵点D在直线BC上，∴当x＝1时，y＝﹣2，则D（1，﹣2），过点D作DG⊥CE于点G，∴DG ＝1，CG ＝1，∴GE ＝CE ﹣CG ＝﹣1＝．在Rt △EGD 中，tan ∠CED ＝＝．②P 1（1﹣，﹣2），P 2（1﹣，﹣）．设OE ＝a ，则GE ＝2﹣a ，当CE 为斜边时，则DG 2＝CG •GE ，即1＝（OC ﹣OG ）•（2﹣a ），∴1＝1×（2﹣a ），∴a ＝1，∴CE ＝2，∴OF ＝OE +EF ＝2∴F 、P 的纵坐标为﹣2，把y ＝﹣2，代入抛物线的函数表达式为y ＝x 2﹣2x ﹣3得：x ＝1+或1﹣∵点P 在第三象限．∴P 1（1﹣，﹣2），当CD 为斜边时，DE ⊥CE ，∴OE ＝2，CE ＝1，∴OF ＝2.5，∴P 和F 的纵坐标为：﹣，把y ＝﹣，代入抛物线的函数表达式为y ＝x 2﹣2x ﹣3得：x ＝1﹣，或1+，∵点P 在第三象限．∴P 2（1﹣，﹣）．综上所述：满足条件为P 1（1﹣，﹣2），P 2（1﹣，﹣）．7．如图，抛物线y ＝ax 2+bx +c 与x 轴交于点A （﹣1，0），点B （3，0），与y 轴交于点C ，且过点D （2，﹣3）．点P 、Q 是抛物线y ＝ax 2+bx +c 上的动点．（1）求抛物线的解析式；（2）当点P 在直线OD 下方时，求△POD 面积的最大值．（3）直线OQ 与线段BC 相交于点E ，当△OBE 与△ABC 相似时，求点Q 的坐标．解：（1）函数的表达式为：y ＝a （x +1）（x ﹣3），将点D 坐标代入上式并解得：a ＝1，故抛物线的表达式为：y ＝x 2﹣2x ﹣3…①；（2）设直线PD 与y 轴交于点G ，设点P （m ，m 2﹣2m ﹣3），将点P 、D 的坐标代入一次函数表达式：y ＝sx +t 并解得：直线PD 的表达式为：y ＝mx ﹣3﹣2m ，则OG ＝3+2m ，S △POD ＝×OG （x D ﹣x P ）＝（3+2m ）（2﹣m ）＝﹣m 2+m +3，∵﹣1＜0，故S△POD有最大值，当m＝时，其最大值为；（3）∵OB＝OC＝3，∴∠OCB＝∠OBC＝45°，∵∠ABC＝∠OBE，故△OBE与△ABC相似时，分为两种情况：①当∠ACB＝∠BOQ时，AB＝4，BC＝3，AC＝，过点A作AH⊥BC于点H，S△ABC＝×AH×BC＝AB×OC，解得：AH＝2，则sin∠ACB＝＝，则tan∠ACB＝2，则直线OQ的表达式为：y＝﹣2x…②，联立①②并解得：x＝，故点Q1（，﹣2），Q2（﹣，2）②∠BAC＝∠BOQ时，tan∠BAC＝＝3＝tan∠BOQ，则点Q（n，3n），则直线OQ的表达式为：y＝﹣3x…③，联立①③并解得：x＝，故点Q3（，），Q4（，）；综上，当△OBE与△ABC相似时，Q1（，﹣2），Q2（﹣，2），Q3（，），Q4（，）．8．如图，在平面直角坐标系中，Rt△ABC的边BC在x轴上，∠ABC＝90°，以A为顶点的抛物线y＝﹣x2+bx+c经过点C（3，0），交y轴于点E（0，3），动点P在对称轴上．（1）求抛物线解析式；（2）若点P从A点出发，沿A→B方向以1个单位/秒的速度匀速运动到点B停止，设运动时间为t秒，过点P作PD⊥AB交AC于点D，过点D平行于y轴的直线l交抛物线于点Q，连接AQ，CQ，当t为何值时，△ACQ的面积最大？最大值是多少？（3）若点M是平面内的任意一点，在x轴上方是否存在点P，使得以点P，M，E，C为顶点的四边形是菱形，若存在，请直接写出符合条件的M点坐标；若不存在，请说明理由．解：（1）将点C、E的坐标代入二次函数表达式得：，解得：，故抛物线的表达式为：y＝﹣x2+2x+3，则点A（1，4）；（2）将点A、C的坐标代入一次函数表达式并解得：直线AC的表达式为：y＝﹣2x+6，点P（1，4﹣t），则点D（，4﹣t），设点Q（，4﹣），S＝×DQ×BC＝﹣t2+t，△ACQ有最大值，当t＝2时，其最大值为1；∵﹣＜0，故S△ACQ（3）设点P（1，m），点M（x，y），①当EC是菱形一条边时，当点M在y轴右方时，点E向右平移3个单位、向下平移3个单位得到C，则点P平移3个单位、向下平移3个单位得到M，则1+3＝x，m﹣3＝y，而MP＝EP得：1+（m﹣3）2＝（x﹣1）2+（y﹣m）2，解得：y＝m﹣3＝，故点M（4，）；当点M在y轴左方时，同理可得：点M（﹣2，3+）；②当EC是菱形一对角线时，则EC中点即为PM中点，则x+1＝3，y+m＝3，而PE＝PC，即1+（m﹣3）2＝4+（m﹣2）2，解得：m＝1，故x＝2，y＝3﹣m＝3﹣1＝2，故点M（2，2）；综上，点M（4，）或（﹣2，3+）或M（2，2）．9．如图，在平面直角坐标系中，抛物线y＝ax2+bx+2（a≠0）与x轴交于A，B两点（点A 在点B的左侧），与y轴交于点C，抛物线经过点D（﹣2，﹣3）和点E（3，2），点P是第一象限抛物线上的一个动点．（1）求直线DE和抛物线的表达式；（2）在y轴上取点F（0，1），连接PF，PB，当四边形OBPF的面积是7时，求点P的坐标；（3）在（2）的条件下，当点P在抛物线对称轴的右侧时，直线DE上存在两点M，N（点M在点N的上方），且MN＝2，动点Q从点P出发，沿P→M→N→A的路线运动到终点A，当点Q的运动路程最短时，请直接写出此时点N的坐标．解：（1）将点D 、E 的坐标代入函数表达式得：，解得：，故抛物线的表达式为：y ＝﹣x 2+x +2，同理可得直线DE 的表达式为：y ＝x ﹣1…①；（2）如图1，连接BF ，过点P 作PH ∥y 轴交BF 于点H ，将点FB 代入一次函数表达式，同理可得直线BF 的表达式为：y ＝﹣x +1，设点P （x ，﹣x 2+x +2），则点H （x ，﹣x +1），S 四边形OBPF ＝S △OBF +S △PFB ＝×4×1+×PH ×BO ＝2+2（﹣x 2+x +2+x ﹣1）＝7，解得：x ＝2或，故点P （2，3）或（，）；（3）当点P 在抛物线对称轴的右侧时，点P （2，3），过点M 作A ′M ∥AN ，过作点A ′直线DE 的对称点A ″，连接PA ″交直线DE 于点M ，此时，点Q 运动的路径最短，∵MN＝2，相当于向上、向右分别平移2个单位，故点A′（1，2），A′A″⊥DE，则直线A′A″过点A′，则其表达式为：y＝﹣x+3…②，联立①②得x＝2，则A′A″中点坐标为（2，1），由中点坐标公式得：点A″（3，0），同理可得：直线A″P的表达式为：y＝﹣3x+9…③，联立①③并解得：x＝，即点M（，），点M沿ED向下平移2个单位得：N（，﹣）．＝1．10．如图1，抛物线y＝（x﹣m）2的顶点A在x轴正半轴上，交y轴于B点，S△OAB（1）求抛物线的解析式；（2）如图2，P是第一象限内抛物线上对称轴右侧一点，过P的直线l与抛物线有且只有一个公共点，l交抛物线对称轴于C点，连PB交对称轴于D点，若∠BAO＝∠PCD，求证：AC＝2AD；（3）如图3，以A为顶点作直角，直角边分别与抛物线交于M、N两点，当直角∠MAN绕A点旋转时，求证：MN始终经过一个定点，并求出该定点的坐标．解：（1）由题意和y＝（x﹣m）2设A（m，0）当x＝0时，y═（0﹣m）2＝，即设B（0，）∴OA＝m，OB＝由S△OAB＝1∴•OA•OB＝1，即m•＝2解得，m＝2∴A（2，0），B（0，1）把y＝（x﹣2）2化为一般式为，y＝x2﹣x+1．（2）由（1）得抛物线对称轴为直线x＝2．D、C两点在直线x＝2上，则设C（2，n），D（2，n'）如图2延长BA交直线PC于点Q并设直线PC交x轴于点E．∵∠BAO＝∠PCD，∠BOA＝∠EAC＝90°∴Rt△BOA∽Rt△EAC∴∠BAO＝∠ECA∴tan∠BAO＝tan∠ECA＝∴＝∴AC＝2AE又∵∠BAO＝∠EAQ，∠BAO＝∠ECA∴∠ECA＝∠EAQ又∵∠ECA+∠CEA＝90°∴∠EAQ+∠QEA＝90°∴BQ⊥PC设直线AB的解析式为y＝kx+b，把A（2，0），B（0，1）代入得，解得∴直线AB的解析式为，y＝﹣x+1由BQ⊥PC设直线PC的解析式为y＝2x+b'．又∵过P的直线l与抛物线有且只有一个公共点∴令2x+b'═（x﹣2）2整理得，x2﹣12x+4﹣4b'＝0，且△＝0即144﹣4（4﹣4b'）＝0解得，b'＝﹣8∴直线PC的解析式为，y＝2x﹣8．∴把点C（2，n）代入y＝2x﹣8中得，n＝2×2﹣8解得，n＝﹣4．∴C点坐标为（2，﹣4），即AC＝4由AC＝2AE得，AE＝2．把b’＝﹣8代入方程x2﹣12x+4﹣4b'＝0中得，x2﹣12x+36＝0解得，x1＝x2＝6再把x＝6代入y＝2x﹣8中得，y＝2×6﹣8解得，y＝4∴P（6，4）设直线PB解析式为y＝k'x+1把P（6，4）代入上式得，4＝6k'+1解得，k'＝∴直线PB的解析式为，y＝x+1又∵D（2，n'）在直线PB上，将其代入y＝x+1中得，n'＝×2+1＝2∴D点坐标为（2，2），即AD＝2∴AD ＝AE∴AC ＝2AD ；（3）如图3中，以A 为原点建立新的坐标系，则抛物线的解析式为y ′＝x 2，在新坐标系中设M （a ， a 2），N （m ， m 2）． ∵AM ⊥AN ，∴＝﹣，∴ma ＝﹣16设直线MN 的解析式为y ′＝kx +b ，则有解得：，∵ma ＝﹣16，∴b ＝4，∴直线MN 的解析式为y ′＝（a +m ）x +4，∴直线MN 经过定点（0，4）（新坐标系中），在原来坐标系中，直线MN 经过点（2，4），∴直线MN 经过定点（2，4）．11．如图，抛物线y ＝ax 2+bx +3与x 轴交于A （﹣3，0），B （9，0）两点，与y 轴交于点C ，连接AC ，BC ．点P 沿AC 以每秒1个单位长度的速度由点A 向点C 运动，同时，点Q 沿BO 以每秒2个单位长度的速度由点B 向点O 运动，当一个点停止运动时，另一个点也随之停止运动，连接PQ ，过点Q 作QD ⊥x 轴，与抛物线交于点D ，连接PD 与BC 交于点E ．设点P的运动时间为t秒（t＞0）（1）求抛物线的表达式；（2）①直接写出P，D两点的坐标（用含t的代数式表示，结果需化简）．②在点P，Q运动的过程中，当PQ＝PD时，求t的值；（3）点M为线段BC上一点，在点P，Q运动的过程中，当点E为PD中点时，是否存在点M使得PM+BM的值最小？若存在，请求出PM+BM的最小值；若不存在，请说明理由．解：（1）将A（﹣3，0），B（9，0）代入y＝ax2+bx+3，得：，解得：，∴抛物线的表达式为y＝﹣x2+x+3…①；（2）由题意得：∠ACO＝∠OBC＝30°，∠ACB＝90°，将点B、C（0，3）的坐标代入一次函数表达式并解得：直线BC的表达式为：y＝﹣x+3…②；①点P的坐标为（﹣3+t， t），点Q（9﹣2t，0），将点Q的坐标代入①式并整理得：点D[9﹣2t，（6t﹣t2）]；②当PQ＝PD时，则DQ中点的纵坐标＝点P的纵坐标，即： [（6t﹣t2）]＝t，解得：t＝；（3）点P的坐标为（﹣3+t， t）、点D[9﹣2t，（6t﹣t2）]，点E是PQ的中点，则点E[3﹣t， t+（6t﹣t2）]，将点E的坐标代入②式并整理得：t2﹣6t+9＝0，解得：t＝3，即点P（﹣，）即点P是AC的中点，作点P关于直线BC的对称点P′，过点P′作P′H⊥x轴、BC于点H、M，过点P作PN ⊥y轴于点N，则MH＝MB，则此时，PM+BM＝PM+MH＝P′H为最小值，∵∠ACB＝90°，PC＝P′C，∠P′CM＝∠NCP，∠P′MC＝∠PNC＝90°，∴△P′MC≌△PNC（AAS），∴MC＝NC＝OC，OM＝OC＝＝P′H，故PM+BM的最小值为．12．抛物线y＝x2+bx+c与x轴负半轴交于点A，与x轴正半轴交于点B，与y轴交于点C．（1）如图1，若OB＝2OA＝2OC①求抛物线的解析式；②若M是第一象限抛物线上一点，若cos∠MAC＝，求M点坐标．（2）如图2，直线EF∥x轴与抛物线相交于E、F两点，P为EF下方抛物线上一点，且P （m，﹣2）．若∠EPF＝90°，则EF所在直线的纵坐标是否为定值，请说明理由．解：（1）①∵x＝0时，y＝x2+bx+c＝c∴C（0，c），OC＝﹣c（c＜0）∴OA＝OC＝﹣c，OB＝2OC＝﹣2c∴A（c，0），B（﹣2c，0）∵抛物线y＝x2+bx+c经过点A、B∴解得：∴抛物线的解析式为y＝x2﹣x﹣②过点M作MD⊥AC于点D，过点D作GH∥x轴，过点A作AG⊥GH于点G，过点M作MH ⊥GH于点H，如图1∴∠ADM＝∠G＝∠H＝90°∴Rt△ADM中，cos∠MAC＝∴AM＝AD∴MD＝＝4AD∵c＝﹣∴A（﹣，0），B（1，0），C（0，﹣）∴OA＝OC∴∠OAC＝45°∴∠GAD＝∠GAO﹣∠OAC＝45°∴△ADG为等腰直角三角形∴∠ADG＝45°∴∠MDH ＝180°﹣∠ADG ﹣∠ADM ＝45°∴△MDH 为等腰直角三角形设AG ＝DG ＝t ，则AD ＝t ∴MD ＝4AD ＝4t ∴DH ＝MH ＝4t∴x M ＝x A +t +4t ＝﹣+5t ，y M ＝4t ﹣t ＝3t∵点M 在抛物线上∴（﹣+5t ）2﹣（﹣+5t ）﹣＝3t解得：t 1＝0（舍去），t 2＝∴x M ＝﹣+＝，y M ＝∴点M 坐标为（，）（2）EF 所在直线的纵坐标是定值，理由如下：过点P 作PQ ⊥EF 于点Q ，如图2∵P （m ，﹣2）在抛物线上∴m 2+bm +c ＝﹣2，即c +2＝﹣m 2﹣bm∵EF ∥x 轴且在点P 上方∴x Q ＝x P ＝m ，设y E ＝y F ＝y Q ＝n ，n ＞﹣2∴PQ ＝n ﹣（﹣2）＝n +2∵x 2+bx +c ＝n ，整理得x 2+bx +c ﹣n ＝0∴x E +x F ＝﹣b ，x E •x F ＝c ﹣n∴∠PQE ＝∠PQF ＝90°∵∠EPF ＝90°∴∠EPQ +∠FPQ ＝∠FPQ +∠PFQ ＝90°∴∠EPQ ＝∠PFQ∴△EPQ ∽△PFQ∴∴PQ2＝EQ•FQ∴（n+2）2＝（m﹣x E）（x F﹣m）∴n2+4n+4＝m•x F﹣m2﹣x E•x F+m•x En2+4n+4＝m（xE+x F）﹣m2﹣x E•x F n2+4n+4＝﹣bm﹣m2﹣（c﹣n）n2+4n+4＝c+2﹣c+n解得：n1＝﹣1，n2＝﹣2（舍去）∴EF所在直线的纵坐标为﹣1，是定值．13．如图所示，二次函数y＝ax2+bx+2的图象经过点A（4，0），B（﹣4，﹣4），且与y轴交于点C．（1）请求出二次函数的解析式；（2）若点M（m，n）在抛物线的对称轴上，且AM平分∠OAC，求n的值．（3）若P是线段AB上的一个动点（不与A、B重合），过P作PQ∥AC，与AB上方的抛物线交于点Q，与x轴交于点H，试问：是否存在这样的点Q，使PH＝2QH？若存在，请直接出点Q的坐标；若不存在，请说明理由．解：（1）将点A、B的坐标代入函数表达式得：，解得：，故抛物线的表达式为：y＝﹣x2+x+2；（2）如图，过点A作∠A的角平分线交y轴于点G，过点G作GN⊥AC于点N，二次函数对称轴交AM、x轴于点M、H，设：OG＝x＝GN，则AN＝OA＝4，AC＝2，OC＝2，CM＝2﹣x，CN＝CA﹣AN＝2﹣4，则由勾股定理得：（2﹣x）2＝x2+（2﹣4）2，解得：x＝4﹣8，∴GH∥O M，则，即：，则n＝GH＝x＝3﹣6；（3）存在，理由：如图：将点B、A的坐标代入一次函数表达式并解得：直线AB的表达式为：y＝x﹣2…①，同理直线AC的表达式为：y＝﹣x+2，∵PQ∥AC，则设直线PQ的表达式为：y＝﹣x﹣c（c＞0）…②，联立①②并解得：x＝2±2（舍去正值），故点Q（2﹣2，﹣1﹣c+），∵PH＝2QH，∴P、Q的纵坐标之比也为2，即﹣c﹣1＝±2（﹣1﹣c+），解得：c＝或，故点Q（﹣，﹣）或（﹣，）．14．如图，抛物线y＝﹣x2+bx+c经过A（0，3），C（2，n）两点，直线l：y＝x+2过C 点，且与y轴交于点B，抛物线上有一动点E，过点E作直线EF⊥x轴于点F，交直线BC于点D（1）求抛物线的解析式．（2）如图1，当点E在直线BC上方的抛物线上运动时，连接BE，BF，是否存在点E使直线BC将△BEF的面积分为2：3两部分？若存在，求出点E的坐标，若不存在说明理由；（3）如图2，若点E在y轴右侧的抛物线上运动，连接AE，当∠AED＝∠ABC时，直接写出此时点E的坐标．解：（1）直线l：y＝x+2过C点，则点C（2，3），y＝x+2过C点，且与y轴交于点B，则点B（0，2），将点A、C的坐标代入二次函数表达式并解得：b＝2，c＝3，故抛物线的表达式为：y＝﹣x2+2x+3；（2）设点E（m，﹣m2+2m+3），则点D（m， m+2），则DE＝﹣m2+m+1，DF＝m+2，＝＝或，解得：m＝或，故点E（，）或（，）；（3）由（2）知：E（m，﹣m2+2m+3），则点D（m， m+2），DE＝﹣m2+m+1，DF＝m+2，①如图2，当点E在直线BC上方时，∵AB∥EF，∠ABD+∠EDB＝180°，∵∠AED＝∠A BC，∴∠AED+∠EDB＝180°，∴AE∥CD，∴四边形ABDE为平行四边形，∴AB＝DE＝1＝﹣m2+m+1，解得：m＝0或（舍去0）；②如图3，当点E在直线BC的下方时，设AE、BD交于点N，作点N作x轴的平行线交DE于点M∵AB∥DE，∴∠ABN＝∠NDE，而∠AED＝∠ABC，∴∠ABN＝∠NDE＝∠AED＝∠ABC，∴△NAB、△DEN都是以点N为顶点的等腰三角形，故点M的纵坐标和AB中点的坐标同为，由中点公式得：（﹣m2+2m+3+m+2）＝，解得：m＝0或（舍去0），综上，点E（，）或（，）．15．如图，直线y＝x﹣3交x轴于点A，交y轴于点C，点B的坐标为（1，0），抛物线y＝ax2+bx+c（a≠0）经过A，B，C三点，抛物线的顶点为点D，对称轴与x轴的交点为点E，点E关于原点的对称点为F，连接CE，以点F为圆心， CE的长为半径作圆，点P为直线y＝x﹣3上的一个动点．（1）求抛物线的解析式；（2）求△BDP周长的最小值；（3）若动点P与点C不重合，点Q为⊙F上的任意一点，当PQ的最大值等于CE时，过P，Q两点的直线与抛物线交于M，N两点（点M在点N的左侧），求四边形ABMN的面积．解：（1）直线y＝x﹣3，令x＝0，则y＝﹣3，令y＝0，则x＝3，故点A、C的坐标为（3，0）、（0，﹣3），则抛物线的表达式为：y＝a（x﹣3）（x﹣1）＝a（x2﹣4x+3），则3a＝﹣3，解得：a＝﹣1，故抛物线的表达式为：y＝﹣x2+4x﹣3…①；（2）过点B作直线y＝x﹣3的对称点B′，连接BD交直线y＝x﹣3于点P，直线B′B交函数对称轴与点G，连接AB′，则此时△BDP周长＝BD+PB+PD＝BD+B′B为最小值，D（2，1），则点G（2，﹣1），即：BG＝EG，即点G是BB′的中点，过点B′（3，﹣2），△BDP周长最小值＝BD+B′B＝；（3）如图2所示，连接PF并延长交圆与点Q，此时PQ为最大值，点A、B、C、E、F的坐标为（3，0）、（1，0）、（0，﹣3）、（2，0）、（﹣2，0），则CE＝，FQ＝CE，则PF＝CE﹣CE＝，设点P（m，m﹣3），点F（﹣2，0），PF2＝13＝（m﹣2）2+（m﹣3）2，解得：m＝1，故点P（1，﹣2），将点P、F坐标代入一次函数表达式并解得：直线PF的表达式为：y＝﹣x﹣…②，联立①②并解得：x ＝，故点M 、N 的坐标分别为：（，）、（，），过点M 、N 分别作x 轴的垂线交于点S 、R ，则S 四边形ABMN ＝S 梯形NRSM ﹣S △ARN ﹣S △SBM ＝．。

九年级数学二次函数的专项培优练习题含详细答案

九年级数学二次函数的专项培优练习题含详细答案一、二次函数1．已知二次函数223y ax ax =-+的最大值为4，且该抛物线与y 轴的交点为C ，顶点为D .（1）求该二次函数的解析式及点C ，D 的坐标；（2）点(,0)P t 是x 轴上的动点，①求PC PD -的最大值及对应的点P 的坐标；②设(0,2)Q t 是y 轴上的动点，若线段PQ 与函数2||23y a x a x =-+的图像只有一个公共点，求t 的取值范围.【答案】（1）2y x 2x 3=-++，C 点坐标为(0,3)，顶点D 的坐标为(1,4)；（2）①最，P 的坐标为(3,0)-，②t 的取值范围为3t ≤-或332t ≤<或72t =. 【解析】【分析】（1）先利用对称轴公式x=2a 12a--=，计算对称轴，即顶点坐标为（1，4），再将两点代入列二元一次方程组求出解析式；（2）根据三角形的三边关系：可知P 、C 、D 三点共线时|PC-PD|取得最大值，求出直线CD 与x 轴的交点坐标，就是此时点P 的坐标；（3）先把函数中的绝对值化去，可知22x 23,0,y x 23,0.x x x x ⎧-++≥=⎨--+<⎩，此函数是两个二次函数的一部分，分三种情况进行计算：①当线段PQ 过点（0，3），即点Q 与点C 重合时，两图象有一个公共点，当线段PQ 过点（3，0），即点P 与点（3，0）重合时，两函数有两个公共点，写出t 的取值；②线段PQ 与当函数y=a|x|2-2a|x|+c （x≥0）时有一个公共点时，求t 的值；③当线段PQ 过点（-3，0），即点P 与点（-3，0）重合时，线段PQ 与当函数y=a|x|2-2a|x|+c （x ＜0）时也有一个公共点，则当t≤-3时，都满足条件；综合以上结论，得出t 的取值．【详解】解：（1）∵2a x 12a-=-=， ∴2y ax ax 3=-+的对称轴为x 1=.∵2y ax ax 3=-+人最大值为4，∴抛物线过点()1,4.得a 2a 34-+=，解得a 1=-.∴该二次函数的解析式为2y x 2x 3=-++.C 点坐标为()0,3，顶点D 的坐标为()1,4.（2）①∵PC PD CD -≤，∴当P,C,D 三点在一条直线上时，PC PD -取得最大值.连接DC 并延长交y 轴于点P ，PC PD CD -===∴PC PD -.易得直线CD 的方程为y x 3=+.把()P t,0代入，得t 3=-.∴此时对应的点P 的坐标为()3,0-.②2y a |x |2a x 3=-+的解析式可化为22x 23,0,y x 23,0.x x x x ⎧-++≥=⎨--+<⎩ 设线段PQ 所在直线的方程为y kx b =+，将()P t,0，()Q 0,2t 的坐标代入，可得线段PQ 所在直线的方程为y 2x 2t =-+.（1）当线段PQ 过点()3,0-，即点P 与点()3,0-重合时，线段PQ 与函数22x 23,0,y x 23,0.x x x x ⎧-++≥=⎨--+<⎩的图像只有一个公共点，此时t 3=-. ∴当t 3≤-时，线段PQ 与函数22x 23,0,y x 23,0.x x x x ⎧-++≥=⎨--+<⎩的图像只有一个公共点. （2）当线段PQ 过点()0,3，即点Q 与点C 重合时，线段PQ 与函数22x 23,0,y x 23,0.x x x x ⎧-++≥=⎨--+<⎩的图像只有一个公共点，此时3t 2=. 当线段PQ 过点()3,0，即点P 与点()3,0重合时，t 3=，此时线段PQ 与函数22x 23,0,y x 23,0.x x x x ⎧-++≥=⎨--+<⎩的图像有两个公共点. 所以当3t 32≤<时，线段PQ 与函数22x 23,0,y x 23,0.x x x x ⎧-++≥=⎨--+<⎩的图像只有一个公共点. （3）将y 2x 2t =-+带入()2y x 2x 3x 0=-++≥，并整理，得2x 4x 2t 30-+-=. ()Δ1642t 3288t =--=-.令288t 0-=，解得7t 2=. ∴当7t 2=时，线段PQ 与函数22x 23,0,y x 23,0.x x x x ⎧-++≥=⎨--+<⎩的图像只有一个公共点.综上所述，t 的取值范围为t 3≤-或3t 32≤<或7t 2=. 【点睛】本题考查了二次函数的综合应用，先利用待定系数法求解析式，同时把最大值与三角形的三边关系联系在一起；同时对于二次函数利用动点求取值问题，从特殊点入手，把函数分成几部分考虑，按自变量从大到小的顺序或从小到大的顺序求解．2．如图，抛物线y ＝ax 2＋bx （a ≠0）过A （4，0），B （1，3）两点，点C 、B 关于抛物线的对称轴对称，过点B 作直线BH ⊥x 轴，交x 轴于点H ．（1）求抛物线的表达式；（2）直接写出点C 的坐标，并求出△ABC 的面积；（3）点P 是抛物线上一动点，且位于第四象限，是否存在这样的点P ，使得△ABP 的面积为△ABC 面积的2倍？若存在，求出点P 的坐标，若不存在，请说明理由；（4）若点M 在直线BH 上运动，点N 在x 轴正半轴上运动，当以点C ，M ，N 为顶点的三角形为等腰直角三角形时，请直接写出此时△CMN 的面积．【答案】（1）y ＝－x 2＋4x ；（2）C （3，3），面积为3；（3）P 的坐标为（5，－5）；（4）52或5．【解析】试题分析：（1）利用待定系数法进行求解即可；（2）先求出抛物线的对称轴，利用对称性即可写出点C 的坐标，利用三角形面积公式即可求面积；（3）利用三角形的面积以及点P 所处象限的特点即可求；（4）分情况进行讨论，确定点M 、N ，然后三角形的面积公式即可求.试题解析：（1）将A （4，0），B （1，3）代入到y ＝ax 2＋bx 中，得16403a b a b +=⎧⎨+=⎩ ，解得14a b =-⎧⎨=⎩ ， ∴抛物线的表达式为y ＝－x 2＋4x ．（2）∵抛物线的表达式为y＝－x2＋4x，∴抛物线的对称轴为直线x＝2．又C，B关于对称轴对称，∴C（3，3）．∴BC＝2，∴S△ABC＝12×2×3＝3．（3）存在点P．作PQ⊥BH于点Q，设P（m，－m2＋4m）．∵S△ABP＝2S△ABC，S△ABC＝3，∴S△ABP＝6．∵S△ABP＋S△BPQ＝S△ABH＋S梯形AHQP∴6＋12×（m－1）×（3＋m2－4m）＝12×3×3＋12×（3＋m－1）（m2－4m）整理得m2－5m＝0，解得m1＝0（舍），m2＝5，∴点P的坐标为（5，－5）．（4）52或5．提示：①当以M为直角顶点，则S△CMN＝52；②当以N为直角顶点，S△CMN＝5；③当以C为直角顶点时，此种情况不存在．【点睛】本题是二次函数的综合题，主要考查待定系数法求解析式，三角形面积、直角三角形的判定等，能正确地根据题意确定图形，分情况进行讨论是解题的关键.3．二次函数y=x2-2mx+3（m＞）的图象与x轴交于点A（a，0）和点B（a+n，0）（n ＞0且n为整数），与y轴交于C点．（1）若a=1，①求二次函数关系式；②求△ABC的面积；（2）求证：a=m-；（3）线段AB（包括A、B）上有且只有三个点的横坐标是整数，求a的值．【答案】（1）y=x2-4x+3；3；（2）证明见解析；（3）a=1或a=−．【解析】试题分析：（1）①首先根据a=1求得A的坐标，然后代入二次函数的解析式，求得m的值即可确定二次函数的解析式；②根据解析式确定抛物线与坐标轴的交点坐标，从而确定三角形的面积；（2）将原二次函数配方后即可确定其对称轴为x=m，然后根据A、B两点关于x=m对称得到a+n-m=m-a，从而确定a、m、n之间的关系；（3）根据a=m-得到A（m-，0）代入y=（x-m）2-m2+3得0=（m--m）2-m2+3，求得m 的值即可确定a的值．试题解析：（1）①∵a=1，∴A（1，0），代入y=x2-2mx+3得1-2m+3=0，解得m=2，∴y=x2-4x+3；②在y=x2-4x+3中，当y=0时，有x2-4x+3=0可得x=1或x=3，∴A（1，0）、B（3，0），∴AB=2再根据解析式求出C点坐标为（0，3），∴OC=3，△ABC的面积=×2×3=3；（2）∵y=x2-2mx+3=（x-m）2-m2+3，∴对称轴为直线x=m，∵二次函数y=x2-2mx+3的图象与x轴交于点A和点B∴点A和点B关于直线x=m对称，∴a+n-m=m-a，∴a=m-；（3）y=x2-2mx+3（m＞）化为顶点式为y=（x-m）2-m2+3（m＞）①当a为整数，因为n＞0且n为整数所以a+n是整数，∵线段AB（包括A、B）上有且只有三个点的横坐标是整数，∴n=2，∴a=m-1，∴A（m-1，0）代入y=（x-m）2-m2+3得（x-m）2-m2+3=0，∴m2-4=0，∴m=2，m=-2（舍去），∴a=2-1=1，②当a不是整数，因为n＞0且n为整数所以a+n不是整数，∵线段AB（包括A、B）上有且只有三个点的横坐标是整数，∴n=3，∴a=m-∴A（m-，0）代入y=（x-m）2-m2+3得0=（m--m）2-m2+3，∴m2=，∴m=，m=-（舍去），∴a=−，综上所述：a=1或a=−．考点：二次函数综合题．4．已知：如图，抛物线y=ax2+bx+c与坐标轴分别交于点A（0，6），B（6，0），C（﹣2，0），点P是线段AB上方抛物线上的一个动点．（1）求抛物线的解析式；（2）当点P运动到什么位置时，△PAB的面积有最大值？（3）过点P作x轴的垂线，交线段AB于点D，再过点P做PE∥x轴交抛物线于点E，连结DE，请问是否存在点P使△PDE为等腰直角三角形？若存在，求出点P的坐标；若不存在，说明理由．【答案】（1）抛物线解析式为y=﹣12x2+2x+6；（2）当t=3时，△PAB的面积有最大值；（3）点P（4，6）．【解析】【分析】（1）利用待定系数法进行求解即可得；（2）作PM⊥OB与点M，交AB于点N，作AG⊥PM，先求出直线AB解析式为y=﹣x+6，设P（t，﹣12t2+2t+6），则N（t，﹣t+6），由S△PAB=S△PAN+S△PBN=12PN•AG+12PN•BM=12PN•OB列出关于t的函数表达式，利用二次函数的性质求解可得；（3）由PH⊥OB知DH∥AO，据此由OA=OB=6得∠BDH=∠BAO=45°，结合∠DPE=90°知若△PDE为等腰直角三角形，则∠EDP=45°，从而得出点E与点A重合，求出y=6时x的值即可得出答案．【详解】（1）∵抛物线过点B（6，0）、C（﹣2，0），∴设抛物线解析式为y=a（x﹣6）（x+2），将点A （0，6）代入，得：﹣12a=6，解得：a=﹣12，所以抛物线解析式为y=﹣12（x ﹣6）（x+2）=﹣12x 2+2x+6；（2）如图1，过点P 作PM ⊥OB 与点M ，交AB 于点N ，作AG ⊥PM 于点G ，设直线AB 解析式为y=kx+b ，将点A （0，6）、B （6，0）代入，得：660b k b =⎧⎨+=⎩，解得：16k b =-⎧⎨=⎩，则直线AB 解析式为y=﹣x+6，设P （t ，﹣12t 2+2t+6）其中0＜t ＜6，则N （t ，﹣t+6）， ∴PN=PM ﹣MN=﹣12t 2+2t+6﹣（﹣t+6）=﹣12t 2+2t+6+t ﹣6=﹣12t 2+3t ， ∴S △PAB =S △PAN +S △PBN=12PN•AG+12PN•BM =12PN•（AG+BM ） =12PN•OB =12×（﹣12t 2+3t ）×6 =﹣32t 2+9t =﹣32（t ﹣3）2+272， ∴当t=3时，△PAB 的面积有最大值；（3）如图2，∵PH ⊥OB 于H ，∴∠DHB=∠AOB=90°，∴DH ∥AO ，∵OA=OB=6，∴∠BDH=∠BAO=45°，∵PE ∥x 轴、PD ⊥x 轴，∴∠DPE=90°，若△PDE 为等腰直角三角形，则∠EDP=45°，∴∠EDP 与∠BDH 互为对顶角，即点E 与点A 重合，则当y=6时，﹣12x 2+2x+6=6，解得：x=0（舍）或x=4，即点P （4，6）．【点睛】本题考查了二次函数的综合问题，涉及到待定系数法、二次函数的最值、等腰直角三角形的判定与性质等，熟练掌握和灵活运用待定系数法求函数解析式、二次函数的性质、等腰直角三角形的判定与性质等是解题的关键.5．如图，已知顶点为(0,3)C -的抛物线2(0)y ax b a =+≠与x 轴交于A ，B 两点，直线y x m =+过顶点C 和点B ．（1）求m 的值；（2）求函数2(0)y ax b a =+≠的解析式；（3）抛物线上是否存在点M ，使得15MCB ∠=︒？若存在，求出点M 的坐标；若不存在，请说明理由．【答案】（1）﹣3；（2）y1 3 =x2﹣3；（3）M的坐标为（33，6）或（3，﹣2）．【解析】【分析】（1）把C（0，﹣3）代入直线y＝x+m中解答即可；（2）把y＝0代入直线解析式得出点B的坐标，再利用待定系数法确定函数关系式即可；（3）分M在BC上方和下方两种情况进行解答即可．【详解】（1）将C（0，﹣3）代入y＝x+m，可得：m＝﹣3；（2）将y＝0代入y＝x﹣3得：x＝3，所以点B的坐标为（3，0），将（0，﹣3）、（3，0）代入y＝ax2+b中，可得：390ba b=-⎧⎨+=⎩，解得：133ab⎧=⎪⎨⎪=-⎩，所以二次函数的解析式为：y13=x2﹣3；（3）存在，分以下两种情况：①若M在B上方，设MC交x轴于点D，则∠ODC＝45°+15°＝60°，∴OD＝OC•tan30°3=设DC为y＝kx﹣33，0），可得：k3=联立两个方程可得：233133y xy x⎧=-⎪⎨=-⎪⎩，解得：121203336x x y y ⎧=⎧=⎪⎨⎨=-=⎪⎩⎩，，所以M 1（33，6）；②若M 在B 下方，设MC 交x 轴于点E ，则∠OEC ＝45°-15°＝30°，∴OE ＝OC •tan60°＝33，设EC 为y ＝kx ﹣3，代入（33，0）可得：k 33=，联立两个方程可得：233133y x y x ⎧=-⎪⎪⎨⎪=-⎪⎩，解得：12120332x x y y ⎧=⎧=⎪⎨⎨=-=-⎪⎩⎩，，所以M 2（3，﹣2）．综上所述M 的坐标为（33，6）或（3，﹣2）．【点睛】此题是一道二次函数综合题，熟练掌握待定系数法求函数解析式等知识是解题关键．6．如图，已知直线y kx 6=-与抛物线2y ax bx c =++相交于A ，B 两点，且点A （1，－4）为抛物线的顶点，点B 在x 轴上。

人教版数学九年级上学期期末备考压轴题培优：二次函数(含答案)

期末备考压轴题培优：二次函数1．如图，在平面直角坐标系中，已知点B的坐标为（﹣1，0），且OA＝OC＝4OB，抛物线y＝ax 2+bx+c（a≠0）图象经过A，B，C三点．（1）求A，C两点的坐标；（2）求抛物线的解析式；（3）若点P是直线AC下方的抛物线上的一个动点，作PD⊥AC于点D，当PD的值最大时，求此时点P的坐标及PD的最大值．2．在平面直角坐标系中，二次函数y＝ax2+bx+2的图象与x轴交于A（﹣3，0），B（1，0）两点，与y轴交于点C．（1）求这个二次函数的关系解析式，x满足什么值时y＜0？（2）点P是直线AC上方的抛物线上一动点，是否存在点P，使△ACP面积最大？若存在，求出点P的坐标；若不存在，说明理由；（3）点M为抛物线上一动点，在x轴上是否存在点Q，使以A、C、M、Q为顶点的四边形是平行四边形？若存在，直接写出点Q的坐标；若不存在，说明理由．3．在平面直角坐标系中，抛物线y＝ax2+bx+c过点A（﹣1，0），B（3，0），与y轴交于点C，连接AC，BC，将△OBC沿BC所在的直线翻折，得到△DBC，连接OD．（1）用含a的代数式表示点C的坐标．（2）如图1，若点D落在抛物线的对称轴上，且在x轴上方，求抛物线的解析式．（3）设△OBD的面积为S1，△OAC的面积为S2，若＝，求a的值．4．如图，已知直线y＝﹣3x+3与x轴交于点A，与y轴交于点C，抛物线y＝ax2+bx+c经过点A和点C，对称轴为直线l：x＝﹣1，该抛物线与x轴的另一个交点为B．（1）求此抛物线的解析式；（2）点P在抛物线上且位于第二象限，求△PBC的面积最大值及点P的坐标．（3）点M在此抛物线上，点N在对称轴上，以B、C、M、N为顶点的四边形能否为平行四边形？若能，写出所有满足要求的点M的坐标；若不能，请说明理由．5．如图，抛物线y＝x2+bx+c与轴交于点A和点B，与y轴交于点C，作直线BC，点B 的坐标为（6，0），点C的坐标为（0，﹣6）．（1）求抛物线的解析式并写出其对称轴；（2）D为抛物线对称轴上一点，当△BCD是以BC为直角边的直角三角形时，求D点坐标；（3）若E为y轴上且位于点C下方的一点，P为直线BC上的一点，在第四象限的抛物线上是否存在一点Q．使以C，E，P，Q为顶点的四边形是菱形？若存在，请求出Q点的横坐标；若不存在，请说明理由．6．如图1，在平面直角坐标系xOy中，直线l：与x轴、y轴分别交于点A和点B （0，﹣1），抛物线经过点B，且与直线l的另一个交点为C（4，n）．（1）求n的值和抛物线的解析式；（2）点D在抛物线上，且点D的横坐标为t（0＜t＜4）．DE∥y轴交直线l于点E，点F 在直线l上，且四边形DFEG为矩形（如图2）．若矩形DFEG的周长为p，求p与t的函数关系式以及p的最大值；（3）M是平面内一点，将△AOB绕点M沿逆时针方向旋转90°后，得到△A1O1B1，点A、O、B的对应点分别是点A1、O1、B1．若△A1O1B1的两个顶点恰好落在抛物线上，请直接写出点A1的横坐标．7．如图，抛物线y＝﹣x2+2x+3与x轴分别交于A、B两点，与y轴的正半轴交于C点，抛物线的顶点为D，连接BC、BD，抛物线上是否存在一点P，使得∠PCB＝∠CBD？若存在，求P点的坐标；若不存在，说明理由．8．如图，已知抛物线经过两点A（﹣3，0），B（0，3），且其对称轴为直线x＝﹣1．（1）求此抛物线的解析式；（2）若点P是抛物线上点A与点B之间的动点（不包括点A，点B），求△PAB的面积的最大值，并求出此时点P的坐标．9．如图，在平面直角标系中，抛物线C：y＝与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C，点D为y轴正半轴上一点．且满足OD＝OC，连接BD，（1）如图1，点P为抛物线上位于x轴下方一点，连接PB，PD，当S△PBD最大时，连接AP，以PB为边向上作正△BPQ，连接AQ，点M与点N为直线AQ上的两点，MN＝2且点N位于M点下方，连接DN，求DN+MN+AM的最小值（2）如图2，在第（1）问的条件下，点C关于x轴的对称点为E，将△BOE绕着点A 逆时针旋转60°得到△B′O′E′，将抛物线y＝沿着射线P A方向平移，使得平移后的抛物线C′经过点E，此时抛物线C′与x轴的右交点记为点F，连接E′F，B′F，R为线段E’F上的一点，连接B′R，将△B′E′R沿着B′R翻折后与△B′E′F重合部分记为△B′RT，在平面内找一个点S，使得以B′、R、T、S为顶点的四边形为矩形，求点S的坐标．10．已知：如图，抛物线y＝ax2+3ax+c（a＞0）与y轴交于C点，与x轴交于A、B两点，A点在B点左侧．点B的坐标为（1，0），OC＝3BO．（1）求抛物线的解析式；（2）若点D是线段AC下方抛物线上的动点，求四边形ABCD面积的最大值；（3）若点E在x轴上，点P在抛物线上．是否存在以A、C、E、P为顶点且以AC为一边的平行四边形？若存在，求出点P的坐标；若不存在，请说明理由．11．如图，在平面直角坐标系中，直线y＝2x+6与x轴交于点A，与y轴交点C，抛物线y ＝﹣2x2+bx+c过A，C两点，与x轴交于另一点B．（1）求抛物线的解析式．（2）在直线AC上方的抛物线上有一动点E，连接BE，与直线AC相交于点F，当EF ＝BF时，求sin∠EBA的值．（3）点N是抛物线对称轴上一点，在（2）的条件下，若点E位于对称轴左侧，在抛物线上是否存在一点M，使以M，N，E，B为顶点的四边形是平行四边形？若存在，直接写出点M的坐标；若不存在，请说明理由．12．如图，在平面直角坐标系中，抛物线y＝ax2+bx+4经过点A（4，0），B（﹣1，0），交y轴于点C．（1）求抛物线的解析式；（2）点D是直线AC上一动点，过点D作DE垂直于y轴于点E，过点D作DF⊥x轴，垂足为F，连接EF，当线段EF的长度最短时，求出点D的坐标；（3）在AC上方的抛物线上是否存在点P，使得△ACP是直角三角形？若存在，求出所有符合条件的点P的坐标；若不存在，说明理由．13．已知二次函数y＝ax2+4x+c，当x＝﹣2时，y＝﹣5；当x＝1时，y＝4（1）求这个二次函数表达式．（2）此函数图象与x轴交于点A，B（A在B的左边），与y轴交于点C，求点A，B，C 点的坐标及△ABC的面积．（3）该函数值y能否取到﹣6？为什么？14．如图，抛物线y＝ax2+bx+c经过A（﹣3，0），B（1，0），C（0，3）三点．（1）求抛物线的函数表达式；（2）如图1，P为抛物线上在第二象限内的一点，若△PAC面积为3，求点P的坐标；（3）如图2，D为抛物线的顶点，在线段AD上是否存在点M，使得以M，A，O为顶点的三角形与△ABC相似？若存在，求点M的坐标；若不存在，请说明理由．15．已知抛物线y＝2x2+bx+c与x轴的交点为A、B，顶点为D．（1）若点A、点B的坐标分别为A（﹣1，0）、B（3，0），求抛物线的解析式；（2）在（1）的条件下，在抛物线的对称轴上是否存在点P使△BCP为直角三角形？若存在，求出P的坐标；若不存在，请说明理由；（3）若抛物线y＝2x2+bx+c与直线y＝x+h交于E、F两点，点M在EF之间的抛物线上运动，MN∥y轴，交直线y＝x+h于点N，是否为定值，并说明理由．参考答案1．解：（1）OA ＝OC ＝4OB ＝4，故点A 、C 的坐标分别为（4，0）、（0，﹣4）；（2）抛物线的表达式为：y ＝a （x+1）（x ﹣4）＝a （x 2﹣3x ﹣4），即﹣4a ＝﹣4，解得：a ＝1，故抛物线的表达式为：y ＝x 2﹣3x ﹣4；（3）直线CA 过点C ，设其函数表达式为：y ＝kx ﹣4，将点A 坐标代入上式并解得：k ＝1，故直线CA 的表达式为：y ＝x ﹣4，过点P 作y 轴的平行线交AC 于点H ，∵OA ＝OC ＝4，∴∠OAC ＝∠OCA ＝45°，∵PH ∥y 轴，∴∠PHD ＝∠OCA ＝45°，设点P （x ，x 2﹣3x ﹣4），则点H （x ，x ﹣4），PD ＝HP sin ∠PFD ＝（x ﹣4﹣x 2+3x+4）＝﹣x 2+2x ，∵＜0，∴PD 有最大值，当x ＝2时，其最大值为2，此时点P （2，﹣6）．2．解：（1）函数表达式为：y ＝a （x+3）（x ﹣1）＝a （x 2+2x ﹣3），﹣3a ＝2，解得：a ＝﹣，抛物线的表达式为：y ＝﹣x 2﹣x+2，当x＜﹣3或x＞1时，y＜0；（2）存在，理由：过点P作平行于y轴的直线交AC于点H，将点A（﹣3，0）、C（0，2）的坐标代入一次函数表达式：y＝kx+b得：，解得：，故直线AC的表达式为：y＝x+2，设点P（x，﹣x2﹣x+2），则点H（x，x+2），△ACP面积S＝×PH×OA＝×3（﹣x2﹣x+2﹣x﹣2）＝﹣x2﹣3x，∵＜0，故当x＝﹣时，S有最大值，此时点P（﹣，）；（3）设点M的坐标为：（m，n），则n＝﹣m2﹣m+2，点Q（s，0），点A、C的坐标分别为：（﹣3，0）、（0，2），①当AC是平行四边形的一条边时，点A向右平移3个单位、向上平移2个单位得到C，同样点M（Q）向右平移3个单位、向上平移2个单位得到Q（M），即：m+3＝s，n+2＝0或m﹣3＝s，n﹣2＝0，且n＝﹣m2﹣m+2，解得：s＝2或﹣5；②当AC是平行四边形的对角线时，则m+s＝﹣3，n+0＝2，且n＝﹣m2﹣m+2，解得：s＝﹣1，故点Q 的坐标为：（﹣1，0）或（﹣5，0）或（2，0）或（2﹣，0）．3．解：（1）抛物线的表达式为：y ＝a （x+1）（x ﹣3）＝a （x 2﹣2x ﹣3），即c ＝﹣3a ，则点C （0，﹣3a ）；（2）过点B 作y 轴的平行线BQ ，过点D 作x 轴的平行线交y 轴于点P 、交BQ 于点Q ，∵∠CDP+∠PDC ＝90°，∠PDC +∠QDB ＝90°，∴∠QDB ＝∠DCP ，设：D （1，n ），点C （0，﹣3a ），∠CPD ＝∠BQD ＝90°，∴△CPD ∽△DQB ，∴，其中：CP ＝n+3a ，DQ ＝3﹣1＝2，PD ＝1，BQ ＝n ，CD ＝﹣3a ，BD ＝3，将以上数值代入比例式并解得：a ＝±，∵a ＜0，故a ＝﹣，故抛物线的表达式为：y ＝﹣x 2+x+；（3）如图2，当点C 在x 轴上方时，连接OD 交BC 于点H ，则DO ⊥BC ，过点H 、D 分别作x 轴的垂线交于点N 、M ，设：OC＝m＝﹣3a，S1＝S△OBD＝×OB×DM＝DM，S2＝S△OAC＝×1×m，而＝，则DM＝，HN＝DM＝＝OC，∴BN＝BO＝，则ON＝3﹣＝，则DO⊥BC，HN⊥OB，则∠BHN＝∠HON，则tan∠BHN＝tan∠HON，则HN2＝ON×BN＝＝（）2，解得：m＝±6（舍去负值），CO＝|﹣3a|＝6，解得：a＝﹣2（不合题意值已舍去），故：a＝﹣2．当点C在x轴下方时，同理可得：a＝2；故：a＝﹣2或a＝2 4．解：（1）直线y＝﹣3x+3与x轴交于点A，与y轴交于点C，当y＝0时，﹣3x+3＝0，解得x＝1，则A点坐标为（1，0）；当x＝0时，y＝3，则C点坐标为（0，3）；抛物线的对称轴为直线x＝﹣1，则B点坐标为（﹣3，0）；把C（0，3）代入y＝a（x﹣1）（x+3）得3＝﹣3a，解得a＝﹣1，则此抛物线的解析式为y＝﹣（x﹣1）（x+3）＝﹣x2﹣2x+3；（2）设P（x，﹣x2﹣2x+3），如图1，过P作PM∥y轴，交BC于点M，设直线BC的关系式为：y＝mx+n，把B（﹣3，0），C（0，3）代入y＝mx+n得，解得，∴直线BC的关系式为y＝x+3，∴PM＝﹣x2﹣2x+3﹣（x+3）＝﹣x2﹣3x，∴△PBC的面积＝S△PBM+S△PCM＝＝×3（﹣x2﹣3x）＝﹣+，∵﹣＜0，∴当x＝﹣时，△PBC的面积有最大值是，∴P点坐标为（﹣，）；（3）①当以BC为对角线，如图2，∵四边形BMCN为平行四边形，∵C点（0，3），N点横坐标为﹣1，B点横坐标为﹣3，∴M点横坐标为﹣2，∴M点纵坐标为y＝﹣4+4+3＝3，∴M点坐标为（﹣2，3）；②当以BC为边时，如图3，∵四边形BCNM为平行四边形，∵C点（0，3），B（﹣3，0），N点横坐标为﹣1，∴M点横坐标为﹣4，∴M点纵坐标为y＝﹣16+8+3＝﹣5，∴M点坐标为（﹣4，﹣5）；同理可知如图4，存在四边形BCMN为平行四边形，可得M的横坐标为2，当x＝2时，y＝﹣4﹣4+3＝﹣5，∴M点坐标为（﹣4，﹣5）或（2，﹣5）．综上所述，M点坐标为（﹣2，3）或（﹣4，﹣5）或（2，﹣5）．5．解：（1）将点B、C的坐标代入二次函数表达式得：，解得：，故抛物线的表达式为：y＝x2﹣2x﹣6，令y＝0，则x＝﹣2或6，则点A（﹣2，0），则函数的对称性x＝2；（2）①当∠BCD＝90°时，将点B、C的坐标代入一次函数表达式得：直线BC的表达式为：y＝x﹣6，则直线CD的表达式为：y＝﹣x﹣6，当x＝2时，y＝﹣8，故点D（2，﹣8）；②当∠DBC＝90°时，同理可得点D（2，4），故点D（2，﹣8）或（2，4）；（3）①当CE为菱形的一条边时，则PQ∥CE，设点P（m，m﹣6），则点Q（m，n），则n＝m2﹣2m﹣6…①，由题意得：CP＝PQ，即m＝m﹣6﹣n…②，联立①②并解得：m＝6﹣2，n＝4﹣8，则点Q（6﹣2，4﹣8）；②当CE为菱形的对角线时，则PQ⊥CE，即PQ∥x轴，设点P（m，m﹣6），则点Q（s，m﹣6），其中m﹣6＝s2﹣2s﹣6…③，则PC＝﹣m，CQ2＝s2+m2，由题意得：CQ＝CP，即：（﹣m）2＝s2+m2…④，联立③④并解得：m＝6或﹣2（舍去6），故点（2，﹣8）；综上，点Q（6﹣2，4﹣8）或（2，﹣8）．6．解：（1）∵直线l：y＝x+m经过点B（0，﹣1），∴m＝﹣1，∴直线l的解析式为y＝x﹣1，∵直线l：y＝x﹣1经过点C（4，n），∴n＝×4﹣1＝2，∵抛物线y＝x2+bx+c经过点C（4，2）和点B（0，﹣1），∴，解得，∴抛物线的解析式为y＝x2﹣x﹣1；（2）令y＝0，则x﹣1＝0，解得x＝，∴点A的坐标为（，0），∴OA＝，在Rt△OAB中，OB＝1，∴AB＝＝＝，∵DE∥y轴，∴∠ABO＝∠DEF，在矩形DFEG中，EF＝DE?cos∠DEF＝DE?＝DE，DF＝DE?sin∠DEF＝DE?＝DE，∴p＝2（DF+EF）＝2（+）DE＝DE，∵点D的横坐标为t（0＜t＜4），∴D（t，t2﹣t﹣1），E（t，t﹣1），∴DE＝（t﹣1）﹣（t2﹣t﹣1）＝﹣t2+2t，∴p＝×（﹣t2+2t）＝﹣t2+t，∵p＝﹣（t﹣2）2+，且﹣＜0，∴当t＝2时，p有最大值；（3）∵△AOB绕点M沿逆时针方向旋转90°，∴A1O1∥y轴时，B1O1∥x轴，设点A1的横坐标为x，①如图1，点O1、B1在抛物线上时，点O1的横坐标为x，点B1的横坐标为x+1，∴x2﹣x﹣1＝（x+1）2﹣（x+1）﹣1，解得x＝，②如图2，点A1、B1在抛物线上时，点B1的横坐标为x+1，点A1的纵坐标比点B1的纵坐标大，∴x2﹣x﹣1＝（x+1）2﹣（x+1）﹣1+，解得x＝﹣，综上所述，点A1的横坐标为或﹣．7．解：连接DC，当y＝0则0＝﹣x2+2x+3，解得：x1＝﹣1，x2＝3，当x＝0，则y＝3，故A（﹣1，0），B（3，0），C（0，3），y＝﹣x2+2x+3＝﹣（x﹣1）2+4，故D（1，4），因此BC＝3，BD＝2，CD＝，故CD2+BC2＝BD2，因此满足△BCD是直角三角形且∠BCD＝90°，过B点作BE垂直于BC，连接EC，且BE＝，∵CO＝OB＝3，∴∠OCB＝∠CBO＝45°，故∠EBx＝45°，则E（4，1），在△ECB和△DBC中，，∴△ECB≌△DBC（SAS），此时CE与抛物线的交点就是满足条件的点P，设直线EC的解析式为：y＝kx+b，则，解得：．则EC直线解析式为：y＝﹣0.5x+3，故﹣0.5x+3＝﹣x2+2x+3，解得：x1＝0（不合题意舍去），x2＝2.5，则y＝1.75，故P1点坐标为：（2.5，1.75）；当y＝0则0＝﹣x2+2x+3，解得：x1＝﹣1，x2＝3，当x＝0，则y＝3，故A（﹣1，0），B（3，0），C（0，3），y＝﹣x2+2x+3＝﹣（x﹣1）2+4，故D（1，4），设直线BD解析式为y＝Kx+b，代入B、D坐标，解得：，因此直线BD为y＝﹣2x+6，只要（1）PC∥BD，则有∠PCB＝∠CBD设直线PC为y＝﹣2x+b，代入C点坐标：则b＝3，直线PC解析式为y＝﹣2x+3联立：﹣2x+3＝﹣x2+2x+3x2﹣4x＝0，解得：x1＝0（舍去），x2＝4，代入x＝4，y＝﹣5因此P2（4，﹣5）．综上所述：P点坐标为：（2.5，1.75）或（4，﹣5）．8．解：（1）∵抛物线对称轴是直线x＝﹣1且经过点A（﹣3，0）由抛物线的对称性可知：抛物线还经过点（1，0）设抛物线的解析式为y＝a（x﹣x1）（x﹣x2）（a≠0）即：y＝a（x﹣1）（x+3）把B（0，3）代入得：3＝﹣3a∴a＝﹣1∴抛物线的解析式为：y＝﹣x2﹣2x+3．（2）设直线AB的解析式为y＝kx+b，∵A（﹣3，0），B（0，3），∴，∴直线AB为y＝x+3，作PQ⊥x轴于Q，交直线AB于M，设P（x，﹣x2﹣2x+3），则M（x，x+3），∴PM＝﹣x2﹣2x+3﹣（x+3）＝﹣x2﹣3x，∴S＝（﹣x2﹣3x）×3＝﹣（x+）2+．当x＝﹣时，S最大＝，y＝﹣（﹣）2﹣2×（﹣）+3＝，∴△P AB的面积的最大值为，此时点P的坐标为（﹣，）9．解：（1）如图1，过点D作DD'∥MN，且DD'＝MN＝2，连接D'M；过点D'作D'J⊥y 轴于点J；作直线AP，过点M作MH⊥AP于点H，过点D'作D'K⊥AP于点K∵y＝＝0解得：x1＝﹣3，x2＝1∴A（﹣3，0），B（1，0）∵x＝0时，y＝＝﹣∴C（0，﹣），OC＝∴OD＝OC＝，D（0，）设P（t，t2+t﹣）（﹣3＜t＜1）设直线PB解析式为y＝kx+b，与y轴交于点G∴解得：∴直线PB：y＝（t+）x﹣t﹣，G（0，﹣t﹣）∴DG＝﹣（﹣t﹣）＝t+∴S△BPD＝S△BDG+S△PDG＝DG?x B+DG?|x P|＝DG?（x B﹣x P）＝（t+）（1﹣t）＝﹣（t2+4t﹣5）∴t＝﹣＝﹣2时，S△BPD最大∴P（﹣2，﹣），直线PB解析式为y＝x﹣，直线AP解析式为y＝﹣x﹣3∴tan∠ABP＝＝∴∠ABP＝30°∵△BPQ为等边三角形∴∠PBQ＝60°，BP＝PQ＝BQ∴BA平分∠PBQ∴PQ⊥x轴，PQ与x轴交点I为PQ中点∴Q（﹣2，）∴Rt△AQI中，tan∠QAI＝∴∠QAI＝∠PAI＝60°∴∠MAH＝180°﹣∠P AI﹣∠QAI＝60°∵MH⊥AP于点H∴Rt△AHM＝90°，sin∠MAH＝∴MH＝AM∵DD'∥MN，DD'＝MN＝2∴四边形MNDD'是平行四边形∴D'M＝DN∴DN+MN+AM＝2+D'M+MH∵D'K⊥AP于点K∴当点D'、M、H在同一直线上时，DN+MN+AM＝2+D'M+MH＝2+D'K最短∵DD'∥MN，D（0，）∴∠D'DJ＝30°∴D'J＝DD'＝1，DJ＝DD'＝∴D'（1，）∵∠P AI＝60°，∠ABP＝30°∴∠APB＝180°﹣∠PAI﹣∠ABP＝90°∴PB∥D'K设直线D'K解析式为y＝x+d，把点D'代入得：+d＝解得：d＝∴直线D'K：y＝x+把直线AP与直线D'K解析式联立得：解得：∴K（﹣，）∴D'K＝∴DN+MN+AM的最小值为（2）连接B'A、BB'、EA、E'A、EE'，如图2∵点C（0，﹣）关于x轴的对称点为E∴E（0，）∴tan∠EAB＝∴∠EAB＝30°∵抛物线C'由抛物线C平移得到，且经过点E∴设抛物线C'解析式为：y＝x2+mx+，∵A（﹣3，0），P（﹣2，﹣），E（0，），B（1，0），∴BE∥PA，BE＝P A，∴抛物线C'经过点A（﹣3，0），∴×9﹣3m+＝0解得：m＝∴抛物线C'解析式为：y＝x2+x+∵x2+x+＝0，解得：x1＝﹣3，x2＝﹣1∴F（﹣1，0）∵将△BOE绕着点A逆时针旋转60°得到△B′O′E′∴∠BAB'＝∠EAE'＝60°，AB'＝AB＝1﹣（﹣3）＝4，AE'＝AE＝∴△ABB'、△AEE'是等边三角形∴∠E'AB＝∠E'AE+∠EAB＝90°，点B'在AB的垂直平分线上∴E'（﹣3，2），B'（﹣1，2）∴B'E'＝2，∠FB'E'＝90°，E'F＝∴∠B'FE'＝30°，∠B'E'F＝60°①如图3，点T在E'F上，∠B'TR＝90°过点S作SW⊥B'E'于点W，设翻折后点E'的对应点为E''∴∠E'B'T＝30°，B'T＝B'E'＝∵△B′E′R翻折得△B'E''R∴∠B'E''R＝∠B'E'R＝60°，B'E''＝B'E'＝2∴E''T＝B'E''﹣B'T＝2﹣∴Rt△RTE''中，RT＝E''T＝2﹣3∵四边形RTB'S是矩形∴∠SB'T＝90°，SB'＝RT＝2﹣3∴∠SB'W＝∠SB'T﹣∠E'B'T＝60°∴B'W＝SB'＝﹣，SW＝SB'＝3﹣∴x S＝x B'﹣B'W＝，y S＝y B'+SW＝3+∴S（，3+）②如图4，点T在E'F上，∠B'RT＝90°过点S作SX⊥B'F于点X∴E'R＝B'E'＝1，点E'翻折后落在E'F上即为点T∴B'S＝RT＝E'R＝1∵∠SB'X＝90°﹣∠RB'F＝30°∴XS＝B'S＝，B'X＝B'S＝∴x S＝x B'+XS＝﹣，y S＝y B'﹣B'X＝∴S（﹣，）③如图5，点T在B'F上，∠B'TR＝90°∴RE''∥E'B'，∠E''＝∠B'E'R＝60°∴∠E'BE''＝∠E'RE''＝120°∴四边形B'E'RE''是平行四边形∵E'R＝E''R∴?B'E'RE''是菱形∴B'E'＝E'R∴△B'E'R是等边三角形∵∠B'SR＝90°，即RS⊥B'E'∴点S为B'E'中点∴S（﹣2，2）综上所述，使得以B′、R、T、S为顶点的四边形为矩形的点S坐标为（，3+）或（﹣，）或（﹣2，2）．10．解：（1）∵B（1，0），∴OB＝1；∵OC＝3BO，∴C（0，﹣3）；（1分）∵y＝ax2+3ax+c过B（1，0）、C（0，﹣3），∴；解这个方程组，得∴抛物线的解析式为：（2分）（2）过点D作DM∥y轴分别交线段AC和x轴于点M、N 在中，令y＝0，得方程解这个方程，得x1＝﹣4，x2＝1∴A（﹣4，0）设直线AC的解析式为y＝kx+b∴解这个方程组，得∴AC的解析式为：（3分）∵S四边形ABCD＝S△ABC+S△ADC＝＝设，（4分）当x＝﹣2时，DM有最大值3此时四边形ABCD面积有最大值（5分）（3）如图所示，①过点C作CP1∥x轴交抛物线于点P1，过点P1作P1E1∥AC交x轴于点E1，此时四边形ACP1E1为平行四边形，∵C（0，﹣3）∴设P1（x，﹣3）∴解得x1＝0，x2＝﹣3∴P1（﹣3，﹣3）；②平移直线AC交x轴于点E，交x轴上方的抛物线于点P，当AC＝PE时，四边形ACEP 为平行四边形，∵C（0，﹣3）∴设P（x，3），∴，x2+3x﹣8＝0解得或，此时存在点和综上所述存在3个点符合题意，坐标分别是P1（﹣3，﹣3），，．11．解：（1）在y＝2x+6中，当x＝0时y＝6，当y＝0时x＝﹣3，∴C（0，6）、A（﹣3，0），∵抛物线y＝﹣2x2+bx+c的图象经过A、C两点，∴，解得，∴抛物线的解析式为y＝﹣2x2﹣4x+6；（2）令﹣2x2﹣4x+6＝0，解得x1＝﹣3，x2＝1，∴B（1，0），∵点E的横坐标为t，∴E（t，﹣2t2﹣4t+6），如图，过点E作EH⊥x轴于点H，过点F作FG⊥x轴于点G，则EH∥FG，∵EF＝BF，∴＝＝＝，∵BH＝1﹣t，∴BG＝BH＝﹣t，∴点F的横坐标为+t，∴F（+t，+t），∴﹣2t2﹣4t+6＝（+t），∴t2+3t+2＝0，解得t1＝﹣2，t2＝﹣1，当t＝﹣2时，﹣2t2﹣4t+6＝6，当t＝﹣1时，﹣2t2﹣4t+6＝8，∴E1（﹣2，6），E2（﹣1，8），当点E的坐标为（﹣2，6）时，在Rt△EBH中，EH＝6，BH＝3，∴BE＝＝＝3，∴sin∠EBA＝＝＝；同理，当点E的坐标为（﹣1，8）时，sin∠EBA＝＝，∴sin∠EBA的值为或；（3）∵点N在对称轴上，∴x N＝＝﹣1，①当EB为平行四边形的边时，分两种情况：（Ⅰ）点M在对称轴右侧时，BN为对角线，∵E（﹣2，6），x N＝﹣1，﹣1﹣（﹣2）＝1，B（1，0），∴x M＝1+1＝2，当x＝2时，y＝﹣2×22﹣4×2+6＝﹣10，∴M（2，﹣10）；（Ⅱ）点M在对称轴左侧时，BM为对角线，∵x N＝﹣1，B（1，0），1﹣（﹣1）＝2，E（﹣2，6），∴x M＝﹣2﹣2＝﹣4，当x＝﹣4时，y＝﹣2×（﹣4）2﹣4×（﹣4）+6＝﹣10，∴M（﹣4，﹣10）；②当EB为平行四边形的对角线时，∵B（1，0），E（﹣2，6），x N＝﹣1，∴1+（﹣2）＝﹣1+x M，∴x M＝0，当x＝0时，y＝6，∴M（0，6）；综上所述，M的坐标为（2，﹣10）或（﹣4，﹣10）或（0，6）．12．解：（1）∵抛物线y＝ax2+bx+4经过点A（4，0），B（﹣1，0），∴，解得：，∴抛物线的解析式为：y＝﹣x2+3x+4；（2）连接OD，由题意知，四边形OFDE是矩形，则OD＝EF，据垂线段最短，可知：当OD⊥AC时，OD最短，即EF最短．由（1）知，在Rt△AOC中，OC＝OA＝4，∴AC＝4．又∵D为AC的中点．∴DF∥OC，∴DF＝OC＝2，∴点D的坐标为（2，2）；（3）假设存在，设点P的坐标为（m，﹣m2+3m+4）．∵点A的坐标为（4，0），点C的坐标为（0，4），∴AP2＝（m﹣4）2+（﹣m2+3m+4﹣0）2＝m4﹣6m3+2m2+16m+32，CP2＝（m﹣0）2+（﹣m 2+3m+4﹣4）2＝m4﹣6m3+10m2，AC2＝（0﹣4）2+（4﹣0）2＝32．分两种情况考虑，．①当∠ACP＝90°时，AP2＝CP2+AC2，即m4﹣6m3+2m2+16m+32＝m4﹣6m3+10m2+32，整理得：m2﹣2m＝0，解得：m1＝0（舍去），m2＝2，∴点P的坐标为（2，6）；②当∠APC＝90°时，CP2+AP2＝AC2，即m4﹣6m3+10m2+m4﹣6m3+2m2+16m+32＝32，整理得：m（m3﹣6m2+6m+8）＝0，∴m（m﹣4）（m2﹣2m﹣2）＝0，解得：m1＝0（舍去），m2＝4（舍去），（舍去），，∴点P的坐标为（1+，3+）．综上所述，假设成立，即存在点P（2，6）或（1+，3+），使得△ACP是直角三角形．13．解：（1）把x＝﹣2时，y＝﹣5；x＝1时，y＝4代入y＝ax2+4x+c得，解得，∴这个二次函数表达式为y＝x2+4x﹣1；（2）令y＝0，则x2+4x﹣1＝0，解得x＝﹣2±，∴A（﹣2﹣，0），B（﹣2+，0），令x＝0，则y＝﹣1，∴C（0，﹣1），∴△ABC的面积：AB?OC＝（﹣2++2+）×1＝；（3）∵y＝x2+4x﹣1＝（x+2）2﹣5，∴函数y的最小值为﹣5，∴函数值y不能取到﹣6．14．解：（1）把A（﹣3，0），B（1，0），C（0，3）代入抛物线解析式y＝ax2+bx+c得，解得，所以抛物线的函数表达式为y＝﹣x2﹣2x+3．（2）如解（2）图1，过P点作PQ平行y轴，交AC于Q点，∵A（﹣3，0），C（0，3），∴直线AC解析式为y＝x+3，设P点坐标为（x，﹣x2﹣2x+3．），则Q点坐标为（x，x+3），∴PQ＝﹣x2﹣2x+3﹣（x+3）＝﹣x2﹣3x．∴S△PAC＝，∴，解得：x1＝﹣1，x2＝﹣2．当x＝﹣1时，P点坐标为（﹣1，4），当x＝﹣2时，P点坐标为（﹣2，3），综上所述：若△P AC面积为3，点P的坐标为（﹣1，4）或（﹣2，3），（3）如解（3）图1，过D点作DF垂直x轴于F点，过A点作AE垂直BC于E点，∵D为抛物线y＝﹣x2﹣2x+3的顶点，∴D点坐标为（﹣1，4），又∵A（﹣3，0），∴直线AD为y＝2x+6，AF＝2，DF＝4，tan∠DAB＝2，∵B（1，0），C（0，3）∴tan∠ABC＝3，BC＝，sin∠ABC＝，直线BC解析式为y＝﹣3x+3．∵AB＝4，∴AE＝AB?sin∠ABC＝＝，BE＝，∴CE＝，∴tan∠ACB＝，∴tan∠ACB＝tan∠PAB＝2，∴∠ACB＝∠P AB，∴使得以M，A，O为顶点的三角形与△ABC相似，则有两种情况，如解（3）图2Ⅰ．当∠AOM＝∠CAB＝45°时，△ABC∽△OMA，即OM为y＝﹣x，设OM与AD的交点M（x，y）依题意得：，解得，即M点为（﹣2，2）．Ⅱ．若∠AOM＝∠CBA，即OM∥BC，∵直线BC解析式为y＝﹣3x+3．∴直线OM为y＝﹣3x，设直线OM与AD的交点M（x，y）．则依题意得：，解得，即M点为（，），综上所述：存在使得以M，A，O为顶点的三角形与△ABC相似的点M，其坐标为（﹣2，2）或（，），15．解：（1）由交点式抛物线表达式得：y＝2（x+1）（x﹣3）＝2x2﹣4x﹣6；（2）存在，理由：设点P坐标为（1，m），则直线BC表达式中的k1值为：2，①当∠BCP＝90°时，如图所示，直线BC⊥CP，则其表达式中的k值为﹣，直线BC的表达式为：y＝﹣x﹣6，当x＝1时，y＝﹣，故：P（1，﹣）；②当∠CBP（P′）＝90°时，同理可得：P（1，1）③当∠CP（P″）B＝90°时，直线BP表达式中的k2值为：﹣，直线PC表达式中的k3值为：m+6，则：﹣（m+6）＝﹣1，解得：m＝﹣3，P（1，﹣3﹣）或（1，﹣3+）；故点P的坐标为（1，﹣）或（1，1）或（1，﹣3﹣）或（1，﹣3+）；（3）设E（x1，y1）、F（x2，y2），联立，整理得2x2﹣5x﹣6﹣h＝0，∴x1+x2＝，x1x2＝﹣，设M（t，2t2﹣4t﹣6）、N（t，t+h），∴MN＝t+h﹣（2t2﹣4t﹣6）＝﹣2t2+5t+h+6，过点E作EG⊥MN于G，过点F作FH⊥MN于H，∴△EGN、△FHN均为等腰直角三角形，∴EN?NF＝EG?NH＝2（t﹣x1）（x2﹣t）═﹣2t2+5t+h+6，∴＝1为定值．。

人教版九年级数学上册第二十二章《二次函数》培优训练题(含答案)

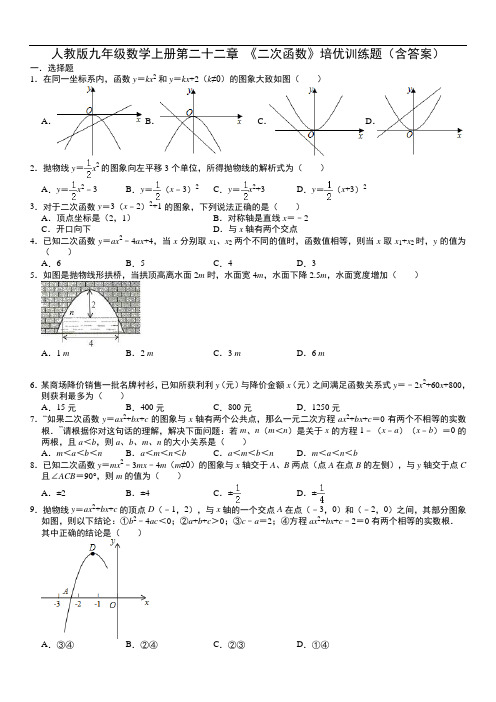
人教版九年级数学上册第二十二章《二次函数》培优训练题（含答案）一．选择题1．在同一坐标系内，函数y＝kx2和y＝kx+2（k≠0）的图象大致如图（）A．B．C．D．2．抛物线y＝x2的图象向左平移3个单位，所得抛物线的解析式为（）A．y＝x2﹣3 B．y＝（x﹣3）2C．y＝x2+3 D．y＝（x+3）23．对于二次函数y＝3（x﹣2）2+1的图象，下列说法正确的是（）A．顶点坐标是（2，1）B．对称轴是直线x＝﹣2C．开口向下D．与x轴有两个交点4．已知二次函数y＝ax2﹣4ax+4，当x分别取x1、x2两个不同的值时，函数值相等，则当x取x1+x2时，y的值为（）A．6 B．5 C．4 D．35．如图是抛物线形拱桥，当拱顶高离水面2m时，水面宽4m，水面下降2.5m，水面宽度增加（）A．1 m B．2 m C．3 m D．6 m6．某商场降价销售一批名牌衬衫，已知所获利利y（元）与降价金额x（元）之间满足函数关系式y＝﹣2x2+60x+800，则获利最多为（）A．15元B．400元C．800元D．1250元7．“如果二次函数y＝ax2+bx+c的图象与x轴有两个公共点，那么一元二次方程ax2+bx+c＝0有两个不相等的实数根．”请根据你对这句话的理解，解决下面问题：若m、n（m＜n）是关于x的方程1﹣（x﹣a）（x﹣b）＝0的两根，且a＜b，则a、b、m、n的大小关系是（）A．m＜a＜b＜n B．a＜m＜n＜b C．a＜m＜b＜n D．m＜a＜n＜b8．已知二次函数y＝mx2﹣3mx﹣4m（m≠0）的图象与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C 且∠ACB＝90°，则m的值为（）A．±2 B．±4 C．±D．±9．抛物线y＝ax2+bx+c的顶点D（﹣1，2），与x轴的一个交点A在点（﹣3，0）和（﹣2，0）之间，其部分图象如图，则以下结论：①b2﹣4ac＜0；②a+b+c＞0；③c﹣a＝2；④方程ax2+bx+c﹣2＝0有两个相等的实数根．其中正确的结论是（）A．③④B．②④C．②③D．①④二．填空题 10．若抛物线的顶点坐标为（2，9），且它在x 轴截得的线段长为6，则该抛物线的表达式为． 11．若抛物线y ＝a （x ﹣h ）2+k 经过（﹣1，0）和（5，0）两点，则关于x 的一元二次方程a （x +h ﹣2）2+k ＝0的解为．12．抛物线经过原点O ，还经过A （2，m ），B （4，m ），若△AOB 的面积为4，则抛物线的解析式为． 13．如图，有一座抛物线形拱桥，在正常水位时水面AB 的宽为20m ，如果水位上升3m 达到警戒水位时，水面CD 的宽是10m ．如果水位以0.25m /h 的速度上涨，那么达到警戒水位后，再过 h 水位达到桥拱最高点O ．14．如图，抛物线解析式为y ＝x 2，点A 1的坐标为（1，1），连接OA 1；过A 1作A 1B 1⊥OA 1，分别交y 轴、抛物线于点P 1、B 1；过B 1作B 1A 2⊥A 1B 1分别交y 轴、抛物线于点P 2、A 2；过A 2作A 2B 2⊥B 1A 2，分别交y 轴、抛物线于点P 3、B 2…；则点P n 的坐标是．三．解答题16．已知抛物线G ：y ＝mx 2﹣2mx ﹣3有最低点P ．（1）求二次函数y ＝mx 2﹣2mx ﹣3的最小值（用含m 的式子表示）；（2）若点P 关于坐标系原点O 的对称点仍然在抛物线上，求此时m 的值；（3）将抛物线G 向右平移m 个单位得到抛物线G 1．经过探究发现，随着m 的变化，抛物线G 1顶点的纵坐标y 与横坐标x 之间存在一个函数关系，求这个函数关系式，并写出自变量x 的取值范围．17．“互联网+”时代，网上购物备受消费者青睐．某网店专售一款休闲裤，其成本为每条40元，当售价为每条80元时，每月可销售100条．为了吸引更多顾客，该网店采取降价措施．据市场调查反映：销售单价每降2元，则每月可多销售10条，设每条裤子的售价为x 元（x 为正整数），每月的销售量为y 条．（1）直接写出y 与x 的函数关系式；（2）设该网店每月获得的利润为w 元，当销售单价降低多少元时，每月获得的利润最大，最大利润是多少？（3）该网店店主热心公益事业，决定每月从利润中捐出200元资助贫困学生，为了保证捐款后每月利润不低于4175元，且让消费者得到最大的实惠，该如何确定休闲裤的销售单价？18．在平面直角坐标系中，抛物线y ＝mx 2﹣4mx +n （m ＞0）与x 轴交于A ，B 两点，点B 在点A 的右侧，顶点为C ，抛物线与y 轴交于点D ，直线CA 交y 轴于E ，且S △ABC ：S △BCE ＝3：4．（1）求点A ，点B 的坐标；（2）将△BCO 绕点C 逆时针旋转一定角度后，点B 与点A 重合，点O 恰好落在y 轴上，①求直线CE 的解析式；②求抛物线的解析式．19．如图，二次函数y＝ax2+bx+4的图象与坐标轴分别交于A、B、C三点，其中A（﹣3，0），点B在x轴正半轴上，连接AC、BC．点D从点A出发，沿AC向点C移动；同时点E从点O出发，沿x轴向点B移动，它们移动的速度都是每秒1个单位长度，当其中一点到达终点时，另一点随之停止移动，连接DE，设移动时间为ts．（1）若t＝3时，△ADE与△ABC相似，求这个二次函数的表达式；（2）若△ADE可以为直角三角形，求a的取值范围．20．某班“数学兴趣小组”对函数y＝﹣x2+3|x|+4的图象和性质进行了探究，探究过程如下，请补充完整．（1）自变量x的取值范围是全体实数，x与y的几组对应值列表如下：x…﹣5 ﹣4 ﹣3 ﹣2 ﹣1 0 1 2 3 4 5 …y…﹣6 0 4 6 6 4 6 6 4 0 m…其中，m＝．（2）根据上表数据，在如图所示的平面直角坐标系中描点，并画出了函数图象的一部分，请画出该函数图象的另一部分．（3）观察函数图象，写出两条函数的性质．（4）直线y＝kx+b经过（，），若关于x的方程﹣x2+3|x|+4＝kx+b有4个不相等的实数根，则b的取值范围为．参考答案一．选择题1．解：由一次函数解析式为：y＝kx+2可知，图象应该与y轴交在正半轴上，故A、B、C错误；D符合题意；故选：D．2．解：∵抛物线y＝x2的图象向左平移3个单位，∴平移后的抛物线的顶点坐标为（﹣3，0），∴所得抛物线的解析式为y＝（x+3）2．故选：D．3．解：A、顶点坐标是（2，1），说法正确；B、对称轴是直线x＝2，故原题说法错误；C、开口向上，故原题说法错误；D、与x轴没有交点，故原题说法错误；故选：A．4．解：∵y＝ax2﹣4ax+4＝a（x﹣2）2﹣4a+4，当x分别取x1、x2两个不同的值时，函数值相等，∴x1+x2＝4，∴当x取x1+x2时，y＝a（4﹣2）2﹣4a+4＝4，故选：C．5．解：建立平面直角坐标系，设横轴x通过AB，纵轴y通过AB中点O且通过C点，则通过画图可得知O为原点，抛物线以y轴为对称轴，且经过A，B两点，OA和OB可求出为AB的一半2米，抛物线顶点C坐标为（0，2），设顶点式y＝ax2+2，把A点坐标（﹣2，0）代入得a＝﹣0.5，∴抛物线解析式为y＝﹣0.5x2+2，当水面下降2.5米，通过抛物线在图上的观察可转化为：当y＝﹣2.5时，对应的抛物线上两点之间的距离，也就是直线y＝﹣2.5与抛物线相交的两点之间的距离，可以通过把y＝﹣2.5代入抛物线解析式得出：﹣2.5＝﹣0.5x2+2，解得：x＝±3，2×3﹣4＝2，所以水面下降2.5m，水面宽度增加2米．故选：B．6．解：对于抛物线y＝﹣2x2+60x+800＝﹣2（x﹣15）2+1250，∵a＝﹣2＜0，∴x＝15时，y有最大值，最大值为1250，故选：D．7．解：∵m、n（m＜n）是关于x的方程1﹣（x﹣a）（x﹣b）＝0的两根，∴二次函数y＝﹣（x﹣a）（x﹣b）+1的图象与x轴交于点（m，0）、（n，0），∴将y＝﹣（x﹣a）（x﹣b）+1的图象往下平移一个单位可得二次函数y＝﹣（x﹣a）（x﹣b）的图象，二次函数y＝﹣（x﹣a）（x﹣b）的图象与x轴交于点（a，0）、（b，0）．画出两函数图象，观察函数图象可知：m＜a＜b＜n．故选：A．8．解：设y＝0，则＝mx2﹣3mx﹣4m＝0，解得：m＝4或m＝﹣1，∵点A在点B的左侧，∴OA＝1，OB＝4，设x＝0，则y＝﹣4m，∴OC＝|﹣4m|，∵∠ACO+∠OCB＝90°，∠CAO+∠ACO＝90°，∴∠CAO＝∠BCO，又∵∠AOC＝∠BOC＝90°，∴△AOC∽△COB，∴，∴OC2＝OA•OB，即16m2＝4，解得：m＝±，故选：C．9．解：∵抛物线与x轴有2个交点，∴△＝b2﹣4ac＞0，所以①错误；∵抛物线y＝ax2+bx+c的顶点D（﹣1，2），∴抛物线的对称轴为直线x＝﹣1，而抛物线与x轴的一个交点A在点（﹣3，0）和（﹣2，0）之间，∴抛物线与x轴的另一个交点A在点（0，0）和（1，0）之间，∴x＝1时，y＜0，∴a﹣b+c＜0，所以②错误；∵抛物线的对称轴为直线x＝﹣＝﹣1，∴b＝2a，∵x＝﹣1时，y＝2，即a﹣b+c＝2，∴a﹣2a+c＝2，即c﹣a＝2，所以③正确；∵抛物线y＝ax2+bx+c的顶点D（﹣1，2），即x＝﹣1时，y有最大值2，∴抛物线与直线y＝2只有一个公共点，∴方程ax2+bx+c﹣2＝0有两个相等的实数根，所以④正确．故选：A．二．填空题（共5小题）10．解：∵抛物线的顶点坐标为（2，9），∴抛物线的对称轴为直线x＝2，∵抛物线在x轴截得的线段长为6，∴抛物线与x轴的交点为（﹣1，0），（5，0），设此抛物线的解析式为：y＝a（x﹣2）2+9，代入（5，0）得，9a+9＝0，解得a＝﹣1，∴抛物线的表达式为y＝﹣（x﹣2）2+9，故答案为y＝﹣（x﹣2）2+9．11．解：将抛物线y＝a（x﹣h）2+k关于y轴对称得新抛物线为y′＝a（x+h）2+k，∵抛物线y＝a（x﹣h）2+k经过（﹣1，0）和（5，0）两点，∴抛物线为y′＝a（x+h）2+k与x轴的交点为（﹣5，0）和（1，0），将新抛物线y′＝a（x+h）2+k向右平移2个单位得抛物线y″＝a（x+h﹣2）2+k，其与x轴的两个交点为（﹣3，0）和（3，0），∴方程a（x+h﹣2）2+k＝0的解为x1＝3，x2＝﹣3，故答案为x1＝3，x2＝﹣3．12．解：∵抛物线经过A（2，m），B（4，m），∴对称轴是：x＝3，AB＝2，∵△AOB的面积为4，∴AB•|m|＝4，m＝±4，当m＝4时，则A（2，4），B（4，4），设抛物线的解析式为：y＝a（x﹣3）2+h，把（0，0）和（2，4）代入得：，解得：，∴抛物线的解析式为：y＝﹣（x﹣3）2+，即y＝﹣x2+3x；当m＝﹣4时，则A（2，﹣4），B（4，﹣4），设抛物线的解析式为：y＝a（x﹣3）2+h，把（0，0）和（2，﹣4）代入得：，解得：，∴抛物线的解析式为：y＝（x﹣3）2﹣＝x2﹣3x；综上所述，抛物线的解析式为：y＝﹣x2+3x或y＝x2﹣3x，故答案为y＝﹣x2+3x或y＝x2﹣3x．13．解：设抛物线解析式为y＝ax2，因为抛物线关于y轴对称，AB＝20，所以点B的横坐标为10，设点B（10，n），点D（5，n+3），由题意：，解得，∴y＝﹣x2，当x＝5时，y＝﹣1，故t＝＝4（h），答：再过4小时水位达到桥拱最高点O．故答案为：4．14．解：∵点A1的坐标为（1，1），∴直线OA1的解析式为y＝x，∵A1B1⊥OA1，∴OP1＝2，∴P1（0，2），设A1P1的解析式为y＝kx+b1，∴，解得，∴直线A1P1的解析式为y＝﹣x+2，解求得B1（﹣2，4），∵A2B1∥OA1，设B1P2的解析式为y＝x+b2，∴﹣2+b2＝4，∴b2＝6，∴P2（0，6），解求得A2（3，9）设A1B2的解析式为y＝﹣x+b3，∴﹣3+b3＝9，∴b3＝12，∴P3（0，12），…∴P n（0，n2+n），故答案为（0，n2+n）．三．解答题（共6小题）15．证明：（1）∵点E为CD中点，∴CE＝DE．∵EF＝BE，∴四边形DBCF是平行四边形．（2）∵四边形DBCF是平行四边形，∴CF∥AB，DF∥BC．∴∠FCG＝∠A＝30°，∠CGF＝∠CGD＝∠ACB＝90°．在Rt△FCG中，CF＝6，∴，．∵DF＝BC＝4，∴DG＝1．在Rt△DCG中，CD＝＝216．解：（1）∵y＝mx2﹣2mx﹣3＝m（x﹣1）2﹣m﹣3，抛物线有最低点，∴二次函数y＝mx2﹣2mx﹣3的最小值为﹣m﹣3；（2）∵y＝mx2﹣2mx﹣3＝m（x﹣1）2﹣m﹣3，∴抛物线的顶点P为（1，﹣m﹣3），∴点P关于坐标系原点O的对称点（﹣1，m+3），∵对称点仍然在抛物线上，∴m+3＝m+2m﹣3，解得m＝3；（3）∵抛物线G：y＝m（x﹣1）2﹣m﹣3∴平移后的抛物线G1：y＝m（x﹣1﹣m）2﹣m﹣3∴抛物线G1顶点坐标为（m+1，﹣m﹣3）∴x＝m+1，y＝﹣m﹣3∴x+y＝m+1﹣m﹣3＝﹣2即x+y＝﹣2，变形得y＝﹣x﹣2∵m＞0，m＝x﹣1∴x﹣1＞0∴x＞1∴y与x的函数关系式为y＝﹣x﹣2（x＞1）．17．解：（1）由题意可得：y＝100+×10＝100+5（80﹣x）＝﹣5x+500，∴y与x的函数关系式为：y＝﹣5x+500；（2）由题意得：w＝（x﹣40）（﹣5x+500）＝﹣5x2+700x﹣20000＝﹣5（x﹣70）2+4500，∵a＝﹣5＜0，∴当x＝70时，w有最大利润，最大利润是4500元；∴应降价80﹣70＝10（元）．∴当销售单价降低10元时，每月获得的利润最大，最大利润是4500元；（3）由题意得：﹣5（x﹣70）2+4500＝4175+200，解得：x1＝65，x2＝75，∵抛物线开口向下，对称轴为直线x＝70，∴当65≤x≤75时，符合该网店要求，而为了让顾客得到最大实惠，故x＝65．∴当销售单价定为65元时，既符合网店要求，又能让顾客得到最大实惠．18．解：（1）如图，过点C作CF⊥AB于F，∵抛物线y＝mx2﹣4mx+n（m＞0），∴对称轴为直线x＝2，∴AF＝BF，点F（2，0），即OF＝2，∵S△ABC ：S△BCE＝3：4，∴S△ABC ＝3S△ABE，∴3××AB×OE＝AB×CF，∴CF＝3OE，∵CF⊥AB，OE⊥AB，∴CF∥OE，∴，∴AF＝3OA，∵OF＝OA+AF＝2，∴OA＝，AF＝，∴点A坐标为（，0），∵AB＝2AF＝3，∴OB＝，∴点B坐标为（，0）；（2）①∵抛物线y＝mx2﹣4mx+n（m＞0）过点A（，0），∴0＝m﹣2m+n，∴n＝m，∴y＝mx2﹣4mx+n＝m（x﹣2）2﹣m，∴点C（2，﹣m），如图2，过点C作CF⊥OB于F，CH⊥y轴于H，又∵∠FOH＝90°，∴四边形OFCH是矩形，∴CF＝OH＝m，∵将△BCO绕点C逆时针旋转一定角度后，点B与点A重合，点O恰好落在y轴上，∴OC＝O'C，OB＝O'A＝，又∵CH⊥OO'，∴OO'＝2OH＝m，∵OA2+O'O2＝O'A2，∴+m2＝，∴m＝，∴点C坐标为（2，﹣），设直线CE的解析式为y＝kx+b，∴，解得：∴直线CE的解析式为y＝﹣x+；②∵m＝，∴y＝x2﹣x+．19．解：（1）∵二次函数y＝ax2+bx+4的图象与y轴交于点C，∴C（0，4），∴OC＝4，∵A（﹣3，0），∴OA＝3，∴AC＝＝＝5，∵t＝3，∴AD＝OE＝3，AE＝6，当△ADE∽△ACB时，∴，即，∴AB＝10，∴B（7，0），∵二次函数y＝ax2+bx+4的图象过点A（﹣3，0），点B（7，0），∴解得：∴抛物线解析式为：，当△ADE∽△ABC时，，即，∴（舍去），综上，二次函数的表达式为：；（2）若△ADE可以为直角三角形，显然∠ADE＝90°，∴△ADE∽△AOC，∴，∴，解得：．设B（x，0），则，设抛物线对称轴为直线，∵A（﹣3，0），∴①．把x＝﹣3，y＝0代入y＝ax2+bx+4，得②，把②代入①，∵a＜0，解得：．20．解：（1）把x＝5代入函数y＝﹣x2+3|x|+4中，得y＝﹣25+15+4＝﹣6，∴m＝﹣6，故答案为：﹣6；（2）连线得，（3）由函数图象可知①该函数的图象关于y轴对称：②该函数的图象有最高点：（答案不唯一）（4）∵直线y＝kx+b经过（，），∴，∴k＝∵关于x的方程﹣x2+3|x|+4＝kx+b有4个不相等的实数根，∴x2﹣3x﹣4+kx+b＝0和方程x2+3x﹣4+kx+b＝0各有两个不相等的实数根，即方程x2﹣（3﹣）x﹣4+b＝和0x2+（3+）x﹣4+b＝0各有两个不相等的实数根，∴，解得b≠，且b＞或b＜，∴b的取值范围为b＞或b＜．故答案为：b＞或b＜．。

【同步培优】人教版2018年九年级数学上册二次函数图象性质专题培优卷(含答案)

2018年九年级数学上册二次函数图象性质专题培优卷一、选择题:1.如图，若a＜0，b＞0，c＜0，则抛物线y=ax2+bx+c的大致图象为( )2.将二次函数y=x2﹣2x+3化为y=(x﹣h)2+k的形式，结果为（）A.y=(x+1)2+4B.y=(x+1)22+2C.y=(x-1)2+4D.y=(x-1)22+23.在平面直角坐标系中，将抛物线y=x2+2x+3绕着它与y轴的交点旋转180°，所得抛物线的解析式是（）．A.y=-(x+1)2+2B.y=-(x-1)2+4C.y=-(x-1)2+2D.y=-(x+1)2+44.若一次函数y=(m+1)x+m的图像过第一、三、四象限，则函数y=mx2-mx( )A.有最大值为0.25mB.有最大值为-0.25mC.有最小值为0.25mD. 有最小值为-0.25m5.若二次函数y=ax2－2ax＋c的图象经过点(-1，0)，则方程ax2－2ax＋c=0的解为( )A.x1=-3，x2=-1B.x1=1，x2=3C.x1=-1，x2=3D.x1=-3，x2=16.向空中发射一枚炮弹，经x秒后的高度为y米，且时间与高度的关系为y=ax2+bx+c(a≠0）,若此炮弹在第7秒与第14秒时的高度相等，则在下列时间中炮弹所在高度最高的是（）A.第8秒B.第10秒C.第12秒D.第15秒7.对于抛物线y=﹣x2+2x+3，有下列四个结论：①它的对称轴为x=1；②它的顶点坐标为（1，4）；③它与y轴的交点坐标为（0，3），与x轴的交点坐标为（﹣1，0）和（3，0）；④当x＞0时，y随x的增大而减小.其中正确的个数为（）A．1 B．2 C．3 D．48.已知A（﹣3，y）、B（﹣2，y2）、C（2，y3）在二次函数y=x2+2x+c的图象上，比较y1、y2、y3的大小( )1A．y1＞y2＞y3B．y2＞y3＞y1C．y2＞y1＞y3D．y3＞y1＞y29.已知点(1，y)、(-2，y2)、(-4，y3)都是抛物线y=-2ax2-8ax+3(a＜0)图象上的点，则下列各式中正确的1是( )A.y1＜y3＜y2B.y3＜y2＜y1C.y2＜y3＜y1D.y1＜y2＜y310.如图，二次函数y=ax2+bx+c的图象与x轴的交点的横坐标分别为﹣1，3，则下列结论正确的个数有（）①ac＜0；②2a+b=0；③4a+2b+c＞0；④对于任意x均有ax2+bx≥a+b．A.1B.2C.3D.411.已知二次函数y=ax2+bx+c的图象如图所示．下列结论：①abc＞0；②2a﹣b＜0；③4a﹣2b+c＜0；④（a+c）2＜b2其中正确的个数有（）A.1B.2C.3D.412.“如果二次函数y=ax2+bx+c的图象与x轴有两个公共点，那么一元二次方程ax2+bx+c=0有两个不相等的实数根”.请根据你对这句话的理解，解决下面问题：若m、n（m<n）是关于x的方程1-(x-a)(x-b)=0的两根，且a < b, 则a、b、m、n 的大小关系是（）A.m<a<b<nB.a<m<n<bC.a<m<b<nD.m<a<n<b二、填空题:13.已知二次函数y=﹣x2+2x+m的部分图象如图所示，则关于x的一元二次方程﹣x2+2x+m=0的解为．14.抛物线y＝2x2＋8x＋m与x轴只有一个公共点，则m的值为．15.如图，二次函数y1＝ax2＋bx＋c(a≠0)与一次函数y2＝kx＋m(k≠0)的图象相交于点A(－2，4)，B(8，2)，则使y1＞y2成立的x的取值范围是__ _．16.二次函数y=ax2+bx的图象如图，若一元二次方程ax2+bx+m=0有实数根，则m的最大值为．17.体育公园的圆形喷水池的水柱（如图1）如果曲线APB表示落点B离点O最远的一条水流（如图2），其上的水珠的高度）y（米）关于水平距离x（米）的函数解析式为y=﹣x2+4x+2.25，那么圆形水池的半径至少为米时，才能使喷出的水流不落在水池外．18.若一元二次方程ax2+bx+1=0有两个相同的实数根，则a2-b2+5的最小值为__________.三、解答题:19.已知函数y=0.5x2+x﹣2.5．请用配方法写出这个函数的对称轴和顶点坐标．20.如图所示，抛物线y=ax2+bx+c与直线y=﹣x+6分别交于x轴和y轴上同一点，交点分别是点B和点C，且抛物线的对称轴为直线x=4．（1）求出抛物线与x轴的两个交点A，B的坐标．（2）试确定抛物线的解析式．21.我们称顶点相同的两条抛物线为同位抛物线，已知抛物线C：y=2x2﹣4x+3．1（1）下列抛物线中，与C1是同位抛物线的是______．A.y=2x2﹣4x+4B.y=3x2﹣6x+4C.y=﹣2x2﹣4x+3D.y=2x2（2）若抛物线C2：y=ax2﹣2ax+c（a≠0）与C1是同位抛物线，则a与c需满足什么关系？22.在坐标系中,已知抛物线y=x2﹣2x+n﹣1与y轴交于点A,其对称轴与x轴交于点B．（1）当△OAB是等腰直角三角形时,求n的值；（2）点C的坐标为（3,0），若该抛物线与线段OC有且只有一个公共点,结合函数的图象求n的取值范围．23.如图，二次函数y=ax2+bx+c的图象与x轴交于A、B两点，交y轴于C点，其中B点坐标为（3，0），C点坐标为（0，3），且图象对称轴为直线x=1．（1）求此二次函数的关系式；（2）P为二次函数y=ax2+bx+c在x轴下方的图象上一点，且S△ABP=S△ABC，求P点的坐标．24.已知关于x的一元二次方程mx2+（3m+1）x+3=0．（1）求证：该方程有两个实数根；（2）如果抛物线y=mx2+（3m+1）x+3与x轴交于A、B两个整数点（点A在点B左侧），且m为正整数，求此抛物线的表达式；（3）在（2）的条件下，抛物线y=mx2+（3m+1）x+3与y轴交于点C，点B关于y轴的对称点为D，设此抛物线在﹣3≤x≤﹣0.5之间的部分为图象G，如果图象G向右平移n（n＞0）个单位长度后与直线CD有公共点，求n的取值范围．参考答案1.A2.D3.B4.B5.C6.B．7.C8.D9.C10.C11.D．12.A13.答案为：x=﹣1或x2=3．114.答案为：_815.答案为：x＜－2或x＞816.答案为3．17.答案为：4.5．18.答案为：1；19.解：y=x2+x﹣，=（x2+2x+1）﹣﹣，=（x+1）2﹣3，20.解：（1）∵抛物线y=ax2+bx+c与直线y=﹣x+6分别交于x轴和y轴上同一点，交点分别是点B和点C，∴将x=0代入y=﹣x+6得，y=6；将y=0代入y=﹣x+6，得x=6．∴点B的坐标是（6，0），点C的坐标是（0，6）．∵抛物线y=ax2+bx+c与x轴交于点A、B两点，对称轴为直线x=4，∴点A的坐标为（2，0）．即抛物线与x轴的两个交点A，B的坐标分别是（2，0），（6，0）．（2）∵抛物线y=ax2+bx+c过点A（2，0），B（6，0），C（0，6），∴4a+2b+c=0,36a+6b+c=0,c=6,解得a=0.5，b=﹣4，c=6．∴抛物线的解析式为：y=0.5x2-4x+6．21.解：抛物线C：y=2x2﹣4x+3．y=2（x2﹣2x+1﹣1）+31y=2（x﹣1）2+1，顶点为（1，1）A、y=2x2﹣4x+4=2（x﹣1）2+2，顶点为（1，2），所以A不正确；B、y=3x2﹣6x+4=3（x﹣1）2+1，顶点为（1，1），所以B正确；C、y=﹣2x2﹣4x+3=﹣2（x+1）2+5，顶点为（﹣1，5），所以C不正确；D、y=2x2，顶点为（0，0），所以D不正确；故选B．（2）抛物线C2：y=ax2﹣2ax+cy=a（x2﹣2x+1﹣1）+cy=a（x﹣1）2﹣a+c，顶点为（1，﹣a+c）由抛物线C2：y=ax2﹣2ax+c（a≠0）与C1是同位抛物线得：﹣a+c=1，c﹣a=1∴a与c需满足的关系式为：c﹣a=122.解：（1）二次函数的对称轴是x=﹣1，则B的坐标是（1，0），当△OAB是等腰直角三角形时，OA=OB=1，则A的坐标是（0，1）或（0，﹣1）．抛物线y=x2﹣2x+n﹣1与y轴交于点A的坐标是（0，n﹣1）．则n﹣1=1或n﹣1=﹣1，解得n=2或n=0；（2）①当抛物线的顶点在x轴上时，△=（﹣2）2﹣4（n﹣1）=0，解得：n=2；②当抛物线的顶点在x轴下方时，如图，由图可知当x=0时，y＜0；当x=3时，y≥0，即，解得：﹣2≤n＜1，综上，﹣2≤n＜1或n=2．23.解：（1）根据题意，得，解得．故二次函数的表达式为y=﹣x2+2x+3．（2）由S△ABP=S△ABC，得y P+y C=0，得y P=﹣3，当y=﹣3时，﹣x2+2x+3=﹣3，解得x1=1﹣，x2=1+．故P点的坐标为（1﹣，﹣3）或（1+，﹣3）．24.（1）证明：由根的判别式，可得：△=（3m+1）2﹣4×m×3=（3m﹣1）2，∵（3m﹣1）2≥0，∴△≥0，∴原方程有两个实数根；（2）解：令y=0，那么mx2+（3m+1）x+3=0，解得：x1=﹣3，x2=﹣，∵抛物线与x轴两个交点的横坐标均为整数，且m为正整数，∴m=1，∴抛物线的解析式为：y=x2+4x+3；（3）如图，∵当x=0时，y=3，∴C（0，3），∵当y=0时，x1=﹣3，x2=﹣1，又∵点A在点B的左侧，∴A（﹣3，0），B（﹣1，0），∵点D与点B关于y轴对称，∴D（1，0），设直线CD的解析式为：y=kx+b，∴，解得：，∴直线CD的表达式为：y=﹣3x+3，又∵当x=﹣时，y=，∴点E（﹣，），∴平移后，点A，E的对应点分别为A′（﹣3+n，0），E′（﹣+n，），当直线y=﹣3x+3经过点A′（﹣3+n，0）时，得：﹣3（﹣3+n）+3=0，解得：n=4，当直线y=﹣3x+3经过点E′（﹣+n，），时，得：﹣3（﹣+n）+3=，解得：n=，∴n的取值范围是≤n≤4．。

二次函数培优专题训练(含答案)

；；；．
A．个B．个C．个D．个
二、填空题
11．若抛物线y=x2﹣2x+m（m为常数）与x轴没有公共点，则实数m的取值范围为．
12．二次函数y=x2-4x+5的最小值是
13．已知（x1，y1），（x2，y2）是抛物线y＝ax2（a≠0）上的两点．当x2＜x1＜0时，y2＜y1，则a的取值范围是_____．
（1）求y与x的函数关系式；
（2）每件文具的售价定为多少元时，月销售利润为2520元？
（3）每件文具的售价定为多少元时可使月销售利润最大？最大的月利润是多少？
参考答案
1．A
【解析】
试题分析：二次函数的一般形式中的顶点式是：y=a（x-h）2+k（a≠0，且a，h，k是常数），它的对称轴是x=h，顶点坐标是（h，k）．
（1）求x=2时，平行四边形AGEF的面积．
（2）当x为何值时，平行四边形AGEF的面积最大？最大面积是多少？
19．某种蔬菜的销售单价y1与销售月份x之间的关系如图1所示，成本y2与销售月份x之间的关系如图2所示.
(1)已知6月份这种蔬菜的成本最低，此时出售每干克的收益是多少元?(收益=售价－成本)
试题解析：A：在对称轴的左侧y随x的增大而增大，在对称轴的右侧y随x的增大而减小．故此选项正确，
B：当x=0，y=1，∴图象与y轴的交点坐标为：（0，1），故此选项错误，
C：∵a=-1，∴函数的开口向下，对称轴是x=1，故此选项错误，
D：∵这个函数的顶点是（1，2），故此选项错误，
故选A．
考点：二次函数的性质．
(2)S是x的什么函数？
(3)当S＝6时，求点P的坐标；
(4)在y＝x2的图象上求一点P′，使△OP′A的两边OP′＝P′A.

2018年中考数学二次函数压轴题集锦(50道含解析)

1．如图1，已知二次函数y=ax2+x+c（a≠0）的图象与y轴交于点A（0，4），与x轴交于点B、C，点C坐标为（8，0），连接AB、AC．（1）请直接写出二次函数y=ax2+x+c的表达式；（2）判断△ABC的形状，并说明理由；（3）若点N在x轴上运动，当以点A、N、C为顶点的三角形是等腰三角形时，请写出此时点N的坐标；（4）如图2，若点N在线段BC上运动（不与点B、C重合），过点N作NM∥AC，交AB于点M，当△AMN面积最大时，求此时点N的坐标．2．对于平面直角坐标系xOy中的图形M，N，给出如下定义：P为图形M上任意一点，Q为图形N上任意一点，如果P，Q两点间的距离有最小值，那么称这个最小值为图形M，N间的“闭距离“，记作d（M，N）．已知点A（﹣2，6），B（﹣2，﹣2），C（6，﹣2）．（1）求d（点O，△ABC）；（2）记函数y=kx（﹣1≤x≤1，k≠0）的图象为图形G．若d（G，△ABC）=1，直接写出k的取值范围；（3）⊙T的圆心为T（t，0），半径为1．若d（⊙T，△ABC）=1，直接写出t 的取值范围．3．如图，在平面直角坐标系中，点A在抛物线y=﹣x2+4x上，且横坐标为1，点B与点A关于抛物线的对称轴对称，直线AB与y轴交于点C，点D为抛物线的顶点，点E的坐标为（1，1）．（1）求线段AB的长；（2）点P为线段AB上方抛物线上的任意一点，过点P作AB的垂线交AB于点H，点F为y轴上一点，当△PBE的面积最大时，求PH+HF+FO的最小值；（3）在（2）中，PH+HF+FO取得最小值时，将△CFH绕点C顺时针旋转60°后得到△CF′H′，过点F'作CF′的垂线与直线AB交于点Q，点R为抛物线对称轴上的一点，在平面直角坐标系中是否存在点S，使以点D，Q，R，S为顶点的四边形为菱形，若存在，请直接写出点S的坐标，若不存在，请说明理由．4．如图，抛物线y=ax2+6x+c交x轴于A，B两点，交y轴于点C．直线y=x﹣5经过点B，C．（1）求抛物线的解析式；（2）过点A的直线交直线BC于点M．①当AM⊥BC时，过抛物线上一动点P（不与点B，C重合），作直线AM的平行线交直线BC于点Q，若以点A，M，P，Q为顶点的四边形是平行四边形，求点P的横坐标；②连接AC，当直线AM与直线BC的夹角等于∠ACB的2倍时，请直接写出点M 的坐标．5．如图，在平面直角坐标系xOy中，以直线x=对称轴的抛物线y=ax2+bx+c与直线l：y=kx+m（k＞0）交于A（1，1），B两点，与y轴交于C（0，5），直线l与y轴交于点D．（1）求抛物线的函数表达式；（2）设直线l与抛物线的对称轴的交点为F，G是抛物线上位于对称轴右侧的一点，若=，且△BCG与△BCD面积相等，求点G的坐标；（3）若在x轴上有且仅有一点P，使∠APB=90°，求k的值．6．如图，抛物线y=ax2+bx（a＜0）过点E（10，0），矩形ABCD的边AB在线段OE上（点A在点B的左边），点C，D在抛物线上．设A（t，0），当t=2时，AD=4．（1）求抛物线的函数表达式．（2）当t为何值时，矩形ABCD的周长有最大值？最大值是多少？（3）保持t=2时的矩形ABCD不动，向右平移抛物线．当平移后的抛物线与矩形的边有两个交点G，H，且直线GH平分矩形的面积时，求抛物线平移的距离．7．抛物线L：y=﹣x2+bx+c经过点A（0，1），与它的对称轴直线x=1交于点B．（1）直接写出抛物线L的解析式；（2）如图1，过定点的直线y=kx﹣k+4（k＜0）与抛物线L交于点M、N．若△BMN的面积等于1，求k的值；（3）如图2，将抛物线L向上平移m（m＞0）个单位长度得到抛物线L1，抛物线L1与y轴交于点C，过点C作y轴的垂线交抛物线L1于另一点D．F为抛物线L1的对称轴与x轴的交点，P为线段OC上一点．若△PCD与△POF相似，并且符合条件的点P恰有2个，求m的值及相应点P的坐标．8．在平面直角坐标系中，点O（0，0），点A（1，0）．已知抛物线y=x2+mx ﹣2m（m是常数），顶点为P．（Ⅰ）当抛物线经过点A时，求顶点P的坐标；（Ⅱ）若点P在x轴下方，当∠AOP=45°时，求抛物线的解析式；（Ⅲ）无论m取何值，该抛物线都经过定点H．当∠AHP=45°时，求抛物线的解析式．9．如图1，四边形OABC是矩形，点A的坐标为（3，0），点C的坐标为（0，6），点P从点O出发，沿OA以每秒1个单位长度的速度向点A出发，同时点Q从点A出发，沿AB以每秒2个单位长度的速度向点B运动，当点P与点A重合时运动停止．设运动时间为t秒．（1）当t=2时，线段PQ的中点坐标为；（2）当△CBQ与△PAQ相似时，求t的值；（3）当t=1时，抛物线y=x2+bx+c经过P，Q两点，与y轴交于点M，抛物线的顶点为K，如图2所示，问该抛物线上是否存在点D，使∠MQD=∠MKQ？若存在，求出所有满足条件的D的坐标；若不存在，说明理由．10．如图①，在平面直角坐标系中，圆心为P（x，y）的动圆经过点A（1，2）且与x轴相切于点B．（1）当x=2时，求⊙P的半径；（2）求y关于x的函数解析式，请判断此函数图象的形状，并在图②中画出此函数的图象；（3）请类比圆的定义（圆可以看成是到定点的距离等于定长的所有点的集合），给（2）中所得函数图象进行定义：此函数图象可以看成是到的距离等于到的距离的所有点的集合．（4）当⊙P的半径为1时，若⊙P与以上（2）中所得函数图象相交于点C、D，其中交点D（m，n）在点C的右侧，请利用图②，求cos∠APD的大小．11．已知顶点为A抛物线经过点，点．（1）求抛物线的解析式；（2）如图1，直线AB与x轴相交于点M，y轴相交于点E，抛物线与y轴相交于点F，在直线AB上有一点P，若∠OPM=∠MAF，求△POE的面积；（3）如图2，点Q是折线A﹣B﹣C上一点，过点Q作QN∥y轴，过点E作EN ∥x轴，直线QN与直线EN相交于点N，连接QE，将△QEN沿QE翻折得到△QEN1，若点N1落在x轴上，请直接写出Q点的坐标．12．在平面直角坐标系xOy中（如图）．已知抛物线y=﹣x2+bx+c经过点A（﹣1，0）和点B（0，），顶点为C，点D在其对称轴上且位于点C下方，将线段DC绕点D按顺时针方向旋转90°，点C落在抛物线上的点P处．（1）求这条抛物线的表达式；（2）求线段CD的长；（3）将抛物线平移，使其顶点C移到原点O的位置，这时点P落在点E的位置，如果点M在y轴上，且以O、D、E、M为顶点的四边形面积为8，求点M的坐标．13．如图1，图形ABCD是由两个二次函数y1=kx2+m（k＜0）与y2=ax2+b（a＞0）的部分图象围成的封闭图形．已知A（1，0）、B（0，1）、D（0，﹣3）．（1）直接写出这两个二次函数的表达式；（2）判断图形ABCD是否存在内接正方形（正方形的四个顶点在图形ABCD上），并说明理由；（3）如图2，连接BC，CD，AD，在坐标平面内，求使得△BDC与△ADE相似（其中点C与点E是对应顶点）的点E的坐标14．小贤与小杰在探究某类二次函数问题时，经历了如下过程：求解体验：（1）已知抛物线y=﹣x2+bx﹣3经过点（﹣1，0），则b=，顶点坐标为，该抛物线关于点（0，1）成中心对称的抛物线表达式是．抽象感悟：我们定义：对于抛物线y=ax2+bx+c（a≠0），以y轴上的点M（0，m）为中心，作该抛物线关于点M对称的抛物线y′，则我们又称抛物线y′为抛物线y的“衍生抛物线”，点M为“衍生中心”．（2）已知抛物线y=﹣x2﹣2x+5关于点（0，m）的衍生抛物线为y′，若这两条抛物线有交点，求m的取值范围．问题解决：（3）已知抛物线y=ax2+2ax﹣b（a≠0）①若抛物线y的衍生抛物线为y′=bx2﹣2bx+a2（b≠0），两抛物线有两个交点，且恰好是它们的顶点，求a、b的值及衍生中心的坐标；②若抛物线y关于点（0，k+12）的衍生抛物线为y1，其顶点为A1；关于点（0，k+22）的衍生抛物线为y2，其顶点为A2；…；关于点（0，k+n2）的衍生抛物线为y n，其顶点为A n…（n为正整数）．求A n A n+1的长（用含n的式子表示）．15．如图，已知抛物线y=ax2+bx（a≠0）过点A（，﹣3）和点B（3，0）．过点A作直线AC∥x轴，交y轴于点C．（1）求抛物线的解析式；（2）在抛物线上取一点P，过点P作直线AC的垂线，垂足为D．连接OA，使得以A，D，P为顶点的三角形与△AOC相似，求出对应点P的坐标；（3）抛物线上是否存在点Q，使得S△AOC =S△AOQ？若存在，求出点Q的坐标；若不存在，请说明理由．16．如图，已知抛物线y=x2﹣4与x轴交于点A，B（点A位于点B的左侧），C 为顶点，直线y=x+m经过点A，与y轴交于点D．（1）求线段AD的长；（2）平移该抛物线得到一条新拋物线，设新抛物线的顶点为C′．若新抛物线经过点D，并且新抛物线的顶点和原抛物线的顶点的连线CC′平行于直线AD，求新抛物线对应的函数表达式．17．如图①，在平面直角坐标系xOy中，抛物线y=ax2+bx+3经过点A（﹣1，0）、B（3，0）两点，且与y轴交于点C．（1）求抛物线的表达式；（2）如图②，用宽为4个单位长度的直尺垂直于x轴，并沿x轴左右平移，直尺的左右两边所在的直线与抛物线相交于P、Q两点（点P在点Q的左侧），连接PQ，在线段PQ上方抛物线上有一动点D，连接DP、DQ．（1）若点P的横坐标为﹣，求△DPQ面积的最大值，并求此时点D的坐标；（Ⅱ）直尺在平移过程中，△DPQ面积是否有最大值？若有，求出面积的最大值；若没有，请说明理由．18．已知抛物线y=ax2+bx+c过点A（0，2）．（1）若点（﹣，0）也在该抛物线上，求a，b满足的关系式；（2）若该抛物线上任意不同两点M（x1，y1），N（x2，y2）都满足：当x1＜x2＜0时，（x1﹣x2）（y1﹣y2）＞0；当0＜x1＜x2时，（x1﹣x2）（y1﹣y2）＜0．以原点O为心，OA为半径的圆与拋物线的另两个交点为B，C，且△ABC有一个内角为60°．①求抛物线的解析式；②若点P与点O关于点A对称，且O，M，N三点共线，求证：PA平分∠MPN．19．如图，在平面直角坐标系中，∠ACB=90°，OC=2OB，tan∠ABC=2，点B的坐标为（1，0）．抛物线y=﹣x2+bx+c经过A、B两点．（1）求抛物线的解析式；（2）点P是直线AB上方抛物线上的一点，过点P作PD垂直x轴于点D，交线段AB于点E，使PE=DE．①求点P的坐标；②在直线PD上是否存在点M，使△ABM为直角三角形？若存在，求出符合条件的所有点M的坐标；若不存在，请说明理由．20．我们不妨约定：对角线互相垂直的凸四边形叫做“十字形”．（1）①在“平行四边形，矩形，菱形，正方形”中，一定是“十字形”的有；②在凸四边形ABCD中，AB=AD且CB≠CD，则该四边形“十字形”．（填“是”或“不是”）（2）如图1，A，B，C，D是半径为1的⊙O上按逆时针方向排列的四个动点，AC与BD交于点E，∠ADB﹣∠CDB=∠ABD﹣∠CBD，当6≤AC2+BD2≤7时，求OE的取值范围；（3）如图2，在平面直角坐标系xOy中，抛物线y=ax2+bx+c（a，b，c为常数，a＞0，c＜0）与x轴交于A，C两点（点A在点C的左侧），B是抛物线与y轴的交点，点D的坐标为（0，﹣ac），记“十字形”ABCD的面积为S，记△AOB，△COD，△AOD，△BOC的面积分别为S1，S2，S3，S4．求同时满足下列三个条件的抛物线的解析式；①=；②=；③“十字形”ABCD的周长为12．21．如图1，抛物线y1=ax2﹣x+c与x轴交于点A和点B（1，0），与y轴交于点C（0，），抛物线y1的顶点为G，GM⊥x轴于点M．将抛物线y1平移后得到顶点为B且对称轴为直线l的抛物线y2．（1）求抛物线y2的解析式；（2）如图2，在直线l上是否存在点T，使△TAC是等腰三角形？若存在，请求出所有点T的坐标；若不存在，请说明理由；（3）点P为抛物线y1上一动点，过点P作y轴的平行线交抛物线y2于点Q，点Q关于直线l的对称点为R，若以P，Q，R为顶点的三角形与△AMG全等，求直线PR的解析式．22．如图，已知直线y=﹣2x+4分别交x轴、y轴于点A、B，抛物线过A，B两点，点P是线段AB上一动点，过点P作PC⊥x轴于点C，交抛物线于点D．（1）若抛物线的解析式为y=﹣2x2+2x+4，设其顶点为M，其对称轴交AB于点N．①求点M、N的坐标；②是否存在点P，使四边形MNPD为菱形？并说明理由；（2）当点P的横坐标为1时，是否存在这样的抛物线，使得以B、P、D为顶点的三角形与△AOB相似？若存在，求出满足条件的抛物线的解析式；若不存在，请说明理由．23．如图，抛物线y=ax2+bx经过△OAB的三个顶点，其中点A（1，），点B （3，﹣），O为坐标原点．（1）求这条抛物线所对应的函数表达式；（2）若P（4，m），Q（t，n）为该抛物线上的两点，且n＜m，求t的取值范围；（3）若C为线段AB上的一个动点，当点A，点B到直线OC的距离之和最大时，求∠BOC的大小及点C的坐标．24．如图，在平面直角坐标系中，抛物线C1：y=ax2+bx﹣1经过点A（﹣2，1）和点B（﹣1，﹣1），抛物线C2：y=2x2+x+1，动直线x=t与抛物线C1交于点N，与抛物线C2交于点M．（1）求抛物线C1的表达式；（2）直接用含t的代数式表示线段MN的长；（3）当△AMN是以MN为直角边的等腰直角三角形时，求t的值；（4）在（3）的条件下，设抛物线C1与y轴交于点P，点M在y轴右侧的抛物线C2上，连接AM交y轴于点K，连接KN，在平面内有一点Q，连接KQ和QN，当KQ=1且∠KNQ=∠BNP时，请直接写出点Q的坐标．25．在平面直角坐标系xOy中，已知抛物线的顶点坐标为（2，0），且经过点（4，1），如图，直线y=x与抛物线交于A、B两点，直线l为y=﹣1．（1）求抛物线的解析式；（2）在l上是否存在一点P，使PA+PB取得最小值？若存在，求出点P的坐标；若不存在，请说明理由．（3）知F（x0，y0）为平面内一定点，M（m，n）为抛物线上一动点，且点M 到直线l的距离与点M到点F的距离总是相等，求定点F的坐标．26．如图，在平面直角坐标系中，二次函数y=ax2+bx+c交x轴于点A（﹣4，0）、B（2，0），交y轴于点C（0，6），在y轴上有一点E（0，﹣2），连接AE．（1）求二次函数的表达式；（2）若点D为抛物线在x轴负半轴上方的一个动点，求△ADE面积的最大值；（3）抛物线对称轴上是否存在点P，使△AEP为等腰三角形？若存在，请直接写出所有P点的坐标，若不存在请说明理由．27．如图，抛物线y=ax2+bx+c（a≠0）与x轴交于点A（﹣4，0），B（2，0），与y轴交于点C（0，4），线段BC的中垂线与对称轴l交于点D，与x轴交于点F，与BC交于点E，对称轴l与x轴交于点H．（1）求抛物线的函数表达式；（2）求点D的坐标；（3）点P为x轴上一点，⊙P与直线BC相切于点Q，与直线DE相切于点R．求点P的坐标；（4）点M为x轴上方抛物线上的点，在对称轴l上是否存在一点N，使得以点D，P，M，N为顶点的四边形是平行四边形？若存在，则直接写出N点坐标；若不存在，请说明理由．28．如图，抛物线y=ax2+bx（a≠0）交x轴正半轴于点A，直线y=2x经过抛物线的顶点M．已知该抛物线的对称轴为直线x=2，交x轴于点B．（1）求a，b的值．（2）P是第一象限内抛物线上的一点，且在对称轴的右侧，连接OP，BP．设点P的横坐标为m，△OBP的面积为S，记K=．求K关于m的函数表达式及K的范围．29．抛物线y=﹣x2﹣x+与x轴交于点A，B（点A在点B的左边），与y轴交于点C，点D是该抛物线的顶点．（1）如图1，连接CD，求线段CD的长；（2）如图2，点P是直线AC上方抛物线上一点，PF⊥x轴于点F，PF与线段AC 交于点E；将线段OB沿x轴左右平移，线段OB的对应线段是O1B1，当PE+EC 的值最大时，求四边形PO1B1C周长的最小值，并求出对应的点O1的坐标；（3）如图3，点H是线段AB的中点，连接CH，将△OBC沿直线CH翻折至△O2B2C的位置，再将△O2B2C绕点B2旋转一周，在旋转过程中，点O2，C的对应点分别是点O3，C1，直线O3C1分别与直线AC，x轴交于点M，N．那么，在△O2B2C的整个旋转过程中，是否存在恰当的位置，使△AMN是以MN为腰的等腰三角形？若存在，请直接写出所有符合条件的线段O2M的长；若不存在，请说明理由．30．综合与探究如图，抛物线y=x﹣4与x轴交于A，B两点（点A在点B的左侧），与y轴交于点C，连接AC，BC．点P是第四象限内抛物线上的一个动点，点P的横坐标为m，过点P作PM⊥x轴，垂足为点M，PM交BC于点Q，过点P作PE ∥AC交x轴于点E，交BC于点F．（1）求A，B，C三点的坐标；（2）试探究在点P运动的过程中，是否存在这样的点Q，使得以A，C，Q为顶点的三角形是等腰三角形．若存在，请直接写出此时点Q的坐标；若不存在，请说明理由；（3）请用含m的代数式表示线段QF的长，并求出m为何值时QF有最大值．31．如图，二次函数y=﹣+bx+2的图象与x轴交于点A、B，与y轴交于点C，点A的坐标为（﹣4，0），P是抛物线上一点（点P与点A、B、C不重合）．（1）b=，点B的坐标是；（2）设直线PB与直线AC相交于点M，是否存在这样的点P，使得PM：MB=1：2？若存在，求出点P的横坐标；若不存在，请说明理由；（3）连接AC、BC，判断∠CAB和∠CBA的数量关系，并说明理由．32．如图，在平面直角坐标系中，二次函数y=（x﹣a）（x﹣3）（0＜a＜3）的图象与x轴交于点A、B（点A在点B的左侧），与y轴交于点D，过其顶点C 作直线CP⊥x轴，垂足为点P，连接AD、BC．（1）求点A、B、D的坐标；（2）若△AOD与△BPC相似，求a的值；（3）点D、O、C、B能否在同一个圆上？若能，求出a的值；若不能，请说明理由．33．如图，已知二次函数y=ax2﹣（2a﹣）x+3的图象经过点A（4，0），与y 轴交于点B．在x轴上有一动点C（m，0）（0＜m＜4），过点C作x轴的垂线交直线AB于点E，交该二次函数图象于点D．（1）求a的值和直线AB的解析式；（2）过点D作DF⊥AB于点F，设△ACE，△DEF的面积分别为S1，S2，若S1=4S2，求m的值；（3）点H是该二次函数图象上位于第一象限的动点，点G是线段AB上的动点，当四边形DEGH是平行四边形，且▱DEGH周长取最大值时，求点G的坐标．34．已知，点M为二次函数y=﹣（x﹣b）2+4b+1图象的顶点，直线y=mx+5分别交x轴正半轴，y轴于点A，B．（1）判断顶点M是否在直线y=4x+1上，并说明理由．（2）如图1，若二次函数图象也经过点A，B，且mx+5＞﹣（x﹣b）2+4b+1，根据图象，写出x的取值范围．（3）如图2，点A坐标为（5，0），点M在△AOB内，若点C（，y1），D（，y2）都在二次函数图象上，试比较y1与y2的大小．35．如图，在平面直角坐标系中，抛物线y=ax2+bx﹣5交y轴于点A，交x轴于点B（﹣5，0）和点C（1，0），过点A作AD∥x轴交抛物线于点D．（1）求此抛物线的表达式；（2）点E是抛物线上一点，且点E关于x轴的对称点在直线AD上，求△EAD 的面积；（3）若点P是直线AB下方的抛物线上一动点，当点P运动到某一位置时，△ABP的面积最大，求出此时点P的坐标和△ABP的最大面积．36．已知抛物线F：y=x2+bx+c的图象经过坐标原点O，且与x轴另一交点为（﹣，0）．（1）求抛物线F的解析式；（2）如图1，直线l：y=x+m（m＞0）与抛物线F相交于点A（x1，y1）和点B（x2，y2）（点A在第二象限），求y2﹣y1的值（用含m的式子表示）；（3）在（2）中，若m=，设点A′是点A关于原点O的对称点，如图2．①判断△AA′B的形状，并说明理由；②平面内是否存在点P，使得以点A、B、A′、P为顶点的四边形是菱形？若存在，求出点P的坐标；若不存在，请说明理由．37．直线y=﹣x+3交x轴于点A，交y轴于点B，顶点为D的抛物线y=﹣x2+2mx ﹣3m经过点A，交x轴于另一点C，连接BD，AD，CD，如图所示．（1）直接写出抛物线的解析式和点A，C，D的坐标；（2）动点P在BD上以每秒2个单位长的速度由点B向点D运动，同时动点Q 在CA上以每秒3个单位长的速度由点C向点A运动，当其中一个点到达终点停止运动时，另一个点也随之停止运动，设运动时间为t秒．PQ交线段AD于点E．①当∠DPE=∠CAD时，求t的值；②过点E作EM⊥BD，垂足为点M，过点P作PN⊥BD交线段AB或AD于点N，当PN=EM时，求t的值．38．如图1，在平面直角坐标系中，直线y=x﹣1与抛物线y=﹣x2+bx+c交于A、B两点，其中A（m，0）、B（4，n），该抛物线与y轴交于点C，与x轴交于另一点D．（1）求m、n的值及该抛物线的解析式；（2）如图2，若点P为线段AD上的一动点（不与A、D重合），分别以AP、DP为斜边，在直线AD的同侧作等腰直角△APM和等腰直角△DPN，连接MN，试确定△MPN面积最大时P点的坐标；（3）如图3，连接BD、CD，在线段CD上是否存在点Q，使得以A、D、Q为顶点的三角形与△ABD相似，若存在，请直接写出点Q的坐标；若不存在，请说明理由．39．如图，点A，B，C都在抛物线y=ax2﹣2amx+am2+2m﹣5（其中﹣＜a＜0）上，AB∥x轴，∠ABC=135°，且AB=4．（1）填空：抛物线的顶点坐标为（用含m的代数式表示）；（2）求△ABC的面积（用含a的代数式表示）；（3）若△ABC的面积为2，当2m﹣5≤x≤2m﹣2时，y的最大值为2，求m的值．40．如图1，在平面直角坐标系xOy中，已知点A和点B的坐标分别为A（﹣2，0），B（0，﹣6），将Rt△AOB绕点O按顺时针方向分别旋转90°，180°得到Rt△A1OC，Rt△EOF．抛物线C1经过点C，A，B；抛物线C2经过点C，E，F．（1）点C的坐标为，点E的坐标为；抛物线C1的解析式为．抛物线C2的解析式为；（2）如果点P（x，y）是直线BC上方抛物线C1上的一个动点．①若∠PCA=∠ABO时，求P点的坐标；②如图2，过点P作x轴的垂线交直线BC于点M，交抛物线C2于点N，记h=PM+NM+BM，求h与x的函数关系式，当﹣5≤x≤﹣2时，求h的取值范围．41．如图，抛物线y=ax2+bx+c与两坐标轴相交于点A（﹣1，0）、B（3，0）、C （0，3），D是抛物线的顶点，E是线段AB的中点．（1）求抛物线的解析式，并写出D点的坐标；（2）F（x，y）是抛物线上的动点：①当x＞1，y＞0时，求△BDF的面积的最大值；②当∠AEF=∠DBE时，求点F的坐标．42．如图，在平面直角坐标系中，矩形ABCD的对称中心为坐标原点O，AD⊥y 轴于点E（点A在点D的左侧），经过E、D两点的函数y=﹣x2+mx+1（x≥0）的图象记为G1，函数y=﹣x2﹣mx﹣1（x＜0）的图象记为G2，其中m是常数，图象G1、G2合起来得到的图象记为G．设矩形ABCD的周长为L．（1）当点A的横坐标为﹣1时，求m的值；（2）求L与m之间的函数关系式；（3）当G2与矩形ABCD恰好有两个公共点时，求L的值；（4）设G在﹣4≤x≤2上最高点的纵坐标为y0，当≤y0≤9时，直接写出L的取值范围．43．已知抛物线y=ax2+bx+c过点A（0，2），且抛物线上任意不同两点M（x1，y1），N（x2，y2）都满足：当x1＜x2＜0时，（x1﹣x2）（y1﹣y2）＞0；当0＜x1＜x2时，（x1﹣x2）（y1﹣y2）＜0．以原点O为圆心，OA为半径的圆与抛物线的另两个交点为B，C，且B在C的左侧，△ABC有一个内角为60°．（1）求抛物线的解析式；（2）若MN与直线y=﹣2x平行，且M，N位于直线BC的两侧，y1＞y2，解决以下问题：①求证：BC平分∠MBN；②求△MBC外心的纵坐标的取值范围．44．如图，抛物线y=x2+bx+c与x轴交于A、B两点，B点坐标为（4，0），与y 轴交于点C（0，4）．（1）求抛物线的解析式；（2）点P在x轴下方的抛物线上，过点P的直线y=x+m与直线BC交于点E，与y轴交于点F，求PE+EF的最大值；（3）点D为抛物线对称轴上一点．①当△BCD是以BC为直角边的直角三角形时，直接写出点D的坐标；②若△BCD是锐角三角形，直接写出点D的纵坐标n的取值范围．45．如图1，抛物线y=ax2+2x+c与x轴交于A（﹣4，0），B（1，0）两点，过点B的直线y=kx+分别与y轴及抛物线交于点C，D．（1）求直线和抛物线的表达式；（2）动点P从点O出发，在x轴的负半轴上以每秒1个单位长度的速度向左匀速运动，设运动时间为t秒，当t为何值时，△PDC为直角三角形？请直接写出所有满足条件的t的值；（3）如图2，将直线BD沿y轴向下平移4个单位后，与x轴，y轴分别交于E，F两点，在抛物线的对称轴上是否存在点M，在直线EF上是否存在点N，使DM+MN的值最小？若存在，求出其最小值及点M，N的坐标；若不存在，请说明理由．46．如图，已知抛物线y=ax2+bx﹣3与x轴交于点A（﹣3，0）和点B（1，0），交y轴于点C，过点C作CD∥x轴，交抛物线于点D．（1）求抛物线的解析式；（2）若直线y=m（﹣3＜m＜0）与线段AD、BD分别交于G、H两点，过G点作EG⊥x轴于点E，过点H作HF⊥x轴于点F，求矩形GEFH的最大面积；（3）若直线y=kx+1将四边形ABCD分成左、右两个部分，面积分别为S1，S2，且S1：S2=4：5，求k的值．47．如图，抛物线顶点P（1，4），与y轴交于点C（0，3），与x轴交于点A，B．（1）求抛物线的解析式．（2）Q是抛物线上除点P外一点，△BCQ与△BCP的面积相等，求点Q的坐标．（3）若M，N为抛物线上两个动点，分别过点M，N作直线BC的垂线段，垂足分别为D，E．是否存在点M，N使四边形MNED为正方形？如果存在，求正方形MNED的边长；如果不存在，请说明理由．48．如图，已知抛物线y=ax2+bx+c（a≠0）的对称轴为直线x=﹣1，且抛物线与x轴交于A、B两点，与y轴交于C点，其中A（1，0），C（0，3）．（1）若直线y=mx+n经过B、C两点，求直线BC和抛物线的解析式；（2）在抛物线的对称轴x=﹣1上找一点M，使点M到点A的距离与到点C的距离之和最小，求出点M的坐标；（3）设点P为抛物线的对称轴x=﹣1上的一个动点，求使△BPC为直角三角形的点P的坐标．49．在平面直角坐标系中，二次函数y=ax2+x+c的图象经过点C（0，2）和点D （4，﹣2）．点E是直线y=﹣x+2与二次函数图象在第一象限内的交点．（1）求二次函数的解析式及点E的坐标．（2）如图①，若点M是二次函数图象上的点，且在直线CE的上方，连接MC，OE，ME．求四边形COEM面积的最大值及此时点M的坐标．（3）如图②，经过A、B、C三点的圆交y轴于点F，求点F的坐标．50．如图，抛物线y=a（x﹣1）（x﹣3）（a＞0）与x轴交于A、B两点，抛物线上另有一点C在x轴下方，且使△OCA∽△OBC．（1）求线段OC的长度；（2）设直线BC与y轴交于点M，点C是BM的中点时，求直线BM和抛物线的解析式；（3）在（2）的条件下，直线BC下方抛物线上是否存在一点P，使得四边形ABPC 面积最大？若存在，请求出点P的坐标；若不存在，请说明理由．一．解答题（共50小题）1．如图1，已知二次函数y=ax 2+x +c （a ≠0）的图象与y 轴交于点A （0，4），与x 轴交于点B 、C ，点C 坐标为（8，0），连接AB 、AC ．（1）请直接写出二次函数y=ax 2+x +c 的表达式；（2）判断△ABC 的形状，并说明理由；（3）若点N 在x 轴上运动，当以点A 、N 、C 为顶点的三角形是等腰三角形时，请写出此时点N 的坐标；（4）如图2，若点N 在线段BC 上运动（不与点B 、C 重合），过点N 作NM ∥AC ，交AB 于点M ，当△AMN 面积最大时，求此时点N 的坐标．【分析】（1）根据待定系数法即可求得；（2）根据抛物线的解析式求得B 的坐标，然后根据勾股定理分别求得AB 2=20，AC 2=80，BC10，然后根据勾股定理的逆定理即可证得△ABC 是直角三角形．（3）分别以A 、C 两点为圆心，AC 长为半径画弧，与x 轴交于三个点，由AC 的垂直平分线与x 轴交于一个点，即可求得点N 的坐标；（4）设点N 的坐标为（n ，0），则BN=n +2，过M 点作MD ⊥x 轴于点D ，根据三角形相似对应边成比例求得MD=（n +2），然后根据S △AMN =S △ABN ﹣S △BMN 得出关于n 的二次函数，根据函数解析式求得即可．【解答】解：（1）∵二次函数y=ax 2+x +c 的图象与y 轴交于点A （0，4），与x 轴交于点B 、C ，点C 坐标为（8，0）， ∴，解得．∴抛物线表达式：y=﹣x2+x+4；（2）△ABC是直角三角形．令y=0，则﹣x2+x+4=0，解得x1=8，x2=﹣2，∴点B的坐标为（﹣2，0），由已知可得，在Rt△ABO中AB2=BO2+AO2=22+42=20，在Rt△AOC中AC2=AO2+CO2=42+82=80，又∵BC=OB+OC=2+8=10，∴在△ABC中AB2+AC2=20+80=102=BC2∴△ABC是直角三角形．（3）∵A（0，4），C（8，0），∴AC==4，①以A为圆心，以AC长为半径作圆，交x轴于N，此时N的坐标为（﹣8，0），②以C为圆心，以AC长为半径作圆，交x轴于N，此时N的坐标为（8﹣4，0）或（8+4，0）③作AC的垂直平分线，交x轴于N，此时N的坐标为（3，0），综上，若点N在x轴上运动，当以点A、N、C为顶点的三角形是等腰三角形时，点N的坐标分别为（﹣8，0）、（8﹣4，0）、（3，0）、（8+4，0）．（4）如图，AB==2，BC=8﹣（﹣2）=10，AC==4，∴AB2+AC2=BC2，∴∠BAC=90°．∴AC⊥AB．∵AC∥MN，∴MN⊥AB．设点N的坐标为（n，0），则BN=n+2，∵MN∥AC，△BMN∽△BAC∴=，∴=，BM==，MN==，AM=AB﹣BM=2﹣==AM•MN∵S△AMN=××=﹣（n﹣3）2+5，当n=3时，△AMN面积最大是5，∴N点坐标为（3，0）．∴当△AMN面积最大时，N点坐标为（3，0）．【点评】本题是二次函数的综合题，解（1）的关键是待定系数法求解析式，解（2）的关键是勾股定理和逆定理，解（3）的关键是等腰三角形的性质，解（4）的关键是三角形相似的判定和性质以及函数的最值等．2．对于平面直角坐标系xOy中的图形M，N，给出如下定义：P为图形M上任意一点，Q为图形N上任意一点，如果P，Q两点间的距离有最小值，那么称这个最小值为图形M，N间的“闭距离“，记作d（M，N）．已知点A（﹣2，6），B（﹣2，﹣2），C（6，﹣2）．（1）求d（点O，△ABC）；（2）记函数y=kx（﹣1≤x≤1，k≠0）的图象为图形G．若d（G，△ABC）=1，直接写出k的取值范围；（3）⊙T的圆心为T（t，0），半径为1．若d（⊙T，△ABC）=1，直接写出t 的取值范围．【分析】（1）根据点A、B、C三点的坐标作出△ABC，利用“闭距离”的定义即可得；（2）由题意知y=kx在﹣1≤x≤1范围内函数图象为过原点的线段，再分别求得经过（1，﹣1）和（﹣1，﹣1）时k的值即可得；（3）分⊙T在△ABC的左侧、内部和右侧三种情况，利用“闭距离”的定义逐一判断即可得．【解答】解：（1）如图所示，点O到△ABC的距离的最小值为2，∴d（点O，△ABC）=2；（2）y=kx（k≠0）经过原点，在﹣1≤x≤1范围内，函数图象为线段，当y=kx（﹣1≤x≤1，k≠0）经过（1，﹣1）时，k=﹣1，此时d（G，△ABC）=1；当y=kx（﹣1≤x≤1，k≠0）经过（﹣1，﹣1）时，k=1，此时d（G，△ABC）=1；∴﹣1≤k≤1，∵k≠0，∴﹣1≤k≤1且k≠0；。

九年级数学上册二次函数(培优篇)(Word版含解析)

九年级数学上册二次函数（培优篇）（Word版含解析）一、初三数学二次函数易错题压轴题（难）1．如图，抛物线y＝﹣x2+bx+c与x轴交于A，B两点，其中A（3，0），B（﹣1，0），与y轴交于点C，抛物线的对称轴交x轴于点D，直线y＝kx+b1经过点A，C，连接CD．（1）求抛物线和直线AC的解析式：（2）若抛物线上存在一点P，使△ACP的面积是△ACD面积的2倍，求点P的坐标；（3）在抛物线的对称轴上是否存在一点Q，使线段AQ绕Q点顺时针旋转90°得到线段QA1，且A1好落在抛物线上？若存在，求出点Q的坐标；若不存在，请说明理由．【答案】（1）2y x2x3=-++；3y x=-+；（2）（﹣1，0）或（4，﹣5）；（3）存在；（1，2）和（1，﹣3）【解析】【分析】（1）将点A，B坐标代入抛物线解析式中，求出b，c得出抛物线的解析式，进而求出点C 的坐标，再将点A，C坐标代入直线AC的解析式中，即可得出结论；（2）利用抛物线的对称性得出BD＝AD，进而判断出△ABC的面积和△ACP的面积相等，即可得出结论；（3）分点Q在x轴上方和在x轴下方，构造全等三角形即可得出结论．【详解】解：（1）把A（3，0），B（﹣1，0）代入y＝﹣x2+bc+c中，得93010b cb c-++=⎧⎨--+=⎩，∴23bc=⎧⎨=⎩，∴抛物线的解析式为y＝﹣x2+2x+3，当x＝0时，y＝3，∴点C的坐标是（0，3），把A（3，0）和C（0，3）代入y＝kx+b1中，得11303k bb+=⎧⎨=⎩，∴113kb=-⎧⎨=⎩∴直线AC的解析式为y＝﹣x+3；（2）如图，连接BC，∵点D是抛物线与x轴的交点，∴AD＝BD，∴S△ABC＝2S△ACD，∵S△ACP＝2S△ACD，∴S△ACP＝S△ABC，此时，点P与点B重合，即：P（﹣1，0），过B点作PB∥AC交抛物线于点P，则直线BP的解析式为y＝﹣x﹣1①，∵抛物线的解析式为y＝﹣x2+2x+3②，联立①②解得，1xy=-⎧⎨=⎩或45xy=⎧⎨=-⎩，∴P（4，﹣5），∴即点P的坐标为（﹣1，0）或（4，﹣5）；（3）如图，①当点Q在x轴上方时，设AC与对称轴交点为Q'，由（1）知，直线AC的解析式为y＝﹣x+3，当x＝1时，y＝2，∴Q'坐标为（1，2），∵Q'D＝AD＝BD＝2，∴∠Q'AB＝∠Q'BA＝45°，∴∠AQ'B＝90°，∴点Q'为所求，②当点Q在x轴下方时，设点Q（1，m），过点A1'作A1'E⊥DQ于E，∴∠A1'EQ＝∠QDA＝90°，∴∠DAQ+∠AQD＝90°，由旋转知，AQ＝A1'Q，∠AQA1'＝90°，∴∠AQD+∠A1'QE＝90°，∴∠DAQ＝∠A1'QE，∴△ADQ≌△QEA1'（AAS），∴AD ＝QE ＝2，DQ ＝A 1'E ＝﹣m ， ∴点A 1'的坐标为（﹣m +1，m ﹣2），代入y ＝﹣x 2+2x +3中，解得，m ＝﹣3或m ＝2（舍）， ∴Q 的坐标为（1，﹣3），∴点Q 的坐标为（1，2）和（1，﹣3）．【点睛】本题考查的是二次函数的综合题，涉及解析式的求解，与三角形面积有关的问题，三角形“k ”字型全等，解题的关键是利用数形结合的思想，设点坐标并结合几何图形的性质列式求解．2．在平面直角坐标系中，O 为坐标原点，抛物线L ：y ＝ax 2﹣4ax （a >0）与x 轴正半轴交于点A ．抛物线L 的顶点为M ，对称轴与x 轴交于点D ．（1）求抛物线L 的对称轴．（2）抛物线L ：y ＝ax 2﹣4ax 关于x 轴对称的抛物线记为L '，抛物线L '的顶点为M '，若以O 、M 、A 、M '为顶点的四边形是正方形，求L '的表达式．（3）在（2）的条件下，点P 在抛物线L 上，且位于第四象限，点Q 在抛物线L '上，是否存在点P 、点Q 使得以O 、D 、P 、Q 为顶点的四边形是平行四边形，若存在，求出点P 坐标，若不存在，请说明理由．【答案】（1）2x =；（2）2122y x x =-+ ；（3）存在，P 点的坐标为(33,3或()33,3--或()13,3-或()13,3+-或31,2⎛⎫- ⎪⎝⎭【解析】【分析】（1）根据抛物线的对称轴公式计算即可．（2）利用正方形的性质求出点M ，M ′的坐标即可解决问题．（3）分OD 是平行四边形的边或对角线两种情形求解即可．【详解】解：（1）∵抛物线L ：y ＝ax 2﹣4ax (a ＞0)， ∴抛物线的对称轴x ＝﹣42aa-＝2．（2）如图1中，对于抛物线y ＝ax 2﹣4ax ，令y ＝0，得到ax 2﹣4ax ＝0，解得x ＝0或4， ∴A (4，0)，∵四边形OMAM ′是正方形， ∴OD ＝DA ＝DM ＝DM ′＝2， ∴M ((2，﹣2)，M ′(2，2) 把M (2，﹣2)代入y ＝ax 2﹣4ax ，可得﹣2＝4a ﹣8a ， ∴a ＝12， ∴抛物线L ′的解析式为y ＝﹣12(x ﹣2)2+2＝﹣12x 2+2x ．（3）如图3中，由题意OD ＝2．当OD 为平行四边形的边时，PQ ＝OD ＝2，设P (m ，12m 2﹣2m )，则Q [m ﹣2，﹣12(m ﹣2)2+2(m ﹣2)]或[m +2，﹣12(m +2)2+2(m +2)]， ∵PQ ∥OD ， ∴12m 2﹣2m ＝﹣12(m ﹣2)2+2(m ﹣2)或12m 2﹣2m ＝﹣12(m +2)2+2(m +2)，解得m ＝33，∴P 33或(333或(133和33，当OD 是平行四边形的对角线时，点P 的横坐标为1，此时P (1，﹣32)，综上所述，满足条件的点P 的坐标为33或(333或(133)和33)或(1，﹣32)．【点睛】本题属于二次函数综合题,考查了二次函数的性质，正方形的性质,平行四边形的判定和性质等知识，解题的关键是理解题意，学会利用参数构建方程解决问题,学会用分类讨论的思想思考问题,属于中考压轴题学会利用参数构建方程解决问题，学会用分类讨论的思想思考问题，属于中考压轴题3．如图，抛物线()250y ax bx a =+-≠经过x 轴上的点1,0A 和点B 及y 轴上的点C ，经过B C 、两点的直线为y x n =+．（1）求抛物线的解析式．（2）点P 从A 出发，在线段AB 上以每秒1个单位的速度向B 运动，同时点E 从B 出发，在线段BC 上以每秒2个单位的速度向C 运动．当其中一个点到达终点时，另一点也停止运动．设运动时间为t 秒，求t 为何值时，PBE △的面积最大并求出最大值．（3）过点A 作AM BC ⊥于点M ，过抛物线上一动点N （不与点B C 、重合）作直线AM 的平行线交直线BC 于点Q ．若点A M N Q 、、、为顶点的四边形是平行四边形，求点N 的横坐标．【答案】（1）265y x x =-+- （2）2t =；2（3）5412或4或5412【解析】【分析】（1）先确定A 、B 、C 三点的坐标，然后用待定系数法解答即可；（2）先求出AB 、BC 的长并说明△BOC 是等腰直角三角形，再求出点P 到BC 的高d 为()24542d BP sin t =⋅︒=-，则12PBESBE d =⨯⨯)()122244222t t t =⨯⨯-=-，再根据二次函数的性质即可确定最大值；（3）先求出2454222AM AB sin =⋅︒=⨯=N 作直线AM 的平行线交直线BC 于点,Q 则，再说明四边形AMNQ 是平行四边形，得到22NQ AM ==；再过点N 作NH x ⊥轴，交x 轴于点,G 交BC 于点,H 结合题意说明NQH 为等腰直角三角形，求得22884NH NQ HQ =+=+=；设()2,65N m m m -+-，则(),0G m ，(),5H m m -，最后分点N 在x 轴上方时、点N 在x 轴下方且5m >时和1m <三种情况解答即可．【详解】解：()1因为直线y x n =+经过B C 、两点，且点B 在x 轴上，点C 在y 轴上， ∵()(),,00,B n C n -∴抛物线25y ax bx =+-经过点1,0A ，点(),0B n -，点()0,C n ，∴250505a b an bn n +-=⎧⎪--=⎨⎪-=⎩，解得51,6n a b =-⎧⎪=-⎨⎪=⎩所以抛物线的解析式为265y x x =-+-．()2∵()()()1,05,0,0,,5,A B C -∴4,AB BC BOC ==为等腰直角三角形， ∴45,ABC ∠=由题意得4,2,02BP t BE t t =-=<≤点P 到BE的距离()4542d BP sin t =⋅︒=- 所以12PBESBE d =⨯⨯)()1244222t t t t =⨯⨯-=-； ∵二次函数()()42f t t =-的函数图象开口向下，零点为0和4, ∴0422t +==时， ∴()()()22422max f t f ==⨯⨯-=即2t =时，PBE △的面积最大，且最大值为()3由题意得454AM AB sin =⋅︒== 过点N 作直线AM 的平行线交直线BC 于点,Q 则,NQ BC ⊥ ∵点,A M N Q 、、为顶点的四边形是平行四边形，∴NQ AM ==过点N 作NH x ⊥轴，交x 轴于点,G 交BC 于点,H ∵:5BC l y x =-，∴NQH 为等腰直角三角形，∴22884,NH NQ HQ =+=+=设()2,65N m m m -+-，则(),0G m ，(),5H m m -，①点N 在x 轴上方时，此时()()2655,NH m m m =-+---∴()()26554m m m -+---=，即()()140,m m --=解得1m =（舍，因为此时点N 与点A 重合）或4m =；②点N 在x 轴下方且5m >时，此时()()2565,NH m m m =---+- ∴()()25654m m m ---+-=，即2540,m m --=解得54152m -=<（舍）或5412m +=③点N 在x 轴下方且1m <时，此时()()2565,NH m m m =---+- ∴()()25654m m m ---+-=，即2540,m m --=解得5412m -=或5412m +=（舍）综上所述，5414,2m m +==，5412m -=符合题意，即若点,A M N Q 、、为顶点的四边形是平行四边形，点N 的横坐标为541-或4或541+．【点睛】本题主要考查了二次函数的性质、平行四边形的判定与性质，掌握二次函数的性质以及分类讨论思想是解答本题的关键4．如图1，抛物线2:C y x =经过变换可得到抛物线()1111:C y a x x b =-，1C 与x 轴的正半轴交于点1A ，且其对称轴分别交抛物线C 、1C 于点1B 、1D ，此时四边形111D OB A 恰为正方形；按上述类似方法，如图2，抛物线()1111:C y a x x b =-经过变换可得到抛物线()2222:C y a x x b =-，2C 与x 轴的正半轴交于点2A ，且对称轴分别交抛物线1C 、2C 于点2B 、2D ，此时四边形222OB A D 也恰为正方形；按上述类似方法，如图3，可得到抛物线()3333:C y a x x b =-与正方形333OB A D ，请探究以下问题：（1）填空：1a = ，1b = ；（2）求出2C 与3C 的解析式；（3）按上述类似方法，可得到抛物线():n n n n C y a x x b =-与正方形n n n OB A D （1n ≥）. ①请用含n 的代数式直接表示出n C 的解析式；②当x 取任意不为0的实数时，试比较2018y 与2019y 的函数值的大小关系，并说明理由.【答案】（1）11a =，12b =；（2）22132y x x =-，23126y x x =-；（3）①()2212123n n y x x n -=-≥⨯，②20182019y y ＞. 【解析】【分析】（1）求与x 轴交点A 1坐标，根据正方形对角线性质表示出B 1的坐标，代入对应的解析式即可求出对应的b 1的值，写出D 1的坐标，代入y 1的解析式中可求得a 1的值；（2）求与x 轴交点A 2坐标，根据正方形对角线性质表示出B 2的坐标，代入对应的解析式即可求出对应的b 2的值，写出D 2的坐标，代入y 2的解析式中可求得a 2的值，写出抛物线C 2的解析式；再利用相同的方法求抛物线C 3的解析式；（3）①根据图形变换后二次项系数不变得出a n =a 1=1，由B 1坐标（1，1）、B 2坐标（3，3）、B 3坐标（7，7）得B n 坐标（2n -1，2n -1），则b n =2（2n -1）=2n +1-2（n ≥1），写出抛物线C n 解析式．②根据规律得到抛物线C 2015和抛物线C 2016的解析式，用求差法比较出y 2015与y 2016的函数值的大小．【详解】解：（1）y 1=0时，a 1x （x -b 1）=0， x 1=0，x 2=b 1， ∴A 1（b 1，0），由正方形OB 1A 1D 1得：OA 1=B 1D 1=b 1， ∴B 1（12b ，12b ），D 1（12b ，12b-）， ∵B 1在抛物线c 上，则12b =(12b )2，解得：b 1=0（不符合题意），b 1=2， ∴D 1（1，-1），把D 1（1，-1）代入y 1=a 1x （x -b 1）中得：-1=-a 1， ∴a 1=1，故答案为1，2；（2）当20y =时，有()220a x x b -=，解得2x b =或0x =，()22,0A b ∴. 由正方形222OB A D ，得2222B D OA b ==，222,22b b B ⎛⎫∴ ⎪⎝⎭，222,22bb D ⎛⎫- ⎪⎝⎭. 2B 在抛物线1C 上，2222222b b b ⎛⎫∴=- ⎪⎝⎭. 解得24b =或20b =（不合舍去），()22,2D ∴-2D 在抛物线2C 上，()22224a ∴-=-.解得212a =. 2C ∴的解析式是()2142y x x =-，即22122y x x =-. 同理，当30y =时，有()330a x x b -=，解得3x b =，或0x =.()33,0A b ∴.由正方形333OB A D ，得3333B D OA b ==，333,22b b B ⎛⎫∴ ⎪⎝⎭，333,22b b D ⎛⎫- ⎪⎝⎭. 3B 在抛物线2C 上，2333122222b b b ⎛⎫∴=-⋅ ⎪⎝⎭. 解得312b =或30b =（不合舍去）， ()36,6D ∴-3D 在抛物线3C 上，()366612a ∴-=-.解得316a =. 3C ∴的解析式是()31126y x x =-，即23126y x x =-. （3）解：①n C 的解析式是()2212123n n y x x n -=-≥⨯. ②由①可得2201820161223y x x =-⨯，2201920171223y x x =-⨯. 当0x ≠时，220182019201620171110233y y x ＞⎛⎫-=- ⎪⎝⎭， 20182019y y ∴＞.【点睛】本题是二次函数与方程、正方形的综合应用，将函数知识与方程、正方形有机地结合在一起．这类试题一般难度较大．解这类问题关键是善于将函数问题转化为方程问题，善于利用正方形的有关性质、定理和二次函数的知识，并注意挖掘题目中的一些隐含条件．就此题而言：①求出抛物线与x 轴交点坐标⇔把y =0代入计算，把函数问题转化为方程问题；②利用正方形对角线相等且垂直平分表示出对应B 1、B 2、B 3、B n 的坐标；③根据规律之间得到解析式是关键．5．二次函数22(0)63m m y x x m m =-+>的图象交y 轴于点A ，顶点为P ，直线PA 与x 轴交于点B ．（1）当m =1时，求顶点P 的坐标；（2）若点Q （a ，b ）在二次函数22(0)63m m y x x m m =-+>的图象上，且0b m ->，试求a 的取值范围；（3）在第一象限内，以AB 为边作正方形ABCD ．①求点D 的坐标（用含m 的代数式表示）；②若该二次函数的图象与正方形ABCD 的边CD 有公共点，请直接写出符合条件的整数m 的值．【答案】（1）P （2，13）；（2）a 的取值范围为：a ＜0或a ＞4；（3）①D （m ，m +3）； ②2，3，4．【解析】【分析】（1）把m =1代入二次函数22(0)63m m y x x m m =-+>解析式中，进而求顶点P 的坐标即可；（2）把点Q （a ，b ）代入二次函数22(0)63m m y x x m m =-+>解析式中，根据0b m ->得到关于a 的一元二次不等式即一元一次不等式组，解出a 的取值范围即可；（3）①过点D 作DE ⊥x 轴于点E ，过点A 作AF ⊥DE 于点F ，求出二次函数与y 轴的交点A 的坐标，得到OA 的长，再根据待定系数法求出直线AP 的解析式，进而求出与x 轴的交点B 的坐标，得到OB 的长；通过证明△ADF ≌△ABO ，得到AF=OA=m ，DF=OB=3，DE=DF+EF= DF+OA=m+3，求出点D 的坐标；②因为二次函数的图象与正方形ABCD 的边CD 有公共点，由①同理可得：C （m+3，3），分当x 等于点D 的横坐标时与当x 等于点C 的横坐标两种情况，进行讨论m 可能取的整数值即可．【详解】解：（1）当m =1时，二次函数为212163y x x =-+， ∴顶点P 的坐标为（2，13）；（2）∵点Q （a ，b ）在二次函数22(0)63m m y x x m m =-+>的图象上， ∴2263m m b a a m =-+，即：2263m m b m a a -=- ∵0b m ->，∴2263m m a a -＞0， ∵m ＞0， ∴2263a a -＞0，解得：a ＜0或a ＞4， ∴a 的取值范围为：a ＜0或a ＞4；（3）①如下图，过点D 作DE ⊥x 轴于点E ，过点A 作AF ⊥DE 于点F ，∵二次函数的解析式为2263m m y x x m =-+， ∴顶点P （2，3m ），当x=0时，y=m ，∴点A （0，m ），∴OA=m ；设直线AP 的解析式为y=kx+b(k≠0)，把点A （0，m ），点P （2，3m ）代入，得： 23m b m k b =⎧⎪⎨=+⎪⎩，解得：3m k b m⎧=-⎪⎨⎪=⎩，∴直线AP 的解析式为y=3m -x+m ，当y=0时，x=3，∴点B （3，0）；∴OB=3；∵四边形ABCD 是正方形，∴AD=AB ，∠DAF+∠FAB=90°，且∠OAB+∠FAB =90°，∴∠DAF=∠OAB ，在△ADF 和△ABO 中，DAF OAB AFD AOB AD AB ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△ADF ≌△ABO （AAS ），∴AF=OA=m ，DF=OB=3，DE=DF+EF= DF+OA=m+3，∴点D 的坐标为：（m ，m+3）；②由①同理可得：C （m+3，3），∵二次函数的图象与正方形ABCD 的边CD 有公共点，∴当x =m 时，3y m ≤+，可得322363m m m m -+≤+，化简得：32418m m -≤． ∵0m >，∴2184m m m -≤，∴218(2)4m m--≤，显然：m =1，2，3，4是上述不等式的解，当5m ≥时，2(2)45m --≥，18 3.6m ≤，此时，218(2)4m m-->， ∴符合条件的正整数m =1，2，3，4；当x = m +3时，y ≥3，可得2(3)2(3)363m m m m m ++-+≥， ∵0m >，∴21823m m m ++≥，即218(1)2m m++≥，显然：m =1不是上述不等式的解，当2m ≥时，2(1)211m ++≥，189m ≤，此时，218(1)2m m++>恒成立， ∴符合条件的正整数m =2，3，4；综上：符合条件的整数m 的值为2，3，4．【点睛】本题考查二次函数与几何问题的综合运用，熟练掌握二次函数的图象和性质、一次函数的图象和性质、正方形的性质是解题的关键．6．已知抛物线2(0)y ax bx c a =++≠过点(0,2)A -．（1）若点(2,0)-也在该抛物线上，请用含a 的关系式表示b ；（2）若该抛物线上任意不同两点()11,M x y 、()22,N x y 都满足：当120x x <<时，()()12120x x y y --<；当120x x <<时，()()12120x x y y -->；若以原点O 为圆心，OA 为半径的圆与抛物线的另两个交点为B 、C （点B 在点C 左侧），且ABC ∆有一个内角为60，求抛物线的解析式；（3）在（2）的条件下，若点P 与点O 关于点A 对称，且O 、M 、N 三点共线，求证：PA 平分MPN ∠．【答案】（1）21b a =-；（2）22y x =-；（3）见解析.【解析】【分析】（1）把点()0,2-、()2,0-代入抛物线解析式，然后整理函数式即可得到答案．（2）根据二次函数的性质可得出抛物线的对称轴为y 轴、开口向上，进而可得出0b =，由抛物线的对称性可得出ABC ∆为等腰三角形，结合其有一个60︒的内角可得出ABC ∆为等边三角形，设线段BC 与y 轴交于点D ，根据等边三角形的性质可得出点C 的坐标，再利用待定系数法可求出a 值，此题得解；（3）由（1）的结论可得出点M 的坐标为1(x ，212)x -+、点N 的坐标为2(x ，222)x -+，由O 、M 、N 三点共线可得出212x x =-，进而可得出点N 及点'N 的坐标，由点A 、M 的坐标利用待定系数法可求出直线AM 的解析式，利用一次函数图象上点的坐标特征可得出点'N 在直线PM 上，进而即可证出PA 平分MPN ∠．【详解】解：（1）把点()0,2-、()2,0-分别代入，得2420c a b c =-⎧⎨-+=⎩．所以21b a =-．（2），如图1，当120x x <<时，()()12120x x y y --<，120x x ∴-<，120y y ->，∴当0x <时，y 随x 的增大而减小；同理：当0x >时，y 随x 的增大而增大，∴抛物线的对称轴为y 轴，开口向上，0b ∴=．OA 为半径的圆与拋物线的另两个交点为B 、C ，ABC ∴∆为等腰三角形，又ABC ∆有一个内角为60︒，ABC ∴∆为等边三角形．设线段BC 与y 轴交于点D ，则BD CD =，且30OCD ∠=︒，又2OB OC OA ===，·303CD OC cos ∴=︒=，·301OD OC sin =︒=．不妨设点C 在y 轴右侧，则点C 的坐标为31)．点C 在抛物线上，且2c =-，0b =，321a ∴-=，1a ∴=，∴抛物线的解析式为22y x =-．（3）证明：由（1）可知，点M 的坐标为1(x ，212)x -，点N 的坐标为2(x ，222)x -．如图2，直线OM 的解析式为()110y k x k =≠．O 、M 、N 三点共线，10x ∴≠，20x ≠，且22121222x x x x --=， 121222x x x x ∴-=-， ()1212122x x x x x x -∴-=-，122x x ∴=-，即212x x =-， ∴点N 的坐标为12(x -，2142)x -．设点N 关于y 轴的对称点为点'N ，则点'N 的坐标为12(x ，2142)x -．点P 是点O 关于点A 的对称点，24OP OA ∴==，∴点P 的坐标为()0,4-．设直线PM 的解析式为24y k x =-，点M 的坐标为1(x ，212)x -，212124x k x ∴-=-，21212x k x +∴=， ∴直线PM 的解析式为21124x y x x +=-． ()222111221111224224·42x x x x x x x +-+-==-，∴点'N在直线PM上，PA∴平分MPN∠．【点睛】本题考查了待定系数法求一次（二次）函数解析式、二次函数的性质、等边三角形的性质以及一次（二次）函数图象上点的坐标特征，解题的关键是：（1）利用二次函数图象上点的坐标特征求出a、b满足的关系式；（2）①利用等边三角形的性质找出点C的坐标；②利用一次函数图象上点的坐标特征找出点'N在直线PM上．7．如图，顶点为M的抛物线y=ax2+bx+3与x轴交于A(﹣1，0)，B两点，与y轴交于点C，过点C作CD⊥y轴交抛物线于另一点D，作DE⊥x轴，垂足为点E，双曲线y=6x(x＞0)经过点D，连接MD，BD．（1）求抛物线的表达式；（2）点N，F分别是x轴，y轴上的两点，当以M，D，N，F为顶点的四边形周长最小时，求出点N，F的坐标；（3）动点P从点O出发，以每秒1个单位长度的速度沿OC方向运动，运动时间为t秒，当t为何值时，∠BPD的度数最大？【答案】（1）y=﹣x2+2x+3；（2）N(57，0)，F(0，53)；（3）t=9﹣15【解析】【分析】（1）由已知求出D点坐标，将点A（-1，0）和D（2，3）代入y=ax2+bx+3即可；（2）作M关于y轴的对称点M'，作D关于x轴的对称点D'，连接M'D'与x轴、y轴分别交于点N、F，则以M，D，N，F为顶点的四边形周长最小即为M'D'+MD的长；（3）设P（0，t），作△PBD的外接圆N，当⊙N与y轴相切时，∠BPD的度数最大；【详解】解；（1）C(0，3)∵CD⊥y，∴D点纵坐标是3．∵D在y=6x上，∴D(2，3)，将点A(﹣1，0)和D(2，3)代入y=ax2+bx+3，∴a=﹣1，b=2，∴y=﹣x2+2x+3；（2）M(1，4)，B(3，0)，作M关于y轴的对称点M'，作D关于x轴的对称点D'，连接M'D'与x轴、y轴分别交于点N、F，则以M，D，N，F为顶点的四边形周长最小即为M'D'+MD的长；∴M'(﹣1，4)，D'(2，﹣3)，∴M'D'直线的解析式为y=﹣73x+53，∴N(57，0)，F(0，53)；（3）设P(0，t)．∵△PBO和△CDP都是直角三角形，tan∠CDP=32t，tan∠PBO=3t，令y =tan ∠BPD =3233123t t t t -+--， ∴yt 2+t ﹣3yt +6y ﹣9=0，△=﹣15y 2+30y +1=0时，y =1515-+-舍)或y =1515+， ∴t =32﹣12×1y ，∴t =9﹣∴P (0，9﹣．【点睛】本题考查二次函数的图象及性质；熟练掌握二次函数的图象及性质，利用轴对称求最短距离，学会利用辅助圆解决问题，属于中考压轴题．8．定义：对于已知的两个函数，任取自变量x 的一个值，当0x ≥时，它们对应的函数值相等；当0x <时，它们对应的函数值互为相反数，我们称这样的两个函数互为相关函数.例如：正比例函数y x =，它的相关函数为(0)(0)x x y x x ≥⎧=⎨-<⎩. （1）已知点()5,10A -在一次函数5y ax =-的相关函数的图像上，求a 的值；（2）已知二次函数2142y x x =-+-. ①当点3,2B m ⎛⎫ ⎪⎝⎭在这个函数的相关函数的图像上时，求m 的值；②当33x -≤≤时，求函数2142y x x =-+-的相关函数的最大值和最小值. （3）在平面直角坐标系中，点M 、N 的坐标分别为1,12⎛⎫-⎪⎝⎭、9,12⎛⎫ ⎪⎝⎭，连结MN .直接写出线段MN 与二次函数24y x x n =-++的相关函数的图像有两个公共点时n 的取值范围.【答案】（1）1；（2）①22- ；②max 432y =，min 12y =-；（3）31n -<≤-，514n <≤【解析】【分析】（1）先求出5y ax =-的相关函数，然后代入求解，即可得到答案；（2）先求出二次函数的相关函数，①分为m ＜0和m ≥0两种情况将点B 的坐标代入对应的关系式求解即可；②当-3≤x ＜0时，y=x 2-4x+12，然后可此时的最大值和最小值，当0≤x≤3时，函数y=-x 2+4x-12，求得此时的最大值和最小值，从而可得到当-3≤x≤3时的最大值和最小值；（3）首先确定出二次函数y=-x 2+4x+n 的相关函数与线段MN 恰好有1个交点、2个交点、3个交点时n 的值，然后结合函数图象可确定出n 的取值范围．【详解】解：（1）根据题意，一次函数5y ax =-的相关函数为5,(0)5,(0)ax x y ax x -≥⎧=⎨-+<⎩， ∴把点()5,10A -代入5y ax =-+，则(5)510a -⨯-+=，∴1a =；（2）根据题意，二次函数2142y x x =-+-的相关函数为2214,(0)214,(0)2x x x y x x x ⎧-+-≥⎪⎪=⎨⎪-+<⎪⎩， ①当m ＜0时，将B （m ，32）代入y=x 2-4x+12得m 2-4m+1322=，解得：m=2当m≥0时，将B （m ，32）代入y=-x 2+4x-12得：-m 2+4m-12=32，解得：或m=2．综上所述：m=2-或m=2+或m=2-②当-3≤x ＜0时，y=x 2-4x+12，抛物线的对称轴为x=2，此时y 随x 的增大而减小， ∴当3x =-时，有最大值，即2143(3)4(3)22y =--⨯-+=， ∴此时y 的最大值为432．当0≤x≤3时，函数y=-x 2+4x 12-，抛物线的对称轴为x=2，当x=0有最小值，最小值为12-，当x=2时，有最大值，最大值y=72．综上所述，当-3≤x≤3时，函数y=-x2+4x12-的相关函数的最大值为432，最小值为12-；（3）如图1所示：线段MN与二次函数y=-x2+4x+n的相关函数的图象恰有1个公共点．∴当x=2时，y=1，即-4+8+n=1，解得n=-3．如图2所示：线段MN与二次函数y=-x2+4x+n的相关函数的图象恰有3个公共点．∵抛物线y=x2-4x-n与y轴交点纵坐标为1，∴-n=1，解得：n=-1．∴当-3＜n≤-1时，线段MN与二次函数y=-x2+4x+n的相关函数的图象恰有2个公共点．如图3所示：线段MN与二次函数y=-x2+4x+n的相关函数的图象恰有3个公共点．∵抛物线y=-x2+4x+n经过点（0，1），∴n=1．如图4所示：线段MN与二次函数y=-x2+4x+n的相关函数的图象恰有2个公共点．∵抛物线y=x2-4x-n经过点M（12，1），∴14+2-n=1，解得：n=54．∴1＜n≤54时，线段MN与二次函数y=-x2+4x+n的相关函数的图象恰有2个公共点．综上所述，n的取值范围是-3＜n≤-1或1＜n≤54．【点睛】本题主要考查的是二次函数的综合应用，解答本题主要应用了二次函数的图象和性质、函数图象上点的坐标与函数解析式的关系，求得二次函数y=-x2+4x+n的相关函数与线段MN 恰好有1个交点、2个交点、3个交点时n的值是解题的关键．9．在平面直角坐标系中，抛物线y=x2+（k﹣1）x﹣k与直线y=kx+1交于A，B两点，点A 在点B的左侧．（1）如图1，当k=1时，直接写出A，B两点的坐标；（2）在（1）的条件下，点P为抛物线上的一个动点，且在直线AB下方，试求出△ABP面积的最大值及此时点P的坐标；（3）如图2，抛物线y=x2+（k﹣1）x﹣k（k＞0）与x轴交于点C、D两点（点C在点D的左侧），在直线y=kx+1上是否存在唯一一点Q，使得∠OQC=90°？若存在，请求出此时k 的值；若不存在，请说明理由．【答案】（1）A(-1,0) ，B(2,3)（2）△ABP 最大面积s=1927322288⨯⨯=; P （12，﹣34）（3）存在；k=25 【解析】【分析】（1）当k=1时，抛物线解析式为y=x 2﹣1，直线解析式为y=x+1，然后解方程组211y x y x ⎧=⎨=+⎩﹣即可；（2）设P （x ，x 2﹣1）．过点P 作PF ∥y 轴，交直线AB 于点F ，则F （x ，x+1），所以利用S △ABP =S △PFA +S △PFB ，，用含x 的代数式表示为S △ABP=﹣x 2+x+2，配方或用公式确定顶点坐标即可．（3）设直线AB ：y=kx+1与x 轴、y 轴分别交于点E 、F ，用k 分别表示点E 的坐标，点F 的坐标，以及点C 的坐标，然后在Rt △EOF 中，由勾股定理表示出EF 的长，假设存在唯一一点Q ，使得∠OQC=90°，则以OC 为直径的圆与直线AB 相切于点Q ，设点N 为OC 中点，连接NQ ，根据条件证明△EQN ∽△EOF ，然后根据性质对应边成比例，可得关于k 的方程，解方程即可.【详解】解：（1）当k=1时，抛物线解析式为y=x 2﹣1，直线解析式为y=x+1．联立两个解析式，得：x 2﹣1=x+1，解得：x=﹣1或x=2，当x=﹣1时，y=x+1=0；当x=2时，y=x+1=3，∴A （﹣1，0），B （2，3）．（2）设P （x ，x 2﹣1）．如答图2所示，过点P 作PF ∥y 轴，交直线AB 于点F ，则F （x ，x+1）．∴PF=y F ﹣y P =（x+1）﹣（x 2﹣1）=﹣x 2+x+2．S △ABP =S △PFA +S △PFB =PF （xF ﹣xA ）+PF （xB ﹣xF ）=PF （xB ﹣xA ）=PF∴S △ABP=（﹣x 2+x+2）=﹣（x ﹣12）2+278 当x=12时，yP=x 2﹣1=﹣34．∴△ABP 面积最大值为，此时点P 坐标为（12，﹣34）．（3）设直线AB ：y=kx+1与x 轴、y 轴分别交于点E 、F ，则E （﹣1k ，0），F （0，1），OE=1k，OF=1．在Rt △EOF 中，由勾股定理得：EF=22111=k k +⎛⎫+ ⎪⎝⎭．令y=x 2+（k ﹣1）x ﹣k=0，即（x+k ）（x ﹣1）=0，解得：x=﹣k 或x=1．∴C （﹣k ，0），OC=k ．假设存在唯一一点Q ，使得∠OQC=90°，如答图3所示，则以OC 为直径的圆与直线AB 相切于点Q ，根据圆周角定理，此时∠OQC=90°．设点N 为OC 中点，连接NQ ，则NQ ⊥EF ，NQ=CN=ON=2k ． ∴EN=OE ﹣ON=1k ﹣2k ． ∵∠NEQ=∠FEO ，∠EQN=∠EOF=90°，∴△EQN ∽△EOF ，∴NQ EN OF EF =，即：1221k k k k-=，解得：25， ∵k ＞0，∴25． ∴存在唯一一点Q ，使得∠OQC=90°，此时25．考点：1.二次函数的性质及其应用；2.圆的性质；3.相似三角形的判定与性质.10．定义：在平面直角坐标系中，O 为坐标原点，设点P 的坐标为（x ，y ），当x ＜0时，点P 的变换点P′的坐标为（﹣x ，y ）；当x≥0时，点P 的变换点P′的坐标为（﹣y ，x ）．（1）若点A （2，1）的变换点A′在反比例函数y=k x的图象上，则k= ；（2）若点B （2，4）和它的变换点B'在直线y=ax+b 上，则这条直线对应的函数关系式为，∠BOB′的大小是度．（3）点P 在抛物线y=x 2﹣2x ﹣3的图象上，以线段PP′为对角线作正方形PMP'N ，设点P 的横坐标为m ，当正方形PMP′N 的对角线垂直于x 轴时，求m 的取值范围．（4）抛物线y=（x ﹣2）2+n 与x 轴交于点C ，D （点C 在点D 的左侧），顶点为E ，点P 在该抛物线上．若点P 的变换点P′在抛物线的对称轴上，且四边形ECP′D 是菱形，求n 的值．【答案】(1) －2；(2) y=13x+103，90；(3) m ＜0，m=12+或m=32；(4) n=﹣8，n=﹣2，n=﹣3．【解析】【分析】（1）先求出A 的变换点A ′，然后把A ′代入反比例函数即可得到结论；（2）确定点B ′的坐标，把问题转化为方程组解决；（3）分三种情形讨论：①当m ＜0时；②当m ≥0，PP '⊥x 轴时；③当m ≥0，MN ⊥x 轴时．（4）利用菱形的性质，得到点E 与点P '关于x 轴对称，从而得到点P '的坐标为（2，﹣n ）．分两种情况讨论：①当点P 在y 轴左侧时，点P 的坐标为（﹣2，﹣n ），代入抛物线解析式，求解即可；②当点P 在y 轴右侧时，点P 的坐标为（﹣n ，﹣2）．代入抛物线解析式，求解即可．【详解】（1）∵A （2，1）的变换点为A ′（－1，2），把A ′（－1，2）代入y =k x中，得到k =－2．故答案为：－2．（2）点B （2，4）的变换点B ′（﹣4，2），把（2，4），（﹣4，2）代入y =ax +b 中．得到：2442a b a b +=⎧⎨-+=⎩，解得：13103a b ⎧=⎪⎪⎨⎪=⎪⎩，∴11033y x =+． ∵OB 2=2224+=20，OB ′2=2224+=20，BB ′2=22(42)(24)--+-=40，∴OB 2+OB ′2=BB ′2，∴∠BOB ′=90°．故答案为：y =13x +103，90．（3）①当m ＜0时，点P 与点P '关于y 轴对称，此时MN 垂直于x 轴，所以m ＜0． ②当m ≥0，PP '⊥x 轴时，则点P '的坐标为（m ，m ），点P 的坐标为（m ，﹣m ）．将点P （m ，﹣m ）代入y =x 2﹣2x ﹣3，得：﹣m =m 2﹣2m ﹣3．解得：121122m m ==（不合题意，舍去）．所以m = ③当m ≥0，MN ⊥x 轴时，则PP '∥x 轴，点P 的坐标为（m ，m ）．将点P （m ，m ）代入y =x 2﹣2x ﹣3，得：m =m 2﹣2m ﹣3．解得：12m m ==所以32m +=．综上所述：m 的取值范围是m ＜0，m =12+或m =32．（4）∵四边形ECP 'D 是菱形，∴点E 与点P '关于x 轴对称．∵点E 的坐标为（2，n ），∴点P '的坐标为（2，﹣n ）．①当点P 在y 轴左侧时，点P 的坐标为（﹣2，﹣n ）．代入y =（x ﹣2）2+n ，得：﹣n =（﹣2﹣2）2+n ，解得：n =﹣8．②当点P 在y 轴右侧时，点P 的坐标为（﹣n ，﹣2）．代入y =（x ﹣2）2+n ，得：﹣2=（﹣n ﹣2）2+n ．解得：n 1=﹣2，n 2=﹣3．综上所述：n 的值是n =﹣8，n =﹣2，n =﹣3．【点睛】本题是二次函数综合题、一次函数的应用、待定系数法、变换点的定义等知识，解题的关键是理解题意，学会用分类讨论的射线思考问题，学会用方程的思想思考问题，属于中考压轴题．。

九年级数学上册二次函数(培优篇)(Word版含解析)

九年级数学上册二次函数（培优篇）（Word 版含解析）一、初三数学二次函数易错题压轴题（难）1．对于函数y ＝ax 2+（b+1）x+b ﹣2（a ≠0），若存在实数x0，使得a 20x +（b+1）x 0+b ﹣2＝x0成立，则称x 0为函数y ＝ax 2+（b+1）x+b ﹣2（a ≠0）的不动点．（1）当a ＝2，b ＝﹣2时，求y ＝ax 2+（b+1）x+b ﹣2（a ≠0）的不动点；（2）若对于任何实数b ，函数y ＝ax 2+（b+1）x+b ﹣2（a ≠0）恒有两相异的不动点，求实数a 的取值范围；（3）在（2）的条件下，若y ＝ax 2+（b+1）x+b ﹣2（a ≠0）的图象上A ，B 两点的横坐标是函数y ＝ax 2+（b+1）x+b ﹣2（a ≠0）的不动点，且直线y ＝﹣x+2121a +是线段AB 的垂直平分线，求实数b 的取值范围．【答案】（1）不动点是﹣1或2；（2）a 的取值范围是0＜a ＜2；（3）b 的取值范围是﹣b ＜0．【解析】【分析】（1）将a ＝2，b ＝﹣2代入函数y ＝ax 2+（b+1）x+b ﹣2（a ≠0），得y ＝2x 2﹣x ﹣4，然后令x ＝2x 2﹣x ﹣4，求出x 的值，即y ＝ax 2+（b+1）x+b ﹣2（a ≠0）的不动点；（2）对于任何实数b ，函数y ＝ax 2+（b+1）x+b ﹣2（a ≠0）恒有两相异的不动点，可以得到x ＝ax 2+（b+1）x+b ﹣2（a ≠0）时，对于任何实数b 都有△＞0，然后再设t ＝△，即可求得a 的取值范围；（3）根据y ＝ax 2+（b+1）x+b ﹣2（a ≠0）的图象上A ，B 两点的横坐标是函数y ＝ax 2+（b+1）x+b ﹣2（a ≠0）的不动点，可知点A 和点B 均在直线y ＝x 上，然后设出点A 和点B 的坐标，从而可以得到线段AB 的中点坐标，再根据直线y ＝﹣x+2121a +是线段AB 的垂直平分线，从而可以求得b 的取值范围．【详解】解：（1）当a ＝2，b ＝﹣2时，函数y ＝2x 2﹣x ﹣4，令x ＝2x 2﹣x ﹣4，化简，得x 2﹣x ﹣2＝0解得，x 1＝2，x 2＝﹣1，即y ＝ax 2+（b+1）x+b ﹣2（a ≠0）的不动点是﹣1或2；（2）令x ＝ax 2+（b+1）x+b ﹣2，整理，得ax 2+bx+b ﹣2＝0，∵对于任何实数b ，函数y ＝ax 2+（b+1）x+b ﹣2（a ≠0）恒有两相异的不动点， ∴△＝b 2﹣4a （b ﹣2）＞0，设t ＝b 2﹣4a （b ﹣2）＝b 2﹣4ab+8a ，对于任何实数b ，t ＞0，故（﹣4a ）2﹣4×1×8a ＜0，解得，0＜a ＜2，即a 的取值范围是0＜a ＜2；（3）由题意可得，点A 和点B 在直线y ＝x 上，设点A （x 1，x 1），点B （x 2，x 2），∵A ，B 两点的横坐标是函数y ＝ax 2+（b+1）x+b ﹣2（a ≠0）的不动点，∴x 1，x 2是方程ax 2+bx+b ﹣2＝0的两个根，∴x 1+x 2＝﹣b a， ∵线段AB 中点坐标为（122x x +，122x x +）， ∴该中点的坐标为（2b a -，2b a -）， ∵直线y ＝﹣x+2121a +是线段AB 的垂直平分线， ∴点（2b a -，2b a -）在直线y ＝﹣x+2121a +上， ∴2b a -＝21221b a a ++∴﹣b ＝221aa ≤+a∴0＜﹣b ≤4，∴﹣4≤b ＜0，即b b ＜0．【点睛】本题是一道二次函数综合题、主要考查新定义、二次函数的性质、二次函数图象上点的坐标特征、一次函数的性质，解答本题的关键是明确题意，利用二次函数的性质解答．2．在平面直角坐标系中，将函数y ＝x 2﹣2mx+m （x≤2m ，m 为常数）的图象记为G ，图象G 的最低点为P(x 0，y 0)．（1）当y 0＝﹣1时，求m 的值．（2）求y 0的最大值．（3）当图象G 与x 轴有两个交点时，设左边交点的横坐标为x 1，则x 1的取值范围是．（4）点A在图象G上，且点A的横坐标为2m﹣2，点A关于y轴的对称点为点B，当点A不在坐标轴上时，以点A、B为顶点构造矩形ABCD，使点C、D落在x轴上，当图象G 在矩形ABCD内的部分所对应的函数值y随x的增大而减小时，直接写出m的取值范围．【答案】（1）51+或﹣1；（2）14；（3）0＜x1＜1；（4）m＝0或m＞43或23≤m＜1【解析】【分析】（1）分m＞0，m＝0，m＜0三种情形分别求解即可解决问题；（2）分三种情形，利用二次函数的性质分别求解即可；（3）由（1）可知，当图象G与x轴有两个交点时，m＞0，求出当抛物线顶点在x轴上时m的值，利用图象法判断即可；（4）分四种情形：①m＜0，②m＝0，③m＞1，④0＜m≤1，分别求解即可解决问题．【详解】解：（1）如图1中，当m＞0时，∵y＝x2﹣2mx+m＝（x﹣m）2﹣m2+m，图象G是抛物线在直线y＝2m的左侧部分（包括点D），此时最底点P（m，﹣m2+m），由题意﹣m2+m＝﹣1，解得m＝512或512（舍弃），当m＝0时，显然不符合题意，当m＜0时，如图2中，图象G是抛物线在直线y＝2m的左侧部分（包括点D），此时最底点P是纵坐标为m，∴m＝﹣1，综上所述，满足条件的m 51或﹣1；（2）由（1）可知，当m＞0时，y0＝﹣m2+m＝﹣（m﹣12）2+14，∵﹣1＜0，∴m＝12时，y0的最大值为14，当m＝0时，y0＝0，当m＜0时，y0＜0，综上所述，y0的最大值为14；（3）由（1）可知，当图象G与x轴有两个交点时，m＞0，当抛物线顶点在x轴上时，4m2﹣4m＝0，∴m＝1或0（舍弃），∴观察观察图象可知，当图象G与x轴有两个交点时，设左边交点的横坐标为x1，则x1的取值范围是0＜x1＜1，故答案为0＜x1＜1；（4）当m＜0时，观察图象可知，不存在点A满足条件，当m＝0时，图象G在矩形ABCD内的部分所对应的函数值y随x的增大而减小，满足条件，如图3中，当m＞1时，如图4中，设抛物线与x轴交于E，F，交y轴于N，观察图象可知当点A在x轴下方或直线x＝﹣m和y轴之间时（可以在直线x＝﹣m上）时，满足条件．则有（2m﹣2）2﹣2m（2m﹣2）+m＜0，解得m＞43，或﹣m≤2m﹣2＜0，解得23≤m＜1（不合题意舍弃），当0＜m≤1时，如图5中，当点A在直线x＝﹣m和y轴之间时（可以在直线x＝﹣m上）时，满足条件．即或﹣m≤2m﹣2＜0，解得23≤m＜1，综上所述，满足条件m 的值为m ＝0或m ＞43或23≤m ＜1．【点睛】本题属于二次函数综合题，考查了二次函数的性质，矩形的性质，最值问题，不等式等知识，解题的关键是理解题意，学会用分类讨论的思想思考问题，学会用转化的思想思考问题，属于中考压轴题．3．二次函数22(0)63m m y x x m m =-+>的图象交y 轴于点A ，顶点为P ，直线PA 与x 轴交于点B ．（1）当m =1时，求顶点P 的坐标；（2）若点Q （a ，b ）在二次函数22(0)63m m y x x m m =-+>的图象上，且0b m ->，试求a 的取值范围；（3）在第一象限内，以AB 为边作正方形ABCD ．①求点D 的坐标（用含m 的代数式表示）；②若该二次函数的图象与正方形ABCD 的边CD 有公共点，请直接写出符合条件的整数m 的值．【答案】（1）P （2，13）；（2）a 的取值范围为：a ＜0或a ＞4；（3）①D （m ，m +3）； ②2，3，4．【解析】【分析】（1）把m =1代入二次函数22(0)63m m y x x m m =-+>解析式中，进而求顶点P 的坐标即可；（2）把点Q （a ，b ）代入二次函数22(0)63m m y x x m m =-+>解析式中，根据0b m ->得到关于a 的一元二次不等式即一元一次不等式组，解出a 的取值范围即可；（3）①过点D 作DE ⊥x 轴于点E ，过点A 作AF ⊥DE 于点F ，求出二次函数与y 轴的交点A 的坐标，得到OA 的长，再根据待定系数法求出直线AP 的解析式，进而求出与x 轴的交点B 的坐标，得到OB 的长；通过证明△ADF ≌△ABO ，得到AF=OA=m ，DF=OB=3，DE=DF+EF= DF+OA=m+3，求出点D 的坐标；②因为二次函数的图象与正方形ABCD 的边CD 有公共点，由①同理可得：C （m+3，3），分当x 等于点D 的横坐标时与当x 等于点C 的横坐标两种情况，进行讨论m 可能取的整数值即可．【详解】解：（1）当m =1时，二次函数为212163y x x =-+， ∴顶点P 的坐标为（2，13）；（2）∵点Q （a ，b ）在二次函数22(0)63m m y x x m m =-+>的图象上， ∴2263m m b a a m =-+，即：2263m m b m a a -=- ∵0b m ->，∴2263m m a a -＞0， ∵m ＞0， ∴2263a a -＞0，解得：a ＜0或a ＞4，∴a 的取值范围为：a ＜0或a ＞4；（3）①如下图，过点D 作DE ⊥x 轴于点E ，过点A 作AF ⊥DE 于点F ，∵二次函数的解析式为2263m m y x x m =-+，∴顶点P （2，3m ），当x=0时，y=m ，∴点A （0，m ），∴OA=m ；设直线AP 的解析式为y=kx+b(k≠0)，把点A （0，m ），点P （2，3m ）代入，得： 23m b m k b =⎧⎪⎨=+⎪⎩，解得：3m k b m⎧=-⎪⎨⎪=⎩，∴直线AP 的解析式为y=3m -x+m ，当y=0时，x=3，∴点B （3，0）；∴OB=3；∵四边形ABCD 是正方形，∴AD=AB ，∠DAF+∠FAB=90°，且∠OAB+∠FAB =90°，∴∠DAF=∠OAB ，在△ADF 和△ABO 中， DAF OAB AFD AOB AD AB ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△ADF ≌△ABO （AAS ），∴AF=OA=m ，DF=OB=3，DE=DF+EF= DF+OA=m+3，∴点D 的坐标为：（m ，m+3）；②由①同理可得：C （m+3，3），∵二次函数的图象与正方形ABCD 的边CD 有公共点，∴当x =m 时，3y m ≤+，可得322363m m m m -+≤+，化简得：32418m m -≤． ∵0m >，∴2184m m m -≤，∴218(2)4m m--≤，显然：m =1，2，3，4是上述不等式的解，当5m ≥时，2(2)45m --≥，18 3.6m ≤，此时，218(2)4m m -->，∴符合条件的正整数m =1，2，3，4；当x = m +3时，y ≥3，可得2(3)2(3)363m m m m m ++-+≥， ∵0m >，∴21823m m m ++≥，即218(1)2m m++≥，显然：m =1不是上述不等式的解，当2m ≥时，2(1)211m ++≥，189m ≤，此时，218(1)2m m++>恒成立， ∴符合条件的正整数m =2，3，4；综上：符合条件的整数m 的值为2，3，4．【点睛】本题考查二次函数与几何问题的综合运用，熟练掌握二次函数的图象和性质、一次函数的图象和性质、正方形的性质是解题的关键．4．如图，抛物线y =ax 2+bx +2经过点A(−1，0)，B(4，0)，交y 轴于点C ；（1）求抛物线的解析式(用一般式表示)；（2）点D 为y 轴右侧抛物线上一点，是否存在点D 使S △ABC =23S △ABD ?若存在，请求出点D 坐标；若不存在，请说明理由；（3）将直线BC 绕点B 顺时针旋转45°，与抛物线交于另一点E ，求BE 的长.【答案】（1）213222y x x =-++（2）存在，D （1，3）或（2，3）或（5，3-）（3）10【解析】【分析】（1）由A 、B 的坐标，利用待定系数法可求得抛物线解析式；（2）由条件可求得点D 到x 轴的距离，即可求得D 点的纵坐标，代入抛物线解析式可求得D 点坐标；（3）由条件可证得BC ⊥AC ，设直线AC 和BE 交于点F ，过F 作FM ⊥x 轴于点M ，则可得BF=BC ，利用平行线分线段成比例可求得F 点的坐标，利用待定系数法可求得直线BE 解析式，联立直线BE 和抛物线解析式可求得E 点坐标，则可求得BE 的长．【详解】解：（1）∵抛物线y=ax 2+bx+2经过点A （-1，0），B （4，0），∴2016420a b a b -+=⎧⎨++=⎩，解得：1232a b ⎧=-⎪⎪⎨⎪=⎪⎩， ∴抛物线解析式为：213222y x x =-++；（2）由题意可知C （0，2），A （-1，0），B （4，0）， ∴AB=5，OC=2，∴S △ABC =12AB•OC=12×5×2=5， ∵S △ABC =23S △ABD ， ∴S △ABD =315522⨯=，设D （x ，y ）， ∴11155222AB y y •=⨯•=，解得：3y =；当3y =时，2132322y x x =-++=，解得：1x =或2x =，∴点D 的坐标为：（1，3）或（2，3）；当3y =-时，2132322y x x =-++=-，解得：5x =或2x =-（舍去），∴点D 的坐标为：（5，-3）；综合上述，点D 的坐标为：（1，3）或（2，3）或（5，-3）；（3）∵AO=1，OC=2，OB=4，AB=5，∴AC ==BC ==∴222AC BC AB +=，∴△ABC 为直角三角形，即BC ⊥AC ，如图，设直线AC 与直线BE 交于点F ，过F 作FM ⊥x 轴于点M ，由题意可知∠FBC=45°，∴∠CFB=45°， ∴25CF BC == ∴AO AC OM CF =，即1525OM = 解得：2OM =， ∴OC AC FM AF =，即2535FM = 解得：6FM =，∴点F 为（2，6），且B 为（4，0），设直线BE 解析式为y=kx+m ，则2640k m k m +=⎧⎨+=⎩，解得312k m =-⎧⎨=⎩， ∴直线BE 解析式为：312y x =-+；联立直线BE 和抛物线解析式可得：231213222y x y x x =-+⎧⎪⎨=-++⎪⎩，解得：40x y =⎧⎨=⎩或53x y =⎧⎨=-⎩， ∴点E 坐标为：(5,3)-， ∴22(54)(3)10BE =-+-=【点睛】本题为二次函数的综合应用，涉及待定系数法、三角形面积、勾股定理及其逆定理、平行线分线段成比例、函数图象的交点、等腰直角三角形的性质、方程思想及分类讨论思想等知识．在（1）中注意待定系数法的应用，在（2）中求得D 点的纵坐标是解题的关键，在（3）中由条件求得直线BE 的解析式是解题的关键．本题考查知识点较多，综合性较强，特别是最后一问，有一定的难度．5．如图，抛物线2(0)y ax bx c a=++≠与坐标轴的交点为()30A-,，()10B,，()0,3C-，抛物线的顶点为D．（1）求抛物线的解析式．（2）若E为第二象限内一点，且四边形ACBE为平行四边形，求直线CE的解析式．（3）P为抛物线上一动点，当PAB∆的面积是ABD∆的面积的3倍时，求点P的坐标．【答案】（1）223y x x=+-；（2）33y x=--；（3）点P的坐标为()5,12-或()3,12．【解析】【分析】（1）本题考查二次函数解析式的求法，可利用待定系数法，将点带入求解；（2）本题考查二次函数平行四边形存在性问题，可根据题干信息结合平行四边形性质确定动点位置，进一步利用待定系数法求解一次函数解析式；（3）本题考查二次函数与三角形面积问题，可先根据题干面积关系假设动点坐标，继而带入二次函数，列方程求解．【详解】（1）∵抛物线2y ax bx c=++与坐标轴的交点为()30A-,，()10B,，()0,3C-，∴9303a b ca b cc-+=⎧⎪++=⎨⎪=-⎩，解得123abc=⎧⎪=⎨⎪=-⎩∴抛物线的解析式为223y x x=+-．（2）如图，过点E作EH x⊥轴于点H，则由平行四边形的对称性可知1AH OB==，3EH OC==．∵3OA =，∴2OH =，∴点E 的坐标为()2,3-．∵点C 的坐标为()0,3-，∴设直线CE 的解析式为()30y kx k =-<将点()2,3E -代入，得233k --=，解得3k =-，∴直线CE 的解析式为33y x =--．（3）∵2223(1)4y x x x =+-=+-，∴抛物线的顶点为()1,4D --．∵PAB ∆的面积是ABD ∆的面积的3倍，∴设点P 为(),12t ．将点(),12P t 代入抛物线的解析式223y x x =+-中，得22312t t +-=，解得3t =或5t =-，故点P 的坐标为()5,12-或()3,12．【点睛】本题考查二次函数与几何的综合，利用待定系数法求解解析式时还可以假设交点式，几何图形存在性问题求解往往需要利用其性质，假设动点坐标，列方程求解．6．如图，抛物线2y x bx c =-++的图象与x 轴交于A 、B 两点（点A 在点B 的左边），与y 轴交于点C ，点D 为抛物线的顶点．点A 坐标的为3,0，点C 的坐标为()0,3．（Ⅰ）求抛物线的解析式；（Ⅱ）点M 为线段AB 上一点（点M 不与点A 、B 重合），过点M 作i 轴的垂线，与直线AC 交于点E ，与抛物线交于点P ，过点P 作//PQ AB 交抛物线于点Q ，过点Q 作QN x ⊥轴于点N ．若点P 在点Q 左边，当矩形PMNQ 的周长最大时，求AEM △的面积；（Ⅲ）在（Ⅱ）的条件下，当矩形PMNQ 的周长最大时，连接DQ ，过抛物线上一点F 作y 轴的平行线，与直线AC 交于点G （点G 在点F 的上方）．若=22FG DQ ，求点F 的坐标．【答案】（Ⅰ）223y x x =--+；（Ⅱ）12；（Ⅲ）()4,5F --或()1,0【解析】【分析】（Ⅰ）将点A ，点C 坐标代入解析式可求解；（Ⅱ）设M （x ，0），P （x ，-x 2-2x+3），利用对称性可求点Q （-2-x ，-x 2-2x+3），可求MP=-x 2-2x+3，PQ=-2-x-x=-2-2x ，则可用x 表示矩形PMNQ 的周长，由二次函数的性质可求当矩形PMNQ 的周长最大时，点P 的坐标，即可求点E ，点M 的坐标，由三角形面积公式可求解；（Ⅲ）先求出点D 坐标，即可求DQ=2，可得FG=4，设F （m ，-m 2-2m+3），则G （m ，m+3），用含有m 的式子表示FG 的长度即可求解．【详解】解:（Ⅰ）依题意()()2330{3b c c --+⨯-+== 解得2{3b c =-= 所以223y x x =--+（Ⅱ）2223(1)4y x x x抛物线的对称轴是直线1x =-(,0)M x ，()2,23P x x x --+，其中31x -<<-∵P 、Q 关于直线1x =-对称设Q 的横坐标为a则()11a x --=--∴2a x =--∴()22,23Q x x x ----+∴223MP x x =--+，222PQ x x x =---=--∴周长()222222232822(2)10d x x x x x x =----+=--+=-++当2x =-时，d 取最大值，此时，(2,0)M -∴2(3)1AM =---=设直线AC 的解析式为y kx b =+则303k b b -+=⎧⎨=⎩，解得13k b =⎧⎨=⎩∴设直线AC 的解析式为3yx 将2x =-代入3yx ，得1y = ∴(2,1)E -，∴1EM =∴11111222AEM S AM ME ∆=⋅=⨯⨯= （Ⅲ）由（Ⅱ）知，当矩形PMNQ 的周长最大时，2x =-此时点()0,3Q ，与点C 重合，∴3OQ =∵2223(1)4y x x x∴()1,4D -过D 作DK y ⊥轴于K ，则1DK =，4OK =∴431OK OK OQ =-=-=∴DKQ 是等腰直角三角形，2DQ =∴224FG DQ ==设()2,23F m m m --+，则(,3)G m m + ()223233FG m m m m m =+---+=+∴234m m +=，解得14m =-，21m =当4m =-时，2235m m --+=-当1m =时，2230m m --+=．∴()4,5F --或()1,0【点睛】本题是二次函数综合题，考查了二次函数的性质，矩形的性质，等腰直角三角形的性质等，利用参数表示线段的长度是本题的关键．7．如图，已知抛物线2y x bx c=-++与x轴交于A，B两点，过点A的直线l与抛物线交于点C，其中点A的坐标是()1,0，点C的坐标是()2,3-，抛物线的顶点为点D．（1）求抛物线和直线AC的解析式．（2）若点P是抛物线上位于直线AC上方的一个动点，求APC∆的面积的最大值及此时点P的坐标．（3）若抛物线的对称轴与直线AC相交于点E，点M为直线AC上的任意一点，过点M作//MN DE交抛物线于点N，以D，E，M，N为顶点的四边形能否为平行四边形？若能，求出点M的坐标；若不能，请说明理由．【答案】（1）y=-x2-2x+3，y=-x+1；（2）最大值为278，此时点P(12-，154)；（3）能，(0，1)，117-+317-)或117--317+【解析】【分析】（1）直接利用待定系数法进行求解，即可得到答案；（2）设点P(m，-m2-2m+3)，则Q(m，-m+1)，求出PQ的长度，结合三角形的面积公式和二次函数的性质，即可得到答案；（3）根据题意，设点M(t，-t+1)，则点N(t，-t2-2t+3)，可分为两种情况进行分析：①当点M在线段AC上时，点N在点M上方；②当点M在线段AC（或CA）延长线上时，点N在点M下方；分别求出点M的坐标即可．【详解】解：（1）∵抛物线y=-x2+bx+c过点A(1，0)，C(-2，3)，∴10423b cb c-++=⎧⎨--+=⎩，，解得：23bc=-⎧⎨=⎩，．∴抛物线的解析式为y=-x2-2x+3．设直线AC的解析式为y=kx+n．将点A，C坐标代入，得023k n k n +=⎧⎨-+=⎩，，解得11k n =-⎧⎨=⎩，． ∴直线AC 的解析式为y=-x+1．（2）过点P 作PQ ∥y 轴交AC 于点Q ．设点P(m ，-m 2-2m+3)，则Q(m ，-m+1)．∴PQ=(-m 2-2m+3)-(-m+1)=-m 2-m+2．∴S △APC =S △PCQ +S △APQ =12PQ·(x A -x C )=12(-m 2-m+2)×3=23127()228m -++． ∴当m=12-时，S △APC 最大，最大值为278，此时点P(12-，154)．（3）能．∵y=-x 2-2x+3，点D 为顶点，∴点D(-1，4)，令x=-1时，y=-（-1）+1=2，∴点E(-1，2)．∵MN ∥DE ，∴当MN=DE=2时，以D ，E ，M ，N 为顶点的四边形是平行四边形．∵点M 在直线AC 上，点N 在抛物线上，∴设点M(t ，-t+1)，则点N(t ，-t 2-2t+3)．①当点M 在线段AC 上时，点N 在点M 上方，则MN=(-t 2-2t+3)-(-t+1)=-t 2-t+2．∴-t 2-t+2=2，解得：t=0或t=-1（舍去）．∴此时点M 的坐标为（0，1）．②当点M 在线段AC （或CA ）延长线上时，点N 在点M 下方，则MN=(-t+1)-(-t 2-2t+3)=t 2+t-2．∴t 2+t-2=2，解得：t=12-+或t=12-． ∴此时点M）．综上所述，满足条件的点M 的坐标为：（0，1（12-，32）．【点睛】本题考查了待定系数法求一次函数解析式、待定系数法求二次函数解析式、二次函数图象上点的坐标特征、一次函数图象上点的坐标特征、二次函数的性质、三角形的面积以及周长，解题的关键是：（1）根据点的坐标，利用待定系数法求出抛物线及直线AC 的函数关系式；（2）利用三角形的面积公式和二次函数的性质解题；（3）利用二次函数图象的对称性结合两点之间线段最短找出点M 的位置．8．如图，已知二次函数1L ：()22311y mx mx m m =+-+≥和二次函数2L ：()2341y m x m =--+-()1m ≥图象的顶点分别为M 、N ，与x 轴分别相交于A 、B 两点（点A 在点B 的左边）和C 、D 两点（点C 在点D 的左边），（1）函数()22311y mx mx m m =+-+≥的顶点坐标为______；当二次函数1L ，2L 的y 值同时随着x 的增大而增大时，则x 的取值范围是_______；（2）判断四边形AMDN 的形状（直接写出，不必证明）；（3）抛物线1L ，2L 均会分别经过某些定点；①求所有定点的坐标；②若抛物线1L 位置固定不变，通过平移抛物线2L 的位置使这些定点组成的图形为菱形，则抛物线2L 应平移的距离是多少？【答案】（1）()1,41m --+，13x ；（2）四边形AMDN 是矩形；（3）①所有定点的坐标，1L 经过定点()3,1-或()1,1，2L 经过定点()5,1-或()1,1-；②抛物线2L 应平移的距离是423+423-．【解析】【分析】（1）将已知抛物线解析式转化为顶点式，直接得到点M 的坐标；结合函数图象填空；（2）利用抛物线解析式与一元二次方程的关系求得点A 、D 、M 、N 的横坐标，可得AD 的中点为（1，0），MN 的中点为（1，0），则AD 与MN 互相平分，可证四边形AMDN 是矩形；（3）①分别将二次函数的表达式变形为1:(3)(1)1L y m x x =+-+和2:(1)(5)1L y m x x =----，通过表达式即可得出所过定点；②根据菱形的性质可得EH 1=EF=4即可，设平移的距离为x ，根据平移后图形为菱形，由勾股定理可得方程即可求解．【详解】解：（1）12b x a=-=-，顶点坐标M 为(1,41)m --+，由图象得：当13x 时，二次函数1L ，2L 的y 值同时随着x 的增大而增大．故答案为：(1,41)m --+；13x ；（2）结论：四边形AMDN 是矩形．由二次函数21:231(1)L y mx mx m m =+-+和二次函数22:(3)41(1)L y m x m m =--+-解析式可得：A 点坐标为41(1m m ---，0)，D 点坐标为41(3m m -+，0)，顶点M 坐标为(1,41)m --+，顶点N 坐标为(3,41)m -，AD ∴的中点为(1,0)，MN 的中点为(1,0)，AD ∴与MN 互相平分，∴四边形AMDN 是平行四边形，又AD MN =，∴□AMDN 是矩形；（3）①二次函数21:231(3)(1)1L y mx mx m m x x =+-+=+-+，故当3x =-或1x =时1y =，即二次函数21:231L y mx mx m =+-+经过(3,1)-、(1,1)两点，二次函数22:(3)41(1)(5)1L y m x m m x x =--+-=----，故当1x =或5x =时1y =-，即二次函数22:(3)41L y m x m =--+-经过(1,1)-、(5,1)-两点，②二次函数21:231L y mx mx m =+-+经过(3,1)-、(1,1)两点，二次函数22:(3)41L y m x m =--+-经过(1,1)-、(5,1)-两点，如图：四个定点分别为(3,1)E -、(1,1)F ，(1,1)H -、(5,1)G -，则组成四边形EFGH 为平行四边形，∴FH ⊥HG ，FH=2，HM=4-x ，设平移的距离为x ，根据平移后图形为菱形，则EH 1=EF=H 1M=4，由勾股定理可得：FH 2+HM 2=FM 2，即22242(4)x =+-，解得：43x =±抛物线1L 位置固定不变，通过左右平移抛物线2L 的位置使这些定点组成的图形为菱形，则抛物线2L 应平移的距离是423+或423-．【点睛】本题考查了二次函数的解析式的求法和与几何图形结合的综合能力的培养．要会利用数形结合的思想把代数和几何图形结合来，利用点的坐标的意义表示线段的长度，从而求出线段之间的关系．9．在平面直角坐标系中，二次函数y=ax 2+bx+2的图象与x 轴交于A(﹣3，0)，B(1，0)两点，与y 轴交于点C ．（1）求这个二次函数的关系解析式；（2）求直线AC 的函数解析式；（3）点P 是直线AC 上方的抛物线上一动点，是否存在点P ，使△ACP 的面积最大？若存在，求出点P 的坐标；若不存在，说明理由；【答案】（1）y=﹣23x 2﹣43x+2；（2）223y x =+；（3）存在，(35,22-) 【解析】【分析】（1）直接用待定系数法即可解答；（2）先确定C 点坐标，设直线AC 的函数解析式y=kx+b ，最后用待定系数法求解即可；（3）连接PO ，作PM⊥x 轴于M ，PN⊥y 轴于N ，然后求出△ACP 面积的表达式，最后利用二次函数的性质求最值即可．【详解】解：（1）∵抛物线y=ax2+bx+2过点A（﹣3，0），B（1，0），∴093202a ba b=-+⎧⎨=++⎩解得2343ab⎧=-⎪⎪⎨⎪=-⎪⎩，∴二次函数的关系解析式为y=﹣23x 2﹣43x+2；（2）∵当x=0时，y=2，∴C（0，2）设直线AC的解析式为y kx b=+，把A、C两点代入得0=32k bb-+⎧⎨=⎩解得232kb⎧=⎪⎨⎪=⎩∴直线AC的函数解析式为223y x=+；（3）存在．如图: 连接PO，作PM⊥x轴于M，PN⊥y轴于N设点P坐标为（m，n）,则n=224233m m--+），PN=-m，AO=3当x=0时，y=22400233-⨯-⨯+=2，∴点C的坐标为（0,2），OC=2∵PAC PAO PCO ACOS S S S=+-212411322()3223322m m m⎛⎫=⨯⋅--++⨯⋅--⨯⨯⎪⎝⎭=23m m--∵a=-1<0∴函数S△PAC=-m2-3m有最大值∴b 当m=()33212-=--⨯- ∴当m=32-时，S △PAC 有最大值n=222423435223332322m m ⎛⎫--+=-⨯-⨯+= ⎪⎝⎭ ∴当△ACP 的面积最大时，P 的坐标为（35,22-）．【点睛】本题是二次函数压轴题，综合考查了二次函数的图象与性质、待定系数法、二次函数极值等知识点，根据题意表示出△PAC 的面积是解答本题的关键．10．在平面直角坐标系xOy 中（如图），已知二次函数2y ax bx c =++（其中a 、b 、c 是常数，且a ≠0）的图像经过点A （0，-3）、B （1，0）、C （3，0），联结AB 、AC ．（1）求这个二次函数的解析式；（2）点D 是线段AC 上的一点，联结BD ，如果:3:2ABD BCD S S ∆∆=，求tan ∠DBC 的值；（3）如果点E 在该二次函数图像的对称轴上，当AC 平分∠BAE 时，求点E 的坐标．【答案】（1）243y x x =-+-；（2）32；（3）E （2，73-）【解析】【分析】（1）直接利用待定系数法，把A 、B 、C 三点代入解析式，即可得到答案；（2）过点D 作DH ⊥BC 于H ，在△ABC 中，设AC 边上的高为h ，利用面积的比得到32AD DC =，然后求出DH 和BH ，即可得到答案；（3）延长AE 至x 轴，与x 轴交于点F ，先证明△OAB ∽△OFA ，求出点F 的坐标，然后求出直线AF 的方程，即可求出点E 的坐标.【详解】解：（1）将A （0，-3）、B （1，0）、C （3，0）代入20y ax bx c a =++≠（）得，03,0934,300a ba bc=+-⎧⎪=+-⎨⎪-=++⎩解得143abc=-⎧⎪=⎨⎪=-⎩，∴此抛物线的表达式是：243y x x=-+-．（2）过点D作DH⊥BC于H，在△ABC中，设AC边上的高为h，则11:():():3:222ABD BCDS S AD h DC h AD DC∆∆=⋅⋅==，又∵DH//y轴，∴25CH DC DHOC AC OA===．∵OA=OC=3，则∠ACO=45°，∴△CDH为等腰直角三角形，∴26355CH DH==⨯=．∴64255BH BC CH=-=-=．∴tan∠DBC=32DHBH=.（3）延长AE至x轴，与x轴交于点F，∵OA=OC=3，∴∠OAC=∠OCA=45°，∵∠OAB=∠OAC-∠BAC=45°-∠BAC，∠OFA=∠OCA-∠FAC=45°-∠FAC，∵∠BAC=∠FAC，∴∠OAB=∠OFA．∴△OAB∽△OFA，∴13 OB OAOA OF==．∴OF=9，即F（9，0）；设直线AF的解析式为y=kx+b（k≠0），可得093k bb=+⎧⎨-=⎩，解得133kb⎧=⎪⎨⎪=-⎩，∴直线AF的解析式为：133y x=-，将x=2代入直线AF的解析式得：73y=-，∴E（2，73 -）.【点睛】本题考查了相似三角形的判定和性质，二次函数的性质，求二次函数的解析式，等腰直角三角形的判定和性质，求一次函数的解析式，解题的关键是掌握二次函数的图像和性质，以及正确作出辅助线构造相似三角形.。

2018年各地市中考《二次函数》压轴题精编(含答案解析)

（1）求抛物线的解析式；
1
（2）若点B C均在抛物线上，其中点B（0,丄），且/BDC=90，求点C的坐
4
标；
（3）如图，直线y=kx+4-k与抛物线交于P、Q两点.
1求证：/PDQ=90；
2求△PDQ面积的最小值.
3.(荆门)如图，抛物线y=ax+bx+c(a^0)与x轴交于原点及点A,且经过点B(4,8),对称轴为直线x=-2.
（1）点A,B,D的坐标分别为,,;
（2）如图①，抛物线翻折后，点D落在点E处.当点E在厶ABC内（含边界）时，求t的取值范围；
（3）如图②，当t=0时，若Q是“M形新图象上一动点，是否存在以CQ为直径的圆与x轴相切于点P?若存在，求出点P的坐标；若不存在，请说明理由.
2.（黄石）已知抛物线y=a（x-1）2过点（3,1）,D为抛物线的顶点.
24
组成一个“M形的新图象.
（1）点A,B,D的坐标分别为,,;
（2）如图①，抛物线翻折后，点D落在点E处.当点E在厶ABC内（含边界）时，求t的取值范围；
（3）如图②，当t=0时，若Q是“M形新图象上一动点，是否存在以CQ为直径的圆与x轴相切于点P?若存在，求出点P的坐标；若不存在，请说明理由.
7.(武汉)抛物线L:y=-x2+bx+c经过点A(0,1),与它的对称轴直线x=1交于点B.
(1)直接写出抛物线L的解析式；
(2)如图1,过定点的直线y=kx- k+4(kv0)与抛物线L交于点M、2若厶BMN的面积等于1，求k的值；
(3)如图2,将抛物线L向上平移m(m>0)个单位长度得到抛物线L,抛物线L1与y轴交于点C,过点C作y轴的垂线交抛物线L于另一点D.F为抛物线L1的对称轴与x轴的交点，P为线段OC上一点.若厶PCD与厶POF相似，并且符合条件的点P恰有2个，求m的值及相应点P的坐标.

2018年九年级数学上册二次函数培优练习卷含答案

（）
A.y=60（300+20x）
B.y=（60﹣x）（300+20x）
C.y=300（60﹣20x）
D.y=（60﹣x）（300﹣20x）
9、已知二次函数 y=﹣x2+2bx+c，当 x＞1 时，y 的值随 x 值的增大而减小，则实数 b 的取值范围是（）
A.b≥﹣1
B.b≤﹣1
C.b≥1
D.b≤1
23、如图，已知二次函数 y=x2+bx+c 的图象经过点 A（0，3）且对称轴是直线 x=2. （1）求该函数的表达式；（2）在抛物线上找点，使△PBC 的面积是△ABC 的面积的 2 倍，求点 P 的坐标.
第5页共8页
24、如图，已知抛物线 y=−x2+bx+c 与 x 轴、y 轴分别相交于点 A（−1，0）、B（0，3）两点，其顶点为 D. （1）求这条抛物线的解析式；（2）若抛物线与 x 轴的另一个交点为 E. 求△ODE 的面积；抛物线的对称轴上是否存在点 P 使得△PAB 的周长最短。若存在请求出 P 点的坐标，若不存在说明理由。
21、已知二次函数 y=x2+bx+c 的图象过点 A（﹣3，0）和点 B（1，0），且与 y 轴交于点 C，D 点在抛物线上且横坐标是﹣2. （1）求抛物线的解析式；（2）抛物线的对称轴上有一动点 P，求出 PA+PD 的最小值.
第4页共8页
22、某服装店购进一批秋衣，价格为每件 30 元.物价部门规定其销售单价不高于每件 60 元，不低于每件 30 元.经市场调查发现：日销售量 y（件）是销售单价 x（元）的一次函数，且当 x=60 时，y=80；x=50 时，y=100. 在销售过程中，每天还要支付其他费用 450 元. （1）求出 y 与 x 的函数关系式，并写出自变量 x 的取值范围. （2）求该服装店销售这批秋衣日获利 w（元）与销售单价 x（元）之间的函数关系式. （3）当销售单价为多少元时，该服装店日获利最大？最大获利是多少元？

九年级数学上册二次函数(培优篇)(Word版含解析)

九年级数学上册二次函数（培优篇）（Word 版含解析）一、初三数学二次函数易错题压轴题（难）1．在平面直角坐标系中，将函数2263,(y x mx m x m m =--≥为常数)的图象记为G ．（1）当1m =-时，设图象G 上一点(),1P a ，求a 的值；（2）设图象G 的最低点为(),o o F x y ，求o y 的最大值；（3）当图象G 与x 轴有两个交点时，设右边交点的横坐标为2,x 则2x 的取值范围是；（4）设1112,,2,16816A m B m ⎛⎫⎛⎫+ ⎪ ⎪⎝⎭⎝⎭，当图象G 与线段AB 没有公共点时，直接写出m 的取值范围．【答案】（1）0a =或3a =-；（2）118；（3）21136x -<<-；（4）18m <-或116m >- 【解析】【分析】（1）将m=-1代入解析式，然后将点P 坐标代入解析式，从而求得a 的值；（2）分m ＞0和m ≤0两种情况，结合二次函数性质求最值；（3）结合二次函数与x 轴交点及对称轴的性质确定取值范围；（4）结合一元二次方程根与系数的关系确定取值范围．【详解】解：（1）当1m =-时，()22613y x x x =++≥ 把(),1P a 代入，得22611a a ++=解得0a =或3a =-（2）当0m >时，,(3)F m m -此时，0o y m =-<当0m ≤时，2223926=2()22y x mx m x m m m =----- ∴239,22F m m m ⎛⎫-- ⎪⎝⎭此时，229911=()22918m m m ---++ ∴0y 的最大值118=综上所述，0y 的最大值为118（3）由题意可知：当图象G 与x 轴有两个交点时，m ＞0 当抛物线顶点在x 轴上时，22=4(6)42()=0b ac m m -=--⨯⨯-△解得：m=0（舍去）或29m =- 由题意可知抛物线的对称轴为直线x=32m 且x ≥3m ∴当图象G 与x 轴有两个交点时，设右边交点的横坐标为x 2，则x 2的取值范围是21136x -<<- （4）18m <-或116m >- 【点睛】本题属于二次函数综合题，考查了二次函数的性质，不等式等知识，解题的关键是理解题意，学会用分类讨论的思想思考问题，学会用转化的思想思考问题，属于中考压轴题． 2．如图，抛物线y=﹣x 2+mx+n 与x 轴交于A 、B 两点，与y 轴交于点C ，抛物线的对称轴交x 轴于点D ，已知A （﹣1，0），C （0，2）．（1）求抛物线的表达式；（2）在抛物线的对称轴上是否存在点P ，使△PCD 是以CD 为腰的等腰三角形？如果存在，直接写出P 点的坐标；如果不存在，请说明理由；（3）点E 时线段BC 上的一个动点，过点E 作x 轴的垂线与抛物线相交于点F ，当点E 运动到什么位置时，四边形CDBF 的面积最大？求出四边形CDBF 的最大面积及此时E 点的坐标．【答案】(1)抛物线的解析式为：y=﹣x 2+x+2 (2)存在，P 1（，4），P 2（，），P 3（，﹣）(3)当点E运动到（2，1）时，四边形CDBF的面积最大，S四边形CDBF的面积最大=．【解析】试题分析：（1）将点A、C的坐标分别代入可得二元一次方程组，解方程组即可得出m、n的值；（2）根据二次函数的解析式可得对称轴方程，由勾股定理求出CD的值，以点C为圆心，CD为半径作弧交对称轴于P1；以点D为圆心CD为半径作圆交对称轴于点P2，P3；作CH 垂直于对称轴与点H，由等腰三角形的性质及勾股定理就可以求出结论；（3）由二次函数的解析式可求出B点的坐标，从而可求出BC的解析式，从而可设设E点的坐标，进而可表示出F的坐标，由四边形CDBF的面积=S△BCD+S△CEF+S△BEF可求出S与a的关系式，由二次函数的性质就可以求出结论．试题解析：（1）∵抛物线y=﹣x2+mx+n经过A（﹣1，0），C（0，2）．解得：，∴抛物线的解析式为：y=﹣x2+x+2；（2）∵y=﹣x2+x+2，∴y=﹣（x﹣）2+，∴抛物线的对称轴是x=．∴OD=．∵C（0，2），∴OC=2．在Rt△OCD中，由勾股定理，得CD=．∵△CDP是以CD为腰的等腰三角形，∴CP1=CP2=CP3=CD．作CH⊥x轴于H，∴HP1=HD=2，∴DP1=4．∴P1（，4），P2（，），P3（，﹣）；（3）当y=0时，0=﹣x2+x+2∴x1=﹣1，x2=4，∴B（4，0）．设直线BC的解析式为y=kx+b，由图象，得，解得：，∴直线BC的解析式为：y=﹣x+2．如图2，过点C作CM⊥EF于M，设E（a，﹣a+2），F（a，﹣a2+a+2），∴EF=﹣a2+a+2﹣（﹣a+2）=﹣a2+2a（0≤x≤4）．∵S四边形CDBF=S△BCD+S△CEF+S△BEF=BD•OC+EF•CM+EF•BN，=+a（﹣a2+2a）+（4﹣a）（﹣a2+2a），=﹣a2+4a+（0≤x≤4）．=﹣（a﹣2）2+∴a=2时，S四边形CDBF的面积最大=，∴E（2，1）．考点：1、勾股定理；2、等腰三角形的性质；3、四边形的面积；4、二次函数的最值3．如图1，抛物线21:C y x b =+交y 轴于()0,1A ．（1）直接写出抛物线1C 的解析式______________．（2）如图1，x 轴上两动点,M N 满足：m n X X n -==．若,B C （B 在C 左侧）为线段MN 上的两个动点，且满足：B 点和C 点关于直线:1l x =对称．过B 作BB x '⊥轴交1C 于B '，过C 作CC x '⊥轴交1C 于C '，连接B C ''．求B C ''的最大值（用含n 的代数式表示）．（3）如图2，将抛物线1C 向下平移78个单位长度得到抛物线2C ．2C 对称轴左侧的抛物线上有一点M ，其横坐标为m ．以OM 为直径作K ，记⊙K 的最高点为Q ．若Q 在直线2y x =-上，求m 的值．【答案】（1）21y x =+；（2）251|n -；（3）14m =-或12m =- 【解析】【分析】（1）将()0,1A 带入抛物线1C 解析式，求得b 的值，即可得到抛物线1C 的解析式；（2）设(),0B q ，则()2,0C q -，求()2B C ''并进行化简，由1n q -≤<且12,qn <-得21n q -<，则当()2max B C ''⎡⎤⎢⎥⎣⎦时，取min 2q q n ==-，带入()2B C ''，即可求得()max B C ''；（3）依题意将抛物线1C 向下平移78个单位长度得到抛物线2C ，求得2C 解析式，根据解析式特点设21,8M m m ⎛⎫+ ⎪⎝⎭，得到222218OM m m ⎛⎫=++ ⎪⎝⎭，由圆的特性易求得，⊙K 的最高点点Q 坐标为：2111,2228m OM m ⎛⎫⎛⎫++ ⎪ ⎪⎝⎭⎝⎭，设Q y k =，则2111228k OM m ⎛⎫=++ ⎪⎝⎭，化简得到22211084k m k m ⎛⎫++-= ⎪⎝⎭，由Q 点在2y x =-上，得2Q k x m =-=-，继而得到231048m m -+=，解得14m =-或12m =-．【详解】解：（1）将()0,1A 带入抛物线21:C y x b =+，得b=1，则21:1C y x =+，（2）设(),0B q ，则()2,0C q -，∴()22222(2)(2)B C q q q q ''⎡⎤=--+--⎣⎦ 2204020q q =-+()2201q =-，∵1n q -≤<且12,q n <- 21n q -<∴，∴()2max B C ''⎡⎤⎢⎥⎣⎦时，min 2q q n ==-，即()22220(21)20(1)B C n n ''=--=-，∴()max 1|B C n ''=-，（3）根据题意，将抛物线1C 向下平移78个单位长度得到抛物线2C ， ∴221:8C y x =+，∴21,8M m m ⎛⎫+⎪⎝⎭， ∴222218OM m m ⎛⎫=++ ⎪⎝⎭， ∴由圆的特性易求得，⊙K 的最高点点Q 坐标为：2111,2228m OM m ⎛⎫⎛⎫++ ⎪ ⎪⎝⎭⎝⎭，设Q y k =，则2111228k OM m ⎛⎫=++ ⎪⎝⎭， ∴222111428OM k m ⎡⎤⎛⎫=-+ ⎪⎢⎥⎝⎭⎣⎦，化简上式得：22211084k m k m ⎛⎫++-= ⎪⎝⎭， ∵Q 点在2y x =-上，则2Q k x m =-=-，∴k m =-为上述方程的一个解， ∴分析可知1()04k m k m ⎛⎫+-= ⎪⎝⎭， 21148m m m -=+∴， ∴231048m m -+=，解得：114m =-，212m =-（经检验114m =-，212m =-是方程231048m m -+=的解），故14m =-或12m =-．【点睛】本题主要考查二次函数的图像及性质、图像平移的性质、及二次函数与一元二次方程的综合应用、最值求法等知识．解题关键是熟练掌握二次函数的性质，充分利用数形结合的思想．4．如图，在平面直角坐标系x O y 中，抛物线y = ax 2+ bx + c 经过A 、B 、C 三点，已知点A （-3，0），B （0，3），C （1，0）．（1）求此抛物线的解析式；（2）点P 是直线AB 上方的抛物线上一动点，（不与点A 、B 重合），过点P 作x 轴的垂线，垂足为F ，交直线AB 于点E ，作PD ⊥AB 于点D ．动点P 在什么位置时，△PDE 的周长最大，求出此时P 点的坐标；（3）在直线x = -2上是否存在点M ，使得∠MAC = 2∠MCA ，若存在，求出M 点坐标．若不存在，说明理由．【答案】（1）y=-x 2-2x+3；（2）点（-32，154），△PDE 的周长最大；（3）点M （-2，3）或（-2，3【解析】【分析】（1）将A 、B 、C 三点代入，利用待定系数法求解析式；（2）根据坐标发现，△AOB 是等腰直角三角形，故只需使得PD 越大，则△PDE 的周长越大.联立直线AB 与抛物线的解析式可得交点P 坐标；（3）作点A 关于直线x=-2的对称点D ，利用∠MAC = 2∠MCA 可推导得MD=CD ，进而求得ME 的长度，从而得出M 坐标【详解】解：（1）∵抛物线y=ax 2+bx+c 经过点A （-3，0），B （0，3），C （1，0），∴93030a b c c a b c -+=⎧⎪=⎨⎪++=⎩，解得：123a b c =-⎧⎪=-⎨⎪=⎩，所以，抛物线的解析式为y=-x 2-2x+3；（2）∵A （-3，0），B （0，3），∴OA=OB=3，∴△AOB 是等腰直角三角形，∴∠BAO=45°，∵PF ⊥x 轴，∴∠AEF=90°-45°=45°，又∵PD ⊥AB ，∴△PDE 是等腰直角三角形，∴PD 越大，△PDE 的周长越大，易得直线AB 的解析式为y=x+3，设与AB 平行的直线解析式为y=x+m ，联立223y x m y x x =+⎧⎨=--+⎩，消掉y 得，x 2+3x+m-3=0，当△=9-4（m-3）=0，即m=214时，直线与抛物线只有一个交点，PD 最长，此时x=-32，y=154，∴点（-32，154），△PDE的周长最大；（3）设直线x=-2与x轴交于点E，作点A关于直线x=-2的对称点D，则D（-1，0），连接MA，MD，MC．∴MA=MD，∠MAC=∠MDA=2∠MCA ，∴∠CMD=∠DCM∴MD=CD=2 ，∴ME=3∴点M（-2，3）或（-2，-3）．【点睛】本题是动点和最值的考查，在解决动点问题时，寻找出不变量来分析是解题关键，最值问题，通常利用对称来简化分析5．如图，若抛物线y＝x2+bx+c与x轴相交于A，B两点，与y轴相交于点C，直线y＝x﹣3经过点B，C．（1）求抛物线的解析式；（2）点P是直线BC下方抛物线上一动点，过点P作PH⊥x轴于点H，交BC于点M，连接PC．①线段PM是否有最大值？如果有，求出最大值；如果没有，请说明理由；②在点P运动的过程中，是否存在点M，恰好使△PCM是以PM为腰的等腰三角形？如果存在，请直接写出点P的坐标；如果不存在，请说明理由．【答案】（1）y＝x2﹣2x﹣3；（2）①有，94；②存在，(2，﹣3)或(32，2﹣2)【解析】【分析】（1）由直线表达式求出点B、C的坐标，将点B、C的坐标代入抛物线表达式，即可求解；（2）①根据PM ＝（x ﹣3）﹣（x 2﹣2x ﹣3）＝﹣（x ﹣32）2+94即可求解； ②分PM ＝PC 、PM ＝MC 两种情况，分别求解即可．【详解】解：（1）对于y ＝x ﹣3，令x ＝0，y ＝﹣3，y ＝0，x ＝3，故点B 、C 的坐标分别为（3，0）、（0，﹣3），将点B 、C 的坐标代入抛物线表达式得：9303b c c ++=⎧⎨=-⎩，解得：32c b =-⎧⎨=-⎩，故抛物线的表达式为：y ＝x 2﹣2x ﹣3；（2）设：点M （x ，x ﹣3），则点P （x ，x 2﹣2x ﹣3），①有，理由：PM ＝（x ﹣3）﹣（x 2﹣2x ﹣3）＝﹣（x ﹣32）2+94， ∵﹣1＜0，故PM 有最大值，当x ＝32时，PM 最大值为：94； ②存在，理由：PM 2＝（x ﹣3﹣x 2+2x+3）2＝（﹣x 2+3x ）2；PC 2＝x 2+（x 2﹣2x ﹣3+3）2；MC 2＝（x ﹣3+3）2+x 2；（Ⅰ）当PM ＝PC 时，则（﹣x 2+3x ）2＝x 2+（x 2﹣2x ﹣3+3）2，解得：x ＝0或2（舍去0），故x ＝2，故点P （2，﹣3）；（Ⅱ）当PM ＝MC 时，则（﹣x 2+3x ）2＝（x ﹣3+3）2+x 2，解得：x ＝0或（舍去0和），故x ＝3，则x 2﹣2x ﹣3＝2﹣，故点P （3，2﹣）．综上，点P 的坐标为：(2，﹣3)或(3，2﹣)．【点睛】本题考查的是二次函数综合运用，涉及到一次函数的性质、等腰三角形的性质等，其中（2）②，要注意分类求解，避免遗漏．6．如图，抛物线2y x bx c =-++的图象与x 轴交于A 、B 两点（点A 在点B 的左边），与y 轴交于点C ，点D 为抛物线的顶点．点A 坐标的为3,0，点C 的坐标为()0,3．（Ⅰ）求抛物线的解析式；（Ⅱ）点M 为线段AB 上一点（点M 不与点A 、B 重合），过点M 作i 轴的垂线，与直线AC 交于点E ，与抛物线交于点P ，过点P 作//PQ AB 交抛物线于点Q ，过点Q 作QN x ⊥轴于点N ．若点P 在点Q 左边，当矩形PMNQ 的周长最大时，求AEM △的面积；（Ⅲ）在（Ⅱ）的条件下，当矩形PMNQ 的周长最大时，连接DQ ，过抛物线上一点F 作y 轴的平行线，与直线AC 交于点G （点G 在点F 的上方）．若=22FG DQ ，求点F 的坐标．【答案】（Ⅰ）223y x x =--+；（Ⅱ）12；（Ⅲ）()4,5F --或()1,0 【解析】【分析】（Ⅰ）将点A ，点C 坐标代入解析式可求解；（Ⅱ）设M （x ，0），P （x ，-x 2-2x+3），利用对称性可求点Q （-2-x ，-x 2-2x+3），可求MP=-x 2-2x+3，PQ=-2-x-x=-2-2x ，则可用x 表示矩形PMNQ 的周长，由二次函数的性质可求当矩形PMNQ 的周长最大时，点P 的坐标，即可求点E ，点M 的坐标，由三角形面积公式可求解；（Ⅲ）先求出点D 坐标，即可求2FG=4，设F （m ，-m 2-2m+3），则G （m ，m+3），用含有m 的式子表示FG 的长度即可求解．【详解】解:（Ⅰ）依题意()()2330{3b c c --+⨯-+==解得2{3b c =-= 所以223y x x =--+（Ⅱ）2223(1)4yx x x抛物线的对称轴是直线1x =-(,0)M x ，()2,23P x x x --+，其中31x -<<-∵P 、Q 关于直线1x =-对称设Q 的横坐标为a 则()11a x --=-- ∴2a x =--∴()22,23Q x x x ----+∴223MP x x =--+，222PQ x x x =---=--∴周长()222222232822(2)10d x x x x x x =----+=--+=-++ 当2x =-时，d 取最大值，此时，(2,0)M - ∴2(3)1AM =---= 设直线AC 的解析式为y kx b =+则303k b b -+=⎧⎨=⎩，解得13k b =⎧⎨=⎩∴设直线AC 的解析式为3y x将2x =-代入3y x，得1y =∴(2,1)E -， ∴1EM=∴11111222AEM S AM ME ∆=⋅=⨯⨯=（Ⅲ）由（Ⅱ）知，当矩形PMNQ 的周长最大时，2x =-此时点()0,3Q ，与点C 重合， ∴3OQ = ∵2223(1)4yx x x∴()1,4D -过D 作DK y ⊥轴于K ，则1DK =，4OK = ∴431OK OK OQ =-=-= ∴DKQ 是等腰直角三角形，2DQ =∴224FG DQ ==设()2,23F m m m --+，则(,3)G m m +()223233FG m m m m m =+---+=+∴234m m +=，解得14m =-，21m = 当4m =-时，2235m m --+=- 当1m =时，2230m m --+=． ∴()4,5F --或()1,0【点睛】本题是二次函数综合题，考查了二次函数的性质，矩形的性质，等腰直角三角形的性质等，利用参数表示线段的长度是本题的关键．7．如图，在平面直角坐标系中，抛物线y ＝﹣12x 2+bx +c 与x 轴交于B ，C 两点，与y 轴交于点A ，直线y ＝﹣12x +2经过A ，C 两点，抛物线的对称轴与x 轴交于点D ，直线MN 与对称轴交于点G ，与抛物线交于M ，N 两点（点N 在对称轴右侧），且MN ∥x 轴，MN ＝7．（1）求此抛物线的解析式．（2）求点N 的坐标．（3）过点A的直线与抛物线交于点F，当tan∠FAC＝12时，求点F的坐标．（4）过点D作直线AC的垂线，交AC于点H，交y轴于点K，连接CN，△AHK沿射线AC 以每秒1个单位长度的速度移动，移动过程中△AHK与四边形DGNC产生重叠，设重叠面积为S，移动时间为t（0≤tS与t的函数关系式．【答案】（1）y＝﹣12x2+32x+2；（2）点N的坐标为（5，-3）；（3）点F的坐标为：（3，2）或（173，﹣509）；（4）25,049,(24549(1044t tS tt⎧⎛≤≤⎪⎪⎝⎭⎪⎪=⎨-<≤⎪⎪⎪+<≤⎪⎩．【解析】【分析】（1）点A、C的坐标分别为（0，2）、（4，0），将点A、C坐标代入抛物线表达式即可求解；（2）抛物线的对称轴为：x＝32，点N的横坐标为：37522+=，即可求解；（3）分点F在直线AC下方、点F在直线AC的上方两种情况，分别求解即可；（4）分0≤t≤5、当5＜t＜t【详解】解：（1）直线y＝﹣12x+2经过A，C两点，则点A、C的坐标分别为（0，2）、（4，0），则c＝2，抛物线表达式为：y＝﹣12x2+bx+2，将点C坐标代入上式并解得：b＝32，故抛物线的表达式为：y＝﹣12x2+32x+2…①；（2）抛物线的对称轴为：x＝32，点N的横坐标为：375 22+=，故点N的坐标为（5，-3）；（3）∵tan∠ACO＝2142AOCO==＝tan∠FAC＝12，即∠ACO＝∠FAC，①当点F在直线AC下方时，设直线AF交x轴于点R，∵∠ACO＝∠FAC，则AR＝CR，设点R（r，0），则r2+4＝（r﹣4）2，解得：r＝32，即点R的坐标为：（32，0），将点R、A的坐标代入一次函数表达式：y＝mx+n得：232nm n=⎧⎪⎨+=⎪⎩，解得：432mn⎧=-⎪⎨⎪=⎩，故直线AR的表达式为：y＝﹣43x+2…②，联立①②并解得：x＝173，故点F（173，﹣509）；②当点F在直线AC的上方时，∵∠ACO＝∠F′AC，∴AF′∥x轴，则点F′（3，2）；综上，点F的坐标为：（3，2）或（173，﹣509）；（4）如图2，设∠ACO＝α，则tanα＝12AOCO=，则sinα5，cosα5①当0≤t≤355时（左侧图），设△AHK移动到△A′H′K′的位置时，直线H′K′分别交x轴于点T、交抛物线对称轴于点S，则∠DST ＝∠ACO ＝α，过点T 作TL ⊥KH ，则LT ＝HH ′＝t ，∠LTD ＝∠ACO ＝α，则DT ＝'52co 5c s 2os L HH T t αα===，DS ＝tan DT α， S ＝S △DST ＝12⨯DT ×DS ＝254t ； 35＜t 35时（右侧图），同理可得：S ＝''DGS T S 梯形＝12⨯DG ×（GS ′+DT ′）＝12⨯3+55﹣323594-； 35＜t 53594+；综上，S ＝2535,023593535,(245435935(5)1044t t t t t t ⎧⎛≤≤⎪ ⎪⎝⎭⎪⎪⎨-<≤⎪⎪⎪+<≤⎪⎩．【点睛】本题考查的是二次函数综合运用，涉及到一次函数、图形平移、图形的面积计算等，其中（3）、（4），要注意分类求解，避免遗漏．8．如图，在平面直角坐标系中，二次函数y ＝﹣x 2+6x ﹣5的图象与x 轴交于A 、B 两点，与y 轴交于点C ，其顶点为P ，连接PA 、AC 、CP ，过点C 作y 轴的垂线l ．（1）P 的坐标，C 的坐标；（2）直线1上是否存在点Q ，使△PBQ 的面积等于△PAC 面积的2倍？若存在，求出点Q 的坐标；若不存在，请说明理由．【答案】（1）（3，4），（0，﹣5）；（2）存在，点Q的坐标为：（92，﹣5）或（212，﹣5）【解析】【分析】（1）利用配方法求出顶点坐标，令x=0，可得y=-5，推出C（0，-5）；（2）直线PC的解析式为y=3x-5，设直线交x轴于D，则D（53，0），设直线PQ交x轴于E，当BE=2AD时，△PBQ的面积等于△PAC的面积的2倍，分两种情形分别求解即可解决问题．【详解】解：（1）∵y＝﹣x2+6x﹣5＝﹣（x﹣3）2+4，∴顶点P（3，4），令x＝0得到y＝﹣5，∴C（0，﹣5）．故答案为：（3，4），（0，﹣5）；（2）令y＝0，x2﹣6x+5＝0，解得：x＝1或x＝5，∴A（1，0），B（5，0），设直线PC的解析式为y＝kx+b，则有534 bk b=-⎧⎨+=⎩，解得：35 kb=⎧⎨=-⎩，∴直线PC的解析式为：y＝3x﹣5，设直线交x轴于D，则D（53，0），设直线PQ 交x 轴于E ，当BE ＝2AD 时，△PBQ 的面积等于△PAC 的面积的2倍， ∵AD ＝23， ∴BE ＝43， ∴E （113，0）或E ′（193，0），则直线PE 的解析式为：y ＝﹣6x +22， ∴Q （92，﹣5），直线PE ′的解析式为y ＝﹣65x +385， ∴Q ′（212，﹣5），综上所述，满足条件的点Q 的坐标为：（92，﹣5）或（212，﹣5）；【点睛】本题考查抛物线与x 轴的交点、二次函数的性质等知识，解题的关键是熟练掌握待定系数法，学会用转化的思想思考问题，属于中考常考题型．9．如图1所示，抛物线223y x bx c =++与x 轴交于A 、B 两点，与y 轴交于点C ，已知C 点坐标为（0，4），抛物线的顶点的横坐标为72，点P 是第四象限内抛物线上的动点，四边形OPAQ 是平行四边形，设点P 的横坐标为m ．（1）求抛物线的解析式；（2）求使△APC 的面积为整数的P 点的个数；（3）当点P 在抛物线上运动时，四边形OPAQ 可能是正方形吗？若可能，请求出点P 的坐标，若不可能，请说明理由；（4）在点Q 随点P 运动的过程中，当点Q 恰好落在直线AC 上时，则称点Q 为“和谐点”，如图（2）所示，请直接写出当Q 为“和谐点”的横坐标的值．【答案】（1）2214433y x x =-+；（2）9个；（3）33,22或44，；（4）33【解析】【分析】（1）抛物线与y 轴交于点C ，顶点的横坐标为72，则472223cb ，即可求解；（2）APC ∆的面积PHAPHCSSS，即可求解；（3）当四边形OPAQ 是正方形时，点P 只能在x 轴的下方，此时OAP 为等腰直角三角形，设点(,)P x y ，则0x y +=，即可求解；（4）求出直线AP 的表达式为：2(1)(6)3y m x ，则直线OQ 的表达式为：2(1)3ym x ②，联立①②求出Q 的坐标，又四边形OPAQ 是平行四边形，则AO 的中点即为PQ 的中点，即可求解．【详解】解：（1）抛物线与y 轴交于点C ，顶点的横坐标为72，则472223cb ，解得1434b c，故抛物线的抛物线为：2214433y x x =-+；（2）对于2214433y x x =-+，令0y =，则1x =或6，故点B 、A 的坐标分别为(1,0)、(6,0)；如图，过点P 作//PH y 轴交AC 于点H ，设直线AC 的表达式为：y kx b =+ 由点A （6，0）、C （0，4）的坐标得460b kb，解得423b k， ∴直线AC 的表达式为：243y x =-+①，设点2214(,4)33P x x x ，则点2(,4)3H x x ，APC ∆的面积221122146(44)212(16)22333PHAPHCSSSPH OA x x x x x，当1x =时，10S =，当6x =时，0S =，故使APC ∆的面积为整数的P 点的个数为9个；（3）当四边形OPAQ 是正方形时，点P 只能在x 轴的下方，此时OAP 为等腰直角三角形，设点(,)P x y ，则0x y +=，即2214433yx x x ，解得：32x =或4，故点P 的坐标为3(2，3)2或(4,4)-；（4）设点2214(,4)33P m m m ，为点(6,0)A ，设直线AP 的表达式为：y kx t =+，由点A ，P 的坐标可得260214433kt kmt m m ，解之得：2(1)326(1)3km tm∴直线AP 的表达式为：2(1)(6)3ym x ， //AP OQ ，则AP 和OQ 表达式中的k 值相同，故直线OQ 的表达式为：2(1)3ym x ②，联立①②得：2(1)3243ym x y x ，解得：446m m y x ，则点6(Q m ，44)m，四边形OPAQ 是平行四边形，则AO 的中点即为PQ 的中点，如图2，作QC x ⊥轴于点C ，PD x ⊥轴于点D ，∴OC AD =,则有，66mm ，解得：33m ，经检验，33m是原分式方程得跟，则633m ，故Q 的横坐标的值为33【点睛】本题考查的是二次函数综合运用，涉及到一次函数的性质、平行四边形正方形的性质、面积的计算等，能熟练应用相关性质是解题的关键．10．在平面直角坐标系中，二次函数y ＝ax 2+bx +2的图象与x 轴交于A （﹣3，0），B （1，0）两点，与y 轴交于点C ．（1）求这个二次函数的关系解析式；（2）点P 是直线AC 上方的抛物线上一动点，是否存在点P ，使△ACP 的面积最大？若存在，求出点P 的坐标；若不存在，说明理由；（3）在平面直角坐标系中，是否存在点Q ，使△BCQ 是以BC 为腰的等腰直角三角形？若存在，直接写出点Q 的坐标；若不存在，说明理由；【答案】（1）224233y x x =--+；（2）存在，点P 35,22⎛⎫- ⎪⎝⎭，使△PAC 的面积最大；（3）存在点Q ，使△BCQ 是以BC 为腰的等腰直角三角形．Q 点坐标为：Q 1（2，3），Q 2（3，1），Q 3（﹣1，﹣1），Q 4（﹣2，1）．【解析】【分析】（1）直接把点A （﹣3，0），B （1，0）代入二次函数y ＝ax 2+bx+2求出a 、b 的值即可得出抛物线的解析式；（2）设点P 坐标为（m ，n ），则n ＝﹣23m 2﹣43m+2，连接PO ，作PM ⊥x 轴于M ，PN ⊥y 轴于N ．根据三角形的面积公式得出△PAC 的表达式，再根据二次函数求最大值的方法得出其顶点坐标即可；（3）以BC 为边，在线段BC 两侧分别作正方形，正方形的其他四个顶点均可以使得“△BCQ 是以BC 为腰的等腰直角三角形”，因此有四个点符合题意要求，再过Q 1点作Q 1D ⊥y 轴于点D ，过点Q 2作Q 2E ⊥x 轴于点E ，根据全等三角形的判定定理得出△Q 1CD ≌△CBO ，△CBO ≌△BQ 2E ，故可得出各点坐标．【详解】（1）∵抛物线y ＝ax 2+bx+2过点A （﹣3，0），B （1，0），∴093202a b a b =-+⎧⎨=++⎩ 2343a b ⎧=-⎪⎪⎨⎪=-⎪⎩解得 ∴二次函数的关系解析式为y ＝﹣23x 2﹣43x+2；（2）存在．∵如图1所示，设点P 坐标为（m ，n ），则n ＝﹣23m 2﹣43m+2．连接PO ，作PM ⊥x 轴于M ，PN ⊥y 轴于N ．则PM＝﹣23m2﹣43m+2．，PN＝﹣m，AO＝3．∵当x＝0时，y＝﹣23×0﹣43×0+2＝2，∴OC＝2，∴S△PAC＝S△PAO+S△PCO﹣S△ACO＝12AO•PM+12CO•PN﹣12AO•CO＝12×3×（﹣23m2﹣43m+2）+12×2×（﹣m）﹣12×3×2＝﹣m2﹣3m∵a＝﹣1＜0∴函数S△PAC＝﹣m2﹣3m有最大值∴当m＝﹣2ba＝﹣32时，S△PAC有最大值．∴n＝﹣23m2﹣43m+2＝﹣23×（﹣32）2﹣43×（﹣32）+2＝52，∴存在点P（﹣32，52），使△PAC的面积最大．（3）如图2所示，以BC为边在两侧作正方形BCQ1Q2、正方形BCQ4Q3，则点Q1，Q2，Q3，Q4为符合题意要求的点．过Q1点作Q1D⊥y轴于点D，过点Q2作Q2E⊥x轴于点E，∵∠1+∠2＝90°，∠2+∠3＝90°，∠3+∠4＝90°，∴∠1＝∠3，∠2＝∠4，在△Q1CD与△CBO中，∵11324Q C BC∠=∠⎧⎪=⎨⎪∠=∠⎩，∴△Q1CD≌△CBO，∴Q1D＝OC＝2，CD＝OB＝1，∴OD＝OC+CD＝3，∴Q1（2，3）；同理可得Q4（﹣2，1）；同理可证△CBO≌△BQ2E，∴BE＝OC＝2，Q2E＝OB＝1，∴OE＝OB+BE＝1+2＝3，∴Q2（3，1），同理，Q3（﹣1，﹣1），∴存在点Q，使△BCQ是以BC为腰的等腰直角三角形．Q点坐标为：Q1（2，3），Q2（3，1），Q3（﹣1，﹣1），Q4（﹣2，1）．【点睛】本题考查的是二次函数综合题，涉及到用待定系数法求二次函数解析式，二次函数极值、全等三角形的判定与性质，正方形及等腰直角三角形的性质等知识，涉及面较广，难度较大．。

人教版九年级数学上册：第22章：二次函数(培优卷)(含答案)(1)

9. 已知函数 y=|x2 -2x-3|的大致图象如图
值范围是 (
)
D．1 个 4，如果方程 |x2 -2x-3|=m(m 为实数 )有 2 个不相等的实数根，则
m 的取
A ． m>3
B． m>4 C． m>3 或 m=0
D． m>4 或 m=0
10. 若实数 a 使关于 x 的二次函数 y=x 2 +(a-1)x-a+2 ，当 x＜ -1 时， y 随 x 的增大而减小，且使关于
)
A．
B．
C．
D．
4. 已知二次函数 y=ax 2 +bx+c(a ≠ 0)的图象如图 1，则下列结论中正确的是 (
)
A ．abc＞ 0
B ．b2 -4ac＜0
C． 9a+3b+c＞ 0
D． c+8a＜ 0
5. 已知二次函数 y=ax 2 +bx+c 的图象如图 2 所示，则下列说法正确的是 (
)
A ．ac＜ 0
15. 函数 y=ax 2 -2x+2 ，若对满足 3＜ x ＜ 4 的任意实数 x 都有 y＞ 0 成立，则实数 a 的取值范围为 16. 已知二次函数 y=(x-m) 2 +2m(m 为常数 )，在自变量 x 的值满足 1≤ x≤ 3 的情况下，与其对应的函数值 y 的最
小值为 4，则 m 的值为三、解答题 (7＇ +8＇ +8＇ +8＇ +9＇+9 ＇ +10＇ +10 ＇ +12＇＝ 72＇ ) 17. 已知二次函数经过 (1，1) ，以 (-1， 4)， (0， 3)．求这个二次函数解析式．

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2018年九年级数学上册二次函数压轴题培优专题1.如图，已知抛物线y=﹣x2﹣x+2与x轴交于A、B两点，与y轴交于点C（1）求点A，B，C的坐标；（2）点E是此抛物线上的点，点F是其对称轴上的点，求以A，B，E，F为顶点的平行四边形的面积；（3）此抛物线的对称轴上是否存在点M，使得△ACM是等腰三角形？若存在，请求出点M的坐标；若不存在，请说明理由．2.如图，已知抛物线经过点A(－1，0)，B(3，0)，C(0，3)三点．(1)求抛物线的解析式；(2)点M是线段BC上的点(不与B，C重合)，过M作NM∥y轴交抛物线于N，若点M的横坐标为m，请用含m 的代数式表示MN的长；(3)在(2)的条件下，连接NB，NC，是否存在点m，使△BNC的面积最大？若存在，求m的值；若不存在，说明理由．3.如图，抛物线y=x2﹣2x﹣3与x轴交于A、B两点（A点在B点左侧），直线l与抛物线交于A、C两点，其中C点的横坐标为2．（1）求A、B、C三点的坐标；（2）在抛物线的对称轴上找到点P，使得△PBC的周长最小，并求出点P的坐标；（3）点G抛物线上的动点，在x轴上是否存在点F，使A、C、F、G为顶点四边形是平行四边形？如果存在，请直接写出F点坐标；如果不存在，请说明理由．4.在平面直角坐标系中，二次函数y=x2+mx+2m﹣7的图象经过点（1，0）．（1）求抛物线的表达式；（2）把﹣4＜x＜1时的函数图象记为H，求此时函数y的取值范围；（3）在（2）的条件下，将图象H在x轴下方的部分沿x轴翻折，图象H的其余部分保持不变，得到一个新图象M．若直线y=x+b与图象M有三个公共点，求b的取值范围．5.如图,抛物线y=ax2+bx+c的顶点为M（﹣2,﹣4），与x轴交于A、B两点,且A（﹣6,0），与y轴交于点C．（1）求抛物线的函数解析式；（2）求△ABC的面积；（3）能否在抛物线第三象限的图象上找到一点P,使△APC的面积最大？若能,请求出点P的坐标；若不能，请说明理由．6.如图，抛物线y=﹣x2+bx+c交x轴于点A（﹣3，0）和点B，交y轴于点C（0，3）．（1）求抛物线的函数表达式；（2）若点P在抛物线上，且S△AOP=4S△BOC，求点P的坐标；（3）如图b，设点Q是线段AC上的一动点，作DQ⊥x轴，交抛物线于点D，求线段DQ长度的最大值．7.如图，关于x的二次函数y=x2＋bx＋c的图象与x轴交于点A(1，0)和点B，与y轴交于点C(0，3)，抛物线的对称轴与x轴交于点D.(1)求二次函数的解析式；(2)在y轴上是否存在一点P，使△PBC为等腰三角形？若存在，请求出点P的坐标；(3)有一个点M从点A出发，以每秒1个单位长度的速度在AB上向点B运动，另一个点N从点D与点M同时出发，以每秒2个单位长度的速度在抛物线的对称轴上运动，当点M到达点B时，点M，N同时停止运动，问点M，N运动到何处时，△MNB面积最大，试求出最大面积.8.如图，矩形的边OA在x轴上，边OC在y轴上，点B的坐标为（10，8），沿直线OD折叠矩形，使点A正好落在BC上的E处，E点坐标为（6，8），抛物线y=ax2+bx+c经过O、A、E三点．（1）求此抛物线的解析式；（2）求A D的长；（3）点P是抛物线对称轴上的一动点，当△PAD的周长最小时，求点P的坐标．9.如图，在直角坐标系中，抛物线经过点A（0，4），B（1，0），C（5，0），其对称轴与x轴相交于点M．（1）求抛物线的解析式和对称轴；（2）在抛物线的对称轴上是否存在一点P，使△PAB的周长最小？若存在，请求出点P的坐标；若不存在，请说明理由；（3）连接AC，在直线AC的下方的抛物线上，是否存在一点N，使△NAC的面积最大？若存在，请求出点N的坐标；若不存在，请说明理由．10.如图,抛物线y=ax2﹣2ax+c(a≠0)与y轴交于点C（0,4）,与x轴交于点A、B,点A坐标为（4,0）．（1）求该抛物线的解析式；（2）抛物线的顶点为N,在x轴上找一点K,使CK+KN最小,并求出点K的坐标；（3）点Q是线段AB上的动点,过点Q作QE∥AC,交BC于点E,连接CQ.当△CQE的面积最大时,求点Q的坐标；（4）若平行于x轴的动直线l与该抛物线交于点P,与直线AC交于点F,点D的坐标为（2,0）.问:是否存在这样的直线l,使得△ODF是等腰三角形？若存在,请求出点P的坐标；若不存在,请说明理由．参考答案1.解：2.解：(1)y ＝－x 2＋2x ＋3(2)易求直线BC 的解析式为y ＝－x ＋3，∴M(m ，－m ＋3)，又∵MN ⊥x 轴，∴N(m ，－m 2＋2m ＋3)，∴MN ＝(－m 2＋2m ＋3)－(－m ＋3)＝－m 2＋3m(0＜m ＜3)(3)S △BNC ＝S △CMN ＋S △MNB ＝21|MN|·|OB|，∴当|MN|最大时，△BNC 的面积最大，MN ＝－m 2＋3m ＝－(m －23)2＋49，所以当m ＝23时，△BNC 的面积最大为21×49×3＝8273.（1）A （﹣1，0）B （3，0）C （2，﹣3）设直线AC 的解析式为：y=kx+b ，解得，k=-1,b=-1，∴直线AC 的函数解析式是y=﹣x ﹣1，由抛物线的对称性可知，点A 与点B 关于对称轴x=1对称，∴连接AC 与x=1交于点P ，点即为所求，当x=1时，y=﹣2，则点P 的坐标为（1，﹣2）；（3）存在4个这样的点F ，F 点坐标是：（﹣3，0）或（1，0）或（4+，0）或（4﹣，0）4.解：（1）∵二次函数y=x 2+mx+2m ﹣7的图象经过点（1，0）， ∴1+m+2m ﹣7=0，解得m=2．∴抛物线的表达式为y=x 2+2x ﹣3；（2）y=x 2+2x ﹣3=（x+1）2﹣4．∵当﹣4＜x ＜﹣1时，y 随x 增大而减小；当﹣1≤x ＜1时，y 随x 增大而增大，∴当x=﹣1，y 最小=﹣4．当x=﹣4时，y=5．∴﹣4＜x＜1时，y的取值范围是﹣4≤y＜5；（3）y=x2+2x﹣3与x轴交于点（﹣3，0），（1，0）．新图象M如右图红色部分．把抛物线y=x2+2x﹣3=（x+1）2﹣4的图象x轴下方的部分沿x轴翻折到x轴上方，则翻折部分的抛物线解析式为y=﹣（x+1）2+4（﹣3≤x≤1），当直线y=x+b经过（﹣3，0）时，直线y=x+b与图象M有两个公共点，此时b=3；当直线y=x+b与抛物线y=﹣（x+1）2+4（﹣3≤x≤1）相切时，直线y=x+b与图象M有两个公共点，即﹣（x+1）2+4=x+b有相等的实数解，整理得x2+3x+b﹣3=0，△=32﹣4（b﹣3）=0，解得b=．结合图象可得，直线y=x+b与图象M有三个公共点，b的取值范围是3＜b＜．5.解：（1）设此函数的解析式为y=a（x+h）2+k，∵函数图象顶点为M（﹣2，﹣4），∴y=a（x+2）2﹣4，又∵函数图象经过点A（﹣6，0），∴0=a（﹣6+2）2﹣4解得a=，∴此函数的解析式为y=（x+2）2﹣4，即y=x2+x﹣3；（2）∵点C是函数y=x2+x﹣3的图象与y轴的交点，∴点C的坐标是（0，﹣3），又当y=0时，有y=x2+x﹣3=0，解得x1=﹣6，x2=2，∴点B的坐标是（2，0），则S△ABC=|AB|•|OC|=×8×3=12；（3）假设存在这样的点，过点P作PE⊥x轴于点E，交AC于点F．设E（x，0），则P（x， x2+x﹣3），设直线AC的解析式为y=kx+b，∵直线AC过点A（﹣6，0），C（0，﹣3），∴，解得，∴直线AC的解析式为y=﹣x﹣3，∴点F的坐标为F（x，﹣x﹣3），则|PF|=﹣x﹣3﹣（x2+x﹣3）=﹣x2﹣x，∴S△APC=S△APF+S△CPF=|PF|•|AE|+|PF|•|OE|=|PF|•|OA|=（﹣x2﹣x）×6=﹣x2﹣x=﹣（x+3）2+，∴当x=﹣3时，S△APC有最大值，此时点P的坐标是P（﹣3，﹣）．6.7.解：8.解：（1）∵四边形ABCD是矩形，B（10，8），∴A（10，0），又抛物线经过A、E、O三点，把点的坐标代入抛物线解析式可得，解得，∴抛物线的解析式为y=﹣x2+x；（2）由题意可知：AD=DE，BE=10﹣6=4，AB=8，设AD=x，则ED=x，BD=AB﹣AD=8﹣x，在Rt△BDE中，由勾股定理可知ED2=EB2+BD2，即x2=42+（8﹣x）2，解得x=5，∴AD=5；（3）∵y=﹣x2+x，∴其对称轴为x=5，∵A、O两点关于对称轴对称，∴PA=PO，当P、O、D三点在一条直线上时，PA+PD=PO+PD=OD，此时△PAD的周长最小，如图，连接OD交对称轴于点P，则该点即为满足条件的点P，由（2）可知D点的坐标为（10，5），设直线OD解析式为y=kx，把D点坐标代入可得5=10k，解得k=，∴直线OD解析式为y=x，令x=5，可得y=，∴P点坐标为（5，）．9.解：（1）根据已知条件可设抛物线的解析式为y=a（x﹣1）（x﹣5），把点A（0，4）代入上式得：a=0.8，∴y=0.8（x﹣1）（x﹣5）=0.8x2﹣4.8x+4=0.8（x﹣3）2﹣4.8，∴抛物线的对称轴是：x=3；（2）P点坐标为（3，1.6）．理由如下：∵点A（0，4），抛物线的对称轴是x=3，∴点A关于对称轴的对称点A′的坐标为（6，4）如图1，连接BA′交对称轴于点P，连接AP，此时△PAB的周长最小．设直线BA′的解析式为y=kx+b，把A′（6，4），B（1，0）代入得6k+b=4,k+b=0，解得k=0.8,b=-0.8，∴y=0.8x﹣0.8，∵点P的横坐标为3，∴y=0.8×3﹣0.8=1.6，∴P（3，1.6）．（3）在直线AC的下方的抛物线上存在点N，使△NAC面积最大．设N点的横坐标为t，此时点N（t，0.8 t2﹣4.8t+4）（0＜t＜5），如图2，过点N作NG∥y轴交AC于G；作AD⊥NG于D，由点A（0，4）和点C（5，0）可求出直线AC的解析式为：y=﹣0.8x+4，把x=t代入得：y=﹣0.8t+4，则G（t，﹣0.8t+4），此时：NG=﹣0.8t+4﹣（0.8t2﹣4.8t+4）=﹣0.8t2+4t，∵AD+CF=CO=5，∴S△ACN=S△ANG+S△CGN=0.5AM×NG+0.5NG×CF=0.5NGOC=0.5×（﹣0.8t2+4t）×5=﹣2t2+10t=﹣2（t﹣2.5）2+12.5，∴当t=2.5时，△CAN面积的最大值为12.5，由t=2.5，得：y=0.8t2﹣4.8t+4=﹣3，∴N（2.5，﹣3）．10.解：（1）∵抛物线经过点C（0，4），A（4，0），∴，解得，∴抛物线解析式为y=﹣；（2）由（1）可求得抛物线顶点为N（1，），如图1，作点C关于x轴的对称点C′（0，﹣4），连接C′N交x轴于点K，则K点即为所求，设直线C′N的解析式为y=kx+b，把C′、N点坐标代入可得，解得，∴直线C′N的解析式为y=，令y=0，解得x=，∴点K的坐标为（，0）；（3）设点Q（m，0），过点E作EG⊥x轴于点G，如图2，由﹣=0，得x1=﹣2，x2=4，∴点B的坐标为（﹣2，0），AB=6，BQ=m+2，又∵QE∥AC，∴△BQE≌△BAC，∴，即，解得EG=；∴S△CQE=S△CBQ﹣S△EBQ===．又∵﹣2≤m≤4，∴当m=1时，S△CQE有最大值3，此时Q（1，0）；（4）存在．在△ODF中，（ⅰ）若DO=DF，∵A（4，0），D（2，0），∴AD=OD=DF=2．又在Rt△AOC中，OA=OC=4，∴∠OAC=45°．∴∠DFA=∠OAC=45°．∴∠ADF=90°．此时，点F的坐标为（2，2）．由﹣=2，得x1=1+，x2=1﹣．此时，点P的坐标为：P1（1+，2）或P2（1﹣，2）；（ⅱ）若FO=FD，过点F作FM⊥x轴于点M．由等腰三角形的性质得：OM=OD=1，∴AM=3．∴在等腰直角△AMF中，MF=AM=3．∴F（1，3）．由﹣=3，得x1=1+，x2=1﹣．此时，点P的坐标为：P3（1+，3）或P4（1﹣，3）；（ⅲ）若OD=OF，∵OA=OC=4，且∠AOC=90°．∴AC=4．∴点O到AC的距离为2．而OF=OD=2＜2，与OF≥2矛盾．∴在AC上不存在点使得OF=OD=2．此时，不存在这样的直线l，使得△ODF是等腰三角形．综上所述，存在这样的直线l，使得△ODF是等腰三角形．所求点P的坐标为：（1+，2）或（1﹣，2）或（1+，3）或（1﹣，3）．。

【专题培优】2018年 九年级数学上册 二次函数压轴题 培优专题(含答案)

2018年九年级数学中考专题 压轴题培优(含答案)

2018年中考数学二次函数压轴题汇编(含答案)

初三数学二次函数的专项培优练习题(含答案)含详细答案

初三数学二次函数的专项培优练习题含详细答案

人教版数学九年级上册 第二十二章 《二次函数》压轴题综合培优训练(含答案)

九年级数学 二次函数的专项 培优练习题含详细答案

人教版数学九年级上学期期末备考压轴题培优：二次函数(含答案)

人教版九年级数学上册第二十二章 《二次函数》培优训练题(含答案)

【同步培优】人教版2018年 九年级数学上册 二次函数图象性质 专题培优卷(含答案)

二次函数培优专题训练(含答案)

2018年中考数学二次函数压轴题集锦(50道含解析)

九年级数学上册 二次函数(培优篇)(Word版 含解析)

九年级数学上册 二次函数(培优篇)(Word版 含解析)

2018年各地市中考《二次函数》压轴题精编(含答案解析)

2018年九年级数学上册二次函数培优练习卷含答案

九年级数学上册 二次函数(培优篇)(Word版 含解析)

人教版九年级数学上册：第22章：二次函数(培优卷)(含答案)(1)

【专题培优】2018年九年级数学上册二次函数压轴题培优专题(含答案)

2018年九年级数学中考专题压轴题培优(含答案)

人教版数学九年级上册第二十二章《二次函数》压轴题综合培优训练(含答案)

九年级数学二次函数的专项培优练习题含详细答案

人教版九年级数学上册第二十二章《二次函数》培优训练题(含答案)

【同步培优】人教版2018年九年级数学上册二次函数图象性质专题培优卷(含答案)

九年级数学上册二次函数(培优篇)(Word版含解析)

九年级数学上册二次函数(培优篇)(Word版含解析)

九年级数学上册二次函数(培优篇)(Word版含解析)