武汉市高一上学期期末数学试卷(I)卷
武汉市高一上学期数学期末考试试卷A卷

武汉市高一上学期数学期末考试试卷A卷姓名:________ 班级:________ 成绩:________一、选择题 (共10题;共20分)1. (2分)若角的终边上有一点(-4,a),则a的值是()A .B .C .D .2. (2分) (2018高三上·丰台期末) 已知集合,,则()A .B .C .D .3. (2分)函数的图象如右图所示,下列说法正确的是()①函数满足②函数满足③函数满足④函数满足A . ①③B . ②④C . ①②D . ③④4. (2分)在△ABC中,PQ分别是AB,BC的三等分点,且AP=AB,BQ=BC,若=,=,则=()A . +B . -+C . -D . --5. (2分)已知且有,则()A . -1B . 1C .D . 06. (2分) (2018高一上·舒兰月考) 定义,如,且当时,有解,则实数k的取值范围是()A .B .C .D .7. (2分)定义在R上的偶函数满足,且,则的值为()A . 3B . -1C . 1D .8. (2分)方程ex﹣x﹣2=0的一个根所在的区间(k,k+1)(k∈N),则k的值为()A . 0B . 1C . 2D . 39. (2分)已知函数f(x)=sin(2x+φ),其中<|φ|<π,若对x∈R恒成立,则f(x)的递增区间是()A .B .C .D .10. (2分) (2016高一上·临川期中) 已知f(x)=3﹣2|x|,g(x)=x2﹣2x,F(x)= ,则F(x)的最值是()A . 最大值为3,最小值为﹣1B . 最大值为3,无最小值C . 最大值为7﹣2 ,无最小值D . 既无最大值,又无最小值二、填空题 (共7题;共7分)11. (1分) (2018高二下·辽宁期末) 若幂函数的图像过点,则的值为________.12. (1分) (2017高一上·福州期末) 若圆锥的侧面展开图是圆心角为90°的扇形,则这个圆锥的侧面积与底面积的比是________.13. (1分)直线y=2与函数y=tan x图象相交,则相邻两焦点间的距离是________ .14. (1分) (2016高三上·新疆期中) 函数f(x)=sin(x+2φ)﹣2sinφcos(x+φ)的最大值为________15. (1分) (2017高三上·苏州开学考) 设a+b=2,b>0,当 + 取得最小值时,a=________.16. (1分)若与为非零向量,|+|=|-|,则与的夹角为________17. (1分) (2016高一上·大名期中) 已知集合A={x|mx2+2x﹣1=0},若集合A中只有一个元素,则实数m 的值为________三、解答题 (共5题;共45分)18. (10分) (2016高一上·饶阳期中) 已知全集U=R,集合A={x|x<﹣4,或x>1},B={x|﹣3≤x﹣1≤2},(1)求A∩B、(∁UA)∪(∁UB);(2)若集合M={x|2k﹣1≤x≤2k+1}是集合A的子集,求实数k的取值范围.19. (10分) (2016高三上·黑龙江期中) 已知向量 =(2cosx,t)(t∈R), =(sinx﹣cosx,1),函数y=f(x)= • ,将y=f(x)的图象向左平移个单位长度后得到y=g(x)的图象且y=g(x)在区间[0, ]内的最大值为.(1)求t的值及y=f(x)的最小正周期;(2)设△ABC的内角A,B,C的对边分别为a,b,c,若 g(﹣)=﹣1,a=2,求BC边上的高的最大值.20. (10分)已知a∈R,函数f(x)=x|x﹣a|(1)判断函数f(x)=x|x﹣a|的奇偶性;(2)当a>0时,求函数f(x)=x|x﹣a|在区间[0,1]上的最大值.21. (5分)设二次函数y=f(x)的最大值为9,且f(3)=f(﹣1)=5,(1)求f(x)的解析式;(2)求f(x)在[0,4]上的最值.22. (10分) (2018高三上·龙泉驿月考) 已知函数.(1)当时,解关于的不等式;(2)若对任意及时,恒有成立,求实数的取值范围.参考答案一、选择题 (共10题;共20分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、二、填空题 (共7题;共7分)11-1、12-1、13-1、14-1、15-1、16-1、17-1、三、解答题 (共5题;共45分) 18-1、18-2、19-1、19-2、20-1、20-2、21-1、22-1、22-2、。
2020-2021武汉市高中必修一数学上期末一模试卷及答案

2020-2021武汉市高中必修一数学上期末一模试卷及答案一、选择题1.设a b c ,,均为正数,且122log aa =,121log 2b b ⎛⎫= ⎪⎝⎭,21log 2cc ⎛⎫= ⎪⎝⎭.则( ) A .a b c << B .c b a << C .c a b << D .b a c <<2.已知集合21,01,2A =--{,,},{}|(1)(2)0B x x x =-+<,则A B =I ( )A .{}1,0-B .{}0,1C .{}1,0,1-D .{}0,1,23.若函数2()2f x mx mx =-+的定义域为R ,则实数m 取值范围是( )A .[0,8)B .(8,)+∞C .(0,8)D .(,0)(8,)-∞⋃+∞4.函数y =a |x |(a >1)的图像是( ) A .B .C .D .5.定义在R 上的偶函数()f x 满足:对任意的1x ,212[0,)()x x x ∈+∞≠,有2121()()0f x f x x x -<-,则( ).A .(3)(2)(1)f f f <-<B .(1)(2)(3)f f f <-<C .(2)(1)(3)f f f -<<D .(3)(1)(2)f f f <<-6.设f(x)=()2,01,0x a x x a x x ⎧-≤⎪⎨++>⎪⎩若f(0)是f(x)的最小值,则a 的取值范围为( ) A .[-1,2] B .[-1,0] C .[1,2]D .[0,2]7.某工厂产生的废气必须经过过滤后排放,规定排放时污染物的残留含量不得超过原污染物总量的0.5%.已知在过滤过程中的污染物的残留数量P (单位:毫克/升)与过滤时间t(单位:小时)之间的函数关系为0ktP P e -=⋅(k 为常数,0P 为原污染物总量).若前4个小时废气中的污染物被过滤掉了80%,那么要能够按规定排放废气,还需要过滤n 小时,则正整数n 的最小值为( )(参考数据:取5log 20.43=) A .8B .9C .10D .148.已知01a <<,则方程log xa a x =根的个数为( ) A .1个B .2个C .3个D .1个或2个或3根9.已知[]x 表示不超过实数x 的最大整数,()[]g x x =为取整函数,0x 是函数()2ln f x x x=-的零点,则()0g x 等于( )A .1B .2C .3D .410.若函数()[)[]1,1,0{44,0,1xx x f x x ⎛⎫∈- ⎪=⎝⎭∈,则f (log 43)=( ) A .13B .14C .3D .411.函数()()212ln 12f x x x =-+的图象大致是( ) A .B .C .D .12.函数y =11x -在[2,3]上的最小值为( ) A .2 B .12 C .13D .-12二、填空题13.已知函数()()22,03,0x x f x x x ⎧+≤⎪=⎨->⎪⎩,则关于x 的方程()()()()200,3f af x a x -=∈的所有实数根的和为_______.14.已知函数()22f x mx x m =-+的值域为[0,)+∞,则实数m 的值为__________15.若关于x 的方程42x x a -=有两个根,则a 的取值范围是_________16.函数22log (56)y x x =--单调递减区间是 .17.若函数()()()()22,0,0x x x f x g x x ⎧+≥⎪=⎨<⎪⎩为奇函数,则()()1f g -=________.18.已知函数()()1123121x a x a x f x x -⎧-+<=⎨≥⎩的值域为R ,则实数a 的取值范围是_____. 19.函数2sin 21=+++xy x x 的最大值和最小值之和为______20.已知函数(2),2()11,22xa x x f x x -≥⎧⎪=⎨⎛⎫-< ⎪⎪⎝⎭⎩,满足对任意的实数12x x ≠,都有1212()()0f x f x x x -<-成立,则实数a 的取值范围为__________.三、解答题21.已知()()()22log 2log 2f x x x =-++. (1)求函数()f x 的定义域; (2)求证:()f x 为偶函数;(3)指出方程()f x x =的实数根个数,并说明理由. 22.设()()12log 10f x ax =-,a 为常数.若()32f =-.(1)求a 的值;(2)若对于区间[]3,4上的每一个x 的值,不等式()12xf x m ⎛⎫>+ ⎪⎝⎭恒成立,求实数m 的取值范围 .23.已知幂函数35()()m f x xm N -+=∈为偶函数,且在区间(0,)+∞上单调递增.(Ⅰ)求函数()f x 的解析式;(Ⅱ)设函数()()21g x f x x λ=+-,若()0<g x 对任意[1,2]x ∈恒成立,求实数λ的取值范围.24.义域为R 的函数()f x 满足:对任意实数x,y 均有()()()2f x y f x f y +=++,且()22f =,又当1x >时,()0f x >.(1)求()()0.1f f -的值,并证明:当1x <时,()0f x <; (2)若不等式()()()222221240f aa x a x ----++<对任意[] 1,3x ∈恒成立,求实数a 的取值范围.25.某群体的人均通勤时间,是指单日内该群体中成员从居住地到工作地的平均用时.某地上班族S 中的成员仅以自驾或公交方式通勤.分析显示:当S 中%x (0100x <<)的成员自驾时,自驾群体的人均通勤时间为()30030180029030100x f x x x x <≤⎧⎪=⎨+-<<⎪⎩,,(单位:分钟),而公交群体的人均通勤时间不受x 影响,恒为40分钟,试根据上述分析结果回答下列问题:(1)当x 在什么范围内时,公交群体的人均通勤时间少于自驾群体的人均通勤时间? (2)求该地上班族S 的人均通勤时间()g x 的表达式;讨论()g x 的单调性,并说明其实26.已知函数2()1f x x x m =-+.(1)若()f x 在x 轴正半轴上有两个不同的零点,求实数m 的取值范围; (2)当[1,2]x ∈时,()1f x >-恒成立,求实数m 的取值范围.【参考答案】***试卷处理标记,请不要删除一、选择题 1.A 解析:A 【解析】试题分析:在同一坐标系中分别画出2,xy =12xy ⎛⎫= ⎪⎝⎭,2log y x =,12log y x =的图象,2xy =与12log y x =的交点的横坐标为a ,12xy ⎛⎫= ⎪⎝⎭与12log y x =的图象的交点的横坐标为b ,12xy ⎛⎫= ⎪⎝⎭与2log y x =的图象的交点的横坐标为c ,从图象可以看出.考点:指数函数、对数函数图象和性质的应用.【方法点睛】一般一个方程中含有两个以上的函数类型,就要考虑用数形结合求解,在同一坐标系中画出两函数图象的交点,函数图象的交点的横坐标即为方程的解.2.A【解析】 【分析】 【详解】由已知得{}|21B x x =-<<,因为21,01,2A =--{,,},所以{}1,0A B ⋂=-,故选A .3.A解析:A 【解析】 【分析】根据题意可得出,不等式mx 2-mx +2>0的解集为R ,从而可看出m =0时,满足题意,m ≠0时,可得出280m m m ⎧⎨=-<⎩V >,解出m 的范围即可. 【详解】∵函数f (x )的定义域为R ; ∴不等式mx 2-mx +2>0的解集为R ; ①m =0时,2>0恒成立,满足题意; ②m ≠0时,则280m m m ⎧⎨=-<⎩V >; 解得0<m <8;综上得,实数m 的取值范围是[0,8) 故选:A . 【点睛】考查函数定义域的概念及求法,以及一元二次不等式的解集为R 时,判别式△需满足的条件.4.B解析:B 【解析】因为||0x ≥,所以1x a ≥,且在(0,)+∞上曲线向下弯曲的单调递增函数,应选答案B .5.A解析:A 【解析】由对任意x 1,x 2 ∈ [0,+∞)(x 1≠x 2),有()()1212f x f x x x -- <0,得f (x )在[0,+∞)上单独递减,所以(3)(2)(2)(1)f f f f <=-<,选A.点睛:利用函数性质比较两个函数值或两个自变量的大小,首先根据函数的性质构造某个函数,然后根据函数的奇偶性转化为单调区间上函数值,最后根据单调性比较大小,要注意转化在定义域内进行6.D解析:D 【解析】 【分析】由分段函数可得当0x =时,2(0)f a =,由于(0)f 是()f x 的最小值,则(,0]-∞为减函数,即有0a ≥,当0x >时,1()f x x a x=++在1x =时取得最小值2a +,则有22a a ≤+,解不等式可得a 的取值范围.【详解】因为当x≤0时,f(x)=()2x a -,f(0)是f(x)的最小值, 所以a≥0.当x >0时,1()2f x x a a x=++≥+,当且仅当x =1时取“=”. 要满足f(0)是f(x)的最小值,需22(0)a f a +>=,即220a a --≤,解得12a -≤≤, 所以a 的取值范围是02a ≤≤, 故选D. 【点睛】该题考查的是有关分段函数的问题,涉及到的知识点有分段函数的最小值,利用函数的性质,建立不等关系,求出参数的取值范围,属于简单题目.7.C解析:C 【解析】 【分析】根据已知条件得出415ke-=,可得出ln 54k =,然后解不等式1200kt e -≤,解出t 的取值范围,即可得出正整数n 的最小值. 【详解】由题意,前4个小时消除了80%的污染物,因为0ktP P e -=⋅,所以()400180%kP Pe --=,所以40.2k e -=,即4ln0.2ln5k -==-,所以ln 54k =, 则由000.5%ktP P e -=,得ln 5ln 0.0054t =-, 所以()23554ln 2004log 2004log 52ln 5t ===⨯5812log 213.16=+=, 故正整数n 的最小值为14410-=.故选:C.【点睛】本题考查指数函数模型的应用,涉及指数不等式的求解,考查运算求解能力,属于中等题.8.B解析:B 【解析】 【分析】在同一平面直角坐标系中作出()xf x a =与()log a g x x =的图象,图象的交点数目即为方程log xa a x =根的个数. 【详解】作出()xf x a =,()log a g x x =图象如下图:由图象可知:()(),f x g x 有两个交点,所以方程log xa a x =根的个数为2.故选:B . 【点睛】本题考查函数与方程的应用,着重考查了数形结合的思想,难度一般.(1)函数()()()h x f x g x =-的零点数⇔方程()()f x g x =根的个数⇔()f x 与()g x 图象的交点数;(2)利用数形结合可解决零点个数、方程根个数、函数性质研究、求不等式解集或参数范围等问题.9.B解析:B 【解析】 【分析】根据零点存在定理判断023x <<,从而可得结果. 【详解】 因为()2ln f x x x=-在定义域内递增,且()2ln 210f =-<,()23ln 303f =->, 由零点存在性定理可得023x <<,根据[]x 表示不超过实数x 的最大整数可知()02g x =, 故选:B. 【点睛】本题主要考查零点存在定理的应用,属于简单题.应用零点存在定理解题时,要注意两点:(1)函数是否为单调函数;(2)函数是否连续.10.C解析:C 【解析】 【分析】根据自变量范围代入对应解析式,化简得结果. 【详解】f (log 43)=log434=3,选C. 【点睛】本题考查分段函数求值,考查基本求解能力,属基础题.11.A解析:A 【解析】函数有意义,则:10,1x x +>∴>-, 由函数的解析式可得:()()21002ln 0102f =⨯-+=,则选项BD 错误; 且211111112ln 1ln ln 402222848f ⎛⎫⎛⎫⎛⎫-=⨯--⨯-+=-=+> ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,则选项C 错误; 本题选择A 选项.点睛:函数图象的识辨可从以下方面入手:(1)从函数的定义域,判断图象的左右位置;从函数的值域,判断图象的上下位置.(2)从函数的单调性,判断图象的变化趋势.(3)从函数的奇偶性,判断图象的对称性.(4)从函数的特征点,排除不合要求的图象.利用上述方法排除、筛选选项.12.B解析:B 【解析】 y =11x -在[2,3]上单调递减,所以x=3时取最小值为12,选B. 二、填空题13.【解析】【分析】由可得出和作出函数的图象由图象可得出方程的根将方程的根视为直线与函数图象交点的横坐标利用对称性可得出方程的所有根之和进而可求出原方程所有实根之和【详解】或方程的根可视为直线与函数图象 解析:3【解析】 【分析】 由()()20fx af x -=可得出()0f x =和()()()0,3f x a a =∈,作出函数()y f x =的图象,由图象可得出方程()0f x =的根,将方程()()()0,3f x a a =∈的根视为直线y a =与函数()y f x =图象交点的横坐标,利用对称性可得出方程()()()0,3f x a a =∈的所有根之和,进而可求出原方程所有实根之和. 【详解】()()()2003f x af x a -=<<Q ,()0f x ∴=或()()03f x a a =<<.方程()()03f x a a =<<的根可视为直线y a =与函数()y f x =图象交点的横坐标, 作出函数()y f x =和直线y a =的图象如下图:由图象可知,关于x 的方程()0f x =的实数根为2-、3.由于函数()22y x =+的图象关于直线2x =-对称,函数3y x =-的图象关于直线3x =对称,关于x 的方程()()03f x a a =<<存在四个实数根1x 、2x 、3x 、4x 如图所示, 且1222+=-x x ,3432x x +=,1234462x x x x ∴+++=-+=, 因此,所求方程的实数根的和为2323-++=. 故答案为:3. 【点睛】本题考查方程的根之和,本质上就是求函数的零点之和,利用图象的对称性求解是解答的关键,考查数形结合思想的应用,属于中等题.14.1【解析】【分析】根据二次函数的值域为结合二次函数的性质列出不等式组即可求解【详解】由题意函数的值域为所以满足解得即实数的值为1故答案为:1【点睛】本题主要考查了二次函数的图象与性质的应用其中解答中解析:1 【解析】 【分析】根据二次函数的值域为[0,)+∞,结合二次函数的性质,列出不等式组,即可求解. 【详解】由题意,函数()22f x mx x m =-+的值域为[0,)+∞,所以满足2440m m ⎧∆=-=⎨>⎩,解得1m =.即实数m 的值为1. 故答案为:1. 【点睛】本题主要考查了二次函数的图象与性质的应用,其中解答中熟记二次函数的图象与性质是解答的关键,着重考查了推理与计算能力,属于基础题.15.【解析】【分析】令可化为进而求有两个正根即可【详解】令则方程化为:方程有两个根即有两个正根解得:故答案为:【点睛】本题考查复合函数所对应的方程根的问题关键换元法的使用难度一般解析:1(,0)4-【解析】 【分析】令20x t =>,42x x a -=,可化为20t t a --=,进而求20t t a --=有两个正根即可. 【详解】令20x t =>,则方程化为:20t t a --=Q 方程42x x a -=有两个根,即20t t a --=有两个正根,1212140100a x x x x a ∆=+>⎧⎪∴+=>⎨⎪⋅=->⎩,解得:104a -<<.故答案为: 1(,0)4-. 【点睛】本题考查复合函数所对应的方程根的问题,关键换元法的使用,难度一般.16.【解析】【分析】先求出函数的定义域找出内外函数根据同增异减即可求出【详解】由解得或所以函数的定义域为令则函数在上单调递减在上单调递增又为增函数则根据同增异减得函数单调递减区间为【点睛】复合函数法:复 解析:(,1)-∞-【解析】 【分析】先求出函数的定义域,找出内外函数,根据同增异减即可求出.【详解】由2560x x -->,解得6x >或1x <-,所以函数22log (56)y x x =--的定义域为(,1)(6,)-∞-+∞U .令256u x x =--,则函数256u x x =--在(),1-∞-上单调递减,在()6,+∞上单调递增,又2log y u =为增函数,则根据同增异减得,函数22log (56)y x x =--单调递减区间为(,1)-∞-.【点睛】复合函数法:复合函数[]()y f g x =的单调性规律是“同则增,异则减”,即()y f u =与()u g x =若具有相同的单调性,则[]()y f g x =为增函数,若具有不同的单调性,则[]()y f g x =必为减函数.17.【解析】根据题意当时为奇函数则故答案为解析:15-【解析】根据题意,当0x <时,()()(),f x g x f x =为奇函数,()()()()()()()()()211113(323)15f g f f f f f f f -=-=-=-=-=-+⨯=-,则 故答案为15-.18.【解析】【分析】根据整个函数值域为R 及分段函数右段的值域可判断出左段的函数为单调性递增且最大值大于等于1即可求得的取值范围【详解】当时此时值域为若值域为则当时为单调递增函数且最大值需大于等于1即解得 解析:10,2⎡⎫⎪⎢⎣⎭【解析】【分析】根据整个函数值域为R 及分段函数右段的值域,可判断出左段的函数为单调性递增,且最大值大于等于1,即可求得a 的取值范围.【详解】当1x ≥时,()12x f x -=,此时值域为[)1,+∞ 若值域为R ,则当1x <时.()()123f x a x a =-+为单调递增函数,且最大值需大于等于1 即1201231a a a ->⎧⎨-+≥⎩,解得102a ≤< 故答案为:10,2⎡⎫⎪⎢⎣⎭【点睛】本题考查了分段函数值域的关系及判断,指数函数的性质与一次函数性质的应用,属于中档题.19.4【解析】【分析】设则是奇函数设出的最大值则最小值为求出的最大值与最小值的和即可【详解】∵函数∴设则∴是奇函数设的最大值根据奇函数图象关于原点对称的性质∴的最小值为又∴故答案为:4【点睛】本题主要考 解析:4【解析】【分析】设()2sin 1x g x x x =++,则()g x 是奇函数,设出()g x 的最大值M ,则最小值为M -,求出2sin 21=+++x y x x 的最大值与最小值的和即可. 【详解】 ∵函数2sin 21=+++x y x x , ∴设()2sin 1x g x x x =++,则()()2sin 1x g x x g x x --=-=-+, ∴()g x 是奇函数,设()g x 的最大值M ,根据奇函数图象关于原点对称的性质,∴()g x 的最小值为M -,又()max max 22g x y M =+=+,()min min 22g x y M =+=-,∴max min 224y y M M +=++-=,故答案为:4.【点睛】本题主要考查了函数的奇偶性与最值的应用问题,求出()2sin 1x g x x x =++的奇偶性以及最值是解题的关键,属于中档题. 20.【解析】若对任意的实数都有成立则函数在上为减函数∵函数故计算得出:点睛:已知函数的单调性确定参数的值或范围要注意以下两点:(1)若函数在区间上单调则该函数在此区间的任意子区间上也是单调的;(2)分段 解析:13,8⎛⎤-∞ ⎥⎝⎦ 【解析】若对任意的实数12x x ≠都有1212()()0f x f x x x -<-成立, 则函数()f x 在R 上为减函数, ∵函数(2),2()11,22x a x x f x x -≥⎧⎪=⎨⎛⎫-< ⎪⎪⎝⎭⎩,故22012(2)12a a -<⎧⎪⎨⎛⎫-≤- ⎪⎪⎝⎭⎩, 计算得出:13,8a ⎛⎤∈-∞ ⎥⎝⎦. 点睛:已知函数的单调性确定参数的值或范围要注意以下两点:(1)若函数在区间[,]a b 上单调,则该函数在此区间的任意子区间上也是单调的;(2)分段函数的单调性,除注意各段的单调性外,还要注意衔接点的取值;(3)复合函数的单调性,不仅要注意内外函数单调性对应关系,而且要注意内外函数对应自变量取值范围.三、解答题21.(1)()2,2-;(2)证明见解析;(3)两个,理由见解析.【解析】【分析】(1)根据对数函数的真数大于0,列出不等式组求出x 的取值范围即可;(2)根据奇偶性的定义即可证明函数()f x 是定义域上的偶函数.(3)将方程()f x x =变形为()22log 4x x -=,即242x x -=,设()242x g x x =--(22x -≤≤),再根据零点存在性定理即可判断.【详解】解:(1) ()()()22log 2log 2f x x x =-++Q2020x x ->⎧∴⎨+>⎩,解得22x -<<,即函数()f x 的定义域为()2,2-; (2)证明:∵对定义域()2,2-中的任意x ,都有()()()()22log 2log 2f x x x f x -=++-=∴函数()f x 为偶函数;(3)方程()f x x =有两个实数根,理由如下:易知方程()f x x =的根在()2,2-内,方程()f x x =可同解变形为()22log 4x x -=,即242x x -= 设()242x g x x =--(22x -≤≤).当[]2,0x ∈-时,()g x 为增函数,且()()20120g g -⋅=-<,则在()2,0-内,函数()g x 有唯一零点,方程()f x x =有唯一实根,又因为偶函数,在()0,2内,函数()g x 也有唯一零点,方程()f x x =有唯一实根, 所以原方程有两个实数根.【点睛】本题考查函数的定义域和奇偶性的应用问题,函数的零点,函数方程思想,属于基础题.22.(1)2a =(2)17,8⎛⎫-∞-⎪⎝⎭ 【解析】【分析】(1)依题意代数求值即可;(2)设()()121log 1022x g x x ⎛⎫=-- ⎪⎝⎭,题设条件可转化为()g x m >在[]3,4x ∈上恒成立,因此,求出()g x 的最小值即可得出结论.【详解】(1)()32f =-Q ,()12log 1032a ∴-=-, 即211032a -⎛⎫-= ⎪⎝⎭,解得2a =; (2)设()()121log 1022xg x x ⎛⎫=-- ⎪⎝⎭, 题设不等式可转化为()g x m >在[]3,4x ∈上恒成立, ()g x Q 在[]3,4上为增函数,()31min2117(3)log (106)28g x g ⎛⎫∴==--=- ⎪⎝⎭, 178m ∴<-, m ∴的取值范围为17,8⎛⎫-∞- ⎪⎝⎭. 【点睛】本题考查函数性质的综合应用,属于中档题.在解决不等式恒成立问题时,常分离参数,将其转化为最值问题解决.23.(Ⅰ)2()f x x =(Ⅱ)3,4⎛⎫-∞- ⎪⎝⎭【解析】【分析】(I )根据幂函数的奇偶性和在区间(0,)+∞上的单调性,求得m 的值,进而求得()f x 的解析式.(II )先求得()g x 的解析式,由不等式()0<g x 分离常数λ得到122x x λ<-,结合函数122x y x =-在区间[]1,2上的单调性,求得λ的取值范围. 【详解】 (Ⅰ)∵幂函数35()()m f x x m -+=∈N 为偶函数,且在区间(0,)+∞上单调递增, 350m ∴-+>,且35m -+为偶数.又N m ∈,解得1m =,2()f x x ∴=.(Ⅱ)由(Ⅰ)可知2()()2121g x f x x x x λλ=+-=+-.当[1,2]x ∈时,由()0<g x 得122x x λ<-. 易知函数122x y x =-在[1,2]上单调递减, min 1123222224x x λ⎛⎫∴<-=-=- ⎪⨯⎝⎭. ∴实数λ的取值范围是3,4⎛⎫-∞-⎪⎝⎭. 【点睛】本小题主要考查幂函数的单调性和奇偶性,考查不等式在给定区间上恒成立问题的求解策略,属于中档题.24.(1)答案见解析;(2)0a <或1a >.【解析】试题分析:(1)利用赋值法计算可得()()02,14f f =--=-,设1x <,则21x ->,利用()22f =拆项:()()22f f x x =-+即可证得:当1x <时,()0f x <;(2)结合(1)的结论可证得()f x 是增函数,据此脱去f 符号,原问题转化为()()2222122a a x a x ----+<-在[]1,3上恒成立,分离参数有:222234x x a a x x +-->-恒成立,结合基本不等式的结论可得实数a 的取值范围是0a <或1a >.试题解析:(1)令,得,令, 得, 令,得,设,则, 因为, 所以; (2)设,, 因为所以, 所以为增函数, 所以, 即, 上式等价于对任意恒成立, 因为,所以 上式等价于对任意恒成立, 设,(时取等), 所以, 解得或. 25.(1) ()45100x ,∈时,公交群体的人均通勤时间少于自驾群体的人均通勤时间;(2)见解析.【解析】【分析】(1)由题意知求出f (x )>40时x 的取值范围即可;(2)分段求出g (x )的解析式,判断g (x )的单调性,再说明其实际意义.【详解】(1)由题意知,当30100x <<时,()180029040f x x x=+->, 即2659000x x -+>,解得20x <或45x >,∴()45100x ∈,时,公交群体的人均通勤时间少于自驾群体的人均通勤时间; (2)当030x <≤时,()()30%401%4010x g x x x =⋅+-=-; 当30100x <<时, ()()218013290%401%585010x g x x x x x x ⎛⎫=+-⋅+-=-+ ⎪⎝⎭;∴()2401013585010x g x x x ⎧-⎪⎪=⎨⎪-+⎪⎩; 当032.5x <<时,()g x 单调递减;当32.5100x <<时,()g x 单调递增;说明该地上班族S 中有小于32.5%的人自驾时,人均通勤时间是递减的;有大于32.5%的人自驾时,人均通勤时间是递增的;当自驾人数为32.5%时,人均通勤时间最少.【点睛】本题考查了分段函数的应用问题,也考查了分类讨论与分析问题、解决问题的能力.26.(1)2m >;(2)m <【解析】【分析】(1)首先>0∆,保证有两个不等实根,又121=x x ,两根同号,因此只要两根的和也大于0,则满足题意;(2)当[1,2]x ∈时,()1f x >-恒成立,转化为2m x x<+在[1,2]x ∈上恒成立即可 ,只要求得2x x+在[1,2]上的最小值即可. 【详解】 (1)由题知210x mx -+=有两个不等正根,则2121240010m x x m x x ⎧∆=->⎪+=>⎨⎪=>⎩,∴2m >;(2)211x mx -+>-恒成立即22mx x <+恒成立,又[1,2]x ∈,故2m x x <+在[1,2]x ∈上恒成立即可 , 又2y x x=+在[1,2]x ∈上的值域为 ,故m <【点睛】本题考查一元二次方程根的分布,考查不等式恒成立问题.一元二次方程根的分布可结合二次函数图象得出其条件,不等式恒成立可采用分离参数法,把问题转化为求函数的最值.。
湖北省武汉市光谷第一中学2019-2020学年高一数学理上学期期末试题含解析

湖北省武汉市光谷第一中学2019-2020学年高一数学理上学期期末试题含解析一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的1. 已知集合A=,B=,则()A. B. C. D.参考答案:A略2. 两条平行线l1:3x-4y-1=0与l2:6x-8y-7=0间的距离为()A、 B、 C、 D、1参考答案:A3. 已知,,则=( )A. B. C. D.参考答案:D略4. 已知,且,那么的值是()A. B. C. D.参考答案:A略5. 在△ABC中,角A,B,C所对的边分别是a,b,c,,,,则B=()A. B=30°或B=150°B. B=150°C. B=30°D. B=60°参考答案:C【分析】将已知代入正弦定理可得,根据,由三角形中大边对大角可得:,即可求得.【详解】解:,,由正弦定理得:故选C.6. 若,则等于()A. B. C.3 D.参考答案:略7. 从存放号码分别为1,2,…,10的卡片的盒子里,有放回地取100次,每次取一张卡片,并记下号码,统计结果如下:A.0.53 B.0.5 C.0.47 D.0.37参考答案:A取到号码为奇数的卡片共有13+5+6+18+11=53(次),所以取到号码为奇数的频率为=0.53.8. 己知全集,集合,,则= ( )A. (0,2) B. (0,2] C. [0,2]D. [0,2)参考答案:D9. (5分)已知函数f(x)是定义在区间上的奇函数,则实数a的值为()A. 1 B.C.0 D.不确定参考答案:考点:函数奇偶性的性质.专题:函数的性质及应用.分析:根据奇偶性函数的定义域特征,得到区间端点满足的条件,得到本题结论.解答:∵函数f(x)为奇函数,∴函数f(x)的定义域关于(0,0)对称.∵函数f(x)定义在区间,∴3a﹣5=﹣2a,∴a=1.故选:A.点评:本题考查了奇偶性函数的特征,本题难度不大,属于基础题.10. 设,则的值为()A.0 B.1 C.2D.2参考答案:C二、填空题:本大题共7小题,每小题4分,共28分11. 已知f(x+1)=2x﹣1,则f(x)= .参考答案:2x﹣3【考点】函数解析式的求解及常用方法.【分析】直接利用配凑法求解函数的解析式即可.【解答】解:f(x+1)=2x﹣1=2(x+1)﹣3,则f(x)=2x﹣3.故答案为:2x﹣3.12. 若函数f(x)=a x(0<a≠1)在[﹣1,2]上的最大值为4,最小值为m,则m= .参考答案:2或【考点】指数函数的图象与性质.【专题】函数思想;综合法;函数的性质及应用.【分析】按a>1,0<a<1两种情况进行讨论:借助f(x)的单调性及最大值先求出a 值,再求出其最小值即可.【解答】解:①当a>1时,f(x)在[﹣1,2]上单调递增,则f(x)的最大值为f(2)=a2=4,解得:a=2,最小值m=f(﹣1)==;②当0<a<1时,f(x)在[﹣1,2]上单调递减,则f(x)的最大值为f(﹣1)==4,解得a=,此时最小值m=f(2)=a2=,故答案为:2或.【点评】本题考查指数函数的单调性及其应用,考查分类讨论思想,对指数函数f(x)=a x(a>0,a≠1),当a>1时f(x)递增;当0<a<1时f(x)递减.13. 定义在R上的函数f(x)既是偶函数又是周期函数,若f(x)的最小正周期是π,且当x∈[0,]时,f(x)=sinx,则f()的值为.参考答案:【考点】H1:三角函数的周期性及其求法.【分析】由题意利用函数的周期性偶函数,转化f()为f(),即可求出它的值.【解答】解:定义在R上的函数f(x)既是偶函数又是周期函数,若f(x)的最小正周期是π,且当x∈[0,]时,f(x)=sinx,所以f()=f(﹣)=f()=sin=.故答案为:.14. 函数的图像恒经过点.参考答案:(1,2)15. 函数f(x)=2|x|+ax为偶函数,则实数a的值为.参考答案:【考点】函数奇偶性的性质.【分析】根据函数奇偶性的定义建立方程关系进行求解即可.【解答】解:∵f(x)=2|x|+ax为偶函数,∴f(﹣x)=f(x),即2|﹣x|﹣ax=2|x|+ax,则a=0,故答案为:0.【点评】本题主要考查函数奇偶性的应用,根据条件建立方程关系是解决本题的关键,比较基础.16. 若为正实数,且满足,则的最大值等于.参考答案:217. 已知函数是定义在上的偶函数,且当时,,那么当时,函数的解析式是______________.参考答案:考点:函数的奇偶性.三、解答题:本大题共5小题,共72分。
湖北省武汉市武昌区2019-2020学年高一上学期期末考试数学试题及答案
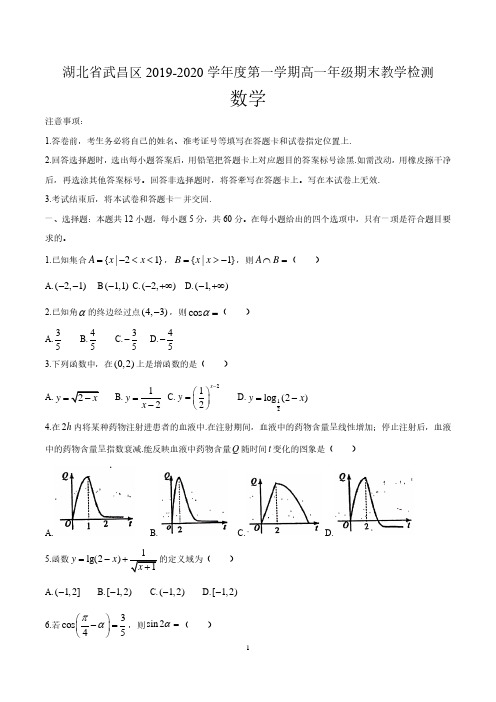
(2)已知
3 tan
=
−2
tan
+
4
,求
cos
2
+
4
的值.
20.(本题满分 12 分)
已知函数 f (x) = −x2 + 2x + 3 + x
(1)求 f ( x) 的定义域;
(2)求 f ( x) 的最小值.
21.(本题满分 12 分)
( ) 已知函数 f (x) = log4 4x +1 + kx(k R) 是偶函数.
(1)求 k 的值;
(2)若方程
f
(x)
=
log4
m 2x
−1 有解,求实数 m
的取值范围.
22.(本题满分 12 分)
用清水洗一堆蔬菜上残留的农药,用水越多,洗掉的农药量也越多,但总还有农药残留在蔬菜上现作如下假
7.已知 a = log0.1 0.2 , b = log1.1 0.2, c = 1.10.2 ,则 a , b , c 的大小关系为( )
A. a b c B. a c b C. c b a D. c a b
8.在同一直角坐标系中,分别作函数
y
=
1 ax
,
y
= loga
lg(2 − x) + 1 的定义域为( ) x +1
A. (−1, 2] B. [−1, 2) C. (−1, 2) D.[−1, 2)
6.若
cos
4
−
=
3 5
(完整版)湖北省武汉市高一数学上册期末考试题

武汉二中2015-2016学年度上学期期末考试高一数学试卷命题学校:武汉二中考试时间:2016年1月27日上午8:00-10:00 试卷满分:150分一、选填题(每小题5分,共60分)1. 已知全集{}1,2,3,4U =,集合{}=12A ,,{}=23B ,,则()=UA B( )A.{}134,,B.{}34,C. {}3D. {}42. 函数y x (1-x )的定义域为( )A. (0,1)B. [0,1)C. (0,1]D. [0,1]3. 用二分法研究函数53()81f x x x =+-的零点时, 第一次经过计算(0)0f < , (0.5)0f >, 则其中一个零点所在的区间和第二次应计算的函数值分别为 ( )A. (0, 0.5) (0.125)fB. (0.5 , 1) (0.25)fC. (0.5 , 1) (0.75)fD. (0 , 0.5) (0.25)f4. 函数2sin(2),[0,]6y x x ππ=-∈为增函数的区间是( )A.[0,]3πB. 7[,]1212ππC. 5[,]36ππD. 5[,]6ππ 5. 如图, 一个大风车的半径为8 m , 每12 min 旋转一周, 最低点离地面为2 m . 若风车翼片从最低点按逆时针方向开始旋转, 则该翼片的端点P 离地面的距离h (m )与时间t (min )之间的函数关系是( )A. h =8cos π6t +10B. h =-8cos π3t +10C. h =-8sin π6t +10D. h =-8cos π6t +106 . 如图, 在ΔABC 中, AD AB ⊥, 23BC BD =, 1AD =, 则AC AD ⋅= ( )A. 233C.32D.337. 设⎪⎩⎪⎨⎧≤->+-=-6,136),1(log )(63x x x x f x 满足98)(-=n f , 则=+)4(n f( )A. 2B. -2C. 1D. -1A OB C8. 如图, 平面内有三个向量,,OA OB OC , 其中OA 与OB 的夹角为120︒, OA 与OC 的夹角为30︒, 且3||2,||,||232OA OB OC ===若(,)OC OA OB λμλμ=+∈R , 则 ( )A. 4,2λμ==B. 83,32λμ==C . 42,3λμ== D. 34,23λμ== 9. 要得到sin 2x y =的图像, 只需将cos 24x y π⎛⎫=- ⎪⎝⎭的图像上的所有点( )A. 向右平移π2B. 向左平移π2C.向左平移4πD. 向右平移4π10. 已知向量a =(2,1), b =(1,2), 则|a +λb |(λ∈R )的最小值为( )A.55B. 255C . 355D. 511. 对于函数f (x )=a sin x +bx +c (其中, a , b ∈R , c ∈Z ), 选取a , b , c 的一组值计算f (1)和f (-1), 所得出的正确结果一定不可能是 ( )A. 4和6B. 3和1C. 2和4D. 1和212. 函数y =11-x 的图像与函数2sin (35)y x x π=-≤≤的图像所有交点的横坐标之和等于( ) A. 2 B. 4 C. 6D. 8二 、填空题(每小题5分,共20分) 13. 若ba cb a +===,2,1且ac ⊥则向量a与b的夹角 .14. 方程()()1122log 95log 322x x ---=-+的解为 . 15. 已知函数()sin f x x=. 若存在1x , 2x , ⋅⋅⋅, m x 满足1206m x x x π≤<<⋅⋅⋅<≤, 且()()()()()()1223112m m f x f x f x f x f x f x --+-+⋅⋅⋅+-=(2m ≥, m *∈N ),则m 的最小值为 .16. 在锐角三角形C AB 中, 1tan 2A =, D 为边CB 上的点, D ∆AB 与CD ∆A 的面积分别为2 和4. 过D 作D E ⊥AB 于E , DF C ⊥A 于F ,则D DF E⋅= . 三、解答题(共70分)17. (10分)计算: (1) 已知2sin cos 0αα-=, 求 sin cos sin cos sin cos sin cos αααααααα-+++-的值.(2) 已知cos 534=⎪⎭⎫ ⎝⎛+x π,求xx x x tan 1cos sin sin 23-+的值.18. (12分)已知向量a , b 满足|a |=|b |=1, 且|k a +b |=3|a -k b |(k >0), 令f (k )=a ·b . (1) 求f (k )=a ·b (用k 表示);(2) 当k >0时, f (k )≥x 2-2tx -12对任意的t ∈[-1,1]恒成立, 求实数x 的取值范围.19. (12分)设a ∈R , f (x )=cos x (a sin x -cos x )+cos 2⎪⎭⎫⎝⎛-x 2π满足f ⎪⎭⎫ ⎝⎛-3π=f (0),(1) 求函数f (x )的解析式; (写成形如y =A sin (wx +φ)+B 的形式, w >0)(2) 画出函数在[0,]π的图像; (3)求函数在[4π,2411π]上的最大值和最小值.20. (12分)某影院共有1000个座位, 票价不分等次. 根据该影院的经营经验, 当每张标价不超过10元时, 票可全部售出, 当每张票价高于10元时, 每提高1元, 将有30张票不能售出, 为了获得更好的收益, 需给影院一个合适的票价, 符合的基本条件是: ①为方便找零和算帐, 票价定为1元的整数倍; ②影院放映一场电影的成本费用支出为5750元, 票房收入必须高于成本支出. 用x (元)表示每张票价, 用y (元)表示该影院放映一场的净收入(除去成本费用支出后的收入).(1) 把y 表示成x 的函数, 并求其定义域;(2) 试问在符合基本条件的前提下, 每张票价定为多少元时, 放映一场的净收入最多?21. (12分)在平面直角坐标系中, O 为坐标原点, A 、B 、C 三点满足1233OC OA OB =+(1) 求证: A 、B 、C 三点共线(2) 已知()()1,cos 1sin ,cos ,0,2A x B x x x π⎡⎤+∈⎢⎥⎣⎦、, f (x )=||3222AB m OC OA ⋅⎪⎭⎫ ⎝⎛+-⋅ 的最小值为12, 求实数m 的值.22. (12分)在△ABC 中.(1)||2,|AC AB AD BC D BAD DAC ︒==⊥∠=∠=︒于,2,45,60AC AB AD BC D BAD DAC ︒==⊥∠=∠=︒于,, 求BD ·AC , BA ·AC .(2) 如果(1)的条件下△ABC 中, PQ 是以A 为圆心, 2为半径的圆的直径, 求CQ BP ⋅的最大值, 最小值, 并指出取最大值, 最小值时向量PQ 与BC 的夹角.武汉二中2015-2016学年度上学期期末考试高一数学试卷参考答案题号 1 2 3 4 5 6 7 8 9 10 11 12答案 D B D C D A B C A C D D13、 120° 14、 2 15、 8 16、 -151617. (10分) (1) -310 (6分) (2)6027 (6分)18 . (12分) 解:(1)由题设得|a |2=|b |2=1, 对|k a +b |=3|a -k b|两边平方得k 2a 2+2k a ·b +b 2=3(a 2-2k a ·b +k 2b 2), 整理易得f (k )=a ·b=k 2+14k(k >0).---------------------------------------------6分(2)f (k )=k 2+14k =k 4+14k ≥12, 当且仅当k =1时取等号.欲使f (k )≥x 2-2tx -12对任意的t ∈[-1,1]恒成立, 等价于12≥x 2-2tx-12,即g (t )=2xt -x 2+1≥0在[-1,1]上恒成立, 而g (t )在[-1,1]上为单调函数或常函数,所以⎩⎪⎨⎪⎧g (1)=2x -x 2+1≥0g (-1)=-2x -x 2+1≥0, 解得1-2≤x ≤2-1. 故实数x的取值范围为[1-2,2-1].-------------------------------------12分19. (12分) (1) 解:22()sin cos cos sin f x a x x x x =-+sin 2cos 2.2ax x =-由31()(0)1,2 3.3222a f f a π-=-⋅+=-=得解得因此()3sin 2cos 22sin(2).6f x x x x π=-=----------------------4分 (2)---------------------8分(3) 当[,],2[,],()43632x x f x πππππ∈-∈时为增函数,当113[,],2[,],()324624x x f x πππππ∈-∈时为减函数,所以11()[,]() 2.443f x f πππ=在上的最大值为又因为11()()424f f ππ==故11()[,]424f x ππ在上的最小值为11()24f π=-----------------12分20. (12分) 解:(1)由题意知当x ≤10时, y =1000x -5750,当x >10时, y =[1000-30(x -10)]x -5750= -30x 2+1300x-57502100057500:301300575005.75x x x x ->⎧⎨-+->⎩<<=解之得又x ∈N ,∴6≤x ≤38 ∴所求表达式为210005750(610,)3013005750(1038,){638,}x x x N y x x x x N x x x N -≤≤∈⎧=⎨-+-<≤∈⎩≤≤∈定义域为------------------------------------6分(2)当425010,),106(57501000max ==∈≤≤-=y x N x x x y 时时 当23013005750(1038,),y x x x x N =-+-<≤∈时2max 652500030(),22833033y x x y =--+==时 所以每张票价定为22元时净收入最多。
2019-2020学年人教A版湖北省武汉市武昌区高一第一学期期末数学试卷 含解析
2019-2020学年高一第一学期期末数学试卷一、选择题1.已知集合A={x|﹣2<x<1},B={x|x>﹣1},则A∩B=()A..(﹣2,﹣1)B.(﹣1,1)C..(﹣2,+∞)D..(﹣1,+∞)2.已知角α的终边经过点(4,﹣3),则cosα等于()A.B.C.﹣D.﹣3.下列函数在(0,2)上是增函数的是()A.B.C.D.4.在2h内将某种药物注射进患者的血液中.在注射期间,血液中的药物含量呈线性增加;停止注射后,血液中的药物含量呈指数衰减.能反映血液中药物含量Q随时间t变化的图象是()A.B.C.D.5.函数的定义域为()A.(﹣1,2] B.[﹣1,2)C.(﹣1,2)D.[﹣1,2)6.若cos(﹣α)=,则sin2α=()A.B.C.﹣D.﹣7.已知a=log0.10.2,b=log1.10.2,c=1.10.2,则a,b,c的大小关系为()A.a>b>c B.a>c>b C.c>b>a D.c>a>b8.在同一直角坐标系中,分别作函数,(a>0,且a≠1)的图象如下,其中,可能正确的个数()A.1 B.2 C.3 D.49.已知函数,将y=f(x)的图象向左平移个单位长度,再向下平移2个单位长度,得到y=g(x)的图象,则g(x)在上的最小值为()A.﹣1 B.﹣2 C.﹣3 D.﹣410.已知m=a++1(a>0),,则m,n之间的大小关系是()A.m>n B.m<n C.m=n D.m≤n11.设函数,已知f(x)在[0,2π]有且仅有5个零点.给出下述三个结论:①y=f(x)+1在(0,2π)有且仅有2个零点;②f(x)在单调递增;③ω的取值范围是其中,所有正确结论的编号是()A.①②B.①③C.②③D.①②③12.已知函数f(x)=ax2﹣bx+c(a<b<c)有两个零点﹣1和m,若存在实数x0,使得f (x0)>0,则实数m的值可能是()A.x0﹣2 B.C.D.x0+3二、填空题13.已知集合A={x|﹣a≤x≤a},B={x|x≤2},若A⊆B,则实数a的取值范围是.14.函数f(x)=3sin(x+)+cos2x的最大值为.15.已知函数在上是增函数,则ω的最大值是.16.已知函数f(x)=x|x|.若对任意的x≥1有f(x+m)+mf(x)<0,则实数m的取值范围是.三、解答题17.给定函数f(x)=x+1,g(x)=(x+1)2,x∈R.(1)在同一坐标系中画出函数f(x),g(x)的图象;(2)对任意实数x,用M(x)表示f(x),g(x)中的较大者,记为M(x)=max{f (x),g(x)}.请分别用图象法和解析法表示函数M(x).18.已知函数f(x)=sinωx cosωx﹣sin2ωx(ω>0)的最小正周期为π.(1)求ω的值;(2)求f(x)在区间[﹣π,0]上的最小值.19.(1)求4cos50°﹣tan40°的值;(2)已知,求的值.20.已知函数.(1)求f(x)的定义域;(2)求f(x)的最小值.21.已知函数为偶函数.(1)求k的值;(2)若方程有解,求实数m的范围.22.用清水洗一堆蔬菜上残留的农药,用水越多,洗掉的农药量也越多,但总还有农药残留在蔬菜上现作如下假定:用x单位的水清洗次后,蔬菜上残留的农药量与本次清洗前残留的农药量之比为函数.(1)(ⅰ)试解释f(0)与f(1)的实际意义;(ⅱ)写出函数f(x)应该满足的条件和具有的性质;(2)现有a(a>0)单位量的水,可以清洗一次,也可以把水平均分成2份后清洗两次.哪种方案清洗后蔬菜上残留的农药量比较少?请说明理由.参考答案一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合A={x|﹣2<x<1},B={x|x>﹣1},则A∩B=()A..(﹣2,﹣1)B.(﹣1,1)C..(﹣2,+∞)D..(﹣1,+∞)【分析】进行交集的运算即可.解:∵A={x|﹣2<x<1},B={x|x>﹣1},∴A∩B=(﹣1,1).故选:B.2.已知角α的终边经过点(4,﹣3),则cosα等于()A.B.C.﹣D.﹣【分析】由条件利用任意角的三角函数的定义,求得cosα的值.解:∵角α的终边经过点(4,﹣3),∴x=4,y=﹣3,r=|OP|=5,则cosα==,故选:A.3.下列函数在(0,2)上是增函数的是()A.B.C.D.【分析】根据常见函数的单调性的性质分别判断即可.解:对于A,函数在(0,2)递减,不合题意;对于B,函数在(0,2)递减,不合题意;对于C,函数在(0,2)递减,不合题意;对于D,函数在(0,2)递增,符合题意;故选:D.4.在2h内将某种药物注射进患者的血液中.在注射期间,血液中的药物含量呈线性增加;停止注射后,血液中的药物含量呈指数衰减.能反映血液中药物含量Q随时间t变化的图象是()A.B.C.D.【分析】根据在注射期间,血液中的药物含量呈线性增加;停止注射后,血液中的药物含量呈指数衰减即可得出.解:在注射期间,血液中的药物含量呈线性增加,则第一段图象为直线,且为增函数,排除A,D,停止注射后,血液中的药物含量呈指数衰减.排除C.能反映血液中药物含量Q随时间t变化的图象是B.故选:B.5.函数的定义域为()A.(﹣1,2] B.[﹣1,2)C.(﹣1,2)D.[﹣1,2)【分析】由对数式的真数大于0,分母中根式内部的代数式大于0联立不等式组求解.解:由,解得﹣1<x<2.∴函数的定义域为(﹣1,2).故选:C.6.若cos(﹣α)=,则sin2α=()A.B.C.﹣D.﹣【分析】法1°:利用诱导公式化sin2α=cos(﹣2α),再利用二倍角的余弦可得答案.法°:利用余弦二倍角公式将左边展开,可以得sinα+cosα的值,再平方,即得sin2α的值解:法1°:∵cos(﹣α)=,∴sin2α=cos(﹣2α)=cos2(﹣α)=2cos2(﹣α)﹣1=2×﹣1=﹣,法2°:∵cos(﹣α)=(sinα+cosα)=,∴(1+sin2α)=,∴sin2α=2×﹣1=﹣,故选:D.7.已知a=log0.10.2,b=log1.10.2,c=1.10.2,则a,b,c的大小关系为()A.a>b>c B.a>c>b C.c>b>a D.c>a>b【分析】利用指数对数函数的单调性即可得出.解:a=log0.10.2∈(0,1),b=log1.10.2<0,c=1.10.2>1,则a,b,c的大小关系为:c>a>b.故选:D.8.在同一直角坐标系中,分别作函数,(a>0,且a≠1)的图象如下,其中,可能正确的个数()A.1 B.2 C.3 D.4【分析】根据对数函数的指数函数的单调性分别进行讨论即可.解:在对数中a>0且a≠1,对数函数的定义域为(,+∞),则②④不正确,①中,对数函数为减函数,则0<a<1,此时函数y=为增函数,故①正确,③中,对数函数为增函数,则a>1,此时函数y=为减函数,故③正确,故正确的有两个,故选:B.9.已知函数,将y=f(x)的图象向左平移个单位长度,再向下平移2个单位长度,得到y=g(x)的图象,则g(x)在上的最小值为()A.﹣1 B.﹣2 C.﹣3 D.﹣4【分析】直接利用三角函数关系式的恒等变换和正弦型函数的性质的应用求出结果.解:知函数=,把图象向左平移个单位长度,再向下平移2个单位长度,得到y=g(x)=的图象,由于x,所以.故.所以函数的最小值为﹣3.故选:C.10.已知m=a++1(a>0),,则m,n之间的大小关系是()A.m>n B.m<n C.m=n D.m≤n【分析】本题运用均值不等式和对数函数的性质分别得到m、n的取值范围,即可判断m,n之间的大小关系.解:由题意,可知m=a++1≥2+1=3,当且仅当a=,即a=1时,等号成立;又x>,根据对数函数性质,可得n=<=3,∴m≥3>n,即m>n.故选:A.11.设函数,已知f(x)在[0,2π]有且仅有5个零点.给出下述三个结论:①y=f(x)+1在(0,2π)有且仅有2个零点;②f(x)在单调递增;③ω的取值范围是其中,所有正确结论的编号是()A.①②B.①③C.②③D.①②③【分析】先通过f(x)在[0,2π]有且仅有5个零点,来确定a的取值范围,再由此判断其他问题的正误.解:当x∈[0,2π]时,,∵f(x)在[0,2π]有且仅有5个零点,∴即,所以③正确;①当<6π即时,函数y=f(x)+1在(0,2π)上有3个零点,即①错误;②当x∈时,,若f(x)在单调递增,则即,∵,∴符合题意,即②正确;所以正确的有②③,故选:C.12.已知函数f(x)=ax2﹣bx+c(a<b<c)有两个零点﹣1和m,若存在实数x0,使得f (x0)>0,则实数m的值可能是()A.x0﹣2 B.C.D.x0+3【分析】由题意可得a<b<c,则a<0,c>0,依题意可得:﹣<<1,然后结合根的对称性分析得答案.解:∵﹣1是函数f(x)=ax2﹣bx+c的一个零点,∴a+b+c=0,∵a<b<c,则a<0,c>0,∵﹣1×m=<0,∴m>0.由a<b,a<0,得<1①,由0=a+b+c>a+b+b=a+2b,得﹣<,即>﹣②,由①②得:﹣<<1.函数f(x)=ax2﹣bx+c的图象是开口向下的抛物线,其对称轴方程为x=,则﹣<<.∴零点﹣1到对称轴的距离d∈(,),另一零点为m>0,∴m﹣(﹣1)=m+1=2d∈(,3),因为f(x0)>0,所以x0∈(﹣1,m),故0<m﹣x0<(2d)min,∴x0<m+x0,综合四个选项,实数m的值可能是+x0.故选:C.二、填空题:本题共4小题,每小题5分,共20分.13.已知集合A={x|﹣a≤x≤a},B={x|x≤2},若A⊆B,则实数a的取值范围是(﹣∞,2] .【分析】直接利用A⊆B即可求解.解:∵集合A={x|﹣a≤x≤a},B={x|x≤2},且A⊆B,∴a≤2,∴实数a的取值范围是:(﹣∞,2],故答案为:(﹣∞,2].14.函数f(x)=3sin(x+)+cos2x的最大值为 4 .【分析】化简函数为cos x的二次函数,根据cos x的范围求得f(x)的最大值.解:∵f(x)=3sin(x+)+cos2x=3cos x+2cos2x﹣1=2(cos x+)2﹣,∵cos x∈[﹣1,1],∴在cos x=1时,f(x)取得最大值为2×(1+)2﹣=4,故答案为:4.15.已知函数在上是增函数,则ω的最大值是2 .【分析】结合正弦函数的性质先求出函数的单调递增区间,然后结合已知区间递增可建立不等式可求.解:由ωx+可得,,故函数的单调递增区间为(﹣,),又f(x)在(0,)上单调递增,故,解可得,0<ω≤2即ω的最大值为2.故答案为:216.已知函数f(x)=x|x|.若对任意的x≥1有f(x+m)+mf(x)<0,则实数m的取值范围是(﹣∞,﹣1] .【分析】讨论当m≥0时,不等式显然不成立;当m=﹣1时,恒成立;当m<﹣1时,去绝对值,由二次函数的对称轴和区间的关系,运用单调性可得恒成立;当﹣1<m<0时,不等式不恒成立.解:由f(m+x)+mf(x)<0得:(x+m)|x+m|+mx2<0,x≥1,当m≥0时,即有(x+m)2+mx2>0,在x≥1恒成立.当m=﹣1时,即有(x﹣1)2﹣x2=1﹣2x<﹣1<0恒成立;当m<﹣1时,﹣m>1,当x≥﹣m>1,即有(x+m)2+mx2=(1+m)x2+2mx+m2,由1+m<0,对称轴为x=﹣<1,则区间[﹣m,+∞)为减区间,即有(1+m)x2+2mx+m2≤m3<0恒成立;当﹣1<m<0时,由x+m>0,可得(x+m)2+mx2<0不恒成立.综上可得当m≤﹣1时,对任意的x≥1有f(x+m)+mf(x)<0恒成立.故答案为:(﹣∞,﹣1].三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.17.给定函数f(x)=x+1,g(x)=(x+1)2,x∈R.(1)在同一坐标系中画出函数f(x),g(x)的图象;(2)对任意实数x,用M(x)表示f(x),g(x)中的较大者,记为M(x)=max{f (x),g(x)}.请分别用图象法和解析法表示函数M(x).【分析】(1)在同一坐标系中画出函数f(x),g(x)的图象(图1).函数M(x)的图象图2.(2)由图1中函数取值情况,结合函数M(x)的定义,可得函数M(x)的图象(图2).由x+1=(x+1)2,解得x,即可得出.解:(1)在同一坐标系中画出函数f(x),g(x)的图象(图1)图1 函数f(x),g(x)的图象图2 函数M(x)的图象(2)由图1中函数取值情况,结合函数M(x)的定义,可得函数M(x)的图象(图2).由x+1=(x+1)2,得x(x+1)=0,解得x=﹣1,或x=0.结合图2,得出函数M(x)=.18.已知函数f(x)=sinωx cosωx﹣sin2ωx(ω>0)的最小正周期为π.(1)求ω的值;(2)求f(x)在区间[﹣π,0]上的最小值.【分析】(1)先结合二倍角公式及辅助角公式对已知函数进行化简,然后结合正弦函数的周期公式即可求解;(2)由已知x的范围,结合正弦函数的性质即可求解函数的最值.解:(1),因为,所以ω=1.(2)由(1)知.因为﹣π≤x≤0,所以.当,即时,f(x)取得最小值.所以f(x)的最小值为.19.(1)求4cos50°﹣tan40°的值;(2)已知,求的值.【分析】(1)利用同角基本关系及二倍角及和差角公式进行化简即可求;(2)先由已知结合两角和的正切公式可求tanα,然后结合二倍角公式及同角基本关系可求.解:(1)=,=.(2)因为,所以tanα=2或.因为,所以,分子分母同除以cos2α,得,将tanα=2或分别代入上式,得.20.已知函数.(1)求f(x)的定义域;(2)求f(x)的最小值.【分析】本题第(1)题根据﹣x2+2x+3≥0即可解得函数f(x)的定义域;第(2)题对f(x)进行变形后运用三角换元法令,将一般函数转化为三角函数求最值问题.解:(1)依题意,由﹣x2+2x+3≥0,解得﹣1≤x≤3.故函数f(x)的定义域为[﹣1,3].(2)由题意,根据,可知(x﹣1)2≤4.令,则,即.∵,∴,∴,∴,故f(x)的最小值为﹣1.21.已知函数为偶函数.(1)求k的值;(2)若方程有解,求实数m的范围.【分析】(1)根据偶函数可知f(x)=f(﹣x),取x=﹣1代入即可求出k的值;(2)问题转化为22x+2x+1﹣m=0有解,令t=2x,则t>0,则t2+t+1﹣m=0有解,从而求出m的范围即可.解:(1)由题意得f(﹣x)=f(x),即log4(4﹣x+1)+k(﹣x)=log4(4x+1)+kx,化简得log4=2kx,从而4(2k+1)x=1,此式在x∈R上恒成立,∴;(2)由(1)若方程有解,则log4(4x+1)=log4(m﹣2x)有解,故22x+2x+1﹣m=0有解,令t=2x,则t>0,则t2+t+1﹣m=0有解,故=m﹣有解,而(t+)2>,故m﹣>,解得:m>1.22.用清水洗一堆蔬菜上残留的农药,用水越多,洗掉的农药量也越多,但总还有农药残留在蔬菜上现作如下假定:用x单位的水清洗次后,蔬菜上残留的农药量与本次清洗前残留的农药量之比为函数.(1)(ⅰ)试解释f(0)与f(1)的实际意义;(ⅱ)写出函数f(x)应该满足的条件和具有的性质;(2)现有a(a>0)单位量的水,可以清洗一次,也可以把水平均分成2份后清洗两次.哪种方案清洗后蔬菜上残留的农药量比较少?请说明理由.【分析】(1)(i)根据函数f(x)的实际意义即可写出,(ii)由题意可得函数f(x)在[0,+∞)上单调递减,并且有0<f(x)≤1;(2)设清洗前蔬菜上的农药量为1,用a单位量的水清洗1次后,残留的农药量为W1,则,如果用单位的水清洗1次,则残留的农药量为,然后再用单位的水清1次后,残留的农药量为,再利用作差法比较即可.解:(1)(ⅰ)f(0)=1,表示没有用水清洗时,蔬菜上的农药量为1,,表示用1个单位的水清洗时,可清除蔬菜上残留的农药的;(ⅱ)函数f(x)在[0,+∞)上单调递减,并且有0<f(x)≤1;(2)设清洗前蔬菜上的农药量为1,用a单位量的水清洗1次后,残留的农药量为W1,则,如果用单位的水清洗1次,则残留的农药量为,然后再用单位的水清1次后,残留的农药量为.由于,所以,W1﹣W2的符号由a2﹣16决定,当a>4时,W1>W2.此时,把a单位的水平均分成2份后,清洗两次,残留的农药量较少;当a=4时,W1=W2.此时,两种清洗方法效果相同;当a<4时,W1<W2.此时,用a单位的水清洗一次,残留的农药量较少.。
湖北省武汉市2020-2021学年高一上学期期末联考数学试卷Word版含解析

湖北省武汉市2020-2021学年高一上学期期末联考数学试卷一、选择题:本大题共12小题,每小题5分,共60分.1.已知全集U={#Ovxv8,xeZ}, A = {2,4,5}, B = {1,3,5,7),则Ac(Q8)=( )A. {2,4)B. {2,4,6}C. {5}D. {6}【答案】A【解析】由题意可得:QB = {2,4,6)•.•A = {245}.•.Ac(q/) = {2,4}故选A2.已知冢函数y = fM得图像过点(2,孝),则/(;)=( )A. ;B.与C. y/2D. 2【答案】D【解析】设某函数y = /(/) = V故选。
3.已知a £(0,与),sin(;r + 2)=手,则cos(a-与)=(A.—立B.正22【答案】B 【解析】•/ s〃7(/r + a =——,..sintz =——— v 72 2(3c 也 cos a — ——=-sin a =—— I 2 ) 2故选54.已知弧度数为2的圆心角所对的弦长也是2,则这个圆心角所对的弧长是( )2A. 2B. ---C. 2sinlD. sin 2sinl【答案】B 【解析】 分析】先由已知条件求出扇形的半径为」一,再结合弧长公式求解即可. sinl【详解】解:设扇形的半径为R, 由弧度数为2的圆心角所对的弦长也是2,可得R = ——,sinl 2由弧长公式可得:这个圆心角所对的弧长是2R =「,sinl故选:B.【点睛】本题考查了扇形的弧长公式,重点考查了运算能力,属基础题.5,函数y = 1lnx + x — 2的零点所在的区间是()2 A.B. (1,2)C. (e ,3)D. (2, e )【答案】BcT^T则。
£【解析】 【分析】应用函数零点存在性定理判断.【详解】易知函数f(X)=!hir + x-2在定义域上连续, 2 且f (1) = -l<0 , f (2) = —In 2>O , f (e) = — +c-2=e- - > 0 ,e e 22 2 2根据函数零点存在性定理,可知零点所在区间为(1,2),故选B.【点睛】本题考查了函数零点的判定定理的应用,判断函数零点所在区间有三种常用方法,①直接法,解 方程判断,②定理法,③图象法.x-5 .x>6)C. 4D. 5【答案】A 【解析】 【分析】 根据自变量范围代入对应解析式,解得结果. 【详解】/(3) = /(3 + 2) = /(5 + 2)=7-5 = 2 故选:A【点睛】本题考查分段函数求值,考查基本分析求解能力,属基础题.\ \7,设/(x) = asinh+Z?sinx_3,若/ + =1,则/ --=( )A. -2B. -5C. -7D. 4【答案】C 【解析】令 g(x) = / (.^) + 3 = osit^x+b sin xg (-x) = -asuv x 一 /? sin x = -g (x)・・・g(x)为奇函数6.已知/(x)h g + 2…<6'则/⑶为( A. 2B. 3g 图+ g1CH 闾+3 + /(一升3 = 0=1【答案】C 【解析】 【分析】去掉绝对值将函数化为分段函数的形式后可得其图象的大体形状.sinx,0<x< —【详解】由题意得丁 =。
新课标人教版高一数学上学期期末试卷及答案

上学期期末考试卷年级:高一科目:英语注意事项: 1.答第I卷前,考生务必将自己的姓名、考生号填写在答题卡上。
2.选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
不能答在本试卷上,否则无效。
(试卷总分:150分;考试时间:120分钟)第I卷第一部分听力(共两节,满分30分)做题时,先将答案标在试卷上。
听力结束后,你将有两分钟的时间将试卷上的答案转涂到答题卡上。
第一节(共5小题;每小题1.5分,满分7.5分)听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有10称钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
例:How much is the shirt?A. £19.15.B. £9.15.C. £9.18.答案是B。
1. What would the man like?A. A cold drink.B. Sleeping pills.C. A cup of coffee.2. Where is the bus station?A. Opposite a stadium.B. Next to a car park.C. On the left of a bridge.3. What does the man dislike about the sweater?A. The price.B. The material.C. The color.4. What does the man think of the course?A. Easy.B. Interesting.C. Difficult.5. What are the speakers mainly talking about?A. A sports game.B. An animal.C. An actor.第二节 (共15小题; 每小题1.5分, 满分22.5分)听下面5段对话或独白。
2022-2023学年湖北省武汉市部分重点中学高一(上)期末数学试卷(含答案解析)
2022-2023学年湖北省武汉市部分重点中学高一(上)期末数学试卷1. 下列四组函数中,同组的两个函数是相同函数的是( )A. y=x与y=(1x)−1 B. y=|x|与y=(√x)2C. y=x与y=e lnxD. y=x与y=√x552. 已知f(x−1)=x2−2x,则f(x)=( )A. x2B. x2−1C. x2+1D. x2+23. 已知幂函数的图象经过点P(16,14),则该幂函数的大致图象是( )A. B.C. D.4. 函数f(x)=lnx−1x的零点所在的大致区间是( )A. (1,2)B. (2,e)C. (e,3)D. (e,+∞)5. 函数f(x)=2x−1,x∈[2,6]的值域是( )A. [13,2] B. [25,2] C. [25,+∞) D. (−∞,2]6. 已知函数f(x)=|log3x|,若a<b,有f(a)=f(b),则a+4b的取值范围是( )A. [2√2,+∞)B. (2√2,+∞)C. [5,+∞)D. (5,+∞)7. 符号[x]表示不超过x的最大整数,如[π]=3,[−1.08]=−2,定义函数{x}=[x]−x,那么下列命题中正确命题的序号是( )①函数{x}的定义域为R,值域为[−1,0];②方程{x}=−12有无数解;③函数{x}是周期函数;④函数{x}是减函数;A. ①②B. ②③C. ③④D. ①④8. 函数f(x)={log 2x (x >0)−√−x (x ≤0)与g(x)=|x +a|+1的图象上存在关于y 轴对称的点,则实数a 的取值范围是( )A. RB. (−∞,−2]C. [2,+∞)D. ⌀9. 设f(x)是定义在R 上的奇函数,且f(x)在(0,+∞)上单调递减,f(−6)=0,则( ) A. f(x)在(−∞,0)上单调递减 B. f(8)<0C. 不等式f(x)>0的解集为(−∞,−6)∪(0,6)D. f(x)的图象与x 轴只有2个交点10. 已知函数f(x)=sin(2x +φ)(0<φ<π)的图象关于直线x =−π3对称,则( ) A. φ=π6 B. f(5π12−x)+f(5π12+x)=0 C. f(π7)=f(4π21)D. f(x)在区间(0,π4)上单调递增11. 已知函数f(x)=log 3(ax 2+bx +c),以下说法正确的有( ) A. 若y =f(x)的定义域是(−1,3),则a >0 B. 若y =f(x)的定义域是R ,则a >0 C. 若f(−x)=f(1+x)恒成立,则a +b =0 D. 若a <0,则y =f(x)的值域不可能是R12. 已知定义域为(0,+∞)的函数f(x)满足:①对任意x ∈(0,+∞),恒有f(2x)=2f(x)成立;②当x ∈(1,2]时,f(x)=2−x.下列结论正确的是( )A. 对任意m ∈Z ,有f(2m )=0B. 函数f(x)的值域为[0,+∞)C. 存在n ∈Z ,使得f(2n +1)=9D. “函数f(x)在区间(a,b)上单调递减”的充要条件是“存在k ∈Z ,使得(a,b)⊆(2k ,2k+1)”13. 函数f(x)=33x−1+√−4x 2+5x −1的定义域为______.14. 已知函数g(x)=6e x +1+ln(√x 2+1+x),则g(3)+g(−3)=______.15. 已知定义在整数集合Z 上的函数f(x),对任意的x ,y ∈Z ,都有f(x +y)+f(x −y)=4f(x)f(y)且f(1)=14,则f(0)+f(1)+f(2)+…+f(2016)=______.16. 函数f(x)={|log 5(1−x)|(x <1)−(x −2)2+2(x ≥1),若关于x 的方程f(x +1x −2)−t =0恰好有8个不同的实数根,则实数t 的取值范围是______.17. 化简求值:(1)2−12+(−4)0√2+1√2+1−√6−2√5+512;(2)log 327+lg25−7log 73+lg4−log 32⋅log 43.18. 已知α为第三象限角,且f(α)=sin(π2−α)cos(−α)tan(π+α)cos(π−α).(1)化简f(α); (2)若f(α)=2√55,求cosα的值. 19. 已知函数f(x)=√2sin(ωx +φ)(ω>0,|φ|≤π2)的部分图像如图所示.(1)求函数f(x)的解析式;(2)将函数f(x)的图像向左平移π4个单位,再将图像上各点的横坐标伸长到原来的2倍(纵坐标不变)得到函数g(x)的图像,若关于x 的方程g(x)−m =0在区间[0,3π4]上有两个不同的实数解,求实数m 的范围.20. 国家质量监督检验检疫局发布的《车辆驾驶人员血液、呼气酒精含量阀值与检验》标准规定:①车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升,小于80毫克/百毫升为酒后驾驶,酒后驾驶,暂扣驾驶证6个月,并处1000元以上2000元以下罚款.如果此前曾因酒驾被处罚,再次酒后驾驶的,处10日以下拘留,并处1000元以上2000元以下罚款,吊销驾驶证.②血液中的酒精含量大于或等于80毫克/百毫升为醉酒驾车.醉酒驾驶,由公安机关约束至酒醒,吊销其驾驶证,依法追究刑事责任,5年内不得重新取得驾驶证.由检验标准规定可知驾驶人员血液中的酒精含量小于20毫克/百毫升才可以正常驾车上路.经过反复试验,喝一瓶啤酒后酒精在人体血液中的含量变化规律的“散点图”如图,该函数近似模型如下:f(x)={a(x −32)2+47.42,0≤x <254.27⋅e −0.3x+10.18,x ≥2,又已知酒后1小时测得酒精含量值为44.42毫克/百毫升,根据上述条件,解答以下问题:现行的酒驾标准类型血液中酒精含量(mg/ml)酒后驾车20−80醉酒驾车≥80(1)当0≤x<2时,确定f(x)的表达式;(2)喝1瓶啤酒后多长时间后才可以驾车?(时间以整分钟计算)(附参考数据:ln982=6.89,ln5427=8.60,ln0.18=−1.71)21. 已知函数f(x)=log a4x+12x(a>0且a≠1).(1)当a=√2时,求函数f(x)的值域;(2)已知g(x)=x−2√x,若∀x1∈[0,2],∃x2∈[0,4],使得f(x1)−g(x2)≤2,求实数a的取值范围.22. 已知函数f(x)=x+ax(其中a为常数).(1)如果存在x∈[1,2],使得不等式f(2x)<2x−14x −14能成立,求实数a的取值范围;(2)设g(x)=1−x1+x ,是否存在正数a,使得对于区间[−35,0]上的任意三个实数m,n,p,都存在以f[g(m)],f[g(n)],f[g(p)]为边长的三角形?若存在,试求出这样的a的取值范围;若不存在,请说明理由.答案和解析1.【答案】D【解析】解:根据题意,依次分析选项:对于A ,y =x ,其定义域为R ,y =(1x)−1,其定义域为{x|x ≠0},故两个函数不是相同函数; 对于B ,y =|x|,其定义域为R ,y =(√x)2,其定义域为{x|x ≥0},故两个函数不是相同函数; 对于C ,y =x ,其定义域为R ,y =e lnx ,其定义域为{x|x >0},故两个函数不是相同函数; 对于D ,y =x ,其定义域为R ,y =√x 55=x ,其定义域为R ,故两个函数是相同函数; 故选:D.根据题意,依次分析选项中函数是否为相同函数,即可得答案. 本题考查函数的定义,注意函数的解析式,属于基础题.2.【答案】B【解析】解:∵f(x −1)=x 2−2x =(x −1)2−1, ∴f(x)=x 2−1, 故选:B.利用f(x −1)=(x −1)2−1,可求得f(x)的解析式. 本题考查函数的解析式的求解,考查运算能力,属于基础题.3.【答案】A【解析】解:设f(x)=x a , 由题意得f(16)=16a =14, 所以a =−12,f(x)=x−12,结合幂函数的性质可知,f(x)的定义域为(0,+∞),排除选项CD , 因为f(x)在(0,+∞)上单调递减,排除选项B. 故选:A.由已知先求出函数解析式,然后结合幂函数性质检验各选项即可判断. 本题主要考查了幂函数的解析式的求解及幂函数性质的应用,属于基础题.4.【答案】A【解析】解:∵y =lnx 在(0,+∞)上单调递增,y =−1x 在(0,+∞)上单调递增, ∴函数f(x)=lnx −1x 在(0,+∞)上单调递增,又f(1)=ln1−1=−1<0,f(2)=ln2−12=ln2−ln √e >0,∴由零点存在性定理得函数f(x)=lnx −1x 的零点所在的大致区间是(1,2), 故选:A.由题意得函数f(x)=lnx −1x 在(0,+∞)上单调递增,根据函数零点的判定定理,即可得出答案. 本题考查函数零点的判定定理,考查转化思想,考查逻辑推理能力和运算能力,属于基础题.5.【答案】B【解析】解:因为f(x)=2x−1在[2,6]上单调递减, 故当x =2时,函数取得最大值2,当x =6时函数取得最小值25. 故选:B.由已知结合函数的单调性即可求解函数的值域.本题主要考查了函数的单调性在函数值域求解中的应用,属于基础题.6.【答案】D【解析】解:因为f(x))=|log 3x|,如图,0<a <b ,且f(a)=f(b),所以−log 3a =log 3b 即log 3a +log 3b =log 3ab =0, 所以ab =1,0<a <1,由对勾函数的单调性可知,a +4b =a +4a ,在(0,1)上单调递减,则a +4a >5. 故选:D.由已知结合对数函数的运算性质可求得ab =1,然后结合对勾函数的单调性即可求解.本题主要考查了对数函数性质的应用及对勾函数单调性在求解函数值域中的应用,属于基础题.7.【答案】B【解析】解:由于[x]表示不超过x 的最大整数,则−1<[x]−x ≤0, 所以函数{x}的定义域为R ,值域为(−1,0],故①错误;②若{x}=−12则x =1.5,2.5,3.5,…, ∴方程{x}=12有无数解,故②正确:③{x +1}=[x +1]−(x +1)=[x]−x ={x}, 所以函数{x}是周期为1的周期函数,故③正确;④因为{3}=3−3=0,{4}=4−4=0,所以{3}={4},而3<4,所以函数{x}在其定义域上不是减函数;故④错误.命题中正确的序号是②③. 故选:B.根据函数的定义结合定义域和值域的概念判断命题①,根据定义解方程判断命题②,根据周期函数的定义判断命题③,根据减函数的定义判断命题④,由此确定正确选项. 本题考查函数的性质,周期性,单调性,定义域与值域,属于中档题.8.【答案】C【解析】解:设y =ℎ(x)与y =f(x)的图象关于y 轴对称, 则ℎ(x)=f(−x)={log 2(−x),x <0−√x,x ≥0,作出y =ℎ(x)与y =g(x)的函数图象如图所示:∵f(x)与g(x)图象上存在关于y 轴对称的点, ∴y =ℎ(x)与y =g(x)的图象有交点, ∴−a ≤−2,即a ≥2. 故选:C.作出f(x)关于y 轴对称的函数ℎ(x)和g(x)的函数图象,根据ℎ(x)与g(x)有交点得出a 的范围. 本题考查了函数零点与函数图象的关系,属于中档题.9.【答案】AC【解析】解:由已知可得函数在(−∞,0)上单调递减,且f(6)=0, 如图所示:则f(8)<0,故A 正确,B 错误,当x <−6或0<x <6时,f(x)>0,故C 正确,函数f(x)与x 轴有三个交点,分别为(−6,0),(0,0),(6,0),故D 错误, 故选:AC.由已知可得函数在(−∞,0)上单调递减,且f(6)=0,然后画出函数的图象,利用数形结合思想对各个选项逐个判断即可求解.本题考查了函数的奇偶性以及单调性,涉及到数形结合思想的应用,属于基础题.10.【答案】ABC【解析】解:由于函数f(x)=sin(2x +φ)(0<φ<π)的图象关于直线x =−π3对称, 故有2×(−π3)+φ=kπ+π2,k ∈Z ,∴φ=π6,f(x)=sin(2x +π6),故A 正确; ∵令x =5π12,求得f(x)=0,故函数f(x)的图象关于点(5π12,0)对称, 故f(5π12−x)+f(5π12+x)=0成立,故B 正确; 根据f(π7)=sin19π42,f(4π21)=sin23π42=sin19π42,故f(π7)=f(4π21),即C 正确;当x ∈(0,π4),则2x +π6∈(π6,2π3),函数f(x)不单调,故D 错误, 故选:ABC.由题意,根据正弦函数的图象和性质,得出结论. 本题主要考查正弦函数的图象和性质,属于中档题.11.【答案】CD【解析】解:对于A 选项,若y =f(x)的定义域是(−1,3),则关于x 的不等式ax 2+bx +c >0的解集为(−1,3),故a <0,A 错;对于B 选项,若函数y =f(x)的定义域为R ,则对任意的x ∈R ,ax 2+bx +c >0, 所以,a =b =0,c >0或a >0,且Δ=b 2−4ac <0,B 错;对于C 选项,由f(−x)=f(1+x)可得f(x)的对称轴为x =12,则有f(0)=f(1), 则有c =a +b +c ,所以,a +b =0,C 对 对于D 选项,当a <0时,则函数y =ax 2+bx+c 的值城为(−∞,4ac−b24a),若函数f(x)的值域为R ,则(0,+∞)⊆(−∞,4ac−b 24a),显然是不可能的,D 对.故选:CD.利用一元二次不等式的解集与系数的关系可判断A 选项;分析可知对任意的x ∈R ,ax 2+bx +c >0,列出关于a 的各种情况,可判断B 选项;利用对数运算求出a +b 的值,可判断C 选项;利用二次函数的基本性质可判断D 选项.本题考查对数函数的性质,考查一元二次不等式,属于中档题.12.【答案】ABD【解析】解:对于A :f(2m )=f(2⋅2m−1)=2f(2m−1)=2m−1⋅f(2),而当x ∈(1,2]时,f(x)=2−x ,所以f(2)=0,所以f(2m )=0故A 正确; 对于B :取x ∈(2m ,2m+1],则x2m∈(1,2];f(x 2m)=2−x2m, 从而f(x)=2f(x2),而f(x)=2m ⋅f(x 2m)=2m+1−x ,其中,m =0,1,2..,从而f(x)∈[0,+∞),所以B 正确;对于C :f(2m +1)=2m+1−2m −1,假设存在n 使f(2n +1)=9,∵2n +1∈[2n ,2n+1),∴f(2n +1)=2n+1−2n −1=2n −1,∴2n −1=9,2n =10, 这与n ∈Z 矛盾,所以该命题错误;对于D :由选项B 知当x ∈(2k ,2k+1)时,f(x)=2k+1−x 单调递减,为减函数, 所以若(a,b)⊆(2k ,2k+1),则函数f(x)在区间(a,b)上单调递减,故正确. 故选:ABD.对于选项A 、B :直接利用关系式的变换和函数的性质求出结果. 对于选项C :利用假设法和关系式的而变换推出矛盾,进一步判定结果. 对于选项D :直接利用函数的单调性判定结果.本题考查的知识要点:函数的性质,关系式的变换,主要考查学生的运算能力和转换能力及思维能力,属于中档题.13.【答案】{x|14≤x ≤1,且x ≠13}【解析】解:要使原函数有意义,则{3x −1≠0−4x 2+5x −1≥0,解得14≤x ≤1,且x ≠13. ∴函数f(x)=33x−1+√−4x 2+5x −1的定义域为{x|14≤x ≤1,且x ≠13}. 故答案为:{x|14≤x ≤1,且x ≠13}.由分式的分母不为0,根式内部的代数式大于等于0联立不等式组求解.本题考查函数的定义域及其求法,是基础题.14.【答案】6【解析】解:∵函数g(x)=6e x+1+ln(√x2+1+x)的定义域为R,且g(−x)+g(x)=61+e−x +ln(√(−x)2+1−x)+6e x+1+ln(√x2+1+x)=6e xe x+1+6e x+1+ln[(x2+1)−x2]=6+ln1=6,∴g(3)+g(−3)=6.故答案为:6.根据已知条件得到g(−x)+g(x)=6,进而求解结论.本题主要考查函数性质的应用以及计算能力,属于基础题.15.【答案】12【解析】解:已知已知定义在整数集合Z上的函数f(x),对任意的x,y∈Z,都有f(x+y)+f(x−y)=4f(x)f(y),令y=1,则f(x+1)+f(x−1)=f(x),即f(x+2)+f(x)=f(x+1),即f(x+2)+f(x−1)=0,即f(x+3)+f(x)=0,即f(x+6)+f(x+3)=0,即f(x+6)=f(x),即函数f(x)的周期为6,又f(0)+f(3)=0,f(1)+f(4)=0,f(2)+f(5)=0,则f(0)+f(1)+f(2)+f(3)+f(4)+f(5)=0,又f(0)+f(1)+f(2)+…+f(2016)=336×[f(0)+f(1)+f(2)+f(3)+f(4)+f(5)]+f(2016)=f(0)令x=1,y=0,则有2f(1)=4f(1)f(0),又f(1)=14,即有f(0)=12,则f(0)+f(1)+f(2)+…+f(2016)=12,故答案为:12.由抽象函数的应用,结合函数的周期性及赋值法求解即可.本题考查了抽象函数的应用,重点考查了函数的周期性,属中档题.16.【答案】(1,2)−2,由对勾函数的性质可知:【解析】解:令m=x+1x−2最多两个解,对于一个确定的m值,关于x的方程m=x+1x−2的图象如下:画出m=x+1x−2值域为(−∞,−4]∪[0,+∞),故m=x+1x作出函数f(x)的图象,如下:令|log5(1−x)|=1,解得:x1=0.8,x2=−4,令|log5(1−x)|=2,解得:x3=0.96,x4=−24,令−(x−2)2+2=0,解得:x5=2+√2,当t<0时,存在唯一的m∈(2+√2,+∞),使得f(m)=t,此时方程m=x+1x−2有两解;当t=0时,存在m1=0,m2=2+√2使得f(m)=0,此时方程m=x+1x−2有三解,其中m1=0时,有1个解,即x=1,m2=2+√2时,有2个解;当t∈(0,1)时,存在m1∈(−4,0),m2∈(0,0.8),m3∈(3,2+√2)使得f(m)=t,此时方程m=x+ 1x−2有四解,m1∈(−4,0)时,无解,m2∈(0,0.8)时,有2个解,m3∈(3,2+√2)时,有2个解;当t=1时,存在m1=−4,m2=0.8,m3=1,m4=3使得f(m)=1,此时方程m=x+1x−2有七解,m1=−4时,有1个解,即x=−1,m2=0.8时,有2个解,m3=1时,有2个解,m4=3时,有2个解;当t∈(1,2)时,存在m1∈(−24,−4),m2∈(0.8,0.96),m3∈(1,2),m4∈(2,3)使得f(m)=t,此时方程m=x+1x−2有八个解,当m1∈(−24,−4)时,有2个解,m2∈(0.8,0.96)时,有2个解,m3∈(1,2)时,有2个解,m4∈(2,3)时,有2个解;当t=2时,存在m1=−24,m2=0.96,m3=2使得f(m)=2,此时方程m=x+1x−2有六解,当m1=−24时,有2个解,m2=0.96时,有2个解,m3=2时,有2个解;当t∈(2,+∞)时,存在m1∈(−∞,−24),m2∈(0.96,1)使得f(m)=t,此时方程m=x+1x−2有四解,当m 1∈(−∞,−24)时,有2个解,m 2∈(0.96,1)时,有2个解; 综上:实数t 的取值范围是(1,2). 故答案为:(1,2).令m =x +1x−2,由对勾函数得到其单调性和值域情况,画出函数f(x)的图象,数形结合得到不同的t 时,根据两函数交点情况,得到答案. 本题考查了复合函数的零点问题,属于中档题.17.【答案】解:(1)原式=1212+√2+√2−1−√(√5−1)2+√5=√22+√22+√2−1−√5+1+√5=2√2.(2)原式=3+(lg25+lg4)−3−lg2lg3⋅lg32lg2=lg100−12=2−12=32.【解析】(1)利用指数的性质和运算法则求解. (2)利用对数的性质和运算法则及换底公式求解.本题考查指数,对数的性质、运算法则及换底公式,属于中档题.18.【答案】解:(1)f(α)=cosα⋅cosα⋅tanα−cosα=−sinα.(2)∵f(α)=−sinα=2√55, ∴sinα=−2√55, 又α为第三象限角,∴cosα=−√1−sin 2α=−1−(−2√55)2=−√55.【解析】(1)根据诱导公式化简即可;(2)利用三角函数平方关系,结合角的象限,计算即可.本题主要考查了诱导公式的应用,考查了同角三角函数间的基本关系,属于基础题.19.【答案】解:(1)由已知函数f(x)=√2sin(ωx +φ)(ω>0,|φ|<π2)的部分图象得{√2sinφ=−1ω⋅π8+φ=0, 解得{ω=2ϕ=−π4,∴f(x)=√2sin(2x −π4);(2)由题意可知,g(x)=√2sin(x +π4),g(x)−m =0在区间[0,3π4]上有两个不同的实数解,则直线y =m 与函数g(x)=√2sin(x +π4)有两个不同的交点,令x +π4=π2+kπ,k ∈Z ,则g(x)对称轴为x =π4+kπ,k ∈Z , ∵x ∈[0,3π4],∴当k =0,x =π4符合题意,即两个交点关于x =π4对称, ∴g(π4)=√2,g(0)=1, ∴m 的取值范围为[1,√2).【解析】(1)由五点法作图以及特殊点的坐标求出ω、φ的值,可得f(x)得解析式;(2)利用函数y =Asin(ωx +φ)的图象变换规律,求得g(x)的解析式,再利用正弦函数的定义域和值域,求出函数g(x)在区间[0,π]上的值域.本题主要考查三角函数的图象,考查转化能力,属于中档题.20.【答案】解:(1)因为酒后1小时测得酒精含量值为44.42毫克/百毫升,所以x =1时,y =44.42,又f(x)=a(x −32)2+47.42,0≤x <2, 所以44.42=a(1−32)2+47.42,解得a =−12, 所以当0≤x <2时,f(x)=−12(x −32)2+47.42. (2)由(1)当0≤x <2时,f(x)=−12(x −32)2+47.42, 所以当0≤x <2时,20.42≤f(x)≤47.42,不可驾车, 令f(x)<20可得,x ≥2且54.27⋅e −0.3x +10.18<20, 化简可得e −0.3x <9825427,所以0.3x >ln5427−ln982,又ln5427=8.60,ln982=6.89,所以x >10(8.60−6.89)3≈5.7,5.7小时等于342分钟,所以喝1瓶啤酒后,需342分钟后才可以驾车.【解析】(1)由已知x =1时,y =44.42,代入函数解析式求a 即可; (2)解不等式f(x)<20求其解可得结果.本题主要考查根据实际问题选择合适的函数模型,属于中档题.21.【答案】解:(1)当a =√2时,f(x)=log √21+4x2x ,因为1+4x2x=2x +12x≥2√2x ⋅12x=2,当且仅当x =0时取等号,属于f(x)≥2,即函数的值域为[2,+∞);(2)若∀x 1∈[0,2],∃x 2∈[0,4],使得f(x 1)−g(x 2)≤2, 则f(x)max ≤[g(x)+2]max ,因为g(x)+2=x −2√x +2=(√x −1)2+1≤2, 因为y =1+4x 2x =2x +12x 在[0,2]上单调递增, 所以y =1+4x 2x=2x +12x≤174, 当a >1时,f(x)在[0,2]上单调递增,f(x)max =f(2)=log a 174≤2, 解得a ≥√172,当0<a <1时,f(x)在[0,2]上单调递减,f(x)max =f(0)=log a 2≤2显然满足题意, 故a 的取值范围为(0,1)∪[√172,+∞).【解析】(1)把a =√2代入已知函数解析式,结合函数的单调性及基本不等式可求; (2)由题意可知x 1∈[0,2],x 2∈[0,4]时,f(x)max ≤[g(x)+2]max ,结合函数的单调性可求. 本题主要考查了基本不等式求解最值,还考查了函数单调性在最值求解中的应用,属于中档题.22.【答案】解:(1)因为f(x)=x +ax ,所以由不等式f(2x)<2x−14x −14可得2x +a 2x <2x−14x −14,即a<−12x −2x4,因为存在x ∈[1,2],使得不等式f(2x )<2x −14x−14能成立,所以存在x ∈[1,2],a <−12x −2x4能成立,即a<(−12x−2x4)max ,因为2x>0,所以12x+2x 4≥2√12x ⋅2x4=1,当且仅当12x =2x4,即x =1时,等号成立,所以在x ∈[1,2]上,−12x−2x4≤−1,即(−12x −2x4)max =−1,故a <−1,即实数a 的取值范围是(−∞,−1); (2)假设存在正数a 满足题意;设t =g(x)=1−x 1+x =−1+21+x ,则t =−1+21+x 在[−35,0]上单调递减, 所以t ∈[1,4],则f(g(x))=f(t)=t +a t;所以对于区间[−35,0]上的任意三个实数m ,n ,p ,都存在以f[g(m)],f[g(n)],f[g(p)]为边长的三角形,等价于2f(t)min >f(t)max , 因为f(x)=x +a x,a >0,任取0<x 1<x 2, 则f(x 1)−f(x 2)=(x 1+a x 1)−(x 2+ax 2)=(x 1−x 2)(x 1x 2−a)x 1x 2, 当0<x 1<x 2<√a 时,x 1−x 2<0,0<x 1x 2<a ,故f(x 1)−f(x 2)>0,即f(x 1)>f(x 2),所以f(x)在(0,√a)上单调递减;当0<√a <x 1<x 2时,x 1−x 2<0,x 1x 2>a >0,故f(x 1)−f(x 2)<0,即f(x 1)<f(x 2),所以f(x)在(√a,+∞)上单调递增;综上:f(x)在(0,√a)上单调递减,在(√a,+∞)上单调递增, 所以对于f(t)=t +a t(t ∈[1,4]),当√a ≤1,即a ≤1时,f(t)在[1,4]上单调递增, 故f(t)min =f(1)=1+a,f(t)max =f(4)=4+a4, 则2(1+a)>4+a4,解得a >87,故a ∈⌀;当1<√a <4,即1<a <16时,f(x)在(1,√a)上单调递减;在(√a,4)上单调递增, 故f(t)min =f(√a)=2√a,f(t)max =max{f(1),f(4)},(i)当f(1)≤f(4)时,1+a ≤4+a4,解得a ≤4,此时f(t)max =f(4)=4+a4, 则2×2√a >4+a 4,整理得a −16√a +16<0,解得8−4√3<√a <8+4√3, 所以(8−4√3)2<a ≤4,即16(7−4√3)<a ≤4,(ii)当f(1)>f(4)时,1+a >4+a4,解得a >4,此时f(t)max =f(1)=1+a , 则2×2√a >1+a ,整理得a −4√a +1<0,解得2−√3<√a <2+√3, 所以4<a <(2+√3)2,即4<a <7+4√3, 所以16(7−4√3)<a <7+4√3;当√a ≥4,即a ≥16时,f(t)在[1,4]上单调递减, 故f(t)min =f(4)=4+a4,f(t)max =f(1)=1+a , 则2(4+a 4)>1+a ,解得a <14,故a ∈⌀; 综上:16(7−4√3)<a <7+4√3,所以存在正数a 满足题意,且a 的取值范围为(16(7−4√3),7+4√3). 【解析】(1)先将问题转化为a <−12x −2x4在x∈[1,2]上能成立,再利用基本不等式求出(−12x−2x4)max,从而得解; (2)先利用反比例函数的单调性求得t =g(x)的值域,再将问题将转化为2f(t)min >f(t)max ,从而分类讨论a ≤1,1<a <16,a ≥16三种情况,结合对勾函数的单调性,列出不等式求解,由此得解.本题考查了函数的恒成立问题,属于难题.。
(附加20套期末模拟试卷)湖北省武汉二中2020年高一上学期期末考试数学试题及答案

湖北省武汉市高一上学期数学期末考试试卷

湖北省武汉市高一上学期数学期末考试试卷姓名:________ 班级:________ 成绩:________一、一.选择题 (共8题;共16分)1. (2分)已知a、b、c为非零实数,代数式 + + + 的值所组成的集合为M,则下列判断中正确的是()A . 0∉MB . ﹣4∉MC . 2∈MD . 4∈M2. (2分)下列函数中,既是奇函数又增函数的为()A . y=x+1B . y=﹣x2C . y=﹣D . y=x|x|3. (2分) (2016高一下·衡阳期中) 已知P1(2,﹣1),P2(0,5)且点P在P1P2的延长线上,| |=2||,则点P的坐标为()A . (2,11)B .C .D . (﹣2,11)4. (2分) (2016高一上·石嘴山期中) 已知函数f(x)是奇函数,当x>0时,f(x)=ax(x>0且a≠1),且f(log 4)=﹣3,则a的值为()A .B . 3C . 9D .5. (2分)若x是三角形的最小内角,则函数y=sinx+cosx﹣sinxcosx的最小值是()A . -+B . +C . 1D .6. (2分) (2018高一下·攀枝花期末) 设是内一点,且,,设,其中、、分别是、、的面积.若,则的最小值是()A . 3B . 4C .D . 87. (2分) (2016·新课标Ⅰ卷理) 若将函数y=2sin 2x的图像向左平移个单位长度,则评议后图象的对称轴为()A . x= –(k∈Z)B . x= + (k∈Z)C . x= –(k∈Z)D . x= + (k∈Z)8. (2分)(2019·南昌模拟) 若函数的值域为,则实数的取值范围为()A .B .C .D .二、二.填空题 (共6题;共15分)9. (1分) (2017高三下·黑龙江开学考) 定义区间[x1 , x2]长度为x2﹣x1(x2>x1),已知函数f(x)=(a∈R,a≠0)的定义域与值域都是[m,n],则区间[m,n]取最大长度时a的值是________.10. (1分) (2016高一上·桓台期中) 三个数a=30.7、b=0.73、c=log30.7的大小顺序为________.11. (1分)在平面直角坐标系xOy中,使角的顶点与原点重合,角的始边与x轴的非负半轴重合.已知点P (x,y)是角θ终边上一点,|OP|=r(r>0),定义f(θ)= .对于下列说法:①函数f(θ)的值域是;②函数f(θ)的图象关于原点对称;③函数f(θ)的图象关于直线θ= 对称;④函数f(θ)是周期函数,其最小正周期为2π;⑤函数f(θ)的单调递减区间是[2kπ﹣,2kπ+ ],k∈Z.其中正确的是________.(填上所有正确命题的序号)12. (1分)设 =(x,3), =(2,﹣1),若⊥ ,则|2 + |=________.13. (1分)函数y=loga(x﹣1)+8(a>0且a≠1)的图象恒过定点P,P在幂函数f(x)的图象上,则f (3)=________14. (10分) (2016高一上·蓟县期中) 已知函数.(1)求f(f(5))的值;(2)画出函数的图象.三、三.解答题 (共5题;共40分)15. (5分) (2016高一上·万全期中) 已知x∈[﹣3,2],求函数f(x)= 的最小值和最大值.16. (10分)已知函数f(x)=sin[ωπ(x+ )]的部分图象如图,其中P为函数图象的最高点,PC⊥x 轴,且tan∠APC=1.(1)求函数f(x)的解析式;(2)若x∈[1,2],求函数f(x)的取值范围.17. (10分) (2018高一上·大石桥期末) 已知角的张终边经过点,且为第二象限.(1)求的值;(2)若,求的值.18. (5分)定义:若函数f(x)对于其定义域内的某一数x0 ,有f(x0)=x0 ,则称x0是f(x)的一个不动点.已知函数f(x)=ax2+(b+1)x+b﹣1(a≠0).(1)当a=1,b=﹣2时,求函数f(x)的不动点;(2)若对任意的实数b,函数f(x)恒有两个不动点,求a的取值范围.19. (10分) (2015高三下·湖北期中) 已知 =(sinx,sin(x﹣)), =(sinx,cos(x+ )),f(x)= • .(1)求f(x)的解析式及周期;(2)求f(x)在x∈[﹣, ]上的值域.参考答案一、一.选择题 (共8题;共16分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、二、二.填空题 (共6题;共15分)9-1、10-1、11-1、12-1、13-1、14-1、14-2、三、三.解答题 (共5题;共40分)15-1、16-1、16-2、17-1、17-2、18-1、19-1、19-2、。
2020-2021学年湖北省武汉市部分高中高一(上)期末数学试卷(附答案详解)

2020-2021学年湖北省武汉市部分高中高一(上)期末数学试卷一、单选题(本大题共8小题,共40.0分)1. 已知集合A ={x|x 2+x −2>0},B ={−3,−2,−1,0,1,2,3},则A ∩B =( )A. {−3,2}B. {−3,2,3}C. {−1,0,1,2}D. {−3,−2,2,3}2. 设命题p :∀n ∈N ,n 2≤2n ,则¬p 为( )A. ∀n ∈N ,n 2>2nB. ∃n ∈N ,n 2≤2nC. ∃n ∈N ,n 2>2nD. ∀n ∈N ,n 2≥2n3. 已知函数f(x)={log 3x,x >0,4x ,x ≤0,则f(f(19))=( )A. −116B. 116C. −16D. 164. 已知p :a ≥0;q :∀x ∈R ,x 2−ax +a >0,则p 是q 的( )A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件5. 下列函数中,既是偶函数又在区间(0,+∞)单调递减的是( )A. y =x 2+1B. y =|x|−1C. y =1x 2D. y =e −x6. 已知正实数a ,b 满足2a +3b =1,则1a +2b 的最小值为( )A. 15B. 8+2√3C. 16D. 8+4√37. 函数y =(x 3−2x)2x4x +1的部分图象大致为( )A.B.C.D.8. 已知定义域为R 的函数f(x)是奇函数,且f(x +2)=−f(x),若f(x)在区间[0,1]是减函数,则f(53),f(1),f(112)的大小关系是( )A. f(112)<f(1)<f(53) B. f(1)<f(112)<f(53) C. f(53)<f(1)<f(112)D. f(53)<f(112)<f(1)二、多选题(本大题共4小题,共20.0分) 9. 若0<a <1,b >c >1,则( )A. (cb )a <1B. c a−1<b a−1C. 1log c a <1log b aD. c−a b−a <cb10. 已知函数f(x)=√x 2−x 4|x+1|−1,下列结论正确的是( )A. f(x)的定义域为[−1,0)∪(0,1]B. f(x)的图象关于坐标原点对称C. f(x)在定义域上是减函数D. f(x)的值域为[−1,1]11. 已知函数f(x)={|log 2(x +1)|,−1<x ≤3,12x 2−5x +252,x >3,若关于x 的方程f(x)=m 有四个不同的实数x 1,x 2,x 3,x 4满足x 1<x 2<x 3<x 4,则下列结论正确的是( )A. x 1x 2=−1B. 1x 1+1x 2=−1C. x 3+x 4=10D. x 3⋅x 4∈[21,25]12. 高斯是德国著名的数学家,近代数学莫基者之一,享有“数学王子”的称号,他和阿基米德、牛顿并列为世界三大数学家,用其名字命名的“高斯函数”为:设x ∈R ,用[x]表示不超过x 的最大整数,则y =[x]称为高斯函数,例如:[−3.5]=−4,[2.1]=2.已知函数f(x)=e x −1e x +1,函数g(x)=[f(x)],以下结论正确的是( )A. f(x)在R 上是增函数B. g(x)是偶函数C. f(x)是奇函数D. g(x)的值域是{−1,0}三、单空题(本大题共4小题,共20.0分)13. 函数f(x)=ln(1−x)+√2+x 的定义域为______ .14. 求值:2log 214−(827)−23−lg 1100= ______ .15.当生物死亡后,它机体内原有的碳14含量会按确定的比率衰减(称为衰减率),大约每经过5730年衰减为原来的一半,这个时间称为“半衰期”.若按照上述变化规律,则死亡生物体内碳14含量每年的衰减率为______ .16.函数f(x)=log a(x2−ax+12)在(2,3)单调递减,则实数a的取值范围是______ .四、解答题(本大题共6小题,共70.0分)17.已知全集U=R,集合A={x|x2+2x−8≤0},B={x|m−1≤x≤m+1}.(1)若m=2,求(∁U B)∩A;(2)若B⊆A,求实数m的取值范围.18.已知函数f(x)=−x2+2|x|.(1)判断函数f(x)的奇偶性;(2)将函数f(x)写成分段函数的形式,并在如图所示的坐标系内作出函数的图象,写出单调区间.19. 已知函数f(x)=log 21+x1−x .(1)求不等式f(x)<1的解集; (2)判断并证明f(x)的单调性.20. (1)已知f(x)=(12)x ,g(x)=(12)−x ,比较f(x)与g(x)的大小;(2)比较log 45,log 56的大小.21. 某品牌手机公司的年固定成本为50万元,每生产1万部手机需增加投入20万元,该公司一年内生产x(x >0)万部手机并全部销售完当年销售量x 不超过40万部时,销售1万部手机的收入R(x)=380−5x 万元;当年销售量x 超过40万部时,销售1万部手机的收入R(x)=9000x−40500x 2万元(1)写出年利润y 万元关于年销售量x 万部的函数解析式; (2)年销售量为多少万部时,利润最大,并求出最大利润.22.已知函数f(x)=log3(9x+1)+kx(k∈R)是偶函数.(1)求实数k的值;(2)若函数y=f(x)−x+a没有零点,求实数a的取值范围;(3)若函数ℎ(x)=3f(x)+x−m⋅3x−1,x∈[0,log35]的最大值为0,求实数m的值.答案和解析1.【答案】B【解析】解:∵A ={x|x <−2或x >1},B ={−3,−2,−1,0,1,2,3}, ∴A ∩B ={−3,2,3}. 故选:B .可求出集合A ,然后进行交集的运算即可.本题考查了描述法和列举法的定义,一元二次不等式的解法,交集及其运算,考查了计算能力,属于基础题.2.【答案】C【解析】解:因为全称命题的否定是特称命题,所以,命题P :∀n ∈N ,n 2≤2n ,则¬P 为:∃n ∈N ,n 2>2n . 故选:C .利用全称命题的否定是特称命题,写出结果即可.本题考查命题的否定,特称命题与全称命题的否定关系,是基础题.3.【答案】B【解析】解:因为函数f(x)={log 3x,x >0,4x ,x ≤0,则f(19)=log 319=log 33−2=−2, 所以f(f(19))=f(−2)=4−2=116. 故选:B .根据自变量的值判断使用哪一段解析式求解,然后利用对数和指数的运算性质求解即可. 本题考查了函数的求值问题,主要考查的是分段函数的求解,解题的关键是确定选用哪一段解析式求解,属于基础题.4.【答案】B【解析】解:因为∀x∈R,x2−ax+a>0,所以△=(−a)2−4a<0,解得0<a<4,所以q:0<a<4,又p:a≥0,因为(0,4)⫋[0,+∞),故p是q的必要不充分条件.故选:B.先利用一元二次不等式恒成立求出q,然后利用两个范围之间的关系结合充分条件与必要条件的定义进行判断即可.本题考查了充分条件与必要条件的判断,解题的关键是掌握充分条件与必要条件的判断方法,属于基础题.5.【答案】C【解析】解:A.y=x2+1是偶函数,当x>0时为增函数,不满足条件.B.y=|x|−1是偶函数,当x>0时,y=x−1为增函数,不满足条件,C.函数是偶函数,当x>0时为减函数,满足条件,D.函数为非奇非偶函数,不满足条件.故选:C.分别判断函数的奇偶性和单调性是否满足条件即可.本题主要考查函数奇偶性和单调性的判断,利用函数奇偶性和单调性的性质是解决本题的关键,是基础题.6.【答案】D【解析】解:∵a>0,b>0,2a+3b=1,∴1a +2b=(1a+2b)(2a+3b)=2+6+3ba+4ab≥8+2√3ba⋅4ab=8+4√3,当且仅当3ba=4a b ,即a=√3−14,b=3−√36时等号成立,∴1a +2b的最小值为:8+4√3.故选:D.根据2a+3b=1可得出1a +2b=(1a+2b)(2a+3b),然后根据基本不等式即可得出1a+2b的最小值.本题考查了基本不等式求最值的方法,注意说明等号成立的条件,考查了计算能力,属于基础题.7.【答案】A【解析】解:f(x)=x 3−2x 2x +2−x,则f(−x)=−x 3+2x 2−x +2x=−f(x),则函数f(x)是奇函数,排除C ,D ,由f(x)=0,得x 3−2x =0,得x =0或x =±√2, 当0<x <1时,f(x)<0,排除B , 故选:A .判断函数的奇偶性和对称性,结合0<x <1时,f(x)<0,进行判断即可.本题主要考查函数图象的识别和判断,利用函数的奇偶性和对称性,以及函数值的符号,利用排除法是解决本题的关键,是基础题.8.【答案】B【解析】解:∵f(x +2)=−f(x),∴f(x +4)=−f(x +2)=f(x),即函数f(x)是周期为4的周期函数, 则f(112)=f(5.5−4)=f(1.5)=f(2−0.5)=−f(−0.5)=f(0.5), f(53)=f(2−13)=−f(−13)=f(13), ∵f(x)在区间[0,1]是减函数,则f(13)>f(0.5)>f(1),即f(1)<f(112)<f(53). 故选:B .根据条件求出函数是周期为4的周期函数,结合函数的周期性和单调性进行转化求解即可.本题主要考查函数值的大小比较,结合函数的周期性和单调性进行转化是解决本题的关键,是中档题.9.【答案】AD【解析】解:选项A:由已知可得0<cb <1,而0<a<1,所以(cb)a<1,故A正确,选项B:因为a−1<0,幂函数y=x a−1是递减函数,而b>c,所以c a−1>b a−1,B 错误,选项C:因为0<a<1,所以函数y=log a x是单调递减函数,所以0>log a c>log a b,所以1log c a >1log b a,故C错误,选项D:因为c−ab−a −cb=bc−ab−bc+ac(b−a)b=a(c−b)(b−a)b,因为0<a<1,b>c>1,所以c−b<0,b−a>0,所以c−ab−a −cb<0,故D正确,故选:AD.选项A,根据已知范围易判断,选项BC,可转化为幂函数的单调性判断大小,选项D,作差比较即可求解.本题考查了不等式的性质,涉及到幂函数的单调性以及作差比较大小的应用,属于基础题.10.【答案】AB【解析】解:x2−x4=x2(1−x2)≥0,|x+1|−1≠0,f(x)定义域为[−1,0)∪(0,1],f(x)=|x|√1−x2(x+1)−1={−√1−x2(x∈[−1,0))√1−x2(x∈(0,1]);对于A,由上述知,A对;对于B,因为f(−x)=−f(x),所以B对;对于C,因为f(−1)=f(1),所以C错;对于D,f(x)=1无解,所以D错.故选:AB.A求出函数定义域,对函数化简;B验证函数奇偶性判断;C特值法判断;D特值法判断.本题以命题的真假判断为载体,考查了函数的基本概念,属基础题.11.【答案】BCD【解析】解:依题意,|log 2(x 1+1)|=|log 2(x 2+1)|且−1<x 1<0<x 2<3,∴log 2(x 1+1)+log 2(x 2+1)=0,即(x 1+1)(x 2+1)=1, ∴x 1x 2+x 1+x 2+1=1,∴1x 1+1x 2=−1,即选项A 错误,选项B 正确;易知,x 3,x 4是方程12x 2−5x +252=m (0<m <2)的根,即方程x 2−10x +25−2m =0的两根,∴x 3+x 4=10,x 3x 4=25−2m ∈(21,25),即选项C ,选项D 均正确. 故选:BCD .作出函数f(x)的图象,可知|log 2(x 1+1)|=|log 2(x 2+1)|,x 3,x 4是方程12x 2−5x +252=m 的两根,由此即可判断出正确选项.本题考查函数零点与方程根的关系,考查数形结合思想,属于中档题.12.【答案】ACD【解析】解:对于A ,因为f(x)=e x +1−2e x +1=1+−2e x +1,因为2e x +1是递减的,所以−2 e x +1是递增的,所以A 对;对于B ,因为e x +1∈(1,+∞)⇒1e x +1∈(0,1)⇒−2 e x +1∈(−2,0)⇒f(x)∈(−1,1), 所以f(x)的值域为(−1,1),所以g(x)={0(x ≥0)−1x <0,g(−1)=−1,g(1)=0≠g(−1),所以B 错; 对于C ,因为f(−x)=e −x −1e −x +1=1−e x 1+e x =−e x −1e x +1=−f(x),根据奇函数定义知,f(x)是奇函数,所以C 对; 对于D ,由B 知,D 对. 故选:ACD .A 根据复合函数单调性判断;B 化简函数并求出分段表达式,根据偶函数定义,用特值法判断;C 根据奇函数定义,用特值法判断;D 由表达式求出值域判断.本题以命题的真假判断为载体,考查了函数的单调性,考查了求函数值域问题,属中档题.13.【答案】[−2,1)【解析】解:要使函数有意义,则{1−x >02+x ≥0,得{x <1x ≥−2,即−2≤x <1,即函数的定义域为[−2,1), 故答案为:[−2,1).根据函数成立的条件建立不等式关系即可.本题主要考查函数的定义域的求解,要求熟练掌握常见函数成立的条件.14.【答案】0【解析】解:2log 214−(827)−23−lg 1100=14−94+2 =0. 故答案为:0.利用指数、对数的性质、运算法则直接求解.本题考查对数式、指数式化简求值,考查指数、对数的性质、运算法则等基础知识,考查运算求解能力,是基础题.15.【答案】1−(12)15730【解析】解:设每年的衰减率为x ,另设原来的碳14含量为A , 则由已知可得:A −A(1−x)5730=A2,所以(1−x)5730=12,即x =1−(12)15730,故答案为:1−(12)15730.设每年的衰减率为x,另设原来的碳14含量为A,则由已知可得:A−A(1−x)5730=A2,解方程即可求解.本题考查了根据实际问题建立函数模型的问题,考查了学生对题干的理解能力,属于基础题.16.【答案】[6,7]∪(0,1)【解析】解:∵函数f(x)=log a(x2−ax+12)在(2,3)单调递减,∴{a>1a2≥39−3a+12≥0①,或{0<a<1a2≤24−2a+12≥0②.解①求得6≤a≤7;解②求得0<a<1.综上可得,实数a的范围为[6,7]∪(0,1),故答案为:[6,7]∪(0,1).由题意利用查复合函数的单调性,二次函数、对数函数的性质,分类讨论a的范围,得到两个不等式组,分别求得不等式组的解集,再取并集,即得所求.本题主要考查复合函数的单调性,二次函数、对数函数的性质,属于中档题.17.【答案】解:(1)m=2,全集U=R,集合A={x|x2+2x−8≤0}={x|−4≤x≤2},B={x|1≤x≤3}.∁U B={x|x<1或x>3},∴(∁U B)∩A={x|−4≤x<1}.(2)∵集合A={x|−4≤x≤2},B={x|m−1≤x≤m+1}≠⌀,B⊆A,∴{m−1≥−4m+1≤2,解得−3≤m≤1.∴实数m的取值范围[−3,1].【解析】(1)m=2,求出集合A,B,从而求出∁U B,由此能求出(∁U B)∩A.(2)求出B={x|m−1≤x≤m+1}≠⌀,再由B⊆A,列不等式组,能求出实数m的取值范围.本题考查补集、交集、实数的取值范围的求法,考查补集、交集、子集定义等基础知识,考查运算求解能力,是基础题.18.【答案】解:(1)f(−x)=−(−x)2+2|−x=−x2+ 2|x|=f(x),则f(x)是偶函数.(2)f(x)={−x 2+2x,x≥0−x2−2x,x<0,作出f(x)的图象如图:则函数的单调递增区间为(−∞,−1]和[0,1],单调递减区间为[−1,0]和[1,+∞).【解析】(1)根据奇偶性的定义进行判断即可.(2)根据绝对值的意义进行转化,结合图象即可得到函数的单调性.本题主要考查函数奇偶性和单调性的判断,结合奇偶性的定义以及利用数形结合是解决本题的关键,是基础题.19.【答案】解:(1)根据题意,函数f(x)=log21+x1−x ,必有1+x1−x>0,解可得−1<x<1,即函数的定义域为(−1,1),若f(x)<1,即0<1+x1−x<2,解可得:−1<x<13,即不等式f(x)<1的解集为(−1,13);(2)根据题意,f(x)在(−1,1)上为增函数;证明:f(x)的定义域为(−1,1),设−1<x1<x2<1,f(x1)−f(x2)=log21+x11−x1−log21+x21−x2=log2(1+x1)(1−x2)(1−x1)(1+x2)=log21−x1x2+(x1−x2)1−x1x2−(x1−x2),又由−1<x1<x2<1,则x1−x2<0,则有1−x1x2+(x1−x2)1−x1x2−(x1−x2)<1,则f(x1)−f(x2)=log21−x1x2+(x1−x2)1−x1x2−(x1−x2)<0,故f(x)在(−1,1)上为增函数,【解析】(1)先分析函数f(x)的定义域,由对数的运算性质可得f(x)<1等价于0<1+x1−x< 2,解可得x的取值范围,即可得答案;(2)根据题意,由作差法分析可得结论.本题考查函数单调性的判断,涉及对数不等式的解法,属于基础题.20.【答案】解:(1)f(x)=(12)x ,g(x)=(12)−x =2x ,在同一直角坐标系中作出f(x)=(12)x ,g(x)=(12)−x =2x 图象如下:结合图象得:当x <0时,f(x)>g(x);当x =0时,f(x)=g(x);当x >0时,g(x)>f(x). (2)设f(x)=log x (x +1),x >1,则f(x)=ln(x+1)lnx,x >1,∴f′(x)=xlnx−(x+1)ln(x+1)x(x+1)(lnx)2,∵g(x)=xlnx 在(1,+∞)上是增函数,∴g(x)−g(x +1)<0, ∴f′(x)<0,∴f(x)在(1,+∞)上是减函数, ∴f(4)>f(5),∴log 45>log 56.【解析】(1)在同一直角坐标系中作出f(x)=(12)x ,g(x)=(12)−x =2x 图象,数形结合能求出结果.(2)设f(x)=log x (x +1),x >1,求出f′(x)=xlnx−(x+1)ln(x+1)x(x+1)(lnx)2,利用导数性质求出f(x)在(1,+∞)上是减函数,从而log 45>log 56.本题考查两数大小的比较,考查函数图象、构造法、导数性质等基础知识,考查运算求解能力,是中档题.21.【答案】解:(1)当0<x ≤40时,y =x(380−5x)−20x −50=−5x 2+360x −50, 当x >40时,y =x(9000x−40500x 2)−20x −50=−40500x−20x +8950,所以年利润y万元关于年销售量x万部的函数解析式为y={−5 x2+360x−50,0<x≤40−40500x−20x+8950,x>40;(2)当0<x≤40时,y=−5(x−36)2+6430,所以当x=36时,y max=6430,当x>40时,y=−(40500x +20x)+8950≤−2√40500x⋅20x+8950=7150,当且仅当40500x=20x,即x=45时取等号,此时y max=7150,综上,年销售量为45万部时,利润最大,且最大利润为7150万元.【解析】(1)根据已知分段求出y,最后以分段函数的形式写出y的关系式即可;(2)根据(1)的结论,分段求出函数的最大值,比较即可求解.本题考查了根据实际问题建立函数模型的问题,涉及到二次函数求最值以及基本不等式求最值的问题,考查了学生的运算能力,属于中档题.22.【答案】解:(1)∵f(x)是偶函数,∴f(−x)=f(x),即log3(9−x+1)−kx=log3(9x+1)+kx对任意x∈R恒成立,∴2kx=log3(9−x+1)−log3(9x+1)=log39−x+19x+1=log33−2x=−2x,∴k=−1.(2)函数y=f(x)−x−a没有零点,即方程log3(9x+1)−2x=a无实数根.令g(x)=log3(9x+1)−2x,则函数y=g(x)的图象与直线y=a无交点,∵g(x)=log3(9x+1)−2x=log3(9x+1)−log39x=log39x+19x =log3(1+19x),又1+19x >1,∴g(x)=log3(1+19x)>0,∴a的取值范围是(−∞,0].(3)由题意ℎ(x)=9x+m⋅3x,x∈[0,log35],令t=3x∈[1,5],φ(t)=t2+mt,t∈[1,5],①当−m2≤3,即m≥−6时,φ(t)max=φ(5)=25+5m=0,m=−5;②当−m2>3,即m<−6时,φ(t)max=φ(1)=1+m=0,解得m=−1(舍去).综上可知,实数m=−5.【解析】(1)利用偶数数的定义f(−x)=f(x),即可求出实数k的值;(2)令f(x)−x−a≠0,得a≠f(x)−x,构造函数g(x)=f(x)−x,将问题转化为直线y=a与函数y=g(x)的图象没有交点,从而求出实数a的取值范围;(3)化简可得ℎ(x)=9x+m⋅3x,x∈[0,log35],运用换元法和二次函数在闭区间上的最值求法,可得所求最大值,再由最大值为0求解m值.本题考查函数奇偶性的性质及应用,考查函数零点的判定及二次函数最值的求法,考查转化思想和运算能力,属于中档题.。
大一高等数学期末考试试卷及复习资料详解

大一高等数学期末考试试卷及复习资料详解大一高等数学期末考试试卷(一)一、选择题(共12分)1.(3分)若/3= 2XXV0,为连续函数,则d的值为().a+ x,x>0(A)I (B) 2 (C)3 (D)-I2.(3分)已知厂⑶=2,则Ii y "7⑶的值为().λ→0 2hOOl (B) 3 (C)-I (D)I23.(3分)定积分∫>Λ∕1-COS23Xdx的值为()•■⑷ 0 (B)-2 (C)I (D) 24.(3分)若/⑴在“勺处不连续,则/3在该点处()・(A)必不可导(B)—定可导(C)可能可导(D)必无极限二、填空题(共12分)1.(3分)平面上过点(0,1),且在任意一点(Λ∙,y)处的切线斜率为3疋的曲线方程为_________________________ .2.( 3 分)∫ ι(x2+x4 Sin XyIX = _______ 1-3.(3 分)IilnX2 Sin丄= ・.r→υX4.(3分)y = 2√ -3√的极大值为________________ —2 (6分)设尸冕,求*JT + 1三、计算题(共42分)1.(6 分)求Iim史S.∙*→υ Sin 3x^3.(6分)求不定积分JXIn(I+十)厶.x .v<ι4.(6 分)求J /(X-1)JΛ∖其中/(x)= < l + cosχ,e' +l,x> 1.5.(6分)设函数y = f(x)由方程JO e,M + [cos∕d∕ = 0所确定,求dy.6.( 6 分)设 f f{x)dx = Sin + C,求j + 3)dx.7.(6 分)求极限IinJI÷-Γn→30k 2/7 7四、解答题(共28分)1.(7 分)设,Γ(lnx) = l+x,且/(0) = 1,求32.(7分)求由曲线y = cosx[-^-<x<^及X轴所围成图形绕着X轴旋I 2 2)转一周所得旋转体的体积.3.(7分)求曲线y = x3-3√÷24x-19在拐点处的切线方程•4.(7分)求函数y = x + √∏7在[-5,1]上的最小值和最大值.五、证明题(6分)设厂(X)在区间[“]上连续,证明i a f^dx = ¥ [/(“) + f(b)]+1 [(X - a)(x - b)fj)dx.(二)一、填空题(每小题3分,共18分)1.设函数/(χ)= 2χ2~1 ,则"1是心)的第_________ 类间断点.X -3x + 23.=∙v→∞V X)4・ 曲线 V 在点(扣)处的切线方程 为 ・5 .函数J = 2X 3-3X 2在[-1,4]上的最大值 _________________ ,最小值 __________ .二、 单项选择题(每小题4分,共20分)1.数列&”}有界是它收敛的( )•(A)必要但非充分条件; (C)充分必要条件; 2.下列各式正确的是((B)充分但非必要条件; (D)无关条件.)・(A) je-χdx=e"x+C i(B) J In X(IX = _ + C ; (C)JI 2∕x=2hl (l 2x)+C ;(D) f —5—JX = Inlllx+ C ・' ,J XInX3-设/(x)在RM 上,广(x)>O 且厂(x)>0,则曲线y = f(x)在[“问上•6.∣∙arctanx J l +x 2(IX(小沿X轴正向上升且为凹(B)沿兀轴正向下降且为凹的;的;(D)沿X轴正向下降且为凸(C)沿兀轴正向上升且为凸的;的.则/(x)在兀=0处的导? :( )•4. 设/(*)=XInX ’⑷等于1;(C)等于O ;(D)不存在•5.已知Ihn/(x)= 2,以下结论正确的是()•G)函数在工=1处有定义且/(1)=2 ; (B)函数在;V = I处的某去心邻域内有定义;(C)函数在2 1处的左侧某邻域内有定义;(D)函数在21处的右侧某邻域内有定义.三、计算(每小题6分,共36分)1.求极限:HlnX2 sinx→0X2.已知y = ln(l + χ2),求几3.求函数J = >0)的导数.5.J X COS XdX ・丄 16.方程y x =X y确定函数y = f(x)f求八四、(H)分)已知/为/(X)的一个原函数,求∫x2∕(x}∕x.五、(6分)求曲线,=壮7的拐点及凹凸区间.六、(10 分)设J广(√∑)/X = X(e、' +1)+C ,求/(X)・(三)填空题(本题共5小题,每小题4分,共20分)・±J_(1)⅛(COSX)r = ________ 石________ .(2)曲线A = Xlnx上及直线X-y + l= °平行的切线方程为y =x-∖(3 )已知f f(e x) = xe~x,且/(D = O ,则大一高等数学期末考试试卷及复习资料详解/(X)= _________ /Cv)= 2(In X)________ .X 211(4)曲线V =3777的斜渐近线方程为 _______ V= 3Λ^9,二、选择题(本题共5小题,每小题4分,共20分)・(1)下列积分结果正确的是(D )(2)函数/W 在[恥]内有定义,其导数广⑴的图形如图1-1所示, 则(D ) •(A)刁宀都是极值点.⑻ g ,/3)),(£,/(£))都是拐点.(C) F 是极值点.,U 是拐点. (D) WJy))是拐点,勺是极值点.(3) 函数y = qe v ÷C 2e-÷A -e'满足的一个微分方程是(D ).(A) /-y-2>∙ = 3xe t . (B) /-y-2y = 3e v . (C) / + y-2y = 3Λ∙e c .(D) / + y~2y = 3e r .lim∕(⅞)-∕(⅞~z0 (4) 设/W 在%处可导,则I h 为(A ) •⑷ 广仇). (B) -f ,M.(C) O. (D)不存在.(5)下列等式中正确的结果是((A) (J* /(x)"∙χ)'Z=/W-(C) 町 /(χ)"χ]=/W -) 微分方程= (V+1)-的通解为三、计算J (本 共4小题,每小题6分,共24分).y =3 _5 "3 O(或令 √Γ+χ = r)四、解答题(本题共4小题,共29分)•1. (本题6分)解微分方程r-5∕÷6j = xe -.解:特征方程r 2-5r + 6 = 0 ------------- 1分 特征解斤=2,r 2 =3. ------------ 1分 3x大一高等数学期末考试试卷及复习资料详解 恤(丄—丄)1∙求极限j X-I In —X 11. xlnx-x+1Iim (—— _ ——)IIm ---------In XIUn I XTl x-1 I---- + In xh ∖x Iim x →,X -1 + xln1.1 + In X 1 IUn -------- =— j 1 + In X +1 2Λ = In Sin t2.方程尸COSWSinf 确定V 为X 的函数,dy y ,(f)-=-一 =∕sm∕, 解 JX 十⑴求dx 及Jx 2 .(3分) (6分)arctan JX3. 4.计算不定积分J石(1+『. arctanA∕√7—— (i + χ)=21 arctan √7t∕ arctan y ∕x ——解 Hatan 仇=2 J √x(l + x)=(arctan2+C ——「一 dx4.计算定积分如+曲.'3χ(l -VTTX) 0解 分)oT7⅛7_ V dx = 一J(:(I-、/i+x)〃X(6分)LL i∖l4/1 «\ ? r V 八2.(本题7分)一个横放着的圆柱形水桶(如图4-1),桶内盛有半桶水,设桶的底半径为R ,水的比重为乙计算桶的一端面上所受的压力.解:建立坐标系如图3.(本题8分)设/B在S】上有连续的导数,f(u) = f(b) = θ9且∫O∕2(X)JΛ =1^试求∫>∕ω∕解:J:Xf(X)f∖x)dx = £ Xf(X)df(x) 2 分= -∫n^^W ------------ 2 分=IV 2(Λ-)⅛-|£72(X)厶一一2 分4.(本题8分)过坐标原点作曲线>, = h^的切线,该切线及曲线y =lnx及X轴围成平面图形D.⑴(3) 求D的面积A;⑵(4) 求D绕直线X = e旋转一周所得旋转体的体积V.解:(1)设切点的横坐标为",则曲线y = In Λ在点(⅞Jn ⅞)处的切线方程y = Inx0 + —(X-X0).氐__I分由该切线过原点知山心-1 = 0,从而心=匕所以该切线的方程为1y = -X.平面图形D的面积1V = -X(2)切线"及X轴及直线Xe所围成的三角形绕直线Xe旋转V I = -7te1所得的圆锥体积为,3 2分曲线尸IZ及X轴及直线所围成的图形绕直线Xe旋转所得的旋转体体积为V2=(oπ(e-e>)2dy9】分因此所求旋转体的体积为V=V l-V2=-^2-e y)2dy = -(5e2-∖2e + 3).五、证明题(本题共1小题,共7分)•1.证明对于任意的实数Y , eJl + x.e x = l + x + —Λ2≥l + x2解法二设fM = e x-x~^则/(0) = 0.因为f f M = e x-∖. 1 分当Xno时,f,M≥o.f(χ)单调增加,/(χ)≥∕(θ)=o.当x≤0时,∕,ω≤0.∕(Λ∙)单调增加,/(X)≥/(0) =0. 所以对于任意的实数X, ∕3≥°∙即e'≥l + I 解法三:由微分中值定理得,R -1 = “ -60 =^(X-O) = ^Xt 其中§位于0 到X 之一1分2分A = V -ey)dy = ~e~^∙解法一:2分2分1分2分间。
武汉市高一上学期数学期末考试试卷(I)卷

武汉市高一上学期数学期末考试试卷(I)卷姓名:________ 班级:________ 成绩:________一、单选题 (共12题;共24分)1. (2分)下列集合表示法正确的是()A . {1,2,2}B . {全体实数}C . {有理数}D . 不等式x2﹣5>0的解集为{x2﹣5>0}2. (2分)已知集合M={y|y=lgx,0<x<1},N={y|y=()x , x>1},则M∩N=()A . {y|y<0}B . {y|y<}C . {y|0<y<}D . ∅3. (2分) (2019高一上·上饶期中) 给出下列关系式:① ;② ;③ ;④ ,其中正确关系式的个数是()A .B .C .D .4. (2分)集合M={x|x=3k-2,k∈Z},P={y|y=3n+1,n∈Z},S={z|z=6m+1,m∈Z}之间的关系是()C . S⫋P=MD . P=M⫋S5. (2分)在下列各组中的集合M与N中,使M=N的是()A . M={(1,﹣3)},N={(﹣3,1)}B . M=∅,N={0}C . M={y|y=x2+1,x∈R},N={(x,y)|y=x2+1,x∈R}D . M={y|y=x2+1,x∈R},N={t|t=(y﹣1)2+1,y∈R}6. (2分)的平方根组成的集合是()A . {16}B . {﹣16,16}C . {4}D . {﹣4,4}7. (2分)下列各组集合中,表示同一集合的是()A . M={(3,2)},N={(2,3)}B . M={3,2},N={2,3}C . M={(x,y)|x+y=1},N={y|x+y=1}D . M={1,2},N={(1,2)}8. (2分) (2016高一上·万全期中) 若集合A={x|y= },B={y|y= },则()A . A=BD . A∪B=A9. (2分)下列对象能构成集合的是()A . 高一年级全体较胖的学生B . sin 30°,sin 45°,cos 60°,1C . 全体很大的自然数D . 平面内到三个顶点距离相等的所有点10. (2分)下列不等式中解集为∅的是()A . x2≤0B . |x﹣5|>0C .D .11. (2分)已知A= ,则a=()A . 1B . 2C . 0D .12. (2分) (2018高二下·辽宁期末) 已知 , ,则是的()A . 充分不必要条件B . 必要不充分条件C . 充分必要条件D . 既不充分也不必要条件二、填空题 (共4题;共4分)13. (1分)若={0,a+b,a2},则a2 016+b2 016的值为________.14. (1分)已知集合A由a﹣1,2a2+5a+1,a2+1组成,且﹣2∈A,求a=________.15. (1分) (2016高一上·大名期中) 已知集合A={x|mx2+2x﹣1=0},若集合A中只有一个元素,则实数m 的值为________16. (1分) (2016高一上·延安期中) 若3∈{1,m+2},则m=________.三、解答题 (共6题;共65分)17. (15分)用列举法表示下列集合:(1) {x|x+y=7,x∈N+,y∈N+};(2) {(x,y)|x+y=7,x∈N+,y∈N+};(3) {y|y=x2﹣1,﹣2<x<3,x∈Z}.18. (15分)(2019·上海) 已知等差数列的公差,数列满足,集合.(1)若,求集合;(2)若,求使得集合恰好有两个元素;(3)若集合恰好有三个元素:,是不超过7的正整数,求的所有可能的值.19. (5分)用反证法证明:钝角三角形最大边上的中线小于该边长的一半.20. (5分)已知集合A={x|x2+x+p=0}.(Ⅰ)若A=∅,求实数p的取值范围;(Ⅱ)若A中的元素均为负数,求实数p的取值范围.21. (10分)设fn(x)是等比数列1,x,x2...,xn的各项和,其中x>0,n N,,n≥2,(1)证明:函数Fn(x)=fn(x)-2在(,1)内有且仅有一个零点(记为xn),且xn=+xnn+1;(2)设有一个与上述等比数列的首项、末项、项数分别相同的等差数列,其各项和为gn(x),比较fn(x)与gn(x)的大小,并加以证明.22. (15分) (2017高一上·西城期中) 已知:集合,其中.,称为的第个坐标分量.若,且满足如下两条性质:① 中元素个数不少于个.② ,,,存在,使得,,的第个坐标分量都是.则称为的一个好子集.(1)若为的一个好子集,且,,写出,.(2)若为的一个好子集,求证:中元素个数不超过.(3)若为的一个好子集且中恰好有个元素,求证:一定存在唯一一个,使得中所有元素的第个坐标分量都是.参考答案一、单选题 (共12题;共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题;共4分)13-1、14-1、15-1、16-1、三、解答题 (共6题;共65分) 17-1、17-2、17-3、18-1、18-2、18-3、19-1、20-1、21-1、21-2、22-1、22-2、22-3、。
2020-2021武汉市高一数学上期末试题(附答案)

2020-2021武汉市高一数学上期末试题(附答案)一、选择题1.已知()f x 在R 上是奇函数,且2(4)(),(0,2)()2,(7)f x f x x f x x f +=∈==当时,则 A .-2B .2C .-98D .982.函数()12cos 12x x f x x ⎛⎫-= ⎪+⎝⎭的图象大致为()A .B .C .D .3.设6log 3a =,lg5b =,14log 7c =,则,,a b c 的大小关系是( ) A .a b c <<B .a b c >>C .b a c >>D .c a b >>4.已知0.11.1x =, 1.10.9y =,234log 3z =,则x ,y ,z 的大小关系是( ) A .x y z >> B .y x z >>C .y z x >>D .x z y >>5.函数()2sin f x x x =的图象大致为( )A .B .C .D .6.已知函数()2log 14x f x x ⎧+=⎨+⎩0x x >≤,则()()3y f f x =-的零点个数为( )A .3B .4C .5D .67.已知()y f x =是以π为周期的偶函数,且0,2x π⎡⎤∈⎢⎥⎣⎦时,()1sin f x x =-,则当5,32x ππ⎡⎤∈⎢⎥⎣⎦时,()f x =( ) A .1sin x +B .1sin x -C .1sin x --D .1sin x -+8.已知函数f (x )=12log ,1,24,1,x x x x >⎧⎪⎨⎪+≤⎩则1(())2f f )等于( )A .4B .-2C .2D .19.已知全集U={1,2,3,4,5,6},集合P={1,3,5},Q={1,2,4},则()UP Q ⋃=A .{1}B .{3,5}C .{1,2,4,6}D .{1,2,3,4,5}10.已知定义在R 上的函数()f x 在(),2-∞-上是减函数,若()()2g x f x =-是奇函数,且()20g =,则不等式()0xf x ≤的解集是( )A .][(),22,-∞-⋃+∞B .][)4,20,⎡--⋃+∞⎣C .][(),42,-∞-⋃-+∞D .][(),40,-∞-⋃+∞11.对任意实数x ,规定()f x 取4x -,1x +,()152x -三个值中的最小值,则()f x ( )A .无最大值,无最小值B .有最大值2,最小值1C .有最大值1,无最小值D .有最大值2,无最小值12.下列函数中,在区间(1,1)-上为减函数的是 A .11y x=- B .cos y x =C .ln(1)y x =+D .2x y -=二、填空题13.()f x 是R 上的奇函数且满足(3)(3)f x f x -=+,若(0,3)x ∈时,()lg f x x x =+,则()f x 在(6,3)--上的解析式是______________.14.已知f (x )是定义域在R 上的偶函数,且f (x )在[0,+∞)上是减函数,如果f (m ﹣2)>f (2m ﹣3),那么实数m 的取值范围是_____. 15.已知()|1||1|f x x x =+--,()ag x x x=+,对于任意的m R ∈,总存在0x R ∈,使得()0f x m =或()0g x m =,则实数a 的取值范围是____________. 16.0.11.1a =,12log 2b =,ln 2c =,则a ,b ,c 从小到大的关系是________. 17.已知11,,1,2,32a ⎧⎫∈-⎨⎬⎩⎭,若幂函数()af x x =为奇函数,且在()0,∞+上递减,则a的取值集合为______.18.若集合{}{}2|560|20A x x x B x ax a Z =-+≤=-=∈,,,且B A ⊆,则实数a =_____.19.定义在R 上的奇函数()f x ,满足0x >时,()()1f x x x =-,则当0x ≤时,()f x =______.20.若函数()22xf x b =--有两个零点,则实数b 的取值范围是_____.三、解答题21.已知二次函数()f x 满足:()()22f x f x +=-,()f x 的最小值为1,且在y 轴上的截距为4.(1)求此二次函数()f x 的解析式;(2)若存在区间[](),0a b a >,使得函数()f x 的定义域和值域都是区间[],a b ,则称区间[],a b 为函数()f x 的“不变区间”.试求函数()f x 的不变区间;(3)若对于任意的[]10,3x ∈,总存在[]210,100x ∈,使得()1222lg 1lg mf x x x <+-,求m 的取值范围. 22.计算或化简:(1)1123021273log 161664π⎛⎫⎛⎫++- ⎪ ⎪⎝⎭⎝⎭; (2)6log 2332log 27log 2log 36lg 2lg 5+⋅-++.23.已知函数2()(,)1ax bf x a b x +=∈+R 为在R 上的奇函数,且(1)1f =. (1)用定义证明()f x 在(1,)+∞的单调性;(2)解不等式()()2341xxf f +≤+.24.攀枝花是一座资源富集的城市,矿产资源储量巨大,已发现矿种76种,探明储量39种,其中钒、钛资源储量分别占全国的63%和93%,占全球的11%和35%,因此其素有“钒钛之都”的美称.攀枝花市某科研单位在研发钛合金产品的过程中发现了一种新合金材料,由大数据测得该产品的性能指标值y (y 值越大产品的性能越好)与这种新合金材料的含量x (单位:克)的关系为:当0≤x <7时,y 是x 的二次函数;当x ≥7时,1()3x m y -=.测得部分数据如表:(1)求y 关于x 的函数关系式y =f (x );(2)求该新合金材料的含量x 为何值时产品的性能达到最佳.25.已知2()12xf x =+,()()1g x f x =-. (1)判断函数()g x 的奇偶性;(2)求101011()()i i f i f i ==-+∑∑的值.26.已知()log a f x x =,()()()2log 2201,1,a g x x a a a =+>+≠∈R ,()1h x x x=+.(1)当[)1,x ∈+∞时,证明:()1h x x x=+为单调递增函数; (2)当[]1,2x ∈,且()()()F x g x f x =-有最小值2时,求a 的值.【参考答案】***试卷处理标记,请不要删除一、选择题 1.A 解析:A 【解析】∵f(x+4)=f(x),∴f(x)是以4为周期的周期函数,∴f(2 019)=f(504×4+3)=f(3)=f(-1).又f(x)为奇函数,∴f(-1)=-f(1)=-2×12=-2,即f(2 019)=-2. 故选A2.C解析:C 【解析】函数f (x )=(1212xx-+)cosx ,当x=2π时,是函数的一个零点,属于排除A ,B ,当x ∈(0,1)时,cosx >0,1212x x -+<0,函数f (x )=(1212xx-+)cosx <0,函数的图象在x 轴下方. 排除D . 故答案为C 。
武汉市高一上学期期末数学试卷A卷(考试)

武汉市高一上学期期末数学试卷A卷姓名:________ 班级:________ 成绩:________一、选择题 (共12题;共24分)1. (2分)如图为一几何体的三视图,则该几何体体积为()A .B . 6C .D .2. (2分)设是不共线的两个向量,已知,,.若三点共线,则m的值为()A . 1B . 2C . -2D . -13. (2分) (2018高二上·合肥期末) 设表示三条不同的直线,表示三个不同的平面,给出下列三个命题:①若,则;②若,是在内的射影,,则;③若则 . 其中真命题的个数为()A . 0B . 1C . 2D . 34. (2分)下列命题中正确的是()A . 经过点P0(x0 , y0)的直线都可以用方程y-y0=k(x-x0)表示B . 经过定点A(0,b)的直线都可以用方程y=kx+b表示C . 经过任意两个不同点P1(x1 , y1),P2(x2 , y2)的直线都可用方程(x2-x1)(y-y1)=(y2-y1)(x-x1)表示D . 不经过原点的直线都可以用方程表示5. (2分)三个等圆O1、O2、O3有公共点M,点A、B、C是其他交点,则点M是△ABC的()A . 外心B . 内心C . 垂心D . 重心6. (2分)圆与圆的位置关系为()A . 内切B . 相交C . 外切D . 相离7. (2分)如图,棱长为1的正方体ABCD﹣A1B1C1D1中,E,F是侧面对角线BC1 , AD1上一点,若BED1F是菱形,则其在底面ABCD上投影的四边形面积()A .B .C .D .8. (2分)两条平行线4x+3y-1=0与8x+6y+3=0之间的距离是()A . 1B .C .D .9. (2分)与直线3x-4y+5=0关于x轴对称的直线方程为()A . 3x+4y-5=0B . 3x+4y+5=0C . -3x+4y-5=0D . -3x+4y+5=010. (2分)(2017·河南模拟) 如图,矩形ABCD中,AB=2AD,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE(A1∉平面ABCD),若M、O分别为线段A1C、DE的中点,则在△ADE翻转过程中,下列说法错误的是()A . 与平面A1DE垂直的直线必与直线BM垂直B . 异面直线BM与A1E所成角是定值C . 一定存在某个位置,使DE⊥MOD . 三棱锥A1﹣ADE外接球半径与棱AD的长之比为定值11. (2分) (2015高二上·西宁期末) 平行于直线2x﹣y+1=0且与圆x2+y2=5相切的直线的方程是()A . 2x﹣y+5=0B . x2﹣y﹣5=0C . 2x+y+5=0或2x+y﹣5=0D . 2x﹣y+5=0或2x﹣y﹣5=012. (2分)如图,在斜三棱柱ABC-A1B1C1中,∠BAC=90°,BC1⊥AC,则点C1在平面ABC上的射影H必在()A . 直线AB上B . 直线BC上C . 直线AC上D . △ABC的内部二、填空题 (共4题;共5分)13. (1分) (2017高一上·潮州期末) 设m,n是两条不同的直线,α,β,γ是三个不同的平面,给出下列四个命题:①若m⊥α,n∥α,则m⊥n;②若α∥β,β∥γ,m⊥α,则m⊥γ;③若m⊥α,n⊥α,则m∥n;④若α⊥γ,β⊥γ,则α∥β;其中正确命题的序号是________.14. (2分) (2017高二下·嘉兴期末) 已知直线与相交于点,若,则 ________,此时点的坐标为________.15. (1分) (2017高二下·成都开学考) 已知A(0,1),B(﹣,0),C(﹣,2),则△ABC内切圆的圆心到直线y=﹣ x+1的距离为________.16. (1分) (2016高二上·黄石期中) 长方体ABCD﹣A1B1C1D1中,底面ABCD是边长为2的正方形,高为4,则顶点A1到截面AB1D1的距离为________.三、解答题 (共6题;共55分)17. (10分)(2017·金山模拟) 如图,在四棱锥P﹣ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PB、PD 与平面ABCD所成的角依次是和,AP=2,E、F依次是PB、PC的中点;(1)求异面直线EC与PD所成角的大小;(结果用反三角函数值表示)(2)求三棱锥P﹣AFD的体积.18. (5分) (2019高二上·慈溪期中) 已知直线在两坐标轴上的截距相等,且点P(2,3)到直线l的距离为2,求直线的方程.19. (5分) (2018高二下·辽宁期末) 已知直线的方程为,圆的参数方程为(为参数),以原点为极点,轴正半轴为极轴,建立极坐标系.(I)求直线与圆的交点的极坐标;(II)若为圆上的动点,求到直线的距离的最大值.20. (10分) (2018高二上·临汾月考) 如图所示,三棱台中,,分别为AC,CB的中点.(1)求证:平面ABED∥平面FGH ;(2)若,,求证:平面平面 .21. (15分) (2016高一下·漳州期末) 设平面直角坐标系xOy中,曲线G:y= + x﹣a2(x∈R),a 为常数.(1)若a≠0,曲线G的图象与两坐标轴有三个交点,求经过这三个交点的圆C的一般方程;(2)在(1)的条件下,求圆心C所在曲线的轨迹方程;(3)若a=0,已知点M(0,3),在y轴上存在定点N(异于点M)满足:对于圆C上任一点P,都有为一常数,试求所有满足条件的点N的坐标及该常数.22. (10分) (2017高一下·衡水期末) 如图,在直三棱柱ABC﹣A1B1C1中,∠ACB=90°.BC=CC1=a,AC=2a.(1)求证:AB1⊥BC1;(2)求二面角B﹣AB1﹣C的正弦值.参考答案一、选择题 (共12题;共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题;共5分)13-1、14-1、15-1、16-1、三、解答题 (共6题;共55分)17-1、17-2、18-1、19-1、20-1、20-2、21-1、21-2、21-3、22-1、22-2、。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
武汉市高一上学期期末数学试卷(I)卷
姓名:________ 班级:________ 成绩:________
一、选择题 (共10题;共20分)
1. (2分)设集合A={0,1},集合B={x|x>a},若A∩B只有一个元素,则实数a的取值范围是()
A . {a|a<1}
B . {a|a≥1}
C . {a|0≤a<1}
D . {a|a≤1}
2. (2分)已知函数,则()
A .
B .
C . 1
D . 7
3. (2分)如图,已知中,点M在线段AC上,点P在线段BM上且满足,若
,则的值为()
A . -2
B . 2
C .
D .
4. (2分)下列函数是奇函数且在(0,+∞)上单调递增的是()
A . y=lnx
B . y=x+
C . y=x2
D .
5. (2分)函数的零点所在区间为()
A .
B .
C .
D .
6. (2分) (2016高三上·黑龙江期中) 设P为△ABC所在平面内一点,且2 +2 + = ,则△PAC 的面积与△ABC的面积之比等于()
A .
B .
C .
D . 不确定
7. (2分) (2019高一上·宁乡期中) 已知函数,其中表示不超过的最大整数.设,定义函数:,,,,则下列说法正确的有()个
① 的定义域为;
②设,,则;
③ ;
④若集合,则中至少含有个元素.
A . 个
B . 个
C . 个
D . 个
8. (2分) (2017高一上·长春期中) 若f(x)是偶函数,且当x∈[0,+∞)时,f(x)=x﹣1,则f(x﹣1)<0的解集是()
A . (﹣1,0)
B . (﹣∞,0)∪(1,2)
C . (1,2)
D . (0,2)
9. (2分) (2017高一下·乾安期末) 已知向量夹角为,且,,则()
A .
B .
C .
D .
10. (2分) (2016高二下·惠阳期中) 已知函数f(x)= .若f(a)+f(1)=0,则实数a的值等于()
A . ﹣3
B . ﹣1
C . 1
D . 3
二、填空题 (共8题;共8分)
11. (1分) (2019高一上·青冈期中) ________.
12. (1分) (2017高一上·上海期中) 若f(x)=ax2+3a是定义在[a2﹣5,a﹣1]上的偶函数,令函数g(x)=f(x)+f(1﹣x),则函数g(x)的定义域为________.
13. (1分)已知不论a为何正实数,y=ax+2﹣3的图象恒过定点,则这个定点的坐标是________.
14. (1分) (2015高二下·椒江期中) 已知空间向量,,若∥ ,则xz=________
15. (1分)(2017·江苏模拟) 若函数f(x)= ,则函数y=|f(x)|﹣的零点个数为________.
16. (1分)(2016·中山模拟) 已知向量为单位向量,向量 =(1,1),且| ﹣ |= ,则向量,的夹角为________.
17. (1分)已知集合A中只含有1,a2两个元素,则实数a不能取的值为________.
18. (1分)函数f(x)=x+1,x∈{﹣1,1,2}的值域是________.
三、解答题 (共4题;共45分)
19. (5分)设集合,且A∩B=C,求实数x,y的值及A∪B.
20. (10分) (2016高一下·溧水期中) 已知在同一平面内,且.
(1)若,且,求m的值;
(2)若| |=3,且,求向量与的夹角.
21. (15分)(2017·黄陵模拟) 已知函数f(x)=x3﹣ax,g(x)= x2﹣lnx﹣.
(1)若f(x)和g(x)在同一点处有相同的极值,求实数a的值;
(2)对于一切x∈(0,+∞),有不等式f(x)≥2x•g(x)﹣x2+5x﹣3恒成立,求实数a的取值范围;
(3)设G(x)= x2﹣﹣g(x),求证:G(x)>﹣.
22. (15分) (2018高一上·广东期末) 已知二次函数满足:,且该函数的最小值为1.
(1)求此二次函数的解析式;
(2)若函数的定义域为(其中),问是否存在这样的两个实数,,使得函数的值域也为?若存在,求出,的值;若不存在,请说明理由.
(3)若对于任意的,总存在使得,求的取值范围.
参考答案一、选择题 (共10题;共20分)
1-1、
2-1、
3-1、
4-1、
5-1、
6-1、
7-1、
8-1、
9-1、
10-1、
二、填空题 (共8题;共8分)
11-1、
12-1、
13-1、
14-1、
15-1、
16-1、
17-1、
18-1、
三、解答题 (共4题;共45分)
19-1、
20-1、
20-2、
21-1、
21-2、
21-3、
22-1、22-2、22-3、。
