培优专题--纸片折叠求角度问题

合集下载

初一数学下学期培优训练小专题06 三角形折叠中的角度问题

初一数学下学期培优训练小专题06 三角形折叠中的角度问题【例题讲解】【原题再现】有这样一道题：如图1，将ABC ∆纸片沿DE 折叠，使点A 落在四边形BCDE 内点A '的位置．试探索A ∠与12∠+∠之间的数量关系，并说明理由．（1）小明提出一种正确的解题思路：连接AA '，则么1∠、2∠分别为AEA '∆、ADA '∆的外角，…… 请你按照小明的思路解决上述问题．（2）【变式探究】如图2，若将原题中“点A 落在四边形BCDE 内点A '的位置”变为“点A 落在四边形BCDE 外点A '的位置”，试猜想此时A ∠与1∠、2∠之间的数量关系，并说明理由．（3）【结论运用】将四边形纸片(90ABCD C ∠=︒，AB 与CD 不平行）沿EF 折叠成图3的形状，若1110∠=︒，240∠=︒，直接写出ABC ∠的度数．解：（1）图1中，结论：2∠BAC =∠1+∠2，理由是：连接AA ′． ∵沿DE 折叠A 和A ′重合，∴∠DAE =∠DA ′E ，∠EA ′A =∠EAA ′，∠DA ′A =∠DAA ′， ∵∠1=∠EA ′A +∠EAA ′，∠2=∠DA ′A +∠DAA ′， ∴∠1+∠2=∠EA ′A +∠EAA ′+∠DA ′A +∠DAA ′=2∠BAC ；（2）如图2，结论：2∠A =∠1-∠2．理由：设EA ′交AC 于J ．∵∠1=∠EJA +∠A ，∠EJA =∠A ′+∠2， ∴∠1=∠A ′+∠A +∠2=2∠A +∠2， ∴2∠A =∠1-∠2；（2）如图，根据折叠知：∠AEF =∠A EF '，∠EFD =∠'EFD ，AEA'=∠AEF=180°-110°=70°，∵∠1=110°，∴∠2∴∠AEF=35°，∵∠2=40°，∴2∠EFD=180°+∠2=220°，∴∠EFD=110°，∴∠A+∠D=360°-(∠AEF+∠EFD)= 215°，∴∠B=360°-(∠A+∠D)-∠C = 55°．【综合演练】1．如图，在△ABC中，点D是BC上的点，将△ABD沿着AD翻折得到△AED，若∠B=∠BAE=50°，则∠CDE的度数是（）A．25°B．30°C．35°D．40°2．如图，△ABC中∠A＝40°，E是AC边上的点，先将△ABE沿着BE翻折，翻折后△ABE的AB边交AC 于点D，又将△BCD沿着BD翻折，点C恰好落在BE上的点G处，此时∠BDC＝82°，则原三角形的∠B 的度数为（）A．57°B．60°C．63°D．70°3．将△ABC纸片沿DE按如图的方式折叠．若∠C=50°，∠1=85°，则∠2的度数等于（）A．10°B．15°C．20°D．25°4．如图，将三角形纸片ABC沿DE折叠，当点A落在四边形BCDE的外部时，测量得∠1＝70°，∠2＝152°，则∠A 为（）A ．40°B ．42°C ．30°D ．52°第II 卷（非选择题）请点击修改第II 卷的文字说明二、填空题(共0分)5．如图，三角形纸片ABC 中，70A ∠=︒，75B ∠=︒．将三角形纸片的一角折叠，使点C 落在ABC 内，那么12∠+∠=_____________︒．6．在△ABC 中，点E 、F 分别为边AB 、AC 上的点，把△ABC 沿EF 翻折，翻折后的图形如图所示．若1+2110∠∠=︒，则A ∠的度数为___________．7．如图，把一张长方形纸片ABCD 沿EF 折叠，∠1＝55°，则∠2＝________°．8．将△ABC 纸片沿DE 按如图的方式折叠．若∠C ＝50°，∠1＝85°，则∠2等于______．三、解答题(共0分)9．如图，将ABC纸片沿DE折叠，使点A落在四边形BCDE内点'A的位置，∠+∠之间的数量关系，并说明理由．(1)探索A∠与12(2)如果点A落在四边形BCDE外点''A的位置，A∠与1∠之间的数量关系有何变化，请说明理由．∠、210．在我们苏科版义务教育教科书数学七下第42页曾经研究过双内角平分线的夹角和内外角平分线夹角问题．聪聪在研究完上面的问题后，对这类问题进行了深入的研究，他的研究过程如下：(1)【问题再现】如图1，在△ABC中，∠ABC、∠ACB的角平分线交于点P，若∠A＝50°．则∠P＝_______；(2)【问题推广】如图2，在△ABC中，∠BAC的角平分线与△ABC的外角∠CBM的角平分线交于点P，过点B作BH⊥AP 于点H，若∠ACB＝80°，求∠PBH的度数．(3)如图3，在△ABC中，∠ABC、∠ACB的角平分线交于点P，将△ABC沿DE折叠使得点A与点P重合，若∠1+∠2＝100°，则∠BPC＝_______；(4)【拓展提升】在四边形BCDE中，EB∥CD，点F在直线ED上运动（点F不与E，D两点重合），连接BF，CF，∠EBF、∠DCF 的角平分线交于点Q ，若∠EBF ＝α，∠DCF ＝β，直接写出∠Q 和α，β之间的数量关系． 11．如图，将一张三角形纸片ABC 的一角折叠，使得点A 落在四边形BCDE 的外部A '的位置且A '与点C 在直线AB 的异侧，折痕为DE ，已知90C ∠=︒，30A ∠=︒．（1）求12∠-∠的度数；（2）若保持A DE '的一边与BC 平行，求ADE ∠的度数．12．将ABC 纸片的一角CAB ∠折叠，使点A 落在点P 的位置，折痕为DE ．（1）如图1，点A 落在ABC 内的点P 的位置．①若//PE AC ，那么PD 与AB 有怎样的位置关系，请说明理由； ②如图2，1∠、2∠与A ∠之间有怎样的数量关系？并说明理由；③连接CP 、BP ，已知CP 、BP 恰好分别平分ACB ∠、ABC ∠（如图3），1∠、2∠与CPB ∠之间有怎样的数量关系，并说明理由；（2）如图4，点A 落在ABC 外的点P 的位置．连接CP 、BP ，如果CP 、BP 恰好分别平分ABC 的两个外角MCB ∠，NBC ∠，那么1∠、2∠与CPB ∠之间的数量关系是______．（请直接写出结果）13．问题1：现有一张△ABC 纸片，点D 、E 分别是△ABC 边上两点，若沿直线DE 折叠．（1）探究1：如果折成图①的形状，使A 点落在CE 上，则∠1与∠A 的数量关系是；（2）探究2：如果折成图②的形状，猜想∠1+∠2和∠A 的数量关系是；（3）探究3：如果折成图③的形状，猜想∠1、∠2和∠A 的数量关系，并说明理由．（4）问题2：将问题1推广，如图④，将四边形ABCD 纸片沿EF 折叠，使点A 、B 落在四边形EFCD 的内部时，∠1+∠2与∠A 、∠B 之间的数量关系是 .14．在△ABC 中，∠BAC ＝90°，点D 是BC 上一点，将△ABD 沿AD 翻折后得到△AED ，边AE 交射线BC 于点F ．（友情提醒：翻折前后的两个三角形的对应边相等，对应角相等．）（1）如图①，当AE ⊥BC 时，求证：DE ∥AC ．（2）若10C B ∠-∠=︒，∠BAD ＝x° ． ①如图②，当DE ⊥BC 时，求x 的值；②是否存在这样的x 的值，使得△DEF 中有两个角相等．若存在，并求x 的值；若不存在，请说明理由． 15．在△ABC 中，∠BAC ＝90°，点D 是BC 上一点，将△ABD 沿AD 翻折后得到△AED ，边AE 交BC 于点F ．(1)如图①，当AE ⊥BC 时，写出图中所有与∠B 相等的角：；所有与∠C 相等的角：．(2)若∠C －∠B ＝50°，∠BAD ＝x °(0＜x ≤45) ． ① 求∠B 的度数；②是否存在这样的x 的值，使得△DEF 中有两个角相等．若存在，并求x 的值；若不存在，请说明理由． 16．如图1，将△ABC 纸片沿DE 折叠，使点C 落在四边形ABDE 内点C ’的位置，（1）①若00120,250∠=∠=，则C ∠= ； ②若042C ∠=，则12∠+∠= ；③探索C ∠ 、1∠与2∠之间的数量关系，并说明理由；（2）直接按照所得结论，填空：①如图中，将△ABC 纸片再沿FG 、MN 折叠，使点A 、B 分别落在△ABC 内点A ’、B ’的位置，则123456∠+∠+∠+∠+∠+∠= ；②如图中，将四边形ABCD 按照上面方式折叠，则128∠+∠++∠= ； ③若将n 边形123n A A A A 也按照上面方式折叠，则122n ∠+∠++∠= ；（3）如图，将△ABC 纸片沿DE 折叠，使点C 落在△ABC 边AC 上方点'C 的位置，探索C ∠、1∠与2∠之间的数量关系，并说明理由.17．直线MN 与直线PQ 垂直相交于O ，点A 在射线OP 上运动，点B 在射线OM 上运动，连接AB, （1）如图，已知AC 、BC 分别是∠BAP 和∠ABM 角的平分线，①点A 、B 在运动的过程中，∠ACB 的大小是否发生变化？若发生变化，请说明理由；若不发生变化，试求出∠ACB 的大小．②如图，将△ABC 沿直线AB 折叠，若点C 落在直线PQ 上，记作点C′，则∠ABO ＝ °；如图，将△ABC 沿直线AB 折叠，若点C 落在直线MN 上，记作点C′′，则∠ABO ＝ °．（2）如图，延长BA至G，已知∠BAO、∠OAG的角平分线与∠BOQ的角平分线及其延长线交于E、F，在△AEF中，如果有一个角是另一个角的32倍，求∠ABO的度数．答案与解析【例题讲解】【原题再现】有这样一道题：如图1，将ABC ∆纸片沿DE 折叠，使点A 落在四边形BCDE 内点A '的位置．试探索A ∠与12∠+∠之间的数量关系，并说明理由．（1）小明提出一种正确的解题思路：连接AA '，则么1∠、2∠分别为AEA '∆、ADA '∆的外角，…… 请你按照小明的思路解决上述问题．（2）【变式探究】如图2，若将原题中“点A 落在四边形BCDE 内点A '的位置”变为“点A 落在四边形BCDE 外点A '的位置”，试猜想此时A ∠与1∠、2∠之间的数量关系，并说明理由．（3）【结论运用】将四边形纸片(90ABCD C ∠=︒，AB 与CD 不平行）沿EF 折叠成图3的形状，若1110∠=︒，240∠=︒，直接写出ABC ∠的度数．解：（1）图1中，结论：2∠BAC =∠1+∠2，理由是：连接AA ′． ∵沿DE 折叠A 和A ′重合，∴∠DAE =∠DA ′E ，∠EA ′A =∠EAA ′，∠DA ′A =∠DAA ′， ∵∠1=∠EA ′A +∠EAA ′，∠2=∠DA ′A +∠DAA ′， ∴∠1+∠2=∠EA ′A +∠EAA ′+∠DA ′A +∠DAA ′=2∠BAC ；（2）如图2，结论：2∠A =∠1-∠2．理由：设EA ′交AC 于J ．∵∠1=∠EJA +∠A ，∠EJA =∠A ′+∠2， ∴∠1=∠A ′+∠A +∠2=2∠A +∠2， ∴2∠A =∠1-∠2；（2）如图，根据折叠知：∠AEF =∠A EF '，∠EFD =∠'EFD ，AEA'=∠AEF=180°-110°=70°，∵∠1=110°，∴∠2∴∠AEF=35°，∵∠2=40°，∴2∠EFD=180°+∠2=220°，∴∠EFD=110°，∴∠A+∠D=360°-(∠AEF+∠EFD)= 215°，∴∠B=360°-(∠A+∠D)-∠C = 55°．【综合演练】1．如图，在△ABC中，点D是BC上的点，将△ABD沿着AD翻折得到△AED，若∠B=∠BAE=50°，则∠CDE的度数是（）A．25°B．30°C．35°D．40°【答案】B【分析】根据翻折的性质得到∠BAD=∠EAD=25°，∠E=∠B=50°，根据三角形内角和定理推出∠ADE=∠ADB=105°，进一步计算即可解答．【解析】解：∵∠B=∠BAE=50°，将△ABD沿着AD翻折得到△AED，∴∠BAD=∠EAD=25°，∠E=∠B=50°，∴∠ADE=∠ADB=180°-50°-25°=105°，∴∠ADC=180°-∠ADB=75°，∴∠CDE=105°-75°=30°，故选：B．【点评】此题考查翻折的性质，三角形内角和定理，关键是掌握翻折的性质．2．如图，△ABC中∠A＝40°，E是AC边上的点，先将△ABE沿着BE翻折，翻折后△ABE的AB边交AC 于点D，又将△BCD沿着BD翻折，点C恰好落在BE上的点G处，此时∠BDC＝82°，则原三角形的∠B 的度数为（）A ．57°B ．60°C ．63°D ．70°【答案】C【分析】根据折叠的性质可知：∠BDG ＝∠BDC ＝82°，∠ABE ＝∠A 'BE ＝∠A 'BG=∠A 'BC ，根据三角形外角性质可得：∠DBA ＝∠BDC ﹣∠A ＝82°﹣40°＝42°，进一步可求出∠ABE ＝∠A 'BE ＝21°，∠ABC ＝3×21°＝63°，即原三角形的∠B =63°．【解析】解：由折叠性质可得，∠BDG ＝∠BDC ＝82°，∠ABE ＝∠A 'BE ＝∠A 'BG=∠A 'BC ， ∵∠BDC 是△BDA 的外角，∴∠DBA ＝∠BDC ﹣∠A ＝82°﹣40°＝42°， ∴∠ABE ＝∠A 'BE ＝21°，∴∠ABC ＝3×21°＝63°，即原三角形的∠B =63°，故选：C ．【点评】此题主要考查的是图形的折叠及三角形外角性质，能够根据折叠的性质发现∠BDG ＝∠BDC ＝82°，∠ABE ＝∠A 'BE ＝∠A 'BG=∠A 'BC 是解答此题的关键．3．将△ABC 纸片沿DE 按如图的方式折叠．若∠C =50°，∠1=85°，则∠2的度数等于（）A ．10°B ．15°C ．20°D ．25°【答案】B【分析】由四边形的内角和及三角形内角和即可求得．【解析】∵180A B C ∠+∠+∠=︒，且∠C =50゜ ∴180130A B C ∠+∠=︒-∠=︒同理，在△CDE 中，180130CDE CED C ∠+∠=︒-∠=︒ 由折叠性质得：A A ∠'=∠，B B '∠=∠ ∴130A B ''∠+∠=︒在四边形A B ED ''中，360A B A DE DEB ''''∠+∠+∠+∠=︒ ∴12360A B CDE CED ''∠+∠+∠+∠+∠+∠=︒ ∴130851302360︒+︒+︒+∠=︒ ∴∠2=15゜故选：B ．【点评】本题考查了折叠的性质，多边形的内角和定理等知识，掌握多边形内角和定理及折叠的性质是关键．4．如图，将三角形纸片ABC 沿DE 折叠，当点A 落在四边形BCDE 的外部时，测量得∠1＝70°，∠2＝152°，则∠A 为（）A ．40°B ．42°C ．30°D ．52°【答案】B【分析】利用四边形的内角和定理求出B C ∠+∠，再利用三角形的内角和定理可得结果．【解析】解：∵1=70∠︒，2=152∠︒，∴3601236070152138B C ∠+∠=︒-∠-∠=︒-︒-︒=︒， ∴180()18013842A B C ∠=︒-∠+∠=︒-︒=︒，故选：B ．【点评】此题考查了多边形内角与外角、三角形内角和定理，熟练掌握相关知识是解题的关键．第II 卷（非选择题）请点击修改第II 卷的文字说明5．如图，三角形纸片ABC 中，70A ∠=︒，75B ∠=︒．将三角形纸片的一角折叠，使点C 落在ABC 内，那么12∠+∠=_____________︒．【答案】70【分析】延长AF、BE交于点D，根据∠A＝70°，∠B＝75°，可得∠D＝35°，由将纸片的一角折叠，使点C落在△ABC内，可得∠DFC+∠DEC＝290°，即可得答案．【解析】解：延长AF、BE交于点D，∵∠A＝70°，∠B＝75°，∴∠D＝180°﹣∠A﹣∠B＝35°，∴∠DFE+∠DEF＝180°﹣∠D＝145°，∵将纸片的一角折叠，使点C落在△ABC内，∴∠CFE＝∠DFE，∠CEF＝∠DEF，∴∠DFC+∠DEC＝2（∠DFE+∠DEF）＝290°，∴∠1+∠2＝（180°﹣∠DFC）+（180°﹣∠DEC）＝360°﹣（∠DFC+∠DEC）＝360°﹣290°＝70°，故答案为：70．【点评】本题考查三角形中的折叠问题，解题的根据是掌握折叠的性质，灵活应用三角形内角和定理．6．在△ABC中，点E、F分别为边AB、AC上的点，把△ABC沿EF翻折，翻折后的图形如图所示．若∠的度数为___________．1+2110∠∠=︒，则A【答案】55︒【分析】如图，延长B′E交C′F的延长线于点A′，连接AA′．证明∠1+∠2=2∠EAF，可得结论．【解析】解：如图，延长B′E交C′F的延长线于点A′，连接AA′．∵∠1=∠EAA′+∠EA′A，∠2=∠F AA′+∠F A′A,∴∠1+∠2=∠EAF+∠EA′F，∵∠EAF=∠EA′F，∴∠1+∠2=2∠EAF=110°，∴∠A=55°．故答案为：55°．【点评】本题考查三角形内角和定理，翻折变换等知识，解题的关键是证明∠1+∠2=2∠EAF．7．如图，把一张长方形纸片ABCD沿EF折叠，∠1＝55°，则∠2＝________°．【答案】70【分析】根据长方形的对边平行知AD∥BC，得∠DEF＝∠1＝55°，再根据折叠的性质知∠GEF＝∠DEF ＝55°，继而由∠AEG＝180°−∠DEF−∠GEF可得答案．【解析】解：由题意知AD∥BC，∠1＝55°，∴∠DEF＝∠1＝55°，根据折叠的性质知∠GEF＝∠DEF＝55°，则∠AEG＝180°−∠DEF−∠GEF＝180°-55°-55°=70°，∴∠2＝70°，故答案为：70．【点评】本题考查了平行线的性质和折叠的性质，解题的关键是掌握两直线平行内错角相等的性质、折叠的性质．8．将△ABC纸片沿DE按如图的方式折叠．若∠C＝50°，∠1＝85°，则∠2等于______．【答案】15︒【分析】利用三角形的内角和定理以及折叠的性质，求出130CDE CED ∠+∠=︒，''130A B ∠+∠=︒，利用四边形内角和为360︒，即可求出∠2．【解析】解：在ABC ∆中，180130A B C ∠+∠=︒-∠=︒，在CDE ∆中，180130CDE CED C ∠+∠=-∠=︒，由折叠性质可知：''130A B A B ∠+∠=∠+∠=︒ ，四边形''DEB A 的内角和为360︒，''''360A B ADE B ED ∴∠+∠+∠+∠=︒，1A DE CDE ∠=∠+∠'，'2B ED CED ∠=∠+∠，''12()360CDE CED A B ∴∠+∠+∠+∠+∠+∠=︒，130CDE CED ∠+∠=︒，''130A B ∠+∠=︒，且∠1＝85°， 215∴∠=︒，故答案为：15︒．【点评】本题主要是考查了三角形和四边形的内角和定理，熟练利用三角形内角和定理，求出两角之和，最后利用四边形的内角和求得某角的度数，这是解决该题的关键．9．如图，将ABC 纸片沿DE 折叠，使点A 落在四边形BCDE 内点'A 的位置，(1)探索A ∠与12∠+∠之间的数量关系，并说明理由．(2)如果点A 落在四边形BCDE 外点''A 的位置，A ∠与1∠、2∠之间的数量关系有何变化，请说明理由．【答案】(1)2∠A =∠1+∠2，理由见解析 (2)∠A =12（∠2-∠1），理由见解析【分析】（1）根据折叠性质得出∠AED=∠A′ED，∠ADE=∠A′DE，根据三角形内角和定理得出∠AED+∠ADE=180°-∠A，代入∠1+∠2=180°+180°-2（∠AED+∠ADE）求出即可；（2）先根据翻折的性质表示出∠1、∠2，再根据四边形的内角和定理列式整理即可得解．（1）2∠A=∠1+∠2，理由是：∵沿DE折叠A和A′重合，∴∠AED=∠A′ED，∠ADE=∠A′DE，∵∠AED+∠ADE=180°-∠A，∠1+∠2=180°+180°-2（∠AED+∠ADE），∴∠1+∠2=360°-2（180°-∠A）=2∠A．（2）∵沿DE折叠A和A'′重合，∴∠AED=∠A′'ED，∠ADE=∠A′'DE，又∵∠1=∠A'ED-∠BED=∠AED-（180°-∠AED）=2∠AED-180°，∠2=180°-2∠ADE，∠AED+∠ADE=180°-∠A，∴12∠1+90°+90°-12∠2=180°-∠A，即∠A=12（∠2-∠1）．【点评】本题考查了折叠的性质，三角形外角性质，三角形内角和定理及四边形内角和的应用，主要考查学生运用定理进行推理和计算的能力．10．在我们苏科版义务教育教科书数学七下第42页曾经研究过双内角平分线的夹角和内外角平分线夹角问题．聪聪在研究完上面的问题后，对这类问题进行了深入的研究，他的研究过程如下：(1)【问题再现】如图1，在△ABC中，∠ABC、∠ACB的角平分线交于点P，若∠A＝50°．则∠P＝_______；(2)【问题推广】如图2，在△ABC中，∠BAC的角平分线与△ABC的外角∠CBM的角平分线交于点P，过点B作BH⊥AP 于点H，若∠ACB＝80°，求∠PBH的度数．(3)如图3，在△ABC中，∠ABC、∠ACB的角平分线交于点P，将△ABC沿DE折叠使得点A与点P重合，若∠1+∠2＝100°，则∠BPC＝_______；(4)【拓展提升】在四边形BCDE中，EB∥CD，点F在直线ED上运动（点F不与E，D两点重合），连接BF，CF，∠EBF、∠DCF的角平分线交于点Q，若∠EBF＝α，∠DCF＝β，直接写出∠Q和α，β之间的数量关系．当F 在D 、E 之间时，如图4-2所示：同理可得112222FBQ EBF QCF DCF αβ∠=∠===，∠∠，180180FBC FCB DCF EBF αβ∠+∠=︒-∠-=︒--∠，∴1801802Q QBC QCB QBF FBC FCB QCF αβ+=︒--=︒----=∠∠∠∠∠∠∠；当点F 在D 点右侧时，如图4-3所示：同理可得1801802Q QBC QCB QBF FBC DCB QCD αβ-=︒--=︒----=∠∠∠∠∠∠∠；综上所述，F 在E 左侧2Q βα-∠=；F 在ED 中间2Q αβ+∠=；F 在D 右侧2Q αβ-∠=．【点评】本题主要考查了三角形内角和定理，角平分线的定义，三角形外角的性质，平行线的性质，垂线的定义，熟知相关知识是解题的关键．11．如图，将一张三角形纸片ABC 的一角折叠，使得点A 落在四边形BCDE 的外部A '的位置且A '与点C 在直线AB 的异侧，折痕为DE ，已知90C ∠=︒，30A ∠=︒．（1）求12∠-∠的度数；（2）若保持A DE '的一边与BC 平行，求ADE ∠的度数．【答案】（1）60°；（2）45°或30°【分析】（1）先求出∠B 的度数，在根据四边形内角和求出∠1+∠BFD 的度数，由∠BFD =∠A ′FE 和∠A ′的度数可求出答案．（2）分EA '∥BC 和DA '∥BC 两种情况讨论．当DA '∥BC 时，先求出∠A ′DA =90°，再根据折叠可得出∠ADE =45°；当EA '∥BC 时，根据平行线的性质求出∠2=∠ABC =60°，由（1）得出∠1=120°，再根据折叠可求出∠ADE 的度数．【解析】解：（1）由折叠可知，30A A '∠=∠=︒在A EF '△中，2180A A FE ''∠+∠+∠=︒2180150A AFE A FE ''∴∠=︒-∠-∠=︒-∠在ABC 中，18060B C A ∠=︒-∠-∠=︒在四边形BCDF 中，1360C B BFD ∠+∠+∠+∠=︒1360210C B BFD BFD ∴∠=︒-∠-∠-∠=︒-∠因为BFD A FE '∠=∠1221015060∴∠-∠=︒-︒=︒（2）①当//DA BC '时，90ADA ACB '∠=∠=︒ADE 沿DE 折叠A DE '1452ADE A DE ADA ''∴∠=∠=∠=︒②当//EA BC '时，260ABC ∠=∠=︒由（1）知，1260∠-∠=︒，1260120∴∠=∠+︒=︒，ADE 沿DE 折叠A DE '()11801302ADE A DE ADA ''∴∠=∠=∠=︒-∠=︒综上，∠ADE 的度数为：45°或30°．【点评】本题考查了翻折变换的性质，三角形的一个外角等于与它不相邻的两个内角的和，三角形的内角和等于180°，平行线的性质，属于综合题，但难度不大．熟记性质准确识图是解题的关键．12．将ABC 纸片的一角CAB ∠折叠，使点A 落在点P 的位置，折痕为DE ．（1）如图1，点A 落在ABC 内的点P 的位置．①若//PE AC ，那么PD 与AB 有怎样的位置关系，请说明理由；②如图2，1∠、2∠与A ∠之间有怎样的数量关系？并说明理由；③连接CP 、BP ，已知CP 、BP 恰好分别平分ACB ∠、ABC ∠（如图3），1∠、2∠与CPB ∠之间有怎样的数量关系，并说明理由；（2）如图4，点A 落在ABC 外的点P 的位置．连接CP 、BP ，如果CP 、BP 恰好分别平分ABC 的两个外角MCB ∠，NBC ∠，那么1∠、2∠与CPB ∠之间的数量关系是______．（请直接写出结果）【答案】（1）①//PD AB ，理由见解析；②122A ∠+∠=∠，理由见解析；③123604CPB ∠+∠+︒=∠，理由见解析；（2）124360CPB ∠+∠+∠=︒，理由见解析【分析】（1）①若//PE AC ，则可推出ADE DEP ∠=∠，然后根据翻折的性质可推出PDE DEA ∠=∠，从而得出结论即可；②根据翻折的性质推出()123602ADE AED ∠+∠=︒-∠+∠，然后结合三角形的内角和推出180A ADE AED ︒-∠=∠+∠，从而代入替换得出结论即可；③根据CP 、BP 恰好分别平分ACB ∠、ABC ∠，可推出()12PCB PBC ACB ABC ∠+∠=∠+∠，然后结合②的结论进行变形整理即可；（2）根据题意可推出()12ACB ABC CPB ∠+∠=∠，然后结合三角形的内角和以及（1）中②的结论，综合整理求解即可．【解析】（1）//PD AB ，理由如下：∵//PE AC ，∴ADE DEP ∠=∠，由翻折的性质可得：ADE PDE ∠=∠，AED PED ∠=∠，∴PDE DEA ∠=∠，∴//PD AB ；②122A ∠+∠=∠，理由如下：由翻折的性质可得：ADE PDE ∠=∠，AED PED ∠=∠，∴11802ADE ∠=︒-∠，21802AED ∠=︒-∠，∴()123602ADE AED ∠+∠=︒-∠+∠，在ADE 中，180A ADE AED ︒-∠=∠+∠，∴()1236021802A A ∠+∠=︒-︒-∠=∠，在ABC 中，由②可知，∠ACB ∠+∠在PBC 中，180CPB ︒-∠12∠+∠+2）1∠+∠CP 、BP 恰好分别平分ABC 的两个外角)ACB ，PBC ∠∴在PBC 中，180PBC ∠=(11801802ABC ︒-∠︒-∠整理得：(12ACB ∠在ABC 中，∠由②可知，∠ACB ∠+∠1118022⎡︒-⎢⎣13．问题1：现有一张△ABC 纸片，点D 、E 分别是△ABC 边上两点，若沿直线DE 折叠．（1）探究1：如果折成图①的形状，使A 点落在CE 上，则∠1与∠A 的数量关系是；（2）探究2：如果折成图②的形状，猜想∠1+∠2和∠A 的数量关系是；（3）探究3：如果折成图③的形状，猜想∠1、∠2和∠A 的数量关系，并说明理由．（4）问题2：将问题1推广，如图④，将四边形ABCD 纸片沿EF 折叠，使点A 、B 落在四边形EFCD 的内部时，∠1+∠2与∠A 、∠B 之间的数量关系是 . 【答案】（1）12A ∠=∠;（2）122A ∠+∠=∠;（3）见解析;（4）1222360A B ∠+∠=∠+∠-︒【分析】（1）根据三角形外角性质可得；（2）在四边形A EAD '中，内角和为360°，∠BDA=∠CEA=180°，利用这两个条件，进行角度转化可得关系式；（3）如下图，根据（1）可得∠1=2∠DAA '，∠2=2∠EAA '，从而推导出关系式；（4）根据平角的定义以及四边形的内角和定理，与（2）类似思路探讨，可得关系式．【解析】（1）∵△'EDA 是△EDA 折叠得到∴∠A=∠A '∵∠1是△'ADA 的外角∴∠1=∠A+∠A '∴12A ∠=∠；（2）∵在四边形A EAD '中，内角和为360°∴∠A+A '+∠A DA '+∠A EA '=360°同理，∠A=∠A '∴2∠A+∠A DA '+∠A EA '=360°∵∠BDA=∠CEA=180∴∠1+∠A DA '+∠A EA '+∠2=360°∴122A ∠+∠=∠ ；（3）数量关系：212A ∠-∠=∠理由：如下图，连接AA '由（1）可知：∠1=2∠DAA '，∠2=2∠EAA '∴212()2EAA DAA DAE ∠-∠=∠-=∠'∠'；（4）由折叠性质知：∠2=180°－2∠AEF ，∠1=180°－2∠BFE相加得：123602(360)22360A B A B ∠+∠=︒-︒-∠-∠=∠+∠-︒．【点评】本题考查角度之间的关系，（4）问的解题思路是相同的，主要运用三角形的内角和定理和四边形的内角和定理进行角度转换．14．在△ABC 中，∠BAC ＝90°，点D 是BC 上一点，将△ABD 沿AD 翻折后得到△AED ，边AE 交射线BC 于点F ．（友情提醒：翻折前后的两个三角形的对应边相等，对应角相等．）（1）如图①，当AE ⊥BC 时，求证：DE ∥AC ．（2）若10C B ∠-∠=︒，∠BAD ＝x°． ①如图②，当DE ⊥BC 时，求x 的值； ②是否存在这样的x 的值，使得△DEF 中有两个角相等．若存在，并求x 的值；若不存在，请说明理由．【答案】（1）见解析；（2）①5x =，②存在，15x =或30．【分析】（1）根据折叠的性质得到∠B=∠E ，根据平行线的判定定理证明；（2）①根据三角形内角和定理分别求出∠C=60°，∠B=30°，根据折叠的性质计算即可；②分∠EDF=∠DFE 、∠DFE=∠E 、∠EDF=∠E 三种情况，列方程解答即可．【解析】（1）∵AE ⊥BC∴∠EAC+∠C=90°∵∠BAC=90°∴∠B+∠C=90°∴∠B=∠EAC∵将△ABD 沿AD 翻折后得到△AED∴∠B=∠E∴∠EAC=∠E∴DE ∥AC（2）①∵∠B+∠C=90°，10C B ∠-∠=︒∴∠B=40°，∠C=50°∵DE ⊥BC∴∠EDF=90°∵将△ABD 沿AD 翻折后得到△AED∴∠B=∠E=40°，∠BAD=∠EAD=x °∴∠DFE=50°∵∠DFE=B BAF ∠+∠∴24050x +=∴5x =②由题意可得，∠ADC=40x +， ∠ABD=140x - ，∠EDF=140(40)1002x x x --+=-∠DFE=402x +（ⅰ）若∠EDF=∠DFE ，可得100-2402x x =+，解得15x =（ⅱ）若∠EDF=∠E ，可得100-240x =解得30x =（ⅲ）若∠DFE =∠E ，可得40240x +=解得0x =（舍去）综上可得15x =或30．【点评】本题考查了三角形折叠中的角度问题，熟知折叠的性质，平行的判定定理是解题的关键．15．在△ABC 中，∠BAC ＝90°，点D 是BC 上一点，将△ABD 沿AD 翻折后得到△AED ，边AE 交BC 于点F ．(1)如图①，当AE ⊥BC 时，写出图中所有与∠B 相等的角：；所有与∠C 相等的角：．(2)若∠C －∠B ＝50°，∠BAD ＝x °(0＜x ≤45) ．① 求∠B 的度数；②是否存在这样的x 的值，使得△DEF 中有两个角相等．若存在，并求x 的值；若不存在，请说明理由．【答案】(1)∠E 、∠CAF ；∠CDE 、∠BAF ； (2)①20°；②30【分析】（1）由翻折的性质和平行线的性质即可得与∠B 相等的角；由等角代换即可得与∠C 相等的角；（2）①由三角形内角和定理可得90B C ∠+∠=︒，再由50C B ∠∠︒-=根据角的和差计算即可得∠C 的度数，进而得∠B 的度数．②根据翻折的性质和三角形外角及三角形内角和定理，用含x 的代数式表示出∠FDE 、∠DFE 的度数，分三种情况讨论求出符合题意的x 值即可．【解析】（1）由翻折的性质可得：∠E ＝∠B ，∵∠BAC ＝90°，AE ⊥BC ，∴∠DFE ＝90°，∴180°－∠BAC ＝180°－∠DFE ＝90°，即：∠B ＋∠C ＝∠E ＋∠FDE ＝90°，∴∠C ＝∠FDE ，∴AC ∥DE ，∴∠CAF ＝∠E ，∴∠CAF ＝∠E ＝∠B故与∠B 相等的角有∠CAF 和∠E ；∵∠BAC ＝90°，AE ⊥BC ，∴∠BAF ＋∠CAF ＝90°, ∠CFA ＝180°－（∠CAF ＋∠C ）＝90°∴∠BAF ＋∠CAF ＝∠CAF ＋∠C ＝90°∴∠BAF ＝∠C又AC ∥DE ，∴∠C ＝∠CDE ，∴故与∠C 相等的角有∠CDE 、∠BAF ；（2）①∵90BAC ∠=︒∴90B C ∠+∠=︒又∵50C B ∠∠︒-=，∴∠C ＝70°，∠B ＝20°;②∵∠BAD ＝x °, ∠B ＝20°则160ADB x ∠︒︒=-,20ADF x ∠︒︒=+,由翻折可知：∵160ADE ADB x ∠∠︒︒==-, 20E B ∠∠︒==,∴1402FDE x ∠︒︒=-, 202DFE x ∠︒︒=+,当∠FDE ＝∠DFE 时，1402202x x ︒︒︒︒-=+, 解得：30x ︒︒=；当∠FDE ＝∠E 时，140220x ︒︒︒-=，解得：60x ︒︒=（因为0＜x ≤45，故舍去）；当∠DFE ＝∠E 时，20220x ︒︒︒+=，解得：0x ︒＝（因为0＜x ≤45，故舍去）；综上所述，存在这样的x 的值，使得△DEF 中有两个角相等．且30x =．【点评】本题考查图形的翻折、三角形内角和定理、平行线的判定及其性质、三角形外角的性质、等角代换，解题的关键是熟知图形翻折的性质及综合运用所学知识．16．如图1，将△ABC 纸片沿DE 折叠，使点C 落在四边形ABDE 内点C ’的位置，（1）①若00120,250∠=∠=，则C ∠= ；②若042C ∠=，则12∠+∠= ；③探索C ∠ 、1∠与2∠之间的数量关系，并说明理由；（2）直接按照所得结论，填空：①如图中，将△ABC 纸片再沿FG 、MN 折叠，使点A 、B 分别落在△ABC 内点A ’、B ’的位置，则123456∠+∠+∠+∠+∠+∠= ；②如图中，将四边形ABCD 按照上面方式折叠，则128∠+∠++∠= ； ③若将n 边形123n A A A A 也按照上面方式折叠，则122n ∠+∠++∠= ；（3）如图，将△ABC 纸片沿DE 折叠，使点C 落在△ABC 边AC 上方点'C 的位置，探索C ∠、1∠与2∠之间的数量关系，并说明理由.【答案】（1）①35︒；②84︒；③212C=+∠∠∠；（2）①360︒；②720︒；③3602(n )︒-；（3）221C=∠∠-∠【分析】（1）①由邻补角的定义可知∠CEC′=160°，∠CDC′=130°，根据折叠的性质可求出∠CED=80°，∠CDE=65°,然后根据三角形内角和定理求解即可；②由三角形内角和可求出∠CED+∠CDE=138°,再由折叠的性质可知∠CEC′+∠CDC′=276°，然后根据邻补角的定义可求出12∠+∠=84°；③由邻补角定义可知1+'=180CEC ∠∠︒，从而2+'=180CDC ∠∠︒，所以，∠1+ ∠CEC′+ ∠2+ ∠CDC′=360 °，结合+'+'+'=360C CEC C CDC ∠∠∠∠︒，可求出2=1+2C ∠∠∠；（2）① 由（1）得12∠∠+=2∠C ，34∠+∠=2∠B ，56∠+∠=2∠A ，从而123456∠+∠+∠+∠+∠+∠=2(∠A+∠B +∠C)，结合三角形内角和求解即可；②由①可知，128∠+∠++∠= 2(∠A+∠B +∠C+∠D)，结合四边形内角和求解即可;③由①可知，()()122218023602n n n ∠+∠++∠=⨯︒⨯-=︒⨯- ；（3）由外角的性质可知∠2=∠3+∠C ，∠3=∠1+∠C ，整理可得2=21C ∠∠-∠.【解析】解：（1）①∵00120,250∠=∠=，∴∠CEC′=160°，∠CDC′=130°，∵ ∠CED=80°，∠CDE=65°,∴∠C= 180°-80°-65°=35°；②∵042C ∠=，∴ ∠CED+∠CDE=180°-42°=138°,∴∠CEC′+∠CDC′=276°，∴12∠+∠=360°-276°=84°；③2=1+2C ∠∠∠，因为1+'=180CEC ∠∠︒，2+'=180CDC ∠∠︒，所以1+'+2+'=360CEC CDC ∠∠∠∠︒，因为在四边形'CEC D 中，+'+'+'=360C CEC C CDC ∠∠∠∠︒，所以1+2=+'C C ∠∠∠∠，因为='C C ∠∠，所以2=1+2C ∠∠∠.（2）① 由①得12∠∠+=2∠C ，34∠+∠=2∠B ，56∠+∠=2∠A ，∴123456∠+∠+∠+∠+∠+∠=2(∠A+∠B +∠C)=360°; ②∵12∠∠+=2∠C ，34∠+∠=2∠B ，56∠+∠=2∠A ，78∠+∠=2∠D ，∴128∠+∠++∠= 2(∠A+∠B +∠C+∠D)=2×360°=720°; ③∵n 边形内角和是()1802n ︒⨯-，∴()()122218023602n n n ∠+∠++∠=⨯︒⨯-=︒⨯- ；（3）2=21C ∠∠-∠.∵∠2=∠3+∠C ，∠3=∠1+∠'C =∠1+∠C ，∴∠2=∠1+∠C +∠C=∠1+2∠C ，∴2=21C ∠∠-∠.【点评】本题考查了折叠性质，三角形内角和定理，多边形的内角和定理，三角形外角的性质及图形类的规律与探究.熟练掌握折叠的性质和三角形内角和定理是解（1）的关键，利用（1）中规律是解（2）的关键，熟练掌握三角形外角的性质是解（3）的关键.17．直线MN 与直线PQ 垂直相交于O ，点A 在射线OP 上运动，点B 在射线OM 上运动，连接AB,（1）如图，已知AC 、BC 分别是∠BAP 和∠ABM 角的平分线，①点A 、B 在运动的过程中，∠ACB 的大小是否发生变化？若发生变化，请说明理由；若不发生变化，试求出∠ACB 的大小．②如图，将△ABC 沿直线AB 折叠，若点C 落在直线PQ 上，记作点C′，则∠ABO ＝ °；如图，将△ABC 沿直线AB 折叠，若点C 落在直线MN 上，记作点C′′，则∠ABO ＝ °．（2）如图，延长BA 至G ，已知∠BAO 、∠OAG 的角平分线与∠BOQ 的角平分线及其延长线交于E 、F ，在△AEF 中，如果有一个角是另一个角的32倍，求∠ABO 的度数．【答案】（1）①∠ACB 的大小不变，∠ACB=45°；②30°，60°；（2）∠ABO 为60°或72°．【分析】（1）①由直线MN 与直线PQ 垂直相交于O ，得到∠AOB=90°，根据三角形的外角的性质得到∠PAB+∠ABM=270°，根据角平分线的定义得到∠BAC=12∠PAB ，∠ABC=12∠ABM ，于是得到结论； ②由于将△ABC 沿直线AB 折叠，若点C 落在直线PQ 上，得到∠CAB=∠BAQ ，由角平分线的定义得到∠PAC=∠CAB ，根据三角形的内角和即可得到结论；根据将△ABC 沿直线AB 折叠，若点C 落在直线MN 上，得到∠ABC=∠ABN ，由于BC 平分∠ABM ，得到∠ABC=∠MBC ，于是得到结论；（2）由∠BAO 与∠BOQ 的角平分线相交于E 可知∠EAO=12∠BAO ，∠EOQ=12∠BOQ ，进而得出∠E 的度数，由AE 、AF 分别是∠BAO 和∠OAG 的角平分线可知∠EAF=90°，在△AEF 中，由一个角是另一。

折叠问题中的角度运算

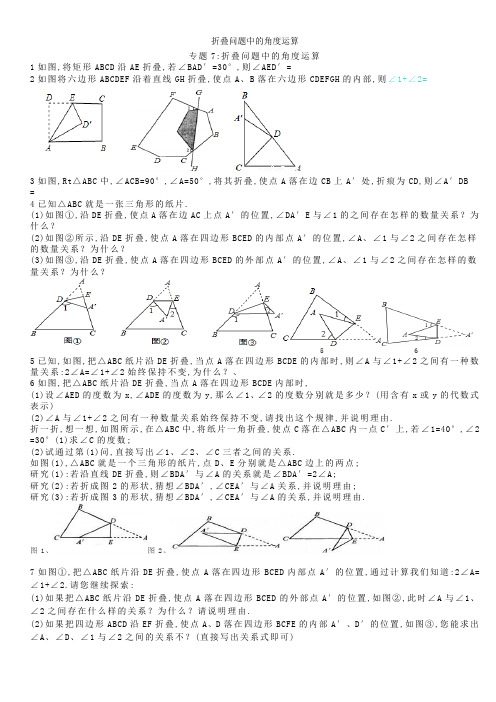
专题7:折叠问题中的角度运算1如图,将矩形ABCD沿AE折叠,若∠BAD′=30°,则∠AED′=2如图将六边形ABCDEF沿着直线GH折叠,使点A、B落在六边形CDEFGH的内部,则∠1+∠2=3如图,Rt△ABC中,∠ACB=90°,∠A=50°,将其折叠,使点A落在边CB上A′处,折痕为CD,则∠A′DB=4已知△ABC就是一张三角形的纸片.(1)如图①,沿DE折叠,使点A落在边AC上点A′的位置,∠DA′E与∠1的之间存在怎样的数量关系？为什么？(2)如图②所示,沿DE折叠,使点A落在四边形BCED的内部点A′的位置,∠A、∠1与∠2之间存在怎样的数量关系？为什么？(3)如图③,沿DE折叠,使点A落在四边形BCED的外部点A′的位置,∠A、∠1与∠2之间存在怎样的数量关系？为什么？5 65已知,如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE的内部时,则∠A与∠1+∠2之间有一种数量关系:2∠A=∠1+∠2始终保持不变,为什么？、6如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,(1)设∠AED的度数为x,∠ADE的度数为y,那么∠1、∠2的度数分别就是多少？(用含有x或y的代数式表示)(2)∠A与∠1+∠2之间有一种数量关系始终保持不变,请找出这个规律,并说明理由.折一折,想一想,如图所示,在△ABC中,将纸片一角折叠,使点C落在△ABC内一点C′上,若∠1=40°,∠2 =30°(1)求∠C的度数;(2)试通过第(1)问,直接写出∠1、∠2、∠C三者之间的关系.如图(1),△ABC就是一个三角形的纸片,点D、E分别就是△ABC边上的两点;研究(1):若沿直线DE折叠,则∠BDA′与∠A的关系就是∠BDA′=2∠A;研究(2):若折成图2的形状,猜想∠BDA′,∠CEA′与∠A关系,并说明理由;研究(3):若折成图3的形状,猜想∠BDA′,∠CEA′与∠A的关系,并说明理由.图1、图2、7如图①,把△ABC纸片沿DE折叠,使点A落在四边形BCED内部点A′的位置,通过计算我们知道:2∠A=∠1+∠2.请您继续探索:(1)如果把△ABC纸片沿DE折叠,使点A落在四边形BCED的外部点A′的位置,如图②,此时∠A与∠1、∠2之间存在什么样的关系？为什么？请说明理由.(2)如果把四边形ABCD沿EF折叠,使点A、D落在四边形BCFE的内部A′、D′的位置,如图③,您能求出∠A、∠D、∠1与∠2之间的关系不？(直接写出关系式即可)8三角形纸片ABC中,∠A=55°,∠B=75°,将纸片的一角折叠,使点C落在△ABC内(如图),则∠1+∠2的度数为度.9如图,已知四边形ABCD,∠C=72°,∠D=81°.沿EF折叠四边形,使点A、B分别落在四边形内部的点A′、B′处,求∠1+∠2的大小.10、如图,△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC边上的点E处.若∠A=22°,则∠BDC等于( )11、将五边形纸片ABCDE按如图方式折叠,折痕为AF,点E、D分别落在E′、D′,已知∠AFC=76°,则∠CFD′等于12如图,在平面内,把矩形ABCD沿EF对折,若∠1=50°,则∠AEF等于13如图,把△ABC沿线段DE折叠,使点A落在点F处,BC∥DE;若∠B=50°,则∠BDF的度数为1 1如图,把一张长方形纸片ABCD,沿EF折叠后,ED′与BC的交点为G,点D,C分别落在D′,C′的位置上.若∠EFG=55°,则∠1等于14将一条两边沿互相平行的纸带按如图折叠.设∠1=x°,则∠α的度数为( )15将长方形ABCD沿折痕EF折叠,使CD落在GH的位置,若∠FGH=55°,则∠HEF=( )16如图,一个宽度相等的纸条按如图所示方法折叠一下,则∠1=( )17如图,D、E分别为△ABC的边AB、AC上的点,DE∥BC,将△ABC沿线段DE折叠,使点A落在BC上的点F处,若∠B=55°,则∠BDF的度数为( )18如图所示,将一张长方形纸片沿EF折叠后,点D,C分别落在D′,C′的位置上,ED′的延长线与BC的交点为G.若∠EFG=80°,则∠BFC′的度数为( )19如图a就是长方形纸带,∠DEF=24°,将纸带沿EF折叠成图b,再沿BF折叠成图c,则图c中的∠CFE的度数( )20如图,三角形纸片ABC,AB=10cm,BC=7cm,AC=6cm,沿过点B的直线折叠这个三角形,使顶点C落在AB边上的点E处,折痕为BD,则△AED的周长为( )21如图,将长方形ABCD沿对角线BD折叠,使点C恰好落在如图C′的位置,若∠DBC=15°,则∠ABC′=( )22一张长方形纸条折成如图的形状,如果∠1=130°,∠2=( )23如图:将一张长方形纸片沿EF折叠后,点D、C分别落在D′、C′的位置,ED′的延长线与BC交于点G.若∠EFG=55°,则∠1=( )24如图,已知长方形ABCD,我们按如下步骤操作可以得到一个特定角:(1)以点A所在直线为折痕,折叠纸片,使点B落在AD上,折痕与BC交于E;(2)将纸片展平后,再一次折叠纸片,以E所在直线为折痕,使点A落在BC上,折痕EF交AD于F,则∠AEF的度数25如图,将纸片△ABC沿着DE折叠压平,且∠1+∠2=72°,则∠A=( )26如图,把△ABC纸片沿DE折叠,当点A落在四边形BCED的外部时,则∠A与∠1与∠2之间有一种数量关系始终保持不变,请试着找一找这个规律,您发现的规律就是( )27如图,三角形纸片ABC,AB=10cm,BC=7cm,AC=6cm,沿过点B的直线折叠这个三角形,使顶点C落在AB边上的点E处,折痕为BD,则△AED的周长为( )28一个宽度相等纸条,按如图所示的方式折叠一下,已知∠3=120°,则∠1的度数为( )29如图,把一张长方形纸条折叠后,若∠AOB′=70°,则∠OGC的度数为( )30如图,∠A=60°,∠B=70°,将纸片的一角折叠,使点C落在△ABC内,若∠2=80°,则∠1的度数为( )31如图(1)就是长方形纸带,∠DEF=α,将纸带沿EF折叠成图(2),再沿BF折叠成图(3),则图(3)中的∠CFE的度数就是( )32如图,生活中,将一个宽度相等的纸条按右图所示折叠一下,如果∠1=140°,那么∠2的度数为( )33如图,四边形ABCD中,点M,N分别在AB,BC上,将△BMN沿MN翻折,得△FMN,若MF∥AD,FN∥DC,则∠B =( )34如图,一张长方形纸条沿AB折叠,如果∠1=124°,那么∠2的度数就是( )35如图,把长方形ABCD沿EF对折后使两部分重合,若∠AEF=110°,则∠1=( )36如图,一张三角形纸片△ABC,沿DE折叠使得顶点C落在边AB上,若DE∥AB,∠A=45°,则∠ADC的度数就是( ) 37如图所示,把一个三角形纸片ABC顶角向内折叠3次之后,3个顶点不重合,那么图中∠1+∠2+∠3+∠4+∠5+∠6的度数与就是( )38如图,将△ABC三个角分别沿DE、HG、EF翻折,三个顶点均落在点O处,则∠1+∠2的度数为( )39如图,正方形纸片ABCD的边长为8,将其沿EF折叠,则图中①②③④四个三角形的周长之与为( )40如图,将五边形ABCDE沿AE对折到如图的位置,其中∠AEC=72°,则∠CED′=( )41如图,在△ABC中,∠A=35°,在平面内沿直线DE将△ABC折叠后,量得∠BDA′=110°,那么∠CEA′的度数为( ) 42如图,把一个长方形纸片沿EF折叠后,点D、C分别落在D′、C′的位置,若∠EFB=65°,则∠AED′等于( )43如图,已知△ABC中,∠BAC=140°,现将△ABC进行折叠,使顶点B、C均与顶点A重合,求∠DAE的度数.。

七年级数学培优竞赛训练：角含答案

角【知识纵横】角，既可以用静止的眼光来观察，也可以用运动的眼光来看待．具有公共端点的两条射线组成的图形或一条射线绕着端点从一个位置旋转到另一位置所成的图形，称为角．角也是几何学的基本图形之一，与角相关的知识有：周角、平角、直角、锐角、钝角、角平分线、数量关系角(如余角、补角)、位置关系角(如邻补角、对顶角)等概念及关系．解与角有关的问题，类似于解与线段相关的问题，常常用到重要概念、分类的思想、代数化的观点等知识与方法．【例题求解】例1.如图1 是一个3×3 的正方形，则图中∠1+∠2+∠3+…+∠9 的度数是．思路点拨除∠3＝∠5＝∠7＝45°外，其他各角的度数无法求出，故不能顺序求和．考虑应用加法的交换律、结合律，关键是对图形进行恰当的处理．图1 图2例2.如图2．A、O、B 在一条直线上，∠1 是锐角，则∠1 的余角是( )．1 1 A．∠2 一∠l B．2 23∠2 一21∠1 C．21（∠2 一∠l）D．3（∠2+∠1）思路点拨∠1 的余角表示为90°一∠1，化简这个代数式，直至与选择项相符为止．1例 3.已知∠1 和∠2 互补，∠3 和∠2 互余，求证∠3=2(∠l 一∠2)．思路点拨依据互补、互余的概念得到含∠l、∠2、∠3 的两个等式，盯住所要达到的目的，恰当处理两个等式．1 例4.如图3，已知∠AOB 与∠BOC 互为补角，OD 是∠AOB 的平分线，OE 在∠BOC 内，∠BOE= ∠2 EOC，∠DOE= 72°，求∠EOC 的度数．图3思路点拨设∠AOB=x 度，∠BOC= y 度，建立x、y 的方程组，用代数方法解几何问题是一种常用的方法．例 5.(1)如图4，已知∠AOB=90°，∠BOC=30°，OM 平分∠AOC，ON 平分之∠BOC，求∠MON 的度数．(2)如果(1)中∠AOB=α，其他条件不求，求∠MON 的度数．(3)如果(1)中∠BOC=β（β为锐角），其他条件不求，求∠MON的度数．(4)从(1)、(2)、<3)的结果中能得出什么结论?(5)线段的计算与角的计算存在着紧密的联系，它们之间可以互相借鉴解法，请你模仿(1)~(4)设计一道以线段为背景的计算题，写出其中的规律，并给出解答．图 4例 6.钟面上从2 点到4 点有几次时针与分针的夹角为60°?分别是几点几分?思路点拨：时钟问题的关键是将时针、分针、秒针转动的速度用角表示出来．时针转动的速度为 0.5°／分，分针为 6°／分，秒针为 360°／分．※巩固训练※1．一个角的补角与这个角的余角的度数比为3：l，则这个角是度．2．钟表时间是2 时15 分时，时针与分针的夹角是．3．由O 点引出的7 条射线如图，若OA⊥OE，OC⊥OC，∠BOC>∠FOC，则图中以O 为顶角的锐角共有个．4．如图，O 是直线AB 上一点，∠AOD＝120°，∠AOC=90°，OE 平分∠BOD，则图中彼此互补的角有对．5．如图，∠AOB=180°，OD 是∠COB 的平分线，OE 是∠AOC 的平分线，设∠BOD=α，则与α的余角相等的角是( )．A．∠OOD B．∠ODE C．∠DOA D．∠COA6．如图，在一个正方体的2 个面上画了两条对角线AB，AC，那么这两条对角线的夹角等于( )．A．60°B．75°C．90°D．135°注：解钟表上的问题，常用到以下知识：(1)钟表上相邻两个数宇之间有 5 个小格，每个小格表示 1 分钟，如与角度联系起来，每小格对应 6°．(2)秒钟每分钟转运 360°，分针每分钟转过 6°，时钟每分钟转过 0.5°．(3)画示意图把这类问题看成是行程问题中的追及问题来解决．7．将一长方形纸片按如图的方式折叠，BC、BD 为折痕，则∠CBD 的度数为( )．A．60°B．75°C．90°D．95°18．如图，∠1>∠2，那么∠2 与(∠1 一∠2)之间的关系是( )．2A．互补B．互余C．和为45°D．和为22．5°9．如图，已知A、O、E 三点在一条直线上，OB 平分∠AOC，∠AOB+∠DOE=90°，试问：∠COD 与∠DOE 之间有怎样的关系?说明理由．10．(1)一副三角板由一个等腰直角三角形和一个含30°角的直角三角形组成．利用这副三角板构成15°角的方法很多，请你画出其中三种不同构成的示意图，并在图上作出必要的标注，不写作法．(2)一个长方形和一个正方形摆放如图，试找出除直角外的互余的角和互补的角．111．α、β、γ中有两个锐角和一个钝角，其数值已经给出，在计算(α+β+γ) 的值时，有三15位同学分别算出了23 °、24 °、25 °这三个不同的结果，其中确有一个是正确的答案，则α+β+γ．12．如图，O 是直线AB 上一点，∠AOE=∠FOD＝90°，OB 平分∠COD，图中与∠DOE 互余的是，与∠DOE 互补的角是．13．以∠AOB 的顶点O 为端点引射线OC，使∠AOC：∠BOC=5：4，若∠AOB=15°，则∠AOC 的度数是．14．光线以图所示的角度α照射到平面镜I 上，然后在乎面镜I、Ⅱ之间来回反射，已知∠α=60°，∠β=50°，则∠γ＝．4 15．若∠β与∠α互补，∠γ与∠α互余，且∠β与∠γ的和是3 1 个平角，则∠β是∠α的( )．A．25倍B．5 倍C．11 倍D．无法确定倍数16．4 点钟后，从时针到分针第二次成90°角，共经过( )分钟(答案四舍五入到整数) ．A．60 B．30 C．40 D．3317．如图，从点 O 引出6 条射线OA、OB、OC、OD、OE、OF，且∠AOB＝100°，OF 平分∠BOC，∠AOE ＝∠DOE，∠EOF=140°，求∠COD 的度数．18．过点 O 任作 7 条直线，求证：以 O 为顶点的角中必有一个小于 26°．19．(1)现有一个 19°的“模板”(如图)，请你设计一种办法，只用这个“模板”和铅笔在纸上画出 1°的角来．(2)现有一个 17°的“模板”与铅笔，你能否在纸上画出一个 1°的角来?(3)用一个 21°的“模板”与铅笔，你能否在纸上画出一个 1°的角来?对于(2)、(3)两问，如果能，请你简述画法步骤；如果不能，请你说明理由．参考答案。

七年级数学尖子生培优竞赛专题辅导专题16折叠问题

专题16折叠问题专题解读】折叠问题是近几年来中考岀现频率较高的一类题型，同学们往往由于对折叠的本质理解不够透彻，因此难以找到解题的方向•折叠是现实生活常见的操作活动，而初中几何学习中，以折叠为活动载体的问题很多，这类问题一般都要经历操作、观察、比较、概括、交流、猜想、推理等过程•研究折叠问题，可以帮助学生提髙观察能力、动手能力、想象能力、综合运用知识的能力，发展合情推理和演绎推理能力.思维索引】例1.数轴是一个非常重要的数学工具，它使数和数轴上的点建立起对应关系，揭示了数与点之间的内在联系，它是“数形结合"的基础.小明在草稿纸上画了一条数轴进行操作研究：操作一：（1）折叠纸面，使1表示的点与-1表示的点重合，则-2表示的点与 ______ 表示的点重合；操作二：（2）折叠纸而，使1表示的点与-3表示的点重合，若数轴上A、B两点之间的距离为8 （A在B的左侧），且A、B两点经折叠重合，则A、B两点表示的数分别是_________ 、_________ : 操作三：（3）在数轴上剪下9个单位长度（从-1到8）的一条线段，并把这条线段沿某点折叠，然后在重叠部分某处剪一刀得到三条线段（如图所示），若这三条线段的长度之比为1： 1： 2,求折痕处对应的点所表示的数？剪1断处折痕例2・如图，ABCD是一张矩形纸片，AD=BC=\. AB=CD=5・在矩形ABCD的边AB上取一点在CD上取一点N,将纸片沿MN折叠，使MB与DN交于点K,得到△MNK.（1）若Zl=70°,求ZMKN的度数.（2）△MNK的面积能否小于丄？若能，求出此时Z1的度数：若不能，试说明理由.2（3）如何折叠能够使△MNK的而积最大？请你利用备用图探究可能出现的情况，画岀相应的图形.素养提升1.如图，把AABC 沿EF 对折，叠合后的图形如图所示.若ZA=60。

，Zl=95°,则Z2的度数为（）A. 24°B. 25°C. 30°D. 35°2.如图，将ZkABC 沿DE 、EF 翻折，顶点A 、B 均落在点O 处，且EA 与EB 重合于线段EO,若ZCDO+ ZCFO=98。

20 专题二十：角度的计算(8)——折叠问题(方法专题);人教版七年级上学期培优专题讲练(含答案)

专题二十：角度的计算（8）——折叠问题专题导入如图，将长方形ABCD折叠，使得点D与点B重合。

思考：①∠BEF与∠DEF的关系；②∠CFE与∠D’FE的关系。

方法点睛折叠的本质是轴对称，折叠前后的图形是“一样的”，所以有以下两个常用结论：①对应角相等；②对应边相等。

在折叠的图形中计算角度，必然用上对应角相等的性质。

典例精讲1．如图，将长方形纸片的一角作折叠，使顶点A落在A′处，EF为折痕，若EA′恰好平分∠FEB．（1）判断∠FEA与∠A′EB的大小关系，并说明理由；（2）求∠FEB的度数．举一反三2．如图，把一张长方形纸片沿EF折叠后，点D，C分别落在点D′，C′的位置，若∠DEF ＝75°，则∠AED′等于多少？3．如图，长方形纸片ABCD，点E、F分别在边AB、CD上，连接EF．将∠BEF对折，点B落在直线EF上的点B′处，得到折痕EC；将∠AEF对折，点A落在直线EF上的点A′处，得到折痕EN．（1）图中有哪几条角平分线，他们各是哪个角的平分线？（2）如果射线NA′平分∠DNE，那么射线CB′平分∠ECF吗？为什么？专题过关4．如图，把一张长方形的纸片沿着EF折叠，点C、D分别落在M、N的位置，且∠MFB=1 2∠MFE．则∠AEN＝（）A．30°B．36°C．45°D．72°5．如图所示，把一张长方形的纸片按折痕EF那样折叠后，C、D两点分别落在N、M点处，若∠AEM＝80°，则∠DEF的度数为．6．如图，将长方形纸片的两角分别折叠，使顶点B落在B′处，顶点A落在A′处，EC、ED为折痕，并且点E、A′、B′在同一条直线上．若∠BED＝32°，求∠CED和∠AEC 的度数．7．如图1，将笔记本活页一角折过去，使角的顶点A落在点A'处，BC为折痕．（1）如图1，若∠1＝25°，求∠A'BD的度数；（2）如果又将活页的另一角斜折过去，使BD边与BA'重合，折痕为BE，如图2所示，求∠CBE的度数．8．如图，长方形纸片ABCD，点E在边AB上，M、N分别在射线BC和射线AD上，连接EM，EN，将三角形MBE沿EM折叠（把物体的一部分翻转和另一部分贴拢），点B落在点B′处；将三角形NAE沿EN折叠，点A落在点A′处．（1）若∠MEB＝30°，∠NEA＝45°，用直尺、量角器画出射线EB′与EA′；（2）若∠MEB＝30°，∠NEA＝45°，求∠A'EB'的度数；（3）若∠MEB＝α，∠NEA＝β，用含α、β的代数式表示∠A'EB'的度数．9．把一长方形（四个角为90°）纸片ABCD的一角折起来，折痕为AE，使∠EAB′＝∠DAB′，如图1．（1）求∠EAD；（2）再沿AC对折长方形ABCD，使B点落在F点上，如图2．若∠EAF＝80°，求∠CAB′．10．如图，长方形纸片ABCD，点E、F分别在边AB、CD上，连接EF，将∠BEF对折，点B落在直线EF上的B′处，得到折痕EC，将点A落在直线EF上的点A′处，得到折痕EN．（1）若∠BEB′＝110°，则∠BEC＝°，∠AEN＝°，∠BEC+∠AEN ＝°．（2）若∠BEB′＝m°，则（1）中∠BEC+∠AEN的值是否改变？请说明你的理由．（3）将∠ECF对折，点E刚好落在F处，且折痕与B′C重合，求∠DNA′．11．已知长方形纸片ABCD，点E在边AB上，点F、G在边CD上，连接EF、EG．将∠BEG对折，点B落在直线EG上的点B′处，得折痕EM；将∠AEF对折，点A落在直线EF上的点A′处，得折痕EN．（1）如图1，若点F与点G重合，求∠MEN的度数；（2）如图2，若点G在点F的右侧，且∠FEG＝30°，求∠MEN的度数；（3）若∠MEN＝α，请直接用含α的式子表示∠FEG的大小．【参考答案】1．解：（1）∠FEA＝∠A′EB，理由如下：由翻折的对称可得：∠FEA＝∠FEA'，∵EA′恰好平分∠FEB，∴∠FEA'＝∠A′EB，∴∠FEA＝∠A′EB；（2）由（1）可知，∠FEA＝∠A′EB＝∠FEA'，又∵∠FEA+∠A′EB+∠FEA'＝180°，∴∠FEA＝∠A′EB＝∠FEA'＝60°，∴∠FEB＝∠FEA'+∠A′EB＝60°+60°＝120°；2．解：由折叠可得，∠DEF＝∠D'EF＝75°，∴∠DED'＝150°，∴∠AED'＝180°﹣∠DED'＝30°．3．解：（1）由翻折可得∠AEN＝∠A′EN，∠ANE＝∠A′NE，∠BCE＝∠B′CE，∠BEC＝∠B′EC，所以，NE是∠AEA′和∠ANA′的平分线，CE是∠BEB′和∠BCB′的平分线；（2）射线CB′平分∠ECF．理由如下：∵射线NA′平分∠DNE，∴∠DNA′＝∠A′NE，∴∠ANE=13×180°＝60°，在Rt△ANE中，∠AEN＝90°﹣∠ANE＝90°﹣60°＝30°，∴∠BEC=12（180°﹣30°×2）＝60°，在Rt△BCE中，∠BCE＝90°﹣60°＝30°，∴∠B′CD＝90°﹣30°×2＝30°，∴∠B′CD＝∠B′CE，∴射线CB′平分∠ECF．4．B．5．50°．6．解：∵EC和ED是折痕，∴∠1＝∠2，∠3＝∠4，又∵∠1+∠2+∠3+∠4＝180°，∴2（∠2+∠3）＝180°，∴∠2+∠3＝90°，即∠CED＝90°．又∠2＝∠1＝32°，∴∠4＝∠3＝90°﹣∠1＝90°﹣32°＝58°，即∠AEC＝58°．7．解：（1）∵角的顶点A落在点A'处，BC为折痕，∴∠1＝∠ABC＝25°．∴∠A'BD＝180°﹣25°﹣25°＝130°；（2）由折叠性质得∠1＝∠ABC=12∠ABA′，∠2＝∠DBE=12∠A'BD，∴∠1+∠2=12∠ABA′+12∠A'BD=12（∠ABA'+∠A'BD）=12×180°＝90°．即∠CBE＝90°．8．解：（1）图形如图1中所示：（2）与翻折可知：∠AEA′＝2∠AEN＝90°，∠BEB′＝2∠BEM＝60°，∴∠A′EB′＝180°﹣90°﹣60°＝30°．（3）当α+β≤90°时，∠A′EB′＝180°﹣2（α+β），当α+β＞90°时，∠A′EB′＝2（α+β）﹣180°．9．解：（1）根据折叠可得：∠BAE＝∠EAB′，∵∠EAB′＝∠B′AD，∴∠BAE＝90°÷3＝30°，∴∠EAD＝90°﹣30°＝60°；（2）根据折叠可得：∠BAC＝∠F AC，∵∠EAF＝80°，∴∠BAF＝80°+30°＝110°，∴∠BAC＝55°，∴∠CAB′＝60°﹣55°＝5°．10．解：（1）55，35，90．（2）不变．由折叠的性质可得：∠BEC＝∠B'EC，∠AEN＝∠A'EN，∵∠BEB′＝m°，∴∠AEA'＝180°﹣m°，可得∠BEC＝∠B'EC=12∠BEB′=12m°，∠AEN＝∠A'EN=12∠AEA'=12（180°﹣m°），∴∠BEC+∠AEN=12m°+12（180°﹣m°）＝90°，故∠BEC+∠AEN的值不变；（3）由折叠的性质可得：∠B'CF＝∠B'CE，∠B'CE＝∠BCE，∴∠B'CF＝∠B'CE＝∠BCE=13×90°＝30°，在Rt△BCE中，∵∠BEC与∠BCE互余，∴∠BEC＝90°﹣∠BCE＝90°﹣30°＝60°，∴∠B'EC＝∠BEC＝60°，∴∠AEA'＝180°﹣∠BEC﹣∠B'EC＝180°﹣60°﹣60°＝60°，∴∠AEN=12∠AEA'＝30°，∴∠ANE＝90°﹣∠AEN＝90°﹣30°＝60°，∴∠ANE＝∠A'NE＝60°，∴∠DNA'＝180°﹣∠ANE﹣∠A'NE＝180°﹣60°﹣60°＝60°．11．解：（1）∵EN平分∠AEF，EM平分∠BEF∴∠NEF=12∠AEF，∠MEF=12∠BEF∴∠MEN＝∠NEF+∠MEF=12∠AEF+12∠BEF=12（∠AEF+∠BEF）=12∠AEB∵∠AEB＝180°∴∠MEN=12×180°＝90°（2）∵EN平分∠AEF，EM平分∠BEG∴∠NEF=12∠AEF，∠MEG=12∠BEG∴∠NEF+∠MEG=12∠AEF+12∠BEG=12（∠AEF+∠BEG）=12（∠AEB﹣∠FEG）∵∠AEB＝180°，∠FEG＝30°∴∠NEF+∠MEG=12（180°﹣30°）＝75°∴∠MEN＝∠NEF+∠FEG+∠MEG＝75°+30°＝105°（3）若点G在点F的右侧，∠FEG＝2α﹣180°，若点G在点F的左侧，∠FEG＝180°﹣2α．。

中考几何——折叠专项

中考几何——折叠专项【一，折叠与平行线性质结合求角度】1．如图，矩形纸片ABCD ，M 为AD 边的中点将纸片沿BM 、CM 折叠，使A 点落在1A 处，D 点落在1D 处，若130∠=︒，则(BMC ∠= )A ．75︒B ．150︒C ．120︒D ．105︒2．将长方形纸片按如图所示的方式折叠，BC 、BD 为折痕，若35ABC ∠=︒，则DBE ∠的度数为( )A ．55︒B ．50︒C ．45︒D ．60︒3．将一张长方形纸片按如图所示的方式折叠，EC ，ED 为折痕，折叠后点A '，B '，E 在同一直线上，则CED ∠的度数为( )A ．75︒B ．95︒C ．90︒D ．60︒4．如图，将一条两边沿互相平行的纸带折叠( )A ．若132∠=∠，则1108∠=︒B ．若122∠=∠，则198∠=︒C ．若12∠=∠，则155∠=︒D ．若1122∠=∠，则140∠=︒5．如图，将对边平行的纸带按如图所示进行折叠，已知165∠=︒，则2∠的大小为( )A ．115︒B ．65︒C ．55︒D ．50︒6．如图①，在长方形ABCD 中，E 点在AD 上，并且30ABE ∠=︒，分别以BE 、CE 为折痕进行折叠并压平，如图②，若图②中AED n ∠=︒，则BCE ∠的度数为( )度．A ．602n+ B ．60n +C ．302n +D ．30n +7．小明将一张正方形纸片按如图所示顺序折叠成纸飞机，当机翼展开在同一平面时（机翼间无缝隙），AOB∠的度数是．8．如图，把一张长方形纸片ABCD沿EF折叠后，点A与点A'重合（点A在BC边上），点∠+∠=︒．B落在点B'的位置上，若40∠'=︒，则12DEA9．如图1，长方形ABCD沿着直线DE和EF折叠，使得AB的对应点A'，B'和点E在同一条直线上．（1）求DEF∠的度数；（2）如图2，若再次沿着直线EM和EN折叠使得A、B的对应点A''、B''分别落在DE和EF上，34∠的度数．∠=︒，求BENAEM10．如图a是长方形纸带（提示：//)AD BC，将纸带沿EF折叠成图b，再沿GF折叠成图c．（1）若20DEF ∠=︒，则图b 中EGB ∠= ，CFG ∠= ；（2）若20DEF ∠=︒，则图c 中EFC ∠= ；（3）若DEF α∠=，把图c 中EFC ∠用α表示为；（4）若继续按EF 折叠成图d ，按此操作，最后一次折叠后恰好完全盖住EFG ∠，整个过程共折叠了9次，问图a 中DEF ∠的度数是．【二.折叠和三角形内角和，外角和结合求角度】1．如图，三角形纸片ABC 中，80A ∠=︒，60B ∠=︒，将纸片的角折叠，使点C 落在ABC ∆内，若30α∠=︒，则β∠的度数是( )A ．30︒B ．40︒C ．50︒D ．60︒2．如图，65A ∠=︒，75B ∠=︒，将纸片的一角折叠，使点C 落在ABC ∆外，若218∠=︒，则1∠的度数为( )A ．50︒B ．98︒C ．75︒D ．80︒3．如图，将一张三角形纸片ABC 的一角折叠，使点A 落在ABC ∆外的A '处，折痕为DE ．如果A α∠=，CEA β∠'=，BDA γ'∠=，那么α，β，γ三个角的关系是．4．如图，将ABC ∆纸片沿DE 折叠，使点A 落在点A '处，且A B '平分ABC ∠，A C '平分ACB ∠，若1288∠+∠=︒，则BA C '∠的度数是．5．将纸片ABC ∆沿DE 折叠使点A 落在A '处的位置．（1）如果A '落在四边形BCDE 的内部（如图1)，A ∠'与12∠+∠之间存在怎样的数量关系？并说明理由．（2）如果A '落在四边形BCDE 的外部（如图2)，这时A ∠'与1∠、2∠之间又存在怎样的数量关系？并说明理由．6．动手操作：一个三角形的纸片ABC，沿DE折叠，使点A落在点A'处．观察猜想（1）如图1，若40∠+∠=︒；∠=︒，则12A若55∠+∠=︒；∠=︒，则12A若A n∠+∠=︒．∠=︒，则12探索证明：（2）利用图1，探索1∠、2∠与A∠有怎样的关系？请说明理由．拓展应用（3）如图2，把ABC∠，若12108∠+∠=︒，利∠，CA'平分ACB∆折叠后，BA'平分ABC用（2）中结论求BAC∠'的度数．【三.折叠和勾股定理结合求边长】1．如图，矩形纸片ABCD中，4AB=，3AD=，折叠纸片使AD边与对角线BD重合，折痕为DG，则AG的长为()A．1 B．43C．32D．22．如图，将矩形纸片ABCD沿直线EF折叠，使点C落在AD边的中点C'处，点B落在点B'处，其中9AB=，6BC=，则FC'的长为()A．103B．4 C．4.5 D．53．如图所示，有一块直角三角形纸片，两直角边6AB=，8BC=，将直角边AB折叠使它落在斜边AC上，折痕为AD，则BD=．4.如图，矩形ABCD中，AD=5,AB=7.点E为DC上一个动点，把△ADE沿AE折叠，当点D的对应点D/落在∠ABC的角平分线上时，DE的长为5.如图，将正方形纸片ABCD 沿MN 折叠，使点D 落在边AB 上，对应点为D ’，点C 落在C ’处.若AB=6，AD ’=2，则折痕MN 的长为 .6．如图，在矩形ABCD 中，点E 是边CD 的中点，将ADE ∆沿AE 折叠后得到AFE ∆，且点F 在矩形ABCD 内部．将AF 延长交边BC 于点G ．若1CG GB k =，则ADAB= 用含k 的代数式表示）．7．如图，在矩形纸片ABCD 中，6AB =，10BC =，点E 在CD 上，将BCE ∆沿BE 折叠，点C 恰落在边AD 上的点F 处；点G 在AF 上，将ABG ∆沿BG 折叠，点A 恰落在线段BF 上的点H 处，①45EBG ∠=︒；②DEF ABG ∆∆∽；③32ABG FGH S S ∆∆=；④AG DF FG +=．则下列结论正确的有( )A ．①②④B ．①③④C ．②③④D ．①②③8.如图，在矩形纸片ABCD 中，AB=6，BC=10，点E 在CD 上，将△BCE 沿BE 折叠，点C 恰落在边AD 上的点F 处；点G 在AF 上，将△ABG 沿BG 折叠，点A 恰落在线段BF 上的点H 处，有下列结论：①∠EBG=45°；②△DEF ∽△ABG ；③S △A B G =S △F G H ；④AG+DF=FG ．其中正确的是．9.如图，长方形ABCD 中，点E 是AD 的中点，将△ABE 沿直线BE 折叠后得到△GBE ，延长BG 交CD 于点F ，连接EF ．若AB=6，BC=8，则DF 的长为( )10.如图，在矩形ABCD 中，AD=5，AB=8，点E 为射线DC 上一个动点，把△ADE 沿直线AE 折叠，当点D 的对应点F 刚好落在线段AB 的垂直平分线上时，则DE 的长为多少？【四.折叠综合证明类型题】FEDB CA1.综合与实践：折纸中的数学数学活动课上，老师组织各学习小组同学动手操作，大胆猜想并加以验证．动手操作：如图，将长与宽的比是2：1 的矩形纸片ABCD 对折，使得点B 与点A 重合，点C 与点D 重合，然后展开，得到折痕EF，BC 边上存在一点G，将角B 沿GH 折叠，点B落到AD 边上的点B′处，点B 在AB 边上；将角C 沿GD 折叠，点C 恰好落到B′G 上的点C′处，HG 和DG 分别交EF 于点M 和点N，B′G 交EF 于点O，连接B′M，B′N．提出猜想：①“希望”小组猜想：HG⊥DG；②“奋斗”小组猜想：B′N⊥DG；③“创新”小组猜想：四边形B′MGN 是矩形．独立思考：（1）请你验证上述学习小组猜想的三个结论；（写出解答过程）（2）假如你是该课堂的一名成员，请你在现有图形中，找出一个和四边形B′MGN 面积相等的四边形．（直接写出其名称，不必证明）2.探究学习：矩形折纸中的数学动手操作：如图1，四边形ABCD 是一张矩形纸片，AB=3cm，AD=4cm，点E,F 分别在AD，BC 边上，连接BE,DF,且BE∥DF。

折叠问题求角度

折叠求角问题
矩形纸片折叠求角的问题
要点： (1) 找平行线 (2) 找平行线构成的同位角、内错角、同旁内角 (3) 找折叠角（折叠角相等）
1、如图，一长方形纸片ABCD沿折痕EF对折，得到点D的对应点D′，点C
的对应点C′，若∠BFE=50°，试求∠BFC′的度数．
分析:由∠BFE=50°,根据邻补角的定义,可求得∠EFC 的度数,又由折叠的性质,可求得∠EFC′的度数,继而可求得∠BFC′的度数．解答：解：∵∠BFE=50°， ∴∠EFC=180°-∠BFE=130°， ∵由折叠的性质可得：∠EFC′=∠EFC=130°， ∴∠BFC′=∠EFC′-∠BFE=130°-50°=80°．
三角形的折叠求角的问题
1、如图，Rt△ABC中，∠ACB=90°，∠A=50°，将其折叠，使点A落在边 CB上A′处，折痕为CD，则∠A′DB= _________ .
解：∵Rt△ABC中，∠ACB=90°，∠A=50°， ∴∠B=90°-50°=40°， ∵将其折叠，使点A落在边CB上A′处，折痕为 CD，则∠CA'D=∠A， ∵∠CA'D是△A'BD的外角， ∴∠A′DB=∠CA'D-∠B=50°-40°=10°．
(1)∵点A沿DE折叠落在点A′的位置，∴∠A=∠DA′E，根据三角形外角性质，∠1=∠A+∠DA′E=2∠DA′E，即∠1=2∠DA′E；
(2)∵点A沿DE折叠落在点A′的位置， ∴∠ADE=∠A′DE，∠AED=∠A′ED， ∴∠ADE=12(180°-∠1)，∠AED=12(180°-∠2)，在△ADE中，∠பைடு நூலகம்+∠ADE+∠AED=180°， ∴∠A+12(180°-∠1)+12(180°-∠2)=180°，整理得，2∠A=∠1+∠2；

初二数学培优专题(5)——折叠问题(答案详解)

折叠问题(一)正方形内的十字架结构结论1：在正方形ABCD中，E、F、G、H分别为AB、CD、BC、AD边上的点，若EF⊥GH，则GH=EF【例1】如图，将边长为4的正方形纸片ABCD折叠，使得点A落在CD的中点E处，折痕为FG，点F 在AD边，求折痕FG的长；【变式2】如图,将边长为的正方形ABCD折叠,使点D落在BC边的中点E处,点A落在F处,折痕为MN.(1)求线段CN的长;(2)求以线段MN为边长的正方形的面积;(3)求线段AM的长度.（二）折痕垂直于对称点的连线结论：折痕上的点到对应点距离相等【例2】如图，在矩形ABCD 中，AB=4，AD=3，将矩形折叠使得点D 与BC 上的点E 重合，折痕分别交AB 、CD 于点G 、F ，若BE=1，求AG 的长．【变式1】如图,四边形ABCD 是边长为9的正方形纸片,将其沿MN 折叠,使点B 落在CD 边上的B'处,点A 对应点为A',且,则AM 的长是______________．【变式2】（2016年山东威海中考题）如图,在矩形ABCD 中,4AB = ,6BC = ,点E 为BC 的中点,将ABE ∆沿AE 折叠,使点B 落在矩形内点F 处,连接CF ,则CF 的长为( )A.95 B.125 C.165 D.185(三) 折叠中动点轨迹与最值【例3】(2015四川自贡)如图，在矩形ABCD 中，4AB = ，6AD = ，E 是AB 边的中点，F 是线段BC 上的动点，将EBF ∆沿EF 所在直线折叠得到'EB F ∆，连接'B D ，则'B D 的最小值是（）。

A. 2B. 6C. 2-D.4【变式】（2014成都）如图，在边长为2的菱形ABCD 中，60A ∠=︒ ，M 是AD 边的中点，N 是AB 边上的一动点，将AMN ∆ 沿MN 所在直线翻折得到'A MN ∆，连接'A C ，则'A C 长度的最小值是_____ 。

折叠问题中的角度运算

专题7：折叠问题中的角度运算1如图，将矩形ABCD沿AE折叠，若∠BAD′=30°，则∠AED′=2如图将六边形ABCDEF沿着直线GH折叠，使点A、B落在六边形CDEFGH的内部，则∠1 +∠2=3如图，Rt△ABC中，∠ACB=90°，∠A=50°，将其折叠，使点A落在边CB上A′处，折痕为CD，则∠A′DB=???4已知△ABC是一张三角形的纸片．（1）如图①，沿DE折叠，使点A落在边AC上点A′的位置，∠DA′E与∠1的之间存在怎样的数量关系？为什么？（2）如图②所示，沿DE折叠，使点A落在四边形BCED的内部点A′的位置，∠A、∠1与∠2之间存在怎样的数量关系？为什么？（3）如图③，沿DE折叠，使点A落在四边形BCED的外部点A′的位置，∠A、∠1与∠2之间存在怎样的数量关系？为什么？5 65已知，如图，把△ABC纸片沿DE折叠，当点A落在四边形BCDE的内部时，则∠A与∠1+∠2之间有一种数量关系：2∠A=∠1+∠2始终保持不变，为什么？.6如图，把△ABC纸片沿DE折叠，当点A落在四边形BCDE内部时，（1）设∠AED的度数为x，∠ADE的度数为y，那么∠1、∠2的度数分别是多少？（用含有x或y的代数式表示）（2）∠A与∠1+∠2之间有一种数量关系始终保持不变，请找出这个规律，并说明理由．折一折，想一想，如图所示，在△ABC中，将纸片一角折叠，使点C落在△ABC内一点C′上，若∠1=40°，∠2=30°（1）求∠C的度数；（2）试通过第（1）问，直接写出∠1、∠2、∠C三者之间的关系．如图（1），△ABC是一个三角形的纸片，点D、E分别是△ABC边上的两点；研究（1）：若沿直线DE折叠，则∠BDA′与∠A的关系是∠BDA′=2∠A；研究（2）：若折成图2的形状，猜想∠BDA′，∠CEA′和∠A关系，并说明理由；研究（3）：若折成图3的形状，猜想∠BDA′，∠CEA′和∠A的关系，并说明理由．图1、图2、7如图①，把△ABC纸片沿DE折叠，使点A落在四边形BCED内部点A′的位置，通过计算我们知道：2∠A=∠1+∠2．请你继续探索：（1）如果把△ABC纸片沿DE折叠，使点A落在四边形BCED的外部点A′的位置，如图②，此时∠A与∠1、∠2之间存在什么样的关系？为什么？请说明理由．（2）如果把四边形ABCD沿EF折叠，使点A、D落在四边形BCFE的内部A′、D′的位置，如图③，你能求出∠A、∠D、∠1与∠2之间的关系吗？（直接写出关系式即可）8三角形纸片ABC中，∠A=55°，∠B=75°，将纸片的一角折叠，使点C落在△ABC内（如图），则∠1+∠2的度数为????度．9如图，已知四边形ABCD，∠C=72°，∠D=81°．沿EF折叠四边形，使点A、B分别落在四边形内部的点A′、B′处，求∠1+∠2的大小．10、如图，△ABC中，∠ACB=90°，沿CD折叠△CBD，使点B恰好落在AC边上的点E处．若∠A=22°，则∠BDC等于（）11、将五边形纸片ABCDE按如图方式折叠，折痕为AF，点E、D分别落在E′、D′，已知∠AFC=76°，则∠CFD′等于12如图，在平面内，把矩形ABCD沿EF对折，若∠1=50°，则∠AEF等于13如图，把△ABC沿线段DE折叠，使点A落在点F处，BC∥DE；若∠B=50°，则∠BDF的度数为1 1 如图，把一张长方形纸片ABCD，沿EF折叠后，ED′与BC的交点为G，点D，C分别落在D′，C′的位置上．若∠EFG=55°，则∠1等于14将一条两边沿互相平行的纸带按如图折叠．设∠1=x°，则∠α的度数为（）15将长方形ABCD沿折痕EF折叠，使CD落在GH的位置，若∠FGH=55°，则∠HEF=（）16如图，一个宽度相等的纸条按如图所示方法折叠一下，则∠1=（）17如图，D、E分别为△ABC的边AB、AC上的点，DE∥BC，将△ABC沿线段DE折叠，使点A落在BC上的点F处，若∠B=55°，则∠BDF的度数为?（）18如图所示，将一张长方形纸片沿EF折叠后，点D，C分别落在D′，C′的位置上，ED′的延长线与BC的交点为G．若∠EFG=80°，则∠BFC′的度数为（）19如图a是长方形纸带，∠DEF=24°，将纸带沿EF折叠成图b，再沿BF折叠成图c，则图c中的∠CFE的度数（）20如图，三角形纸片ABC，AB=10cm，BC=7cm，AC=6cm，沿过点B的直线折叠这个三角形，使顶点C落在AB边上的点E处，折痕为BD，则△AED的周长为（）21如图，将长方形ABCD沿对角线BD折叠，使点C恰好落在如图C′的位置，若∠DBC=15°，则∠ABC′=（）22一张长方形纸条折成如图的形状，如果∠1=130°，∠2=（）23如图：将一张长方形纸片沿EF折叠后，点D、C分别落在D′、C′的位置，ED′的延长线与BC交于点G．若∠EFG=55°，则∠1=（）24如图，已知长方形ABCD，我们按如下步骤操作可以得到一个特定角：（1）以点A所在直线为折痕，折叠纸片，使点B落在AD上，折痕与BC交于E；（2）将纸片展平后，再一次折叠纸片，以E所在直线为折痕，使点A落在BC上，折痕EF交AD于F，则∠AEF的度数25如图，将纸片△ABC沿着DE折叠压平，且∠1+∠2=72°，则∠A=（）26如图，把△ABC纸片沿DE折叠，当点A落在四边形BCED的外部时，则∠A与∠1和∠2之间有一种数量关系始终保持不变，请试着找一找这个规律，你发现的规律是（）27如图，三角形纸片ABC，AB=10cm，BC=7cm，AC=6cm，沿过点B的直线折叠这个三角形，使顶点C落在AB边上的点E处，折痕为BD，则△AED的周长为（）28一个宽度相等纸条，按如图所示的方式折叠一下，已知∠3=120°，则∠1的度数为（）29如图，把一张长方形纸条折叠后，若∠AOB′=70°，则∠OGC的度数为（）30如图，∠A=60°，∠B=70°，将纸片的一角折叠，使点C落在△ABC内，若∠2=80°，则∠1的度数为（）31如图（1）是长方形纸带，∠DEF=α，将纸带沿EF折叠成图（2），再沿BF折叠成图（3），则图（3）中的∠CFE的度数是（）32如图，生活中，将一个宽度相等的纸条按右图所示折叠一下，如果∠1=140°，那么∠2的度数为（）33如图，四边形ABCD中，点M，N分别在AB，BC上，将△BMN沿MN翻折，得△FMN，若MF∥AD，FN∥DC，则∠B =（）34如图，一张长方形纸条沿AB折叠，如果∠1=124°，那么∠2的度数是（）35如图，把长方形ABCD沿EF对折后使两部分重合，若∠AEF=110°，则∠1=（）36如图，一张三角形纸片△ABC，沿DE折叠使得顶点C落在边AB上，若DE∥AB，∠A=45°，则∠ADC的度数是（）37如图所示，把一个三角形纸片ABC顶角向内折叠3次之后，3个顶点不重合，那么图中∠1+∠2+∠3+∠4+∠5+∠6的度数和是（）38如图，将△ABC三个角分别沿DE、HG、EF翻折，三个顶点均落在点O处，则∠1+∠2的度数为（）39如图，正方形纸片ABCD的边长为8，将其沿EF折叠，则图中①②③④四个三角形的周长之和为（）40如图，将五边形ABCDE沿AE对折到如图的位置，其中∠AEC=72°，则∠CED′=（）41如图，在△ABC中，∠A=35°，在平面内沿直线DE将△ABC折叠后，量得∠BDA′=110°，那么∠CEA′的度数为（）42如图，把一个长方形纸片沿EF折叠后，点D、C分别落在D′、C′的位置，若∠EFB=65°，则∠AED′等于（）43如图，已知△ABC中，∠BAC=140°，现将△ABC进行折叠，使顶点B、C均与顶点A重合，求∠DAE的度数．。

培优专题01 与三角形模型有关的角度计算-解析版

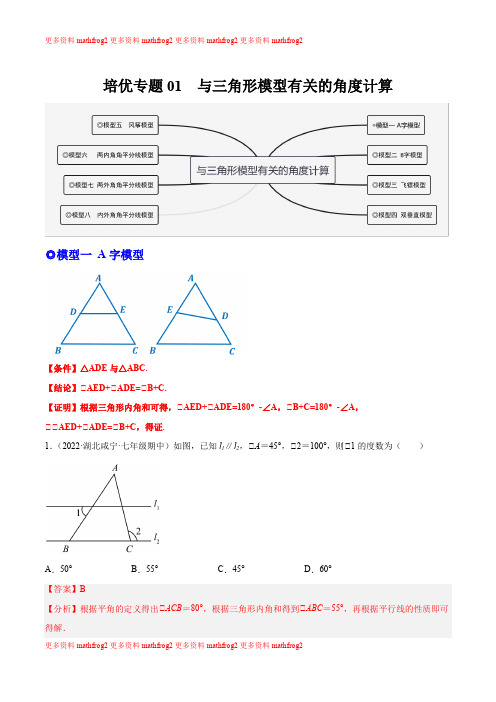
培优专题01 与三角形模型有关的角度计算◎模型一A字模型【条件】△ADE与△ABC.【结论】∠AED+∠ADE=∠B+C.【证明】根据三角形内角和可得，∠AED+∠ADE=180°-∠A，∠B+C=180°-∠A，∠∠AED+∠ADE=∠B+C，得证.1．（2022·湖北咸宁·七年级期中）如图，已知l1∥l2，∠A＝45°，∠2＝100°，则∠1的度数为（）A．50°B．55°C．45°D．60°【答案】B【分析】根据平角的定义得出∠ACB＝80°，根据三角形内角和得到∠ABC＝55°，再根据平行线的性质即可得解．【详解】解：∠∠2＝100°，∠∠ACB ＝180°−100°＝80°， ∠∠A ＝45°，∠∠ABC ＝180°−45°−80°＝55°， ∠l 1∥l 2，∠∠1＝∠ABC ＝55°，故选：B ．【点睛】此题考查了平行线的性质，熟记“两直线平行，内错角相等”是解题的关键．2．（2022·全国·八年级课时练习）如图，ABC 中，65A ∠=︒，直线DE 交AB 于点D ，交AC 于点E ，则BDE CED ∠+∠=（）．A ．180︒B ．215︒C ．235︒D ．245︒【答案】D【分析】根据三角形内角和定理求出ADE AED ∠+∠，根据平角的概念计算即可．【详解】解：65A ∠=︒，18065115ADE AED ∴∠+∠=︒-︒=︒， 360115245BDE CED ∴∠+∠=︒-︒=︒，故选：D ．【点睛】本题考查的是三角形内角和定理的应用，掌握三角形内角和等于180︒是解题的关键． 3．（2022·全国·八年级课时练习）如图是某建筑工地上的人字架，若1120∠=︒，那么32∠-∠的度数为_________．【答案】60︒【分析】根据平角的定义求出4，再利用三角形的外角的性质即可解决问题．【详解】解：如图14180∠+∠=︒，1120∠=︒， 460∴∠=︒，324，32460∴∠-∠=∠=︒，故答案为：60︒．【点睛】本题考查三角形外角的性质、平角的性质等知识，解题的关键是熟练掌握基本知识，属于中考基础题．4．（2020·湖南·常德市第二中学九年级期中）如图，在ABC ∆中，90C ∠=︒，6BC =，D ，E 分别在AB 、AC 上，将ADE ∆沿DE 折叠，使点A 落在点A '处，若A '为CE 的中点，则折痕DE 的长为__．DE BC ，故∆BC ．【详解】解：ABC ∆沿90DEA =∠'=︒，AED ∆∽，的中点，AE =∴=．ED2故答案为：2．【点睛】本题考查相似三角形的判定和性质，掌握“A ”字形三角形相似的判定和性质为解题关键． 5．（2022·全国·八年级课时练习）如图所示，DAE ∠的两边上各有一点,B C ，连接BC ，求证180DBC ECB A +∠=︒∠+∠．【答案】见解析【分析】根据三角形的外角等于与它不相邻的两个内角的和证明即可．【详解】解：DBC ∠和ECB ∠是ABC 的外角， ,DBC A ACB ECB A ABC ∴∠=∠+∠∠=∠+∠．又180A ABC ACB ∠+∠+∠=︒，180DBC ECB A ACB ABC A A ∴∠+∠=∠+∠+∠+∠︒=+∠．【点睛】本题主要考查三角形外角的性质，熟知三角形的外角等于与它不相邻的两个内角的和是解题的关键．◎模型二 8字模型【条件】AD 、BC 相交于点O.【结论】∠A +∠B =∠C +∠D.(上面两角之和等于下面两角之和)【证明】在∠ABO 中，由内角和定理：∠A +∠B +∠BOA =180°，在∠CDO 中，∠C +∠D +∠COD =180°， ∠∠A +∠B +∠BOA =180°=∠C +∠D +∠COD ，由对顶角相等：∠BOA =∠COD ∠∠A +∠B =∠C +∠D ，得证.6．（2022·全国·八年级课时练习）如图，AB 和CD 相交于点O ，∠A ＝∠C，则下列结论中不能完全确定正确的是（）A．∠B＝∠D B．∠1＝∠A＋∠D C．∠2＞∠D D．∠C＝∠D【答案】D【分析】利用三角形的外角性质，对顶角相等逐一判断即可．【详解】∠∠A＋∠AOD＋∠D＝180°，∠C＋∠COB＋∠B＝180°，∠A＝∠C，∠AOD＝∠BOC，∠∠B＝∠D，∠∠1＝∠2＝∠A＋∠D，∠∠2＞∠D，故选项A，B，C正确，故选D．【点睛】本题考查了对顶角的性质，三角形外角的性质，熟练掌握并运用两条性质是解题的关键．7．（2022·全国·八年级课时练习）如图，∠1=60°，则∠A+∠B+∠C+∠D+∠E+∠F=（）A．240°B．280°C．360°D．540°【答案】A【分析】根据三角形内角和定理得到∠B与∠C的和，然后在五星中求得∠1与另外四个角的和，加在一起即可．【详解】解：由三角形外角的性质得：∠3=∠A+∠E，∠2=∠F+∠D，∠∠1+∠2+∠3=180°，∠1=60°，∠∠2+∠3=120°，即：∠A+∠E+∠F+∠D=120°，∠∠B+∠C=120°，∠∠A+∠B+∠C+∠D+∠E+∠F=240°．故选A．【点睛】本题考查了三角形的外角和三角形的内角和的相关知识，解决本题的关键是将题目中的六个角分成两部分来分别求出来，然后再加在一起．8．（2022·全国·八年级课时练习）如图，求∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠I＝__．【答案】900°【分析】根据多边形的内角和，可得答案．【详解】解：连EF，GI，如图，∠6边形ABCDEFK的内角和＝（6－2）×180°＝720°，∠∠A＋∠B＋∠C＋∠D＋∠E＋∠F＝720°－（∠1＋∠2），即∠A＋∠B＋∠C＋∠D＋∠E＋∠F＋（∠1＋∠2）＝720°，∠∠1＋∠2＝∠3＋∠4，∠5＋∠6＋∠H＝180°，∠∠A＋∠B＋∠C＋∠D＋∠E＋∠F∠H＋（∠3＋∠4）＝900°，∠∠A＋∠B＋∠C＋∠D＋∠E＋∠F（∠3＋∠4）＋∠5＋∠6＋∠H＝720°＋180°，∠∠A＋∠B＋∠C＋∠D＋∠E＋∠F＋∠G＋∠H＋∠I＝900°，故答案为：900°．【点睛】本题考查了n边形的内角和定理：n边形的内角和为（n－2）×180°（n≥3的整数）．9．（2022·全国·八年级课时练习）如图，∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠I+∠K的度数为__．【答案】1080°【分析】连KF，GI，根据n边形的内角和定理得到7边形ABCDEFK的内角和＝（7－2）×180°＝900°，则∠A＋∠B＋∠C＋∠D＋∠E＋∠F＋∠K＋（∠1＋∠2）＝900°，由三角形内角和定理可得到∠1＋∠2＝∠3＋∠4，∠5＋∠6＋∠H＝180°，则∠A＋∠B＋∠C＋∠D＋∠E＋∠F＋∠K＋（∠3＋∠4）＋∠5＋∠6＋∠H＝900°＋180°，即可得到∠A＋∠B＋∠C＋∠D＋∠E＋∠F＋∠G＋∠H＋∠I＋∠K的度数．【详解】解：连KF，GI，如图，∠7边形ABCDEFK的内角和＝（7－2）×180°＝900°，∠∠A＋∠B＋∠C＋∠D＋∠E＋∠F＋∠K＝900°－（∠1＋∠2），即∠A＋∠B＋∠C＋∠D＋∠E＋∠F＋∠K＋（∠1＋∠2）＝900°，∠∠1＋∠2＝∠3＋∠4，∠5＋∠6＋∠H＝180°，∠∠A＋∠B＋∠C＋∠D＋∠E＋∠F＋∠K＋（∠3＋∠4）＝900°，∠∠A＋∠B＋∠C＋∠D＋∠E＋∠F＋∠K＋（∠3＋∠4）＋∠5＋∠6＋∠H＝900°＋180°，∠∠A＋∠B＋∠C＋∠D＋∠E＋∠F＋∠G＋∠H＋∠I＋∠K＝1080°．故∠A＋∠B＋∠C＋∠D＋∠E＋∠F＋∠G＋∠H＋∠I＋∠K的度数为1080°．故答案为：1080°．【点睛】本题考查了n边形的内角和定理：n边形的内角和为（n－2）×180°（n≥3的整数）．10．（2022·全国·八年级课时练习）如图，OAB和OCD中，OA＝OB，OC＝OD，∠AOB＝∠COD＝α，AC、BD交于M（1）如图1，当α＝90°时，∠AMD 的度数为 °；（2）如图2，当α＝60°时，求∠AMD 的度数；（3）如图3，当OCD 绕O 点任意旋转时，∠AMD 与α是否存在着确定的数量关系？如果存在，请你用α表示∠AMD ，并用图3进行证明；若不确定，说明理由．【答案】（1）90；（2）120︒；（3）180α︒-【分析】（1）如图1，设OA 交BD 于K ，只要证明△≌△BOD AOC ，推出OBD OAC ∠=∠，由BKO AKM ∠=∠，可得90AMK BOK ∠=∠=︒；（2）如图2，设OA 交BD 于K ，只要证明△≌△BOD AOC ，推出OBD OAC ∠=∠，由BKO AKM ∠=∠，可得60AMK BOK ∠=∠=︒；（3）如图3，设OA 交BD 于K ，只要证明△≌△BOD AOC ，推出OBD OAC ∠=∠，由BKM AKO ∠=∠，可得BMK AOK α∠=∠=，可得180AMD α∠=︒-；【详解】解：（1）如图1中，设OA 交BD 于K∠OA OB OC OD ==，，90AOB COD ∠=∠=︒ ∠BOD AOC ∠=∠ ∠△≌△()BOD AOC SAS ∠OBD OAC ∠=∠ ∠BKO AKM ∠=∠ ∠90AMK BOK ∠=∠=︒ ∠90AMD ∠=︒ 故答案为90︒（2）如图2，设OA 交BD 于K ，∠OA OB OC OD ==，，60AOB COD ∠=∠=︒ ∠BOD AOC ∠=∠ ∠△≌△()BOD AOC SAS ∠OBD OAC ∠=∠ ∠BKO AKM ∠=∠ ∠60AMK BOK ∠=∠=︒ ∠180120AMD AMK ∠=︒-∠=︒ 故答案为120︒（3）如图3，设OA 交BD 于K ，∠OA OB OC OD ==，，AOB COD α∠=∠= ∠BOD AOC ∠=∠ ∠△≌△()BOD AOC SAS ∠OBD OAC ∠=∠ ∠AKO BKM ∠=∠ ∠BMK AOK α∠=∠=∠180180AMD BMK α∠=︒-∠=︒- 故答案为180α︒-【点睛】本题考查了几何变换综合题，全等三角形的判定，三角形内角和性质，解题的关键是灵活运用所学知识解决问题，学会利用“8字型”证明角相等．◎模型三飞镖模型【条件】四边形ABDC 如上左图所示.【结论】∠D =∠A +∠B +∠C.(凹四边形凹外角等于三个内角和) 【证明】如上右图，连接AD 并延长到E ，则：∠BDC =∠BDE +∠CDE =(∠B +∠1)+(∠2+∠C )=∠B +∠BAC +∠C.本质为两个三角形外角和定理证明. 11．（2022·全国·八年级课时练习）在社会实践手工课上，小茗同学设计了一个形状如图所示的零件，如果52,25A B ︒︒∠=∠=，30,35,72C D E ︒︒︒∠=∠=∠=，那么F ∠的度数是（）．A ．72︒B ．70︒C ．65︒D ．60︒【答案】A【分析】延长BE 交CF 的延长线于O ，连接AO ，根据三角形内角和定理求出,BOC ∠再利用邻补角的性质求出DEO ∠，再根据四边形的内角和求出DFO ∠，根据邻补角的性质即可求出DFC ∠的度数．【详解】延长BE 交CF 的延长线于O ，连接AO ，如图，∠180,OAB B AOB ∠+∠+∠=︒∠180,AOB B OAB ∠=︒-∠-∠ 同理得180,AOC OAC C ∠=︒-∠-∠ ∠360,AOB AOC BOC ∠+∠+∠=︒ ∠360BOC AOB AOC ∠=︒-∠-∠360(180)(180)B OAB OAC C =︒-︒-∠-∠-︒-∠-∠ 107,B C BAC =∠+∠+∠=︒ ∠72,BED ∠=︒∠180108,DEO BED ∠=︒-∠=︒ ∠360DFO D DEO EOF ∠=︒-∠-∠-∠36035108107110,=︒-︒-︒-︒=︒∠180********DFC DFO ∠=︒-∠=︒-︒=︒, 故选：A ．【点睛】本题考查三角形内角和定理，多边形内角和，三角形的外角的性质，邻补角的性质，解题关键是会添加辅助线，将已知条件联系起来进行求解．三角形外角的性质：三角形的一个外角等于与它不相邻的两个内角的和；邻补角性质：邻补角互补；多边形内角和：180(2)n ︒-．12．（2022·全国·八年级课时练习）如图，已知BE ，CF 分别为△ABC 的两条高，BE 和CF 相交于点H ，若△BAC=50°，则△BHC 为（）A ．115°B ．120°C ．125°D ．130°【答案】D【详解】∠BE 为∠ABC 的高，∠BAC=50°， ∠∠ABE=90°-50°=40°， ∠CF 为∠ABC 的高， ∠∠BFC=90°，∠∠BHC=∠ABE+∠BFC=40°+90°=130°．故选D．13．（2022·全国·八年级课时练习）如图，若115∠+∠+∠+∠+∠+∠=EOC∠=︒，则A B C D E F____________．【答案】230°【分析】根据三角形外角的性质，得到∠EOC=∠E+∠2=115°，∠2=∠D+∠C，∠EOC=∠1+∠F=115°，∠1=∠A+∠B，即可得到结论．【详解】解：如图∠∠EOC=∠E+∠2=115°，∠2=∠D+∠C，∠∠E+∠D+∠C=115°，∠∠EOC=∠1+∠F=115°，∠1=∠A+∠B，∠∠A+∠B+∠F=115°，∠∠A+∠B+∠C+∠D+∠E+∠F=230°，故答案为：230°．【点睛】本题主要考查三角形内角和定理和三角形外角的性质，解决本题的关键是要熟练掌握三角形外角性质．14．（2022·山东德州·七年级期末）如图，则∠A+∠B+∠C+∠D+∠E的度数是__．【答案】180°【分析】由三角形的一个外角等于与它不相邻的两个内角的和，得∠4＝∠A＋∠2，∠2＝∠D＋∠C，进而利用三角形的内角和定理求解．【详解】解：如图可知：∠∠4是三角形的外角，∠∠4＝∠A＋∠2，同理∠2也是三角形的外角，∠∠2＝∠D＋∠C，在∠BEG中，∠∠B＋∠E＋∠4＝180°，∠∠B＋∠E＋∠A＋∠D＋∠C＝180°．故答案为：180°．【点睛】本题考查三角形外角的性质及三角形的内角和定理，解答的关键是沟通外角和内角的关系．15．（2022·全国·八年级课时练习）模型规律：如图1，延长CO交AB于点D，则∠=∠+∠=∠+∠+∠．因为凹四边形ABOC形似箭头，其四角具有“BOC A B C 1BOC B A C B∠=∠+∠+∠”这个规律，所以我们把这个模型叫做“箭头四角形”．模型应用（1）直接应用：∠如图2，60,20,30A B C∠=︒∠=︒∠=︒，则BOC∠=__________︒；∠如图3，A B C D E F∠+∠+∠+∠+∠+∠=__________︒；（2）拓展应用：∠如图4，ABO∠、ACO∠的2等分线（即角平分线）1BO、1CO交于点1O，已知120BOC∠=︒，50BAC∠=︒，则1BO C∠=__________︒；∠如图5，BO、CO分别为ABO∠、ACO∠的10等分线1,2,3,,(,)89i=⋯．它们的交点从上到下依次为1O、2O、3O、…、9O．已知120BOC∠=︒，50BAC∠=︒，则7BO C∠=__________︒；∠如图6，ABO∠、BAC∠的角平分线BD、AD交于点D，已知120,44BOC C∠=︒∠=︒，则ADB=∠__________︒；∠如图7，BAC∠、BOC∠的角平分线AD、OD交于点D，则B、C∠、D∠之同的数量关系为__________．【详解】解：（1）∠∠BOC=∠A+∠B+∠C=60°+20°+30°=110°；◎模型四双垂直模型【条件】∠B=∠D=∠ACE=90°.【结论】∠BAC=∠DCE，∠ACB=∠CED.【证明】∠∠B=∠D=∠ACE=90°；∠∠BAC+∠ACB=90°；又∠ECD+∠ACB=90°；∠∠BAC=∠DCE同理,∠ACB+∠DCE=90°，且∠CED+∠DCE=90°；∠∠ACB=∠CED，得证.16．（2021·青海海东·八年级期中）如图，已知∠ABC∠∠CDE，∠B＝90°，点C为线段BD上一点，则∠ACE的度数为（）A．94°B．92°C．90°D．88°【答案】C【分析】由全等三角形的性质得出∠ACB＝∠CED，则可得出答案．【详解】解：∠∠ABC∠∠CDE，∠∠ACB＝∠CED，∠B＝∠D＝90°，∠∠CED+∠ECD＝90°，∠∠ACB+∠ECD＝90°，∠∠ACB+∠ECD+∠ACE＝180°，∠∠ACE＝90°．故选：C．【点睛】本题考查了全等三角形的性质；熟练掌握三角形全等的性质定理是解题的关键．17．（2020·河南·郑州市第八中学模拟预测）如图所示，一副三角尺摆放置在矩形纸片的内部，三角形的三个顶点恰好在矩形的边上，若16FGC ∠=︒，则AEF ∠等于（）A ．106︒B ．114︒C ．126︒D ．134︒【答案】D【分析】根据矩形的性质可得∠C=90°，AD∠BC ，利用直角三角形的两个锐角互余求出∠GFC ，从而求出∠EFB ，然后根据平行线的性质可得∠AEF ＋∠EFB=180°，从而求出结论．【详解】解：∠四边形ABCD 为矩形 ∠∠C=90°，AD∠BC ∠16FGC ∠=︒∠∠GFC=90°－∠FGC=74° 由三角尺可知：∠EFG=60° ∠∠EFB=180°－∠GFC －∠EFG=46° ∠AD∠BC∠∠AEF ＋∠EFB=180° ∠∠AEF=180°－∠EFB=134° 故选D ．【点睛】此题考查的是矩形的性质、直角三角形的性质和平行线的性质，掌握矩形的性质、直角三角形的两个锐角互余和平行线的性质是解决此题的关键．18．（2022·山东青岛·七年级期末）如图，小虎用10块高度都是4cm 的相同长方体小木块，垒了两堵与地面垂直的木墙，木墙之间刚好可以放进一个等腰直角三角板（AC BC =，90ACB ∠=︒），点C 在DE 上，点A 和B 分别与木墙的顶端重合，则两堵木墙之间的距离为______．【答案】40 cm【分析】根据题意可得AC＝BC，∠ACB＝90°，AD∠DE，BE∠DE，进而得到∠ADC＝∠CEB＝90°，再根据等角的余角相等可得∠BCE ＝∠DAC ，再证明∠ADC ∠∠CEB 即可，利用全等三角形的性质进行解答．【详解】解：由题意得：AC ＝BC ，∠ACB ＝90°，AD ∠DE ，BE ∠DE ， ∠∠ADC ＝∠CEB ＝90°，∠∠ACD ＋∠BCE ＝90°，∠ACD ＋∠DAC ＝90°， ∠∠BCE ＝∠DAC ，在∠ADC 和∠CEB 中，ADC CEB DAC BCE AC BC ∠∠⎧⎪∠∠⎨⎪⎩＝＝＝， ∠∠ADC ∠∠CEB （AAS ）；由题意得：AD ＝EC ＝12cm ，DC ＝BE ＝28cm ， ∠DE ＝DC ＋CE ＝40（cm ），答：两堵木墙之间的距离为40cm ，故答案为：40 cm ．【点睛】此题主要考查了全等三角形的应用，涉及到垂直的定义、直角三角形的性质和连个三角形全等的判定与性质等知识点，解题的关键是正确找出证明三角形全等的条件．19．（2021·江苏盐城·七年级期中）将含有30角的直角三角板（30A ∠=︒）和直尺按如图方式摆放，已知136∠=︒，则2∠=______︒．【答案】24【分析】过点B 作BC //MN ，由平行线传递性，可得BC //KL ，再由平行线的性质可得1=LBC ∠∠ ，2=ABC ∠∠ ，最后由在直角三角形中两锐角互余的关系，求出2=24∠︒ ．【详解】解：过点B 作BC //MN ，如图所示：MN //KH∴ BC //KL1LBC ∴∠=∠又1=36∠︒=36LBC ∴∠︒又 BC //MN2=ABC ∴∠∠又=30A ∠︒=60ABL ∴∠︒又=ABL LBC ABC ∠∠+∠603624ABC ∴∠=︒-︒=︒224∴∠=︒故答案为：24【点睛】本题考查了平行线的判定与性质(两直线平行，内错角相等)，平行线传递性(如果两条直线都与第三条直线平行，那么这两条直线也互相平行)，直角三角形中两锐角互余，角的和差计算等综合知识点．难点是作已知直线的平行线．20．（2022·全国·八年级专题练习）如图1，已知ABC ∆中，90ACB ∠=︒，AC BC =，BE 、AD 分别与过点C 的直线垂直，且垂足分别为E ，D ．(1)猜想线段AD 、DE 、BE 三者之间的数量关系，并给予证明．(2)如图2，当过点C 的直线绕点C 旋转到ABC ∆的内部，其他条件不变，如图2所示，∠线段AD 、DE 、BE 三者之间的数量关系是否发生改变？若改变，请直接写出三者之间的数量关系，若不改变，请说明理由；∠若 2.8AD =， 1.5DE =时，求BE 的长．【答案】(1)DE AD BE =+，证明见解析 (2)∠发生改变，DE AD BE =-；∠1.3【分析】（1）证明ACD CBE ∆≅∆，可得AD CE =，CD ＝BE ，即可求解；（2）∠证明ACD CBE ∆≅∆，可得AD CE =，CD ＝BE ，即可求解；∠由∠可得DE AD BE =-，从而得到BE AD DE =-，即可求解．（1）解：DE AD BE =+，理由如下： ∠BE 、AD 分别与过点C 的直线垂直， ∠90BEC ADC ∠∠=︒＝， ∠90ACD CAD ∠∠+︒＝， ∠90ACB ∠=︒， ∠90ACD BCE ∠+∠=︒， ∠CAD BCE ∠=∠，在ACD ∆和CBE ∆中，ADC BECCAD BCE AC BC ∠=∠⎧⎪∠=∠⎨⎪=⎩，()ACD CBE AAS ∴∆≅∆，AD CE ∴=，CD ＝BE ，∠ DE ＝EC ＋CD ，DE AD BE ∴=+；（2）解：∠发生改变．∠BE 、AD 分别与过点C 的直线垂直，∠90BEC ADC ∠∠=︒＝，∠90ACD CAD ∠∠+︒＝， ∠90ACB ∠=︒， ∠90ACD BCE ∠+∠=︒， ∠CAD BCE ∠=∠，在ACD ∆和CBE ∆中，ADC BEC CAD BCE AC BC ∠=∠⎧⎪∠=∠⎨⎪=⎩，()ACD CBE AAS ∴∆≅∆，AD CE ∴=，CD ＝BE ，∠ DE ＝CE -CD ， ∠DE AD BE=-； ∠由∠知：DE AD BE =-， ∠ 2.8 1.5 1.3BE AD DE =-=-=， ∠BE 的长为1.3.【点睛】本题主要考查了全等三角形的判定和性质、等角的余角相等，熟练掌握全等三角形的判定和性质是解题的关键．◎模型五风筝模型【条件】四边形ABPC ，分别延长AB 、AC 于点D 、E ，如上左图所示. 【结论】∠PBD+∠PCE =∠A +∠P .【证明】如上右图，连接AP ，则：∠PBD =∠PAB +∠APB ，∠PCE =∠PAC +∠APC ，∴∠PBD+∠PCE=∠PAB +∠APB+∠PAC +∠APC=∠BAC +∠BPC ，得证.21．（2022·内蒙古赤峰·八年级期末）如图，将ABC 的一角折叠，若12130∠+∠=︒，则B C ∠+∠=（）A．50°B．65°C．115°D．130°【答案】C【分析】根据折叠性质证得∠3=∠4，∠5=∠6，再根据平角定义求得∠4+∠5=115°，然后根据三角形的内角和定理求解即可．【详解】解：如图，由折叠性质得：∠3=∠4，∠5=∠6，∠∠1+∠3+∠4=180°，∠5+∠6+∠2=180°，∠∠1+∠2+2∠4+2∠5=360°，∠∠1+∠2=130°，∠2∠4+2∠5=360°－130°=230°，∠∠4+∠5=115°，∠∠4+∠5+∠A=180°，∠A+∠B+∠C=180°，∠∠B+∠C=∠4+∠5=115°，故选：C．【点睛】本题考查三角形折叠中的角度问题，熟练掌握折叠性质是解答的关键.22．（2022·海南海口·七年级期末）如图，把∠ABC纸片沿MN折叠，使点C落在∠ABC内部点C′处，若∠C=36°，则∠1+∠2等于（）A ．54°B ．62°C ．72°D ．76°【答案】C【分析】根据折叠可知∠C =∠'C ，四边形内角和为360°，即可求出'CMC ∠+'CNC ∠，用平角的定义即可求出∠1+∠2【详解】∠∠CMN 折叠得到'C MN ∠∠C =∠'C∠∠1=180°-'CMC ∠，∠2=180°-'CNC ∠∠∠1+∠2=180°-'CMC ∠+180°-'CNC ∠=360°-（'CMC ∠+'CNC ∠） ∠'CMC ∠+'CNC ∠=360°-∠C -'C ∠=360°-36°-36°=288° ∠∠1+∠2=360°-288°=72° 故选：C【点睛】本题主要考查了折叠问题，掌握三角形的内角和定理，四边形的内角和以及平角的定义是解题的关键．23．（2022·山东烟台·七年级期中）如图，在三角形纸片ABC 中65A ∠=︒，75B ∠=︒，将纸片的一角折叠，使点C 落在∠ABC 内，若150∠=︒，则∠2的度数为_________.【答案】30°##30度【分析】根据题意，已知∠A =65°，∠B =75°，可结合三角形内角和定理和四边形内角和求解．【详解】解：如图，设折痕为DE ；∠65A ∠=︒，75B ∠=︒，∠180180657540C A B ∠=︒-∠+∠=︒-︒+︒=︒（）（）， ∠180140CDE CED C ∠+∠=︒-∠=︒，又∠150∠=︒，∠2360(1)36030030A B CED CDE ∠=︒-∠+∠+∠+∠+∠=︒-︒=︒，故答案为：30°．【点睛】本题主要是考查了三角形、四边形内角和，即三角形的内角和为180°，四边形的内角和为360°；熟练掌握三角形的内角和定理是解题的关键．24．（2022·湖北恩施·一模）图，把等边ABC 沿直线DE 折叠，点A 落在'A 处，若150∠=︒，则2∠=______．【答案】40︒【分析】先求出AED ∠的度数，再根据折叠得到AED A ED '∠=∠，即可求出2∠的度数．【详解】∠等边ABC 沿直线DE 折叠 ∠60A ∠=︒，AED A ED '∠=∠ ∠150∠=︒∠180170AED A ∠=︒-∠-∠=︒ ∠70AED A ED '∠=∠=︒∠420180AED A ED ∠=︒-'∠-∠=︒ 故答案为：40︒【点睛】此题考查翻折问题，折叠问题的实质是“轴对称”，解题关键是找出经轴对称变换所得的等量关系．25．（2022·江苏·扬州市竹西中学七年级期末）如图∠，把∠ABC纸片沿DE折叠，使点A落在四边形BCED内部点A′的位置，通过计算我们知道：2∠A＝∠1+∠2．请你继续探索：(1)如果把∠ABC纸片沿DE折叠，使点A落在四边形BCED的外部点A′的位置，如图∠，此时∠A与∠1、∠2之间存在什么样的关系？为什么？请说明理由．(2)如果把四边形ABCD沿EF折叠，使点A、D落在四边形BCFE的内部A′、D′的位置，如图∠，你能求出∠A、∠D、∠1与∠2之间的关系吗？（直接写出关系式即可）（1）解：如图所示，连接AA'，◎模型六两内角角平分线模型【条件】△ABC 中，BI 、CI 分别是∠ABC 和∠ACB 的角平分线，且相交于点I. 【结论】A I ∠+︒=∠2190 【证明】∵BI 是∠ABC 平分线，∴ABC ∠=∠212∵CI 是∠ACB 平分线，∴ACB ∠=∠213 由A →B →I →C →A 的飞镖模型可知： ∠I =∠A +∠2+∠3=∠A +ABC ∠21+ACB ∠21=∠A +)180(21A ∠-︒=A ∠+︒2190. 26．（2022·山东东营·七年级期末）如图，在△ABC 中，BF 平分△ABC ，CF 平分△ACB ，△BFC =125°，则△A 的度数为（）A ．60°B ．80°C ．70°D ．45°【答案】C【分析】先根据三角形内角和定理得出CBF BCF ∠+∠的度数，再由角平分线的性质得出ABC ACB ∠+∠的度数，根据三角形内角和定理即可得出结论．【详解】解：∠125BFC ∠=︒， ∠18012555BCF CBF ∠+∠=︒︒=︒﹣． ∠BF 平分ABC ∠，CF 平分ACB ∠，∠()2110ABC ACB BCF CBF ∠+∠=∠+∠=︒， ∠180A ABC ACB ∠+∠+∠=︒，∠18011070﹣．A∠=︒︒=︒故选：C ．【点睛】本题考查的是三角形内角和定理，以及三角形角平分线的定义，熟知三角形内角和是180°是解答此题的关键．27．（2022·福建·泉州五中七年级期末）如图，在四边形ABCD 中，∠A +∠D ＝α，∠ABC 的平分线与∠BCD 的平分线交于点P ，则∠P ＝（）A ．90°﹣12α B ．12αC ．90°+12α D ．360°﹣α28．（2022·河南鹤壁·七年级期末）已知ABC 中，A α∠=．在图1中B 、C ∠的平分线交于点1O ，则可计算得11902BO C α∠=︒+；在图2中，设B 、C ∠的两条三等分角线分别对应交于2O 、3O ，则3BO C ∠=_______________．【详解】解：Aα∠=，180ACB=︒-B∠、C∠的两条三等分角线分别对应交于332 ( 3CBO BCO ABC ∴∠+=∠3(BO C CBO∴∠=-∠+故答案为：【点睛】本题考查三角形内角和定理，解题的关键是熟练运用三等分角线求解．29．（2022·江苏常州·七年级期中）如图，在∠MBC中，∠ABC、∠ACB的角平分线OB、OC交于点O，若∠O=m°，则∠A的度数是______________________________°（用含m的代数式表示）．【答案】（2m-180）【分析】先由角平分线的定义得到∠ABC=2∠OBC，∠ACB=2∠OCB，再利用三角形内角和定理求解即可．【详解】解：∠OB，OC分别是∠ABC和∠ACB的角平分线，∠∠ABC=2∠OBC，∠ACB=2∠OCB，∠∠O+∠OBC+∠OCB=180°，∠∠OBC+∠OCB=180°-∠O=180°-m°，∠∠ABC+∠ACB=2∠OBC+2∠OCB=360°-2m°，∠∠A=180°-∠ABC-∠ACB=2m°-180°，故答案为：（2m-180）．【点睛】本题主要考查了三角形内角和定理，角平分线的定义，熟知相关知识是解题的关键．30．（2021·重庆·垫江第八中学校七年级阶段练习）在∠ABC中，BD，CE是它的两条角平分线，且BD，CE相交于点M，MN∠BC于点N．将∠MBN记为∠1，∠MCN记为∠2，∠CMN记为∠3．(1)如图1，若∠A=110°，∠BEC=130°，则∠2= °，∠3－∠1= °；(2)如图2，猜想∠3－∠1与∠A的数量关系，并证明你的结论；(3)若∠BEC=α，∠BDC=β，用含α和β的代数式表示∠3－∠1的度数．（直接写出结果即可）∠BD平分∠ABD，【点睛】本题主要考查了三角形内角和定理，三角形外角的像这种，角平分线的定义，垂直的定义，熟知三角形内角和为180度是解题的关键．◎模型七两外角角平分线模型【条件】△ABC 中，BI 、CI 分别是△ABC 的外角的角平分线，且相交于点O. 【结论】A O ∠-︒=∠2190. 【证明】∵BO 是∠EBC 平分线，∴EBC ∠=∠212，∵CO 是∠FCB 平分线，∴FCB ∠=∠215 由△BCO 中内角和定理可知：∠O =180°-∠2 -∠5 =180°-EBC ∠21 -FCB ∠21 =180°-)180(21ABC ∠-︒ -)180(21ACB ∠-︒=)(21ACB ABC ∠+∠=)180(21A ∠-︒=A O ∠-︒=∠2190. 31．（2022·江苏·江阴市祝塘第二中学七年级阶段练习）如图，在△ABC 中，设∠A ＝x °，∠ABC 与∠ACD 的平分线交于点A 1，得∠A 1；∠A 1BC 与∠A 1CD 的平分线相交于点A 2，得∠A 2；…；∠A 2021BC 与∠A 2021CD 的平分线相交于点A 2022，得∠A 2022，则∠A 2022是（）度．A ．202012x B ．202112x C ．202212x D ．202312x∠∠A＝∠ACD−∠ABC，∠A1＝∠A1CD−∠A1BC，∠BA1和CA1分别是∠ABC和∠ACD的角平分线，32．（2022·浙江·八年级专题练习）如图，ABC 中，56A ∠=︒，BD 平分ABC ∠，CD 平分ABC 的外角ACE ∠，BD 、CD 交于点D ，则D ∠的度数（）A ．28︒B ．56︒C ．30D ．26︒BD 平分平分ABC 的外角DBC ∴∠=12DCE ACE =∠根据外角性质：DBC D +∠28D DCE α∴∠=∠-=︒．故选：A ．33．（2022·陕西·西安博爱国际学校八年级期末）如图，在∠ABC中，∠ABC=75°，∠A=40°，∠ACD是∠ABC的外角，若∠ABC与∠ACD的平分线交于点P，则∠BPC的大小为_____．∠34．（2022·陕西·西安市曲江第一中学八年级期末）如图，在ABC中，ABC的内角CAB∠和外角CBD 的角平分线交于点P，已知42∠=︒，则CAPB∠的度数为____________．【答案】84︒##84度为ABC外角CBD=∠C+∠以求出答案．【详解】解：如下图，。

培优专题--纸片折叠求角度问题

点拨：解决折叠问题,挖掘出隐含在题中的条件,要抓住折叠前后对应角相等、对应边相等这些不变量，同时也要注意平行线性质的应用.1.如图，把一张长方形纸片ABCD 沿EF折叠后，点C 、D 分别落在'C 、'D 的位置上，'EC 交AD 于点G ，若∠EFG ＝58°,试求∠BEG 的度数.2.如图，把一条两边互相平行的纸条ABCD 沿EF 折叠，若∠1＝x ，请用关于x 的代数式表示∠α的度数.3.如图，小敏拿一张上下两边平行的纸条，任意得折痕AB ，然后过点A 折叠，使折痕AB 与边AD 重合，得折痕AC ；然后她由过点B 折叠，使折痕BA 与边BC 重合，得折痕BD. 在此过程中，折痕BD 与折痕AC 交于点E ，由此求∠AEB 的度数.4321E B CAD4.如图a 是长方形纸带，∠DEF=20°，将纸带沿EF 折叠成图b ，再沿BF 折叠成图c ，求图c 中的∠CFE 的度数。

5.如图，D E ，分别为ABC △的AC ，BC 边的中点，将此三角形沿DE 折叠，使点C 落在AB 边上的点P 处．若48CDE ∠=°，求APD ∠的度数。

G C 'D 'F D C E BA α3421N M G F E DCB A6.如图，Rt△ABC 中，∠ACB =90°，∠A =50°，将其折叠，使点A 落在边CB 上A ′处，折痕为CD ，求A DB '∠的度数。

7.如图所示，把一个长方形纸片沿EF 折叠后，点D ，C 分别落在D ′，C ′的位置．若∠EFB ＝65°，求∠AED ′的度数。

8.如图，在ABC ∆中，AB AC =，若将ABC ∆绕点C 顺时针旋转得A B C ''∆，使点B '落在线段AB 上，如果65B ∠=︒，则ACA '∠= 度.9.如图，在等腰直角三角形ABC 中，90,B AB BC ∠=︒=，O 是斜边AC 的中点，P 是斜边AC 上的一个动点，D 为射线BC 上的一点，且PB PD =，过D 点作射线AC 上的垂线DE ，垂足为E .（1）当点P 在线段AO 上时，PE BO =吗？为什么？（2）当点P 在线段OC 上时，PE BO =吗？为什么？A 'B DA E DB C′F CD ′ AA A ′B ′ B CAPO ECBA BOC（备用图）B6.如图6，△ABC 中，AD 是BC 边上的中线，E 是AD 上一点，且BE=AC ，延长BE 交AC 于F 。

折叠问题中的角度运算

专题7：折叠问题中的角度运算1如图，将矩形ABCD沿AE折叠，若∠BAD′=30°，则∠AED′=2如图将六边形ABCDEF沿着直线GH折叠，使点A、B落在六边形CDEFGH的内部，则∠1+∠2=3如图，Rt△ABC中，∠ACB=90°，∠A=50°，将其折叠，使点A落在边CB上A′处，折痕为CD，则∠A′DB=4已知△ABC是一张三角形的纸片．（1）如图①，沿DE折叠，使点A落在边AC上点A′的位置，∠DA′E与∠1的之间存在怎样的数量关系？为什么？（2）如图②所示，沿DE折叠，使点A落在四边形BCED的内部点A′的位置，∠A、∠1与∠2之间存在怎样的数量关系？为什么？（3）如图③，沿DE折叠，使点A落在四边形BCED的外部点A′的位置，∠A、∠1与∠2之间存在怎样的数量关系？为什么？5 65已知，如图，把△ABC纸片沿DE折叠，当点A落在四边形BCDE的内部时，则∠A与∠1+∠2之间有一种数量关系：2∠A=∠1+∠2始终保持不变，为什么？.6如图，把△ABC纸片沿DE折叠，当点A落在四边形BCDE内部时，（1）设∠AED的度数为x，∠ADE的度数为y，那么∠1、∠2的度数分别是多少？（用含有x或y的代数式表示）（2）∠A与∠1+∠2之间有一种数量关系始终保持不变，请找出这个规律，并说明理由．折一折，想一想，如图所示，在△ABC中，将纸片一角折叠，使点C落在△ABC内一点C′上，若∠1 =40°，∠2=30°（1）求∠C的度数；（2）试通过第（1）问，直接写出∠1、∠2、∠C三者之间的关系．如图（1），△ABC是一个三角形的纸片，点D、E分别是△ABC边上的两点；研究（1）：若沿直线DE折叠，则∠BDA′与∠A的关系是∠BDA′=2∠A；研究（2）：若折成图2的形状，猜想∠BDA′，∠CEA′和∠A关系，并说明理由；研究（3）：若折成图3的形状，猜想∠BDA′，∠CEA′和∠A的关系，并说明理由．图1、图2、7如图①，把△ABC纸片沿DE折叠，使点A落在四边形BCED内部点A′的位置，通过计算我们知道：2∠A=∠1+∠2．请你继续探索：（1）如果把△ABC纸片沿DE折叠，使点A落在四边形BCED的外部点A′的位置，如图②，此时∠A 与∠1、∠2之间存在什么样的关系？为什么？请说明理由．（2）如果把四边形ABCD沿EF折叠，使点A、D落在四边形BCFE的内部A′、D′的位置，如图③，你能求出∠A、∠D、∠1与∠2之间的关系吗？（直接写出关系式即可）8三角形纸片ABC中，∠A=55°，∠B=75°，将纸片的一角折叠，使点C落在△ABC内（如图），则∠1+∠2的度数为度．9如图，已知四边形ABCD，∠C=72°，∠D=81°．沿EF折叠四边形，使点A、B分别落在四边形内部的点A′、B′处，求∠1+∠2的大小．10、如图，△ABC中，∠ACB=90°，沿CD折叠△CBD，使点B恰好落在AC边上的点E处．若∠A=22°，则∠BDC 等于（）11、将五边形纸片ABCDE按如图方式折叠，折痕为AF，点E、D分别落在E′、D′，已知∠AFC=76°，则∠CFD′等于12如图，在平面内，把矩形ABCD沿EF对折，若∠1=50°，则∠AEF等于13如图，把△ABC沿线段DE折叠，使点A落在点F处，BC∥DE；若∠B=50°，则∠BDF的度数为1 1如图，把一张长方形纸片ABCD，沿EF折叠后，ED′与BC的交点为G，点D，C分别落在D′，C′的位置上．若∠EFG=55°，则∠1等于14将一条两边沿互相平行的纸带按如图折叠．设∠1=x°，则∠α的度数为（）15将长方形ABCD沿折痕EF折叠，使CD落在GH的位置，若∠FGH=55°，则∠HEF=（）16如图，一个宽度相等的纸条按如图所示方法折叠一下，则∠1=（）17如图，D、E分别为△ABC的边AB、AC上的点，DE∥BC，将△ABC沿线段DE折叠，使点A落在BC上的点F处，若∠B=55°，则∠BDF的度数为（）18如图所示，将一张长方形纸片沿EF折叠后，点D，C分别落在D′，C′的位置上，ED′的延长线与BC的交点为G．若∠EFG=80°，则∠BFC′的度数为（）19如图a是长方形纸带，∠DEF=24°，将纸带沿EF折叠成图b，再沿BF折叠成图c，则图c中的∠CFE的度数（）20如图，三角形纸片ABC，AB=10cm，BC=7cm，AC=6cm，沿过点B的直线折叠这个三角形，使顶点C落在AB边上的点E处，折痕为BD，则△AED的周长为（）21如图，将长方形ABCD沿对角线BD折叠，使点C恰好落在如图C′的位置，若∠DBC=15°，则∠ABC′=（）22一张长方形纸条折成如图的形状，如果∠1=130°，∠2=（）23如图：将一张长方形纸片沿EF折叠后，点D、C分别落在D′、C′的位置，ED′的延长线与BC交于点G．若∠EFG=55°，则∠1=（）24如图，已知长方形ABCD，我们按如下步骤操作可以得到一个特定角：（1）以点A所在直线为折痕，折叠纸片，使点B落在AD上，折痕与BC交于E；（2）将纸片展平后，再一次折叠纸片，以E所在直线为折痕，使点A落在BC 上，折痕EF交AD于F，则∠AEF的度数25如图，将纸片△ABC沿着DE折叠压平，且∠1+∠2=72°，则∠A=（）26如图，把△ABC纸片沿DE折叠，当点A落在四边形BCED的外部时，则∠A与∠1和∠2之间有一种数量关系始终保持不变，请试着找一找这个规律，你发现的规律是（）27如图，三角形纸片ABC，AB=10cm，BC=7cm，AC=6cm，沿过点B的直线折叠这个三角形，使顶点C落在AB边上的点E处，折痕为BD，则△AED的周长为（）28一个宽度相等纸条，按如图所示的方式折叠一下，已知∠3=120°，则∠1的度数为（）29如图，把一张长方形纸条折叠后，若∠AOB′=70°，则∠OGC的度数为（）30如图，∠A=60°，∠B=70°，将纸片的一角折叠，使点C落在△ABC内，若∠2=80°，则∠1的度数为（）31如图（1）是长方形纸带，∠DEF=α，将纸带沿EF折叠成图（2），再沿BF折叠成图（3），则图（3）中的∠CFE 的度数是（）32如图，生活中，将一个宽度相等的纸条按右图所示折叠一下，如果∠1=140°，那么∠2的度数为（）33如图，四边形ABCD中，点M，N分别在AB，BC上，将△BMN沿MN翻折，得△FMN，若MF∥AD，FN∥DC，则∠B =（）34如图，一张长方形纸条沿AB折叠，如果∠1=124°，那么∠2的度数是（）35如图，把长方形ABCD沿EF对折后使两部分重合，若∠AEF=110°，则∠1=（）36如图，一张三角形纸片△ABC，沿DE折叠使得顶点C落在边AB上，若DE∥AB，∠A=45°，则∠ADC的度数是（）37如图所示，把一个三角形纸片ABC顶角向内折叠3次之后，3个顶点不重合，那么图中∠1+∠2+∠3+∠4+∠5+∠6的度数和是（）38如图，将△ABC三个角分别沿DE、HG、EF翻折，三个顶点均落在点O处，则∠1+∠2的度数为（）39如图，正方形纸片ABCD的边长为8，将其沿EF折叠，则图中①②③④四个三角形的周长之和为（）40如图，将五边形ABCDE沿AE对折到如图的位置，其中∠AEC=72°，则∠CED′=（）41如图，在△ABC中，∠A=35°，在平面内沿直线DE将△ABC折叠后，量得∠BDA′=110°，那么∠CEA′的度数为（）42如图，把一个长方形纸片沿EF折叠后，点D、C分别落在D′、C′的位置，若∠EFB=65°，则∠AED′等于（）43如图，已知△ABC中，∠BAC=140°，现将△ABC进行折叠，使顶点B、C均与顶点A重合，求∠DAE的度数．（此文档部分内容来源于网络，如有侵权请告知删除，文档可自行编辑修改内容，供参考，感谢您的配合和支持）。

折叠问题中的角度运算

专题 7：折叠问题中的角度运算1 如图，将矩形 ABCD沿 AE折叠，若∠BAD′=30°，则∠AED′=2 如图将六边形 ABCDEF沿着直线 GH折叠，使点 A、B落在六边形 CDEFGH的内部，则∠1+∠2=3 如图，Rt △ ABC 中，∠ ACB=90 °，∠ A=50 °，将其折叠，使点 A 落在边 CB 上 A′处，折痕为 CD，则∠ A′DB=4已知△ABC是一张三角形的纸片．（1）如图①，沿 DE折叠，使点 A落在边 AC上点 A′的地点，∠DA′E与∠1 的之间存在如何的数目关系？为何？（2）如图②所示，沿 DE折叠，使点 A落在四边形 BCED的内部点 A′的地点，∠ A、∠ 1 与∠2 之间存在如何的数目关系？为何？（3）如图③，沿 DE折叠，使点 A落在四边形 BCED的外面点 A′的地点，∠ A、∠ 1 与∠2 之间存在如何的数目关系？为何？565 已知，如图，把△ABC纸片沿 DE折叠，当点 A落在四边形 BCDE的内部时，则∠A与∠1+∠2 之间有一种数目关系：2∠A=∠1+∠2一直保持不变，为何？.6 如图，把△ABC纸片沿 DE折叠，当点 A落在四边形 BCDE内部时，（1）设∠ AED 的度数为 x ，∠ ADE 的度数为 y ，那么∠ 1 、∠ 2 的度数分别是多少？（用含有 x 或y 的代数式表示）（2）∠A与∠1+∠2 之间有一种数目关系一直保持不变，请找出这个规律，并说明原因．折一折，想想，以下图，在△ABC中，将纸片一角折叠，使点 C落在△ABC内一点 C′上，若∠1=40°，∠2=30°（ 1）求∠C的度数；（2）试经过第（1）问，直接写出∠1、∠2、∠C三者之间的关系．如图（1），△ABC是一个三角形的纸片，点 D、E分别是△ABC边上的两点；研究（1）：若沿直线 DE折叠，则∠BDA′与∠A的关系是∠BDA′=2∠A；研究（2）：若折成图 2 的形状，猜想∠BDA′，∠CEA′和∠A关系，并说明原因；研究（3）：若折成图3 的形状，猜想∠BDA′，∠CEA′和∠A的关系，并说明原因．图 1、图 2、7如图①，把△ABC纸片沿 DE折叠，使点 A落在四边形 BCED内部点 A′的地点，经过计算我们知道：2∠A=∠1+∠2．请你持续探究：（1）假如把△ABC纸片沿 DE折叠，使点 A落在四边形 BCED的外面点 A′的地点，如图②，此时∠A与∠1、∠2 之间存在什么样的关系？为何？请说明原因．（2）假如把四边形 ABCD沿 EF折叠，使点 A、D落在四边形 BCFE的内部 A′、D′的地点，如图③，你能求出∠A、∠D、∠1 与∠2 之间的关系吗？（直接写出关系式即可）8三角形纸片 ABC 中，∠A=55°，∠B=75°，将纸片的一角折叠，使点 C 落在△ABC内（如图），则∠1+∠2 的度数为度．9如图，已知四边形 ABCD，∠C=72°，∠D=81°．沿 EF折叠四边形，使点 A、B分别落在四边形内部的点 A′、B′处，求∠1+∠2的大小．10、如图，△ABC中，∠ACB=90°，沿 CD折叠△CBD，使点 B 恰巧落在 AC边上的点 E 处．若∠A=22°，则∠BDC等于（）11、将五边形纸片 ABCDE按如图方式折叠，折痕为 AF，点 E、D分别落在 E′、D′，已知∠AFC=76°，则∠CFD′等于12如图，在平面内，把矩形 ABCD沿 EF对折，若∠1=50°，则∠AEF等于13 如图，把△ABC沿线段 DE折叠，使点 A落在点 F处，BC∥DE；若∠B=50°，则∠BDF的度数为 11如图，把一张长方形纸片 ABCD，沿 EF 折叠后，ED′与 BC的交点为 G，点 D，C分别落在 D′，C′的地点上．若∠EFG=55°，则∠1 等于14 将一条两边沿相互平行的纸带按如图折叠．设∠ 1=x °，则∠ α的度数为（）15 将长方形 ABCD沿折痕 EF折叠，使 CD落在 GH的地点，若∠ FGH=55°，则∠ HEF=（）16 如图，一个宽度相等的纸条按以下图方法折叠一下，则∠1=（）17如图，D、E分别为△ABC的边 AB、AC上的点，DE∥BC，将△ABC沿线段 DE折叠，使点 A落在 BC上的点 F处，若∠18以下图，将一张长方形纸片沿 EF折叠后，点 D，C分别落在 D′，C′的地点上，ED′的延伸线与 BC的交点为 G．若∠EFG=80°，则∠ BFC′的度数为（）19 如图 a 是长方形纸带，∠ DEF=24 °，将纸带沿 EF 折叠成图 b ，再沿 BF 折叠成图 c ，则图 c 中的∠ CFE 的度数（）20如图，三角形纸片 ABC， AB=10cm ， BC=7cm， AC=6cm，沿过点 B 的直线折叠这个三角形，使顶点 C 落在 AB 边上的点 E 处，折痕为 BD，则△AED的周长为（）21 如图，将长方形 ABCD沿对角线 BD折叠，使点 C恰巧落在如图 C′的地点，若∠DBC=15°，则∠ABC′=（）22 一张长方形纸条折成如图的形状，假如∠1=130°，∠2=（）23如图：将一张长方形纸片沿 EF 折叠后，点 D、C分别落在 D′、C′的地点，ED′的延伸线与 BC交于点 G．若∠EFG=55°，则∠1=（）24如图，已知长方形 ABCD，我们按以下步骤操作能够获得一个特定角：（1）以点 A所在直线为折痕，折叠纸片，使点 B落在 AD上，折痕与 BC交于 E；（2）将纸片展平后，再一次折叠纸片，以 E所在直线为折痕，使点 A落在 BC上，折痕 EF交 AD于 F，则∠AEF的度数25 如图，将纸片△ABC沿着 DE折叠压平，且∠1+∠2=72°，则∠A=（）26如图，把△ABC纸片沿 DE折叠，当点 A落在四边形 BCED的外面时，则∠A与∠1和∠2 之间有一种数目关系一直保持不变，请试着找一找这个规律，你发现的规律是（）27如图，三角形纸片 ABC， AB=10cm ， BC=7cm， AC=6cm，沿过点 B 的直线折叠这个三角形，使顶点 C 落在 AB 边上的点 E 处，折痕为 BD，则△AED的周长为（）28一个宽度相等纸条，按以下图的方式折叠一下，已知∠3=120°，则∠1的度数为（）29如图，把一张长方形纸条折叠后，若∠AOB′=70°，则∠OGC的度数为（）30如图，∠A=60°，∠B=70°，将纸片的一角折叠，使点 C落在△ABC内，若∠2=80°，则∠1的度数为（）31如图（ 1 ）是长方形纸带，∠ DEF= α，将纸带沿 EF 折叠成图（ 2 ），再沿 BF 折叠成图（ 3），则图（ 3 ）中的∠ CFE 的度数是（）32如图，生活中，将一个宽度相等的纸条按右图所示折叠一下，假如∠1=140°，那么∠2 的度数为（）33如图，四边形 ABCD中，点 M，N 分别在 AB，BC 上，将△ BMN沿 MN 翻折，得△ FMN，若 MF∥ AD，FN∥ DC，则∠ B =（）34如图，一张长方形纸条沿 AB折叠，假如∠1=124°，那么∠2的度数是（）35如图，把长方形 ABCD沿 EF对折后使两部分重合，若∠AEF=110°，则∠1=（）36如图，一张三角形纸片△ABC，沿 DE折叠使得极点 C落在边 AB上，若 DE∥AB，∠ A=45°，则∠ADC的度数是（）37以下图，把一个三角形纸片 ABC顶角向内折叠 3 次以后，3 个极点不重合，那么图中∠1+∠2+∠3+∠4+∠5+∠6 的度数和是（）38 如图，将△ABC三个角分别沿 DE、HG、EF翻折，三个极点均落在点 O处，则∠1+∠2的度数为（）39如图，正方形纸片 ABCD的边长为 8，将其沿 EF折叠，则图中①②③④四个三角形的周长之和为（）40如图，将五边形 ABCDE沿 AE对折到如图的地点，此中∠AEC=72°，则∠CED′=（）41如图，在△ABC中，∠A=35°，在平面内沿直线 DE将△ABC折叠后，量得∠BDA′=110°，那么∠CEA′的度数为（）42如图，把一个长方形纸片沿 EF折叠后，点 D、C分别落在 D′、C′的地点，若∠EFB=65°，则∠AED′等于（）43如图，已知△ABC中，∠BAC=140°，现将△ABC进行折叠，使极点 B、C均与极点 A重合，求∠DAE的度数．。

折叠问题中角度运算

专题7：折叠问题中的角度运算1如图，将矩形ABCD沿AE折叠，假设∠BAD′=30°，那么∠AED′=2如图将六边形ABCDEF沿着直线GH折叠，使点A、B落在六边形CDEFGH的内部，那么∠1+∠2=3如图，Rt△ABC中，∠ACB=90°，∠A=50°，将其折叠，使点A落在边CB上A′处，折痕为CD，那么∠A′DB=△ABC是一张三角形的纸片．1〕如图①，沿DE折叠，使点A落在边AC上点A′的位置，∠DA′E与∠1的之间存在怎样的数量关系为什么2〕如图②所示，沿DE折叠，使点A落在四边形BCED的内部点A′的位置，∠A、∠1与∠2之间存在怎样的数量关系为什么3〕如图③，沿DE折叠，使点A落在四边形BCED的外部点A′的位置，∠A、∠1与∠2之间存在怎样的数量关系为什么5 65，如图，把△ABC纸片沿DE折叠，当点A落在四边形BCDE的内部时，那么∠A 与∠1+∠2之间有一种数量关系：2∠A=∠1+∠2始终保持不变，为什么.6如图，把△ABC纸片沿DE折叠，当点A落在四边形BCDE内部时，1〕设∠AED的度数为x，∠ADE的度数为y，那么∠1、∠2的度数分别是多少〔用含有x或y的代数式表示〕2〕∠A与∠1+∠2之间有一种数量关系始终保持不变，请找出这个规律，并说明理由．折一折，想一想，如下图，在△ABC中，将纸片一角折叠，使点C落在△ABC内一点C′上，假设∠1=40°，∠2=30°〔1〕求∠C的度数；〔2〕试通过第〔1〕问，直接写出∠1、∠2、∠C三者之间的关系．如图〔1〕，△ABC是一个三角形的纸片，点D、E分别是△ABC边上的两点；研究〔1〕：假设沿直线DE折叠，那么∠BDA′与∠A的关系是∠BDA′=2∠A；研究〔2〕：假设折成图2的形状，猜测∠BDA′，∠CEA′和∠A关系，并说明理由；研究〔3〕：假设折成图3的形状，猜测∠BDA′，∠CEA′和∠A的关系，并说明理由．图1、图2、（如图①，把△ABC纸片沿DE折叠，使点A落在四边形BCED内部点A′的位置，通过计算我们知道：2 （∠A=∠1+∠2．请你继续探索：（1〕如果把△ABC纸片沿DE折叠，使点A落在四边形BCED的外部点A′的位置，如图②，此时∠A与∠1、∠2之间存在什么样的关系为什么请说明理由．（2〕如果把四边形ABCD沿EF折叠，使点A、D落在四边形BCFE的内部A′、D′的位置，如图③，你能求出∠A、∠D、∠1与∠2之间的关系吗〔直接写出关系式即可〕三角形纸片ABC中，∠A=55°，∠B=75°，将纸片的一角折叠，使点C落在△ABC内〔如图〕，那么∠1+∠2的度数为度．如图，四边形ABCD，∠C=72°，∠D=81°．沿EF折叠四边形，使点A、B分别落在四边形内部的点A′、B′处，求∠1+∠2的大小．10、如图，△ABC中，∠ACB=90°，沿CD折叠△CBD，使点B恰好落在AC边上的点E处．假设∠A=22°，那么∠BDC等于〔〕11、将五边形纸片ABCDE按如图方式折叠，折痕为AF，点E、D分别落在E′、D′，∠AFC=76°，那么∠CFD′等于20如图，在平面内，把矩形ABCD沿EF对折，假设∠1=50°，那么∠AEF等于2113如图，把△ABC沿线段DE折叠，使点A落在点F处，BC∥DE；假设∠B=50°，那么∠BDF的度数为1122如图，把一张长方形纸片ABCD，沿EF折叠后，ED′与BC的交点为G，点D，C分别落在D′，C′的位置上．假设∠EFG=55°，23那么∠1等于2414将一条两边沿互相平行的纸带按如图折叠．设∠1=x°，那么∠α的度数为〔〕2515将长方形ABCD沿折痕EF折叠，使CD落在GH的位置，假设∠FGH=55°，那么∠HEF=〔〕2616如图，一个宽度相等的纸条按如下图方法折叠一下，那么∠1=〔〕27282930313233如图，D、E分别为△ABC的边AB、AC上的点，DE∥BC，将△ABC沿线段DE折叠，使点A落在BC上的点F处，假设∠3435如下图，将一张长方形纸片沿EF折叠后，点D，C分别落在D′，C′的位置上，ED′的延长线与BC的交点为G．假设36∠EFG=80°，那么∠BFC′的度数为〔〕3719如图a是长方形纸带，∠DEF=24°，将纸带沿EF折叠成图b，再沿BF折叠成图c，那么图c中的∠CFE的度数〔〕383940414243如图，三角形纸片ABC，AB=10cm，BC=7cm，AC=6cm，沿过点B的直线折叠这个三角形，使顶点C落在AB边上的点E处，折痕为BD，那么△AED的周长为〔〕21如图，将长方形ABCD沿对角线BD折叠，使点C恰好落在如图C′的位置，假设∠DBC=15°，那么∠ABC′=〔〕22一张长方形纸条折成如图的形状，如果∠1=130°，∠2=〔〕如图：将一张长方形纸片沿EF折叠后，点D、C分别落在D′、C′的位置，ED′的延长线与BC交于点G．假设∠EFG=55°，那么∠1=〔〕24如图，长方形ABCD，我们按如下步骤操作可以得到一个特定角：〔1〕以点A所在直线为折痕，折叠纸片，使B落在AD上，折痕与BC交于E；〔2〕将纸片展平后，再一次折叠纸片，以E所在直线为折痕，使点A落在BC上，折痕EF交AD于F，那么∠AEF 的度数25如图，将纸片△ABC沿着DE折叠压平，且∠1+∠2=72°，那么∠A=〔〕如图，把△ABC纸片沿DE折叠，当点A落在四边形BCED的外部时，那么∠A与∠1和∠2之间有一种数量关系始终保持不变，请试着找一找这个规律，你发现的规律是〔〕如图，三角形纸片ABC，AB=10cm，BC=7cm，AC=6cm，沿过点B的直线折叠这个三角形，使顶点C落在AB边上的点E处，折痕为BD，那么△AED的周长为〔〕28一个宽度相等纸条，按如下图的方式折叠一下，∠3=120°，那么∠1的度数为〔〕29如图，把一张长方形纸条折叠后，假设∠AOB′=70°，那么∠OGC的度数为〔〕30如图，∠A=60°，∠B=70°，将纸片的一角折叠，使点C落在△ABC内，假设∠2=80°，那么∠1的度数为〔〕如图〔1〕是长方形纸带，∠DEF=α，将纸带沿EF折叠成图〔2〕，再沿BF折叠成图〔3〕，那么图〔3〕中的∠CFE的度数是〔〕32如图，生活中，将一个宽度相等的纸条按右图所示折叠一下，如果∠1=140°，那么∠2的度数为〔〕33如图，四边形ABCD中，点M，N分别在AB，BC上，将△BMN沿MN翻折，得△FMN，假设MF∥AD，FN∥DC，那么∠B=〔〕34如图，一张长方形纸条沿AB折叠，如果∠1=124°，那么∠2的度数是〔〕35如图，把长方形ABCD沿EF对折后使两局部重合，假设∠AEF=110°，那么∠1=〔〕36如图，一张三角形纸片△ABC，沿DE折叠使得顶点C落在边AB上，假设DE∥AB，∠A=45°，那么∠ADC的度数是〔〕37如下图，把一个三角形纸片ABC顶角向内折叠3次之后，3个顶点不重合，那么图中∠1+∠2+∠3+∠4+∠5+∠6的度数和是〔〕38如图，将△ABC三个角分别沿DE、HG、EF翻折，三个顶点均落在点O处，那么∠1+∠2的度数为〔〕39如图，正方形纸片ABCD的边长为8，将其沿EF折叠，那么图中①②③④四个三角形的周长之和为〔〕40如图，将五边形ABCDE沿AE对折到如图的位置，其中∠AEC=72°，那么∠CED′=〔〕41如图，在△ABC中，∠A=35°，在平面内沿直线DE将△ABC折叠后，量得∠BDA′=110°，那么∠CEA′的度数为〔〕42如图，把一个长方形纸片沿EF折叠后，点D、C分别落在D′、C′的位置，假设∠EFB=65°，那么∠AED′等于〔〕43如图，△ABC中，∠BAC=140°，现将△ABC进行折叠，使顶点B、C均与顶点A重合，求∠DAE的度数．。

折叠问题中的角度运算

专题7：折叠问题中的角度运算1如图，将矩形ABCD沿AE折叠，若∠BAD′=30°，则∠AED′=2如图将六边形ABCDEF沿着直线GH折叠，使点A、B落在六边形CDEFG H的内部，则∠1+∠2=3如图，Rt△ABC中，∠ACB=90°，∠A=50°，将其折叠，使点A落在边CB上A′处，折痕为CD，则∠A′DB=???4已知△ABC是一张三角形的纸片．（1）如图①，沿DE折叠，使点A落在边AC上点A′的位置，∠DA′E 与∠1的之间存在怎样的数量关系？为什么？（2）如图②所示，沿DE折叠，使点A落在四边形BCED的内部点A′的位置，∠A、∠1与∠2之间存在怎样的数量关系？为什么？（3）如图③，沿DE折叠，使点A落在四边形BCED的外部点A′的位置，∠A、∠1与∠2之间存在怎样的数量关系？为什么？5 65已知，如图，把△ABC纸片沿DE折叠，当点A落在四边形BCDE的内部时，则∠A与∠1+∠2之间有一种数量关系：2∠A=∠1+∠2始终保持不变，为什么？.6如图，把△ABC纸片沿DE折叠，当点A落在四边形BCDE内部时，（1）设∠AED的度数为x，∠ADE的度数为y，那么∠1、∠2的度数分别是多少？（用含有x或y的代数式表示）（2）∠A与∠1+∠2之间有一种数量关系始终保持不变，请找出这个规律，并说明理由．折一折，想一想，如图所示，在△ABC中，将纸片一角折叠，使点C落在△ABC内一点C′上，若∠1=40°，∠2=30°（1）求∠C的度数；（2）试通过第（1）问，直接写出∠1、∠2、∠C三者之间的关系．如图（1），△ABC是一个三角形的纸片，点D、E分别是△ABC边上的两点；研究（1）：若沿直线DE折叠，则∠BDA′与∠A的关系是∠BDA′=2∠A；研究（2）：若折成图2的形状，猜想∠BDA′，∠CEA′和∠A关系，并说明理由；研究（3）：若折成图3的形状，猜想∠BDA′，∠CEA′和∠A的关系，并说明理由．图1、图2、7如图①，把△ABC纸片沿DE折叠，使点A落在四边形BCED内部点A′的位置，通过计算我们知道：2∠A=∠1+∠2．请你继续探索：（1）如果把△ABC纸片沿DE折叠，使点A落在四边形BCED的外部点A′的位置，如图②，此时∠A与∠1、∠2之间存在什么样的关系？为什么？请说明理由．（2）如果把四边形ABCD沿EF折叠，使点A、D落在四边形BCFE的内部A′、D′的位置，如图③，你能求出∠A、∠D、∠1与∠2之间的关系吗？（直接写出关系式即可）8三角形纸片ABC中，∠A=55°，∠B=75°，将纸片的一角折叠，使点C落在△ABC内（如图），则∠1+∠2的度数为????度．9如图，已知四边形ABCD，∠C=72°，∠D=81°．沿EF折叠四边形，使点A、B分别落在四边形内部的点A′、B′处，求∠1+∠2的大小．10、如图，△ABC中，∠ACB=90°，沿CD折叠△CBD，使点B恰好落在AC边上的点E处．若∠A=22°，则∠BDC等于（）11、将五边形纸片ABCDE按如图方式折叠，折痕为AF，点E、D分别落在E′、D′，已知∠AFC=76°，则∠CFD′等于12如图，在平面内，把矩形ABCD沿EF对折，若∠1=50°，则∠AEF等于13如图，把△ABC沿线段DE折叠，使点A落在点F处，BC∥DE；若∠B=50°，则∠BDF的度数为1 1如图，把一张长方形纸片ABCD，沿EF折叠后，ED′与BC的交点为G，点D，C分别落在D′，C′的位置上．若∠EFG=55°，则∠1等于14将一条两边沿互相平行的纸带按如图折叠．设∠1=x°，则∠α的度数为（）15将长方形ABCD沿折痕EF折叠，使CD落在GH的位置，若∠FGH=55°，则∠HEF=（）16如图，一个宽度相等的纸条按如图所示方法折叠一下，则∠1=（）17如图，D、E分别为△ABC的边AB、AC上的点，DE∥BC，将△ABC沿线段DE折叠，使点A落在BC 上的点F处，若∠B=55°，则∠BDF的度数为?（）18如图所示，将一张长方形纸片沿EF折叠后，点D，C分别落在D′，C′的位置上，ED′的延长线与BC的交点为G．若∠EFG=80°，则∠BFC′的度数为（）19如图a是长方形纸带，∠DEF=24°，将纸带沿EF折叠成图b，再沿BF折叠成图c，则图c中的∠CFE的度数（）20如图，三角形纸片ABC，AB=10cm，BC=7cm，AC=6cm，沿过点B的直线折叠这个三角形，使顶点C 落在AB边上的点E处，折痕为BD，则△AED的周长为（）21如图，将长方形ABCD沿对角线BD折叠，使点C恰好落在如图C′的位置，若∠DBC=15°，则∠ABC′=（）22一张长方形纸条折成如图的形状，如果∠1=130°，∠2=（）23如图：将一张长方形纸片沿EF折叠后，点D、C分别落在D′、C′的位置，ED′的延长线与BC 交于点G．若∠EFG=55°，则∠1=（）24如图，已知长方形ABCD，我们按如下步骤操作可以得到一个特定角：（1）以点A所在直线为折痕，折叠纸片，使点B落在AD上，折痕与BC交于E；（2）将纸片展平后，再一次折叠纸片，以E 所在直线为折痕，使点A落在BC上，折痕EF交AD于F，则∠AEF的度数25如图，将纸片△ABC沿着DE折叠压平，且∠1+∠2=72°，则∠A=（）26如图，把△ABC纸片沿DE折叠，当点A落在四边形BCED的外部时，则∠A与∠1和∠2之间有一种数量关系始终保持不变，请试着找一找这个规律，你发现的规律是（）27如图，三角形纸片ABC，AB=10cm，BC=7cm，AC=6cm，沿过点B的直线折叠这个三角形，使顶点C 落在AB边上的点E处，折痕为BD，则△AED的周长为（）28一个宽度相等纸条，按如图所示的方式折叠一下，已知∠3=120°，则∠1的度数为（）29如图，把一张长方形纸条折叠后，若∠AOB′=70°，则∠OGC的度数为（）30如图，∠A=60°，∠B=70°，将纸片的一角折叠，使点C落在△ABC内，若∠2=80°，则∠1的度数为（）31如图（1）是长方形纸带，∠DEF=α，将纸带沿EF折叠成图（2），再沿BF折叠成图（3），则图（3）中的∠CFE的度数是（）32如图，生活中，将一个宽度相等的纸条按右图所示折叠一下，如果∠1=140°，那么∠2的度数为（）33如图，四边形ABCD中，点M，N分别在AB，BC上，将△BMN沿MN翻折，得△FMN，若MF∥AD，FN∥DC，则∠B =（）34如图，一张长方形纸条沿AB折叠，如果∠1=124°，那么∠2的度数是（）35如图，把长方形ABCD沿EF对折后使两部分重合，若∠AEF=110°，则∠1=（）36如图，一张三角形纸片△ABC，沿DE折叠使得顶点C落在边AB上，若DE∥AB，∠A=45°，则∠ADC的度数是（）37如图所示，把一个三角形纸片ABC顶角向内折叠3次之后，3个顶点不重合，那么图中∠1+∠2+∠3+∠4+∠5+∠6的度数和是（）38如图，将△ABC三个角分别沿DE、HG、EF翻折，三个顶点均落在点O处，则∠1+∠2的度数为（）39如图，正方形纸片ABCD的边长为8，将其沿EF折叠，则图中①②③④四个三角形的周长之和为（）40如图，将五边形ABCDE沿AE对折到如图的位置，其中∠AEC=72°，则∠CED′=（）41如图，在△ABC中，∠A=35°，在平面内沿直线DE将△ABC折叠后，量得∠BDA′=110°，那么∠CEA′的度数为（）42如图，把一个长方形纸片沿EF折叠后，点D、C分别落在D′、C′的位置，若∠EFB=65°，则∠AED′等于（）43如图，已知△ABC中，∠BAC=140°，现将△ABC进行折叠，使顶点B、C均与顶点A重合，求∠DAE的度数．。

折叠问题中的角度运算

专题7:折叠问题中的角度运算1如图,将矩形ABCD沿AE折叠，若∠BAD′=30°，则∠AED′=2如图将六边形ABCDEF沿着直线GH折叠，使点A、B落在六边形CDEFGH的内部，则∠1+∠2=3如图,Rt△ABC中，∠ACB=90°，∠A=50°,将其折叠，使点A落在边CB上A′处，折痕为CD，则∠A′DB=4已知△ABC是一张三角形的纸片．(1）如图①，沿DE折叠，使点A落在边AC上点A′的位置，∠DA′E与∠1的之间存在怎样的数量关系?为什么？（2)如图②所示，沿DE折叠，使点A落在四边形BCED的内部点A′的位置，∠A、∠1与∠2之间存在怎样的数量关系？为什么？（3)如图③,沿DE折叠，使点A落在四边形BCED的外部点A′的位置，∠A、∠1与∠2之间存在怎样的数量关系?为什么?5 65已知,如图,把△ABC纸片沿DE折叠，当点A落在四边形BCDE的内部时，则∠A与∠1+∠2之间有一种数量关系：2∠A=∠1+∠2始终保持不变，为什么？。

6如图，把△ABC纸片沿DE折叠，当点A落在四边形BCDE内部时，（1）设∠AED的度数为x，∠ADE的度数为y，那么∠1、∠2的度数分别是多少?（用含有x或y的代数式表示）（2）∠A与∠1+∠2之间有一种数量关系始终保持不变，请找出这个规律，并说明理由．折一折，想一想,如图所示，在△ABC中,将纸片一角折叠,使点C落在△ABC内一点C′上，若∠1=40°，∠2=30°（1)求∠C的度数;（2)试通过第（1)问，直接写出∠1、∠2、∠C三者之间的关系．如图（1），△ABC是一个三角形的纸片，点D、E分别是△ABC边上的两点;研究（1）:若沿直线DE折叠，则∠BDA′与∠A的关系是∠BDA′=2∠A；研究（2）：若折成图2的形状,猜想∠BDA′,∠CEA′和∠A关系，并说明理由；研究（3）：若折成图3的形状,猜想∠BDA′,∠CEA′和∠A的关系,并说明理由．图1、图2、7如图①，把△ABC纸片沿DE折叠，使点A落在四边形BCED内部点A′的位置，通过计算我们知道：2∠A=∠1+∠2．请你继续探索：（1)如果把△ABC纸片沿DE折叠，使点A落在四边形BCED的外部点A′的位置，如图②，此时∠A与∠1、∠2之间存在什么样的关系?为什么？请说明理由．(2）如果把四边形ABCD沿EF折叠，使点A、D落在四边形BCFE的内部A′、D′的位置，如图③,你能求出∠A、∠D、∠1与∠2之间的关系吗？（直接写出关系式即可)8三角形纸片ABC中，∠A=55°，∠B=75°,将纸片的一角折叠,使点C落在△ABC内（如图），则∠1+∠2的度数为度．9如图,已知四边形ABCD，∠C=72°，∠D=81°．沿EF折叠四边形，使点A、B分别落在四边形内部的点A′、B′处，求∠1+∠2的大小．10、如图,△ABC中，∠ACB=90°，沿CD折叠△CBD,使点B恰好落在AC边上的点E处．若∠A=22°，则∠BDC等于（）11、将五边形纸片ABCDE按如图方式折叠，折痕为AF，点E、D分别落在E′、D′，已知∠AFC=76°，则∠CFD′等于12如图，在平面内，把矩形ABCD沿EF对折，若∠1=50°,则∠AEF等于13如图,把△ABC沿线段DE折叠，使点A落在点F处，BC∥DE；若∠B=50°,则∠BDF的度数为1 1如图，把一张长方形纸片ABCD，沿EF折叠后，ED′与BC的交点为G,点D，C分别落在D′,C′的位置上．若∠EFG=55°，则∠1等于14将一条两边沿互相平行的纸带按如图折叠．设∠1=x°,则∠α的度数为（）15将长方形ABCD沿折痕EF折叠，使CD落在GH的位置，若∠FGH=55°，则∠HEF=( ）16如图，一个宽度相等的纸条按如图所示方法折叠一下,则∠1=( ）17如图，D、E分别为△ABC的边AB、AC上的点，DE∥BC，将△ABC沿线段DE折叠，使点A落在BC上的点F处,若∠B=55°，则∠BDF的度数为（）18如图所示,将一张长方形纸片沿EF折叠后,点D，C分别落在D′,C′的位置上，ED′的延长线与BC的交点为G．若∠EFG=80°，则∠BFC′的度数为（）19如图a是长方形纸带，∠DEF=24°，将纸带沿EF折叠成图b，再沿BF折叠成图c，则图c中的∠CFE的度数（）20如图,三角形纸片ABC,AB=10cm，BC=7cm，AC=6cm,沿过点B的直线折叠这个三角形，使顶点C落在AB边上的点E处,折痕为BD,则△AED的周长为( )21如图，将长方形ABCD沿对角线BD折叠，使点C恰好落在如图C′的位置，若∠DBC=15°，则∠ABC′=( ）22一张长方形纸条折成如图的形状，如果∠1=130°，∠2=（）23如图：将一张长方形纸片沿EF折叠后,点D、C分别落在D′、C′的位置,ED′的延长线与BC交于点G．若∠EFG=55°，则∠1=（）24如图，已知长方形ABCD，我们按如下步骤操作可以得到一个特定角：（1）以点A所在直线为折痕，折叠纸片，使点B落在AD上，折痕与BC交于E；（2)将纸片展平后，再一次折叠纸片，以E所在直线为折痕,使点A落在BC上，折痕EF交AD于F，则∠AEF的度数25如图，将纸片△ABC沿着DE折叠压平，且∠1+∠2=72°，则∠A=（)26如图,把△ABC纸片沿DE折叠,当点A落在四边形BCED的外部时，则∠A与∠1和∠2之间有一种数量关系始终保持不变，请试着找一找这个规律,你发现的规律是（)27如图，三角形纸片ABC,AB=10cm，BC=7cm，AC=6cm，沿过点B的直线折叠这个三角形，使顶点C落在AB边上的点E 处，折痕为BD，则△AED的周长为（）28一个宽度相等纸条，按如图所示的方式折叠一下，已知∠3=120°，则∠1的度数为( ）29如图,把一张长方形纸条折叠后，若∠AOB′=70°，则∠OGC的度数为（)30如图，∠A=60°,∠B=70°，将纸片的一角折叠，使点C落在△ABC内，若∠2=80°，则∠1的度数为( ）31如图（1)是长方形纸带，∠DEF=α,将纸带沿EF折叠成图（2），再沿BF折叠成图（3），则图（3）中的∠CFE的度数是（）32如图，生活中，将一个宽度相等的纸条按右图所示折叠一下,如果∠1=140°，那么∠2的度数为（）33如图，四边形ABCD中，点M，N分别在AB,BC上，将△BMN沿MN翻折,得△FMN，若MF∥AD，FN∥DC，则∠B =（）34如图,一张长方形纸条沿AB折叠，如果∠1=124°,那么∠2的度数是（）35如图，把长方形ABCD沿EF对折后使两部分重合，若∠AEF=110°，则∠1=( ）36如图，一张三角形纸片△ABC，沿DE折叠使得顶点C落在边AB上,若DE∥AB，∠A=45°，则∠ADC的度数是（) 37如图所示，把一个三角形纸片ABC顶角向内折叠3次之后，3个顶点不重合，那么图中∠1+∠2+∠3+∠4+∠5+∠6的度数和是（）38如图，将△ABC三个角分别沿DE、HG、EF翻折,三个顶点均落在点O处，则∠1+∠2的度数为( ）39如图，正方形纸片ABCD的边长为8，将其沿EF折叠，则图中①②③④四个三角形的周长之和为（）40如图，将五边形ABCDE沿AE对折到如图的位置，其中∠AEC=72°，则∠CED′=（)41如图，在△ABC中,∠A=35°，在平面内沿直线DE将△ABC折叠后,量得∠BDA′=110°,那么∠CEA′的度数为（) 42如图，把一个长方形纸片沿EF折叠后，点D、C分别落在D′、C′的位置，若∠EFB=65°,则∠AED′等于（）43如图，已知△ABC中,∠BAC=140°，现将△ABC进行折叠，使顶点B、C均与顶点A重合，求∠DAE的度数．。

折叠问题中的角度运算

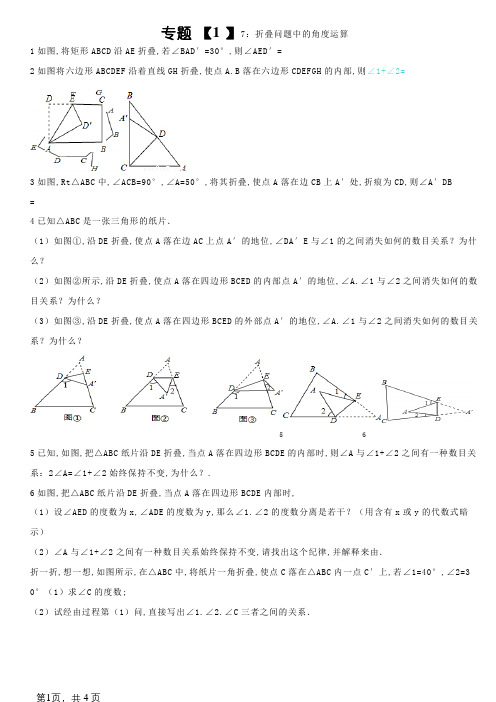
专题【1 】7：折叠问题中的角度运算1如图,将矩形ABCD沿AE折叠,若∠BAD′=30°,则∠AED′=2如图将六边形ABCDEF沿着直线GH折叠,使点A.B落在六边形CDEFGH的内部,则∠1+∠2=3如图,Rt△ABC中,∠ACB=90°,∠A=50°,将其折叠,使点A落在边CB上A′处,折痕为CD,则∠A′DB=4已知△ABC是一张三角形的纸片．（1）如图①,沿DE折叠,使点A落在边AC上点A′的地位,∠DA′E与∠1的之间消失如何的数目关系？为什么？（2）如图②所示,沿DE折叠,使点A落在四边形BCED的内部点A′的地位,∠A.∠1与∠2之间消失如何的数目关系？为什么？（3）如图③,沿DE折叠,使点A落在四边形BCED的外部点A′的地位,∠A.∠1与∠2之间消失如何的数目关系？为什么？5 65已知,如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE的内部时,则∠A与∠1+∠2之间有一种数目关系：2∠A=∠1+∠2始终保持不变,为什么？.6如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,（1）设∠AED的度数为x,∠ADE的度数为y,那么∠1.∠2的度数分离是若干？（用含有x或y的代数式暗示）（2）∠A与∠1+∠2之间有一种数目关系始终保持不变,请找出这个纪律,并解释来由．折一折,想一想,如图所示,在△ABC中,将纸片一角折叠,使点C落在△ABC内一点C′上,若∠1=40°,∠2=3 0°（1）求∠C的度数;（2）试经由过程第（1）问,直接写出∠1.∠2.∠C三者之间的关系．如图（1）,△ABC是一个三角形的纸片,点D.E分离是△ABC边上的两点;研讨（1）：若沿直线DE折叠,则∠BDA′与∠A的关系是∠BDA′=2∠A;研讨（2）：若折成图2的外形,猜测∠BDA′,∠CEA′和∠A关系,并解释来由;研讨（3）：若折成图3的外形,猜测∠BDA′,∠CEA′和∠A的关系,并解释来由．图1.图2.7如图①,把△ABC纸片沿DE折叠,使点A落在四边形BCED内部点A′的地位,经由过程盘算我们知道：2∠A=∠1+∠2．请你持续摸索：（1）假如把△ABC纸片沿DE折叠,使点A落在四边形BCED的外部点A′的地位,如图②,此时∠A与∠1.∠2之间消失什么样的关系？为什么？请解释来由．（2）假如把四边形ABCD沿EF折叠,使点A.D落在四边形BCFE的内部A′.D′的地位,如图③,你能求出∠A.∠ D.∠1与∠2之间的关系吗？（直接写出关系式即可）8三角形纸片ABC中,∠A=55°,∠B=75°,将纸片的一角折叠,使点C落在△ABC内（如图）,则∠1+∠2的度数为度．9如图,已知四边形ABCD,∠C=72°,∠D=81°．沿EF折叠四边形,使点A.B分离落在四边形内部的点A′.B′处,求∠1+∠2的大小．10.如图,△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B正好落在AC边上的点E处．若∠A=22°,则∠BDC等于（）11.将五边形纸片ABCDE按如图方法折叠,折痕为AF,点 E.D分离落在E′.D′,已知∠AFC=76°,则∠CFD′等于12如图,在平面内,把矩形ABCD沿EF半数,若∠1=50°,则∠AEF等于13如图,把△ABC沿线段DE折叠,使点A落在点F处,BC∥DE;若∠B=50°,则∠BDF的度数为11如图,把一张长方形纸片ABCD,沿EF折叠后,ED′与BC的交点为G,点D,C分离落在D′,C′的地位上．若∠EFG=55°,则∠1等于14将一条双方沿互相平行的纸带按如图折叠．设∠1=x°,则∠α的度数为（）15将长方形ABCD沿折痕EF折叠,使CD落在GH的地位,若∠FGH=55°,则∠HEF=（）16如图,一个宽度相等的纸条按如图所示办法折叠一下,则∠1=（）17如图,D.E分离为△ABC的边AB.AC上的点,DE∥BC,将△ABC沿线段DE折叠,使点A落在BC上的点F处,若∠B=55°,则∠BDF的度数为（）18如图所示,将一张长方形纸片沿EF折叠后,点D,C分离落在D′,C′的地位上,ED′的延伸线与BC的交点为G．若∠EFG=80°,则∠BFC′的度数为（）19如图a是长方形纸带,∠DEF=24°,将纸带沿EF折叠成图b,再沿BF折叠成图c,则图c中的∠CFE的度数（）20如图,三角形纸片ABC,AB=10cm,BC=7cm,AC=6cm,沿过点B的直线折叠这个三角形,使极点C落在AB边上的点E处,折痕为BD,则△AED的周长为（）21如图,将长方形ABCD沿对角线BD折叠,使点C正好落在如图C′的地位,若∠DBC=15°,则∠ABC′=（）22一张长方形纸条折成如图的外形,假如∠1=130°,∠2=（）23如图：将一张长方形纸片沿EF折叠后,点D.C分离落在D′.C′的地位,ED′的延伸线与BC交于点G．若∠EFG=55°,则∠1=（）24如图,已知长方形ABCD,我们按如下步调操纵可以得到一个特定角：（1）以点A地点直线为折痕,折叠纸片,使点B落在AD 上,折痕与BC交于E;（2）将纸片展平后,再一次折叠纸片,以E地点直线为折痕,使点A落在BC上,折痕EF交AD于F,则∠AEF的度数25如图,将纸片△ABC沿着DE折叠压平,且∠1+∠2=72°,则∠A=（）26如图,把△ABC纸片沿DE折叠,当点A落在四边形BCED的外部时,则∠A与∠1和∠2之间有一种数目关系始终保持不变,请试着找一找这个纪律,你发明的纪律是（）27如图,三角形纸片ABC,AB=10cm,BC=7cm,AC=6cm,沿过点B的直线折叠这个三角形,使极点C落在AB边上的点E处,折痕为BD,则△AED的周长为（）28一个宽度相等纸条,按如图所示的方法折叠一下,已知∠3=120°,则∠1的度数为（）29如图,把一张长方形纸条折叠后,若∠AOB′=70°,则∠OGC的度数为（）30如图,∠A=60°,∠B=70°,将纸片的一角折叠,使点C落在△ABC内,若∠2=80°,则∠1的度数为（）31如图（1）是长方形纸带,∠DEF=α,将纸带沿EF折叠成图（2）,再沿BF折叠成图（3）,则图（3）中的∠CFE的度数是（）32如图,生涯中,将一个宽度相等的纸条按右图所示折叠一下,假如∠1=140°,那么∠2的度数为（）33如图,四边形ABCD中,点M,N分离在AB,BC上,将△BMN沿MN翻折,得△FMN,若MF∥AD,FN∥DC,则∠B =（）34如图,一张长方形纸条沿AB折叠,假如∠1=124°,那么∠2的度数是（）35如图,把长方形ABCD沿EF半数后使两部分重合,若∠AEF=110°,则∠1=（）36如图,一张三角形纸片△ABC,沿DE折叠使得极点C落在边AB上,若DE∥AB,∠A=45°,则∠ADC的度数是（）37如图所示,把一个三角形纸片ABC顶角向内折叠3次之后,3个极点不重合,那么图中∠1+∠2+∠3+∠4+∠5+∠6的度数和是（）38如图,将△ABC三个角分离沿DE.HG.EF翻折,三个极点均落在点O处,则∠1+∠2的度数为（）39如图,正方形纸片ABCD的边长为8,将其沿EF折叠,则图中①②③④四个三角形的周长之和为（）40如图,将五边形ABCDE沿AE半数到如图的地位,个中∠AEC=72°,则∠CED′=（）41如图,在△ABC中,∠A=35°,在平面内沿直线DE将△ABC折叠后,量得∠BDA′=110°,那么∠CEA′的度数为（）42如图,把一个长方形纸片沿EF折叠后,点D.C分离落在D′.C′的地位,若∠EFB=65°,则∠AED′等于（）43如图,已知△ABC中,∠BAC=140°,现将△ABC进行折叠,使极点B.C均与极点A重合,求∠DAE的度数．。

培优专题--纸片折叠求角度问题

初一数学下学期培优训练小专题06 三角形折叠中的角度问题

折叠问题中的角度运算

七年级数学培优竞赛训练 ：角 含答案

七年级数学尖子生培优竞赛专题辅导专题16折叠问题

20 专题二十：角度的计算(8)——折叠问题(方法专题);人教版七年级上学期培优专题讲练(含答案)

中考几何——折叠专项

折叠问题求角度

初二数学培优专题(5)——折叠问题(答案详解)

折叠问题中的角度运算

培优专题01 与三角形模型有关的角度计算-解析版

培优专题--纸片折叠求角度问题

折叠问题中的角度运算

折叠问题中的角度运算

折叠问题中的角度运算

折叠问题中角度运算

折叠问题中的角度运算

折叠问题中的角度运算

折叠问题中的角度运算

七年级数学培优竞赛训练：角含答案