第二讲基本概念
第二讲 局放基本概念

图1.7 空气的击穿场强
SJTU-OMRC
电气工程系 在线监测技术研究中心
2.1 内部放电 导致实际击穿电压小于预测值的因素:
气隙表壁覆盖了静止电荷 导致击穿电压有多达20%的变化.
在气隙表壁会形成了半导体层 导致场强大幅增加,使气隙击穿.
杂质
污垢、纸屑、纸纤维、金属碎片以及其他的外来离子 杂质击穿 → 形成气隙 → 发生气体放电
4.1 基本参数
b 放电重复率N
单位时间内局部放电的平均脉冲个数,通常以每秒放电次数表示
ucm
uC'
uCB
ur
uC
-ur -uCB
(2)计算 N
n = ucm = um ⋅ Cb ucB ucB Cb + Cc
电晕放电也可以采用a-b-c三电容模型来描 述,但放电的重复不同于其他几种放电 空间电荷会在很短时间内消散。
SJTU-OMRC
电气工程系 在线监测技术研究中心
3.3 交直流电压下的电晕放电
(1)
_
E
+_ +_ +_ +_
(2)
+
_
E
+ ___ + ___ + ___ + ___
(3)
+
_
(4)
E
+
_
⋅U i
or
Vi
= Ui (1+
ε
d ⋅Δ
)
气隙与固体介质串联时的击穿
Vi = f (Δ)
SJTU-OMRC
2
电气工程系 在线监测技术研究中心
2.2 表面放电
Vi
=
f (Δ) = Ui (1+
C语言第2讲-C语言基本概念

注意事项:
①键入数据可用一个或多个空格、Tab、回车键分隔; ②指定宽度时,键入就不要分隔符,按 个数读 ③当含有其它普通字符时,则键入时必须一一对应完全相同;
①scanf ( " %d %d %d " , &a , &b , &c ) ; 键入3 _ 4 _ 5 ②scanf ( " %3d%3d " , &a , &b ) ; 键入 123 456 7 ③scanf ( " %3c " , &ch) ; 键入abc ④scanf ( " %2d %3d%2d " , &a , &b ) 键入12345678 ⑤不能写成scanf ( " %7.2f " , &x ) ; ⑥scanf ( " %d , %d " , &a , &b ); ⑦scanf ( " %c %c %c " , &c1 , &c2 , &c3 ) ;
3.实数:(实型常量、实型常数)又称之为浮点数; (1)小数表示法:用十进制小数形式表示实数:如:12.34、2.0、0.234等 (2)指数表示形式:如:2E2 或2e2,2.341E-4等等。 注意:①e(E)之前必须有数字;②e之后必须是整数; 4.字符型常量 (1)用一对单引号(单撇)括起来的一个字符;如:‘a‟、‘A‟、 ‘#‟;这种方式表示可显示的字符。 (2)转义字符:用一反斜杠\将后面的字符转变为另一些特殊字符 (非显示/打印字符); 一个字符常量放到一个字符变量中时,是将该字
地址表列:必须是变量的地址; 即:输入项为:&变量;
注意:格式控制中格式描述符应与地址表
第二讲翻译学的基本概念

• 宁信而不顺(鲁迅语) rather to be faithful than smooth (“I’d rather be faithful than smooth”) • 神似(傅雷语) spiritual resemblance • 化境(钱钟书语)sublimation(升华) • 信、达、切(刘重德语)faithfulness, expressiveness and closeness (to the original style) • 三美: 音美, 形美, 意美(许渊冲语)the three beauties: beauty in sound, beauty in form and bea• •
选词diction 补偿compensation 视点转换shift of perspective 套译/仿译/仿拟imitation 信/忠实faithfulness/ 达/易懂intelligibility/expressiveness 通顺smoothness 流畅fluency 自然naturalness /idiomaticity(语言的表达习惯) 雅/优美elegance/gracefulness
• • • • • • • • •
东方语言Oriental languages 西方语言Occidental languages 佛经Buddhist Scriptures/sutra['su:trə] 梵语Sanskrit 鸠摩罗什Kumarajiva 泰特勒(Alexander Fraser )Tytler 奈达(Eugene A.) Nida 机器翻译machine translation(MT) 人工智能artificial intelligence(AI)
注意:英译汉中长句化短即采用分译法的 依据是:英语多用长句,汉语多用中短 句。长句化短要根据翻译实际需要为转 移。
计量经济学讲义第二讲(共十讲)

第二讲 普通最小二乘估计量 一、基本概念:估计量与估计值对总体参数的一种估计法则就是估计量。
例如,为了估计总体均值为u ,我们可以抽取一个容量为N 的样本,令Y i 为第i 次观测值,则u 的一个很自然的估计量就是ˆiY uY N==∑。
A 、B 两同学都利用了这种估计方法,但手中所掌握的样本分别是12(,,...,)A A AN y y y 与12(,,...,)B B B N y y y 。
A 、B 两同学分别计算出估计值ˆAiA y uN=∑与ˆBiB y uN=∑。
因此,在上例中,估计量ˆu是随机的,而ˆˆ,A B u u 是该随机变量可能的取值。
估计量所服从的分布称为抽样分布。
如果真实模型是:01y x ββε=++,其中01,ββ是待估计的参数,而相应的OLS 估计量就是:1012()ˆˆˆ;()iiix x yy x x x βββ-==--∑∑ 我们现在的任务就是,基于一些重要的假定,来考察上述OLS 估计量所具有的一些性质。
二、高斯-马尔科夫假定●假定一:真实模型是:01y x ββε=++。
有三种情况属于对该假定的违背:(1)遗漏了相关的解释变量或者增加了无关的解释变量;(2)y 与x 间的关系是非线性的;(3)01,ββ并不是常数。
●假定二:在重复抽样中,12(,,...,)N x x x 被预先固定下来,即12(,,...,)N x x x 是非随机的(进一步的阐释见附录),显然,如果解释变量含有随机的测量误差,那么该假定被违背。
还存其他的违背该假定的情况。
笔记:12(,,...,)N x x x 是随机的情况更一般化,此时,高斯-马尔科夫假定二被更改为:对任意,i j ,i x 与j ε不相关,此即所谓的解释变量具有严格外生性。
显然,当12(,,...,)N x x x 非随机时,i x 与j ε必定不相关,这是因为j ε是随机的。
●假定三:误差项期望值为0,即()0,1,2i E i N ε==。
砼施工基本概念

流动性:指砼拌合物在自重作用下,自由展开或流动的
性能、反映拌合物 的稀稠程度。 坍落度 拌合物太稠,砼难以振捣,易造成内部孔隙; 拌合物过稀,会分层离析,影响砼的均匀性。
粘聚性:指砼拌合物抗离析的能力。
保水性:指砼拌合物保持水分不易析出(泌水)的能力。
2
坍落度
◆泵送混凝土除去考虑捣实施工外,还要考虑其可泵性, 即要求泵送效率高、不阻塞。
硬度越高,管道磨损越快
28
磨削与方向
B端
磨削少
A端
磨薄
29
吸料三要素
30
闸板阀: a.落差大
b.叶片效果好 c.流动性好
d.容积效率80%
31
3
2
1
S阀:
a.落差小 b.叶片效果差
c.流动性差
主轴体将做三种不同的运动: 1 = S阀的左右摆动 2 = 泵送混凝土时泵管上下颤动 3 = S阀所被提供的轴向预紧力推动
其中:
R为输送管半径,单位为m。
K1=(3.0-0.1S)×102为粘着系数,单位为Pa。
K2=(4.0-0.1S)×102为速度系数(Pa/m/s)。 S为混凝土的坍落度,单位为cm。
t2为拖泵分配阀的切换时间。
t1为砼活塞单个冲程所用时间。
V2为 混凝土在管道内的流速 v
Q 4Q A d 2
8
坍落度观察
测定坍落度后,观察拌合物的下述性质:
粘聚性:用捣棒在已坍落的拌和物锥体侧面轻轻敲打,如果锥体 逐步下沉,表示粘聚性良好;如果突然倒塌,或部分崩裂, 则为粘聚性不好的表现。
保水性:当提起坍落度筒后如有较多的稀浆从底部析出,锥体部 分的拌和物也因失浆 而骨料外露,则表明保水性不好。 如无这种现象,则表明保水性良好。
西经重点第二讲 需求曲线和供给曲线概述以及有关的基本概念

第二讲需求曲线和供给曲线概述以及有关的基本概念本章主要内容是需求和供给曲线,内容较简单,大家只需掌握基本概念即可。
名词解释:需求函数,需求曲线,需求弹性,供给函数,供给曲线,供给弹性,恩格尔定律等,同时要了解影响需求,供给弹性的因素。
总体上来说,本章考点不多。
1.合乎理性的人(理性人,经济人)⑴基本特征⑵另一定义:偏好的完全性,可传递性,非饱和性⑶意义:微观经济学的基本假设条件。
2.需求⑴定义:一定的时期,在一既定的价格水平下,消费者愿意并且能够购买的商品数量;⑵影响需求的因素:①商品本身价格;②相关商品的价格;③消费者的收入水平;④消费者的偏好;⑤消费者对未来商品的价格预期;⑶需求函数:假定商品的价格与需求量的变化具有无限的分割性,把商品价格视为自变量,把需求量作为依变量;⑷需求表:一张某种商品的各种价格和与各种价格相对应的该商品的需求量之间关系的数字序列表;⑸需求曲线:根据需求表中的商品的不同的价格与需求量的组合,在平面上拟合的一条曲线;⑹需求规律:当影响商品需求量的其他因素不变时,商品的需求量随着商品价格的上升而减少,随着商品价格下降而增加;需求规律的特例:吉芬商品;⑺需求量变动与需求变动:需求量变动是在某一时期内,在某一价格水平上,消费者购买的商品数量由于商品价格的变动引起购买量的变动,表现为该曲线上的点的变动,不表示整个需求状态的变化。
在商品价格不变的条件下,非价格因素的变动所引起了购买量变动(如收入变动等)称之为需求的变动,表现为需求曲线的移动,表示整个需求状态的变化。
3.供给⑴定义:一定的时期,在一既定的价格水平下,生产者愿意并且能够生产的商品数量;⑵影响供给的因素:①商品本身的价格;②厂商能生产的相关商品价格;③生产的成本;④技术水平;⑤生产者对未来商品的价格预期;⑶供给函数:假定商品的供给量与商品的价格具有无限的分割性,并把商品的价格视为自变量,把供给量作为依变量;⑷供给表:一张某种商品的价格与对应的供给量间关系的数字序列表;⑸供给曲线:是根据供给表中的商品的价格——供给量组合在平面图上所绘制的一条曲线;⑹供给规律:当影响商品供给的其他因素不变时,商品的供给量随着商品价格的上升而增加,随着商品的价格的下降而减少。
控制工程(自动控制)第二讲 基本概念

执行元件:直接推动被控对象,使其被控量发生变 化; 校正元件:也叫补偿元件,它是结构或参数便于调 整的元部件,用串联或反馈连接在系统中,以改善 系统的性能。
自动控制系统基本控制方式
开环控制方式 控制装置与被控对象之间只有顺向作用而没有反向 联系的控制过程,其特点是系统的输出量不会对 系统的控制作用发生影响。
电炉
给定电压
-
+
热电偶
+
+ 电压 放大 功率 放大
+
SM
220V ~
电阻丝
扰动 给定电压 热电偶 电压 放大 功率 放大 伺服 电动机 减速器 调压器 电炉 温度T
执行机构 放大元件 恒温箱自动控制系统方块图
被控对象 测量元件
反馈控制系统组成
输入量 比较元件 串联补偿元件 反馈补偿元件 局部反馈 比较元件 放大元件 执行元件
控制工程基础
主 讲 陈 青 林
本次课的主要内容
1、自动控制的基本概念 2、自动控制与自动控制系统 3、开环控制系统 4、△闭环控制系统 5、△闭环控制系统的组成与工作原理 6、自动控制系统的分类 7、△对自动控制系统的基本要求
第一章 自动控制的一般概念
1-1 自动控制的基本原理与方式
3、程序控制系统
系统的输入量按预定规律随时间变化,要求被控 量迅速、准确地加以复现。
其它分类方法
按时间概念分:定常系统、时变系统 按输入输出信号的数量分:单输入单输出系统、多 输入多输出系统 按控制方式分:开环控制系统、闭环控制系统、复 合控制系统 按系统功用分类:温度控制系统、位置控制系 统…… 按元件类型分类:机电系统、气动系统、液压系统、 生物系统……
2 第二讲定量研究的基本概念和研究设计

区分变量的数据类型,是进行定量研究的 重要基础 无序分类、有序分类、连续
课堂测验:区分以下数据的类型
高度、重量、温度,年收入
能力倾向测试,成就测验 性别,宗教,民族,大学专业,政党身份
学校类型,父母婚姻状况
学生留级(留级还是不留级)
学校规模、班级规模 自尊水平,平均绩点,师生比 使用的母语,教学方法,社会阶层 职业满意度得分 年龄,花在作业上的时间 拼写正确率,阅读成绩,辍学率
学习投入-引起长时记忆 中的知识输入和组织-学 习成绩
某种教学方法对于学习成 绩水平不同学生的影响不 同 学习成绩提高可能是学习 时间更长,也有可能是学 习策略不同
(四)变量之间的关系
差异;相关;因果;
不同性别的学生在语文学习成绩上的差异显著; 年龄和注意力集中时间呈显著正相关; 家庭社会经济背景对学业成绩有显著正影响;
注意,尽管因果比较研究含有因果二字,但 它属于非实验研究的一种方法,没有操纵自变 量,基本上也不控制无关变量,因而得出的结 果并非是真正的因果关系
相关研究 连续变量与连续变量
三、定量研究中的抽样
为什么要抽样? 应该怎样抽样?
美国的《文学文摘》杂志成功地预测了1920年、1924 年、1928年、1932年4次总统大选结果,一时名声大 噪。 1936年大选前,《文学文摘》综合了240万人的意见后, 认为兰登将当选; 而盖洛普(George Gallup)领导的美国舆论研究所 (AIPO)在对5000人进行了问卷调查后,认为罗斯福 将当选。 结果是,5000击败了240万。
中介变量 (mediating variable)
北大行政领导学课件第二讲 行政领导的基本概念

它包括以下要点:
它都有相应的职权。它是领导者行使职权、履行职责的 前提。
(2)职位的特点:
职位是以“事”为中心,而不是以“人”为中心确定 的。即它是由工作性质、工作范围、工作内容等因素 决定; 职位的数量是有限的。它由领导机构的规模、任务及 经费等因素决定 它具有相对稳定性,不因领导者的变动而变动
被领导者对抗权的来源:
专长
掌握重要的信息和物质资源
熟悉规章制度 密切的关系 集体行动
(四)追随者的准备就绪程度理论
准备就绪程度(Readiness Levels)理论:保罗· 赫西
和杜威· 约翰逊提出的。是指追随者所表现出的完成某 一任务的能力和意愿的程度。 准备就绪程度的四个等级:
工作责任
从工作内容上看领导的主要职责: 毛泽东精辟概括为:出主意,用干部两件事。 “一切计划、决议、命令、指示等,都属于出 主意一类;而使一切主意见之实行,必须团结 干部,推动他人去做,则属于用干部一类。”
——《毛泽东选集》第2卷,人民社64年版,P515
具体职责:规划、组织、指挥、决策、用人、思政工作 等。
领导= f(领导者、被领导者、环境) 它们的相互作用 构成有效的领导活动。
一、领导者
“领导者的唯一定义是其后面有追随者。
一些人是思想家,一些人是预言家,这 些人都很重要,而且也很急需,但是没 有追随者,就不会有领导者。” ——彼得· 德鲁克
(一)领导者的定义
领导者通常是指在人类群体活动中负责组织、
怎么办?
二、被领导者
(一)定义:
被领导者是指在领导活动中执行具体决策方案、 命令、任务 辽宁铁岭市有9个副市长、20个副秘书长。 河南新乡市有11个副市长、16个副秘书长。
第二讲 关于初等教育的基本概念与特征

第二讲关于初等教育的基本概念与特征一、什么是教育?1.广义的教育广义的教育是指对人产生影响的各种社会活动,是属于社会现象。
在中外教育史上,尽管对于教育的解说各不相同,但却存在着一个共同的基本点,即把教育看作是培养人的活动,这是教育区别于其他事物现象的根本特征。
2.狭义的教育狭义的教育特指学校教育。
学校教育是根据一定社会的现实和未来的需要,遵循年轻一代身心发展的规律,有目的、有计划、有组织地引导受教育者获得知识技能,陶冶思想品德、发展智力和体力的一种活动,以便把受教育者培养成为适应一定社会(或一定阶级)的需要和促进社会发展的人。
3.更狭义的教育更狭义的教育是特指道德教育。
道德教育是教育者按照一定社会或阶级的要求,有目的、有计划、系统地对受教育者施加思想、政治和道德影响,通过受教育者积极的认识、体验、身体力行,以形成他们的品德和自我修养能力的教育活动。
二、什么是初等教育?1.广义的初等教育:对5、6~11、12岁的儿童所提供的影响身心发展的活动。
2.狭义的初等教育:指学校教育制度中的一个阶段——小学教育,指为5、6~11、12岁的儿童所提供的基础的、义务的、全民性的教育活动。
三、初等教育的主要特征1.基础性基础性是指初等教育是各级各类教育的基础、初等教育为培养身心全面发展的人奠定基础、是一个个体继续不断发展的基础。
2.义务性义务性是指国家以法律形式规定对适龄儿童和青少年实施一定年限的普及的、强迫的、免费的学校教育。
在我国实施的是九年义务教育。
3.免费性免费性是指实施免费的学校教育。
实施免费教育是普及初等义务教育的重要措施之一。
4.全民性全民性是指初等教育面向所有儿童,接受初等教育是所有国民应享有的权利,亦是应尽的义务。
5.生活性生活性是指初等教育必须与儿童的生活密切相关,帮助儿童养成良好的生活习惯,学会生活。
6.民族性初等教育的民族性可以说是从近代开始初等教育所逐渐具有的特性之一,最早的近代初等教育机构的产生恰恰与民族性密切相关。
第二讲家庭治疗基本概念和原则2

第二讲家庭治疗中的基本内容家庭治疗过程中的重要事项一、治疗目的1.短期目的:消除家庭目前的症状,又不产生新的症状。
2.长期目的:帮助家庭完成与发展相适应的任务和学会应对问题的技能技巧。
上述两个目的可以通过完成下列目标来实现:(1 )增加或减少与原生家庭、扩展家庭及家庭外系统的接触与交往。
如果交往带来积极的后果,使家庭获得有益的社会支持,则增加交往;如果交往带来消极的后果,使家庭的困难进一步增加,或者形成解决问题的“ 三角关系” ,则应减少交往。
(2 )形成更加清楚的沟通,如直接对话,直接表达自己的愿望和想法,在说明自己的看法时用具体事实加以说明等等。
(3 )自我的分化,形成独立而分化的自我。
(4)采用合作解决问题的方法解决冲突,避免使用淹没个别化、避免冲突及竞争的方法解决冲突。
(5)夫妻冲突或者家庭成员间的冲突尽量避免引入第三者,以避免使矛盾复杂化(6)形成强有力的夫妻亚系统和父母同盟,确保父母在家庭中的地位和对孩子的养育。
(7)使家庭成员有更多的独立性和自主性,使他们能够更大程度地发挥自己作为家庭一员的作用。
(8)减少家庭成员的移情和投射,使家庭成员更现实地了解彼此的想法和情感。
(9)使家庭成员间自发且适当分享情感。
(10)使家庭成员对家庭生活感到乐观、满意,并喜欢家庭生活。
二、治疗时间1.两次治疗间隔时间的长短:1次/周或1次/2周;2.每次治疗持续时间的长短:对于每周见1次的来说,60分钟/次;对于两周见1次的来说, 90分钟至120分钟/次;3.整个治疗过程持续的时间的长短:(1)根据治疗的过程来确定,到治疗师认为治疗起作用,症状消失的时候,就结束整个治疗;(2)有些治疗师会事先确定整个治疗持续的时间,需要见面的次数。
三、治疗涉及的对象在治疗开始的时候,一般要求与患者住在一起的人都来参与面谈。
只有这样,才能有助于治疗师了解究竟哪些家庭成员与症状的产生和维持有关。
但是,随着治疗的进行,当治疗师明确诊断出哪些家庭成员与问题有关之后,就可以只让那些起参与有助于问题解决或者不参与就会阻碍问题解决的人参与治疗。
第二讲 经济学的假设、基本概念和研究方法

2020/5/3
8
例4 买车和总统投票
你要买一辆新车,花时间“货比三家” 你要对选举总统投票,几秒种就“搞定” 为什么?
2020/5/3
9
小结
理性假设往往比其它假设能更好地预测人 的行为
可能有例外,但预测的许多人的总体行为, 而不是个体行为
预测的是特定条件下的特定对象的行为, 而不是所有的人
2020/5/3
10
二、经济学的基本概念
概念 ➢ 阅读和理解经济学文献的工具 ➢ 分析和探讨经济问题的“武器”
2020/5/3
11
选择:人们受各种欲望的控制
吸烟:有害健康,但 为什么还有人照吸不 误呢?
2020/5/3
12
翻越马路上的栏杆: 可能会被车撞!为什 么还有那么多人干?
QUANTITY
150
31
Market Clearing(市場均衡)
买卖双方對價格及數量的妥協; 买卖双方的行為,共同決定的均衡價格水準——Invisible
Hand(看不見的手)。 在这场合,像在其他许多场合一样,他受着一只看不
见的手的指导,去尽力达到一个并非他本意想要达到的目 的。也并不因为事非出于本意,就对社会有害。他追求自 己的利益,往往使他能比在真正出于本意的情况下更有效 地促进社会利益-------《国富论》 亚当. 斯密 市场不足或过剩?
2020/5/3
13
购买食品:超市琳琅 满目,挑什么呢?
2020/5/3
14
小结:对个人来说,人生就是在选 择中度过
有欲望和需求 (自然、社会)提供的机会多 与个人的财富、收入有关 与个人拥有该物品的数量有关 经济学研究人的行为,实际上就是研究人
第二讲 传播学的基本概念

一篇惊动教育部的小学生作文
今天,老师带领我们到烈士纪 念馆参观,使我很受感动。那些 革命烈士,为了革命,不怕严刑 拷打,不怕枪林弹雨,为了穷人 的解放,献出了自己宝贵的生命。 我要向他们学习,做革命的接班 人,长大为人民服务。 我热爱那些为穷人打天下的烈 士,我痛恨那些资本家反动派。 听爷爷说,刚解放那会,日子虽 然苦,但那时当官的一心为老百 姓,不像现在,到处是贪污犯。 我对爷爷说,我长大了就专门抓 贪官,给他们灌辣椒水,上老虎 凳,叫他们把贪污的钱交出来, 分给穷人。
一、传播的概念
“传播”在印欧语系的文字中,是 communication或kommunikation,它源 于古希腊的两个词根,一个是com,指 与别人建立一种关系;一个是munus, 指效用、产品、作品、利益、服务等 等。两个词根合起来,意为“共有”、 “共享”。 古罗马的著名演说家西塞罗(Cicero, 前106-43),将communication定义 为与别人建立一种联系或把握一件事 情。
中国人民大学新闻学院教授博导陈力丹陈力丹闫伊默传播学纲要26万字242页图115张设置基本概念人际传播组织传播大众传播文艺传播跨文化传播传播控制大众传播批判等九章陈力丹易正林编著传播学关键词北师大出版社2009搜集了关于25个传播学概念的外国学者原始论证对每个概念进行学术梳理
传播学的基本概念
中国人民大学新闻学院教授、博导 陈力丹
姬无命:这有什么区别吗? 秀才:举个例子,但我用我这个代号来进行对话的 同时,你的代号也是我,这意味着什么呢,这是否 意味着,你就是我,而我也就是你? 姬无命:这这,这个问题没什么意义嘛。 秀才:那就问几个有意义的,我生从何来,死往何 处,我为何要出现在这个世界上,我的出现对这个 世界来说意味着什么,是世界选择了我,还是我选 择了世界? 姬无命:够了! 秀才:我和宇宙之间有必然的联系吗?宇宙是否有 尽头?时间是否有长短?过去的时间在哪里消失? 未来的时间又在何处停止?我在这一刻提出的问题, 还是你刚才听到的问题? 姬无命:我杀了你! 秀才:是谁杀了我,而我又杀了谁! 姬无命:是我杀了我! 秀才:回答正确,动手吧! 姬无命:啊!!(自杀)
语言学习的基本概念

(三)第一语言和母语的关系
• 第一语言和母语是两个不同 的概念 • 就多数人而言,母语是他们 的第一语言。但由于种种原 因,有些人习得的第一语言 并非母语。 • 母语失却现象的存在,也有 力地说明了第一语言和母语 的不同。
二、第一语言的获得
• 人是怎样获得第一语言的呢? • 大致分为两个阶段: • 第一阶段是早期的潜意识的语言习得;
•第二讲 •语言学习的基本概念
一、第一语言和母语
(一)第一语言
First Language
第一语言: 是指一个人出生之后 最先 接触并
获得的语言。
• 一个人的第一语言通常是他的母语。
(二)母语
母语(教材P31):
母语就是指本国或本民族的语言,通常是指本 国或本民族通用的语言。
对母语不同的看法: ① mother language 是指“一个人最初学会的一种语言,在一般 情况下是本民族的标准语或某一种方言”。
• 当儿童接触到具体语言时,就 会不断地通过假设--验证的演 绎过程对“普遍语法”的参数 进行定值以形成具体语言的规 则系统,从而习得一种语言。
对先天论的评价
• goed,comed等不正确的动词形态,是儿童常出 现的语言规则过度概括的错误,正说明他们在检 验和评价对语言规则的假设。 • 人脑中存在的语言习得机制只是一种假说,究竟 有没有LAD很难通过实验来证明。 • 人类的语言千差万别,即使能找到普遍特征,是 否能为人类天生所有? 说儿童一生下来就懂得基 本语法关系、语法范畴和转换规律,是很难令人 信服的。 • 对环境的作用不够重视。
(二)第一语言习得理论
教材P34-37
1、强化论 (斯金纳)
• 语言不是先天所有而是后天习得的 , 是后天形成的一套习惯。 • 语言是人类的一种行为,同人类的其 他行为一样,语言也是通过剌激--反 应 -- 强化 ( 反应后的刺激 ) 的模式而 获得的。 • 儿童学话就是对环境所给予的刺激 做出相应的反应,开始是对成人语 言的模仿,如果模仿得比较接近, 就从成人那里得到赞许或奖励,这 样他的反应就得到了强化。
第二讲光与颜色的基本概念(1)
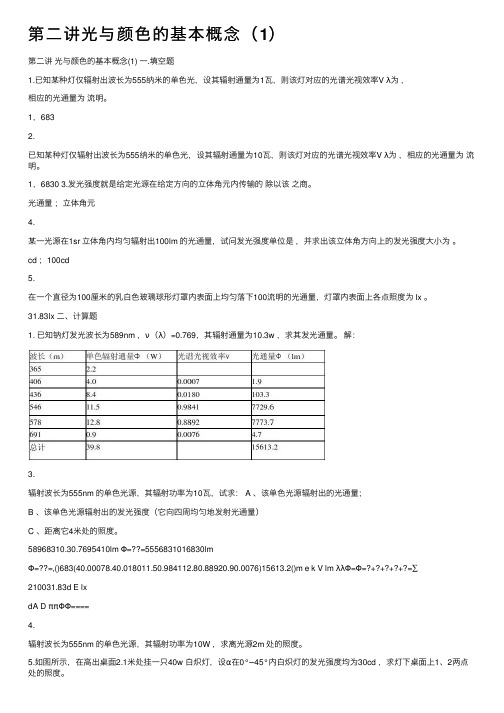
第⼆讲光与颜⾊的基本概念(1)第⼆讲光与颜⾊的基本概念(1) ⼀.填空题1.已知某种灯仅辐射出波长为555纳⽶的单⾊光,设其辐射通量为1⽡,则该灯对应的光谱光视效率V λ为,相应的光通量为流明。
1,6832.已知某种灯仅辐射出波长为555纳⽶的单⾊光,设其辐射通量为10⽡,则该灯对应的光谱光视效率V λ为,相应的光通量为流明。
1,6830 3.发光强度就是给定光源在给定⽅向的⽴体⾓元内传输的除以该之商。
光通量;⽴体⾓元4.某⼀光源在1sr ⽴体⾓内均匀辐射出100lm 的光通量,试问发光强度单位是,并求出该⽴体⾓⽅向上的发光强度⼤⼩为。
cd ;100cd5.在⼀个直径为100厘⽶的乳⽩⾊玻璃球形灯罩内表⾯上均匀落下100流明的光通量,灯罩内表⾯上各点照度为 lx 。
31.83lx ⼆、计算题1. 已知钠灯发光波长为589nm ,ν(λ)=0.769,其辐射通量为10.3w ,求其发光通量。
解:3.辐射波长为555nm 的单⾊光源,其辐射功率为10⽡,试求: A 、该单⾊光源辐射出的光通量;B 、该单⾊光源辐射出的发光强度(它向四周均匀地发射光通量)C 、距离它4⽶处的照度。
58968310.30.7695410lm Φ=??=5556831016830lmΦ=??=,()683(40.00078.40.018011.50.984112.80.88920.90.0076)15613.2()m e k V lm λλΦ=Φ=?+?+?+?+?=∑210031.83d E lxdA D ππΦΦ====4.辐射波长为555nm 的单⾊光源,其辐射功率为10W ,求离光源2m 处的照度。
5.如图所⽰,在⾼出桌⾯2.1⽶处挂⼀只40w ⽩炽灯,设α在0°─45°内⽩炽灯的发光强度均为30cd ,求灯下桌⾯上1、2两点处的照度。
6.⼀个直径为250mm 的乳⽩⾊玻璃球形灯罩,内装⼀个光通量为1260lm 的⽩炽灯,设灯罩的光透射⽐为0.60,求灯罩外表⾯亮度?解:直径D=250mm=0.25m球的表⾯积为S=4πR^2=π×D^2=0.196m2透过乳⽩⾊玻璃球形灯罩的光通量Φ=1260×0.6=756lm 发光强度Ι=d Φ/d Ω=Φ/(4π) 灯罩外表⾯亮度L α=Ι/dAcos α=d Φ/(d ΩdAcos0)=φ/(4π×πD^2)7.⼀个直径为400毫⽶的乳⽩玻璃球形灯罩,内装⼀个光通量为1179流明的⽩炽灯,设灯罩的光透射⽐为0.7,求灯罩外表⾯亮度(不考虑灯罩的内反射影响)。
第二讲 集合的基本概念

第一讲集合的基本概念一【新课讲解】知识点一:集合的概念集合是某些指定的元素集在一起就构成一个集合。
通常用大写字母 A,B,C,D...来表示集合,用小写字母a,b,c,d来表示元素。
如{}c baA,,=注意:(1)构成集合的元素除了常见的数、式、点等,还可以是其它任何的对象。
(2)构成集合的元素必须是确定的(所指对象明确)(3)集合与元素之间的关系:若a是集合A的元素,记做Aa∈;若a不是集合A的元素,记做Aa∉。
【即时练习】1.判断下列各组对象是否可以构成集合,若能,请指出该集合的元素;若不能,请说明理由?①接近于0的数的全体;②比较小的正整数全体;③平面上的到坐标原点的距离为1的点的全体;④身高大于1米7的人。
2.设集合{}4,32,13==≤=baxxA,则a,b与A间的关系为知识点二:常用数集的表示方法1.非负整数集(或自然数集),记做N;2.正整数集,记做N*(或N+);3.整数集记做Z;4.有理数集记做Q;5.实数集记做R;6.不含任何元素的集合叫做空集,记做:φ【即时练习】3.下列选项正确的是( )A. N+∈0 B. R∉π C. Q∉1 D.Z∈知识点三:集合的四种表示方法1.列举法:把集合中的元素一一列举出来,并用大写的“{}”括起来,每两个元素间用“,”隔开。
适用于集合中的元素的个数有限。
如1:{}cba,,如2:方程0322=--xx的解集可以表示成集合{}1,3-例1.用列举法表示下列集合(1)(){}NyNxyxyx∈∈=+,,3,()⎭⎬⎫⎩⎨⎧∈+∈ZxZx262☆变式训练☆1.用列举法表示下列集合:(1)一次函数xy=与12-=xy图像的交点组成的集合。
()⎭⎬⎫⎩⎨⎧∈+∈NxNx262()⎭⎬⎫⎩⎨⎧∈∈+ZxZx2632.描述法:用集合所含元素的共同特征表示集合。
适用于集合中的元素的个数是无限多个。
描述法的一般格式是:{}的属性x x ,其中,x 是代表元素。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
样本空间:样本所有可能的取值构成的空间
(Sample Space)
在统计中,对总体的推断,实际上是推断
总体的分布,即确定总体的分布。为此,我
们可以根据对总体了解程度,假设总体的分
布属于某个分布族 {P , }, 至于其中哪一
个分布最适合还得通过统计推断来确定,因
此往往将 {P , } 称为统计模型。 其中
k
Q j~ 2(nj ) n j n. j1
t 分布
设随机变量 X ~ N (0,1), Y ~ 2(n), 且 X 与Y 相互独立,则称随机变量
T X Y n
所服从的分布为自由度是 n 的 t 分布, 记为
T ~ t(n).
F 分布
设随机变量 X ~ 2(n1 ), Y ~ 2(n2 ), 且 X 与Y 相互独立,则称随机变量
个体:总体中的每个对象,如例1中的每个 产品。
(S样am本p:le)X1, X2 , , Xn , 样本的实现称为样本 的一组观察值(Observation or data), 记为 x1, x2 , , xn .
今后,为了方便若不加特别声明,用 x1, x2 , , xn既表示样本,又表示样本观察值。
有关参数的信息,而剔除无关的信息,这在
统计上就反映为构造样本的已知函数,即
统计量(Statistic)。
例2 设总体X服从两点(正品和次品)分布,即
P( X 1) , P( X 0) 1
X
是来自总体的样本,考虑样本
n
的函数
T ( X1, X2 ,
, Xn)
S
1 n1
n i 1
(Xi
X
)2 .
样本矩(Sample Moment)
k阶原点矩
Ak
1 n
n i 1
X
k i
,
k
1,2
.
k阶中心矩
Bk
1
n
n i 1
(
X
i
X )k ,
k
1,2
.
2. 充分统计量
统计量既然是对样本的加工或压缩,在这 个过程中可能有损失有关参数的一部分信息, 现在问题是在这个过程中是否存在某些统计 量,既起到压缩作用,又不损失参数的信息, 这样的统计量称为充分统计量。
定理1 设统计模型为{P , },统计量T ( X )
是充分的,当且仅当存在一个定义在I
上的函数g(t, )及定义在Rn上函数h( x)使得
p( x, ) g(T ( x), )h( x)
对所有的x Rn都成立,其中I是T( x)的值域,
p( x, )是样本的联合概率密度函数或分布率。
例4
X F n1
Y n2
所服从的分布为自由度是 n1, n2 的 F 分布, 记为 F ~ F(n1, n2 ).
正态总体样本和方差的分布
定理6 设 X1, X2 , , Xn 是来自正态总体 N (, 2 ) 的一个简单样本, A是 p n 阶矩阵,则
Y1 X1
Y
Y2
Yp
A
X2 Xn
1
2
n
(Xi
i 1
)2 ~
2(n)
定理3 设 X ~ 2(n),则
(1)X
的特征函数为(t)
Ee itX
n
(1 2it) 2
(2) E( X ) n, D( X ) 2n
定理4 设 X1~ 2(n1 ), X 2~ 2(n2 ), 且相互独立, 则 X1 X2~ 2(n1 n2 ).
第二讲 基本概念
一、总体,样本和统计模型 二、统计量及其分布
一、总体、样本和统计模型
例1 有一批产品,总数为N。在N件产品中
有N件次品,是这批产品的次品率。
是我们感兴趣的参数,通常是未知的,需
要利用统计方法对参数做出推断。
总体:研究对象的全体,如例1中的这批产
(Population)
产品就构成总体。通常用 X ,Y等表示。
三大分布
2 分布
设随机变量 X1, X2, , Xn 相互独立且同服从 标准正态分布N (0,1),称随机变量
2
X
2 1
X
2 2
X
2 n
所服从的分布为自由度是 n 的 2 分布,记为
2~ 2(n)
定理2 假设简单样本 X1, X2, , Xn 来自正态总 体 N (, 2 ),则有
2
称为参数空间。 (Statistical Model)
(Parameter Space)
如例1中,统计模型为{P , } ,其中
N N N
P { X k}
k
n k N
,
n
max((n N (1 ),0) k min( N , n),
其中X表示一次试验中抽取的 n件产品的
1, n
s
定义2 设统计模型为{P , },T ( X )是统计
量。如果在给定T (X ) t的条件下,X的条
件分布与参数无关,则称统计量T ( X )是 参数的充分统计量(Sufficient Statistics)
一般情况下,利用条件分布证明统计量的 充分性是比较困难的。但存在证明充分性的
一个充分必要准则,就是下面的因子分解定 理(Factorization theorem)。
设样本X 1 ,
X2 ,
,
X
是来源于正态总体
n
N (, 2 ),令参数 (, 2 ),试证明
(1)
T ( X ) n i1
n
Xi,
i 1
X
2 i
及
(2)
T(
X
)
1 n
n i 1
Xi
,
1 n
n i 1
(
Xi
X )2
都是的充分统计量。
3. 抽样分布
特征函数
设 X 随机变量, 称函数
Fp (n2 , n1)
1 F1 p (n1, n2 )
P{X zp} p
由对称性有 z1 p zp
2
(n)
分布:用
2 p
(n)
表示
p 分位点,即
P{ 2
2 p
(n)}
p
t(n)分布:用 tp (n)表示 p 分位点,即
P{T tp (n)} p
F(n1, n2 )分布:用 Fp (n1, n2 ) 表示 p 分位点,即
P{F Fp (n1, n2 )} p
Sw
11 n1 n2
其中
S12
X1 n1
1 n1 1
n1
i 1 n1
i 1
Xi, (Xi
Y X
1 n2
n2
Yi
i 1
)2,
S22
1 n2 1
n2 i 1
(Yi
Y
)2
Sw2
(n1
1)S12 (n2 1)S22 n1 n2 2
定理9 设 X1, X 2 ,L , X n1 和 Y1,Y2 ,L ,Yn2是分别来自
正态总体
N
(
1
,
2 1
)
和
N
(
2
,
2 2
)
的两个简单样本,
且两样本独立,则
F
S12 S22
12
2 2
~ F(n1 1, n2 1)
4. 分位点
定义 设随机变量 X 的分布函数为F(x),对任意 给定的实数 p (0 p 1) ,若存在 xp 使得
P{X xp} F(xp ) p
成立,则称 xp为此概率分布的 p 分位点。 常见分布分位点记号: 标准正态分布 N (0,1):用 z p 表示,即
次品数。
{ : 0 1}为参数空间。
二、统计量及其分布
设统计模型为 P , ,我们仅知道
总体的分布属于此分布族,但哪个最合适 还需经过统计推断。推断总体的分布,实际
上就是确定参数 ,为此,需抽取样本。
样本来源于总体,它应当包含参数的所有 相关信息,但观察值呈现为一堆杂乱无章 数据,故需对数据进行加工或压缩,提取
n
如例2中
X
是统计量,因为它不含任何未
i
i 1
知的参数。
常用统计量(Statistic):
样本均值(Sample Mean):
X
1 n
n i 1
Xi.
样本方差(Sample Variance):
S 2
1 n1
n i 1
(Xi
X
)2 .
样本标准差(Sample Standard Deviation):
X (t) E(eitX )
为 X 特征函数。 常见分布的特征函数:
二项分布 B(n, p) :(t) ( peit (1 p))n
Poisson分布P() :(t) exp{(eit 1)} 正态分布 N (, 2 ) :(t) exp{it 1 2t}
2
特征函数的性质:
(1)有界性 对任意t R,有|(t) | (0) 1。
n
Xi.
T实际上表
i 1
示样本中所含的次品个数,对不同观察值
可能对应相同的T值,这样实际上是对样本 起到了加工或压缩的作用。
1. 统计量
定义1 设X1, X2 , , Xn是来自总体X的一个样 本,T ( X1, X2 , , Xn )是样本的函数。如果 T ( X1, X2 , , Xn )不包含任何未知参数,则称 其为总体X的统计量,简记为T。
(2)设Y aX b,其中 a,b为常数,则 Y (t) eibtX (at)
(3)若 X与 Y 相互独立,则有
