金属丝杨氏模量的测定
测金属丝的杨氏模量

测金属丝的杨氏模量
杨氏模量是材料力学中重要的一个参量,它描述了材料在受到外力作用下产生形变的程度,是衡量材料刚度和弹性的指标。
许多物理学实验都涉及到测量杨氏模量,这篇文章将介绍如何测定金属丝的杨氏模量。
首先,我们需要准备一段长度为L,截面积为A的金属丝,以及一组实验仪器:定压电源、可变电阻、恒定电流源、滑动电阻、计长度器和显微镜。
接下来,我们需要进行实验测定杨氏模量。
具体步骤如下:
1. 首先,将金属丝固定在两个支架上,使其处于水平状态。
2. 在金属丝的中央处加上一个重物,使其产生一个小的弯曲,同时记录下金属丝和重物的位置(这里用到计长度器和显微镜)。
3. 将恒定电流源与金属丝相连,使电流通过金属丝。
4. 使用滑动电阻测量电流,同时使用可变电阻器调节电流,使其维持一个恒定的数值。
5. 使用定压电源对金属丝施加一个保持不变的电压。
6. 记录下金属丝的弯曲变形,重复实验三次并取平均数。
根据上述实验数据,可以使用下面的公式计算出金属丝的杨氏模量:
E = (4FL^3) / (πd^4ΔL)
其中,E是金属丝的杨氏模量,F是重物的分力,L是金属丝的长度,d是金属丝的直径,ΔL是金属丝受到的弯曲变形。
需要注意的是,实验中应尽可能减小误差,比如使用精度更高的仪器、避免金属丝受到外力等。
同时,实验数据的准确性也至关重要,需要尽可能多地进行实验测量,减小随机误差的影响,以保证实验结果的准确性和可靠性。
总之,通过上述实验方法,我们可以测定金属丝的杨氏模量,并且可以得到一个准确可靠的数值,为材料力学和其他相关领域的研究提供重要的实验数据和参考依据。
金属丝杨氏模量的测定实验报告

一、实验目的1. 了解杨氏模量的概念和意义;2. 掌握用拉伸法测量金属丝杨氏模量的原理和方法;3. 学会使用实验仪器进行测量,并学会数据处理和误差分析;4. 培养实验操作能力和科学思维。
二、实验原理杨氏模量(E)是描述材料弹性性能的物理量,定义为材料在弹性形变时,单位应力所引起的单位应变。
其计算公式为:E = σ / ε其中,σ为应力,ε为应变。
应力是指单位面积上的力,应变是指单位长度的形变量。
本实验采用拉伸法测量金属丝的杨氏模量。
在实验过程中,对金属丝施加一定的拉力,使其产生弹性形变。
通过测量金属丝的伸长量和所受拉力,根据上述公式计算出杨氏模量。
三、实验仪器与材料1. 金属丝:直径约为1mm,长度约为100mm;2. 拉伸仪:用于施加拉力;3. 量角器:用于测量金属丝的伸长角度;4. 标尺:用于测量金属丝的伸长量;5. 计算器:用于计算数据。
四、实验步骤1. 将金属丝固定在拉伸仪上,确保金属丝与拉伸仪的轴线一致;2. 将金属丝的另一端固定在支架上,确保支架与拉伸仪的轴线一致;3. 调整量角器,使其与金属丝轴线垂直;4. 拉伸金属丝,使其产生弹性形变;5. 记录金属丝的伸长角度和伸长量;6. 重复上述步骤,进行多次实验,以确保数据的准确性;7. 根据实验数据,计算金属丝的杨氏模量。
五、数据处理与结果分析1. 计算金属丝的应力:σ = F / S其中,F为拉力,S为金属丝的横截面积。
2. 计算金属丝的应变:ε = ΔL / L其中,ΔL为金属丝的伸长量,L为金属丝的原始长度。
3. 根据实验数据,计算金属丝的杨氏模量:E = σ / ε4. 分析实验结果,与理论值进行比较,讨论误差来源。
六、实验结论通过本次实验,我们成功测量了金属丝的杨氏模量。
实验结果表明,金属丝的杨氏模量与理论值基本吻合。
在实验过程中,我们学会了使用拉伸法测量金属丝的杨氏模量,掌握了数据处理和误差分析的方法。
同时,本次实验也提高了我们的实验操作能力和科学思维。
金属丝杨氏模量的测定实验报告

金属丝杨氏模量的测定实验报告金属丝杨氏模量的测定实验报告引言:杨氏模量是描述材料刚性和弹性的重要参数,对于材料的力学性能评估和工程设计具有重要意义。
本实验旨在通过测定金属丝的杨氏模量,探索金属材料的力学性能,并了解测量过程中的误差来源及其对结果的影响。
实验原理:杨氏模量是描述材料在弹性变形过程中应力与应变关系的物理量。
在弹性区域内,应力与应变成正比,比例系数即为杨氏模量。
实验中,我们采用悬挂法测定金属丝的杨氏模量。
将金属丝固定在两个支撑点上,并在中间加挂一负重。
通过测量金属丝的长度变化和负重的重量,可以计算得到杨氏模量。
实验步骤:1. 准备工作:选择一根细丝材料,如铜丝或钢丝,并测量其直径和长度。
准备两个支撑点,保证丝材能够悬挂在中间。
2. 悬挂装置搭建:将金属丝固定在两个支撑点上,并调整支撑点的高度,使金属丝水平悬挂。
3. 测量初始长度:使用游标卡尺等测量工具,准确测量金属丝的初始长度。
注意避免外力对丝材的影响。
4. 加挂负重:在金属丝的中间位置加挂一负重,记录下负重的重量。
5. 测量变形长度:使用测微计等精确测量工具,测量金属丝在负重作用下的长度变化。
注意避免外力对丝材的影响。
6. 数据处理:根据测量结果计算金属丝的应变和应力,并绘制应力-应变曲线。
通过线性拟合得到斜率,即为金属丝的杨氏模量。
实验结果与讨论:根据实验数据和测量结果,我们得到了金属丝的杨氏模量。
然而,实验中可能存在一些误差来源,如测量长度的精确度、负重的不均匀分布等。
这些误差会对最终的结果产生影响。
为了减小误差,我们可以采取以下措施:1. 使用更加精确的测量工具,如激光测距仪等,提高测量长度的准确性。
2. 在金属丝上均匀分布负重,避免负重集中在某一点导致丝材变形不均匀。
3. 进行多次实验,取平均值,减小随机误差的影响。
此外,我们还可以探索不同材料的杨氏模量差异,比较不同金属材料的力学性能。
不同材料的杨氏模量差异可能源于其晶格结构、原子间键的强度等因素。
金属丝杨氏模量的测定
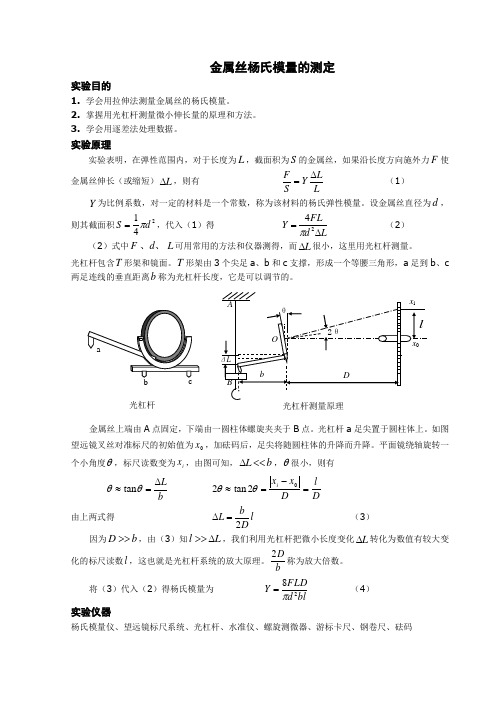
金属丝杨氏模量的测定实验目的1. 学会用拉伸法测量金属丝的杨氏模量。
2. 掌握用光杠杆测量微小伸长量的原理和方法。
3. 学会用逐差法处理数据。
实验原理实验表明,在弹性范围内,对于长度为L ,截面积为S 的金属丝,如果沿长度方向施外力F 使金属丝伸长(或缩短)L ∆,则有LL YS F ∆= (1)Y 为比例系数,对一定的材料是一个常数,称为该材料的杨氏弹性模量。
设金属丝直径为d ,则其截面积241d S π=,代入(1)得Ld FLY ∆=24π (2)(2)式中L d F 、、可用常用的方法和仪器测得,而L ∆很小,这里用光杠杆测量。
光杠杆包含T 形架和镜面。
T 形架由3个尖足a 、b 和c 支撑,形成一个等腰三角形,a 足到b 、c 两足连线的垂直距离b 称为光杠杆长度,它是可以调节的。
金属丝上端由A 点固定,下端由一圆柱体螺旋夹夹于B 点。
光杠杆a 足尖置于圆柱体上。
如图望远镜叉丝对准标尺的初始值为0x ,加砝码后,足尖将随圆柱体的升降而升降。
平面镜绕轴旋转一个小角度θ,标尺读数变为i x ,由图可知,b L <<∆,θ很小,则有bL ∆=≈θθtan Dl Dx x i =-=≈02tan 2θθ 由上两式得l Db L 2=∆(3)因为b D >>,由(3)知L l ∆>>,我们利用光杠杆把微小长度变化L ∆转化为数值有较大变化的标尺读数l ,这也就是光杠杆系统的放大原理。
bD 2称为放大倍数。
将(3)代入(2)得杨氏模量为bld FLDY 28π=(4)实验仪器杨氏模量仪、望远镜标尺系统、光杠杆、水准仪、螺旋测微器、游标卡尺、钢卷尺、砝码光杠杆光杠杆测量原理操作要点1. 利用水准仪调节杨氏模量仪的底脚螺钉使支架保持铅直。
2. 调节望远镜标尺装置,使望远镜和光杠杆等高,且使望远镜镜身和标尺在平面镜中的像在一条直线上。
3. 调节望远镜目镜使十字叉丝清晰,调节物镜,并适当移动标尺系统,使标尺像清晰。
金属丝杨氏模量的测定

物理实验报告【实验名称】杨氏模量的测定【实验目的】1. 掌握用光杠杆测量微小长度变化的原理和方法,了解其应用。
2. 掌握各种长度测量工具的选择和使用。
3. 学习用逐差法和作图法处理实验数据。
【实验仪器】MYC-1型金属丝杨氏模量测定仪(一套)、钢卷尺、米尺、螺旋测微计、重垂、砝码等。
【实验原理】 一、杨氏弹性模量设金属丝的原长L ,横截面积为S ,沿长度方向施力F 后,其长度改变ΔL ,则金属丝单位面积上受到的垂直作用力F/S 称为正应力,金属丝的相对伸长量ΔL/L 称为线应变。
实验结果指出,在弹性范围内,由胡克定律可知物体的正应力与线应变成正比,即LLYS F ∆= (1) 则E LL SF Y ∆=(2) 比例系数E 即为杨氏弹性模量。
在它表征材料本身的性质,Y 越大的材料,要使它发生一定的相对形变所需要的单位横截面积上的作用力也越大。
Y 的国际单位制单位为帕斯卡,记为Pa (1Pa =12m N ;1GPa =910Pa )。
本实验测量的是钢丝的杨氏弹性模量,如果钢丝直径为d ,则可得钢丝横截面积S42d S π=则(2)式可变为EL d FLY ∆=24π (3)可见,只要测出式(3)中右边各量,就可计算出杨氏弹性模量。
式中L (金属丝原长)可由米尺测量,d (钢丝直径),可用螺旋测微仪测量,F (外力)可由实验中钢丝下面悬挂的砝码的重力F=mg 求出,而ΔL 是一个微小长度变化(在此实验中 ,当L ≈1m时,F 每变化1kg 相应的ΔL 约为0.3mm)。
因此,本实验利用光杠杆的光学放大作用实现对钢丝微小伸长量ΔL 的间接测量。
二、光杠杆测微小长度变化尺读望远镜和光杠杆组成如图2所示的测量系统。
光杠杆系统是由光杠杆镜架与尺读望远镜组成的。
光杠杆结构见图2(b )所示,它实际上是附有三个尖足的平面镜。
三个尖足的边线为一等腰三角形。
前两足刀口与平面镜在同一平面内(平面镜俯仰方位可调),后足在前两足刀口的中垂线上。
金属丝杨氏弹性模量的测定及其实验数据

金属丝杨氏弹性模量的测定及其实验数据【实验目的】1.学习静态拉伸法测金属丝的杨氏模量。
2.掌握用光杠杆法测量微小长度变化的原理和方法。
3.利用有效的多次测量,及相应处理方法来减小误差。
【实验仪器】杨氏模量测量仪,光杠杆,望远镜尺组,米尺,游标卡尺【实验原理】根据胡克定律,金属丝的杨氏弹性模量, L是一个微小长度变化量,当金属丝直径为0.5毫米时, L约为10-5米。
实验中采用光杠杆镜尺法测量。
利用光杠杆镜尺法由几何原理可得,光杠杆的放大倍数为β=2D/b,一般D=1.5—2.0米,b=7.0厘米,所以放大倍数约为40倍。
通过在增加(减)砝码的同时测出标尺读数Xi和其他的长度量L、D、d、b,就能求得金属丝的杨氏弹性模量Y. 【实验内容】1.调整支架,使金属丝处于铅直位置2.调光杠杆和望远镜,使能在望远镜中看清标尺像,并无视差。
3.通过增减砝码,测出相应的标尺读数Xi′和Xi″(共加五个砝码),由Xi= Xi′/ Xi″,用逐差法求出?Xi。
重复一次。
4.测出L、D、d、b,重复六次,求出杨氏模量,【注意事项】1.仪器一经调好,测量开始,切勿碰撞移动仪器,否则要重新调节,老师检查数据前也不要破坏调节好的状态,否则一旦有错误,将难以查找原因或补作数据。
2.望远镜、光杠杆属精密器具,应细心使用操作。
避免打碎镜片,勿用手或他物触碰镜片。
3.调节旋钮前应先了解其用途,并预见到可能产生的后果或危险,不要盲目乱调,以免损坏仪器,调节旋钮时也不要过分用力,防止滑丝。
4.用螺旋测微计测量钢丝直径时,要端平测微计,避免钢丝弯曲,【数据处理】1.增减重量时钢丝伸缩量的记录数【思考题】1.在本实验中,为什么可以用不同精确度的量具测量多种长度量?为什么有些需要多次测量,有些单次测量就可以?2. 如何用十几个砝码即快又精确地测量出金属丝的平均伸长量,应该用什么方法来计算?3.光杠杆法可测微小长度变化,其主要是采用了光放大原理,放大率为β=2D/b 。
金属丝杨氏模量的测定实验报告

金属丝杨氏模量的测定实验报告实验报告金属丝杨氏模量的测定一、实验目的通过实验测定金属丝的杨氏模量,掌握杨氏模量的测定方法及其原理。
二、实验原理杨氏模量是材料的一种物理量,它是表征材料在受力情况下的刚度。
杨氏模量越大,表明力作用下材料变形越小,其刚度越大。
杨氏模量的测定方法一般采用悬线法或悬挂法,本实验采用的是悬线法。
实验原理如下:当金属丝受外力作用时,形成一个悬挂状态,其自身重力受到张力的平衡,成为拉伸状态。
设金属丝的直径为d,长度L,所加载重物的重量为F,则金属丝所受拉力为F,而张力均匀分布在金属丝的横截面上,张力大小为F/π(d/2)^2。
令金属丝的长度为L0,其自身重量为G,则金属丝在外力作用下的总长度L为L0+δ,δ为金属丝的伸长量。
根据胡克定律,当金属丝受到张力时,其伸长量与张力成正比。
则有:δ=(FL0)/AEl其中A是金属丝的截面积,E为杨氏模量,I为金属丝的惯性矩。
从上述公式可以得到:E=FL0/δAI在实验中,由于金属丝受到外力的作用会有摆动,会引起对实验结果的影响,因此需要仔细控制稳定性。
三、实验步骤1. 将衡盘放在支架上,将经过钩子的紫铜丝绳穿过轮子,将两端悬挂在衡盘钩子上,轻轻震动衡盘,使丝绳震动到稳定位置,将衡盘调整至HorizonTal水平。
2. 当稳定之后,开启溶液灯,扯动指示灯片的变压器,使其显出最明亮的横向梯纹,然后调整可调光圈,调整至红、绿烛强度相等。
这时就得到成功的平面梯纹。
3. 用高清显微镜读取最上面一篇横向梯纹上下测线之差h1和水准仪板上面的读数H1。
4. 加上适当载荷,然后用高清显微镜读取最下面一篇横向梯纹上下测线之差h2和水准仪板上面的读数H2。
5. 改变重物的质量,重复上述操作,每递增一定量,再读一次上下两个梯纹的位移离差和水准仪的读数,使绘出不同载荷下的荷载荷距图。
6. 根据实验数据求出图像中 e 及 L 的数值,代入E=FL/δAI 计算得杨氏模量。
金属丝杨氏模量的测定

金属丝杨氏模量的测定实验报告【实验目的】1. 学会测量杨氏模量的一种方法,掌握“光杠杆镜”测量微小长度变化的原理。
2. 学会用“对称测量”消除系统误差。
3. 学习如何依实际情况对各个测量量进行误差估算。
4. 练习用逐差法和作图法处理实验数据。
【实验仪器】杨氏模量仪测量仪、钢卷尺、螺旋测微器、望远镜(附标尺)、游标卡尺、砝码等。
【实验原理】(一)、设金属丝的原长L ,横截面积为S ,沿长度方向施力F 后,其长度改变ΔL ,则金属丝单位面积上受到的垂直作用力F/S 称为正应力,金属丝的相对伸长量ΔL/L 称为线应变。
实验结果指出,在弹性范围内,由胡克定律可知物体的正应力与线应变成正比,即LL E S F ∆= (1) 则LS FL E ∆= (2) 比例系数即为杨氏弹性模量。
国际单位制单位为-2m ⋅N 。
在它表征材料本身的性质,越大的材料,要使它发生一定的相对形变所需要的单位横截面积上的作用力也越大。
本实验测量的是钢丝的杨氏弹性模量,如果钢丝直径为,则可得钢丝横截面积则(2)式可变为 Ld FL E ∆=24π (3)可见,只要测出式(3)中右边各量,就可计算出杨氏弹性模量。
式中(金属丝原长)可由米尺测量,(钢丝直径),可用螺旋测微仪测量,F (外力)可由实验中钢丝下面悬挂的砝码的重力F=求出,而ΔL 是一个微小长度变化(在此实验中 ,当L ≈1m时,F 每变化1kg 相应的ΔL 约为0.3mm)。
因此,本实验利用光杠杆的光学放大作用实现对钢丝微小伸长量ΔL 的间接测量。
(二)、尺读望远镜和光杠杆组成测量系统。
光杠杆系统是由光杠杆镜架与尺读望远镜组成的。
光杠杆结构实际上是附有三个尖足的平面镜。
三个尖足的边线为一等腰三角形。
前两足刀口与平面镜在同一平面内(平面镜俯仰方位可调),后足在前两足刀口的中垂线上。
尺读望远镜由一把竖立的毫米刻度尺和在尺旁的一个望远镜组成。
将光杠杆和望远镜放置好,按仪器调节顺序调好全部装置后,就会在望远镜中看到经由光杠杆平面镜反射的标尺像。
金属丝杨氏模量的测定

金属丝杨氏模量的测定金属丝杨氏模量的测定是一个重要的物理实验,它用来测量金属材料的弹性性质。
杨氏模量是一个表征材料刚度的物理量,它反映了材料在弹性范围内变形时的抵抗力。
杨氏模量的测定对于金属丝的性能评估以及材料科学的深入研究都具有重要意义。
一、实验原理杨氏模量是指在线性弹性范围内,垂直于材料轴向的单位面积上所承受的拉伸力与材料伸长量之比。
数学表达式为:E = σ / ε其中,E为杨氏模量,σ为应力(单位面积上所承受的拉伸力),ε为应变(材料的伸长量)。
二、实验步骤1.样品准备:选取一段金属丝,长度约数十厘米,直径约数毫米。
用细线将金属丝悬挂起来,让其自然下垂。
2.测量初始长度:使用测量显微镜或读数显微镜,测量金属丝的自然下垂长度(原始长度)。
3.加荷:通过砝码或压力器将一定的重力施加于金属丝的下端,使其产生拉伸形变。
根据所施加的重力,可以计算出应力和应变的关系。
4.测量形变:使用测量显微镜或读数显微镜,测量金属丝在重力作用下的伸长量。
5.数据记录:将不同重力的拉伸形变数据记录在表格中,用于后续的数据分析和处理。
6.数据分析:利用实验数据计算金属丝的杨氏模量。
三、数据处理根据实验数据,利用线性拟合的方法,将应力和应变的关系绘制在直角坐标系中,得到一条直线。
该直线的斜率即为金属丝的杨氏模量。
四、误差分析在实验过程中,可能存在以下误差来源:1.测量误差:由于测量显微镜或读数显微镜的精度限制,可能导致对金属丝长度和伸长量的测量存在误差。
可以通过使用更高精度的测量设备来减小这种误差。
2.加荷误差:由于砝码或压力器的重力不准确,可能导致对金属丝应力的测量存在误差。
可以通过使用更高精度的加荷设备来减小这种误差。
3.环境误差:环境温度和湿度的变化可能影响金属丝的力学性能,从而产生误差。
为了减小这种误差,实验过程中应保持稳定的实验环境。
4.操作误差:由于实验操作不当(如金属丝放置不直、受力不均匀等),可能导致实验结果存在误差。
大学物理实验-金属丝的杨氏弹性模量的测量

大学物理实验-金属丝的杨氏弹性模量的测量实验目的:1. 掌握金属丝杨氏弹性模量的测量方法。
2. 加深对杨氏弹性模量的了解。
实验原理:杨氏弹性模量是描述固体材料在轴向拉伸时所表现出来的弹性和形变特性的物理量。
弹性模量表示单位面积上在轴向拉伸应力与相应的应变之间的比值。
在弹性极限以内,应力和应变成正比关系,弹性模量即为斜率。
实验步骤:1. 实验仪器:万能试验机、金属丝、游标卡尺、千分尺、比重大约为水的液体、密度计、小刻度尺。
2. 将金属丝卷绕在试验机的夹具上,并调整夹具间距使其长度充分展开。
3. 利用游标卡尺测量金属丝的直径,取3个位置进行测量,取平均值做准确度提高。
4. 将金属丝悬挂在试验机上,处于自重状态。
5. 连接数字万用表,用微调盒调整滑动器位置。
6. 微调座向上调节送电触点,金属丝受拉后试验机起始点的值就被纪录下来了。
7. 通过调节位移控制器上的微调座,使其向下缓慢移动,以强制拉伸金属丝,使其长度发生变化。
8. 根据数字万用表读数,可以计算出不同负载下金属丝伸长量的数据。
9. 根据相关公式,计算出金属丝的杨氏弹性模量值。
1. 利用游标卡尺测量金属丝直径,取平均值为$D_{av}$。
2. 量测每个加权的载荷方法下的金属丝的伸长量,分别纪录数据。
3. 计算出每个载荷下的金属丝的应力和应变。
4. 作出载荷和伸长量的关系曲线并求出其斜率$S$。
5. 利用公式$S = \dfrac {4FL}{\pi D^2 d}$求出弹性模量$E$。
6. 汇总数据并作出数据汇总表。
实验数据:金属丝数量:1根金属丝直径:$D_{av}=0.0985cm$金属丝的长度 $L=60.00cm$金属丝的密度:$\rho=8.96g/cm^3$负载(N)伸长量(mm)应力(Pa)应变($10^{-3}$)0 0 0 0100 0.17 13196440 6200 0.34 26392879 12300 0.57 39589319 18400 0.79 52785758 23500 1.02 65982197 29600 1.24 79178637 35实验结果:通过数据处理可以得到如下结果:弹性模量 $E = 1.12 \cdot 10^{11} N/m^2$讨论和结论:在本实验中,我们学习了如何测量金属丝的杨氏弹性模量。
金属丝杨氏模量的测量实验报告

金属丝杨氏模量的测量实验报告一、实验目的1、学会用伸长法测量金属丝的杨氏模量。
2、掌握光杠杆放大原理和测量微小长度变化的方法。
3、学会使用游标卡尺、螺旋测微器等测量长度的工具。
4、学习数据处理和误差分析的方法。
二、实验原理1、杨氏模量的定义杨氏模量是描述固体材料抵抗形变能力的物理量。
对于一根长度为L、横截面积为 S 的金属丝,在受到沿长度方向的拉力 F 作用时,伸长量为ΔL。
根据胡克定律,在弹性限度内,应力与应变成正比,即:\F = Y \times \frac{\Delta L}{L} \times S\其中,Y 就是杨氏模量。
2、光杠杆放大原理本实验中,由于金属丝的伸长量ΔL 非常小,难以直接测量,因此采用光杠杆放大法进行测量。
光杠杆是一个带有三个尖足的平面镜,前两尖足放在一个固定的平台上,后尖足放在一个可移动的小平台上,小平台与金属丝的下端相连。
当金属丝伸长或缩短时,小平台会随之升降,带动光杠杆转动一个微小的角度θ。
通过望远镜和标尺,可以测量出光杠杆转动前后标尺的读数变化Δn,从而计算出角度θ 的变化。
根据几何关系,有:\\tan \theta \approx \theta =\frac{\Delta n}{D}\其中,D 为光杠杆平面镜到标尺的距离。
又因为:\\Delta L =\frac{b}{2} \times \theta\其中,b 为光杠杆后足到两前足连线的垂直距离。
联立上述式子,可得:\\Delta L =\frac{b \times \Delta n}{2D}\将其代入杨氏模量的表达式,可得:\Y =\frac{8FLD}{S\pi d^2 \Delta n b}\其中,d 为金属丝的直径。
三、实验仪器1、杨氏模量测定仪2、光杠杆及望远镜尺组3、螺旋测微器4、游标卡尺5、砝码6、米尺四、实验步骤1、调整仪器(1)将杨氏模量测定仪放在水平桌面上,调节底座上的三个调节螺丝,使立柱铅直。
物理实验报告金属丝杨氏模量的测定

实验名称:金属丝杨氏弹性模量的测定一、引言:金属杨氏弹性模量是反映物体在受外力作用下发生形变难易程度的重要物理量。
二、实验目的:1.学会用光杠杆法测量杨氏弹性模量;2.掌握光杠杆法测量微小伸长量的原理;3.学会用逐差法处理实验数据;三、实验原理:在外力作用下,固体所发生的形状变化成为形变。
它可分为弹性形变和塑性形变两种。
本实验中,只研究金属丝弹性形变,为此,应当控制外力的大小,以保证外力去掉后,物体能恢复原状。
最简单的形变是金属丝受到外力后的伸长和缩短。
金属丝长L,截面积为S,沿长度方向施力F后,物体的伸长L,则在金属丝的弹性限度内,有:F S =Y?LL0,Y=FL0S?L.我们把Y称为杨氏弹性模量,单位N/m2S=14πd2,则有Y=4FLπd2?L如上图:tanθ≈θ=?L b ,tan2θ≈2θ=|n 2−n 1|D =?nD 解出:?L =b2D ?n四、实验仪器:杨氏弹性模量测量仪,螺旋测微器,游标卡尺,钢卷尺,望远镜五、实验内容:仪器调整加重2kg 杨氏弹性模量测定仪底座调节水平;平面镜镜面放置与测定仪平面垂直;将望远镜放置在平面镜正前方左右位置上;粗调望远镜:将镜面中心、标尺零点、望远镜调节到等高,望远镜上的缺口、准星对准平面镜中心,并能在望远镜上方看到尺子的像;细调望远镜:调节目镜焦距能清晰的看到叉丝,并先调节物镜焦距找到平面镜,然后继续调节物镜焦距并能看到尺子清晰的像。
测量计下加重2kg 时刻度尺的读数0n ;依次挂上kg 1的砝码,七次,计下7654321,,,,,,n n n n n n n ;依次取下kg 1的砝码,七次,计下'7'65'4'3'2'1,,,,,,'n n n n n n n ;用米尺测量出金属丝的长度L (两卡b口之间的金属丝)、镜面到尺子的距离D ;用游标卡尺测量出光杠杆x 、用螺旋测微器测量出金属丝直径d 。
测金属丝的杨氏模量

测金属丝的杨氏模量对固体来说,弹性形变可分为四种:①伸长或压缩的形变(应变);②切向形变(切变);③扭转形变(扭变);④弯曲形变。
杨氏弹性模量是描述固体材料抵抗形变的能力的物理量,它与固体材料的几何尺寸无关,与外力大小无关,只决定于金属材料的性质,它的国际单位为:牛/米^2(N/m^2),它是表征固体材料性质的重要物理量,是选择固体材料的依据之一,是工程技术中常用的参数。
杨氏模量的测量方法很多,现总结出以下几种常用方法:1、万能试验机法:在万能试验机上做拉伸或压缩试验,自动记录应力和应变的关系图线,从而计算出杨氏弹性模量。
2、静态拉伸法:它适用于有较大形变的固体和常温下的测量。
缺点是:①因为载荷大,加载速度慢,含有驰豫过程。
所以它不能很真实地反映出材料内部结构的变化。
②对脆性材料不能用拉伸法测量;③不能测量材料在不同温度下的杨氏弹性模量。
3、动态悬挂法:将试样(圆棒或矩形棒)用两根线悬挂起来并激发它作横向振动。
在一定条件下,试样振动的固有频率取决于它的几何形状、尺寸、质量以及它的杨氏弹性模量,如果我们在实验中测出了试样在不同温度下的固有频率,就可以算出试样在不同温度下的杨氏弹性模量。
此法克服了静态拉伸法的缺点,具有实用价值,是国家标准规定的一种测量方法。
在本实验中,采用静态拉伸法。
基本原理如下:一根粗细均匀的金属丝,长度为L,截面积为S。
将其上端固定,下端悬挂砝码。
于是,金属丝受外力F作用而发生形变,伸长了ΔL,比值F/S是金属丝单位面积上的作用力,称为胁强(正应力);比值ΔL/L是金属丝的相对伸长,称为胁变(线应变)。
根据虎克定律,金属丝在弹性限度内,它的胁强与胁变成正比,即F/s=EΔL/L式中比例系数Y就是杨氏弹性模量。
由于伸长量ΔL的值很小,用一般量具不易测准。
本实验采用光杠杆望远镜尺组进行放大测量(简称光杠杆放大法)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
α1S1 (T1
− T20 ) n2 − T10 ) n1
若两种金属样品的形状和尺寸都大致基本相同,则可认为 S1 = S2 ;若两种样品的表面状况也基本相
同(如涂层、色泽等),又处于同一环境中进行观察,那么周围介质(空气)的性质当然也相同,则可认
为α1 = α 2 , n1 = n2 。于是,当周围介质温度不变(即室温 T10 = T20 = T0 恒定),而两种样品又处于相同 温度 T1 = T2 = T 时,上式可简化为如下形式:
4
5
6
7
8
9 10
温度 T(℃)
时间 t(分) 11 12 13 14 15 16 17 18 19 20 21
温度 T(℃)
时间 t(分) 22 23 24 25 26 27 28 29 30
温度 T(℃)
表二:铝盘散热数据记录
m2 =_______g
时间 t(分) 0
1
2
3
4
5
6
7
8
9 10
温度 T(℃)
实验要点
1. 把加热盘放到隔热板上,设定加热盘加热所需的温度值(70℃),然后再把温度指示选择换档开关旋至 “加热盘温度”档,使加热盘加热到 70℃左右。
2. 记录铜盘和铝盘的质量分别为 m1 和 m2 。 3. 测量标准铜盘在温度 T =50℃时的自然冷却速率:
加热标准铜盘,当标准铜盘温度上升到 60℃左右时,让标准铜盘通过外表面直接向环境散热(自然冷 却)。记录铜盘的散热情况(记录铜盘散热温度区间 55℃-45℃,记录起始时刻为 t=0 时刻,每隔一分钟记 录一个数据) 4. 测量待测铝盘在温度 50℃附近的自然冷却速率:
(1)
式中, c1 为该金属样品在温度 T1 时的比热容。又根据牛顿冷却定律有:
ΔQ Δt
= α 1S1 (T1
− T10 ) n1
(2)
式中,α1 为热交换系数, S1 为该样品外表面的面积, n1 为与周围介质的状况有关的系数, T1 为金属
样品的温度, T10 为周围介质的温度。由式(1)﹑(2),可得:
确定度为:
E = cAl − c2 ×100% = _________
c Al
误差分析及讨论
加热待测铝盘,当待测铝盘温度上升到 60℃左右时,让待测铝盘通过外表面直接向环境散热(自然冷 却)。记录铝盘的散热情况(记录铝盘散热温度区间 55℃-45℃,记录起始时刻为 t=0 时刻,每隔一分钟记 录一个数据)
数据处理
1. 表一:铜盘散热数据记录
m1 =_______g
时间 t(分) 0
1
2
3
c1 m1
ΔT1 Δt
= α1S1 (T1 − T10 ) n1
(3)
同理,对质量为 m2 、比热容为 c2 的另一种金属样品,可有同样的表达式:
c2 m2
ΔT2 Δt
= α 2 S2 (T2
− T20 )n2
(4)
由式(3)﹑(4),可得:
c2
=
c1
m1
ΔT1 Δt
α 2S2
(T2
m2
ΔT2 Δt
时间 t(分) 11 12 13 14 15 16 17 18 19 20 21
温度 T(℃)
时间 t(分) 22 23 24 25
温度 T(℃)
2.根据所记录数据作出散热铜盘及铝盘的散热冷却曲线(T∼t 图)。
3.根据铜盘及铝盘的散热冷却曲线分别求出铜盘及铝盘在温度 50℃附近的冷却速率 ΔT1 和 ΔT2 。 Δt Δt
实验目的 实验原理 实验仪器及图片 实验要点 数据处理
冷却法测量金属比热容
实验目的
1. 了解金属的冷却速率和它与环境之间温差的关系。 2. 学会用冷却法对金属的比热容进行测量。
实验原理
比热容是物质的一种属性。单位质量的物质,其温度每升高(或降低)1K(或 1℃)所需吸收(或放出)
的热量叫做该物质的比热容。任何物质都有自己的比热容,其值大小会随物质温度的高低而发生变化。
将质量为 m1 的金属样品加热后,放到较低温度的介质(例如室温的空气)中,样品将会逐渐冷却。
由于金属样品的直径和厚度都很小,而导热性能又很好,所以可认为样品各处的温度相同,则其在单位时
间内的热量损失(△Q/△t)应与其温度下降速率(△T1/△t)成正比,满足如下关系式:
ΔQ Δt
=
c1 m1
Δ T1 Δt
4.已知铜在 50℃时的比热容为: ccu = 393 J (Kg⋅o C) ,求出铝盘在温度 T =50℃时的比热容 c2 。源自c2=c1
m1 m2
Δ T1
Δt ΔT2
Δt
= _________
5. 已知铝在 50℃时的比热容理论值为: cAl = 904J / Kg ⋅ °C ,根据以上测量结果可得本次测量的相对不
c2
=
c1
m1 m2
Δ T1
Δt ΔT2
Δt
(5)
由上式可知,如果已知标准金属样品的比热容 c1 、质量 m1 、待测样品的质量 m2 及两样品在温度 T 时
的温度下降速率之比 ΔT1 和 ΔT2 ,就可求出待测的金属比热容c2。
Δt Δt
实验仪器及图片
FT-EH-IV 数字智能化综合实验仪,测量实验装置(包括测温台,加热盘,铜盘,铝盘各一件)
