最优化工程设计
min ������
������. ������ ∇������(������������)������������ − ������ ∇������������(������������)������������ + ������ ≥ 0, ������
（1-28）
其中 Y 是设计变量，X 是状态变量。设计变量是完全独立的，状态变量是非独立的，利 用状态变量去满足约束
对于第一个目标函数和约束函数而言： 其中
（1-29）
即那个初始 X 满足约束，对于向量 X 的任何改变，必须满足 约束才是满足的。所以
进而有：
，这样，X+dX 处 （1-30）
（1-31）
输出������������，否则令W = (������������������)−1������，∇������(������������) = [������������]，其中 u 和 v 分别对应于������1和 E，如果u ≥
0，则停止迭代，输出������������；如果，u < 0，则在 u 中选择一个负分量，修正������1，得到新的矩 阵���̂���1，令������1 = ���̂���1，转到第三步；
设 是第 i 次迭代的初始点。(
（1-17） 严格满足)，我们可以找到 ：
是 在矩阵 P 下的投影。如果 ：
（1-18） 那么从 出发，沿着方向 可以找到点
（1-19）
如果 其中
那么：
（1-20） （1-21）
上式表明，目标函数的负梯度可以通过在 处的有效约束的线性组合给出。如果所有的
都是非负的，那么 Kuhn-Tucker 条件满足，迭代可以被终止。
（1-11） （1-12）
（1-13）
求解 S 得到：
（1
（1-14）
如果 S 被标准化， 不为 0，由此：
所以：
（1-15）
其中 P 就是投影矩阵。忽略常数 ，可以看出，投影矩阵将向量
（1-16） 投影到约
束向量的正交平面的相交面上。如果
是独立的，那么矩阵 N 的列向量线性无关，
则
是非奇异矩阵并可以被转置。向量 S 可以被标准化如下：
的可行点，因此所有方向都是可行方向。
（1-5）
当点 位于某一起作用约束的边界 和对应的约束函数在该点的梯度相交成钝角，即使
，为了满足上述条件，必须使方向 S （1-6）
因为约束条件定义为
的形式，所以约束函数的梯度
是指向可行
域之外的。并且在该梯度方向上约束函数的值增大得最快。故与该梯度成钝角的方向必定 是指向可行域内的可行方向。
1.3.2 理论基础
广义简约梯度法（GRG）是简约梯度法的延伸，要求
的最小值，约束为：
通过在不等式约束上添加一个非负的松弛变量，将约束转化为：
（1-25） （1-26）
由此可以将问题写做有 n+m 个变量
的形式：
（1-27） GRG 方法的算法思想是对等式约束中的变量进行消元。从理论上来说，一个方程可以 解出一个变量，可以将 n+m 个变量分为两个系列：
令������������+1 = ������������ + ������������������，k = k + 1，返回第二步。 注意：计算实践和理论分析表明，该算法可能失效或者出现锯齿现象，使算法可能收 敛很慢甚至不收敛到最优点或 K—T 点。
1.1.4 适用范围
这种方法主要对线性不等式约束较为有效，对非线性不等式约束优化问题效果不佳。
1.2.4 适用范围
这种方法主要对线性不等式约束较为有效，对非线性不等式约束优化问题效果不佳。
1.3Generalized Reduced Gradient Method 方法概述
1.3.1 算法思想
1963 年,Wolfe 将线性规划的单纯形法推广到具有非线性目标函数的问题，提出了产生 可行下降方向的另一类方法，称为即约梯度法。随后推广到求解带非线性等式约束的情 形，即现在的 Generalized Reduced Gradient Method，该方法是目前求解约束非线性最优化 问题的最有效的方法之一。
������������ (������������������ )−1 ������ 4：构造可行下降方向，令������������ = −������∇������(������������)，若‖������������‖ ≤ ������，则进行第 5 步，否则，进行
第6步 5：检查起作用的约束数，判定迭代点������������是否在可行域内部，若 M 为空则停止迭代，
最佳下降可行方向可以在满足可行条件的前提下，通过极小化目标函数的方向导数得 到。由此构成如下寻求最佳下降可行方向 S 的最优化问题：
（1-7）
上式中，
。
由于点 上的梯度
和
的目标函数和约束函数都是变量
都是已知的常数向量，所以上式中 的线性函数。因此这个问题变成了线性规划
问题。利用求解线性规划问题的单纯形算法可以方便得求出最佳下降可行方向 。
1.1.3 算法实现
1：选取初始数据，选取初始可行点������0，允许误差ε > 0，令k = 0； 2：确定起作用约束，确定点������������外起作用约束的指标集，������(������������) = |������|������������(������������) ≥ 0; ������ = 1,2 ⋯ ������
Rosen’s Gradient Projection Method 的基本思想为：当迭代点在可行域内部时，取该点 处的负梯度方向为可行下降方向；当迭代点在可行域边界上时，取该点处负梯度方向在可 行域边界上的投影产生一个可行下降方向。
1.2.2 理论基础
梯度投影算法并不通过进行线性规划求解，而是通过将目标函数的负梯度投影到当前 的有效约束上。问题描述为：
如果一些 是负的，且
则一些约束梯度 方向与
在 处的角度
是钝角，这表明这些约束虽然是有效约束但是并不应该包括在内。在使用时，当 为负
时，并不需要忽略所有的有效约束，新的矩阵 N 为：
（1-22）
由此计算投影矩阵 P：
搜索方向为：
（1-23）
（1-24）
1.2.3 算法实现
1：选取初始数据，选取初始可行点������0，允许误差允许误差ε > 0，令k = 0； 2：分解出起作用的约束，在������������处分解A = [������������12]，b = [������������12]，使得������1������������ = ������1，������2������������ = ������2 3：确定投影矩阵，令M = [������������1]，若 M 为空，则令������ = ������������，否则令������ = ������������ −
≤ ∈
0 ������(������������)的最优解（������������,
������������）
{ −1 ≤ ������������ ≤ 1, ������ = 1,2 ⋯ ������
4：构造可行下降方向，若|������������| ≤ ������，停止迭代，输出������������；否则，得到可行下降方向 ������������，进入下一步；
1.2Rosen’s Gradient Projection Method 方法概述
1.2.1 算法思想
Rosen’s Gradient Projection Method 是利用梯度的投影技巧求约束非线性规划问题最优 解的一种方法。该方法可以处理一般的非线性规划问题，但在实际上它最适宜于处理约束 条件为线性函数的非线性规划问题。在一般工程中，功能函数呈现线性状态，采用 Rosen’s Gradient Projection Method 方法能够有效的处理非线性功能函数，而且计算效率和精度 高，通用性强。
5：进行一维搜索，求解 min
0≤������≤������������������������
������(������������
+
������������������)，得到最优解������������。其中������������������������按照下式计
算：ቤተ መጻሕፍቲ ባይዱ
������������������������ = sup|������|������������(������������ + ������������������) ≥ 0, ������ = 1,2 ⋯ ������;
1.1.2 理论基础
函数在一点的梯度方向是函数在该点函数值上升得最快的方向，与梯度值成锐角的方
向是函数值上升的方向，与梯度成钝角的方向是函数值下降的方向。因此，函数在点
的下降方向就是满足以下关系的方向 S：
（1-4）
可行方向是那些指向可行域内的方向。当点 位于可行域内时，从该点出发的任意方向
S 上都必然存在满足：
3：求即约梯度，计算∇������(������������) = [∇∇������������������������������������((������������������������))]，求r {���������(���������)} = ∇������������������(������������) − (������−1������)������∇������������������(������������)
工程优化设计方法研究报告
一、三种约束方法概述
1.1 Zoutendijk’s Method 概述
工程设计的优化与控制
工程设计的优化与控制一、概述工程设计的优化与控制是指在工程设计阶段进行最优化设计和控制，以达到最佳的经济、技术和管理效益。
这是工程设计的重要组成部分，是工程质量和效率的重要保证。
二、工程设计的优化工程设计的优化指的是在设计方案中寻求最佳的选择，以达到经济、技术和管理效益的最优化。
其原则可归纳如下：1. 考虑全面。
全面地考虑设计的各个方面，如技术、质量、安全、环保和经济等，进行综合平衡，以达到最佳化设计的目标。
2. 灵活变通。
根据工程实际情况和变化，灵活变通，寻求新的最佳化方案。
3. 利用工具。
运用现代化工具和方法，如计算机仿真、优化软件等，以快速提高设计的效率和准确性。
4. 遵循规范。
遵循国家和地方的有关规范和标准，保证设计的合法性和合理性。
5. 持续改进。
通过不断地改进设计方案和工程实施方案，实现设计的优化和控制。
三、工程设计的控制工程设计的控制主要是指在设计过程中对设计方案的严格控制和管理，以确保设计质量和效率。
其原则可归纳如下：1. 设计过程的掌控。
对设计过程的各个环节进行全面掌控和管理，确保设计按照规定的流程和标准进行。
2. 设计资料的保密。
对设计资料进行保密处理，避免泄露和损失。
3. 质量控制。
通过质量控制体系，确保设计方案的质量和合理性。
4. 项目进度的控制。
对设计进度进行科学的控制和管理，以确保工程实施的顺利进行。
5. 合理预算。
对设计方案进行合理预算，避免超预算或消耗过多资源。
四、结论工程设计的优化和控制是工程设计中的重要组成部分，可以提高设计效率和设计质量，降低工程成本和风险。
因此，在工程设计中，应该注重优化和控制，提高设计的水平和经济效益。
工程设计中的优化方法教学课件PPT
（4）数学模型 建立数学模型是解决优化设计的关键 优化设计的数学模型是实际设计的数学抽象。
任何一个优化设计问题可归结为如下描述：
在给定的约束条件下，选择适当的设计变量X， 使其目标函数 f (X)达到最优值。
其数学表达式(数学模型)为
设计变量
X= (x1, x2, ···, xn)T X∈Rn
在满足约束方程
无约束优化方法的特点和适用范围
计算方法
消去 黄金分割法 法 Fibonacci
直 插值 二次插值法
接 搜
法
三次插值法
索 爬山 坐标轮换法
法
法非导
共轭方向法
数法 单纯形法
最速下降法
间 接 寻 优 法
爬山 法导数 法
共轭梯度法 牛顿法
变尺度法
特点及适用范围
黄金分割法计算过程简单，收敛较快，应用较广
二次插值法算法成熟，收敛较快，应用广。函数性态较好时， 其效果比消去法好
所用数据为：F1=120kN， F2=12kN，[σ]=140MPa
表5-1 箱形梁设计结果比铰
跨度 l(cm)
常规设计（mm）
x1
x2
x3
x4
1050 760 340 6 10 1350 880 390 6 10 1650 1010 440 6 10
优化设计(mm)
x1
x2
x3
x4
790 310 5
计算简单，占内存少，收敛慢，可靠性差，适用于维数n<10 收敛较快，可靠性较好，占用内存少，特别适用于n<10-20 的二次函数 计算简单,收敛快,效果好，适用于中小型设计问题 计算简单，占用内存少，对初始点的选择要求低。最初几步 迭代函数值下降很快，但越靠近极值点越慢。和他法混用 所用公式结构简单，收敛速度较快，要求内存量少。适用于 多维优化问题求解 算法复杂，计算是大，对初始点要求高。一定条件下收敛速 度很快。高维优化问题不宜采用 收敛速度快，稳定性好，是目前最有效的方法之一，适用于 求解多维优化问题8Βιβλιοθήκη 870 380 66
LabVIEW最优化在工程设计中的应用
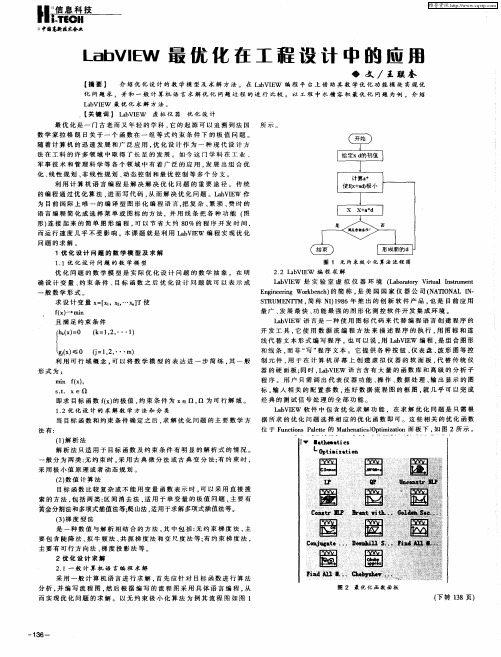
形 ） 接 起 来 的 简单 图形 编 程 ， 以 节 省 大 约 ８ ％的 程 序 开 发 时 间 ， 连 可 ０ 而 运 行 速 度 几 乎 不 受 影 响 。本 课 题 就 是 利 用 Ｌ ｂ Ｅ 编 程 实 现 优 化 ａＶＩｗ
问题 的求 解 。
１优 化 设 计 问题 的 数 学 模 型 及 求 解
器 的 硬 面 板 ： 时 ． ａＶＩＷ 语 言 含 有 大 量 的 函 数 库 和 高 级 的 分 析 子 同 Ｌｂ Ｅ 程 序 。 用 户 只 需 调 出 代 表 仪 器 功 能 、 作 、 据 处 理 、 出 显 示 的 图 操 数 输
（ （） ｇ ｘ ≤０ ｊ
形 式为 ：
（＝１２ … ｍ） ｊ ，，
（ ＝ ， ， １ ｋ １２ … ）
开 发 工 具 ， 使 用 数 据 流 编 程 方 法 来 描 述 程 序 的 执 行 ， 图 标 和 连 它 用 线 代 替 文 本 形 式 编 写 程 序 。 可 以 说 。 Ｌｂ ＩＷ 编 程 ， 组 合 图 形 也 用 ａ ＶＥ 是 和 线 条 ． 非 “ ” 序 文 本 。 它 提 供 各 种 按 钮 、 表 盘 、 形 图 等 控 而 写 程 仪 波
最 优 化 是 一 门 古 老 而 又 年 轻 的 学 科 ， 的 起 源 可 以 追 溯 到 法 国 所 示 。 它
数 学 家拉 格 朗 日关于 一 个 函 数在 一 组 等 式 约束 条 件 下 的 极值 问题 。
随 着 计 算 机 的 迅 速 发 展 和 广 泛 应 用 ， 化 设 计 作 为 一 种 现 代 设 计 方 优 法 在 工科 的许 多领 域 中取 得 了长 足的 发 展 。如 今 这 门 学 科 在 工业 、 军 事 技 术 和 管 理 科 学 等 各 个 领 域 中 有 着 广 泛 的 应 用 ， 展 出 组 合 优 发 化 、 性 规 划 、 线性 规 划 、 态控 制 和 最优 控 制 等 多个 分 支 。 线 非 动 利 用 计 算 机 语 言 编 程 是 解 决 解 决 优 化 问 题 的 重 要 途 径 。 传 统 的 编 程 通 过 优 化 算 法 ． 而 写 代 码 ． 而 解 决 优 化 问 题 。Ｌｂ ＩＷ 作 进 从 ａＶＥ 为 目 前 国 际 上 唯 一 的 编 译 型 图 形 化 编 程 语 言 ． 复 杂 、 琐 、 时 的 把 繁 费 语 言 编 程 简 化 成 选 择 菜 单 或 图 标 的 方 法 ，并 用 线 条 把 各 种 功 能 （ 图
工程结构优化设计与分析
工程结构优化设计与分析一、简介工程结构优化设计与分析是通过对结构进行综合评价和分析，优化设计和修改，提高结构的技术性能、经济性能和可靠性能，从而使结构更加安全、经济、美观和环保的工程技术方法。
它是现代工程设计的一项重要内容，对于建造保证高质量、高效率的工程具有重要意义。
二、优化设计的方法和步骤1.结构形式优化：通过对结构形式的创新，可以在不增加材料消耗的情况下提高结构强度和稳定性。
2.结构模拟：通过计算机模拟等数学方法，预测结构在不同载荷下的受力情况，以此为依据进行优化设计。
3.结构参数调整：通过对结构的材料、截面形状和尺寸等参数进行调整，使其在承受相同荷载的情况下更加合理和经济。
4.多重协同：通过结构、材料、施工工艺、设备等多方面的协同作用，提高结构质量，从而达到优化设计的目的。
三、分析方法1.有限元分析法：在结构力学中，有限元是一种处理大而复杂的结构问题的数值分析方法。
它利用计算机模拟大量离散物理元件，将其连接在一起形成整个结构，再通过计算机求解方法得到结构的应力应变分布和变形等相关参数的分析方法。
2.最优化设计方法：通过寻找结构的最优化组合方式，从而实现对结构性能和经济性的全面考虑。
这种方法一般是在给定的质量标准和经济预算下，确定结构的最优解。
3.材料试验：通过材料试验对材料进行分析，了解材料的性能和机械性质，利用这些数据作为设计的参考依据。
四、优化设计的重点1.结构强度和刚度的分析和提高。
2.结构的稳定性和可靠性的分析和优化。
3.结构的经济性和美观性等因素的考虑。
4.结构的环保性和施工的可行性的分析和优化。
五、优化设计的效果1.显著提高结构质量，使其更加安全可靠。
2.降低工程投资成本，提高经济效益。
3.优化结构形式和材料选用，减少环境污染。
4.提高施工工艺和效率，缩短建造周期。
六、结语在现代工程建设中，结构优化设计与分析已成为一项不可或缺的技术手段。
通过与其他领域的协调和共同创新，将有助于实现工程建设的高品质、高效率、低成本和可持续发展。
最优化设计
“最优化设计”是在现代计算机广泛应用的基础上发展起来的一项新技术，是根据最优化原理和方法，综合各方面的因索，以人机配合方式或用“自动探索”的方式，在计算机上进行的半自动或自动设计，以选出在现有工程条件下的最好设计方案的一种现代设计方法[1]。
实践证明，最优化设计是保证产品具有优良的性能，减轻自重或体积，降低工程造价的一种有效设计方法。
同时也可使设计者从大量繁琐和重复的计算工作中解脱出来，使之有更多的精力从事创造性的设计，并大大提高设计效率。
最优化设计方法己陆续应用到建筑结构、化工、冶金、铁路、航空、造船，机床、汽车、自动控制系统、电力系统以及电机、电器等工程设计领域，并取得了显著效果。
设计上的“最优值”是指在一定条件(各种设计因素)影响下所能得到的最佳设计值。
最优值是一个相对的概念。
它不同于数学上的极值，但有很多情况下可以用最大值或最小值来表示。
概括起来，最优化设计工作包括以下两部分内容[1]1）将设计问题的物理模型转变为数学模型。
建立数学模型时要选取设计变量，列出目标函数，给出约束条件。
目标函数是设计问题所要求的最优指标与设计变量之间的函数关系式;2）采用适当的最优化方法，求解数学模型。
可归结为在给定的条件(例如约束条件)下求目标函数的极值或最优值问题。
本章将根据前几章所提供的理论基础，以理论排量50/q ml r =、压力16MPa 、转速为1500r/min 时单位体积排量最大为目标，建立多齿轮泵优化设计的数学模型，并用C 语言编制优化设计的计算程序。
5.1 数学模型[1][11]任何一个最优化问题均可归结为如下的描述，即：在满足给定的约束条件(可行域D 内)下，选取适当的设计变量X ，使其目标函数()f X 达到最优值其数学表达式(数学模型)为：设计变量：12[...]T n X x x x = n X D E ∈⊂在满足约束条件：()0v h X = （1,2,...,v p =）()0u g X ≤ （1,2,...,u m =）的条件下，求目标函数11()()qj j f X f X ω==⋅∑的最优值。
建筑工程结构设计中的优化设计分析
建筑工程结构设计中的优化设计分析建筑工程结构设计是建筑工程的重要组成部分，它在保证建筑安全的前提下，力求在材料投入、建筑体积、施工工期等方面实现最优化设计。
优化设计是指通过分析工程设计所涉及的诸多参数输入和输出，以及不同变量之间的相互作用关系，选择最佳的方案，实现最优化的设计目的。
本文将介绍建筑工程结构设计中的优化设计分析。
1. 目标函数的确定工程结构设计中的目标函数一般是指对工程的投资成本、工程的运营维护成本、工程的使用寿命等进行综合评价的函数。
在设计变量有限且已知条件下，通过建立应力、位移等性能指标的优化模型，可以得到目标函数值，并最终实现优化设计目的。
2. 变量的选取在工程结构设计过程中，需要确定哪些变量是可以改变的，哪些变量是不可变的。
通常，可变的变量比较多，如截面形状、截面尺寸、材料类型、寿命要求等，而不可变的变量则比较少，如建筑的用途、建筑要求的稳定性等。
正确地选取变量是优化设计的前提。
3. 变量的离散化在确定变量后，需要对这些变量进行离散化处理。
离散化可以将连续的变量从连续域转换为离散域，从而方便计算。
在离散化后，可以利用已有的数学工具对变量进行分析和优化计算。
4. 可行性分析在执行优化设计时，需要对每个可行的参数组合进行验证，以确保方案的可行性。
在这个过程中，需要考虑诸如应力、变形、刚度、破坏等方面的限制条件，以及施工和运行维护的实际情况，从而得出最终的建议设计参数组合。
5. 多目标优化在实际生产中，往往需要考虑多种因素，不同的因素之间往往具有一定的矛盾性。
对于这种实际情况，可以采用多目标优化方法，通过制定不同的优化目标函数，同时考虑多种优化目的，最终得到综合最优方案。
6. 结构优化结构优化是在确定目标函数、变量选取、变量离散化、可行性分析的基础上，采用数学工具来对结构进行参数化建模、分析和优化的过程。
结构优化的本质是将结构设计问题转化为数学优化问题，利用数学分析方法进行计算分析。
什么是工程方案优化
什么是工程方案优化引言工程方案优化是指在工程设计、施工或运营过程中，通过合理的分析、比较和调整，使得工程方案的经济性、技术性、可行性以及社会环境影响达到最佳状态的一种方法。
工程方案优化可以通过调整工程设计方案，优化施工进度，提高工程质量，减少资源消耗等方式来实现。
在工程领域中，工程方案优化是一个非常重要的环节，它直接影响到工程项目的效益和可行性，也是工程技术的重要组成部分。
一、工程方案优化的内容工程方案优化主要包括工程设计方案的优化、施工方案的优化和运营方案的优化。
在不同的阶段，具体的优化内容也会有所不同。
1.工程设计方案的优化工程设计方案的优化是指通过优化工程的设计方案，来提高工程的经济性、技术性、安全性和环保性。
在工程设计的过程中，常常会有不同的设计方案可供选择，通过对比和分析这些方案的优缺点，找出最为合适的设计方案，从而实现工程项目的最佳化。
在设计方案优化的过程中，可以从工程结构、工程材料、施工工艺等方面进行调整，以达到最佳的设计方案。
2.施工方案的优化施工方案的优化主要针对工程施工过程中的安全性、效率性和质量控制进行优化。
通过对施工方案中的工序、工艺、材料选择、施工技术等进行分析和比较，找出最佳的施工方案，以提高施工效率，降低施工成本，提高工程质量和安全性。
3.运营方案的优化工程项目竣工之后，需要进行长期的运营和维护工作。
运营方案的优化主要是针对工程项目的运营管理、设备维护、效益分析等方面进行优化，从而实现工程项目的经济性、可靠性和可维护性的最佳化。
二、工程方案优化的原则在进行工程方案优化时，需要遵循一些基本的原则，以确保优化的结果符合工程项目的实际情况和需求。
1.多方案比较原则在工程方案优化的过程中，需要通过比较和分析多种不同的方案，来找出最佳的方案。
只有通过比较，才能发现各个方案的优缺点，找到最为适合的方案。
2.经济性原则工程方案的优化首先要考虑其经济性，即在满足工程项目要求的前提下，尽可能降低成本，提高效益。
工程设计优化重点(仅供参考)
根据老师最后一节课画的重点，考试总共有两种题。
一种是道40-50分的答题，另外一种是计算题。
看来看去，总体感受是难题看不会，简单题稍微看一下也不难。
个人觉得对着老师画的重点去看几个例题，过应该是没问题吧。
1.大题（40-50分）
涉及内容：
对综合优化基本思想的认识，铁路的投资模型，铁路的运营模型以及模型的约束条件。
可参考的复习资料：
王柢教授写的书《工程决策中的综合优化-以铁路为例》
老师上课用的ppt
2.具体计算
涉及内容：
最优化问题的求解方法
①用直接搜索法求解无约束非线性函数极值问题
②无约束问题的梯度解法
③罚函数法——将有约束的优化问题化成无约束的优化问题
④有约束最优化问题
可参考的复习资料：
天津大学解可新写的《最优化方法》老师上课的PPT。
工程最优化设计课程设计
工程最优化设计课程设计一、课程设计背景随着时代的变迁，工程设计也在不断地发展和进步。
然而，随着工程设计的复杂度不断提高，需要对设计方案进行有效地优化，以达到更好的效果和降低成本。
因此，需要培养具备工程最优化设计能力的工程师，来满足社会的需求。
二、课程设计目标本门课程旨在培养学生具备工程最优化设计的理论基础和实践能力，并帮助学生了解如何进行多种设计模型的最优化处理。
在课程结束后，学生将能够：•熟悉各种最优化方法，如模拟退火算法、遗传算法等；•掌握最优化理论及其应用；•能够进行实际的最优化设计项目；•能够评估设计方案，并提出有针对性的优化建议。
三、课程设计内容1.最优化理论基础–单变量函数的最大值和最小值求解–多元函数的最大值和最小值求解–约束条件下的最优化问题2.最优化方法介绍–模拟退火算法–遗传算法–粒子群算法–梯度下降法3.实际案例分析与解决–车辆行驶路径最优化设计–工业生产线的时间和资源调度优化–城市交通路网规划的最优化设计4.实践项目–学生自主选择一个工程最优化设计项目，进行实际设计和优化，并撰写完整的报告。
四、课程设计评估1.学生的平时表现（占总分20%）–课堂讨论活跃度–作业完成情况–课程笔记清晰度和完整度2.期末项目（占总分80%）–项目完成度–最优化解决方案的优越性–报告质量五、总结本门课程将为学生的职业发展提供有力的帮助，为他们以后工程最优化设计的实践提供强有力的支持。
相信在这门课程的学习中，学生将不仅拥有最新的方法和技能，还能开拓视野，加深对工程最优化设计的理解和掌握。
关于建筑设计优化合理化建议书
建筑⼯程在设计优化的过程中，我们可以提出合理化建议。
店铺为⼤家精⼼准备了建筑设计优化建议书，欢迎⼤家前来阅读。
建筑设计优化建议书篇⼀ 本⼯程的结构设计咨询⼯作是在⼯程初步设计已经完成，并经建设⾏政主管部门审批后介⼊的。
进⾏的⽅式是介⼊后的结构设计全过程控制，包括对初步设计的修改完善，对施⼯图设计过程的控制和对施⼯图成果的审核三个⽅⾯的⼯作内容。
本⼯程位于⼭东淄博，地下⼀层车库，地上⼀⼆层营业、办公，三⾄⼗⼋层住宅，框架—剪⼒墙结构，平板式筏形基础。
⼯程抗震设防类别为丙类，抗震设防烈度为7度，地震基本加速度值为0.10g，剪⼒墙抗震等级为⼆级，框架抗震等级为三级，设计使⽤年限为50年，地基基础设计等级为甲级。
本⼯程设计⽅案原为剪⼒墙结构，并已通过了建设⾏政主管部门的审查。
考虑到下部楼层为营业和办公，在咨询过程中⾸先探讨采⽤框架—剪⼒墙结构的可⾏性和优点，配合设计单位对结构⽅案进⾏了调整，由剪⼒墙结构改为框架剪⼒墙结构，并合理的⽽布置剪⼒墙和框架柱，优化了地基基础的设计⽅法，通过多次的设计计算、分析⽐较、合理调整来满⾜规范规程的⽽要求，保证结构的安全性和经济性。
在结构施⼯图设计过程中，多次与结构设计⼈员交流沟通，统⼀了设计的做法和上机计算数据，事先控制保证了结构的施⼯图设计沿着安全、合理、经济的思路进⾏，使最终的结构施⼯图成果⽂件差错少、质量优、经济性好。
施⼯图绘制完成后，对结构设计的成果进⾏了审核，并提出了审核意见。
配合设计⽅对施⼯图审查咨询中⼼的审核意见进⾏了修改，对部分审查意见与审查专家进⾏了沟通说明，修改后的施⼯图交付建设单位。
设计咨询⼯作和精益求精的结构设计保证了结构设计的技术质量和经济质量，达到了使营业、办公空间布置的⽅便合理，地下车位的增加，合理的混凝⼟⽤量，较低的⽤钢量等多⽅⾯效益。
通过结构设计的咨询优化，给投资⽅带来了很好的效益，使投资⽅⾮常满意。
建筑设计优化建议书篇⼆ ⾼层建筑项⽬投资⼤，建设周期长，对其进⾏优化设计能够有效的减少投资⾦，但是，由于设计变量、约束条件、计算量过于庞⼤的原因，⾼层建筑的结构优化设计并未有效的展开。