矩阵论系列课件09 矩阵微分方程
矩阵及其应用ppt课件

线性方程组
• 根据矩阵乘法的定义,第三页中的线性方 程组可以表示成:
• Ax = y • 其中A是第五页中的系数矩阵,x是列向量
[x1, x2, ..., xn],y是列向量[y1, y2, ..., ym]。 • 当n=m时,A是n阶方阵,如果A可逆,那么:
• x = A-1y
方阵的幂
• 已知n阶方阵A和正整数m,计算Am。其中n 不超过50,m不超过1000000。
方阵的幂(二)
• 已知n阶方阵A和正整数m,计算A1 + A2 + ... + Am。其中n不超过50,m不超过1000000。
路径计数
• 给定一个有向图,问从A点恰好经过k步 (允许多次经过同一条边)走到B点的方案 总数。图中顶点数不超过50,边数不超过 1000000。
线性递推式
已知x1, x2 ,...,xn的值和线性递推关系 xk a1xk1 a2xk2 ... an xkn , 其中k n, a1, a2,...,an是常数。对于任给的正整 数m,计算xm的值。(n不超过50,m 不超过1000000)
数乘矩阵
类似地,矩阵与数c相乘定义为cy1, ..., cym的系数所对应的矩阵:
a11 ... a1n ca11 ... ca1n c ... ... ... ... ... mn
矩阵乘法
设有如下两个方程组:
z1 a11 y1 ... a1m ym .................................. zk ak1 y1 ... akm ym 和 y1 b11x1 ... b1n xn ................................ ym bm1x1 ... bmnxn
矩阵微分方程

定解问题(4.3)的解为 y (1, 0, 0, , 0) x(t ) (1, 0, 0, , 0)e x(0) y0 y0 ' At , 0)e ( n 1) y0
At
(1, 0, 0,
n阶常系数线性非齐次方 程的定解问题: y
(n) (i )
(n) (i )
a1 y
( n 1)
a2 y
(i ) 0
( n2)
an y 0 (4.3)
y (t )
t 0
y , i 0,1,, n 1
令x1 y, x2 y ' x '1 ,
x '1 x2 , x2 ' x3 , x 'n 1 xn ,
x1n (t , t0 ) x11 (t , t0 ) x12 (t , t0 ) x (t , t ) x (t , t ) x ( t , t ) 0 22 0 2n 0 21 xnn (t , t0 ) xn1 (t , t0 ) xn 2 (t , t0 ) dx(t ) 为方程组 A(t ) x (t )的转移矩阵,有时又称它为基本矩阵。 dt 显然 (t0 , t0 ) I n
dx(t ) 性质1 n阶方阵(t , t0 )是方程组 A(t ) x(t )的转移矩阵的 dt dx(t ) A(t ) x(t ) 充要条件是(t , t0 )是定解问题 dt 的解。 x(t ) |t t I n 0
dx(t ) 性质2 设(t , t0 )是方程组 A(t ) x(t )的转移矩阵, dt dx(t ) A(t ) x(t ) 则定解问题 dt x(t ) |t t x(t0 ) 0 的解为x(t ) (t , t0 ) x(t0 )。
线性代数矩阵的分解与微分方程应用

线性代数矩阵的分解与微分方程应用线性代数是数学中的一个重要分支,它研究的是线性空间以及其上的线性变换。
线性代数在不同领域中都有广泛的应用,比如说在计算机图形学、物理学、经济学等领域中都起着非常重要的作用。
其中,矩阵的分解和微分方程的应用是线性代数的两大重要内容。
一、矩阵的分解矩阵的定义是一个由数字排成的矩形表格。
在线性代数中,矩阵是一个重要的工具,矩阵的分解是矩阵理论中的一个基本问题。
矩阵的分解通常是指将一个矩阵分解成几个特定形式的矩阵的乘积。
常见的矩阵分解包括LU分解、QR分解、SVD分解等。
1、LU分解LU分解是线性代数中的一种矩阵分解方法,可以将一个矩阵分解成一个下三角矩阵L和一个上三角矩阵U的乘积。
LU分解可以用于求解线性方程组、求矩阵的逆以及计算矩阵的行列式等问题。
在实际应用中,使用LU分解求解线性方程组比直接求解更加高效和准确。
2、QR分解QR分解是一个将一个矩阵分解成一个正交矩阵Q和一个上三角矩阵R的乘积的方法。
QR分解在求解最小二乘问题、特征值问题以及解非线性方程组等问题中都有广泛的应用。
3、SVD分解SVD分解是一种将一个矩阵分解成三个矩阵的乘积的方法,包括一个左奇异矩阵、一个右奇异矩阵和一个奇异值矩阵。
SVD分解可以用于降维、信号处理、图像处理等方面。
二、微分方程的应用微分方程是研究变化的数学分支,它研究的是变量与其变化率的关系。
微分方程在科学、工程和经济等领域中都有广泛的应用。
微分方程的解法中涵盖了矩阵分解的知识。
1、矩阵微分方程矩阵微分方程指的是方程中包含了一个矩阵与它的导数。
矩阵微分方程在控制系统、差分方程的研究中都有广泛的应用。
解矩阵微分方程时,可以使用矩阵指数函数或拉普拉斯变换等方法。
2、级数解法级数解法是一种用级数求微分方程解的方法。
在级数解法中,将未知函数表示为级数的形式,将其代入微分方程中,然后通过逐项比较系数来求解微分方程。
级数解法在近似计算和数值解法方面都有重要应用。
《矩阵论》课件 共39页PPT资料

n
x 1
xi ;
i1
1
x
2
n i1
xi
2 2
;
x
max
1 i n
xi
;
1
x
n p i 1
xi
p p ,
p1
x , x , x , x ( p 1)都是 C n上的向量范数。
1
2
p
引6理 .1.1 如 果p实 1,q数 1且111,则 对 pq
向 量 范,数1,,n为V的 一 组,V基中 任 一 向量
n
可唯一地表示为xii, x(x1,, xn)T Pn. i1
则 是x1,, xn的连续函. 数
定义6.1.2 设 , 是n维线性V空 上间 定义的 ab
种 向 量,范 如数 果 存 在 两 无个关与的 正 常
其中p 实 1,q 数 1且 111. pq
定理6.1.2(Minkowski不等式)
设 x ( x 1 , ,x n ) T ,y ( y 1 , ,y n ) T C n ,则
1
1
1
i n1xiyi p p i n1xi p p i n1yi p p
定理6.1.5 设V是 数 域 P上 的n维 线 性 空,间 1,,n 为V的 一 组,基 则V中 任 一 向可 量唯 一 地 表 示
n
xii , x (x1,, xn)T Pn.又 设 是Pn上 的
i1
向 量 范,数 令 v
x,
则 是V上的向量范. 数 v
定理6.1.6 设 是数域 P上n维线性空V上 间的任一
矩阵与常微分方程
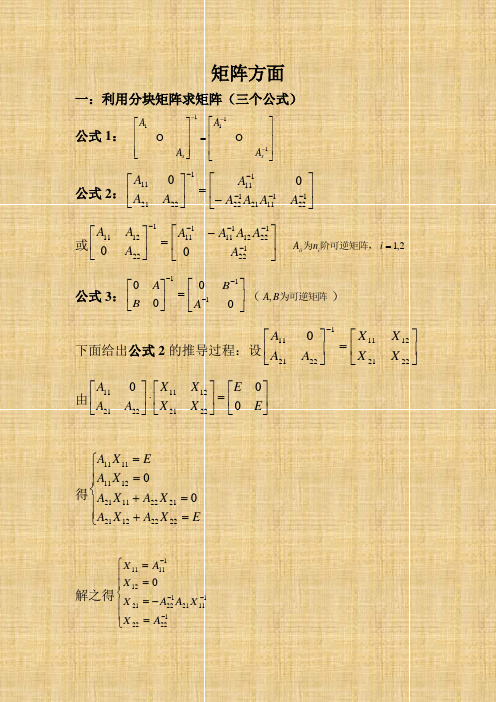
一:利用分块矩阵求矩阵(三个公式) 公式1:⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---11111s s A A A A公式2:⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡-----12211121122111122211100A A A A A A AA或⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡-----1221221211111112212110A A A A A A A A2,1=i n A i ii 阶可逆矩阵,为公式3:⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡---0000111ABBA (为可逆矩阵B A ,)下面给出公式2的推导过程:设⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡-2221121112221110X X X X A AA由⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡⋅⎥⎦⎤⎢⎣⎡E EX X X X A A A 00022211211222111得⎪⎪⎩⎪⎪⎨⎧=+=+==EXA X A X A X A X A E X A 22221221212211211211111100解之得⎪⎪⎩⎪⎪⎨⎧=-===----12222111211222112111110A X X A A XX A X^-^习题1:1,11210000520021-⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡---=A A 求 习题2:1,20120031204312-⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=A A 求答案:习题1:⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡-=-313100323100001200251A习题2:⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡------=-2100412*******2101658541211A二:利用定义求矩阵 例1:设n 阶方阵A 满足022=--E A A ,求证A 可逆并求1-A证明:由022=--E A A ,得:E E A A 2)(=-即EEA A =-⋅2,从而A 可逆且21E A A-=-例2:设B A ,为同阵且满足ABB A =+,证明E A -可逆并求其逆,BAAB =证明:BE A B AB A )(-=-=,故BE A E E A )()(-=+-从而有E E B E A =--))((即E A -可逆且EB E A -=--1)( 故))(())((E A E B E B E A --=--即EB A BA E B A AB +--=+--从而BAAB =例3:已知n 阶方阵A 满足3)(2A E A A =-,求1)(--A E证明:由3)(2A E A A =-,得02223=+-A A A所以E E A A A-=-+-2223从而有EE A A A E =+--))((2即EA A A E +-=--21)(下面就检查下自己的学习能力^-^ 习题1:设)(0为正整数k Ak=,证明:12-1)(-++++=-k AA A E A E习题2:设B A ,为n 阶方阵,且AB E -与BA E -均可逆,证明A AB E B E BA E 11)()(---+=-习题3:若n 阶方阵A 满足E A =2,求证E A 2-可逆习题4:设A A =2,试证明E A 2-为可逆阵例题1:设)(x f 为可微函数,且满足方程)0()()1()(0>+=⎰⎰x dtt tf x dt t f x xx求)(x f解:方程两边对x 求导,得:)()1()()()(0x xf x dt t tf x xf dt t f xx++=+⎰⎰化简得:⎰⎰=+xxdt t f x f x dt t tf 002)()()(两边再对)(x f 求导,化简得:0)(13)(2=-+'x f x x f x )( 这是一阶线性齐次方程,分离变量得:dx xx x f x df 231)()(-=两边积分得x xCe x f ln 31--=)(即)(13为任意常数)(C eCxx f x--=下面就检查下自己的学习能力^-^ 习题1:设连续函数)(x f 满足方程20)(2)(xdt t f x f x=+⎰,求)(x f习题2:设连续函数)(x y 满足方程⎰+=xxedt t y x y 0)()(,求)(x y答案:习题1:xex x f 22121)(-+-=习题2:x e x x y )1()(+=。
矩阵论简介及线性代数复习PPT课件

的矩阵叫做复矩阵, (1)式也简记为
A = (aij)m×n 或 A = (aij) ,
m×n 矩阵 A 也记作 Am×n .
-
16
2) 方阵 列矩阵 行矩阵
对 (1) 式, 当 m = n 时, A 称为 n 阶方阵. 当 m = 1 时, A 称为行矩阵. 当 n = 1 时, A 称为列矩阵.
n
cij aikbkj
k 1
( i = 1,2, … , s ; j = 1, 2, … , m),
AB 称为 A 与 B 的积. 设 k 为实数, 定义 kA = (kaij)
则称 kA 为 A 与数 k 的乘积.
-
22
矩阵乘法的定义源于二个线性变换的复合运算
yy21 aa1211xx11 aa1222xx22 aa1233xx33
是成立的, 即
|AB| = |A||B | = |B||A| = |BA| .
-
34
3. 若 AB = AC 能推出 B = C 吗? 答 不能. 因为矩阵的乘法不满足消去律.
例如
A 1 00 0 ,B 0 01 0 ,C 0 00 0 ,
则 AB = AC , 但 B C.
A11 A21
A*
A12
A22
A1n
A2n
An1
An2
,
Ann
叫做方阵 A 的伴随矩阵. 伴随矩阵具有重要性质: AA* = A*A =|A|E.
-
32
思考
1. 任何两个矩阵 A、B 都能进行加(减), 相乘 运算吗?
答 不是. (1) 只有当 A,B 为同型矩阵时, 才能 进行加(减)运算. (2) 只有当第一个矩阵 A 的列数与 第二个矩阵 B 的行数相同时, A 与 B 才能相乘, 这 时 AB 才存在.
矩阵论ppt

a
则称方阵范数 A 与向量范数 x a 是相容的.
4 February 2018 河北科技大学
机动 目录 上页 下页 返回 结束
矩阵论
性质:
(1 ) P n n 上的每一个方阵范数,在 P n 上都存在与它 相容的向量范数;
(2 ) P n n 上任意两种方阵范数 A a , A b 都是等价的, 即 存 在 两 个 与 A 无 关 的 正 的 常 数 C1 , C2 , 使 得 对
证
矩阵论
j H n n H n
1 H n
j 1
j 1 i 1
4 February 2018
河北科技大学
机动 目录 上页 下页 返回 结束
矩阵论
注 (1 ) F - 范数的优点之一是矩阵乘以酉矩阵U 之 后 F -范数不变,即: UA F A F AU F . 事实上:
H A ( A A); (3) 2
nn
n n Cc ,则
列模和最大者
行模和最大者
H
H
( A A) 是 A A 的最大特征值
2
(4) A
F
a
j 1 i 1
n
m
ij
tr A A ;
H
F -范数
4 February 2018
河北科技大学
机动 目录 上页 下页 返回 结束
河北科技大学
机动 目录 上页 下页 返回 结束
矩阵论
矩阵序列的极限计算具有以下性质:
设 Am 和 Bm 为两个 n阶矩阵序列
lim Am A ,则对 Cnn 中任何方阵范数 , Am 有界; (1 ) 如果 m
矩阵论系列课件 矩阵微分方程

第九讲矩阵微分方程一、矩阵的微分和积分1.矩阵导数定义:若矩阵ij m ×n A(t)=(a (t))的每一个元素a (t)ij 是变量t 的可微函数,则称A(t)可微,其导数定义为'ij m ×n da dA=A (t)=()dt dt由此出发,函数可以定义高阶导数,类似地,又可以定义偏导数。
2.矩阵导数性质:若A(t),B(t)是两个可进行相应运算的可微矩阵,则(1)d dA dB[A(t)±B(t)]=±dt dt dt(2)d dA dB [A(t)B(t)]=B +A dt dt dt (3)d da dA[a(t)A(t)]=A +a dt dt dt (4)()()()()()()()t A t A t Ad dde =A e =e Ac o s t A =-A s i n t A s i n t A =A c o s t Ad td t d t(A 与t 无关)此处仅对tA tA tAd (e )=Ae =e A dt加以证明证: tA 2233223d d 111(e )=(I+tA +t A +t A +)=A +tA +t A +dt dt 2!3!2!22tA1=A(I+tA+t A +)=Ae 2!又22tA 1=(I+tA+t A +)A=e A 2!3.矩阵积分定义:若矩阵A(t)=(a (t))m ×n ij的每个元素ij a (t)都是区间01[t ,t ]上的可积函数,则称A(t)在区间01[t ,t ]上可积,并定义A(t)在01[t ,t ]上的积分为⎛⎫⎰⎰ ⎪⎝⎭1100ij t t A(t)dt =a (t)dt t t m ×n4.矩阵积分性质(1)⎰⎰⎰111t t t t t t [A(t)±B(t)]dt =A(t)dt±B(t)dt(2)⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎰⎰⎰⎰11110000t t t t t t t t [A(t)B]dt =A (t)dt B,[AB(t)]dt =A B(t)dt (3)'''⎰⎰t ba adA(t )dt =A(t),A (t)dt =A(b)-A(a)dt 二、阶线性齐次常系数常微分方程组设有一阶线性其次常系数常微分方程组⎧⎪⎪⎪⎪⎨⎪⎪⎪⎪⎩ 11111221n n 22112222n n n n11n22nn ndx =a x(t)+a x (t)++a x (t)dt dx =a x(t)+a x (t)++a x (t)dt dx =a x(t)+a x (t)++a x (t)dt式中t 是自变量,i ix =x(t)是t 的一元函数 ij (i=1,2,,n),a (i,j=1,2,,n)是常系数。
矩阵论课件

第一讲线性空间一、线性空间的定义及性质[知识预备]★集合:笼统的说是指一些事物(或者对象)组成的整体集合的表示:枚举、表达式集合的运算:并(),交()另外,集合的“和”(+):并不是严格意义上集合的运算,因为它限定了集合中元素须有可加性。
★数域:一种数集,对四则运算封闭(除数不为零)。
比如有理数域、实数域(R)和复数域(C)。
实数域和复数域是工程上较常用的两个数域。
线性空间是线性代数最基本的概念之一,也是学习现代矩阵论的重要基础。
线性空间的概念是某类事物从量的方面的一个抽象。
1.线性空间的定义:设V是一个非空集合,其元素用x,y,z等表示;K是一个数域,其元素用k,l,m等表示。
如果V满足[如下8条性质,分两类](I)在V中定义一个“加法”运∈时,有唯一的和算,即当x,y V+∈(封闭性),且加法运算x y V满足下列性质(1)结合律()()++=++;x y z x y z(2)交换律 x y y x +=+;(3)零元律 存在零元素o ,使x +o x =;(4)负元律 对于任一元素x V ∈,存在一元素y V ∈,使x y +=o ,且称y 为x 的负元素,记为(x -)。
则有()x x +-= o 。
(II )在V 中定义一个“数乘”运算,即当x V ∈,k K ∈时,有唯一的kx V ∈(封闭性),且数乘运算满足下列性质(5)数因子分配律()+=+;k x y kx ky(6)分配律()+=+;k l x kx lx(7)结合律()()=;k lx kl x=;(8)恒等律1x x [数域中一定有1]则称V为数域K上的线性空间。
注意:1)线性空间不能离开某一数域来定义,因为同一个集合,如果数域不同,该集合构成的线性空间也不同。
(2)两种运算、八条性质数域K中的运算是具体的四则运算,而V中所定义的加法运算和数乘运算则可以十分抽象。
(3)除了两种运算和八条性质外,还应注意唯一性、封闭性。
唯一性一般较显然,封闭性还需要证明,出现不封闭的情况:集合小、运算本身就不满足。
矩阵理论课程介绍.ppt

、数乘.
轾犏犏犏犏犏犏犏臌xxxMn21
每个分量是实 数
处理器:m xn矩阵 骣 çççççççç桫aamM111
L M L
a1n M
am 3
÷÷÷÷÷÷÷÷÷
每个分量是实 数
本科线性代数
研究:由n维实矢量组成的欧式空间和其上的变换/映 射。
矩阵理论
处理对象:线性空间(欧式空间、多项式、函数、实 数、复数、矩阵等)
主要内容
矩阵理论和本科线性代数有什么区别? 为什么电气工程(EE)需要矩阵理论? 课程安排 本科线性代数的回顾
本科线性代数
处理系统(DSP/控制器/电路)
轾犏x 1 犏犏x 2 犏犏M 犏犏臌x n
骣 çççççççç桫aamM111
L M L
a1n M
am 3
÷÷÷÷÷÷÷÷÷
轾犏犏犏犏犏犏犏臌yyyMn21
输入
输出
将向量理解为被处理的对象
例如:信号、控制量/被控制量、参数向量等
将矩阵理解为处理装置
例如:数字信号处理器、线性控制器、图像降噪算法、线 性电路等
矩阵有多少列,输入就有多少分量,矩阵有多少行, 输出就有多少分量。
本科线性代数
处理对象:n维向量(欧式空间中),代数运算:加
参考书籍
教材:刘西奎,矩阵分 析讲义,2006.
参考书:
刘丁酉. 矩阵分析. 武汉大 学出版社, 武汉, 2003.
董增福. 矩阵分析教程. 哈 尔滨工业大学出版社. 哈 尔滨, 2005.
张明淳. 工程矩阵理论. 东 南大学出版社. 1999。
参考书籍
David, C. Lay. Linear Algebra and Its Applications (3rd). 电子工业出版社. 2004 (中文版、英文版)
矩阵法求解微分方程组

矩阵法求解微分方程组在数学的世界里,有一个神奇的地方,那就是微分方程组。
听上去就像个高深莫测的术语,对吧?其实这就像一场探险,特别是用矩阵法去解这些方程的时候,简直像打开了一个新世界。
想象一下,微分方程组就像一群小朋友在操场上追逐打闹,每个小朋友都有自己的个性和特点,他们有时候会一起玩,有时候又会分开。
但是一旦我们用矩阵这个大玩具把他们聚在一起,哇,事情就变得简单多了。
咱们得搞清楚什么是矩阵。
矩阵就像是一张表格,上面摆满了数字。
看上去有点复杂,其实它就像我们每天用的购物清单,只不过这里面装的不是苹果和香蕉,而是方程的系数。
对了,矩阵的每一行每一列都可以看作是微分方程组中的一个方程,简直是一目了然。
用矩阵把这些方程整理在一起,就像把那些小朋友们排成整齐的队伍,马上就显得有条理多了。
我们来聊聊如何用矩阵法求解这个微分方程组。
步骤其实不复杂。
把方程转化成矩阵的形式。
听上去好像是个数学魔法,其实就是把各个方程的系数和变量按照一定的规则摆在一起。
比如,假设你有两个方程,像“y' = 2x + 3”和“z' = 4y + 5”,那么就可以把它们整理成一个大矩阵。
这样,咱们就把问题浓缩成了一张图表,看着舒服多了。
矩阵法的“主角”就是特征值和特征向量。
说到特征值,那可是个大咖!它决定了整个系统的行为。
特征值就像是那些小朋友的性格,有的活泼好动,有的安静内敛。
不同的特征值会导致方程组的解有不同的表现,就像小朋友们的游戏风格,千奇百怪,各有特色。
通过计算特征值,我们可以了解到系统的长远趋势,是朝着繁荣昌盛的方向,还是走向凋零的边缘。
然后,咱们还得求解特征向量。
这个过程就像是在找合适的搭档,谁和谁在一起最默契。
特征向量能告诉我们,如何从特征值出发,找到具体的解。
也就是说,特征向量会为我们指明道路,让我们在解的海洋中找到方向。
通过这些特征值和特征向量的组合,我们就能把微分方程组的解找出来,真是令人惊喜!如果你觉得这些步骤听上去太复杂,不用担心,实际操作起来并没有想象中那么麻烦。
矩阵论课件

P 是数域, 若 n是正整数, 则系数属于 P 而未知元为 x 的
所有次数不超过 n 的多项式的集合,此集合连同零多 项式在内按通常多项式的加法及数与多项式的乘法, 构成数域 P 上的一个线性空间全体记作: Pn [ x ].
4 December 2014 河北科技大学
机动 目录 上页 下页 返回 结束
, t 可以由1 , 2 ,
, s 线性表
, t 线性相关.
推论1 若 1 , 2 ,
, t 可 以 由 1 , 2 ,
, s 线 性 表 示 , 且
1 , 2 , , t 线性无关,则 t s .
推论2 若 1 , 2 ,
, t 与 1 , 2 , , s 等 价 ,且 均 线性 无
实数域 R 上的线性空间简称为实线性空间; 复数域 C 上的线性空间简称为复线性空间.
下面看几个线性空间的例子.
4 December 2014
河北科技大学
机动 目录 上页 下页 返回 结束
矩阵论
例1 若 P= 是数域,V 是分量属于 P= 的 n元有序数组的集合
V a1 , a2 ,
, an | ai P,i 1, 2,
矩阵论
例4 所有定义在区间 a , b a t b 上的实值连续
函数全体构成的集合, 按照函数的加法及数与函数 的数量乘法,构成实数域 R 上的一个线性空间,记 作: R a , b .
例5 实(复)系数齐次线性方程组 Ax 0( A R mn
或 C mn ; x R n 或 C n ;行向量和列向量不做区别) 的解空间 S 构成 R 或C 上的一个线性空间.
才成立,称 x1 , x2 ,
矩阵论简明教程整理全PPT课件

k
ei
e
H j
E ei , ej , k
第45页/共188页
Remark
det E u,v, det In uvH det 1 vHu
1 vHu (由n Im AB m In BA 得到)
第46页/共188页
四、其他特殊矩阵
1幂零矩阵:Ak 0, k : 某正整数; 2幂等矩阵:A2 A; 3 实对称正定矩阵:
a a jn 1 j1 2 j2
anjn
j1 j2 jn
第13页/共188页
二、块矩阵的行列式
1、设A Cmm , B Cmn , C Cnm , D Cnn , 则
1 A
0A
BA
0 AD
0D 0D CD
2 A B 1mn C D 1mn B A
CD
AB
DC
3 A B m A B
minrank A, rank B
第30页/共188页
推论1
设ACmn , B Cnk ,且AB 0,则
rank A rank B n
第31页/共188页
§1.4 特殊矩阵
一、 几类基本的特殊矩阵
1、零矩阵,单位矩阵 2、对角矩阵
a11
D
a22
diag
a11
,
a22
,
ann
第50页/共188页
§2.1 矩阵的特征值与特征向量
一、特征值与特征向量 1、定义 定义1
设ACnn ,若存在数 C和x Cn , x 0使得 Ax x
则称是A的特征值,x称为A属于的特征向量。
第51页/共188页
2、特征多项式 定义2
设ACnn , 称In A为A的特征矩阵,称detIn A 为A的特征多项式,称detIn A 0为A的特征方程。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
则原方程组变成如下矩阵方程
dx = Ax(t) dt
其解为
x(t)= etAx(0)= etAc
对该解求导,可以验证
更一般的
x(t)= e(t-t0 )Ax(t0 )
dx(t) = AetAc = Ax(t) 且 t=0 时, x(t)= e0A c =Ic = c = x(0) dt
0
e -sA b(s) ds + c(0)
由积分性质(3)可验证 c(t)是解。
加上初始条件 x(0)= c(0),有
x(t)= e tA[x(0)+ e -sA b(s)ds]
0
t
说明:高阶常微分方程常常可以化为一阶常微分方程组来处理, 如: 令 x1 = y,x2 =
d2 y dy a 2 + b + cy = f dt dt
令
x(t)=[x(t), x2(t), , xn(t)]T 1 b(t)=[b(t), b2(t), , bn(t)]T 1 a11 a12 a a 21 22 a a n1 n2 a1n a2n ann
方程组化为矩阵方程
dx = Ax + b dt
表明 x(t)确为方程的解,积分常数亦正确
dx1 = x2 dt 例:求解微分方程组 , dx 2 = -x1 dt
x (0) r 初始条件为 1 = 1 x2(0) r2
解: A =
0
, f(A)= e -1 0
1
tA
f(λ)= etλ λ -1 2 =(λ +1)=(λ-j)(λ+j) , 1 λ
1o 求 出 A 的 特 征 多 项 式 , (λ)= j = -1
λ λ 1 = j,m1 = 1; 2 = -j,m 2 = 1
m=n=2
2o 定义待定系数的多项式 g(λ)= c0 + cλ 1 3 解方程
4. 矩阵积分性质
t1
dt = (1) [A(t)±B(t)]
t0
t1
t1
t0
A(t)dt± B(t)dt
t0
t1
t1 t1 t1 [A(t)B] dt = A(t)dt B, [AB(t)] dt = A B(t) dt (2) t0 t0 t0 t0
第九讲 矩阵微分方程
一、矩阵的微分和积分 1. 矩阵导素 a (t)是变量 t 的 ij 可微函数,则称 A(t)可微,其导数定义为
da dA = A (t)=( ij )m×n dt dt
由此出发,函数可以定义高阶导数,类似地,又可以定义偏导数。 2. 矩阵导数性质:若 A(t),B(t)是两个可进行相应运算的可微矩阵,则 (1) (2) (3) (4)
三、 一阶线性非齐次常系数常微分方程组
dx1 (t)+ +a1nxn(t)+b(t) 1 12x2 1 dt = a11x(t)+a dx2 = a21x(t)+a (t)+ +a2nxn(t)+b2(t) 1 22x2 dt dxn = a x(t)+a x (t)+ +a x (t)+b (t) n1 1 n2 2 nn n n dt
(A 与 t 无关)
此处仅对 证:
d tA (e )= AetA = etAA 加以证明 dt
d tA d 1 1 1 (e )= (I+ tA + t2A2 + t3A3 + )= A + tA2 + t2A3 + dt dt 2! 3! 2!
1 = A(I+tA+ t2A2 + )= AetA 2! 1 2 2 )A =etAA 又 =(I+tA+ t A + 2!
o
g(λ)= f(λ)= ejt = cost +jsint = c0 +jc1 1 1 g(λ)= f(λ)= e-jt = cost -jsint = c -jc
2 2 0
1
c0 = cost c1 = sint
4o
g(A)= c0I+ c1A =
cost 0 cost
采用常数变易法求解之;齐次方程的解为 etA c ,可设非齐次方程的解为
etA c(t),
代入方程,得:
dx d tA dc dc = (e )c(t)+ e tA = Ax(t)+ e tA = Ax(t)+ b(t) dt dt dt dt dc = e -tA b(t) dt
c(t)=
t
dy ,则可得 dt
d x1 = x2 dt d x 2 = 1( f - c x 1 - b x 2 ) = - c x 1 - b x 2 + f dt a a a a
一般地,n 阶常微分方程可以化为 n 个一阶常微分方程组成的方程组。
作业:p170-171 p177 3、4
t
b
xi = x(t) ,n),aij(i, j = 1,2, ,n) 式中 t 是自变量, 是 t 的一元函数(i= 1,2, i
是常系数。 令
a11 a12 a a T x(t)=[x(t),x ,xn(t)] , A = 21 22 1 2(t), a n1 an2 a1n a2n ann
d A(t) dt = A(t), A(t) dt = A(b)- A(a) (3) dt a a
二、 阶线性齐次常系数常微分方程组 设有一阶线性其次常系数常微分方程组
dx1 dt = a11x1(t)+ a12 x2(t)+ + a1n xn(t) dx 2 = a21x1(t)+ a22 x2(t)+ + a2n xn(t) dt dxn = a x (t)+ a x (t)+ + a x (t) n1 1 n2 2 nn n dt
5、9
0 0 sint cost sint tA + = = f(A)= e cost -sint 0 -sint cost
x(t)= etA x(0)=
sint r1 rcost +rsint x(t) 1 2 1 = = -rsint x2(t) 2 1 -sint cost r2 rcost
3. 矩阵积分定义:若矩阵 A(t)=(a (t))m× 的每个元素 aij(t)都是区间 n ij
[t0 ,t1]上的可积函数, 则称 A(t)在区间[t0 ,t1]上可积, 并定义 A(t)在[t0 ,t1]
上的积分为
t1 t1 A(t) dt = a (t)dt ij t0 t0 m×n
d dA dB [A(t)±B(t)]= ± dt dt dt
d dA dB [A(t)B(t)]= B+A dt dt dt d da dA [a(t)A(t)]= A +a dt dt dt d costA =-AsintA dt d sintA =AcostA dt
d tA e =AetA =etAA dt
