第02章 热力学第一定律作业
第二章 热力学第一定律

第二章 热力学第一定律英文习题1. Cooling of a hot fluid in a tankA rigid tank contains a hot fluid that is cooled while being stirred by apaddle wheel. Initially, the internal energy of the fluid is 800 kJ. During the cooling process, the fluid loses 500 kJ of heat, and the paddle wheel does 100 kJ of work on the fluid. Determine the final internal energy of the fluid. Neglect the energy stored in the paddlewheel.2. Heating of a gas by a resistance heaterA piston-cylinder device initially contains 0.5 m 3of nitrogen gas at 400 kPa and 27℃. An electric heater within the device is turned on and is allowed to pass a current of 2 A for 5 min from a 120-V source. Nitrogen expands at constant pressure, and a heat loss of 2800 J occursduring the process. Determine the final temperature of nitrogen.3. Cooling of an iron block by watercontains 0.5 A 50-kg iron block at 80℃ is dropped into an insulated tanks that equilibriumm 3of liquid water at 25℃. Determine the temperature when thermal is reached.4. Deceleration of air in a diffuserAir at 10℃ and 80 kPa enter the diffuser of a jet engine steadily with a velocity of 200 m/s. The inlet area of the diffuser is 0.4 m 2. The air leaves the diffuser with a velocity that isvery small compared with the inlet velocity. Determine (a) themass flow rate of the air and (b) the temperature of the air leaving the diffuser.5. Energy balance in turbineConsider a gas turbine power plant with air as the working fluid, Air enters at 100 kPa, 20ºC (ρ=1.19 kg/m 3), with a velocity of 130m/s through an opening 0.112 m 2cross-sectional area. After being compressed, heated and expanded through a turbine, the air leaves at 180 kPa, 150ºC (ρ=1.48 kg/m 3), through an opening of 0.100 m 2cross-sectional area. The power output of the plant is 375 kW. The internal energy and enthalpy of the air are given in kJ/kg byU=0.717T and h=1.004T, where T istemperature on the Kelvin scale. Determine the net amountofheatadded tothe air in kJ/kg.FIGURE 2-1FIGURE 2-2FIGURE 2-3FIGURE 2-42113111112.0/130/19.120100mA s m c m k g CT k Pa p f ===︒==ρ2112WsQ223222100.0/48.1150180m A m kg CT kPap ==︒==ρFIGURE 2-56. Air is compressed in a frictionless steady-flow processAir is compressed in a frictionless steady-flow process from 90 kPa, 150ºC (v=0.918 m 3/kg) to 130 kPa in such a manner that p(v+0.250)=constant, where v is in m 3/kg, inlet velocity is negligible small, and discharge velocity is 110 m/s. Calculate the work required per kilogram of air.7. Mixture processA mixture of air and water vapor with an enthalpy of 120 kJ/kg enters the dehumidifying section of an air-conditioning system at a rate of 320 kg/hr, liquid water drains out of the dehumidifier with an enthalpy of 42 kJ/kg at a rate of 7.0 kg/hr. An air vapor mixture leaves with an enthalpy of 47 kJ/kg.Determine the rate of heat removal from the fluids passing through the dehumidifier.8. Reviews problemA piston-cylinder device contains helium gas initially at 150 kPa, 20℃, and0.5 m 3. The helium is now compressed in a polytropic process (PV n=constant) to 400 kPa and 140℃. Determine the heat loss or gainduring this process.9. Two rigid tanks are connected by a valve. Tank Acontains 0.2 m 3of water at 400 kPa and 80 percent quality. Tank B contains 0.5 m 3of water at 200 kPa and 250℃. The valve is now opened, and the two tanks eventually come to the same state. Determine the pressure and the amount of heat transfer whenthe system reaches thermal equilibrium with the surrounding at 25 ℃.10. Consider a well-insulated horizontal rigid cylinder that isdividedm m 112233dehumidifierkgkJ h hrkg /126/32011==∙kgkJ h hr kg /42/0.722==∙kgkJ h /473=FIGURE 2-7FIGURE 2-8W in1122/918.0901311===f c kg m v kPa p sm c kPa p f /11013022==FIGURE 2-6FIGURE 2-9FIGURE 2-10into two compartments by a piston that is free to move but does not allow either gas to leak into the other side. Initially, one side of the piston contains 1 m 3of N 2 gas at 500 kPa and 80℃ while the other side contains 1 m 3of He gas at 500 kPa and 25℃. Now thermal equilibrium is established in the cylinder as a result of heat transfer through the piston. Using constant specific heats at room temperature, determine the final equilibrium temperature in the cylinder. What would your answer be if the piston were not free to move?工程热力学与传热学第二章 热力学第一定律 习题1. 一绝热刚性容器,中间用隔板分为两部分,左边盛有空气,右边为真空,抽掉搁板,空气将充满整个容器。
《物理化学》第二章热力学第一定律练习题(含答案)

《物理化学》第二章热力学第一定律练习题(含答案)第二章练习1,填入1,根据系统与环境之间的能量和物质交换,系统可分为,,2,强度性质显示了体系的特征,与物质的量无关。
容量属性体现了系统的特征,它与物质的数量有关,具有性别。
3年,热力学平衡态同时达到四种平衡,即,,,4,系统状态改变称为进程常见的过程有、、、和,5.从统计热力学的观点来看,功的微观本质是热的微观本质6,每种气体的真空膨胀功w = 0.7,在绝热钢瓶内的化学反应△ u = 0.8,焓定义为2.真或假:1。
当系统的状态不变时,所有状态函数都有一定的值(√) 2。
当系统的状态改变时,所有状态函数的值也相应地改变。
(χ) 3。
因为=δH和=δU,所以和都是状态函数(χ)4,密闭系统在恒压过程中吸收的热量等于系统的焓(χ)误差只有当封闭系统不做非膨胀功等压过程δH = QP5且状态被给定时,状态函数才有固定值;在状态函数被确定之后,状态也被确定(√) 6。
热力学过程中的W值由具体过程(√)7和1摩尔理想气体从同一初始状态经过不同的循环路径后返回初始状态决定,其热力学能量保持不变(√) 3。
单一主题1。
系统中的以下几组物理量都是状态函数:(C) A,T,P,V,Q B,M,W,P,H C,T,P,V,N,D,T,P,U,W2,对于内能是系统的单值函数的概念,误解是(C)系统A处于某一状态,某一内能B对应于某一状态,内能只能有一个值,不能有两个以上的值c的状态改变,内部能量也必须随着对应于内部能量值的d而改变。
可以有多种状态3以下语句不具有状态函数的特征:(d)当系统A的状态确定后状态函数值也确定时,状态函数值的变化值只由系统C的恒定状态通过循环过程来确定。
状态函数值是常数。
D态函数的可加性为4。
在下面的描述中正确的是(a)A物体的温度越高,它的内能越大,B物体的温度越高,它包含的热量越多。
当系统温度升高时,一定是它吸收了热量。
当系统温度恒定时,解释它既不吸热也不放热。
第二章 热力学第一定律自测题资料讲解

第二章热力学第一定律自测题一、选择题1.物质的量为n的理想气体,该气体的下列物理量中,其值确定后,其他状态函数方有定值的是()。
(a) p(b) V(c) T, U(d) T, p2.有一真空绝热瓶子,通过阀门和大气相隔。
当阀门打开时,大气(视为理想气体)进入瓶内,此时瓶内气体的温度将()。
(a) 升高(b) 降低(c) 不变(d) 不确定3.公式 H=Q p适用于下列过程中的()。
(a) 理想气体从1013.25kPa反抗恒定的外压101.325kPa膨胀(b) 273K,101.325kPa下冰融化成水(c) 298K,101.325kPa下电解CuSO4水溶液(d) 气体从状态Ⅰ等温可逆变化到状态Ⅱ4.反应C(金刚石) + 0.5O2(g)—CO(g)的热效应为△rHmθ,问此△rHmθ值为()A CO(g) 的生成焓B C(金刚石)的燃烧焓C C的燃烧焓D 全不是5.对于一定量的理想气体,有可能发生的过程是()。
(1)对外做功且放出热量(2)恒容绝热升温、无非膨胀功(3)恒压绝热膨胀(4)恒温绝热膨胀(a) (1),(4) (b) (2),(3) (c) (3),(4) (d) (1),(2) 6.实际气体经节流膨胀后,( )。
(a) Q <0, ∆H =0, ∆p <0 (b) Q =0, ∆H =0, ∆T <0 (c) Q =0, ∆H <0, ∆p <0 (d) Q =0, ∆H =0, ∆p <07.某气体的状态方程为pV m =RT +bp (b 为大于零的常数),此气体向真空绝热膨胀后的温度将( )。
(a) 不变 (b) 上升 (c) 下降 (d) 不确定 8.根据定义等压膨胀系数pT V V ⎪⎭⎫⎝⎛∂∂=1α,等容压力系数V T p p ⎪⎭⎫⎝⎛∂∂=1β,等温压缩系数Tp V V ⎪⎪⎭⎫⎝⎛∂∂-=1κ。
α,β,κ 三者间的关系为( )。
第二章 热力学第一定律自测题

第二章热力学第一定律自测题与答案. I选择题1.物质的量为n的纯理想气体,该气体的下列物理量中,其值确定后,其他状态函数方有定值打得是(d)。
(a)p(b)V (c)T,U (d)T,p2.有一真空绝热瓶子,通过阀门和大气相隔。
当阀门打开时,大气(视为理想气体)进入瓶内,此时瓶内气体的温度将(a)。
(a)升高(b)降低(c)不变(d)不确定3.公式∆H=Q p适用于下列过程中的(b)。
(a)理想气体从1013.25 kPa反抗很定的外压101.325 kPa膨胀(b)273 K,1013.25 kPa下冰融化成水(c)298 K,下电解CuSO4水溶液(d)气体从状态I等温可逆变化到状态II4.可逆机的效率为η,冷冻机的冷冻系数为β,则β和η的数值满足(d)。
(a)η<1,β<1 (a)η<1,β<1(a)η<1,β>1 (a)η<1,β可能小于、等于或大于15.对于一定量的理想气体,有可能发生的过程是(a)。
(1)对外做功且放出热量(2)很容绝热升温、无非膨胀功(3)恒压绝热膨胀(4)恒温绝热膨胀(a)(1),(4)(b)(2),(3)(c)(3),(4)(d)(1),(2)6.实际气体经节流膨胀后,(d)。
(a)Q<0,∆H=0,∆p<0(a)Q=0,∆H=0,∆T<0(a)Q=0,∆H<0,∆p<0(a)Q=0,∆H=0,∆p<07.某气体的状态方程为pV m=RT+bp(b为大于零的常数)。
此气体向真空绝热膨胀后的温度将(a)。
(a)升高(b)降低(c)不变(d)不确定8.根据定义:等压膨胀系数1=pVV Tα∂⎛⎫⎪∂⎝⎭,等容压力系数1=Vpp Tβ∂⎛⎫⎪∂⎝⎭,等温压缩系数1=TVV pκ⎛⎫∂⎪∂⎝⎭。
,,αβκ三者间的关系为(d)。
(a)α⋅β=p⋅κ(b)α⋅β⋅κ=1(c)α⋅κ=β/p(d)α=p⋅β⋅κ9.van der waals 气体经Joule实验后(绝热向真空膨胀),气体的温度将(b)。
第二章 热力学第一定律-2
压力下, 例 在0℃,1000kPa压力下,10.00dm3理想气体经下列三 ℃ 压力下 种途径膨胀至压力为100kPa的末态,求各过程的。 种途径膨胀至压力为100kPa的末态,求各过程的。设该 100kPa的末态 体的C ,m 气 体的 V,m=12.471kJ.mol-1. ⑴等温可逆膨胀; 等温可逆膨胀; ⑵绝热可逆膨胀; 绝热可逆膨胀; ⑶在恒定外压为100kPa下绝热膨胀。 在恒定外压为100kPa下绝热膨胀。 100kPa下绝热膨胀 解:气体的物质的量为
理想气体 : dU = CV dT nRT nCV ,m dT = − dV V dT dV CV ,m = −R T V CV ,m d ln T + Rd ln V = 0
d ln T = −(γ − 1)d ln V V2 T2 ln = ln V T1 1 T2 V2 T V 1 1
W = ∆U = nCV ,m (T2 − T1 )
可逆条件: 用过程方程解出T 用过程方程解出T2和 便可得W. T1,便可得W.
p1 ,V1 , T
p
Q= 0
T = 常数 p2 ,V2 , T
p2,V',T'
V
例2.6.1. 某双原子理想气体4mol, 从始态50kPa, 160dm 经绝热可逆 某双原子理想气体4mol, 从始态50kPa, 求末态温度T 及过程的W, W,△ 压缩到末态压力=200kPa,求末态温度T2及过程的W,△U及△H. 分析: 分析: n=4mole n=4mole
(完整版)《物理化学》第二章热力学第一定律练习题(含答案)

(完整版)《物理化学》第⼆章热⼒学第⼀定律练习题(含答案)第⼆章练习题⼀、填空题1、根据体系和环境之间能量和物质的交换情况,可将体系分成、、。
2、强度性质表现体系的特征,与物质的数量⽆关。
容量性质表现体系的特征,与物质的数量有关,具有性。
3、热⼒学平衡状态同时达到四种平衡,分别是、、、。
4、体系状态发⽣变化的称为过程。
常见的过程有、、、、。
5、从统计热⼒学观点看,功的微观本质是,热的微观本质是。
6、⽓体各真空膨胀膨胀功W= 07、在绝热钢瓶中化学反应△U= 08、焓的定义式为。
⼆、判断题(说法对否):1、当体系的状态⼀定时,所有的状态函数都有⼀定的数值。
(√)2、当体系的状态发⽣变化时,所有的状态函数的数值也随之发⽣变化。
(χ)3.因= ΔH, = ΔU,所以与都是状态函数。
(χ)4、封闭系统在压⼒恒定的过程中吸收的热等于该系统的焓。
(χ)错。
只有封闭系统不做⾮膨胀功等压过程ΔH=Q P5、状态给定后,状态函数就有定值;状态函数确定后,状态也就确定了。
(√)6、热⼒学过程中W的值应由具体过程决定( √ )7、1mol理想⽓体从同⼀始态经过不同的循环途径后回到初始状态,其热⼒学能不变。
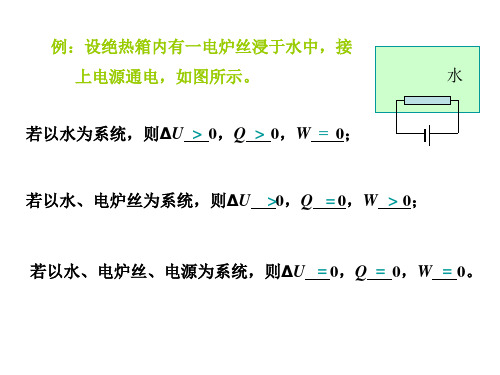
( √ )三、单选题1、体系的下列各组物理量中都是状态函数的是( C )A 、T、P、V、QB 、m、W、P、HC、T、P、V、n、D、T、P、U、W2、对于内能是体系的单值函数概念,错误理解是( C )A体系处于⼀定的状态,具有⼀定的内能B对应于某⼀状态,内能只能有⼀数值不能有两个以上的数值C状态发⽣变化,内能也⼀定跟着变化D对应于⼀个内能值,可以有多个状态3下列叙述中不具有状态函数特征的是(D )A体系状态确定后,状态函数的值也确定B体系变化时,状态函数的改变值只由体系的始终态决定C经循环过程,状态函数的值不变D状态函数均有加和性4、下列叙述中正确的是( A )A物体温度越⾼,说明其内能越⼤B物体温度越⾼,说明其所含热量越多C凡体系温度升⾼,就肯定是它吸收了热D凡体系温度不变,说明它既不吸热也不放热5、下列哪⼀种说法错误( D )A焓是定义的⼀种具有能量量纲的热⼒学量B只有在某些特定条件下,焓变△H才与体系吸热相等C焓是状态函数D焓是体系能与环境能进⾏热交换的能量6、热⼒学第⼀定律仅适⽤于什么途径(A)A同⼀过程的任何途径B同⼀过程的可逆途径C同⼀过程的不可逆途径D不同过程的任何途径7. 如图,将CuSO4⽔溶液置于绝热箱中,插⼊两个铜电极,以蓄电池为电源进⾏电解,可以看作封闭系统的是(A)(A) 绝热箱中所有物质; (B) 两个铜电极;(C) 蓄电池和铜电极;(D) CuSO4⽔溶液。
热力学第一定律作业

第二章热力学第一定律1.始态为25 °C,200 kPa的5 mol某理想气体,经途径a,b两不同途径到达相同的末态。
途经a先经绝热膨胀到-28.47 °C,100 kPa,步骤的功;再恒容加热到压力200 kPa的末态,步骤的热。
途径b为恒压加热过程。
求途径b的及。
2. 2 mol某理想气体,。
由始态100 kPa,50 dm3,先恒容加热使压力体积增大到150 dm3,再恒压冷却使体积缩小至25 dm3。
求整个过程的。
文档来自于网络搜索3.单原子理想气体A与双原子理想气体B的混合物共5 mol,摩尔分数,始态温度,压力。
今该混合气体绝热反抗恒外压膨胀到平衡态。
求末态温度及过程的。
文档来自于网络搜索4. 1.00mol(单原子分子)理想气体,由10.1kPa、300K按下列两种不同的途径压缩到25.3kPa、300K,试计算并比较两途径的Q、W、ΔU及ΔH。
文档来自于网络搜索(1)等压冷却,然后经过等容加热;(2)等容加热,然后经过等压冷却。
5.在一带活塞的绝热容器中有一固定的绝热隔板。
隔板靠活塞一侧为2 mol,0 °C的单原子理想气体A,压力与恒定的环境压力相等;隔板的另一侧为6 mol,100 °C的双原子理想气体B,其体积恒定。
今将绝热隔板的绝热层去掉使之变成导热板,求系统达平衡时的T及过程的。
文档来自于网络搜索6.1mol 理想气体从300K,100kPa下等压加热到600K,求此过程的Q、W、∆U、∆H。
已知此理想气体C p,m=30.0 J·K-1·mol-1。
文档来自于网络搜索7. 5 mol双原子气体从始态300 K,200 kPa,先恒温可逆膨胀到压力为50 kPa,在绝热可逆压缩到末态压力200 kPa。
求末态温度T及整个过程的及。
文档来自于网络搜索8.一水平放置的绝热恒容的圆筒中装有无摩擦的绝热理想活塞,活塞左、右两侧分别为50 dm3的单原子理想气体A和50 dm3的双原子理想气体B。
热力学第一定律作业

热力学第一定律作业一、 选择题(每题2分,共20分)1.1mol 单原子理想气体经一循环过程后,W =400J ,则该过程的Q 为:( )A 、 0B 、因未指明是可逆过程,无法确定C 、400 JD 、–400 J2.理想气体经一不可逆循环( )。
A 、ΔU >0,ΔH =0B 、ΔU >0,ΔH >0C 、ΔU =0,ΔH =0D 、ΔU=0,ΔH >03.物质的量为n 的理想气体的何组物理量确定后,其它状态函数方有定值:( )A 、pB 、VC 、T ,UD 、T ,p4.在一带活塞的绝热气缸中发生某一化学反应,系统终态温度升高,体积增大,则此过程的S ∆( )。
A 、大于零B 、小于零C 、等于零D 、无法确定5.下列各摩尔反应焓中,属于摩尔生成焓的是( )。
A 、2222()()2()H g O g H O g +→B 、221()()()2CO g O g CO g +→ C 、2221()()()2H g O g H O l +→ D 、2222443()()()C H g C H g C H g +→+6.在一保温良好、门窗紧闭的房间内,放有电冰箱,若将电冰箱门打开,不断向冰箱供给电能,室内的温度将( )A 、 逐渐降低B 、 逐渐升高C 、不变D 、无法确定7.甲烷燃烧反应:4222CH (g)+2O (g)=CO (g)+2H O(l),在绝热恒压条件下反应,终态温度升高,体积增大,其过程的ΔU 和ΔH 分别为( )。
A 、=0,>0B 、<0,=0C 、=0,<0D 、无法确定8.下列物质中,“完全氧化”后的最终产物错误的是( )。
2232A C CO (g)B H H O(l)C S SO (g)D N N (g)→→→→、、、、9.理想气体从同一始态(p 1,V 1,T 1)出发,分别经恒温可逆压缩(T)、绝热可逆压缩(i)到终态体积为V 2时,环境对体系所做功的绝对值比较( )。
衡水学院 《物理化学》第二章 热力学第一定律 作业及答案

[90-1] 求1 mol 理想气体,在恒定压力下温度升高1℃,求过程的功。
解:理想气体变温过程:W = - n R ∆T = - 1 ⨯ 8.314 ⨯ 1 = - 8.314 (J)[90-2] 1 mol 水蒸气在100℃,101.325 kPa 下全部凝结成液态水。
求过程的功。
假设:相对于水蒸气的体积,液态水的体积可以忽略不计。
解:有理想气体参加的相变过程: W = - (∆n )g RT = n RT = 1 ⨯ 8.314 ⨯ 373.15 = 3102 (J) [91-3] 25℃在恒定压力下,电解1 mol 水求过程的体积功。
H 2 O (l) = H 2 (g) + (1/2) O 2 (g)解:有理想气体参加的化学变化: W = - (∆n )g RT = -1.5 ⨯ 8.314 ⨯ 298.15 = -3718 (J) [91-4] 系统由相同的始态经过不同途径达到相同的末态,若途径a 的Q a = 2 .078 kJ ,W a = -4 .157 kJ ,而途径 b 的 Q b = - 0 .692 kJ 。
求W b 解:对于状态函数U 有 ∆U a = ∆U b 所以 Q a + W a = Q b + W b即 2.078 kJ + (-4 .157) kJ = -0 .692 kJ + W b , 解得: W b = -1.387 kJ[91-5] 始态为25℃,200 kPa 的5mol 某理想气体,经a,b 两不同途径到达相同的末态。
途径a 先经绝热膨胀到-28.57 ℃,100 kPa ,步骤的功W a = -5.57 kJ ;再恒容加热到压力200 kPa 的末态,步骤的热Q a = 25.42 kJ 。
途径b 为恒压加热过程。
求途径b 的W b 及Q b 。
解:)(10 167.10102)57.2815.273(314.85)(10 197.6102)2515.273(314.8532-5232-5111m pnRT V m p nRT V ⨯=⨯-⨯⨯==⨯=⨯+⨯⨯==W b = - p amb (V 2 – V 1 )= - 200 ⨯103(10.167–6.194) ⨯10-2 = - 7. 94 (kJ) Q b = ∆U b - W b因为U 为状态函数,所以 ∆U b = ∆U a ∆U a = ∆U a,1 + ∆U a,2=(Q a,1 + W a,1) + (Q a,2 + W a,2) = (0 - 5.57) + (25.42 + 0) = 19.85 (kJ)Q b = 19.85 - (-7. 94)= 27.79 (kJ)[91-6] 4mol 的某理想气体,温度升高20℃,求∆H - ∆U 的值。
第二章热力学第一定律练习题及答案

第一章热力学第一定律练习题一、判断题(说法对否):1.当系统的状态一定时,所有的状态函数都有一定的数值。
当系统的状态发生变化时,所有的状态函数的数值也随之发生变化。
2.在101.325kPa、100℃下有lmol的水和水蒸气共存的系统,该系统的状态完全确定。
3.一定量的理想气体,当热力学能与温度确定之后,则所有的状态函数也完全确定。
4.系统温度升高则一定从环境吸热,系统温度不变就不与环境换热。
5.从同一始态经不同的过程到达同一终态,则Q和W的值一般不同,Q + W的值一般也不相同。
6.因Q P= ΔH,Q V= ΔU,所以Q P与Q V都是状态函数。
7.体积是广度性质的状态函数;在有过剩NaCl(s) 存在的饱和水溶液中,当温度、压力一定时;系统的体积与系统中水和NaCl的总量成正比。
8.封闭系统在压力恒定的过程中吸收的热等于该系统的焓。
9.在101.325kPa下,1mol l00℃的水恒温蒸发为100℃的水蒸气。
若水蒸气可视为理想气体,那么由于过程等温,所以该过程ΔU = 0。
10.一个系统经历了一个无限小的过程,则此过程是可逆过程。
11.1mol水在l01.325kPa下由25℃升温至120℃,其ΔH= ∑C P,m d T。
12.因焓是温度、压力的函数,即H = f(T,p),所以在恒温、恒压下发生相变时,由于d T = 0,d p = 0,故可得ΔH = 0。
13.因Q p = ΔH,Q V = ΔU,所以Q p - Q V = ΔH - ΔU = Δ(p V) = -W。
14.卡诺循环是可逆循环,当系统经一个卡诺循环后,不仅系统复原了,环境也会复原。
15.若一个过程中每一步都无限接近平衡态,则此过程一定是可逆过程。
16.(∂U/∂V)T = 0 的气体一定是理想气体。
17.一定量的理想气体由0℃、200kPa的始态反抗恒定外压(p环= 100kPa) 绝热膨胀达平衡,则末态温度不变。
第二章 热力学第一定律-附答案

(A)V1 V2
(B)V1 V2
(C)V1 V2
(D) 无法确定
答案:C(因绝热过程无法从环境吸热,则同样温度下压力较低,体积较小。) 16. 始态(p1,T1)完全相同的一个理想气体体系和另一个范德华气体体系,分别进行绝热恒
答案:B。 H Q p 成立的条件是恒压、W' 0 。
13. 某化学反应在恒压、绝热和只作体积功的条件下进行,体系温度由 T1 升高 T2 ,则此过
程的焓变 H :
(A)小于零 (B)大于零
(C)等于零 (D)不能确定
答案:C。因恒压、不做其它功, H Q p ,又因绝热故 H 0 。
14. 体系的状态改变了,其内能值: (A)必定改变 (B) 必定不变 (C) 不一定改变 (D) 状态与内能无关 答案:C。例如,理想气体恒温下体积发生变化其内能不变。
二、选择题
1. 热力学第一定律中的 W 是指______ C A. 体积功 B. 非体积功 C. 各种形式功之和
D. 机械功
2. 热力学第一定律ΔU=Q+W 只适用于
(A) 单纯状态变化
(B) 相变化
(C) 化学变化
(D) 封闭物系的任何变化
答案:D
3.关于热和功, 下面的说法中, 不正确的是
(A) 功和热只出现于系统状态变化的过程中, 只存在于系统和环境间的界面上
C. T2 ' T2 ,V2 ' V2
答案:C
D. T2 ' T2 ,V2 ' V2
22.分子数增加的放热化学反应在一绝热钢瓶中进行,则( )
第二章热力学第一定律习题和答案

第二章热力学第一定律一选择题1.某绝热体系在接受了环境所做的功之后,其温度() AA.一定升高B.一定降低C.一定不变D.不一定改变2.当体系将热量传递给环境后,体系的焓() DA.必定减少B.必定增加C.没有变化D.不一定改变3.热力学状态和热力学状态函数的关系为() BA.状态函数一定,状态就单一的确定B.状态一定,状态函数就单值的确定C .A、B 都对 D. A、B 都不对4.系统的状态函数,定义为H=U+pV 若系统发生状态变化时,则焓的变化为△H=△U+△(pV),式中△(pV)的意思是() BA. △(pV) = △P△VB.△(pV) = p2V2-p1V1C. △(pV) = p△V+V△p5.在一个密闭绝热的房间里放置一台电冰箱,将冰箱门打开,接通电源使冰箱工作,过一段时间后,室内的平均气温将如何变化?()A.升高B.降低C.不变D.先升后降 A6.分子数增加的放热化学反应在一绝热钢瓶中进行,则() DA. B.C. D.7.1mol 单原子理想气体,从p1=202650Pa,T1=273K 经p/T=常数的途径加热使压力增加到p2=405300Pa,则体系做的功为() CA.大于零B.小于零C.零D.无法确定8. 氧气的燃烧热应为何值() DA.大于零B.小于零C.等于零D.不存在9.下述说法中,哪一个正确?() BA.水蒸气的生成热即是氢气的燃烧热B.水的生成热即是氢气的燃烧热C.水的生成热即是氧气的燃烧热D.水蒸气的生成热即是氧气的燃烧热9.298K 及101325Pa 条件下,1mol 过冷水蒸气变成1mol 的液态水则ΔG 为 ( )A.ΔG < 0B.ΔG > 0C.ΔG = 0D.不一定 A10.关于焓,下述说法不正确的是() AA.△H=Q 适用于封闭体系等压只做功的过程B.对于常压下的凝聚相,过程△H≈△UC.对理想气体的恒容过程△H=△U+V△PD 对于任何体系等压只做体积功的过程△H=△U-W11.将某理想气体从温度T1加热到T2,若此变化为非恒容途径,则其热力学能的变化△U 应() BA.= 0B.= Cv(T2-T1)C.不存在D.等于其他值12.对于封闭体系,当过程的始终态确定后,下列值中不能确定的是()A.恒容、无其它功过程的QB.可逆过程的WC.任意过程的Q+WD.绝热过程的W D13.化学反应在只做体积功的定温定压条件下,若从反应物开始进进行反应,由此过程为() CA.是热力学可逆过程B.是热力学不可逆过程C.是否过逆不能确定 C.是不能进行的过程14.下面陈述中,正确的是() C A.虽然Q 和W 是过程量,但由于Q v=△U,Q p=△H,而U 和H 是状态函数,所以Q v 和Q p 是状态函数B.热量是由于温度差而传递的能量,它总是倾向于从含热量较多的高温物体流向含热量较少的低温物体C.封闭系统与环境之间交换能量的形式非功即热D.两物体之间只有存在温差,才可传递能量,反过来系统与环境间发生热量传递后, 必然要引起系统温度变化15.物质的量为n 的纯理想气体,若该气体的哪一组物理量确定之后,其它状态函数方有定值。
热学习题第二章热力学第一定律及应用

第二章热力学第一定律及应用2.1 人们是怎样认识热的本质的?【答】“热是能量的一种形式。
”这就是热的本质。
回顾过去,人们为了认识热的本质曾走过了一段很长的弯路。
这里,我们不想过多地叙述物理学史中诸如“热质说”等人们认识热的本质时所走过的歧路。
但人们是怎样抛弃了热是物质的假说而承认热是能量的一种形式呢?我们认为这与当时著名的物理学家焦耳的辛勤工作分不开,重温这一历程对于我们认识热的本质也是很有益处的。
焦耳做过的最有名的实验如今已收集在教科书中,他把一个金属奖状搅拌器装到一个盛水的大铁罐中,当搅拌器被一个向下运动的重物驱动时,它就搅拌大铁罐中的水而产生热,产生热量的多少可以根据测量温度上升的多少及大铁罐中水的质量而计算出来。
而消耗的机械能量可以从重物下落的距离和重物的重量计算出来。
这个实验看起来很简单,但是,为了防止热量从实验装置上损失是很不容易的,焦耳采取了许多巧妙的措施才比较好地解决了这一问题。
为了使实验更令人信服,焦耳还曾把大铁罐中的水,换成水银、油等重做这个实验,其结果与水完全一样。
焦耳通过上述实验发现,一定数量的机械能总是产生柑同数量的热量。
也就是说,机械能和热量之间的转换率是一定的。
:焦耳根据自己的实验正确地指出’,热是机械能的另一 种形式,从而道出了热的本质。
实际上,在焦耳之前,有一些物理学家,象牛顿和玻意耳等人就已经认识到热与动能有关,并且推测到热可能是运动的一种形式。
现在人们认为热是分子的无规则运动,换句话说,热是物体分子运动的动能。
例如,当物体的机械能转变成热能时,用分子运动论的观点,我们可以用下述的物理图象来理解。
假定一个下落的物体,当它与地面碰撞时不反弹起来。
在物体下落的过程中,它损失了势能获得了动能。
这时物体中所有的分子都具有向下的运动,平均说来,它们是向一个方向运动,也就是说,运动是定向有规则的。
当物体到达地面而停止运动时,分子的定向有规则运动变成了杂乱的无规则的运动。
即分子的无规则热运动代替了有规则的定向运动。
自测习题 第2章 热力学第一定律

第2章 热力学第一定律思考题:1. 对一定量的理想气体,下列单纯PVT 过程是否可能:① 等温下绝热膨胀。
② 等压下绝热压缩。
③ 体积不变,而温度上升,且过程绝热。
④ 吸热而温度不变。
⑤ 温度不变,且压力不变。
2. 在一个带有无摩擦、无质量的绝热活塞的绝热气缸内充入一定量的气体。
气缸内壁绕有电阻丝,活塞上方施以一恒定压力,并与缸内气体成平衡状态,如图所示。
现通入一微小电流,使气体缓慢膨胀。
此过程为一等压过程,故Q p =ΔH ,该系统为一绝热系统,则Q p =0,所以此过程的ΔH=0。
此结论对否?3. 已知下述反应的ΘΔmr H : ① C(石墨) + 0.5 O 2(g)== CO(g) )(I H m r ΘΔ ② CO+ 0.5 O 2(g) == CO 2(g) )(II H mr ΘΔ ③ H 2(g) + 0.5 O 2(g) == H 2O(g) )(III H mr ΘΔ ④ 2H 2(g) + O 2(g) == 2H 2O(l) )(IV H mr ΘΔ (i) )(I H mr ΘΔ,)(II H m r ΘΔ,)(III H m r ΘΔ,)(IV H m r ΘΔ是否分别是CO(g) ,CO 2(g) ,H 2O(g), H 2O(l)的ΘΔm f H ?(ii) )(I H mr ΘΔ,)(II H m r ΘΔ,)(III H m r ΘΔ是否分别是C(石墨),CO (g),H 2(g)的ΘΔm C H ?4. 什么情况下,一个化学反应的ΘΔmr H 不随温度变化?选择题:1. 绝热水箱中装有水,水中绕有电阻丝,由蓄电池供给电流。
假设电池放电过程中无热效应,通电后电阻丝和水的温度皆有升高。
A .Q=0,W<0,ΔU<0 B. Q<0,W>0,ΔU>0 C .Q>0,W=0,ΔU>0D. Q=0,W>0,ΔU>0E. Q<0,W=0,ΔU<0① 以电池为系统,水和电阻丝为环境,上述正确的是② 以电阻丝为系统,水和电池为环境,上述正确的是③ 以水为系统,电阻丝和电池为环境,上述正确的是④ 以水和电阻丝为系统,电池为环境,上述正确的是⑤ 以电池和电阻丝为系统,水为环境,上述正确的是2. 使公式p p Q H =Δ成立的条件是A 开放体系,只作膨胀功,P 体=P 外=常数B 封闭体系,可作任何功,P 体=P 外=常数C 封闭体系,只作有用功,P 体=P 外=常数D 封闭体系,只作膨胀功,P 体=P 外=常数E 封闭体系,只作膨胀功,P 始=P 终=P 外=常数3. 根据热力学第一定律,关于封闭体系的描述正确的是A. 吸热Q 是状态函数B. 对外做功W 是状态函数C. Q-W 是状态函数D. 热力学能U 是状态函数4. 下列说法,哪一种不正确?A. 焓只有在特定条件下,才与系统吸热相等B. 焓是人为定义的一种具有能量量纲的热力学量C. 焓是状态函数D. 焓是体系可以与环境进行热交换的能量5.下列说法正确的是A. 热容C不是状态函数B. 热容C与途径无关C. 恒压热容C p不是状态函数D. 恒容热容C v不是状态函数6.某体系经历一不可逆循环后,下列说法错误的是A. Q=0B. W=0C. ΔU=0D. ΔC p=0E. ΔC v=0F. ΔH=07.公式ΔU=Q+W适用于什么体系A. 开放体系B. 封闭体系C. 孤立体系8.下列说法正确的是A. 理想气体经历绝热自由膨胀后,其热力学能变化为零;B. 非理想气体经历绝热自由膨胀后,其热力学能变化不一定为零;C. 非理想气体经历绝热自由膨胀后,其温度不一定降低。
(完整版)第二章热力学第一定律习题

第二章热力学第一定律选择题1.热力学第一定律ΔU=Q+W 只适用于(A) 单纯状态变化 (B) 相变化(C) 化学变化 (D) 封闭物系的任何变化答案:D2.关于热和功, 下面的说法中, 不正确的是(A) 功和热只出现于系统状态变化的过程中, 只存在于系统和环境间的界面上(B) 只有在封闭系统发生的过程中, 功和热才有明确的意义(C) 功和热不是能量, 而是能量传递的两种形式, 可称之为被交换的能量(D) 在封闭系统中发生的过程中, 如果内能不变, 则功和热对系统的影响必互相抵消答案:B3.关于焓的性质, 下列说法中正确的是(A) 焓是系统内含的热能, 所以常称它为热焓(B) 焓是能量, 它遵守热力学第一定律(C) 系统的焓值等于内能加体积功(D) 焓的增量只与系统的始末态有关答案:D。
因焓是状态函数。
4.涉及焓的下列说法中正确的是(A) 单质的焓值均等于零(B) 在等温过程中焓变为零(C) 在绝热可逆过程中焓变为零(D) 化学反应中系统的焓变不一定大于内能变化答案:D。
因为焓变ΔH=ΔU+Δ(pV),可以看出若Δ(pV)<0则ΔH<ΔU。
5.下列哪个封闭体系的内能和焓仅是温度的函数(A) 理想溶液 (B) 稀溶液 (C) 所有气体 (D) 理想气体答案:D6.与物质的生成热有关的下列表述中不正确的是(A) 标准状态下单质的生成热都规定为零(B) 化合物的生成热一定不为零(C) 很多物质的生成热都不能用实验直接测量(D) 通常所使用的物质的标准生成热数据实际上都是相对值答案:A。
按规定,标准态下最稳定单质的生成热为零。
7.dU=CvdT及dUm=Cv,mdT适用的条件完整地说应当是(A) 等容过程(B)无化学反应和相变的等容过程(C) 组成不变的均相系统的等容过程(D) 无化学反应和相变且不做非体积功的任何等容过程及无反应和相变而且系统内能只与温度有关的非等容过程答案:D8.下列过程中, 系统内能变化不为零的是(A) 不可逆循环过程 (B) 可逆循环过程(C) 两种理想气体的混合过程 (D) 纯液体的真空蒸发过程答案:D 。
第二章 能量与热力学第一定律作业

1 2 q h2 h1 C 2 C f2 f1 2
41.6 500 4.1868 102 1002 103 / 2 1924.2kJ/kg
即每千克蒸汽在冷凝器中放热量为1924.2 kJ。
热力学习题参考答案
[2-10]某燃气轮机装置如图2-19所示。已知h1=286kJ/kg的燃料和空气的混合 物,在截面1处以20m/s的速度进入燃烧室,并在定压下燃烧,使工质吸入热 量q=879kJ/kg,燃烧后燃气进入喷管绝热膨胀到状态3,h3=502kJ/kg,流速 增加到cf3,此后燃气进入动叶,推动转轮作功。若燃气在动叶中的热力状态 不变,最后离开燃气轮机的速度cf4=150m/s。求: ⑴ 燃气在喷管出口的流速cf3; ⑵ 每千克燃气在燃气轮机中所作的功; ⑶ 燃气流量为5.23kg/s时,燃气轮机的功率(kW)。 解: ⑴燃气流速c f3
热力学习题参考答案
⑵每千克燃气作功 取截面3至截面4作热力系,燃气的热力状态不变,稳定流动能量方程为
2 q h4 h3 C 2 C f4 f 3 / 2 wnet
其中, q 0 , h3 h4
2 2 2 3 wnet C 2 C / 2 1151.7 150 10 / 2 651.95kJ / kg f3 f4
热力学习题参考答案
一、是非题 1. 2. 3. 4.
×, ×, √; ×, √;
√; ×.
热力学习题参考答案 二、选择题 1. 2. 3. 4.
c a1 b a
; , a2 ; ; , a , c , c .
热力学习题参考答案
[2-2]为了确定高压下稠密气体的性质,取2kg气体在25 MPa下从350K定压 加热到370K,气体初终状态下的容积分别为0.03m3及0.035m3,加入气体 的热量为700KJ,试确定初终状态下的内能之差。 解: 定压下加热
物理化学-第二章-热力学第一定律-经典习题及答案

。由始态 100 kPa,50 dm3,先恒容加热使
压力体积增大到 150 dm3,再恒压冷却使体积缩小至 25 dm3。求整个过程的
。
解:过程图示如下
n = 2mol
n = 2mol
n = 2mol
理想气体
理想气体
T1 = ?
恒容 → T2 = ?
理想气体 恒压 → T3 = ?
p1 = 100kPa
解:环境对体系做最小的功,必然是一个可逆过程
(1)
n = 1mol
n = 1mol
理想气体 T1 = 300K p1 = p外
理想气体 恒温可逆压缩 → T2 = 300K
p2 = p外
V1 = 0.040m3
V2 = 0.010m3
∫ ∫ Wr = −
pdV = − V2 nRT dV = nRT ln V1
n = 5mol 理想气体
T3 = ? p3 = 200kPa V3 = V2
两种过程始终态相同,先确定系统的始、末态 由理想气体状态方程
V1
=
nRT1 p1
=
5×8.314× 298.15 200 ×103
=
0.06197m3
V3
= V2
=
nRT2 p2
=
5×8.314× 244.18 100 ×103
解:
CV ,m = 20.92J ⋅ mol−1 ⋅ K −1
n = 1mol
n = 1mol
n = 1mol
理想气体
理想气体
理想气体
恒温
恒容
T1 = 300.15K p1 = 101.325kPa
→ p外 = p2
T2 p2
第二章--热力学第一定律

第二章热力学第一定律一.判断题1、理想气体的内能U与p和V均无关,所以U与pV也无关。
()2、对于同一热力学体系,其在p~V图上的两条绝热可逆过程线绝不可能相交。
()3、因为Q V= U,Q p = H,而U和H是状态函数的增量,所以Q V和Q p也只取决于系统的始末态,与过程的具体途径无关。
()4、理想气体恒温膨胀过程中U = 0,Q = W,即膨胀过程中系统所吸收的热全部变成了膨胀功,这是热力学第一定律的必然结果,但却违反了热力学第二定律。
( )二.选择题1、2000K时反应CO(g)+1/2O2(g)=CO2(g)的K p为 6.443,则在同温度下反应为2CO2(g)=2CO(g)+O2(g)的K p应为()A、 1/6.443B、 (6.443)1/2 C.、(1/6.443)2 D.、1/(6.443)1/22、 A和B能形成理想溶液。
已知在100℃时纯液体A的饱和蒸汽压为133.3kPa, 纯液体B 的饱和蒸汽压为66.7 kPa, 当A和B的二元溶液中A的摩尔分数为0.5时,与溶液平衡的蒸气中A的摩尔分数是()A、 1B、 0.75C、 0.667D、 0.53、理想气体的真空自由膨胀,哪个函数不变()A。
、ΔS=0 B、 V=0 C、ΔG=0 D、ΔH=04、一体积的氢气在0℃,101.3kPa下等温膨胀至原来体积的3倍,其内能变化是多少?(设氢气是理想气体) ()A、 0.4JB、 0JC、 6JD、0.04J5、已知反应CO(g)+1/2O2(g)=CO2(g)的ΔH,下列说法中何者不正确()A.、ΔH是CO2(g)的生成热B.、ΔH是CO(g)的燃烧热 C、ΔH是负值 D、ΔH与反应ΔU的数值不等6、已知下列反应的平衡常数:()H2(g) + S(s)= H2S(g) K1 ;S(s) + O2(g) = SO2(g) K2;则反应H2S(g) + O2(g)= H2(g) + SO2(g) 的平衡常数为A、 K2/K1B、 K1—K2 C.、K1×K2 D、 K1/K27、对于N2和H2混合气体的绝热可逆压缩(没有生产NH3),则()A.、ΔU=0 B 、 ΔH=0 C 、 ΔS=0 D、 ΔG=08.、298K 时反应Zn+Fe 2+=Zn 2++Fe 的E 0为0.323V ,则其平衡常数为( )A 、 2.89×105 B.、8.34×1010 C 、 5.53×104 D 、 2.35×1029、将H 2O(l)变成同温同压的H 2O(g),则体系的( )A 、内能不变B 、内能可能减少,也可能增加C 、内能增大D 、内能减少10、今有①T②P③U④U m ⑤H⑥H m ⑦Cp⑧Cpm,对于理想气体上述量中随物质的量而改变的量有( )A.、①②③ B 、②④⑥ C 、③⑤⑦ D 、③④11、有关CO 2(g)的标准生成热△f H m 有以下说法①C(金刚石)+O 2(g) → CO 2(g) △r H m =△f H m ②CO(g)+0.5O 2→ CO 2(g) △r H m =△f H m③C(无定形)+O 2(g) → CO 2(g) △r H m =△f H m④C(石墨)+O 2(g) →CO 2(g) △r H m =△f H m⑤CO(g)+0.5O 2(g) → CO 2(g) C(石墨)+0.5O 2(g)→ CO(g)可通过此二式的标准反应热效应,计算出CO 2(g)的△f Hm ,其中正确的是( )A 、①②B 、②③C 、④⑤D 、③④ 12 、查得298K 时Fe 3O 4,Fe 2O 3,FeO 的标准生成自由能分别为-1014,-741,-257(KJ.mol -1)则在298K101.3KPa 的空气中最稳定的物质是( )A.、Fe 3O 4B.、Fe 2O 3 C 、FeO D 、无法判断13、理想气体经历绝热不可逆过程从状态1(P 1,V 1,T 1)变化到状态2(P 2,V 2,T 2),所做的功为 ( )A 、P 2 V 2 - P 1 V 1B 、P 2(V 2 - V 1)C 、[])/1/1()1/(111222----γγγγV V V PD 、(P 2 V 2 - P 1 V 1)/(1-γ)14、在458K -475K 间,反应:2C 2H 5OH (g)=CH 3COOC 2H 5(g)+2H 2(g)的平衡常数与T 的关系为lgKp=-2100/T+4.66,已知△ f H m (C 2H 5OH,g,473K)=-235.34KJ.mol -1,则△ f H m (CH 3COOC 2H 5,g,473K)等于:( )A 、-4.305×105J.mol -1B 、-1.951×105J.mol -1 o oC 、5.109×105J.mol -1D 、 2.756×105J.mol-1 15、反应C(s)+2H 2(g)→CH 4(g)在873K 时△r H m =-85 kJmol -1,为获得CH 4的更大平衡产率,问温度和压力怎样选择?( ) A 、降低温度,减少压力 B 、升高温度,减少压力C 、升高温度,增加压力D 、降低温度,增加压力16、对于反应3H 2(g)+N 2(g)=2NH 3(g),当其中N 2因反应消耗了0.3 mol 时,反应进度等于:( )A 、1.8 molB 、0.9 molC 、0.6 molD 、0.3 mol17、物质能以液体形式存在的最高温度是:( )A 、沸腾温度T bB 、临界温度T cC 、对比温度T rD 、熔融温度T m18、自发过程(即天然过程)的基本特征是 ( )A 、系统能够对外界作功B 、过程进行时不需要外界作功C 、过程发生后, 系统和环境不可能同时恢复原态D 、系统和环境间一定有功和热的交换19、下列说法不正确的是 ( )A 、热力学和统计热力学的研究对象都是大量粒子的集合体;B 、热力学和统计热力学的研究方法都是宏观的方法;C 、1900年,普朗克提出了量子论,引入了能量量子化的概念;D 、吉布斯创立了统计系综的方法,建立了系综理论;20、关于粒子配分函数的概念,不正确的说法是 ( )A 、分函数是无量纲量;B 、配分函数是对体系中所有粒子的所有可能状态的玻兹曼因子求和,故又称状态和;C 、配分函数中任意两项之比等于在该两能级上最概然分布的粒子数之比;D 、配分函数中任意一项与配分函数本身的比值等于粒子分配在该任意能级上的分数;21、对于O 2和N 2混合气体的可逆绝热压缩过程 ( )A 、0=∆UB 、0=∆FC 、0=∆SD 、0=∆G22、1mol 物质A 与1mol 物质B 形成的理想溶液(即理想液态混合物),在压力p 下达气-液两相平衡,已知**B A p p >,则 ( )A 、A A y x =B 、B A y y =C 、A A y x <D 、A A y x >23、100g 的2Cl 与一定量的8S 按反应式628SCl 8Cl 24S =+反应,当2Cl 全部转变成6SCl 时的反应进度ξ (单位:mo1)是 ( )A 、0.0587B 、0.470C 、0.587D 、0.04724、在2000K 时反应)(CO )(1/2O CO(g)22g g =+的标准平衡常数(θK )为6.443,则在同温度下反应)(O CO(g)2)(CO 222g g +=的标准平衡常数为( )A 、443.6/1B 、443.6C 、2)443.6/1(D 、443.6/125反应)(CH )(2H C(s)42g g →+在873K 时185-⋅-=∆mol kJ H m r θ,为提高CH 4的平衡产率,温度和压力应如何选择 ( )A 、降低温度,减少压力B 、升高温度,减少压力C 、升高温度,增加压力D 、降低温度,增加压力26、在配制理想溶液(即理想液态混合物)时,下列效应正确的是 ( )A 、H mix = 0 B 、S mix = 0 C 、G mix 0 D 、V mix 027、 封闭体系,当状态从Ⅰ到Ⅱ发生变化时经历二条任意的不同途径,则 ( )A 、21Q Q =B 、21W W =C 、2211W Q W Q +=+D 、0=∆U28、热力学第一定律ΔU=Q+W 只适用于( )(A) 单纯状态变化 (B) 相变化(C) 化学变化 (D) 封闭物系的任何变化29、关于热和功, 下面的说法中, 不正确的是( )(A) 功和热只出现于系统状态变化的过程中, 只存在于系统和环境间的界面上(B) 只有在封闭系统发生的过程中, 功和热才有明确的意义(C) 功和热不是能量, 而是能量传递的两种形式, 可称之为被交换的能量(D) 在封闭系统中发生的过程中, 如果内能不变, 则功和热对系统的影响必 互相抵消30、关于焓的性质, 下列说法中正确的是 ( )(A) 焓是系统内含的热能, 所以常称它为热焓(B) 焓是能量, 它遵守热力学第一定律(C) 系统的焓值等于内能加体积功(D) 焓的增量只与系统的始末态有关31、涉及焓的下列说法中正确的是( )(A) 单质的焓值均等于零(B) 在等温过程中焓变为零(C) 在绝热可逆过程中焓变为零(D) 化学反应中系统的焓变不一定大于内能变化32、下列哪个封闭体系的内能和焓仅是温度的函数 ( )(A) 理想溶液 (B) 稀溶液 (C) 所有气体 (D) 理想气体33、与物质的生成热有关的下列表述中不正确的是( )(A) 标准状态下单质的生成热都规定为零(B) 化合物的生成热一定不为零(C) 很多物质的生成热都不能用实验直接测量(D) 通常所使用的物质的标准生成热数据实际上都是相对值34、dU=CvdT 及dUm=Cv,mdT 适用的条件完整地说应当是( )(A) 等容过程(B)无化学反应和相变的等容过程(C) 组成不变的均相系统的等容过程(D) 无化学反应和相变且不做非体积功的任何等容过程及无反应和相变而且系统内能只与温度有关的非等容过程35、下列过程中, 系统内能变化不为零的是()(A) 不可逆循环过程 (B) 可逆循环过程(C) 两种理想气体的混合过程 (D) 纯液体的真空蒸发过程36、第一类永动机不能制造成功的原因是()(A) 能量不能创造也不能消灭(B) 实际过程中功的损失无法避免(C) 能量传递的形式只有热和功(D) 热不能全部转换成功37、盖斯定律包含了两个重要问题, 即()(A) 热力学第一定律和热力学第三定律(B) 热力学第一定律及热的基本性质(C) 热力学第三定律及热的基本性质(D) 热力学第一定律及状态函数的基本特征38.当某化学反应ΔrCp,m<0,则该过程的随温度升高而()(A) 下降 (B) 升高 (C) 不变 (D) 无规律39、在下面涉及盖斯定律的表述中, 不正确的是()(A) 对在等温等压且不做非体积功的条件下, 发生的各个化学反应过程和相变过程, 可使用盖斯定律(B) 对在等温等容且不做功的条件下, 发生的各个化学反应过程, 可使用盖斯定律(C) 同一物质在盖斯定律涉及的几个反应中都出现时, 只要无溶解等现象, 相态不同也可加减(D) 利用盖斯定律求某个反应的热效应时可引入一些别的反应,设想一些中间步骤, 无论实际反应是否按这些中间步骤进行都可以40、下面的说法符合热力学第一定律的是()(A) 在一完全绝热且边界为刚性的密闭容器中发生化学反应时,其内能一定变化(B) 在无功过程中, 内能变化等于过程热, 这表明内能增量不一定与热力学过程无关(C) 封闭系统在指定的两个平衡态之间经历绝热变化时, 系统所做的功与途径无关(D) 气体在绝热膨胀或绝热压缩过程中, 其内能的变化值与过程完成的方式无关41、关于热平衡, 下列说法中正确的是()(A) 系统处于热平衡时, 系统的温度一定等于环境的温度(B) 并不是所有热力学平衡系统都必须满足热平衡的条件(C) 若系统A与 B成热平衡, B与C成热平衡, 则A与 C直接接触时也一定成热平衡(D) 在等温过程中系统始终处于热平衡42、对于功, 下面的说法中不正确的是()(A) 在系统对环境做功或环境对系统做功时, 环境中一定会留下某种痕迹(B) 功的量值与系统的始末态有关(C) 无论做什么功都伴随着系统中某种物质微粒的定向运动(D) 广义功=广义力³广义位移。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
物理化学---热力学第一定律作业题
习题1 看仿P27-29所有课后习题,参考答案及解题思路见书后
习题2 (1)如果一系统从环境接受了160J 的功,内能增加了200J ,试问系统将吸收或是放出多少热?(2)一系统在膨胀过程中,对环境做了10540J 的功,同时吸收了27110J 的热,试问系统的内能变化为若干?
[答案:(1) 吸收40J ;(2) 16570J]
习题3 一蓄电池其端电压为12V ,在输出电流为10A 下工作2小时,这时蓄电池的内能减少了1265000J ,试求算此过程中蓄电池将吸收还是放出多少热?
[答案:放热401000J]
习题4 体积为4.10dm 3的理想气体作定温膨胀,其压力从106 Pa 降低到105 Pa,计算此过程所能作出的最大功为若干?
[答案:9441J]
习题5 在25℃下,将50gN 2作定温可逆压缩,从105Pa 压级到2×106Pa ,试计算此过程的功。
如果被压缩了的气体反抗恒定外压105Pa 作定温膨胀到原来的状态,问此膨胀过程的功又为若干?
[答案:–1.33×104J ;4.20×103J]
习题6 计算1mol 理想气体在下列四个过程中所作的体积功。
已知始态体积为25dm 3终态体积为100dm 3;始态及终态温度均为100℃。
(1)向真空膨胀;
(2)在外压恒定为气体终态的压力下膨胀;
(3)先在外压恒定为体积等于50dm 3时气体的平衡压力下膨胀,当膨胀到50dm 3(此时温度仍为100℃)以后,再在外压等于100 dm 3时气体的平衡压力下膨胀;
(4)定温可逆膨胀。
试比较这四个过程的功。
比较的结果说明了什么问题?
[答案:0;2326J ;310l J ;4299J]
习题7 试证明对遵守范德华方程的1mol 实际气体来说,其定温可逆膨胀所作的功可用下式求算。
)11()ln(2
,12,1,2,V V a b V b V RT W m m m -----= 已知范德华方程为 RT b V V a p m m
=-+))((2 习题8 1mol 液体水在100℃和标准压力下蒸发,试计算此过程的体积功。
(1)已知在100℃和标准压力下,水蒸气的比体积(体积除以质量)为1677cm 3·g -1,水的比体积为1.043cm 3·g -1。
(2)假设水的体积比之蒸气的体积可略去不计,蒸气作为理想气体。
比较两者所得的结果,说明(2)的省略是否合理。
[答案:3.057×103J ;3.101×103J]
习题9 在373K 和标推压力下,水的蒸发热为 4.067×104J·mol -1,1mol 液态水体积为18.08cm 3,蒸气则为30200cm 3。
试计算在该条件下1mol 水蒸发成气的ΔU 和ΔH 。
[答案:3.761×104J ;4.067×104J]
习题10 试由0=⎪⎭⎫ ⎝⎛∂∂T V U 及0=⎪⎭⎫ ⎝⎛∂∂T V H 证明理想气体的 0=⎪⎪⎭⎫ ⎝⎛∂∂T p U 及
0=⎪⎪⎭⎫ ⎝⎛∂∂T
p U 习题11 有1mol 单原子分子理想气体在0℃,105Pa 时经一变化过程,体积增大一倍,△H =2092J ,Q=1674J 。
(1)试求算终态的温度、压力及此过程的△U 和W ;(2)如果该气体经定温和定容两步可逆过程到达上述终态,试计算Q 、W 、△U 和△H 。
[答案:(1)373.7K ,6.84×104Pa ,1255J ,419J , (2)2828J ,1573J ,1255J, 2092J]
习题12 已知任何物质的 TV C C v p β
α2
=- 其中α为膨胀系数,β为压缩系数。
现已查得25℃时液体水的定容热容C v,m =75.2J·K -1·mol -1, α=2.1×10-4K -1, β=4.44×10-10Pa -1,而水的V m =18×10-6m 3·mol -1。
试计算液体水在25℃时的C p,m 。
[答案:75.7J·K -1·mol -1 ]
习题13 已知N 2和O 2的定压摩尔热容与温度的关系式分别为
113
2,)1027.487.27()(---⋅⋅⨯+=mol K J K T N C p m 1121
32,))
/(1031.410845.0162.31()(----⋅⋅⨯-⨯+=mol K J K T K T O C p m 试求空气的C p,m 与温度的关系式应为如何?
习题14 某理想气体的C p,m =35.90J·K -1·mol -1,⑴当2mol 此气体在25℃,1.5×106 Pa 时,作绝热可逆膨胀到最后压力为5×105 Pa ;⑵当此气体在外压恒定为5×105 Pa 时作绝热快速膨胀;试分别求算上述两过程终态的T 和V 及过程的W 、△U 和△H 。
[答案:⑴231K ;7.68dm 3;-3697J ;-3697J ;-4811J ;⑵252K ;8.38 dm 3;2538J ;-2538J ;-3303J]
习题15 已知下列反应在25℃时的热效应为
1
221
422142221
23.92);()(2
1)(21)4(8.1382);()(2)()(2)3(8.800);()(2)()()2(411);()(2
1)()1(-Θ-Θ-Θ-Θ⋅-=∆=+⋅-=∆=++⋅-=∆=++⋅-=∆=+m ol kJ H g HCl g Cl g H m ol kJ H s SO Na g O s S s Na m ol kJ H l SO H g O s S g H m ol kJ H s NaCl g Cl s Na m r m r m r m r
计算反应2NaCl(s)+H 2SO 4(l)=Na 2SO 4(s)+2HCl(g)在25℃时的Θ∆m r H 和Θ∆m r U
[答案:55.4; 50.4 kJ·mol -1]
习题16 已知反应
(1)C(金刚石)+O 2(g)=CO 2(g); )298(K H m r Θ∆=-395.4kJ·mol -1
(2) C(石墨)+O 2(g)=CO 2(g); )298(K H m r Θ∆=-393.5kJ·mol -1
求C(石墨)=C(金刚石)的 )298(K H m r Θ∆
[答案: 1.9kJ·mol -1]
习题17 利用下列数据计算HCl(g)的生成焓
1
3221
42221441
1
331
4302.46)298();()(2
3)(21)6(8.313)298();()(2
1)(2)(21)5(32.16)298();,()()4(22.73)298();,()()3(56.35)298();,()()2(21.50)298();,(),(),()1(-Θ-Θ-Θ-Θ-Θ-Θ⋅-=∆=+⋅-=∆=++⋅=∆∞=+⋅-=∆∞=+⋅-=∆∞=+⋅-=∆∞=∞+∞m ol kJ K H g NH g H g N m ol kJ K H s Cl NH g Cl g H g N m ol kJ K H aq Cl NH s Cl NH m ol kJ K H aq HCl g HCl m ol kJ K H aq NH g NH m ol kJ K H aq Cl NH aq HCl aq NH m r m r m r m r m r m r 水水水
[答案:-92.5kJ·mol -1]
习题18 试计算在20 ℃及标准压力下,1mol 液态水蒸发成水蒸气的气化焓。
已知100 ℃ 焓及及标准压力下液态水蒸发成水蒸气的气化焓为2259J·g -1,在此温度区间内,水和水蒸气的平均摩尔等压热容分别为75.3 J·K -1·mol -1和 33.2 J·K -1·mol -1。
[答案:43.8kJ·mol -1]
习题19 某工厂中生产氯气的方法如下:将比例为1:2的18℃的氧气和氯化氢混合物连续地通过一个386℃的催化塔。
如果气体混合物通得很慢,在塔中几乎可达成平衡,即有80%的HCl 转化成Cl 2和H 2O(g)。
试求算欲使催化塔温度保持不变,则每通过1molHCl 时,需从系统取出多少热?
[答案:约7kJ]。
