倒立摆系统的最优控制应用研究
基于LQR的直线一级倒立摆最优控制系统研究

Ree rh o n o t l ie riv re e d lm o to y tm a e n L sa c na pi n a etd p n uu c nr l se b sd o QR ma l n s
XN i —u C E i o gJA G Mig IG J gh , H N Q — n ,I N n n g
力 , 为 小 车位 置 , 为 摆 杆 与
垂 直 向上方 向 的夹 角 , 0为摆 杆 与垂 直 向下 方 向 的 夹 角 ( 虑 考 到摆 杆初 始位 置 为竖直 向下 ) 。
图 1 直 线 一 级 倒 立 摆 系 统
0 l
然不 稳定 的系统 , 立 摆 系 统 通 常 用来 检 验 控 制 策 倒 略 的效果 , 是控 制理 论研 究 中较 为理想 的实 验装 置 。 又 因其与 火箭 飞行 器及单 足 机器人 有很 大 的相 似之
维普资讯
20 0 7年 第 6期
工 业 仪 表 与 自动 化 装 置
・3 ・
基 于 LQR 的 直 线 一 级 倒 立 摆 最 优 控 制 系 统 研 究
邢景虎 , 陈其工 , 江 明
( 安徽 工程 科技 学 院 电气传 动与控 制 安徽 省 高校重 点 实验 室 , 徽 芜湖 2 10 ) 安 4 00 摘 要 : 理 论和 实践 上对 直线 一级 倒立摆 作 了深 入 的研 究。 用牛 顿一 欧拉 方 法建 立 了倒 立摆 从 的数 学模 型 , 此基 础 上 采 用 线 性 二 次 型 最 优 控 制 方 法 设 计 了倒 立摆 的 控 制 器。 通过 固高 公 司 在
倒立摆系统控制方法的研究的开题报告

倒立摆系统控制方法的研究的开题报告一、选题背景倒立摆系统作为一种重要的非线性系统,其具有复杂的动态特性,包含了多种不同的振动模式,其中包括摆臂旋转、摆杆摆动等。
在实际应用中,倒立摆系统被广泛应用于机器人控制、无人机飞行稳定性控制以及动态控制系统等领域。
倒立摆系统具有高度的不确定性和非线性性,因此如何设计有效的控制策略,使其稳定地控制成为了研究人员的热点问题。
二、研究目标本研究旨在探究倒立摆系统的控制方法,以实现系统的稳定控制并提高其动态性能。
三、研究内容1. 倒立摆系统的建模及数学描述2. 常用的倒立摆控制方法:包括经典PID控制、模糊控制、神经网络控制、自适应控制等3. 基于模型预测控制算法的倒立摆控制方法研究4. 倒立摆控制算法的性能评估四、研究难点和挑战倒立摆系统具有非线性、时变性强、不确定性大的特点,在应用中存在稳定性差、控制精度低、鲁棒性不足的问题。
因此,在设计控制策略时需要解决这些难点和挑战。
五、研究方法本研究将采用理论分析和实验验证相结合的方法,建立数学模型,并针对不同的倒立摆控制方法进行对比分析,评估其性能及优缺点。
六、研究意义本研究的意义在于:1. 为倒立摆系统的控制提供了新的思路与方法,有助于提高系统的稳定性和控制精度。
2. 对于其他非线性系统控制算法的研究和应用提供了借鉴和参考。
3. 促进了控制理论及其在实际应用中的发展。
七、预期成果1. 完成倒立摆系统的建模及数学描述。
2. 实现常用的控制算法,并对其稳定性和性能进行评估。
3. 基于模型预测控制算法,实现倒立摆系统的控制,提高其稳定性和控制精度。
4. 优化控制算法,提高系统的鲁棒性和动态性能。
八、研究计划本研究计划于2021年12月开始,预计2022年12月完成。
计划分为以下几个阶段:1. 研究倒立摆系统的基本原理和常用控制方法,完成控制算法的设计和建模,预计时间:3个月。
2. 基于模型预测控制算法,实现倒立摆系统的控制,进行实验验证,评估其性能及优缺点,预计时间:6个月。
三级倒立摆的LQG最优控制应用研究

Th plc to s Re e r h o r p e I e t d e Ap i a i n s a c fTh i l nv r e
P n uu B sd o QG p i l o to e d lm a e n L O t ma C n r l
YE in bn。 Ja - i GUO n - Ho gwu
Ke r s til n etd p n uu s se !LQG t l o to ! alb smuain ywo d rpeiv re e d lm y tm z Op i nr lM t i lt ma c a o
感器 的量测误 差 , 些对 系统 的稳定 控 制都 产生 了 这
立摆 的动态平 衡 。仿 真 结果表 明 , 控制 系统 取得 该
了预期 的效果 。
的是 线性 二 次最 优控制 ( QR) L 方法 , 献 [ ] 文 2 重点
研究 了 三级倒 立 摆 系统 L QR方 法 的加 权 阵 Q 的 选择 , 献 [ ] 三 级倒 立 摆 的 数 学模 型 设 计 了模 文 3对 糊 控 制器 和 L QR控 制器 的混 合控 制 器 , 进行 了 并 仿 真 , 献[ ] 二级 倒 立 摆 的 线性 化 数 学模 型设 文 4就
l e r udai Gas pi l o t lo al i l i ,einaL G o t l radep r n o ta tepee- i a a rt us t nr [r t bs n q c o ma c o M a mua o d s Q C nr l ,n ei t h w th rsn tn g oe x me s h
二级倒立摆系统的最优控制

∞
ut
+
B
+
1 /S
x
C
y
A
R-1BT
P
五、仿真分析
将某二级倒立摆系统模型各参数代入式1-8,得出系数矩阵 设, 写出Matlab程序如下:
A=[0,0,0,1,0,0;0,0,0,0,1,0;0,0,0,0,0,1; 0,-2.57163,0.164291,-16.6674,0.0124145,0.005; 0,29.9499,-15.1957,40.3167,-0.204856,0.17380; 0,29.9499,65.4455,-49.3949,0.463474,-0.59148]; B=[0;0;0;8.64636;-20.9146;25.9146]; C=[1 0 0 0 0 0;0 1 0 0 0 0;0 0 1 0 0 0];D=[0;0;0]; %求开环特征值 r1=eig(A) %加入最优反馈器 q1=100;q2=10;q3=5000;q4=0;q5=0;q6=0; Q=[q1 0 0 0 0 0;0 q2 0 0 0 0;0 0 q3 0 0 0;0 0 0 q4 0 0;0 0 0 0 q5 0;0 0 0 0 0 q6];R=1; %求最优增益矩阵、黎卡提方程的解、闭环特征值 [K,P,r2]=lqr(A,B,Q,R) Ac=[(A-B*K)];Bc=[B];Cc=[C];Dc=[D]; T=0:0.02:20;U=zeros(size(T)); x0=[0;-0.05;0.1;0;0;0]; [Y,X]=lsim(Ac,Bc,Cc,Dc,U,T,x0); %绘制下摆偏离垂直方向的角度变化曲线 figure(1);plot(T,Y(:,1)); xlabel('Time/sec');ylabel('01/rad');grid; %绘制上下摆角度之差的曲线 figure(2);plot(T,Y(:,2)); xlabel('Time/sec');ylabel('02-01/rad');grid; %绘制小车位移曲线 figure(3);plot(T,Y(:,3)) xlabel('Time/sec');ylabel('x(小车)/m');grid;
倒立摆控制算法的研究与优化

倒立摆控制算法的研究与优化第一章:引言倒立摆是一种经典的控制理论案例,它是一个由一个倒立的杆和底座组成的系统。
通过应用适当的控制算法,倒立摆可以稳定在立直的位置上。
倒立摆的研究对于理解和应用控制算法有着重要的作用。
本文将对倒立摆控制算法的研究和优化进行探讨。
第二章:倒立摆控制算法的基本原理倒立摆控制算法的基本原理是通过对摆杆的力矩进行控制,使其保持在立直的位置上。
常用的控制算法包括PID控制、模糊控制和神经网络控制等。
PID控制是一种常见且简单的控制算法,通过对比实际位置和期望位置的偏差来控制力矩的大小。
模糊控制是一种基于模糊逻辑的控制算法,通过设置一系列的模糊规则来控制力矩。
神经网络控制则通过训练神经网络来得到最优的控制策略。
第三章:倒立摆控制算法的研究进展在过去的几十年中,倒立摆控制算法得到了广泛的研究。
研究者们不断提出新的控制算法,并对已有的算法进行改进和优化。
例如,有学者通过将PID控制与模糊控制相结合,提出了模糊PID控制算法,使控制效果更加稳定和精确。
另外,研究者们还通过使用进化算法对控制算法进行优化,提高了控制的性能。
此外,一些新兴的控制算法如深度强化学习等也被应用于倒立摆控制中。
第四章:倒立摆控制算法的优化方法为了提高倒立摆控制算法的性能,研究者们提出了一系列的优化方法。
首先,一些参数整定技巧被应用到控制算法中,例如Ziegler-Nichols方法和系统辨识方法,可以提高控制算法的稳定性和鲁棒性。
其次,优化算法如遗传算法和粒子群算法被用于优化控制算法的参数,实现更好的控制效果。
另外,研究者们还将深度学习方法引入倒立摆控制中,通过训练神经网络来得到更优的控制策略。
这些优化方法使得倒立摆控制算法在实际应用中得到了更好的效果。
第五章:倒立摆控制算法的应用与展望倒立摆控制算法在现实世界中有着广泛的应用。
例如,它可以应用在机器人控制、航天器操纵和工业自动化等领域。
随着科技的不断发展,倒立摆控制算法也将不断演化和完善。
单级倒立摆三种控制方法的对比研究

单级倒立摆三种控制方法的对比研究一、本文概述倒立摆系统作为经典的控制理论实验平台,被广泛用于研究和验证各种控制算法的有效性。
单级倒立摆作为倒立摆系统中最简单的形式,其动态特性和控制难度适中,成为了许多学者研究的焦点。
本文将重点探讨三种常见的单级倒立摆控制方法,并通过对比分析,揭示各方法的优缺点以及在不同场景下的适用性。
本文将简要介绍单级倒立摆的基本结构和动力学特性,为后续控制方法的研究奠定基础。
随后,将详细介绍三种控制方法:PID控制、模糊控制和最优控制,并阐述各自的基本原理和实现过程。
在此基础上,本文将通过仿真实验和实物实验,对比三种控制方法在单级倒立摆稳定控制中的表现,评估其控制精度、响应速度和鲁棒性等方面的性能。
通过本文的研究,旨在为倒立摆控制领域的研究者提供有益的参考,并为实际工程应用中的控制策略选择提供理论支持。
也希望本文的研究能够推动倒立摆控制技术的发展,为智能控制领域的发展做出一定的贡献。
二、单级倒立摆系统概述单级倒立摆系统是一种典型的非线性、不稳定、不可控系统,是控制理论研究和教学实验中常用的典型实验对象。
该系统由一个支点、一个摆杆和一个小球组成,摆杆一端通过支点与地面相连,另一端固定一个小球。
小球受到重力作用,会自然下垂,而摆杆则可以在垂直平面内自由摆动。
当系统受到外部扰动时,小球会偏离平衡点,导致摆杆摆动,系统变得不稳定。
单级倒立摆系统的控制目标是通过施加一定的控制力,使小球能够稳定地倒立在摆杆顶端,即保持系统平衡。
由于该系统具有非线性、不稳定和不可控等特性,控制难度较大。
为了实现这一控制目标,需要设计合适的控制器,并采用合适的控制策略。
在单级倒立摆系统的控制中,常用的控制方法包括PID控制、模糊控制、神经网络控制等。
PID控制是一种基于误差反馈的控制方法,通过不断调整控制量来减小误差,使系统达到稳定状态。
模糊控制则是一种基于模糊逻辑的控制方法,通过模糊化输入和输出变量,实现对系统的非线性控制。
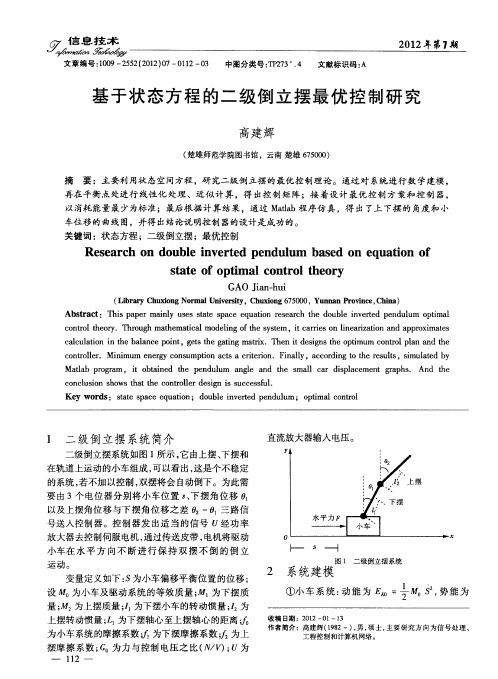
基于状态方程的二级倒立摆最优控制研究
0
卜一 S — _ — —1
图 1 二 级 倒立 摆 系统
变量 定义 如下 : . s为小车偏 移 平衡 位 置 的位移 ; 设 为小 车及 驱动 系统 的等效 质 量 ; 为下 摆质 M。
量 ; 为上摆 质量 ; 为下摆 小车 的转 动惯 量 ;2 , 1 为
车位 移的 曲线 图,并得 出结论说 明控制 器的设 计是成 功的 。
关键 词 :状 态方程 ;二级倒 立摆 ;最优控 制
Re e r h o o b e i v r e e d l n a e n e u to f s a c n d u l n e t d p n u u l b s d o q a i n o sa e o p i a o t o h o y t t fo tm lc n r lt e r
Ke r s s t p c q a in; d u l n e e e d l m ; o t lc n o y wo d : t e s a e e u t a o o beiv r d p n uu t pi o t l ma r
1 二 级 倒立 摆 系统 简介
二 级倒立 摆 系统如 图 1所示 ,介 :高建辉 (9 2一) 男 , 士, 18 , 硕 主要研究 方向 为信 号处理、 工程控制和计算机网络 。
摘
要 :主 要利 用状 态空间方程 ,研 究二 级倒 立摆 的 最优 控 制理 论 。通过 对 系统进 行 数 学建模 ,
再在 平衡点 处进 行 线性 化 处 理 、近 似计 算 ,得 出控 制 矩 阵 ;接 着设 计 最优 控 制 方 案 和 控 制 器 , 以消耗 能量 最 少为标准 ;最后根 据 计 算结 果 ,通过 Maa 序仿 真 ,得 出 了上 下摆 的 角度 和 小 l fb程
一级倒立摆系统最优控制

摘要倒立摆系统是一个典型的快速、多变量、非线性、不稳定系统,许多抽象的控制理论概念都可以通过倒立摆实验直观的表现出来。
因此,倒立摆系统经常被用来检验控制策略的实际效果。
应用上,倒立摆广泛应用于航空航天控制、机器人,朵项顶杆表演等领域,研究倒立摆的精确控制对工业复杂对象的控制也有着重要的工程应用价值。
本文以固高公司生产的GIP-100-L型一阶倒立摆系统为研究对象,对直线一级倒立摆模型进行了建模,控制算法的仿真对比,并得出了相应的结论。
文中介绍了倒立摆的分类、特性、控制訂标、控制方法等以及倒立摆控制研究的发展及其现状。
利用牛顿力学方法推到了直线以及倒立摆的动力学模型,求出其传递函数及其状态空间方程。
在建立了系统模型的基础下,本文还研究了倒立摆系统的线性二次型最优控制问题,并且使用了MATLAB软件进行仿真,通过改变LQR模块及状态空间模块中的参数,在仿真中取得了不同的控制效果,最终得到了最好的控制效果。
关键字:一级倒立摆线性系统、数学建模、最优控制、LQR、仿真目录1 一阶倒立摆的概述 01」倒立摆的起源与国内外发展现状 01.2倒立摆系统的组成 01.3倒立摆的分类: 01.4倒立摆的控制方法: (1)2. 一阶倒立摆数学模型的建立 (2)2.1概述 (2)2.2数学模型的建立 (3)2.4实际参数代入: (4)3・定量、定性分析系统的性能 (6)3」对系统的稳定性进行分析 (6)3.2对系统的能空性和能观测性进行分析: (7)4.线性二次型最优控制设计 (8)4」线性二次最优控制简介 (8)4.2直线一级倒立摆LQR控制算法 (9)4.3 最优控制MATLAB仿真 (17)总结 (20)参考文献 (21)1 一阶倒立摆的概述1.1倒立摆的起源与国内外发展现状倒立摆的最初研究开始于二十世纪五十年代,麻省理工学院的控制理论专家根据火箭助推器原理设讣出来一级倒立摆实验设备。
倒立摆作为一个典型的不稳定,严重非线性例证被正式提出于二十世纪六十年代后期。
倒立摆控制系统的研究

倒立摆控制系统研究【关键词】 状态空间、可控可观、状态反馈、降维观测器、Simulink 非线性系统仿真一、研究背景基于自动控制原理课程设计《倒立摆控制系统研究》以及3号楼实验室具有硬件实验平台,我们在已知系统的非线性模型、简化线性模型的条件下对系统进行设计控制,有利于我们将控制理论真正地应用到实际中去解决问题。
同时也能有利于我们对Matlab 软件具有较好的应用。
二、研究目的1、学会使用Simulink 软件分析复杂的控制系统。
2、学会状态反馈进行控制系统设计。
3、了解状态观测器的实现。
4、加深对现代控制理论的理解。
三、实验平台装有Matalab 的计算机以及打印机 一台 实际倒立摆系统 一套四、倒立摆的数学模型1、实际的非线性模型)(cos 00144.00061.0212001θθθ--+=⋅⋅B A 2121121222)sin(2.1)cos(2.1sin 2.61⋅⋅⋅⋅⋅⋅⋅-----=θθθθθθθθθθ其中:⋅⋅---++=11212110]0168.0)cos()sin(00144.0[sin 2979.00236.0θθθθθθθu A 2221212210])sin()[cos(0012.0sin )cos(0734.0⋅⋅---+--=θθθθθθθθθB2、简化的线性模型 状态空间表达式为X AX BU Y CX DU⎧=+⎨=+⎩其中:''1212x θθθθ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦ ,12y θθ⎡⎤=⎢⎥⎣⎦,⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----=3444.16254.42122.822122.822760.07062.38751.168751.6510000100A ,⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=5125.62184.500B⎥⎦⎤⎢⎣⎡=00100001C ,⎥⎦⎤⎢⎣⎡=00D3、系统研究方法 由现代控制理论知识知,原系统的状态空间模型为BU AX X+= ,若系统的状态是完全能控的,则引入状态反馈调节器KX R U -=。
倒立摆系统__实验设计报告

倒立摆系统__实验设计报告一、实验目的本实验旨在通过对倒立摆系统的研究与实验,探讨倒立摆的运动规律,并分析其特点和影响因素。
二、实验原理与方法1.实验原理倒立摆是指在重力作用下,轴心静止在上方的直立摆。
倒立摆具有自然的稳定性,能够保持在平衡位置附近,且对微小干扰具有一定的抵抗能力。
其本质是控制系统的一个重要研究对象,在自动控制、机器人控制等领域有广泛的应用。
2.实验方法(1)搭建倒立摆系统:倒立摆由摆杆、轴心和电机组成,摆杆在轴心上下运动,电机用于控制倒立摆的运动。
(2)调节电机控制参数:根据实验需要,调节电机的参数,如转速、力矩等,控制倒立摆的运动状态。
(3)记录数据:通过相机或传感器等手段,记录倒立摆的位置、速度、加速度等相关数据,用于后续分析。
(4)分析数据:根据记录的数据,分析倒立摆的运动规律、特点和影响因素,在此基础上进行讨论和总结。
三、实验步骤1.搭建倒立摆系统:根据实验需要,选取合适的材料和设备,搭建倒立摆系统。
2.调节电机参数:根据实验目的,调节电机的转速、力矩、控制信号等参数,使倒立摆能够在一定范围内保持平衡。
3.记录数据:利用相机或传感器等设备,记录倒立摆的位置、速度、加速度等相关数据。
4.分析数据:通过对记录的数据进行分析,研究倒立摆的运动规律和特点,并探讨影响因素。
5.总结讨论:根据实验结果,进行总结和讨论,对倒立摆的运动规律、特点和影响因素进行深入理解和探究。
四、实验设备与器材1.倒立摆系统搭建材料:包括摆杆、轴心、电机等。
2.记录数据设备:相机、传感器等。
五、实验结果与分析通过实验记录的数据,分析倒立摆的运动规律和特点,找出影响因素,并进行讨论和总结。
六、实验结论根据实验结果和分析,得出倒立摆的运动规律和特点,并总结影响因素。
倒立摆具有一定的稳定性和抵抗干扰的能力,在控制系统中具有重要的应用价值。
七、实验感想通过参与倒立摆系统的搭建和实验,深入了解了倒立摆的运动规律和特点,对控制系统有了更深刻的理解。
倒立摆的原理及应用

倒立摆的原理及应用1. 倒立摆的基本原理倒立摆是一种非线性系统,它的基本原理可以通过以下几个方面来解释:•平衡态分析:倒立摆的平衡态是指竖立在竖直方向上的摆,此时摆的角度为零。
平衡态分析是倒立摆研究的重要内容之一,可以通过力矩平衡来进行分析和计算。
•线性化:倒立摆的一阶线性化模型可以通过泰勒展开来实现。
将非线性系统在某一工作点处进行一阶泰勒展开,可以得到一个近似的线性模型,进而用线性系统的理论和方法进行分析。
•设计控制器:倒立摆需要一个控制器来保持其稳定性。
常用的控制方法有经典的PID控制器、模糊控制、自适应控制等。
这些控制器采用传感器(如陀螺仪)来测量倒立摆的角度,并通过调节摆的力矩来保持其平衡。
2. 倒立摆的应用倒立摆具有很高的研究和应用价值,以下是一些常见的倒立摆应用领域:•机器人控制:倒立摆经常被用作机器人控制的实验平台。
通过控制倒立摆的平衡,可以实现对移动机器人、工业机器人等的稳定控制。
倒立摆可以模拟真实场景中的复杂动力学问题,是一个理想的研究工具。
•交通工具:倒立摆在交通工具领域也有广泛的应用。
例如,自平衡电动车就是一种基于倒立摆原理的交通工具。
它能够通过控制摆杆的角度来保持平衡,使人们在不用脚踏的情况下也能稳定骑行。
•能源系统:倒立摆也可以应用于能源系统,例如储能系统中的能量转换和稳定控制。
倒立摆可以帮助储能系统实现能量的高效转换和稳定输出,提高能源利用率和储能效果。
3. 倒立摆的发展趋势倒立摆作为一种非线性控制系统,其相关研究及应用也在不断发展。
以下是倒立摆的一些发展趋势:•智能控制:随着人工智能的发展,倒立摆的控制也越来越智能化。
例如,基于深度学习的控制方法可以通过学习大量的数据来进行控制决策,提高控制器的性能。
•多摆联合控制:将多个倒立摆通过机械结构连接起来,并进行联合控制,可以实现更复杂的动力学和控制策略,扩展倒立摆的应用领域。
•仿生机器人:仿生机器人是倒立摆在机器人领域的一种应用形式。
倒立摆研究报告(DOC)

基于LQR控制的二级倒立摆系统研究作者:牛娟031210308王晨琳031210307王鹤彬031210312 学院:自动化指导老师:王晶、陆宁云摘要倒立摆系统是一种高阶次、不稳定、多变量、非线性、强耦合的系统,是进行控制理论研究的典型实验平台。
本文采用最优控制的方法设计二级倒立摆系统的控制器。
首先简要介绍了倒立摆以及倒立摆的几种常见控制方法,着重介绍了最优控制理论,其次对二级倒立摆系统进行了数学建模,最后对线性二次型最优控制原理进行了分析并使用MATLAB进行了仿真。
关键词:二级倒立摆,最优控制目录一、绪论 (3)1.1、倒立摆系统简介 (3)1.2、倒立摆系统的控制算法 (3)1.3、小结 (4)二、直线倒立摆的建模 (4)2.1、直线二级倒立摆的建模 (4)2.2、直线二级倒立摆的定性分析 (6)三、基于MATLAB的LQR仿真 (9)3.1、最优控制(LQR)简介 (9)3.2、线性二次型最有调节器原理 (9)3.3、MATLAB仿真 (10)3.4、SIMULINK仿真 (11)四、结束语 (13)4.1、小结 (13)4.2、未解决问题展望 (13)五、附录 (13)一、绪论1.1、倒立摆系统简介倒立摆系统是一种高阶次、不稳定、多变量、非线性、强耦合的系统,是进行控制理论研究的典型实验平台。
许多抽象的控制理论概念如系统稳定性、可控性和系统抗干扰能力等等,都可以通过倒立摆系统实验直观的表现出来。
在控制理论发展的过程中,某种控制理论的正确性及可行性需要通过设计一个控制器去控制一个典型的控制对象去加以验证。
倒立摆系统正是这样一种比较典型的控制对象。
最简单的倒立摆可由一个可在水平轨道上自由移动的小车和倒置摆铰链组成。
倒立摆的种类繁多,分类方法也多种多样:按结构来分有直线倒立摆,环形倒立摆,平面倒立摆;按级数来分有一级摆,二级摆,三级摆乃至更高级摆;按运动轨道来分有水平轨道倒立摆,倾斜轨道倒立摆;按控制电机数目来分有单电机倒立摆,多电机倒立摆。
倒立摆与自动控制原理实验报告

倒立摆与自动控制原理实验报告摘要:本实验以倒立摆为研究对象,通过对倒立摆与自动控制原理的结合研究,探讨其在实际控制系统中的应用。
实验采用模拟倒立摆系统,使用PID控制算法对倒立摆进行控制,并对控制系统进行参数调整和性能测试。
实验结果表明,PID控制算法能够有效地实现倒立摆的平衡控制,具有较好的控制性能和稳定性。
1.引言倒立摆是一种经典的非线性动力学系统,具有重要的理论和应用价值。
倒立摆在自动控制中常被用作教学和研究对象,深入研究其动态特性可以帮助我们更好地理解自动控制原理。
2.实验原理倒立摆系统由摆杆和摆轮组成,通过控制摆杆的角度使得摆轮保持垂直状态。
实验中我们使用模拟倒立摆系统,通过转动电机控制摆杆的角度。
控制系统采用PID控制算法对摆杆进行控制,其中比例、积分和微分控制器的参数需要根据实际情况进行调整。
3.实验过程3.1系统建模根据倒立摆的运动学和动力学方程,我们可以建立系统的数学模型。
并结合实际参数进行仿真得到系统的状态响应。
3.2控制器设计在实验中,我们采用PID控制算法对倒立摆进行控制,其中比例、积分和微分控制器的参数需要根据实际情况进行调整。
实验中我们使用试错法进行参数调整,通过观察系统的响应曲线来判断参数是否合理,并逐步调整参数使系统达到最佳控制效果。
3.3性能测试在控制器设计完成后,我们对系统进行性能测试。
通过控制器输出信号,观察摆杆的运动轨迹和角度,并记录下对应的数据。
通过计算和分析可以评估控制系统的性能。
4.实验结果与分析实验结果表明,经过参数调整的PID控制系统能够有效地控制倒立摆的角度。
通过观察运动轨迹可以看出,当摆杆偏离垂直方向时,控制系统会通过调整控制信号,使得摆杆返回到垂直状态。
实验中我们进行了多组测试,通过计算平均偏差和稳定时间等指标,验证了控制系统的性能。
5.结论本实验通过对倒立摆与自动控制原理的结合研究,验证了PID控制算法在倒立摆控制中的有效性。
实验结果表明,经过参数调整的PID控制系统能够实现倒立摆的平衡控制,并具有较好的控制性能和稳定性。
倒立摆系统的智能控制研究的开题报告

倒立摆系统的智能控制研究的开题报告
一、选题背景
倒立摆系统是一种具有非线性、高度敏感、动态不稳定等特点的控制系统,具有广泛的应用领域,在机器人控制、智能控制、自适应控制等领域都有着重要的应用。
然而,传统的控制方法难以应对其高度复杂的动态特性,如何提高控制系统的稳定性和鲁棒性是解决该问题的关键所在。
本文将研究利用智能控制方法对倒立摆系统进行控制,以提高控制系统的稳定性和鲁棒性,并验证其控制效果。
二、研究内容
1.分析倒立摆系统的动态特性,建立倒立摆系统的控制模型,并对其特点进行分析。
2.利用智能控制方法设计倒立摆系统控制器。
具体来说,采用模糊控制、神经网络控制、深度强化学习等智能控制策略,针对倒立摆系统的动态特性进行优化,提高控制器的稳定性和鲁棒性。
3.搭建实验平台,进行仿真和实验验证。
通过模拟实验验证不同智能控制策略对倒立摆系统的控制效果,同时利用实验平台进行实际实验验证,对实验结果进行分析和解释。
三、研究意义
本文将通过对倒立摆系统的智能控制研究,旨在提高控制系统的稳定性和鲁棒性,具有以下研究意义:
1.对倒立摆系统的控制方法进行研究和探索,加深对智能控制技术的理解和应用。
2.提高倒立摆系统的控制效果,为实际应用提供有力支撑。
3.促进控制领域的发展,扩展控制技术的应用范围。
四、预期成果
1.建立倒立摆系统的控制模型,分析其动态特性。
2.设计出基于智能控制方法的倒立摆控制器。
3.通过仿真实验和实际实验对控制器进行验证和分析,得出相应的实验结果和结论。
4.撰写论文,对本文研究内容进行总结和归纳,提出可能的改进方案和研究展望。
倒立摆研究报告

倒立摆研究报告摘要:本研究报告主要对倒立摆进行研究。
倒立摆是一种常见的动态系统,具有许多实际应用。
本报告首先介绍了倒立摆的基本原理和数学模型,并分析了其稳定性。
接着,我们探讨了倒立摆的控制方法,包括PID控制和模糊控制等。
最后,我们进行了实验验证,并对结果进行了分析和总结。
通过本研究,我们可以更好地理解倒立摆的控制原理,并为实际应用提供参考。
1.引言倒立摆是一种常见的动态系统,广泛应用于机器人技术、控制系统等领域。
其基本原理是通过控制系统对倒立摆进行控制,使其保持平衡。
本研究将对倒立摆进行研究,并探讨其控制方法和稳定性。
2.倒立摆的原理和数学模型倒立摆由一个过渡段和一个摆杆组成。
过渡段通过一个电机控制摆杆的角度,并通过传感器测量摆杆的角度。
根据动力学原理,可以得到倒立摆的数学模型。
通过对数学模型进行分析,可以推导出倒立摆的运动方程。
3.倒立摆的稳定性分析对于倒立摆系统,稳定性是一个重要的性质。
稳定性分析能够帮助我们理解系统的行为,并为控制系统的设计提供参考。
本研究通过线性化分析和Lyapunov稳定性理论,对倒立摆的稳定性进行了分析。
4.倒立摆的控制方法倒立摆的控制方法有很多种,常用的包括PID控制和模糊控制等。
本研究对比了不同控制方法的优缺点,并提出了一种基于模糊控制的倒立摆控制策略。
5.实验验证与结果分析我们设计了一个倒立摆实验平台,并进行了实验验证。
通过实验数据的采集和分析,我们对控制系统的性能进行了评估,并与理论分析进行了比较。
6.结论与展望通过本研究,我们对倒立摆的原理和控制方法有了更深入的了解。
我们的实验结果验证了我们的控制策略的有效性。
未来,我们将进一步改进控制算法,提高倒立摆的控制精度,并将其应用于实际工程中。
二级倒立摆的 LQG 最优控制研究

1 系统 建 模
直线 二级 倒立 摆 系统 的模 型结 构 如图 1 所 示 。图 1中 , , 一 为 小车 位移 ( 右 为正 方 向 ) ; , 分 别 为 下 摆 杆、 上摆 杆 与垂 直方 向的夹 角 ( 顺 时针 为正方 向) 。 为使研 究对 象的 模 型不 过 于 复 杂 , 简 化 数 学模 型
二级 倒 立摆 的 L QG 最优 控 制 研 究 与 电 气工 程 学 院 。 山东 青岛 2 6 6 5 9 0 )
摘 要 : 为 实 现 二级 倒 立摆 系统 的稳 摆 控 制 ,应 用 了 线 性 二 次 高 斯 最 优 控 制 。 根 据 L Q G 的 分 离 原 理 . 首 先 利 用 最 优 控制 设 计 控制 律 ,得 到状 态 反馈 ; 由于 系统 状 态 不 能 完全 测 得 , 而 且 系统 也 不 可避 免地 会 受 到 噪 声 的 影 响 , 在 详 细 给 出相 应 参 数取 值 规 则 的 基 础 上 ,采 用 了卡 尔 曼滤 波 对 系统 输 出做 出最 优 估 计 。 最 后 的 仿 真 结 果 表 明 . 设 计 的 控制 器 能 够 较好 地 对 二 级倒 立摆 进 行 稳定 控制 ,且 具 有 抑 制 噪 声 和 抗 干 扰 能 力 。
第 l 期( 总第 1 8 2期 )
2 O I 4年 O 2月
机 械 工 程 与 自 动 化
ME CI { ANI CAL ENGI NEE Rl NG & AUT( ) M ATl ( ) N
No.1 Fe b.
文章编号 : l 6 7 2 — 6 4 1 3 ( 2 0 1 4 ) 0 l 一 0 1 5 0 — 0 3
倒立摆控制技术研究

倒立摆控制技术研究近年来,倒立摆控制技术的发展已经引起了人们广泛的关注。
此技术主要应用于工控、自动控制、航空航天等领域,然而其最为显著的应用就是在机器人领域中。
倒立摆的控制技术在工业生产中的应用已经非常广泛,其主要功能是通过控制倒立摆的运动实现对特定物件的精准定位和控制。
同时,倒立摆控制技术在拓扑稳定性控制、模糊控制,甚至是神经网络控制技术中都有广泛的应用。
近年来,随着自动化和人工智能技术的飞速发展,机器人技术的应用也越来越成为人们特别关注的一种技术。
而控制倒立摆技术在机器人领域的应用,更是得到了广泛的关注和研究。
那么,什么是倒立摆?倒立摆,简而言之就是一种物理系统,在平衡状态下,其表现出各种不同的动态效应。
它通常由一个摆杆和一个连接在摆杆上的小球组成,当摆杆在倾斜过程中,小球就会在其中振荡、滑动或者甚至是飞跃。
对于这种物理系统,在控制理论和控制工程领域中,研究人员经过很长一段时间的努力,已经开发出了各种不同的倒立摆控制技术,这些技术主要是通过调整和控制倒立摆的倾斜方向来控制其运动。
那么,倒立摆控制技术的优势和特点有哪些?首先,倒立摆控制技术可以帮助机器人在维持平衡方面更加稳定,从而实现更加精准的定位和控制。
其次,倒立摆控制技术还可以帮助机器人更加灵活地运动,从而扩展其使用范围。
对于倒立摆的控制技术,研究人员们通常采用模型预测控制、自适应控制和滑模控制等不同的技术路线。
而这些控制技术的核心点,都是如何建立一个合适的倒立摆控制模型来实现对机器人的控制。
在倒立摆控制模型的建立中,首先需要确定倒立摆的控制目标,确定控制目标之后,就可以根据目标模型建立控制模型。
在控制模型中,通常需要确定摆杆的质量、长度、重心、弹性等一些基本的参数,并且在控制系统中需要使用一些传感器来检测倒立摆的位置、速度、加速度等状态信息。
此外,倒立摆控制模型还需要根据摆杆的运动情况,建立一个回馈控制系统,在控制系统中需要通过精密的计算和控制算法来调整摆杆的偏角,进而实现对机器人运动的控制。
以最优控制法实现旋转式倒立摆系统的控制

[ ( s +c0] 一2 凰n-Li2 。c0 g o-Lo2 ‘ + z ) n m (i +s0】Rs 0 s 【 z ) 。 - 0 n
=m g s l 2 0 一m R 2 i( 1 2 一m2 L 2O ( 1 2 . 2g i 0 —m R 1 2 L s 0 —0 ) n n R 2 CS 0 —0 ) 0
表 1 主 要 机 械 参 数
Ta . M a n m a h n r a a e e b1 i c i e y p r m tr
0 2
采用实验和计算相结合的方法 , 可以得到各主要机械参数值( 1 。 表 )
机械参数
取值
机械参数
取值
旋臂质量 m 1
旋臂质心到转轴的距离 L .
76 4
西
安
科
技
大 学 学
报
20 08隹
哪
+ c- 【 i m o 0 m 2 R 2 : z s) ( 蚴+ 0 1
l i n O s
:
2 蚴 s i
¨ ㈩ 卜
=
=
【】 l l2i】 “ m +gn . + g ,R L ns
i
:
令0 1 , — 则 0 —0 0,n0 , 1 2 s 1 ls 2 , i ,i 0一 2则有 线性 化模 型 n
学建模过 程 , 究 了倒 立摆 系统 的二 次型 最优控 制 器设计 , 研 并运 用 MA L B程 序 对最 优控 制 器进 TA 行 了仿 真 , 通过 仿真 实验表 明这 种控 制方 案是 可行 的 , 其效 果 良好 。
关键 词 : 转倒 立摆 ;最优控 制 器 ;M T A 旋 A L B仿 真
最优控制Project对单级倒立摆系统进行控制的研究对单级倒立摆系统

对单级倒立摆系统进行控制的研究组别: 第二小组成员: 余凯 3103036026 刘烃 3103041027陶敬 3103041001导师: 管晓宏 专业: 系统工程 班级: 硕325/硕330院所: 西安交通大学系统工程研究所 日期: 2004.05.18最优控制 PROJECT目录一、倒立摆系统简介-----------------------------------------------------------------3二、单级倒立摆系统控制问题的提出------------------------------------------3三、单级倒立摆系统控制问题的分析------------------------------------------4四、对单级倒立摆系统进行控制并利用SIMULINK进行仿真---------8五、不同控制(调节)方案的比较----------------------------------------------54六、本次Project与实际中对单级倒立摆系统进行控制的区别-------55七、工作情况和心得体会---------------------------------------------------------56八、感谢和小结----------------------------------------------------------------------56对单级倒立摆系统进行控制的研究一、倒立摆系统简介1. 引言倒立摆系统是一个典型的高阶次、多变量、严重不稳定和强耦合的非线性系统。
由于它的行为与火箭飞行以及两足机器人行走有很大的相似性,因而对其研究在理论上、实践上和方法论上具有重大意义。
由于倒立摆系统本身所具有的上述特点,使它成为人们深入学习、研究和证实各种控制理论有效性的实验系统。
对倒立摆系统进行研究可归结为对非线性多变量绝对不稳定系统的研究,其控制方法和思路对处理一般工业过程亦有广泛的用途。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
[1] Fan Xingzhe, Cheng Ning, ZhangNaiyao. Two Fuzzy Cascade Control Schemes of a Trip le Inverted Pendulum[A]. Proceedings of the 3 thWorld Congress on Intelligent Control and Automation: Vol 3 [C].Hefei: IEEE, 2000, 1721-1726.
图6 直线一级倒立摆LQR控制仿真结果2
从图中可以看出,系统响应时间有明显的改善,增大
Q
1,
1
和
Q
3,
,系统的响应还会更快,但是对于实际离散控制
3
系统,过大的控制量会引起系统振荡。
3 直线一级倒立摆L Q R实时控制 实时控制实验在MATALB Simulink 环境下进行,直线
一级倒立摆L Q R 实时控制模块如图 7 所示。
Matlab 语句为K=lqr(A,B,Q,R)。求得 K=[-1 -1.7855 25.422 4.6849] 在S i m u l i n k 中建立直线一级倒立摆的模型如图 2真结果1
可以发现,Q 矩阵中,增加 Q1,1 使稳定时间和上升时间 变短,并且使摆杆的角度变化减小。这里取Q1,1= 1 0 0 0,Q3,3 =200。
图7 直线一级倒立摆LQR控制实时控制程序
实时控制模块“Real Control”模块如图8 所示。 (下转第35 页)
32
《自动化与仪器仪表》2011 年第 2 期(总第 154 期)
(2) 误码率:按瑞利衰落法计算,在信噪比≥2 0 d B 时, 基站、移动终端接收端的比特误码率≦ 4 %;
“Pendulum”模块内部结构如图9 所示。
图9 “Pendulum”模块内部结构
其中“Set Cart’s Acc and Vel”模块的作用是设置 小车运动的速度和加速度,“Get Cart’s Position”模块 的作用是读取小车当前的实际位置,“Get Pend’s Angle” 的作用是读取摆杆当前的实际角度。 4 结 论
图4 K值输入窗口
得到如下仿真结果: LQR 控制的阶跃响应如图5 所示,其中CartPos 为小车 的位置曲线,CartSpd 为小车的速度曲线,PendAng 为摆杆 角度曲线,P e n d S p d 为摆杆角速度曲线,从图中可以看出, 闭环控制系统响应的超调量很小,但稳定时间和上升时间 偏大,我们可以通过增大控制量来缩短稳定时间和上升时 间。
《自动化与仪器仪表》2011 年第 2 期(总第 154 期)
倒立摆系统的最优控制应用研究*
易 杰1,谢贤金2 (1 湖南工学院电气与信息工程系 湖南衡阳,4210 02)
(2 重庆工业自动化仪表研究所 重庆,401121)
摘 要:针对倒立摆系统的不稳定性,对最优控制理论在倒立摆控制系统中的应用进行了分析, 设计 L Q R 控制 器,并在倒立摆实验装置上进行了实验。实验结果表明设计的控制器是有效的,对倒立摆系统的平衡稳定控制效果 好,提高了系统的抗干扰能力。
0 引 言 倒立摆作为典型的快速、多变量、非线性、不确定系
统, 一直是控制领域研究的热点。许多研究人员一直将它 视为典型的研究对象,不断从中发掘出新的控制策略和控 制方法。其控制方法在军工、航天、机器人领域及一般工 业过程中都有着广泛的应用。针对不稳定的倒立摆系统的 平衡控制,应用最优控制理论设计控制器。
1 线性二次最优控制L Q R 基本原理及分析 线性二次最优控制L Q R 基本原理,由系统方程:
确定下列最佳控制向量的矩阵 K :
使得性能指标达到最小值:
时间越短。但是Q 不能过大。 2 倒立摆LQR控制参数调节及仿真
针对直线型一级倒立摆系统应用 L Q R 法设计与调节控 制器,控制摆杆保持竖直向上平衡的同时,跟踪小车的位 置,倒立摆最优控制L Q R 控制原理图如图1 所示。
31
个参数用来平衡输入量和状态量的权重。 最简单的情况是假设R=1,Q=C T* C 。当然,也可以通过
改变 Q 矩阵中的非零元素来调节控制器以得到期望的响 应。
倒立摆系统的最优控制应用研究 易 杰,等
其中,Q1,1 代表小车位置的权重,而 Q3,3 是摆杆角度的 权重,输入的权重 R 是 1 。
[5] 郑 科,徐建明,俞 立.基于 T-S 模型的倒立摆最优保性能模糊 控制[J].控制理论与应用,2004,21(5)703-708.
[6] 吴晓莉.Matlab 辅助模糊系统设计[M].西安:西安电子科技大学 出版社,2002.
35
重庆地铁一号线T E T R A 无线调度系统的网络基础设施 由交换控制中心M S O ( 与三号线合用) 、双载频基站构成; 有线台由分别位于控制中心、车辆段等地的调度终端构 成;无线台由固定电台、车载电台、便携电台等共同构成, 组网结构如图2 所示。
4 结束语 本文简述了重庆地铁一号线T E T R A 无线调度系统的覆
[2] 祁玉生.现代移动通信系统[M].人民邮电出版社,1999 年. [3] SJ/T11228-2000,数字集群移动通信系统体制. [4] 北京邮电设计院编著. 电信工程设计手册—移动通信分册
[M].人民邮电出版社,1994 年.
(上接第3 2 页)
图8 Real Control模块内部结构
其中“P e n d u l u m ”模块为倒立摆系统输入输出模块, 输入为小车的速度“V e l ”和“A c c ”,输出为小车的位置 “P o s ”和摆杆的角度“A n g l e ”。
四个状态量x、 、 、 分别代表小车位移、小车速度、 摆杆角度和摆杆角速度,输出y 包括小车位置和摆杆角度。 应用线性反馈控制器,设计控制器使得当给系统施加一个 阶跃输入时,摆杆会摆动,然后仍然回到垂直位置,小车 可以到达新的指定位置。
假设全状态反馈可以实现(四个状态量都可测),找 出确定反馈控制规律的向量K 。在M a t l a b 中得到最优控制 器对应的K。Lqr 函数允许你选择两个参数——R 和Q ,这两
则 K=[-31.623 -20.151 72.718 13.155] 输入参数,运行得到响应曲线如图 6 所示。
图2 直线一级倒立摆LQR控制仿真模型
“LQR Controller”为一封装好的模块,结构如图3 所 示。
图3 LQR Controller内部结构
双击“M a t r i x g a i n K ”即可输入控制参数(见图 4 )。
图1 倒立摆最优控制LQR控制原理图
直线一级倒立摆系统的以小车加速度作为输入的系 统状态方程:
式中,Q 为正定( 或正半定) 厄米特或实对称阵;R 为正 定厄米特或实对称阵。
方程右端第二项是考虑到控制能量的损耗而引进的, 矩阵 Q 和 R 确定了误差和能量损耗的相对重要性。并且假 设控制向量 u ( t ) 是无约束的。
[2] 薛安克, 王惠姣. 基于鲁棒 L Q 控制的倒立摆系统分析和设计 [J].上海交通大学学报,2002,36(增刊)1-7.
[3] 王正林,王胜开.MATLAB/Simulink 与控制系统仿真[M].北京:电 子工业出版社,2005.
[4] 薛安克,吕应权,孙优贤等.不确定线性系统鲁棒二次最优控制 的时频域方法[J].控制与决策,2001,16(1)20-24.
输入参数 K 值:K=[-31.623 -20.151 72.718 13.155] 运行结果如图1 0 所示。
图10 直线一级倒立摆LQR控制实时控制结果
其 中 图 片 上 半 部 分 为 小 车 的 位 置 曲 线 ,下 半 部 分 为 摆杆角度的变化曲线,从图中可以看出,在给定外界干扰 后,小车可以在1 . 5 秒内回到平衡位置。达到了较好的控 制效果。
( 3 ) 最小接收电平:接收机动态灵敏度 - 1 0 3 d B m ,考虑 瞬时瑞利衰落储备及上行链路余量储备后,列车车内的整 体覆盖性能应确保在手持台和车载台接收机端的最小接 收电平为-85dBm(95% 时间、地点概率),话音质量达到3 级 以 上;
台、站厅、车站办公区及出入口,场强覆盖指标满足在任 何4 0 米连续区段内无缝覆盖时间及地点概率不小于9 5 % 。 3.2 系统组网结构
关键词:倒立摆;最优控制;M A T L A B 仿真 Abstract: This paper reviews the applications of theory of optimal control for inverted pendulum, design a LQR Controller. Simulation and experiment show that the presented method is effective. and system has good stability and good robustness. Key words: Inverted pendulum ; Optimal control ; Matlab simulation 中图分类号:T P 1 3 文献标识码:B 文章编号:1 0 0 1 - 9 2 2 7 ( 2 0 1 1 ) 0 2 - 0 0 3 1 - 0 3
对线性系统:
根据期望性能指标选取Q 和R,利用MATLAB 命令lqr 就
可以得到反馈矩阵K 的值。
K=lqr(A,B,Q,R)
改变矩阵 Q 的值,可以得到不同的响应效果,Q 的值越
大( 在一定的范围之内) ,系统抵抗干扰的能力越强,调整
收稿日期: 2 0 1 0 - 1 1 - 0 1 作者简介: 易杰( 1 9 6 5 - ) , 男, 湖南人, 高级工程师, 主要研究 方向为智能控制。 * 基金项目: 湖南省教育厅科研项目( 0 8 c2 4 4 ) : 基于模糊控 制器参数最优调整的倒立摆控制研究
