初一几何练习题及答案
初一数学几何图形练习题及答案20题

初一数学几何图形练习题及答案20题1. 填空题:a. 正方形的对角线长度是________(1词)。
b. 两个互相垂直的角的和为________度(1词)。
2. 判断题(正确为T,错误为F):a. 直角三角形的两个直角边可以相等。
()b. 一个平行四边形的对角线相等。
()c. 所有的矩形都是正方形。
()d. 一个凸四边形的内角和为360度。
()3. 简答题:a. 请解释平行四边形的定义及性质。
(至少2句)b. 解释锐角、钝角和直角分别是什么角度范围。
(至少1句)4. 计算题:在下图中,ΔABC是个等边三角形,边长为4cm。
a. 请计算三角形ABC的周长。
(2词)b. 请计算三角形ABC的面积。
(2词)5. 应用题:桌子的形状为长方形,长为120cm,宽为80cm。
在桌子的边上画出一个同样形状的长方形,使得它的宽比原来的桌子短一半,长比原来的桌子长一半。
请计算这个新长方形的面积。
(2词)答案:1. a. 简答题b. 902. a. Fb. Tc. Fd. T3. a. 平行四边形是一个有四个边的四边形,且相对的两边是平行的。
其性质包括:对角线互相平分;相邻角互补;相对角相等。
b. 锐角是指小于90度的角;钝角是指大于90度小于180度的角;直角是指等于90度的角。
4. a. 12cmb. 4√3 cm²5. 1800 cm²通过以上20道初一数学几何图形练习题及答案的训练,可以帮助学生巩固和加深对于几何图形的理解和应用能力。
请同学们认真学习,并通过解答这些问题来提高自己的数学技能。
初中数学几何题练习与参考答案

初中数学几何题练习与参考答案答案如下:初中数学几何题练习与参考答案练习题一:直角三角形的性质1. 在直角三角形ABC中,已知∠A=90°,BC=6cm,AC=8cm,求AB的长。
解:根据勾股定理,有AB² + BC² = AC²代入已知数据,得到AB² + 6² = 8²化简得AB² = 64 - 36 = 28再开方得到AB = √28 cm练习题二:相似三角形的特征2. 若△ABC ~ △DEF,且AB=10cm,BC=6cm,DE=12cm,求DF 的长度。
解:由相似三角形的性质,可以得到以下比例:AB/DE = BC/DF 代入已知数据,得到10/12 = 6/DF交叉相乘得到DF = 6*12/10 = 7.2cm练习题三:平行线和梯形的性质3. 若AB // CD, AB = 8cm, CD = 10cm,且ABCD为梯形,高为6cm,求梯形的面积。
解:由梯形的面积公式,可以得到以下计算步骤:梯形面积 = (底1 + 底2) * 高 / 2代入已知数据,得到梯形面积 = (8 + 10) * 6 / 2 = 54cm²练习题四:圆的性质4. 已知半径为3cm的圆,求其周长和面积。
解:圆的周长公式为2πr,圆的面积公式为πr²。
代入已知半径3cm,得到周长= 2π * 3 = 6π cm,面积= π * 3² = 9π cm²练习题五:体积与表面积的计算5. 已知正方体的棱长为4cm,求其体积和表面积。
解:正方体的体积公式为边长的立方,表面积公式为边长的平方乘以6。
代入已知边长4cm,得到体积 = 4³ = 64cm³,表面积 = 4² * 6 =96cm²练习题六:二次曲线的图像探究6. 若抛物线y = ax² + bx + c的顶点为(-2, 3),且过点(1, 5),求a、b、c的值。
人教版七年级数学上册第四章《几何图形初步》单元练习题(含答案)
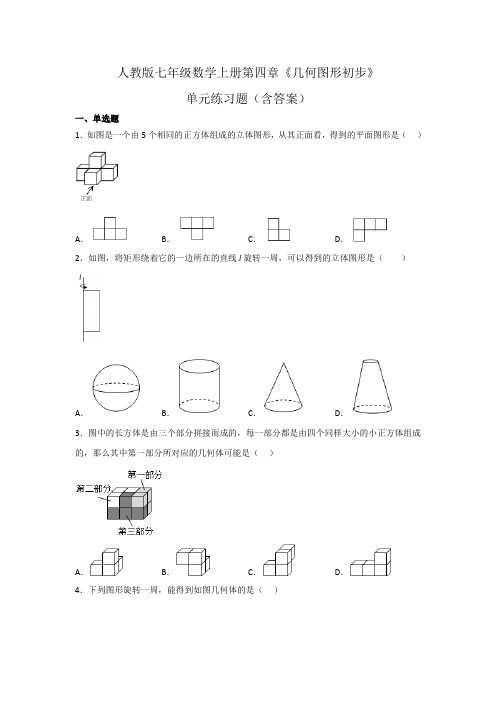
人教版七年级数学上册第四章《几何图形初步》单元练习题(含答案)一、单选题1.如图是一个由5个相同的正方体组成的立体图形,从其正面看,得到的平面图形是()A.B.C.D.2.如图,将矩形绕着它的一边所在的直线l旋转一周,可以得到的立体图形是()A.B.C.D.3.图中的长方体是由三个部分拼接而成的,每一部分都是由四个同样大小的小正方体组成的,那么其中第一部分所对应的几何体可能是()A.B.C.D.4.下列图形旋转一周,能得到如图几何体的是()A.B.C.D.5.如图,用一个平行于圆锥底面的平面截圆锥,截面的形状是()A.B.C. D.6.数学源于生活,并用于生活,要把一根木条固定在墙上至少需要钉两颗钉子,其中的数学原理是()A.过一点有无数条直线B.线段中点的定义C.两点之间线段最短D.两点确定一条直线7.下列图形是正方体展开图的个数为()A .1个B .2个C .3个D .4个8.下列说法中正确的有( ).(1)线段有两个端点,直线有一个端点; (2)由两条射线组成的图形叫角(3)角的大小与我们画出的角的两边的长短无关; (4)线段上有无数个点;(5)两个锐角的和必定是直角或钝角;(6)若AOC ∠与AOB ∠有公共顶点,且AOC ∠的一边落在AOB ∠的内部,则AOB AOC ∠>∠.A .1个B .2个C .3个D .4个9.如果一个角的度数比它的补角的度数2倍多30°,那么这个角的度数是( ) A .50°B .70°C .130°D .160°10.圆柱与圆锥的体积之比为2:3,底面圆的半径相同,那么它们的高之比为( ) A .2:3B .4:5C .2:1D .2:911.几何图形都是由点、线、面、体组成的,点动成线,线动成面,面动成体,下列生活现象中可以反映“线动成面”的是( ) A .笔尖在纸上移动划过的痕迹 B .长方形绕一边旋转一周形成的几何体 C .流星划过夜空留下的尾巴 D .汽车雨刷的转动扫过的区域12.己知点M 是线段AB 上一点,若14AM AB =,点N 是直线AB 上的一动点,且AN BN MN -=,则MNAB 的( ) A .34B .12C .1或12D .34或2二、填空题13.有一块积木,每一块的各面都涂上红绿黑白蓝黄六种不同的颜色,下面是它摆放的三种不同方向的图像,请根据图像判断绿色面的对面是_____色14.将两个三角尺的直角顶点重合为如图所示的位置,若108∠=︒,则AOD∠=_________.COB15.如图是用一副七巧板拼成的正方形,边长是10cm.图中小正方形(涂色部分)的面积是( )2cm.16.如图是一个正方体的展开图,将它拼成正方体后,“神”字对面的字是________.17.圆柱的侧面展开图是一个相邻的两边长分别为4,2π的长方形,则圆柱体的体积为_____.18.有一个正方体,六个面上分别写有数字1,2,3,4,5,6,如图是我们能看到的三种情况,如果记6的对面数字为a,2的对面数字为b,那么a+b的值为_____.三、解答题19.如图,点E是线段AB的中点,C是EB上一点,AC=12,(1)若EC:CB=1:4,求AB的长;(2)若F为CB的中点,求EF长。
七年级数学几何图形练习题及答案

七年级数学几何图形练习题及答案[答案表]以下是七年级数学几何图形练习题的答案。
1. 判断下列说法是否正确,并用对或错来回答:a) 正方形有四个直角。
答案:对。
b) 所有矩形都是正方形。
答案:错。
c) 所有正方形都是矩形。
答案:对。
d) 所有正方形都是长方形。
答案:对。
2. 根据图形的描述,选择正确的图形并填写在括号内:a) 一个有两条等长直角边的三角形是( )。
①直角三角形②等腰三角形③锐角三角形④钝角三角形答案:②等腰三角形b) 一条边为直径的圆叫作( )。
①半圆②椭圆③圆锥④圆答案:④圆c) 具有四条边且都相等的四边形是( )。
①正方形②长方形③梯形④平行四边形答案:①正方形3. 请计算下列图形的周长:a) 边长为4 cm的正方形的周长是多少?答案:正方形的四边相等,所以周长=4cm+4cm+4cm+4cm=16cm。
b) 边长分别为5 cm和8 cm的长方形的周长是多少?答案:长方形的周长=5cm+8cm+5cm+8cm=26cm。
c) 一张和纸短边长7 cm,长边长10 cm的长方形纸片,它的周长是多少?答案:周长=7cm+10cm+7cm+10cm=34cm。
4. 请计算下列图形的面积:a) 边长为6 cm的正方形的面积是多少?答案:正方形的面积=边长 ×边长 = 6cm × 6cm = 36cm²。
b) 边长分别为3 cm和7 cm的长方形的面积是多少?答案:长方形的面积=长 ×宽 = 3cm × 7cm = 21cm²。
c) 一张长边长为12 cm,短边长为5 cm的长方形纸片,它的面积是多少?答案:面积=长 ×宽 = 12cm × 5cm = 60cm²。
5. 请判断图形是否相似,并用是或否来回答:a) 下图中的两个三角形是否相似?答案:是。
(图形描述省略)b) 下图中的两个四边形是否相似?答案:否。
人教版七年级数学下册《相交线与平行线中的四种几何模型》专项练习题-附含答案

人教版七年级数学下册《相交线与平行线中的四种几何模型》专项练习题-附含答案类型一、猪脚模型例.问题情境:如图① 直线AB CD ∥ 点E F 分别在直线AB CD 上.(1)猜想:若1130∠=︒ 2150∠=︒ 试猜想P ∠=______°;(2)探究:在图①中探究1∠ 2∠ P ∠之间的数量关系 并证明你的结论;(3)拓展:将图①变为图② 若12325∠+∠=︒ 75EPG ∠=︒ 求PGF ∠的度数. 【答案】(1)80︒(2)36012P ∠=︒-∠-∠;证明见详解(3)140︒【详解】(1)解:如图过点P 作MN AB ∥∵AB CD ∥∵AB MN CD ∥∥.∵1180EPN ∠+∠=︒2180FPN ∠+∠=︒.∵1130∠=︒ 2150∠=︒∵12360EPN FPN ∠+∠+∠+∠=︒∵36013015080EPN FPN ∠+=︒-︒-︒=︒.∵P EPN FPN ∠=∠+∠∵∵P =80°.故答案为:80︒;(2)解:36012P ∠=︒-∠-∠ 理由如下:如图过点P 作MN AB ∥∵AB CD ∥∵AB MN CD ∥∥.∵1180EPN ∠+∠=︒2180FPN ∠+∠=︒.∵12360EPN FPN ∠+∠+∠+∠=︒∵EPN FPN P ∠+∠=∠36012P ∠=︒-∠-∠.(3)如图分别过点P 、点G 作MN AB ∥、KR AB ∥∵AB CD ∥∵AB MN KR CD ∥∥∥.∵1180EPN ∠+∠=︒180NPG PGR ∠+∠=︒2180RGF ∠+∠=︒.∵12540EPN NPG PGR RGF ∠+∠+∠+∠++∠=︒∵75EPG EPN NPG ∠=∠+∠=︒PGR RGF PGF ∠+∠=∠12325∠+∠=︒∵12540PGF EPG ∠+∠+∠+∠=︒∵54032575140PGF ∠=︒-︒-︒=︒故答案为:140︒.【变式训练1】已知直线a b ∥ 直线EF 分别与直线a b 相交于点E F 点A B 分别在直线a b 上 且在直线EF 的左侧 点P 是直线EF 上一动点(不与点E F 重合)设∵P AE =∵1 ∵APB =∵2 ∵PBF =∵3.(1)如图1 当点P 在线段EF 上运动时 试说明∵1+∵3=∵2;(2)当点P 在线段EF 外运动时有两种情况.①如图2写出∵1 ∵2 ∵3之间的关系并给出证明;②如图3所示 猜想∵1 ∵2 ∵3之间的关系(不要求证明).【答案】(1)证明见详解(2)①312∠=∠+∠;证明见详解;②123∠=∠+∠;证明见详解【详解】(1)解:如图4所示:过点P 作PC a ∥∵a b ∥∵PC a b ∥∥∵1APC ∠=∠ 3BPC ∠=∠∵2APC BPC ∠=∠+∠∵213∠=∠+∠;(2)解:①如图5过点P 作PC a ∥∵a b ∥∵PC a b ∥∥∵3BPC ∠=∠ 1APC ∠=∠∵2BPC APC ∠=∠+∠∵312;②如图6过点P 作PC a ∥∵a b ∥∵PC a b ∥∥∵1APC ∠=∠ 3BPC ∠=∠∵2APC BPC ∠=∠+∠∵123∠=∠+∠.【变式训练2】阅读下面内容 并解答问题.已知:如图1 AB CD 直线EF 分别交AB CD 于点E F .BEF ∠的平分线与DFE ∠的平分线交于点G .(1)求证:EG FG ⊥;(2)填空 并从下列①、②两题中任选一题说明理由.我选择 题.①在图1的基础上 分别作BEG ∠的平分线与DFG ∠的平分线交于点M 得到图2 则EMF ∠的度数为 .②如图3 AB CD 直线EF 分别交AB CD 于点E F .点O 在直线AB CD 之间 且在直线EF 右侧 BEO ∠的平分线与DFO ∠的平分线交于点P 则EOF ∠与EPF ∠满足的数量关系为 . GH ABAB CD AB GH CD ∴BEG EGH DFG FGH ∠∠∠∠∴==,180BEF DFE ∴∠+∠=︒EG 平分GEB ∴∠=GEB ∴∠+在EFG ∆中EGF ∴∠=EM 平分BEM ∴∠45EMF BEM MFD ∴∠=∠+∠=︒故答案为:45︒;②结论:2EOF EPF ∠=∠.理由:如图3中 由题意 EOF BEO DFO ∠=∠+∠ EPF BEP DFP ∠=∠+∠PE 平分BEO ∠ PF 平分DFO ∠2BEO BEP ∴∠=∠ 2DFO DFP ∠=∠2EOF EPF ∴∠=∠故答案为:2EOF EPF ∠=∠.【变式训练3】如图:(1)如图1 AB CD ∥ =45ABE ∠︒ 21CDE ∠=︒ 直接写出BED ∠的度数.(2)如图2 AB CD ∥ 点E 为直线AB CD 间的一点 BF 平分ABE ∠ DF 平分CDE ∠ 写出BED ∠与F ∠之间的关系并说明理由.(3)如图3 AB 与CD 相交于点G 点E 为BGD ∠内一点 BF 平分ABE ∠ DF 平分CDE ∠ 若60BGD ∠=︒ 95BFD ∠=︒ 直接写出BED ∠的度数. 【答案】(1)∵BED =66°;(2)∵BED =2∵F 见解析;(3)∵BED 的度数为130°.【详解】(1)解:(1)如图 作EF ∵AB∵直线AB ∵CD∵EF ∵CD∵∵ABE =∵1=45° ∵CDE =∵2=21°∵∵BED =∵1+∵2=66°;(2)解:∵BED =2∵F理由是:过点E作EG∥AB延长DE交BF于点H∵AB∥CD∵AB∥CD∥EG∵∵5=∵1+∵2∵6=∵3+∵4又∵BF平分∵ABE DF平分∵CDE∵∵2=∵1∵3=∵4则∵5=2∵2∵6=2∵3∵∵BED=2(∵2+∵3)又∵F+∵3=∵BHD∵BHD+∵2=∵BED∵∵3+∵2+∵F=∵BED综上∵BED=∵F+12∵BED即∵BED=2∵F;(3)解:延长DF交AB于点H延长GE到I∵∵BGD=60°∵∵3=∵1+∵BGD=∵1+60° ∵BFD=∵2+∵3=∵2+∵1+60°=95°∵∵2+∵1=35° 即2(∵2+∵1) =70°∵BF平分∵ABE DF平分∵CDE∵∵ABE=2∵2∵CDE=2∵1∵∵BEI=∵ABE +∵BGE=2∵2+∵BGE∵DEI=∵CDE+∵DGE=2∵1+∵DGE ∵∵BED=∵BEI+∵DEI=2(∵2+∵1)+( ∵BGE+∵DGE)=70°+60°=130°∵∵BED的度数为130°.类型二、铅笔模型例.问题情景:如图1 AB ∵CD ∵P AB =140° ∵PCD =135° 求∵APC 的度数.(1)丽丽同学看过图形后立即口答出:∵APC =85° 请补全她的推理依据.如图2 过点P 作PE ∵AB因为AB ∵CD 所以PE ∵CD .( )所以∵A +∵APE =180° ∵C +∵CPE =180°.( )因为∵P AB =140° ∵PCD =135° 所以∵APE =40° ∵CPE =45°∵APC =∵APE +∵CPE =85°.问题迁移:(2)如图3 AD ∵BC 当点P 在A 、B 两点之间运动时 ∵ADP =∵α ∵BCP =∵β 求∵CPD 与∵α、∵β之间有什么数量关系?请说明理由.(3)在(2)的条件下 如果点P 在A 、B 两点外侧运动时(点P 与点A 、B 、O 三点不重合) 请直接写出∵CPD 与∵α、∵β之间的数量关系.【答案】(1)平行于同一条直线的两条直线平行(或平行公理推论) 两直线平行 同旁内角互补;(2)CPD αβ∠=∠+∠ 理由见解析;(3)CPD βα∠=∠-∠或CPD αβ∠=∠-∠【详解】解:(1)如图2 过点P 作PE ∵AB因为AB ∵CD 所以PE ∵CD .(平行于同一条直线的两条直线平行)所以∵A +∵APE =180° ∵C +∵CPE =180°.(两直线平行同旁内角互补)因为∵P AB=140° ∵PCD=135°所以∵APE=40° ∵CPE=45°∵APC=∵APE+∵CPE=85°.故答案为:平行于同一条直线的两条直线平行;两直线平行同旁内角互补;(2)∵CPD=∵α+∵β理由如下:如图3所示过P作PE∵AD交CD于E∵AD∵BC∵AD∵PE∵BC∵∵α=∵DPE∵β=∵CPE∵∵CPD=∵DPE+∵CPE=∵α+∵β;(3)当P在BA延长线时如图4所示:过P作PE∵AD交CD于E同(2)可知:∵α=∵DPE∵β=∵CPE∵∵CPD=∵β-∵α;当P在AB延长线时如图5所示:同(2)可知:∵α=∵DPE∵β=∵CPE∵∵CPD=∵α-∵β.综上所述∵CPD与∵α、∵β之间的数量关系为:∵CPD=∵β-∵α或∵CPD=∵α-∵β.【变式训练1】已知直线AB∥CD(1)如图(1)点G为AB、CD间的一点联结AG、CG.若∵A=140° ∵C=150° 则∵AGC 的度数是多少?(2)如图(2)点G为AB、CD间的一点联结AG、CG.∵A=x° ∵C=y° 则∵AGC的度数是多少?(3)如图(3)写出∵BAE、∵AEF、∵EFG、∵FGC、∵GCD之间有何关系?直接写出结论.【答案】(1)70°;(2)∵AGC=(x+y)°;(3)∵BAE+∵EFG+∵GCD=∵AEF+∵FGC.【详解】解:(1)如图过点G作GE∥AB∵AB∥GE∵∵A+∵AGE=180°(两直线平行同旁内角互补).∵∵A=140°∵∵AGE=40°.∵AB∥GE AB∥CD∵GE∥CD.∵∵C+∵CGE=180°(两直线平行同旁内角互补).∵∵C=150°∵∵CGE=30°.∵∵AGC=∵AGE+∵CGE=40°+30°=70°.(2)如图过点G作GF∥AB∵AB∥GF∵∵A=AGF(两直线平行内错角相等).∵AB∥GF AB∥CD∵GF∥CD.∵∵C=∵CGF.∵∵AGC=∵AGF+∵CGF=∵A+∵C.∵∵A=x° ∵C=y°∵∵AGC=(x+y)°.(3)如图所示过点E作EM∥AB过点F作FN∥AB过点G作GQ∥CD∵AB∥CD∵AB∥EM∥FN∥GQ∥CD.∵∵BAE=∵AEM∵MEF=∵EFN∵NFG=∵FGQ∵QGC=∵GCD(两直线平行内错角相等).∵∵AEF=∵BAE+∵EFN∵FGC=∵NFG+GCD.∵∵EFN+∵NFG=∵EFG∵∵BAE+∵EFG+∵GCD=∵AEF+∵FGC.【变式训练2】问题情境:如图1 AB∵CD∵P AB=130° ∵PCD=120° 求∵APC度数.思路点拨:小明的思路是:如图2 过P作PE∵AB通过平行线性质可分别求出∵APE、∵CPE的度数从而可求出∵APC的度数;小丽的思路是:如图3 连接AC通过平行线性质以及三角形内角和的知识可求出∵APC的度数;小芳的思路是:如图4 延长AP交DC的延长线于E通过平行线性质以及三角形外角的相关知识可求出∵APC的度数.问题解决:请从小明、小丽、小芳的思路中任选一种思路进行推理计算你求得的∵APC的度数为°;问题迁移:(1)如图5 AD∵BC点P在射线OM上运动当点P在A、B两点之间运动时∵ADP=∵α ∵BCP=∵β.∵CPD、∵α、∵β之间有何数量关系?请说明理由;(2)在(1)的条件下如果点P在A、B两点外侧运动时(点P与点A、B、O三点不重合)请你直接写出∵CPD、∵α、∵β间的数量关系.【答案】问题解决:110°;问题迁移:(1)∵CPD=∵α+∵β 理由见解析;(2)∵CPD=∵β﹣∵α 理由见解析【详解】解:小明的思路:如图2 过P作PE∵AB∵AB∵CD∵PE∵AB∵CD∵∵APE=180°﹣∵A=50° ∵CPE=180°﹣∵C=60°∵∵APC=50°+60°=110°故答案为:110;(1)∵CPD=∵α+∵β 理由如下:如图5 过P作PE∵AD交CD于E∵AD∵BC∵AD∵PE∵BC∵∵α=∵DPE∵β=∵CPE∵∵CPD=∵DPE+∵CPE=∵α+∵β;(2)当P在BA延长线时∵CPD=∵β﹣∵α;理由:如图6 过P作PE∵AD交CD于E∵AD∵BC∵AD∵PE∵BC∵∵α=∵DPE∵β=∵CPE∵∵CPD=∵CPE﹣∵DPE=∵β﹣∵α;当P在BO 之间时 ∵CPD =∵α﹣∵β.理由:如图7 过P 作PE ∵AD 交CD 于E∵AD ∵BC∵AD ∵PE ∵BC∵∵α=∵DPE ∵β=∵CPE∵∵CPD =∵DPE ﹣∵CPE =∵α﹣∵β.类型三、锄头模型例.已知 AB ∵CD .点M 在AB 上 点N 在CD 上.(1)如图1中 ∵BME 、∵E 、∵END 的数量关系为: ;(不需要证明) 如图2中 ∵BMF 、∵F 、∵FND 的数量关系为: ;(不需要证明)(2)如图3中 NE 平分∵FND MB 平分∵FME 且2∵E +∵F =180° 求∵FME 的度数;(3)如图4中 ∵BME =60° EF 平分∵MEN NP 平分∵END 且EQ ∵NP 则∵FEQ 的大小A BC D P123是否发生变化若变化请说明理由若不变化求出∵FEQ的度数.【答案】(1)∵BME=∵MEN﹣∵END;∵BMF=∵MFN+∵FND;(2)120°;(3)不变30°【详解】解:(1)过E作EH∵AB如图1∵∵BME=∵MEH∵AB∵CD∵HE∵CD∵∵END=∵HEN∵∵MEN=∵MEH+∵HEN=∵BME+∵END即∵BME=∵MEN﹣∵END.如图2 过F作FH∵AB∵∵BMF=∵MFK∵AB∵CD∵FH∵CD∵∵FND=∵KFN∵∵MFN=∵MFK﹣∵KFN=∵BMF﹣∵FND即:∵BMF=∵MFN+∵FND.故答案为∵BME=∵MEN﹣∵END;∵BMF=∵MFN+∵FND.(2)由(1)得∵BME=∵MEN﹣∵END;∵BMF=∵MFN+∵FND.(2)观察图(2)已知AB∵CD猜想图中的∵BPD与∵B、∵D的关系并说明理由.(3)观察图(3)和(4)已知AB∵CD猜想图中的∵BPD与∵B、∵D的关系不需要说明理由.【答案】(1)∵B+∵BPD+∵D=360° 理由见解析;(2)∵BPD=∵B+∵D理由见解析;(3)∵BPD=∵D-∵B或∵BPD=∵B-∵D理由见解析【详解】解:(1)如图(1)过点P作EF∵AB∵∵B+∵BPE=180°∵AB∵CD EF∵AB∵EF∵CD∵∵EPD+∵D=180°∵∵B+∵BPE+∵EPD+∵D=360°∵∵B+∵BPD+∵D=360°.(2)∵BPD=∵B+∵D.理由:如图2 过点P作PE∵AB∵AB∵CD∵PE∵AB∵CD∵∵1=∵B∵2=∵D∵∵BPD=∵1+∵2=∵B+∵D.(3)如图(3)∵BPD=∵D-∵B.理由:∵AB∵CD∵∵1=∵D∵∵1=∵B+∵BPD∵∵D=∵B+∵BPD即∵BPD=∵D-∵B;如图(4)∵BPD=∵B-∵D.理由:∵AB ∵CD∵∵1=∵B∵∵1=∵D +∵BPD∵∵B =∵D +∵BPD即∵BPD =∵B -∵D .【变式训练2】已知//AM CN 点B 为平面内一点 AB BC ⊥于B .(1)如图1 点B 在两条平行线外 则A ∠与C ∠之间的数量关系为______; (2)点B 在两条平行线之间 过点B 作BD AM ⊥于点D . ①如图2 说明ABD C ∠=∠成立的理由;②如图3 BF 平分DBC ∠交DM 于点,F BE 平分ABD ∠交DM 于点E .若180,3FCB NCF BFC DBE ∠∠∠∠+=︒= 求EBC ∠的度数.【答案】(1)∵A +∵C =90°;(2)①见解析;②105°【详解】解:(1)如图1 AM 与BC 的交点记作点O∵AM ∵CN∵∵C =∵AOB∵AB ∵BC∵∵A +∵AOB =90°∵∵A +∵C =90°;(2)①如图2 过点B作BG∵DM∵BD∵AM∵DB∵BG∵∵DBG=90°∵∵ABD+∵ABG=90°∵AB∵BC∵∵CBG+∵ABG=90°∵∵ABD=∵CBG∵AM∵CN BG∵DMBG CN//,∵∵C=∵CBG∵ABD=∵C;②如图3 过点B作BG∵DM∵BF平分∵DBC BE平分∵ABD∵∵DBF=∵CBF∵DBE=∵ABE由(2)知∵ABD=∵CBG∵∵ABF=∵GBF设∵DBE=α∵ABF=β则∵ABE=α∵ABD=2α=∵CBG∵GBF=∵AFB=β∵BFC=3∵DBE=3α∵∵AFC=3α+β∵∵AFC+∵NCF=180° ∵FCB+∵NCF=180° ∵∵FCB=∵AFC=3α+β∵BCF中由∵CBF+∵BFC+∵BCF=180°得:2α+β+3α+3α+β=180°∵AB∵BC∵β+β+2α=90°∵α=15° ∵∵ABE=15°∵∵EBC=∵ABE+∵ABC=15°+90°=105°.类型四、齿距模型例.如图AB∵EF设∵C=90° 那么x y z的关系式为______.【答案】y=90°-x+z.【详解】解:作CG//AB DH//EF∵AB//EF∵AB//CG//HD//EF∵∵x=∵1 ∵CDH=∵2 ∵HDE=∵z∵∵BCD=90°∵∵1+∵2=90°∵y=∵CDH+∵HDE=∵z+∵2∵∵2=90°-∵1=90°-∵x∵∵y=∵z+90°-∵x.即y=90°-x+z.【变式训练1】如图1 已知AB ∵CD ∵B =30° ∵D =120°;(1)若∵E =60° 则∵F = ;(2)请探索∵E 与∵F 之间满足的数量关系?说明理由;(3)如图2 已知EP 平分∵BEF FG 平分∵EFD 反向延长FG 交EP 于点P 求∵P 的度数.【答案】(1)90︒;(2)30F E ∠=∠+︒ 理由见解析;(3)15︒【详解】(1)解:如图1 分别过点E F 作//EM AB //FN AB////EM AB FN ∴30B BEM ∴∠=∠=︒ MEF EFN ∠=∠又//AB CD //AB FN//CD FN ∴180D DFN ∴∠+∠=︒又120D ∠=︒60DFN ∴∠=︒30BEF MEF ∴∠=∠+︒ 60EFD EFN ∠=∠+︒60EFD MEF ∴∠=∠+︒3090EFD BEF ∴∠=∠+︒=︒;故答案为:90︒;(2)解:如图1 分别过点E F 作//EM AB //FN AB////EM AB FN ∴30B BEM ∴∠=∠=︒ MEF EFN ∠=∠又//AB CD //AB FN//CD FN ∴又120D ∠=60DFN ∴∠=BEF MEF ∴∠=∠EFD MEF ∴∠=∠(3)解:如图设2BEF ∠=EP 平分PEF ∴∠=//FH EP HFG ∠=【变式训练2】如图1 点A 、B 分别在直线GH 、MN 上 GAC NBD ∠=∠ C D ∠=∠.(1)求证://GH MN ;(提示:可延长AC 交MN 于点P 进行证明) (2)如图2 AE 平分GAC ∠ DE 平分BDC ∠ 若AED GAC ∠=∠ 求GAC ∠与ACD ∠之间的数量关系;(3)在(2)的条件下 如图3 BF 平分DBM ∠ 点K 在射线BF 上 13KAG GAC ∠=∠ 若AKB ACD ∠=∠ 直接写出GAC ∠的度数.∵ACD C ∠=∠∵//AP BD∵NBD NPA ∠=∠∵GAC NBD ∠=∠∵GAC NPA ∠=∠∵//GH MN ;(2)延长AC 交MN 于点P 交DE 于点Q∵180E EAQ AQE ∠+∠+∠=° 180AQE AQD ∠+∠=° ∵AQD E EAQ ∠=∠+∠∵//AP BD∵AQD BDQ ∠=∠∵BDQ E EAQ ∠=∠+∠∵AE 平分GAC ∠ DE 平分BDC ∠∵2GAC EAQ ∠=∠ 2CDB BDQ ∠=∠∵2CDB E GAC ∠=∠+∠∵AED GAC ∠=∠ ACD CDB ∠=∠∵23ACD GAC GAC GAC ∠=∠+∠=∠;(3)当K 在直线GH 下方时 如图 设射线BF 交GH 于I⎫.⎪⎭上方时如图-∠(180GAC⎫.⎪⎭°︒。
初一几何练习题及答案

相交线及平行线 练习题及答案(1)一、填空题1.如图,直线、相交于点O ,假设∠1=28°,那么∠2=.2. 直线AB CD ∥,60ABE =∠,20CDE =∠,那么BED =∠ 度.3. 如图,∥,分别交、于点E 、F ,∠1=60°,那么∠2=度.4. 如图,直线∥,∠A =70°,∠B =40°,那么∠P =_____.5.设a 、b 、c 为平面上三条不同直线,(1) 假设//,//a b b c ,那么a 及c 的位置关系是; (2) 假设,ab bc ⊥⊥,那么a 及c 的位置关系是; (3) 假设//ab ,bc ⊥,那么a 及c 的位置关系是.6.如图,填空:⑴∵1A ∠=∠〔〕∴〔 〕 ⑵∵2B ∠=∠〔〕第2PBM A N第1第3第4∴〔〕⑶∵1D∠=∠〔〕∴〔〕第6二、解答题7.如图,AOC∠及BOC∠的平分线,试推∠是邻补角,、分别是AOC∠及BOC断及的位置关系,并说明理由.8.如图,直线及交于点O,⊥,垂足为O,假设∠=3∠,求∠的度数.9.如图,直线//a b,求证:12∠=∠.10.如图,∥,试问∠B、∠E、∠有什么关系.解:∠B+∠E=∠过点C作∥,那么B∠=∠〔〕又∵∥,∥,∴〔 〕 ∴∠E =∠〔 〕∴∠B +∠E =∠1+∠2 即∠B +∠E =∠.11.如第10题图,当∠B 、∠E 、∠有什么关系时,有∥.12如图,∥,那么∠B 、∠、∠D 有什么关系?13、如图9,直线a ∥b ,∠1=28°,∠2=50°,那么∠3=____。
∠3+∠4+∠5=___。
14、假设两条平行线被第三条直线所截得的八个角中,有一个角的度数,那么〔 〕A 只能求出其余3个角的度数B 只能求出其余5个角的度数C 只能求出其余6个角的度数D 只能求出其余7个角的度数 15、如图,∥,平分∠,假设∠=40°,那么∠=〔 〕A 60°B 70°C 80°D 90° 16、设A 、B 、C 是直线a 上的三点,P 为直线a外一点,假设=2,=3,=5,那么点P 到直线a 的间隔 〔 〕 A 等于2 B 小于2 C 不小于2 D 不大于2。
七年级数学上册第四单元《几何图形初步》-解答题专项经典练习题(含答案解析)

一、解答题1.如图,已知点C 为线段AB 上一点,15cm AC =,35CB AC =,D ,E 分别为线段AC ,AB 的中点,求线段DE 的长.解析:5cm【分析】根据线段的中点定义即可求解.【详解】解:因为15cm AC =,35CB AC =, 所以3159(cm)5CB =⨯=, 所以15924(cm)AB =+=.因为D ,E 分别为线段AC ,AB 的中点,所以112cm 2AE BE AB ===,17.5cm 2DC AD AC ===. 所以127.5 4.5(cm)DE AE AD =-=-=. 【点睛】本题考查了两点间的距离,解决本题的关键是利用线段的中点定义.2.如图,已知点C 是线段AB 的中点,点D 在线段CB 上,且DA =5,DB =3.求CD 的长.解析:1【解析】【分析】根据线段的和差,可得AB 的长,根据线段中点的性质,可得AC 的长,根据线段的和差,可得答案.【详解】由线段的和差,得AB=AD+BD=5+3=8.由线段中点的性质,得AC=CB=12AB=4. 由线段的和差,得CD=AD−AC=5−4=1.【点睛】此题考查两点间的距离,解题关键在于掌握各性质定义.3.如图所示,∠AOB =35°,∠BOC =50°,∠COD =22°,OE 平分∠AOD ,求∠BOE 的度数.解析:5°【解析】【分析】首先根据角的和差关系算出∠AOD 的度数,再根据角平分线的性质可得∠AOE =12∠AOD ,进而得到答案.【详解】 ∵∠AOB =35°,∠BOC =50°,∠COD =22°,∴∠AOD =35°+50°+22°=107°.∵OE 平分∠AOD ,∴∠AOE =12∠AOD =12×107°=53.5°,∴∠BOE =∠AOE -∠AOB =53.5°-35°=18.5°.【点睛】本题考查了角平分线的性质,关键是掌握角平分线的定义:从一个角的顶点出发,把这个角分成相等的两个角的射线叫做这个角的平分线.4.如图是由若干个正方体形状的木块堆成的,平放于桌面上。
完整版)初一几何练习题及答案

完整版)初一几何练习题及答案初一几何:三角形一、选择题(本大题共24分)1.以下列各组数为三角形的三条边,其中能构成直角三角形的是()A。
17,15,8B。
1/3,1/4,1/5C。
4,5,6D。
3,7,112.如果三角形的一个角的度数等于另两个角的度数之和,那么这个三角形一定是()A。
锐角三角形B。
直角三角形C。
钝角三角形D。
等腰三角形3.下列给出的各组线段中,能构成三角形的是()A。
5,12,13B。
5,12,7C。
8,18,7D。
3,4,84.如图已知:Rt△ABC中,∠C=90°,AD平分∠BAC,AE=AC,连接DE,则下列结论中,不正确的是()A。
DC=DEB。
∠___∠ADEC。
∠DEB=90°D。
∠___∠DAE5.一个三角形的三边长分别是15,20和25,则它的最大边上的高为()A。
12B。
10C。
8D。
56.下列说法不正确的是()A。
全等三角形的对应角相等B。
全等三角形的对应角的平分线相等C。
角平分线相等的三角形一定全等D。
角平分线是到角的两边距离相等的所有点的集合7.两条边长分别为2和8,第三边长是整数的三角形一共有()A。
3个B。
4个C。
5个D。
无数个8.下列图形中,不是轴对称图形的是()A。
线段MNB。
等边三角形C。
直角三角形D。
钝角∠AOB9.如图已知:△ABC中,AB=AC,BE=CF,AD⊥BC于D,此图中全等的三角形共有()A。
2对B。
3对C。
4对D。
5对10.直角三角形两锐角的平分线相交所夹的钝角为()A。
125°B。
135°C。
145°D。
150°11.直角三角形两锐角的平分线相交所夹的钝角为()A。
125°B。
135°C。
145°D。
150°12.___已知:∠A=∠D,∠C=∠F,如果△ABC≌△DEF,那么还应给出的条件是()A。
AC=DEB。
AB=DFC。
七年级数学几何练习题及答案

七年级数学几何练习题及答案练题一:直线的性质1. 试述直线的定义和特点。
答案:直线是由一连串无限延伸的点组成,它没有弯曲和拐角。
直线上的任意两点可以用唯一一条直线连接。
2. 画出以下直线的标志并写出它们的名称:水平线、垂直线、倾斜线、平行线、相交线。
答案:- 水平线:⎕,两端点的纵坐标相同。
- 垂直线:⎈,两端点的横坐标相同。
- 倾斜线:/,连接两个不同的点。
- 平行线://,在同一平面内永不相交的两条直线。
- 相交线:+,两条直线在同一点相交。
练题二:三角形的性质1. 试述三角形的定义和特点。
答案:三角形是由三条线段组成的图形。
它的特点是三条边相连的三个点不在一条直线上。
2. 根据三角形的边长关系,判断以下三角形的类型:等边三角形、等腰三角形、直角三角形、锐角三角形、钝角三角形。
答案:- 等边三角形:三条边的长度都相等。
- 等腰三角形:两条边的长度相等。
- 直角三角形:有一个角度为90度。
- 锐角三角形:三个角都小于90度。
- 钝角三角形:有一个角度大于90度。
练题三:四边形的性质1. 试述四边形的定义和特点。
答案:四边形是由四条线段组成的图形。
它的特点是四条边相连的四个点不在一条直线上。
2. 根据四边形的边长关系,判断以下四边形的类型:平行四边形、矩形、正方形、菱形、梯形。
答案:- 平行四边形:有两对平行的边。
- 矩形:有四个直角。
- 正方形:既是矩形又是菱形,四个边的长度相等且都是直角。
- 菱形:四个边的长度相等。
- 梯形:有一对平行的边。
练题四:圆的性质1. 试述圆的定义和特点。
答案:圆是平面上所有到中心点距离相等的点的集合。
圆由一个中心点和半径组成。
2. 根据圆的性质,判断以下说法的正误:半径相等的圆周长相等、直径相等的圆周长相等。
答案:半径相等的圆周长相等是正确的,直径相等的圆周长相等也是正确的。
以上是七年级数学几何练习题及答案的简要概述,希望对你的学习有所帮助。
七年级上册《数学》几何图形专项练习题((含答案)

七年级上册《数学》几何图形专项练习题第1课时几何图形一、能力提升1.下列所列举的物体中,与圆锥的形状类似的是()A.足球B.字典C.易拉罐D.标枪的尖头2.下列图形属于柱体的是()3.下列第一行所示的四个图形,每个图形均是由四种简单的图形a,b,c,d(圆、直线、三角形、长方形)中的两种组成.例如由a,b组成的图形记作a☉b,那么由此可知,下面第二行的图中可以记作a☉d的是()4.如图,下面各几何体中,是三棱柱的是.(只填序号)5.下列说法:①圆锥和圆柱的底面都是圆;②棱锥底面边数与侧棱数相等;③棱柱的上、下底面是形状、大小相同的多边形;④四棱柱是长方体.其中正确的是.(填序号)6.有一个几何体,形状如图所示,这个几何体的面数为.7.如图,下列各图形主要由哪些简单的几何图形组成?二、创新应用8.请利用图中的几何体拼出蘑菇、台灯等图案,并和同伴一起交流,尽量拼出最多的图案.答案一、能力提升1.D.2.C.3.A.根据题意,知a代表长方形,d代表直线,因此记作a☉d的图形是长方形和直线的组合,故选A.4.④.5.①②③.6.6.7.解:(1)由圆组成;(2)由长方形和正方形组成;(3)由菱形(或四边形)组成;(4)由圆和圆弧组成(或由一个圆和两个小半圆组成).二、创新应用8.分析:本题是开放性试题,只要所给答案合理即可.解:答案不唯一,如图.第2课时几何图形的三种形状图与展开图一、能力提升1.如图,小李书桌上放了一本书,从上往下看得到的平面图形是()2.如图,一个带有方形空洞、圆形空洞的儿童玩具.如果用下列几何体作为塞子,那么既可以堵住方形空洞又可以堵住圆形空洞的几何体是()3.一张桌子上摆放有若干个大小、形状完全相同的碟子,现从三个方向看到的图形如图所示,则这张桌子上碟子的总数为()A.11B.12C.13D.144.有3块正方体积木,每一块的各面都涂上不同的颜色,3块的涂法完全相同.现把它们摆放成不同的位置(如图),请你根据图形判断涂成绿色一面的对面的颜色是()A.白B.红C.黄D.黑5.图①是一个小正方体的侧面展开图,小正方体从图②所示的位置依次翻到第1格、第2格、第3格,这时小正方体朝上一面的字是.图①图②6.根据下列多面体的平面展开图,填写多面体的名称:(1),(2),(3).7.如图,将下列图形剪去一个小正方形,使余下的部分恰好能折成一个正方体,应剪去.(填序号)8.如图,画出所给几何体的从正面看、从左面看和从上面看得到的图形.9.如图①,在正方体中,点P,Q,S分别是所在边的中点,将此正方体展开,请在展开图②中标出点P,Q,S的位置.二、创新应用10.火箭的示意图如图所示(火箭圆柱底面的周长不等于圆柱的高),请你画出火箭的平面展开图.11.如图,在一个长方体的展开图上,每一面上都标注了字母(标字母的面是外表面),根据要求回答问题:(1)如果D面在多面体的左面,那么F面在哪里?(2)B面和哪个面是相对的面?(3)如果C面在前面,从上面看是D面,那么左面是哪个面?(4)如果B面在后面,从左面看是D面,那么前面是哪个面?(5)如果A面在右面,从下面看是F面,那么B面在哪里?答案一、能力提升1.A.2.B.从正面与上面分别看圆柱体所得的平面图形分别是长方形和圆,它既可以堵住方形空洞又可以堵住圆形空洞.3.B.因为右上角的碟子有5个,左下角的碟子有3个,左上角的碟子有4个,所以碟子的总数为3+4+5=12.4.C.根据第一个图和第二个图可知,与绿色相邻的四个面的颜色分别为白、黑、蓝、红,从第三个图可知第六个面为黄色,即为绿色一面的对面.5.国.翻到题图②第1格时朝下的为“了”字,第2格为“害”字,第3格为“厉”字,其对面为“国”字,即为这时小正方体朝上一面的字.6.(1)长方体.(2)三棱柱.(3)三棱锥.7.1或2或6.8.解:9.解:如图所示.二、创新应用10.解:11.解:(1)右面.(2)E面.(3)B面.(4)E面.(5)后面.4.1.2点、线、面、体一、能力提升1.如图,将下面的平面图形绕直线l旋转一周,得到的立体图形是()2.下列几何体有6个面的有()①长方体;②圆柱;③四棱柱;④正方体;⑤三棱柱.A.1个B.2个C.3个D.4个3.如果一个直棱柱有12个顶点,那么它的面的个数是()A.10B.9C.8D.74.下列说法正确的有()①四面体的各个面都是三角形;②棱柱的顶点数一定是偶数,棱的条数一定是3的倍数;③圆柱是由两个面围成的;④长方体的面不可能是正方形.A.1个B.2个C.3个D.4个5.观察下图,把左边的图形绕着给定的直线旋转一周后可能形成的立体图形是()6.薄薄的硬币在桌面上转动时,看上去像球,这说明了.7.航天飞机拖着“长长的火焰”,我们用数学知识可解释为点动成线.用数学知识解释下列现象:(1)一只小蚂蚁爬行留下的路线可解释为.(2)电动车车辐条运动形成的图形可解释为.8.如图,正方形ABCD的边长为3cm,以直线AB为轴,将正方形旋转一周,所得几何体从正面看的图形的面积是cm2.9.观察右图,填空:(1)这个图形的名称是;(2)这个几何体有个面,有个底面,有个侧面,底面是形,侧面是形.(3)侧面的个数与底面多边形的边数有什么关系?10.用数学的眼光去观察问题,你会发现很多图形都能看成是动静结合,舒展自如的.下面所给的三排图形都存在着某种联系,用线将它们连起来.11.如图①,把一张长为6厘米、宽为10厘米的长方形纸板分成两个相同的直角三角形.(1)甲三角形(如图②)绕轴旋转一周,可以形成一个怎样的几何体?它的体积是多少立方厘米?(2)乙三角形(如图③)绕轴旋转一周,可以形成一个怎样的几何体?它的体积是多少立方厘米?二、创新应用12.十八世纪瑞士数学家欧拉证明了简单多面体中顶点数(V)、面数(F)、棱数(E)之间存在的一个有趣的关系式,被称为欧拉公式.请你观察下列几种简单多面体模型,解答下列问题:(1)根据上面多面体模型,完成表格中的空格:顶点数多面体面数(F) 棱数(E)(V)四面体 4 4长方体8 6 12正八面体8 12正十二面20 12 30体你发现顶点数(V)、面数(F)、棱数(E)之间存在的关系式是.(2)若一个多面体的面数比顶点数大8,且有30条棱,则这个多面体的面数是.(3)某个玻璃饰品的外形是简单多面体,它的外表面是由三角形和八边形两种多边形拼接而成,且有24个顶点,每个顶点处都有3条棱.设该多面体外表三角形的个数为x,八边形的个数为y,求x+y的值.答案一、能力提升1.D.2.C.3.C.直棱柱有12个顶点,一定是六棱柱,因此它的面的个数是8.4.B.5.D.由题中图形可以看出,左边的长方形的竖直的两条边与已知的直线平行,因而这两条边旋转形成两个柱形表面,旋转一周后可能形成的立体图形是一个管状的物体.6.面动成体.从运动的观点可知,薄薄的硬币在桌面上转动时,看上去像球,这种现象说明面转动成体.7.(1)点动成线.(2)线动成面.8.18.将正方形旋转一周所形成的图形是圆柱,从正面看圆柱是一个长方形,长方形的一边长为3cm,另一边长为6cm.因此面积为18cm2. 9.解:(1)六棱柱.(2)8;2;6;六边;长方.(3)侧面的个数与底面多边形的边数相等.10.解:从第一行的平面图形绕某一边旋转或沿某一方向平移可得到第二行的立体图形,从第二行的立体图形的上面看可得到第三行的平面图形.(1)→(三)→(D);(2)→(二)→(C);(3)→(四)→(B);(4)→(一)→(A).11.解:(1)甲三角形绕它的一条直角边所在直线旋转一周,形成一个底面半径是6厘米,高是10厘米的圆锥,它的体积是×π×62×10=120π(立方厘米).(2)乙三角形(如题图③)绕轴旋转一周,形成一个圆柱,且中间挖去了一个和圆柱同底等高的圆锥,它的体积是π×62×10-π×62×10=240π(立方厘米).二、创新应用12.解:(1)四面体的棱数为6;正八面体的顶点数为6;关系式为V+F-E=2.(2)由题意,得F-8+F-30=2,解得F=20.(3)因为有24个顶点,每个顶点处都有3条棱,两点确定一条直线,所以共有24×3÷2=36条棱.由(1)得24+F-36=2,解得F=14,所以x+y=14.。
2024年数学七年级下册几何基础练习题(含答案)

2024年数学七年级下册几何基础练习题(含答案)试题部分一、选择题(每题2分,共20分)1. 在一个等边三角形中,每个角的度数是()。
A. 60°B. 90°C. 120°D. 180°2. 下列哪个图形是一个四边形?()A. 圆B. 三角形C. 正方形D. 直线3. 一个三角形的两个角分别是30°和60°,那么第三个角的度数是()。
A. 30°B. 60°C. 90°D. 120°4. 下列哪个图形是一个平行四边形?()A. 矩形C. 正方形D. 菱形5. 一个等腰三角形的底边长度是10厘米,腰长是12厘米,那么这个三角形的周长是()厘米。
A. 22B. 24C. 26D. 286. 下列哪个图形是一个圆形?()A. 正方形B. 长方形C. 椭圆D. 三角形7. 一个三角形的两个边长分别是5厘米和8厘米,那么这个三角形的周长最小可能是()厘米。
A. 10B. 12C. 13D. 148. 下列哪个图形是一个梯形?()A. 正方形B. 矩形C. 平行四边形9. 一个等腰三角形的底边长度是8厘米,腰长是10厘米,那么这个三角形的周长是()厘米。
A. 18B. 20C. 22D. 2410. 下列哪个图形是一个正方形?()A. 长方形B. 梯形C. 菱形D. 圆二、判断题(每题2分,共10分)1. 一个等边三角形的每个角都是60°。
()2. 一个四边形的内角和是360°。
()3. 一个等腰三角形的两个腰长相等。
()4. 一个正方形的四个角都是90°。
()5. 一个三角形的两个边长分别是5厘米和8厘米,那么这个三角形的周长最小可能是13厘米。
()以上是一个练习题的示例,你可以根据实际情况进行调整和扩展。
希望对你有所帮助!一、选择题(每题2分,共20分)1. 在一个等边三角形中,每个角的度数是()。
初一几何作图题试题及答案

初一几何作图题试题及答案试题一:题目:已知线段AB,求作一个等边三角形ABC,使得点C在AB的延长线上。
作法:1. 以点A为圆心,以线段AB的长度为半径画圆。
2. 以点B为圆心,同样以线段AB的长度为半径画圆。
3. 两圆相交于点C。
4. 连接AC和BC,得到等边三角形ABC。
答案:按照上述作法,我们可以得到一个等边三角形ABC,其中AC=BC=AB。
试题二:题目:已知线段AB和线段CD,求作一个平行四边形ABCD,使得AB平行于CD。
作法:1. 延长线段AB到点E,使得AE=CD。
2. 以点B为圆心,以BE为半径画圆。
3. 以点D为圆心,以DE为半径画圆。
4. 两圆相交于点C。
5. 连接AC和BC,得到平行四边形ABCD。
答案:按照上述作法,我们可以得到一个平行四边形ABCD,其中AB平行于CD。
试题三:题目:已知圆O和点A,求作点A在圆O上的切线。
作法:1. 以点A为圆心,任意长度为半径画圆,与圆O相交于点B和点C。
2. 连接点A和点B,再连接点A和点C。
3. 延长线段AB和AC,使其相交于点D。
4. 线段AD即为点A在圆O上的切线。
答案:按照上述作法,我们可以得到点A在圆O上的一条切线AD。
试题四:题目:已知点A和点B,求作一个矩形ABCD,使得AB=CD。
作法:1. 以点A为圆心,以AB为半径画圆。
2. 以点B为圆心,同样以AB为半径画圆。
3. 两圆相交于点C。
4. 连接AC和BC。
5. 以点C为圆心,以AC为半径画圆,与线段AB相交于点D。
6. 连接AD和CD,得到矩形ABCD。
答案:按照上述作法,我们可以得到一个矩形ABCD,其中AB=CD。
结束语:通过以上四个几何作图题的练习,同学们可以加深对几何图形性质和作图方法的理解,提高空间想象能力和几何作图技能。
希望这些练习能帮助同学们在几何学习中取得更好的成绩。
初一几何体试题及答案

初一几何体试题及答案一、选择题(每题2分,共10分)1. 下列几何体中,属于多面体的是:A. 球体B. 圆柱C. 圆锥D. 立方体答案:D2. 如果一个几何体有8个顶点和12条棱,那么它可能是:A. 立方体B. 正四面体C. 正八面体D. 正十二面体答案:A3. 正方体的每个面都是:A. 圆形B. 椭圆形C. 长方形D. 正方形答案:D4. 一个长方体的长、宽、高分别是a、b、c,那么它的体积是:A. abcB. a+b+cC. ab+bc+caD. a^2+b^2+c^2答案:A5. 一个正四面体的每个面都是:A. 等边三角形B. 等腰三角形C. 直角三角形D. 等腰直角三角形答案:A二、填空题(每题2分,共10分)6. 一个长方体的长为5厘米,宽为3厘米,高为2厘米,它的表面积是______平方厘米。
答案:627. 一个正方体的棱长为4厘米,它的体积是______立方厘米。
答案:648. 如果一个几何体的底面是一个正方形,且边长为x厘米,高为y厘米,那么它的体积是______立方厘米。
答案:xy^29. 一个圆锥的底面半径为r厘米,高为h厘米,它的体积是______立方厘米。
答案:πrh^2/310. 一个圆柱的底面半径为r厘米,高为h厘米,它的体积是______立方厘米。
答案:πr^2h三、简答题(每题5分,共10分)11. 描述一个正方体的特征。
答案:正方体是一个有6个面,每个面都是正方形的立体图形。
它的12条棱的长度相等,每个顶点连接3条棱。
12. 解释为什么球体不属于多面体。
答案:球体是一个连续的曲面,没有平面的面和棱,因此它不属于多面体。
多面体是由多个平面多边形面、直线棱和顶点组成的立体图形。
结束语:通过本试题的练习,同学们应该对初一几何体的基本概念和计算方法有了更深入的理解。
希望同学们能够继续努力,掌握更多的几何知识,为今后的学习打下坚实的基础。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初一几何三角形一.选择题 (本大题共 24 分)1.以下列各组数为三角形的三条边,其中能构成直角三角形的是()(A)17,15,8 (B)1/3,1/4,1/5 (C) 4,5,6 (D) 3,7,112.如果三角形的一个角的度数等于另两个角的度数之和,那么这个三角形一定是()(A)锐角三角形(B)直角三角形(C)钝角三角形(D)等腰三角形3.下列给出的各组线段中,能构成三角形的是()(A)5,12,13 (B)5,12,7 (C)8,18,7 (D)3,4,84.如图已知:Rt△ABC中,∠C=90°,AD平分∠BAC,AE=AC,连接DE,则下列结论中,不正确的是()(A) DC=DE (B) ∠ADC=∠ADE (C) ∠DEB=90°(D) ∠BDE=∠DAE5.一个三角形的三边长分别是15,20和25,则它的最大边上的高为()(A)12 (B)10 (C) 8 (D) 56.下列说法不正确的是()(A)全等三角形的对应角相等(B)全等三角形的对应角的平分线相等(C)角平分线相等的三角形一定全等(D)角平分线是到角的两边距离相等的所有点的集合7.两条边长分别为2和8,第三边长是整数的三角形一共有()(A)3个(B)4个(C)5个(D)无数个8.下列图形中,不是轴对称图形的是()(A)线段MN (B)等边三角形(C) 直角三角形(D) 钝角∠AOB9.如图已知:△ABC中,AB=AC,BE=CF,AD⊥BC于D,此图中全等的三角形共有()(A)2对(B)3对(C)4对(D)5对10.直角三角形两锐角的平分线相交所夹的钝角为()(A)125°(B)135°(C)145°(D)150°11.直角三角形两锐角的平分线相交所夹的钝角为()(A)125°(B)135°(C)145°(D)150°12.如图已知:∠A=∠D,∠C=∠F,如果△ABC≌△DEF,那么还应给出的条件是()(A) AC=DE (B) AB=DF (C) BF=CE (D) ∠ABC=∠DEF二.填空题 (本大题共 40 分)1.在Rt△ABC中,∠C=90°,如果AB=13,BC=12,那么AC= ;如果AB=10,AC:BC=3:4,那么BC=2.如果三角形的两边长分别为5和9,那么第三边x的取值范围是。
3.有一个三角形的两边长为3和5,要使这个三角形是直角三角形,它的第三边等于4.如图已知:等腰△ABC中,AB=AC,∠A=50°,BO、CO分别是∠ABC和∠ACB的平分线,BO、CO 相交于O。
则:∠BOC=5.设α是等腰三角形的一个底角,则α的取值范围是( )(A)0<α<90°(B)α<90°(C) 0<α≤90°(D) 0≤α<90°6.如图已知:△ABC≌△DBE,∠A=50°,∠E=30°则∠ADB= 度,∠DBC= 度7.在△ABC中,下列推理过程正确的是( )(A)如果∠A=∠B,那么AB=AC(B)如果∠A=∠B,那么AB=BC(C) 如果CA=CB ,那么∠A=∠B(D) 如果AB=BC ,那么∠B=∠A8.如果三角形的一个外角小于与它相邻的内角,那么这个三角形一定是三角形。
9.等腰△ABC中,AB=2BC,其周长为45,则AB长为10.命题“对应角相等的三角形是全等三角形”的逆命题是:其中:原命题是命题,逆命题是命题。
11.如图已知:AB∥DC,AD∥BC,AC、BD,EF相交于O,且AE=CF,图中△AOE≌△,△ABC ≌△,全等的三角形一共有对。
12.如图已知:在Rt△ABC和Rt△DEF中∵AB=DE(已知)= (已知)∴Rt△ABC≌Rt△DEF (________)13.如果三角形的一个外角小于与它相邻的内角,那么这个三角形一定是三角形。
14.如图,BO、CO分别是∠ABC和∠ACB的平分线,∠BOC=136°,则= 度。
15.如果等腰三角形的一个外角为80°,那么它的底角为度16.在等腰Rt△ABC中,CD是底边的中线,AD=1,则AC= 。
如果等边三角形的边长为2,那么它的高为。
17.等腰三角形的腰长为4,腰上的高为2,则此等腰三角形的顶角为( )(A)30°(B)120°(C) 40°(D)30°或150°18.如图已知:AD是△ABC的对称轴,如果∠DAC=30˚,DC=4cm,那么△ABC的周长为cm。
19.如图已知:△ABC中,AB=AC,AB的垂直平分线DE交AC于E,垂足为D,如果∠A=40˚,那么∠BEC= ;如果△BEC的周长为20cm,那么底边BC= 。
20.如图已知:Rt△ABC中,∠ACB=90˚˚,DE是BC的垂直平分线,交AB于E,垂足为D,如果AC=√3,BC=3,那么,∠A= 度。
△CDE的周长为。
三.判断题 (本大题共 5 分)1.有一边对应相等的两个等边三角形全等。
()2.关于轴对称的两个三角形面积相等()3.有一角和两边对应相等的两个三角形全等。
()4.以线段a、b、c为边组成的三角形的条件是a+b>c ()5.两边和其中一边上的中线对应相等的两个三角形全等。
()四.计算题 (本大题共 5 分)1.如图已知,△ABC中,∠B=40°,∠C=62°,AD是BC边上的高,AE是∠BAC的平分线。
求:∠DAE的度数。
五.作图题 (本大题共 6 分)1.如图已知△ABC,用刻度尺和量角器画出:∠A的平分线;AC边上的中线;AB边上的高。
2.如图已知:∠α和线段α。
求作:等腰△ABC,使得∠A=∠α, AB=AC,BC边上的高AD=α。
3.在铁路的同旁有A、B两个工厂,要在铁路旁边修建一个仓库,使与A、B两厂的距离相等,画出仓库的位置。
六.解答题 (本大题共 5 分)1.如图已知:RtΔABC中,C=90°,DE⊥AB于D,BC=1,AC=AD=1。
求:DE、BE的长。
七.证明题 (本大题共 15 分)1.若ΔABC的三边长分别为m2-n2,m2+n2,2mn。
(m>n>0)求证:ΔABC是直角三角形2.如图已知:△ABC中,BC=2AB,D、E分别是BC、BD的中点。
求证:AC=2AE3.如图已知:△ABC中,∠ABC的平分线与∠ACB的外角平分线交于D,DE∥BC交AB于E,交AC 于F。
求证:BE=EF+CF初二几何---三角形——答案一.选择题 (本大题共 24 分)1.:A2.:B3.:A4.:D5.:A6.:C7.:A8.:C9.:C10.:B11.:B12.:C二.填空题 (本大题共 40 分)1.:5,82.:4<x<143.:4或√344.:115°5.:A6.:50,207.:C8.:钝角9.:1810.:全等三角形的对应角相等。
假,真。
11.:COF,CDA,612.:AC=DF,SAS13.:钝角14.:9215.:4016.:√2,√317.:D18.:2419.:30˚,8cm20.:60˚,1/2(3√3+3)三.判断题 (本大题共 5 分)1.:√2.:√3.:×4.:×5.:√四.计算题 (本大题共 5 分)1.:解:∵AD⊥BC(已知)∴∠CAD+∠C=90°(直角三角形的两锐角互余)∠CAD=90°-62°=28°又∵∠BAC+∠B+∠C=180°(三角形的内角和定理)∴∠BAC=180°-∠B-∠C=180°-40°-62°=78°而AE平分∠BAC,∴∠CAE= ∠BAC=39°∠DAE=∠CAE-∠CAD=39°-28=11°五.作图题 (本大题共 6 分)1.:画图略2.:作法:(1)作∠A=∠α,(2)作∠A的平分线AD,在AD上截取AD=α(3)过D作AD的垂线交∠A的两边于B、C△ABC即为所求作的等腰三角形3.:作法:作线段AB的垂直平分线交铁路于C,点C即为仓库的位置。
六.解答题 (本大题共 5 分)1.:解:∵BC=AC=1∠C=90°,则:∠B=45°AB2=BC2+AC2=2,AB=√2又∵DE⊥AB,∠B=45°∴DE=DB=AB-AD=√2-1∴BE=√2DE=√2(√2-1)=2-√2七.证明题 (本大题共 15 分)1.:证明:∵(m2-n2)+(2mn)2=m4-2m2n2+n4+4m2n2=m4+2m2n2+n4=(m2+n2)∴ΔABC是直角三角形2.:证明:延长AE到F,使AE=EF,连结DF,在△ABE和△FDE 中,BE=DE,∠AEB=∠FEDAE=EF∴△ABE ≌△FDE (SAS)∴∠B=∠FDE,DF=AB∴D为BC中点,且BC=2AB∴DF=AB= BC=DC而:BD= BC=AB,∴∠BAD=∠BDA∠ADC=∠BAC+∠B,∠ADF=∠BDA+∠FDE∴∠ADC=∠ADFDF=DC (已证)∴△ADF ≌△ACD (SAS)∠ADF=∠ADC (已证)AD=AD (公共边)∴AF=AC ∴AC=2AE3.:证明:∵DE∥BCDB平分∠ABC,CD平分∠ACM∴∠EBD=∠DBC=∠BDE,∠ACD=∠DCM=∠FDC∴BE=DE,CF=DF而:BE=EF+DF∴BE=EF+CF。
