确定性信号谱分析
【精品课件】高效液相色谱定性定量分析方法

定量分析基本要求
• 要有纯物质做标准 • 被定量组分峰要与其他组分达到基线分离 • 符合定性参数要求 • 选择合适定量方法
定量分析基本公式
• 在某些限定条件下,被测组分的浓度与检测器的 响应值成正比的关系。(蒸发光散射检测器浓度 与峰面积不成线性,分别取对数后呈线性。)
两谱联用技术
1 如果标准物质缺乏或难以获得;或由于结构、理 化性质相似,很多物质具有十分接近,甚至相同 的保留值,则保留值定性准确度存在疑问。
2 可以运用红外光谱、紫外光谱、核磁共振光谱和 质谱对化合物进行定性,目前两用技术有: HPLC-紫外光谱,HPLC-红外光谱,HPLC-MS, HPLC-NMR等。
高效液相色谱定性定量分析方法
色谱分析的目的:
对未知组分进行定性分析 对已知组分进行定量分析
根据色谱图上某个色谱峰的保留时间和该色谱峰 在检测器上的响应信号强度,对该谱峰进行初步定性 定量分析。
液相色谱定性分析 液相色谱定量分析 影响定量分析的因素
色谱峰的定性鉴别:
通过保留值(通常指保留时间)进行定性 需要制定保留时间误差范围
• 相关系数—用来表示线性关系的好坏程度;
• 相关系数越接近1,说明线性关系越好;
• 绘制标准工作曲线时一般选取3-6个不同浓度 的标准样品,相关系数起码应在0.95以上。
如达不到要求,可பைடு நூலகம்存在以下原因:
1 所选浓度范围使检测器的响应值超出了该检测器
2
响应值的线性范围;
2 实验数据的精密度太差,过于分散。
3 无论何种原因,都应重新绘制标准工作曲线 。
气相色谱分析法-定性定量分析

利用保留值定性(3)
色谱操作条件不稳定时的定性 相对保留值定性:相对保留值只受柱温和固定相性质的影响, 而柱长、固定相的填充情况和载气的流速均不影响相对保留 值的大小。 用已知标准物增加峰高法定性:在得到未知样品的色谱图后, 在未知样品中加入一定量的已知标准物质,然后在同样的色 谱条件下,作已知标准物质的未知样品的色谱图。对比这两 张色谱图,哪个峰增高了,则说明该峰就是加入的已知纯物 质的色谱峰。
f 'i f ' S 分别为组分i和内标物S的质量校正因子
Ai、AS分别为组分i和内标物S的峰面积
问题:内标法中,如以内标物为基准,则其相应 计算公式如何? 提示:此时 f ' S =1.0。
内标物的选择
内标物应是试样中不存在的纯物质; 内标物的性质应与待测组分性质相近,以使内标物的色谱峰 与待测组分色谱峰靠近并与之完全分离; 内标物与样品应完全互溶,但不能发生化学反应; 内标物加入量应接近待测组分含量。
一般来说,对浓度型检测器,常用峰高定量;对质量型检测器, 常用峰面积定量。
校正因子
校正因子分为相对校正因子和绝对校正因子。 绝对校正因子:表示单位峰面积或单位峰高所代表的物质质量。
mi fi = Ai
或
f i(h)
mi = hi
绝对校正因子的测定一方面要准确知道进入检测器的组分的 量mi,另一方面要准确测量出峰面积或峰高,并要求严格控制色 谱操作条件,这在实际工作中是有一定的困难的。
答:没有。由测定过程和计算公式我们可以发现,进样量的大小不影 响最终的测定结果。
内标法应用实例:甲苯试剂纯度的测定
标准溶液和试样溶液的配制 标准溶液的配制 甲苯试样溶液的配制 相对校正因子的测定 仪器开机、点火、调试; 标准溶液的分析 相对校正因子的计算: 甲苯试样中甲苯含量的测定 甲苯试样溶液的分析
4窗函数及频谱分析

窗函数及频谱分析实验目的:1. 掌握各类窗函数的时域和频率特性;2. 掌握合理运用窗函数分析信号频谱的方法;3. 掌握利用DFT 分析连续信号频谱的方法;4. 掌握谱分析中参数的选取方法。
实验原理:一、窗函数分析在确定信号谱分析中,截短无穷长的序列会造成频率泄漏,合理选取窗函数的类型,可以改善泄露现象。
1. 常用窗函数矩形窗w=boxcar(N)汉明窗w=hamming(N)汉宁窗w=hanning(N)布莱克曼窗w=blackman(N)凯泽窗w=Kaiser(N,beta)例:N=50;w=boxcar(N);W=fft(w,256);subplot(2,1,1);stem([0:N-1],w);subplot(2,1,2); plot([-128:127],abs(fftshift(W)))MATLAB中提供了fft函数,FFT是DFT的快速算法。
X=fft(x,n) :补零或截短的n 点傅立叶变换;fftshift(x)将fft计算输出的零频移到输出的中心。
例:N=50;w=hamming(N);W=fft(w,256);subplot(2,1,1);stem([0:N-1],w);subplot(2,1,2); plot([-128:127],abs(fftshift(W)))例:已知一连续信号为x(t) cos(2 f1t) cos(2 f2t)其中f i=100Hz, f2=120Hz,若以抽样频率fsam=600Hz对该信号进行抽样,试用DFT近似分析其频谱:利用不同宽度N的矩形窗截短该序列,N分别取15, 40, 80观察不同长度的窗对谱分析结果的影响;利用汉明窗重做( 1)。
用矩形窗分析:N=input('请输入N的值:’);L=512;f1=100;f2=120;fs=600;ws=2*pi*fs;t=(0:N-1)*(1/fs);x=cos(2*pi*f1*t)+cos(2*pi*f2*t);subplot(211);stem(t,x);W=fft(x,L);f=((-L/2:L/2-1)*(2*pi/L)*fs)/(2*pi);% f=((-L/2:L/2-1)*(1/L)*fs);subplot(212);plot(f,abs(fftshift(W))) 用汉明窗重做上述谱分析:N=input('请输入N的值:’);L=512;f1=100;f2=120;fs=600;ws=2*pi*fs;t=(0:N-1)*(1/fs);x=cos(2*pi*f1*t)+cos(2*pi*f2*t);wh=hamming(N)';x=x.*wh;subplot(211);stem(t,x);W=fft(x,L);f=((-L/2:L/2-1)*(2*pi/L)*fs)/(2*pi);subplot(212);plot(f,abs(fftshift(W)))例:已知连续信号为x(t) cos(2 f1t) 0.15cos(2 f2t),其中f i=100Hz, f2=150Hz,若以抽样频率fsam=600Hz对该信号进行抽样,利用不同宽度N的矩形窗截短该序列,N 分别取15,40,80 观察不同长度的窗对谱分析结果的影响;用汉明窗重做上述谱分析。
实验二 确定性信号谱分析
实验报告课程名称: 数字信号处理 指导老师: 成绩:__________________实验名称:DFT 的应用之一 − 确定性信号谱分析一、实验目的和要求谱分析即求信号的频谱。
本实验采用DFT 技术对周期性信号进行谱分析。
通过实验,了解用X(k)近似地表示频谱X(e j ω)带来的栅栏效应、混叠现象和频谱泄漏,了解如何正确地选择参数(抽样间隔T 、抽样点数N )。
二、实验内容和步骤2-1 选用最简单的周期信号:单频正弦信号、频率f=50赫兹,进行谱分析。
2-2 谱分析参数可以从下表中任选一组(也可自定)。
对各组参数时的序列,计算:一个正弦周期是否对应整数个抽样间隔?观察区间是否对应整数个正弦周期?2-3 对以上几个正弦序列,依次进行以下过程。
2-3-1观察并记录一个正弦序列的图形(时域)、频谱(幅度谱、频谱实部、频谱虚部)形状、幅度谱的第一个峰的坐标(U ,V )。
2-3-2 分析抽样间隔T 、截断长度N (抽样个数)对谱分析结果的影响; 2-3-3 思考X(k)与X(e j ω)的关系;2-3-4 讨论用X(k)近似表示X(e j ω)时的栅栏效应、混叠现象、频谱泄漏。
专业:________________ 姓名: 陈斌斌学号: 3120104034 日期:________________ 地点:________________实验名称:_______________________________姓名:______________学号:__________________ P.三、主要仪器设备MATLAB编程。
四、操作方法和实验步骤(参见“二、实验内容和步骤”)五、实验数据记录和处理程序清单:t =linspace(0,0.04,16);xn = sin(100*pi*t);N=length(xn);WNnk=dftmtx(N);Xk=xn*WNnk;subplot(2,2,1),stem(1:N,xn),title('时域离散序列x(n)');subplot(2,2,2),stem(1:N,abs(Xk)),title('幅度谱');subplot(2,2,3),stem(1:N,real(Xk)),title('频谱实部');subplot(2,2,4),stem(1:N,imag(Xk)),title('频谱虚部');六、实验结果与分析本实验以第五组参数为基准:采样频率:400 Hz6-1 实验前预习有关概念,并根据上列参数来推测相应频谱的形状、谱峰所在频率(U)和谱峰的数值(V)、混叠现象和频谱泄漏的有无。
谱分析的原理与

谱分析在大数据处理中的应用
数据降维
利用谱分析对高维数据 进行降维处理,提取主 要特征,降低计算复杂
度。
异常检测
通过谱分析检测大数据 中的异常值和异常模式, 提高数据质量和可靠性。
数据分类与聚类
利用谱分析对大数据进 行分类和聚类,发现数
据间的关联和模式。
数据可视化
将谱分析应用于数据可 视化,生成更直观、易
析、滤波器设计等。
小波变换谱分析
小波变换谱分析是一种将时间序列分 解为不同频率和尺度成分的方法,通 过分析小波系数,可以揭示信号的局 部特性和非平稳性。
小波变换在信号处理、图像处理、语 音识别等领域有着广泛的应用,如信 号去噪、特征提取、图像压缩等。
小波变换的基本思想是将一个信号表 示为一组小波函数的叠加,这些小波 函数具有不同的尺度参数和位移参数。
06
谱分析的未来发展与挑战
谱分析算法的优化与改进
算法效率
优化谱分析算法,提高计算效率,减少计算 时间和资源消耗。
适应性增强
增强算法的适应性,使其能够处理更广泛的 数据类型和复杂情况。
精度提升
改进算法以提高谱分析的精度和准确性,减 少误差和不确定性。
可解释性增强
提高谱分析结果的解释性和可理解性,使其 更易于理解和应用。
于理解的数据图像。
谱分析在物联网中的应用
信号处理
利用谱分析对物联网中的信号 进行滤波、去噪和特征提取,
提高信号质量。
设备监测与故障诊断
通过谱分析监测物联网设备的 运行状态,及时发现故障并进 行诊断。
数据分析与决策支持
利用谱分析对物联网数据进行 深入分析和挖掘,为决策提供 支持。
物联网安全
通过谱分析检测物联网中的异 常行为和攻击,提高网络安全
现代通信原理 第2章 确定信号分析

设x1(t)和x2(t)都为功率信号,则它们的互相关函数定义为
(2.38)
式中, T的含义与式(2.14)中相同,为功率信号的截断区间。
44
第2章
确定信号分析
当x1(t)=x2(t)=x(t)时,定义
(2.39)
为功率信号x(t)的自相关函数。
45
第2章
确定信号分析
由式(2.39)可得到周期信号x(t)的自相关函数为
41
第2章
确定信号分析
2.3.2 能量信号的相关定理 若能量信号x1(t)和x2(t)的频谱分别是X1(ω)和X2(ω),则信号 x1(t)和x2(t)的互相关函数R12(τ)与X1(ω)的共轭乘以X2(ω)是傅立 叶变换对,即
(2.36)
式(2.36)称为能量信号的相关定理。它表明两个能量信号在时 域内相关,对应频域内为一个信号频谱的共轭与另一信号的频 谱相乘。
30
第2章
确定信号分析
2.3 相关函数与功率谱密度函数
2.3.1 能量信号的相关函数
设信号x1(t)和x2(t)都为能量信号,则定义它们的互相关函 数R12(τ)为 (2.32) 若x1(t)=x2(t)=x(t),则定义 (2.33) 为x(t)的自相关函数。
31
第2章
确定信号分析
【例2.2】
5
第2章
确定信号分析
设xT(t)为x(t)在一个周期内的截断信号,即
(2. 6)
而
6
第2章
确定信号分析
则有:
(2. 7)
比较式(2. 5)与式(2. 7)可得:
(2. 8) 由此可见,由于引入了δ(· )函数,对周期信号和非周期信
号都可统一用信号的傅立叶变换(即频谱密度函数)来表示。
第四章 平稳随机过程的谱分析

1 2
S
X
(
)e
j
d
自相关函数和功率谱密度皆为偶函数
若随机过程X t是平稳的,自相关函数绝对可积,则自相关函数
jt
ddt
1
2
XX
()
x(t)e jt dtd
1
2
X
X
()X
* X
()d
1
2
X
X
()
2d
4.1、平稳随机过程的功率谱密度 ❖功率谱
功率型信号:能量无限、平均功率有限的信号
P lim 1 T s(t) 2 dt T 2T T 其能谱不存在,而功率谱存在
持续时间无限长的信号一般能量无限
4.1、平稳随机过程的功率谱密度
❖如何计算随机信号的平均功率?
2)时域计算方法
任一样本函数的平均功率为
W
lim
T
1 2T
T x2(t, )dt
T
随机过程的平均功率为
W
E[W
]
lim
T
1 2T
T E{X 2(t)}dt
T
若为各态历经过程:
W =W
4.1、平稳随机过程的功率谱密度 ❖如何计算随机信号的平均功率?
2020/5/20
6
4.1、平稳随机过程的功率谱密度
❖傅立叶变换
则 x(t)的傅立叶变换为:
X () x(t)e jt dt
其反变换为:
x(t) 1 X ()e jt d
2
频谱密度存在的条件为:
频谱密度
x(t)dt
2020/5/即20 信号为绝对可积信号
包含:振幅谱 相位谱
求各样本函数功率谱密度的统计平均
现代通信原理答案WORD版( 罗新民)指导书 第二章 确定信号分析 习题详解

第二章 确定信号分析2-1图E2.1中给出了三种函数。
图 E2.1①证明这些函数在区间(-4,4)内是相互正交的。
②求相应的标准正交函数集。
③用(2)中的标准正交函数集将下面的波形展开为标准正交级数:⎩⎨⎧≤≤=为其它值t t t s ,040,1)(④利用下式计算(3)中展开的标准正交级数的均方误差: ⎰∑-=-=44231])()([dt t u a t s k k k ε⑤对下面的波形重复(3)和(4):⎪⎩⎪⎨⎧≤≤-=为其它值t t t t s ,044),41cos()(π ⑥图E2.1中所示的三种标准正交函数是否组成了完备正交集?解:①证明:由正交的定义分别计算,得到12()()0u t u t dt +∞-∞⋅=⎰,23()()0u t u t dt +∞-∞⋅=⎰,31()()0u t u t dt +∞-∞⋅=⎰,得证。
②解:424()8,k C u t dt k -== =1,2,3⎰,对应标准正交函数应为()(),1,2,3k k q t t k ==因此标准正交函数集为123123{(),(),()}(),()()}q t q t q t t t t =③解:用标准正交函数集展开的系数为4()(),1,2,3k k a s t q t dt k =⋅ =⎰,由此可以得到4110()()a s t t dt ===⎰4220()()a s t t dt ===⎰4330()()0a s t t dt ==⎰。
所以,121211()()()()()22s t t t u t u t ==-④解:先计算得到312111()()()()()()022k k k t s t a u t s t u t u t ε==-=-+=∑ ⑤解:用标准正交集展开的系数分别为441141()())04a s t t dt t dt π--===⎰⎰,44224011()()cos()cos()044a s t t dt t dt t dt ππ--==-=⎰⎰⎰,433422442()()111cos()))444a s t t dtt dt t dt t dt ππππ----= =-+- =⎰⎰⎰⎰。
光谱定性、定量分析

c.标准加入法 无合适内标物时,采用该法。 取若干份体积相同的试液(cX),依次按比例加入不同量的 待测物的标准溶液(cO),浓度依次为: cX , cX +cO , cX +2cO , cX +3cO , cX +4 cO …… 在相同条件下测定:RX,R1,R2,R3,R4……。 以R对浓度c做图得一直线,图中cX点即待测溶液浓度。 R=Acb b=1时,R=A(cx+ci ) R=0时, cx = – ci
三、原子发射光谱分析法的应用
原子发射光谱分析在鉴定金属元素方面(定性分析)具 有较大的优越性,不需分离、多元素同时测定、灵敏、快捷 ,可鉴定周期表中约70多种元素,长期在钢铁工业(炉前快 速分析)、地矿等方面发挥重要作用; 在定量分析方面,原子吸收分析有着优越性; 80年代以来,全谱光电直读等离子体发射光谱仪发展迅 速,已成为无机化合物分析的重要仪器。
(3)摄谱过程 )
摄谱顺序:碳电极(空白)、铁谱、试样; 摄谱顺序 分段暴光法:先在小电流(5A)激发光源摄取易挥发元素 分段暴光法 光谱调节光阑,改变暴光位置后,加大电流(10A),再次暴光 摄取难挥发元素光谱; 采用哈特曼光阑,可多 次暴光而不影响谱线相对位 置,便于对比。
二、 光谱定量分析
§1-3 光谱定性、定量分析 光谱定性、
一、 光谱定性分析
定性依据:元素不同 电子结构不同 光谱不同→特征光谱 电子结构不同→光谱不同 定性依据:元素不同→电子结构不同 光谱不同 特征光谱 元素的原子结构不同时,产生不同的光谱,也就是说, 元素的原子结构不同时,产生不同的光谱,也就是说,通过 谱线存在否,确某元素可否存在。 谱线存在否,确某元素可否存在。 1.元素的分析线、最后线、灵敏线 元素的分析线、最后线、 分析线: 分析线:复杂元素的谱线可能多至数千条,只选择其中几条 特征谱线检验,称其为分析线; 最后线: 最后线:浓度逐渐减小,谱线强度减小,最后消失的谱线; 灵敏线: 灵敏线:最易激发的能级所产生的谱线,每种元素都有一条 或几条谱线最强的线,即灵敏线。最后线也是最灵敏线; 共振线:由第一激发态回到基态所产生的谱线;通常也是最 共振线 灵敏线、最后线;
信号分析基础

确定性信号又可分为周期信号和非周期信号 随机信号又可分平稳和非平稳的信号两种
周期信号是经过一定时间可以重复出现的信号, 满足条件:
x(t)=x(t+Nt) 式中:T——周期,T=2π/ω0;
ω0——基频 N=0,十1…
确定信号与随机信号
• 当信号是一确定的时间函数时,给定某一时 间值,就可以确定一相应的函数值。这样的 信号称为确定信号。
x(t)x(t) x(t )x(t ) 2x(t)x(t )
两边取时间T的平均值并取极限
lim 1
T
x(t)x(t)dt lim
1
T
x(t )x(t )dt
lim
1
T
2x(t)x(x )dt
T T 0
T T 0
T T 0
R(0) R( )
这个性质极为重要,它是相关技术 确定同名点的依据
3、数字相关
数字相关是利用计算机对数字影像进 行数值计算的方式完成影像的相关 二维相关
搜 索 区
目标区
测相 度似
性
c,r
maxij
i j
i0 j0
l
2 k
2
n 2
, , i0
l 2
n 2
m 2
, , i0
k 2
m 2
4.工程应用
2.4 信号的频域分析
确定信号的时间特性
• 表示信号的时间函数,包含了信号的全部 信息量,信号的特性首先表现为它的时间 特性。
R( ) lim 1
T
x(t)x(t )dt
T 2T T
lim 1
T
x(t )x(t)dt
T 2T T
lim
T
第三章 定性和定量分析

式中W0.15和 W0.85分别为峰高0.15倍和0.85倍处的峰宽。
35
(3)对于同系物-峰高乘保留时间法 在一定操作条件下,同系物之间存在半峰宽规律: W1/2=btR+a
对于难于测量半峰宽的窄峰、重叠峰(未完全重叠),
组分X
18
[例]图19-15为某组分在阿皮松L柱上的流出曲线 (柱温100℃)。测得调整保留时间以记录纸距离表 示为310.0mm。又测得正庚烷和正辛烷的调整保留时 间分别为174.0mm,373.4mm,求组分X的保留指数 并判断是什么组分。 解: 已知Z=7
lg 310.0 lg174.0 I x 100 [7 ] 775.6 lg 373.4 lg174.0
16
保留指数的测定
将被测组分与相邻两正构烷烃混合在 一起(或分别进行),在相同色谱条件下 进行分析,测出保留值,按上式计算出被 测组分保留指数Ix。将测定出的Ix值与文 献值对照定性。
17
[例]图19-15为某组分在阿皮松L柱上的流出曲线 (柱温100℃)。测得调整保留时间以记录纸距离 表示为310.0mm。又测得正庚烷和正辛烷的调整保 留时间分别为174.0mm,373.4mm,求组分X的保 留指数并判断是什么组分。
从文献上查得,在该色谱条件下,乙酸乙酯保留指数为 775.6,再用纯乙酸乙酯对照实验,可以确认该组分是乙酸乙酯。 在与文献值对照时,一定要重视文献值的实验条件,如 固定液、柱温等。而且要用几个已知组分进行验证。
19
保留指数的应用特点
保留指数仅与柱温和固定相性质有关,与色
谱操作条件无关。不同的实验室测定的保留指数 的重现性较好,精度可达±0.03个指数单位。所
色谱定性定量分析方法

⑥稳定性(stability):
意义: 考察分析样品与试剂在一定时间内稳定性。 内容:
根据样品与试剂测定时实际可能所处的环 境进行考察。
⑦耐用性( robustness ):
意义: 考察测定条件发生小变动时测定结果的变化。
内容:
流动相的组成和pH、商品柱的品牌尺寸、 柱温等
广泛用于药物中的杂质、体内外代谢产物的结构鉴定
重现性: 不同实验室,不同人测定的精密度 1、色谱信号的测量:
意义: 待测物浓度与响应值成线性关系的浓度范围;
相对保留值 α, (t-t0)/(tr -t0)
2、选择合适的离子源,利用LC-MS获得杂质的准分量不同浓度的对照品,比较测定值和加入值确定。
ELSD响应的自然对数与样品的浓度或质量呈线 性关系;
质谱(MS-ESI)检测器高浓度时的响应与样品 的质量可能呈二次或更复杂的方式。
四、色谱分析方法验证
目的:
证明所采用的色谱分析方法适合于相应的检验 要求,判断能否用于药品分析。
效能指标:评价分析方法的尺度
效能指标包括: 精密度、准确度、专属性、检测限、定量限、
tr
内容: LC-ESI-MS的
要求,判断能否用于药品分析。 内容: 药物制剂含量测定时的专属性考察内容:
重复性 广药泛品用 质于量药标物准中分的析杂方质法:、验体证内外代同谢产一物的实结构验鉴定室,同一人多次测定的精密度
中间精密度 2药、品选质择量合标适准的分离析子方源法,验利证用LC:-MS同获得一杂质实的准验分子室离子,峰。不同人,不同仪器测定的精密度
线性与范围、耐用性、稳定性、系统适用性等
不同分析测定方法的要求
药品质量标准分析方法验证 药物制剂人体生物利用度和生物等效性试验
第十一章 色谱分析法——定性定量分析
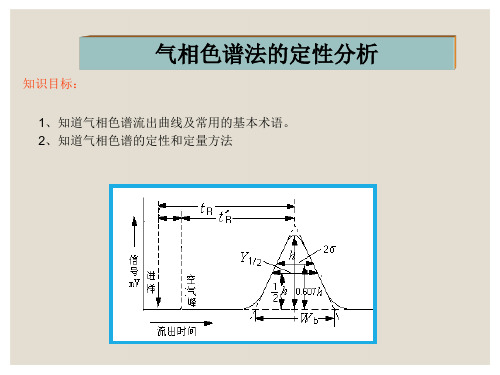
气相色谱法的定性分析
1、知道气相色谱流出曲线及常用的基本术语。 2、知道气相色谱的定性和定量方法
一、色谱流出曲线
色谱流出曲线:以组分电信号为纵坐标,流出时间为横坐标所得的曲线称为色谱流 出曲线或色谱图。该曲线反映了试样在色谱柱分离的效果,是组分定性和定量的依 据,同时也是研究色谱动力学和热力学的依据。
空气峰有时有,有时没有。
tM
②保留时间(tR):组分从进样到柱后出现浓度极大值时所需的时间。
③调整保留时间(t R ’): (1) t′R = tR-tM (2)反映组分在固定相中停 留的时间
(3)在实验条件一定时, t′R 决定于组分的性质,是定性 的基本参数。
(2) 相对保留值r21 组分2与组分1调整保留值之比:
内标法 当组分不能全部流出色谱柱,或检测器对样品中某些组分不产生信号,或只测
定样品中某一组分,采用内标法可获得准确结果。
1、测定步骤 (1)称取样品m样(其中:样品中待测组分i的质量用mi表示) (2)选定内标物。称取内标物ms。 (3)将内标物加入到已准确称量的样品中去。 (4)进样,测定待测组分的峰面积Ai和内标物的峰面积As。
气相色谱的定量分析 一、定量依据
样品中组分的质量与组分色谱峰的面积或峰高成正比。
m i = f i ·A i 或 m i = f i ·h i
组
绝色
分
对谱
的
校峰
质
正面
量
因积
子
文献查出
①准确测定Ai和hi ②准确求出f i ③计算mi
峰 高
峰面积A 1、定义:色谱峰与峰底基线所围成区域的面积叫峰面积。
c.将所测组分的相对保留值ris与手册数据对比作出定性判断。
信号的分析与处理

结论:1)周期信号的Rx(τ)不会衰减,非周期信号的Rx(τ)
一定会衰减至零。 2)如果某信号的Rx(τ)没有衰减至零,则一定含有周期成分。
信号的相关分析
2.2.3 互相关(Cross-Correlation)分析
x2
0
2 x 2 x
自相关函数的性质
信号的相关分析 周期函数的自相关函数仍为同频率的周期函数
1 T Rx ( nT ) lim x(t nT ) x(t nT )d(t nT ) T T 0 1 T lim x(t ) x(t )d(t ) Rx ( ) T T 0
有上述结论。
信号的相关分析
6) 两个不同频率的周期信号,其互相关为零。
1 T Rxy ( ) lim x(t ) y (t )dt T T 0 1 T lim x0 y0 sin(1t 1 ) sin[(2 (t ) 2 ]dt T T 0
测试信号分析与处理测试信号分析与处理确定性信号确定性信号非确定性信号非确定性信号周期信号周期信号非周期信号非周期信号随机信号随机信号时域分析频域分析时域分析频域分析时域分析频域分析窗函数窗函数滤波器滤波器三角函数展开式三角函数展开式复指数展开式复指数展开式测试信号常用的时域与频域分析与处理方法测试信号常用的时域与频域分析与处理方法信号特征值求取信号特征值求取信号时域运算滤波处理相关分析相关分析和卷积运算信号重组和波形修正频谱分析频谱分析功率谱分析功率谱分析希尔波特变换相干分析联合时域分析概率密度函数分析概率密度函数分析倒谱分析倒谱分析2121信号的时域分析信号的时域分析signalanalysistimedomainsignalanalysistimedomain离散时间序列统计参数离散时间序列统计参数211211特征值分析特征值分析离散信号的绝对平均值绝对平均值absolutemeanabsolutemean离散信号的均值均值meanmean离散信号的均方值均方值meansquaremeansquare信号的均方根值均方根值rootmeansquarerootmeansquare即为有效值离散信号的方差方差variancevariance信号的时域分析212212概率密度概率密度probabilitydensityprobabilitydensity函数分析函数分析正弦信号正弦加随机噪声窄带随机信号宽带随机信号概率密度函数概率密度函数常见信号的概率密度函数
气相色谱的原理及定性定量分析

气相色谱的原理及定性定量分析基本原理气相色谱是将有机物分离的一种方法,它也可以对混合物的组成进行定性定量分析。
混合物是通过在流动相和固定相中的相作用而分离的。
流动相和固定相构成色谱法的基础。
流动相可以有气体和液体两种状态,固定相则有液体和固体两种状态。
流动相是气体的称作气相色谱。
流动相是液体的称做液相色谱。
气相色谱是一种分配色谱,其固定相是由特定的液体黏附在一些固体基质上组成的。
各种气相色谱仪虽然在功能、价格和操作上有所不同,但其都是由气流系统、分离系统、检测系统和数据处理系统所组成的。
如下图:气相色谱的气流系统主要包括气源和气体纯化及调节装置。
气源一部分是作为流动相的载气,我们所使用的载气是氮气。
气源的另一部分是作为后期检测所用的燃烧气体,主要是氢气和空气。
由于进入分离系统的气体纯度需要保证,所以不论气源纯度如何,都应通过气体净化装置才能进入色谱分离系统。
虽然根据检测器或色谱柱不同,气相色谱的气体纯度有所差异,但所有气体的纯度至少要达到99 %以上,许多情况下应达99?99 %。
气相色谱分离系统包括样品汽化室和色谱柱两部分。
气相色谱分离技术需要所测有机物样品必须在气态才能进行,因此,首先需要将液态或固态的样品加热(100 —300 C )汽化才能进入色谱柱进行分离。
这样气相色谱进样是用人工或自动注射的方式将有机样品首先注入汽化室。
气相色谱的定性定量分析气相色谱主要功能不仅是将混合有机物中的各种成分分离开来,而且还要对结果进行定性定量分析。
所谓定性分析就是确定分离出的各组分是什么有机物质,而定量分析就是确定分离组分的量有多少。
色谱在定性分析方面远不如其它的有机物结构鉴定技术,但在定量分析方面则远远优于其它的仪器方法。
有机物进入气相色谱后得到两个重要的测试数据:色谱峰保留值和面积,这样气相色谱可根据这两个数据进行定性定量分析。
色谱峰保留值是定性分析的依据,而色谱峰面积则是定量分析的依据。
㈠定性分析气相色谱的定性分析主要有保留值定性法、化学试剂定性法和检测器定性法。
定性试验质控

一 质控目的
为满足检测的目的而采取一定的程序和方 法监控和维持检测方法学或试剂盒的性能 指标稳定在一定范围内,这个范围由实验 室依据行业标准、临床需求、制造商规定 以及实验室的实际设置。 免疫定量分析的室内质控方法参照临床化 学的执行,本节只针对用读数仪根据CUT OFF 值或域值判定结果的量值化的标记免 疫定性试验如ELISA、发光技术定性试验 等。
Division of Viral Hepatitis National Center for Infectious Diseases
HIV抗体筛查试验流程图
样 品 筛查试剂 筛查检测 阳性反应 阴性反应
原有试剂加另外一种筛查试剂
重复检测
均阳性反应 送确认实验室 进行确认
一阴一阳
均阴性反应
阴性报告
诊断试验 用来评价具有可疑给予特征(如一种感染 的特殊类型)的人。 敏感性和特异性应该处于相对平衡状态。 如果此特征对治疗或预后考虑很重要,那 么敏感性要尽可能的高;而且后续已有准 确的确证试验,可以不需要高的特异性。 感染性疾病的大多数临床试验是用于诊断。
确证试验 获得筛选或诊断试验阳性结果后,增加的 试验用于证明和确认此人前面的阳性结果。 在这种情况下,主要考虑的性能常常是特 异性和阳性预测值,而不是敏感性和阴性 预测值;特异性应该超过98到99%。确证 试验可以是非免疫化学的(如,培养或脱 氧核糖核酸研究)或免疫化学的(包括免 疫印迹和抗原或抗体中和试验)。 如果筛选和诊断试验已具有高的特异性和 阳100%)敏感性、特异 性或预测值。Cut off值的选择和来自一个检测的结果 报告应该考虑这些性能指标哪个更重要。 下面是Galen和Gambino推荐的标准: (1)当疾病是严重的,并且是可治疗的,应该不能漏 检;当假阳性结果不会导致严重的精神或经济创伤;和 不合适的治疗有轻微的后果(如没有青霉素变态反应的, A群链球菌快速试验阳性个体的治疗)需要高敏感性。 (2)当疾病是严重的,但是不能治疗;当没有疾病时 具有心理或公众健康价值;或如果假阳性结果可能引起 严重的精神或经济上的创伤(如HIV抗体的确证试验) 需要高特异性。
第一章_信号及其特征分析
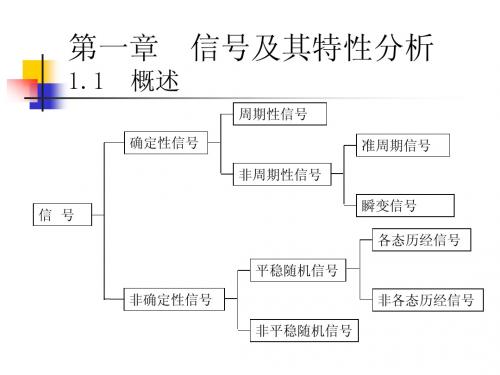
x t1 lim
N
x t N
i 1 i 1
随机过程两个不同时刻,如t1和t1+时刻之值的相关性,可以 用t1和t1+时刻瞬时值乘积的集合平均来计算,即自相关函数为:
Rx t1 , t1 lim
N
1 N xi t1 xi t1 N i 1
2. 对称性 若 xt 的傅里叶变换为 X f ,即
则
X t x f
3. 奇偶虚实性
利用欧拉公式,将公式改写为:
X f xt e j 2ftdt X R f jX I f
式中 实部— X
R
f xt cos2ft
二、周期信号的均方值、均方根值、平均 功率和相关函数
均值、绝对均值、均方值和均方根值都是描述信号强度的 量。 所谓均值是周期信号 xt 在一周期内对时间的平均值,均 值就是信号的常量分量,即 1 T x xt dt T 0
周期信号全波整流后的均值就是信号的绝对均值,即
1 x T
I
f xt cos2ft
4. 时间尺度改变
在信号 xt 幅值不变的条件下,若 xt X f ,则
1 f xkt X k k
5. 时移特性 若 xt X f 则 即把时域信号沿时间轴平移一常值t0,则使其频域引起相应的 相移 2ft0
则
d n xt n j 2 f Xf n dt
f0
,则相当于在对应
1 xt dt j 2f X f
t
8. 卷积特性 两个函数 x1 t 和 x2 t ,定义 x1 t x2 t d 为函数 x1 t 与 x2 t 的卷积,记作 x1 x2 t
高效液相色谱定性定量分析方法

1
134.2
220.2
0 100 125 150 175 200 225 250 275 300 325 350 375 400 425 450 475 500 Counts vs. Mass-to-Charge (m/ z)
由分子量及其 质谱图可以确 定该代谢物为 乙酰化氨脒
定性分析—两谱联用定性
定性分析—其他方法
1 收集洗脱物后进行定性分析
` 收集色谱分离后的每一个分离组分 ` 对所得组分分别进行仪器、化学分析或其他物理
参数(如熔点、沸点、折光、旋光等)测定
定性分析—其他方法
收集组分时应注意
` 某些情形,如色谱分析,宜采用非破坏性检测器,电化 学检测器不可;
` 如使用破坏性检测器,则须在检测器前分流,使分离后 的一小部分组分进入检测器
` 可根据文献数据和对照品选用已知标准物 ,再用已知标准物进行定性
定性分析—保留值定性
3 利用已知物增加峰高法定性
将已知标准物质加到待测样品,若某一峰 增高,且改变色谱柱或流动相组成后仍能使 该峰增高,则可基本认定该峰与已知标准物 为同一物质
定性分析—保留值定性
4 用三维图谱检测器定性
` 如果HPLC仪配备有三维图谱检测器,除比较未 知组分与已知标准物保留时间外,还可比较两 峰的立体构形
条件下应该有相同的保留值; 但相反结论却不成立,即相同色谱条件下
,具有相同保留值的两个物质不一定是同一 个物质。尚需一些辅助技术 ` 利用两谱联用定性;
其他方法定性
定性分析—保留值定性
1 已知物保留值直接对照法定性
` 未知峰保留值(t’R或V’R)与某标准物完全 相同,可初步确定为同一物质
` 改变色谱柱或流动相组成,二者保留值仍 完全相同,则可认定为同一物质
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验报告课程名称:数字信号处理指导老师:刘英成绩:__________________ 实验名称:DFT/FFT的应用之一——确定性信号谱分析一、实验目的和要求谱分析即求信号的频谱。
本实验采用DFT/FFT技术对周期性信号进行谱分析。
通过实验,了解用X(k)近似地表示频谱X(e j )带来的栅栏效应、混叠现象和频谱泄漏,了解如何正确地选择参数(抽样间隔T、抽样点数N)。
二、实验内容和步骤2-1 考虑下列序列()cos(0.48)cos(0.52)x n n n求出它基于有限个样本的频谱。
a)当0≤n≤10 时,分别确定并画出x(n)的基于N=10点DFT和N=100点的DFT b)当0≤n≤100 时,确定并画出x(n) 的基于N=100点的DFT比较(a)、(b)基于N=100的DFT的异同,说明补零(高密度频谱)和采集更多数据(高分辨率频谱)之间的区别。
2-2 谱分析参数可以从下表中任选一组(也可自定)。
对各组参数时的序列,计算:一个正弦周期是否对应整数个抽样间隔?观察区间是否对应整数个正弦周期?2-3-1观察并记录一个正弦序列的图形(时域)、频谱(幅度谱、频谱实部、频谱虚部)形状、幅度谱的第一个峰的坐标(U,V)。
2-3-2分析抽样间隔T、截断长度N(抽样个数)对谱分析结果的影响;2-3-3思考X(k)与X(ejω)的关系;2-3-4讨论用X(k)近似表示X(ejω)时的栅栏效应、混叠现象、频谱泄漏。
三、主要仪器设备MATLAB编程。
四、操作方法和实验步骤(参见“二、实验内容和步骤”)五、实验数据记录和处理2-1%0<=n<=9,N=10n=0:1:9;x=cos(0.48*pi*n)+cos(0.52*pi*n);X=fft(x,10);figure(1);subplot(2,1,1);stem(n,x);xlabel('n');ylabel('x');title('signal x(n),0<=n<=9');axis([0 10 -2.5 2.5]);subplot(2,1,2);stem(n/5,abs(X));axis([0 1 0 10]);xlabel('n');ylabel('|X|');title('Magnitude of X');%0<=n<=9,N=100,²¹Áãn=0:1:9;x=cos(0.48*pi*n)+cos(0.52*pi*n);x=[x,zeros(1,90)];X=fft(x,100);N=0:1:99;figure(2);subplot(2,1,1);stem(N,x);xlabel('n');ylabel('x');title('signal x(n),0<=n<=9');axis([0 100 -2.5 2.5]);subplot(2,1,2);stem(N/50,abs(X));axis([0 1 0 10]);xlabel('n');ylabel('|X|');title('Magnitude of X');%0<=n<=99,N=100n=0:1:99;x=cos(0.48*pi*n)+cos(0.52*pi*n);X=fft(x,100);figure(3);subplot(2,1,1);stem(N,x);xlabel('n');ylabel('x');title('signal x(n),0<=n<=9');axis([0 100 -2.5 2.5]);subplot(2,1,2);stem(N/50,abs(X));axis([0 1 0 60]);xlabel('n');ylabel('|X|');title('Magnitude of X'); 2-2%program 2-2-1clear;clf;clc;%清除缓存length=32;T=0.000625;t=0:0.001:31;%设置区间以及步长n=0:length-1;xt=sin(2*pi*50*t);xn=sin(2*pi*50*T*n);figure(1);subplot(2,1,1);plot(t,xt);xlabel('t');ylabel('x(t)');axis([0 0.1 -1 1]);title('原序列');subplot(2,1,2);stem(n,xn);xlabel('n');ylabel('xn)');title('抽样后序列');axis([0 length -1 1]);figure(2); %画出序列的实部、虚部、模、相角subplot(2,2,1);stem(n,real(xn));xlabel('n');ylabel('real(xn)');title('序列的实部');axis([0 length -1 1]);subplot(2,2,2);stem(n,imag(xn));xlabel('n');ylabel('imag(xn)');title('序列的虚部');axis([0 length -1 1]);subplot(2,2,3);stem(n,abs(xn));xlabel('n');ylabel('abs(xn)');title('序列的模');axis([0 length -1 1]);subplot(2,2,4);stem(n,angle(xn));xlabel('n');ylabel('angle(xn)');title('序列的相角');axis([0 length -1 pi]);F=fft(xn,length); %计算DFTfigure(3); %画出DFT的幅度,实部和虚部subplot(3,1,1);stem(n,abs(F));xlabel('k');ylabel('abs(F)');title('DFT幅度谱');axis([0 length 0 20]);subplot(3,1,2);stem(n,real(F));xlabel('k');ylabel('real(F)');title('DFT实部');axis([0 length -2*10^-15 2*10^-15]);subplot(3,1,3);stem(n,imag(F));xlabel('k');ylabel('imag(F)');title('DFT虚部');axis([0 length -20 20]);六、实验结果与分析2-1为了得到一个较密的频谱,显然,我们的采样频率应更小一些,也就是说,应增加N的长度。
有两种方法,一种是取样时就采集更多的样本;另一种是在序列后面添加一定长度的零,叫做填零运算填零是给原始序列填零的运算。
这导致较长的DFT,它会给原始序列的离散时间傅氏变换提供间隔更密的样本。
填零运算提供了一个较密的频谱和较好的图示形式,但因为在信号中只是附加了零,而没有增加任何新的信息,还是原始连续谱的N点取样,只是补零观察到了更多的频点,但这并不意味着补零能够提高真正的频谱分辨率。
采集更多的数据,可以获得更多的信息,可以真正提高频谱分辨率。
2-2第二组参数第三组参数第四组参数第五组参数2-3-1观察并记录一个正弦序列的图形(时域)、频谱(幅度谱、频谱实部、频谱虚部)形状、幅度谱的第一个峰的坐标(U,V)。
如图所示可知结果。
2-3-2分析抽样间隔T、截断长度N(抽样个数)对谱分析结果的影响;抽样间隔决定是否发生混叠,抽样的时间长短决定是否发生频谱泄漏,抽样间隔决定栅栏效应。
2-3-3思考X(k)与X(ejω)的关系;X(k)是对X(ejω)的抽样。
2-3-4讨论用X(k)近似表示X(ejω)时的栅栏效应、混叠现象、频谱泄漏。
用X(k)近似表示X(ejω)时,一定会产生栅栏效应,但取样间隔决定了栅栏效应强弱。
取样时间决定了混叠,抽样多少决定了频谱泄漏。
6-1 实验前预习有关概念,并根据上列参数来推测相应频谱的形状、谱峰所在频率(U)和谱峰的数值(V)、混叠现象和频谱泄漏的有无。
候,即满足奈奎斯特定律的时候不会出现频率的混叠现象。
由于采样后,信号的频谱在频域上周期上延拓,而且截断后,相当于频谱在频域上与sinc函数进行卷积,因此采样后的信号总是存在高频分量,因此总是存在频域混叠的现象,也会存在频域泄露的现象。
6-2 观察实验结果(数据及图形)的特征,做必要的记录。
1、抽样间隔不同会影响谱峰所在位置以及峰值2、泄露现象可能出现了泄漏6-3 用基本理论、基本概念来解释各种现象。
(1)混叠序列的频谱是被采样信号频谱的周期延拓,当采样速率不满足Nyquist定理时,就会发生频谱混叠,使得采样后的信号序列频谱不能真实的反映原信号的频谱。
避免混叠现象的唯一方法是保证采样速率足够高,使频谱混叠现象不致出现,即在确定采样频率之前,必须对频谱的性质有所了解。
在一般情况下,为了保证不出现频谱混叠,在采样前,先进行抗混叠滤波。
(2)泄漏用截短的序列来近似很长的甚至是无限长的序列,这样可以使用较短的DFT来对信号进行频谱分析,这种截短等价于给原信号序列乘以一个矩形窗函数,也相当于在频域将信号的频谱和矩形窗函数的频谱卷积,所得的频谱是原序列频谱的扩展。
泄漏不能与混叠完全分开,因为泄漏导致频谱的扩展,从而造成混叠。
为了减少泄漏的影响,可以选择适当的窗函数使频谱的扩散减至最小。
