贪婪算法在排课问题中分析与应用
基于贪婪算法的自动排课表系统的研究与实现

的 时 候 直 接 指 定 课 程 班 的 老 师 ,在 预 防 老 师 授 课 的 冲 突 上 进 行一个冲突检测。这样,排课表的基本要素为教室和课程班[7]。
在 排 课 表 之 前 ,算 法 将 排 课 表 的 各 要 素 初 始 化 。 在 教 室 和课程班的初始化上,依据算法的数据结构定义,首先将课程 班 按 照 上 课 的 人 数 依 据 从 大 到 小 进 行 排 序 ,这 样 做 的 目 的 是 保 证 在 一 个 基 本 排 课 表 过 程 中 ,大 的 班 级 可 以 优 先 排 课 表 ,这 也 符 合 我 们 进 行 排 课 表 算 法 设 计 的 目 的 。接 着 将 教 室 按 照 课 室 的 人 数 将 课 室 节 点 排 序 成 为 一 棵 二 叉 排 序 树 ,基 本 的 结 构 示意如图 3 所示。这里考虑到排课表的整体方便性,没有将 课室的功能作为排序的参考因素,将教室排成二叉排序树,考 虑的机理在于降低排课表过程中查找匹配的时间复杂度。对二 叉排序树我们可以进行二分查找,其时间复杂度为 O (log N) , [5] 能够起到较好的时间效果。
课室 2 人数 40
课室 1 人数 50
课室 3 人数 55
课室 4 人数 40
课室 5 人数 45
课室 6 人数 52
课室 7 人数 60
课室 8 人数 30
课室 9 人数 43
课室 10 人数 58
图 3 教室二叉树结构
课室 11 人数 70
当 初 始 化 进 行 之 后 ,算 法 就 可 以 进 行 排 课 表 了 。 在 一 个 基 本 的 排 课 表 过 程 中 ,首 先 我 们 从 课 程 信 息 链 中 读 出 第 一 个 课程班(即为人数最大的课程班),去到教室信息表中查找合适 的 教 室 。 这 里 采 用 贪 婪 法 ,遇 到 根 节 点 合 适 ,马 上 提 取 教 室 , 不合适情况下,如果人数小于根节点,转向教室二叉树的左子 树 寻 找 合 适 的 节 点 。当 找 到 节 点 后 退 出 ,提 取 教 室 ,如 果 都 还 没 有 找 到 合 适 的 教 室 ,再 回 到 根 节 点 的 右 子 树 进 行 上 述 同 样 的 查 找 ,如 果 还 是 没 有 找 到 合 适 的 教 室 ,就 退 出 查 找 ,这 个 课 程 班 就 排 课 表 不 成 功 ,无 法 安 排 教 室 ,转 向 下 一 个 课 程 班 。在 查找合适的教室中,如何有效的进行查找是关键,算法采用的 是 在 查 找 过 程 中 将 节 点 归 入 队 列 中 ,当 一 次 查 找 不 成 功 时 可 以 容 易 转 向 队 列 中 的 其 它 节 点 ,保 证 查 找 的 成 功 率 。
用顶点着色问题的贪婪算法解决排课问题

Ab ta t ne poeueo rcs vr xclr gpolm wt ged to clr galte vr xsi vn odrS- sr c: l rcd r fpoes et oo n rbe i re yme d(o i l h e ee n ag e re U e i h h on t i
c n i es e e y rc r a e e . o s es e ey s e t n a s h o i tbe a a b x wi i e n o ra d d- o sd r v r e od s a v r x c n i r v r h e t d i c ol t a l s o t df r tc l , n me h fe o
排课 是学校教学管理 中十 分重要 ,又相 当复杂 的管理 工作之一 , 为学校所设置 的课 程安排 时间、 点和授课 教 是 地 师, 使整个学校 能够有计划有秩序地 进行。 课表编排是 一个 涉及 多种 因素 的组合规划 问题 , 要保证在课程 安排 中教师 , 学生 , 室不能产生冲突 ( 教 所谓 冲突 , 就是将 需上不 同课程 的两个或 多个班排在 同一时间、 同一教室 ; 或为 同一个教师 在 同一 时间段安排 了多门课程等 情况 ),并且要满 足教师 的要求和 教室 资源等约束条件【 l 1 。 随着我 国教育体制 改革 深入 , 学生人数 的不 断上升 , 课 程设置不 断向深度 和广 度发展 ,排课 系统的研 发变得尤为
Ke wo d Shd l rgme tAgrh y r : c eueAr e n l i m a ot
贪心算法原理及应用

贪心算法原理及应用随着人工智能技术的不断发展,算法的种类也越来越多,其中贪心算法作为一种最基础的算法,也在不断优化和升级。
本文将简要介绍贪心算法原理及其应用,探讨贪心算法的优劣和适用场景。
一、贪心算法原理贪心算法是一种常见的优化算法,它的基本思想是:在每一步选择中都采取当前状态下最优的选择,从而希望最终得到全局最优的解。
贪心算法在每一步选择中都依赖于以前的选择结果,但不依赖于将来的选择结果。
这种贪心选择性质是该算法能达到最终全局最优解的保证。
然而,即使每个局部最优的选择都是正确的,但最终的全局最优解并不一定会得到,因此贪心算法不一定能得到全局最优解,但是在实际问题中,贪心算法通常可以得到非常接近最优解的结果。
二、贪心算法应用1.最小生成树最小生成树是图论中的一个经典算法问题,它可以用贪心算法来解决。
在给定一个带权无向图时,我们需要找到一棵生成树,使得生成树所有边的权值之和最小。
Prim算法和Kruskal算法都是基于这一思想建立的。
2.背包问题背包问题是一种经典的动态规划问题,也可以用贪心算法来解决。
在背包问题中,我们需要找到一种最佳的方案,使得放入背包的物品的总价值最大。
3.活动安排在一组活动中,每个活动都有一个开始时间和结束时间。
如何安排这些活动,使得可以安排的最多?可以用贪心算法进行解决。
三、贪心算法的优劣1.优点优点是:简单,易于实现;对于一些问题可以快速得到答案。
2.缺点缺点是:贪心算法不能保证得到全局最优解,只能得到最终结果接近最优解的结果。
在一些问题中会出现无解的情况。
此外,贪心算法需要根据实际问题进行调整,否则可能会得到错误的答案。
3.适用场景对于一些特殊的问题,贪心算法通常可以得到非常好的效果。
例如上文提到的最小生成树、背包问题和活动安排等等。
在这些问题中,贪心算法可以得到接近最优解的结果。
但是,在一些问题中,贪心算法的结果会偏离真实结果。
四、结语贪心算法是一种简单而实用的算法,它在很多实际问题中都有广泛的应用。
贪心算法在高校排课系统中的应用

( 4 )为 了便 于 阅读 程序 ,用 户还 需为 内
I 址 另 加注 释 。
中应用在对算法 的优化及对 新技术的应用上。
L o g i x 5 0 0 0平 台 自 动 内存 管 理 的 面 向 “ 对象” 技术 在河 南 中烟南 阳卷烟 厂 电子皮 带秤 P L C
一
3排课算法简介
排 课 问题早在 7 0年 代 就 证 明 是 一 个 NP
】 课程 。
( 2 )一位教师在 某一 时刻最 多只能教授
上接 2 2 4页
地址 对 应 表 ,记 忆 对 于 的 I / 0 位置 ;
加 至 8个或 1 6个,也 无需再 定义标 签 ,只需 动 存 储 这 些 数据 结 构 ,开 发者 无 需知 道 数 据 具 将s e n s o r 对象 的下标加长 ,相应 从 4改成 8或 体存放 的物理单元 ,因而开发者可 以把精力集
在 高校 中,科 学合 理 高效 的
课表 是教 学活动顺 利开展 的前提 , 课 表 的优 劣直接 影 响 着 高校 的教 学质 量。人 工排 课 工作 量 十分 繁 重 ,常 出现 各 种 冲 突,例 如 两个 班 级 同时 使用 一 间教 室等。 随着 计 算机 技 术 的发展 , 出现 了多种
}
如实验课 。 ( 5 )合班教 学时尽量 为同一专业 或邻近
2贪心算法 简介
贪心算法,又叫贪婪算法 ( G  ̄d y 砷h m) ,
专业 ,高数 、英语 等基础 课除外。
( 6 )教室使 用时利 用率尽量 高,即不 出 指在 问题求解时 ,总是做 出在当前看来是最好 排课 算法,有效地解决了排课 困 I 难 的 问题 。本文 就 贪 心算 法在 排 I 现十几人 的小班 占用容量 为几 百人的大教室。 的选 择 , 也就是说 , 不 从 整 体 0 0 开 发平 台的P L O 开 发 电 6编 程 Z 带秤 的数据管理
贪心算法的分析与实际应用

XX师大学计算机与信息工程学院算法设计与分析结课论文题目贪心算法的分析与实际应用专业计算机科学与技术班级1402班学号1430090056XX王悦宁任课教师洋完成日期2015-1-18贪心算法的分析与实际应用王悦宁摘要:贪心算法是指,在对问题求解时,总是做出在当前看来是最好的选择。
也就是说,不从整体最优上加以考虑,他所做出的仅是在某种意义上的局部最优解。
贪心算法不是对所有问题都能得到整体最优解,但对围相当广泛的许多问题他能产生整体最优解或者是整体最优解的近似解。
本文主要介绍了贪心算法的核心、特点及算法本身存在的问题。
关键词:贪心算法;最优解;背包问题;马踏棋盘The greedy algorithm analysis and practical application王悦宁Tianjin normal university puter and Information Engineering College Tianjin 300387Abstract:Greedy algorithm refers to, in the solution of the problem, always make in the current view is the best choice. That is to say, not to be considered as a whole, he made only in a sense of the local optimal solution. The greedy algorithm is not able to obtain the global optimal solution for all problems, but for a wide range of problems, he can produce the global optimal solution or the approximate solution of the global optimal solution. This paper mainly introduces the core of the greedy algorithm, the characteristics and the existing problems of the algorithm itself..Key words:greedy algorithm; optimal solution; knapsack problem;0引言研究背景:为了满足人们对大数据量信息处理的渴望,为了解决各种实际问题,计算机算法学得到了飞速的发展,线性规划、动态规划、贪心策略等一系列运筹学模型纷纷运用到计算机算法学中,产生了解决各种现实问题的有效算法。
贪心法思想及其运用

贪心法思想及其运用摘要:主要介绍贪心算法(又称贪婪算法)的基本思想,以及如何利用贪心算法来求解问题,如何选择最佳的贪心算法的策略,以及贪心算法在一些数学问题上的运用。
关键词:贪心算法最优策略正文:贪心算法(又称贪婪算法)是指,在对问题求解时,总是做出在当前看来是最好的选择。
也就是说,不从整体最优上加以考虑,他所做出的仅是在某种意义上的局部最优解。
贪心算法不是对所有问题都能得到整体最优解,但对一些问题它能产生整体最优解或者是整体最优解的近似解。
贪心算法没有固定的算法框架,算法设计的关键是贪婪策略的选择。
一定要注意,选择的贪婪策略要具有无后向性,即某阶段状态一旦确定以后,不受这个状态以后的策略影响,也就是说某个状态以后的过程不会影响以前的状态,只与当前状态有关,也称为这种特性为无后效性。
因此,适应用贪婪策略解决的问题类型较少,对所采用的贪婪策略一定要仔细分析其是否满足无后效性。
为了说明在使用贪心算法中选择策略是关键,下面这个例子可以充分的说明这个问题:题目:设有n个正整数,将他们连接成一排,组成一个最大的多位整数。
例如:n=3时,3个整数13,312,343,连成的最大整数为:34331213第一种策略:把整数按从大到小的顺序连接起来,题目中的例子正好符合这个策略;第二种策略:先把整数化成字符串,然后再比较a+b和b+a,如果a+b>b+a,就把a排在b 的前面,反之则把a排在b的后面。
许多同学开始看到这个题目的时候会毫不犹豫的选择第一种策略,这种策略表面上看起来是对的,从大到小排列之后,最终的数肯定会是最大的结果,但实际上这种策略师错误的,反例有很多,比如说当n=2时,2个整数为12,121 按照第一种策略就会组成12112,而正确的结果为12121,按照第二种策略的结果正是12121。
由此可见算法策略的选择是非常关键的,会直接影响到最终结果的正确性。
当然上面的例子也可以不用贪心算法来实现,但是我们发现用贪心算法来解决这个问题还是比较简单的,很容易理解其实现过程。
贪婪算法在高校排课系统中的运用

同时,为了使排 出的课表更合理、源自具人性化,排课还应考虑以下因素: ( 1) 每门课程在一
周内的上课时间尽可能分布合理; ( 2) 尽可能使同一个班级连续的两门课之间更换教室的机率小, 或就近安排; ( 3) 同一课程的不同讲次尽可能安排在同一教室,而且要隔一天以上安排,使教师 有充足的时间备课和批改作业,学生也有足够的时间复习消化; ( 4 ) 学生每天的必修课安排尽可 能趋于平衡; ( 5 ) 尽可能满足每门课程教学的客观要求; ( 6) 满足个别教师 ( 如外聘教师) 的特 殊上课时间要求。 在排课中必须遵守的基本原则、人性化因素和特殊要求构成了排课约束条件 。 ( 二 ) 排课问题数学模型 排课问题涉及班级、课程、时间、教师、教室五个方面数据,是一个典型的排列组合问题。 由于排课前课程与教师的关系已经在教学计划中确定,因而,在排课时,只要对学校所有班级开 设的每 门课程,安排课程、教师、教室具有共同的空闲时间片上课即可,排课算法也就简化为班 级、教师、教室三方面数据在具有共同的空闲时间片前提下的排列组合问题,三者关系如图 1 所 示。它们在三维空间上的交点 P 表示一个排课组合的选择,即可能的教学安排。排课问题就是遵 循一定的约束规则, 在这个三维空间搜索空闲时间片集合, 如果该集合存在, 说明排课问题有解。
摘 要: 贪婪算法在解决诸如排课等 N 完全问 P 题中具有实用价值。本文通过描述排课问题及其数学模型, 分析了基于优先级的贪婪算法在高校排课系统中的运用。利用该算法,既可以简化排课过程,缩短排课所花费 的时间,同时也能提高排课结果的满意度。 关健词: 排课问题; 数学模型; 优先级; 贪婪算法 中圈分类号: 023 文献标识码: A 文章编号: 1009- 4768 (2007) 12- 0045- 05
基于贪心算法的自动排课方法研究

基于贪心算法的自动排课方法研究一、引言在当今信息化社会,自动排课系统在许多领域中发挥着重要作用。
从学校的教学安排到企业的会议组织,合理的排课安排能够提高效率,降低错误,并提升用户体验。
贪心算法作为一种简单而有效的优化方法,在自动排课问题上具有独特的优势。
本文将围绕基于贪心算法的自动排课方法展开研究。
二、贪心算法在排课中的应用贪心算法在排课问题中的应用,主要是通过选择最简单、最直接的课程安排,以获得整体最优的解决方案。
具体来说,贪心算法会按照一定的规则,将课程安排在时间片内,尽可能减少冲突,并逐步优化整个排课方案。
三、自动排课系统设计1. 需求分析:明确排课系统的需求,包括可用的时间段、教室资源、教师资源等。
2. 算法设计:根据需求,设计适合的贪心算法,以实现自动排课。
3. 实现与测试:实现算法,并进行测试,确保系统能够正确地完成排课任务。
四、实验与结果我们将通过模拟实验来验证基于贪心算法的自动排课方法的可行性。
实验结果表明,该方法能够有效减少冲突,提高排课的合理性,与传统的排课方法相比,具有更高的效率和准确性。
五、结论本文通过对基于贪心算法的自动排课方法的研究,证明了贪心算法在排课问题上的有效性。
通过合理的算法设计和实现,我们可以得到更加合理、高效的排课方案,对于实际应用具有重要意义。
然而,贪心算法在处理一些复杂问题时可能存在局限性,因此在实际应用中,还需要结合其他算法和技术,以获得更加全面和优化的排课方案。
六、未来工作未来研究可以从多个方面展开,如进一步优化贪心算法,考虑更多的约束条件,如教室容量、教师时间等;开发更加智能的排课系统,引入人工智能技术,实现更加自动化的排课;研究如何提高排课的用户体验,如提供更灵活的时间段选择、教室资源推荐等。
总之,基于贪心算法的自动排课方法研究为解决排课问题提供了一种新的思路和方法。
通过不断完善和优化算法,我们可以得到更加合理、高效的排课方案,对于实际应用具有重要意义。
贪心算法解决活动安排问题

表1 安排活动非减序时间表
-
5
贪心算法实现
贪心算法的计算过 程如下图所示。图 中每行相应于算法 的一次迭代。阴影 长条表示的活动是 已选入集合A的活动 ,而空白长条表示 的活动是当前正在 检查相容性的活动 。
图-1 贪心算法的计算过程图
减序算法
贪心算法
时间复杂度 O(n2)
O(nlogn) O(n)
-
8
小组任务分工
1. 算法: 2. 李文治 3. 2. PPT: 4. 制作:陈平,谢华欣,韩月梅 5. 3.文档: 6. 制作:陈平,谢华欣,韩月梅
-
-
返回
-
贪心算法算法思想及分析 Nhomakorabea活动安排运用贪心算法的思路为,尽可能多的使更多的 事件得到资源的安排。按这种方法选择相容活动为未安 排活动留下尽可能多的时间。也就是说,该算法的贪心 选择的意义是使剩余的可安排时间段极大化,以便安排 尽可能多的相容活动。实现方法是在满足相容的条件下, 使结束时间靠前的活动得到资源,这样就为后续时间留 下更多的安排时间,以使更多的活动得到安排。
运用贪心算法解决活动安排问题
Using the greedy algorithm to solve the problem of activity arrangement
组长:李文治 组员: 陈平 谢华欣 韩月梅
内容提要
1 问题描述 2 算法思想及分析 3 实验及结果 4 实验总结
-
问题描述
问题描述
陈平谢华欣韩月梅运用贪心算法解决活动安排问题usingthegreedyalgorithmtosolvetheproblemofactivityarrangement问题描述实验及结果实验总结算法思想及分析问题描述设有n个活动的集合e12n其中每个活动都要求使用同一资源如演讲会场等而在同一时间内只有一个活动能使用这一资源
贪婪算法思想及其应用

贪婪算法思想及其应用贪婪算法(Greedy algorithm)是一种常用的算法思想,它根据当前情况做出局部最优的选择,从而希望获得全局最优的解决方案。
贪婪算法通常用于求解优化问题,其特点是简单、高效,并且不需要进行完全的。
贪婪算法的基本思想是通过每一步的局部最优解来建立起全局最优解。
每一步做出的选择依赖于前一步的选择结果,所以贪婪算法通常具有递归的特点。
贪婪算法的目的是使每一步的选择都是最有利的,从而达到整体的最优解。
贪婪算法的应用广泛,下面分别介绍几个常见的应用场景。
1.找零钱问题:假设有一定面值的硬币,要找零钱给客户。
贪婪算法可以选择最大面值的硬币作为找零的一部分,然后继续选择最大面值的硬币,直到完成找零。
这样可以保证找零的硬币数量最少。
2.背包问题:给定一些物品和一个背包,每个物品有一定的重量和价值。
目标是找到一个物品组合,使得其总重量不超过背包容量,但总价值最大。
贪婪算法可以根据每个物品的单位价值(即价值与重量的比值)来选择物品放入背包,以获得最大的总价值。
3.最小生成树问题:给定一个带权无向图,要找到一个包含所有顶点的子图,且该子图的边权重之和最小。
贪婪算法可以从一个顶点开始,每次选择权重最小的边连接到已经选择的顶点集合中的顶点,直到所有顶点都被包含在选择的子图中。
4.哈夫曼编码:哈夫曼编码是一种最优前缀编码方法,用于将字符编码为二进制序列。
贪婪算法可用于构建哈夫曼树,根据字符的出现频率构建最小的二叉树,然后将字符编码为哈夫曼树的路径。
以上只是贪婪算法的一些常见应用,实际上贪婪算法还可以应用于很多其他领域,如任务调度、排序、图着色等。
贪婪算法的优点是简单、高效,但也有一定的局限性,它不能保证一定能得到全局最优解。
因此,在应用贪婪算法时需要根据具体情况来评估其适用性,并结合其他算法和方法来求解问题。
贪心算法解决活动安排问题报告

1.引言:贪心法是一种改进了的分级处理方法。
用贪心法设计算法的特点是一步一步地进行,每一步上都要保证能获得局部最优解。
每一步只考虑一个数据,它的选取满足局部优化条件。
若下一个数据与部分最优解连在一起不再是可行解时,就不把该数据添加到部分解中,直到把所有数据枚举完,或者不能再添加为止。
这种能够得到某种度量意义下的最优解的分级处理方法称为贪心法。
贪心算法总是做出在当前看来是最优的选择,也就是说贪心算法并不是从整体上加以考虑,它所做出的选择只是在某种意义上的局部最优解,而许多问题自身的特性决定了该题运用贪心算法可以得到最优解或较优解。
2.贪心算法的基本思想及存在问题贪心法的基本思想:从问题的某一个初始解出发逐步逼近给定的目标,以尽可能快的地求得更好的解。
当达到某算法中的某一步不能再继续前进时,算法停止。
1.建立数学模型来描述问题。
2.把求解的问题分成若干个子问题。
3.对每一子问题求解,得到子问题的局部最优解。
4.把子问题的解局部最优解合成原来解问题的一个解。
3.活动安排问题:3.1 贪心算法解决活动安排问题学校举办活动的安排问题是用贪心算法有效求解的一个很好例子。
活动安排问题要求安排一系列争用某一公共资源的活动。
用贪心算法可使尽可能多的活动能兼容的使用公共资源。
设有n个活动的集合{0,1,2,…,n-1},其中每个活动都要求使用同一资源,如会场等,而在同一时间内只有一个活动能使用这一资源。
每个活动i都有一个要求使用该资源的起始时间starti和一个结束时间endi,且starti<endi。
如选择了活动i,则它在半开时间区间[starti,endi)内占用资源。
若区间[starti,endi)与区间[startj,endj)不相交,称活动i与活动j是相容的。
也就是说,当start j≥endi或starti≥endj时,活动i与活动j相容。
活动安排问题就是在所给的活动集合中选出最大的相容子活动集合。
贪婪算法的分析与实现

这篇文章我们共同学习贪婪算法,贪婪策略是一种非常简单的问题解决策略。
教室调度问题假设目前有如下的课程表,你希望将尽可能多的课程安排在某间教室上。
如果我们安排了美术课之后,英语课就不能安排到这间教室了你希望在这间教室上尽可能多的课,那么如何选出尽可能多且时间不冲突的课程呢?具体做法这里给你:1、先选出结束最早的课,即就是这间教室上的第一堂课2、由于第一节课是10点结束的,因此我们要选从第一节课结束的时间才开始上的课,同样,我们选出结束最早的课,这将是这间教室上的第二堂课重复第二步,这样我们就能找出这间教室既不冲突也可以安排尽可能多的课。
于是,我们就得出了这间教室可以上三堂课,如图所示:你看到这里一定说这有啥难的!但这就是贪婪算法的优势——简单易行,因为每一步都是局部最优解,那么最终得到的就是全局最优解。
当然贪婪算法有其局限性,正是其简单易实现的优点才没有被弃用。
我们再看一个问题——集合覆盖问题假设存在如下表的需要付费的广播台,以及广播台信号可以覆盖的地区。
如何选择最少的广播台,让所有的地区都可以接收到信号每个广播台播出都需要支付费用,因此要力图在尽可能少的广播台播出并且覆盖的州要尽可能多。
每个广播台都覆盖特定的区域,不同广播台的覆盖区域可能重叠是不是想想都挺难的,但是贪婪算法可以解决这一问题,具体做法:1、选出覆盖了最多的地区的广播台,即使下次选择的广播台已经覆盖了上次已经覆盖过的地区,也没有关系,只要它是覆盖最多的就可以。
2、重复第一步,直到覆盖了所有的地区这是一种近似算法。
在获得精确解需要的时间太长时,可使用近似算法。
判断近似算法优劣的标准如下:i.速度有多快ii.得到的近似解与最优解的接近程度贪婪算法不仅简单,而且通常运行速度很快。
代码实现。
贪心算法及其应用doc资料

贪心算法及其应用湖州师范学院实验报告课程名称:算法实验三:贪心算法一、实验目的1、理解贪心算法的概念,掌握贪心算法的基本要素。
2、掌握设计贪心算法的一般步骤,针对具体问题,能应用贪心算法求解。
二、实验内容1、问题描述活动安排问题设有n个活动的集合E={1,2,…,n},其中每个活动都要求使用同一资源,如演讲会场等,而在同一时间内只有一个活动能使用这一资源。
每个活动i都有一个要求使用该资源的起始时间si和一个结束时间fi,且si <fi 。
如果选择了活动i,则它在半开时间区间[si, fi)内占用资源。
若区间[si, fi)与区间[sj, fj)不相交,则称活动i与活动j是相容的。
也就是说,当si≥fj或sj≥fi时,活动i与活动j相容。
2、数据输入:文件输入或键盘输入。
3、要求:1)完成上述两个问题中1个或全部,时间为 1 次课。
2)独立完成实验及实验报告。
三、实验步骤1、理解方法思想和问题要求。
2、采用编程语言实现题目要求。
3、上机输入和调试自己所写的程序。
4、附程序主要代码:2、活动规划问题#include<stdio.h>#include<iostream>#include<algorithm>using namespace std;struct node{int start;int end;} a[11111];bool cmp(node x,node y){if(x.end<y.end) return true;else if(x.end==y.end && x.start>y.start) return true; return false;}int main(){int n,i,j,ans,end;cin>>n;for(i=0;i<n;i++) cin>>a[i].start>>a[i].end;sort(a,a+n,cmp);ans=0;end=-1e9-100;for(i=0;i<n;i++) {if(a[i].start>=end) {ans++;end=a[i].end;}}cout<<ans<<endl;return 0;}5、实验结果:四、实验分析活动安排问题:结束时间越早的活动优先。
贪心算法理解贪心算法的基本原理和应用场景

贪心算法理解贪心算法的基本原理和应用场景贪心算法:理解贪心算法的基本原理和应用场景简介:贪心算法(Greedy Algorithm)是一种常用的算法设计和解决问题的方法。
它以一种贪婪的方式做出每一步的选择,希望最终能够达到整体上的最优解。
本文将介绍贪心算法的基本原理和常见应用场景。
一、贪心算法的基本原理贪心算法的基本原理是每次都做出当前最优的选择,希望最终能够达到整体上的最优解。
贪心算法的优点在于简单、高效,但由于它只关注当前最优解,因此可能无法得到全局最优解。
贪心算法的基本步骤如下:1. 将问题划分为若干子问题,每个子问题都有多个选择;2. 分析子问题的选择,以及每个选择的最优解;3. 根据每个子问题的最优解,做出当前最优的选择;4. 更新已做出选择的子问题集合;5. 重复步骤3和4,直到解决全部子问题。
二、贪心算法的应用场景1. 零钱兑换问题零钱兑换问题是指给定一个金额和一组零钱的面值,如何用最少数量的零钱找零。
贪心算法可以从面值最大的零钱开始,每次找零选择当前面值最大的零钱,直到达到目标金额。
2. 区间调度问题区间调度问题是指给定一组区间,如何选择最多数量的不相交区间。
贪心算法可以根据区间的结束时间进行排序,每次选择结束时间最早的区间,并排除与之重叠的其他区间。
3. 背包问题背包问题是指给定一组物品和一个固定容量的背包,如何选择物品放入背包,使得背包中物品的总价值最大。
贪心算法可以通过计算每个物品的单位价值(即物品的价值与重量的比值)来选择单位价值最高的物品放入背包。
4. 最短路径问题最短路径问题是指在一个有向图或无向图中,找到两个节点之间的最短路径。
贪心算法可以使用Dijkstra算法,每次选择离起始节点最近的未访问节点进行扩展,直到找到目标节点。
5. 活动选择问题活动选择问题是指在一组活动中,选出最大的互相兼容的活动子集合。
贪心算法可以根据活动的结束时间进行排序,每次选择结束时间最早的活动,并排除与之重叠的其他活动。
算法贪婪法实验报告

一、实验背景与目的随着计算机科学的不断发展,算法在解决实际问题中的应用日益广泛。
贪婪法作为一种重要的算法设计方法,在许多领域都得到了广泛应用。
本实验旨在通过实际案例,让学生了解和掌握贪婪法的基本原理、设计方法以及应用场景。
二、实验内容与步骤1. 实验内容本实验选取两个经典问题作为案例,分别是“最小生成树”和“硬币找零问题”,分别使用贪婪法进行求解。
2. 实验步骤(1)最小生成树问题① 确定问题背景:给定一个无向连通图,要求找到一棵包含图中所有顶点的最小生成树。
② 设计贪心算法:以图中的任意一个顶点为根,选择与根顶点距离最短的顶点作为下一个顶点,并添加到最小生成树中。
重复此步骤,直到所有顶点都被包含在最小生成树中。
③ 实现代码:使用C++语言实现贪心算法,计算最小生成树的总权值。
(2)硬币找零问题① 确定问题背景:给定一系列不同面值的硬币和找零金额,要求找出最少硬币数来凑齐该金额。
② 设计贪心算法:从面值最大的硬币开始,尽可能地使用硬币凑齐金额。
若当前硬币面值大于剩余金额,则尝试使用面值较小的硬币,重复此步骤,直到金额为0。
③ 实现代码:使用C++语言实现贪心算法,计算最少硬币数。
三、实验结果与分析1. 最小生成树问题实验结果表明,使用贪心法求解最小生成树问题时,能够得到一棵包含图中所有顶点的最小生成树。
在实验过程中,我们发现贪心法在求解最小生成树问题时,存在一定的局限性。
例如,当图中存在多个顶点距离相同的情况下,贪心法可能会得到次优解。
2. 硬币找零问题实验结果表明,使用贪心法求解硬币找零问题时,能够得到最少硬币数来凑齐给定金额。
在实验过程中,我们发现贪心法在求解硬币找零问题时,具有较好的性能。
四、实验总结与讨论1. 贪婪法的基本原理贪婪法是一种在每一步都选择当前最优解的算法。
它通过在每一步选择局部最优解,期望得到全局最优解。
然而,贪婪法并不保证能够得到全局最优解,因为它的决策过程是基于局部最优解的。
贪婪算法的基本原理及应用论文

贪婪算法的基本原理及应用论文摘要贪婪算法是一种基于贪心策略的算法,其通过每一步的局部最优选择来达到整体最优的解。
本文将介绍贪婪算法的基本原理,包括选择策略和求解过程。
同时,将引入一些贪婪算法的应用案例,并分析其优缺点。
1. 引言贪婪算法是解决优化问题的一种常用方法,其思想简单而直观,可以快速得到一个近似最优解。
本文将重点阐述贪婪算法的基本原理和应用,以帮助读者更好地理解贪婪算法的特点和使用方法。
2. 贪婪算法的基本原理贪婪算法的基本原理是通过每一步的局部最优选择来达到整体最优的解。
其选择策略通常是基于某种优先级的排序方式,可以是按照权重、代价、效益等进行决策。
贪婪算法的求解过程通常分为以下几个步骤:•初始化:根据问题的具体特点,进行相关变量的初始化。
•贪心选择:根据选择策略,选择当前步骤的局部最优解。
•约束更新:根据问题约束条件对解进行更新,使之符合问题要求。
•判断终止:根据问题的终止条件,判断是否达到最终解。
3. 贪婪算法的应用案例3.1 零钱找零问题零钱找零问题是贪婪算法的典型应用之一。
假设我们需要找零的金额为N,同时可以使用的货币面额有d1、d2、…、dn。
贪婪算法的解决思路是选择面额最大且小于等于N的货币进行找零,然后继续在剩余金额中进行相同的操作,直到找零金额为0为止。
3.2 背包问题背包问题是贪婪算法的另一个典型应用。
假设我们有一个背包,其最大承载重量为W,同时有一组物品,每个物品都有自己的重量和价值。
贪婪算法的解决思路是按照单位重量的价值进行排序,然后依次选择单位重量价值最高的物品放入背包,直到背包装满或物品耗尽。
3.3 最小生成树问题最小生成树问题是贪婪算法在图论中的一个重要应用。
给定一个带权重的无向连通图,找到一个子图使得该子图包含图中的所有顶点,并且边的权重之和最小。
贪婪算法的解决思路是从任意一个顶点开始,选择与当前子图相连的最小权重边,并将其加入子图中,直到子图包含所有顶点。
基于优先级贪婪算法排课系统

基于优先级贪婪算法的排课系统研究摘要:运用计算机进行自动排课既是高校教务管理的迫切需要,同时也有重要的理论研究意义。
由于排课的条件约束多且复杂多变,所以几十年来还没有定型的最优实现方案。
本文提出了大学校级排课问题的数学模型和排课算法,研究了计算机辅助排课问题的数学解决方法,且在设计上注意避免了班级排课冲突、教师排课冲突和教室排课冲突三个关键问题。
该算法已在校级排课系统中实现,和同类模型和算法相比较,更具有设计思路简洁、排课速度快,冲突少,可移植性强等优点。
关键词:排课算法;排课冲突;贪婪算法;数学模型;调度算法abstract: automatic course scheduling by computer is not only the urgent need of college educational administration,but also is an important theoretical significance.a steady optimal project has not been worked out for several decades because thecourse scheduling is complex and changeable.in this paper,a mathematical model and algorithm of thecollege course schedulingis proposed ,and the mathematical solution of computer aidedcourse schedulingis discussed. this algorithm has settled three key problems such as class scheduling collide, teacher scheduling collide and classroom scheduling collide . and this algorithm has been applied inthe school timetable management system .comparing with other similar model and algorithm , sms has the characteristics of simple in design,fast speed , less conflictand better portability.key words : course scheduling algorithm ; course scheduling collide; greedy algorithm ; mathematical model ; dispatch algorithm0 引言课程安排是高校教学中的一项重要且繁琐的工作,因为安排的结果的好坏会直接影响教学计划的执行及教师授课和学生学习的效果[1],传统排课方式下,课程表安排是手工实现的,主要依靠个人经验、很容易出现冲突,且排课质量不高。
浅谈贪心算法在排课系统中的应用

() 1初始化
就是删 除系统数 据库 中部 分或全 部数据表 中的 内容 , 以
便于新学期开始时输入新的数据 。采用手工输入方式时, 应保 留班级 、 教师、 教室 等基 本数据, 以减小输入 工作量 ; 而采用 自 动导入方式时, 应清空所有数据表, 以避免数据重复 。
() 取 记 录 2读
局保证整体利益。
() 2 在保 证时间无冲突的情况下 , 尽量将课程 安排在上此 类课 效果最好的时间。每周 的周二 、 周三 、 四是最佳学习 日, 周 每天上午是教学 的最佳课 时, 应该把难度大 、 关键 的课程安排 在此 时间段。其它课程 , 例如体育课则安排在下午教学。 () 3 根据人类大脑 皮层 活动的优势规律 , 应该交 替编排课 程 。理论课与实践课要交替编排 ; 人文学科与 自然学科课程交 替编排 ; 同一 门课程不应连排 ,中间应 该保持适 当的时间间
取 该 记 录 的班 级 、 师 、 室 信 息 向回 找 已经 排 过 的 最 近 的相 教 教
贪 心算法不在整体上考虑最优 ,而是把整个 问题分 成若干个
同信息 , 提取 该信 息对应 的记录 , 重新从这条记录开始编排【 3 ] 。
4. 总结
阶段, 保证在 每个阶段做 出当前看来 的最优 决策, 并且一旦做
4 排 课 系 统算 法 的 实现 .
() I课程表是一所高校开展教 学工 作的运行指挥 图, 全校 师生正是 依据 课程 表来进行教学活动 的。课程 表要根据教 学 计划 , 将讲授课程 的教师 、 实施教学活动 的教室和学习课程 的 学 生等 资源遵 守 时问不 冲突 的原 则在某 个 时间片 段 结合起 来 。课表是面 向全校 学生, 安排上 百门课 程 , 要 因此必须从全
活动安排

贪心算法解决活动安排问题软件02 1311611006 张松彬问题描述:现有一个阶梯教室,有n个活动(A1A2A3A4...An)需要申请这个教室,但是这个教室同一时间只能被一个活动使用。
已知每个活动的起始时间Ts和结束时间Te。
问怎样安排活动才能使尽可能多的活动使用到教室。
、问题解决:1、为了使得每次贪心选择后面向唯一的一个子问题,我们将活动按结束时间单调递增排序。
2、活动安排问题的贪心算法特性证明:贪心选择性:由于结束时间的单调递增排序,可以知道第一次贪心选择的是A1,如果能够证明A1必属于某一个全局最优解(这里的全局最优解可能有多个),就证明了问题的贪心选择特性。
怎么证明呢?设已有全局最优解Sk,其中Aj是Sk中结束时间最早的活动,讨论A1和Aj,如若给A1=Aj,则问题已证。
如果A1 != Aj。
因为A1.endTime <= Aj.endTime。
那么即使将Aj替换成A1得到的新的Sk'应该也是相容的,因为Sk'包含的活动个数等于Sk 包含的活动个数,所以Sk‘也是一个全局最优解,则特性得证,即A1必属于某个全局最优解。
进而推论,每次做出的局部贪心选择都属于全局最优解中的一个子问题。
代码:public class ActivitySelection {public static void main(String[] args) {Activity[] activities = new Activity[5];activities[0] = new Activity(0,0);activities[1] = new Activity(1,2);activities[2] = new Activity(3,7);activities[3] = new Activity(2,9);activities[4] = new Activity(8,10);ArrayList<Activity> resultList = new ArrayList<Activity>();resultList = resolve(activities);for(Activity a:resultList) {System.out.println("(" + a.getStart() + "," + a.getEnd() + ") ");}}/*** 求解问题* @param startTimes 活动的开始时间数组* @param endTimes 活动的结束时间数组* @return*/public static ArrayList<Activity> resolve(Activity[] activityList) {int n = activityList.length;ArrayList<Activity> result = new ArrayList<Activity>();int k = 1;result.add(activityList[1]);for(int m=2;m<n;m++) {//选择下一个兼容与当前活动兼容的活动,if(activityList[m].getStart() >= activityList[k].getEnd()) {result.add(activityList[m]);k = m;}}return result;}}class Activity {int start;int end;public Activity(int start, int end) {super();this.start = start;this.end = end;}public int getStart() {return start;}public void setStart(int start) {this.start = start;}public int getEnd() {return end;}public void setEnd(int end) {this.end = end;}}运行结果:(1,2)(3,7)(8,10)。
贪婪算法活动安排问题
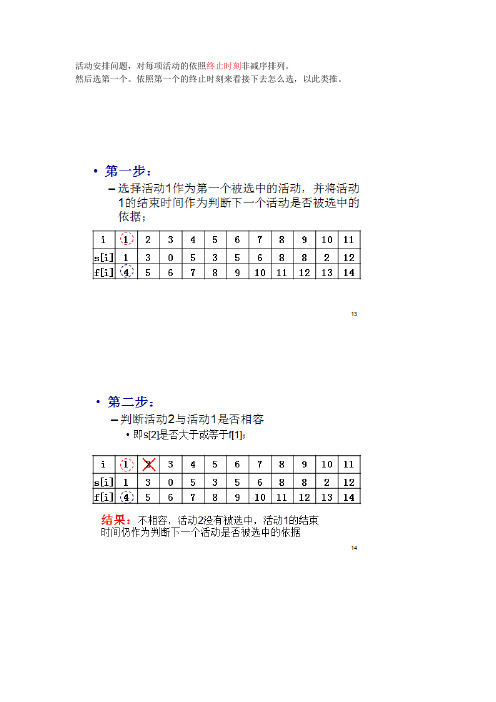
活动安排问题,对每项活动的依照终止时刻非减序排列。
然后选第一个。
依照第一个的终止时刻来看接下去怎么选,以此类推。
贪婪选择性质的证明:
1.活动安排问题的一个最优解是以贪婪选择开始。
即最优解包括第一个活动(叫做活动1)。
证明:假设有一个最优解叫做A。
它的活动也是以终止时刻的非减序进行排列。
假设A中第一个活动叫做K。
若是K是咱们的活动1,那么A确实是以活动1开始的。
若是K不是活动1.那么把K从A中去掉,并加上活动1,而且活动1是相容的是因为活动1
的终止时刻最先。
因此证明了活动安排问题的一个最优解是以贪婪选择开始。
最优子结构的证明:
把起始时刻大于活动1的终止时刻的活动去掉,A也能够把K去掉,如此子有一个递推的关系确实是(总活动中)接下去那个与活动1相容的解必然能够相容在最优解(A-K)里面。
(因它又能够化为一个贪婪选择的开始)因此每一步做出的贪婪选择将使得原问题化为规模变小的相似的子问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
贪婪算法在排课问题中分析与应用
摘要:排课问题是教学管理中重要的问题,对教学质量起到十分重要的影响。
随着计算机和信息技术的快速发展,通过合理的算法编制排课系统是十分合适的。
本文通过排课问题算法的分析,选择贪婪算法来解决排课问题。
通过实验表明,目前的算法能够很好的解决排课问题,对问题的解决的复杂度大大降低,使得排课变得十分简单和高效。
关键字:排课,贪婪算法,优先级
1、绪论
在高校日常管理中,教学计划是重要的组成部分。
而教学计划的重要体现方式之一就是排课表,其在教学管理中的地位和作用不可低估,课表的管理对教学管理是起到基础和重要的作用。
因此排课问题是教学管理中重要的问题,对教学质量起到十分重要的影响。
由于上课约束条件多,课表的编制十分复杂,是一个耗时耗力的工作。
目前随着高校人数的越来越多,其很难用手工去编制课表,其工作时间长,工作量大和繁琐的编制过程是一般人很难驾驭的。
随着计算机和信息技术的快速发展,通过合理的算法编制排课系统是十分合适的。
通过计算机算法的求解来对问题进行抽象和解决。
2、排课算法算法简介
目前对于排课问题的算法较多,主要有蚁群算法、模拟退火算法、遗传算法、整数规划法和贪婪算法等。
(1)蚁群算法
蚁群算法就是将模拟蚂蚁的活动,对参数设置较少。
这种算法具备较强的全局搜索能力,但其效率较低,且容易出现停滞[1]。
(2)模拟退火算法
这个算法被较多的学者用来解决排课问题,它是模拟退火的现象,对自然事物进行抽象而来。
其比较适合约束条件较少的问题。
如果约束条件少,其很快就能获得最优解。
但这种算法的参数选择较难,且资源开销大[2]。
(3)遗传算法
遗传算法是基于自然选择和生物遗传的全局优化策略。
其优点在于在非线性问题上能够表现出全局最优,可以并行处理而且算法效率相对较高[3]。
但遗传算法本身较为复杂,由于排课问题的约束条件较多,其算法的效率较低,如果排课要求十分严格的话,很有可能造成找不到解。
(4)整数规划法
整数规划法来解决排课问题计算量很大,只适合规模较小排课问题,对于规模较大的,至今都很难找到一个可行算法。
(5)贪婪算法
贪婪算法是指在解决问题的时候,不会考虑整体最优,而是采取局部最优的思想进行最优思想[4]。
也就是说,该算法将解决问题分解为每一个步骤,根据其难易程度进行解决,通过满足局部最优的方式来尽可能的获得最满意的解决。
虽然在某些情况下,贪婪算法并不能得到最优解,但能得到相对满意的解。
3、排课问题综述
(1)排课原则
排课问题的本质是一个优化问题,是对教师、上课课程、上课时间和上课地点等因素的优化。
其目的就是将全校所开设课程在有限的时间和地点下进行合理的安排,确保教学的顺利进行,以达到最优的效果。
为了能够产出一张满意合格的排课表,在排课中要满足一些约束条件。
我们将一些约束
条件进行归纳和整理,将约束分为基本硬约束、硬约束和软约束。
①基本硬约束:这个约束是指在排课中绝对不能发生的事情。
主要有:一个教室在同一时间只能安排一门课程;一个学生不能在同一时间只能上一门课程;一个教师只在同一时间只能教授一门课程。
②硬约束:这个约束是指排课过程中需要遵守,不然就毫无意义的约束。
主要有每一个课程有特定的功能教室类型进行匹配;有一部分课程由于特殊原因,可以在与系统之前进行手工确定安排;上课按照时段形式进行组织安排;课程的学时分配有一定的规律;课程被安排在特定的预分配区域中
③软约束:这个约束是指,如果在排课过程中,如果能够满足这些约束,那么其效果将更好。
主要有班级课程表尽量在一周内分布平均;教师对上课时间有某些偏好;周末尽量不安排课程,一般学生安排在白天,夜校的学生安排在晚上
(2)排课目标
排课问题其本质是一个多目标规划求最优解的问题。
在目前问题规模越来越多的情况下,使得其方案增加越来越快。
如何对目标进行限制是排课的关键问题。
在排课过程中,其思想就是放弃寻找单个最优解,而是在满足基本硬约束和硬约束的前提下,尽可能的满足软约束。
所以我们的排课目标主要有:①没有硬性冲突:这个目标首先要满足基本硬约束,同时也需要对硬约束进行满足;②安排可行,体现人性化;③不能出现没有安排的课程。
4、基于贪婪算法的排课分析
(1)算法选择
对常用的算法进行了综述,各个算法都有优缺点,目前没有非常成熟的排课算法和系统,在我们系统中,为了取得较为满意的效果,根据实际,我们采用贪婪算法。
贪婪算法只考虑获得较为满意的解,不追求全局最优,虽然贪婪算法并不能对所有的问题找到最优解,但他是一种最直接的算法,通过寻求局部最优以达到全局最优[5]。
(2)贪婪算法的排课流程
笔者采用贪婪算法进行对人工排课进行仿照,对资源进行最优的利用。
为了降低算法的复杂度,采用优先级的贪婪算法。
其排课步骤如下:
开始
确定排课班
计算各班每门课
优先权
根据优先权值逐个班
级、逐门课程排课
出现冲突?
人工干预
结束排课N
1)确定排课班
在班级划分上,行政班是从行政角度进行划分的,而排课班是指在同一课程教室上课的班级。
假如有M,N行政班,而他们需要进行合并上课,形成Z排课班,每个排课班都有自己的一张课程表。
2)确定优先原则
排课时间、排课地点等因素都可以成为优先因素,其关系十分复杂,且排课原则也会对其产生影响。
由于课程本身和教师自身的癖好等因素,很多教师在排课前都会提出自己的特殊要求,比如上课时间最好在晚上、上课地点必须安排有多媒体的教室等最优因素。
在优先级原则确定需要根据学校自身情况。
笔者认为在排课过程中将排课原则确定如下:①唯一特殊的要求优先;②对资源占用较大、资源紧缺、课程重要的优先,比如政治基础课程或者实验类课程等优先;③对没有特殊要求的进行最后考虑。
3)计算优先权值
在排课过程中,需要对优先级进行量化,这样有利于系统处理。
为了对优先级进行量化,引入优先权值概念。
这里对一些相关变量进行定义:一周排课时间片总数为FT,某一课程可以安排的时间片数量为AT,可以排课的教室数量为FR,符合排课要求的(对教师大小、硬件设备等符合要求的)教室数量为AR,课程的课时单元数为M,课程的合班的数量为
N,则这门课程的优先级权重值计算方式如下:=FT FR
W M N
AT AR
⨯⨯⨯。
假如某一个高校有排课时间片为4个,而一周可安排时间为5天,学校可用教室为150个,某一个课程的课时单元为3个,合并班为2个,上课人数为100人,其上课需要使用多媒体教师,且安排在下午,而学校大于100的多媒体教室只有30间。
故这门课程的优先级权值为40。
将所有需要安排的课程进行优先权值计算,然后按照这个值进行排序。
如果出现优先级相同,则随机选取进行再排序。
(3)死锁问题处理
死锁问题就是在输入正确有效的情况下,目前的排课资源无法满足排课需求。
造成这种情况的原因有很多,但主要原因是资源约束条件和排课原则产生了冲突。
由于目前并不存在一个十分完备的排课算法,所以死锁的出现也比较正常。
当遇到死锁时,系统对中断目前的排课运行,同时弹出提示框告诉管理者出现死锁的原因,并告知其进入人工调整步骤。
目前的人工调整主要有以下几个方法:①通过对排课条件进行适当的放宽;②对课程相关信息进行调整;③对某一课程进行重新时间,以转向解空间的其他区域;④对系统重新运行,重新排课。
以上方式依据不同的情况,进行选择。
5、结论
本文通过排课问题算法的分析,选择贪婪算法来解决排课问题。
通过实验表明,目前的算法能够很好的解决排课问题,对问题的解决的复杂度大大降低,使得排课变得十分简单和高效。
参考文献
[1]张忠.蚁群算法在课程表问题中的应用.华南金融电脑,2007,10(6):91-93.
[2]刘继清,陈传波.模拟退火算法在排课中的应用.武汉船舶职业技术学院学
报,2003(3):41-43
[3]陈远.基于遗传算法的排课系统的设计.高等函授学报(自然科学版),2009(4):47-49.
[4]曾光清.贪婪算法在高校排课系统中的运用.福建金融管理干部学院学报,2007(6):49-45.
[5]聂小东,李振坤,陈平华.基于贪婪算法的排课系统的探讨与实现.现代计算
机,2007,11:109-112.。
