重庆大学数理统计试题
重庆大学研究生数理统计习题答案

()(){}{}()22222111221121221164~,~(8),89111,01(1)11~(0,1)1.28 1.280.281(2)0.261 1.8360.2619818ni i n X N S S X S n X X X X E X X n n n n n D X X DX DX DX X X N n n n P X X P U X P X S P μχσμ=-=--=--=---⎛⎫-=+==⇒- ⎪⎝⎭->=>=⎛ -⎧⎫ <-+<=<⎨⎬ ⎩⎭⎝∑解:由题可知(,)且与相互独立(){}22222222241164. 1.836896464 = 2.08814.688=~(9)991188= 2.08814.688=0.90.01=0.89423948i i i S X X P S S P X X χχχμ=⎧⎫⎫⎪⎪⎪⎪⎪⎪+<⎨⎬⎪⎪⎪⎪⎪⎪⎭⎩⎭⎧⎫⎛⎫⎛⎫⎪⎪ ⎪ ⎪--⎪⎪⎪ ⎪<+<+⎨⎬ ⎪ ⎪⎪⎪⎪ ⎪⎪⎪⎝⎭⎝⎭⎩⎭<<-⎛⎫- ⎪⎝⎭=⋅∑,其中原式()()()()(){}24882255448822554821584~(0,1)=~4998244~(4)8944 2.132= 2.132=0.1i ii i i i i i i i i ii i N X X X t t X XP X XP t μμχμμμμμμ======⎛⎫ ⎪⎛⎫⎛⎫ ⎪-- ⎪ ⎪ ⎪⎝⎭⎝⎭ ⎪⎝⎭⎛⎫⎛⎫⎛⎫-- ⎪⎪⎪⎝⎭⎝⎭==--⎧⎫⎛⎫⎪⎪-≤-≤⎨⎬ ⎪⎝⎭⎪⎪⎩⎭∑∑∑∑∑∑∑∑∑()则,()()()(){}222222222891(4)=8~1~(1,8)6498911=(1,8)58.82(8,1)10.90.158.8258.82XXX F FSSXP P F P FSμμμχμ-⎛⎫⎪--==⎧⎫-⎪⎪⎧⎫<<=<=-=⎨⎬⎨⎬⎩⎭⎪⎪⎩⎭(),则也可以用T分布与F分布的关系.0020001111()()1ln(1)11,,ˆˆˆ1ln(1),,ln(1)ln(1)2(;,...,)(;)ln (;,...,)=01ˆ=()()似然方程:得到参数的极大似然估计,再由i A nnx n n xn i i i n P X A F A e p p A EX DX A EX p EX X A EX p X p L x x f x e e d L x x nnx d Xλλλλλλλλλλλλλλλ---==<==-=-=-===--=∴=--=--====-∏∏ 0000010000ln(1)ˆln(1)ˆln(1)ˆ(3)=ln(1)=ln(1)==ˆln (;,...,)ln(1){[ln(1)][]}ln(1)ˆ()ln(1)ˆˆ极大似然估计的不变性,推出的极大似然估计为是的无偏估计且是的无偏估计是有效n A p A X p p EA E X p p EX A AA d L x x p n n nx X p d p n AA p AA A λλλλλλ-=-=----⎡⎤----⎣⎦∴-=-=-----=--∴ ()202ˆlim ln(1)ˆlim lim 0ˆ估计又是相合估计量n n n EA A p DA n Aλ→∞→∞→∞⎧=⎪⎨-⎪==⎩∴221212121222122222222221222121.422,2~222(1)(1)~01~(2) (1)(1)(1)(1)2=222X YX Y X YX X X X Nn mX X n S m SU N n mn S m S n S m S X X Sn mX Xtωσσμμμμμμχχσσσσ+++++-+--==++----+-+++-+-+==的无偏估计为且(,+)(,)又且与独立,记则()()()()()()()121212212121211221212122222=22=22222=12122t n mP t t n mX XP t n m t n mP X X t n m S X X t n m SX X t n m Sαααααωαμμμμαμμα-----+-⎧⎫≤+-⎨⎬⎩⎭⎧⎫⎪⎪+-+⎪⎪+-≤≤+-⎨⎬⎪⎪⎪⎪⎩⎭⎧⎪+-+-≤+≤+++-⎨⎪⎩-+-+±+-因此构造的置信区间为{}{}121201212120121212121212.222=022,22=02=02=0=的无偏估计为,在:成立的条件下,大于某个常数应该是小概率事件,因此构造拒绝域:以下确定常数由X X H X X c K X X c cP X X c P P t t μμμμμμμμμμα+++++>+>+⎧⎫⎪⎪⎪=>+⎬⎪⎪⎭⎧⎫⎪⎪⎪⎪=>+=⎨⎬⎪⎪⎪⎪⎩⎭()()122n m c t n m S ααω--+-⇒=+-拒绝域为:3133011331122333333111~(1,).~(3)220.220.230.20.20.80.20.104220.4因为所以,类错误(弃真):为真类错误(纳伪):为真i i i i i i i i i i i i i i X B p X B p P X H P X p P X p P X p C C P X H P X p αβ=======I ⎧⎫⎧⎫=≥=≥=⎨⎬⎨⎬⎩⎭⎩⎭⎧⎫⎧⎫===+==⎨⎬⎨⎬⎩⎭⎩⎭=+=II ⎧⎫⎧=<=<=⎨⎬⎨⎩⎭⎩∑∑∑∑∑∑∑313311223333120.4120.430.410.40.60.40.648i i i i i i P X p P X p P X p C C ===⎫⎬⎭⎧⎫=-≥=⎨⎬⎩⎭⎧⎫⎧⎫=-==-==⎨⎬⎨⎬⎩⎭⎩⎭=--=∑∑∑()()221221111211=200ˆnE i i i n n nEi i i i i i i i i ni ii nii S y x dS y x x y x x d x yxββββββ======-=--=⇒-==∑∑∑∑∑∑解:()利用最小二乘估计使残差平方和最小参数的最小二乘估计量为2211222111111221111ˆ2=~(,)ˆˆˆ~(,)111ˆ===11ˆ(),由正态分布的性质推知服从正态分布ni ii i i i ni ii nnni i iiiinnni i i i i ii i i ni i nn i i i i i x YY x N x xN E D E E x Y x EY x x x x xD D x Y x x ββεβσβββββββ============+⎛⎫ ⎪ ⎪= ⎪ ⎪⎝⎭⎛⎫⎛ ⎪ ⎪ == ⎪ ⎪⎝⎭⎝∑∑∑∑∑∑∑∑∑∑∑()()()()()222211221222111112211ˆ~(,)ˆˆˆ3=ˆˆˆ2(,)ˆ(,)(,)因此,()nii ni ii n i i nnE i iiiiii i nni i i i i ii i ni ii ii i i i nniii i xDY xN x ES E Y x D Y x E Y x D Y x DY D x Cov Y x x Yx Cov Y x Cov Y x C xxσσβββββββββ==========⎫⎪⎪=⎪ ⎪⎭⎡⎤-=-+-⎣⎦⎡⎤=-=+-⎣⎦==∑∑∑∑∑∑∑∑∑∑()222221112222222222221111(,)(,)221则ni i i i i i i nni iii i nni i Enni i iii i x x ov Y x Y Cov Y Y xxx x ESn n n xxσσσσσσσσ==========+-=+-=-∑∑∑∑∑∑∑因素:车型水平:3种不同的车型A,B,C方差分析前提假设:正态性,方差齐次性,独立性对比分位数:0.95(2,9) 4.26F F >=,拒绝原假设0123:H μμμ==,认为这三种车型耗油量有显著差异。
重庆大学数理统计试题3

n Xi
i 1 m n m
( 1 ) Y1
m
2
i m 1
X
; ( 2 ) Y2
2 i
n X i 2 m Xi
i m 1 i 1 mn 2
n n 2 i 1 2 1 e 2 ) ( 2 2 ) 2 e 2 2 n xi2
xi2
n
L( 2 , X 1 , X 2 ,
Xn) (
i 1
ln( L( 2 , X 1 , X 2 , ln( L( 2 , X 1 , X 2 , d 2
xi2 n X n )) ln( 2 ) ln 2 i 1 2 2 2 X n )) n 1 n 1 n 2 i 1 ( xi 2 ) 2 2 2 4 2 2( ) 2 n i 1
s
2
c1
1 1 2 (n 1), c2 2 (n 1) n 1 2 n 1 1 2 s2
k0 :{
2
c2或
s2
2
c1}
(2) H0 : 2 1, H1 : 2 2
2 拒绝域 k0 : (n 1)s 2 12 (n 1);22s 2 0.95 (22) 33.92; :
m
2 i m1
X
n X i 2 m Xi
i m 1 i 1 mn 2
Y2 ~ F (m, n)
2 i
n
Xi
(3)
i 1
m
m n
m
~ N (0,1),
最新重庆大学数理统计大作业

研究生课程考核试卷(适用于课程论文、提交报告)科目:数理统计教师:刘琼荪姓名: xxx 学号: 20150702xxx 专业:机械工程类别:学术上课时间: 2016 年 3 月至 2016 年 4 月考生成绩:卷面成绩平时成绩课程综合成绩阅卷评语:阅卷教师 (签名)我国上世纪70-90年代民航客运量回归分析摘要:中国民航从上实际50年代发展至今已有60多年的历史,这期间中国民航经历了曲折的发展。
随着改革开发以来,中国人民的生活水平日渐提高,出行坐乘飞机逐渐人们可选的交通方式。
我国民航客运量逐年提高,为了研究其历史变化趋势及其成因,现以民航客运量作为因变量y,假设以国民收入x1、消费额x2、铁路客运量x3、民航航线里程x4、来华旅游入境人数x5为影响民航客运量的主要因素。
利用SPSS和excel软件通过建立回归模型分析我国民航客运量主要受到其中哪些因素的影响,并就回归模型分析具体可能的成因。
关键词:民航客运量影响因素回归模型一、问题提出及问题分析2004年,民航行业完成运输总周转量230亿吨公里、旅客运输量1.2亿人、货邮运输量273万吨、通用航空作业7.7万小时。
截止2004年底,我国定期航班航线达到1200条,其中国内航线(包括香港、澳门航线)975条,国际航线225条,境内民航定期航班通航机场133个(不含香港、澳门),形成了以北京、上海、广州机场为中心,以省会、旅游城市机场为枢纽,其它城市机场为支干,联结国内127个城市,联结38个国家80个城市的航空运输网络。
民航机队规模不断扩大,截止至2004年底,中国民航拥有运输飞机754架,其中大中型飞机680架,均为世界上最先进的飞机。
2004年中国民航运输总周转量达到230亿吨公里(不包括香港、澳门特别行政区以及台湾省),在国际民航组织188个缔约国中名列第3位。
从上述事实可以看出我国民航的发展所取得的成果显著。
当前我国民航客运量相当巨大,而影响我国航运客运量的因素有很多,例如第三产业增加值(亿元),城市居民消费水平(绝对元),定期航班航线里程(万千里)等[1]。
重庆大学研究生数理统计总复习

* 故任意样本(X1,…,Xn)的概率分布统一为:
n
f (x1, x2,, xn ) f (xi )
i 1
7、统计量
1)定义:设X1,…,Xn为总体X 的一个样本,
f (x1,, xn ) 为关于n维变量 x1,, xn 的连续函 数,且该函数中不含任何未知参数 ( x1,, xn 取定值时),则称 f (X1,, X n ) 为统 计量,很明显,统计量是一个随机变量。
3 . X ~ P ()E XD X
4 . X ~ U ( a ,b )E X a bD X 1 ( b a ) 2
2
1 2
1
1
5 . X ~ () E X D X 2
6 . X ~ N ( a , 2 )E X a D X 2
4、二维随机变量的数学期望:(EX,EY)
2)Poisson分布X~P(λ): P X k k e , k 0,1,2,( 0)
k!
4)均匀分布X~U[a,b]:
f
( x;
a,
b)
b
1
a
,
a xb
F(x)
x
f(t)dt
10bxaa,abxxxab
0
,其它
5)指数分布X~Γ(λ):
f
(
x;
)
e
x
,
x0
0 , x 0
分 布 函 数 F (x ) x f( t) d t 1 0 , e x ,0 x 0 0
D(aX bY ) a2DX b2DY 2ab cov(X ,Y )
4)若X与Y独立,则:
E( XY ) EXEY
D(aX bY ) a 2 DX b2 DY
第二学期概率论与数理统计试卷 参考答案
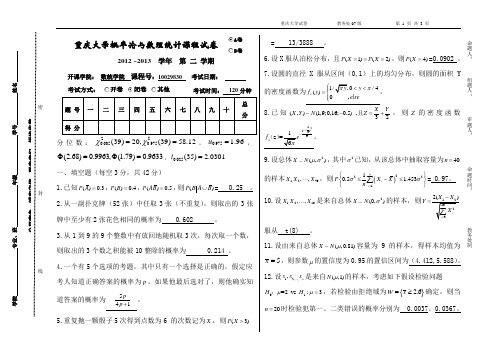
重庆大学概率论与数理统计课程试卷A卷B卷2012 ~2013 学年 第 二 学期开课学院: 数统学院 课程号:10029830 考试日期:考试方式:开卷闭卷 其他 考试时间: 120分钟分位数:220.0050.975(39)20,(39)58.12χχ==,0.975 1.96u =,(2.68)0.9963,(1.79)0.9633Φ=Φ=,0.025(35) 2.0301t =一、填空题(每空3分,共42分)1.已知()0.3P A =,()0.4P B =,()0.5P AB =,则()P B A B ⋃= 0.25 。
2.从一副扑克牌(52张)中任取3张(不重复),则取出的3张牌中至少有2张花色相同的概率为 0.602 。
3.从1到9的9个整数中有放回地随机取3次,每次取一个数,则取出的3个数之积能被10整除的概率为 0.214 。
4.一个有5个选项的考题,其中只有一个选择是正确的。
假定应 考人知道正确答案的概率为p 。
如果他最后选对了,则他确实知道答案的概率为541pp +。
5.重复抛一颗骰子5次得到点数为6 的次数记为X ,则(3)P X >= 13/3888 。
6.设X 服从泊松分布,且(1)(2)P X P X ===,则(4)P X ==0.0902 。
7.设圆的直径X 服从区间(0,1)上的均匀分布,则圆的面积Y 的密度函数为1//4()0 ,Y y f y elseπ⎧<<⎪=⎨⎪⎩。
8.已知(,)(1,9;0,16;0.5) ,32X YX Y N Z -=+且,则Z 的密度函数21()36z Z f --(z )。
9.设总体2(,)X N μσ,其中2σ已知,从该总体中抽取容量为40n =的样本1,240,,X X X ,则()222110.5 1.453nii P X X n σσ=⎧⎫≤-≤⎨⎬⎩⎭∑= 0.97。
10.设1,210,,X X X 是来自总体2(0,)XN σ的样本,则Y =服从 t(8) 。
重庆大学概率统计试题(A上期解答)

2002级重大概率论和数理统计试题(A )一、 填空题(每空3分,共45分)1、已知P(A) = 0.92, P(B) = 0.93, P(B|A ) = 0.85, 则P(A|B ) = 0.8286 。
P( A ∪B) = 0.988 。
2、设事件A 与B 独立,A 与B 都不发生的概率为19,A 发生且B 不发生的概率与B发生且A 不发生的概率相等,则A 发生的概率为: 2/3 ;3、一间宿舍内住有6个同学,求他们之中恰好有4个人的生日在同一个月份的概率:14212661112C C ⨯ ,没有任何人的生日在同一个月份的概率61266!12C ;4、已知随机变量X 的密度函数为:,0()1/4,020,2x Ae x x x x ϕ⎧<⎪=≤<⎨⎪≥⎩, 则常数A= 1/2 , 分布函数F (x )= 1,021,02241,2xe x xx x ⎧≤⎪⎪⎪+<≤⎨⎪>⎪⎪⎩, 概率{0.51}P X -<<= 0.53142e --;5、设随机变量X~ B(2,p)、Y~ B(1,p),若{1}5/9P X ≥=,则p = 1/3 ,若X与Y 独立,则Z=max(X,Y)的分布律: Z 0 1 2P 8/27 16/27 3/27;6、设~(200,0.01),~(4),X B Y P 且X 与Y 相互独立,则D(2X-3Y)= 43.92 , COV(2X-3Y , X)= 3.96 ;7、设125,,,X X X 是总体~(0,1)X N 的简单随机样本,则当k =~(3)Y t =;8、设总体~(0,)0X U θθ>为未知参数,12,,,n X X X 为其样本,11ni i X X n==∑为样本均值,则θ的矩估计量为: 2X 。
9、设样本129,,,X X X 来自正态总体(,1.44)N a ,计算得样本观察值10x =,求参数a 的置信度为95%的置信区间: [9.216,10.784] ;二、 计算题(35分)1、 (12分)设连续型随机变量X 的密度函数为:1,02()20,x x x ϕ⎧≤≤⎪=⎨⎪⎩其它求:1){|21|2}P X -<;2)2Y X =的密度函数()Y y ϕ;3)(21)E X -; 1) 9{|21|2}{0.5 1.5}16P X P X -<=-<<=2)(0()0,01,0440,X X Y y y y y ϕϕϕ+>=≤⎩⎧≤≤⎪=⎨⎪⎩其它3)45(21)212133E X E X -=-=⨯-=2、(12分)设随机变量(X,Y)的密度函数为1/4,||,02,(,)0,y x x x y ϕ<<<⎧=⎨⎩其他1) 求边缘密度函数(),()X Y x y ϕϕ; 2) 问X 与Y 是否独立?是否相关? 3) 计算Z = X + Y 的密度函数()Z z ϕ;解:1)1,02,02()(,)420,0,x X x x dy x x x x y dy ϕϕ+∞--∞⎧⎧<<<<⎪⎪===⎨⎨⎪⎪⎩⎩⎰⎰其它其它2||1,||22||,||24()(,)0,0,y Y dx y y y y x y dx ϕϕ+∞-∞⎧<-<⎧⎪===⎨⎨⎩⎪⎩⎰⎰其它其它2)显然,(,)()()X Y x y x y ϕϕϕ≠,所以X 与Y 不独立。
第二学期概率论与数理统计试卷 参考答案

重庆大学概率论与数理统计课程试卷A卷B卷2012 ~2013 学年 第 二 学期开课学院: 数统学院 课程号:10029830 考试日期:考试方式:开卷闭卷 其他 考试时间: 120分钟分位数:220.0050.975(39)20,(39)58.12χχ==,0.975 1.96u =,(2.68)0.9963,(1.79)0.9633Φ=Φ=,0.025(35) 2.0301t =一、填空题(每空3分,共42分)1.已知()0.3P A =,()0.4P B =,()0.5P AB =,则()P B A B ⋃= 0.25 。
从一副扑克牌(52张)中任取3张(不重复),则取出的3张牌中至少有2张花色相同的概率为 0.602 。
从1到9的9个整数中有放回地随机取3次,每次取一个数,则取出的3个数之积能被10整除的概率为 0.214 。
4.一个有5个选项的考题,其中只有一个选择是正确的。
假定应 考人知道正确答案的概率为p 。
如果他最后选对了,则他确实知道答案的概率为541pp +。
5.重复抛一颗骰子5次得到点数为 6 的次数记为X ,则(3)P X > = 13/3888 。
6.设X 服从泊松分布,且(1)(2)P X P X ===,则(4)P X ==0.0902 。
7.设圆的直径X 服从区间(0,1)上的均匀分布,则圆的面积Y的密度函数为1//4()0 ,Y y f y elseπ⎧<<⎪=⎨⎪⎩。
8.已知(,)(1,9;0,16;0.5) ,32X YX Y N Z -=+且,则Z 的密度函数21()36z Zf --(z )。
9.设总体2(,)X N μσ,其中2σ已知,从该总体中抽取容量为40n =的样本1,240,,X X X ,则()222110.5 1.453n i i P X X n σσ=⎧⎫≤-≤⎨⎬⎩⎭∑= 0.97。
10.设1,210,,X X X 是来自总体2(0,)XN σ的样本,则Y =服从 t(8) 。
重庆大学数理统计试题答案版

涉及到的有关分位数:()()()()()()()()()()()()20.950.950.950.9750.9750.9752222220.9750.0250.0250.9750.950.97520.95 1.645,16 1.746,15 1.753,16 2.12,15 2.131,1628.851527.49,16 6.91,15 6.26,1 5.02,1 3.84,27.382 5.99u t t t t χχχχχχχχ=============一、设123,,X X X 是来自总体~(0,3)X N 的样本。
记()2332i 1111,32i i i X X S X X====-∑∑,试确定下列统计量的分布:(1)3113i i X =∑;(2)23119i i X =⎛⎫⎪⎝⎭∑;(3)()23113i i X X=-∑;(4X解:(1)由抽样分布定理,311~(0,1)3i i X X N ==∑(2)因311~(0,1)3i i X N =∑,故223321111~(1)39i i i i X X χ==⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭∑∑(3)由抽样分布定理,()()()2223321131211~(2)3323i i i i S X X X X χ==-=⋅-=-∑∑(4)因()222~(0,1),~23X N S χ,X 与2S独立,故()~2X t 。
二、在某个电视节目的收视率调查中,随机调查了1000人,有633人收看了该节目,试根据调查结果,解答下列问题:(1)用矩估计法给出该节目收视率的估计量;(2)求出该节目收视率的最大似然估计量,并求出估计值;(3)判断该节目收视率的最大似然估计是否是无偏估计;(4)判断该节目收视率的最大似然估计是否是有效估计。
解:总体X 为调查任一人时是否收看,记为~(1,)X B p ,其中p 为收视率(1)因EX p =,而^E X X =,故收视率的矩估计量为^Xp =(2)总体X 的概率分布为()1()1,0,1xxf x p p x -=-=1111()(1)(1)(1)ln ()ln (1)ln(1)ln ()(1)01nniii ii i nx n x x x n X n n Xi L p p p pp p p L p nX p n X p d L p nX n X dp p p==---=∑∑=-=-=-=+---=-=-∏解得收视率p 的最大似然估计量为^Xp =现有一参量为1000的样本121000,,X X X ……,,且10001633ii X==∑则6330.6331000X ==,故收视率的极大似然估计值为0.633.(3)因E X p =,故^X p =是无偏估计(4)因()ln ()(1)1(1)d L p nX n X nX p dp p p p p -=-=---,又E X p=故收视率的最大似然估计X 是p 的有效估计。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
涉及到的有关分位数:
()()()()()()()()()()()()2
0.950.950.950.9750.9750.9752222220.9750.0250.0250.9750.950.97520.95 1.645,16 1.746,15 1.753,16 2.12,15 2.131,1628.851527.49,16 6.91,15 6.26,1 5.02,1 3.84,27.382 5.99
u t t t t χχχχχχχχ=============
一、设123,,X X X 是来自总体~(0,3)X N 的样本。
记()2
332
i 11
11,32i i i X X S X X
====-∑∑,
试确定下列统计量的分布:
(1)3113i i X =∑;(2)2
3119i i X =⎛⎫ ⎪⎝⎭∑;(3)()
2
3
1
13i i X X
=-∑;(4。
解:(1)由抽样分布定理,3
1
1~(0,1)3i i X X N ==∑
(2)因311~(0,1)3i i X N =∑,故2
2
3321111~(1)39i i i i X X χ==⎛⎫⎛⎫
= ⎪ ⎪⎝⎭⎝⎭
∑∑
(3)由抽样分布定理,
()()
()
2
2
23
3
21
1
31211~(2)3
323i i i i S X X X X χ==-=⋅-=-∑∑
(4)因()222~(0,1),
~23
X N S χ,X 与2S
()~2t 。
二、在某个电视节目的收视率调查中,随机调查了1000人,有633人收看了该节目,试根
据调查结果,解答下列问题:
(1)用矩估计法给出该节目收视率的估计量;
(2)求出该节目收视率的最大似然估计量,并求出估计值; (3)判断该节目收视率的最大似然估计是否是无偏估计; (4)判断该节目收视率的最大似然估计是否是有效估计。
解:总体X 为调查任一人时是否收看,记为~(1,)X B p ,其中p 为收视率 (1)因EX p =,而^
E X X =,故收视率的矩估计量为
^
X p =
(2)总体X 的概率分布为()
1()1,0,1x
x
f x p p x -=-=
11
11
()(1)(1)
(1)ln ()ln (1)ln(1)ln ()(1)
01n
n
i
i
i i i i n
x n x x x n X n n X
i L p p p p p p p L p nX p n X p d L p nX n X dp p p
==-
--=∑∑=-=-=-=+---=-=-∏
解得收视率p 的最大似然估计量为
^
X p =
现有一参量为1000的样本121000,,X X X ……,, 且1000
1
633i
i X
==∑
则633
0.6331000
X =
=,故收视率的极大似然估计值为0.633. (3)因EX p =,故^
X p =是无偏估计
(4)因
()
ln ()(1)1(1)
d L p nX n X n
X p dp p p p p -=-=---, 又EX p =
故 收视率的最大似然估计X 是p 的有效估计。
三、甲制药厂进行有关麻疹疫苗效果的研究,用X 表示一个人用这种疫苗注射后的抗体强
度,假定X 服从正态分布。
另一家与之竞争的乙制药厂生产的同种疫苗的平均抗体强度是1.9。
现甲厂声称其产品有更高的平均抗体强度,为证实这一点,检测了16个志愿者注射甲厂疫苗后的抗体强度,得样本均值 2.225X =,样本方差为2
0.2687S =。
请回答下列问题: (1)提出该问题的原假设与备择假设;
(2)写出犯第一类错误的概率表达式,并说明犯第一类错误的实际后果;
(3)根据样本数据,在显著性水平0.05α=时,检验你的假设,验证甲厂疫苗是否有更高的平均抗体强度;
(4)求甲厂疫苗抗体强度方差的置信度为0.95的置信区间。
解:设22
~(,).,X N μσμσ未知
(1)0010: 1.9;: 1.9H H μμμμ==>=
(2)犯第一类错误的概率为:{}
00P H H 拒绝成立
犯第一类错误误认为甲厂疫苗有更高的平均抗体强度,其实际后果是可能对人的生命健康安全造成威胁。
(3)由于2
σ未知,n 16=,
0H 的拒绝域为:0010.95( 1.9K X t n X t αμ-⎧⎧=->-=->⎨⎨⎩⎩ 又
0.950.5184
1.9
2.225 1.90.325, 1.7530.2274X t -=-==⨯=
因0.3250.227>,故拒绝0H ,接受1H 。
即在0.05α=时可以认为甲厂疫苗有更高
的平均抗体强度。
(4)因2~(,).X N μσμ未知,
()()222
0.9750.02510.95,16,0.2687,1527.49,15 6.26n S αχχ-=====
()()()()()()
0.975
0.025
22212
2
222
1150.2687150.26870.14711527.491150.2687150.26870.644115 6.26n S n n S n ααχχχχ-
-⨯⨯===--⨯⨯===-
故方差2
σ的置信度为0.95的置信区间为()0.147,0.644。
试判断慢性支气管炎与吸烟量是否有关系。
(取) 解:此为独立性检验
0H :慢性支气管炎与吸烟量无关,1H :慢性支气管炎与吸烟量有关
拒绝域:(){}
22
011K αχχ-=>
()22
2
112221120.951212
() 1.3211 3.84n n n n n n n n n χχ⋅⋅⋅⋅-==<
=
故接受0H ,认为慢性气管炎与吸烟量无关。
五、为了决定在老鼠中血糖的减少量和注射胰岛素A 的剂量间的关系,将同样条件下繁殖的7只老鼠注射不同剂量的胰岛素A ,获得以下数据: 通过计算得知0.343,43.714,x y ==
()
()
()()
2
2
7
7
7
1
1
1
0.092,1301.429,10.186
xx i yy i xy i i i i i l x x
l y y
l x x y y ====-==-==--=∑∑∑(1)试根据以上数据,建立血糖减少量对胰岛素A 的剂量的样本回归直线方程;
(2
)求出
^
σ
=
(3)写出回归系数显著性检验的原假设与备择假设; (4)若用t 检验法,写出回归系数显著性检验的拒绝域;
(5)根据以上数据判断胰岛素A 的剂量与血糖减少量之间是否存在线性关系。
(0.05α=) 解:(1)^
110.186
110.7170.092
xy xx
l l β=
=
=
^
^
0143.714110.7170.343 5.738y x ββ=-=-⨯=
得血糖减少量对胰岛素A 的剂量的回归方程为:^
5.738110.717y x =+。
(2)2
^^
2111301.429110.71710.186173.666E
yy xx yy xy S l l l l ββ=-=-=-⨯=
^
5.893σ
∴
===
(3)0111:0;:0H H ββ=≠
(4) ()^^01122K n αβ-⎧⎫⎪⎪
=>-⎨⎬⎪⎪
⎩⎭
(5
(
)^
0.9755 2.57149.951=
= 因
^
1110.71749.951β=>,故拒绝0H ,认为存在线性关系。
六、现有某种型号的电池3批,它们分别是A ,B ,C 这3个工厂生产的,为评比其质量,
若用方差分析方法来分析各厂电池寿命有无显著差异,请问: (1)该问题的指标是什么?因素是什么?因素的水平是什么? (2)数据应该满足的基本假定有哪些? (3)提出该问题的原假设与备择假设。
解:(1)指标是寿命,因素是工厂,因素的水平是A ,B ,C 三个不同的工厂 (2)同一工厂的电池寿命数据是来自同一个正态总体的样本
不同工厂的电池寿命数据是来自相互独立的正态总体,各总体方差相同 (3)0H :不同水平下的平均电池寿命相同
1H :至少有两个水平下的平均电池寿命不同
七、请简述为什么正交试验设计可以用较少的试验次数找到较优的水平搭配。
答:正交表保证所做的试验的水平搭配均衡地分散在所有各种水平搭配之中,因而代表性强,容易从中找到较优的水平搭配。
这是正交表的均衡分散性。
另外,对于每个因子,在它各个水平下的jt K 中,其他因子的各个水平出现的次数都相同。
这保证了jt K 中最大限度地排除了其他因子的干扰,因而有可能通过比较好的12,j j jr K K K , 值来找出较优的水
平。
这是正交表的整齐可比性。
