精馏塔理论塔板数计算

合集下载

化工实验精馏实验单板效率计算

化工实验精馏实验单板效率计算精馏是一种重要的分离和纯化技术，在化工实验中被广泛应用。

在精馏过程中，通过加热和冷却装置，将混合物中的组分按照其沸点的差异进行分离，从而获得所需纯化的物质。

精馏实验中，板塔效率是评价精馏塔分离性能的重要指标之一、本文将详细介绍精馏实验中板塔效率的计算方法。

板塔效率是指在一定条件下，塔板上产生的蒸馏液与塔板上所存在的组分间的传质情况。

计算板塔效率的方法主要有理论计算和实验计算两种。

理论计算方法是利用传质方程和物料平衡方程，结合扩散系数和溶解度等参数，通过数学模型计算得到。

而实验计算方法则是通过实际进行精馏实验，测量实验数据后，利用实验结果进行计算。

常用的实验计算方法包括：用塔板温度测定法、用馏头和下塔液的成分测定法、用馏液进出口温度比辐射法等。

其中，用塔板温度测定法是最为常用的实验计算方法之一、它基于塔板上蒸馏液和下塔液的物质平衡，通过测量不同塔板上的温度，计算得到塔板效率。

在实验中，首先需要确定实验所使用的精馏塔的塔板数。

其次，对精馏塔进行加热，使混合物开始蒸发。

然后，通过温度计等仪器测量各塔板上的温度，记录数据。

根据实验数据，可以通过下述的计算公式来计算板塔效率：塔板效率=(x进-x出)/(x进-x平衡)其中，x进和x出分别为进塔液和出塔液的组分浓度，x平衡为精馏塔平衡液的组分浓度。

需要注意的是，实验计算方法的精确程度受多种因素的影响，如实验操作技巧、仪器的准确度等。

因此，在进行板塔效率的计算时，需要进行多次实验，取平均值，使结果更加准确。

此外，为了进一步提高实验计算方法的精确性，还可以采用其他辅助手段，如红外光谱和质谱等仪器的应用，以辅助测量组分浓度。

总之，板塔效率的计算是精馏实验中一个重要的步骤，对于评价精馏技术的有效性具有重要意义。

通过实验计算方法，可以有效地获得精馏塔的分离性能，为其进一步优化提供依据。

精馏过程工艺参数的确定(理论塔板数计算)

（不包括塔釜）（包括塔釜）
2、图解法图解法求理论塔板数的基本原
理与逐板计算法相同，所不同的是用相平衡曲线和操作线分别代替相平衡方程和操作线方程。用图解法求理论塔板层数的具体步骤如下：
（1）绘相平衡曲线（2）绘操作线绘出精馏段操作线和提馏段操作线
（3）绘直角梯级从（xD,xD）点开始，在精馏段操作线与平衡线之间绘水平线与垂直线构成直角梯级，当梯级跨过两段操作线交点d时，则改在提馏段操作线与平衡线之间作直角梯级，直至梯级的垂线达到或跨过(xW,xW)点为止。梯级总数即为所需的理论塔板数（包括塔釜）。
职业教育环境监测与治理技术专业教学资源库《化工单元操作》课程
项目八蒸馏及设备操作
南京科技职业学院
项目八：精馏及设备操作
任务2：精馏过程工艺参数的确定 ---理论塔板数计算回流比计算
南京科技职业学院化学工程系
一、理论塔板数计算
（一）理论塔板概念若汽液两相能在塔板上充分接触，使离
开塔板的汽液两相温度相等，且组成互为平衡，则称该塔板为理论塔板。
❖ 试用（1）逐板计算法，（2）图解法分别求出所需的理论板层数及进料板位置。
（三）实际塔板数确定全塔效率在指定的分离条件下，所需的理论塔板数NT（不包括塔釜）与实际塔板数N之比称为全塔效率，用符
号ET表E示T 。N即NT
实际塔板数：
N NT ET
L
泡罩塔塔板效率关系曲线
y3
xn-1
精馏段操作线方程
yn
yn
相平衡方程求
xn≤ xd
直到xn xd（xd为两段操作线交点坐标x数值）时，说明第n 层板为加料板，该板应属于提馏段。因此精馏段所需理论板数为n -1块。

理论塔板数的计算

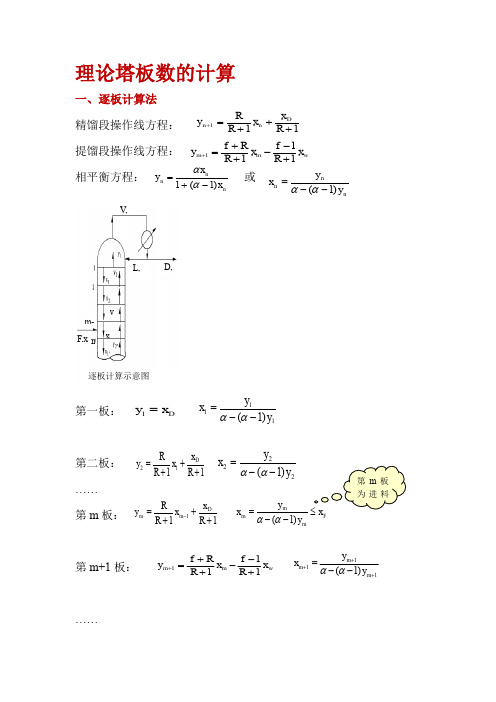
理论塔板数的计算一、逐板计算法精馏段操作线方程：提馏段操作线方程：相平衡方程：或第一板：第二板：…… 第m 板：第m+1板： (1)11+++=+R x x R R y D n n w m m x R f x R R f y 1111+--++=+nn n x x y )1(1-+=ααnn n y y x )1(--=ααD, V, L, xD F,xx y m m-逐板计算示意图 111)1(y y x --=ααDx y =11112+++=R x x R R y D 222)1(y y x --=αα111+++=-R x x R R y D m m F m m m x y y x ≤--=)1(αα第m 板为进料111)1(+++--=m m m y y x ααw m m x R f x R R f y 1111+--++=+第N 板：在计算过程中, 每使用一次平衡关系, 表示需要一层理论板. 由于一般再沸器相当于一层理论板.结果: 塔内共有理论板N 块, 第N 板为再沸器, 其中精馏段m-1块, 提馏段N-m+1块 (包括再沸器), 第m 板为进料板。

二、图解法图解法求理论板层数的基本原理与逐板计算法的完全相同,只不过是用平衡曲线和操作线分别代替平衡方程和操作线方程,用简便的图解法代替繁杂的计算而已。

1、操作线的作法首先根据相平衡数据, 在直角坐标上绘出待分离混合物的x-y 平衡曲线, 并作出对角线.W NN N x y y x ≤--=)1(ααw N N x R f x R R f y 1111+--++=-在x=xD 处作铅垂线, 与对角线交于点a, 再由精馏段操作线的截距xD /(R+1) 值, 在y 轴上定出点b, 联ab. ab为精馏段操作线.在x=xF 处作铅垂线, 与精馏段操作线ab交于点d.在x=xW 处作铅垂线, 与对角线交于点c, 联cd. cd为提留段操作线.2、求N 的步骤自对角线上a点始, 在平衡线与精馏段操作线间绘出水平线及铅垂线组成的梯级.当梯级跨过两操作线交点d 时, 则改在平衡线与提馏操作线间作梯级, 直至某梯级的垂直线达到或小于xw为止.每一个梯级代表一层理论板. 梯级总数即为所需理论板数.3、梯级含义：如第一梯级:由a点作水平线与平衡线交于点1(y1, x1), 相当于用平衡关系由y1求得x1；再自点1作垂线与精馏段操作线相交, 交点坐标为(y2, x1), 即相当于用操作线关系由x1求得y2。

精馏塔理论塔板数计算

2 0.398 0.612
0.392 0.612
3 0.392 0.602
精馏塔逐板计算
解除密码：
wulijian2710
塔板编号 xi yi
1 0.952 0.980
2 0.913 0.963
3 0.860 0.938
4 0.795 0.905
5 0.721 0.863
6 0.645 0.817
说明:这里给出了最小Rmin算法,偏差比较大,可以调整点在平衡线上,回流比最小,记入Rmin计算理
平衡线方程y
精馏段方程yn＋1
画提馏段方程yn＋1 图 q线方程xq 数 q线方程yq 据
区精折线
0.000
0.400 0.400 塔板编号 x: y:
0.048 0.048 0.357 0.409 0.456 0.363 0.376 0.376 0.479 0.501
-0.011 0.020 0.020 0.278 0.333
FALSE 0.001 0.003
FALSE -0.004 -0.009
FALSE -0.007 -0.017
FALSE -0.009 -0.022
FALSE -0.010 -0.025
FALSE 0.406 0.619
FALSE -0.001 -0.003
FALSE
0.406 0.619
0.406 0.619
FALSE
-0.012 -0.012 -0.030 -0.030
FALSE
0.406 0.619
0.406 0.619
FALSE
-0.012 -0.012 -0.030 -0.030
FALSE
0.406 0.619

精馏塔塔径与塔高计算

y1 yq Rmin Rmin 1 xP xq
或
xP yq Rmin Rmin 1 xP xq
整理得：其中对饱和液进料（xq=xF）：
Rmin xP y F y F xF
Rmin
xP y q yq xq
yq
xq 1 ( 1) xq
5）最小回流比的计算 — 操作参数
根据： y R x 1 x n 1 n P R 1 R 1 其中：R= L / P 当系统处于全回流状态时 R＝∞。精馏段操作线为y=x（斜率最大、截距为零）理论塔板数NT=NTmin。当系统处于R＝Rmin状态（斜率最小、截距最大）时，精馏段操作线、加料线（q 线）、相平衡方程线交汇于同一点（x=xq、y=yq ）理论塔板数NT→∞。即方程满足：
符号意义：
y f x yn 1
y` f x` ym 1
R x xn D R 1 R 1
Wx L` xm W L`W L`W
y f qx y
q 1 x xF q 1 q 1
x y f x y 1 ( 1) x
Z
NT HT ET
其中：Z —板式塔有效高度（传质段），m NT —理论塔板数（不包括塔釜） HT —塔板间距（经验值：见P344表8—2） ET —全塔效率（＜1，实测）
应掌握：1. 全塔操作线绘制 2. 图解法求NT 3. Rmin（图解法、解析法） 4. Z的计算
附二：理论板数的求解思路
而实际操作中的回流比： R=(1.1～2) Rmin. R↑：斜率↑、板数↓（分离效率↑）、设备造价↓、产品↓。 R↓：则与上述相反
yF

连续精馏理论塔板数的计算

5.3 连续精馏理论塔板数的计算本节重点：理论塔板数的计算。

本节难点：理论塔板数的计算—逐板计算法和图解法；双组分连续精馏塔所需理论板数，可采用逐板计算法和图解法。

5.3.1逐板计算法假设塔顶冷凝器为全凝器，泡点回流，塔釜为间接蒸汽加热，进料为泡点进料如图5－5所示。

因塔顶采用全凝器，即y 1=x D 5－24而离开第1块塔板的x 1与y 1满足平衡关系，因此x 1可由汽液相平衡方程求得。

即111)1(y y x --=αα 5－25第2块塔板上升的蒸汽组成y 2与第1块塔板下降的液体组成x1满足精馏段操作线方程，即Dx R x R R y 11112+++=5－26同理，交替使用相平衡方程和精馏段操作线方程，直至计算到x n <x q (即精馏段与提馏段操作线的交点)后，再改用相平衡方程和提馏段操作线方程计算提馏段塔板组成，至x w ’<x w 为止。

现将逐板计算过程归纳如下：相平衡方程： x1 x2 x3……x n <x q-------x w ’<x w 操作线方程： x D =y1 y2 y3在此过程中使用了几次相平衡方程即可得到几块理论塔板数（包括塔釜再沸器）。

5.3.2 图解法应用逐板计算法求精馏塔所需理论板数的过程，可以在y-x 图上用图解法进行。

具体求解步骤如下：1、相平衡曲线在直角坐标系中绘出待分离的双组分物系y-x 图，如图5－13。

2、精馏段操作线3、提馏段操作线4、画直角梯级从a 点开始，在精馏段操作线与平衡线之间作水平线及垂直线，当梯级跨过q 点时，则改在提馏段操作线与平衡线之间作直角梯级，直至梯级的水平线达到或跨过b 点为止。

其中过q 点的梯级为加料板，最后一个梯级为再沸器。

最后应注意的是，当某梯级跨越两操作线交点q 时（此梯级为进料板），应及时更换操图5-13 理论板数图解法示意图作线，因为对一定的分离任务，此时所需的理论板数最少，这时的加料板为最佳加料板。

板式精馏塔进料口最佳位置的确定及理论塔板数的求解

板式精馏塔进料口最佳位置的确定及理论塔板数的求解王中麟(南京师范大学,南京,210042)摘要精馏是一种重要的工业单元操作,广泛用于石油、化工、轻工、制药、原子能等工业及生物工程、环境保护工程中。

精馏是一种高投入的操作。

其中塔板数和进料位置对投资、操作费用及产品质量影响重大。

主要讨论五种进料热状态下的进料口最佳位置的确定和精、提馏操作段内理论塔板数的确定。

关键词理论塔板;精馏操作段;提馏操作段;相平衡分类号TQ028. 13The Discussion of Determination about the Best Entrance of Raw Materials and the Number of Theoretical Plates inRectifying Tower/ Wang Zhonglin (Nanjing Normal University , Nanjing 210042 , P. R. China) / / Journal of NortheastForest ry University. - 2004 ,32 (2) . - 91～93Rectification is one kind of important unit - operation of indust ry , which has been used in wide - ranging of indus2t ry , such as oil indust ry , chemical engineering , light indust ry , pharmacy , indust ry of atom , bioengineering and engi2neering of environmental protection. Rectification is a kind of unit - operation that needs high cost . The number of theo2retical plates and ent rance of raw materials can affect the cost of investment and o peration as well as the quality of produc2tion greatly. The determination about the best ent rance of raw materials and the number of theoreticalplates in rectifyingsection and st ripping section with five kinds of heat - states is discussed.Key words Theoretical plate ; Rectifying section ; St ripping section ; Vapour - liquid phase equilibrium精馏在工业生产中是一种重要的,且应用非常广泛的传质单元操作。

7.5.6其它类型精馏塔及理论塔板数的计算

yn 1 R x xn D 0.5 xn 0.45 R1 R1
第二段:两股进料之间，其下降液量和上升气量与第一段进料热状态有关
L=RD=1×7.35=7.35kmol/h; V=(R+1)D=2×7.35=14.7kmol/h
饱和液体进料,q1=1。则第二段进料口以上的上升气量和下降液量为
L’=L+q1F1=7.35+10=17.35kmol/h; V’=V-(1-q1)F1=V=14.7kmol/h GLL
对第二股进料口以上作物料衡算
F1xF1 V' y s1 L'xs DxD
其它类型精馏塔理论板数的确定直接蒸汽加热当水是重组分时,可将加热蒸汽直接通入塔釜加热。直接蒸汽加热不影响精馏操作线由于塔底多了一股蒸汽流，其提馏段的操作线与间接蒸汽加热过程不同。其推导如下：总物料衡算轻组分衡算
L' S V' W
加热蒸气 S V F, xF L D, xD
V’ L’
F, xF D, xD
Q
W, xW
无回流的回收塔 GLL
其操作线方程与一般精馏塔的提馏段操作线方程相同。
ym 1 L' W ' xm ' xW V V
D V , V' D 1 q F ,
ym 1
冷液进料时
L' qF
提馏段操作线方程为
WxW qF xm D 1 q F D 1 q F
1.0 1
1
D1 xD1
q 2
yD2 y
q 2
1
y
3
F, xF
2 3
D2 xD2 (yD2)

6-2 理论塔板数的计算(简版)

逐板法图解法捷算法
23:29:19
6-2 理论塔板数计算（48）
2
双组分连续精馏塔的计算
理论板理论板是指离开塔板的蒸汽和液体呈平衡的塔板，它是人为的理想化的塔板。理论板可以作为衡量实际塔板分离效果的一个标准。
23:29:19
6-2 理论塔板数计算（48）
3
例1 环己烷 80.8℃ 苯 80.1℃ 常压下沸点糠醛 161.7℃ 苯酚 180℃
环己烷-苯恒沸物 77℃
糠醛能显著降低苯的饱和蒸汽压，而对环己烷影响不明显，使苯从易挥发组分变为难挥发组分，而且使环己烷-苯的增大至2以上。
23:29:19
6-2 理论塔板数计算（48）
22
萃取剂的选择原则：
6-2 理论塔板数计算（48）
23:29:19
说明：（1）EmV(n)和 EmL(n)不一定相等，（2）一般情况单板效率小于 1，特殊情况它们会大于 1，通常出现在塔径较大的精馏塔中。
16
2．全塔效率E0
又称总板效率，其定义为：
D, xD
理论板数 N E0 实际板数 N e
恒沸精馏特殊精馏萃取精馏
23:29:19
6-2 理论塔板数计算（48）
x
19
1．恒沸精馏
加入的第三组分与原溶液中的一个或者两个组分形成最低恒沸物，从而形成了“恒沸物－纯组分”的精馏体系，恒沸物从塔顶蒸出，纯组分从塔底蒸出，这种形式的精馏称为恒沸精馏，其中所添加的第三组分称为恒沸剂或者夹带剂。
ym+1 xm yN-1 xm+1
x N1 1 y N1 2 x N1 2 y N1 3

精馏塔理论板计算

精馏塔理论板计算精馏塔是一种重要的分离设备，广泛应用于石油化工、化学工程、食品工业等领域。

精馏塔的设计和计算涉及多个方面，包括塔型选择、传热、质量传递、能量平衡等等。

下面我们将重点介绍精馏塔的理论板计算。

在精馏过程中，将混合物加热至汽化温度后，引入精馏塔顶部。

混合物在塔内上升时，会发生质量传递与能量转移，使得不同组分在塔内逐渐分离。

在塔内设置一些平行分离表面，称为理论板，用于增加塔内相对运动，增强分离效果。

理论板数的计算是精馏塔设计的一项关键工作。

理论板数决定了塔的高度和尺寸，直接关系到精馏塔的经济性和操作性能。

一般来说，塔板数越多，分离效果越好，但也会增加塔的复杂性和成本。

因此，确定适当的理论板数非常重要。

常用的理论板计算方法有剪切力方法、传质阻力方法和蒸汽平衡法。

其中，剪切力方法是最常用的一种方法。

剪切力方法通过计算流体在理论板上的剪切力来确定塔板数。

该方法的基本原理是，在理论板上，当上升相和下降相的速度逐渐相等时，流体单位质量通过塔板上的剪切应力会阻碍下一板的流体上升，从而形成塔板。

因此，通过剪切力的大小，可以推导出理论板数。

剪切力方法的计算步骤如下：1.确定需要分离的组分物质和混合物的性质参数，包括物质的相对挥发度、密度、粘度等。

2.根据塔板上升流体和下降流体的速度差异，计算剪切力。

剪切力的计算公式为：F=ρL×g×(Ud-Uu)其中，F为塔板上的剪切力，ρL为流体密度，g为重力加速度，Ud 为下降相（液相）速度，Uu为上升相（气相）速度。

3.根据剪切力的大小，选择适当的理论板间距。

根据经验公式或实验数据，可以确定不同剪切力值对应的理论板间距。

4.根据塔高度和理论板间距，计算理论板数。

塔高度H除以理论板间距L，即可得到理论板数N。

需要注意的是，精馏塔的理论板计算还需要考虑一些其他因素，如进料浓度、热力学性质、操作压力等等。

因此，在实际设计中，还需要结合具体情况进行综合考虑和优化。

化工基础精馏实验理论塔板数的图解法计算

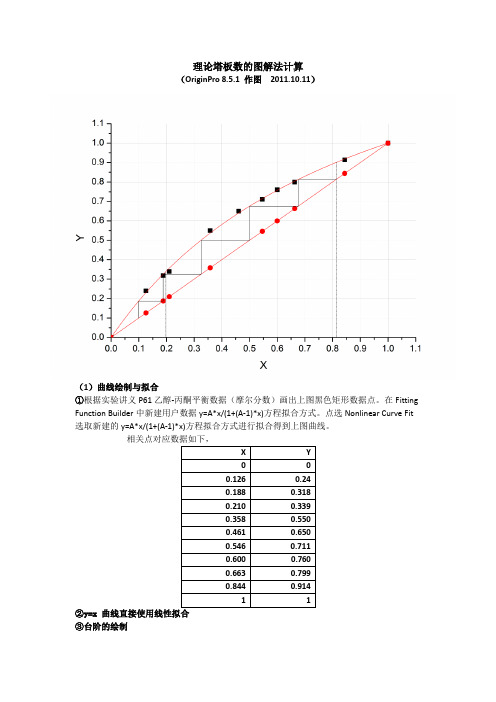
理论塔板数的图解法计算
（OriginPro 8.5.1 作图2011.10.11）
（1）曲线绘制与拟合
①根据实验讲义P61乙醇-丙酮平衡数据（摩尔分数）画出上图黑色矩形数据点。

在Fitting Function Builder中新建用户数据y=A*x/(1+(A-1)*x)方程拟合方式。

点选Nonlinear Curve Fit 选取新建的y=A*x/(1+(A-1)*x)方程拟合方式进行拟合得到上图曲线。

②y=x 曲线直接使用线性拟合
③台阶的绘制
根据塔顶的乙醇摩尔分数0.813，算出该y值下曲线上对应的x点，并依次求算下一个点的x值。

（根据OriginPro 8.5.1的拟合功能中的Find Special X from Y来实现）
用绘图中
④在图中标出塔顶和塔底的乙醇摩尔分数
塔顶 0.813
塔底 0.196
（2）理论塔板数
N完整=3
N不完整=（第三个台阶对应x值-塔底摩尔分数）/（第三个台阶对应x值第二个台阶对应x值）=（0.32493-0.196）/（0.32493-0.18773）= 0.12893 / 0.13720 ≈0.94 N理论=N完整+N不完整= 3 + 0.94 = 3.94 个
即根据2011.10.07日测定的数据处理后图解法求解的精馏塔的理论塔板数为3.94。

精馏塔理论塔板数计算

0.940 0.940 0.979 0.923 1.358 0.940 0.513 0.423 0.476
0.950 0.950 0.983 0.941 1.388 0.950 0.517 FALSE 0.423 0.476 -0.009 -0.029
0.990 0.990 0.997 0.950 1.403 0.990 0.530 0.423 0.476
FALSE 0.423 0.476 FALSE -0.009 -0.029 -0.009 -0.029 0.423 0.476
FALSE 0.423 0.476 FALSE -0.009 -0.029 -0.009 -0.029 0.423 0.476
FALSE 0.423 0.476 FALSE -0.009 -0.029 -0.009 -0.029 0.423 0.476
交点在平衡线上,回流比最小,记入Rmin计算理论塔
0.605 0.605 0.821 0.608 0.836 0.605 0.402 0.423 0.476
0.630 0.630 0.836 0.640 0.888 0.630 0.410 FALSE 0.423 0.476 -0.007 -0.021
FALSE -0.009 -0.028
FALSE -0.009 -0.029
FALSE -0.009 -0.029
FALSE -0.009 -0.029
FALSE -0.009 -0.029
FALSE -0.009 -0.029
FALSE -0.009 -0.029
FALSE -0.009 -0.029
7 0.044 0.120
8 0.017 0.050
FALSE 0.004 0.011

初步掌握精馏原理和塔板数的计算

反馈控制
通过测量精馏产品的质量或关键工艺参数，并对其进行调节，使产品达到预设的质量指标。
串级控制
将两个或多个控制器串联起来，一个控制器的输出作为另一个控制器的输入，以提高控制精度和稳定性。
过程参数的优化
进料流量
根据原料的性质和精馏塔的处理能力，合理调整进料流量，以实现最佳的分离效果。
塔板温度
3
预测控制
利用模型预测未来的输出，并通过优化算法找到最佳的控制策略，以实现最优的过程控制。
06 精馏过程的节能与环保
节能技术应用
热集成精馏
通过优化精馏塔内热量传递和回收，减少能量损失，提高能源利用效率。
低温余热利用
利用低温余热驱动精馏过程，降低能耗，提高能源回收率。
高效换热器
采用高效换热器，减小换热温差，降低热量损失，提高换热效率。
02 塔板数的计算
塔板数的定义
塔板数定义
01
塔板数是指精馏塔内，用以分离液体混合物的理论塔板的数量。
理论塔板
02
理论塔板是假设的一种理想化的塔板，其上的液体和蒸汽分布
均匀，无停留时间，且满足平衡关系。
塔板效率
03
实际塔板与理论塔板的接近程度，用塔板效率表示。
塔板数的计算方法
01
02
03
逐板计算法
提高精馏塔效率的方法
优化操作条件
通过调整加热温度、压力、进料流量等操作条件，可以改善精馏塔内的传热和传质过程，从而提
高精馏塔的效率。
采用高效填料
在精馏塔内采用高效填料可以增加气液接触面积，提高传质效率，从而提高精馏塔的效率。
改进设备结构
通过改进精馏塔的结构设计，例如增加塔板数、改变进料位置等，可以提高精馏塔的分离能力和效率。

精馏塔板数无限多的计算问题

精馏塔板数无限多的计算问题众所周知，精馏塔的分离能力随着塔板数的增加而增加，即塔顶产品与塔釜产品的纯度会随着塔板数的增加而增加，假设精馏塔板数达到无限多块，对于二元精馏而言，塔顶产品与塔釜产品的纯度会不会都达到100%呢？我们说一般不会，因为精馏塔的分离能力不但与塔板数有关，还严格的受到相平衡规律、物料衡算规律的限制。

相平衡规律、物料衡算规律是解决精馏塔板数无限多的计算问题的核心。

下面，我们通过两个例子说明解决精馏塔板数无限多的计算问题的要点所在。

例1.在常压连续提馏塔中分离含乙醇0.033(摩尔分数)的乙醇-水混合液。

饱和液体进料，直接蒸汽加热。

若要求塔顶产品中乙醇回收率为99%，试求：(1)在理论板层数为无限多时，计算1mo1进料所需蒸汽量；(2)若蒸汽量取为最小蒸汽量的2倍时，求所需理论板层数及两产品的组成。

假设塔内气、液相为恒摩尔流动。

常压下气液平衡数据列于本题下表中。

分析：要求解本问题，首先要比较透彻得了解提馏塔和直接水蒸气加热条件下的操作线方程的画法。

我们知道，提馏塔没有精馏段，进料加入塔顶的第一块板，所以提馏塔的操作线方程只有一条，且该操作线的上端点就是q线与y=x D(塔顶产品组成)的交点。

若采用直接水蒸气加热，该操作线的下端点就是(x w,0)点，x w为塔釜产品组成。

图1(1)通过上面的分析可知，提馏塔操作线的上端点在q线上，且上端点的纵坐标就是塔顶产品组成x D。

现塔板无穷多，意味着x D会尽可能增大，即上端点会沿q线尽可能向上移动。

但上端点会不会无限向上移动呢？如图1所示，上端点向上移动的极限点就是q线与平衡线的交点。

上端点如果向上移动超过极限点的话，意味着塔内的精馏操作将被破坏。

因此，当提馏塔塔板无限多时，塔顶产品组成x D的极限点的纵坐标。

根据题意，饱和液体进料，q 线的方程为x=x F，平衡线可通过上表的数据做出，则极限点的纵坐标就是0.27，即x D=0.27。

另外一方面，塔板无穷多，也意味着塔釜组成x w将尽可能减小，即提馏塔操作线的下端点会尽可能沿着横轴向左移动，下端点会不会向左移动到横轴与平衡线的交点，即原点，以至于x w=0呢？不会的，根据物料衡算，如果发生这种情况，意味着进料的全部乙醇都会从塔顶产品馏出，那么乙醇在塔顶的回收率就会达到100%，和题意中的乙醇在塔顶的回收率为99%矛盾。

精馏过程工艺参数的确定(理论塔板数计算)讲解

x D = y1
x 根据 x y 根据 y x 根据 x y
相平衡方程求
1
1
精馏段操作线方程
相平衡方程求
2
2
2
精馏段操作线方程
2
3
xn-1
yn

精馏段操作线方程
相平衡方程求
yn
x n≤ x d

直到xn xd（xd为两段操作线交点坐标x数值）时，说明第n 层板为加料板，该板应属于提馏段。因此精馏段所需理论板数为n -1块。
理论塔板数与哪些参数有关？与物料量的多少是否有关？
NT f xF , xD , xW , q, R,
与进料位置也有关，提前进料和推迟进料都会使理论塔板数增多
某理想混合液用常压精馏塔进行分离。进料组成含 A81.5％，含B18.5％（摩尔百分数，下同），饱和液体进料，塔顶为全凝器，塔釜为间接蒸气加热。要求塔顶产品为含A95％，塔釜为含B95％，此物系的相对挥发度为2.0，回流比为4.0。试用（1）逐板计算法，（2）图解法分别求出所需的理论板层数及进料板位置。
根据 y2 xm-1 ym
相平衡方程求
提馏段操作线方程
相平衡方程求

如此重复计算直至xm xW为止。由于离开塔釜的汽液两相组成达到平衡，故塔釜相当于一块理论板，提馏段所需的理论塔板数为m-1块。
WxW L y m1 xm L W L W
x A yA 1 ( 1) x A
全塔所需的理论塔板数NT为
N n m 2
T
（不包括塔釜）（包括塔釜）
N n m 1
T
2、图解法图解法求理论塔板数的基本原理与逐板计算法相同，所不同的是用相平衡曲线和操作线分别代替相平衡方程和操作线方程。用图解法求理论塔板层数的具体步骤如下：（1）绘相平衡曲线（2）绘操作线绘出精馏段操作线和提馏段操作线

化工原理理论塔板计算

精馏过程的物料衡算和塔板数的计算一、理论塔板连续精馏计算的主要对象是精馏塔的理论塔板数。

所谓的理论塔板是指气液在塔板上充分接触，有足够长的时间进行传热传质，当气体离开塔板上升时与离开塔板下降的液体已达平衡，这样的塔板称为理论塔板。

实际上，由于塔板上气液接触的时间及面积均有限，因而任何形式的塔板上气液两相都难以达到平衡状态，也就是说理论塔板是不存在的，它仅是一种理想的板，是用来衡量实际分离效率的依据和标准。

通常在设计中先求出按生产要求所需的理论塔板数N T然后用塔板效率η予以校正，即可求得精馏设备中的实际塔板数N P二、计算的前提由于精馏过程是涉及传热、传质的复杂过程，影响因素众多。

为处理问题的方便作如下假设，这些就是计算的前提条件。

（1）塔身对外界是绝热的，即没有热损失。

（2）回流液由塔顶全凝器供给，其组成与塔顶产品相同。

（3）塔内上升蒸气由再沸器加热馏残液使之部分气化送入塔内而得到。

（4）恒摩尔气化在精馏操作时，在精馏段内，每层塔板上升的蒸气的摩尔流量都是相等的，提馏段内也是如此，即：精馏段：V1 = V2 = …………＝Ｖn= Vmol/s(下标为塔板序号，下同）提馏段：Ｖ′n+1 =V′n+2 =…………＝V′m= V′mol/s但Ｖn不一定与Ｖ′m相等，这取决于进料状态。

（５）恒摩尔溢流（或称为恒摩尔冷凝）精馏操作时，在精馏段内每层塔板下降的液体的摩尔流量都是相等的，提馏段也是如此，即：Ｌ1 = L2=…………= L n = L mol/sL′n+1= L′n+2=………… = L′m= L′ mol/s但Ｌ不一定与Ｌ′相等，这也取决于进料的状态。

（６）塔内各塔板均为理论塔板。

三、物料衡算和操作线方程１、全塔物料衡算图4-10 全塔物料衡算示意图如图４－１０所示，设入塔进料流量为Ｆ，轻组分含量为x F,塔顶产量流量为Ｄ，轻组分含量为x D,塔底产品流量为Ｗ，轻组分含量为x w，流量单位均为mol/s，含量均为摩尔分率。

图解法求理论板数

一、图解法求理论板数图解法计算精馏塔的理论板数和逐板计算法一样，也是利用汽液平衡关系和操作关系，只是把气液平衡关系和操作线方程式描绘在y x -相图上，使繁琐数学运算简化为图解过程。

两者并无本质区别，只是形式不同而己。

（1）精馏段操作线的作法由精馏段操作线方程式可知精馏段操作线为直线，只要在x y -图上找到该线上的两点，就可标绘出来。

若略去精馏段操作线方程中变量的下标， 11+++=R x x R R y D 上式中截距为1+R x D ，在图7－12中以c 点表示。

当D x x =时，代入上式得D x y =，即在对角线上以a 点表示。

a 点代表了全凝器的状态。

联ac 即为精馏段操作线。

（2）提馏段操作线的作法由q 线ef ，即可求得它和精馏段操作线的交点，而q 线是两操作线交点的轨迹，故这一交点必然也是两操作线的交点d,联接bd 即得提馏段操作线。

（3）图解法求理论板数的步骤①在直角坐标纸上绘出待分离的双组分混合物在操作压强下的y x -平衡曲线，并作出对角线。

如图7-14所示。

②依照前面介绍的方法作精馏段的操作线ac ，q 线ef ，提馏段操作线bd 。

③从a 点开始，在精馏段操作线与平衡线之间作水平线及垂直线构成直角梯级，当梯级跨过d 点时，则改在提馏段与平衡线之间作直角梯级，直至梯级的水平线达到或跨过b 点为止。

④梯级数目减一即为所需理论板数。

每一个直角梯级代表一块理论板，这结合逐板计算法分析不难理解。

其中过d 点的梯级为加料板，最后一级为再沸器。

因再沸器相当于一块理论板，故所需理论板数应减一。

在图7-14中梯级总数为７。

第四层跨过d 点，即第４层为加料板，精馏段共3层，在提馏段中，除去再沸器相当的一块理论板，则提馏段的理论板数为4-1=3。

该分离过程共需6块理论板（不包括再沸器）。

图解法较为简单，且直观形象，有利于对问题的了解和分析，目前在双组分连续精馏计算中仍广为采用。

但对于相对挥发度较小而所需理论塔板数较多的物系，结果准确性较差。

精馏塔的简洁计算公式

精馏塔的简洁计算公式精馏塔是一种用于分离液体混合物的设备，通过不同组分的沸点差异来实现分离。

在工程设计和操作中，需要对精馏塔进行计算和分析，以确保其正常运行和达到预期的分离效果。

在本文中，我们将介绍精馏塔的简洁计算公式，帮助读者更好地理解和应用这些公式。

1. 精馏塔的传质效率公式。

精馏塔的传质效率是评价其性能的重要指标之一。

传质效率通常用塔板数或高度来表示，其计算公式如下：N = HETP × (n-1)。

其中，N表示塔板数或塔高度，HETP表示每塔板传质高度，n表示理论板数。

2. 精馏塔的塔板压降公式。

塔板压降是精馏塔运行中需要考虑的重要参数之一。

塔板压降的计算公式如下：ΔP = ρ× g × H × (1-ε) + ΔPv。

其中，ΔP表示塔板压降，ρ表示液体密度，g表示重力加速度，H表示塔板高度，ε表示塔板孔隙率，ΔPv表示气体速度压降。

3. 精馏塔的塔顶温度计算公式。

精馏塔的塔顶温度是其操作中需要重点关注的参数之一。

塔顶温度的计算公式如下：T = T0 + ΔT。

其中，T表示塔顶温度，T0表示进料温度，ΔT表示塔顶降温。

4. 精馏塔的塔板液体高度计算公式。

塔板液体高度是精馏塔操作中需要实时监测和控制的参数之一。

塔板液体高度的计算公式如下：H = H0 + ΔH。

其中，H表示塔板液体高度，H0表示初始液位高度，ΔH表示液位变化量。

5. 精馏塔的塔板塔顶气体速度计算公式。

塔板塔顶气体速度是精馏塔操作中需要关注的参数之一。

塔板塔顶气体速度的计算公式如下：V = Q / A。

其中，V表示塔板塔顶气体速度，Q表示气体流量，A表示塔板横截面积。

总结。

精馏塔是一种重要的分离设备，其性能和操作参数需要通过计算和分析来进行评估和控制。

本文介绍了精馏塔的传质效率、塔板压降、塔顶温度、塔板液体高度和塔板塔顶气体速度的计算公式，希望能对读者有所帮助。

当然，精馏塔的计算和分析涉及到更多的参数和复杂的情况，需要结合具体的工程实际情况进行综合分析和计算。

精馏塔理论塔板数计算

精馏塔理论塔板数计算精馏塔是一种常用的分离和纯化混合物的设备。

在精馏过程中，混合物中的组分会根据其挥发性的差异，通过塔板分离为不同纯度的组分。

塔板数是衡量精馏塔分离效果的重要指标之一、本文将介绍精馏塔的理论塔板数计算方法，并简要解析其应用。

精馏塔的理论塔板数是指在无质量和热量传递损失的情况下，实现完全的分离所需的等效塔板数。

其计算可以使用Teope方程进行估算。

Teope方程是一个基于传递单元理论的简化模型，可以用于估算理论塔板数。

Teope方程的基本形式为：Nt=Nf+Nr+Nz其中，Nt为总塔板数，Nf为塔底下部的传质单元数，Nr为塔顶上部的传质单元数，Nz为塔体的塔板数。

传质单元数是通过传递单元量化描述的，可以根据不同的物理现象进行选择。

一般来说，传递单元可以是汽-液平衡单元、传质过程单元或传热过程单元等。

在使用Teope方程计算理论塔板数时，需要根据实际情况选择适当的传递单元。

常用的选择有根据挥发度平均法选择传质单元，或者根据物理性质（如热扩散系数）选择传质过程单元。

对于质量传输控制塔板，传质单元的选择可以通过挥发度平均法来实现。

挥发度是指组分在液相和气相中分配的平衡性质，可以通过实验或计算得到。

根据挥发度平均法，可以将塔板上的传质单元数定义为:Nf = ΔHF / ln(αi)其中，ΔHF为进料组分的化学势差，αi为塔底和塔顶组分浓度的挥发度比。

对于能量传输控制塔板，传热过程单元的选择可以使用传热系数的平均法。

传热系数是描述传热过程的性质，可以根据传热模型或实验来确定。

传热过程单元的计算可以使用下式：Nr=ΔHR/(KlA)其中，ΔHR为进料组分的焓差，Kl为液相传热系数，A为塔板有效面积。

总的塔板数Nt的计算可以通过对Nf、Nr和Nz进行求和得到。

需要注意的是，由于Teope方程是一个估算模型，其计算结果只能作为初步参考，并不能完全准确地预测塔板数。

精馏塔的理论塔板数计算是精馏塔设计的重要一步。