广州市中考问答题常考题型讲解

合集下载

详解广州中考数学最后两道大题!

详解广州中考数学最后两道大题!广州中考数学试卷中最后两道大题通常难度较大，对于大部分考生来说，能够得到满分是非常困难的。

但是，只要掌握了正确的解题方法，我们也可以攻克这些难题。

本文将详细解析广州中考数学最后两道大题的解题思路和方法，帮助考生更好地应对中考数学考试。

一、最后一道大题——函数综合题这类题目主要考察函数的性质、图像以及运用函数知识解决实际问题的能力。

解题关键在于要熟练掌握函数的基础知识，并能够灵活运用。

常见考点包括：1. 一次函数、二次函数图像的绘制、性质和应用；2. 函数图像的变化和趋势的判断；3. 函数与几何的综合应用，如利用函数图像解决几何问题；4. 函数与方程的综合问题，如函数的最值问题、零点问题等。

解题步骤：1. 根据题意画出函数图像，并根据图像分析变化趋势；2. 根据函数的性质寻找解题的关键点；3. 综合运用数学知识解决问题。

例题解析：（2023年广州中考数学最后一题）某地区天气预报显示，该地区未来一段时间内每天的降雨量都为x毫米，已知该地区某水库的警戒水位为a毫米，若该水库的排水量为每天8毫米，求该水库水位每天上升8毫米后与警戒水位相比是上升还是下降？请说明理由。

解题思路：1. 根据预报降雨量x和排水量8毫米，计算出新水位y；2. 与警戒水位a比较，判断上升还是下降。

解：上升。

因为警戒水位为a毫米，而每天的降雨量都为x毫米，且水库的排水量为每天8毫米，所以每天水位上升8毫米后与警戒水位相比是上升。

二、倒数第二道大题——几何综合题这类题目主要考察几何图形的性质、特征、判定方法以及几何知识在实际问题中的应用。

解题关键在于要能够正确识别图形，找到解题的关键点，并综合运用几何和代数知识解决问题。

常见考点包括：1. 图形变换问题；2. 角度、弦、切、距离等问题；3. 几何模型的应用；4. 代数方法解决几何问题。

解题步骤：1. 仔细阅读题意，识别图形特征；2. 找到解题的关键点；3. 综合运用几何和代数知识解决问题；4. 检验答案是否正确。

广州市中考各科题型

广州市中考各科题型及答题技巧，具体如下：* 语文：1. 选择题。

尽量不翻阅资料，直接在卷面上作答。

注意合理安排时间。

2. 非选择题。

答题步骤为：①先审题（关键步骤），②下笔（落笔之前，一定要深思熟虑），③留空（答完题后，至少要在答答题卡时间上留有富裕），④复查（如果有时间，一定要复查）。

* 数学：1. 填空题。

要做到答案准确，书写规范。

2. 综合题。

要注重条理和逻辑清晰，按步骤答题。

遇到难题，先跳过做简单题，待心情和精力稳定下来后，再回头做难题。

* 英语：1. 单项选择。

注重积累，了解语境，联系上下文答题。

2. 完形填空。

通读全文，了解全文大意，再逐个答题。

3. 阅读理解。

针对问题，找寻答案。

答题步骤为：①读清题干要求，划出文章中心。

②扫读全文，领会大意。

③通览全卷，合理推断。

④细读全文，核实答案。

* 物理：1. 单项选择题。

主要考查学生对基本概念、规律及定律的记忆和理解。

答题时，注意仔细分析选项，排除错误选项。

2. 填空题。

注意理清题意，找出正确信息。

3. 作图题。

按照规范要求作图，注意用笔和标度。

* 化学：1. 选择题。

在理解化学原理的基础上进行答题。

2. 简答题。

简述化学变化过程时，尽量用学科语言描述。

对于推断题，应搞清楚相关物质的化学性质，理清推导过程。

3. 实验题。

根据题目所给信息进行分析，注意审题。

在广州市中考中，注重基础知识的考察，同时也会对思维能力和解题技巧有一定的要求。

考生应保持良好的心态，根据自身情况合理安排答题策略，并在考场上发挥出自己的最佳水平。

以上内容仅供参考，建议查阅广州市教育局发布的官方中考指南以获取更准确的信息。

广州2012中考数学简答题分析

# #
4、为打造“书香校园” ，某学校计划用不超过 1900 本科技类书籍和 1620 本人文类书籍，组建中、小型两类图书角共 30 个.已知组建一个中型图书角需科技类书籍 80 本，人文类书籍 50 本；组建一个小型图书角需科技类书籍 30 本，人文类书籍 60 本．（1）问符合题意的组建方案有几种？请你帮学校设计出来；（2）若组建一个中型图书角的费用是 860 元，组建一个小型图书角的费用是 570 元，试说明在（1）中哪种方案费用最低？最低费用是多少元？
中小学个性化教育专家
精锐教育学科教师辅导讲义精锐教育学科教师辅导讲义学科教师
讲义编号________
学员编号：学员编号：学员姓名：学员姓名：
年级：初三辅导科目：辅导科目：数学
课时数及课时进度：课时数及课时进度：及课时进度（学科教师：
/
）
学科组长/带头人签名及日期学科组长带头人签名及日期带头人签名课题
教学目标
重点、重点、难点
考点及考试要求
教学内容
广州中考试卷中简答题有 9 道题，其中 17-22 是属于简单的解答题，一般情况下学 17生只要够细心，都能够很好哦解答，而简答题的难点主要在 23、24、25 三道大题，这是 23、24、高、中档学生的分档题。所以，如果一个学生要考好成绩，这些前面的六道大题必须拿满分。现在，我们对中考的前面六道大题做一下分析。
60°
P
45°
C
B 第 21 题图 7、已知：如图，在直角梯形 ABCD 中，AD∥BC，∠ABC=90°，DE⊥AC 于点 F，交 BC 于点 G，交 AB 的延长线于点 E，且 AE = AC ． D A （1）求证： BG = FG ；（2）若 AD = DC = 2 ，求 AB 的长． B E （20 题） F G C

广州近三年中考数学试题分析

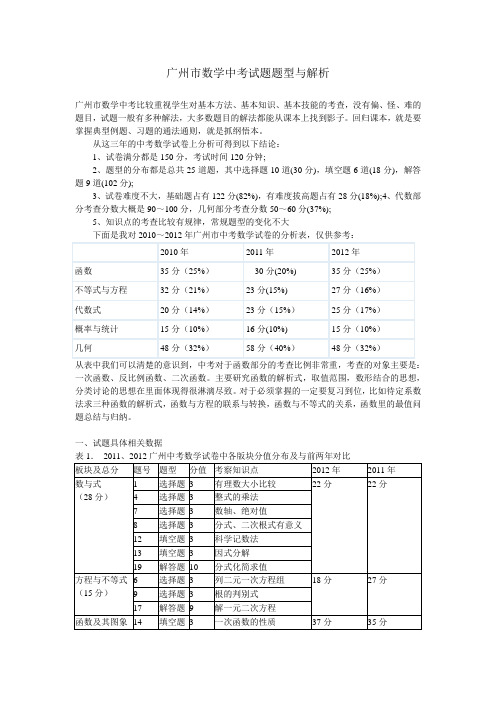
广州市数学中考试题题型与解析广州市数学中考比较重视学生对基本方法、基本知识、基本技能的考查，没有偏、怪、难的题目，试题一般有多种解法，大多数题目的解法都能从课本上找到影子。

回归课本，就是要掌握典型例题、习题的通法通则，就是抓纲悟本。

从这三年的中考数学试卷上分析可得到以下结论：1、试卷满分都是150分，考试时间120分钟;2、题型的分布都是总共25道题，其中选择题10道(30分)，填空题6道(18分)，解答题9道(102分);3、试卷难度不大，基础题占有122分(82%)，有难度拔高题占有28分(18%);4、代数部分考查分数大概是90～100分，几何部分考查分数50～60分(37%);5、知识点的考查比较有规律，常规题型的变化不大下面是我对2010～2012年广州市中考数学试卷的分析表，仅供参考：从表中我们可以清楚的意识到，中考对于函数部分的考查比例非常重，考查的对象主要是：一次函数、反比例函数、二次函数。

主要研究函数的解析式，取值范围，数形结合的思想，分类讨论的思想在里面体现得很淋漓尽致。

对于必须掌握的一定要复习到位，比如待定系数法求三种函数的解析式，函数与方程的联系与转换，函数与不等式的关系，函数里的最值问题总结与归纳。

一、试题具体相关数据注：2011及2012年对比加粗部分为占比变化较大的板块。

表2 2013广州中考数学试卷中各版块分值分布注：灰色部分为多个知识点综合题.二、试题分析1.在内容上，2013年广州中考数学在各板块所占比重与上年基本持平，但函数部分占比下降明显，2012年填选题3题，解答题2题，2013年填空题1题，解答题2题。

数与式部分题目量增加，所占分值较上年有所增加。

本卷统计与概率结合同一解答题考查，统计概论板块所占分值下降。

2.2013年广州中考数学没有考查找规律，也没考查方程、不等式或函数的应用题，而增加了尺规作图的考查，还是要求考生掌握基本作图方法。

3.在难度上，与上年相比，2013年中考数学试题前22题难度相对较小，考察的题型也比较常规，基本上都是基础的知识，如有理数大小比较、数与式部分基础题型、全等三角形的判定和尺规作图、四边形的性质。

广州中考物理问答题

问答题1.问题：电风扇是一种常用家电，它在工作时涉及到很多物理知识，请你回答如下问题：⑴电风扇在工作过程中，能量是如何转化的？实现它主要功能的部件是什么？⑵当我们在炎热的夏天吹电风扇的时候，会感觉到凉爽。

请你分析其中的原因。

答案、⑴电风扇的能量转化主要是电能转化为机械能和内能。

（1分）实现这种转化的部件是电动机。

（1分）⑵吹风扇是加快了身体表面的空气的流速（1分），使身体的体液蒸发加快（1分），而蒸发有至冷作用，所以让人感到凉快（1分）。

2.问题月我国成功地发射并回收了“神舟”7号载人飞船。

(1)火箭发射时，高温的火焰向下喷射，大量的“白气”从发射台底部的大水池中涌出，这些“白气”是怎么形成的？（3分）(2)返回舱穿越大气层时与空气摩擦生热，舱的表面温度非常高，但由于返回舱表面涂有一层非常厚的特殊涂料发生了一些物态变化，使舱内温度保持正常。

请说明涂料是怎样起降温作用的？（2分）答案：(1)这些“白气”是水池中的水吸热汽化成的大量水蒸汽遇到周围低温的空气放出热量液化成的“小水珠”--------3分(2)特殊涂料在温度升高时熔化并汽化，从返回舱表面吸收大量的热，使舱内温度保持正常。

问题3．小明在烈日当空的海边玩耍，发现沙子烫脚，而海水却是凉凉的；远处，钢铁制造的轮船正在海面上航行着；海鸥在天空中飞翔……好美的景色啊！在玩耍的过程中，小明提出了下面两个问题，请你帮他解释：（1）为什么沙子烫脚，而海水却是凉凉的？（2）实心的铁块总是下沉到水底，为什么钢铁制造的轮船却能漂浮在海面？答案：（1）因为海水的比热容比沙子的大，在相同光照下（或吸收相同热量）时，沙子的温度升得比水高。

所以沙子很烫脚，而海水却是凉凉的。

（2）实心铁块的密度比水大，而轮船的平均密度比水小，所以铁块在水中下沉，而轮船却能漂浮中水面上。

（或实心铁块浸没在水中时受到的浮力比重力小，所以下沉；而轮船排开海水的所受到的浮力等于轮船本身的重力，所以轮船能漂浮在水面上。

广州中考笔试考试题型分析及解题策略

教学建议
1、渗透句子结构意识，培养学生句子结构分析能力；
2、知识点教学，可适当联系相关点，引导学生对比分析
完形填空
考查方向
逻辑分析
推理判断
1、上下文整体感知能力（阅读理解能力）
语言基础知识运用能力（词汇运用能力）
2、重点考查名词、代词、动词、形容词（实词，词义辨析）
&介词、连词（虚词）
失分研究
1、基础知识：词汇不扎实，易混词难区分；
2、句型：it作形式主宾；感叹句型；比较句型
失分研究
1、句意与句子比较不清晰，不知要填什么；
2、知道要填内容，但不会用英语表达；
3、知道所缺语义，但第一反应表达不符合句子结构；
4、拼写、缩写、主谓一致等方面考虑不全
解题策略
1、对比中文意思与给出句子，确定所缺语义部分；
2、分析句子结构，确定所缺成分；
3、根据语义与句子结构，对语义进行多方面同义变化；
4、选取符合句子结构的表达，注意考虑考点各细节问题
教学建议
1、基础教学：侧重词性运用，积累同、反义词句，
多进行同义变化练习；
知识点各考查方向系统、清晰化；
2、强化句子结构分析，将所学词汇、语法运用于句子表达
失分研究
1、阅读基础：词汇掌握不过关，问题、文章均一知半解；
2、阅读习惯：中文式理解，速度慢，花费时间多；
思路不清晰，犹豫，没方向，浪费时间；
感性阅读，“看懂才能做”，畏难，易慌乱焦躁；
3、阅读技巧：极欠缺，或有认识，但机械模仿，缺乏条理性清晰性；
解题策略
1、阅读前：审题，把握5个问题的关键（明确阅读的目的）；
解题策略
1、根据句子结构，清晰把握句意，确定所缺词性；

2021~2024年广东中考各题型分布和试题分析

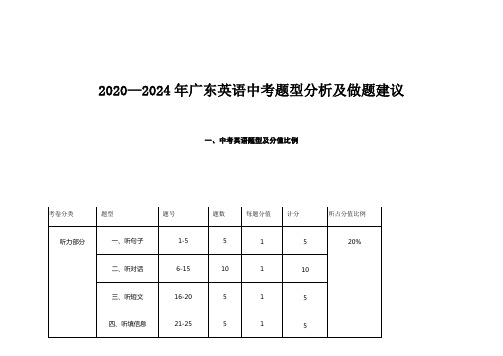
2020—2024年广东英语中考题型分析及做题建议一、中考英语题型及分值比例考卷分类题型题号题数每题分值计分所占分值比例听力部分一、听句子1-5 5 1520%二、听对话6-15 10 1 10三、听短文16-20 5 1 5四、听填信息21-25 5 1 5笔试部分一、情境对话26-30 5 1 5 80%二、语法选择31-40 5 1 5三、完型填空41-50 10 1 10四、阅读理解51-65 15 2 30五、短文填空66-75 10 1.5 15六、读写综合 A.回答问题 5 2 10B.书面表达 1 15 15二、2020-2024年广东中考英语各题型分析比较:（一）语法填空题型/号 2020 年 2021年 2022年 2023年 2024年单选31 介词(with 表伴随) 形容词最高级介词(in) 形容词比较级时态，一般过去时32 被动语态加时态感叹句加时态（how 型感叹句）状从引导词(连词when) 代词（him ）被动语态加时态33 非谓语动词（表目的，to do ）代词（it ）形容词性物主代词（teachers ’）被动语态加时态 There be 句型34 形容词原级、比较级介词(between) 非谓语动词tell sb. to do 介词(in) 被形容词和副词（ing 和ed 的区别）35 代词（her ）加最高级的用冠词形容词和副词感叹句（how 型形容词性物主代词（hours ’）法感叹句）36 时态，一般过去时名词形容词原级、比较级冠词非谓语动词（表目的，to do）37 连词时态，一般将来时被动语态加时态连词宾从引导词how情态动词38 冠词非谓语动词（表目的，to do）冠词状从引导词(连词why)39 感叹句（how型感叹句）被动语态加时态时态，一般过去时非谓语动词形容词和副词（need to do））40 状从引导词(连词why) 形容词和副词不定代词（her）时态，现在进行时冠词注意：形容词的解法可以多从情绪出发（贬义褒义）（二）完形填空2020 年2021年2022年2023年2024年完形41 语境上下文联系短语搭配look for 线索（胡萝卜）依线索辨别词意（有个姐姐）辨依线索辨别词意(上文提及了生物学家)42 短语搭配ask for 辨依线索辨别词意（四副词)短语搭配take away 线索（时间变快）线索（人类健康）43 线索nose 依线索辨别词意（四形容词）依线索辨别词意（四名词）线索（the上文提及，看到宝宝）惯用搭配从未想过44 线索change longhair线索（特点）线索（带食物过来帮助）依线索辨别词意（四名词）线索（联系上文doctor）45 辨别词意(四副词) 线索（联系上下文，依线索辨别词意（四形容固定搭配draw a picture 画惯用搭配重要品质space）词，来帮助，感动）画46 线索（后面的五官）线索（联系上下文，wrote to）依线索辨别词意（在花园里面工作）固定搭配（叶子改变了他们的颜色）理解句意（结构，上文已经出现了一个原因，another）47 固定搭配（完全不同）固定搭配（protect..from）线索（联系上下文，在花园工作）理解句意（按时间顺序）理解句意（并列，前文is provedright）48 线索（上文对于样貌的改变）线索（联系上下文）理解句意（转折，but）依线索辨别词意（四动词短语）理解句意（转折）49 语境联系上下文（berefused to,所以才造成困扰）依线索辨别词意（四动词，在办公室看到你）依线索辨别词意（四形容词）固定搭配（在手臂上抱着宝宝）依线索辨别词意（失败是成功之母）50 辨别词意（名词）辨别词意（形容词）线索（联系上下文，日子线索（联系上下文，双胞胎）线索（全文都是讲科学家）困难）（三）阅读理解（46-65）题型类别细节理解题（易）推理判断题（中/难）补充句子（中，2024新题型）词义猜测题（中）综合归纳题/主旨大意（难）2020年 5 3 1 1 2021年 3 5 1 1 2022年3511 2023年4312 2024年 5 2 1 1 1（四）短文填空题型/号2020年2021年2022年2023年2024年短文填空66 语法加上下文语境连接两个句子，线索为only 固定搭配makesb do sth结合上下文推断成分分析+联系上文缺少代词固定搭配one of +名词复数结合上下文67 固定搭配at theage of+数字习惯搭配for+时间表示一段，结合前文现在完成时语法感叹句惯用搭配guess what itis成分分析+结合上下文缺乏状语68 惯用搭配衣服是用来穿的固定搭配叫他+名字固定搭配be good for 惯用搭配清理牙齿惯用搭配兴趣成长69 惯用搭配thinkabout what to do 固定搭配worked as+职业固定搭配be 成分分析缺少谓语→找动成分分析两个句子结构和动词produced in+地点词并列70 惯用搭配raisemoney（结合上下文）固定搭配not....until惯用搭配年+ago 多少年前用于过去的时间固定搭配as time wentby成分分析两个句子状语从句71 惯用搭配come upwith an idea 惯用搭配+时态写了十三本书结合上下文推断成分分析连接两个句子联系上下文线索chengdu和beijing72 固定搭配set up建立固定搭配beproud of结合上下文使用惯用搭配become popularin固定搭配hundreds of 成分分析缺乏主语联系下文yes73 固定搭配a little+不可数名词一些结合上下文推断写了信给惯用搭配drink tea喝茶联系上文+惯用搭配变得流行成分分析作状语缺乏介词74 成分分析主谓宾齐全找定状语法成分考察并列连接两个成分语法知识比较级的使用固定搭配have a goodhabit of惯用搭配正如一个大家庭一样75 语法+固定搭配more than 惯用搭配成分分析缺少宾语宾语从句where to buy 成分分析缺乏谓语动词（五）书面表达题型/号2017年2018年2019年2020年书面表达主题：语言的力量，议论文主题：共享图书馆，议论文主题：介绍传统文化，应用文主题：表达爱，记叙文题型/号2021年2022年2023年2024书面表达主题：课外活动（介绍校园广播），应用文主题：户外活动，，邀请函主题：介绍有趣的梦，说明+议论文（思维导图）主题：课外活动（共读伙伴，自荐信），应用文二、2017年至2024年广东英语中考选择题主要语法点概述（一）基础词法1.名词（1）单复数形式（2）所有格（'s与of结构）2.冠词（1）不定冠词a/an（2）定冠词the（3）零冠词情况3.代词（1）人称代词（主格、宾格、形容词性物主代词、名词性物主代词）（2）反身代词（3）不定代词（如some, any, every, no等）（4）指示代词（this, that, these, those）4.形容词与副词（1）原级、比较级、最高级（2）修饰作用（形容词修饰名词，副词修饰动词、形容词、其他副词）（3）易混易错词辨析5.动词（1）时态（一般现在时、一般过去时、一般将来时、现在进行时、过去进行时、现在完成时等）（2）语态（主动语态、被动语态）（3）主谓一致（4）非谓语动词（不定式to do, 动名词-ing, 过去分词done）（二）句法1.简单句（1）五大基本句型（主语+谓语、主语+谓语+宾语、主语+谓语+表语、主语+谓语+双宾语、主语+谓语+宾语+宾语补足语）（2）复合句2.名词性从句（主语从句、宾语从句、表语从句、同位语从句）（1）状语从句（时间状语从句、地点状语从句、原因状语从句、条件状语从句等）（2）定语从句（关系代词which, that, who, whom及关系副词where, when, why引导）3.特殊句式（1）倒装句（2）感叹句（3）省略句（4）祈使句三、具体中考语法点举例（基于近几年趋势）•名词：名词单复数、所有格（如David's book, the students' books）•冠词：不定冠词a/an的选择，定冠词the的特定用法•代词：形容词性物主代词、名词性物主代词的选择（如his book, mine）•形容词与副词：比较级与最高级的正确使用（如taller, the tallest; more carefully, the most carefully）•动词：时态与语态的综合考查（如一般过去时的被动语态was/were done）•从句：宾语从句的引导词与语序（如I don't know what he said.），定语从句的关系代词与关系副词（如The book which/that you gave me is interesting.）四、根据历年真题分析中考英语命题规律：1、从难易度上看，近五年中考卷“注重基础，提升能力”。

广州中考语文讲题型分析.doc

技巧三：分别匹配，看组合是否合理
技巧四：自问自答，知不知道选项具体在讲什么,能不能用自己的话再表述出来。
5.语言表达（3分）
（1）出题类型
类型一:语言表达是否得体（词语：语体色彩；语句:考虑语境及对话者双方身份）；
类型二:语义是否偏离主体/主旨；
类型三:描述图片（语言是否符合图片事实）；
类型四：改句与原句是否意义一致（不能看形式,要体会意义）语言表达的题目类型繁多，但总的要求不夕卜乎两点:语义的一致性，结构的合理性。
（2）答题技巧（仅以A类为例）：
A.读音相同题
技巧一:对于完全相同的两个字,看它们的意义、词性、色彩是否相同。一般来说意义毫无联系音不同，词性不同音不同，色彩不同音不同，当三者都一致时读音相同。
实例：贝寿/金蝉脱売（色彩不同：口语与书面语）
解数/不求甚解（词性不同：名词与动词；语义也不同）
背影/芒刺在背边搴/舉翁失马（各项一致，读音相同）
技巧二:对于偏旁/部首相同的两个字，看他们的常见同类字（具有这个部首的字）读音是否相同。所有常见同类字读音都相同的话，这两个字读音应该也相同；常见同类字有两个或多个读音,那这两个极有可能不同音。
实例:
请责/扌吉据（读音相同，常见同类字:结婚、整洁、劭、桔梗、麦秸……）
沉湎/腼腆（读音相同，常见同类字：缅、価、麺……）
(1)出题类型(从问题划分)：
类型一:找出读音全都正确的一项；
类型二:找出读音完全相同的一项;
补充类型:找出读音全都错误的一项;
找出读音全都不同的一项;
找出读音错误最多的一项（难度最大1
总体上可归为两类：A.读音相同题；B.读音正确题。从选项上看，A又分为三种情况，
即整字相同，偏旁/部首相同，偏旁/部首音同或音近；

广东省中考各种题型分析

题型题数分值命题特点备注 14 综合1 分析说明题及综合探探究究题一般各3问。问题一般围绕“是什么、为什么、怎么做”来设置，不一定是三方面俱全。综合探究题的最后一问，往往会落脚在考生身上，提建议，或者自己(中学生)怎么做。小计 32 100
思想品德
首页
末页
题型题数分值命题特点备注 10 辨析1 辨析题的广东省中考思品题辨点基本科主观题一直是上是两个四大题型，分别角度或者是简答、辨析、两层意思，分析说明、综合考查到的探究。其中简答考点也一题8分、辨析题般为两个 10 分、分析说明或以上。题 12 分，综合探究题 14 分，共 44分。
题型题数简答1 题
分值 8
命题特点备注简答题基本广东省中考思品科上都是2问；主观题一直是四大第一问基本题型，分别是简答、是问“是什辨析、分析说明、么”，第二综合探究。其中简问问“为什答题8分、辨析题10 么”或“怎分、分析说明题 12 么样”。考分，综合探究题 14 查的考点范分，共 44分。围比较窄，一般是一到两个考点。
第四部分
中考题型解题方法及专项训练广东省中考各种题型分析Fra bibliotek思想品德
首页
末页
一、广东省中考各种题型分析题型题数分值命题特点备注 56 在各题的选择题作为客观单项 28 选择四个选项试题的代表，是题中，只有广东省思想品德一项是最中考的一种重要符合题意题型，其分值占的答案。总分的 56 分，每小题 2 地位极其重要。分。
题型题数分值命题特点备注 12 分析1 辨析题的广东省中考思品说明辨点基本科主观题一直是题上是两个四大题型，分别角度或者是简答、辨析、两层意思，分析说明、综合考查到的探究。其中简答考点也一题8分、辨析题般为两个 10 分、分析说明或以上。题 12 分，综合探究题 14 分，共 44分。

广州中考物理试题分析

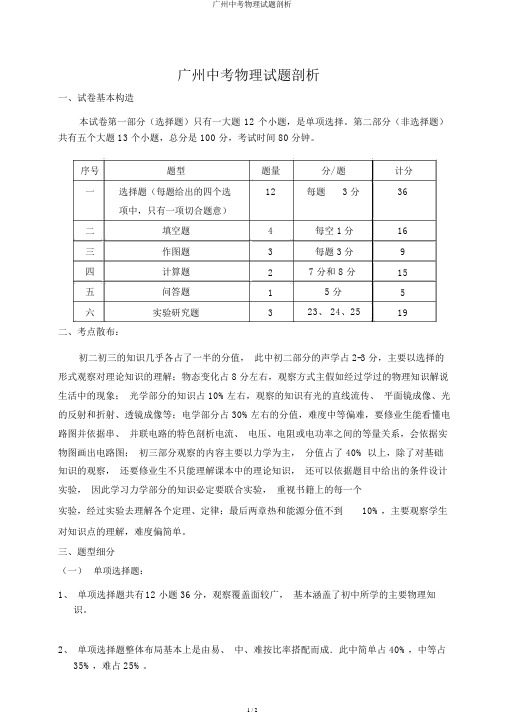
广州中考物理试题剖析一、试卷基本构造本试卷第一部分（选择题）只有一大题 12 个小题，是单项选择。

第二部分（非选择题）共有五个大题 13 个小题，总分是 100 分，考试时间 80 分钟。

序号题型题量分/ 题计分一选择题（每题给出的四个选12每题 3 分36项中，只有一项切合题意）二填空题4每空 1分16三作图题3每题 3分9四计算题27 分和 8 分15五问答题1 5 分5六实验研究题323、 24、2519二、考点散布：初二初三的知识几乎各占了一半的分值，此中初二部分的声学占 2-3 分，主要以选择的形式观察对理论知识的理解；物态变化占 8 分左右，观察方式主假如经过学过的物理知识解说生活中的现象；光学部分的知识占 10%左右，观察的知识有光的直线流传、平面镜成像、光的反射和折射、透镜成像等；电学部分占 30%左右的分值，难度中等偏难，要修业生能看懂电路图并依据串、并联电路的特色剖析电流、电压、电阻或电功率之间的等量关系，会依据实物图画出电路图；初三部分观察的内容主要以力学为主，分值占了 40% 以上，除了对基础知识的观察，还要修业生不只能理解课本中的理论知识，还可以依据题目中给出的条件设计实验，因此学习力学部分的知识必定要联合实验，重视书籍上的每一个实验，经过实验去理解各个定理、定律；最后两章热和能源分值不到10%，主要观察学生对知识点的理解，难度偏简单。

三、题型细分（一）单项选择题：1、单项选择题共有12 小题 36 分，观察覆盖面较广，基本涵盖了初中所学的主要物理知识。

2、单项选择题整体布局基本上是由易、中、难按比率搭配而成．此中简单占 40%，中等占35%，难占 25%。

3、单项选择题观察的方式是紧扣课本，观察课本中常有的知识点，因此要修业生一定熟习课本上的每个知识点。

（二）填空题1.填空题有 4 小题 16 分，以观察力学知识为主，所观察的内容也是力学的要点部分。

2.观察的重视点是书籍上出现过的图形及涵盖的知识点，侧重于观察学生对课本的熟习程度和对知识的应用能力。

近六年广东省中考数学试题各小题的考点分析

近六年广东省中考数学试题各小题的考点分析（一）年年考的题型有（12点）1．数的简单计算（相反数、绝对值、算术平方根、倒数等，其中08年绝对值，09年算术平方根，10年相反数，11年倒数，12年绝对值，预测今年算术平方根、相反数）；以及数的综合计算（往往综合零指数、负指数、方根、特殊角的三角函数、绝对值化简等）。

通常是一大一小（3+6=9分）；2．科学记数法（都是与当年最热时事相关的数据，近几年都是以正整数指数为主，预测今年也是考正指数幂的科学记数法。

分值一般是3分或4分）3．式的简单计算（幂的计算、乘法公式、根式与分式等计算）；以及式的综合计算（有时还设计成化简求值的题，主要考查整式与分式的基本计算），分值一般是3分、4分或6分。

预测今年中考一小一大。

（2）[2010广东第2题]下列运算正确的是（）A ．abba 532=+B ．b a b a -=-4)2(2C ．22))((bab a b a -=-+D ．222)(bab a +=+（3）[2012广东第12题]先化简，再求值：（x+3）（x ﹣3）﹣x （x ﹣2），其中x=4．（4）[2009广东第2题] 计算23)(a 的结果是A. 6aB. 9aC.5aD. 8a4．作图题（用尺规作图或者方格纸中作图，纯作图的题已不太会出现，一般以三角形、四边形或圆等几何图形为背景，设计一、两问的回答）。

分值一般为6分。

07年作线段的垂直平分线并求线段的长；08年作中线并求线段的长；09年过点作已知线的垂线并证明边相等；10年作平移和旋转后的直角三角形；11年作平移后的圆并求面积。

12年角平分线，今年预测中线、垂直线的作法。

如：（1）[2012广东第14题]如图，在△ABC 中，AB=AC ，∠ABC=72°．（1）用直尺和圆规作∠ABC 的平分线BD 交AC 于点D （保留作图痕迹，不要求写作法）；（2）在（1）中作出∠ABC 的平分线BD 后，求∠BDC 的度数．5．探究规律（数的计算、式的计算、图形计数、图形计算等，往往设计在第10题和解答题，近三年都设计为一大一小。

《2022年广州市中考数学真题及重点题型分析》——与去年相比，还算可以！

《2022年广州市中考数学真题及重点题型分析》——与去年
相比，还算可以！
关于将来中考的趋势，以下说法，喜门表示认同！
今年（2022）广州市中考数学满分120分，考试时间120分钟。

题数25题，选择10题，填空6题，其余都是解答题，和福建中考类似。

选择题，总体都不难，第9、10题还是不错的题目；
第16题，考查主从联动模型，涉及最值问题，都是比较难的题目；
第17-23题，常规题，没太大难度；
第24题代数压轴题，后面两问都是有难度的，需要小伙伴认真细心，一不小心，可能就解不出来了；
第25题，几何压轴题，最后一问涉及最值问题，而且是两个最值，难度一下子就提高了；
来个总结：整体难度和区分度还可以，出题属于比较传统，和福建中考相似。

“做对一题你已会的题目，只是一时爽；研透一题你不全会的题目，将会时时爽。

”
说明：文末附有参考答案，如有疑问，可以私信联系喜门（微信号：Ci-Men），欢迎交流探讨！
欢迎其他省市或学校的同侪、小伙伴，如果您刚好有自己省市的
质检卷子，或学校期末、期中卷子等，我们可以交换学习与交流！
试卷电子版
试卷重点题型分析
试卷参考答案。

广东省广州市2021-2023三年中考数学真题分类汇编-03解答题(提升题)知识点分类

广东省广州市2021-2023三年中考数学真题分类汇编-03解答题（提升题）知识点分类一．一次函数的应用（共1小题）1．（2023•广州）因活动需要购买某种水果，数学活动小组的同学通过市场调查得知：在甲商店购买该水果的费用y1（元）与该水果的质量x（千克）之间的关系如图所示；在乙商店购买该水果的费用y2（元）与该水果的质量x（千克）之间的函数解析式为y2＝10x （x≥0）．（1）求y1与x之间的函数解析式；（2）现计划用600元购买该水果，选甲、乙哪家商店能购买该水果更多一些？二．反比例函数综合题（共1小题）2．（2023•广州）已知点P（m，n）在函数y＝﹣（x＜0）的图象上．（1）若m＝﹣2，求n的值；（2）抛物线y＝（x﹣m）（x﹣n）与x轴交于两点M，N（M在N的左边），与y轴交于点G，记抛物线的顶点为E．①m为何值时，点E到达最高处；②设△GMN的外接圆圆心为C，⊙C与y轴的另一个交点为F，当m+n≠0时，是否存在四边形FGEC为平行四边形？若存在，求此时顶点E的坐标；若不存在，请说明理由．三．二次函数综合题（共2小题）3．（2022•广州）已知直线l：y＝kx+b经过点（0，7）和点（1，6）．（1）求直线l的解析式；（2）若点P（m，n）在直线l上，以P为顶点的抛物线G过点（0，﹣3），且开口向下．①求m的取值范围；②设抛物线G与直线l的另一个交点为Q，当点Q向左平移1个单位长度后得到的点Q′也在G上时，求G在≤x≤+1的图象的最高点的坐标．4．（2021•广州）已知抛物线y＝x2﹣（m+1）x+2m+3．（1）当m＝0时，请判断点（2，4）是否在该抛物线上；（2）该抛物线的顶点随着m的变化而移动，当顶点移动到最高处时，求该抛物线的顶点坐标；（3）已知点E（﹣1，﹣1）、F（3，7），若该抛物线与线段EF只有一个交点，求该抛物线顶点横坐标的取值范围．四．全等三角形的判定与性质（共1小题）5．（2023•广州）如图，B是AD的中点，BC∥DE，BC＝DE．求证：∠C＝∠E．五．四边形综合题（共3小题）6．（2023•广州）如图，在正方形ABCD中，E是边AD上一动点（不与点A，D重合）．边BC关于BE对称的线段为BF，连接AF．（1）若∠ABE＝15°，求证：△ABF是等边三角形；（2）延长FA，交射线BE于点G．①△BGF能否为等腰三角形？如果能，求此时∠ABE的度数；如果不能，请说明理由；②若，求△BGF面积的最大值，并求此时AE的长．7．（2022•广州）如图，在菱形ABCD中，∠BAD＝120°，AB＝6，连接BD．（1）求BD的长；（2）点E为线段BD上一动点（不与点B，D重合），点F在边AD上，且BE＝DF．①当CE⊥AB时，求四边形ABEF的面积；②当四边形ABEF的面积取得最小值时，CE+CF的值是否也最小？如果是，求CE+CF的最小值；如果不是，请说明理由．8．（2021•广州）如图，在菱形ABCD中，∠DAB＝60°，AB＝2，点E为边AB上一个动点，延长BA到点F，使AF＝AE，且CF、DE相交于点G．（1）当点E运动到AB中点时，证明：四边形DFEC是平行四边形；（2）当CG＝2时，求AE的长；（3）当点E从点A开始向右运动到点B时，求点G运动路径的长度．六．圆的综合题（共2小题）9．（2023•广州）如图，在平面直角坐标系xOy中，点A（﹣2，0），B（0，2），所在圆的圆心为O．将向右平移5个单位，得到（点A平移后的对应点为C）．（1）点D的坐标是，所在圆的圆心坐标是；（2）在图中画出，并连接AC，BD；（3）求由，BD，，CA首尾依次相接所围成的封闭图形的周长．（结果保留π）10．（2021•广州）如图，在平面直角坐标系xOy中，直线l：y＝x+4分别与x轴，y轴相交于A、B两点，点P（x，y）为直线l在第二象限的点．（1）求A、B两点的坐标；（2）设△PAO的面积为S，求S关于x的函数解析式，并写出x的取值范围；（3）作△PAO的外接圆⊙C，延长PC交⊙C于点Q，当△POQ的面积最小时，求⊙C 的半径．七．作图—基本作图（共1小题）11．（2021•广州）如图，在四边形ABCD中，∠ABC＝90°，点E是AC的中点，且AC＝AD．（1）尺规作图：作∠CAD的平分线AF，交CD于点F，连结EF、BF（保留作图痕迹，不写作法）；（2）在（1）所作的图中，若∠BAD＝45°，且∠CAD＝2∠BAC，证明：△BEF为等边三角形．八．相似形综合题（共1小题）12．（2023•广州）如图，AC是菱形ABCD的对角线．（1）尺规作图：将△ABC绕点A逆时针旋转得到△ADE，点B旋转后的对应点为D（保留作图痕迹，不写作法）；（2）在（1）所作的图中，连接BD，CE．①求证：△ABD∽△ACE；②若tan∠BAC＝，求cos∠DCE的值．九．解直角三角形（共1小题）13．（2022•广州）如图，AB是⊙O的直径，点C在⊙O上，且AC＝8，BC＝6．（1）尺规作图：过点O作AC的垂线，交劣弧于点D，连接CD（保留作图痕迹，不写作法）；（2）在（1）所作的图形中，求点O到AC的距离及sin∠ACD的值．一十．解直角三角形的应用-仰角俯角问题（共1小题）14．（2022•广州）某数学活动小组利用太阳光线下物体的影子和标杆测量旗杆的高度．如图，在某一时刻，旗杆AB的影子为BC，与此同时在C处立一根标杆CD，标杆CD的影子为CE，CD＝1.6m，BC＝5CD．（1）求BC的长；（2）从条件①、条件②这两个条件中选择一个作为已知，求旗杆AB的高度．条件①：CE＝1.0m；条件②：从D处看旗杆顶部A的仰角α为54.46°．注：如果选择条件①和条件②分别作答，按第一个解答计分．参考数据：sin54.46°≈0.81，cos54.46°≈0.58，tan54.46°≈1.40．一十一．频数（率）分布直方图（共1小题）15．（2022•广州）某校在九年级学生中随机抽取了若干名学生参加“平均每天体育运动时间”的调查，根据调查结果绘制了如下不完整的频数分布表和频数分布直方图．频数分布表运动时间t/min频数频率30≤t＜6040.160≤t＜9070.17590≤t＜120a0.35120≤t＜15090.225150≤t＜1806b合计n1请根据图表中的信息解答下列问题：（1）频数分布表中的a＝，b＝，n＝；（2）请补全频数分布直方图；（3）若该校九年级共有480名学生，试估计该校九年级学生平均每天体育运动时间不低于120min的学生人数．广东省广州市2021-2023三年中考数学真题分类汇编-03解答题（提升题）知识点分类参考答案与试题解析一．一次函数的应用（共1小题）1．（2023•广州）因活动需要购买某种水果，数学活动小组的同学通过市场调查得知：在甲商店购买该水果的费用y1（元）与该水果的质量x（千克）之间的关系如图所示；在乙商店购买该水果的费用y2（元）与该水果的质量x（千克）之间的函数解析式为y2＝10x （x≥0）．（1）求y1与x之间的函数解析式；（2）现计划用600元购买该水果，选甲、乙哪家商店能购买该水果更多一些？【答案】（1）y1与x之间的函数解析式为y1＝；（2）在甲商店购买更多一些．【解答】解：（1）当0≤x≤5时，设y1与x之间的函数解析式为y1＝kx（k≠0），把（5，75）代入解析式得：5k＝75，解得k＝15，∴y1＝15x；当x＞5时，设y1与x之间的函数解析式为y1＝mx+n（m≠0），把（5，75）和（10，120）代入解析式得，解得，∴y1＝9x+30，综上所述，y1与x之间的函数解析式为y1＝；（2）在甲商店购买：9x+30＝600，解得x＝63，∴在甲商店600元可以购买63千克水果；在乙商店购买：10x＝600，解得x＝60，∴在乙商店600元可以购买60千克，∵63＞60，∴在甲商店购买更多一些．二．反比例函数综合题（共1小题）2．（2023•广州）已知点P（m，n）在函数y＝﹣（x＜0）的图象上．（1）若m＝﹣2，求n的值；（2）抛物线y＝（x﹣m）（x﹣n）与x轴交于两点M，N（M在N的左边），与y轴交于点G，记抛物线的顶点为E．①m为何值时，点E到达最高处；②设△GMN的外接圆圆心为C，⊙C与y轴的另一个交点为F，当m+n≠0时，是否存在四边形FGEC为平行四边形？若存在，求此时顶点E的坐标；若不存在，请说明理由．【答案】（1）1；（2）①m＝﹣；②假设存在，E（﹣，﹣），或（，﹣）．【解答】解：（1）把m＝﹣2代入y＝﹣（x＜0）得n＝﹣＝1；故n的值为1；（2）①在y＝（x﹣m）（x﹣n）中，令y＝0，则（x﹣m）（x﹣n）＝0，解得x＝m或x＝n，∴M（m，0），N（n，0），∵点P（m，n）在函数y＝﹣（x＜0）的图象上，∴mn＝﹣2，令x＝，得y＝（x﹣m）（x﹣n）＝﹣（m﹣n）2＝﹣2﹣（m+n）2≤﹣2，即当m+n＝0，且mn＝﹣2，则m2＝2，解得：m＝﹣（正值已舍去），即m＝﹣时，点E到达最高处；②假设存在，理由：对于y＝（x﹣m）（x﹣n），当x＝0时，y＝mn＝﹣2，即点G（0，﹣2），由①得M（m，0），N（n，0），G（0，﹣2），E（，﹣（m﹣n）2），对称轴为直线x＝，由点M（m，0）、G（0，﹣2）的坐标知，tan∠OMG＝＝，作MG的中垂线交MG于点T，交y轴于点S，交x轴于点K，则点T（m，﹣1），则tan∠MKT＝﹣m，则直线TS的表达式为：y＝﹣m（x﹣m）﹣1．当x＝时，y＝﹣m（x﹣m）﹣1＝﹣，则点C的坐标为：（，﹣）．由垂径定理知，点C在FG的中垂线上，则FG＝2（y C﹣y G）＝2×（﹣+2）＝3．∵四边形FGEC为平行四边形，则CE＝FG＝3＝y C﹣y E＝﹣﹣y E，解得：y E＝﹣，即﹣（m﹣n）2＝﹣，且mn＝﹣2，则m+n＝，∴E（﹣，﹣），或（，﹣）．三．二次函数综合题（共2小题）3．（2022•广州）已知直线l：y＝kx+b经过点（0，7）和点（1，6）．（1）求直线l的解析式；（2）若点P（m，n）在直线l上，以P为顶点的抛物线G过点（0，﹣3），且开口向下．①求m的取值范围；②设抛物线G与直线l的另一个交点为Q，当点Q向左平移1个单位长度后得到的点Q′也在G上时，求G在≤x≤+1的图象的最高点的坐标．【答案】（1）y＝﹣x+7；（2）①m＜10且m≠0；②（﹣2，9）或（2，5）．【解答】解：（1）将点（0，7）和点（1，6）代入y＝kx+b，∴，解得，∴y＝﹣x+7；（2）①∵点P（m，n）在直线l上，∴n＝﹣m+7，设抛物线的解析式为y＝a（x﹣m）2+7﹣m，∵抛物线经过点（0，﹣3），∴am2+7﹣m＝﹣3，∴a＝，∵抛物线开口向下，∴a＜0，∴a＝＜0，∴m＜10且m≠0；②∵抛物线的对称轴为直线x＝m，∴Q点与Q'关于x＝m对称，∴Q点的横坐标为m+，联立方程组，整理得ax2+（1﹣2ma）x+am2﹣m＝0，∵P点和Q点是直线l与抛物线G的交点，∴m+m+＝2m﹣，∴a＝﹣2，∴y＝﹣2（x﹣m）2+7﹣m，∴﹣2m2+7﹣m＝﹣3，解得m＝2或m＝﹣，当m＝2时，y＝﹣2（x﹣2）2+5，此时抛物线的对称轴为直线x＝2，图象在≤x≤上的最高点坐标为（2，5）；当m＝﹣时，y＝﹣2（x+）2+，此时抛物线的对称轴为直线x＝﹣，图象在﹣2≤x≤﹣1上的最高点坐标为（﹣2，9）；综上所述：G在≤x≤+1的图象的最高点的坐标为（﹣2，9）或（2，5）．4．（2021•广州）已知抛物线y＝x2﹣（m+1）x+2m+3．（1）当m＝0时，请判断点（2，4）是否在该抛物线上；（2）该抛物线的顶点随着m的变化而移动，当顶点移动到最高处时，求该抛物线的顶点坐标；（3）已知点E（﹣1，﹣1）、F（3，7），若该抛物线与线段EF只有一个交点，求该抛物线顶点横坐标的取值范围．【答案】（1）点（2，4）不在抛物线上；（2）（2，5）；（3）x顶点＜﹣或x顶点＞或x顶点＝1．【解答】解：（1）当m＝0时，抛物线为y＝x2﹣x+3，将x＝2代入得y＝4﹣2+3＝5，∴点（2，4）不在抛物线上；（2）抛物线y＝x2﹣（m+1）x+2m+3的顶点为（，），化简得（，），顶点移动到最高处，即是顶点纵坐标最大，而＝﹣（m﹣3）2+5，∴m＝3时，纵坐标最大，即是顶点移动到了最高处，此时该抛物线解析式为y＝x2﹣4x+9，顶点坐标为：（2，5）；（3）设直线EF解析式为y＝kx+b，将E（﹣1，﹣1）、F（3，7）代入得：，解得，∴直线EF的解析式为y＝2x+1，由得：或，∴直线y＝2x+1与抛物线y＝x2﹣（m+1）x+2m+3的交点为：（2，5）和（m+1，2m+3），而（2，5）在线段EF上，∴若该抛物线与线段EF只有一个交点，则（m+1，2m+3）不在线段EF上，或（2，5）与（m+1，2m+3）重合，∴m+1＜﹣1或m+1＞3或m+1＝2（此时2m+3＝5），∴此时抛物线顶点横坐标x顶点＝＜﹣或x顶点＝＞或x顶点＝＝＝1．四．全等三角形的判定与性质（共1小题）5．（2023•广州）如图，B是AD的中点，BC∥DE，BC＝DE．求证：∠C＝∠E．【答案】证明见解析．【解答】证明：∵B是AD的中点，∴AB＝BD，∵BC∥DE，∴∠ABC＝∠D，在△ABC和△BDE中，，∴△ABC≌△BDE（SAS），∴∠C＝∠E．五．四边形综合题（共3小题）6．（2023•广州）如图，在正方形ABCD中，E是边AD上一动点（不与点A，D重合）．边BC关于BE对称的线段为BF，连接AF．（1）若∠ABE＝15°，求证：△ABF是等边三角形；（2）延长FA，交射线BE于点G．①△BGF能否为等腰三角形？如果能，求此时∠ABE的度数；如果不能，请说明理由；②若，求△BGF面积的最大值，并求此时AE的长．【答案】（1）见解析；（2）①22.5°；②；．【解答】（1）证明：由轴对称的性质得到BF＝BC，∵四边形ABCD是正方形，∴∠ABC＝90°，∵∠ABE＝15°，∴∠CBE＝75°，∵BC关于BE对称的线段为BF，∴∠FBE＝∠CBE＝75°，∴∠ABF＝∠FBE﹣∠ABE＝60°，∴△ABF是等边三角形；（2）解：①能，∵边BC关于BE对称的线段为BF，∴BC＝BF，∵四边形ABCD是正方形，∴BC＝AB，∴BF＝BC＝BA，∵E是边AD上一动点，∴BA＜BE＜BG，∴点B不可能是等腰三角形BGF的顶点，若点F是等腰三角形BGF的顶点，则有∠FGB＝∠FBG＝∠CBG，此时E与D重合，不合题意，∴只剩下GF＝GB了，连接CG交AD于H，∵BC＝BF，∠CBG＝∠FBG，BG＝BG，∴△CBG≌△FBG（SAS），∴FG＝CG，∴BG＝CG，∴△BGF为等腰三角形，∵BA＝BC＝BF，∴∠BFA＝∠BAF，∵△CBG≌△FBG，∴∠BFG＝∠BCG，∵AD∥BC，∴∠AHG＝∠BCG，∴∠BAF+∠HAG＝∠AHG+∠HAG＝180°﹣∠BAD＝90°，∴∠FGC＝180°﹣∠HAG﹣∠AHG＝90°，∴∠BGF＝∠BGC＝＝45°，∵GB＝GC，∴∠GBC＝∠GCB＝（180°﹣∠BGC）＝67.5°，∴∠ABE＝∠ABC﹣∠GBC＝90°﹣67.5°＝22.5°；②由①知，△CBG≌△FBG，要求△BGF面积的最大值，即求△BGC面积的最大值，在△GBC中，底边BC是定值，即求高的最大值即可，如图2，过G作GP⊥BC于P，连接AC，取AC的中点M，连接GM，作MN⊥BC于N，设AB＝2x，则AC＝2x，由①知∠AGC＝90°，M是AC的中点，∴GM＝＝x，MN＝＝x，∴PG≤GM+MN＝（）x，当G，M，N三点共线时，取等号，∴△BGF面积的最大值＝＝（1）×＝；如图3，设PG与AD交于Q，则四边形ABPQ是矩形，∴AQ＝PB＝x，PQ＝AB＝2x，∴QM＝MP＝x，GM＝x，∴，∵QE+AE＝AQ＝x，∴，∴＝2（）x＝2（×（）＝．7．（2022•广州）如图，在菱形ABCD中，∠BAD＝120°，AB＝6，连接BD．（1）求BD的长；（2）点E为线段BD上一动点（不与点B，D重合），点F在边AD上，且BE＝DF．①当CE⊥AB时，求四边形ABEF的面积；②当四边形ABEF的面积取得最小值时，CE+CF的值是否也最小？如果是，求CE+CF的最小值；如果不是，请说明理由．【答案】（1）6（2）①7；②是，最小值为12．【解答】解：（1）过点D作DH⊥AB交BA的延长线于H，如图：∵四边形ABCD是菱形，∴AD＝AB＝6，∵∠BAD＝120°，∴∠DAH＝60°，在Rt△ADH中，DH＝AD•sin∠DAH＝6×＝3，AH＝AD•cos∠DAH＝6×＝3，∴BD＝＝＝6；（2）①设CE⊥AB交AB于M点，过点F作FN⊥AB交BA的延长线于N，如图：菱形ABCD中，∵AB＝BC＝CD＝AD＝6，AD∥BC，∠BAD＝120°，∴∠ABC+∠BAD＝180°，∴∠ABC＝180°﹣∠BAD＝60°，在Rt△BCM中，BM＝BC•cos∠ABC＝6×＝3，∵BD是菱形ABCD的对角线，∴∠DBA＝ABC＝30°，在Rt△BEM中，ME＝BM•tan∠DBM＝3×＝，BE＝＝＝2，∵BE＝DF，∴DF＝2，∴AF＝AD﹣DF＝4，在Rt△AFN中，∠FAN＝180°﹣∠BAD＝60°，∴FN＝AF•sin∠FAN＝4×＝2，AN＝AF•cos∠FAN＝4×＝2，∴MN＝AB+AN﹣BM＝6+2﹣3＝5，∴S四边形ABEF＝S△BEM+S梯形EMNF﹣S△AFN＝EM•BM+（EM+FN）•MN﹣AN•FN＝3+（+2）×5﹣2×2＝+﹣2＝7；②当四边形ABEF的面积取最小值时，CE+CF的值是最小，理由：设DF＝x，则BE＝DF＝x，过点C作CH⊥AB于点H，过点F作FG⊥CH 于点G，过点E作EY⊥CH于点Y，作EM⊥AB于M点，过点F作FN⊥AB交BA的延长线于N，如图：∴EY∥FG∥AB，FN∥CH，∴四边形EMHY、FNHG是矩形，∴FN＝GH，FG＝NH，EY＝MH，EM＝YH，由①可知：ME＝BE＝x，BM＝BE＝x，AN＝AF＝（AD﹣DF）＝3﹣x，FN＝AF＝，CH＝BC＝3，BH＝BC＝3，∴AM＝AB﹣BM＝6﹣x，AH＝AB﹣BH＝3，YH＝ME＝x，GH＝FN＝，EY＝MH＝BM﹣BH＝x﹣3，∴CY＝CH﹣YH＝3﹣x，FG＝NH＝AN+AH＝6﹣，CG＝CH﹣GH＝3﹣＝x，∴MN＝AB+AN﹣BM＝6+3﹣x﹣x＝9﹣2x，∴S四边形ABEF＝S△BEM+S梯形EMNF﹣S△AFN＝EM•BM+（EM+FN）•MN﹣AN•FN＝x×x+（x+）•（9﹣2x）﹣（3﹣x）•＝x2﹣x+9＝（x﹣3）2+，∵＞0，∴当x＝3时，四边形ABEF的面积取得最小值，方法一：CE+CF＝+•＝+＝+×＝+×＝+，∵（x﹣3）2≥0，当且仅当x＝3时，（x﹣3）2＝0，∴CE+CF＝+≥12，当且仅当x＝3时，CE+CF＝12，即当x＝3时，CE+CF的最小值为12，∴当四边形ABEF的面积取最小值时，CE+CF的值也最小，最小值为12．方法二：如图：将△BCD绕点B逆时针旋转60°至△BAG，连接CG，在Rt△BCG中，CG＝2BC＝12，∵＝＝，∠CDF＝∠GBE＝60°，∴△BEG∽△DFC，∴＝＝，即GE＝CF，∴CE+CF＝CE+GE≥CG＝12，即当且仅当点C、E、G三点共线时，CE+CF的值最小，此时点E为菱形对角线的交点，BD中点，BE＝3，DF＝3，∴当四边形ABEF的面积取最小值时，CE+CF的值也最小，最小值为12．解法二：如图，在BD上截取DM，使得DM＝2，在DA上取点F，连接DF，使得△DFM∽△BEC．则有CE＝FM，作点M关于AD的对称点M′，∴CE+CF＝FM+CF＝（CF+FM）＝（CF+FM′），∴C，F，M′共线时，最小，此时DF＝3，可得CE+CF的值也最小，最小值为12．8．（2021•广州）如图，在菱形ABCD中，∠DAB＝60°，AB＝2，点E为边AB上一个动点，延长BA到点F，使AF＝AE，且CF、DE相交于点G．（1）当点E运动到AB中点时，证明：四边形DFEC是平行四边形；（2）当CG＝2时，求AE的长；（3）当点E从点A开始向右运动到点B时，求点G运动路径的长度．【答案】见试题解答内容【解答】解：（1）证明：连接DF，CE，如图所示：，∵E为AB中点，∴AE＝AF＝AB，∴EF＝AB＝CD，∵四边形ABCD是菱形，∴EF∥CD，∴四边形DFEC是平行四边形．（2）作CH⊥BH，设AE＝FA＝m，如图所示，，∵四边形ABCD是菱形，∴CD∥EF，∴△CDG∽△FEG，∴，∴FG＝2m，在Rt△CBH中，∠CBH＝60°，BC＝2，sin60°＝，CH＝，cos60°＝，BH＝1，在Rt△CFH中，CF＝2+2m，CH＝，FH＝3+m，CF2＝CH2+FH2，即（2+2m）2＝（）2+（3+m）2，整理得：3m2+2m﹣8＝0，解得：m1＝，m2＝﹣2（舍去），∴．（3）G点轨迹为线段AG，证明：如图，（此图仅作为证明AG轨迹用），延长线段AG交CD于H，作HM⊥AB于M，作DN⊥AB于N，∵四边形ABCD是菱形，∴BF∥CD，∴△DHG∽△EGA，△HGC∽△AGF，∴，，∴，∵AE＝AF，∴DH＝CH＝1，在Rt△ADN中，AD＝2，∠DAB＝60°．∴sin60°＝，DN＝．cos60°＝，AN＝1，在Rt△AHM中，HM＝DN＝，AM＝AN+NM＝AN+DH＝2，tan∠HAM＝，G点轨迹为线段AG．∴G点轨迹是线段AG．如图所示，作GH⊥AB，∵四边形ABCD为菱形，∠DAB＝60°，AB＝2，∴CD∥BF，BD＝2，∴△CDG∽△FBG，∴，即BG＝2DG，∵BG+DG＝BD＝2，∴BG＝，在Rt△GHB中，BG＝，∠DBA＝60°，sin60°＝，GH＝，cos60°＝，BH＝，在Rt△AHG中，AH＝2﹣＝，GH＝，AG2＝（）2+（）2＝，∴AG＝．∴G点路径长度为．解法二：如图，连接AG，延长AG交CD于点W．∵CD∥BF，∴＝，＝，∴＝，∵AF＝AE，∴DW＝CW，∴点G在AW上运动．下面的解法同上．六．圆的综合题（共2小题）9．（2023•广州）如图，在平面直角坐标系xOy中，点A（﹣2，0），B（0，2），所在圆的圆心为O．将向右平移5个单位，得到（点A平移后的对应点为C）．（1）点D的坐标是　（5，2）　，所在圆的圆心坐标是　（5，0）　；（2）在图中画出，并连接AC，BD；（3）求由，BD，，CA首尾依次相接所围成的封闭图形的周长．（结果保留π）【答案】（1）（5，2）、（5，0）；（2）见解答；（3）2π+10．【解答】解：（1）如下图，由平移的性质知，点D（5，2），所在圆的圆心坐标是（5，0），故答案为：（5，2）、（5，0）；（2）在图中画出，并连接AC，BD，见下图；（3）和长度相等，均为×2πr＝×2＝π，而BD＝AC＝5，则封闭图形的周长＝++2BD＝2π+10．10．（2021•广州）如图，在平面直角坐标系xOy中，直线l：y＝x+4分别与x轴，y轴相交于A、B两点，点P（x，y）为直线l在第二象限的点．（1）求A、B两点的坐标；（2）设△PAO的面积为S，求S关于x的函数解析式，并写出x的取值范围；（3）作△PAO的外接圆⊙C，延长PC交⊙C于点Q，当△POQ的面积最小时，求⊙C 的半径．【答案】（1）A（﹣8，0），B（0，4）；（2）S＝2x+16（﹣8＜x＜0）；（3）4．【解答】解：（1）∵直线y＝x+4分别与x轴，y轴相交于A、B两点，∴当x＝0时，y＝4；当y＝0时，x＝﹣8，∴A（﹣8，0），B（0，4）；（2）∵点P（x，y）为直线l在第二象限的点，∴P（x，），∴S△APO＝＝2x+16（﹣8＜x＜0）；∴S＝2x+16（﹣8＜x＜0）；（3）∵A（﹣8，0），B（0，4），∴OA＝8，OB＝4，在Rt△AOB中，由勾股定理得：AB＝，在⊙C中，∵PQ是直径，∴∠POQ＝90°，∵∠BAO＝∠Q，∴tan Q＝tan∠BAO＝，∴，∴OQ＝2OP，∴S△POQ＝，∴当S△POQ最小时，则OP最小，∵点P在线段AB上运动，∴当OP⊥AB时，OP最小，∴S△AOB＝，∴，∵sin Q＝sin∠BAO，∴，∴，∴PQ＝8，∴⊙C半径为4．七．作图—基本作图（共1小题）11．（2021•广州）如图，在四边形ABCD中，∠ABC＝90°，点E是AC的中点，且AC＝AD．（1）尺规作图：作∠CAD的平分线AF，交CD于点F，连结EF、BF（保留作图痕迹，不写作法）；（2）在（1）所作的图中，若∠BAD＝45°，且∠CAD＝2∠BAC，证明：△BEF为等边三角形．【答案】（1）作图见解析部分．（2）证明见解析部分．【解答】（1）解：如图，图形如图所示．（2）证明：∵AC＝AD，AF平分∠CAD，∴∠CAF＝∠DAF，AF⊥CD，∵∠CAD＝2∠BAC，∠BAD＝45°，∴∠BAE＝∠EAF＝∠FAD＝15°，∵∠ABC＝∠AFC＝90°，AE＝EC，∴BE＝AE＝EC，EF＝AE＝EC，∴EB＝EF，∠EAB＝∠EBA＝15°，∠EAF＝∠EFA＝15°，∴∠BEC＝∠EAB+∠EBA＝30°，∠CEF＝∠EAF+∠EFA＝30°，∴∠BEF＝60°，∴△BEF是等边三角形．八．相似形综合题（共1小题）12．（2023•广州）如图，AC是菱形ABCD的对角线．（1）尺规作图：将△ABC绕点A逆时针旋转得到△ADE，点B旋转后的对应点为D（保留作图痕迹，不写作法）；（2）在（1）所作的图中，连接BD，CE．①求证：△ABD∽△ACE；②若tan∠BAC＝，求cos∠DCE的值．【答案】（1）作法、证明见解答；（2）①证明见解答；②cos∠DCE的值是．【解答】解：（1）如图1，作法：1．以点D为圆心，BC长为半径作弧，2．以点A为圆心，AC长为半径作弧，交前弧于点E，3．连接DE、AE，△ADE就是所求的图形．证明：∵四边形ABCD是菱形，∴AD＝AB，∵DE＝BC，AE＝AC，∴△ADE≌△ABC（SSS），∴△ADE就是△ABC绕点A逆时针旋转得到图形．（2）①如图2，由旋转得AB＝AD，AC＝AE，∠BAC＝∠DAE，∴＝，∠BAC+∠CAD＝∠DAE+∠CAD，∴∠BAD＝∠CAE，∴△ABD∽△ACE．②如图2，延长AD交CE于点F，∵AB＝AD，BC＝DC，AC＝AC，∴△ABC≌△ADC（SSS），∴∠BAC＝∠DAC，∵∠BAC＝∠DAE，∴∠DAE＝∠DAC，∵AE＝AC，∴AD⊥CE，∴∠CFD＝90°，设CF＝m，CD＝AD＝x，∵＝tan∠DAC＝tan∠BAC＝，∴AF＝3CF＝3m，∴DF＝3m﹣x，∵CF2+DF2＝CD2，∴m2+（3m﹣x）2＝x2，∴解关于x的方程得x＝m，∴CD＝m，∴cos∠DCE＝＝＝，∴cos∠DCE的值是．九．解直角三角形（共1小题）13．（2022•广州）如图，AB是⊙O的直径，点C在⊙O上，且AC＝8，BC＝6．（1）尺规作图：过点O作AC的垂线，交劣弧于点D，连接CD（保留作图痕迹，不写作法）；（2）在（1）所作的图形中，求点O到AC的距离及sin∠ACD的值．【答案】（1）详见解答；（2）点O到AC的距离为4，sin∠ACD＝．【解答】解：（1）分别以A、C为圆心，大于AC为半径画弧，在AC的两侧分别相交于P、Q两点，画直线PQ交劣弧于点D，交AC于点E，即作线段AC的垂直平分线，由垂径定理可知，直线PQ一定过点O；（2）∵AB是⊙O的直径，∴∠ACB＝90°，在Rt△ABC中，且AC＝8，BC＝6．∴AB＝＝10，∵OD⊥AC，∴AE＝CE＝AC＝4，又∵OA＝OB，∴OE是△ABC的中位线，∴OE＝BC＝3，由于PQ过圆心O，且PQ⊥AC，即点O到AC的距离为3，连接OC，在Rt△CDE中，∵DE＝OD﹣CE＝5﹣3＝2，CE＝4，∴CD＝＝＝2∴sin∠ACD＝＝＝．一十．解直角三角形的应用-仰角俯角问题（共1小题）14．（2022•广州）某数学活动小组利用太阳光线下物体的影子和标杆测量旗杆的高度．如图，在某一时刻，旗杆AB的影子为BC，与此同时在C处立一根标杆CD，标杆CD的影子为CE，CD＝1.6m，BC＝5CD．（1）求BC的长；（2）从条件①、条件②这两个条件中选择一个作为已知，求旗杆AB的高度．条件①：CE＝1.0m；条件②：从D处看旗杆顶部A的仰角α为54.46°．注：如果选择条件①和条件②分别作答，按第一个解答计分．参考数据：sin54.46°≈0.81，cos54.46°≈0.58，tan54.46°≈1.40．【答案】（1）BC的长为8m；（2）旗杆AB的高度约为12.8m．【解答】解：（1）∵BC＝5CD，CD＝1.6m，∴BC＝5×1.6＝8（m），∴BC的长为8m；（2）若选择条件①：由题意得：＝，∴＝，∴AB＝12.8，∴旗杆AB的高度为12.8m；若选择条件②：过点D作DF⊥AB，垂足为F，则DC＝BF＝1.6m，DF＝BC＝8m，在Rt△ADF中，∠ADF＝54.46°，∴AF＝DF•tan54.46°≈8×1.4＝11.2（m），∴AB＝AF+BF＝11.2+1.6＝12.8（m），∴旗杆AB的高度约为12.8m．一十一．频数（率）分布直方图（共1小题）15．（2022•广州）某校在九年级学生中随机抽取了若干名学生参加“平均每天体育运动时间”的调查，根据调查结果绘制了如下不完整的频数分布表和频数分布直方图．频数分布表运动时间t/min频数频率30≤t＜6040.160≤t＜9070.17590≤t＜120a0.35120≤t＜15090.225150≤t＜1806b合计n1请根据图表中的信息解答下列问题：（1）频数分布表中的a＝　14　，b＝　0.15　，n＝　40　；（2）请补全频数分布直方图；（3）若该校九年级共有480名学生，试估计该校九年级学生平均每天体育运动时间不低于120min的学生人数．【答案】见试题解答内容【解答】解：（1）由题意可知，n＝4÷0.1＝40，∴a＝40×0.35＝14，b＝6÷40＝0.15，故答案为：14；0.15；40；（2）补全频数分布直方图如下：（3）480×＝180（名），答：估计该校九年级学生平均每天体育运动时间不低于120min的学生人数为180名．。

广东中考题型解题方法与技巧(四)

返回
道德与法治
推动城乡、区域协调发展，走共同富裕道路等。 ②政治建设：坚持中国共产党的领导，走中国特色社会主义道路；践行“三个代表”重要思想；坚持依法治国基本方略，建设社会主义法治社会；政府要依法行政；坚持和完善人民代表大会制度，加强社会主义民主政治建设，充分保障人民当家作主等。
返回
道德与法治
返回
道德与法治第四种格式：体现什么观点，直接写观点即可。
【例】2010年省中考题第30题分析说明题：(1)材料一体现了《思想品德》课中的哪些观点？【参考答案】(1)落实保护环境的基本国策；节约资源；实现社会经济的可持续发展；实现人与自然的和谐发展。(答其中的两点即可)
返回
道德与法治第五种格式：双向联系型。提问方式有：A和B之间有什么关系(联系)；材料一和材料二之间有什么关联等。答题步骤是：(1)二者之间是相互联系、相互影响、相互促进的。(2)A对B的影响：A的实施有助于B，然后说明理由。B对A的影响：B的实施有助于A，这促进了(有助于、有利于)A。(3)总结：所以……
返回
道德与法治
③落实科学发展观，坚持走可持续发展道路，促进人与自然的和谐发展。 ④坚持和完善我国的基本经济制度，促进经济又好又快发展等。 (2)关于青少年(公民个人)方面的答题策略。常用的观点有(典型人物具有的品质)：调控情绪；主动交往；战胜挫折；磨砺坚强意志；自尊自爱；
返回
道德与法治
自立自强；珍爱生命，提升人生价值；文明礼貌；诚实守信；平等待人；换位思考，与人为善；理解宽容他人；敢于竞争，善于合作；勇于承担责任，积极参加公益活动；崇尚公平，维护正义；发扬团队精神，正确处理个人与集体的关系；学法守法用法；自觉抵制不良诱惑，防微杜渐；正确行使权利，自觉履行义务；珍惜受教育的权利；发扬中华民族精神、时代精神、传统美德、艰苦奋斗精神等。

2021广东省中考数学试卷25题第三问详解分析

2021广东省中考数学试卷25题第三问分析一、呈现2020 广东省中考数学压轴题之---代数与几何（代几）综合题25二、试题情境分析首先谈一谈各省市中考数学卷中以“二次函数”为背景的代数（几何）综合题的状况。

往往以探索性问题（动点、动线导致的）作为压轴大戏，举例：探索三角形相似、全等，探索平行四边形存在性、探索等腰三角形存在性、探索三角形面积的最值问题、探索函数的取值范围等等。

对于此类压轴题的设计题材背景一般有以下显著特点：1.一般试题背景考生都很熟悉（以平面直角坐标系为依托），本着有易到难，利于学生们入题上手，渐入佳境的原则题目的设问层层推进，难度结构合理，多数设问为“常规题”，，体现了中考试题的学业水平检测功能，但随着问题解决的推进，解决问题难度逐步上升，体现了中考试题的选拔性。

2.有些试题背景的设计考生不很熟悉，那些题目一般是新定义或新情境问题（首都中考数学试题常见），但相对于任何学生而言是公平的，人人不熟悉情境和人人熟悉情境同一道理，很好体现了中考试题的公平性。

3.命题者对于此类题目的设计非常注意各小问解题方法的多样性和灵活性，但不同的解题方法繁简程度可能大相径庭，充分照顾了不同数学学习层次能力的学生，通过检测让不同的学生得到不同的收获，但有保证优秀学生的脱颖而出。

对于此类压轴题的问题设计中考查的知识点或区域一般有以下几个：1.利用待定系数法求函数解析式2.利用两个函数解析式联立方程组（直线或抛物线）求点坐标方法3.抛物线的性质、点关于直线对称。

4.直线的平移，点的平移（图形三大变换：对称、旋转、平移）5.两个三角形相似，对应边上的高特性6.三角形全等、相似7.平面直角坐标系中不规则四边形面积求法8.一次、二次函数与圆相结合的题目，考查圆的知识（与圆有“缘”），2003年新课改后此类题目一般不多见。

因为新课标上建了一些圆的知识。

再看本题，它以平面直角坐系为依托，全面覆盖了对学生初中阶段与一次、二次函数学习相关的基本知识、基本技能、基本数学思想方法和基本数学活动经验的考查。