人教版数学高一-新人教A版必修四测试题 第三章 三角恒等变换测试题2
高中数学必修4第三章三角恒等变换综合检测题(人教A版)

第三章三角恒等变换综合检测题本试卷分第I 卷选择题和第U 卷非选择题两部分,满分150分,时间120 分钟。
第I 卷(选择题共60分)一、选择题(本大题共12个小题,每小题 5分,共60分,在每小题给出的四个选项中 只有一个是符合题目要求的 )n 3 41 .已知 0v av 2v 3<n 又 sin a= 5, cos (a+ ®= — 5,贝V sin ()B . 0 或 2424 C.25 24 D . ±25 [答案]Cn 3 4[解析]•/ 0v av 2 v 3v n 且 sin a= 5, COS ( a+ 3 = — 54 n3 3• cos a= 5 , 2< a+ 3v ㊁ n, • sin( a+ 3 = ±5,=sin( a+ 3cos a — cos( a+ 3)sin a才< 3v n ••• sin 3> 0•故排除 A , B , D.4 3 4⑵由 cos( a+ 3)= — 5及 Sin a= 3可得 sin 3= §(1 + cos 3)代入 sin 2 3+ cos 2 3= 1 中可解得 cos37 n=—1或一25,再结合2<仟n 可求sin 32.若sin Bv 0, cos2 0v 0,则在(0,2 内)B 的取值范围是()3 n3=0.sin3=- 5x 4-又氏才,n j, • sin 3> 0,故 sin 3= 24当 sin( a+ 3 =,sin 3= sin [( a+ a[点评](1)可用排除法求解,T=器53 245 = 25;A . n< 0< 25 nB.5T <e< ¥3 nC.y <e< 2 nD.严< 0<孕4 4[答案]B[解析]2 2 2•/ cos2 e< 0, • 1 —2sin < 0,即sin e>2或sin < —"2,又已知sin < 0, •— 1 < sin e<—亠2,2由正弦曲线得满足条件的e取值为54n<e< ¥3. 函数y= sin2x+ cos2x的图象,可由函数y= sin2x —cos2x的图象()A .向左平移f个单位得到B .向右平移f个单位得到8c.向左平移n个单位得到4D .向右平移4个单位得到[答案]C[解析]y= sin2x+ cos2x= , 2sin(2x+J=2si n2(x +》_ n _ ny= sin2x—cos2x= 2sin(2x—4)= . 2sin2(x—§)n n n其中x+8=(x+ 4)—8n•••将y= sin2x—cos2x的图象向左平移:个单位可得y= sin2x+ cos2x的图象.44. 下列各式中,值为~2的是()A . 2sin 15 cos15 °2 2B. cos 15。
高中数学第三章三角恒等变换3.1.3二倍角的正弦、余弦、正切公式课时提升作业1新人教A版必修4

二倍角的正弦、余弦、正切公式(25分钟60分)一、选择题(每小题5分,共25分)1.下列各式中,值为的是( )A.2sin 15°cos 15°B.cos215°-sin215°C.2sin215°D.sin215°+cos215°【解析】选B.cos215°-sin215°=cos 30°=.2.已知sin=,cos=-,则角α所在的象限是( )A.第一象限B.第二象限C.第三象限D.第四象限【解析】选C.因为sinα=2sin cos=2××=-<0,cosα=cos2-sin2=-=-<0,所以α是第三象限角.3.(2015·乐山高一检测)若tanα=3,则的值等于( )A.2B.3C.4D.6【解析】选D.==2tanα=2×3=6.【延伸探究】若本题条件不变,则的值如何?【解析】==2+2tanα=2+2×3=8.4.已知α∈R,sinα+2cosα=,则tan2α=( )A. B. C.- D.-【解析】选C.本题考查三角函数同角间的基本关系.将sinα+2cosα=两边平方可得sin2α+4sinαcosα+4cos2α=.将左边分子分母同除以cos2α得,=,解得tanα=3或-,所以tan2α==-.5.(2015·成都高一检测)在△ABC中,若||=2sin15°,||=4cos15°,且∠ABC=30°,则·的值为( )A. B.- C.2 D.-2【解析】选B.因为||=2sin15°,||=4cos15°,且∠ABC=30°,所以·=||||cos150°=2sin15°·4cos15°·=-2sin30°=-2×=-.二、填空题(每小题5分,共15分)6.(2015·合肥高一检测)已知α∈,sinα=,则tan2α=________.【解析】由α∈,sinα=,得cosα=-,tanα==-,tan2α==-.答案:-7.化简:tan70°cos10°·(tan20°-1)的结果是________.【解析】原式=·cos10°=cos10°-cos10°·=cos10°-====-1.答案:-1【误区警示】解答本题在切化弦通分后易忽视应用辅助角公式进一步化简.【补偿训练】计算cos·cos·cos=________.【解析】原式======.答案:8.已知角α的终边经过点(-8,-6),则=________.【解题指南】先利用定义求出α的三角函数,而后化简所求式即可.【解析】因为点(-8,-6)到原点的距离r==10,所以sinα==-,cosα==-.==-2cosα-2sinα=-2×-2×=.答案:三、解答题(每小题10分,共20分)9.(2015·泰州高一检测)已知α为第二象限角,且sinα=,求的值. 【解析】原式==.因为α为第二象限角,且sinα=,所以sinα+cosα≠0,cosα=-,所以原式==-.【补偿训练】已知sin sin=,α∈,求sin4α的值.【解析】因为sin sin=sin cos=,所以sin=,即cos2α=.因为α∈,所以2α∈(π,2π).所以sin2α=-=-.所以sin4α=2sin2αcos2α=2××=-.10.(2015·吉林高一检测)已知向量m=(cosα-,-1),n=(sinα,1),m与n为共线向量,且α∈.(1)求sinα+cosα的值.(2)求的值.【解析】(1)因为m与n为共线向量,所以×1-(-1)×sinα=0,即sinα+cosα=.(2)因为1+sin2α=(sinα+cosα)2=,所以sin2α=-,因为(sinα+cosα)2+(sinα-cosα)2=2,所以(sinα-cosα)2=2-=.又因为α∈,所以sinα-cosα<0,sinα-cosα=-.因此,=.(20分钟40分)一、选择题(每小题5分,共10分)1.若α∈,且sin2α+cos2α=,则tanα的值等于( )A. B. C. D.【解析】选D.由二倍角公式可得sin2α+1-2sin2α=,即-sin2α=-,sin2α=,又因为α∈,所以sinα=,即α=,所以tanα=.2.(2015·昆明高一检测)若=-,则sinα+cosα的值为( )A.-B.-C.D.【解析】选C.cos2α=sin=-sin=-sin2=-2sin·cos,==-,所以2cos=1,展开得2=1,即cosα+sinα=.二、填空题(每小题5分,共10分)3.(2015·黄冈高一检测)若sin=,则cos=________.【解析】已知sin=,且+=,则cos=sin=,故cos=2cos2-1=-.答案:-4.已知θ是第三象限角,且sin4θ+cos4θ=,那么sin2θ等于________.【解析】sin4θ+cos4θ=(sin2θ+cos2θ)2-2sin2θcos2θ=1-sin22θ,又sin4θ+cos4θ=,所以1-sin22θ=,即sin22θ=,因为θ是第三象限角.所以2kπ+π<θ<2kπ+(k∈Z),所以4kπ+2π<2θ<4kπ+3π(k∈Z),所以sin2θ>0,所以sin2θ=.答案:【延伸探究】若cos2θ=,试求sin4θ+cos4θ.【解析】因为cos2θ=,所以sin22θ=.所以sin4θ+cos4θ=1-2sin2θcos2θ=1-sin22θ=.三、解答题(每小题10分,共20分)5.已知向量a=(1+sin2x,sinx-cosx),b=(1,sinx+cosx),函数f(x)=a·b.(1)求f(x)的最大值及相应的x值;(2)若f(θ)=,求cos2的值.【解题指南】用向量数量积表示出f(x)转化成三角函数问题求解.【解析】(1)因为a=(1+sin2x,sinx-cosx),b=(1,sinx+cosx),所以f(x)=1+sin2x+sin2x-cos2x=1+sin2x-cos2x=sin+1.因此,当2x-=2kπ+,即x=kπ+(k∈Z)时,f(x)取得最大值+1.(2)由f(θ)=1+sin2θ-cos2θ及f(θ)=得sin2θ-cos2θ=,两边平方得1-sin4θ=,即sin4θ=. 因此,cos2=cos=sin4θ=.6.某同学在一次研究性学习中发现,以下五个式子的值都等于同一个常数:①sin213°+cos217°-sin13°cos17°;②sin215°+cos215°-sin15°cos15°;③sin218°+cos212°-sin18°cos12°;④sin2(-18°)+cos248°-sin(-18°)cos48°;⑤sin2(-25°)+cos255°-sin(-25°)cos55°.(1)请根据②式求出这个常数.(2)根据(1)的计算结果,将该同学的发现推广为三角恒等式,并证明你的结论.【解析】方法一:(1)计算如下:sin215°+cos215°-sin15°cos15°=1-sin30°=1-=.(2)三角恒等式为sin2α+cos2(30°-α)-sinαcos(30°-α)=.证明如下:sin2α+cos2(30°-α)-sinαcos(30°-α)=sin2α+(cos30°cosα+sin30°sinα)2-sinα(cos30°cosα+sin30°sinα)=sin2α+cos2α+sinαcosα+sin2α-sinαcosα-sin2α=sin2α+cos2α=.方法二:(1)同方法一.(2)三角恒等式为sin2α+cos2(30°-α)-sinαcos(30°-α)=.证明如下:sin2α+cos2(30°-α)-sinαcos(30°-α)=+-sinα(cos30°cosα+sin30°sinα)=-cos2α++(cos60°cos2α+sin60°·sin2α)-sinαcosα-sin2α=-cos2α++cos2α+sin2α-sin2α-(1-cos2α)=1-cos2α-+cos2α=.。
高中数学(人教A版)必修4第3章 三角恒等变换 测试题(含详解)

第三章测试(时间:120分钟,满分:150分)一、选择题(本大题共12小题,每题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.sin105°cos105°的值为( ) A.14 B .-14C.34D .-34解析 原式=12sin210°=-12sin30°=-14.答案 B2.若sin2α=14,π4<α<π2,则cos α-sin α的值是( )A.32B .-32C.34D .-34解析 (cos α-sin α)2=1-sin2α=1-14=34.又π4<α<π2, ∴cos α<sin α,cos α-sin α=-34=-32. 答案 B3.sin15°sin30°sin75°的值等于( ) A.14 B.34 C.18D.38解析 sin15°sin30°sin75° =sin15°cos15°sin30° =12sin30°sin30°=12×12×12=18. 答案 C4.在△ABC 中,∠A =15°,则 3sin A -cos(B +C )的值为( ) A. 2 B.22C.32D. 2解析 在△ABC 中,∠A +∠B +∠C =π, 3sin A -cos(B +C ) =3sin A +cos A =2(32sin A +12cos A ) =2cos(60°-A )=2cos45°= 2. 答案 A5.已知tan θ=13,则cos 2θ+12sin2θ等于( )A .-65B .-45C.45D.65解析 原式=cos 2θ+sin θcos θcos 2θ+sin 2θ=1+tan θ1+tan 2θ=65.答案 D6.在△ABC 中,已知sin A cos A =sin B cos B ,则△ABC 是( ) A .等腰三角形 B .直角三角形 C .等腰直角三角形D .等腰三角形或直角三角形解析 ∵sin2A =sin2B ,∴∠A =∠B ,或∠A +∠B =π2.答案 D 7.设a =22(sin17°+cos17°),b =2cos 213°-1,c =32,则( ) A .c <a <b B .b <c <a C .a <b <c D .b <a <c 解析 a =22sin17°+22cos17°=cos(45°-17°)=cos28°,b =2cos 213°-1=cos26°,c =32=cos30°, ∵y =cos x 在(0,90°)内是减函数, ∴cos26°>cos28°>cos30°,即b >a >c . 答案 A8.三角形ABC 中,若∠C >90°,则tan A ·tan B 与1的大小关系为( ) A .tan A ·tan B >1 B. tan A ·tan B <1 C .tan A ·tan B =1D .不能确定解析 在三角形ABC 中,∵∠C >90°,∴∠A ,∠B 分别都为锐角. 则有tan A >0,tan B >0,tan C <0. 又∵∠C =π-(∠A +∠B ),∴tan C =-tan(A +B )=-tan A +tan B1-tan A ·tan B <0,易知1-tan A ·tan B >0, 即tan A ·tan B <1. 答案 B9.函数f (x )=sin 2⎝⎛⎭⎫x +π4-sin 2⎝⎛⎭⎫x -π4是( ) A .周期为π的奇函数 B .周期为π的偶函数 C .周期为2π的奇函数 D .周期为2π的偶函数解析 f (x )=sin 2⎝⎛⎭⎫x +π4-sin 2⎝⎛⎭⎫x -π4 =cos 2⎝⎛⎭⎫π4-x -sin 2⎝⎛⎭⎫x -π4 =cos 2⎝⎛⎭⎫x -π4-sin 2⎝⎛⎭⎫x -π4 =cos ⎝⎛⎭⎫2x -π2 =sin2x . 答案 A10.y =cos x (cos x +sin x )的值域是( ) A .[-2,2] B.⎣⎢⎡⎦⎥⎤1+22,2C.⎣⎢⎡⎦⎥⎤1-22,1+22D.⎣⎡⎦⎤-12,32 解析 y =cos 2x +cos x sin x =1+cos2x 2+12sin2x=12+22⎝⎛⎭⎫22sin2x +22cos2x =12+22sin(2x +π4).∵x ∈R , ∴当sin ⎝⎛⎭⎫2x +π4=1时,y 有最大值1+22; 当sin ⎝⎛⎭⎫2x +π4=-1时,y 有最小值1-22. ∴值域为⎣⎢⎡⎦⎥⎤1-22,1+22.答案 C11.已知θ为第二象限角,sin(π-θ)=2425,则cos θ2的值为( )A.335 B.45 C .±35D .±45解析 由sin(π-θ)=2425,得sin θ=2425.∵θ为第二象限的角,∴cos θ=-725.∴cos θ2=±1+cos θ2=± 1-7252=±35. 答案 C12.若α,β为锐角,cos(α+β)=1213,cos(2α+β)=35,则cos α的值为( )A.5665 B.1665C.5665或1665D .以上都不对解析 ∵0<α+β<π,cos(α+β)=1213>0,∴0<α+β<π2,sin(α+β)=513.∵0<2α+β<π,cos(2α+β)=35>0,∴0<2α+β<π2,sin(2α+β)=45.∴cos α=cos [(2α+β)-(α+β)]=cos(2α+β)cos(α+β)+sin(2α+β)sin(α+β) =35×1213+45×513=5665. 答案 A二、填空题(本大题共4小题,每题5分,共20分.将答案填在题中横线上) 13.若1+tan α1-tan α=2012,则1cos2α+tan2α=______.解析1cos2α+tan2α=1+sin2αcos2α=sin 2α+cos 2α+2sin αcos αcos 2α-sin 2α=tan 2α+1+2tan α1-tan 2α=(tan α+1)21-tan 2α=1+tan α1-tan α=2012.答案 201214.已知cos2α=13,则sin 4α+cos 4α=________.解 ∵cos2α=13,∴sin 22α=89.∴sin 4α+cos 4α=(sin 2α+cos 2α)2-2sin 2αcos 2α =1-12sin 22α=1-12×89=59.答案 5915.sin (α+30°)+cos (α+60°)2cos α=________.解析 ∵sin(α+30°)+cos(α+60°)=sin αcos30°+cos αsin30°+cos αcos60°-sin αsin60°=cos α,∴原式=cos α2cos α=12.答案 1216.关于函数f (x )=cos(2x -π3)+cos(2x +π6),则下列命题:①y =f (x )的最大值为2; ②y =f (x )最小正周期是π;③y =f (x )在区间⎣⎡⎦⎤π24,13π24上是减函数;④将函数y =2cos2x 的图像向右平移π24个单位后,将与已知函数的图像重合.其中正确命题的序号是________. 解析 f (x )=cos ⎝⎛⎭⎫2x -π3+cos ⎝⎛⎭⎫2x +π6 =cos ⎝⎛⎭⎫2x -π3+sin ⎣⎡⎦⎤π2-⎝⎛⎭⎫2x +π6 =cos ⎝⎛⎭⎫2x -π3-sin ⎝⎛⎭⎫2x -π3 =2·⎣⎡⎦⎤22cos ⎝⎛⎭⎫2x -π3-22sin ⎝⎛⎭⎫2x -π3 =2cos ⎝⎛⎭⎫2x -π3+π4 =2cos ⎝⎛⎭⎫2x -π12, ∴y =f (x )的最大值为2,最小正周期为π,故①,②正确.又当x ∈⎣⎡⎦⎤π24,13π24时,2x -π12∈[0,π],∴y =f (x )在⎣⎡⎦⎤π24,13π24上是减函数,故③正确. 由④得y =2cos2⎝⎛⎭⎫x -π24=2cos ⎝⎛⎭⎫2x -π12,故④正确. 答案 ①②③④三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤) 17.(10分)已知向量m =⎝⎛⎭⎫cos α-23,-1,n =(sin x,1),m 与n 为共线向量,且α∈⎣⎡⎦⎤-π2,0.(1)求sin α+cos α的值; (2)求sin2αsin α-cos α的值.解 (1)∵m 与n 为共线向量, ∴⎝⎛⎭⎫cos α-23×1-(-1)×sin α=0, 即sin α+cos α=23. (2)∵1+sin2α=(sin α+cos α)2=29,∴sin2α=-79.∴(sin α-cos α)2=1-sin2α=169. 又∵α∈⎣⎡⎦⎤-π2,0,∴sin α-cos α<0. ∴sin α-cos α=-43.∴sin2αsin α-cos α=712. 18.(12分)求证:2-2sin ⎝⎛⎭⎫α+3π4cos ⎝⎛⎭⎫α+π4cos 4α-sin 4α=1+tan α1-tan α. 证明 左边=2-2sin ⎝⎛⎭⎫α+π4+π2cos ⎝⎛⎭⎫α+π4(cos 2α+sin 2α)(cos 2α-sin 2α) =2-2cos 2⎝⎛⎭⎫α+π4cos 2α-sin 2α =1-cos ⎝⎛⎭⎫2α+π2cos 2α-sin 2α=1+sin2αcos 2α-sin 2α=(sin α+cos α)2cos 2α-sin 2α=cos α+sin αcos α-sin α=1+tan α1-tan α. ∴原等式成立.19.(12分)已知函数f (x )=2cos2x +sin 2x -4cos x . (1)求f ⎝⎛⎭⎫π3的值;(2)求f (x )的最大值和最小值. 解 (1)f ⎝⎛⎭⎫π3=2cos 2π3+sin 2π3-4cos π3 =2×⎝⎛⎭⎫-12+⎝⎛⎭⎫322-4×12 =-1+34-2=-94.(2)f (x )=2(2cos 2x -1)+(1-cos 2x )-4cos x =3cos 2x -4cos x -1=3⎝⎛⎭⎫cos x -232-73, ∵x ∈R ,cos x ∈[-1,1],∴当cos x =-1时,f (x )有最大值6; 当cos x =23时,f (x )有最小值-73.20.(12分)已知cos ⎝⎛⎭⎫x -π4=210,x ∈⎝⎛⎭⎫π2,3π4. (1)求sin x 的值; (2)求sin ⎝⎛⎭⎫2x +π3的值. 解 (1)解法1:∵x ∈⎝⎛⎭⎫π2,3π4, ∴x -π4∈⎝⎛⎭⎫π4,π2, 于是sin ⎝⎛⎭⎫x -π4= 1-cos 2⎝⎛⎭⎫x -π4=7210.sin x =sin ⎣⎡⎦⎤⎝⎛⎭⎫x -π4+π4=sin ⎝⎛⎭⎫x -π4cos π4+cos ⎝⎛⎭⎫x -π4sin π4 =7210×22+210×22=45. 解法2:由题设得22cos x +22sin x =210, 即cos x +sin x =15.又sin 2x +cos 2x =1, 从而25sin 2x -5sin x -12=0, 解得sin x =45,或sin x =-35,因为x ∈⎝⎛⎭⎫π2,3π4,所以sin x =45. (2)∵x ∈⎝⎛⎭⎫π2,3π4,故 cos x =-1-sin 2x =-1-⎝⎛⎭⎫452=-35. sin2x =2sin x cos x =-2425.cos2x =2cos 2x -1=-725.∴sin ⎝⎛⎭⎫2x +π3 =sin2x cos π3+cos2x sin π3=-24+7350.21.(12分)已知函数 f (x )=4cos x sin ⎝⎛⎭⎫x +π6-1. (1)求f (x )的最小正周期;(2)求f (x )在区间⎣⎡⎦⎤-π6,π4上的最大值和最小值. 解 (1)因为f (x )=4cos x sin ⎝⎛⎭⎫x +π6-1 =4cos x ⎝⎛⎭⎫32sin x +12cos x -1=3sin2x +2cos 2x -1=3sin2x +cos2x =2sin ⎝⎛⎭⎫2x +π6所以f (x )的最小正周期为π.(2)-π6≤x ≤π4,所以-π6≤2x +π6≤2π3,当2x +π6=π2时,即x =π6,f (x )取得最大值2;当2x +π6=-π6时,即x =-π6,f (x )取得最小值-1.22.(12分)已知函数f (x )=sin ⎝⎛⎭⎫x +7π4+cos ⎝⎛⎭⎫x -3π4,x ∈R . (1)求f (x )的最小正周期和最小值;(2)已知cos(β-α)=45,cos(β+α)=-45,0<α<β≤π2,求证:[f (β)]2-2=0.解 (1)∵f (x )=sin ⎝⎛⎭⎫x +7π4-2π+sin ⎝⎛⎭⎫x -3π4+π2 =sin ⎝⎛⎭⎫x -π4+sin ⎝⎛⎭⎫x -π4=2sin ⎝⎛⎭⎫x -π4, ∴T =2π,f (x )的最小值为-2.(2)证明:由已知得cos βcos α+sin βsin α=45,cos βcos α-sin βsin α=-45.两式相加,得2cos βcos α=0, ∵0<α<β≤π2,∴β=π2.∴[f (β)]2-2=4sin 2π4-2=0.。
数学人教A版必修4单元检测:第三章三角恒等变换 含解

数学人教A 必修4第三章 三角恒等变换单元检测(时间:45分钟,满分:100分)一、选择题(本大题共8小题,每小题6分,共48分) 1.化简22ππcos sin 44αα⎛⎫⎛⎫---⎪ ⎪⎝⎭⎝⎭得到( ) A .sin 2α B .-sin 2αC .cos 2αD .-cos 2α 2.已知cos θ=13,θ∈(0,π),则3cos π22θ⎛⎫+ ⎪⎝⎭=( )A .9-B .79-C .9D .793.已知tan α=12,tan(α-β)=25-,那么tan(β-2α)的值为( )A .34-B .112- C .98- D .984.已知函数f (x )ωx +cos ωx (ω>0),y =f (x )的图象与直线y =2的两个相邻交点的距离等于π,则f (x )的单调递增区间是( )A .π5ππ,π1212k k ⎡⎤-+⎢⎥⎣⎦,k ∈Z B .5π11ππ+,π+1212k k ⎡⎤⎢⎥⎣⎦,k ∈Z C .πππ,π+36k k ⎡⎤-⎢⎥⎣⎦,k ∈ZD .π2ππ+,π+63k k ⎡⎤⎢⎥⎣⎦,k ∈Z 5.2cos10sin 20sin 70︒-︒︒的值是( )A .12B .2CD 6.22sin 2cos 1cos 2cos 2αααα⋅+等于( )A .tan αB .tan 2αC .1D .127.已知等腰三角形顶角的余弦值等于45,则这个三角形底角的正弦值为( )A B .C D .8.已知(sin x -2cos x )(3+2sin x +2cos x )=0,则2sin 22cos 1tan x xx++的值为( )A .85 B .58 C .25 D .52二、填空题(本大题共3小题,每小题6分,共18分)9.已知α,β为锐角,且cos(α+β)=sin(α-β),则tan α=________. 10.已知0<x <π2,化简:2lg cos tan 12sin 2x x x ⎛⎫⋅+- ⎪⎝⎭+πlg 4x ⎤⎛⎫- ⎪⎥⎝⎭⎦-lg(1+sin 2x )=________.11.设函数f (x )=2cos 2x x +a ,已知当x ∈π0,2⎡⎤⎢⎥⎣⎦时,f (x )的最小值为-2,则a =________.三、解答题(本大题共3小题,共34分)12.(10分)已知 3π5sin 413α⎛⎫+= ⎪⎝⎭,π3cos 45β⎛⎫-= ⎪⎝⎭,且ππ44α-<<,π3π44β<<,求cos 2(α-β)的值.13.(10分)已知πcos 4x ⎛⎫-= ⎪⎝⎭x ∈π3π,24⎛⎫⎪⎝⎭. (1)求sin x 的值; (2)求πsin 23x ⎛⎫+⎪⎝⎭的值. 14.(14分)已知函数f (x )=π3π2cos 2sin 32x x ⎛⎫⎛⎫-+- ⎪ ⎪⎝⎭⎝⎭. (1)求函数f (x )的单调减区间;(2)求函数f (x )的最大值并求f (x )取得最大值时的x 的取值集合; (3)若f (x )=65,求πcos 23x ⎛⎫- ⎪⎝⎭的值.参考答案1答案:A解析:原式=πcos 24α⎛⎫-⎪⎝⎭=πcos22α⎛⎫-⎪⎝⎭=sin 2α.2答案:C解析:3cosπ22θ⎛⎫⎪⎝⎭+=sin 2θ=2sin θcos θ=123=.3答案:B解析:tan(β-2α)=tan[(β-α)-α]=1 12 -.4答案:C解析:f(x)ωx+cos ωx=π2sin6xω⎛⎫+⎪⎝⎭,由已知得周期T=π.∴ω=2,即f(x)=π2sin26x⎛⎫+⎪⎝⎭.由ππ2π226k x-≤+(k∈Z)得ππππ36k x k-≤≤+(k∈Z).5答案:C解析:原式=2cos(3020)sin20sin70︒-︒-︒︒=2(cos30cos20sin30sin20)sin20sin70︒⋅︒+︒⋅︒-︒︒=.6答案:B解析:原式=22222 2sin2cos2sin cos2tan12cos1cos2cos sin1tanαααααααααα⋅⋅==+---=tan2α.7答案:C解析:设等腰三角形的底角为π2αα⎛⎫<<⎪⎝⎭,则其顶角为π-2α.由已知cos(π-2α)=45,∴cos 2α=45-.故1-2sin2α=45-,sin2α=910.又0<α<π2,∴sin α.8答案:C解析:由已知条件知tan x=2,原式=22cos(sin cos)2cos(1tan)1tan1tanx x x x xx x++=++=2cos2x=2221tan5x=+.9答案:1解析:∵cos(α+β)=sin(α-β),∴cos αcos β-sin αsin β=sin αcosβ-cos αsin β.∴cos α(sin β+cos β)=sin α(sin β+cos β).∵β为锐角,∴sin β+cos β≠0,∴cos α=sin α,∴tan α=1.10答案:0解析:原式=lg(sin x+cos x)+lg(sin x+cos x)-lg(sin x+cos x)2=0.11答案:-2解析:f(x)=1+cos 2x x+a=π2sin216x a⎛⎫+++⎪⎝⎭.∵x∈π0,2⎡⎤⎢⎥⎣⎦,∴ππ7π2,666x⎡⎤+∈⎢⎥⎣⎦.∴sπ1sin2,162x⎛⎫⎡⎤+∈-⎪⎢⎥⎝⎭⎣⎦,∴f (x )min =2×12⎛⎫-⎪⎝⎭+a +1=a .∴a =-2. 13答案:解:∵ππ44α-<<,∴π3ππ24α<+<.∴312cos π413α⎛⎫+=- ⎪⎝⎭. ∵π3π44β<<,∴ππ024β-<-<.∴π4sin 45β⎛⎫-==-⎪⎝⎭.∴cos(α-β)=3πcos π44αβ⎡⎤⎛⎫⎛⎫-++- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦ =3π3π16sin πsin cos πcos 444465αβαβ⎛⎫⎛⎫⎛⎫⎛⎫+⋅--+⋅-= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭.∴cos 2(α-β)=2cos 2(α-β)-1=216371321=654225⎛⎫⨯-- ⎪⎝⎭. 13答案:解:(1)∵x ∈π3π,24⎛⎫⎪⎝⎭,∴πππ,442x ⎛⎫-∈ ⎪⎝⎭,∵πcos 410x ⎛⎫-= ⎪⎝⎭∴πsin 410x ⎛⎫-=⎪⎝⎭. ∴sin x =ππsin 44x ⎡⎤⎛⎫-+ ⎪⎢⎥⎝⎭⎣⎦=ππππ4sin cos cos sin 44445x x ⎛⎫⎛⎫-+-= ⎪ ⎪⎝⎭⎝⎭.(2)由(1)可得cos x =35-,∴sin 2x =2425-,cos 2x =725-,∴πsin 23x ⎛⎫+ ⎪⎝⎭=πsin 2cos 3x +πcos 2sin 3x=. 14答案:解:f (x )=π2cos cos3x +π2sin sin 3x -2cos x=cos x x -2cos x x -cos x=π2sin 6x ⎛⎫- ⎪⎝⎭.(1)令ππ32π2ππ262k x k +≤-≤+ (k ∈Z ),∴2k π+2π3≤x ≤2k π+5π3(k ∈Z ), ∴单调递减区间为2π5π2π,2π33k k ⎡⎤++⎢⎥⎣⎦(k ∈Z ).(2)f (x )取最大值2时,ππ2π62x k -=+(k ∈Z ),则x =2k π+2π3(k ∈Z ).∴f (x )的最大值是2,取得最大值时的x 的取值集合是2π2π,3x x k k ⎧⎫+∈⎨⎬⎩⎭Z .(3)f (x )=65即π62sin 65x ⎛⎫-= ⎪⎝⎭,∴π3sin 65x ⎛⎫-= ⎪⎝⎭.∴2ππcos 212sin 36x x ⎛⎫⎛⎫--- ⎪ ⎪⎝⎭⎝⎭==23712525-⨯=.。
高中数学第三章三角恒等变换3.1.2两角和与差的正弦、余弦、正切公式练习新人教A版必修4(2021

2017-2018学年高中数学第三章三角恒等变换3.1.2 两角和与差的正弦、余弦、正切公式练习新人教A版必修4编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(2017-2018学年高中数学第三章三角恒等变换3.1.2 两角和与差的正弦、余弦、正切公式练习新人教A版必修4)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为2017-2018学年高中数学第三章三角恒等变换3.1.2 两角和与差的正弦、余弦、正切公式练习新人教A版必修4的全部内容。
3.1。
2 两角和与差的正弦、余弦、正切公式题号1234567891011得分答案一、选择题(本大题共7小题,每小题5分,共35分)1.sin 7°cos 37°-sin 83°cos 53°=()A.-错误! B.错误!C。
错误! D.-错误!2.已知α+β=错误!π,则(1+tan α)·(1+tan β)=()A.-1 B.-2C.2 D.33.已知△ABC的三个内角分别是A,B,C,若sin C=2cos Asin B,则△ABC一定是( ) A.直角三角形 B.正三角形C.等腰三角形 D.等腰直角三角形4.已知tan (α+β)=13,tan β=错误!,则tan α=( ) A 。
错误! B 。
错误!C.711D.13185.在△ABC 中,若tan B =错误!,则这个三角形是( )A .锐角三角形B .直角三角形C .等腰三角形D .等腰三角形或直角三角形6.若0<α〈错误!,-错误!<β<0,cos(错误!+α)=错误!,cos (错误!-错误!)=错误!,则cos (α+错误!)=( )A.错误! B .-错误!C.错误! D .-错误!7.已知sin 2α=错误!(错误!<2α〈π),tan(α-β)=错误!,则tan (α+β)=( )A .-2B .-1C .-错误! D.错误!二、填空题(本大题共4小题,每小题5分,共20分)8.若cos (α+β)cos α+sin (α+β)sin α=-错误!,且450°〈β<540°,则sin (60°-β)=________.9.已知sin x -sin y =-23,cos x -cos y =错误!,且x,y 均为锐角,则tan(x -y )=________.10.“在△ABC 中,cos Acos B =________+sin Asin B”,已知横线处是一个实数.甲同学在横线处填上一个实数a ,这时C 是直角;乙同学在横线处填上一个实数b ,这时C 是锐角;丙同学在横线处填上一个实数c ,这时C 是钝角.实数a,b ,c 的大小关系是________________.11.下列式子的结果为错误!的有________(填序号).①tan 25°+tan 35°+错误!tan 25°tan 35°;②2(sin 35°cos 25°+sin 55°cos 65°);③错误!.三、解答题(本大题共2小题,共25分)得分12.(12分)已知向量a=(cos α,sin α),b=(cos β,sin β),|a-b|=错误!。
人教A版数学必修四习题第三章 三角恒等变换 3.1 两角和与差的正弦、余弦和正切公式 分层训练 含答案

分层训练·进阶冲关A组基础练(建议用时20分钟)1.已知cos x=,则cos 2x= ( D )A.-B.C.-D.2.已知α∈,tan=,那么sin 2α+cos 2α的值为( A )A.-B.C.-D.3.已知α为锐角,且7sin α=2cos 2α,则sin= ( A )A. B.C. D.4.sin 20°cos10°-cos 160°sin 10°=( D )A.-B.C.-D.5.(2018·贵阳高一检测)已知sin+sin α=,则sin的值是( D )A.-B.C.D.-6.如果tan θ=2,那么1+sin θcos θ= ( B )A. B. C. D.7.计算:cos cos=.8.的值是2.9.若θ∈(0,π),且sin 2θ=-,则cos θ-sin θ=-.10.tan 20°+tan 40°+tan 20°tan40°=.11.已知tan α=,tanβ=,且α,β均为锐角,求α+2β的值.【解析】tan 2β==,tan(α+2β)==1.因为α,β均为锐角,且tan α=<1,tan β=<1,所以α,β∈,所以α+2β∈,所以α+2β=.12.已知cos α-sin α=,且π<α<,求的值.【解析】因为cos α-sin α=,所以1-2sin αcos α=,2sin αcos α=.又因为α∈,所以sin α+cos α=-=-,所以====-.B组提升练(建议用时20分钟)13.已知sin 2α=,则cos2= ( A )A. B. C. D.14.若α∈,且3cos 2α=sin,则sin 2α的值为( D )A. B.- C. D.-15.已知α是第二象限角,且sin(π-α)=,则sin 2α的值为-.16.已知0<α<,0<β<,tan(α+β)=2tan α,4tan=1-tan2,则α+β=.17.已知0<α<,sin α=.(1)求的值.(2)求tan的值.【解析】(1)由0<α<,sin α=,得cos α=,所以===20.(2)因为tan α==,所以tan===.18.已知cos=,x∈.(1)求sin x的值.(2)求sin的值.【解析】(1)因为x∈,所以x-∈.sin= =,sin x=sin=sin cos+cos sin =×+×=.(2)因为x∈,所以cos x=-=-=-,sin 2x=2sin xcos x=-,cos 2x=2cos2x-1=-.所以sin=sin 2xcos +cos 2xsin=-.C组培优练(建议用时15分钟)19.已知角θ的顶点与原点重合,始边与x轴的正半轴重合,终边在直线y=2x上,则cos 2θ= ( B )A.-B.-C.D.20.已知向量a=(3sin α,cos α),b=(2sin α,5sin α-4cos α),α∈,且a⊥b.(1)求tan α的值.(2)求cos的值.【解析】(1)因为a⊥b,所以a·b=6sin2α+5sin αcos α-4cos2α=0,由于cos α≠0, 所以6tan2α+5tan α-4=0,解得tan α=-或tan α=.因为α∈,所以tan α<0,所以tan α=-.(2)因为α∈,所以∈.由tan α=-,求得tan =-或tan =2(舍去).所以sin =,cos =-,所以cos=cos cos -sin sin=-×-×=-.关闭Word文档返回原板块。
2019_2020学年高中数学第三章三角恒等变换3.1.3二倍角的正弦、余弦、正切公式练习新人教A版必修4

3.1.3 二倍角的正弦、余弦、正切公式[A 基础达标]1.已知sin ⎝ ⎛⎭⎪⎫π4-x =35,则cos ⎝ ⎛⎭⎪⎫π2-2x 的值为( ) A.1925 B.1625 C.1425D.725解析:选D.因为sin ⎝⎛⎭⎪⎫π4-x =35,所以cos ⎝ ⎛⎭⎪⎫π2-2x =cos ⎣⎢⎡⎦⎥⎤2⎝ ⎛⎭⎪⎫π4-x=1-2sin 2⎝⎛⎭⎪⎫π4-x =725.2.已知sin α=55,则cos 4α-sin 4α的值为( ) A .-35B .-15C.15D.35解析:选 D.cos 4α-sin 4α=(cos 2α+sin 2α)(cos 2α-sin 2α)=cos 2α=1-2sin 2α=1-25=35.3.设-3π<α<-5π2,化简1-cos (α-π)2的结果是( )A .sin α2B .cos α2C .-cos α2D .-sin α2解析:选 C.因为-3π<α<-5π2,-3π2<α2<-5π4,所以1-cos (α-π)2=1+cos α2=⎪⎪⎪⎪⎪⎪cos α2=-cos α2.4.已知cos ⎝ ⎛⎭⎪⎫α-π4=-13,则sin(-3π+2α)=( ) A.79B .-79C.35 D .-35解析:选A.易得cos ⎝ ⎛⎭⎪⎫2α-π2=2cos 2⎝ ⎛⎭⎪⎫α-π4-1=2×⎝ ⎛⎭⎪⎫-132-1=-79.又cos ⎝⎛⎭⎪⎫2α-π2=cos ⎝ ⎛⎭⎪⎫π2-2α=sin 2α,所以sin(-3π+2α)=sin(π+2α)=-sin 2α=-⎝ ⎛⎭⎪⎫-79=79.故选A.5.化简tan 14°1-tan 214°·cos 28°的结果为( ) A.sin 28°2B .sin 28°C .2sin 28°D .sin 14°cos 28°解析:选A.tan 14°1-tan 214°·cos 28°=12×2tan 14°1-tan 214°·cos 28°=12tan 28°·cos 28°=sin 28°2,故选A. 6.已知sin α-2cos α=0,则tan 2α=________. 解析:由sin α-2cos α=0,得tan α=sin αcos α=2,tan 2α=2tan α1-tan 2α=2×21-22=-43. 答案:-437.已知tan α=-13,则sin 2α-cos 2α1+cos 2α=________.解析:sin 2α-cos 2α1+cos 2α=2sin αcos α-cos 2α1+2cos 2α-1 =2sin αcos α-cos 2α2cos 2α=tan α-12=-56. 答案:-568.1-2sin 20°cos 20°2cos 210°-1-cos 2160°-1=________.解析:1-2sin 20°cos 20°2cos 210°-1-cos 2160°-1=(cos 20°-sin 20°)2cos 20°-sin 20°=cos 20°-sin 20°cos 20°-sin 20°=1.答案:19.已知sin 2α=513,π4<α<π2,求sin 4α,cos 4α的值.解:由π4<α<π2,得π2<2α<π.因为sin 2α=513,所以cos 2α=-1-sin 22α=-1-⎝ ⎛⎭⎪⎫5132=-1213. 于是sin 4α=2sin 2αcos 2α=2×513×⎝ ⎛⎭⎪⎫-1213=-120169;cos 4α=1-2sin 22α=1-2×⎝ ⎛⎭⎪⎫5132=119169.10.已知π2<α<π,sin α=45.(1)求tan 2α的值; (2)求cos ⎝ ⎛⎭⎪⎫2α-π4的值.解:(1)由题意得cos α=-35,所以tan α=-43,所以tan 2α=2tan α1-tan 2α=-831-169=247. (2)因为sin α=45,所以cos 2α=1-2sin 2α=1-2×⎝ ⎛⎭⎪⎫452=-725,sin 2α=2sin α·cos α=2×45×⎝ ⎛⎭⎪⎫-35=-2425.所以cos ⎝ ⎛⎭⎪⎫2α-π4=cos 2α·cos π4+sin 2α·sin π4=⎝ ⎛⎭⎪⎫-725×22+⎝ ⎛⎭⎪⎫-2425×22=-31250. [B 能力提升]11.已知tan x =2,则tan ⎣⎢⎡⎦⎥⎤2⎝⎛⎭⎪⎫x -π4等于( )A.43 B .-43C.34D .-34解析:选C.tan ⎣⎢⎡⎦⎥⎤2⎝⎛⎭⎪⎫x -π4=tan ⎝ ⎛⎭⎪⎫2x -π2=sin ⎝ ⎛⎭⎪⎫2x -π2cos ⎝ ⎛⎭⎪⎫2x -π2=-cos 2x sin 2x =-1tan 2x=-1-tan 2x 2tan x =4-12×2=34.12.已知θ∈⎝ ⎛⎭⎪⎫π2,π,1sin θ+1cos θ=22,则sin ⎝ ⎛⎭⎪⎫2θ+π3=________. 解析:1sin θ+1cos θ=22⇒sin θ+cos θsin θcos θ=2 2 ⇒sin θ+cos θ=22sin θcos θ⇒1+sin 2θ=2sin 22θ,因为θ∈⎝ ⎛⎭⎪⎫π2,π,所以2θ∈(π,2π), 所以sin 2θ=-12,所以sin θ+cos θ<0,所以θ∈⎝⎛⎭⎪⎫3π4,π,所以2θ∈⎝ ⎛⎭⎪⎫3π2,2π,所以cos 2θ=32,所以sin ⎝⎛⎭⎪⎫2θ+π3=sin 2θ·cos π3+sin π3cos 2θ=12.答案:1213.已知sin ⎝ ⎛⎭⎪⎫π4-x =513,0<x <π4,求cos 2x cos ⎝ ⎛⎭⎪⎫π4+x 的值.解:因为0<x <π4,所以0<π4-x <π4.又因为sin ⎝⎛⎭⎪⎫π4-x =513, 所以cos ⎝ ⎛⎭⎪⎫π4-x =1213.因为cos 2x =sin ⎝ ⎛⎭⎪⎫π2-2x=2sin ⎝ ⎛⎭⎪⎫π4-x cos ⎝ ⎛⎭⎪⎫π4-x =2sin ⎣⎢⎡⎦⎥⎤π2-⎝ ⎛⎭⎪⎫π4+x cos ⎝ ⎛⎭⎪⎫π4-x=2cos ⎝⎛⎭⎪⎫π4+x cos ⎝ ⎛⎭⎪⎫π4-x ,所以cos 2x cos ⎝ ⎛⎭⎪⎫π4+x =2cos ⎝ ⎛⎭⎪⎫π4-x =2413.14.(选做题)已知sin x 2-2cos x2 =0.(1)求tan x 的值;(2)求cos 2xcos ⎝ ⎛⎭⎪⎫5π4+x sin (π+x )的值.解:(1)由sin x 2-2cos x2=0,知cos x 2≠0,所以tan x2=2,所以tan x =2tanx21-tan 2 x 2=2×21-22=-43.(2)由(1)知tan x =-43,所以cos 2xcos ⎝ ⎛⎭⎪⎫5π4+x sin (π+x )=cos 2x -cos ⎝ ⎛⎭⎪⎫π4+x (-sin x )=cos 2x -sin 2x⎝ ⎛⎭⎪⎫22cos x -22sin x sin x=(cos x -sin x )(cos x +sin x )22(cos x -sin x )sin x=2×cos x +sin xsin x=2×1+tan x tan x =24.。
人教版高一数学必修四测试题(含详细答案)

高一数学试题(必修4)(特别适合按14523顺序的省份)必修4 第一章三角函数(1)一、选择题:1.已知A={第一象限角},B={锐角},C={小于90°的角},那么A、B、C关系是()A.B=A∩C B.B∪C=C C.AC D.A=B=C2 等于()A B C D3.已知的值为()A.-2 B.2 C.D.-4.下列函数中,最小正周期为π的偶函数是()A.y=sin2xB.y=cos C .sin2x+cos2x D. y=5 若角的终边上有一点,则的值是()A B C D6.要得到函数y=cos()的图象,只需将y=sin的图象()A.向左平移个单位 B.同右平移个单位C.向左平移个单位 D.向右平移个单位7.若函数y=f(x)的图象上每一点的纵坐标保持不变,横坐标伸长到原来的2倍,再将整个图象沿x轴向左平移个单位,沿y轴向下平移1个单位,得到函数y=sinx的图象则y=f(x)是()A.y= B.y=C.y=D.8. 函数y=sin(2x+)的图像的一条对轴方程是()A.x=-B. x=- C .x=D.x=9.若,则下列结论中一定成立的是()A. B. C. D.10.函数的图象()A.关于原点对称 B.关于点(-,0)对称 C.关于y轴对称 D.关于直线x=对称11.函数是()A.上是增函数 B.上是减函数C.上是减函数D.上是减函数12.函数的定义域是()A.B.C. D.二、填空题:13. 函数的最小值是 .14 与终边相同的最小正角是_______________15. 已知则 .16 若集合,,则=_______________________________________三、解答题:17.已知,且.a)求sinx、cosx、tanx的值.b)求sin3x – cos3x的值.18 已知,(1)求的值(2)求的值19. 已知α是第三角限的角,化简20.已知曲线上最高点为(2,),由此最高点到相邻的最低点间曲线与x轴交于一点(6,0),求函数解析式,并求函数取最小值x的值及单调区间必修4 第一章三角函数(2)一、选择题:1.已知,则化简的结果为()A. B. C. D. 以上都不对2.若角的终边过点(-3,-2),则( )A.sin tan>0 B.cos tan>0C.sin cos>0 D.sin cot>03 已知,,那么的值是()A B C D4.函数的图象的一条对称轴方程是()A. B. C. D.5.已知,,则tan2x= ( ) A. B. C. D.6.已知,则的值为()A. B. 1 C. D. 2 7.函数的最小正周期为()A.1 B. C. D.8.函数的单调递增区间是()A. B.C. D.9.函数,的最大值为()A.1 B. 2 C. D.10.要得到的图象只需将y=3sin2x的图象()A.向左平移个单位B.向右平移个单位C.向左平移个单位 D.向右平移个单位11.已知sin(+α)=,则sin(-α)值为()A. B. — C. D. —12.若,则()A. B. C. D.二、填空题13.函数的定义域是14.的振幅为初相为15.求值:=_______________16.把函数先向右平移个单位,然后向下平移2个单位后所得的函数解析式为________________________________三、解答题17 已知是关于的方程的两个实根,且,求的值18.已知函数,求:(1)函数y的最大值,最小值及最小正周期;(2)函数y的单调递增区间19.已知是方程的两根,且,求的值20.如下图为函数图像的一部分(1)求此函数的周期及最大值和最小值(2)求与这个函数图像关于直线对称的函数解析式必修4 第三章三角恒等变换(1)一、选择题:1.的值为 ( )A 0BC D2.,,,是第三象限角,则()A B C D3.设则的值是( )A B C D4. 已知,则的值为()A B C D5.都是锐角,且,,则的值是()A B C D6. 且则cos2x的值是()A B C D7.在中,的取值域范围是 ( )A B C D8. 已知等腰三角形顶角的余弦值等于,则这个三角形底角的正弦值为()A B C D9.要得到函数的图像,只需将的图像()A、向右平移个单位B、向右平移个单位C、向左平移个单位D、向左平移个单位10. 函数的图像的一条对称轴方程是()A、 B、 C、 D、11.若是一个三角形的最小内角,则函数的值域是( )A B C D12.在中,,则等于 ( )A B C D二、填空题:13.若是方程的两根,且则等于14. .在中,已知tanA ,tanB是方程的两个实根,则15. 已知,则的值为16. 关于函数,下列命题:①若存在,有时,成立;②在区间上是单调递增;③函数的图像关于点成中心对称图像;④将函数的图像向左平移个单位后将与的图像重合.其中正确的命题序号(注:把你认为正确的序号都填上)三、解答题:17. 化简18. 求的值.19. 已知α为第二象限角,且sinα=求的值.20.已知函数,求(1)函数的最小值及此时的的集合。
人教A版数学必修四培优教程练习:第3章 三角恒等变换3-1-2-1a

A 级:基础巩固练一、选择题1.化简cos(x +y )sin y -sin(x +y )cos y 等于( ) A .sin(x +2y ) B .-sin(x +2y ) C .sin x D .-sin x答案 D解析 cos(x +y )sin y -sin(x +y )cos y =sin[y -(x +y )]=-sin x . 2.已知cos ⎝⎛⎭⎪⎫α-π6+sin α=435,则sin ⎝⎛⎭⎪⎫α+7π6的值为( )A .-235B .235C .-45D .45答案 C解析 cos ⎝ ⎛⎭⎪⎫α-π6+sin α=32cos α+12sin α+sin α=32cos α+32sin α=3⎝ ⎛⎭⎪⎫12cos α+32sin α=3sin ⎝ ⎛⎭⎪⎫α+π6=435, ∴sin ⎝⎛⎭⎪⎫α+π6=45,∴sin ⎝ ⎛⎭⎪⎫α+7π6=-sin ⎝ ⎛⎭⎪⎫α+π6=-45.3.设tan α,tan β是方程x 2-3x +2=0的两根,则tan(α+β)的值为( )A .-3B .-1C .1D .3答案 A解析 由根与系数的关系可知tan α+tan β=3, tan αtan β=2,tan(α+β)=tan α+tan β1-tan αtan β=31-2=-3.4.函数f (x )=sin x -cos ⎝ ⎛⎭⎪⎫x +π6的值域为( )A .[-2,2]B .[-3,3]C .[-1,1]D .⎣⎢⎡⎦⎥⎤-32,32答案 B解析 因为f (x )=sin x -cos ⎝ ⎛⎭⎪⎫x +π6 =sin x -cos x cos π6+sin x sin π6 =sin x -32cos x +12sin x=3⎝ ⎛⎭⎪⎫32sin x -12cos x=3sin ⎝ ⎛⎭⎪⎫x -π6(x ∈R ),所以f (x )的值域为[-3,3].5.△ABC 中,若0<tan A ·tan B <1,则△ABC 是( ) A .锐角三角形 B .钝角三角形 C .直角三角形 D .无法确定答案 B解析 ∵0<tan A ·tan B <1, ∴tan A >0,tan B >0,tan(A +B )=-tan C =tan A +tan B1-tan A ·tan B >0.∴tan C <0,又∵0<C <π,∴π2<C <π. 二、填空题6.cos23°+sin15°sin8°sin23°-cos15°sin8°的值为________.答案 2+ 3解析 原式=cos (15°+8°)+sin15°sin8°sin (15°+8°)-cos15°sin8°=cos15°cos8°sin15°cos8° =cos15°sin15°=cos (45°-30°)sin (45°-30°)=22⎝⎛⎭⎪⎫32+1222⎝⎛⎭⎪⎫32-12=2+ 3. 7.若点P (-3,4)在角α的终边上,点Q (-1,-2)在角β的终边上,则sin(α-β)=________,cos(α+β)=________.答案 -255 11525解析 因为点P (-3,4)在角α的终边上,所以r =5, 故sin α=45,cos α=-35.又因为点Q (-1,-2)在角β的终边上, 所以r ′=5,故sin β=-255,cos β=-55,则sin(α-β)=sin α·cos β-cos α·sin β=45×⎝ ⎛⎭⎪⎫-55-⎝ ⎛⎭⎪⎫-35×⎝ ⎛⎭⎪⎫-255=-255.cos(α+β)=cos αcos β-sin αsin β=⎝ ⎛⎭⎪⎫-35×⎝ ⎛⎭⎪⎫-55-45×⎝⎛⎭⎪⎫-255=11525.8.在△ABC 中,A =120°,则sin B +sin C 的最大值为________. 答案 1解析 由A =120°,A +B +C =180°,得sin B +sin C =sin B +sin(60°-B )=32cos B +12sin B =sin(60°+B ).显然当B =30°时,sin B +sin C 取得最大值1.三、解答题 9.化简下列各式:(1)sin ⎝ ⎛⎭⎪⎫x +π3+2sin ⎝ ⎛⎭⎪⎫x -π3-3cos ⎝ ⎛⎭⎪⎫2π3-x ; (2)sin (2α+β)sin α-2cos(α+β).解 (1)原式=sin x cos π3+cos x sin π3+2sin x cos π3-2cos x sin π3-3cos 2π3cos x -3sin 2π3sin x=12sin x +32cos x +sin x -3cos x +32cos x -32sin x=⎝ ⎛⎭⎪⎫12+1-32sin x +⎝ ⎛⎭⎪⎫32-3+32cos x =0.(2)原式=sin[(α+β)+α]-2cos (α+β)sin αsin α =sin (α+β)cos α-cos (α+β)sin αsin α =sin[(α+β)-α]sin α =sin βsin α.10.(1)已知sin α=35,cos β=-513,且α为第一象限角,β为第二象限角,求sin(α+β)和sin(α-β)的值;(2)求值:3sin π12+cos π12;(3)在△ABC 中,tan B +tan C +3tan B tan C =3,且3tan A +3tan B +1=tan A tan B ,判断△ABC 的形状.解 (1)因为α为第一象限角,β为第二象限角, sin α=35,cos β=-513,所以cos α=45,sin β=1213,∴sin(α+β)=sin αcos β+cos αsin β=35×⎝⎛⎭⎪⎫-513+45×1213=3365,sin(α-β)=sin αcos β-cos αsin β=35×⎝ ⎛⎭⎪⎫-513-45×1213=-6365.(2)原式=2⎝ ⎛⎭⎪⎫32sin π12+12cos π12=2⎝ ⎛⎭⎪⎫sin π12cos π6+cos π12sin π6 =2sin ⎝⎛⎭⎪⎫π12+π6=2sin π4= 2.(3)tan A =tan[180°-(B +C )]=-tan(B +C )=tan B +tan Ctan B tan C -1=3-3tan B tan Ctan B tan C -1=-3,而0°<A <180°,∴A =120°.tan C =tan[180°-(A +B )]=-tan(A +B )=tan A +tan Btan A tan B -1=tan A +tan B 3tan A +3tan B=33,而0°<C <180°,∴C =30°,∴B =180°-120°-30°=30°,∴△ABC 是顶角为120°的等腰三角形.B 级:能力提升练1.在△ABC 中,3sin A +4cos B =6,3cos A +4sin B =1,则C 的大小为( )A .π6B .5π6C .π6或5π6D .π3或2π3答案 A解析 由已知可得(3sin A +4cos B )2+(3cos A +4sin B )2=62+12,即9+16+24sin(A +B )=37.所以sin(A +B )=12.所以在△ABC 中sin C =12,所以C =π6或C =5π6.又1-3cos A =4sin B >0,所以cos A <13.又13<12,所以A >π3,所以C <2π3. 所以C =5π6不符合题意,所以C =π6.2.已知0<α<π2<β<π,sin ⎝ ⎛⎭⎪⎫α-π3=4-3310,cos(β-α)=210. (1)求sin α的值; (2)求β的值.解 (1)∵0<α<π2<β<π,∴-π3<α-π3<π6,0<β-α<π. 由sin ⎝ ⎛⎭⎪⎫α-π3=4-3310,cos(β-α)=210得 cos ⎝ ⎛⎭⎪⎫α-π3=3+4310,sin(β-α)=7210. 于是sin α=sin ⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫α-π3+π3=sin ⎝ ⎛⎭⎪⎫α-π3cos π3+cos ⎝ ⎛⎭⎪⎫α-π3sin π3 =4-3310×12+3+4310×32=45.(2)由(1)知sin α=45且0<α<π2,所以cos α=35.于是cos β=cos[(β-α)+α]=cos(β-α)cos α-sin(β-α)sin α=210×35-7210×45=-22,因为π2<β<π,所以β=3π4.由Ruize收集整理。
人教版高一数学必修四测试题(含详细答案)

高一数学试题(必修4)(特殊适合按14523依次的省份)必修4第一章三角函数(1)一、选择题:l已知A={第一象限角}'B={锐角}'C={小千90°的角},那么A、B、C关系是()A. B=Anc2.✓sin2120° 等千忒i A土——- B. B U C=CC. A宝D. A=B=C()五2B五2c1_2n i sin a —2cosa3已知=-5, 那么tana的值为3 sin a + 5 c os aA.—2B. 2C .23164. 下列函数中,最小正周期为兀的偶函数是A.y =sin 2xXB y =c s—2A , 4✓3B -4✓3C .s in 2x+c s 2x 5, 若角600°的终边上有一点(-4,a),则a的值是()23 D.16( )1-tan 2 xD. y =1 + tan2 x()c .土4✓3D✓3X冗X6. 要得到函数y=co s (—-—)的图象,只需将y=sin —的图象( )2 4 2冗冗A. 向左平移—个单位B 同右平移—个单位22冗冗C. 向左平移—个单位D. 向右平移—个单位4 47. 若函数y=f (x)的图象上每一点的纵坐标保持不变,横坐标伸长到原来的2倍,再将冗l整个图象沿x轴向左平移—个单位,沿y轴向下平移l个单位,得到函数y =-sin x 的图象22测y=f (x)是()l 兀A. y=—sin(2x+—) +12 2 l 兀C.y =—sin(2x+—) +1 2 4l 兀B.y =—sin(2x -—) +12 2 l 冗D. —sin(2x -—) +12 45兀8. 函数y=sin (2x+—-)的图像的一条对方程是2冗A.x=-— 冗B. x =-— 冗_8__ xc 19. 若sin0·cos0=—,则下列结论中肯定成立的是A .si n 0 = ✓22B. 五sin 0 = -—C. si n 0+cos0 = 1(三4(_ x D))冗10 函数y = 2si n (2x+—)的图象3冗A. 关千原点对称B.关千(——,0)对称c.6 冗11 函数y =s n (x+—)X E R 是2 兀冗A . [-—,—]上是增函数2 2C. [-冗OJ 上是减函数12函数y =✓2c o sx l的定义域是A . [2k三三}k EZ)C. [2k冗十f,2k冗+气}k EZ)D. si n 0—cos0=0()冗关千y 对称D .关千直线x =—对称6( )B. [O五上是减函数D. [-冗冗上是减函数()B. [2k 二,2k 兀三}k E Z ) 6 6D. [2k 兀一气,2k兀+气}k E Z ) 二、填空题:冗冗213. 函数y = cos (x -—) (x E [—,—兀)的最小值是8 6 314。
高中数学第三章三角恒等变换3.1.4二倍角的正弦、余弦、正切公式练习(含解析)新人教A版必修4

高中数学第三章三角恒等变换3.1.4二倍角的正弦、余弦、正切公式练习(含解析)新人教A 版必修41.设α是第四象限角,已知sin α=-35,则sin2α,cos2α和tan2α的值分别为( )A .-2425,725,-247B .2425,725,247C .-2425,-725,247D .2425,-725,-247答案 A解析 因为α是第四象限角,且sin α=-35,所以cos α=45,所以sin2α=2sin αcos α=-2425,cos2α=2cos 2α-1=725,tan2α=sin2αcos2α=-247.2.已知sin ⎝ ⎛⎭⎪⎫α+π4=7210,cos2α=725,则cos α=( )A .45B .-45C .-35D .35 答案 A解析 ∵sin ⎝ ⎛⎭⎪⎫α+π4=7210,∴22sin α+22cos α=7210,即sin α+cos α=75,∵cos2α=725,∴cos 2α-sin 2α=725,即(cos α-sin α)(cos α+sin α)=725,∴cos α-sin α=15,可得cos α=45,故选A .3.1-tan 215°2t an15°等于( )A . 3B .33C .1D .-1 答案 A解析 原式=12tan15°1-tan 215°=1tan30°=3.4.cos 275°+cos 215°+cos75°cos15°的值等于( ) A .62 B .32 C .54 D .1+34答案 C解析 原式=sin 215°+cos 215°+sin15°cos15°=1+12sin30°=1+14=54.5.sin65°cos25°+cos65°sin25°-tan 222.5°2tan22.5°等于( )A .12 B .1 C .3 D .2 答案 B解析 原式=sin90°-tan 222.5°2tan22.5°=1-tan 222.5°2tan22.5°=1tan45°=1.6.3-sin70°2-cos 210°的值是________. 答案 2 解析3-sin70°2-cos 210°=3-sin70°2-1+cos20°2=23-cos20°3-cos20°=2. 7.若cos(75°-α)=13,则cos(30°+2α)=________.答案 79解析 由cos(75°-α)=13,得cos(150°-2α)=2cos 2(75°-α)-1=-79,则cos(30°+2α)=cos[180°-(150°-2α)] =-cos(150°-2α)=79.8.若α∈2,2,则1+sin α+1-sin α的值为( )A .2cos α2B .-2cos α2 C .2sin α2 D .-2sin α2 答案 D解析 ∵α∈5π2,7π2,∴α2∈5π4,7π4,∴原式=sin α2+cos α2+sin α2-cos α2=-sin α2-cos α2-sin α2+cos α2=-2sin α2. 9.已知角α在第一象限且cos α=35,则1+2cos2α-π4sin α+π2等于( )A .25B .75C .145D .-25 答案 C解析 ∵cos α=35且α在第一象限,∴sin α=45.∴cos2α=cos 2α-sin 2α=-725,sin2α=2sin αcos α=2425,∴原式=1+2cos2αcos π4+sin2αsinπ4cos α=1+cos2α+sin2αcos α=145.10.已知sin x 2-2cos x2=0.(1)求tan x 的值;(2)求cos2xcos ⎝ ⎛⎭⎪⎫5π4+x sin π+x 的值.解 (1)由sin x 2-2cos x 2=0,知cos x2≠0,∴tan x2=2,∴tan x =2tanx21-tan 2x 2=2×21-22=-43.(2)由(1),知tan x =-43,∴cos2xcos ⎝ ⎛⎭⎪⎫5π4+x sin π+x =cos2x-cos ⎝ ⎛⎭⎪⎫π4+x -sin x=cos 2x -sin 2x⎝ ⎛⎭⎪⎫22cos x -22sin x sin x=cos x -sin x cos x +sin x22cos x -sin x sin x=2×cos x +sin x sin x =2×1+tan x tan x =24.对应学生用书P90一、选择题1.12-sin 215°=( ) A .64 B .6-24 C .32 D .34答案 D解析 原式=12-1-cos 2×15°2=cos30°2=34.2.函数f (x )=2sin 2⎝ ⎛⎭⎪⎫x 2+π4-1是( )A .最小正周期为π的奇函数B .最小正周期为π的偶函数C .最小正周期为2π的奇函数D .最小正周期为2π的偶函数 答案 C解析 ∵f (x )=2sin 2⎝ ⎛⎭⎪⎫x 2+π4-1=-cos2x 2+π4=-cos ⎝ ⎛⎭⎪⎫x +π2=sin x ,∴函数f (x )=2sin 2⎝ ⎛⎭⎪⎫x 2+π4-1是最小正周期为2π的奇函数.3.已知cos π4-x =35,则sin2x 的值为( )A .1825B .725C .-725D .-1625 答案 C解析 因为sin2x =cos π2-2x =cos2π4-x =2cos 2π4-x -1,所以sin2x =2×352-1=1825-1=-725.4.已知cos2θ=23,则sin 4θ+cos 4θ的值为( ) A .1318 B .1118 C .79 D .-1 答案 B解析 sin 4θ+cos 4θ=(sin 2θ+cos 2θ)2-2sin 2θcos 2θ =1-12sin 22θ=1-12(1-cos 22θ)=1118.5.若cos2αsin α-π4=-22,则cos α+sin α的值为( )A .-72 B .-12C .12D .72 答案 C解析 cos2αsin α-π4=cos 2α-sin 2α22sin α-cos α=cos α+sin αcos α-sin α22sin α-cos α=-2(cos α+sin α)=-22. ∴sin α+cos α=12.二、填空题6.已知tan x +π4=2,则tan xtan2x 的值为________.答案 49解析 ∵tan x +π4=2,∴tan x +11-tan x =2,∴tan x =13.∴tan x tan2x =tan x 2tan x 1-tan 2x=1-tan 2x2=1-192=49. 7.已知sin 22α+sin2αcos α-cos2α=1,α∈0,π2,则 α=________.答案π6解析 ∵sin 22α+sin2αcos α-(cos2α+1)=0. ∴4sin 2αcos 2α+2sin αcos 2α-2cos 2α=0. ∵α∈0,π2.∴2cos 2α>0.∴2sin 2α+sin α-1=0.∴sin α=12(sin α=-1舍).∴α=π6.8.设a =12cos7°-32sin7°,b =2cos12°·cos78°,c =1-cos50°2,则a ,b ,c 的大小关系是________.答案 c >b >a解析 a =12cos7°-32sin7°=sin30°cos7°-cos30°sin7°=sin(30°-7°)=sin23°,b =2cos12°cos78°=2sin12°·cos12°=sin24°,c =1-cos50°2=1-1-2sin 225°2=sin 225°=sin25°,所以c >b >a .三、解答题9.求下列各式的值:(1)sin π8sin 3π8;(2)cos 215°-cos 275°;(3)2cos25π12-1;(4)tan30°1-tan 230°; (5)求s in10°sin30°sin50°sin70°的值. 解 (1)∵sin 3π8=sin ⎝ ⎛⎭⎪⎫π2-π8=cos π8,∴sin π8sin 3π8=sin π8cos π8=12·2sin π8cos π8=12sin π4=24.(2)∵cos 275°=cos 2(90°-15°)=sin 215°, ∴cos 215°-cos 275°=cos 215°-sin 215°=cos30°=32. (3)2cos25π12-1=cos 5π6=-32. (4)tan30°1-tan 230°=12×2tan30°1-tan 230°=12tan60°=32. (5)解法一:∵sin10°sin50°sin70°=sin20°sin50°sin70°2cos10°=sin20°cos20°sin50°2cos10°=sin40°sin50°4cos10°=sin40°cos40°4cos10°=sin80°8cos10°=18,∴sin10°sin30°sin50°sin70°=116.解法二:sin10°sin30°sin50°sin70°=12cos20°cos40°cos80°=2sin20°cos20°cos40°cos80°4sin20°=sin40°cos40°cos80°4sin20°=sin80°cos80°8sin20°=116·sin160°sin20°=116.10.已知α为钝角,且tan π4-α=2.(1)求tan α的值;(2)求sin2αcos α-sin αcos2α的值.解 (1)tan π4-α=1-tan α1+tan α,所以1-tan α1+tan α=2,1-tan α=2+2tan α,所以tan α=-13.(2)sin2αcos α-sin αcos2α=2sin αcos 2α-sin αcos2α=sin α2cos 2α-1cos2α=sin αcos2αcos2α=sin α.因为tan α=-13,所以cos α=-3sin α,又sin 2α+cos 2α=1,所以sin 2α=110,又α为钝角,所以sin α=1010, 所以sin2αcos α-sin αcos2α=1010.。
5.5.2三角恒等变换(典例精讲)-【巅峰课堂】2021-2022学年高一数学同步精讲+检测(人教A
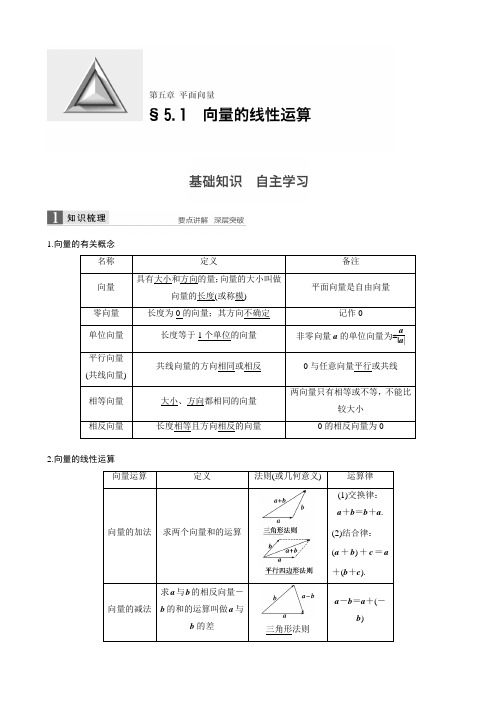
1.向量的有关概念名称 定义备注向量 具有大小和方向的量;向量的大小叫做向量的长度(或称模) 平面向量是自由向量零向量 长度为0的向量;其方向不确定记作0单位向量 长度等于1个单位的向量非零向量a 的单位向量为±a|a |平行向量(共线向量) 共线向量的方向相同或相反0与任意向量平行或共线 相等向量 大小、方向都相同的向量 两向量只有相等或不等,不能比较大小 相反向量长度相等且方向相反的向量0的相反向量为02.向量的线性运算向量运算定义法则(或几何意义)运算律 向量的加法求两个向量和的运算(1)交换律: a +b =b +a .(2)结合律: (a +b )+c =a +(b +c ).向量的减法 求a 与b 的相反向量-b 的和的运算叫做a 与b 的差三角形法则a -b =a +(-b )数乘向量求实数λ与向量a 的积的运算(1)|λa |=|λ||a |; (2)当λ>0时,λa 的方向与a 的方向相同;当λ<0时,λa 的方向与a 的方向相反;当λ=0或a =0时,λa =0(1)(λ+μ)a =λa+μa ; (2)λ(μa )=(λμ)a ; (3)λ(a +b )=λa+λb3.平行向量基本定理如果a =λb ,则a ∥b ;反之,如果a ∥b ,且b ≠0,则一定存在唯一一个实数λ,使a =λb . 【思考辨析】判断下面结论是否正确(请在括号中打“√”或“×”)(1)向量与有向线段是一样的,因此可以用有向线段来表示向量.( × ) (2)|a |与|b |是否相等与a ,b 的方向无关.( √ ) (3)若a ∥b ,b ∥c ,则a ∥c .( × )(4)向量AB →与向量CD →是共线向量,则A ,B ,C ,D 四点在一条直线上.( × ) (5)当两个非零向量a ,b 共线时,一定有b =λa ,反之成立.( √ ) (6)△ABC 中,D 是BC 中点,则AD →=12(AC →+AB →).( √ )1.给出下列命题:①零向量的长度为零,方向是任意的;②若a ,b 都是单位向量,则a =b ;③向量AB →与BA →相等.则所有正确命题的序号是( ) A.① B.③ C.①③ D.①②答案 A解析 根据零向量的定义可知①正确;根据单位向量的定义可知,单位向量的模相等,但方向不一定相同,故两个单位向量不一定相等,故②错误;向量AB →与BA →互为相反向量,故③错误. 2.如图所示,向量a -b 等于( )A.-4e 1-2e 2B.-2e 1-4e 2C.e 1-3e 2D.3e 1-e 2解析 由题图可得a -b =BA →=e 1-3e 2.3.(2015·课标全国Ⅰ)设D 为△ABC 所在平面内一点,BC →=3CD →,则( ) A.AD →=-13AB →+43AC →B.AD →=13AB →-43AC →C.AD →=43AB →+13AC →D.AD →=43AB →-13AC →答案 A解析 ∵BC →=3CD →,∴AC →-AB →=3(AD →-AC →), 即4AC →-AB →=3AD →,∴AD →=-13AB →+43AC →.4.(教材改编)已知▱ABCD 的对角线AC 和BD 相交于O ,且OA →=a ,OB →=b ,则DC →=________,BC →=________(用a ,b 表示). 答案 b -a -a -b解析 如图,DC →=AB →=OB →-OA →=b -a ,BC →=OC →-OB →=-OA →-OB →=-a -b .5.已知a 与b 是两个不共线向量,且向量a +λb 与-(b -3a )共线,则λ=________. 答案 -13解析 由已知得a +λb =-k (b -3a ),∴⎩⎪⎨⎪⎧λ=-k ,3k =1.解得⎩⎨⎧λ=-13,k =13.题型一 平面向量的概念例1 下列命题中,正确的是________.(填序号) ①有向线段就是向量,向量就是有向线段;②向量a 与向量b 平行,则a 与b 的方向相同或相反; ③向量AB →与向量CD →共线,则A 、B 、C 、D 四点共线; ④两个向量不能比较大小,但它们的模能比较大小.解析 ①不正确,向量可以用有向线段表示,但向量不是有向线段,有向线段也不是向量;②不正确,若a 与b 中有一个为零向量,零向量的方向是不确定的,故两向量方向不一定相同或相反; ③不正确,共线向量所在的直线可以重合,也可以平行;④正确,向量既有大小,又有方向,不能比较大小;向量的模均为实数,可以比较大小.思维升华 (1)相等向量具有传递性,非零向量的平行也具有传递性.(2)共线向量即为平行向量,它们均与起点无关.(3)向量可以平移,平移后的向量与原向量是相等向量.解题时,不要把它与函数图象的移动混为一谈.(4)非零向量a 与a |a |的关系:a|a |是与a 同方向的单位向量.设a 0为单位向量,①若a 为平面内的某个向量,则a =|a |a 0;②若a 与a 0平行,则a =|a |a 0;③若a 与a 0平行且|a |=1,则a =a 0.上述命题中,假命题的个数是( ) A.0 B.1 C.2 D.3答案 D解析 向量是既有大小又有方向的量,a 与|a |a 0的模相同,但方向不一定相同,故①是假命题;若a 与a 0平行,则a 与a 0的方向有两种情况:一是同向,二是反向,反向时a =-|a |a 0,故②③也是假命题.综上所述,假命题的个数是3. 题型二 平面向量的线性运算 命题点1 向量的线性运算例2 (1)设D ,E ,F 分别为△ABC 的三边BC ,CA ,AB 的中点,则EB →+FC →等于( ) A.BC → B.12AD → C.AD →D.12BC → (2)在△ABC 中,AB →=c ,AC →=b ,若点D 满足BD →=2DC →,则AD →等于( ) A.23b +13c B.53c -23b C.23b -13c D.13b +23c 答案 (1)C (2)A解析 (1)EB →+FC →=12(AB →+CB →)+12(AC →+BC →)=12(AB →+AC →)=AD →. (2)∵BD →=2DC →,∴AD →-AB →=BD →=2DC →=2(AC →-AD →), ∴3AD →=2AC →+AB →,∴AD →=23AC →+13AB →=23b +13c .命题点2 根据向量线性运算求参数例3 (1)在△ABC 中,已知D 是AB 边上的一点,若AD →=2DB →,CD →=13CA →+λCB →,则λ等于( )A.23B.13C.-13D.-23(2)在△ABC 中,点D 在线段BC 的延长线上,且BC →=3CD →,点O 在线段CD 上(与点C ,D 不重合),若AO →=xAB →+(1-x )AC →,则x 的取值范围是( ) A.⎝⎛⎭⎫0,12 B.⎝⎛⎭⎫0,13 C.⎝⎛⎭⎫-12,0 D.⎝⎛⎭⎫-13,0 答案 (1)A (2)D 解析 (1)∵AD →=2DB →, 即CD →-CA →=2(CB →-CD →), ∴CD →=13CA →+23CB →,∴λ=23.(2)设CO →=yBC →, ∵AO →=AC →+CO →=AC →+yBC →=AC →+y (AC →-AB →) =-yAB →+(1+y )AC →.∵BC →=3CD →,点O 在线段CD 上(与点C ,D 不重合), ∴y ∈⎝⎛⎭⎫0,13, ∵AO →=xAB →+(1-x )AC →, ∴x =-y ,∴x ∈⎝⎛⎭⎫-13,0. 思维升华 平面向量线性运算问题的常见类型及解题策略 (1)向量加法或减法的几何意义.向量加法和减法均适合三角形法则.(2)求已知向量的和.一般共起点的向量求和用平行四边形法则;求差用三角形法则;求首尾相连向量的和用三角形法则.(3)求参数问题可以通过研究向量间的关系,通过向量的运算将向量表示出来,进行比较求参数的值.如图,一直线EF 与平行四边形ABCD 的两边AB ,AD 分别交于E ,F两点,且交对角线AC 于K ,其中,AE →=25AB →,AF →=12AD →,AK →=λAC →,则λ的值为( ) A.29 B.27 C.25 D.23答案 A解析 ∵AE →=25AB →,AF →=12AD →,∴AB →=52AE →,AD →=2AF →.由向量加法的平行四边形法则可知, AC →=AB →+AD →, ∴AK →=λAC →=λ(AB →+AD →) =λ⎝⎛⎭⎫52AE →+2AF → =52λAE →+2λAF →, 由E ,F ,K 三点共线,可得λ=29,故选A.题型三 平行向量基本定理的应用 例4 设两个非零向量a 与b 不共线,(1)若AB →=a +b ,BC →=2a +8b ,CD →=3(a -b ),求证:A 、B 、D 三点共线; (2)试确定实数k ,使k a +b 和a +k b 共线.(1)证明 ∵AB →=a +b ,BC →=2a +8b ,CD →=3(a -b ), ∴BD →=BC →+CD →=2a +8b +3(a -b ) =2a +8b +3a -3b =5(a +b )=5AB →. ∴AB →、BD →共线,又∵它们有公共点B , ∴A 、B 、D 三点共线.(2)解 ∵k a +b 和a +k b 共线, ∴存在实数λ,使k a +b =λ(a +k b ), 即k a +b =λa +λk b .∴(k -λ)a =(λk -1)b . ∵a 、b 是两个不共线的非零向量, ∴k -λ=λk -1=0,∴k 2-1=0.∴k =±1.思维升华 (1)证明三点共线问题,可用向量共线解决,但应注意向量共线与三点共线的区别与联系.当两向量共线且有公共点时,才能得出三点共线.(2)向量a 、b 共线是指存在不全为零的实数λ1,λ2,使λ1a +λ2b =0成立,若λ1a +λ2b =0,当且仅当λ1=λ2=0时成立,则向量a 、b 不共线.(1)已知向量AB →=a +3b ,BC →=5a +3b ,CD →=-3a +3b ,则( )A.A ,B ,C 三点共线B.A ,B ,D 三点共线C.A ,C ,D 三点共线D.B ,C ,D 三点共线(2)设D ,E 分别是△ABC 的边AB ,BC 上的点,AD =12AB ,BE =23BC .若DE →=λ1AB →+λ2AC →(λ1,λ2为实数),则λ1+λ2的值为________. 答案 (1)B (2)12解析 (1)∵BD →=BC →+CD →=2a +6b =2(a +3b )=2AB →, ∴BD →、AB →共线,又有公共点B , ∴A ,B ,D 三点共线.故选B. (2)DE →=DB →+BE →=12AB →+23BC →=12AB →+23(AC →-AB →) =-16AB →+23AC →,∵DE →=λ1AB →+λ2AC →,∴λ1=-16,λ2=23,故λ1+λ2=12.10.方程思想在平面向量线性运算中的应用典例 (12分)如图所示,在△ABO 中,OC →=14OA →,OD →=12OB →,AD 与BC 相交于点M ,设OA →=a ,OB →=b .试用a 和b 表示向量OM →.思维点拨 (1)用已知向量来表示另外一些向量是用向量解题的基本要领,要尽可能地转化到平行四边形或三角形中去求解.(2)既然OM →能用a 、b 表示,那我们不妨设出OM →=m a +n b . (3)利用向量共线建立方程,用方程的思想求解. 规范解答解 设OM →=m a +n b ,则AM →=OM →-OA →=m a +n b -a =(m -1)a +n b .AD →=OD →-OA →=12OB →-OA →=-a +12b .[3分]又∵A 、M 、D 三点共线,∴AM →与AD →共线. ∴存在实数t ,使得AM →=tAD →, 即(m -1)a +n b =t ⎝⎛⎭⎫-a +12b .[5分] ∴(m -1)a +n b =-t a +12t b .∴⎩⎪⎨⎪⎧m -1=-t ,n =t2,消去t 得,m -1=-2n , 即m +2n =1.① [7分]又∵CM →=OM →-OC →=m a +n b -14a =⎝⎛⎭⎫m -14a +n b , CB →=OB →-OC →=b -14a =-14a +b .又∵C 、M 、B 三点共线,∴CM →与CB →共线.[10分] ∴存在实数t 1,使得CM →=t 1CB →, ∴⎝⎛⎭⎫m -14a +n b =t 1⎝⎛⎭⎫-14a +b , ∴⎩⎪⎨⎪⎧m -14=-14t 1,n =t 1. 消去t 1得,4m +n =1. ②由①②得m =17,n =37,∴OM →=17a +37b .[12分]温馨提醒 (1)本题考查了向量的线性运算,知识要点清楚,但解题过程复杂,有一定的难度.(2)易错点是找不到问题的切入口,想不到利用待定系数法求解.(3)数形结合思想是向量加法、减法运算的核心,向量是一个几何量,是有“形”的量,因此在解决向量有关问题时,多数习题要结合图形进行分析、判断、求解,这是研究平面向量最重要的方法与技巧.如本题易忽视A 、M 、D 三点共线和B 、M 、C 三点共线这个几何特征.(4)方程思想是解决本题的关键,要注意体会.[方法与技巧]1.向量的线性运算要满足三角形法则和平行四边形法则,做题时,要注意三角形法则与平行四边形法则的要素.向量加法的三角形法则要素是“首尾相接,指向终点”;向量减法的三角形法则要素是“起点重合,指向被减向量”;平行四边形法则要素是“起点重合”.2.证明三点共线问题,可用向量共线来解决,但应注意向量共线与三点共线的区别与联系,当两向量共线且有公共点时,才能得出三点共线.3.对于三点共线有以下结论:对于平面上的任一点O ,OA →,OB →不共线,满足OP →=xOA →+yOB →(x ,y ∈R ),则P ,A ,B 共线⇔x +y =1. [失误与防范]1.解决向量的概念问题要注意两点:一是不仅要考虑向量的大小,更重要的是要考虑向量的方向;二是考虑零向量是否也满足条件.要特别注意零向量的特殊性.2.在利用向量减法时,易弄错两向量的顺序,从而求得所求向量的相反向量,导致错误.A 组 专项基础训练 (时间:30分钟)1.设O 是正方形ABCD 的中心,则向量AO →,BO →,OC →,OD →是( ) A.相等的向量 B.平行的向量 C.有相同起点的向量 D.模相等的向量答案 D解析 这四个向量的模相等.2.设a 0,b 0分别是与a ,b 同向的单位向量,则下列结论中正确的是( ) A.a 0=b 0 B.a 0·b 0=1 C.|a 0|+|b 0|=2 D.|a 0+b 0|=2 答案 C解析 因为是单位向量,所以|a 0|=1,|b 0|=1.3.在四边形ABCD 中,AB ∥CD ,AB =3DC ,E 为BC 的中点,则AE →等于( )A.23AB →+12AD →B.12AB →+23AD →C.56AB →+13AD →D.13AB →+56AD → 答案 A解析 BC →=BA →+AD →+DC →=-23AB →+AD →,AE →=AB →+BE →=AB →+12BC →=AB →+12⎝⎛⎭⎫AD →-23AB →=23AB →+12AD →. 4.已知平面内一点P 及△ABC ,若P A →+PB →+PC →=AB →,则点P 与△ABC 的位置关系是( ) A.点P 在线段AB 上 B.点P 在线段BC 上 C.点P 在线段AC 上 D.点P 在△ABC 外部答案 C解析 由P A →+PB →+PC →=AB →得P A →+PC →=AB →-PB →=AP →,即PC →=AP →-P A →=2AP →,所以点P 在线段AC 上. 5.已知点O 为△ABC 外接圆的圆心,且OA →+OB →+OC →=0,则△ABC 的内角A 等于( ) A.30° B.60° C.90° D.120° 答案 B解析 由OA →+OB →+OC →=0,知点O 为△ABC 的重心, 又∵O 为△ABC 外接圆的圆心, ∴△ABC 为等边三角形,A =60°.6.已知O 为四边形ABCD 所在平面内一点,且向量OA →,OB →,OC →,OD →满足等式OA →+OC →=OB →+OD →,则四边形ABCD 的形状为________. 答案 平行四边形解析 由OA →+OC →=OB →+OD →得OA →-OB →=OD →-OC →, 所以BA →=CD →.所以四边形ABCD 为平行四边形.7.设点M 是线段BC 的中点,点A 在直线BC 外,BC →2=16,|AB →+AC →|=|AB →-AC →|,则|AM →|=________. 答案 2解析 由|AB →+AC →|=|AB →-AC →|可知,AB →⊥AC →,则AM 为Rt △ABC 斜边BC 上的中线, 因此,|AM →|=12|BC →|=2.8.(2015·北京)在△ABC 中,点M ,N 满足AM →=2MC →,BN →=NC →.若MN →=xAB →+yAC →,则x =________;y =________. 答案 12 -16解析 MN →=MC →+CN →=13AC →+12CB → =13AC →+12(AB →-AC →) =12AB →-16AC →,∴x =12,y =-16.9.在△ABC 中,D 、E 分别为BC 、AC 边上的中点,G 为BE 上一点,且GB =2GE ,设AB →=a ,AC →=b ,试用a ,b 表示AD →,AG →.解 AD →=12(AB →+AC →)=12a +12b .AG →=AB →+BG →=AB →+23BE →=AB →+13(BA →+BC →)=23AB →+13(AC →-AB →)=13AB →+13AC →=13a +13b .10.设两个非零向量e 1和e 2不共线.(1)如果AB →=e 1-e 2,BC →=3e 1+2e 2,CD →=-8e 1-2e 2,求证:A 、C 、D 三点共线;(2)如果AB →=e 1+e 2,BC →=2e 1-3e 2,CD →=2e 1-k e 2,且A 、C 、D 三点共线,求k 的值.(1)证明 ∵AB →=e 1-e 2,BC →=3e 1+2e 2,CD →=-8e 1-2e 2,∴AC →=AB →+BC →=4e 1+e 2=-12(-8e 1-2e 2)=-12CD →,∴AC →与CD →共线.又∵AC →与CD →有公共点C ,∴A 、C 、D 三点共线.(2)解 AC →=AB →+BC →=(e 1+e 2)+(2e 1-3e 2)=3e 1-2e 2,∵A 、C 、D 三点共线,∴AC →与CD →共线,从而存在实数λ使得AC →=λCD →,即3e 1-2e 2=λ(2e 1-k e 2),得⎩⎪⎨⎪⎧ 3=2λ,-2=-λk ,解得λ=32,k =43.B 组 专项能力提升(时间:15分钟)11.设a ,b 不共线,AB →=2a +p b ,BC →=a +b ,CD →=a -2b ,若A ,B ,D 三点共线,则实数p 的值是() A.-2 B.-1 C.1 D.2答案 B解析 ∵BC →=a +b ,CD →=a -2b ,∴BD →=BC →+CD →=2a -b .又∵A ,B ,D 三点共线,∴AB →,BD →共线.设AB →=λBD →,∴2a +p b =λ(2a -b ),∴2=2λ,p =-λ,∴λ=1,p =-1.12.如图,已知AB 是圆O 的直径,点C ,D 是半圆弧的两个三等分点,AB →=a ,AC →=b ,则AD →等于( )A.a -12bB.12a -bC.a +12b D.12a +b 答案 D解析 连接CD ,由点C ,D 是半圆弧的三等分点,得CD ∥AB 且CD →=12AB →=12a , 所以AD →=AC →+CD →=b +12a . 13.设G 为△ABC 的重心,且sin A ·GA →+sin B ·GB →+sin C ·GC →=0,则B 的大小为( )A.45°B.60°C.30°D.15°答案 B解析 ∵G 是△ABC 的重心,∴GA →+GB →+GC →=0,GA →=-(GB →+GC →),将其代入sin A ·GA →+sin B ·GB →+sinC ·GC →=0,得(sin B -sin A )GB →+(sin C -sin A )GC →=0.又GB →,GC →不共线,∴sin B -sin A =0,sin C -sin A =0,则sin B =sin A =sin C .根据正弦定理知b =a =c ,∴△ABC 是等边三角形,则角B =60°.故选B.14.在▱ABCD 中,AB →=a ,AD →=b ,AN →=3NC →,M 为BC 的中点,则MN →=____________.(用a ,b 表示)答案 -14a +14b 解析 由AN →=3NC →得AN →=34AC →=34(a +b ),AM →=a +12b ,所以MN →=AN →-AM → =34(a +b )-⎝⎛⎭⎫a +12b =-14a +14b . 15.如图,经过△OAB 的重心G 的直线与OA ,OB 分别交于点P ,Q ,设OP →=mOA →,OQ→=nOB →,m ,n ∈R ,则1n +1m的值为________. 答案 3解析 设OA →=a ,OB →=b ,由题意知OG →=23×12(OA →+OB →)=13(a +b ),PQ →=OQ →-OP →=n b -m a ,PG →=OG →-OP →=⎝⎛⎭⎫13-m a +13b ,由P ,G ,Q 三点共线得,存在实数λ,使得PQ →=λPG →,即n b -m a =λ⎝⎛⎭⎫13-m a +13λb , 从而⎩⎨⎧ -m =λ⎝⎛⎭⎫13-m ,n =13λ,消去λ得1n +1m =3.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《三角恒等变换》单元测试一、选择题(本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一个是符合题目要求的) 1、已知3cos 5α=-,,2παπ⎛⎫∈ ⎪⎝⎭,12sin 13β=-,β是第三象限角,则()cos βα-的值是 ( ) A 、3365-B 、6365C 、5665D 、1665- 2、已知α和β都是锐角,且5sin 13α=,()4cos 5αβ+=-,则sin β的值是( ) A 、3365 B 、1665 C 、5665 D 、63653、已知32,244x k k ππππ⎛⎫∈-+ ⎪⎝⎭()k Z ∈,且3cos 45x π⎛⎫-=- ⎪⎝⎭,则cos2x 的值是 ( ) A 、725-B 、2425-C 、2425D 、7254、设()()12cos sin sin cos 13x y x x y x +-+=,且y 是第四象限角,则2ytan 的值是( ) A 、23±B 、32±C 、32-D 、23- 5、函数()sincos22f x x x ππ=+的最小正周期是 ( )A 、πB 、2πC 、1D 、25'、若函数()()()sin g x f x x π=为以2为最小正周期的奇函数,则函数()f x 可以是( )A 、()sin x πB 、cos 2x π⎛⎫⎪⎝⎭ C 、sin 2x π⎛⎫⎪⎝⎭D 、sin 2x π⎛⎫⎪⎝⎭6、某物体受到恒力是(1,3F =,产生的位移为()sin ,cos s t t =-,则恒力物体所做的功是 ( )A 1B 、2C 、6'、已知向量()2cos ,2sin a ϕϕ=,()90,180ϕ∈,()1,1b =,则向量a 与b 的夹角为( )A 、ϕB 、45ϕ-C 、135ϕ-D 、45ϕ+ 7、要得到函数2sin 2y x =的图像,只需要将函数2cos 2y x x =-的图像( ) A 、向右平移6π个单位 B 、向右平移12π个单位C 、向左平移6π个单位 D 、向左平移12π个单位8、已知12sin 41342x x πππ⎛⎫⎛⎫+=<<⎪ ⎪⎝⎭⎝⎭,则式子cos 2cos 4x x π⎛⎫- ⎪⎝⎭的值为( )A 、1013-B 、2413C 、513D 、1213- 9、函数sin 22x xy =的图像的一条对称轴方程是 ( )A 、x =113πB 、x =53π C 、53x π=- D 、3x π=- 10、已知1cos sin 21cos sin x xx x-+=-++,则sin x 的值为 ( )A 、45 B 、45- C 、35- D、5-11、已知0,4πα⎛⎫∈ ⎪⎝⎭,()0,βπ∈,且()1tan 2αβ-=,1tan 7β=-,则2αβ-的值是 ( ) A 、56π-B 、23π-C 、 712π-D 、34π- 12、已知不等式()2cos 04442x x x f x m =+--≤对于任意的566x ππ-≤≤恒成立,则实数m 的取值范围是 ( ) A、m ≥ B、m ≤ C、m ≤、m ≤≤二、填空题(本大题共4小题,每小题4分,共16分.请把答案填在题中的横线上)13、已知1sin 3x =,()sin 1x y +=,则()sin 2y x += 14、函数sin 234y x x π⎛⎫=+++ ⎪⎝⎭的最小值是 15、函数1sin cosxy x-=图像的对称中心是(写出通式)16、关于函数()cos2cos f x x x x =-,下列命题: ①、若存在1x ,2x 有12x x π-=时,()()12f x f x =成立; ②、()f x 在区间,63ππ⎡⎤-⎢⎥⎣⎦上是单调递增; ③、函数()f x 的图像关于点,012π⎛⎫⎪⎝⎭成中心对称图像; ④、将函数()f x 的图像向左平移512π个单位后将与2sin 2y x =的图像重合.其中正确的命题序号 (注:把你认为正确的序号都填上)三、解答题(本大题共6个小题,共74分.解答应写出文字说明,证明过程或演算步骤)17、(本小题满分12分) 已知02πα<<,15tan22tan2αα+=,试求sin 3πα⎛⎫- ⎪⎝⎭的值.18、(本小题满分12分)已知()3sin ,cos a x x ωω=-,()cos ,cos b x x ωω=()0ω>,令函数()f x a b =,且()f x 的最小正周期为π.(1) 求ω的值;(2) 求()f x 的单调区间.(选做)18'、设()1cos ,sin a αα=+,()1cos ,sin b ββ=-,()1,0c =,()0,απ∈,(),2βππ∈,设a 与c 的夹角为1θ,b 与c 夹角为2θ,且126πθθ-=.求sin8αβ-的值.19、(本小题满分12分)已知1tan 42πα⎛⎫+=- ⎪⎝⎭,试求式子2sin 22cos 1tan ααα--的值.20、(本小题满分12分)已知x R ∈,()211sin tan 222tan 2x f x x x x ⎛⎫⎪=-⎪ ⎪⎝⎭. (1) 若02x π<<,求()f x 的单调的递减区间;(2) 若()2f x =,求x 的值.21、(本小题满分12分) 已知函数()f x 满足下列关系式: (i )对于任意的,x y R ∈,恒有 ()()222f x f y f x y f x y ππ⎛⎫⎛⎫=-+---⎪ ⎪⎝⎭⎝⎭; (ii )12f π⎛⎫=⎪⎝⎭. 求证:(1)()00f =; (2)()f x 为奇函数;(3)()f x 是以2π为周期的周期函数.《三角恒等变换》单元测试题1、∵3cos 5α=-,,2παπ⎛⎫∈ ⎪⎝⎭,∴4sin 5α=,又12sin 13β=-,β是第三象限角,∴5cos 13β=-,∴()cos βα-531243313513565⎛⎫⎛⎫=-⨯-+-⨯=-⎪ ⎪⎝⎭⎝⎭ 2、依题意,∵5sin 13α=,∴12cos 13α=,又()4cos 5αβ+=-,∴2παβπ<+<,∴()3sin 5αβ+=,∵()sin sin[]βαβα=+-,因此有,3124556sin 51351365β⎛⎫=⨯--⨯=⎪⎝⎭ 3、∵32,244x k k ππππ⎛⎫∈-+ ⎪⎝⎭,∴cos sin 0x x ->,即)sin cos sin 042x x x π⎛⎫--> ⎪⎝⎭,∴4sin 45x π⎛⎫-= ⎪⎝⎭,又∵cos 2sin 22sin cos 244x x x x πππ⎛⎫⎛⎫⎛⎫=-=-- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,∴4324cos 225525x ⎛⎫=⨯⨯-=-⎪⎝⎭4、由()()12cos sin sin cos 13x y x x y x +-+=得()12sin sin 13x x y y -+=-=⎡⎤⎣⎦,又∵y 是第四象限角,∴5cos 13y =,∵22sin 1cos 2tan2sin 2sin cos 22y y y y y y-==5121312313-==-- 5因为()()()1sin1cos 122f x x x ππ+=+++sin cos 2222x x ππππ⎛⎫⎛⎫=+++ ⎪ ⎪⎝⎭⎝⎭()cossin22x x f x ππ=+-=,∴最小正周期是1T = 5'、∵()()g x g x -=-,∴()()()()sin sin f x x f x x ππ--=-,即得:()()f x f x -=成立,∴()f x 为偶函数,又∵()()2g x g x +=,∴()()2f x f x +=,即()f x 的周期为2,选C6、∵功sin 2sin 3w F s t t t π⎛⎫===- ⎪⎝⎭,∴2w ≤ 6'、∵()2cos 2sin 45a b ϕϕϕ=+=+,2a =,2b =,因此,()()()cos ,sin 45cos 9045cos 45a b a b a bϕϕϕ⎡⎤==+=-+=-⎣⎦,6' ∴,45a b ϕ=-7、∵12cos 222cos 22y x x x x ⎫=-=-⎪⎪⎝⎭2sin 26x π⎛⎫=- ⎪⎝⎭2sin 212x π⎛⎫=- ⎪⎝⎭, ∵12122sin 22sin 212y x y x πππ⎛⎫−−−−−→==-←−−−−− ⎪⎝⎭向右平移得向左平移得选D8、∵42x ππ<<,∴5244x πππ<+<,则5cos 413x π⎛⎫+=-⎪⎝⎭,则式为sin 22sin cos 2442sin 4cos cos 44x x x x x x ππππππ⎛⎫⎛⎫⎛⎫--- ⎪ ⎪ ⎪⎛⎫⎝⎭⎝⎭⎝⎭===- ⎪⎛⎫⎛⎫⎝⎭-- ⎪ ⎪⎝⎭⎝⎭2cos 4x π⎛⎫=+ ⎪⎝⎭9、∵sin 22x x y =2sin 23x π⎛⎫=+ ⎪⎝⎭,令22323x k x k πππππ+=+⇒=+()k Z ∈,当1k =-时,53x π=-10、∵()()222sin 2sin cos1cos sin 222tan1cos sin 22cos 2sin cos 222x x x x x x x x xx x ⎛⎫+ ⎪-+⎝⎭==+++2=-,∴22tan42sin 51tan 2xx x ==-+11、∵()11127tan tan 113127ααββ-=-+==⎡⎤⎣⎦⎛⎫-⨯- ⎪⎝⎭,∴()()tan 2tan αβαβα-=-+⎡⎤⎣⎦1132111132+==-⨯,又∵()0,βπ∈,1tan 7β=-,0,4πα⎛⎫∈ ⎪⎝⎭,∴20παβ-<-<,∴2αβ-34π=-12、∵()26x f x π⎛⎫=+ ⎪⎝⎭0m -≤对于566x ππ-≤≤恒成立,即()max m f x ≥=13、∵()sin 1x y +=,∴22x y k ππ+=+,∴22y k xππ=+-,∴()sin 2sin (2)2y x k y ππ⎡⎤+=++⎢⎥⎣⎦sin cos 2y yπ⎛⎫=+= ⎪⎝⎭cos 22k x ππ⎛⎫=+- ⎪⎝⎭1cos sin 23x x π⎛⎫=-==⎪⎝⎭14、令cos 4t x π⎛⎫=+ ⎪⎝⎭,∴cos 2324y x x ππ⎛⎫⎛⎫=-++++ ⎪ ⎪⎝⎭⎝⎭2225215222t ⎛⎛=--+≥---+=- ⎝⎭⎝⎭15、∵1cos tan sin 2x xy x -==∴对称中心为()(),0k k Z π∈16、∵()552sin 22sin 22sin 26612f x x x x πππ⎛⎫⎛⎫⎛⎫=-=+=+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,∴周期T π=,①正确;∵递减区间是532262x πππ≤+≤,解之为,63ππ⎡⎤-⎢⎥⎣⎦,②错误;∵对称中心的横坐标5526212k x k x ππππ+=⇒=-,当1k =时,得③正确;应该是向右平移,④不正确.17、解:由15tan22tan2αα+=,得1cos 1cos 54sin sin sin 25ααααα-++=⇒=,又02πα<<,∴3cos 5α=,所以4134sin 3525210πα-⎛⎫-=⨯-⨯=⎪⎝⎭ 18、(1)∵()f x a b=,∴()2cos cos f x x x xωωω=+()11cos 2222x x ωω=+1sin 262x πω⎛⎫=-+ ⎪⎝⎭,即()5sin 26f x x πω⎛⎫=+ ⎪⎝⎭12+,∴2221T ππωωπ==⇒=;(2)令5222,262k x k k Z πππππ-≤+≤+∈,解之()f x 在2,36k k ππππ⎡⎤--⎢⎥⎣⎦()k Z ∈上递增;同理可求递减区间为,63k k ππππ⎡⎤-+⎢⎥⎣⎦()k Z ∈. 18'依题意:1cos cos22a b a bαθ====+,又()0,απ∈,则0,22απ⎛⎫∈ ⎪⎝⎭,∴12αθ=,同理2cos sin 2βθ=cos 22βπ⎛⎫=- ⎪⎝⎭,因(),2βππ∈,所以0,222βππ⎛⎫-∈ ⎪⎝⎭,∴222βπθ=-,将1θ、2θ代入126πθθ-=有23αβπ-=-,从而有sinsin sin 81264αβπππ-⎛⎫⎛⎫=-=-=⎪ ⎪⎝⎭⎝⎭.19、2sin 22cos 1tan ααα--()222cos tan 12cos tan 1tan 4ααπααα-⎛⎫==- ⎪+⎝⎭cos 241cos 222sin 24ππααππα⎡⎤⎛⎫+- ⎪⎢⎥+⎝⎭⎣⎦=-⎡⎤⎛⎫+- ⎪⎢⎥⎝⎭⎣⎦()11cos222cos2tan 4ααπα=-+=+⎛⎫+ ⎪⎝⎭24tan 422sin 2221tan 4παπαπα⎛⎫+ ⎪⎛⎫⎝⎭=++=+ ⎪⎛⎫⎝⎭++ ⎪⎝⎭2142225112⎛⎫- ⎪⎝⎭=+=⎛⎫+- ⎪⎝⎭20、()211cos 1cos sin 22sin sin x x f x xx x x +-⎛⎫=- ⎪⎝⎭212cos 1sin cos 2sin 2cos 22sin 222x x x x x x =+=+sin 23x π⎛⎫=+ ⎪⎝⎭ (1)∵02x π<<,∴42233x πππ≤+<,即122x ππ≤<时,()f x 为减函数,故()f x 的递减区间为,122ππ⎡⎫⎪⎢⎣⎭;(2)∵sin 232x π⎛⎫+= ⎪⎝⎭,∴()x k k Z π=∈,或()6x k k Z ππ=+∈.21、(1)令0x y ==,()()22000022f f f f ππ⎛⎫⎛⎫=-=⇒= ⎪ ⎪⎝⎭⎝⎭;(2)令2x π=,y R ∈,()()()22f f y f y f y π⎛⎫=-- ⎪⎝⎭,∵12f π⎛⎫= ⎪⎝⎭,∴()()f y f y =--,故()f x 为奇函数;(3)令2y π=,x R ∈,有()()()21f x f x f x π=---,即()()f x f x π-=……①,再令2x π=-,y x =有()()()()21f x f x f x ππ-=+--()()f x f x π+-,即()()()f x f x f x ππ+=-=-,令x t π-=,则2x t ππ+=+,所以()()2f t f t π=+,即()f x 是以2π为周期的周期函数.。
