初中数学奥林匹克模拟试卷1_10套

合集下载

初中数学奥林匹克竞赛题包括答案.docx

初中数学奥林匹克竞赛题及答案奥数题一一、选择题（每题 1 分，共 10 分）1．如果 a，b 都代表有理数，并且a＋b=0 ，那么 ( ) A．a，b 都是 0B．a，b 之一是 0C．a，b 互为相反数D． a，b 互为倒数答案： C解析：令 a=2 ， b= － 2，满足 2+( － 2)=0 ，由此 a、b 互为相反数。

2．下面的说法中正确的是( )A．单项式与单项式的和是单项式B．单项式与单项式的和是多项式C．多项式与多项式的和是多项式D．整式与整式的和是整式答案： D3都是单项式．两个单项式33A。

两个单项式解析： x2， x x ， x2之和为 x +x 2是多项式，排除x2， 2x2之和为3x2是单项式，排除 B。

两个多项式x3+x2 与 x3－x2之和为2x3 是个单项式，排除 C，因此选 D。

3．下面说法中不正确的是( )A.有最小的自然数B．没有最小的正有理数Word资料C．没有最大的负整数D．没有最大的非负数答案： C解析：最大的负整数是-1 ，故 C 错误。

4．如果 a，b 代表有理数，并且a＋b 的值大于 a－ b 的值，那么( ) A．a，b 同号B．a，b 异号C．a＞0D． b＞ 0答案： D5．大于－π并且不是自然数的整数有( )A．2 个B．3 个C．4 个D．无数个答案： C解析：在数轴上容易看出：在－π右边0的左边（包括0 在）的整数只有－3，－ 2，－1 ，0 共 4 个．选 C。

6．有四种说法：甲．正数的平方不一定大于它本身；乙．正数的立方不一定大于它本身；丙．负数的平方不一定大于它本身；丁．负数的立方不一定大于它本身。

Word资料这四种说法中，不正确的说法的个数是( )A．0 个B．1 个C．2 个D． 3 个答案： B解析：负数的平方是正数，所以一定大于它本身，故 C 错误。

7．a 代表有理数，那么， a 和－ a 的大小关系是( )A．a 大于－ aB．a 小于－ aC．a 大于－ a 或 a 小于－ aD． a 不一定大于－ a答案： D解析：令 a=0 ，马上可以排除A、 B、 C，应选 D。

初中数学奥林匹克模拟试卷1-10套

数学奥林匹克模拟试卷（一）一、选择题：1、已知311=-=-b b a a ，且3>+b a ，则33a b b a -的值是（）。

（A ）521（B ）1321（C ）533（D ）13332、如果二次函数()522++++=k x k x y 的图象与x 轴的两个不同交点的横坐标是正的，那么k 值应为（）（A ）4>k 或5.-<k （B ）45-<<-k （C ）4.-≥k 或5-≤k （D ）45-≤≤-k3、如图，∆ABC 为锐角三角形，BE ⊥AC 于F ，则ABCAEF S S ∆∆:的值为（）（A ）A sin （B ）A cos （C ）A 2sin （D ）A 2cos 4、方程1997111=+y x 的正整数解的组数为（）（A ）1（B ）2（C ）3（D ）大于等于45、P 为∆ABC 内一点，PA 、PB 、PC 把∆ABC 的面积分成三等分，则P 点是∆ABC 的（）（A ）内心（B ）外心（C ）垂心（D ）重心6、抛物线122++=bx x y 与直线ab ax y 22+=的图象至多有一个交点，则的最大值是（）（A ）1（B ）23（C ）22（D ）0 二、填空题：1、已知四个实数的乘积为1，其中任意一个数与其余三个数的积的和都等于1000，则此四数的和是_________。

2、如果c yz b xz a xy ===,,，而且它们都不等于0，则222z y x ++=_________。

3、若抛物线()242+++=a x ax y 全在x 轴的上方，a 的范围是_________。

4、如图，在图形ABCD 中，AB ∥CD ，∠A=900，E 为BC 重点，GE ⊥BC 于，交DA 延长线于G ，DC=17cm ，AB=25cm ，BC=10cm ，则CE=_________。

AB CEFABC E DG三、解答题：1、已知∠ACE=∠CDE=900，点B 在CE 上，CA=CB=CD ，过点A 、C 、D 三点的圆交AB 于F ，求证：F 是∆CDE 的内心。

数学奥林匹克初中训练模拟试题附答案(四)

数学奥林匹克初中训练题附答案（四）第一试一、选择题(每小题7分，共42分)1.如图，已知在Rt △ABC 中，AB=35，一个边长为12的正方形CDEF 内接于△ABC.则△ABC 的周长为( ).(A)35 (B)40 (C)81 (D)842.设n=9+99+…+99…9(99个9).则n 的十进制表示中，数码1有( )个. (A)50 (B)90 (C)99 (D)1003.已知f(x)=x 2+6ax-a ，y=f(x)的图像与x 轴有两个不同的交点(x 1，0)，(x 2，0)，且)x -6a -)(1x -6a -(13)x )(1x (1a2121-++=8a-3.则a 的值是( ).(A)1 (B)2 (C)0或21 (D)214.若不等式ax 2+7x-1>2x+5对-1≤a≤1恒成立，则x 的取值范围是( ). (A)2≤x≤3 (B)2<x<3 (C)-1≤x≤1 (D)-1<x<15.在Rt △ABC 中，∠B=60°，∠C=90°，AB=1，分别以AB 、BC 、CA 为边长向△ABC 外作等边△ABR 、等边△BCP 、等边△CAQ ，联结QR 交AB 于点T.则△PRT 的面积等于( ). (A)3239 (B)43 (C)21 (D)336.在3×5的棋盘上，一枚棋子每次可以沿水平或者垂直方向移动一小格，但不可以沿任何斜对角线移动.从某些待定的格子开始，要求棋子经过全部的小正方格恰好一次，但不必回到原来出发的小方格上.在这15个小方格中，有( )个可以是这枚棋子出发的小方格. (A)6 (B)8 (C)9 (D)10二、填空题(每小题7分，共28分)1.正方形ABCD 的边长为5，E 为边BC 上一点，使得BE=3，P 是对角线BD 上的一点，使得PE+PC 的值最小.则PB= .2.设a 、b 、c 为整数，且对一切实数x ，(x-a)(x-8)+1=(x-b)(x-c) 恒成立.则a+b+c 的值为 .3.如图，在以O 为圆心的两个同心圆图2中，MN 为大圆的直径，交小圆于点P 、Q ，大圆的弦MC 交小圆于点A 、B.若OM=2，OP= 1，MA=AB=BC ，则△MBQ 的面积为 .4.从1， 2，…， 2 006中，至少要取出个奇数，才能保证其中必定存在两个数，它们的和为2 008.第二试一、(20分)实数x 、y 、z 、w 满足x≥y≥z≥w≥0，且5x+4y+3z+6w=100.求x+y+z+w 的最大值和最小值.二、(25分)如图，在Rt △ABC 中，∠B=90°，它的内切圆分别与边BC 、CA 、AB 相切于点D 、E 、F ，联结AD 与内切圆相交于另一点P ，联结PC 、PE 、PF.已知PC ⊥PF.求证:(1)EP/DE=PD/DC;(2)△EPD 是等腰三角形.三、(25分)在]20082008[],20082[],20081[222中，有多少个不同的整数(其中，[x]表示不大于x的最大整数)?数学奥林匹克初中训练题参考答案第一试一、1.D. 设BC=a ，AC=b.则a 2+b 2=352=1 225.①又Rt △AFE ∽Rt △ACB ，则FE/CB=AF/AC ，. 故12(a+b)=ab.由式①、②得(a+b)2=1 225+24(a+b).解得a+b=49(a+b=-25舍去).所以，周长为84. 2.C.因为n=(10-1)+(100-1)+…+(100…0(99个0)-1)=11…1(99个1)0-99=11…1(97个1)011，所以，n 的十进制表示中，数码1有97+2=99(个). 3.D.由Δ=36a 2+4a>0，得a>0或a<-1/9.由题意可设f(x)=x 2+6ax-a=(x-x 1)(x-x 2). 则(1+x 1)(1+x 2)=f(-1)=1-7a ， (1-6a-x 1)(1-6a-x 2)=f(1-6a)=1-7a. 所以，7a-13-a =8a-3.解得a=1/2或a=0(舍去). 4.B.由题意知，不等式ax 2+7x-1>2x+对-1≤a≤1恒成立，即关于a 的不等x 2a+5x-6>0对-1≤a≤1恒成立.令g(a)=x 2a+5x-6.则g(-1)=-x 2+5x-6>0，g(1)=x 2+5x-6>0.解得2<x<3. 5.A.如图，联结PQ.由题设得BC=1/2 ，AC=3 /2，∠QAT=90°， ∠QCP=150°，P 、B 、R 三点共线. 因为S △AQT =21 AT·AQ=21 AT·AC=43AT ，而S △ART /S △ARB =AT/AB ，所以，S △ART =43AT=S △AQT.从而，QT=RT.于是，S △PRT =21 S △PQR =21 (S △ABC +S △ABR +S △BCP +S △CAQ +S △CPQ -S △AQR )=3239.6.B.如图5，将3×5的棋盘黑白染色.图5中有8个黑色小方格和7个白色小方格，棋子每次移动都是黑白交替的，则7个白格不能作为出点.另一方面，如图6的8个黑格中的任一个都可以作为出发点.二、1.152 /8.因为PE+PC=PE+PA ，所以，当A 、P 、E 三点共线时，PE+PA 最小.如图，建立直角坐标系，设B 为坐标原点，BA 为x 轴.则l BD :y=x ， l AE :3x+5y=15.所以，P(15/8，15/8).故PB=15 2 /8.2.20或28.因x 2-(8+a)x+8a+1=x 2-(b+c)x+bc 恒成立，所以，8+a=b+c ，8a+1=bc. 消去a 可得bc-8(b+c)=-63，即(b-8)(c-8)=1.因为b 、c 都是整数，所以，b-8=c-8=1或b-8=c-8=-1. 从而，a+b+c=20或28. 3.315/8.设MA=x.由MA·MB=MP·MQ ，得x·2x=1×3.解得x=23.联结CN.在Rt △MCN 中，MC=3x=323，MN=4.所以，NC=25，S △MCN =4153.又S △MQB /S △MCN =1/2，则S △MQB =8153.4.503.从1，2，…，2 006中选出两个奇数，和为2 008的共有如下501组: 3+2 005，5+2 003，…，1 003+1 005.由于1与其中的任意一个奇数的和都不会等于2 008，因此，至少要取出503个奇数，才能保证其中一定有两个数，它们的和为2 008. 第二试一、设z=w+a ，y=w+a+b ，x=w+a+b+c.则a 、b 、c≥0，且x+y+z+w=4w+3a+2b+c. 故100=5(w+a+b+c)+4(w+a+b)+3(w+a)+6w=18w+12a+9b+5c=4(4w+3a+2b+c)+(2w+b+c) ≥4(x+y+z+w). 因此，x+y+z+w≤25.当x=y=z=25/3，w=0时，上式等号成立.故x+y+z+w 的最大值为25. 又100=18w+12a+9b+5c=5(4w+3a+2b+c)-(2w+3a+b)≤5(x+y+z+w)，则 x+y+z+w≥20.当x=20，y=z=w=0时，上式等号成立.故x+y+z+w 的最小值为20. 二、(1)如图，联结DF.则△BDF 是等腰直角三角形.于是，∠FPD=∠FDB=45°.故∠DPC=45°.又因为∠PDC=∠PFD ，所以，△PFD ∽△PDC. 从而，PF/FD=PD/DC.①由∠AFP=∠ADF ，∠AEP=∠ADE ，得△AFP ∽△ADF ，△AEP ∽△ADE. 于是，EP/DE=AP/AE=AP/AF=FP/DF. 故由式①得EP/DE=PD/DC.(2)因为∠EPD=∠EDC ，结合式②得△EPD’∽△EDC.所以，△EPD 也是等腰三角形. 三、设f(n)=0082n2.当n=2，3，…，1 004时，有f(n)-f(n-1)=00821-2n <1.而f(1)=0，f(1 004)=1 0042/2 008=502，以，从0到502的整数都能取到.当n=1 005，1 006，…，2 008时，有f(n)-f(n-1)= 00821-2n >1.而f(1 005)=1 0052/2 008=(1 004+1)2/2 008=502+1+1/2 008>503，故]20082008[],20082[],20081[222是互不同的整数.从而，在]20082008[],20082[],20081[222中，共有503+1 004=1 507个不同的整数.。

初中数学奥林匹克模拟试卷1-10套

1数学奥林匹克模拟试卷（一）一、选择题：1、已知311b baa，且3b a，则33ab ba 的值是（）。

（A ）521（B ）1321（C ）533（D ）13332、如果二次函数522k x k xy的图象与x 轴的两个不同交点的横坐标是正的，那么k 值应为（）（A ）4k或5.k（B ）45k（C ）4.k或5k （D ）45k 3、如图，?ABC 为锐角三角形，BE ⊥AC 于F ，则AB C AE F S S :的值为（）（A ）A sin （B ）A cos （C ）A 2sin （D ）A2cos 4、方程1997111y x 的正整数解的组数为（）（A ）1（B ）2（C ）3（D ）大于等于 4 5、P 为?ABC 内一点，PA 、PB 、PC 把?ABC 的面积分成三等分，则P 点是?ABC 的（）（A ）内心（B ）外心（C ）垂心（D ）重心6、抛物线122bx xy 与直线ab ax y 22的图象至多有一个交点，则的最大值是（）（A ）1（B ）23（C ）22（D ）0二、填空题：1、已知四个实数的乘积为1，其中任意一个数与其余三个数的积的和都等于1000，则此四数的和是_________。

2、如果c yz b xz a xy,,，而且它们都不等于0，则222z yx=_________。

3、若抛物线242a x axy全在x 轴的上方，a 的范围是_________。

4、如图，在图形ABCD 中，AB ∥CD ，∠A=900，E 为BC 重点，GE ⊥BC 于，交DA 延长线于G ，DC=17cm ，AB=25cm ，BC=10cm ，则CE=_________。

ABCEFABCEDG。

七年级数学奥林匹克竞赛题(一)解析

初中一年级奥赛训练题(一)及解析一、选择题（每题1分，共10分）1．如果a，b都代表有理数，并且a＋b=0，那么( C)A．a，b都是0 B．a，b之一是0C．a，b互为相反数D．a，b互为倒数2．下面的说法中正确的是( D)A．单项式与单项式的和是单项式B．单项式与单项式的和是多项式C．多项式与多项式的和是多项式D．整式与整式的和是整式3．下面说法中不正确的是( C)A. 有最小的自然数B．没有最小的正有理数C．没有最大的负整数D．没有最大的非负数4．如果a，b代表有理数，并且a＋b的值大于a－b的值，那么( D) A．a，b同号B．a，b异号C．a＞0 D．b＞05．大于－π并且不是自然数的整数有( B)A．2个B．3个C．4个D．无数个6．有四种说法：甲．正数的平方不一定大于它本身；乙．正数的立方不一定大于它本身；丙．负数的平方不一定大于它本身；丁．负数的立方不一定大于它本身。

这四种说法中，不正确的说法的个数是( B)A．0个B．1个C．2个D．3个解析：负数的平方是正数，所以一定大于它本身，故丙错误。

7．a代表有理数，那么a和－a的大小关系是( D)A．a大于－a B．a小于－aC．a大于－a或a小于－a D．a不一定大于－a解析：令a=0，马上可以排除A、B、C，应选D。

8．在解方程的过程中，为了使得到的方程和原方程同解，可以在原方程的两边( D)A．乘以同一个数B．乘以同一个整式C．加上同一个代数式D．都加上1解析：对方程同解变形，要求方程两边同乘不等于0的数，所以排除A。

我们考察方程x－2=0，易知其根为x=2．若该方程两边同乘以一个整式x－1，得(x－1)(x －2)=0，其根为x=1及x=2，不与原方程同解，排除B。

同理应排除C．事实上方程两边同时加上一个常数，新方程与原方程同解，D所加常数为1，因此选D．9．杯子中有大半杯水，第二天较第一天减少了10%，第三天又较第二天增加了10%，那么，第三天杯中的水量与第一天杯中的水量相比的结果是( C) A．一样多B．多了C．少了D．多少都可能解析：设杯中原有水量为a，依题意可得，第二天杯中水量为(1－10%)a=0.9a；第三天杯中水量为0.9a(1+10%)=0.9×1.1a；第三天杯中水量与第一天杯中水量之比为0.99∶1，所以第三天杯中水量比第一天杯中水量少了，选C。

数学奥林匹克初中训练题15套

数学奥林匹克初中训练题(一)第一试一. 选择题 1、已知33333a b c abca b c++-=++，则22()()()()a b b c a b b c -+-+--的值为:A ．1B ．2C ．3D ．42、规定”Δ”为有序实数对的运算，如果(,)a b Δ(,)(,).c d ac bd ad bc =++如果对任意实数,a b 都有(,)a b Δ(,)(,),x y a b =则(,)x y 为: A ．（0,1） B ．（1,0） C ．（-1,0） D ．（0，-1）3、在ΔABC 中，211a b c=+，则∠A:A ．一定是锐角B ．一定是直角C ．一定是钝角D ．非上述答案4、下列五个命题:①若直角三角形的两条边长为3与4，则第三边长是5;②2();a a =③若点(,)P a b 在第三象限，则点1(,1)P a b --+在第一象限;④连结对角线垂直且相等的四边形各边中点的四边形是正方形;⑤两边及其第三边上的中线对应相等的两个三角形全等.其中正确的命题的个数是:A ．2个B ．3个C ．4个D ．5个5、设P 为等腰Rt ΔABC 斜边AB 上或其延长线上一点，22S AP BP =+，那么: A ． 22CP S < B ．22CP S = C ．22CP S > D ．不确定6、满足方程222()x y x y xy +=++的所有正整数解有:A ．一组B ．二组C ．三组D ．四组二. 填空题1、一辆客车，一辆货车和一辆小轿车在同一条直线上朝同一方向行驶，在某一时刻，货车在中，客车在前，小轿车在后，且它们的距离相等.走了10分钟，小轿车追上了货车;又走了5分钟，小轿车追上了客车.问再过分钟，货车追上了客车.2、若多项式2228171642070P a ab b a b =-+--+，那么P 的最小值是 .3、如图1， ∠AOB=30O ， ∠AOB 内有一定点P ，且OP=10.在OA 上有一点Q ，OB 上有一点R.若ΔPQR 周长最小，则最小周长是 .4、已知二次函数2(1)y ax a =≥的图象上两点A ，B 的横坐标分别为1,2-，O 是坐标原点，如果ΔAOB 是直角三角形，则ΔAOB 的周长为 .第二试一、已知实数,,a b c 满足不等式,a b c b c a ≥+≥+，c a b ≥+，求a b c ++的值.二、如图2，点D 在ΔABC 的边BC 上，且与B ，C 不重合，过点D 作AC 的平行线DE 交AB 于E ，作AB 的平行线DF 交AC 于点F.又知BC=5.（1）设ΔABC 的面积为S.若四边形AEFD 的面积为25S .求BD 长.（2）若2,AC AB =且DF 经过ΔABC 的重心G ，求E ，F 两点的距离.三、已知定理:”若三个大于3的质数,,a b c 满足关系式25a b c +=，则a b c ++是整数n 的倍数.”试问:上述定理中整数n 的最大可能值是多少?并证明你的结论.数学奥林匹克初中训练题(二)第一试一、选择题1、有铅笔，练习本，圆珠笔三种学习用品.若购铅笔3支，练习本7本，圆珠笔1支共需3.15元;若购铅笔4支，练习本10本，圆珠笔1支共需4.2元.现购铅笔，练习本，圆珠笔各1件，共需:A ．1.2元B ．1.05元C ．0.95元D ．0.9元2、三角形的三边,,a b c 都是整数，且满足7abc bc ca ab a b c ++++++=，则此三角形的面积等于: A ．32B ．24C ．34D ．223、如图1，ΔABC 为正三角形，PM ⊥AB ，PN ⊥AC.设四边形AMPN ， ΔABC 的周长分别是,m n ，则有: A ．5321<<n m B ．4332<<nm C ．%79%78<<nm D ．%83%80<<nm4、满足22(3)(3)6x y -+-=的所有实数对(,)x y ，使y x取最大值，此最大值为:A ．322+B ．42+C ．533+D ．53+5、设333717171p a b c =+++++371d ++.其中,,,a b c d 是正实数，且满足1a b c d +++=.则p 满足:A ．p ＞5B ．p ＜5C ．p ＜2D ．p ＜36、如图2，点O 是正六边形ABCDEF 的中心，OM ⊥CD ，N 为OM 的中点.则:ABN BC N S S 等于:A ．9:5B ．7:4C ．5:3D ．3:2二、填空题1、若实数,x y 满足22(1)(1)1x x y y ++++=，则 x y += .2、如图3，CD 为直角ΔABC 斜边AB 上的高，DE ⊥AC.设ΔADE ，ΔCDB ，ΔABC 的周长分别是12,,p p p .当12p p p +取最大值时，∠A= .3、若函数2543kx y kx kx +=++中自变量的取值范围是一切实数，则实数k 的取值范围是 .4、如图4所示，线段AB 与CD 都是⊙O 中的弦，其 108,,36,O O AB AB a CDCD b ====，则⊙O 的半径R= .第二试一.(共20分)n 是一个三位数，b 是一个一位数，且22,1a a bb ab ++都是整数，求a b +的最大值与最小值.二.(共25分)如图5，在ΔABC 中，∠A=60O ，O ，I ，H 分别是它的外心，内心，垂心.试比较ΔABC 的外接圆与ΔIOH 的外接圆的大小，证明你的论断.三.(共25分)求方程组33333x y z x y z ++=⎧⎨++=⎩的所有整数解.数学奥林匹克初中训练题(三)第一试一、选择题1、在112,,0.2002,(3222),7223n n π----(n 是大于3的整数)这5个数中，分数的个数为:A ．2B ．3C ．4D ．52、如图1，正方形ABCD 的面积为256，点F 在AD 上，点E 在AB 的延长线上，Rt ΔCEF 的面积为200，则BE 的长为: A ．10 B ．11 C ．12 D ．153、已知,,a b c 均为整数，且满足2223a b c +++＜32ab b c ++.则以,a b c b +-为根的一元二次方程是:A ．2320x x -+=B ．2280x x +-=C ．2450x x --=D ．2230x x --=4、如图2，在Rt ΔABC 中，AF 是高，∠BAC=90O，且 BD=DC=FC=1，则AC 为:A ．32 B ．3 C ．2 D ．335、若222a b c a b c k cba+++===，则k 的值为:A ．1B ．2C ．3D ．非上述答案6、设0,0,26x y x y ≥≥+=，则224363u x xy y x y =++--的最大值是: A ．272B ．18C ．20D ．不存在二、填空题1、方程222111013x x x x++=+的实数根是 .2、如图3，矩形ABCD 中，E ，F 分别是BC ，CD 上的点，且4,3,2===∆∆∆ADF CEF ABE S S S ，则AEF S ∆= .3、已知二次函数2(1)y x a x b =+++(,a b 为常数).当3x =时，3;y =当x 为任意实数时，都有y x ≥.则抛物线的顶点到原点的距离为 .4、如图4，半径为2cm ，圆心角为90O 的扇形OAB 的 AB 上有一运动的点P .从点P 向半径OA 引垂线PH 交OA 于点H.设ΔOPH 的内心为I ，当点P 在 AB 上从点A 运动到点B 时，内心I 所经过的路径长为 .第二试一、（20分）在一个面积为1的正方形中构造一个如下的小正方形;将单位正方形的各边n 等分，然后将每个顶点和它相对应顶点最接近的分点连结起来，如图5所示.若小正方形的面积恰为13281，求n 的值.二、（25分）一条笔直的公路l 穿过草原，公路边有一卫生站A ，距公路30km 的地方有一居民点B ，A ，B 之间的距离为90km .一天某司机驾车从卫生站送一批急救药品到居民点.已知汽车在公路上行驶的最快速度是60/km h ，在草地上行驶的最快速度是30/km h .问司机应以怎样的路线行驶，所用的行车时间最短?最短时间是多少?三、(25分)从1，2，3，……，3919中任取2001个数。

初中数学奥数题综合模拟试卷及答案

初中数学奥数题综合模拟试卷及答案初中数学奥数题:综合模拟试卷及答案篇一：初中数学模拟试题及答案初四数学试题一、选择题：本题共12小题，在每小题所给出的四个选项中，只有一个是正确的，请将第i卷选择题所选选项填入下表，第1～3小题每题3分，第4～12小题每题4分，错选、不选或选出的答案超过一个，均记零分．1．例如图，数轴的单位长度为1，如果点a，b则表示的数的绝对值成正比，那么点a则表示的数是（a）－4（b）－2（c）0（d）42．以下排序恰当的就是（a）（－p2q）3＝－p5q3（b）（12a2b3c）÷（6ab2）＝2ab2－（c）3m÷（3m－1）＝m－3m2（d）（x2－4x）x1＝x－43．长方体的主视图、俯视图如图所示，则其左视图面积为（a）3（b）4（c）12（d）164．未知m＝??221，则存有3??（a）5＜m＜6（b）4＜m＜5（c）－5＜m＜－4（d）－6＜m＜－55．下列命题中，假命题是（a）平行四边形就是中心对称图形（b）三角形三边的垂直平分线相交于一点，这点到三角形三个顶点的距离相等（c）对于直观的随机样本，可以用样本的方差回去估算总体的方差（d）若x2＝y2，则x＝y6．如图，将周长为8的△abc沿bc方向平移1个单位得到△def，则四边形abfd的周长为（a）6（b）8（c）10（d）127．如图，b处在a处的南偏西45°方向，c处在a处的南偏东15°方向，c处在b处的北偏东80°方向，则∠acb等于（a）40°（b）75°（c）85°（d）140°8．未知一组数据：1，3，5，5，6，则这组与数据的方差就是（a）16（b）5（c）4（d）3.29．如图，在直角坐标系中，矩形oabc的顶点o在坐标原点，边oa在x轴上，oc在y轴上，如果矩形oa′b′c′与矩形oabc关于点o位似，且矩形oa′b′c′的面积等于矩形oabc面积的1，那么点b′的坐4（－∠abc线段点标是（a）（－2，3）（b）（2，－3）c）（3，－2）或（－2，3）（d）2，3）或（2，－3）10．如图，△abc是等边三角形，p是的平分线bd上一点，pe⊥ab于点e，bp的垂直平分线交bc于点f，垂足为q．若bf＝2，则pe的长为（a）23（b）3（c）2（d）311．例如图，在rt△abo中，斜边ab＝1．若oc∥ba，∠aoc＝36°，则（a）点b到ao的距离为sin54°（b）点b到ao的距离为tan36°（c）点a到oc 的距离为sin36°sin54°（d）点a到oc的距离为cos36°sin54°12．如图，点a是反比例函数y?23（x＞0）的图象上任意一点，ab∥x轴交反比例函数y??的xx图象于点b，以ab为边作□abcd，其中c，d在x轴上，则s□abcd为（a）5（b）4（c）3（d）2二、填空题：本题共5小题，满分20分，13．水解因式：3m3－18m2n＋27mn2＝．14．例如图，在菱形abcd中，点e，f分别就是bd，cd的中点，ef＝6cm，那么存有ab＝15．如果代数式x2＋3x＋2可以则表示为（x－1）2＋a（x－1）＋b的形式，则a＋b的值是．16．当阔为3cm的刻度尺的一边与圆切线时，另一边与圆的两个交点处的读数如图所示（单位：cm），那么该圆的半径为cm．17．二次函数y＝－（x－2）2＋9的图象与x4轴围整数利用说道一个变成的半封闭区域内（包含边界），斜、纵坐标都就是的点有个．（提示信息：必要时可以．三、答疑题：本大题共7小题，共55分后．答疑必须写下必要的文字清、证明过程或编程语言步骤．18．（本题满分6分后）x?x2?x?x化简分式?，并从－1≤x＜3中选出?2??2x1x1x2x1你认为合适的整数x代入求值．19．（本题满分6分后）如图，在△abc中，ab＝ac，ad是高，am是△abc外角∠cae的平分线．（1）用尺规作图方法，并作∠adc的平分线dn；（留存作图痕迹，不文学创作法和证明）（2）设dn与am处设点f，推论△adf的形状，并详述理由．20．（本题满分8分）关于x的一元二次方程x2＋3x＋m－1＝0的两个实数根分别为x1，x2．（1）谋m的值域范围．（2）若2（x1＋x2）＋x1x2＋10＝0，谋m的值．21．（本题满分8分）某校八年级为介绍学生课堂讲话情况，随机提取该年级部分学生，对他们某天在课堂上讲话的次数展开了统计数据，其结果如下表中，并绘制了如图所示的两幅不完备的统计图，未知b，e两组发言人数的比为5：2，恳请融合图中有关数据提问以下问题：（1）求出样本容量，并补全直方图；（2）该年级共计学生500人，恳请估算全年级在这天里讲话次数不少于12的人数；（3）已知a组发言的学生中恰有1位女生，e组发言的学生中有2位男生，现从a组与e组中分别抽一位学生写报告，请用列表法或画树状图的方法，求所抽的两位学生恰好是一男一女的概率．22．（本题满分9分）某学校为了提升办学条件，计划添置一批电子白板和一批笔记本电脑，经投标，出售1块电子白板比卖3台笔记本电脑多3000元，出售4块电子白板和5台笔记本电脑共需80000元．（1）求购买1块电子白板和一台笔记本电脑各需多少元？（2）根据该校实际情况，须要出售电子白板和笔记本电脑的总数为40，建议出售的总费用不少于300000元，并且出售笔记本电脑的台数不少于出售电子白板数量的3倍，该校存有哪几种出售方案？（3）上面的哪种购买方案最省钱？按最省钱方案购买需要多少钱？23．（本题满分9分）例如图，梯形abcd就是全等梯形，且ad∥bc，o就是腰cd的中点，以cd短为直径作圆，交bc于e，过e作eh⊥ab于h．（1）澄清：oe∥ab；1cd，澄清：ab就是⊙o的切线；2bh（3）在（2）的条件下，若be＝4bh，谋的值．ce（2）若eh＝24．（本题满分9分）例如图，顶点为p（4，－4）的二次函数图象经过原点（0，0），点a在该图象上，oa缴其对称轴l于点m，点m，n关于点p等距，相连接an，on．（1）求该二次函数的关系式．（2）若点a的座标就是（6，－3），谋△ano的面积．（3）当点a在对称轴l右侧的二次函数图象上运动，请解答下列问题：①证明：∠anm＝∠onm．②恳请从∠ona、∠nao中挑选出一个推论其若想为直角，并详细表明理由．一、选择题1.与无理数最吻合的整数就是a．1b．22.以下运算恰当的就是c．3d．4篇二：2021年初中奥数题及答案2021年初中奥数题及答案初中奥数题试题一一、选择题（每题1分，共10分）1．如果a，b都代表有理数，并且a＋b=0，那么()a．a，b都就是0b．a，b之一就是0c．a，b互为相反数d．a，b互为倒数答案：c解析：令a=2，b=－2，满足2+(－2)=0，由此a、b互为相反数。

数学奥林匹克初中训练题(6套)综述

数学奥林匹克初中训练题(1)第一试一. 选择题 .( 每题 7 分,共 42 分)()1.已知 a3b3c33abc 3 ,则(a b)2(b c)2(a b)(b c) 的值为:a b c(A)1(B)2(C)3(D)4()2.规定” Δ”为有序实数对的运算, 假如(a, b)(c, d)( ac bd, ad bc ). 如果对随意实数a, b 都有 ( a, b)( x, y)( a,b), 则 (x, y) 为:(A) (0,1)(B)(1,0)(C)(1,0)(D) (0,1)()3.在ABC中 ,211, 则∠A:a b c(A) 必定是锐角(B)必定是直角(C)必定是钝角(D)非上述答案()4.以下五个命题 : ①若直角三角形的两条边长为3与4,则第三边长是5; ②( a )2a; ③若点P(a, b)在第三象限,则点 P1 (a,b1)在第一象限;④连结对角线垂直且相等的四边形各边中点的四边形是正方形; ⑤两边及其第三边上的中线对应相等的两个三角形全等. 此中正确的命题的个数是:(A)2 个(B)3个(C)4个(D)5个()5.设 P 为等腰Rt ABC斜边 AB上或其延伸线上一点, S AP2BP2,那么:(A) S2CP 2(B)S2CP 2(C)S2CP 2(D)不确立()6.知足方程 x2y22( x y)xy 的全部正整数解有:(A) 一组(B)二组(C)三组(D)四组二. 填空题 .( 每题 7分,共28分 )1. 一辆客车 , 一辆货车和一辆小轿车在同一条直线上朝同一方向行驶, 在某一时辰 ,货车在中 , 客车在前 , 小轿车在后 , 且它们的距离相等.走了 10分钟 , 小轿车追上了货车 ; 又走了5分钟 , 小轿车追上了客车. 问再过分钟 , 货车追上了客车 .2. 若多项式P2a28ab 17b2 16 a 4b2070,那么 P 的最小值是.3. 如图 1,O∠ AOB内有必定点 P, 且 OP=10.∠ AOB=30,在 OA 上有一点Q,OB 上有一点 R.若PQR 周长最小 , 则最小周长是.4.已知二次函数yax 2 (a 1) 的图象上两点A,B的横坐标分别为1,2 ,O 是坐标原点 ,假如AOB 是直角三角形, 则AOB 的周长为第二试.一 .(20分 )已知实数a,b,c知足不等式ab c, bc a , ca b, 求a bc 的值 .二.(25 分) 如图2, 点 D 在 ABC 的边 BC 上 , 且与 B,C 不重合 , 过点D 作 AC 的平行线DE 交 AB 于 E, 作 AB 的平行线 DF 交 AC 于点 F. 又知 BC=5. (1) 设 ABC 的面积为 S. 若四边形 AEFD 的面积为 2S . 求5BD 长 .(2) 若 AC2AB, 且 DF 经过 ABC 的重心 G,求 E,F 两点的距离 .三 .(25 分 )已知定理 :”若三个大于 3 的质数 a, b, c 知足关系式 2a5b c ,则 a b c是整数 n 的倍数 .”试问 :上述定理中整数 n 的最大可能值是多少?并证明你的结论 .数学奥林匹克初中训练题(2)第一试一. 选择题 .( 每题 7 分,共 42 分)( )1.有铅笔,练习本,圆珠笔三种学惯用品. 若购铅笔 3 支 , 练习本 7 本 , 圆珠笔 1 支共需 3.15 元 ; 若购铅笔4 支,练习本 10 本, 圆珠笔 1 支共需4.2 元 . 现购铅笔 ,练习本 , 圆珠笔各 1 件,共需:元元元元( )2.三角形的三边 a,b,c 都是整数 , 且知足 abc bc caab a bc 7 , 则此三角形的面积等于:(A)3 2(C)3 2(B)4(D) 224( )3.如图 1,ABC 为正三角形 ,PM ⊥AB,PN ⊥AC.设四边形 AMPN,ABC 的周长分别是 m,n , 则有 :1 m 3 (B)2 m3 80% m m(A)n53n(C)83% (D) 78% 79%24nn( )4.知足 ( x3)2( y 3)26 的全部实数对( x, y) , 使y取最大值 , 此最大值x为 :(A) 32 2 (B)42 (C) 5 33 (D) 5 3( )5.设 p 37a 1 37b 1 37c137d1 . 此中 a,b,c, d 是正实数 , 且满足 ab c d 1. 则 p 知足 : (A) p ＞ 5(B) p ＜ 5 (C)p ＜2(D)p ＜ 3( )6.如图 2, 点 O 是正六边形 ABCDEF 的中心 ,OM ⊥ CD,N为 OM 的中点 .则 S ABN :S BCN 等于:(A)9:5 (B)7:4 (C)5:3 (D)3:2二 . 填空题 .(每题 7 分 ,共 28 分)1. 若实数 x, y 知足 ( xx 2 1)( yy21)1则,x y.2.如图 3,CD 为直角 ABC 斜边 AB 上的高 ,DE ⊥AC.设p 1 p 2ADE, CDB, ABC 的周长分别是 p 1 , p 2 , p . 当p取最大值时 , ∠A= .3. 若函数 ykx 5 中自变量的取值范围是4kx kx 2 3一确实数 , 则实数 k 的取值范围是.4. 如图 4 所示 , 线段 AB 与 CD 都是⊙ O 中的弦 , 此中AB 108O , AB a, CD 36O ,CD b ,则⊙O的半径R=.第二试一.( 共 20分 ) n是一个三位数 , b是一个一位数 , 且a,a2b2都是整数 , 求a b 的b ab1最大值与最小值 .二.( 共 25分)如图 5, 在ABC中, ∠A=60O,O,I,H 分别是它的外心, 心里 , 垂心 . 试比较ABC的外接圆与IOH 的外接圆的大小, 证明你的论断 .x y z 3的全部三 .(共 25 分 )求方程组3y3z3x3整数解 .参照答案一.1.(B)数学奥林匹克初中训练题( 四 )第一试三. 选择题 .( 每题 7 分,共 42 分)(1,0.2002,13 2 22),n n2)1.在,(3( n是大于 3 的整数 )这 5 个722数中 ,分数的个数为 :(A)2(B)3(C)4(D)5()2.如图 1,正方形 ABCD的面积为256,点 F 在 AD 上,点E在AB的延伸线上 ,Rt CEF 的面积为200,则 BE 的长为 :(A)10(B)11(C)12(D)15 ()3.已知a, b, c均为整数 ,且知足a2b2 c 23＜ ab3b 2c .则以 a b,c b 为根的一元二次方程是 :(A) x23x20(B) x2 2 x80(C) x24x50(D) x2 2 x30()4.如图 2,在 Rt ABC 中 ,AF 是高 ,∠ BAC=90 O,且BD=DC=FC=1, 则 AC 为:(A) 32(B)3(C)2(D)33()5.若k 2a b2c a2b cc b a,则k的值为 :(A)1(B)2(C)3(D) 非上述答案()6.设x0, y0,2 x y 6 ,则u 4x23xy y 2 6x 3y 的最大值是:(A)27(B)18(C)20(D) 不存在2四 . 填空题 .(每题7 分,共 28分)1.方程1x2110的实数根是.x21x23x2.如图 3,矩形 ABCD中 ,E,F分别是 BC,CD上的点 ,且SABE 2 , S C E F 3 ,S ADF,4则SAEF=.3.已知二次函数数时,都有为.y x2( a 1)x b (a, b为常数).当x 3 时, y 3; 当x为随意实y x .则抛物线的顶点到原点的距离4.如图 4,半径为2cm ,圆心角为90O的扇形 OAB 的AB上有一运动的点 P.从点 P 向半径 OA 引垂线 PH 交 OA 于点 H.设OPH 的心里为 I,当点 P 在AB上从点 A 运动到点 B 时 ,心里I 所经过的路径长为.第二试一.(20 分 ) 在一个面积为 1 的正方形中结构一个以下的小正方形 ; 将单位正方形的各边n均分 , 而后将每个顶点和它相对应极点最靠近的分点连接起来,如图5所示 . 若小正方形的面积恰为1, 求n的值 . 3281二 .(25 分)一条笔挺的公路l 穿过草原,公路边有一卫生站A, 距公路30km的地方有一居民点B,A,B 之间的距离为 90km .一天某司机驾车从卫生站送一批抢救药品到居民点.已知汽车在公路上行驶的最迅速度是60km / h ,在草地上行驶的最迅速度是30km / h .问司机应以如何的路线行驶,所用的行车时间最短 ?最短时间是多少 ?三.(25 分 )从 1，2，3，， 3919 中任取 2001 个数。

数学奥林匹克初中训练题

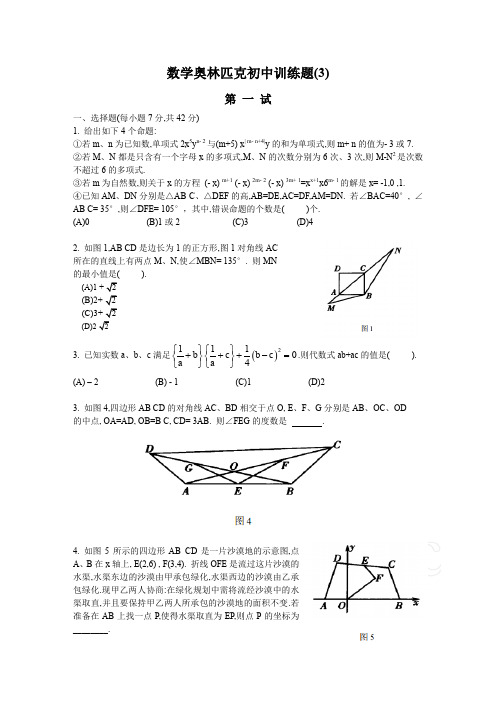
数学奥林匹克初中训练题(3)第一试一、选择题(每小题7分,共42分)1. 给出如下4个命题:①若m 、n 为已知数,单项式2x 5y n- 2与(m+5) x | m- n+4|y 的和为单项式,则m+ n 的值为- 3或7. ②若M 、N 都是只含有一个字母x 的多项式,M 、N 的次数分别为6次、3次,则M-N 2是次数不超过6的多项式.③若m 为自然数,则关于x 的方程 (- x) m+1 (- x) 2m- 2 (- x) 3m+ 1=x x+1x6m- 1的解是x= -1,0 ,1. ④已知AM 、DN 分别是△AB C 、△DEF 的高,AB=DE,AC=DF,AM=DN. 若∠BAC=40°, ∠AB C= 35°,则∠DFE= 105°，其中,错误命题的个数是( )个.(A)0 (B)1或2 (C)3 (D)42. 如图1,AB CD 是边长为1的正方形,图1对角线AC所在的直线上有两点M 、N,使∠MBN= 135°. 则MN的最小值是( ).3. 已知实数a 、b 、c 满足()211104b c b c a a ⎧⎫⎧⎫+++-=⎨⎬⎨⎬⎩⎭⎩⎭.则代数式ab+ac 的值是( ). (A) – 2 (B) - 1 (C)1 (D)23. 如图4,四边形AB CD 的对角线AC 、BD 相交于点O, E 、F 、G 分别是AB 、OC 、OD 的中点, OA=AD, OB=B C, CD= 3AB. 则∠FEG 的度数是.4. 如图5所示的四边形AB CD 是一片沙漠地的示意图,点A 、B 在x 轴上, E(2,6) , F(3,4). 折线OFE 是流过这片沙漠的水渠,水渠东边的沙漠由甲承包绿化,水渠西边的沙漠由乙承包绿化.现甲乙两人协商:在绿化规划中需将流经沙漠中的水渠取直,并且要保持甲乙两人所承包的沙漠地的面积不变.若准备在AB 上找一点P,使得水渠取直为EP,则点P 的坐标为________.。

初中数学奥林匹克竞赛全真试题

初中数学奥林匹克竞赛全真试题题目一：1. 解方程$\frac{1}{3}x+2=\frac{2}{5}x-1$，求$x$的值。

2. 若直线$y=kx-3$与直线$y=\frac{1}{2}x-5$平行，求$k$的值。

3. 已知$a$是正整数，满足方程$a^2-4a-5=0$，求$a$的值。

题目二：1. 华华跑步比赛中，他以每分钟1.5米的速度匀速前进。

比赛开始后30分钟，华华忘记带水了，于是他以每分钟2米的速度奔回去取水，然后再以每分钟1.5米的速度继续往前跑。

已知比赛结束时，华华总共跑了120米。

请问比赛一共进行了多少分钟？2. 有一条宽为6米的小溪，小明骑自行车沿着小溪一端的水平直线岸边骑行。

小明的自行车速度是每小时10千米，溪水的流速是每小时4千米。

小明骑行了10分钟后，他发现自行车打了个铃，遇到了沿小溪反方向划独木舟的小红。

小红的独木舟速度是每小时5千米。

请问小红划独木舟一共需要多少时间才能追上小明？3. 小玲和小华共同参加一场马拉松比赛。

小玲的速度是每分钟2.5米，小华的速度是每分钟3米。

他们同时从起点出发，一起向终点前进。

已知终点距离起点500米，当小华到达终点时，小玲还剩下100米没有到达终点。

请问比赛结束时，小华比小玲多走了多少米？解答：1. 解方程$\frac{1}{3}x+2=\frac{2}{5}x-1$，求$x$的值。

首先，将方程两边的分数化成相同的分母，得到$\frac{5}{15}x+\frac{30}{15}=\frac{6}{15}x-\frac{15}{15}$。

继续化简得到$\frac{1}{15}x=-\frac{45}{15}$。

通过消去分数，可知$x=-45$。

2. 若直线$y=kx-3$与直线$y=\frac{1}{2}x-5$平行，求$k$的值。

平行的直线具有相同的斜率，所以$k=\frac{1}{2}$。

3.已知$a$是正整数，满足方程$a^2-4a-5=0$，求$a$的值。

初中数学奥林匹克训练题及答案

初中数学奥林匹克训练题第一试一、选择题(每小题7分，共42分)1.已知m 、n 是两个连续正整数，m<n ，且a=mn ，设x=m -a n a ++，y=m -a n a -+.下列说法正确的是( ).(A)x 为奇数，y 为偶数 (B)x 为偶数，y 为奇数 (C)x 、y 都为奇数 (D)x 、y 都为偶数2.设a 、b 、c 和S 分别为三角形的三边长和面积，关于x 的方程b 2x 2+(b 2+c 2-a 2)x+c 2=0的判别式为Δ.则Δ与S 的大小关系为( ).(A)Δ=16S 2 (B)Δ=-16S 2 (C)Δ=16S (D)Δ=-16S 3.设a 为5353--+的小数部分，b 为336336--+的小数部分.则ab12-的值为( ). (A)6 +2 -1 (B) 6- 2+1 (C) 6- 2-1 (D) 6+2+14.如图，D 、E 分别为△ABC 的边AB 、AC 上的点，△ACD 与△BCD的周长相等，△ABE 与△CBE 的周长相等，记△ABC 的面积为S.若∠ACB=90°，则AD ·CE 与S 的大小关系为( ).(A)S=AD·CE(B)S>AD·CE(C)S<AD ·CE(D)无法确定5.如图，在△ABC 中，AB=8，BC=7，AC=6，延长边BC 到点P ，使得△PAB 与△PCA 相似.则PC 的长是( ).(A)7 (B)8 (C)9 (D)10 6.如图，以PQ=2r(r ∈Q)为直径的圆与一个以R(R ∈Q)为半径的圆相切于点P .正方形ABCD 的顶点A 、B 在大圆上，小圆在正方形的外部且与边CD 切于点Q.若正方形的边长为有理数，则R 、r 的值可能是( ).(A)R=5，r=2 (B)R=4，r=3/2(C)R=4，r=2 (D)R=5，r=3/2 二、填空题(每小题7分，共28分) 1.已知方程x 2+x-1=0的两个根为α、β.则αββα33+的值为 .2.把1，2，…，2 008个正整数分成1 004组:a 1，b 1;a 2，b 2;…;a 1 004，b 1 004，且满足a 1+b 1=a 2+b 2=…=a 1004+b 1004.对于所有的i(i=1，2，…，1 004)，a i b i 的最大值为 .3.AD 、BE 、CF 为△ABC 的内角平分线.若BD+BF=CD+CE=AE+AF ，则∠BAC 的度数为 .4.下列四个命题:①一组对边相等且一组对角相等的四边形是平行四边形; ②一组对边相等且一条对角线平分另一条对角线的四边形是平行四边形;③一组对角相等且这一组对角的顶点所联结的对角线被另一条对角线平分的四边形是平行四边形;④一组对角相等且这一组对角的顶点所联结的对角线平分另一条对角线的四边形是平行四边形.其中，正确命题的序号是.第二试一、(20分)已知△ABC中，∠A>∠B>∠C，且∠A=2∠B.若三角形的三边长为整数，面积也为整数，求△ABC面积的最小值.二、(25分)已知G是△ABC内任一点，BG、CG分别交AC、AB于点E、F.求使不等式S△BGF ·S△CGE≤kS2△ABC恒成立的k的最小值.三、(25分)已知(x+1y2+)(y+1x2+)=1.求证:x+y=0.初中数学奥林匹克训练题参考答案第一试一、1.C.x=n+m=m+m+1=2m+1，y=n-m=1.所以，x 、y 都是奇数. 2.B. 因为Δ=(b 2+c 2-a 2)2-4b 2c 2=(b 2+c 2-a 2+2bc)(b 2+c 2-a 2-2bc) =[(b+c)2-a 2][(b-c)2-a 2]=(b+c+a)(b+c-a)(b-c+a)(b-c-a). 记p=21 (a+b+c)，所以，Δ=2p·2(p-a)·2(p-c)[-2(p-b)]=-16p(p-a)(p-b)(p-c).由海伦公式知S 2=p(p-a)(p-b)(p-c). 故Δ=-16S 2.3.B.4.A.设BC=a ，CA=b ，AB=c.由题意知AD+AC=BC+CE=21 (a+b+c).故AD=21 (a+c-b)，CE=21 (b+c-a).则AD ·CE=41 (a+c-b)(b+c-a)=41[c 2-(a-b)2]=41(c 2-a 2-b 2)+12ab.由∠ACB=90°，知a 2+b 2=c 2，S=21ab.于是，AD ·CE=S.5.C.由题意知只能是△PAB ∽△PCA.则有PA/PC=PB/PA=AB/AC=8/6=4/3.故PB=34PA ，PB=PC+BC=PC+7，PA=34PC.又PA 2=PB ·PCPC=9. 6.D.辅助线如图.由题意知OA 2=OE 2+AE 2.设AB=2x ，则AE=x. 于是，R 2=[2x-(R-2r)]2+x 2.化简得5x 2-4(R-2r)x+4(r 2-Rr)=0.①要使AB 为有理数，只要x 为有理数，也即方程①的Δ=[-4(R-2r)]2-4×5×4(r2-Rr)=16(R 2+Rr-r 2)为完全平方式，也即只需R 2+Rr-r 2为完全平方式. 经验证知，只有选项(D)符合题意. 二、1.-7. 令A=αββα33+，B=ββαα33+=α2+β2.由已知有α+β=-1，αβ=-1.故B=(α+β)2-2αβ=1+2=3.① A+B=)=(α3+β3)(1/α+1/β)=-4.②由式①、②得A=-4-3=-7. 2.1 009 020. 注意到a i b i =41[(a i +b i )2-(a i -b i )2]，a i +b i =(1+2 008)×1 004/1 004=2 009.要使a i b i 的值最大，须a i -b i 的值最小，而a i -b i 的最小值为1，此时a i +b i =2 009，a i -b i =1.于是，a i =1 005，b i =1 004，此时，a i b i 的最大值为1 005×1 004=1 009 020. 3.60°.记BC=a ，CA=b ，AB=c.由内角平分线定理知 BD=cb ac +，CD=cb ab +，BF=ba ac +，CE=ca ab +.由BD+BF=CD+CE ，.去分母并化简得a 2c+2ac 2+2bc 2+c 3=a 2b+2ab 2+2b 2c+b 3，即 (c-b)(a 2+2ac+2ab+b 2+c 2+3bc)=0.显然a 2+2ac+2ab+2bc+b 2+c 2+bc=(a+b+c)2+bc>0. 于是，c-b=0，即b=c.同理，当CD+CE=AE+AF 时，有c=a.所以，a=b=c ，△ABC 为等边三角形. 故∠BAC=60°. 4.④.命题①、②、③可分别给出如下反例:命题①:如图5(a)中的四边形ABCD ，其中，△ABD △CDE.命题②:如图5(b)，作等腰△ADE ，延长底边ED 到任意点O ，以O 为对角线的交点可作出 ABCE ，而此时四边形ABCD 满足条件AD=(AE=)BC ，且AO=CO ，但不是平行四边形.命题③:如图5(c)中的四边形ABCD ，其中，A 、C 是BD 垂直平分线上的任意两点.图5 以下证明命题④是正确的.如图5(d)，已知∠BAD=∠DCB ，且OB=OD.以点O 为中心，将△ABD 逆时针旋转180°.因为OB=OD ，所以，点D 与B 重合，点B 与D 重合，点A 与射线OC 上某点A 1重合.如果A 1不是C ，则∠BA 1D>∠BCD(A 1在线段OC 内部)或∠BA 1D<∠BCD(A 1在OC 的延长线上)，都与∠BA 1D=∠BAD=∠BCD 矛盾，从而，A 1即是C ，即OA=OA 1=OC.所以，四边形ABCD 是平行四边形. 第二试一、记BC=a ，CA=b ，AB=c.如图，作∠BAC 的平分线AD ，则∠BAD=∠DAC=∠B ，∠ADC=∠B+∠BAD=2∠B.故△ACD △BCA.于是，b/a=CD/b.①又由角平分线定理知b/c=CD/BD.从而，cb b +=BDCD CD + =aCD .②由式①、②得ac b +=ba .故a 2=b(b+c).若(b ，c)=d ，则由式①知d|a ，故不妨设(b ，c)=1.于是，可令 b=m 2，b+c=n 2.则a=mn ，c=n 2-m 2.由∠A>∠B>∠C ，知a>b>c ，即mn>m 2>n 2-m 2. 故m<n<2 m.③又m 、n 为正整数，从而，2m-m>1，即m>2 +1.④设△ABC 的面积为S ，由海伦公式知 S=41n(n+m)(n-m)·n)-n)(2m (2m +.由式④知m ≥3.又由式③容易验证:当3≤m ≤7时，只有m=5时，n=6，n)-n)(2m (2m + =8(有理数)，此时， S=14×6×11×1×8=132.下证当m ≥8，n ≥9时，S>162. 由式③、④知(2m+n)(2m-n)>3m(2m-2m)=(6-32)m 2>(6-42)m 2=(2-2)2m 2，n(n+m)(n-m)>n(1+22n)×1=21 (2+ 2)n 2.由式⑤知 S>14×12(2+ 2)n 2(2- 2)m=14n 2则当m ≥8，n ≥9时，有S>162.故S 的最小值为132，此时，m=5，n=6.所以，a=30，b=25，c=11时，△ABC 面积最小，最小值为132.二、如图，设AF/AB=x ，AE/AC=y.则0<x 、y<1.在△ABE 中，由梅涅劳斯定理有BG/GE·EC/CA·AF/FB=1..从而，u 2+(t-2)u+2t=0在[0，2]内有实根，则Δ=(t-2)2-8t ≥0 t ≥6+42或t ≤6-42.从而t ≤6-4 2. 所以，tmax=6-4 2，此时u=22 -2.因此，当u=22-2，x=y ，即x=y=2-1时，(S △BFG ·S △CEG /S 2△ABC )max=41(6-4 2)2=17-122.故k ≥17-122，kmin=17-12 2.三、用反证法证明.(1)先证x=0时y=0，或y=0时x=0.如若不然，假设x=0时，y>0.则 (x+1y 2+)(y+1x 2+)=1y 2+ (y+1)>1，与已知矛盾.当x=0，y<0时，又有 (x+1y 2+)(y+1x 2+)=1y 2+ (y+1)<12y 2+-y (1+y)=(1-y)(1+y)=1-y 2<1，与已知矛盾.故x=0时，y=0. 同理，y=0时，x=0.(2)再证x ≠0，y ≠0时，x+y=0.为此先证xy<0. 如若不然，则x>0，y>0或x<0，y<0.当x>0，y>0时，(x+1y 2+)(y+1x 2+)>1，与已知矛盾.当x<0，y<0时，(x+1y 2+)(y+1x 2+)=y)-1x x)(-1y ()y -1)(x x -1(y 222222++++=y)-1x x)(-1y ()x -(y -122222++≤y)-1x x)(-1y (122++.但(1y 2+-x>1，1x 2+-y>1，则y)-1x x)(-1y (122++<1，与已知矛盾.从而，xy<0. 以下分两种情形讨论.(i)若x+y>0，由于原式关于x 、y 对称，不妨设x>0，y<0.则x>-y ，x2>y2，有(x+1y 2+)(y+1x 2+)>(1y 2+-y)(1y 2++y)=1，与已知矛盾.同理，当x<0，y>0时，也与已知矛盾. (ii)若x+y<0，不妨设x>0，y<0.则x<-y ，x 2<y 2，有(x+1y 2+)(y+1x 2+)<(1y 2+-y)(1y 2++y)=1，与已知矛盾.由(i)、(ii)知，x+y>0和x+y<0均不成立. 因此，x+y=0. 综上知x+y=0.。

数学奥林匹克初中训练题(128)

数学奥林匹克初中训练题(128)
《数学奥林匹克初中训练题（128）》
一、选择题（每题5分，共20分）
1. 在等差数列{an}中，Sn = n(a1 + an)，且a2-a1=3，那么a8 = （）
A. 25
B. 24
C. 31
D. 30
2. 如果a = 2,b = -2,那么a-b的绝对值等于（）
A. -4
B. 4
C. 0
D. 2
3. 在△ABC中，若a＝3，b＝4，C＝90°，则cosC的值等于（）
A. -3/5
B. 3/4
C. 3/5
D. -3/4
4. 把一个正方形沿对角线分割成两个相似的四边形，那么这两个四边形的面积之比等于（）
A. 1：1
B. 2：1
C. 1：2
D. 4：1
5. 已知等比数列{an}的前n项和为Sn，S4＝24，a1＝2，则a5的值是（）
A. 8
B. 32
C. 48
D. 128
二、填空题（每题5分，共20分）
6. 圆锥的体积公式为V= πR2h ________，其中R、h分别表示圆锥底面半径和高。

7. 将等差数列{an}中的各项乘以一个常数k，所得到的序列叫做________数列。

8. 已知正方形边长为a，则它的面积为________。

9. 若a,b,c均为正实数，且a>b>c，则a3-b3-c3的值为________。

10. 在△ABC中，若a = 3, b = 4, c = 5, 则sinA等于________。

初中数学奥林匹克模拟试卷(10)

数学奥林匹克模拟试卷（十）一、选择题：1、若0<=-=-=-abc cx z b z y a y x ，则c b a ,,中负数的个数有（）（A ）1个（B ）2个（C ）3个（D ）4个 2、若a 是方程0663232=--x x 的一个实根，则32444316643⎪⎭⎫ ⎝⎛--a a 的值是（）（A ）1（B ）–1（C ）8（D ）–83、已知梯形的两条对角线分别为m 与n ，两对角线的夹角为60 0，那么，该梯形的面积为（）（A ）mn 3（B ）mn 23（C ）mn 43（D ）mn 83 4、已知三个实数321,,x x x ，它们中任何一个数加其余两个数的积的5倍总等于6，这样的三元数组（321,,x x x ），共有（）（A ）2组（B ）3组（C ）4组（D ）5组5、已知A ⎪⎭⎫ ⎝⎛a 1,31、B ⎪⎭⎫ ⎝⎛b 1,41、C ⎪⎭⎫ ⎝⎛c 1,51满足31=+c b a ，21=+c a b 则A 、B 、C 三边的位置适合（）（A ）在同一直线上（B ）组成锐角三角形（C ）组成直角三角形（D ）组成钝角三角形6、Rt ∆ABC 中，AB=3，AC=4，BC=5，现在记A 、B 、C 到某一直线l 的距离分别为C B A d d d ,,，若，则3:2:1::=C B A d d d ，满足条件的直线l 共有（）（A ）1条（B ）2条（C ）3条（D ）4条二、填空题：1、若a x <<0，化简()⎥⎥⎦⎤⎢⎢⎣⎡-++-⎪⎭⎫ ⎝⎛+----222211x a x a ax x x a x a x a a 。

2、如图，已知∆ABC ，∠B 的平分线交边AC 于P ，∠A 的平分线交边BC 于Q ，如果过点P 、Q 、C 的圆也过∆ABC 的内心R ，且PQ=1，则PR 的长等于。

3、对于满足2||≤p 的所有实数p ，使不等式p x px x +>++212恒成立的x 的取值范围是。

初中数学奥林匹克训练题10(试卷)

初中数学奥林匹克训练题（10）第一试一、填空题1、设H 为锐角三角形ABC 的垂心，已知30A ∠=︒，3BC =，则AH =___________.2、有六张分别写有数字1，2，3，4，5，6的卡片，每次从中抽取一张，记下上面的数字，然后放回. 这样取了4次，则抽到的最大数与最小数的差等于5的概率为__________.3、已知三个正数,,a b c 满足3a b c a ≤+≤，223()5b a a c b ≤+≤，则2b c a -的最小值是________.4、设x R ∈，则函数()f x =的最小值为 .5、从前2008个正整数构成的集{}1,2,,2008M = 中取出一个k 元子集A ，使得A 中任两数之和不能被这两数之差整除，则k 的最大值为．6、已知()()2222212f x x a b x a ab b =++-++-的对称轴是y 轴，则函数图象与y 轴交点的纵坐标的最大值是7、＝。

8、设,,,a b c d 为非负实数，满足a b c d b c d a c d a b d a b c ===++++++++，则 a b b c c d d a c d a d a b b c+++++++++++＝。

9、设实系数一元二次方程2220x ax b ++-=有两个相异实根，其中一根在区间(0,1)内，另一根在区间(1,2)内，则41b a --的取值范围是。

10、考虑集合{}1,2,,10S = 的所有非空子集，若一个非空子集中的偶数的数目不少于奇数的数目，称这个子集是“好子集”，则“好子集”的数目有（）个.11、考虑44⨯的正方形方格表中的25个格点，则通过至少3个格点的不同直线的数目为 .12、设[]x 表示不超过x 的最大整数，则2008120082009k k =⎡⎤⎢⎥⎣⎦∑的值是 . 13、如右图，已知,,L M N 分别为ABC ∆的三边,,BC CA AB 的中点，,D E 分别是,BC AB 上的点，并满足,AD CE 均平分ABC ∆的周长，,P Q 分别是,D E 关于,L N 的对称点，PQ 与LM 交于点F ，若AB AC >，则AF 一定过ABC ∆的（）.()A 内心 ()B 外心 ()C 重心 ()D 垂心14、设不定方程222100x y z xyz ++-+=的正整数解(),,x y z 中满足,,x y z 均大于2008的不同解的数目为k ，则k 满足（）.()0A k = ()12008B k ≤≤ ()2008C k >，但k 是有限的数 ()D k 是无穷大二、解答题1、已知锐角ABC ∆的三边,,BC CA AB 的中点分别为,,D E F ，在,,EF FD DE 的延长线上分别取点,,P Q R ，若AP BQ CR ==，证明PQR ∆的外心为ABC ∆的垂心.2、有10个选手1210,,,A A A ，他们的积分分别为9,8,7,6,5,4,3,2,1,0，名次分别为第1,2,3,4,5,6,7,8,9,10. 现进行单循环比赛，即任意两个选手之间都恰进行一场比赛，且每场比赛都要分出胜负. 若名次靠前的选手胜了名次靠后的选手，则胜者得1分，负者得0分；若名次靠后的选手胜了名次靠前的选手，则胜者得2分，负者得0分，全部比赛结束后计算每个选手的累计积分（即这次单循环所得的分数与之前的积分相加所得的和），并根据累计积分进行重新排名，求新的冠军累计积分的最小值（名次并列是允许的）.311x ≥--。

初中数学奥林匹克模拟试卷1_10套

初中数学奥林匹克竞赛题包括答案.docx

初中数学奥林匹克模拟试卷1-10套

数学奥林匹克初中训练模拟试题附答案(四)

初中数学奥林匹克模拟试卷1-10套

七年级数学奥林匹克竞赛题(一)解析

数学奥林匹克初中训练题15套

初中数学奥数题综合模拟试卷及答案

数学奥林匹克初中训练题(6套)综述

数学奥林匹克初中训练题

初中数学奥林匹克竞赛全真试题

初中数学奥林匹克训练题及答案

数学奥林匹克初中训练题(128)

初中数学奥林匹克模拟试卷(10)

初中数学奥林匹克训练题10(试卷)

最新整理初中奥数试题大全及解析汇总