02第二章 热一律2-1热力学第一定律的实质及表达式
第2章热力学第一定律

技术功:技术上可以利用的功
1 2 wt c gz wi 2
q u w
wt w pv w p2 v2 p1v1
可逆过程
wt pdv p1v1 p2v2 pdv d pv vdp
2 2 2 2 1 1 1 1
第二章 热力学第一定律
本章要求
理解热力学第一定律的实质—能量守恒定律 掌握流动功,轴功及技术功的概念 注意热力学能,焓的引入及定义
掌握热力学第一定律能量方程的基本表达式 及稳定流动能量方程
本章学习流程
热力学第一定律的提出
热力系能量的组成
能量之间的传递和转化 + 焓
闭口系能量方程 + 开口系能量方程 (第一定律数学表达式)
热力学能只取决于热力系内部的状态,且具有 可加性,是一个具有广延性质的状态参数
2
1
du u 2 u1
du 0
2u 2u Tv vT
u u du dT dv T v v T
二.外储存能
工质在参考坐标系中作为一个整体,因有宏观 速度而具有动能,因有高度差而具有位能
热力学能:是指储存于热力系内部的能量. 用U表示,单位是J或 kJ,单位质量工质的热力 学能称为比热力学能,用u表示,单位是J/kg或 kJ/Kg
热力学能是工质的状态参数,完全取决于工 质的初态和终态,与过程的途径无关
热力学能为两个独立状态参数的函数: u=f(T,v)或u=f(T,p)或u=f(p,v)
能量方程式的应用
确定研究对象—选好热力系统
写出所研究热力系对应的能量方程
针对具体问题,分析系统与外界的相互作用, 作出某些假设和简化,使方程简单明了 求解简化后的方程,解出未知量
工程热力学 第2章 热力学第一定律

δWtot
δmi ei
δQ
E
δm j e j
E+dE
δQ = dE + ⎡Σ ( ej δmj ) −Σ ( eiδmi ) ⎤ + δWtot ⎣ ⎦
或
τ
τ + dτ
Q = ΔE + ∫ ⎡Σ( ej δmj ) −Σ( eiδmi ) ⎤ +Wtot ⎦ τ1 ⎣
τ2
dE Φ= + ⎡Σ ( ej qmj ) −Σ ( ei qmi ) ⎤ + P ⎣ ⎦ tot dτ
二、总(储存)能(total stored energy of system) 热力学能,内部储存能
E =U+Ek +Ep
宏观动能 宏观位能 总能 外部储存能
e =u+ek +ep
3
外部储存能 宏观动能:质量为m的物体以速度cf运动时,该物 体具有的宏观运动动能为:
1 2 Ek = mc f 2
重力位能:在重力场中质量为m的物体相对于系统 外的参数坐标系的高度为z时,具有的重力位能为:
1 2 q − Δu = Δc f + gΔz + Δ( pv ) + wi 2
维持工质流动所需的流动功
21
稳定能量方程的物理意义:工质在状态变化过程 中,从热能转变而来的机械能总和等于膨胀功。 技术功:技术上可资用的功,其数学表达式为:
由
1 2 wt = wi + Δc f + gΔz 2 q − Δu = w
E p = mgz
4
宏观动能与内动能的区别
三、热力学能是状态参数∂U ⎞ ⎛ ∂U ⎞ dU = ⎜ ⎟ dT + ⎜ ⎟ dV = cV dT + ⎢T ⎜ ⎟ − p ⎥ dV ⎝ ∂T ⎠V ⎝ ∂V ⎠T ⎣ ⎝ ∂T ⎠V ⎦
《工程热力学》第二章—热力学基本定律

五、功量与热力过程直接相关
在既定的始、终状态之间,可以有许多过程途径。 在既定的始、终状态之间,可以有许多过程途径。不同 过程中的功量交换是完全不同的。 过程中的功量交换是完全不同的。即:功的大小除与过程的 有关——功 初、终状态有关外,还与描述过程的函数p=f(v)有关 终状态有关外,还与描述过程的函数 有关 功 过程量。 而不能用dw表示 是一个过程量 微元过程功只能用δw而不能用 表示, 是一个过程量。微元过程功只能用 而不能用 表示,即
在孤立系统中,能的形式可以相互转换, ● 在孤立系统中,能的形式可以相互转换,但能 的总量保持不变。 的总量保持不变。 第一类永动机是不可能制成的。 ● 第一类永动机是不可能制成的。 ● 工程热力学中常以热力系统为对象来研究能量 的传递、转换和守恒。 的传递、转换和守恒。 对任一热力系统,热力学第一定律可表述为: ● 对任一热力系统,热力学第一定律可表述为: 进入系统的能量 - 离开系统的能量 = 系统中储存能量的变化
无论哪一种情况, 无论哪一种情况,当系统与外界发生功量 交换时,总与系统本身所经历的过程有关。 交换时,总与系统本身所经历的过程有关。
三、功量交换的基本表达式
δW = F • dx
W = ∫ F ( x)dx
x1
x2
热力学最常见的功——容积功 容积功 热力学最常见的功
δW = F • dx = pA • dx = pdV
宏观位能(位能):系统在外力场作用下, ):系统在外力场作用下 ◆ 宏观位能(位能):系统在外力场作用下,相对于 某参考坐标系中某一位置所具有的能量。 某参考坐标系中某一位置所具有的能量。
E p = mgz
二、内能
储存于系统内部的能量称为内能 内能, ● 储存于系统内部的能量称为内能,内能与物质 的分子结构和微观运动形式有关。 的分子结构和微观运动形式有关。 ● 对于闭口系统来说,工质经历一个循环之后又 对于闭口系统来说, 回复到原来的状态, 回复到原来的状态,所以系统储存能量的变化为 零,即:进入系统的能量(吸热量)等于离开系 进入系统的能量(吸热量) 统的能量(对外做功量)。 统的能量(对外做功量)。
热力学第一定律

流入: 流出:
qm1
h1
1 2
cf21
gz1
qm2
h3
1 2
cf23
gz3
qm1
h2
1 2
cf22
gz2
qm2
h4
1 2
cf24
gz4
与外界无功和热量交换
系统内增加: 0
若忽略动能差、位能差,方程为:
h4
不花费能量就可以产生功的第一类永动机是 不可能制造成功的。
3
2–2 热力学能和总能
一、热力学能(internal energy)
Uch-化学能
U
Unu-原子核能 平移动能
Uth
Uk
转动动能 振动动能
f1 T
U U (T, v)
Up— 内位能 f 2 T , v
在无化学反应及原子核反应的过程中,化学能和原子 核能都不变化,可以不考虑,热力学能的变化只是内位能 和内动能的变化。
12
二、开口系统能量方程
工质流进(出)开口系统时,必将其本身所具有的各种 形式的能量,带入(出)开口系统。因此,开口系统除了 通过作功与传热的方式传递能量外,还可以借助物质的流 动来转移能量。 分析开口系统时,除了能量平衡外,还必须考虑质量平衡:
13
1. 推动功(Flow work)
因工质出、入开口系统 而传递的功,叫推动功(推 进功) 。
36
外部储存能包括宏观动能和重力位能,它们的大 小要借助在系统外的参考坐标系测得的参数来表示。
热力学第一定律

P29, 2.10
∵ Q=-25kJ
1
本题10分
h 是一个复合状态参数。 可表示为两个任意独立的状态参数的函数。 如 : h=f(P,T) 对理想气体: h = CvT+RgT = (Cv+Rg)T = CpT 2) 焓的物理意义 a 不论工质是否流动,焓都是状态参数 b 对流动工质: h 是随工质流动而转移的能量 c 对非流动工质:h 仅是复合状态参数,无能量含义
U 比热力学能: u m
J/kg
u=u(T, )
由上述可见: 比热力学能仅是状态参数T、 的函数,它 只与工质的状态有关,而与过程无关。
结论:比热力学能 u(简称热力学能)是状态参数。
简单可压缩系统(两个独立的状态参数=1+1)
u=f(T,p) 或 u=f(p,)…… 对理想气体:内位能=0,热力学能=内动能,即
(2) 轴功、流动功(推动功)
1)轴功:通过机轴对外界输出的机械功,记作Wsh
或 Ws
2)流动功(推动功): 推动工质流动所须消耗的功,记作Wf
如图所示,将dm工质推入系统,所消耗流动功为:
Wf p ·A ·dx p dV
p ·dm · dm ·p
对mkg工质: Wf m p pV
吸入系统的热量-系统对外做的功= 闭口系热力学能增量 即 或 对1kg工质:
Q W E
Q U W
,
Q W U
闭口系能 量方程式
q u w
w pd
对微元过程: Q dU W 或 q du w
由 对可逆过程:
适用于任何工 质、任何过程
即
(Q E1 p1V1 ) (Wsh E2 p2V2 ) Esy
第二章 热力学第一定律

入口处: p1A1 d x = p1 d V1 = p1 v1 d m1
出口处: p2A2 d x = p2 d V2 = p2 v2 d m2
流动功:系统为维持工质流动所需的功。 (p v ) = p2 v2 – p1 v1 3. 几点说明: (1)是工质在开口系统中流动而传递的能量; (2)只有在工质流动过程中才出现; (3)工质在传递流动功时,没有热力状态的变化, 也没有能量形态的变化
1 2 2 (c f 2 c f 1 ) h1 h2 2
说明 :工质流经喷管时,动能的增加等于 焓值的减少。
同学们:
上课铃声即将敲响, 你们准备好了吗?!
同学们:
现在开始上课。 请翻开你们的书、笔记本,
拿起笔。 并请保持课堂安静。谢谢!
例1:对定量的某种气体加热100kJ,使之由状态1 沿路径1a 2变化到状态2,同时对外作功60kJ。若外 界对气体作功40kJ,使之从状态2沿路径2b1返回状 态1,如图,问返回过程中工质与外界交换的热量 是多少?是吸热用力的存在所具有 的位能,与气体的比体积有关。 化学能,原子核能,电磁能。
单位:焦耳 J,符号 U 比热力学能:单位质量物质的热力学能,u, J / kg 2. 热力学能是温度和比体积的函数,是状态参数。 3. 热力学能的大小是相对的。 二. 宏观动能和宏观位能 1. 宏观动能:由于宏观运动速度而具有的动能。EK 2. 宏观位能:由于其在重力场中的位置而具有的位 能。 EP 三. 总储存能 (stored energy) 总储存能:系统的热力学能,宏观动能,宏观位 能之和,用E表示,单位J,KJ。 比储存能 e = u + e k+ ep
Q = W + U = W + U2 - U1
3第二章热力学第一定律

●闭口热力系统总储存能的变化: △E=△U=U2-U1 闭口热力系统总储存能的变化:
热力学第一定律: 热力学第一定律: Q -W=△E=△U 或 Q =△U+ W
Q
W
一、闭口系统能量方程式
Q = U + W 一 δQ = dU + δW
般 式 q = u + w
Q
W
δq = du + δw δq = du + pdv
2
单位工质
适用条件: ) 适用条件:1)任何工质 2) 任何过程
●过程量
符号w ●符号
轴功
●定义 ●符号 ●实例
系统通过机械轴与外界传递的机械功 ws 规定系统输出轴功为正,输入为负 规定系统输出轴功为正, ws
…………… …………… …………… …………… ……………
ws
闭口系统
开口系统
2-4 焓enthalpy
流动工质传递的总能量 pV + U + 0.5mc2 + mgz h= u + pv 定义焓: 定义焓:H=U+ pV 单位: 单位: J(kJ) kJ) J/kg(kJ/kg) J/kg(kJ/kg) 对理想气体:h=u+pv=u+RT=f( ●H是状态参数 ,对理想气体:h=u+pv=u+RT=f(T) 是 H为广延参数 h为比参数 ● H为广延参数 H=U+pV= m(u+pv)= mh, h为比参数 物理意义: ●物理意义:
第二章 热力学第一定律

令
u pv h
U pV H
,h 称为比焓。
, H 称为焓
焓的定义:焓=热力学能+推动功。
2-4 开口系统的稳定流动能量方程式
由于p、v 、u都是状态参数,所以焓也是工质的一个
1 2 Ws m u2 cf2 gz2 mp2v2 2 1 2 Ws m u2 cf2 gz2 p2v2 2
2-4 开口系统的稳定流动能量方程式
根据热力学第一定律可得
1 2 Q m u1 p1v1 2 cf1 gz1
本章主要内容
1 2 3 4 5
热力系统的储存能 热力学第一定律的实质 闭口系统的热力学第一定律表达式 开口系统的稳定流动能量方程式 稳定流动能量方程式的应用
2-1 热力系统的储存能
热力学能
热力学储存能
U
宏观动能与宏观位能
热力学能的定义:
Ek , E p
物体因热运动而具有的能量 , 是存储于物体内部的能量 。 内动能 内位能 原子能 化学能
对于单位质量工质的可逆过程 ,
q du pdv
q u pdv
1
2
2-3 闭口系统的热力学第一定律表达式
适用条件:
闭口系;可逆、不可逆; 理想和实际气体;初、终态为平衡态
符号规定:
吸热q为正,放热为负 系统对外作功为正,反之为负
系统内能增大 U为正,反之为负
2-3 闭口系统的热力学第一定律表达式
热力学能(内能)
2-3 闭口系统的热力学第一定律表达式
Q ΔU
热力学第一定律

热能工程教研室
例3 一刚性绝热容器内储有水蒸气,通过电热器向蒸 汽输入80kJ的能量,问水蒸气的热力学能变化多少?
解 方法一: 取图中虚线所包围水蒸气和电热器为系 统。控制质量系统。 2)列出能量方程
Q U W
U W
0
3)根据边界上热功交换情况,对能量方程进行简化
4)带入数据(注意热量和功量的正负号)
2 1 2 2
热能工程教研室
第二章 热力学第一定律
2-1 热力学第一定律的实质
基本内容
2-2 热力学能和总能
2-3 能量的传递和转化
2-4 焓
2-5 热力学第一定律的基本能量方程式 2-6 开口系统能量方程式 2-7 能量方程式的应用
热能工程教研室
2-4焓
1.定义: H=U+pV h=u+pv 2.焓的物理意义: 表示物质流入或流出系统所携带的能量 3.焓是一个组合状态参数,单位:J ,KJ,KJ/Kg 4.一般关心 h
思考:开口系存在焓,闭口系不存在焓,对吗?
热能工程教研室
第二章 热力学第一定律
2-1 热力学第一定律的实质
基本内容
2-2 热力学能和总能
2-3 能量的传递和转化
2-4 焓
2-5 热力学第一定律的基本能量方程式 2-6 开口系统能量方程式 2-7 能量方程式的应用
热能工程教研室
2-4、闭口系能量方程 ——热力学第一定律的基本能量方程式
4)带入数据(注意热量和功量的正负号)
Q 80kJ
U 80kJ
热能工程教研室
讨论:
本例题再次证明了,解决涉及热现象的能量传递和转换问题时
,首先必须正确合理的选取系统(研究对象)。系统不同不但 与外界交换的功、热不同,能量方程的形式也会有所不同。
热力学基本定律热一律

Q与W类比
能量传递方式 性质 推动力 标志参数 公式 公式适用条件 图示
W 过程量
Δp dV , dv
w pdv
准静态或可逆
P-V(示功图)
p
W
Q 过程量
ΔT dS , ds
q Tds
可逆
T-s(示热图)
T
Q
V
S
3、随物质传递的能量
1.流动工质本身携带的能量:u + c2/2 + g z
2.流动功(或推动功)
1)对于准静态、可逆过程,用上述公式计算,但还需要已 知p-v函数关系。
2)对于非平衡过程,不能用上述公式计算,但有些情况可 利用外界条件计算:
系统膨胀功=-外界反力对系统所做的功 若外力R已知,则:
2
w 1 Rdx
[例1]
空气从状态1 (p1,V1)膨胀到状态2 (p2,V2), (1) p-V图上过程线为直线;(2)可逆定温过 程。求w
系统
dE
δW
储存能的变化量:dE 循环后: dE = 0
热一律:进入的能量 – 离开的能量 = 储存能的变化量
(2)能的导出
p1
对于循环1a2c1:
b
( Q W ) ( Q W ) 0
1a 2
2c1
a c
对于循环1b2c1:
2
( Q W ) ( Q W ) 0
V
1b 2
2c1
( Q W ) ( Q W )
p1
(1)
(2)
2
V
[例2]
大气压pb =0.1MPa,活塞+重物共195kg,面积 100cm2,初始状态下弹簧与活塞接触但不受力,弹 簧刚度150N/cm,把重物拿去100kg后,活塞无摩 擦上升20cm。求w
第二章 热力学第一定律

(二)热力学第一定律
热力学第一定律实质就是能量守恒和转换 定律在热现象上的应用。 表述1:热可以变为功,功也可以变为热;一 定量的热消灭,必产生一定量的功;消耗一 定量的功时,必出现与之相应数量的热。
表述2:第一类永动机是造不成的
First Law of Thermodynamics
In 1843, at the age of 25, James Prescott Joule did a series of careful experiments to prove the equivalence of heat and work.
A p V
dl
对推进功的说明
1、与宏观流动有关,流动停止,推进功不存在 2、作用过程中,工质仅发生位置变化,无状态变化
3、w推=pv与所处状态有关,是状态量 4、并非工质本身的能量(动能、位能)变化引起, 而由外界(泵与风机)做出,流动工质所携带的能量
可理解为:由于工质的进出,外界与系统之
间所传递的一种机械功,表现为流动工质进 出系统使所携带和所传递的一种能量
4、物理意义:开口系中随工质流动而携带的、取决 于热力状态的能量。
三、稳定流动能量方程
Energy balance for steady-flow systems
稳定流动条件
(P22)
1、
•
•
•
mout min m
2、
•
Q Const
min
uin 1 2
c
2 in
gzin
3、
•
•
Wnet ConstWs
三、总能
热力系统的储存能: 储存于热力系统的能量。 (1)内部储存能———热力学能 (2)外部储存能———宏观动能,宏观位能。
第二章 热力学第一定律 主要公式及使用条件

第二章 热力学第一定律主要公式及使用条件1. 1. 热力学第一定律的数学表示式W Q U +=Δ或'amb δδδd δdU Q W Q p V W =+=−+规定系统吸热为正,放热为负。
系统得功为正,对环境作功为负。
式中 p amb 为环境的压力,W ’为非体积功。
上式适用于封闭体系的一切过程。
2. 2. 焓的定义式pVU H +=3. 3. 焓变(1) )(pV U H Δ+Δ=Δ式中为乘积的增量,只有在恒压下)(pV ΔpV )()(12V V p pV −=Δ在数值上等于体积功。
(2) 2,m 1d p H nC Δ=∫T 此式适用于理想气体单纯pVT 变化的一切过程,或真实气体的恒压变温过程,或纯的液体、固体物质压力变化不大的变温过程。
4. 4. 热力学能(又称内能)变此式适用于理想气体单纯pVT 变化的一切过程。
2,m 1d V U nC Δ=∫T5. 5. 恒容热和恒压热(d V Q U =Δ0,'0)V W ==p Q H =Δ(d 0,'0)p W ==6. 6. 热容的定义式(1)定压热容和定容热容δ/d (/)p p C Q T H T p ==∂∂δ/d (/)V V C Q T U T ==∂∂V p V R 3(2)摩尔定压热容和摩尔定容热容,m m /(/)p p C C n H T ==∂∂,m m /(/)V V C C n U T ==∂∂上式分别适用于无相变变化、无化学变化、非体积功为零的恒压和恒容过程。
(3)质量定压热容(比定压热容),m //p p p c C m C M==式中m 和M 分别为物质的质量和摩尔质量。
(4),m ,m p V C C −=此式只适用于理想气体。
(5)摩尔定压热容与温度的关系2,m p C a bT cT dT =+++式中a , b , c 及d 对指定气体皆为常数。
(6)平均摩尔定压热容21,m ,m 21d /()T p p T C T T T C =−∫7. 7. 摩尔蒸发焓与温度的关系21v ap m 2vap m 1v ap ,m ()()d T p T H T H T C T Δ=Δ+Δ∫或 vap m vap ,m (/)p p H T ∂Δ∂=ΔC d amb ∑−=−−=−−=式中 = C (g) —C (l),上式适用于恒压蒸发过程。
高中物理 第二章热力学第一定律 - 热能工程

第二章 热力学第一定律一、目的及要求:掌握热力学第一定律在闭口系统及开口系统的表达式,掌握状态参数热力学能U 及焓H 的含义,掌握各种功(流动功、推动功、容积变化功、技术功等)的含义。
二、内容:2.1热力学第一定律的实质 2.2热力学能和总能 2.3能量的传递与转化 2.4焓及热力学第一定律的基本能量方程式 2.5 开口系统的能量方程式及能量方程式的应用三、重点及难点:2.1 深入理解热力学第一定律的实质,熟练掌握热力学第一定律及其表达式。
能够正确、灵活地应用热力学第一定律表达式来分析计算工程实际中的有关问题。
2.2 掌握能量、储存能、热力学能、总能的概念。
2.3 掌握体积变化功、推动功、轴功和技术功的要领及计算式。
2.4 注意焓的引出及其定义式。
四、主要外语词汇:enthalpy, first law of thermodynamics,五、本章节采用多媒体课件六、复习思考题及作业:思考题:1、热力学第一定律的实质是什么?2、闭口系热力学第一定律的两个数学表达式q du w δδ=+和t q dh w δδ=+的适用范围有何不同?3、工质进行膨胀时是否必须对工质加热?工质吸热后热力学能是否一定增加?对工质加热其温度反而降低是否有可能?4、膨胀功、推动功、轴功和技术功四者之间有何联系和区别?5、为什么推动功出现在开口系能量方程式中,而不出现在闭口系能量方程式中?6、什么是焓?它的物理意义是什么?为什么说它是工质的状态参数?7、如图中过程1-2与过程1-a-2,有相同的初态和终态,试比较两过程的功谁大谁小?热量谁大谁小?热力学能的变化量谁大谁小?8、如图所示一内壁绝热的容器,中间用隔板分为两部分,A 中存有高压空气,B 中保持高度真空。
如果将隔板抽出,容器中空气的热力学能如何变化?为什么?作业:2-3,2-5,2-6,2-8,2-9,2-11,2-12第二章热力学第一定律热力学第一定律是热力学的基本定律之一,它给出了系统与外界相互作用过程中,系统能量变化与其它形式能量之间的数量关系。
02-物理化学第二章 热力学第一定律
H
m
298
K
H1
H
2
r
H
m
298
K
298K
T
eCP,E fC P,F dT
T
298K gCP,G hCP,H dT
X = f(T,P)o=rf(T,V)… 双变量坐标
强度性质—— 与量n无关
整体 = 部分 (T、P)
广延性质—— 与量n成正比 整体 = ∑部分
强度量 = 广延量/广延量
本章任务:
计算能量变化:
状态函数 U、H + 过程量 Q、W 理想气体,纯物质的 U、H 性质
步骤: ㈠ 不需第一定律即能计算的Q和W ㈡ 第一定律及内能 ㈢ 用于计算过程热及焓 ㈣ 用于绝热功的计算
§2-1
热和功
过程量——计算时一定要看具体过程 2·1·1 热Q
显热的计算
用热容
QB n CB,mdT
利用手册中数据,只能计算恒压或恒容热
QP or V
n
C dT T2
T1
P or V ,m
2·1·2 功W
体积功的计算
2
W 1 PexdV
eg. 恒容过程 W = 0
等外压过程 Pex=constant
Ⅱ:192.5kPa
298.15K
352.15K
求:Q、W、△U、△H
解: Q=0
U n CV ,mdT
nCV ,m T2 T1 1.366kJ
H n CP,mdT
n CV ,m R T2 T1 1.814kJ
W U Q 1.366kJ
例2·5·2 1mol双原子理想气体于27℃, 101.325 kPa 状态下,受某恒定外压恒温 压缩到平衡,再由该状态恒容升温至 97 ℃,则压力升到 1013.25 kPa。求整个过 程的W、Q、 △U及△H。
第二章热力学第一定律

m out
u pv c / 2 gz min
in
流动时,总一起存在
焓的引入
定义:焓
h = u + pv
Q dEcv / W net u pv c / 2 gz h
2 2 out
m out
u pv c / 2 gz min h
总结: 开口系能量方程一般表达式:
Q =dEcv + ∑(h+ + gz)out mout ∑(h+ c2/2 + gz)in min + Wnet
2/2 c
以流率表示的开口系能量方程:
Q dEcv / W net u pv c / 2 gz h
2 2 out
1 q h c 2 g z ws 2
稳定流动能量方程
1 2 q h c g z ws 2
适用条件:
任何流动工质
任何稳定流动过程
技术功
Wt
1 2 Q mh mc mg z Ws 2 1 2 q h c g z ws 2 动能 位能 轴功 wt 机械能 工程技术上可以直接利用
间所传递的一种机械功,表现为流动工质进 出系统使所携带和所传递的一种能量
开口系能量方程的推导
uin pvin gzin Wnet mout uout pvout 1 2 cout gzout 2 min 1 2 cin 2
Q
Q + min(u + c2/2 + gz)in - mout(u + c2/2 + gz)out - Wnet = dEcv
第二章热力学第一定律概念及公式总结

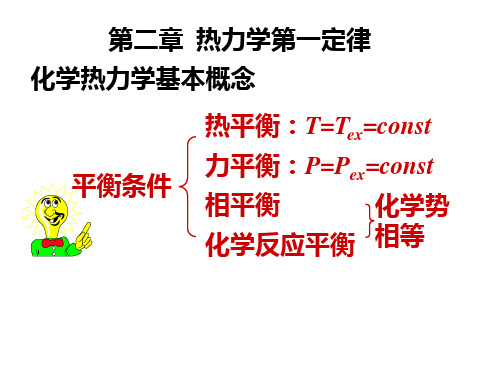
第二章 热力学第一定律2.3热力学基本概念 1.系统:● 隔离系统:没有物质或能量的交换 ● 封闭系统:有能量交换● 敞开系统:有能量或物质的交换 2.热力学平衡态:(当系统的各种性质不随时间而改变,则系统就处于热力学平衡状态)热力学必须同时满足的条件平衡:热动平衡、力学平衡、相平衡、化学平衡。
2.3.1状态函数(当系统的状态发生变化时,它的一系列性质也随之变化,改变的多少取决于始态和终态)【异途同归,值变相等;周而复始,数值还原】 《m 、T 、、P 、V 、浓度、黏度、折光率、热力学能、焓、熵》 2.3.2 状态方程(),ν=T f p 与系统性质有关的函数2.3.3 过程和途径2.3.3.1 常见的变化过程有:● 等温过程:只有始终态温度不变● 恒温过程:在过程中温度一直持续不变 ● 等压过程:始终态压力相等且等于环境温度● 等容过程:系统变化过程中体积不变(刚性容器)● 绝热过程:系统与环境没有热交换(爆炸、快速燃烧)Q=0 ● 环状过程:系统经一系列变化又回到了原来的状态d 0∮ν= 、d 0∮=p 、d 0∮=U 、d 0∮=T状态函数的变化值仅取决于系统的始终态,而与中间具体的变化无关。
过程函数的特点:只有系统发生一个变化时才有过程函数 过程函数不仅与始终态有关还与途径有关没有全微分,只有微小量。
用δQ 、δw 表示环积分不一定为0 (不一定0∮δ=Q )2.3.4 热和功热的本质是分子无规则运动强度的一种体现,系统内部的能量交换不可能是热。
功和热都不是状态函数,其值与过程无关。
2.4热力学第一定律热力学能是指系统内分子运动的平动能、转动能、振动能、电子及核的能量,以及分子与分子之间相互作用的位能等能量的总和。
文字表述:第一类永动机是不可能造成的(既不靠外界提供能量,本身也不减少能量,却可以不断对外做功的机器称为第一类永动机)能量总量在转化过程中保持不变 系统热力学能的变化是:21∆=-=+U U U Q W系统发生微小变化,热力学能的变化d U 为:d δδ=+U Q W (状态函数)对于物质的量为定值的封闭系统,则微小变量的热力学能变化可以表示为:d d d ν⎛⎫∂∂⎛⎫=+ ⎪ ⎪∂∂⎝⎭⎝⎭p TU U T p T p 2.5准静态过程与可逆过程2.5.1功与过程系统做的膨胀功为:e e d δ=-=-W F dl p V膨胀功分为 :✧ 自由膨胀(向真空膨胀)<W=0>:外压e p 为零的膨胀过程,由于e p =0所以,,10δ=e W ,系统对外不做功。
《工程热力学》第二章 热力学第一定律

6
2-2 热力学能和总能
能量是物质运动的度量,运动有各种不同的 形态,相应的就有各种不同的能量。
系统储存的能量称为储存能,它有内部储存 能与外部储存能之分。系统的内部储存能即为热 力学能
Q U W
Q 0 W ? 0 U 0 即U1 U2
强调:功是通过边界传递的能量。
30
h1 a 2
h1 b 2
2
dh
1
h2 h1
dh 0
21
三、焓的意义:
焓是物质进出开口系统时带入或带出的热力学 能与推动功之和,是随物质一起转移的能量。
焓是一种宏观存在的状态参数,不仅在开口系 统中出现,而且在分析闭口系统时,它同样存 在。
焓是随着质量交换而交换的一种“转移能”, 只有在质量跨越边界的前提下,焓的物理意义 及其能量属性才能体现出来。
第二章 热力学第一定律
1
本章基本要求
深刻理解热能、储存能、功的概念,深刻理解内 能、焓的物理意义;
理解膨胀(压缩)功、轴功、技术功、流动功的 联系与区别;
本章重点
熟练应用热力学第一定律解决具体问题
2
2-1 热力学第一定律的实质
19世纪30-40年代,迈耶,焦耳等发现并确 定了能量转换与守恒定律。恩格斯将这列为19世纪 三大发现之一(细胞学说、达尔文进化论)。
在热能与其它形式能的互相转换过程中,能的 总量始终不变。
不花费能量就可以产生功的第一类永动机是不 可能制造成功的。
4
5
进入系统的能量-离开系统的能量 = 系 统储存能量的变化
在工程热力学的范围内,主要考虑热能与机 械能之间的相互转换与守恒,因此热力学第一定 律可表述为:热可以变为功,功也可以变为热, 在相互转变时能的总量是不变的。
热力学第一定律及其表达式

热力学第一定律及其表达式
热力学第一定律是能量守恒定律在热系统中的应用,它表明在任何一个封闭系统中,能量的增量等于系统所做的功加上系统所吸收的热量。
这一定律的表达式为ΔU=Q-W,其中ΔU表示系统内能量的增量,Q表示系统吸收的热量,W表示系统所做的功。
热力学第一定律的实质是能量不能自行消失,只能从一种形式转变为另一种形式。
这一定律对于热力学的研究具有重要的意义,它为热力学第二定律提供了理论基础,并为工程技术的发展提供了指导。
热力学第一定律的表达式ΔU=Q-W可以用于热力学系统的能量平衡分析。
例如,在化学反应中,反应物和产物的内能差可以通过测量反应热来确定,从而可以计算反应所做的功或吸收的热量。
在热机和制冷机中,热力学第一定律的表达式也被广泛应用。
总之,热力学第一定律是热力学研究的基础,它为热力学的发展和应用提供了重要的理论支持。
- 1 -。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
吸热膨胀作功(参看图2-3c) 吸热膨胀作功 外界供给热量 –Q 膨胀功 –W 热力学能 –U2
排气过程中(参看图2-3d) 排气过程中 外界消耗排气功 外界获得推动功 排气后(参看图2-3a) 排气后 质量 m = 0 总能量 E2 = 0
开口系在一个工作周期中的能量进出情况
Q=Q ∆E = 0
1 2 2 w = ( p2 v2 − p1v1 ) + (c2 − c1 ) + g ( z 2 − z1 ) + wsh 2
(2-16)
总功(Wtot )、膨胀功(W )、技术功( W t )和轴功 (W sh )之间的区别和内在联系 膨胀功、技术功、轴功孰大孰小取决于 ( p 2 v2 − p1v1 ) 1 2 2 (c2 − c1 ) 、 g ( z 2 − z1 ) 的大小和正负。
二、热力学第一定律表达式
1、一般热力系能量方程
- 热力学第一定律基本表达式
热力系总能量(total stored energy of system)为E(图2-1a)。它是 热力学能(U)、宏观动能(EK)和重力位能(EP)的总和: 热力学能,内部储存能 热力学能,
E =U+Ek +Ep
宏观动能 总能 宏ቤተ መጻሕፍቲ ባይዱ位能 外部储存能
e =u+ek +ep
根据质量守恒定律可知:热力系质量的变化等于流进和流出 质量的差:
dm = δm1 − δm2
根据热力学第一定律可知:
热力系输出的能量的总和= 加入热力系的能量的总和 - 热力系输出的能量的总和=热力系总能量的增量
(δQ + e1δm1) (δW总 + e2δm2 ) = ( E + dE ) − E −
Wt = W进气 + W − W排气
代入式(2-8)可得
Q = H 2 − H + Wt
(2-9)
每千克工质
q = h2 − h1 + wt
微分式 δq = dh + δwt
适用条件:开口系、任何工质、 适用条件 任何(无摩擦或摩擦)过程。
4、稳定流动的能量方程 、
稳定流动是指流道中任何位置上流体的流速及其它状态参数 状态参数 (温度、压力、比体积、比热力学能等)都不随时间而变化 不随时间而变化 的流动。
第二章 热力学第一定律
First law of thermodynamics
2-1 热力学第一定律的实质及表达式
一、热力学第一定律的实质 • 实质是能量守恒与转换原理在热力学中 的具体体现。 • 在工程热力学中,热力学第一定律主要 热能和机械能在转移和转换时,能 说明热能和机械能 热能和机械能 量的总量必定守恒。
适用条件:闭口系、任何工质、 适用条件:闭口系、任何工质、 任何(无摩擦或有摩擦)过程。 任何(无摩擦或有摩擦)过程。
Q = ∆U + W q = ∆u + w
δQ = dU + δW δq = du + δw
3、开口系的能量方程
进气前(参看图2-3a) 进气前 质量 m = 0 总能量 E1 = 0 进气过程中(参看图2-3b) 进气过程中 热力学能 – U1 进出口气体的重力位能基本不变 外界对气体作了推动功 – p1V1 外界获得了进气功 – +W
q = (u2 + p2 v2 ) − (u1 + p1v1 ) + w进气 + w − w排气
因为
w进气= p1v1 , w排气 = p2 v2
所以
q = u2 − u1 + w
归根结底,反映热能和机械能转换的是式(2-6)。将其改写为
w = (u1 − u 2 ) + q
在任何情况下,膨胀功都只能从热力系本身的热力学 能减少或从外界供给的热量转变而来。所不同的是, 因热力系的不同而输出的功的形式有所不同。
微分式
δQ = dE + (e2δm2 − e1δm1 ) + δWtot
积分式
Q = ∆E + ∫ (τ ) (e2δm2 − e1δm1 ) + Wtot
适用条件:任何热力系、任何工质、任何 (无摩擦或有摩擦)过程
2、闭口系的能量方程
设一带活塞的气缸,取封闭在活塞气缸中虚线包围的 气体工质为研究对象(闭口系)
w 在闭口系中- 膨胀功()全部向外界输出
在开口系中- 膨胀功中有一分要用来弥补排气推动功和 进气推动功的差值 p2 v2 − p1v1),剩下的部分(即为 ( 技术功)可供输出
w = ( p2 v2 − p1v1 ) + wt
(2-15)
在稳定流动中,膨胀功除用于弥补排气推动和进气 推动功的差值外,还要用于 1 2 ] [ (c2 − c12) , 增加流体的位能 [ g ( z 2 − z1 )] 增加流体的功能 2 剩下的部分(即为轴功)才供输出
∫
(τ)
(e2δm2 − e1δm1 ) = U 2 − U1
Wtot = − p1V1 + W进气 + W − W排气 + p2V2
根据式(2-4)可得
Q = U 2 − U1 + p2V2 − p1V1 + W进气 + W − W排气 (2-8)
动力机械在一个工作周期中获得的功称为技术功,用 Wt 表示
这样,式(2-13)和式(2-11)完 全一样了,即
1 2 2 q = h2 − h1 + [ (c2 − c1 ) + g ( z2 − z1 ) + wsh ] 2 = h2 − h1 + wt
q = h2 − h1 + wt
如果再把式(2-14)中的焓写为热力学能和推动功之和, 把技术功写为进气功、 膨胀功及排气功的代数和,便可以 得到式(2-6)
( )
(e2δ m2 − e1δ m1 ) = (e2 − e1 ) ∫ (τ )δ m = e2 − e1 Wtot = wsh − p1v1 + p2 v2
q = e2 − e1 + wsh − p1v1 + p2 v2 = (e2 + p2 v2 ) − (e1 + p1v1 ) + wsh
2 c2 + gz2 式中 e2 + p2 v2 = u 2 + ek 2 + e p 2 + p2 v2 = h2 + 2 c12 e1 + p1v1 = u1 + ek1 + e p1 + p1v1 = h1 + + gz1 2 1 2 2 最后得 q = ( h2 − h1 ) + (c2 − c1 ) + g ( z 2 − z1 ) + wsh 2
2
初态热力学能 - U1 吸热 - Q 对外界作膨胀功 - W
∆Ek = ∆E p = 0
终态热力学能 - U2 动能和重力位能均无变化与外界无物质交换
δm1 = δm2 = 0
积分式 每千克工质 微分式
Q = ∆U + W = U 2 − U1 + W
q = u2 − u1 + w
δq = du + δw
适用条件:稳定流动开口系、任何工质、任何过程。 对流动工质,焓可以理解为流体向下游 传送的热力 学能和推动功之和。
5、能量方程之间的内在联系、热变功的实质 、能量方程之间的内在联系、
若把稳定流动能量方程中流体动能的增量和重力位能的增量看 作是暂存于流体(热力系)本身,并把它们和轴功合并在一 起,合并以后的功也就相当于开口系能量方程中的技术功。
出口截面
进口截面
p1,v1,u1,c1,z1,e1
p2,v2,u2,c2,z 2,e2
取一段时间τ ,设在这段时间内恰好有1kg 流体流过通道,同 时有热量q 传入又有轴功 wsh 作出。对这样一个稳定流动的开 口系,式(2-4)中各项为
Q=q ∆E = 0 E = 定值) (
∫τ
根据式(2-4)可得
