考研数学:高等数学知识要点思维导图
考研数学 知识结构思维导图(数二)
1.分离变量,物以类聚人以群分 2.y'在等式左侧,右侧应写成乘积形式
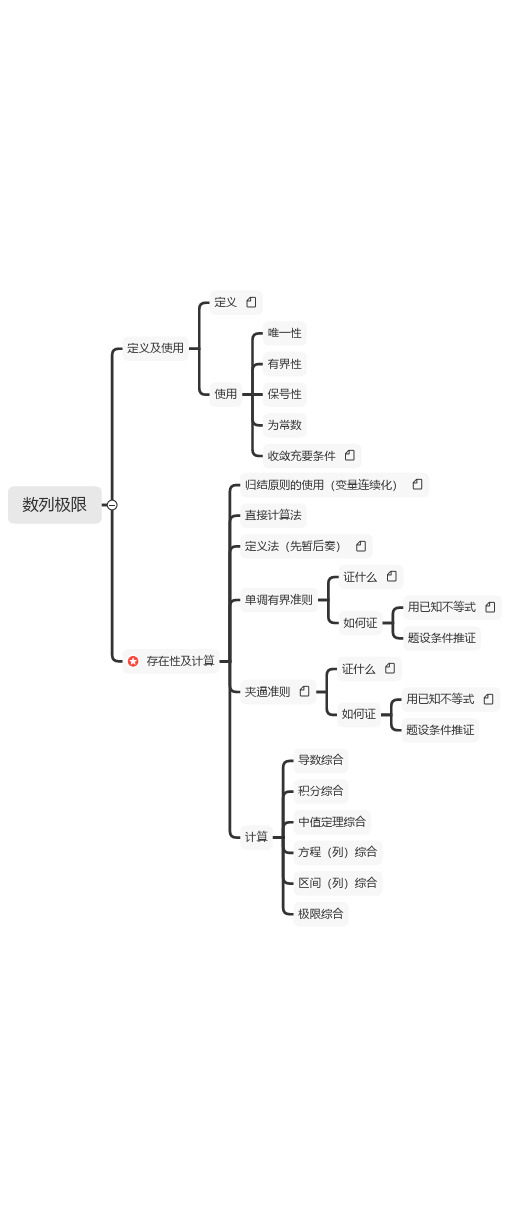
一阶微分方程的求解
齐次型
y'=f(y/x)
对x求导
1/y'=f(x/y)
对y求导
换元后分离变量,交换x和y的地位
一阶线性型(或可换元为它)
y'+p(x)y=q(x) 伯努利方程
y'+p(x)y=q(x)的特殊形式
伯努利方程可理解为一 阶线性方程的普遍形式
符号函数 抽象函数
复合函数
偏导函数
换元法
一元函数积分换元法 二元函数积分换元法
应用
面积
1.积分变化口诀:后积先定限,限内画直 线,先交先下限,后交写上限;
2.注意对称性得0的应用可以极大地化简计 算
微分方程
可分离变量
y'=f(x).g(y)
分离变量
y'=f(ax+by+c)
换元后再分离变量
一般一层积分不易处理,化成两层积分,在交换 积分次序
分部积分法
换序型
反常积分的计算
研究对象
常规题型取绝对值时取值范围
曲线平移时相关符号不同取值范围所对应的面积
切线综合
函数列综合
题型总结
在平面极坐标系中,如果极径ρ随极角θ的 增加而成比例增加(或减少),这样的动
点所形成的轨迹叫做螺线。
阿基米德螺旋线
数列极限
定义
定义及使用
唯一性 有界性
使用
保号性
为常数
收敛充要条件
归结原则的使用(变量连续化)
直接计算法
定义法(先暂后奏)
考研数学一思维导图

数学一(By 风吟)高等数学线性代数概率论与数理统计函数、极限、连续一元函数微分学一元函数积分学向量代数和空间解析几何多元函数微分学多元函数积分学无穷级数常微分方程行列式矩阵向量线性方程组矩阵的特征值和特征向量二次型随机事件和概率随机变量及其分布多维随机变量及其分布随机变量的数字特征大数定律和中心极限定理数理统计的基本概念参数估计假设检验函数的概念及表示法函数的有界性、单调性、周期性和奇偶性 复合函数、反函数、分段函数和隐函数 基本初等函数的性质及其图形 初等函数 函数关系的建立数列极限与函数极限的定义及其性质 函数的左极限和右极限无穷小量和无穷大量的概念及其关系 无穷小量的性质及无穷小量的比较 极限的四则运算极限存在的两个准则:单调有界准则和夹逼准则两个重要极限函数连续的概念 函数间断点的类型 初等函数的连续性 闭区间上连续函数的性质 导数和微分的概念 导数的几何意义和物理意义 函数的可导性与连续性之间的关系 平面曲线的切线和法线 导数和微分的四则运算 基本初等函数的导数复合函数、反函数、隐函数以及参数方程所确定的函数的微分法 高阶导数一阶微分形式的不变性 微分中值定理洛必达(L’Hospital )法则 函数单调性的判别 函数的极值函数图形的凹凸性、拐点及渐近线 函数图形的描绘 函数的最大值与最小值 弧微分 曲率的概念 曲率圆与曲率半径原函数和不定积分的概念 不定积分的基本性质 基本积分公式定积分的概念和基本性质 定积分中值定理 积分上限的函数及其导数牛顿-莱布尼茨(Newton-Leibniz )公式 不定积分和定积分的换元积分法与分部积分法 有理函数、三角函数的有理式和简单无理函数的积分 反常(广义)积分 定积分的应用向量的概念 向量的线性运算 向量的数量积和向量积 向量的混合积两向量垂直、平行的条件 两向量的夹角向量的坐标表达式及其运算 单位向量 方向数与方向余弦曲面方程和空间曲线方程的概念 平面方程 直线方程平面与平面、平面与直线、直线与直线的夹角以及平行、垂直的条件 点到平面和点到直线的距离球面 柱面 旋转曲面常用的二次曲面方程及其图形 空间曲线的参数方程和一般方程 空间曲线在坐标面上的投影曲线方程多元函数的概念二元函数的几何意义 二元函数的极限与连续的概念 有界闭区域上多元连续函数的性质 多元函数的偏导数和全微分全微分存在的必要条件和充分条件 多元复合函数、隐函数的求导法 二阶偏导数 方向导数和梯度 空间曲线的切线和法平面 曲面的切平面和法线 二元函数的二阶泰勒公式 多元函数的极值和条件极值多元函数的最大值、最小值及其简单应用 二重积分与三重积分的概念、性质、计算和应用 两类曲线积分的概念、性质及计算 两类曲线积分的关系 格林(Green )公式平面曲线积分与路径无关的条件二元函数全微分的原函数两类曲面积分的概念、性质及计算 两类曲面积分的关系 高斯(Gauss )公式 斯托克斯(Stokes )公式 散度、旋度的概念及计算 曲线积分和曲面积分的应用 常数项级数的收敛与发散的概念 收敛级数的和的概念级数的基本性质与收敛的必要条件 几何级数与p 级数及其收敛性正项级数收敛性的判别法 交错级数与莱布尼茨定理 任意项级数的绝对收敛与条件收敛函数项级数的收敛域与和函数的概念幂级数及其收敛半径、收敛区间(指开区间)和收敛域 幂级数的和函数幂级数在其收敛区间内的基本性质 简单幂级数的和函数的求法 初等函数的幂级数展开式函数的傅里叶(Fourier )系数与傅里叶级数 狄利克雷(Dirichlet )定理常微分方程的基本概念 变量可分离的微分方程 齐次微分方程 一阶线性微分方程 伯努利(Bernoulli )方程 全微分方程可用简单的变量代换求解的某些微分方程 可降阶的高阶微分方程线性微分方程解的性质及解的结构定理 二阶常系数齐次线性微分方程高于二阶的某些常系数齐次线性微分方程 简单的二阶常系数非齐次线性微分方程 欧拉(Euler )方程 微分方程的简单应用行列式的概念和基本性质 行列式按行(列)展开定理矩阵的概念 矩阵的线性运算矩阵的乘法 方阵的幂方阵乘积的行列式矩阵的转置逆矩阵的概念和性质 矩阵可逆的充分必要条件伴随矩阵 矩阵的初等变换初等矩阵 矩阵的秩 矩阵的等价 分块矩阵及其运算向量的概念向量的线性组合与线性表示 向量组的线性相关与线性无关向量组的极大线性无关组等价向量组 向量组的秩向量组的秩与矩阵的秩之间的关系向量空间及其相关概念n 维空间向量的基变换和坐标变换过渡矩阵 向量的内积线性无关向量组的正交规范化方法规范正交基 正交矩阵及其性质线性方程组的克拉默(Cramer )法则 齐次线性方程组有非零解的充分必要条件 非齐次线性方程组有解的充分必要条件线性方程组解的性质和解的结构 齐次线性方程组的基础解系和通解解空间非齐次线性方程组的通解矩阵的特征值和特征向量的概念、性质相似变换、相似矩阵的概念及性质矩阵可相似对角化的充分必要条件及相似对角矩阵 实对称矩阵的特征值、特征向量及其相似对角矩阵二次型及其矩阵表示 合同变换与合同矩阵二次型的秩 惯性定理二次型的标准形和规范形用正交变换和配方法化二次型为标准形二次型及其矩阵的正定性随机事件与样本空间 事件的关系与运算完备事件组 概率的概念 概率的基本性质古典型概率 几何型概率 条件概率 概率的基本公式 事件的独立性 独立重复试验 随机变量随机变量分布函数的概念及其性质离散型随机变量的概率分布 连续型随机变量的概率密度常见随机变量的分布 多维随机变量及其分布二维离散型随机变量的概率分布、边缘分布和条件分布 二维连续型随机变量的概率密度、边缘概率密度和条件密度随机变量的独立性和不相关性常用二维随机变量的分布两个及两个以上随机变量简单函数的分布随机变量的数学期望(均值)、方差、标准差及其性质 随机变量函数的数学期望 矩、协方差、相关系数及其性质切比雪夫(Chebyshev )不等式切比雪夫大数定律伯努利(Bernoulli )大数定律 辛钦(Khinchine )大数定律棣莫弗-拉普拉斯(De Moivre-Laplace )定理列维-林德伯格(Levy-Lindberg )定理总体 个体简单随机样本统计量 样本均值样本方差和样本矩X2分布t 分布 T 分布 分位数正态总体的常用抽样分布随机变量函数的分布点估计的概念 估计量与估计值矩估计法 最大似然估计法 估计量的评选标准 区间估计的概念单个正态总体的均值和方差的区间估计 两个正态总体的均值差和方差比的区间估计显著性检验假设检验的两类错误单个及两个正态总体的均值和方差的假设检验。
高等数学考研复习思维导图 脑图

高等数学函数特性:有界性、单调性、奇偶性、周期性反函数、复合函数、分段函数初等函数极限无穷小两个重要极限间断点连续零点定理、介值定理洛必达法则、泰勒公式导数和微分求导反函数求导复合函数求导高阶导数隐函数求导参数方程求导拐点、凹凸性最大值、最小值微分微分中值定理罗尔定理朗格拉日中值定理*柯西中值定理曲率、弧微分不定积分换元法分部积分法定积分反常积分微分方程可分离变量的微分方程齐次方程一阶线性微分方程齐次非齐次伯努利方程可降阶的高阶微分方程高/二阶线性微分方程解的结构常系数齐次线性微分方程常系数非齐次线性微分方程欧拉方程空间解析几何向量数量积向量积混合积曲面一次曲面二次曲面柱面圆柱面椭圆住吗抛物柱面椭圆锥面椭球面单叶双曲面双叶双曲面椭圆抛物面双曲抛物面(马鞍面)空间曲线空间曲线的一般方程空间曲线的参数方程空间曲线在坐标面上的投影平面及方程平面一般方程两平面夹角平面束方程空间直线及方程空间直线的一般方程空间直线的对称式方程空间直线的参数方程两直线夹角直线与平面的夹角多元函数微分法多元函数点集极限连续性偏导数全微分多元函数复合求导隐函数求导一个方程的情况方程组的情况几何应用一元向量值函数及导数空间曲线的切线和法平面曲面的切平面和法线(偏导数有关)方向导数和梯度(偏导数有关)多元函数的极值(偏导数有关)条件极值重积分二重积分性质极坐标计算二重积分三重积分柱面坐标计算三重积分球面坐标计算三重积分曲线积分对弧长的曲线积分(线密度)对坐标的曲线积分(力做功)两类曲线积分之间的关系格林公式路径无关原函数的一个全微分曲面积分对面积的曲面积分对坐标的曲面积分两类曲面积分之间的联系高斯公式无穷级数基本知识常数项级数、收敛、发散收敛级数的基本性质正项级数定义审敛比较审敛法比较审敛法的极限形式比值审敛法*根值审敛法(柯西审敛法)极限审敛法交错级数绝对收敛、条件收敛幂级数阿贝尔定理性质和运算收敛半径函数展开成幂级数傅立叶级数。
考研数学思维导图高等数学篇

= o(α )
如果lim β = ∞,那么就说β是比α低阶的无穷小 α
如果lim β = c ≠ 0,那么就说β与α是同阶无穷小 α
如果
lim
β αk
= c ≠ 0, k
> 0,那么就说β是关于α的k阶无穷小
如果lim β = 1,那么就说β与α是等价无穷小,记作α ~ β α
⑨
sin x =
x
−
1 6
(x) − kx] = lim[ f x→-∞
(x) − kx] = b,则y
=
kx + b是曲线y
=
f
( x)的一条斜渐近线
2/31
数列极限的定义
lim
n→∞
xn =A
⇔
∀ε
>
0, ∃N
>
0,当n
>
N 时, 有
xn
−
A
<
ε
极限性质
是常数 唯一性 有界性 保号性
设数列{xn}收敛,则( )
(A)当 lim sin n→∞
中值定理证明方法(上) .................................................... 10
第十章 重积分...............................................................................25
② 设函数f (x)在闭区间[a,b]上连续,且f (a)与f (b)异号(即f (a) • f (b) < 0),
则在开区间(a,b)内至少有一点 ξ,使f (ξ ) = 0.
③ 设函数f (x)在闭区间[a,b]上连续,且在这区间的端点取不同的函数值,f (a) = A, f (b) = B,
大学高数常微分方程思维导图_高等数学各章节知识点框架常微分方程.pdf

⼤学⾼数常微分⽅程思维导图_⾼等数学各章节知识点框架常微分⽅程.pdf【微信公众号:给⼒考研资料】免费分享常微分⽅程1.概念,2.⼀阶微分⽅程求解3.⾼阶微分⽅程求解4.应⽤题1.概念(7个概念,了解即可)微分⽅程—含有未知函数的导数或者微分的⽅程常微分⽅程—未知函数为⼀元函数的微分⽅程偏微分⽅程—未知函数为多元函数的微分⽅程微分⽅程的阶—未知函数的导数的最⾼阶数为⽅程的阶数微分⽅程的解—将函数代⼊⽅程,为恒等式,则该函数为解微分⽅程的通解与特解—通解—解中独⽴常数的个数等于⽅程的阶数,特解—解中没有任何常数初始条件(定解条件)—确定通解中的常数的条件2.⼀阶微分⽅程求解⼀阶⽅程(4个)1.可分离变量型(两边直接积分)2.可化成可分离变量型形如y'=f(ax+by+c)型 (令u=ax+by+c,相应对x求导,则化成可分离变量)⻬次型—形如y'=f(y/x) (令p=y/x,相应求导,则可化为分离变量型)Note :1.对于式⼦中出现lnu中u不知正负,则要带上绝对值,除过⼀阶线性2.对于⼀阶线性⽅程,不⽤带绝对值(18版18讲P217有分析)3.所求的通解可以不是全部解(线性:通解=全部解,⾮线性:通解不等于全部解)4.在求通解中,⼀定要带上对独⽴常数C的限定5.若出现不属于⼀阶⽅程四种类型,则考虑调换x ,y的地位6.能写成显⽰解就写要写成显⽰解3.⼀阶线性⽅程(要掌握推导解的公式,利⽤求导公式逆⽤法)—形如y'+p(x)y=q(x)4.伯努利⽅程(这⾥可以将其化成⼀阶线性,利⽤恒等变形中三种⽅法中换元)形如y'+p(x)y=q(x)yn(令y1-n=u ,相应求导,化成⼀阶线性)5.全微分⽅程利⽤积分与路径⽆关的性质,⽤折线法来求原函数=C⼆阶可降阶⽅程1.形如y''=f(x,y') 缺y型——将y斩草除根(令y'=u,y''=u',化成了⼀阶)2.形如y''=f(y,y')缺x型——将x斩尽杀绝(令y'=u,y'=udu/dy,化成⼀阶)要注意两种类型不同的处理⽅法Note :还有⼀种可降阶的n阶⽅程,连续求导即可3.⾼阶微分微分⽅程的求解(2~4阶)⼆阶线性微分⽅程的概念(详⻅18讲P218)1.⻬次与⾮⻬次2.变系数与常系数注意若真的出现了变系数⼆阶,要想到换元,化成⼆阶(或者是欧拉⽅程)解的结构与解的性质(各2个)(详⻅⾼数18讲P218)1.⼆阶常系数⻬次线性微分⽅程的通解结构(两个线性⽆关的解(通俗理解就是相除不为常数)可以构成起通解)2.⾮⻬次的解的结构——⻬次的特解+⾮⻬次的特解3.两个⾮⻬次的特解相加为⼀个全新⾮⻬次的特解(叠加原理)【微信公众号:给⼒考研资料】免费分享4.两个⾮⻬次的特解相减为其⻬次的⼀个解⼆阶常系数⻬次线性微分⽅程求解(背公式)⾮⻬次的特解(背公式)n阶常系数线性⻬次微分⽅程求解(背公式)注意特征⽅程的特征根各种情况(四种情况)4.欧拉⽅程(仅数⼀)(18讲259)形如x2y''+pxy'+qy=f(x)换元:当x⼤于0当x⼩于04.应⽤题:1.背景公平——信息给予2.翻译成数学表达式Note :注意⽐例系数应是正号,或负号,应根据题意主动添上。
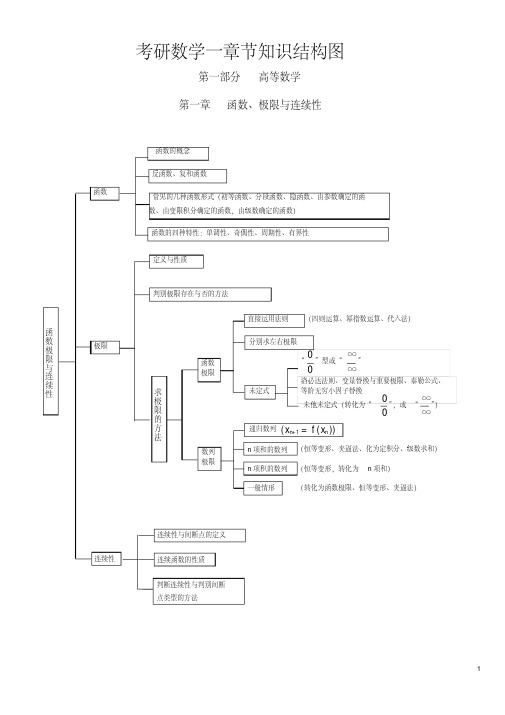
考研数学一章节知识结构图
重积分
计算公式 二重积分的极坐标变换面积微元 重积分变量替换 三重积分柱坐标变换,体积微元
d σ= rdrd θ dV = rdrd θ dz
三重积分球坐标变换、体积微元
几何应用 应用 物理应用 多元函数积 分学 平面图形面积、体积 质量、质心、转动惯量
dV = ρ sin ? dρ d? dθ
2
基本概念、性质
8
第九章
常微分方程
基本概念 一阶微分方程 基本类型 变量可分离方程 一阶线性方程 全微分方程 伯努力方程 可化为基本类型 齐次方程 用某些简单的变量代换求解某些微分方程
常 微 分 方 程
解的叠加原理 性质 通解的结构 可降阶的 高 阶微分方程 基本概念 可降阶的类型 二阶,高阶微分方程
基本概念 二阶线性常系数方程 高阶线 性微 分方程 二阶微分方程(含 某些高阶情形) 特殊的二阶线性变系数方程 可化为求解微分方程的情形(含变限积分的方程)
奇偶性与周期函数的导数性质 隐函数与反函数求导法 分阶函数求导法 基本求导法则 含参数方程所确定的函数的求导 对数求导法及幂指数求导法 导 数的 计 算与 高 阶导数 高阶导数
导 数 与 微 分
高阶导数的定义
极大值、极小值
微分 中值 定理 与 导数的应用
几种微分中值定理
( 费马定理、罗尔定理、拉格朗日中值定理、泰勒公定、柯西定理)
17
第三章
多维随机变量及其概率分布
基本概念
多维,二维随机变量 离散型
考研数学一章节知识结构图
第一部分 第一章 高等数学 函数、极限与连续性
函数的概念 反函数、复和函数 函数 常见的几种函数形式(初等函数、分段函数、隐函数、由参数确定的函 数、由变限积分确定的函数,由级数确定的函数) 函数的四种特性:单调性、奇偶性、周期性、有界性
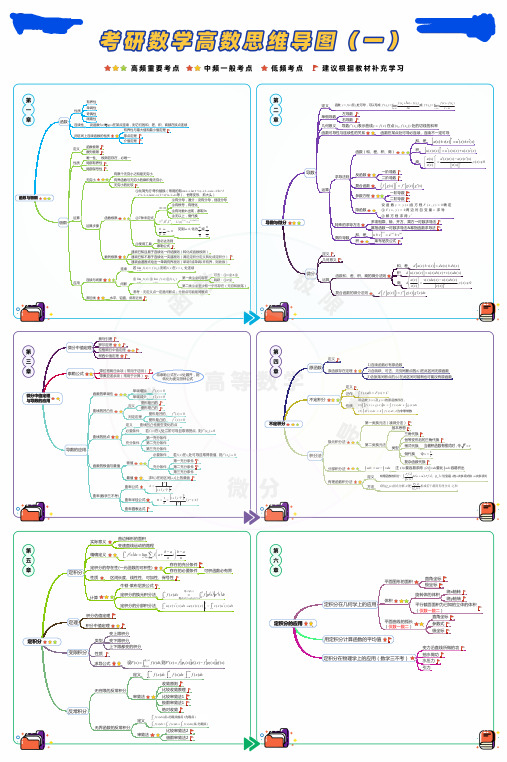
23考研高数命题点思维导图
3 2
(y ′′ ≠ 0 )
曲率圆表达式
定积分
定积分
实际意义
曲边梯形的面积 变速直线运动的路程
精确定义
b a
f (x)dx
=
lim
n→∞
n i =1
f a +
b
− n
a
i
b
− n
a
定积分的存在性(一元函数的可积性)
存在的充分条件 存在的必要条件
性质
区间长度、线性性、可加性、保号性
可积函数必有界
有理函数的积分: QPnm((xx))dx (n < m ), Pn (x)、Qm (x)分别是 x的n次多项式和 m次多项式
1)将
Qm
(
x
)因式分解;2
)把
Pn (x) Qm (x)
拆成若干最简有理分式
之和
定积分的应用
定积分在几何学上的应用
平面图形的面积
直角坐标 极坐标
旋转体的体积 绕x轴转
体积
有限个无穷小之和是无穷小
无穷小
有界函数与无穷小的乘积是无穷小
运算
运算步骤
无穷小的比较
①化简先行:等价替换(常用的有sinx~x,ln(1+x)~x,1-cosx~1/2x^2 ,e^x-1~x,tanx~x,(1+x)^α-1~αx等)、恒等变形、抓大头)
①有分母,通分;没有分母,创造分母
∞-∞
导数的应用
函数的单调性 曲线的凹凸性 曲线的拐点 函数的极值与最值 曲率(数学三不考)
单调增加 单调减少
f ′(x) > 0 f ′(x) < 0
定义
图形是凹的 图形是凸的
考研数学二命题人归纳每章知识结构图

*
*
AA = A A = A E
可交换矩阵 AB=BA
共轭矩阵 A 为 A 的共轭矩阵 反对称矩阵 AT = - A ? aij = - a ji,aii = 0
A+B ,kA, AB,A T→方阵的幂 A n
矩 阵
逆矩阵
定义法 AB=E (或 BA=E ),则 A 可逆, A-1=B
伴随矩阵法
A- 1 = 1 A* A
基本公式
牛顿—莱布尼茨公式 变限积分所定义的函数的连续性、可导性及可导公式
定
积
分
的
计
定积分的性质
算
及
其
应
用
积分中值定理 等式表示的与不等式表示的 奇偶函数与周期函数的积分性质 非负连续函数的积分性质
积
基本积分表
分项积分法
分
的
积
计
分
分段积分法
算
法
则
换元积分法
分部积分法
几何应用
应 用
平面图形的面积与旋转体的体积 平面曲线的弧长、旋转体的侧面积、平行截面面积、已知的立体体积
定义 ( CT AC = B , C 可逆; A,B 实对称 A≌B)
标准形
合同
充分条件 ( A ~B )
充要条件 ( x7 Ax 与 xT Bx 有相同的正负惯性指数)
二
次
型
惯性定理
正、负惯性指数
定义
xT Ax > 0( ? x ≠0 )A 为正定矩阵
正定
充分条件
aii > 0 A >0
充要条件
正惯性指数 P=n λi > 0( i = 1, , n ) A = CT C ,其中 C 可逆
