改进欧拉法求解初值问题教学提纲
改进的欧拉算法课程设计

改进的欧拉算法课程设计一、课程目标知识目标:1. 理解欧拉算法的基本原理及其在数值分析中的应用;2. 掌握改进的欧拉算法的计算步骤和推导过程;3. 能够运用改进的欧拉算法解决简单的数值问题。
技能目标:1. 培养学生运用数学软件或编程语言实现改进的欧拉算法的能力;2. 提高学生分析数值问题、设计算法及解决问题的能力;3. 培养学生通过合作学习,进行算法优化和调试的能力。
情感态度价值观目标:1. 培养学生对数值分析学科的兴趣,激发其探究精神;2. 增强学生的团队合作意识,学会倾听、尊重他人意见;3. 培养学生严谨、踏实的科学态度,提高其面对问题的勇气和信心。
本课程针对高年级学生,结合数值分析学科特点,注重理论知识与实践操作的结合。
通过本课程的学习,使学生能够深入理解并掌握改进的欧拉算法,培养其运用所学知识解决实际问题的能力,同时提高学生的情感态度价值观,为后续学习和工作打下坚实基础。
二、教学内容本章节教学内容以《数值分析》教材中关于改进的欧拉算法的相关章节为基础,进行以下组织:1. 回顾欧拉算法的基本原理,对比其与改进的欧拉算法的优缺点;- 教材章节:3.2 欧拉方法及其改进2. 详细讲解改进的欧拉算法的推导过程和计算步骤;- 教材章节:3.3 改进的欧拉方法3. 分析改进的欧拉算法在数值求解常微分方程中的应用;- 教材章节:3.4 数值求解常微分方程实例4. 通过实例演示,让学生动手实践改进的欧拉算法,提高其编程和解决问题的能力;- 教学实例:求解一维非线性常微分方程初值问题5. 组织课堂讨论,分析改进的欧拉算法在求解过程中的误差来源及优化方法;- 教材章节:3.5 改进的欧拉方法的误差分析6. 总结改进的欧拉算法的特点、适用范围及其在工程和科学研究中的应用。
教学内容安排和进度如下:第1-2课时:回顾欧拉算法,引入改进的欧拉算法;第3-4课时:详细讲解改进的欧拉算法的推导和计算步骤;第5-6课时:分析改进的欧拉算法在数值求解中的应用;第7-8课时:实例演示,学生动手实践;第9-10课时:课堂讨论,总结和拓展。
欧拉方法解决微分方程初值问题

欧拉⽅法解决微分⽅程初值问题
微分⽅程初值问题
初值问题\begin{cases}y^{\prime}=f(x, y)\\ y(x_{0})=y_{0}\end{cases}的解y=y(x)代表通过点(x_0, y_0)的⼀条称为微分⽅程的积分曲线。
积分曲线上的每⼀个点(x, y)的切线斜率等于函数y^{\prime}在这点的值.
欧拉⽅法画出函数图像
在最⼀开始的(x_0, y_0)位置开始,每次我们都给x⼀个步长\Delta x,如果这个步长⽐较⼩我们就可以认为(x, g(x))和(x+\Delta x, g(x+\Delta x))两点构成的直线的斜率近似为函数在x处的导数。
这样每次都画出这样⼀条“线段”,然后x跳到x+\Delta x这个位置,重复上⾯的过程就可以近似的画出这条直线的图像。
代码实现
import matplotlib.pyplot as plt
x, y = 0.0, 1.0
step = 0.1
X, Y = [x], [y]
def f(x:float, y:float):
return y - 2 * x / y
while x < 10.0:
k = f(x, y)
y = y + k * step
x = x + step
X.append(x)
Y.append(y)
print(X, Y, sep='\n')
plt.plot(X, Y)
plt.show()
Processing math: 0%。
分别利用欧拉法和改进欧拉法求解微分方程组的数值解

分别利用欧拉法和改进欧拉法求解微分方程组的数值解欧拉法(Euler’s Method)和改进欧拉法(Improved Euler’s Method),是求解常微分方程数值解的两种常用方法。
它们都属于一阶精度的显式迭代算法。
首先,我们来介绍一下欧拉法。
欧拉法是一种简单的数值求解算法,它基于微分方程的定义,将微分方程转化为差分方程。
考虑一个一阶常微分方程 dy/dx = f(x, y),并给定初始条件 y(x0)= y0,我们希望求解在给定区间 [x0, xn] 上方程的数值解。
首先,我们将区间 [x0, xn] 平均分成 N 个小区间,每个小区间的长度为 h = (xn - x0) / N。
然后,我们可以使用以下的欧拉迭代公式计算数值解:y[i+1] = y[i] + h * f(x[i], y[i])其中,x[i] = x0 + i * h,y[i] 是在点 x[i] 处的数值解。
通过不断迭代上述公式,我们可以获得[x0, xn] 上微分方程的数值解。
欧拉法的优点在于简单易懂,计算速度较快。
然而,欧拉法的缺点是精度较低,误差随着步长h 的增大而增大。
为了提高精度,我们可以使用改进欧拉法。
改进欧拉法,也称为龙格–库塔算法(Runge-Kutta Method)或四阶龙格–库塔方法,是一种基于欧拉法的改进算法。
改进欧拉法使用了更多的近似取值,以减小误差。
与欧拉法类似,我们将区间 [x0, xn] 平均分成 N 个小区间,每个小区间的长度为 h = (xn - x0) / N。
然后,我们可以使用以下的公式计算数值解:k1 = h * f(x[i], y[i])k2 = h * f(x[i] + h/2, y[i] + k1/2)y[i+1] = y[i] + k2其中,k1 和 k2 是计算过程中的辅助变量。
通过不断迭代上述公式,我们可以获得 [x0, xn] 上微分方程的数值解。
改进欧拉法相对于欧拉法而言,计算精度更高。
第8章 常微分方程数值解法 本章主要内容: 1.欧拉法、改进欧拉法 2

第8章 常微分方程数值解法本章主要内容:1.欧拉法、改进欧拉法. 2.龙格-库塔法。
3.单步法的收敛性与稳定性。
重点、难点一、微分方程的数值解法在工程技术或自然科学中,我们会遇到的许多微分方程的问题,而我们只能对其中具有较简单形式的微分方程才能够求出它们的精确解。
对于大量的微分方程问题我们需要考虑求它们的满足一定精度要求的近似解的方法,称为微分方程的数值解法。
本章我们主要讨论常微分方程初值问题⎪⎩⎪⎨⎧==00)(),(yx y y x f dx dy的数值解法。
数值解法的基本思想是:在常微分方程初值问题解的存在区间[a,b]内,取n+1个节点a=x 0<x 1<…<x N =b (其中差h n = x n –x n-1称为步长,一般取h 为常数,即等步长),在这些节点上把常微分方程的初值问题离散化为差分方程的相应问题,再求出这些点的上的差分方程值作为相应的微分方程的近似值(满足精度要求)。
二、欧拉法与改进欧拉法欧拉法与改进欧拉法是用数值积分方法对微分方程进行离散化的一种方法。
将常微分方程),(y x f y ='变为()*+=⎰++11))(,()()(n xn x n n dtt y t f x y x y1.欧拉法(欧拉折线法)欧拉法是求解常微分方程初值问题的一种最简单的数值解法。
欧拉法的基本思想:用左矩阵公式计算(*)式右端积分,则得欧拉法的计算公式为:Nab h N n y x hf y y n n n n -=-=+=+)1,...,1,0(),(1 欧拉法局部截断误差11121)(2++++≤≤''=n n n n n x x y h R ξξ或简记为O (h 2)。
我们在计算时应注意欧拉法是一阶方法,计算误差较大。
欧拉法的几何意义:过点A 0(x 0,y 0),A 1(x 1,y 1),…,A n (x n ,y n ),斜率分别为f (x 0,y 0),f (x 1,y 1),…,f (x n ,y n )所连接的一条折线,所以欧拉法亦称为欧拉折线法。
改进Euler法

y0 ?
h 6
(
K1
?
2K2 ? 2K3 ?
K4)
n ? N ? 1; N
x1 ? x0, y1 ? y0
n? N?
Y
结束
输出 x1,y1
例题4
例4 求(3阶、4阶R ? K公式 )解初值问题 (步长 h ? 0.1)
? ?
y??
?
y?
2x y
?? y(0) ? 1
(0 ? x ? 1)
解 f (x, y) ? y ? 2x / y
f ( x , y( x ))dx ?
xn
2
f ( x n , y( x n )) ? f ( x n?1, y( x n?1 )) ? O(h3 )
?
yn?1 ?
yn ?
h 2
[
f
(
x
n
,
yn
)
?
f ( x n? 1 , yn? 1 )]
梯形格式
梯形格式是显式 Euler 格式与隐式 Euler 格式的 算术平均
平均化形式:
? y p ? yn ? hf ( xn , yn )
? ?? yc ? yn ? hf ( x n?1, y p )
? ? yn?1 ?
?
1 2
(
y
p
?
yc )
?? y( x0 ) ? y0
? 改进 Euler 方法计算框图 开始
输入 x0 , y0 , h, b
n?1
x1 ? x0 ? h
K 2 ? f ( xn ? ph , yn ? phK1 ) ? f ( xn , yn ) ? phf x ( xn , yn ) ? phK1 f y ( xn , yn ) ? O(h2 ) ? y ?( x n ) ? phy ??( x n ) ? O ( h 2 )
课题10常微分方程初值问题的数值方法

课题10. 常微分方程初值问题的数值方法一.问题提出(1)利用欧拉方法和改进的欧拉方法求解初值问题:dy/dx=4*x/y-x*y; y(0)=3; 其中0<x<=2二.问题算法、c语言编程和上机运算结果1.欧拉法算法:输入微分方程f(x,y);输入积分部数n;输入初值x0,y0;输入步长h;利用k1=f(xn,yn)y(n+1)=yn+k1*h;n=0,1,2……采取不断循环计算;输出x1,x2,……xn.程序:/*微分方程*/float f(x,y)float x,y;{float z;z=4*x/y-x*y;return(z);}/* 欧拉法*/float EULAR(f)float (*f)();{int i,n;float x0,y0,x,y,k1,h;printf("\n请输入积分步数n:");scanf("%d",&n);printf("\n请输入初值x(0) y(0):");scanf("%f%f",&x0,&y0);printf("\n请输入步长h:");scanf("%f",&h);printf("\n x y"); printf("\n %f %f",x0,y0); for(i=1;i<=n;i++){x=x0+h;k1=(*f)(x0,y0);y=y0+h*k1;printf("\n %f %f",x,y); x0=x;y0=y;}}main(){EULAR(f);}结果:(1)h=0.1时(2)h=0.2时(3)h=0.4时2.改进的欧拉法算法:输入微分方程f(x,y);输入积分部数n;输入初值x0,y0;输入步长h;利用k1=f(xn,yn)k2=f(xn+h,yn+h*k1)y(n+1)=yn+(k1+k2)/2;n=0,1,2……采取不断循环计算;输出x1,x2,……xn.程序:/*微分方程*/float f(x,y)float x,y;{float z;z=y-2.0*x/y;return(z);}/* 改进欧拉法*/float EULAR(f)float (*f)();{int i,n;float x0,y0,x,y,k1,k2,h;printf("\n请输入积分步数n:");scanf("%d",&n);printf("\n请输入初值x(0) y(0):");scanf("%f%f",&x0,&y0);printf("\n请输入步长h:");scanf("%f",&h);printf("\n x y"); printf("\n %f %f",x0,y0); for(i=1;i<=n;i++){x=x0+h;k1=(*f)(x0,y0);k2=(*f)(x,y0+h*k1);y=y0+h*(k1+k2)/2.0;printf("\n %f %f",x,y); x0=x;y0=y;}}main(){EULAR(f);}结果:(1)当h=0.1时(2)当h=0.2时(3)当h=0.4时三.结果分析讨论1.对比欧拉法,改进的欧拉法和精确解的结果可知,改进的欧拉法所得到结果的精度比欧拉法的大,这是因为改进的欧拉法融入了属于隐式公式的梯形公式,它的计算数值解的精度要比欧拉公式好。
Euler法与改进Euler法知识讲解

yn1 yn dy h dx
常用方法
(2) 用数值积分近似积分
dy xn1
xn1
dx f ( x, y)dx (n 0,1, )
xn dx
xn
即
y( xn1) y( xn )
xn1 f ( x, y( x))dx
xn
进一步: 令 yn1 y( xn1) , yn y( xn )
xn x0 nh, n 0,1,2 .
二、建立数值解法的常用方法
建立微分方程数值解法,首先要将微分方程离散化.
一般采用以下几种方法: (1) 用差商近似导数
dy
y xn1 yxn
xn1 xn
f xn , y(xn )
dx x y , n n
进一步 : 令 yn1 y(xn1) , yn y(xn )
y0 ( x x0 ) f ( x0 , y0 )
dx x y , 0 0
几何意义
等步长为h,则 x1 x0 h,可由切线算出y1 : y1 y0 hf(x0 , y0)
逐步计算出y
y( x)
在
xn
点
1
的
值
:
yn1 yn hf(xn , yn) n 0,1,2,
注意:这是“折线法”而非“切线法” y 除第一个点是曲线切线外,其他点不是!
能用解析方法求出精确解的微分方程为数不多, 而且有的方程即使有解析解,也可能由于解的表达 式非常复杂而不易计算,因此有必要研究微分方程 的数值解法
常微分方程数值解法
重点 研究一阶常微分方程的初值问题的数值解
其一般形式为:
dy
dx
f (x, y)
y( x0 ) y0
a xb
21讲:Euler法与改进Euler法

hy'( xn )
h2 2!
y''( )
h2 y( xn ) hy'( xn ) 2! y''( xn )
进一步: 令 yn1 y( xn1 ) , yn y( xn )
yn1 yn hf ( xn , yn )
h2
y( xn1 ) yn1
max y''( x) 2 axb
三、Euler方法
已知初值问题的一般形式为:
dy
dx
f
( x,
y)
y( x0 ) y0
a xb
(1)
用差商近似导数 问题转化为
yn1 yn dy
h
dx
yn1 y0
y(
yn x0 )
hf
(
xn
,
yn
)
(n 0,1,2,3,...)
Euler方法的迭代公式
逐步计算出y y( x) 在 xn1点的值 : yn1 yn hf(xn , yn) n 0,1,2,
注意:这是“折线法”而非“切线法” y 除第一个点是曲线切线外,其他点不是!
Y=y(x)
a
x1χx0
χ1χ2
2
χ3
b
χ
四、Euler方法的误差估计
为简化分析,先考虑计算一步所产生的误差,即假设
( xn1 ,
y(k) n1
)
(k 0,1,2,)
如果用中心差商代替导数,则可导出Euler两步公式。
六、向后Euler方法
用向后差商:yxn1
yxn1
h
(完整word版)计算方法 用欧拉预估-校正法求初值问题

《计算方法》实验指导书实验1 方程求根一、实验目的1.通过对二分法、牛顿法、割线法作编程练习,进一步体会它们各自不同的特点;2.了解二分法,切线法,割线法。
3.能熟练运用二分法,牛顿法进行方程求根4.通过上机调试运行,对方程求根的几种方法程序进行改进。
二、实验要求1.上机前作好充分准备,包括复习编程所需要的语言工具。
2.上机时要遵守实验室的规章制度,爱护实验设备。
3.记录调试过程及结果,记录并比较与手工运算结果的异同。
4.程序调试完后,须由实验辅导教师在机器上检查运行结果。
5.给出本章实验单元的实验报告。
三、实验环境、设备1.硬件设备:IBM PC以上计算机,有硬盘和一个软驱、单机和网络环境均可。
2.软件环境:C语言运行环境。
四、实验原理、方法二分算法计算步骤:(1)输入有根区间的端点a、b及预先给定的精度ε;(2)计算中点x=(a+b)/2;(3)若f(x)f(b)<0,则a=x,转向下一步;否则b=x,转向下一步;(4)若b-a<ε,则输出方程满足精度要求的根x,结束;否则转向步骤(2)。
迭代法:牛顿法:牛顿迭代法是一种逐步线性化方法,即将非线性方程f(x)=0的求根问题归结为计算一系列线性方程的根。
设x k 是方程f(x)=0的一个近似根,将f(x)在x k 处作一阶泰勒展开,即f(x)≈f(x k )+f′(x k )(x- x k )于是得到如下的近似方程f(x k )+f′(x k )(x- x k )=0 (2.7)设f′(x k )≠0,则式(2.7)的解为)()('k k k x f x f x x -= 取x 作为原方程的新的近似根x k+1,即令)()('1k k k k x f x f x x -=+ k=0,1,2, … (2.8)则称式(2.8)为牛顿迭代公式。
用牛顿迭代公式(2.8)求方程近似根的方法称为牛顿迭代法,简称牛顿法,又称切线法。
改进Euler方法

第九章 解常微分方程初值问题4. 改进Euler 方法我们先用Euler 公式求的一个初步的近似值,再用梯形公式将它校正一次,即按(5)迭代一次得y 1+n ,这个结果称为校正值,这样建立的校正系统通常成为改进Euler 公式.y 1+n = y n +h /2(f (n n y x ,) + f (x n +1, n y + h* f (n n y x ,))) (6)即迭代公式为:⎪⎪⎪⎨⎧+=+=+),,(*),,(*1p n n c n n n p y x f h y y y x f h y y(7)进过计算得出改进Euler 法比Euler 法 明显改善了精度.上机实验⑷上机题目:贬值求一阶常微分方程的初值问题实验目的:掌握各种Euler 方法和梯形法。
进过计算结果来分析四种方法的优缺点,掌握规律。
分析结果。
实验要求:用不同的方法来解同一个例子。
① 上机前充分准备,复习有关内容,写出计算步骤,查对程 序。
②改进Euler 法在Matlab 环境中运算,并分析出最好的方法,再给出它的流程图。
③实验结束后写出完整的实验报告。
算法说明:①经过所给出的方程组和初值初步改变方程组。
②由以上四种方法的计算公式来逐步计算y 的每个值。
③最后为了方便比较列为表最适合。
上机例题:例1.后退Euler 方法解初值问题,h =0.1⎩⎨⎧=〈〈='1y(0)1x 0 2x/y,-y y Matlab 程序:function[x,y]=gaijing(f,x0,y0,a,b,n)h=(b-a)/n; %定义并计算步长 for k=1:n+1x(k)=a+(k-1)*h; %计算x(k) endy(1)=y0; for i=1:nyp=y(i)+h*subs(subs(f,x(i)),y(i)); %由改进Euler 的公式计算. yc=y(i)+h*subs(subs(f,x(i+1)),yp); y(i+1)=(1/2)*(yp+yc); enddisp(sprintf(' i x(i) y(i)')); %为了方便以规定格式先输出 i,x(i),y(i). for i=1:ndisp(sprintf(' %d %f %f',i,x(i+1),y(i+1))); %为了方便观察结果在先输出的格式下输出结果end s=y(i);运行结果:[x,y]=gaijing('y-2*x/y',0,1,0,1,10) i x(i) y(i) 1 0.100000 1.0959092 0.200000 1.1840973 0.300000 1.2662014 0.400000 1.3433605 0.500000 1.4164026 0.600000 1.4859567 0.700000 1.5525148 0.800000 1.6164759 0.900000 1.678166 10 1.000000 1.737867改进Euler 的流程图:流程图解释:1) 输入N h y x 最大循环次序,,,00;2)1腻给n;3)把 10x h x 腻给+ 把1000002)(,),(,),(y y y y y x hf y y y x hf y c p c p p 腻给腻给腻给+++;4)输出1x ,1y ;5)判断n 是否等于 N ,若n=N ,那么停止;否则到第6步;6)把n+1 赋给 n,把1x 赋给0x ,把1y 腻给0y 到步骤3;上机结果分析:梯形方法是Euler 的校正,它比Euler 方法好的多,改进Euler 是梯形方法的校正。
欧拉法、改进的欧拉法、龙格-库塔法求解初值问题

欧拉法、改进的欧拉法、龙格-库塔法求解初值问题欧拉法、改进的欧拉法、龙格-库塔法求解初值问题简介通过求解简单的初值问题:dudx =f (x ,u )(1)u (x 0)=u 0(2)引⼊欧拉法、改进的欧拉法、龙格-库塔法等。
前期准备数值解法的基本思想就是先对x 和u(x)在区间[x0,∞)上进⾏离散化,然后构造递推公式,再进⼀步得到u(x)u(x) u(x)u(x)u(x)u(x)在这些位置的近似取值。
取定步长h ,令x n =x 0+nh (n =±1,±2,⋯)得到离散的位置:x 1,x 2,⋯,x n ,u(x)在这些点精确取值为:u (x 1),u (x 2),⋯,u (x n )利⽤数值解法得到的这些点的近似取值,u 1,u 2,⋯,u n欧拉法欧拉法的核⼼就是将导数近似为差商。
将导数近似为向前差商,则有:du dxx =x n≈u x n +1−u x nh代⼊(1)式,有:u x n +1=y x n +hf x n ‖u x n⽤u n +1和 u n 代替u (x n +1)和u (x n ),得:u n +1=u n +hf x n ,u n因此,若知道u 0我们就可以递归出u 1,u 2,⋯如果将导数近似为向后差商:du dxx =x n≈u x n −u x n −1h类似的,就可以得到:u n −1=u n −hf x n ,u n这样,若知道u 0我们就可以递归出u −1,u −2⋯改进的欧拉法对(1)式在[x n ,x n +1]上积分,可得:u x n +1=u x n +∫xn +1x nf (x ,u )dx其中,n =0,1,⋯⽤不同⽅式来近似上式的积分运算,就会得到不同的递推公式。
若使⽤左端点计算矩形⾯积并取近似:∫x n +1x nf (x ,u )dx ≈hf x n +1,u x n +1代⼊上式得:{|()()()()(())()|()()()()()(())u n +1=u n +hf (x n ,u n )若使⽤梯形的⾯积做近似:∫x n +1x nf (x ,y )dx ≈h2f x n ,u x n+f x n +1,ux n +1得到:u n +1=u n +h2f x n ,u n +f x n +1,u n +1欧拉法虽然精度偏低,但它是显式的,可直接得到结果。
用改进欧拉法和梯形法解初值问题

在数值分析领域,求解初值问题是一个非常重要的课题。
常见的数值方法有欧拉法和梯形法,但它们都存在一定的局限性。
本文将深入探讨如何改进欧拉法和梯形法,以更高效、精确地解决初值问题。
让我们回顾一下初值问题的基本概念。
初值问题是指,在已知微分方程初值条件的情况下,求解微分方程的数值解。
通常情况下,微分方程很难直接求解,因此需要借助数值方法来逼近微分方程的解。
欧拉法和梯形法是最常见的数值方法之一,它们都是通过离散化微分方程来逼近微分方程的解。
接下来,让我们讨论欧拉法的改进方法。
欧拉法是一种一阶精度的数值方法,它的局限性在于步长选择较大时,数值解会出现较大的误差。
为了改进欧拉法,可以考虑使用改进的欧拉法,如改进的Euler-Cauchy法,它通过使用更复杂的插值公式来提高精度。
也可以考虑使用四阶Runge-Kutta法等更高阶的方法来提高数值解的精度和稳定性。
另让我们分析梯形法的改进方法。
梯形法是一种二阶精度的数值方法,它对微分方程积分过程进行了更加精确的近似。
但梯形法在处理刚性微分方程时会出现数值不稳定的情况。
为了改进梯形法,可以考虑使用隐式的Runge-Kutta法,它可以更好地处理刚性微分方程,提高数值解的稳定性和精度。
总结来说,改进欧拉法和梯形法是为了解决数值解精度不高、数值不稳定等问题。
在实际应用中,根据不同的初值问题特性,选择合适的数值方法很关键。
只有综合考虑数值解精度、稳定性等因素,才能更好地求解初值问题。
从我个人的观点来看,改进欧拉法和梯形法是数值分析领域的一个重要研究方向。
随着科学技术的不断发展,解决初值问题需要更高效、精确的数值方法。
改进欧拉法和梯形法对于提高数值解的精度和稳定性具有重要意义。
在本文中,我们深入探讨了如何改进欧拉法和梯形法,以更高效、精确地解决初值问题。
通过对不同的改进方法进行分析,我们可以更好地理解数值方法的优缺点,为实际问题的求解提供参考。
希望本文能够对初值问题的数值解求解提供一定的帮助,也希望读者可以从中获得一定的启发和思考。
方程的改进欧拉公式

2013-2014(1)专业课程实践论文题目:方程的改进欧拉公式一、算法理论按照⎪⎩⎪⎨⎧=++=+=+++++ ,2,1,0)],,(),([2)(1)(11)1(,1)0(k y x f y x f h y yy x hf y y n k n n n n n k n n n n 计算⎪⎩⎪⎨⎧=≤≤=0)(),,(y a y b x a y x f dx dy的数值解时候,如果每次只迭代一次,相当于将欧拉公式与梯形格式结合使用:先用欧拉公式求出1+n y ,称为预测值,然后用梯形格式校正求得近似值1+n y ,即 预测: ),(1n n n n y x hf y y +=+;校正: )],(),([2111+++++=n n n n n n y x f y x f hy y将上式称为由欧拉公式和梯形格式得到的预测—校正系统,也叫改进的欧拉公式。
它是显式的单步法。
为了便于编制程序上机,上式常改写成),(n n n p y x hf y y +=),(p n n q y h x hf y y ++=)(211q p n y y y +=+ 改进的欧拉方法算法如下:(1)输入),,(,,y x f b a 区间等分数N ,初始值0y 。
(2)输出)(x y 在x 的N 个点处的近似值y 。
(3)置0,,0,y y a x n Nab h ===-=。
(4)计算),(),,(p q p y h x hf y y y x hf y y ++=+=,置,),(21x h x y y y q p ⇒+⇒+输出),(y x 。
(5)若1n,置,x<N-+1,转(4);否则,停机.计算框图见二。
n⇒#include <stdio.h>#include <math.h>#include <stdlib.h>double fun(double x,double y){return x*y;}void Euler(double (*fun)(double ,double), double h,double x0,double y0 ,double low,double up){int n =0,i=0,j=0;double x1 = x0,y1=y0;n = (up-low)/h;printf("第n个变量变量的值xn 函数值yn\n");printf("%lf %lf \n",x0,y0);for ( i = 1 ; i<=n ; i++){x1 = x0 + i*h;y1 = y1+ h*fun(x1,y1);printf("%d %lf %lf\n",i,x1,y1);}}void main(){double h,x0,y0,low,up;printf("*****输入初始值x0=");scanf("%lf",&x0);printf("********输入初始值y0=");scanf("%lf",&y0);printf("************请输入利用“改进的欧拉公式”使用变量的范围\n");printf("****************输入区间下界low=");scanf("%lf",&low);printf("********************输入区间上界up=");scanf("%lf",&up);printf("************************输入步长h="); scanf("%lf",&h);Euler(fun,h,x0,y0,low,up);return 0;}四、算法实现例1.用改进的欧拉公式,求解常微分方程初值问题的解。
用Euler法、改进的Euler法及四阶的龙格库塔法求解初值问题

微分方程数值解课程设计题目1(30分)分别用Euler 法、改进的Euler 法及四阶的龙格库塔法求解初值问题:⎪⎩⎪⎨⎧=-=1)0(2'u ut u u 10≤<th 分别取0.1和0.2,要求计算并绘出图形,最后比较三种算法的精度。
(1).先构建初值问题的函数M 文件: function z=fun(x,y)z=y-2*x/y; (2).Euler 法 M 文件:function E=Euler(fun,x0,y0,h,N) x=zeros(1,N+1);y=zeros(1,N+1); x(1)=x0;y(1)=y0;for n=1:Nx(n+1)=x(n)+h;y(n+1)=y(n)+h*feval(fun,x(n),y(n)); end T=[x;y]① .当h=0.1时>> Euler('fun',0,1,0.1,10) T = Columns 1 through 100 0.1000 0.2000 0.3000 0.4000 0.5000 0.6000 0.7000 0.8000 0.90001.0000 1.1000 1.1918 1.2774 1.3582 1.4351 1.5090 1.5803 1.6498 1.7178 Column 11 1.00001.7848②.当h=0.2时>> Euler('fun',0,1,0.2,5)T = 0 0.2000 0.4000 0.6000 0.8000 1.00001.0000 1.2000 1.3733 1.5315 1.6811 1.8269(3).改进的Euler 法:M 文件:Euler_modify.mfunction E=Euler_modify(fun,x0,y0,h,N) x=zeros(1,N+1);y=zeros(1,N+1);x(1)=x0;y(1)=y0;for n=1:Nx(n+1)=x(n)+h;z0=y(n)+h*feval(fun,x(n),y(n));y(n+1)=y(n)+h/2*(feval(fun,x(n),y(n))+feval(fun,x(n+1),z0));endT=[x;y]①.当h=0.1时>> Euler_modify('fun',0,1,0.1,10)T = Columns 1 through 90 0.1000 0.2000 0.3000 0.4000 0.5000 0.60000.7000 0.80001.0000 1.0959 1.1841 1.2662 1.3434 1.4164 1.4860 1.5525 1.6165Columns 10 through 110.9000 1.00001.6782 1.7379②.当h=0.2时>> Euler_modify('fun',0,1,0.2,5)T = 0 0.2000 0.4000 0.6000 0.8000 1.00001.0000 1.1867 1.3483 1.4937 1.6279 1.7542(4).四阶R_K方法:M文件:function [x,y]=Rk_N4(f,x0,y0,h,N)x=zeros(1,N+1);y=zeros(1,N+1);x(1)=x0;y(1)=y0;for n=1:Nx(n+1)=x(n)+h;k1=h*feval(f,x(n),y(n));k2=h*feval(f,x(n)+1/2*h,y(n)+1/2*k1);k3=h*feval(f,x(n)+1/2*h,y(n)+1/2*k2);k4=h*feval(f,x(n)+h,y(n)+k3);y(n+1)=y(n)+1/6*(k1+2*k2+2*k3+k4);end①.当h=0.1时>> [x,y]=Rk_N4('fun',0,1,0.1,10)x = Columns 1 through 90 0.1000 0.2000 0.3000 0.4000 0.5000 0.6000 0.7000 0.8000Columns 10 through 110.9000 1.0000y = Columns 1 through 91.0000 1.0954 1.1832 1.2649 1.3416 1.4142 1.4832 1.5492 1.6125Columns 10 through 111.6733 1.7321②.当h=0.2时>> [x,y]=Rk_N4('fun',0,1,0.2,5)x = 0 0.2000 0.4000 0.6000 0.8000 1.0000y = 1.0000 1.1832 1.3417 1.4833 1.6125 1.7321(5)作图:1): h=0.1>> x=0:0.1:1;>> y_euler=[1.0000 1.1000 1.1918 1.2774 1.3582 1.4351 1.5090 1.5803 1.6498 1.7178 1.7848];>> y_euler_modify=[1.0000 1.0959 1.1841 1.2662 1.3434 1.4164 1.4860 1.5525 1.6165 1.6782 1.7379];>> y_RK_N4=[1.0000 1.0954 1.1832 1.2649 1.3416 1.4142 1.4832 1.5492 1.6125 1.6733 1.7321];plot(x,y_euler,'bo:',x,y_euler_modify,'r*-',x,y_RK_N4,'gv--');title('误差分析');xlabel('x轴');y label('y轴');text(0.3,1.3,'Euler法');text(0.4,1.35,'Euler改进法');text(0.5,1.4,'R-k法'); text(0.8,1.0 2,'作者:李靖');text(0.8,1.07,'日期:2010.6.19');text(0.4,1.75,'h=0.1');legend('Euler','Euler改进法','R_K法');grid on2): h=0.2>> x=0:0.2:1;>> y_euler=[1.0000 1.2000 1.3733 1.5315 1.6811 1.8269];>> y_euler_modify=[1.0000 1.1867 1.3483 1.4937 1.6279 1.7542];>> y_RK_N4=[ 1.0000 1.1832 1.3417 1.4833 1.6125 1.7321];plot(x,y_euler,'bo:',x,y_euler_modify,'r*-',x,y_RK_N4,'gv--');title('误差分析');xlabel('x轴');y label('y轴');text(0.3,1.3,'Euler法');text(0.4,1.35,'Euler改进法');text(0.5,1.4,'R-k法'); text(0.8,1.0 2,'作者:xx');text(0.8,1.07,'日期:2010.6.19'); text(0.4,1.75,'h=0.2');legend('Euler','Euler改进法', 'R_K法');grid on0.10.20.30.40.50.60.70.80.9111.11.21.31.41.51.61.71.8误差分析x 轴y 轴Euler 法Euler 改进法R-k 法作者:李靖日期:2010.6.19h=0.1EulerEuler 改进法R K 法00.10.20.30.40.50.60.70.80.9111.11.21.31.41.51.61.71.81.9误差分析x 轴y 轴Euler 法Euler 改进法R-k 法作者:李靖日期:2010.6.19h=0.2EulerEuler 改进法R K 法2.(20分)编写一个程序用tylor 级数法求解问题:⎩⎨⎧==1)0('u ut u 10≤<t取tylor 级数法的截断误差为O(21h ),即要用u(t),u ’(t),…,u (20)(t)的值。
用欧拉法、改进欧拉法、四阶龙格-库塔法解初值问题

常微分方程的数值解一、实验名称:用欧拉法、改进欧拉法、四阶龙格-库塔法解初值问题[])( b a, x ),(00⎪⎩⎪⎨⎧=∈=y x y y x f dx dy 要求输出:x ,真值,欧拉法,改进欧拉法,龙格库塔法二、算法:(1)欧拉法公式:),(1n n n n y x f h y y +=+(2)改进欧拉法公式:[]),(),(2111+++++=n n n n n n y x f y x f h y y (3)龙格—库塔法公式: ()⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧++=⎪⎭⎫ ⎝⎛++=⎪⎭⎫ ⎝⎛++==++++=+342312143211,2,212,21),()22(6hk y h x f k k h y h x f k k h y h x f k y x f k k k k k h y y n n n n n n n n n n 三、源程序(见附件)1. 常微分方程见f.m2. 欧拉法、改进欧拉法、龙格库塔法及真值对比见cwffc.m四、数值例子以讲义例9.2为例:⎪⎩⎪⎨⎧=-=1)0(2y y x y dxdy 在区间[0,1.5]上,取h=0.11.在命令窗口输入: cwffc(@f,1,0.1,0,1.5)、回车输出:欧拉法、改进欧拉法、龙格库塔法的计算结果及真值五、分析总结由以上的实例可以看出这三种方法的计算精度:龙格库塔>改进欧拉法>欧拉法,由于欧拉法采取的实际是左矩形公式,随着计算次数的增多,其误差越来越大,改进欧拉法较欧拉法的精度要高,而龙格库塔法具有收敛、稳定、计算过程中可以改变步长等优点。
六、操作手册1.双击启动matlab;2.在命令窗口依次输入cwffc(@fx,y0,h,a,b),回车(输入时给y0赋初始值,h赋步长,a赋左端点值,b赋右端点值,常微分方程的修改在f.m 中进行),即可输出真值和欧拉法、改进欧拉法、龙格库塔法的计算结果。
常微分方程的数值解法(欧拉法、改进欧拉法、泰勒方法和龙格库塔法)
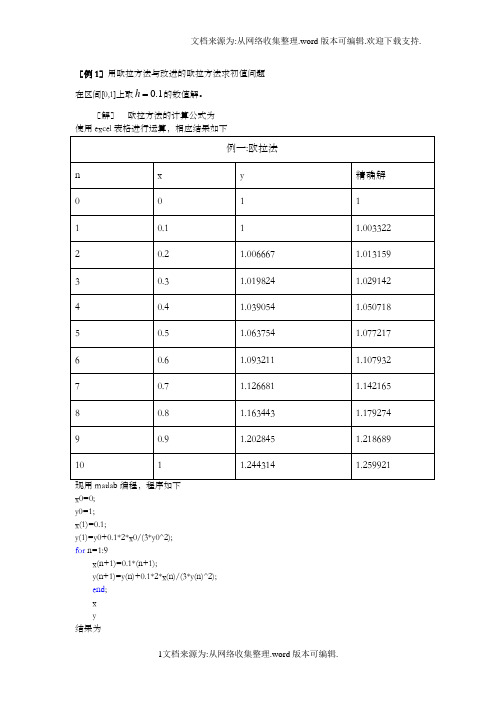
[例1]用欧拉方法与改进的欧拉方法求初值问题h 的数值解。
在区间[0,1]上取0.1[解]欧拉方法的计算公式为x0=0;y0=1;x(1)=0.1;y(1)=y0+0.1*2*x0/(3*y0^2);for n=1:9x(n+1)=0.1*(n+1);y(n+1)=y(n)+0.1*2*x(n)/(3*y(n)^2);end;xy结果为x =Columns 1 through 80.1000 0.2000 0.3000 0.4000 0.5000 0.6000 0.7000 0.8000 Columns 9 through 100.9000 1.0000y =Columns 1 through 81.0000 1.0067 1.0198 1.0391 1.0638 1.0932 1.1267 1.1634 Columns 9 through 101.2028 1.2443改进的欧拉方法其计算公式为本题的精确解为()y x=x0=0;y0=1;ya(1)=y0+0.1*2*x0/(3*y0^2);y(1)=y0+0.05*(2*x0/(3*y0^2)+2*x0/(3*ya^2));for n=1:9x(n+1)=0.1*(n+1);ya(n+1)=ya(n)+0.1*2*x(n)/(3*ya(n)^2);y(n+1)=y(n)+0.05*(2*x(n)/(3*y(n)^2)+2*x(n+1)/(3*ya(n+1)^2));end;xy结果为x =Columns 1 through 80.1000 0.2000 0.3000 0.4000 0.5000 0.6000 0.7000 0.8000 Columns 9 through 100.9000 1.0000y =Columns 1 through 81.0000 1.0099 1.0261 1.0479 1.0748 1.1059 1.1407 1.1783 Columns 9 through 101.2183 1.2600[例2]用泰勒方法解x=0.1, 0.2, …, 1.0处的数值解,并与精确解进行比较。
(完整word版)计算方法 用欧拉预估-校正法求初值问题

《计算方法》实验指导书实验1 方程求根一、实验目的1.通过对二分法、牛顿法、割线法作编程练习,进一步体会它们各自不同的特点;2.了解二分法,切线法,割线法。
3.能熟练运用二分法,牛顿法进行方程求根4.通过上机调试运行,对方程求根的几种方法程序进行改进。
二、实验要求1.上机前作好充分准备,包括复习编程所需要的语言工具。
2.上机时要遵守实验室的规章制度,爱护实验设备。
3.记录调试过程及结果,记录并比较与手工运算结果的异同。
4.程序调试完后,须由实验辅导教师在机器上检查运行结果。
5.给出本章实验单元的实验报告。
三、实验环境、设备1.硬件设备:IBM PC以上计算机,有硬盘和一个软驱、单机和网络环境均可。
2.软件环境:C语言运行环境。
四、实验原理、方法二分算法计算步骤:(1)输入有根区间的端点a、b及预先给定的精度ε;(2)计算中点x=(a+b)/2;(3)若f(x)f(b)<0,则a=x,转向下一步;否则b=x,转向下一步;(4)若b-a<ε,则输出方程满足精度要求的根x,结束;否则转向步骤(2)。
迭代法:牛顿法:牛顿迭代法是一种逐步线性化方法,即将非线性方程f(x)=0的求根问题归结为计算一系列线性方程的根。
设x k 是方程f(x)=0的一个近似根,将f(x)在x k 处作一阶泰勒展开,即f(x)≈f(x k )+f′(x k )(x- x k )于是得到如下的近似方程f(x k )+f′(x k )(x- x k )=0 (2.7)设f′(x k )≠0,则式(2.7)的解为)()('k k k x f x f x x -= 取x 作为原方程的新的近似根x k+1,即令)()('1k k k k x f x f x x -=+ k=0,1,2, … (2.8)则称式(2.8)为牛顿迭代公式。
用牛顿迭代公式(2.8)求方程近似根的方法称为牛顿迭代法,简称牛顿法,又称切线法。
欧拉方法求解初值问题

欧拉方法是一种数值求解微分方程初值问题的方法。
该方法假设微分方程在给定点的斜率近似等于在该点处的斜率,并利用该斜率计算出微分方程在下一个点的近似解。
具体步骤如下:
1. 将时间轴分成若干个小段,步长为 h 。
2. 初始条件为 y0,即微分方程在 t0 时刻的初始值。
3. 用斜率公式(斜率为 y')来近似计算 y1 的值:
y1 = y0 + h * f(t0, y0)
其中,f(t0, y0) 表示在 t0 时刻 y0 点的导数。
4. 重复步骤 3,利用 y1 和 t1 来计算 y2,y3 等等,直到求得满足要求的
解。
需要注意的是,欧拉方法的精度不高,当步长过大时,会导致计算误差增大。
因此,在实际运用中,需要根据所求解的特点,选择合适的步长,以保证计算精度和计算效率的平衡。
