运筹学(胡运权版)第三章运输问题课后习题答案
清华大学运筹学教程胡运权主编课后习题答案
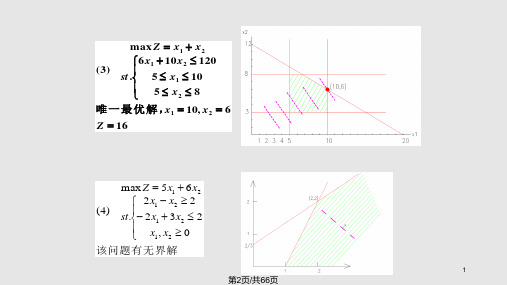
8 10
x1 , x2 0
目标函数最优值(下界)为:6.4
17
第18页/共66页
l.7 分别用单纯形法中的大M法和两阶 段法求解下列线性规划问题,并指出属哪—
类解。
max Z 3x1 x2 2x3
x1 x2 x3 6
(1)
st
2x1 2x2
x3 x3
0
2
x j 0(, j 1,,3)
所以最优解为X*=(1,3/2,0,0)T
第11页/共66页
0点
A1点 A2点
max Z 2x1 x2 3x1 5x2 15
(2) st.6x1 2x2 24 x1, x2 0
11
第12页/共66页
第13页/共66页
第14页/共66页
d
x
2
,
l.5 讨论c
,
上题(1)中,若目标函数变为max Z = d的值如何变化,使该问题可行域的每个
8
第9页/共66页
1.4 分别用图解法和单纯形法求解下述 线性规划问题,并对照指出单纯形表中的各 基可行解对应图解法中可行域的哪一顶点。
max Z 10x1 5x2
(1)
st.35xx11
4 x2 2 x2
9 8
x1, x2 0
9
第10页/共66页
cj
10
5 00
CB
xB
b
x1
x2
max Z x1 x2
(3)
st
6 .
x1 10x2 5 x1
120 10
5 x2 8
唯 一 最 优 解 ,x1 10, x2 6
Z 16
max Z 5x1 6x2 2x1 x2 2
运筹学胡运权第三版第三章运输问题

§1运 输 问 题 及 其 数 学 模 型
二、运输问题数学模型的特点: 运输问题一定有最优解;基变量的个数=m+n-1 运输问题约束条件的系数矩阵:
x1m
x2m
xm1
xmm
x11
x12
…
x21
x22
…
xm2
…
…
m行
n行
§1运 输 问 题 及 其 数 学 模 型
解 的 最 优 性 检 验
运输问题及其数学模型
用表上作业法求解运输问题
运输问题的进一步讨论
应用问题举例
本章内容
3运输问题进一步讨论
01.
产销不平衡的运输问题 有转运的运输问题
02.
1.当产大于销时,即 产销不平衡问题 平衡后的数学模型为: 加入假想销地(假想仓库),销量为 ,由于实际并不运 送,它们的运费为 = 0;
解 的 最 优 性 检 验
解 的 最 优 性 检 验
销地产地
B1
B2
B3
B4
产量
ui
A1
16
u1(1)
A2
10
u2(0)
A3
22
u3(-4)
销量
8
14
12
14
48
vj
v1(2)
v2(9)
v3(3)
v4(10)
4
2
8
12
5
4
10
11
3
9
6
11
表3-9
1.增加一位势列和位势行并计算位势
其中
8
10
2
6
8
产量
A1
胡运权《运筹学教程》(第5版)配套题库-考研真题精选及课后习题(第一~三章)【圣才出品】

2.μ是关于可行流 f 的一条增广链,则在μ上有:对一切(i,j)∈μ-,有 fij>0。( ) [暨南大学 2019 研]
【答案】√ 【解析】由增广链定义可知,当边(i,j)属于μ的反向边集时,该条边的流量大于 0。
3.事件 j 的最早时间 TE(j)是指以事件 j 为开工事件的工序最迟必须开工时间。( ) [暨南大学 2019 研]
零元素的最少直线数目的集合。结果如下:
4 / 113
圣才电子书 十万种考研考证电子书、题库视频学习平台
(4)在未被覆盖的元素中找最小元素,未被覆盖的行分别减去该最小元素,在出现负
数的列上整列加上最小元素,得到新矩阵 C′:
0 2 6 1 0 0 4
表 1-1-1
解:(1)先对各行减去本行的最小元素,再对各列减去本列最小元素,得到矩阵 C 如
下:
0 2 6 9
C 1 4 4 0 1 0 0 3 2 3 6 0
(2)确定独立零元素,对 C 加圈,得到
◎ 2 6 9
C
1
1
4 ◎
4
◎ 3
2
3
6
(3)由于只有 3 个独立零元素,少于系数矩阵阶数 n=4,故需要确定能够覆盖所有
A.没有无穷多最优解 B.没有最优解 C.有无界解 D.有最优解 【答案】B 【解析】有最优解的前提是有可行解,该题无可行解,则也无最优解。
2.如果某种资源的影子价格大于其市场价格,则说明( )。[暨南大学 2019 研] A.该资源稀缺 B.该资源过剩 C.企业应尽快处理该资源 D.企业应充分利用该资源,开辟新的生产途径 【答案】A 【解析】当资源的影子价格不为 0 时,表明该种资源在生产中已耗费完毕;且若影子 价格大于其市场价格,说明企业应买进该种资源,该种资源稀缺。
运筹学基础及应用第五版 胡运权第三章

例3
设有三个化肥厂供应四个地区的农用化肥,假
定等量的化肥在这些地区使用效果相同,已知各化肥厂 年产量,各地区年需要量及从各化肥厂到各地区单位化 肥的运价表如下,试决定使总的运费最节省的化肥调拨 方案。
解:这是一个产销不平衡的运输问题,总产量为
160万t,四个地区最低需求为110万t ,最高需求为无限。 当其它地区都是满足最低需求时,第Ⅳ地区每年最多能 分配到60万t ,这样最高需求就是210万t,大于产量。 为建立产销平衡表,在表中增加一假想化肥厂D , 其年产量为50万t 。并把各地区的最低需求和额外需求 区分开来,建立产销平衡表。
例1
现在把问题概括一下,在线性规划中我们研究这样 一类运输问题:有某种物资需要调运,这种物资的计量
单位可以是重量、包装单位或其他。已知有m个地点可以
供应该种物资(以后通称产地,用 i 1,, m 表示),有 n个地点需要该种物资(以后通称销地,用 j 1,, n 表示),又知这m个产地的可供量(以后通称产量)为 (可通写为 a i ),n个销地的需要量(以后 a1 , a2 ,, am
第三章 运输问题
§1.运输问题的典例和数学模型
§ 2.表上作业法
§ 3.产销不平衡的运输问题及其应用
§1.运输问题的典例和数学模型
某食品公司经销主要产品之一是糖果,它下面 设有三个加工厂,每天的糖果生产量分别为: A1 7t , A3 9t。该公司把这些糖果分别运往四个地区 A2 4t , 的门市部销售,各地区每天的销售量: B1 3t , B2 6t, B4 6t 。已知从每个加工厂到各销售门市部每 B3 5t, 吨糖果的运价如下表: 单位:元/t
产 销 平 衡 表
当一个产地的产量不能运往某一个销地的时候,认为 运价为M(表示任意大正数)。额外需求部分的销量,由于 是否满足都可以,所以假想厂运往这些销地的运价定为 0。
运筹学胡运权第五版课件(第3章)分析

B3
B4
ai
11 ④
3 ③
10 7
1
9
2
③
①
7
4
⑥
10 ③
84 59
3
6
5
6 20
24 (8 3) (2 10) 1
表示新方案的费用要减少1元
综上,得到检验数表如下: B1 B2 B3 B4
A1 1 2 0 0 A2 0 1 0 -1 A3 10 0 12 0 注意:有数字格(基变量)的检验数为0。
则总费用为:
34
min z = cijxij i=1 j=1
x11+x12+x13+x14=7
产
x21+x22+x23+x24=4
量 限
制
x31+x32+x33+x34=9
x11+x21+x31=3
s.t.
x12+x22+x32=6
销 量
限
x13+x23+x33=5
制
x14+x24+x34=6 xij0,(i=1,2, 3;j=1,2,3,4)
最优性判别准则: 当所有ij 0时,运输问题达到最优解。
(1)若有负检验数,则该方案需要改进;
(2)若空格的检验数全为正数,则该问题有唯 一最优方案;
(3)若检验数全非负,且有空格的检验数为0, 则该问题有无穷多最优解。
4、改进方案的方法------闭回路法
在检验数表中,确定绝对值最大的负检验 数对应的空格,利用该空格的闭回路在满足供 需关系下调整各顶点的运量,得到费用更小的 调运方案。
5、运输问题解的情况
运筹学基础及应用第3章-运输问题(胡运权)

产量<销量
1.运输规划问题的典例和数学模型 特征:
1、平衡运输问题必有可行解,也必有最优解; 2、运输问题的基本可行解中应包括 m+n-1 个 基变量。
运筹学基础及应用
Operations Research
运 筹 帷 幄 之 中
第三章
运输问题
决 胜 千 里 之
Transportation Problem
外
目
1
运输规划问题的典例和数学模型 表上作业法 运输问题的应用
录
CONTENTS
2
3
1.运输规划问题的典例和数学模型
例3.1 某公司从两个产地A1、A2将物品运往三个销地B1, B2, B3,各产地的产量、各销地的销量和各产地运往各销地每件 物品的运费如下表所示,问:应如何调运可使总运输费用最 小?
48
列差额
例3.4 某运输资料如下表所示:
销地 产地 A1 2 10
2.表上作业法
B2 B3
12 4
B1
4
B4
11
产量
行差额
16 3 9
0
A2
10
1
8 A3
5
11
6 22 2
14
销量 8 2 14 12 1
8
14 3 48
列差额
2.表上作业法
例3.4 某运输资料如下表所示:
销地 产地 A1 2 10 3 9 B1 4 B2 12 B3 4 B4 11 16 0 产量
二三版兼用《运筹学教程》胡运权主编课后习题答案(第三章)

城市
电站
1
2
3
Ⅰ
15
18
22
Ⅱ
21
25
16
第三章习题解答
习题3.12的解答
城市 城市
电站
1-1
城市 1-2
城市2
城市 3-1
城市 3-2
产量
Ⅰ
150 15
15 250 18
22
22 400
Ⅱ
140 21
第三章习题解答
表3-35
食品厂
面粉厂
1
2
3
产量
Ⅰ
3 10
2 20
Ⅱ
4 11
8 30
Ⅲ
8 11
4 20
销量
15 25 20
第三章习题解答
习题3.10的解答
食品厂 面粉厂
Ⅰ Ⅱ Ⅲ 销量
1
3 15 4
8 15
2
10 5 11 20 11 25
3
20 2 8 4
20
4
0 10 0
0 10
产量
20 30 20
B3
B4 产量
A1 A2 A3 销量
3
7
6
45
2
4
3
22
4
3
8
56
3
3
2
2
第三章习题解答
习题3.9的解答
销地
产地
B1 B2 B3 B4 B5 产量A1源自33 7 6 24 0 5
A2
2 4 23 2 0 2
A3 销量
4 33 8 5 30 6 33223
第三章习题解答
3.10 某市有三个面粉厂,它们供给三个面食加工 厂所需的面粉。各面粉厂的产量、各面食加工厂加工 面粉的能力、各面食加工厂和各面粉厂之间的单位运 价,均表示于表3-35中。假定在第1,2和3面食加工厂 制作单位面粉食品的利润分别为12元、16元和11元, 试确定使总效益最大的面粉分配计划(假定面粉厂和面 食加工厂都属于同一个主管单位)。
运筹学胡运权 部分课后习题答案
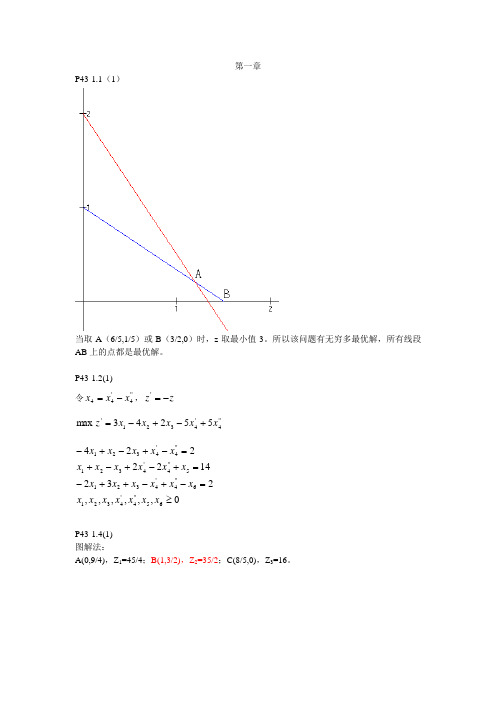
第一章P43-1.1(1)当取A (6/5,1/5)或B (3/2,0)时,z 取最小值3。
所以该问题有无穷多最优解,所有线段AB 上的点都是最优解。
P43-1.2(1)令''4'44x x x -=,z z -='''4'4321'55243max x x x x x z +-+-=,,,,,,232142222465''4'43216''4'43215''4'4321''4'4321≥=-+-++-=+-+-+=-+-+-x x x x x x x x x x x x x x x x x x x x x x x xP43-1.4(1) 图解法:A(0,9/4),Z 1=45/4;B(1,3/2),Z 2=35/2;C(8/5,0),Z 3=16。
单纯形法:10 5 0 0C b X b b x1x2x3x4θ0 x39 3 4 1 0 30 x48 5 2 0 1 8/5δ10 5 0 00 x321/5 0 14/5 1 -3/5 3/210 x18/5 1 2/5 0 1/5 4δ0 1 0 -25 x23/2 0 1 5/14 -3/1410 x1 1 1 0 -1/7 2/7δ0 0 -5/14 -25/14依次相当于:原点;C;B。
P44-1.7(1)2 -1 2 0 0 0 -M -M -MC b X b b x1x2x3x4x5x6x7x8x9θ无界解。
两阶段法:阶段二:P45-1.10证明:CX (0)>=CX*,C*X*>=C*X (0) CX (0)-CX*+C*X*-C*X (0)>=0,即(C*-C)(X*-X (0))>=0。
P45-1.13设饲料i 使用x i (kg ),则543218.03.04.07.02.0m in x x x x x z ++++=s.t. 7001862354321≥++++x x x x x 305.022.05.054321≥++++x x x x x1008.022.05.054321≥++++x x x x x0,,,,54321≥x x x x x第二章P74-2.1(1)321532m ax y y y w ++=22321≤++y y y 243321≤++y y y 4334321=++y y y 无约束321,0,0y y y ≤≥P75-2.4(1),06353322232max 212121212121≥≥≤-≤+≤-≤++=y y y y y y y y y y y y w(2) (8/5,1/5)(3) 无穷多最优解。
运筹学(胡运权版)第三章运输问题课后习题答案
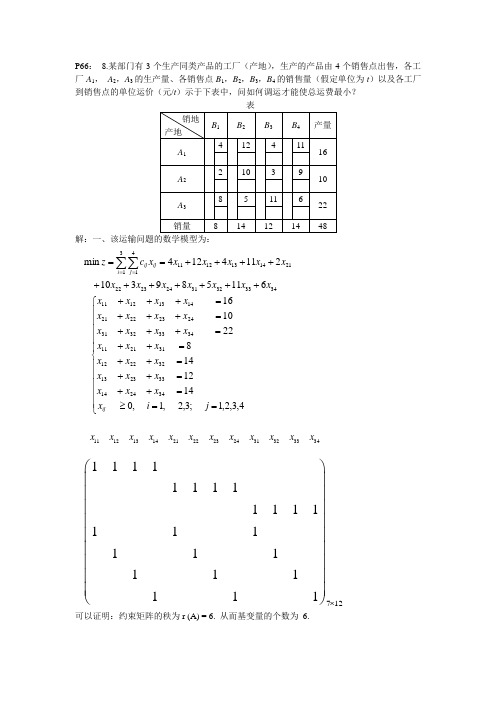
P66: 8.某部门有3个生产同类产品的工厂(产地),生产的产品由4个销售点出售,各工厂A 1, A 2,A 3的生产量、各销售点B 1,B 2,B 3,B 4的销售量(假定单位为t )以及各工厂到销售点的单位运价(元/t )示于下表中,问如何调运才能使总运费最小?解:一、该运输问题的数学模型为:可以证明:约束矩阵的秩为r (A) = 6. 从而基变量的个数为 6.34333231242322213141141312116115893102114124min x x x x x x x x x x x x x c z i j ij ij +++++++++++==∑∑==⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧==≥=++=++=++=++=+++=+++=+++4,3,2,1;3,2,1,01412148221016342414332313322212312111343332312423222114131211j i x x x x x x x x x x x x x x x x x x x x x x x x x ij 111213142122232431323334x x x x x x x x x x x x 712111111111111111111111111⨯⎛⎫ ⎪⎪⎪ ⎪⎪⎪ ⎪⎪ ⎪⎝⎭二、给出运输问题的初始可行解(初始调运方案)1. 最小元素法思想:优先满足运价(或运距)最小的供销业务。
其余(非基)变量全等于零。
此解满足所有约束条件,且基变量(非零变量)的个数为6(等于m+n-1=3+4-1=6).总运费为(目标函数值) ,1013=x ,821=x ,223=x ,1432=x ,834=x ,614=x ∑∑===3141i j ij ij x c Z 246685143228116410=⨯+⨯+⨯+⨯+⨯+⨯=2. 伏格尔(Vogel)法伏格尔法的基本思想:运输表中各行各列的最小运价与次小运价之差值(罚数)应尽可能地小。
《运筹学》课堂作业及相应答案解析

第一部分绪论第二部分线性规划与单纯形法1 判断下列说法是否正确:(a)图解法同单纯形法虽然求解的形式不同,但从几何上理解,两者是一致的;(b)线性规划模型中增加一个约束条件,可行域的范围一般将缩小,减少一个约束条件,可行域的范围一般将扩大;(c)线性规划问题的每一个基解对应可行域的一个顶点;(d)如线性规划问题存在可行域,则可行域一定包含坐标的原点;(e)对取值无约束的变量x i,通常令其中,在用单纯形法求得的最优解中有可能同时出现(f)用单纯形法求解标准型的线性规划问题时,与对应的变量都可以被选作换入变量;(g)单纯形法计算中,如不按最小比值原则选取换出变量,则在下一个解中至少有一个基变量的值为负;(h)单纯形法计算中,选取最大正检验数δk对应的变量x k作为换入变量,将使目标函数值得到最快的增长;(i)一旦一个人工变量在迭代中变为非基变量后,则该变量及相应列的数字可以从单纯形表中删除,而不影响计算结果;(j)线性规划问题的任一可行解都可以用全部基可行解的线性组合表示;(k)若x1,x2分别是某一线性规划问题的最优解,则也是该线性规划问题的最优解,其中λ1,λ2可以为任意正的实数;(1)线性规划用两阶段法求解时,第一阶段的目标函数通常写为X ai为人工变量),但也可写为,只要所有k i均为大于零的常数;(m)对一个有n个变量、m个约束的标准型的线性规划问题,其可行域的顶点恰好为个;(n)单纯形法的迭代计算过程是从一个可行解转转换到目标函数值更大的另一个可行解;(o)线性规划问题的可行解如为最优解,则该可行解一定是基可行解;(p)若线性规划问题具有可行解,且其可行域有界,则该线性规划问题最多具有有限个数的最优解;(q)线性规划可行域的某一顶点若其目标函数值优于相邻的所有顶点的目标函数值,则该顶点处的目标函数值达到最优;(r)将线性规划约束条件的“≤”号及“≥”号变换成“=”号,将使问题的最优目标函数值得到改善;(s)线性规划目标函数中系数最大的变量在最优解中总是取正的值;(t)一个企业利用3种资源生产4种产品,建立线性规划模型求解得到的最优解中,最多只含有3种产品的组合;(u)若线性规划问题的可行域可以伸展到无限,则该问题一定具有无界解;(v)一个线性规划问题求解时的迭代工作量主要取决于变量数的多少,与约束条件的数量关系相对较小。
最新《运筹学》胡运权 第4版 第三章 运输问题培训讲学

i=1 j=1
10 x22 3 x23 9 x24 8 x31 5 x32 11x33 6x34
x11 x12 x13 x14 =1 6
x
2
1
x22
x23
x24 =10
x
31
x32
x33
x34 = 22
s
.
t
.
x11 x12
x21 x22
x31 = 8 x32 =14
始
的产量(销量)已满足,则把
基
该行(列)的其他格划去。如
可
此进行下去,直至得到一个基
行
本可行解。
解
2.西北角法
寻 找 初 始
销地
产地
B1
B2
B3 B4 产量
A1 A2 A3 销量
4
8 12
4
11 16
②
82
6 10 4 3
9 10
④
8
5 8 11 14 6 22
⑥
8
14
12
14
48
基
①
③⑤
⑥
可
34
型
§1
对产销平衡运输问题,除上述
运
两个特点外,还有以下特点:
输
(1) 所有结构约束条件都是等式
问
约束;
题
(2) 各产地产量之和等于各销地
及
销量之和。
其
数
学
模
型
§1 运 输 问 题 及 其 数 学 模 型
例1 某部门有3个生产同类产品的工厂(产地),生产
的产品由4个销售点(销地)出售,各工厂的生产量、 各销售点的销售量(假定单位均为t)以及各工厂到 各销售点的单位运价(元/t)示于表3-2中,要求研 究产品如何调运才能使总运费最小?
运筹学第三章课后习题答案

量 1 2 34
4 51 34
6 8 302
④
A2 A3 销量
31
2
25
30 8 1 1 5
⑤
3
7 15
1 4 224 ⑥
6
5
6
3
列12 罚22 数3
vj 4
111 11 11 1
②
①⑦
③
2020/1/1
9
从上表计算知:x12=5,x13=3,x21=3,x23=2,x24=3, x33=1。总费用=5×1+3×4+3×1+2×5+3×0+ 1×5=35,在上述三种计算方法中,这种方法计算所需 运输费用是最省的。但还不知是否最优。现用闭回路法 检验如下: 闭回路法检验如下:
2020/1/1
10
第一个闭回路σ11,走4→1→5→4线路
产地 销地
A1
B1
B2
B3
45 13 4
B4
6
A2 3 1
22 5 3 0
A3 销量
3
71 5
1
6
5
6
3
产量
8 8 4
σ11=4-1+5-4=4
2020/1/1
11
第二闭回路σ14,走6→0→5→4线路
产地 销地
A1
B1
B2
B3
45 13 4
2020/1/1
17
①最小元素法求解:
销地 B1
B2
产地
A1
13
7
A2
22
4
A3
4
33
销量
3
3
B3
B4 B5 产量
6 3 28 2
1 4 30
运筹学胡运权第五版课件(第3章)分析

B1 3 1 7
3
B2 11 9 4
6
B3 3 2
10
5
B4
ai
10 7
84
59
6 20
3、运输问题的数学模型
对于m产n销运输问题,设xij表示产地 i 运往销地 j 的物资 数量,则其数学模型如下:
mn
min z
cij xij
i1 j1
n
xij ai
空格(A3,B1)的闭回路
Ïú µØ ²ú µØ
A1 A2 A3 bj
B1 3
③1
B2
B3
B4
ai
11 ④
3 ③
10 7
9
2
①
84
7
4
⑥
3
6
10 ③
59
5
6 20
31 (7 10 2) (5 3 1) 10
表示新方案的费用要增加10元
空格(A3,B3)的闭回路
Ïú µØ ²ú µØ
x24 1, x23 0, x13 5, x14 2
此时x23=0,可看成非基变量。
得到新的调运方案:
Ïú µØ ²ú µØ
A1
B1 3
B2
B3
B4
ai
11 ⑤
3 ②
10 7
1
A2
③
9
2 ①
84
A3
7
4
⑥
10 ③
59
bj
3
6
5
6 20
该方案就是用沃格尔法得到的初始方案。
其检验数表为
2 - 12 2-1-
运筹学基础及应用运输问题胡运权

x12
…
c21
c22
A2
x21
x22
…
Bn c1n
x1n c2n
x2n
产量 a1 a2
┇
Am 销量
┇
┇
┇
cm
cm
1
2
…
xm1
xm2
b1
b1
…
┇
┇
cmn
xmn
am
bn
1.运输规划问题的典例和数学模型 运输问题的求解思路
基本可行解
是
是否最优解
结束
否
换基
2.表上作业法
计算步骤: (1) 找出初始调运方案。即在(m×n)产销平衡表上给出 m+n-1个数字格。(最小元素法、西北角法或伏格尔法)
运筹学基础及应用
Operations Research
运
第三章
决
筹
胜
帷
运输问题
千
幄
里
之
之
中
Transportation Problem
外
1 运输规划问题的典例和数学模型 2 表上作业法 3 运输问题的应用
CONTENTS
目
录
1.运输规划问题的典例和数学模型
例B33,.1各某产公地司的从产两量个、产各地销A地1、的A销2将量物和品各运产往地三运个往销各地销B地1每, B件2, 物品的运费如下表所示,问:应如何调运可使总运输费用最 小?
步骤
描述
方法
第一步 求初始基行可行解(初始调运方案)
最小元素法、西 北角法、 伏格尔法
第二步
求检验数并判断是否得到最优解当非基变量的检验
数σi j全都非负(求min)时得到最优解,若存在检 验数σi j <0,说明还没有达到最优,转第三步。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
x11
x21
x12 x22
x13 x23
x14 x24
x31 x11
x32 x21
x33 x31
x34 8
x12
x22
x32
14
x13
x23
x33
12
x14 x24 x34 14
xij 0, i 1, 2,3;
16 10 22
j 1,2,3,4
10 0
8
②
A3
8
5
14
销量
8
14
①
④
此时得到一个初始调运方案(初始可行解):
11
10 ③
6
22 0
8
14
14 0
48
⑤
⑥
x13 10, x14 6, x21 8, x23 2, x32 14, x34 8,
其余(非基)变量全等于零。此解满足所有约束条件,且基变量(非零变量)的个数为 6(等 于 m+n-1=3+4-1=6). 总运费为(目标函数值)
B3
B4 产量
产地
4 12 4 11
A1
16
2 10 3 9
A2
10
8 5 11 6
A3
22
销量 8 14 12 14 48 解:一、该运输问题的数学模型为:
34
min z
cij xij 4x11 12x12 4x13 11x14 2x21
i1 j1
10x22 3x23 9x24 8x31 5x32 11x33 6x34
14
产量
16
10
8
2
22 48
B4
产量
11 16
9
10
8
②
6 22
14
48
B4 11 9 6
14
产量
16 6 10
10
8
②
22 48
学习必备
欢迎下载
产地
销地
A1 A2
A3 销量
B1 4
B2 12
2 8
8
8 ①
10
5 14
14 ④
B3
4 10
3 2
11
10 ③
B4 11 9 6
14
产量
16 6 10
1
②
14
12
14
48
1
3
产地
销地
A1 A2
A3
销量 列差额
B1
B2
B3
B4
产量
行差额
4 2 8
12
4
11
7
12
16 4
12
10
3
9 10 0
6
⑤
2
8
8
5
14
11
6
8
22 0
1
②
14
8
14
12
14
48
2
5
1
3
③
①
④
产地
销地
B1
B2
B3
B4
产量
行差额
4
12
4
11
7
A1
12
4
16 0
12
A2
2
10
3
9 10 0
产地
销地 A1
A2
A3
销量 列差额
B1
B2
B3
B4
产量
行差额
4
12
4
11
16
0
2
10
3
9
10
1
8
5
11
6
22
1
8
14
12
14
48
2
5
1
3
产地
销地 A1
A2
A3
销量 列差额
B1
B2
B3
B4
产量
行差额
4
12
4
11
16
0
2
10
3
9
10
1
8
5
14
8
14
2
5
①
11
6
22 8
1→2
14
12
14
48
1
3
产地
销地 A1
x11 x12 x13 x14 x21 x22 x23 x24 x31 x32 x33 x34
1 1 1 1
1111
1 1 1 1
1
1
1
1
1
1
1
1
1
1
1
1 712
可以证明:约束矩阵的秩为 r (A) = 6. 从而基变量的个数为 6.
学习必备
欢迎下载
二、给出运输问题的初始可行解(初始调运方案) 1. 最小元素法 思想:优先满足运价(或运距)最小的供销业务。
6
⑤
8
2
8
A3
8
5
14
11
6
8
22 0
1
②
14
销量
8
14
12
14 0
48
列差额
2
5
1
3
③
①
④
⑥
此时得到一个初始调运方案(初始可行解):x13 = 12, x14 = 4, x21 = 8, x24 = 2, x32 = 14, x34 = 8
其余(非基)变量全等于零。此解满足所有约束条件,且基变量(非零变量)的个数为 6(等 于 m+n-1=3+4-1=6)。
A2 A3
销量 列差额
B1
B2
4
12
2
10
8
5
14
8
14
2
5
①
B3
B4
产量
行差额
4
11
16
0
3
9
10
1
11
6
8
22 0
1
②
14
12
14
48
1
3
学习必备
欢迎下载
产地
销地 A1
A2 A3
销量 列差额
B1
B2
4
12
2
10
8
8
5
14
8
14
2
5
③
①
B3
B4
产量
行差额
4
11
16
0
3
9 10 2
1
8
11
6
8
22 0
2
10
8
8 14 5
8
14
B3 4
10 3
2 11
12
B4 6 11
9 6 8 14
产量 16 10 22 48
σ12 = C12 + C34 - (C14 + C32) = 12 + 6 –( 11 + 5 ) =2
总运费为(目标函数值):
34
Z cij xij 124 41182 29 14586 244 i1 j1
学习必备
欢迎下载
三、解的最优性检验 ⒈ 闭回路法(以下的闭回路都是顺时针方向)
看非基变量的检验数是否满足:ij 0.
(1)首先对用最小元素法所确定的初始基本可行解进行检验。参见前面的计算结果,可知 非基变量分别为:x11,x12,x22,x24,x31,x33。
34
Z
cij xij
i1 j1
学习必备
欢迎下载
104 61182 2314586 246
2. 伏格尔(Vogel)法 伏格尔法的基本思想:运输表中各行各列的最小运价与次小运价之差值(罚数)应尽可能地 小。或者说:优先供应罚数最大行(或列)中最小运费的方格,以避免将运量分配到该行(或 该列)次小运距的方格中。
产地
销地 A1
A2
A3 销量
B1 X11 4
B2 12
B3 10 4
82
10
8
5
14
8
14
3 2
11 12
B4 11
6 9
6 8
14
产量 16 10 22 48
σ11 = C11 + C23 - (C13 + C21) = 4 + 3 –( 4 + 2 ) =1
产地
销地 A1
A2
A3 销量
B1 4
B2 X12 12
产地
销地 A1
A2
A3 销量
B1 4
2 8
8
8 ①
B2 12 10 5
14
B3 4 3 11
12
产地
销地
A1 A2
A3 销量
B1 4
2 8
8
8 ①
B2 12
B3 4
10
3
2
5
11
14
10
产地
销地
A1 A2
A3 销量
B1 4
2 8
8
8 ①
B2 12 10 5
B3
4 10
3 2
11
14
10
③
B4 11 9 6
10
8
②
22 8 14
48
产地
销地
A1 A2
A3
销量
B1 4
B2 12
2 8
8
8 ①
10
5 14
