管理运筹学》(第二版)课后习题参考答案
《管理运筹学》第二版习题答案(韩伯棠教授)高等教育出版社,超详细版

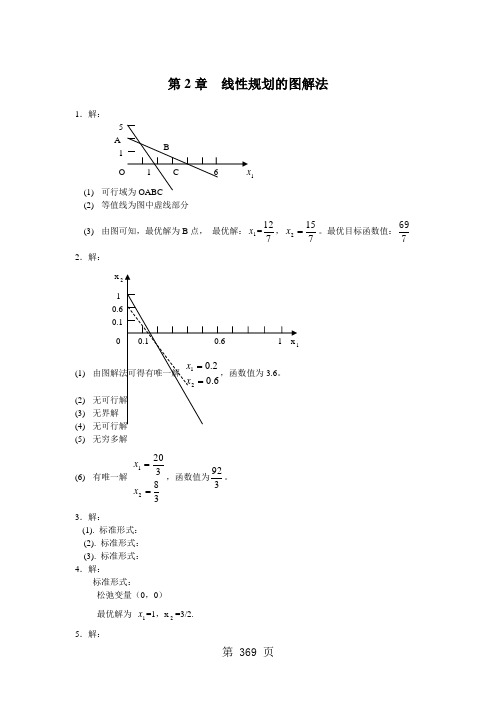
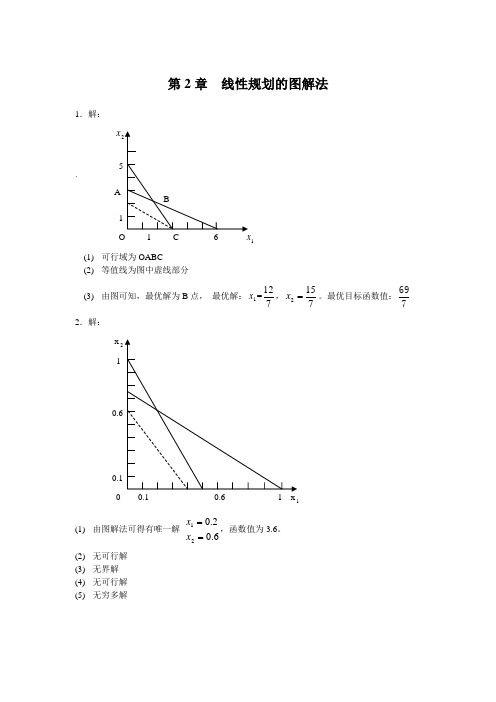
《管理运筹学》第二版习题答案(韩伯棠教授)高等教育出版社第 2 章 线性规划的图解法11a.可行域为 OABC 。
b.等值线为图中虚线所示。
12c.由图可知,最优解为 B 点,最优解: x 1 = 769 。
7 2、解:15 x 2 =7, 最优目标函数值:a x 210.60.1O1有唯一解x 1 = 0.2函数值为 3.6x 2 = 0.6b 无可行解c 无界解d 无可行解e 无穷多解1 2 2 1 2f 有唯一解20 x 1 =3 8函数值为 92 33、解:a 标准形式:b 标准形式:c 标准形式:x 2 = 3max fmax f= 3x 1 + 2 x 2 + 0s 1 + 0s 2 + 0s 3 9 x 1 + 2x 2 + s 1 = 303x 1 + 2 x 2 + s 2 = 13 2 x 1 + 2x 2 + s 3 = 9 x 1 , x 2 , s 1 , s 2 , s 3 ≥= −4 x 1 − 6x 3 − 0s 1 − 0s 23x 1 − x 2 − s 1 =6x 1 + 2x 2 + s 2 = 10 7 x 1 − 6 x 2 = 4x 1 , x 2 , s 1 , s 2 ≥max f = −x ' + 2x ' − 2 x ''− 0s − 0s'''− 3x 1 + 5x 2 − 5x 2 + s 1 = 70 2 x ' − 5x ' + 5x '' = 50122' ' ''3x 1 + 2 x 2 − 2x 2 − s 2 = 30'' ''4 、解:x 1 , x 2, x 2, s 1 , s 2 ≥ 0标准形式: max z = 10 x 1 + 5x 2 + 0s 1 + 0s 23x 1 + 4 x 2 + s 1 = 9 5x 1 + 2 x 2 + s 2 = 8 x 1 , x 2 , s 1 , s 2 ≥ 0s 1 = 2, s 2 = 0标准形式: min f = 11x 1 + 8x 2 + 0s 1 + 0s 2 + 0s 310 x 1 + 2x 2 − s 1 = 203x 1 + 3x 2 − s 2 = 18 4 x 1 + 9x 2 − s 3 = 36 x 1 , x 2 , s 1 , s 2 , s 3 ≥ 0s 1 = 0, s 2 = 0, s 3 = 136 、解:b 1 ≤c 1 ≤ 3c 2 ≤ c 2 ≤ 6d x 1 = 6 x 2 = 4e x 1 ∈ [4,8]x 2 = 16 − 2x 1f 变化。
管理运筹学课后习题答案

管理运筹学课后习题答案管理运筹学课后习题答案一、线性规划线性规划是管理运筹学中的一种重要方法,它通过建立数学模型,寻找最优解来解决实际问题。
下面我们来讨论一些常见的线性规划习题。
1. 一家工厂生产两种产品A和B,每单位产品A需要3小时的加工时间和2小时的装配时间,每单位产品B需要2小时的加工时间和4小时的装配时间。
工厂每天有8小时的加工时间和10小时的装配时间。
已知产品A的利润为300元,产品B的利润为400元。
如何安排生产,使得利润最大化?解答:设生产产品A的数量为x,生产产品B的数量为y。
根据题目中的条件,可以得到以下线性规划模型:目标函数:max 300x + 400y约束条件:3x + 2y ≤ 82x + 4y ≤ 10x, y ≥ 0通过求解上述线性规划模型,可以得到最优解,即生产4个产品A和1个产品B时,利润最大化,为2000元。
2. 一家超市有两种品牌的洗衣液,品牌A和品牌B。
品牌A每瓶售价20元,每瓶利润为5元;品牌B每瓶售价25元,每瓶利润为7元。
超市每天销售洗衣液的总利润不能超过100元,并且每天至少要销售10瓶洗衣液。
如何安排销售,使得利润最大化?解答:设销售品牌A的瓶数为x,销售品牌B的瓶数为y。
根据题目中的条件,可以得到以下线性规划模型:目标函数:max 5x + 7y约束条件:20x + 25y ≤ 100x + y ≥ 10x, y ≥ 0通过求解上述线性规划模型,可以得到最优解,即销售5瓶品牌A和5瓶品牌B时,利润最大化,为60元。
二、排队论排队论是管理运筹学中研究排队系统的一种方法,它通过数学模型和概率统计来分析和优化排队系统。
下面我们来讨论一些常见的排队论习题。
1. 一家银行有两个窗口,每个窗口的服务时间服从指数分布,平均服务时间分别为3分钟和4分钟。
顾客到达的间隔时间也服从指数分布,平均间隔时间为2分钟。
如果顾客到达时,两个窗口都有空闲,顾客会随机选择一个窗口进行服务。
卫生管理运筹学第二版答案薛迪,复旦大学出版社.doc

习题参考答案习题一设选用第1种、第2种.第3种、第4种、第5种饲料的量分别为x p x 2,x 3,x 45x 5oMinZ = 0.2x∣ + OAx 2 + 0.7x 3 + 0.3x 4 + 0.8x 53x 1 + Ix l +x 3 + 6X 4 +1 8X 5 ≥ 700 X l + O.5X 2 + 0.2X 3 + 2X A + O.5Λ5 ≥ 30 0.5X I +x 2 + 0.2X i + 2X 4 + O.8X 5 ≥ 100 x 1,x 2,x 3,x 4,x 5 ≥0设“为生产第i 种食品所使用的第j 种原料数,i = b 2, 3分别代表甲.乙、丙.j = MaX Z = 2x l +x 2 + 4X 31. 2. 1, 2, 3分别代表A 、B. C 。
其数学模型为:MaX Z = 2.9 ×(x 11 +x 12 + X 13) + 2.45 × (x 2l + x 22 + x 23) + 1.95 × (X il + x 32 + X 33) -2×(x 11 +x 2l +⅞∣)-1.5×(X ∣2 +x 22 +X32)-1・O X (“3 +X23 +%33)I X Il + X 21 + x 3l ≤ 2000x∣2 + X ll + X il ≤ 2500X li +X 23 +X33 S 1200————≥0.6 X 11 +X 12 +X 13“3s. t≤0.2X 11 +x l2 +X 13——乜——≥0.15X 2I+x22 +x 23x2i≤0.6x 2l +x 22 +X 23X33≤0.5⅞1 + “32 + ⅞3心 ≥0,(∕ = UΛy = lΛ3)3.将下列线性规划问题化为标准形式 <1)引入剩余变量耳,松弛变:⅛%2x l + 3X2+2X3+J2 = 15-X I一3X2+2X3 = 7xι,X2,X3 > O, S i9S2≥0(2)令X2 = -X2 , X3 = A3 " x3 引入松弛变量SlMaX Z = —5Xl- Sx f2 + Ix f3— 7x;6x∣ —Xy — Xy + Xj + 5| =1057/ 5x l + 4毘 + 2牙;—2x; = 15x^x91,x∖,x↑.s x≥04.(1)唯一最优解J1=I. 7143, X2 =2. 1429, MaX Z =9. 8571: (2)无可行解:(3)无界解:(4)无可行解:(5)多重最优解,MaXZ二66,其中一个解为x, =4, X2 =6:(6)唯一最优解,为X1 =6. 6667, X2 =2. 6667, MaX Z =30. 6667O5.可行解:(A), (C)t (E), (F):基本解:(A), (B), (F):基本可行解:(A), (F)6. (1)标准型为:MaX Z = 5x1 + 9x20.5X l +x2 + 51 =8x l+x y + Sy = 10 s.ts ~ 'X I + 0.5‰ 一$3 = 6(2)至少有2个变量的值取零,因为有3个基本变量、2个非基本变量,非基本变量的取值为零。
《管理运筹学》课后习题答案

《管理运筹学》课后习题答案第2章线性规划的图解法1.解决方案:X25`a1bo1c6x1可行的区域是oabc等值线为图中虚线部分从图中可以看出,最优解是B点,最优解是x1=121569,x2?。
最优目标函数值:7772.解:x21零点六0.100.10.61x1有唯一解、无可行解、无界解、无可行解和无限解x1?0.2x2?0.6,函数值为3.6。
三百六十九20923有唯一解,函数值为。
83x2?3x1?3.解决方案:(1).标准形式:麦克斯夫?3x1?2x2?0s1?0s2?0s39x1?2x2?s1?303x1?2x2?s2?132x1?2x2?s3?9x1,x2,s1,s2,s3?0(2).标准形式:明夫?4x1?6x2?0s1?0s23x1?x2?s1?6x1?2x2?s2?107x1?6x2?4x1,x2,s1,s2?0(3).标准形式:明夫?x1?2x2?2x2?0s1?0s2“”?3x1?5x2?5x2?s1?七十 '''2x1'?5x2?5x2?503x?2x?2x?s2?30'''x1',x2,x2,s1,s2?0'1'2''2标准形式:麦克斯?10x1?5x2?0s1?0s23x1?4x2?s1?95x1?2x2?s2?8x1,x2,s1,s2?0松弛变量(0,0)的最优解为X1=1,X2=3/23705.解决方案:标准形式:明夫?11x1?8x2?0s1?0s2?0s310x1?2x2?s1?203x1?3x2?s2?184x1?9x2?s3?36x1,x2,s1,s2,s3?0剩余变量(0.0.13)最优解为x1=1,x2=5.6.解决方案:(10)最优解为x1=3,x2=7.(11)1?c1?3(12)2?c2?6(13)x1?6x2?四(14)最优解为x1=8,x2=0.(15)不变化。
卫生管理运筹学第二版答案

习题参考答案习题一1.设选用第1种、第2种、第3种、第4种、第5种饲料的量分别为12345,,,,x x x x x 。
Min 543218.03.07.04.02.0x x x x x Z ++++=12345123451234512345326187000.50.220.530..0.50.220.8100,,,,0x x x x x x x x x x s t x x x x x x x x x x ++++≥⎧⎪++++≥⎪⎨++++≥⎪⎪≥⎩2.设x ij 为生产第i 种食品所使用的第j 种原料数,i =1,2,3分别代表甲、乙、丙,j =1,2,3分别代表A 、B 、C 。
其数学模型为:Max Z =)(0.1)(5.1)(2)(95.1)(45.2)(9.2332313322212312111333231232221131211x x x x x x x x x x x x x x x x x x ++⨯-++⨯-++⨯-++⨯+++⨯+++⨯s.t.)3,2,1,3,2,1(,05.06.015.02.06.01200250020003332313323222123232221211312111313121111332313322212312111==≥≤++≤++≥++≤++≥++≤++≤++≤++j i x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x ij3.将下列线性规划问题化为标准形式(1)引入剩余变量1s ,松弛变量2sMax 32142x x x Z ++=123112321231231225623215..327,,0,,0x x x s x x x s s t x x x x x x s s +--=⎧⎪+++=⎪⎨--+=⎪⎪≥≥⎩ (2)令'22x x =-,'''333x x x =-,引入松弛变量1s Max 33217785x x x x Z ''-'+'--= ⎪⎩⎪⎨⎧≥''''=''-'+'+=+''+'-'-0,,,,152245106..13321332113321s x x x x x x x x s x x x x t s4.(1)唯一最优解 1x =1.7143,2x =2.1429,Max Z =9.8571;(2)无可行解; (3)无界解;(4)无可行解;(5)多重最优解,Max Z=66,其中一个解为1x =4,2x =6; (6)唯一最优解,为1x =6.6667,2x =2.6667,Max Z =30.6667。
《管理运筹学》课后习题答案59页word
第2章 线性规划的图解法1.解: 5 A 11 (1) (2) 等值线为图中虚线部分(3) 由图可知,最优解为B 点, 最优解:1x =712,7152=x 。
最优目标函数值:7692.解: x 2 1 0(1) (2) (3) 无界解 (4) (5)无穷多解(6) 有唯一解 3832021==x x ,函数值为392。
3.解:(1). 标准形式: (2). 标准形式:(3). 标准形式: 4.解:标准形式:松弛变量(0,0) 最优解为 1x =1,x 2=3/2. 5.解:标准形式:剩余变量(0.0.13) 最优解为 x 1=1,x 2=5. 6.解:(1) 最优解为 x 1=3,x 2=7. (2) 最优解为 x 1=8,x 2=0. (3) 不变化。
因为当斜率31121-≤-≤-c c ,最优解不变,变化后斜率为1,所以最优解不变. 7.解:模型:(1) 1501=x ,702=x ,即目标函数最优值是103000 (2) 2,4有剩余,分别是330,15,均为松弛变量. (3) 50,0,200,0。
(4) 在[]500,0变化,最优解不变。
在400到正无穷变化,最优解不变. (5) 因为143045021-≤-=-c c ,所以原来的最优产品组合不变. 8.解:(1) 模型:b a x x f 38min +=基金a,b 分别为4000,10000,回报率为60000。
(2) 模型变为:b a x x z 45max +=推导出:180001=x 30002=x ,故基金a 投资90万,基金b 投资30万。
第3章 线性规划问题的计算机求解1.解:(1) 1501=x ,702=x 。
目标函数最优值103000。
(2) 1,3车间的加工工时已使用完;2,4车间的加工工时没用完;没用完的加工工时数为2车间330小时,4车间15小时. (3) 50,0,200,0含义:1车间每增加1工时,总利润增加50元;3车间每增加1工时,总利润增加200元;2车间与4车间每增加一个工时,总利润不增加。
运筹学课后答案2

运筹学(第2版)习题答案2第1章 线性规划 P36~40第2章 线性规划的对偶理论 P68~69 第3章 整数规划 P82~84 第4章 目标规划 P98~100 第5章 运输与指派问题 P134~136 第6章 网络模型 P164~165 第7章 网络计划 P185~187 第8章 动态规划 P208~210 第9章 排队论 P239~240 第10章 存储论 P269~270 第11章 决策论 Pp297-298 第12章 博弈论 P325~326 全书360页由于大小限制,此文档只显示第6章到第12章,第1章至第5章见《运筹学课后答案1》习题六6.1如图6-42所示,建立求最小部分树的0-1整数规划数学模型。
【解】边[i ,j ]的长度记为c ij ,设⎩⎨⎧=否则包含在最小部分树内边0],[1j i x ij数学模型为:,12132323243434364635365612132434343546562324463612132446362335244656121324354656m in 52,22,233344,510ij ijij i j ij Z c x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x ==++≤++≤++≤++≤+++≤+++≤+++≤++++≤++++≤+++++≤=∑或,[,]i j ⎧⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎩所有边6.2如图6-43所示,建立求v 1到v 6的最短路问题的0-1整数规划数学模型。
图6-42【解】弧(i ,j )的长度记为c ij ,设⎩⎨⎧=否则包含在最短路径中弧0),(1j i x ij数学模型为:,1213122324251323343524344546253545564656m in 100,00110,(,)ijiji jij Z cx x x x x x x x x x x x x x x x x x x x x x i j =⎧+=⎪---=⎪⎪+--=⎪⎪+--=⎨⎪++-=⎪⎪+=⎪=⎪⎩∑或所有弧 6.3如图6-43所示,建立求v 1到v 6的最大流问题的线性规划数学模型。
管理运筹学第二版习题答案

12-2《管理运筹学》课后习题详解 第2章 线性规划的图解法1. ( 1)可行域为0, 3, A ,3围成的区域。
(2) 等值线为图中虚线所示。
(3) 如图,最优解为 A 点(12/7,15/7 ),对应最 优目标函数值 Z=69/7。
2.( 1)有唯一最优解 A 点,对应最优目标函数 值 Z=3.6。
(2)无可行解。
(3)有无界解。
40.7 0-33X 1+ X2(4)无可行解。
9y -F 2.r, + 6 = 30 3x x+2X2 + s2 =13 2x{—2xi+6=9 gx”片宀宀二0max f = 一4形—— 0町—Os2(5)无可行解。
X22max最优解A点最优函数值3. (1)标准形式(2)标准形式Xj + 2X2 H-S2 = 107,v:—6.v* = 4M , .Y2 , % 出> O(3)标准形式|!_|_fifmax f = —x 1 + 2 屯—2 込—0® — 0^2—3x x * 5X 2 — 5X 2 + s x = 70 2x x — 5X 2 + 5X 2 = 50 3xj + 2X 2 — 2X 2 —=305x ;,歩1 .s 2 土 0max z = 10.^! + 5.Y 2 \ 0^t 1 0©3x 】十 4X 2 + S J = 95.巧 +2.Y 2 -b >s 2 = 8 x t ,x 2 ^s lr>s 2 > 04.解: (1)标准形式求解:3X 〔 4X 2 9 5X 〔 2X 28X , 1 X 21.5S , S 25.标准形式:x , x 2 6 x , 3.6 S 3 S 2 0 4x , 9x 2 16x 2 2.4s , 11.27. 模型: (1) X 1=150, X 2=150;最优目标函数值 Z=103000。
(2) 第2、4车间有剩余。
剩余分别为: 330、15,均为松弛变量。
《管理运筹学》(第二版)课后习题参考答案汇总

《管理运筹学》(第二版)课后习题参考答案第1章线性规划(复习思考题)1.什么是线性规划线性规划的三要素是什么答:线性规划(Linear Programming,LP)是运筹学中最成熟的一个分支,并且是应用最广泛的一个运筹学分支。
线性规划属于规划论中的静态规划,是一种重要的优化工具,能够解决有限资源的最佳分配问题。
建立线性规划问题要具备三要素:决策变量、约束条件、目标函数。
决策变量是决策问题待定的量值,取值一般为非负;约束条件是指决策变量取值时受到的各种资源条件的限制,保障决策方案的可行性;目标函数是决策者希望实现的目标,为决策变量的线性函数表达式,有的目标要实现极大值,有的则要求极小值。
2.求解线性规划问题时可能出现几种结果,哪种结果说明建模时有错误答:(1)唯一最优解:只有一个最优点;(2)多重最优解:无穷多个最优解;(3)无界解:可行域无界,目标值无限增大;(4)没有可行解:线性规划问题的可行域是空集。
当无界解和没有可行解时,可能是建模时有错。
3.什么是线性规划的标准型松弛变量和剩余变量的管理含义是什么答:线性规划的标准型是:目标函数极大化,约束条件为等式,右端常数项,决策变量满足非负性。
如果加入的这个非负变量取值为非零的话,则说明该约束限定没有约束力,对企业来说不是紧缺资源,所以称为松弛变量;剩余变量取值为非零的话,则说明“≥”型约束的左边取值大于右边规划值,出现剩余量。
4.试述线性规划问题的可行解、基础解、基可行解、最优解的概念及其相互关系。
答:可行解:满足约束条件的解,称为可行解。
基可行解:满足非负性约束的基解,称为基可行解。
可行基:对应于基可行解的基,称为可行基。
最优解:使目标函数最优的可行解,称为最优解。
最优基:最优解对应的基矩阵,称为最优基。
它们的相互关系如右图所示:5.用表格单纯形法求解如下线性规划。
.解:标准化.列出单纯形表412b02[8]2 /80868 /641241/41/81/8]/8(1/4/(1/813/265/4/43/4(13/2/(1/4 0-1/23/21/222806-221-12-502故最优解为,即,此时最优值为.6.表1—15中给出了求极大化问题的单纯形表,问表中为何值及变量属于哪一类型时有:(1)表中解为唯一最优解;(2)表中解为无穷多最优解之一;(3)下一步迭代将以代替基变量;(4)该线性规划问题具有无界解;(5)该线性规划问题无可行解。
运筹学(胡运权第二版)习题答案(第二章)

对偶问题: st34yy11
y2 4y3 2 3y2 3y3 4
y1 0, y2 0, y3无限制
School of Management
运筹学教程
page 3 5/17/2021
第二章习题解答
maxZ 5x1 6x2 3x3
x1 2x2 2x3 5
(2)
st
4xx1175xx22
3x3 3x3
运筹学教程
第二章习题解答
page 2 5/17/2021
2.1 写出下列线性规划问题的对偶问题。
min Z 2x1 2x2 4x3
x1 3x2 4x3 2
(1)
st
2x1x3
3 5
x1, x2 , 0, x3无约束
maxW 2y1 3y2 5y3
y1 2y2 y3 2
page 4 5/17/2021
School of Management
运筹学教程
第二章习题解答
m
maxZ cjxj
j1
n
aijxj
bi
(i 1,,m1 m)
(4)
j1 st n aijxj bi
(i m1 1,m1 2,,m)
j1
xj 0 (j 1,,n1,n),xj无约束j( n1 1,,n)
(4)
由于(1)和(4)是矛盾约束,故对偶问题无可行解。 所以原问题目标函数值无界。
page 16 5/17/2021
School of Management
运筹学教程
第二章习题解答
2.7 给出线性规划问题
min Z 2 x1 4 x 2 x3 x 4
x1 3 x2 x4 8
st .
运筹学课后答案2

运筹学(第2版)习题答案2第1章 线性规划 P36~40第2章 线性规划的对偶理论 P68~69 第3章 整数规划 P82~84 第4章 目标规划 P98~100 第5章 运输与指派问题 P134~136 第6章 网络模型 P164~165 第7章 网络计划 P185~187 第8章 动态规划 P208~210 第9章 排队论 P239~240 第10章 存储论 P269~270 第11章 决策论 Pp297-298 第12章 博弈论 P325~326 全书360页由于大小限制,此文档只显示第6章到第12章,第1章至第5章见《运筹学课后答案1》习题六6.1如图6-42所示,建立求最小部分树的0-1整数规划数学模型。
【解】边[i ,j ]的长度记为c ij ,设⎩⎨⎧=否则包含在最小部分树内边0],[1j i x ij数学模型为:,12132323243434364635365612132434343546562324463612132446362335244656121324354656m in 52,22,233344,510ij ijij i j ij Z c x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x ==++≤++≤++≤++≤+++≤+++≤+++≤++++≤++++≤+++++≤=∑或,[,]i j ⎧⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎩所有边6.2如图6-43所示,建立求v 1到v 6的最短路问题的0-1整数规划数学模型。
图6-42【解】弧(i ,j )的长度记为c ij ,设⎩⎨⎧=否则包含在最短路径中弧0),(1j i x ij数学模型为:,1213122324251323343524344546253545564656m in 100,00110,(,)ijiji jij Z cx x x x x x x x x x x x x x x x x x x x x x i j =⎧+=⎪---=⎪⎪+--=⎪⎪+--=⎨⎪++-=⎪⎪+=⎪=⎪⎩∑或所有弧 6.3如图6-43所示,建立求v 1到v 6的最大流问题的线性规划数学模型。
《管理运筹学》课后习题参考标准答案

《管理运筹学》(第二版)课后习题参考答案第1章 线性规划(复习思考题)1.什么就是线性规划?线性规划的三要素就是什么?答:线性规划(Linear Programming,LP)就是运筹学中最成熟的一个分支,并且就是应用最广泛的一个运筹学分支。
线性规划属于规划论中的静态规划,就是一种重要的优化工具,能够解决有限资源的最佳分配问题。
建立线性规划问题要具备三要素:决策变量、约束条件、目标函数。
决策变量就是决策问题待定的量值,取值一般为非负;约束条件就是指决策变量取值时受到的各种资源条件的限制,保障决策方案的可行性;目标函数就是决策者希望实现的目标,为决策变量的线性函数表达式,有的目标要实现极大值,有的则要求极小值。
2.求解线性规划问题时可能出现几种结果,哪种结果说明建模时有错误? 答:(1)唯一最优解:只有一个最优点; (2)多重最优解:无穷多个最优解; (3)无界解:可行域无界,目标值无限增大;(4)没有可行解:线性规划问题的可行域就是空集。
当无界解与没有可行解时,可能就是建模时有错。
3.什么就是线性规划的标准型?松弛变量与剩余变量的管理含义就是什么? 答:线性规划的标准型就是:目标函数极大化,约束条件为等式,右端常数项0≥i b ,决策变量满足非负性。
如果加入的这个非负变量取值为非零的话,则说明该约束限定没有约束力,对企业来说不就是紧缺资源,所以称为松弛变量;剩余变量取值为非零的话,则说明“≥”型约束的左边取值大于右边规划值,出现剩余量。
4.试述线性规划问题的可行解、基础解、基可行解、最优解的概念及其相互关系。
答:可行解:满足约束条件0≥=X b AX ,的解,称为可行解。
基可行解:满足非负性约束的基解,称为基可行解。
可行基:对应于基可行解的基,称为可行基。
最优解:使目标函数最优的可行解,称为最优解。
最优基:最优解对应的基矩阵,称为最优基。
它们的相互关系如右图所示:5.用表格单纯形法求解如下线性规划。
管理运筹学韩伯棠答案

管理运筹学韩伯棠答案【篇一:管理运筹学(第四版)第五章习题答案】时间为x2小时;产品i加班生产时间为x3小时,产品ii加班生产时间为x4小时。
minzp1d1p2d2p3d3s.t.3x1?2.5x2?d1??d1??1203x3?2.5x4?d2?d2?4010x1?8x2??10?1.5?x3??8?1?x4?d3??d3??640xj,di?,di??0,i?1,2,3;j?1,2,3,4运行结果:5.10解:设a电视机生产x1台,b电视机生产x2台,c电视机生产x3台。
minz?p1d1??p2d2?p3d3??d3??d4?d4?d5??d5s.t.500x1?650x2?900x3?d1??d1??18000??6x1?8x2?10x3?d2?d2?224x1?d3??d3??14x2?d4?d4?15x3?d5??d5??10xj,di?,di??0,i?1,2,3,4,5;j?1,2,3运行结果:5.10解:设电台a时间x1分钟,电台b时间x2分钟,电台c时间x3分钟。
minz?p1d1p22d2?d2?p3d3?s.t.400x1?600x2?80x3?24002000x1?4000x2?1000x3?d1??d1??80000 ??x1?x2?x3?d2?d2?30x3?d3??d3??0xj,di?,di??0,i?1,2,3;j?1,2,3运行结果:【篇二:《管理运筹学》第二版习题答案(韩伯棠教授)1】txt>11a.可行域为 oabc。
b.等值线为图中虚线所示。
c.由图可知,最优解为 b 点,最优解: x1 = 1215x2=69 7,7 。
2、解: a x210.60.1o1有唯一解x1= 0.2x函数值为 3.62= 0.6b 无可行解c 无界解d 无可行解e 无穷多解最优目标函数值:20 x1=3 函数值为92f 有唯一解8 3x2=33、解:a 标准形式:b 标准形式:max f = 3x1 + 2 x2+ 0s1 + 0s2+ 0s3 9 x1 + 2x2+ s1= 30 3x1 + 2 x2+ s2= 13 2 x1 + 2x2+ s3= 9 x1 , x2 , s1 , s2 , s3≥ max f = ?4 x1 ? 6x3 ? 0s1 ? 0s23x1 ? x2? s1=6x1 + 2x2+ s2= 10 7 x1 ? 6 x2= 4c 标准形式:x1 , x2 , s1 , s2≥max f = ?x1 + 2x2 ? 2 x? 0s ? 0s 2 1 23x1 + 5x2 5x2+ s1= 70 2 x 5x + 5x = 50123x1 + 2 x 2? 2x2? s2= 302x, x, x, s1 , s2≥ 04 、解:标准形式: max z = 10 x1 + 5x2+ 0s1 + 0s23x1 + 4 x2+ s1= 9 5x1 + 2 x2+ s2= 8 x1 , x2 , s1 , s2≥ 0s1 = 2, s2= 01 225 、解:标准形式: min f = 11x1 + 8x2+ 0s1 + 0s2+ 0s310 x1 + 2x2? s1= 203x1 + 3x2? s2= 18 4 x1 + 9x2? s3= 36 x1 , x2 , s1 , s2 , s3≥ 0s1 = 0, s2= 0, s3 = 136 、解:b 1 ≤ c1≤ 3 c 2 ≤ c2≤ 6 d x1= 6 x2= 4e x1 ∈ [4,8] x2= 16 ? 2x1 2f 变化。
运筹学课后答案2

运筹学(第2版)习题答案2第1章 线性规划 P36~40第2章 线性规划的对偶理论 P68~69 第3章 整数规划 P82~84 第4章 目标规划 P98~100 第5章 运输与指派问题 P134~136 第6章 网络模型 P164~165 第7章 网络计划 P185~187 第8章 动态规划 P208~210 第9章 排队论 P239~240 第10章 存储论 P269~270 第11章 决策论 Pp297-298 第12章 博弈论 P325~326 全书360页由于大小限制,此文档只显示第6章到第12章,第1章至第5章见《运筹学课后答案1》习题六6.1如图6-42所示,建立求最小部分树的0-1整数规划数学模型。
【解】边[i ,j ]的长度记为c ij ,设⎩⎨⎧=否则包含在最小部分树内边0],[1j i x ij数学模型为:,12132323243434364635365612132434343546562324463612132446362335244656121324354656m in 52,22,233344,510ij ijij i j ij Z c x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x ==++≤++≤++≤++≤+++≤+++≤+++≤++++≤++++≤+++++≤=∑或,[,]i j ⎧⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎩所有边6.2如图6-43所示,建立求v 1到v 6的最短路问题的0-1整数规划数学模型。
图6-42【解】弧(i ,j )的长度记为c ij ,设⎩⎨⎧=否则包含在最短路径中弧0),(1j i x ij数学模型为:,1213122324251323343524344546253545564656m in 100,00110,(,)ijiji jij Z cx x x x x x x x x x x x x x x x x x x x x x i j =⎧+=⎪---=⎪⎪+--=⎪⎪+--=⎨⎪++-=⎪⎪+=⎪=⎪⎩∑或所有弧 6.3如图6-43所示,建立求v 1到v 6的最大流问题的线性规划数学模型。
管理运筹学课后答案
(4)在负无穷到5.5的范围内变化,其最优解不变,但此时最优目标函数值变化。
(5)在0到正无穷的范围内变化,其最优解不变,但此时最优目标函数值变化。
5.解:
(1)约束条件2的右边值增加1个单位,目标函数值将增加3.622;
(2) 目标函数系数提高到0.703,最优解中 的取值可以大于零;
总成本最小为264元,能比第一问节省:320-264=56元。
3.解:设生产A、B、C三种产品的数量分别为x1,x2,x3,则可建立下面的
数学模型:
max z=10 x1+12x2+14x3
s.t. x1+1.5x2+4x3 2000
2x1+1.2x2+x3 1000
x1 200
x2 250
x3 100
x3+x4+x5+x6+y4+y5+y6+2 3
x4+x5+x6+x7+y5+y6+y7+1 6
x5+x6+x7+x8+y6+y7+y8+2 12
x6+x7+x8+y7+y8+y9+2 12
x7+x8+y8+y9+1 7
x8+y9+1 7
x1,x2,x3,x4,x5,x6,x7,x8,y1,y2,y3,y4,y5,y6,y7,y8,y9 0
x6+x7+x8+x9+2 12
x7+x8+x9+x10+1 7
x8+x9+x10+x11+1 7
x1,x2,x3,x4,x5,x6,x7,x8,x9,x10,x11 0
用管理运筹学软件我们可以求得此问题的解为:
x1=8,x2=0,x3=1,x4=1,x5=0,x6=4,x7=0,x8=6,x9=0,x10=0,x11=0
(5)在400到正无穷的范围内变化,最优产品的组合不变。
运筹学(第二版)课后答案

max z 4 x1 5 x 2 x3 3 x1 2 x 2 x3 x 4 x6 18 2 x x x 4 1 2 5 st x1 x 2 x3 x7 5 x j 0, ( j 1, ,7)
406
附录四习题参考答案
1 0 1 σj 1 0 1 σj
X6 X1 X7 X6 X2 X7
0 1 0 0 -1 2 -1 2
1/2 1/2 1/2 -1 0 1 0 0
1 0 -1 0 1 0 -1 0
-1 0 0 1 -1 0 0 1
-3/2 1/2 -1/2 2 -2 2 -1 3
1 0 0 0 1 0 0 0
0 0 1 0 0 0 1 0
12 2 3 10 4 1
表 1.4-1.2 在第一阶段的最优解中人工变量不为零,则原问题无可行解。 注:在第二阶段计算时,初始表中的检验数不能引用第一阶段最优表的检 验数,必须换成原问题的检验数。 (2) 无穷多最优解,如 X1=(4,0,0) ;X2=(0,0,8) (3) 无界解 (4) 唯一最优解 X*=(5/2,5/2,5/2,0) (5) 唯一最优解 X*=(24,33) (6) 唯一最优解 X*=(14,0,-4) 1.5 (1) X*仍为最优解,max z=λCX; (2) 除 C 为常数向量外,一般 X*不再是该问题的最优解; (3) 最优解变为λX*,目标函数值不变。 1.6 (1) d≥0,c1<0, c2<0 (2) d≥0,c1≤0, c2≤0,但 c1,c2 中至少一个为零 (3) d=0 或 d>0,而 c1>0 且 d/4=3/a2 (4) c1>0,d/4>3/a2 (5) c2>0,a1≤0 (6) x5 为人工变量,且 c1≤0, c2≤0 1.7 解: 设 xj 表示第 j 年生产出来分配用于作战的战斗机数; yj 为第 j 年已 培训出来的驾驶员; (aj-xj)为第 j 年用于培训驾驶员的战斗机数;zj 为第 j 年用于培训驾驶员的战斗机总数。则模型为 max z = nx1+(n-1)x2+…+2xn-1+xn s.t. zj=zj-1+(aj-xj) yj=yj-1+k(aj-xj) x1+x2+…+xj≤yj xj,yj,zj≥0 (j=1,2, …,n) 1.8
运筹学(胡运权第二版)习题答案(第二章)

2.9 用对偶单纯形法求解下列线性规划问题。
minZ 4x1 12x2 18x3
(1)
st.
x1 3x3 3 2x2 2x3 5
xj 0,( j 1,,3)
minZ 5x1 2x2 4x3
3x1 x2 2x3 4
(2) st.6x1 3x2 5x3 10
xj
0, (
j
1,,3)
School of Management
page 11 5/17/2021
School of Management
运筹学教程
第二章习题解答
min W 2 y1 3 y2
y1 2 y2 2
(1)
对偶问题:
st
.
2 3
y1 y1
y2 y2
3 5
y1
3y2
6
y1 0, y2 0
(2) 最优解是:y1=-8/5,y2=1/5,目标函数值-19/5。 (3)由于 y1=-8/5,y2=1/5都不等于零,原问题中的约 束取等号。又上面第4个约束不等号成立,故x4=0,令 x3=0就可以得到最优解: x1=8/5,x2=1/5。
page 5 5/17/2021
School of Management
运筹学教程
第二章习题解答
minWb1y1b2y2 bmym
m
aijyi
cj
(j 1,2,,n1)
对偶问题s: tim 1 aijyi cj
(j n11,n12,,n)
i1 yi 0
(i 1,,m1)
yi无约束j( m1 1,,m)
2x3 5x3
4 10
xj
0, (
j
1,,3)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《管理运筹学》(第二版)课后习题参考答案第1章 线性规划(复习思考题)1.什么是线性规划线性规划的三要素是什么答:线性规划(Linear Programming ,LP )是运筹学中最成熟的一个分支,并且是应用最广泛的一个运筹学分支。
线性规划属于规划论中的静态规划,是一种重要的优化工具,能够解决有限资源的最佳分配问题。
建立线性规划问题要具备三要素:决策变量、约束条件、目标函数。
决策变量是决策问题待定的量值,取值一般为非负;约束条件是指决策变量取值时受到的各种资源条件的限制,保障决策方案的可行性;目标函数是决策者希望实现的目标,为决策变量的线性函数表达式,有的目标要实现极大值,有的则要求极小值。
2.求解线性规划问题时可能出现几种结果,哪种结果说明建模时有错误 答:(1)唯一最优解:只有一个最优点; (2)多重最优解:无穷多个最优解;(3)无界解:可行域无界,目标值无限增大; (4)没有可行解:线性规划问题的可行域是空集。
当无界解和没有可行解时,可能是建模时有错。
3.什么是线性规划的标准型松弛变量和剩余变量的管理含义是什么答:线性规划的标准型是:目标函数极大化,约束条件为等式,右端常数项0≥i b ,决策变量满足非负性。
如果加入的这个非负变量取值为非零的话,则说明该约束限定没有约束力,对企业来说不是紧缺资源,所以称为松弛变量;剩余变量取值为非零的话,则说明“≥”型约束的左边取值大于右边规划值,出现剩余量。
4.试述线性规划问题的可行解、基础解、基可行解、最优解的概念及其相互关系。
答:可行解:满足约束条件0≥=X b AX ,的解,称为可行解。
基可行解:满足非负性约束的基解,称为基可行解。
可行基:对应于基可行解的基,称为可行基。
最优解:使目标函数最优的可行解,称为最优解。
最优基:最优解对应的基矩阵,称为最优基。
它们的相互关系如右图所示:5.用表格单纯形法求解如下线性规划。
. ⎪⎩⎪⎨⎧≥≤++≤++0,,86238321321321x x x x x x x x x 解:标准化 32124max x x x Z ++=. ⎪⎩⎪⎨⎧≥=+++=+++0,,,,862385432153214321x x x x x x x x x x x x x 列出单纯形表故最优解为T X )6,0,2,0,0(*=,即2,0,0321===x x x ,此时最优值为4*)(=X Z . 6.表1—15中给出了求极大化问题的单纯形表,问表中d c c a a ,,,,2121为何值及变量属于哪一类型时有:(1)表中解为唯一最优解;(2)表中解为无穷多最优解之一;(3)下一步迭代将以1x 代替基变量5x ;(4)该线性规划问题具有无界解;(5)该线性规划问题无可行解。
表1—15 某极大化问题的单纯形表解:(1)0,0,021<<≥c c d ;(2)中至少有一个为零)(2121,0,0,0c c c c d ≤≤≥; (3)22134,0,0a d a c >>>; (4)0,012≤>a c ;(5)1x 为人工变量,且1c 为包含M 的大于零的数,234a d >;或者2x 为人工变量,且2c 为包含M 的大于零的数,0,01>>d a .7.用大M 法求解如下线性规划。
. ⎪⎪⎩⎪⎪⎨⎧≥=++≤++≤++0,,101632182321321321321x x x x x x x x x x x x 解:加入人工变量,进行人造基后的数学模型如下:. ⎪⎪⎩⎪⎪⎨⎧=≥=+++=+++=+++)6,,2,1(0101632182632153214321 i x x x x x x x x x x x x x i 列出单纯形表故最优解为T X )0,0,4,0,4,6(*=,即0,4,6321===x x x ,此时最优值为42*)(=X Z . 8.A ,B ,C 三个城市每年需分别供应电力320,250和350单位,由I ,II 两个电站提供,它们的最大可供电量分别为400单位和450单位,单位费用如表1—16所示。
由于需要量大于可供量,决定城市A 的供应量可减少0~30单位,城市B 的供应量不变,城市C 的供应量不能少于270单位。
试建立线性规划模型,求将可供电量用完的最低总费用分配方案。
表1—16 单位电力输电费(单位:元)解:设ij x 为“第i 电站向第j 城市分配的电量”(i =1,2; j =1,2,3),建立模型如下:. ⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧==≥≤+≥+=+≤+≥+=++=++3,2,1;2,1,035027025032029045040023132313221221112111232221131211j i x x x x x x x x x x x x x x x x x ij9.某公司在3年的计划期内,有4个建设项目可以投资:项目I 从第一年到第三年年初都可以投资。
预计每年年初投资,年末可收回本利120%,每年又可以重新将所获本利纳入投资计划;项目II 需要在第一年初投资,经过两年可收回本利150%,又可以重新将所获本利纳入投资计划,但用于该项目的最大投资不得超过20万元;项目III 需要在第二年年初投资,经过两年可收回本利160%,但用于该项目的最大投资不得超过15万元;项目IV 需要在第三年年初投资,年末可收回本利140%,但用于该项目的最大投资不得超过10万元。
在这个计划期内,该公司第一年可供投资的资金有30万元。
问怎样的投资方案,才能使该公司在这个计划期获得最大利润解:设)1(i x 表示第一次投资项目i ,设)2(i x 表示第二次投资项目i ,设)3(i x 表示第三次投资项目i ,(i =1,2,3,4),则建立的线性规划模型为. ⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧=≥≤≤≤----+++=+--+≤+≤+4,3,2,1,0,,101520302.15.12.1302.130)3()2()1()1(4)1(3)1(2)1(3)2(1)1(2)1(1)1(1)1(2)2(1)1(4)3(1)1(2)1(1)1(1)1(3)2(1)1(2)1(1i x x x x x x x x x x x x x x x x x x x x x x i i i 通过LINGO 软件计算得:44,12,0,20,10)2(1)2(1)1(3)1(2)1(1=====x x x x x . 10.某家具制造厂生产五种不同规格的家具。
每种家具都要经过机械成型、打磨、上漆几道重要工序。
每种家具的每道工序所用的时间、每道工序的可用时间、每种家具的利润由表1—17给出。
问工厂应如何安排生产,使总利润最大表1—17 家具生产工艺耗时和利润表解:设i x 表示第i 种规格的家具的生产量(i =1,2,…,5),则. ⎪⎪⎩⎪⎪⎨⎧=≥≤++++≤++++≤++++5,,2,1,0280034332395046534360032643543215432154321 i x x x x x x x x x x x x x x x x i 通过LINGO 软件计算得:3181,642,0,254,38,054321======Z x x x x x .11.某厂生产甲、乙、丙三种产品,分别经过A ,B ,C 三种设备加工。
已知生产单位产品所需的设备台时数、设备的现有加工能力及每件产品的利润如表2—10所示。
表1—18 产品生产工艺消耗系数(1)建立线性规划模型,求该厂获利最大的生产计划。
(2)产品丙每件的利润增加到多大时才值得安排生产如产品丙每件的利润增加到6,求最优生产计划。
(3)产品甲的利润在多大范围内变化时,原最优计划保持不变(4)设备A 的能力如为100+10q ,确定保持原最优基不变的q 的变化范围。
(5)如合同规定该厂至少生产10件产品丙,试确定最优计划的变化。
解:(1)设321,,x x x 分别表示甲、乙、丙产品的生产量,建立线性规划模型. ⎪⎪⎩⎪⎪⎨⎧≥≤++≤++≤++0,,3006226005410100321321321321x x x x x x x x x x x x 标准化得. ⎪⎪⎩⎪⎪⎨⎧≥=+++=+++=+++0,,,,,3006226005410100654321632153214321x x x x x x x x x x x x x x x x x x 列出单纯形表故最优解为0,3/200,3/100321===x x x ,又由于321,,x x x 取整数,故四舍五入可得最优解为0,67,33321===x x x ,732max =Z .(2)产品丙的利润3c 变化的单纯形法迭代表如下:要使原最优计划保持不变,只要0333≤-=c σ,即67.6363≈≤c .故当产品丙每件的利润增加到大于时,才值得安排生产。
如产品丙每件的利润增加到6时,此时6<,故原最优计划不变。
(3)由最末单纯形表计算出0611,03210,0611151413≤-=≤+-=≤--=c c c σσσ,解得1561≤≤c ,即当产品甲的利润1c 在]15,6[范围内变化时,原最优计划保持不变。
(4)由最末单纯形表找出最优基的逆为⎪⎪⎪⎭⎫⎝⎛---=-10206/13/206/13/51B ,新的最优解为 解得54≤≤-q ,故要保持原最优基不变的q 的变化范围为]5,4[-.(5)如合同规定该厂至少生产10件产品丙,则线性规划模型变成. ⎪⎪⎪⎩⎪⎪⎪⎨⎧≥≥≤++≤++≤++0,,1030062260054101003213321321321x x x x x x x x x x x x x 通过LINGO 软件计算得到:708,10,58,32321====Z x x x .第2章 对偶规划(复习思考题)1.对偶问题和对偶向量(即影子价值)的经济意义是什么答:原问题和对偶问题从不同的角度来分析同一个问题,前者从产品产量的角度来考察利润,后者则从形成产品本身所需要的各种资源的角度来考察利润,即利润是产品生产带来的,同时又是资源消耗带来的。
对偶变量的值i y 表示第i 种资源的边际价值,称为影子价值。
可以把对偶问题的解Y 定义为每增加一个单位的资源引起的目标函数值的增量。
2.什么是资源的影子价格它与相应的市场价格有什么区别答:若以产值为目标,则i y 是增加单位资源i 对产值的贡献,称为资源的影子价格(Shadow Price )。
即有“影子价格=资源成本+影子利润”。
因为它并不是资源的实际价格,而是企业内部资源的配比价格,是由企业内部资源的配置状况来决定的,并不是由市场来决定,所以叫影子价格。
