线性时不变系统
线性时不变系统

第6章线性时不变系统尹霄丽6.1 引言MATLAB •••利用函数,和计算LTI系统的输出;研究离散时间LTI系统的多conv ls 个性质主要;连续i 时内容:间卷积m 的filter 数值近似;例1[][][][]1, 040, n x n n y n x n x n ≤≤⎧=⎨⎩=∗考虑如下有限长信号其余(a)用解析方法计算。
[][][](b) 编程实现% exe2_1_a.m, see also exe2_1_b.mx=ones(1,5);nx=0:4;y=conv(x,x);ny=(min(nx)+min(nx)):(max(nx)+max(nx)); h=stem(ny,y);set(h,'linewidth',2);xlabel('n');ylabel('x[n]*x[n]');作业3[][][][][][][]1, 050, , 050, (a) ;(b) MATLAB(c)conv y n x n nn n h n ny n x n h n x n h n ≤≤⎧=⎨⎩≤≤⎧=⎨⎩=∗考虑下面有限长信号:其余其余不用编程,请计算卷积和用生成信号和,并画出相应的图形。
用计算卷积和,并用stem画出其图形。
注:图形请加上必要的标注。
6.3 MATLAB函数filterfilterFILTER One-dimensional digital filter.Y = FILTER(B,A,X) filters the data in vector X with the filter described by vectors A and B to create the filtered data Y. The filter is a "Direct Form II Transposed"implementation of the standard difference equation:a(1)*y(n) + a(2)*y(n-1) + ... + a(na+1)*y(n-na) =b(1)*x(n) + b(2)*x(n-1) + ... + b(nb+1)*x(n-nb)[][][][]00LTI 1 filte r KMk mk m x x x a y n k b x n m x n n n n N y n ==−=−≤≤+−∑∑命令计算由线性常系数差分方程表征的因果系统在某一给定输入时的输出。
LinearTimeinvariantSystem(线性时不变系统)

Linear Time-invariant System(线性时不变系统)2-1:Discrete-Time LTI System:The Convolution Sum(离散LTI系统:卷和)本节的关键在于:把任意离散信号x[n]表示为若干个脉冲信号的叠加。
这样,信号x[n]输入某一个系统的输出y[n],便可以等效为把这些脉冲信号分别输入这个系统之后,再把它们的输出结果叠加。
当系统是LTI系统时,对应每个脉冲信号输入的输出函数都可以由对应单位冲激函数的响应δ[n]的输出h[n]进行时移和乘以系数得到。
把每个脉冲输入的输出叠加便得到了输入信号x[n]的输出y[n]。
用脉冲信号表示任意信号:可以把x[n]看作x[0].δ[n]+ δ[n-1].x[1]+ δ[n-2].x[2]……即P75 2-2式对一个系统LTI,当输入信号为δ[n]时的输出信号h[n]称为单位冲激响应(unit impulse response)卷和而对于每个x[k].δ[n-k],输入系统后的输出为hk[n]=x[k].h[n-k],因此,x[n]输入后的输出y[n]便应当是全部hk[n](k从负无穷取到正无穷)的累加。
换言之得到了P78 2-6式(公式请自己看啦,输入太麻烦了,呵呵呵呵)该公式称作x[n]和h[n]的卷和或卷积和(Convolution Sum)。
写作x[n]*h[n]。
是一种基本的运算方式,由两个函数卷和得到一个新函数。
对LTI系统而言,就是输入x[n]与单位冲激响应卷和,得到输出信号y[n]。
x[n]*h[n]=y[n]对于有限长序列卷和的运算:竖式法比较简单。
2-2:continuous-time LTI systems:the convolution integral(连续时间LTI系统:卷积)与离散系统类似,本节的核心也是把输入的一个连续时间信号从时间上拆分成无数个冲激信号的叠加,然后对于每个冲激信号去求它输入这个系统得到的输出,再把所有的这些输出叠加起来,从而得到原信号输入系统的输出。
线性时不变系统

线性时不变系统
传递函数
• 在考虑扰动的情况下,系统的传递函数可以写成
y (t ) = G (q )u (t ) + H (q )e(t )
(2.12)
y (kT ) =
∫τ
∞ =0
g (τ )u (kT − τ )dτ
线性时不变系统
稳定性
• 系统的传递函数如果满足以下条件
G (q ) =
∞ ∞
∑
k =1
线性时不变系统
传递函数
• 我们定义q算子
qu (t ) = u (t + 1)
• 同样
q −1u (t ) = u (t − 1)
(2.9)
(2.10)
• 那么(2.6)就可以写成
y (t ) =
∞ k =1
∑ g (k )u(t − k ) =∑ g (k )q
k =1
∞
−k
u (t )
(2.11)
y (t ) = G (q )u (t )
y (kT ) =
∫τ
∞ =0
g (τ )u (kT − τ )dτ
线性时不变系统
传递函数
• 如果系统是稳定的,随着k的增大,g(k)趋近于0, 则上式可以简化为
G (q ) = ∑ g (k )q − k
k =1
n
• 其中g(n+1),g(n+2),…接近于0,可以忽略不计
(2.3)
y (kT ) =
∫τ
∞ =0
g (τ )u (kT − τ )dτ
线性时不变系统
单位脉冲响应模型
• 将(2.3)带入(2.2)
y (kT ) = =
∫τ
第2章 线性时不变系统

0 t
2.4 LTI系统的性质
举例:累加系统(accumulator)
y[n]
k
x[k ]
n
它是LTI系统,其单位脉冲响应为
h[n] u[n]
h[n] k [n] Memory h[n] 0, n 0 Causal
2.4 LTI系统的性质
从以上推导得出以下结论: DT LTI 系统的单位阶跃响应是其单位脉冲响应的求和函数; DT LTI 系统的单位脉冲响应是其单位阶跃响应的一次差分 同理,对于CT LTI 系统: 单位阶跃响应是其单位冲激响应的积分函数
s(t ) h( )d
t
单位冲激响应是其单位阶跃响应的一阶导数
2.7小结
2.1概述
(1)线性与时不变性(Linearity and Time-Invariance): 很多物理过程都具有这两个性质 这些物理过程能用LTI系统表征 可以对LTI系统进行详细的分析:
能够将LTI系统的输入用一组基本信号的线性组合表示 根据该系统对基本信号的响应,利用叠加性质求得整个系统的输出
2.4 LTI系统的性质
离散时间LTI系统用 卷积和表示
连续时间LTI系统用 卷积积分表示
LTI系统的特性可以 完全由其单位冲激响 应决定
2.4 LTI系统的性质
卷积的交换律性质 The Commutative Property of Convolution
2.4 LTI系统的性质
卷积的三个代数性质:交换律、结合律、分配律 Three algebraic properties of convolution
线性系统理论全

稳定性判据与判定方法
稳定性判据
在控制工程中,常用的稳定性判据有Routh判据、Nyquist判据、 Bode判据等。这些判据通过分析系统的特征方程或频率响应来判 断系统的稳定性。
判定方法
除了使用稳定性判据外,还可以通过时域仿真、频域分析、根轨 迹法等方法来判定系统的稳定性。这些方法各有优缺点,适用于 不同类型的线性系统和不同的问题背景。
100%
线性偏差分方程
处理离散空间和时间的问题,如 数字滤波器和图像处理等。
80%
初始条件与边界条件
在差分方程中,初始条件确定系 统的起始状态。
状态空间模型
状态变量与状态方程
表示系统内部状态的变化规律 ,揭示系统动态特性。
输出方程
描述系统输出与状态变量和输 入的关系,反映系统对外部激 励的响应。
状态空间表达式的建立
复频域分析法
拉普拉斯变换
将时域信号转换为复频域信号,便于分析系统的稳定性和动态性 能。
系统函数
描述Байду номын сангаас统传递函数的复频域表示,反映系统的固有特性和对输入信 号的响应能力。
极点、零点与稳定性
通过分析系统函数的极点和零点分布,可以判断系统的稳定性以及 动态性能。
04
线性系统稳定性分析
BIBO稳定性
01
线性系统理论全
目
CONTENCT
录
• 线性系统基本概念 • 线性系统数学模型 • 线性系统分析方法 • 线性系统稳定性分析 • 线性系统能控性与能观性分析 • 线性系统优化与综合设计
01
线性系统基本概念
线性系统定义与性质
线性系统定义
满足叠加性与均匀性的系统。
线性系统性质
§1-6 线性时不变系统的基本特性

一、 线性 线性包含叠加性与均匀(齐次)性。 1、叠加性:
若
x1 (t ) x2 (t )
x(t ) x1 (t ) x2 (t )
系统
y1 (t ) y2 (t ) y(t ) y1 (t ) y2 (t )
称系统满足叠加性。
2、齐次性
x(t ) axi (t )
x(t t0 )
系统
y (t )
y (t t0 )
例如:设系统的输入输出之间的关系为:
y (t ) tx(t )
y1 (t ) tx(t t0 ) y (t t0 )
系统是时变的。 y(t t0 ) (t t0 ) x(t t0 ) 因为 再如: 设系统的输入输出之间的关系为:
y(t ) ax(t ) b
y1 (t ) ax(t t0 ) b y (t t0 )
所以系统是时不变的。
判断一个系统是否满足某种特性,只要能找到一个例 子不满足,就可证明其不满足此特性。
例如: 设系统的输入输出之间的关系为: y(t ) x(2t ) 即如图所示:
x(t ) ak xk (t t k )
k 1 N
y (t ) ak yk (t t k )
k 1
N
系统同时满足线性与时不变性,称为线性时不变系统, 记为LTI(linear-time-invariant)系统。
例如: 设LTI系统的输入x(t)与输出y(t)之间的关系由下图描述, 试作出当输入分别为x1(t)与x2(t)时,输出y1(t)与y2(t)的波 形图。
y(t ) ayi (t )
称系统满足齐次性。同时满足叠加性与齐次性的系统称为 线性系统。
信号处理与系统分析 第2章线性时不变系统

从波形的角度来观察离散时间信号,它可以 看成是由许多加权了的单位冲激信号组合 而成的
x[n] x[1] [n 1] x[0] [n] x[2] [n 2]
对于任意的离散时间信号:
累加序号 自变量
加权值 移位的冲激信号
x[n]
k
x[k ] [n k ]
n
卷积公式是无穷多项求和,而我们实际遇到的常 常是有限长度序列,特别是在计算机离线处理的场 合,因为计算机不可能处理无穷多的信息。 在进行有限长度的序列的卷积时候,长度为N和M 的2个序列作卷积时,反转序列从左到右进入重叠 直至移出重叠,只有存在重叠项时,卷积和才可能 非零。 卷积序列的长度为M+N-1。
求解系统响应的卷积方法是系统分析的重要工具。
单位冲激响应h[n]完全描述了线性时不变系统的变换 规律。不同的系统输入,都在h[n]的作用下产生相应的 响应,因此,给定了一个LTI系统的单位冲激响应h[n]就 等于给定了该系统。
从计算某一个特定点的角度来看
yy [n [n 0]
k k
第2章 线性时不变系统
线性时不变(简称LTI,Linear, Time-invariant)系统
为什么引入LTI ?
如果不对系统的性质加以限制,那么分析 一个系统将是十分困难的。 给系统加上线性和时不变性的限制,那么 系统的分析将变得十分简便。 LTI系统的分析还为非线性系统的分析方法 提供了思路。例如,线性时不变系统可以 用冲激响应来表达,非线性系统可以用 Volterra级数来表达。
上式应该理解为许多以为n自变量的函数的相 加,而不是数值相加。
许多移了位的冲激信号的加权和,构成了x[n] 。
特别地,我们有
线性时不变系统--习题

dt
dt
dt
et t et t
t t t
t
方法二没有注意利用冲激函数的性质,求解过
程较繁。另外,对冲激偶信号的性质
f t t f 0 t f 0 t
往往被错误写成
f t t f 0 t
从而得出错误结论。
(2) f t t e3 δτ d τ
1 O t 3 1
t
t 3 1
t
3
1
即2 t 4
g(t) 1 1(t )d t 2 t 2
t3 2
42
T4
1 f1
f2 t
t
1 O
1 t3
t-31
即t 4
gt 0
卷积结果
f1t
1
1 O 1 t
f2 t
3
2
O
3t
t2 t 1
g(t
)
4 t
t
2
2
4
x(t t0 ) h(t) x(t) h(t t0 ) y(t t0 )
例1 粗略绘出下列各函数式的波形图
(1) f1t u t2 1
(2)
f2 t
d dt
et cos tut
描绘信号波形是本课程的一项基本训练,在绘 图时应注意信号的基本特征,对所绘出的波形,应标 出信号的初值、终值及一些关键的值,如极大值和极 小值等,同时应注意阶跃、冲激信号的特点。
设x3(t) ax1 t bx2 t x3 t y3 t x32 t ax1 t bx2 t 2 a2 x12 t b2 x22 t 2abx1 t x2 t
a2 y1 t b2 y2 t 2abx1 t x2 t ay1 t by2 t
第2章-线性时不变系统

卷积和:对位相乘法
计算 x 1n x 2n ,其中
x 1 n 2 n n 1 4 n 2 n 3 x 2n 3 n n 1 5 n 2
x1 n : x2 n:
2 1 41 3 15
10 5 20 5
21 4 1
6 3 12 3
x1n x2 n: 6 5 23 12 21 5
用的。
例1: x (t) e a tu (t), a 0 h(t)u(t)
y(t) x(t) h(t) x( )h(t )
ea u( )u(t )d
t ea d 1 (1 eat )u(t)
0
a
u(t )
x ( )
1
1
0
0t
例2 :
x(t)10
0tT otherwise
x(k)
t
0
k (k1)
引用 (t,) 即:
(t) 1/0
0t otherwise
则有: (t) 1 0
0t otherwise
第 个k 矩形可表示为: x (k ) (t k )
这些矩形叠加起来就成为阶梯形信号 x ,( t )
即: x(t) x(k)(tk) k 当 0时, k d (t k ) (t ) x(t)x(t)
etut*ut 1ut 1
1[e(t1) 1]u(t 1) 1[e(t1) 1]u(t 1)
信号与系统
举例
❖ 已知某线性时不变系统的单位冲激响应和激
励信号分别为:e2tut ,ut1ut2,则系
利用z变换求解
❖ x1nnn1n2 x2nn1n2
X 1zX 2z1z 1z 2 z 1z 2
z 1z 2z 2z 3z 3z 4
第三章线性时不变系统的标准形与最小实现

A=
0 an
1 1
an1 an2
1
P
1 a1
h
hA
hA2
hAn1
其中, hAn anh an1hA an2hA2 (凯莱 哈密尔顿定理)
a1hAn1
6
另一方面,注意到U1U I
1 0 0
[b
Ab
An1b] I= 0
h
0
1
我们有 hb 0,hAb 0, ,hAn2b 0,hAn1b 1
A1 PAT P1, b1 PcT , c1 bT P1
24
对
A1 PAT P1, b1 PcT , c1 bT P1
转置处理后有:
A1T (PT )1APT
A
c1T (PT )1b
b
令
b1T cPT
c
A : A1T , b (PT )1b, c cPT
则(A,b, c)就是可观标准形。
0
00
0
00
0
01
0
1
29
p
0 0
0 0
1
0 0
B= 0 0
0
1
0
0
0 0
0 0
0
0
1
0
0
2
0
0 1
p
C=CP1 没有任何特点
30
下面介绍变换的具体做法。
1). 不失一般性,假设B=[b1 b2,……bp]列满秩;
2). 列出可控性矩阵:
U [b1 b2 b p Ab1 Ab2 Ab p
A P2AP21, B P2B,C CP21
34
讨论:1)P2的可逆性证明:
只要证明:若有列向量 ,满足P2 0 0即可。
第二章线性时不变系统

引 言
2.0
分析LTI系统时,问题的实质是什么?
1)研究信号的分解:即以什么样的信号作为构成任意 信号的基本信号单元,如何用基本信号单元的线性组合来 构成任意信号; 引 言 2.0 3 2)研究如何得到LTI系统对基本单元信号的响应。
基本单元的信号应满足以下要求是什么?
1)尽可能简单,并且用它的线性组合能够表示尽可能 广泛的其他信号; 2)LTI系统对这种信号的响应易于求的。
h( )
2T
1 x(t )
0
2T
t T
0
t
① 当
t0
时,
y (t ) 0
② 当 0 t T 时,
③ 当 T t 2T时,
连 续 时 间 系 统 : 卷 积 积 分 19 LTI
④ 当 2T t 3T时,
⑤ 当 t 3T 时,
1 2 y(t ) d t 0 2 t 1 2 y(t ) d Tt T t T 2 2T 1 2 y(t ) d 2T (t T ) 2 t T 2 y (t ) 0
对应点相乘,再把乘积的各点值累加,得到 n 时刻的 y n
x n nu n 例1 已知 h n u n
0 1 ,求LTI系统对输
入信号的响应 y n 。
解:采用图解法
y n
k
x k h n k
上式表明: LTI系统可以完全由它的单位脉冲响应 h(t )来表征。这种求得系统响 应的运算关系称为卷积积分(The convolution integral)。
三.卷积积分的计算(分5步移动法) 卷积积分与卷积和类似,求解的方法有图解法、解析法 和数值解法。
第2章__线性时不变系统

g (t ) u(t ) h(t ) h()d
求系统零状态响应举例:如图所示系统, hD (t ) (t 1 ) hG (t ) u(t ) u(t 3) , ,输入 x(t ) u(t ) u (t 1),求零状态响应y(t)
k
h[k ]x[n k ]
2、分配律
x[n] (h1[n] h2 [n]) x[n] h1[n] x[n] h2 [n]
x(t ) (h1 (t ) h2 (t )) x(t ) h1 (t ) x(t ) h2 (t )
物理意义: (1)LTI系统对两个输入的和的响应等于对 单个输入响应的和
y[n]
k
x[k ]h [n]
k
• 若该线性系统又是时不变的 ,则有
hk [n] h[n k ]
其中h[n]是系统输入为δ[n]时的零状态响应, 称为单位脉冲(样本)(序列)响应 y[n] x[k ]h[n k ] 所以对LTI系统,有 : k 对照卷积的定义,有: y[n] x[n] h[n] 称为卷积和
通信中的编码器都是可逆的 例: y(t ) 2 x(t ) w(t ) 1 y(t )
2
y[n]
k
x[k ]
n
w[n] y[n] y[n 1]
不可逆:
y[n] c
y(t ) x (t )
2
2.2.3 因果性
因果系统 :系统在任何时刻的输出只决定于现在 的输入以及过去的输入
y (t )
因此当 h(t ) dt 时,输出为有界-充分性 亦可证必要性 h(t ) dt 连续时间LTI系统的稳定性 离散时间LTI系统的稳定性 h[n]
2.2 线性不变系统
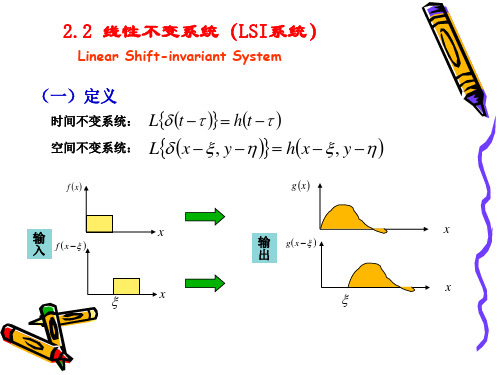
输入一个单 一频率的余 弦信号 系统 输出
只有输入频率的余弦信号,则是线性不变系统; 只有输入频率的余弦信号,则是线性不变系统; 还含有其他的频率,则不是线性不变系统! 还含有其他的频率,则不是线性不变系统!
g (t ) = K1 A2 sin ω1 (t − t0 ) + K 2 AB cos ω 2 (t − t0 ) = K1 g1 (t ) + K 2 g 2 (t )
从上式看出,此滤波器具有均匀性和叠加性, 从上式看出,此滤波器具有均匀性和叠加性,因此是一个 线性滤波器。 线性滤波器。
即
τ ' f 1 (t ) = A sin ω 1 (t − τ ) = f 1 (t − τ )
即:
{
}
g (x, y ) = f ( x, y ) * h( x, y )
输出函数 = 输入函数 * 单位脉冲响应
说明:系统的输出函数等于输入函数与系统的单位 说明:系统的输出函数等于输入函数与系统的单位 输出函数等于输入函数与系统的 脉冲响应的卷积 的卷积。 脉冲响应的卷积。
(二)线性不变系统的传递函数
如果例子中的输入有一个时间延迟
则输出响应可以表示成: 则输出响应可以表示成:
g '1 (t ) = A 2 sin ω 1 (t − τ − t 0 ) = g 1 (t − τ )
即输出响应同样有一个延迟 , 因此这个理想的滤波器是一个线性时间不变滤波器。 线性时间不变滤波器 因此这个理想的滤波器是一个线性时间不变滤波器。
线性时不变滤波器与系统

h( ) x(n )
| h( ) | | x(n ) |
C | h( ) | , 即 y ( n) 有界。 这说明该
系统具有BIBO稳定性。 2. 能量有限稳定性 对于一个系统或滤波器,如果其输入信号的能量 有限时,其输出信号的能量也是有限的, 则称该系统 或滤波器具有能量有限稳定性。 定理2 线性时不变系统 h(n) 具有能量有限稳定性 的充要条件是:h(n) 的频谱 H ( ) 是有界的, 即存在
二、稳定性
所谓系统的稳定性,是指当输入信号为有限时,输 信号也是有限的。而信号是有限的,有两种含义:
一是信号本身是有界的,即存在一正数 C , 使得
n, 均有 | x(n) | C;二是指信号的能量ຫໍສະໝຸດ 有限的,即n
x 2 ( n) .
1. 有界输入有界输出稳定性 当系统的输入信号 x(n) 有界时,输出信号 y (n) 也是有界的,则称该系统或滤波器具有有界输入有界 输出(BIBO)稳定性。 定理1 线性时不变系统 h(n) 具有有界输入有界输 出(BIBO)稳定性的充要条件是
n
| h(n) | .
证
必要性:对任何输入信号 x(n), 输出信号
y ( n) x ( n) h( n)
h( ) x(n ).
在上式中取 n 0, 得 y (0)
1, h( ) 0, 再取 x( ) 此时 x(n) 有界, 1, h( ) 0,
一是信号本身是有界的即存在一正数有界输入有界输出稳定性当系统的输入信号也是有界的则称该系统或滤波器具有有界输入有界输出bibo稳定性
线性时不变系统模型

线性时不变系统模型
ARMAX模型 模型
• 重新整理(4.14),在两边同时加上[1-C(q)] y(t|θ)
ˆ ˆ y (t | θ ) = B(q)u (t ) + [1 − A(q)] y (t ) + [C (q) − 1][ y (t ) − y (t | θ )]
(4.15)
• 在(4.15)中我们可以看出,历史的预测误差被 考虑了进来
线性时不变系统模型
ARX模型 模型
• 这样(4.6)就可以用一种更加简洁的方法表达
ˆ y (t | θ ) = θ T ϕ (t ) = ϕ T (t )θ
(4.7)
• 向量φ(t)是系统的输入和输出的历史数据,是已 知的 • θ是需要估计的参数,是未知的 • 这样的模型叫做线性自回归(linear regression),其中φ(t)是回归向量(regression vector) • 如何使用数学工具来估计参数向量θ,是我们系 统辨识的一项重要研究内容
(4.13) (4.14)
ˆ C (q) y (t | θ ) = B (q)u (t ) + [C (q) − A(q)] y (t )
• 由(4.14)可以看出,不同于ARX模型,如果要 计算ARMAX模型的一步预测值,我们不但要知 道系统输入u(t)和系统输出y(t)的历史值,我们还 要知道预测的历史值y(t|θ)的历史值
线性时不变系统模型
线性时不变系统模型组
• 对于y(t)的一步预测值,我们可以重写(3.6)
ˆ y (t | θ ) = H −1 (q, θ )G (q )u (t ) + [1 − H −1 (q, θ )] y (t ) (4.3)
• 与(4.2)是一个概率模型组不同的是,(4.3) 是一个预测模型组 • (4.3)里面包含了模型结构的信息,下面将使用 几种数学形式来描述(4.3)的模型结构
线性时不变系统

f1 (t )
C 11 C
C1 f1 (t )
f 2 (t )
C 22 C
H [[•]] H•
C2 f 2 (t )
∑
C1 H [ f1 (t )]
H [•]
H [C1 f1 (t ) + C2 f 2 (t )]
H [•]
H [ f (t ) ]
y (t )
f (t − τ )
τ
H[•]
y (t − τ )
H [ f (t − τ ) ]
f (t )
若
τ
H[ f (t −τ)] = y(t −τ)
是非时变系统,否则是时变系统。 则 系统 H • 是非时变系统,否则是时变系统。
[]
三.线性时不变系统的微分特性
线性时不变系统满足微分特性、积分特性 线性时不变系统满足微分特性、积分特性 微分特性
e(t )
de(t ) dt
r (t )
H
dr (t ) dt
H
∫
t
−∞
e(τ )dτ
∫
H
t
−∞
r (τ )dτ
三.线性时不变系统的微分特性
利用线性和时不变性证明,可推广至高阶。 利用线性和时不变性证明,可推广至高阶。 首先由时不变性可知, 首先由时不变性可知,激励 e(t ) 对应输出 r (t ) ,则激励 e(t − ∆t ) 再由叠加性与均匀性,时不变性可知, 产生 r (t − ∆t ) 。再由叠加性与均匀性,时不变性可知, 若激励为 e(t ) − e(t − ∆t ) 则响应为 r (t ) − r (t − ∆t )
线性时不变系统的应用

线性时不变系统(LTI system)是一类非常重要的信号处理系统,它在很多领域都有着广泛的应用。
本文将对线性时不变系统的定义、特性以及其在信号处理、控制系统、通信系统等方面的应用进行详细的介绍。
首先,我们来解释一下什么是线性时不变系统。
线性系统是指输出信号是输入信号的线性函数,即对于任意的输入信号x1和x2,以及任意的常数a1和a2,都有输出信号y1=ax1+by1和y2=ax2+by2。
时不变系统是指系统的输出信号只与输入信号的形态有关,而与时间无关。
因此,线性时不变系统就是既是线性系统又是时不变系统。
线性时不变系统有着许多优秀的特性,使得它在信号处理、控制系统、通信系统等领域都有着广泛的应用。
其中,最重要的优秀特性就是线性性和时不变性。
因为线性性使得系统的输出信号可以通过线性变换得到,而时不变性使得系统的输出信号与时间无关,这为信号的分析和处理带来了巨大的便利。
在信号处理领域,线性时不变系统可以用来模拟各种不同的信号处理器。
例如,低通滤波器就是一种常见的线性时不变系统,它可以用来消除高频噪声,使得信号更加平稳。
此外,线性时不变系统还可以用来提取信号的特征,例如通过频谱分析来获取信号的频率成分。
在控制系统领域,线性时不变系统也有着重要的应用。
例如,在飞行控制系统中,可以使用线性时不变系统来模拟飞机的运动方程,并通过调节系统的参数来实现飞机的姿态控制。
此外,在工业生产过程中,也可以使用线性时不变系统来控制生产设备的运行状态,从而实现生产过程的自动化。
在通信系统领域,线性时不变系统也有着广泛的应用。
例如,在数字通信系统中,可以使用线性时不变系统来模拟信道的传输特性,并通过调节系统的参数来实现信号的增益控制。
此外,在无线电通信系统中,也可以使用线性时不变系统来模拟电磁波的传播特性,并通过调节系统的参数来实现信号的功率控制。
总之,线性时不变系统是一类非常重要的信号处理系统,它在信号处理、控制系统、通信系统等领域都有着广泛的应用。
5-6线性时不变系统

线性时不变系统系统参数不随时间的变化而变化【系统参数一般为电路中的各种元件及激励源】从响应角度上看,系统响应与激励加入的时刻无关。
为什么这么说?例1:系统激励与响应之间的关系如下,判断是否为时不变系统?)()(2)0(*3cos )(t u t tf x t t y +=解:因为系统的初始状态【)0(x 】与激励【)(t f 】的系数均不是常数【初始状态)0(x 系数为t 3cos ,激励)(t f 的系数为t 2】,所以系统)(t y 是时变系统。
例2:判断系统)()(2)0(*3cos )(t u t tf x t t y +=是否为线性系统?分析:如何系统)(t y 满足可分解性,即)()()(t y t y t y zs zi +=,并且零输入响应)()()(21t y t y t y zi zi zi +=【即零输入响应zi y 满足零输入线性】,且)()(21t y t y y zs zs zs +=【即零状态响应zs y 也满足零状态线性】:1、对于零输入响应---判断是否满足零输入线性令)0(*3cos 11x t y zi =,)0(*3cos 22x t y zi =,因为212121)]0()0([*3cos )0(*3cos )0(*3cos zi zi y y x x t x t x t +=+=+,所以此系统的零输入响应满足零输入线性。
)]()0([),0(*3cos )()0(11111t y x x t t y x zi zi 对应输出状态状态=→,)]()0([),0(*3cos )()0(22222t y x x t t y x zi zi 对应输出状态状态=→ )]0()0([*3cos )0()0(2121x x t x x +=+2、对于零状态响应----判断是否满足零状态线性令)(2)(),(2)(2211t tf t y t tf t y zs zs ==,那么)]()([2)(2)(2)()(212121t f t f t t tf t tf t y t y zs zs +=+=+,所以,该系统也满足零状态线性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
x(k∆τ).∆τ.h(t −k∆τ)
则系统对输入x(t)的总响应为所有冲激响应之和: 则系统对输入x(t)的总响应为所有冲激响应之和: x(t)的总响应为所有冲激响应之和
yf (t) ≈ ∑x(k∆τ).∆τ.h(t −k∆τ)
当:
∞
∆τ →dτ,k∆τ →τ
∞ −∞
∞
k=−∞
求和符号改为积分符号
x1 (t ) = e −t 和x2 (t ) = 5e −t 求分别输入
时的输出y(t)。 。 时的输出
解:
y1 (t ) = (e −2t + e − t )u (t )
y2 (t ) = (−3e
−2 t
+ 5e )u (t )
−t
2.2 单位冲激响应
单位冲激响应: 单位冲激响应:线性时不变系统在单位冲激信 的激励下产生的零状态响应。 表示。 号 δ (t ) 的激励下产生的零状态响应。用h(t)表示。 表示 即:
x(t) = ∫ x(τ )δ (t −τ )dτ
−∞
y f (t) = ∫ x(τ )h(t −τ )dτ
上述积分是x(t)与h(t)之间的一种二元运算, 上述积分是x(t)与h(t)之间的一种二元运算,用 x(t) 之间的一种二元运算 y(t)=x(t)*h(t)表示 表示。 y(t)=x(t)*h(t)表示。即
第二章 线性时不变系统 (LTI:Linear Time Invarient) :
重点: 重点: 理解并掌握卷积积分与卷积和的概念与相关性质; 理解并掌握卷积积分与卷积和的概念与相关性质; 掌握LTI系统的性质; 系统的性质; 掌握 系统的性质 难点: 难点: 深刻理解卷积积分与卷积和的概念; 深刻理解卷积积分与卷积和的概念;
h(t ) ≡ T[{0},δ (t )]
分析如下电路:已知: 分析如下电路:已知:uc(0-)=0,求uc(t)。 , 。
2Ω + 1.5δ(t) + 0.25F -
解:建立系统的微分方程: 建立系统的微分方程:
uc(t)
-
du c RC + u c = 1.5δ (t ) dt du c 即: + 2u c = 3δ (t ) dt
∫
t
−∞
( x(τ ) ∗ h(τ ))dτ = ∫ x(τ )dτ ∗ h(t ) = x(t ) ∗ ∫ h(τ )dτ
−∞ −∞
t
t
应用类似的推演可以到处卷积的高阶导数或 多重积分之运算规律: 多重积分之运算规律: 则有: 设 y (t ) = x1 (t ) ∗ x2 (t ) ,则有:
y ( i ) (t ) = x1 (t ) ∗ x2
y(t) = x(t) *h(t) = ∫ x(τ )h(t −τ )dτ
−∞
∞
卷积积分的图解法 卷积的图解法有助于我们理解卷积的物理意义以及求 解步骤, x(t)*h(t)为例: (t)为例 解步骤,以x(t)* (t)为例: 1、将h(τ)反折,得h(-τ) 、 )反折, ) 2、将h(-τ)沿τ轴时延 秒,得得 -τ) 、 轴时延t秒 得得h(t- ) ) 轴时延 3、将x(τ)与 h(t-τ)相乘 ,得x(τ) h(t-τ) 、 ) - ) ) - ) 4、沿τ轴对 (τ) h(t-τ)积分 轴对x 、 轴对 ) - )
i =0 n
y x (t ) = T [( y(t0 ), }] {0
−
y f (t ) = T [{0} x(t )] ,
λi t
y f (t ) = ∑ c f i e λi t + y p (t )
i =0
n
例:已知一系统的微分方程为: 已知一系统的微分方程为:
y ' (t ) + 2 y (t ) = x(t ),且y (0 − ) = 2
(t ) ∗ x2 ' (t )
4.与冲激函数或阶跃函数的卷积 4.与冲激函数或阶跃函数的卷积
由于冲激函数是在t=0时给系统注入了一定的能量,而在 由于冲激函数是在 时给系统注入了一定的能量,而在t>0 时给系统注入了一定的能量 时刻, 时,系统的激励为0。相当于在 -到0+时刻,使系统具有了一 系统的激励为 。相当于在0 定的初始能量。因此, 定的初始能量。因此,系统的冲激响应与系统的零输入响应具 有相同的形式。这里, 表示系统的冲激响应。 有相同的形式。这里,用h(t)表示系统的冲激响应。即: 表示系统的冲激响应
h(t − τ )
1
x(τ )
(3)
− -2+t 2 1
0 1 tτ
3 1≤ t < 时 2 1 1 3 3 y (t ) = ∫ 1 (t − τ )dτ = t − − 2 4 16 2
(4)
h(t − τ )
1
x(τ )
3 ≤t <3 2
t τ
−
1 -2+t 2 0
1
1 t2 t 3 y (t ) = ∫ (t − τ )dτ = + + t −2 2 4 2 4
微分方程的特解形式: 微分方程的特解形式:
输入信号x(t) 输入信号x(t) 常数C 常数C
e at a ≠ λi
特解y 特解yp(t) 常数A 常数A
Ae at
j =0 L
e
at
a = λi
Ck t k ∑
k =0 L
λi为σ i重根
A j t j e at ∑
σi
Aj t j ∑
j =0
t
cos(ωt + β )
1
(5)
− 1 2
1
x(τ )
h(t − τ )
t > 3时,y (t ) = 0
0 1 -2+t t τ
y(t)
5 16
y(t)的时域波形如图所示: 的时域波形如图所示: 的时域波形如图所示
9 16
− 1 2
0
1
3 2
2
3
t
例:
x1(t) 1
x2(t) 1
-1
0
1
t
-2
0
2
t
求
y1 (t ) = x1 (t ) * x1 (t )
x(t) h1(t) h2(t) y(t)
(4)卷积的微分: 卷积的微分: 两个函数卷积后的导数等于其中一函数导数 与另一函数之卷积。即: 与另一函数之卷积。
( x(t ) ∗ h(t ))' = x' (t ) ∗ h(t ) = x(t ) ∗ h' (t )
(5)卷积的积分: )卷积的积分:
i =1
n −1
为无时限的信号, 设x(t)为无时限的信号,将它分解为一系列宽度为 ∆τ 的 为无时限的信号 窄脉冲之和。 窄脉冲之和。
x (t ) x ( k∆ τ )
0
k∆ τ
+∞
∆τ
t
当
∆τ → 0
则: x(t) ≈
k=−∞
∑x(k∆τ).∆τ.δ(t −k∆τ)
设系统的单位冲激响应为h(t),则系统对应于 τ t 设系统的单位冲激响应为h(t),则系统对应于 =k∆ 的 h(t), 冲激响应为
x(t ) ∗ [h1 (t ) + h2 (t )] = x(t ) ∗ h1 (t ) + x(t ) ∗ h2 (t )
h1(t) x(t) h2(t) y(t)
(3)卷积的结合律: 卷积的结合律:
( x(t ) ∗ h1 (t )) * h2 (t ) = x(t ) ∗ (h1 (t ) ∗ h2 (t ))
y1 (t) 2
y2 (t ) = x1 (t ) * x2 (t )
y2 (t) 2
解:
-2 0
2
t
-3
-1
1
3
t
例:已知
x(t ) = e − at u (t )
a>0
h(t ) = u (t )
求:
y (t ) = x(t ) * h(t )
x(τ) (
1
h( τ) (
1
t
t
例:已知
x(t ) = e u (−t ) h(t ) = u (t − 3)
h(t ) ≡ L[{0},δ (t )] = ceλt u(t )的形式。 这里,λ=-2。即h(t ) = ce-2t u(t )代入方程中: -2ce-2t u(t )+cδ (t ) + 2ce-2t u(t ) = 3δ (t ) ⇒c=3 ∴ h(t ) = 3e-2t u(t )
注意:单位冲击响应为系统的零状态响应。 注意:单位冲击响应为系统的零状态响应。
h(t) 1 1 t
x(t) 2 1 2 4 t
h(t-τ)
x(τ)
τ
t=0 t-1 t t<1
τ
1<t<2
τ
2<t<3
τ
3<t<4
τ
4<t<5
τ
如图所示, 例:设x(t)与h(t)如图所示,求y(t)=x(t)*h(t) 与 如图所示
x(t) 1
h(t) 1
−
1 2
0
1
t
0
2
t
h(−τ )
反折: 反折:
2.1
线性时不变连续系统的时域解法
连续时间系统处理连续时间信号, 连续时间系统处理连续时间信号,通常用微分 方程来描述系统。 方程来描述系统。
微分方程的经典解。 微分方程的经典解。 微分方程
∑a y
i =0 i
n
(i )
(t ) = ∑ b j x ( j ) (t )
