现代控制理论 离散时间系统、 时变系统和非线性系统的状态空间表达式
现代控制理论状态空间法

根据系统微分方程建立状态空间表达式.
1.输入项中不含输入导数项的线性系统空间状态 表达式
• 系统描述为:
y (n ) a1 y (n1) an1 y an y u
(1)
讨论:状态如何选择
y(t) C (t)x(t) D(t)u(t)
2)线性时不变系统: x Ax Bu y Cx Du
在通常情况下,大多数还是研究线性时不变 系 统,即线性定常系统,因此本课程的主要研究对 象是线性定常系统。
4.状态空间描述的结构图(或称状态变量图)
• 例:根据上例画出结构图. • 解:先将例子写成下述形式
现代控制理论
第一章 状态空间法
控制系统的状态空间描述
一.问题的引出 1 --古典控制理论的局限性 1、仅适用于SISO的线性定常系统(外部描述,
时不变系统) 2、古典控制理论本质上是复频域的方法.(理论) 3、设计是建立在试探的基础上的.(应用) 4、系统在初始条件为零,或初始松驰条件下,才
能采用传递函数.
定义2.状态变量
状态变量是确定系统状态的最小一组变量,如果以最
少的n个变量 x1 (t ), x2 (t ), , xn (t ) 可以完全描述系
统的行为 (即当t≥ 时输入和
t0
在t= t0初始状态给定后,系统的状态完全可以确定),那 么
x1 (t ), x2 (t ), 是一, xn组(t )状态变量.
(2)状态变量选取不唯一,有时选取状态变量仅为数 学描述所需,而非明确的物理意义。
(3)状态变量是系统的内部变量,一般情况下输出是 状态的函数,但输出总是希望可量测的。
(4)仅讨论有限个状态变量的系统。 (5)有限个数的状态变量的集合,称为状态向量。 (6)状态向量的取值空间称为状态空间。
现代控制理论知识点汇总

现代控制理论知识点汇总Revised at 2 pm on December 25, 2020.第一章 控制系统的状态空间表达式1. 状态空间表达式 n 阶DuCx y Bu Ax x+=+= 1:⨯r u 1:⨯m y n n A ⨯: r n B ⨯: n m C ⨯:r m D ⨯:A 称为系统矩阵,描述系统内部状态之间的联系;B为输入(或控制)矩阵,表示输入对每个状态变量的作用情况;C 输出矩阵,表示输出与每个状态变量间的组成关系,D直接传递矩阵,表示输入对输出的直接传递关系。
2. 状态空间描述的特点①考虑了“输入-状态-输出”这一过程,它揭示了问题的本质,即输入引起了状态的变化,而状态决定了输出。
②状态方程和输出方程都是运动方程。
③状态变量个数等于系统包含的独立贮能元件的个数,n 阶系统有n 个状态变量可以选择。
④状态变量的选择不唯一。
⑤从便于控制系统的构成来说,把状态变量选为可测量或可观察的量更为合适。
⑥建立状态空间描述的步骤:a 选择状态变量;b 列写微分方程并化为状态变量的一阶微分方程组;c 将一阶微分方程组化为向量矩阵形式,即为状态空间描述。
⑦状态空间分析法是时域内的一种矩阵运算方法,特别适合于用计算机计算。
3. 模拟结构图(积分器 加法器 比例器)已知状态空间描述,绘制模拟结构图的步骤:积分器的数目应等于状态变量数,将他们画在适当的位置,每个积分器的输出表示相应的某个状态变量,然后根据状态空间表达式画出相应的加法器和比例器,最后用箭头将这些元件连接起来。
4. 状态空间表达式的建立① 由系统框图建立状态空间表达式:a 将各个环节(放大、积分、惯性等)变成相应的模拟结构图;b 每个积分器的输出选作i x ,输入则为i x;c 由模拟图写出状态方程和输出方程。
② 由系统的机理出发建立状态空间表达式:如电路系统。
通常选电容上的电压和电感上的电流作为状态变量。
利用KVL 和KCL 列微分方程,整理。
现代控制理论第版课后习题答案

现代控制理论第版课后习题答案Prepared on 22 November 2020《现代控制理论参考答案》第一章答案1-1 试求图1-27系统的模拟结构图,并建立其状态空间表达式。
解:系统的模拟结构图如下: 系统的状态方程如下: 令y s =)(θ,则1x y =所以,系统的状态空间表达式及输出方程表达式为1-2有电路如图1-28所示。
以电压)(t u 为输入量,求以电感中的电流和电容上的电压作为状态变量的状态方程,和以电阻2R 上的电压作为输出量的输出方程。
解:由图,令32211,,x u x i x i c ===,输出量22x R y =有电路原理可知:•••+==+=++3213222231111x C x x x x R x L ux x L x R 既得22213322222131111111111x R y x C x C x x L x L R x u L x L x L R x =+-=+-=+--=•••写成矢量矩阵形式为:1-4 两输入1u ,2u ,两输出1y ,2y 的系统,其模拟结构图如图1-30所示,试求其状态空间表达式和传递函数阵。
解:系统的状态空间表达式如下所示: 1-5系统的动态特性由下列微分方程描述列写其相应的状态空间表达式,并画出相应的模拟结构图。
解:令..3.21y x y x y x ===,,,则有相应的模拟结构图如下: 1-6 (2)已知系统传递函数2)3)(2()1(6)(+++=s s s s s W ,试求出系统的约旦标准型的实现,并画出相应的模拟结构图解:ss s s s s s s s W 31233310)3(4)3)(2()1(6)(22++++-++-=+++= 1-7 给定下列状态空间表达式[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡321321321100210311032010x x x y u x x x x x x ‘(1) 画出其模拟结构图 (2) 求系统的传递函数 解:(2)⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+-+-=-=31103201)()(s s s A sI s W 1-8 求下列矩阵的特征矢量(3)⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=6712203010A 解:A 的特征方程 061166712230123=+++=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+---=-λλλλλλλA I 解之得:3,2,1321-=-=-=λλλ当11-=λ时,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---3121113121116712203010p p p p p p 解得: 113121p p p -== 令111=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1113121111p p p P(或令111-=p ,得⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1113121111p p p P ) 当21-=λ时,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---32221232221226712203010p p p p p p 解得: 1232122221,2p p p p =-= 令212=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1423222122p p p P(或令112=p ,得⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=21213222122p p p P )当31-=λ时,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---33231333231336712203010p p p p p p 解得: 133313233,3p p p p =-= 令113=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=3313323133p p p P1-9将下列状态空间表达式化成约旦标准型(并联分解)(2)⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡32121321321110021357213311201214x x x y y u x x x x x x解:A 的特征方程 0)3)(1(311212142=--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡------=-λλλλλλA I 当31=λ时,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--3121113121113311201214p p p p p p 解之得 113121p p p == 令111=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1113121111p p p P当32=λ时,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--1113311201214312111312111p p p p p p 解之得 32222212,1p p p p =+= 令112=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=0013222122p p p P当13=λ时,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--332313332313311201214p p p p p p 解之得3323132,0p p p == 令133=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1203323133p p p P约旦标准型1-10 已知两系统的传递函数分别为W 1(s)和W 2(s)试求两子系统串联联结和并联连接时,系统的传递函数阵,并讨论所得结果 解:(1)串联联结 (2)并联联结1-11 (第3版教材)已知如图1-22所示的系统,其中子系统1、2的传递函数阵分别为求系统的闭环传递函数解:1-11(第2版教材) 已知如图1-22所示的系统,其中子系统1、2的传递函数阵分别为求系统的闭环传递函数 解:1-12 已知差分方程为试将其用离散状态空间表达式表示,并使驱动函数u 的系数b(即控制列阵)为(1)⎥⎦⎤⎢⎣⎡=11b解法1: 解法2:求T,使得⎥⎦⎤⎢⎣⎡=-111B T 得⎥⎦⎤⎢⎣⎡=-10111T 所以 ⎥⎦⎤⎢⎣⎡-=1011T 所以,状态空间表达式为第二章习题答案2-4 用三种方法计算以下矩阵指数函数At e 。
现代控制理论-第二章 控制系统的状态空间描述

DgXu
2.2.1.由物理机理直接建立状态空间表达式: 例2.2.1 系统如图所示
L
R2
u
iL
R1
uc
选择状态变量:
x1 iL , x2 uC ,
13 中南大C diL 1 iL (u L ) C dt R1 dt duC diL L uC C R2 u dt dt
y(s) [C(sI A) B D]U (s)
1
1
得
9
G(s) C (sI A) B D
命题得证
中南大学信息学院自动化系
1
DgXu
例2.1.3
已知系统的状态空间描述为
x1 0 1 0 x1 0 x 0 1 1 x 1 u 2 2 x3 0 0 3 x3 1
28 中南大学信息学院自动化系
DgXu
故有(n-1) 个状态方程:
对xl求导数且考虑式 (2.3.12),经整理有:
则式 (2.3.12) bn=0 时的动态方程为:
(2.3.16)
式中:
29 中南大学信息学院自动化系
DgXu
30 中南大学信息学院自动化系
DgXu
3)
化输入-输出描述为状态空间描述
11 中南大学信息学院自动化系
DgXu
2.3. 线性定常连续系统状态空间表达式的建立
建立状态空间表达式的方法主要有两种: 一是直接根据系统的机理建立相应的微分方程或差分方 程,继而选择有关的物理量作为状态变量,从而导出其状态 空间表达式; 二是由已知的系统其它数学模型经过转化而得到状态达 式。由于微分方程和传递函数是描述线性定常连续系统常用 的数学模型,故我们将介绍已知 n 阶系统微分方程或传递函 数时导出状态空间表达式的一般方法,以便建立统一的研究 理论,揭示系统内部固有的重要结构特性。
现代控制理论-第1章

它的模拟结构图示于下图
再以三阶微分方程为例: 将最高阶导数留在等式左边,上式可改写成 它的模拟结构图示于下图
同样,已知状态空间表达式,也可画出相应的模拟结构图,下图是下列 三阶系统的模拟结构图。
试画出下列二输入二输出的二阶系统的模拟结构图。
1.3 状态变量及状态空间表达式的建立(一)
(63)
故U—X间的传递函数为:
它是一个
的列阵函数。
间的传递函数为:
它是一个标量。
2.多输入一多输出系统 已知系统的状态空间表达式:
(64)
(66) 式中, 为r×1输入列矢量; 为m×1输出列矢量;B为n×r控制矩阵; C为m×n输出矩阵;D为m×r直接传递阵;X,A为同单变量系统。
同前,对式(66)作拉氏变换并认为初始条件为零,得:
(9)
2021/3/11
11
2021/3/11
12
因而多输入一多输出系统状态空间表达式的矢量矩阵形式为: (10)
式中,x和A为同单输入系统,分别为n维状态矢量和n×n系统矩阵;
为r维输入(或控制)矢量;
为m维输出矢量;
为了简便,下面除特别申明,在输出方程中,均不考虑输入矢量的直接 传递,即令D = 0 。注意:矢量是小写字母,矩阵是大写字母。
1.4.2 传递函数中有零点时的实现 此时,系统的微分方程为:
相应地,系统传递函数为:
设待实现的系统传递函数为:
因为
上式可变换为
(26)
令 则 对上式求拉氏反变换,可得:
2021/3/11
31
每个积分器的输出为一个状态变量,可得系统的状态空问表达式: 或表示为: 推广到 阶系统,式(26)的实现可以为:
现代控制理论--刘豹优秀PPT

1.3.1 从系统框图出发建立状态空间表达式 该法是首先将系统的各个环节,变换成相应的模拟结构图,并把每个积
1.4.2 传递函数中有零点时的实现
22
此时,系统的微分方程为: 相应地,系统传递函数为:
设待实现的系统传递函数为:
因为
上式可变换为
(26)
23
令 则 对上式求拉氏反变换,可得: 每个积分器的输出为一个状态变量,可得系统的状态空问表达式:
24
或表示为:
推广到 阶系统,式(26)的实现可以为:
25
(4)
6
在经典控制理论中,用指定某个输出量的高阶微分方程来描述系统的 动态过程。如上图一所示的系统,在以 作输出时,从式(1)消去中间变量 i,得到二阶微分方程为:
(5)
其相应的传递函数为:
(6)
回到式(5)或式(6)的二阶系统,若改选 和 作为两个状态变量,
即令
则得一阶微分方程组为:
7
设单输入一单输出定常系统,其状态变量为 状态方程的一般形式为:
2
1.1.3 状态方程 以状态变量
为坐标轴所构成的 维空间,称为
状态空间。
1.1.4 状态方程
由系统的状态变量构成的一阶微分方程组称为系统的状态方程。 用图下所示的 网络,说明如何用状态变量描述这一系统。
图一
3
根据电学原理,容易写出两个含有状态变量的一阶微分方程组:
亦即
(1)
式(1)就是图1.1系统的状态方程,式中若将状态变量用一般符号 ,
现代控制理论 第1章 状态空间描述

得动态方程组 1 x2 x k b 1 x 2 y y u y m m m k b 1 x1 x2 u m m m y x 1
问题:到底有 何区别?
13
状态空间表达式为
1 0 x k x 2 m
如果将储能元件的物理变量选为系统的状态变量,则状态变量的个数 等于系统中独立储能元件的个数
5
基本概念
状态方程:系统状态方程描述的结构图如下图所示
假设:causal system ——现在的输出只取决 于现在和过去的输入, 而与将来的输入无关。
输入引起状态的变化是一个动态过程,每个状态变量的一阶导数与所有 状态变量和输入变量的数学表达(常微分方程ODE)称为状态方程,一般形式 为:
1896192019872006状态变量和状态空间表达式状态变量和状态空间表达式化输入化输入输出方程为状态空间表达式输出方程为状态空间表达式系统的线性变换对角线标准型和约当标准型系统的线性变换对角线标准型和约当标准型由状态空间表达式导出传递函数阵由状态空间表达式导出传递函数阵离散时间系统的状态空间表达式离散时间系统的状态空间表达式时变系统的状态空间表达式时变系统的状态空间表达式从系统黑箱的输入输出因果关系中获悉系统特性传递函数描述属系统的外部描述系统的内部描述白箱系统完整地表征了系统的动力学特征状态空间表达式属系统的内部描述状态变量
x1 f1 ( x1 , x2 f 2 ( x1 , xn f n ( x1 , , xn , u1 , , xn , u1 , , xn , u1 , , um , t ) , um , t ) , um , t )
标量形式,繁琐!
6
矢量形式
现代控制理论(第二章)讲解

sI
A 1
s 2
s3
1 1 s 3
(s
1)(s 2
2)
(s 1)(s 2)
1
(s
1)(s s
2)
(s 1)(s 2)
s3
e At
L1
(s
1)( s 2
2)
(s 1)(s 2)
EAST CHINA INSTITUTE OF TECHNOLOgy
第二章 控制系统状态空间表达式的解
2.1 线性定常齐次状态方程的解(自由解) 2.2 矩阵指数函数——状态转移矩阵 2.3 线性定常系统非齐次方程的解 2.4 * 线性时变系统的解 2.5 * 离散时间系统状态方程的解 2.6* 连续时间状态空间表达式的离散化
(s
1)( s 2
2)
(s 1)(s 2)
1
(s
1)( s s
2)
(s 1)(s 2)
eAt L1
sI A 1
2et e2t 2et 2e2t
et e2t
et
2e2t
et
2e2t
例2-6,利用凯莱-哈密顿定理— -----------------自学! 例2-3与例2-7也请注意自学!
EAST CHINA INSTITUTE OF TECHNOLOgy
2.3 线性定常系统非齐次方程的解
现在讨论线性定常系统在控制作用 方程为非齐次矩阵微分方程:
现代控制理论基础-第2章-控制系统的状态空间描述精选全文完整版

(2-18)
解之,得向量-矩阵形式的状态方程
(2-19)
输出方程为
(2-20)
(5) 列写状态空间表达式
将式(2-19)和式(2-20)合起来即为状态空间表达式,若令
则可得状态空间表达式的一般式,即
(2-21)
例2.2 系统如图
取状态变量:
得:
系统输出方程为:
写成矩阵形式的状态空间表达式为:
1.非线性系统
用状态空间表达式描述非线性系统的动态特性,其状态方程是一组一阶非线性微分方程,输出方程是一组非线性代数方程,即
(2-7)
2. 线性系统的状态空间描述
若向量方程中 和 的所有组成元都是变量 和 的线性函数,则称相应的系统为线性系统。而线性系统的状态空间描述可表示为如下形式: (2-8) 式中,各个系数矩阵分别为 (2-9)
4.线性定常系统的状态空间描述
式中的各个系数矩阵为常数矩阵
当系统的输出与输入无直接关系(即 )时,称为惯性系统;相反,系统的输出与输入有直接关系(即 )时,称为非惯性系统。大多数控制系统为惯性系统,所以,它们的动态方程为
(2-11)
1.系统的基本概念 2. 动态系统的两类数学描述 3. 状态的基本概念
2.2 状态空间模型
2.2.1状态空间的基本概念
1.系统的基本概念
■系统:是由相互制约的各个部分有机结合,且具有一定功能的整体。 ■静态系统:对于任意时刻t,系统的输出惟一地取决于同一时刻的输入,这类系统称为静态系统。静态系统亦称为无记忆系统。静态系统的输入、输出关系为代数方程。 ■动态系统:对任意时刻,系统的输出不仅与t时刻的输入有关,而且与t时刻以前的累积有关(这种累积在t0(t0<t)时刻以初值体现出来),这类系统称为动态系统。由于t0时刻的初值含有过去运动的累积,故动态系统亦称为有记忆系统。动态系统的输入、输出关系为微分方程。
现代控制理论知识点汇总

第一章控制系统的状态空间表达式1. 状态空间表达式n 阶 DuCx y Bu Ax x +=+= 1:⨯r u 1:⨯m y n n A ⨯: r n B ⨯: n m C ⨯:r m D ⨯:A 称为系统矩阵,描述系统内部状态之间的联系;B为输入(或控制)矩阵,表示输入对每个状态变量的作用情况;C 输出矩阵,表示输出与每个状态变量间的组成关系,D直接传递矩阵,表示输入对输出的直接传递关系。
2. 状态空间描述的特点①考虑了“输入-状态-输出”这一过程,它揭示了问题的本质,即输入引起了状态的变化,而状态决定了输出。
②状态方程和输出方程都是运动方程。
③状态变量个数等于系统包含的独立贮能元件的个数,n 阶系统有n 个状态变量可以选择。
④状态变量的选择不唯一。
⑤从便于控制系统的构成来说,把状态变量选为可测量或可观察的量更为合适。
⑥建立状态空间描述的步骤:a 选择状态变量;b 列写微分方程并化为状态变量的一阶微分方程组;c 将一阶微分方程组化为向量矩阵形式,即为状态空间描述。
⑦状态空间分析法是时域内的一种矩阵运算方法,特别适合于用计算机计算。
3. 模拟结构图(积分器 加法器 比例器)已知状态空间描述,绘制模拟结构图的步骤:积分器的数目应等于状态变量数,将他们画在适当的位置,每个积分器的输出表示相应的某个状态变量,然后根据状态空间表达式画出相应的加法器和比例器,最后用箭头将这些元件连接起来。
4. 状态空间表达式的建立① 由系统框图建立状态空间表达式:a 将各个环节(放大、积分、惯性等)变成相应的模拟结构图;b 每个积分器的输出选作i x ,输入则为i x;c 由模拟图写出状态方程和输出方程。
② 由系统的机理出发建立状态空间表达式:如电路系统。
通常选电容上的电压和电感上的电流作为状态变量。
利用KVL 和KCL 列微分方程,整理。
③由描述系统的输入输出动态方程式(微分方程)或传递函数,建立系统的状态空间表达式,即实现问题。
现代控制理论第版课后习题答案

现代控制理论第版课后习题答案Document number:WTWYT-WYWY-BTGTT-YTTYU-2018GT《现代控制理论参考答案》第一章答案1-1 试求图1-27系统的模拟结构图,并建立其状态空间表达式。
解:系统的模拟结构图如下: 系统的状态方程如下: 令y s =)(θ,则1x y =所以,系统的状态空间表达式及输出方程表达式为1-2有电路如图1-28所示。
以电压)(t u 为输入量,求以电感中的电流和电容上的电压作为状态变量的状态方程,和以电阻2R 上的电压作为输出量的输出方程。
解:由图,令32211,,x u x i x i c ===,输出量22x R y =有电路原理可知:•••+==+=++3213222231111x C x x x x R x L ux x L x R 既得22213322222131111111111x R y x C x C x x L x L R x u L x L x L R x =+-=+-=+--=•••写成矢量矩阵形式为:1-4 两输入1u ,2u ,两输出1y ,2y 的系统,其模拟结构图如图1-30所示,试求其状态空间表达式和传递函数阵。
解:系统的状态空间表达式如下所示: 1-5系统的动态特性由下列微分方程描述列写其相应的状态空间表达式,并画出相应的模拟结构图。
解:令..3.21y x y x y x ===,,,则有相应的模拟结构图如下: 1-6 (2)已知系统传递函数2)3)(2()1(6)(+++=s s s s s W ,试求出系统的约旦标准型的实现,并画出相应的模拟结构图解:ss s s s s s s s W 31233310)3(4)3)(2()1(6)(22++++-++-=+++= 1-7 给定下列状态空间表达式[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡321321321100210311032010x x x y u x x x x x x ‘(1) 画出其模拟结构图 (2) 求系统的传递函数 解:(2)⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+-+-=-=31103201)()(s s s A sI s W 1-8 求下列矩阵的特征矢量(3)⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=6712203010A 解:A 的特征方程 061166712230123=+++=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+---=-λλλλλλλA I 解之得:3,2,1321-=-=-=λλλ当11-=λ时,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---3121113121116712203010p p p p p p 解得: 113121p p p -== 令111=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1113121111p p p P(或令111-=p ,得⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1113121111p p p P ) 当21-=λ时,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---32221232221226712203010p p p p p p 解得: 1232122221,2p p p p =-= 令212=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1423222122p p p P(或令112=p ,得⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=21213222122p p p P )当31-=λ时,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---33231333231336712203010p p p p p p 解得: 133313233,3p p p p =-= 令113=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=3313323133p p p P1-9将下列状态空间表达式化成约旦标准型(并联分解)(2)⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡32121321321110021357213311201214x x x y y u x x x x x x解:A 的特征方程 0)3)(1(311212142=--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡------=-λλλλλλA I 当31=λ时,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--3121113121113311201214p p p p p p 解之得 113121p p p == 令111=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1113121111p p p P当32=λ时,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--1113311201214312111312111p p p p p p 解之得 32222212,1p p p p =+= 令112=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=0013222122p p p P当13=λ时,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--332313332313311201214p p p p p p 解之得3323132,0p p p == 令133=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1203323133p p p P约旦标准型1-10 已知两系统的传递函数分别为W 1(s)和W 2(s)试求两子系统串联联结和并联连接时,系统的传递函数阵,并讨论所得结果 解:(1)串联联结 (2)并联联结1-11 (第3版教材)已知如图1-22所示的系统,其中子系统1、2的传递函数阵分别为求系统的闭环传递函数解:1-11(第2版教材) 已知如图1-22所示的系统,其中子系统1、2的传递函数阵分别为求系统的闭环传递函数 解:1-12 已知差分方程为试将其用离散状态空间表达式表示,并使驱动函数u 的系数b(即控制列阵)为(1)⎥⎦⎤⎢⎣⎡=11b解法1: 解法2:求T,使得⎥⎦⎤⎢⎣⎡=-111B T 得⎥⎦⎤⎢⎣⎡=-10111T 所以 ⎥⎦⎤⎢⎣⎡-=1011T 所以,状态空间表达式为第二章习题答案2-4 用三种方法计算以下矩阵指数函数At e 。
第1章 控制系统的状态空间表达式

1 选择状态变量 每一个方块的后面,除比例环节。 2 列写状态方程 4 列写状态空间形式
3 列写输出方程
1.3 状态空间表达式的建立(一)
例1.3-2 系统方块图如下,输入为u,输出为y,试求其状态空间表达式
例1.3-3 系统方块图如下,输入为u,输出为y,试求其状态空间表达式
1.3 状态空间表达式的建立(一)
1.1 状态变量及状态空间表达式
例题 1.1-1 【解答】 3 列写状态方程和输出方程
(2)输出方程
y uC x1
x1 y 1 0 x2
4 列写状态空间表达式
x Ax Bu y Cx Du
1 0 0 C A ,B 1 1 R L L L C 1 0 , D 0
绪论
本章结构 • 第1章 控制系统的状态空间表达式
1.1 状态变量及状态空间表达式 1.2 状态空间表达式的模拟结构图 1.3 状态空间表达式的建立(一) 1.4 状态空间表达式的建立(二) 1.5 状态变量的线性变换 1.6 从状态空间表达式求传递函数 1.7 离散时间系统的状态空间表达式 1.8 时变系统和非线性系统的状态空间表达式
7 状态空间表达式
状态方程+输出方程,构成一个系统完整的动态描述:
x(t ) Ax(t ) Bu (t ) (1.1 5) y (t ) Cx(t ) Du (t )
1.1 状态变量及状态空间表达式
例1.1-1 求R-L-C电路的状态空间表 达式,输出为电容两端电压
R1 R1 1 di1 i i u 1 2 dt L1 L1 L1 u R R2 di2 R1 i2 1 i2 c L2 L2 L2 dt du c 1 i2 C dt
王孝武主编《现代控制理论基础》(第3版)课件

x1 x2
xn
0 u 0
1
x1
y b0
b1
bn1
xn
注:如果输入项的导数阶次和输出项导数阶次相同,则有d。
Y (s) R(s)
bn s n an s n
b1s b0 a1s a0
d
bn1sn1 b1s b0 ansn a1s a0
例1-4 已知描述系统的微分方程为 y18y 192y 640y 160u 640u
0
0
0 1 an1
x1 x2
xn
0
0
b0
u
系统的状态图如下:
x1
y 1
0
0
xn
1.2.2 微分方程中含有输入信号导数项
(一)待定系数法
首先考察三阶系统,其微分方程为 y a2 y a1 y a0 y b3u b2u b1u b0u
┆ xn1 xn z(n1)
xn z(n) a0 x1 a1x2 an1xn b0u
y
b z (n1) n1
b1z
b0 z
b0 x1
b1x2
bn1xn
写成矩阵形式
x1
x2
xn
0
0
0
a0
1 0 0 a1
0 1 0 a2
0 0 0 a3
0
0
0 1 an1
2. 线性时变系统: x A(t)x B(t)u y C(t)x D(t)u
3. 非线性定常系统:
x = f(x, u) y = g(x, u)
4. 非线性时变系统:
x = f(x, u, t ) y = g(x, u, t )
1.1.3 状态变量的选取 (1) 状态变量的选取可以视问题的性质和输入特性而定
《现代控制理论》刘豹著(第3版)课后习题答案(最完整版)

第一章习题答案1-1 试求图1-27系统的模拟结构图,并建立其状态空间表达式。
11K s K K p +sK s K p 1+s J 11sK n 22s J K b -++-+-)(s θ)(s U 图1-27系统方块结构图解:系统的模拟结构图如下:)(s U )(s θ---+++图1-30双输入--双输出系统模拟结构图1K pK K 1pK K 1+++pK n K ⎰⎰⎰11J ⎰2J K b ⎰⎰-1x 2x 3x 4x 5x 6x系统的状态方程如下:u K K x K K x K K x X K x K x x x x J K x J x J K x J K x x J K x x x pp p p n p b1611166131534615141313322211+--=+-==++--===∙∙∙∙∙∙令y s =)(θ,则1x y =所以,系统的状态空间表达式及输出方程表达式为[]⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡-----=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡∙∙∙∙∙∙654321165432111111112654321000001000000000000010010000000000010x x x x x x y uK K x x x x x x K K K K K K J K J J K J K J K x x x x x x p p pp n p b1-2有电路如图1-28所示。
以电压)(t u 为输入量,求以电感中的电流和电容上的电压作为状态变量的状态方程,和以电阻2R 上的电压作为输出量的输出方程。
R1L1R2L2CU---------Uc---------i1i2图1-28 电路图解:由图,令32211,,x u x i x i c ===,输出量22x R y =有电路原理可知:∙∙∙+==+=++3213222231111x C x x x x R x L ux x L x R 既得22213322222131111111111x R y x C x C x x L x L R x u L x L x L R x =+-=+-=+--=∙∙∙写成矢量矩阵形式为:[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡----=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡32121321222111321000*********x x x R y u L x x x CC L L R L L R x x x 。
现代控制理论第3版课后答案
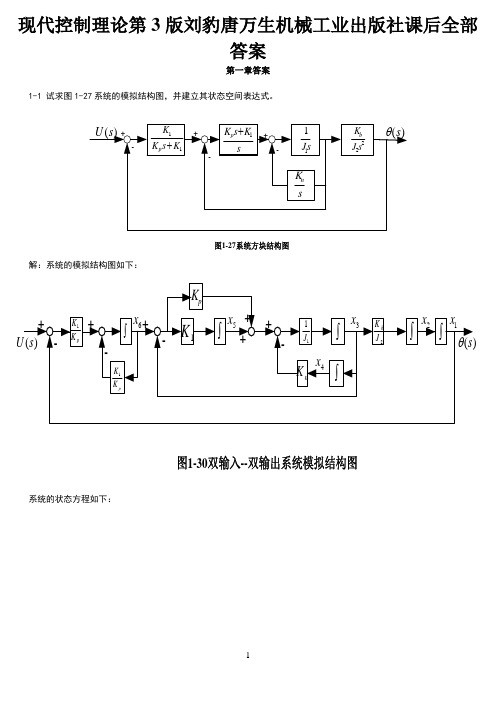
现代控制理论第3版刘豹唐万生机械工业出版社课后全部答案第一章答案1-1 试求图1-27系统的模拟结构图,并建立其状态空间表达式。
图1-27系统方块结构图解:系统的模拟结构图如下:图1-30双输入--双输出系统模拟结构图系统的状态方程如下:u K K x K K x K K x X K x K x x x x J K x J x J K x J K x x J K x x x pp p p n p b1611166131534615141313322211+--=+-==++--===••••••令y s =)(θ,则1x y =所以,系统的状态空间表达式及输出方程表达式为[]⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡-----=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡••••••654321165432111111112654321000001000000000000010010000000000010x x x x x x y uK K x x x x x x K K K K K K J K J J K J K J K x x x x x x p p pp npb1-2有电路如图1-28所示。
以电压)(t u 为输入量,求以电感中的电流和电容上的电压作为状态变量的状态方程,和以电阻2R 上的电压作为输出量的输出方程。
U图1-28 电路图解:由图,令32211,,x u x i x i c ===,输出量22x R y =有电路原理可知:•••+==+=++3213222231111x C x x x x R x L ux x L x R 既得22213322222131111111111x R y x C x C x x L x L R x u L x L x L R x =+-=+-=+--=•••写成矢量矩阵形式为:[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡----=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡32121321222111321000*********x x x R y u L x x x CCL L R L L R x x x 。
现代控制理论第版课后习题答案

现代控制理论参考答案第一章答案1-1 试求图1-27系统的模拟结构图,并建立其状态空间表达式; 解:系统的模拟结构图如下: 系统的状态方程如下: 令y s =)(θ,则1x y =所以,系统的状态空间表达式及输出方程表达式为1-2有电路如图1-28所示;以电压)(t u 为输入量,求以电感中的电流和电容上的电压作为状态变量的状态方程,和以电阻2R 上的电压作为输出量的输出方程; 解:由图,令32211,,x u x i x i c ===,输出量22x R y =有电路原理可知:•••+==+=++3213222231111x C x x x x R x L ux x L x R 既得22213322222131111111111x R y x C x C x x L x L R x u L x L x L R x =+-=+-=+--=•••写成矢量矩阵形式为:1-4 两输入1u ,2u ,两输出1y ,2y 的系统,其模拟结构图如图1-30所示,试求其状态空间表达式和传递函数阵;解:系统的状态空间表达式如下所示: 1-5系统的动态特性由下列微分方程描述列写其相应的状态空间表达式,并画出相应的模拟结构图; 解:令..3.21y x y x y x ===,,,则有 相应的模拟结构图如下: 1-6 2已知系统传递函数2)3)(2()1(6)(+++=s s s s s W ,试求出系统的约旦标准型的实现,并画出相应的模拟结构图解:ss s s s s s s s W 31233310)3(4)3)(2()1(6)(22++++-++-=+++=1-7 给定下列状态空间表达式[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡321321321100210311032010x x x y u x x x x x x ‘(1) 画出其模拟结构图(2) 求系统的传递函数 解:2⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+-+-=-=31103201)()(s s s A sI s W 1-8 求下列矩阵的特征矢量3⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=6712203010A 解:A 的特征方程 061166712230123=+++=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+---=-λλλλλλλA I 解之得:3,2,1321-=-=-=λλλ当11-=λ时,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---3121113121116712203010p p p p p p 解得: 113121p p p -== 令111=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1113121111p p p P 或令111-=p ,得⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1113121111p p p P 当21-=λ时,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---32221232221226712203010p p p p p p解得: 1232122221,2p p p p =-= 令212=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1423222122p p p P或令112=p ,得⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=21213222122p p p P 当31-=λ时,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---33231333231336712203010p p p p p p 解得: 133313233,3p p p p =-= 令113=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=3313323133p p p P 1-9将下列状态空间表达式化成约旦标准型并联分解2⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡32121321321110021357213311201214x x x y y u x x x x x x解:A 的特征方程 0)3)(1(311212142=--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡------=-λλλλλλA I 当31=λ时,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--3121113121113311201214p p p p p p 解之得 113121p p p == 令111=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1113121111p p p P 当32=λ时,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--1113311201214312111312111p p p p p p解之得 32222212,1p p p p =+= 令112=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=0013222122p p p P 当13=λ时,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--332313332313311201214p p p p p p 解之得3323132,0p p p == 令133=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1203323133p p p P约旦标准型1-10 已知两系统的传递函数分别为W 1s 和W 2s试求两子系统串联联结和并联连接时,系统的传递函数阵,并讨论所得结果 解:1串联联结 2并联联结1-11 第3版教材已知如图1-22所示的系统,其中子系统1、2的传递函数阵分别为 求系统的闭环传递函数 解:1-11第2版教材 已知如图1-22所示的系统,其中子系统1、2的传递函数阵分别为 求系统的闭环传递函数 解:1-12 已知差分方程为试将其用离散状态空间表达式表示,并使驱动函数u 的系数b 即控制列阵为 1⎥⎦⎤⎢⎣⎡=11b 解法1: 解法2:求T,使得⎥⎦⎤⎢⎣⎡=-111B T 得⎥⎦⎤⎢⎣⎡=-10111T 所以 ⎥⎦⎤⎢⎣⎡-=1011T 所以,状态空间表达式为第二章习题答案2-4 用三种方法计算以下矩阵指数函数At e ;2 A=1141⎛⎫⎪⎝⎭解:第一种方法: 令0I A λ-=则11041λλ--=-- ,即()2140λ--=;求解得到13λ=,21λ=- 当13λ=时,特征矢量11121p p p ⎡⎤=⎢⎥⎣⎦由 111Ap p λ=,得11112121311341p p p p ⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦即112111112121343p p p p p p +=⎧⎨+=⎩,可令112p ⎡⎤=⎢⎥⎣⎦当21λ=-时,特征矢量12222p p p ⎡⎤=⎢⎥⎣⎦由222Ap p λ=,得121222221141p p p p -⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦即1222121222224p p p p p p +=-⎧⎨+=-⎩ ,可令212p ⎡⎤=⎢⎥-⎣⎦则1122T ⎡⎤=⎢⎥-⎣⎦,111241124T -⎡⎤⎢⎥=⎢⎥⎢⎥-⎢⎥⎣⎦第二种方法,即拉氏反变换法:第三种方法,即凯莱—哈密顿定理 由第一种方法可知13λ=,21λ=-2-5 下列矩阵是否满足状态转移矩阵的条件,如果满足,试求与之对应的A 阵;3()22222222t tt t ttt t e e e e t e e e e --------⎡⎤--Φ=⎢⎥--⎣⎦ 4()()()()3333112412t t t t t tt t e e e e t e e e e ----⎡⎤+-+⎢⎥Φ=⎢⎥⎢⎥-++⎢⎥⎣⎦解:3因为 ()10001I ⎡⎤Φ==⎢⎥⎣⎦,所以该矩阵满足状态转移矩阵的条件 4因为()10001I ⎡⎤Φ==⎢⎥⎣⎦,所以该矩阵满足状态转移矩阵的条件2-6 求下列状态空间表达式的解:初始状态()101x ⎡⎤=⎢⎥⎣⎦,输入()u t 时单位阶跃函数;解: 0100A ⎡⎤=⎢⎥⎣⎦ 因为 01B ⎡⎤=⎢⎥⎣⎦,()()u t I t =2-9 有系统如图所示,试求离散化的状态空间表达式;设采样周期分别为T=和1s,而1u 和2u 为分段常数; 图 系统结构图 解:将此图化成模拟结构图 列出状态方程则离散时间状态空间表达式为 由()At G T e =和()0TAt H T e dtB =⎰得:当T=1时 ()()()()11111001111k e e x k x k u k e ke ----⎡⎤-⎡⎤+=+⎢⎥⎢⎥--⎢⎥⎣⎦⎣⎦当T=时 ()()()()()0.10.10.10.11001110.90.1k e e x k x k u k e k e ----⎡⎤-⎡⎤⎢⎥+=+⎢⎥⎢⎥---⎣⎦⎣⎦第三章习题3-1判断下列系统的状态能控性和能观测性;系统中a,b,c,d 的取值对能控性和能观性是否有关,若有关,其取值条件如何 1系统如图所示: 解:由图可得: 状态空间表达式为:由于•2x 、•3x 、•4x 与u 无关,因而状态不能完全能控,为不能控系统;由于y 只与3x 有关,因而系统为不完全能观的,为不能观系统; 3系统如下式:解:如状态方程与输出方程所示,A 为约旦标准形;要使系统能控,控制矩阵b 中相对于约旦块的最后一行元素不能为0,故有0,0≠≠b a ;要使系统能观,则C 中对应于约旦块的第一列元素不全为0,故有0,0≠≠d c ; 3-2时不变系统试用两种方法判别其能控性和能观性; 解:方法一:方法二:将系统化为约旦标准形;⎥⎦⎤⎢⎣⎡=1-111T ,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=21212121T 1- B T -1中有全为零的行,系统不可控;CT 中没有全为0的列,系统可观; 3-3确定使下列系统为状态完全能控和状态完全能观的待定常数i i βα和 解:构造能控阵:要使系统完全能控,则211αα≠+,即0121≠+-αα 构造能观阵:要使系统完全能观,则121αα-≠-,即0121≠+-αα 3-4设系统的传递函数是1当a 取何值时,系统将是不完全能控或不完全能观的 2当a 取上述值时,求使系统的完全能控的状态空间表达式; 3当a 取上述值时,求使系统的完全能观的状态空间表达式; 解:1 方法1 :)6)(3)(1()()()(++++==s s s as s u s y s W 系统能控且能观的条件为Ws 没有零极点对消;因此当a=1,或a=3或a=6时,系统为不能控或不能观; 方法2:系统能控且能观的条件为矩阵C 不存在全为0的列;因此当a=1,或a=3或a=6时,系统为不能控或不能观;2当a=1, a=3或a=6时,系统可化为能控标准I 型3根据对偶原理,当a=1, a=2或a=4时,系统的能观标准II 型为 3-6已知系统的微分方程为:u y y y y 66116...=+++试写出其对偶系统的状态空间表达式及其传递函数; 解:63611603210=====b a a a a ,,,,系统的状态空间表达式为 传递函数为其对偶系统的状态空间表达式为: 传递函数为61166)(23+--=s s s s W 3-9已知系统的传递函数为 试求其能控标准型和能观标准型;解:345213486)(222++++=++++=s s s s s s s s W系统的能控标准I 型为 能观标准II 型为3-10给定下列状态空间方程,试判别其是否变换为能控和能观标准型;解:[]100210311032010=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=C b A ,, 3-11试将下列系统按能控性进行分解1[]111,100,340010121-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=C b A 解:[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--==9310004102b A Ab bM rankM=2<3,系统不是完全能控的; 构造奇异变换阵c R :⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-==⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡==010*********R Ab R b R ,,,其中3R 是任意的,只要满足c R 满秩;即⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=031100010c R 得⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=-010*******c R 3-12 试将下列系统按能观性进行结构分解1 []111,100,340010121-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=C b A 解: 由已知得[]111,100,340010121-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=C b A 则有⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=4742321112CA CA C Nrank N=2<3,该系统不能观构造非奇异变换矩阵10R -,有10111232001R --⎡⎤⎢⎥=-⎢⎥⎢⎥⎣⎦ 则0311210001R --⎡⎤⎢⎥=-⎢⎥⎢⎥⎣⎦3-13 试将下列系统按能控性和能观性进行结构分解1[]211,221,102322001=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=C b A 解:由已知得211121226202M A Ab Ab ⎡⎤⎢⎥⎡⎤==⎣⎦⎢⎥⎢⎥-⎣⎦rank M=3,则系统能控 rank N=3,则系统能观所以此系统为能控并且能观系统取211121226202c T ⎡⎤⎢⎥=⎢⎥⎢⎥-⎣⎦,则1217344173215344c T -⎡⎤-⎢⎥⎢⎥⎢⎥=--⎢⎥⎢⎥⎢⎥-⎢⎥⎣⎦则002105014A ⎡⎤⎢⎥=-⎢⎥⎢⎥⎣⎦,12100c B T b -⎡⎤⎢⎥==⎢⎥⎢⎥⎣⎦,[]271323c c cT == 3-14求下列传递函数阵的最小实现; 1 ()111111w s s ⎡⎤=⎢⎥+⎣⎦解: 01α=,01111B ⎡⎤=⎢⎥⎣⎦,1001c A -⎡⎤=⎢⎥-⎣⎦ 1001c B ⎡⎤=⎢⎥⎣⎦,1111c C ⎡⎤=⎢⎥⎣⎦,0000c D ⎡⎤=⎢⎥⎣⎦ 系统能控不能观取101101R -⎡⎤=⎢⎥⎣⎦,则01101R -⎡⎤=⎢⎥⎣⎦所以10010ˆ01A R AR --⎡⎤==⎢⎥-⎣⎦,1011ˆ01c B R B -⎡⎤==⎢⎥⎣⎦ 010ˆ10c C C R ⎡⎤==⎢⎥⎣⎦,00ˆ00D ⎡⎤=⎢⎥⎣⎦所以最小实现为ˆ1m A =,[]ˆ11m B =,1ˆ1m C ⎡⎤=⎢⎥⎣⎦,00ˆ00m D ⎡⎤=⎢⎥⎣⎦ 验证:()()1111ˆˆˆ111m mm C sI A B w s s -⎡⎤-==⎢⎥+⎣⎦3-15设1∑和2∑是两个能控且能观的系统1试分析由1∑和2∑所组成的串联系统的能控性和能观性,并写出其传递函数; 2试分析由1∑和2∑所组成的并联系统的能控性和能观性,并写出其传递函数; 解: 11∑和2∑串联当1∑的输出1y 是2∑的输入2u 时,331222x x x x =-++010*********x x u ⎡⎤⎡⎤⎢⎥⎢⎥=--+⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦,[]001y x = 则rank M=2<3,所以系统不完全能控; 当2∑得输出2y 是1∑的输入1u 时011034100021x x u ⎡⎤⎡⎤⎢⎥⎢⎥=--+⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦,[]210y x = 因为 2001016124M bAbA b ⎡⎤⎢⎥⎡⎤==-⎣⎦⎢⎥⎢⎥--⎣⎦rank M=3 则系统能控因为2210321654c N cA cA ⎡⎤⎡⎤⎢⎥⎢⎥==--⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦rank N=2<3 则系统不能观 21∑和2∑并联010*********x x u ⎡⎤⎡⎤⎢⎥⎢⎥=--+⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦,[]211y x = 因为rank M=3,所以系统完全能控 因为rank N=3,所以系统完全能观现代控制理论第四章习题答案4-1判断下列二次型函数的符号性质:1222123122313()31122Q x x x x x x x x x x =---+-- 2222123122313()4262v x x x x x x x x x x =++--- 解:1由已知得110∆=-<,2112013-∆==>-,31111711302411112--∆=--=-<--- 因此()Q x 是负定的 2由已知得110∆=>,2113014-∆==>-,3111143160131--∆=--=-<--因此()Q x 不是正定的 4-2已知二阶系统的状态方程:试确定系统在平衡状态处大范围渐进稳定的条件;解:方法1:要使系统在平衡状态处大范围渐进稳定,则要求满足A 的特征值均具有负实部;即:有解,且解具有负实部; 即:1122112212210a a a a a a +<>且方法2:系统的原点平衡状态0e x =为大范围渐近稳定,等价于T A P PA Q +=-;取Q I =,令11121222PP P P P ⎡⎤=⎢⎥⎣⎦,则带入TA P PA Q +=-,得到 若 11211211222111221122122112222204()()0022a a a a a a a a a a a a a a +=+-≠,则此方程组有唯一解;即 其中11221221det A A a a a a ==- 要求P 正定,则要求 因此11220a a +<,且det 0A >4-3试用lyapunov 第二法确定下列系统原点的稳定性;11123x x -⎡⎤=⎢⎥-⎣⎦ 21111x x -⎡⎤=⎢⎥--⎣⎦解:1系统唯一的平衡状态是0e x =;选取Lyapunov 函数为2212()0V x x x =+>,则 ()V x •是负定的;x →∞,有()V x →∞;即系统在原点处大范围渐近稳定;2系统唯一的平衡状态是0e x =;选取Lyapunov 函数为2212()0V x x x =+>,则 ()V x •是负定的;x →∞,有()V x →∞;即系统在原点处大范围渐近稳定;4-6设非线性系统状态方程为: 试确定平衡状态的稳定性;解:若采用克拉索夫斯基法,则依题意有: 取P I =很明显,()Q x 的符号无法确定,故改用李雅普诺夫第二法;选取Lyapunov 函数为2212()0V x x x =+>,则()V x •是负定的;x →∞,有()V x →∞;即系统在原点处大范围渐近稳定;4-9设非线性方程:试用克拉索夫斯基法确定系统原点的稳定性; 解:1采用克拉索夫斯基法,依题意有:x →∞,有()V x →∞; 取P I =则2121013()132x Q x x ⎡⎤-+=⎢⎥-+⎣⎦,根据希尔维斯特判据,有: 2221121210310310132x x x -∆=∆==->-+,(),()Q x 的符号无法判断; 2李雅普诺夫方法:选取Lyapunov 函数为421233()042V x x x =+>,则 ()V x •是负定的;x →∞,有()V x →∞;即系统在原点处大范围渐近稳定;4-12试用变量梯度法构造下列系统的李雅普诺夫函数 解:假设()V x 的梯度为: 计算()V x 的导数为:选择参数,试选112212211,0a a a a ====,于是得:12x V x ⎛⎫∇= ⎪⎝⎭,显然满足旋度方程12122121,0V V x xx x x x ∂∇∂∇∂∂===∂∂∂∂即,表明上述选择的参数是允许的;则有:如果121211202x x x x -><或,则()V x •是负定的,因此,1212x x <是12x x 和的约束条件; 计算得到()V x 为:()V x 是正定的,因此在121211202x x x x -><即范围内,0e x =是渐进稳定的;现代控制理论第五章习题答案5-1已知系统状态方程为:试设计一状态反馈阵使闭环系统极点配置为-1,-2,-3; 解:依题意有:2011012112M bAbA b ⎡⎤⎢⎥⎡⎤==⎣⎦⎢⎥⎢⎥⎣⎦3rankM =,系统能控; 系统0(,,)A b C =∑的特征多项式为:则将系统写成能控标准I 型,则有010*********x x u ⎡⎤⎡⎤⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦; 引入状态反馈后,系统的状态方程为:()x A bK x bu =++,其中3K ⨯为1矩阵,设[]012K k k k =,则系统(,,)K A bK C =∑的特征多项式为:根据给定的极点值,得到期望特征多项式为:比较*()()f f λλ与各对应项系数,可解得:012599k k k =-=-=-,则有:[]-5-9-9K =;5-3有系统:(1) 画出模拟结构图;(2) 若动态性能不满足要求,可否任意配置极点 (3) 若指定极点为-3,-3,求状态反馈阵; 解1系统模拟结构图如下:2系统采用状态反馈任意配置极点的充要条件是系统0(,,)A b C =∑完全能控; 对于系统0(,,)A b C =∑有: []0111M bAb ⎡⎤==⎢⎥-⎣⎦2rankM =,系统能控,故若系统动态性能不满足要求,可任意配置极点;3系统0(,,)A b C =∑的特征多项式为:则将系统写成能控标准I 型,则有010231x x u ⎡⎤⎡⎤=+⎢⎥⎢⎥--⎣⎦⎣⎦; 引入状态反馈后,系统的状态方程为:()x A bK x bu =++,设[]01K k k =,则系统(,,)KA bK C =∑的特征多项式为:根据给定的极点值,得到期望特征多项式为:比较*()()f f λλ与各对应项系数,可解得:[]017373k k K =-=-=--,; 5-4设系统传递函数为试问能否利用状态反馈将传递函数变成 若有可能,试求出状态反馈K ,并画出系统结构图;解:6522)3)(2)(1()2)(1()(232--+-+=+-++-=s s s s s s s s s s s W由于传递函数无零极点对消,因此系统为能控且能观; 能控标准I 型为 令[] 210k k k K =为状态反馈阵,则闭环系统的特征多项式为由于状态反馈不改变系统的零点,根据题意,配置极点应为-2,-2,-3,得期望特征多项式为比较 )(λf 与 )(*λf 的对应项系数,可得 即[]52118---=K 系统结构图如下:5-5使判断下列系统通过状态反馈能否镇定;11222 A 011,01011b ---⎡⎤⎡⎤⎢⎥⎢⎥=-=⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦解:系统的能控阵为:2240010115M bAbA b -⎡⎤⎢⎥⎡⎤==⎣⎦⎢⎥⎢⎥-⎣⎦3rankM =,系统能控; 由定理 5.2.1可知,采用状态反馈对系统0(,,)A b C =∑任意配置极点的充要条件是(,,)A b C =∑完全能控;又由于3rankM =,系统0(,,)A b C =∑能控,可以采用状态反馈将系统的极点配置在根平面的左侧,使闭环系统镇定; 5-7设计一个前馈补偿器,使系统 解耦,且解耦后的极点为1,1,2,2----; 解:0()()() d W s W s W s = 5-10已知系统:试设计一个状态观测器,使观测器的极点为-r,-2rr>0;解:因为1001c N cA ⎡⎤⎡⎤==⎢⎥⎢⎥⎣⎦⎣⎦满秩,系统能观,可构造观测器; 系统特征多项式为[]21det det 0I A λλλλ-⎡⎤-==⎢⎥⎣⎦,所以有10010,0,10a a L ⎡⎤===⎢⎥⎣⎦ 于是11001100x T ATx T bu x u --⎡⎤⎡⎤=+=+⎢⎥⎢⎥⎣⎦⎣⎦ 引入反馈阵12g G g ⎡⎤=⎢⎥⎣⎦,使得观测器特征多项式:根据期望极点得期望特征式:比较()f λ与()*f λ各项系数得:即223r G r ⎡⎤=⎢⎥⎣⎦,反变换到x 状态下2201321023r r G TG r r ⎡⎤⎡⎤⎡⎤===⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦ 观测器方程为:。
现代控制理论控制系统的状态空间模型

线性时变系统的特点
线性时变系统的动态行为由线性时变微 分方程描述,其特点是系统参数随时间 变化。
线性时变系统的稳定性分析较为复杂,需要 考虑参数变化对系统稳定性的影响。
线性时变系统在航空航天、机器人、 化工等领域有广泛应用,其控制策 略需要根据具体应用场景进行设计。
05
非线性系统的状态空间 模型
状态空间模型的近似线性化
线性化方法
由于非线性系统的分析和设计通常比较复杂,因此常常采 用近似线性化的方法将非线性系统转化为线性系统进行分 析。
泰勒级数展开
一种常用的近似线性化方法是使用泰勒级数展开,将非线 性函数展开成多项式形式,并保留低阶项以获得近似的线 性模型。
局部线性化
另一种常用的近似线性化方法是局部线性化,即将非线性 系统在某个平衡点附近进行线性化处理,以获得该点附近 的线性模型。
线性微分方程具有叠加性和时不变性,即对于任意常数c,若x(t) 是方程的解,则cx(t)也是方程的解;同时,若在时间t=t0时, x(t0)=x0,则对于任意时间t>t0,x(t)都等于x0。
状态空间模型的建立
状态空间模型是一种描述控制系统动态行为的方法,它由状态方程和输出方程组成。状态方程描述了系统内部状态的变化规 律,输出方程描述了系统输出与内部状态和输入的关系。
状态空间模型的建立需要确定系统的状态变量、输入变量和输出变量,然后根据系统的物理特性和实际需求来选择合适的系 统矩阵A、B和C。
线性时不变系统的特点
01
线性时不变系统具有叠加性、 均匀性和时不变性,这些性质 使得线性时不变系统在分析和 设计上相对简单。
02
线性时不变系统的动态行为可 以通过系统的极点和零点来描 述,这些极点和零点决定了系 统的动态响应特性和稳定性。
现代控制理论复习知识点

xe渐近稳定。 渐近稳定时,若||x||时, V(x) : xe大范围渐近
M满秩,M=?注意矩阵维数
能观
特殊情况判别:对角线,特征值互异;约当阵,特征值 有重复
N满秩,N=?注意矩阵维数
离散时间系统的能控能观性判别M, N->G, H。
第三章复习要点
3、标准型及转化 (单输入单输出,系统能控)
标准型:
能控标准I型 A (I在右上角),B=(0, … 0, 1)T,C 能控标准II型 A (I在左下角), B=(1, 0, … 0)T ,C 能观标准I型 A (I在右上角) ,B,C=(1, 0, …, 0) 能观标准II型 A(I在左下角),B,C= (0, …, 0 1) 直接写出传递函数: 能控I,能观II
原理:状态反馈增益矩阵K… 结构图? 特点:改变闭环系统的特征值,可配置极点
2、输出反馈
原理:输出反馈增益矩阵H… 结构图? 特点:
3、闭环系统的能控性、能观性
状态反馈不改变系统的能控性,但不保证能观性不变 输出反馈不改变系统的能控性和能观性
第五章复习要点
4、极点配置
状态反馈:前提:系统完全能控
第二章 系统解的表达式
要求内容:
包括线性定常系统状态方程齐次解,矩阵指数函数和 状态转移矩阵的概念及其计算方法,线性定常系统状 态方程的非齐次解,离散系统状态方程解,连续时间 系统状态方程离散化
第1章控制系统的状态空间表达式

u
X
y
●状态方程的一般形式为:
x Ax Bu
§1-1 状态空间变量及状态空间表达式
五. 输出方程
在指定系统输出y 的情况下,输出y 与状态变量x 及系统输入u 的
函数关系式,称为系统的输出方程 。
●系统的状态和输入决定了系统输出的变化 。
2.根据给定的数学模型,画出相应的加法器和比例器。
3.用箭头将这些元件连接起来。
§1-2 状态空间表达式的模拟结构图
二. 绘制状态空间模拟结构图的例子
例1 一阶标量微分方程x: ax bu
u
b+
x x
+
a
§1-2 状态空间表达式的模拟结构图
二. 绘制状态空间模拟结构图的例子
例2 三阶微分方程 : x a2 x a1x a0 x bu
值以及t≥t0时间的输入,就完全能够确定系统在任何t≥t0时间的动态行 为;
●状态变量的最小性,体现在减少变量个数就不能够完全表征系统的动态
行为,而增加变量数则是完全表征系统动态行为所不需要的。
●状态变量在数学上是线性无关的。
●状态变量的选取不是唯一的。
●对于一个实际的物理系统,状态变量个数等于系统独立储能元件的个数。
Kn
J2 x2
x1
Kb
x2
x1
§1-3 状态空间表达式的建立(一)
由以上方框图可知:x1 x2
x2
J2 Kb
x4
x3 K n x4
状态方程:
x4
1 J1
x3
Kp J1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《现代控制理论》MOOC课程
1.5 离散时间系统、时变系统和非线性系统的状态空间表达式
一. 时间离散系统
离散系统的状态空间表达式可用差分方程组表示为
x(k +1)=Gx(k)+Hu (k)y k =Cx k +Du(k)
二. 线性时变系统
其系数矩阵的元素中至少有一个元素是时间t 的函数;
线性时变系统的状态空间表达式为:
x =A t x +A t u y=C t x +D t u
三. 非线性系统
x =f (x,u , t )
y=g (x,u,t)
1.非线性时变系统的状态空间表达式
式中,f ,g 为函数向量;
x =f (x,u )
y=g (x,u)
2.非线性定常系统的状态空间表达式
当非线性系统的状态方程中不显含时间t 时,则称为非线性定常系统
3.非线性系统的线性化
x =f (x,u )
y =g (x,u)
设是非线性系统x 0,u 0的一个平衡状态, 即。
f (x 0,u 0)=0 , y 0=
g (x 0,u 0)若只考虑附近小范围的行为,则可将非线性系统取一次近似而予以线性化。
x 0,u 0,y 0将非线性函数f 、g 在附近作泰勒级数展开,并忽略高次项,仅保留一次项:
x 0,u 0f x,u =f x 0,u 0
+ðf ðx x 0,u 0δx +ðf ðu x 0,u 0δu g x,u =g x 0,u 0+ðg ðx x 0,u 0δx +ðg ðu x 0,u 0
δu
则非线性系统的一次线性化方程可表示为:δx =x −x 0=ðf ðx x 0,u 0δx +ðf ðu x
0,u 0δu δy =y −y 0=ðg ðx x 0,u 0δx +ðg ðu x 0,u 0
δu 将微增量用符号表示,线性化状态方程就表示为:
δx ,δu ,δy x ,u ,y x
=A x +B u y
=C x +D u 其中,A =ðf ðx x 0,u 0,B =ðf ðu x 0,u 0,C =ðg ðx x 0,u 0,D =ðg ðu x 0,u 0
第一章控制系统的状态空间表达式第一章小结
状态变量、状态空间、状态空间表达式的定义
建立系统状态空间表达式的方法,特别是状态变量选取的方法;
状态空间表达式非奇异线性变换的方法;
由状态空间表达式导出传递函数矩阵的方法;
组合系统状态空间表达式的建立方法;
离散系统、非线性系统状态空间的基本形式;。
