第3章习题答案

合集下载

第三章练习题答案

第三章练习题一、判断正误并解释1.所谓商品的效用，就是指商品的功能。

分析：这种说法是错误的。

商品的效用指商品满足人的欲望的能力，指消费者在消费商品时所感受到的满足程度2.不同的消费者对同一件商品的效用的大小可以进行比较。

分析：这种说法是错误的。

同一个消费者对不同商品的效用大小可以比较。

但由于效用是主观价值判断，所以同一商品对不同的消费者来说，其效用的大小是不可比的。

3.效用的大小，即使是对同一件商品来说，也会因人、因时、因地而异。

分析：这种说法是正确的。

同一商品给消费者的主观心理感受会随环境的改变而改变。

4.边际效用递减规律是指消费者消费某种消费品时，随着消费量的增加，其最后一单位消费品的效用递减。

分析：这种说法是错误的。

必须在某一特定的时间里，连续性增加。

5.预算线的移动表示消费者的货币收入发生变化。

分析：这种说法是错误的。

只有在收入变动，商品价格不变，预算线发生平移时，预算线的移动才表示消费者的收入发生了变化。

6.效应可以分解为替代效应和收入效应，并且替代效应与收入效应总是反向变化。

分析：这种说法是错误的。

正常物品的替代效应和收入效应是同向变化的。

二、选择1.当总效用增加时，边际效用应该：（A ）A.为正值，但不断减少；B.为正值，且不断增加；C.为负值，且不断减少；D.以上都不对２.当某消费者对商品Ｘ的消费达到饱合点时，则边际效用ＭＵχ为：（C ）Ａ.正值Ｂ.负值Ｃ.零Ｄ.不确定３.正常物品价格上升导致需求量减少的原因在于：（C ）Ａ.替代效应使需求量增加，收入效应使需求量减少；Ｂ.替代效应使需求量增加，收入效应使需求量增加；Ｃ.替代效应使需求量减少，收入效应使需求量减少；Ｄ.替代效应使需求量减少，收入效应使需求量增加。

4.无差异曲线的形状取决于（C ）A.消费者收入；B.所购商品的价格；Ｃ.消费者偏好；Ｄ.商品效用水平的大小。

5.无差异曲线为斜率不变的直线时，表示相组合的两种商品是（B ）Ａ.可以替代的；Ｂ.完全替代的；Ｃ.互补的；Ｄ.互不相关的。

第3章习题答案

思考题：题3.1.1 组合逻辑电路在结构上不存在输出到输入的，因此状态不影响状态。

答：反馈回路、输出、输入。

题3.1.2 组合逻辑电路分析是根据给定的逻辑电路图，而确定。

组合逻辑电路设计是根据给定组合电路的文字描述，设计最简单或者最合理的。

答：逻辑功能、逻辑电路。

题3.2.1 一组合电路输入信号的变化顺序有以下三种情况，当时，将可能出现竞争冒险。

（A ）00→01→11→10 （B ）00→01→10→11 （C ）00→10→11→01 答：B题3.2.2 清除竞争冒险的常用方法有（1）电路输出端加；（2）输入加；（3）增加。

答：电容，选通脉冲，冗余项。

题3.2.3 门电路的延时时间是产生组合逻辑电路竞争与冒险的唯一原因。

（）答：×题3.2.4 根据毛刺产生的方向，组合逻辑的冒险可分为冒险和冒险。

答：1型、0型。

题3.2.5 传统的判别方法可采用和法来判断组合电路是否存在冒险。

答：代数法、卡诺图。

题3.3.1 进程行为之间执行顺序为，进程行为内部执行顺序为。

答：同时、依次。

题3.3.2 行为描述的基本单元是，结构描述的基本单元是。

答：进程、调用元件语句。

题3.3.3 结构体中的每条VHDL 语句的执行顺序与排列顺序。

答：无关题3.4.1串行加法器进位信号采用传递，而并行加法器的进位信号采用传递。

（A ）超前，逐位（B ）逐位，超前（C ）逐位，逐位（D ）超前，超前答：B题3.4.2 一个有使能端的译码器作数据分配器时，将数据输入端信号连接在。

答：使能端题 3.4.3 优先编码器输入为70I I -（0I 优先级别最高），输出为2F 、1F 、0F （2F 为高位）。

当使能输入00,651====I I I S 时，输出012F F F 应为。

答：110题3.4.4 用4位二进制比较器7485实现20位二进制数并行比较，需要片。

数据与计算机通信答案(第3章)

上述两种方案由于每个原色强度过少，色彩单调，图象层次感差，对于数字电视无实际应用价值。如果可以提高三倍数据率，以每三个连续的 5 比特组分别表示一个像素，三种颜色各有 32 种强度值，共有 32768 种色彩，这对于计算机显示器而言，色彩并不算丰富，
而对于数字彩色电视机，相当不错了。如果不提高数据率，还可以通过降低分辨率或刷新速率，来换取色彩数的提高，但这也不实用的方法。
已知视频带宽 B=5MHz，所以有 5=P/105，则每行的像素数 P=5x105=525。然而，通常 CCIR-M/NTSC 制式每行只约有 450 像素，带宽 B=P/105=450/105=4.3MHz (实际技术指标 4.2Hz) 。带宽由 4.2MHz 增加到 5MHz 时，水平分辨率约增加 75 像素，增幅 16.7%。（2）计算垂直分辨率的增幅由于信号最高频率 fH=5MHz，即最短的信号周期 1/fH=0.2υs。又因为每个最短周期包含 2 个像素，则有 225 周期/行。那么，每行扫描时间为 0.2υs×225=45υs。加上水平回扫 11υs，每行往返扫描时间为 56υs ，即 56x10-6 s，假定每屏 V 行，每秒扫描 30 场（帧、屏），则每秒扫描行数为 30V。因此对于画面刷新，有 30V×56x10-6 = 1s，V = 595 行/屏。目前 NSTL 制式每行只有 525 行。垂直分辨率增加了 70 行，增幅 13.3%。
cos 2 t = cos t cos t = 1 (cos 2t + cos 0) = 1 (cos 2t + 1)
2
2
所以， f (t) = (10 cos t)2 = 100 cos 2 t = 50 + 50 cos 2t

第三章习题解答

第3章力学基本定律与守恒律习题及答案1．作用在质量为10 kg 的物体上的力为i t F)210(+=N ，式中t 的单位是s ，(1)求4s 后，这物体的动量和速度的变化．(2)为了使这力的冲量为200 N ·s ，该力应在这物体上作用多久，试就一原来静止的物体和一个具有初速度j 6-m ·s -1的物体,回答这两个问题．解: (1)若物体原来静止，则i t i t t F p t 1401s m kg 56d )210(d -⋅⋅=+==∆⎰⎰,沿x 轴正向，ip I imp v111111s m kg 56s m 6.5--⋅⋅=∆=⋅=∆=∆ 若物体原来具有6-1s m -⋅初速，则⎰⎰+-=+-=-=t tt F v m t m F v m p v m p 000000d )d (,于是⎰∆==-=∆t p t F p p p 0102d,同理， 12v v ∆=∆,12I I=这说明，只要力函数不变，作用时间相同，则不管物体有无初动量，也不管初动量有多大，那么物体获得的动量的增量(亦即冲量)就一定相同，这就是动量定理． (2)同上理，两种情况中的作用时间相同，即⎰+=+=tt t t t I 0210d )210(亦即 0200102=-+t t 解得s 10=t ，(s 20='t 舍去)2．一颗子弹由枪口射出时速率为10s m -⋅v ，当子弹在枪筒内被加速时，它所受的合力为 F =(bt a -)N(b a ,为常数)，其中t 以秒为单位：(1)假设子弹运行到枪口处合力刚好为零，试计算子弹走完枪筒全长所需时间；(2)求子弹所受的冲量．(3)求子弹的质量．解: (1)由题意，子弹到枪口时，有0)(=-=bt a F ,得ba t =(2)子弹所受的冲量⎰-=-=tbt at t bt a I 0221d )(将bat =代入，得 ba I 22=(3)由动量定理可求得子弹的质量202bv a v I m == 3．如图所示，一质量为m 的球，在质量为M 半径为R 的1/4圆弧形滑槽中从静止滑下。

第3章习题答案

习题31.名词解释：栈、队列、循环队列。

解：栈是只能在一端进行插入和删除操作的线性表，允许插入和删除的一端叫栈顶，另一端叫栈底。

最后插入的元素最先删除，故栈也称后进先出表。

队列是允许在一端插入而在另一端删除的线性表，允许插入的一端叫队尾，允许删除的一端叫队头。

最后插入的元素最先删除，故栈也称先进先出表。

最先入队的元素最先删除，故队列也称先进先出表。

用常规意义下顺序存储结构的一维数组表示队列，由于队列的性质（队尾插入，队头删除），容易造成“假溢出”现象，即队尾已达到一维数组的高下标，不能再插入，然而队中元素个数小于队列的长度。

循环队列是解决“假溢出”的一种方法。

通常把一维数组看成首尾相接。

在循环队列下，通常采用“牺牲一个存储空间”的方法解决“队满”和“队空”的判定问题。

2.如果输入序列为1，2，3，4，5，6，试问能否通过栈结构得到以下两个序列：4，3，5，6，1，2和1，3，5，4，2，6；请说明为什么不能或如何才能得到。

解：输入序列为1，2，3，4，5，6，不能得到4，3，5，6，1，2，其理由是：输出序列最后两个元素是1，2，前面四个元素（4，3，5，6）得到后，栈中元素剩下1，2，且2在栈顶，栈底元素1不可能在栈顶元素2出栈之前出栈。

得到序列1，3，5，4，2，6的过程是：1入栈并出栈；然后2和3依次入栈，3出栈，部分输出序列是1，3；紧接着4和5入栈，5，4和2依次出栈，此时输出序列为1，3，5，4，2；最后6入栈并出栈，得到最终结果序列是1，3，5，4，2，6。

3.试证明：若借助栈由输入序列1，2，…，n 得到序列1p ，2p ，…，n p (它是输入序列的一个全排列)，则在输出序列中不可能出现下列情形：存在着i <j <k ，使得j p <k p <i p 。

解：如果i <j ，说明i p 在j p 入栈前先出栈。

而对于i p >j p 的情况，则说明要将j p 压到i p 之上，也就是在j p 出栈之后i p 才能出栈。

第三章习题参考答案

第三章习题参考答案一、填空题1、指令格式是由操作码和操作数所组成，也可能仅由操作码组成。

2、若用传送指令访问MCS-51的程序存储器，它的操作码助记符应为MOVC 。

3、若用传送指令访问MCS-51的片内数据存储器，它的操作码助记符应为MOV 。

4、若访问MCS-51的片外数据存储器，它的操作码助记符应为MOVX 。

5、累加器（A）=80H，执行完指令ADD A，#83H后，进位位C= 1 。

6、执行ANL A，#0FH指令后，累加器A的高4位= 0000 。

7、JZ rel的操作码地址为1000H，rel=20H，它的转移目的地址为1022H 。

8、JBC 00H，rel 操作码的地址为2000H，rel=70H，它的转移目的地址为2073H 。

9、累加器（A）=7EH，（20H）= #04H，MCS-51执行完ADD A，20H指令后PSW.0= 0 。

10、MOV PSW，#10H是将MCS-51的工作寄存器置为第 2 组。

11、指令LCALL 37B0H，首地址在2000H，所完成的操作是2003H 入栈，37B0H →PC。

12、MOVX A，@DPTR源操作数寻址方式为寄存器间接寻址。

13、ORL A，#0F0H是将A的高4位置1，而低4位保持不变。

14、SJMP rel的指令操作码地址为0050H，rel=65H，那么它的转移目标地址为 00B7H 。

15、设DPTR=2000H，（A）=80H，则MOVC A，@A+DPTR的操作数的实际地址为2080H 。

16、MOV C，20H源寻址方式为位寻址。

17、在直接寻址方式中，只能使用8 位二进制数作为直接地址，因此其寻址对象只限于片内RAM 。

18、在寄存器间接寻址方式中，其“间接”体现在指令中寄存器的内容不是操作数，而是操作数的地址。

19、在变址寻址方式中，以 A 作变址寄存器，以PC 或DPTR 作基址寄存器。

20、假定累加器A中的内容为30H，执行指令1000H：MOVC A,@A+PC后，把程序存储器1031H 单元的内容送入累加器A中。

第3章本量利练习题(答案版)

第3章本量利分析一、单项选择题：1、生产单一品种产品企业，保本销售额=（ B ）A. 保本销售量×单位利润B. 固定成本总额÷贡献边际率C. 固定成本总额÷（单价一单位变动成本）D. 固定成本总额÷综合贡献边际率E. 固定成本总额÷贡献边际2、生产多品种产品企业测算综合保本销售额=固定成本总额÷（ D ）A.单位贡献边际B.贡献边际率C.单价一单位变动成本D.加权平均贡献毛益率3、某企业只生产一种产品，单价6元，单位变动生产成本4元，单位销售和管理变动成本0.5元，销量为500件，则其产品贡献边际为（ B ）元A.650B.750C.850D.9504、下属因素中导致保本销售量下降的是（ D ）A.销售量上升B.产品单价下降C.固定成本上升D.产品单位变动成本下降5、在变动成本法下，其利润表所提供的中间指标是（ A ）A.贡献边际B.营业利润C.营业毛利D.期间成本6、在下列指标中，可据以判断企业经营安全程度的指标是（ C ）A.保本量B.贡献边际C.保本作业率D.保本额7、保本作业率与安全边际率之间的关系是（ D ）A.两者相等B.前者一般大于后者C.后者一般大于前者D.两者之和等于18、销售量不变，保本点越高，则能实现的利润（ A ）A.越小B.不变C.越大D.不一定9、销售量不变，单价单独变动时，会使安全边际（ C ）A.不变B.不一定变动C.同方向变动D.反方向变动10、下列因素单独变动时，不对实现目标利润的销售量产生影响的是（ D ）A.单价B.目标利润C.成本水平D.销售量二、多项选择题：1、安全边际率=（ AC ）A.安全边际量÷实际销售量B.保本销售量÷实际销售量C.安全边际额÷实际销售额D.保本销售额÷实际销售额E.安全边际量÷安全边际额2、从传统式保本图得知（ CE ）A.保本点右边，成本大于收入，是亏损区B.销售量一定的情况下，保本点越高，盈利区越大C.实际销售量超过保本点销售量部分即是安全边际D.在其他因素不变的情况，保本点越低，盈利面积越小E.安全边际越大，盈利面积越大3、贡献边际率的计算公式可表示为（ABDE ）A.1-变动成本率B.贡献边际/销售收入C.固定成本/保本销售量D.固定成本/保本销售额E.单位贡献边际/单价4、在盈亏临界图中，盈亏临界点的位置取决于（ ABD ）等因素。

第三章习题解答及参考答案

(
)
①
2 式中 m 为整数。令 u = αr ，显然上式是 u 的周期函数，周期为 2π ，故可展开成傅里 ∞ 1 1 + sgn (cos u ) = ∑ Cn e inu 2 2 n = −∞
叶级数：
其中，
Cn =
1 2π
∫
π 2
−π 2
e −inu du =
sin (nπ 2) nπ
②
遂有：
∞ 1 1 sin (nπ 2 ) inαr 2 e + sgn cos αr 2 = ∑ 2 2 nπ n= −∞
②
σ ( f x ,0 ) 2λd i =1− f x = 1− f x f0 σ0 l
l l ≤ λd i f x ≤ (见附图3 - 4(b)) 4 2
2 1 l l σ ( f x ,0 ) = (l − λd i f x ) l − = − λd i l f x 2 2 2
λd ；两个一级分量与中央亮斑 L
附图 3-2
习题[3-2]图示
附图 3-3
归一化强度分布
[3-3]
将面积为 10 mm × 10 mm 的透射物体置于一傅里叶变换透镜的前焦面上作频谱分析。
用波长 λ = 0.5 µ m 的单色平面波垂直照明，要求在频谱面上测得的强度在频率 140 线/mm 以下能准确代表物体的功率谱。并要求频率为 140 线/mm 与 20 线/mm 在频谱面上的间隔为 30mm,问该透镜的焦距和口径各为多少？解：取面积为10mm ×10mm 的透射物体的对角线方向为 x 轴。因要求在 140 线/mm 以下的空间频率成分不受到有限孔径的渐晕效应的影响，故透镜的口径 D 应满足条件：

第三章习题(含答案)

第三章会计等式与复式记账一、单项选择题1、总分类账户与明细分类账户平行登记四要点中的“依据相同”是指（）。

A.总分类账要根据明细分类账进行登记B.明细分类账要根据总分类账进行登记C.根据同一会计凭证登记D.由同一人员进行登记2、某企业原材料总分类科目的本期借方发生额为25 000元，贷方发生额为24 000元，其所属的三个明细分类账中；甲材料本期借方发生额为8 000元，贷方发生额为6 000；乙材料借方发生额为13 000元，贷方发生额为16 000元；则丙材料的本期借、贷方发生额分别为（）。

A.借方发生额为12 000元，贷方发生额为2 000元B.借方发生额为4 000元，贷方发生额为2 000元C.借方发生额为4 000元，贷方发生额为10 000元D.借方发生额为6 000元，贷方发生额为8 000元3、甲公司月末编制的试算平衡表中，全部科目的本月贷方发生额合计为120万元，除银行存款外的本月借方发生额合计104万元，则银行存款科目（）。

A.本月借方余额为16万元B.本月贷方余额为16万元C.本月贷方发生额为16万元D.本月借方发生额为16万元4、下列记账错误中，不能通过试算平衡检查发现的是（）。

A.将某一分录的借方发生额600元，误写成6 000元B.某一分录的借贷方向写反C.借方的金额误记到贷方D.漏记了借方的发生额5、下列关于试算平衡法的说法，正确的是（）。

A.漏记某项经济业务影响试算平衡B.包括发生额试算平衡法和余额试算平衡法C.试算平衡了，账户记录一定正确D.发生额试算平衡法理论的依据是会计等式6、企业购入原材料10 000元，已开出支票支付6 000元，另4 000元暂欠。

下列会计分录正确的是（）。

A.借：原材料10 000贷：银行存款10 000B.借：原材料10 000贷：应付账款10 000C.借：原材料10 000贷：银行存款6 000应付账款4 000D.借：原材料10 000贷：应付票据6 000应付账款4 0007、企业计算应交所得税时，正确的会计分录是（）。

大学物理课后习题答案第三章

第3章力学基本定律与守恒律习题及答案1．作用在质量为10 kg 的物体上的力为i t F)210(+=N ，式中t 的单位是s ，(1)求4s 后，这物体的动量和速度的变化．(2)为了使这力的冲量为200 N ·s ，该力应在这物体上作用多久，试就一原来静止的物体和一个具有初速度j6-m ·s -1的物体,回答这两个问题．解: (1)若物体原来静止，则i t i t t F p t 1401s m kg 56d )210(d -⋅⋅=+==∆⎰⎰,沿x 轴正向，ip I imp v111111s m kg 56s m 6.5--⋅⋅=∆=⋅=∆=∆ 若物体原来具有6-1s m -⋅初速，则⎰⎰+-=+-=-=t tt F v m t m F v m p v m p 000000d )d (,于是⎰∆==-=∆t p t F p p p 0102d,同理， 12v v ∆=∆,12I I=这说明，只要力函数不变，作用时间相同，则不管物体有无初动量，也不管初动量有多大，那么物体获得的动量的增量(亦即冲量)就一定相同，这就是动量定理． (2)同上理，两种情况中的作用时间相同，即⎰+=+=tt t t t I 0210d )210(亦即 0200102=-+t t 解得s 10=t ，(s 20='t 舍去)2．一颗子弹由枪口射出时速率为10s m -⋅v ，当子弹在枪筒内被加速时，它所受的合力为 F =(bt a -)N(b a ,为常数)，其中t 以秒为单位：(1)假设子弹运行到枪口处合力刚好为零，试计算子弹走完枪筒全长所需时间；(2)求子弹所受的冲量．(3)求子弹的质量．解: (1)由题意，子弹到枪口时，有0)(=-=bt a F ,得ba t =(2)子弹所受的冲量⎰-=-=tbt at t bt a I 0221d )(将bat =代入，得 ba I 22= (3)由动量定理可求得子弹的质量202bv a v I m == 3．如图所示，一质量为m 的球，在质量为M 半径为R 的1/4圆弧形滑槽中从静止滑下。

第三章习题及答案

第三章练习题一、填空题1、从国际经济地理的分布上看，发达国家大都分布在北方，发展中国家大都分布在南方，因此，国际经济学界有时将这种发达国家与发展中国家的产业间贸易称作。

2、规模经济指企业的平均成本随着整个行业生产规模的不断扩大而下降。

3、不以要素禀赋差异为基础，而以规模经济和差异产品为基础的国际贸易是贸易。

4、外部规模经济下的国际分工与贸易模式是不可预测的，在很大程度上由因素决定。

5、从技术转移的角度探讨比较优势动态演变的贸易理论是技术差距理论和理论。

6、重叠需求理论认为，是影响一国需求结构的最主要因素。

7、1961年瑞典经济学家提出了重叠需求理论，从需求的角度探讨了国际贸易发生的原因。

8、国际贸易理论最新的发展方向之一是将技术作为贸易的内生变量来分析，既研究技术变化的原因，也研究作为生产和贸易结果的技术进步对与社会福利的影响。

9、在国内投资乘数理论的基础上，凯恩斯的追随们引申出理论。

10、战略性贸易理论的基本内容是利用关税分享外国企业的垄断利润和。

11、贸易政策有两大基本类型，即和保护贸易政策。

12、美国1988年在中修订过301条款。

13、就是以国内生产的工业品代替进口产品的政策。

14、指用工业制成品和半制成品的出口代替初级产品出口的政策。

15、除比较优势外，成为国际贸易的一个独立的基础和源泉。

16、某种商品的进口大国设置一定程度的关税会使贸易条件向有利于本国不利于外国的方向转化，使国内实际收入最大化，这种程度关税叫。

二、判断题1、如果厂商的生产具有规模报酬递增的特征，那么该厂商一定存在规模经济，但规模经济不一定要求规模报酬递增。

2、一个只存在外部规模经济的行业一般由大量较小的厂商构成。

3、外部规模经济下的国际分工与贸易格局在很大程度上由历史或偶然因素决定。

4、市场规模大的国家生产的差异化产品种类一般较多。

5、新制度经济学认为，所有交易集中在一个地方可以改进交易效率，只要交易效率改进带来的收益大于该地区地价上升产生的成本，行业还会进一步向该地区及其周边集中。

第三章习题参考答案

第三章缓冲溶液习题参考答案1. 在1L 1.0×10-5mol ·L -1 NaOH 溶液中，加入0.001molNaOH 或HCl ，溶液的pH 怎样改变？解：ΔpH 1≈11-9=2；ΔpH 2≈3-9=-62. 设有下列三种由乳酸和乳酸钠组成的缓冲溶液，分别计算它们的pH 值（25℃时乳酸的K a = 1.4×10-4）。

（1）1L 溶液中含有0.1mol 乳酸和0.1mol 乳酸钠。

（2）1L 溶液中含0.1mol 乳酸和0.01mol 乳酸钠。

（3）1L 溶液中含0.01mol 乳酸和0.1mol 乳酸钠。

解：（1）85.31.01.0lg )104.1lg(lg p [HB]][B lg p pH 4HB B a a =+⨯-=+=+=--n n K K （2）85.21.001.0lg )104.1lg(lg [HB]][B lg p pH 4HB B a a =+⨯-=+=+=--n n pK K （3）85.401.01.0lg )104.1lg(lg [HB]][B lg p pH 4HB B a a =+⨯-=+=+=--n n pK K 3. 正常血浆中具有H 2PO 4-－HPO 42-缓冲系，H 2PO 4-的p K a2 = 6.8（校正后），已知正常血浆中[HPO 42-]/[H 2PO 4-]为4/1，试求血浆的pH 值；尿中[HPO 42-]/[H 2PO 4-]为1/9，试求尿的pH 值。

解：血浆的pH 值：40.714lg 8.6[HB]][B lg p pH a =+=+=-K 尿液的pH 值：84.591lg 8.6[HB]][B lg p pH a =+=+=-K 4. 将0.15mol ·L -1 NaOH 溶液0.1mL 加于10mL pH 值为4.74的缓冲溶液中，溶液的pH 值变为4.79，试求此缓冲溶液的缓冲容量。

习题第3章答案

所示。
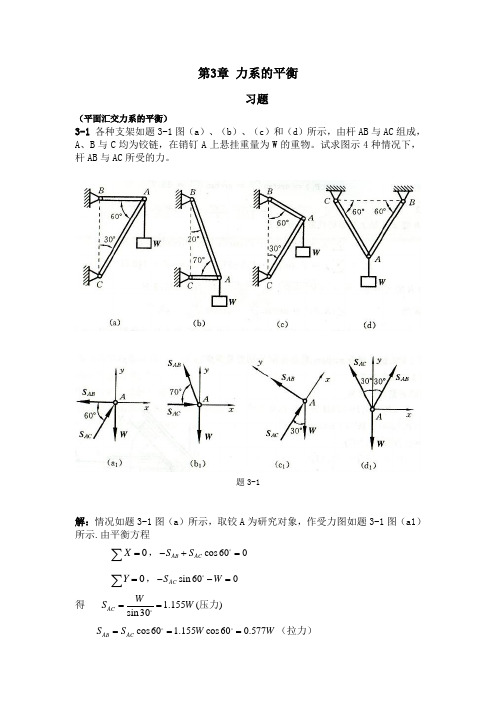
由平衡方程
，
，
，
得，
，
（c）解除题3-7图（c）所示梁的支座，代之以支座反力，作受力图（c1）
所示。
由平衡方程
，
，
，
得，
，
（d）解除题3-7图（d）所示梁的支座，代之以支座反力，作受力图（d1）
所示。
由平衡方程
，
，
，
得，
，
3-8试求题3-8图所示各梁的支座反力。
题3-8图
解：（a）解除题3-8图（a）所示悬臂梁的约束，代之以支座反力，作受力图（a1）
题3-6图
解：分别取杆AE和BD为研究对象，销子C作用于导槽的反力因垂直于AE，因此决定了铰A处的反力应于等值、反向。杆BD上的反力应于等值、反向，铰B处的反力应于等值、反向，作杆AE和BD的受力图如题3-6图（b）和（c）所示。由题3-6图（a）中的几何关系，可得
由题3-6图（b）的平衡条件
，
，
得 (拉力)
3-2题3-2图（a）所示的电动机重，放在水平梁AC的中间，A和B为固定铰链，C为中间铰链。试求A点反力及杆BC所受的力。
题3-2图
解：解除题3-2图（a）所示电动机支架的支座，代之以约束反力，利用三力平衡汇交定理，作受力图如题3-2图（b）所示。由平衡方程
，
，
得
所以A点的反力为，杆BC为二力杆，B点受的力就是杆BC受的力，为。
题3-5图
解：因杆AB是二力杆，所以杆AB俩端的铰A和B的约束力应沿杆的轴线方向，题3-5图（b）所示。因此，杆和杆的铰B和铰A处的约束反力的方向应如题3-5图（c）、（d）所示。因杆和杆的外力均为力偶，所以约束反力及分别应与及等值、反向，并有

概率论课后习题第3章答案

第三章多维随机向量及其概率分布(一)基本题答案1、设X 和Y 的可能取值分别为.2,1,0;3,2,1,0,==j i j i 则与因盒子里有3种球，在这3种球中任取4个，其中黑球和红球的个数之和必不超过4.另一方面，因白球只有2个，任取的4个球中，黑球和红球个数之和最小为2个，故有j i 与ٛ且,42≤+≤j i ./),(474223C C C C j Y i X p j i j i −−===因而或0),(===j Y i X P 2).2,1,0;3,2,1,0,4(<+j i ==>+j i j i于是 ,0)0,0(1111======y Y x X P P ,0)0,0(2112======y Y x X P p.35/1/)0,0(472212033113=======C C C C y Y x X P p即 2、X 和. ⎥⎦⎤⎢⎣⎡04.032.064.0210~X ⎥⎦⎤⎢⎣⎡25.05.025.0210~Y 由独立性知，X 和Y 的联合分布为3、Y 的分布函数为显知有四个可能值：).0(0)(),0(1)(≤=>−=−y y F y e y F y ),(21X X }{{}{}11−=e ,2,10,0).1,1(),0,1(),1,0(),0,0(121−≤=≤≤===Y P Y Y P X X P 易知{}{}{}{}{},221−−−=e e 12<=P ,10,1,02,11,02121≤≤>====>≤===Y Y Y P X X P Y Y P X X P{}{}{},212,10,12121−=≤<=≤>===e e Y P Y Y P X X P {}−− {}{}.22,11,1221−=>=>>===e Y P Y Y P X X P于是，可将X 1和X 24、∑=====nm m n P n X P 0),()(ηζ∑=−−−−=nm mn m n e m n m p p 0)!(!)1(λλ()[]).,2,1,0(!1!)1()!(!!!==−+=−−=−−−=−∑n n e p p n e p p m n m n n e n n n mn m nm n λλλλλλ即X 是服从参数为λ的泊松分布.∑∑∞=−−∞=−−−−−=−−==mn mn m n mn m m mn m n m n p m e p em n m p p m Y P )!()1(!)!(!)1()(λλλλλ).,2,1,0(,!)(!)()1( ==⋅=−−−−m m ep e e m ep pmp mλλλλλλ即Y 是服从参数为λp 的泊松分布.5、由定义F （y x ,）=P {}∫∫∞−∞−=≤≤x y dxdy y x y Y x X .),(,ϕ因为ϕ（y x ,）是分段函数，要正确计算出F （y x ,;1>y ），必须对积分区域进行适当分块：等5个部分.10,10,1;1,1;10,100≤≤≤≤>>>≤≤<x y x y x y y x 或;0<≤≤x （1）对于有 F （,00<<y x 或y x ,）=P{X ≤,x Y ≤y}=0; （2）对于有 ;,10,10≤≤≤≤y x 2204),(y x vdudv u y x F x y ==∫∫（3）对于, 有 10,1≤≤>y x {};,1),(2y y Y X P y x F =≤≤= （4）对于, 有 10,1≤≤>x y {}21,),(x Y x X P y x F =≤≤=; （5）对于有 ,1,1>>y x 1),(=y x F .故X 和Y 的联合分布函数⎪⎪⎪⎩⎪⎪⎪⎨⎧<<≤≤<<≤≤≤≤≤≤<<=.1,1,.1,10,1,,1,10,,10,10,,00,0),(2222y x y x y y x x y x y x y x y x F 或6、（1） ,0,0;0),(,00>>=≤≤y x y x F y x 或),(y x F =∫∫+−x y t s dsdt ze)2())(())((200202yt x s y t x se e dt e ds e−−−−−−==∫∫=)1)(1(2y x e e −−−−即⎩⎨⎧>>−−=−−.,0,0,0),1)(1(),(2其它y x e e y x F y x （2）P ()()220(),22x x y x yxy xY X f x y dxdy dx e dy e e d +∞+∞−−−−<≤===−∫∫∫∫∫x∫∫∞+−−−∞+−−=−−=03220)(2)1(2dx e e dx e e x x x x .312131(2)2131(2023=−−=−=∞+−−x x e e7、（1）时，0>x ,0)(,0;)(=≤==∫∞+−−x f x e dy e x f X Xx y X 时即 ⎩⎨⎧≤>=−.0,0,0,)(x x e x f x X （2）{}2/111210121),(1−−≤+−−−+===≤+∫∫∫∫e e dy e dxdxdy y x f Y X P y x x xy8、（1）（i ）时,，;),()(计算根据公式∫∞+∞−=dy y x f x f X 0≤x 当10;0)(<<=x x f X 当时()();24.224.2)2(8.4)(202x x x y dy x y x f xx X −=−=−=∫0)(,1=≥x f x X 时当即⎩⎨⎧<<−=.,0;10),2(4.2)(2其它x x x x f X （ii ）利用公式计算. 当∫∞+∞−=dx y x f y f Y ),()(;0)(,0=≤y f y Y 时,10时当<<y112)22(8.4)2(8.4)(y y Y x x y dx x y y f ∫−=−=⎥⎥⎦⎤⎢⎢⎣⎡⎟⎟⎠⎞⎜⎜⎝⎛−−⎟⎠⎞⎜⎝⎛−=222128.42y y y );43(4.2)2223(8.422y y y y y y +−=+−=当时，1≥y .0)(=y f Y 即⎩⎨⎧<<+−=.0;10),43(4.2)(2其它y y y y y f Y 121111222211111(2)((1(,1(,)1.22222P X Y P X Y f x y dxdy dx dxdy +∞+∞⎧⎫<<=−≥≥=−=−=⎨⎬⎩⎭∫∫∫∫∪58、47809、本题先求出关于x 的边缘概率密度，再求出其在2=x 之值. 由于平面区域D 的面积为)2(X f ,2121=dx =∫x S e D 故（X,Y ）的联合概率密度为⎪⎩⎪⎨⎧∈=.,0;),(,21),其它D y x y x (f易知，X 的概率密度为∫∞+∞−⎪⎩⎪⎨⎧<<==,,0,1,21),()(2其它e x xdy y x f x f X 故.41221)2(=×=X f 10、（1）有放回抽取：当第一次抽取到第个数字时，第二次可抽取到该数字仍有十种可能机会，即为 k {}).9, ,1,0(101====i k Y i X P （2）不放回抽取：（i ）当第一次抽取第)90(≤≤k k 个数时，则第二次抽到此（第个）数是不可能的，故 k {}.)9,,1,0,; =k i k (0====i k Y i X P（ii ）当第一次抽取第个数时，而第二次抽到其他数字（非k ）的机会为，知)90(≤≤k k 9/1{}.)9,,1,0,; =k i k (9/1≠===i k Y i X P 11、（1）因∫−=−=12,)1(12)1(24)(yy y ydx x y f η.,0)(;10其它=≤≤y f y n 故在0≤y ≤1时，⎩⎨⎧≤≤−−=;1)1/()1(2)(2其它x y y x y x f ηξ因()∫−=−=x y x ydy x x f 022,)1(12124)(ξ.,0)(;10其它=≤≤x f x ξ故在0≤x ≤1时，⎩⎨⎧≤≤=.0,0/2)(2其它x y x y x y f ξη（2）因;1,121)(2/12∞≤≤==∫x x nxdy y x X f x x ξ;,0)(其它=x f ξ故在1≤x<时，∞⎪⎩⎪⎨⎧<<=.,1121)(其它x y xnxy x y f ξη因 ⎪⎪⎪⎩⎪⎪⎪⎨⎧∞<<=≤<==∫∫∞∞,002121102121)(22/12其它y y dx y x y dx y x y f y y η 故在10≤<y 时,⎪⎩⎪⎨⎧∞<<=;011)(2其它x y y x x y f ξη 而在,1时∞<<y ⎪⎩⎪⎨⎧∞<<=.0)(2其它x y x yx y f ξη（3）在x >0,.0,0)(;0,)(≤=>==∫∞−−x x f x e dy e x f x xy ξξ⎪⎩⎪⎨⎧>=−.0,)(其它x y e x y f y x ξη ;0,)(0>==∫−−y ye dx e y f y yy η .故在y>0时，0,0)(≤=y y f η⎪⎩⎪⎨⎧<<=.0,01)(其它y x y y x f ηξ12、1(1)(2)2(),0(1)(1)X n n n n n f x dy x x y x ∞−−−−==+++∫>，故12(1)(2)0,(/1)0.n nY X n y y f y −⎧−+>=⎨⎩其它 13、X 和Y 是否独立，可用分布函数或概率密度函数验证.方法一：X 的分布函数的分布函数分别为 Y x F X 和)()(y F Y ⎩⎨⎧<≥−=+∞=−,0001),()(5.0x x e x F x F x X ⎩⎨⎧<≥−=+∞=−.0001),()(5.0y y e y F y F yY 由于独立.Y X y F x F y x F Y X 和知),()(),(={}{}{}[][]1.005.005.0)1.0(1)1.0(11.01.01.0,1.0−−−=⋅=−⋅−=>⋅>=>>=e e e F F Y P X P Y X P Y X αY X Y X x f x f y x f Y X 和分别表示和),,()()(),,(方法二：以的概率密度，可知 ⎩⎨⎧≥≥=∂∂∂=+−.00,025.0),(),()(5.02其它y x e y x y x F y x f y x ∫∞+∞−−⎩⎨⎧<≥==,0005.0),()(5.0x x e dy y x f x f x X ∫∞+∞−−⎩⎨⎧<≥==.00,05.0),()(5.0y y e dx y x f y f yY ∫∫∞+∞+−+−==>>==1.01.01.0)(5.0.25.0}1.0,1.0{.),()(),(e dxdy e Y X P a Y X y f x f y x f y x Y X 独立和知由于)()(),(j i j i y Y P x x P y Y x X P =⋅====14、因知X 与Y 相互独立，即有 . )3,2,1,2,1(==j i 首先，根据边缘分布的定义知 .2418161),(11=−===y Y x X P 又根据独立性有),(61)()(},{2411111i x X p y Y p x X p y Y x X p ===⋅===== 解得41)(==i x X P ,从而有 1218124141),(31=−−===y Y x X P 又由 )()(),(2121y Y P x X P y Y x X P =⋅====, 可得 ),(41812y Y P == 即有21)(2==y Y P , 从而 838121),(22=−===y Y x X P .类似地，由),()(),(3131y Y P x X P y Y x X P ===== 有),(411213y Y P ==得31)(3==y Y P ,从而,.111),(31=−===y Y x X P 最后=)(2x X P =1+3+1=3. 将上述数值填入表中有1x1/24 1/8 1/12 1/4 2x1/8 3/8 1/4 3/4 {}j P y X P j ⋅==1/6 1/2 1/3115、本题的关键是由题设P{X 1X 2=0}=1，可推出P{X 1X 2≠0}=0；再利用边缘分布的定义即可列出概率分布表.(1)由P{X 1X 2=0}=1,可见易见,0}1,1{}1,1{2121=====−=X X P X X P 25.0}1{}0,1{121=−===−=X P X X P 5.0}1{}1,0{221=====X P X X P 25.0}1{}0,1{121=====X P X X P 0}0,0{21===X X P121212.16、(1) ⎩⎨⎧<<=,,0,10,1)(其他x x f X ⎪⎩⎪⎨⎧≤>=−.0,0,021)(2y y ey f yY 因为X ，Y 独立，对任何y x ,都有 ).,()()y x f y f x Y =⋅(f X ⎪⎩⎪⎨⎧><<=−.,0,0,10,21),(2其他所以有y x e y x f y（2）二次方程有实根，△ t Y Xt t 中022=++,04)2(2≥−=Y X ,02≥−Y X 即,2X Y ≤ 故=)(有实根t P dydx e dydx y x f X Y P yx y x 2122221),(}{−≤∫∫∫∫==≤∫−−=1022)(dx ex y=dx edx edx x x x 2101010222221211)21(−−∫∫−=−=−πππ21−=［∫∫∞−∞−−−−1022222121dx edx exx ππ］.1445.08555.01]5.08413.0[21)]0()1([21=−≈−−≈Φ−Φ−=ππ17、（1）因为X ，Y 独立，所以 .⎩⎨⎧>>==+−.,0,0,0,)()(),()(其他y x e y f x f y x f uy x Y X λλμ（2）根据Z 的定义，有 P{z=1}=P{Y ≥X}∫∫∫∫∞+∞−+−≥==)(),(xy x xy dydx e dydx y x f μλλμ∫∫∞+∞+−−=)(dx dy e e xy x μλμλ ),0u dx ee x x +=⋅=∫∞+−−λλλμλ{}{110=−==Z P Z P Z 的分布函数为⎪⎪⎩⎪⎪⎨⎧≥<≤+<=.1,1,10,,0,0)(z z z z F Z μλμ18、∵X 、Y 分别仅取0，1两个数值，∴Z 亦只取0，1两个数值. 又∵X 与Y 相互独立，∴{}{}{}{}==========00)0,0(0),max(0Y P X P Y X P Y X P Z P 1/2×1/2=1/4，故{}{}.4/34/110111=−==−===Z P Z P 19、 X 由2×2阶行列式表示，仍是一随机变量，且X=X 1X 4--X 2X 3，根据X 1，X 2，X 3，X 4的地位是等价且相互独立的，X 1X 4与X 2X 3也是独立同分布的，因此可先求出X 1X 4和X 2X 3的分布律，再求X 的分布律. ,则X=Y 1--Y 2.随机变量Y 1和Y 2独立同分布：322411,X X Y X X Y ==记}{}{}{{}.84.016.01}0{0112121=−========Y P Y Y P Y P 16.01,132===P X X P 显见, 随机变量X=Y 1--Y 2有三个可能值--1,0,1.易见 P{X=--1}=P{Y 1=0,Y 2=1}=0.84×0.16= 0.1344， P{X=1}=P{Y 1=1,Y 2=0}=0.16×0.84=0.1344, P{X=0}=1--2×0.1344=0.7312. 于是，行列式的概率分布为 4321X X X X X =~ ⎥⎦⎤⎢⎣⎡−1344.07312.01344.010120、因为{Z=i }={X+Y=i }={X=0,Y=i }}.0,{}1,1{==−==Y i X i Y X ∪ ∪∪ 由于上述各事件互不相容，且注意到X 与Y 相与独立，则有 ∑∑==−===−====i k ik k i Y P k X P k i Y k X P i Z P 00}{}{},{}{∑=+−−−−−=−−=iik ki n ki k i nkn kk n P p pC P p c 022111()1()1∑=−−+ik k i n k n in n C Cp 02121)(,,1,0,)1(212121n n i p p C i n n i i n n+=−=−++).,(~21p n n B Y X Z ++=故注：在上述计算过程中，已约定：当r>n 时，用到了公式并,0=rnC .12121∑=+−=ik i n n k i n k n C C C21、X 和Y 的概率分布密度为},2)(exp{21)(22σσπy x x f X −−=);(+∞<<−∞x ⎩⎨⎧≤≤−=.,0,),2/(1)(其它πππy y f Y 因X 和Y 独立，考虑到 )仅在[)(y f Y ππ,−]上才有非零值，故由卷积公式知Z 的概率密度为.221)()()(222)(dy edy y f y z f z f a y z Y X Z ∫∫−−−−∞+∞−=−=ππμσππ令σμ−−=y z t ,则上式右端等于.(2122122⎥⎦⎤⎢⎣⎡⎟⎠⎞⎜⎝⎛−−Φ−−+Φ=∫−+−−−σμπσμππππσμπσμπz z dt e z z t 22、（1）由题设知 {}y X X P y M P y F n M ≤=≤=),,max()()(1),,(1y X y X P n ≤≤= )()()()()(121y F y F y X P y X P y X P Xn X n =≤≤≤=.∵),1(],0[~:,,1n i U X X X i n ≤≤θ独立且同分布 ∴⎪⎩⎪⎨⎧><<≤=,0,1,0,,0,0)(x x x x x F i X θθ∴⎪⎪⎩⎪⎪⎨⎧≥<<≤=.,1,0,,0,0)(θθθy y y y y F n n M 故⎪⎩⎪⎨⎧<<=−.,0,0,)(1其它θθy ny y f n n M（2）{}y X X P y N P y N P y F n N >−=>−=≤=),,min(1)(1)()(1()y X P y X P y X P y X y X y X P n n >>>−=>>>−= )()(1,,,12121()[])(11)(11y F y X P i X i ni −−=>Π−==故 ⎪⎩⎪⎨⎧<<−=⎪⎩⎪⎨⎧<<−−−=−−其它其它,0,00,)(,001(1()(11y y n y y n y f n n n N θθθθθ 23、由题设容易得出随机变量（X ，Y ）的概率密度，本题相当于求随机变量X 、Y 的函数S=XY 的概率密度，可用分布函数微分法求之.依题设，知二维随机变量（X ，Y ）的概率密度为()()()⎩⎨⎧∉∈=G y x Gy x y x f ,,0,2/1,若若设为S 的分布函数,则当{s S P s F ≤=)(}0≤s 时,()0=s F ；当时, .2≥s ()1=s F 现设0<s<2. 曲线s xy =与矩形G 的上边交于点(s,1);位于曲线s xy =上方的点满足s xy >,位于下方的点满足s xy <. 故(){}{}{}).ln 2ln 1(2211211121s sdy dx dxdy S XY P s XY P s S P s F s x s sxy −+=−=−=>−=≤=≤=∫∫∫∫>于是,⎩⎨⎧≥≤<<−=.20,0,20,2/)ln 2(ln )(s s s s s f 或若若（二）、补充题答案1.由于即{},0)(),,min(,,max =<==Y X P Y X 故知ηξηξ{}{}{}03,23,12,1=========Y X P Y X P Y X P ；又易知{}{}{}{},9/1111,11,1==⋅=======ηξηξP P P Y X P{}{},9/12,22,2======ηξP Y X P {}{},9/13,33,3======ηξP Y X P {}{}{},9/29/19/11,22,11,2=+===+=====ηξηξP P Y X P{}{}{},9/22,33,22,3===+=====ηξηξP P Y X P {}.9/29/711,3=−===Y X P 所以2.（1）x{}.,2,1,0,0,)1( =≤≤−===n n m P P C n X m Y P m n {}（2）{}{}n X P n X m Y P m Y n X P ======,.,2,1,0,0,!)1( =≤≤⋅⋅−=−−n n m e P P C n m n mm n λλ3.22)1()1()1()0()0()1(p p Y P X P Y P X P z P +−===+====)1(2)0()1()1()0()0(p p Y P X P Y P X P z P −===+====而，由2)1,1()1,1(p Y X P Z X P ======),1()1()1,1(=====Z P X P Z X P 得. 2/1=p 5.:设随机变量ξ和η相互独立，都服从分 )1,0(N 布.则⎭⎬⎫⎩⎨⎧+−⋅=)(21exp 21),(22y x y x p π.显然， ,),(),(∫∫∫∫<SGdxdy y x p dxdy y x p,其中 G 和S 分别是如图所示的矩形ABCD 和圆.22/)21(),(2∫∫∫−−=a ax Gdx e dxdy y x p π，令,sin ,cos ϕγϕγ==y x 则 ∫∫∫∫=ππ20221),(a aSdxdy y x p 所以221212/a aaxe dx e −−−−<∫π.6.设这类电子管的寿命为ξ，则（1）三个管子均不要替换的概率为；（2）三个管子均要替换的概率为 .∫∞+==>1502.3/2)/(100)150(dx x P ξ21(−27/8)3/2(3=27/1)3/3=7.假设总体X 的密度函数为，分布函数为，第次的观察值为，独立同分布，其联合密度函数)(x f ,(1x f )(x F )()2x f i (n x )1(n i X i ≤≤i X )(),1n f x f x =.依题意，所求的概率为{}∫∫∫∫∫∫∞+∞−∞−∞−∞−−−−=−==>>><n n n nx i x x x x n n nn nn n i n n n n dx x f dx x f dx x f dx x f dx dx xx f X X X X X X P 112211111,...,2,1121)(...)()()(),,(.,...,,∫∫∞+∞−∞+∞−−−==)()()()(11n n n n n n n x dF x F dx x f x F.1)(1n x F nn n=∞−∞+=8.)(),()(21211211n P n k P n k P =+=+===+=ξξξξξξξξ)()()(2121n P k n P k P =+−===ξξξξ.由普哇松分布的可加性，知服从参数为的普哇松分布，所以 21ξξ+21λλ+)(21212112121!)()!(!)(λλλλλλλλξξξ+−−−−+−⋅==+=e n e k n ek n k P n k n k.1211211kn kk n −⎟⎟⎠⎞⎜⎜⎝⎛+−⎟⎟⎠⎞⎜⎜⎝⎛+⎟⎟⎠⎞⎜⎜⎝⎛=λλλλλλ9.当，0≤z (),0)(=≤=z Z P z F z ,0>z 当()z Z P z F z ≤=)(∫∫−+−=20)2(02xz y x z dy e dx∫∫−−−−−−−==202012x z z z y z x ze e dy e dxe ，所以 Y X z 2+=的分布函数为 ⎩⎨⎧>+−≤=−.0,)1(1,0,0),(z e z z y x F z10.由条件知X 和Y 的联合密度为⎪⎩⎪⎨⎧≤≤≤≤=其他若,0,31,31,41),(y x y x p以表示随机{})()(∞<<−∞≤=u u U P u F 变量U 的分布函数.显然，当0≤u 时， 0)(=u F ；当时，； 2≥u 1)(=u F 当，则20<<u []∫∫∫∫≤−uy x y x p ||,(≤−−−=−−===uy x u u dxdy dxdy u F ||2)2(411)2(44141))(2u−于是，随机变量的密度为⎪⎩⎪⎨⎧<<−=其他,0;20),2(21)(u u u p .11.记为这3个元件无故障工作的时间，则的分布函数321,,X X X ),,min(321X X X T ={}[][].)(1),,min(1(31321t X P t X X X P t F T −=>−(11)13X P t ≤−−=>)()t T P =≤=⎩⎨⎧≤>−=∴⎩⎨⎧=≤>−=−−,0,0,0,1)()3,2,1(,0,0,0,1)(~3t t e t F i t t e t F X t T t i λλ∵ 故 ⎪⎩⎪⎨⎧≤>==−.0,0,0,3)(')(3t t e t F t f t T T λλ。

电工学第三章习题答案

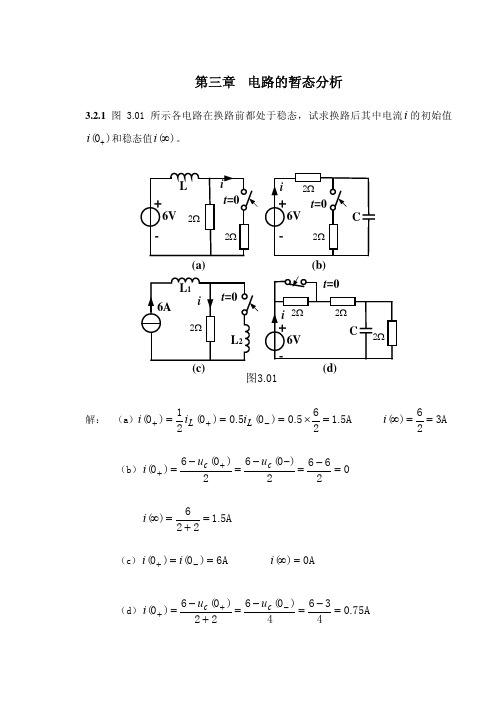
第三章电路的暂态分析3.2.1 图3.01所示各电路在换路前都处于稳态，试求换路后其中电流i 的初始值(0)i +和稳态值()i ∞。

(b)(a)(c)(d)图3.01解：（a ）A 5.1265.0)0(5.0)0(21)0(=×===−++L L i i i A 326)(==∞i（b ）02662)0(62)0(6)0(=−=−−=−=++c c u u iA 5.1226)(=+=∞i （c ）A 6)0()0(==−+i i A 0)(=∞i（d ）A 75.04364)0(622)0(6)0(=−=−=+−=−++c c u u iA 12226)(=++=∞i3.4.1 在图3.07(a)的电路中，u 为一阶跃电压，如图3.07(b)所示，试求3i 和c u 。

设V 1)0(c =−u 。

(a)图3.07(b)解：s 102)(331312−×=++=C R R R R R τV 22224)(C =+×=∞u V 1)0()0(C C ==−+u u V 2)(500C t e t u −−=mA 75.0)(1)(4)0(31131312322323213=+++++++=+R R R R R R R R R R R R R R R R i mA 144)(3==∞imA 25.01)(5003t e t i −−=3.4.2 电路如图3.08所示，求0t ≥时(1)电容电压C u ，(2)B 点电位B v 和(3)A 点电位A v 的变化规律。

换路前电路处于稳态。

Sk 10图3.08解：(1)求0≥t 时的电容电压C uV 15255)6(0)0()0(C =×+−−==−+C u uV 5.1525510)6(6)(C =×++−−=∞u[]s 1044.010100105//)2510(6123−−×=×××+=τ故V 5.05.1)5.11(5.1)(66103.21044.0C t t e et u ×−×−−=−+=−t =0_时k 10t =0+时+6V Ωk 10（2）求0≥t 时的B 点电位B v注意，+=0t 时，由于电容中存在电流，0CC ≠=dtdu Ci 因此，10K 和5K 电阻中的电流不等。

第三章习题答案

第三章热力学第二定律1、在T1=750K的高温热源与T2=300K的低温热源间工作一卡诺可逆热机,当其从高温热源Q1=250kJ时,该热机对环境所做的功W= -150 Kj，放至低温热的热Q2= -100 kJ。

2、以汞为工作物质时，可逆卡诺热机效率为以理想气体为工作物质时的100% 。

（可逆热机效率与工质无关）3、液体苯在其沸点下恒温蒸发，则此过程的△U 大于零；△H 大于零；△S 大于零；△G 等于零。

4、将1mol 温度为100℃、压力为101.325kPa的液体水投入一密封真空容器中，并刚好完全蒸发为同温同压的水蒸气，则此过程的△H 大于零；△S 大于零；△G 等于零。

5、H2与O2均为理想气体，当经历如下所示的过程后，则系统的△U 等于零; △H 等于零; △S 等于零; △G 等于零。

6、732 K时，反应NH4Cl(s)==NH3(g)+HCl(g)的∆r G=－20.8 kJ·mol-1，∆r H=154 kJ·mol-1，则该反应的∆r S = 239 J·K-1·mol-1 。

7、某双原子理想气体3 mol从始态300 K，200 KPa下经过恒温可逆膨胀到150KPa ，则其过程的功W是－2152.6 J。

8、某双原子理想气体3 mol从始态350K，200 KPa下经过绝热可逆膨胀到235.5 K平衡，则其过程的功W是－7139.6 J。

9、在真空密封的容器中,1mol温度为100℃、压力为101.325 kPa的液体水完全蒸发为100℃、101.325 kPa的水蒸气, 测得此过程系统从环境吸热37.53kJ,则此过程的△H= 40.63 kJ, △S= 108.88 J·K-1, △G= 0 kJ。

判断题1、绝热过程都是等熵过程。

×2、理想气体的熵变公式∆S nC V V nC p p p V =⎛⎝ ⎫⎭⎪+⎛⎝ ⎫⎭⎪,,ln ln m m 2121只适用于可逆过程。

第三章习题(答案)

第三章辛亥革命与君主专制制度的终结一、单项选择题1. 1903年6月，（）在上海《苏报》发表《驳康有为论革命书》，批驳康有为所谓“中国之可立宪，不可革命”的谬论A.陈天华B.邹容C.章炳麟D.梁启超2.1903年邹容写的（）是中国近代史上第一部宣传革命和资产阶级共和国思想的著作A.《猛回头》B.《警世钟》C.《革命军》D.《驳康有为论革命书》3.中国近代第一个资产阶级革命政党是()A.强学会B.兴中会C.同盟会D.国民党4. 孙中山三民主义思想的核心是()A.驱除鞑虏B.恢复中华C.创立民国D.平均地权5.1905年11月，孙中山在《民报》发刊词中将中国同盟会的政治纲领概括为（）A.创立民国、平均地权B.驱除鞑虏、恢复中华、创立合众政府C.民族主义、民权主义、民生主义D.联俄、联共、扶助农工6.武昌起义前同盟会领导的影响最大的武装起义是()A.广州起义B.萍浏醴起义C.镇南关起义D.黄花岗起义7.中国历史上第一部具有资产阶级共和国宪法性质的法典是（）A.《钦定宪法大纲》B.《中华民国临时约法》C.《中华民国约法》D.《试训政纲领》8. 辛亥革命取得的最大成就是（）A.推翻了封建帝制B.促进了资本主义的发展C.使人民获得了一些民主自由权利D.打击了帝国主义的殖民势力9. 南京临时政府的局限性表现为（）A.承认清政府与列强所订的一切不平等条约和一切外债有效B.没有提出任何可以满足农民土地要求的政策和措施C.维护封建土地制度以及官僚、地主所占有的土地财产D.主体是资产阶级革命派10. 二次革命失败的最重要原因是()A.革命党人军队不足B.国民党力量涣散C.袁世凯军队强大D.袁世凯得到帝国主义的支持11.1915年，（）在云南率先举起反袁护国的旗帜，发动护国战争A.黄兴B.段祺瑞C.蔡锷D.孙中山12.资产阶级革命派开展护国运动的主要原因是()A.袁世凯指使刺杀宋教仁B.袁世凯强迫国会选举他为正式大总统C.袁世凯解散国会D.袁世凯复辟帝制13. 袁世凯为复辟帝制不惜出卖主权，与日本签订了卖国的（）A.中日共同防敌军事协定B.承认外蒙自治C.“二十一条”D.出让川汉、粤汉铁路14. 1917年孙中山针对（）指出“以假共和之面孔，行真专制之手段”，并举起“护法”旗帜A.黎元洪B.张勋C.张作霖D.段祺瑞15.标志着整个中国民族资产阶级领导的旧民主主义革命终结的是（）A.二次革命的失败B.护国运动的失败C.护法运动的失败D.保路风潮的失败16.20世纪初主张“实业救国”的著名实业家楷模是()A.张謇B.周学熙C.荣宗敬D.荣德生二、多项选择题1.《辛丑条约》的签订，标志着（）。

第3章测量技术基础习题参考答案

第3章测量技术基础习题参考答案1、测量的实质是什么？一个完整的测量过程包括哪几个要素？答：⑴测量的实质是将被测几何量L与作为计量单位的标准量μ进行比较，以确定被测量的量值的操作过程，即L/μ=q,或L=μq。

⑵一个完整的测量过程包括被测对象，计量单位、测量方法和测量精度四个要素。

2、量块的作用是什么？其结构上有何特点？答：⑴量块的作用：a、用于计量器具的校准和鉴定；b、用于精密设备的调整、精密划线和精密工件的测量；c、作为长度尺寸传递的实物基准等。

⑵非测量面；测量面的表面非常光滑平整，具有研合性，两个测量面间具有精确的尺寸。

量块上标的尺寸称为量块的标称长度ln。

当ln<6mm的量块可在上测量面上作长度标记，ln>6mm的量块，有数字的平面的右侧面为上测量面。

3、量块分等、分级的依据各是什么？在实际测量中，按级和按等使用量块有何区别？答：⑴量块分等的依据是量块测量的不确定度和量块长度变动量的允许值来划分的。

量块分级主要是根据量块长度极限偏差和量块长度变支量的最大允许值来划分的。

⑵区别是：量块按“级”使用时，是以量块的标称长度作为工作尺寸。

该尺寸包含了量块的制造误差，制造误差将被引入到测量结果中去，但固不需要加修正值，故使用较方便。

量块按“等”使用时，是以量块栏定书列出的实例中心长度作为工作尺寸的，该尺寸排除了量块的制造误差，只包含栏定时较小的测量误差。

量块按“等”使用比按“级”使用的测量精度高。

4、说明分度间距与分度值；示值范围与测量范围；示值误差与修正值有何区别？答：其区别如下：⑴分度间距（刻度间距）是指计量器具的刻度标尺或度盘上两面三刀相邻刻线中心之间的距离，般为1-2.5mm；而分度值(刻度值)是指计量器具的刻度尺或度盘上相邻两刻线所代表的量值之差。

⑵示值范围是指计量器具所显示或指示的最小值到最大值的范围；而测量范围是指在允许的误差限内，计量器具所能测出的最小值到最大值的范围。

⑶示值误差是指计量器具上的示值与被测量真值的代数差；而修正值是指为消除系统误差，用代数法加到未修正的测量结果上的值。

第3章习题答案

第三章 练习题答案

第3章习题答案

数据与计算机通信答案(第3章)

第三章习题解答

第3章习题答案

第三章习题参考答案

第3章 本量利练习题(答案版)

第三章习题解答及参考答案

第三章习题(含答案)

大学物理课后习题答案第三章

第三章习题及答案

第三章习题参考答案

习题第3章答案

概率论课后习题第3章答案

电工学第三章习题答案

第三章习题答案

第三章习题(答案)

第3章测量技术基础习题参考答案

第三章练习题答案

第3章本量利练习题(答案版)