专题4 平面向量与不等式结合
11第十一讲 平面向量、不等式

∥
=
( 0)
· ( y 3 y1 )=( x3 x1 ) · ( y 2 y1 ) ( x 2 x1 ) ④两个向量 a 、 b 的夹角公式:
cos x1 x 2 y1 y 2
2 x1 2 2 2 y1 x2 y2
⑤线段的定比分点公式: ( 0 和 1) 1 设 P1P = PP2 (或 P2P = PP1 ) ,且 P1 , P, P2 的坐标分别是 (x1 , y1) , ( x, y), ( x2 , y2 ) ,则 推广
abc ] 2
⑸已知⊙O 是△ABC 的内切圆,若 BC=a,AC=b,AB=c [注:s 为△ABC 的半周长,即 则:①AE= s a =1/2(b+c-a) ②BN= s b =1/2(a+c-b) ③FC= s c =1/2(a+b-c) 综合上述:由已知得,一个角的邻边的切线长,等于半周长减去对边(如图 4). 特例:已知在 Rt△ABC,c 为斜边,则内切圆半径 r=
1 ab ba ac (a b c) 2 ( a b c时取等) 3
⑶绝对值不等式:
a 1 a 2 a 3 a 1 a 2 a 3 a b a b a b (ab 0时,取等)
⑷算术平均≥几何平均(a1、a2…an 为正数) : ⑸柯西不等式:设 a i ,b i R(i
c
A
F b
b
O a B
E F
ra
C
1图
图2
图3
B N
附:三角形的五个“心” ; 重心:三角形三条中线交点. 外心:三角形三边垂直平分线相交于一点. 内心:三角形三内角的平分线相交于一点.
平面向量常见题型汇编2 向量基本定理与不等式

向量基本定理与不等式,、三角函数相结合例题1: 在Rt ABC ∆中,090A ∠=,点D 是边BC 上的动点,且3AB =,4AC =,(0,0)AD AB AC λμλμ=+>>,则当λμ取得最大值时, AD 的值为 解析:由090A ∠=可将三角形放入平面直角坐标系中,建立如图坐标系,其中()00A ,,()30B ,,()04C ,∵(0,0)AD AB AC λμλμ=+>>∴1λμ+= ∵2λμλμ+≥14λμ≤当且仅当12λμ==时取等号 ()()111133004222222AD AB AC AB AC λμ⎛⎫=+=+=+= ⎪⎝⎭,,, ∴2235222AD ⎛⎫=+= ⎪⎝⎭变式1: 已知点A 在线段BC 上(不含端点),O 是直线BC 外一点,且20OA aOB bOC --=,则221a b a b b+++的最小值是___________ 分析:本题主要考查了不等式,不等式求最值问题,属于中档题。
解决此类问题,重要的思路是如何应用均值不等式或其他重要不等式,很多情况下,要根据一正、二定、三取等的思路去思考,本题根据条件构造21a b +=,研究的式子分别加1后变形,即可形成所需条件,应用均值不等式.解析:由20OA aOB bOC --=可得, 2OA aOB bOC =+,根据A 、B 、C 三点共线可得21a b +=,且0,0a b >>,所以()222222211222221222a b a b a a b b a b a b a b b a b a b b a b a b+++++++=-+-=+-≥+++++++ 所以最小值为222,故填222.变式2: 给定两个长度为1的平面向量,OA OB ,它们的夹角为120.如图1所示,点C 在以O 为圆心的圆弧AB 上变动.若,OC xOA yOB =+其中,x y R ∈,则x y +的最大值是______. 思考方向一 :考虑特值法解法1 当C 与A 重合时,10,OC OA OB =⨯+⨯1x y +=,当C 与B 重合时,01,OC OA OB =⨯+⨯1x y +=,当C 从AB 的端点向圆弧内部运动时,1x y +>,于是猜想当C 是AB 的中点时,x y +取到最大值.当C 是AB 的中点时,由平面几何知识OACB 是菱形,∴,OC OA OB =+∴11 2.x y +=+=猜想x y +的最大值是2.思考方向二:考虑坐标法建立如图3,所示的平面直角坐标系,设AOC α∠=,则13(1,0),(,),(cos ,sin )22A B C αα-. 于是OC xOA yOB =+可化为:13(cos ,sin )(1,0)(,)22x y αα=+-, ∴1cos ,23sin .2x y y αα⎧=-⎪⎪⎨⎪=⎪⎩(1)解法2:函数法求最值由方程组(1)得: 1cos sin ,32sin .3x y ααα⎧=+⎪⎪⎨⎪=⎪⎩∴3sin cos 2sin(30)x y ααα+=+=+,又0120α≤≤,∴当30α=时,max () 2.x y +=解法3:不等式法求最值由方程组(1)得:222221sin cos ()3x y xy x y xy αα=+=+-=+-, ∴211()33xy x y =+-,由0,0x y >>,及2x y xy +≥得:2()4x y xy +≥, ∴2()4x y +≤,∴2x y +≤,当且仅当1x y ==时取等号,∴max () 2.x y +=思考方向三:考虑向量的数量积的运算解法:两边点乘同一个向量∵,OC xOA yOB =+∴,.OC OA xOA OA yOB OA OC OB xOA OB yOB OB ⎧⋅=⋅+⋅⎪⎨⋅=⋅+⋅⎪⎩ 设AOC α∠=,则 120BOC α∠=-,又||||||1OC OA OB ===,∴1cos ,21cos(120).2x y x y αα⎧=-⎪⎪⎨⎪-=-+⎪⎩,∴2[cos cos(120)]2sin(30)x y ααα+=+-=+, ∴当30α=时,max () 2.x y +=解法5:两边平方法∵,OC xOA yOB =+∴22(),OC xOA yOB =+∴2221()3x y xy x y xy =+-=+- 222()()()344x y x y x y ++≥+-⋅=, ∴2x y +≤,当且仅当1x y ==时取等号,∴max () 2.x y +=思考方向四:考虑平行四边形法则过C 作CM ∥OB 交OA 于M ,作CN ∥OA 交OB 于N ,则OMCN 是平行四边形,由向量加法的平行四边形法则得:OC OM ON =+,在OMC ∆中,设AOC α∠=, 则 120BOC α∠=-, 且||,||.OM x MC y ==解法6:利用正弦定理sin sin sin OM MC OC OCM COM OMC==∠∠∠, 1sin(60)sin sin 60x y αα==+,由等比性值得:1sin(60)sin sin 60x y αα+=++, ∴2sin(30)x y α+=+,∴当30α=时,max () 2.x y +=解法7:利用余弦定理222||||||2||||cos60,OC OM MC OM MC =+-⋅∴2221()3x y xy x y xy =+-=+-222()()()344x y x y x y ++≥+-⋅=, ∴2x y +≤,当且仅当1x y ==时取等号,∴max () 2.x y +=小结:仔细研究上面的解法,可以发现在解决向量问题时一般有三种转化策略,一是利用向量的坐标运算,二是利用向量的代数运算特别是数量积的运算,三是利用向量的几何意义转化为平面几何问题求解.在解答最值问题时,本文利用了函数法和不等式法.当然,本题作为一个填空题或者选择题,能够利用特值和猜想的办法是很好的.变式3: 若非零向量a b 、满足a b b -=,则下列不等式恒成立的为( ) A. 22b a b >- B. 22b a b <- C. 22a a b >- D. 22a a b <-解析:若两向量共线,则由于非零向量a b 、,且a b b -=,∴必有a =2b ;代入可知只有A. C 满足;若两向量不共线,注意到向量模的几何意义, ∴可以构造如图所示的三角形,使其满足OB =AB =BC ;令OA =a ,OB =b ,则BA =a b - ∴CA =2a b -且a b b -=;又BA +BC >AC ∴a b -+b >2a b -∴22b a b >-。
【巧解妙解】高考数学向量与其他问题结合的经典题型

平面向量综合应用与解题技巧【命题趋向】由2019年高考题分析可知:1.这部分内容高考中所占分数一般在10分左右.2.题目类型为一个选择或填空题,一个与其他知识综合的解答题. 3.考查内容以向量的概念、运算、数量积和模的运算为主. 【考点透视】“平面向量”是高中新课程新增加的内容之一,高考每年都考,题型主要有选择题、填空题,也可以与其他知识相结合在解答题中出现,试题多以低、中档题为主. 透析高考试题,知命题热点为:1.向量的概念,几何表示,向量的加法、减法,实数与向量的积. 2.平面向量的坐标运算,平面向量的数量积及其几何意义. 3.两非零向量平行、垂直的充要条件. 4.图形平移、线段的定比分点坐标公式.5.由于向量具有“数”与“形”双重身份,加之向量的工具性作用,向量经常与数列、三角、解析几何、立体几何等知识相结合,综合解决三角函数的化简、求值及三角形中的有关问题,处理有关长度、夹角、垂直与平行等问题以及圆锥曲线中的典型问题等.6.利用化归思想处理共线、平行、垂直问题向向量的坐标运算方面转化,向量模的运算转化为向量的运算等;利用数形结合思想将几何问题代数化,通过代数运算解决几何问题. 【例题解析】1. 向量的概念,向量的基本运算(1)理解向量的概念,掌握向量的几何意义,了解共线向量的概念. (2)掌握向量的加法和减法.(3)掌握实数与向量的积,理解两个向量共线的充要条件.(4)了解平面向量的基本定理,理解平面向量的坐标的概念,掌握平面向量的坐标运算. (5)掌握平面向量的数量积及其几何意义,了解用平面向量的数量积可以处理有关长度、角度和垂直的问题,掌握向量垂直的条件. (6)掌握平面两点间的距离公式.例1(北京卷理)已知O 是ABC △所在平面内一点,D 为BC 边中点,且2OA OB OC ++=0,那么( ) A.AO OD = B.2AO OD = C.3AO OD = D.2AO OD = 命题意图:本题考查能够结合图形进行向量计算的能力.解: 22()(,22.OA OB OC OA DB OD DC OD DB DC OA OD AO OD ∴∴++=++++=-+==)=0,0, 故选A . 例2.(安徽卷)在ABCD 中,,,3AB a AD b AN NC ===,M 为BC 的中点,则MN =______.(用a b 、表示)命题意图: 本题主要考查向量的加法和减法,以及实数与向量的积. 解:343A =3()AN NC AN C a b ==+由得,12AM a b =+,所以,3111()()4244MN a b a b a b =+-+=-+. 例3.(广东卷)如图1所示,D 是△ABC 的边AB 上的中点,则向量=( ) (A )BA BC 21+- (B ) 21--(C ) 21- (D )21+命题意图: 本题主要考查向量的加法和减法运算能力. 解:21+-=+=,故选A.例4. (重庆卷)与向量a =71,,22b ⎛⎫= ⎪⎝⎭⎪⎭⎫ ⎝⎛27,21的夹解相等,且模为1的向量是 ( ) (A) ⎪⎭⎫- ⎝⎛53,54 (B) ⎪⎭⎫- ⎝⎛53,54或⎪⎭⎫ ⎝⎛-53,54 (C )⎪⎭⎫- ⎝⎛31,322 (D )⎪⎭⎫- ⎝⎛31,322或⎪⎭⎫ ⎝⎛-31,322 命题意图: 本题主要考查平面向量的坐标运算和用平面向量处理有关角度的问题.解:设所求平面向量为,c 由433,,, 1.555c c ⎛⎫⎛⎫=-= ⎪ ⎪⎝⎭⎝⎭4或-时5另一方面,当7413431,,cos ,.5527a c c a c a c ⎛⎫⨯+⨯- ⎪⋅⎛⎫=-=== ⎪⋅⎝⎭⎛⎫时 当7413431,,cos ,.5527a c c a c a c ⎛⎫⎛⎫⨯-+⨯ ⎪ ⎪⋅⎛⎫=-==- ⎪⋅⎝⎭⎛⎫时 故平面向量c 与向量a =71,,22b ⎛⎫= ⎪⎝⎭⎪⎭⎫ ⎝⎛27,21的夹角相等.故选B. 例5.(天津卷)设向量a 与b 的夹角为θ,且)3,3(=a,)1,1(2-=-a b ,则=θcos __. 命题意图: 本题主要考查平面向量的坐标运算和平面向量的数量积,以及用平面向量的数量积处理有关角度的问题.解: ()()()()(),,22,3,323,231,1.b x y b a x y x y =-=-=--=-设由 ()2311,1,2.231 2.x xb y y -=-=⎧⎧⇒∴=⎨⎨-==⎩⎩得 2cos ,33a b a b a b⋅===⋅+例6.(2006年湖北卷)已知向量()3,1a =,b 是不平行于x 轴的单位向量,且3a b ⋅=,则b = ()(A ) ⎪⎪⎭⎫⎝⎛21,23 (B ) ⎪⎪⎭⎫ ⎝⎛23,21 (C )⎪⎪⎭⎫ ⎝⎛433,41 (D ) ()0,1 命题意图: 本题主要考查应用平面向量的坐标运算和平面向量的数量积,以及方程的思想解题的能力.解:设(),()b x y x y =≠,则依题意有1,y +=1,2x y ⎧=⎪⎪⎨⎪⎪⎩ 故选B.例7.设平面向量1a 、2a 、3a 的和1230a a a ++=.如果向量1b 、2b 、3b ,满足2i i b a =,且i a 顺时针旋转30o 后与i b 同向,其中1,2,3i =,则( )(A )1230b b b -++= (B )1230b b b -+= (C )1230b b b +-= (D )1230b b b ++=命题意图: 本题主要考查向量加法的几何意义及向量的模的夹角等基本概念.常规解法:∵1230a a a ++=,∴ 1232220.a a a ++=故把2i a (i=1,2,3),分别按顺时针旋转30 后与i b 重合,故1230b b b ++=,应选D.巧妙解法:令1a =0,则2a =3a -,由题意知2b =3b -,从而排除B ,C ,同理排除A ,故选(D). 点评:巧妙解法巧在取1a =0,使问题简单化.本题也可通过画图,利用数形结合的方法来解决.2. 平面向量与三角函数,解析几何等问题结合(1) 平面向量与三角函数、三角变换、数列、不等式及其他代数问题,由于结合性强,因而综合能力较强,所以复习时,通过解题过程,力争达到既回顾知识要点,又感悟思维方法的双重效果,解题要点是运用向量知识,将所给问题转化为代数问题求解.(2)解答题考查圆锥曲线中典型问题,如垂直、平行、共线等,此类题综合性比较强,难度大. 例8.(2007年陕西卷理17.)设函数f (x )=a-b ,其中向量a =(m,cos2x ),b =(1+sin2x ,1),x ∈R ,且函数y=f (x )的图象经过点⎪⎭⎫⎝⎛2,4π,(Ⅰ)求实数m 的值;(Ⅱ)求函数f (x )的最小值及此时x 的值的集合. 解:(Ⅰ)()(1sin 2)cos 2f x a b m x x ==++,由已知πππ1sin cos 2422f m ⎛⎫⎛⎫=++=⎪ ⎪⎝⎭⎝⎭,得1m =.(Ⅱ)由(Ⅰ)得π()1sin 2cos 2124f x x x x ⎛⎫=++=+⎪⎝⎭,∴当πsin 214x ⎛⎫+=- ⎪⎝⎭时,()f x 的最小值为1,由πsin 214x ⎛⎫+=- ⎪⎝⎭,得x 值的集合为3ππ8x x k k ⎧⎫=-∈⎨⎬⎩⎭Z , 例2.(2007年陕西卷文17)设函数b a x f 、=)(.其中向量2)2π(R,),1,sin 1(),cos ,(=∈+==f x x b x m a 且.(Ⅰ)求实数m 的值; (Ⅱ)求函数)(x f 的最小值.解:(Ⅰ)()(1sin )cos f x m x x ==++a b ,πππ1sin cos 2222f m ⎛⎫⎛⎫=++=⎪ ⎪⎝⎭⎝⎭,得1m =.(Ⅱ)由(Ⅰ)得π()sin cos 114f x x x x ⎛⎫=++=++ ⎪⎝⎭,∴当πsin 14x ⎛⎫+=- ⎪⎝⎭时,()f x 的最小值为1例9.(湖北卷理16)已知ABC △的面积为3,且满足06AB AC ≤≤,设AB 和AC 的夹角为θ. (I )求θ的取值范围;(II )求函数2()2sin 24f θθθ⎛⎫=+⎪⎝⎭π的最大 解:(Ⅰ)设ABC △中角A B C ,,的对边分别为a b c ,,, 则由1sin 32bc θ=,0cos 6bc θ≤≤,可得0cot 1θ≤≤,ππ42θ⎡⎤∈⎢⎥⎣⎦,∴.(Ⅱ)2π()2sin 24f θθθ⎛⎫=+⎪⎝⎭π1cos 222θθ⎡⎤⎛⎫=-+ ⎪⎢⎥⎝⎭⎣⎦(1sin 2)2θθ=+-πsin 2212sin 213θθθ⎛⎫=-+=-+ ⎪⎝⎭.ππ42θ⎡⎤∈⎢⎥⎣⎦,∵,ππ2π2363θ⎡⎤-∈⎢⎥⎣⎦,,π22sin 2133θ⎛⎫-+ ⎪⎝⎭∴≤≤.即当5π12θ=时,max ()3f θ=;当π4θ=时,min ()2f θ=. 例10.(广东卷理)已知ABC 的三个顶点的直角坐标分别为A(3,4)、B(0,0)、C(c,0) (1)若c=5,求sin ∠A 的值;(2)若∠A 为钝角,求c 的取值范围; 解:(1)(3,4)AB =--,(3,4)AC c =--,若c=5, 则(2,4)AC =-,∴cos cos ,A AC AB ∠=<>=sin ∠A ; (2)∠A 为钝角,则39160,0,c c -++<⎧⎨≠⎩解得253c >,∴c 的取值范围是25(,)3+∞例11.(山东卷文17)在ABC △中,角A B C ,,的对边分别为tan a b c C =,,,(1)求cos C ;(2)若52CB CA =,且9a b +=,求c .解:(1)sin tan cos CC C=∴=又22sin cos 1C C +=解得1cos 8C =±. tan 0C >,C ∴是锐角. 1cos 8C ∴=. (2)52CB CA =, 5cos 2ab C ∴=,20ab ∴=. 又9a b += 22281a ab b ∴++=. 2241a b ∴+=.2222cos 36c a b ab C ∴=+-=.6c ∴=.例12. (湖北卷)设函数()()f x a b c =⋅+,其中向量()()sin ,cos ,sin ,3cos a x x b x x =-=-, ()cos ,sin ,c x x x R =-∈.(Ⅰ)求函数()x f 的最大值和最小正周期;(Ⅱ)将函数()x f y =的图像按向量d 平移,使平移后得到的图像关于坐标原点成中心对称,求长度最小的d . 命题意图:本小题主要考查平面向量数量积的计算方法、三角公式、三角函数的性质及图像的基本知识,考查推理和运算能力.解:(Ⅰ)由题意得,f(x)=a ·(b c +)=(sinx,-cosx)·(sinx-cosx,sinx -3cosx)=sin 2x -2sinxcosx+3cos 2x =2+cos2x -sin2x =2+2sin(2x+43π).所以,f(x)的最大值为2+2,最小正周期是22π=π.(Ⅱ)由sin(2x+43π)=0得2x+43π=k.π,即x =832ππ-k ,k ∈Z ,于是d =(832ππ-k ,-2),(k d π=-k ∈Z.因为k 为整数,要使d 最小,则只有k =1,此时d =(―8π,―2)即为所求.例13.(2006年全国卷II )已知向量a =(sin θ,1),b =(1,cos θ),-π2<θ<π2.(Ⅰ)若a ⊥b ,求θ;(Ⅱ)求|a +b |的最大值. 命题意图:本小题主要考查平面向量数量积和平面向量的模的计算方法、以及三角公式、三角函数的性质等基本知识,考查推理和运算能力.解:(Ⅰ)若a ⊥b ,则sin θ+cos θ=0,由此得 tan θ=-1(-π2<θ<π2),所以 θ=-π4;(Ⅱ)由a =(sin θ,1),b =(1,cos θ)得|a +b |=(sin θ+1)2+(1+cos θ)2=3+2(sin θ+cos θ)=3+22sin(θ+π4),当sin(θ+π4)=1时,|a +b |取得最大值,即当θ=π4时,|a +b |最大值为2+1.例14.(2006年陕西卷)如图,三定点(2,1),(0,1),(2,1);A B C --,,AD t AB BE tBC == ,[0,1].DM tDE t =∈(I )求动直线DE 斜率的变化范围; (II )求动点M 的轨迹方程。
不等式及平面向量

二、平面向量的基本定理及向量坐标运 算
坐标运算
二、平ห้องสมุดไป่ตู้向量的基本定理及向量坐标运 算
坐标运算(共线、垂直?)
练习题
练习题
练习题
三、平面向量的数量积
数量积
练习题
不等式
一、不等关系与不等式 二、一元二次不等式的解法
三、不等式组和线性规划问题
四、均值不等式及其应用
一、不等关系与不等式
练习题
练习题
4、若m<0,n>0,且m+n<0,则下列不等式中成立的是() A:-n<m<n<-m B:-n <m <-m <n
C:m <-n <-m <n
D:m <-n <n <-m
二、一元二次不等式的解法
练习题
练习题
三、不等式组和线性规划问题
结论:用不等式组表示区域 一般地总结出了结论:
不等到式Ax+By+C>0(或Ax+By+C<0)(其中A、B不同时为零)在平面直角坐 标系上表示的点集组成的图形是直线Ax+By+C=0的同侧的所有点组成的平 面区域。
练习题
练习题
四、均值不等式及其应用
练习题
练习题
平面向量
一、平面向量的线性运算 二、平面向量的基本定理及向量坐标运算
三、平面向量的数量积
一、平面向量的线性运算
三角形法则和平行四边形法则
一、平面向量的线性运算
运算定理
练习题
二、平面向量的基本定理及向量坐标运 算
基本定理
平面向量与不等式结合专题

g ( x) 1 1 进行化简,得 x 2 5 ,然后利用 f ( x) x2
不等式 a b 2 ab 求函数的最值.
b b b 2 [答案](1)由已知得 A( ,0), B (0, b), 则 AB { , b} ,于是 k , k k b 2
故当 a c 1 时,上式成立,本题应选 (C). [规律小结]
(1)平面向量与不等式结合的问题,经常以向量为载体考查不等式的知识,解题的关 键是利用向量的知识将问题转化为不等式的问题:解不等式,求最大值(最小值) ,转化时 不要把向量与实数搞混淆。 (2)向量与不等式的结合,既符合在知识的“交汇处”构题,又加强了对双基的考查, 特别是向量的坐标表示及运算, 这类问题的解决思路通常是将向量的数量积的运算与模用坐 标运算后,转化为三角函数问题,然后用三角函数基本公式求解,基中涉及到的有关向量的 知识有:①向量的坐标表示及加法、减法、数乘向量;②向量的数量积;③向量平行、垂直 的充要条件;④向量的模、夹角;⑤ a b a b ;若 a ( x1 , y1 ) , b
2
因为 0≤ x ≤ ,所以
4
<x<
3 ; 4
专题4 平面向量压轴小题(解析版)

专题4平面向量压轴小题一、单选题1.(2021·重庆九龙坡·高三期中)已知12AB AB ⊥,121OB OB ==,12AP AB AB =+,12OP <,则||OA 的取值范围( )A .B .C .D . 【答案】B 【分析】根据题设易知四边形12B AB P 为矩形,构建以A 为原点直角坐标系,将问题转化为平面上满足1211,2OB OB OP ==<的情况下,结合两点距离公式求,O A 两点距离的范围. 【详解】由题设,四边形12B AB P 为矩形,构建以A 为原点的直角坐标系,如下图,若12(0,),(,0)B n B m ,则(,)P m n ,设(,)O x y ,∴22()1x y n +-=,22()1x m y -+=且2210()()4x m y n ≤-+-<, 又22222||2[()()]OA x y x m y n =+=--+-,∴27||24OA <≤||2OA <≤ 故选:B 【点睛】关键点点睛:构建直角坐标系,将平面向量的模长问题转化为平面上两点的距离问题,应用解析法求范围. 2.(2021·浙江丽水·高三期中)已知平面向量1e ,2e ,a ,121e e ==,若()122a e e ⋅+≥,()121a e e ⋅-≥,则( )A .a 的最小值是32B .a 的最大值是32C .a 的最小值是94D .a 的最大值是94【答案】A 【分析】令1212,u e e v e e =+=-,可得u v ⊥,且2||u +2||4v =,设(2cos ,0),(0,2sin )u v αα== ,||a r =,a =(sin ,cos )r r ββ,根据已知条件及三角函数的有界性即可求解. 【详解】令1212,u e e v e e =+=-,则22120u v e e ⋅=-=,故u v ⊥,且2||u +()22212||24v e e =+=,假设(2cos ,0),(0,2sin )u v αα== ,||a r =,a =(sin ,cos )r r ββ, 所以根据已知条件有2cos sin 22sin cos 1a u r a v r αβαβ⎧⋅=⋅⋅≥⎪⎨⋅=⋅⋅≥⎪⎩,所以22(|cos sin ||sin cos |)3r r αβαβ≥⋅+⋅≥,即32r ≥, 当且仅当3sin ,22r παβα==-=时等号成立, 所以||a 的最小值是32,故选:A.3.(2021·安徽·淮南第一中学高三月考(理))已知点M 是ABC 所在平面内一点,若1123AM AB AC =+,则ABM 与BCM 的面积之比为( ) A .83B .52C .2D .43【答案】C 【分析】作出图形,结合三点共线性质可得,()1AG AB AC λλ=+-,同时设AG tAM =,联立解出,t λ,进而确定GM GA关系,同时满足CG CB λ=,进而求出BGGC关系,即可求解两三角形面积之比. 【详解】如图,延长AM 交BC 于G ,则()1AG AB AC λλ=+-,因为A ,M ,G 三点共线,所以AG tAM =,即()11123AB AC t AB AC λλ⎛⎫+-=+ ⎪⎝⎭,所以12113λλ=-,则312λλ=-,故35λ=且65t =,又CG CB λ=,故35CG CB =,所以23BG GC =,16GM GA =,所以55112252BMC BGM BAM BAM S S S S ==⨯=△△△△,所以2BAM BMC S S =△△.故答案为:C4.(2021·浙江·模拟预测)在正三棱柱111ABC A B C -中,11AB AA ==,点P 满足1(1)(01)BP BC BB λλλ=+-<<,则( )A .存在P 点使得1BP A C ⊥B .存在P 点使得1BP AC ⊥ C .存在P 点使得BP AC ⊥D .存在P 点使得1BP AB ⊥ 【答案】A 【分析】通过题干条件可得:P 点一定在线段1B C 上运动,即BP 一定在平面11BCC B 上,所以找到选项中的目标线段的特点,只有A 选项中A 1C 中含有的A 1点能够使得 A 1D (D 为B 1C 1的中点)垂直平面BCC 1B 1. 【详解】因为1(1)(01)BP BC BB λλλ=+-<<,由平面向量基本定理可得:P 点一定在线段1B C 上,所以取11B C 的中点D ,连接CD ,过B 作BP CD ⊥交CD 于点H ,交1B C 于点P ,因为1A D ⊥11C B ,1A D ⊥1BB ,1111C B BB B =,所以1A D ⊥平面11BCC B ,因为BP ⊂平面11BCC B ,所以1A D ⊥BP ,因为1A DDC D =,所以BP ⊥平面1A DC ,因为1AC ⊂平面1A DC ,所以1BP A C ⊥,其余均不可能. 故选:A5.(2021·广东肇庆·模拟预测)如图,在平行四边形ABCD 中,13AE AD =,14BF BC =,CE 与DF 交于点O .设AB a =,AD b =,若AO a b λμ=+,则λμ+=( )A .817B .1917C .317D .1117【答案】B 【分析】根据,,D O F 和,,E O C 三点共线,可得AO x AD y AF =+和AO mAE nAC =+,利用平面向量线性运算可用,a b 表示出AO ,由此可得方程组求得,x y ,进而得到λμ+的值.【详解】 连接AF ,AC ,,,D O F 三点共线,∴可设AO x AD y AF =+,则1x y +=, ()1144AO xAD y AB BF xAD y AB AD x y b ya ⎛⎫⎛⎫∴=++=++=++ ⎪ ⎪⎝⎭⎝⎭;,,E O C 三点共线,∴可设AO mAE nAC =+,则1m n +=, ()33m m AO AD n AD AB n b na ⎛⎫=++=++ ⎪⎝⎭; 11143x y m n mx y ny n +=⎧⎪+=⎪⎪∴⎨+=+⎪⎪=⎪⎩,解得:917817x y ⎧=⎪⎪⎨⎪=⎪⎩,8111717AO a b ∴=+,即81119171717λμ+=+=. 故选:B. 【点睛】思路点睛:本题考查平面向量基本定理的应用,基本思路是根据O 为两线段交点,利用两次三点共线,结合平面向量基本定理构造出方程组求得结果.6.(2021·云南师大附中高三月考(文))已知a ,b ,e 是平面向量,e 与a 是单位向量,且a e ⊥,向量b 满足24830b e b -⋅+=,则||a b -的最大值与最小值之和是( )A .B .C .4D .【答案】A 【分析】将24830b e b -⋅+=变形为(2)(23)0b e b e -⋅-=,从而可得322e e b b ⎛⎫⎛⎫-⊥- ⎪ ⎪⎝⎭⎝⎭,设(10)e =,,由向量减法及数量积可知b 的终点在以(10),为圆心,以12为半径的圆周上,结合圆的性质可得答案. 【详解】由24830b e b -⋅+=得(2)(23)0b e b e -⋅-=,322e e b b ⎛⎫⎛⎫-⊥- ⎪ ⎪⎝⎭⎝⎭∴.不妨设(10)e =,,则b 的终点在以(10),为圆心,以12为半径的圆周上. 因为e 与a 是单位向量,所以||a b -的最大值是(01),与圆心距离加12,12,最小值是(01),与圆心距离减1212,故和为故选:A .7.(2021·云南·峨山彝族自治县第一中学高三月考(文))已知ABCD 是矩形,且满足3,4AB BC ==.其所在平面内点,M N 满足:3,2BM MC BN NC ==,则AD MN →→⋅的取值范围是( )A .4080,93⎡⎤⎢⎥⎣⎦B .20,403⎡⎤⎢⎥⎣⎦C .[]44,44-D .[]40,40-【答案】B 【分析】建立平面直角坐标系,根据题意得到点M ,N 的轨迹方程,然后作出图形,进而结合数量积的定义和坐标运算得到答案. 【详解】如图所示,建立平面直角坐标系,则()()()()0,0,4,0,4,3,0,3B C D A设(),M x y ,由3BM MC =,所以=221924x y ⎛⎫++= ⎪⎝⎭,记为圆1C ,设(),N a b ,由2BN NC =,所以=22166439a b ⎛⎫-+= ⎪⎝⎭,记为圆2C ,即为22166439x y ⎛⎫-+= ⎪⎝⎭, 两圆圆心距为:1116135||326C C =+=,半径和为:123825236r r +=+=, 所以1112||C C r r >+,则两圆相离,如图所示,对圆1C ,令y =0,得:()()2,0,1,0E F -, 令圆2C ,令y =0,得:()8,0,8,03G H ⎛⎫⎪⎝⎭,所以5,03FG →⎛⎫= ⎪⎝⎭,()10,0EH →=,又()4,0AD →=, 结合平面向量数量积的定义可知,AD MN →→⋅的最小值为()5204,0,033F DG A →→⎛⎫=⋅= ⎪⎝⎭⋅,AD MN →→⋅的最大值为()()4,010,040A H D E →→=⋅=⋅.故选:B.8.(2021·全国·高三专题练习)已知动直线l 与圆224x y +=相交于A ,B 两点,且满足2AB =,点C 为直线l 上一点,且满足52CB CA =,若M 为线段AB 的中点,O 为坐标原点,则OC OM ⋅的值为( )A .3B .C .2D .3-【答案】A 【分析】先利用圆的方程和弦长判定OAB 为等边三角形,设出符合条件的一条直线,再利用平面向量共线得到点的坐标,再利用数量积的坐标运算进行求解. 【详解】动直线l 与圆O :224x y +=相交于A ,B 两点, 且满足2AB =,则OAB 为等边三角形, 所以不妨设动直线l为2y =+, 根据题意可得()2,0B -,(A -, ∵M 是线段AB的中点,∴32M ⎛- ⎝⎭,设(),C x y ,∵52CB CA =,∴()()52,12x y x y ---=--, ∴())521252x x y y ⎧--=--⎪⎪⎨⎪-=⎪⎩,解得13x y ⎧=-⎪⎪⎨⎪=⎪⎩13C ⎛- ⎝⎭, ∴OC OM ⋅=131533222⎛⎛-⋅-=+= ⎝⎭⎝⎭.故选:A .9.(2021·湖南·高三月考)在ABC 中,D 为三角形所在平面内一点,且1132AD AB AC →→→=+,则BCD ACDS S =()A .16B .12C .13D .23【答案】B 【分析】设AD 交BC 于E ,然后根据条件得到点E 的位置,进而根据向量关系得到线段间的比例,最后得出面积比. 【详解】如图,设AD 交BC 于E ,且32AE xAD A x x B AC →→→→==+,由B ,E ,C 三点共线可得:61325x x x +=⇒=,∴2355AE AB AC →→→=+, ∴323255AE AB AC AE BE EC →→→→→→⎛⎫⎛⎫=⇒ ⎪ ⎪⎭⎭=⎝⎝--. 设2CEDSy =,则3BEDSy =,∴5BCDSy =.又655AE AD AD DE →→→→⇒==,∴10ACDS y =,∴51102BCD ACDS y Sy ==. 故选:B.10.(2021·重庆一中高三月考)设G 为△ABC 的重心,若0,2BG AG AB ⋅==,则()22CA CB AB AC +⋅的取值范围为( ) A .(-80,160) B .(-80,40) C .(-40,80) D .(-160,80)【答案】A 【分析】由题设知BG AG ⊥、D 为AB 的中点且2CG GD =,结合已知求出CD ,利用向量数量积的运算律有224()()CA CB CA CB CA CB ⋅=+--求得CA CB⋅,再由目标式中向量线性关系的几何意义及三角形三边关系,即可求范围. 【详解】∵0BG AG ⋅=,∴BG AG ⊥,连接CG 并延长交AB 于D ,则D 为AB 的中点,且2CG GD =, 在Rt AGB △中,12ABGD ==,则3CD =, ∵22224()()4432CA CB CA CB CA CB CD AD ⋅=+--=-=, ∴8CA CB ⋅=,2222()[()2]()(3616)(8)CB AB AC CB CA CA CA AC B CB A C AC C =-⋅-⋅=--+⋅+220(8)AC =-,∵CD AD AC CD AD +>>-,即42AC >>, ∴()22(80,160)CB AB AC CA ∈-+⋅.故选:A 【点睛】关键点点睛:连接CG 并延长交AB 于D ,根据重心的性质可知D 为AB 的中点且2CG GD =,再由向量数量积的运算律求CA CB ⋅,结合相关向量线性关系的几何意义及三角形三边关系求目标式范围.11.(2021·山东·烟台二中三模)在等腰梯形ABCD 中,//AB DC ,222AB BC CD ===,P 是腰AD 上的动点,则2PB PC -的最小值为( )A B .3C D .274【答案】C 【分析】过D 作DE AB ⊥,垂足为E ,过C 作CF AB ⊥,垂足为F ,以E 为原点,分别以EB ,ED 所在的直线为x轴,y 轴,建立平面直角坐标系,运用坐标表示出2(2,PB PC x -=-,再由向量的数量积运算求得2PB PC -,根据二次函数的性质可得最值得选项. 【详解】过D 作DE AB ⊥,垂足为E ,过C 作CF AB ⊥,垂足为F ,以E 为原点,分别以EB ,ED 所在的直线为x 轴,y 轴,建立平面直角坐标系,如图所示:由已知可得:1,1CD BC AD EF ====, 12AE BF ==,所以DE ==1.(0,0),(,0),2E A D -,3(1,0),(,0)2C F B , 因为P 是腰AD 上的点,所以设点P 的横坐标为 1(0)2x x -≤≤,因为直线AD的方程为112=-x,即=y(P x +,所以3(,2PB x =-,(1,)PC x =-,2(2,PB PC x ∴-=-,所以|2|(2PB PC -=当11,042x ⎡⎤=-∈-⎢⎥⎣⎦,|2|PB PC -, 故选:C. 【点睛】关键点睛:本题考查求向量的模的最值,关键在于建立平面直角坐标系,运用向量的坐标运算求得向量的模,再利用函数的性质求得最值.12.(2021·辽宁葫芦岛·二模)在ABC 中,点P 满足2BP PC =,过点P 的直线与AB ,AC 所在的直线分别交于点M ,N ,若AM x AB =,()0,0AN yAC x y =>>,则2x y +的最小值为( ) A .3 B .C .1D .13【答案】A 【分析】由向量加减的几何意义可得233AB AC AP =+,结合已知有233AM AN AP x y =+,根据三点共线知21133x y +=,应用基本不等式“1”的代换即可求最值,注意等号成立的条件. 【详解】由题设,如下图示:23333BC AC AB AB ACAP AB BP AB AB -=+=+=+=+,又AM x AB =,()0,0AN yAC x y =>>,∴233AM AN AP x y=+,由,,M P N 三点共线,有21133x y +=,∴215225)33333332(2)(x y x y y x x y y x +=+=++≥+=+,当且仅当x y =时等号成立. 故选:A 【点睛】关键点点睛:利用向量线性运算的几何表示,得到AP 、AM 、AN 的线性关系,根据三点共线有21133x y+=,再结合基本不等式求最值.13.(2021·浙江省宁海中学模拟预测)已知平面非零向量,,,a b c d 满足{}()(){},{||},0a b u u d u d c v v a v b ⊆-=⋅∈-⋅-=∣∣,则对于任意的d 使得()()//a d b d --( )A .()()0d c d ⋅≤恒有解B .()()10d c d -⋅≤恒有解C .()()20d c d -⋅≤恒无解D .()()30d c d -⋅≤恒无解【答案】B 【分析】设()(),0,,OD d r OU u x y ====,其中0r >,记,,OA a OB b OC c ===rx =,即()222120r x rx r y --++=,然后分1r =,01r <<,1r >三种情况讨论,再根据直线AB 是过点D 的直线与圆锥曲线E 的两个不同的交点和点C 在以AB 为直径的圆M 上,分析圆M 与相应准线的位置关系,即可求解. 【详解】解:设()(),0,,OD d r OU u x y ====,其中0r >,记,,OA a OB b OC c ===rx =,即()222120.r x rx r y --++=若1r =,则点U 的轨迹是拋物线,方程为E :221y x =-,点D 恰为抛物线E 的焦点, 则AB 是过点D 的直线与抛物线E 的两个不同的交点,点C 在以AB 为直径的圆M 上, 此时0c d ⋅≥.若01r <<,则点U 的轨迹是椭圆,方程为E :()222224241111r r r x y r r r --⎛⎫-+= ⎪-⎝⎭, 点D 为椭圆E 的左焦点,y 轴是椭圆的左准线,AB 是过点D 的直线与椭圆E 的两个不同的交点,点C 在以AB 为直径的圆M 上,此时圆M 与准线相离,故0.c d ⋅>若1r >,则点U 的轨迹是双曲线,方程为E :()222224241111r r r x y r r r --⎛⎫--= ⎪-⎝⎭, 点D 为双曲线E 的右焦点,y 轴是双曲线的右准线,AB 是过点D 的直线与双曲线E 的两个不同的交点,点C 在以AB 为直径的圆M 上,此时圆M 与准线相交,故c d ⋅可正,可负,可零.所以,当01r <<时,恒有()()0d c d ⋅⋅>,故A 错误; 当1r >时,()()20d c d -⋅⋅≤,与()()30d c d -⋅⋅≤均有解,故,C D 错误;故选:B. 【点睛】关键点点睛:利用坐标法,设()(),0,,OD d r OU u x y ====,其中0r >,记,,OA a OB b OC c ===则有rx =,即()222120r x rx r y --++=,然后分1r =,01r <<,1r >三种情况讨论,将原问题转化为判断圆M 与准线的位置关系,从而解决问题.14.(2021·全国全国·模拟预测)设||=1a →,||b →,且a b →→⊥,若向量c →满足2c a b a b →→→→→--=-,则||c →的最大值是( ) A .5 B .6 C .7 D .8【答案】B 【分析】设OA a →→=,OB b →→=,OC c →→=,OD a b →→→=+,根据条件,借助平面图形得到点C 的轨迹,即可得到结果. 【详解】 如图,设OA a →→=,OB b →→=,OC c →→=,OD a b →→→=+,连接AD ,BD , 则由a b →→⊥可知四边形OBDA 为矩形,则||||2a b a b →→→→+=-=. 由|()|2||c a b a b →→→→→-+=-,可得|()|4c a b →→→-+=,连接CD ,则4DC →=,所以点C 在以点D 为圆心,4为半径的圆上, 所以OC →的最大值为246OD DC →→+=+=. 故选:B. 【点睛】对于向量模的最值或者范围的问题,我们往往采取数形结合的方式进行解决.首先我们要根据题目的条件将几个向量的起点平移到同一点,作出图形,最后根据所求向量的条件得出终点的轨迹. 15.(2021·上海市建平中学高三开学考试)已知ABC 的外接圆圆心为O ,6A π∠=,若(),AO xAB yAC x y R =+∈,则x y +的最大值为( )A.4+B.4- CD【答案】B 【分析】过点O 作⊥OD AB ,OE AC ⊥,利用圆的性质知,D E 为AB ,AC 中点,设AB a =,AC b =,利用向量的数量积结合已知条件得到22221212a xa yab b ya ⎧=⎪⎪⎨⎪=⎪⎩,求出x y +,利用基本不等式求最值即可. 【详解】如图,过点O 作⊥OD AB ,OE AC ⊥OA OB =,OA OC =,OAB ∴和OAC 是等腰三角形,D ∴为AB 中点,E 为AC 中点,设AB a =,AC b =,则cos 6AB AC AB AC π⋅=⋅=21cos 2AB AO AB AO BAO AB AD a ⋅=⋅∠=⋅=21cos 2AC AO AC AO CAO AB AE b ⋅=⋅∠=⋅=AO xAB yAC =+,()2xAB y AB AO A AC xAB y B A A C B ∴⋅=⋅=⋅++,即2212a a a x b y =()2xAB y AC AO AC A AC y AC x AC B +=⋅+∴⋅=⋅,即2212b a a y b x =联立解得:2x =2y =22444b a x y a b ⎫+==+≤-=-⎪⎭当且仅当ba ab=,即a b =时,等号成立.所以x y +的最大值为4-故选:B【点睛】关键点点睛:本题考查圆的性质,平面向量的数量积以及基本不等式求最值,利用圆的性质结合平面向量的数量积得到关于x ,y 的方程,进而求出x y +是解题的关键,考查学生的逻辑推理与运算能力,属于难题. 16.(2021·浙江浙江·模拟预测)已知非零平面向量a ,b ,c 满足2a =,1b c -=,若a 与b 的夹角为π3,则a c -的最小值为( )A 1BC 1D 【答案】A 【分析】解法一利用绝对值三角不等式得到1a c a b -≥--,然后求a b -的最小值即可;解法二 设OA a =,OB b =,OC c =,易得1BC =,则C 的轨迹是以B 为圆心,半径为1的圆,连接AB ,然后又A ,C ,B 三点共线且C 在A ,B 中间时,a c -取得最小值求解. 【详解】解法一 由题可得,1a c a b b c a b b c a b -=-+-≥---=--, 所以要求a c -的最小值,需求a b -的最小值. 因为2a =,a 与b 的夹角为π3,所以a b -的最小值为πsin3a = 所以131a c ab -≥--≥, 即a c -的最小值为1, 解法二 如图,设OA a =,OB b =,OC c =,则c b BC -=,a c CA -=.由1b c c b -=-=,知1BC =,点C 的轨迹是以B 为圆心,半径为1的圆,连接AB ,结合图形可知,当A ,C ,B 三点共线且C 在A ,B 中间时,a c -取得最小值.由正弦定理得:πsin sin 3AB OAOBA =∠,所以AB =≥故a c -的最小值为1. 故选:A 【点睛】关键点点睛:本题关键是根据a 与b 的夹角为π3,由a b -的最小值为πsin 3a 而得解.17.(2021·山东·模拟预测)在ABC 中,2BC=,若AB =,则BC BA ⋅的取值范围是( )A .(6-+B .6⎡-+⎣C .(8-+D .8⎡-+⎣【答案】C 【分析】建立平面直角坐标系,由AB 得到A 的轨迹,最后结合图形及向量的数量积运算可得结果. 【详解】以BC 的中点O 为坐标原点,BC 所在直线为x 轴建立如图所示的平面直角坐标系,则()1,0B -,()1,0C .设点()(),0A x y y ≠,由AB =,可得()()2222121x y x y ⎡⎤++=-+⎣⎦,化简得()23x - (()220y y +=≠,故点A 的轨迹为圆(不包含与x 轴的交点),记圆()(2223x y -+=与x 轴的交点分别为M ,N (M 在N的左侧)则4MB =-4NB =+所以BC BA BC BA ⋅=⋅cos 8ABC BC BM ⋅∠>⋅=-8BC BA BC BN ⋅<⋅=+ 故选:C.【点睛】关键点睛:解决本题的关键一是建立坐标后根据几何关系建立等式然后得到点A 的轨迹方程,二是求最值. 18.(2021·宁夏中卫·模拟预测(理))已知2a b ==,且a ,b 的夹角为60,若向量1c a -≤,则b c ⋅的取值范围是( )A .[]4,4-B .⎡-⎣C .0,⎡⎣D .[]0,4【答案】D 【分析】设()2,0a =,()1,3b =,(),c x y =.由1c a -≤得()2221x y -+≤,设2cos x r α=+,sin y r α=,得22sin 6b c r πα⎛⎫⋅=++ ⎪⎝⎭可得答案.【详解】不妨设()2,0a =,()1,3b =,(),c x y =,且1cos 2a b =,, 因为1c a -≤,所以()2221x y -+≤,设2cos x r α=+,sin y r α=,01r ≤≤,α∈R ,所以32cos sin 22sin 6b c x r r πααα⎛⎫⋅=+=+=++ ⎪⎝⎭,由于1sin 16r r r πα⎛⎫-≤-≤+≤≤ ⎪⎝⎭,故[]0,4b c ⋅∈.故选:D . 【点睛】本题考查了用向量的坐标运算求取值范围的问题,解题的关键点是设()2,0a =,()1,3b =,(),c x y =转化为坐标运算,考查了学生分析问题、解决问题的能力.19.(2021·全国·高三专题练习(理))半径为2的圆O 上有三点A 、B 、C 满足0OA AB AC ++=,点P 是圆内一点,则PA PO PB PC ⋅+⋅的取值范围为( )A .[414)-,B .[0)4,C .[414],D .[416],【答案】A 【分析】设OA 与BC 交于点D ,由0OA AB AC ++=得四边形OBAC 是菱形,D 是对角线中点,,,,PA PO PB PC 用PD 和其他向量表示并计算数量积后可得PA PO PB PC ⋅+⋅=224PD -,由点与的位置关系可得PD 的取值范围,得结论. 【详解】如图, OA 与BC 交于点D ,由0OA AB AC ++=得: 0OB AC +=,所以四边形OBAC 是菱形,且2OA OB ==,则1AD OD ==,BD DC == 由图知PB PD DB =+,PC PD DC =+,而DB DC =-, ∴22222||||||3PB PC PD DB PD DB PD ⋅=-=-=-, 同理PA PD DA =+,PO PD DO =+,而DA DO =-,∴22222||||||1PA PO PD DO PD DO PD ⋅=-=-=-, ∴22||4PA PO PB PC PD ⋅+⋅=-,∵点P 是圆内一点,则03PD ≤<,∴414PA PO PB PC -≤⋅+⋅<, 故选:A. 【点睛】关键点点睛:本题考查平面向量数量积的运算,解题关键是是利用线段的中点的性质,把,,,PA PO PB PC 用PD 和其他向量相加,然后求数量积可化化简.二、多选题 20.(2021·全国·高三专题练习)如图,正方形ABCD ,()AE AB λλ=∈R ,P 为以A 为圆心、AB 为半径的四分之一圆弧上的任意一点,设向量AC xDE y AP =+,x y +,则λ可取( )A B C .3 D .2+【答案】BD 【分析】设BAP α∠=,根据向量运算得cos 1sin 1x y y x λαα+=⎧⎨-=⎩,进而得x y +(1)(sin 1)1sin cos λαλαα++=-+,(1)(sin 1)()1sin cos f λααλαα++=-+,[0,]2πα∈,求函数导数,得函数最小值2min 221()1f λλαλ+-==+,解方程求解即可. 【详解】设BAP α∠=,则cos sin A AP A B D αα=+, 由AC xDE y AP =+,可得()(cos sin )(cos )(sin )AC x AE AD y AD x y B B x A A y AD ααλαα=-++=++-又AC AB AD =+,所以cos 1sin 1x y y x λαα+=⎧⎨-=⎩,解得sin cos sin cos 1sin cos x y ααλααλλαα-⎧=⎪⎪+⎨+⎪=⎪+⎩,所以sin cos 1sin cos sin cos x y ααλλααλαα-++=+++(1)sin (sin cos )1sin cos sin cos λαλααλλααλαα+-++=+++(1)(sin 1)1sin cos λαλαα++=-+,令(1)(sin 1)()1sin cos f λααλαα++=-+,[0,]2πα∈则21sin cos ()(sin cos )f αλααλαα+-'=+,(sin [0,])2πϕϕϕ==∈[0,]2πα∈,[,]2παϕϕϕ-∈--,记0sin()αϕ-=0()0f α'=,易得0min 000(1)(sin 1)()()1sin cos f f λαααλαα++==-+,此时由0cos()αϕ-=,可得2000021sin sin[()]sin()cos cos()sin 1λααϕϕαϕϕαϕϕλ-=-+=-+-=+,000022cos cos[()]cos()cos sin()sin 1λααϕϕαϕϕαϕϕλ=-+=---=+,所以222min022221(1)(1)211()()112111f f λλλλλααλλλλλλ-+++-+==-==-++++解得λ=2 故选:BD. 【点睛】关键点点睛:在处理x y +(1)(sin 1)1sin cos λαλαα++=-+的最小值时,利用函数求导是本题的关键点,也是难点,借助辅助角公式得函数的极值点即为最值点,从而得解,本题的运算量较大,属于难题.21.(2021·湖北黄石·高三开学考试)在平面直角坐标系中,O 是坐标原点,,n n M N 是圆222:O x y n +=上两个不同的动点,n P 是n n M N 的中点,且满足()220n n n OM ON OP n *⋅+=∈N .设,n n M N到直线20l y n n +++=的距离之和的最大值为n a ,则下列说法中正确的是( ) A .向量n OM 与向量n ON 所成角为120︒ B .n OP n = C .22n a n n =+D .若2n n a b n =+,则数列12{}(21)(21)n nn b b b +--的前n 项和为11121n +-- 【答案】ACD 【分析】对于A ,用n OM 与n ON 表示n OP ,结合给定向量等式计算判断;对于B ,求出||n OP 的值即可判断;对于C , 转化为点n P 到直线l 距离最大值并计算判断;对于D ,求出数列{}n b 的通项,代入并利用裂项相消法计算判断作答. 【详解】依题意,||||n n OM ON n ==,而点n P 是弦n n M N 的中点,则1()2n n n OP OM ON =+,2222111(2)422n n n n n n n OP OM OM ON ON OM ON n =+⋅+=+⋅,而220n n n OM ON OP ⋅+=,于是得212n n O n OM N ⋅=-,1cos 2||,||n n n n n n OM ON OM ON OM ON 〈〉==-⋅⋅,即120,n n OM ON 〈〉=,A 正确; 显然n n OM N 是顶角120n n M ON ∠=的等腰三角形,则1|||co60|s 2n n OP OM n ==,B 不正确;依题意,点,n n M N 到直线2:0l y n n +++=的距离之和等于点n P 到直线l 距离的2倍, 由1|2|n OP n =知,点n P 在以原点O 为圆心,12n 为半径的圆上,则点n P 到直线l 距离的最大值是点O 到直线l的距离加上半径12n ,而点O 到直线l 距离222n n d +==,则点n P 到直线l 距离的最大值是22n n +,因此,222()22n n a n n n =+=+,C 正确;由2n n a b n =+得,n b n =,则111122(21)(21)(21)(21)(21)(21)(21)(21)n n n b n n n b b n n n n ++++---==------1112121n n +=---,因此,数列12{}(21)(21)n n n b b b +--的前n 项和2231111111111212121212121n n n n T ++⎛⎫⎛⎫⎛⎫=-+-++-=- ⎪ ⎪ ⎪------⎝⎭⎝⎭⎝⎭,D 正确.故选:ACD22.(2021·广东深圳·高三月考)在ABC 中,角,,A B C 所对的边分别为,,a b c ,6A π=,2a =,O 为ABC的外接圆,OP mOB nOC =+,给出下列四个结论正确的是( ) A .若1m n ==,则||23OP =;B .若P 在O 上,则m n +的最大值为2;C .若P 在O 上,则221m n mn ++=;D .若,[0,1]m n ∈,则点P的轨迹所对应图形的面积为 【答案】ACD 【分析】根据向量的线性运算以及向量的求模公式可判断A ,根据向量的线性运算,结合点与圆的位置关系及基本不等式可判断BC ,根据向量的线性运算,结合点的轨迹及三角形的面积公式可判断D. 【详解】 6A π=,2a =,O 为ABC 的外接圆∴22421sin 2a R R A ===⇒= 260,2BOC A OB OC ∠=∠===对于A :若1m n ==,则OP OB OC =+()222221223OP OB OCOB OC OB OC OP =+=++⋅=⇒=故A 正确对于BC :由()22OP mOB nOC OP mOB nOC =+⇒=+ 22222m OB n OC mnOB OC =++⋅()22224444m n mn m n mn =++=++若P 在O 上,则2OP =()2222441m n mn m n mn ++=⇒++=()()222311124m n m n mn m n+⎛⎫∴+=+≤+⇒+≤ ⎪⎝⎭m n ∴+≤m n =时取等号) 故B 错误,C 正确;对于D :若,[0,1]m n ∈,则点P 的轨迹:当0,[0,1]m n =∈时,OP nOC =,此时点P 在线段OC ; 当0,m [0,1]n =∈时, OP mOB =,此时点P 在线段OB ;当1,[0,1]m n =∈时,OP OB nOC =+,构造平行四边形OBCD ,此时点P 在线段BD 上;当1,m [0,1]n =∈时,OP mOB OC =+,构造平行四边形OBCD ,此时点P 在线段CD 上;当(),0,1m n ∈时,OP mOB nOC =+,此时点P 在菱形OBCD 内部,综上P 点的轨迹为菱形OBCD 组成的图形区域,则12222sin 60232OBCOBCD S S ==⨯⨯⨯⨯=菱形故D 正确. 故选:ACD. 【点睛】本题考查了向量的线性运算以及向量的求模公式,点与圆的位置关系,基本不等式,点的轨迹及三角形的面积公式,熟悉以上内容综合运用是解题的关键.23.(2021·广东天河·高三月考)对于△ABC ,其外心为O ,重心为G ,垂心为H ,则下列结论正确的是( ) A .OA OB OA OC OB OC ⋅=⋅=⋅ B .212AO AB AB ⋅=C .向量AH 与cos cos AB AC AB BAC C+共线D .过点G 的直线l 分别与AB 、AC 交于E 、F 两点,若AE AB λ=,AF AC μ=,则113λμ+=【答案】BCD 【分析】A :由外心的性质,结合向量数量积的几何意义判断;B :根据||cos AO OAB ∠的几何意义即可判断正误;C :应用向量数量积的运算律及定义化简()cos cos AB AC BC AB BAC C+⋅,再根据AH BC ⊥判断正误;D :根据平面向量基本定理可得1133AG AE AF λμ=+,再由三点共线即可证. 【详解】A :O 为外心,则OA OB OC ==,仅当AOB AOC BOC ∠=∠=∠时才有OA OB OA OC OB OC ⋅=⋅=⋅,错误; B :由||||cos AO AB AO AB OAB ⋅=∠,又||||cos 2AB AO OAB ∠=,故212AO AB AB ⋅=,正确;C :||||cos()()cos cos cos cos cos AB AC AB BC AC BC AB BC B BC AB BAC CAB BAC CAB Bπ⋅⋅-+⋅=+=+||||cos ||||0cos AC BC CBC BC AC C =-+=,即cos cos AB AC AB BAC C+与BC 垂直,又AH BC ⊥,所以AH 与cos cos AB AC AB BAC C+共线,正确;D :2111()3333AG AD AB AC AE AF λμ==+=+,又,,E G F 三点共线,则11133λμ+=,故113λμ+=,正确.故选:BCD 【点睛】关键点点睛:综合应用外心、垂心、重心的性质,结合平面向量数量积的运算律、几何含义以及平面向量基本定理判断各选项正误.24.(2021·广东华侨中学高三月考)已知向量()1,sin θ=a ,(cos b θ=,则下列命题正确的是( )A .存在θ,使得//a bB .当tan 2θ=时,a 与b 垂直C .对任意θ,都有a b ≠D .当3a b ⋅=-时,a 在b 方向上的投影为【答案】BD 【分析】A 选项考察向量平行坐标之间的关系;B 选项考察向量垂直时坐标之间的关系;C 选项分别求出,a b ,可以得到是否存在θ,使得a b =;D 选项中根据数量积求出θ角的三角函数值,可以求出a 在b 方向上的投影 【详解】选项A 中,若//a b sin cos =θθ,sin 2θ=θ,所以A 错误选项B 中,若a b ⊥,则cos 0θθ=,cos θ=θ,得:tan θ=,所以选项B 正确 选项C 中,1sin a =+2cos b =+2πθ=时,a b =,所以C 错误选项D 中,cos a b ⋅==θθ两边同时平方得:2222cos 2sin cos 3cos 3sin θ+θ+θθ=θ+θ ,化简得:222cos sin cos 0θ+θ-θθ=,同除2cos θ得:2tan 20θ-θ+=,(2tan 0θ=,所以tan θ=22sin 2cos θ=θ,解得:21cos 3θ=,设a 与b 的夹角为α,所以a 在b 方向上的投影cos 2cos a b a b ⋅-=⋅α===+D 选项正确故选:BD.25.(2021·全国·高三专题练习)奔驰定理:已知O 是ABC 内的一点,BOC ,AOC △,AOB 的面积分别为A S ,B S ,C S ,则0A B C S OA S OB S OC ⋅+⋅+⋅=.“奔驰定理”是平面向量中一个非常优美的结论,因为这个定理对应的图形与“奔驰”轿车(Mercedesbenz )的logo 很相似,故形象地称其为“奔驰定理”.若O 、P 是锐角ABC 内的点,A 、B 、C 是ABC 的三个内角,且满足13PA PB PC CA ++=,OA OB OB OC OC OA ⋅=⋅=⋅,则( )A .::4:2:3PAB PBC PCA S S S =△△△ B .πA BOC ∠+∠=C .::cos :cos :cos OA OB OC A B C =D .tan tan tan 0⋅+⋅+⋅=A OA B OB C OC 【答案】ABCD 【分析】13PA PB PC CA ++=变形后表示为2433PB PA PC =--,再由奔驰定理得出向量,,PB PA PC 的关系,利用平面向量基本定理判断A ,利用数量积的运算,变形后证明O 是ABC 的重心,由平面几何知识判断B ,利用数量积的定义表示已知数量积的等式,结合选项B 的结论可证明C ,求出,,AOB BOC COA △△△的面积,利用选项B 的结论转化,再利用选项C 的结论可得面积比,然后结合奔驰定理可判断D . 【详解】因为13PA PB PC CA ++=,所以1()3PA PB PC PA PC ++=-,即24033PA PB PC ++=,所以2433PB PA PC =--,又由奔驰定理0PBC PCA PAB S PA S PB S PC ++=△△△得PBC PAB PCA PCAS SPB PA PC S S =--△△△△, 因为,PA PC 不共线,所以24,33PBC PAB PCA PCA S S S S -=--=-△△△△, 所以::4:2:3PAB PBC PCA S S S =△△△,A 正确;延长,,AO BO CO 分别与对边交于点,,D E F ,如图,由OA OB OB OC ⋅=⋅得()0OB OA OC OB CA ⋅-=⋅=,所以OB AC ⊥,同理,OC AB OA BC ⊥⊥,所以O 是ABC 的垂心,所以四边形AEOF 中BAC EOF π∠+∠=,EOF BOC ∠=∠,所以A BOC π∠+∠=,B 正确; 由OA OB OB OC OC OA ⋅=⋅=⋅得cos cos cos OA OB AOB OB OC BOC OC OA AOC ∠=∠=∠, 所以::cos :cos :cos OA OB OC BOC AOC AOB =∠∠∠,由选项B 得cos cos BOC A ∠=-,cos cos AOC B ∠=-,cos cos AOB C ∠=-, 所以::cos :cos :cos OA OB OC A B C =,C 正确; 由上讨论知, 11sin sin 22OBC S OB OC BOC OB OC A =∠=△, 11sin sin 22OAC S OA OC AOC OA OC B =∠=△11sin sin 22OAB S OA OB AOB OA OB C =∠=∠△, 所以sin sin sin ::::OBC OAC OAB A B CS S S AO OB OC=△△△, 又由选项C :::cos :cos :cos OA OB OC A B C =, 得sin sin sin ::::tan :tan :tan cos cos sin OBC OAC OAB A B CS S S A B C A B C==△△△, 由奔驰定理:0A B C S OA S OB S OC ⋅+⋅+⋅=得tan tan tan 0⋅+⋅+⋅=A OA B OB C OC ,D 正确. 故选:ABCD .【点睛】本题考查平面向量基本定理的应用,考查学生的创新能力,理解新知识、应用新知识的能力.解题关键一是利用平面向量基本定理知用基底表示平面上任一向量的方法是唯一的,由此可得等量关系,二是利用数量积的运算得出O 是三角形的垂心,由此利用平面几何知识得出角的关系,再利用三角函数知识进行推导得出相应结论.26.(2021·全国·高三专题练习(理))设1A ,2A ,3A ,4A 是两两不同的四个点,若1312A A A A λ=,1412A A A A μ=,且112λμ+=,则称3A ,4A 调和分割1A ,2A .现已知平面上两点C ,D 调和分割A ,B ,则下列说法正确的是( )A .点C 可能是线段AB 的中点 B .点D 不可能是线段AB 的中点C .点C ,D 可能同时在线段AB 上D .点C ,D 不可能同时在线段AB 的延长线上 【答案】BD 【分析】由题意设()0,0A ,()10B ,,(),0C c ,(),0D d ,结合已知条件得112c d +=,根据选项考查112c d+=的解,用排除法选择答案即可. 【详解】由已知不妨设()0,0A ,()10B ,,(),0C c ,(),0D d , 由C ,D 调和分割A ,B 可知,()(),01,0c λ=,()(),01,0d μ=,,c d λμ∴== 代入112λμ+=得112c d+=(∗) 对于AB ,若C 是线段AB 的中点,则12c =,代入(∗)得,d 不存在,故C 不可能是线段AB 的中点,同理D 不可能是线段AB 的中点,故A 错误,B 正确;对于C , 若C ,D 同时在线段AB 上,则01c ≤≤,01d ≤≤代入(∗)得,1c d ==, 此时C 和D 点重合,与已知矛盾,故C 错误;对于D ,若C ,D 同时在线段AB 的延长线上时,则1c >,1d >,则112c d +<,这与112c d+=矛盾,所以C ,D 不可能同时在线段AB 的延长线上,故D 正确; 故选:BD. 【点睛】关键点点睛:本题考查新定义的应用问题,正确理解新定义的含义是解题的关键,考查学生的逻辑推理与特殊与一般思想,属于较难题.27.(2021·山东济宁·高三月考)如图,已知点,,A B C 是O 上三个不同定点,Q 为弦AB 的中点,*)(n D n N ∈是劣弧BC 上异于,B C 的一系列动点,连接n AD 交BC 于n P ,点()*n P n N ∈满足()1221n n n n n P C a P a P A Q →→→+-+⋅⋅=,其中数列{}n a 是首项为1的正项数列,n S 是数列{}n a 的前n 项和,则下列结论正确的是( )A .数列{1}n a +是等比数列B .37a =C .21n a n =-D .22nn S n =+-【答案】AB 【分析】由平面向量线性运算和向量共线可得到()12212=n n a a λλ+⎧-+=⎨-⎩,由此可确定递推关系式,得到121n n a a +=+,进而得数列{1}n a +是等比数列可判断A 选项;利用等比数列通项公式求得21nn a =-,可确定BC 正误;利用分组求和法,结合等比数列求和公式可求得n S ,知D 错误. 【详解】解:因为Q 为弦AB 的中点,所以12n n n P P Q A B P →→→=+⎛⎫⎪⎝⎭,所以2n n n P B A P P Q →→→=-,因为,,n B C P 三点共线,所以=,n n P C P R B λλ→→∈, 又因为()1221n n n n n P C a P a P A Q →→→+-+⋅⋅=,所以()122122n n n n n n n n A Q Q A Q a P a P A P P P P λλλ→→→→→→+⎛⎫-+⋅=-=- ⎪⎝⋅⎭,所以()12212=n n a a λλ+⎧-+=⎨-⎩,消去λ得121n n a a +=+,所以()()1121n n a a ++=+,即1121n n a a ++=+()*n N ∈, 所以数列{}1n a +是等比数列,公比为2,首项为112a +=,故A 选项正确;所以12nn a +=,故21n n a =-,所以33217a =-=,故B 选项正确,C 选项错误;此时数列{}n a 的前n 项和()()()()123123212*********n n n nS =-+-+-++-=++++-()12122212n n n n +-=-=---,故D 选项错误.故选:AB 【点睛】关键点点睛:本题考查数列与向量的综合应用问题,解题关键是能够根据平面向量的线性运算和向量共线的性质推导得到数列的递推关系式,由此构造出所需的等比数列进行求解.28.(2021·全国·高三专题练习)对于给定的ABC ,其外心为O ,重心为G ,垂心为H ,则下列结论正确的是( ) A .212AO AB AB ⋅=B .OA OB OA OC OB OC ⋅=⋅=⋅C .过点G 的直线l 交AB AC 、于E F 、,若AE AB λ=,AF AC μ=,则113λμ+=D .AH 与cos cos AB AC AB BAC C+共线【答案】ACD【分析】根据外心在AB 上的射影是AB 的中点,利用向量的数量积的定义可以证明A 正确;利用向量的数量积的运算法则可以OA OB OA OC =即OA BC ⊥,在一般三角形中易知这是不一定正确的,由此可判定B 错误;利用三角形中线的定义,线性运算和平面向量基本定理中的推论可以证明C 正确;利用向量的数量积运算和向量垂直的条件可以判定cos cos AB AC AB BAC C+与BC 垂直,从而说明D 正确.【详解】如图,设AB 中点为M,则OM AB ⊥,AO cos OAM AM ∴∠=()21·cos cos ?22AB AO AB AO AB OAB AB AO OAB AB AB ∴=∠=∠==,故A 正确; ··OAOB OAOC =等价于()·0OA OB OC -=等价于·0OACB =,即OA BC ⊥,对于一般三角形而言,O 是外心,OA 不一定与BC 垂直,比如直角三角形ABC 中, 若B 为直角顶点,则O 为斜边AC 的中点,OA 与BC 不垂直.故B 错误; 设BC 的中点为D ,则()211111133333AG AD AB AC AE AF AE AF λμλμ⎛⎫==+=+=+ ⎪⎝⎭, ∵E,F ,G 三点共线,11133λμ∴+=,即113λμ+=,故C 正确;cos cos cos cos AB AC AB BC AC BC BC AB B AC C AB B AC C ⎛⎫⋅⋅ ⎪+⋅=+ ⎪⎝⎭()cos cos cos cos AB BC B AC BC C AB B AC C π⋅-⋅=+ 0BC BC =-+=,∴cos cos AB AC AB BAC C+与BC 垂直,又AH BC ⊥,∴cos cos AB AC AB BAC C+与AH 共线,故D 正确.故选:ACD. 【点睛】本题考查平面向量线性运算和数量及运算,向量垂直和共线的判定,平面向量分解的基本定理,属综合小题,难度较大,关键是熟练使用向量的线性运算和数量积运算,理解三点共线的充分必要条件,进而逐一作出判定.29.(2021·全国·高三专题练习)如图,直角ABC 的斜边BC 长为2,30C ∠=︒,且点B ,C 分别在x 轴正半轴和y 轴正半轴上滑动,点A 在线段BC 的右上方则( )A .||OA OC +有最大值也有最小值B .OA OC ⋅有最大值无最小值 C .||OA BC +有最小值无最大值D .OA BC ⋅无最大值也无最小值【答案】BD 【分析】设OCB α∠=,则()30,090ABx αα∠=+<<,所以()()2sin ,0,0,2cos B C αα,)30),sin(30)Aαα++, ()2sin ,2cos BC αα=-.由2OA OC +化简为54sin(230)α++根据α的范围可判断A ;由OA OC ⋅化简为1sin(230)2α++根据α的范围可判断B ;由2OA BC +化简为460)α++根据α的范围可判断C ;由OA BC ⋅化简为214sin α-根据α的范围可判断D.【详解】由题意30BCA ∠=,2,90BC A =∠=,所以1AC AB =,设OCB α∠=, 则ABO ∠的补角即AB 与x 轴正半轴的夹角()30,090ABx αα∠=+<<, 所以)30),sin(30)Aαα++,()()2sin ,0,0,2cos B C αα,()2sin ,2cos BC αα=-,所以()330),sin(30)2cos OA OC ααα+=+++,。
高考数学(理)之平面向量 专题04 平面向量在平面几何、三角函数、解析几何中的应用(解析版)

平面向量04 平面向量在平面几何、三角函数、解析几何中的应用一、具本目标: 一)向量的应用1.会用向量方法解决某些简单的平面几何问题.2.会用向量方法解决简单的力学问题与其他一些实际问题. 二)考点解读与备考:1.近几年常以考查向量的共线、数量积、夹角、模为主,基本稳定为选择题或填空题,难度较低;2.常与平面几何、三角函数、解析几何等相结合,以工具的形式进行考查,常用向量的知识入手.力学方面应用的考查较少.3.备考重点:(1) 理解有关概念是基础,掌握线性运算、坐标运算的方法是关键;(2)解答与平面几何、三角函数、解析几何等交汇问题时,应注意运用数形结合的数学思想,将共线、垂直等问题,通过建立平面直角坐标系,利用坐标运算解题.4.难点:向量与函数、三角函数、解析几何的综合问题.以向量形式为条件,综合考查了函数、三角、数列、曲线等问题.要充分应用向量的公式及相关性质,会用向量的几何意义解决问题,有时运用向量的坐标运算更能方便运算. 二、知识概述:常见的向量法解决简单的平面几何问题: 1.垂直问题:(1)对非零向量a r 与b r ,a b ⊥⇔r r.(2)若非零向量1122(,),(,),a x y b x y a b ==⊥⇔r r r r.2.平行问题:(1)向量a r 与非零向量b r共线,当且仅当存在唯一一个实数λ,使得 .(2)设1122(,),(,)a x y b x y ==r r是平面向量,则向量a r 与非零向量b r 共线⇔ .【考点讲解】3.求角问题:(1)设,a b r r是两个非零向量,夹角记为α,则cos α= .(2)若1122(,),(,)a x y b x y ==r r是平面向量,则cos α= .4.距离(长度)问题:(1)设(,)a x y =r,则22a a ==r r ,即a =r .(2)若1122(,),(,)A x y B x y ,且a AB =r u u u r ,则AB AB ==u u u r.【答案】1.1212(1)0,(2)0.a b x x y y ⋅=+=r r2.(1)a b λ=r r,(2)12210x y x y -=3.(1)a b a b ⋅⋅r r r r.4.(1)22x y +【优秀题型展示】 1. 在平面几何中的应用:已知ABC D 中,(2,1),(3,2),(3,1)A B C ---,BC 边上的高为AD ,求点D 和向量AD u u u r的坐标.【解析】设点D 坐标(x ,y ),由AD 是BC 边上的高可得⊥,且B 、D 、C 共线,∴⎪⎩⎪⎨⎧=⋅//0∴⎩⎨⎧=+---+=--⋅+-0)1)(3()2)(3(0)3,6()1,2(y x y x y x ∴⎩⎨⎧=+---+=+---0)1)(3()2)(3(0)1(3)2(6y x y x y x ∴⎩⎨⎧=+-=-+012032y x y x解得⎩⎨⎧==11y x ∴点D 坐标为(1,1),AD =(-1,2). 【答案】AD =(-1,2)【变式】已知四边形ABCD 的三个顶点(02)A ,,(12)B --,,(31)C ,,且2BC AD =u u u r u u u r,则顶点D 的坐标为 ( ) A .722⎛⎫ ⎪⎝⎭,B .122⎛⎫- ⎪⎝⎭,C .(32),D .(13),【解析】设22(,),(3,1)(1,2)(4,3),(,2),,37222x x D x y BC AD x y y y 祆==镲镲镲=---==-\\眄镲-==镲镲铑u u u r u u u rQ , 【答案】A【变式】已知正方形OABC 的边长为1,点D E 、分别为AB BC 、的中点,求cos DOE ∠的值.【解析】以OA OC 、为坐标轴建立直角坐标系,如图所示.由已知条件,可得114.225⋅==∴∠=⋅u u u r u u u ru u u r u u u r u u u r u u u r (1,),(,1),cos =OD OE OD OE DOE OD OE2.在三角函数中的应用:已知向量3(sin ,)4a x =r ,(cos ,1)b x =-r .设函数()2()f x a b b =+⋅r r r ,已知在ABC ∆中,内角A B C 、、的对边分别为a bc 、、,若a =2b =,sin B =()4cos(2)6f x A π++([0,]3x π∈)的取值范围.【解析】 由正弦定理得或 . 因为,所以4A π=.因为+.所以, ,, 所以. 【答案】()⎥⎦⎤⎢⎣⎡--∈⎪⎭⎫ ⎝⎛++212,12362cos 4πA x f sin ,sin sin 24a b A A A B π===可得所以43π=A a b >()2())4f x a b b x π=+⋅=+r r r 32()⎪⎭⎫⎝⎛++62cos 4πA x f =)4x π+12-0,3x π⎡⎤∈⎢⎥⎣⎦Q 112,4412x πππ⎡⎤∴+∈⎢⎥⎣⎦()21262cos 4123-≤⎪⎭⎫ ⎝⎛++≤-πA x f3.在解析几何中的应用:(1)已知直线x +y =a 与圆x 2+y 2=4交于A 、B 两点,且|OA →+OB →|=|OA →-OB →|,其中O 为坐标原点,则实数a 的值为________.【解析】如图所示,以OA 、OB 为边作平行四边形OACB , 则由|OA →+OB →|=|OA →-OB →|得, 平行四边形OACB 是矩形,OA →⊥OB →.由图象得,直线y =-x +a 在y 轴上的截距为±2.【答案】±2(2)椭圆的焦点为F F ,点P 为其上的动点,当∠F P F 为钝角时,点P 横坐标的取值范围是 .【解析】法一:F 1(-,0)F 2(,0),设P (3cos ,2sin ).为钝角,.∴=9cos 2-5+4sin 2=5 cos 2-1<0.解得: ∴点P 横坐标的取值范围是(). 14922=+y x ,121255θθ21PF F ∠Θ123cos ,2sin )3cos ,2sin )PF PF θθθθ⋅=-⋅-u u u r u u u u r(θθθ55cos 55<<-θ553,553-ODC BA【答案】() 法二:F 1(-,0)F 2(,0),设P (x,y ).为钝角,∴ ()()125,5,PF PF x y x y •=--⋅-u u u r u u u u r225x y =+-=25109x -<. 解得:353555x -<<.∴点P 横坐标的取值范围是(). 【答案】() 2. 在物理学中的应用:如图所示,用两条成120º的等长的绳子悬挂一个灯具,已知灯具的重量为10N ,则每根绳子的拉力是 .]【解析】 ∵绳子的拉力是一样的(对称) ,∴OA =OB ,∴四边形OADB 为菱形 .∵∠AOB =120º ,∴∠AOD =60º .又OA =OB =AD , ∴三角形OAD 为等边三角形 ,∴OD =OA . 又根据力的平衡得OD =OC =10 , ∴OA =10 ,∴OA =OB =10 . ∴每根绳子的拉力大小是10N. 【答案】10N553,553-5521PF F ∠Θ553,553-553,553-【真题分析】1.【2017年高考全国II 卷理数】已知ABC △是边长为2的等边三角形,P 为平面ABC 内一点,则()PA PB PC ⋅+u u u r u u u r u u u r的最小值是( )A .2-B .32-C .43- D .1-【解析】如图,以BC 为x 轴,BC 的垂直平分线DA 为y 轴,D 为坐标原点建立平面直角坐标系,则A ,(1,0)B -,(1,0)C ,设(,)P x y ,所以()PA x y =-u u u r ,(1,)PB x y =---u u u r,(1,)PC x y =--u u u r ,所以(2,2)PB PC x y +=--u u u r u u u r ,22()22)22(PA PB PC x y y x y ⋅+=-=+-u u u r u u u r u u u r233)222-≥-,当(0,2P 时,所求的最小值为32-,故选B . 【答案】B2.【2018年高考上海卷】在平面直角坐标系中,已知点()10A -,、()20B ,,E 、F 是y 轴上的两个动点,且||2EF =u u u r ,则AE BF ⋅u u u r u u u r的最小值为___________.【解析】根据题意,设E (0,a ),F (0,b );∴2EF a b =-=u u u r;∴a =b +2,或b =a +2;且()()1,2,AE a BF b ==-u u u r u u u r ,;∴2AE BF ab ⋅=-+u u u r u u u r; 当a =b +2时,()22222AE BF b b b b ⋅=-++⋅=+-u u u r u u u r;∵b 2+2b ﹣2的最小值为8434--=-; ∴AE BF ⋅u u u r u u u r 的最小值为﹣3,同理求出b =a +2时,AE BF ⋅u u u r u u u r的最小值为﹣3.故答案为:﹣3.【答案】-33.【2018年高考江苏卷】在平面直角坐标系xOy 中,A 为直线:2l y x =上在第一象限内的点,()5,0B ,以AB 为直径的圆C 与直线l 交于另一点D .若0AB CD ⋅=u u u r u u u r,则点A 的横坐标为___________.【解析】设(),2(0)A a a a >,则由圆心C 为AB 中点得5,,2a C a +⎛⎫⎪⎝⎭易得()()():520C x x a y y a --+-=e ,与2y x =联立解得点D 的横坐标1,D x =所以()1,2D .所以()55,2,1,22a AB a a CD a +⎛⎫=--=-- ⎪⎝⎭u u u r u u u r ,由0AB CD ⋅=u u u r u u u r 得()()()2551220,230,32a a a a a a a +⎛⎫--+--=--== ⎪⎝⎭或1a =-,因为0a >,所以 3.a = 【答案】34.【2017年高考全国I 卷理数】已知向量a ,b 的夹角为60°,|a |=2,|b |=1,则| a +2b |=___________. 【解析】方法一:222|2|||44||4421cos60412+=+⋅+=+⨯⨯⨯+=oa b a a b b ,所以|2|+==a b .方法二:利用如下图形,可以判断出2+a b 的模长是以2为边长,一夹角为60°的菱形的对角线的长度,则为【答案】5.【2017年高考江苏卷】如图,在同一个平面内,向量OA u u u r ,OB uuu r ,OC uuu r 的模分别为1,1,2,OA u u u r 与OCuuu r的夹角为α,且tan α=7,OB uuu r 与OC uuu r 的夹角为45°.若OC mOA nOB =+u u u r u u u r u u u r(,)m n ∈R ,则m n +=___________.【解析】由tan 7α=可得sin 10α=,cos 10α=,根据向量的分解,易得cos 45cos sin 45sin 0n m n m αα⎧︒+=⎪⎨︒-=⎪⎩0210n m +=-=⎩,即510570n m n m +=⎧⎨-=⎩,即得57,44m n ==,所以3m n +=. 【答案】36.【2017年高考浙江卷】已知向量a ,b 满足1,2,==a b 则++-a b a b 的最小值是________,最大值是___________.【解析】设向量,a b 的夹角为θ,则-==a b+==a b ++-=a b a b令y =[]21016,20y =+,据此可得:()()maxmin 4++-==++-==a b a ba b a b ,即++-a b a b 的最小值是4,最大值是【答案】4,7. 【2016·江苏卷】如图,在△ABC 中,D 是BC 的中点,E ,F 是AD 上的两个三等分点,BA →·CA →=4, BF →·CF →=-1,则BE →·CE →的值是________.【解析】 设AB →=a ,AC →=b ,则BA →·CA →=(-a )·(-b )=a ·b =4.又∵D 为BC 中点,E ,F 为AD 的两个三等分点,则AD →=12(AB →+AC →)=12a +12b ,AF →=23AD →=13a +13b ,AE →=13AD →=16a +16b ,BF →=BA →+AF →=-a +13a +13b =-23a +13b ,CF →=CA →+AF →=-b +13a +13b =13a -23b ,则BF →·CF →=⎝⎛⎭⎫-23a +13b ·⎝⎛⎭⎫13a -23b =-29a 2-29b 2+59a ·b =-29(a 2+b 2)+59×4=-1. 可得a 2+b 2=292.又BE →=BA →+AE →=-a +16a +16b =-56a +16b ,CE →=CA →+AE →=-b +16a +16b =16a -56b ,则BE →·CE →=⎝⎛⎭⎫-56a +16b ·⎝⎛⎭⎫16a -56b =-536(a 2+b 2)+2636a ·b =-536×292+2636×4=78.【答案】 788.【2017年高考江苏卷】已知向量(cos ,sin ),(3,[0,π].x x x ==∈a b (1)若a ∥b ,求x 的值;(2)记()f x =⋅a b ,求()f x 的最大值和最小值以及对应的x 的值.【解析】(1)因为co ()s ,sin x x =a,(3,=b ,a ∥b,所以3sin x x =. 若cos 0x =,则sin 0x =,与22sin cos 1x x +=矛盾,故cos 0x ≠.于是tan 3x =-.又[]0πx ∈,,所以5π6x =.(2)π(cos ,sin )(3,3cos ())6f x x x x x x =⋅=⋅=-=+a b . 因为[]0πx ∈,,所以ππ7π[,]666x +∈,从而π1cos()62x -≤+≤. 于是,当ππ66x +=,即0x =时,()f x 取到最大值3; 当π6x +=π,即5π6x =时,()f x取到最小值-【答案】(1)5π6x =;(2)0x =时,()f x 取到最大值3;5π6x =时,()f x取到最小值-.1.已知数列{}n a 为等差数列,且满足32015BA a OB a OC =+u u u r u u u r u u u r ,若()AB AC R λλ=∈u u u r u u u r,点O 为直线BC 外一点,则12017a a +=( )A. 0B. 1C. 2D. 4【解析】∵32015BA a OB a OC =+u u u r u u u r u u u r , ∴32015OA OB a OB a OC -=+u u u r u u u r u u u r u u u r, 即()320151OA a OB a OC =++u u u r u u u r u u u r , 又∵()AB AC R λλ=∈u u u r u u u r,∴3201511a a ++=, ∴12017320150a a a a +=+=. 【答案】A2.直角ABC V 中, AD 为斜边BC 边的高,若1AC =u u u r , 3AB =u u u r,则CD AB ⋅=u u u r u u u r ( )【模拟考场】A .910 B . 310 C . 310- D . 910-【解析】依题意BC =22,AC AC CD CB CD CB =⋅==103cos ==BC AB B,所以有9cos 310CD AB CD AB B ⋅=⋅⋅==u u u r u u u r u u u r u u u r . 【答案】A3.已知正三角形ABC 的边长为,平面ABC 内的动点P ,M 满足1AP =uu u r ,PM MC =uuu r uuu r ,则2BMuuu r 的最大值是( ) A.B. C. D.【解析】本题考点是向量与平面图形的综合应用.由题意可设D 为三角形的内心,以D 为原点,直线DA 为x 轴建立平面直角坐标系,由已知易得1220,DA ADC ADB D D BDC B C ∠=∠====∠=︒u u u r u u u r u u u r. 则()((2,0,1,,1,.A B C --设(),,P x y 由已知1AP =u u u r ,得()2221x y -+=,又11,,,,,22x x PM MC M BM ⎛⎛-+=∴∴= ⎝⎭⎝⎭u u u u r u u u u r u u u u r()(22214x y BM -++∴=u u u u r ,它表示圆()2221x y -+=上点().x y 与点(1,--距离平方的14,()22max149144BM⎫∴==⎪⎭u u u u r ,故选B.【答案】B4.已知曲线C :x =直线l :x=6.若对于点A (m ,0),存在C 上的点P 和l 上的点Q 使得0AP AQ +=u u u r u u u r r,则m 的取值范围为 .【解析】本题考点是向量线性运算与解析几何中点与直线的位置关系的应用.由0AP AQ +=u u u r u u u r r知A 是PQ的中点,设(,)P x y ,则(2,)Q m x y --,由题意20x -≤≤,26m x -=,解得23m ≤≤.3244344943637+433237+【答案】[2,3]5.在平面直角坐标系中,O 为原点,()),0,3(),3,0(,0,1C B A -动点D 满足CD u u u r=1,则OA OB OD ++u u u r u u u r u u u r 的最大值是_________.【解析】本题的考点是参数方程中的坐标表示, 圆的定义与 三角函数的值域.由题意可知C 坐标为()3,0且1CD =,所以动点D 的轨迹为以C 为圆心的单位圆,则D 满足参数方程3cos sin D D x y θθ=+⎧⎨=⎩(θ为参数且[)0,2θπ∈),所以设D 的坐标为()[)()3cos ,sin 0,2θθθπ+∈, 则OA OB OD ++=u u u r u u u r u uu r=因为2cos θθ+=所以OA OB OD ++的最大值为1==+故填1【答案】1+6.在△ABC 中,∠ABC =120°,BA =2,BC =3,D ,E 是线段AC 的三等分点,则BD →·BE →的值为________. 【解析】 由题意得BD →·BE →=(BA →+AD →)·(BC →+CE →)=⎝⎛⎭⎫BA →+13AC →·⎝⎛⎭⎫BC →+13CA → =⎣⎡⎦⎤BA →+13(BC →-BA →)·⎣⎡⎦⎤BC →+13(BA →-BC →)=⎝⎛⎭⎫13BC →+23BA →·⎝⎛⎭⎫23BC →+13BA → =29BC →2+59BC →·BA →+29BA →2=29×9+59×2×3×cos 120°+29×4=119. 【答案】1197.已知菱形ABCD 的边长为2,∠BAD =120°,点E ,F 分别在边BC ,DC 上,BC =3BE ,DC =λDF . 若AE →·AF →=1,则λ的值为________. 【解析】法一、 如图,AE →=AB →+BE →=AB →+13BC →,AF →=AD →+DF →=AD →+1λDC →=BC →+1λAB →,所以AE →·AF →=⎝⎛⎭⎫AB →+13BC →·⎝⎛⎭⎫BC →+1λAB →=⎝⎛⎭⎫1+13λAB →·BC →+1λAB →2+13BC →2=⎝⎛⎭⎫1+13λ×2×2×cos 120°+4λ+43=1,解得λ=2.法二、 建立如图所示平面直角坐标系.由题意知:A (0,1),C (0,-1),B (-3,0),D (3,0).由BC =3BE ,DC =λDF .可求点E ,F 的坐标分别为E ⎝⎛⎭⎫-233,-13,F ⎝⎛⎭⎫3⎝⎛⎭⎫1-1λ,-1λ, ∴AE →·AF →=⎝⎛⎭⎫-233,-43·⎝⎛⎭⎫3⎝⎛⎭⎫1-1λ,-1λ-1=-2⎝⎛⎭⎫1-1λ+43⎝⎛⎭⎫1+1λ=1,解得λ=2. 【答案】28.在△ABC 中,∠A =60°,AB =3,AC =2,若BD →=2DC →,AE →=λAC →-AB →(λ∈R ),且AD →·AE →=-4,则λ的值为________.【解析】AB →·AC →=3×2×cos 60°=3,AD →=13AB →+23AC →,则AD →·AE →=⎝⎛⎭⎫13AB →+23AC →·(λAC →-AB →)=λ-23AB →·AC →-13AB →2+2λ3AC →2=λ-23×3-13×32+2λ3×22=113λ-5=-4,解得λ=311.【答案】3119.在△ABC 中,点M ,N 满足AM →=2MC →,BN →=NC →.若MN →=xAB →+yAC →,则x =__________;y =__________.【解析】MN →=MC →+CN →=13AC →+12CB →=13AC →+12(AB →-AC →)=12AB →-16AC →,∴x =12,y =-16.【答案】 12 -1610.在等腰梯形ABCD 中,已知AB ∥DC ,AB =2,BC =1,∠ABC =60°,动点E 和F 分别在线段BC 和DC 上,且BE →=λBC →,DF →=19λDC →,则AE →·AF →的最小值为________.【解析】法一 在梯形ABCD 中,AB =2,BC =1,∠ABC =60°,可得DC =1,AE →=AB →+λBC →,AF →=AD →+19λDC →,∴AE →·AF →=(AB →+λBC →)·(AD →+19λDC →)=AB →·AD →+AB →·19λDC →+λBC →·AD →+λBC →·19λDC →=2×1×cos 60°+2×19λ+λ×1×cos 60°+λ·19λ×cos 120°=29λ+λ2+1718≥229λ·λ2+1718=2918,当且仅当29λ=λ2,即λ=23时,取得最小值为2918.法二 以点A 为坐标原点,AB 所在的直线为x 轴建立平面直角坐标系,则B (2,0),C ⎝⎛⎭⎫32,32,D ⎝⎛⎭⎫12,32.又BE →=λBC →,DF →=19λDC →,则E ⎝⎛⎭⎫2-12λ,32λ,F ⎝⎛⎭⎫12+19λ,32,λ>0,所以AE →·AF →=⎝⎛⎭⎫2-12λ⎝⎛⎭⎫12+19λ+34λ=1718+29λ+12λ≥1718+229λ·12λ=2918,λ>0, 当且仅当29λ=12λ,即λ=23时取等号,故AE →·AF →的最小值为2918.【答案】291811.已知矩形ABCD 的边AB =2,AD =1.点P ,Q 分别在边BC ,CD 上,且∠P AQ =π4,则AP →·AQ →的最小值为________.【解析】法一(坐标法) 以A 为坐标原点,AB 所在直线为x 轴,AD 所在直线为y 轴建立平面直角坐标系,则A (0,0),B (2,0),D (0,1).设∠P AB =θ,则AP →=(2,2tan θ),AQ →=⎝⎛⎭⎫tan ⎝⎛⎭⎫π4-θ,1,0≤tan θ≤12. 因为AP →·AQ →=(2,2tan θ)·⎝⎛⎭⎫tan ⎝⎛⎭⎫π4-θ,1=2tan ⎝⎛⎭⎫π4-θ+2tan θ=2(1-tan θ)1+tan θ+2tan θ=41+tan θ+2tan θ-2=41+tan θ+2(tan θ+1)-4≥42-4,当且仅当tan θ=2-1时,“=”成立,所以AP →·AQ →的最小值为42-4.法二(基底法) 设BP =x ,DQ =y ,由已知得,tan ∠P AB =x2,tan ∠QAD =y ,由已知得∠P AB +∠QAD =π4,所以tan ∠P AB +tan ∠QAD 1-tan ∠P AB tan ∠QAD =1,所以x +2y 2=1-xy2,x +2y =2-xy ≥2x ·2y ,解得0<xy ≤6-42,当且仅当x =2y 时,“=”成立.AP →·AQ →=22·(4+x 2)(1+y 2)=22·(xy )2+(x +2y )2-4xy +4=22·(xy )2+(2-xy )2-4xy +4=(xy )2-4xy +4=2-xy ≥42-4. 【答案】 42-412.设O 为坐标原点,C 为圆(x -2)2+y 2=3的圆心,且圆上有一点M (x ,y )满足OM →·CM →=0,则y x =________.【解析】 ∵OM →·CM →=0,∴OM ⊥CM ,∴OM 是圆的切线,设OM 的方程为y =kx , 由|2k |1+k 2=3,得k =±3,即yx =± 3.【答案】 ±313.在△ABC 中,已知AB =1,AC =2,∠A =60°,若点P 满足AP →=AB →+λAC →,且BP →·CP →=1,则实数λ的值为________.【解析】 由AB =1,AC =2,∠A =60°,得BC 2=AB 2+AC 2-2AB ·AC ·cos A =3,即BC = 3.又AC 2=AB 2+BC 2,所以∠B =90°.以点A 为坐标原点,AB →,BC →的方向分别为x 轴,y 轴的正方向建立平面直角坐标系,则B (1,0),C (1,3).由AP →=AB →+λAC →,得P (1+λ,3λ),则BP →·CP →=(λ,3λ)·(λ,3λ-3)=λ2+3λ(λ-1)=1,即4λ2-3λ-1=0,解得λ=-14或λ=1.【答案】 -14或114.证明:同一平面内,互成120°的三个大小相等的共点力的合力为零.【证明】如图,用r a ,r b ,r c 表示这3个共点力,且r a ,r b ,rc 互成120°,模相等,按照向量的加法运算法则,有:r a +r b +r c = r a +(r b +r c )=r a +u u u rOD .又由三角形的知识知:三角形OBD 为等边三角形, 故r a 与u u u r OD 共线且模相等,所以:u u u r OD = -r a ,即有:r a +r b +r c =0r .15.在直角坐标系xOy 中,已知点(1,1),(2,3),(3,2)A B C ,点(,)P x y 在ABC ∆三边围成的区域(含边界)上,且(,)OP mAB nAC m n R =+∈u u u r u u u r u u u r.(1)若23m n ==,求||OP u u u r ;(2)用,x y 表示m n -,并求m n -的最大值.【解析】(1)(1,1),(2,3),(3,2)A B C Q (1,2)AB ∴=u u u r ,(2,1)AC =u u u r.Q OP mAB nAC =+u u u r u u u r u u u r ,又23m n ==.22(2,2)33OP AB AC ∴=+=u u u r u u u r u u u r,|OP ∴u u u r(2)OP mAB nAC =+u u u r u u u r u u u rQ (,)(2,2)x y m n m n ∴=++即22x m ny m n=+⎧⎨=+⎩,两式相减得:m n y x -=-.令y x t -=,由图可知,当直线y x t =+过点(2,3)B 时,t 取得最大值1,故m n -的最大值为1.【答案】(1)(2)m n y x -=-,1.16.如图,在直角梯形ABCD 中,AB ∥CD ,∠DAB =90°,AD =AB =4,CD =1,动点P 在边BC 上,且满足AP →=mAB →+nAD →(m ,n 均为正实数),求1m +1n的最小值.【解析】 如图,建立平面直角坐标系,得A (0,0),B (4,0),D (0,4),C (1,4),则AB →=(4,0),AD →=(0,4).设AP →=(x ,y ),则BC 所在直线为4x +3y =16. 由AP →=mAB →+nAD →,即(x ,y )=m (4,0)+n (0,4),得x =4m ,y =4n (m ,n >0), 所以16m +12n =16,即m +34n =1,那么1m +1n =⎝⎛⎭⎫1m +1n ⎝⎛⎭⎫m +34n =74+3n 4m +m n ≥74+23n 4m ·m n =74+3=7+434(当且仅当3n 2=4m 2时取等号). 17.已知向量m =(cos α,-1),n =(2,sin α),其中α∈⎝⎛⎭⎫0,π2,且m ⊥n . (1)求cos 2α的值; (2)若sin(α-β)=1010,且β∈⎝⎛⎭⎫0,π2,求角β的值. 【解析】 (1)由m ⊥n ,得2cos α-sin α=0,sin α=2cos α,代入cos 2α+sin 2α=1,得5cos 2α=1, 又α∈⎝⎛⎭⎫0,π2,则cos α=55,cos 2α=2cos 2α-1=-35. (2)由α∈⎝⎛⎭⎫0,π2,β∈⎝⎛⎭⎫0,π2,得α-β∈⎝⎛⎭⎫-π2,π2.因为sin(α-β)=1010,所以cos(α-β)=31010,而sin α=1-cos 2α=255, 则sin β=sin[α-(α-β)]=sin αcos(α-β)-cos αsin(α-β)=255×31010-55×1010=22.因为β∈⎝⎛⎭⎫0,π2,所以β=π4.。
2021年高考数学经典例题 专题四:平面向量与不等式【含解析】

真题四 平面向量与不等式一、单选题1.已知向量()()2332a b ==,,,,则|–|a b =( ) A 2B .2 C .2D .50【答案】A 【解析】由已知,(2,3)(3,2)(1,1)a b -=-=-, 所以22||(1)12a b -=-+=故选A2.已知向量()2,3a =,()1,b λ=-,若向量2a b -与向量a 共线,则b =( ) A .32-B .132 C 13 D .134【答案】B 【解析】由向量坐标运算得到2a b -,根据向量共线可构造方程求得λ,由模长的坐标运算得到结果. 【详解】()24,32a b λ-=-,又向量2a b -与向量a 共线,()432λλ∴=--,解得:32λ=-,()2239131124b ⎛⎫∴=-+-=+= ⎪⎝⎭. 故选:B. 【点睛】结论点睛:若()11,a x y =与()22,b x y =共线,则1221x y x y =. 3.在ABC 中,D 是AB 边上的中点,则CB =( )A .2CD CA +B .2CD CA -C .2CD CA - D .2CD CA +【答案】C 【解析】根据向量的加减法运算法则算出即可. 【详解】()222CB CA AB CA AD CA CD CA CD CA -=+=+=+-=故选:C4.已知,,a b c 均为单位向量,且22a b c +=,则a c ⋅=( ) A .12-B .14-C .14D .12【答案】C 【解析】由22a b c +=两边平方得14-⋅=a b ,又因为22a b c +=可得()1=22+c a b ,再计算a c ⋅即可得结果. 【详解】 由()()2222+=a bc 得222444++⋅=ab a b c因为,,a b c 均为单位向量,则1a b c ===,所以14-⋅=a b , 又()1=22+c a b ,所以()()21111122122224⎛⎫⋅=⋅+=+⋅=-= ⎪⎝⎭a c a a b a a b故选:C .5.已知,a b 是相互垂直的单位向量,与,a b 共面的向量c 满足2,a c b c ⋅⋅==则c 的模为( ) A .1 B 2C .2D .22【答案】D 【解析】根据,a b 是相互垂直的单位向量,利用坐标法以及数量积的坐标表示,建立方程进行求解即可. 【详解】,a b 是相互垂直的单位向量,不妨设()1,0a =,()0,1b =, 设(),c x y =,由2,a c b c ⋅⋅== 可得2x y ==,即()2,2c =, 则c 的模为2222822c =+==.故选:D6.若实数x ,y 满足约束条件31030x y x y -+≤⎧⎨+-≥⎩,则z =x +2y 的取值范围是( )A .(,4]-∞B .[4,)+∞C .[5,)+∞D .(,)-∞+∞【答案】B 【解析】首先画出可行域,然后结合目标函数的几何意义确定目标函数在何处能够取得最大值和最小值从而确定目标函数的取值范围即可. 【详解】绘制不等式组表示的平面区域如图所示,目标函数即:1122y x z =-+,其中z 取得最大值时,其几何意义表示直线系在y 轴上的截距最大, z 取得最小值时,其几何意义表示直线系在y 轴上的截距最小, 据此结合目标函数的几何意义可知目标函数在点A 处取得最小值, 联立直线方程:31030x y x y -+=⎧⎨+-=⎩,可得点A 的坐标为:()2,1A ,据此可知目标函数的最小值为:min 2214z =+⨯= 且目标函数没有最大值.故目标函数的取值范围是[)4,+∞. 故选:B.7.已知单位向量a ,b 的夹角为60°,则在下列向量中,与b 垂直的是( ) A .2a b + B .2a b +C .2a b -D .2a b -【答案】D 【解析】根据平面向量数量积的定义、运算性质,结合两平面向量垂直数量积为零这一性质逐一判断即可. 【详解】由已知可得:11cos 601122a b a b ︒⋅=⋅⋅=⨯⨯=. A :因为215(2)221022a b b a b b +⋅=⋅+=+⨯=≠,所以本选项不符合题意;B :因为21(2)221202a b b a b b +⋅=⋅+=⨯+=≠,所以本选项不符合题意;C :因为213(2)221022a b b a b b -⋅=⋅-=-⨯=-≠,所以本选项不符合题意;D :因为21(2)22102a b b a b b -⋅=⋅-=⨯-=,所以本选项符合题意.故选:D.8.已知向量ab a ,b 满足||5a =,||6b =,6a b ⋅=-,则cos ,=a a b +( ) A .3135-B .1935-C .1735D .1935【答案】D 【解析】计算出()a ab ⋅+、a b +的值,利用平面向量数量积可计算出cos ,a a b <+>的值. 【详解】5a =,6b =,6a b ⋅=-,()225619a a b a a b ∴⋅+=+⋅=-=. ()22222526367a b a b a a b b +=+=+⋅+=-⨯+,因此,()1919cos ,5735a a ba ab a a b⋅+<+>===⨯⋅+. 故选:D.9.已知P 是边长为2的正六边形ABCDEF 内的一点,则AP AB ⋅ 的取值范围是( ) A .()2,6- B .(6,2)- C .(2,4)- D .(4,6)-【答案】A 【解析】首先根据题中所给的条件,结合正六边形的特征,得到AP 在AB 方向上的投影的取值范围是(1,3)-,利用向量数量积的定义式,求得结果. 【详解】AB 的模为2,根据正六边形的特征,可以得到AP 在AB 方向上的投影的取值范围是(1,3)-, 结合向量数量积的定义式,可知AP AB ⋅等于AB 的模与AP 在AB 方向上的投影的乘积, 所以AP AB ⋅的取值范围是()2,6-, 故选:A.10.若x ,y 满足|1|x y ≤-,且y ≥−1,则3x+y 的最大值为( ) A .−7 B .1C .5D .7【答案】C 【解析】 由题意1,11yy x y -≤⎧⎨-≤≤-⎩作出可行域如图阴影部分所示.设3,3z x y y z x =+=-,当直线0:3l y z x =-经过点()2,1-时,z 取最大值5.故选C.11.设2log 3a =,24log 3b =,则2a b +,ab ,ba 的大小关系为( ) A .2ab b ab a +>> B .2a b b ab a +>> C .2a b b ab a +>> D .2b a bab a +>> 【答案】C 【解析】由已知得1,0a b >>且2a b +=,然后结合基本不等式与中间值1比较,用不等式的性质比较大小可得. 【详解】易知:0,0a b >>,12a b +=,()214a b ab +<=,1b ab a a >⇔>,显然成立. 所以2a b bab a+>>.故选:C .12.已知,a b 是平面向量,满足||2,||1a b =≤,且322b a -≤,记a 与b 的夹角为θ,则cos θ的最小值是( ) A .1116B .78C 15D 315【答案】B 【解析】先给322b a -≤两边平方然后展开,代入2a =,得到2143a b b⋅≥+,然后利用23||113||4cos 8||||2||2||b a b b a b b b θ+⋅=≥=+⋅,然后当1b ≤时,求解cos θ的最小值. 【详解】由322b a -≤得,()2223294124b ab a a b -=+-⋅≤,所以2143a b b ⋅≥+.则23||113||4cos 8||||2||2||b a b b a b b b θ+⋅=≥=+⋅⋅ 令函数13()28xf x x =+,因为()f x 在[]0,1上单调递减. 又因为1b ≤,故当1b =时,cos θ取得最小值,最小值为78. 故选:B 【点睛】本题考查向量间夹角余弦值的取值范围的计算问题,解答的一般思路为:当已知a ,b 和a b λμ+(其中,λμ为常数)时,一般采用平方法,得到2a b λμ+然后展开,得到cos θ的值.13.已知a ,b ,R c ∈,若关于x 不等式01a cx b x x≤++≤-的解集为[]{}()123321,0x x x x x x ⋃>>>,则( )A .不存在有序数组(,,)a b c ,使得211x x -=B .存在唯一有序数组(,,)a b c ,使得211x x -=C .有且只有两组有序数组(,,)a b c ,使得211x x -=D .存在无穷多组有序数组(,,)a b c ,使得211x x -= 【答案】D 【解析】根据1>0x ,不等式转化为一元二次不等式的解的问题,利用两个一元二次不等式解集有交集的结论,得出两个不等式解集的形式,从而再结合一元二次方程的根与系数关系确定结论. 【详解】由题意不等式20x bx a c x ≤++≤-的解集为[]{}()123321,0x x x x x x ⋃>>>,即220x bx a x bx a c x ⎧++≥⎨++≤-⎩的解集是[]{}123,x x x ⋃,则不等式20x bx a ++≥的解是{|x 2x x ≤或3x x ≥},不等式2x bx a c x ++≤-的解集是13{|}x x x x ≤≤, 设1x m =,21x m =+,3x n =(1)m n +<, 所以0c n -=,n c =,1m +和n 是方程20x bx a ++=的两根,则11b m n m c -=++=++,(1)a m n mc c =+=+, 又22(1)m bm a m m m c mc c c m ++=+---++=-, 所以m 是2x bx a c x ++=-的一根, 所以存在无数对(,,)a b c ,使得211x x -=. 故选:D .14.已知a ,b ∈R 且ab ≠0,对于任意x ≥0 均有(x –a )(x–b )(x–2a–b )≥0,则( ) A .a <0 B .a >0C .b <0D .b >0【答案】C 【解析】对a 分0a >与0a <两种情况讨论,结合三次函数的性质分析即可得到答案. 【详解】因为0ab ≠,所以0a ≠且0b ≠,设()()()(2)f x x a x b x a b =----,则()f x 的零点 为123,,2x a x b x a b ===+当0a >时,则23x x <,1>0x ,要使()0f x ≥,必有2a b a +=,且0b <, 即=-b a ,且0b <,所以0b <;当0a <时,则23x x >,10x <,要使()0f x ≥,必有0b <. 综上一定有0b <. 故选:C15.已知22220,0,3,3a b a b ab a b >>+-=-≤,则+a b 的最小值是( )A .22B .3C .23D .4【答案】B 【解析】将223a b ab +-=,变形为223324b b a ⎛⎫-+= ⎪⎝⎭,令3233ba θθ⎧-=⎪⎪=,根据0,0a b >>确定203θπ<<,得到22a b -2323πθ⎛⎫=+ ⎪⎝⎭,然后由223a b -≤,,进一步确定62ππθ≤≤,然后由33sin 236a b πθθθ⎛⎫+=+=+ ⎪⎝⎭,利用三角函数性质求解.【详解】因为222222344b b a b ab a b ab +-=+-++, 223324b b a ⎛⎫=-+= ⎪⎝⎭,令3233ba θθ⎧-=⎪⎪=,则3sin 2sin 32sin a b πθθθθ⎧⎛⎫=+=+⎪ ⎪⎝⎭⎨⎪=⎩, 因为0,0a b >>,所以sin 03sin 0πθθ⎧⎛⎫+>⎪ ⎪⎝⎭⎨⎪>⎩,即030πθπθπ⎧<+<⎪⎨⎪<<⎩, 解得203θπ<<, 所以)()22223sin 2sin a b θθθ-=+-,2223cos 23sin cos sin 4sin θθθθθ=++-,()223cos sin 23cos θθθθ=-+3cos23sin 2θθ=,2323πθ⎛⎫=+ ⎪⎝⎭,因为203θπ<<, 所以52333ππθπ<+<,因为223a b -≤,所以33sin 23πθ⎛⎫≤+≤⎪⎝⎭ 解得242333ππθπ≤+≤, 所以62ππθ≤≤,则2363πππθ≤+≤, 所以33sin 233,236a b πθθθ⎛⎫⎡⎤+=+=+∈ ⎪⎣⎦⎝⎭, 所以+a b 的最小值是3, 故选:B关键点点睛:本题关键是将223a b ab +-=,变形为223324b b a ⎛⎫-+= ⎪⎝⎭,利用三角换元,转化为三角函数求解. 二、多选题16.已知0a b c >>>且1abc =,则下列结论中一定成立的是( ) A .1b = B .1ab >C .01bc <<D .22a c +>【答案】BCD 【解析】由0a b c >>>且1abc =,可以得到1a >,01c <<,然后结合不等式的性质容易对A ,B ,C 选项进行判断,然后利用基本不等式可对D 选项进行判断. 【详解】A :因为0a b c >>>且1abc =,所以331c abc a <=<,即1a >,01c <<,b 不一定等于1,故A 项不一定成立;B :因为01c <<,所以11ab c =>,所以B 项一定成立; C :因为1a >,所以101bc a<=<,C 项一定成立;D :22211222a a c a a ab ab b+=+≥⋅,D 项一定成立. 17.已知,a b 均为正实数,且1a b +=,则( ) A .ab 的最大值为14B .2b a b+的最小值为22C .221155a b ⎛⎫⎛⎫++ ⎪⎪⎝⎭⎝⎭的最小值为15D .2221a b a b +++的最小值为94 【答案】AC 【解析】对于选项A ,直接根据基本不等式可求得结果;对于选项B ,化为积为定值的形式后,根据基本不等式求出最小值可得答案; 对于选项C ,变形后利用二次函数求出最小值可得答案; 对于选项D ,变形后利用基本不等式求出最小值可得答案. 【详解】对于选项A ,2124a b ab +⎛⎫≤= ⎪⎝⎭,当且仅当12a b ==时取“=”,故A 正确;对于选项B ,22222b b a b b aa b a b a b++=+=++≥222, 当且仅当222b a ==“=”,故B 错误;对于选项C ,22222111()55525a b a b ab +⎛⎫⎛⎫++=++ ⎪⎪⎝⎭⎝⎭ 222121111()()5525555ab a b ab ab ⎛⎫=++-+=-+≥ ⎪⎝⎭,当且仅当15ab =时取“=”,故C 正确; 对于选项D ,22a a ++222(22)(11)121b a b b a b +-+-=++++ 41241221a b a b =+-+++-+++ 41221a b =+-++, 令2s a =+,1t b =+,则4s t +=,所以4121a b +++=141(4s s t ⎛⎫++ ⎪⎝⎭14)414t s t s t ⎛⎫=+++⎪⎝⎭ 1495244t s s t ⎛≥+⋅= ⎝, 当且仅当2s t =,即43t =,83s =时取“=”,所以41221a b +-++91244≥-=, 所以221214a b a b +≥++,当且仅当23a =,13b =时取“=”,故选项D 错误. 故选:AC. 【点睛】方法点睛:利用基本不等式求解最值问题常采用常数代换法,其解题步骤为:(1)根据已知条件或其变形确定定值(常数);(2)把定值(常数)变形为1;(3)把“1”的表达式与所求最值的表达式相乘或相除,进而构造和或积为定值的形式;(4)利用基本不等式求解最值. 18.已知a >0,b >0,且a +b =1,则( ) A .2212a b +≥B .122a b ->C .22log log 2a b +≥-D 2a b 【答案】ABD 【解析】根据1a b +=,结合基本不等式及二次函数知识进行求解. 【详解】对于A ,()222221221a b a a a a +=+-=-+21211222a ⎛⎫⎪⎭+ ⎝≥-=,当且仅当12a b ==时,等号成立,故A 正确; 对于B ,211a b a -=->-,所以11222a b-->=,故B 正确; 对于C ,2222221log log log log log 224a b a b ab +⎛⎫+=≤==- ⎪⎝⎭, 当且仅当12a b ==时,等号成立,故C 不正确; 对于D ,因为(21212a bab a b =+≤++=,2a b 12a b ==时,等号成立,故D 正确; 故选:ABD 三、填空题19.已知向量(),1a x =,()1,2b =-,且a b ⊥,则a b -=___________. 10【解析】由垂直的坐标表示求得x ,再由模的坐标运算求解. 【详解】由a b ⊥得20a b x ⋅=-=,2x =,则(1,3)a b -=,所以221310a b -=+= 10.20.已知点(),C x y 在线段():41,AB x y x y ++=∈R 上运动,则xy 的最大值是____________.【答案】116【解析】直接利用基本不等式计算可得; 【详解】解:由题设()41,x y x y ++=∈R 可得:4124x y xy +=≥142xy ≤, ∴144xy ≤,即116xy ≤,当且仅当142x y ==时取“=”, 故答案为:116.21.已知a ,b 为实数,则221214a b ++______2ab a +.(填“>”、“<”、“≥”或“≤”)【答案】≥ 【解析】利用作差法,配方即可比较大小. 【详解】()2222112121042a b ab a a b a ⎛⎫++--=-+-≥ ⎪⎝⎭,当且仅当1a =,2b =取等号. 故答案为:≥22.若x ,y 满足约束条件1121,x y x y x y +≥-⎧⎪-≥-⎨⎪-≤⎩,,则2z x y =+的最大值是__________.【答案】8 【解析】在平面直角坐标系内画出不等式组表示的平面区域,然后平移直线12y x =-,在平面区域内找到一点使得直线1122y x z =-+在纵轴上的截距最大,求出点的坐标代入目标函数中即可.【详解】不等式组表示的平面区域为下图所示:平移直线12y x =-,当直线经过点A 时,直线1122y x z =-+在纵轴上的截距最大,此时点A 的坐标是方程组121x y x y -=-⎧⎨-=⎩的解,解得:23x y =⎧⎨=⎩,因此2z x y =+的最大值为:2238+⨯=. 故答案为:8.23.若02030x x y x y ≥⎧⎪-≤⎨⎪+-≥⎩,则3z x y =-的最大值是___________.【答案】1- 【解析】根据约束条件作出可行域以及直线3z x y =-过点A 时在y 轴上的截距最小,z 有最大值,得出答案. 【详解】根据约束条件02030x x y x y ≥⎧⎪-≤⎨⎪+-≥⎩作出可行域如图所示,由2030x y x y -=⎧⎨+-=⎩解得()2,1A将目标函数3z x y =-化为133z y x =-, z 表示直线133z y x =-在y 轴上的截距的相反数的13故当直线133zy x =-在y 轴上的截距最小时,z 有最大值.当直线133zy x =-过点(2,1)时在y 轴上的截距最小,z 最大,由A (2,1)知z 的最小值为2311-⨯=- 故答案为:1-24.已知向量a ,b 满足3a b +=,0a b ⋅=.若()1c λa λb =+-,且c a c b ⋅=⋅,则c 的最大值为______. 【答案】32【解析】令M a A =,MB b =,利用已知作出以AB 为直径作直角三角形ABM 的外接圆O ,令AN MB =,连接MN .设c AC =,由已知点C 在直线MN 上,【详解】令M a A =,MB b =,则a b AM MB AB =++=,故3AB =,又0a b ⋅=,所以AM MB ⊥.以AB 为直径作直角三角形ABM 的外接圆O ,进而得出当NM AB ⊥时,AC 即c 取得最大值.令AN MB =,连接MN .设c AC =,因为()1c λa λb =+-⋅,所以点C 在直线MN 上,又c a c b ⋅=⋅,所以()0c a b ⋅-=,即0AC NM ⋅=,所以AC NM ⊥.结合图形可知,当NM AB ⊥时,AC 即c 取得最大值,且32c AO ==.故答案为:3225.已知单位向量a →,b →的夹角为45°,k a b →→-与a →垂直,则k =__________. 【答案】22【解析】首先求得向量的数量积,然后结合向量垂直的充分必要条件即可求得实数k 的值. 【详解】由题意可得:211cos 452a b →→⋅=⨯⨯=, 由向量垂直的充分必要条件可得:0k a b a →→→⎛⎫-⋅= ⎪⎝⎭,即:2202k a a b k →→→⨯-⋅=-=,解得:22k =. 故答案为:22. 26.设,a b 为单位向量,且||1a b +=,则||a b -=______________. 3【解析】整理已知可得:()2a b a b +=+,再利用,a b 为单位向量即可求得21a b ⋅=-,对a b -变形可得:222a b a a b b -=-⋅+,问题得解.【详解】因为,a b 为单位向量,所以1a b == 所以()2222221a b a ba ab b a b +=+=+⋅+=+⋅=解得:21a b ⋅=- 所以()22223a b a ba ab b -=-=-⋅+=327.平面向量OA 、OB 、OC ,满足24OA OB ==,()()20OC OA OC OB -⋅-=,0OA OB ⋅=,则对任意[]0,2θπ∈,11cos sin 42OC OA OB θθ--⋅的最大值为___________. 【答案】221 【解析】建立平面直角坐标系,可得点C 的轨迹方程为()()22112x y -+-=,然后化简所求式子,转化为两个圆的点之间的最大值问题,简单判断即可. 【详解】由0OA OB ⋅=,24OA OB ==,可设()()()4,0,0,2,,A B C x y由()()20OC OA OC OB -⋅-=,把坐标代入化简可得:()()22112x y -+-= 所以点点C 的轨迹方程为()()22112x y -+-= 又()()11cos sin ,cos ,sin 42OC OA OB x y θθθθ--⋅=-, 所以求11cos sin 42OC OA OB θθ--⋅的最大值即两个圆()()22112x y -+-=、221x y +=上动点最大值,如图所示;当过两圆的圆心时,有最大即221MN = 故答案为:22128.已知向量a ,b ,c 满足22a b c b -+==,b a -与a 的夹角为34π,则c 的最大值为______.【答案】22【解析】根据题意设OA b a =-,OB b =,OC c =,则a AB =,b a c OA OC CA --=-=,1OB =,2CA =由条件可得4OAB π∠=,1OB =后能结合正弦定理得到动点A 的轨迹,利用2CA =C 的轨迹,然后数形结合得到OC 的最大值,即c 的最大值. 【详解】 因为22a b c b -+==,所以2a b c -+=,1b =.设OA b a =-,OB b =,OC c =,则a AB =,b ac OA OC CA --=-=,1OB =,2CA =因为b a -与a 的夹角为34π,所以4OAB π∠=,OAB 的外接圆的直径为:122sin sin4OB R AOB π===∠ 则动点A 2D 中的优弧OB (不含点O ,B ), 由2CA =C 的轨迹是以A 2结合图形可知,当点O ,D ,A ,C四点共线,且C 在线段OA 的延长线上时,OC 最大,且最大值是22 故c 的最大值为22 故答案为:22【点睛】关键点睛:本题考查向量的运算和模长的最值问题,解答本题的关键是在OAB 中,根据题意得到4OAB π∠=,1OB =后能结合正弦定理得到动点A 的轨迹,利用2CA =C 的轨迹,然后数形结合得到OC 的最大值,即c 的最大值.属于中档题.29.李明自主创业,经营一家网店,每售出一件A 商品获利8元.现计划在“五一”期间对A 商品进行广告促销,假设售出A 商品的件数m (单位:万件)与广告费用x (单位:万元)符合函数模型231m x =-+.若要使这次促销活动获利最多,则广告费用x 应投入_______万元. 【答案】3 【解析】设李明获得的利润为()f x 万元,求出()f x 关于x 的表达式,利用基本不等式可求得()f x 的最小值及其对应的x 的值. 【详解】设李明获得的利润为()f x 万元,则0x ≥, 则()()()21616168832425125211111f x m x x x x x x x x x ⎛⎫⎡⎤=-=--=--=-++≤-+ ⎪⎢⎥++++⎝⎭⎣⎦25817=-=,当且仅当1611x x +=+,因为0x ≥,即当3x =时,等号成立. 故答案为:3.30.已知正实数x ,y ,a ,b 满足a bx yxy ==,其中1x >,1y >,则4911a b +--的最小值为______. 【答案】12 【解析】 解法一根据ab x y xy ==可知11()a b xy xy +=,得到a b ab +=,然后变形所求的式子并结合基本不等式可知结果. 解法二对a b x y xy ==取对数可知lg lg lg x y a x +=,lg lg lg x yb y+=,然后代入所求式子并结合基本不等式可知结果. 【详解】解法一 由abxyxy ==得1()a xy x =,1()b xy y =,所以11()a b xy xy +=,所以111a b+=,即a b ab +=,所以4949139413941311(1)(1)()1b a a b a b a b a b ab a b +-+-+===+------++. 因为111a b +=,所以114994(94)1325b a a b a b a b a b ⎛⎫+=++=++≥ ⎪⎝⎭,当且仅当49b a a b =时等号成立.故491211a b +≥--,所以4911a b +--的最小值为12. 解法二 对a b x y xy ==两边同时取对数,得lg lg lg x y a x +=,lg lg lg x yb y+=,所以494lg 9lg 1211lg lg x y a b y x +=+≥--,当且仅当23x y =时等号成立,所以4911a b +--的最小值为12. 故答案为:12 【点睛】关键点定睛:解法一关键在于得到111a b+=,解法二结合对数,同时两种解法都使用基本不等式. 31.已知数列{}n a 是等差数列,11a ≥-,22a ≤,30a ≥,则153z a a =-的最大值是______. 【答案】16 【解析】由等差数列得通项公式可的1111220a a d a d ≥-⎧⎪+≤⎨⎪+≥⎩设1a x =,d y =,则不等式组等价为1220x x y x y ≥-⎧⎪+≤⎨⎪+≥⎩,15324z a a x y =-=-,利用线性规划知识求最值即可.【详解】设等差数列{}n a 的公差为d ,由题设知,1111220a a d a d ≥-⎧⎪+≤⎨⎪+≥⎩,设1a x =,d y =,则不等式组等价为1220x x y x y ≥-⎧⎪+≤⎨⎪+≥⎩,对应的可行域为如图所示的三角形ABC 及其内部,由15132424a a a d x y -=-=-,由24z x y =-可得124z y x =-, 作12y x =沿着可行域的方向平移,当直线过点A 时,z 取得最大值. 由220x y x y +=⎧⎨+=⎩ 解得()4,2A -, 所以 ()max 244216z =⨯-⨯-=, 故答案为:1632.设1e ,2e 为单位向量,满足21|22|-≤e e ,12a e e =+,123b e e =+,设a ,b 的夹角为θ,则2cos θ的最小值为_______. 【答案】2829【解析】利用复数模的平方等于复数的平方化简条件得1234e e ⋅≥,再根据向量夹角公式求2cos θ函数关系式,根据函数单调性求最值. 【详解】12|2|2e e -≤, 124412e e ∴-⋅+≤,1234e e ∴⋅≥, 222121222121212(44)4(1)()cos (22)(106)53e e e e a b e e e e e e a bθ+⋅+⋅⋅∴===+⋅+⋅+⋅⋅12424228(1)(1)3332953534e e =-≥-=+⋅+⨯. 故答案为:2829. 四、双空题33.如图,在四边形ABCD 中,60,3B AB ︒∠==,6BC =,且3,2AD BC AD AB λ=⋅=-,则实数λ的值为_________,若,M N 是线段BC 上的动点,且||1MN =,则DM DN ⋅的最小值为_________.【答案】16 132【解析】可得120BAD ∠=,利用平面向量数量积的定义求得λ的值,然后以点B 为坐标原点,BC 所在直线为x 轴建立平面直角坐标系,设点(),0M x ,则点()1,0N x +(其中05x ≤≤),得出DM DN ⋅关于x 的函数表达式,利用二次函数的基本性质求得DM DN ⋅的最小值. 【详解】AD BC λ=,//AD BC ∴,180120BAD B ∴∠=-∠=,cos120AB AD BC AB BC ABλλ⋅=⋅=⋅1363922λλ⎛⎫=⨯⨯⨯-=-=- ⎪⎝⎭,解得16λ=, 以点B 为坐标原点,BC 所在直线为x 轴建立如下图所示的平面直角坐标系xBy ,()66,0BC C =∴,,∵3,60AB ABC =∠=︒,∴A 的坐标为3332A ⎛ ⎝⎭,∵又∵16AD BC =,则5332D ⎛ ⎝⎭,设(),0M x ,则()1,0N x +(其中05x ≤≤), 533,2DM x ⎛=- ⎝⎭,333,2DN x ⎛=- ⎝⎭,()22253332113422222DM DN x x x x x ⎛⎫⎛⎫⋅=--+=-+=-+ ⎪⎪⎝⎭⎝⎭⎝⎭, 所以,当2x =时,DM DN ⋅取得最小值132. 故答案为:16;132. 五、解答题34.某乡镇响应“绿水青山就是金山银山”的号召,因地制宜的将该镇打造成“生态水果特色小镇”.经调研发现:某珍惜水果树的单株产量W (单位:千克)与施用肥料x (单位:千克)满足如下关系:()253,02()50,251x x W x x x x⎧+≤≤⎪=⎨<≤⎪+⎩,肥料成本投入为10x 元,其它成本投入(如培育管理、施肥等人工费)20x元.已知这种水果的市场售价大约15元/千克,且销售畅通供不应求,记该水果单株利润为()f x (单位:元)(1)写单株利润()f x (元)关于施用肥料x (千克)的关系式; (2)当施用肥料为多少千克时,该水果单株利润最大?最大利润是多少?【答案】(1)27530225,02()75030,251x x x f x x x x x⎧-+⎪=⎨-<⎪+⎩(2)故当施肥量为4千克时,该水果树的单株利润最大,最大利润为480元. 【解析】(1)用销售额减去成本投入得出利润()f x 的解析式;(2)分段判断()f x 的单调性,及利用基本不等式求出()f x 的最大值即可. 【详解】(1)依题意()15()1020f x W x x x =--,又()253,02()50,251x x W x xx x⎧+≤≤⎪=⎨<≤⎪+⎩ 所以27530225,02()75030,251x x x f x x x x x⎧-+⎪=⎨-<⎪+⎩.(2)当02x 时,2()7530225f x x x =-+,开口向上,对称轴为15x =, ()f x ∴在[0,1]5上单调递减,在1(5,2]上单调递增,()f x ∴在[0,2]上的最大值为()2465f =.当25x <时,2525()78030(1)78030(1)48011f x x x x x=-++-⨯+++, 当且仅当2511x x=++时,即4x =时等号成立. 因为465480<,所以当4x =时,()480max f x =.答:当投入的肥料费用为40元时,种植该果树获得的最大利润是480元.。
2021届高考数学总复习:平面向量与函数、不等式的综合应用

2021届高考数学总复习:平面向量与函数、不等式的综合应用【例】 设θ是两个非零向量a ,b 的夹角,若对任意实数t ,|a +t b |的最小值为1,则下列判断正确的是( )A .若|a |确定,则θ唯一确定B .若|b |确定,则θ唯一确定C .若θ确定,则|b |唯一确定D .若θ确定,则|a |唯一确定解析 设g (t )=(a +t b )2=b 2t 2+2t a ·b +a 2,当且仅当t =-2a ·b 2b 2=-|a |cos θ|b |时,g (t )取得最小值1,所以b 2×|a |2cos 2θ|b |2-2a ·b ×|a |cos θ|b |+a 2=1,化简得a 2sin 2θ=1,所以当θ确定时,|a |唯一确定。
答案 D通过向量的数量积运算把向量运算转化为实数运算,再结合函数、不等式的知识解决,同时也要注意平面向量的坐标运算在这方面的应用。
【变式训练】 (2019·福州四校联考)已知向量a ,b 为单位向量,且a ·b =-12,向量c 与a +b 共线,则|a +c |的最小值为( )A .1B .12 C.34 D.32解析 因为向量c 与a +b 共线,所以可设c =t (a +b )(t ∈R ),所以a +c =(t +1)a +t b ,所以(a +c )2=(t +1)2a 2+2t (t +1)a ·b +t 2b 2,因为向量a ,b 为单位向量,且a ·b =-12,所以(a +c )2=(t+1)2-t (t +1)+t 2=t 2+t +1≥34,所以|a +c |≥32,所以|a +c |的最小值为32。
故选D 。
解析:因为向量a ,b 为单位向量,且a ·b =-12,所以向量a ,b 的夹角为120°,在平面直角坐标系中,不妨设向量a =(1,0),b =⎝ ⎛⎭⎪⎫-12,32,则a +b =⎝ ⎛⎭⎪⎫12,32,因为向量c 与a +b 共线,所以可设c =t ⎝ ⎛⎭⎪⎫12,32(t ∈R ),所以a +c =⎝⎛⎭⎪⎫1+t 2,32t ,所以|a +c |=⎝ ⎛⎭⎪⎫1+t 22+3t 24=t 2+t +1≥32,所以|a +c |的最小值为32。
基础专项练(二) 平面向量、不等式

专项练(二) 平面向量、不等式一、单项选择题1.(2021·天津卷)已知a ∈R ,则“a >6”是“a 2>36”的( ) A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件答案 A解析 由题意,若a >6,则a 2>36,故充分性成立;若a 2>36,则a >6或a <-6,推不出a >6,故必要性不成立; 所以“a >6”是“a 2>36”的充分不必要条件.2.已知向量OA →=(3,-4),OB →=(6,-3),OC →=(2m ,m +1).若AB →∥OC →,则实数m 的值为( ) A.15 B.-35 C.-3 D.-17答案 C解析 易知AB →=(3,1),且OC →=(2m ,m +1),由AB →∥OC →,得2m =3(m +1),∴m=-3.3.(2021·浙江卷)已知非零向量a ,b ,c ,则“a ·c =b ·c ”是“a =b ”的( ) A.充分不必要条件 B.必要不充分条件 C.充分必要条件 D.既不充分也不必要条件答案 B解析 由a ·c =b ·c 可得(a -b )·c =0,所以(a -b )⊥c 或a =b ,所以“a ·c =b ·c ”是“a =b ”的必要不充分条件.故选B.4.已知P (a ,b )为圆x 2+y 2=4上任意一点,则当1a 2+4b 2取最小值时,a 2的值为( )A.45B.2C.43D.3答案 C解析 因为P (a ,b )为圆x 2+y 2=4上任意一点,所以a 2+b 2=4. 所以1a 2+4b 2=14⎝ ⎛⎭⎪⎫1a 2+4b 2(a 2+b 2)=14⎝ ⎛⎭⎪⎫5+b 2a 2+4a 2b 2≥14⎝⎛⎭⎪⎫5+2b 2a 2·4a 2b 2=94, 当且仅当b 2=2a 2=83时取等号,故a 2=43.5.(2021·青岛调研)已知a ,b 是平面内两个互相垂直的单位向量,若向量c 满足(a -c )·(b -c )=0,则|c |的最大值是( ) A.1 B.2 C. 2 D.22答案 C解析 因为(a -c )·(b -c )=0,所以(a -c )⊥(b -c ).如图所示,设OC→=c ,OA →=a ,OB →=b , 则CA →=a -c ,CB →=b -c , 所以AC→⊥BC →. 又因为OA→⊥OB →,所以O ,A ,C ,B 四点共圆,当且仅当OC 为圆的直径时,|c |最大,且最大值为 2.6.(2021·长沙一模)在平面直角坐标系xOy 内,已知直线l 与圆O :x 2+y 2=8相交于A ,B 两点,且|AB |=4,若OC →=2OA →-OB →且M 是线段AB 的中点,则OC →·OM →的值为( ) A. 3 B.2 2 C.3D.4解析 由OC→=2OA →-OB →,知A ,B ,C 三点共线.因为|AB |=4,M 是线段AB 的中点,则OM ⊥AB , 所以|OM |=R 2-22=8-4=2.在直角△CMO 中,OC →·OM →=|OM →|·|OC→|cos ∠COM =|OM →|2=4.7.已知单位向量a ,b 满足|a -b |+23a ·b =0,则|t a +b |(t ∈R )的最小值为( ) A.23 B.32 C.223 D.22答案 B解析 由|a -b |+23a ·b =0,得|a -b |=-23a ·b , 平方得a 2-2a ·b +b 2=12(a ·b )2, 整理得(2a ·b +1)(3a ·b -1)=0, 所以a ·b =-12或a ·b =13.因为|a -b |=-23a ·b ≥0,所以a ·b ≤0, 所以a ·b =-12,所以|t a +b |=|t a +b |2=t 2+1+2t a ·b =t 2-t +1=⎝ ⎛⎭⎪⎫t -122+34≥32⎝ ⎛⎭⎪⎫当且仅当t =12时取“=”. 8.若对任意的x ,y ∈R ,不等式x 2+y 2+xy ≥3(x +y -a )恒成立,则实数a 的取值范围为( ) A.(-∞,-1] B.(-∞,1] C.[-1,+∞)D.[1,+∞)解析 不等式x 2+y 2+xy ≥3(x +y -a )对任意x ,y ∈R 恒成立等价于x 2+(y -3)x +y 2-3y +3a ≥0对任意x ,y ∈R 恒成立,∴Δ=(y -3)2-4(y 2-3y +3a )=-3y 2+6y +9-12a ≤0, ∴4a ≥-y 2+2y +3=-(y -1)2+4, 当y =1时,-y 2+2y +3取得最大值4, ∴4a ≥4,解得a ≥1.因此,实数a 的取值范围是[1,+∞). 二、多项选择题9.(2021·湖南四校联考)在△ABC 中,D ,E ,F 分别是边BC ,CA ,AB 的中点,AD ,BE ,CF 交于点G ,则( ) A.EF →=12CA →-12BC → B.BE →=-12BA →+12BC → C.AD →+BE →=FC → D.GA→+GB →+GC →=0 答案 CD解析 如图,因为点D ,E ,F 分别是边BC ,CA ,AB 的中点,所以EF→=12CB →=-12BC →,故A 不正确;BE →=BC →+CE →=BC →+12CA →=BC →+12(CB →+BA →)=BC →-12BC →-12AB →=-12AB →+12BC →,故B 不正确;FC →=AC →-AF →=AD →+DC →+F A →=AD →+12BC →+F A →=AD →+FE →+F A →=AD→+FB →+BE →+F A →=AD→+BE →,故C 正确; 由题意知,点G 为△ABC 的重心,所以AG→+BG →+CG →=23AD →+23BE →+23CF →=23×12(AB→+AC →)+23×12(BA →+BC →)+23×12(CB →+CA →)=0,即GA →+GB →+GC →=0,故D 正确.故选CD.10.(2021·山东质检)若a >0,b >0,且a +b =4,则下列不等式恒成立的是( )A .0<1ab ≤14 B.ab <2 C.1a +1b ≥1 D.1a 2+b 2≤18答案 CD解析 A 选项,由ab ≤a +b 2=2知ab ≤4.因为a >0,b >0,所以ab >0,所以1ab ≥14,当且仅当a =b =2时等号成立,故A 错误;B 选项,ab ≤a +b2=2,当且仅当a =b =2时等号成立,故B 错误; C 选项,1a +1b ≥21a ·1b =2ab≥2×12=1,当且仅当a =b =2时等号成立,故C 正确;D 选项,因为a 2+b 2≥(a +b )22=8,当且仅当a =b =2时等号成立,所以1a 2+b 2≤18,故D 正确.故选CD. 11.(2021·南京、盐城一模)下列关于向量a ,b ,c 的运算,一定成立的是( ) A.(a +b )·c =a·c +b·c B.(a·b )·c =a·(b·c ) C.a·b ≤|a|·|b| D.|a -b|≤|a|+|b|答案 ACD解析 对于A ,因为向量满足分配律,所以A 一定成立;对于B ,因为(a·b )·c =|a||b|cos 〈a ,b 〉·c 表示一个与c 平行的向量,a·(b·c )=|b||c| cos 〈b ,c 〉·a 表示一个与a 平行的向量,而c 与a 不一定共线,所以B 不一定成立;对于C ,a·b =|a|·|b|cos 〈a ,b 〉≤|a|·|b|,所以C 一定成立;对于D ,因为|a -b|2=|a|2+|b|2-2a·b =|a|2+|b|2-2|a||b|cos 〈a ,b 〉≤|a|2+|b|2+2|a||b|=(|a|+|b|)2,所以|a -b|≤|a|+|b|,所以D 一定成立.综上所述,选ACD. 12.(2021·济南统考)设a ,b 为正实数,下列命题正确的是( ) A.若a 2-b 2=1,则a -b <1 B.若1b -1a =1,则a -b <1 C.若|a -b |=1,则|a -b |<1D.若|a 3-b 3|=1,则|a -b |<1 答案 AD解析 若a 2-b 2=1,则a 2-1=b 2, 即(a +1)(a -1)=b 2.∵a +1>a -1,∴a -1<b <a +1, ∴a -b <1,故A 正确;若1b -1a =1,则可取a =7,b =78,而a -b >1,故B 错误; 若|a -b |=1,则可取a =9,b =4,而|a -b |=5>1,故C 错误; 若|a 3-b 3|=1,当a >b >0时,得a 3-b 3=1,a 3-1=b 3, 即(a -1)(a 2+a +1)=b 3.∵a 2+a +1>b 2,∴a -1<b ,即a -b <1; 当0<a <b 时,得b 3-a 3=1,b 3-1=a 3, 即(b -1)(b 2+1+b )=a 3. ∵b 2+1+b >a 2,∴b -1<a ,即b -a <1.故|a -b |<1,D 正确.故选AD. 三、填空题13.(2021·全国乙卷)已知向量a =(1,3),b =(3,4),若(a -λb )⊥b ,则λ=________. 答案 35解析 法一 a -λb =(1-3λ,3-4λ),∵(a -λb )⊥b , ∴(a -λb )·b =0,即(1-3λ,3-4λ)·(3,4)=0, ∴3-9λ+12-16λ=0,解得λ=35.法二 由(a -λb )⊥b 可知,(a -λb )·b =0,即a ·b -λb 2=0,从而λ=a ·bb2=(1,3)·(3,4)32+42=1525=35.14.(2021·天津卷)若a >0,b >0,则1a +ab 2+b 的最小值为________. 答案 2 2解析 ∵a >0,b >0,∴1a +ab 2+b ≥21a ·a b 2+b =2b +b ≥22b ·b =22,当且仅当1a =a b 2且2b =b ,即a=b =2时等号成立, ∴1a +ab2+b 的最小值为2 2. 15.(2021·枣庄模拟)如图,由四个全等的三角形与中间的一个小正方形EFGH 拼成的一个大正方形ABCD 中,AF →=3AE →.设AF →=xAB →+yAD →,则x +y 的值为________.答案 65解析 连接BD 交AF 于点M (图略). 令|BF |=1,则|AF |=3,所以tan ∠ABF =3, 所以tan ∠FBM =tan(∠ABF -45°)=3-11+3=12, 所以|FM |=12,|AM |=52,则|AM ||AF |=56, 所以AM→=56AF →=56xAB →+56yAD →. 因为点M 在BD 上,所以56x +56y =1,即x +y =65. 16.(2021·福州质检)已知a >b ,b >0,若不等式m 3a +b≤3a +1b 恒成立,则m 的最大值为________. 答案 16解析 由题意,不等式m 3a +b≤3a +1b 恒成立,且a >0,b >0,即有m ≤(3a +b )⎝ ⎛⎭⎪⎫3a +1b 恒成立,即m ≤⎣⎢⎡⎦⎥⎤(3a +b )⎝ ⎛⎭⎪⎫3a +1b min 成立.由(3a +b )⎝ ⎛⎭⎪⎫3a +1b =10+3a b +3b a ≥10+23ab·3ba=16,当且仅当3ab=3ba,即a=b时,取得等号,即有m≤16,则m的最大值为16.。
中考数学专题复习向量问题(四)
中考数学专题复习向量问题(四)学校:___________姓名:___________班级:___________考生__________评卷人 得分 一、单选题1.已知在△ABC 中,AD 是中线,设,AB m AD n == ,那么向量BC 用向量,m n 表示为( ) A .22m n - B .22m n + C .22n m - D .n m -2.如图,点G 是△ABC 的重心,联结AG 并延长交BC 边于点D .设AB a =,GDb=,那么向量BC 用向量a 、b 表示为( )A .32BC b a =-B .32BC b a =+ C .62BC b a =-D .62BC b a =+ 评卷人得分二、填空题 3.如果向量AB 与向量CD 方向相反,且5AB CD ==,那么AB CD +=______. 4.在平行四边形ABCD 中,如果AB a =,AD b =,那么AC =__________,BC =__________.(用a 、b 表示)5.如图,在ABC 中,点D 在边AC 上,已知ABD △和BCD △的面积比是2:3,,AB a AC b ==,那么向量BD (用向量,a b 表示)是________.6.已知向量a 与单位向量e 的方向相反,|a |=3,那么向量a 用单位向量e 表示为_______.7.已知点G 是ABC ∆的重心,如果,AB a AC b ==,那么向量AG 用向量、a b 表示为_____.8.如图,在△ABC中,点D在边AC上,且CD=2AD.设AB a=,AC b=,那么BD =_____.(结果用向量a、b的式子表示)9.如图,已知梯形ABCD,AD△BC,BC=3AD,如果AD a=,AB b=,那么DC=_____(用a,b表示).10.在△ABC中,D、E分别在边AB、AC上,DE△BC,DE经过△ABC的重心,如果AB=π,AC n=,那么DE=_____.(用π、n表示)11.如图,在正六边形ABCDEF中,如果向量AB a=,AF b=,那么向量AD用向量a,b表示为____.12.如图,在△ABC中,AD为边BC上的中线,DE△AB,已知ED a=,BC b=,那么用a,b表示AD=_____.13.已知平行四边形ABCD,E是边AB的中点.设AB a=,BC b,那么DE=_____.(结果用a、b表示).14.如图,在△ABC中,点D在边AB上,AB=4AD,设AB a=,AC b=,那么向量DC用向量a、b表示为_____.15.如图,点M是△ABC的边AB上的中点,设AC=a,AB=b,那么CM用a,b 表示为_____.16.如图,已知△ABC中,点D、E分别在边AB、AC上,DE△BC,DC、BE交于点O,AB=3AD,设BD=a,DE=b,那么向量DO用向量a、b表示是__.17.ABC中,点D在边AB上,点E在边AC上,联结DE,DE是ABC的一条中位线,点G是ABC的重心,设AG a=,AB b=,则DE=________(用含a,b的式子表示)参考答案:1.C【解析】【分析】根据向量的三角形法则求出BD,即可得到BC.【详解】△,==,AB m AD n△AD ABD m=-=-,B n△AD是△ABC中线,△2 22=-=,BC BD n m故选:C.【点睛】此题考查平面向量,掌握三角形的向量法则是解题的关键.2.C【解析】【分析】G是△ABC的重心,推出AG=2DG,推出AD=3DG,利用三角形法则求出BD即可解决问题.【详解】解:△G是△ABC的重心,△AG=2DG,△AD=3DG,△AD=3GD=3b,△BD=BA+AD=﹣a+3b,DB=BD,△BC=2BD=6b﹣2a,故选:C.【点睛】此题考查三角形的重心,平面向量,三角形法则,解题的关键是熟练掌握基本知识,属于中考常考题型.3.0【解析】【分析】根据题意可知AB CD =- ,然后计算即可得出答案.【详解】△向量AB 与向量CD 方向相反,且5AB CD ==,△AB CD =-,△0AB CD CD CD +=-+=故答案为:0.【点睛】本题主要考查向量的运算,能够根据题意得出AB CD =-是解题的关键.4. +b a ()b a +-【解析】【分析】根据向量的性质求解即可.【详解】△AB a =,AD b =△AC =+b a ,BC =()b a +-故答案为:+b a , ()b a +-.【点睛】本题考查了向量的问题,掌握向量的性质是解题的关键.5.25b a - 【解析】【分析】先根据ABD △和BCD △的面积比是2:3得出:2:3AD DC =,再根据向量计算公式求算即可.【详解】△ABD △和BCD △的面积比是2:3△:2:3AD DC =△2255AD AC b == △22=-55BD BA AD AB AD a b b a =+=-++=- 故答案为:25b a - 【点睛】本题考查向量相关的求算,掌握向量的表示是解题关键.6.-3e【解析】【分析】由向量a 与单位向量e 的方向相反,且长度为3,根据向量的定义,即可求得答案.【详解】解:△向量a 与单位向量e 的方向相反,|a |=3,△a =-3e .故答案为:-3e .【点睛】本题考查的是平面向量的知识,即长度不为0的向量叫做非零向量,向量包括长度及方向,而长度等于1个单位长度的向量叫做单位向量,注意单位向量只规定大小没规定方向.7.1133a b + 【解析】【分析】如图,延长AE 到H ,使得EH=AE ,连接BH ,CH .求出AH ,证明13AG AH =即可解决问题.【详解】如图,延长AE 到H ,使得EH=AE ,连接BH ,CH .△AE=EH,BE=EC,△四边形ABHC是平行四边形,△AC=BH,AC△BH,△AH AB BH a b=+=+,△G是重心,△23AG AE=,△AE=EH,△13AG AH=,△1133aAG b+=.【点睛】本题考查三角形的重心,平行四边形的判定和性质等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.8.13b a-【解析】【分析】首先由向量的知识,得到AD和AB的值,即可得到BD的值.【详解】△在△ABC中,点D在边AC上,且CD =2AD,△13AD AC==13b,又△AB a=△BD=AD-AB=13b-a故答案为13b a-【点睛】本题考查了平面向量,找到向量关系是解题的关键. 9.2a b+【解析】【分析】根据DC DA AB BC=++,只要求出BC,问题即可解决.【详解】解:△AD△BC,BC=3AD,△33BC AD a==,△DC DA AB BC=++,△32DC a b a a b=-++=+.故答案为:2a b+.【点睛】本题考查了平面向量和三角形法则等知识,解题的关键是掌握向量的基本知识.10.2233nπ-【解析】【分析】由DE△BC推出AD:AB=AG:AF=DE:BC=2:3,推出DE=23BC,求出BC即可解决问题.【详解】解:如图设G是重心,作中线AF.△DE△BC,△AD:AB=AG:AF=DE:BC=2:3,△DE=23BC,△BC BA AC=+△BC nπ=-,△()222333DE n nππ=-=-故答案为:2233nπ-.【点睛】本题考查三角形的重心、平行线的性质、平面向量等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.11.2a+2b.【解析】【分析】如图,连接BE交AD于O.则AOB∆是等边三角形,OA OD=,根据三角形法则求出AO 即可解决问题.【详解】如图,连接BE交AD于O.△ABCDEF是正六边形,△△AOB是等边三角形,AO=OD,△△F AO=△AOB=60°,OB=AB=AF,△AF△OB,△BO AF b==,△AO AB BO a b=+=+,△AD=2AO,△AD=2a+2b.故答案为:2a+2b.【点睛】本题考查正多边形与圆,平面向量,等边三角形的判定和性质,平行线的判定和性质等知识,熟练掌握基本知识是解题的关键.12.2a+1 b 2【解析】【分析】根据题意利用三角形法则可知:A AB BDD=+,求出AB,BD即可解决问题.【详解】解:△AD是中线,△BD=DC,△DE△AB,△AE=EC,△AB△DE,AB=2DE,△AB=2a,△BD=12BC=1b2,A AB BDD=+,△AD=2a+1b2,故答案为:2a+1b2.【点睛】本题考查平面向量,三角形法则,平行线等分线段定理,三角形的中位线定理等知识,解题的关键是熟练掌握基本知识.13.12-+b a【解析】【分析】根据平行四边形的性质可得AD=BC=b,然后求出AE,根据ED=DA+AE即可求出结论.【详解】解:如图,△四边形ABCD是平行四边形,△AD=BC,AD△BC △AD=BC=b,△E是AB的中点,△AE=12AB=12a,△ED=DA+AE,△ED=﹣b+12 a,故答案为:﹣b+12 a.【点睛】此题考查了平面向量的知识.此题难度不大,注意掌握三角形法则与平行四边形法则的应用,注意掌握数形结合思想的应用.14.14a b -+【解析】【分析】利用三角形法则:DC=DA+AC求解即可.【详解】△AB=4AD,△AD=14 AB,△AD=14AB,△DC=DA+AC,△DC=14a b -+故答案为:14a b-+.【点晴】考查了平面向量,三角形法则等知识,解题关键是熟练掌握基本知识.15.﹣a+1 2 b→【解析】【分析】利用三角形法则可知:CM CA AM →→→=+,只要求出AM →即可解决问题.【详解】解:△M 是AB 的中点,△AM =12AB , △1122AM AB b →→→==, △CM CA AM →→→=+,△12CM a b →→→=-+, 故答案为:12a b →→-+. 【点睛】本题考查平面向量,三角形法则等知识.解题的关键是熟练掌握向量运算的三角形法则.16.﹣14a +34b 【解析】【分析】利用平行线分线段成比例定理求出BC →,根据三角形法则求出DC →,证明DO =14DC 即可. 【详解】解:△DE △BC ,AB AD =DE BC =13, △BC =3DE ,△DE →=b→, △BC →=3b→, △△DOE△△COB ,△OD OC=DE BC =13, △OD =13OC =14CD , △DC →=DB →+BC→, △DC →=﹣a →+3b→,△DO→=﹣14a→+34b→,故答案为:﹣14a→+34b→【点睛】本题考查了平行线分线段成比例和平面向量的知识点17.32a b-【解析】【分析】延长AG交BC于点F,根据重心的性质可得出32AF a=,由DE为ABC的中位线可得出12DE BC BF==,根据AB b=,结合BF AF AB=-,即可用含,a b的式子表示出DE.【详解】解:延长AG交BC于点F,如图所示.△点G是ABC的重心,△ 2AG GF a==,△32AF AG GF a=+=.△DE是ABC的一条中位线,△1322DE BC BF AF AB a b===-=-.故答案为:32a b-.【点睛】本题考查了三角形的重心、三角形中位线定理以及平面向量,根据三角形重心的性质找出32AF a=是解题的关键.。
高考数学压轴专题《平面向量及其应用》难题汇编

一、多选题1.已知非零平面向量a ,b ,c ,则( )A .存在唯一的实数对,m n ,使c ma nb =+B .若0⋅=⋅=a b a c ,则//b cC .若////a b c ,则a b c a b c =++++D .若0a b ⋅=,则a b a b +=- 2.正方形ABCD 的边长为1,记AB a =,BC b =,AC c =,则下列结论正确的是( )A .()0a b c -⋅= B .()0a b c a +-⋅= C .()0a c b a --⋅=D .2a b c ++=3.已知ABC 的三个角A ,B ,C 的对边分别为a ,b ,c ,若cos cos A bB a=,则该三角形的形状是( ) A .等腰三角形B .直角三角形C .等腰直角三角形D .等腰或直角三角形4.已知点()4,6A ,33,2B ⎛⎫- ⎪⎝⎭,与向量AB 平行的向量的坐标可以是( ) A .14,33⎛⎫⎪⎝⎭B .97,2⎛⎫ ⎪⎝⎭C .14,33⎛⎫-- ⎪⎝⎭D .(7,9)5.已知向量a =(2,1),b =(1,﹣1),c =(m ﹣2,﹣n ),其中m ,n 均为正数,且(a b -)∥c ,下列说法正确的是( ) A .a 与b 的夹角为钝角B .向量a 在bC .2m +n =4D .mn 的最大值为26.已知向量()1,0a =,()2,2b =,则下列结论正确的是( ) A .()25,4a b += B .2b = C .a 与b 的夹角为45°D .()//2a a b +7.已知ABC ∆是边长为2的等边三角形,D ,E 分别是AC 、AB 上的两点,且AE EB =,2AD DC =,BD 与CE 交于点O ,则下列说法正确的是( )A .1AB CE ⋅=- B .0OE OC +=C .3OA OB OC ++=D .ED 在BC 方向上的投影为768.在△ABC 中,若cos cos a A b B =,则△ABC 的形状可能为( )A .直角三角形B .等腰三角形C .等腰直角三角形D .等边三角形9.在ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,则下列结论中正确的是( )A .若a b >,则sin sin AB >B .若sin 2sin 2A B =,则ABC 是等腰三角形 C .若cos cos a B b A c -=,则ABC 是直角三角形D .若2220a b c +->,则ABC 是锐角三角形10.已知a 、b 是任意两个向量,下列条件能判定向量a 与b 平行的是( ) A .a b =B .a b =C .a 与b 的方向相反D .a 与b 都是单位向量11.对于菱形ABCD ,给出下列各式,其中结论正确的为( ) A .AB BC =B .AB BC =C .AB CD AD BC -=+D .AD CD CD CB +=-12.已知实数m ,n 和向量a ,b ,下列说法中正确的是( ) A .()m a b ma mb -=- B .()m n a ma na -=-C .若ma mb =,则a b =D .若()0ma na a =≠,则m n =13.对于ABC ∆,有如下判断,其中正确的判断是( ) A .若sin 2sin 2A B =,则ABC ∆为等腰三角形 B .若A B >,则sin sin A B >C .若8a =,10c =,60B ︒=,则符合条件的ABC ∆有两个D .若222sin sin sin A B C +<,则ABC ∆是钝角三角形14.已知ABC ∆中,角A,B,C 的对边分别为a ,b ,c ,且满足,3B a c π=+=,则ac=( ) A .2B .3C .12 D .1315.下列说法中错误的是( )A .向量AB 与CD 是共线向量,则A ,B ,C ,D 四点必在一条直线上 B .零向量与零向量共线 C .若,a b b c ==,则a c =D .温度含零上温度和零下温度,所以温度是向量二、平面向量及其应用选择题16.在矩形ABCD 中,3,2AB BC BE EC ===,点F 在边CD 上,若AB AF 3→→=,则AE BF→→的值为( )A .0B .833C .-4D .417.如图,测量河对岸的塔高AB 时,选与塔底B 在同一水平面内的两个测点C 与D .现测得15BCD ∠=︒,45BDC ∠=︒,302CD m =,并在点C 测得塔顶A 的仰角为30,则塔高AB 为( )A .302mB .203mC .60mD .20m18.如图,ADC 是等边三角形,ABC 是等腰直角三角形,90ACB ∠︒=,BD 与AC 交于E 点.若2AB =,则AE 的长为( )A 62B .1(62)2C 62D .1(62)219.在ABC ∆中,6013ABC A b S ∆∠=︒=,,,则2sin 2sin sin a b cA B C-+-+的值等于( ) A 239B 2633C 833D .2320.ABC 中,5AB AC ==,6BC =,则此三角形的外接圆半径是( ) A .4B .72C .258D .25921.已知1a =,3b =,且向量a 与b 的夹角为60︒,则2a b -=( ) A 7B .3C 11D 1922.已知圆C 的方程为22(1)(1)2x y -+-=,点P 在直线3y x上,线段AB 为圆C的直径,则PA PB ⋅的最小值为() A .2B .52C .3D .7223.已知向量(22cos m x =,()1,sin2n x =,设函数()f x m n =⋅,则下列关于函数()y f x =的性质的描述正确的是( )A .关于直线12x π=对称B .关于点5,012π⎛⎫⎪⎝⎭对称 C .周期为2πD .()y f x =在,03π⎛⎫-⎪⎝⎭上是增函数 24.已知非零向量AB 与AC 满足0AB AC BC AB AC ⎛⎫ ⎪+⋅= ⎪⎝⎭且12AB AC AB AC ⋅=,则ABC 的形状是( ) A .三边均不相等的三角形 B .等腰直角三角形 C .等边三角形 D .以上均有可能 25.在ABC 中,若 cos a b C =,则ABC 的形状是( )A .直角三角形B .等腰三角形C .等腰直角三角形D .等腰或直角三角形26.题目文件丢失!27.已知,m n 是两个非零向量,且1m =,2||3m n +=,则||+||m n n+的最大值为 A BC .4D .528.在ABC ∆中,8AB =,6AC =,60A ∠=,M 为ABC ∆的外心,若AM AB AC λμ=+,λ、R μ∈,则43λμ+=( )A .34B .53C .73D .8329.已知ABC ∆的内角A 、B 、C 满足()()1sin 2sin sin 2A ABC C A B +-+=--+,面积S 满足12S ≤≤,记a 、b 、c 分别为A 、B 、C 所对的边,则下列不等式一定成立的是( )A .()8bc b c +>B .()ab a b +>C .612abc ≤≤D .1224abc ≤≤30.奔驰定理:已知O 是ABC ∆内的一点,BOC ∆,AOC ∆,AOB ∆的面积分别为A S ,B S ,C S ,则0A B C S OA S OB S OC ⋅+⋅+⋅=.“奔驰定理”是平面向量中一个非常优美的结论,因为这个定理对应的图形与“奔驰”轿车(Mercedes benz )的logo 很相似,故形象地称其为“奔驰定理”若O 是锐角ABC ∆内的一点,A ,B ,C 是ABC ∆的三个内角,且点O 满足OA OB OB OC OC OA ⋅=⋅=⋅,则必有( )A .sin sin sin 0A OAB OBC OC ⋅+⋅+⋅= B .cos cos cos 0A OA B OB C OC ⋅+⋅+⋅= C .tan tan tan 0A OA B OB C OC ⋅+⋅+⋅=D .sin 2sin 2sin 20A OA B OB C OC ⋅+⋅+⋅= 31.已知1a b ==,12a b ⋅=,(),1c m m =-,(),1d n n =-(m ,n R ∈).存在a ,b ,对于任意实数m ,n ,不等式ac bd T -+-≥恒成立,则实数T 的取值范围为( ) A .(32-∞B .)32,⎡+∞⎣C .(32-∞D .)32,⎡+∞⎣32.ABC 中,内角,,A B C 所对的边分别为,,a b c .若()226,c a b =-+3C π=,则ABC 的面积为( )A .6B 33C .33D 333.在ABC ∆中,内角,,A B C 的对边分别是,.a b c ,若cos 2aB c=,则ABC ∆一定是( ) A .等腰三角形B .等边三角形C .直角三角形D .等腰直角三角形34.题目文件丢失!35.在ABC 中,()2BC BA AC AC +⋅=,则ABC 的形状一定是( ) A .等边三角形B .等腰三角形C .等腰直角三角形D .直角三角形【参考答案】***试卷处理标记,请不要删除一、多选题 1.BD【分析】假设与共线,与,都不共线,即可判断A 错;根据向量垂直的数量积表示,可判断B 正确;向量共线可以是反向共线,故C 错;根据向量数量积法则,可判断D 正确. 【详解】A 选项,若与共线,与,都 解析:BD 【分析】假设a 与b 共线,c 与a ,b 都不共线,即可判断A 错;根据向量垂直的数量积表示,可判断B 正确;向量共线可以是反向共线,故C 错;根据向量数量积法则,可判断D 正确. 【详解】A 选项,若a 与b 共线,c 与a ,b 都不共线,则ma nb +与c 不可能共线,故A 错;B 选项,因为a ,b ,c 是非零平面向量,若0⋅=⋅=a b a c ,则a b ⊥,a c ⊥,所以//b c ,即B 正确;C 选项,因为向量共线可以是反向共线,所以由////a b c 不能推出a b c a b c =++++;如a 与b 同向,c 与a 反向,且a b c +>,则a b c a b c =+-++,故C 错;D 选项,若0a b ⋅=,则()222222a b a b a b a b a b+=+=++⋅=+,()222222a b a ba b a b a b -=-=+-⋅=+,所以a b a b +=-,即D 正确.故选:BD. 【点睛】本题主要考查共线向量的有关判定,以及向量数量积的相关计算,属于基础题型.2.ABC 【分析】作出图形,利用平面向量加、减法法则与正方形的性质可判断A 、B 选项的正误;利用平面向量的减法法则与向量的数乘运算可判断C 选项的正误;利用平面向量的加法法则可判断D 选项的正误. 【详解解析:ABC 【分析】作出图形,利用平面向量加、减法法则与正方形的性质可判断A 、B 选项的正误;利用平面向量的减法法则与向量的数乘运算可判断C 选项的正误;利用平面向量的加法法则可判断D 选项的正误. 【详解】 如下图所示:对于A 选项,四边形ABCD 为正方形,则BD AC ⊥,a b AB BC AB AD DB -=-=-=,()0a b c DB AC ∴-⋅=⋅=,A 选项正确;对于B 选项,0a b c AB BC AC AC AC +-=+-=-=,则()00a b c a a +-⋅=⋅=,B 选项正确;对于C 选项,a c AB AC CB -=-=,则0a c b CB BC --=-=,则()0a c b a --⋅=,C 选项正确;对于D 选项,2a b c c ++=,222a b c c ∴++==,D 选项错误. 故选:ABC. 【点睛】本题考查平面向量相关命题正误的判断,同时也考查了平面向量加、减法法则以及平面向量数量积的应用,考查计算能力,属于中等题.3.D 【分析】在中,根据,利用正弦定理得,然后变形为求解. 【详解】 在中,因为, 由正弦定理得, 所以,即, 所以或, 解得或.故是直角三角形或等腰三角形. 故选: D. 【点睛】 本题主要考查解析:D 【分析】 在ABC 中,根据cos cos A b B a =,利用正弦定理得cos sin cos sin A BB A=,然后变形为sin 2sin 2A B =求解. 【详解】在ABC 中,因为cos cos A bB a =, 由正弦定理得cos sin cos sin A BB A=, 所以sin cos sin cos A A B B =,即sin 2sin 2A B =, 所以22A B =或22A B π=-,解得A B =或2A B π+=.故ABC 是直角三角形或等腰三角形. 故选: D. 【点睛】本题主要考查利用正弦定理判断三角形的形状,还考查了运算求解的能力,属于基础题.4.ABC 【分析】先求出向量的坐标,然后由向量平行的条件对选项进行逐一判断即可. 【详解】 由点,,则选项A . ,所以A 选项正确. 选项B. ,所以B 选项正确. 选项C . ,所以C 选解析:ABC 【分析】先求出向量AB 的坐标,然后由向量平行的条件对选项进行逐一判断即可. 【详解】由点()4,6A ,33,2B ⎛⎫- ⎪⎝⎭,则972,AB ⎛⎫=-- ⎪⎝⎭选项A . 91473023⎛⎫-⨯--⨯= ⎪⎝⎭,所以A 选项正确. 选项B. 9977022⎛⎫-⨯--⨯= ⎪⎝⎭,所以B 选项正确. 选项C . ()91473023⎛⎫⎛⎫-⨯---⨯-= ⎪ ⎪⎝⎭⎝⎭,所以C 选项正确.选项D. 979702⎛⎫-⨯--⨯≠ ⎪⎝⎭,所以选项D 不正确 故选:ABC 【点睛】本题考查根据点的坐标求向量的坐标,根据向量的坐标判断向量是否平行,属于基础题. 5.CD【分析】对于A,利用平面向量的数量积运算判断;对于B,利用平面向量的投影定义判断;对于C,利用()∥判断;对于D,利用C 的结论,2m+n=4,结合基本不等式判断.【详解】对于A,向量(解析:CD【分析】对于A,利用平面向量的数量积运算判断;对于B,利用平面向量的投影定义判断;对于C,利用(a b-)∥c判断;对于D,利用C的结论,2m+n=4,结合基本不等式判断.【详解】对于A,向量a=(2,1),b=(1,﹣1),则2110a b⋅=-=>,则,a b的夹角为锐角,错误;对于B,向量a=(2,1),b=(1,﹣1),则向量a在b方向上的投影为2a bb⋅=,错误;对于C,向量a=(2,1),b=(1,﹣1),则a b-=(1,2),若(a b-)∥c,则(﹣n)=2(m ﹣2),变形可得2m+n=4,正确;对于D,由C的结论,2m+n=4,而m,n均为正数,则有mn12= (2m•n)12≤(22m n+)2=2,即mn的最大值为2,正确;故选:CD.【点睛】本题主要考查平面向量的数量积运算以及基本不等式的应用,属于基础题.6.AC【分析】利用向量线性的坐标运算可判断A;利用向量模的坐标求法可判断B;利用向量数量积的坐标运算可判断C;利用向量共线的坐标表示即可求解.【详解】由向量,,则,故A正确;,故B错误;解析:AC【分析】利用向量线性的坐标运算可判断A ;利用向量模的坐标求法可判断B ;利用向量数量积的坐标运算可判断C ;利用向量共线的坐标表示即可求解. 【详解】由向量()1,0a =,()2,2b =,则()()()21,022,25,4a b +=+=,故A 正确;222222b =+=,故B 错误;22222cos ,1022a b a b a b⋅<>===⋅+⋅+,又[],0,a b π<>∈,所以a 与b 的夹角为45°,故C 正确; 由()1,0a =,()25,4a b +=,140540⨯-⨯=≠,故D 错误. 故选:AC 【点睛】本题考查了向量的坐标运算,考查了基本运算能力,属于基础题.7.BCD 【分析】以E 为原点建立平面直角坐标系,写出所有点的坐标求解即可. 【详解】由题E 为AB 中点,则,以E 为原点,EA ,EC 分别为x 轴,y 轴正方向建立平面直角坐标系,如图所示: 所以,,解析:BCD 【分析】以E 为原点建立平面直角坐标系,写出所有点的坐标求解即可. 【详解】由题E 为AB 中点,则CE AB ⊥,以E 为原点,EA ,EC 分别为x 轴,y 轴正方向建立平面直角坐标系,如图所示:所以,1(0,0),(1,0),(1,0),(,)33E A B C D -,设1(0,),(1,),(,3O y y BO y DO y ∈==-,BO ∥DO ,所以133y y -=-,解得:2y =, 即O 是CE 中点,0OE OC +=,所以选项B 正确;32OA OB OC OE OC OE ++=+==,所以选项C 正确; 因为CE AB ⊥,0AB CE ⋅=,所以选项A 错误;1(,33ED =,(1,BC =,ED 在BC 方向上的投影为127326BC BCED +⋅==,所以选项D 正确.故选:BCD 【点睛】此题考查平面向量基本运算,可以选取一组基底表示出所求向量的关系,对于特殊图形可以考虑在适当位置建立直角坐标系,利于计算.8.ABCD 【分析】应用正弦定理将边化角,由二倍角公式有即或,进而有△ABC 可能为:直角三角形,等腰三角形,等腰直角三角形,等边三角形 【详解】 根据正弦定理 , 即. , 或. 即或解析:ABCD 【分析】应用正弦定理将边化角,由二倍角公式有sin 2sin 2A B =即A B =或2A B π+=,进而有△ABC 可能为:直角三角形,等腰三角形,等腰直角三角形,等边三角形 【详解】根据正弦定理sin sin a b A B= cos cos a A b B =sin cos sin cos A A B B =, 即sin 2sin 2A B =. 2,2(0,2)A B π∈,22A B =或22A B π+=. 即A B =或2A B π+=,△ABC 可能为:直角三角形,等腰三角形,等腰直角三角形,等边三角形. 故选:ABCD 【点睛】本题考查了正弦定理的边化角,二倍角公式解三角形判断三角形的形状,注意三角形内角和为180°9.AC 【分析】对选项A ,利用正弦定理边化角公式即可判断A 正确;对选项B ,首先利用正弦二倍角公式得到,从而得到是等腰三角形或直角三角形,故B 错误;对选项C ,利用正弦定理边化角公式和两角和差公式即可判解析:AC 【分析】对选项A ,利用正弦定理边化角公式即可判断A 正确;对选项B ,首先利用正弦二倍角公式得到sin cos sin cos A A B B =,从而得到ABC 是等腰三角形或直角三角形,故B 错误;对选项C ,利用正弦定理边化角公式和两角和差公式即可判断C 正确;对D ,首先根据余弦定理得到A 为锐角,但B ,C 无法判断,故D 错误. 【详解】对选项A ,2sin 2sin sin sin a b r A r B A B >⇒>⇒>,故A 正确; 对选项B ,因为sin 2sin 2sin cos sin cos A B A A B B =⇒= 所以A B =或2A B π+=,则ABC 是等腰三角形或直角三角形.故B 错误;对选项C ,因为cos cos a B b A c -=,所以()sin cos sin cos sin sin A B B A C A C -==+,sin cos sin cos sin cos cos sin A B B A A B A B -=+,sin cos cos sin B A A B -=,因为sin 0B ≠,所以cos 0A =,2A π=,ABC 是直角三角形,故③正确;对D ,因为2220a b c +->,所以222cos 02a b c A ab+-=>,A 为锐角.但B ,C 无法判断,所以无法判断ABC 是锐角三角形,故D 错误.故选:AC【点睛】本题主要考查正弦定理和余弦定理解三角形,同时考查学三角函数恒等变换,属于中档题. 10.AC【分析】根据共线向量的定义判断即可.【详解】对于A选项,若,则与平行,A选项合乎题意;对于B选项,若,但与的方向不确定,则与不一定平行,B选项不合乎题意;对于C选项,若与的方向相反,解析:AC【分析】根据共线向量的定义判断即可.【详解】对于A选项,若a b=,则a与b平行,A选项合乎题意;=,但a与b的方向不确定,则a与b不一定平行,B选项不合乎题对于B选项,若a b意;对于C选项,若a与b的方向相反,则a与b平行,C选项合乎题意;对于D选项,a与b都是单位向量,这两个向量长度相等,但方向不确定,则a与b不一定平行,D选项不合乎题意.故选:AC.【点睛】本题考查向量共线的判断,考查共线向量定义的应用,属于基础题.11.BCD【分析】由向量的加法减法法则及菱形的几何性质即可求解.【详解】菱形中向量与的方向是不同的,但它们的模是相等的,所以B结论正确,A结论错误;因为,,且,所以,即C结论正确;因为,解析:BCD【分析】由向量的加法减法法则及菱形的几何性质即可求解.【详解】菱形中向量AB 与BC 的方向是不同的,但它们的模是相等的, 所以B 结论正确,A 结论错误;因为2AB CD AB DC AB -=+=,2AD BC BC +=,且AB BC =, 所以AB CD AD BC -=+,即C 结论正确; 因为AD CD BC CD BD +=+=,||||CD CB CD BC BD -=+=,所以D 结论正确.故选:BCD 【点睛】本题主要考查了向量加法、减法的运算,菱形的性质,属于中档题.12.ABD 【分析】根据向量数乘运算判断AB 选项的正确性,通过的特殊情况判断C 选项的正确性,根据向量运算判断D 选项的正确性. 【详解】根据向量数乘的运算可知A 和B 正确;C 中,当时,,但与不一定相等,解析:ABD 【分析】根据向量数乘运算判断AB 选项的正确性,通过m 的特殊情况判断C 选项的正确性,根据向量运算判断D 选项的正确性. 【详解】根据向量数乘的运算可知A 和B 正确;C 中,当0m =时,0ma mb ==,但a 与b 不一定相等,故C 不正确;D 中,由ma na =,得()0m n a -=,因为0a ≠,所以m n =,故D 正确. 故选:ABD 【点睛】本小题主要考查向量数乘运算,属于基础题.13.BD 【分析】对于A ,根据三角函数的倍角公式进行判断;对于B ,根据正弦定理即可判断证明;对于C ,利用余弦定理即可得解;对于D ,根据正弦定理去判断即可. 【详解】 在中,对于A ,若,则或, 当A =解析:BD【分析】对于A ,根据三角函数的倍角公式进行判断;对于B ,根据正弦定理即可判断证明;对于C ,利用余弦定理即可得解;对于D ,根据正弦定理去判断即可. 【详解】 在ABC ∆中,对于A ,若sin 2sin 2A B =,则22A B =或22A B π+=, 当A =B 时,△ABC 为等腰三角形; 当2A B π+=时,△ABC 为直角三角形,故A 不正确,对于B ,若A B >,则a b >,由正弦定理得sin sin a b A B=,即sin sin A B >成立.故B 正确;对于C ,由余弦定理可得:b C 错误; 对于D ,若222sin sin sin A B C +<,由正弦定理得222a b c +<,∴222cos 02a b c C ab+-=<,∴C 为钝角,∴ABC ∆是钝角三角形,故D 正确;综上,正确的判断为选项B 和D . 故选:BD . 【点睛】本题只有考查了正弦定理,余弦定理,三角函数的二倍角公式在解三角形中的综合应用,考查了转化思想,属于中档题.14.AC 【分析】将两边同时平方,可得一个关系式,再结合余弦定理可得结果. 【详解】 ∵, ∴①,由余弦定理可得,②, 联立①②,可得, 即, 解得或. 故选:AC. 【点睛】本题考查余弦定理的应解析:AC 【分析】将a c +=两边同时平方,可得一个关系式,再结合余弦定理可得结果. 【详解】∵,3B a c π=+=,∴2222()23a c a c ac b +=++=①, 由余弦定理可得,2222cos3a c acb π+-=②,联立①②,可得222520a ac c -+=,即22520a a c c ⎛⎫⎛⎫-+= ⎪ ⎪⎝⎭⎝⎭, 解得2ac =或12a c =. 故选:AC. 【点睛】本题考查余弦定理的应用,考查计算能力,是基础题.15.AD 【分析】利用零向量,平行向量和共线向量的定义,判断各个选项是否正确,从而得出结论. 【详解】向量与是共线向量,则A ,B ,C ,D 四点不一定在一条直线上,故A 错误; 零向量与任一向量共线,故B解析:AD 【分析】利用零向量,平行向量和共线向量的定义,判断各个选项是否正确,从而得出结论. 【详解】向量AB 与CD 是共线向量,则A ,B ,C ,D 四点不一定在一条直线上,故A 错误; 零向量与任一向量共线,故B 正确; 若,a b b c ==,则a c =,故C 正确; 温度是数量,只有正负,没有方向,故D 错误. 故选:AD 【点睛】本题考查零向量、单位向量的定义,平行向量和共线向量的定义,属于基础题.二、平面向量及其应用选择题16.C 【分析】先建立平面直角坐标系,求出B,E,F 坐标,再根据向量数量积坐标表示得结果. 【详解】 如图所示,AB AF2232,3cos 1133BE EC BE BC AF DF α=⇒==→→=⇒=⇒=.以A 为原点建立平面直角坐标系,AD 为x 轴,AB 为y 轴,则()()230,3,3,1,,33B FE ⎛⎫⎪ ⎪⎝⎭,因此()BFAEBF233,2,3232643→=-→→=⨯-⨯=-=-,故选C.【点睛】平面向量数量积的类型及求法(1)求平面向量数量积有三种方法:一是夹角公式cos a b a b θ⋅=⋅;二是坐标公式1212a b x x y y ⋅=+;三是利用数量积的几何意义.(2)求较复杂的平面向量数量积的运算时,可先利用平面向量数量积的运算律或相关公式进行化简. 17.D 【分析】由正弦定理确定BC 的长,再tan30AB BC 求出AB .【详解】15BCD ∠=︒,45BDC ∠=︒120CBD302sin 45BC302sin 45203sin120BC3tan 3020320ABBC故选D【点睛】本题是正弦定理的实际应用,关键是利用正弦定理求出BC ,属于基础题. 18.A 【分析】由条件求得∠BCD =150°,∠CBE =15°,故∠ABE =30°,可得∠AEB =105°.计算sin105°,代入正弦定理sin30sin105AE AB=︒︒,化简求得AE =-. 【详解】由题意可得,AC =BC =CD =DA =BAC =45°,∠BCD =∠ACB +∠ACD =90°+60°=150°.又△BCD 为等腰三角形,∴∠CBE =15°,故∠ABE =45°﹣15°=30°,故∠BEC =75°,∠AEB =105°.再由 sin105°=sin (60°+45°)=sin60°cos45°+cos60°sin45°=, △ABE 中,由正弦定理可得sin30sin105AE AB=︒︒,∴124AE=,∴AE =), 故选:A . 【点睛】本题考查勾股定理、正弦定理的应用,两角和的正弦公式,属于中档题. 19.A 【解析】分析:先利用三角形的面积公式求得c 的值,进而利用余弦定理求得a ,再利用正弦定理求解即可.详解:由题意,在ABC ∆中, 利用三角形的面积公式可得011sin 1sin 6022ABC S bc A c ∆==⨯⨯⨯=, 解得4c =,又由余弦定理得22212cos 116214132a b c bc A =+-=+-⨯⨯⨯=,解得a =,由正弦定理得2sin 2sin sin sin a b c a A B C A -+===-+,故选A. 点睛:本题主要考查了利用正弦定理和三角函数的恒等变换求解三角形问题,对于解三角形问题,通常利用正弦定理进行“边转角”寻求角的关系,利用“角转边”寻求边的关系,利用余弦定理借助三边关系求角,利用两角和差公式及二倍角公式求三角函数值. 利用正、余弦定理解三角形问题是高考高频考点,经常利用三角形内角和定理,三角形面积公式,结合正、余弦定理解题. 20.C 【分析】在ABC 中,根据5AB AC ==,6BC =,由余弦定理求得7cos 25A =,再由平方关系得到sin A ,然后由正弦定理2sin BCR A=求解. 【详解】在ABC 中,5AB AC ==,6BC =,由余弦定理得:2222225567cos 225525AB AC BC A AB AC +-+-===⋅⨯⨯,所以24sin 25A ==, 由正弦定理得:625224sin 425BC R A ===, 所以258R =, 此三角形的外接圆半径是258故选:C 【点睛】本题主要考查余弦定理,正弦定理的应用,还考查了运算求解的能力,属于中档题. 21.A 【分析】根据向量的数量积的运算公式,以及向量的模的计算公式,准确运算,即可求解. 【详解】因为1a =,3b =,a 与b 的夹角为60︒,所以2224424697a a b b a b =-⋅+=-+=-,则27a b -=. 故选:A. 【点睛】本题主要考查了向量的数量积的运算,以及向量的模的求解,其中解答中熟记向量的数量积的运算公式是解答的关键,着重考查推理与运算能力. 22.B 【分析】将PA PB ⋅转化为2||2PC -,利用圆心到直线的距离求得||PC 的取值范围求得PA PB⋅的最小值. 【详解】()()()()PA PB PC CA PC CB PC CA PC CA ⋅=+⋅+=+⋅-2222||||||22PC CA PC =-=-≥-52=.故选B. 【点睛】本小题主要考查向量的线性运算,考查点到直线距离公式,考查化归与转化的数学思想方法,属于中档题. 23.D 【详解】()22cos 2cos 2212sin(2)16f x x x x x x π=+=+=++,当12x π=时,sin(2)sin163x ππ+=≠±,∴f (x )不关于直线12x π=对称;当512x π=时,2sin(2)116x π++= ,∴f (x )关于点5(,1)12π对称; f (x )得周期22T ππ==, 当(,0)3x π∈-时,2(,)626x πππ+∈-,∴f (x )在(,0)3π-上是增函数. 本题选择D 选项. 24.C 【分析】ABAB 和ACAC 分别表示向量AB 和向量AC 方向上的单位向量,0AB AC BC AB AC ⎛⎫⎪+⋅= ⎪⎝⎭表示A ∠平分线所在的直线与BC 垂直,可知ABC 为等腰三角形,再由12AB AC ABAC⋅=可求出A ∠,即得三角形形状。
春季课程 不等式与平面向量
教学过程一、考纲解读不等式1.对本部分的考查,不等式性质常与简易逻辑结合考查选择填空题;2.不等式解法主要以一元二次不等式为主,兼顾简单分式不等式、含绝对值的不等式、指对数不等式、与分段函数有关的不等式,常与集合,导数相结合。
3.线性规划为必考且难度不大。
4.基本不等式求最值要引起足够的重视;5.不等式的恒成立问题也应当反复训练。
向量1.对本部分的考查,在选择填空中要重视向量的几何运算和代数运算;必须掌握向量共线、垂直、夹角、模、投影等;2.要重视在其它知识中的工具作用,主要在解析几何中。
二、复习预习不等式:(1)不等关系 (2)一元二次不等式(3)二元一次不等式组与简单线性规划问题(4)基本不等式:()0,2>≥+b a ab ba ① 了解基本不等式的证明过程.② 会用基本不等式解决简单的最大(小)值问题. 平面向量(1)平面向量的实际背景及基本概念(2)向量的线性运算(3)平面向量的基本定理及坐标表示 (4)平面向量的数量积 (5)向量的应用①会用向量方法解决某些简单的平面几何问题.②会用向量方法解决简单的力学问题与其他一些实际问题.三、知识讲解考点1 不等式(1)不等关系了解现实世界和日常生活中的不等关系,了解不等式(组)的实际背景. (2)一元二次不等式① 会从实际情境中抽象出一元二次不等式模型.② 通过函数图像了解一元二次不等式与相应的二次函数、一元二次方程的联系. ③ 会解一元二次不等式,对给定的一元二次不等式,会设计求解的程序框图. (3)二元一次不等式组与简单线性规划问题 ① 会从实际情境中抽象出二元一次不等式组.② 了解二元一次不等式的几何意义,能用平面区域表示二元一次不等式组.③ 会从实际情境中抽象出一些简单的二元线性规划问题,并能加以解决.(4)基本不等式:()0,2>≥+b a ab ba ① 了解基本不等式的证明过程. ② 会用基本不等式解决简单的最大(小)值问题.考点2 平面向量(1)平面向量的实际背景及基本概念①了解向量的实际背景.②理解平面向量的概念,理解两个向量相等的含义.③理解向量的几何表示.(2)向量的线性运算①掌握向量加法、减法的运算,并理解其几何意义.②掌握向量数乘的运算及其意义,理解两个向量共线的含义.③了解向量线性运算的性质及其几何意义.(3)平面向量的基本定理及坐标表示①了解平面向量的基本定理及其意义.②掌握平面向量的正交分解及其坐标表示.③会用坐标表示平面向量的加法、减法与数乘运算.④理解用坐标表示的平面向量共线的条件.(4)平面向量的数量积①理解平面向量数量积的含义及其物理意义.②了解平面向量的数量积与向量投影的关系.③掌握数量积的坐标表达式,会进行平面向量数量积的运算.④能运用数量积表示两个向量的夹角,会用数量积判断两个平面向量的垂直关系.(5)向量的应用①会用向量方法解决某些简单的平面几何问题.②会用向量方法解决简单的力学问题与其他一些实际问题.四、例题精析例1 [2014全国1卷] 已知集合A={x |2230x x --≥},B={}22x x -≤<,则A B ⋂=( )A .[-2,-1]B .[-1,2)C .[-1,1]D .[1,2)【规范解答】解法1.选A (演绎法)∵A={x |2230x x --≥}={}13x x x ≤-≥或,B={}22x x -≤<, ∴A B ⋂={}21x x -≤≤, 解法2.选A (特值法)取元素2-,代入集合A 与集合B 验证,发现既在集合A 中,也在集合B 中,只有选项A 中含有元素2-,排除其它选项,选A【总结与反思】 (1)本题考查了一元二次不等式的解法与集合的交集运算,容易出错的地方是审错题目,把不等式的等号漏掉。
高考数学中平面向量与其它知识的交汇

高考数学中平面向量与其它知识的交汇向量由于具有几何形式和代数形式的“双重身份”,使它成为中学数学知识的一个交汇点,成为联系多项内容的媒介。
向量与平面解析几何,特别是其中直线部分保持着天然的联系,同时平面向量是处理其它问题的重要方法,通过将元素间的关系转化为数量关系,将过去的形式逻辑证明转化为数值计算,化繁难为简易,是一种重要的解决问题的手段和方法。
平面向量的高考考查要求,其一是主要考查平面向量的性质和运算法则,向量的坐标表示及运算。
其三是和其他数学内容结合在一起,如可以和曲线、数列等基础知识结合,考查逻辑推理和运算能力等综合运用数学知识解决问题的能力。
本文例析高考数学中平面向量与其它知识的交汇及解题策略. 一、平面向量与不等式的交汇例1 设a 、b 为不相等的正数,求证:2332244)())((b a b a b a +>++证明: 设m =(a,b), n =(a 2,b 2), 利用向量的数量积不等式有|m | |n |≥|m·n | , 由于a ≠b ,故ab 2-a 2b ≠0,也即向量m 与n 不是平行向量,故|m | |n |>|m·n |, |m |2|n |2>|m·n |2 即2332244)())((b a b a b a +>++成立.金点子:从整体结构上发现不等式与向量不等式有相似之处,避免了取差比较的繁琐。
二、平面向量与函数的交汇例2 已知平面向量),1,3(-=→a ),23,21(=→b 若存在实数x 和k,使,)3(2→→→-+=b x a c ,→→→+-=b x a k d.→→⊥d c 且(1)试求函数关系式k=f(x);(2)讨论函数k=f(x)的单调性并求出极大值与极小值.解:(1) 0,1,422=⋅==→→→→b a b a . ,0=⋅⇒⊥→→→→d c d c ,0)3(222=-+-∴→→b x x a k,0)3(42=-+-∴x x k ).(4)3(2R x x x k ∈-=∴ (2) ).1)(1(43)1(432'-+=-=x x x k 当x 变化时,'k , k 的变化情况如下表: x(-∞,-1) -1 (-1,1) 1 (1,+∞) 'k+ 0 - 0 + k↗极大值0.5↘极小值-0.5↗∴k=f(x)在(-∞,-1)及(1,+∞)上是增函数,在(-1,1)上是减函数. 当x=-1时,k=f(x)有极大值0.5,当x=1时,k=f(x)有极小值-0.5金点子:第(1)小题关键是发现0=⋅→→b a ,以简化计算,利用0=⋅→→d c ,建立函数表达式;第(2)小题利用导数不难解决.三、平面向量和三角函数的交汇例3 平面直角坐标系内有点P(1,cosx),Q(cosx,1), ]4,4[ππ-∈x , (1)求向量OP OQ与的夹角θ的余弦用x 表示的函数f(x); (2)求θ的最值.解:(1)21cos ,OP x OQ =+= O P O Q ⋅ 2c o s ,x = .c o s 1c o s 2c o s 2xx +=∴θ (2),cos 1cos 2cos xx +=θ ],4,4[ππ-∈∴x ,1c o s 22≤≤∴x ,223c o s 1c o s 2≤+≤∴x x ,1c o s 232≤≤∴θ .232a r c c o s 0≤≤∴θ .4,232a r c c o s ;0,0m a x m i n πθθθ±====∴此时此时x金点子:第(1)小题利用向量夹角公式,cos →→→→⋅=ba b a θ 问题便可解决;第(2)题注意到0≤θ≤π,要求出θ的最值,只需求出cos θ的最值. 四、平面向量与解析几何中的交汇例4 已知椭圆,1162422=+y x 直线,1812:=+y x l P 是l 上一点,射线OP 交椭圆于R ,又Q 在OP 上且满足,2OR OP OQ =⋅ 当点P 在l 上移动时,求点Q 的轨迹方程,并说明轨迹是什么曲线.解:如下图不妨设(,),OQ x y =(,),P P OP x y =(,).R R OR x y =因为OP OQ 、同方向,且,2OR OP OQ =⋅ 所以22.OP OR OP OQ OQ OQ OQ =⋅=⋅ 所以,有,,2222y OQOR y x OQ OR x P P ⋅=⋅= 并将其代入直线l 方程,得,1)812(22=+y x OQ OR…① 同理,OR OQ 、同方向, 所以知有,,y OQOR y x OQ OR x R R ⋅=⋅=代入椭圆方程,得,1)1624(2222=+y x OQ OR…② 由①、②得)不全为,(0,812162422y x y x y x +=+ 所以点Q 的轨迹方Q PRlxy程为椭圆 原点除外).(135)1(25)1(22=-+-y x 金点子:利用两个非零向量a 与b 共线的充要条件是有且只有一实数λ,使得b =λa .当a 与b 同方向时,有b =λa ;当a 与b 反方向时,有b =-λa .五、平面向量在物理中的应用例5一重物m 用绳悬起如下图,绳的另一端系在天花板上,绳长l =0.5m ,重物经推动后,在一水平面内作匀速圆周运动,转速n=1转/秒,求这时绳和竖直方向所成的角度(g 取10米/秒2). 解:重物作匀速圆周运动时,加速度是向心加速度,由牛顿第二定律知:在竖直方向上,|T |cosθ=|G |=mg(其中为绳与竖直方向所成的角)①,在水平面内,重力所受合力大小|f |=|T |sinθ,即|T |sinθ=|f |=m|a | (其中a 为向心加速度),…② 由①②得ga =θtan …③ 圆半径R=l sinθ,圆周长为2πl sinθ,故重物在圆周上的速度大小为|v |=|2πl nsinθ| 而θπsin 422l n R==2v a …④ 把④代入③ 得l n g 224cos πθ= …⑤ 代入已知数字得cos =0.5,故θ=60o 由⑤可知,物体转速n 愈大,θ也愈大.金点子:本题是利用向量求解物理问题,物理中力的合成,速度的合成等都与向量有关. 六、平面向量与其它知识的综合交汇例6(2002年江西、山西、天津高考试题)已知两点M (-1,0),N (1,0),且点P 使,,MP MN PM PN NM NP ⋅⋅⋅成公差小于零的等差数列。
必胜秘诀向量与不等式

高考数学必胜秘诀在哪?――概念、方法、题型、易误点及应试技巧总结五、平面向量1、向量有关概念:(1)向量的概念:既有大小又有方向的量,注意向量和数量的区别。
向量常用有向线段来表示,注意不能说向量就是有向线段,为什么?(向量可以平移)。
如已知A (1,2),B (4,2),则把向量AB 按向量a =(-1,3)平移后得到的向量是_____(答:(3,0))(2)零向量:长度为0的向量叫零向量,记作:0,注意零向量的方向是任意的;(3)单位向量:长度为一个单位长度的向量叫做单位向量(与AB 共线的单位向量是||AB AB ±); (4)相等向量:长度相等且方向相同的两个向量叫相等向量,相等向量有传递性;(5)平行向量(也叫共线向量):方向相同或相反的非零向量、叫做平行向量,记作:∥,规定零向量和任何向量平行。
提醒:①相等向量一定是共线向量,但共线向量不一定相等;②两个向量平行与与两条直线平行是不同的两个概念:两个向量平行包含两个向量共线, 但两条直线平行不包含两条直线重合;③平行向量无传递性!(因为有0);④三点A B C 、、共线⇔ AB AC 、共线;(6)相反向量:长度相等方向相反的向量叫做相反向量。
a 的相反向量是-a 。
如下列命题:(1)若a b =,则a b =。
(2)两个向量相等的充要条件是它们的起点相同,终点相同。
(3)若AB DC =,则ABCD 是平行四边形。
(4)若ABCD 是平行四边形,则AB DC =。
(5)若,a bb c ==,则a c =。
(6)若/,/a bb c ,则//a c 。
其中正确的是_______(答:(4)(5)) 2、向量的表示方法:(1)几何表示法:用带箭头的有向线段表示,如,注意起点在前,终点在后;(2)符号表示法:用一个小写的英文字母来表示,如,,等;(3)坐标表示法:在平面内建立直角坐标系,以与x 轴、y 轴方向相同的两个单位向量,j 为基底,则平面内的任一向量可表示为(),a xi y j x y =+=,称(),x y 为向量的坐标,=(),x y 叫做向量的坐标表示。
2020高考复习专题之平面向量与不等式
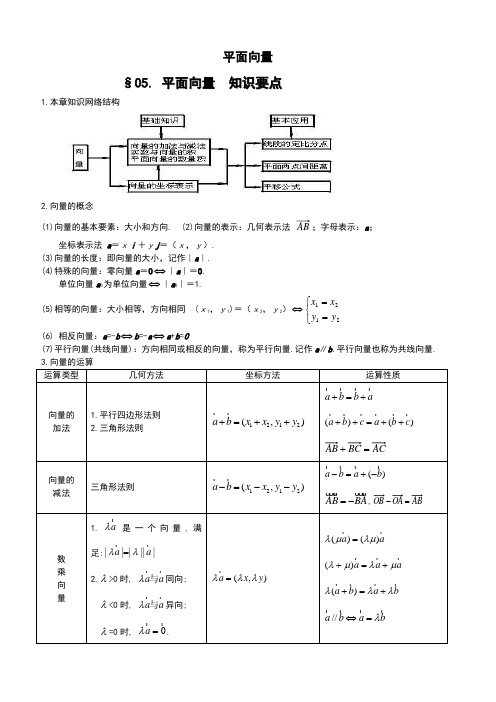
平面向量§05. 平面向量 知识要点1.本章知识网络结构2.向量的概念(1)向量的基本要素:大小和方向.(2)向量的表示:几何表示法 AB ;字母表示:a ;坐标表示法 a =xi+yj =(x,y). (3)向量的长度:即向量的大小,记作|a |. (4)特殊的向量:零向量a =O ⇔|a |=O .单位向量a O 为单位向量⇔|a O |=1.(5)相等的向量:大小相等,方向相同(x1,y1)=(x2,y2)⎩⎨⎧==⇔2121y y x x(6) 相反向量:a =-b ⇔b =-a ⇔a +b =0(7)平行向量(共线向量):方向相同或相反的向量,称为平行向量.记作a ∥b .平行向量也称为共线向量. 3.向量的运算 运算类型几何方法坐标方法运算性质向量的 加法1.平行四边形法则2.三角形法则1212(,)a b x x y y +=++r ra b b a +=+r r r r()()a b c a b c ++=++r r r r r rAC BC AB =+向量的 减法三角形法则1212(,)a b x x y y -=--r r()a b a b -=+-r r r rAB BA =-u u u r u u u r,AB OA OB =- 数 乘 向 量1.a λr是一个向量,满足:||||||a a λλ=r r2.λ>0时, a a λr r与同向; λ<0时, a a λr r与异向;λ=0时, 0a λ=r r.(,)a x y λλλ=r()()a a λμλμ=r r()a a a λμλμ+=+r r r()a b a b λλλ+=+r r r r//a b a b λ⇔=r r r r向 量 的 数 量 积a b •r r是一个数1.00a b ==r r r r或时, 0a b •=r r. 2.00||||cos(,)a b a b a b a b ≠≠=r r r r r r r r g 且时, 1212a b x x y y •=+r ra b b a •=•r r r r()()()a b a b a b λλλ•=•=•r r r r r r()a b c a c b c +•=•+•r r r r r r r2222||||=a a a x y =+r r u r即 ||||||a b a b •≤r r r r4.重要定理、公式(1)平面向量基本定理e 1,e 2是同一平面内两个不共线的向量,那么,对于这个平面内任一向量,有且仅有一对实数λ1, λ2,使a =λ1e 1+λ2e 2.(2)两个向量平行的充要条件a ∥b ⇔a =λb (b ≠0)⇔x 1y 2-x 2y 1=O. (3)两个向量垂直的充要条件a ⊥b ⇔a ·b =O ⇔x 1x 2+y 1y 2=O. (4)线段的定比分点公式设点P 分有向线段21P P 所成的比为λ,即P P 1=λ2PP ,则OP =λ+111OP +λ+112OP (线段的定比分点的向量公式) ⎪⎪⎩⎪⎪⎨⎧++=++=.1,12121λλλλy y y x x x (线段定比分点的坐标公式) 当λ=1时,得中点公式:OP =21(1OP +2OP )或⎪⎪⎩⎪⎪⎨⎧+=+=.2,22121y y y x x x (5)平移公式设点P (x ,y )按向量a =(h,k)平移后得到点P ′(x ′,y ′), 则P O '=OP +a 或⎩⎨⎧+='+='.,k y y h x x曲线y =f (x )按向量a =(h,k)平移后所得的曲线的函数解析式为:y -k=f (x -h) (6)正、余弦定理 正弦定理:.2sin sin sin R CcB b A a === 余弦定理:a 2=b 2+c 2-2bc cos A , b 2=c 2+a 2-2ca cos B ,c 2=a 2+b 2-2ab cos C .(7)三角形面积计算公式:设△ABC 的三边为a ,b ,c ,其高分别为h a ,h b ,h c ,半周长为P ,外接圆、内切圆的半径为R ,r . ①S △=1/2ah a =1/2bh b =1/2ch c ②S △=Pr ③S △=abc/4R④S △=1/2sin C ·ab=1/2ac ·sin B=1/2cb ·sin A ⑤S △=()()()c P b P a P P --- [海伦公式] ⑥S △=1/2(b+c-a )r a [如下图]=1/2(b+a-c )r c =1/2(a+c-b )r b[注]:到三角形三边的距离相等的点有4个,一个是内心,其余3个是旁心. 如图:图1 图2 图3 图4图1中的I 为S △ABC 的内心, S △=Pr图2中的I 为S △ABC 的一个旁心,S △=1/2(b+c-a )r a附:三角形的五个“心”; 重心:三角形三条中线交点.外心:三角形三边垂直平分线相交于一点. 内心:三角形三内角的平分线相交于一点. 垂心:三角形三边上的高相交于一点.旁心:三角形一内角的平分线与另两条内角的外角平分线相交一点.⑸已知⊙O 是△ABC 的内切圆,若BC =a ,AC =b ,AB =c [注:s 为△ABC 的半周长,即2cb a ++] 则:①AE=a s -=1/2(b+c-a ) ②BN=b s -=1/2(a+c-b ) ③FC=c s -=1/2(a+b-c )综合上述:由已知得,一个角的邻边的切线长,等于半周长减去对边(如图4). 特例:已知在Rt △ABC ,c 为斜边,则内切圆半径r =cb a abc b a ++=-+2(如图3). ⑹在△ABC 中,有下列等式成立C B A C B A tan tan tan tan tan tan =++. 证明:因为,C B A -=+π所以()()C B A -=+πtan tan ,所以C BA BA tan tan tan 1tan tan -=-+,∴结论!⑺在△ABC 中,D 是BC 上任意一点,则DC BD BCBCAB BD AC AD ⋅-+=222.证明:在△ABCD 中,由余弦定理,有ΛB BD AB BD AB AD cos 2222⋅⋅-+=① 在△ABC 中,由余弦定理有ΛBC AB AC BC AB B ⋅-+=2cos 222②,②代入①,化简可得,DC BD BCBCAB BD AC AD ⋅-+=222(斯德瓦定理)AB C Oa b cI A BC D E F IA B C D EF r ar ar abc a ab c ACB N E FA图5①若AD 是BC 上的中线,2222221a cb m a -+=; ②若AD 是∠A 的平分线,()a p p bc cb t a -⋅+=2,其中p 为半周长; ③若AD 是BC 上的高,()()()c p b p a p p ah a ---=2,其中p 为半周长.⑻△ABC 的判定:⇔+=222b a c △ABC 为直角△⇔∠A + ∠B =2π2c <⇔+22b a △ABC 为钝角△⇔∠A + ∠B <2π 2c >⇔+22b a △ABC 为锐角△⇔∠A + ∠B >2π 附:证明:abc b a C 2cos 222-+=,得在钝角△ABC 中,222222,00cos c b a c b a C πππ+⇔-+⇔⑼平行四边形对角线定理:对角线的平方和等于四边的平方和.)(22222b a b a b a +=-++空间向量1.空间向量的概念:具有大小和方向的量叫做向量 注:⑴空间的一个平移就是一个向量⑵向量一般用有向线段表示同向等长的有向线段表示同一或相等的向量 ⑶空间的两个向量可用同一平面内的两条有向线段来表示 2.空间向量的运算定义:与平面向量运算一样,空间向量的加法、减法与数乘向量运算如下b a AB OA OB ϖρ+=+= b a OB OA BA ρρ-=-=)(R a OP ∈=λλρ运算律:⑴加法交换律:a b b a ϖϖϖρ+=+⑵加法结合律:)()(c b a c b a ϖϖϖϖρϖ++=++⑶数乘分配律:b a b a ϖϖϖϖλλλ+=+)(3共线向量表示空间向量的有向线段所在的直线互相平行或重合,则这些向量叫做共线向量或平行向量.a ρ平行于bρ记作b a ρϖ//.当我们说向量a ρ、b ρ共线(或a ρ//b ρ)时,表示a ρ、b ρ的有向线段所在的直线可能是同一直线,也可能是平行直线.4.共线向量定理及其推论:共线向量定理:空间任意两个向量a ρ、b ρ(b ρ≠0ρ),a ρ//b ρ的充要条件是存在实数λ,使a ρ=λb ρ.推论:如果l 为经过已知点A 且平行于已知非零向量a ρ的直线,那么对于任意一点O ,点P 在直线l 上的充要条件是存在实数t 满足等式t OA OP +=a ρ.其中向量a ρ叫做直线l 的方向向量. 5.向量与平面平行:已知平面α和向量a r ,作OA a =u u u r r ,如果直线OA 平行于α或在α内,那么我们说向量a r平行于平面α,记作://a αr.通常我们把平行于同一平面的向量,叫做共面向量 说明:空间任意的两向量都是共面的 6.共面向量定理:如果两个向量,a b r r 不共线,p r 与向量,a b rr 共面的充要条件是存在实数,x y 使p xa yb =+r r r推论:空间一点P 位于平面MAB 内的充分必要条件是存在有序实数对,x y ,使MP xMA yMB =+u u u r u u u r u u u r或对空间任一点O ,有OP OM xMA yMB =++u u u r u u u u r u u u r u u u r① ①式叫做平面MAB 的向量表达式7空间向量基本定理:如果三个向量,,a b c r r r不共面,那么对空间任一向量p r,存在一个唯一的有序实数组,,x y z ,使p xa yb zc =++r r r r推论:设,,,O A B C 是不共面的四点,则对空间任一点P ,都存在唯一的三个有序实数,,x y z ,使OP xOA yOB zOC =++u u u r u u u r u u u r u u u r8空间向量的夹角及其表示:已知两非零向量,a b rr ,在空间任取一点O ,作,OA a OB b ==u u u r u u u r r r ,则AOB ∠叫做向量a r 与b r 的夹角,记作,a b <>r r ;且规定0,a b π≤<>≤r r ,显然有,,a b b a <>=<>r r r r ;若,2a b π<>=rr ,则称a r 与b r 互相垂直,记作:a b ⊥r r .9.向量的模:设OA a =u u u r r ,则有向线段OA uuu r 的长度叫做向量a r 的长度或模,记作:||a r.10.向量的数量积: a b ⋅=r r ||||cos ,a b a b ⋅⋅<>r rr r .已知向量AB a =u u u r r 和轴l ,e r是l 上与l 同方向的单位向量,作点A 在l 上的射影A ',作点B 在l 上的射影B ',则A B ''u u u u r 叫做向量AB u u u r 在轴l 上或在e r 上的正射影.可以证明A B ''u u u u r 的长度||||cos ,||A B AB a e a e ''=<>=⋅u u u u r u u u r r r r r .11.空间向量数量积的性质:(1)||cos ,a e a a e ⋅=<>r r r r r.(2)0a b a b ⊥⇔⋅=r r r r .(3)2||a a a =⋅r r r .12.空间向量数量积运算律:(1)()()()a b a b a b λλλ⋅=⋅=⋅r r r r r r.(2)a b b a ⋅=⋅r r r r (交换律)(3)()a b c a b a c ⋅+=⋅+⋅r r r r r r r (分配律).空间向量的坐标运算一.知识回顾:(1)空间向量的坐标:空间直角坐标系的x 轴是横轴(对应为横坐标),y 轴是纵轴(对应为纵轴),z 轴是竖轴(对应为竖坐标).①令a =(a 1,a 2,a 3),),,(321b b b b =,则),,(332211b a b a b a b a ±±±=+))(,,(321R a a a a ∈=λλλλλ332211b a b a b a b a ++=⋅ a ∥)(,,332211R b a b a b a b ∈===⇔λλλλ332211b a b a b a ==⇔0332211=++⇔⊥b a b a b a b a 222321a a a a a a ++=⋅=(用到常用的向量模与向量之间的转化:a a a a a a ⋅=⇒⋅=2)232221232221332211||||,cos b b b a a a b a b a b a b a ba b a ++⋅++++=⋅⋅>=<ρρρρρρ②空间两点的距离公式:212212212)()()(z z y y x x d -+-+-=.(2)法向量:若向量a 所在直线垂直于平面α,则称这个向量垂直于平面α,记作α⊥a ,如果α⊥a 那么向量a 叫做平面α的法向量.(3)用向量的常用方法:①利用法向量求点到面的距离定理:如图,设n 是平面α的法向量,AB 是平面α的一条射线,其中α∈A ,则点B 到平面α的距离为||||n n AB ⋅.②利用法向量求二面角的平面角定理:设21,n n 分别是二面角βα--l 中平面βα,的法向量,则21,n n 所成的角就是所求二面角的平面角或其补角大小(21,n n 方向相同,则为补角,21,n n 反方,则为其夹角). ③证直线和平面平行定理:已知直线≠⊄a 平面α,α∈⋅∈⋅D C a B A ,,且CDE 三点不共线,则a ∥α的充要条件是存在有序实数对μλ⋅使CE CD AB μλ+=.(常设CE CD AB μλ+=求解μλ,若μλ,存在即证毕,若μλ,不存在,则直线AB 与平面相交).α▲nBCAαβ▲n 2n 1αCED AB高中数学第六章-不等式考试内容:不等式.不等式的基本性质.不等式的证明.不等式的解法.含绝对值的不等式. 考试要求:(1)理解不等式的性质及其证明.(2)掌握两个(不扩展到三个)正数的算术平均数不小于它们的几何平均数的定理,并会简单的应用. (3)掌握分析法、综合法、比较法证明简单的不等式. (4)掌握简单不等式的解法.(5)理解不等式│a │-│b │≤│a+b │≤│a │+│b │§06. 不 等 式 知识要点1. 不等式的基本概念(1) 不等(等)号的定义:.0;0;0b a b a b a b a b a b a <⇔<-=⇔=->⇔>- (2) 不等式的分类:绝对不等式;条件不等式;矛盾不等式. (3) 同向不等式与异向不等式.(4) 同解不等式与不等式的同解变形. 2.不等式的基本性质(1)a b b a <⇔>(对称性)(2)c a c b b a >⇒>>,(传递性)(3)c b c a b a +>+⇒>(加法单调性)(4)d b c a d c b a +>+⇒>>,(同向不等式相加) (5)d b c a d c b a ->-⇒<>,(异向不等式相减) (6)bc ac c b a >⇒>>0,.(7)bc ac c b a <⇒<>0,(乘法单调性)(8)bd ac d c b a >⇒>>>>0,0(同向不等式相乘)(9)0,0a b a b c d c d>><<⇒>(异向不等式相除) 11(10),0a b ab a b>>⇒<(倒数关系) (11))1,(0>∈>⇒>>n Z n b a b a n n 且(平方法则)(12))1,(0>∈>⇒>>n Z n b a b a n n 且(开方法则) 3.几个重要不等式(1)0,0||,2≥≥∈a a R a 则若(2))2||2(2,2222ab ab b a ab b a R b a ≥≥+≥+∈+或则、若(当仅当a=b 时取等号) (3)如果a ,b 都是正数,那么 .2a b ab +≤(当仅当a=b 时取等号)极值定理:若,,,,x y R x y S xy P +∈+==则:○1如果P 是定值, 那么当x=y 时,S 的值最小; ○2如果S 是定值, 那么当x =y 时,P 的值最大. 利用极值定理求最值的必要条件: 一正、二定、三相等.3,3a b c a b c R abc +++∈≥(4)若、、则(当仅当a=b=c 时取等号) 0,2b aab a b>+≥(5)若则(当仅当a=b 时取等号)2222(6)0||;||a x a x a x a x a x a x a a x a >>⇔>⇔<-><⇔<⇔-<<时,或(7)||||||||||||,b a b a b a R b a +≤±≤-∈则、若 4.几个著名不等式(1)平均不等式: 如果a ,b 都是正数,那么 222.1122a ba b ab a b++≤≤≤+(当仅当a=b 时取等号)即:平方平均≥算术平均≥几何平均≥调和平均(a 、b 为正数):特别地,222()22a b a b ab ++≤≤(当a = b 时,222()22a b a b ab ++==)),,,(332222时取等c b a R c b a c b a c b a ==∈⎪⎭⎫ ⎝⎛+++≥++ ⇒幂平均不等式:22122221)...(1...n n a a a na a a +++≥+++ 注:例如:22222()()()ac bd a b c d +≤++.常用不等式的放缩法:①21111111(2)1(1)(1)1n n n n n n n n n n -==-≥++--p p②11111(1)121n n n n n n n nn n +-==--≥+++-pp(2)柯西不等式: 时取等号当且仅当(则若nn n n n n n n b a b a b a b a b b b b a a a a b a b a b a b a R b b b b R a a a a ====+++++++≤++++∈∈ΛΛΛΛΛΛ332211223222122322212332211321321))(();,,,,,,,,(3)琴生不等式(特例)与凸函数、凹函数若定义在某区间上的函数f(x),对于定义域中任意两点1212,(),x x x x ≠有12121212()()()()()().2222x x f x f x x x f x f x f f ++++≤≥或则称f(x)为凸(或凹)函数.5.不等式证明的几种常用方法比较法、综合法、分析法、换元法、反证法、放缩法、构造法.6.不等式的解法(1)整式不等式的解法(根轴法).步骤:正化,求根,标轴,穿线(偶重根打结),定解. 特例① 一元一次不等式ax >b 解的讨论;②一元二次不等式ax 2+bx +c >0(a ≠0)解的讨论.(2)分式不等式的解法:先移项通分标准化,则()()0()()0()()0;0()0()()f x g x f x f x f x g x g x g x g x ≥⎧>⇔>≥⇔⎨≠⎩ (3)无理不等式:转化为有理不等式求解 ○1()0()()()0()()f x f x g x g x f x g x ⎧≥⎫⇒⎪⎬>⇔≥⎨⎭⎪>⎩定义域○2⎩⎨⎧<≥⎪⎩⎪⎨⎧>≥≥⇔>0)(0)()]([)(0)(0)()()(2x g x f x g x f x g x f x g x f 或 ○3⎪⎩⎪⎨⎧<≥≥⇔<2)]([)(0)(0)()()(x g x f x g x f x g x f (4).指数不等式:转化为代数不等式()()()()()(1)()();(01)()()(0,0)()lg lg f x g x f x g x f x a a a f x g x a a a f x g x a b a b f x a b>>⇔>><<⇔<>>>⇔⋅>(5)对数不等式:转化为代数不等式()0()0log ()log ()(1)()0;log ()log ()(01)()0()()()()a a a a f x f x f x g x a g x f x g x a g x f x g x f x g x >>⎧⎧⎪⎪>>⇔>><<⇔>⎨⎨⎪⎪><⎩⎩(6)含绝对值不等式○1应用分类讨论思想去绝对值; ○2应用数形思想; ○3应用化归思想等价转化 ⎩⎨⎧>-<>≤⇔>⎩⎨⎧<<->⇔<)()()()(0)()0)(),((0)()(|)(|)()()(0)()(|)(|x g x f x g x f x g x g x f x g x g x f x g x f x g x g x g x f 或或不同时为注:常用不等式的解法举例(x 为正数): ①231124(1)2(1)(1)()22327x x x x x -=⋅--≤=②2222232(1)(1)12423(1)()223279x x x y x x y y --=-⇒=≤=⇒≤类似于22sin cos sin (1sin )y x x x x ==-,③111||||||()2x x x x x x+=+≥与同号,故取等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题4 平面向量与不等式结合考点动向:向量与不等式的交汇是当今高考命题的一个热点.自从新教材实施以来,在高考中,不时考查平面向量与不等式有关知识的结合。
这些题实际上是以向量为载体考查不等式的知识,解题的关键是利用向量的数量积等知识将问题转化为不等式的问题,转化时不要把向量与实数搞混淆,一般来说向量与不等式结合的题目难度不大。
向量与不等式结合,既符合在知识的“交汇处”构题,又加强了对双基的考查。
这类题目常常包括向量与不等式的性质、均值不等式、解不等式、求值包括(求最大值、最小值)的交汇等几个方面.可以预测到,明年仍至今后的高考中,还会继续出现向量与不等式结合的题目。
方法范例例1、(2005年,上海卷)已知函数b kx x f +=)(的图象与y x ,轴分别相交于点A 、B ,22+=(,分别是与y x ,轴正半轴同方向的单位向量),函数6)(2--=x x x g 。
(1) 求b k ,的值;(2)当x 满足)()(x g x f >时,求函数)(1)(x f x g +的最小值。
[解析] (1)通过交点坐标求出向量的坐标表示,列方程组,求b k ,的值;(2)先由),()(x g x f > 得 ,42<<-x 再对)(1)(x f x g +进行化简,得5212-+++x x ,然后利用不等式ab b a 2≥+求函数的最值.[答案](1)由已知得},{),,0(),0,(b k b b B k b A =-则,于是 .21,22⎩⎨⎧==∴⎪⎩⎪⎨⎧==b k b k b (2)由,62),()(2-->+>x x x x g x f 得 即 ,42,0)4)(2(<<-<-+x x x 得,521225)(1)(2-+++=+--=+x x x x x x f x g 由于3)(1)(,02-≥+>+x f x g x 则, 其中等号当且仅当x +2=1,即x =-1时成立,∴)(1)(x f x g +时的最小值是-3. 例2、(2005年·黄岗模拟)已知二次函数)(x f 对任意x R ∈,都有)1()1(x f x f +=-成立,设向量)2,(sin x a =,)21,sin 2(x b =,)1,2(cos x c =,)2,1(=d ,当x ],0[π∈时,求不等式)()(d c f b a f ∙>∙的解集.[解析] 二次函数图象开口方向不确定,要分类讨论. 由)1()1(x f x f +=-,知二次函数)(x f 关于直线x =1对称.先求出向量数量积b a ∙与d c ∙,[答案]二次函数图象开口方向不确定,要分类讨论.由)1()1(x f x f +=-,知二次函数)(x f 关于直线x =1对称.当二次项系数A >0时,)(x f 在),1[+∞∈上递增,当A <0时,)(x f 在),1[+∞∈上递减.因为=∙b a )2,(si n x )21,s i n 2(x ∙=1sin 22+x ≥1,=∙d c )1,2(cos x )2,1(∙=22cos +x ≥1,所以当A >0时,由)()(d c f b a f ∙>∙,得1sin 22+x >22cos +x ,即02cos <x ,又因为0≤x ≤π,所以4π<x <π43; 当A <0时,由)()(d c f b a f ∙>∙,得1sin 22+x <22cos +x ,即02cos >x ,又因为0≤x ≤π,所以0≤x <4π或π43<x ≤π. 综上所述,当二次函数)(x f 二次项系数A >0时,不等式的解集{x ∣4π<x <π43};当二次函数)(x f 二次项系数A <0时,不等式的解集{x ∣0≤x <4π或π43<x ≤π}. 例3、(2005年,浙江卷)已知向量a ≠e ,|e |=1,对任意t ∈R ,恒有|a -t e |≥|a - e |,则( ).(A) a ⊥e , (B) a ⊥(a -e ), (C) e ⊥(a -e ), (D) (a +e )⊥(a -e ).[解析] 对|a -t e |≥|a -e |进行平方,化成关于t 的二次不等式,利用二次函数性质,得0∆≤恒成立,从而得1a c ⋅=.[答案]解:对任意t ∈R ,恒有|a -t e |≥|a -e |,故两边平方得2222221,2210a t a c t a a c t t a c t a c -⋅⋅+≥-⋅⋅+-⋅⋅+⋅⋅-≥即:.又上式对任意t ∈R ,恒成立,即有:0∆≤恒成立.22421410c c c ∆⋅-⋅-=⋅-≤即=4(a )(a )(a ).故当1a c ⋅=时,上式成立,本题应选 (C ).[规律小结](1)平面向量与不等式结合的问题,经常以向量为载体考查不等式的知识,解题的关键是利用向量的知识将问题转化为不等式的问题:解不等式,求最大值(最小值),转化时不要把向量与实数搞混淆。
(2)向量与不等式的结合,既符合在知识的“交汇处”构题,又加强了对双基的考查,特别是向量的坐标表示及运算,这类问题的解决思路通常是将向量的数量积的运算与模用坐标运算后,转化为三角函数问题,然后用三角函数基本公式求解,基中涉及到的有关向量的知识有:①向量的坐标表示及加法、减法、数乘向量;②向量的数量积;③向量平行、垂直的充要条件;④向量的模、夹角;⑤b a b a ⋅≤⋅;若a ),(11y x =,b ),(22y x =,有))(()(2221222122121y y x x y y x x ++≤+;⑥向量不等式:b a b a b a +≤±≤-|,||||||||||||a b a b a b -≤±≤+.(3)可能涉及不等式的内容有:①解分式不等式()()()0≠>a a x g x f 的一般解题思路:移项通分,分子分母分解因式,x 的系数变为正值,标根及奇穿过偶弹回.②含有两个绝对值的不等式:一般是根据定义分类讨论、平方转化或换元转化③解含参不等式常分类等价转化,必要时需分类讨论.注意:按参数讨论,最后按参数取值分别说明其解集,但若按未知数讨论,最后应求并集. ④利用重要不等式ab b a 2≥+ 以及变式2()2a b ab +≤等求函数的最值时,务必注意a ,b +∈R (或a ,b 非负),且“等号成立”时的条件是积ab 或和a +b 其中之一应是定值(一正二定三等).2211a b a b+≥≥+(根据目标不等式左右的运算结构选用) a 、b 、c ∈R ,222a b c ab bc ca ++≥++(当且仅当a b c ==时,取等号) ⑥比较大小的方法和证明不等式的方法主要有:差比较法、商比较法、函数性质法、综合法、分析法和放缩法.⑦含绝对值不等式的性质:a b 、同号或有0⇔||||||a b a b +=+≥||||||||a b a b -=-;a b 、异号或有0⇔||||||a b a b -=+≥||||||||a b a b -=+.⑧不等式的恒成立,能成立等问题1).恒成立问题:若不等式()A x f >在区间D 上恒成立,则等价于在区间D 上()min f x A >;若不等式()B x f <在区间D 上恒成立,则等价于在区间D 上()max f x B <.2).能成立问题:若在区间D 上存在实数x 使不等式()A x f >成立,即()A x f >在区间D 上能成立 ,则等价于在区间D 上()max f x A >;若在区间D 上存在实数x 使不等式()B x f <成立,即()B x f <在区间D 上能成立 ,则等价于在区间D 上的()min f x B <.考点误区分析:(1)对于||||||||||||a b a b a b -≤±≤+,要注意: ① a b 、同向或有0⇔||||||a b a b +=+≥||||||||a b a b -=-; ② a b 、反向或有0⇔||||||a b a b -=+≥||||||||a b a b -=+; ③ a b 、不共线⇔||||||||||||a b a b a b -<±<+.(这些和实数集中类似)(2)解不等式是求不等式的解集,最后务必有集合的形式表示;不等式解集的端点值往往是不等式对应方程的根或不等式有意义范围的端点值.(3)有些取值范围、最值问题,虽然没有直接用向量作为已知条件出现,但如果运用向量知识来解决,也会显得自然、简便,而且易入手。
考生经常没想到而陷入困境.(4)注意对“整式、分式、绝对值不等式”的放缩途径,“配方、函数单调性等”对放缩的影响.同步训练:1、(2000年,全国卷)椭圆14922=+y x 的焦点为F ,1F 2,点P 为其上的动点,当 ∠F 1P F 2为钝角时,点P 横坐标的取值范围是___。
2、(2005年,江苏卷)在△ABC 中,O 为中线AM 上的一个动点,若AM =2,则OA OB OC ∙+()的最小值是 .3、已知向量a =(2,2),向量b 与a 的夹角为π43,且a ∙b =-2. (1)求向量b ;(2)若t =(1,0)且b ⊥t ,c =(A c o s ,2cos 22C ),其中A 、C 是ABC ∆的内角,若三角形的三个内角依次成等差数列,试求c b +的取值范围.4、已知定点A(-1,0)和B(1,0),P 是圆(x-3)2+(y-4)2=4上的一动点,求22PA PB +的最大值和最小值.5、若(cos ,sin ),(cos ,sin )a b ααββ==,且a k -=+),0(R k k ∈>(1)试用k 表示b a ∙;(2) 求∙的最小值,并求出此时a 与b 的夹角θ的大小.[参考答案]1、[解析]解决与角有关的一类问题,总可以从平面向量数量积入手,通过坐标运算列出不等式。
F 1(-5,0)F 2(5,0),设P (3cos θ,2sin θ),21PF F ∠ 为钝角∴123cos ,2sin )3cos ,2sin )PF PF θθθθ⋅=-⋅-( =9cos 2θ-5+4sin 2θ=5 cos 2θ-1<0,解得:55cos 55<<-θ ∴点P 横坐标的取值范围是(553,553-)[答案] (553,553-) 2、[解析]如图设||,||202OA x OM x x ==-≤≤则,()2M BC OC OM ∴+=为的中点,OB ,222OA O OC OA OM x x ∴∙+=∙=-∙︒(B )()cos180222421202,x x x x =-=--≤≤()() 1 2.x ∴=-当时,取最小值[答案]-2.3、[解析](1)设b =(y x ,),由a ∙b =-2,得y x 22+=-2,即y x +=-1① 因为向量b 与a 的夹角为π43,a =2222+=22, 所以b =π43cos ∙∙a b a =⎪⎪⎭⎫ ⎝⎛-∙-22222=1,因此22y x +=1. ② 联立①、②,解得⎩⎨⎧=-=0,1y x 或⎩⎨⎧-==1,0y x .所以b =(-1,0)或b =(0,-1).(2)根据题意,得B =3π,A+C =32π,由于t =(1,0)且b ⊥t ,故b =(0,-1),b +c =(A cos ,C cos ),2c b +=A 2cos +C 2cos=1+)2cos 2(cos 21C A ++1+⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-+A A π322cos 2cos 21=1+)32cos(21π+A , 因为0<A <32π,所以3π<2A+3π<35π,-1≤)32cos(π+A <21, 因此,2c b +⎪⎭⎫⎢⎣⎡∈45,21,c b +⎪⎪⎭⎫⎢⎣⎡∈25,22. [答案](1) b =(-1,0)或b =(0,-1);(2)⎪⎪⎭⎫⎢⎣⎡25,22 4、[分析]利用向量把问题转化为求向量OP 的最值。
