c++求解非线性方程组的牛顿顿迭代法

合集下载

数值分析求解非线性方程根的二分法简单迭代法和牛顿迭代法

实验报告一：实验题目一、实验目的掌握求解非线性方程根的二分法、简单迭代法和牛顿迭代法，并通过数值实验比较两种方法的收敛速度。

二、实验内容1、编写二分法、并使用这两个程序计算02)(=-+=x e x x f 在[0, 1]区间的解，要求误差小于 410- ，比较两种方法收敛速度。

2、在利率问题中，若贷款额为20万元，月还款额为2160元，还期为10年，则年利率为多少？请使用牛顿迭代法求解。

3、由中子迁移理论，燃料棒的临界长度为下面方程的根，用牛顿迭代法求这个方程的最小正根。

4、用牛顿法求方程的根，精确至8位有效数字。

比较牛顿迭代法算单根和重根的收敛速度，并用改进的牛顿迭代法计算重根。

第1题：02)(=-+=x e x x f 区间[0,1] 函数画图可得函数零点约为0.5。

画图函数：function Test1()% f(x) 示意图, f(x) = x + exp(x) - 2; f(x) = 0r = 0:0.01:1;y = r + exp(r) - 2plot(r, y);grid on 二分法程序：计算调用函数：[c,num]=bisect(0,1,1e-4)function [c,num]=bisect(a,b,delta)%Input –a,b 是取值区间范围% -delta 是允许误差%Output -c 牛顿迭代法最后计算所得零点值% -num 是迭代次数ya = a + exp(a) - 2;yb = b + exp(b) - 2;if ya * yb>0return;endfor k=1:100c=(a+b)/2;yc= c + exp(c) - 2;if abs(yc)<=deltaa=c;b=c;elseif yb*yc>0b=c;yb=yc;elsea=c;ya=yc;endif abs(b-a)<deltanum=k; %num为迭代次数break;endendc=(a+b)/2;err=abs(b-a);yc = c + exp(c) - 2;牛顿迭代法程序：计算调用函数：[c,num]=newton(@func1,0.5,1e-4) 调用函数：function [y] = func1(x)y = x + exp(x) - 2;end迭代算法：function[c,num]=newton(func,p0,delta)%Input -func是运算公式% -p0是零点值% -delta是允许误差%Output -c牛顿迭代法最后计算所得零点值% -num是迭代次数num=-1;for k=1:1000y0=func(p0);dy0=diff(func([p0 p0+1e-8]))/1e-8;p1=p0-y0/dy0;err=abs(p1-p0);p0=p1;if(err<delta)num=k;%num为迭代次数break;endendc=p0;第2题：由题意得到算式：计算调用函数：[c,num]=newton(@func2,0.02,1e-8)程序：先用画图法估计出大概零点位置在0.02附近。

C++二元非线性方程组

二元非线性方程牛顿迭代法C++代码。

小弟需要解一个二元非线性方程组，虽然说matlab的解法是一两个代码的事，但是我的情况是需要在C++ 里面实现。

由于自己不熟悉C++代码和牛顿迭代法的解法，小弟最近在网上找了一些资料。

发现很多有问题的例子，纯粹是在误导别人，浪费别人的时间。

于是小弟自己在看了解法（牛顿迭代法）的基础上，自己通过C++ 语言实现了一些简单方程组的解法，分享给给大家。

1. 非线性方程组的解法原理我在网上找了一个资料，应该是中南大学计算机学院的教程，如下：注意，他这里的例子第二个方程应该是，x1*x2*x2+x1-10*x2+8经过观察，我发现其实对于2元方程来说：f(x1,x2)和g(x1,x2)。

牛顿迭代法里面的迭代量(Δx 1 和Δx 2) 可以如下表示。

(我看到网上很多例子用矩阵来表示，我表示看不太懂，而且根据网上贴出来的程序，发现有错误。

而我发现对于2元方程来说，用下面的表示方法更直观，更简单。

2元方程并不需要再学习矩阵的相关知识。

)()()()221121211,,,x x x f x x x f x x f x ∂∂+∂∂-=∆ ()()()221121212,x x x x g x ∂+∂-=∆2. 代码(运行环境, VS 2010, WIN 7 64)// Nonlinear.cpp : Defines the entry point for the console application.//#include"stdafx.h"#include<math.h>#include<iostream>using namespace std;int _tmain(int argc, _TCHAR* argv[]){double x1,x2; //变量x1,x2;double x1_0,x2_0; //变量x1,x2迭代前的值double x1_1,x2_1; //变量x1,x2迭代后的值double delta_x1,delta_x2; //变量double function_F,function_G; //方程f(x1,x2) 和g(x1,x2)double F_x1,F_x2; //方程f的偏导double G_x1,G_x2; //方程g的偏导double Error=1e-10; //给定的误差double Error_cout; //用来计算的误差int Steps; //运行步骤int Max_Steps=100000; //最大运行步骤x1 = 0.5;x2 = 0.5; //初始化初值x1_0 = x1;x2_0 = x2;for(Steps=1;Steps<=Max_Steps;Steps++){// 方程组, f(x1,x2), g(x1,x2)function_F = x1_0*x1_0-10.0*x1_0+x2_0*x2_0+8.0; // 10.0的意思是double类型，10 是指整数类型function_G = x1_0*x2_0*x2_0+x1_0-10.0*x2_0+8.0;// 偏导,F_x1 = 2.0*x1_0-10.0;F_x2 = 2.0*x2_0;G_x1 = x1_0*x1_0+1.0;G_x2 = 2.0*x1_0*x2_0-10.0;// 迭代delta_x1 = -function_F/(F_x1+F_x2);delta_x2 = -function_G/(G_x1+G_x2);x1_1 = x1_0 + delta_x1;x2_1 = x2_0 + delta_x2;x1_0 = x1_1; //迭代，将新计算的变量赋值给原始变量x2_0 = x2_1;Error_cout = fabs(delta_x1)+fabs(delta_x2);if(Error_cout<Error)break; //当迭代到某个次数时，变量变化不大的时候就不运行了}printf(" Run steps is %d\n",Steps);printf(" x1 is %lf\n",x1_0);printf(" x2 is %lf\n",x2_0);return 0;}运行结果为：当然，对于有些方程用这个方法是解不了的，大家可以查一下阻尼牛顿法！。

非线性方程求根—牛顿迭代法(新)

非线性方程求根——牛顿迭代法一、牛顿迭代法的基本思想基本思想：将非线性方程逐步归结为某种线性方程求解。

设方程f (x )=0有近似根x k （f `(x k )≠0），将f (x )在x k 展开：（ξ在x 和x k 之间）2()()()()()()2!k k k k f f x f x f x x x x x ξ'''=+-+-()()()()k k k f x f x f x x x '≈+-可设记该线性方程的根为x k +1，则()()()0k k k f x f x x x '+-=1()()k k k k f x x x f x +=-'故f (x )=0可近似表示为即为Newton 法迭代格式。

（k =0,1,……）例：用Newton 迭代法求方程310x x --=在x 0=1.5附近的近似实根。

解：32()1,()31f x x x f x x '=--=-迭代公式为312131kk k k k x x x x x +--=--计算步骤如下:（1）取初值x 0=1.5;（2）按照迭代公式计算x 1；（3）若|x 1-x 0|<=0.00001，终止迭代；否则，x 0=x 1；转(2)；（4）输出迭代次数和近似根.二、牛顿迭代法的实现MATLAB求解程序设计：方程及一阶导数函数：function[fun,dfun]=fun0(x)fun=x^3-x-1;%求原函数的值dfun=3*x^2-1;%求一阶导数的值计算主程序：clearx0=1.5;[fun,dfun]=fun0(x0);x1=x0-fun/dfun;i=1;while abs(x1-x0)>1e-5x0=x1;[fun,dfun]=fun0(x0);x1=x0-fun/dfun;i=i+1;enddisp('the solution is x1=')x1disp('the iter time is ')i计算结果为：the solution is x1=x1 =1.3247the iter time isi =4可见经过4次迭代即到达要求的精度，原方程的一个近似实数根为1.3247.三、牛顿迭代法的收敛性牛顿迭代法的迭代函数：)()()(x f x f x x '-=ϕ222)]([)()()]([)()()]([1)(x f x f x f x f x f x f x f x '''='''-'-='ϕ设f (x *)=0，f `(x *)≠0，则ϕ`(x *)=0，故Newton 迭代法在x *附近至少平方收敛。

牛顿迭代法求解非线性方程组的解

10 简化牛顿法简化牛顿法又称平行弦法，其迭代公式为
xk1 xk Cf (xk ),C 0, k 0,1,
(4-7)
从不动点迭代法的角度看，简化牛顿法的迭代函数(x) x Cf (x) ，下面讨论简
化牛顿法的收敛性。
若| '(x) ||1 Cf '(x) | 1 ,即取 0 Cf ' (x) 2 .在根 x* 附近成立，则迭代法
x k 的点 Pk 引切线，并将该切线与 x 轴的交点的横坐标 x k1 作为 x* 的新的近似值。注意到切线方程为
y f (xk ) f '(xk )(x xk )
(4-4)
这样求得的值 x k1 比满足 f (xk ) f '(xk )(x xk ) 0 ，从而就是牛顿公式
x
k 1
| f (xk1) || f (xk ) |
(4-8)
满足此要求的算法称为下山法。
将牛顿法和下山法一起使用时，即在下山法保证函数值稳定下降的前提下，
用牛顿法加快收敛速度。为此，为此将牛顿法的计算结果
xk 1
xk
f (xk ) f ' (xk )
(4-9)
与前一步的近似值 xk 的适当加权平均作为新的改进值
代法中所遇到的 jacobi 矩阵难求的问题。
关键词：非线性方程组、牛顿迭代法、MATLAB、 jacobi 矩阵
一、前言非线性方程组在实际问题中经常出现，并且在科学与工程计算中的地位越来
越来重要，很多常见的线性模型都是在一定条件下由非线性问题简化得到的，为得到更符合实际的解答，往往需要直接研究非线性模型，然而从线性到非线性是一个质的飞跃，方程的性质的不同，所以求解方法也有很大差别。本文主要介绍关于非线性方程及方程组的数值解法，先分析非线性方程的数值解法，然后再延伸到方程组的解法。

c++ 牛顿迭代法解方程组

c++ 牛顿迭代法解方程组牛顿迭代法是一种求解方程的数值方法，它通过迭代逼近的方式，不断接近方程的解。

首先，我们需要定义要解的方程组。

假设我们要求解的方程组为：f1(x1, x2, ..., xn) = 0f2(x1, x2, ..., xn) = 0...fn(x1, x2, ..., xn) = 0其中，f1, f2, ..., fn是方程组中的各个方程，x1, x2, ..., xn是方程组的未知数。

接下来，我们可以利用牛顿迭代法来求解这个方程组。

具体步骤如下：1. 首先，我们需要给出方程组的初始猜测解。

设初始解为x^(0) = (x1^(0), x2^(0), ..., xn^(0))。

2. 然后，我们计算方程组在初始解处的Jacobi矩阵J^(0)，即：J^(0) = [[∂f1/∂x1, ∂f1/∂x2, ..., ∂f1/∂xn],[∂f2/∂x1, ∂f2/∂x2, ..., ∂f2/∂xn],...[∂fn/∂x1, ∂fn/∂x2, ..., ∂fn/∂xn]]其中，∂f/∂x表示方程f对未知数x的偏导数。

3. 接下来，我们计算方程组在初始解处的函数值向量F^(0)，即：F^(0) = [f1(x1^(0), x2^(0), ..., xn^(0)),f2(x1^(0), x2^(0), ..., xn^(0)),...fn(x1^(0), x2^(0), ..., xn^(0))]4. 然后，我们可以利用牛顿迭代公式来更新解，即：x^(k+1) = x^(k) - (J^(k))^(-1) * F^(k)其中，x^(k)表示第k次迭代的解，J^(k)表示第k次迭代的Jacobi矩阵，F^(k)表示第k次迭代的函数值向量。

5. 将更新后的解x^(k+1)代入方程组，并重新计算Jacobi矩阵和函数值向量。

6. 重复步骤4和步骤5，直到满足迭代停止的条件。

常见的迭代停止条件有：达到最大迭代次数、解的变化小于某个阈值、函数值的范数小于某个阈值等。

c++ 牛顿迭代法解方程组

c++ 牛顿迭代法解方程组牛顿迭代法（Newton's Method）是一种用于解方程的迭代算法，可以用于解非线性方程组。

下面是使用 C++ 实现牛顿迭代法解方程组的示例：#include <iostream>#include <cmath>// 定义方程组中的函数double f1(double x, double y) {return x * x + y * y - 1;}double f2(double x, double y) {return x - y * y;}// 定义方程组中的偏导数double df1_dx(double x, double y) {return 2 * x;}double df1_dy(double x, double y) {return 2 * y;}double df2_dx(double x, double y) {return 1;}double df2_dy(double x, double y) {return -2 * y;}// 牛顿迭代法解方程组void newtonIteration(double x0, double y0, int maxIterations) { double epsilon = 1e-6; // 迭代精度double x = x0;double y = y0;for (int i = 0; i < maxIterations; i++) {double det = df1_dx(x, y) * df2_dy(x, y) - df1_dy(x, y) * df2_dx(x, y);double dx = (-f1(x, y) * df2_dy(x, y) + f2(x, y) * df1_dy(x, y)) / det;double dy = (f1(x, y) * df2_dx(x, y) - f2(x, y) * df1_dx(x, y)) / det;x += dx;y += dy;if (std::abs(dx) < epsilon && std::abs(dy) < epsilon) { std::cout << "Converged to solution: x = " << x << ", y = " << y << std::endl;return;}}std::cout << "Iteration did not converge to a solution" << std::endl;}int main() {double initialX = 0.5;double initialY = 0.5;int maxIterations = 100;newtonIteration(initialX, initialY, maxIterations);return 0;}在上述示例中，我们定义了一个方程组，包含两个方程 f1(x, y) = x^2 + y^2 - 1和f2(x, y) = x - y^2。

非线性方程的牛顿法

求函数 f x x 10 x 精度要求： 106
3

例题2
2
19.68x 10.944 的正实根
用Matlab画图，查看根的分布情形
从图形中我们可以看出：在x=7和x=8 之间有一单根；在x=1和x=2 之间有一重根。
初值x0＝8.0 时,计算的是单根, The iterative number is 28,The numerical solution is 7.600001481 初值x0＝1.0 ,计算的是重根, The iterative number is 1356,The numerical solution is 1.198631981
重复上述过程
xk 1
f ( xk ) xk f ( xk )
牛顿法的几何意义
Tangent line : y f ( x0 ) f ( x0 )( x x0 )
y
f ( x0 ) x1 x0 f ( x0 )
x*
x2
x
x1 x0
牛顿法也称为切线法
f ( x1 ) x2 x1 f ( x1 )
例3:设C为正实数,导出用牛顿法求 C 的公式,并证明 2 en 迭代序列的误差 en xn C 满足 en 1 2 xn 2 x C 解：设 x C ，则于是有
f ( x) x 2 C, f ' ( x) 2x, f ' ' ( x) 2
由于 f (0) C, f ( C 1) 2 C 1 0 ], 所以在 [0,1 C ] 内有一正根.又在 [0,1 C 内 f ' ( x) 0, f ' ' ( x) 0根据定理得牛顿迭代格式为:

非线性方程组的牛顿迭代法-最速下降法

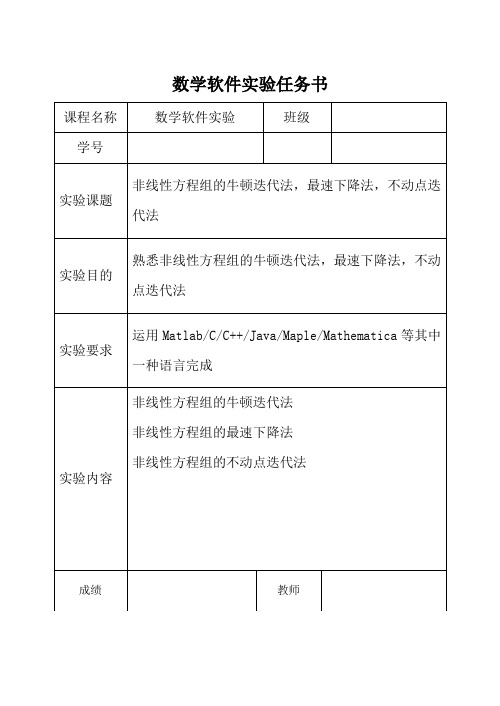
数学软件实验任务书实验一非线性方程组的牛顿迭代法 1 实验原理对于非线性方程11221212(,,,)(,,,)(,,,)n n n n f x x x f x x x f f x x x ⎛⎫ ⎪ ⎪= ⎪ ⎪⎝⎭ 在x (k )处按照多元函数的泰勒展开，并取线性项得到 ()()()()(1)()1111()()()()(1)()()122()()()()(1)()1(,,,)(,,,)()0(,,,)k k k k k k n n k k k k k k k n n n k k k k k k n n n nn f x x x x x f x x x x x f x f x x x x x +++⎛⎫⎛⎫- ⎪ ⎪- ⎪ ⎪'+= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭ 其中1111()n n n n f f x x f x f f x x ∂∂⎛⎫ ⎪∂∂ ⎪' ⎪= ⎪∂∂ ⎪ ⎪∂∂⎝⎭(1)()()()()()1111(1)()()()()()()1221(1)()()()()()1(,,,)(,,,)[()](,,,)k k k k k k n n k k k k k k k n n n k k k k k k n n n n n x x f x x x x x f x x x f x x x f x x x ++-+⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪'=- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ 2 数据来源计算非线性方程组22220.50440x x y x y ⎧--+=⎨+-=⎩ 初值取11x y ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦3 实验步骤步骤一：编写牛顿迭代法的基本程序。

打开Editor 编辑器，输入以下语句：function [x,n,data]=new_ton(x0,tol)if nargin==1tol=1e-10;endx1=x0-f1(x0)/df1(x0);MATLAB 241 数值分析与应用n=1;%迭代过程while (norm(x1-x0)>tol)x0=x1;x1=x0-f1(x0)/df1(x0);n=n+1;%data 用来存放中间数据data(:,n)=x1;endx=x1;以文件名new_ton.m保存。

非线性方程的数值求法牛顿迭代法和弦截法PPT课件

26
Newton下山法
原理：若由 xk 得到的 xk+1 不能使 | f | 减小，则在 xk 和 xk+1 之间找一个更好的点 xk1，使得 f ( xk1) f ( xk ) 。
xk
xk+1
xk1 (1 )xk , [0, 1]
xk 1
[xk
)g( xn
)

n1

n

mng(xn ) mg( xn ) n g(
xn
)

n2 g( xn )
mg( xn ) n g( xn )

n1

2 n

g( xn )
mg( xn ) n g( xn )
若 xn 收敛，即
n 0 (n ),
没有具体的描述，而且若x0 的值没有取好，有可能得不到收敛的结果。
以下定理，给出了 f x 满足一定的条件时，要使得牛顿
迭代法收敛，x0 应满足什么条件。
又 f ( ) 0
( ) 0 1,
牛顿迭代法局部收敛于
又 ( ) 0
即有：牛顿迭代法具有二阶（平方）收敛速度。
注. 定理要求 x0 充分接近 (局部收敛)，充分的程度
没有具体的描述，而且若x0 的值没有取好，有可能得不到收敛的结果。
以下定理，给出了 f x 满足一定的条件时，要使得牛顿
迭代法收敛，x0 应满足什么条件。
定理设 f x 在区间 a,b 上的二阶导数存在，且满足： ① f (a) f (b) 0; （保证 a, b中至少存在一个根）
若 xn 收敛，即 n 0 (n )
lim n1 lim[1

牛顿法解非线性方程(MATLAB和C++)

41 end
42 time = toc;
43
44 fprintf('\nIterated times is %g.\n', times);
45 fprintf('Elapsed time is %g seconds.\n', time);
46
47 root = x_iter;
48
49 % subfunction
5
6 // 功能描述：求解非线性方程根，并输出最终解 7 // 迭代式：x(k+1) = x(k) - f(x(k))/df(x(k)). 8 // 使用：修改标出的“修改”部分即可自定义参数
9
10 // 输入：函数 fun，函数导数 dfun，初值 x0，
4
11 // 最大迭代次数 maxiter，停止精度 tol 12 // 输出：迭代数值解 x_iter2
2
Listing 1: MATLAB EXAMPLE 1 % 2013/11/20 15:14:38
2
3 f = @(x)x^2 − 2; 4 df = @(x)2*x; 5 x0 = 3; 6 root = newton(f, df, x0);
C++ 以 C++ 实现的方法并未编写成为一般可调用的方法，而作为一个独立的文件（包含一个实例），修改部分即可求解对应的方程。具体参照 cpp 文件内注释。
A 附录
A.1 MATLAB
Listing 2: MATLAB CODE 1 function root = newton(f, df, x0, maxiter, tol) 2 %NEWTON Newton's method for nonlinear equations. 3% 4 % NEWTON's method: x(k+1) = x(k) - f(x(k))/f'(x(k)). 5% 6 % Inputs 7 % f - nonlinear equation. 8 % df - derivative of f(x). 9 % x0 - initial value. 10 % maxiter - maximum iterated times. 11 % tol - precision. 12 % 13 % Outputs 14 % root - root of f(x) = 0.

解非线性方程组的牛顿迭代法

3 x3 1.425497619 1.414213562 1.414213562
19
计算三步，方法（2）及（3）均达到10位有效数字，而用牛顿法只有线性收敛，要达到同样精度需迭代30次.
20
7.5 弦截法与抛物线法
用牛顿法求方程（1.1）的根，每步除计算 f (xk ) 外还要算 f (xk )，当函数 f (x)比较复杂时，计算 f (x) 往往较困难，为此可以利用已求函数值 f (xk ), f (xk1), 来回避导数值 f (xk ) 的计算.
的导数为
(x) x f (x)
f (x)
(x*) 1 1 0
m
且 (x*) 1，所以牛顿法求重根只是线性收敛. 若取
16
(x) x m f (x) ,
f (x)
则 (x*) 0
. 用迭代法
xk 1

xk
m
f ( xk ) f (xk )
(k 0,1,)
7.5.1 弦截法
设 xk , xk 1是 f (x) 0的近似根，利用 f (xk ), f (xk1) 构造一次插值多项式 p1(x)，并用 p1(x) 0的根作为新的近似根 xk 1 . 由于
p1(x)
f (xk )
f
( xk ) xk

f xk 1
xk 1

10
在（4.7）中取C 1 ，则称为简化牛顿法，这
f ( x0 )
类方法计算量省，但只有线性收敛，其几何意义是用平行弦与 x轴交点作为 x *的近似. 如图7-4所示.
图7-4
11
（2）牛顿下山法.
牛顿法收敛性依赖初值 x0的选取. 如果x0 偏离所求根 x *较远，则牛顿法可能发散.

牛顿迭代法求根c语言

牛顿迭代法求根c语言牛顿迭代法是一种常用的数值计算方法，其可以用来求解非线性方程的根。

本文将介绍牛顿迭代法的基本原理和实现方法，并提供一些使用C语言实现牛顿迭代法求根的示例代码。

一、牛顿迭代法的原理在介绍牛顿迭代法的原理之前，我们先来看一个简单的例子。

假设我们要求解方程f(x) = 0的近似根，其中f(x)是一个可导函数。

我们可以通过利用切线来逼近方程f(x) = 0的根。

具体地，我们可以选择一个起始点x0，然后在x0处取得f(x0)的切线，将其延长到x轴上的交点x1，那么x1就是f(x) = 0的一个近似根。

可以通过数学方法得到x1的表达式：x1 = x0 - f(x0) / f'(x0)其中f'(x0)表示函数f(x)在x0处的导数。

换句话说，我们使用f(x)在x0处的切线来近似替代f(x)的图形，直到得到f(x) = 0的一个近似根为止。

这就是牛顿迭代法的基本思想。

牛顿迭代法的具体步骤如下：1. 选择一个起始点x0；2. 使用f(x)在x0处的切线来近似替代f(x)的图形；3. 在切线上取得x轴的交点x1； 4. 将x1作为新的起始点，重复步骤2和3，直到得到近似根。

二、牛顿迭代法的实现牛顿迭代法的实现过程比较简单，但需要注意一些细节。

具体实现可以分为以下几个步骤：1. 定义一个函数f(x)，表示待求解的方程；2. 定义一个函数f_prime(x)，表示函数f(x)在x处的导数；3. 定义一个起始点x0；4. 通过牛顿迭代公式计算出x1； 5. 将x1作为新的起始点，重复步骤4，直到满足精度要求为止。

下面，我们提供一段使用C语言实现牛顿迭代法求根的代码示例：```c #include<stdio.h> #include<math.h>#define EPSILON 0.0001double f(double x) { // 表示待求解的非线性方程 return x*x*x - x*x + 2; }double f_prime(double x) { // 表示f(x)在x 处的导数 return 3*x*x - 2*x; }double newton_raphson(double x) { // 牛顿迭代法求根 double x0 = x;while (1) { double x1 = x0 - f(x0) / f_prime(x0);if (fabs(x1 - x0) < EPSILON) return x1;x0 = x1; } }int main() { double x = 0;printf("The root is: %lf\n",newton_raphson(x));return 0; } ```代码中，定义了非线性方程f(x)和它在x处的导数f_prime(x)，然后利用牛顿迭代法计算出方程的近似根。

解非线性方程组的牛顿法

§6 解非线性方程组的迭代法
考虑非线性方程组
f1(x1, x2, , xn ) 0,
f2(x1, x2, , xn ) 0,
fn (x1, x2, , xn ) 0. 利用向量记号写为
F (X ) O. 这里F (X )是定义在某区域D Rn上向量值函数. 若存在 X* D, 使得F (X*) O, 则称X*为非线性方程组的解.
.
逐次迭代得结果.
Step 5 Set x x y
Step 6 If y TOL then OUTPUT(x)
Step7 Set k k 1
STOP.
Step8 OUTPUT (‘Maximum number of iterations exceeded’) STOP.
为了说明上述算法，我们可以看看下面的例子。设
s1
145 272
，
145 272
T
.
x2 x1 s1 0.092，3.092 T .
显然，我们只经过两步计算，所得到的 x2就已经非常靠近解 0，3T .
例1 用牛顿法求解方程组
k x (k) 0 (1.5, 1.0)T
f1( f2(
x1 x1
,x2 ,x2
) )
x1 2 x12
定理 2 设G : D Rn Rn在D内有一不动点X *且G在X *可导,
(G(X*)) 1, 则存在开球 S S( X*, ) D, 对X (0) S, 迭代序列{X (k)}
收敛于X *.
牛顿迭代公式：
X (k1) X (k) F( X (k) ) 1 F ( X (k) ),
其中
f1
F
(
X
(k
)
)

c语言牛顿迭代法

c语言牛顿迭代法牛顿迭代法（Newton-Raphson法）是一种求解方程近似解的方法，它是利用泰勒级数展开函数在某点的值，然后用一阶泰勒展开式的根近似表示函数的零点，因此也被称为牛顿拉弗森法。

它可以高效地解决复杂的非线性方程组，是科学计算领域中最为常用和基础的方法之一。

牛顿迭代法的基本思想是：在第k次迭代时，求出曲线f(x)在点xk的一次导数斜率，以此确定x轴上的一个点xk+1，和该点处曲线的一次切线。

这条切线和x轴交点的横坐标就是极值点的估计值。

这个过程可以迭代多次，直到达到满足一定的误差精度或者迭代次数的要求。

C语言实现牛顿迭代法需要先定义一个函数，这个函数就是需要求解方程的函数。

定义完函数之后，需要实现牛顿迭代公式来求出下一次迭代的估计值，然后不断迭代。

具体实现过程如下：1. 定义函数f(x)，即需要求解方程的函数。

2. 定义函数f_prime(x)，即f(x)的一次导数。

3. 定义变量x和x_next，初始化它们的值。

4. 在循环中，首先计算f(x)和f_prime(x)，然后计算下一个迭代点的估计值x_next = x - f(x) / f_prime(x)。

5. 如果x_next和x的差异满足预设的精度要求，则退出循环。

6. 否则，将x_next的值赋值给x，并重复执行第4步。

C语言实现牛顿迭代法的代码如下：#include <stdio.h>#include <math.h>定义函数f(x)double f(double x) {return x * x - 2;}定义函数f_prime(x)double f_prime(double x) {return 2 * x;}int main() {定义变量double x, x_next, epsilon;int iter;初始化变量x = 1.0;epsilon = 1e-6;iter = 0;迭代求解do {x_next = x - f(x) / f_prime(x);iter++;printf("Iteration %d: x = %lf\n", iter, x_next);x = x_next;} while (fabs(x_next - x) >= epsilon);输出结果printf("Final result: x = %lf\n", x);return 0;}在这个代码中，我们使用了do-while循环来不断执行迭代过程，直到达到预设的精度要求。

C语言编程_牛顿迭代法求方程2

牛顿迭代公式设r是f(x) = 0的根，选取x0作为r初始近似值，过点（x0,f(x0)）做曲线y = f(x)的切线L，L的方程为y = f(x0)+f'(x0)(x-x0)，求出L与x轴交点的横坐标 x1 = x0-f(x0)/f'(x0)，称x1为r的一次近似值。

过点（x1,f(x1)）做曲线y = f(x)的切线，并求该切线与x轴交点的横坐标 x2 = x1-f(x1)/f'(x1)，称x2为r的二次近似值。

重复以上过程，得r的近似值序列，其中x(n+1)=x(n)－f(x(n))/f'(x(n))，称为r的n+1次近似值，上式称为牛顿迭代公式。

解非线性方程f(x)=0的牛顿法是把非线性方程线性化的一种近似方法。

把f(x)在x0点附近展开成泰勒级数 f(x) = f(x0)+(x－x0)f'(x0)+(x－x0)^2*f''(x0)/2! +… 取其线性部分，作为非线性方程f(x) = 0的近似方程，即泰勒展开的前两项，则有f(x0)+f'(x0)(x－x0)-f(x)=0 设f'(x0)≠0则其解为x1=x0－f(x0)/f'(x0) 这样，得到牛顿法的一个迭代序列：x(n+1)=x(n)－f(x(n))/f'(x(n))。

牛顿迭代法又称牛顿切线法，它采用以下方法求根：先任意设定一个与真实的根接近的值x0作为第一个近似根，由x0求出f(x0)，过(x0,f(x0))点做f(x)的切线，交x轴于x1，把它作为第二次近似根，再由x1求出f(x1)，再过(x1,f(x1))点做f(x)的切线，交x轴于x2，再求出f(x2)，再作切线……如此继续下去，直到足够接近真正的x*为止。

就是牛顿迭代公式。

例1 用牛顿迭代法求方程2x3-4x2+3x-6=0在1.5附近的根。

本题中，f(x)= 2x3-4x2+3x-6=((2x-4)x+3)x-6f’(x)= 6x2-8x+3=(6x-8)x+3#include "stdio.h"#include "math.h"voidmain(){ float x1,x0,f,f1;x1=1.5;do{ x0=x1;f=((2*x0-4)*x0+3)*x0-6;f1=(6*x0-8)*x0+3;x1=x0-f/f1;}while(fabs(x1-x0)>=1e-5);printf("THe root of equation is %5.2f\n",x1);}例题2 #include <math.h>main(){float x,x0,d,f,fd;x0=0;do {f=2*x0*x0*x0-4*x0*x0+3*x0-6;fd=6*x0*x0-8*x0+3;d=f/fd;x=x0-d;x0=x;}while(fabs(d)>1e-3);printf("x=%f\n",x); }X+=X-=X*X赋值表达式此表达式为自右向左赋值，如X的初值为12，此表达式赋值步骤如下：1. 先进行“X-=X*X”的运算，它相当于X=X-X*X，X的值为12-144=-1322. 再进行“X+=-132”的运算，相当于X=X+(-132)，X的值为-132-132=-264。

C++牛顿法：快速求解非线性方程的利器!

C++牛顿法：快速求解非线性方程的利器！C++牛顿法是一种高效求解非线性方程的方法，通过不断迭代逼近方程的根，达到求解的目的。

本文将详细介绍C++牛顿法的实现原理、优点、缺点及在科学计算中的应用，并给出相应的代码实现和示例。

一、C++牛顿法的实现原理牛顿法是一种迭代算法，通过不断逼近非线性方程的根，达到求解的目的。

具体实现方法如下：选择一个初始值x0，作为迭代起点；计算函数f(x)在x0处的切线，得到切线方程的截距和斜率；通过切线方程求得下一个迭代点x1；重复步骤2和3，直到满足收敛条件为止。

二、C++牛顿法的优点和缺点1、优点：收敛速度快，一般情况下只需几次迭代就能得到精度较高的解；代码实现简单，易于掌握；可以处理具有多个根的情况。

2、缺点：收敛速度受初始值影响较大，若初始值选择不当，可能会导致算法不收敛；对于某些非线性方程，可能存在局部最小值或最大值，导致算法无法找到全局最优解。

三、C++牛顿法在科学计算中的应用牛顿法在科学计算中有着广泛的应用，例如：求解非线性方程组，如牛顿法可以用于求解二元二次方程组；求函数的零点，如牛顿法可以用于求平方根、对数等函数的零点；求函数的极值点，如牛顿法可以用于求函数的最小值或最大值。

四、C++牛顿法的代码实现和示例下面是一个示例的C++代码，用牛顿法求解方程f(x) = 0的根：#include <iostream>#include <cmath>// 定义函数f(x)double f(double x) {return x * x - 4;}// 定义函数f'(x)的导数double f_derivative(double x) {return 2 * x;}// 牛顿法求解方程的根double newton_method(double x0, double epsilon, int max_iterations) {double x = x0;int iterations = 0;while (iterations < max_iterations) {double fx = f(x);double fx_derivative = f_derivative(x);// 判断是否接近根if (std::abs(fx) < epsilon)break;// 更新xx = x - fx / fx_derivative;iterations++;}return x;}int main() {double x0 = 1.0; // 初始近似解double epsilon = 1e-6; // 精度int max_iterations = 1000; // 最大迭代次数// 使用牛顿法求解方程的根double root = newton_method(x0, epsilon, max_iterations);std::cout << "The root is: " << root << std::endl;return 0;}在上面的代码中，定义了函数f(x)和f'(x)的导数，然后使用牛顿法求解方程f(x) = 0的根。

6.解非线性方程组的牛顿迭代法

eN TN (1 hL) eN 1
TN (1 hL) TN 1 (1 hL) eN 2
TN (1 hL) TN 1
(1 hL)2 TN 2 (1 hL)N 1 T1

N 1 k 0
(1
function f=myfun syms x; syms y f=[x^2+y^2-1;x^3-y]; x0=[0.8;0.6];
>> newton (myfun,x0,1e-6) n=
4 ans =
0.8260 0.5636
7. 最速下降法

f1( x, f2 (x,
y) y)

f1 y f2 y

y1

y0

1 J0
f1 f2
f1 f2 ( x0 , y0 ) f1x f2x
(**)
例： x 2 ( x
y2 5 0 1) y (3x
1)

0
求
(1,1) 附近的解
f1x

f2x
f1 y f2 y

2x y3
Tn1 y( xn1 ) yn1 一步产生的误差
其中是由公式根据前一步的准确值获得的。
y( xn1 ) y( xn h)

y( xn ) hf ( xn ,
y(xn ))
h2 2
y( )
xn xn!
yn1 y( xn ) hf (xn , y( xn )) (Euler方法)
f
(x,
y ( x))dx

(完整word版)c++求解非线性方程组的牛顿顿迭代法

}
void inv_jacobian(float yy[N][N],float inv[N][N])
{float aug[N][N2],L;
int i,j,k;
cout<<"开始计算雅克比矩阵的逆矩阵："<<endl;
for (i=0;i<N;i++)
{ for(j=0;j<N;j++)
aug[i][j]=yy[i][j];
ff(x0,y0);//计算雅克比矩阵jacobian
ffjacobian(x0,jacobian);//计算雅克比矩阵的逆矩阵invjacobian
inv_jacobian(jacobian,invjacobian);//由近似解向量x0计算近似解向量x1
newdundiedai(x0, invjacobian,y0,x1);//计算差向量的1范数errornorm
yy[0][0]=2*x-2;
yy[0][1]=-1;
yy[1][0]=2*x;
yy[1][1]=8*y;
cout<<"雅克比矩阵是："<<endl;
for( i=0;i<N;i++)
{for(j=0;j<N;j++)
cout<<yy[i][j]<<" ";
cout<<endl;
}
cout<<endl;
{ for(j=0;j<N2;j++)
cout<<aug[i][j]<<" ";