emd 希尔伯特黄变换程序

希尔伯特黄变换信号处理

希尔伯特黄变换信号处理
希尔伯特黄变换（Hilbert Huang Transform，简称HHT）是一个信
号处理的方法，常常用于分析非线性和非平稳信号。

它是由黄其炎教
授于1996年开发的，因此也叫做黄变换。

HHT的主要目的是将复杂的信号分解成数个瞬时频率相近的固有模态
函数（Intrinsic Mode Function，简称IMF）。

IMF是自然界中任何非线性现象的基本构建块，因此它们的分析在很多领域都非常重要。

HHT算法通常包括以下几个步骤：
1. 将待处理的信号（无论是时域信号还是频域信号）分解成数个组成
部分，即IMF。

2. 对每个IMF进行希尔伯特变换，得到复信号。

3. 计算每个复信号在复平面上的相位角和振幅。

4. 根据每个IMF在时域上的相位角和振幅，重建原信号的相位角和振幅。

5. 最后，将所有IMF的相位角和振幅相加得到原信号的相位角和振幅。

HHT的优点在于它不需要对信号做任何假设或模型。

它可以处理时域
和频域的信号，非常适合于分析非线性和非平稳信号，例如心电图、语音、天气数据和金融数据等。

HHT也有一些缺点，比如计算复杂度比较高，有时候需要选择合适的参数来得到比较准确的结果。

总的来说，希尔伯特黄变换是一个非常有用的信号处理方法，可以帮助我们了解自然界中复杂的现象。

它在科学、工程和医学等领域都得到了广泛应用。

emd 希尔伯特黄变换程序

（一）简单的EMD程序function imf = emd(x)% Empiricial Mode Decomposition (Hilbert-Huang Transform)% imf = emd(x)% Func : findpeaksx = transpose(x(:));%转置imf = [];while ~ismonotonic(x) %当x不是单调函数，分解终止条件x1 = x;sd = Inf;%均值%直到x1满足IMF条件，得c1while (sd > 0.1) | ~isimf(x1) %当标准偏差系数sd大于0.1或x1不是固有模态函数时，分量终止条件s1 = getspline(x1);%上包络线s2 = -getspline(-x1);%下包络线x2 = x1-(s1+s2)/2;%此处的x2为文章中的hsd = sum((x1-x2).^2)/sum(x1.^2);x1 = x2;endimf{end+1} = x1;x = x-x1;endimf{end+1} = x;% FUNCTIONSfunction u = ismonotonic(x)%u=0表示x不是单调函数，u=1表示x为单调的u1 = length(findpeaks(x))*length(findpeaks(-x));if u1 > 0, u = 0;else, u = 1; endfunction u = isimf(x)%u=0表示x不是固有模式函数，u=1表示x是固有模式函数N = length(x);u1 = sum(x(1:N-1).*x(2:N) < 0);u2 = length(findpeaks(x))+length(findpeaks(-x));if abs(u1-u2) > 1, u = 0;else, u = 1; endfunction s = getspline(x)%三次样条函数拟合成元数据包络线N = length(x);p = findpeaks(x);s = spline([0 p N+1],[0 x(p) 0],1:N);-------------------------------------------------------------------------------- function n = findpeaks(x)% Find peaks.找到极值% n = findpeaks(x)n = find(diff(diff(x) > 0) < 0);u = find(x(n+1) > x(n));n(u) = n(u)+1;------------------------------------------------------------------------------------------ ---------------------------------------------------------------------------------------- function plot_hht00(x,Ts)% 双边带调幅信号的EMD分解% Plot the HHT.% plot_hht(x,Ts)%% :: Syntax% The array x is the input signal and Ts is the sampling period.% Example on use: [x,Fs] = wavread('Hum.wav');% plot_hht(x(1:6000),1/Fs);% Func : emd% Get HHT.clear all;close all;Ts=0.0005;t=0:Ts:1; % 采样率2000HZ% 调幅信号x=sin(2*pi*t).*sin(40*pi*t);s1 = getspline(x);%上包络线s2 = -getspline(-x);%上包络线x1 = (s1+s2)/2;%此处的x2为文章中的hfigure;plot(t,x);xlabel('Time'), ylabel('Amplitude');title('双边带调幅信号');hold on;plot(t,s1,'-r');plot(t,s2,'-r');plot(t,x1,'g');imf = emd(x);for k = 1:length(imf)b(k) = sum(imf{k}.*imf{k});th = angle(hilbert(imf{k}));d{k} = diff(th)/Ts/(2*pi);end[u,v] = sort(-b);b = 1-b/max(b);% Set time-frequency plots.N = length(x);c = linspace(0,(N-2)*Ts,N-1);%figure;for k = v(1:2)plot(c,d{k},'k.','Color',b([k k k]),'MarkerSize',3); hold on;set(gca,'FontSize',8,'XLim',[0 c(end)],'YLim',[0 50]);%设置x、y轴句柄xlabel('Time'), ylabel('Frequency');title('原信号时频图');end% Set IMF plots.M = length(imf);N = length(x);c = linspace(0,(N-1)*Ts,N);for k1 = 0:4:M-1figurefor k2 = 1:min(4,M-k1), subplot(4,1,k2), plot(c,imf{k1+k2});set(gca,'FontSize',8,'XLim',[0 c(end)]);title('EMD分解结果');endxlabel('Time');end(二)function imf = emd(x)% Empiricial Mode Decomposition (Hilbert-Huang Transform)% imf = emd(x)% Func : findpeaksx = transpose(x(:));%转置imf = [];while ~ismonotonic(x) %当x不是单调函数，分解终止条件x1 = x;sd = Inf;%均值%直到x1满足IMF条件，得c1while (sd > 0.1) | ~isimf(x1) %当标准偏差系数sd大于0.1或x1不是固有模态函数时，分量终止条件s1 = getspline(x1);%上包络线s2 = -getspline(-x1);%下包络线x2 = x1-(s1+s2)/2;%此处的x2为文章中的hsd = sum((x1-x2).^2)/sum(x1.^2);x1 = x2;endimf{end+1} = x1;x = x-x1;endimf{end+1} = x;% FUNCTIONSfunction u = ismonotonic(x)%u=0表示x不是单调函数，u=1表示x为单调的u1 = length(findpeaks(x))*length(findpeaks(-x));if u1 > 0, u = 0;else, u = 1; endfunction u = isimf(x)%u=0表示x不是固有模式函数，u=1表示x是固有模式函数N = length(x);u1 = sum(x(1:N-1).*x(2:N) < 0);u2 = length(findpeaks(x))+length(findpeaks(-x));if abs(u1-u2) > 1, u = 0;else, u = 1; endfunction s = getspline(x)%三次样条函数拟合成元数据包络线N = length(x);p = findpeaks(x);s = spline([0 p N+1],[0 x(p) 0],1:N);--------------------------------------------------------------------------------------------------------------------------------------------------------------- function n = findpeaks(x)% Find peaks.找到极值% n = findpeaks(x)n = find(diff(diff(x) > 0) < 0);u = find(x(n+1) > x(n));n(u) = n(u)+1;------------------------------------------------------------------------------------------ ---------------------------------------------------------------------------------------- function plot_hht00(x,Ts)% 双边带调幅信号的EMD分解% Plot the HHT.% plot_hht(x,Ts)%% :: Syntax% The array x is the input signal and Ts is the sampling period.% Example on use: [x,Fs] = wavread('Hum.wav');% plot_hht(x(1:6000),1/Fs);% Func : emd% Get HHT.clear all;close all;Ts=0.0005;t=0:Ts:1; % 采样率2000HZ% 调幅信号x=sin(2*pi*t).*sin(40*pi*t);s1 = getspline(x);%上包络线s2 = -getspline(-x);%上包络线x1 = (s1+s2)/2;%此处的x2为文章中的hfigure;plot(t,x);xlabel('Time'), ylabel('Amplitude');title('双边带调幅信号');hold on;plot(t,s1,'-r');plot(t,s2,'-r');plot(t,x1,'g');imf = emd(x);for k = 1:length(imf)b(k) = sum(imf{k}.*imf{k});th = angle(hilbert(imf{k}));d{k} = diff(th)/Ts/(2*pi);end[u,v] = sort(-b);b = 1-b/max(b);% Set time-frequency plots.N = length(x);c = linspace(0,(N-2)*Ts,N-1);%figure;for k = v(1:2)plot(c,d{k},'k.','Color',b([k k k]),'MarkerSize',3); hold on;set(gca,'FontSize',8,'XLim',[0 c(end)],'YLim',[0 50]);%设置x、y轴句柄xlabel('Time'), ylabel('Frequency');title('原信号时频图');end% Set IMF plots.M = length(imf);N = length(x);c = linspace(0,(N-1)*Ts,N);for k1 = 0:4:M-1figurefor k2 = 1:min(4,M-k1), subplot(4,1,k2), plot(c,imf{k1+k2}); set(gca,'FontSize',8,'XLim',[0 c(end)]);title('EMD分解结果');endxlabel('Time');endplot_hht00(x,Ts)只画出了时频图，没有三维图。

希尔伯特-黄变换说明及程序(标准程序)

目录∙ 1 本质模态函数(IMF)∙ 2 经验模态分解(EMD)∙ 3 结论∙ 4 相关条目∙ 5 参考文献∙ 6 外部链接[编辑]本质模态函数(IMF)任何一个资料，满足下列两个条件即可称作本质模态函数。

⒈局部极大值(local maxima)以及局部极小值(local minima)的数目之和必须与零交越点(zero crossing)的数目相等或是最多只能差1，也就是说一个极值后面必需马上接一个零交越点。

⒉在任何时间点，局部最大值所定义的上包络线(upper envelope)与局部极小值所定义的下包络线，取平均要接近为零。

因此，一个函数若属于IMF，代表其波形局部对称于零平均值。

此类函数类似于弦波（sinusoid-like），但是这些类似于弦波的部分其周期与振幅可以不是固定。

因为，可以直接使用希尔伯特转换，求得有意义的瞬时频率。

[编辑]经验模态分解(EMD)EMD算法流程图建立IMF是为了满足希尔伯特转换对于瞬时频率的限制条件之前置处理，也是一种转换的过程。

我们将IMF来做希尔伯特转换可以得到较良好的特性，不幸的是大部分的资料并不是IMF，而是由许多弦波所合成的一个组合。

如此一来，希尔伯特转换并不能得到正确的瞬时频率，我们便无法准确的分析资料。

为了解决非线性（non-linear）与非稳态（non-stationary）资料在分解成IMF时所遇到的困难，便发展出EMD。

经验模态分解是将讯号分解成IMF的组合。

经验模态分解是借着不断重复的筛选程序来逐步找出IMF。

以讯号为例，筛选程序的流程概述如下:步骤 1 : 找出中的所有局部极大值以及局部极小值，接着利用三次样条(cubic spline)，分别将局部极大值串连成上包络线与局部极小值串连成下包络线。

步骤 2 : 求出上下包络线之平均，得到均值包络线。

步骤 3 : 原始信号与均值包络线相减，得到第一个分量。

步骤 4 : 检查是否符合IMF的条件。

matlab hht变换代码

matlab hht变换代码
在MATLAB中，可以使用以下代码实现希尔伯特-黄变换（HHT）：
% 读取信号
Fs = 1000; % 采样频率
t = (0:1/Fs:length(x)-1/Fs); % 时间向量
x = sin(2*pi*50*t) + sin(2*pi*120*t); % 合成信号
% 希尔伯特-黄变换
[imf,t,A,f] = eemd(x,5); % 使用EEMD方法进行HHT变换
% 绘制原始信号和IMFs
figure;
subplot(2,1,1);
plot(t,x);
title('原始信号');
subplot(2,1,2);
for k = 1:length(imf)
plot(t,imf(k));
end
title('IMFs');
在上述代码中，x是一个合成信号，它由两个正弦波组成。

使用eemd函数对信号进行希尔伯特-黄变换，该函数使用经验模式分解（EMD）方法进行分解。

eemd函数的输出包括：
●imf：固有模式函数（IMFs）
●t：时间向量
●A：每个IMF的瞬时幅度
●f：每个IMF的瞬时频率
最后，使用subplot和plot函数绘制原始信号和IMFs。

希尔伯特黄变换和经验模态分解

希尔伯特黄变换和经验模态分解下载温馨提示：该文档是我店铺精心编制而成，希望大家下载以后，能够帮助大家解决实际的问题。

文档下载后可定制随意修改，请根据实际需要进行相应的调整和使用，谢谢!并且，本店铺为大家提供各种各样类型的实用资料，如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等，如想了解不同资料格式和写法，敬请关注!Download tips: This document is carefully compiled by the editor. I hope that after you download them, they can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you!In addition, our shop provides you with various types of practical materials, such as educational essays, diary appreciation, sentence excerpts, ancient poems, classic articles, topic composition, work summary, word parsing, copy excerpts, other materials and so on, want to know different data formats and writing methods, please pay attention!希尔伯特黄变换和经验模态分解：理论与应用导言希尔伯特黄变换（Hilbert-Huang Transform，HHT）和经验模态分解（Empirical Mode Decomposition，EMD）是近年来在信号处理领域备受关注的两大方法。

以希尔伯特-黄转换法为GPS接收机抑制调频干扰

任何一個資料序列，滿足下列兩個條件即可稱作本質模態函數(IMF)。
5
1. 在整個資料中，局部極大值(local maxima)及局部極小值(local minima)的數目之和必須與零交越點(zero crossing)的數目相等或是最多只能差 1。 2. 在任一時間點上，由局部極大值所定義的上包絡線(upper envelope)與局部極小值所定義的下包絡線(lower envelope)之平均值為零。
3
II. GPS 訊號特性與接收機架構在 GPS 訊號方面[1]，其通訊方法是採用展頻通訊的系統，而此展頻碼可分為 C/A 碼(Coarse/Acquisition Code)及 P 碼(Precision Code)，P 碼是用以提供精確定位服務，一般限用於美國軍方和政府單位，C/A 碼則開放給民間使用。而 C/A 碼和 P 碼的碼率(chip rate)分別是 1.023MHz 及 10.23MHz。衛星所傳送的定位資訊是 50Hz 的二位元訊號，該訊號會乘上展頻碼以達到展頻之目的，之後乘上載波，將展頻後的訊號調變至 L1 及 L2 的通道頻帶後，再將訊號發射出去，而 L1 及 L2 的頻率分別為 1575.42MHz 及 1227.60MHz。在此我們僅考慮 GPS 訊號乘上 C/A 碼調變至 L1 的通道頻帶，將傳送的訊號以數學式表示為
(6)
接著將 r1 t 當作新的資料，重複經由篩選程序解析出第二個 IMF 分量 c2 t ，並將其由 r1 t 中減去，以得到新的殘餘量 r2 t 。如此重複分解 n 次
r2 t r1 t c2 t r3 t r2 t c3 t rn t rn 1 t cn t

用希尔伯特黄变换(HHT)求时频谱和边际谱

【原创】用希尔伯特黄变换(HHT 求时频谱和边际寒假将至，精心将自己最近做的东西总结了一下，能跟大家分享讨论是我的荣幸源代码也贴出来了，希望大家能提出宝贵意见~顺祝大家寒假快乐，新年快乐 1.什么是HHTHHT 就是先将信号进行经验模态分解(EMD 分解)，然后将分解后的每个IMF 分量进行Hilbert 变换，得到信号的时频属性的一种时频分析方法。

2.EMD 分解的步工1^1,*-1(0- 12SD = ~y -------------z is ⑴ r ：-05(/)-q(Z) = /;(/)EMD分解的流程图如下:3.实例演示给定频率分别为10Hz和35Hz的两个正弦信号相叠加的复合信号，采样频率fs=2048Hz 的信号，表达式如下：y=5sin(2*pi*10t)+5*sin(2*pi*35t)(1)为了对比，先用fft对求上述信号的幅频和相频曲线。

复制内容到剪贴板代码:fun cti on fftfenxi clear;clc;N=2048;%fft默认计算的信号是从0开始的t=li nspace(1,2,N);deta=t(2)-t(1);1/detax=5*si n(2*pi*10*t)+5*si n( 2*pi*35*t);% N仁256;N2=512;w1=0.2*2*pi;w2=0.3*2*pi;w3=0.4*2*pi;%x=(t>=-200&t<=-200+N1*deta).*si n(w1*t)+(t>-200+N1*deta&t<=-200+N2*det a).*si n(w2*t)+(t>-200+N2*deta&t<=200).*si n(w3*t);y = x;m=0:N-1;f=1./(N*deta)*m;% 可以查看课本就是这样定义横坐标频率范围的济面计算的丫就是x(t)的傅里叶变换数值%Y=exp(i*4*pi*f).*fft(y)% 将计算出来的频谱乘以exp(i*4*pi*f) 得到频移后[-2,2]之间的频谱值Y=fft(y);z=sqrt(Y.*conj(Y));plot(f(1:100),z(1:100));title(' 幅频曲线')xia ngwei=a ngle(Y);figure(2)plot(f,xia ngwei)title(' 相频曲线')figure(3)plot(t,y,'r')%axis([-2,2,0,1.2])title(' 原始信号')H站惜号(2) 用Hilbert 变换直接求该信号的瞬时频率复制内容到剪贴板代码：clear;clc;clf;%假设待分析的函数是z=t A3N=2048;%fft 默认计算的信号是从0开始的t=li nspace(1,2,N);deta=t(2)-t(1);fs=1/deta; x=5*si n(2*pi*10*t)+5*sin( 2*pi*35*t);z=x; 6D0D4CQ _ALi W 20 i | .qwM atlib. c:n用且由样;hx=hilbert(z); xr=real(hx);xi=imag(hx);%计算瞬时振幅sz=sqrt(xr.A2+xi.A2);%计算瞬时相位sx=a ngle(hx);%计算瞬时频率dt=diff(t);dx=diff(sx);sp=dx./dt;plot(t(1:N-1),sp) title(' 瞬时频率')小结：傅里叶变换不能得到瞬时频率，即不能得到某个时刻的频率值。

用希尔伯特黄变换(HHT)求时频谱和边际谱

用希尔伯特黄变换（HHT）求时频谱和边际谱1.什么是HHT？HHT就是先将信号进行经验模态分解（EMD分解），然后将分解后的每个IMF分量进行Hilbert变换，得到信号的时频属性的一种时频分析方法。

2.EMD分解的步骤。

EMD分解的流程图如下：3.实例演示。

给定频率分别为10Hz和35Hz的两个正弦信号相叠加的复合信号，采样频率fs=2048Hz的信号，表达式如下：y=5sin(2*pi*10t)+5*sin(2*pi*35t)(1)为了对比，先用fft对求上述信号的幅频和相频曲线。

代码:function fftfenxiclear;clc;N=2048;%fft默认计算的信号是从0开始的t=linspace(1,2,N);deta=t(2)-t(1);1/detax=5*sin(2*pi*10*t)+5*sin(2*pi*35*t);% N1=256;N2=512;w1=0.2*2*pi;w2=0.3*2*pi;w3=0.4*2*pi;%x=(t>=-200&t<=-200+N1*deta).*sin(w1*t)+(t>-200+N1*deta&t<=-200+N2*det a).*sin(w2*t)+(t>-200+N2*deta&t<=200).*sin(w3*t);y = x;m=0:N-1;f=1./(N*deta)*m;%可以查看课本就是这样定义横坐标频率范围的%下面计算的Y就是x(t)的傅里叶变换数值%Y=exp(i*4*pi*f).*fft(y)%将计算出来的频谱乘以exp(i*4*pi*f)得到频移后[-2,2]之间的频谱值Y=fft(y);z=sqrt(Y.*conj(Y));plot(f(1:100),z(1:100));title('幅频曲线')xiangwei=angle(Y);figure(2)plot(f,xiangwei)title('相频曲线')figure(3)plot(t,y,'r')%axis([-2,2,0,1.2])title('原始信号')（2）用Hilbert 变换直接求该信号的瞬时频率代码:clear;clc;clf;%假设待分析的函数是z=t^3N=2048;%fft 默认计算的信号是从0开始的t=linspace(1,2,N);deta=t(2)-t(1);fs=1/deta;x=5*sin(2*pi*10*t)+5*sin(2*pi*35*t);z=x;hx=hilbert(z);xr=real(hx);xi=imag(hx);%计算瞬时振幅sz=sqrt(xr.^2+xi.^2);%计算瞬时相位sx=angle(hx);%计算瞬时频率dt=diff(t);dx=diff(sx);sp=dx./dt;plot(t(1:N-1),sp)title('瞬时频率')小结：傅里叶变换不能得到瞬时频率，即不能得到某个时刻的频率值。

用希尔伯特黄变换(HHT)求时频谱和边际谱

用希尔伯特黄变换（HHT）求时频谱和边际谱1.什么是HHT？HHT就是先将信号进行经验模态分解（EMD分解），然后将分解后的每个IMF分量进行Hilbert变换，得到信号的时频属性的一种时频分析方法。

2.EMD分解的步骤。

3.实例演示。

给定频率分别为10Hz和35Hz的两个正弦信号相叠加的复合信号，采样频率fs=2048Hz的信号，表达式如下：y=5sin(2*pi*10t)+5*sin(2*pi*35t)(1)为了对比，先用fft对求上述信号的幅频和相频曲线。

复制内容到剪贴板代码:function fftfenxiclear;clc;N=2048;%fft默认计算的信号是从0开始的t=linspace(1,2,N);deta=t(2)-t(1);1/detax=5*sin(2*pi*10*t)+5*sin(2*pi*35*t);% N1=256;N2=512;w1=0.2*2*pi;w2=0.3*2*pi;w3=0.4*2*pi;%x=(t>=-200&t<=-200+N1*deta).*sin(w1*t)+(t>-200+N1*deta&t<=-200+N2*deta).*sin(w2*t)+(t >-200+N2*deta&t<=200).*sin(w3*t);y = x;m=0:N-1;f=1./(N*deta)*m;%可以查看课本就是这样定义横坐标频率范围的%下面计算的Y就是x(t)的傅里叶变换数值%Y=exp(i*4*pi*f).*fft(y)%将计算出来的频谱乘以exp(i*4*pi*f)得到频移后[-2,2]之间的频谱值Y=fft(y);z=sqrt(Y.*conj(Y));plot(f(1:100),z(1:100));title('幅频曲线')xiangwei=angle(Y);figure(2)plot(f,xiangwei)title('相频曲线')figure(3)plot(t,y,'r')%axis([-2,2,0,1.2])title('原始信号')（2）用Hilbert变换直接求该信号的瞬时频率复制内容到剪贴板代码:clear;clc;clf;%假设待分析的函数是z=t^3N=2048;%fft默认计算的信号是从0开始的t=linspace(1,2,N);deta=t(2)-t(1);fs=1/deta;x=5*sin(2*pi*10*t)+5*sin(2*pi*35*t);z=x;hx=hilbert(z);xr=real(hx);xi=imag(hx);%计算瞬时振幅sz=sqrt(xr.^2+xi.^2);%计算瞬时相位sx=angle(hx);%计算瞬时频率dt=diff(t);dx=diff(sx);sp=dx./dt;plot(t(1:N-1),sp)title('瞬时频率')小结：傅里叶变换不能得到瞬时频率，即不能得到某个时刻的频率值。

希尔伯特-黄变换方法

IMF 1; iteration 2 1.5 1 0.5 0 -0.5 -1 -1.5 10 20 30 40 50 60 70 80 90 100 110 120
residue 1.5 1 0.5 0 -0.5 -1 -1.5 10 20 30 40 50 60 70 80 90 100 110 120
IMF 1; iteration 1 1.5 1 0.5 0 -0.5 -1 -1.5 10 20 30 40 50 60 70 80 90 100 110 120
residue 1.5 1 0.5 0 -0.5 -1 -1.5 10 20 30 40 50 60 70 80 90 100 110 120
IMF 1; iteration 1 1.5 1 0.5 0 -0.5 -1 -1.5 10 20 30 40 50 60 70 80 90 100 110 120
residue 1.5 1 0.5 0 -0.5 -1 -1.5 10 20 30 40 50 60 70 80 90 100 110 120
IMF 1; iteration 1 1.5 1 0.5 0 -0.5 -1 -1.5 10 20 30 40 50 60 70 80 90 100 110 120
residue 1.5 1 0.5 0 -0.5 -1 -1.5 10 20 30 40 50 60 70 80 90 100 110 120
residue 1 0.5 0 -0.5 -1 10 20 30 40 50 60 70 80 90 100 110 120
IMF 1; iteration 4 1 0.5 0 -0.5 -1 10 20 30 40 50 60 70 80 90 100 110 120

几种时频分析方法综述2——希尔伯特黄变换

几种时频分析方法综述2——希尔伯特黄变换EMD是希尔伯特-黄变换的第一步，它是一种数据驱动的自适应信号处理方法。

EMD将非平稳信号分解为一组努力总体分量（Intrinsic Mode Functions，IMFs），每个IMF均满足以下两个条件：1.在整个信号时域上的局部振动特征呈现出类似正弦波的形状。

2.任意一对相邻IMFs的频率没有任何交叉。

EMD的具体过程如下：1.对于给定的非平稳信号，从中提取出包含极值与香农熵最大的分量，并称之为第一IMF。

2.将第一IMF从原信号中去除，得到原信号的一个残差。

3.对残差信号重复步骤1和步骤2，直到得到一组IMF。

EMD的特点在于它不依赖于任何先验知识或设定的基函数，而是根据信号本身的特性进行自适应分解。

这使得EMD可以较好地适应具有非线性和非平稳特性的信号。

在得到一组IMFs后，就可以进行下一步的希尔伯特谱分析。

HSA使用希尔伯特变换来计算每个IMF的瞬时频率和瞬时振幅。

希尔伯特变换是将信号从时域转换到时频域的一种方法，其中每个频率的成分均具有固定的相位。

希尔伯特谱分析的具体步骤如下：1.对每个IMF进行希尔伯特变换，得到每个IMF的解析信号。

2.通过解析信号计算每个IMF的瞬时频率和瞬时振幅。

瞬时频率是指在每个时间点上信号的主要振动频率，瞬时振幅是指信号在每个时间点上的能量大小。

通过对每个IMF的瞬时频率和瞬时振幅进行时频分析，可以得到信号的能量随时间和频率变化的情况。

希尔伯特-黄变换在许多领域都有广泛的应用，例如信号处理、振动分析、气象预测等。

它可以有效地揭示非平稳信号中的时频特性，提供更准确的时频分析结果。

然而，希尔伯特-黄变换也存在一些问题。

例如，EMD方法对于噪声敏感，噪声可能会引入额外的IMF。

此外，EMD方法的计算量较大，对于较长的信号会消耗较长的时间。

综上所述，希尔伯特-黄变换是一种非平稳信号时频分析方法，通过经验模态分解和希尔伯特谱分析实现时域和频域的联合分析。

希尔伯特黄变换matlab程序

下面是一个简单的MATLAB 程序，用于实现希尔伯特-黄变换（Hilbert-Huang Transform）：% 原始信号
t = linspace(0, 1, 100); % 时间范围
x = sin(2*pi*10*t) + sin(2*pi*20*t) + 0.5*randn(size(t)); % 生成一个含有两个频率成分的信号，加上噪声
% 进行希尔伯特-黄变换
[imf, ~] = emd(x); % 对信号进行经验模态分解（Empirical Mode Decomposition）
hht = hilbert(imf); % 对每个分量进行希尔伯特变换
% 绘制结果
figure;
subplot(2, 1, 1);
plot(t, x);
xlabel('时间');
ylabel('原始信号');
title('原始信号');
subplot(2, 1, 2);
plot(t, abs(hht(1, :))); % 绘制第一个分量的振幅
xlabel('时间');
ylabel('振幅');
title('希尔伯特-黄变换结果');
在这个示例中，首先定义了一个时间范围t，然后生成一个包含两个频率成分的信号x，并添加了一些高斯噪声。

接下来，使用emd 函数对信号进行经验模态分解（Empirical Mode Decomposition），得到一组称为内禀模态函数（IMF）的分量。

然后，利用hilbert 函数对每个分量进行希尔伯特变换，得到复数形式的希尔伯特谱。

最后，绘制原始信号和第一个分量的振幅。

希尔伯特—黄变换方法的仿真研究

希尔伯特—黄变换方法的仿真研究希尔伯特—黄变换（Hilbert-Huang Transform，简称HHT）是一种广泛应用于信号处理领域的方法。

该方法由希尔伯特空间和黄-恩博特变换（EMD，Empirical Mode Decomposition）两部分组成。

HHT 方法能够适应非线性、非平稳信号的特点，将信号分解为固有模态函数（Intrinsic Mode Functions，简称IMF），并计算出每个IMF的瞬时频率和振幅。

本文将介绍HHT方法的原理和算法实现，并对其进行仿真研究。

HHT方法的第一步是EMD，它可以将复杂的信号分解为多个IMF。

每个IMF都是信号的局部特征表现，具有非线性和非平稳性。

EMD算法的基本步骤是：将输入信号x(t)进行平滑处理，得到信号x'(t)。

找到信号x'(t)的局部极大值和极小值点，将它们分别连接成上包络线和下包络线。

对上、下包络线进行拟合，得到信号x''(t)。

将x''(t)与x'(t)相减，得到一个残差信号r(t)。

将残差信号r(t)作为新的输入信号，重复步骤1-4，直到r(t)成为一个IMF。

得到IMF后，可以利用希尔伯特变换对每个IMF进行包络线和瞬时相位计算，进而得到IMF的瞬时频率和振幅。

希尔伯特变换算法如下：计算IMF'的导数，得到瞬时相位p(t)。

对瞬时相位进行积分，得到瞬时频率f(t)。

利用IMF和瞬时频率、瞬时相位，计算出希尔伯特变换的结果。

为了验证HHT方法的可行性，我们进行了一系列仿真实验。

实验平台为MATLAB R2021a，实验数据为合成信号和实际信号。

合成信号由多个正弦波和随机噪声组成，实际信号为心电图信号。

实验步骤如下：将合成信号和实际信号作为输入，进行EMD分解，得到多个IMF。

对每个IMF进行希尔伯特变换，得到瞬时频率和振幅。

对瞬时频率和振幅进行绘图，以便观察和分析。

用希尔伯特黄变换(HHT)求时频谱和边际谱

1.什么是HHT？HHT就是先将信号进行经验模态分解（EMD分解），然后将分解后的每个IMF 分量进行Hilbert变换，得到信号的时频属性的一种时频分析方法。

2.EMD分解的步骤。

EMD分解的流程图如下：3.实例演示。

给定频率分别为10Hz和35Hz的两个正弦信号相叠加的复合信号，采样频率fs=2048Hz的信号，表达式如下：y=5sin(2*pi*10t)+5*sin(2*pi*35t)(1)为了对比，先用fft对求上述信号的幅频和相频曲线。

1.function fftfenxi2.clear;clc;3.N=2048;4.%fft默认计算的信号是从0开始的5.t=linspace(1,2,N);deta=t(2)-t(1);1/deta6.x=5*sin(2*pi*10*t)+5*sin(2*pi*35*t);7.%N1=256;N2=512;w1=0.2*2*pi;w2=0.3*2*pi;w3=0.4*2*pi;8.%x=(t>=-200&t<=-200+N1*deta).*sin(w1*t)+(t>-200+N1*deta&t<=-200+N2*deta).*sin(w2*t)+(t>-200+N2*deta&t<=200).*sin(w3*t);9.y=x;10.m=0:N-1;11.f=1./(N*deta)*m;%可以查看课本就是这样定义横坐标频率范围的12.%下面计算的Y就是x(t)的傅里叶变换数值13.%Y=exp(i*4*pi*f).*fft(y)%将计算出来的频谱乘以exp(i*4*pi*f)得到频移后[-2,2]之间的频谱值14.Y=fft(y);15.z=sqrt(Y.*conj(Y));16.plot(f(1:100),z(1:100));17.title('幅频曲线')18.xiangwei=angle(Y);19.figure(2)20.plot(f,xiangwei)21.title('相频曲线')22.figure(3)23.plot(t,y,'r')24.%axis([-2,2,0,1.2])25.title('原始信号')复制代码（2）用Hilbert变换直接求该信号的瞬时频率1.clear;clc;clf;2.%假设待分析的函数是z=t^33.N=2048;4.%fft默认计算的信号是从0开始的5.t=linspace(1,2,N);deta=t(2)-t(1);fs=1/deta;6.x=5*sin(2*pi*10*t)+5*sin(2*pi*35*t);7.z=x;8.hx=hilbert(z);9.xr=real(hx);xi=imag(hx);10.%计算瞬时振幅11.sz=sqrt(xr.^2+xi.^2);12.%计算瞬时相位13.sx=angle(hx);14.%计算瞬时频率15.dt=diff(t);16.dx=diff(sx);17.sp=dx./dt;18.plot(t(1:N-1),sp)19.title('瞬时频率')复制代码小结：傅里叶变换不能得到瞬时频率，即不能得到某个时刻的频率值。

Hilbert-HuangTransform：matlab希尔伯特-黄变换：matlab实现

Hilbert-HuangTransform：matlab希尔伯特-黄变换：matlab实现关于Hilbert-Huang的matlab实现，材料汇总，⽐较杂...感谢所有⽹络上的贡献者们:)核⼼：以下代码计算HHT边际谱及其对应频率⼯具包要求：G-Rilling EMD Toolbox，TFTB Toolbox附：黄锷先⽣课题组开发的⼯具包（可以在找到），这⾥并未⽤到。

% Empirical mode decomposition, resulting in intrinc mode functions.% Without parameter 'MAXMODES' the process may be seriously delayed by% decompose original signals into too many IMFs (not necessary, 9 is% enough generally)imfs = emd(oriSig, 'MAXMODES', 9);% HHT spectrum: hhtS[A, f, t] = hhspectrum(imfs);[hhtS, ~, fCent] = toimage(A, f, t);% Marginal hilbert spectrum: hhtMS, xf: correspondig frequencyfor k = 1 : size(hhtS, 1)hhtMS(k) = sum(hhtS(k, : )) * 1 / fs;endxf = fCent(1, :) .* fs;简单来说，设置好路径之后输⼊install_emd即可。

hhspectrum 函数说明（8楼：⽼⽼的学⽣）% [A,f,tt] = HHSPECTRUM(imf,t,l,aff)% Input:%- imf : matrix with one IMF per row % 将emd分解得到的IMF代⼊就可以，就是你的程序中写的c变量，不⽤加最后⼀⾏的趋势项%- t : time instants % 瞬时时间或持续时间？？（写[1:信号长度]就可以，真实的时间可以根据采样率转换%- l : estimation parameter for instfreq % 瞬时频率的估计参数？？（写1就可以，决定瞬时频率估计时的边界从第⼏个点开始%- aff : if 1, displays the computation evolution % 显⽰计算进程选项，不想显⽰写0就可以%% Output:% - A : amplitudes of IMF rows% - f : instantaneous frequencies% - tt : truncated time instants % 截⽌时间？？（截断时间，返回的是瞬时频率对应的时间，要⽐原来信号的时间按短，由前⾯的l值决定）%% calls:% - hilbert : computes the analytic signal% - instfreq : computes the instantaneous frequency % 瞬时频率%% Example：[A,f,tt] = hhspectrum(c(1:end-1,:),[1:n],1,0);[im,tt,ff] = toimage(A,f,tt,512);disp_hhs(im,tt,[],fs);9楼：⽼⽼的学⽣关于时频图的概念，我认为是与诸如⼩波，gabor等联合时频分析⽅法联系在⼀起的。

用希尔伯特黄变换HHT求时频谱和边际谱

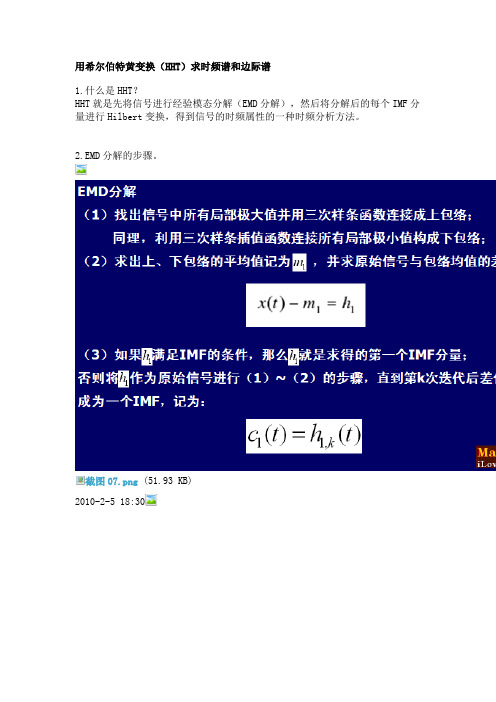
用希尔伯特黄变换（HHT）求时频谱和边际谱1.什么是HHT？HHT就是先将信号进行经验模态分解（EMD分解），然后将分解后的每个IMF分量进行Hilbert变换，得到信号的时频属性的一种时频分析方法。

2.EMD分解的步骤。

截图07.png (51.93 KB)2010-2-5 18:302010-2-5 18:30EMD分解的流程图如下：2010-2-5 18:493.实例演示。

给定频率分别为10Hz和35Hz的两个正弦信号相叠加的复合信号，采样频率fs=2048Hz的信号，表达式如下：y=5sin(2*pi*10t)+5*sin(2*pi*35t)(1)为了对比，先用fft对求上述信号的幅频和相频曲线。

复制内容到剪贴板代码:function fftfenxiclear;clc;N=2048;%fft默认计算的信号是从0开始的t=linspace(1,2,N);deta=t(2)-t(1);1/detax=5*sin(2*pi*10*t)+5*sin(2*pi*35*t);% N1=256;N2=512;w1=0.2*2*pi;w2=0.3*2*pi;w3=0.4*2*pi;%x=(t>=-200&t<=-200+N1*deta).*sin(w1*t)+(t>-200+N1*deta&t<=-200+N2*det a).*sin(w2*t)+(t>-200+N2*deta&t<=200).*sin(w3*t);y = x;m=0:N-1;f=1./(N*deta)*m;%可以查看课本就是这样定义横坐标频率范围的%下面计算的Y就是x(t)的傅里叶变换数值%Y=exp(i*4*pi*f).*fft(y)%将计算出来的频谱乘以exp(i*4*pi*f)得到频移后[-2,2]之间的频谱值Y=fft(y);z=sqrt(Y.*conj(Y));plot(f(1:100),z(1:100));title('幅频曲线')xiangwei=angle(Y);figure(2)plot(f,xiangwei)title('相频曲线')figure(3)plot(t,y,'r')%axis([-2,2,0,1.2])title('原始信号')102.PNG (57.26 KB) 2010-2-5 18:42103.PNG (24.85 KB)2010-2-5 18:42104.PNG (25.65 KB)2010-2-5 18:42（2）用Hilbert变换直接求该信号的瞬时频率复制内容到剪贴板代码:clear;clc;clf;%假设待分析的函数是z=t^3N=2048;%fft默认计算的信号是从0开始的t=linspace(1,2,N);deta=t(2)-t(1);fs=1/deta;x=5*sin(2*pi*10*t)+5*sin(2*pi*35*t);z=x;hx=hilbert(z);xr=real(hx);xi=imag(hx);%计算瞬时振幅sz=sqrt(xr.^2+xi.^2);%计算瞬时相位sx=angle(hx);%计算瞬时频率dt=diff(t);dx=diff(sx);sp=dx./dt;plot(t(1:N-1),sp)title('瞬时频率')106.PNG (35.92 KB)2010-2-5 18:42小结：傅里叶变换不能得到瞬时频率，即不能得到某个时刻的频率值。