用希尔伯特黄变换(HHT)求时频谱和边际谱
Hilbert边际谱.doc
1、Hilbert边际谱我觉得既然已经做出EMD了,也就是得到了IMF。
这个时候就是做hilbert幅值谱,然后对它积分就可以了。
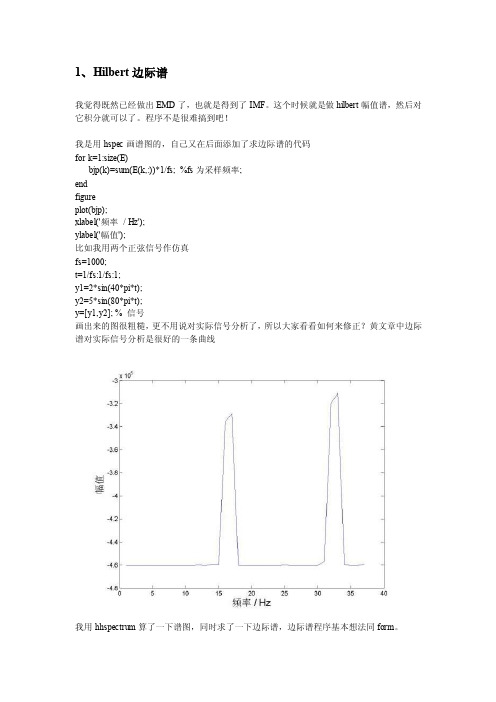
程序不是很难搞到吧!我是用hspec画谱图的,自己又在后面添加了求边际谱的代码for k=1:size(E)bjp(k)=sum(E(k,:))*1/fs; %fs为采样频率;endfigureplot(bjp);xlabel('频率/ Hz');ylabel('幅值');比如我用两个正弦信号作仿真fs=1000;t=1/fs:1/fs:1;y1=2*sin(40*pi*t);y2=5*sin(80*pi*t);y=[y1,y2]; % 信号画出来的图很粗糙,更不用说对实际信号分析了,所以大家看看如何来修正?黄文章中边际谱对实际信号分析是很好的一条曲线我用hhspectrum算了一下谱图,同时求了一下边际谱,边际谱程序基本想法同form。
结果也不太好,20HZ处还行,40HZ就有些问题了,见附图你自己再用这个试试我没有用rilling的hhspectrumnspab:function h1= nspab(data,nyy,minw,maxw,dt)% The function NSPAB generates a smoothed HHT spectrum of data(n,k)% in time-frequency space, where% n specifies the length of time series, and% k is the number of IMF components.% The frequency-axis range is prefixed.% Negative frequency sign is reversed.%% MA TLAB Library function HILBERT is used to calculate the Hilbert transform. %% Example, [h,xs,w] = nspab(lod78_p',200,0,0.12,1,3224).%% Functions CONTOUR or IMG can be used to view the spectrum,% for example contour(xs,w,h) or img(xs,w,h).%% Calling sequence-% [h,xs,w] = nspab(data,nyy,minw,maxw,t0,t1)%% data - 2-D matrix data(n,k) of IMF components% nyy - the frequency resolution% minw - the minimum frequency% maxw - the maximum frequency% t0 - the start time% t1 - the end time% Output-% h - 2-D matrix of the HHT spectrum, where% the 1st dimension specifies the number of frequencies, % the 2nd dimension specifies the number of time values % xs - vector that specifies the time-axis values% w - vector that specifies the frequency-axis values% Z. Shen (JHU) July 2, 1995 Initial%----- Get dimensions (number of time points and components)[npt,knb] = size(data);%----- Get time interval%----- Apply Hilbert Transformdata=hilbert(data);a=abs(data);omg=abs(diff(unwrap(angle(data))))/(2*pi*dt);%----- Smooth amplitude and frequencyfiltr=fir1(8,.1);for i=1:knba(:,i)=filtfilt(filtr,1,a(:,i));omg(:,i)=filtfilt(filtr,1,omg(:,i));end%----- Limit frequency and amplitudefor i=1:knbfor i1=1:npt-1if omg(i1,i) >=maxw,omg(i1,i)=maxw;a(i1,i)=0;elseif omg(i1,i)<=minw,omg(i1,i)=minw;a(i1,i)=0;endendendclear filtr data%va=var(omg(200:1200))%----- Get local frequencydw=maxw - minw;wmx=maxw;wmn=minw;%----- Construct the ploting matrixclear p;h1=zeros(npt-1,nyy+1);p=round(nyy*(omg-wmn)/dw)+1;for j1=1:npt-1for i1=1:knbii1=p(j1,i1);h1(j1,ii1)=h1(j1,ii1)+a(j1,i1);endend%----- Do 3-point to 1-point averaging[nx,ny]=size(h1);%n1=fix(nx/3);%h=zeros(n1,ny);%for i1=1:n1%h(i1,:)=(h1(3*i1,:)+h1(3*i1-1,:)+h1(3*i1-2,:)); %end%clear h1;%----- Do 3-points smoothing in x-directionfltr=1./3*ones(3,1);for j1=1:nyh1(:,j1)=filtfilt(fltr,1,h1(:,j1));endclear fltr;%----- Define the results%w=linspace(wmn,wmx,ny-1)';%xs=linspace(t0,t1,nx)';h1=flipud(rot90(h1));h1=h1(1:ny-1,:);form求边际谱时所用程序是没有问题的,用的是矩形积分公式。
hht边际谱计算

hht边际谱计算
在光学中,Hartmann–Hartmann–Tscherning(HHT)边际谱计算是一种用于分析眼睛的光学性能的方法。
它可以用来评估眼睛的像差、波前畸变和其他光学特性。
HHT边际谱计算的过程通常包括以下步骤:
1. 采集数据:首先,需要采集眼睛通过适当的仪器(如自动视力检查仪或自适应光学系统)所产生的数据。
这可能包括从点光源发出的光线通过眼睛后在屏幕上形成的光斑的信息。
2. 分析数据:接下来,通过计算机程序对采集到的数据进行分析。
这可能涉及将数据转换成波前形状或像差的信息。
通常使用Zernike多项式来表示波前形状。
3. 边际谱计算:在分析数据的过程中,可以利用边际谱计算方法来评估眼睛的光学性能。
这个过程会衡量不同波长下的像差水平以及光学系统的性能。
总的来说,HHT边际谱计算是一个用于评估眼睛光学性能的重要工具,它可以帮助我们理解眼睛的视觉质量以及潜
在的视觉问题。
这对于眼科医生和光学工程师来说都非常有价值。
Hilbert_Huang变换在谱分析中的应用

(上接第 142 页)
把 r1(t)作为新的原信号重复以上过程。对后面得 r1(t)也进行同 样得筛选, 这样依次得到第二阶 IMF、、第 N 阶剩余信号:
r1(t)- c2(t)=r2(t)
┇
(6)
rN-1(t)- cN(t)=rN(t) 最后得到得 rN(t)是一个常量或者变化足够小。从以上得分解
(1.East China Normal University, Shanghai 200062, China; 2.China Ship Scientific R esearch Center, Wuxi 214082, China) Abs tract: Simulation of Hilbert- Huang transform is researched in this paper. Simulation experiment has proved that the non- stationary sig- nal is decomposed according to their intrinsic characteristic scales into a number of intrinsic mode function components by using empirical mode decomposition method. Instantaneous frequency and amplitude spectrum- time- frequency distribution are achieved by Hilbert transform to in- trinsic mode function components. Finally Hilbert- Huang transform has a more intrinsic characteristic of the original data, and better congrega- tiveness in time- frequency, more excellent process in mutational and non- stationary signal by having compared with short time Fourier trans- form and wavelet transform. Key words : Hilbert- Huang Transform; Empirical Mode Decomposition; Intrinsic Mode Function; Spectrum Analysis
python希尔伯特黄变换的时频谱

Python希尔伯特黄变换(Python Hilbert-Huang Transform,简称HHT)是一种复杂非线性信号分析方法,结合了希尔伯特变换和黄变换的优势,能够有效地对非线性和非平稳信号进行时频谱分析。
本文将从HHT的原理、基本步骤和Python实现方法三个方面进行介绍。
一、HHT的原理1.希尔伯特变换希尔伯特变换是一种将实数信号转换为解析信号的数学方法,通过对原信号进行傅立叶变换得到频谱信息,再对频谱信息进行一定的处理得到解析频谱,从而实现信号的解析表示。
希尔伯特变换的核心是求出原信号的解析函数,即原信号的复数形式,其中实部是原信号本身,虚部是原信号的希尔伯特变换。
希尔伯特变换在信号处理领域有着广泛的应用,能够提取信号的瞬时特征,对非平稳信号进行时频分析具有很高的效果。
2.黄变换黄变换是一种局部线性和非线性信号分解方法,可以将非线性和非平稳信号分解成若干个固有模态函数(Intrinsic Mode Function,简称IMF)的线性组合。
黄变换首先对原信号进行极值点的提取,然后通过极值点之间的插值得到包络线,再将原信号减去包络线得到一维信号,并对得到的一维信号进行数据挑选和插值,最终得到IMF。
多次重复以上步骤,直到原信号能够被分解为若干个IMF,再通过IMF的线性组合得到原信号的近似表示。
3.HHT的结合HHT将希尔伯特变换和黄变换结合在一起,利用希尔伯特变换提取信号的瞬时特征,再通过黄变换将信号分解成若干个IMF,从而能够更准确地描述信号的时频特性。
HHT的优势在于能够适用于非线性和非平稳信号,对信号的局部特征具有很好的描述能力,因此在振动信号分析、生物医学信号处理等领域有着广泛的应用。
二、HHT的基本步骤1.信号分解HHT首先对原信号进行希尔伯特变换,得到信号的瞬时频率特征,然后通过黄变换将信号分解成若干个IMF。
2.IMF的提取针对得到的IMF,需要对每个IMF进行较为严格的判别,确定其是否符合IMF的特征:极值点交替出现、包络线对称、局部频率单调。
(完整版)希尔伯特-黄变换(Hilbert-HuangTransform,HHT)

希尔伯特-黄变换(Hilbert-Huang Transform,HHT)0 前言传统的数据分析方法都是基于线性和平稳信号的假设,然而对实际系统,无论是自然的还是人为建立的,数据最有可能是非线性、非平稳的。
希尔伯特-黄变换(Hilbert-Huang Transform,HHT)是一种经验数据分析方法,其扩展是自适应性的,所以它可以描述非线性、非平稳过程数据的物理意义。
1 HHT简介[贺礼平.希尔伯特-黄变换在电力谐波分析中的应用研究[D].湖南:中南大学,2009]HHT的发展。
1995年,Norden E.Huang为研究水表面波构思出一种所谓“EMD--HSA”的时间序列分析法,通过这种方法他发现水波的演化不是连续的,而是突变、离散、局部的。
1998年,Norden E.Huang等人提出了经验模态分解方法,并引入了Hilbert谱的概念和Hilbert谱分析的方法,美国国家航空和宇航局(NASA)将这一方法命名为Hilbert-Huang Transform,简称HHT,即希尔伯特-黄变换。
HHT是一种新的分析非线性非平稳信号的时频分析方法,由两部分组成:第一部分为经验模态分解(Empirical Mode Decomposition,EMD)(the sifting process,筛选过程),它是由Huang提出的,基于一个假设:任何复杂信号都可以分解为有限数目且具有一定物理定义的固有模态函数(Intrinsic Mode Function,IMF;也称作本征模态函数);EMD方法能根据信号的特点,自适应地将信号分解成从高到低不同频率的一系列IMF;该方法直接从信号本身获取基函数,因此具有自适应性,同时也存在计算量大和模态混叠的缺点。
第二部分为Hilbert谱分析(Hilbert Spectrum Analysis,HSA),利用Hilbert变换求解每一阶IMF 的瞬时频率,从而得到信号的时频表示,即Hilbert谱。
频谱管理中基于希尔伯特 - 黄变换的干扰诊断

频谱管理中基于希尔伯特 - 黄变换的干扰诊断张长根;王玉文;孟凡计【摘要】为了给频谱管理的干扰协调机制提供科学有效的依据,在分析系统间EMC 干扰的特点基础上,采用希尔伯特 - 黄变换分析接收机端的干扰信号样本的时 - 频信息、希尔伯特谱和边际谱,得到干扰信号的时频特征.采用多级频率搬移的方法,解决信号的经验模态分解中出现的模态混叠.文章以互调干扰信号的诊断分析为例,验证此法能够将互调干扰从信号样本中分离.【期刊名称】《软件》【年(卷),期】2011(032)006【总页数】4页(P70-72,77)【关键词】干扰诊断;多级频率搬移;希尔伯特;-;黄变换;模态混叠【作者】张长根;王玉文;孟凡计【作者单位】电子科技大学空天科学技术研究院,成都,610054;电子科技大学空天科学技术研究院,成都,610054;电子科技大学空天科学技术研究院,成都,610054【正文语种】中文【中图分类】TP391由于信息技术的不断发展,电磁环境越来越复杂,这使得电磁兼容性(Electromagnetic com patibility,即EMC)问题越来越突出。
为了保障正常的通信,有效地利用有限的频谱资源,建立有效的干扰协调机制显得尤为重要[1]。
为了给干扰协调提供科学、准确的技术依据,就需掌握干扰信号特征,包括基本参数和频谱特性参数。
信号的干扰是非常复杂的,可能是平稳信号或非平稳信号,频域上也可能非常相近。
传统的方法主要是从信号的频率、频率误差、射频电平、发射带宽和调制度等方面来测量信号的特征[1]。
这些方法大都只适用于平稳信号,并且对平稳信号的分析能力还是有限的,特别是频率相近的干扰[2]。
因此,本文从分析系统间电磁兼容性干扰场景出发,根据受干扰台站提供的干扰信号样本,采用希尔伯特-黄变换[3](H ilbert-Huang Transform,HHT)对干扰信号进行细化分析,获得详细的干扰信号的时频特征和边际谱。
希尔伯特黄变换

而且能够表示可变的频率。因此,新方法突破了傅立叶变
换的束缚。用Hilbert谱可以进一步定义边际谱为:
(12)
H H,tdt
这里由HHT得到的边际谱与Fourier频谱有相似之 处,从统计观点上来看,它表示了该频率上振幅 (能量)在时间上的累加,能够反映各频率上的能 量分布,但因为瞬时频率定义为时间的函数,不 同以往Fourier等需要完整的振荡波周期来定义局 部的频率值,而且求取的能量值不是全局定义的 。因此对信号的局部特征反映更准确,在这方面 优于Fourier谱。尤其是在分析非平稳信号时,这 种
2.4 Hilbert谱和边际谱
• 在IMF定义和EMD的基础上,Huang等人系统地
提出了一种分析信号的新理论或新方法。它包
括两个大组成部分,EMD和与之相应的Hilben
谱分析方法。即首先用EMD将任意信号s(t)分解
成有限个IMF的和
n
s(t)cjtrnt
j1
然后分别对每一个IMF分量用Hilbert变换进行谱 分析。最后得到信号的瞬时频率表示:
2.2时间特征尺度
• 现在有三种测量时间尺度的方法:相邻两过零点间隔 的时间尺度,相邻两极值点间隔的时间尺度,相邻两 曲率极值点间隔的时间尺度。三种情况中,时间间隔 都是用来局部测量事物时间变化的。局部极值时间间 隔和曲率时间间隔尺度代表了整个波形,无论波形是 否穿过零线。Huang等人分析认为,时间尺度代表了 信号的局部震荡尺度,并且仅表示一种震荡模式。这 种震荡从一个极值点到另一个相反的极值点,因此时 间尺度是震荡本身所隐含的尺度,称为特征时间尺度。 EMD方法使用的时间尺度是极值点间隔,它当然提供 了一个很好的对时间尺度测量的方法。所谓的局部是 特征尺度是指信号重量邻近极大值点或者极小值点的 时间间隔。HHT分析方法是通过对信号本身的局部特 征进行分析,从局部特征时间尺度入手,获得不同时 间尺度特征的有限个IMF分量。
基于希尔伯特黄变换的刀具磨损特征提取

基于希尔伯特黄变换的刀具磨损特征提取
孙惠斌;牛伟龙;王俊阳
【期刊名称】《振动与冲击》
【年(卷),期】2015(000)004
【摘要】概述了希尔伯特黄变换(HHT)的基本理论和算法,对信号经过经验模态分解(EMD)后得到的固有模态函数(IMF)求取振幅均值,差值筛选出与刀具磨损相关的 IMF 分量,并对单分量固有模态函数求取边际谱,获取边际谱最大幅值点,建立他们与刀具磨损之间的映射关系,进行特征提取,将其作为神经网络的输入特征向量,结合希尔伯特三维时频谱进行刀具磨损状态的判断。
研究结果证明,该方法可以作为刀具磨损监测中信号特征提取的一种简单和可靠的方法。
【总页数】8页(P158-164,183)
【作者】孙惠斌;牛伟龙;王俊阳
【作者单位】西北工业大学机电学院,西安 710072;西北工业大学机电学院,西安 710072;西北工业大学机电学院,西安 710072
【正文语种】中文
【中图分类】TH165;TN911
【相关文献】
1.基于希尔伯特-黄变换和等距特征映射的刀具磨损状态监测 [J], 宋伟杰;关山;庞弘阳
2.钛合金车削加工过程中刀具磨损状态监测的小波包子带能量变换特征提取新方法
[J], 陈侃;傅攀;李威霖;曹伟青
3.基于Hough变换的刀具磨损监测加工表面纹理特征提取 [J], 郑建明;李鹏阳;李言;朱云飞
4.基于改进希尔伯特黄的故障特征提取方法研究 [J], 沈颉; 郭欣; 何嘉
5.基于改进希尔伯特黄的故障特征提取方法研究 [J], 沈颉;郭欣;何嘉
因版权原因,仅展示原文概要,查看原文内容请购买。
HHT方法在山丹地电场数据处理中的应用

收 稿 日期 : 2 0 1 3— 0 4— 2 8
第二 , 信号上任意一点 , 由局部极大值点确定 的包 络 线和 由局 部极 小值 点确 定 的包 络线 的均 值 均为零 , 即信号关于时间轴局部对称。
第一 , 在 整个 数 据序 列 中 , 极值 点 数 目与过 零
点 的数 量相 当或 至 多相差 一个 :
的优势 。 但也有各 自的缺陷: 最大熵谱法存在滤波
器 阶数 的选 择 问 题 , 而 小 波 变 换 方 法 存 在 小 波 基
的选择问题 [ 5 ] 。为避免 传统分析方法 的缺陷 , 本 文 拟 将 希 尔 伯 特 一黄 变 换 ( H i l b e  ̄ . H u a n g T r a n s f o r m。 简称 HH T ) 方 法 应 用 于 山 丹 地 电 场 数
究结果 一致 , 验 证 了该方法处理地 电场数据是有 效的。
关键词 : H H T方法; 地 电场 ; 周期 ; 变 化
中图分类 号 : P 3 1 5 . 6 3
文献标识码 : A
文章编 号 : 1 6 7 3— 8 0 4 7 ( 2 0 1 3 ) 0 3— 0 0 6 1—0 6
O 引吉 F = I
地 电场 是指 地 球 表 面 天 然 存 在 的 电场 , 根 据 场 源 的不 同可分 为大 地 电场 和 自然 电场 。大地 电
处理中将有广阔的应用前景 。 1 HHT方 法
H H T方法 是 由华 裔 科 学 家 N . E . H u a n g等 [ 6 ]
部 分组 成 , 核 心 是 经 验 模 态 分解 ( E m p i r i c a l Mo d e D e c o m p o s i t i o n , 简称 E MD) 。通 过 E MD可 以 自适
用希尔伯特黄变换(HHT)求时频谱和边际谱

用希尔伯特黄变换(HHT)求时频谱和边际谱1.什么是HHT?HHT就是先将信号进行经验模态分解(EMD分解),然后将分解后的每个IMF分量进行Hilbert变换,得到信号的时频属性的一种时频分析方法。
2.EMD分解的步骤。
EMD分解的流程图如下:3.实例演示。
给定频率分别为10Hz和35Hz的两个正弦信号相叠加的复合信号,采样频率fs=2048Hz的信号,表达式如下:y=5sin(2*pi*10t)+5*sin(2*pi*35t)(1)为了对比,先用fft对求上述信号的幅频和相频曲线。
function fftfenxiclear;clc;N=2048;%fft默认计算的信号是从0开始的t=linspace(1,2,N);deta=t(2)-t(1);1/detax=5*sin(2*pi*10*t)+5*sin(2*pi*35*t);% N1=256;N2=512;w1=0.2*2*pi;w2=0.3*2*pi;w3=0.4*2*pi;%x=(t>=-200&t<=-200+N1*deta).*sin(w1*t)+(t>-200+N1*deta&t<=-200+N2*deta).*sin(w2*t)+(t>-200+N2*deta &t<=200).*sin(w3*t);y = x;m=0:N-1;f=1./(N*deta)*m;%可以查看课本就是这样定义横坐标频率范围的%下面计算的Y就是x(t)的傅里叶变换数值%Y=exp(i*4*pi*f).*fft(y)%将计算出来的频谱乘以exp(i*4*pi*f)得到频移后[-2,2]之间的频谱值Y=fft(y);z=sqrt(Y.*conj(Y));plot(f(1:100),z(1:100));title('幅频曲线')xiangwei=angle(Y);figure(2)plot(f,xiangwei)title('相频曲线')figure(3)plot(t,y,'r')%axis([-2,2,0,1.2])title('原始信号')复制代码(2)用Hilbert变换直接求该信号的瞬时频率clear;clc;clf;%假设待分析的函数是z=t^3N=2048;%fft默认计算的信号是从0开始的t=linspace(1,2,N);deta=t(2)-t(1);fs=1/deta;x=5*sin(2*pi*10*t)+5*sin(2*pi*35*t);z=x;xr=real(hx);xi=imag(hx);%计算瞬时振幅sz=sqrt(xr.^2+xi.^2);%计算瞬时相位sx=angle(hx);%计算瞬时频率dt=diff(t);dx=diff(sx);sp=dx./dt;plot(t(1:N-1),sp)title('瞬时频率')复制代码小结:傅里叶变换不能得到瞬时频率,即不能得到某个时刻的频率值。
HHT在震动信号处理中的应用

HHT在震动信号处理中的应用肖玲;吴建星;刘佳;陶慧畅【摘要】希尔伯特-黄变换是一种处理非线性、非平稳信号的方法,它的核心是经验模态分解(EMD),但是EMD分解存在模态混叠等不足现象,针对这个问题引入了总体平均经验模分解(EEMD)算法.对实测的震动信号分别做两种算法的分解得到固有模态函数(IMF),再对其结果进行能量分析,绘制瞬时频率图、希尔伯特谱,得到信号震源的真实时频特征量,以便进一步分析震源类型,从而可以更好地实时预测震动灾害发生的可能情况.【期刊名称】《工业安全与环保》【年(卷),期】2013(039)004【总页数】5页(P32-36)【关键词】希尔伯特-黄变换;经验模态分解;总体平均经验模分解;固有模态函数【作者】肖玲;吴建星;刘佳;陶慧畅【作者单位】武汉科技大学冶金矿产资源高效利用与造块湖北省重点实验室武汉430081;武汉科技大学冶金矿产资源高效利用与造块湖北省重点实验室武汉430081;武汉科技大学冶金矿产资源高效利用与造块湖北省重点实验室武汉430081;武汉科技大学冶金矿产资源高效利用与造块湖北省重点实验室武汉430081【正文语种】中文0 引言目前,井下实时在线监测监控技术广泛应用于安全领域,而对于实时监测的信号分析还有待进一步加强,震动信号是井下监测信号的一种,它可以预测预报井下采动地质灾害、瓦斯突涌以及井下突水等情况。
因此,对实时监测的震动信号进行准确、快速的分析判断是预测的前提。
现在对震动信号进行时频分析应用比较多的方法就是希尔伯特-黄变换(Hilbert-Huang Transform,HHT),它是一种处理非线性、非平稳信号的方法,克服了传统傅里叶变换发生频谱泄漏和栅栏效应、小波变换不能分离相近谐波等方法的缺点,创造性的提出了经验模态分解法(Empirical Mode Decomposition,EMD),从本质上对信号进行平稳化处理。
它能够将一个复杂信号分解成多个固有模态函数(IMF)分量之和,每个IMF 分量都反应了信号本身的物理信息,再对数据进行Hilbert 变换,计算各分量的瞬时频率等,得到信号的Hilbert 谱。
Hilbert变换及谱分析
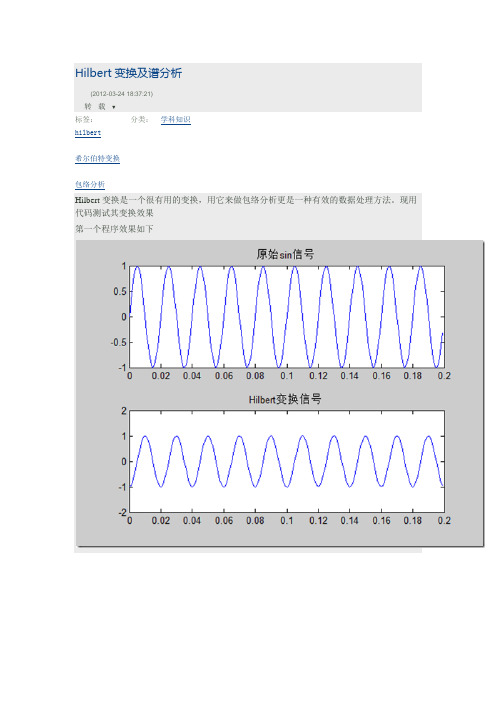
Hilbert变换及谱分析(2012-03-24 18:37:21)转载▼标签:hilbert希尔伯特变换包络分析分类:学科知识Hilbert变换是一个很有用的变换,用它来做包络分析更是一种有效的数据处理方法。
现用代码测试其变换效果第一个程序效果如下% Hilbert变换测试clcclear allclose allts = 0.001;fs = 1/ts;N = 200;f = 50;k = 0:N-1;t = k*ts;% 信号变换% 结论:sin信号Hilbert变换后为cos信号y = sin(2*pi*f*t);yh = hilbert(y); % matlab函数得到信号是合成的复信号yi = imag(yh); % 虚部为书上定义的Hilbert变换figuresubplot(211)plot(t, y)title('原始sin信号')subplot(212)plot(t, yi)title('Hilbert变换信号')% 检验两次Hilbert变换的结果(理论上为原信号的负值)% 结论:两次Hilbert变换的结果为原信号的负值yih = hilbert(yi);yii = imag(yih);max(y + yii)% 信号与其Hilbert变换的正交性% 结论:Hilbert变换后的信号与原信号正交sum(y.*yi)% 谱分析% 结论:Hilbert变换后合成的复信号的谱没有大于奈氏频率的频谱,即其谱为单边的NFFT = 2^nextpow2(N);f = fs*linspace(0,1,NFFT);Y = fft(y, NFFT)/N;YH = fft(yh, NFFT)/N;figuresubplot(211)plot(f,abs(Y))title('原信号的双边谱')xlabel('频率f (Hz)')ylabel('|Y(f)|')subplot(212)plot(f,abs(YH))title('信号Hilbert变换后组成的复信号的双边谱')xlabel('频率f (Hz)')ylabel('|YH(f)|')第二个效果如下第一个包络测试可以看到,此包络分析得到的包络信号频率为20Hz,包络信号的波形为余弦信号的绝对值信号,这是因为计算包络时是取绝对值得到的,从而使信号频率加倍。
Hilbert边际谱
1、Hilbert边际谱我觉得既然已经做出EMD了,也就是得到了IMF。
这个时候就是做hilbert幅值谱,然后对它积分就可以了。
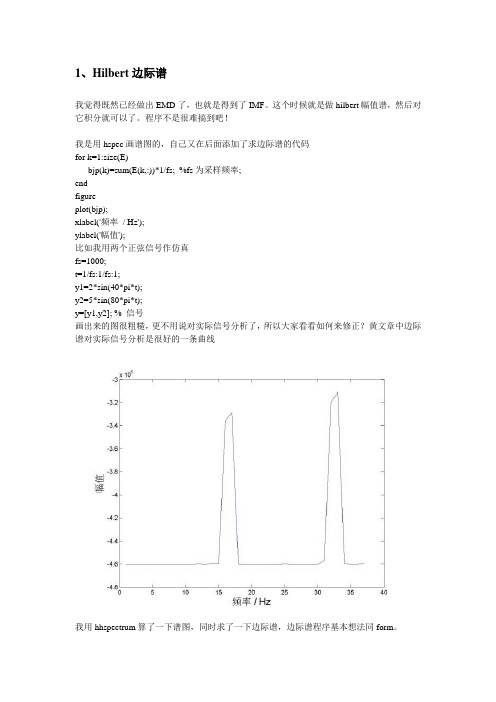
程序不是很难搞到吧!我是用hspec画谱图的,自己又在后面添加了求边际谱的代码for k=1:size(E)bjp(k)=sum(E(k,:))*1/fs; %fs为采样频率;endfigureplot(bjp);xlabel('频率/ Hz');ylabel('幅值');比如我用两个正弦信号作仿真fs=1000;t=1/fs:1/fs:1;y1=2*sin(40*pi*t);y2=5*sin(80*pi*t);y=[y1,y2]; % 信号画出来的图很粗糙,更不用说对实际信号分析了,所以大家看看如何来修正?黄文章中边际谱对实际信号分析是很好的一条曲线我用hhspectrum算了一下谱图,同时求了一下边际谱,边际谱程序基本想法同form。
结果也不太好,20HZ处还行,40HZ就有些问题了,见附图你自己再用这个试试我没有用rilling的hhspectrumnspab:function h1= nspab(data,nyy,minw,maxw,dt)% The function NSPAB generates a smoothed HHT spectrum of data(n,k)% in time-frequency space, where% n specifies the length of time series, and% k is the number of IMF components.% The frequency-axis range is prefixed.% Negative frequency sign is reversed.%% MATLAB Library function HILBERT is used to calculate the Hilbert transform. %% Example, [h,xs,w] = nspab(lod78_p',200,0,0.12,1,3224).%% Functions CONTOUR or IMG can be used to view the spectrum,% for example contour(xs,w,h) or img(xs,w,h).%% Calling sequence-% [h,xs,w] = nspab(data,nyy,minw,maxw,t0,t1)%% data - 2-D matrix data(n,k) of IMF components% nyy - the frequency resolution% minw - the minimum frequency% maxw - the maximum frequency% t0 - the start time% t1 - the end time% Output-% h - 2-D matrix of the HHT spectrum, where% the 1st dimension specifies the number of frequencies, % the 2nd dimension specifies the number of time values % xs - vector that specifies the time-axis values% w - vector that specifies the frequency-axis values% Z. Shen (JHU) July 2, 1995 Initial%----- Get dimensions (number of time points and components)[npt,knb] = size(data);%----- Get time interval%----- Apply Hilbert Transformdata=hilbert(data);a=abs(data);omg=abs(diff(unwrap(angle(data))))/(2*pi*dt);%----- Smooth amplitude and frequencyfiltr=fir1(8,.1);for i=1:knba(:,i)=filtfilt(filtr,1,a(:,i));omg(:,i)=filtfilt(filtr,1,omg(:,i));end%----- Limit frequency and amplitudefor i=1:knbfor i1=1:npt-1if omg(i1,i) >=maxw,omg(i1,i)=maxw;a(i1,i)=0;elseif omg(i1,i)<=minw,omg(i1,i)=minw;a(i1,i)=0;endendendclear filtr data%va=var(omg(200:1200))%----- Get local frequencydw=maxw - minw;wmx=maxw;wmn=minw;%----- Construct the ploting matrixclear p;h1=zeros(npt-1,nyy+1);p=round(nyy*(omg-wmn)/dw)+1;for j1=1:npt-1for i1=1:knbii1=p(j1,i1);h1(j1,ii1)=h1(j1,ii1)+a(j1,i1);endend%----- Do 3-point to 1-point averaging[nx,ny]=size(h1);%n1=fix(nx/3);%h=zeros(n1,ny);%for i1=1:n1%h(i1,:)=(h1(3*i1,:)+h1(3*i1-1,:)+h1(3*i1-2,:)); %end%clear h1;%----- Do 3-points smoothing in x-directionfltr=1./3*ones(3,1);for j1=1:nyh1(:,j1)=filtfilt(fltr,1,h1(:,j1));endclear fltr;%----- Define the results%w=linspace(wmn,wmx,ny-1)';%xs=linspace(t0,t1,nx)';h1=flipud(rot90(h1));h1=h1(1:ny-1,:);form求边际谱时所用程序是没有问题的,用的是矩形积分公式。
Hilbert-HuangTransform:matlab希尔伯特-黄变换:matlab实现

Hilbert-HuangTransform:matlab希尔伯特-黄变换:matlab实现关于Hilbert-Huang的matlab实现,材料汇总,⽐较杂...感谢所有⽹络上的贡献者们:)核⼼:以下代码计算HHT边际谱及其对应频率⼯具包要求:G-Rilling EMD Toolbox,TFTB Toolbox附:黄锷先⽣课题组开发的⼯具包(可以在找到),这⾥并未⽤到。
% Empirical mode decomposition, resulting in intrinc mode functions.% Without parameter 'MAXMODES' the process may be seriously delayed by% decompose original signals into too many IMFs (not necessary, 9 is% enough generally)imfs = emd(oriSig, 'MAXMODES', 9);% HHT spectrum: hhtS[A, f, t] = hhspectrum(imfs);[hhtS, ~, fCent] = toimage(A, f, t);% Marginal hilbert spectrum: hhtMS, xf: correspondig frequencyfor k = 1 : size(hhtS, 1)hhtMS(k) = sum(hhtS(k, : )) * 1 / fs;endxf = fCent(1, :) .* fs;简单来说,设置好路径之后输⼊install_emd即可。
hhspectrum 函数说明(8楼:⽼⽼的学⽣)% [A,f,tt] = HHSPECTRUM(imf,t,l,aff)% Input:%- imf : matrix with one IMF per row % 将emd分解得到的IMF代⼊就可以,就是你的程序中写的c变量,不⽤加最后⼀⾏的趋势项%- t : time instants % 瞬时时间或持续时间??(写[1:信号长度]就可以,真实的时间可以根据采样率转换%- l : estimation parameter for instfreq % 瞬时频率的估计参数??(写1就可以,决定瞬时频率估计时的边界从第⼏个点开始%- aff : if 1, displays the computation evolution % 显⽰计算进程选项,不想显⽰写0就可以%% Output:% - A : amplitudes of IMF rows% - f : instantaneous frequencies% - tt : truncated time instants % 截⽌时间??(截断时间,返回的是瞬时频率对应的时间,要⽐原来信号的时间按短,由前⾯的l值决定)%% calls:% - hilbert : computes the analytic signal% - instfreq : computes the instantaneous frequency % 瞬时频率%% Example:[A,f,tt] = hhspectrum(c(1:end-1,:),[1:n],1,0);[im,tt,ff] = toimage(A,f,tt,512);disp_hhs(im,tt,[],fs);9楼:⽼⽼的学⽣关于时频图的概念,我认为是与诸如⼩波,gabor等联合时频分析⽅法联系在⼀起的。
HHT变换讲义

HHT变换讲义1.1简介传统的信号处理方法,如傅立叶分析是一种纯频域的分析方法。
它用频率不同的各复正弦分量的叠加来拟合原函数,也即用()ωf。
而()ωF在有F来分辨()ω限频域上的信息不足以确定在任意小范围内的函数()ωf,特别是非平稳信号在时间轴上的任何突变,其频谱将散布在整个频率轴上。
而且,非平稳动态信号的统计特性与时间有关,对非平稳信号的处理需要进行时频分析,希望得到时域和频域中非平稳信号的全貌和局域化结果。
在傅立叶变换中,人们若想得到信号的时域信息,就得不到频域信息。
反之亦然。
后来出现的小波(Wavelet)变换通过一种可伸缩和平移的小波对信号变换,从而达到时频局域化分析的目的。
但这种变换实际上没有完全摆脱傅立叶变换的局限,它是一种窗口可调的傅立叶变换,其窗内的信号必须是平稳的。
另外,小波变换是非适应性的,小波基一旦选定,在整个信号分析过程中就只能使用这一个小波基了。
HHT(Hilbert-Huang Transform)技术是(1998年由NASA的Norden E Huang 等提出的新的信号处理方法。
该方法适用于非线性非平稳的信号分析,被认为是近年来对以傅立叶变换为基础的线性和稳态谱分析的一个重大突破。
目前HHT 技术已用于地球物理学和生物医学等领域的研究,并取得了较好的结果。
存在的问题尽管HHT技术在处理非线性、非稳态信号方面有很大的优势,但是这个方法本身还是有许多的问题有待进一步研究。
正如Huang 在文章中指出的那样,对于这种新的信号处理方法,其基的完备性还需要严密的证明。
另外,在做Hilbert变换时出现的边界效应也需要更好的方法来解决。
但是,HHT技术中最严重,也是现今研究的最多的是EMD 分解中的包络过程。
从对EMD分解方法的介绍可以看出,包络线的构造影响着整个分解的结果,也决定了后面的Hilbert变换。
Huang 采用的三次样条插值来拟和包络线。
在实际应用中,发现这样做会产生严重的边界效应,污染了原始数据。
边际谱和HHT谱的画法

看到版上总有人在问边际谱和HHT谱的画法,又搜索了一下,好像没有这方面的主题帖子,就发两个以前写的小程序,权作抛砖引玉吧。
% 边际谱与FFT比较clearT = 1; % 仿真时间f1 = 15.2;f2 = 40;fs = 1000; % 采样率N = T*fs;n = 1:N;s = sin(2*pi*f1/fs*n) + sin(2*pi*f2/fs*n);s_fft = abs(fft(s))/N;imf = emd(s);[A, fa, tt] = hhspectrum(imf);[E, tt1] = toimage(A,fa,tt,length(tt));for k=1:size(E,1)bjp(k) = sum(E(k,:))*1/fs*1/T;endf = (0:N-3)/N*(fs/2);figure(1);plot(f,bjp);xlabel('频率/ Hz');ylabel('幅值');figure(2);plot(0:fs/N:fs/2-fs/N, s_fft(1:end/2))% 实际信号的HHT谱和边际谱clearrand('seed', 0);T = 0.01; % 仿真时间R = 5000; % 码速率fd = 10000; % 载波频差fc = 20000; % 载波频率fs = 200000; % 采样率samp = fs/R; % 每个码元上的采样点数N = T*fs;n = 1:N;x = randint(1, R*T, 2);y = fskmod(x, 2, fd, samp, fs);y = y .* exp(i*2*pi*fc/fs*n);y = real(y);% z = awgn(y, 20, 'measured');z = y;imf = emd(z);[A, fa, tt] = hhspectrum(imf);if size(imf,1) > 1[A,fa,tt] = hhspectrum(imf(1:end-1, :));else[A,fa,tt] = hhspectrum(imf);end[E, tt1] = toimage(A,fa,tt,length(tt));disp_hhs(E, tt1);% 使用灰度图显示% colormap(gray(255))for k = 1:size(E,1)bjp(k) = sum(E(k,:))*1/fs*1/T; endf = (0:N-3)/N*(fs/2);figure(2);plot(f, bjp);。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
用希尔伯特黄变换(HHT)求时频谱和边际谱1.什么是HHT?HHT就是先将信号进行经验模态分解(EMD分解),然后将分解后的每个IMF分量进行Hilbert变换,得到信号的时频属性的一种时频分析方法。
2.EMD分解的步骤。
EMD分解的流程图如下:3.实例演示。
给定频率分别为10Hz和35Hz的两个正弦信号相叠加的复合信号,采样频率fs=2048Hz的信号,表达式如下:y=5sin(2*pi*10t)+5*sin(2*pi*35t)(1)为了对比,先用fft对求上述信号的幅频和相频曲线。
代码:function fftfenxiclear;clc;N=2048;%fft默认计算的信号是从0开始的t=linspace(1,2,N);deta=t(2)-t(1);1/detax=5*sin(2*pi*10*t)+5*sin(2*pi*35*t);% N1=256;N2=512;w1=0.2*2*pi;w2=0.3*2*pi;w3=0.4*2*pi;%x=(t>=-200&t<=-200+N1*deta).*sin(w1*t)+(t>-200+N1*deta&t<=-200+N2*det a).*sin(w2*t)+(t>-200+N2*deta&t<=200).*sin(w3*t);y = x;m=0:N-1;f=1./(N*deta)*m;%可以查看课本就是这样定义横坐标频率范围的%下面计算的Y就是x(t)的傅里叶变换数值%Y=exp(i*4*pi*f).*fft(y)%将计算出来的频谱乘以exp(i*4*pi*f)得到频移后[-2,2]之间的频谱值Y=fft(y);z=sqrt(Y.*conj(Y));plot(f(1:100),z(1:100));title('幅频曲线')xiangwei=angle(Y);figure(2)plot(f,xiangwei)title('相频曲线')figure(3)plot(t,y,'r')%axis([-2,2,0,1.2])title('原始信号')(2)用Hilbert 变换直接求该信号的瞬时频率代码:clear;clc;clf;%假设待分析的函数是z=t^3N=2048;%fft 默认计算的信号是从0开始的t=linspace(1,2,N);deta=t(2)-t(1);fs=1/deta;x=5*sin(2*pi*10*t)+5*sin(2*pi*35*t);z=x;hx=hilbert(z);xr=real(hx);xi=imag(hx);%计算瞬时振幅sz=sqrt(xr.^2+xi.^2);%计算瞬时相位sx=angle(hx);%计算瞬时频率dt=diff(t);dx=diff(sx);sp=dx./dt;plot(t(1:N-1),sp)title('瞬时频率')小结:傅里叶变换不能得到瞬时频率,即不能得到某个时刻的频率值。
Hilbert变换是求取瞬时频率的方法,但如果只用Hilbert变换求出来的瞬时频率也不准确。
(出现负频,实际上负频没有意义!)(3)用HHT求取信号的时频谱与边际谱代码:function HHTclear;clc;clf;N=2048;%fft默认计算的信号是从0开始的t=linspace(1,2,N);deta=t(2)-t(1);fs=1/deta;x=5*sin(2*pi*10*t)+5*sin(2*pi*35*t);z=x;c=emd(z);%计算每个IMF分量及最后一个剩余分量residual与原始信号的相关性[m,n]=size(c);for i=1:m;a=corrcoef(c(i,:),z);xg(i)=a(1,2);endxg;for i=1:m-1%-------------------------------------------------------------------- %计算各IMF的方差贡献率%定义:方差为平方的均值减去均值的平方%均值的平方%imfp2=mean(c(i,:),2).^2%平方的均值%imf2p=mean(c(i,:).^2,2)%各个IMF的方差mse(i)=mean(c(i,:).^2,2)-mean(c(i,:),2).^2;end;mmse=sum(mse);for i=1:m-1mse(i)=mean(c(i,:).^2,2)-mean(c(i,:),2).^2;%方差百分比,也就是方差贡献率mseb(i)=mse(i)/mmse*100;%显示各个IMF的方差和贡献率end;%画出每个IMF分量及最后一个剩余分量residual的图形figure(1)for i=1:m-1disp(['imf',int2str(i)]) ;disp([mse(i) mseb(i)]);end;subplot(m+1,1,1)plot(t,z)set(gca,'fontname','times New Roman')set(gca,'fontsize',14.0)ylabel(['signal','Amplitude'])for i=1:m-1subplot(m+1,1,i+1);set(gcf,'color','w')plot(t,c(i,:),'k')set(gca,'fontname','times New Roman')set(gca,'fontsize',14.0)ylabel(['imf',int2str(i)])endsubplot(m+1,1,m+1);set(gcf,'color','w')plot(t,c(m,:),'k')set(gca,'fontname','times New Roman')set(gca,'fontsize',14.0)ylabel(['r',int2str(m-1)])%画出每个IMF分量及剩余分量residual的幅频曲线figure(2)subplot(m+1,1,1)set(gcf,'color','w')[f,z]=fftfenxi(t,z);plot(f,z,'k')set(gca,'fontname','times New Roman')set(gca,'fontsize',14.0)ylabel(['initial signal',int2str(m-1),'Amplitude'])for i=1:m-1subplot(m+1,1,i+1);set(gcf,'color','w')[f,z]=fftfenxi(t,c(i,:));plot(f,z,'k')set(gca,'fontname','times New Roman')set(gca,'fontsize',14.0)ylabel(['imf',int2str(i),'Amplitude'])endsubplot(m+1,1,m+1);set(gcf,'color','w')[f,z]=fftfenxi(t,c(m,:));plot(f,z,'k')set(gca,'fontname','times New Roman')set(gca,'fontsize',14.0)ylabel(['r',int2str(m-1),'Amplitude'])hx=hilbert(z);xr=real(hx);xi=imag(hx);%计算瞬时振幅sz=sqrt(xr.^2+xi.^2);%计算瞬时相位sx=angle(hx);%计算瞬时频率dt=diff(t);dx=diff(sx);sp=dx./dt;figure(6)plot(t(1:N-1),sp)title('瞬时频率')%计算HHT时频谱和边际谱[A,fa,tt]=hhspectrum(c);[E,tt1]=toimage(A,fa,tt,length(tt));figure(3)disp_hhs(E,tt1) %二维图显示HHT时频谱,E是求得的HHT谱pausefigure(4)for i=1:size(c,1)faa=fa(i,:);[FA,TT1]=meshgrid(faa,tt1);%三维图显示HHT时频图surf(FA,TT1,E)title('HHT时频谱三维显示')hold onendhold offE=flipud(E);for k=1:size(E,1)bjp(k)=sum(E(k,:))*1/fs;endf=(1:N-2)/N*(fs/2);figure(5)plot(f,bjp);xlabel('频率 / Hz');ylabel('信号幅值');title('信号边际谱')%要求边际谱必须先对信号进行EMD分解function [A,f,tt] = hhspectrum(x,t,l,aff)error(nargchk(1,4,nargin));if nargin < 2t=1:size(x,2);endif nargin < 3l=1;endif nargin < 4aff = 0;endif min(size(x)) == 1if size(x,2) == 1x = x';if nargin < 2t = 1:size(x,2);endendNmodes = 1;elseNmodes = size(x,1);endlt=length(t);tt=t((l+1):(lt-l));for i=1:Nmodesan(i,:)=hilbert(x(i,:)')';f(i,:)=instfreq(an(i,:)',tt,l)'; A=abs(an(:,l+1:end-l));if affdisprog(i,Nmodes,max(Nmodes,100)) endendfunction disp_hhs(im,t,inf)% DISP_HHS(im,t,inf)% displays in a new figure the spectrum contained in matrix "im" % (amplitudes in log).%% inputs : - im : image matrix (e.g., output of "toimage")% - t (optional) : time instants (e.g., output of "toimage")% - inf (optional) : -dynamic range in dB (wrt max)% default : inf = -20%% utilisation : disp_hhs(im) ; disp_hhs(im,t) ; disp_hhs(im,inf) % disp_hhs(im,t,inf)figurecolormap(bone)colormap(1-colormap);if nargin==1inf=-20;t = 1:size(im,2);endif nargin == 2if length(t) == 1inf = t;t = 1:size(im,2);elseinf = -20;endendif inf >= 0error('inf doit etre < 0')endM=max(max(im));im = log10(im/M+1e-300);inf=inf/10;imagesc(t,fliplr((1:size(im,1))/(2*size(im,1))),im,[inf,0]);set(gca,'YDir','normal')xlabel(['time'])ylabel(['normalized frequency'])title('Hilbert-Huang spectrum')function [f,z]=fftfenxi(t,y)L=length(t);N=2^nextpow2(L);%fft默认计算的信号是从0开始的t=linspace(t(1),t(L),N);deta=t(2)-t(1);m=0:N-1;f=1./(N*deta)*m;%下面计算的Y就是x(t)的傅里叶变换数值%Y=exp(i*4*pi*f).*fft(y)%将计算出来的频谱乘以exp(i*4*pi*f)得到频移后[-2,2]之间的频谱值Y=fft(y);z=sqrt(Y.*conj(Y));4.总结。
