2.5 矩阵的秩及其求法

合集下载

矩阵求秩方法

矩阵求秩方法
求矩阵的秩是线性代数中常见的问题，以下是关于矩阵求秩的10条方法及其详细描述：
1. 奇异值分解法：通过对矩阵进行奇异值分解，将矩阵变换为一个对角矩阵，其中非零元素的个数即为矩阵的秩。

2. 初等变换法：利用矩阵的初等行（列）变换，将矩阵化简为行简化阶梯型矩阵，其中非零行的个数即为矩阵的秩。

3. 极大线性无关组法：通过逐步选择矩阵中的列，构建一个极大线性无关组，其中向量的个数即为矩阵的秩。

4. 秩-零空间法：矩阵的秩与其零空间的维数之和为矩阵的列数。

可以通过计算矩阵的零空间 (null space) 的维数来求解矩阵的秩。

5. 行列式法：矩阵的行列式非零的最大子阵的阶数就是矩阵的秩。

6. 直接检验法：将矩阵转换为梯形矩阵或行阶梯矩阵，其中非零行的个数即为矩阵的秩。

7. 特征值法：矩阵的秩等于其特征值不为零的个数。

8. 与单位矩阵求秩法：通过将矩阵与单位矩阵进行连接，得到一个增广矩阵，进而将其化简为行简化阶梯型矩阵，其中非零行的个数即为矩阵的秩。

9. Gauss-Jordan消元法：通过高斯消元法和高斯约当消元法将矩阵化简为行简化阶梯型矩阵，其中非零行的个数即为矩阵的秩。

10. 极大线性无关组与生成组比较法：利用极大线性无关组与生成组的关系来求解矩阵的秩，其中生成组的个数等于矩阵的秩。

矩阵的秩计算

矩阵的秩计算矩阵的秩是线性代数中一个重要的概念，它可以用来描述矩阵的线性相关性和线性无关性。

在计算机科学、工程学和物理学等领域中，矩阵的秩也有着广泛的应用。

本文将从基本概念、计算方法和应用三个方面介绍矩阵的秩。

一、基本概念矩阵的秩指的是矩阵中线性无关的行或列的最大个数。

具体来说，对于一个m行n列的矩阵A，如果它的秩为r，那么就意味着存在r 个线性无关的行或列，且没有更多的线性无关行或列。

同时，矩阵的秩也等于它的列空间或行空间的维度。

二、计算方法对于一个矩阵A，可以通过进行初等行变换或初等列变换来求解其秩。

初等行变换包括交换两行、某行乘以一个非零常数、某行加上另一行的k倍。

初等列变换与之类似。

通过这些变换，可以将矩阵A转化为行简化阶梯形或列简化阶梯形，从而求得其秩。

可以通过矩阵的特征值来计算矩阵的秩。

具体来说，对于一个n阶矩阵A，如果它有n个非零的特征值，那么它的秩为n。

反之，如果它只有k个非零特征值，那么它的秩就是n-k。

三、应用1. 线性方程组的解：对于一个m行n列的矩阵A和n行1列的矩阵X，可以通过求解AX=0来得到线性方程组的解。

如果矩阵A的秩等于n，那么线性方程组有唯一解；如果矩阵A的秩小于n，那么线性方程组有无穷多解；如果矩阵A的秩小于m，那么线性方程组无解。

2. 矩阵的相似性：矩阵的秩还可以用于判断两个矩阵是否相似。

如果两个矩阵A和B相似，那么它们的秩相等。

3. 矩阵的逆：对于一个n阶矩阵A，如果它的秩等于n，那么它是可逆的，即存在一个n阶矩阵B，使得AB=BA=I，其中I是单位矩阵。

反之，如果矩阵A的秩小于n，那么它是不可逆的。

4. 图像处理：在图像处理中，可以使用矩阵的秩来判断图像的信息量。

如果一个图像的秩较高，那么它包含了更多的信息；反之，如果一个图像的秩较低，那么它的信息量较少。

总结起来，矩阵的秩是描述矩阵线性相关性和线性无关性的重要指标。

它可以通过初等行变换、初等列变换或特征值来计算。

2.5 矩阵的秩及其求法

求 R( A).
1 0 2 −4 1 0 2 −4 −4 → 0 1 −1 2 r 2r ，解 A 2 − 0 1 −1 2 r1 → r3 + 1 0 −1 1 − 2 0 0 0 0
R(A) = 2
13
1 −1 1 2 例5 设A = 3 λ −1 2, 且R（A） 2 = ，求λ, µ 5 3 µ 6
∴ R( A) = 3
A为满秩方阵。
19
若求A 若求的标准型矩阵
1 − 2 1 − 4 0 −1 −1 3 → 0 0 1 9 0 0 0 0
2 1 1 0 →0 2 0 0
0 −1 2 1 0 0
4 0 12 3 1 9 2 0 0 0
矩阵A 的第一、三行，第二、四列相交处的元素所构成的二阶子式为
2 −1 D2 = 0 −1
3 5 为 A 的一个三阶子式。
而
1 2 D3 = 4 6
1 0 −1
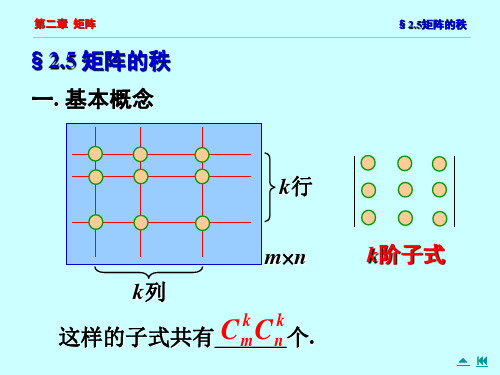
k k m× n 矩阵 A 共有 cmcn 个 k 阶子式。显然，
4
设
A = (aij )m×n 当 A＝0 时，它的任何子式都为零。
⑤ R（AB）≤ min{R（A），R（B）} ⑥ 若 Am×nBn×s=0，则 R（A）+R（B）≤n
24
例8
设A为n阶矩阵，证明R（A+E）+R（A-E）≥n 证： ∴ 而 ∴ ∵ （A+E）+（E-A）=2E r（A+E）+ r（ E-A ）≥ r（2E）=n r（ E-A ）= r（ A-E ） r（A+E）+r（A-E）≥n
7
矩阵秩的求法二、矩阵秩的求法 1、子式判别法定义。、子式判别法(定义定义)。

2.6-矩阵的秩

001
1 0 5 1 0 5 1 0 5 1 0 0
E(1, 3(5)) = 0 1 0 , 0 1 0 0 1 0 = 0 1 0 .
00 1 001 00 1 001
第二章矩阵
§2.6 方阵的逆矩阵
2. 可逆矩阵的分解
***
(1) * * *
** * ***
***
= ***
10 0
010.
000 *** 000 001
第二章矩阵
2 0 4 1
0 1 3 2 的3阶子式有14个:
4 0 8 2
§2.5矩阵的秩
2 0 4 2 0 1 2 4 1 0 4 1
0 1 3 = 0 1 2 = 0 3 2 = 1 3 2 = 0. 4 0 8 4 0 2 4 8 2 0 8 2
第二章矩阵
§2.5矩阵的秩
问题: 假若一个56的矩阵中所有3阶子式都等
1 0
0 1
3/2 1
3 1
5/2 1
1 3 2 故A1 = 3/2 3 5/2 .
1 1 1
第二章矩阵
§2.6 方阵的逆矩阵
三. 用初等变换解矩阵方程
设A可逆, 则A可以经过有限次初等行变换化为行最简形——单位矩阵E.
下面用初等变换解矩阵方程AX = B. 注意到X = A1B.
(A B) … (E ?)
第二章矩阵
§2.5 矩阵的秩
定理2. 设A是满秩方阵，则存在初等方阵
P1, P2, , Ps. 使得 Ps Ps1 , P2P1A E
第二章矩阵
§2.5 矩阵的秩
定理3. mn矩阵A, m阶初等矩阵
P1, P2, …, Ps 及m阶初等矩阵

矩阵的秩及其求法矩阵秩求法演示文稿

5 3 6
0
8
5
4
1 1 1 2
0 3 4 4 0 5 1 0
R(A) 2, 5 0, 1 0
5, 1
三、满秩矩阵定义3 A 为 n 阶方阵时，
RA n, 称 A 是满秩阵，（非奇异矩阵）
RA n, 称 A 是降秩阵，（奇异矩阵）可见：RA n A 0
RA n A ~ E
RA n A ~ En
例如 1 A 2 3
2 1 1
3 2 2
1 0 0
2 3 2
3 1 4 0 3 0
0 1 2
0 1 3
1 0 0
0 0
1 0 E 0 1
RA 3
A为满秩方阵。
关于矩阵的秩的一些重要结论：
定理5
R(AB) R(A), R(AB) R(B),即
对于满秩方阵A施行初等行变换可以化为单位阵E, 又根据初等阵的作用：每对A施行一次初等行变换，相当于用一个对应的初等阵左乘A, 由此得到下面的定理
定理3 设A是满秩方阵，则存在初等方阵
P1, P2,, Ps. 使得 Ps Ps1 , P2P1A E
对于满秩矩阵A，它的行最简形是 n 阶单位阵 E .
2 1 所构成的二阶子式为 D2 0 1
12 3 而 D3 4 6 5 为 A 的一个三阶子式。
1 0 1
显然， m n 矩阵 A 共有 cmk cnk 个 k 阶子式。
2. 矩阵的秩
定义2 设 A aij mn ，有r 阶子式不为0，任何r+1阶
子式(如果存在的话)全为0 , 称r为矩阵A的秩，
0 1
2 3
4 6
求 RA.
1 1 1 2

求矩阵的秩的步骤

矩阵秩的计算方法：将矩阵A按初等行数变换为梯形矩阵B，梯形矩阵B的非零行数即为矩阵A的秩。

在线性代数中，矩阵A的列秩是A的线性独立列数的最大值，类似地，行秩是A的线性独立的水平行数的最大值，一般说来，如果将矩阵看作行向量或列向量，则秩是这些行向量或列向量的秩，即包含在最大不相关群中的向量的个数。

矩阵秩的性质；
1.矩阵的行秩、列秩、秩均相等。

2.初等变换不改变矩阵的秩。

3.矩阵Rab<=min{Ra，Rb}乘积的秩。

4.如果p和q是可逆矩阵，则r(PA)=r(A)=r(AQ)=r(PAQ)。

5.当r(A)<=n-2时，最高阶非零子公式的阶数<=n-2，n-1阶子公式为零，而伴随矩阵中的每个元素都是n-1阶子公式加一个符号，所以伴随矩阵是零矩阵。

6.当r(A)<=n-1时，最高阶非零子公式的阶数为<=n-1，因此n-1
阶子公式可能不为零，因此伴随矩阵可能为非零(等号成立时伴随矩阵必须为非零)。

矩阵的秩

D4 3 0 21 D5 3 6 2 4 0
D3
1 6 0 4 0 6
4
2 7
D6 7 4 42 Nhomakorabea高等代数
●矩阵的秩的概念
定义2.5.2 矩阵A中所有不为零的子式的最高阶数，称为矩阵A的秩，记作 R(A) 或 r(A)。如果 R(A)=r，则 A 中至少有一个 r 阶子式不等于零，
高等代数
定理2.5.2 n阶矩阵A可逆的充要条件是R(A)=n
定理2.5.3 n阶矩阵A可逆的充要条件是方阵A满秩序。
定理2.5.4 一个方阵满秩的充要条件是它能表示为初等矩阵的乘积
高等代数
所有高于 r 阶的子式都为零。
例如
1 2 3 A 2 2 1 3 4 4
因为所以
高等代数
A 0
1 2 2 0 2 2
R( A) 2
1 3 2 2 0 2 1 3 的秩. 例求矩阵A= 2 0 1 5 解: 因为 1 3 2 0, 计算A的3阶子式. 0 2 1 3 2 0 2 1 0, 2 0 1 1 2 2 0 1 3 0, 2 1 5 1 3 2 0 2 3 0, 2 0 5 3 2 2 2 1 3 0. 0 1 5 所以, R(A)=2.
高等代数
●利用矩阵的初等变换求矩阵的秩
定理2.5.1 设矩阵A经过初等变换化为B，则A有不等于零的 K阶子式当且仅当B有不等于零的K阶子式推论2.5.1 矩阵的初等变换不改变矩阵的秩。
初等变换求矩阵秩的方法: 用初等行变换把矩阵变成为行阶梯形矩阵, 行阶梯形矩阵中非零行的行数就是矩阵的秩.
一、矩阵的秩概念二、矩阵的秩求法

线性代数-矩阵的秩

设A
=
2 −2 3
−4 4 −6
8 −2 0
−036 , b
=
2 43
求矩阵A及矩阵B = ( A b)的秩. 解分析：设 B 的行阶梯形矩阵为 B~ = ( A~,b~),
则 A~ 就是 A 的行阶梯形矩阵，故从 B~ = ( A~,b~) 中可同时看出 R( A) 及 R(B).
1 − 2 2 − 1 1
故 R(AT A) = R(A).
又由于 B 也可经一次初等变换变为 A, 故也有 R(B) ≤ R( A).
因此 R( A) = R(B).
经一次初等行变换矩阵的秩不变，即可知经有限次初等行变换矩阵的秩仍不变．
设A经初等列变换变为 B,也有R( A) = R(B).
设 A 经初等列变换变为 B, 则 AT 经初等行变换变为 BT , R( AT ) = R(BT ),
6 11
则这个子式便是A 的一个最高阶非零子式.
设 n 阶可逆矩阵 A， A ≠ 0, ∴ A 的最高阶非零子式为 A, R( A) = n, 故 A 的标准形为单位阵 E, A ~ E.
可逆矩阵的秩等于阶数，故称可逆矩阵为满秩矩阵. 奇异矩阵为降秩矩阵 .
1 − 2 2 − 1 1
例5
− 2 0 1 5
解
13 02 −2 0
1 0
3 = 2 ≠ 0, 2
计算A的3阶子式，
−2
1 3 2 1 −2 2
− 1 = 0, 0 2 3 = 0, 0 − 1 3 = 0,
1
−2 0 5 −2 1 5
3 −2 2
2 − 1 3 = 0, ∴ R(A) = 2.
015
1 3 − 2 2 另解对矩阵 A = 0 2 − 1 3 做初等变换，

求矩阵的秩的三种方法

求矩阵的秩的三种方法矩阵是线性代数中的一个重要概念，它由一个数域中的矩形阵列组成，是线性变换的一种表现形式。

矩阵的秩是矩阵的重要性质之一，它可以告诉我们矩阵中行向量或列向量之间的关系。

在实际应用中，求解矩阵的秩是非常常见的问题。

本文将介绍矩阵的三种求解秩的方法。

方法一：高斯消元法高斯消元法是求解矩阵秩的一种基础方法。

对于一个矩阵A，如果它的秩为r，则A必然存在一个大小为r的非零行列式。

我们可以通过对矩阵A进行初等行变换将矩阵转化为行简化阶梯矩阵，然后统计矩阵中非零行的个数来确定矩阵的秩。

具体步骤如下：1. 对矩阵A进行高斯列变换，将A转化为行简化阶梯矩阵形式。

2. 统计矩阵中非零行的个数，即为矩阵的秩。

对于下面的矩阵A，我们可以通过高斯消元法求解矩阵的秩：$$A=\begin{bmatrix}1 &2 & 3\\4 &5 & 6\\7 & 8 & 9\end{bmatrix}$$按照高斯消元法的步骤对A进行初等行变换，得到行简化阶梯矩阵：方法二：矩阵的列空间对于一个矩阵A，其列空间是由A中所有列向量所张成的向量空间。

矩阵的秩等于它的列空间的维度。

我们可以先求解矩阵A的列空间的维度，然后确定矩阵A的秩。

具体步骤如下：2. 取矩阵A中与非零列对应的列向量，将它们作为张成列空间的一组基。

3. 求解列空间的维度，即为矩阵A的秩。

阶梯矩阵中非零列的位置分别是1和2，因此取A中的第1列和第2列作为列空间的一组基。

可以看出，这组基中存在一个线性关系：第2列 = 2*第1列。

矩阵A的列空间实际上只由A中的第1列张成，其维度为1，因此矩阵A的秩为1。

总结：本文介绍了求解矩阵秩的三种方法：高斯消元法、矩阵的列空间和矩阵的行空间。

对于一般的矩阵，三种方法的求解结果并不一定相同。

但无论采用哪种方法，都能够有效地求解矩阵的秩。

还有一些特殊的矩阵，它们的秩具有一些特殊性质：1. 对于一个n阶矩阵A，如果它是一个可逆矩阵，那么它的秩为n。

矩阵的秩及其求法求秩的技巧

第五节：矩阵的秩及其求法一、矩阵秩的概念1. ｋ阶子式定义1 设在A 中任取k 行ｋ列交叉处元素按原相对位置组成的阶行列式,称为A 的一个k 阶子式。

例如共有个二阶子式，有个三阶子式矩阵A 的第一、三行,第二、四列相交处的元素所构成的二阶子式为而为 A 的一个三阶子式。

显然, 矩阵 A 共有个 k 阶子式。

２. 矩阵的秩定义2 设有r 阶子式不为0，任何ｒ+1阶子式(如果存在的话)全为0 , 称ｒ为矩阵Ａ的秩,记作R (Ａ）或秩(A )。

规定：零矩阵的秩为 0 .注意：(1) 如 R ( A ) = r ，则 A 中至少有一个 r 阶子式所有 r + 1 阶子式为 0,且更高阶子式均为 0,r 是 A 中不为零的子式的最高阶数，是唯一的 .（2) 有行列式的性质, （3) R(Ａ) ≤m , R (A ) ≤n ，０ ≤R (A ） ≤min { m , n } ．(4) 如果 An ×ｎ , 且则 R( A ） = n .反之，如 R ( Ａ ) = n ,则因此,方阵Ａ可逆的充分必要条件是 R ( A ) = n ．二、矩阵秩的求法1、子式判别法（定义)。

例1 设为阶梯形矩阵,求Ｒ（B ）。

解由于存在一个二阶子式不为0,而任何三阶子式全为0,则Ｒ(B ) = 2.结论：阶梯形矩阵的秩=台阶数。

例如()n m ij a A ⨯={}),m in 1(n m k k ≤≤⎪⎪⎪⎭⎫ ⎝⎛----=110145641321A 182423=C C 43334=C C 10122--=D 1015643213-=D n m ⨯k n k m c c ()n m ij a A ⨯=0,r D ≠()().T R A R A =0,A ≠0.A ≠⎪⎪⎪⎭⎫ ⎝⎛=000007204321B 02021≠⎪⎪⎪⎭⎫ ⎝⎛=010*********A ⎪⎪⎪⎭⎫ ⎝⎛=001021B ⎪⎪⎪⎭⎫ ⎝⎛=100010011C 125034000D ⎛⎫ ⎪= ⎪ ⎪⎝⎭21235081530007200000E ⎛⎫ ⎪ ⎪= ⎪ ⎪⎝⎭()3=A R ()2=B R ()3=C R ()2R D =()3R E =一般地，行阶梯形矩阵的秩等于其“台阶数”—— 非零行的行数。

矩阵的秩_精品文档

1 1
4 1
r2 r4
2 3
0 2
1 0
5 3 5 0
3 2 0 5 0
A
3 2
2 0
3 1
6 1 5 3
1 6 4 1 4
r1 r4 r2 r4 r3 2r1 r4 3r1
1 6 4 1 4 0 4 3 1 1 0 12 9 7 11 0 16 12 8 12
把矩阵用初等行变换变成为阶梯形矩阵，阶梯形矩阵中阶梯上元素的个数就是矩阵的秩
或者：
把矩阵用初等变换变成为标准形矩阵，标准形矩阵1的个数就是矩阵的秩.
3 2 0 5 0
例4
设
A
3 2
2 0
3 1
6 5
1 3
,
求矩阵
A
的
1 6 4 1 4
秩，并求 A 的一个最高阶非零子式．
解对A作初等行变换，变成行阶梯形矩阵：
F
Er O
O O
显然，F有一个r阶子式 Er 1 0 ，而F中的任一个
(r+1)阶子式都至少有一个零行和零列，从而为0
R(F) r
从而：标准形矩阵的秩等于其中1的个数
（2）阶梯形矩阵
由例3知，对于阶梯形矩阵，当我们选定阶梯上的元素所在的行、列后所得的r阶子式不等于0，
而任一个(r+1)阶子式必含有至少一个零行，从而为0
解分析：设 B 的行阶梯形矩阵为B~ ( A~,b~),
则 A~ 就是 A的行阶梯形矩阵，
故从 B~ ( A~,b~) 中可同时看出R( A) 及 R(B).
1 2 2 1 1
B
2 2
4 4
8 2
0 3

2.5 矩阵的秩及其求法

2 1
0 1
2
1 2 3 1 2 2 共有C 3 例如设 A 4 6 5 4 ， C 4 18 1 0 1 1 3 3 个二阶子式，有 C 4 C 3 4 个三阶子式。
1 2
而
3 5 为 A 的一个三阶子式。
D3 4 6
1 0 1

E
16
关于秩的一些结论（熟记）：规定：零矩阵的秩为 0 . T R ( A ) R ( A ). (1) 根据行列式的性质， (2) A为m×n矩阵, 0 ≤R(A) ≤min { m , n } .
R(AB) R(A), R(AB) R(B),即 R(AB) min{R(A)，R(B)}。设A是 m n 矩阵， B是 n t 矩阵，定理4 R( A) R( B ) n R( AB). 定理3 推论1 推论2 推论3 如果 A B = 0 则 R( A) R( B) n. 则 B = 0。如果 R(A)= n, A B = 0
6
a 1 1 例3 设 A 1 a 1 如果 R A 3 , 求 a . 1 1 a 分析：R（A)<3,A所有的3阶子式为零，即A的行列式为零。
解 R A 3 A 1 1 a 1 或 a 2
a 1 1 a 1 (a 2)(a 1) 0
1
12
Ex1.
求矩阵A 的秩，并求A 的一个最高阶非零子式。解先求A 的秩，对A 作初等行变换化为行阶梯形：
故R（A）= 3 。
再求A 的一个最高阶非零子式。
因R（A）= 3 ，知A 的最高阶非零子式为 3 阶，易计算A 的前三行构成的子式
因此这个子式便是A 的一个最高阶子式。

矩阵的秩与运算

矩阵的秩与运算
一·矩阵秩的求法
求矩阵的秩主要有三种方法；(1)定义
法，利用定义寻找矩阵中非零子式的最高
阶数。

(2)初等变换法，对矩阵实施初等行变
换，将其变成为行阶梯形矩阵，行阶梯形矩
阵中非零行的行数就是矩阵的秩；(3)标准
形法，求矩阵的标准形，l的个数即为矩阵
的秩。

二·矩阵的秩与行列式
对于一个方阵A，如何判断它是
否可逆，除了根据它的行列式是否为零，还
可以根据方阵秩的大小来判断。

比如方阵A（nn）
其秩R, ，若R ＜ n，则显然矩阵行列式为零，不可逆；
若R = n ,则矩阵行列式不为零，矩阵可逆。

三·矩阵的秩与线性方程组
1齐次的
齐次线性方程组
●系数矩阵R = n ，则有且仅有一个0解
●系数矩阵R ＜ n，则有无数个解。

2非齐次的
费齐次线性方程组，设系数矩阵A ,增广矩阵B
●若R(A) = R(B) = n ，则有且仅有一个解；
●若R(A) = R(B)＜n，则有无数个解；
●若R(A)≠R(B) ，则方程组无解。

四·矩阵的秩与二次曲面
说二次曲面，其实就是与二次型的关系。

有定义知道，
二次型的秩定义为其矩阵的秩，这就为解决二次曲面问题找到了一个可转移的办法。

正所谓遇难则变，变则通。

道家之言，诚哉大哉！！
下面将具体举例阐述，二次型总可以经线性变换成CY化为标准形（比如合同变换），而且，同的非退化线性变换化为不同的标准形，但这些标准形中所含平方项的个数是相同的，所含平方项的个数就等于二次型的秩，也就是矩阵的秩。

2.5 矩阵的秩

Байду номын сангаас
可逆矩阵， O 为什么？ r r . 1 2 I r2 O O O
返回
2 0 0 0 2 0 0 0
2 4 2 6 2 2 0 0 1 1 0 0
1 2 1 3 1 0 1 0
1 0 5 1
r2 2 1 0 r3 r2 0 r4 3r2 0
R( A) 2,
R( B ) 3.
返回
A
m n
A
m n
A
m n
推论对任意矩阵A, R(PA)=R(AQ)=R(PAQ)=R(A)，其中P, Q分别为可逆矩阵. 证因为Q可逆，存在初等矩阵E1, …, Et使得 Q= E1• • • Et，
AQ =A E1• • • Et，
即 AQ 为A经列初等变换所得. 故 R(AQ)= R(A). 同理可证其他.
显然对任意矩阵A， A的秩唯一，但其最高阶非零子式一般不唯一.
返回
例1 求矩阵的秩：
1 (1) A 2 1 2 ; ( 2) B 2 1 4 2 1 8 ; ( 3) C 2 1 3 2 4 6 4 8 2 1 2 0
解 (1)、（2）易
O P1 I r2 O O P2 Q2 O O
I r1 O O O O P2 O
O Q2
A 所以，秩 O
I r1 O O O O 秩 B O
返回
三、矩阵的标准形（分解）
定理2
对任意矩阵A , 都存在可逆矩阵P , Q 使得
m n m m n n
I PAQ O
r

求矩阵的秩有下列基本方法(1)用初等变换.即用矩阵的初等行(.

(2) XA B
~
A 初等列变换
B
E BA1
X
BA1
或者
初等行变换
~ ( AT BT)
( E (AT )1BT )
X T (AT )1BT X BA1
例 3.设
A
103
0 1 1
104 , 且AX
A
2 X , 求矩阵X .
解：AX A 2X (A - 2E)X A
X
(A - 2E)1 A
1 1 1 1 1 0 1 0
A～
1
1 3
2 1 2
1 1 3
2 11
~
0
0 0
1 0 0
0 0 0
0
0 1
从而得方程组的通解为
x1 1
x
x2 x3 x4
k
0 1 0
(k为任意常数)
当a 2 时,把系数矩阵A化为行最简矩阵为
A～
1
1
1 3
1 2 1 2
1 1 2 3
1 2
1 a 3
2 a1
~
0 0 0
1 2 5
0 a 1
0
1 a23
1 1 1 1
~
0
0 0
1 0 0
0 a 1
0
1
a
0
2
当a 1 or a 2 时，R( A) 4，此时方程组
有非零解，可仿照解法一求出它的通解。
四、解矩阵方程的初等变换法
(1) AX B
初等行变换
~ (A B)
(E A1B) X A1B
1 1 1 1 1 1 1 1
解一：A
1 1

25矩阵的秩及习题处理

T34(4)：解： 2
3 2 2 3 令A 1 1 0 ，则 | A | 1 1 0 1 0，且： 1 2 1 1 2 1 2
A11
1 0 2 1
2 3 2 1
2 3
1, A12
4, A22
1
3
0
1 1
1, A13
T
3)当r ( A) min{ m , n}时，称矩阵 A为满秩矩阵。
注： (1) 非奇异矩阵（可逆矩阵）A，有 | A | 0，
A的秩就等于它的阶数，A为满秩矩阵。
(2) 奇异矩阵A，也称为降秩矩阵。
3 2 2 1 0 3 1 2 5 0 观察：求矩阵 B 的秩. 0 0 0 4 3 0 0 0 0 0
1 已知 A 0 例1： 2 1 3 2 0, 解 0 2
1 0 3 2 1 1 , 2 1 00 3 2
3 2 2 2 1 3 ，求秩． 0 1 5
计算A的3阶子式，
2 2
3 2 2 1 0 , 2 3 2 , 1 3 00 0 1 5 2
§2.5 矩阵的秩
1. k 阶子式
定义 : 设A (a ij )是m n矩阵，从 A中任取 k行k列 ( k min{ m , n}), 把位于这些行和列的相保持它们原来的相对位矩阵 A的一个 k阶子式。
1 0 A 0 2 0 0
交处的元素，
置所构成的 k阶行列式，称为
B , A
1 - 2 A 1 BA1 1 1 ，且 A 则D 0 1 ， 1 A 0 1 - 2 3 4 1 - 2 1 1 1 A BA 0 1 2 3 0 1 2 1 ， 1 0 1 2 1 2 1 0 1 所以 A . 0 0 1 2 0 0 0 1

矩阵的秩及初等矩阵

第二章矩阵
§2.4 矩阵的秩
记为r(A 记为r(A)或秩(A) 2. 矩阵A的秩矩阵A A中有一个r阶子式不为零中有一个r r(A) = r r(A A的所有l（l>r）阶子式都等于零的所有l l>r）零矩阵的秩规定为0. 零矩阵的秩规定为0. 1 −1 1 1 2 −2 0 6 0 4 1 −4 5 7 5 −1 0 4 的秩=? 的秩=? −3 4
命题：初等行变换不减小命题：初等行变换不减小矩阵的秩不减小矩阵的秩
初等初等由于矩阵A B，则 B A. 由于矩阵，行变换行变换
定理：初等行变换不改变不改变矩阵的秩定理：初等行变换不改变矩阵的秩
1 −1 1 1 2 −2 0 6 0 4 1 −4 5 7 5 −1 0 4 的秩=? 的秩=? −3 4
a b c a b c a x 1 x y z = x y z , b y 2 k 2k 3k c z 3 1 2 3
a x k 1 0 0 0 1 0 = b y 2k , c z 3k 0 0 k
第二章矩阵
§2.5 初等矩阵
1 k 0 0 1 0 0 0 1
a b c a+kx b+ky c+kz +kx +ky +kz x y z = x y z , 1 2 3 1 2 3
第二章
§2.4 §2.5
矩
阵
矩阵的秩初等矩阵
2011. 10. 17
第二章矩阵
§2.4 矩阵的秩
秩的概念
1. 矩阵A的子式矩阵A
k行 m× n k列 k阶子式
第二章矩阵
§2.4 矩阵的秩
记为r(A 记为r(A)或秩(A) 2. 矩阵A的秩矩阵A A中有一个r阶子式不为零中有一个r r(A) = r r(A A的所有l（l>r）阶子式都等于零的所有l l>r）零矩阵的秩规定为0. 零矩阵的秩规定为0.

矩阵的秩

5−λ =0 , 即5=λ . µ−1=0 µ =1
下页
矩阵秩的性质 (1)0≤R(Am×n)≤min{m, n}. (2)R(AT)=R(A). (3)若A~B, 则R(A)=R(B). (4)若P、Q可逆, 则R(PAQ)=R(A). (5)若A可逆，则R(AB)= R(B). (6) R(AB)≤min{R(A), R(B)}.
1 0 −1 2 r3 − 2 r2 0 −1 3 1 = B → 0 0 0 0
显然B是阶梯型矩阵，显然是阶梯型矩阵，R(B)=2，所以，由定理是阶梯型矩阵，所以，由定理2.5 知R(A)=2。。
进一步，变为C：进一步，将B变为：变为
1 0 −1 2 1 0 −1 2 0 −1 3 1 0 1 −3 −1 = C −r2 B= → 0 0 0 0 0 0 0 0
下页
矩阵的秩设在矩阵A中有一个不等于0的r阶子式D, 且所有r+1阶子式(如果存在的话)全等于0, 那么D称为矩阵A的最高阶非零子式, 数r称为矩阵A的秩, 记作R(A). 并规定零矩阵的秩等于0. 几个简单结论 (1)若矩阵A中有某个s阶子式不为0, 则R(A)≥s; 若A中所有 t阶子式全为0, 则R(A)<t. (2)若A为m×n矩阵, 则0≤R(A)≤min{m, n}. (3)R(AT)=R(A).
首页上页返回下页结束铃
k阶子式在m×n矩阵A中, 任取k行与k列(k≤m, k≤n), 位于这些行列交叉处的k2个元素, 不改变它们在A中所处的位置次序而得的 k阶行列式, 称为矩阵A的k阶子式. 例如
1 1 −2 1 4 A= 2 −1 −1 1 2 , 2 −3 1 −1 2 −3 −1 3 6 −9 7 9 D= 1 1 是A的一个二阶子式. −3 −1 k k m×n 矩阵A 的k 阶子式有CmCn 个.