MATLAB-欧拉方法和龙格库塔方法的小实例
MATLAB改进欧拉法与四阶龙格-库塔求解一阶常微分方程

姓名:樊元君学号:02 日期:一、实验目的掌握MATLAB语言、C/C++语言编写计算程序的方法、掌握改进欧拉法与四阶龙格-库塔求解一阶常微分方程的初值问题。
掌握使用MATLAB程序求解常微分方程问题的方法。
:二、实验内容1、分别写出改进欧拉法与四阶龙格-库塔求解的算法,编写程序上机调试出结果,要求所编程序适用于任何一阶常微分方程的数值解问题,即能解决这一类问题,而不是某一个问题。
实验中以下列数据验证程序的正确性。
求,步长h=。
*2、实验注意事项的精确解为,通过调整步长,观察结果的精度的变化^)三、程序流程图:●改进欧拉格式流程图:~|●四阶龙格库塔流程图:]四、源程序:●改进后欧拉格式程序源代码:function [] = GJOL(h,x0,y0,X,Y)format longh=input('h=');…x0=input('x0=');y0=input('y0=');disp('输入的范围是:');X=input('X=');Y=input('Y=');n=round((Y-X)/h);\i=1;x1=0;yp=0;yc=0;for i=1:1:nx1=x0+h;yp=y0+h*(-x0*(y0)^2);%yp=y0+h*(y0-2*x0/y0);%·yc=y0+h*(-x1*(yp)^2);%yc=y0+h*(yp-2*x1/yp);%y1=(yp+yc)/2;x0=x1;y0=y1;y=2/(1+x0^2);%y=sqrt(1+2*x0);%fprintf('结果=%.3f,%.8f,%.8f\n',x1,y1,y);:endend●四阶龙格库塔程序源代码:function [] = LGKT(h,x0,y0,X,Y)。
format longh=input('h=');x0=input('x0=');y0=input('y0=');disp('输入的范围是:');"X=input('X=');Y=input('Y=');n=round((Y-X)/h);i=1;x1=0;k1=0;k2=0;k3=0;k4=0;for i=1:1:n~x1=x0+h;k1=-x0*y0^2;%k1=y0-2*x0/y0;%k2=(-(x0+h/2)*(y0+h/2*k1)^2);%k2=(y0+h/2*k1)-2*(x0+h/2)/(y0+h/2*k1);% k3=(-(x0+h/2)*(y0+h/2*k2)^2);%k3=(y0+h/2*k2)-2*(x0+h/2)/(y0+h/2*k2);% k4=(-(x1)*(y0+h*k3)^2);%k4=(y0+h*k3)-2*(x1)/(y0+h*k3);%…y1=y0+h/6*(k1+2*k2+2*k3+k4);%y1=y0+h/6*(k1+2*k2+2*k3+k4);%x0=x1;y0=y1;y=2/(1+x0^2);%y=sqrt(1+2*x0);%fprintf('结果=%.3f,%.7f,%.7f\n',x1,y1,y);end·end*五、运行结果:改进欧拉格式结果:;}四阶龙格库塔结果:步长分别为:和时,不同结果显示验证了步长减少,对于精度的提高起到很大作用,有效数字位数明显增加。
数值分析matlab作业龙格库塔欧拉方法解二阶微分方程

Matlab 应用使用Euler 和Rungkutta 方法解臂状摆的能量方程背景 单摆是常见的物理模型,为了得到摆角θ的关于时间的函数,来描述单摆运动。
由角动量定理我们知道εJ M =化简得到0sin 22=+θθlgdt d在一般的应用和计算中,只考虑摆角在5度以内的小摆动,因为可以吧简化为θ,这样比较容易解。
实际上这是一个解二阶常微分方程的问题。
在这里的单摆是一种特别的单摆,具有均匀的质量M 分布在长为2的臂状摆上, 使用能量法建立方程WT =hmg ∆=2J 21ω 化简得到θθcos 35499.722=dtd重力加速度取9.806651使用欧拉法令dxdy z =,这样降阶就把二阶常微分方程转化为一阶微分方程组,再利用向前Euler 方法数值求解。
y(i+1)=y(i)+h*z(i);z(i+1)=z(i)+h*7.35499*cos(y(i)); y(0)=0 z(0)=0精度随着h 的减小而更高,因为向前欧拉方法的整体截断误差与h 同阶,(因为是用了泰勒公式)所以欧拉方法的稳定区域并不大。
2.RK4-四阶龙格库塔方法使用四级四阶经典显式Rungkutta 公式稳定性很好,RK4法是四阶方法,每步的误差是h5阶,而总积累误差为h4阶。
所以比欧拉稳定。
运行第三个程序:在一幅图中显示欧拉法和RK4法,随着截断误差的积累,欧拉法产生了较大的误差h=0.01h=0.0001,仍然是开始较为稳定,逐渐误差变大总结:RK4是很好的方法,很稳定,而且四阶是很常用的方法,因为到五阶的时候精度并没有相应提升。
通过这两种方法计算出角度峰值y=3.141593,周期是1.777510。
三个程序欧拉法clear;clch=0.00001;a=0;b=25;x=a:h:b;y(1)=0;z(1)=0;for i=1:length(x)-1 % 欧拉y(i+1)=y(i)+h*z(i);z(i+1)=z(i)+h*7.35499*cos(y(i));endplot(x,y,'r*');xlabel('时间');ylabel('角度');A=[x,y];%y(find(y==max(y)))%Num=(find(y==max(y)))[y,T]=max(y);fprintf('角度峰值等于%d',y) %角度的峰值也就是πfprintf('\n')fprintf('周期等于%d',T*h) %周期legend('欧拉');龙格库塔方法先定义函数rightf_sys1.mfunction w=rightf_sys1(x,y,z)w=7.35499*cos(y);clear;clc;%set(0,'RecursionLimit',500)h=0.01;a=0;b=25;x=a:h:b;RK_y(1)=0; %初值RK_z(1)=0; %初值for i=1:length(x)-1K1=RK_z(i);L1=rightf_sys1(x(i),RK_y(i),RK_z(i)); % K1 and L1 K2=RK_z(i)+0.5*h*L1;L2=rightf_sys1(x(i)+0.5*h,RK_y(i)+0.5*h*K1,RK_z(i)+0.5*h*L1);K3=RK_z(i)+0.5*h*L2;L3=rightf_sys1(x(i)+0.5*h,RK_y(i)+0.5*h*K2,RK_z(i)+0.5*h*L2);K4=RK_z(i)+h*L3;L4=rightf_sys1(x(i)+h,RK_y(i)+h*K3,RK_z(i)+h*L3); % K4 and L4RK_y(i+1)=RK_y(i)+1/6*h*(K1+2*K2+2*K3+K4);RK_z(i+1)=RK_z(i)+1/6*h*(L1+2*L2+2*L3+L4);endplot(x,RK_y,'b+');xlabel('Variable x');ylabel('Variable y');A=[x,RK_y];[y,T]=max(RK_y);legend('RK4方法');fprintf('角度峰值等于%d',y) %角度的峰值也就是πfprintf('\n')fprintf('周期等于%d',T*h) %周期两个方法在一起对比使用跟上一个相同的函数rightf_sys1.mclear;clc; %清屏h=0.0001;a=0;b=25;x=a:h:b;Euler_y(1)=0;Euler_z(1)=0; %欧拉的初值RK_y(1)=0;RK_z(1)=0; %龙格库塔初值for i=1:length(x)-1%先是欧拉法Euler_y(i+1)=Euler_y(i)+h*Euler_z(i);Euler_z(i+1)=Euler_z(i)+h*7.35499*cos(Euler_y(i));%龙格库塔K1=RK_z(i); L1=rightf_sys1(x(i),RK_y(i),RK_z(i)); % K1 and L1 K2=RK_z(i)+0.5*h*L1;L2=rightf_sys1(x(i)+0.5*h,RK_y(i)+0.5*h*K1,RK_z(i)+0.5*h*L1);% K2 and L2K3=RK_z(i)+0.5*h*L2;L3=rightf_sys1(x(i)+0.5*h,RK_y(i)+0.5*h*K2,RK_z(i)+0.5*h*L2);% K3 and L3K4=RK_z(i)+h*L3;L4=rightf_sys1(x(i)+h,RK_y(i)+h*K3,RK_z(i)+h*L3); % K4 and L4RK_y(i+1)=RK_y(i)+1/6*h*(K1+2*K2+2*K3+K4);RK_z(i+1)=RK_z(i)+1/6*h*(L1+2*L2+2*L3+L4);endplot(x,Euler_y,'r-',x,RK_y,'b-');[y,T]=max(RK_y);fprintf('角度峰值等于%d',y) %角度的峰值也就是πfprintf('\n')fprintf('周期等于%d',T*h) %周期xlabel('时间');ylabel('角度');legend('欧拉','RK4');文- 汉语汉字编辑词条文,wen,从玄从爻。
龙哥库塔法or欧拉法求解微分方程matlab实现

龙哥库塔法or欧拉法求解微分⽅程matlab实现举例:分别⽤欧拉法和龙哥库塔法求解下⾯的微分⽅程我们知道的欧拉法(Euler)"思想是⽤先前的差商近似代替倒数",直⽩⼀些的编程说法即:f(i+1)=f(i)+h*f(x,y)其中h是设定的迭代步长,若精度要求不⾼,⼀般可取0.01。
在定义区间内迭代求解即可。
龙哥库塔法⼀般⽤于⾼精度的求解,即⾼阶精度的改进欧拉法,常⽤的是四阶龙哥库塔,编程语⾔如下:y(i+1)=y(i)+h*(k1+2*K2+2*k3+k4)/6;k1=f(xi,yi)k2=f(xi+h/2,yi+h*k1/2);k3=f(xi+h/2,yi+h*k2/2);k4=f(xi+h,yi+h*k3);设置终⽌条件迭代求解。
matlab实现程序如下:%% 龙哥库塔or欧拉法求解微分⽅程t=0:0.01:3; %⾃变量范围f = [];g = [];f(1) = 0.1; %f初值g(1) = 1; %g初值h=0.001;for i=1:length(t)%% 欧拉法% f(i+1) =f(i)+h*(exp(f(i)*sin(t(i)))+g(i));% g(i+1) =g(i)+h*(exp(g(i)*cos(t(i)))+f(i));%% 龙哥库塔kf1 = exp(f(i)*sin(t(i)))+g(i);%g(i)相当于常值kf2 = exp((f(i)+kf1*h/2)*sin(t(i)+h/2))+g(i);kf3 = exp((f(i)+kf2*h/2)*sin(t(i)+h/2))+g(i);kf4 = exp((f(i)+kf3*h)*sin(t(i)+h))+g(i);f(i+1) = f(i) + h*(kf1+2*kf2+2*kf3+kf4)/6;kg1 = exp(f(i)*cos(t(i)))+f(i);%f(i)相当于常值kg2 = exp((f(i)+kg1*h/2)*cos(t(i)+h/2))+f(i);kg3 = exp((f(i)+kg2*h/2)*cos(t(i)+h/2))+f(i);kg4 = exp((f(i)+kg3*h)*cos(t(i)+h))+f(i);g(i+1) = g(i) + h*(kg1+2*kg2+2*kg3+kg4)/6;endfigure(1)plot(t,f(1:length(t)),t,g(1:length(t)));legend('f函数','g函数')。
使用Matlab进行微分方程求解的方法

使用Matlab进行微分方程求解的方法引言微分方程是数学中非常重要的一部分,广泛应用于物理、经济、工程等领域。
对于大部分微分方程的解析解往往难以求得,而数值解法则成为了一种常用的解决手段。
Matlab作为一种强大的科学计算软件,也提供了丰富的工具和函数用于求解微分方程,本文将介绍一些常见的使用Matlab进行微分方程求解的方法。
一、数值求解方法1. 欧拉方法欧拉方法是最简单的一种数值求解微分方程的方法,它将微分方程的微分项用差分的方式进行近似。
具体的公式为:y(n+1) = y(n) + hf(x(n), y(n))其中,y(n)表示近似解在第n个点的值,h为步长,f(x, y)为微分方程的右端项。
在Matlab中使用欧拉方法进行求解可以使用ode113函数,通过设定不同的步长,可以得到不同精度的数值解。
2. 中点法中点法是较为精确的一种数值求解微分方程的方法,它的计算公式为:k1 = hf(x(n), y(n))k2 = hf(x(n) + h/2, y(n) + k1/2)y(n+1) = y(n) + k2中点法通过计算两个斜率的平均值来得到下一个点的值,相较于欧拉方法,中点法能提供更精确的数值解。
3. 4阶龙格库塔法龙格库塔法是一类高阶数值求解微分方程的方法,其中4阶龙格库塔法是最常用的一种。
它的计算公式为:k1 = hf(x(n), y(n))k2 = hf(x(n) + h/2, y(n) + k1/2)k3 = hf(x(n) + h/2, y(n) + k2/2)k4 = hf(x(n) + h, y(n) + k3)y(n+1) = y(n) + (k1 + 2k2 + 2k3 + k4)/64阶龙格库塔法通过计算多个斜率的加权平均值来得到下一个点的值,相较于欧拉方法和中点法,它的精度更高。
二、Matlab函数和工具除了可以使用以上的数值方法进行微分方程求解之外,Matlab还提供了一些相关的函数和工具,方便用户进行微分方程的建模和求解。
有限差分的欧拉法

西北农林科技大学实习报告学院:理学院 专业年级:信计061 姓名:袁金龙 学号:15206012 课程:微分方程数值解 报告日期:2008-11-26实习一、一维问题的有限差分方法-----Euler 法一)实习问题:用欧拉法,龙格库塔法,米尔恩法求解下面的初值问题:'2(0)1tu u e u ⎧+=⎨=⎩二)算法描述:⑴欧拉法:1(,),0,1,2,...,1m m m m u u hf t u m n +=+=-⑵龙格库塔法的中点法:111(,(,)),0,1,2,...,122m m m m m m u u hf t h u hf t u m n +=+++=-⑶米尔恩法:2211(4),0,1,2,...,23m m m m m u u h f f f m n +++=+++=-⑷初始值的确定: 泰勒级数法1'1000()()()...()(1)q q j jh u u t u t jh ut q --=+++- ⑸雅可比迭代法1[1][]0[0]11(,)()()k n n m k k m k m k j m j j m j j m km k m k u h f t u u h f u uhf Euler βαβ-++++++=++-+-⎧=--⎪⎨⎪=⎩∑三)matlab 程序: ⑴问题函数:function [f1]=f(t,u) f1=-2*u+exp(t);*************************************************** ⑵欧拉法:function []=oula(a,b,u0,n) %[a,b]表示t 的取值区间%u0表示初值%n表示将[0,1]区间分成的分数h=(b-a)/n;t0=a;u(1)=u0+h*(f(t0,u0));for i=1:nt(i)=a+i*h;endtfor i=2:nu(i)=u(i-1)+h*f(t(i-1),u(i-1));endu%精确解的求法for i=1:nu1(i)=(2/3)*exp(-2*t(i))+(1/3)*exp(t(i));endu1plot(t,u,t,u1)title('欧拉法中的预测值与真实值的比较');xlabel('采样点');ylabel('幅度');grid;legend('预测值','真实值');*********************************************************** ⑶龙格库塔法的中点法:function []=zhongdian(a,b,u0,n)%[a,b]表示t的取值区间%u0表示初值%n表示将[0,1]区间分成的分数h=(b-a)/n;t0=a;u(1)=u0+h*(f((t0+(1/2)*h),(u0+(1/2)*h*f(t0,u0))));for i=1:nt(i)=a+i*h;endtfor i=2:nu(i)=u(i-1)+h*(f((t(i-1)+(1/2)*h),(u(i-1)+(1/2)*h*f(t(i-1),u(i-1))))); endu%精确解的求法for i=1:nu1(i)=(2/3)*exp(-2*t(i))+(1/3)*exp(t(i));endu1plot(t,u,t,u1)title('中点法中的预测值与真实值的比较');xlabel('采样点');ylabel('幅度');grid;legend('预测值','真实值');**************************************************************⑷米尔恩法:function []=Milne(n,e)%n表示区间[0,1]要分的份数%对于初值精度我们选择q=3阶的%初值的求解%经过计算运用泰勒级数法求解初值%q(i)表示第i次迭代满足精度的最终值t0=0;for i=1:nt(i)=(1/n)*i;endu0=1;h=1/n;u2(1,1)=1-h+2.5*h*h%Jacobi迭代求解隐式法u2(2,1)=u2(1,1)+h*f(t(1),u2(1,1))for i=2:1000000u2(2,i)=h*(1/3)*f(t(2),u2(2,i-1))+u0+h*(1/3)*f(t0,u0)+h*(4/3)*f(t(1),u2(1,1));if abs(u2(2,i)-u2(2,(i-1)))<eu2(3,1)=u2(2,i)+h*f(t(2),u2(2,i));break;endendfor i=3:nfor j=2:1000000u2(i,j)=h*(1/3)*f(t(i),u2(i,j-1))+u2(i-2,1)+h*(1/3)*f(t(i-2),u2(i-2,1))+h*(4/3)*f(t(i-1),u2(i-1,1));if abs(u2(2,j)-u2(2,(j-1)))<eu2(i+1,1)=u2(i,j)+h*f(t(i),u2(i,j));break;endendendq(1)=u2(1,1);for i=2:n-1q(i)=u2(i+1,1);end%精确解的求法for i=1:n-1t1(i)=(1/n)*i;endfor i=1:n-1u1(i)=(2/3)*exp(-2*t(i))+(1/3)*exp(t(i));endu1;plot(t1,q,t1,u1)title('Milne法中的预测值与真实值的比较');xlabel('采样点');ylabel('幅度');grid;legend('预测值','真实值');*********************************************************四)图形显示的计算结果:⑴欧拉法:表1:欧拉法中的预测值与真实值的比较(n=20时)真实值预测值误差(%)0.9500 0.9536 0.38260.9076 0.9142 0.72710.8721 0.8812 1.03170.8430 0.8540 1.29550.8197 0.8324 1.51810.8020 0.8158 1.70050.7893 0.8041 1.84400.7813 0.7968 1.95110.7777 0.7938 2.02490.7784 0.7948 2.06860.7830 0.7997 2.08620.7913 0.8082 2.08150.8033 0.8202 2.05850.8188 0.8356 2.02070.8376 0.8544 1.97160.8597 0.8764 1.91430.8850 0.9017 1.85140.9135 0.9301 1.78530.9451 0.9616 1.71790.9799 0.9963 1.6506表2:欧拉法中的预测值与真实值的比较(n=10时)真实值 预测值 误差(%)0.9000 0.9142 1.5544 0.8305 0.8540 2.7514 0.7866 0.8158 3.5882 0.7642 0.7968 4.0910 0.7606 0.7948 4.3105 0.7733 0.8082 4.31150.8009 0.8356 1.638 0.8421 0.8764 1.6736 0.8962 0.9301 1.6943 0.96290.99631.70540.10.20.30.40.50.60.70.80.910.750.80.850.90.951欧拉法中的预测值与真实值的比较采样点幅度图1:欧拉法中的预测值与真实值的比较(分成20份时)说明:从图1及表1和表2中可以看出:采用欧拉法对初值问题的近似比较准确,且从算法中可以推断,随着n (将[a,b]区间分成的分数)值的增大,误差将会越来越小。
0计算方法及MATLAB实现简明讲义课件PPS8-1欧拉龙格法

第8章常微分方程初值问题数值解法8.1 引言8.2 欧拉方法8.3 龙格-库塔方法8.4 单步法的收敛性与稳定性8.5 线性多步法8.1 引 言考虑一阶常微分方程的初值问题00(,),[,],().y f x y x a b y x y '=∈=(1.1) (1.2)如果存在实数 ,使得121212(,)(,).,R f x y f x y L y y y y -≤-∀∈(1.3)则称 关于 满足李普希茨(Lipschitz )条件, 称为 的李普希茨常数(简称Lips.常数). 0>L f y L f (参阅教材386页)计算方法及MATLAB 实现 所谓数值解法,就是寻求解 在一系列离散节点)(x y<<<<<+121n n x x x x 上的近似值 .,,,,,121+n n y y y y 相邻两个节点的间距 称为步长.n n n x x h -=+1 如不特别说明,总是假定 为定数, ),2,1( ==i h h i 这时节点为 . ),2,1,0(0 =+=i nh x x n 初值问题(1.1),(1.2)的数值解法的基本特点是采取 “步进式”.即求解过程顺着节点排列的次序一步一步地向前推进.00(,),[,],().y f x y x a b y x y '=∈=描述这类算法,只要给出用已知信息 ,,,21--n n n y y y 计算 的递推公式.1+n y 一类是计算时只用到前一点的值 ,称为单步法. 1+n y n y 另一类是用到 前面 点的值, 1+n y k 11,,,+--k n n n y y y 称为 步法.k 其次,要研究公式的局部截断误差和阶,数值解 与 精确解 的误差估计及收敛性,还有递推公式的计算 稳定性等问题.n y )(n x y 首先对方程 离散化,建立求数值解的递推 公式.),(y x f y ='8.2 简单的数值方法8.2.1 欧拉法与后退欧拉法积分曲线上一点 的切线斜率等于函数 的 值.),(y x ),(y x f 如果按函数 在平面上建立一个方向场,那么, ),(y x f xy 积分曲线上每一点的切线方向均与方向场在该点的方向相一致.在 平面上,微分方程的解 称 作它的积分曲线.xy )(x y y =),(y x f y ='基于上述几何解释,从初始点 出发, ),(000y x P 先依切线 在该点的方向推进到 上一点 ,然后再 1x x =1P 从 依切线 的方向推进到 上一点 ,循此前进 1P 2x x =2P 做出一条折线 (图8-1).210P P P 图8-179一般地,设已做出该折线的顶点 ,过 依 切线 的方向再推进到 ,显然两个顶点的坐标有关系 ),(n n n y x P nP ),(111+++n n n y x P 1,+n n P P 11n n n n y y x x ++-=-反解,得).,(1n n n n y x hf y y +=+(2.1)这就是著名的欧拉(Euler )方法. 欧拉法实际上是对常微分方程中的导数用差商近似,即1()()n n y x y x h+-≈直接得到的.(,)d d n n x y y x =(,)n n f x y 00(,),[,],().y f x y x a b y x y '=∈=1n n y y h +-=()(,())n n n y x f x y x '=111(,)n n n n y y hf x y +=+例欧拉方法13若初值已知,则依公式(2.1)可逐步算出 0y ),,(0001y x hf y y +=),,(1112y x hf y y +=).,(1n n n n y x hf y y +=+(2.1)例1 求解初值问题⎪⎩⎪⎨⎧=<<-='.1)0(),10(2y x y x y y (2.2)解 欧拉公式的具体形式为).2(1nnn n n y x y h y y -+=+取步长 ,计算结果见表8-1.1.0=h 初值问题(2.2)的解为 ,按这个解析式 子算出的准确值 同近似值 一起列在表8-1中,两者相比较可以看出欧拉方法的精度不高.x y 21+=)(n x y n y 1(,)n n n n y y hf x y +=+12y x=+81()()0.1 1.1000 1.09540.6 1.5090 1.48320.2 1.1918 1.18320.7 1.5803 1.54920.3 1.2774 1.26490.8 1.6498 1.61250.4 1.3582 1.34160.9 1.7178 1.67330.51.43511.41421.01.78481.7321n nn n nn x y y x x y y x -表计算结果对比 还可以通过几何直观来考察欧拉方法的精度.假设 ,即顶点 落在积分曲线 上,那么,按欧拉方法做出的折线 便是 过点 的切线(图8-2). )(n n x y y =nP )(x y y =1+n n P P )(x y y =nP图8-2从图形上看,这样定出的顶点 显著地偏离了原来 的积分曲线,可见欧拉方法是相当粗糙的.1+n P 为了分析计算公式的精度,通常可用泰勒展开将)(1+n x y在处展开,则有n x)()(1h x y x y n n +=+在 的前提下, )(n n x y y =)())(,(),(n n n n n x y x y x f y x f '==11()n n y x y ++-=称为此方法的局部截断误差.()()n n y x y x h '=++于是可得欧拉法(2.1)的误差 (2.3)),(22n x y h ''≈如果对方程 从 到积分,得 n x 1+n x ),(y x f y =').,(1n n n n y x hf y y +=+(2.1) 2()2n h y ξ''1(,)n n n x x ξ+∈1(,)n n n n y y hf x y +=+(上一值精确相等时,估计下一值误差!) 2()2n h y ξ''1()n y x +=(2.4)1()(,())n nx n xy x f t y t dt++⎰18右端积分用左矩形公式 近似.))(,(n n x y x f h 再以 代替 n y ),(n x y 如果在(2.4)中右端积分用右矩形公式 ))(,(11++n n x y x f h 111(,)n n n n y y hf x y +++=+(2.5)称为后退的欧拉法.代替也得到(2.1), )(1+n x y 1+n y 局部截断误差也是(2.3). 近似,则得另一个公式它也可以通过利用均差近似导数 ,即11()()n n n ny x y x x x ++-≈-)(1+'n x y 1(,)n n n n y y hf x y +=+2()2n hy ξ''1()(,())n nx n x y x f t y t dt++⎰111()(,())n n n y x f x y x +++'=欧拉公式是关于 的一个直接的计算公式,这类公式称作是显式的;1+n y 后退欧拉公式的右端含有未知的 ,它是关于 的一个函数方程,这类公式称作是隐式的.1+n y 1+n y 1(,)n n n n y y hf x y +=+111(,)n n n n y y hf x y +++=+隐式方程通常用迭代法求解,而迭代过程的实质是逐步显示化. 设用欧拉公式),()0(1n n n n y x f h y y+=+给出迭代初值 ,用它代入(2.5)式的右端,使之转化 为显式,直接计算得)0(1+n y ),,()0(11)1(1++++=n n n n yx f h y y然后再用 代入(2.5)式,又有)1(1+n y ).,()1(11)2(1++++=n n n n yx f h y y111(,)n n n n y y hf x y +++=+(2.5)21如此反复进行,得).,1,0(),,()(11)1(1=+=++++k yx f h y yk n n n k n (2.6)由于 对 满足李普希茨条件(1.3). ),(y x f y 由(2.6)减(2.5)得(1)11k n n yy +++-=.1)(1++-≤n k n y y hL 由此可知,只要迭代法(2.6)就收敛到解 . 1<hL 1+n y 从积分公式可以看到后退欧拉方法的公式误差与欧拉法是相似的.111(,)n n n n y y hf x y +++=+(2.5) ()1111(,)(,)k n n n n h f x y f x y ++++-121212(,)(,).,Rf x y f x y L y y y y -≤-∀∈8.2.2 梯形方法 若用梯形求积公式近似等式(2.4)右端的积分并分别用 代替 则可得到比欧拉法 精度高的计算公式1,+n n y y ),(),(1+n n x y x y 111[(,)(,)]2n n n n n n h y y f x y f x y +++=++(2.7) 称为梯形方法. 梯形方法是隐式单步法,可用迭代法求解.⎰+1))(,(n nx x dtt y t f .))(,()()(11⎰++=+n nx xn n dt t y t f x y x y (2.4) 1()(,())n nx n xy x f t y t dt++⎰111(,())[(,)(,)]2n n x n n n n x hf t y t dt f x y f x y +++≈+⎰23⎪⎪⎩⎪⎪⎨⎧+=+);,()0(1n n n ny x f h y y 为了分析迭代过程的收敛性,将(2.7)与(2.8)式相减,得)],(),([2)(11)1(1k nn n n n k n y x f y x f h y y ++++++=(2.8) ).,2,1,0( =k 同后退的欧拉方法一样,仍用欧拉方法提供迭代初值, 则梯形法的迭代公式为111[(,)(,)]2n n n n n n h y y f x y f x y +++=++(2.7) (1)()111111[(,)(,)]2k k n n n n n n h y yf x y f x y +++++++-=-如果选取 充分小,使得h 12hL<则当 时有 , ∞→k 1)(1++→n k n y y 此时迭代过程是收敛的.于是有(1)11k n n y y+++-≤式中 为关于 的李普希茨常数. ),(y x f y L (1)()111111[(,)(,)]2k k n n n n n n h y yf x y f x y +++++++-=-121212(,)(,).,Rf x y f x y L y y y y -≤-∀∈()112k n n hL y y ++-计算方法及MATLAB 实现8.2.3 改进欧拉公式梯形方法虽然提高了精度,但其算法复杂. 在应用迭代公式(2.8)进行实际计算时,每迭代一次,都要重新计算函数 的值.),(y x f 为了控制计算量,通常只迭代一两次就转入下一步的 计算,这就简化了算法.具体地,先用欧拉公式求得一个初步的近似值 , 1n y + 而迭代又要反复进行若干次,计算量很大,而且往往难以预测.称之为预测值,)],(),([2)(11)1(1k n n n n n k n y x f y x f h y y ++++++=计算方法及MATLAB 实现这样建立的预测-校正系统通常称为改进的欧拉公式: 预测值 的精度可能很差,再用梯形公式(2.7)将它校正一次,即按(2.8)式迭代一次得 ,这个结果称校正值. 1+n y 1+n y 预测 ),,(1n n n n y x f h y y +=+校正)].,(),([2111+++++=n n n n n n y x f y x f hy y (2.9)也可以表为下列平均化形式),,(n n n p y x f h y y +=),,(1p n n c y x f h y y ++=).(1y y y +=111[(,)(,)]2n n n n n n h y y f x y f x y +++=++(2.7) )],(),([2)(11)1(1k n n n n n k n y x f y x f h y y ++++++=(参阅教材392页!)计算方法及MATLAB 实现例2 用改进的欧拉方法求解初值问题(2.2).解 这里 改进的欧拉公式为⎪⎪⎪⎩⎪⎪⎪⎨⎧-+=),2(nnn n p y x y h y y ⎪⎩⎪⎨⎧=<<-='.1)0(),10(2y x y x y y (2.2)2(,)(),xf x y y y=-),2(1p n p n c y x y h y y +-+=).(211c p n y y y +=+),,(n n n p y x f h y y +=),,(1p n n c y x f h y y ++=).(211c p n y y y +=+计算方法及MATLAB 实现282(,)xf x y y y=-),,(n n n p y x f h y y +=),,(1p n n c y x f h y y ++=).(211c p n y y y +=+取 ,计算结果见表8-2.1.0=h 同例1中欧拉法的计算结果比较,改进欧拉法明显改善了精度.()()0.11.0959 1.09540.6 1.4860 1.48320.2 1.1841 1.18320.7 1.5525 1.54920.3 1.2662 1.26490.8 1.6153 1.61250.4 1.3434 1.34160.9 1.6782 1.67330.51.41641.41421.01.73791.7321n n n n n n x y y x x y y x -表8212y x=+9.2.4 单步法的局部截断误差与阶 初值问题(1.1),(1.2)的单步法可用一般形式表示为),,,,(11h y y x h y y n n n n n +++=ϕ(2.10)其中多元函数 与 有关,ϕ),(y x f 当 含有 时,方法是隐式的,若不含 则为显式方法,ϕ1+n y 1+n y ),,,(1h y x h y y n n n n ϕ+=+(2.11) 称为增量函数, ),,(h y x ϕ).,(),,(y x f h y x =ϕ所以显式单步法可表示为 例如对欧拉法(2.1)有 它的局部截断误差已由(2.3)给出.⎩⎨⎧=='.)(),,(00y x y y x f y (1.1) (1.2) ).,(1n n n n y x hf y y +=+(2.1) )(2)(211n n n y h y x y ξ''=-++(2.3) ),(22n x y h ''≈对一般显式单步法则可如下定义. 定义1 设 是初值问题(1.1),(1.2)的准确解, 称 )(x y y =)),(,()()(11h x y x h x y x y T n n n n n ϕ--=++(2.12) 为显式单步法(2.11)的局部截断误差. 之所以称为局部的,是假设在 前各步没有误差.1+n T n x 当 时,计算一步,则有 )(n n x y y =11()n n y x y ++-=1()()(,(),)n n n n y x y x h x y x h ϕ+=--⎩⎨⎧=='.)(),,(00y x y y x f y (1.1)(1.2) ),,,(1h y x h y y n n n n ϕ+=+(2.11)1()[(,,)]n n n n y x y h x y h ϕ+-+1.n T +=1(,)n n n n y y hf x y +=+).,(),,(y x f h y x =ϕ在前一步精确的情况下用显式单步公式计算产生的公式误差. 根据定义,欧拉法的局部截断误差 ))(,()()(11n n n n n x y x hf x y x y T --=++即为(2.3)的结果. 这里 称为局部截断误差主项. )(22n x y h '')(2h O T =局部截断误差可理解为用显式单步方法计算一步的误差,即 ()()n n y x h y x =+-22()()2n h y x o h ''=+显然 ),,,(1h y x h y y n n n n ϕ+=+(2.11))(2)(211n n n y h y x y ξ''=-++(2.3) ),(22n x y h ''≈()n hy x '-(,)y f x y '=1()()n n y x y x h +=+(泰勒公式) (小o 高阶,大O 同阶)计算方法及MATLAB 实现 定义2 设 是初值问题(1.1),(1.2)的准确解, 若存在最大整数使显式单步法(2.11)的局部截断误差满足 )(x y p ),(),,()()(11++=--+=p n h O h y x h x y h x y T ϕ(2.13) 则称显式单步法具有 阶精度. p 若将(2.13)展开式写成),())(,(211++++=p p n n n h O h x y x T ψ则 称为局部截断误差主项. 1))(,(+p n n hx y x ψ 以上定义对隐式单步法(2.10)也是适用的.⎩⎨⎧=='.)(),,(00y x y y x f y (1.1) (1.2) ),,,,(11h y y x h y y n n n n n +++=ϕ(2.10) 1(,,)n n n n y y h x y h ϕ+=+(小o 高阶,大O 同阶)对后退欧拉法(2.5)其局部截断误差为))(,()()(1111++++--=n n n n n x y x hf x y x y T 这里 ,是1阶方法,局部截断误差主项为 . 1=p )(22n x y h ''-23()()()2n n h hy x y x O h '''=++).()(232h O x y h n +''-=),,(111++++=n n n n y x hf y y (2.5)2[()()()]n n h y x hy x O h '''-++对梯形法(2.7)有)]()([2)()(111+++'+'--=n n n n n x y x y h x y x y T 所以梯形方法是二阶的,其局部误差主项为 )(123n x y h '''-23()()()23!n n n h h hy x y x y x ''''''=++).()(1243h O x y h n +'''-=)],,(),([2111+++++=n n n n n n y x f y x f h y y (2.7) 24[()()()()]()22n n n n h h y x y x hy x y x O h '''''''-++++3364h h -8.3龙格-库塔方法8.3.1 显式龙格-库塔法的一般形式 上节给出了显式单步法的表达式),,,(1h y x h y y n n n n ϕ+=+其局部截断误差为),(),,()()(11++=--+=p n h O h y x h x y h x y T ϕ对欧拉法 ,即方法为阶, )(21h O T n =+1=p ))].,(,(),([21n n n n n n n n y x hf y h x f y x f h y y ++++=+(3.1)若用改进欧拉法,它可表为此时增量函数 ))].,(,(),([21),,(n n n n n n n n y x hf y h x f y x f h y x +++=ϕ(3.2)与欧拉法的 相比,增加了计算一个 右函数 的值,可望 .),(),,(n n n n y x f h y x =ϕf 2=p 若要使得到的公式阶数 更大, 就必须包含更多的值.p ϕf ,))(,()()(11⎰+=-+n n x x n n dx x y x f x y x y (3.3)从方程 等价的积分形式(2.4),即),(y x f y ='若要使公式阶数提高,就必须使右端积分的数值求积公式 精度提高,必然要增加求积节点.为此可将(3.3)的右端用求积公式表示为线性组合1(,())n n x x f x y x dx +≈⎰点数 越多,精度越高, r 上式右端相当于增量函数 , ),,(h y x ϕ为得到便于计算的显式方法,可类似于改进欧拉法,将公式表示为),,,(1h y x h y y n n n n ϕ+=+(3.4)其中1(,())r i n i n i i h c f x h y x h λλ=++∑,))(,()()(11⎰+=-+n n x x n n dx x y x f x y x y (3.3)(可变步长因子!) (组合系数!),),,(1∑==r i i i n n K c h y x ϕ),,(1n n y x f K =),(11∑-=++=i j j ij n i n i K h y h x f K μλ(3.5),,,2r i =这里 均为常数. ij i i c μλ,, (3.4)和(3.5)称为 级显式龙格-库塔(Runge-Kutta )法, r 简称R-K 方法.当 时,就是欧拉法,),(),,(,1n n n n y x f h y x r ==ϕ此时方法的阶为. 1=p 当 时,改进欧拉法(3.1),(3.2)也是其中的一种,2=r ),,,(1h y x h y y n n n n ϕ+=+(3.4) ),,(1h y x h y y n n n n ϕ+=+))].,(,(),([21),,(n n n n n n n n y x hf y h x f y x f h y x +++=ϕ).,(1n n n n y x hf y y+=+1(,,)n n n n y y h x y h ϕ+=+(步长调节因子) (组合系数) (斜率组合系数)8.3.2 二阶显式R-K 方法 1(,,)rn n i ii x y h c K ϕ==∑1(,,)n n n n y y h x y h ϕ+=+ 对 的R-K 方法,计算公式如下2=r 11122122211()(,)(,)n n n n n n y y h c K c K K f x y K f x h y hK λμ+=++⎧⎪=⎨⎪=++⎩(3.6)这里 均为待定常数.21221,,,μλc c ),(11∑-=++=i j j ij n i n i K h y h x f K μλ若取 得计算公式,2/1,1,021221====μλc c 12n n y y hK +=+称为中点公式,相当于数值积分的中矩形公式.上式也可表示为1(,(,))22n n n n n n h hy y hf x y f x y +=+++1(,)n n K f x y =(3.10)21(,)22n n h hK f x y K =++)).,(2,2(1n n n n n n y x f hy h x hf y y +++=+11122122211()(,)(,)n n n n n n y y h c K c K K f x y K f x h y hK λμ+=++⎧⎪=⎨⎪=++⎩继续上述过程,经过较复杂的数学演算,可以导出各 种四阶龙格-库塔公式,下列经典公式是其中常用的一个:可以证明其截断误差为 . )(5h O 四阶龙格-库塔方法的每一步需要计算四次函数值 ,f ⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧++=++=++==++++=+).,(),2,2(),2,2(),,(),22(6342312143211hK y h x f K K h y h x f K K h y h x f K y x f K K K K K h y y n n n n n n n n n n (3.13) (凸线性组合!) (中点公式!) (欧拉公式!)例 设取步长 ,从 到 用四阶龙格-库塔方法求解 初值问题 ⎪⎩⎪⎨⎧=<<-='.1)0(),10(2y x y xy y 解 这里 ,经典的四阶龙格-库塔公式为 yx y y x f 2),(-=),22(643211K K K K hy y n n ++++=+,2nx y K -=2.0=h 0=x 1=x 112341213243(22),6(,),(,),22(,),22(,).n n n nn n n n n n h y y K K K K K f x y h h K f x y K h hK f x y K K f x h y hK +⎧=++++⎪⎪⎪=⎪⎪⎪=++⎨⎪⎪=++⎪⎪⎪=++⎪⎩计算方法及MATLAB 实现,222223K h y h x K h y K n n n ++-+=,222112K h y h x K hy K n n n ++-+=.)(2334hK y h x hK y K n n n ++-+= 表8-3列出了计算结果,同时了出了相应的精确解. 龙格-库塔方法的精度较高.112341213243(22)6(,),(,),22(,),22(,).n n n nn n n n n n h y y K K K K K f x y h h K f x y K h h K f x y K K f x h y hK +⎧=++++⎪⎪⎪=⎪⎪⎪=++⎨⎪⎪=++⎪⎪⎪=++⎪⎩yxy y x f 2),(-=,21nnn y x y K -=83()0.2 1.1832 1.18320.4 1.3417 1.34160.6 1.4833 1.48320.8 1.6125 1.61251.01.73211.7321n n n x y y x 表计算结果。
matlab-欧拉方法和龙格库塔方法的小实例
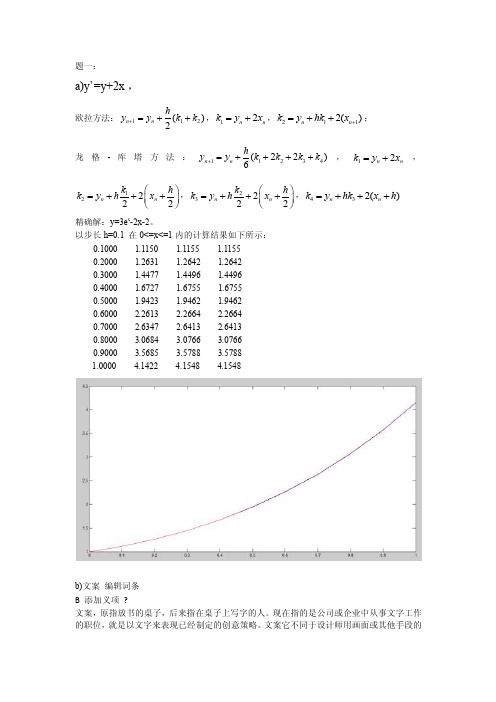
题一:a)y’=y+2x , 欧拉方法:112()2n n h y y k k +=++,12n n k y x =+,2112()n n k y hk x +=++; 龙格-库塔方法:11234(22)6n n h y y k k k k +=++++,12n n k y x =+,12222n n k h k y h x ⎛⎫=+++ ⎪⎝⎭,23222n n k h k y h x ⎛⎫=+++ ⎪⎝⎭,432()n n k y hk x h =+++ 精确解:y=3e x -2x-2。
以步长h=0.1 在0<=x<=1内的计算结果如下所示:0.1000 1.1150 1.1155 1.11550.2000 1.2631 1.2642 1.26420.3000 1.4477 1.4496 1.44960.4000 1.6727 1.6755 1.67550.5000 1.9423 1.9462 1.94620.6000 2.2613 2.2664 2.26640.7000 2.6347 2.6413 2.64130.8000 3.0684 3.0766 3.07660.9000 3.5685 3.5788 3.57881.0000 4.1422 4.1548 4.1548b)文案 编辑词条B 添加义项 ?文案,原指放书的桌子,后来指在桌子上写字的人。
现在指的是公司或企业中从事文字工作的职位,就是以文字来表现已经制定的创意策略。
文案它不同于设计师用画面或其他手段的表现手法,它是一个与广告创意先后相继的表现的过程、发展的过程、深化的过程,多存在于广告公司,企业宣传,新闻策划等。
基本信息中文名称文案外文名称Copy目录1发展历程2主要工作3分类构成4基本要求5工作范围6文案写法7实际应用折叠编辑本段发展历程汉字"文案"(wén àn)是指古代官衙中掌管档案、负责起草文书的幕友,亦指官署中的公文、书信等;在现代,文案的称呼主要用在商业领域,其意义与中国古代所说的文案是有区别的。
MATLAB常微分方程数值解——欧拉法、改进的欧拉法与四阶龙格库塔方法

MATLAB常微分⽅程数值解——欧拉法、改进的欧拉法与四阶龙格库塔⽅法MATLAB常微分⽅程数值解作者:凯鲁嘎吉 - 博客园1.⼀阶常微分⽅程初值问题2.欧拉法3.改进的欧拉法4.四阶龙格库塔⽅法5.例题⽤欧拉法,改进的欧拉法及4阶经典Runge-Kutta⽅法在不同步长下计算初值问题。
步长分别为0.2,0.4,1.0.matlab程序:function z=f(x,y)z=-y*(1+x*y);function R_K(h)%欧拉法y=1;fprintf('欧拉法:x=%f, y=%f\n',0,1);for i=1:1/hx=(i-1)*h;K=f(x,y);y=y+h*K;fprintf('欧拉法:x=%f, y=%f\n',x+h,y);endfprintf('\n');%改进的欧拉法y=1;fprintf('改进的欧拉法:x=%f, y=%f\n',0,1);for i=1:1/hx=(i-1)*h;K1=f(x,y);K2=f(x+h,y+h*K1);y=y+(h/2)*(K1+K2);fprintf('改进的欧拉法:x=%f, y=%f\n',x+h,y);endfprintf('\n');%龙格库塔⽅法y=1;fprintf('龙格库塔法:x=%f, y=%f\n',0,1);for i=1:1/hx=(i-1)*h;K1=f(x,y);K2=f(x+h/2,y+(h/2)*K1);K3=f(x+h/2,y+(h/2)*K2);K4=f(x+h,y+h*K3);y=y+(h/6)*(K1+2*K2+2*K3+K4);fprintf('龙格库塔法:x=%f, y=%f\n',x+h,y);end结果:>> R_K(0.2)欧拉法:x=0.000000, y=1.000000欧拉法:x=0.200000, y=0.800000欧拉法:x=0.400000, y=0.614400欧拉法:x=0.600000, y=0.461321欧拉法:x=0.800000, y=0.343519欧拉法:x=1.000000, y=0.255934改进的欧拉法:x=0.000000, y=1.000000改进的欧拉法:x=0.200000, y=0.807200改进的欧拉法:x=0.400000, y=0.636118改进的欧拉法:x=0.600000, y=0.495044改进的欧拉法:x=0.800000, y=0.383419改进的欧拉法:x=1.000000, y=0.296974龙格库塔法:x=0.000000, y=1.000000龙格库塔法:x=0.200000, y=0.804636龙格库塔法:x=0.400000, y=0.631465龙格库塔法:x=0.600000, y=0.489198龙格库塔法:x=0.800000, y=0.377225龙格库塔法:x=1.000000, y=0.291009>> R_K(0.4)欧拉法:x=0.000000, y=1.000000欧拉法:x=0.400000, y=0.600000欧拉法:x=0.800000, y=0.302400改进的欧拉法:x=0.000000, y=1.000000改进的欧拉法:x=0.400000, y=0.651200改进的欧拉法:x=0.800000, y=0.405782龙格库塔法:x=0.000000, y=1.000000龙格库塔法:x=0.400000, y=0.631625龙格库塔法:x=0.800000, y=0.377556>> R_K(1)欧拉法:x=0.000000, y=1.000000欧拉法:x=1.000000, y=0.000000改进的欧拉法:x=0.000000, y=1.000000改进的欧拉法:x=1.000000, y=0.500000龙格库塔法:x=0.000000, y=1.000000龙格库塔法:x=1.000000, y=0.303395注意:在步长h为0.4时,要将for i=1:1/h改为for i=1:0.8/h。
matlab解状态方程

Matlab解状态方程详解
一、引言
状态方程是描述系统动态行为的重要工具,广泛应用于控制工程、电子工程、机械工程等领域。
在Matlab中,可以使用各种方法来解状态方程,包括直接法、迭代法和优化法等。
本文将详细介绍Matlab解状态方程的几种常用方法,并给出相应的示例代码。
二、直接法
直接法是解状态方程最简单的方法之一。
对于简单的一阶或二阶线性时不变系统,可以通过简单的代数运算得到状态变量的解。
对于更复杂的多阶非线性系统,可能需要使用数值方法进行求解。
在Matlab中,可以使用以下代码实现直接法:
三、迭代法
迭代法是一种通过不断迭代来逼近状态变量解的方法。
常用的迭代法包括欧拉法、龙格-库塔法和雅可比迭代法等。
在Matlab中,可以使用以下代码实现欧拉法:
四、优化法
优化法是一种通过最小化某个代价函数来求解状态方程的方法。
常用的优化法包括梯度下降法、牛顿法和拟牛顿法等。
在Matlab中,可以使用以下代码实现梯度下降法:。
龙格库塔方法及其matlab实现

资料范本本资料为word版本,可以直接编辑和打印,感谢您的下载龙格库塔方法及其matlab实现地点:__________________时间:__________________说明:本资料适用于约定双方经过谈判,协商而共同承认,共同遵守的责任与义务,仅供参考,文档可直接下载或修改,不需要的部分可直接删除,使用时请详细阅读内容龙格-库塔方法及其matlab实现摘要:本文的目的数值求解微分方程精确解,通过龙格-库塔法,加以利用matlab为工具达到求解目的。
龙格-库塔(Runge-Kutta)方法是一种在工程上应用广泛的高精度单步算法,用于数值求解微分方程。
MatLab软件是由美国Mathworks公司推出的用于数值计算和图形处理的科学计算系统环境。
MatLab 是英文MATrix LABoratory(矩阵实验室)的缩写。
在MratLab环境下,用户可以集成地进行程序设计、数值计算、图形绘制、输入输出、文件管理等各项操作。
关键词:龙格-库塔 matlab 微分方程前言1.1:知识背景龙格-库塔法(Runge-Kutta)是用于非线性常微分方程的解的重要的一类隐式或显式迭代法。
这些技术由数学家卡尔·龙格和马丁·威尔海姆·库塔于1900年左右发明。
通常所说的龙格库塔方法是相对四阶龙格库塔而言的,成为经典四阶龙格库塔法。
该方法具有精度高,收敛,稳定,计算过程中可以改变步长不需要计算高阶导数等优点,但是仍需计算在一些点上的值,比如四阶龙格-库塔法没计算一步需要计算四步,在实际运用中是有一定复杂性的。
Matlab是在20世纪七十年代后期的事:时任美国新墨西哥大学计算机科学系主任的Cleve Moler教授出于减轻学生编程负担的动机,为学生设计了一组调用LINPACK和EISPACK库程序的“通俗易用”的接口,此即用FORTRAN编写的萌芽状态的MATLAB。
经几年的校际流传,在Little的推动下,由Little、Moler、Steve Bangert合作,于1984年成立了MathWorks公司,并把MATLAB正式推向市场。
matlab编写龙格库塔法或欧拉法求解常微分方程数值解

龙格库塔法(Runge-Kutta method)和欧拉法(Euler's method)是两种常用的数值求解常微分方程的方法。
这里分别给出它们的MATLAB实现:1. 龙格库塔法(Runge-Kutta method):```matlabfunction [y, t] = runge_kutta(f, y0, t0, tf, h)% f: 微分方程函数,输入为[y, t],输出为dy/dt% y0: 初始值% t0: 初始时间% tf: 结束时间% h: 步长N = round((tf - t0) / h); % 计算迭代次数t = zeros(1, N + 1); % 初始化时间向量y = zeros(size(y0), N + 1); % 初始化解向量t(1) = t0;y(:, 1) = y0;for i = 1:Nk1 = h * f(y(:, i), t(i));k2 = h * f(y(:, i) + k1 / 2, t(i) + h / 2);k3 = h * f(y(:, i) + k2 / 2, t(i) + h / 2);k4 = h * f(y(:, i) + k3, t(i) + h);y(:, i + 1) = y(:, i) + (k1 + 2 * k2 + 2 * k3 + k4) / 6;t(i + 1) = t(i) + h;endend```2. 欧拉法(Euler's method):```matlabfunction [y, t] = euler_method(f, y0, t0, tf, h)% f: 微分方程函数,输入为[y, t],输出为dy/dt% y0: 初始值% t0: 初始时间% tf: 结束时间% h: 步长N = round((tf - t0) / h); % 计算迭代次数t = zeros(1, N + 1); % 初始化时间向量y = zeros(size(y0), N + 1); % 初始化解向量t(1) = t0;y(:, 1) = y0;for i = 1:Ny(:, i + 1) = y(:, i) + h * f(y(:, i), t(i));t(i + 1) = t(i) + h;endend```使用这两个函数时,需要定义一个表示微分方程的函数`f`,例如:```matlabfunction dydt = my_ode(y, t)dydt = -y; % 一个简单的一阶线性微分方程:dy/dt = -yend```然后调用相应的求解函数,例如:```matlaby0 = 1; % 初始值t0 = 0; % 初始时间tf = 5; % 结束时间h = 0.1; % 步长[y_rk, t_rk] = runge_kutta(@my_ode, y0, t0, tf, h);[y_euler, t_euler] = euler_method(@my_ode, y0, t0, tf, h);```。
MATLAB中的差分方程建模与求解方法

MATLAB中的差分方程建模与求解方法引言差分方程是数学中常见的一种方程类型,是一种离散形式的微分方程。
在实际问题中,差分方程能够提供对系统的离散描述,对于动态模型的建立和求解具有重要作用。
MATLAB作为一种功能强大的数值计算软件,其内置了丰富的工具箱和函数,为差分方程的建模和求解提供了便利。
一、差分方程的建模差分方程的建模是将实际问题转化为数学方程的过程。
在MATLAB中,差分方程的建模可以通过定义离散系统的状态和状态转移方程来实现。
下面以一个简单的例子说明差分方程的建模过程。
假设有一个人口增长模型,人口数在每年增加10%,则差分方程可以表示为:P(n+1) = P(n) + 0.1 * P(n),其中P(n)表示第n年的人口数,P(n+1)表示第n+1年的人口数。
在MATLAB中,可以通过定义一个函数来描述差分方程的状态转移方程,代码如下:```matlabfunction Pn = population_growth(Pn_minus_1)growth_rate = 0.1;Pn = Pn_minus_1 + growth_rate * Pn_minus_1;end```上述代码定义了一个名为"population_growth"的函数,该函数的输入参数为上一年的人口数"Pn_minus_1",输出为当前年的人口数"Pn"。
其中,growth_rate表示人口增长率,根据差分方程的定义,将上一年的人口数乘以增长率再加上本身,即可得到当前年的人口数。
二、差分方程的求解方法在MATLAB中,差分方程的求解可以通过多种方法实现。
下面介绍两种常用的差分方程求解方法:欧拉法和四阶龙格-库塔法。
1. 欧拉法(Euler's method)欧拉法是差分方程求解中最简单直观的一种方法。
其基本思想是通过离散化的方式逐步逼近连续函数的解。
具体步骤如下:1) 将时间段分割成若干个小区间;2) 根据差分方程的状态转移方程,在每个小区间内进行计算;3) 迭代计算直到达到指定的时间点。
MATLAB数值分析实验五(欧拉法,荣格-库塔法解常微分方程)

佛山科学技术学院实 验 报 告课程名称 数值分析 实验项目 常微分方程问题初值问题数值解法 专业班级 姓 名 学 号 指导教师 陈剑 成 绩 日 期一. 实验目的1、理解如何在计算机上实现用Euler 法、改进Euler 法、Runge -Kutta 算法求一阶常微分方程初值问题⎩⎨⎧=∈='1)(],[),,()(y a y b a x y x f x y 的数值解。
2、利用图形直观分析近似解和准确解之间的误差。
二、实验要求(1) 按照题目要求完成实验内容; (2) 写出相应的Matlab 程序;(3) 给出实验结果(可以用表格展示实验结果); (4) 分析和讨论实验结果并提出可能的优化实验。
(5) 写出实验报告。
三、实验步骤1、用Matlab 编写解常微分方程初值问题的Euler 法、改进Euler 法和经典的四阶Runge-Kutta 法。
2、给定初值问题⎪⎩⎪⎨⎧=≤≤-=;1)1(,21,1')1(2y x xy x y⎪⎩⎪⎨⎧=≤≤++-=31)0(10,25050')2(2y x x x y y 要求:(a )用Euler 法和改进的Euler 法(步长均取h=0.05)及经典的四阶Runge-Kutta 法(h=0.1)求(1)的数值解,并打印)10,....2,1,0(1.01=+=i i x 的值。
(b) 用经典的四阶Runge-Kutta 方法解(2),步长分别取h=0.1, 0.05,0.025,计算并打印)10,....2,1,0(1.0==i i x 个点的值,与准确解25031)(x e x y x +=-比较,并列表写出在x=0.2,0.5,0.8处,对于不同步长h 下的误差,讨论同一节点处,误差随步长的变化规律。
(c )用Matlab 绘图函数绘制(2)的精确解和近似解的图形。
四、实验结果 %Euler.mfunction y = Euler(x0,xn,y0,h) %Euler 法解方程f_xy ; %x0,y0为初始条件; %x0,xn 为求值区间; %h 为步长; %求区间个数: n = (xn-x0)/h;%矩阵x 存储n+1个节点: x = [x0:h:xn]';%矩阵y 存储节点处的值: y = [y0;zeros(n,1)];%矩阵y_存储节点处导数值: y_(1)= f_xy(x0,y0); y_ = [y_(1);zeros(n,1)];%进行迭代(欧拉法迭代;求导数): for i = 2:n+1y (i) = y(i-1)+h*y_(i-1); y_(i) = f_xy(x(i),y(i)); end%Imp_Euler.mfunction y = Imp_Euler(x0,xn,y0,h)%改进的Euler法解方程f_xy;%x0,y0为初始条件;%x0,xn为求值区间;%h为步长;%求区间个数:n = (xn-x0)/h;%矩阵x存储n+1个节点:x = [x0:h:xn]';%矩阵y存储节点处的值:y = [y0;zeros(n,1)];%矩阵y_存储节点处导数值:y_(1)= f_xy(x0,y0);y_ = [y_(1);zeros(n,1)];%使用改进Euler法求值(欧拉法求近似;近似点导数;梯形校正;求导):for i = 2:n+1y_l = y(i-1) + h*y_(i-1);y_l = f_xy(x(i),y_l);y(i) = y(i-1) + (h/2)*(y_(i-1)+y_l);y_(i)= f_xy(x(i),y(i));end%R_Kutta4.mfunction y = R_Kutta4(x0,xn,y0,h)%Runger_Kutta法解方程f_xy;%x0,y0为初始条件;%x0,xn为求值区间;%h为步长;%求区间个数:n = (xn-x0)/h;%矩阵x存储n+1个节点:x = [x0:h:xn]';%矩阵y存储节点处的值:y = [y0;zeros(n,1)];%矩阵k1,k2,k3,k4存储各节点(中点)数值:k1(1)= f_xy(x0,y0);k1 = [k1(1);zeros(n,1)];k2(1)= f_xy(x0+h/2,y0+h*k1(1)/2);k2 = [k2(1);zeros(n,1)];k3(1)= f_xy(x0+h/2,y0+h*k2(1)/2);k3 = [k3(1);zeros(n,1)];k4(1)= f_xy(x0+h,y0+h*k3(1));k4 = [k4(1);zeros(n,1)];for i= 2:n+1y(i) = y(i-1)+(h/6)*(k1(i-1)+2*k2(i-1)+2*k3(i-1)+k4(i-1));k1(i)= f_xy(x(i),y(i));k2(i)= f_xy(x(i)+h/2,y(i)+h*k1(i)/2);k3(i)= f_xy(x(i)+h/2,y(i)+h*k2(i)/2);k4(i)= f_xy(x(i)+h,y(i)+h*k3(i));end(a):%f_xy.mfunction y_=f_xy(x,y)%求解第五次作业第一题的点(x,y)处的导数;y_ = 1/(x^2) - y/x;%run521.mclc,clear;x0 = 1;xn = 2;h = 0.05;y0 = 1;%便于显示出x,与y对应:x = [x0:h:xn]';y = Euler(x0,xn,y0,h);YE =[x,y];y = Imp_Euler(x0,xn,y0,h); YIE= [x,y];h = 0.1;x = [x0:h:xn]';y = R_Kutta4(x0,xn,y0,h); YRK= [x,y];(b): %f_xy.mfunction y_=f_xy(x,y) %求第二个方程的导数: y_ = -50*y+50*(x^2)+2*x;%run522.mclc,clear; x0 = 0; xn = 1; y0 = 1/3; %步长0.1: h = 0.1; x = [x0:h:xn]';y = R_Kutta4(x0,xn,y0,h); y_r= f_Real(x); Y1 = [x,y,y_r];%步长0.05: h = 0.05; x = [x0:h:xn]';y = R_Kutta4(x0,xn,y0,h); y_r= f_Real(x); Y2 = [x,y,y_r]; %步长0.025: h = 0.025; x = [x0:h:xn]';y = R_Kutta4(x0,xn,y0,h); y_r= f_Real(x); Y3 = [x,y,y_r];五、讨论分析(a)从结果可以看出使用RK 方法,步长较大但是结果也更加精确; (b)分析求值结果的误差,可以发现当步长取0.1时,误差是超级大的(10^8数量级),但是当步长缩小一半取0.05时,误差就很小了,再缩小一半,误差就更小了。
数学实验“欧拉数值算法,Runge-Kutta数值算法”实验报告(内含matlab程序)
西京学院数学软件实验任务书实验二十四实验报告一、实验名称:欧拉数值算法(显式,隐式,欧拉预估-校正法),Runge-Kutta 数值算法。
二、实验目的:进一步熟悉欧拉数值算法(显式,隐式,欧拉预估-校正法),Runge-Kutta 数值算法。
三、实验要求:运用Matlab/C/C++/Java/Maple/Mathematica 等其中一种语言完成程序设计。
四、实验原理:1.欧拉数值算法(显式):微分方程里最简单的方程形式莫过于一阶常微分方程的初值问题,即:0(,)()dy f x y a x b dx y a y ⎧=≤≤⎪⎨⎪=⎩其中a ,b 为常数。
因为其简单但又是求解其他方程的基础,所以发展了许多典型的解法。
所有算法中的f 就是代表上式中(,)f x y ,而y f 表示(,)f x y y ∂∂,x f 表示(,)f x y x∂∂。
简单欧拉法是一种单步递推算法。
简单欧拉法的公式如下所示:1(,)n n n n y y hf x y +=+简单欧拉法的算法过程介绍如下:给出自变量x 的定义域[,]a b ,初始值0y 及步长h 。
对0,1,()/k b a h =-,计算1(,)k k k k y y hf x y +=+2.欧拉数值算法(隐式):隐式欧拉法也叫退欧拉法,隐式欧拉法的公式如下所示:111(,)n n n n y y hf x y +++=+隐式欧拉法是一阶精度的方法,比它精度高的公式是:111[(,)(,)]2n n n n n n h y y f x y f x y +++=++ 隐式欧拉的算法过程介绍如下。
给出自变量x 的定义域[,]a b ,初始值0y 及步长h 。
对0,1,()/k b a h =-,用牛顿法或其他方法求解方111(,)k k k k y y hf x y +++=+得出1k y +。
3.欧拉预估-校正法:改进欧拉法是一种二阶显式求解法,其计算公式如下所示:1[,(,)]22n n n n n n h h y y hf x y f x y +=+++11(,)[(,)(,)]2n n n n n n n n t y hf x y h y y f x y f x t ++=+⎧⎪⎨=++⎪⎩ 4.Runge-Kutta 数值算法:二阶龙格-库塔法有多种形式,除了改进的欧拉法外,还有中点法。
解微分方程欧拉法RK法及其MATLAB实例

解微分方程的欧拉法,龙格-库塔法及其MATLAB简单实例欧拉方法(Euler method)用以对给定初值的常微分方程(即初值问题)求解分为前进EULER法、后退EULER法、改进的EULER法。
缺点:欧拉法简单地取切线的端点作为下一步的起点进行计算,当步数增多时,误差会因积累而越来越大。
因此欧拉格式一般不用于实际计算。
改进欧拉格式:为提高精度,需要在欧拉格式的基础上进行改进。
采用区间两端的斜率的平均值作为直线方程的斜率。
改进欧拉法的精度为二阶。
算法为:微分方程的本质特征是方程中含有导数项,数值解法的第一步就是设法消除其导数值。
对于常微分方程:?x∈[a,b]y(a) = y0可以将区间[a,b]分成n段,那么方程在第xi点有y'(xi) = f(xi,y(xi)),再用向前差商近似代替导数则为:在这里,h是步长,即相邻两个结点间的距离。
因此可以根据xi点和yi点的数值计算出yi+1来:i=0,1,2,L这就是向前欧拉格式。
改进的欧拉公式:将向前欧拉公式中的导数f(xi,yi)改为微元两端导数的平均,即上式便是梯形的欧拉公式。
可见,上式是隐式格式,需要迭代求解。
为了便于求解,使用改进的欧拉公式:数值分析中,龙格-库塔法(Runge-Kutta)是用于模拟常微分方程的解的重要的一类隐式或显式迭代法。
实际上,龙格-库塔法是欧拉方法的一种推广,向前欧拉公式将导数项简单取为f(xn,yn),而改进的欧拉公式将导数项取为两端导数的平均。
龙格-库塔方法的基本思想:在区间[xn,xn+1]内多取几个点,将他们的斜率加权平均,作为导数的近似。
龙格库塔法的家族中的一个成员如此常用,以至于经常被称为“RK4”或者就是“龙格库塔法”。
令初值问题表述如下。
则,对于该问题的RK4由如下方程给出:其中这样,下一个值(y n+1)由现在的值(y n)加上时间间隔(h)和一个估算的斜率的乘积决定。
该斜率是以下斜率的加权平均:k1是时间段开始时的斜率;k2是时间段中点的斜率,通过欧拉法采用斜率k1来决定y在点tn + h/2的值;k3也是中点的斜率,但是这次采用斜率k2决定y值;k4是时间段终点的斜率,其y值用k3决定。
matlab ppt_13_龙格-库塔法

龙格――库塔法
1.1 数值法解常微分方程 已知 y = f (x, y ), (a ≤ x ≤ b) y (x 0 ) = y 0 取步长为h = (b − a)/n,将区间分成n个子区间, a = x0 < x 1 · · · < x i < · · · < x n = b 求离散点上的y (xi), y (xi+1) − y (xi) 由中值定理, = y (xi + θh) h 得 y (xi+1) = y (xi) + hkave 平均斜率为 kave = f (xi + θh, y (xi + θh)) 。 1.2 欧拉公式 取kave = f (xi, yi),得欧拉公式 yi+1 = yi + hf (xi, yi) 取kave = (K1 + K2)/2,则得改进的欧拉公式 h yi+1 = yi + (K1 + K2) 2 其中K1和K2分别为xi 和xi+1 两点的斜率值。 其中K2 的计算为:先用欧拉法得到y (xi+1)的预报值 y i+1 = yi + hK1 = yi + hf (xi, yi) 再用预报值计算xi+1处的斜率值 K2 = f (xi+1, y i+1) = f (xi+1, yi + hf (xi, yi)) 可得 h yi+1 = yi + (K1 + K2) 2 h = yi + [f (xi, yi) + f (xi+1, yi + hf (xi, yi))] 2 (0 < θ < 1)
数值分析Matlab作业龙格库塔欧拉方法解二阶微分方程

Matlab 应用使用Euler 和Rungkutta 方法解臂状摆的能量方程背景 单摆是常见的物理模型,为了得到摆角θ的关于时间的函数,来描述单摆运动。
由角动量定理我们知道εJ M =化简得到0sin 22=+θθl g dt d 在一般的应用和计算中,只考虑摆角在5度以内的小摆动,因为可以吧简化为,这样比较容易解。
实际上这是一个解二阶常微分方程的问题。
θ在这里的单摆是一种特别的单摆,具有均匀的质量M 分布在长为2的臂状摆上,使用能量法建立方程W T =h mg ∆=2J 21ω化简得到四阶龙格库塔方法使用四级四阶经典显式Rungkutta公式稳定性很好,RK4法是四阶方法,每步的误差是h5阶,而总积累误差为h4阶。
所以比欧拉稳定。
运行第三个程序:在一幅图中显示欧拉法和RK4法,随着截断误差的积累,欧拉法产生了较大的误差h=0.01h=0.0001,仍然是开始较为稳定,逐渐误差变大总结:RK4是很好的方法,很稳定,而且四阶是很常用的方法,因为到五阶的时候精度并没有相应提升。
通过这两种方法计算出角度峰值y=3.141593,周期是1.777510。
三个程序欧拉法clear;clch=0.00001;a=0;b=25;x=a:h:b;y(1)=0;z(1)=0;for i=1:length(x)-1 % 欧拉y(i+1)=y(i)+h*z(i);z(i+1)=z(i)+h*7.35499*cos(y(i));endplot(x,y,'r*');xlabel('时间');ylabel('角度');A=[x,y];%y(find(y==max(y)))%Num=(find(y==max(y)))[y,T]=max(y);fprintf('角度峰值等于%d',y) %角度的峰值也就是πfprintf('\n')fprintf('周期等于%d',T*h)%周期legend('欧拉');龙格库塔方法先定义函数rightf_sys1.mfunction w=rightf_sys1(x,y,z)w=7.35499*cos(y);clear;clc;%set(0,'RecursionLimit',500)h=0.01;a=0;b=25;x=a:h:b;RK_y(1)=0; %初值%RK_z(1)=0;初值for i=1:length(x)-1K1=RK_z(i); L1=rightf_sys1(x(i),RK_y(i),RK_z(i));%K1 and L1K2=RK_z(i)+0.5*h*L1;L2=rightf_sys1(x(i)+0.5*h,RK_y(i)+0.5*h*K1,RK_z(i)+0.5*h*L1);K3=RK_z(i)+0.5*h*L2;L3=rightf_sys1(x(i)+0.5*h,RK_y(i)+0.5*h*K2,RK_z(i)+0.5*h*L2);K4=RK_z(i)+h*L3;% K4L4=rightf_sys1(x(i)+h,RK_y(i)+h*K3,RK_z(i)+h*L3);and L4RK_y(i+1)=RK_y(i)+1/6*h*(K1+2*K2+2*K3+K4);RK_z(i+1)=RK_z(i)+1/6*h*(L1+2*L2+2*L3+L4);endplot(x,RK_y,'b+');xlabel('Variable x');ylabel('Variable y');A=[x,RK_y];[y,T]=max(RK_y);legend('RK4方法');fprintf('角度峰值等于%d',y) %角度的峰值也就是πfprintf('\n')%周期fprintf('周期等于%d',T*h)两个方法在一起对比使用跟上一个相同的函数rightf_sys1.mclear;clc; %清屏h=0.0001;a=0;b=25;x=a:h:b;Euler_y(1)=0;%欧拉的初值Euler_z(1)=0;RK_y(1)=0;%龙格库塔初值RK_z(1)=0;for i=1:length(x)-1%先是欧拉法Euler_y(i+1)=Euler_y(i)+h*Euler_z(i);Euler_z(i+1)=Euler_z(i)+h*7.35499*cos(Euler_y(i));%龙格库塔K1=RK_z(i); L1=rightf_sys1(x(i),RK_y(i),RK_z(i)); % K1 andL1K2=RK_z(i)+0.5*h*L1;L2=rightf_sys1(x(i)+0.5*h,RK_y(i)+0.5*h*K1,RK_z(i)+0.5*h*L1);% K2 and L2K3=RK_z(i)+0.5*h*L2;L3=rightf_sys1(x(i)+0.5*h,RK_y(i)+0.5*h*K2,RK_z(i)+0.5*h*L2);% K3 and L3K4=RK_z(i)+h*L3; L4=rightf_sys1(x(i)+h,RK_y(i)+h*K3,RK_z(i)+h*L3); K4 and L4RK_y(i+1)=RK_y(i)+1/6*h*(K1+2*K2+2*K3+K4);RK_z(i+1)=RK_z(i)+1/6*h*(L1+2*L2+2*L3+L4);endplot(x,Euler_y,'r-',x,RK_y,'b-');[y,T]=max(RK_y);%角度的峰值也就是πfprintf('角度峰值等于%d',y)fprintf('\n')%周期fprintf('周期等于%d',T*h)xlabel('时间');ylabel('角度');legend('欧拉','RK4');。
后退欧拉法的例题

后退欧拉法的例题
一、实验目的
1.学习matlab的使用方法。
2.掌握常微分方程的几种数值解法:后退欧拉法,龙格库塔法三阶方法,龙格库塔法四阶方法。
3.比较各方法的数值解及误差,了解各方法的优缺点。
二、实验题目
给定的初值问题
y′=-y+x+2,0≤x≤1
y(0)=-1,
取精确解y(x)=exp(-x)+x
按(1)后退欧拉法,步长h=0.003, h=0.1;
(2)龙格库塔法三阶方法,步长h=0.1;
(3)龙格库塔法四阶方法,步长h=0.1;
求在节点x k=1+0.1k (k=1,2,3……10)处的数值解及误差比较各方法的优缺点。
三、实验原理
1.对于后退欧拉法:
利用Yn+1 = Yn + 1/2*K1 + 1/2*K2①n = 1, 2, 3……
K1 = hf(Xn, Yn)②
K2 = hf(Xn + h, Yn + K1)③三式可以完成计算
需要将微分方程表达式和精度计算表达式作为两个函数保存在m文件里并在程序中调用:
①微分方程(oulei_wf)
function z=oulei_wf(x,y)
z=-y+x+2
end
②精确解计算(ouleij_q)
function z=ouleij_q(x)
z=exp(-x)+x
end
2.对于龙哥库塔三阶:
利用Yn+1 = Yn + h/6(K1 + 4K2 + K3 )。
