阀控液压马达速度伺服系统仿真分析报告
阀控液压马达速度伺服系统仿真分析资料报告

阀控液压马达速度伺服系统仿真分析引言阀控液压马达速度伺服系统的负载具有较大的惯性和很小的阻尼,其传递函数常可近似由一对实部为零的极点组成,并有很低的动态响应,由于负载处在系统的闭环之中,所以它对阀控液压马达的动态品质有很大的影响。
此外,系统的负载常是可变的,系统设计只能针对一种特定负载,负载一旦改变,系统的动态品质就会变坏,有时甚至失去稳定性,严重的影响了伺服系统的跟踪性能。
本文主要针对干扰力矩对系统的影响,利用结构不变性原理,消除干扰力矩对系统的影响,同时利用PID 控制理论来提高系统的动态性能。
1 阀控液压马达速度伺服系统模型建立阀控液压马达速度伺服系统的结构如图1所示。
液压马达的力矩方程为:fm m s l m T G s C J P +++=θ)(D (1)负载流量方程为:l em m l tm l sP Vs D P C βθ4Q +== (2)伺服阀的线性流量方程为:L p x l P K x k Q -= (3)电液伺服阀近似看成二阶振荡环节:122^2^)()(++=s S K s i s x svsvsv svv ωξω (4) 伺服放大器输出电流ΔI 与输入电压Ue 近似成正比,其传递函数可用伺服放大器增益Ka 表示:错误!未指定书签。
但通常的速度控制系统采用积分放大器,对原系统加以校正才能稳定工作。
校正后的积分放大器增益Ka 表示为:测速机速度传感器(测速机)的数学模型为:错误!未指定书签。
在上述公式中:v x 为电液伺服阀阀芯位移;i 为电液伺服阀输入电流;v sv k s sv ωξ、、分别为电液伺服阀的增益、阻尼系数和固有频率;m D 为马达排量;L Q 为马达的负载流量;x K 为流量增益系数;p K 为流量一压力系数;只为供油压力;s P 为负载压力;m θ为马达转速;e β为从油液有效体积弹性模数;V 为马达的总容积;J 为折算到马达输出轴上的转动惯量;f T 为外干扰力矩;tm C 为马达泄露系数;m C 为粘性阻尼系数;G 为扭簧梯度。
阀控液压马达速度伺服系统仿真分析

阀控液压马达速度伺服系统仿真分析引言阀控液压马达速度伺服系统的负载具有较大的惯性与很小的阻尼,其传递函数常可近似由一对实部为零的极点组成,并有很低的动态响应,由于负载处在系统的闭环之中,所以它对阀控液压马达的动态品质有很大的影响。
此外,系统的负载常就是可变的,系统设计只能针对一种特定负载,负载一旦改变,系统的动态品质就会变坏,有时甚至失去稳定性,严重的影响了伺服系统的跟踪性能。
本文主要针对干扰力矩对系统的影响,利用结构不变性原理,消除干扰力矩对系统的影响,同时利用PID 控制理论来提高系统的动态性能。
1 阀控液压马达速度伺服系统模型建立阀控液压马达速度伺服系统的结构如图1所示。
液压马达的力矩方程为:fm m s l m T G s C J P +++=θ)(D (1)负载流量方程为:l em m l tm l sP Vs D P C βθ4Q +== (2)伺服阀的线性流量方程为:L p x l P K x k Q -= (3)电液伺服阀近似瞧成二阶振荡环节:122^2^)()(++=s S K s i s x svsvsv svv ωξω (4) 伺服放大器输出电流ΔI 与输入电压Ue 近似成正比,其传递函数可用伺服放大器增益Ka 表示:但通常的速度控制系统采用积分放大器,对原系统加以校正才能稳定工作。
校正后的积分放大器增益Ka 表示为:测速机速度传感器(测速机)的数学模型为:在上述公式中:v x 为电液伺服阀阀芯位移;i 为电液伺服阀输入电流;v sv k s sv ωξ、、分别为电液伺服阀的增益、阻尼系数与固有频率;m D 为马达排量;L Q 为马达的负载流量;x K 为流量增益系数;p K 为流量一压力系数;只为供油压力;s P 为负载压力;m θ为马达转速;e β为从油液有效体积弹性模数;V 为马达的总容积;J 为折算到马达输出轴上的转动惯量;f T 为外干扰力矩;tm C 为马达泄露系数;m C 为粘性阻尼系数;G 为扭簧梯度。
机电液压系统仿真与应用实验报告-A14机电

实验报告书
课程名称:机电液压系统仿真与应用班级:A14机电
学号:______________________ 姓名:______________________ 学期:2016-2017第2学期
课程实验项目目录
仿真条件:输入的压力:在10s内,压力从-1bar 升到5bar
四、实验操作步骤
、在子模型模式选择子模型
、在参数模式下设置仿真所需参数、绘制仿真曲线图
四、实验操作步骤
搭建该元件模型的步骤:
、仿真模型草图搭建
)柱塞运动单元仿真模型
表3.1元件参数设置
值
3.2元件参数设置
5)柱塞泵完整仿真模型搭建
2、在子模型模式选择子模型
3、在参数模式下设置仿真所需参数
将1-5个的超级元件的angular displacement分别设置为0、72、144的旋转速度设置为650r/min。
4、运行仿真,选择元件15,绘制端口2的流量。
5、绘制仿真曲线图
五、实验数据处理
搭建该元件模型的步骤:
、仿真模型草图搭建
、在子模型模式选择子模型
、在参数模式下设置仿真所需参数
四、实验操作步骤
3)确认通流面积4)确认可变容积
2、在子模型模式选择子模型
3、在参数模式下设置仿真所需参数、绘制仿真曲线图
四、实验操作步骤
搭建该元件模型的步骤:
四、实验操作步骤
搭建该元件模型的步骤:
31。
泵控马达速度伺服系统建模与仿真分析

S H E N W ), CUI Xia2
(1. Shanghai Ocean U n iv e rs ity ,C ollege o f E n g in e e rin g ,Shanghai 2 0 1 3 0 6 ,C h in a ;
摘 要 :泵控闭式系统工作效率高且油液不易被污染,因此大功率伺服系统都乐于采用此种控制方式。特别是电液比例变量泵和定
量马达组成的闭式液压控制系统,在泵控闭式系统中最为常见。该文运用MATLAB软 件 Srniul m k 模 块 和 SrniSCape模块,建立了交流
电动机驱动的电液比例变量泵控定量马达恒速控制系统时域仿真模型,取得了较好的仿真效果。通过仿真验证了泵马达流量耦合特
domain model is
desirable.By sim ulation,the influence on
constant speed control
performance
by f
hydraulic m otor,load disturbance and variable pump in p u t speed disturbance is ve rified . The influence on model sim plification of electro
恒转速控制是泵控马达速度伺服的一项重要内 容 。要实现马达的恒速控制,通常认为主要需克服三 方面的不利因素。首先是泵控马达闭式系统流量耦合
收 稿 日 期 :2017-12-20 作 者 简 介 :沈伟(1973- ) ,男 ,江苏常州人,讲师,博士,从事控制 理论与控制技术领域的科学研究。
泵控马达速度控制系统PID控制器的设计与仿真综述

泵控马达速度控制系统P I D控制器的设计与仿真综述(总52页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--石家庄铁道大学毕业设计泵控马达速度控制系统PID控制器的设计与仿真Design of PID Controller for Pump Controlled Motor Speed Control System2016 届电气与电子工程学院专业电气工程及其自动化学号学生姓名武云飞指导教师郑海青完成日期 2016年6月 11 日摘要随着科学水平的发展,泵控马达系统越来越多的应用于民用以及军用领域,这是由于泵控马达具有一些其他系统不具备的优点,该系统效率高、转动惯量小同时其响应速度迅速。
然而泵控马达系统在实际的生产生活中常常会出现系统负载频繁变化的情况,这种情况会导致系统的输出速度不稳定,严重时可能导致系统的瘫痪。
本设计的目的就是为了寻找一个较为适合泵控马达系统的控制系统用以克服外负载以及模型变化对系统产生的影响。
通过对泵控马达系统的组成的学习和研究以及对液压回路的工作原理的分析,建立起泵控马达速度控制系统的数学模型,借此来实现对泵控马达速度控制系统的仿真模拟。
在该数学模型的基础上,采用PID控制器作为系统的控制环节,分别对传统PID控制器、位置式PID控制器、增量式PID控制器以及抗积分饱和PID控制器进行系统的仿真模拟,通过对系统进行仿真,比较在外负载干扰的情况下马达转速的响应曲线,从而得出哪种PID控制器更适合泵控马达调速系统。
经过仿真分析对比,可以看出,抗积分饱和PID控制器较其他三种PID控制器有着更短的调节时间以及平滑的曲线,能更符合系统对于马达转速控制的要求。
所以最终选择抗积分饱和PID控制器作为系统的控制环节。
关键词:泵控马达;PID控制器;仿真AbstractWith the development of technology, pump controlled motor system more and more applied in civil and military fields, this is because the pump controlled motor system has some advantages that other systems do not have, this system is highly efficient, low mom -ent of inertia, and fast response. However, pump controlled motor system often appears system load change in actually, the load change can cause the system output speed not stable, severe cases may lead to paralysis of the system. The purpose of this design is to find a suitable control system that can solve to the impact of load changes.Through to the study of pump controlled motor system and the analysis of the hydraulic circuit, we establish the mathematical model of pump controlled motor system, with the system, we can realize the simulation of the pump controlled motor control system. On the basis of the mathematical model, we simulate the traditional PID controller, posi -tional PID controller, incremental PID controller and anti-windup PID controller for respectively. By compare the motor speed response curve which in the case of external load disturbance, which PID controller we can draw is more suitable for pump controlled motor speed control system. Through simulation comparison, we can get that anti-windup PID controller has a more smooth curve and a shorter adjusting time. So we finally choose anti-windup PID controller as the control link of the system.Key words:pump motor control;t he PID controller;simulation目录第1章绪论 0课题研究的背景意义 0PID控制器简介 (2)主要内容 (4)第2章泵控马达调速系统模型的建立 (5)泵控马达调速系统基本原理 (5)时域数学模型 (6)电-机械转换元件的模型建立 (6)比例方向控制阀4WRA6的模型建立 (7)变量泵的阀控液压缸模型的建立 (8)活塞-斜盘倾角环节模型的建立 (10)建立泵控马达的回路模型 (11)速度传感器以及比例放大器的模型建立 (13)建立系统的开环传递函数 (14)系统中各环节参数的整定 (16)求解比例放大器的增益系数 (16)比例方向控制阀的增益系数 (16)系统的流量增益系数 (16)活塞斜盘倾角传递函数 (16)泵-马达环节的参数整定 (17)对系统稳定性的检测 (18)控制系统的基本要求 (18)系统稳定性检测 (18)本章小结 (19)第3章泵控马达PID控制器设计与仿真 (20)PID控制器的基本原理 (20)四种PID控制器简介 (20)位置式PID控制算法 (20)增量式PID控制算法 (22)抗积分饱和PID控制算法 (23)PID控制器设计 (24)PID控制器参数的整定 (25)PID控制器仿真 (25)关于Simulink的简介 (25)PID控制器的仿真分析 (25)泵控马达速度控制系统的仿真模拟 (27)本章小结 (32)第4章结论与展望 (33)结论 (33)展望 (33)参考文献 (35)致谢 (37)附录 (39)附录A 外文资料翻译 (39)英文 (39)译文 (44)附录B 泵控马达速度控制系统仿真图 (47)第1章绪论课题研究的背景意义随着时代的发展,各种科技也在飞快的发展着,工业自动化水平的高低早已经成为了衡量各个部门现代化水平的标志,而工业自动化必然离不开动力的源泉——马达。
基于AMESim的阀控液压缸液压伺服系统仿真解读

・28・计算机应用技术机械 2008年第 1期总第 35卷基于AMESim 的阀控液压缸液压伺服系统仿真邬国秀(襄樊学院机械工程系,湖北襄樊 441003)摘要:AMESim 是法国IMAGINE 公司开发的高级工程系统仿真建摸环境,为机械、液压、控制等工程系统提供了一个较为完善的仿真环境。
首先介绍了AMESim 软件的功能和特点,并以阀控液压缸液压伺服系统为例,探讨了基于AMESim 的液压伺服系统的模型建立、参数设置和仿真方法,得出了仿真结果,并对改变系统元件参数下的仿真结果进行了比较与分析。
关键词:AMESim ;建模;参数设置;仿真;液压伺服系统中图分类号:TP391.9 文献标识码:A 文章编号:1006-0316(200800-0028-03Simulation of valve-controlled cylinder hydraulic servo system based on AMESimWU Guo-xiu(Department of Mechanical Engineering,Xiangfan University,Xiangfan 441003,chinaAbstract :AMESim is an advanced modelling environment for performing simulations of engineering systems produced by IMAGINE inc. of France, and it provides a whole modelling environment for mechanism, hydraulic and control system. The functions and characteristics of AMESim software are introduced in this paper. Taking valve-controlled cylinder hydraulic servo system as an example, this paperdiscusses the modeling, parameter setting and simulation method of hydraulic servo system based on AMESim, and gives the results of simulation. The comparision and analylsis of the results of simulation by changing the components parameters have been performed.Key words:AMESim ;modeling ;parameter setting;simulation ;hydraulic servo system随着仿真理论及计算机技术的不断发展,工程系统的设计开发中,仿真技术可使企业在最短时间内以最低成本将新产品投放市场;科学研究中,可利用仿真技术缩短研究周期,降低科研成本与风险,提高研究水平,加速科研成果转化为生产力的进程。
阀控液压马达速度伺服系统仿真分析

阀控液压马达速度伺服系统仿真分析引言阀控液压马达速度伺服系统的负载具有较大的惯性和很小的阻尼,其传递函数常可近似由一对实部为零的极点组成,并有很低的动态响应,由于负载处在系统的闭环之中,所以它对阀控液压马达的动态品质有很大的影响。
此外,系统的负载常是可变的,系统设计只能针对一种特定负载,负载一旦改变,系统的动态品质就会变坏,有时甚至失去稳定性,严重的影响了伺服系统的跟踪性能。
本文主要针对干扰力矩对系统的影响,利用结构不变性原理,消除干扰力矩对系统的影响,同时利用PID 控制理论来提高系统的动态性能。
1 阀控液压马达速度伺服系统模型建立阀控液压马达速度伺服系统的结构如图1所示。
液压马达的力矩方程为:fm m s l m T G s C J P +++=θ)(D (1)负载流量方程为:l em m l tm l sP Vs D P C βθ4Q +== (2)伺服阀的线性流量方程为:L p x l P K x k Q -= (3)电液伺服阀近似看成二阶振荡环节:122^2^)()(++=s S K s i s x svsvsv svv ωξω (4) 伺服放大器输出电流ΔI 与输入电压Ue 近似成正比,其传递函数可用伺服放大器增益Ka 表示:错误!未找到引用源。
但通常的速度控制系统采用积分放大器,对原系统加以校正才能稳定工作。
校正后的积分放大器增益Ka 表示为:测速机速度传感器(测速机)的数学模型为:错误!未找到引用源。
在上述公式中:v x 为电液伺服阀阀芯位移;i 为电液伺服阀输入电流;v sv k s sv ωξ、、分别为电液伺服阀的增益、阻尼系数和固有频率;m D 为马达排量;L Q 为马达的负载流量;x K 为流量增益系数;p K 为流量一压力系数;只为供油压力;s P 为负载压力;m θ为马达转速;e β为从油液有效体积弹性模数;V 为马达的总容积;J 为折算到马达输出轴上的转动惯量;f T 为外干扰力矩;tm C 为马达泄露系数;m C 为粘性阻尼系数;G 为扭簧梯度。
液压伺服控制系统的建模与分析

F(t)
( 1 t)
t
(t)
sin wt e t
F(s)
1 s
1 s2 1
s s2 w2 1
s
第3章 液压动力元件
本章摘要
液压动力元件是由液压放大元件和液压执行 元件组成。 有四种基本型式的液压动力元件:阀控液压 缸、阀控液压马达、泵控液压缸、泵控液压马达。 本章将建立几种基本的液压动力元件的传递 函数,分析它们的动态特性和主要性能参数。
由方框图求得液压缸输出位移传递函数:
Xp
mtVt
4e Ap2
s3
Kq Ap
Xv
Kce Ap2
1
Vt
4 e K ce
s FL
mt Kce Ap2
BpVt
4e Ap2
s2
1
Bp Kce Ap2
KVt
4e Ap2
s
KKce Ap2
式中,Kce为总的流量系数,Kce=Kc+Ktc
Khmin 4 A 2 P e / Vt
2、液压谐振频率的概念 设活塞及负载在总质量是m,在没有阻尼的情 况下,由于存在两种储能元件(弹性和质 量),位能和动能反复转换,系统出现谐振, 无阻尼谐振频率为:
Wh Kh / m Ap2e (1/V10 V20 ) / m
当V10 V20时
Wh 4 Ap2eVt / m
s
s2
h2
2 h h
s
1
s FL
液压固有频率: 液压阻尼比:
h
4e Ap2
mtVt
h
Kce Ap
emt Bp
Vt 4 Ap
Vt
emt
忽略Bp后近似为:
阀控马达轮边驱动系统仿真分析

阀控马达轮边驱动系统仿真分析杨霞;白雪银;张伟【摘要】以单泵双马达阀控速度闭环控制系统作为工程车辆的轮边驱动单元为研究背景,分析了车辆调速与转向控制原理,提出了应用负反馈闭环控制技术调整发动机转速的节能思路,并进行了AMESim仿真分析.结果表明:该系统能够实现两个驱动轮转速的独立控制,对复杂路面工况具有较强的自适应性,能够实时调整发动机转速,减少溢流,具有显著的节能效果.【期刊名称】《液压与气动》【年(卷),期】2015(000)002【总页数】4页(P62-65)【关键词】轮边驱动;阀控马达;调速;节能;AMESim【作者】杨霞;白雪银;张伟【作者单位】内蒙古化工职业学院测控与机电工程系,内蒙古呼和浩特010070;内蒙古化工职业学院测控与机电工程系,内蒙古呼和浩特010070;秦皇岛港股份有限公司,河北秦皇岛066002【正文语种】中文【中图分类】TH137引言目前,随着液压技术的不断创新发展,以液压马达为驱动单元的轮边驱动形式在工程车辆领域得到了广泛应用[1-3]。
其基本形式为发动机-量泵-变量马达-驱动轮,它通过改变泵的排量实现车速控制,改变马达排量以调节驱动轮输出转矩,应用液压缸转向机构改变车辆行进方向。
该传动形式有效利用了恒压系统下各并联元件可以互不干涉独立工作的特性,实现了驱动轮转速、转矩和转向的独立控制,而且采用泵控马达闭式系统,节能效果显著[4-6],但存在动态调节响应慢、系统成本高等缺陷。
本研究提出了一种发动机-定量泵-比例阀-定量马达-驱动轮的传动形式,该系统充分发挥了阀控系统响应快的特点,有效地改善了车辆操作性能,而且降低了成本。
1 原理分析和仿真模型搭建工程车辆阀控马达行走系统基本原理如图1所示。
用两套独立的比例阀控定量马达速度闭环控制系统分别驱动左右两个车轮,通过调节比例阀开口大小来改变进入定量马达的流量,进而改变驱动轮的转速,以实现车辆的速度控制。
引入转向控制系数,将其与速度控制信号作乘除运算后,分别作为两套阀控马达系统的输入信号,进而使得两个驱动轮的输出转速成比例关系,当左轮转速大于右轮转速,车辆即实现右转,当左轮转速小于右轮转速,车辆即实现左转。
液压马达速度伺服系统研究_马俊功

( 1) 泵控液压马达速度伺服系统 泵控液压 马达速度 伺服 系 统是 由变 量泵 和 定量 马
达组成的传动 装置。这 种系 统 的工 作原 理是 通 过改 变
变量泵的斜盘倾角来控制供给液压马达的流量, 从而 调节液压马达 的转速 。按其 结 构形 式和 控制 指 令给 定
方式可分开环泵控液压马达速度伺服系统 ( 图 1) 、带 位置环的闭环泵控液压马达速度伺服系统 ( 图 2) 和 不带位置环的闭环泵控液压马达速度伺服系统 ( 图 3) 三种。
馈, 系统受负载和温度的影响大, 如当压力从无负载 变化到额定负载时, 系统流量变化大约 8% ~ 12% , 故精度很低 。只适用于要 求不高的场 合。
为了改善精度, 可以采用压力反馈补偿, 用压力 传感器检测负载压力, 作为第二指令输入变量泵伺服 机构, 使变量泵的流量随负载压力的升高而增加, 以 此来补偿变量 泵驱动 电机 转差 和泄 漏所 造 成的 流量 减 少。由于这个压力反馈是正反馈, 因此有可能造成稳
# 100 #
的影响。提高补油压力, 可以提高系统的响应速度。 该系统适 于解决大 功率 系 统高 效与 快速 调 节的 问
题, 特别对有些系统重点要求在阶跃负载作用时的动 态调节性能时, 可采用此系统。
图 6 补油式并联阀控液压马达速度伺服系统
( 3) 阀泵联合控制液压马达速度伺服系统 对于大功率速度伺服系统, 传统的阀控形式无法 解决溢流损失造成的系统温升高、散热难的问题, 因 此必须采用效 率较高 的容 积控 制系 统以 解决 发 热量 大 的问题, 但容积控制系统虽然效率较高, 可动态性能 较差, 不适于高精度的场合。因此研究一种动态性能 好、精度高、适 于大功 率场 合 的液 压马 达速 度 伺服 系 统成为必要 。该类系统 按其 结 构形 式和 控制 方 式的 不 同分为以下两种类型: 阀泵串联控制液压马达速度调 节系统 ( 图 7 和图 8) , 阀泵并联控制液压马达速度调 节系统 ( 图 9) 。 ¹ 阀泵串联控制液压马达速度调节系统 这种系统 的结构是 在伺 服 变量 泵和 液压 马 达之 间 再用一个电液伺服阀来控制泵的输出流量, 其工作原 理与具体系统构成有关。图 7 为用同一指令同时控制 伺服阀和油泵 的系统 形式 。系 统用 同一 误差 信 号来 控 制伺服阀的开度和变量泵的斜盘倾角, 因斜盘倾角的 变化速度低于伺服阀开口的变化速度, 故用一个给定 信号 C来保证液压泵时刻都有一个固定输出 Q 0。这个 Q 0 应足以满足执行机构瞬时加速度和速度的要求, 即 Q 0 要足够大; 另一方面, 当负载需求量较小时, Q 0 的大 部分将以溢流阀调定的压力流回油箱, 造成能量的无用 损耗, 并引起系统温度的升高, 故要求 Q0 尽量小。因此 C的选择 是本系统设 计的关键之 一。C的 选择 要视具 体 指标而定, 如执行机构初始速度的要求, 系统长期工作 温升的要求等 。 阀泵串联控制的另一种形式如图 8 所示。系统的 工作原理为: 变量泵斜盘变量机构的控制信号取自能 源压力和负载压力之差, 使能源压力跟随负载压力的 变化, 这样可以消除恒压油源的溢流损失, 并减少压 力油通过伺服 阀的节 流损 失以 及系 统和 液压 泵 的泄 漏 损失。液压泵 也必须有 一个 高 于负 载压 力的 设 计信 号 $, 当泵出口压力高于负载压力时, 经比较后得到的差
比例调速阀控马达液压回路仿真分析

DOI:10.13733/j.jcam.issn.2095-5553.2014.06.033中国农机化学报Journal of Chinese Agricultural Mechanization 第35卷第6期2014年11月Vol .35No .6Nov.2014比例调速阀控马达液压回路仿真分析陈鹏伟,解宁,郭津津摘要:从比例调速阀的工作机能出发,分析了比例调速阀中的起压力补偿作用的定差减压阀对流量的影响,其始终保持节流阀阀口前后的压差基本恒定不变,减弱了负载变化对系统流量的影响,然后扩展到液压系统,从系统整体分析了比例调速阀控马达系统的稳定性及其压力和流量的动态特性,最终达到马达的运动速度均匀平稳,从而为节流调速系统的设计改进提供技术上的支持。
关键词:比例调速阀;AMESim ;动态特性;仿真分析中图分类号:TH137.5文献标识码:A文章编号:2095-5553(2014)06-0131-04陈鹏伟,解宁,郭津津.比例调速阀控马达液压回路仿真分析[J].中国农机化学报,2014,35(6):131~134Chen Pengwei,Xie Ning,Guo Jinjin.Simulative analysis of motor hydraulic circuit by proportional speed valve control [J].Journal of Chinese A -gricultural Mechanization,2014,35(6):131~134(天津理工大学复杂系统控制理论及应用重点实验室,天津市,300384)收稿日期:2013年9月12日修回日期:2013年10月12日第一作者:陈鹏伟,男,1986年生,河北石家庄人,硕士研究生;研究方向为液压系统动态特性。
E-mail:chenpw8612@0引言液压系统的动静态特性受元件参数等多种因素的影响,当参数调整不当时,调速系统的作用无法发挥,甚至会影响整个液压系统的稳定性。
(小刘辉)阀控液压缸伺服系统的动态特性分析

阀控液压缸伺服系统的动态特性分析摘 要顾名思义,就是利用阀来控制油缸的各种参数,又称阀控,还有泵控,是利用变量泵来控制执行件的各项运动参数,阀控简单便宜,但不节能,是以牺牲能量为代价的,泵控复杂较贵,但很节能。
前者是节流调控,后者是容积调控。
阀控系统中关键的控制量是兼做动力元件的控制阀或电液伺服阀的阀口节流面积a ,即主阀芯位移x 或Δx 或VX 、VY ;一、建立阀控伺服系统的数学模型阀控系统如图1-1所示。
可将阀控系统分成输入元件、校正部分、放大元件、阀控操纵装置、反馈元件以及由输入x 到输出y 的“系统执行部分”。
图中 x-四通滑阀(这里是零开口)液压放大器的输入量,即电液伺服阀主芯的位移量;Δe-误差电信号; Px 油源的恒定油压力;L Q -滑阀放大器输出负载量;P1,P2-液压缸活塞两腔的压力;L Q -液压缸漏损流量;V0-活塞处于缸体中间时两腔中油液体积(包括油路直到阀芯出口)相等,都用V0表示,等于液压腔总油量的½,不在中位时,V0等于2V1V2/(V1+V2); V1、V2分别是油缸活塞两边腔内油液的容积;y-油缸活塞位移量,即负载位移量。
将电液伺服阀的动态特性放在放在阀的操纵装置框内,系统就是电液伺服系统。
对别的多级控制阀,只要将其前面放大的动态特性包括在阀的操纵装置的动态特性中就行了。
因此,图6-8的形式具有普遍意义。
假定其它部分的特性都已知,只分析滑阀-液压缸-负载部分的特性。
按照一般情况分析,参考图6-8,可得流量连续性方程1L Q =Ady /dt +V0dp1/βdt+L P L 0+L0P1(6-1)2L Q =-Ady /dt +V0dp2/βdt -LmPL +L0P2A-活塞腔有效作用面积;Lm-执行元件的内漏系统数; L0-系统(执行元件加上管路)上的外漏损系数;L P =P1-P2这是负载压差。
元件的流量特性1L Q =KqX -KlP1QL2=-(KqX +KlP1) Kq=|XL Q ∂∂1=XL Q ∂∂2 (6-2)L K =2121P Q P Q L L ∂∂=∂∂式6-1与式6-2联立得KqX -L k Kl P1= Ady /dt +V0dp1/βdt +LmPL +L0P1KqX +KlP2= Ady /dt-V0dp2/βdt+LmPL-L0P2 两式相加得KqX= Ady /dt +V0dp1/βdt+m K LP (6-3)式中,系统漏损系数 m k =( Lm+L0+L K /2) (6-4)活塞上的力平衡-力平衡特性 假定活塞杆及负载绝对刚性,暂不考虑结构柔度,则=L AP =f K F y C dtdy Bdtdy m +++220(6-5)1. 系统执行部分传递函数将式6-5代入6-3,并引入算符整理得=X A K q [22202202032002122A K C S A BK C A V S A k m AB V S A m V mK mK m +⎪⎪⎭⎫⎝⎛+++⎪⎪⎭⎫⎝⎛++βββ]Y+⎪⎪⎭⎫⎝⎛+S V K A F m f β202(6-6)输出y 对输入x 的部分传递函数为222022020320021221)()(A K C S A BK A C V S A k m AB V S A m V A k S X S Y mK m K m q+⎪⎪⎭⎫⎝⎛+++⎪⎪⎭⎫⎝⎛++=βββ (6-7)输出y 对干扰力的部分传递函数 =)()(S F S Y f 220220203200022122)2(1A C S A BK A C V S A k m A B V S A m V s v K AKmK m m +⎪⎪⎭⎫⎝⎛+++⎪⎪⎭⎫⎝⎛+++-ββββ(6-8)系统在输入信号x 下和干扰力作用下的总输出为=)(S Y +=)(0)()(s X F S X S Y f)(0)()(s F X S F S Y f f = (6-9)2. 系统方块图有式6-3及6-5可得执行部分的方块图,其余部分的传递函数已知,则系统方块图如图6-9所示图6-9执行部分方块图整理为6-7、6-8。
基于AMESim 的电液伺服速度控制系统仿真分析

基于AMESim 的电液伺服速度控制系统仿真分析王强吴张永李红星武鹏飞刘建强(昆明理工大学流体控制工程研究所,云南昆明650093)摘要:在电液伺服控制系统设计分析中,由于传统的数学建模方法比较复杂,本文利用面向工程设计的高级建模软件AMESim 对阀控液压马达电液伺服速度控制系统进行建模,并对其动态特性进行了仿真分析,得到了较好的分析结果。
关键词:电液伺服控制系统;AMESim;仿真分析中图分类号:TH137 文献标识码:A 文章编号:1008- 0813(2008)04- 0031- 03 Simulation Analysis of Electro- Hydraulic Servo Velocity Control System Based on AMESim WANG Qiang WU Zhang-yong LI Hong-xing WU Peng-fei LIU Jian-qiang (Institute of Fluid Power Control Engineering, Kunming University of Science and Technology,Kunming 650093, China)Abstract: Conventional mathematical modeling, which is used in analysis of designing eletro-hydraulic servo control system, is comparative complex. This paper use AMESim software, which orients engineering design ,modeling hydraulic valve- controlled velocity system, analyzing dynamic characteristics of this system, getting a better analytical result.Key Words: eletro-hydraulic servo control system;AMESim;simulation analysis0 引言在实际工程中,经常需要进行速度控制,如机床进给装置的速度控制,雷达天线、炮塔、转台的姿态跟踪以及发电机、气轮机和水轮机的调速系统等。
电液伺服阀控活塞式液压摆动马达位置控制系统设计讲解

电液伺服阀控活塞式液压摆动马达位置控制系统设计姓名:洪敏学号:101201205班级:机械1002班专业:机械设计与制造及其自动化学院:机械工程学院第一章、设计任务和要求1.1活塞式液压摆动马达的组成及工作原理活塞式液压摆动马达是将直线运动转换为旋转摆动的液压—机械复合传动机构,其中结构原理如图所示。
它由滚珠螺旋副、滚珠花键导轨副、旋转输出套以及液压油缸等组成。
摆动马达的工作原理为:液压油进入油缸驱动滚珠螺旋丝杆轴往复直线运动,滚珠螺旋丝杆轴驱动螺旋旋转输出套做往复旋摆运动,滚珠花键导轨副防止螺旋丝杆轴转动。
1.活塞式液压摆动马达是将直线运动转换为旋转摆动的液压—机械复合传动机构,其中结构原理如图所示。
它由滚珠螺旋副、滚珠花键导轨副、旋转输出套以及液压油缸等组成。
摆动马达的工作原理为:液压油进入油缸驱动滚珠螺旋丝杆轴往复直线运动,滚珠螺旋丝杆轴驱动螺旋旋转输出套做往复旋摆运动,滚珠花键导轨副防止螺旋丝杆轴转动。
2设计并仿真分析电液伺服阀控活塞式液压摆动马达位置控制系统设计参数及性能要求:马达的最大旋转摆角为50°;最大转速s /30max ︒=ω,最大角加速度;液压缸以外运动部件受到干摩擦力矩为kgM m =150为m kg M m ⋅=150;液压缸的粘性摩擦系数为s m kg B m /105.125⋅⨯=;负载转动惯量为218.4s m N J ⋅⋅=,静态误差︒≤2.0c e ;速度误差︒≤1.0v e ;相位裕量︒=50][γ;增益裕量dB L g 10][=;液压弹性模量为25/107000mNe⨯=β。
1)计算液压缸的传递函数,并绘制系统控制方框图;2)建立电液控制系统的数学模型;3)用PI调节器对系统进行性能校正和仿真分析(校正前、后的伯德图、单位阶跃响应以及正弦响应)。
第二章、元器件选用2.1液压油源开式泵选用德国力士乐原装进口的轴向柱塞恒压变量泵,特别适合开式回路,具有良好的自吸特性,连续工作压力可达35Mpa,噪声低、使用寿命长、功率重量比高,排量为125mL/r。
(完整word版)电液伺服阀控液压缸仿真

华中科技大学电液控制工程四通电液伺服阀控液压缸控制系统仿真摘要:本文通过对电液伺服四通滑阀控液压缸系统进行数学建模和Matlab仿真研究系统的传递函数、响应特性以及波特图。
关键词:四通 伺服 建模 仿真 响应特性 波特图引言:电液伺服控制系统是电液控制技术最早出现的一种应用形式。
通常所说的电液伺服控制系统,从其构成来说,就是指以电液伺服阀作为电液转换和放大元件实现某种控制规律的系统,它的输出信号能跟随输入信号快速变化,所以有时也成为随动系统。
电液伺服控制系统将液压技术和电气、电子技术有机地结合起来,既有快速易调和高精度的响应能力,又有控制大惯量实现大功率输出的优势,因而在国防和国民经济建设的各个技术领域得到了广泛的应用.作为电液伺服系统中不可缺少的组成部分,液压动力机构由液压控制元件、执行元件和负载组成,又称为液压动力元件,它的动态特性对大多数液压伺服系统的性能有着决定性影响,因此,其传递函数是分析整个液压伺服系统的基础.液压动力元件可以分为四种基本形式:阀控液压缸、阀控液压马达、泵控液压缸和泵空液压马达.四种液压动力元件虽然结构不同,但其特性是类似的,本文通过建立数学模型,分析零开口四通滑阀和对称液压缸组成的液压系统的流量特性、力平衡方程和控制传递函数,获得系统的响应特性。
系统组成和原理:电液伺服控制系统根据输出信号的不同分为电液位置伺服系统、电液速度伺服系统和电液力伺服系统。
本文四通阀控液压缸属于电液位置伺服系统,其原理如右图1所示,四通滑阀控制液压缸拖动带有弹性和粘性阻尼的负载作往复运动。
该液压伺服控制系统的结构框图则如下图2所示.u i + u g i q L F L图 1 四通阀控液压缸原理图放大器 伺服阀 液压缸负载 反馈装置图 2 系统原理方框建立系统数学模型:流量方程由图1可知,从阀进入液压缸做强的流量除了推动活塞运动外,还要补偿液体的压缩量和管道等的膨胀量,补偿液压缸内、外泄漏,即q1=A p dx p/dt+V1/βe(dp1/dt)+Ci(p1-p2)+C e p1 (1)q2=A p dx p/dt-V2/βe(dp2/dt)+Ci(p1—p2)-C e p2 (2)式中,A p为活塞面积,x p为活塞位移,分别为左右进油腔容积,为液压弹性模量,分别为液压缸左右腔压力。
阀泵联合控制大功率速度伺服系统,一起来看看!
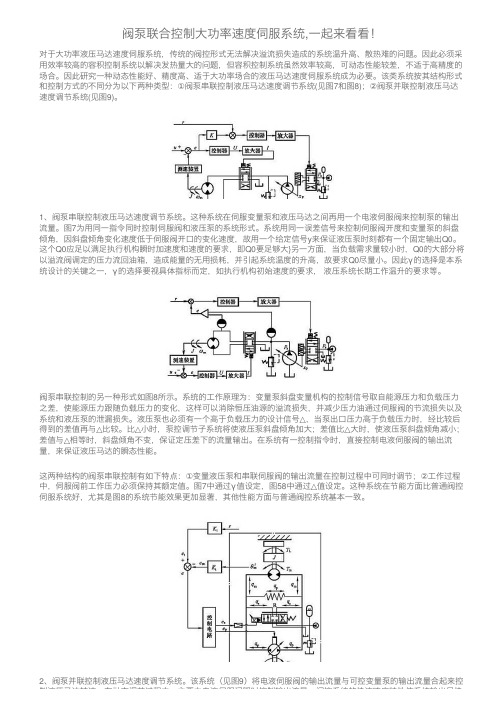
阀泵联合控制⼤功率速度伺服系统,⼀起来看看!对于⼤功率液压马达速度伺服系统,传统的阀控形式⽆法解决溢流损失造成的系统温升⾼、散热难的问题。
因此必须采⽤效率较⾼的容积控制系统以解决发热量⼤的问题,但容积控制系统虽然效率较⾼,可动态性能较差,不适于⾼精度的场合。
因此研究⼀种动态性能好、精度⾼、适于⼤功率场合的液压马达速度伺服系统成为必要。
该类系统按其结构形式和控制⽅式的不同分为以下两种类型:①阀泵串联控制液压马达速度调节系统(见图7和图8);②阀泵并联控制液压马达速度调节系统(见图9)。
1、阀泵串联控制液压马达速度调节系统。
这种系统在伺服变量泵和液压马达之间再⽤⼀个电液伺服阀来控制泵的输出流量。
图7为⽤同⼀指令同时控制伺服阀和液压泵的系统形式。
系统⽤同⼀误差信号来控制伺服阀开度和变量泵的斜盘倾⾓,因斜盘倾⾓变化速度低于伺服阀开⼝的变化速度,故⽤⼀个给定信号y来保证液压泵时刻都有⼀个固定输出Q0。
这个Q0应⾜以满⾜执⾏机构瞬时加速度和速度的要求,即Q0要⾜够⼤}另⼀⽅⾯,当负载需求量较⼩时,Q0的⼤部分将以溢流阀调定的压⼒流回油箱,造成能量的⽆⽤损耗,并引起系统温度的升⾼,故要求Q0尽量⼩。
因此γ的选择是本系统设计的关键之⼀,γ的选择要视具体指标⽽定,如执⾏机构初始速度的要求,液压系统长期⼯作温升的要求等。
阀泵串联控制的另⼀种形式如图8所⽰。
系统的⼯作原理为:变量泵斜盘变量机构的控制信号取⾃能源压⼒和负载压⼒之差,使能源压⼒跟随负载压⼒的变化,这样可以消除恒压油源的溢流损失,并减少压⼒油通过伺服阀的节流损失以及系统和液压泵的泄漏损失。
液压泵也必须有⼀个⾼于负载压⼒的设计信号△,当泵出⼝压⼒⾼于负载压⼒时,经⽐较后得到的差值再与△⽐较。
⽐△⼩时,泵控调节⼦系统将使液压泵斜盘倾⾓加⼤;差值⽐△⼤时,使液压泵斜盘倾⾓减⼩;差值与△相等时,斜盘倾⾓不变,保证定压差下的流量输出。
在系统有⼀控制指令时,直接控制电液伺服阀的输出流量,来保证液压马达的瞬态性能。
液压凿岩机阀控液压马达转速伺服系统的建模与仿真

液压凿岩机阀控液压马达转速伺服系统的建模与仿真李明超;陈可【摘要】凿岩机中液压马达的转速一般情况下随实际工况的变化产生一定程度的波动,随着液压马达负载的增大,系统泄漏增加和溢流阀溢流增加,使得液压马达转速低于期望转速.如此凿岩效率降低且容易发生转钎卡死.基于独立旋转凿岩机的工作原理,为了使凿岩机转速稳定且可控,提高凿岩的效率,设计了凿岩机转速伺服控制系统,试图使凿岩机中的液压马达转速保持稳定且可控.通过AMESim对凿岩机内液压马达速度控制系统建模与仿真,结果显示新模型的响应速度、稳定性满足实际使用要求.【期刊名称】《机械工程师》【年(卷),期】2017(000)008【总页数】3页(P14-16)【关键词】凿岩机;液压马达;PID调节【作者】李明超;陈可【作者单位】四川大学制造科学与工程学院,成都610065;四川大学制造科学与工程学院,成都610065【正文语种】中文【中图分类】TU631;TP273凿岩机是凿岩台车与岩石直接作业的结构,在进行凿岩台车设计时,通常使其与台车臂对点机构具有独立的液压系统,以便于根据不同型号的凿岩机对液压系统进行调整。
目前常用的凿岩机种类繁多,根据工作方式不同分为冲击型凿岩机和独立旋转式凿岩机。
某品牌HYD200型独立旋转式凿岩机旋转机构工作原理图如图1所示,凿岩机中有一个液压马达,凿岩机中一系列的机构通过液压马达的旋转带动转钎的旋转。
由转钎直接对岩石进行作用。
凿岩机中液压马达的转速一般情况下随实际工况的变化产生一定程度的波动,随着液压马达负载的增大、系统泄漏增加和溢流阀溢流增加,使得液压马达转速低于期望转速。
如此凿岩效率降低且容易发生转钎卡死。
如图1所示,凿岩机中有一个液压马达,凿岩机中一系列的机构通过液压马达的旋转带动转钎的旋转。
由转钎直接对岩石进行作用。
1)转钎处于停止状态:当换向阀4的阀芯处于右位(如图1所示位置)时,由液压泵2输出的压力油经过溢流阀5,沿回油管直接回到油箱。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
阀控液压马达速度伺服系统仿真分析
引言
阀控液压马达速度伺服系统的负载具有较大的惯性和很小的阻尼,其传递函数常可近似由一对实部为零的极点组成,并有很低的动态响应,由于负载处在系统的闭环之中,所以它对阀控液压马达的动态品质有很大的影响。
此外,系统的负载常是可变的,系统设计只能针对一种特定负载,负载一旦改变,系统的动态品质就会变坏,有时甚至失去稳定性,严重的影响了伺服系统的跟踪性能。
本文主要针对干扰力矩对系统的影响,利用结构不变性原理,消除干扰力矩对系统的影响,同时利用PID 控制理论来提高系统的动态性能。
1 阀控液压马达速度伺服系统模型建立
阀控液压马达速度伺服系统的结构如图1所示。
液压马达的力矩方程为:
f
m m s l m T G s C J P +++=θ)(D (1)
负载流量方程为:
l e
m m l tm l sP V
s D P C βθ4Q +== (2)
伺服阀的线性流量方程为: L p x l
P K x k Q -= (3)
电液伺服阀近似看成二阶振荡环节:
1
22^2^)()(++=
s S K s i s x sv
sv
sv sv
v ωξω (4) 伺服放大器输出电流ΔI 与输入电压Ue 近似成正比,其传递函数可用伺服放大器增益Ka 表示:
但通常的速度控制系统采用积分放大器,对原系统加以校正才能稳定工作。
校正后的积分放大器增益Ka 表示为:
测速机速度传感器(测速机)的数学模型为:
在上述公式中:v x 为电液伺服阀阀芯位移;i 为电液伺服阀输入电流;v sv k s sv ωξ、、分别为电液伺服阀的增益、阻尼系数和固有频率;m D 为马达排量;L Q 为马达的负载流量;x K 为流量增益系数;
p K 为流量一压力系数;只为供油压力;s P 为负载压力;m θ为马达转
速;e β为从油液有效体积弹性模数;V 为马达的总容积;J 为折算到
马达输出轴上的转动惯量;f T 为外干扰力矩;tm C 为马达泄露系数;
m C 为粘性阻尼系数;G 为扭簧梯度。
Ue 为积分放大器额定电压,;Ka 为积分放大器增益。
为传感器电压;为速度传感器增益。
2 电液速度控制系统原理
首先给出阀控液压马达速度控制系统的实际物理模型:
如图所示,该系统由伺服放大器、电液伺服阀、液压马达、测速电动机等组成。
测速电机轴与负载机轴相联,用于检测负载轴的速度,检测到的速度信号与指令信号差(误差信号)经伺服放大器进行功率放大,产生的电流用来控制电液伺服阀的阀芯位置,电液伺服阀输出压力油驱动液压马达及负载旋转。
根据所建立的物理模型,可以建立相对应的闭环控制系统原理的方框图:
伺服放大器
伺服阀
液压马达
测速机
速度信号电压
+
-
仿真系统动态方块图
根据所给出的系统原理方框图以及所求得的各环节数学模型,
可以得出仿真系统经过积分环节校正后的系统动态方块图如下:
K a
s
K sv
s2
ωsv2
+2ξh
ωsv
s+1
K s
s2
ωh2+
2ξh
ωh s+1
K fs s
Ur
Uf
Ue
+
-
θm
3 问题描述
现有一阀控液压伺服速度控制系统,其原理图如图1,考虑伺服阀的动态,伺服参数为:=3060e-6,=600,=0.5,液压缸的参数为=1.25e6,=388,=0.94,放大器增益=0.05,试用simulink对该系统进行动态分析,并比较校正前后系统稳定性,分析校正前后的变化。
4 解题步骤
(1)根据给定的参数,利用simulink对该系统进行未加积分环节校正的系统建模,如下图所示:
未校正系统的simulink模型
(2)绘制未校正系统的伯德图。
Matlab程序如下:
clear all;clc;
Wsv=600;zuni1=0.5;Ksv=3060e-6;Ka=0.05;i=3;Kf=0.175;
Wh=388;zuni2=0.94;Kh=1.25e6;
sys=tf(Ka*Ksv*i*Kf*Kh,conv([1/Wsv^2 2*zuni1/Wsv 1],[1/Wh^2 2*zuni2/Wh 1]));
Figure;margin(sys);
grid;
分析bode图:
从图可看出系统的稳定裕量(Gm=-32.6dB,Pm=-128°)为负,可以断定其闭环系统是不稳定的。
及时K0值调很低,对数幅频特性曲线也是以-80dB/dec或-40dB/dec的斜率穿过零分贝线,系统的相位裕量和幅值裕量都趋于负值,使系统不稳定。
为了使系统有一定的稳定裕度量,必须加校正环节。
在速度控制系统中,可以用运算放大器组成积分放大器代替原来的放大器。
积分放大器如下图所示:
积分放大器
其传递函数为:
其中,Ka=0.05。
加了校正之后的系统仿真方框图如下:
校正后速度控制系统的仿真框图
矫正后的MATLAB程序:
clear all;clc;
Wsv=600;zuni1=0.5;Ksv=3060e-6;Ka=0.05;i=3;Kf=0.175;
Wh=388;zuni2=0.94;Kh=1.25e6;
sys=tf(Ka*Ksv*Kh,conv([1/Wsv^2 2*zuni1/Wsv 1 0],[1/Wh^2 2*zuni2/Wh 1]));
figure;margin(sys);
grid;
从伯德图看出校正后的系统穿越频率下降到247 rad/s,Gm=4.09dB,Pm=26.7deg,可看出系统有正的相角裕度,因而该系统闭环是稳定的。
阀控液压马达速度伺服系统仿真分析
专业:机械设计制造及其自动化
班级:(2)班
:王仲凯
学号:120312005
指导老师:董甲东。
