选择填空专题训练十

合集下载

平面向量选择填空压轴题专练-2021届高考数学(理)培优专题提升训练(解析版)

第23讲平面向量选择填空压轴题专练A 组一、选择题1．(2018天津)如图，在平面四边形ABCD 中，AB BC ⊥，AD CD ⊥，120BAD ∠=︒，1AB AD ==．若点E 为边CD 上的动点，则⋅AE BE 的最小值为A ．2116B ．32C ．2516D ．3【答案】A【解析】以A 为坐标原点，AB 所在直线为x 轴，建立如图的平面直角坐标系，因为在平面四边形ABCD 中，1AB AD ==，120BAD ∠=︒，所以(0,0)A ，(1,0)B，1(,22D -，设(1,)C m ,(,)E x y ，所以3(,22DC m =-，1(,)22AD =-，因为AD CD ⊥，所以31(,(022m ⋅-=，即31()022m ⨯--=，解得m =，即(1C ，因为E 在CD上，所以2y ≤，由CE CD k k =，得21112y x =-+，即2x -，因为(,)AE x y =，(1,)BE x y =-，所以2222(,)(1,)2)2AE BE x y x y x x y y ⋅=⋅-=-+=-++246y =-+，令2()46f y y =-+，[2y ∈． E DCB因为函数2()46f y y =-+在上单调递减，在上单调递增，所以2min 21()4616f y =⨯-+=．所以⋅AE BE 的最小值为2116，故选A ．2．已知ABC ∆是边长为2的等边三角形，P 为平面ABC 内一点，则()PA PB PC ⋅+的最小值是（） A.2- B.32- C. 43- D.1- 【答案】B【解析】以BC 为x 轴，BC 的垂直平分线AD 为y 轴，D 为坐标原点建立坐标，则A ，(1,0)B -，(1,0)C ，设(,)P x y ，所以()PA x y =-，(1,)PB x y =---，(1,)PC x y =--所以(2,2)PB PC x y +=--，22233()22)22(22PA PB PC x y y x y ⋅+=-=+-≥-当P 时，所求的最小值为32-，故选B 。

[必刷题]2024三年级英语上册听力理解专项专题训练(含答案)

[必刷题]2024三年级英语上册听力理解专项专题训练（含答案）试题部分一、选择题：10道1. Listen and choose the right answer. What's the boy's name?A. MikeB. TomC. John2. Listen and choose the correct answer. What's the weather like today?A. SunnyB. RainyC. Cloudy3. Listen and choose the right answer. What's the girl's favorite fruit?A. AppleB. BananaC. Orange4. Listen and choose the correct answer. Where does the cat sleep?A. On the bedB. Under the tableC. In the box5. Listen and choose the right answer. What time does the school start?A. At 7:30B. At 8:00C. At 8:306. Listen and choose the correct answer. What does the teacher ask the students to do?A. Read a bookB. Write a letterC. Draw a picture7. Listen and choose the right answer. Which animal can fly?A. ElephantB. TigerC. Bird8. Listen and choose the correct answer. How many days are there in a week?A. FiveB. SixC. Seven9. Listen and choose the right answer. What's the mother doing?A. CookingB. Washing clothesC. Watching TV10. Listen and choose the correct answer. What's the opposite of "hot"?A. ColdB. WarmC. Cool二、判断题：5道1. Listen and decide if the statement is true or false. The girl likes playing basketball. ( )2. Listen and decide if the statement is true or false. The boy goes to school bus. ( )3. Listen and decide if the statement is true or false. The cat is sleeping on the sofa. ( )4. Listen and decide if the statement is true or false. There are twelve months in a year. ( )5. Listen and decide if the statement is true or false. The teacher is reading a story to the students. ( )三、填空题：20道1. The cat is _______ on the table.2. I go to school _______ foot.3. There are _______ days in a week.4. My mother is _______ dinner.5. The sun is _______ in the sky.6. Apples are _______ the basket.7. She is _______ a red dress today.8. We have English class _______ Monday.9. The bird is _______ in the tree.10. My birthday is in _______.11. I can _______ a bike.12. The dog is _______ the bone.13. They are playing _______ the park.14. I like to _______ to music.15. The book is _______ the table.16. She _______ her hair every morning.17. He is _______ a story to the children.18. We eat breakfast _______ the morning.19. The car is _______ the garage.20. The flowers are _______ in the garden.四、简答题：10道1. What is your favorite color? Why do you like it?2. Describe your best friend.3. What do you usually do after school?4. What is your favorite day of the week? Why?5. Where do you go on vacation?6. What do you like to do on weekends?7. Who is your favorite teacher? Why?8. What do you want to be when you grow up?9. Describe your favorite animal.10. What is your favorite season? Why do you like it?本套试题答案如下一、选择题答案：1. A2. A3. C4. B5. B6. C7. C8. C9. A10. A二、判断题答案：1. √2. √3. ×4. √5. √三、填空题答案：1. sitting2.3. seven4. making5. shining6. in7. wearing8. on9. singing10. June11. ride12. chasing13. in14. listen15. on16. brushes17. reading18. in19. in20. blooming四、简答题答案：1. My favorite color is blue because it reminds me of the ocean.2. My best friend is tall and has short brown hair. We like to play soccer together.3. After school, I usually do my homework and then play video games.4. My favorite day of the week is Saturday because Idon't have school.5. We usually go to the beach on vacation.6. On weekends, I like to go cycling with my family.7. My favorite teacher is my English teacher because she makes learning fun.8. When I grow up, I want to be a doctor.9. My favorite animal is a panda because it's cute and eats bamboo.10. My favorite season is autumn because I like the colorful leaves.。

高考数学客观题训练【6套】选择、填空题

数学PA高考数学客观题训练【6套】选择、填空题专题练习（一）1．已知全集U=R ，集合)(},021|{},1|{N M C x x x N x x M U则≥-+=≥=（）A ．{x |x <2}B ．{x |x ≤2}C ．{x |－1<x ≤2}D ．{x |－1≤x <2}2．设,0,0<>b a 已知),(a b m ∈且0≠m ，则m1的取值范围是： ( )A ．)1,1(a b B.)1,1(b a C.)1,0()0,1(a b ⋃ D.),1()1,(+∞⋃-∞ab 3．设)(x f '是函数)(x f 的导函数,)(x f y '=的图象如图所示，则)(x f y =的图象最有可能的是4．直线052)3(057)3()1(2=-+-=-+-++yx m m y m x m 与直线垂直的充要条件是（）A ．2-=mB ．3=mC ．31=-=m m 或D ．23-==m m 或5．命题“042,2≤+-∈∀x x R x ”的否定为（）(A) 042,2≥+-∈∀x x R x (B) 042,2>+-∈∃x x R x (C)042,2≤+-∉∀x x R x (D) 042,2>+-∉∃x x R x6. 若平面四边形ABCD 满足0AB CD +=,()0AB AD AC -⋅=,则该四边形一定是A ．直角梯形B ．矩形C ．菱形D ．正方形7．有一棱长为a 的正方体框架，其内放置一气球，是其充气且尽可能地膨胀（仍保持为球的形状），则气球表面积的最大值为 A ．2a πB ．22a πC ．32a πD ．42a π8．若22πβαπ<<<-，则βα-一定不属于的区间是 ( )A ．()ππ,- B ．⎪⎭⎫⎝⎛-2,2ππ C ．()π,0 D ． ()0,π-9．等差数列{a n } 中，a 3 =2，则该数列的前5项的和为( ) A ．10 B ．16C ． 20D ．3210．不等式10x x->成立的充分不必要条件是 A ．10x -<<或1x > B ．1x <-或01x << C ．1x >-D ．1x >二、填空题（每题5分，满分20分，请将答案填写在题中横线上） 11. 线性回归方程ˆybx a =+必过的定点坐标是________. 12. .在如下程序框图中，已知：x xe x f =)(0，则输出的是__________.13. 如图，一个粒子在第一象限运动，在第一秒末，它从原点运动到（0，1），接着它按如图所示的x 轴、y 轴的平行方向来回运动，（即（0，0）→（0，1）→（1，1）→（1，0）→ （2，0）→…），且每秒移动一个单位，那么第2008秒末这个粒子所处的位置的坐标为______。

选词填空练习题初二

选词填空练习题初二
下面是一些选词填空练习题，适合初二学生练习，通过填写适当的
词语来完整句子。

这些练习题可以帮助学生巩固词汇、理解词语用法，并提高句子构建的能力。

请根据提示，用适当的词语填空。

1. 我们在游泳池玩得很高兴，水很______。

2. 这本小说很______，我一下子就读完了。

3. 我每天都坚持锻炼，身体感觉______了很多。

4. 好好学习，天天向上是我们的______。

5. 爷爷喜欢在花园里种花，每个季节都有______的花开。

6. 她努力学习，终于______考试的第一名。

7. 天气预报说今天会下雨，我们最好带上______。

8. 这个问题太难了，我需要更多的______来解决。

9. 我们去公园玩，看到很多人在大声______。

10. 我们要积极参加社区活动，为社会做出______贡献。

参考答案：
1. 清凉
2. 有趣
3. 健康
4. 座右铭
5. 不同种类
6. 考到
7. 雨伞
8. 信息
9. 喊叫
10. 积极的。

苏教版二年级数学上册填空专项专题训练

苏教版二年级数学上册填空专项专题训练1. 在41÷5中，余数是______，它比______小。

2. 我会填。

24棵白菜，平均放在8个篮子里，求每个篮子放几棵，列式为24÷8。

方法一：24-(______)-(______)-(______)=0(棵)。

方法二：(______)× 8=24，所以每个篮子放(______)棵。

方法三：还可以用(______)计算。

3. 想一想，再比较大小。

3分______ 30秒 4时______ 400分240秒______ 4分100秒______ 2分半时______ 40分100秒______ 1分4. 估弹珠。

5. 12厘米＝______毫米9米＝______分米200毫米＝______厘米6. 李群在船快靠岸时，连续拍摄了几张图片，请你按先后顺序选择序号排列．______7. 接着写。

5，50，500，______，______。

8. 下面的时间对不对错误的订正过来。

9. 把口诀补充完整．______十五______五得五______二十五______二十______五一十四五______10. 写出下面的时间。

11. 填一填。

（1）520+90=______思考：①先算20加90得______，再算______加500得______；②520是______个十，加上______个十，得______个十，就是______。

（2）480-50=______思考：①先算80减去______得______，再算______加上______得______；②480是______个十，减去______个十，得______个十，就是______。

12. 比大小（在横线上填上“＞”“＜”或者“＝”）1时______ 50分13. 小新跑60米要12______。

14. 用乘法解决问题．（1）（2）（3）买5只15. 标准地图通常是按照上______、下______、左______、右______的顺序绘制的。

初三化学填空题专题训练

初三化学填空题专题训练一、题目及解析1. 保持水的化学性质的最小粒子是________。

-解析：分子是保持物质化学性质的最小粒子，水是由水分子构成的，所以保持水的化学性质的最小粒子是水分子。

-答案：水分子。

2. 空气中含量最多的气体是________。

-解析：空气中含量最多的气体是氮气，约占空气体积的78%。

-答案：氮气。

3. 地壳中含量最多的元素是________。

-解析：地壳中含量最多的元素是氧元素。

-答案：氧元素。

4. 元素的化学性质主要决定于原子的________。

-解析：元素的化学性质主要决定于原子的最外层电子数。

-答案：最外层电子数。

5. 2 个氧分子的符号是________。

-解析：氧分子用O₂表示，2 个氧分子就是2O₂。

-答案：2O₂。

6. 写出硫酸铝的化学式________。

-解析：硫酸铝中铝元素显+3 价，硫酸根显-2 价，根据化合物中正负化合价代数和为零，其化学式为Al₂(SO₂)₂。

-答案：Al₂(SO₂)₂。

7. 相对分子质量最小的氧化物是________。

-解析：相对分子质量最小的氧化物是水，化学式为H₂O。

-答案：H₂O。

8. 点燃氢气前必须要________。

-解析：氢气是可燃性气体，点燃氢气前必须要检验氢气的纯度，防止发生爆炸。

-答案：检验氢气的纯度。

9. 二氧化碳能使澄清石灰水变浑浊，反应的化学方程式为________。

-解析：二氧化碳与氢氧化钙反应生成碳酸钙沉淀和水，化学方程式为CO₂ + Ca(OH)₂ = CaCO₂↓ + H₂O。

-答案：CO₂ + Ca(OH)₂ = CaCO₂↓ + H₂O。

10. 实验室制取氧气的方法有多种，其中一种方法是加热高锰酸钾，反应的化学方程式为________。

-解析：高锰酸钾受热分解生成锰酸钾、二氧化锰和氧气，化学方程式为2KMnO₂ =₂ K₂MnO₂ + MnO₂ + O₂↑。

-答案：2KMnO₂ =₂ K₂MnO₂ + MnO₂ + O₂↑。

初中生物选择健康的生活方式填空题专题训练含答案

初中生物选择健康的生活方式填空题专题训练含答案姓名：__________ 班级：__________考号：__________一、填空题（共30题）1、健康的生活习惯包括生活有规律、合理、合理及拒绝吸烟、酗酒、吸毒等。

2、是休息方式中最重要的一种，另外还有，闭目养神、散步、参加。

3、吸烟会影响的健康，长期吸烟会引起。

4、一个人的健康与他的日常生活习惯有着密切的关系。

健康的生活习惯包括生活有、合理、合理用药及拒绝吸烟、酗酒、吸毒等。

5、当今社会威胁人类健康的主要疾病是和。

6、与心血管疾病有关的三个重要因素是、和。

7、“吸食毒品犹如玩火”对于“玩火者”，吸毒时有毒物质首先接触的是他们的______黏膜，会使其受到伤害，吸毒对______、______和__________等器官系统也有影响。

8、健康是指一种身体上、和方面的良好状态。

维持心理健康和良好的，是健康生活的重要内容。

9、健康与密切相关。

10、选择健康的生活方式有利于提高人们的健康水平，青少年尤其要注意抵制吸烟、酗酒和吸毒的诱惑。

（1）烟草燃烧时，烟雾有和等有毒物质，吸烟不仅诱发多种系统疾病，还可诱发肺癌。

（2）吸食毒品会损害人的系统降低人的免疫功能，严重会导致死亡。

11、健康的生活方式不仅有利于预防__________，特别是一些______________，而且有利于提高人们的__________，提高__________。

12、“吸食毒品犹如玩火”对于“玩火者”，吸毒时有毒物质首先接触的是他们的______黏膜，会使其受到伤害，吸毒对______、______和__________等器官系统也有影响。

13、健康新概念：、、、。

14、我国常见的癌症中，死亡人数和死亡率最高的是___________。

15、拥有愉快的心情是我们中学生健康的核心。

16、第64届世界卫生大会于5月16日在日内瓦举行。

本次会议的议题包括流感疫情的防控、流感病毒和疫苗的共享、慢性病的防治等。

人教版三年级语文上册填空题专项专题训练

人教版三年级语文上册填空题专项专题训练1. 在横线上填入适当的字或量词，把词语补充完整。

清______见底全神______注胆大______为气______吁吁响______云霄 ______不可及一______谎言一______装饰一______石狮子一______扫帚一______画一______旗杆2. 词语搭配连线。

哀痛的______ 朋友风筝飞得______ 很高高尚的______ 日子日子过得______ 茂盛尴尬的______ 眼光花儿开得______ 鲜艳羡慕的______ 局面树木长得______ 飞快3. 选词填空。

抽长①春天树木______出新的枝条，______出嫩绿的叶子。

挡封遮②夏天，树木长得葱葱茏茏，密密层层的枝叶把森林______得严严实实，______住了人们的视线，______住了蓝蓝的天空。

4. 我会根据课文在横线上填上恰当的词语。

______的空调列车______的地方______的客人______的燕子______的大雪______的山路5. 选择下划线字的正确读音。

在充满噪（zào zhào）______音的厂房里，母亲用龟(guī jūn)______裂的手指数完毛票后把钱塞(sāi sài)______给我，紧接着又又陷(xiàn xuàn)______入了工作中。

我不敢耽(dān diān)______误她工作，拿了钱跑了出去……6. 给下面加下划线字选择正确的读音。

人未还______（hái huán）飞将_______（jiāng jiàng）在生当______（dāng dàng）作人杰死亦为______（wéi wèi）鬼雄不教______（jiāo jiào）胡马度______（dùduó）阴7. 找出括号中不正确的读音。

中考专题名校优选训练-倍长中线法和路径问题(填空选择部分)

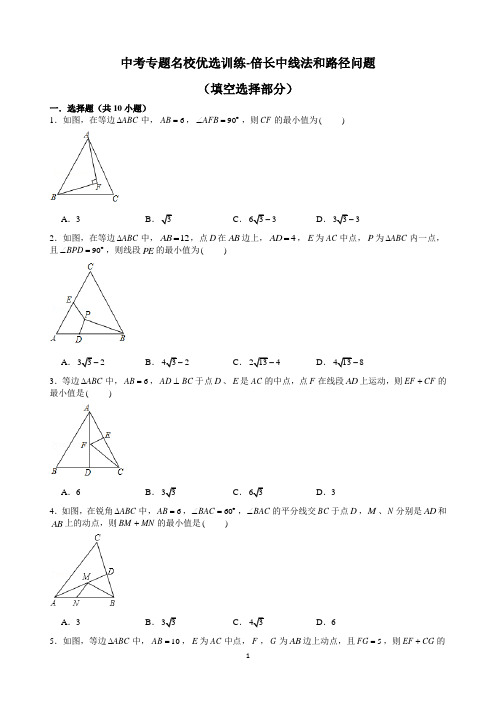
中考专题名校优选训练-倍长中线法和路径问题（填空选择部分）一．选择题（共10小题）1．如图，在等边ABC ∆中，6AB =，90AFB ∠=︒，则CF 的最小值为( )A ．3B ．3C ．633-D ．333-2．如图，在等边ABC ∆中，12AB =，点D 在AB 边上，4AD =，E 为AC 中点，P 为ABC ∆内一点，且90BPD ∠=︒，则线段PE 的最小值为( )A ．332-B ．432-C ．2134-D ．4138-3．等边ABC ∆中，6AB =，AD BC ⊥于点D 、E 是AC 的中点，点F 在线段AD 上运动，则EF CF +的最小值是( )A ．6B ．33C ．63D ．34．如图，在锐角ABC ∆中，6AB =，60BAC ∠=︒，BAC ∠的平分线交BC 于点D ，M 、N 分别是AD 和AB 上的动点，则BM MN +的最小值是( )A ．3B ．33C ．43D ．65．如图，等边ABC ∆中，10AB =，E 为AC 中点，F ，G 为AB 边上动点，且5FG =，则EF CG +的最小值是()A．57B．56C．535+D．156．如图，在等边ABC∆中，9AB=，N为AB上一点，且3AN=，BC的高线AD交BC于点D，M是AD上的动点，连接BM，MN，则BM MN+的最小值是()A．62B．932C．1073D．377．如图，在Rt ABC∆中，90BAC∠=︒，30ACB∠=︒，6AB=，点P为BC上任意一点，连接PA，以PA，PC为邻边作平行四边形PAQC，连接PQ，则PQ的最小值为()A．3B．23C．6D．338．如图，在Rt ABC∆中，90ACB∠=︒，6AC BC==，D为AC的中点，E是线段AB边上一动点，连接ED、EC，则CDE∆周长的最小值为()A．35B．33C．333D．3539．如图，边长为a的等边ABC∆的顶点A，B分别在x轴正半轴和y轴正半轴上运动，则动点C到原点O 的距离的最大值是()A ．3122a a -B ．3122a a + C ．6122a a - D ．6122a a + 10．如图，MNP ∆中，60P ∠=︒，MN NP =，MQ PN ⊥，垂足为Q ．延长MN 至G ，取NG NQ =，若MNP ∆的周长为12，则MGQ ∆周长是( )A ．823+B ．643+C ．843+D ．623+二．填空题（共7小题）11．如图在Rt ACB ∆中，C 为直角顶点，25ABC ∠=︒，O 为斜边中点．将OA 绕着点O 逆时针旋转(0180)θθ︒<<至OP ，当BCP ∆恰为轴对称图形时，θ的值为．12．如图，在Rt ABC ∆中，C 为直角顶点，20ABC ∠=︒，O 为斜边的中点，将OA 绕着点O 逆时针旋转(0180)θθ︒<<至OP ，当BCP ∆恰为轴对称图形时，θ的值为．13．如图，在ABC ∆中，D 是BC 的中点，E 是AD 上一点，BE AC =，BE 的延长线交AC 于点F ．若60ACB ∠=︒，44DAC ∠=︒，则FBC ∠的度数是．14．如图，ABC ∆中，D 为边AB 的中点，E 为边BC 上一点，ED 延长线交CA 延长线于点F ，以下结论正确的有． ①若AB BC =，BE DE =，则AF AD =；②若90ACB ∠=︒，CE DE =，则AD BD CE CB =；③当13BE CE =时，则13FA AC =； ④当CA x CF =，CB y CE=时，则2x y +=．15．如图，等边ABC ∆中，4AB =，E 是线段AC 上的任意一点，BAC ∠的平分线交BC 于D ，23AD =，F 是AD 上的动点，连接CF 、EF ，则CF EF +的最小值为．16．如图，在边长为63的等边ABC ∆中，点D 、点E 分别是边BC 、AC 上的点，且BD CE =，连接BE 、AD ，相交于点F ．连接CF ，则CF 的最小值为．17．定理：直角三角形斜边上的中线等于斜边的一半，即：如图1，在Rt ABC ∆中，90ACB ∠=︒，若点D是斜边AB 的中点，则12CD AB =，运用：如图2，ABC ∆中，90BAC ∠=︒，2AB =，3AC =，点D 是BC 的中点，将ABD ∆沿AD 翻折得到AED ∆连接BE ，CE ，DE ，则CE 的长为．参考答案与试题解析一．选择题（共10小题）1．【解答】解：如图取AB 的中点E ，连接EF 、EC ．ABC ∆是等边三角形，AE EB =，6AB BC ∴==，60CBE ∠=︒，sin 6033CE BC ∴=︒=，90AFB ∠=︒，AE EB =，132EF AB ∴==， CF EC EF ∴-， ∴当E 、F 、C 共线时，FC 的值最小，最小值为333-，故选：D ．2．【解答】解：以BD 为直径作O ，连接OE 交O 于点P ，则OE 的长度最小，即EP 最小，过点E 作EF AB ⊥于点F ，在Rt AEF ∆中，60A ∠=︒，6AE =，3AF ∴=，33EF =，在Rt OEF ∆中，33EF =，5OF =，213OE ∴=，2134PE ∴=-，即线段PE 的最小值为2134-，故选：C ．3．【解答】解：如图，作点E 关于直线AD 的对称点E '，连接CE '交AD 于F '．EF FC FE FC +='+，∴当C 、E '、F 共线时，EF CF +最小值CE ='，ABC ∆是等边三角形，6AB BC AC ===，3AE AE ='=，3AE E B ∴'='=，60ACB ∠=︒，30ACE BCE ∴∠'=∠'=︒，CE AB '⊥，3332CE BC ∴'==，故选：B ．4．【解答】解：在AC 上取一点E ，使得AE AB =，过E 作EN AB '⊥于N '，交AD 于M ，连接BM ，BE ，BE 交AD 于O ，则BM MN +最小（根据两点之间线段最短；点到直线垂直距离最短）， AD 平分CAB ∠，AE AB =，EO OB ∴=，AD BE ⊥，AD ∴是BE 的垂直平分线（三线合一）， E ∴和B 关于直线AD 对称，EM BM ∴=，即BM MN EM MN EN +'=+'='，EN AB '⊥，90ENA ∴∠=︒，60CAB ∠=︒，30AEN ∴∠'=︒，6AE AB ==，132AN AE ∴==，在AEN ∆中，由勾股定理得：22226333EN AE AN =-'=-=，即BM MN +的最小值是33．故选：B ．5．【解答】解：如图：作C 点关于AB 的对称点C '，取BC 的中点Q ，连接C Q '，交AB 于点G ，此时CG EF +最小，作C H BC '⊥交BC 的延长线于点H ，10BC BC ='=，120CBC ∠'=︒， 53HC ∴'=，5HB =， 10HQ ∴=，7510057C Q ∴'=+=，EF CG ∴+的最小值是57．故选：A ．6．【解答】解：连接CN ，与AD 交于点M ．则CN 就是BM MN +的最小值．取BN 中点E ，连接DE ，等边ABC ∆的边长为9，3AN =，936BN AC AN ∴=-=-=，3BE EN AN ∴===，又AD BC ⊥，DE ∴是BCN ∆的中位线，2CN DE ∴=，//CN DE ，又N 为AE 的中点，M ∴为AD 的中点，MN ∴是ADE ∆的中位线，2DE MN ∴=，24CN DE MN ∴==，34CM CN ∴=．在直角CDM ∆中，1 4.52CD BC ==，19324DM AD ==， 22974CM CD MD ∴=+=， 37CN ∴=．BM MN CN +=，BM MN ∴+的最小值为37．故选：D ．7．【解答】解：设PQ 与AC 交于点O ，作OP BC '⊥于P '．如图所示：在Rt ABC ∆中，30ACB ∠=︒，212BC AB ∴==，363AC AB ==，四边形PAQC 是平行四边形，33OA OC ∴==，OP BC '⊥，30ACB ∠=︒，13322OP OC '∴==，当P 与P '重合时，OP 的值最小，则PQ 的值最小， PQ ∴的最小值233OP ='=．故选：D ．8．【解答】解：过点D 作D 点关于直线AB 的对称点D '，连接D C '，交AB 于E ，连接AD '，此时DE CE D E EC D C +='+='的值最小．在Rt ABC ∆中，90ACB ∠=︒，6AC BC ==，D 为AC 的中点，45BAC ∴∠=︒，3DC =，由对称性可知45D AE DAE ∠'=∠=︒，AD AD '=，90DAD ∴∠'=︒，D 是AC 边的中点，6AC =，3AD ∴'=，根据勾股定理可得：22226335D C AC AD '=+'=+=，CDE ∴∆周长的最小值：353DE CE DC D C DC ++='+=+故选：D ．9．【解答】解：取AB 的中点D ，连接OD ，CD ，在OCD ∆中，OC OD CD <+，只有当O ，D ，C 三点在一条线上时，OC OD CD =+，此时OC 最大，如图所示，OC AB ⊥， AOB ∆为等腰直角三角形，AB a =，1122OD AB a ∴==，在Rt BCD ∆中，BC a =，12BD a =，根据勾股定理得：32CD a =，则1322OC OD DC a a =+=+．故选：B ．10．【解答】解：MNP ∆中，60P ∠=︒，MN NP =，PMN ∴∆是等边三角形，60PMN PNM ∴∠=∠=︒，PM MN PN ==，MNP ∆的周长为12，4MN PN PM ∴===，MQ PN ⊥，2NQ PQ ∴==，90MQN ∠=︒，1302QMN PMN ∠=∠=︒，在Rt MQN ∆中，由勾股定理得：22224223MQ MN NQ --=， NG NQ =，G GQN ∴∠=∠，60G GQN PNM ∠+∠=∠=︒，30G ∴∠=︒， 30NMQ ∠=︒，G GQN ∴∠=∠，23GQ AQ ∴==，4MN =，2NG NQ ==，MGQ ∴∆周长是(42)2323643MG GQ MQ ++=+++ 故选：B ．二．填空题（共7小题）11．【解答】解：BCP ∆恰为轴对称图形，BCP ∴∆是等腰三角形，如图1，连接AP ，O 为斜边中点，OP OA =，BO OP OA ∴==，90APB ∴∠=︒，当BC BP =时，BCP BPC ∴∠=∠，90BCP ACP BPC APC ∴∠+∠=∠+∠=︒，ACP APC ∴∠=∠，AC AP ∴=，AB ∴垂直平分PC ，25ABP ABC ∴∠=∠=︒，22550θ∴=⨯︒=︒，当BC PC =时，如图2，连接CO 并延长交PB 于H ，BC CP =，BO PO =，CH ∴垂直平分PB ，90CHB ∴∠=︒，OB OC =，25BCH ABC ∴∠=∠=︒，65CBH ∴∠=︒，40OBH ∴∠=︒，24080θ∴=⨯︒=︒，当PB PC =时，如图3，连接PO 并延长交BC 于G ，连接OC ，90ACB ∠=︒，O 为斜边中点，OB OC ∴=，PG ∴垂直平分BC ，90BGO ∴∠=︒，25ABC ∠=︒，65BOG θ∴=∠=︒，综上所述：当BCP ∆恰为轴对称图形时，θ的值为50︒或65︒或80︒，故答案为：50︒或65︒或80︒．12．【解答】解：BCP ∆恰为轴对称图形，BCP ∴∆是等腰三角形，如图1，连接AP ， O 为斜边中点，OP OA =，BO OP OA ∴==，90APB ∴∠=︒，当BC BP =时，BCP BPC ∴∠=∠，90BCP ACP BPC APC ∴∠+∠=∠+∠=︒，ACP APC ∴∠=∠，AC AP ∴=，AB ∴垂直平分PC ，20ABP ABC ∴∠=∠=︒，22040θ∴=⨯︒=︒，当BC PC =时，如图2，连接CO 并延长交PB 于H ，BC CP =，BO PO =，CH ∴垂直平分PB ，90CHB ∴∠=︒，OB OC =，20BCH ABC ∴∠=∠=︒，70CBH ∴∠=︒，50OBH ∴∠=︒，250100θ∴=⨯︒=︒；当PB PC =时，如图3，连接PO 并延长交BC 于G ，连接OC ，90ACB ∠=︒，O 为斜边中点，OB OC ∴=，PG ∴垂直平分BC ，90BGO ∴∠=︒，20ABC ∠=︒，70BOG θ∴=∠=︒，综上所述：当BCP ∆恰为轴对称图形时，θ的值为40︒或100︒或70︒，故答案为：40︒或100︒或70︒．13．【解答】解：如图，延长AD 到G 使DG AD =，连接BG ，在ACD ∆与GBD ∆中，CD BD ADC BDG AD DG =⎧⎪∠=∠⎨⎪=⎩，ACD GBD ∴∆≅∆，CAD G ∴∠=∠，AC BG =，BE AC =，BE BG ∴=，G BEG ∴∠=∠，BEG AEF ∠=∠，AEF EAF ∴∠=∠，60ACB ∠=︒，44DAC ∠=︒，180604476ADC ∴∠=︒-︒-︒=︒，44BED AEF DAC ∠=∠=∠=︒， 764432FBC ADC BED ∴∠=∠-∠=︒-︒=︒，故答案为：32︒14．【解答】解：①如图1中，=，BE BD∴∠=∠=∠，BDE BED ADCBED F F∠=∠+∠，∴∠<∠，F BEDF ADF∴∠<∠，∴<，故①错误．AD AF②如图2中，∠=︒，AD DBACB90=，∴==，DC AD DB∴∠=∠，DCB B=，EC ED∴∠=∠，DCE CDE∠=∠，∴∠=∠，DCE BCD CDE B∽，DCE BCD∴∆∆∴DC CE CB DC=， 2DC CE CB ∴=，AD DB EC CB ∴=，故②正确．③如图3中，作//AN BC 交EF 于N ．//AN CB ，NAD EBD ∴∠=∠，在ADN ∆和BDE ∆中，ADN BDE NAD EBD AD DB ∠=∠⎧⎪∠=∠⎨⎪=⎩，ADN BDE ∴∆≅∆，AN BE ∴=，∴13BE AN AF CE CE FC ===， :1:2AF AC ∴=，故③错误．④由③可知：BE AF CE FC=， CA x CF =，CB y CE=， ∴1111y x --=， 2x y ∴+=，故④正确．故答案为②④．15．【解答】解：AD 是等边ABC ∆的BAC ∠的平分线，AD BC ∴⊥，BD CD =，∴点B 、C 关于AD 对称，过点B 作BE AC ⊥于E ，交AD 于F ，连接CF ，由轴对称确定最短路线问题，点E 、F 即为使CF EF +的最小值的点， ABC ∆是等边三角形，AD 、BE 都是高，23BE AD ∴==CF EF ∴+的最小值23BE ==．故答案为：23．16．【解答】解：如图，ABC ∆是等边三角形，AB BC AC ∴==，60ABC BAC BCE ∠=∠=∠=︒，BD CE =，在ABD ∆和BCE ∆中，AB CB ABC BCE BD CE =⎧⎪∠=∠⎨⎪=⎩，()ABD BCE SAS ∴∆≅∆，BAD CBE ∴∠=∠，又AFE BAD ABE ∠=∠+∠，AFE CBE ABE ABC ∴∠=∠+∠=∠，60AFE ∴∠=︒，120AFB ∴∠=︒，∴点F 的运动轨迹是O 为圆心，OA 为半径的弧上运动此时120AOB ∠=︒，6OA =，212OC OA ∴==，连接OC 交O 于N ，当点F 与N 重合时，CF 的值最小，最小值1266OC ON =-=-=．故答案为6．17．【解答】解：如图，连接BE 交AD 于O ，作AH BC ⊥于H ．在Rt ABC ∆中，90BAC ∠=︒，2AB =，3AC =，由勾股定理得13BC =由题可得13AD DC DB ===1122BC AH AB AC =，∴113123222⨯=⨯⨯ 61313AH ∴=， AE AB =，DE DB =， ∴点A 在BE 的垂直平分线上，点D 在BE 的垂直平分线上， AD ∴垂直平分线段BE ， 1122AD BO BD AH =， 61313OB ∴=， 1213213BE OB ∴==，在Rt BCE ∆中，222212135(13)()131313EC BC BE =-=-=．故答案为51313．。

高考英语语法填空专题强化训练10+Word版含答案

专题强化训练(十)Ⅰ.语法填空A(2019·广西玉林市期末)Speaking of talented people, we will think of the young. Mozart created his first piano concert at 11. Yet I can 't help but draw much 1.____________(inspire) from those who succeeded at an old age.2.____________(give) hope, I am convinced that our dreams can come true if we have faith 3____________ ourselves and keep learning and working for 4.______________.Consider the story of Mary Declany, a 72-year-old woman from the UK, who invented a new art form in the 1770s. On a visit to a friend, she met two plant experts who 5.____________( take) a trip with an explorer through the South Pacific. Interested in their work, she picked up a pair of 6.______________(scissor) and began making flower collages with cut paper.7．____________ surprised us most was that her works of art were so unique and 8.____________(value) that they were on display in the British Museum. There's the modern version 9.______________(create) our lives, without worrying about our age. And away from the mysterious world, Colonel Sanders didn 't open his first KFC restaurant 10.______________ he was 62, while Fauja Singh ran his first marathon at 89.语篇解读：文章讲述了一些大器晚成，勇于追梦的人，只要对自己有信心，什么年龄去实现梦想都不晚。

2021高考英语单项选择专题训练精品题（10）(1)

2021高考英语单项选择专题训练精品题（10）【2021安徽省屯溪一中月考卷】单项填空(共15小题；每题1分，总分值15分)请认真阅读下面各题，从题中所给的A、B、C、D四个选项中，选出最正确选项。

21. Having lived in China for 8 years, Helen has ____ good command of_____ Chinese language.A. the ; /B. a ; aC. the; aD. a; the22. The description of these events _______ other accounts written at the time closely.A. contributes toB. subscribes toC. corresponds withD. submits to23. you’d better take down all the key points ______the memory is still fresh in your mind.A. unlessB. whileC. beforeD. untilYour daughter is in her thirties. I can’t understand ______ married again and again.---- Now she is at the peak of her career. Work means more to her than anything else.A. her to delay to getB. her delaying to getC. her to delay gettingD. her delaying getting25. --- Have you ever been to Dunhuang?--- No, I’d like to, _________.A. tooB. thoughC. yetD. either26. She has been in doctors describe as a vegetative （植物的）state for sixyears．A．what B．which C．that D．how27. Be ______ ---- you can’t expect me to finish all this work in so little time.A. reasonableB. confidentC. creativeD. abundant28. This girl _____ a cry of surprise upon seeing a snake coming outof the room.A. let outB. figure outC. give outD. put out29. --- When shall we start the reconstruction of the historic building?--- Not until ________ by the authority.A. will our program be approvedB. our program will be approvedC. has our program been approvedD. our program has been approved30. --- I need to advertise for a roommate for next term.--- __________? Mary is interestedA. Why botherB. Why notC. So whatD. what for31. Guan Lu’s sacrifices for the country were never officially _______ until 1982.A. appealedB. acknowledgedC. recommendedD. evaluated32. A wireless smart pillbox can remind patients to take their daily vitamins, ________we all find hard to believe.A. thatB. whatC. whichD. it33. Ladies and gentlemen, please remain _____ until the plane has come to acomplete stop.A. seatedB. seatingC. to seatD. seat34．, I believe, and you will find the boy is very outgoing．A．Having a talk with the student B. One talk with the studentC．Given a talk with the student D. If you have a talk with the student35. The dance performed by the disabled actors is really a hit, but years ago no one_______ have imagined they were to achieve such great success.A. mustB. couldC. shouldD. can【参考答案】单项选择：21—25 D C B D B 26—30 A A A D A 31—35 B C A B B第一组10分钟1．Tuesday being ________windy，cold day in Beijing，US President Barack Obama Toured ________Forbidden City in Beijing, wearing ________blue shirt with no tie and a casual leather jacket．A．a；the；the B．a；/；a C．/；/；a D．a；the；a 2．---Where is your mother working? ---In a hospital ________ our town．A．is located in B．located in C．set in D．is set in3．I like a house with a beautiful garden in front, but I don’t have enough money to buy_________．A．one B．it C．this D．that4．---The research on the new bird flu virus vaccine is challenging and demanding．Who do you think can do the job? ---________ mystudents have a try?A．Shall B．Must C．Will D．May5．---Oh，how depressed！I’m bound to lose to him in tomorrow’s competition．---Cheer up！In fact，he is ________ than you．A．not more nervous B．no more nervousC．no less nervous D．a little less nervous6．In Beijing Olympics，Michael Phelps swam into Olympic history，________ the first athlete ________ the most gold medals ever．A．became；to win B．becoming；to winC．becoming；winning D．to become；to win7．---Liu Xiang shouldn’t have given up．．．---What？His injury was so serious，or he ________from the race．A．would never have withdrawn B．would have withdrawnC．would withdraw D．would never withdraw8．For all the professional athletes，________to the Olympics means that they have a chance to enter the history books．A．access B．attachment C．appeal D．approach9．I think it was on the playground on ________ we played basketball with some boys yesterday ________you lost your handbag．A．that；which B．which；thatC．where；that D．that；where10．Mary was so tired that she fell asleep _________ her book．A．by B．over C．in D．through 11．In Australia, surfing is a popular sport among young people _________ they can seek excitement and adventure．A．that B．which C．where D．how12．---What’s all that noise?---Just in front of the bus __________ an injured man, all covered with blood．A．where lies B．lies C．does lie D．lying is 13．To improve the quality of the products, we asked for advice from _________ had used the products．A．no matter who B．who C．anyone D．whoever 14．_________ her home, Lily went to the kitchen and began to prepare supper．A．As soon as she returned B．On arrivingC．After she got D．Immediately she reached15．---How long do you suppose it is _________ he arrived here?----No more than ten minutes．A．when B．before C．since D．after【参考答案】DBAAC BAABB CBDDC1．(201*年山东实验中学一模)Don't worry too much about ________mistakes. They are ________natural part of learning.A．不填；a B．the；不填C．不填；the D．the；the解析：句意：别太担忧(你有)错误，它们是学习进程中很正常的一部份。

2019年中考数学真题分类训练——专题十：三角形

2019年中考数学真题分类训练——专题十：三角形一、选择题1．（2019滨州）如图，在OAB △和OCD △中，,,,40OA OB OC OD OA OC AOB COD ==>∠=∠=︒，连接,AC BD 交于点M ，连接OM ．下列结论：①AC BD =；②40AMB ∠=︒；③OM 平分BOC ∠；④MO 平分BMC ∠．其中正确的个数为A ．4B ．3C ．2D ．1【答案】B2．（2019陕西）如图，在△ABC 中，∠B =30°，∠C =45°，AD 平分∠BAC 交BC 于点D ，DE ⊥AB ，垂足为E ．若DE =1，则BC 的长为A ．2B 23+C 32D ．3【答案】A3．（2019衢州）“三等分角”大约是在公元前五世纪由古希腊人提出来的，借助如图所示的“三等分角仪”能三等分任一角．这个三等分角仪由两根有槽的棒OA ，OB 组成，两根棒在O 点相连并可绕O 转动，C 点固定，OC =CD =DE ，点D 、E 可在槽中滑动．若∠BDE =75°，则∠CDE 的度数是A．60°B．65°C．75°D．80°【答案】D4．（2019重庆A卷）如图，在△ABC中，D是AC边上的中点，连接BD，把△BDC′沿BD翻折，得到BDC'△，DC与AB交于点E，连接AC'，若AD=AC′=2，BD=3则点D到BC的距离为A．332B．3217C．7D．13【答案】B5．（2019南通）小明学了在数轴上画出表示无理数的点的方法后，进行练习：首先画数轴，原点为O，在数轴上找到表示数2的点A，然后过点A作AB⊥OA，使AB=3（如图）．以O为圆心，OB的长为半径作弧，交数轴正半轴于点P，则点P所表示的数介于A．1和2之间B．2和3之间C．3和4之间D．4和5之间【答案】C6．（2019宁波）勾股定理是人类最伟大的科学发现之一，在我国古算书《周髀算经》中早有记载．如图1，以直角三角形的各边为边分别向外作正方形，再把较小的两张正方形纸片按图2的方式放置在最大正方形内．若知道图中阴影部分的面积，则一定能求出A．直角三角形的面积B．最大正方形的面积C．较小两个正方形重叠部分的面积D．最大正方形与直角三角形的面积和【答案】C7．（2019青岛）如图，BD是△ABC的角平分线，AE⊥BD，垂足为F．若∠ABC=35°，∠C=50°，则∠CDE的度数为A．35°B．40°C．45°D．50°【答案】C9．（2019天水）如图，等边OAB△的边长为2，则点B的坐标为A ．(11)，B ．(13)，C ．(31)，D ．(33)，【答案】B10．（2019宁波）已知直线m ∥n ，将一块含45°角的直角三角板ABC 按如图方式放置，其中斜边BC 与直线n 交于点D ．若∠1=25°，则∠2的度数为A ．60°B ．65°C ．70°D ．75°【答案】C11．（2019宿迁）一副三角板如图摆放（直角顶点C 重合），边AB 与CE 交于点F ，DE BC ∥，则BFC ∠等于A ．105︒B ．100︒C ．75︒D ．60︒【答案】A12．（2019临沂）如图，D 是AB 上一点，DF 交AC 于点E ，DE FE =，FC AB ∥，若4AB =，3CF =，则BD 的长是A ．0.5B ．1C ．1.5D ．2【答案】B13．（2019绍兴）如图，墙上钉着三根木条a ，b ，c ，量得∠1=70°，∠2=100°，那么木条a ，b 所在直线所夹的锐角是A ．5°B ．10°C ．30°D ．70°【答案】B14．（2019潍坊）如图，已知AOB ∠．按照以下步骤作图：①以点O 为圆心，以适当的长为半径作弧，分别交AOB ∠的两边于C ，D 两点，连接CD ．②分别以点C ，D 为圆心，以大于线段OC 的长为半径作弧，两弧在AOB ∠内交于点E ，连接CE ，DE ．③连接OE 交CD 于点M ．下列结论中错误的是A ．CEO DEO ∠=∠B ．CM MD =C ．OCD ECD ∠=∠D ．12OCED S CD OE =⋅四边形【答案】C15．（2019梧州）如图，DE 是ABC △的边AB 的垂直平分线，D 为垂足，DE 交AC 于点E ，且85AC BC ==，，则BEC △的周长是A ．12B ．13C ．14D ．15【答案】B16．（2019杭州）在△ABC 中，若一个内角等于另外两个内角的差，则 A ．必有一个内角等于30° B ．必有一个内角等于45°C ．必有一个内角等于60°D ．必有一个内角等于90° 【答案】D17．（2019河南）如图，在四边形ABCD 中，AD ∥BC ，∠D =90°，AD =4，BC =3．分别以点A ，C 为圆心，大于12AC 长为半径作弧，两弧交于点E ，作射线BE 交AD 于点F ，交AC 于点O ．若点O 是AC 的中点，则CD 的长为A ．2B ．4C ．3D 10【答案】A18．（2019张家界）如图，在ABC △中，90C ∠=︒，8AC =，13DC AD =，BD 平分ABC ∠，则点D 到AB 的距离等于A．4 B．3 C．2 D．1【答案】C19．（2019台州）下列长度的三条线段，能组成三角形的是A．3，4，8 B．5，6，10C．5，5，11 D．5，6，11【答案】B20．（2019台湾）如图，△ABC中，AC=BC<AB．若∠1、∠2分别为∠ABC、∠ACB的外角，则下列角度关系何者正确A．∠1<∠2 B．∠1=∠2C．∠A+∠2<180°D．∠A+∠1>180°【答案】C21．（2019长春）如图，在ABC∠为钝角．用直尺和圆规在边AB上确定一点D．使△中，ACB∠=∠，则符合要求的作图痕迹是ADC B2A．B．C ．D ．【答案】B22．（2019金华）若长度分别为a ，3，5的三条线段能组成一个三角形，则a 的值可以是 A ．1 B ．2C ．3D ．8【答案】C23．（2019广西）如图，在ABC ∆中，,40AC BC A =∠=︒，观察图中尺规作图的痕迹，可知BCG ∠的度数为A ．40︒B ．45︒C ．50︒D ．60︒【答案】C24．（2019大庆）如图，在△ABC 中，BE 是∠ABC 的平分线，CE 是外角∠ACM 的平分线，BE 与CE 相交于点E ，若∠A =60°，则∠BEC 是A ．15°B ．30°C ．45°D ．60°【答案】B25．（2019荆门）将一副直角三角板按如图所示的位置摆放，使得它们的直角边互相垂直，则1∠的度数是A ．95︒B ．100︒C ．105︒D ．110︒【答案】C26．（2019百色）三角形的内角和等于 A ．90︒B ．180︒C ．270︒D ．360︒【答案】B27．（2019徐州）下列长度的三条线段，能组成三角形的是 A ．2，2，4 B ．5，6，12 C ．5，7，2 D ．6，8，10【答案】D 二、填空题28．（2019临沂）如图，在ABC △中，120ACB ∠=︒，4BC =，D 为AB 的中点，DC BC ⊥，则ABC △的面积是__________．【答案】329．（2019南京）如图，在△ABC 中，BC 的垂直平分线MN 交AB 于点D ，CD 平分∠ACB ．若AD =2，BD =3，则AC 的长为__________．【答案】1030．（2019威海）如图，在四边形ABCD 中，AB CD ∥，连接AC ，BD ．若90ACB ∠=︒，AC BC =，AB BD =，则ADC ∠=__________︒．【答案】10531．（2019北京）如图所示的网格是正方形网格，则∠PAB +∠PBA =__________°（点A ，B ，P 是网格线交点）．【答案】4532．（2019成都）如图，在△ABC 中，AB =AC ，点D ，E 都在边BC 上，∠BAD =∠CAE ，若BD =9，则CE 的长为__________．【答案】933．（2019黄冈）如图，AC BD ，在AB 的同侧，288AC BD AB ===，，，点M 为AB 的中点，若120CMD ∠=︒，则CD 的最大值是__________．【答案】1434．（2019舟山）如图，一副含30°和45°角的三角板ABC和EDF拼合在一个平面上，边AC与EF重合，AC=12cm．当点E从点A出发沿AC方向滑动时，点F同时从点C出发沿射线BC方向滑动．当点E 从点A滑动到点C时，点D运动的路径长为__________cm；连接BD，则△ABD的面积最大值为__________cm2．【答案】（24–122），（243+362-126）35．（2019长沙）如图，要测量池塘两岸相对的A，B两点间的距离，可以在池塘外选一点C，连接AC，BC，分别取AC，BC的中点D，E，测得DE=50 m，则AB的长是__________m．【答案】10036．（2019南京）在△ABC中，AB=4，∠C=60°，∠A>∠B，则BC的长的取值范围是__________．【答案】4<BC≤3337．（2019枣庄）把两个同样大小含45︒角的三角尺按如图所示的方式放置，其中一个三角尺的锐角顶点与另一个三角尺的直角顶点重合于点A ，且另外三个锐角顶点B C D ，，在同一直线上．若AB =2，则CD =__________．【答案】62-38．（2019兰州）在△ABC 中，AB =AC ，∠A =40°，则∠B =__________．【答案】70°39．（2019盐城）如图，在ABC △中，62BC =+，45C ∠=︒，2AB AC =，则AC 的长为__________．【答案】240．（2019伊春）一张直角三角形纸片ABC ，90ACB ∠=︒，10AB =，6AC =，点D 为BC 边上的任一点，沿过点D 的直线折叠，使直角顶点C 落在斜边AB 上的点E 处，当BDE △是直角三角形时，则CD 的长为__________．【答案】3或24741．（2019襄阳）如图，已知ABC DCB ∠=∠，添加下列条件中的一个：①A D ∠=∠，②AC DB =，③AB DC =，其中不能确定ABC △≌△DCB △的是__________（只填序号）．【答案】②42．（2019南通）如图，△ABC 中，AB =BC ，∠ABC =90°，F 为AB 延长线上一点，点E 在BC 上，且AE =CF ，若∠BAE =25°，则∠ACF =__________度．【答案】7043．（2019哈尔滨）在ABC △中，50A ∠=︒，30B ∠=︒，点D 在AB 边上，连接CD ，若ACD △为直角三角形，则BCD ∠的度数为__________．【答案】60︒或10︒44．（2019怀化）若等腰三角形的一个底角为72︒，则这个等腰三角形的顶角为__________．【答案】36°45．（2019通辽）腰长为5，高为4的等腰三角形的底边长为__________．【答案】6或25或4546．（2019大庆）如图，在△ABC 中，D 、E 分别是BC ，AC 的中点，AD 与BE 相交于点G ，若DG =1，则AD =__________．【答案】347．（2019江西）如图，在ABC △中，点D 是BC 上的点，40BAD ABC ∠=∠=︒，将ABD △沿着AD 翻折得到AED △，则CDE ∠=__________°．【答案】20三、证明题48．（2019南京）如图，D是△ABC的边AB的中点，DE∥BC，CE∥AB，AC与DE相交于点F．求证：△ADF≌△CEF．证明：∵DE∥BC，CE∥AB，∴四边形DBCE是平行四边形，∴BD=CE，∵D是AB的中点，∴AD=BD，∴AD=EC，∵CE∥AD，∴∠A=∠ECF，∠ADF=∠E，∴△ADF≌△CEF．49．（2019益阳）已知，如图，AB=AE，AB∥DE，∠ECB=70°，∠D=110°，求证：△ABC≌△EAD．证明：由∠ECB=70°得∠ACB=110°，又∵∠D=110°，∴∠ACB=∠D，∵AB∥DE，∴∠CAB=∠E，∴在△ABC和△EAD中，==ACB DCAB E AB AE∠∠⎧⎪∠∠⎨⎪=⎩，∴△ABC≌△EAD．50．（2019山西）已知：如图，点B，D在线段AE上，AD=BE，AC∥EF，∠C=∠F．求证：BC=DF．证明：∵AD=BE，∴AD-BD=BE-BD，∴AB=ED，∵AC∥EF，∴∠A=∠E，在△ABC和△EDF中，C FA E AB ED∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△ABC≌△EDF（AAS），∴BC=DF．51．（2019兰州）如图，AB=DE，BF=EC，∠B=∠E，求证：AC∥DF．证明：∵BF=EC，∴BF+FC=EC+FC，∴BC=EF，在△ABC和△DEF中，AB DEB E BC EF=⎧⎪∠=∠⎨⎪=⎩，∴△ABC≌△DEF（SAS），∴∠ACB=∠DFE，∴AC∥DF．52．（2019广州）如图，D是AB上一点，DF交AC于点E，DE=FE，FC∥AB，求证：ADE CFE△≌△．证明：∵FC∥AB，∴∠A=∠FCE，∠ADE=∠F，所以在△ADE与△CFE中，A FCEADE F DE EF∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△ADE≌△CFE．53．（2019泸州）如图，AB CD ∥，AD 和BC 相交于点O ，OA OD =．求证：OB OC =．证明：∵AB CD ∥，∴A D ∠=∠，B C ∠=∠，在AOB △和DOC △中，A D B C OA OD ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴AOB DOC △≌△， ∴OB OC =．54．（2019重庆A 卷）如图，在△ABC 中，AB =AC ，D 是BC 边上的中点，连结AD ，BE 平分∠ABC 交AC 于点E ，过点E 作EF ∥BC 交AB 于点F ．（1）若∠C =36°，求∠BAD 的度数．（2）若点E 在边AB 上，EF ∥AC 叫AD 的延长线于点F ．求证：FB =FE ．证明：（1）∵AB AC =，∴C ABC ∠=∠， ∵36C ∠=︒， ∴36ABC ∠=︒，∵D 为BC 的中点，∴AD BC ⊥，∴90903654BAD ABC ∠=-∠=-︒=︒︒︒．（2）∵BE 平分ABC ∠，∴ABE EBC ∠=∠，又∵EF BC ∥，∴EBC BEF ∠=∠，∴EBF FEB ∠=∠， ∴BF EF =．55．（2019桂林）如图，AB =AD ，BC =DC ，点E 在AC 上．（1）求证：AC 平分∠BAD ；（2）求证：BE =DE ．证明：（1）在△ABC 与△ADC 中，AB AD AC AC BC DC =⎧⎪=⎨⎪=⎩∴△ABC ≌△ADC （SSS ）， ∴∠BAC =∠DAC ，即AC 平分∠BAD ．（2）由（1）∠BAE =∠DAE ，在△BAE 与△DAE 中，得BA DA BAE DAE AE AE =⎧⎪∠=∠⎨⎪=⎩，∴△BAE ≌△DAE （SAS ）， ∴BE =DE ．56．（2019黄石）如图，在ABC △中，90BAC ∠=︒，E 为边BC 上的点，且AB AE =，D 为线段BE 的中点，过点E 作EF AE ⊥，过点A 作AF BC ∥，且AF 、EF 相交于点F ．（1）求证：C BAD ∠=∠；（2）求证：AC EF =．证明：（1）如图，∵AB AE =，∴ABE △是等腰三角形，又∵D 为BE 的中点，∴AD BE ⊥，在Rt ABC △和Rt DBA △中，∵B Ð为公共角，90BAC BDA ∠=∠=︒， ∴C BAD ∠=∠．（2）∵AF BC ∥，∴EAF AEB ∠=∠， ∵AB AE =，∴ABE AEB ∠=∠， ∴EAF ABC ∠=∠，又∵90BAC AEF ∠=∠=∠︒， ∴BAC AEF △≌△， ∴AC EF =．57．（2019重庆）如图，在△ABC 中，AB =AC ，AD ⊥BC 于点D ．（1）若∠C =42°，求∠BAD 的度数；（2）若点E 在边AB 上，EF ∥AC 交AD 的延长线于点F ．求证：AE =FE ．证明：（1）∵AB =AC ，AD ⊥BC 于点D ， ∴∠BAD =∠CAD ，∠ADC =90°，又∠C =42°，∴∠BAD =∠CAD =90°-42°=48°．（2）∵AB =AC ，AD ⊥BC 于点D ， ∴∠BAD =∠CAD ， ∵EF ∥AC ， ∴∠F =∠CAD ， ∴∠BAD =∠F ， ∴AE =FE ．58．（2019苏州）如图，ABC △中，点E 在BC 边上，AE AB =，将线段AC 绕点A 旋转到AF 的位置，使得CAF BAE ∠=∠，连接EF ，EF 与AC 交于点G ．（1）求证：EF BC =；（2）若65ABC ∠=︒，28ACB ∠=︒，求FGC ∠的度数．证明：（1）∵CAF BAE ∠=∠， ∴BAC EAF ∠=∠，∵AE AB AC AF ==，， ∴BAC EAF △≌△， ∴EF BC =．（2）∵65AB AE ABC =∠=︒，， ∴18065250BAE ∠=︒-︒⨯=︒， ∴50FAG ∠=︒， ∵BAC EAF △≌△， ∴28F C ∠=∠=︒， ∴502878FGC ∠=︒+︒=︒．59．（2019无锡）如图，在△ABC 中，AB =AC ，点D 、E 分别在AB 、AC 上，BD =CE ，BE 、CD 相交于点O ．求证：（1）DBC ECB △≌△；（2）OB OC =．证明：（1）∵AB =AC ， ∴∠ECB =∠DBC ，在DBC △与ECB △中，BD CEDBC ECB BC CB =⎧⎪∠=∠⎨⎪=⎩，∴DBC △≌ECB △．（2）由（1）DBC △≌ECB △， ∴∠DCB =∠EBC ，∴OB =OC ．60．（2019枣庄）在ABC △中，90BAC ∠=︒，AB AC =，AD BC ⊥于点D ．（1）如图1，点M ，N 分别在AD ，AB 上，且90BMN ∠=︒，当30AMN =︒∠，2AB =时，求线段AM 的长；（2）如图2，点E ，F 分别在AB ，AC 上，且90EDF ∠=︒，求证：BE AF =；（3）如图3，点M 在AD 的延长线上，点N 在AC 上，且90BMN ∠=︒，求证：2AB AN AM +=．证明：（1）∵90BAC ∠=︒，AB AC =，AD BC ⊥，∴AD BD DC ==，45ABC ACB ∠=∠=︒，45BAD CAD ∠=∠=︒， ∵2AB =，∴2,AD BD DC ===，∵30AMN ∠=︒，∴180903060BMD ∠=︒-︒-︒=︒， ∴30BMD ∠=︒，∴2BM DM =，由勾股定理得，222BM DM BD -=，即222(2)(2)DM DM -=，解得23DM = ∴2323AM AD DM =-=．（2）∵AD BC ⊥，90EDF ∠=︒，∴BDE ADF ∠=∠，在BDE △和ADF △中，B DAF DB DA BDE ADF ∠=∠=∠=∠⎧⎪⎨⎪⎩，∴BDE ADF △≌△， ∴BE AF =．（3）如图，过点M 作//ME BC 交AB 的延长线于E ，∴90AME ∠=︒，则2AEAB =，45E ∠=︒，∴ME MA =，∵90AME ∠=︒，90BMN ∠=︒， ∴BME AMN ∠=∠，在BME △和AMN △中，E MAN ME MA BME AMN ∠=∠=∠=∠⎧⎪⎨⎪⎩，∴BME AMN △≌△，∴BE AN =， ∴2AB AN AB BE AE AM +=+==．61．（2019温州）如图，在△ABC 中，AD 是BC 边上的中线，E 是AB 边上一点，过点C 作CF ∥AB 交ED 的延长线于点F ．（1）求证：△BDE ≌△CDF ；（2）当AD ⊥BC ，AE =1，CF =2时，求AC 的长．证明：（1）∵CF AB ∥， ∴B FCD BED F ∠=∠∠=∠，， ∵AD 是BC 边上的中线，∴BD CD =，∴△BDE ≌△CDF ．（2）∵△BDE ≌△CDF ， ∴2BE CF ==，∴123AB AE BE =+=+=． ∵AD BC BD CD ⊥=，， ∴3AC AB ==．62．（2019杭州）如图，在△ABC 中，AC ＜AB ＜BC ．（1）已知线段AB 的垂直平分线与BC 边交于点P ，连接AP ，求证：∠APC =2∠B ．（2）以点B 为圆心，线段AB 的长为半径画弧，与BC 边交于点Q ，连接AQ ．若∠AQC =3∠B ，求∠B 的度数．证明：（1）∵线段AB 的垂直平分线与BC 边交于点P ， ∴PA =PB ， ∴∠B =∠BAP ， ∵∠APC =∠B +∠BAP ， ∴∠APC =2∠B ；（2）根据题意可知BA =BQ ， ∴∠BAQ =∠BQA ，∵∠AQC =3∠B ，∠AQC =∠B +∠BAQ ， ∴∠BQA =2∠B ，∵∠BAQ+∠BQA+∠B=180°，∴5∠B=180°，∴∠B=36°．四、解答题63．（2019河北）已知：整式A=（n2-1）2+（2n）2，整式B>0．尝试化简整式A．发现A=B2，求整式B．联想由上可知，B2=（n2-1）2+（2n）2，当n>1时，n2-1，2n，B为直角三角形的三边长，如图．填写下表中B的值：直角三角形三边n2-1 2n B勾股数组Ⅰ/ 8 __________勾股数组Ⅱ35 / __________解：A=（n2-1）2+（2n）2=n4-2n2+1+4n2=n4+2n2+1=（n2+1）2，∵A=B2，B>0，∴B=n2+1，当2n=8时，n=4，∴n2+1=42+1=15；当n2-1=35时，n2+1=37．64．（2019大庆）如图，一艘船由A港沿北偏东60°方向航行10 km至B港，然后再沿北偏西30°方向航行10 km至C港．（1）求A ，C 两港之间的距离（结果保留到0.1 km ，参考数据：2≈1.414，3≈1.732）；（2）确定C 港在A 港的什么方向．解：（1）由题意可得，∠PBC =30°，∠MAB =60°， ∴∠CBQ =60°，∠BAN =30°，∴∠ABQ =30°， ∴∠ABC =90°． ∵AB =BC =10，∴AC =22AB BC +=102≈14.1．答：A 、C 两地之间的距离为14.1 km ．（2）由（1）知，△ABC 为等腰直角三角形， ∴∠BAC =45°，∴∠CAM =15°， ∴C 港在A 港北偏东15°的方向上．65．（2019金华）如图，在76⨯的方格中，ABC △的顶点均在格点上，试按要求画出线段EF （E ，F 均为格点），各画出一条即可．【答案】如图所示：。

[必刷题]2024九年级英语上册语法填空专项专题训练(含答案)

[必刷题]2024九年级英语上册语法填空专项专题训练（含答案）试题部分一、选择题：1. Choose the correct form of the verb to plete the sentence. "He _______ to the library every weekend to read books."A. goB. goesC. goingD. gone2. Identify the correct tense to plete the sentence. "By next month, she _______ for the pany for three years."A. will workB. has workedC. workedD. is working3. Select the appropriate preposition to plete the sentence. "He is responsible _______ the project."A. forB. toC. in4. Choose the correct form of the adjective to plete the sentence. "She is _______ than her sister."A. beautifullerB. more beautifulC. beautifullestD. beauty5. Which sentence uses the correct parative form of the adjective? "He is _______ tall than his brother."A. tallerB. tallC. tallestD. tallerly6. Fill in the blank with the correct form of the pronoun. "_________ is going to the movies tonight."A. SheB. HeC. ItD. They7. Choose the correct conjunction to plete the sentence. "She loves singing, _______ she doesn't like dancing."A. andB. butC. or8. Identify the correct past participle form of the verb. "The book was _______ the famous author."A. writeB. wroteC. writtenD. writed9. Select the correct article to plete the sentence. "I saw _______ interesting movie last night."A. aB. anC. theD. no10. Fill in the blank with the correct form of the verb. "If I _______ you, I would study harder for the exam."A. amB. wereC. beD. have been二、判断题：1. The sentence "She has been to Beijing twice" is in the present perfect tense. ( )2. The phrase "look forward to" is followed a gerund. ( )3. "Whose" is a possessive pronoun. ( )4. The sentence "I like apples, but she likes bananas" uses a correct contrast. ( )5. "Than" is a subordinating conjunction. ( )三、填空题：1. The past tense of the verb "do" is _______.2. The plural form of "child" is _______.3. The present perfect continuous tense of "play" is_______.4. "I have _______ a letter from my pen pal." (Use the correct past participle form of "send".)5. The correct form of "there is" in the plural is_______.6. The opposite of "expensive" is _______.7. "I _______ (be) to London last year." (Fill in the correct verb form.)8. "The sun _______ (rise) in the east." (Fill in the correct verb form.)9. "She _______ (go) to the store and _______ (buy) some milk." (Fill in the correct verb forms.)10. "If it _______ (rain) tomorrow, we will stay at home." (Fill in the correct verb form.)11. "The cat _______ (be) on the table." (Fill in the correct form of "be".)12. "He _______ (read) a book when I called him." (Fill in the correct past continuous form of "read".)13. "They _______ (not go) to the party because they_______ (be) tired." (Fill in the correct verb forms.)14. "She _______ (can) speak three languages fluently." (Fill in the correct modal verb.)15. "_______ you like some coffee?" (Fill in the correct form of "do".)16. "He _______ (should) have finished his homework now." (Fill in the correct modal verb form.)17. "The movie _______ (be) very interesting." (Fill in the correct form of "be".)18. "We _______ (be) happy to help you." (Fill in the correct form of "be".)19. "They _______ (be) going to the zoo next week." (Fill in the correct form of "be".)20. "I wish I _______ (can) fly." (Fill in the correct modal verb form.)四、简答题：1. What is the difference between "affect" and "effect"?2. Explain the difference between "its" and "it's".3. What is the past perfect tense and give an example sentence.4. What is a gerund and how is it used in a sentence?5. How do you form the present continuous tense?6. What is a modal verb? Give three examples.7. What is the difference between "some" and "any"?8. Explain the use of "used to" in a sentence.9. How do you form questions in the present simple tense?10. What is the difference between "there", "their", and "they're"?本套试题答案如下一、选择题：1. B2. B3. A4. B5. A6. A7. B8. C9. A10. B二、判断题：1. √2. √3. ×4. √5. ×三、填空题：1. did2. children3. has been playing4. received5. there are6. cheap7. was8. rises9. went, bought10. rains11. is12. was reading13. didn't go, were14. can15. Would16. should17. is18. are19. are20. could四、简答题：1. "Affect" is a verb, "effect" is a noun.2. "Its" is a possessive adjective, "it's" is a contraction of "it is".3. The past perfect tense is used to describe an action that was pleted before another past action. Example: "By the time he arrived, the meeting had already started."4. A gerund is a verb form ending in ing that functionsas a noun. Example: "Reading is my favorite hob."5. The present continuous tense is formed with thepresent tense of "be" followed the ing form of the verb. Example: "She is singing."6. Modal verbs are auxiliary verbs that express possibility, permission, or ability. Examples: can, may, must.7. "Some" is used in positive sentences, "any" is used in negative sentences and questions.8. "Used to" is used to describe a past habit or state that is no longer true. Example: "He used to smoke, but he quit."9. To form questions in the present simple tense, invert the subject and the verb "do" or "does". Example: "Do youlike coffee?"10. "There" indicates a place, "their" is a possessive adjective, "they're" is a contraction of "they are".。

分数-选择填空之压轴题训练第一学期六年级压轴题训练(沪教版)(原卷版)

专题03 分数选择、填空之压轴题训练一、选择题（本大题共12题）1. （华理附中2019期中19）下列分数中，能化成有限小数的是（） A.740; B.124; C. 415; D. 5122.（2019浦东四署10月6）两根同样长的铁丝，一根用去了13，另一根用去了13米，剩下的铁丝相比（）A.第一根长；B.第二根长；C.一样长；D.无法比较哪根长.3.（2019上南中学10月考6）下列各题，用分数表示图中阴影部分与整体的关系，正确的个数有（）A. 1个；B. 2个；C. 3个；D. 4个.4.（2019上南东校9月6）小明将8米长的绳子对折3次，那么每段绳子的长度为（） A.81米 B.83米 C.1米 D.38米 5.（2019建平西校10月考6）把分数b a 的分子扩大为原来的4倍，分母缩小为原来的31，所得的分数比原来（）A.扩大到原来的7倍B.缩小到原来的12倍C.不变D.扩大到原来的12倍 6. （青教院附中2019期中4）如图，三个大小相同的长方形拼在一起，组成一个大长方形，把第二个长方形平均分成2份，再把我第三个长方形平均分成3份，那么图中阴影部分的面积是大长方形面积的( ) A 、56 B 、23 C 、12 D 、7187102533147.（华师大附中2019期中5）甲、乙、丙三位同学比赛跑1000米，如果甲同学用时4分16秒，乙同学用时413分钟，丙同学用时4.2分钟，那么三位同学中，跑得最慢的是（） A 、甲 B 、乙 C 、丙 D 、不能确定 8.（2019大同期中6）修一条小路，第一天修了全长的35，第二天修了全长的16，还剩70米没修，求小路的全长是多少米，可列计算式为（）A. 3170（-）56⨯ ；B.3170（-）56÷； C. 3170（1--）56⨯；D.3170（1--）56÷ 9.（2020普陀期末6）班级开展“迎新”活动，预计活动费用200元，实际用了180元，下列结论错误的是（） A.实际费用是计划费用的910； B.实际费用比计划费用少110； C.计划费用比实际费用多110； D. 实际费用比计划费用少20元. 10.（2019崇明期中20）若312a+是分母为12的最简真分数，则a 可取的自然数个数是（）A. 1； B. 2； C. 3； D. 4. 11.（2020浦东四署10月6）如果在分数38的分子上加上6，要分数的大小不变，分母应（）A. 加上6； B. 乘以6； C. 加上3； D.乘以3.12.（2019普陀期中6）七巧板是中国一种古老的传统智力玩具，如图2是用七巧板拼成的正方形，其中图形7和图形貌4的面积之和占这个正方形面积的（） A.12； B. 13； C. 14； D. 27.二、填空题（本大题共14题）13.（2020浦东四署10月18）一个分数，分子和分母的和是221，约分后，得89，原分数是 . 14.（2019曹阳二中9月11）一个分数，它的分母加上1，可约分为最简分数21，分母减去1，可约为32，则这个分数为 . 15.(2019南模初中10月考12)小敏看一本书，第一周看了全书的73，第二周看了全书的52，第三周看完，第三周看了全书的 .16.（2019徐汇教院期中14）如果()14125<<，那么括号内可取的整数有_______.（写出所有可能）17. （奉贤2019期中20）如图，两个四边形重叠部分（图中阴影）面积占四边形B 的211，占四边形A 的13，则四边形A 面积比四边形B 的面积少（填“几分之几”）.18.（浦东南片2019期中18）31213223233223321-=⨯-⨯=⨯-=⨯ 以上过程，是逆用异分母分数减法的方法得到.采用该方法同样可得：4131431-=⨯ 请直接计算=⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯1091981871761651541431321 .19.（2020奉贤期末18）规定了一种新运算：1111a b a b a b⨯*=+，计算：(34)5**= . 20.（2020长宁期末14）我们规定max{,}a b 表示数a 与数b 中较大的一个数，如max{3,4}4=.按这样的规定，如果7max{,1}max{,2.3}133xx +-=，那么x 的值为 .21.（2019宝山期中15）我们把分子为1的分数称为“单位分数”，一个单位分数可以分成两个分母不同的单位分数之和，例如：131********+===+. 请将15分成两个分母不同的单位分数之和，则15= . 22.（2019闵行期中18）如图，把一个长方形平均分成上下两部分，上半部分再平均分成4块，下半部分平均分成5块，若图形A 、B 、C 的面积和为2，则阴影部分的面积是 .23.（2019复旦实验期中16）规定：1( 2.5)(1)8a b a b *=---，计算：135(3.5)416**= .24.（2019静安期中18）瓶内装满一瓶水，第一次倒出全部水的12，然后再灌入同样多的酒精，第二次倒出全部溶液的13，又用酒精灌满，第三次倒出全部溶液的14，再用酒精灌满，依次类推，一直到第九次倒出全部溶液的110，再用酒精灌满，那么这时的酒精占全部溶液的 . 25.（2021松江期末20）六年级（1）班学生去野外郊游，无意中发现了一口枯井，外号“神童”的小明想了个办法测出井深，他的方法是：用绳子测量井深，将一根绳子先折成三折来量，量出井外还余213米，将一根绳子先折成四折来量，量出井外还余15米，请你算算看，这口枯井深为米.26.（浦东四署2019期中18）阅读理解：1211122112-==-⨯，1321163223-==-⨯，14311124334-==-⨯，……阅读以上材料后计算：111111111357911131517612203042567290++++++++= .。

名词专题训练及答案

名词专题阶段测试一、选择填空1.All the _____ have three _____ each.A. hero; photoB. heros; photosC. heros; photoesD. heroes; photos2. A group of _____ are eating _____ and _____ at the foot of the hillA. sheep; grass; leavesB. sheep; grasses; leavesC. sheep; grass; leafD. sheeps; grass; leafs3.—Some of the _____ are made of _____ , and some are plastics.A. glass; glassB. glasses; glassC. glass; glassesD. glasses; glasses4.—What did you see?—I saw _____ police there.A. manyB. muchC. littleD. the5. _____fish are there in that bowl?A. How muchB. How manyC. Do you know how muchD. What’s the number of6. The _____ we saw yesterday come out to the farm once in a while.A. cowB. dogC. deerD. horse7. _____is needed in cold countries.A. A lot of clothesB. Much clothesC. Many a clothD. lots of clothes8. I tried every _____to make him give up smoking, nut failed.A. meanB. wayC. meaningD. means9. Two _____years ago, he lived in America.A. scoresB. scoreC. score of theD. scores of10. _____are sold in the new store.A. Men and child’s shoesB. Men’s and children’s shoesC. Men and children shoesD. Men and child’s shoes11. They are _____ in name, but they are no longer in practiceA. woman doctorsB. women doctorsC. lady doctorsD. ladies doctors12. Julie went to the _____ to buy a pair of shoes.A. shoes storeB. shoe storeC. shoe’s storeD. shoes’ store13. —What would you like to drink?—I will have_____, please.A. a coffee cupB. small coffeeC. a little coffeeD. a cup of coffee14. In Britain _____ are all painted red.A. letter boxesB. letters boxesC. letter boxD. letters box15.Biology is _____.A. science of lifeB. science of the lifeC. the science of the lifeD. the science of life16. I will give you _____ to finish it.A. two-weeks timeB. two weeks timeC. two weeks’ timeD. two week’s time17. _____is more useful than gold.A. IronsB. IronC. An ironD. The iron18. _____ are a hard-working people.A. The GermanyB. The GermanC. The GermanD. The Germen19.—Whose hat is it?—It’s_____ hatA. somebody else’sB. somebody elseC. somebody’s else’sD. somebody’s else20. Mike and John’s _____.A. father is a teacherB. fathers are teachersC. father are teachersD. fathers are teacher21. How many _____ do you want?A. breadB. breadsC. piece of breadD. pieces of bread22. Miss Smith is a friend of _____A. Mary’s mother’sB. Mary’s motherC. Mother’s of MaryD. Mary mother23. If these trousers are too big, buy a smaller _____A. setB. oneC. copyD. pair24. The number of people invited _____ fifty, but a number of them _____ absent for different reasons.A. were; wasB. was; wasC. was; wereD. were; were25. All but one _____ here just now.A. isB. wasC. has beenD. wereKeys 1~5 DABDB6~10 CBDBB11~15 BBCAD16~20 CBCAA21~25 DADCD。

高三英语语法填空专题训练10篇(含答案)

原创力文档是网络服务平台方若您的权利被侵害侵权客服qq
高三英语语法填空专题训练十篇
高三语法填空专题训练1
The Sahara Desert is the world’s largest hot desert, located in North Africa. 1. ___________ (it) area is about 3.5 million square miles. This makes it almost as large 2. ____________ the United States of America.
In June 2018, the World Health Organization (WHO) 4. ___________ (add) gaming disorder to its list of diseases and health conditions. a person may have the disorder if gaming has damaged his or her relationships 5. ___________ family and friends, and if it has affected his or her daily activities.
Sussman suggests 8. _____________ (record) how long you play. He says you should take at least an hour-long break after every hour of play, as the brain needs time to recover. Young gamers 9. ___________ think they might have a problem should ask a grown-up for help. He also suggests you should first answer a simple question: “Are you in control, 10. _____________ is thegame in control?”

选择填空专题

选择、填空专项训练班级：.姓名：.学号.一、选择题（本题8小题．每小题3分，共24分）完成时间：8分钟1.如图所示是生活中常见的物品,其中使用时属于费力杠杆的是（ A ）2.关于中山市期末体育测试项目,下列说法正确的是( )A.“引体向上”身体上升时,重力势能减小B.篮球测试中,用手拍球手会感到疼,说明力的作用是相互的C.足球测试中,用脚踢球,球在水平草地上滚动一段距离,球的重力做了功D.抛出去的实心球,在惯性力的推动下会继续向前运动3.下列与自行车有关的说法中正确的是( )A.车坐垫又宽又软是为了减小压力B.骑车匀速下坡时,机械能减小C.车把手上的花纹是为了增大压力D.在水平路面上匀速骑行时,车前进的动力大于车受到的阻力4.如图所示,小明将压强计的探头放入水中某一深度处,记下U型管中两液面的高度差h,下列操作能够使高度差h增大的是( )A.将探头向下移动一段距离B.将探头水平向左移动一段距离C.将探头放在酒精中的同样深度处(p酒精<p水)D.将探头在原深度处向其他方向任意转动一个角度5交通规则规定,机动车驾驶人不系安全带属违法行为,正确系好安全带可以( )A.减小机动车惯性,防止发生事故B.减小因机动车突然加速对人员造成的伤害C.减小驾驶员惯性,防止发生事故D.减小因机动车紧急刹车对人员造成的伤害6.下列关于于飞机的说法中,不正确的是( )A.客机飞得越高,大气压强也越小B.客机采用密度较小的新材料,可以减轻它的自重C.客机飞行的速度越大,惯性也越大D.客机升空利用了“流体压强与流速关系”的原理7.一个苹果静止在水平桌面上。

下列说法正确的是( )A.苹果受到的重力与苹果对桌面的压力是一对平衡力B.桌面对苹果的支持力大于苹果对桌面的压力C.苹果对桌面的压力与桌面对苹果的支持力是一对平衡力D.苹果受到的重力与桌面对苹果的支持力是一对平衡力8.三个材料不同但是体积相同的小球分别放入同种液体中,所处状态如图所示,则下列说法正确的是( )A.小球受到的浮力F甲> F乙> F丙B.小球受到的浮力F甲< F乙< F丙C.小球受到的浮力F甲< F乙= F丙D.小球受到的浮力F甲> F乙= F丙二．填空题（共8小题，每空1分）完成时间：14分钟9.2017年1月,中山正式迎来“高铁时代”。

高考真题与模拟训练专题10 等差数列(解析版)

专题10 等差数列第一部分真题部分一、选择题1．（2021·北京高考真题）{}n a 和{}n b 是两个等差数列，其中()15kka kb ≤≤为常值，1288a =，596=a ，1192b =，则3b =（）A ．64B ．128C ．256D ．512【答案】B【解析】由已知条件可得5115a a b b =，则51519619264288a b b a ⨯===，因此，1531926412822b b b ++===. 故选：B.2．（2021·北京高考真题）数列{}n a 是递增的整数数列，且13a ≥，12100n a a a ++⋅⋅⋅+=，则n 的最大值为（） A ．9 B ．10C ．11D ．12【答案】C【解析】若要使n 尽可能的大，则1a ，递增幅度要尽可能小，不妨设数列{}n a 是首项为3，公差为1的等差数列，其前n 项和为n S ，则2n a n =+，1131311881002S +=⨯=<，12314121021002S +=⨯=>，所以n 的最大值为11. 故选：C.3．（2020·浙江高考真题）已知等差数列{a n }的前n 项和S n ，公差d ≠0，11a d≤．记b 1=S 2，b n+1=S 2n+2–S 2n ，n *∈N ，下列等式不可能．．．成立的是（） A ．2a 4=a 2+a 6 B ．2b 4=b 2+b 6C ．2428a a a = D ．2428b b b =【答案】D【解析】对于A ，因为数列{}n a 为等差数列，所以根据等差数列的下标和性质，由4426+=+可得，4262a a a =+，A 正确；对于B ，由题意可知，21212222n n n n n b S a a S ++++=+=-，1212b S a a ==+， ∴234b a a =+，478b a a =+，61112b a a =+，81516b a a =+． ∴()47822b a a =+，26341112b b a a a a +=+++．根据等差数列的下标和性质，由31177,41288+=++=+可得()26341112784=2=2b b a a a a a a b +=++++，B 正确；对于C ，()()()()2224281111137222a a a a d a d a d d a d d d a -=+-++=-=-，当1a d =时，2428a a a =，C 正确；对于D ，()()22222478111213452169b a a a d a a d d =+=+=++，()()()()2228341516111125229468145b b a a a a a d a d a a d d =++=++=++，()22428112416832b b b d a d d d a -=-=-．当0d >时，1a d ≤，∴()113220d a d d a -=+->即24280b b b ->；当0d <时，1a d ≥，∴()113220d a d d a -=+-<即24280b b b ->，所以24280b b b ->，D 不正确．故选：D.4．（2019·全国高考真题（理））记n S 为等差数列{}n a 的前n 项和．已知4505S a ==，，则 A ．25n a n =- B ． 310n a n =- C ．228n S n n =-D ．2122n S n n =- 【答案】A【解析】由题知，41514430245d S a a a d ⎧=+⨯⨯=⎪⎨⎪=+=⎩，解得132a d =-⎧⎨=⎩，∴25n a n =-，故选A ．二、填空题5．（2021·江苏高考真题）已知等比数列{}n a 的公比为q ，且116a ，24a ，3a 成等差数列，则q 的值是___________. 【答案】4【解析】因为{}n a 为等比数列，且公比为q ，所以21a a q =⋅，231a a q =⋅且10a ≠，0q ≠. 因为116a ，24a ，3a 成等差数列，所以1321624a a a +=⨯，有21111624a a q a q +⋅=⨯⋅，28160q q -+=，解得4q =. 故答案为：4.6．（2020·海南高考真题）将数列{2n –1}与{3n –2}的公共项从小到大排列得到数列{a n }，则{a n }的前n 项和为________．【答案】232n n -【解析】因为数列{}21n -是以1为首项，以2为公差的等差数列，数列{}32n -是以1首项，以3为公差的等差数列，所以这两个数列的公共项所构成的新数列{}n a 是以1为首项，以6为公差的等差数列，所以{}n a 的前n 项和为2(1)16322n n n n n -⋅+⋅=-，故答案为：232n n -.7．（2020·全国高考真题（文））记n S 为等差数列{}n a 的前n 项和．若1262,2a a a =-+=，则10S =__________．【答案】25 【解析】{}n a 是等差数列，且12a =-，262a a +=设{}n a 等差数列的公差d根据等差数列通项公式：()11n a a n d +-= 可得1152a d a d +++= 即：()2252d d -++-+= 整理可得：66d =解得：1d =根据等差数列前n 项和公式：*1(1),2n n n S na d n N -=+∈ 可得：()1010(101)1022045252S ⨯-=-+=-+=∴1025S =.故答案为：25.8．（2019·江苏高考真题）已知数列*{}()n a n ∈N 是等差数列，n S 是其前n 项和.若25890,27a a a S +==，则8S 的值是_____. 【答案】16.【解析】由题意可得：()()()25811191470989272a a a a d a d a d S a d ⎧+=++++=⎪⎨⨯=+=⎪⎩，解得：152a d =-⎧⎨=⎩，则8187840282162S a d ⨯=+=-+⨯=. 9．（2019·全国高考真题（理））记S n 为等差数列{a n }的前n 项和，12103a a a =≠，，则105S S =___________. 【答案】4.【解析】因213a a =，所以113a d a +=，即12a d =，所以105S S =11111091010024542552a d a a a d⨯+==⨯+．三、解答题10．（2021·天津高考真题）已知{}n a 是公差为2的等差数列，其前8项和为64．{}n b 是公比大于0的等比数列，1324,48b b b =-=．（I ）求{}n a 和{}n b 的通项公式；（II ）记2*1,n n nc b b n N =+∈，（i ）证明{}22n n c c -是等比数列；（ii）证明)*nk n N =∈【答案】（I ）21,n a n n N *=-∈，4,n n N b n *=∈；（II ）（i ）证明见解析；（ii ）证明见解析.【解析】（I ）因为{}n a 是公差为2的等差数列，其前8项和为64．所以12818782642a a a a ⨯++⋅⋅⋅+=+⨯=，所以11a =，所以()12121,n n n n N a a *=+-=-∈；设等比数列{}n b 的公比为(),0q q >，所以()221321484q b b b q q b q ==-=--，解得4q =（负值舍去），所以114,n n n b q n N b -*==∈；（II ）（i ）由题意，221441n n n n n b c b =++=，所以22224211442444n n nn nnn c c ⎛⎫⎛⎫=+-+=⋅ ⎪ ⎪⎝⎭⎝⎭-，所以220nn c c ≠-，且212222124424n n n n nn c c c c +++⋅==⋅--，所以数列{}22n n c c -是等比数列；（ii ）由题意知，()()22122222121414242222n n n n n n n n n a n n c c a +-+-==<-⋅⋅⋅，12n n-==，所以112nn k k k k-==<，设10121112322222nn k n k k nT --===+++⋅⋅⋅+∑，则123112322222n n nT =+++⋅⋅⋅+，两式相减得21111111122121222222212nn n n nn n n n T -⎛⎫⋅- ⎪+⎝⎭=+++⋅⋅⋅+-=-=--，所以1242n n n T -+=-，所以1112422n nk nk kk n--==+⎫=-<⎪⎭11．（2021·全国高考真题）记n S是公差不为0的等差数列{}n a的前n项和，若35244,a S a a S==．（1）求数列{}n a的通项公式n a；（2）求使n nS a>成立的n的最小值．【答案】(1)26na n=-；(2)7.【解析】(1)由等差数列的性质可得：535S a=，则：3335,0a a a=∴=，设等差数列的公差为d，从而有：()()22433a a a d a d d=-+=-，()()()41234333322S a a a a a d a d a a d d=+++=-+-++-=-，从而：22d d-=-，由于公差不为零，故：2d=，数列的通项公式为：()3326na a n d n=+-=-.(2)由数列的通项公式可得：1264a=-=-，则：()()214252nn nS n n n-=⨯-+⨯=-，则不等式n nS a>即：2526n n n->-，整理可得：()()160n n-->，解得：1n<或6n>，又n为正整数，故n的最小值为7.12．（2021·全国高考真题）已知数列{}n a满足11a=，11,,2,.nnna naa n++⎧=⎨+⎩为奇数为偶数（1）记2n nb a=，写出1b，2b，并求数列{}n b的通项公式；（2）求{}n a的前20项和.【答案】（1）122,5b b==；（2）300.【解析】（1）由题设可得121243212,1215b a a b a a a==+===+=++=又22211k ka a++=+，2122k ka a+=+，*()k N∈故2223k ka a+=+，即13n nb b+=+，即13n nb b+-=所以{}n b为等差数列，故()21331nb n n=+-⨯=-.（2）设{}n a 的前20项和为20S ，则2012320S a a a a =++++，因为123419201,1,,1a a a a a a =-=-=-，所以()20241820210S a a a a =++++-()1291091021021023103002b b b b ⨯⎛⎫=++++-=⨯⨯+⨯-= ⎪⎝⎭.13．（2021·全国高考真题（理））已知数列{}n a 的各项均为正数，记n S 为{}n a 的前n 项和，从下面①②③中选取两个作为条件，证明另外一个成立．①数列{}n a 是等差数列：②数列是等差数列；③213aa =．注：若选择不同的组合分别解答，则按第一个解答计分．【答案】答案见解析【解析】选①②作条件证明③：(0)an b a =+>，则()2n S an b =+，当1n =时，()211a S a b ==+；当2n ≥时，()()221n n n a S S an b an a b -=-=+--+()22a an a b =-+；因为{}n a 也是等差数列，所以()()222a b a a a b +=-+，解得0b =；所以()221n aa n =-，所以213a a =.选①③作条件证明②：因为213a a =，{}n a 是等差数列，所以公差2112d a a a =-=，所以()21112n n n S na d n a -=+==，)1n =+=，所以是等差数列.选②③作条件证明①：(0)an b a =+>，则()2n S an b =+，当1n =时，()211a S a b ==+；当2n ≥时，()()221n n n a S S an b an a b -=-=+--+()22a an a b =-+；因为213a a =，所以()()2323a a b a b +=+，解得0b =或43a b =-；当0b =时，()221,21n a a a a n ==-，当2n ≥时，2-1-2n n a a a =满足等差数列的定义，此时{}n a 为等差数列；当43a b =-4=3an b an a =+-03a=-<不合题意，舍去.综上可知{}n a 为等差数列.14．（2021·全国高考真题（理））记n S 为数列{}n a 的前n 项和，n b 为数列{}n S 的前n 项积，已知212n nS b +=．（1）证明：数列{}n b 是等差数列; （2）求{}n a 的通项公式．【答案】（1）证明见解析；（2）()3,121,21n n a n n n ⎧=⎪⎪=⎨⎪-≥+⎪⎩.【解析】（1）由已知212n n S b +=得221n n n b S b =-,且0n b ≠，12n b ≠, 取1n =,由11S b =得132b =, 由于n b 为数列{}n S 的前n 项积，所以1212222212121n n n b b b b b b b ⋅⋅⋅⋅=---, 所以1121121222212121n n n b b b b b b b +++⋅⋅⋅⋅=---，所以111221n n n nb bb b +++=-,由于10n b +≠所以12121n n b b +=-，即112n n b b +-=,其中*n N ∈ 所以数列{}n b 是以132b =为首项，以12d =为公差等差数列; （2）由（1）可得，数列{}n b 是以132b =为首项，以12d =为公差的等差数列，()3111222n nb n ∴=+-⨯=+, 22211n n n b nS b n+==-+,当n =1时，1132a S ==, 当n ≥2时,()121111n n n n n a S S n n n n -++=-=-=-++,显然对于n =1不成立, ∴()3,121,21n n a n n n ⎧=⎪⎪=⎨⎪-≥+⎪⎩.15．（2019·江苏高考真题）定义首项为1且公比为正数的等比数列为“M －数列”. （1）已知等比数列{a n }满足：245132,440a a a a a a =-+=，求证:数列{a n }为“M －数列”；（2）已知数列{b n }满足:111221,n n n b S b b +==-，其中S n 为数列{b n }的前n 项和． ①求数列{b n }的通项公式；②设m 为正整数，若存在“M －数列”{c n }，对任意正整数k ，当k ≤m 时，都有1k k k c b c +成立，求m 的最大值．【答案】（1）见解析；（2）①b n =n ()*n ∈N ；②5.【解析】（1）设等比数列{a n }的公比为q ，所以a 1≠0，q ≠0.由245321440a a a a a a =⎧⎨-+=⎩，得244112111440a q a q a q a q a ⎧=⎨-+=⎩，解得112a q =⎧⎨=⎩．因此数列{}n a 为“M —数列”.（2）①因为1122n n n S b b +=-，所以0n b ≠．由1111,b S b ==得212211b =-，则22b =. 由1122n n n S b b +=-，得112()n n n n n b b S b b ++=-，当2n ≥时，由1n n n b S S -=-，得()()111122n n n nn n n n n b b b b b b b b b +-+-=---，整理得112n n n b b b +-+=．所以数列{b n }是首项和公差均为1的等差数列. 因此，数列{b n }的通项公式为b n =n ()*n N ∈.②由①知，b k =k ，*k N ∈.因为数列{c n }为“M –数列”，设公比为q ，所以c 1=1，q >0. 因为c k ≤b k ≤c k +1，所以1k k q k q -≤≤，其中k =1，2，3，…，m .当k =1时，有q ≥1；当k =2，3，…，m 时，有ln ln ln 1k kq k k ≤≤-．设f （x ）=ln (1)x x x >，则21ln ()xf 'x x-=．令()0f 'x =，得x =e .列表如下：x(1,e)e(e ，+∞) ()f 'x+0 –f （x ）极大值因为2663=<=，所以max ()(3)3f k f ==．取q =k =1，2，3，4，5时，ln ln k q k，即k k q ≤，经检验知1k q k -≤也成立．因此所求m 的最大值不小于5．若m ≥6，分别取k =3，6，得3≤q 3，且q 5≤6，从而q 15≥243，且q 15≤216，所以q 不存在.因此所求m 的最大值小于6. 综上，所求m 的最大值为5．16．（2019·北京高考真题（文））设{a n }是等差数列，a 1=–10，且a 2+10，a 3+8，a 4+6成等比数列．（Ⅰ）求{a n }的通项公式；（Ⅱ）记{a n }的前n 项和为S n ，求S n 的最小值．【答案】（Ⅰ）212n a n =-；（Ⅱ）30-. 【解析】（Ⅰ）设等差数列{}n a 的公差为d ，因为234+10+8+6a a a ，，成等比数列，所以2324(+8)(+10)(+6)a a a =，即2(22)(34)d d d -=-，解得2d =，所以102(1)212n a n n =-+-=-.（Ⅱ）由（Ⅰ）知212n a n =-, 所以22102121112111()224n n S n n n n -+-=⨯=-=--；当5n =或者6n =时，n S 取到最小值30-.第二部分模拟训练1．若数列{}n a 为等差数列，且16a π=，32a π=，则20cos a =（）A ．12B C ．12-D ．【答案】C 【解析】3126a a d π-== 201101963a a ππ=+⋅=201041cos coscos cos 3332a ππππ⎛⎫===+=- ⎪⎝⎭ 故选：C2．记n S 为数列{}n a 的前项和，已知点(,)n n a 在直线102y x =-上，若有且只有两个正整数n 满足n S k ≥，则实数k 的取值范围是（） A ．(8,14] B ．(14,18] C ．(18,20] D ．81(18,]4【答案】C【解析】解：由已知可得102n a n =-，由12n n a a --=-，所以数列{}n a 为等差数列，首项为8，公差为-2，所以2(1)8(2)92n n n S n n n -=+⨯-=-+，当n =4或5时， n S 取得最大值为20，因为有且只有两个正整数n 满足n S k ≥，所以满足条件的4n =和5n =，因为3618S S ==，所以实数k 的取值范围是(]18,20．故选：C ．3．已知n S 为等差数列{}n a 的前n 项和，3518a S +=-，63a a =-，则下列数值中最大的是（）A ．416S B ．525S C ．636SD ．749S【答案】D【解析】设等差数列{}n a 的公差为d，3518a S +=-，63a a =-，()111154+2+5+182+5+2a d a d a d a d ⨯⎧=-⎪∴⎨⎪=-⎩，解得17a =-，2d =，()217282n n n S n n n -=-+⨯=-，281n S n n ∴=-，可得2n S n ⎧⎫⎨⎬⎩⎭是单调递增数列，所以在416S ，525S ，536S ，749S 中，最大的为749S ．故选：D.4．在正项等比数列{}n a 中.24a =.416a =.满足123m a a a a =21ma +.则m =（） A ．4 B ．3C ．5D ．8【答案】A【解析】由题意得公比2q ===，首项21422a a q ===， ∴111222n n nn a a q --==⨯=，由21231m m a a a a a +=，()(1)12212331 (2)2222222m m m m m++++++===可得(1)2(1)222m m m ++=，解得4m =,故选：A.5．已知数列{}n a 的前n 项和为n S ，且21122n S n n =+，若()1211n n n n n b a a ++=-⋅，则数列{}n b 的前n 项和n T =______.【答案】,12,1n nn n T n n n ⎧-⎪⎪+=⎨+⎪-⎪+⎩为偶数为奇数【解析】21122n S n n =+，当1n =时，111a S ==，当2n ≥时，()()2211111112222n n n a S S n n n n n -⎡⎤=-=+--+-=⎢⎥⎣⎦，满足11a =， n a n ∴=，()()()()12111++121111+1nn n n n n n n b a n n a n n +++=-⋅=-⋅=⎛⎫∴⋅ ⎪⎝⎭-，当n 为偶数时，111111111+122334111n n T n n n n ⎛⎫⎛⎫⎛⎫⎛⎫=-++-++++=-+=- ⎪ ⎪ ⎪ ⎪+++⎝⎭⎝⎭⎝⎭⎝⎭，当n 为奇数时，1111111121+122334111n n T n n n n +⎛⎫⎛⎫⎛⎫⎛⎫=-++-++-+=--=- ⎪ ⎪ ⎪ ⎪+++⎝⎭⎝⎭⎝⎭⎝⎭， ,12,1n n n n T n n n ⎧-⎪⎪+∴=⎨+⎪-⎪+⎩为偶数为奇数.故答案为：,12,1n nn n T n n n ⎧-⎪⎪+=⎨+⎪-⎪+⎩为偶数为奇数6．数列{}n a 的前n 项和为n S ，23nn n a S +=，数列{}n b 满足()()211332n bn n a a n N *++=-∈，则数列{}n b 的前10项和为______．【答案】65【解析】由23nn n a S +=知：11123n n n a S ++++=，则1112233n n n n n n a S a S ++++--=-，得1323n n n a a +-=⨯，∴121323n n n a a +++-=⨯，而()()211332n bn n a a n N *++=-∈， ∴1n b n =+，故数列{}n b 的前10项和为1010(211)652T ⨯+==，故答案为：65.7．设公差不为0的等差数列{}n a 的前n 项和为n S .若数列{}n a 满足：存在三个不同的正整数,,r s t ，使得,,r s t a a a 成等比数列，222,,r s t a a a 也成等比数列，则1990nnS S a +的最小值为___________.【答案】45【解析】设1(1)n a a n d =+-，0d ≠，由题意,,r s t a a a 成等比数列，s t r s a a a a =，所以s t s t r s r s a a a a s t a a a a r s--===--， 222,,r s t a a a 也成等比数列，2222s t r s a a a a =，所以222222222222s t s t r s r s a a a a s t s t a a a a r s r s---====---，所以s t r s a a a a =2222s t r s a a a a ==，所以s t r s a a a a =2222s t r s a a a a ==2222s s r r a a s s sa a r r r--===--， 1111(1)(1)s r a a s d a d sd s a a r d a d rd r+--+===+--+，所以10a d -=，1d a =． 1111(1)99099099012(1)22nnn n a na dS S n a a n d n -+++==+++-，4445<<，设9901()22n f n n =++，由勾形函数性质知()f n在上递减，在)+∞上递增，又*n N ∈， (45)45f =，990441(44)454422f =++=，所以()f n 的最小值为45．即1990nnS S a +的最小值为45．故答案为：45．8．已知定义在[0,)+∞上的函数()f x 满足()()151,0222,2x x f x f x x ⎧--≤<⎪=⎨--≥⎪⎩.设()f x 在[)()*22,2n n n -∈N上的最大值记作n a ，n S 为数列{}n a 的前n 项和，则n S 的最大值为___________. 【答案】64【解析】由题意，函数()()151,0222,2x x f x f x x ⎧--≤<⎪=⎨--≥⎪⎩，当1n =时，[0,2)x ∈，此时()151f x x =--，此时函数()f x 在[0,2)上的最大值为()1151115f =--=，所以115a =，当2n =时，[2,4)x ∈，此时()()22f x f x =--，此时2[0,2)x -∈，所以()()2215212133f x f x x x =--=----=--，此时函数()f x 在[2,4)[0,2)上的最大值为()3133313f =--=，所以213a =，当[22,2)x n n ∈-时，()15[(22)]2(1)15(22)12(1)f x f x n n x n n =-----=------，此时函数()f x 的最大值为()172f n n =-，所以172n a n =-，当18,n n N +≤≤∈时，0n a >，当9,n n N +≥∈时，0n a <，所以n S 的最大值为8818()8(151)6422a S a +⨯+===. 故答案为：64.9．设等差数列{}n a 的前n 项和为n S ，首项11a =，且41412S S -=.数列{}n b 的前n 项和为n T ，且满足111,21n n b b T +==+.（1）求数列{}n a 和{}n b 的通项公式；（2）求数列n n a b ⎧⎫⎨⎬⎩⎭的前n 项和.【答案】（1）21n a n =-，13n n b -=；（2）1133n n n T -+=-. 【解析】解：（1）设数列{}n a 的公差为d ，且11a =，又41412S S -=，则()12341412312a a a a a d +++-=++=，所以2d =，则1(1)221n a n n =+-⋅=-；由121n n b T +=+可得121(2)n n b T n -=+≥，两式相减得12n n n b b b +-=，13(2)n n b b n +=≥，又21213b T =+=，所以213b b =，故{}n b 是首项为1，公比为3的等比数列，所以13n n b -=.（2）设1213n n n n a n c b --==，记{}n c 的前n 项和为n T .则0121135213333n n n T --=++++， 12311352133333n n n T -=++++，两式相减得：121222221133333n n n n T --=++++-，11112212233122133313n n n n n n T -⎛⎫⨯- ⎪-+⎝⎭=+⨯-=--，所以1133n n n T -+=-.10．已知数列{}n a 满足31212311212121212n n n a a a a ++++=-++++，n *∈N ．（1）求数列{}n a 的通项公式；（2）设等差数列{}n b 的前n 项和为n S ，且21122n S n n k =-+，令2n n n c b a kn =-+，求数列{}n c 的前n 项和n T ．【答案】（1）112n n a =--；（2）()11122n n n n T +=+- ．【解析】（1）当1n =时，11132a =-，132a ∴=-；当2n ≥时，由31212311212121212n n n a a a a ++++=-++++，①得31121231111212121212nn n a a a a ---++++=-++++，② ①-②得，111121222n n n n n a -=-=-+，112n n a ∴=--，132=-a 也符合，因此，数列{}n a 的通项公式为112n n a =--；（2）由题意，设等差数列{}n b 的公差为d ，则()221111122222n n n d d d S nb n b n n n k -⎛⎫=+=+-=-+ ⎪⎝⎭， 11221220d d b k ⎧=⎪⎪⎪∴-=-⎨⎪=⎪⎪⎩，解得，1010b d k =⎧⎪=⎨⎪=⎩，()111n b b n d n ∴=+-=-；由（1）知，212n n n nc b a kn n =-+=+，故123231*********2n n nT c c c c n ⎛⎫=++++=+++++++++ ⎪⎝⎭()()111111*********n n n n n n ⎛⎫- ⎪++⎝⎭=+=+--． 11．已知数列{}n a 满足0n a ≠恒成立.（1）若221n n n a a ka ++=且0n a >，当{}lg n a 成等差数列时，求k 的值；（2）若2212n n n a a a ++=且0n a >，当11a =、4a =2a 以及n a 的通项公式；（3）若21312n n n n a a a a +++=-，11a =-，3[4,8]a ∈，20200a <，设n S 是{}n a 的前n 项之和，求2020S 的最大值.【答案】（1）1 ；（2）2a ，()21n n a -=；（3）505143-【解析】（1）若221n n n a a ka ++=且0n a >，所以221lg lg n n n a a ka ++=，即21lg lg 2lg lg n n n a a k a ++=++，当{}lg n a 成等差数列时，21lg lg 2lg n n n a a a ++=+，所以lg 0k =，解得：1k = ；（2）2212n n n a a a ++=，令1n =可得21322a a a =，即2322a a =，令2n =可得22432a a a =，即2232a =所以42224a =⨯，因为0n a >，所以32a =，解得2a =，由2212n n n a a a ++=可得2112n n n na aa a +++=，所以1n n a a +⎧⎫⎨⎬⎩⎭是首项为21a a =2的等比数列，所以112n n na a -+=，所以0212a a =，1322a a =，2432a a =，212n nn a a --=，以上式子累乘得：()()()()()()21211112101222122n n n n n n n n n na a --------++++-=⨯=⨯=⨯=，所以()21n n a -=，（3）由21312n n n n a a a a +++=-可得132412n n n n a a a a ++++=-，所以22424111224n n n n n n a a a a a a +++++⎛⎫=-- ⎪=⎝⎭⨯，因为0n a ≠，所以414n n a a +=，即44n n a a +=，所以2505504202020162012444444k k a a a a a -=====，因为20200a <，所以504440a <，所以40a <，因为213412a a a a =-，所以341220a a a a =+即2432a a a =， ()()()202015920172610201837112019S a a a a a a a a a a a a =++++++++++++++()48122020a a a a +++++()()250425041214441444a a =+++++++++()250431444a +++++()250441444a +++++()()250412341444a a a a =+++++++，因为2432a a a =，3[4,8]a ∈，所以240a a >，因为40a <，所以20a <，所以()24a a +-≥=-24a a +≤-所以123431a a a a a +++≤-+-，令31y a =-+-2,t ⎡=⎣，21y t =--，对称轴为t =，是开口向上的抛物线，在2,t ⎡∈⎣单调递增，所以t =时取得最大值，故1234a a a a +++最大值为(211-=-，所以()()2504202012341444S a a a a =+++++++最大值为50550514141143---⨯=-.。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

细心审题，快速做题，小题小做，小题巧做
山西大学附中高三年级（下）专题复习编号17
选择填空专题训练十
制作人：孙娟审核人：代婷时间：2012年4月（第9周）
一、选择题（每小题5分，共60分）
1. 复数)1(i i z +-=（i 为虚数单位)在复平面内所对应的点位于
A.第一象限
B.第二象限 C .第三象限 D.第四象限
2.等比数列{}n a 的前n 项和为n S ，且41a ，22a ，3a 成等差数列。

若1a =1，则4S =
A.7
B.8
C.15
D.16
3．已知流程图如右图所示，
该程序运行后，为使输出的
b 值为16，则循环体的判断框
内①处应填的是
A ．2
B ．3
C ．4
D ．16
4．一个空间几何体的三视图如下，
则这个空间几何体的体积是
A ．423π+
B ．823
π+ C ．413
π+ D ．108π+ 5.5()a x x +（x R ∈）展开式中3x 的系数为10，则实数a 等于 A.-1 B.12
C. 1
D. 2 6. 设⎪⎩⎪⎨⎧≥-<=-,
2),1(log ,2,2)(231x x x e x f x 则不等式2)(>x f 的解集为 A ．),3()2,1(+∞⋃ B ．),10(+∞ C ．),10()2,1(+∞⋃ D ．（1，2）
7．设函数()f x 定义在实数集上，它的图像关于直线1x =对称，且当1x ≥时， ()ln f x x x =-，则有
A ．132()()()323f f f <<
B ．231()()()323
f f f << C ．213()()()332f f f << D ．321()()()233
f f f << 8．若不等式组0220x y x y y x y a
-≥⎧⎪+≤⎪⎨≥⎪⎪+≤⎩，
，，
表示的平面区域是一个四边形，则a 的取值范围是（）
A ．43a ≥
B ．01a <≤
C ．413a <<
D ．01a <≤或43a ≥
9．在ABC ∆中，O 为边BC 中线AM 上的一点，若4=AM ，则)(+∙的（）
A ．最大值为8
B ．最大值为4
C ．最小值－4
D ．最小值为－8
10. 已知1F ,2F 分别是双曲线122
22=-b
y a x ()0,0>>b a 的左、右焦点，过2F 且平行于y 轴的直线交双曲线的渐近线N M ,两点.若1MNF ∆为锐角三角形,则该双曲线的离心率的取值范围是 A.)3,1( B.),3(+∞ C.)5,1( D.),5(+∞
11．某游戏中，一个珠子从如右图所示的通道（图中的斜线）
由上至下滑下，从最大面的六个出口出来，规定猜中出口者为胜．
如果你在该游戏中，猜得珠子从出口3出来，那么你取胜的概率为
A ．
165 B ．325 C ．61 D ．以上都不对 12．设).,(),,(2121b b b a a a == ．定义一种向量积),(2211b a b a b a =⊕．已知)0,3(),21,2(π==，点),(y x P 在x y sin =的图象上运动,点Q 在)(x f y =的图象上运动，且满足+⊕=（其中O 为坐标原点），则)(x f y =的最大值A 及
最小正周期T 分别为 A ．2, π B ．2, 4π C ．π4,21 D ．π,21 二、填空题（每小题5分，共20分）
13.在ABC ∆中，角,,A B C 所对的边分别为c b a ,,若a =，2b =，
sin cos B B +=A 的大小为 . A=30
14．已知一个公园的形状如图所示，现有4种不同的植物要种在此公
园的,,,,A B C D E 这五个区域内，要求有公共边界的的两块相邻区域
种不同的植物，共有种不同的种法．144
15．设曲线cos y x =与x 轴、y 轴、直线6
x π
=围成的封闭图形的面积为b ，若2()2ln 2g x x bx kx =--在[1,)+∞上单调递减，则实数k 的取值范围
是．0k ≥
16. 已知集合},,),().()()(|)({22R y x y x f y x f y f x f x f M ∈-+=-=有下列命题
①若⎩
⎨⎧<-≥=,0,1,0,1)(1x x x f 则;)(1M x f ∈②若,2)(2x x f =则;)(2M x f ∈；③若,)(3M x f ∈则)(3x f y =的图象关于原点对称；④若,)(4M x f ∈则对于任意不等的实数,,21x x 总有0)()(2
12414<--x x x f x f 成立.其中所有正确命题的序号是．②③
13． 14． 15． 16．。