初中数学难题精选附答案解析
初中数学难题精选(附答案)

经典难题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初二)2、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150. 求证:△PBC 是正三角形.(初二)APCDB AFGCEBOD3、如图,已知四边形ABCD、A1B1C1D1都是正方形,A2、B2、C2、D2分别是AA1、BB1、CC1、DD1的中点.求证:四边形A2B2C2D2是正方形.(初二)4、已知:如图,在四边形ABCD中,AD=BC,M、NBC的延长线交MN于E、F.求证:∠DEN=∠F.D2C2B2A2D1C1B1C BD AA1B经典难题(二)1、已知:△ABC中,H为垂心(各边高线的交点),O为外心,且OM⊥BC于M.(1)求证:AH=2OM;(2)若∠BAC=600,求证:AH=AO.(初二)2、设MN是圆O外一直线,过O作OA⊥MN于A,自A及D、E,直线EB及CD分别交MN于P、Q.求证:AP=AQ.(初二)F3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE于P 、Q . 求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.经典难题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P是正方形ABCD一边BC上的任一点,PF⊥AP,CF平分∠DCE.4、如图,PC切圆O于C,AC为圆的直径,B、D.求证:AB=DC,BC=AD.(初三)经典难题(四)1、已知:△ABC是正三角形,P是三角形内一点,PA=3,PB=4,PC=5.求:∠APB的度数.(初二)2、设P是平行四边形ABCD内部的一点,且∠PBA=∠PDA.求证:∠PAB=∠PCB.(初二)3、设ABCD为圆内接凸四边形,求证:AB·CD+AD·BC=AC·BD.4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二)经典难题(五)1、设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L <2.FP DE CBAAPCB2、已知:P是边长为1的正方形ABCD内的一点,求PA+PB+PC的最小值.3、P为正方形ABCD内的一点,并且PA=a,PB=2a,PC=3a4、如图,△ABC中,∠ABC=∠ACB=800,D、E分别是AB、AC上的点,∠DCA=300,∠EBA=200,求∠BED的度数.经典难题(一)1.如下图做GH⊥AB,连接EO。
初二数学经典难题(带答案及解析)

初二数学经典难题一、解答题(共10小题,满分100分)1.(10分)已知:如图,P是正方形内点,∠∠15°.求证:△是正三角形.(初二)2.(10分)已知:如图,在四边形中,,M、N分别是、的中点,、的延长线交于E、F.求证:∠∠F.3.(10分)如图,分别以△的边、为一边,在△外作正方形和,点P是的中点,求证:点P到的距离是的一半.4.(10分)设P是平行四边形内部的一点,且∠∠.求证:∠∠.5.(10分)P为正方形内的一点,并且,2a,3a,求正方形的边长.6.(10分)一个圆柱形容器的容积为V立方米,开始用一根小水管向容器内注水,水面高度达到容器高度一半后,改用一根口径为小水管2倍的大水管注水.向容器中注满水的全过程共用时间t分.求两根水管各自注水的速度.7.(10分)(2009•郴州)如图1,已知正比例函数和反比例函数的图象都经过点M(﹣2,﹣1),且P(﹣1,﹣2)为双曲线上的一点,Q为坐标平面上一动点,垂直于x轴,垂直于y轴,垂足分别是A、B.(1)写出正比例函数和反比例函数的关系式;(2)当点Q在直线上运动时,直线上是否存在这样的点Q,使得△与△面积相等?如果存在,请求出点的坐标,如果不存在,请说明理由;(3)如图2,当点Q在第一象限中的双曲线上运动时,作以、为邻边的平行四边形,求平行四边形周长的最小值.8.(10分)(2008•海南)如图,P是边长为1的正方形对角线上一动点(P与A、C不重合),点E在线段上,且.(1)求证:①;②⊥;(2)设,△的面积为y.①求出y关于x的函数关系式,并写出x的取值范围;②当x取何值时,y取得最大值,并求出这个最大值.9.(10分)(2010•河南)如图,直线1与反比例函数(x>0)的图象交于A (1,6),B(a,3)两点.(1)求k1、k2的值.(2)直接写出时x的取值范围;(3)如图,等腰梯形中,∥,,边在x轴上,过点C作⊥于点E,和反比例函数的图象交于点P,当梯形的面积为12时,请判断和的大小关系,并说明理由.10.(10分)(2007•福州)如图,已知直线与双曲线交于A,B两点,且点A的横坐标为4.(1)求k的值;(2)若双曲线上一点C的纵坐标为8,求△的面积;(3)过原点O的另一条直线l交双曲线于P,Q两点(P点在第一象限),若由点A,B,P,Q为顶点组成的四边形面积为24,求点P的坐标.初二数学经典难题参考答案与试题解析一、解答题(共10小题,满分100分)1.(10分)已知:如图,P是正方形内点,∠∠15°.求证:△是正三角形.(初二)2.(10分)已知:如图,在四边形中,,M、N分别是、的中点,、的延长线交于E、F.求证:∠∠F.∴∥,且3.(10分)如图,分别以△的边、为一边,在△外作正方形和,点P是的中点,求证:点P到的距离是的一半.,则()4.(10分)设P是平行四边形内部的一点,且∠∠.求证:∠∠.5.(10分)P为正方形内的一点,并且,2a,3a,求正方形的边长.22,中,即正方形的边长为6.(10分)一个圆柱形容器的容积为V立方米,开始用一根小水管向容器内注水,水面高度达到容器高度一半后,改用一根口径为小水管2倍的大水管注水.向容器中注满水的全过程共用时间t分.求两根水管各自注水的速度.解之得:经检验得:∴小口径水管速度为立方米7.(10分)(2009•郴州)如图1,已知正比例函数和反比例函数的图象都经过点M(﹣2,﹣1),且P(﹣1,﹣2)为双曲线上的一点,Q为坐标平面上一动点,垂直于x轴,垂直于y轴,垂足分别是A、B.(1)写出正比例函数和反比例函数的关系式;(2)当点Q在直线上运动时,直线上是否存在这样的点Q,使得△与△面积相等?如果存在,请求出点的坐标,如果不存在,请说明理由;(3)如图2,当点Q在第一象限中的双曲线上运动时,作以、为邻边的平行四边形,求平行四边形周长的最小值.)为双曲线)坐标代入得,所以正比例函数解析式为,,××m×(﹣所以有,)(﹣)﹣,由勾股定理得+2=28.(10分)(2008•海南)如图,P是边长为1的正方形对角线上一动点(P与A、C不重合),点E在线段上,且.(1)求证:①;②⊥;(2)设,△的面积为y.①求出y关于x的函数关系式,并写出x的取值范围;②当x取何值时,y取得最大值,并求出这个最大值.,﹣ו×x﹣2.x2)x2﹣﹣+<时,.9.(10分)(2010•河南)如图,直线1与反比例函数(x>0)的图象交于A (1,6),B(a,3)两点.(1)求k1、k2的值.(2)直接写出时x的取值范围;(3)如图,等腰梯形中,∥,,边在x轴上,过点C作⊥于点E,和反比例函数的图象交于点P,当梯形的面积为12时,请判断和的大小关系,并说明理由.()在>,即12=,即10.(10分)(2007•福州)如图,已知直线与双曲线交于A,B两点,且点A的横坐标为4.(1)求k的值;(2)若双曲线上一点C的纵坐标为8,求△的面积;(3)过原点O的另一条直线l交双曲线于P,Q两点(P点在第一象限),若由点A,B,P,Q为顶点组成的四边形面积为24,求点P的坐标.代入是直线与双曲线(在双曲线××=×)))。
初二数学经典难题(带答案及解析)

初二数学经典难题一、解答题(共10小题,满分100分)1.(10分)已知:如图,P是正方形ABCD内点,∠PAD=∠PDA=15°.求证:△PBC是正三角形.(初二)2.(10分)已知:如图,在四边形ABCD中,AD=BC,M、N分别是AB、CD的中点,AD、BC的延长线交MN 于E、F.求证:∠DEN=∠F.3.(10分)如图,分别以△ABC的边AC、BC为一边,在△ABC外作正方形ACDE和CBFG,点P是EF的中点,求证:点P到AB的距离是AB的一半.4.(10分)设P是平行四边形ABCD内部的一点,且∠PBA=∠PDA.求证:∠PAB=∠PCB.5.(10分)P为正方形ABCD内的一点,并且PA=a,PB=2a,PC=3a,求正方形的边长.6.(10分)一个圆柱形容器的容积为V立方米,开始用一根小水管向容器内注水,水面高度达到容器高度一半后,改用一根口径为小水管2倍的大水管注水.向容器中注满水的全过程共用时间t分.求两根水管各自注水的速度.7.(10分)(2009•郴州)如图1,已知正比例函数和反比例函数的图象都经过点M(﹣2,﹣1),且P(﹣1,﹣2)为双曲线上的一点,Q为坐标平面上一动点,PA垂直于x轴,QB垂直于y轴,垂足分别是A、B.(1)写出正比例函数和反比例函数的关系式;(2)当点Q在直线MO上运动时,直线MO上是否存在这样的点Q,使得△OBQ与△OAP面积相等?如果存在,请求出点的坐标,如果不存在,请说明理由;(3)如图2,当点Q在第一象限中的双曲线上运动时,作以OP、OQ为邻边的平行四边形OPCQ,求平行四边形OPCQ周长的最小值.8.(10分)(2008•海南)如图,P是边长为1的正方形ABCD对角线AC上一动点(P与A、C不重合),点E在线段BC上,且PE=PB.(1)求证:①PE=PD;②PE⊥PD;(2)设AP=x,△PBE的面积为y.①求出y关于x的函数关系式,并写出x的取值范围;②当x取何值时,y取得最大值,并求出这个最大值.9.(10分)(2010•河南)如图,直线y=k1x+b与反比例函数(x>0)的图象交于A(1,6),B(a,3)两点.(1)求k1、k2的值.(2)直接写出时x的取值范围;(3)如图,等腰梯形OBCD中,BC∥OD,OB=CD,OD边在x轴上,过点C作CE⊥OD于点E,CE和反比例函数的图象交于点P,当梯形OBCD的面积为12时,请判断PC和PE的大小关系,并说明理由.10.(10分)(2007•福州)如图,已知直线y=x与双曲线交于A,B两点,且点A的横坐标为4.(1)求k的值;(2)若双曲线上一点C的纵坐标为8,求△AOC的面积;(3)过原点O的另一条直线l交双曲线于P,Q两点(P点在第一象限),若由点A,B,P,Q为顶点组成的四边形面积为24,求点P的坐标.初二数学经典难题参考答案与试题解析一、解答题(共10小题,满分100分)1.(10分)已知:如图,P是正方形ABCD内点,∠PAD=∠PDA=15°.求证:△PBC是正三角形.(初二)考点:正方形的性质;全等三角形的判定与性质;等边三角形的性质;等边三角形的判定。
初中数学难题附答案

经典难题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初二)2、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150. 求证:△PBC 是正三角形.(初二)APCDB AFGCEBOD3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC的延长线交MN 于E 、F . 求证:∠DEN =∠F .D 2 C 2B 2A 2 D 1C 1B 1CBDA A 1ANFECDMB经典难题(二)1、已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且OM ⊥BC 于M . (1)求证:AH =2OM ;(2)若∠BAC =600,求证:AH =AO .(初二)2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 引圆的两条直线,交圆于B 、C及D 、E ,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)· ADHE M CBO· GA O DB ECQP NMP C GFBQA DE 3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN于P 、Q . 求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.(初二)经典难题(三)·O QPB DECN M · A1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)AF DECBEDACBF3、设P 是正方形ABCD 一边BC 上的任一点,PF ⊥AP ,CF 平分∠DCE .求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEF 为圆的割线,AE 、AF 与直线PO 相交于B 、D .求证:AB =DC ,BC =AD .(初三)经典难题(四)DFEPCBAOD BFAEC P1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC =5.求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .(初三)APCBP ADCBCBDA4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二)经典难题(五)1、设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L <2.FP DE CBAAPCB2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.A CBPDA CBPD4、如图,△ABC中,∠ABC=∠ACB=800,D、E分别是AB、AC上的点,∠DCA=300,∠EBA=200,求∠BED的度数.经典难题(一)1.如下图做GH⊥AB,连接EO。
初中数学难题精选(附问题详解)
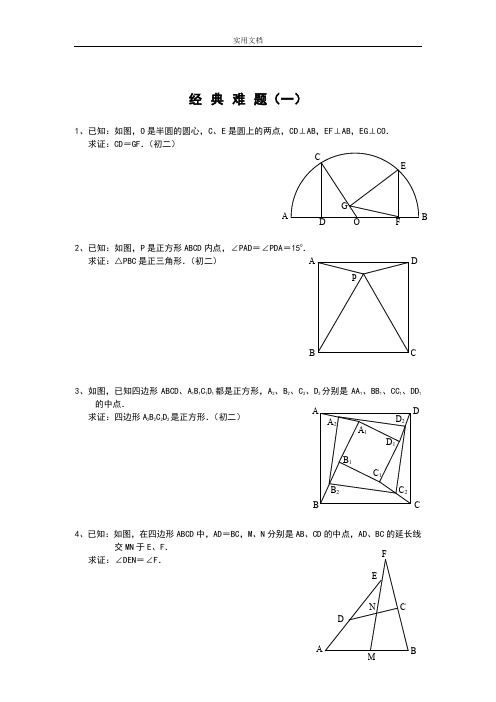
3、设P是正方形ABCD一边BC上的任一点,PF⊥AP,CF平分∠DCE.
求证:PA=PF.(初二)
4、如图,PC切圆O于C,AC为圆的直径,PEF为圆的割线,AE、AF与直线PO相交于B、D.求证:AB=DC,BC=AD.(初三)
经典难题(四)
1、已知:△ABC是正三角形,P是三角形内一点,PA=3,PB=4,PC=5.
经典难题(一)
1、已知:如图,O是半圆的圆心,C、E是圆上的两点,CD⊥AB,EF⊥AB,EG⊥CO.
求证:CD=GF.(初二)
2、已知:如图,P是正方形ABCD内点,∠PAD=∠PDA=150.
求证:△PBC是正三角形.(初二)
3、如图,已知四边形ABCD、A1B1C1D1都是正方形,A2、B2、C2、D2分别是AA1、BB1、CC1、DD1的中点.
2、设MN是圆O外一直线,过O作OA⊥MN于A,自A引圆的两条直线,交圆于B、C及D、E,直线EB及CD分别交MN于P、Q.
求证:AP=AQ.(初二)
3、如果上题把直线MN由圆外平移至圆内,则由此可得以下命题:
设MN是圆O的弦,过MN的中点A任作两弦BC、DE,设CD、EB分别交MN于P、Q.
求证:AP=AQ.(初二)
经典难题(四)
1.顺时针旋转△ABP 600,连接PQ,则△PBQ是正三角形。
可得△PQC是直角三角形。
所以∠APB=1500。
2.作过P点平行于AD的直线,并选一点E,使AE∥DC,BE∥PC.
可以得出∠ABP=∠ADP=∠AEP,可得:
AEBP共圆(一边所对两角相等)。
可得∠BAP=∠BEP=∠BCP,得证。
经典难题(一)
1.如下图做GH⊥AB,连接EO。由于GOFE四点共圆,所以∠GFH=∠OEG,
(完整版)初中数学经典难题(含答案)
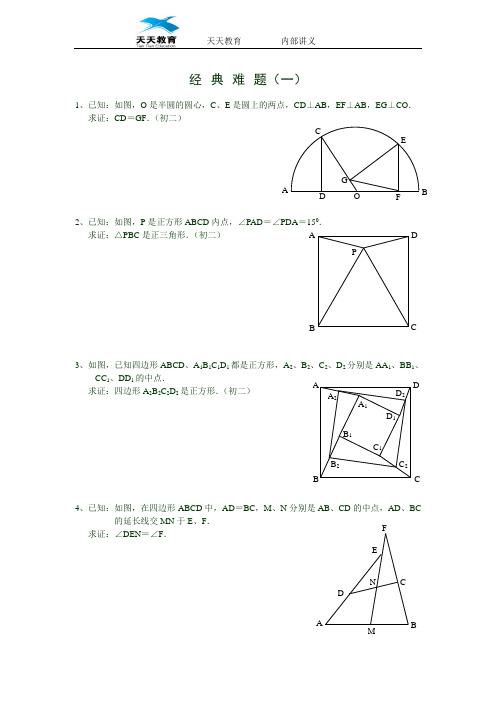
经典难题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初二)2、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150. 求证:△PBC 是正三角形.(初二)3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC的延长线交MN 于E 、F .求证:∠DEN =∠F .A P C DB A F G CE BO D D 2 C 2B 2 A 2D 1 C 1 B 1C B DA A 1 A N FE CDMBP CG FB QA D E1、已知:△ABC 中,H 为垂心(各边高线的交点),O (1)求证:AH =2OM ; (2)若∠BAC =600,求证:AH =AO .(初二)2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 及D 、E ,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.(初二)· A D HE M C B O · GAO D B EC Q P NM · O Q PB DEC N M · A1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边BC 上的任一点,PF ⊥AP ,CF 平分∠DCE .求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEF 为圆的割线,AE 、AF 与直线PO 相交于B 、D .求证:AB =DC ,BC =AD .(初三)D AF D E C B E DA CB F A E PC B A OD BFAECP1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC =5.求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二)3、Ptolemy (托勒密)定理:设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD . (初三)4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二)AP C B P A D CB C B DAF PD E C B A1、设P 是边长为1的正△ABC 内任一点,l =PA +PB +PC ,求证:3≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.4、如图,△ABC 中,∠ABC =∠ACB =800,D 、E 分别是AB 、AC 上的点,∠DCA =300,∠EBA =200,求∠BED 的度数.APCBACBPDEDCB AA CBPD经典难题(一)1、2、3、4、经典难题(二)1、2、4、经典难题(三)1、3、4、1、2、3、4、证明:过D 作DQ ⊥AE ,DG ⊥CF,并连接DF 和DE ,如右图所示 则S △ADE =21S ABCD =S △DFC ∴21 AE ﹒DQ = 21 DG ﹒FC 又∵AE=FC,∴DQ=DG,∴PD 为∠APC 的角平分线,∴∠DPA=∠DPC1、2、3、3、4、。
初三数学难题精选答案及讲解

1、如果将点P 绕定点M 旋转180°后与点Q 重合,那么称点P 与点Q 关于点M 对称,定点M 叫做对称中心。
此时,M 是线段PQ 的中点。
如图,在平面直角坐标系中,△ABO 的顶点A ,B ,O 的坐标分别为(1,0),(0,1),(0,0)。
点列P 1,P 2,P 3,…中的相邻两点都关于△ABO 的一个顶点对称:点P 1与点P 2关于点A 对称,点P 2与点P 3关于点B 对称,点P 3与点P 4关于点O 对称,点P 4与点P 5关于点A 对称,点P 5与点P 6关于点B 对称,点P 6与点P 7关于点O 对称…对称中心分别是A ,B ,O ,A ,B ,O ,…,且这些对称中心依次循环。
已知点P 1的坐标是(1,1),则点P 2017的坐标为 。
解:P 2的坐标是(1,-1),P 2017的坐标是(1,-1)。
理由:作P 1关于A 点的对称点,即可得到P 2(1,-1),P 3(-1,3),P 4(1,-3),P 5(1,3),P 6(-1,-1),又回到原来P 1的坐标,P 7(-1,-1);由此可知,每6个点为一个周期,作一次循环,2017÷6=336…1,循环了336次后又回到了原来P 1的坐标,故P 2017的坐标与P 1的坐标一样为(1,1)。
点评:此题主要考查了平面直角坐标系中中心对称的性质,以及找规律问题,根据已知得出点P 的坐标每6个一循环是解题关键.2、如图①,已知△ABC 是等边三角形,点E 在线段AB 上,点D 在直线BC 上,且DE=EC ,将△BCE 绕点C 顺时针旋转60°至△ACF ,连接EF 。
试证明:AB=DB+AF 。
【类比探究】(1)如图②,如果点E 在线段AB 的延长线上,其它条件不变,线段AB 、DB 、AF 之间又有怎样的数量关系?请说明理由。
(2)如果点E 在线段BA 的延长线上,其他条件不变,请在图③的基础上将图形补充完整,并写出AB ,DB ,AF 之间数量关系,不必说明理由。
七年级数学试卷超难的答案

一、选择题1. 题目:若一个等腰三角形的底边长为8cm,腰长为10cm,则该三角形的周长为多少?答案:24cm解析:等腰三角形的两腰相等,因此周长为8cm(底边)+ 10cm(腰)+ 10cm(腰)= 24cm。
2. 题目:一个正方形的对角线长为20cm,则该正方形的面积是多少?答案:200cm²解析:正方形的对角线等于边长的√2倍,因此边长为20cm / √2 ≈ 14.14cm。
正方形面积为边长的平方,即14.14cm × 14.14cm ≈ 200cm²。
3. 题目:一个圆的半径为5cm,其面积是多少?答案:78.54cm²解析:圆的面积公式为πr²,其中π≈3.14,r为半径。
因此面积为3.14 × 5cm × 5cm ≈ 78.54cm²。
4. 题目:一个长方体的长、宽、高分别为3cm、4cm、5cm,则其体积是多少?答案:60cm³解析:长方体的体积公式为长×宽×高,因此体积为3cm × 4cm × 5cm = 60cm³。
5. 题目:若一个数的平方根为±2,则该数是多少?答案:4解析:一个数的平方根为±2,即该数的平方为4,因此该数为4。
二、填空题1. 题目:若一个数的倒数是2,则该数为多少?答案:1/2解析:一个数的倒数是其与1的商,因此该数为1 ÷ 2 = 1/2。
2. 题目:若一个数的平方根是√3,则该数是多少?答案:3解析:一个数的平方根是√3,即该数的平方为3,因此该数为3。
3. 题目:一个圆的直径为12cm,则其半径是多少?答案:6cm解析:圆的半径等于直径的一半,因此半径为12cm ÷ 2 = 6cm。
4. 题目:若一个数的立方根是∛8,则该数是多少?答案:8解析:一个数的立方根是∛8,即该数的立方为8,因此该数为8。
(完整版)初二数学经典难题(带答案及解析)

初二数学经典难题一、解答题(共10小题,满分100分)1.(10分)已知:如图,P是正方形ABCD内点,∠PAD=∠PDA=15°.求证:△PBC是正三角形.(初二)2.(10分)已知:如图,在四边形ABCD中,AD=BC,M、N分别是AB、CD的中点,AD、BC的延长线交MN 于E、F.求证:∠DEN=∠F.3.(10分)如图,分别以△ABC的边AC、BC为一边,在△ABC外作正方形ACDE和CBFG,点P是EF的中点,求证:点P到AB的距离是AB的一半.4.(10分)设P是平行四边形ABCD内部的一点,且∠PBA=∠PDA.求证:∠PAB=∠PCB.5.(10分)P为正方形ABCD内的一点,并且PA=a,PB=2a,PC=3a,求正方形的边长.6.(10分)一个圆柱形容器的容积为V立方米,开始用一根小水管向容器内注水,水面高度达到容器高度一半后,改用一根口径为小水管2倍的大水管注水.向容器中注满水的全过程共用时间t分.求两根水管各自注水的速度.7.(10分)(2009•郴州)如图1,已知正比例函数和反比例函数的图象都经过点M(﹣2,﹣1),且P(﹣1,﹣2)为双曲线上的一点,Q为坐标平面上一动点,PA垂直于x轴,QB垂直于y轴,垂足分别是A、B.(1)写出正比例函数和反比例函数的关系式;(2)当点Q在直线MO上运动时,直线MO上是否存在这样的点Q,使得△OBQ与△OAP面积相等?如果存在,请求出点的坐标,如果不存在,请说明理由;(3)如图2,当点Q在第一象限中的双曲线上运动时,作以OP、OQ为邻边的平行四边形OPCQ,求平行四边形OPCQ周长的最小值.8.(10分)(2008•海南)如图,P是边长为1的正方形ABCD对角线AC上一动点(P与A、C不重合),点E在线段BC上,且PE=PB.(1)求证:①PE=PD;②PE⊥PD;(2)设AP=x,△PBE的面积为y.①求出y关于x的函数关系式,并写出x的取值范围;②当x取何值时,y取得最大值,并求出这个最大值.9.(10分)(2010•河南)如图,直线y=k1x+b与反比例函数(x>0)的图象交于A(1,6),B(a,3)两点.(1)求k1、k2的值.(2)直接写出时x的取值范围;(3)如图,等腰梯形OBCD中,BC∥OD,OB=CD,OD边在x轴上,过点C作CE⊥OD于点E,CE和反比例函数的图象交于点P,当梯形OBCD的面积为12时,请判断PC和PE的大小关系,并说明理由.10.(10分)(2007•福州)如图,已知直线y=x与双曲线交于A,B两点,且点A的横坐标为4.(1)求k的值;(2)若双曲线上一点C的纵坐标为8,求△AOC的面积;(3)过原点O的另一条直线l交双曲线于P,Q两点(P点在第一象限),若由点A,B,P,Q为顶点组成的四边形面积为24,求点P的坐标.初二数学经典难题参考答案与试题解析一、解答题(共10小题,满分100分)1.(10分)已知:如图,P是正方形ABCD内点,∠PAD=∠PDA=15°.求证:△PBC是正三角形.(初二)考点:正方形的性质;全等三角形的判定与性质;等边三角形的性质;等边三角形的判定。
初中数学难题试题及答案

初中数学难题试题及答案1. 已知函数f(x) = 2x^2 - 4x + 3,求f(x)的最小值。
答案:首先求导数f'(x) = 4x - 4,令f'(x) = 0,解得x = 1。
将x = 1代入原函数,得到f(1) = 2(1)^2 - 4(1) + 3 = 1。
因此,f(x)的最小值为1。
2. 一个数列的前三项为1, 2, 3,从第四项开始,每一项是前三项的和。
求数列的第10项。
答案:数列的前几项为1, 2, 3, 6, 11, 20, 37, 68, 125, 230。
因此,数列的第10项为230。
3. 一个圆的半径为5,求圆内接正方形的面积。
答案:圆内接正方形的对角线等于圆的直径,即10。
设正方形的边长为a,则对角线与边长的关系为a^2 + a^2 = 10^2,解得a = 5√2。
因此,正方形的面积为(5√2)^2 = 50。
4. 已知三角形ABC中,∠A = 30°,∠B = 45°,求∠C的度数。
答案:根据三角形内角和定理,三角形的内角和为180°。
因此,∠C = 180° - ∠A - ∠B = 180° - 30° - 45° = 105°。
5. 计算(2x - 3)(x + 4)的展开式。
答案:根据多项式乘法法则,(2x - 3)(x + 4) = 2x^2 + 8x - 3x - 12 = 2x^2 + 5x - 12。
6. 一个长方体的长、宽、高分别为2cm、3cm和4cm,求其体积。
答案:长方体的体积计算公式为V = 长× 宽× 高,所以V = 2cm × 3cm × 4cm = 24cm³。
7. 一个等差数列的前三项为2, 5, 8,求第10项。
答案:等差数列的通项公式为an = a1 + (n - 1)d,其中a1为首项,d为公差。
八年级数学经典难题(答案 解析)

初二数学经典难题一、解答题(共10小题,满分100分)1.(10分)已知:如图,P是正方形ABCD内点,∠PAD=∠PDA=15°.求证:△PBC是正三角形.(初二)2.(10分)已知:如图,在四边形ABCD中,AD=BC,M、N分别是AB、CD的中点,AD、BC的延长线交MN 于E、F.求证:∠DEN=∠F.3.(10分)如图,分别以△ABC的边AC、BC为一边,在△ABC外作正方形ACDE和CBFG,点P是EF的中点,求证:点P到AB的距离是AB的一半.4.(10分)设P是平行四边形ABCD内部的一点,且∠PBA=∠PDA.求证:∠PAB=∠PCB.5.(10分)P为正方形ABCD内的一点,并且PA=a,PB=2a,PC=3a,求正方形的边长.6.(10分)一个圆柱形容器的容积为V立方米,开始用一根小水管向容器内注水,水面高度达到容器高度一半后,改用一根口径为小水管2倍的大水管注水.向容器中注满水的全过程共用时间t分.求两根水管各自注水的速度.7.(10分)(2009•郴州)如图1,已知正比例函数和反比例函数的图象都经过点M(﹣2,﹣1),且P(﹣1,﹣2)为双曲线上的一点,Q为坐标平面上一动点,PA垂直于x轴,QB垂直于y轴,垂足分别是A、B.(1)写出正比例函数和反比例函数的关系式;(2)当点Q在直线MO上运动时,直线MO上是否存在这样的点Q,使得△OBQ与△OAP面积相等?如果存在,请求出点的坐标,如果不存在,请说明理由;(3)如图2,当点Q在第一象限中的双曲线上运动时,作以OP、OQ为邻边的平行四边形OPCQ,求平行四边形OPCQ周长的最小值.8.(10分)(2008•海南)如图,P是边长为1的正方形ABCD对角线AC上一动点(P与A、C不重合),点E在线段BC上,且PE=PB.(1)求证:①PE=PD;②PE⊥PD;(2)设AP=x,△PBE的面积为y.①求出y关于x的函数关系式,并写出x的取值范围;②当x取何值时,y取得最大值,并求出这个最大值.9.(10分)(2010•河南)如图,直线y=k1x+b与反比例函数(x>0)的图象交于A(1,6),B(a,3)两点.(1)求k1、k2的值.(2)直接写出时x的取值范围;(3)如图,等腰梯形OBCD中,BC∥OD,OB=CD,OD边在x轴上,过点C作CE⊥OD于点E,CE和反比例函数的图象交于点P,当梯形OBCD的面积为12时,请判断PC和PE的大小关系,并说明理由.10.(10分)(2007•福州)如图,已知直线y=x与双曲线交于A,B两点,且点A的横坐标为4.(1)求k的值;(2)若双曲线上一点C的纵坐标为8,求△AOC的面积;(3)过原点O的另一条直线l交双曲线于P,Q两点(P点在第一象限),若由点A,B,P,Q为顶点组成的四边形面积为24,求点P的坐标.初二数学经典难题参考答案与试题解析一、解答题(共10小题,满分100分)1.(10分)已知:如图,P是正方形ABCD内点,∠PAD=∠PDA=15°.求证:△PBC是正三角形.(初二)2.(10分)已知:如图,在四边形ABCD中,AD=BC,M、N分别是AB、CD的中点,AD、BC的延长线交MN 于E、F.求证:∠DEN=∠F.GM=BCADMG=BC3.(10分)如图,分别以△ABC的边AC、BC为一边,在△ABC外作正方形ACDE和CBFG,点P是EF的中点,求证:点P到AB的距离是AB的一半.PQ=(PQ=PQ=5.(10分)P为正方形ABCD内的一点,并且PA=a,PB=2a,PC=3a,求正方形的边长.PE=2PE==2CF=EF=CE===即正方形的边长为6.(10分)一个圆柱形容器的容积为V立方米,开始用一根小水管向容器内注水,水面高度达到容器高度一半后,改用一根口径为小水管2倍的大水管注水.向容器中注满水的全过程共用时间t分.求两根水管各自注水的速度.解之得:经检验得:∴小口径水管速度为立方米7.(10分)(2009•郴州)如图1,已知正比例函数和反比例函数的图象都经过点M(﹣2,﹣1),且P(﹣1,﹣2)为双曲线上的一点,Q为坐标平面上一动点,PA垂直于x轴,QB垂直于y轴,垂足分别是A、B.(1)写出正比例函数和反比例函数的关系式;(2)当点Q在直线MO上运动时,直线MO上是否存在这样的点Q,使得△OBQ与△OAP面积相等?如果存在,请求出点的坐标,如果不存在,请说明理由;(3)如图2,当点Q在第一象限中的双曲线上运动时,作以OP、OQ为邻边的平行四边形OPCQ,求平行四边形OPCQ周长的最小值.Y=上的一点,所以,所以正比例函数解析式为x,|OB×m|所以有,)=))﹣OP=(=28.(10分)(2008•海南)如图,P是边长为1的正方形ABCD对角线AC上一动点(P与A、C不重合),点E在线段BC上,且PE=PB.(1)求证:①PE=PD;②PE⊥PD;(2)设AP=x,△PBE的面积为y.①求出y关于x的函数关系式,并写出x的取值范围;②当x取何值时,y取得最大值,并求出这个最大值..BE PF=x﹣xx xx x=()<时,9.(10分)(2010•河南)如图,直线y=k1x+b与反比例函数(x>0)的图象交于A(1,6),B(a,3)两点.(1)求k1、k2的值.(2)直接写出时x的取值范围;(3)如图,等腰梯形OBCD中,BC∥OD,OB=CD,OD边在x轴上,过点C作CE⊥OD于点E,CE和反比例函数的图象交于点P,当梯形OBCD的面积为12时,请判断PC和PE的大小关系,并说明理由.y=的图象上,﹣=12=,即PE=CE10.(10分)(2007•福州)如图,已知直线y=x与双曲线交于A,B两点,且点A的横坐标为4.(1)求k的值;(2)若双曲线上一点C的纵坐标为8,求△AOC的面积;(3)过原点O的另一条直线l交双曲线于P,Q两点(P点在第一象限),若由点A,B,P,Q为顶点组成的四边形面积为24,求点P的坐标.xx与双曲线在双曲线××=×)))。
初中数学经典难题(含问题详解)

经典难题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初二)2、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150.求证:△PBC 是正三角形.(初二)3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN 于E 、F .求证:∠DEN =∠F .A PC D B A FG C EBO D D 2 C 2B 2 A 2D 1 C 1 B 1 C B DA A 1 BF经典难题(二)1、已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且OM ⊥BC 于M .(1)求证:AH =2OM ;(2)若∠BAC =600,求证:AH =AO .(初二)2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 引圆的两条直线,交圆于B 、C 及D 、E ,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q .求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.经典难题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边BC 上的任一点,PF ⊥AP ,CF 平分∠DCE .求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEF 为圆的割线,AE 、AF 与直线PO 相交于B 、D .求证:AB =DC ,BC =AD .(初三)经典难题(四)E1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC =5.求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二)3、Ptolemy (托勒密)定理:设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD . (初三)4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二)经典难题(五)1、设P 是边长为1的正△ABC 内任一点,l =PA +PB +PC ,求证:3≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.4、如图,△ABC 中,∠ABC =∠ACB =800,D 、E 分别是AB 、AC 上的点,∠DCA =300,∠EBA=200,求∠BED 的度数.经典难题(一)1、2、3、4、经典难题(二)1、2、3、4、经典难题(三)1、2、3、4、经典难题(四)2、3、4、证明:过D 作DQ ⊥AE ,DG ⊥CF,并连接DF 和DE ,如右图所示 则S △ADE =21S ABCD =S △DFC∴21 AE ﹒DQ = 21 DG ﹒FC 又∵AE=FC,∴DQ=DG,∴PD 为∠APC 的角平分线,∴∠DPA=∠DPC经典难题(五)2、3、3、4、。
初中数学经典难题(含答案)
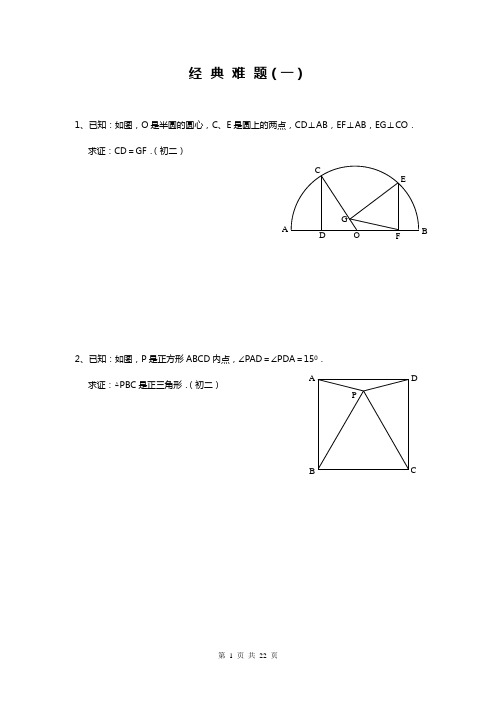
经典难题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初二)2、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150. 求证:△PBC 是正三角形.(初二)APCDB AFGCEBOD3、如图,已知四边形ABCD、A1B1C1D1都是正方形,A2、B2、C2、D2分别是AA1、BB1、CC1、DD1的中点.求证:四边形A2B2C2D2是正方形.(初二)4、已知:如图,在四边形ABCD中,AD=BC,M、NBC的延长线交MN于E、F.求证:∠DEN=∠F.D2C2B2A2D1C1B1C BD AA1B经典难题(二)1、已知:△ABC中,H为垂心(各边高线的交点),O为外心,且OM⊥BC于M.(1)求证:AH=2OM;(2)若∠BAC=600,求证:AH=AO.(初二)2、设MN是圆O外一直线,过O作OA⊥MN于A,自A及D、E,直线EB及CD分别交MN于P、Q.求证:AP=AQ.(初二)F3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE于P 、Q . 求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.经典难题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P是正方形ABCD一边BC上的任一点,PF⊥AP,CF平分∠DCE.4、如图,PC切圆O于C,AC为圆的直径,B、D.求证:AB=DC,BC=AD.(初三)经典难题(四)1、已知:△ABC是正三角形,P是三角形内一点,PA=3,PB=4,PC=5.2、设P是平行四边形ABCD内部的一点,且∠PBA=∠PDA.求证:∠PAB=∠PCB.(初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .4、平行四边形ABCD 中,设E 、F分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二)经典难题(五)1、设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a4、如图,△ABC中,∠ABC=∠ACB=800,D、E分别是AB、AC∠EBA=200,求∠BED的度数.经典难题(一)1.如下图做GH⊥AB,连接EO。
初中数学经典难题含答案

经典难题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初二)2、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150. 求证:△PBC 是正三角形.(初二)3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC的延长线交MN 于E 、F .求证:∠DEN =∠F .A P C DB A F G CE BO D D 2 C 2B 2 A 2D 1 C 1 B 1C B DA A 1 BF1、已知:△ABC 中,H 为垂心(各边高线的交点),O(1)求证:AH =2OM ; (2)若∠BAC =600,求证:AH =AO .(初二)2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 及D 、E ,直线EB及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边BC 上的任一点,PF ⊥AP ,CF 平分∠DCE .求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEF 为圆的割线,AE 、AF 与直线PO 相交于B 、D .求证:AB =DC ,BC =AD .(初三)E1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC =5.求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二)3、Ptolemy (托勒密)定理:设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD . (初三)4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二)1、设P 是边长为1的正△ABC 内任一点,l =PA +PB +PC ,求证:3≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.4、如图,△ABC 中,∠ABC =∠ACB =800,D 、E 分别是AB 、AC 上的点,∠DCA =300,∠EBA =200,求∠BED 的度数.经典难题(一)1、2、3、4、经典难题(二)1、2、4、经典难题(三)1、3、4、1、2、3、4、证明:过D 作DQ ⊥AE ,DG ⊥CF,并连接DF 和DE ,如右图所示 则S △ADE =21S ABCD =S △DFC ∴21 AE ﹒DQ = 21 DG ﹒FC 又∵AE=FC,∴DQ=DG,∴PD 为∠APC 的角平分线,∴∠DPA=∠DPC1、2、3、3、4、。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
.难题(一)经典.,EF⊥ABEG⊥CO1、已知:如图,O是半圆的圆心,C、E是圆上的两点,CD⊥AB,(初二)求证:CD=GF.CEG A B O D F0.PAD=∠PDA=15P2、已知:如图,是正方形ABCD内点,∠D A (初二)求证:△PBC 是正三角形.PC BDD、BB、CC、C、D分别是AA、BC3、如图,已知四边形ABCD、ABD都是正方形,A、112112111212的中点.A D(初二)CD是正方形.求证:四边形AB D2222A2 2 A 1D 1B1C1 BC2 2C B的延长线、BCAD分别是AB、CD的中点,MAD4、已知:如图,在四边形ABCD中,=BC,、N .、于EF交MNFF=∠.求证:∠DEN EC N DAB.M.难题(二)经典M.⊥BC于,ABC中,H为垂心(各边高线的交点)O为外心,且OM1、已知:△A=2OM;(1)求证:AH0.=AO(初二))若∠BAC=60,求证:AH (2O ·H EB C D M,、EB、C及DMN作OA⊥于A,自A引圆的两条直线,交圆于是圆2、设MNO外一直线,过OQ.MN于P、直线EB及CD分别交GE (初二)=求证:APAQ.O ·CB DNM Q AP由圆外平移至圆内,则由此可得以下命题:3、如果上题把直线MN Q.于EB分别交MNP、、是圆MNO的弦,过MN的中点A任作两弦BCDE,设CD、设E(初二)求证:AP=AQ.C A Q M ·N P·O BD,和正方形CBFGBC和为一边,在△ABC的外侧作正方形ACDEABC4、如图,分别以△的AC 的中点.点P是EFD (初二)ABP求证:点到边AB的距离等于的一半.GCEP FABQ..经典难题(三)1、如图,四边形ABCD为正方形,DE∥AC,AE=AC,AE与CD相交于F.求证:CE=CF.(初二)DAFEB C.交DA延长线于F,且DE∥ACCE=CA,直线EC2、如图,四边形ABCD为正方形,(初二)AE=AF.求证:DA FB CEDCE.CFPF⊥AP,平分∠ABCD3、设P是正方形一边BC上的任一点,.(初二)求证:PA=PFD AFB EP C求D相交于B、.POAEACO、4如图,PC切圆于C,为圆的直径,PEF为圆的割线,、AF与直线.(初三)BCAB证:=DC,=ADAD O BPEFC..经典难题(四)1、已知:△ABC是正三角形,P是三角形内一点,PA=3,PB=4,PC=5.求:∠APB的度数.(初二)APC BPDA.内部的一点,且∠PBA=∠2、设P是平行四边形ABCD (初二)PCBPAB=∠.求证:∠A DPB C(初三).=AC·BD+3、设ABCD为圆内接凸四边形,求证:AB·CDAD·BCADB C4、平行四边形ABCD中,设E、F分别是BC、AB上的一点,AE与CF相交于P,且AE=CF.求证:∠DPA=∠DPC.(初二)A D FP..经典难题(五),求证:≤L<2+PB+PC. PAP1、设是边长为1的正△ABC内任一点,L=AP CB的最小值.PCPA+PB+的正方形2、已知:P是边长为1ABCD内的一点,求DAP C B3a,求正方形的边长.PCPB=a,=2a,=PAABCDP3、为正方形内的一点,并且PC B..00EBA,∠DCA=30分别是D、EAB、AC上的点,∠=∠4、如图,△ABC中,∠ABCACB=80,A0,求∠BED=20的度数.DCB经典难题(一)OEG, GFH=∠。
由于AB,连接EOGOFE四点共圆,所以∠⊥1.如下图做GH COEOGO得证。
CD=GF∽即△GHF△OGE,可得==,又CO=EO,所以CDGFGH全等,可得△PDG为等边△,从而可得ADP2. 如下图做△DGC使与△015PC=AD=DC,CGP,≌△DGC△≌APD△得出和∠PCG∠DCG==0所以∠DCP=30PBC,从而得出△是正三角形..3.连接BC和AB分别找其中点F,E.连接CF与AE并延长相交于Q点,如下图2121连接EB并延长交CQ于H点,连接FB并延长交AQ于G点,222211110AB=BC= FB,EB由AE==C,又∠GFQ+∠Q=90和AB=BC=F 1 121212 122220=BB+,EB B又∠FC∠GE=所以∠∠Q=90,GE∠A∠GFQ222222,CB=B FC可得△B≌△AEB,所以A222222220 , A∠EB∠GFQ+HBF=90和∠GFQ=又∠2220,BA C=90从而可得∠222同理可得其他边垂直且相等,是正方形。
B从而得出四边形ACD2222..4.连接AC并取其中点Q,连接QN和QM,所以可得∠QMF=如下图∠F,∠QNM=∠DEN。
=∠F,从而得出∠QMN=∠QNMDEN和∠经典难题(二)1.(1)延长AD到F连BF,做OG⊥AF,又∠F=∠ACB=∠BHD,可得BH=BF,从而可得HD=DF,AH=GF+HG=GH+HD+DF+HG=2(GH+HD)=2OM又0既得OC,连接OB,(2),BOC=120 ∠0, BOM=60 从而可得∠OB=2OM=AH=AO,所以可得得证。
..3.作OFCD,OG⊥BE,连接OP,OA,OF,AF,OG,AG,⊥OQ。
ADACCD2FDFD====,由于ABAEBE2BGBG由此可得△ADF≌△ABG,从而可得∠AFC=∠AGE。
又因为PFOA与QGOA四点共圆,可得∠AFC=∠AOP和∠AGE=∠AOQ,。
,从而可得AP=AQ∠AOP=∠AOQEG+FH PQ=FH。
可得AB点分别作所在直线的高EG,CI,4.过E,C,F。
2≌EG=AI,由△BFH△CBI,可得FH=BI。
,可得△EGA 由△≌AIC AI+BIAB PQ== ,从而得证。
从而可得22..经典难题(三)1.顺时针旋转△ADE,到△ABG,连接CG.000由于 +45ABG=∠ADE=90=135∠从而可得B,G,D在一条直线上,可得△AGB≌△CGB。
推出AE=AG=AC=GC,可得△AGC为等边三角形。
000∠AGB=30,既得∠EAC=30,从而可得∠A EC=75。
000又∠EFC=∠DFA=45+30=75.。
CE=CF 可证:2.连接BD作CH⊥DE,可得四边形CGDH是正方形。
..由AC=CE=2GC=2CH,00可得∠CEH=30,所以∠CAE=∠CEA=∠AED=15,0000又∠FAE=90+45+15=150,0。
,从而得出AE=AF从而可知道∠F=153.作FGCD,FE⊥BE,可以得出⊥GFEC为正方形。
令AB=Y ,BP=X ,CE=Z ,可得PC=Y-X 。
XZ2=,可得YZ=XY-X+XZ,EPF= tan∠BAP=tan∠Y-X+ZY即Z(Y-X)=X(Y-X) ,既得X=Z ,得出△ABP≌△PEF ,。
,得证=得到PAPF经典难题(四)1.顺时针旋转0ABP 60△,连接PQ ,则△PBQ是正三角形。
可得△PQC是直角三角形。
..0。
所以∠APB=1502.作过P点平行于AD的直线,并选一点E,使AE∥DC,BE∥PC.可以得出∠ABP=∠ADP=∠AEP,可得:AEBP共圆(一边所对两角相等)。
可得∠BAP=∠BEP=∠BCP,得证。
3.在BD取一点E,使∠BCE=∠ACD,既得△BEC∽△ADC,可得:BEAD=,即AD?BC=BE? AC,①ACBC又∠ACB=∠DCE,可得△ABC∽△DEC,既得ABDE=,即AB?CD=DE? AC,②DCAC由①+②可得:AB?CD+AD?BC=AC(BE+DE)= AC·BD ,得证。
..S ABCD SS AQ4.过D作,可得:= =,由CF ⊥AE ,AG⊥DFCADE2AEPQAEPQ,由AE=FC。
=22。
(角平分线逆定理)DPA=∠DPC 可得DQ=DG,可得∠经典难题(五)顺时针旋转(11.,可得△PBE为等边三角形。
△BPC 60既得PA+PB+PC=AP++PE+EF 0)要使最小只要AP,PE,EF在一条直线上,即如下图:可得最小L= ;..(2)过P点作BC的平行线交AB,AC与点D,F。
由于∠APD>∠ATP=∠ADP,推出AD>AP ①又BP+DP>BP ②和PF+FC>PC ③又DF=AF ④由①②③④可得:最大L< 2 ;)既得:≤L<)和(22 。
由( 12.,可得△PBE为等边三角形。
△BPC 60既得PA+PB+PC=AP+PE+EF要使0顺时针旋转最小只要AP,PE,EF在一条直线上,。
即如下图:可得最小PA+PB+PC=AF..4+231321)+(+3+2AF=既得== 242221)(3+(3+1) = = 226+2。
=23.,可得如下图:△ABP 900顺时针旋转..2222a()(2++)a225+。
= L = 既得正方形边长22FAB4.在上找一点,∠BCF=600,使连接EF,DG,既得△BGC为等边三角形,00 ,推出△ABE≌△ACF ,可得∠DCF=10∠ , FCE=20 得到BE=CF , FG=GE 。
0,,可得∠AFE=80 FGE推出:△为等边三角形0①DFG=40 既得:∠00 DGF=40 ②BD=BC=BG 又,既得∠BGD=80 ,既得∠ DFE≌△,DGE 得到:△推得: DF=DG ,0。
∠FED=从而推得:∠BED=30..。
同进步我们共去,让坚持下习惯,常好的一种非学习是阅读和建议。
意见或保贵的您好,欢您提出,希望读过后印。
阅直接打也可以修改,可编辑文档WOR本文章,读我的迎您阅.。
