【精品】等腰三角形性质及判定 基础知识点练习题
等腰三角形的性质与判定综合练习 #(精选.)

1 / 3word.等腰三角形的性质与判定综合练习1、若等腰三角形的顶角为60°,则它底角的度数为( )A 、40°B 、50°C 、60°D 、70°2、如图,在△ABC 中,点D 在BC 上,AB =AD =DC ,∠B =80°,则C 的度数为( )A 、30°B 、40°C 、45°D 、60°3、如图,在△ABC 中,D 为BC 的中点,AD ⊥BC ,E 为AD 上一点,∠ABC =60°,∠ECD=40°,则∠ABE =( ) A 、10° B 、15° C 、20° D 、25°4、等腰△ABC 中,AB =AC=6cm ,∠A =150°,则△ABC 的面积为( )A 、9cm ²B 、18cm ²C 、6cm ²D 、36cm ²5、如图,在△ABC 中,AB =AC ,∠A =36°,DM 是AB 的垂直平分线,则图中的等腰三角形有( )A 、5个B 、4个C 、3个D 、2个 6、如图,在△ABC 中,∠A =60°,BE ⊥AC ,垂足为E ,CF ⊥AB , 垂足为F ,BE 、CF 交于点M 。
如果CM =4,FM =5,则BE 等于( ) A 、9 B 、12 C 、13 D 、14 7、如图,已知AB =AC ,∠A =36°,AB 的中垂线MD 交AC 于点D ,交AB 于点M 。
下列结论:①BD 是∠ABC 的平分线;②△BCD 是等腰三角形;③DC+BC=AB 。
正确的有( )A 、3个B 、2个C 、1个D 、0个8、如图,△ABC 中,AB =AC ,△DEF 为等边三角形,则γβα、、之间的关系为( )A 、2γαβ+= B 、2γβα+= C 、2γαβ—= D 、2γβα—=二、填空题9、如图,AB//CD ,CD =BD ,∠ABD =68°,则∠C 的度数为 。
等腰三角形的性质练习(含答案)

等腰三角形的性质练习(含答案)等腰三角形的性质1.选择题:1) 等腰三角形的底角与相邻外角的关系是()A。
底角大于相邻外角 B。
底角小于相邻外角C。
底角大于或等于相邻外角 D。
底角小于或等于相邻外角2) 等腰三角形的一个内角等于100°,则另两个内角的度数分别为()A。
40°,40° B。
100°,20°C。
50°,50° D。
40°,40°或100°,20°3) 等腰三角形中的一个外角等于100°,则这个三角形的三个内角分别为()A。
50°,50°,80° B。
80°,80°,20°C。
100°,100°,20° D。
50°,50°,80°或80°,80°,20°4) 如果一个等腰三角形的一个底角比顶角大15°,那么顶角为()A。
45° B。
40° C。
55° D。
50°5) 等腰三角形一腰上的高与底边所成的角等于()A。
顶角 B。
顶角的一半C。
顶角的2倍 D。
底角的一半6) 已知:如图1所示,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,则∠A的度数为()A。
30° B。
45° C。
36° D。
72°2.填空题:1) 如图2所示,在△ABC中,①因为AB=AC,所以∠A=∠C;②因为AB=AC,∠1=∠2,所以BD=BC,BD⊥AC.2) 若等腰三角形的顶角与一个底角之和为110°,则顶角的度数为70°.3) 已知等腰三角形的一个角是80°,则顶角为20°.4) 在等腰三角形ABC中,一腰上的高是1cm,这条高与底边的夹角是45°,则△ABC的面积为1/2 cm².5) 如图3所示,O为△ABC内一点,且OA=OB=OC,∠ABO=20°,∠BCO=30°,则∠CAO=30°.3.等腰三角形两个内角的度数比为4:1,求其各个角的度数.设两个内角的度数为4x和x,则三角形的第三个角的度数为180°-5x.因为三角形内角和为180°,所以4x+4x+180°-5x=180°,解得x=36°,因此两个内角的度数分别为144°和36°,第三个角的度数为100°.4.如图,已知线段a和c,用圆规和直尺作等腰三角形ABC,使等腰三角形△ABC以a和c为两边,这样的三角形能作无数个.5.如图,在△ABC中,D是BC边上一点,AD=BD,AB=AC=CD,求∠BAC的度数.连接AD和AC,因为AD=BD,AB=AC,所以△ABD≌△ACD,故∠ABD=∠ACD.又因为AB=CD,所以△ABC为等腰三角形,所以∠BAC=180°-∠ABC=180°-2∠ABD=80°.6.如图所示,AB=AE,∠ABC=∠AED,BC=ED,点F是CD的中点.1) AF与CD不垂直.因为∠ABC=∠AED,所以△ABC≌△AED,故AB=AE,又因为BC=ED,所以AC=AD,所以AF垂直于BC的中点,而CD的中点是F,所以AF与CD不垂直.二、拓展延伸训练右下图是人字型层架的设计图,由AB、AC、BC、AD四根钢条焊接而成,其中A、B、C、D均为焊接点,且AB=AC,D为BC的中点,现在焊接所需的四根钢条已截好,且已标出BC的中点D。
人教版八年级上册数学等腰三角形知识点及对应练习(附参考解析)

等腰三角形一、知识梳理:专题一:等腰三角形概念及性质;等腰三角形的判定.二、考点分类考点一:等腰三角形的概念有两边相等的三角形是等腰三角形。
【类型一】利用等腰三角形的概念求边长或周长【例1】如果等腰三角形两边长是6cm和3cm,那么它的周长是()A.9cm B.12cm C.15cm或12cm D.15cm解析:当腰为3cm时,3+3=6,不能构成三角形,因此这种情况不成立.当腰为6cm 时,6-3<6<6+3,能构成三角形;此时等腰三角形的周长为6+6+3=15(cm).故选D.方法总结:在解决等腰三角形边长的问题时,如果不明确底和腰时,要进行分类讨论,同时要养成检验三边长能否组成三角形的好习惯,把不符合题意的舍去.考点二:等腰三角形的性质1、等腰三角形的性质:(1)等腰三角形的两个底角相等(简写成“等边对等角”).(2)等腰三角形的顶角平分线,底边上的中线、•底边上的高互相重合(通常称作“三线合一”).2、解题方法:设辅助未知数法与拼凑法.3、重要的数学思想方法:方程思想、整体思想和转化思想.【类型一】利用“等边对等角”求角度【例2】等腰三角形的一个内角是50°,则这个三角形的底角的大小是()A .65°或50° B.80°或40° C .65°或80° D.50°或80°解析:当50°的角是底角时,三角形的底角就是50°;当50°的角是顶角时,两底角相等,根据三角形的内角和定理易得底角是65°.故选A.方法总结:等腰三角形的两个底角相等,已知一个内角,则这个角可能是底角也可能是顶角,要分两种情况讨论.【类型二】 利用方程思想求等腰三角形角的度数【例3】 如图①,在△ABC 中,AB =AC ,点D 在AC 上,且BD =BC =AD ,求△ABC 各角的度数.解析:设∠A =x ,利用等腰三角形的性质和三角形内角和定理即可求得各角的度数.解:设∠A =x .∵AD =BD ,∴∠ABD =∠A =x .∵BD =BC ,∴∠BCD =∠BDC =∠ABD +∠A=2x .∵AB =AC ,∴∠ABC =∠BCD =2x .在△ABC 中,∠A +∠ABC +∠ACB =180°,∴x +2x+2x =180°,∴x =36°,∴∠A =36°,∠ABC =∠ACB =72°.方法总结:利用等腰三角形的性质和三角形外角的性质可以得到角与角之间的关系,当这种等量关系或和差关系较多时,可考虑列方程解答,设未知数时,一般设较小的角的度数为x .① ②【类型三】 利用“等边对等角”的性质进行证明【例4】 如图②,已知△ABC 为等腰三角形,BD 、CE 为底角的平分线,且∠DBC =∠F ,求证:EC ∥DF .解析:先由等腰三角形的性质得出∠ABC =∠ACB ,根据角平分线定义得到∠DBC =12∠ABC ,∠ECB =12∠ACB ,那么∠DBC =∠ECB ,再由∠DBC =∠F ,等量代换得到∠ECB =∠F ,于是根据平行线的判定得出EC ∥DF .证明:∵△ABC 为等腰三角形,AB =AC ,∴∠ABC =∠ACB .又∵BD 、CE 为底角的平分线,∴∠DBC =12∠ABC ,∠ECB =12∠ACB ,∴∠DBC =∠ECB .∵∠DBC =∠F ,∴∠ECB =∠F ,∴EC ∥DF .方法总结:证明线段的平行关系,主要是通过证明角相等或互补.【类型四】 利用等腰三角形“三线合一”的性质进行证明【例5】 如图①,点D 、E 在△ABC 的边BC 上,AB =AC .(1)若AD =AE ,求证:BD =CE ;(2)若BD =CE ,F 为DE 的中点,如图②,求证:AF ⊥BC .解析:(1)过A 作AG ⊥BC 于G ,根据等腰三角形的性质得出BG =CG ,DG =EG 即可证明;(2)先证BF =CF ,再根据等腰三角形的性质证明.证明:(1)如图①,过A 作AG ⊥BC 于G .∵AB =AC ,AD =AE ,∴BG =CG ,DG =EG ,∴BG-DG =CG -EG ,∴BD =CE ;(2)∵BD =CE ,F 为DE 的中点,∴BD +DF =CE +EF ,∴BF =CF .∵AB =AC ,∴AF ⊥BC .方法总结:在等腰三角形有关计算或证明中,会遇到一些添加辅助线的问题,其顶角平分线、底边上的高、底边上的中线是常见的辅助线.【类型五】 与等腰三角形的性质有关的探究性问题【例6】 如图①,已知△ABC 是等腰直角三角形,∠BAC =90°,BE 是∠ABC 的平分线,DE⊥BC ,垂足为D .(1)请你写出图中所有的等腰三角形;(2)请你判断AD 与BE 垂直吗?并说明理由.(3)如果BC =10,求AB +AE 的长.解析:(1)由△ABC 是等腰直角三角形,BE 为角平分线,可证得△ABE ≌△DBE ,即AB =BD ,AE =DE ,所以△ABD 和△ADE 均为等腰三角形;由∠C =45°,ED ⊥DC ,可知△EDC 也符合题意;(2)BE 是∠ABC 的平分线,DE ⊥BC ,根据角平分线定理可知△ABE 关于BE 与△DBE对称,可得出BE ⊥AD ;(3)根据(2),可知△ABE 关于BE 与△DBE 对称,且△DEC 为等腰直角三角形,可推出AB +AE =BD +DC =BC =10.解:(1)△ABC ,△ABD ,△ADE ,△EDC .(2)AD 与BE 垂直.证明:由BE 为∠ABC 的平分线,知∠ABE =∠DBE ,∠BAE =∠BDE =90°,BE =BE ,∴△ABE ≌△DBE ,∴△ABE 沿BE 折叠,一定与△DBE 重合,∴A 、D 是对称点,∴AD ⊥BE .(3)∵BE 是∠ABC 的平分线,DE ⊥BC ,EA ⊥AB ,∴AE =DE .在Rt △ABE 和Rt △DBE 中,∵⎩⎪⎨⎪⎧AE =DE ,BE =BE ,∴Rt △ABE ≌Rt △DBE (HL),∴AB =BD .又∵△ABC 是等腰直角三角形,∠BAC =90°,∴∠C =45°.又∵ED ⊥BC ,∴△DCE 为等腰直角三角形,∴DE =DC ,∴AB +AE =BD +DC =BC=10.① ②考点三:等腰三角形的判定方法(1)根据定义判定;(2)两个角相等的三角形是等腰三角形.【类型一】 确定等腰三角形的个数 【例7】 如图②,在△ABC 中,AB =AC ,∠A =36°,BD 、CE 分别是∠ABC 、∠BCD 的角平分线,则图中的等腰三角形有( )A .5个B .4个C .3个D .2个解析:共有5个.(1)∵AB =AC ,∴△ABC 是等腰三角形;(2)∵BD 、CE 分别是∠ABC 、∠BCD的角平分线,∴∠EBC =12∠ABC ,∠ECB =12∠BCD .∵△ABC 是等腰三角形,∴∠EBC =∠ECB ,∴△BCE 是等腰三角形;(3)∵∠A =36°,AB =AC ,∴∠ABC =∠ACB =12(180°-36°)=72°.又∵BD 是∠ABC 的角平分线,∴∠ABD =12∠ABC =36°=∠A ,∴△ABD 是等腰三角形;同理可证△CDE 和△BCD 也是等腰三角形.故选A.方法总结:确定等腰三角形的个数要先找出相等的边和相等的角,然后确定等腰三角形,再按顺序不重不漏地数出等腰三角形的个数.【类型二】 在坐标系中确定三角形的个数【例8】 已知平面直角坐标系中,点A 的坐标为(-2,3),在y 轴上确定点P ,使△AOP 为等腰三角形,则符合条件的点P 共有( )A .3个B .4个C .5个D .6解析:因为△AOP 为等腰三角形,所以可分三类讨论:(1)AO =AP (有一个).此时只要以A 为圆心AO 长为半径画圆,可知圆与y 轴交于O 点和另一个点,另一个点就是点P ;(2)AO=OP (有两个).此时只要以O 为圆心AO 长为半径画圆,可知圆与y 轴交于两个点,这两个点就是P 的两种选择;(3)AP =OP (一个).作AO 的中垂线与y 轴有一个交点,该交点就是点P 的最后一种选择.综上所述,共有4个.故选B. 方法总结:解决此类问题的方法主要是线段垂直平分线与辅助圆的灵活运用以及分类讨论时做到不重不漏.【类型三】 判定一个三角形是等腰三角形【例9】如图,在△ABC中,∠ACB=90°,CD是AB边上的高,AE是∠BAC的角平分线,AE与CD交于点F,求证:△CEF是等腰三角形.解析:根据直角三角形两锐角互余求得∠ABE=∠ACD,然后根据三角形外角的性质求得∠CEF=∠CFE,根据等角对等边求得CE=CF,从而求得△CEF是等腰三角形.证明:∵在△ABC中,∠ACB=90°,∴∠B+∠BAC=90°.∵CD是AB边上的高,∴∠ACD+∠BAC=90°,∴∠B=∠ACD.∵AE是∠BAC的角平分线,∴∠BAE=∠EAC,∴∠B+∠BAE=∠ACD+∠EAC,即∠CEF=∠CFE,∴CE=CF,∴△CEF是等腰三角形.方法总结:“等角对等边”是判定等腰三角形的重要依据,是先有角相等再有边相等,只限于在同一个三角形中,若在两个不同的三角形中,此结论不一定成立.【类型四】等腰三角形性质和判定的综合运用【例10】如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC边上,且BE=CF,BD=CE.(1)求证:△DEF是等腰三角形;(2)当∠A=50°时,求∠DEF的度数.解析:(1)根据等边对等角可得∠B=∠C,利用“边角边”证明△BDE和△CEF全等,根据全等三角形对应边相等可得DE=EF,再根据等腰三角形的定义证明即可;(2)根据全等三角形对应角相等可得∠BDE=∠CEF,然后求出∠BED+∠CEF=∠BED+∠BDE,再利用三角形的内角和定理和平角的定义求出∠B=∠DEF.(1)证明:∵AB =AC ,∴∠B =∠C .在△BDE 和△CEF 中,∵⎩⎪⎨⎪⎧BD =CE ,∠B =∠C ,BE =CF ,∴△BDE ≌△CEF (SAS),∴DE =EF ,∴△DEF 是等腰三角形;(2)解:∵△BDE ≌△CEF ,∴∠BDE =∠CEF ,∴∠BED +∠CEF =∠BED +∠BDE .∵∠B +∠BDE =∠DEF +∠CEF ,∴∠B =∠DEF .∵∠A =50°,AB =AC ,∴∠B =12×(180°-50°)=65°,∴∠DEF =65°.方法总结:等腰三角形提供了好多相等的线段和相等的角,判定三角形是等腰三角形是证明线段相等、角相等的重要手段.经典例题考点一:等腰三角形的概念【例1】等腰三角形的两边长分别为4和9,则这个三角形的周长为考点二:等腰三角形的性质【例3】已知等腰△ABC 中,AB=AC ,D 是BC 边上一点,连接AD ,若△ACD 和△ABD 都是等腰三角形,求∠C 的度数。
初中数学等腰三角形及性质练习题(附答案)

初中数学等腰三角形及性质练习题一、单选题1・以下列各组线段为边,能组成三角形的是()A. 2 cm, 2 cm,5 cm B ・ 3cn ι4c π‰7 CmC. 4 cm, 6 cm,8 cmD. 5cm,6cm,12cm2•如图,在LABC 中・ZB = 60o . ZC = 50。
,如果AD 平分ZBAC ,那么ZADB 的度数是()A. 35oB.70oC.85oD.95o 3. 下列命题为真命题的是()A. 直角三角形的两个锐角互余B. 任意多边形的内角和为360。
C. 任意三角形的外角中最多有一个钝角D. 一个三角形中最多有一个锐角4. 将一副直角三角板按如图所示的位置放宜,使含30°角的三角板的一条直角边和含45。
角的三角 板的一条直角边放在同一条直线上,则厶,的度数是()A. 房屋顶的支撑架B. 自行车上的三脚架C. 伸缩的拉闸门A.45oB.60oC.75o 5 •下列图形中,没有运用三角形的稳左性的是()D.85oD.在木门上钉一根木条6 •如图AB// DF, AC丄BC于C, BC与DF交于点E ,若ZA = 20°,则ZCEF等于()A.IlO oB.100oC.80oD.70o7.如图,在ZvlBC中,AB = AC, AQ平分ABAC, DE丄AB,DF丄AC, E,F分别为垂足,则下列四个结论:(I)ZDEF = ZDFE ;(2) AE = AFX⑶AD平分ZEDF ;⑷AD垂直平分矿.其中正确的有()A.1个B.2个C.3个D.4个&如图BF = £CZB = ZE请问添加下而哪个条件不能判断AABC ^DEF()A. ZA = ZD B・ AB = ED C. DF//AC D. AC = DF9.如图,点P为ZAOB内一点,分别作点P关于04,03的对称点P l,P2,连接人,出交OA于M,交OB于N,若∕>Λ=6,则APMN的周长为()10•如图,在正五边形ABa)E中,连接BE侧ZABE的度数为()A.30oB.36°C.54oD.72°11・已知点P(-1-2<Λ5)关于x轴的对称点和点Q(3,b)关于y轴的对称点相同,则点Aab)关于X轴对称的点的坐标为()A.(l,-5)B.(l,5)C. (-1,5)D.(-l,-5)12.在正方形网格中,ZAoB的位宜如图所示,到ZAoB两边距离相等的点是()A.M点B.N点、C.P点 D・Q点二S解答题E如图所示,ZA = 27。
(完整)等腰三角形性质与判定练习题

等腰三角形性质与判定练习题一、选择题1、等腰三角形一腰上的中线把等腰三角形的周长分成9和12两部分,则腰长为()A、6B、8C、10D、6或82、等腰三角形的周长为19cm,其中一边长为5cm,则该等腰三角形的底边边长为()A、9cmB、5cmC、9cm或5cmD、10cm3、等腰三角形的腰长等于2m,面积等于1m2,则它的顶角等于()A、150°B、30°C、150°或30°D、60°4、若等腰三角形的周长为10,一边长为4,则此等腰三角形的腰长为()A、2B、3C、4D、3或45、下列说法中正确的是()A、等腰三角形的两个底角的角平分线所夹的角是这个等腰三角形顶角的两倍B、在等腰三角形中“三线合一”是指等腰三角形的中线、高线、角平分线重合C、等边对等角D、有一个角等于60°的等腰三角形是等边三角形6、等腰三角形有两条边长为3和5,则它的周长可以是()A、12B、11C、10D、11或137、等腰三角形的对称轴有( )A、一条B、二条C、三条D、一条或三条8、等腰三角形周长为36cm,两边长之比为4:1,则底边长为()A、16cmB、4cmC、20cmD、16cm或4cm9、等腰三角形的周长是18cm,其中一边长为4cm,其它两边长分别为()A、4cm,10cmB、7cm,7cmC、4cm,10cm或7cm,7cmD、无法确定10、一个等腰而非等边的三角形,它的所有的内角平分线、中线和高的条数为()A、9B、6C、7D、311、已知等腰三角形的两边长分别为8与16,则其周长为()A、32B、40C、32或40D、8或1612、一个等腰三角形的周长是16,其中一边长是6,另两边长分别是()A、6和10B、6和4C、5和5D、5和5或4和613、等腰三角形ABC,其中AB=8cm,周长为20cm,则这个等腰三角形的腰长是( )A、8cmB、4cmC、6cmD、6cm或8cm14、等腰三角形的周长为18cm,其中一边长为4cm,则该等腰三角形的腰长为()A、4cm或10cmB、4cm或7cmC、4cmD、7cm15、如右图,在△ABC中,AB=AC,BD=BC,AD=DE=EB,则∠A是( )A、30°B、45°C、60°D、20°16、有下列命题说法:①锐角三角形中任何两个角的和大于90°;②等腰三角形一定是锐角三角形;③等腰三角形有一个外角等于120°,这个三角形一定是等边三角形;④等腰三角形中有一个是40°,那么它的底角是70°;⑤一个三角形中至少有一个角不小于60度.其中正确的有()A、2个B、3个C、4个D、5个17、等腰三角形中一个角是40°,则另外两个角的度数分别是()A、70°,70°B、40°,100°C、40°,40°D、70°,70°或40°,100°18、如右图,一钢架中,∠A=15°,焊上等长的钢条来加固钢架.若A P1=P1P2,则这样的钢条最多只能焊上()条.A、4B、5C、6D、719、若△ABC的三边a,b,c满足(a﹣b)(b﹣c)(c﹣a)=0,那么△ABC的形状是( )A、等腰三角形B、直角三角形C、等边三角形D、锐角三角形20、如果一个三角形的一条角平分线恰好是对边上的高,那么这个三角形一定是( )A、直角三角形B、等边三角形C、等腰三角形D、等腰直角三角形二、填空题1、一个等腰三角形的两边长分别是2cm、5cm,则它的周长为_______2、等腰三角形的两边长分别为4和9,则第三边长为_________ .3、等腰三角形的对称轴最多有_________ 条.4、一个等腰三角形周长为5,它的三边长都是整数,则底边长为_________ .5、若等腰三角形的三条边长分别为a2+1,a+1,4a﹣3,则a可以取的值为_________ .6、等腰三角形一个底角为36°,则此等腰三角形顶角为_________ 度.7、等腰三角形的两边长为5cm,10cm,则它的周长等于_________ cm.8、一个等腰三角形的顶角是底角的2倍,则它的各个内角的度数是_________ .9、在等腰△ABC中,AB=AC,AC腰上的中线BD将三角形周长分为15和21两部分,则这个三角形的底边长为_________ .10、如图,B在AC上,D在CE上,AD=BD=BC,∠ACE=25°,∠ADE=_______度.10题图 11题图 13题图 15题图11、如图,在△ABC中,∠C=25°,AD⊥BC,垂足为D,且AB+BD=CD,则∠BAC的度数是_______ 度.12、一个三角形有两条边相等,周长为18cm,三角形的一边长为4cm,则其他两边长分别为_________ cm.13、如图,△ABC中,∠A=36°,AB=AC,BD平分∠ABC,DE∥BC,则图中等腰三角形有______个.14、在△ABC中,AD⊥BC于D,且BD=CD,若AB=3,则AC= _________ .15、如图,在△ABC中,BC=5cm,BP、CP分别是∠ABC和∠ACB的角平分线,且PD∥AB,PE∥AC,则△PDE的周长是_________ cm.16、如右图,在Rt△ABC中,∠ACB=90°,∠ABC=60°,在直线BC或AC上取一点P,使得△PAB为等腰三角形,则符合条件的点P共有_________个.17、如图,在下列三角形中,若AB=AC,则能被一条直线分成两个小等腰三角形的是(填序号)______三、解答题1、如图,在△ABC和△DCB中,AC与BD相交于点O.AB=DC,AC=BD.试判断△OBC的形状,并证明2、已知:如图,△ABC是等腰三角形,AB=AC,∠1=∠2.求证:OA平分∠BAC.3、已知:点D是△ABC的边BC的中点,DE⊥AC,DF⊥AB,垂足分别为E,F,且BF=CE.求证:△ABC是等腰三角形.4、如图,在△ABC中,点E在AB上,点D在BC上,BD=BE,∠BAD=∠BCE,AD与CE相交于点F,试判断△AFC的形状,并说明理由.5、已知,如图△ABC中,AB=AC,D点在BC上,且BD=AD,DC=AC.求∠B的度数.6、如图,在△ABC中,BO平分∠ABC,CO平分∠ACB,DE过O且平行于BC,已知△ADE的周长为10cm,BC 的长为5cm,求△ABC的周长.7、△ABC中,AB=AC,BD是△ABC的角平分线,E在BC的延长线上,且CE=CD。
等腰三角形的性质基础练习

等腰三角形的性质基础练习一.选择题(共10小题)1.若一个等腰三角形的两边长分别是2和5,则它的周长为()A.12 B.9 C.12或9 D.9或72.已知一个等腰三角形的两边长a、b 满足方程组,则此等腰三角形的周长为()A.5 B.4 C.3 D.5或43.已知等腰三角形的一个内角为50°,则这个等腰三角形的顶角为()A.50° B.80° C.50°或80°D.40°或65°4.如图,在△ABC中,AB=AC,D为BC中点,∠BAD=35°,则∠C的度数为()A.35° B.45° C.55° D.60°5.如图,在等腰△ABC中,AB=AC,BD⊥AC,∠ABC=72°,则∠ABD=()A.36° B.54° C.18° D.64°6.如图,等腰三角形ABC中,AB=AC,BD平分∠ABC,∠A=36°,则∠1的度数为()A.36° B.60° C.72° D.108°7.在等腰△ABC中,AB=AC,其周长为16cm,则AB边的取值范围是()A.1cm<AB<4cm B.3cm<AB<6cm C.4cm<AB<8cm D.5cm<AB<10cm8.若x,y满足|x﹣3|+=0,则以x,y的值为两边长的等腰三角形的周长为()A.12 B.14 C.15 D.12或159.如图,AB=AC=AD,若∠BAD=80°,则∠BCD=()A.80° B.100°C.140°D.160°二.填空题(共5小题)10.如图,△ABC中,D是BC上一点,AC=AD=DB,∠BAC=102°,则∠ADC=度.11.等腰三角形的一个外角是60°,则它的顶角的度数是.12.等腰三角形一腰上的高与另一腰的夹角的度数为20°,则顶角的度数是.第4题第5题第6题第9题13.如图,在等腰△ABC 的两腰AB 、BC 上分别取点D 和E ,使DB=DE ,此时恰有∠ADE=∠ACB,则∠B 的度数是.14.如图,在△ABC 中,AB=AC,且D 为BC 上一点,CD=AD ,AB=BD ,则∠B 的度数为 .三.解答题15.如图,已知AB=AC=AD ,且AD∥BC,求证:∠C=2∠D.16.如图,在△ABC 中,AB=AC ,AD 是BC 边上的中线,BE⊥AC 于点E .求证:∠CBE=∠B AD .17.如图,在△ABC 中,AB=AC ,D 、E 在BC 上,且AD=AE ,求证:BD=CE .如有侵权请联系告知删除,感谢你们的配合!第13题第14题。
等腰三角形的判定定理(2个知识点+12大题型+18道强化训练)(学生) 24-25学年八年级数学上册

第04讲等腰三角形的判定定理(2个知识点+12大题型+18道强化训练)知识点01:等腰三角形的判定等腰三角形的判定①有两条边相等的三角形是等腰三角形。
②有两个角相等的三角形是等腰三角形。
(简称“等角对等边”)总结:【即学即练1】已知等腰三角形的一边长为5cm ,另一边长为11cm ,则它的周长为( )A .16cmB .27cmC .21cmD .21cm 或27cm【即学即练2】如图,在ABC D 中,AB AC =,AD BD =,DE AB ^于点E ,若4BC =,BDC D 的周长为10,则AE 的长为( )A .2.5B .3C .3.5D .4知识点02:等边三角形的判定1、判定:①三条边都相等的三角形是做等边三角形②三个角都相等的三角形是等边三角形③有一个角是60°的等腰三角形是等边三角形。
2、等腰三角形和等边三角形的判定【即学即练3】下列四个说法中,正确的有( )①三个角都相等的三角形是等边三角形;②有两个角等于60°的三角形是等边三角形;③有一个角是60°的等腰三角形是等边三角形;④有两个角相等的等腰三角形是等边三角形.A .1个B .2个C .3个D .4个【即学即练4】若一个三角形有两条边相等,且有一内角为60°,那么这个三角形一定为( )A .钝角三角形B .等腰三角形C .直角三角形D .正三角形题型01 格点中画等腰三角形1.如图,在33´的网格中,以AB 为一边,点P 在格点处,使ABP V 为等腰三角形的点P 有( )个A .2个B .5个C.3个D .1个2.在正方形网格中,网格线的交点成为格点,如图,A 、B 分别在格点处,若C 也是图中的格点,且使得ABC V 是以AB 为腰的等腰三角形,则符合条件的点C 有( )A .7个B .6个C .5个D .4个3.如图,在正方形网格中,网格线的交点称为格点.已知A 、B 是网格中的两个格点,如果C 也是网格中的格点,且使ABC V 为等腰三角形,那么符合条件的点C 有 个.4.如图,在4×5的点阵图中,每两个横向和纵向相邻阵点的距离均为1,该点阵图中已有两个阵点分别标为A ,B ,请在此点阵中找一个阵点C ,使得以点A ,B ,C 为顶点的三角形是等腰三角形,则符合条件的点C 有 个.5.如图,在方格纸中,每一个小正方形的边长为1,按要求画一个三角形,使它的顶点都在小方格的顶点上.(1)在图1中画一个以AB 为直角边且面积为3的直角三角形.(2)在图2中画一个以AC 为腰的等腰三角形.题型02 找出图中的等腰三角形1.如图,在ABC V 中,AB AC =,72B Ð=°,CD 平分ACB Ð交AB 于点D ,DE AC ∥交BC 于点E ,则图中共有等腰三角形( )A .3个B .4个C .5个D .6个2.如图,已知线段AB 的端点B 在直线l 上(AB 与l 不垂直)请在直线l 上另找一点C ,使ABC V 是等腰三角形,这样的点能找( )A .2个B .3个C .4个D .5个3.如图,在ABC V 中,已知边AB 的垂直平分线与边BC 的垂直平分线交于点P ,连接PA PB PC 、、,则图中有 个等腰三角形.4.如图,已知ABC V 中,37AB BC ==,,在ABC V 所在平面内一条直线,使其中有一个边长为3的等腰三角形,则这样的直线最多可画 条.5.如图,在四边形ABCD 中,AB ∥CD ,∠1=∠2,DB=DC .(1)求证:AB+BE=CD .(2)若AD=BC ,在不添加任何补助线的条件下,直接写出图中所有的等腰三角形.题型03 根据等角对等边证明等腰三角形1.一个三角形两个内角的度数分别如下,这个三角形是等腰三角形的是( )A .40°,70°B .30°,90°C .60°,50°D .40°,20°2.在ABC V 中,36A Ð=°,72B Ð=°,则ABC V 是( )A .钝角三角形B .等腰三角形C .等边三角形D .等腰直角三角形3.在ABC V 中,若50B Ð=°,65C =°∠,则ABC V 等腰三角形.(填“是”或“不是”)4.在ABC V 中,90A Ð=°,当B Ð= 度时,ABC V 是等腰三角形.5.如图,在ABC V 中,60,40,BAC C ABC Ð=°Ð=°Ð的平分线BD 交AC 于点D .判断BCD △是否为等腰三角形?请说明理由.题型04 根据等角对等边证明边相等1.如图,在ABC V 中,6BC =,边AB 的垂直平分线交BC 于M ,点N 在MC 上,连接AM ,AN ,C NAC Ð=Ð,则MAN △的周长为( )A .6B .4C .3D .122.在ABC V 中,AD 平分235BAC B ADB AB CD ÐÐ=Ð==,,,,则AC 的长为( )A .6B .7C .8D .93.如图,在ABC V 中,ABC Ð和ACB Ð的平分线交于点E ,过点E 作MN BC ∥交AB 于M ,交AC 于N ,若8BM CN +=,则线段MN 的长为 .4.如图,在ABC V 中,4AB =,6AC =,ABC Ð和ACB Ð的平分线交于O 点,过点O 作BC 的平行线交AB 于M 点,交AC 于N 点,则AMN V 的周长为 .5.如图,ABC V 中,CA CB =,点D 在BC 的延长线上,连接AD AE ,平分CAD Ð交CD 于点E ,过点E 作EF AB ^,垂足为点F ,与AC 相交于点G ..(1)求证:CG CE =;(2)若30B Ð=°,40CAD Ð=°,求AEF Ð和D Ð的度数;(3)求证:2D AEF Ð=Ð.题型05 根据等角对等边求边长1.如图,在ABC V 中,B C Ð=Ð,4AB =,则AC 的长为( )A .2B .3C .4D .52.如图,在ABC V 中,ABC Ð的平分线交AC 于点D ,6AD =,过点D 作DE BC ∥交AB 于点E ,若AED △的周长为16,则边AB 的长为( )A .10B .8C .6D .163.如图,在ABC V 中,12AB =,9AC =,沿过点A 的直线折叠这个三角形,使点C 落在AB 边上的点E 处,折痕为AD ,若12ADE C Ð=Ð,则BD 的长是 .4.如图,在Rt ABC △中,90C Ð=°,10AC =,12BC =,点D 是AC 边的中点,点E 是BC 边上一动点,将CDE V 沿DE 折叠得到C DE ¢V ,连接BC ¢,当BEC ¢△是直角三角形时,BE 的长为 .5.如图,100,40203BAC B D AB Ð=°Ð=°Ð=°=,,,求CD 的长.题型06 直线上与已知两点组成等腰三角形的点1.点A ,B 在直线l 同侧,若点C 是直线l 上的点,且ABC V 是等腰三角形,则这样的点C 最多有( )A .5个B .4个C .3个D .2个2.在平面直角坐标系中,O 为坐标原点,点A 的坐标为(3,4),点P 是坐标轴上的一点,使OAP V 为等腰三角形的点P 的个数有( )A .5个B .6个C .7个D .8个3.如图,点O 在直线l 上,点A 在直线l 外.若直线l 上有一点P 使得APO △为等腰三角形,则满足条件的点P 位置有 个.4.如图,已知Rt ABC △中,90,30Ð=°Ð=°C A .在直线BC 或AC 上取一点P ,使得PAB V 是等腰三角形,则符合条件的P 点有 个.5.如图,在直线EF 上有一点A ,直线外有一点B ,点C 在直线EF 上,ΔABC 是以AB 、AC 为腰的等腰三角形.(1)在图中画出ΔABC(2)已知40BAF Ð=°,求BCAÐ题型07 求与图形中任意两点构成等腰三角形的点1.已知ABC V 中,AB AC =.108A Ð=°,在平面内找一点P ,使得PAB V ,PAC V ,PBC V 都是等腰三角形,则这样的P 点有( )个A .4B .6C .8D .102.已知:如图ABC V 中,=60B а,80C Ð=°,在直线BA 上找一点D ,使ACD V 或BCD △为等腰三角形,则符合条件的点D 的个数有( )A .7个B .6个C .5个D .4个3.如图,在ABC V 中,25,100B A Ð=°Ð=°,点P 在ABC V 的三边上运动,当PAC V 成为等腰三角形时,其顶角的度数是 .4.如图,60AOB Ð=°,C 是OB 延长线上一点,若18cm OC =,动点P 从点C 出发沿CB 以2cm/s 的速度移动,动点Q 从点O 沿OA 以1cm/s 的速度移动,如果点P 、Q 同时出发,用()t s 表示移动的时间,当t = s时,POQ △是等腰三角形?5.如图,在ABC V 中,AB AC BC ==,ABC V 所在的平面上有一点P (如图中所画的点1P ),使PAB V ,PBC △, PAC V 都是等腰三角形,问:具有这样性质的点P 有几个(包括点1P )?在图中画出来.题型08 作等腰三角形(尺规作图)1.如图,已知直线m n P ,线段AC 分别与直线m ,n 相交于点B 、点C ,以点A 为圆心,AB 的长为半径画弧交直线m 于点B 、点D .若70A Ð=°,则a 的度数为( )A .45°B .50°C .55°D .60°2.如图,已知直线l 及直线l 外一点P ,过点P 作直线l 的平行线,下面四种作法中错误的是( )A .B .C .D .3.如图,在Rt △ABC 中,∠ACB =90°,∠A =50°,以点B 为圆心,BC 长为半径画弧,交AB 于点D ,连接CD ,则∠ACD 的度数是 .4.如图,直线a b ,相交于点O ,150а=,点A 是直线上的一个定点,点B 在直线b 上运动,若以点O ,A ,B 为顶点的三角形是等腰三角形,则OAB Ð的度数是 .5.已知:线段a ,h ,求作等腰ABC V ,使底边BC a =,高AD h =,(要求:用尺规作图,保留作图痕迹,不必写作法和证明).题型09 等腰三角形的性质和判定1.如图,ABC V 中,AB AE =,且AD BC EF ^,垂直平分AC ,交AC 于点F ,交BC 于点E ,若ABC V 周长为166AC =,,则DC 为( )A .5B .8C .9D .102.如图,在ABC V 中,16AB AC ==,点E 是BC 边上任意一点,过点E 分别作AB AC ,的平行线,交AC 于点F ,交AB 于点D ,则四边形ADEF 的周长是( )A .32B .24C .16D .83.如图,在ABC V 中,BD 和CD 分别是ABC Ð和ACB Ð的平分线,EF 过点D ,且EF BC ∥,若,BE CF ==34,则EF 的长为 .4.如图,在Rt ABC △中,90A Ð=°,30C Ð=°,作边BC 的垂直平分线,交AC 于点D ,交BC 于点E .若3AD =,则DE 的长为 .5.如图,在ABC V 中,点E 在AB 上,点D 在BC 上,BD BE =,BAD BCE Ð=Ð,AD 与CE 相交于点F .(1)证明:BA BC =;(2)求证:AFC V 为等腰三角形.题型10 三角形边角的不等关系1.若等腰三角形的一边长等于2,另一边长等于3,则它的周长等于( ).A .7B .8C .9D .7或82.如图,ABC V 中,5,9,10,AB AC BC EF ===垂直平分BC ,点P 为直线EF 上的任一点,则ABP V 周长的最小值是( )A .10B .14C .15D .193.等腰三角形周长为20,一边长为4,则另两边长为 .4.等腰三角形的一边是7,另一边是4,其周长等于 .5.已知a 、b 、c 为ABC V 的三边长,a 、b 满足2(2)|3|0a b -+-=,且c 为方程|6|3x -=的解,求ABC V 的周长并判断ABC V 的形状.题型11 等边三角形的判定1.在下列命题中:①有一个外角是120°的等腰三角形是等边三角形;②有两个外角相等的等腰三角形是等边三角形;③有一边上的高也是这边上的中线的三角形是等边三角形;④三个外角都相等的三角形是等边三角形.正确的命题有( )A .4个B .3个C .2个D .1个2.在ABC V 中,60A Ð=°,添加下列一个条件后,仍不能判定ABC V 为等边三角形的是( )A .AB AC =B .AD BC ^C .B C Ð=ÐD .A CÐ=Ð3.在ABC V 中,B C Ð=Ð,若添加一个条件使ABC V 是等边三角形,则添加的条件可以是 .(写出一个即可)4.已知a ,b ,c 为ABC V 三边的长,当222222ab a b c bc +=++时,则ABC V 的形状是 .5.如图,在四边形ABCD 中,AD BC ∥,B D Ð=Ð,点E 在BA 的延长线上,连接CE .(1)求证:E ECD Ð=Ð;(2)若60E Ð=°,CE 平分BCD Ð,请判断BCE V 的形状并说明理由.题型12 等边三角形的判定和性质1.如图,30AOB Ð=°,点P 在AOB Ð的内部,点C ,D 分别是点P 关于OA OB 、的对称点,连接CD 交OA OB 、分别于点E ,F ;若PEF !的周长的为9,则线段OP =( )A .8B .9C .10D .112.若一个等腰三角形一腰上的高等于腰的一半,则这个等腰三角形的底角为( )A .75°B .15°C .30°或150°D .15°或75°3.如图,已知30AOB Ð=°,P 是AOB Ð内部的一个定点,且1OP =,点E 、F 分别是OA 、OB 上的动点,则PEF !周长的最小值等于 .4.如图,等边ABC V 的边长为4cm ,点Q 是AC 的中点,若动点P 以2cm /秒的速度从点A 出发沿A B A ®®方向运动设运动时间为t 秒,连接PQ ,当APQ △是等腰三角形时,则t 的值为 秒.5.如图,D 是等边ABC V 外的一点,3BC =,DB DC =,120BDC Ð=°,点E 、F 分别在AB 和AC 上.(1)求证:AD 是BC 的垂直平分线(2)若ED 平分BEF Ð,①证明:FD 平分EFC Ð;②求AEF △的周长.1.如图,ABC V 中,AB AE =,且AD BC ^,EF 垂直平分AC ,交AC 于点F ,交BC 于点E ,若ABC V 周长为16,6AC =,则DC 为( )A .5B .8C .9D .102.如图,在ABC V 中,AB AC =,45BAC Ð=°,AD BC ^于点D ,BE AC ^于点E ,交AD 于点F ,若10AF =,则BD 的长为( )A .4B .5C .8D .103.如图,在ABC V 中,AB AC =,120A Ð=°,6cm BC =,AB 的垂直平分线交BC 于点M ,交AB 于点E ,AC 的垂直平分线交BC 于点N ,交AC 于点F ,则MN 的长为( )A .4cmB .3cmC .2cmD .1cm4.如图,D 为ABC V 内一点,CD 平分ACB Ð,BD CD ^,A ABD Ð=Ð,若5AC =,3BC =,则BD 的长为( )A .1B .1.5C .2D .2.55.如图,在AOB V 和COD △中,OA OB =,OC OD =,OA OC <,36AOB COD Ð=Ð=°.连接AC BD 、交于点M ,连接OM .下列结论:①BOM COM Ð=Ð;②AC BD =;③OM 平分AMD ∠;④144AOD Ð=°,⑤MOC MOD V V ≌其中正确的结论个数有( )个.A .5B .4C .3D .26.如图,在四边形OAPB 中,120AOB Ð=°,OP 平分AOB Ð,且2OP =,若点M 、N 分别在直线OA OB 、上,且PMN V 为等边三角形,则满足上述条件的PMN V 有( )A .1个B .2个C .3个D .3个以上7.如图,ABC V 中,BO 、CO 分别平分ABC Ð和ACB Ð,过点O 平行于BC 的直线分别交AB 、AC 于点D 、E ,已知9cm AB =,8cm AC =,ADE V 的周长为 .8.如图,60AOB Ð=°,C 是BO 延长线上一点,12cm OC =,动点M 从点C 出发沿射线CB 以2cm /s 的速度移动,动点N 从点O 出发沿射线OA 以1cm /s 的速度移动,如果点M 、N 同时出发,设运动的时间为s t ,那么当t = s 时,MON △是等腰三角形.9.已知,在ABC V 中,AB AC =,BD AC ^于点D ,AE BC ^于点E ,若50BAC Ð=°,则DCO Ð= °.10.如图,在ABC V 中,AB AC =,AD 是ABC V 的中线,点E 在AC 上,且AE AD =,连接DE ,若20CDE Ð=°,则B Ð的度数为 °.11.定义:如果一个三角形能被过顶点的一条线段分割成两个等腰三角形,则称这个三角形为特异三角形,如图,ABC V 中,36,A B Ð=°Ð为钝角,则使得ABC V 是特异三角形所有可能的B Ð的度数为 .12.已知在ABC V 中,40A Ð=°,D 为边AC 上一点,ABD △和BCD △都是等腰三角形,则C Ð的度数可能是 .13.如图,在ABC V 中,AB AC D =,是BC 边上一点,以AD 为边在AD 右侧作ADE V ,使AE AD =,连接108CE BAC DAE Ð=Ð=°,(1)求证:BAD CAE V V ≌;(2)若DE DC =,求CDE Ð的度数.14.如图,点D 、E 在ABC V 的边BC 上,AD AE =,BD CE =.(1)求证:AB AC =.(2)若108,2180BAC DAE BAC Ð=°Ð+Ð=°,直接写出图中除ABC V 与ADE V 外所有等腰三角形.15.如图,在等边ABC V 中,点D 在边BC 上,过点D 作DE AB ∥交AC 于点E ,过点E 作EF DE ^,交BC 的延长线于点F .(1)求F Ð的度数;(2)求证:DC CF =.16.如图,已知ABC V 中,D 为BC 上一点,AB AD =,E 为ABC V 外部一点,满足AC AE =,连结DE ,与AC 交于点O ,且CAE BAD Ð=Ð.(1)求证:ABC ADE △≌△;(2)若25BAD Ð=°,求EDC Ð的度数.17.如图,已知在ABC V 中,10AB AC ==厘米,8BC =厘米,点D 为AB 的中点,点P 在线段BC 上以3厘米/秒如果点P 在线段BC 上以3厘米每秒的速度由B 点向C 点运动,同时,点Q 在线段CA 上由C 点向A 点运动.(1)若点Q 的运动速度与点p 的运动速度相等,经一秒后,三角形BPD 与三角形CQP 是否全等,请说明理由;(2)若点Q 的运动速度与点P 的运动速度不相等,当点Q 的运动速度是多少时,能够使三角形BPD 与三角形CQP 全等?18.(1)【问题提出】如图1,在Rt ABC △和Rt CDE △,已知90ACE B D Ð=Ð=Ð=°,AC CE =,B 、C 、D 三点在一条直线上,5AB =, 6.5DE =,则BD 的长度为______.(2)【问题提出】如图2,在Rt ABC △中,90ABC Ð=°,4BC =,过点C 作CD AC ^,且CD AC =,求BCD △的面积.(3)【问题解决】某市打造国家级宜居城市,优化美化人居生态环境.如图3所示,在河流BD 的周边规划一个四边形ABCD 巨无霸森林公园,按设计要求,在四边形ABCD 中,45ABC CAB ADC Ð=Ð=Ð=°,AC BC =,ACD V 面积为212km ,且CD 的长为6km ,则河流另一边森林公园BCD △的面积为______2km .。
等腰三角形的性质及判定含答案

等腰三角形的性质及判定一.选择题(共30小题)1.如图,已知AB=AC=BD,那么()A.∠1=∠2B.2∠1+∠2=180°C.∠1+3∠2=180°D.3∠1﹣∠2=180°2.如图,△ABC中,CA=CB,∠A=20°,则三角形的外角∠BCD的度数是()A.20°B.40°C.50°D.140°3.若C也是图中的格点,且使得△ABC为等腰三角形,则符合条件的点C有()个.A.2个B.3个C.4个D.5个4.如果某等腰三角形的两条边长分别为4和8,那么它的周长为()A.16B.20C.20或16D.不确定5.△ABC中,AB=AC,顶角是120°,则一个底角等于()A.120°B.90°C.60°D.30°6.已知等腰三角形ABC的两边满足+|6﹣BC|=0,则此三角形的周长为()A.12B.15C.12或15D.不能确定7.如图,在△ABC中,AB=AC=5,BC=8,D是线段BC上(不含端点B,C)的动点.若线段AD长为正整数,则点D的个数共有()A.5个B.3个C.2个D.1个8.已知等腰三角形的两边长分别为6和1,则这个等腰三角形的周长为()A.13B.8C.10D.8或139.若等腰三角形的周长为26cm,底边为11cm,则腰长为()A.11cm B.11cm或7.5cmC.7.5cm D.以上都不对10.若实数m、n满足|m﹣3|+(n﹣6)2=0,且m、n恰好是等腰△ABC的两条边的边长,则△ABC的周长是()A.12B.15C.12或15D.911.已知△ABC中,∠ACB=90°,AC=8,BC=6.在射线BC上取一点D,使得△ABD 为等腰三角形,这样的等腰三角形有几个?()A.2个B.3个C.4个D.5个12.若等腰三角形的一边长等于6,另一边长等于4,则它的周长等于()A.15或17B.16C.14D.14或1613.若等腰三角形的顶角为70°,则它的一个底角度数为()A.70°或55°B.55°C.70°D.65°14.如图,在3×3的正方形网格中,点A、B在格点上,要找一个格点C,使△ABC是等腰三角形(AB是其中一腰),则图中符合条件的格点有()A.2个B.3个C.4个D.5个15.等腰三角形的一个角是30°,则这个等腰三角形的底角为()A.75°B.30°C.75°或30°D.不能确定16.如图,在△ABC中,AB=AC,∠A=36°,BD平分∠ABC交AC于E,CD平分∠ACB 交BE于D,图中等腰三角形的个数是()A.3个B.4个C.5个D.6个17.如图,直线l1,l2相交于点A,点B是直线外一点,在直线l1,l2上找一点C,使△ABC 为一个等腰三角形,满足条件的点C有()A.2个B.4个C.6个D.8个18.如图,已知OA=OB=OC,BC∥AO,若∠A=36°,则∠B等于()A.54°B.60°C.72°D.76°19.如图,△ABC中,∠B=∠C,BD=CD,则下列判断不一定正确的是()A.AB=AC B.AD⊥BCC.∠BAD=∠CAD D.△ABC是等边三角形20.等腰三角形的边长为2和3,那么它的周长为()A.8B.7C.8或7D.以上都不对21.等腰三角形的顶角是40°,则它的底角是()A.55°B.70°C.40°或70°D.55°或70°22.如图所示,在三角形ABC中,AB=AC,∠BAC=108°,在BC上分别取点D,E使∠BAD=∠B,∠CAE=∠C,则图中的等腰三角形有()A.3个B.4个C.5个D.6个23.三角形三个内角的比是∠A:∠B:∠C=1:1:2,则△ABC是()A.等腰三角形B.等腰直角三角形C.等边三角形D.不能确定24.小方画了一个有两边长为3和5的等腰三角形,则这个等腰三角形的周长为()A.11B.13C.8D.11或1325.如图钢架中,∠A=a,焊上等长的钢条P1P2,P2P3,P3P4,P4P5…来加固钢架.若P1A =P1P2,且恰好用了4根钢条,则α的取值范围是()A.15°≤a<18°B.15°<a≤18°C.18°≤a<22.5°D.18°<a≤22.5°26.已知等腰△ABC中,∠A=120°,则底角的大小为()A.60°B.30°或120°C.120°D.30°27.如图,在△ABC中,AB=AC=13,该三角形的面积为65,点D是边BC上任意一点,则点D分别到边AB,AC的距离之和等于()A.5B.6.5C.9D.1028.如图,直线L1∥L2,点A、B在L1上,点C在L2上,若AB=AC、∠ABC=70°,则∠1的大小为()A.20°B.40°C.35°D.70°29.若等腰△ABC中有一个内角为40°,则这个等腰三角形的一个底角的度数为()A.40°B.100°C.40°或100°D.40°或70°30.等腰三角形的周长为18,其中一条边的长为8,则另两条边的长是()A.5、5B.2、8C.5、5或2、8D.以上结果都不对二.填空题(共15小题)31.等腰三角形的一个内角为30°,那么其它两个角的度数为______.32.已知AD是△ABC的高,若AB=AC,BC=4,则CD=______,33.如图,在平面直角坐标系中,点A,B分别在y轴和x轴上,∠ABO=60°,在y轴上找一点P,使△P AB是等腰三角形,则符合条件的P点共有______个.34.如图,直线a、b相交于点O,∠1=50°,点A在直线a上,直线b上存在点B,使以点O、A、B为顶点的三角形是等腰三角形,这样的B点有______.35.若等腰三角形的两边的长分别为3和10,则它的周长为______.36.如果等腰三角形的两边长分别是6、8,那么它的周长是______.37.如图,Rt△ABC中,AC⊥BC,AE=AO,BF=BO,则∠EOF的度数是______.38.等腰△ABC的边长分别为6和8,则△ABC的周长为______.39.已知等腰三角形中顶角的度数是底角的3倍,那么底角的度数是______.40.已知等腰三角形的周长为20,底长为x,则x的取值范围是______.41.用一条长为20cm的细绳围成一个等腰三角形,已知一边长是另一边长的2倍,则腰长为______cm.42.如图,△ABC中,AB=AC,D、E是BC边上两点,AD=AE,BE=6,DE=4,则EC =______.43.如图,△ABC中,AB=AC,∠C═30°,DA⊥BA于点A,BC=16cm,则AD=______.44.如图,AB=AC=CD,∠BAC=56°,则∠B=______,∠D=______.45.如图,已知每个小方格的边长为1,A,B两点都在小方格的顶点上,请在图中找一个顶点C,使△ABC为等腰三角形,则这样的顶点C有______个.三.解答题(共5小题)46.如图,在△ABC中,∠C=∠ABC=2∠A,BD是AC边上的高,求∠DBC的度数.47.在△ABC中,AD平分∠BAC,E是BC上一点,BE=CD,EF∥AD交AB于F点,交CA的延长线于P,CH∥AB交AD的延长线于点H,①求证:△APF是等腰三角形;②猜想AB与PC的大小有什么关系?证明你的猜想.48.如图,在△ABC中,AB=AC,点D在BC上,且BD=BA,点E在BC的延长线上,且CE=CA.(1)若∠BAC=90°(图1),求∠DAE的度数;(2)若∠BAC=120°(图2),求∠DAE的度数;(3)当∠BAC>90°时,探求∠DAE与∠BAC之间的数量关系,直接写出结果.49.已知等腰三角形的周长为24cm,其中两边之差为6cm,求这个等腰三角形的腰长.50.如图,在△ABC中,AB=AC,CE平分∠ACB,EC=EA.(1)求∠A的度数;(2)若BD⊥AC,垂足为D,BD交EC于点F,求∠1的度数.等腰三角形的性质及判定参考答案与试题解析一.选择题(共30小题)1.解:∵AB=AC=BD,∴∠B=∠C,∠BAD=∠1,∵∠1=∠C+∠2,∴∠BAD=∠1=∠C+∠2,∵∠B+∠1+∠BAD=180°,∴∠C+2∠1=180°,∵∠C=∠1﹣∠2,∴∠1﹣∠2+2∠1=180°,即3∠1﹣∠2=180°.故选:D.2.解:∵CA=CB,∠A=20°,∴∠B=∠A=20°,∴∠BCD=∠A+∠B=40°,故选:B.3.解:如图:分情况讨论.①AB为等腰△ABC底边时,符合条件的C点有2个;②AB为等腰△ABC其中的一条腰时,符合条件的C点有2个.故选:C.4.解:若4为腰,8为底边,此时4+4=8,不能构成三角形,故4不能为腰;若4为底边,8为腰,此时三角形的三边分别为4,8,8,周长为4+8+8=20,综上三角形的周长为20.故选:B.5.解:∵△ABC中,AB=AC,顶角是120°,∴∠B=∠C,∠A=120°∵∠A+∠B+∠C=180°,∴∠B=∠C==30°,故选:D.6.解:∵+|6﹣BC|=0,∴AB﹣3=0,6﹣BC=0,解得AB=3,BC=6,(1)若AB是腰长,BC为底,则三角形的三边长为:3、3、6,不能能组成三角形,(2)若AB是底边长,BC为腰,则三角形的三边长为:3、6、6,能组成角形,周长为3+6+6=15.故此三角形的周长为15.故选:B.7.解:过A作AE⊥BC,∵AB=AC,∴EC=BE=BC=4,∴AE==3,∵D是线段BC上的动点(不含端点B、C).∴3≤AD<5,∴AD=3或4,∵线段AD长为正整数,∴AD的可以有三条,长为4,3,4,∴点D的个数共有3个,故选:B.8.解:当等腰三角形的腰为1时,三边为1,1,6,1+1=2<6,三边关系不成立,当等腰三角形的腰为6时,三边为1,6,6,三边关系成立,周长为1+6+6=13.故选:A.9.解:∵11cm是底边,∴腰长=(26﹣11)=7.5cm,故选:C.10.解:|m﹣3|+(n﹣6)2=0,∴m﹣3=0,n﹣6=0,解得m=3,n=6,当m=3作腰时,三边为3,3,6,不符合三边关系定理;当n=6作腰时,三边为3,6,6,符合三边关系定理,周长为:3+6+6=15.故选:B.11.解:在Rt△ABC中,AB==10,①如图1,当AB=AD=10时,CD=CB=6时,CD=CB=6,得△ABD的等腰三角形.②如图2,当AB=BD=10时,△ABD是等腰三角形;③如图3,当AB为底时,AD=BD时,△ABD是等腰三角形.故选:B.12.解:当4为底边时,腰长为6,则这个等腰三角形的周长=4+6+6=16;当6为底边时,腰长为4,则这个等腰三角形的周长=4+4+6=14;故选:D.13.解:∵等腰三角形的顶角为70°,∴它的一个底角度数为(180°﹣70°)=55°,故选:B.14.解:如图所示:由勾股定理得:AB==,①若AB=BC,则符合要求的有:C1,C2,C3共4个点;②若AB=AC,则符合要求的有:C4,C5共2个点;若AC=BC,则不存在这样格点.∴这样的C点有5个.故选:D.15.解:①当这个角为顶角时,底角=(180°﹣30°)÷2=75°;②当这个角是底角时,底角=30°;故选:C.16.解:∵AB=AC,∠A=36°,∴△ABC是等腰三角形.∴∠C=∠ABC=72°.∵BD平分∠ABC交AC于E,∴∠ABE=∠EBC=36°,∵∠A=∠ABE=36°,∴△ABE是等腰三角形.∵∠BEC=∠A+∠ABE=72°=∠C,∴△BEC是等腰三角形.∵∠DBC=∠DCB=36°,∴△BCD是等腰三角形,∵∠EDC=∠DBC+∠DCB=72°=∠DEC,∴△CDE是等腰三角形,∴共有5个等腰三角形.故选:C.17.解:以A为圆心,AB长为半径画弧,交l1、l2于4个点;以B为圆心,AB长为半径画弧交l1、l2于2个点,再作AB的垂直平分线交l1、l2于2个点,共有8个点,故选:D.18.解:∵OA=OC,∴∠ACO=∠A=36°,∵BC∥AO,∴∠BCA=∠A=36°,∴∠BCO=72°,∵OB=OC,∴∠B=72°.故选:C.19.解:∵∠B=∠C,∴AB=AC,∴选项A不符合题意;∵∠B=∠C,∴AB=AC,BD=CD,∴AD⊥BC,∠BAD=∠CAD,∴选项B、选项C不符合题意;当△ABC中有一个角为60°时,△ABC是等边三角形,∴选项D符合题意;故选:D.20.解:分两种情况讨论:当这个三角形的底边是2时,三角形的三边分别是2、3、3,能够组成三角形,则三角形的周长是8;当这个三角形的底边是3时,三角形的三边分别是2、2、3,能够组成三角形,则三角形的周长是7.故等腰三角形的周长为8或7.故选:C.21.解:因为等腰三角形的两个底角相等,又因为顶角是40°,所以其底角为=70°.故选:B.22.解:∵AB=AC,∠BAC=108°,∴∠B=∠C=36°,△ABC是等腰三角形,∵∠BAD=∠B=36°,∴△ABD是等腰三角形,∵∠CAE=∠C=36°,∴△AEC是等腰三角形,∴∠ADC=∠DAC=72°,∴△ADC是等腰三角形,同理,△ABE是等腰三角形,∴∠ADE=∠AED=72°,∴△ADE是等腰三角形,故选:D.23.解:∵∠A+∠B+∠C=180°,∠A:∠B:∠C=1:1:2,∴∠A=∠B=45°,∠C=90°.则该三角形的等腰直角三角形.故选:B.24.解:由题意知,应分两种情况:(1)当腰长为3时,能构成三角形,周长=2×3+5=11;(2)当腰长为5时,能构成三角形,周长=2×5+3=13.故选:D.25.解:∵AP1=P1P2,P1P2=P2P3,P3P4=P2P3,P3P4=P4P5,∴∠A=∠P1P2A,∠P2P1P3=∠P2P3P1,∠P3P2P4=∠P3P4P2,∠P4P3P5=∠P4P5P3,∴∠P3P5P4=4∠A=4α°,∵要使得这样的钢条只能焊上4根,∴∠P5P4B=5α°,由题意,∴18°≤α<22.5°.故选:C.26.解:∵在等腰△ABC中,∵∠A=120°,∴∠A为等腰三角形的顶角,∴∠B=∠C,∵∠A=120°,∴∠B=∠C=30°;故选:D.27.解:连接AD,∵在△ABC中,AB=AC=13,该三角形的面积为65,∴三角形ABC的面积=△ABD的面积+△ACD的面积=AB•DN+AC•DM=AB•(DN+DM)=×13×(DN+DM)=65,解得:DN+DM=10.故选:D.28.解:∵AB=AC,∴∠ACB=∠ABC=70°,∵直线l1∥l2,∴∠1+∠ACB+∠ABC=180°,∴∠1=180°﹣∠ABC﹣∠ACB=180°﹣70°﹣70°=40°.故选:B.29.解:当40°的角为等腰三角形的顶角时,底角的度数==70°;当40°的角为等腰三角形的底角时,其底角为40°,故它的底角的度数是70°或40°.故选:D.30.解:当腰长为8时,底长为:18﹣8×2=2;2+8>8,能构成三角形;当底长为8时,腰长为:(18﹣8)÷2=5;5+5>8,能构成三角形.故另两条边的长是5、5或2、8.故选:C.二.填空题(共15小题)31.解:①30°是顶角,则底角=(180°﹣30°)=75°;②30°是底角,则顶角=180°﹣30°×2=120°.∴另两个角的度数分别是75°、75°或30°、120°.故答案为75°、75°或30°、120°.32.解:∵AD是△ABC的高,AB=AC,∴CD=BD=BC=4=2,故答案为:2.33.解:①当AB=AP时,在y轴上有2点满足条件的点P.②当AB=BP时,在y轴上有1点满足条件的点P.③当AP=BP时,在y轴上有一点满足条件的点P.综上所述:符合条件的点P共有4个.故答案为:434.解:要使△OAB为等腰三角形分三种情况讨论:①当OB=AB时,作线段OA的垂直平分线,与直线b的交点为B,此时有1个;②当OA=AB时,以点A为圆心,OA为半径作圆,与直线b的交点,此时有1个;③当OA=OB时,以点O为圆心,OA为半径作圆,与直线b的交点,此时有2个,1+1+2=4,故答案为:435.解:(1)若3为腰长,10为底边长,由于3+3<10,则三角形不存在;(2)若10为腰长,则符合三角形的两边之和大于第三边.所以这个三角形的周长为10+10+3=23.故答案为:23.36.解:当6是腰长时,周长=6+6+8=20;当8是腰长时,周长=6+8+8=22.故周长是20或22.故答案为:20或22.37.解:∵Rt△ABC中,AC⊥BC,∴∠A+∠B=90°,∵AE=AO,BF=BO,∴∠AOE=∠AEO=,∠BOF=∠BFO=,∴∠EOF=180°﹣∠AOE﹣∠BOF=180°﹣(+)=(∠A+∠B)=45°,故答案为45°.38.解:当6为底时,三角形的三边为6,8、8可以构成三角形,周长为6+8+8=22;当8为底时,三角形的三边为8,6、6可以构成三角形,周长为8+6+6=20.则△ABC的周长为22或20.故答案为:22或20.39.解:设底角为x°,则顶角为3x°,根据题意得:x+x+3x=180解得:x=36;故答案为:36°.40.解:根据三角形的三边关系,x<(20﹣x),解得x<10,∴x的取值范围是0<x<10.故答案为:0<x<10.41.解:设较短的边长为xcm,则较长的边长为2xcm,①若较短的边为底边,较长的边为腰,则x+2x+2x=20,解得x=4,此时三角形三边长分别为4cm,8cm,8cm,能组成三角形;②若较短的边为腰,较长的边为底边,则x+x+2x=20,解得x=5,此时三角形三边长分别为5cm,5cm,10cm,∵5+5=10,∴不满足三角形任意两边之和大于第三边,故不能围成三角形;综上所述,等腰三角形的腰长8cm,故答案为8.42.证明:∵BE=6,DE=4,∴BD=BE﹣DE=2,过A作AP⊥BC于P,∵AB=AC,AP⊥BC,∴BP=CP,同理有DP=EP,∴CE=BD=2,故答案为:2.43.解:∵AB=AC,∴∠B=∠C=30°,∴∠BAC=180°﹣2×30°=120°,∵DA⊥BA,∴∠BAD=90°,∴∠CAD=120°﹣90°=30°,∴∠CAD=∠C,∴AD=CD,在Rt△ABD中,∵∠B=30°,∠BAD=90°,∴BD=2AD,∴BC=BD+CD=2AD+AD=3AD,∵BC=16cm,∴AD=cm,故答案为:cm.44.解:∵AB=AC,∠BAC=56°∴∠B=∠ACB==62°,∵AC=CD,∴∠CAD=∠D,∵∠ACB=∠CAD+∠D,∴∠D=∠ACB=31°,故答案为:62°,31°.45.解:当AB为底时,作AB的垂直平分线,可找出格点C的个数有5个,当AB为腰时,分别以A、B点为顶点,以AB为半径作弧,可找出格点C的个数有3个;∴这样的顶点C有8个.故答案为:8.三.解答题(共5小题)46.解:∵∠C=∠ABC=2∠A,∴∠C+∠ABC+∠A=5∠A=180°,∴∠A=36°.则∠C=∠ABC=2∠A=72°.又BD是AC边上的高,则∠DBC=90°﹣∠C=18°.47.①证明:∵EF∥AD,∴∠1=∠4,∠2=∠P,∵AD平分∠BAC,∴∠1=∠2,∴∠4=∠P,∴AF=AP,即△APF是等腰三角形;②AB=PC.理由如下:证明:∵CH∥AB,∴∠5=∠B,∠H=∠1,∵EF∥AD,∴∠1=∠3,∴∠H=∠3,在△BEF和△CDH中,∵,∴△BEF≌△CDH(AAS),∴BF=CH,∵AD平分∠BAC,∴∠1=∠2,∴∠2=∠H,∴AC=CH,∴AC=BF,∵AB=AF+BF,PC=AP+AC,∴AB=PC.48.解:(1)如图1,∵AB=AC,∠BAC=90°,∴∠B=∠ACB=45°,∵BD=BA,∴∠BAD=∠BDA=(180°﹣∠B)=67.5°,∵CE=CA∴∠CAE=∠E=∠ACB=22.5°,∴∠BAE=180°﹣∠B﹣∠E=112.5°,∴∠DAE=∠BAE﹣∠BAD=45°,(2)如图2,∵AB=AC,∠BAC=90°,∴∠B=∠ACB=30°,∵BA=BD,∴∠BAD=∠BDA=75°,∴∠DAC=45°,∵CA=CE,∴∠E=∠CAE=15°,∴∠DAE=∠DAC+∠CAE=60°;(3)∠DAE=∠BAC,理由:设∠CAE=x,∠BAD=y,则∠B=180°﹣2y,∠E=∠CAE=x,∴∠BAE=180°﹣∠B﹣∠E=2y﹣x,∴∠DAE=∠BAE﹣∠BAD=2y﹣x﹣y=y﹣x,∠BAC=∠BAE﹣∠CAE=2y﹣x﹣x=2y﹣2x ∴∠DAE=∠BAC.49.解:设三角形的腰为x,底为y,根据题意得或,解得或,又知6+6<12,不能构成三角形,即等腰三角形的腰长为:10cm.50.解:(1)∵EA=EC,∴设∠A=∠2=x,∵EC平分∠ACB,∴∠ACB=2x,∵AB=AC,∴∠ABC=∠ACB=2x,在△ABC中,∴x+2x+2x=180°,∴x=36°,∴∠A=36°;(2)∵∠A=∠2,∴∠2=36°,∵BD⊥AC,∴∠DFC=90°﹣36°=54°,∴∠1=∠DFC=54°.第1页(共1页)。
【基础练习】《等腰三角形》(数学沪科版八上)【含答案】

15.3 《等腰三角形》基础练习第 1 课时《等腰三角形的性质定理及推论》一、选择题1.已知等腰三角形的顶角为40°,则这个等腰三角形的底角为()A.40°B.70°C. 100 °D.140 °2.若等腰三角形中有两边长分别为 2 和5,则这个三角形的第三条边长为()A.2 或5B. 3C. 4D. 53.如图,AB∥ CD, AD=CD,∠ 1=65 °,则∠ 2 的度数是()A.50°B.60°C. 65°D.70°4.如图, AD,CE分别是△ ABC的中线和角均分线.若AB=AC,∠ CAD=20°,则∠ACE的度数是()A.20°B.35°C. 40°D. 70°5.若实数 m、n 知足等式 |m ﹣ 2|+=0,且 m、 n 恰巧是等腰△ ABC 的两条边的边长,则△ ABC的周长是()A.12B.10C.8 D.66.若等腰三角形的一个外角等于140 °,则这个等腰三角形的顶角度数为()A.40°B.100 °C. 40°或 70°D. 40°或 100 °7.如图,已知DE∥ BC, AB=AC,∠ 1=125 °,则∠ C 的度数是()A.55°B.45°C. 35°D. 65°8.如图,△ ABC中, AD⊥ BC, AB=AC,∠ BAD=30°,且 AD=AE,则∠ EDC等于()A.10°B. 12.5 °C. 15°D. 20°二、填空题9.等腰三角形的一个底角为50°,则它的顶角的度数为.10.一个等腰三角形的两边长分别为4cm 和 9cm ,则它的周长为cm.11.已知等腰三角形的一个外角为130 °,则它的顶角的度数为.12.如图,△ ABC中.点 D 在 BC边上, BD=AD=AC, E 为 CD 的中点.若∠CAE=16°,则∠ B 为度.13.我们规定:等腰三角形的顶角与一个底角度数的比值叫做等腰三角形的“特点值”,记作k,若 k=,则该等腰三角形的顶角为度.三、解答题14.如图,点D、 E 在△ ABC 的 BC 边上, AB=AC,AD=AE.求证: BD=CE.15.如图,△ ABC是等边三角形,BD 是中线,延伸BC 至 E,CE=CD,(1)求证: DB=DE.(2)在图中过 D 作 DF⊥ BE交 BE于 F,若 CF=4,求△ ABC 的周长.第2课时一、选择题1.以以下各组数据为边长,能够组成等腰三角形的是()A.1, 1, 2B. 1,1,3C. 2,2, 1D. 2,2,52.在△ABC 中,其两个内角以下,则能判断△ABC为等腰三角形的是()A.∠ A=40°,∠ B=50B.∠ A=40°,∠ B=60°C.∠ A=40°,∠ B=70D.∠ A=40°,∠ B=80°AB 于点E,3.如图,在△ABC中,∠ A=36°,∠ C=72°,点 D 在AC 上, BC=BD, DE∥ BC交则图中等腰三角形共有()A.3 个B.4 个C.5 个D.6 个4.如图,正方形网格中,网格线的交点称为格点,已知A, B 是两格点,假如 C 也是图中C 的个数是()的格点,且使得△ABC为等腰三角形,则点A.6B. 8C.9D.105.以下条件中,不可以判断△ABC 是等腰三角形的是()A.a=3,b=3 ,c=4B. a: b: c=2: 3: 4C.∠ B=50°,∠ C=80°D.∠ A:∠ B:∠ C=1: 1:26.已知△ ABC 的三条边长分别为3,4,6,在△ ABC所在平面内画一条直线,将△ABC切割成两个三角形,使此中的一个是等腰三角形,则这样的直线最多可画()A.5 条B.6 条C.7 条D.8 条7.以下三角形,不必定是等边三角形的是()A.有两个角等于60°的三角形B.有一个外角等于120 °的等腰三角形C.三个角都相等的三角形D.边上的高也是这边的中线的三角形8.如图, A、B 两点在正方形网格的格点上,每个方格都是边长为 1 的正方形,点 C 也在格点上,且△ABC是等腰三角形,则切合条件是点C共有()个.A.8B.9C. 10D. 11二、填空题9.如图,在△ABC中,∠ ACB=90°,∠ BAC=40°,在直线 AC上找点 P,使△ ABP 是等腰三角形,则∠ APB的度数为.10.如图已知OA=a, P 是射线 ON 上一动点,∠ AON=60°,当 OP=时,△ AOP为等边三角形.11.如图,在3× 3 的网格中有A、B 两点,任取一个格点E,则知足△EAB是等腰三角形的点 E 有个.12.在△ ABC中,∠ A=80°,当∠ B= 13.如图,以下 4 个三角形中,均有这个三角形分红两个小等腰三角形的是时,△ ABC 是等腰三角形.AB=AC,则经过三角形的一个极点的一条直线不可以够将(填序号).三、解答题14.如图, BD 是△ ABC的角均分线,DE∥ BC 交 AB 于点 E.(1)求证: BE=DE;(2)若 AB=BC=10,求 DE 的长.15.已知:如图,AB=AC,∠ ABD=∠ ACD,求证: BD=CD.第3课时一、选择题1.如图∠ AOP=∠ BOP=15°, PC∥ OA, PD⊥ OA,若 PC=10,则 PD 等于()A.10B.C. 5D.2.52.如图,在Rt△ ABC中,∠C=90°, AB=2BC,则∠A=()A.15°B. 30°C. 45°D. 60°3.如图,在Rt△ ABC中,∠ C=90°,∠ A=30°, BC=4cm,则 AB 等于()A.9 cm B. 8 cm C. 7cm D. 6cm4.如图,在等边△ABC中,BD 均分∠ABC交AC于点D,过点D 作 DE⊥BC于点E,且AB=6,则 EC的长为()A 3B 4.5C 1.5D 7.55.△ ABC中,∠A:∠ B:∠ C=1: 2: 3,最小边BC=3cm,则最长边AB 的长为()A.9cm B. 8cm C. 7cm D. 6cm6.如图,在△ABC中,∠ ACB=90°, CD是高,∠A=30°,AB=8,则BD=()A.2B.3C. 4D.67.某市为了美化环境,计划在以下图的三角形空地上栽种草皮,已知这类草皮每平方米售价为 a 元,则购置这类草皮起码需要()A.450a 元B. 225a 元C.150a 元D. 300a 元8.如图是屋架设计图的一部分,点D是斜梁AB的中点,立柱BC,DE垂直于横梁AC,AB=6m,∠ A=30°,则 DE等于()A.1.5m B. 2m C. 2.5m D. 3m二、填空题9.在 Rt△ ABC中,∠ A=30°,∠ B=90°, AC=10,则 BC=10.如图,在△A BC 中,∠ ACB=90°,∠ A=30°,以点 C 为圆心, CB 长为半径作圆弧,交AB 于点 D,若 CB=4,则 BD 的长为.11.如图,在Rt△ ABC 中,∠ C=90°,∠ ABC=60°, AB 的垂直均分线分别交AB 与 AC 于点 D 和点 E,若 CE=2,则 AB 的长为12.已知等腰三角形的底角为15°,腰长为 8cm,则腰上的高为.13.如图,在△A BC 中,∠ B=∠ C=60°,点 D 在 AB 边上, DE⊥ AB,并与 AC 边交于点E.如果 AD=1, BC=6,那么 CE等于.三、解答题14.如图,在△A BC 中, BA=BC,∠ B=120°,线段AB 的垂直均分线MN 交 AC 于点 D,且AD=8cm.求:(1)∠ ADG 的度数;(2)线段 DC的长度.15.某轮船由西向东航行,在 A 处测得小岛 P 的方向是北偏东 75°,又持续航行 7 海里后,在 B处测得小岛 P 的方向是北偏东 60°,求:( 1)此时轮船与小岛P 的距离 BP 是多少海里.(2)小岛点 P 方圆 3 海里内有暗礁,假如轮船持续向东履行,请问轮船有没有触礁的危险?请说明原因.参照答案第1课时1.解:∵等腰三角形的顶角为50°,∴这个等腰三角形的底角为:( 180°﹣ 40°)÷ 2=70°,应选: B.2.解:当腰为 5 时,依据三角形三边关系可知此状况建立,这个三角形的第三条边长为5;当腰长为 2 时,依据三角形三边关系可知此状况不建立;应选: D.3.解:∵ AB∥ CD,∴∠ 1=∠ ACD=65°,∵ AD=CD,∴∠ DCA=∠ CAD=65°,∴∠ 2 的度数是: 180°﹣ 65°﹣ 65°=50°.应选: A.4.解:∵ AD 是△ ABC 的中线, AB=AC,∠ CAD=20°,∴∠ CAB=2∠ CAD=40°,∠ B=∠ ACB=(180°﹣∠ CAB)=70°.∵ CE是△ ABC的角均分线,∴∠ ACE= ∠ ACB=35°.应选: B.5.解:∵ |m ﹣ 2|+=0,∴m﹣2=0, n﹣ 4=0,解得 m=2, n=4,当 m=2 作腰时,三边为 2,2, 4,不切合三边关系定理;当 n=4 作腰时,三边为2, 4, 4,切合三边关系定理,周长为:2+4+4=10.应选: B.6.解:①若顶角的外角等于140 °,那么顶角等于 40°,两个底角都等于70°;②若底角的外角等于140°,那么底角等于40°,顶角等于100°.应选: D.7.解:∵∠ 1=125 °,∴∠ ADE=180°﹣125°=55°,∵DE∥BC, AB=AC,∴AD=AE,∠ C=∠ AED,∴∠ AED=∠ ADE=55°,又∵∠ C=∠ AED,∴∠C=55°.应选:A.8.解:∵△ ABC中, AD⊥ BC, AB=AC,∠ BAD=30°,∴∠ DAC=∠BAD=30°(等腰三角形的顶角均分线、底边上的中线、底边上的高互相重合),∵AD=AE(已知),∴∠ ADE=75°∴∠ EDC=90°﹣∠ADE=15°.应选: C.9.解:∵等腰三角形底角相等,∴180°﹣50°×2=80°,∴顶角为 80°.故填 80°.10.解:①当腰是4cm ,底边是9cm 时:不知足三角形的三边关系,所以舍去.②当底边是4cm,腰长是9cm 时,能组成三角形,则其周长=4+9+9=22cm.故填 22.11.解:当50°为顶角时,其余两角都为65°、 65°,当50°为底角时,其余两角为50°、80°,所以等腰三角形的顶角为 50°或 80°.故答案为: 50°或 80°.12.解:∵ AD=AC,点 E 是 CD 中点,∴AE⊥ CD,∴∠ AEC=90°,∴∠ C=90°﹣∠CAE=74°,∵ AD=AC,∴∠ADC=∠C=74°,∵ AD=BD,∴2∠ B=∠ ADC=74°,∴∠ B=37°,故答案为 37°.13.解:∵△ ABC中, AB=AC,∴∠ B=∠ C,“特点值”,记作k,若k=,∵等腰三角形的顶角与一个底角度数的比值叫做等腰三角形的∴∠ A:∠ B=1: 2,即 5∠ A=180°,∴∠ A=36°,故答案为: 36.14.证明:如图,过点 A 作 AP⊥ BC于 P.∵ AB=AC,∴BP=PC;∵ AD=AE,∴DP=PE,∴BP﹣ DP=PC﹣ PE,∴BD=CE.15.( 1)证明:∵△ ABC是等边三角形,BD 是中线,∴∠ ABC=∠ ACB=60°.∠DBC=30°(等腰三角形三线合一).又∵ CE=CD,∴∠ CDE=∠CED.又∵∠ BCD=∠ CDE+∠CED,∴∠ CDE=∠CED=∠ BCD=30°.∴∠ DBC=∠ DEC.∴ DB=DE(等角平等边);(2)∵∠ CDE=∠ CED= ∠ BCD=30°,∴∠ CDF=30°,∵ CF=4,∴ DC=8,∵ AD=CD,∴ AC=16,∴△ ABC的周长 =3AC=48.第2课时1.解: A、∵ 1+1=2,∴本组数据不可以够组成等腰三角形;故本选项错误;B、∵ 1+1< 3,∴本组数据不可以够组成等腰三角形;故本选项错误;C、∵1+2>2,且有两边相等,∴本组数据能够组成等腰三角形;故本选项正确;D、∵ 2+2<5,∴本组数据不可以够组成等腰三角形;故本选项错误;应选: C.2.解;当顶角为∠A=40°时,∠ C=70°≠ 50°,当顶角为∠ B=50°时,∠ C=65°≠40°所以 A 选项错误.当顶角为∠ B=60°时,∠ A=60°≠40°,当∠ A=40°时,∠ B=70°≠ 60°,所以 B 选项错误.当顶角为∠ A=40°时,∠ C=70°=∠ B,所以 C 选项正确.当顶角为∠ A=40°时,∠ B=70°≠ 80°,当顶角为∠ B=80°时,∠ A=50°≠40°所以 D 选项错误.应选: C.3.解:∵在△ABC中, AB=AC,∠ A=36°,∴∠ ABC=∠ C==72°,△ ABC是等腰三角形,∵BD 均分∠ ABC,∴∠ABD=∠ DBC=36°,∵DE∥BC,∴∠ EDB=∠ DBC=36°,∴∠ ABD=∠ EDB=∠A,∴AD=BD, EB=ED,即△ ABD 和△ EBD是等腰三角形,∵∠ BDC=180°﹣∠ DBC﹣∠ C=72°,∴∠ BDC=∠ C,∴BD=BC,即△ BCD是等腰三角形,∵DE∥BC,∴∠ AED=∠ ABC,∠ ADE=∠ C,∴∠ AED=∠ ADE,∴AE=AD,即△ AED是等腰三角形.∴图中共有 5 个等腰三角形.应选: C.4.解:如图,分状况议论:① AB 为等腰△ ABC的底边时,切合条件的C点有 6 个;② AB 为等腰△ ABC此中的一条腰时,切合条件的 C 点有4 个.应选: D.5.解: A、∵ a=3, b=3,c=4,∴ a=b,∴△ ABC是等腰三角形;B、∵ a: b: c=2: 3: 4∴ a≠ b≠ c,∴△ ABC不是等腰三角形;C、∵∠ B=50°,∠ C=80°,∴∠ A=180°﹣∠ B﹣∠ C=50°,∴∠ A=∠ B,∴ AC=BC,∴△ ABC是等腰三角形;D、∵∠ A:∠ B:∠ C=1: 1: 2,∵∠ A=∠ B,∴ AC=BC,∴△ ABC是等腰三角形.应选: B.6.解:以下图:当 BC1=AC1, AC=CC2,AB=BC3, AC4=CC4, AB=AC5, AB=AC6, BC7=CC7时都能获得切合题意的等腰三角形.应选: C.7.解: A、依占有两个角等于60°的三角形是等边三角形,不合题意,故此选项错误;B、有一个外角等于120 °的等腰三角形,则内角为60°的等腰三角形,此三角形是等边三角形,不合题意,故此选项错误;C、三个角都相等的三角形,内角必定为60°是等边三角形,不合题意,故此选项错误;D、边上的高也是这边的中线的三角形,也可能是等腰三角形,故此选项正确.应选:D.8.解:①点 C 以点 A 为标准,AB 为底边,切合点 C 的有 5 个;②点 C 以点 B 为标准, AB 为等腰三角形的一条边,切合点 C 的有4 个.所以切合条件的点C共有 9 个.应选: B.9.解:∵在Rt△ ABC中,∠ C=90°,∠ A=40°,∴当 AB=BP1时,∠ BAP1=∠ BP1A=40°,当 AB=AP3 时,∠ ABP3=∠AP3B= ∠ BAC= × 40°=20°,当 AB=AP4 时,∠ ABP4=∠AP4B= ×( 180°﹣40°)=70°,当 AP2=BP2时,∠ BAP2=∠ ABP2,∴∠ AP2B=180°﹣ 40°× 2=100°,∴∠ APB 的度数为: 20°、40°、70°、 100°.故答案为: 20°或 40°或 70°或 100°.10.解:∵ AON=60°,∴当 OA=OP=a时,△ AOP 为等边三角形.故答案是: a.11.解:如图,知足△ EAB是等腰三角形的点 E 有5 个,故答案为: 5.12.解:∵∠A=80°,∴①当∠ B=80°时,△ ABC是等腰三角形;②当∠ B=( 180°﹣ 80°)÷ 2=50°时,△ ABC 是等腰三角形;③当∠ B=180°﹣ 80°× 2=20°时,△ ABC是等腰三角形;故答案为: 80°、 50°、20°.13.解:由题意知,要求“被一条直线分红两个小等腰三角形”,①中分红的两个等腰三角形的角的度数分别为:36°,36°,108°和 36°,72°72°,能;②不可以;③明显原等腰直角三角形的斜边上的高把它还分为了两个小等腰直角三角形,能;④中的为36°, 72, 72°和 36°, 36°, 108°,能.故答案为:②14.( 1)证明:∵ BD 是△ ABC 的角均分线,∴∠ EBD=∠ CBD.∵DE∥BC,∴∠EDB=∠CBD.∴∠EDB=∠ EBD.∴BE=DE.( 2)∵ AB=BC, BD 是△ ABC 的角均分线,∴ AD=DC.∵DE∥BC,∴,∴.∴DE=5.15.证明:连结BC.∵AB=AC(已知),∴∠ 1=∠ 2(等边平等角).又∠ ABD=∠ ACD(已知),∴∠ ABD﹣∠ 1=∠ ACD﹣∠ 2(等式运算性质).即∠ 3=∠ 4.∴ BD=DC(等角平等边).第3课时1.解:∵ PC∥ OA,∴∠ CPO=∠ POA,∵∠ AOP=∠ BOP=15°,∴∠ AOP=∠ BOP=∠ CPO=15°,过点 P 作∠ OPE=∠CPO交于 AO 于点 E,则△ OCP≌△ OEP,∴PE=PC=10,∵∠ PEA=∠OPE+∠ POE=30°,∴PD=10× =5.应选: C.2.解:∵在Rt△ ABC中,∠ C=90°, AB=2BC,即 BC= AB,∴∠ A=30°,应选: B.3.解:∵在Rt△ ABC中,∠ C=90°,∠ A=30°, BC=4cm,∴AB=2BC=8cm,应选: B.4.解:∵△ ABC是等边三角形,∴∠ C=60°, AC=AB=BC=6,∵BD 均分∠ ABC交 AC 于点 D,∴CD= AC=3,∵ DE⊥BC,∴∠ CDE=30°,∵EC= CD=1.5.应选: C.5.解:设∠ A、∠ B、∠ C 分别为 k、2k、 3k,则 k+2k+3k=180°,解得 k=30°,2k=60 °,3k=90 °,∵最小边BC=3cm,∴最长边AB=2BC=2×3=6cm.应选: D.6.解:∴ CD 是高,∴∠ BDC=90°,∵∠ ACB=90°,∠ A=30°,∴∠ B=60°,BC= AB=× 8=4,∴∠ BCD=30°,∴BD= BC=2,应选: A.7.解:如图,作BH⊥ AC于 H,则∠ ABH=180°﹣∠ BAC=30°,在 Rt△ ABH 中, BH= AB=10,所以 S△ ABC=× 10× 30=150,所以购置这类草皮起码需要150a 元.应选: C.8.解:∵立柱BC、 DE 垂直于横梁AC,∴BC∥ DE,∵D是 AB中点,∴ AD=BD,∴ AE: CE=AD: BD,∴ AE=CE,∴ DE 是△ ABC的中位线,∴DE= BC,在 Rt△ ABC中, BC= AB=3,∴ DE=1.5.应选: A.9.解:∵∠ A=30°,∠ B=90°,∴BC= AC=5,故答案为: 5.10.解:如图,过 C 点作 BD 的垂直均分线交BD 于点 E,∵在△ ABC中,∠ ACB=90°,∠ A=30°, BC=4,∴∠ BCE=∠ A=30°, BE=BD,∴BE=2∴BD=2BE=4故答案为: 4.11.解:∵在Rt△ ABC中,∠ C=90°,∠ ABC=60°,∴∠ A=30°,∵DE 是线段 AB 的垂直均分线,∴ EA=EB, ED⊥ AB,∴∠ A=∠ EBA=30°,∴∠ EBC=∠ ABC﹣∠ EBA=30°,又∵ BC⊥ AC, ED⊥ AB,∴DE=CE=2.在直角三角形ADE 中, DE=2,∠ A=30°,∴AE=2DE=4,∴ AD==2 ,∴ AB=2AD=4.故答案为: 4.12.解:如图,过C作CD⊥AB,交BA延长线于D,∵∠ B=15°,AB=AC,∴∠ DAC=30°,∵CD 为 AB 上的高, AC=8cm,∴CD= AC=4cm.故答案为: 4cm.13.解:∵在△ABC 中,∠ B=∠ C=60°,∴∠ A=60°,∵DE⊥AB,∴∠ AED=30°,∵AD=1,∴AE=2,∵ BC=6,∴AC=BC=6,∴CE=AC﹣ AE=6﹣ 2=4,故答案为 4.14.解:(1 )∵在△ ABC中,已知BA=BC,∴∠ A=∠ C(等边平等角);又∵∠ B=120°,∴∠ A=(180°﹣120°)=30°(三角形内角和定理),∴∠ ADG=90°﹣30°=60°;( 2)连结 BD.∵ AB 的垂直均分线DG 交 AC 于点 D,∴AD=BD,∠ A=∠ABD=30°,∴∠ CBD=90°;由( 1)知∠ A=∠ C=30°,∴BD= CD( 30°所对的直角边是斜边的一半),∴CD=2AD=2BD,∴AC=AD+CD=AD+2AD=3AD;又∵ AD=8cm,∴DC=16cm.15.解:(1 )过 P 作 PD⊥AB 于点 D,∵∠ PBD=90°﹣ 60°=30°且∠ PBD=∠ PAB+∠ APB,∠ PAB=90﹣ 75=15°∴∠ PAB=∠ APB,∴BP=AB=7(海里).( 2)作 PD⊥ AB于 D,∵ A 处测得小岛 P 在北偏东 75°方向,∴∠ PAB=15°,∵在 B 处测得小岛 P 在北偏东 60°方向,∴∠ APB=15°,∴AB=PB=7海里,∵∠ PBD=30°,∴PD= PB=3.5> 3,∴该船持续向东航行,没有触礁的危险.。
等腰三角形知识点+经典例题

等腰三角形知识点+经典例题等腰三角形知识点+经典例题等腰三角形是一种特殊的三角形,它具有两条边相等的性质。
在几何学中,等腰三角形有着独特的特点和应用。
本文将介绍等腰三角形的基本性质和解题技巧,并通过经典例题加深对该知识点的理解。
一、等腰三角形基本性质1. 两边相等:等腰三角形的两条边长相等,通常表示为AB = AC。
2. 两底角相等:等腰三角形的两个底角(即底边两侧的角)相等,通常表示为∠B = ∠C。
3. 对顶角平分底边:等腰三角形的对顶角(即顶点处的角)平分底边,即顶角的平分线与底边相等和垂直。
4. 底角是钝角:当等腰三角形的顶角大于90度时,底角为钝角。
二、等腰三角形的特殊性质1. 高线重合:等腰三角形的高线与底边重合,且高线上的高度等于底边的中线和中线的一半。
2. 内切圆:等腰三角形的内切圆与底边相切,且圆心在高线上。
3. 外接圆:等腰三角形的外接圆的圆心位于底边的中点,且外接圆的半径等于底边长度的一半。
三、等腰三角形的解题技巧1. 利用等腰三角形的两边相等性质,可在题目中找到相等的边长,进而推导其他角度和边长的关系。
2. 利用等腰三角形的两底角相等性质,可在题目中找到已知角度与未知角度的关系,从而推导解题过程。
3. 利用等腰三角形的对顶角平分底边性质,和底角是钝角的特点,可应用角平分线定理解题。
四、经典例题例题1:在等腰三角形ABC中,AB = AC = 6cm,∠B = 60°,求角A的度数和三角形的面积。
解析:由于AB = AC,可知三角形ABC是等腰三角形。
又∠B =∠C = 60°,由等腰三角形的两底角相等性质可得∠A = 180° - 2∠B = 60°。
三角形ABC的三个角度均为60°,是等边三角形。
根据等边三角形的性质,三角形ABC的面积为√3/4 * AB^2 = √3/4 * 6^2 = 9√3 cm^2。
例题2:在等腰三角形ABC中,AB = AC = 8cm,∠A = 100°,求顶角B的度数和三角形的周长。
七年级数学下册专题第13讲等腰三角形重点、考点知识总结及练习

专题 第13讲等腰三角形知识点1 等腰三角形的相关概念---分类讨论求边角的值1.等腰三角形的两个腰相等,两个底角也相等.2.直角三角形30°的角所对的直角边等于斜边的一半.【典例】1.若等腰三角形一腰上的高等于腰长的一半,求此三角形的底角.【解析】解:①如下图,当高在三角形内部时,12BD AB =,∴∠A=30°,∴∠ABC=∠ACB=75°,②如下图,当高在三角形外部时,12BD AB =,则∠BAD=30°,∴∠BAC=150°,∴∠ABC=∠ACB=15°,所以此三角形的底角等于75°或15°.【方法总结】本题考查了等腰三角形的性质,以及含特殊角的直角三角形,熟记三角形的高相对于三角形的三种位置关系(三角形内部,三角形的外部,三角形的边上),解题时注意需要分类讨论.2.如果一等腰三角形的周长为27,且两边的差为12,求这个等腰三角形的腰长.【解析】解:设等腰三角形的腰长为x,则底边长为x﹣12或x+12,当底边长为x﹣12时,根据题意,得2x+x﹣12=27,解得x=13,∴腰长为13,此时底边长为13-12=1,满足三角形的两边之和大于第三边,两边之差小于第三边,当底边长为x+12时,根据题意,得2x+x+12=27,解得x=5,此时底边长为5+12=17,因为5+5<17,所以构不成三角形,故这个等腰三角形的腰的长为13.【方法总结】已知等腰三角形的周长和两边之差来求等腰三角形的底或腰时,我们需要分类讨论,分为两种情况:一种是“腰-底=某个值”,第二种是“底-腰=某个值”,可将底或腰设为未知数,再根据等腰三角形的周长列出方程,求出三边以后根据三角形的三边关系进行验证,选择合理的数值.【随堂练习】1.(2017秋•洛阳期末)若等腰三角形的一个内角比另一个内角大30°,则这个等腰三角形的顶角的度数为_____.【解答】解:在△ABC中,设∠A=x,∠B=x+30°,分情况讨论:当∠A=∠C为底角时,2x+(x+30°)=180°,解得x=50°,顶角∠B=80°;当∠B=∠C为底角时,2(x+30)+x=180°,解得x=40°,顶角∠A=40°.故这个等腰三角形的顶角的度数为80°或40°.故答案为:80°或40°.2.(2017秋•襄州区期末)在等腰△ABC中,AB=AC,一边上的中线BD将这个三角形的周长分为15和12两个部分,则该等腰三角形的底边长为______.【解答】解:根据题意,①当15是腰长与腰长一半时,AC+AC=15,解得AC=10,所以底边长=12﹣×10=7;②当12是腰长与腰长一半时,AC+AC=12,解得AC=8,所以底边长=15﹣×8=11.所以底边长等于7或11.故答案为:7或11.3.(2017秋•枣阳市期末)一个等腰三角形的周长为20,一条边的长为6,则其两腰之和为______.【解答】解:①底边长为6,则腰长为:(20﹣6)÷2=7,所以另两边的长为7,7,能构成三角形,7+7=14;②腰长为6,则底边长为:20﹣6×2=8,能构成三角形,6+6=12.故答案为:12或144.(2017秋•诸暨市期末)已知等腰三角形的周长为8,其中一边长为2,则该等腰三角形的腰长为_____.【解答】解:①2是腰长时,底边为:8﹣2×2=4,三角形的三边长分别为2、2、4,∵2+2=4,∴不能组成三角形,②2是底边长时,腰长为:×(8﹣2)=3,三角形的三边长分别3、3、2,能组成三角形,综上所述,该等腰三角形的腰长是3.故答案为:3.5.(2018春•李沧区期中)若等腰三角形一腰上的高与另一腰的夹角为48°,则其顶角度数为_______°.【解答】解:①如图1,当等腰三角形的顶角是钝角时,腰上的高在外部.根据三角形的一个外角等于与它不相邻的两个内角的和,即可求得顶角是90°+48°=138°;②如图1,当等腰三角形的顶角是锐角时,腰上的高在其内部,故顶角是90°﹣48°=42°.故答案为:42或138.6.(2018春•邗江区期中)已知等腰三角形的一条边等于4,另一条边等于9,那么这个三角形的第三边是_____.【解答】解:当4为底时,其它两边都为9,4、9、9可以构成三角形;当4为腰时,其它两边为4和9,因为4+4=8<9,所以不能构成三角形.故答案为:9.知识点2 等腰三角形的性质---边角关系等腰三角形的两底角相等(简称“等边对等角”),即在△ABC,AB=AC,可得∠B=∠C.【典例】1.如图,在△ABC中,∠ACB=90°,AD=AC,BE=BC,求∠DCE的大小.【解析】解:设∠ACE=x,∠ECD=y,∠DCB=z,∵BC=BE,+,∴∠CED=∠ECB=y z∵AC=AD,+,∴∠ADC=∠ACD=x y+-,在△CDB中,∠B=x y z+-,在△ACE中,∠A=y z x在△ABC中,∠ACB=90°,+-++-=90°,∴∠A+∠B=90°,即x y z y z x∴2y=90°,解得y=45°.于是∠DCE=45°.【方法总结】本题考查了等腰三角形的性质,解答此题的关键是建立起各角之间的关系,结合图形列出方程进行解答.2.如图,在△ABC中,AB=AC,AB的垂直平分线交边AB于D点,交边AC于E点,若△ABC 与△EBC的周长分别是40,24,求AB的长.【解析】解:∵DE是AB的垂直平分线,∴AE=BE,∵△ABC的周长=AB+AC+BC,△EBC的周长=BE+EC+BC=AE+EC+BC=AC+BC,∴△ABC的周长﹣△EBC的周长=(AB+AC+BC)-(AC+BC)=AB,∴AB=40﹣24=16.【方法总结】本题考查了等腰三角形的性质和垂直平分线上的性质,根据垂直平分线上的点到线段两端点的距离相等,得出相等的线段,把三角形的周长表示出来,再利用相等的线段进行转化求解. 【随堂练习】1.(2017春•成华区期末)如图△ABC中,AB=AC,点E、D、F分别是边AB、BC、AC边上的点,且BE=CD,CF=BD.若∠EDF=50°,则∠A的度数为_____.【解答】解:∵AB=AC,∴∠B=∠C,在△BDE与△CEF中,∴△BDE≌△CFE.∴∠BDE=∠CFD,∵∠EDF=50°,∴∠BDE+∠CDF=∠CDF+∠CFD=130°,∴∠C=50°∵AB=AC,∴∠C=∠B=50°,∴∠A=180°﹣50°﹣50°=80°,故答案为:80°.2.(2017秋•浦东新区校级期末)如图所示,已知△ABC中,AB=AC,∠BAD=30°,AD=AE,求∠EDC的度数.【解答】解:设∠EDC=x,∠B=∠C=y,∠AED=∠EDC+∠C=x+y,又因为AD=AE,所以∠ADE=∠AED=x+y,则∠ADC=∠ADE+∠EDC=2x+y,又因为∠ADC=∠B+∠BAD,所以2x+y=y+30,解得x=15.所以∠EDC的度数是15°.知识点3等腰三角形的性质---三线合一等腰三角形底边上的高线、中线及顶角平分线重合.例:已知△ABC是等腰三角形,AB=AC,①AD⊥BC ②BD=CD ③AD平分∠BAC,上述三个条件,任意满足一个,可得到另外两个.即①⇒②,③;②⇒①,③;③⇒①,②.【典例】1.如图,在△ABC中,AB=AC,AD是BC边上的中线,E是AC 边上的一点,且∠CBE=∠CAD.求证:BE⊥AC.【解析】证明:∵AB=AC,AD是BC边上的中线,∴AD⊥BC,∴∠CAD+∠C=90°,又∵∠CBE=∠CAD,∴∠CBE+∠C=90°,∴∠BEC=90°,即BE⊥AC.【方法总结】本题主要是利用等腰三角形的三线合一,根据三线合一的性质可知,等腰三角形底边上的中线也是底边的高线.注:等腰三角形常作的辅助线是,过顶角的顶点向底边作垂线,再利用三线合一得到一些相等的关系式,当题目中给出等腰三角形底边上的中点时,常常将等腰三角形的顶角顶点和它直接相连.【随堂练习】1.(2017秋•莘县期末)如图,在等腰三角形△ABC中,AB=AC,BD平分∠ABC,在BC的延长线上取一点E,使CE=CD,连接DE,求证:BD=DE.【解答】证明:∵AB=AC∴∠ABC=∠ACB,∵BD平分∠ABC,∵CD=CE,∴∠E=∠CDE,∵∠ACB=∠E+∠CDE,∴∠E=∠ACB,∴∠E=∠DBE,∴BD=DE.2.(2017秋•东城区期末)如图,在△ABC中,AB=AC,AD⊥于点D,AM是△ABC的外角∠CAE的平分线.(1)求证:AM∥BC;(2)若DN平分∠ADC交AM于点N,判断△ADN的形状并说明理由.【解答】证明:(1)∵AB=AC,AD⊥BC,∴∠BAD=∠CAD=.∵AM平分∠EAC,∴∠EAM=∠MAC=.∴∠MAD=∠MAC+∠DAC==.∵AD⊥BC∴∠ADC=90°∴AM∥BC.(2)△ADN是等腰直角三角形,理由是:∵AM∥AD,∴∠AND=∠NDC,∵DN平分∠ADC,∴∠ADN=∠NDC=∠AND.∴AD=AN,∴△ADN是等腰直角三角形.知识点4等腰三角形的判定与性质1.等腰三角形的判定定理:有两个角相等的三角形是等腰三角形(简称“等角对等边”).2.等腰三角形的两个底角相等(简称“等边对等角”).3. 等腰三角形底边上的高线、中线及顶角平分线重合.【典例】1.如图,A、B两点在正方形网格的格点上,每个方格都是边长为1的正方形,点C也在格点上,且△ABC是等腰三角形,则符合条件是点C共有_______ 个.【答案】9【解析】解:①以AB作为等腰三角形的底边,则符合条件的C一定在线段AB的垂直平分线上,且处于格点上,图中红线上的点,共5个;②以AB作为等腰三角形的一个腰,当点A是等腰三角形的顶角顶点时,符合条件的点在紫色线上,共有2个,当点B是等腰三角形的顶角顶点时,符合条件的点在蓝色线上,共有2个,综合①②可知,符合条件的点C共有9个.故答案是:9.【方法总结】本题考查的等腰三角形的判定,利用的是数形结合思想,当已知两个格点找寻第三个格点时,需要分类讨论,将这条边作为底和作为腰时可以构建的等腰三角形的个数之和,即为所求的点的个数.2.如图,∠BOC=60°,点A是BO延长线上的一点,OA=10cm,动点P从点A出发沿AB 以2cm/s的速度移动,动点Q从点O出发沿OC以1cm/s的速度移动,如果点P、Q同时出发,用t(s)表示移动的时间,当t=_____________s时,△POQ是等腰三角形.【答案】10或103【解析】解:当PO=QO时,△POQ是等腰三角形;如图1所示:当P点在O的左侧时,∵PO=AO﹣AP=10﹣2t,OQ=1t∴当PO=QO时,10﹣2t=t;解得t=103时,△POQ是等腰三角形;即当t=103如图2所示:当P点在O的右侧,△POQ是等腰三角形,∵∠BOC=60°,∴△POQ是等边三角形,∴PO=QO=PQ∵PO=AP﹣AO=2t﹣10,OQ=1t;∴2t﹣10=t;解得t=10;故答案为:10或10.3【方法总结】本题主要考查了等腰三角形的性质,由等腰三角形的两个腰相等得出方程是解决问题的关键,注意本题分类讨论时,由于∠POQ=60°,可得出△POQ是等边三角形,再根据PO=QO进行求解.3.如图,在△ABC中,AB=AC,CD是∠ACB的平分线,DE∥BC,交AC于点E.(1)求证:DE=CE.(2)若∠CDE=35°,求∠A的度数.【解析】证明:(1)∵CD是∠ACB的平分线,∴∠BCD=∠ECD.∵DE∥BC,∴∠EDC=∠BCD,∴∠EDC=∠ECD,∴DE=CE.(2)解:∵∠ECD=∠EDC=35°,∴∠ACB=2∠ECD=70°.∵AB=AC,∴∠ABC=∠ACB=70°,∴∠A=180°﹣70°﹣70°=40°.【方法总结】本题主要考查的是“平行+角分线” 模型,在之后学习菱形证明题时也会用到,需记牢.模型如下:如图所示,①∠1=∠2;②AC∥BD;③AB=AC(△ABC是等腰三角形)上述条件任意两个成立则第三个也成立.即①②⇒③;①③⇒②;②③⇒①.【随堂练习】1.(2018•安徽模拟)如图,在△ABC中,BC=4,BD平分∠ABC,过点A作AD⊥BD于点D,过点D作DE∥CB,分別交AB、AC于点E、F,若EF=2DF,则AB的长为()A.4 B.6 C.8 D.10【解答】解:如图,延长AD,BC交于点G,∵BD平分∠ABC,AD⊥BD于点D,∴∠BAD=∠G,∴AB=BG,∴D是AG的中点,又∵DE∥BG,∴E是AB的中点,F是AC的中点,∴DE是△ABG的中位线,EF是△ABC的中位线,∴EF=BC=2,又∵EF=2DF,∴DF=1,∴DE=3,∴BG=2DE=6,∴AB=6,故选:B.2.(2018•河东区二模)如图,在△ABC中,∠ABC=90°,AB=6,BC=8,∠BAC,∠ACB的平分线相交于点E,过点E作EF∥BC交AC于点F,则EF的长为_____.【解答】解:过E作EG∥AB,交AC于G,则∠BAE=∠AEG,∵AE平分∠BAC,∴∠BAE=∠CAE,∴∠CAE=∠AEG,∴AG=EG,同理可得,EF=CF,∵AB∥GE,BC∥EF,∴∠BAC=∠EGF,∠BCA=∠EFG,∴△ABC∽△GEF,∵∠ABC=90°,AB=6,BC=8,∴AC=10,∴EG:EF:GF=AB:BC:AC=3:4:5,设EG=3k=AG,则EF=4k=CF,FG=5k,∵AC=10,∴3k+5k+4k=10,∴k=,∴EF=4k=.故答案为:.3.(2017春•平南县期中)如图,在Rt△ABC中,∠C=90°,D为AB上的点,BD=CD=5,则AD=______.【解答】解:在Rt△ABC中,∠C=90°,∵BD=DC,∴∠B=∠DCB,∵∠B+∠A=90°,∠DCB+∠DCA=90°,∴∠A=∠DCA,∴AD=DC=5,故答案为5.综合运用1. 如图,正方形网格中的每个小正方形边长都是1.已知A、B是两格点,若△ABC为等腰三角形,且S△ABC=1.5,则满足条件的格点C有________个.【答案】2【解析】解:如上图:分情况讨论.①AB为等腰△ABC底边时,符合△ABC为等腰三角形的C点有4个;②AB为等腰△ABC其中的一条腰时,符合△ABC为等腰三角形的C点有4个.因为S△ABC=1.5,所以满足条件的格点C只有两个,如图中蓝色的点.故答案为:2.2.如图,C是△ABE的BE边上一点,F在AE上,D是BC的中点,且AB=AC=CE,下列结论:①AD⊥BC;②CF⊥AE;③∠1=∠2;④AB+BD=DE其中正确的结论有_________.【答案】①④【解析】解:①∵D是BC的中点,AB=AC,∴AD⊥BC,故①正确;②∵虽然AC=CE,F在AE上,但F点不一定是AE的中点,∴无法证明CF⊥AE,故②错误;③由②可知,CF不一定垂直于AE,则无法证明∠1=∠2,故③错误;21④∵D 是BC 的中点,∴BD=DC ,∵AB=CE ,∴AB+BD=CE+DC=DE ,故④正确.故其中正确的结论有①④.故答案为:①④.3.如图,△ABC 中,AB=AC ,D 是BC 的中点,E 、F 分别是AB 、AC 上的点,且AE=AF ,求证:DE=DF .【解析】证明:连接AD ,∵AB=AC ,D 是BC 的中点,∴∠EAD=∠FAD ,在△AED 和△AFD 中,AE AF EAD FAD AD AD =⎧⎪=⎨⎪=⎩∠∠,∴△AED ≌△AFD (SAS ),∴DE=DF .4.如图,AD∥BC,∠BAC=70°,DE⊥AC于点E,∠D=20°.(1)求∠B的度数,并判断△ABC的形状;(2)若延长线段DE恰好过点B,试说明DB是∠ABC的平分线.【解析】解:(1)∵DE⊥AC于点E,∴∠AED=90°,∵∠D=20°,∴∠CAD=90°-∠D =90°-20°=70°,∵AD∥BC,∴∠C=∠CAD=70°,∵∠BAC=70°,∴∠BAC=∠C,∠B=180°-∠BAC- ∠C =40°,∴AB=AC,∴△ABC是等腰三角形.(2)∵延长线段DE恰好过点B,DE⊥AC,∴BD⊥AC,23∵△ABC 是等腰三角形,∴DB 是∠ABC 的平分线.5.已知等腰三角形△ABC ,AB=AC ,一腰上的中线把这个三角形的周长分成12和15两部分,求这个三角形的三边长.【解析】解:如图,在△ABC 中,AB=AC ,且AD=BD .设AB=AC=x ,BC=y ,(1)当AC+AD=15,BD+BC=12时, 根据题意得,152x x +=,122x y +=, 解得x=10,y=7.(2)当AC+AD=12,BC+BD=15时, 根据题意得,122x x +=,152x y +=, 解得x=8,y=11,故得这个三角形的三边长分别为10,10,7或8,8,11.6.如图,O 是△ABC 的∠ABC ,∠ACB 的角平分线的交点,OD ∥AB 交BC 于D ,OE ∥AC 交BC 于E ,若BC=16,求△ODE 的周长.【解析】解:∵BO平分∠ABC,∴∠ABO=∠DBO,又OD∥AB,∴∠ABO=∠DOB,∴∠DBO=∠DOB,∴OD=BD,同理OE=CE,∵BC=16,则△ODE的周长为:OD+DE+OE=BD+DE+EC=BC=16.。
专题:等腰三角形的性质与判定(答案)
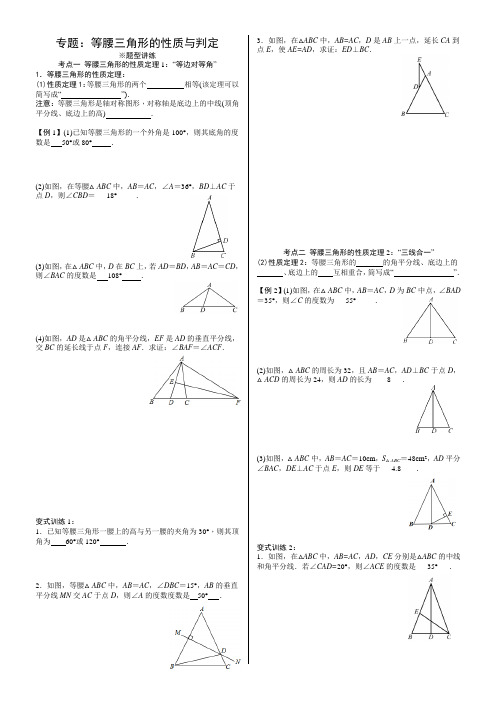
专题:等腰三角形的性质与判定※题型讲练考点一等腰三角形的性质定理1:“等边对等角”1.等腰三角形的性质定理:(1)性质定理1:等腰三角形的两个相等(该定理可以简写成“”).注意:等腰三角形是轴对称图形,对称轴是底边上的中线(顶角平分线、底边上的高) .【例1】(1)已知等腰三角形的一个外角是100°,则其底角的度数是50°或80°.(2)如图,在等腰△ABC中,AB=AC,∠A=36°,BD⊥AC于点D,则∠CBD=___18°_____.(3)如图,在△ABC中,D在BC上,若AD=BD,AB=AC=CD,则∠BAC的度数是108°.(4)如图,AD是△ABC的角平分线,EF是AD的垂直平分线,交BC的延长线于点F,连接AF.求证:∠BAF=∠ACF.变式训练1:1.已知等腰三角形一腰上的高与另一腰的夹角为30°,则其顶角为60°或120°.2.如图,等腰△ABC中,AB=AC,∠DBC=15°,AB的垂直平分线MN交AC于点D,则∠A的度数度数是50°.3.如图,在△ABC中,AB=AC,D是AB上一点,延长CA到点E,使AE=AD,求证:ED⊥BC.考点二等腰三角形的性质定理2:“三线合一”(2)性质定理2:等腰三角形的的角平分线、底边上的、底边上的互相重合,简写成“”.【例2】(1)如图,在△ABC中,AB=AC,D为BC中点,∠BAD =35°,则∠C的度数为___55°_____.(2)如图,△ABC的周长为32,且AB=AC,AD⊥BC于点D,△ACD的周长为24,则AD的长为____8___.(3)如图,△ABC中,AB=AC=10cm,S△ABC=48cm2,AD平分∠BAC,DE⊥AC于点E,则DE等于___4.8____.变式训练2:1.如图,在△ABC中,AB=AC,AD,CE分别是△ABC的中线和角平分线.若∠CAD=20°,则∠ACE的度数是___35°___.2.如图,△ABC中,AB=AC,点D是BC边的中点,作∠EAB =∠BAD,AE边交CB的延长线于点E,延长AD到点F,使AF=AE,连接CF.试证明:BE=CF.考点三等腰三角形的判定定理:“等角对等边”1.等腰三角形的判定定理:如果一个三角形有相等,那么这两个角所对的边也相等(简写成“”).【例2】(1)如图,∠B=∠C=36°,∠ADE=∠AED=72°,则图中的等腰三角形的个数为( D )A.3个B.4个C.5个D.6个(2)如图,在△ABC中,∠ACB=90°,CD是AB边上的高,AE是∠BAC的角平分线,AE与CD交于点F,求证:△CEF是等腰三角形.(3)如图,AD是△ABC的角平分线,BE⊥AD交AD的延长线于点E,EF∥AC交AB于点F.求证:AF=FB.变式训练3:1.如图,在△ABC中,BP平分∠CBA,AP平分∠CAB,且DE∥AB,若CB=12,AC=18,则△CDE的周长是____30____.2.如图,△ABC中,∠B=2∠C,AD是∠BAC的平分线.求证:AC=AB+BD.考点四等腰三角形的综合问题【例4】如图,在△ABC中,AB=AC,点D、E、F分别在AB 、BC 、AC边上,且BE=CF,BD=CE.(1)求证:△DEF是等腰三角形;(2)当∠A=50°时,求∠DEF的度数.※课后练习1.等腰三角形是轴对称图形,它的对称轴是( D )A.过顶点的直线B.腰上的高所在的直线C.顶角的角平分线D.底边的垂直平分线2.如图,在△ABC中,AB=AC,∠A=30°,以B为圆心,BC 的长为半径画弧,交AC于点D,连接BD,则∠ABD=(B) A.30°B.45°C.60°D.90°3.如图所示,已知AB=AC=BD,那么∠1和∠2之间的关系是(D)A.∠1=2∠2 B.2∠1-∠2=180°C.∠1+3∠2=180°D.3∠1-∠2=180°4.已知等腰三角形中有一个内角为70°,则该等腰三角形的顶角度数为70°或40°.5.如图,已知OC平分∠AOB,CD∥OB,若OD=4 cm,则CD等于____4 cm ___.6.如图,在△ABC中,∠B=∠C,点E在CA延长线上,EP⊥BC于点P,交AB于点F.若AF=3,BF=5,则CE的长度为11.7.在平面直角坐标系中,O为坐标原点,已知点A(2,4),在坐标轴上确定一点P,使△AOP为等腰三角形,则所有符合条件的点P有8 个.8.如图,在△ABC中,AB=AC,D,E分别在AC,AB边上,且BC=BD,AD=DE=EB.则∠A的度数为45°.9.如图所示,在△ABC中,∠BAC=90°,AD⊥BC于D,BE 交AD于F,交AC于E.(1)若BE平分∠ABC,试判断△AEF的形状,并说明理由;(2)若AE=AF,请证明BE平分∠ABC.10.如图,AD是∠BAC的平分线,AB=AC+DC.求证:∠C=2∠B.证明:在AB上截取AE=AC,连接DE.∵AB=AC+DC,AE=AC,∴BE=DC.∵AD是∠BAC的平分线,∴∠EAD=∠CAD,∴△AED≌△ACD( SAS ).∴DE=DC=BE,∠AED=∠C,∴∠B=∠EDB.∵∠AED=∠B+∠EDB,∴∠AED=2∠B,∴∠C=2∠B.11.如图,在△ABC中,AB=AC,D是BC上任意一点,过点D 分别向AB,AC引垂线,垂足分别为E,F.(1)当点D在BC的什么位置时,DE=DF?请给出证明.(2)过点C作AB边上的高CG,请问DE,DF,CG的长度之间存在怎样的数量关系?并加以证明.解:(1)当D为BC的中点时,DE=DF.∵D为BC的中点,∴BD=CD.∵AB=AC,∴∠B=∠C.∵DE⊥AB,DF⊥AC,∴∠DEB=∠DFC=90°,∴△BED≌△CFD( AAS ),∴DE=DF.(2)CG=DE+DF.连接AD,∵S△ABC=S△ADB+S△ADC,AB×CG=AB×DE+AC×DF,又∵AB=AC,∴CG=DE+DF.12.在△ABC中,∠C=90°,AC=BC=2,将一块三角板的直角顶点放在斜边AB的中点P处,将此三角板绕点P旋转,三角板的两直角边分别交射线AC,CB于点D,E,图1,图2,图3是旋转得到的三种图形.(1)以图2为例证明:PD=PE;(2)△PBE能否构成等腰三角形?若能,求出∠PEB的度数;若不能,请说明理由.。
专题04等腰三角形的性质和判定综合题(原卷版)

专题04 等腰三角形的性质和判定(综合题)知识互联网易错点拨知识点1:等腰三角形的定义的三角形,叫做等腰三角形,其中叫做腰,另一边叫做,两腰所夹的角叫做,叫做底角.如图所示,在△ABC中,,则它叫等腰三角形,其中AB、AC为,BC为,∠A是,∠B、∠C是.细节剖析:等腰直角三角形的 相等,且都等于 .等腰三角形的底角只能为 ,不能为 ,但顶角可为 .∠A =180°-2∠B ,∠B =∠C = . 知识点2:等腰三角形的性质1.等腰三角形的性质性质1:等腰三角形的 (简称“ ”).性质2:等腰三角形的 互相重合(简称“ ”).2.等腰三角形的性质的作用性质1证明 相等.是证明角相等的一个重要依据.性质2用来证明 等.3.等腰三角形是轴对称图形等腰三角形 所在直线是它的对称轴,通常情况 对称轴. 知识点3:等腰三角形的判定如果一个三角形中有两个角相等,那么这 也相等(简称“ ”).要点诠释:等腰三角形的判定是证明两条线段相等的重要定理,是将三角形中的角的相等关系转化为边的相等关系的重要依据.等腰三角形的性质定理和判定定理是互逆定理.一.选择题 1.(2022秋•朝阳区校级月考)如图,BO 平分∠ABC ,CO 平分∠ACB ,MN ∥BC ,AB =15,AC =18,则△AMN 的周长为( )1802A ︒-∠易错题专训A.15B.18C.30D.332.(2021秋•微山县期末)如图,在△ABC中,∠A=60°,∠ABC=40°,BD平分∠ABC,CE⊥BD,交AB 于点E.关于下面两个结论,说法正确的是()结论①∠ADE=20°;结论②BC=BE.A.结论①②都正确B.结论①②都错误C.只有结论①正确D.只有结论②正确3.(2021秋•建昌县期末)如图所示,在△ABC中,∠ABC与∠ACB的平分线交于点P,过点P作MN∥BC 交AB于点M,交AC于点N,那么下列结论:①BP=CP;②MN=BM+CN;③△BMP和△CNP都是等腰三角形;④△AMN的周长等于AB+AC,其中正确的有()A.4个B.3个C.2个D.1个4.(2021秋•覃塘区期末)如图,在△ABC中,AB=AC,点E、F分别在BA、BC的延长线上,∠EAC、∠ABC、∠ACF的平分线相交于点D.对于以下结论:①AD∥BC;②AD=AC;③∠ADC=∠ACB;④∠ADB与∠ADC互余.其中正确结论的个数为()A.4B.3C.2D.15.(2021秋•巢湖市期末)如图,在△ABC中,AB=AC,AD=BD,∠A=36°,下列结论错误的是()A.BD是AC边上的中线B.BD是∠ABC的平分线C.图中共有3个等腰三角形D.∠DBC=36°6.(2021•太仓市自主招生)如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过O点作EF∥BC 交AB于点E,交AC于点F,过点O作OD⊥AC于D,下列四个结论.①EF=BE+CF;②∠BOC=90°+∠A;③点O到△ABC各边的距离相等;④设OD=m,AE+AF=n,则S△AEF=mn,正确的结论有()个.A.1个B.2个C.3个D.4个二.填空题7.(2022春•五华区校级期中)如图,在△ABC中,ED∥BC,∠ABC和∠ACB的平分线分别交ED于点G、F,若FG=4,ED=8,求EB+DC=.8.(2021秋•句容市期末)如图,BD平分∠ABC,DE∥BC交BA于点E,若DE=,则EB=.9.(2021秋•市中区期末)如图,△ABC中,AC=DC=4,AD平分∠BAC,BD⊥AD于D,E为AC的中点,则图中两个阴影部分面积之差的最大值为.10.(2021秋•澄城县期末)如图,在Rt△ABC中,∠A=90°,CM平分∠ACB交AB于点M,过点M作MN ∥BC交AC于点N,且MN平分∠AMC,若AN=2,则BC的长为.11.(2021秋•崇川区期末)如图,在△ABC中,AB=AC=3,∠ABC和∠ACB的平分线交于点E,过点E 作EM∥BC分别交AB,AC于M,N,则△AMN的周长为.12.(2021秋•宁津县期末)如图,△ABC中,∠A=∠ACB,CP平分∠ACB,BD,CD分别是△ABC的两外角的平分线,下列结论中:①CP⊥CD;②∠P=∠A;③BC=CD;④∠D=90°﹣∠A;⑤PD∥AC.其中正确的结论是(直接填写序号).13.(2021•长沙模拟)如图,△ABC中,AD平分∠BAC,∠ACB=3∠B,CE⊥AD,AC=8,BC=BD,则CE=.三.解答题14.(2021秋•祥云县期末)如图,在△ABC中,∠ABC与∠ACB的角平分线交于点O,过点O作DE∥BC,分别交AB、AC于点D、E.若△ADE的周长为7,△ABC的周长为12,求BC的长度.15.(2021秋•海沧区期末)定义:一个三角形,若过一个顶点的线段将这个三角形分为两个三角形,其中一个是直角三角形,另一个是等腰三角形,则称这个三角形是等直三角形,这条线段叫做这个三角形的等直分割线段.例如:如图1,在△ABC中,∵AD⊥BC于D,且BD=AD,∴△ACD是直角三角形,△ABD是等腰三角形,∴△ABC是等直三角形,AD是△ABC的一条等直分割线段.(1)如图2,已知Rt△ABC中,∠C=90°,DE是AB的垂直平分线,请说明AD是△ABC的一条等直分割线段;(2)若△ABC是一个等直三角形,恰好有两条等直分割线,∠B和∠C均小于45°,求证:△ABC是等腰三角形.16.(2022春•会宁县期末)已知:如图,E为△ABC的外角平分线上的一点,AE∥BC,BF=AE,求证:(1)△ABC是等腰三角形;(2)AF=CE.17.(2021秋•开福区校级期末)如图,在四边形ABCD中,BD所在的直线垂直平分线段AC,过点A作AF ∥BC交CD于F,延长AB、DC交于点E.(1)求证:AC平分∠EAF;(2)求证:∠F AD=∠E;(3)若∠EAD=90°,AE=5,AF=3,求CF的长.18.(2021秋•伊通县期末)如图,△ABC中,AB=AC,∠A=36°,AB的垂直平分线交AC于点D,交AB 于点M,证明:△BCD是等腰三角形.19.(2021秋•雨花区校级月考)已知△ABC中,∠ACB的平分线CD交AB于点D,DE平分∠ADC,DE∥BC.(1)如图1,如果点E是边AC的中点,AC=10,求DE的长;(2)在(1)的条件下,求证:△ADC是等腰三角形.(3)如图2,若∠ABC=30°,在BC边上取点F使BF=DF,若BC=18,求DF的长.20.(2021春•项城市校级期末)如图①,△ABC中,AB=AC,∠B、∠C的平分线交于O点,过O点作EF ∥BC交AB、AC于E、F.(1)图中有几个等腰三角形?猜想:EF与BE、CF之间有怎样的关系,并说明理由.(2)如图②,若AB≠AC,其他条件不变,图中还有等腰三角形吗?如果有,分别指出它们.在第(1)问中EF与BE、CF间的关系还存在吗?(3)如图③,若△ABC中∠B的平分线BO与三角形外角平分线CO交于O,过O点作OE∥BC交AB 于E,交AC于F.这时图中还有等腰三角形吗?EF与BE、CF关系又如何?说明你的理由.。
等腰三角形的性质和判定练习题

等腰三角形的性质和判定一、单选题1.以下判断中错误的是( )A .等边三角形的每条高线都是角平分线和中线B .有一内角为60︒的等腰三角形是等边三角形C .等腰三角形一定是锐角三角形D .等腰三角形顶角的平分线,底边上的中线,底边上的高相互重合2.如图,在ABC 中,AB AC =,65C ︒∠=,点D 是BC 边上任意一点,过点D 作//DF AB 交AC 于点E ,则FEC ∠的度数是( ).A .120︒B .130︒C .145︒D .150︒3.如图,直线a ,b 相交形成的夹角中,锐角为52°,交点为O ,点A 在直线a 上,直线b 上存在点B ,使以点O ,A ,B 为顶点的三角形是等腰三角形,这样的点B 有( )A .1个B .2个C .3个D .4个4.等腰三角形一腰上的高与另一腰的夹角为30,则顶角的度数为( )A .60︒B .120︒C .60︒或150︒D .60︒或120︒5.如图,已知△ABC 是等边三角形,点B ,C ,D ,E 在同一直线上,且CG =CD ,DF =DE ,则△E =( )A .15°B .20°C .25°D .30°二、填空题6.已知△ABC 是等腰三角形.若△A =40°,则△ABC 的顶角度数是____.7.如图,AB AC =,若AD 平分BAC ∠,则AD 与BC 的位置关系是_______.8.已知:如图,ABC 中,,BO CO 分别是ABC ∠和ACB ∠的平分线,过O 点的直线分别交AB 、AC 于点D 、E ,且//DE BC .若6cm,8cm AB AC ==,则ADE 的周长为______.9.如图,在ABC 中,AB AC =,点E 在CA 延长线上,EP BC ⊥于点P ,交AB 于点F ,若10CE =,3AF =,则BF 的长度为______.三、解答题10.等腰三角形一腰上的中线将三角形的周长分成了21和27两个部分,求等腰三角形的底边和腰长.11.如图,BD 是ABC 的角平分线,DE BC ∥,交AB 于点E .(1)求证:EBD EDB ∠=∠.(2)当AB AC =时,请判断CD 与ED 的大小关系,并说明理由.12.如图,已知点D 、E 在ABC 的边BC 上,AB AC =,AD AE =.(1)求证:BD CE =;(2)若AD BD DE CE ===,求BAE ∠的度数.13.如图,在△ABC 中,AB =AC ,D 是BC 边上的中点,连结AD ,BE 平分△ABC 交AC 于点E ,过点E 作EF △BC 交AB 于点F .(1)若△C =36°,求△BAD 的度数.(2)求证:FB =FE .。
八年级上册数学等腰三角形知识点和典型习题分类汇总附答案

第7讲等腰三角形❖基本知识(熟记,会画图,要提问.)(1)(等边对等角).【证明之】(2)等腰三角形的性质2:等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合(三线合一).【证明之】(3)等腰三角形的判定:如果一个三角形有两个角相等,那么这两个角所对的边也相等(等角对等边).【证明之】❖等腰三角形的性质【方程思想计算角度】1、【易】如图,求下列等腰三角形的所有角的度数。
(1)顶角30° (2)底角30°2、【易】计算:(1)等腰三角形的一个角是110°,求其余内角。
(2)等腰三角形的一个角是80°,求其余内角。
(3)已知一个等腰三角形的两角分别为(2x-2)°,(3x-5)°,求这个等腰三角形各角的度数。
3、【易】如图所示,在△ABC中,AB=AD=DC,△BAD=26°,求△B和△C的度数.4、【易】如图,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,求△A、△ADB和△C的度数.5、【中】如图所示,五角星的五个角都是顶角为36°的等腰三角形,则△AMB的度数为______.6、【中】如图,AB=AC,△A=40°,AB的垂直平分线MN交AC于点D,求△DBC的度数.7、【中】如图,等腰△ABC中,AB=AC,△DBC=15°,AB的垂直平分线MN交AC于点D,则△A的度数是_______.【基础证明题】8、【易】如图,AD△BC,点E在AB的延长线上,CB=CE,试猜想△A与△E的大小关系,并说明理由.9、【中】已知:CD平分AB,且CD=AD=BD,求证:△ABC是直角三角形.【如果一个三角形一条边上的中线等于这条边的一半,那么这个三角形是直角三角形。
这句话倒过来也是对的,学到矩形时会证明。
】10、【中】如图,点D,E在△ABC的边BC上,AB=AC,AD=AE,求证:BD=CE.【全等法或三线合一法】11、【中】【仿上题】如图,点D 、E 在△ABC 的边BC 上,AB=AC .若BD=CE ,F 为DE 的中点,求证:AF△BC .12、【中】如图,在△ABC 中,AB=AC ,D 为BC 边上一点,△B=30°,△DAB=45°.(1)求△DAC 的度数;(2)求证:DC=AB .13、【难】如图,在△ABC 中,AB=AC ,△ABC 、△ACB 的平分线BD ,CE 相交于O 点,且BD 交AC 于点D ,CE 交AB 于点E .某同学分析图形后得出以下结论:△△BCD△△CBE ;△△BAD△△BCD ;△△BDA△△CEA ;△△BOE△△COD ;△△ACE△△BCE ;上述结论一定正确的是________.14、【中】已知:如图,在△ABC 中,AB=AC ,D 是BC 的中点,DE△AB ,DF△AC ,E ,F 分别是垂足,求证:AE=AF .15、【中】如图,已知:AB=AC ,△CAE 是△ABC 的外角,△1=△2.求证:AD △ BC .参考答案1、(1)底角75°;(2)底角30°,顶角120°.2、(1)35°,35°;(2)50°,50°;或80°,20°。
人教版八年级下册数学专题复习及练习(含解析):等腰三角形

专题13.3 等腰三角形知识点1:等腰三角形1.等腰三角形的定义:有两条边相等的三角形叫做等腰三角形.相等的两边叫做腰,另一边叫做底边,两腰所夹的角叫做顶角,底边与腰的夹角叫底角.2.等腰三角形的性质:(1)等腰三角形的两个底角相等(简写成“等边对等角”).(2)等腰三角形的顶角平分线,底边上的中线、 底边上的高互相重合(通常称作“三线合一”).3.等腰三角形的判定定理:如果一个三角形有两个角相等,那么这两个角所对的边也相等(简写成“等角对等边”).知识点2:等边三角形1.定义:三条边相等的三角形叫做等边三角形.2.等边三角形的性质和判定:(1)等边三角形的三个内角都相等,并且每一个角都等于60°。
(2)三个角都相等的三角形是等边三角形。
(3)有一个角是60°的等腰三角形是等边三角形。
知识点3:直角三角形的一个定理在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.【例题1】如图,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,求:△ABC各角的度数.【例题2】证明:在直角三角形中,如果一个锐角等于30°, 那么它所对的直角边等于斜边的一半. 已知:如图,在Rt △ABC 中,∠C=90°,∠BAC=30°.求证:BC=AB .【例题7】已知等边三角形的边长为3,点P 为等边三角形内任意一点,则点P 到三边的距离之和为( )A .B .C .D .不能确定【例题3】如图,已知AC ⊥BC ,BD ⊥AD ,AC 与BD 交于点O ,AC=BD.求证:(1)BC=AD ;(2)△OAB 是等腰三角形.一、选择题1.已知等边三角形的边长为3,点P 为等边三角形内任意一点,则点P 到三边的距离之和为( )12C AA.B.C.D.不能确定2.如图所示,点D是△ABC的边AC上一点(不含端点),AD=BD,则下列结论正确的是()A.AC>BC B.AC=BC C.∠A>∠ABC D.∠A=∠ABC3.如图,∠AOB=120°,OP平分∠AOB,且OP=2.若点M,N分别在OA,OB上,且△PMN 为等边三角形,则满足上述条件的△PMN有()A.1个B.2个C.3个D.3个以上4.如图所示,底边BC为2,顶角A为120°的等腰△ABC中,DE垂直平分AB于D,则△ACE的周长为()A.2+2B.2+C.4 D.3二、解答题5.已知:在△ABC中,AB=AC,D为AC的中点,DE⊥AB,DF⊥BC,垂足分别为点E,F,且DE=DF.求证:△ABC是等边三角形.6.如图,在△ABC中,过C作∠BAC的平分线AD的垂线,垂足为D,DE∥AB交AC于E.求证:AE=CE.7.求证:如果三角形一个外角的平分线平行于三角形的一边,那么这个三角形是等腰三角形.已知:∠CAE 是△ABC 的外角,∠1=∠2,AD ∥BC (如图).求证:AB=AC .8.已知:如图,AD ∥BC ,BD 平分∠ABC .求证:AB=AD .9.证明:等腰三角形两底角的平分线相等.已知:如图,在△ABC 中,AB=AC ,BD 、CE 是△ABC 的平分线.求证:BD=CE .10.证明:等腰三角形两腰上的高相等.已知:如图,在△ABC 中,AB=AC ,BE 、CF 分别是△ABC 的高.E DCAB11.证明:等腰三角形两腰上的中线相等.已知:如图,在△ABC 中,AB=AC ,BD 、CE 分别是两腰上的中线.求证:BD=CE .12.已知:如图,在△ABC 中,AB=AC=2a ,∠ABC=∠ACB=15°,CD 是腰AB 上的高.求:CD 的长.13.已知:如图,△ABC 中,∠ACB=90°,CD 是高,∠A=30°.求证:BD=AB .14.已知直角三角形的一个锐角等于另一个锐角的2倍,这个角的平分线把对边分成两条线段.求证:其中一条是另一条的2倍.已知:在Rt △ABC 中,∠A=90°,∠ABC=2∠C ,BD 是∠ABC 的平分线.1415.已知:如图,在Rt △ABC 中,∠C=90°,BC=AB .求证:∠BAC=30°.16.已知,如图,点C 为线段AB 上一点,△ACM 、△CBN 是等边三角形.求证:AN=BM .17.一个直角三角形房梁如图所示,其中BC ⊥AC ,∠BAC=30°,AB=10cm , CB 1⊥AB ,B 1C ⊥AC 1,垂足分别是B 1、C 1,那么BC 的长是多少?18.如图,△ABC 中,AB=AC ,∠A=36°,AC 的垂直平分线交AB 于E ,D 为垂足,连接EC .(1)求∠ECD 的度数;(2)若CE=5,求BC 长.12专题13.3 等腰三角形知识点1:等腰三角形1.等腰三角形的定义:有两条边相等的三角形叫做等腰三角形.相等的两边叫做腰,另一边叫做底边,两腰所夹的角叫做顶角,底边与腰的夹角叫底角.2.等腰三角形的性质:(1)等腰三角形的两个底角相等(简写成“等边对等角”).(2)等腰三角形的顶角平分线,底边上的中线、 底边上的高互相重合(通常称作“三线合一”).3.等腰三角形的判定定理:如果一个三角形有两个角相等,那么这两个角所对的边也相等(简写成“等角对等边”).知识点2:等边三角形1.定义:三条边相等的三角形叫做等边三角形.2.等边三角形的性质和判定:(1)等边三角形的三个内角都相等,并且每一个角都等于60°。
第一章第01讲 等腰三角形的性质与判定(6类热点题型讲练)(解析版)

第01讲 等腰三角形的性质与判定(6类热点题型讲练)1.经历“探索一发现一猜想一证明”的过程,逐步掌握综合法证明的方法,发展推理能力.2.进一步了解作为证明基础的几条基本事实的内容,能证明等腰三角形的性质.3.有意识地培养学生对文字语言、符号语言和图形语言的转换能力,关注证明过程及其表达的合理性.知识点01 等腰三角形的性质(1)等腰三角形性质1:等腰三角形的两个底角相等(简称:等边对等角)(2)等腰三角形性质2:文字:等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合(简称:等腰三角的三线合一)图形:如下所示;符号:在ABC D 中,AB =AC ,1212,,;,,;,12.BD CD AD BC AD B BD CD AD BC C BD CD Ð=Ðìï=^Ð=Ð^Ð=Ðíï^î==若则若则若,则 知识点02 等腰三角形的判定(1)等腰三角形的判定方法1:(定义法)有两条边相等的三角形是等腰三角形;(2)等腰三角形的判定方法2:有两个角相等的三角形是等腰三角形;(简称:等角对等边)21D C B A题型01根据等腰三角形腰相等求第三边或周长【例题】(2023上·河南商丘·八年级商丘市实验中学校考阶段练习)一个等腰三角形的两条边长分别为8cm 和4cm,则第三边的长为cm.【答案】8【分析】本题考查等腰三角形的性质及三角形的三边关系;已知没有明确腰和底边的题目一定要想到两种情况,分类进行讨论,还应验证各种情况是否能构成三角形进行解答,是解题的关键.【详解】解:①若一腰长为8cm,则底边为4cm,则第三边的长为8cm,488+>,故能组成三角形;②若一腰长为4cm,则底边为8cm,则第三边的长为4cm,+=,故不能组成三角形.448故答案为:8.【变式训练】解得:4a =,5b =,当4为等腰三角形的腰长,5为等腰三角形的底边时,则等腰三角形的周长为44513++=,当5为等腰三角形的腰长,4为等腰三角形的底边时,则等腰三角形的周长为55414++=,故答案为:13或14.题型02 根据等腰三角形等边对等角求角的度数题型03 根据等腰三角形三线合一进行求解【答案】25【详解】解:如图,作BE∵AB BC =,∴AE CE =,∵AC CD ^,90BAD Ð=°∴EBA BAE BAE Ð+Ð=Ð+Ð【答案】10【详解】解:AB Q 5BD CD \==,210BC BD \==,故答案为:10.(1)求AF 的长.(2)求CD 的长.【详解】(1)解:连接AF ,如下图,根据题意,90BAC Ð=°,AB ∴222(2)BC AB AC =+=+∴190452B ACB Ð=Ð=´°=°,∵F 为BC 中点,题型04 根据等腰三角形三线合一进行证明 (1)若106BAC DAE ÐÐ=°,(2)求证:BD EC =.【详解】(1)解:∵AB AC =(1∵,AB AC AD AE ==,∴,BF CF DF EF ==,∴BD CE =.【变式训练】1.(2023上·山东威海·七年级校联考期中)如图,已知AB AE ABC AED BC ED =Ð=Ð=,,,点F 是CD 的中点,连接AF ,请判断AF 与CD 的位置关系.【答案】垂直【分析】此题考查全等三角形的判定和性质,等腰三角形三线合一的性质:连接AC AD ,,证明ABC AED ≌△△,得到AC AD =,根据等腰三角形三线合一的性质得到AF CD ^,熟练掌握全等三角形的判定定理及等腰三角形的性质是解题的关键.【详解】答:AF CD^连接AC AD ,∵AB AE ABC AED BC ED =Ð=Ð=,,∴ABC AED≌△△∴AC AD=又∵点F 是CD 的中点∴AF CD ^.2.如图,在ABC V 中,AB AC =,40BAC а=,AD 是BC 边上的高.线段AC 的垂直平分线交AD 于点E ,交AC 于点F ,连接BE .(1)试问:线段AE 与BE 的长相等吗?请说明理由;(2)求EBD Ð的度数.【详解】(1)解:线段AE 与BE 的长相等,理由如下:连接CE ,如图所示:=,AD∵AB AC=,∴BD CD∴AD为BC的垂直平分线,∵点E在AD上,=,∴BE CE又∵线段AC的垂直平分线交题型05根据等角对等边证明等腰三角形Ð,【例题】(2023上·广西玉林·八年级统考期中)如图,点E在BA的延长线上,已知AD平分CAE ∥.求证:ABCAD BCV是等腰三角形.【答案】证明见解析【分析】本题主要考查了等角对等边,平行线的性质与角平分线的定义,先根据平行线的性质得到EAD B CAD C Ð=ÐÐ=Ð,,再由角平分线的定义和等量代换得到B C Ð=Ð,即可证明ABC V 是等腰三角形.【详解】证明:∵AD BC ∥,∴EAD B CAD C Ð=ÐÐ=Ð,,∵AD 平分CAE Ð,∴EAD CAD Ð=Ð,∴B C Ð=Ð,∴ABC V 是等腰三角形.【变式训练】【答案】ABC V 是等腰三角形,理由见解析【分析】本题主要考查了等腰三角形的判定,三角形外角的性质,角平分线的定义,设4ACD x Ð=,3ECD x =∠,由角平分线的定义得到1【答案】证明见解析【分析】本题考查了平行线的性质,等腰三角形的性质和判定,证明根据角平分线的定义可得,以及直线平行的性质证明题型06 等腰三角形的性质和判定综合应用【例题】如图,在ABC V 中,AB AC =,D 是BC 边的中点,连接AD ,BE 平分ABC Ð交AC 于点E .(1)若40C Ð=°,求BAD Ð的度数;(2)过点E 作EF BC ∥交AB 于点F ,求证:BEF △是等腰三角形.(3)若BE 平分ABC V 的周长,AEF △的周长为15,求ABC V 的周长.【详解】(1)解:AB AC =Q ,C ABC \Ð=Ð,∵40C Ð=°,∴40ABC Ð=°,AB AC =Q ,D 为BC 的中点,AD BC \^,90BDA \Ð=°,∴90904050BAD ABC °°°°Ð=-Ð=-=;(2)证明:BE Q 平分ABC Ð,ABE EBC \Ð=Ð,又∵EF BC ∥,∴EBC BEF Ð=Ð,∴EBF FEB Ð=Ð,BF EF \=,BEF \V 是等腰三角形;(3)解:AEF QV 的周长为15,15AE AF EF \++=,BF EF =Q ,15AE AF BF \++=,即15AE AB +=,BE Q 平分ABC V 的周长,=15AE AB BC CE \++=,ABC \V 的周长+1515=30AE AB BC CE ++=+.【变式训练】1.如图,在ABC V 中,AB AC =,D 为CA 延长线上一点,DE BC ^于点E ,交AB 于点F .(1)求证:ADF △是等腰三角形(1)试判断折叠后重叠部分△的面积.(2)求重叠部分AFC△【详解】(1)解:AFC∵四边形ABCD是长方形,∥,∴AD BC一、单选题1.(2023上·河南许昌·八年级统考期中)等腰三角形的一个底角为80°,则这个等腰三角形的顶角为( ).A .20°B .80°C .100°D .20°或100°【答案】A【分析】本题主要查了等腰三角形的性质.根据“等腰三角形两底角相等”,即可求解.【详解】解:∵等腰三角形的一个底角为80°,∴等腰三角形的顶角为180808020°-°-°=°.故选:A2.(2024下·全国·七年级假期作业)如图,在ABC V 中,,AB AC AD =为BC 边上的中线,30B Ð=°,则CAD Ð的度数为( )A .50°B .60°C .70°D .80°【答案】B【解析】略3.(2023上·广东珠海·八年级校考阶段练习)下列条件中,可以判定ABC V 是等腰三角形的是( )A .40B Ð=°,80C Ð=°B .123A BC ÐÐÐ=::::C .2A B CÐ=Ð+ÐD .三个角的度数之比是2:2:1【答案】D【分析】本题考查了等腰三角形的判定,三角形内角和定理,熟练掌握等腰三角形的判定是解题的关键.利A.16【答案】A【分析】此题考查的是全等三角形的判定与性质、等腰三角形的性质,解题关键是掌握并会运用全等三角形的判定与性质、等腰三角形性质定理.二、填空题【答案】117°/117度【分析】本题考查等腰三角形的性质,三角形内角和定理与外角的性质,根据等边对等角可得54BAC BCA °Ð=Ð=,CAE CEA Ð=Ð127CAE ACB Ð=Ð=°,1BAD Ð=Ð【答案】10°,80°,140°或20°【详解】本题考查了等腰三角形的性质,先利用三角形内角和定理可得:AP AB =时;当AP AB =时;当BA BP =解:∵130ABC Ð=°,30ACB Ð=°,+ ∵BAC Ð是ABP V 的一个外角,∴20BAC APB ABP Ð=Ð+Ð=°,∵AB AP =,∵AB AP =,20BAP Ð=°,∴180802BAP ABP APB °-ÐÐ=Ð==°;当BA BP =时,如图:∵BA BP =,∴20BAP BPA Ð=Ð=°,∴180140ABP BAP BPA Ð=°-Ð-Ð=°;当PA PB =时,如图:∵PA PB =,∴20BAP ABP Ð=Ð=°;综上所述:当ABP V 是等腰三角形时,故答案为:10°,80°,140°或20°.11.(2023上·广东汕尾·八年级校联考阶段练习)用一条长为21cm 的细绳围成一个等腰三角形.(1)如果腰长是底边长的3倍,那么各边的长是多少?(1)求BD的长.(2)求BE的长.【答案】(1)4 (2)5,AE CD ^Q ,AD AC =AE \平分CAD Ð,CAE DAE \Ð=Ð,在CAE V 和DAE V 中,当AD BC^时,Q AB AC=,\142BD CD BC===,Q DEFV的周长DE DF EF=++,\DEFV的周长CE EF CD=+++(1)若120BAC Ð=°,求BAD Ð(2)求证:ADF △是等腰三角形.【答案】(1)60度(2)见解析(1)求证:BD CE =;(2)若BD AD =,B DAE Ð=Ð,求【答案】(1)见解析(2)108BAC Ð=°∵,AB AC AD AE ==.∴,BF CF DF EF ==,∴BD CE =.(2)∵,AB AC AD AE ==,AF ^∴BAF CAF Ð=Ð,DAF EAF Ð=Ð【答案】(1)等腰;(2)3;(3)12;(4)30;(5)5cm【分析】本题考查平行线的性质,角平分线的定义,对角对等边.(1)平行线的性质结合角平分线平分角,得到B C Ð=Ð,即可得出结果;(2)平行线的性质结合角平分线平分角,得到A ABC CB =Ð∠,进而得到AB AC =即可;(3)同法(2)可得:BD DE =,利用AB AD BD =+,求解即可;(4)同法(2)得到,FD BD CE EF ==,推出ADE V 的周长等于+AB AC ,即可得出结果;(5)同法(2)得到,PD BD PE CE ==,推出PDE △的周长等于BC 的长即可.掌握平行线加角平分线往往存在等腰三角形,是解题的关键.【详解】解:(1)∵AE BC ∥,∴,DAE B CAE C Ð=ÐÐ=Ð,∵AE 平分DAC Ð,∴DAE CAE Ð=Ð,∴B C Ð=Ð,∴ABC V 是等腰三角形;故答案为:等腰;(2)∵BC 平分ABD Ð,AC BD ∥,∴,ABC DBC ACB DBC Ð=ÐÐ=Ð,∴A ABC CB =Ð∠,∴3AB AC ==;故答案为:3;(3)同法(2)可得:7BD DE ==,∴5712AB AD BD =+=+=;故答案为:12;(4)同法(2)可得:,FD BD CE EF ==,∴ADE V 的周长30AD AE DE AD AE DF EF AD AE BD CE AB AC =++=+++=+++=+=;故答案为:30;(5)同法(2)可得:,PD BD PE CE ==,∴PDE △的周长5cm PD PE DE BD CE DE BC =++=++==;故答案为:5cm .理解概念:(1)如图1,在Rt ABC △中,90ACB Ð=°,CD AB ^,请写出图中两对概念应用:(2)如图2,在ABC V 中,CD 为角平分线,40A Ð=°,60B Ð=°.求证:动手操作:(3)当ACD V 是等腰三角形,DA DC =时,如图,则50ACD A Ð=Ð=°,BCD Ð=∴100ACB ACD BCD Ð=Ð+=°∠当ACD V 是等腰三角形,DA AC =则65ACD ADC Ð=Ð=°,BCD Ð∴5065115ACB Ð=°+°=°;当ACD V 是等腰三角形,CD AC =则1803ACD BCD B °-Ð=Ð=Ð=∴2603ACB ACD BCD Ð=+=∠∠当BCD △是等腰三角形,DB =则BDC BCD Ð=Ð,设BDC BCD x Ð=Ð=,则B Ð=则1802ACD B x Ð=Ð=°-,由题意得,180250x x °-+°=,230x °。
等腰三角形知识点及习题

1、掌握三角形的性质、判定2、考点:三角形的性质 中位线 30度的直角三角形性质 直角三角形的斜边中线 三角形的判定3、三角形的三边关系定理及推论(1)三角形三边关系定理:三角形的两边之和大于第三边。
推论:三角形的两边之差小于第三边。
(2)三角形三边关系定理及推论的作用: ①判断三条已知线段能否组成三角形 ②当已知两边时,可确定第三边的范围。
③证明线段不等关系。
7、三角形的内角和定理及推论三角形的内角和定理:三角形三个内角和等于180°。
推论:①直角三角形的两个锐角互余。
②三角形的一个外角等于和它不相邻的来两个内角的和。
注:在同一个三角形中:等角对等边;等边对等角;大角对大边;大边对大角。
8、 三角形的面积=21×底×高 9、新知: 新知:等腰三角形1、等腰三角形的性质(1)等腰三角形的性质定理及推论:定理:等腰三角形的两个底角相等(简称:等边对等角)推论1:等腰三角形的顶角平分线、底边上的中线、底边上的高重合。
推论2:等边三角形的各个角都相等,并且每个角都等于60°。
(2)等腰三角形的其他性质:①等腰直角三角形的两个底角相等且等于45°②等腰三角形的底角只能为锐角,不能为钝角(或直角),但顶角可为钝角(或直角)。
④等腰三角形的三角关系:设顶角为顶角为∠A ,底角为∠B 、∠C ,则∠A=180°—2∠B ,∠B=∠C=180A∠-︒2、等腰三角形两腰上的高相等,并且它们的交点和底边两端点距离相等。
那么这个三角形是等腰三角形; 2、有两条高相等的三角形是等腰三角形。
角 等边对等角等角对等边边底的一半<腰长<周长的一半两边相等的三角形是等腰三角形4、三角形中的中位线,要会区别三角形中线与中位线。
三角形中位线定理:三角形的中位线平行于第三边,并且等于它的一半。
三角形中位线定理的作用:位置关系:可以证明两条直线平行。
数量关系:可以证明线段的倍分关系知识点一:等腰三角形的性质——等边对等角,等腰三角形的两个底角 .例1:(2009年贵州黔东南州)如图,在△ABC 中,AB =AC ,点D 在AC 上,且BD =BC =AD ,则∠A 等于( )A .30oB .40oC .45oD .36o同步检测一:1.在△ABC 中,AB =AC ,①若∠A =70°,则∠B = °,∠C = °②若∠B =40°, 则∠A = °2.)已知等腰三角形的一个内角为50°,则这个等腰三角形的顶角为( ) A.50° B.80° C.50°或80° D.40°或65° 知识点二:等腰三角形的性质——三线合一等腰三角形的 、 、 互相重合。
专题01 等腰三角形的性质与判定(十六大题型+跟踪训练)(原卷版)

专题01等腰三角形的性质与判定(十六大题型+跟踪训练).....在ABC 中,若AB =,则ABC 是(.不等边三角形B .等边三角形C .直角三角形.等腰三角形.以下列线段为边不能组成等腰三角形的是(),4,51,1,1,则周长是()7cm 或8cm .条件不足,无法求出A .5cm B中,AB 15.如图,ABCA.80︒B 16.如图,在△ABC中,A.50︒B60中,17.如图,在ABCA.30︒B.18.如图,70∠=︒,AOBA.20°B.25°题型4:等边对等角的综合应用20.如图所示,在ABC 中,30A ∠=︒,80ACB ∠=︒,DE 垂直平分AC 交AB 于E ,垂足为D ,则BCE ∠=______.21.如图,直线a ∥b ,AB AC =,140 ∠=,则∠BAC 的度数是()A .100B .110C .120D .13022.如图,在∠ECF 的边CE 上有两点A 、B ,边CF 上有一点D ,其中BC =BD =DA 且∠ECF =27°,则∠ADF 的度数为()A .54°B .91°C .81°D .101°23.如图,在ABC 中,DE 垂直平分BC ,若6428CDE A ∠=︒∠=︒,,则ABD ∠的度数为()A .100︒B .128︒C .108︒D .98︒70B ∠=︒,则BDF ∠等于(A .65︒B .26.如图,在ABC 中,AB =27.如图,,∥DE AB AE 平分∠28.如图,在ABC 中,AB (1)求证:ABD △≌△(2)若3BD =,5CD =题型6:等腰三角形的“三线合一”30.等腰三角形的“三线合一”指的是()A .中线,高线,角平分线互相重合B .顶角的平分线,中线,高线三线互相重合C .腰上的中线,腰上的高线,底角的平分线互相重合D .顶角的平分线,底边上的中线及底边上的高线三线互相重合31.如图,在ABC 中,AB AC =,D 是BC 边上的中点,54B ∠=︒,则DAC ∠等于()A .36°B .45°C .54°D .72°32.在ABC 中,AB AC =,AD BC ⊥于点D ,若6BC =,则BD =()A .2B .3C .4D .533.下列说法错误的是()A .等腰三角形两腰上的高相等B .等腰三角形两腰上的中线相等C .等腰三角形两底角的平分线相等D .等腰三角形高、中线和角平分线重合34.已知点P 到ABC 的两边AB ,AC 所在直线的距离相等,且PB PC =,则下列命题为假命题的是()A .若点P 在边BC 上,则AB AC=B .若点P 在ABC 内部,则AB AC=C .若点P 在ABC 外部,则AB AC=D .若AB AC =,则点P 可能在边BC 上,可能在ABC 内部,也可能在ABC 外部题型7:等腰三角形的“三线合一”有关的最值问题35.如图,在ABC 中,AB AC =,=4BC ,面积是10;AB 的垂直平分线ED 分别交AC ,AB 边于E 、D 两点,若点F 为BC 边的中点,点P 为线段ED 上一动点,则PBF △周长的最小值为()A .7B .9C .10D .1436.如图,等腰ABC 中AB AC =,AD BC ⊥,EF 垂直平分AB ,交AB 于点E ,交BC 于点F ,点G 是线段EF 上的一动点,若ABC 的面积是26cm ,6cm BC =,则ADG △的周长最小值是()A .4.5cmB .5cmC .5.5cmD .6cm37.如图ABC 中,5AC BC ==,6AB =,CD 为ABC 的中线,点E 、点F 分别为线段CD 、CA 上的动点,连接AE 、EF ,则AE EF +的最小值为()A .2.4B .4.8C .5D .6题型8:等腰三角形“三线合一”的综合问题38.如图,在ABC 中,AB AC =,AD 是BC 边的中线,DE AB ⊥于点E ,DF AC ⊥于点F ,下列结论:①DE DF =;②BE CF =;③BDE CDF ∠=∠;④BDE DAF ∠=∠.其中正确的是()A .①②③B .①②④C .②③④D .①②③④39.如图,在 ABC 中,AB AC =,AD BC ⊥于点D ,DE AB ⊥于点E ,BF AC ⊥于点F ,5DE =cm ,则BF =()A .8cmB .10cmC .12cmD .14cm40.如图,ACB △和DCE △均为等腰直角三角形,且90ACB DCE ∠=∠=︒,点A 、D 、E 在同一条线上,CM 平分DCE ∠,连接BE ,下列结论:①AD CE =;②CM BE ∥;③2AE BE CM =+;④COE BOE S S = ,其中正确的有()A .1个B .2个C .3个D .4个题型9:等腰三角形“三线合一”的解答证明41.如图,点D ,E 分别在BA ,AC 的延长线上,且AB AC =,AD AE =.求证:DE BC ⊥.42.如图,在ABC 中,AB AC =,40BAC ∠︒=,AD 是BC 边上的高.线段AC 的垂直平分线交AD 于点E ,交AC 于点F ,连接BE .(1)试问:线段AE 与BE 的长相等吗?请说明理由;(2)求EBD ∠的度数.43.如图,在ABC 中,2AC AB =,AD 平分BAC ∠交BC 于点D ,E 是AD 上一点,且EA EC =.求证:EB AB ⊥.题型10:等角对等边证明等腰三角形44.如图,在ABC 中,B C ∠=∠,AD 平分BAC ∠,=5AB ,=6BC ,则=BD ()A .3B .4C .5D .645.已知一个三角形中两个内角分别是50︒和80︒,则这个三角形一定是()A .钝角三角形B .直角三角形C .等腰三角形D .不能确定46.ABC 的三边分别是a ,b ,c ,不能判定是等腰三角形的是()A .::2:2:3ABC ∠∠∠=B .::2:2:3a b c =C .50B ∠=︒,80C ∠=︒D .2A B C∠=∠+∠47.如图,在ABC 中,BD 平分ABC ∠,2C CDB ∠=∠,12AB =,3CD =,则ABC 的周长为()A .2B .24C .27D .3题型11:等角对等边证明等腰三角形的解答证明48.已知:如图,在ABC 中,点D 在CA 边的延长线上,AE 平分DAB ∠,AE BC ∥.求证:ABC 为等腰三角形.49.如图,在ABD △和ACD 中,AB AC =,BD CD =.(1)求证:ABD ACD △≌△;(2)过点D 作∥DE AC 交AB 于点E ,求证:AED △是等腰三角形.50.已知ABC 中,AD 平分BAC ∠交BC 于点D ,且2B C ∠=∠.(1)如图1,求证:AB BD AC +=;(2)如图2,延长CB 至点E ,使BE AB =,连接AE ,若36C ∠=︒,直接写出图中所有的等腰三角形(ABC 和ADE V 除外).题型12:等角对等边证明边长相等、求边长51.如图,已知12∠=∠,B C ∠=∠,不正确的等式是()A .AB AC =B .BAE CAD ∠=∠C .BE DC =D .BD DE=52.如图,ABC 中,BD 平分ABC ∠交AC 于点D ,过点D 作DE BC ∥交AB 于点E ,若12AB =,7DE =,则AE 的长为()A .5B .6C .7D .853.如图,点P 是AOB ∠的角平分线OC 上一点,点Q 是OA 上一点,且PQ OB ∥,若2PQ =,则线段OQ 的长是()A .1.8B .2.5C .3D .254.如图,在ABC 中,BE 平分ABC ∠,DE BC ∥.若8DE =,5AD =,则AB 的长为()A .13B .12C .10D .955.如图,在ABC 中,45AB AC ==,,ABC ∠和ACB ∠的平分线交于点E ,过点E 作MN BC ∥分别交AB AC ,于M ,N ,则AMN 的周长为()A .8B .9C .10D .不确定56.如图,ABC DEF ≌△△,点E 在AC 上,B ,F ,C ,D 四点在同一条直线上.若40,35A CED ∠=︒∠=︒,则下列结论正确的是()A .,EF EC AB FC ==B .,EF EC AE FC≠=C .,EF EC AE FC =≠D .,EF EC AE FC≠≠57.如图,在ABC 中,AB AC =,AD BC ⊥于点D .(1)若37B ∠=︒,求CAD ∠的度数;(2)若点E 在边AC 上,EF AB ∥交AD 的延长线于点F .求证:AE FE =.58.如图,在四边形ABCD 中,AD BC ∥,E 是AB 的中点,连接DE 并延长交CB 的延长线于点F ,点G 在边BC 上,且GDF ADF ∠=∠.连接EG ,判断EG 与DF 的位置关系,并说明理由.题型13:直线上与已知两点组成等腰三角形的点59.如图,ABC ,点P 为直线AC 上的一个动点,若使得ABP 是等腰三角形.则符合条件的点P 有()A .1个B .2个C .3个D .4个60.如图,线段AB 的一个端点B 在直线m 上,直线m 上存在点C ,使ABC 为等腰三角形,这样的点C 有()A .2个B .3个C .4个D .5个61.如图,直线a b ,相交于点O ,150∠=︒,点A 在直线a 上,直线b 上存在点B ,使以点O A B 、、为顶点的三角形是等腰三角形,这样的B 点有()A .1个B .2个C .3个D .4个题型14:等腰三角形有关的尺规作图62.如图,给出了尺规作等腰三角形的三种作法,认真观察作图痕迹,下面的已知分别对应作图顺序正确的是()①已知等腰三角形的底边和底边上的高;②已知等腰三角形的底边和腰;③已知等腰三角形的底边和一底角.A .①②③B .②①③C .③①②D .②③①63.如图(1),锐角ABC 中,AB BC AC >>,要用尺规作图的方法在AB 边上找一点D ,使ACD 为等腰三角形,关于图(2)中的甲、乙、丙三种作图痕迹,下列说法正确的是()A .甲、乙、丙都正确B .甲、丙正确,乙错误C .甲、乙正确,丙错误D .只有甲正确64.已知锐角40AOB ∠=︒,如图,按下列步骤作图:①在OA 边取一点D ,以O 为圆心,OD 长为半径画 MN ,交OB 于点C .②以D 为圆心,DO 长为半径画 GH, GH 与OB 交于点E ,连接DC 并延长,使DC 的延长线交 GH于点P ,连接DE ,则POC ∠的度数为__________.题型15:格点中画等腰三角形(网格问题)65.由24个边长为1的小正方形组成的64⨯的网格中,线段AB 的两个端点都在格点(小正方形的顶点)上.请在所给的网格中各画一个△ABC ,使得△ABC 是轴对称图形,并画出其对称轴.(画出两种情况即可,全等图形视为一种情况)66.图1,图2均是44⨯的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点称为格点,点A ,B ,C 均为格点.只用无刻度的直尺,分别在给定的网格中找一格点M ,按下列要求作图:(1)在图1中,连接MA ,MB ,使MA MB =;(2)在图2中,连接MA ,MB ,MC ,使MA MB MC ==.67.如图,在每个小正方形的边长均为1的方格纸中,有线段AB 和线段DE ,点A 、B 、D 、E 均在小正方形的顶点上.(1)在方格纸中画出以AB 为底的等腰ABC (2)在方格纸中画出以DE 为一边的等腰DEF 直接写出DC 的长度.题型16:等腰三角形的性质和判定综合题68.如图,在ABC 中,90BAC ∠=︒,AB 90EDF ∠=︒,下列结论:①BED AFD △≌△积,则1211142S S S ≤≤;④EF AD =;所有正确的结论是(A .①③B .①③④69.如图,在Rt ABC 中,90CAB ∠=︒,AB 于点F ,且AE AF ⊥,AH BF ⊥,下列说法:A FCB S BF AH =⋅四边形⑤.正确的有()个A .2B .370.在Rt ABC △中,AC BC =,点D 为AB 中点,BC 交于E ,F 两点.下列结论:①AE BF +=④2222AE CE DF +=.其中正确的是(A .①②③④B .①②③C .①④D .②③71.在ABC 中,90ACB ∠=︒,AC BC =,点D 在射线BC 上(不与B ,C 重合),连接AD ,过点B 作BF AD ⊥,垂足为F .(1)如图1,点D 在线段BC 上,若AF 恰好平分CAB ∠,求证:AB AC CD =+.(2)如图2,点D 在线段BC 上,点M 是直线BF 上的一点,且AF 平分MAC ∠,探究AC 、CD 、AM 之间的数量关系,并说明理由.(3)如图3,若点D 在线段BC 的延长线上()CD BC <,点M 是直线BF 上的一点,且AF 平分MAC ∠,4AM =,8BD =,求CD 的长度.一、单选题1.等腰三角形的三边均为整数,且周长为13,则底边是()A .1或3B .3或5C .1或5D .1或3或52.如图,ABC 中,AC AD BD ==,80CAD ︒∠=,则B ∠等于()A .25︒B .30︒C .35︒D .40︒3.在等腰△ABC 中,AB=AC ,其周长为16cm ,则AB 边的取值范围是()A .1cm <AB <4cm B .3cm <AB <6cmC .4cm <AB <8cmD .5cm <AB <10cm4.如图,在ABC 中,B C ∠=∠,点,D E 都在边BC 上,且BD CE =,若3AD =,则AE 的长为()A .90αβ+=︒B 6.如图,在ABC 中,心,大于12AD 长为半径作弧,两弧交于点()A .10︒B 7.如图,ABC 中,CAB ∠()A .75︒B 8.如图,在ABC 中,定ADE V 是等腰三角形的是(A .122∠=∠B .1∠+A .7B .810.如图,在等腰ABC 中,BE ,若8BC =,则BCE 的面积为(A .16B .2411.如图,AOB ∠是一角度为且OE EF FG GH ===…,在A .4根B .5根12.在ABC 中,45ACB ∠=︒,过C 交于点F ,过点E 作EH CD ⊥分别交的中点,连接EQ .下面结论:①ABE 2GQPAHP S CQ S PH =△△.其中正确的是(A .①②③④B .①②③⑤二、填空题13.用一条长为20cm 的细绳围成一个边长为20.如图,在ABC 中,点F 是高21.如图,在ABC 中,BAC ∠22.已知()0,2A 、()4,0B ,点C 在x 轴上,若23.如图,在ABC 中,B ∠与C ∠的平分线交于点若5AB =,4AC =,则ADE V 的周长是24.如图,AD 和CD 分别为ABC 的两个外角的平分线,E 和F 给出以下结论:①ED DF =;②确的是.三、解答题25.如图,已知A B ∠=∠,AD BC =,AC 和BD 相交于点E .求证:BDC ACD ∠=∠.26.如图,在ABC 中,AB AC =,CE 平分ACB ∠,EC EA =.(1)求A ∠的度数;(2)若BD AC ⊥,垂足为D ,BD 交EC 于点F ,求1∠的度数.27.在由6个大小相同的小正方形组成的方格中,(1)如图1,A ,B ,C 是三个格点(即小正方形的顶点),判断AB 与BC 的关系,并说明理由;(2)如图2,连接三格和两格的对角线,求αβ∠+∠的度数.28.如图,将ABC 绕点A 逆时针旋转得到AB C ''△.若点B 的对应点B '恰好落在BC 上,84,BAB AB B C '''∠=︒=,(1)求C ∠的度数;(2)求BAC ∠的度数.29.如图,已知在ABC 中,AB AC =,AD BC ⊥,垂足为D .过点C 作CE AB ∥,连接ED 并延长交AB 于点F ,65BCE ∠=︒.(1)求CAD ∠的大小;(2)求证:CDE BDF △△≌;(3)直接写出线段AC ,AF ,CE 之间的数量关系______.30.如图,在AOB 中,90AOB ∠=︒,OA OB =,C 是AB 边上一点(点C 与A ,B 不重合),连结OC ,将线段OC 绕点O 按逆时针方向旋转90︒得到线段OD ,连结CD 交OB 于点E ,连结BD .(1)求证:AOC BOD ≌ .(2)当BE AC =时,求BDE ∠的度数.31.如图,在ABC 中,90C ∠=︒,4cm AC BC ==,点D 是斜边AB 的中点.点E 从点B 出发以1cm /s 的速度向点C 运动,点F 同时从点C 出发以一定的速度沿射线CA 方向运动,规定当点E 到终点C 停止运动,设运动的时间为x 秒,连接DE 、DF .(1)求ABC 的面积;(2)当1x =且点F 运动的速度也是1cm /s 时,求证:DE DF =;(3)若动点F 以3cm /s 的速度沿射线CA 方向运动,在点E 、点F 运动过程中,如果存在某个时间x ,使得ADF 的面积是BDE 面积的两倍,请你求出时间x 的值.32.如图,在ABC 中,90BAC ∠=︒,AB AC =,D E ,是平面内两点,135ADC ∠=︒(1)如图1,若AD BE =,20∠=∠=︒ABE BCD ,求BAE ∠的大小;(2)如图2,若BD CE =,180AEC ADB ∠+∠=︒,BF CD ∥交AD 延长线于F ,求证:+=AD AE DF ;(3)如图3,若BD CE =,180AEC ADB ∠+∠=︒,3CD =,直接写出CED △的面积.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
等腰三角形性质及判定
等腰三角形的性质
知识点一:等腰三角形的定义
1.等腰三角形的两边的长为3和5,则其周长为_____________
2.等腰三角形的两边的长分别为2和4,则取周长为__________
3.等腰三角形的周长为29,其中一边长为7,则它的底边长为________
4.等腰三角形的一个角为40°,则其余角度为_____________
5.等腰三角形的一个角为120°,则其余角为____________
知识点二等边对等角
6.△ABC中,AB=AC,∠B=70°,则∠A的度数是___________
7.如图,AB∥CD,点E在BC上,且CD=CE,∠D=80°,则∠B的度数为_________。
第7题第8题第9题
8.如图,在△ABC中,AB=AC,AD∥BC,若∠1=70°,则∠BAC=___________
9.如图,△ABC中,AB=AC,∠B=40°,CD=AC,则∠DAC=_________,∠DAB=__________-
10.如图,△ABC中,AB=AC,AE平分△ABC的外角∠DAC,求证:AE∥BC。
知识点三:等腰三角形的“三线合一”
11.在△ABC中,AB=AC,AD⊥BC于点D,若AB=6,CD=4,则△ABC的周长为_________-
12.在△ABC中,AB=AC,D为BC的中点,若∠BAD=20°,则∠C=_________
13.如图,在△ABC中,AB=AC,BD=CD,DE⊥AB于E,DF⊥AC于F,求证:DE=DF
14.如图,已知AB=AC=AD,且AD∥BC,求证:∠C=2∠D
15.在△ABC中,AC=AB,点D在AB上,BC=BD,∠ACD=15°,求∠B的度数。
16.如图,AB=AC=CD,AD=BD,求∠BAC的度数。
17.如图1.在△ABC中,AB=AC,BD⊥AC于D.
(1)若∠A=50°,则∠DBC=__________,∠A= ,则∠DBC=____________
(2)如图2,若∠BAC为钝角,猜想:∠DBC与∠BAC之间的数量关系,并给予证明。
18.如图,△ABC中,AC=BC,∠C=90°,E为AC上一点,F为CB延长线上一点,AE=BF,EF交AB于点G,EH⊥AB于点H。
(1)画出△AEH关于直线EH对称的三角形;
(2)求GH AB
等腰三角形的判定:
1.在△ABC中:
(1)若∠B=∠C,AB=5,则AC=_______
(2)若∠B =50°,∠C=65°,则△ABC的形状是______
(3)若∠A:∠B:∠C=1:1:2,则△ABC的形状是____________.
2.如图,△ABC中,AB=AC,D为AC上一点,∠A=36°,BD平分∠ABC,BE=BC,则图中共有_________个等腰三角形。
3.如图,已知△ABC的角平分线CD交AB于D,DE∥BC交AC于E,若DE=3,AE=4,
则AC=________
4.如图,在△ABC中,AD平分∠BAC交BC于D,EF∥AD,交AC于E,交BA的延长线于F,求证:△AEF 为等腰三角形。
5.如图,在△ABC中,BO平分∠ABC,CO平分∠ACB,MN经过点O,且MN∥BC分别交AB,AC于M,N.
(1)求证:MN=BM+CN
(2)若AB=12,AC=18,求△AMN的周长。
6.如图,在△ABC中,点D,E分别在BC,AB上,BD=BE,∠BAD=∠BCE,AD与CE交于点F.
(1)求证:BA=BC
(2)判断△AFC的形状,并说明理由。
7.如图,点F是∠ABC的平分线和外角∠ACG的平分线的交点,线段DE、DB、EC之间有何数量关系,并证明。
8.如图,在△ABC中,AB=AC,D为BC边上一点,∠B=30°,∠DAB=45°
(1)求∠DAC的度数
(2)求证:DC=AB
9.如图,已知CE为△ABC的角平分线,D为BC上一点,AD交CE于F,若∠BAC=∠ADC=90°。
(1)求证:∠DAC=∠B
(2)求证:AE=AF
10.如图,在△ABD中,∠ABC=45°,AC,BF为高,AC,BF相交于E点,(1)求证:BE=AD
(2)过点C点作CM∥AB交AD于M点,连接EM,求证:BE=AM+EM
利用等腰三角形的性质求角度
练习题
1.如图,AB=AD=CD,∠BAD=20°,则∠B=_______,∠C=__________
第1题第2题第3题
2.如图,AB=BC=CD,EC=ED=EF,∠A=20°,则∠DEF=___________
3.如图,点K,B,C分别在GH,GA,KA上,且AB=AC,BG=BH,KA=KG,则∠BAC的度数为___________
4.如图,在△ABC中,AB=AC,点D在AC上,且BD=AD=BC,求△ABC的各角的度数
5.如图,点D在AC上,点E在AB上,且AB=AC,BC=BD,AD=DE=BE,求∠A的度数
6.如图,AB=AC,AB的垂直平分线交AC于D点,若AD=BC
(1)求∠B的度数
(2)若点E在BC的延长线上,且CE=CD,连接AE,求∠CAE的度数
整体思想求角度
7.已知△ABC中,∠A= ,点E,D,F分别在BC,BA,AC上
(1)如图1,若BE=BD,CD=CF,则∠EDF=_________
(2)如图2,若BD=DE,DC=DF,则∠EDF=_________
(3)如图3,若BD=CF,CD=BE,AB=AC,则∠EDF=________
(4)如图4,若DE⊥AB,DF⊥BC,AB=AC,则∠EDF=____________.
等腰三角形中的分类讨论
1.等腰三角形的两边的长为5和6,则其周长为_____________.
2.等腰三角形的两边的长为4和9,则其周长为____________。
3.若等腰三角形的一个角为70°,则其顶角的度数为_________
4.若等腰三角形的一个角为100°,则其底角的度数为_________
5.等腰三角形一腰上的高于另一腰的夹角为45°,则其顶角的度数为_________
6.等腰三角形一腰上的中线把三角形分成两个三角形,两个三角形的周长之差为8,底边是5,则腰长为_________.
7.已知△ABC中,CA=CB,AD⊥BC于点D,∠CAD=40°,则∠B的度数为_________
8.△ABC的高AD、BE所在的直线交于点M,若BM=AC,求∠ABC的度数。
动点引起的分类讨论
9.已知△ABC中,AC=AB,∠BAC=30°,点D为直线BC上异于B,C的一点,若△ABD是等腰三角形,求∠D 的度数。
10.已知点P为线段CB上方一点,CA⊥CB,PA⊥PB,且PA=PB,PM⊥BC于M,若CA=1,PM=4,求CB的长。
