北大高微讲义第4章 需求
高级微观经济学 讲义4

如果给定效用水平 ∈ , 根据值域的定义, 存在某个 ∈ | 得 ,从而保证 ∈ 不是空集。 3.
。如何证明这一结 目标函数 ⋅ 在 上连续(或在 上连续) 论?在 中任取一点 ,证明对收敛于 的每个点数列 , ⋅ → ⋅ 。 再看约束集 ∈ | 的特征。 时,这一集合非空。
4.
非空集:当 ∈
∗
证明:取 , ,设 。不难看出,
9
5.
,
在 上为一阶齐次函数
证明:取 0。我们证明在 , 和 , 下,支出最小化问题的解 相同。设前者的解为 ,后者的解为 。不难看出, , 因此, , , 就是说, , , 证毕 6. , 在 上为凹函数 , ,取λ ∈ 0,1 。 ≡λ 设在 因此, , 因此, λ , 1 λ λ , λ ⋅ ∗ 1 λ ⋅ 1
,
∗∗
。也就是说, ,
函数 ⋅ 在 上连续,因此,存在 并且, ⋅ 这与
∗∗ ∗
1使得
∗
,
。 证毕
是
,
下的最优解的前提矛盾。
4.
,
在 上递减
3
设
。求证: , , ;在 。 , 下,消费者选择 。
证明:设在 , 下,消费者选择 因为 ,所以, 由于 整理得到 ⋅ 因此, ⋅ 就是说,在价格为 , ,因此, ⋅
并且,效用函数严格单调,因此, ,∀ ∈ 就是说, min 在 取 中最小值时,支出最小化问题为 min
∈
。
。
⋅
. .
min
它的解显然为 。因为商品束 满足约束条件: min 同时实现最小支出: 0 ⋅ ⋅ ∀ ∈ ∈ | min 证毕 2. 在其定义域 上连续
8
定理 A2.21 最大值定理 3. 对所有的 ≫ ,在 上严格递增且无上界 。设 。我们要
高级微观经济学讲义(清华 白重恩) Notes2-04

四、偏好关系与选择规则之间的关系1. Question :Can the choice structure be generated (or rationalized) by a rational preference relation? In other words, can we find some rational preference relation such that *()(,)C C =i i ? A natural candidate of such a is the * that is implied by C(•). ()**(,*)C C →→i i Question: ()*(,*)?C C =i iIn order for C to be rationalized by some preference relation, we need C to satisfy:and ', , and ',(),(')B B x y B B x C B y C B ∀∈∈∈(i.e. x is chosen when y is also available and y is chosen when x is also available), then (),(')y C B x C B ∈∈.Another way of expressing this is:定义6:(WARP or Weak Axiom of Revealed Preference )Suppose B ∈B ,,, and ()x y B x c B ∈∈. Then B ′∀∈B ,with , and ()x y B y c B ′′∈∈, we must have ()x c B ′∈.In the two earlier examples, C 1 satisfies WARP but C 2 does not.Recall the definition of C*, the choice rule implied by :B ∀∈B {}*(, ): for every assumeC B x x y y B φ=∈≠ Q :If is rational, does *(, C i satisfy WARP?A :Yes, i.e., WARP is a necessary condition for C to be rationalized by a rational preference relation. 证明:假定,,*(),,,,*()x y B x C B B x y B y C B ∈∈Β∈′′′∈Β∈∈且 要证:*(x C B ′∈) *(),,*(), , for all *()x C B x y y C B y z for z B x z z B x C B ∈⇒′′∈⇒∀∈′∴∈′∈ 由即 利用了理性偏好的传递性2、 Question: Is WARP also a sufficient condition? (choice rule →preference relation)Suppose C satisfies WARP, can we always find a s.t *()(,)C C =i i ?A: No!Counter example :{}{}{}{}{}x z z y z y x X ,,,,y,x,B ,,=={}{}{}(,){}(,){}(,){}.C x y x C y z y C z x z ===可以证明这样的()C i 是满足WARP 的,但是它所产生的* 却是非理性的:but .x y y x x y ≥⇒ Similarly, and ,y z z x contradictory to rationality.3、 命题3:给定choice structure (B ,()C i ),假定a) Satisfy WARP ;b) B contains all subsets of X with three or less elements 。
北大高微讲义第3章 显示偏好理论

所以,有(x1j − x0j ) = (x2j − x0j ) + (x1j − x2j )
两边同除以∆pj
,得:
(x1j − x0j ) ∆p j
=
(x2j − x0j ) ∆p j
+
(x1j − x2j ) ∆p j
(2)
以(1)替代(2)中最后一项的∆pj ,有:
(x1j − x0j ) ∆p j
设 x t 是 价 格 p t时 被 选 择 的 商 品 束 , x是使得pt xt > pt x 的另一个商品束, 则 称 x t 直 接 地 显 示 出 严 格 优 于 x。 记为:xt P D x
4
3.1 显示偏好公理
3、间接显示偏好( indirectly revealed preference) 亦称:传递闭包关系(transitive closure)
即: ∆p∆x ≤ 0
22
3.4 希克斯补偿和斯拉茨基补偿
二、显示偏好和两种补偿的符号:
结论:
对于两种不同定义的补偿效应的符
号来说,均有
∆p∆x ≤ 0
23
3.4 希克斯补偿和斯拉茨基补偿
三、希克斯补偿需求曲线和斯拉茨基补偿 需求曲线
24
第3章 显示偏好理论
• 3.1 显示偏好公理 • 3.2 显示偏好和无差异曲线 • 3.3 显示偏好和斯拉茨基方程 • 3.4 希克斯补偿和斯拉茨基补偿 • 3.5 显示偏好和生活水平比较
第1部分 消费者行为理论
• 第1章 消费者的最优决策 • 第2章 比较静态分析 • 第3章 显示偏好理论 • 第4章 需求 • 第5章 消费者的福利变化 • 第6章 库恩 --- 塔克条件 • 第7章 不确定条件下的个人选择
高等代数课件(北大版)第四章-矩阵§4-2

则称 A 为反对称矩阵.
a1n a2n
ann
a1n a2n
0
§4.2 2024/3/7 矩阵的运算
数学与计算科学学院
性质
(1) A, B 对称 A B, A B 对称 ; A, B 反对称 A B, A B 反对称.
(2) A 对称,k P kA 对称 ; A 反对称,k P kA 反对称.
(3) 奇数级反对称矩阵的行列式等于零.
A A A A A (1)n A ,
n 为奇数时,A A A 0.
§4.2 2024/3/7 矩阵的运算
数学与计算科学学院
想一想 A, B 皆为 n 级对称矩阵, i) A, B 对称,积 AB对称吗? ii) A, B 反对称,积 AB 反对称吗?
例7 已知 A, B 皆为 n 级对称矩阵,证明:
AB 对称 AB BA.
证: 若AB对称,则有
AB ( AB) BA BA .
反过来,若AB=BA,则有 ( AB) BA BA AB. 所以 AB 对称.
§4.2 2024/3/7 矩阵的运算
数学与计算科学学院
例8 设 A 为 n 级实对称矩阵,且 A2 0,证明:
1
1,
12,
1 3
23
3,
An 3n1
1
3n1 3n1 A 3n1 2
3
1 2 1
3 2
1
3 2
3 1
.
§4.2 2024/3/7 矩阵的运算
数学与计算科学学院
附: 共轭矩阵
定义
当 A aij 为复矩阵时,用 aij 表示 aij 的共轭 复数, 记 A aij , A 称为 A 的共轭矩阵.
北大测试全套课件和教案 9. 第4章 第3讲

北大测试全套课件和教案 9. 第4章第3讲《软件测试基础》授课教案授课内容:第四章白盒测试技术授课课次:第9次课授课时数:2学时授课日期: 上课教室: 目的与要求:掌握白盒测试中基本路经测试的概念和方法;了解程序插桩的概念和方法。
教学重点:基本路经测试教学难点:程序插桩教学方式:1. 运用《白盒测试技术》课件进行课堂讲授,让学生理解基本路径测试的概念,掌握基本路径测试方法;2. 进行课堂练习,加深对基本路径测试的理解和使用。
教学内容:1.程序结构分析 2.DD路径测试 3.基本路径测试 4.程序插桩内容提要及时间分配:1、课前引导(8分钟)? 回顾6种覆盖法的基本思想。
? 白盒测试中有哪些常用方法?2、本课内容(75分钟)? 程序结构分析 ? DD路径测试 ? 基本路径测试 ? 程序插桩3、课后小结(5分钟)4、布置作业(2分钟)教学参考书:1. 软件测试方法和技术朱少民清华大学出版社2. 软件测试Paul C.Jorgensen 机械工业出版社讨论与思考:把第2章的NextDate问题的伪代码转换成为控制流图,并简化。
作业:1.请把下面的程序流程图转化成控制流图。
12364791181052.重新编写程序片断14~20,用嵌套if-then-else语句替代复合条件。
14. if(a=b)AND (b=c) 15. T hen Output(“Equilateral”)16. Else If(a<>b)AND(a<>c)AND(b<>c) 17. Then Output(“Scalence”) 18. Else Output(“Isosecles”) 19. EndIf 20. EndIf比较你改写后的程序和上面程序片断的圈复杂度。
复问题目:序号 1 2 3 题目学生成绩教学内容与方法步骤4.2.3程序结构分析引言:程序的结构形式是白盒测试的主要依据。
这一部分将从控制流分析和数据流分析的不同方面讨论如何分析程序结构。
高级微观经济学讲义(清华 白重恩) Notes6-04

1 1 1 ( , , ) 2 4 4
但是,心理学家的测试认为这样的等同可能会有问题,例如下面这样一个复合彩票
1 1 1 ( , ,0) = L1′ 2 2 2 1 1 1 ′ ( ,0, ) = L2 2 2 2
equivalent to ( ,
1 1 1 , ) 2 4 4
但消费者对这两种复合彩票的认识可能不同。 注意:本章后面假定 Consequentialist view,即只注重结果,认为上述等同成立。
2
X1 (1,0,0)
2004 年秋季
高级微观经济学
L = p1 x1 + p2 x2 + px3
其中,Pi≥0
p1 + p 2 + p3 = 1
定义 2:复合彩票(compound lottery) 若 L1……,LK 是简单彩票,α 1, ,α k 是得到相应简单彩票的概率, 为复合彩票。
∑α
∑p
i =1
N
i
=1 , x N }和相应的概率 {P1 , , p N }。
定义 1: 简单彩票 (Simple lottery) 定义为可能的结果 {x1 , Given X , the set of all lotteries ∆ = {( p1 ,..., pn ) pi ≥ 0 &
∑p
.
i
Î contradiction [2]下面证无差异曲线是平行的。 Choose L1 ~ L2 on one of the indifference line
∃α1 , L4 = α1L3 + (1 − α1 ) L2 ~ α1L3 + (1 − α1 ) L1 = L6 ≠ L5
北大高微讲义第5章 消费者的福利变化

∫
p q
x1 ( t ) d t
µ (t ; q , m )
=
∫
p q
p q
x1 ( t ) d t
µ ( p; q, m ) − µ (q; q, m ) = µ ( p; q, m ) = 即
∫
p q
x1 ( t )dt ( 1)
∫
x1 ( t ) d t + m
= ∆CS + m µ ( p; q, m ) = ∆C S + m
已知 :拟线性效用函数 下 的需求函数为 x1 ( p1) 其 可积性 方程 为 d µ (t ; q , m ) = x1 (t ) dt µ ( q; q, m ) = m 求: µ ( p; q , m )
21
5.2 CV、EV和ΔCS三者之间的关系
解:∫
p q
d µ (t ; q , m ) dt = dt
p1 p1
0 p1
∂e( p, u1 ) dp1 ∂p1
= ∫ 1 h1 ( p, u1 )dp1 显然,h1 ( p, u1 )是与u1相联系的商品1的补偿需求函数。
10
p0
5.1 消费者剩余变化、补偿变化和 等价变化的定义
3、 定义三:由支出函数到补偿需求曲线
结论: CV 是 当 u= u 0时 , 补 偿 需 求 曲 线 h1 ( p , u 0 )
26
5.3 加总:社会总福利
• 中心结论
V (P ) =
∫ ∑
P
∞
n
i =1
xi (t )d t = S C S
∂V (P ) = X (P ) ∂P
• 推导
27
5.3 加总:社会总福利
高级微观经济学讲义(清华 白重恩) Notes3-04
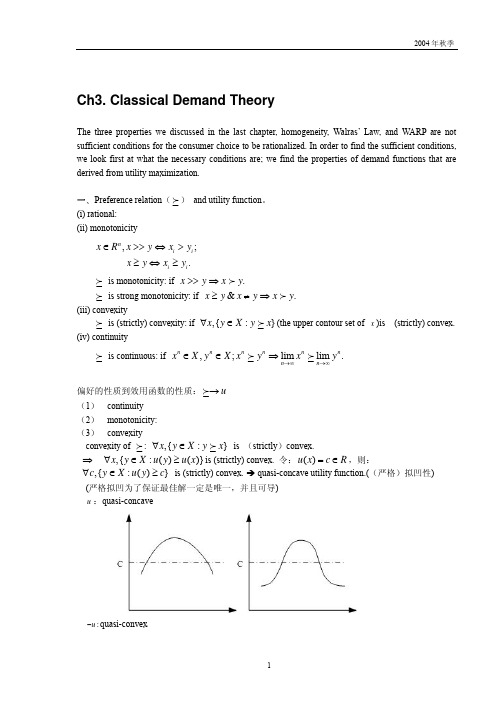
Ch3. Classical Demand TheoryThe three properties we discussed in the last chapter, homogeneity, Walras’ Law, and WARP are not sufficient conditions for the consumer choice to be rationalized. In order to find the sufficient conditions, we look first at what the necessary conditions are; we find the properties of demand functions that are derived from utility maximization.一、Preference relation ( ) and utility function 。
(i) rational: (ii) monotonicity,; .n i i i i x R x y x y x y x y ∈>>⇔>≥⇔≥is monotonicity: if .x y x y >>⇒is strong monotonicity: if &.x y x y x y ≥≠⇒(iii) convexityis (strictly) convexity: if ,{:}x y X y x ∀∈ (the upper contour set of x )is (strictly) convex. (iv) continuityis continuous: if ,;lim lim .nnnnnnn n x X y X x y x y →∞→∞∈∈⇒偏好的性质到效用函数的性质:u → (1) continuity (2) monotonicity:(3) convexity convexity of : ,{:}x y X y x ∀∈ is (strictly )convex.⇒ ,{:()()}x y X u y u x ∀∈≥is (strictly) convex. 令:()u x c R =∈,则:,{:()}c y X u y c ∀∈≥ is (strictly) convex. Î quasi-concave utility function.((严格)拟凹性)(严格拟凹为了保证最佳解一定是唯一,并且可导) u :quasi-concave:u −quasi-convexQuasi-concave and quasi-convex: monotone function; special e.g. line functionAnother proposition: if u is concave (convex) , f is strictly increasing, then f u is quasi-concave (quasi-convex).二、效用最大化问题(utility maximization problem )(UMP)1、 效用最大化问题 给定p ,w ,11max ()s.t. or (budget constraint)xn n u x px w px p x p x ≤=+⋅⋅⋅+性质1:只要u 是连续的,UMP 有解重写UMP {},max ()s.t. :,0xp w u x x B x px w x ∈=≤≥解的存在性和唯一性: B p,w 是闭集,并且有上下界,⇒B p,w 是紧集(compact set ),紧集上的连续函数最大化问题一定有解。
第6章 北大高微讲义库恩-塔克条件汇总

第1部分消费者行为理论•第1章消费者的最优决策•第2章比较静态分析•第3章显示偏好理论•第4章需求•第5章消费者的福利变化•第6章库恩---塔克条件•第7章不确定条件下的个人选择1第6章库恩---塔克条件(Kuhn —Tucker condition)一、K —T 条件•在最优化问题中,若–选择变量要求非负–约束条件是不等式则需要用K —T 条件来解决问题。
1、K —T 条件初步理解(1)关于选择变量非负的要求Max y =f (xs .. t x ≥0f ' (x ≤0, x ≥0, and f ' (x ⋅x =02第6章库恩---塔克条件(2)关于约束条件是不等式的要求:P1在(1)的基础上加入不等约束的要求Max x y =f (x 1, x 2, x 3 s . t . g 1(x 1, x 2, x 3 ≤r 1g 2(x 1, x 2, x 3 ≤r 2且x 1, x 2, x 3≥03()第6章库恩---塔克条件(3)关于(P1)最优解的推导第一步:加入两个虚设变量s 1、s 2 ≥0,将(P1)处理成以下的等价形式(P2)。
(即:去掉不等式约束条件)Max y =f (x 1, x 2, x 3 x , s(P2)s . t . g (x 1, x 2, x 3 +s 1=r 1g (x 1, x 2, x 3 +s 2=r 221且x 1, x 2, x 3, s 1, s 2≥04第6章库恩---塔克条件(3)关于(P1)最优解的推导第二步:假设去掉选择变量的非负要求,于是有:Z (x 1, x 2, x 3, s 1, s 2, λ1, λ2=f (x 1, x 2, x 3 +λ1(r 1−g (x1, x 2, x 3 −s 1 +λ2(r 2−g (x 1, x 2, x 3 −s 2 (P2' )∂z ∂z ∂z F . O . C . ===0∂x 1∂x 2∂x 3∂z ∂z ==0∂s 1∂s 2∂z ∂z ==0∂λ1∂λ2512第6章库恩---塔克条件(3)关于(P1)最优解的推导第三步:加上选择变量非负的要求。
北京大学裴伟伟有机化学讲义Chapter4精品PPT课件

第五节 卤代烷的化学性质 一 预备知识 二 亲核取代反应 三 消除反应 四 卤代烷的还原 五 卤仿的分解
一 预备知识
1. 电子效应
诱导效应
定义:因分子中原子或基团的极性(电负性)不同 而引起成键电子云沿着原子链向某一方向移动的效 应称为诱导效应。
O
特点 *沿原子链传递。 *很快减弱(三个原子)
三 偶极矩与有机分子的极性 偶极矩大,有机分子的极性大。
四 电负性与键的分类
C (2.5)
差值
F (4.1) 1.6
Cl (2.8) Br (2.7)
0.3
0.2
I (2.2) 0.3
极性共价键
共价键
第三节 卤代烷的构象
1,2-二氯乙烷的构象
有范德华吸引力
Cl
H
Cl
H C H 无范德华吸引力l
有偶极-偶极排斥力 H
氟化物(fluoride)
(CH3)3CI 三级丁基碘 Tert--butyl iodide 碘化物(iodide)
第二节 卤代烷的结构
一 碳卤键的特点
二 键长
C 成键轨道
sp 3
等性杂化
极性共价键, 成键电子对 偏向X.
Xsp 3
不等性杂化
C—H C—F C—C C—Cl C—Br C— I 110 139 154 176 194 214 (pm)
C+
••
H
电性特点:亲电性
结构特点: 平面型, sp2杂化。
R 1 +
C R 3
R 2
稳定性: 3oC+ > 2oC+ , 烯丙基C+ > 1oC+ > +CH3
高级微观经济学讲义(清华 白重恩) Notes1-04

⇒ u(x) ≥ u(y), u(y) ≥ u(z) ⇒ u(x) ≥ u(z) ⇒x z ⇒ 传递性
7、Question: if
is rational preference relation, can we find a U function representation?
答案:不一定能找到一个效用函数与之对应。 一个反例: X = ( x1 , x2 ) : x1 ∈ [ o, ∞ ) , x2 ∈ [ o, ∞ ) ,定义偏好关系为字典顺序,即,
∀x1,
( x1 ,2)
( x1 ,1)
u ( x1 ,2) > u ( x1 ,1) ⇒ ∃有理数ϕ ( x1 ),u ( x1 ,2) > ϕ ( x1 ) > u ( x1 ,1)
可以证明 x1 → ϕ ( x1 ) 是一个一一对应
设x1 < x 2
⇒ u ( x1 ,1) < u ( x1 ,2) < u ( x 2 ,1) < u ( x 2 ,2) ⇒ ϕ ( x1 ) < ϕ ( x 2 )
y.
∀x ∈ R n . define: e ≡ (1,1,...,1) ∃λ1 , λ2 ∈ R, s.t. λ1e ≥ x ≥ λ2 e ⇒ λ1e
define: set A,B.
x
λ2 e; (单调性的定义)
A ≡ {λ1 ∈ R : λ1e B ≡ {λ2 ∈ R : x
x};
λ2 e}.
Î
( x1 , x2 ) ( y1 , y2 ), if x1 > y1 , or x1 = y1 andx2 ≥ y2
{
}
可以证明字典序是理性的。 问题:是否存在一个函数 u, s.t , ( x1 , x 2 ) ( y1 , y 2 ) iff u ( x1 , x 2 ) ≥ ( y1 , y 2 ) ? Answer: No! 证明:反设存在这样一个 u 满足上述条件。
教学课件:第4章-章末复习课

理解难点内容
难点内容1
深入理解第4章中难以理解的概念和 理论,如“XXX”的内在含义和实际 应用。
难点内容2
掌握解决第4章中复杂问题的思路和方 法,如“XXX”问题的解题思路和技 巧。
提高应用能力
应用能力1
通过实际案例和习题,提高运用第4章知识解决实际问题的能 力。
应用能力2
培养学生对第4章知识的综合运用和创新思维能力,激发学生 的学习热情和兴趣。
教学课件:第4章-章末复习课
contents
பைடு நூலகம்目录
• 复习目标 • 知识回顾 • 重点难点解析 • 习题解答与解析 • 总结与展望
01 复习目标
掌握重点知识
重点知识1
掌握第4章中的核心概念和理论, 如“XXX”、“XXX”等。
重点知识2
理解第4章中重点公式和计算方法 ,如“XXX”公式的应用和计算 技巧。
习题三答案与解析
总结词:难题
详细描述:这道题难度较大,对学生的思维能力有较高的要求。在解题时,需要仔细分析题目中的条 件和要求,运用所学知识进行推理和判断。同时,要注意解题思路的清晰和严谨,避免出现逻辑错误 或遗漏。
05 总结与展望
本章总结
01
知识点回顾
02
回顾了第4章中涉及的核心知识点,包括但不限于课程内 容、重点概念、公式和例题解析。
鼓励学生在学习过程中积极思考、勇于探索,培养自主 学习和解决问题的能力。
THANKS FOR WATCHING
感谢您的观看
强调与第4章的关联,说明学习第5章需要具备哪些前导知识和技能。
学习建议
学习方法指导
提醒学生注意时间管理,合理安排学习进度,确保按时 完成学习任务。
数学讲义(高微)

(2) x* 为函数的全局最小值的解
,对于任意非零 dx 都成立。
⇒ d 2 y = f ''(x)(dx)2 ≥ 0
在满足必要条件的前提下,若函数取得唯一的最值的解,它的充分条件为
(1) d 2 y = f ''(x)(dx)2 < 0 ,对于任意非零 dx 都成立 ⇒ x* 为函数唯一的全局最大值
(4)函数为严格拟凸函数 ⇐ Bk (x) < 0(k = 1, 2,..., n)
3 函数间关系
(1) f (x) 是(严格)凹函数 ⇔ − f (x) 是(严格)凸函数; (2) f (x) 是(严格)拟凹函数 ⇔ − f (x) 是(严格)拟凸函数; (3) f (x) 是(严格)凹函数 ⇒ f (x) 是(严格)拟凹函数(反之不成立); (4) f (x) 是(严格)凸函数 ⇒ f (x) 是(严格)拟凸函数(反之不成立);
f1(x1, x2 ) f11(x1, x2 ) f21(x1, x2 )
f2 (x1, x2 ) f12 (x1, x2 ) 。 f22 (x1, x2 )
Bkπ
(x1, x2 )
=
0
∇f
πT k
∇fkπ
H
π k
,其中 H π (x) 表示海塞矩阵 H (x) 的指标(1,2,3,…,n)的任意
排序,
(5)单调函数既是拟凹函数也是拟凸函数 (6)凹(凸)函数相加后仍为凹(凸)函数,拟凹和拟凸函数则没有类似关系。
4 常见的拟凹函数
拟凹的效用函数 ⇔ 上等值集为凸集 ⇒ 凸的无差异曲线。
因为等产量曲线的概念几乎与无差异曲线是一致的,我们可以类推:
拟凹的生产函数 ⇔ 上等值集为凸集 ⇒ 凸的等产量曲线。
北大编译原理讲义chapter4_2

4.5.1 规范归约 归约 G=(VT,VN,S,P),α, β ∈(VT∪VN)*,A→β∈P, αAw αβw 。归约的过程是,已知αβw和产生 式A→β,用产生式A→β左部A替换αβw中的β, 得到符号串αAw。 从输入符号串出发 ,每次 从被归约的句型中找到一个产生式的右部 , 用其左部替换之,得到新的句型 ,直至归约到 文法的开始符号。 因为从左至右读入输入符号串,自然在被 归约的句型中找最左边的某个产生式的右部 (句柄)进行归约。
4.5 自底向上分析 把一个输入符号串逐步归约到文法的开始符 号。 这种方法的大致过程是,用一个栈,把输 入符号一个一个地移进到栈里,当栈顶形成某 个产生式的右部( 句柄)时,把栈顶的这一部 分替换成(归约为)它的左部符号。称作“移 进—归约”分析。 4.5.1 规范归约 句柄
4.5.2 “移进—归约”分析的栈实现
例4.12 G[S](4.12),其产生式如下: ①S→aABe ② A→b ③ A→Abc ④ B→d (4.12) 输入串 abbcde aAbcde aAde aABe S S S aABe SaABe aAde aAbcde A abbcde aAde B A aAbcde abbcde a b b c d e
· >
· > · >
$
$ $ $
归约
归约 归约 接受
算法4.5 算符优先分析法 方法: if (ab) or (ab) then begin /* 移进* / 把b推入栈中; 使ip前进到下一个符 号; end if a· then /* 归约* / b repeat 从栈中弹出符号 until 栈顶终结符号最近弹出的终结 else error 符号
找右句型的可归约串 的方法 $ <· · + <· · * <· · $ id > id > id > 1· 找可归约串 的右端; 2 · 找可归约串 的左端; 3· 归约 使用下面的优先关系表,分析过程如下:
北大高微讲义第2章 比较静态分析

20
2.1 斯拉茨基方程
3、斯拉茨基方程组
一 般 地 , 有 ∂x1(p,m) ∂h ∂h ∂x1(p,m) 1( p,u) 1( p,u) ∂ x1(p, m) ⋅⋅⋅⋅⋅ ⋅⋅⋅⋅⋅ , , ∂p ∂p ∂ p ∂ p n n 1 1 ∂m ∂x2( p, m) ∂x2(p,m) ∂h2( p,u) ∂h2(p,u) ∂x2(p, m) ∂p ,⋅⋅⋅⋅⋅ ∂p ∂p ,⋅⋅⋅⋅⋅ ∂p ( x1(p,m),⋅⋅⋅⋅⋅xn(p,m)) = − m ∂ n n 1 1 ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅ ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅ ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅ ∂xn(p,m) ∂ ( , ) ∂ ( , ) h p u h p u x p m x p m ( , ) ( , ) ∂ ∂ n n n n ∂p ,⋅⋅⋅⋅⋅ ∂p ∂p ,⋅⋅⋅⋅⋅ ∂p m ∂ 1 1 n n 共 n×n个 斯 拉 茨 基 方 程 。
13
2.1 斯拉茨基方程
(Slutsky equation)
写 成 矩 阵 形 式 为 : u11 u 21 − p1 u12 u 22 − p2 − p1 − p2 0 ∂ x1 ∂m ∂x2 ∂m ∂λ ∂m 0 = 0 −1
2
2.1 斯拉茨基方程
(Slutsky equation)
一、斯拉茨基方程的推导 1、利用最优决策的一阶条件:传统的推导方法 • 思路:(以n=2 为例)
∂ x1 求总效应 ∂ p = ? 1 ∂x1 求替代效应 ∂p u =u0 = ? 1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
21
4.2 复合商品
2、复合商品:函数的可分性和效用最大化
Key: • 在效用函数可分性的基础上,将最大化问题 分解为:子效用最大化和总效用最大化 • 将子效用最大化问题的约束条件设定为 px=mx • 令子效用函数v(x)为一次齐次效用函数
22
4.2 复合商品
2、函数的可分性和效用最大化
令:效用函数u ( x, z ) = U (v( x), z )是弱可分的。 • 子效用最大化
• 效用最大化模型
M ax s .t . u (c, L ) pc + wL = w L + m c( p, w, L, m ) L ( p, w, L, m )
最优解为需求函数:
8
4.1 禀赋的收入效应
• 理解劳动(即禀赋)的供给(曲线)特征
根据(3)式,可得关于闲暇的相应表达式如下: ∂L( p, w, L, m) ∂L( p, w, u ) ∂L( p, w, L, m) ( L − L) = + ∂w ∂w ∂m 即闲暇的总效应=闲暇的替代效应+闲暇的收入效应 ∂L( p, w, L, m) 在上式中,由于闲暇是正常品,故 > 0, ∂m 且总有 禀赋量 L > 闲暇量L 。
16
4.2 复合商品
二、希克斯可分性 1、希克斯可分性和效用最大化
结论: 在价格指数 P = t 时,X = p 0 x是关于x − goods的复合商品 一个合适的数量指数。 在(P2)中,将商品复合以后,maxU ( X , P )得到的解X ; 与在(P1)中,先max u ( x, z ), 然后“加总”即X = g ( x) = p 0 x 求出的X 是相同的。
由 于效用 函数 u ( x , z ) = U (v ( x ), z )是 弱 可分的 , 则 子 效用最 大 化 模型 为 Max v ( x ) s.t . px = m x
( P1 )
最优解为: x * = x ( p , m x )
23
4.2 复合商品
2、函数的可分性和效用最大化 • 总效用最大化
5
• 理解:关于禀赋的(交叉)收入效应
∂xi ( p, pω) • 如果消费者是净买者即ω j − x j < 0, 则有 (ω j − x j ) < 0。 ∂m 意味: 若净商品的价格p j上升(下降),则消费者的实际收入 ∂e ∂m 减少(增加)。 即 (ω j − x j ) = = < 0。 ∂p j ∂p j
于是,闲暇的收入效应符号总为正。 (任何商品的替代效应总是负的。) ( à 闲暇的替代效应和收入效应符号总是相 反。 9
4.1 禀赋的收入效应
• 理解劳动的供给(曲线)特征 进一步有
• 当 w较 低 时 , 一 般 有 闲 暇 的 S .E > I .E , 则 闲 暇 的 T .E 符 号 为 负 。 • 当 w较 高 时 , 一 般 有 闲 暇 的 S .E < I .E , 则 闲 暇 的 T .E 符 号 为 正 。 ⇒ 由闲暇的需求曲线特征到劳动的供给 曲线特征
2
4.1 禀赋的收入效应
一、禀赋形式的预算约束和禀赋的收入效应
令:消费者拥有的各种物品的初始禀赋向量 和相应的价格向量分别为 ω = ( ω 1 L L ω n) p = ( p1 L L p n)
M ax s .t . u (x) p x = pω
• 模型
最 优 解 : x ( p , pω )
M ax s .t . u (x, z) px + qz = m ( P 1)
最 优 解 为 : x( p,q,m ) z( p,q,m )
12
4.2 复合商品
• 要解决的问题是: 是否能将x组合的商品(x--goods)复合成 一种商品? 如果能的话,且令复合商品的数量指数和 价格指数分别为X和P, 那么,效用最大化问题 可以写为:
P ,q
s .t .
PX + qz = m
18
4.2 复合商品
3、应用:两种商品的模型 以复合商品的价格指数为基础,表达某 一种商品的价格及需求函数。
令 : 单 种 商 品 z ; 另 有 商 品 向 量 x。 于 是 , 有 M ax u (x, z)
x,z
s .t . 分 析 :
px + qz = m
6
4.1 禀赋的收入效应
二、劳动的供给:由闲暇的需求与劳动的供给之视角 • 令: – 某消费者的初始禀赋为: • 全部可用于劳动的时间 L • 非劳动收入m – 该消费者消费两种商品: • 一种商品:数量为c, 价格为p • 另一种商品为闲暇: 闲暇时间为L, 闲暇价格为工资率w
7
4.1 禀赋的收入效应
第1部分 消费者行为理论
• 第1章 消费者的最优决策 • 第2章 比较静态分析 • 第3章 显示偏好理论 • 第4章 需求 • 第5章 消费者的福利变化 • 第6章 库恩 --- 塔克条件 • 第7章 不确定条件下的个人选择
1
第4章 需求
• 4.1 禀赋的收入效应 • 4.2 复合商品 • 4.3 单个需求函数和总需求函数之间 的关系: 高曼形式的间接效用函数 • 4.4 需求函数与反需求函数
• 结论:关于禀赋的收入效应的符号
∂xi ( p, pω ) ∂hi ( p, u ) ∂xi ( p, pω ) = + (ω j − x j ) ∂p j ∂p j ∂m
3
4.1 禀赋的收入效应
一、禀赋形式的预算约束和禀赋的收入效应 • 推导:关于禀赋的收入效应的符号
将 最 优 解 : x* i = x i ( p , pω ) 对 p j 求 偏 导 , 有 : ∂ xi ( p , pω ) ∂ xi ( p , pω ) = ∂p j ∂p j ∂ x i ( p , pω ) + ωj ∂m (1)
根 据 希 克 斯 可 分 法 , 在 x − g o o d s的 价 格 同 比 例 变 化 的 前 提 下 , 将 x − g o o d s归 并 成 一 种 复 合 商 品 , 则 有 M ax u(X , z)
X ,z
s .t .
PX + qz = m
19
最 优 解 : z* = z ( P , q , m )
14
4.2 复合商品
一、希克斯可分性和复合商品 1、复合商品:希克斯可分性和效用最大化 Key: • 假定x组合内所有商品的价格都以相同比例变 化。 • 运用罗伊恒等式。
15
4.2 复合商品
二、希克斯可分性 ቤተ መጻሕፍቲ ባይዱ、希克斯可分性和效用最大化
令 : x 组合内的商品价格都以相同的比例变化,即p = tp 0 , 其中,p 0为给定的基础价格向量。于是,有价格指数P = t 。 问题:当价格指数 P = t 时,是否可以合理地推导出相应的数量 指数X 呢? 推导:当价格指数 P = t 时,原效用最大化问题(P1)可以写为 Max u ( x, z ) s.t. P ⋅ p 0 x + qz = m ( P3) 可求出间接效用函数 : v( P, q, m) ∂v( P, q, m) / ∂P = p 0 x x ( P , q , m ) = X ( P, q, m) 由R.I 可得 : − ∂v( P, q, m) / ∂m 即数量指数为 : X ( P, q, m) = p 0 x
4.2 复合商品
3、应用:两种商品的模型 以复合商品的价格指数为基础,表达某 一种商品的需求函数。
由 于 z * = z ( P , q , m ) 在 价 格 P, q 和 收 入 m 上 1 是 零 次 齐 次 的 , 故 令 P , q , m同 时 乘 以 , 则 有 P q m * z =z( , ) P P
10
第4章 需求
• 4.1 禀赋的收入效应 • 4.2 复合商品 • 4.3 单个需求函数和总需求函数之间 的关系: 高曼形式的间接效用函数 • 4.4 需求函数与反需求函数
11
4.2 复合商品
• 问题的提出 令:商品的消费组合被划分为两个子组合x、z, 即有 消费向量x, 相应的价格向量p; 消费向量z, 相应的价格向量q。 于是,效用最大化问题为
M ax s .t . u(X , z) PX + qz = m (P 2)
最 优 解 为 : X (P, q, m ) z (P, q, m )
13
4.2 复合商品
• 在什么条件下,可以将一组商品归并成一个 复合商品呢? – 希克斯可分性 – 函数的可分性 ( 由P à X ) ( 由X à P )
24
最优解为X ( P , q, m,)
4.2 复合商品
2、函数的可分性和效用最大化 小结
(1)效用函数本身是弱可分的,所以有子效用v(x)最大化问 题,从而有了数量指数X=v。 (2)给可分的效用函数施加一个假定,即v(x)是一次齐次 的,从而找出相应的价格指数P=e(p)。 (3)一种具体运用:可以先从总效用最大化问题求出复合商 品的需求X (P,q,m), 以及单种商品需求的z (P,q,m)。然 后,由子效用最大化问题求出每一种商品的需求 xi(p,mx)。
17
4.2 复合商品
二、希克斯可分性 2、分析的扩展: 关于复合商品的对偶性的应用
由 直 接 效 用 函 数 到 间 接 效 用 函 数 : V (P , q, m ) = M ax u(X , z)
X ,z
s .t .
PX + qz = m
由 间 接 效 用 函 数 到 直 接 效 用 函 数 : U ( X , z ) = M in V ( P , q , m )
令 : 最 优 子 效 用 水 平 为 v, 则 总 效 用 最 大 化 模 型 为 M a x U (v , z ) s .t . e( p, v) + qz = m (P2) 可 见 , v是 一 个 恰 当 的 数 量 指 数 , 即 X = v , 但相应的价格指数是什么? 为 此 , 令 v ( x )是 一 次 齐 次 效 用 函 数 , 则 有 e ( p , v ) = e ( p ,1) v = e ( p ) v 数 量 指 数 X = v 价 格 指 数 P = e( p) 总 效 用 最 大 化 模 型 ( P2) 则 可 改 写 为 M ax U ( X , z ) 于 是 , 由 ( P2) 有 s .t . PX + qz = m ( P3)
