孟生旺《非寿险精算学》(第三版)参考答案
风险模型与非寿险精算学 (26)

1 承保风险的一般特征 2 短期保险合同模型 3 聚合风险模型 4 真2.1题基本模型 2.2 关于基本模型简化的讨论 2.3 符号和假设
短期保险合同的一个重要特点是,保费的水平仅限于保险 期(短期)内发生的索赔.这与寿险保单形成了鲜明对比,因为死亡 率随着年龄的增长而增加,意味着早期的(水平)年保费将足以覆 盖早期的预期索赔,然后,超额金额将累计作为准备金,在以后 的几年中使用,因为单独的保费不足以满足预期的索赔成本.
响.
风险模型与非寿险精算学
1 承保风险的一般特征 2 短期保险合同模型 3 聚合风险模型 4 真2.1题基本模型 2.2 关于基本模型简化的讨论 2.3 符号和假设
将要研究的问题是: 在有、无简单再保险的情况下,根 据N 和Xi的矩和分布推导出S的矩和分布. 此外,还将研究再保 险人的相应问题,即推导再保险人在本年度支付的索赔总额的矩 和分布.
另一个简化是,假设一旦引起索赔的事件发生,索赔就会无时 滞解决,例如,保险公司的利润在年底就已经知道了.在实践 中,理赔时效平均1-3天,在某些情况下,赔付延迟可能长达多 年.当损失的程度难以确定时尤其如此,例如损失要在法院作出 决定.
风险模型与非寿险精算学
1 承保风险的一般特征 2 短期保险合同模型 3 聚合风险模型 4 真2.1题基本模型 2.2 关于基本模型简化的讨论 2.3 符号和假设
在本章中,假设所有索赔均为非负金额,因此对于 x < 0,P (Xi x) = 0.本章中的许多公式将使用 S, N 和Xi的矩 母函数(从现在起缩写为MGFs)得出.这些MGFs将分别表示 为MS(t), MN (t) and MX (t)并假定变量t取正值.对于正值t,非 负随机变量的MGF可能不存在;例如,对于任何正 值t的pareto和lognormal分布的MGF都不存在.然而,在本章中借 助MGFs推导出的所有公式都可以推导出来,不需要假设MGFs存 在正的t值.
2021精算师考试《非寿险精算》真题模拟及答案(5)

2021精算师考试《非寿险精算》真题模拟及答案(5)1、一个决策者拥有财产50,其效用函数为u(ω)=lnω,该决策者面临着发生概率为1/2,损失额为36的潜在损失,若该决策者为此投保一保额为20的保单,则其愿意支付的最大保费为()。
(单选题)A. 11.72B. 12.98C. 13.29D. 14.36E. 15.75试题答案:D2、已知在2010年发生的赔案在各进展年的已报告索赔的赔案准备金如表1。
表1单位:千元并且保险人还知道在2010年发生的赔案在各进展年的索赔支付额如表2。
表2则在进展年2的PO比率与CED比率分别为()。
(单选题)A. 0.688,1.55B. 0.788,1.55C. 1.55,0.788D. 1.55,0.688E. 1.55.0.888试题答案:B3、一个决策者拥有财产50,其效用函数为u(ω)=lnω,该决策者面临着发生概率为1/2,损失额为36的潜在损失,若该决策者为此投保一保额为20的保单,则其愿意支付的最大保费为()。
(单选题)A. 11.72B. 12.98C. 13.29E. 15.75试题答案:D4、已知:则到2011年7月1日的整体指示费率的变化量为()。
(单选题)A. 0.1661B. 0.1551C. 0.1441D. 0.1771E. 0.1331试题答案:A5、已知小李有36元人民币,效用函数为:小张有65元人民币,效用函数为u2(x)=x2。
现两人进行游戏,规则如下:(1)盒中装有100个球,有红、蓝两种颜色;(2)从盒中随机取出一球;(3)若抽到红球,小李给小张4元人民币;(4)若抽到蓝球,小张给小李20元人民币。
设只有当两人参与游戏的期望效用和不参与游戏的期望效用相当时,才进行游戏,那么盒中红球的数目为()时,两人都愿意进行游戏。
(单选题)A. 18B. 19C. 33D. 49E. 81试题答案:E6、某NCD设三个折扣等级:0%,20%,40%。
寿险精算学(第3版)习题答案2

【解2.1】(1)可以被写成=(90−p(r200)18000,又由于达到极限寿命时=0,故=90。
(2)证明:因为,0=1;其次,达到极限寿命=90时,有90=0;且,的导数−110−218000<0,>0。
由此,生存函数的三个条件都被满足。
(3)93333.0)0()10(00010==S S p (4)(030−050)020(5)=−0'(p/0==110+218000−110−2因此,40=0.015833。
【解2.2】作为生存函数的基本属性有:(0)1,S =函数是单调递减的,同时lim ()0x S x →∞=。
(1)由于()exp[0.7(21)](10.72ln 2)xxS x x '=---⨯⨯,(0)0.51480S '=>,说明该函数不满足单调递减的性质。
所以,它不能作为生存函数。
(2)由于(0)1S =,3()2(1)0S x x -'=-+<,21lim ()lim0(1)x x S x x →∞→∞==+。
该函数可以作为生存函数。
(3)由于(0)1S =,()2()(2)0x S x ex -'=-<,lim ()0x S x →∞=。
该函数可以作为生存函数。
【解2.3】(1)4320751001)75(1)75(=--=-=S F (2)20017510040175)()75(=-==-=x x S dx d f (3)501412001)75()75()75(===S f μ【解2.4】(40)40(40)(40)40(40)(40)60(),060(40)60(40)1(),060(40)601()(),06060T t T T t T S t tS t p t S S t t t S t tf x p t t μμ+-===<≤'+=-=<≤+-==<≤【解2.5】()18)100(9)100(6)100(3100)100()100(2)]([2)]([3100)100()100()]([)100()100(222210002221000100022100022x x x x dt x t x t x T E dt p t x T Var xdt x t x dt p x T E x t x l l p xxx t xxx tx t x x t -=---=⎪⎭⎫⎝⎛------=-=-=---==---==⎰⎰⎰⎰----+【解2.6】所有表达式均为非负,因此需要验证是否满足0∞B =∞,使得0)(=∞S (1)∞==∞∞⎰0ln C BC dx BC xx,可以(2)∞=+=+∞∞-⎰001)ln()(x b a dx x b a ,可以(3)21)1(21)1(023=+-=+∞∞-⎰x dx x ,不可以【解2.7】把30.250x q +=代入120.170x q +=式中,得11232120.1700.680x x x x x x q p p q p p ++++++=⋅⋅=⇒=上式与已知条件11210.090x x x q p q+++=⋅=联立求解,解出10.770x p +=,20.117x q +=最后得1212(1)0.230.1170.347x x x x q q p q +++++=-+=+=【解2.8】由()1xS x ω=-,可知~(0,)X U ω,且有(20)~(0,20)T U ω-则[()]2x E T x ω-=,2()[()]12x Var T x ω-=已知020e 40=,即20401002ωω-=⇒=所以2(20)Var[T(20)]533.312ω-==【解2.9】首先计算K 的生存函数k012197k p +1015415则210414()09715151502210422()(21)13509715151513422()()[()]225E K p k k E K k p k k Var K E K E K ==++=∑==+⋅=⋅+⋅+⋅=∑==-=【解2.10】证明:(1)x t x x x t q t T t T p -=<-=≥=1)Pr(1)Pr((2)xu t x t x x x x ut p p u t T t T u t T t q +-=+≥-≥=+≤≤=)Pr()Pr()Pr((3)()()()tx u x t t x x x ut p p u T t T p ++⋅=≥⋂≥=Pr 【解2.11】(1)证明:110111111111+∞+∞+-∞∞+=+≤⋅+=+==⎰⎰⎰⎰⎰⎰x x x t x x t x t x t x t x e dt p dtp p dt p dt p dt p dt p e (2)证明:由于是关于的递减函数,因此有K1B≥所以xk x k k k kx tx t x e p dtp dt p e =≥==∑∑⎰⎰∞=+∞=+∞101【解2.12】证明:()()()()()()()t x t x x t S x t f x t S x t x t p p t t S x S x S x μμ+∂∂++-++====∂∂【解2.13】318.02005exp 20025exp 20015exp )5()25()15(200exp 100exp )(2225101020=⎪⎪⎭⎫⎝⎛-⎪⎪⎭⎫⎝⎛--⎪⎪⎭⎫ ⎝⎛-=-=⎪⎪⎭⎫⎝⎛-=⎭⎬⎫⎩⎨⎧-=⎰S S S q x dt t x S x 【解2.14】[][]8684284p =其中86l 已知,而[][][][][]2848484184841(1)(1)p p p q q ++==--由已知条件推导出[][][]85841848483144508030360.3225550803343640050800.20644556400q q q q q ++-=⋅=⋅=-==⋅⋅=⋅=【解2.15】(1)7[76]=83[76]=1192816608=0.718208(2)6|275+1=82−8475+1=0.084631【解2.16】40+1=40(1−40),40+2=402p [40],43=40+2−40∗2|40,46=43−40+1∗2|340+1.因此343=46/43=1−(1−40)2|340+1/(2p [40]−2|40)=1−(1−0.01608)×0.08964/(0.95977-0.02383)=0.905765【解2.17】151025:2525152540015100.040.04150.06015.40667t t tte p dt p p dtedt eedt--⨯-=+=+=⎰⎰⎰⎰【解2.18】(1)0.752.5=1−53.252.5=1−0.853+0.2540.552+0.553=0.0068381.7|1.252.5=54.2−55.452.5=0.854+0.255−0.655−0.4560.552+0.553=0.022690(2)0.752.5=1−0.5p 52.50.2p 53=1−520.5530.2=0.0068351.7|1.252.5=1.7p 52.51−1.2p 54.2=0.5p 52.5530.2p 541−0.8p 54.20.4p 55=520.553540.21−540.8550.4=0.022668【解2.19】因为{}10102102221exp ()=1exp 2()1exp ()1()1(1)2x x x x x q x t dt x t dt x t dt p q q q μμμ⎡⎤''=--+⎢⎥⎣⎦⎡⎤--+⎢⎥⎣⎦⎡⎤=--+⎢⎥⎣⎦=-=--=-⎰⎰⎰由此推出2x xq q '<。
中国精算师《非寿险精算》过关必做500题(含历年真题)(第3章 非寿险费率厘定)【圣才出品】

A.179.750 B.351.625 C.355.750 D.358.825 E.361.875 【答案】E 【解析】用 t 来表示时间变量,单位为年,并令初始时间为 2009 年 1 月 1 日。由于每 个季度签单保单的签单时间、风险分布都在相应季度中均匀分布,因此,在 2009 年第一个 季度,t 时刻瞬间签发的保单数量为
【答案】B
【解析】由题意知:
V 6 20 8 0.355,Q 0.05,G 5 0.1
80 100
50
其中,V 为可变费用因子,Q 为利润因子,G 为固定费用因子
0 . 2 05 .25
1 / 81
圣才电子书 十万种考研考证电子书、题库视频学习平台
0.75 83 tdt 51.875 , 1 96 tdt 84 。而在 2010 年 t 时刻签发的保单在 2010 年的已
0.5 0.25
0.75 0.25
承担的风险量为 1-t,因此在 2010 年各季度签发的保单在 2010 年的已承担的风险量为:
f (t) 78 312 ,在 2009 年的已承担风险量为1 t ,在 2010 年的已承担风险量为 t 。 0.25
0.25
因此该季度签发的保单在 2010 年的已承担的风险量为: 312tdt 9.75 。同理可得 2009 0
年 各 季 度 签 发 的 保 单 在 2010 年 的 已 承 担 的 风 险 量 为 : 0 . 5 98 tdt 36.75 ,
4.已知费用比率数据:
则目标损失率 T 为( )。[2011 年秋季真题] A.T<0.66 B.0.66≤T<0.68 C.0.68≤T<0.70 D.0.70≤T<0.72
非寿险精算答案整理

一:假设某保单的损失服从指数分布,概率密度函数为)0();(>=-x e x f x λλ其中,λ为未知参数,如果该保单过去各年的损失观测值为),(21n x x x ,求参数λ的极大似然估解:利用极大似然估计的方法,可以得到xxnni i1ˆ1==∑=λ二:假设某保险业务的累积损失S 服从复合泊松分布,泊松参数为20,而每次损失的金额服从均值为100的指数分布,用正态近似求累积损失的99%的分位数。
解:[]400000)100100(20)()()()()(200010020)()(222=+=+==⨯==X E N VAR N E X VAR S VAR X E S E λ分位数=3471)(326.2)(=⨯+S VAR S E加二、某保单规定的免赔额为20,该保单的损失服从参数为0.2的指数分布,求该保险人对该保险保单的期望赔款。
解: 令⎩⎨⎧≥-≤=2020200X X X Y ,,为保险人的赔款随机变量4202.052.0)20()2020()(-∞-=-=>-=⎰e dx e x X X E Y E x三、假设某公司承保的所有汽车每年发生交通事故的次数都服从泊松分布,而不同汽车的泊松分布参数不同,假设只取两个值(1或2),进一步假设λ的先验分布为4.0)2(,6.0)1(====λλp p ,如果汽车一年内发生4次事故,求该汽车索赔频率λ的后验分布。
解:λλλ-==e x P !4)4(41241)14(-===e x P λ 22416)24(-===e x P λ 2031.04.024166.0246.024)41(211=⨯+⨯⨯===---e e e x P λ7969.04.024166.0246.02416)42(212=⨯+⨯⨯===---e e e x P λ=)(λE 1)41(⨯==x P λ+2)42(⨯==x P λ=1.7969四:假设某险种的损失次数服从参数为0.2的泊松分布,对于一次保险事故,损失为5000元的概率是80%,损失为10000元的概率是20%,请计算保险公司的累积损失的分布 解:为简化计算,假设一个货币单位为5000元,解:818731.0)0(2.0===--e e f s λ ,130997.08.02.0)0()1()1(2.0=⨯⨯==-e f f f S X s λ043229.0))0()2(2)1()1((2)2(=+=S X S X s f f f f f λ五:假设某保险人签发了两份保单六:假设保险业务在一年内是均匀分布,保险期限为1年,各日历年的已赚保费如下,2000解:如果把1998年生效的相对费率看做是1,则1999年生效的相对费率为1.08,2001年生效的相对费率为1772.19.01*8.01=,2000年的相对费率为7.01.5%87*8.01.5%12*1=+,2001年的相对费率为1.08*12.5%+1.1772*12.5%=1.09215,2002年的相对费率为1.08*12.5%+1.1772*87.5%=1.16505,将所有年费的已赚保费调整到2002年的水平,可得等水平已赚保费为3100*1.1772/1.07+3200*1.1772/1.09215+3500*1.1772/1.16505=10396.28 八:某险种当年的相对费率和保费收入、过去三年的等水平已赚保费和经验损失数据如下表所示,假设A 为基础类别,经验数据的可信度为40%,如果整体保费需要上调15%,请计算调整后的相对费率。
20XX中国准精算师考试《非寿险精算》经典习题2第5页-精算师考试.doc

2013中国准精算师考试《非寿险精算》经典习题2第5页-精算师考试整理了2013年中国准精算师考试《非寿险精算》经典习题,望给广大考友带来帮助,预祝大家取得优异的成绩!第1页:单项选择题第3页:多项选择题第4页:综合解答题第5页:单项选择题答案第7页:多项选择题答案第8页:综合解答题答案解题思路:1.解:2.解:因为B忽略了独立条件,即要使讨论成立,必须要X1X2,…,Xn相互独立。
选B。
3.解:由熵的定义选D。
4.解:由纯保费法及损失率法公式:可以判断选项C不正确,关键要区分开纯保费P与均衡保费的区别。
选C。
5.解:在损失率法中,则:指示费率整体水平变动量为:选C。
6.解:在索赔额为常数的情况下:(次)(次)选C。
7,解?由八分法可知年来应提取未到期责任准备金为:(万元)选B。
8.解:0.2分位点为0.25,0.7分位点为0.875,分别令0.2及得:和将0.25和0.875代人上面两式有:整理得:选E。
9.解:5根线为100万元,风险单位A自留额20万元,剩余30万元,再保险人只承担100万元,占总保额的,故其摊赔应为:120×=80(万元)。
选C。
10.自留额在成数再保险中可以表示成数α,溢额再保险可以表示成线数m,超额再保险可表示成优先额r,停止损失再保险可以表示成优先额ρP,若α、m、γ、ρP越大,自留风险越大。
选E。
中国精算考试教材 非寿险精算

中国精算考试教材非寿险精算
对于中国精算考试中的非寿险精算,以下是一些常用的教材推荐:
1. 《非寿险精算学》(作者:张宇):这本教材是中国精算师协会(CIAA)编写的非寿险精算教材,涵盖了非寿险精算的基本理论和实际应用,并结合了大量的案例分析。
2. 《非寿险精算学习指导》(作者:中国精算协会):该教材是由中国精算协会编写的,提供了非寿险精算学习的指导方针和重点内容,可以帮助考生更好地理解和掌握非寿险精算的知识。
3. 《非寿险精算方法与实务》(作者:李中华):这本书介绍了非寿险精算方法和实务,包括不同类型的非寿险产品的风险评估、保费计算、赔付准备金计算等内容,适合深入学习非寿险精算的人士。
4. 《非寿险科目考点精讲》(作者:某精算培训机构):这本教材主要针对非寿险精算考试的科目内容进行详细解析和讲解,可以帮助考生更好地理解考试重点和难点,提高
备考效果。
以上是一些常用的非寿险精算教材推荐,考生可以根据自己的需求和学习情况选择适合的教材来进行学习。
另外,还可以参考相关的考试指南、模拟试题和辅导资料,以全面准备考试。
孟生旺非寿险精算学》 第三版 参考答案

Var( K ) E[Var( I N )] Var[E( I N )] q(1 q)*E( N ) q 2 *Var( N )
0.00001 0.99999 68.6 0.000012 1.372 0.000686
2011 日历年总已赚车年=5+10=15
(2)截至 2010 年 12 月 31 日,
2010 保单年保单 A 承保车年数=5×2=10;2010 保单年保单 B 承保车年数=10×2=20;
因此,2010 保单年承保的总车年数=10+20=30
(3)2010 日历年,保单 A 承保车年数=5×2=10;保单 B 承保车年数=10×2=20;
E( N ) n1 p1 68.6, Var( N ) n1 p1 (1 p1 ) 70 0.98 0.02 1.372
P 表示飞机上的人员数,M 表示飞机上的乘客数, M ~ B(n2 , p2 ) , n2 200 , p2 0.9 ,
则
P 6M ,
孟生旺、刘乐平、肖争艳 编著,非寿险精算学(第三版)
,中国人民大学出版社,2015。
《非寿险精算学》
(第三版)参考答案
第1章
非寿险简介(略)
第2章
损失模型
2.1
首先将 2005 年和 2006 年的损失折现到 2004 年中:
2005 年平均损失金额的折现值为: 1200
2006 年平均损失金额的折现为: 1500
f S (2)
2
f X (1) f S (1) 2 f X (2) f S (0) 0.043229
寿险精算学(第3版)习题答案3

【解3.1】因为()()ln ()Pr Pr Pr T z F z Z z e z T δδ-⎛⎫=≤=≤=≥ ⎪-⎝⎭且由条件知剩余寿命服从De Moivre 分布,即()0,70T U ,故70ln ln 1ln ()Pr 17070z z z F z T dt δδδ-⎛⎫=≥==+ ⎪-⎝⎭⎰密度函数等于分布函数求导()ln 117070Z z f z zδδ'⎛⎫=+= ⎪⎝⎭已知0.05δ=,0.6z =代入上式得()0.60.48Z f =【解3.2】(40)的剩余寿命T 服从均匀分布(0,70),其生存函数为407070t tP -=,070t ≤≤由题意,可得ln 70ln ln ()Pr()Pr()Pr()ln 70t z z v F z Z z v z t v-=≤=≤=≥=Z 的90%置信上限即为使()0.9F z =的z 值,即ln 70ln 0.970zv -=解得exp[(70700.9)ln ]0.84z v =-⨯=【解3.3】在恒定死亡力和恒定利息力场合,容易验证趸缴净保费等于x A μδμ=+在调整以前有0.60.05μμ=+则求得0.075μ=调整以后0.0750.020.095μ'=+=,0.04δ'=则调整后的趸缴净保费为0.0950.7040.0950.04x A μμδ'===''++【解3.4】(1)()()tx A E Z E v ==,则()()2200.055001 1.250.031252500.0312522Pr[0]t x T x tt t A e f t dtedte dte Y δ∞-∞--+⎛⎫∞- ⎪⎝⎭====≥⎰⎰⎰其中~( 1.25,25)Y N -,则()1.25Pr(0)Pr(0.25)10.255Y Y +≥=≥=-Φ()0.031252[10.25]0.83x A e =-Φ=(2)因为22()x x Var Z A A =-,其中()()()2220.100.15001 2.50.1252500.12522[10.5]0.70t x T x tt t A e f t dte dte dte ∞-∞--+⎛⎫∞- ⎪⎝⎭====-Φ=⎰⎰⎰所以222()0.700.830.014x x Var Z A A =-=-=【解3.5】给付函数和贴现函数都已知,容易得到现时值函数为1(10.2)t t Z b v t -==+密度函数已知()()40400.02,050T t f t p t t μ=+=≤≤则趸缴净保费等于()()505000ln 10.21110.020.2410.2500.210t E Z dt t +⎛⎫=⨯=== ⎪+⎝⎭⎰两倍利息力下,趸缴净保费等于()()50502200110.020.020.091(10.2)0.210.2E Z dt t t -=⨯=⨯=++⎰所以现值变量的方差等于222()()[()]0.09090.23980.0334Var Z E Z E Z =-=-=【解3.6】一般情况下,如果剩余寿命T 服从()0,ω的均匀分布,即1(),0T f t t ωω=≤≤可以得到()0111t x T tt A e f t dte dtev a δωδωδωωωωδωδω∞---==-=-==⎰⎰本题中,T 服从(0,60)的均匀分布,故所求的净保费为604040100010001000666.76060a A =⨯=⨯=【解3.7】令3z 为()x 岁的人投保期末赔付1的n 年定期生存保险的现时值变量,根据已知条件有3()0.20.450.09n n x E z v p =⋅=⨯=223()0.040.450.018n n x E z v p =⋅=⨯=根据定期两全保险与定期寿险和定期生存险的关系,有213z z z =+则213123()()()()()()0.350.090.26E z E z E z E z E z E z =+⇒=-=-=[][]222213222212322()()()()()()()()0.060.0180.350.1645Var z E z E z E z E z Var z E z E z =+-⇒=-+=-+=推导出()[]2221110.16450.260.0969Var Z E Z E Z ⎡⎤=-=-=⎣⎦【解3.8】因为死亡服从De Moivre 分布,故40岁的人剩余寿命的密度函数为()160T f t =,060t ≤≤由于延期20年,所以赔付现值变量为0,020,2060TT Z e T δ-≤≤⎧=⎨<≤⎩所以,0z =点为重概率点,该点概率值为20201Pr(0)Pr(020)()603T Z T f t dt ==≤≤===⎰【解3.9】该保单可以视为一个10000元的终身寿险和10000元的20年定期寿险的组合,则该保单趸缴净保费为14545:201000010000A A +已知450.25A =,下面求145:20A 的值。
非寿险精算学

概论 风险与保险的基本关系
1、保险是将风险由被保险人向保险人的转移;
2、保险人也需要对其所承保的超额风险寻求保险保障;
3、风险集合包含的个体风险越多,其相对风险越少;
4、不同的保险人具有不同的风险水平;
5、在很多情况下,少数巨灾风险所造成的损失找到总损失的很大比重。
理赔次数0123456
保 单 数427536501500450100205
试分析索赔次数是否服从泊松分布( )。
解:第一步,计算理赔次数X的均值;
则有:
第二步,计算皮尔逊统计量
理赔次数ki)观测次数( )
理论次数( )
042754274.150.0002
136503633.030.0793
k=1, 2, …
几何分布的方差大于均值,均值为 ,方差为
二、损失(索赔)金额(强度)模型
1、指数分布
假设损失金额X服从参数为 的指数分布,则其分布函数和密度函数分别为:
其中, ,x>0
?指数分布的均值和方差分别为: 和
2、对数正态分布
假设损失金额X服从参数为 的对数正态分布,则其分布函数和密度函数分别为:
第一章非寿险和非寿险精算
非寿险是与寿险相对而言的,是指寿险以外的其它保险业务,主要包括财产保险、责任保险、健康保险和意外伤害保险等。
一、财产保险
财产保险是以有形的物质财富及相关利益为保险标的的一种保险。主要包括火灾保险、运输保险和工程保险等。
1、火灾保险
特点:首先,火灾保险的保险标的只能存放于固定场所并处于相对静止状态下的各种财产物资;其次,火灾保险承报财产的地址不能随意变动,如果被保险人确实需要变动保险财产的存放地点,必须征得保险人的同意。
风险模型与非寿险精算学 (32)

SI = Y1 + Y2 + · · · + YN
(1)
再保险人的总索赔为
SR = Z1 + Z2 + ... + ZN
(2)
风险模型与非寿险精算学
1 比例和超额赔款再保险的总索赔分布 2 个体风险模型 3 参数可1.变1 性比/例不再确保定险性 14.2真超题额赔款再保险
例如,N ∼ Poi(λ),SI 满足泊松参数为λ的复合泊松分布, 第i单个索赔金额为Yi.类似地,SR 服从一个泊松参数为λ的复合 泊松分布,而第i个索赔金额为Zi.但是注意到如果F (M ) > 0, 则Zi取0.换句话说再保险人可能的索赔金额可能取0.保险人可以 观察到N 的值,但再保险人可能只知道超过自留额M 的索赔次 数,因为保险人仅在索赔高于自留额时通知再保险人.
风险模型与非寿险精算学
1 比例和超额赔款再保险的总索赔分布 2 个体风险模型 3 参数可变性/不确定性 4 真题
导论 I
1 根据索赔次数和个人索赔金额,构建适合短期保险合同的模 型.
2 描述(iii)中模型的主要简化假设. 3 推导出复合二项、复合泊松和复合负二项随机变量的均值、
方差和偏度系数. 4 在简单形式的比例超额赔款再保险操作之后,进一步推导出
2 2 个体风险模型
3 3 参数可变性/不确定性
3.1 简介 3.2 各种组合中的可变性
3.2.1 例 3.2.2 例 3.3 同质组合的可变性 3.3.1 例子 3.4 索赔次数和索赔金额的可变性和参数不确定性 3.4.1 例 3.4.2 例
4 4 真题
风险模型与非寿险精算学
1 比例和超额赔款再保险的总索赔分布 2 个体风险模型 3 参数可变性/不确定性 4 真题
非寿险精算学2孟生旺
.
160
未决赔款准备金评估
.
161
.
162
.
163
.
164
.
165
.
166
.
167
.
168
.
169
常用未决赔款准备金评估方法:
链梯法 期望赔付法 案均赔款法 Bornhuetter-Ferguson法(B-F) 准备金进展法
.
170
.
171
基于已付赔款数据的链梯法
.
.
131
.
132
.
133
请同学们思考:
两年期或三年期保单的未到期责任准备金的月 比例法应如何操作?
.
134
.
135
选取原则:
日比例法不要求保费收入在各月均匀分布,能 更真实反映现实,评估准确性高。仅从这一点 出发,日比例法优于月比例法和季比例法;
日比例法计算量大,需要数据系统及时记录更 新保单信息,因此对IT系统不够完善的公司最 好采用月比例法。
代入可得各等级概率的稳定分布:
1 = 0 .0 7 4 7 3
2
0 .0 6 1 1 8
3 4
0 .0 6 9 4 1 0 .1 4 4 0 5
5
0 .1 1 7 9 4
6 0 . 5 3 2 6 9
.
114
这一万个投保人在6个等级中的稳定人数为
折扣率等级 人数
0% 20% 30% 40% 50% 60% 747 612 694 1441 1179 5327
假设全额保费是100元,则总保费收入为
p 1 1 0 0 * 7 4 7 8 0 * 6 1 2 7 0 * 6 9 4 6 0 * 1 4 4 1 5 0 * 1 1 7 9 4 0 * 5 3 2 7 5 3 0 7 3 0 元
2021精算师考试《非寿险精算》真题模拟及答案(2)

2021精算师考试《非寿险精算》真题模拟及答案(2)1、《护照法》第9条第2款规定,“外交护照、公务护照的签发范围、签发办法以及公务护照的具体类别,由()规定”。
(单选题)A. 县级以上公安机关B. 外交部C. 国务院D. 以上都不是试题答案:B2、某保险公司自2005年起所承保的某种业务的有关信息如下:(1)2005年已赚保费为495000元,之后已赚保费每年以35%的速度增长;(2)2005事故年的期望赔付率为68%;(3)2008年12月31日,公司准备金精算师认为自公司开始承保该业务以来,期望赔付率每年增长两个百分点。
准备金评估时采用已报案赔款数据,选择的进展因子如表1所示。
表1则使用预算IBNR方法计算2008年12月31日的总IBNR准备金为()元。
(单选题)A. 897040.8B. 793488.3C. 993713D. 657389.1E. 873576试题答案:C3、预报信号是指()时,驻站联络员应立即向现场防护员发出预报。
(单选题)A. 车站对作业区间办理闭塞B. 车站已向施工区间发车C. 列车已经接近D. 刚刚发过的预报(或确报)信号已予取消试题答案:A4、某保险公司就家庭财产保险与再保险人签定合同进行再保险,合同规定原保险人的赔付率在85%~125%时,由再保险人承担责任。
假定原保险人当年家庭财产保险费收入1000万元,赔款总额为1300万元,则再保险人承担保险赔款()万元。
(单选题)A. 0B. 100C. 200D. 300E. 400试题答案:E5、某决策者的效用函数为当前财富为9元,他可以通过支付5元来转移某种风险给付。
已知该风险给付的额度分别为0,12,21,相应的概率为1-p-p2,p,p2,其中0<p<1。
若假设这个决策对他的期望效用无差异,则p为()。
(单选题)A. 1/2B. 1/3C. 1/4D. 1/5E. 1/6试题答案:B6、走私、贩卖、运输毒品罪的认定不正确的是()。
风险模型与非寿险精算学 (23)

证明 我们希望计算积分的值:
∞
x
1 √
e−
1 2
(
log
x−µ σ
)2
dx
xσ 2π
α
换元,
u
=
log x−µ σ
−σ
.
所以积分变成:
∞
√1
e−
1 2
(u+σ)2
σeµ+uσ+σ2
du
σ 2π
log
a−µ σ
−σ
指数项部分进行合并,我们得到:
第二个积分就是我们在第(ii)(a)部分计算出的概率.所以:
E(R) = 2.26164 − 25 × 0.05745 = 0.8253
风险模型与非寿险精算学
0 导论 1 分保协议 2 特定分布 3 通货膨胀 4 估计 5 超额保单 6 真题
同样,第二个分保协议(其中R是再保险人支付的超过30的金 额),我们得到:
Y = 0, if X ≤ L Y = X − L, if X > L
风险模型与非寿险精算学
0 导论 1 分保协议 2 特定分布 3 通货膨胀 4 估计 5 超额保单 6 真题
显然,任何超额保单的到期保费将低于无超额保单的保费. 超额保单的保险人情况与超额损失再保险的再保险人相同.投 保人在损失方面的情况与超额损失再保险合同的保险人完全相 同.
自留额 25 30
保费 48.5 38.2
根据每个再保险安排,计算发生索赔涉及再保险人的概率. 通过调查分出给再保险人的每项索赔的平均金额,计算出哪一个 自留额最有价值(忽略保险人对风险的态度) 第2年,假设所有其他条件相同,保险公司认为通货膨胀将使其 组合中索赔的均值和标准偏差增加8%.如果再保险人收取与以前 相同的保险费,那么下一年哪一个自留额将是最有价值的.
2020精算师考试《非寿险精算》真题模拟及答案(2)

2020精算师考试《非寿险精算》真题模拟及答案(2)1、中等突水点的突水量为()m3/h。
(单选题)A. >60~600B. >60~500C. >50~600D. >50~500试题答案:A2、某保险公司在其未满期业务中有19307张保险单。
其总的风险保费为366833美元,一年内索赔总额为340575美元。
保险公司在下一年对每张保险合同应收取的风险保费的完全可信性估计值为()美元。
(单选题)A. 17B. 18C. 19D. 20E. 21试题答案:C3、设某险种的损失额X具有密度函数(单位:万元)为假定最高赔偿限额D=4万元,赔付率p=3.2%,则净保费是()元。
(单选题)A. 214.8B. 238.8C. 269.8D. 294.8E. 320.8试题答案:D4、在实际工作中评价一个完整的江河水系需要设置几个断面()(单选题)A. 1B. 2C. 3D. 4试题答案:D5、对于超过100万元之后的100万元事故巨灾超赔保障合同,如果一次暴风雪延续9天,如规定连续72小时为一次事故发生,9天认为发生了3次巨灾事故,如果每次发生的巨灾损失分别为150万,200万,50万,即总的赔款是400万元,则原保险人与再保险人承担的赔款分别为()万元。
(单选题)A. 100,300B. 150,250C. 250,150D. 300,100E. 350,50试题答案:C6、假设一个保单组合包含5份保单,每份保单的风险单位数相同,它们在近4年的索赔次数数据如表所示。
用Bühlmann方法估计保单A在下一保险年度的索赔频率为()。
(单选题)A. 0.97B. 0.86C. 0.75D. 0.64E. 0.53试题答案:C7、下列情况中适合瞬间采样的是()(单选题)A. 连续流动的水流B. 水和废水特性不稳定时C. 测定某些参数,如溶解气体、余氯、可溶解性硫化物、微生物、油脂、有机物和pH 时试题答案:C8、地下水的运动要素有:①流向、②流量、③流速、④水头、⑤水力坡度、⑥流网、⑦渗透系数。
非寿险精算(孟生旺)课后答案

2.15 X 的矩母函数为 M x ( z ) = ∫ e
0
N 的母函数为 PN ( z ) = [1 − β ( z − 1) ]
kh da w. co m
案 网
zx 5 ni Ai2 n A2 + 0.04∑ i i = 1.7072 × 109 4 i =1 12
1
θ
e
− x /θ
dx =
1
θ
n
2.5 2.6
M x (t ) = E(etx ) = ∫ etx ∑ ai λi e − λi x dx = ∑ ai (1 −
0 i =1 i =1
E ( S ) = λ E ( X ) = 20 × 100 = 2000
Var ( S ) = Var ( X ) E ( N ) + Var ( N ) [ E ( X ) ] = λ Var ( X ) + [ E ( X ) ]
课后答案网
《非寿险精算学》
(孟生旺 刘乐平 编著,中国人民大学出版社 2007 版)
参考答案
(2008 年 2 月)
0, x ≤ 0 ⎧ ⎪ f (x + d ) 其密度函数为 f Y ( x ) = ⎨ ,x > 0 ⎪ ⎩ 1 − F (d )
w.
=
1⎞ ⎛ f ⎜x+ ⎟ ∞ ∞ ∞ f (x + d) λ⎠ E (Y ) = ∫ xfY ( x )dx = ∫ x ⋅ dx = ∫ x ⎝ dx 0 0 0 1− F (d ) ⎛1⎞ 1− F ⎜ ⎟ ⎝λ⎠
+∞
1 16 −2 λ 4 −λ e , P ( x = 4 λ = 1) = e−1 , P (x = 4 λ = 2) = e 24 4! 24
寿险精算学(第3版)习题答案7

【解 7.2】 根据题意有
所以
t
t px00 exp( 01 02dt ) e 0.05 t
0
t
t p1x1 exp( 12dt ) e 0.05 t
0
t
t px01
s
px00 01
t
s
p11 x s
dt
0.02te
0.05 t
0
p 00
10 x
10 px00 10 px01
e 0.5
所以
35
p40
p 25 25,50 p 15 25
0.2 0.9
2 9
【解 7.16】
由 i 0.04 1 ,得 d i 1 ,且延付年金和初付年金之间具有如下关系
25
i 1 26
ax ax 1 11 , ay ay 1 16 , axy axy 1 10
则根据题意,该保单的精算现值等于
t
p60,55
t
p6s0
t
p5n5
20 t 20
2
25 t 25
则他们还能共同生活的期望时间为
0
e
20 0
t
p60,55dt
20 0
20 20
t
2
25 25
tdt
5.33
【解 7.25】
qx 1 px 1 e 1 e 1.2 0.6988
qx3
qx
3
0.6988
o
e70,75
35 0
p70,75dt
35 1
0
75t t 1400
2
dt
12.40
【解 7.9】 则
t q70
t 40
风险模型与非寿险精算学 (30)
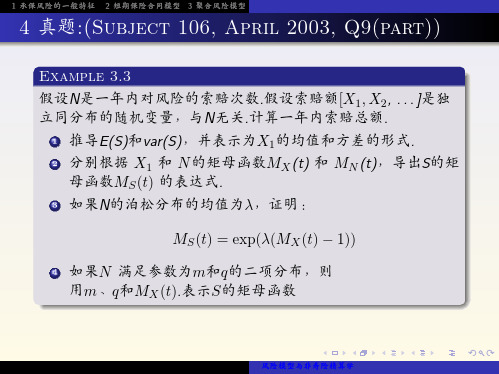
母函数MS(t) 的表达式exp(λ(MX (t) − 1)) 4 如果N 满足参数为m和q的二项分布,则
Acknowledgement
T HAN KS
风险模型与非寿险精算学
4 二项分布 查表可知,如果 N ∼ Bin(m, q), 则 MN (t) = (1 − q + qet)m 根据(ii)的结果,我们得出: MS(t) = (1 − q + qeln MX(t))m = (1 − q + qMX (t))m
风险模型与非寿险精算学
1 承保风险的一般特征 2 短期保险合同模型 3 聚合风险模型 4 真题
2 (ii) MGF S的矩母函数的定义是 MS(t) = E[etS] 再次,我们使用条件法来做 E etS = E E etS |N = E E et(X1+X2+...+XN ) |N = E E etX1 E etX2 ...E etXN |N = E E etX1 N = E (MX (t))N = E [exp (N ln MX (t))] = M N (lnM X (t))
3 泊松分布 查表可知,如果 N ∼ P oi(λ),则 MN (t) = exp[λ(et − 1)]. 根据(ii)的结果,我们得出: MS(t) = exp[λ(elnMX(t) − 1)]
风险模型与非寿险精算学
1 承保风险的一般特征 2 短期保险合同模型 3 聚合风险模型 4 真题
真题答案 (Subject 106 , April 2003,Q9(part)) III
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
20(1002 1002 ) 400000 分位数= E(S) 2.326 Var(S) 3471
2.6
令Y
0, X
X
20 20, X
为保险人的赔款随机变量。
20
E(Y) = E(X-20|X>20)×P(X>20)+0×P(X<20)
,x≥0
2.12 设 N 表示下个月出行的航班数, N ~ B(n1, p1) , n1 70 , p1 0.98
E(N) n1 p1 68.6, Var(N) n1 p1(1 p1) 700.980.02 1.372 P 表示飞机上的人员数,M 表示飞机上的乘客数, M ~ B(n2, p2 ) , n2 200 , p2 0.9 ,
qi
0.04 (80 10000 35 20000 25 30000 15 50000 5 100000) 70000 2
Var(S)
5
5
niui2qi
(1
qi
)
ni
2 i
qi
0.04
0.96
i 1
i 1
ni Ai2 4
5
0.04
2006
年平均损失金额的折现为:1500
1
1
10%2
1239.7
2004 年的平均损失金额为: E x 1 1090.9 2 1239.7 1190.1
3
3
而 Pareto, 分布的期望是 E x
1
用损失次数进行加权,得 1 1090.9 2 1239.7 1190.1 ,得 λ = 2380.2
etx
0
n i1
ai i e i xdx
n i1
ai (1
t )1, (t i
i )
2.5
1
孟生旺、刘乐平、肖争艳 编著,非寿险精算学(第三版),中国人民大学出版社,2015。
E(S) E( X ) 20100 2000
Var(S) Var( X )E(N ) Var(N )E( X )2
2.3 ������(������1, ������2, … ������������; ������) = ������������������−������ ∑������������=1 ������������
������
L(������1, ������2, … ������������; ������) = ������������ ������(������1, ������2, … ������������; ������) = ������������������������ − ������ ∑ ������������
第3章 费率厘定基础
3.1 赔付率=已发生损失/已赚保费=125000/200000=0.625 综 合 成 本 率 = 赔 付 率 + 经 营 费 用 率 = 赔 付 率 × (1+ 理 赔 费 用 率 )+ 承 保 费 用 率 =0.625×(1+0.14)+0.25=0.9625 3.2 (1)2011 日历年,保单 A 已赚车年=5×2×0.5=5;保单 B 已赚车年=10×2×0.5=10; 2011 日历年总已赚车年=5+10=15 (2)截至 2010 年 12 月 31 日, 2010 保单年保单 A 承保车年数=5×2=10;2010 保单年保单 B 承保车年数=10×2=20; 因此,2010 保单年承保的总车年数=10+20=30 (3)2010 日历年,保单 A 承保车年数=5×2=10;保单 B 承保车年数=10×2=20; 2010 日历年承保的总车年数=10+20=30
0
,
0
b
有,
5ln a xi ln a
xi ln b ln yi xi 2 ln b xi ln yi
由 ∑ xi= 15, ∑ xi2=55, ∑ ln yi= 34.78659, ∑ xiln yi= 105.24673 代 入 上 面 方 程 组 解 得 ,
i 1
ni Ai2 12
1.7072 109
ห้องสมุดไป่ตู้
PS (1 )
E(S)
99%
P
S
E(S
)
E(S )
99%
Var(S) Var(S)
E(S)
99%
,
Var(S)
E(S) Var(S )
1 (0.99)
2.325
2.325 Var(S) E(S)
1.3724
2.11
X
的矩母函数为������������(������)
=
∫0∞
������ ������������
1 ������
������ −������/������ d������
=
1 ������
∫0∞
������ (������−���1���)������ d������
3
3
31
2.2
E(x)
0
x
2 2 ( x)3
dx
2 1
由题意可知,2007 年平均索赔金额的期望值为:
( 500×1.053×100+600×1.052×150+700×1.05×200 ) ÷ 450 = 675.8
即:E(x) = 675.8 = λ
从而,λ 的矩估计值为 675.8。
j 1,2,..., N
E(K) qE(N) 0.00001 68.6 0.000686 Var(K) E[Var(I N)] Var[E(I N)] q(1 q)*E(N) q2 *Var(N)
0.00001 0.99999 68.6 0.000012 1.372 0.000686
=
(1
−
������������)−1,������
<
1 ������
N 的母函数为 PN (z) 1 (z 1) 1
S 的矩母函数为 MS (z) PN MS (z)
1 (1 z)1 1
1
1 (1 ) z 1
1
2
fX
(2)
fS
(0)
0.043229
依此类推,其他计算结果如下表所示。
x
fS (x)
0
0.818731
1
0.130997
2
0.043229
3
0.005799
4
0.001097
5
0.000128
6
0.000018
FS (x)
0.818731 0.949728 0.992957 0.998756 0.999853 0.999981 0.999999
其中对每个
i,
Y
i j
,(j
=
1,…,ni)独立分布,设其分布与
IBi
相同,
Bi
U
(0,Ai),ui
=
E
(Bi)
=
Ai
/
2,
2 i
var(Bi ) Ai2 /12 ,则总赔付额 S
为:
S X1 X2 X5
E(S)
5 i 1
ni ui qi
5 i 1
ni Ai 2
2.8
E(S) E(X ) 20100 2000
2 Var(S) Var(X )E(N ) Var(N )E(X )2
Var(X ) E(X )2
20(1002 1002 ) 400000
E[(S
E(S))3] 3
2
孟生旺、刘乐平、肖争艳 编著,非寿险精算学(第三版),中国人民大学出版社,2015。
fS (0) e e0.2 0.818731, fS (1) f X (1) fS (0) 0.2 0.8 e0.2 0.130997
fS
(2)
2
fX
(1)
fS
(1)
1
1
3
孟生旺、刘乐平、肖争艳 编著,非寿险精算学(第三版),中国人民大学出版社,2015。
这是一个两点混合分布。
fs
(x)
1
1
,
(1 )2
exp
x (1
)
x =0 ,x 0
FS(x)=1-
β 1+β
exp
(-
θ(1x+β))
=
+∞
∫ (x-20)f(x|x>20)dx
×P(X>20)=
∫2+0∞(x-20)f(x)dx
×P(X>20)
20
P(X>20)
+∞
+∞
= ∫ (x-20)f(x)dx= ∫ (x-20)0.2e-0.2xdx=5e-4
20
2.7 P x 4
20
4
e 4!
,P x
4
1 1 e 1 , P x 4 2 16 e2
