实验2-1-答案
2022学年九年级化学上仁爱版 学生实验实验1--2过关测试题附答案

学生实验实验1实验基本操作一、单选题1.下列实验操作不当的是( )A.将腐蚀性药品放在已知质量的烧杯里用托盘天平称量B.将试管夹从试管底部往上套,夹在试管的中上部C.振荡试管时,用手紧握试管,拇指堵住试管口,上下晃动D.滴加液体时,滴瓶滴管的尖嘴不能触及试管内壁2.图图图图图图图图图图图图()A.B.C.D.3.下列实验操作的先后顺序错误的是()A.连接玻璃管和胶皮管时,应先把玻璃管口用水润湿,然后稍用力把玻璃管插入胶皮管中B.检验装置气密性时,先用手握住试管再将导管伸入水中C.给物质加热时,先预热再定点加热D.称取一定量药品时,先调节砝码和游码再添加或减少药品4.下列为“节约用水”标志的是(9 )A.B.C.D.5.某同学从量筒中取用一定量的液体,开始时仰视读数得38毫升,取出一部分后仰视读数得18毫升,则他实际取出液体的体积是()A.大于20毫升B.等于20毫升C.小于20毫升D.无法确定6.能直接在酒精灯上加热的玻璃仪器是()A.蒸发皿B.试管C.烧杯D.坩埚7.下列仪器能用于取用液体药品的是()A.镊子B.纸槽C.药匙D.胶头滴管8.试剂的用量应按实验规定。
如果没有规定用量,试管取用液体一般取用()A.0.1~0.5mL B.1~2mL C.5~6mL D.10mL9.如图所示,龙龙同学采用手握试管外壁的方法检查装置的气密性,若装置的气密性良好,则将双手移开一会后,烧杯内导管处的现象(画圈部分)是()A.A B.B C.C D.D10.已知NaOH固体具有强烈的腐蚀性,且易吸水潮解。
实验室欲配制质量分数为20%的NaOH溶液,下列说法正确的是( )A.称量时将NaOH固体直接放在托盘上B.将称量好的NaOH固体倒入量筒中加水溶解C.该实验中需要用到的仪器有酒精灯、托盘天平、胶头滴管和烧杯D.若在量取水时俯视凹液面的最低处,则配制溶液的质量分数大于20%11.组装一套较为复杂的装置时,组装的顺序一般是()A.从上到下,从右到左B.从下到上,从左到右C.从下到上,从右到左D.从上到下,从左到右12.长期盛放石灰水的试剂瓶内壁有一层白膜,除去这层白膜的最好方法是()A.用蒸馏水冲洗B.用钢丝刷刷洗C.用稀盐酸洗涤D.用热水冲洗13.某同学制氧气时,试管炸裂了,造成试管炸裂的原因可能是下列中的()①没有给试管均匀预热;②试管外壁潮湿;③试管口没有略微向下倾斜;④忘了在试管口加一团棉花;⑤加热时试管与灯芯接触;⑥收集完氧气,先撤酒精灯;A.全部B.除④外C.除④⑤外D.①②③⑤14.粗盐的提纯实验中,不需要用到的仪器是()A.玻璃棒B.烧杯C.酒精灯D.导管15.利用铜和浓硫酸加热反应,制取二氧化硫和硫酸铜晶体,下列操作正确的是()A.用图甲装置制取并收集二氧化硫B.用图乙装置向反应后的混合物中加水稀释C.用图丙装置过滤出稀释后混合物中的不溶物D.用图丁装置将硫酸铜溶液蒸发浓缩后冷却结晶二、综合应用题16.某兴趣小组用如图1所示流程制取氧气,并回收提纯氯化钾和二氧化锰。
五年级上册科学练习-1、2 种子发芽实验(二) 教科版(含答案)

《种子发芽实验(二)》练习一、填空题1.种子发芽的适宜温度是()。
2.在研究种子发芽是否需要水分的对比实验中,需要改变的条件是(),不需要改变的条件是()和()。
3.将绿豆完全浸没在水中,四五天之后种子会停止发芽,这种实验现象说明种子发芽需要()。
4.绿豆种子发芽的必需条件是()、()和()。
二、判断题1.在地球的南极看不到植物,是因为那里一年四季都非常寒冷,植物的种子即使到了那里也无法发芽、生长。
()2.光照是种子发芽所必需的条件。
()3.种子要发芽除了要满足一定能够的条件之外,还要求种子必须是活的、结构完整、饱满的、保存时间短,已度过休眠期等自身条件。
()4.把种子放到任何条件下,都可以发芽。
()三、选择题1.“碧玉妆成一树高,万条垂下绿丝绦”千万枝条及其绿叶都是由()发育成的。
A.种皮B.花C.根D.芽2.已被虫蛀过的种子,一般不能萌发,原因是()。
A.种子的胚被破坏,无法存活B.外界条件不适宜C.感染虫子的病毒,无法生存D.种子还在休眠期3.下列常见的食物中,()不是种子。
A.花生B.菜豆C.大蒜D.黄豆4.在测定绿豆种子发芽的试验中,下列绿豆种子中,()最符合条件。
A.随机抽取的绿豆种子B.挑选颗粒饱满的绿豆种子C.被虫子蛀过的绿豆种子D.种皮破损的绿豆种子5.下面()不是种子发芽最关键的因素。
A.肥料B.温度C.水分D.空气四、简答题1.选择豆子时,为什么要选择绿豆,而不是选择黄豆?2.种子萌发必需的外界条件三要素是什么?《种子发芽实验(二)》练习答案一、填空题1.0-40℃解析:植物种子的发芽温度可以从0-40℃的范围,但每一种植物都有其发芽适温,也就是最适合于发芽的温度。
植物的发芽适温因原产地而异,一般而言,温带植物以15-20℃为最适,亚热带及热带植物以25-30℃为适。
[来源:学|科|网Z|X|X|K]2.水、空气、光解析:在做对照实验时,我们所要控制的是一个条件,是可以改变的,其余的是都是不变的。
实验2-1-答案
白盒测试用例练习
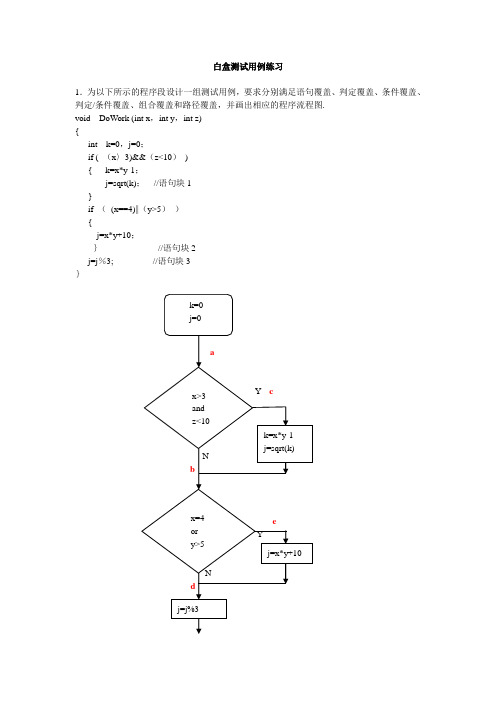
1.为以下所示的程序段设计一组测试用例,要求分别满足语句覆盖、判定覆盖、条件覆盖、判定/条件覆盖、组合覆盖和路径覆盖,并画出相应的程序流程图.
void DoWork (int x,int y,int z)
{
int k=0,j=0;
if ( (x〉3)&&(z<10))
{ k=x*y-1;
j=sqrt(k);//语句块1
}
if ((x==4)||(y>5))
{
j=x*y+10;
}//语句块2
j=j%3; //语句块3
}
由这个流程图可以看出,该程序模块有4条不同的路径:
P1:(a-c—e)P2:(a-c-d)
P3:(a—b-e)P4:(a—b—d)
将里面的判定条件和过程记录如下:
判定条件M={x〉3 and z<10}
判定条件N={x=4 or y〉5}
1、语句覆盖
2、判定覆盖
也可以让测试用例测试路径P2和P3.相应的两组输入数据如下:
3、条件覆盖
对于M:x>3取真时T1,取假时F1;
z〈10取真时T2,取假时F2;
对于N:x=4取真时T3,取假时F3;
y>5取真时T4,取假时F4。
条件:x〉3,z〈10,x=4,y>5
条件:x〈=3,z>=10,x!=4,y〈=5
5、组合覆盖
条件组合
1)x>3,z〈10 2)x>3,z〉=10
3) x〈=3,z<10 4)x〈=3,z〉=10
5)x=4,y〉5 6)x=4,y<=5
6。
人教版高中物理选修2-1 第二章 磁场 练习【含答案】

高中物理选修2-1第二章磁场一、单选题1.通电直导线所受安培力的方向与磁场方向、电流方向的关系,下列图示正确的是()A. B. C. D.2.磁场中任一点的磁场方向规定为小磁针在磁场中()A. 受磁场力的方向B. 北极受磁场力的方向C. 南极受磁场力的方向D. 受磁场力作用转动的方向3.如图所示,均匀绕制的螺线管水平放置,在其正中心的上方附近用绝缘线水平吊起通电直导线A.A与螺线管垂直,“×”表示导线中电流的方向垂直于纸面向里.电键闭合后,A受到通电螺线管磁场的作用力的方向是( )A. 水平向左B. 水平向右C. 竖直向下D. 竖直向上4.10 .用两根细线把两个完全相同的圆形导线环悬挂起来,让两者等高平行放置,如图所示.当两导线环中通入方向相同的电流I1、I2时,则有( )A. 两导线环相互吸引B. 两导线环相互排斥C. 两导线环无相互作用力D. 两导线环先吸引后排斥5.一个长螺线管中通有电流,把一个带电粒子沿中轴线射入(若不计重力影响),粒子将在管中( )A. 做圆周运动B. 沿轴线来回运动C. 做匀加速直线运动D. 做匀速直线运动6.关于磁场和磁感线,下列说法中正确的是()A. 磁场看不见、摸不到,但在磁体周围确实存在着磁场;而磁感线是一种假想曲线,是不存在的B. 磁场对放入其中的磁体产生力的作用,当其中没放入磁体时,则无力的作用,也就不存在磁场C. 在磁场中画出磁感线处存在磁场,在磁感线间的空白处不存在磁场D. 磁体周围的磁感线是从磁体北极出来,回到南极,所以磁体内部不存在磁场,也画不出来7.如图所示,在圆环状导体圆心处,放一个可以自由转动的小磁针.现给导体通以顺时针方向的恒定电流,不计其他磁场的影响,则( )A. 小磁针保持不动B. 小磁针的N极将向下转动C. 小磁针的N极将垂直于纸面向里转动D. 小磁针的N极将垂直于纸面向外转动8.发电机和电动机的发明使人类步入电气化时代,其中电动机依据的原理是()A. 磁场对电流的作用B. 磁铁间的相互作用C. 惯性定律D. 万有引力定律9.在物理学史上,发现电流周围存在磁场的著名科学家是A. 奥斯特B. 伽利略C. 焦耳D. 库仑二、多选题10.图中标出了磁场B的方向、通电直导线中电流I的方向以及通电直导线所受磁场力F的方向,其中正确的是()A. B. C. D.11.在赤道处沿东西方向水平放置一根长直导线,导线正下方放一小磁针,下列现象可能发生的是()A. 长直导线通电时,小磁针仍然静止B. 长直导线通电时,小磁针逆时针转动90°C. 长直导线通电时,小磁针顺时针转动90°D. 长直导线通电时,小磁针静止,将长直导线在水平面内稍作转动,小磁针转动近180°12.(多选)如图,一束带电粒子沿着水平方向平行地飞过磁针上方时,磁针的S极向纸内偏转,这一束带电粒子可能是()A. 向右飞行的正离子B. 向左飞行的正离子C. 向右飞行的负离子D. 向左飞行的负离子13.如图1,两根光滑平行导轨水平放置,间距为L,其间有竖直向下的匀强磁场,磁感应强度为B.垂直于导轨水平对称放置一根均匀金属棒.从t=0时刻起,棒上有如图2的变化电流I、周期为T,电流值为I m,图1中I所示方向为电流正方向.则金属棒()A. 位移随时间周期性变化B. 速度随时间周期性变化C. 受到的安培力随时间周期性变化D. 受到的安培力在一个周期内做正功14.图中装置可演示磁场对通电导线的作用.电磁铁上下两磁极之间某一水平面内固定两条平行金属导轨,L是置于导轨上并与导轨垂直的金属杆.当电磁铁线圈两端a、b,导轨两端e、f,分别接到两个不同的直流电源上时,L便在导轨上滑动.下列说法正确的是()A. 若a接正极,b接负极,e接正极,f接负极,则L向右滑动B. 若a接正极,b接负极,e接负极,f接正极,则L向右滑动C. 若a接负极,b接正极,e接正极,f接负极,则L向左滑动D. 若a接负极,b接正极,e接负极,f接正极,则L向左滑动15.如图所示,直导线处于足够大的匀强磁场中,与磁感线成θ=30°角,导线中通过的电流为I为了增大导线所受的磁场力,采取了下列四种办法,其中正确的是()A. 增大电流IB. 增加直导线的长度C. 使导线在纸面内顺时针转30°D. 使导线在纸面内逆时针转60°三、填空题16.通电螺线管的极性跟螺线管中的________方向有关,它们之间的关系可以用________定则来判定.内容是:用________手握住螺线管,让________弯向螺线管中电流的方向,则________所指的那端就是螺线管的N极.17.________是世界上最早研究磁现象的国家.并制成了指向仪器________,它是用天然磁石磨制成的________,静止时其________指向南方.指南针是我国________之一,其最早记载于北宋学者________的《梦溪笔谈》.18.一个磁场的磁感线如图所示,一个小磁针被放入磁场中,则小磁针沿顺时针转动,则磁场方向________。
大学物理(2-1)(山东联盟)智慧树知到答案章节测试2023年中国石油大学(华东)

绪论单元测试1.大学物理是面向理工科大学生的一门重要的必修基础课,该课程讲授的物理学知识、思想和方法是构成学生科学素养的重要组成部分.A:对B:错答案:A第一章测试1.质点由一点运动到另外一点,则下列说法正确的是A:各点的位置矢量是唯一的B:位移的大小等于路程C:路程是唯一的D:位移是唯一的答案:D2.以下关于加速度的说法中错误的是A:物体加速度大小越来越小时,物体的速度仍将可能增加B:加速度为零的物体速度不一定为零C:加速度决定了物体速度的变化D:物体速度大,加速度一定大答案:D3.质点沿半径为R的圆周作匀速率运动,每T秒转一圈。
在2T时间间隔中,其平均速度大小与平均速率大小分别为A:0 ,2πR/TB:2πR/T , 0C:2πR/T ,2πR/TD:0 , 0答案:A4.气球正在上升,气球下系有一重物,当气球上升到离地面100m高处,系绳突然断裂,重物下落,这重物下落到地面的运动与另一个物体从100m高处自由落到地面的运动相比,下列哪一个结论是正确的A:下落的路程相同B:下落的时间相同C:下落的位移相同D:落地时的速度相同答案:C5.某人骑自行车以速率v向正西方向行驶,遇到由北向南刮的风(设风速大小也是v),则他感到风是从A:西南方向吹来B:东南方向吹来C:东北方向吹来D:西北方向吹来答案:D6.电子很小可以视为质点,而太阳很大不能视为质点.A:对B:错答案:B7.质点做匀加速运动,其轨迹一定是直线.A:错B:对答案:A8.物体具有恒定的速度,但仍有变化的速率是不可能的.A:错B:对答案:B9.质点作匀速圆周运动时速度一定不变.A:对B:错答案:B10.同一物体的运动,如果选取的参考系不同,对它的运动描述也不同.A:对B:错答案:A第二章测试1.在下列关于力与运动关系的叙述中,正确的是A:若质点从静止开始,所受合力恒定,则一定作匀加速直线运动B:若质点所受合力越大,则质点速度必定越大C:若质点所受合力的大小不变,则一定作匀加速直线运动D:若质点所受合力恒定,肯定不会作曲线运动E:若质点所受合力的方向不变,则一定作直线运动答案:A2.质量为m的物体自空中落下,它除受重力外,还受到一个与速度平方成正比的阻力的作用,比例系数为k,k为正值常量.该下落物体的收尾速度(即最后物体作匀速运动时的速度)将是A:B:C:D:答案:A3.体重、身高相同的甲乙两人,分别用双手握住跨过无摩擦轻滑轮的绳子各一端.他们从同一高度由初速为零向上爬,经过一定时间,甲相对绳子的速率是乙相对绳子速率的两倍,则到达顶点的情况是A:甲先到达B:同时到达C:乙先到达D:谁先到达不能确定答案:B4.功的概念有以下几种说法:1)保守力作正功时,系统内相应的势能增加.2)质点运动经一闭合路径,保守力对质点做的功为零.3)作用力与反作用力大小相等,方向相反,所以两者所做功的代数和必为零.上列说法中A:2)、3)正确B:3)正确C:1)、2)正确D:2)正确答案:D5.在下列关于动量的表述中,不正确的是A:系统的内力无论为多大,只要合外力为零,系统的动量必守恒B:动量守恒是指运动全过程中动量时时(处处)都相等C:内力对系统内各质点的动量没有影响D:内力不影响系统的总动量,但要影响其总能量答案:C6.物体只有作匀速直线运动和静止时才有惯性.A:错B:对答案:A7.摩擦力总和物体运动的方向相反.A:对B:错答案:B8.质量为m的质点以速度v沿一直线运动,则它对空间任一点的角动量都为零.A:对B:错答案:B9.牛顿运动定律在任何参考系中都成立.A:对B:错答案:B10.一个不受外力作用的系统,它的动量和机械能都守恒.A:错答案:A第三章测试1.下面几种运动属于定轴转动的是A:陀螺的运动B:滚动车轮的运动C:抽油机活塞的运动D:电风扇叶片的运动答案:D2.刚体绕定轴作匀变速转动时,刚体上距轴为r的任一点的A:切向、法向加速度的大小均随时间变化B:切向加速度的大小恒定,法向加速度的大小变化C:切向、法向加速度的大小均保持恒定D:法向加速度的大小恒定,切向加速度的大小变化答案:B3.刚体角动量守恒的充分而必要的条件是A:刚体所受的合外力和合外力矩均为零B:刚体的转动惯量和角速度均保持不变C:刚体不受外力矩的作用D:刚体所受合外力矩为零答案:D4.有两个力作用在一个有固定转轴的刚体上(1) 这两个力都平行于轴作用时,它们对轴的合力矩一定是零; (2) 这两个力都垂直于轴作用时,它们对轴的合力矩可能是零; (3) 当这两个力的合力为零时,它们对轴的合力矩也一定是零; (4) 当这两个力对轴的合力矩为零时,它们的合力也一定是零.在上述说法中A:(1) 、(2)正确,(3) 、(4) 错误B:(1) 、(2) 、(3) 、(4)都正确C:(1)、(2) 、(3) 都正确,(4)错误D:只有(1)是正确的答案:A5.一个人站在有光滑固定转轴的转动平台上,双臂水平地拿着二哑铃.在该人把此二哑铃水平收缩到胸前的过程中,人、哑铃与转动平台组成的系统的A:机械能不守恒,角动量也不守恒B:机械能不守恒,角动量守恒C:机械能守恒,角动量不守恒D:机械能守恒,角动量守恒答案:B6.刚体的转动惯量只与转轴和刚体总质量有关.A:错答案:A7.一均匀细直棒,可绕通过其一端的光滑固定轴在竖直平面内转动.使棒从水平位置自由下摆,棒作匀角加速转动.A:对B:错答案:B8.刚体定轴转动时所有质点的角速度和角加速度都相同.A:错B:对答案:B9.刚体作定轴转动时,刚体角动量守恒的条件是刚体所受的合外力等于零.A:对B:错答案:B10.一个质量为m的小虫,在有光滑竖直固定中心轴的水平圆盘边缘上,此时圆盘转动的角速度为ω.若小虫沿着半径向圆盘中心爬行,则圆盘的角速度变大.A:对B:错答案:A第四章测试1.有下列几种说法:(1)所有惯性系对物理基本规律都是等价的;(2)在真空中,光的速度与光的频率、光源的运动状态无关;(3)在任何惯性系中,光在真空中沿任何方向的传播速率都相同.其中说法是正确的是A:全部说法都是正确的B:只有(1)、(3)是正确的C:只有(1)、(2)是正确的D:只有(2)、(3)是正确的答案:A2.在狭义相对论中,下列说法中正确的是:(1)一切运动物体相对于观察者的速度都不能大于真空中的光速;(2)质量、长度、时间的测量结果都是随物体与观察者的相对运动状态而改变的;(3)在一惯性系中发生于同一时刻,不同地点的两个事件在其他一切惯性系中也是同时发生的;(4)惯性系中的观察者观察一个与他作匀速相对运动的时钟时,会看到这时钟比与他相对静止的相同的时钟走得慢些.A:(2),(3),(4)B:(1),(3),(4)C:(1),(2),(4)D:(1),(2),(3)答案:C3.宇宙飞船相对于地面以速度0.8c直线飞行,一光脉冲从船尾传到船头.飞船的静止长度是100m,则地球观察者测出光脉冲从船尾到船头两个事件的空间间隔为A:60mB:100mC:500/3mD:300m答案:D4.在某地发生两件事,静止位于该地的甲测得时间间隔为4 s,若相对于甲作匀速直线运动的乙测得时间间隔为5 s,则乙相对于甲的运动速度是(c表示真空中光速)A:(1/5) cB:(3/5) cC:(2/5) cD:(4/5) c答案:B5.粒子在加速器中被加速,当其质量为静止质量的3倍时,其动能为静止能量的A:3倍B:5倍C:2倍D:4倍答案:C6.经典力学中的所有基本定律,如动量守恒定律,角动量守恒定律,机械能守恒定律都具有伽利略变换不变性.A:错B:对答案:B7.狭义相对论的两条基本原理是狭义相对性原理和光速不变原理.A:对B:错答案:A8.我们把与物体保持静止的参考系所测得的长度称为物体的固有长度.A:对B:错答案:A9.光子的静止质量为零.A:错答案:B10.在某个惯性系中有两个同时同地发生的事件,在对该系有相对运动的其他惯性系中,这两个事件不一定是同时同地发生的.A:对B:错答案:B第五章测试1.一质量为m的物体挂在劲度系数为k的轻弹簧下面,振动角频率为f ,若把此弹簧分割成四等份,将物体m挂在分割后的一根弹簧上,则振动角频率是A:3fB:0.5fC:2fD:f答案:C2.一质点作简谐振动,周期为T. 质点由平衡位置向x轴正方向运动时,由平衡位置到二分之一最大位移这段路程所需要的时间为A:T/8B:T/4C:T/12D:T/6答案:C3.一弹簧振子,当把它水平放置时,它可以作简谐振动,若把它竖直放置或放在固定的光滑斜面上,试判断下面哪种情况是正确的A:竖直放置可作简谐振动,放在光滑斜面上不能作简谐振动B:竖直放置不能作简谐振动,放在光滑斜面上可作简谐振动C:两种情况都不能作简谐振动D:两种情况都可作简谐振动答案:D4.一弹簧振子作简谐振动,总能量为E,如果简谐振动振幅增加为原来的两倍,重物的质量增为原来的四倍,则它的总能量变为A:E/4B:E/2C:2ED:4E答案:D5.一弹簧振子作简谐振动,当位移为振幅的一半时,其动能为总能量的A:1/2B:3/4C:3/2答案:B6.质点作简谐振动时,从平衡位置运动到最远点需时1/4周期,因此走过该距离的一半需时1/8周期.A:对B:错答案:B7.一个作简谐振动的物体,其位移与加速度的相位始终相差π.A:对B:错答案:A8.一个作简谐振动的物体处于平衡位置处时具有最大的速度和最大的加速度.A:错B:对答案:A9.简谐运动的动能和势能都随时间作周期性的变化,且变化频率与位移变化频率相同.A:对B:错答案:B10.两个相同的弹簧挂着质量不同的物体,当它们以相同的振幅作简谐振动时,振动总能量相同.A:对B:错答案:A第六章测试1.在相同的时间内,某种波长的单色光在空气中和在玻璃中A:传播的路程不相等,走过的光程不相等B:传播的路程不相等,走过的光程相等C:传播的路程相等,走过的光程相等D:传播的路程相等,走过的光程不相等答案:B2.用白光光源进行双缝实验,若用一个纯红色的滤光片遮盖一条缝,用一个纯蓝色的滤光片遮盖另一条缝,则A:不产生干涉条纹B:干涉条纹的宽度将发生改变C:干涉条纹的亮度将发生改变D:产生红光和蓝光两套彩色条纹答案:A3.在双缝干涉实验中,两条缝的宽度原来是相等的,若其中一缝的宽度略变窄(缝中心位置不变),则A:不再发生干涉现象B:干涉条纹的间距变宽C:干涉条纹的间距不变D:干涉条纹的间距变窄答案:C4.在光栅衍射实验中,与缺级级数有关的量为A:入射光波长B:屏到光栅的距离C:光栅常数D:入射光强度答案:C5.一束白光垂直照射在一光栅上,在形成的同一级光栅光谱中,偏离中央明纹最远的是A: 红光B:绿光C:黄光D:紫光答案:A6.获得相干光源只能用波阵面分割和振幅分割这两种方法来实现.A:错B:对答案:A7.发光的本质是原子、分子等从具有较高能级的激发态到较低能级的激发态跃迁过程中释放能量的一种形式.A:错B:对答案:B8.光波的相干叠加服从波的叠加原理,不相干叠加不服从波的叠加原理.A:对B:错答案:B9.光程是将光在不同介质中走过的实际路程折合成在真空中走过的路程.A:错B:对答案:A10.双折射现象是光从光疏介质进入光密介质时发生的一种现象.A:错B:对答案:A第七章测试1.水蒸气分解成同温度的氢气和氧气,内能增加了A:66.7%B: 0C:25%D:50%答案:C2.一瓶氦气和一瓶氮气密度相同,分子平均平动动能相同,而且它们都处于平衡状态,则它们A:温度相同,但氦气的压强小于氮气的压强B:温度、压强都不相同C:温度相同,但氦气的压强大于氮气的压强D:温度相同、压强相同答案:C3.关于温度的意义,有下列几种说法:(1)气体的温度是分子平均平动动能的量度.(2)气体的温度是大量气体分子热运动的集体表现,具有统计意义. (3)温度的高低反映物质内部分子热运动剧烈程度的不同.(4)从微观上看,气体的温度表示每个气体分子的冷热程度.这些说法中正确的是A:(1)、(3) 、(4)B:(1)、(2)、(4)C:(2)、(3)、(4)D:(1)、(2)、(3)答案:D4.下列各图所示的速率分布曲线,哪一图中的两条曲线能是同一温度下氮气和氦气的分子速率分布曲线A:B:C:D:答案:D5.玻尔兹曼分布律表明:在某一温度的平衡态,(1)分布在某一区间(坐标区间和速度区间)的分子数,与该区间粒子的能量成正比. (2)在同样大小的各区间(坐标区间和速度区间)中,能量较大的分子数较少;能量较小的分子数较多. (3)在大小相等的各区间(坐标区间和速度区间)中比较,分子总是处于低能态的概率大些. (4)分布在某一坐标区间内、具有各种速度的分子总数只与坐标区间的间隔成正比,与粒子能量无关.以上四种说法中A:只有(2)、(3)是正确的B:只有(1)、(2)、(3)是正确的C:只有(1)、(2)是正确的D:全部是正确的答案:A6.只有对大量分子的集体,温度的微观意义才成立.A:错B:对答案:B7.物体的熔解、凝固、蒸发等现象都属于热现象.A:对B:错答案:A8.一切互为热平衡的热力学系统不一定具有相同的温度.A:错B:对答案:A9.表征系统热平衡的宏观性质的物理量为压强.A:错B:对答案:A10.每个分子的质量、速度和能量属于微观量.A:对B:错答案:A第八章测试1.关于可逆过程和不可逆过程的判断: (1)可逆热力学过程一定是准静态过程. (2)准静态过程一定是可逆过程. (3)不可逆过程就是不能向相反方向进行的过程. (4)凡有摩擦的过程,一定是不可逆过程.以上四种判断,其中正确的是A: (1)、(2)、(3)B: (2)、(4)C: (1)、(2)、(4)D: (1)、(4)答案:D2.质量一定的理想气体,从相同状态出发,分别经历等温过程、等压过程和绝热过程,使其体积增加一倍,那么气体温度的改变(绝对值)在A:等压过程中最大,绝热过程中最小B:绝热过程中最大,等压过程中最小C:绝热过程中最大,等温过程中最小D:等压过程中最大,等温过程中最小答案:D3.两个相同的容器,容积固定不变,一个盛有氨气,另一个盛有氢气(看成刚性分子的理想气体),它们的压强和温度都相等,现将5J的热量传给氢气,使氢气温度升高,如果使氨气也升高同样的温度,则应向氨气传递的热量是A:6JB:5JC:2JD:3J答案:D4.1mol的单原子分子理想气体从状态A变为状态B,如果不知是什么气体,变化过程也不知道,但A、B两态的压强、体积和温度都知道,则可求出A:气体所作的功B:气体的质量C:气体传给外界的热量D:气体内能的变化答案:D5.一定量的某种理想气体起始温度为T,体积为V,该气体在下面循环过程中经过三个平衡过程:(1)绝热膨胀到体积为2V,(2)等体变化使温度恢复为T,(3)等温压缩到原来体积V,则此整个循环过程中A:气体内能减少B:气体对外界作正功C:气体向外界放热D:气体内能增加答案:C6.用旋转的叶片使绝热容器中的水温上升(焦耳热功当量实验),这一过程是可逆的.A:对B:错答案:B7.不规则地搅拌盛于绝热容器中的液体,液体温度在升高,若将液体看作系统,则外界对系统作功,系统的内能增加.A:对B:错答案:A8.热力学系统的状态发生变化时,其内能的改变量只决定于初末态的温度而与过程无关.A:错B:对答案:B9.不作任何热交换也可以使系统温度发生变化.A:错B:对答案:B10.对物体加热也可以不致升高物体的温度.A:对B:错答案:A。
2.实验二MATLAB绘图一答案

2.实验⼆MATLAB绘图⼀答案实验⼆ MATLAB 绘图⼀1. 编程绘制y=sin(t)/t 的曲线,t 的定义域是[-10Π,10Π],绘图时加⽹格解:t=[-10*pi:0.2:10*pi];y=sin(t)./t;plot(t,y),grid on-40-30-20-10010203040-0.4-0.20.20.40.60.812. 在[0,10]之间⽤⼀张图画出y=sin(t),y1=cos(t)的曲线,y ⽤红⾊实线绘制,y1⽤蓝⾊长划线绘制,绘图时加⽹格,横纵坐标⽐例相同,横轴标明“时间”,纵轴标明“正弦、余弦”,图题“正弦和余弦曲线”,要有图例说明,且⽤⿏标拖动来标注“sin(t)”、“cos(t)”。
解: t=0:0.1:10;y1=sin(t);y2=cos(t);plot(t,y1,'r',t,y2,'b--'); title('正弦和余弦曲线'); legend('正弦','余弦')xlabel('时间t'),ylabel('正弦、余弦') grid axis squaregtext('sin(t)'),gtext('cos(t)')246810-1-0.8-0.6-0.4-0.200.20.40.60.81正弦和余弦曲线时间t正弦、余弦3. ⽤三种⽅法编程,同时在⼀张图上观察常⽤对数、⾃然对数函数在[0,10]之间的曲线,其中在两种⽅法中,常⽤对数曲线⽤⿊⾊实线绘制,⾃然对数曲线⽤红⾊“+”绘制,绘图时,MATLAB 不要提⽰“W arning ” 解⼀: t=[0.1:0.1:10]; y1=log10(t); y2=log(t);plot(t,y1,'-k'),hold on plot(t,y2,'+r'),hold off246810-2.5-2-1.5-1-0.500.511.522.5解⼆: t=[0.1:0.1:10]; y1=log10(t); y2=log(t); plot(t,[y1;y2])246810-2.5-2-1.5-1-0.500.511.522.5解三: t=[0.1:0.1:10]; y1=log10(t); y2=log(t); plot(t,y1,'-k',t,y2,'+r')246810-2.5-2-1.5-1-0.500.511.522.54.曲线y=x+2x2+3x3,x的定义域为[-3,3],在⼀张图上⽤排成⼀⾏的三幅⼦图分别显⽰该曲线:⿊⾊实线图、脉冲图、条形图,每幅图均有图题及横纵坐标轴说明解:x=[-3:0.1:3];y=x+2*x.^2+3*x.^3;subplot(1,3,1),plot(x,y,'k')title('plot(x,y)')xlabel('x'),ylabel('y')subplot(1,3,2),stem(x,y)title(' stem(x,y)')xlabel('x'),ylabel('y')subplot(1,3,3),bar(x,y)title(' bar(x,y)')xlabel('x'),ylabel('y')5.通过MATLAB的help功能⾃学如何绘制饼图,在⼀张图上分上下两幅分别绘制“通信08-1”、“通信08-2”、“电⼦08-1”、“电⼦08-2”的“MATLAB ⼤侠”⽐例为3:3:2:2的饼图和⽴体饼图,其中,“通信08-1”的饼被抽出。
北理大学计算机实验基础 实验二 实验报告表答案精编版
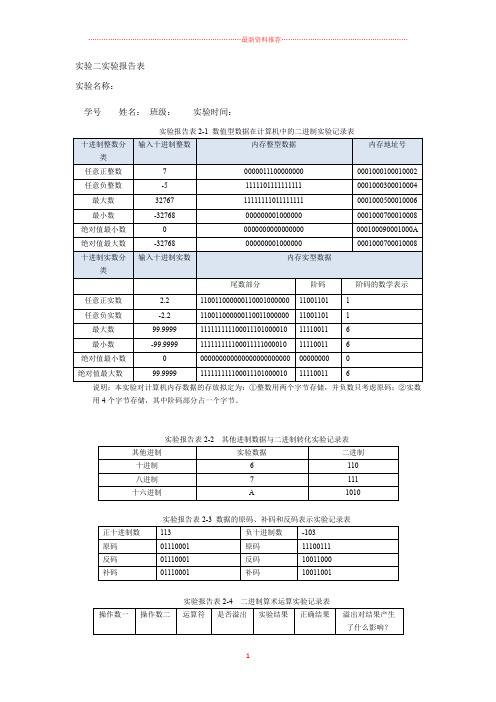
实验二实验报告表
实验名称:
学号姓名:班级:实验时间:
实验报告表2-1 数值型数据在计算机中的二进制实验记录表
说明:本实验对计算机内存数据的存放拟定为:①整数用两个字节存储,并负数只考虑原码;②实数用4个字节存储,其中阶码部分占一个字节。
实验报告表2-2 其他进制数据与二进制转化实验记录表
实验报告表2-3 数据的原码、补码和反码表示实验记录表
实验报告表2-4 二进制算术运算实验记录表
实验报告表2-5溢出实验记录表
实验报告表2-6浮点数的小数点浮动实验记录表
实验报考表2-7 表示浮点数的二进制串中阶码位数改变实验记录表。
操作系统实验答案-实验2Linux的基本操作及vi的使用(答案)

实验二Linux的基本命令操作及vi的使用实验目的:1、熟悉Linux操作系统环境2、熟悉Linux操作系统的文件结构3、熟悉Linux操作系统的基本命令4、熟悉Linux操作系统的文件组织方式5、学习使用vi编辑器建立、编辑、显示以及加工处理文本文件。
实验内容及要求:1、登陆实验室的Linux服务器。
启动电脑,进入Windows操作系统,在“开始”-〉“运行”中输入“Telnet 10.200.41。
178”,即可登陆实验室的Linux服务器.在“Login:”提示后输入“stu”+学号(如02号同学输入stu02),按下回车键。
在“Password:”提示后输入“123”(注意输入密码时屏幕上不会有“*”等符号出现,这和Windows 不同),按下回车键,若出现“[os@root os]$”或“-bash—2。
05b$”,表示已成功登陆系统,可以开始输入指令操作。
思考:(用pwd指令)查看自己登陆后位于Linux的哪个目录,写出该目录的路径,与自己周围的同学比较,看是否相同.(可查阅Linux资料了解“/home"目录的功能介绍)2、在Linux中进行以下基本操作:1)在当前目录下新建一个名为(自己姓名首字母缩写+学号后3位数)的子目录。
写出你所用的指令.(例如:mkdir zq000 )2)进入刚创建的子目录环境下.(提示:指令cd)3)在刚创建的子目录下新建一个名为abc.txt的文件。
写出你所用的指令。
(提示:新建文件的指令是touch)4)将/目录下(即根目录下)的welcome.txt文件复制到自己的子目录下,写出你所用的指令.cp –i /root/stu62/abc.txt /home/welcome.txt5)写出welcome.txt文件的内容。
(提示:用cat指令查看)Hello, Boys and girls ,welcome to the wonderful Linux world!3、在Linux中进行以下基本操作:1)进入自己的主目录。
2022学年九年级化学上仁爱版 学生实验实验1--2内容测试题附答案

实验1 实验基本操作一、单选题1.给3mL液体加热,需使用的仪器有①试管②烧杯③试管夹④酒精灯⑤蒸发皿⑥石棉网⑦铁架台(带铁圈)()A. ①③④⑤B. ②④⑥C. ①③④D. ②④⑥⑦2.一氧化氮是汽车尾气中的一种大气污染物,它是无色气体,难溶于水,密度比空气略大,在空气中能与氧气迅速反应生成红棕色的二氧化氮.在实验中,收集一氧化氮时可选用的收集方法是()A. 向下排空气法B. 向下排空气法C. 排水集气法D. 排水集气法或向下排空气法3.实验结束后,下图中仪器的处理方式正确的是()A. B. C. D.4.用量筒量取溶液,视线与量筒内液体的凹液面最低处保持水平,读数为15mL;倒出部分液体后,仰视凹液面的最低处,读数为9mL。
则该学生实际倒出的溶液体积()A. 大于6mLB. 小于6mLC. 等于6mLD. 以上都不对5.某同学用天平称量5g食盐时,天平指针向右偏转,此时应进行的操作为()A. 添加药品B. 减少药品C. 增加砝码D. 减少砝码6.用酒精灯给试管里的液体加热时,造成试管破裂,可能的原因有:①用酒精灯外焰加热②试管外壁有水③试管底部接触灯芯④没有先预热就直接集中加热液体.你认为可能的原因是()A. ①③④B. ②④C. ②③④D. ③④7.给试管里的物质加热时,切忌将试管底部接触灯芯的原因是()A.易使试管底部熔化B.会使酒精燃烧不充分C.会使酒精灯熄灭D.灯芯处温度低,易使热的试管骤冷而破裂8.下列能直接加热,且为玻璃仪器的是()A. 烧杯B. 试管C. 集气瓶D. 蒸发皿9.用量筒量取20mL的水,读数时视线仰望,则所取水的实际体积()A. 20mLB. 大于20mLC. 小于20mLD. 无法估计10.某气体既能用向上排空气法收集,也能用排水法收集,则该气体具备下列性质中的哪几项()①不易溶于水②易溶于水③密度比空气小④密度比空气大.A. ①③B. ①④C. ②③D. ②④二、填空题11.洗过的玻璃仪器内壁附着的水既________,也不________流下时,表明仪器已洗干净.12.从现在起我们应该帮助爸爸、妈妈做一些家务事,锻炼独立生活能力,刷洗碗碟的过程是________,判断是否刷净的标准是________.13.使用量筒时,量筒必须________ ,视线要与液体的________保持水平,读数时如果俯视刻度,则读数偏________ (填大、小),量出的液体体积比读数要________(填大、小).14.________是实验室常用的加热仪器.是使用时绝对禁止________,也绝对禁止________,以免失火.用完后必须用________盖灭.三、解答题15.我们都知道:KTV房间内的空气质量不如室外的清新,长时间呆在里面有头晕感觉,现有环境监测人员到某KTV房抽取空气样品进行检测,你知道他是如何抽取的吗?(请写出具体的操作)四、实验探究题16.如图是实验室常用的仪器,请用图中仪器的名称按要求填空:(1)用于取用粉末状固体药品的仪器是________;(2)用于吸取和滴加少量液体药品的仪器是________;(3)常用于给物质加热的仪器是________;(4)既可用作反应容器又能直接受热的是________;(5)用来收集和贮存少量气体的仪器是________.五、综合题17.正确的操作是试验成功的重要保证.(1)现用50mL 量筒量取46mL 氯化钠溶液,请你在图中画出所取氯化钠溶液的液面.(2)在过滤的操作中,需要的仪器除铁架台(含铁圈)、烧杯、漏斗,还需要________ ;过滤中要注意“一贴二低三靠”,“二低”中的其中“一低”是指滤纸边缘略低于漏斗边缘,这样操作的原因是________18.某同学准备称量一定量的食盐和量取一定量的水做实验:(1)称量食盐:用托盘天平称量3g食盐。
苏州南京师范大学苏州实验学校高中数学选修2-1第二章《空间向量与立体几何》检测(含答案解析)

一、选择题1.已知三棱锥P ABC -的所有棱长均为2,点M 为BC 边上一动点,若AN PM ⊥且垂足为N ,则线段CN 长的最小值为( )A .2133-B .2733-C .73D .12.如图,四边形ABCD 和ABEF 都是正方形,G 为CD 的中点,60DAF ∠=,则直线BG 与平面AGE 所成角的余弦值是( )A .25B .105C .155D .2153.在正四棱锥P ABCD -中,1PA PB PC PD AB =====,点Q ,R 分别在棱AB ,PC 上运动,当||QR 达到最小值时,||||PQ CQ 的值为( ) A .7010 B .355 C .3510 D .7054.如图,在60︒二面角的棱上有两点A 、B ,线段AC 、BD 分别在这个二面角的两个面内,并且都垂直于棱AB ,若AB =4,AC =6,BD =6,则线段CD 的长为( )A 29B .10C .241D .2135.若直线1l 、2l 的方向向量分别为(1,2,2)a =-,(2,3,2)b =-,则1l 与2l 的位置关系是( )A .12l l ⊥B .12l lC .1l 、2l 相交不垂直D .不能确定 6.在边长为2的菱形ABCD 中,23BD =ABCD 沿对角线AC 对折,使二面角B AC D --的余弦值为13,则所得三棱锥A BCD -的内切球的表面积为( ) A .43π B .π C .23π D .2π 7.将直角三角形ABC 沿斜边上的高AD 折成120︒的二面角,已知直角边43,46AB AC ==,那么下面说法正确的是( ) A .平面ABC ⊥平面ACDB .四面体D ABC -的体积是86 C .二面角A BCD --的正切值是423 D .BC 与平面ACD 所成角的正弦值是2178.在棱长为2的正方体1111ABCD A BC D -中,E ,F 分别为棱1AA 、1BB 的中点,M 为棱11A B 上的一点,且1(02)A M λλ=<<,设点N 为ME 的中点,则点N 到平面1D EF 的距离为( )A .3λB .22C .23λD .559.如图,在棱长为2的正方体1111ABCD A BC D -中,点E F 、分别是棱AB 、BC 的中点,则点1C 到平面1B EF 的距离等于( )A .23B .223C .233D .4310.如图所示,平行六面体1111ABCD A BC D -中,以顶点A 为端点的三条棱长都为1,且两两夹角为60︒.求1BD 与AC 夹角的余弦值是( )A .33B .66C .217D .21311.如图,在长方体ABCD ﹣A 1B 1C 1D 1中,DC =2,DA =DD 1=1,点M 、N 分别为A 1D 和CD 1上的动点,若MN ∥平面AA 1C 1C ,则MN 的最小值为( )A .53B .23C .56D .5212.已知正方体ABCD ﹣A 1B 1C 1D 1,点E 为平面BCC 1B 1的中心,则直线DE 与平面ACD 1所成角的余弦值为( )A .14B .13C .33D .233二、填空题13.如图,在四面体ABCD 中,若截面PQMN 是正方形,则有以下四个结论,其中结论正确的是__________________.(请将你认为正确的结论的序号都填上,注意:多填、错填、少填均不得分.)①//AC 截面PQMN ;②AC BD ⊥;③AC BD =;④异面直线PM 与BD 所成的角为045.14.若平面α的一个法向量为()n 122=,,,A(1,0,2),B(0,-1,4),A ∉α,B ∈α,则点A 到平面α的距离为__________.15.如图,四棱锥P ABCD -中,ABCD 是矩形,PA ⊥平面ABCD ,1==PA AB ,2BC =,四棱锥外接球的球心为O ,点E 是棱AD 上的一个动点.给出如下命题:①直线PB 与直线CE 是异面直线;②BE 与PC 一定不垂直;③三棱锥E BCO -的体积为定值;④CE PE +的最小值为22.其中正确命题的序号是______________.(将你认为正确的命题序号都填上)16.如图,正方体1111ABCD A BC D -的棱长为1,P 为BC 的中点,Q 为线段1CC 上的动点,过点A ,P ,Q 的平面截该正方体所得的截面为S ,则下列命题正确的是__________(写出所有正确命题的编号).①当102CQ <<时,S 为四边形;②当12CQ =时,S 为等腰梯形; ③当34CQ =时,S 与11C D 的交点R 满足114C R =; ④当314CQ <<时,S 为五边形; ⑤当1CQ =时,S 的面积为6.17.若向量()()()1,1,,1,2,1,1,1,1a x b c ===,满足条件()()·22c a b -=-,则x = __________.18.如图,四边形ABCD 和ADPQ 均为正方形,它们所在的平面互相垂直,,,M E F 分别为,,PQ AB BC 的中点,则直线ME 与平面ABCD 所成角的正切值为________;异面直线EM 与AF 所成角的余弦值是________.19.已知,若向量互相垂直,则k 的值为____. 20.正三棱锥底面边长为1,侧面与底面所成二面角为45°,则它的全面积为________三、解答题21.如图,直三棱柱ABC-A 1B 1C 1中,ABC 是边长为6的等边三角形,D ,E 分别为AA 1,BC 的中点.(1)证明:AE //平面BDC 1;(2)若123AA =,求DE 与平面BDC 1所成角的正弦值. 22.如图,在三棱锥P ABE -中,AB AE ⊥,PA ⊥平面ABE ,D 是AE 的中点,C 是线段BE 上的一点,且5AC =,122AB AP AE ===.(1)求证://CD 平面PAB ;(2)求直线PE 与平面PCD 所成角的正弦.23.如图,在四棱锥P ABCD -中,PD ⊥平面ABCD ,4PD =,底面ABCD 是边长为2的正方形,E ,F 分别为PB ,PC 的中点.(1)求证:平面ADE ⊥平面PCD ;(2)求直线BF 与平面ADE 所成角的正弦值.24.如图,在四棱锥P ABCD -中,PD ⊥平面//ABCD AB CD AD CD ⊥,,,且22AD CD PD AB ====.(I )求证:AB ⊥平面PAD ;(Ⅱ)求二面角P BC A --的余弦值.25.如图,在等腰直角三角形PAD 中,90A ∠=︒,8AD =,3AB =,B ,C 分别是PA ,PD 上的点,且//AD BC ,M ,N 分别为BP ,CD 的中点,现将BCP 沿BC 折起,得到四棱锥P ABCD -,连结MN .(1)证明://MN 平面PAD ;(2)在翻折的过程中,当4PA =时,求二面角B PC D --的余弦值.26.如图,在直三棱柱111ABC A B C -中,AB AC ⊥,2AB AC ==,14AA =,点D 是BC 的中点.(1)求异面直线1A B 与1C D 所成角的余弦值;(2)求平面1ADC 与平面1A BA 所成的二面角(是指不超过90的角)的余弦值.【参考答案】***试卷处理标记,请不要删除一、选择题1.A解析:A【分析】取PA 中点O ,得点N 在以O 为球心,半径为1的球面上,进一步可得N 的轨迹为一段圆弧,设点O 在平面PBC 的投影点为1O ,则点N 在以1O 为圆心的圆弧上,可得当点N 在1CO 上时,CN 取最小值,求解三角形计算得答案.【详解】解:取PA 中点O ,AN PM ⊥,∴点N 在以O 为球心,半径为1的球面上, 又点N 在平面PBC 上,故N 的轨迹为一段圆弧,设点O 在平面PBC 的投影点为1O ,且点1(O PS S ∈为BC 中点),则点N 在以1O 为圆心的圆弧上,3PS AS ==,设A 到PS 的距离为h ,则221132(3)122h =⨯- 即26h =,得163OO =,21631()3PO =-,22213PS =-=由N 在PS 上时,求得13NO =Rt △1CO S ,得2212313213CO ⎛⎫=+ ⎪ ⎪=⎝⎭,则当点N 在1CO 上时,CN 取最小值2133-, 故选:A .【点睛】本题考查空间中点、线、面间的距离计算,考查空间想象能力与思维能力,考查运算求解能力,解答的关键是弄清动点的轨迹;2.C解析:C【分析】以A 为原点,以AD 、AB 的方向分别为x 、y 轴的正方向,过A 作垂直平面ABCD 的直线作z 轴建立空间直角坐标系,设2AB =,利用空间向量法可求得直线BG 与平面AGE 所成角的正弦值,再利用同角三角函数的基本关系可求得结果.【详解】以A 为原点,以AD 、AB 的方向分别为x 、y 轴的正方向,过A 作垂直平面ABCD 的直线作z 轴,建立如图所示的空间直角坐标系A xyz -.设2AB =,得()0,0,0A 、()2,1,0G 、()0,2,0B 、(1,3E ,则()2,1,0AG =,(3AE =,()2,1,0BG =-,设平面AGE 的法向量为(),,n x y z =, 则20230n AG x y n AE x y z ⎧⋅=+=⎪⎨⋅=+=⎪⎩,取1x =,则2y =-,3z = 所以,平面AGE 的一个法向量为(1,3n =-,从而410cos ,5225n BGn BG n BG ⋅<>===⨯⋅, 故直线BG 与平面AGE 所成角的余弦值是21015155⎛⎫-= ⎪ ⎪⎝⎭. 故选:C.【点睛】方法点睛:计算线面角,一般有如下几种方法:(1)利用面面垂直的性质定理,得到线面垂直,进而确定线面角的垂足,明确斜线在平面内的射影,即可确定线面角;(2)在构成线面角的直角三角形中,可利用等体积法求解垂线段的长度h ,从而不必作出线面角,则线面角θ满足sin h lθ=(l 为斜线段长),进而可求得线面角; (3)建立空间直角坐标系,利用向量法求解,设a 为直线l 的方向向量,n 为平面的法向量,则线面角θ的正弦值为sin cos ,a n θ=<>.3.A解析:A【分析】建立空间直角坐标系,利用三点共线的思想,分别求出点R ,Q ,利用两点距离公式求解,后利用导数求最值,进一步求出答案.【详解】以P 在底面的投影O 为坐标原点,建立如图所示的坐标系,设1(,,0)2Q a ,(,,)R m n q 因为211(0(,0),222P C -,,112(,222PC =-, 又因为R 在PC 上,PR PC λ=所以(,m m q =,11(,),22λλ-, 所以R 11(,),2222λλ=--+,所以2222111222QR a λλ⎛⎛⎫⎛⎫=--+-++ ⎪ ⎪ ⎝⎭⎝⎭⎝⎭221324a a λλλ=+-++ 因为[]11,,0,122a λ⎡⎤∈-∈⎢⎥⎣⎦ 设2213()24f a a a λλλ=+-++,2213()24g a a λλλλ=+-++ 对其求导()2f a a λ'=-,1()22g a λλ'=-+ 当二个导数同时为0时,取最小值,即20a λ-=,1202a λ-+= 所以11,36a λ==时取最小值, 所以1121,,,1,,02623PQ CQ ⎛⎫⎛⎫=-=- ⎪ ⎪ ⎪⎝⎭⎝⎭所以PQ CQ =所以当||QR 达到最小值时,||||PQ CQ 故选:A.【点睛】 空间直角坐标系距离公式的理解:(1)两点间的距离公式其形式与平面向量的长度公式一致,它的几何意义是表示长方体的对角线的长度.(2)两点间的距离公式与坐标原点的选取无关,经过适当转化也可以求异面直线间的距离,点到面以及平面与平面的距离等.本题主要是R 的坐标利用三点共线的思想去求.4.D解析:D【解析】【分析】CD CA AB BD =++,利用数量积运算性质可得2222222CD CA AB BD CA AB CA BD AB BD =+++++.根据CA AB ⊥,BD AB ⊥,可得0CA AB =,0BD AB =,由60︒二面角可得;cos120CA BD CA BD =︒,代入计算即可得出. 【详解】解:CD CA AB BD =++,∴2222222CD CA AB BD CA AB CA BD AB BD =+++++,CA AB ⊥,BD AB ⊥,∴0CA AB =,0BD AB =,1cos12066182CA BD CA BD =︒=-⨯⨯=-.∴222264621852CD =++-⨯=, ∴213CD =故选:D . 【点睛】本题考查了利用向量的多边形法则、数量积的运算性质、向量垂直与数量积的关系,考查了空间想象能力,考查了推理能力与计算能力,属于中档题5.A解析:A 【分析】求出直线1l 、2l 的方向向量数量积为0,由此得到1l 与2l 的位置关系. 【详解】由题意,直线1l 、2l 的方向向量分别为(1,2,2)a =-,(2,3,2)b =-,2640a b ⋅=-+-=,∴1l 与2l 的位置关系是12l l ⊥.故选A . 【点睛】本题主要考查了两直线的位置关系的判断,考查直线与直线垂直的性质等基础知识,着重考查运算求解能力,属于基础题.6.C解析:C 【分析】作出图形,利用菱形对角线相互垂直的性质得出DN ⊥AC ,BN ⊥AC ,可得出二面角B ﹣AC ﹣D 的平面角为∠BND ,再利用余弦定理求出BD ,可知三棱锥B ﹣ACD 为正四面体,可得出内切球的半径R ,再利用球体的表面积公式可得出答案. 【详解】 如下图所示,易知△ABC 和△ACD 都是等边三角形,取AC 的中点N ,则DN ⊥AC ,BN ⊥AC . 所以,∠BND 是二面角B ﹣AC ﹣D 的平面角,过点B 作BO ⊥DN 交DN 于点O ,可得BO ⊥平面ACD .因为在△BDN 中,3BN DN ==,所以,BD 2=BN 2+DN 2﹣2BN •DN •cos ∠BND 1332343=+-⨯⨯=, 则BD =2.故三棱锥A ﹣BCD 为正四面体,则其内切球半径为正四面体高的14,又正四面体的高为棱长的63,故662126R ==. 因此,三棱锥A ﹣BCD 的内切球的表面积为226244(3R πππ=⨯=. 故选C . 【点睛】本题考查几何体的内切球问题,解决本题的关键在于计算几何体的棱长确定几何体的形状,考查了二面角的定义与余弦定理,考查计算能力,属于中等题.7.C解析:C 【分析】先由图形的位置关系得到CDB ∠是二面角C AD B --的平面角,120CDB ∠=,故A不正确;B 由于11132684sin12042332D ABC A BCD BCD V V S AD --⎛⎫==⋅=⨯⨯= ⎪⎝⎭故得到B 错误;易知AFD ∠为二面角A BC D --的平面角,4242tan 4217AD AFD DF ∠===∠BDC 为B ﹣AD ﹣C 的平面角,即∠BDC=120°,作DF ⊥BC 于F ,连结AF ,sin ∠BCO=BOBC. 【详解】 沿AD 折后如图,AD BC ⊥,易知CDB ∠是二面角C AD B --的平面角,120CDB ∠=,12,4,42,CD BD AD ===由余弦定理得2222BC CD BD CD =+-cos120BD ⋅,可得47BC =过D 作DF BC ⊥于F ,连接AF ,则AF BC ⊥,由面积相等得11sin12022CD BD DF BC ⋅=⋅,可得421DF =. 根据AD BC ⊥,易知CDB ∠是二面角C AD B --的平面角, 120CDB ∠=故A 平面ABC 与平面ACD 不垂直,A 错;B 由于11132684sin12042332D ABC A BCD BCD V V S AD --⎛⎫==⋅=⨯⨯⨯= ⎪⎝⎭,B 错; C 易知AFD ∠为二面角A BC D --的平面角,4242tan 421AD AFD DF ∠===C 对;D 故如图,由题意可知∠BDC 为B ﹣AD ﹣C 的平面角,即∠BDC=120°,作DF ⊥BC 于F ,连结AF ,AF=4217,BD=4,DC=8,AD=4,过O 作BO 垂直BO ⊥CO 于O ,则∠BCO 就是BC 与平面ACD 所成角,3OD=2,2247BO CO +sin ∠BCO=232147BO BC ==. 选.C 【点睛】本题考查了平面的翻折问题,考查了面面垂直的证明,线面角的求法,面面角的求法以及四面体体积的求法,求线面角,一是可以利用等体积计算出直线的端点到面的距离,除以线段长度就是线面角的正弦值;还可以建系,用空间向量的方法求直线的方向向量和面的法向量,再求线面角即可.面面角一般是要么定义法,做出二面角,或者三垂线法做出二面角,利用几何关系求出二面角,要么建系来做.8.D解析:D【分析】由几何体为正方体,以D 为原点,DA 为x 轴,DC 为y 轴,DD 1为z 轴,建立空间直角坐标系,求出平面D 1EF 的法向量n ,结合向量的点到平面距离公式求得点M 到平面D 1EF 的距离,结合N 为EM 中点即可求解 【详解】以D 为原点,DA 为x 轴,DC 为y 轴,DD 1为z 轴,建立空间直角坐标系, 则M (2,λ,2),D 1(0,0,2),E (2,0,1),F (2,2,1),1ED =(﹣2,0,1),EF =(0,2,0),EM =(0,λ,1),设平面D 1EF 的法向量n =(x ,y ,z ),则12020n ED x z n EF y ⎧⋅=-+=⎪⎨⋅==⎪⎩ ,取x =1,得n =(1,0,2),∴点M 到平面D 1EF 的距离为:d =||225||55EM n n ⋅==,N 为EM 中点,所以N 到该面的距离为55故选:D .【点睛】本题考查利用向量法求解点到平面距离,建系法与数形结合是解题关键,属于中档题9.D解析:D 【分析】建立空间直角坐标系,找到平面1B EF 的法向量,利用向量法求点到平面的距离求解即可. 【详解】以1D 为坐标原点,分别以11D A ,11D C ,1D D 的方向为x 轴、y 轴、z 轴的正方向建立空间直角坐标系,则1(2,2,0)B ,1(0,2,0)C ,(2,1,2)E ,(1,2,2)F .设平面1B EF 的法向量为(,,)n x y z =,1(0,1,2)B E =-1(1,0,2)B F =-则1100n B E n B F ⎧⋅=⎪⎨⋅=⎪⎩,即2020y z x z -+=⎧⎨-+=⎩令1z =,得(2,2,1)n =. 又11(2,0,0)BC =-, ∴点1C 到平面1B EF 的距离1122|||243||221n B C h n ⋅-===++,故选:D . 【点睛】本题用向量法求点到平面的距离,我们也可以用等体积法求点到平面的距离,当然也可以找到这个垂线段,然后放在直角三角形中去求.10.B解析:B 【分析】以1,,AB AD AA 为空间向量的基底,表示出1BD 和AC ,由空间向量的数量积求出向量的夹角的余弦值即得. 【详解】由题意11111cos 602AB AD AB AA AD AA ⋅=⋅=⋅=⨯⨯︒=. 以1,,AB AD AA 为空间向量的基底,AC AB AD =+,111BD AD AB AD AA AB =-=+-,221111()()AC BD AB AD AD AA AB AB AD AB AA AB AD AD AA AB AD ⋅=+⋅+-=⋅+⋅-++⋅-⋅1=,222()23AC AB AD AB AB AD AD =+=+⋅+=222211111()2222BD AD AA AB AD AA AB AD AA AD AB AA AB =+-=+++⋅-⋅-⋅=,∴11116cos ,632AC BD AC BD AC BD ⋅<>===⋅⋅.∴1BD 与AC 夹角的余弦值为66.故选:B . 【点睛】本题考查用空间向量法求异面直线所成的角,解题时选取空间基底,把其他向量用基底表示,然后由数量积的定义求得向量的夹角,即得异面直线所成的角.11.A解析:A 【分析】先建立空间坐标系,设出(),0,M m m ,()0,22,N n n -+,转化条件得1m n +=,利用函数即可得解. 【详解】如图建系,由题意可设(),0,M m m ,()0,22,N n n -+,∴(),22,MN m n n m =---,又 ()10,0,1AA =,()1,2,0AC =-,∴平面11AAC C 的法向量()2,1,0n =,又 //MN 面11AACC ,∴=0MN n ⋅即1m n +=,∴()()2222222941MN m n n m m m =+-+-=-+, ∴MN 最小值为5故选:A. 【点睛】本题考查了空间向量的应用,考查了转化化归和函数思想,属于中档题.12.B解析:B【分析】如图所示,建立空间之间坐标系,设正方体边长为1,则()0,0,0D ,11,1,22E ⎛⎫⎪⎝⎭.易知平面1ACD 的法向量为()1,1,1n =,计算夹角得到答案. 【详解】如图所示,建立空间之间坐标系,设正方体边长为1,则()0,0,0D ,11,1,22E ⎛⎫⎪⎝⎭. 根据1,n AC n AD ⊥⊥得到平面1ACD 的法向量为()1,1,1n =,11,1,22DE ⎛⎫= ⎪⎝⎭, 故22cos 3n DE n DEα⋅==⋅,故1sin 3α=, 直线DE 与平面ACD 1所成角θ,满足1cos sin 3θα==. 故选:B .【点睛】本题考查了线面夹角,意在考查学生的空间想象能力和计算能力.二、填空题13.①②④【分析】根据线面平行的判定定理可判断①;同①以及正方形的特征可判断②;根据异面直线所成的角可判断④;根据题中条件若不是其所在线段中点时可判断③【详解】因为是正方形所以所以平面又平面平面于所以所解析:①②④ 【分析】根据线面平行的判定定理可判断①;同①以及正方形的特征可判断②;根据异面直线所成的角可判断④;根据题中条件,若P Q M N 、、、不是其所在线段中点时可判断③ 【详解】因为PQMN 是正方形,所以//PQ MN ,所以//PQ 平面ACD ,又平面ACD ⋂平面ABC 于AC ,所以//AC PQ ,所以//AC 截面PQMN ,故①正确;同理可得//BD MQ ,所以AC BD ⊥,即②正确;又//BD MQ ,PMQ 45∠=︒,所以异面直线PM 与BD 所成的角为045,故④正确;根据已知条件,无法确定AC BD 、长度之间的关系,故③错. 故答案为①②④ 【点睛】本题主要考查空间中点线面位置关系,熟记相关知识点即可求出结果,属于常考题型.14.【分析】利用点到直线的距离公式借助平面的法向量利用公式即可求解【详解】由题意平面的一个法向量为且则所以点A 到平面的距离为【点睛】本题主要考查了点到平面的距离的求法其中解答中熟记空间向量在几何问题中的解析:13【分析】利用点到直线的距离公式,借助平面的法向量,利用公式,即可求解. 【详解】由题意,平面α的一个法向量为,,(1)22n =,且(1,0,2),(0,1,4),,A B A B αα-∉∈,则(1,1,2)BA =-, 所以点A 到平面α的距离为1131BA n d n⋅+===+.【点睛】本题主要考查了点到平面的距离的求法,其中解答中熟记空间向量在几何问题中的应用,以及点到直线的距离公式,准确计算是解答的关键,着重考查了推理与计算能力,属于基础题.15.①③④【分析】由题意画出图形由异面直线的概念判断①;利用线面垂直的判定与性质判断②;找出球心由棱锥底面积与高为定值判断③;设列出关于的函数式结合其几何意义求出最小值判断④【详解】解:对于①直线经过平解析:①③④ 【分析】由题意画出图形,由异面直线的概念判断①;利用线面垂直的判定与性质判断②;找出球心,由棱锥底面积与高为定值判断③;设AE x =,列出PE EC +关于x 的函数式,结合其几何意义求出最小值判断④. 【详解】 解:对于①,直线PB 经过平面ABCD 内的点B ,而直线CE 在平面ABCD 内不过C ,∴直线PB 与直线CE 是异面直线,故①正确;对于②,当E 与D 重合时,BE AC ⊥,因为PA ⊥平面ABCD ,BE ⊂平面ABCD ,所以PA BE ⊥,又PAAC A =,PA ⊂平面PAC ,AC ⊂平面PAC ,BE ∴⊥平面PAC ,则BE 垂直AC ,故②错误;对于③,由题意知,四棱锥P ABCD -的外接球的球心为O 是PC 的中点,则△BCE 的面积为定值,且O 到平面ABCD 的距离为定值,∴三棱锥E BCO -的体积为定值,故③正确;对于④,设AE x =,则2DE x =-,2211(2)PE EC x x ∴+=+++-.由其几何意义,即平面内动点(,1)x 与两定点(0,0),(2,0)距离和的最小值知,其最小值为22,故④正确. 故答案为:①③④.【点睛】本题考查命题的真假判断与应用,考查空间想象能力和思维能力,属于中档题.16.①②④【解析】①项时为而时线段上同理存在一点与平行此时为四边形且是梯形故命题①为真;②项是等腰梯形故命题②为真;③项当时如图所示∵点是的中点∴∴∴与的交点满足故命题③为假④项如图所示为五边形故命题④解析:①②④ 【解析】 ①项,12CQ =时,S 为APQD , 而102CQ <<时,线段1DD 上同理,存在一点,与PQ 平行, 此时,S 为四边形,且是梯形,故命题①为真;②项,1AP D Q =,1AD PQ ,1APQD 是等腰梯形,故命题②为真;③项当34CQ =时,如图所示,0AP DC ⋂=, ∵点P 是BC 的中点,∴CO CD AB ==, ∴1113C R C Q CO QC ==, ∴S 与11CD 的交点R 满足113C R =, 故命题③为假.④项,如图所示,S 为五边形,故命题④为真;⑤项,如图所示,S 221526222222⎛⎫⎛⎫-= ⎪ ⎪ ⎪⎝⎭⎝⎭,故命题⑤为假.综上所述,命题正确的是:①②④.17.2【解析】因为向量所以则解之得应填答案解析:2 【解析】因为向量(1,1,),(1,2,1),(1,1,1)a x b c ===,所以(0,0,1),2(2,4,2)c a x b -=-=,则()(2)222c a b x -⋅=-=-,解之得2x =,应填答案2。
最新国家开放大学电大《MySQL数据库应用》网络核心课实验训练1及2答案

最新国家开放大学电大《MySQL数据库应用》网络核心课实验训练1及2答案盗传必究本课程分为形成性考核和终结性末考两种考核形式,形成性考核占50%(满分100分),末考为网络考试占50%(满分100),其中形成性考核为完成课程网站上的形考作业任务,形考作业均为主观题,包括四个实训:实训一:在MYSQL创建数据库和表,25分;实训二:数据查询操作,25分;实训三:数据增删改操作,25分;实训四:数据库系统维护,25分。
实验训练1 在MySQL中创建数据库和表答案:步骤:1、使用 show 语句找出在服务器上当前存在什么数据库:mysql>show databases;2、创建一个数据库 test :mysql>create database test;3、选择你所创建的数据库:mysql>use test;4 创建一个数据表:首先查看刚才创建的数据库中存在什么表:mysql>show tables;(说明刚才创建的数据库中还没有数据库表)接着我们创建一个关于 students 的数据表:包括学生的学号 (id) ,姓名 (name) ,性别 (sex) ,年龄 (age) 。
mysql>create table students(id int unsigned not null auto_increment primary key,name char(8) not null,sex char(4) not null,age tinyint unsigned not null,);解释:以 "id int unsigned not null auto_increment primary key" 行进行介绍 :"id" 为列的名称 ;"int" 指定该列的类型为 int( 取值范围为 -8388608 到 8388607), 在后面我们又用 "unsigned" 加以修饰 , 表示该类型为无符号型 , 此时该列的取值范围为 0 到 16777215;"not null" 说明该列的值不能为空 , 必须要填 , 如果不指定该属性 , 默认可为空 ;"auto_increment" 需在整数列中使用 , 其作用是在插入数据时若该列为 NULL, MySQL 将自动产生一个比现存值更大的唯一标识符值。
2020高中化学必修二实验题总结实验大全附答案

一.科学探究【B02-05】1.将一干燥的坩埚加热,同时取一小块钾,擦干表面的煤油后,迅速投到热坩埚中,观察现象。
2.在培养皿中放入一些水,然后取绿豆大的钾,用滤纸吸干表面的煤油,投入培养皿中,观察现象。
〖思考作答〗该实验说明了什么?实验1-1【B02-08】1.将少量氯水分别加热盛有NaBr溶液和KI溶液的试管中,用力振荡后加入少量四氯化碳,振荡、静置。
2.将少量溴水加入盛有KI溶液的试管中,用力振荡后加入少量四氯化碳,振荡、静置。
〖思考作答〗该实验说明了什么?二.科学探究【B02-15】1.取一小段镁带,用砂纸除去表面的氧化膜,放入试管中。
向试管中加入2mL水,并滴入2滴酚酞溶液。
观察现象。
过一会儿加热试管至水沸腾。
观察现象。
〖思考作答〗该实验说明了什么?2.取一小段镁带和一小片铝,用砂纸磨去它们表面的氧化膜,分别放入两支试管,再各加入2mL 1mol/L盐酸。
观察现象。
〖思考作答〗该实验说明了什么?实验1-2【B02-21】取一块绿豆大的金属钠(切去氧化层),用滤纸吸净煤油,放在石棉网上,用酒精灯微热。
待钠熔化球状时,将盛有氯气的集气瓶迅速倒扣在钠的上方。
观察现象。
〖思考作答〗写出化学方程式,用电子式表示NaCl的形成过程实验2-1、2-2【B02-33】在一支试管中加入2~3mL 6mol/L的盐酸,再插入用砂纸打磨光的铝条。
观察现象,并用温度计测量溶液温度的变化。
实验现象是将约20g Ba(OH)2·8H2O晶体研细后与约10g NH4Cl晶体一起放入烧杯中,并将烧杯放在滴有几滴水的玻璃片或小木板上,用玻璃棒快速搅拌,闻气味,用手接触杯壁下部,试着用手拿起烧杯。
实验现象是〖思考作答〗总结吸热和放热反应实验2-3【B02-34】在50mL烧杯中加入20mL 2mol/L的盐酸,测其温度。
另用量筒量取20mL 2mol/L的NaOH溶液,测其温度,并缓缓地倾入烧杯中,边加边用玻璃棒搅拌。
大学物理2-1第七章(波动光学)习题答案

习 题 七7-1 如图所示,O S O S 21=。
若在O S 1中放入一折射率为n ,厚度为e 的透明介质片,求O S 1与O S 2之间的光程差。
如果1S 和2S 是两个波长为λ的同相位的相干光源,求两光在O 点的相位差。
[解] O S 1与O S 2的几何路程相等 光程差为()e n 1-=δ 位相差为()e n 122-==∆λπδλπϕ7-2 一束绿光照射到两相距 0.6mm 的双缝上,在距双缝2.5m 处的屏上出现干涉条纹。
测得两相邻明条纹中心间的距离为2.27mm ,试求入射光的波长。
[解] 由杨氏双缝干涉知,dD x λ=∆ 所以5448m 10448.55.21060.01027.2733=⨯=⨯⨯⨯=∆=---D xd λÅ7-3 如图所示,在双缝干涉实验中,21SS SS =,用波长为λ的单色光照S ,通过空气后在屏幕E 上形成干涉条纹。
已知点P 处为第3级干涉明条纹,求1S 和2S 到点P 的光程差。
若整个装置放于某种透明液体中,点P 为第4级干涉明条纹,求该液体的折射率。
[解] 1S 和2S 到P 点的光程差满足λλδ312==-=k r r 整个装置放置于液体中,1S 和2S 到P 点的光程差满足()λδ412=-=r r nλλ43=n 所以得到 33.134==n7-4 如习题7-1图所示,1S 和2S 是两个同相位的相干光源,它们发出波长λ=5000Å的光波,设O 是它们中垂线上的一点,在点1S 与点O 之间的插入一折射率n =1.50的薄玻璃,点O 恰为第4级明条纹的中心,求它的厚度e 。
[解] 在O 点是第4级明条纹的中心 光程差 λδ4=-=e ne所以 410414⨯=-=n e λÅ7-5 初位相相同的两相干光源产生的波长为6000Å的光波在空间某点P 相遇产生干涉,其几何路径之差为6102.1-⨯m 。
如果光线通过的介质分别为空气(11=n )、水(=2n 1.33)或松节油(=3n 1.50)时,点P 的干涉是加强还是减弱。
上海青浦区实验中学高中数学选修2-1第三章《圆锥曲线与方程》测试题(含答案解析)

一、选择题1.设双曲线C :22221x y a b-=(0a >,0b >)的左、右焦分别是1F ,2F ,过1F 的直线交双曲线C 的左支于M ,N 两点若212=MF F F ,且112MF NF =,则双曲线C 的离心率是( ) A .2B .32C .54D .532.P 是椭圆221169x y +=上的点,1F 、2F 是椭圆的左、右焦点,设12PF PF k ⋅=,则k的最大值与最小值之和是( ) A .16 B .9 C .7 D .253.人们已经证明,抛物线有一条重要性质:从焦点发出的光线,经过抛物线上的一点反射后,反射光线平行于抛物线的轴.探照灯、手电筒也是利用这个原理设计的.已知抛物线()220y px p =>的焦点为F ,从点F 出发的光线第一象限内抛物线上一点P 反射后的光线所在直线方程为2y =,若入射光线FP 的斜率为43,则抛物线方程为 ( ) A .28y x =B .26y x =C .24y x =D .22y x =4.已知双曲线221(0,0)x y m n m n-=>>和椭圆22174x y +=有相同的焦点,则11m n +的最小值为( )A .12 B .32 C .43D .95.若圆222210x y ax y +-++=与圆221x y +=关于直线1y x =-对称,过点()2,C a a -的圆P 与y 轴相切,则圆心P 的轨迹方程为( )A .24480y x y -++=B .22220y x y +-+=C .2210y x y ---=D .24250y x y +-+=6.已知1F ,2F 是双曲线22221(0,0)x y a b a b-=>>的左右焦点,若在右支上存在点A 使得点2F 到直线1AF ,则离心率e 的取值范围是( )A .⎛ ⎝⎭B .⎫+∞⎪⎪⎝⎭C .⎛ ⎝⎭D .⎫+∞⎪⎪⎝⎭7.已知抛物线22(0)y px p =>的焦点为F ,点P 在抛物线上,点9,02Q p ⎛⎫⎪⎝⎭.若2QF PF =,且PQF △的面积为p =( )A .1B .2C .3D .48.椭圆22221x y a b+=(0a b >>)上一点M 关于原点的对称点为N ,F 为椭圆的一个焦点,若0MF NF ⋅=,且3MNF π∠=,则该椭圆的离心率为( ) A .212-B .22 C .33D .31-9.如图所示,12FF 分别为椭圆2222x y 1a b+=的左右焦点,点P 在椭圆上,2POF 的面积为3的正三角形,则2b 的值为( )A 3B .23C .33D .4310.抛物线224y x x =-的焦点坐标是( ) A .F (0,18) B .F (1,-158) C .F (0,-158) D .(1,18) 11.(2018·太原一模)已知抛物线y 2=2px(p>0)的焦点为F ,△ABC 的顶点都在抛物线上,且满足0FA FB FC ++=,则111AB BC CAk k k ++= ( ) A .0 B .1 C .2D .2p12.已知椭圆r :()222210x y a b a b+=>>的右焦点为()1,0F ,且离心率为12,三角形ABC 的三个顶点都在椭圆r 上,设它的三条边AB 、BC 、AC 的中点分别为D 、E 、M ,且三条边所在直线的斜率分别为1k 、2k 、3k ,且1k 、2k 、3k 均不为0.O 为坐标原点,若直线OD 、OE 、OM 的斜率之和为1.则123111k k k ++=( ) A .43-B .-3C .1813-D .32-二、填空题13.设12,F F 为双曲线22212x y a -=的两个焦点,已知点P 在此双曲线上,且123F PF π∠=,若此双曲线的离心率等于62,则点P 到y 轴的距离等于__________. 14.已知双曲线2222:1(0,0)x y C a b a b-=>>)的左,右焦点分别是1F ,2F ,直线:(10)l y k x =-过点2F ,且与双曲线C 在第一象限交于点P .若(22()0OP OF PF +⋅=(O 为坐标原点),且()121PF a PF +=,则双曲线C 的离心率为__________.15.已知双曲线()2222:10,0x y C a b a b-=>>的左、右焦点分别是1F ,2F ,直线:36l y x =+过点1F ,且与双曲线C 在第二象限交于点P ,若点P 在以12F F 为直径的圆上,则双曲线C 的离心率为_____________.16.已知椭圆22221(0)x y a b a b+=>>与直线11:2l y x =,21:2l y x =-,过椭圆上一点P作12,l l 的平行线,分别交12,l l 于,M N 两点,若||MN 为定值,则ab=__________. 17.如图,将桌面上装有液体的圆柱形杯子倾斜α角(母线与竖直方向所成角)后,液面呈椭圆形,当30α=︒时,该椭圆的离心率为____________.18.双曲线221916x y -=的左焦点到渐近线的距离为________.19.在平面直角坐标系中,曲线C 是由到两个定点1,0A 和点()1,0B -的距离之积等于2C ,有下列四个结论:①曲线C 是轴对称图形; ②曲线C 是中心对称图形;③曲线C 上所有的点都在单位圆221x y +=内; 其中,所有正确结论的序号是__________.20.已知双曲线的方程为221916x y -=,点12,F F 是其左右焦点,A 是圆22(6)4x y +-=上的一点,点M 在双曲线的右支上,则1||||MF MA +的最小值是__________.三、解答题21.在平面直角坐标系xOy 中,椭圆()2222:10x yC a b a b+=>>的离心率为12,过点()03,,且BMN ∆是椭圆C 的内接三角形.(1)若点B 为椭圆C 的上顶点,且原点O 为BMN ∆的垂心,求线段MN 的长; (2)若点B 为椭圆C 上的一动点,且原点O 为BMN ∆的重心,求原点O 到直线MN 距离的最小值.22.已知抛物线26y x =焦点为F ,一条直线过焦点与抛物线相交于A ,B 两点,直线的倾斜角为60.(1)求线段AB 的长度.(2)过点()3,0Q 的直线l 与抛物线C 交于M ,N 两点,点P 为直线3x =-上的任意一点,设直线PM ,PQ ,PN 的斜率分别为1k ,2k ,3k ,且满足132k k k μ+=,μ能否为定值?若为定值,求出μ的值;若不为定值,请说明理由.23.已知离心率22e =的椭圆C :()222210x y a b a b +=>>的一个焦点为()1,0-.(1)求椭圆C 的方程;(2)若斜率为1的直线l 交椭圆C 于A ,B 两点,且423AB =,求直线l 的方程. 24.已知椭圆2222:1(0)x y C a b a b+=>>的短轴为2,椭圆上的点到焦点的最短距离为23-.(1)求椭圆的标准方程;(2)已知椭圆的右顶点和上顶点分别为,M N ,斜率为12的直线l 与椭圆C 交于P Q 、两点,求证:直线MP 与NQ 的斜率之和为定值;(3)过右焦点2F 作相互垂直的弦,AB CD ,求||||AB CD +的最小值.25.椭圆C :22221(0)x y a b a b+=>>的一个焦点与抛物线243y x =的焦点重合,短轴的一个端点与两焦点围成的三角形面积为3. (1)求椭圆C 的方程;(2)设过点(0,4)的直线l 与椭圆C 交于,A B 两点,且坐标原点O 在以AB 为直径的圆上,求直线l 的斜率.26.在平面直角坐标系xOy 中,动点M 到点(1,0)A -和(1,0)B 的距离分别为1d 和2d ,2AMB θ∠=,且212cos 1d d θ=.(1)求动点M 的轨迹E 的方程;(2)是否存在直线l 过点B 与轨迹E 交于P ,Q 两点,且以PQ 为直径的圆过原点O ?若存在,求出直线l 的方程,若不存在,请说明理由.【参考答案】***试卷处理标记,请不要删除一、选择题 1.D 解析:D 【分析】根据题意画出图形,结合图形建立关于c 、a 的关系式,再求离心率ce a=的值. 【详解】 解:如图所示,取1F M 的中点P ,则2122MF FF c ==,MP c a =-,1F P c a =-;又112NF MF =,则()14NF c a =-,242NF c a =-; 在2Rt NPF △中,22222NP PF NF +=, 在2Rt MPF △中,22222MP PF MF +=,得()()()()22224252c a c a c c a ---=--⎡⎤⎣⎦, 化简得223850c ac a -+=, 即()()350c a c a --=, 解得c a =或35c a =; 又1e >, ∴离心率53c e a ==. 故选:D .【点睛】本题考查求双曲线的离心率,解题关键是建立,a c 的等量关系,结合等腰三角形的性质与双曲线的定义可得.2.D解析:D 【分析】设(),P x y ,根据标准方程求得271616k x =-,再由椭圆的几何性质可得最大值与最小值,从而可得结论. 【详解】因为椭圆方程为椭圆221169x y +=,所以4,7a c =设(),P x y , 则()()22222127·771616k PF PF x y x y x ==-+-+-, 又2016x ≤≤.∴max min 16,9k k ==. 故max min +16+925k k ==. 所以k 的最大值与最小值的和为25. 故选:D. 【点睛】关键点点睛:解决本题的关键在于将所求得量表示成椭圆上的点的坐标间的关系,由二次函数的性质求得其最值.3.D解析:D 【分析】由抛物线方程可得焦点坐标,设出P 点坐标,由性质求出P 点坐标,表示出FP 的斜率,解出p ,即可得抛物线方程. 【详解】,02p F ⎛⎫⎪⎝⎭,设()00,P x y由题意有02y =将02y =代入()220y px p =>得02x p=2,2P p ⎛⎫∴ ⎪⎝⎭,又,02p F ⎛⎫⎪⎝⎭,且FP 的斜率为43,有204232p p -=-解得:1p =故抛物线方程为:22y x = 故选:D 【点睛】抛物线方程中,字母p 的几何意义是抛物线的焦点F 到准线的距离,2p等于焦点到抛物线顶点的距离.牢记它对解题非常有益.4.C解析:C 【分析】本题首先可根据双曲线和椭圆有相同的焦点得出3m n +=,然后将11m n+转化为123m n n m ⎛⎫++ ⎪⎝⎭,最后利用基本不等式即可求出最小值. 【详解】因为双曲线221x y m n-=和椭圆22174x y +=有相同的焦点,所以743m n ,则()111111233m n m n m n n m n m ⎛⎫⎛⎫+=++=++ ⎪ ⎪⎝⎭⎝⎭ 142233m n n m,当且仅当m n =时取等号, 故11m n+的最小值为43,故选:C. 【点睛】关键点点睛:本题考查双曲线与椭圆焦点的相关性质的应用,双曲线有222+=a b c ,椭圆有222a b c =+,考查利用基本不等式求最值,是中档题.5.D解析:D 【分析】首先根据两圆的对称性,列式求a ,再利用直接法求圆心P 的轨迹方程. 【详解】由条件可知222210x y ax y +-++=的半径为1,并且圆心连线所在直线的斜率是1-,()()2222222101x y ax y x a y a +-++=⇔-++=,,圆心(),1a -,22r a =,所以2111a a -⎧=-⎪⎨⎪=⎩,解得:1a =,即()2,1C -设(),P x y ,由条件可知PC x =x =,两边平方后,整理为24250y x y +-+=. 故选:D 【点睛】方法点睛:一般求曲线方程的方法包含以下几种:1.直接法:把题设条件直接“翻译”成含,x y 的等式就得到曲线的轨迹方程.2.定义法:运用解析几何中以下常用定义(如圆锥曲线的定义),可从曲线定义出发,直接写出轨迹方程,或从曲线定义出发建立关系式,从而求出轨迹方程.3.相关点法:首先要有主动点和从动点,主动点在已知曲线上运动,则可以采用此法.6.D解析:D 【分析】设直线1AF 的方程,利用点2F 到直线的距离建立等式,解出斜率k ,因为0bk a<<,从而求出,a c 的不等关系,进而解出离心率的范围. 【详解】设1AF :()y k x c =+,因为点A 在右支上,则0b k a<<,,所以222222343a b k c a a =<-,即2247c a >,解得:2e > 故选:D . 【点睛】本题考查双曲线求离心率,属于中档题.方法点睛:(1)利用点到直线的距离建立等量关系; (2)解出斜率k 与,a b 的关系;(3)由点在右支和左焦点的位置关系,求出斜率k 的范围; (4)利用斜率k 的范围,建立,a c 的不等式,求出离心率的范围.7.B解析:B 【分析】根据题意得||4QF p =,||2PF p =,进而根据抛物线的定义得P 点的横坐标为32P x p =,设点P 在x 轴上方,故P ,再结合三角形PQF △面积即可得答案.【详解】 解:由条件知(,0)2p F ,所以||4QF p =,所以1||||22PF QF p ==, 由抛物线的准线为2p x =-,及抛物线的定义可知,P 点的横坐标为3222p p p -=,不妨设点P 在x 轴上方,则P ,所以142PQFSp =⨯=2p =. 故选:B 【点睛】本题解题的关键在于根据抛物线的定义得P 点的横坐标为32P x p =,进而求出P 的纵坐标并结合三角形PQF △面积求解,考查运算求解能力,是中档题.8.D解析:D 【分析】E 是另一个焦点,由对称性知MENF 是平行四边形,从而得MENF 是矩形.3MEF MNF π∠=∠=,在直角三角形MEF 中用c 表示出两直角边,再上椭圆定义得,a c 的等式,求得离心率. 【详解】如图,E 是另一个焦点,由对称性知MENF 是平行四边形, ∵0MF NF ⋅=,∴MF NF ⊥,∴MENF 是矩形.3MNF π∠=,∴3MEF π∠=,∴1cos232ME EF c c π==⨯=,2sin3MF c π==,∴1)2MF ME c a +==,∴1c e a ===. 故选:D .【点睛】关键点点睛:本题考查求椭圆的离心率,解题关键是找到,a c 的关系,本题利用椭圆的对称性,引入另一焦点E 后形成一个平行四边形MENF ,再根据向量数量积得垂直,从而得到矩形,在矩形中利用椭圆的定义构造出,a c 的关系.求出离心率.9.B解析:B 【分析】由2POF 3233=.c 把(3P 代入椭圆方程可得:22131a b+=,与224a b =+联立解得即可得出. 【详解】 解:2POF 3233= 解得2c =.(3P ∴代入椭圆方程可得:22131a b+=,与224a b =+联立解得:223b = 故选B . 【点睛】本题考查了椭圆的标准方程及其性质、等边三角形的面积计算公式,考查了推理能力与计算能力,属于中档题.10.B解析:B 【分析】右边配方后,利用抛物线的标准方程结合图象平移变换求解. 【详解】已知抛物线方程为22(1)2y x =--,即21(1)(2)2x y -=+,它的图象是由抛物线212x y =向右平移1单位,再向下平移2个单位得到的,抛物线212x y =中122p =,14p =,焦点坐标为1(0,)8,011+=,115288-=-,因此所求焦点坐标为15(1,)8-, 故选:B . 【点睛】本题考查求抛物线的焦点坐标,掌握抛物线的标准方程与图象变换是解题关键.11.A解析:A 【解析】设11(,)A x y ,22(,)B x y ,33(,)C x y . ∵抛物线22(0)y px p =>的焦点为F ∴(,0)2p F ∵0FA FB FC ++= ∴112233(,)(,)(,)(0,0)222p p px y x y x y -+-+-= ∴1230y y y ++=∵2221212121211()122AB y y x x y y p k y y y y p--+===--,同理可知3212BC y y k p +=,3112CA y y k p +=. ∴3231123212()11102222AB BC CA y y y y y y y y y k k k p p p p+++++++=++== 故选A.12.A解析:A 【分析】根据椭圆的右焦点为()1,0F ,且离心率为12,求出椭圆方程,由三角形ABC 的三个顶点都在椭圆r 上,利用点差法求解. 【详解】因为椭圆的右焦点为()1,0F ,且离心率为12, 所以11,2c c a ==,解得 22,3a b ==, 所以椭圆方程为:22143x y +=,设 ()()()112233,,,,,A x y B x y C x y ,则222212121,14343y x y x +=+=, 两式相减得:()()1212121243+-=--+y y x x y y x x , 即143OD AB k k =-, 同理1414,33OM OE AC BC k k k k =-=-, 又直线OD 、OE 、OM 的斜率之和为1,所以()1231114433OD OM OE k k k k k k ++=-++=-, 故选:A 【点睛】本题主要考查椭圆方程的求法以及直线与椭圆的位置关系和中点弦问题,还考查了运算求解的能力,属于中档题.二、填空题13.【解析】依题意由解得根据双曲线焦点三角形面积公式有解得代入双曲线方程解得解析:【解析】依题意,由222{b c a c a b ===+,解得2,a c =,根据双曲线焦点三角形面积公式有212F F 21b cotπ22tan6P S y∠===⋅,解得y =,代入双曲线方程解得x =14.【分析】取的中点则根据得则设根据结合双曲线的定义得到然后在中利用勾股定理求解即可【详解】如图取的中点则因为所以即因为是的中位线所以由题意可得设则由双曲线的定义可知则即故在中由勾股定理得即整理得解得故解析:2【分析】取2PF 的中点H ,则22OP OF OH +=,根据22()0OP OF PF +⋅=,得2OH PF ⊥,则12PF PF ⊥,设2PF m =,根据()121PF a PF +=结合双曲线的定义得到2||2PF =,122PF a =+,然后在12Rt PF F 中,利用勾股定理求解即可.【详解】 如图,取2PF 的中点H ,则22OP OF OH +=, 因为22()0OP OF PF +⋅=,所以20OH PF ⋅=,即2OH PF ⊥.因为OH 是12PF F △的中位线,所以12PF PF ⊥.由题意可得10c =,设2PF m =,则()11PF a m =+, 由双曲线的定义可知12||2PF PF a -=,则2am a =,即2m =, 故2||2PF =,122PF a =+.在12Rt PF F 中,由勾股定理得2221122||||PF PF F F +=, 即()242240a ++=,整理得2280a a +-=, 解得2a =.故双曲线C 的离心率为102c a =. 故答案为:102【点睛】本题主要考查双曲线的几何性质和定义的应用以及平面几何的知识,平面向量垂直问题,还考查了数形结合的思想和运算求解的能力,属于中档题.15.【分析】利用直线l 的斜率和点P 在以为直径的圆周上在直角三角形中求出和用定义求出代入离心率公式求解即可【详解】由题意可得则因为直线l 的斜率是3则因为点P 在以为直径的圆周上所以所以则故双曲线C 的离心率为 解析:102【分析】利用直线l 的斜率和点P 在以12F F 为直径的圆周上,在直角三角形12PF F 中,求出1PF和2PF ,用定义求出a ,代入离心率公式求解即可.【详解】由题意可得2c =,则2124F F c ==. 因为直线l 的斜率是3,则12sin PF F ∠=,12cos PF F ∠=. 因为点P 在以12F F 为直径的圆周上,所以1290F PF ∠=︒,所以11212cos PF F F PF F =∠=,21212sin PF F F PF F =∠=,则212PF PF a -==,故双曲线C的离心率为c a =【点睛】本题考查双曲线的性质,考查双曲线定义的应用,考查学生的计算能力,属于中档题.16.4【解析】当点时过椭圆上点作的平行线分别为联立可得同理可得所以当点时过椭圆上点作的平行线分别为联立可得同理可得所以所以为定值则所以点睛:本题考查了直线与椭圆的位置关系此类问题的解答中主要特例法的应用解析:4 【解析】当点(0,)P b 时,过椭圆上点P 作12,l l 的平行线分别为11,22y x b y x b =+=-+, 联立1212y x b y x⎧=-+⎪⎪⎨⎪=⎪⎩,可得(,)2b M b ,同理可得(,)2b N b -,所以2MN b =,当点(,0)P a 时,过椭圆上点P 作12,l l 的平行线分别为11,2222a ay x y x =-=-+, 联立12212a y x y x⎧=-+⎪⎪⎨⎪=⎪⎩,可得(,)24a a M ,同理可得(,)24a a N -,所以2a MN =,所以MN 为定值,则22ab =,所以4a b=. 点睛:本题考查了直线与椭圆的位置关系,此类问题的解答中主要特例法的应用,是解答选择题的一种方法,本题的解答中取点P 分别为长轴和短轴的端点,联立方程组,求得MN ,得出,a b 的关系式是解答关键,平时应注意特殊值等方法在选择题解答中的应用.17.【分析】由图知椭圆的短轴长为圆柱的直径椭圆的长半轴与底面半径构成夹角为的直角三角形由此可求得椭圆离心率【详解】设圆柱形杯子的底面半径为画示意图如图所示:则是椭圆的长半轴长是椭圆的短半轴长则又则故答案 解析:12【分析】由图知椭圆的短轴长为圆柱的直径,椭圆的长半轴与底面半径构成夹角为30的直角三角形,由此可求得椭圆离心率. 【详解】设圆柱形杯子的底面半径为b ,画示意图如图所示:则OC 是椭圆的长半轴长,OB 是椭圆的短半轴长,则22BC a b c =-=,又30COB α∠==︒,则1sin 2c e a α===. 故答案为:12【点睛】本题考查了圆柱的截面为椭圆的问题,根据椭圆的性质求出椭圆的离心率,考查了学生的分析能力,空间想象能力,属于中档题.18.4【分析】首先根据题中所给的双曲线方程求出其左焦点坐标和渐近线方程之后利用点到直线的距离公式求得结果【详解】根据题意双曲线的方程为其中所以所以其左焦点的坐标为渐近线方程为即则左焦点到其渐近线的距离为解析:4 【分析】首先根据题中所给的双曲线方程,求出其左焦点坐标和渐近线方程,之后利用点到直线的距离公式求得结果. 【详解】根据题意,双曲线的方程为221916x y -=,其中3,4a b ==,所以5c =,所以其左焦点的坐标为(5,0)-,渐近线方程为43y x =±,即430x y ±=,则左焦点到其渐近线的距离为2045d ===, 故答案为:4. 【点睛】该题考查的是有关双曲线的问题,涉及到的知识点有根据双曲线的方程求其焦点坐标以及渐近线方程,点到直线的距离公式,属于简单题目.19.①②【分析】由题意曲线是平面内与两个定点和的距离的积等于常数设动点坐标为得到动点的轨迹方程然后由方程特点即可加以判断【详解】由题意设动点坐标为利用题意及两点间的距离公式的得:对于①分别将方程中的被﹣解析:①② 【分析】由题意曲线C 是平面内与两个定点1,0A 和()1,0B -标为(),x y ,得到动点的轨迹方程,然后由方程特点即可加以判断. 【详解】由题意,设动点坐标为(),x y ,利用题意及两点间的距离公式的得:=对于①,分别将方程中的x 被﹣x 代换y 不变,y 被﹣ y 代换x 不变,方程都不变,故关于y 轴对称和x 轴对称,故曲线C 是轴对称图形,故①正确对于②,把方程中的x 被﹣x 代换且y 被﹣y 代换,方程不变,故此曲线关于原点对称,曲线C 是中心对称图形,故②正确;对于③,令y =0=x 21>,此时对应的点不在单位圆x 2+y 2=1内,故③错误. 故答案为:①② 【点睛】本题考查了利用直接法求出动点的轨迹方程,考查了运算能力和转化能力,属于中档题.20.【分析】设点的坐标为利用双曲线的定义可得于是转化求解即可【详解】解:由题意可得即则的坐标分别为由双曲线的定义得又是圆上的点圆的圆心为半径为2由图可知则的最小值为故答案为:【点睛】本题主要考查双曲线的解析:【分析】设点C 的坐标为(0,6),利用双曲线的定义,可得12||||26MF MF a -==,于是1||||MF MA +=2||||2||MF CM a CA ++-2||62CF ≥+-,转化求解即可.【详解】解:由题意可得,291625c =+=,即5c =,则1F ,2F 的坐标分别为(5,0)-,(5,0),由双曲线的定义,得12||||26MF MF a -==,又A 是圆22(6)4x y +-=上的点,圆的圆心为(0,6)C ,半径为2, 由图可知,22||||||CM MF CF +≥,12||||||||2||MF MA MF CM a CA +=++-2||62461CF ≥+-=则1||||MF MA +的最小值为4+61 故答案为:4+61 【点睛】本题主要考查双曲线的几何性质,熟练掌握双曲线的性质及其圆外一点到圆上一点距离的最小值是解题的关键,属于中档题.三、解答题21.(143323 【分析】(1)根据题意,先求出椭圆的方程,由原点O 为BMN △的垂心可得BO MN ⊥,//MN x 轴,设(),M x y ,则(),N x y -,22443x y =-,根据·=0BM ON 求出线段MN 的长;(2)设MN 中点为D ,直线OD 与椭圆交于A ,B 两点,O 为BMN △的重心,则2BO OD OA ==,设MN :y kx m =+,()11,M x y ,()22,N x y ,则()1212,A x x y y ++,当MN 斜率不存在时,则O 到直线MN 的距离为1,由斜率存在时根据()()222222121211221434343x x y y x y x y +++=+=+=,即1212346x x y y +=-,由方程联立得出22443m k =+,再由点到直线的距离求出最值. 【详解】解:(1)设焦距为2c,由题意知:22212b b ac c a ⎧⎪=⎪=-⎨⎪⎪=⎩,22431a b c ⎧=⎪=⎨⎪=⎩因此,椭圆C 的方程为:22143x y +=;由题意知:BO MN ⊥,故//MN x 轴,设(),M x y ,则(),N x y -,22443x y =-,2227·403BM ON x y y =-+=-=,解得:y =, B ,M不重合,故y =213249x =,故2MN x ==(2)设MN 中点为D ,直线OD 与椭圆交于A ,B 两点,O 为BMN △的重心,则2BO OD OA ==,当MN 斜率不存在时,点D 在x 轴上,所以此时点B 在长轴的端点处 由2OB =,则1OD =,则O 到直线MN 的距离为1;当MN 斜率存在时,设MN :y kx m =+,()11,M x y ,()22,N x y , 则1212,22x x y y D ++⎛⎫⎪⎝⎭,所以()1212,A x x y y ++, 所以()()222222121211221434343x x y y x y x y +++=+=+=,即1212346x x y y +=- 也即()()1212346x x kx m kx m +++=-()()221212434460kx x mk x x m +++++=223412y kx m x y =+⎧⎨+=⎩,则()2224384120k x mkx m +++-= ()2248430k m∆=+->,x =则:122843mk x x k -+=+,212241243m x x k -=+,代入式子得: 22223286043m k m k --=+,22443m k =+设O 到直线MN 的距离为d,则d ===0k =时,min 32d =; 综上,原点O 到直线MN 距离的最小值为32.【点睛】关键点睛:本题考查椭圆的内接三角形的相关性质的应用,解答本题的关键是设MN 中点为D ,直线OD 与椭圆交于A ,B 两点,O 为BMN △的重心,则2BO OD OA ==,根据点,,M N A 均在椭圆上,得出1212346x x y y +=-,由方程联立韦达定理得到22443m k =+,属于中档题.22.(1)8;(2)是,定值为2. 【分析】(1)联立直线与抛物线得出韦达定理,即可求出弦长;(2)设出直线方程,联立直线与抛物线方程,利用韦达定理表示出13k k +,即可得出定值. 【详解】 (1)可得3,02F ⎛⎫⎪⎝⎭,直线的倾斜角为603 则直线方程为332y x ⎫=-⎪⎭, 设()()1122,,,A x y B x y ,联立直线与抛物线23326y x y x ⎧⎫=-⎪⎪⎭⎨⎪=⎩可得242090x x -+=, 则121295,4x x x x +==, 123538AB x x =++=+=;(2)可知直线l 的斜率不为0,则设直线l 的方程为3x my =+,m R ∈, 设()3,P t -,()11,M x y ,()22,N x y , 把3x my =+代入26y x =得26180y my --= ∴126y y m +=,1218y y =-,∴12121312123366y t y t y t y tk k x x my my ----+=+=+++++ ()()()()()()1221126666y t my y t my my my -++-+=++()()()1212212122612636my y tm y y t m y y m y y +-+-=+++()()()221866121866363m tm m t t m m m ⨯-+-⋅-==-⨯-+⋅+,26tk =-,132k k k μ+=,36t t μ⎛⎫∴-=⨯- ⎪⎝⎭,P 为3x =-上的任意一点,t ∴不恒为0,2μ∴=,即μ为定值2.【点睛】方法点睛:解决直线与圆锥曲线相交问题的常用步骤: (1)得出直线方程,设交点为()11A x y ,,()22B x y ,; (2)联立直线与曲线方程,得到关于x (或y )的一元二次方程; (3)写出韦达定理;(4)将所求问题或题中关系转化为1212,x x x x +形式; (5)代入韦达定理求解.23.(1)2212x y +=;(2)1y x =+或1y x =-.【分析】(1)由离心率求出a ,再求出b ,可得椭圆方程;(2)设直线l 的方程为y x m =+,点()11,A x y ,()22,B x y ,直线方程代入椭圆方程整理后应用韦达定理得1212,x x x x +,然后代入弦长公式12AB x =-可求得参数m 值得直线方程.【详解】(1)由题意知,1c =,2c e a ==,∴a = 1b =, ∴椭圆C 的方程为2212x y +=.(2)设直线l 的方程为y x m =+,点()11,A x y ,()22,B x y ,联立方程组2212x y y x m ⎧+=⎪⎨⎪=+⎩,化简,得2234220x mx m ++-=.由已知得,()2221612228240m m m ∆=--=-+>,即23m <,∴m <<1243m x x +=-,212223m x x -=.∴21AB x =-== 解得1m =±,符合题意,∴直线l 的方程为1y x =+或1y x =-. 【点睛】方法点睛:本题考查直线与椭圆相交弦长问题.解题方法是设而不求的思想方法,即设交点坐标1122(,),(,)A x y B x y ,设出直线方程,代入椭圆方程后应用韦达定理得1212,x x x x +,代入弦长公式12AB x =-求解.24.(1)2214x y +=;(2)证明见解析;(3)3.【分析】(1)由题知1b=,2a c -=222a b c =+即可得椭圆的标准方程为2214x y +=; (2)由题意得(2,0),(0,1)M N ,设112211,,,22P x x m Q x x m ⎛⎫⎛⎫++ ⎪ ⎪⎝⎭⎝⎭,直线l 为12y x m =+,直线与椭圆联立化简得212122,22x x m x x m +=-=-,进而0MP NQ k k =+;(3)当直线AB 斜率不存在时,22||||23b AB CD a a+=+=,当直线AB 斜率存在时,设直线AB 为y kx =,直线CD为1y x k =-+2245||||54174AB CD k k+=-++,再结合基本不等式即可得答案. 【详解】(1)因为短轴为2,所以22,1b b ==,又因为椭圆上的点到焦点的最短距离为ac -,所以2a c -= 又因为222a b c =+,解得2,1,a b c ===所以椭圆的标准方程为2214x y +=;(2)由题意得(2,0),(0,1)M N ,设直线l 为12y x m =+,与2214x y +=联立得:222220x mx m ++-=设112211,,,22P x x m Q x x m ⎛⎫⎛⎫++ ⎪ ⎪⎝⎭⎝⎭,则212122,22x x m x x m +=-=- 所以()12121212122111(1)222222MP NQ x m x m x x m x x m k k x x x x x ++-+-+-++=+=--22222(1)(2)220222m m x m m m x -+---+==--,所以MP 与NQ 的斜率之和为定值0;(3)当直线AB 斜率不存在时,2225b AB CD a a+=+=当直线AB 斜率存在时,设直线AB为y kx =,直线CD为1y x k =-+得()2222411240k x x k +-+-=,所以23434212441k x x x x k -+==+,所以()224141AB k k +==+,同理()2241||4k CD k +=+,所以()()2222224141445||||5414417k AB CD k k k kk +++=+=-++++因为22448k k +≥=,所以1635AB CD +≥>,当且仅当1k =±时取等号, 所以AB CD +的最小值为3. 【点睛】本题考查直线与椭圆的位置关系,椭圆中的最值问题,考查运算能力与化归转化思想,是中档题.本题解题的关键在于巧设点的坐标,结合韦达定理,设而不求,达到求解目标,化简运算;同时还要注意再设直线方程时,需要考虑斜率存在与否,做到周密解答.25.(1)2214x y +=;(2)【分析】(1)根据抛物线2y=的焦点为),解得c =122c b⨯⨯=b即可.(2)设直线l方程为4y kx=+,与椭圆方程联立,根据坐标原点O在以AB为直径的圆上,由OA OB⊥,即1212x x y y⋅+⋅=求解.【详解】(1)因为抛物线2y=的焦点为),由题意得:c=所以122c b⨯⨯=解得1b=,24a=,所以椭圆C的方程为2214xy+=;(2)由题意设过点(0,4)的直线l方程为4y kx=+,设()()1122,,,A x yB x y,由22414y kxxy=+⎧⎪⎨+=⎪⎩,得()221432600k x kx+++=,则1212223260,1414kx x x xk k+=-⋅=++,()()2232240140k k∆=-+>,解得k>k<,因为坐标原点O在以AB为直径的圆上,所以OA OB⊥,即1212x x y y⋅+⋅=,即()()2121214160k x x k x x+⋅+++=,所以()()2226032141601414kk kk k++-+=++,即219k=,解得k=适合0∆>,所以直线l的斜率是.【点睛】易错点点睛:易错点是由坐标原点O在以AB为直径的圆上,转化为OA OB⊥,由1212x x y y⋅+⋅=,求得斜率,而忽视要满足.0∆>.26.(1)2212xy+=;(2)存在;1)y x=-.【分析】(1)由余弦定理可得12d d+=.(2)设P ,Q 两点的坐标依次为()11,x y ,()22,x y ,以线段PQ 为直径的圆过原点得,0OP OQ ⋅=,即12120x x y y +=,先假设存在直线l 满足题设,设直线l 的方程为(1)y k x =-,与椭圆方程联立,韦达定理代入求出k 的值,再检验斜率不存在的情况.【详解】(1)当0θ≠时,在ABM 中,由余弦定理得:22121242cos2d d d d θ=+-. 又212cos1d d θ=,整理得,12d d +=所以点M 的轨迹E 是以(1,0)A -和(1,0)B为焦点,长轴长为个端点)又当点M 为该椭圆的长轴的两个端点时,0θ=,也满足212cos1d d θ=.所以点M 的轨迹E 的方程是2212x y +=.(2)假设存在直线l 满足题设,设直线l 的方程为(1)y k x =-,由22(1)12y k x x y =-⎧⎪⎨+=⎪⎩ 得()2222124220k x k x k +-+-= 设P ,Q 两点的坐标依次为()11,x y ,()22,x y ,由韦达定理得,2122412k x x k +=+,21222212k x x k-=+. 由题意以线段PQ 为直径的圆过原点得,0OP OQ ⋅=,即12120x x y y +=.又()()()212121212111y y k x k x k x x x x =--=-++⎡⎤⎣⎦, 整理得:()212121210x k x x x x x =⎡-+⎤⎣⎦++.代入整理得:22222222222410121212k k k k k k k ⎛⎫--+-+= ⎪+++⎝⎭,即k = 当直线l 的斜率不存在时,直线l 的方程为1x =,此时1,2P ⎛ ⎝⎭、1,2Q ⎛- ⎝⎭,经验证0OP OQ ⋅≠不满足题意.综上所述,所求直线l存在,其方程为1)y x =-. 【点睛】关键点睛:本题考查求轨迹方程和根据条件求直线方程,解答本题的关键是由以线段PQ 为直径的圆过原点,得0OP OQ ⋅=,即12120x x y y +=,转化为方程联立韦达定理代入求解,将条件转化为向量的数量积为0,进而转化为利用韦达定理求解的方法,属于中档题.。
上海行知实验中学高中数学选修2-1第一章《常用逻辑用语》检测题(有答案解析)

一、选择题1.以下四个命题中,真命题的个数是( )①存在正实数M ,N ,使得()log log log a a a M N MN +=;②“若函数()f x 满足()()201920200f f ⋅<,则()f x 在()2019,2020上有零点”的否命题;③函数()()()log 320,1a f x x a a =->≠的图象过定点()1,0; ④“1x =-”是“2230x x --=”的必要不充分条件. A .1B .2C .3D .42.已知:11p x -≤, 2:230q x x --≥, 则p 是q ⌝的( ) A .充分不必要条件 B .必要不充分条件 C .充分必要条件 D .既不充分也不必要条件3.已知1:12p x ≥-,:2q x a -<,若p 是q 的充分不必要条件,则实数a 的取值范围为( ) A .(],4-∞B .[]1,4C .(]1,4D .()1,44.“函数()2()311f x ax a x =--+在区间[)1+∞,上是增函数”是“01a ≤≤”的( ) A .充分不必要条件 B .必要不充分条件 C .充分必要条件D .既不充分也不必要条件5.已知命题p :在ABC 中,若A B >,则cos cos A B <,命题q :()0,x ∃∈+∞,sin x x >,则下列命题中为真命题的是( )A .p q ∧B .()p q ⌝∧C .()p q ∨⌝D .()()p q ⌝∧⌝6.已知三个正数a ,b ,c 满足3a b c a ≤+≤,()2235b a a c b ≤⋅+≤,则以下四个命题正确的是( )1p :对任意满足条件的a ,b ,c ,均有b c ≤;2p :存在一组实数a ,b ,c ,使得b c >; 3p :存在满足条件的a ,b ,c ,使得64b a c ≤+; 4p :对任意满足条件的a ,b ,c ,均有64b a c >+.A .1p ,3pB .1p ,4pC .2p ,3pD .2p ,4p7.已知命题():0,p x ∀∈+∞,1102xm ⎛⎫+-> ⎪⎝⎭;命题():0,q x ∃∈+∞,2410mx x +-=,则命题p 是命题q 的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件8.已知命题p :23100x x -->,命题q :23x m m +>﹣,若p ⌝是q ⌝的充分不必要条件,则实数m 的取值范围是( ) A .[﹣1,2]B .(﹣∞,﹣1]∪[2,+∞)C .(﹣∞,﹣1)∪(2,+∞)D .(﹣1,2)9.已知p :2+2=5;q :3>2,则下列判断错误的是( )A .“p ∨q ”为真,“¬q ”为假B .“p ∧q ”为假,“¬p ”为真C .“p ∧q ”为假,“¬p ”为假D .“p ∨q ”为真,“¬p ”为真10.01a <<是函数()221=+f x ax 取值恒为正的( )条件 A .充分非必要B .必要非充分C .充要D .既不充分又不必要11.已知函数()222f x x x =-+,2log g xx t ,对[]10,2x ∀∈,21,162x ⎡⎤∃∈⎢⎥⎣⎦使得()()12f x g x =,则实数t 的取值范围( ) A .(],2-∞- B .[)2+∞,C .()2,2-D .[]22-,12.已知2:11xp x <+,:()(3)0q x a x -->,p 为q 的充分不必要条件,则a 的范围是( ) A .[)1,+∞B .()1,+∞C .[)0,+∞D .()1,-+∞二、填空题13.已知{}|13A x x =-<<, {}11|B x x m =-<<+,若x B ∈成立的一个必要不充分条件是x A ∈,则实数m 的取值范围是_______________. 14.下列说法中:①命题“对任意的1x >,有21x >”的否定为“存在1x ≤,有21x ≤”;②“对于任意的x D ∈,总有()f x M ≥(M 为常数)”是“函数()y f x =在区间D 上的最小值为M ”的必要不充分条件;③若1x ,()20,x ∈+∞,则函数()log a f x x =满足()()()1212f x f x f x x +=; ④若1x ,2x ∈R ,12x x ≠,则函数()2xf x =满足()()121222f x f x x x f ++⎛⎫> ⎪⎝⎭.所有正确说法的序号______.(把满足条件的序号全部写在横线上) 15.若0, 0a >b >,则“4a b +≤”是 “4ab ≤”的_____条件 16.关于以下结论: ①*n N ∀∈,22n n ≤;②函数44()sin cos f x x x =-的最小正周期为π; ③若向量0a b ⋅=,则向量a b ⊥; ④20182019log 2019log 2020>. 以上结论正确的个数为______.17.“对任意的正数x ,结论21a x x+≥恒成立”的充要条件为______.18.已知集合{}|A x x a =>,{}|22,B x x x R =-<∈,若“x A ∈”是“x B ∈”的必要不充分条件,则a 的取值范围_________.19.命题“0x R ∃∈,使()200110m x mx m +-+-≤”是假命题,则实数m 的取值范围为__________.20.已知命题p :存在[]0,1x ∈,使得0x a e -≥成立,命题:q 对任意x ∈R ,240x x a ++> 恒成立,若命题p q ∧⌝是真命题,则实数a 的取值范围是______________.三、解答题21.已知命题{}:2131p A x a x a =-<<+,命题{}:14q B x x =-<<.(1)若p 是q 的充分条件,求实数a 的取值范围.(2)是否存在实数a ,使得p 是q 的充要条件?若存在,求出a 的值;若不存在,请说明理由.22.命题P :函数()log a f x x =在0,上是增函数;命题Q :x R ∃∈,使得240x x a -+= .(1)若命题Q 为真,求实数a 的取值范围;(2)若命题“P 且Q ”为真,求实数a 的取值范围.23.设{}2:8200p P x x x =--≤,:q 非空集合{}11S x m x m =-≤≤+,且p 是q 的充分不必要条件,求实数m 的取值范围.24.设命题p :实数x 满足22430x ax a -+<,命题q :实数x 满足|3|1x -<. (1)若1a =,且p q ∨为真,求实数x 的取值范围;(2)若0a >且p ⌝是q ⌝的充分不必要条件,求实数a 的取值范围. 25.已知命题“x R ∃∈,不等式220x x m --≤”成立是假命题. (1)求实数m 的取值集合A ;(2)若:44q m a -<-<是集合A 的充分不必要条件,求实数a 的取值范围. 26.已知2:,2p x R x x a ∀∈+≥,()2:431q x -≤,2:(21)(1)0r x a x a a -+++≤. (1)若命题p 为真命题,求实数a 的取值范围; (2)若q 是r 的充分不必要条件,求实数a 的取值范围.【参考答案】***试卷处理标记,请不要删除一、选择题1.B 解析:B 【分析】根据对数的运算判断①;根据零点存在性定理判断②;根据对数函数的性质判断③,根据充分条件、必要条件判断④; 【详解】解:对于①,根据对数运算法则知正确;对于③,无论a 取何值都有()10f =,所以函数()f x 的图象过定点()1,0,故正确; 对于②,函数()f x 在()2019,2020上有零点时,函数()f x 在2019x =和2020x =处的函数值不一定异号,故其逆命题是错误的,所以否命题也是错误的;对于④,当1x =-时,2230x x --=,当2230x x --=时,1x =-或3x =,所以是充分不必要条件,故④错误. 故选:B 【点睛】本题考查命题真假性的判断以及相关知识点,属于中档题.2.A解析:A 【分析】利用不等式的解法求出p , q ,然后求出q ⌝,即可得到答案 【详解】:11p x -≤,化为111x -≤-≤,解得02x ≤≤ 2:230q x x --≥,解得3x ≥或1x ≤-则q ⌝:13x -<<则p 是q ⌝的充分不必要条件 故选A 【点睛】本题主要考查了必要条件,充分条件以及充要条件的判定定理,不等式的解法,属于基础题.3.C解析:C【分析】求出p 、q 中的不等式,根据p 是q 的充分不必要条件可得出关于实数a 的不等式组,由此可解得实数a 的取值范围. 【详解】 解不等式112x ≥-,即131022x x x --=≤--,解得23x <≤, 解不等式2x a -<,即22x a -<-<,解得22a x a -<<+,由于p 是q 的充分不必要条件,则(]2,3()2,2a a -+,所以2223a a -≤⎧⎨+>⎩,解得14a <≤. 因此,实数a 的取值范围是(]1,4. 故选:C. 【点睛】本题考查利用充分不必要条件求参数,同时也考查了分式不等式和绝对值不等式的求解,考查计算能力,属于中等题.4.C解析:C 【解析】0a <时,“函数()()2311f x ax a x =--+在区间[)1,+∞上不是增函数”,0a =时,()1f x x =+在[)1,+∞上是增函数,0a >时,令3112a a-≤,得01a <≤,∴“()()2311f x ax a x =--+在区间[)1,+∞上是增函数” 的充分必要条件“01a ≤≤”,故选C.5.C解析:C 【分析】由函数cos y x =在(0,)π上的单调性即可判断p 为真命题;当(0,)2x π∈时,令()sin f x x x =-,利用导数判断函数()f x 在(0,)2π上的单调性从而证明sin x x <,当[,)2x π∈+∞时,根据图象判断sin x x <,即可确定q 为假命题,利用复合命题的真假判断规则进行判断即可. 【详解】命题p :在ABC 中,,(0,)A B π∈,因为函数cos y x =在(0,)π上单调递减,所以若A B >,则cos cos A B <,命题p 为真命题.命题q :令()sin f x x x =-,当(0,)2x π∈时,cos 10y x '=-<,函数()sin f x x x=-在(0,)2π上单调递减,所以()(0)0f x f <=,即sin x x <;当[,)2x π∈+∞时,由下图可知sin x x <,所以q 为假命题.所以()p q ∨⌝为真命题. 故选:C 【点睛】本题考查复合命题的真假判断,涉及正、余弦函数的图象与性质,利用导数证明不等式,属于中档题.6.C解析:C 【分析】取特殊值,结合原命题与否定的真假关系,即可得出答案. 【详解】取2,1,3b c a ===,满足条件3a b c a ≤+≤,()2235b a a c b ≤⋅+≤,此时b c >则2p 为真命题,由于2p 的否定为1p ,则1p 为假命题取1,2a b c ===,满足条件3a b c a ≤+≤,()2235b a a c b ≤⋅+≤,此时也满足64b a c ≤+,则3p 为真命题,由于3p 的否定为4p ,则4p 为假命题故选:C 【点睛】本题主要考查了判断命题的真假,属于中档题.7.A解析:A 【分析】分别计算得到m 1≥和4m ≥-,根据范围大小判断得到答案. 【详解】():0,p x ∀∈+∞,1102xm ⎛⎫+-> ⎪⎝⎭,即112xm ⎛⎫>- ⎪⎝⎭,易知函数()112xf x ⎛⎫=- ⎪⎝⎭单调递增,故m 1≥.命题():0,q x ∃∈+∞,2410mx x +-=, 2214124m x x x ⎛⎫=-=-- ⎪⎝⎭,故4m ≥-. 故命题p 是命题q 的充分不必要条件. 故选:A . 【点睛】本题考查了根据命题求参数,充分不必要条件,意在考查学生的推断能力.8.B解析:B 【分析】由p ⌝是q ⌝的充分不必要条件,则q 是p 的充分不必要条件, 由23100x x -->得5x >或2x <-,只需235m m -+≥,即可.【详解】由23100x x -->得5x >或2x <-,因为p ⌝是q ⌝的充分不必要条件,所以q 是p 的充分不必要条件,所以235m m -+≥,解得2m ≥或1m ≤-. 故选:B . 【点睛】本题考查充分必要条件求参数取值范围问题,难度一般.9.C解析:C 【分析】先判定命题p 为假命题,命题q 为真命题,再结合复合命题的真假判定,即可求解. 【详解】由题意,命题:225p +=为假命题,命题:32q >为真命题,所以命题p q ∧为假命题,p ⌝为真命题,命题p q ∨为真命题,q ⌝为假命题, 故选:C . 【点睛】本题主要考查了复合命题的真假判定,其中解答中正确判定命题,p q 的真假,熟记复合命题的真假判定方法是解答的关键,着重考查了分析问题和解答问题的能力,属于基础题.10.A解析:A 【分析】根据一元二次函数的图象与性质,结合充分条件、必要条件的定义,进行判定,即可求解. 【详解】由题意,当01a <<时,函数()2210f x ax =+>恒成立,所以充分性成立;例如:当0a =时,函数()22110f x ax =+=>恒成立,所以函数()2210f x ax =+>恒成立时,01a <<不一定成立,所以必要性不成立,所以01a <<是函数()221=+f x ax 取值恒为正的充分非必要条件.故选:A . 【点睛】本题主要考查了充分条件、必要条件的判定,其中解答中熟记一元二次函数的图象与性质是解答的关键,着重考查了推理与论证能力,属于基础题.11.D解析:D 【分析】求出()(),f x g x 的值域,A B ,由题意可得A B ⊆,列不等式求解即可. 【详解】()222f x x x =-+,当[]0,2x ∈时,()f x 的值域为[]1,2A =,2log g xx t ,1,162x ⎡⎤∈⎢⎥⎣⎦,()g x 的值域[]1,4t t B =-+,由条件可知A B ⊆,即[][]1,21,4t t ⊆-+,从而有1142t t -≤⎧⎨+≥⎩,可得22t -≤≤. 故选:D. 【点睛】本题主要考查全称命题与特称命题的综合应用,关键是要将问题进行转化,转化为值域之间的包含问题,是中档题.12.A解析:A 【分析】由p 为q 的充分不必要条件可得211xx <+的解集是()(3)0x a x -->的解集的真子集,从而可求出答案. 【详解】 解:∵211x x <+,∴2101x x x --<+,即101x x -<+, ∴()()110x x +-<,解得11x -<<, ∴:11p x -<<,由p 为q 的充分不必要条件可得211xx <+的解集是()(3)0x a x -->的解集的真子集, 当3a =时,解得:3q x ≠,满足条件; 当3a >时,解得:q x a >或3x <,满足条件; 当3a <时,解得:3q x >或x a <,∴13a ≤<, 综上:1a ≥, 故选:A . 【点睛】本题主要考查充分条件和必要条件的应用,根据不等式的性质求出命题的等价条件是解决本题的关键,属于基础题.二、填空题13.【分析】先依题意判断集合B 是集合A 的真子集再讨论集合B 是否空集求参数m 的取值范围即可【详解】因为成立的一个必要不充分条件是所以推不出且可推出故集合B 是集合A 的真子集当时即集合A 的真子集符合题意;当时 解析:{}|2m m <【分析】先依题意判断集合B 是集合A 的真子集,再讨论集合B 是否空集求参数m 的取值范围即可. 【详解】因为x B ∈成立的一个必要不充分条件是x A ∈,所以x A ∈推不出x B ∈,且x B ∈可推出x A ∈,故集合B 是集合A 的真子集.当11m +≤-时即2m ≤-,B =∅集合A 的真子集,符合题意;当11m +>-时即2m >-,要使集合B 是集合A 的真子集,则需13m +<,即2m <,故22m -<<;综上,实数m 的取值范围是2m <. 故答案为:{}|2m m <. 【点睛】结论点睛:本题考查必要不充分条件的应用,一般可根据如下规则判断: (1)若p 是q 的必要不充分条件,则q 对应集合是p 对应集合的真子集; (2)若p 是q 的充分不必要条件, 则p 对应集合是q 对应集合的真子集; (3)若p 是q 的充分必要条件,则p 对应集合与q 对应集合相等;(4)若p 是q 的既不充分又不必要条件, q 对的集合与p 对应集合互不包含.14.②③④【分析】①直接利用命题的否定判断;②函数的最小值和必要不充分条件的应用;③对数的运算关系式的应用;④根据基本不等式可得答案;【详解】①命题对任意的有的否定为存在有故①错误;②对于任意的总有(为解析:②③④ 【分析】①直接利用命题的否定判断;②函数的最小值和必要不充分条件的应用; ③对数的运算关系式的应用; ④根据基本不等式可得答案; 【详解】①命题“对任意的1x >,有21x >”的否定为“存在1x >,有21x ≤”,故①错误; ②“对于任意的x D ∈,总有()f x M ≥(M 为常数)”由于没有说明0x D ∈()0f x M =,所以“函数()y f x =在区间D 上的最小值为M ”不一定成立;函数()y f x =在区间D 上的最小值为M ,总有()f x M ≥(M 为常数)成立,故②正确;③若1x ,()20,x ∈+∞,则函数()log a f x x =满足()1212log log log a a a x x x x =+, 所以()()()1212f x f x f x x +=成立,故③正确;④若1x ,2x ∈R ,12x x ≠,()()1212,33x x f x f x ==,1212232x xx x f ++⎛⎫= ⎪⎝⎭, 因为()30xf x =>,所以()()1212122322x x f x f x x x f +++⎛⎫>=== ⎪⎝⎭,故④正确.故答案为:②③④.【点睛】本题考查了命题的否定、函数的最小值和充分条件和必要条件的应用、对数的运算关系、不等式比较大小的问题.15.充分不必要【分析】根据题意利用基本不等式可判定充分性是成立的可举出反例说明必要性不成立即可得到答案【详解】当时由基本不等式可得当时有解得充分性是成立的;例如:当时满足但此时必要性不成立综上所述是的充解析:充分不必要 【分析】根据题意,利用基本不等式,可判定充分性是成立的,可举出反例,说明必要性不成立,即可得到答案. 【详解】当0,0a b >>时,由基本不等式,可得a b +≥当4a b +≤时,有4a b +≤,解得4ab ≤,充分性是成立的; 例如:当1,4a b ==时,满足4ab ≤,但此时=5>4a+b ,必要性不成立, 综上所述,“4a b +≤”是“4ab ≤”的充分不必要条件. 故答案为充分不必要条件. 【点睛】本题主要考查了充分不必要条件的判定,其中解答中熟记充分条件、必要条件的判定方法,以及合理利用基本不等式求解是解答的关键,着重考查了分析问题和解答问题的能力,属于基础题.16.2【分析】对命题逐一分析正误得出结论即可【详解】解:对于①当时∴;故①错误;②函数所以的最小正周期为;故②正确;③若向量则向量;当时或当时但不垂直于;故③错误;④;④正确证明如下:∵;而∴;∴故②④解析:2 【分析】对命题逐一分析正误,得出结论即可.【详解】解:对于①*n N ∀∈,22n n ≤,当3n =时,29n =,28n =,∴22n n >;故①错误;②函数44()sin cos cos2f x x x x =-=-,所以()f x 的最小正周期为T π=;故②正确;③若向量0a b ⋅=,则向量a b ⊥;当0a =时或当0b =时,0a b ⋅=,但a 不垂直于b ;故③错误;④20182019log 2019log 2020>;④正确,证明如下: ∵220182019lg2019lg2020(lg2019)lg2018lg2020log 2019log 2020lg2018lg2019lg2018lg2019-⋅-=-=⋅;而22lg 2018lg 2020lg 2018lg 2020()2+⋅<= 2220182020(lg )(lg 2019)2+<=. ∴2(lg2019)lg2018lg20200-⋅>;∴20182019log 2019log 2020>.故②④正确;正确的个数为2个;故答案为:2.【点睛】本题考查命题判断真假的方法,需要逐个判断,属于基础题.17.∪【分析】对任意的正数x 结论恒成立等价于a2≥(xx2)max(x >0)令y=x2+x(x >0)利用二次函数的单调性即可得出【详解】对任意的正数x 结论恒成立等价于a2≥(xx2)maxx >0令y=x 解析:12⎛⎤-∞- ⎥⎝⎦,∪12⎡⎫+∞⎪⎢⎣⎭, 【分析】 “对任意的正数x ,结论21a x x+≥恒成立”等价于a 2≥(x -x 2)max (x >0).令y =-x 2+x (x >0),利用二次函数的单调性即可得出.【详解】“对任意的正数x ,结论21a x x+≥恒成立”等价于a 2≥(x -x 2)max ,x >0. 令y =-x 2+x =-21()2x -+14≤14,当x =12时,取等号. ∴a 2≥14.解得a 12≥或a ≤-12. 故答案为:12⎛⎤-∞- ⎥⎝⎦,∪12⎡⎫+∞⎪⎢⎣⎭,. 【点睛】本题考查了二次不等式的恒成立问题,考查了充要条件的判定方法,考查了推理能力与计算能力,属于基础题.18.【分析】根据必要不充分条件得到集合之间的关系从而求解出参数的取值范围【详解】因为是的必要不充分条件所以又因为所以因为所以即的取值范围是:【点睛】集合:若是的必要不充分条件则有:;若是的充分不必要条件 解析:0a ≤【分析】根据必要不充分条件得到集合,A B 之间的关系,从而求解出参数的取值范围.【详解】因为“x A ∈”是“x B ∈”的必要不充分条件,所以B A ,又因为{}|22,B x x x R =-<∈,所以()0,4B =,因为(),A a =+∞,所以0a ≤,即a 的取值范围是:0a ≤.【点睛】集合()(){|},{|}A x x p x B x x q x =∈=∈:若“x A ∈”是“x B ∈”的必要不充分条件,则有:B A ; 若“x A ∈”是“x B ∈”的充分不必要条件,则有:A B .19.【分析】使是假命题则使是真命题对是否等于进行讨论当时不符合题意当时由二次函数的图像与性质解答即可【详解】使是假命题则使是真命题当即转化为不是对任意的恒成立;当使即恒成立即第二个式子化简得解得或所以【解析:3m >【分析】 0x R ∃∈,使()200110m x mx m +-+-≤是假命题,则x R ∀∈,使()2110m x mx m +-+->是真命题,对1m +是否等于0进行讨论,当10m +=时不符合题意,当10m +≠时,由二次函数的图像与性质解答即可.【详解】0x R ∃∈,使()200110m x mx m +-+-≤是假命题,则x R ∀∈,使()2110m x mx m +-+->是真命题, 当10m +=,即1m =-,()2110m x mx m +-+->转化为20x ->,不是对任意的x ∈R 恒成立;当10m +≠,x R ∀∈,使()2110m x mx m +-+->即恒成立,即 ()()()2104110m m m m +>⎧⎪⎨--+-<⎪⎩ ,第二个式子化简得234m >,解得3m >或3m <-所以3m >【点睛】 本题考查命题间的关系以及二次函数的图像与性质,解题的关键是得出x R ∀∈,使()2110m x mx m +-+->是真命题这一条件,属于一般题.20.【分析】先确定各命题为真时实数的取值范围再根据复合命题真假得各命题真假最后求交集得结果【详解】命题:存在使得成立所以最小值1即所以;命题对任意恒成立所以;因为命题是真命题所以是真命题是假命题即【点睛 解析:[]1,4a ∈【分析】先确定各命题为真时实数a 的取值范围,再根据复合命题真假得各命题真假,最后求交集得结果.【详解】命题p :存在[]0,1x ∈,使得0x a e -≥成立,所以x a e ≥的最小值1,即所以1a ≥; 命题:q 对任意x R ∈,240x x a ++> 恒成立,所以24404a a ,-; 因为命题p q ∧⌝是真命题,所以p 是真命题,q 是假命题,即14a ≤≤【点睛】本题考查命题真假以及不等式恒成立与存在性问题,考查基本分析转化与求解能力,属中档题.三、解答题21.(1)(][],20,1-∞-;(2)不存在,理由见解析. 【分析】(1)由已知得A B ⊆,分为A =∅或A ≠∅两种情况来讨论,建立不等式(组),求解可得出实数a 的取值范围.(2)由已知可得A B =,根据集合相等建立不等式组可得结论.【详解】(1)集合{}2131A x a x a =-<<-,集合{}14B x x =-<<.因为p 是q 的充分条件,所以A B ⊆,∴集合A 可以分为A =∅或A ≠∅两种情况来讨论:当A =∅时,满足题意,此时2131a a -≥-,解得:2a ≤-;当A ≠∅时,要使A B ⊆成立,需满足211314012131a a a a a -≥-⎧⎪+≤⇒≤≤⎨⎪-<+⎩, 综上所得,实数a 的取值范围(][],20,1-∞-.(2)假设存在实数a ,使得p 是q 的充要条件,那么A B =,则必有211314a a -=-⎧⎨+=⎩,解得01a a =⎧⎨=⎩,综合得a 无解. 故不存在实数a ,使得A B =,即不存在实数a ,使得A 是B 的充要条件.【点睛】本题考查充分必要条件,集合间的关系,根据集合间的关系求参数的范围,属于中档题. 22.(1)4a ≤;(2)14a <≤.【分析】(1)根据条件将问题转化为方程有解,从而得到1640a ∆=-≥,由此求解出a 的取值范围;(2)根据含逻辑联结词的复合命题的真假判断出,P Q 的真假,由此求解出a 的取值范围.【详解】(1)因为x R ∃∈使得240x x a -+=,所以240x x a -+=在R 上有解,所以1640a ∆=-≥,所以4a ≤;(2)因为“P 且Q ”为真,所以,P Q 均为真,当P 为真时,1a >;当Q 为真时,4a ≤,所以14a <≤.【点睛】本题考查根据命题、复合命题的真假求解参数范围,着重考查了含逻辑联结词的复合命题的分析方法,难度一般.23.[)9,+∞【分析】首先求出集合P ,再根据p 是q 的充分不必要条件,可得所以P S ,即可得到不等式组,解得即可;【详解】解:由28200x x --,解得210x -.{}|210P x x ∴=-≤≤. 非空集合{}11S x m x m =-≤≤+.因为p 是q 的充分不必要条件,所以P S ,所以11012m m +≥⎧⎨-≤-⎩解得9m ≥即[)9,m ∈+∞【点睛】本题考查了不等式的解法、简易逻辑的判定方法,考查了推理能力与计算能力,属于中档题.24.(1)(1,4);(2)4,23⎡⎤⎢⎥⎣⎦. 【分析】(1)分别求解当命题p 命题q 为真时x 的取值范围,在分“p 真q 假”和“q 真p 假”两种情况求对应的实数x 的取值范围即可.(2)根据0a >再因式分解求得命题p :3a x a <<,再根据p ⌝是q ⌝的充分不必要条件可知p ⌝对应的集合是q ⌝对应的集合的子集,再根据集合区间端点的位置关系求出实数a 的取值范围即可.【详解】(1)由22430x ax a -+<得()(3)0x a x a --<,当1a =时,13x <<,即p 为真时,(1,3)x ∈.由|3|1x -<,得131x -<-<,得24x <<,即q 为真时,(2,4)x ∈.若p q ∨为真,则p 真或q 真,所以实数的取值范围是(1,4).(2)由22430x ax a -+<得()(3)0x a x a --<,0,a >3a x a ∴<<.由|3|1x -<,得131x -<-<,得24x <<.设{|3},A x x a x a =≤≥或{|24}B x x x =≤≥或,若p ⌝是q ⌝的充分不必要条件,则A 是B 的真子集,故0234a a <≤⎧⎨≥⎩, 所以实数a 的取值范围为4,23⎡⎤⎢⎥⎣⎦. 【点睛】本题主要考查了根据充分与必要条件求解参数的范围问题.需要根据参数的范围求解对应的集合区间,再根据区间端点的位置关系列式求出参数的范围.属于中档题.25.(1){}1A m m =<-;(2)(,5]-∞-.【分析】(1)本题首先可根据题意得出命题的否定“x R ∀∈,不等式220x x m -->”成立是真命题,然后根据求解440m ∆=+<即可得出结果;(2)本题可根据题意得出集合{}44B m a m a =-<<+是集合A 的真子集,然后通过计算即可得出结果.【详解】(1)因为命题“x R ∃∈,不等式220x x m --≤”成立是假命题,所以命题的否定“x R ∀∈,不等式220x x m -->”成立是真命题,即440m ∆=+<,解得1m <-,集合{}1A m m =<-.(2)因为44m a -<-<,即44a m a -<<+,所以:44q a m a -<<+,因为:44q a m a -<<+是集合A 的充要不必要条件, 所以令集合{}44B m a m a =-<<+,集合B 是集合A 的真子集,即41a +≤-,解得5a ≤-,实数a 的取值范围是(,5]-∞-.【点睛】关键点点睛:若命题p 是命题q 的充分不必要条件,则命题p 对应的集合是命题q 对应的集合的真子集;若命题p 是命题q 的必要不充分条件,则命题q 对应的集合是命题p 对应的集合的真子集.26.(1)(],1-∞-;(2)10,2⎡⎤⎢⎥⎣⎦. 【分析】(1)由全称命题为真,结合一元二次不等式恒成立即可得解;(2)由一元二次不等式结合命题间的关系可转化条件为112x x ⎧⎫≤≤⎨⎬⎩⎭ {}1x a x a ≤≤+,即可得解. 【详解】(1)若命题p 为真,则不等式220x x a +-≥对x R ∀∈恒成立,所以440a ∆=+≤,1a ≤-,所以实数a 的取值范围为(],1-∞-;(2)命题q 等价于112x ≤≤,命题r 等价于1a x a ≤≤+, 因为q 是r 的充分不必要条件,所以112x x ⎧⎫≤≤⎨⎬⎩⎭ {}1x a x a ≤≤+, 所以1211a a ⎧≤⎪⎨⎪+≥⎩且上述等号不同时成立,所以102a ≤≤, 所以实数a 的取值范围为10,2⎡⎤⎢⎥⎣⎦. 【点睛】解决本题的关键是合理转化条件:将全称命题为真转化为一元二次不等式恒成立,将命题间的关系转化为集合间的关系.。
四川省广安市2022-2023学年高一上学期期末检测模拟化学(B卷 )试题含答案

广安市名师工作室2022年秋高一期末检测化学模拟试题(B 卷)(答案在最后) 注意事项:考试时间100分钟,满分100分可能用到的相对原子质量:H -1 C -12 N -14 O -16 Na -23 Cl -35.5 K -39第Ⅰ卷 选择题一、选择题(单项选择题,每小题2分,共44分)化学与生活密切相关,下列有关物质的性质与用途,不具有对应关系的是( ) A.氧化铁——油漆、涂料 B.3Al(OH)——治疗胃酸过多C.次氯酸钠——消毒液D.食盐()NaCl ——制作馒头和面包的膨松剂2.化学的世界,多姿多彩.下列物质颜色描述不正确的是( ) A.23Fe O 黑色B.2Cl 黄绿色C.22Na O 淡黄色D.()3Fe OH 红褐色3.社会的进步与时代的发展充满了人类智慧的结晶.下列有关说法中错误的是( ) A.合金为纯净物,具有许多优良的物理、化学或机械性能 B.不锈钢是最常见的一种合金钢,不容易生锈. C.商朝的“后母戊鼎”是我国较早使用的铜制品之一D.近年来,人们又设计和合成了许多新型合金.如储氢合金、钛合金等4.节日燃放的五彩缤纷的烟花,就是锂、钠、锶、钾、钡等金属化合物所呈现的各种艳丽色彩.下列金属元素中,透过蓝色钴玻璃看到火焰呈紫色的是( ) A.NaB.CuC.KD.Ca5.下列物质中属于盐的是( ) A.2Ca(ClO)B.2Ba(OH)C.HClD.34Fe O6.下列关于“摩尔”的说法,正确的是( ) A.是一种物理量B.是物质的量的单位C.1mol 任何物质都含有A N 个原子D.可以用“摩尔”描述宏观物体7.下列过程不涉及氧化还原反应的是( ) A.食物的腐败B.铁的生锈C.将海水晒干获得粗盐D.燃料的燃烧8.下列物质属于电解质( ) A.金属铜B.氢氧化钠C.2CO D.氯水9.实验室配制1100mL1.0mol L KOH -⋅溶液时,不需要用到的仪器是( )A.烧杯B.玻璃棒C.容量瓶D.漏斗10.下列电离方程式中,不正确的是( ) A.()322443Al SO 2Al3SO +-=+B.233NaHCO Na H CO ++-=++ C.22Ba(OH)Ba 2OH +=+D.2233Na CO 2Na CO +=+11.下列物质间的转化,不能一步完成的是( ) A.233Fe O Fe(OH)→ B.22Na Na O →C.232Al O NaAlO →D.2Cl HClO →12.在无色透明的溶液中可以大量共存的离子组是( ) A.H +、K +、3HCO -、4SO -B.Na +、K +、2Cu +、Cl -C.2Mg +、Na +、24SO -、Cl -D.Ag +、K +、Cl -、3NO -13.工业上利用3FeCl 溶液腐蚀覆铜板制作印刷电路板,其反应原理为:3222FeCl Cu 2FeCl CuCl +=+下列对该反应的分析正确的是( ) A.3FeCl 做还原剂B.2CuCl 是还原产物C.该反应说明Cu 比Fe 活泼D.反应后的废液经回收处理后可以循环利用14.10mL 、()421mol /LKAl SO 溶液中各离子浓度表达正确的是( ) A.K +为0.2mol /LB.24SO -为2mol /L C.3Al +为m 0.02ol /LD.24SO -为1mol /L15.除去3FeCl 溶液中混有的2FeCl 杂质,应选用的试剂是( ) A.氯水B.KSCN 溶液C.NaOH 溶液D.4KMnO16.下列指定反应的离子方程式正确的是( )A.稀硫酸滴在铁片上:322Fe 6H 2Fe 3H +++=+↑B.少量金属铝放入氢氧化钠中:222Al 2OH 2AlO H -+=-↑ C.醋酸溶解水垢中的碳酸钙:2322CaCO 2H Ca H O CO +++=++↑ D.金属钠放入冷水中:222Na 2H O 2Na 2OH H +-+=++↑17.“沐雾迎霞褶皱延,高登俯瞰石奇观.天池湖水鱼欢月,云鹤楼台鸟唱山.协兴故居思缅远,华蓥热土铸红岩.慕追遗韵巴渝舞,幺妹风情岂比攀.”这首诗赞美的是广安四大名片之一华蓥山.下列说法不正确的是( )A.诗中的雾是一种气溶胶B.3Fe(OH)胶体是比较稳定的液体,而浊液不稳定C.胶体的特征现象是丁达尔效应D.胶体是纯净物18.用A N 代表阿伏加德罗常数的值,下列说法正确的是( ) A.21L0.2mol /LCaCl 溶液含Cl -数目为0.2A N B.标准状况下,222.4LH O 含有分子数目为A NC.2.3gNa 与足量的氧气反应生成22Na O 转移的电子数为0.1A ND.222gCO 中含有的氧原子数为2A N19.关于等物质的量的NO 和2NO ,则下列说法不正确的是( ) A.氧原子数目比为1:2B.摩尔质量之比为15:23C.同温同压下,密度之比为23:15D.常温常压下,所占体积比为1:120.下列实验操作或事实与预期实验目的或所得结论对应正确的是( )21.下图是Al 及其化合物之间的转化图,则关于Al 及其化合物转化关系描述正确的是( )A.Al 是地壳中含量最多的元素B.Al 还原性强,能与空气中的氧气反应,所以抗腐蚀性差C.23Al O 既能与盐酸反应,又能与氢氧化钠溶液反应D.2NaAlO 属于氧化物22.价一类二维图是学习元素化合物知识的重要模型和工具,它以元素的化合价为纵坐标,以物质类别为横坐标.下图为铁元素的价一类二维图,其中的箭头表示部分物质间的转化关系.下列说法正确的是( )A.用铁丝与水蒸气高温下反应可实现上述转化①B.加热3Fe(OH)发生转化③C.实现转化⑤可以加入NaOH 溶液D.Fe 与强氧化剂可以发生转化⑥第Ⅱ卷(非选择题,共4个大题,共56分)23.(14分)钠是一种非常活泼、具有广泛应用的金属.(1)根据钠原子的结构示意图分析,钠在反应中容易_________电子(填“得到”或“失去”),表现强的_________(填“氧化性”或“还原性”)(2)钠的一种常见淡黄色的氧化物,常用作呼吸面具的供氧剂.该淡黄色固体物质的阴阳离子个数比为_________,写出2CO 与该物质的化学反应方程式______________(3)钠的另一种化合物碳酸钠,它的俗名为:____________,向碳酸钠溶液中通入足量2CO 气体时,发生的化学反应方程式为:________________(4)小苏打的化学式为:____________,碳酸钠固体中混有碳酸氢钠,除杂的化学方程式为:___________ 24.(14分)小组同学探究23Na CO 的性质及工业制法.(1)用23Na CO 固体配制123500mL0.200mol L Na CO -⋅溶液.i.用到的仪器有:天平、药匙、量筒、烧杯、玻璃棒、胶头滴管、___________. ii.计算需要23Na CO 固体的质量是________g.iii.下列主要操作步骤的正确顺序是___________(填字母). a.称取一定质量的碳酸钠固体,放入烧杯中,加入适量蒸馏水溶解;b.向容量瓶中加水至液面离容量瓶刻度线下1-2cm ,改用胶头滴管向容量瓶中加入蒸馏水至凹液面与刻度线相切;c.将溶液转移到500mL 容量瓶中;d.盖好瓶塞,反复翻转,摇匀;e.用少量的蒸馏水洗涤烧杯内壁和玻璃棒2~3次,洗涤液转移到容量瓶中. iv.下列情况中,会使所配溶液浓度偏高的是__________(填字母).a.转移时,没有洗涤烧杯和玻璃棒b.定容时,眼睛俯视刻度线c.摇匀后,发现液面低于刻度线,继续加水至液面与刻度线相切(2)探究23Na CO 与盐酸的反应.向1230.200mol L Na CO -⋅溶液中滴加稀盐酸,开始无气泡,继续滴加,产生气泡,反应的离子方程式为:233CO H HCO -+-+=、______________.(3)我国化学家侯德榜发明的“联合制碱法”为世界制碱工业做出了巨大贡献.通过“联合制碱法”得到的纯碱产品中往往含少量NaCl ,为测定产品中23Na CO 的质量分数,进行如下操作: ①称取50g 样品放入烧杯内加水溶解.②加入过量的氯化钙溶液充分反应,经过滤、______________等操作,称量沉淀的质量为40g .则样品中23Na CO 的质量分数为____________.25.(14分)化学小组同学为研究氯气制备和氯水的成分及性质进行了如下实验. 【实验1】制备氯气.下图是实验室制取纯净、干燥氯气装置图.(1)M 仪器的名称是_____________,①中反应的反应的化学方程式是______________________________. (2)③中存放的试剂是________________.(3)⑤中反应的离子方程式是___________________________. 【实验2】研究氯水性质.实验操作及现象如下表. 资料:淀粉的特征反应——遇2I 变蓝色(4)实验2-1可证明氧化性2Cl ______2I (填“>”或“<”);实验2-2中使溶液褪色的粒子是_______.(5)证明氯水中含有氯离子的方案是_________________________________________________.(6)同学们发现久置的氯水会失去漂白性,溶液由黄绿色变为无色.为探究氯水失效的原因,进行实验:用强光照射盛有氯水的密闭广口瓶,并用传感器测定广口瓶中数据,得到如下曲线.上两图中曲线变化的原因是___________________________________________________.26.(14 分)已知:单质A 为目前人类使用最广泛的金属,氧化物B 为具有磁性的黑色晶体,根据下列转化关系填空.(1)金属单质A与水蒸气生成固体B的反应中,每生成1molB,转移的电子数为_________.(2)写出固体A与水蒸气反应的化学反应方程式_________________________________.(3)写出D+A→C的离子方程式_______________________________________.(4)实验室要检验C溶液中的金属阳离子,可滴加NaOH溶液,当观察到的现象为_________________,则证明含该阳离子;此过程中发生的氧化还原反应化学方程式为_____________________________________.FeCl溶液、(5)将D饱和溶液滴入沸水中,并继续煮沸至溶液呈红褐色,制得分散系是____________,它与3Fe(OH)浊液的本质区别是___________________________________.3广安市化学名师工作室2022年秋高一期末检测化学模拟试题(B卷)参考答案方程式扣分标准:“浓”、“加热”、“↑”等漏掉或者多写共扣一分,化学式写错、未配平不得分;化学方程式写成离子方程式扣一分,离子方程式写成化学方程式不得分.一、选择题(单项选择题,每小题2分,共44分)23.(14分)(除标注外每空2分) (1)失去(1分)还原性(1分)(2)1:2 2222322Na O 2CO 2Na CO O +=+(3)纯碱或苏打(写对一种即可得分)23223Na CO CO H O 2NaHCO ++=(4)3NaHCO 323222NaHCO Na CO CO H O +↑+△ 24.(14分)(每空2分)(1)i.500mL 容量瓶 ii.10.6g iii.acebd iv.b(2)322HCO H CO H O -++=↑+(3)洗涤、干燥 84.8%25.(14分)(除标注外每空2分) (1)分液漏斗 2222MnO 4HCl()MnCl Cl 2H O ++↑+△浓(2)浓硫酸(3)22Cl 2OH Cl ClO H O ---+=++(4)>(1分)HClO (1分)(5)取氯水于一支洁净试管中,加入过量稀3HNO 使其酸化,再加入3AgNO 溶液,若产生白色沉淀,则含有Cl -(6)氯水中的HClO 分解生成HCl 和2O ,2O 的量和溶液中的()c Cl -均增加26.(14分)(每空2分) (1)A 8N(2)()23423Fe 4H O g Fe O 4H +=+↑(条件为高温) (3)322Fe Fe 3Fe +++=(4)产生白色絮状沉淀,迅速变为灰绿色,最后变成红褐色沉淀22234Fe(OH)O 2H O 4Fe(OH)++==(5)3Fe(OH)胶体分散质的直径大小。
2020高中化学人教版必修二教师用书:2-2-1 化学能与电能 Word版含答案

姓名,年级:时间:第二节化学能与电能第一课时化学能转化为电能一、一次能源和二次能源二次能源中的电能是应用最广泛,使用最方便,污染最小的能源。
二、化学能转化为电能1.燃煤发电的能量转化(1)过程:化学能错误!热能错误!机械能错误!电能(2)化石燃料的燃烧(氧化还原反应)是使化学能转换为电能的关键。
2.原电池(1)实验(2)原电池概念:将化学能转变为电能的装置(3)铜锌原电池工作原理电池总反应:Zn+H2SO4===ZnSO4+H2↑。
(4)反应本质:原电池反应的本质是氧化还原反应.(5)构成原电池的条件理论上,自发的氧化还原反应均可设计成原电池。
①两个活动性不同的电极(或一个为金属,一个为能导电的非金属)电极。
②具有电解质溶液。
③形成闭合回路。
1.正误判断(1)HCl+NaOH===NaCl+H2O是放热反应,可以设计成原电池()(2)在铜—锌—稀硫酸原电池中,电子由锌通过导线流向铜,再由铜通过电解质溶液到达锌()(3)原电池中阳离子向正极移动 ( )(4)原电池中的负极反应一定是电极材料失电子()(5)把锌粒放入盛有盐酸的试管中,加入几滴CuCl2溶液,气泡放出速率加快( )[答案] (1)×(2)×(3)√(4)×(5)√2.下列叙述不正确的是( )A.根据一次能源和二次能源的划分,氢气为二次能源B.电能是现代社会中应用最广泛、使用最方便、污染最小的一种二次能源C.火力发电是将燃料中的化学能直接转化为电能的过程D.在火力发电过程中,化学能转化为热能实际上是氧化还原反应发生的过程,伴随着能量的变化[答案]A3.下列设备工作时,将化学能转化为电能的是( )[答案]C4.(1)下列装置属于原电池的是________。
(2)在选出的原电池中,________是负极,发生________反应,________是正极,该极的现象是________________.(3)此原电池反应的化学方程式为______________________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
白盒测试用例练习
1.为以下所示的程序段设计一组测试用例,要求分别满足语句覆盖、判定覆盖、条件覆盖、判定/条件覆盖、组合覆盖和路径覆盖,并画出相应的程序流程图。
( z)
{
00;
( (x>3)(z<10) )
{ *1;
(k); 语句块1
}
( (4)(y>5) )
{
*10;
} 语句块2
3; 语句块3
}
a
Y c
N
b
由这个流程图可以看出,该程序模块有4条不同的路径:
P1:() P2:()
P3:() P4:()
将里面的判定条件和过程记录如下:
判定条件M={x>3 z<10}
判定条件{4 y>5}
1、语句覆盖
2、判定覆盖
p1和p4可以作为测试用例,其中p1作为取真的路径,p4作为取反的路径。
也可以让测试用例测试路径P2和P3。
相应的两组输入数据如下:
3、条件覆盖
对于M:x>3取真时T1,取假时F1;
z<10取真时T2,取假时F2;
对于N:4取真时T3,取假时F3;
y>5取真时T4,取假时F4。
条件:x>3<104>5
条件:x<=3>=104<=5
根据条件覆盖的基本思路,和这8个条件取值,组合测试用例如表所示:
4、判定/条件覆盖
5、组合覆盖
条件组合
1)x>3<10 2)x>3>=10
3) x<=3<10 4)x<=3>=10
5)4>5 6)4<=5
7)4>5 8)4<=5
6、路径覆盖。
