中国证券市场的非线性特征与分形维分析
我国股市非线性特征的检验与分形验证

本 文 通过 对 上证 综 指 和 深圳 成 指 日收益 率 、 周
收益率、 月收益率 的基本统计量 、 和K 检验 、 J B S 直方
表2 深 圳成 指 收 益 率 指 数 的 统 计特 征
( A M)套 利 定 价 模 型 ( )Bak Shls 权 CP 、 A 、lc — co 期 e 定 价模 型 ( P 等 都依赖 于 理性投 资 者 、 效市 场 、 O M) 有 随机游 动 等几 个核 心 假设 。 特点 是对 正 态 分布 及 其 有 限方 差 的存 在有 着 很 强 的依 赖 , 即特别 强 调序 列 独立( 不相 关 )然 而 股票 市 场 的参 与 者 不 一定 在 任 。 何 时候 都 回避 风 险 , 市场 也不 是 一 直 井 然 有 序 , 如 “ 节效 应 ” 小 公 司效 应 ” 季 和“ 的普遍 存 在 , 在实 际 生 活 中人 们往 往 以一 种非 线 性 方 式对 信 息 做 出反 应 。
一
RS 析方 法验 证 了我 国股票 市场 具有 分形 特征 。 /分
二 、 我 国股 票 市场 的 非 正 态特 征 检 验 对
数 据选取 上证 综指 19 年 1月2 90 2 4日 ̄ 2 1年 1 100 2 1 月2 日之 间 的 日收盘指 数 、 收盘 指数 、 收盘 指数 3 周 月
表 1 上 证 综 指 收 益率 指 数 的统 计 特 征
21 年第2 总第 16 01 期( 3 期)
注 :— 统计量在5 JB %和l %显著性水平 下的临界值分别为59 1 和9 13 K S .95 . 0 , — 统计量在5 2 %和 l %显著性水 平下( 双尾 ) 的临界值
分析分形是市场分析的必经之路1.2.3.4.5.6.7.9.

分析分形是市场分析的必经之路1.2.3.4.5.6.7.9.姚⼯讲分形(1):分析分形是市场分析的必经之路(1)发布时间:2018-05-04 ⽂章来源:量学⼤讲堂受“最⼩努⼒原则”的制约,⼈们⾯对复杂问题总是⽤⼀种简化的办法进⾏线性化处理。
这虽然不是很精确,但也能满⾜当时⼈们的需求。
遗憾的是这种措施仅能解决⼈们⾯对世界的⼤约5%左右的问题,现在⼤学的课程花费95%的时间学习的就是这种解决问题的知识。
随着社会的发展,⼈们不得不⾯对像⽣命系统,社会系统以及⽓象预报,⾦融市场分析这类复杂系统的,看似带有随机性的复杂问题。
⾯对这类问题,像以前那样地简化,线性化的处理⽅法是⾛不下去了!这使得⼈们对现实世界的认知彷徨了相当长的⼀段时间。
直⾄上世纪60年代后期伴随着⾮线性动⼒学研究的进展,⼈们先后发现了耗散结构理论,混沌理论和分形理论。
这些前沿科学理论的相继发现对⼈们的世界观和⽅法论形成了巨⼤地冲击,使⼈们对真实的⾮线性世界的认知发⽣了⾰命性变⾰。
市场分形分析⽅法就是在这种背景下逐步出现的。
美国⼈的脚步⽐较快,⽐尔.威廉姆先⽣⾸先出版了《混沌操作法》,此书离分形分析还⽐较远,但是它论述了⾦融交易市场是⼀个混沌系统,以及市场价格沿着最⼩阻⼒⽅向运⾏。
这对⼈们认识市场是有帮助的;埃德加E⽐德斯先⽣写了⼀本书《分形市场分析》,这本书距真正的分形分形进了⼀⼤步,因为它的时间序列R/分析从数理上证明了“市场是有长期记忆功能的”,这可是个不得了的结论,对⾦融交易分析产⽣了巨⼤影响;曼德博罗先⽣是分形⼏何的祖师爷,他通过“曼德博罗集合”向世⼈展⽰了黄⾦分割率及其衍⽣⽐率是⾃然界客体向前演进过程中遵循的⼀种⼗分重要分形维度,是⼀种极其普遍的⾃然现象。
这也对⾦融市场分析产⽣了重⼤影响!⼀度风靡世界的“⾼频交易”就是俄罗斯⼈应⽤分形分形的杰作。
现在看来分形市场分析是正确解读市场的必经之路。
另:请参阅《⼈类⾏为与最⼩努⼒原则——⼈类⽣态学引论》——齐普夫(美哈佛教授)姚⼯讲分形(2):分析分形是市场分析的必经之路(2)发布时间:2018-05-04 ⽂章来源:量学⼤讲堂北⼤博雅特训班刚把我推为“量学三⽼”之⾸,今天突然封了我在178448⽹站的账号,逻辑上似乎出了点问题。
我国股票市场收益率序列的非线性分析

变化的大小和 向只取决于 、前的信息 , 以前的变 l 化情况 尤荚 . 没存 }忆和趋辨性 . 己 电就是说 . 其有马尔科 夫性 主流资4= 市场理 ’几 所有的命题承 缔论, 它 l 如马 柯维菠 的资产组合理沦 . A M. C P 套利定价理论 ( F ) A' . F Bak : e 期权 定价模 删等. l 一 ̄l s c ml 椰匙以此为坫础. 曾几 何时这种范式 l擗蒋证券 市场研究的很长时问 0 , 然而这种瓶式并非充奖无缺的 . 钉效市场的研究者 之 一的奥斯奉 ( s re 9 4 标绘股氍市场收益率 O t n .16 ) m 的街鹰甬数时注意到了在其 分布的尾部较 正态分 应
选用深 份指数母 ¨收盘指数 .样乖区问 为 19 午 I 诚 I 9
4月 3门鼋 2 0 年 4月 1日。股票收益 毕 R 定义为 : 03 .
R =f ~P ./ . 巾 P 我示 【 ) P .其 . 时期 的股价指数 , P 表永滞后一期的股价指数. t
市场收 艋牢足服从 ・ 种他称为稳定帕累托的分布. 其分 布在均值处厩钉尖峰 . 也有胖尾 . 方差足 见定义或咒 限
有『 肥胖 .『 绕均值的峰部比正态分布预 占的更高, l { I I ; I 也就是所谓的” 尖峰” 和” 胖尾” 看来J 禁『场 的收益 } } =
疑非线 性范式 给予 人们解 决 问题纳 一种新 方泼 和思
路。奉 文就从 描述性统 计和 I S分析剥 我 股票T 场 I / f ,
收盐率序列的非线形进行探讨 . 要指 出的 屉 F 为了 需 丽
分析的 便我们有时 以一个市场 为侧 . 似基 _情况足一 本
致的
二、 我国股票市场的描述性统计分析
I 数 据 泉 源 和描 逮 性 统 计 .
新常态下中国证券市场发展现状及趋势研究

新常态下中国证券市场发展现状及趋势研究近年来,中国证券市场发生了较大的变革。
随着新常态下中国经济社会发展的新形势,证券市场不断调整结构、优化服务,也逐步向规范化、国际化方向发展。
本文将从市场规模、结构、制度等多个角度研究新常态下中国证券市场的发展现状及趋势。
一、市场规模截至2021年6月底,中国A股市场总市值达到116.67万亿元人民币,位列全球第二,仅次于美国纳斯达克市场。
同时,A股市场已有超过5.5亿户股民,成为全球最大的股票投资人口数量。
证监会不断开放市场,如不断推进沪港通、深港通的改革,引入外资进入中国市场,中国资本市场国际化步伐加快,有助于推动未来证券市场进一步发展。
二、市场结构在市场结构方面,目前中国证券市场已大致形成了“股债并举、多层次、多元化发展”的格局。
其中,股票市场作为最为常见的融资工具之一,与资本市场的其他工具合作,形成了多种融资渠道,满足了企业不同层次和领域的融资需求。
此外,在债券和期货市场方面,也形成了规模庞大、产品多样、交易活跃的市场体系。
三、市场制度在加强市场监管方面,证监会出台了一系列重要的制度调整,如《期货保障基金管理办法》、《股票交易规则》、《公开发行证券募集说明书格式》等。
并且,证监会进一步加强了对上市公司的财务监管,推动上市公司信息披露制度更加规范、透明、公正。
此外,还加强了交易所的市场监管,优化市场运行机制,加大对违规行为的处罚力度,推动市场牢固树立风险意识和风险防范意识。
总之,新常态下中国证券市场的发展已经取得重大进展,市场规模和活力都大幅提高,市场结构日趋成熟,市场制度不断完善。
未来,中国证券市场将进一步实现国际化,加强与全球各主要资本市场的联系,开放更多的金融衍生品品种,加强市场信用体系,提高市场透明度和商品化程度,使市场在稳步发展的同时,具备更大的活力和竞争力。
中国金融市场的效率和多重分形分析

中国金融市场的效率和多重分形分析中国金融市场的效率和多重分形分析随着中国经济的迅速发展,金融市场在其中扮演着至关重要的角色。
金融市场的效率对经济稳定和发展至关重要。
然而,金融市场的效率一直是一个备受争议的话题。
多重分形分析作为一种研究金融市场效率的方法,被广泛应用于中国金融市场。
首先,我们来了解一下金融市场的效率是什么。
金融市场的效率是指市场价格能否充分反映市场信息,并能提供有效资源配置和定价功能。
高效的金融市场可以有效地为实体经济提供融资和风险管理工具,促进资源的合理配置和经济的稳定发展。
多重分形分析是一种非线性的数据分析方法,可以用来研究金融市场的效率。
它基于分形理论,通过分析金融市场的时间序列数据,来探索其中的内在规律和结构。
在中国金融市场中,多重分形分析的应用涵盖了各个方面。
一方面,研究人员通过多重分形分析来探讨中国股市的效率问题。
例如,他们可以通过分析股票价格的时间序列数据,来研究股市的波动性和波动的规律性。
通过多重分形分析,他们可以发现价格的波动不是完全随机的,而是存在一定程度的自相似性和自相关性。
这些内在规律的存在对于股票市场的投资者具有重要意义,可以帮助他们制定更合理的投资策略。
另一方面,多重分形分析还被应用于研究中国债券市场的效率。
债券市场作为中国金融市场的重要组成部分,其效率的高低直接关系到经济的稳定发展。
通过多重分形分析,研究人员可以分析债券价格的变化和债券市场的波动性,以评估债券市场的效率水平。
他们发现债券价格的波动具有一定的规律性,存在一定程度的自相关性。
这些发现可以为债券市场投资者提供有价值的信息,帮助他们更好地预测债券市场的走势和制定投资策略。
除了股票市场和债券市场,多重分形分析还被广泛应用于研究其他金融市场,如汇率市场、期货市场和商品市场等。
通过对这些市场的多重分形分析,研究人员可以揭示出市场内在规律,为投资者提供更可靠的决策依据。
尽管多重分形分析在中国金融市场中的应用已经取得了一些成果,但研究人员还面临着一些困境和挑战。
A股市场是否具有弱有效性的实证检验

有效市场 只是其 中的一个特例 , 因此分形市场理 市场参与者数量庞大 , 任何单个参与者都无法对市场产生重大影 近于真实市场 , 论开始演变为有效市场理论的检验方 法之一 , 如果能够提示出 A 响; 所有参与者都具有完全的信 息 , 同样的市场进入途径 , 做 有 并 出各种理性行为 ; 不存在交易成本 。有效市场理论 的实质是信息 股市场存在长期记忆性 ,那 么也就 间接证 明了 A股市场不是一
三、 实证 分析
P S分析法 旨在 通过对股价 行为是否存 在长期记 忆性 的检 d
( ) R T指 数实 证 研 究 一 HU S
息, 股票价格过去 的变动趋势对于判断价格的未来走势没有任何 验 若用表示时期以
列为鞅过程具有等价性。
二、 弱有 效性检 验 方法 评价 及分 形市场 理论
( ) 价 及 收 益 率序 列 的统 计 特 征 一 股
泸州 老窖 ( 058 006 ) 中集集 团 ( 009 003 ) 陆家 嘴 (00 3 6 06 ) 深 发展 A (00 1 00 0 )
一 致药业 ( 008 0 02 ) 大 冷股份 (0 50 0 03 ) i 沙 隆达 A (0 53 00 5) ; 佛 山照 明 ( 051 0 04 )
效率 理论 ,按照股价变化对相关信 息作 出迅速准确反映的程度 , 个有效市场 。
将有效市场化分为弱式效性 、 半强式有效 、 强式有效三个层次 , 股 票市场弱有效是指股票价格 反映 了股票所有历 史价格包含 的信
关系, 股票价格是相对 独立 的 , 因此对弱有效性 的检 验就是检验
中的鞅具有的特 性 , 因此股票市场弱有效 与股价或收益率波动序 本文通过大智慧行情软件从大盘股 、 中盘股、 小盘股中各选取 ( 表二 : 样本列表 )
上海证券市场混沌特征分析
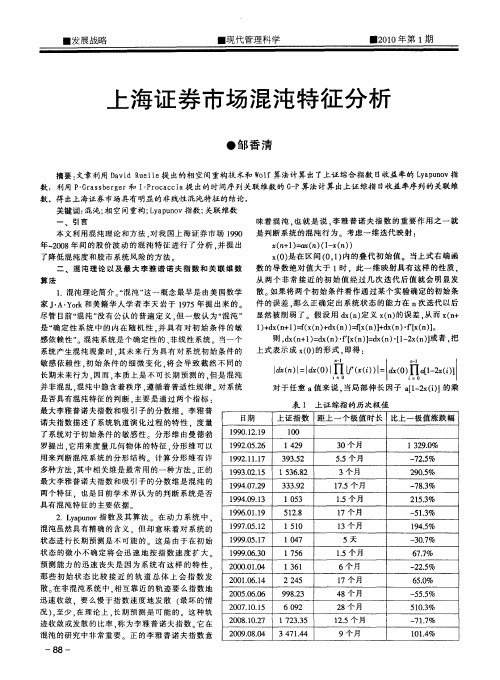
55个 月 .
3个 月 1 . 月 75个 1 . 月 5个 l 7个 月
- 25 7 .%
2 O5 9 .% 一 83 7- % 2 53 1 .% 一 13 5 .%
多种 方法 . 其中相 关维是 最常 用 的一 种方 法 。 的 正
最 大 李 雅 普 诺 夫 指 数 和 吸 引 子 的 分 数 维 是 混 沌 的
上 式 表 示 成 x0 的 形 式 , 得 : () 即
1 .混沌理论 简介 “ 混沌 ” 这一概 念最 早是 由美 国数学 家 J A. ok和美籍 华人 学 者李 天 岩于 17 . Yr 9 5年 提 出来 的 。 尽管 目前 “ 混沌 ” 有公认 的普遍 定 义 . 没 但一 般认 为 “ 沌” 混 是 “ 定 性系 统 中的 内在 随 机性 . 具有 对 初 始 条件 的 敏 确 并 感依 赖性 ” 。混沌 系统是 个确 定性 的 、 线性 系统 。当一个 非 系统 产生混 沌现象 时 . 其未 来行 为 具有 对 系统初 始条 件 的 敏 感依 赖性 . 初始 条件 的细微 变 化 . 将会 导 致截 然 不 同 的 长期未来 行为 , 因而 , 质 上是不 可 长期 预测 的 , 本 但是 混沌 并 非混乱 , 混沌 中隐含着 秩序 , 遵循着 普适 性规 律 。 对系统 是 否具有混沌 特征 的判断 , 主要 是通 过两 个指 标 : 最大 李雅普诺 夫指数 和吸 引子 的分 数 维 。李 雅普 诺夫 指数描 述了系统 轨道 演化 过程 的 特性 .度量 了系统对 于初 始条件 的敏 感性 。分形 维 由曼德勃
i =0 l i =0 l
对 于任 意 a值来 说 , 当局 部伸 长 因子 al 2 () l一 x i】的乘 表 1 上证 综指 的 历次极值
证券市场交易数据序列多重分形分析

a n o n , h ti t sY h r li gp e ii s n r a e y tmig p i t t a a , te am yn r cs n i i ce s d b b r n so o i ma ̄ g 4 Ke r s s c r y b ran d t ; mu t r c l g n rl e i n i y wo d : e u i ag i aa t l f t ; e e ai d d me s n; sr g n s ia a z o t wle e s
l e Wi ol er a e acl u iat er,s ttsadaa s r O e esc yd z t nni a ym t m ta m lf c lhoy t ii n nl i a vnt t e— h n l h i tr a t a sc ys c oh
第2卷 4
第 2期
证 券 市 场 交 易 数 据 序 列 多重 分 形 分 析
张金 良,李光泉 ,扬 忠直 ,杜厌 芳
( 天津大学 管理学 院 ,天津 3x 7 ) f0 2 3
[ 摘
要 】本 文以沪深证 券市场的 实时数 据为基础 ,应用非线性数 学的 多重分形理论 ,分析 了
交易数 据的局部 变化趋向 的多重分形特性 和转折 点的数 字特征 ,得 到 了证 券交 易数据 序 列 多 重分形广义维数在雏数空 间上的分布规律 和任意 交 易数 据序 列的推广性 质。样本计 算和统计 蛄果表 明 ,证 券 交易数据序列具有显著的 多重分 形特性 和在 转折 点 附近 存在 突变奇异性 ,分 析精度 也 大太提 高。
Z NG J - a g L u n -u n Y NG h n -h , D ml a g HA i l n , IG a gq a , A n i Z o gz i U Y - n f
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2005年5月系统工程理论与实践第5期 文章编号:100026788(2005)0520068206中国证券市场的非线性特征与分形维分析宿成建1,缪晓波2,刘 星3(11汕头大学商学院,广东汕头515063;21成都高新区经贸发展局,四川成都610041;31重庆大学经济与工商管理学院,重庆400044)摘要: 采用Cao方法清楚地观测到中国证券市场的月收益率序列是确定性混沌序列,而日收益率序列和周收益率序列却接近于随机波动信号,不适宜做分形维的研究.对我国股市各指数分别作了分形维计算后,同时用替代数据法进行非线性检验,拒绝了中国股市为线性过程的可能性,从而保证了非线性前提下分维数结果的可靠性.结果显示:深证A股市场最为复杂,需要五个变量来建立动力学模型(D2=416150),而上证A股需要四个变量来建立模型(D2=312411).因此,深圳股市的效率弱于上海股市.而我国B股市场已经接近于发达国家股市的复杂性程度(D2=313195(上B);D2=215875(深B)),说明B股的效率比A股的效率高.关键词: 非线性;混沌;收益率序列;相关维数中图分类号: F830191 文献标识码: A N onlinear Characteristics and Fractal Dimension Analysisof Chinese Stock MarketsS U Cheng2jian1,MI AO X iao2bo2,LI U X ing3(11School of Business,Shantou Univ,Shantou515063,China;21Bureau of Economic and T rade Development of Chengdu Hi2tech Z one 610041,China;31C ollege of Business Administration&Economy,Chongqing Univ,Chongqing400044,China)Abstract: Cao’s method is employed in this article to make sure the m onthly return series of Chinese S tock Marketis chaotic but daily return series and weekly return series were found noisy.Thus m onthly return series were analyzedusing correlation dimension as well as its surrogate data.Apparent difference of correlation dimension from the m onthlyreturn series and its surrogate data rejects the null hypothesis that the m onthly return series is derived from a linearsystem,which con firms that the fractal dimension of Chinese S tock Market stems from an inner nonlinear dynamics.Itwas concluded that Shanghai A Share’s efficiency outweighs Shenzheng A Share’s and in general B Share’s efficiencyoutweighs A Share’s.Shenzheng A Share is m ost complex(D2=416150)compared with its Shanghai’s counterpart(D2=312411).B Share(D2=313195(Shanghai B);D2=215875(Shenzheng B))approaches the stockcomplexity of Western countries’.K ey w ords: nonlinearity;chaos;return series;correlation dimension1 引言近年来,随着人们对证券市场的非线性特征认识的深入,应用混沌理论研究股票市场越来越成为金融学者们感兴趣的问题.在国外的研究中,对于日收益率的第一个完整研究是Fama,Eugene F.(1965)作的,他发现收益率是负斜的:在左边(负的)尾部的观测值比右边的尾部的观测值更多[1].Chen Ping(1985)第一个验证了美国的证券市场呈现混沌行为[2],从此揭开了应用混沌理论研究证券市场的序幕.Scheinkman和LeBaron(1989)发现了美国股票市场CRSP日收益率序列与周收益序列中存在非线性的证据[1].Turner和Weigel(1990)使用自1928~1990年的S&P指数的日收益率,作了一个对于易变性的全面研究,得出了类似的结果.他们发现,道琼斯和S&P的日收益率分布是负斜的[1].Edgar E.Peters(1990)在其《资本市场的混沌与秩序》中则宣布了有效市场的失败和不成立,并揭示了美国资本市场的非线性与混沌行为[1,2].在我国的收稿日期:2003211226作者简介:宿成建(1966-),汉族,男,四川郫县人,汕头大学商学院副教授,金融学博士,研究方向:财务与金融.证券市场的非线性特征的研究中,林晓明和王美今(1997)对我国股票市场的混沌现象与市场有效性进行了研究,其研究认为我国股票市场存在混沌现象同时也具有弱式有效性[3].樊智和张世英(2002)应用分维数来分析中、美股市的分形及非线性的结构特征,认为中国股市的非线性程度要强于美国[4].唐奎、宿成建和王宗笠(2003)通过对中国与海外股指的混沌特征的比较实证研究发现,中国深沪股市收益率不服从正态分布,收益率是负斜的,呈现出胖尾和峰态.并存在着非周期循环等混沌特征[5].张永东(2003)则应用BDS 检验和临近返回检验对上海股票市场非线性与混沌进行了实证研究,其检验结果表明,上证综合指数对数收益率不是完全随机的,其中存在着非线性相关结构.但是,通过临近返回检验,没有得到上证综合指数每日对数收益率序列存在混沌的证据[6].现有研究一般要么直接对某一种收益率序列计算分形维值(一般都是关联维数),而没有考虑该序列是否确定性混沌序列;要么在算出分形维值就直接用之进行证券市场的分形特性讨论,而没有求证该分形维值是否来自非线性系统,因为有些线性系统,比如随机噪声(如1Πf 噪声)等自然现象同样可能具有分形维[7].本文在对我国沪深股市进行分形维分析之前,首先用Cao 方法考证了沪深股市的日、周、月对数收益率是否混沌序列,结果发现,日和周对数收益率都没有显示出明显的混沌序列特征,而表现出较强的随机序列特征,而月对数收益率则呈现出混沌序列的特征,因此我们以月对数收益率作为研究序列.在计算月对数收益率序列的关联维数后,同时用替代数据法作非线性检验,保证了月收益率序列分形维数结果的科学性和可靠性,进而用之探讨我国沪深股市的动力学演化行为.2 政券市场的分形维分析211 数据选择和预处理以每日收盘价作为原始数据,再将之转换为收益率R (t )作为分析序列.这里我们以月收益率作为待分析的时间序列,一方面由于以日或周收益率作为分析序列难以避免信号的随机波动,即日收益率序列和周收益率序列都受到比较严重的随机噪声的影响,在原理上不适合做分形维的计算和分析(具体分析见下文).另一方面以式(1)求得的月收益率还具有趋势消除的作用[1,2],这在我们的实验分析中得到体现,故而我们选择月收益率时间序列作为分形市场的刻划对象.R (t )=ln P (t +22)-ln P (t ),(1)在求得月收益率序列后,再对其进行归一化,以降低计算结果的变动性.212 关联维数算法分维特性一般常用分形维数(fractal dimension )来刻划,而关联维数是应用最为广泛的一种分形维数,其最具代表性的计算方法主要就是G 2P 算法[8,9].G 2P 算法是1983年,G rassberger 和Procaccia 根据延迟时间重构思想[10]提出来的,它直接从时间序列计算相关维数D 2.其计算一般分为以下几个步骤:1)相空间重构:设{x k :k =1,…,N }是观测得到的某一时间序列,将其嵌入到m 维欧氏空间R m 中,得到一个点(或向量)集J (m ),其元素记作X n (m ,τ)=(x n ,x n +τ,…,x n +(m -1)τ), n =1,…,N m .(2)式中L =KΔt 是固定时间间隔,即时间延迟,Δt 是两次采样的时间间隔,K 是整数N m =N -(m -1)L .2)欧式距离计算:从这N m 个点中任意选定一个参考点X i ,计算其余N m -1个点到X i 的距离:r ij =d (X i ,X j )=∑m -1k =0(x i +k ×l -x j +k ×l )21Π2, (i ≠j ).(3) 3)相关积分求解:相关积分C m (r )定义为“参考点周围半径为r 的m 维空间所能包含矢量的概率”.C m (r )=1N 2m -N m ∑N m i =1∑N m j =1θ(r -r ij ),(4)式中θ是Heaviside 函数(if x >0,θ=1;if x <0,θ=0).4)关联维数估计:对于充分小的ln r ,相关积分逼近下式:ln C m (r )=ln C +D (m )ln r .(5)96第5期中国证券市场的非线性特征与分形维分析 因此得到R m 中的子集J (m )的相关维:D (m )=lim r →0(5ln C m (r ))Π5ln (r ),(6)D 2=lim m →∞D (m ).(7)这就是吸引子的关联维数.D 2的值可从ln C m (r )相对ln (r )曲线的线性刻度区的斜率估计得到.G 2P 算法从数学定义出发求解混沌时间信号的分维数值,物理意义鲜明,易于实现.因此,被广泛采用.213 参数选择基于G 2P 算法的关联维数根植于延迟时间相空间重构法,延迟时间重构最关键的环节在于延迟时间和嵌入维数两个参数的选取,至今仍是一个开放的问题.这两个参数的合理优化选择直接关系到所求得的关联维数值的真实性和可靠性[7].其中选取延迟时间的方法有自相关函数法,最小互信息法等,其中以最小互信息被广泛采用,该法以序列的的第一个最小互信息值作为优化的延迟时间[7].我们用最小互信息法估计得到优化的延迟时间在16左右(见图1(a )).嵌入维数的选择一般有系统饱和法,伪最近领域点法等[7],其中国际上以伪最近领域点法采用最多.这里我们介绍一种基于伪最近领域点法,但优于伪最近领域点法的最小嵌入维数确定法,它是由Liangyue Cao 于1997年提出,所以我们暂且称之为Cao 方法.该方法定义了两个参数E 1(m )和E 2(m ).其中E 1(m )用于确定最小的嵌入维数(m ),指出E 1(m )在随m 的演变中趋于平稳时对应的m 值即为最小嵌入维数.同时该方法还引入另一个关于m 的参数E 2(m ),E 2(m )不用于确定最小嵌入维数,但E 2(m )有一个非常良好的性能在于:对于任何的m ,如果E 2(m )都等于1(或在1附近)时,则表明这个时间序列是随机序列;而对于确定性混沌序列则不可能对任何m ,E 2(m )都等于1,一般对确定性混沌序列E 2(m )会渐渐趋向1.这就为我们判别一个时间序列是否具有分维特性的混沌序列提供了一种直观而简便的方法.关于Cao 方法的具体的算法可参考Cao 的原始论文[11],这里不作详述.根据Cao 方法,我们确定优化的最小嵌入维数在11左右(见图1(b )).图1 延迟时间和最小嵌入维数的选取.其中(a )是最小互信息法确定优化延迟时间;(b )是Cao 方法确定优化嵌入维数,其中实线表示E 1,虚线表示E 23 混沌和非线性检验在用分形维刻划混沌吸引子特性的历史进程中,研究人员逐渐发现,并非只有混沌吸引子才具有分形维,随机噪声(如1Πf 噪声)等自然现象同样可能具有分形维[7].因而在对一个时间序列进行分形维刻划的时候,必须要求证的一点是该序列是否混沌序列?是否可以用分形维等参数刻划?因此,我们在进行股票07系统工程理论与实践2005年5月市场的分形维研究时,首先应该考证所研究的收益指数序列是否混沌序列,在算得分形维值后还应考证其是否来自非线性系统.这是很多研究所欠缺的.我们在本文中应用Cao 方法实证了月收益率序列是混沌序列,并用替代数据法拒绝了沪深股市来自线性系统的可能性,故而用所计算得出的分形维值进行证券市场的分形分析是可靠的.下面分别阐述之.311 C ao 方法根据上面介绍的Cao 方法,我们从图2中观测到月收益率序列是确定性混沌序列.但是,日收益率序列和周收益率序列却接近于随机波动信号,因而我们认为这两种收益率序列均不适宜用在分形维的计算和分析上.图2 日收益率序列,周收益率序列,以及月收益率的Cao 方法计算得到的E2(m )结果.其中第一列表示日收益率结果;第二列表示周收益率结果;第三列表示月收益率结果.第一行(a )是深综指的结果;第二行(b )是上综指的结果;第三行(c )是深B 指的结果;第四行(d )是上B 指的结 果;第五行(e )是深成指的结果312 替代数据法另一方面,我们用国际上流行的替代数据法[8,12],计算出月收益率序列的替代数据,替代数据只保留了原信号的线性特征,而去掉了原信号的所有非线性特征.如果对原信号和替代数据分别计算分形维的话,如果二者的结果一致,则表明原信号是线性信号;如果不一致,则表明原信号是非线性信号.这就很大程度上可以排除那些虽然也具有分形维但实质上是却是线性信号的序列(如上面提到的随机噪声等).图3(a )所示是原始的深综指月收益率序列及其自相关函数(图3(b )),原始序列的替代序列((图3(c ))及其自相关函数(图3(d )).如图所示原始数据和替代数据的自相关函数大致相同,表明二者的线性特征是相同的.但是计算发现原始的月收益率序列和其替代数据二者的关联维数不一致(如深综指的月收益率关联维数是41615;而其替代数据的关联维数却是1117562),这就有力地证明了深综指月收益率序列是非线性的,非整数维数刻划出其内秉性的分形结构.Cao 方法和替代数据两种方法从不同角度都得到了一致的结论,即月收益率序列具有确定性混沌特性,并来自与非线性系统,因而可以研究其内在的动力学演化,为投资和决策提供参考.17第5期中国证券市场的非线性特征与分形维分析图3 归一化后的深综指的月收益率序列(a )及其自相关函数(b );深综指的月收益率序列的替代序列(c )及其自相关函数(d )4 结果分析通过上述分析,我们计算得出了中国股市各种指数月收益率的分形维值(关联维数)D 2,结果如表1所示.其中Surr D 2是对应的替代数据结果.可以看出,原始数据的关联维值和替代数据的关联维值均不一致,表明每种股指均是非线性的,而且具有分形结构,可用确定性混沌理论加以刻划.表1 中国股指的关联维数计算结果(M =11,L =16)深综指(月)上综指(月)深B 指(月)上B 指(月)深成指(月)D 2 4.615 3.24112.58753.31954.3665Surr D 211.75627.08977.908732.5083 6.3625为对比中外股市的混沌特性,将Edgar E.Peters (1990)根据相关维数的方法计算得出的欧美发达股市的分形维列出,如表2所示.表2 海外股指分形维指数分形维S&P500 2.33MSCI 日本 3.05MSCI 德国 2.41MSCI 英国 2.94比较国外主要股票市场与我国股市的复杂性可知,我国股市从总体上看比国外股市要复杂一些.从表2可知,美国、英国和德国股票指数的分形维都在2到3之间.这意味着可以用三个变量给这些市场的动力学建立模型.而日本的分形维是3105,这意味着需要四个变量.日本市场比其它市场复杂[1].而从表1可以看出,除深B 指外,其它股指的分形维均在312以上,这就意味着我国股市比国外发达股市复杂很多.其中,深证A 股市场比上海A 股市场还要复杂,需要五个变量来建立动力学模型.而上证A 股和B 股则需要四个变量来建立模型.相比之下,只有深证B 股需要三个变量建立模型.5 结论通过以上分析得出如下结论:1)中国沪深股市均是混沌的,具有内秉性的分形结构.2)中国股市从总体上看比欧美股市具有更高的复杂性.3)中国股市日和周对数收益率都没有显示出明显的混沌序列特征,而表现出较强的随机序列特征,而月对数收益率则呈现出混沌序列的特征.4)相对A 股市场,中国B 股市场已经接近于发达国家股市的复杂性程度,说明B 股的效率比A 股的效率高.5)深证A 股市场最为复杂,需要五个变量来建立动力学模型,而上证A 股需要四个变量来建立模型.27系统工程理论与实践2005年5月因此,深圳股市的效率弱于上海股市.参考文献:[1] Edgar E.Peters.Chaos and order in the capital markets :A New View of Cycles ,Prices ,and Market V olatility ,Second Edition[M],John Wiley and S ons ,Inc ,1996.[2] 陈平.经济混沌和经济波动的非线性动力学理论[C].北京大学中国经济研究中心讨论稿系列,N o.C2000015,2000,10.Chen Ping.N onlinear dynamics theory of Economic chaos and fluctuations [C ].W orking paper ,National center for Economic research at Peking University ,2000,10N o.C2000015.[3] Scheinkman J A ,LeBaron B.N onlinear dynamics and stock returns[J ].Journal of Business ,1989,62:311-337.[4] 林小明,王美今.我国股票市场的混沌现象与市场有效性[J ].数量经济技术经济研究,1997,4:51-53.Ling X iao 2ming ,Wang Mei 2jin.The chaos phenomenon and market efficiency in Chinese stock markets [J ].The Journal of Quantitative &T echnical Economics ,1997,4:51-53.[5] 樊智,张世英.金融市场的效率与分形市场理论[J ].系统工程理论与实践,2003,23(3):13-19.Fan Zhi ,Zhang Shi 2ying.The efficiency of financial markets and fractal market theory[J ].Journal of Systems Engineering 2Theory &Practice ,2003,23(3):13-19.[6] 唐奎,宿成建,王宗笠.中国与海外股指的混沌特征的比较实证[J ].重庆大学学报,2003,7:139-142.T ang K ui ,Su Cheng 2jian ,Wang Zhong 2li.The comparative analysis of chaos characteristics between Chinese stock index and overseas[J ].Journal of Chongqing University ,2003,7:139-142.[7] 张永东.上海股票市场非线性与混沌的检验[J ].管理工程学报,2003,3:21-25.Zhang Y ong 2dong.The empirical tests of nonlinear and chaos of Shanghai stock market [J ].Journal of Industrial Engineering and Engineering Management ,2003,3:21-25.[8] H olger K antz ,Thomas Schreiber.N onlinear time series analysis[M].Cambridge University Press ,1997.[9] G rassberger P ,Procaccia I.Measuring the strangeness of strange attractors[J ].Physica D.1983,9:189-208.[10] T akens F.Detecting strange attactors in turbulence[J ]Lecture N otes in Mathematics.S pringer 2Verlag ,1981,898:366-381.[11] Cao Liangyue.Practical method for oletermining the minimum embedding dimension of a scalar time series[J ].Physica D ,1997,110:43-50.[12] Thomas Schreiber ,Andreas Schmitz.Surrogate time series[J ].Physica D ,2000,142:346-382.37第5期中国证券市场的非线性特征与分形维分析。
