数学实验练习题杨振华(MATLAB)
matlab数学实验一2015(答案版)

Matlab数学实验一——matlab初体验一、实验目的及意义[1] 熟悉MATLAB软件的用户环境;[2] 了解MATLAB软件的一般目的命令;[3] 掌握MATLAB数组操作与运算函数;通过该实验的学习,使学生能熟悉matlab的基础应用,初步应用MATLAB软件解决一些简单问题。
二、实验内容1.认识matlab的界面和基本操作2.了解matlab的数据输出方式(format)3. MATLAB软件的数组(矩阵)操作及运算练习;三、实验任务根据实验内容和步骤,完成以下具体实验,要求写出实验报告(实验目的→问题→原理→算法与编程→计算结果或图形→心得体会)完成如下题目,并按照实验报告格式和要求填写实验报告1.在command window中分别输入如下值,看它们的值等于多少,并用matlab的help中查询这些缺省预定义变量的含义,用中文写出它们的意义。
i j eps inf nan pi realmax realmin2.分别输入一个分数、整数、小数等,(如:a=1/9),观察显示结果,并使用format 函数控制数据的显示格式,如:分别输入format short、format long、format short e、format long g、format bank、format hex 等,然后再在命令窗口中输入a,显示a的值的不同形式,并理解这些格式的含义。
3.测试函数clear、clc的含义及所带参数的含义(利用matlab的help功能)。
4. 写出在命令窗口中的计算步骤和运行结果。
(1)计算1.2210(ln log)81eππ+-;>> (log(pi)+log(pi)/log(10)-exp(1.2))^2/81 >>ans =0.0348(2)>> x=2;y=4;>> z=x^2+exp(x+y)-y*log(x)-3z =401.6562(3)输入变量135.3,25a b⎡⎤==⎢⎥⎣⎦,在工作空间中使用who,whos,并用save命令将变量存入”D:\exe01.mat”文件。
数学实验第一次测验选题答案(08)

数学实验第一次测验题及参考答案一、写出下列MATLAB命令的运算结果.1. a=[1 2 3 4].\ [2 1 3 2], b=[1 2 3 4].* [2 1 3 2]a =2.0000 0.5000 1.0000 0.5000b =2 2 9 82. A=[1 2; 3 4]; a=A(2, :) , b=A(: , 2), c=A(:)'a =3 4b =24c =1 32 43. a=linspace(0, 10, 5), b=0:2.5:10a =0 2.5000 5.0000 7.5000 10.0000b =0 2.5000 5.0000 7.5000 10.00004. A=[1,2,3; 4,5,6]; b=A(2, 3), c=A([1 2], [1,3]) , d=size(A)b =6c =1 34 6d =2 35. x=7.1; [fix(x), floor(x) ceil(x) round(x)]ans = 7 7 8 7x=-7.1; [fix(x), floor(x) ceil(x) round(x)]ans = -7 -8 -7 -76. syms x y, z='x^2+x*y-y'; zx=diff(z, x), zy=diff(z, y)zx =2*x+yzy =x-17. syms t, x=[exp(t), cos(t), sin(t)]; dx=diff(x, t)dx =[ exp(t), -sin(t), cos(t)]8. syms x y, f=x*y; y=x^2; f1=subs(f, 'y', y)f =x^39. a=[1 2 3]; b=[4 5 6]; x=dot(a, b), y=cross(a, b)x = 32y = -3 6 -310. v=[1, 2, 3, 4]; A=diag(v); det(A)ans =24二、写出下列MATLAB 命令的实验目的. 1. f=inline('sum(1./(1:n).^2)', 'n'); f(10) 求∑=nk k121当10=n 时的值.2. syms x, limit(sin(x)/x, x, 0) 求极限xxx sin lim0→.3. x=0: 0.1: 5; y=zeros(1, length(x)); plot(x, y, 'r')画出函数0=y ,50≤≤x 的图形.4. syms x, f=3*x^2-x+2; c=roots([3, -1, 2]) 求多项式方程0232=+-x x 的解.syms x, x=-3:0.1:3; f=inline('x.^2 -4*x-10'); c1=fzero(f, [-3,0]) 求函数1042--x x 在区间]0,3[-的零点.5. f='x/(1+x.^2)'; [xmin, ymin]=fminbnd(f, -10,10) 求函数21x xf +=在区间]10,10[-的最小值.6. syms x, int('x^2*sin(x)', x, 0,1) 计算定积分⎰12sin xdx x 的值.syms x, quad('sin(x)./x', 0.001, 1) 求定积分⎰10sin dx x x的近似值.7. ezplot3('cos(t)', 'sin(t)', 't', [0, 8*pi])作出空间曲线⎪⎩⎪⎨⎧===t z t y t x sin cos 当]8,0[π∈t 时的图形.8. [x,y]=meshgrid(-2:0.1:2, -2:0.1:2); z=x.^2-y.^2; contour(x, y, z, 20) 作函数22y x z -=的等高线.9. s= solve( 'x^2 + x*y + y = 3', 'x^2 - 4*y + 3 = 0'), [s.x, s.y]求方程组 ⎩⎨⎧=+-=++034322y x y xy x 的解.10. syms x y; int( int(x*y^2, y, 0, x), x, 0, 1) 计算重积分⎰⎰1002xdx dy xy 的值.dblquad(inline('sin(exp(x.*y))'), 0, 1, 0, 1) 求重积分⎰⎰101)sin(dx dy exy的近似值.三、为下列实验目的写MATLAB 指令.1. 作出星形线t x 3cos 2=,t y 3sin 2=(π20≤≤t )的图形.ezplot('2*cos(t)^3','2*sin(t)^3',[0,2*pi])作出摆线)sin (2t t x -=, )cos 1(2t y -=(π40≤≤t )的图形.ezplot('2*(t-sin(t))','2*(1-cos(t))',[0,4*pi])2. 用极坐标命令, 作出五叶玫瑰线θρ5sin 4=的图形.theta=0:0.1:2*pi; rho=4*sin(5*theta); polar(theta,rho)用隐函数命令作出椭圆322+=+xy y x 的图形和双曲线3322+=+xy y x 的图形. ezplot('x^2+y^2-x*y-3',[-3,3,-3,3])ezplot('x^2+y^2-3*x*y-3',[-10,10,-10,10]) 3. 求!100的近似值. prod(1:100) 求∑=101!1n n 的近似值. s=0;for n=1:10s=s+prod(1./(1:n)); end s4. 求极限 1512lim 33++∞→n n n .syms nlimit((2*n^3+1)/(5*n^3+1),n,inf)5. 求函数x x x f 3cos sin )(=的一阶导数. 并求)1(f '. syms xdaoshu=diff('sin(x)*cos(3*x)') x=1;daoshuzhi=eval(daoshu)求由方程0122222=++++-y x y xy x 确定的隐函数的导数. 并求)1(f '. syms x yz=2*x^2-2*x*y+y^2+x+2*y+1; daoshu=-diff(z,x)/diff(z,y) x=1;daoshuzhi=eval(daoshu)6. 求由参数方程⎩⎨⎧==ty tx 33sin cos 确定的函数的导数. syms t x=cos(t)^3; y=sin(t)^3;daoshu=diff(y,t)/diff(x,t) daoshu=simple(daoshu)求由参数方程⎪⎩⎪⎨⎧+=+=3231616t t y t t x 确定的函数的导数. syms tx=6*t/(1+t^3); y=6*t^2/(1+t^3);daoshu=diff(y,t)/diff(x,t)7. 求⎰)(cos 02)(x dx x w dxd .diff(int('w(x)',0,(cos(x))^2))8. 求⎰-ππ2222sin xdx ex.syms xint('exp(2*x)*sin(2*x)^2',x,-pi,2*pi)9. 绘制曲面22y x z +=的图形 x=-2:0.1:2; y=-2:0.1:2;[x,y]=meshgrid(x,y); z=x.^2+y.^2; surf(x,y,z)作出空间曲线t t x cos =,t t y sin =,t z 2=(π60≤≤t )的图形. ezplot3('t*cos(t)','t*sin(t)','2*t',[0,6*pi])10. 作双曲抛物面4122y x z -=的图形,其中66≤≤-x ,1414≤≤-y . x=-6:0.1:6;y=-14:0.1:14;[x,y]=meshgrid(x,y); z=x.^2-y.^2./4; mesh(x,y,z)11. 设y xy z )1(+=,求x z ∂∂,yz ∂∂. syms x yz='(1+x*y)^y'; diff(z,x),diff(z,y)设),(y xy f z =,求22x z ∂∂,22y z ∂∂,yx z∂∂∂2.syms x y z='f(x*y,y)'; zxx=diff(z,x,2) zyy=diff(z,y,2)zxy=diff(diff(z,x),y)12. 求级数∑∞=12k kk的和.syms k;s1=symsum(k/(2^k),k,1,inf) 求级数∑∞=-12)12(1k k 的和. syms k;s2=symsum(1/((2*k-1)^2),k,1,inf)13. 求函数)1ln()1(x x ++的6阶麦克劳林多项式. clear; syms xser3=taylor((1+x)*log(1+x),7)四、为下列实验目的编写MATLAB 程序.1. 作出分段函数⎪⎩⎪⎨⎧>≤<--≤+=1,11,11,23)(2x x x x x x f 的图形.y=[];for x=-3:0.1:3; if x<=-1y=[y, 3+2*x]; elseif x<=1y=[y, 1]; elsey=[y, x^2]; end endx=-3:0.1:3; plot(x,y)作出分段函数⎩⎨⎧>≤+=0,0,sin 1)(x e x x x h x 的图形.y=[ ];for x=-4:0.1:4 if x<=0y=[y, 1+sin(x)]; elsey=[y, exp(x)]; end endx=-4:0.1:4; plot(x, y)2. 设D 为由2=+y x ,y x =,2=y 所围成的有界区域.(1) 作出区域D 的图形;(2) 根据图形确定积分限. 先对x 后对y 积分计算⎰⎰Ddxdy xy2.x=0:0.01:2; y1=2-x; y2=x.^2; y3=2;plot(x, y1,'r-', x, y2,'b-', x, y3,'k-') syms x y;int(int(x*y^2, x, 2-y, sqrt(y)), y, 1,2) 3. 计算⎰⎰+-Dy x dxdy e )(22, 其中D 为122≤+y x .提示:用极坐标变换 22y x r +=,⎰⎰⎰⎰-+-=πθ201)(222rdrd e dxdy er Dy xtheta=0:0.1:2*pi; x=cos(theta); y=sin(theta);plot(x,y,'r-')clear;syms r theta; f=exp(-(r^2))*r ;int(int(f,r,0,1),theta,0,2*pi)4. 求曲线x x x g 2sin )(=)0(π≤≤x 与x 轴所围成的图形分别绕x 轴, y 轴旋转所成的旋转体体积,并写出作该旋转体的图形的指令. (1) 在图形绕x 轴旋转时,体积dx x g v ⎰=ππ02)(.syms xv=int('pi*(x*sin(x)^2)^2', x, 0, pi)v= 1/8*pi^4-15/64*pi^2 即)86415(22ππ+-=v .(2) 图形绕y 轴旋转时,体积 dx x xg v ⎰=ππ0)(2syms xquad('2*pi*x.^2*sin(x).^2', 0, pi) 则得到体积的近似值为 ans = 27.5349(3) 绕x 轴旋转所得旋转体图形的作图指令 r=0:0.1:pi; t=-pi:0.1:pi; [r, t]=meshgrid(r,t); x=r;z=r.*sin(t).*sin(r).^2; y=r.*cos(t).*sin(r).^2; surf(x,y,z)title('绕x 轴旋转');xlabel('x 轴'); ylabel('y 轴'); zlabel('z 轴')(4) 绕y 轴旋转所得旋转体图形的作图指令 r=0:0.1:pi; t=-pi:0.1:pi; [r, t]=meshgrid(r,t); x=r.*cos(t); z=r.*sin(t); y=r.*sin(r).^2; surf(x,y,z)title('绕y 轴旋转');xlabel('x 轴'); ylabel('y 轴'); zlabel('z 轴')5. 作出抛物柱面2y x =和平面1=+z x 相交的图形.u=-2:0.1:2; v=-2:0.1:2; [u,v]=meshgrid(u,v); x=u.^2; y=u; z=v;mesh(x,y,z) hold onx1=-2:0.1:2; y1=-2:0.1:2; [x1,y1]=meshgrid(x1,y1); z1=1-x1;mesh(x1,y1,z1) hold off6. 作出球面22222=++z y x 和柱面1)1(22=+-y x 相交的图形.解:提示:柱面1)1(22=+-y x 的参数方程:⎪⎪⎪⎩⎪⎪⎪⎨⎧=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛==⎪⎭⎫ ⎝⎛=+=z z t t t y t t x 2cos 2sin 2sin 2cos 2)cos(12t=0:0.1:pi; r=0:0.1:2*pi;[r,t]=meshgrid(r,t); x=2*sin(t).*cos(r); y=2*sin(t).*sin(r); z=2*cos(t); mesh(x,y,z) hold onu=-pi/2:0.1:pi/2; v=-3:0.1:3;[u,v]=meshgrid(u,v); x1=2*cos(u).^2; y1=sin(2*u); z1=v;mesh(x1,y1,z1) hold off 7. 求⎰Lds z y x f ),,(,其中y x z y x f 10301),,(2++=,路径L 为: t x =,2t y =,23t z =,20≤≤t .解:首先把曲线积分化为定积分. 因为dt z y x ds t t t 222++=,clear; syms t;x= t; y=t^2; z= 3*t^2; f=sqrt(1+30*x^2+10*y);f1=f*sqrt(diff(x,t)^2+diff(y,t)^2+diff(z,t)^2); s=int(f1,t,0,2)8. 计算曲面积分⎰⎰∑++ds zx yz xy )(,其中∑为锥面22y x z +=被柱面 x y x 222=+所截得的有限部分.解:因为面积微元dxdy z z ds y x 221++=,根据曲面积分化作二重积分的计算公式, 并采用极坐标计算重积分. 注意到投影曲线x y x 222=+的极坐标方程为t r cos 2=,22ππ≤≤-t .clear;syms x y z r t f=x*y+y*z+z*x; z= sqrt(x^2+y^2); f=subs(f, 'z ', z);mj=sqrt(1+diff(z,x)^2+diff(z,y)^2); x= r*cos(t); y = r*sin(t); f=eval(f); mj=eval(mj); f1=f*mj*r;int(int(f1, r, 0, 2*cos(t)), t,-pi/2,pi/2) 输出为64/15*2^(1/2).五.其它练习1. 作函数2470722234++-+=x x x x y 及其二阶导函数在区间]7,8[-上的图形,并求函数的凹凸区间和拐点.syms xddf=diff(x^4+2*x^3-72*x^2+70*x+24,x,2) ddf =12*x^2+12*x-144>>ezplot('x^4+2*x^3-72*x^2+70*x+24',[-8,7])>>ezplot('12*x^2+12*x-144',[-8,7])>> x=-8:0.1:8;y1=x.^4+2*x.^3-72*x.^2+70.*x+24;y2=12*x.^2+12.*x-144;y3=zeros(1,length(x));plot(x,y1,'r',x,y2,'b',x,y3,'g')ddf=inline('12*x^2+12*x-144');c1=fzero(ddf,[-8,0])c2=fzero(ddf,[0,7])c1 =-4c2 =3>> ddf=inline('12*x^2+12*x-144')>> zhi1=ddf(-5),zhi2=ddf(0),zhi3=ddf(4)zhi1 =96zhi2 =-144zhi3 =96>> f=inline('x^4+2*x^3-72*x^2+70*x+24','x'); zhi4=f(-4),zhi5=f(3)zhi4 =-1280zhi5 =-279函数的下凸(向上凹)区间为[-8,-4],[3,+∞],下凹(向上凸)区间为[-4,3];拐点(-4,-1280), (3,-279).2. 设⎪⎭⎫ ⎝⎛=-πx e x f x cos )(162,45sin )(23+=x x g . 作它们在区间],0[π上的图形. 并求方程)()(x g x f =在该区间内的近似根.x=0:0.1:pi;y1=exp(-x.^2/16).*cos(x./pi);y2=sin(x.^(3/2))+5/4; plot(x,y1,'r',x,y2,'b')clear; syms xf=inline('exp(-x^2/16)*cos(x/pi)-(sin(x^(3/2))+5/4)');x0=fzero(f,2.5)x0 =2.5411>> x0=fzero(f,3)x0 =2.9746 为所求近似根.3. 求曲面14),(22++=y x y x k 在点)2164,21,41(处的切平面方程,并把曲面和它的切平面作在同一图形里.syms x y zF='4/(x^2+y^2+1)-z';f=diff(F,x);g=diff(F,y);h=diff(F,z);x=1/4;y=1/2;z=64/21;a=eval(f);b=eval(g);c=eval(h);x=-1:0.1:1;y=-1:0.1:1;[x,y]=meshgrid(x,y);z1=a*(x-1/4)+b*(y-1/2)+64/21;z2=4*(x.^2+y.^2+1).^(-1);mesh(x,y,z1)hold onmesh(x,y,z2)4. 求函数22y x z +=在条件0122=-+++y x y x 下的极值.syms x y rg=x^2+y^2;h=x^2+y^2+x+y-1;la=g+r*h;lx=diff(la,x)ly=diff(la,y)lr=diff(la,r)输出lx = 2*x+r*(2*x+1)ly = 2*y+r*(2*y+1)lr = x^2+y^2+x+y-1输入solve('2*x+r*(2*x+1)=0', '2*y+r*(2*y+1)=0', 'x^2+y^2+x+y-1=0','x,y,r')得到输出ans =r: [2x1 sym]x: [2x1 sym]y: [2x1 sym]再分别输入rxy得到r =[ -1+1/3*3^(1/2)][ -1-1/3*3^(1/2)]x =[ 1/2*3^(1/2)-1/2][ -1/2-1/2*3^(1/2)]y =[ 1/2*3^(1/2)-1/2][ -1/2-1/2*3^(1/2)]即有解:1(33r =--,1(12x =-,1(12y =--;1(33r =-+,1(12x =-+,1(12y =-+. 因此有两个极值可疑点. 再输入x = 1/2*3^(1/2)-1/2;y = 1/2*3^(1/2)-1/2;f1=eval(g)x = -1/2-1/2*3^(1/2);y = -1/2-1/2*3^(1/2);f2=eval(g)得到输出0.26793.7321即得到两个可能是条件极值的函数值{2+3,2-3}. 但是否真的取到条件极值呢?可利用等高线作图来判断:输入[x,y]=meshgrid(-2:0.1:2,-2:0.1:2);z=x.^2+y.^2;contour(x,y,z,30)hold onezplot('x^2+y^2+x+y-1')5. 求∑∞=+-021)3(4n nn n x 的收敛域与和函数. clear;syms n x;a1=4^(2*n)*(x-3)^n/(n+1);a2=subs(a1, n, n+1);p=limit(a2/a1, n, inf)输出为p =16*x-48注意这里对a2和a1都没有加绝对值. 因此上式的绝对值小于1时,幂级数收敛,大于1时发散. 为了求出收敛区间的端点,输入x=solve('abs(16*x-48)=1')输出为x =[ 49/16][ 47/16] 由此可知16491647<<x 时收敛,1647<x 或1649>x 时发散. 为了判断端点的敛散性,输入 simplify(subs(a1, 'x', 49/16))得到x 为右端点时幂级数的一般项为ans =1/(n+1), 因此当1649=x 时发散. 再输入 simplify(subs(a1, 'x', 47/16))输出结果为ans =1/(n+1)*(-1)^n, 因此当4716x =时, 级数收敛. 也可以在收敛域内求得这个级数的和函数. 输入clear;syms n xs4=symsum(4^(2*n)*(x-3)^n/(n+1), n, 0, inf )输出为 s4 =-1/(16*x-48)*log(49-16*x)。
(完整版)实验报告第2章参考答案yangh1

xlabel('X'),ylabel('Y'),zlabel('Z')
pause
figure(2)
contour(x,y,z)
pause
figure(3)
contour3(x,y,z)
思考
及
习题
结合实验结果及相关理论完成思考及习题内容
1.怎样对隐函数的图形进行显示?
(1) ;
>> syms a b x
>>(3*a*x^2+4*b*x^(1/2))/(x-1)
ans=(3*a*x^2+4*b*x^(1/2))/(x-1)
(2) ;
>> syms x
>> (sin(2*x+pi/4)-log(3*x))/sqrt(x^2+1)
ans=(sin(2*x+1/4*pi)-log(3*x))/(x^2+1)^(1/2)
end
end
end
在命令窗口中运行以下部分:
score =[71 80 87 89 69;85 92 74 94 65;74 90 90 81 92;81 84 82 91 71;70 90 76 70 74;86 85 86 94 85;76 75 81 73 74;91 74 78 73 79;91 75 86 91 67;83 81 84 87 95];
>> a=sqrt(exp(exp(1))); b=tan(pi^2/3);>> a=sqrt(exp(exp(1))); b=tan(pi^2/3);
>> 2*a^2+3*a*b^3-5*a^3*b^5>> sec(atan(a))
MATLAB数学实验答案(全)

MATLAB数学实验答案(全)第⼀次练习教学要求:熟练掌握Matlab 软件的基本命令和操作,会作⼆维、三维⼏何图形,能够⽤Matlab 软件解决微积分、线性代数与解析⼏何中的计算问题。
补充命令vpa(x,n) 显⽰x 的n 位有效数字,教材102页fplot(‘f(x)’,[a,b]) 函数作图命令,画出f(x)在区间[a,b]上的图形在下⾯的题⽬中m 为你的学号的后3位(1-9班)或4位(10班以上) 1.1 计算30sin limx mx mx x →-与3sin lim x mx mxx →∞-syms xlimit((902*x-sin(902*x))/x^3) ans =366935404/3limit((902*x-sin(902*x))/x^3,inf)//inf 的意思 ans = 0 1.2 cos1000xmxy e =,求''y syms xdiff(exp(x)*cos(902*x/1000),2)//diff 及其后的2的意思 ans =(46599*cos((451*x)/500)*exp(x))/250000 - (451*sin((451*x)/500)*exp(x))/250 1.3 计算221100x y edxdy +??dblquad(@(x,y) exp(x.^2+y.^2),0,1,0,1)//双重积分 ans = 2.13941.4 计算4224x dx m x +? syms xint(x^4/(902^2+4*x^2))//不定积分 ans =(91733851*atan(x/451))/4 - (203401*x)/4 + x^3/12 1.5 (10)cos ,x y e mx y =求//⾼阶导数syms xdiff(exp(x)*cos(902*x),10) ans =-356485076957717053044344387763*cos(902*x)*exp(x)-3952323024277642494822005884*sin(902*x)*exp(x)1.6 0x =的泰勒展式(最⾼次幂为4).syms xtaylor(sqrt(902/1000+x),5,x)//泰勒展式 ans =-(9765625*451^(1/2)*500^(1/2)*x^4)/82743933602 +(15625*451^(1/2)*500^(1/2)*x^3)/91733851-(125*451^(1/2)*500^(1/2)*x^2)/406802 + (451^(1/2)*500^(1/2)*x)/902 +(451^(1/2)*500^(1/2))/500 1.7 Fibonacci 数列{}n x 的定义是121,1x x ==12,(3,4,)n n n x x x n --=+=⽤循环语句编程给出该数列的前20项(要求将结果⽤向量的形式给出)。
数学实验(matlab版)过程考试试卷及答案完整版

试绘出三种产品产量与季度的三维垂直方向条形图(分组式). >> x=[8,8,9;11,7,8;12,6,9;10,6,10]; bar3(x,'group') 图形如下:
2/2
第一题:编程计算下面问题, x 值由键≥ 1 y = x 2 , −1 ≤ x < 1 2 x − 1, x < −1
>> x=input('输入 x:'); if x>=1 y=x^2+1; end if x<-1 y=x^2-1; end if x>=-1&x<1 y=x^2; end y 输入 x:5 y= 26 第二题:某人做一种材料的伸缩实验,t 为温度(℃),L 为长度(mm),实验数据见下表 t 20 25 30 35 40 L 81 82.3 84 86.8 89
f = x 4 − xy + y 2 ,求
>> syms x y
∂f ∂ 3 f , ∂x ∂y 3
1/1
f=x^4-x*y+y^2; dx=diff(f,x,1) dy3=diff(f,y,3) dx = 4*x^3-y dy3 = 0 第四题:某厂生产三种产品,某年四季度的产量如下 A 产品产量 笫一季度 笫二季度 笫三季度 笫四季度 8 11 12 10 B 产品产量 8 7 6 6 C 产品产量 9 8 9 10
用二阶拟合法,求 L 与 t 的表达式.要求:1.编程;2.写出 L 与 t 的关系式. >> t=[20,25,30,35,40]; L=[81,82.3,84,86.5,89]; k=polyfit(t,L,2) k= 0.0091 -0.1446 80.2114 L=0.0091 t^2 —0.1446t+ 80.2114 第三题:求微分与积分(编程)
MATLAB数学实验第二版课后练习题含答案

MATLAB数学实验第二版课后练习题含答案课后练习题MATLAB数学实验第二版的课后练习题如下:第一章课后练习题1.编写MATLAB程序,计算并输出下列公式的结果:y = \\frac{1}{\\sqrt{2\\pi\\sigma^2}} e^{-\\frac{(x-\\mu)^2}{2\\sigma^2}}其中,x, $\\mu$, $\\sigma$ 分别由用户输入。
要求输出结果精确至小数点后两位。
答案如下:x=input('请输入 x 的值:');mu=input('请输入 mu 的值:');sigma=input('请输入 sigma 的值:');y=1/sqrt(2*pi*sigma^2) *exp(-(x-mu)^2/ (2*sigma^2));fprintf('y = %.2f\', y);2.编写MATLAB程序,求解下列方程的解:4x + y = 11\\\\x + 2y = 7答案如下:A= [4,1;1,2];B= [11;7];X=inv(A) *B;fprintf('x = %.2f, y = %.2f\', X(1), X(2));第二章课后练习题1.编写MATLAB程序,计算下列多项式的值:P(x) = x^4 - 2x^3 + 3x^2 - x + 1其中,x 由用户输入。
要求输出结果精确至小数点后两位。
答案如下:x=input('请输入 x 的值:');y=x^4-2*x^3+3*x^2-x+1;fprintf('P(%.2f) = %.2f\', x, y);2.编写MATLAB程序,绘制下列函数的图像:f(x) = \\begin{cases} x + 1, & x < 0 \\\\ x^2, & 0 \\leq x < 1 \\\\ 2x - 1, & x \\geq 1 \\end{cases}答案如下:x=-2:0.01:2;y1=x+1;y2=x.^2.* ((x>=0) & (x<1));y3=2*x-1;plot(x,y1,x,y2,x,y3);legend('y1 = x + 1','y2 = x^2','y3 = 2x - 1');总结本文提供了《MATLAB数学实验第二版》的部分课后练习题及其答案。
matlab数学实验考试题及答案

matlab数学实验考试题及答案一、选择题(每题2分,共10分)1. MATLAB中用于生成0到1之间均匀分布的随机数的函数是?A. randB. randiC. randnD. randperm答案:A2. 下列哪个命令可以计算矩阵的行列式?A. detB. rankC. eigD. inv答案:A3. MATLAB中用于求解线性方程组的命令是?A. solveB. linsolveC. fsolveD. ode45答案:A4. 在MATLAB中,如何创建一个3x3的单位矩阵?A. eye(3)B. ones(3)C. zeros(3)D. identity(3)答案:A5. MATLAB中用于绘制二维图形的函数是?A. plotB. surfC. meshD. contour答案:A二、填空题(每题3分,共15分)1. MATLAB中,使用________函数可以计算矩阵的迹。
答案:trace2. 若要在MATLAB中创建一个从1到10的向量,可以使用________函数。
答案:1:103. MATLAB中,使用________函数可以计算矩阵的特征值。
答案:eig4. 若要在MATLAB中绘制一个正弦波,可以使用________函数。
答案:sin5. MATLAB中,使用________函数可以计算矩阵的逆。
答案:inv三、简答题(每题10分,共20分)1. 描述MATLAB中如何使用循环结构来计算并打印1到100之间所有奇数的和。
答案:可以使用for循环结构,初始化一个变量sum为0,然后遍历1到100之间的每个数,使用模运算符判断是否为奇数,如果是,则将其加到sum上,最后打印sum的值。
2. 简述MATLAB中如何使用条件语句来检查一个数是否为素数,并打印出所有小于100的素数。
答案:可以使用for循环遍历2到99之间的每个数,对于每个数,使用一个while循环检查它是否有除1和它本身之外的因数,如果没有,则使用if语句判断该数是否为素数,如果是,则打印该数。
MATLAB数学实验 练习题(附答案)教学教材

%2、求100~999之间的水仙花数 clear all; clc; for n=100:999 n1=floor(n/100); %取出百位数字n1 n2=mod(floor(n/10),10); %取出十位数字n2 n3=mod(n,10) ; %取出个位数字n3 if n1^3+n2^3+n3^3==n
MATLAB数学实验 练习题(附答 案)
4.作yoz面上的曲线z=sin(y)+1绕z轴旋转所得到的图形。
5.作xoy面上的曲线(x-a)2+y2=r2绕z轴旋转所得到的图形 (0<r<a),取r=1,a=2. 6. 作x2/2-y2/3=2z图形. 7. 作x2/2+字符,若输入一个大写字母,则输出其对应的小写字母,若输入一个 小写字母,则输出其对应的大写字母;若为其它字符,则原样输出。 clear all,clc; ch=input('请输入一个字符:','s'); if ch>='A' && ch<='Z'%判断条件 ch=char(ch+32);%大写字母与小写字母ASCII值相差32 else ch=char(ch); end ch
此课件下载可自行编辑修改,仅供参考! 感谢您的支持,我们努力做得更好!谢谢
%6. 作x2/2-y2/3=2z图形. clear,clf,clc; [X,Y,Z]=meshgrid(-1:0.1:1); V=X.^2./2+Y.^2./2-2*Z; fv=isosurface(X,Y,Z,V,0);%显示V=0等值面 p=patch(fv); set(p,'FaceColor','blue','EdgeColor','none');%设置图形的相关属性 view(3) hold on camlight
数学实验(MATLAB)课后习题答案
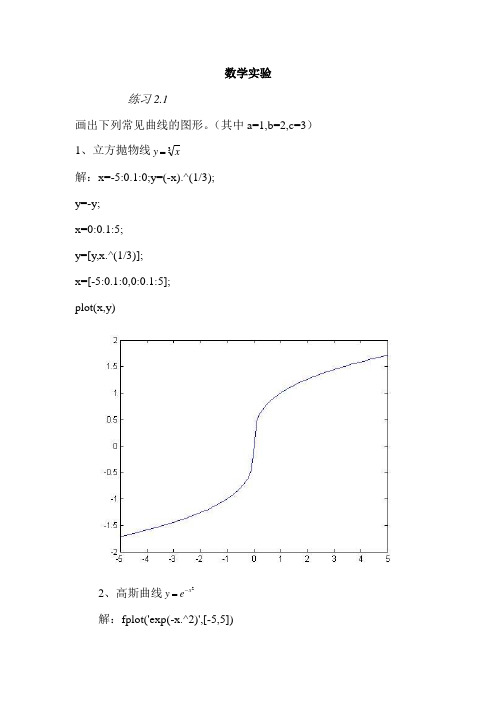
数学实验练习2.1画出下列常见曲线的图形。
(其中a=1,b=2,c=3)1、立方抛物线3xy=解:x=-5:0.1:0;y=(-x).^(1/3);y=-y;x=0:0.1:5;y=[y,x.^(1/3)];x=[-5:0.1:0,0:0.1:5];plot(x,y)2、高斯曲线2x e=y-解:fplot('exp(-x.^2)',[-5,5])3、笛卡儿曲线)3(13,1333222axy y x t at y t at x =++=+=解:ezplot('x.^3+y.^3-3*x*y',[-5,5])xyx.3+y.3-3 x y = 0或t=-5:0.1:5; x=3*t./(1+t.^2); y=3*t.^2./(1+t.^2); plot(x,y)4、蔓叶线)(1,1322322xa x y t at y t at x -=+=+=解:ezplot('y.^2-x.^3/(1-x)',[-5,5])xyy.2-x.3/(1-x) = 0或t=-5:0.1:5; x=t.^2./(1+t.^2); y=t.^3./(1+t.^2); plot(x,y)5、摆线)cos 1(),sin (t b y t t a x -=-= 解:t=0:0.1:2*pi;x=t-sin(t); y=2*(1-cos(t)); plot(x,y)6、星形线)(sin ,cos 32323233a y x t a y t a x =+== 解:t=0:0.1:2*pi; x=cos(t).^3; y=sin(t).^3;plot(x,y)或ezplot('x.^(2/3)+y.^(2/3)-1',[-1,1])xyx.2/3+y.2/3-1 = 07、螺旋线ct z t b y t a x ===,sin ,cos 解:t=0:0.1:2*pi; x=cos(t); y=2*sin(t); z=3*t; plot3(x,y,z) grid on8、阿基米德螺线θa r = 解:x =0:0.1:2*pi; r=x; polar(x,r)902701809、对数螺线θa e r = 解:x =0:0.1:2*pi; r=exp(x); polar(x,r)90270180010、双纽线))()((2cos 22222222y x a y x a r -=+=θ 解:x=0:0.1:2*pi; r=sqrt(cos(2*x)); polar(x,r)90270或ezplot('(x.^2+y.^2).^2-(x.^2-y.^2)',[-1,1]) grid onxy(x.2+y.2).2-(x.2-y.2) = 011、双纽线)2)((2sin 222222xy a y x a r =+=θ 解:x=0:0.1:2*pi; r=sqrt(sin(2*x)); polar(x,r)90270或ezplot('(x.^2+y.^2).^2-2*x*y',[-1,1]) grid onxy(x.2+y.2).2-2 x y = 012、心形线)cos 1(θ+=a r 解:x =0:0.1:2*pi; r=1+cos(x); polar(x,r)90270练习2.21、求出下列极限值。
matlab数学实验复习题(有答案)

matlab数学实验复习题(有答案)复习题1、写出3个常用的绘图函数命令2、inv (A )表示A 的逆矩阵;3、在命令窗口健入clc4、在命令窗口健入clear 5、在命令窗口健入6、x=-1:0.2:17、det (A )表示计算A 的行列式的值;8、三种插值方法:拉格朗日多项式插值,分段线性插值,三次样条插值。
9、若A=123456789⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦,则fliplr (A )=321654987⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦A-3=210123456--⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦A .^2=149162536496481⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦tril (A )=100450789⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦ triu (A ,-1)=123456089⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦diag (A )=100050009⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦A(:,2),=258A(3,:)=369 10、normcdf (1,1,2)=0.5%正态分布mu=1,sigma=2,x=1处的概率[t,x]=ode45(@f,[a,b],x0),中参数的涵义是@fun 是求解方程的函数M 文件,[a,b]是输入向量即自变量的范围a 为初值,x0为函数的初值,t function 开头;1721、设x )的功能是作出将X 十等分的直方图22、interp1([1,2,3],[3,4,5],2.5)Ans=4.523、建立一阶微分方程组⎩⎨⎧+='-='yx t y y x t x 34)(3)(2的函数M 文件。
(做不出来)二、写出运行结果:1、>>eye(3,4)=1000010000102、>>size([1,2,3])=1;33、设b=round (unifrnd (-5,5,1,4)),则=3 5 2 -5 >>[x,m]=min(b);x=-5;m=4,[x,n]=sort(b)-5 2 3 5 4 3 1 2mean(b)=1.25,median (b )=2.5,range (b )=104、向量b 如上题,则>>any(b),all(b<2),all(b<6)Ans=1 0 15、>>[5 6;7 8]>[7 8;5 6]=00116、若1234B ⎡⎤=⎢⎥⎣⎦,则 7、>>diag(diag(B))=10048、>>[4:-2:1].*[-1,6]=-4 129、>>acos(0.5),atan(1)ans=1.047197551196598ans=0.78539816339744810、>>norm([1,2,3])Ans=3.74165738677394111、>>length([1,3,-1])=312、>>x=0:0.4:2;plot(x,2*x,’k*’)13、>>zeros(3,1);ans=14、>>ones(3)=111111111,vander([2,3,5])=421931255116、>>floor(1:0.3:3)=1 1 1 12 2 218、>>subplot(2,2,1); fplot('sin',[0,2*pi]);subplot(2,2,2);plot([1,2,-1]);>>x=linspace(0,6*pi);subplot(2,2,3);plot3(cos(x),sin(x),x);>>subplot(2,2,4);polar(x,5*sin(4*x/3));19、>>t=linespace(0,2,11)0.0 0.2 0.4 0.6 0.8 1.0 1.2 1.4 1.6 1.8 2.020、>>[a,b]=binostat(15,0.2)a=3 b=2.4>>y1=binopdf(5,10,0.7)=0.1029,y2=binocdf(5,10,0.7)=0.15031 1 1 11 1 1 1>>y=-poissrnd(8,2,4)-16 -10 8 -7-7 -8 -6 -9>>sign(y)-1 -1 -1 -1-1 -1 -1 -135、>>[a1,b1]=binostat(20,0.4) a1=8 b1=4.8 >>[a2,b2]=poisstat(8)ans=8,8>>[a3,b3]=chi2stat(15)ans=[15 30]36、运行M文件:chi2fign=5;a=0.9;xa=chi2inv(a,n);x=0:0.1:15;y=chi2pdf(x,n);plot(x,y,'b');hold on;xf=0:0.1:xa;yf=chi2pdf(xf,n);fill([xf,xa],[yf,0],'g');text(xa*1.01,0.005,num2str(xa));text(2.5,0.05,'alpha=0.9','fontsize',20); text(9,0.09,'X~{\chi}^2(4)','fontsize',16);37、>>t=linspace(0,2*pi);>>polar(t,3*t,’g*’)38、>>quadl(’exp(2*x).*log(3*x)’,1,3)ans =398.635239、x0=0:2*pi/6:2*pi;y0=sin(x0).*cos(x0);x=[linspace(0,2*pi,100)];y=sin(x).*cos(x);y1=spline(x0,y0,x); [x;y;y1]'plot(x,y,'k',x,y1,'b-')注:此处省略100组数据40、>>A=round(unifrnd(0,100,3,3));>>[L,U]=lu(A)L =0.9897 0.4699 1.00000.1649 1.0000 01.0000 0 0U =97.0000 80.0000 92.00000 35.8041 26.82470 0 -89.656841、a=sparse([1 3 3],[2 3 5],[1 2 3],4,5);s=full(a)s =0 1 0 0 00 0 0 0 00 0 2 0 30 0 0 0 0三、编程1、 分别用矩形公式、梯形公式、辛普森公式、Gauss-Lobatto 公式及随机模拟方法计算数值积分/230sin 2x e xdx π⎰,并与符号运算计算的结果进行比较。
matlab与数学实验的考试试题

matlab与数学实验的考试试题一、单项选择题(每题2分,共10分)1. MATLAB的全称是什么?A. Matrix LaboratoryB. Microprocessor Application ToolC. Microsoft Advanced Technology ToolD. Microprocessor Application Technology2. 在MATLAB中,以下哪个命令用于绘制函数f(x)=x^2在闭区间[0,1]上的图像?A. plot(0:1, 0:1)B. plot(0:0.01:1, 0:0.01:1)C. plot(0:1, 0:1:1)D. plot(0:0.01:1, 0.^2)3. 以下哪个MATLAB命令用于求解线性方程组?A. solveB. linsolveC. equationD. linear4. 在MATLAB中,用于生成一个3x3单位矩阵的命令是什么?A. eye(3)B. unit(3)C. identity(3)D. I(3)5. 如果变量x和y在MATLAB中分别表示为x = [1 2 3; 4 5 6] 和 y= [1; 2; 3],那么表达式x * y的结果是什么?A. [5; 15; 29]B. [14; 32; 50]C. [7; 15; 23]D. [3; 6; 9]二、简答题(每题5分,共20分)1. 简述MATLAB在数学实验中的作用和重要性。
2. 解释MATLAB中向量和矩阵的区别,并给出创建它们的基本命令。
3. 在MATLAB中,如何使用for循环生成一个从1到100的奇数向量?4. 描述在MATLAB中使用函数文件的过程,包括如何定义和调用函数。
三、编程题(每题10分,共30分)1. 编写一个MATLAB函数,该函数接受一个向量作为输入,并返回向量中所有元素的和。
```matlabfunction S = sumVector(V)% 请在此处编写代码end```2. 编写一个MATLAB脚本,该脚本生成一个5x5的随机矩阵,并计算其行列式。
数学实验试题库写出完成下列运算的Matlab代码

如对您有帮助,欢迎下载支持,谢谢!1写出完成下列运算的Matlab 代码实验1 Matlab 概述 121. 36,4==x y ,求x 、y 的最大公因子和最小公倍数。
答案:x=36;y=4; ………1分 gcd(x,y) ………2分 lcm(x,y) ………2分2. 设3.6,4.3==x y ,分别对x 和y 进行向下取整和四舍五入取整操作。
答案:x=3.6;y=4.3; ………1分 floor(x) ………2分 round(y) ………2分3.绘制22x y e-=在[-3,3]上以0.3为步长各数据点的条形图。
如对您有帮助,欢迎下载支持,谢谢!2答案: X=-3:0.3:3; Y= exp(-X.^2); bar(X,Y)4.72,45x y ==,求x 、y 的最大公因子和x 对y 的余数。
答案:x=36;y=4; ………1分 gcd(x,y) ………2分 rem(x,y) ………2分4.bar(y)实验2 函数图形绘图 3一元函数图形(平面曲线)5.作函数sin ,cos y t x t ==在区间[2,2]ππ-上的图形.clear;close;t=0:2*pi/30:2*pi; x=cos(t);y=sin(t); plot(x,y); axis equal如对您有帮助,欢迎下载支持,谢谢!36. 画出星形线33()2cos ()2sin ⎧=⎪⎨=⎪⎩x t ty t t的图形。
答案:t=linspace(0,2*pi,500) ; ………1分 x=2*(cos(t)).^3; ………1分 y=2*(sin(t)).^3; ………1分 plot(x,y) ………2分7.作出以参数方程]2,0[,sin ,cos π∈==t t y t x 表示的平面曲线(单位圆), 相应的MATLAB 程序代码为:clear; close;t=0:2*pi/30:2*pi; x=cos(t); y=sin(t); plot(x,y)8.作出以极坐标方程]2,0[,1),cos 1(πϕϕ∈=+=a a r 表示的心脏线 相应的MA TLAB 程序代码为:t=0:2*pi/30:2*pi; r=1+cos(t);x=r.*cos(t); y=r.*sin(t); %极坐标转化为直角坐标 plot(x,y)9. 画出立方曲线3x y =在[-1,1]上的图形 x=-1:0.01:1; y=x.^3; plot(x,y)10. 画出立方抛物线3x y =在[-1,1]上的图形 x=0:0.01:1; y=x.^(1/3);如对您有帮助,欢迎下载支持,谢谢!4plot(x,y,-x,-y)11. 画出高斯曲线2x e y -=在[-3,3]上的图形 x=-3:0.01:3; y=exp(-x.^2); plot(x,y)12. 画出奈尔抛物线32,x t y t ==在t ∈[-3,3]上的图形 t=-3:0.01:3; x=t.^3; y=t.^2; plot(x,y)13. 画出半立方抛物线23,x t y t ==在t ∈[-3,3]上的图形 t=-3:0.01:3; x=t.^2; y=t.^3; plot(x,y)14. 画出迪卡尔曲线22233,11at at x y t t ==++的图形,a=1, t ∈[-π, π] t=-pi:0.01:pi;a=1;x=a*t./(1+t.^2);y=3*a*t.^2./(1+t.^2); plot(x,y)15. 画出蔓叶线2322,11at at x y t t ==++的图形, a=1, t ∈[-3,3] t=-3:0.01:3;a=1;x=a*t.^2./(1+t.^2);如对您有帮助,欢迎下载支持,谢谢!5y=a*t.^3./(1+t.^2); plot(x,y)16. 画出摆线)cos 1(),sin (t b y t t a x -=-= 的图形,1,2a b ==, t ∈[0,4 π]。
数学实验模拟试题2

数学实验模拟试题2数学实验模拟试题一、Matlab软件题目,不定项选择(共34题,每题2分,共68分,多选不得分)1、MATLAB常用窗口有(a b c d)A. 命令窗口B. M文件窗口C. 工作空间窗口D. 图形窗口2、命令窗口可用于(a c)A. 数值计算B. 函数作图C. 符号计算D. 编写循环结构语句3、关于命令窗口进行编程时的说法正确的是(a b d)A.如果某个语句运行发现错误,可直接对其进行编辑修改B.语句运行后如出现红色字体提示,说明语句有语法错误C.向下方向键可重调前一行进行重新编辑D.表达式后面跟分号,运行不会进行计算4、M文件窗口可用于(a b c d)A.变量赋值B.自定义函数C.函数作图D.编写条件结构语句5、关于M文件描述正确的有(bcd)A.第一行必须为function开头B.以%开头的命令行不参与运算C.M文件的文件名规则必须与变量命名规则相同D.函数M文件调用时要调用文件名6、通过帮助学习得到命令legend的功能为(c)A.计算矩阵的行列数B.二维作图函数C.图形标注函数D. 生成特殊矩阵7、下面变量命名错误的有(a)A.123aB.a123C.piD.xa_b_68、命令format rat功能为(d)A.5位定点表示数据格式B. 15位定点表示数据格式C.变量之间有空行D.以有理数显示9、结果为[1 3 5 7 9 ]的是(a b c)A. 1:2:9B. linspace(1,9,5)C.[1,3,5,7,9]D.logspace(1,2,9)10、命令行A=[1 2 3;4 5 6;7 8 9];C=A(2:-1:1,[3 1])的结果是(c d)A.[1 3;4 6]B.[2 1;3 1]C.[6 4;3 1]D.[6,4;3,1]11、结果为:1 0 0 10 1 0 10 0 1 11 2 3 1的是(ab)A. a=eye(3);b=[1 2 3];c=ones(4,1);[[a;b],c]B. a=eye(3);b=[1 2 3 1];c=ones(3,1);[a,c;b]C. a=eye(3);b=[1 2 3];c=ones(4,1);[[a;b,c]D. a=eye(3);b=[1 2 3 1];c=ones(3,1);[b;a,c]12、g=[l 2 3;2 4 6;7 8 9];h=[1 1 l;2 2 2;3 3 3];g*h结果为(a)A . 14 14 1428 28 2850 50 50B. 1 2 34 8 1221 24 27C. 10 14 1820 28 3630 42 54D.以上都不对13、下面语句表达正确的有(a d)A.x^2/(1-x^2)B. e^x*sin(x)-x*(x+1)C. x=1:20;y=sinx;plot(x,y)D. (x+3^x)^(1/x)14、结果为-6的有(a c)A.fix(-6.51)B.floor(-6.51)C.ceil(-6.51)D.round(-6.51)15、a=[-4.5 10 7 -2.8 3.5 10 5];[x,y]=max(a)结果为(d)A.x=10,y=6B.x=-4.5,y=1C.x=10,y=[2,6]D.x=10,y=216、下面二维作图语句正确的有(a c d)A.x=-5:0.5:5;y1=x.^2;y2=x.^3;y3=x.^4; plot(x,y1,x,y2,x,y3)B. x=linspace(-5,5,100);y=exp(-x^2); plot(x,y)C.theta=linspace(0,2*pi,100);rou=sin(2*theta);polar(theta,rou)D.ezplot('3*t/(1+t^3)','3*(t^2)/(1+t^3)',[0 20])E.y=linspace(-0.9,0.9,100);x=[log((1+sqrt(1-y.^2))./y)-sqrt(1-y.^2),log((1-sqrt(1-y.^2))./y)+sqrt(1-y.^2)];plot(y,x)17、下面三维做图语句正确的有(a b)A. ezmesh('sin(pi*sqrt(x.^2+y.^2))')B. x='(1+cos(u)).*cos(v)';y='(1+cos(u)).*sin(v)';z='sin(u)';ezmesh(x,y,z,[0,2*pi,0,2*pi])C.x=-7.5:0.5:7.5;y=x;r=sqrt(x.^2+y.^2);z=sin(r)./r;mesh(x,y,z)D.x=1:0.1:10;y=sin(x);subplot(x,y)18、关于作图控制和标注的说法错误的有(b c)A.y:-可表示画黄色实线B.axis square表示x轴、y轴单位长度相同C.gtext(1,2),'sinx')表示在点(1,2)处标记sinxD.itle为图形加标题19、下面符号表达式正确的有(a d)A.syms x;y=2+cos(x)B. sym x;y=2+cos(x)C. y=sym(2+cos(x))D. y=sym('2+cos(x)')20、程序y='x^5+6*x-18';subs(y,'x',5)结果为(a)A.3137B.3200D.以上都不对21、下面求函数极限语句正确的有(c)A. limit((x+3^x)^(1/x),x,inf)B. limit((exp(x)*sin(x)-x*(x+1))/x^3,x,0)C.syms x; limit((x+3^x)^(1/x),x,inf)D. limit(‘(exp(x)*sin(x)-x*(x+1))/x^3’,x,0)22、下面求函数导数语句正确的有( ac )A. syms x;f=(x^2+2*x+1)/(exp(-x)*sin(x)+1);diff(f,x)B. diff(‘(x^2+2*x+1)/(exp(-x)*sin(x)+1)’,x)C. syms x;f=x^2/(1-x^2);diff(f,x,3)D. sym x;diff(x^2/(1-x^2),x)23、下面求函数积分语句正确的有(b c)A. syms x;diff(exp(2*x)/(exp(x)+2),x)B. syms x;int(exp(2*x)/(exp(x)+2))C. syms x;int(exp(2*x)/(exp(x)+2),x)D. syms x;diff(exp(2*x)/(exp(x)+2))24、方程101*x^7+5*x^3-101=0的实数解约为(a)A.0.99B.10.78C.8.41D.以上都不对25、微分方程dy/dx=1-y^2,y(0)=1的解为()A.tan(x+1/4*pi)B. 1C. 0D.以上都不对26、调用自定义函数ddd(7)结果为(c)function f=ddd(a)n=1;x(n+1)=(x(n)+a/x(n))/2;while abs(x(n+1)-x(n))>=10^(-5)n=n+1;x(n+1)=(x(n)+a/x(n))/2;endf=x(n+1);A.2.4495B.2.8284C. 2.6458D.以上都不对27、调用自定义函数shui(3500)结果为(a)function y=shui(x)cx=x-3500if cx<=0y=0;elseif cx<=1500y=cx*0.03;elseif cx<=4500y=cx*0.1-105;elseif cx<=9000y=cx*0.2-555;elseif cx<=35000y=cx*0.25-1005;elseif cx<=55000y=cx*0.3-2755;elseif cx<=80000y=cx*0.35-5505;elsey=cx*0.45-13505endendA. 0B. 1C.-1D.以上都不对28、下面程序的结果为(c)sum=0;for i=1:2:100sum=sum+i;endsumA.5500B. 5050C.2500D. 以上都不对29、关于下面程序描述正确的有(d b)n=0;EPS=1;while(1+EPS)>1EPS=EPS/2;n=n+1;endn,EPSA.程序使用了条件语句B.程序使用了循环语句C.程序会进入死循环D.程序会生成matlab最小的正数30、关于matlab软件中分号的功能描述正确的有(a b c)A. 表达式后面跟分号,该语句不进行运算B. 矩阵输入时分号用来行分隔C. 同一行有多个语句,可用分号做分隔D 作图语句后面跟分号将隐藏图形31、关于matlab软件中,括号的功能描述正确的有(a c)A.通常每个命令后面跟小括号,用来放置参数B.大括号可用于组织运算C.中括号可用来数组输入D.组织运算时小括号可不限次数的使用32、关于矩阵拼接描述正确的有(b d)A.只有行数和列数均相同的矩阵才可以拼接B.左右拼接矩阵时可以列数不相同C.上下拼接矩阵时可以列数不相同D.矩阵拼接为矩阵输入带来方便,减少手工输入量33、关于matlab软件功能述正确的有(a b c d)A.数值分析B.方程求解C. 绘图功能D.图像处理34、关于matlab编程描述正确的有(a b c d)A. 变量命名要统一B.为程序加注释可增加程序的可读性C. 有效的排版可增加程序的可读性D.程序错误时会给出错误提示二、数学实验题目,不定项选择(共8题,每题4分,共32分,多选不得分)35、下面哪些问题可用微分方程模型描述(c d)A. 飞机如何定价问题B. 新商品销售规律C. 人口增长问题D. 计算机网络可靠性分析36、下面哪个是用图形放大法得到方程10*x^5+2*x^2-14=0最准确的根(d)A. 1.035B. 1.045C.1.025D.以上都不是37、区间迭代法求得方程10*x^5+2*x^2-14=0在[-5,5]的根为()A.1.0347B.1.0351C.1.0451D. 以上都不是38、下面koch曲线程序空白处应填写(b)function koch(a,b,n)if (n==0)plot([a(1);b(1)], [a(2);b(2)], 'r');hold on;elsex=pi/3;T=[cos(x),-sin(x);sin(x),cos(x)];c =(2*a+b)/3;e =(a+2*b)/3;d=c+T*(e-c);koch(a, c, n-1);;koch(d, e, n-1);koch(e, b, n-1);endA. koch(a, c, n-1)B. koch(c, d, n-1)C. koch(d, e, n-1)D. koch(e, b, n-1)39、下面程序是用哪种图示示法观察数列的散敛性和周期性(a)clear;clc;x=[0.2000 0.6080 0.9057 0.3246 0.8331];k=1:5;plot(k,x,'o')hold on,plot(k,x)hold offA. 线性联结图B.蛛网图C.费根鲍姆图D.以上都不是40、下面程序是用哪种方法求解微分方程的数值解(b)clear;clc;n=10;h=0.1;f=inline('-y+x+1','x','y');x(1)=0;y(1)=1;for k=1:nx(k+1)=x(k)+h;y(k+1)=(y(k)+h*x(k+1)+h)/(1+h);endyA.向前欧拉公式B.向后欧拉公式C.梯形公式D.改进欧拉公式E.隐式欧拉公式41、已知观察数据x=1:5;y=[5 8 9 15 25],用分段线性插值计算2.5的插值结果()A. 6.5B. 8.5C.8.75D.以上都不对42、已知观察数据x=1:5;y=[5 18 29 15 25],用三次样条线性插值计算2.5的插值结果()A. 25.3B.26.3C.26D.以上都不对。
MATLAB数学实验课后答案

数学实验MATLAB参考答案(重要部分)P20,ex1(5) 等于[exp(1),exp(2);exp(3),exp(4)](7) 3=1*3, 8=2*4(8) a为各列最小值,b为最小值所在的行号(10) 1>=4,false, 2>=3,false, 3>=2, ture, 4>=1,ture(11) 答案表明:编址第2元素满足不等式(30>=20)和编址第4元素满足不等式(40>=10)(12) 答案表明:编址第2行第1列元素满足不等式(30>=20)和编址第2行第2列元素满足不等式(40>=10)P20, ex2(1)a, b, c的值尽管都是1,但数据类型分别为数值,字符,逻辑,注意a与c相等,但他们不等于b(2)double(fun)输出的分别是字符a,b,s,(,x,)的ASCII码P20,ex3>> r=2;p=0.5;n=12;>> T=log(r)/n/log(1+0.01*p)T =11.5813P20,ex4>> x=-2:0.05:2;f=x.^4-2.^x;>> [fmin,min_index]=min(f)fmin =-1.3907 %最小值min_index =54 %最小值点编址>> x(min_index)ans =0.6500 %最小值点>> [f1,x1_index]=min(abs(f)) %求近似根--绝对值最小的点f1 =0.0328x1_index =24>> x(x1_index)ans =-0.8500>> x(x1_index)=[];f=x.^4-2.^x; %删去绝对值最小的点以求函数绝对值次小的点>> [f2,x2_index]=min(abs(f)) %求另一近似根--函数绝对值次小的点f2 =0.0630x2_index =65>> x(x2_index)ans =1.2500P20,ex5>> z=magic(10)z =92 99 1 8 15 67 74 51 58 4098 80 7 14 16 73 55 57 64 414 81 88 20 22 54 56 63 70 4785 87 19 21 3 60 62 69 71 2886 93 25 2 9 61 68 75 52 3417 24 76 83 90 42 49 26 33 6523 5 82 89 91 48 30 32 39 6679 6 13 95 97 29 31 38 45 7210 12 94 96 78 35 37 44 46 5311 18 100 77 84 36 43 50 27 59>> sum(z)ans =505 505 505 505 505 505 505 505 505 505 >> sum(diag(z))ans =505>> z(:,2)/sqrt(3)ans =57.157746.188046.765450.229553.693613.85642.88683.46416.928210.3923>> z(8,:)=z(8,:)+z(3,:)z =92 99 1 8 15 67 74 51 58 40 98 80 7 14 16 73 55 57 64 41 4 81 88 20 22 54 56 63 70 4785 87 19 21 3 60 62 69 71 2886 93 25 2 9 61 68 75 52 34 17 24 76 83 90 42 49 26 33 6523 5 82 89 91 48 30 32 39 6683 87 101 115 119 83 87 101 115 11910 12 94 96 78 35 37 44 46 5311 18 100 77 84 36 43 50 27 59P 40 ex1先在编辑器窗口写下列M函数,保存为eg2_1.m function [xbar,s]=ex2_1(x)n=length(x);xbar=sum(x)/n;s=sqrt((sum(x.^2)-n*xbar^2)/(n-1));例如>>x=[81 70 65 51 76 66 90 87 61 77];>>[xbar,s]=ex2_1(x)xbar =72.4000s =12.1124P 40 ex2s=log(1);n=0;while s<=100n=n+1;s=s+log(1+n);endm=n计算结果m=37P 40 ex3clear;F(1)=1;F(2)=1;k=2;x=0;e=1e-8; a=(1+sqrt(5))/2;while abs(x-a)>ek=k+1;F(k)=F(k-1)+F(k-2); x=F(k)/F(k-1); enda,x,k计算至k=21可满足精度P 40 ex4clear;tic;s=0;for i=1:1000000s=s+sqrt(3)/2^i;ends,toctic;s=0;i=1;while i<=1000000s=s+sqrt(3)/2^i;i=i+1;ends,toctic;s=0;i=1:1000000;s=sqrt(3)*sum(1./2.^i);s,tocP 40 ex5t=0:24;c=[15 14 14 14 14 15 16 18 20 22 23 25 28 ...31 32 31 29 27 25 24 22 20 18 17 16];plot(t,c)P 40 ex6(1)clear;fplot('x^2*sin(x^2-x-2)',[-2,2])x=-2:0.1:2;y=x.^2.*sin(x.^2-x-2);plot(x,y)y=inline('x^2*sin(x^2-x-2)');fplot(y,[-2 2]) (2)参数方法t=linspace(0,2*pi,100);x=2*cos(t);y=3*sin(t); plot(x,y)(3)x=-3:0.1:3;y=x;[x,y]=meshgrid(x,y);z=x.^2+y.^2;surf(x,y,z)(4)x=-3:0.1:3;y=-3:0.1:13;[x,y]=meshgrid(x,y);z=x.^4+3*x.^2+y.^2-2*x-2*y-2*x.^2.*y+6;surf(x,y,z)(5)t=0:0.01:2*pi;x=sin(t);y=cos(t);z=cos(2*t);plot3(x,y,z)(6)theta=linspace(0,2*pi,50);fai=linspace(0,pi/2,20); [theta,fai]=meshgrid(theta,fai);x=2*sin(fai).*cos(theta);y=2*sin(fai).*sin(theta);z=2*cos(fai);surf(x,y,z)(7)x=linspace(0,pi,100);y1=sin(x);y2=sin(x).*sin(10*x);y3=-sin(x);plot(x,y1,x,y2,x,y3)page41, ex7x=-1.5:0.05:1.5;y=1.1*(x>1.1)+x.*(x<=1.1).*(x>=-1.1)-1.1*(x<-1.1);plot(x,y)page41,ex8分别使用which trapz, type trapz, dir C:\MATLAB7\toolbox\matlab\datafun\page41,ex9clear;close;x=-2:0.1:2;y=x;[x,y]=meshgrid(x,y);a=0.5457;b=0.7575;p=a*exp(-0.75*y.^2-3.75*x.^2-1.5*x).*(x+y>1);p=p+b*exp(-y.^2-6*x.^2).*(x+y>-1).*(x+y<=1);p=p+a*exp(-0.75*y.^2-3.75*x.^2+1.5*x).*(x+y<=-1);mesh(x,y,p)page41, ex10lookfor lyapunovhelp lyap>> A=[1 2 3;4 5 6;7 8 0];C=[2 -5 -22;-5 -24 -56;-22 -56 -16]; >> X=lyap(A,C)X =1.0000 -1.0000 -0.0000-1.0000 2.0000 1.0000-0.0000 1.0000 7.0000Chapter 3%Exercise 1>> a=[1,2,3];b=[2,4,3];a./b,a.\b,a/b,a\bans =0.5000 0.5000 1.0000ans =2 2 1ans =0.6552 %一元方程组x[2,4,3]=[1,2,3]的近似解ans =0 0 00 0 00.6667 1.3333 1.0000%矩阵方程[1,2,3][x11,x12,x13;x21,x22,x23;x31,x32,x33]=[2,4,3]的特解Exercise 2(1)>> A=[4 1 -1;3 2 -6;1 -5 3];b=[9;-2;1];>> rank(A), rank([A,b]) %[A,b]为增广矩阵ans =3ans =3 %可见方程组唯一解>> x=A\bx =2.38301.48942.0213Exercise 2(2)>> A=[4 -3 3;3 2 -6;1 -5 3];b=[-1;-2;1]; >> rank(A), rank([A,b])ans =3ans =3 %可见方程组唯一解>> x=A\bx =-0.4706-0.2941Exercise 2(3)>> A=[4 1;3 2;1 -5];b=[1;1;1];>> rank(A), rank([A,b])ans =2ans =3 %可见方程组无解>> x=A\bx =0.3311-0.1219 %最小二乘近似解Exercise 2(4)>> a=[2,1,-1,1;1,2,1,-1;1,1,2,1];b=[1 2 3]';%注意b的写法>> rank(a),rank([a,b])ans =3ans =3 %rank(a)==rank([a,b])<4说明有无穷多解>> a\bans =110 %一个特解Exercise 3>> a=[2,1,-1,1;1,2,1,-1;1,1,2,1];b=[1,2,3]'; >> x=null(a),x0=a\bx =-0.62550.6255-0.20850.4170x0 =11%通解kx+x0Exercise 4>> x0=[0.2 0.8]';a=[0.99 0.05;0.01 0.95]; >> x1=a*x, x2=a^2*x, x10=a^10*x >> x=x0;for i=1:1000,x=a*x;end,xx =0.83330.1667>> x0=[0.8 0.2]';>> x=x0;for i=1:1000,x=a*x;end,xx =0.83330.1667>> [v,e]=eig(a)v =0.9806 -0.70710.1961 0.7071e =1.0000 00 0.9400>> v(:,1)./xans =1.17671.1767 %成比例,说明x是最大特征值对应的特征向量Exercise 5%用到公式(3.11)(3.12)>> B=[6,2,1;2.25,1,0.2;3,0.2,1.8];x=[25 5 20]';>> C=B/diag(x)C =0.2400 0.4000 0.05000.0900 0.2000 0.01000.1200 0.0400 0.0900>> A=eye(3,3)-CA =0.7600 -0.4000 -0.0500-0.0900 0.8000 -0.0100-0.1200 -0.0400 0.9100>> D=[17 17 17]';x=A\Dx =37.569625.786224.7690%Exercise 6(1)>> a=[4 1 -1;3 2 -6;1 -5 3];det(a),inv(a),[v,d]=eig(a) ans =-94ans =0.2553 -0.0213 0.04260.1596 -0.1383 -0.22340.1809 -0.2234 -0.0532v =0.0185 -0.9009 -0.3066-0.7693 -0.1240 -0.7248-0.6386 -0.4158 0.6170d =-3.0527 0 00 3.6760 00 0 8.3766%Exercise 6(2)>> a=[1 1 -1;0 2 -1;-1 2 0];det(a),inv(a),[v,d]=eig(a) ans =1ans =2.0000 -2.0000 1.00001.0000 -1.0000 1.00002.0000 -3.0000 2.0000v =-0.5773 0.5774 + 0.0000i 0.5774 - 0.0000i -0.5773 0.5774 0.5774-0.5774 0.5773 - 0.0000i 0.5773 + 0.0000id =1.0000 0 00 1.0000 + 0.0000i 00 0 1.0000 - 0.0000i%Exercise 6(3)>> A=[5 7 6 5;7 10 8 7;6 8 10 9;5 7 9 10]A =5 76 57 10 8 76 8 10 95 7 9 10>> det(A),inv(A), [v,d]=eig(A)ans =1ans =68.0000 -41.0000 -17.0000 10.0000 -41.0000 25.0000 10.0000 -6.0000 -17.0000 10.0000 5.0000 -3.0000 10.0000 -6.0000 -3.0000 2.0000v =0.8304 0.0933 0.3963 0.3803-0.5016 -0.3017 0.6149 0.5286-0.2086 0.7603 -0.2716 0.55200.1237 -0.5676 -0.6254 0.5209d =0.0102 0 0 00 0.8431 0 00 0 3.8581 00 0 0 30.2887%Exercise 6(4)、(以n=5为例)%关键是矩阵的定义%方法一(三个for)n=5;for i=1:n, a(i,i)=5;endfor i=1:(n-1),a(i,i+1)=6;endfor i=1:(n-1),a(i+1,i)=1;enda%方法二(一个for)n=5;a=zeros(n,n);a(1,1:2)=[5 6];for i=2:(n-1),a(i,[i-1,i,i+1])=[1 5 6];enda(n,[n-1 n])=[1 5];a%方法三(不用for)n=5;a=diag(5*ones(n,1));b=diag(6*ones(n-1,1));c=diag(ones(n-1,1));a=a+[zeros(n-1,1),b;zeros(1,n)]+[zeros(1,n);c,zeros(n-1,1)] %下列计算>> det(a)ans =665>> inv(a)ans =0.3173 -0.5865 1.0286 -1.6241 1.9489-0.0977 0.4887 -0.8571 1.3534 -1.62410.0286 -0.1429 0.5429 -0.8571 1.0286 -0.0075 0.0376 -0.1429 0.4887 -0.5865 0.0015 -0.0075 0.0286 -0.0977 0.3173 >> [v,d]=eig(a)v =-0.7843 -0.7843 -0.9237 0.9860 -0.9237 0.5546 -0.5546 -0.3771 -0.0000 0.3771 -0.2614 -0.2614 0.0000 -0.1643 0.0000 0.0924 -0.0924 0.0628 -0.0000 -0.0628 -0.0218 -0.0218 0.0257 0.0274 0.0257d =0.7574 0 0 0 00 9.2426 0 0 00 0 7.4495 0 00 0 0 5.0000 00 0 0 0 2.5505%Exercise 7(1)>> a=[4 1 -1;3 2 -6;1 -5 3];[v,d]=eig(a) v =0.0185 -0.9009 -0.3066-0.7693 -0.1240 -0.7248-0.6386 -0.4158 0.6170d =-3.0527 0 00 3.6760 00 0 8.3766>> det(v)ans =-0.9255 %v行列式正常, 特征向量线性相关,可对角化>> inv(v)*a*v %验算ans =-3.0527 0.0000 -0.00000.0000 3.6760 -0.0000-0.0000 -0.0000 8.3766>> [v2,d2]=jordan(a) %也可用jordanv2 =0.0798 0.0076 0.91270.1886 -0.3141 0.1256-0.1605 -0.2607 0.4213 %特征向量不同d2 =8.3766 0 00 -3.0527 - 0.0000i 00 0 3.6760 + 0.0000i>> v2\a*v2ans =8.3766 0 0.00000.0000 -3.0527 0.00000.0000 0.0000 3.6760>> v(:,1)./v2(:,2) %对应相同特征值的特征向量成比例ans =2.44912.44912.4491%Exercise 7(2)>> a=[1 1 -1;0 2 -1;-1 2 0];[v,d]=eig(a)v =-0.5773 0.5774 + 0.0000i 0.5774 - 0.0000i-0.5773 0.5774 0.5774-0.5774 0.5773 - 0.0000i 0.5773 + 0.0000id =1.0000 0 00 1.0000 + 0.0000i 00 0 1.0000 - 0.0000i>> det(v)ans =-5.0566e-028 -5.1918e-017i %v的行列式接近0, 特征向量线性相关,不可对角化>> [v,d]=jordan(a)v =1 0 11 0 01 -1 0d =1 1 00 1 10 0 1 %jordan标准形不是对角的,所以不可对角化%Exercise 7(3)>> A=[5 7 6 5;7 10 8 7;6 8 10 9;5 7 9 10]A =5 76 57 10 8 76 8 10 95 7 9 10>> [v,d]=eig(A)v =0.8304 0.0933 0.3963 0.3803-0.5016 -0.3017 0.6149 0.5286-0.2086 0.7603 -0.2716 0.55200.1237 -0.5676 -0.6254 0.5209d =0.0102 0 0 00 0.8431 0 00 0 3.8581 00 0 0 30.2887>> inv(v)*A*vans =0.0102 0.0000 -0.0000 0.00000.0000 0.8431 -0.0000 -0.0000-0.0000 0.0000 3.8581 -0.0000-0.0000 -0.0000 0 30.2887%本题用jordan不行, 原因未知%Exercise 7(4)参考6(4)和7(1), 略%Exercise 8 只有(3)对称, 且特征值全部大于零, 所以是正定矩阵. %Exercise 9(1)>> a=[4 -3 1 3;2 -1 3 5;1 -1 -1 -1;3 -2 3 4;7 -6 -7 0]>> rank(a)ans =3>> rank(a(1:3,:))ans =2>> rank(a([1 2 4],:)) %1,2,4行为最大无关组ans =3>> b=a([1 2 4],:)';c=a([3 5],:)';>> b\c %线性表示的系数ans =0.5000 5.0000-0.5000 1.00000 -5.0000%Exercise 10>> a=[1 -2 2;-2 -2 4;2 4 -2]>> [v,d]=eig(a)v =0.3333 0.9339 -0.12930.6667 -0.3304 -0.6681-0.6667 0.1365 -0.7327d =-7.0000 0 00 2.0000 00 0 2.0000>> v'*vans =1.0000 0.0000 0.00000.0000 1.0000 00.0000 0 1.0000 %v确实是正交矩阵%Exercise 11%设经过6个电阻的电流分别为i1, ..., i6. 列方程组如下%20-2i1=a; 5-3i2=c; a-3i3=c; a-4i4=b; c-5i5=b; b-3i6=0; %i1=i3+i4;i5=i2+i3;i6=i4+i5;%计算如下>> A=[1 0 0 2 0 0 0 0 0;0 0 1 0 3 0 0 0 0;1 0 -1 0 0 -3 0 0 0;1 -1 0 0 0 0 -4 0 0;0 -1 1 0 0 0 0 -5 0;0 1 0 0 0 0 0 0 -3;0 0 0 1 0 -1 -1 0 0;0 0 0 0 -1 -1 0 1 0;0 0 0 0 0 0 -1 -1 1];>>b=[20 5 0 0 0 0 0 0 0]'; A\b ans =13.34536.44018.54203.3274-1.18071.60111.72630.42042.1467>> A=[1 2 3;4 5 6;7 8 0];>> left=sum(eig(A)), right=sum(trace(A))left =6.0000right =6>> left=prod(eig(A)), right=det(A) %原题有错, (-1)^n应删去left =27.0000right =27>> fA=(A-p(1)*eye(3,3))*(A-p(2)*eye(3,3))*(A-p(3)*eye(3,3)) fA =1.0e-012 *0.0853 0.1421 0.02840.1421 0.1421 0-0.0568 -0.1137 0.1705>> norm(fA) %f(A)范数接近0ans =2.9536e-013roots([1 1 1])%Exercise 1(2)roots([3 0 -4 0 2 -1])%Exercise 1(3)p=zeros(1,24);p([1 17 18 22])=[5 -6 8 -5];roots(p)%Exercise 1(4)p1=[2 3];p2=conv(p1, p1);p3=conv(p1, p2);p3(end)=p3(end)-4; %原p3最后一个分量-4roots(p3)%Exercise 2fun=inline('x*log(sqrt(x^2-1)+x)-sqrt(x^2-1)-0.5*x'); fzero(fun,2)】%Exercise 3fun=inline('x^4-2^x');fplot(fun,[-2 2]);grid on;fzero(fun,-1),fzero(fun,1),fminbnd(fun,0.5,1.5)%Exercise 4fun=inline('x*sin(1/x)','x');fplot(fun, [-0.1 0.1]);x=zeros(1,10);for i=1:10, x(i)=fzero(fun,(i-0.5)*0.01);end;x=[x,-x]%Exercise 5fun=inline('[9*x(1)^2+36*x(2)^2+4*x(3)^2-36;x(1)^2-2*x(2)^2-20*x(3);1 6*x(1)-x(1)^3-2*x(2)^2-16*x(3)^2]','x');[a,b,c]=fsolve(fun,[0 0 0])%Exercise 6fun=@(x)[x(1)-0.7*sin(x(1))-0.2*cos(x(2)),x(2)-0.7*cos(x(1))+0.2*sin(x(2))]; [a,b,c]=fsolve(fun,[0.5 0.5])%Exercise 7clear; close; t=0:pi/100:2*pi;x1=2+sqrt(5)*cos(t); y1=3-2*x1+sqrt(5)*sin(t);x2=3+sqrt(2)*cos(t); y2=6*sin(t);plot(x1,y1,x2,y2); grid on; %作图发现4个解的大致位置,然后分别求解y1=fsolve('[(x(1)-2)^2+(x(2)-3+2*x(1))^2-5,2*(x(1)-3)^2+(x(2)/3)^2-4]',[ 1.5,2])y2=fsolve('[(x(1)-2)^2+(x(2)-3+2*x(1))^2-5,2*(x(1)-3)^2+(x(2)/3)^2-4]',[ 1.8,-2])y3=fsolve('[(x(1)-2)^2+(x(2)-3+2*x(1))^2-5,2*(x(1)-3)^2+(x(2)/3)^2-4]',[ 3.5,-5])y4=fsolve('[(x(1)-2)^2+(x(2)-3+2*x(1))^2-5,2*(x(1)-3)^2+(x(2)/3)^2-4]',[ 4,-4])%Exercise 8(1)clear;fun=inline('x.^2.*sin(x.^2-x-2)');fplot(fun,[-2 2]);grid on; %作图观察x(1)=-2;x(3)=fminbnd(fun,-1,-0.5);x(5)=fminbnd(fun,1,2);fun2=inline('-x.^2.*sin(x.^2-x-2)');x(2)=fminbnd(fun2,-2,-1);x(4)=fminbnd(fun2,-0.5,0.5);x(6)=2feval(fun,x)%答案: 以上x(1)(3)(5)是局部极小,x(2)(4)(6)是局部极大,从最后一句知道x(1)全局最小,x(2)最大。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
注意:在下面的题目中m 为你的学号的后3位(1-9班)或4位(10班以上).
第一次练习题
1.求解下列各题:
1)3
sin lim
x m x m x
x
->- 2)
(4)
cos
,1000.0
=x
m x y e y
求
3)
2
1/20
mx
e
dx ⎰
(求近似值,可以先用inline 定义被积函数,然后用quad 命令)
4)
4
2
2
4x
dx m
x
+⎰
5
0x =展开(最高次幂为8).
2.对矩阵2110
20
41
A m -⎛⎫ ⎪=
⎪ ⎪-⎝
⎭
,分别求逆矩阵,特征值,特征向量,行列式,并求矩阵,P D (D 是对角矩阵),使得1A PDP -=。
3.
已知2
2
1(),()2f x e
x μσ
=
--
分别在下列条件下画出)(x f 的
图形:
(1)/600m σ=,μ分别为0,1,1-(在同一坐标系上作图); (2)0μ=,σ分别为1,2,4,/100m (在同一坐标系上作图).
4.画 (1)sin 020
cos 02100x u t t y u t
u t z m ⎧
⎪=≤≤⎪
=⎨
≤≤⎪⎪=
⎩
(2)
sin()
03,03z mxy x y =≤≤≤≤
(3)
sin()(/100cos )02cos()(/100cos )02sin x t m u t y t m u u z u π
π=+⎧≤≤⎪
=+⎨≤≤⎪=⎩
的图
(第4题只要写出程序).
5.对于方程
5
0.10
200
m x x -
-=,先画出左边的函数在合适的区间上的
图形,借助于软件中的方程求根的命令求出所有的实根,找出函数的单调区间,结合高等数学的知识说明函数为什么在这些区间上是单调的,以及该方程确实只有你求出的这些实根。
最后写出你做此题的体会.
第二次练习题
判断迭代收敛速度的程序
x0=1;stopc=1;eps=10^(-8);a=1;c=1;b=2*c;d=a;k=0; f=inline('(a*x+b)/(c*x+d)'); kmax=100;
while stopc>eps&k<kmax k=k+1
x0=f(a,b,c,d,x0) stopc=abs(x0^2-2); end
1.设11
()/23n n
n m x x x x +⎧
=+⎪⎨⎪=⎩,数列}{n x 是否收敛?若收敛,其值为多少?精确到8
位有效数字。
2,3,4.实验四练习1,2,7(1) 5.能否找到分式函数
2
ax bx c dx e
+++以及分式函数
2
ax b cx dx e
+++,使它产生的迭代序列
17位有效数字。
有一个要求:,,,,a b c d e 必须全部是整数)?并研究如果迭代收敛,那么
迭代的初值与收敛的速度有什么关系.写出你做此题的体会.
第三次练习题
随机数应用例题
对于第一象限的正方形01,01x y ≤≤≤≤,内画出四分之一个圆
向该正方形区域内随即投点,则点落在扇形区域内的概率为4
π
.
投n 次点,落在扇形内的次数为nc ,则4
nc n
π
≈
,因此4nc n
π≈
.
程序如下
n=10000;nc=0; for i=1:n
x=rand;y=rand; if(x^2+y^2<=1) nc=nc+1; end end pi=4*nc/n
1. 练习16(Page95,取自实验七,选取20m 对随机数)
2. 练习7(Page132,取自实验十)(选取20m 对随机数,随机数的范围:1到10^9). 提示:(1)最大公约数的命令:gcd(a,b)
(2)randint(1,1,[u,v])产生一个在[u,v]区间上的随机整数
书上习题:(实验八)
1. 若数列n a 满足12121,1,n n n a a a ma a --===+,编程求出4039/a a 的8位有效数字.
写出n a 的通项公式,在理论上求出1lim n n n
a a +→∞
的值,并与求出的4039/a a 的近似值作对
比.
2. 练习18
3. 练习19(注:只要对a m =,
精确到8位有效数字,
为整数的学号,
4. 练习20
5. 练习21(注:只要对a m =,
8位有效数字,
为整数的学号,
6. 练习23(将方程改为321412/100x x x m +--=,精确到8位有效数字)
7. 练习24
选做题目:练习25,26
在第三次练习题中至少选择一道题目写出做题体会。
第四次练习题
1. 练习9,10,12,15,20(Page142起 取自实验十一)
圆柱体易拉罐的最优化问题
设一个355毫升的易拉罐是圆柱体,上底面与下底面的厚度分别为侧面厚度的a 倍与b 倍.问在圆柱体的高度与上下底面的半径为多少时,该易拉罐所用的材料最省.(求解时取 2.85, 2.31a b ==)
解:设底面厚度其侧面厚度为d ,上底面的厚度为a d ,下底面的厚度为b d ,圆柱体的高度为H ,上下底面的半径为R ,则该圆柱的容积为2V R H π=,所用的材料的体积为222R ad R bd RHd πππ++,为使所用的材料最省,我们得到如下的数学模型
2
2
m in [()2]..
3550,0
S d a b R RH s t R H R H ππ=++=>>
模型求解:
由约束条件解得2
355
H R
π=
,代入到目标函数中得到2710
[()]
S d a b R R
ππ=++
下面通过程序给出该目标函数在 2.85, 2.31a b ==时的最优解.
h=1;Smin=100000;
for R=0.001:h:1000
S=5.16*R^2+710/(pi*R);
if S<Smin
Smin=S;Rmin=R;
end
end
for i=1:5
h=h/10;
for R=Rmin-20*h:h:Rmin+20*h
S=5.16*R^2+710/(pi*R);
if S<Smin
Smin=S;
Rmin=R;
end
end
end
fprintf('Rmin=%10.5f,Hmin=%10.5f,Smin=%10.5f\n',Rmin,355/(pi*Rmin^2), Smin)
2.分别取1
==,/300,/400
a b
==运行程序,你能否验证所得到的解是最优
a m
b m
解?
3. 若易拉罐的形状是一个圆台加圆柱,即中截面如下的图形,其上底面,下底面与圆台的侧面的厚度分别为侧面厚度的a倍,b倍与c倍. 问在圆柱体的高度,圆台的高度与上下底面的半径为多少时,该易拉罐所用的材料最省.(求解时分别取1
===以及/300,/400,/100
a b c
===)
a m
b m
c m
写出做此题的体会.
总结题目:这一段时间学习数学实验,你有什么体会?对课程的内容等方面有什么建议?。
