Matlab数学实验一2015(标准答案版)

合集下载

实验一 MATLAB软件应用复习含具体答案

，其中E,R,O,S分别为单位阵、随机阵、零阵和对角阵，试通过数值计算验证
。 2．某零售店有9种商品的单件进价（元）、售价（元）及一周的销量如表1.1，问哪种商品的利润最大，哪种商品的利润最小；按收入由小到大，列出所有商品及其收入；求这一周该9种商品的总收入和总利润。表1.1
货号
1
2
3. 用两种方法在同一个坐标下作出这四条曲线的图形，并要求用两种方法在图上加各种标注。 4．用subplot分别在不同的坐标系下作出下列四条曲线，为每幅图形加上标题， 1）概率曲线； 2）四叶玫瑰线； 3）叶形线
4）曳物线
。 5．作出下列曲面的3维图形， 1）； 2）环面
（2）新建一个M文件输入命令如下： v=0:0.01:2*pi; u=v; [U,V]=meshgrid(u,v); X=(1+cos(U)).*cos(V); Y=(1+cos(U)).*sin(V); Z=sin(U); mesh(X,Y,Z) 保存并运行，运行结果如下：
T6 新建一个M文件输入命令如下： function shuixianhuashu for m=100:999; a=fix(m/100); b=rem(fix(m/10),10); c=rem(m,10); if m==a.^3+b.^3+c.^3 disp(m) end end 保存，再在命令窗口输入shuixianhuashu结果如下： >> shuixianhuashu 153
探究实验自由发挥：自己提出问题，实验探索，广泛联想，发现规律，大胆猜想。比如函数cos(1/x)在 x=0附近的振荡现象，有无规律可寻？
T1
新建一个M文件输入命令如下： E=eye(3,3); R=rand(3,2); O=zeros(2,3); S=diag([3,7]); A=[E,R;O,S]; AA=A*A; B=[E,R+R*S;O,S*S]; if B==AA disp('命题成立'); else disp('命题不成立'); end 保存并运行，结果如下：命题成立由运行结果可知，得以验证。

数学实验(MATLAB)课后习题答案

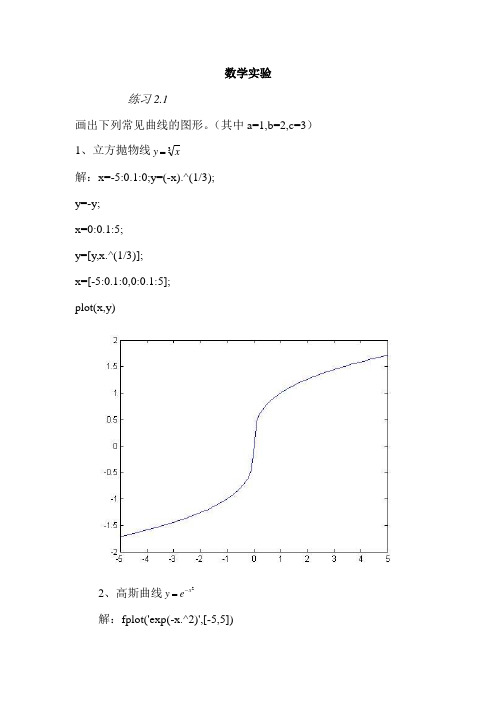
数学实验练习2.1画出下列常见曲线的图形。

（其中a=1,b=2,c=3）1、立方抛物线3xy=解：x=-5:0.1:0;y=(-x).^(1/3);y=-y;x=0:0.1:5;y=[y,x.^(1/3)];x=[-5:0.1:0,0:0.1:5];plot(x,y)2、高斯曲线2x e=y-解：fplot('exp(-x.^2)',[-5,5])3、笛卡儿曲线)3(13,1333222axy y x t at y t at x =++=+=解：ezplot('x.^3+y.^3-3*x*y',[-5,5])xyx.3+y.3-3 x y = 0或t=-5:0.1:5; x=3*t./(1+t.^2); y=3*t.^2./(1+t.^2); plot(x,y)4、蔓叶线)(1,1322322xa x y t at y t at x -=+=+=解：ezplot('y.^2-x.^3/(1-x)',[-5,5])xyy.2-x.3/(1-x) = 0或t=-5:0.1:5; x=t.^2./(1+t.^2); y=t.^3./(1+t.^2); plot(x,y)5、摆线)cos 1(),sin (t b y t t a x -=-= 解：t=0:0.1:2*pi;x=t-sin(t); y=2*(1-cos(t)); plot(x,y)6、星形线)(sin ,cos 32323233a y x t a y t a x =+== 解：t=0:0.1:2*pi; x=cos(t).^3; y=sin(t).^3;plot(x,y)或ezplot('x.^(2/3)+y.^(2/3)-1',[-1,1])xyx.2/3+y.2/3-1 = 07、螺旋线ct z t b y t a x ===,sin ,cos 解：t=0:0.1:2*pi; x=cos(t); y=2*sin(t); z=3*t; plot3(x,y,z) grid on8、阿基米德螺线θa r = 解：x =0:0.1:2*pi; r=x; polar(x,r)902701809、对数螺线θa e r = 解：x =0:0.1:2*pi; r=exp(x); polar(x,r)90270180010、双纽线))()((2cos 22222222y x a y x a r -=+=θ 解：x=0:0.1:2*pi; r=sqrt(cos(2*x)); polar(x,r)90270或ezplot('(x.^2+y.^2).^2-(x.^2-y.^2)',[-1,1]) grid onxy(x.2+y.2).2-(x.2-y.2) = 011、双纽线)2)((2sin 222222xy a y x a r =+=θ 解：x=0:0.1:2*pi; r=sqrt(sin(2*x)); polar(x,r)90270或ezplot('(x.^2+y.^2).^2-2*x*y',[-1,1]) grid onxy(x.2+y.2).2-2 x y = 012、心形线)cos 1(θ+=a r 解：x =0:0.1:2*pi; r=1+cos(x); polar(x,r)90270练习2.21、求出下列极限值。

MATLAB全部实验及答案

MATLAB全部实验及答案实验一、MATLAB基本操作实验内容及步骤1、命令窗口的简单使用（1）简单矩阵的输入（2）求[12+2×(7-4)]÷32的算术运算结果2、有关向量、矩阵或数组的一些运算（1）设A=15；B=20；求C=A+B与c=a+b？（2）设A=[1 2 3;4 5 6;7 8 9]，B=[9 8 7;6 5 4;3 2 1]；求A*B与A.*B？A*B就是线代里面的矩阵相乘 A.*B是对应位置的元素相乘（3）设a=10，b=20；求i=a/b=0.5与j=a\b=2？（4）设a=[1 -2 3;4 5 -4;5 -6 7]请设计出程序，分别找出小于0的矩阵元素及其位置（单下标、全下标的形式），并将其单下标转换成全下标。

clear,clca=[1 -2 3;4 5 -4;5 -6 7];[x,y]=find(a<0);c=[];for i=1:length(x)c(i,1)=a(x(i),y(i));c(i,2)=x(i);c(i,3)=y(i);c(i,4)=(y(i)-1)*size(a,2)+x(i);endc（5）在MATLAB命令行窗口运行A=[1,2;3,4]+i*[5,6;7,8]；看结果如何？如果改成运行A=[1,2;3,4]+i[5,6;7,8]，结果又如何？前面那个是虚数矩阵，后面那个出错（6）请写出完成下列计算的指令：a=[1 2 3;3 4 2;5 2 3]，求a^2=？,a.^2=？a^2= 22 16 1625 26 2326 24 28a.^2=1 4 99 16 425 4 9（7）有一段指令如下，请思考并说明运行结果及其原因clearX=[1 2;8 9;3 6];X( : ) 转化为列向量（8）使用三元组方法，创建下列稀疏矩阵2 0 8 00 0 0 10 4 0 06 0 0 0方法一：clear,clcdata=[2 8 1 4 6];ir=[1 1 2 3 4 ];jc=[1 3 4 2 1];s=sparse(ir,jc,data,4,4);full(s)方法二：不用三元组法clear,clca=zeros(4,4);a(1,[1,3])=[2,8];a(2,4)=1;a(3,2)=4;a(4,1)=6;a（9）写出下列指令的运行结果>> A = [ 1 2 3 ]; B = [ 4 5 6 ];>> C = 3.^A>> D = A.^B3、已知⎪⎭⎫ ⎝⎛+⋅=-334sin 234πt e y t 若需要计算t ∈[-1,1]，取间隔为0.01，试计算出相对应的y 值。

MATLAB数学实验答案（全）

MATLAB数学实验答案（全）第⼀次练习教学要求：熟练掌握Matlab 软件的基本命令和操作，会作⼆维、三维⼏何图形，能够⽤Matlab 软件解决微积分、线性代数与解析⼏何中的计算问题。

补充命令vpa(x,n) 显⽰x 的n 位有效数字，教材102页fplot(‘f(x)’,[a,b]) 函数作图命令，画出f(x)在区间[a,b]上的图形在下⾯的题⽬中m 为你的学号的后3位（1-9班）或4位（10班以上） 1.1 计算30sin limx mx mx x →-与3sin lim x mx mxx →∞-syms xlimit((902*x-sin(902*x))/x^3) ans =366935404/3limit((902*x-sin(902*x))/x^3,inf)//inf 的意思 ans = 0 1.2 cos1000xmxy e =，求''y syms xdiff(exp(x)*cos(902*x/1000),2)//diff 及其后的2的意思 ans =(46599*cos((451*x)/500)*exp(x))/250000 - (451*sin((451*x)/500)*exp(x))/250 1.3 计算221100x y edxdy +??dblquad(@(x,y) exp(x.^2+y.^2),0,1,0,1)//双重积分 ans = 2.13941.4 计算4224x dx m x +? syms xint(x^4/(902^2+4*x^2))//不定积分 ans =(91733851*atan(x/451))/4 - (203401*x)/4 + x^3/12 1.5 (10)cos ,x y e mx y =求//⾼阶导数syms xdiff(exp(x)*cos(902*x),10) ans =-356485076957717053044344387763*cos(902*x)*exp(x)-3952323024277642494822005884*sin(902*x)*exp(x)1.6 0x =的泰勒展式(最⾼次幂为4).syms xtaylor(sqrt(902/1000+x),5,x)//泰勒展式 ans =-(9765625*451^(1/2)*500^(1/2)*x^4)/82743933602 +(15625*451^(1/2)*500^(1/2)*x^3)/91733851-(125*451^(1/2)*500^(1/2)*x^2)/406802 + (451^(1/2)*500^(1/2)*x)/902 +(451^(1/2)*500^(1/2))/500 1.7 Fibonacci 数列{}n x 的定义是121,1x x ==12,(3,4,)n n n x x x n --=+=⽤循环语句编程给出该数列的前20项（要求将结果⽤向量的形式给出）。

（完整版）MATLAB）课后实验答案[1]

（完整版）MATLAB）课后实验答案[1]实验⼀ MATLAB 运算基础1. 先求下列表达式的值，然后显⽰MATLAB ⼯作空间的使⽤情况并保存全部变量。

(1) 0122sin 851z e =+(2) 21ln(2z x =，其中2120.455i x +??=?- (3) 0.30.330.3sin(0.3)ln , 3.0, 2.9,,2.9,3.022a a e e az a a --+=++=--L (4) 2242011122123t t z t t t t t ?≤=-≤，其中t =0:0.5:2.5 解：4. 完成下列操作：(1) 求[100,999]之间能被21整除的数的个数。

(2) 建⽴⼀个字符串向量，删除其中的⼤写字母。

解：(1) 结果：(2). 建⽴⼀个字符串向量例如：ch='ABC123d4e56Fg9';则要求结果是：实验⼆ MATLAB 矩阵分析与处理1. 设有分块矩阵33322322E R A O S=?，其中E 、R 、O 、S 分别为单位矩阵、随机矩阵、零矩阵和对⾓阵，试通过数值计算验证2 2E R RS A O S +??=。

解: M ⽂件如下；5. 下⾯是⼀个线性⽅程组：1231112340.951110.673450.52111456x x x ??=???(1) 求⽅程的解。

(2) 将⽅程右边向量元素b 3改为0.53再求解，并⽐较b 3的变化和解的相对变化。

(3) 计算系数矩阵A 的条件数并分析结论。

解： M ⽂件如下：123d4e56g9实验三选择结构程序设计1. 求分段函数的值。

2226035605231x x x x y x x x x x x x ?+-<≠-?=-+≤<≠≠??--?且且及其他⽤if 语句实现，分别输出x=-5.0,-3.0,1.0,2.0,2.5,3.0,5.0时的y 值。

解：M ⽂件如下：2. 输⼊⼀个百分制成绩，要求输出成绩等级A、B、C、D、E。

MATLAB实验及答案详解

《MATLAB原理及应用》实验报告实验一MATLAB环境熟悉及基本操作一、实验目的熟悉MATLAB软件的工作环境和练习MATLAB命令窗口的基本操作。

二、实验内容1.命令窗口（Command Window）运行如入门【实验1-1】求23)]47(212[÷-⨯+的算术运算结果。

用键盘在MATLAB命令窗口中命令提示符“>>”后输入一下内容：(12+2*(7-4))/(3^2)在上述表达式输入完成后，按【Enter】键，该命令被执行。

在命令执行后，MATLAB命令窗口中将显示结果。

ans =2【实验1-2】简单矩阵⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----=15524974111415412869811105132316A的输入步骤。

(1)用键盘在MATLAB命令窗口中命令提示符“>>”后输入一下内容：A=[16 3 2 13 -1 -4;5 10 11 8 7 9;9 6 8 12 -4 2;4 15 14 1 -5 15](2)按【Enter】键，该命令被执行。

(3)在命令执行后，MATLAB命令窗口中将显示结果.(4)采用分行输入，在命令窗口输入：A=[16 3 2 13 -1 -45 10 11 8 7 99 6 8 12 -4 24 15 14 1 -5 15]【实验1-3】用简短命令计算并绘制在0≤x≤6范围内的sin(Ax)、sinAx2、sin2(Ax)。

( A代表你的学号）在命令窗口输入：x=0:0.01:6;y=[sin(1*x);sin(1*x.^2);sin(1*x).^2];plot(x,y)(2) 按【Enter】键，该命令执行结果如图1图1 函数曲线图(3)在命令窗口输入：x=0:0.01:6;y1=sin(1*x);y2=sin(1*x.^2);y3=sin(1*x).^2; subplot(2,2,1),plot(x,y1),title('sin(1*x)') subplot(2,2,2),plot(x,y2),title('sin(1*x.^2)') subplot(2,2,3),plot(x,y3),title('sin(1*x) .^2') (4) 按【Enter】键，该命令执行结果如图2图2子图形式函数曲线图2.命令窗口（Command Window）常用的基本操作【实验1-4】命令行操作过程示例。

Matlab实验及答案

实验一、MATLAB基本操作一、实验目的2．学习使用图形函数计算器命令funtool及其环境。

3. 学习使用help命令进行帮助4. 掌握向量与矩阵的创建以及矩阵的基本操作5. 掌握数组与矩阵的概念二、实验内容熟悉Matlab操作环境，认识命令窗口、内存工作区窗口、历史命令窗口；学会使用format命令调整命令窗口的数据显示格式；学会使用变量和矩阵的输入，并进行简单的计算；掌握数组与矩阵的概念；学会使用help命令进行帮助；学会使用who和whos命令查看内存变量信息；学会使用图形函数计算器funtool；1.命令窗口的简单使用（1）简单矩阵的输入（自由创建）x=[1 3 5;2 4 6]x =1 3 52 4 6（2）求[12+2×(7-4)]÷32的算术运算结果，总结算术运算符先级[12+2*(7-4)]/3^2ans =22.有关向量、矩阵或数组的一些运算（1）设A=15；B=20；求C=A+B与c=a+b的区别A=15;B=20;>> C=A+BC =35>> c=a+bUndefined function or variable 'a'.（2）设A=[1 2 3;4 5 6;7 8 9]，B=[9 8 7;6 5 4;3 2 1]；求A*B与A.*B，分析原因？(A*B是两个矩阵相乘，A.*B是对应元素相乘)A=[1 2 3;4 5 6;7 8 9];B=[9 8 7;6 5 4;3 2 1];>> A*Bans =30 24 1884 69 54138 114 90>> A.*Bans =9 16 2124 25 2421 16 9（3）设a=10，b=20；求i=a/b与j=a\ba=10;>> b=20;>> i=a/bi =0.5000>> j=a\bj =2（4）设a=[1 -2 3;4 5 -4;5 -6 7]请设计出程序，分别找出小于0的矩阵元素的线性索引以及行列索引（sub2ind/ind2sub）。

重庆大学数学实验一 matlab的基本应用参考答案

《数学实验》第一次上机实验1．设有分块矩阵⎥⎦⎤⎢⎣⎡=⨯⨯⨯⨯22322333S O R E A ，其中E,R,O,S 分别为单位阵、随机阵、零阵和对角阵，试通过数值计算验证⎥⎦⎤⎢⎣⎡+=22S 0RS R E A 。

程序及结果：E=eye(3); %创建单位矩阵E% R=rand(3,2); %创建随机矩阵R% O=zeros(2,3); %创建0矩阵% S=diag(1:2); %创建对角矩阵% A=[E,R;O,S]; %创建A 矩阵%B=[E,(R+R*S);zeros(2,3),S^2] %计算等号右边的值%A^2 %计算等号左边的值%运行结果：B =1.00 0 0 1.632.74 0 1.00 0 1.81 1.90 0 0 1.00 0.25 0.29 0 0 0 1.00 0 0 0 0 0 4.00 ans =1.00 0 0 1.632.740 1.00 0 1.81 1.90 0 0 1.00 0.25 0.29 0 0 0 1.00 0 0 0 0 0 4.002．某零售店有9种商品的单件进价（元）、售价（元）及一周的销量如表1.1，问哪种商品的利润最大，哪种商品的利润最小；按收入由小到大，列出所有商品及其收入；求这一周该10种商品的总收入和总利润。

表1.11)程序：a=[7.15 8.25 3.20 10.30 6.68 12.03 16.85 17.51 9.30]; b=[11.10 15.00 6.00 16.25 9.90 18.25 20.80 24.15 15.50]; c=[568 1205 753 580 395 2104 1538 810 694];s=sum((b-a).*c)i=b.*cmax((b-a).*c)min((b-a).*c)[m,n]=sort(b.*c)2）运行结果：s =4.6052e+004i =1.0e+004 *0.6305 1.8075 0.4518 0.9425 0.3911 3.8398 3.1990 1.95621.0757ans =1.3087e+004ans =1.2719e+003m =1.0e+004 *0.3911 0.4518 0.6305 0.9425 1.0757 1.8075 1.9562 3.1990 3.8398n =5 3 1 4 9 2 8 7 63. 近景图将x的取值范围局限于较小的区间内可以画出函数的近景图,用于显示函数的局部特性。

MATLAB实验一：参考--答案

7. 写出下列函数的作用： clc Clear ones det triu fliplr zeros cat
清除命令窗口的记录清除已声明的变量和函数的记录生成全 1 矩阵求一个方阵的行列式取一个矩阵的上三角对矩阵进行左右旋转产生一个零矩阵拼接两个数组或者矩阵
8. 建立如下矩阵
0 0 2015 2015 0 0 （1） 0 0 2015 1010
3．
计算 1.369 sin
2
7 26.48 2.9 的值（输入程序） 10
1.369^2+sin(7/10*pi)*26.48^(1/2)/2.9
4．
1 3 3 1 1 2 输入矩阵 A 4 4 6 , B 2 2 2 ，指出下列命令的含义 6 8 9 3 3 3
实验一：MATLAB 软件环境及基本操作
实验目的：
1、熟悉 MATLAB 软件的工作环境； 2、熟悉 MATLAB 基本命令与操作； 3、掌握数组（矩阵）的算术运算、逻辑运算和关系运算的方法
实验内容
MATLAB 基本命令与实际操作、矩阵运算
实验要求
1、学生在实验操作过程中自己动手独立完成，1 人为 1 组。 2、完成实验报告：按照试验的每个题目的具体要求完成。
评语：
教师签字：
日期：
年
月
日
（1）A=2015*eye(10) （2）A=8*(ones(8)-eye(8))
0 8 （2） 8
8 0 8Leabharlann 8 8 0 88
9. 设有分块矩阵 A
E33 O23

MATLAB上机实验1答案

实验1 Matlab 初步一、问题已知矩阵A 、B 、b 如下：⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡-------------=031948118763812654286174116470561091143A ⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡------=503642237253619129113281510551201187851697236421B []1187531=b应用Matlab 软件进行矩阵输入及各种基本运算。

二、实验目的学会使用Matlab 软件构作已知矩阵对应的行（列）向量组、子矩阵及扩展矩阵，实施矩阵的初等变换及线性无关向量组的正交规范化，确定线性相关相关向量组的一个极大线性无关向量组，且将其余向量用极大线性无关向量组线性表示，并能编辑M 文件来完成所有的实验目的。

三、预备知识1、线性代数中的矩阵及其初等变换、向量组的线性相关性等知识。

2、 Matlab 软件的相关命令提示如下；（1）选择A 的第i 行做一个行向量：ai=A(i,:)；（2）选择A 的第j 行做一个列向量：ai=A(j,:)；（3）选择A 的某几行、某几列上的交叉元素做A 的子矩阵：A([行号],[列号])；（4） n 阶单位阵：eye(n)；n 阶零矩阵：zeros(n)；（5）做一个n 维以0或1为元素的索引向量L ，然后取A(:,L)，L 中值为1的对应的列将被取到。

（6）将非奇异矩阵A 正交规范化，orth(A) ；验证矩阵A 是否为正交阵，只需做A*A'看是否得到单位阵E 。

（7）两个行向量a1和a2的内积：a1*a2'。

（8）让A 的第i 行与第j 列互换可用赋值语句：A([i,j],:)=A([j,i],:)；（9）让K乘以A的第i行可用赋值语句：A(i,:)=K*A(i,:)；（10）让A的第i行加上第j行的K倍可用赋值语句：A(i,:)=A(i,:)+K*A(j,:)；（11）求列向量组的A的一个极大线性无关向量组可用命令：rref(A)将A化成阶梯形行的最简形式，其中单位向量对应的列向量即为极大线性无关向量组所含的向量，其它列向量的坐标即为其对应向量用极大线性无关组线性表示的系数。

Matlab实验第一次实验答案

实验一Matlab使用方法和程序设计一、实验目的1、掌握Matlab软件使用的基本方法；2、熟悉Matlab的数据表示、基本运算和程序控制语句3、熟悉Matlab绘图命令及基本绘图控制4、熟悉Matlab程序设计的基本方法二、实验内容：1、帮助命令使用help命令，查找sqrt（开方）函数的使用方法；'解：sqrtSquare rootSyntaxB = sqrt(X)DescriptionB = sqrt(X) returns the square root of each element of the array X. For the elements of X that are negative or complex, sqrt(X) produces complex results.RemarksSee sqrtm for the matrix square root.Examples;sqrt((-2:2)')ans =0 +0 +2、矩阵运算（1）矩阵的乘法/已知A=[1 2;3 4]; B=[5 5;7 8];求A^2*B解：A=[1 2;3 4 ];B=[5 5;7 8 ];A^2*B（2）矩阵除法已知A=[1 2 3;4 5 6;7 8 9]; `B=[1 0 0;0 2 0;0 0 3];A\B,A/B解：A=[1 2 3;4 5 6;7 8 9 ];B=[1 0 0;0 2 0;0 0 3 ];A\B,A/B（3）矩阵的转置及共轭转置已知A=[5+i,2-i,1;6*i,4,9-i];*求A.', A'解：A=[5+1i,2-1i,1;6*1i,4,9-1i ];A1=A.',A2=A'（4）使用冒号表达式选出指定元素已知：A=[1 2 3;4 5 6;7 8 9];<求A中第3列前2个元素；A中所有列第2，3行的元素；方括号[]解：A=[1 2 3;4 5 6;7 8 9 ];B=A([1,2],[3]),C=A(2:end, : )用magic 函数生成一个4阶魔术矩阵，删除该矩阵的第四列'3、多项式（1）求多项式 42)(3--=x x x p 的根解：A=[1 0 -2 -4];B=roots(A)（2）已知A=[ 3 5 ;5 5 6;3 9 0 1;1 2 3 4] ，求矩阵A 的特征多项式;解：/A=[ 3 5 .9 ; 5 5 6 ;3 9 0 1 ;1 2 3 4];A=poly(A);A=poly2sym(A)把矩阵A作为未知数代入到多项式中；4、基本绘图命令（1）绘制余弦曲线y=cos(t)，t∈[0，2π]解：t=0:.1:2*pi;y=cos(t);plot(t,y),grid~（2）在同一坐标系中绘制余弦曲线y=cos和正弦曲线y=sin，t∈[0，2π] t=0:.1:2*pi; y1=cos;y2=sin;plot(t,y1，t,y2)grid》5、基本绘图控制绘制[0，4π]区间上的x1=10sint曲线，并要求：（1）线形为点划线、颜色为红色、数据点标记为加号；（2）坐标轴控制：显示范围、刻度线、比例、网络线（3）标注控制：坐标轴名称、标题、相应文本；t=0:.01:4*pi;y=10*sin(t);plot(t,y,'-.',t,y,'r')grid\6、基本程序设计（1）编写命令文件：计算1+2+…+n<2000 时的最大n值；解法1：s=0;i=0;while(s<2000) i=i+1;s=s+i; ends=s-i,i=i-1解法2：s=0;for i=1:1000; s=s+i;if(s>2000) ,break;endend；s=s-i,i=i-1（2）编写函数文件：分别用for和while循环结构编写程序，求2的0到n次幂的和。

Matlab实验一答案

MATLAB 实验一答案1.3 先自定义一个变量，然后分别用8种不同的数字显示格式显示查看。

>> a=pia =3.1416>> format long>> aa =3.14159265358979>> format short>> aa =3.1416>> format short e>> aa =3.1416e+000>> format long e>> aa =3.141592653589793e+000>> format hex>> aa =400921fb54442d18>> format bank>> aa =3.14>> format +>> aa =+>> format rat>> aa =355/1131.4 下面的语句用于画出函数()0.22x y x e -=在[0,10]区间的值x = 0:0.1:10;y = 2*exp(-0.2*x);plot(x,y)1.5 用Matlab 编辑器创建一个m 文件，把上述语句写入这个m 文件并命名为“test1.m ”，保存在当前路径中，然后在命令窗中键入test1，观察结果和运行程序后工作空间的变化.工作空间和结果均与1.4一样1.6 如何清空工作区间数据？键入 clear ；如何关闭图像窗口？键入close ；除了在命令窗输入文件名，还可以怎样运行一个m 文件程序？点击file ，打开m 文件，点击Run 按钮，运行m 文件程序。

1.7 通过以下两种方式得到关于exp 函数的帮助：(1) 在命令窗中输入help exp 命令；(2) 运用帮助空间窗口。

思考，用什么指令可以直接打开帮助空间中关于exp 函数的说明？键入doc exp1.8 假设x =3，y = 4，用Matlab 计算下列表达式：(1) ()232x y x y - (2) 43x y (3) 24x x π- (4) 33x x x y- >> x=3,y=4;>> x^2*(y^3)/(x-y)^2ans =576>> 4*x/(3*y)ans =1>> 4/x*(pi*x^(-2))ans =0.4654>> x^3/(x^3-y^x)ans =-0.72971.9 在当前目录下创建一个m文件，键入以下程序并保存，先把文件保存为“2.m”，运行后观察结果，总结m文件的文件名（包括Matlab标识符）命名规则。

MATLAB全部实验及答案

MATLAB全部实验及答案MATLAB全部实验及答案实验一、MATLAB基本操作实验内容及步骤4、有关向量、矩阵或数组的一些运算（1）设A=15；B=20；求C=A+B与c=a+b？（2）设A=[1 2 3;4 5 6;7 8 9]，B=[9 8 7;6 5 4;3 2 1]；求A*B 与A.*B？A*B就是线代里面的矩阵相乘A.*B是对应位置的元素相乘（3）设a=10，b=20；求i=a/b=0.5与j=a\b=2？（4）设a=[1 -2 3;4 5 -4;5 -6 7]请设计出程序，分别找出小于0的矩阵元素及其位置（单下标、全下标的形式），并将其单下标转换成全下标。

clear,clca=[1 -2 3;4 5 -4;5 -6 7];[x,y]=find(a<0);c=[];for i=1:length(x)c(i,1)=a(x(i),y(i));c(i,2)=x(i);c(i,3)=y(i);c(i,4)=(y(i)-1)*size(a,2)+x(i);endc（5）在MATLAB命令行窗口运行A=[1,2;3,4]+i*[5,6;7,8]；看结果如何？如果改成运行A=[1,2;3,4]+i[5,6;7,8]，结果又如何？前面那个是虚数矩阵，后面那个出错（6）请写出完成下列计算的指令：a=[1 2 3;3 4 2;5 2 3]，求a^2=？,a.^2=？a^2= 22 16 1625 26 2326 24 28a.^2=1 4 99 16 425 4 9（7）有一段指令如下，请思考并说明运行结果及其原因clearX=[1 2;8 9;3 6];X( : ) 转化为列向量（8）使用三元组方法，创建下列稀疏矩阵2 0 8 00 0 0 10 4 0 06 0 0 0方法一：clear,clcdata=[2 8 1 4 6];ir=[1 1 2 3 4 ];jc=[1 3 4 2 1];s=sparse(ir,jc,data,4,4);full(s)方法二：不用三元组法clear,clca=zeros(4,4);a(1,[1,3])=[2,8];a(2,4)=1;a(3,2)=4;a(4,1)=6;a（9）写出下列指令的运行结果>> A = [ 1 2 3 ]; B = [ 4 5 6 ];>> C = 3.^A>> D = A.^B5、已知+?=-334sin 234πt e y t 若需要计算t ∈[-1,1]，取间隔为0.01，试计算出相对应的y 值。

Matlab实验及答案-推荐下载

a.^2= 149 9 16 4 25 4 9
（7）有一段指令如下，请思考并说明运行结果及其原因 clear
X=[1 2;8 9;3 6]; X( : ) 转化为列向量
>> clear >> X=[1,2;8,9;3,6]; >> X(:) ans =
1 8 3 2 9 6 （8）使用 help 命令，明白什么是稀疏矩阵 sparse( )，并用采用两种方法创
实验一、MATLAB 基本操作
一、实验目的
2．学习使用图形函数计算器命令 funtool 及其环境。 3. 学习使用 help 命令进行帮助 4. 掌握向量与矩阵的创建以及矩阵的基本操作 5. 掌握数组与矩阵的概念二、实验内容
熟悉 Matlab 操作环境，认识命令窗口、内存工作区窗口、历史命令窗口；学会使用 format 命令调整命令窗口的数据显示格式；学会使用变量和矩阵的输入，并进行简单的计算；掌握数组与矩阵的概念；学会使用 help 命令进行帮助；学会使用 who 和 whos 命令查看内存变量信息；学会使用图形函数计算器 funtool；
Error: Unbalanced or misused parentheses or brackets. 前面那个是虚数矩阵，后面那个出错（6）请写出完成下列计算的指令：
a=[1 2 3;3 4 2;5 2 3]，求 a^2=？,a.^2=？
a^2= 22 16 16 25 26 23 26 24 28
并将其单下标转换成全下标。
clear,clc
a=[1 -2 3;4 5 -4;5 -6 7];
b=find(a<0)
[x,y]=ind2sub(size(a),find(a<0))

东北大学MATLAB实验答案

东北大学《MATLAB语言与应用》实验东北大学MATLAB实验课习题答案第一部分MATLAB语言编程、科学绘图与基本数学问题求解2、>> A=[1,2,3,4;4,3,2,1;2,3,4,1;3,2,4,1]A =1 2 3 44 3 2 12 3 4 13 24 1B=[1+4j,2+3j,3+2j,4+1j;4+1j,3+2j,2+3j,1+4j;2+3j,3+2j,4+1j,1+4j;3+2j,2+3j,4+1j,1+4j]B =1.0000 + 4.0000i2.0000 +3.0000i 3.0000 + 2.0000i4.0000 + 1.0000i4.0000 + 1.0000i 3.0000 + 2.0000i 2.0000 + 3.0000i 1.0000 + 4.0000i2.0000 +3.0000i 3.0000 + 2.0000i4.0000 + 1.0000i 1.0000 + 4.0000i3.0000 + 2.0000i 2.0000 + 3.0000i4.0000 + 1.0000i 1.0000 + 4.0000i >> A(5,6)=5A =1 2 3 4 0 04 3 2 1 0 02 3 4 1 0 03 24 1 0 00 0 0 0 0 53、A=magic(8)A =64 2 3 61 60 6 7 579 55 54 12 13 51 50 1617 47 46 20 21 43 42 2440 26 27 37 36 30 31 3332 34 35 29 28 38 39 2541 23 22 44 45 19 18 4849 15 14 52 53 11 10 568 58 59 5 4 62 63 1 >> B=A(2:2:end,:)B =9 55 54 12 13 51 50 1640 26 27 37 36 30 31 3341 23 22 44 45 19 18 488 58 59 5 4 62 63 1 4．i=0:63;s=sum(2.^i)s =1.8447e+0195、(1) >> z=sin(1./t);Warning: Divide by zero.>> plot(t,z)-1-0.8-0.6-0.4-0.20.20.40.60.81-1-0.8-0.6-0.4-0.200.20.40.60.81(2)>> t=[-pi:0.05:-1.8,-1.799:.001:-1.2,-1.2:0.05:1.2,1.201:0.001:1.8,1.81:0.05:pi]; >> y=sin(tan(t))-tan(sin(t)); >> plot(t,y)-4-3-2-101234-3-2-11236.三视图>> surf(x,y,z),shading flat;zlim([0,15])>> xx=[-2:.1:-1.2,-1,1:0.02:-0.9,-0.8:0.1:0.8,0.9:0.02:1.1,1.2:0.1:2]; >> yy=[-1:0.1:-0.2,-0.1:0.02:0.1,0.2:.1:1];>> [x,y]=meshgrid(xx,yy);>> subplot(224),surf(x,y,z)>> subplot(221),surf(x,y,z),view(0,90);>> subplot(222),surf(x,y,z),view(90,0);>> subplot(223),surf(x,y,z),view(0,0);1-2-1012-1-0.500.51-1-0.500.510204060-2-11202040607.（1）>> syms x;f=(3.^x+9.^x)^(1./x);L=limit(f,x,inf) L = 9（2）>>syms x y;f=x*y/(sqrt(x*y+1)-1);L1=limit(limit(f,x,0),y,0) L1 = 2 （3）>> syms x y;>> f=(1-cos(x^2+y^2))/((x^2+y^2)*exp(x^2+y^2)); >> L=limit(limit(f,x,0),y,0) L = 08．先建立M文件：function result=paradiff(y,x,t,n)if mod(n,1)~=0,error('n should positive integer,please correct') elseif n==1,result=diff(y,t)/diff(x,t);else,result=diff(paradiff(y,x,t,n-1),t)/diff(x,t);end,end然后调用函数：>> syms t;x=log(cos(t));y=cos(t)-t*sin(t);>> f=paradiff(y,x,t,1);>> [n,d]=numden(f);>> F=simple(n)/simple(d)F =(2*sin(t)+t*cos(t))*cos(t)/sin(t)>> syms t;x=log(cos(t));y=cos(t)-t*sin(t);>> f=paradiff(y,x,t,1);>> syms t;x=log(cos(t));y=cos(t)-t*sin(t);>> f=paradiff(y,x,t,2);>> [n,d]=numden(f);>> F=simple(n)/simple(d)F =-cos(t)*(3*cos(t)^2*sin(t)+cos(t)^3*t-2*sin(t)-2*t*cos(t))/sin(t)^3 >> subs(F,t,pi/3)ans =1.53879.>> syms x y t;>> f=exp(-t^2);>> I=simple(int(f,t,0,x*y))I =1/2*pi^(1/2)*erf(x*y)>> F=x/y*diff(I,x,2)-2*diff(diff(I,x),y)+diff(I,y,2)F =2*x^2*y^2*exp(-x^2*y^2)-2*exp(-x^2*y^2)-2*x^3*y*exp(-x^2*y^2) >> K=simple(F)K =-2*exp(-x^2*y^2)*(-x^2*y^2+1+x^3*y)10.（1）>> syms n;>> S=symsum(1/((2*n)^2-1),n,1,inf)S =1/2（2）>> syms k n>> limit(n*symsum(1/(n^2+k*pi),k,1,n),n,inf)ans =111.（1）>> syms t;>> syms a positive;>> x=a*(cos(t)+t*sin(t));>> y=a*(sin(t)-t*cos(t));>> I=int((x^2+y^2)*sqrt(diff(x,t)^2+diff(y,t)^2),t,0,2*pi)I =2*a^3*pi^2+4*a^3*pi^4（2）>> syms t;>> syms a b c positive;>> x=c/a*cos(t);>> y=c/b*sin(t);>> F=[y*x^3+exp(y),x*y^3+x*exp(y)-2*y];>> ds=[diff(x,t);diff(y,t)];>> I=int(F*ds,t,pi,0)I =2/15*c*(-2*c^4+15*b^4)/a/b^412.首先编写M程序：function A=vander(v)n=length(v);v=v(:);A=sym(ones(n));for j=n-1:-1:1,A(:,j)=v.*A(:,j+1);end>> syms a b c d e;>> A=[a,b,c,d,e];>> V=vander(A)V =[ a^4, a^3, a^2, a, 1][ b^4, b^3, b^2, b, 1][ c^4, c^3, c^2, c, 1][ d^4, d^3, d^2, d, 1][ e^4, e^3, e^2, e, 1]>> det(V),simple(ans)ans =(c-d)*(b-d)*(b-c)*(a-d)*(a-c)*(a-b)*(-d+e)*(e-c)*(e-b)*(e-a) 13.>> A=[-2,0.5,-0.5,0.5;0,-1.5,0.5,-0.5;2,0.5,-4.5,0.5;2,1,-2,-2]; >> [V J]=jordan(sym(A))V =[ 0, 1/2, 1/2, -1/4][ 0, 0, 1/2, 1][ 1/4, 1/2, 1/2, -1/4][ 1/4, 1/2, 1, -1/4]J =[ -4, 0, 0, 0][ 0, -2, 1, 0][ 0, 0, -2, 1][ 0, 0, 0, -2]14.先编写M文件：function X=lyap(A,B,C)if nargin==2,C=B;B=A';end[nr,nc]=size(C);A0=kron(A,eye(nc))+kron(eye(nr),B');tryC1=C';x0=-inv(A0)*C1(:);X=reshape(x0,nc,nr)';catch,error('singular matrix found.'),end数值解为：>> A=[3,-6,-4,0,5;1,4,2,-2,4;-6,3,-6,7,3;-13,10,0,-11,0;0,4,0,3,4]; >> B=[3,-2,1;-2,-9,2;-2,-1,9];>> C=[-2,1,-1;4,1,2;5,-6,1;6,-4,-4;-6,6,-3];>> X=lyap(A,B,C)X =-4.0569 -14.5128 1.56530.0356 25.0743 -2.74089.4886 25.9323 -4.41772.6969 21.6450 -2.88517.7229 31.9100 -3.7634>> norm(A*X+X*B+C)ans =3.9870e-013解析解为：>> X=lyap(sym(A),B,C)X =[ -434641749950/107136516451, -4664546747350/321409549353, 503105815912/321409549353][ 3809507498/107136516451, 8059112319373/321409549353, -880921527508/321409549353][ 1016580400173/107136516451, 8334897743767/321409549353, -1419901706449/321409549353][ 288938859984/107136516451, 6956912657222/321409549353, -927293592476/321409549353][ 827401644798/107136516451, 10256166034813/321409549353, -1209595497577/321409549353]>> A*X+X*B+Cans =[ 0, 0, 0][ 0, 0, 0][ 0, 0, 0][ 0, 0, 0][ 0, 0, 0]15.（1）>> A=[-4.5,0,0.5,-1.5;-0.5,-4,0.5,-0.5;1.5,1,-2.5,1.5;0,-1,-1,-3];>> A=sym(A);syms t;>> expm(A*t)ans =[ 1/2*exp(-5*t)+1/2*exp(-3*t)-1/2*t*exp(-3*t)+1/2*t^2*exp(-3*t), t*exp(-3*t)-1/2*exp(-3*t)+1/2*exp(-5*t),1/2*t^2*exp(-3*t)+1/2*t*exp(-3*t),1/2*t^2*exp(-3*t)-1/2*t*exp(-3*t)-1/2*exp(-3*t)+1/2*exp(-5*t)][ -1/2*exp(-3*t)+1/2*exp(-5*t)+1/2*t*exp(-3*t), 1/2*exp(-5*t)+1/2*exp(-3*t),1/2*t*exp(-3*t),-1/2*exp(-3*t)+1/2*exp(-5*t)+1/2*t*exp(-3*t)][ 1/2*exp(-3*t)-1/2*exp(-5*t)+1/2*t*exp(-3*t), 1/2*exp(-3*t)-1/2*exp(-5*t),1/2*t*exp(-3*t)+exp(-3*t),1/2*exp(-3*t)-1/2*exp(-5*t)+1/2*t*exp(-3*t)][ -1/2*t^2*exp(-3*t), -t*exp(-3*t), -t*exp(-3*t)-1/2*t^2*exp(-3*t), exp(-3*t)-1/2*t^2*exp(-3*t)]（2）编写M程序function F=funm(A,fun,x)[V,J]=jordan(A);v1=[0,diag(J,1)'];v2=[find(v1==0),length(v1)+1];for i=1:length(v2)-1v_lambda(i)=J(v2(i),v2(i));v_n(i)=v2(i+1)-v2(i);endm=length(v_lambda);F=sym([]);for i=1:mJ1=J(v2(i):v2(i)+v_n(i)-1,v2(i):v2(i)+v_n(i)-1);fJ=funJ(J1,fun,x);F=diagm(F,fJ);endF=V*F*inv(V);function fJ=funJ(J,fun,x)lam=J(1,1);f1=fun;fJ=subs(fun,x,lam)*eye(size(J));H=diag(diag(J,1),1);H1=H;for i=2:length(J)f1=diff(f1,x);a1=subs(f1,x,lam);fJ=fJ+a1*H1;H1=H1*H/i;endfunction A=diagm(A1,A2)A=A1;[n,m]=size(A);[n1,m1]=size(A2);A(n+1:n+n1,m+1:m+m1)=A2;>> A=[-4.5,0,0.5,-1.5;-0.5,-4,0.5,-0.5;1.5,1,-2.5,1.5;0,-1,-1,-3];>> syms x t;>> A1=funm(sym(A),sin(x*t),x)A1 =[ -1/2*sin(5*t)+1/2*sin(3*t)*t^2-1/2*cos(3*t)*t-1/2*sin(3*t), -1/2*sin(5*t)+cos(3*t)*t+1/2*sin(3*t),1/2*cos(3*t)*t+1/2*sin(3*t)*t^2,-1/2*sin(5*t)+1/2*sin(3*t)+1/2*sin(3*t)*t^2-1/2*cos(3*t)*t][ -1/2*sin(5*t)+1/2*cos(3*t)*t+1/2*sin(3*t), -1/2*sin(5*t)-1/2*sin(3*t),1/2*cos(3*t)*t, -1/2*sin(5*t)+1/2*cos(3*t)*t+1/2*sin(3*t)] [ 1/2*sin(5*t)+1/2*cos(3*t)*t-1/2*sin(3*t), 1/2*sin(5*t)-1/2*sin(3*t),-sin(3*t)+1/2*cos(3*t)*t,1/2*sin(5*t)+1/2*cos(3*t)*t-1/2*sin(3*t)][ -1/2*sin(3*t)*t^2, -cos(3*t)*t, -cos(3*t)*t-1/2*sin(3*t)*t^2, -sin(3*t)-1/2*sin(3*t)*t^2]（3）>> A=[-4.5,0,0.5,-1.5;-0.5,-4,0.5,-0.5;1.5,1,-2.5,1.5;0,-1,-1,-3];>> syms x t;>> A1=funm(sym(A),exp(x*t)*sin(x^2*exp(x*t)*t),x)A1 =[ 1/2*exp(-5*t)*sin(25*exp(-5*t)*t)+1/2*t^2*exp(-3*t)*sin(9*exp(-3*t)*t)+t*exp(-3* t)*cos(9*exp(-3*t)*t)*(-6*exp(-3*t)*t+9*t^2*exp(-3*t))-1/2*exp(-3*t)*sin(9*exp(-3* t)*t)*(-6*exp(-3*t)*t+9*t^2*exp(-3*t))^2+1/2*exp(-3*t)*cos(9*exp(-3*t)*t)*(2*exp( -3*t)*t-12*t^2*exp(-3*t)+9*t^3*exp(-3*t))-1/2*t*exp(-3*t)*sin(9*exp(-3*t)*t)-1/2*e xp(-3*t)*cos(9*exp(-3*t)*t)*(-6*exp(-3*t)*t+9*t^2*exp(-3*t))+1/2*exp(-3*t)*sin(9* exp(-3*t)*t),1/2*exp(-5*t)*sin(25*exp(-5*t)*t)+t*exp(-3*t)*sin(9*exp(-3*t)*t)+exp(-3*t)*cos(9* exp(-3*t)*t)*(-6*exp(-3*t)*t+9*t^2*exp(-3*t))-1/2*exp(-3*t)*sin(9*exp(-3*t)*t),1/2*t*exp(-3*t)*sin(9*exp(-3*t)*t)+1/2*exp(-3*t)*cos(9*exp(-3*t)*t)*(-6*exp(-3*t)* t+9*t^2*exp(-3*t))+1/2*t^2*exp(-3*t)*sin(9*exp(-3*t)*t)+t*exp(-3*t)*cos(9*exp(-3 *t)*t)*(-6*exp(-3*t)*t+9*t^2*exp(-3*t))-1/2*exp(-3*t)*sin(9*exp(-3*t)*t)*(-6*exp(-3*t)*t+9*t^2*exp(-3*t))^2+1/2*exp(-3*t)*cos(9*exp(-3*t)*t)*(2*exp(-3*t)*t-12*t^2 *exp(-3*t)+9*t^3*exp(-3*t)),1/2*exp(-5*t)*sin(25*exp(-5*t)*t)-1/2*exp(-3*t)*sin(9*exp(-3*t)*t)+1/2*t^2*exp(-3 *t)*sin(9*exp(-3*t)*t)+t*exp(-3*t)*cos(9*exp(-3*t)*t)*(-6*exp(-3*t)*t+9*t^2*exp(-3 *t))-1/2*exp(-3*t)*sin(9*exp(-3*t)*t)*(-6*exp(-3*t)*t+9*t^2*exp(-3*t))^2+1/2*exp(-3*t)*cos(9*exp(-3*t)*t)*(2*exp(-3*t)*t-12*t^2*exp(-3*t)+9*t^3*exp(-3*t))-1/2*t*ex p(-3*t)*sin(9*exp(-3*t)*t)-1/2*exp(-3*t)*cos(9*exp(-3*t)*t)*(-6*exp(-3*t)*t+9*t^2* exp(-3*t))][1/2*exp(-5*t)*sin(25*exp(-5*t)*t)+1/2*t*exp(-3*t)*sin(9*exp(-3*t)*t)+1/2*exp(-3*t) *cos(9*exp(-3*t)*t)*(-6*exp(-3*t)*t+9*t^2*exp(-3*t))-1/2*exp(-3*t)*sin(9*exp(-3*t) *t),1/2*exp(-5*t)*sin(25*exp(-5*t)*t)+1/2*exp(-3*t)*sin(9*exp(-3*t)*t),1/2*t*exp(-3*t)*sin(9*exp(-3*t)*t)+1/2*exp(-3*t)*cos(9*exp(-3*t)*t)*(-6*exp(-3*t)* t+9*t^2*exp(-3*t)),1/2*exp(-5*t)*sin(25*exp(-5*t)*t)+1/2*t*exp(-3*t)*sin(9*exp(-3*t)*t)+1/2*exp(-3*t)*cos(9*exp(-3*t)*t)*(-6*exp(-3*t)*t+9*t^2*exp(-3*t))-1/2*exp(-3*t)*sin(9*exp(-3*t) *t)][-1/2*exp(-5*t)*sin(25*exp(-5*t)*t)+1/2*t*exp(-3*t)*sin(9*exp(-3*t)*t)+1/2*exp(-3*t )*cos(9*exp(-3*t)*t)*(-6*exp(-3*t)*t+9*t^2*exp(-3*t))+1/2*exp(-3*t)*sin(9*exp(-3* t)*t),-1/2*exp(-5*t)*sin(25*exp(-5*t)*t)+1/2*exp(-3*t)*sin(9*exp(-3*t)*t),exp(-3*t)*sin(9*exp(-3*t)*t)+1/2*t*exp(-3*t)*sin(9*exp(-3*t)*t)+1/2*exp(-3*t)*cos( 9*exp(-3*t)*t)*(-6*exp(-3*t)*t+9*t^2*exp(-3*t)),-1/2*exp(-5*t)*sin(25*exp(-5*t)*t)+1/2*t*exp(-3*t)*sin(9*exp(-3*t)*t)+1/2*exp(-3*t )*cos(9*exp(-3*t)*t)*(-6*exp(-3*t)*t+9*t^2*exp(-3*t))+1/2*exp(-3*t)*sin(9*exp(-3* t)*t)][-1/2*t^2*exp(-3*t)*sin(9*exp(-3*t)*t)-t*exp(-3*t)*cos(9*exp(-3*t)*t)*(-6*exp(-3*t) *t+9*t^2*exp(-3*t))+1/2*exp(-3*t)*sin(9*exp(-3*t)*t)*(-6*exp(-3*t)*t+9*t^2*exp(-3*t))^2-1/2*exp(-3*t)*cos(9*exp(-3*t)*t)*(2*exp(-3*t)*t-12*t^2*exp(-3*t)+9*t^3*e xp(-3*t)),-t*exp(-3*t)*sin(9*exp(-3*t)*t)-exp(-3*t)*cos(9*exp(-3*t)*t)*(-6*exp(-3*t)*t+9*t^2 *exp(-3*t)),-t*exp(-3*t)*sin(9*exp(-3*t)*t)-exp(-3*t)*cos(9*exp(-3*t)*t)*(-6*exp(-3*t)*t+9*t^2 *exp(-3*t))-1/2*t^2*exp(-3*t)*sin(9*exp(-3*t)*t)-t*exp(-3*t)*cos(9*exp(-3*t)*t)*(-6 *exp(-3*t)*t+9*t^2*exp(-3*t))+1/2*exp(-3*t)*sin(9*exp(-3*t)*t)*(-6*exp(-3*t)*t+9* t^2*exp(-3*t))^2-1/2*exp(-3*t)*cos(9*exp(-3*t)*t)*(2*exp(-3*t)*t-12*t^2*exp(-3*t) +9*t^3*exp(-3*t)),exp(-3*t)*sin(9*exp(-3*t)*t)-1/2*t^2*exp(-3*t)*sin(9*exp(-3*t)*t)-t*exp(-3*t)*cos(9 *exp(-3*t)*t)*(-6*exp(-3*t)*t+9*t^2*exp(-3*t))+1/2*exp(-3*t)*sin(9*exp(-3*t)*t)*(-6*exp(-3*t)*t+9*t^2*exp(-3*t))^2-1/2*exp(-3*t)*cos(9*exp(-3*t)*t)*(2*exp(-3*t)*t-12*t^2*exp(-3*t)+9*t^3*exp(-3*t))]第二部分数学问题求解与数据处理1.(1)>> syms a t;>> f=sin(a*t)/t;laplace(f)ans =atan(a/s)(2)>> syms t a;f=t^5*sin(a*t);laplace(f)ans =60*i*(-1/(s-i*a)^6+1/(s+i*a)^6)(3)>> syms t a;>> f=t^8*cos(a*t);laplace(f)ans =20160/(s-i*a)^9+20160/(s+i*a)^92.(1)>> syms s a b;F=1/(s^2*(s^2-a^2)*(s+b));ilaplace(F)ans =1/2/a^3/b^2/(a^2-b^2)*(2*t*a*b^3+2*(1-exp(-b*t)-b*t)*a^3+( -2*a+exp(a*t)*(a-b)+exp(-a*t)*(a+b))*b^2)（2）>> syms a b s;F=sqrt(s-a)-sqrt(s-b);ilaplace(F)ans =1/2/t^(3/2)/pi^(1/2)*(exp(b*t)-exp(a*t))（3）>> syms a b s; F=log((s-a)/(s-b));ilaplace(F)ans =(exp(b*t)-exp(a*t))/t3(1)>> syms x;f=x^2*(3*sym(pi)-2*abs(x));F=fourier(f) F =-6*(4+pi^2*dirac(2,w)*w^4)/w^4>> ifourier(F)ans =x^2*(-4*x*heaviside(x)+3*pi+2*x)(2)>> syms t;f=t^2*(t-2*sym(pi))^2;F=fourier(f)F =2*pi*(dirac(4,w)-4*pi^2*dirac(2,w)+4*i*pi*dirac(3,w)) >> ifourier(F)ans =x^2*(-2*pi+x)^24.(1)>> syms k a T;f=cos(k*a*T);F=ztrans(f)(z-cos(a*T))*z/(z^2-2*z*cos(a*T)+1)>> f1=iztrans(F)f1 =cos(a*T*n)(2)>> syms k T a;f=(k*T)^2*exp(-a*k*T);F=ztrans(f)F =T^2*z*exp(-a*T)*(z+exp(-a*T))/(z-exp(-a*T))^3>> f1=iztrans(F)f1 =T^2*(1/exp(a*T))^n*n^2(3)>> syms a k T;f=(a*k*T-1+exp(-a*k*T))/a;>> F=ztrans(f)F =1/a*(a*T*z/(z-1)^2-z/(z-1)+z/exp(-a*T)/(z/exp(-a*T)-1)) >> iztrans(F)ans =(-1+a*T*n+(1/exp(a*T))^n)/a5.用数值方法求解(1)>> syms x;>> x1=solve('exp(-(x+1)^2+pi/2)*sin(5*x+2)')x1 =-2/5验证过程>> subs('exp(-(x+1)^2+pi/2)*sin(5*x+2)',x,x1)ans =(2)>> syms x;>> y1=solve('(x^2+y^2+x*y)*exp(-x^2-y^2-x*y)=0','y')y1 =(-1/2+1/2*i*3^(1/2))*x(-1/2-1/2*i*3^(1/2))*x验证过程>>y2=simple(subs('(x^2+y^2+x*y)*exp(-x^2-y^2-x*y)=0','y',y1)) y2 =(x^2+(-1/2+1/2*i*3^(1/2))^2*x^2+x^2*(-1/2+1/2*i*3^(1/2)))* exp(-x^2-(-1/2+1/2*i*3^(1/2))^2*x^2-x^2*(-1/2+1/2*i*3^(1/2) )) = 0(x^2+(-1/2-1/2*i*3^(1/2))^2*x^2+x^2*(-1/2-1/2*i*3^(1/2)))*e xp(-x^2-(-1/2-1/2*i*3^(1/2))^2*x^2-x^2*(-1/2-1/2*i*3^(1/2))) = 06.首先求出积分：>> syms x c;y=int((exp(x)-c*x)^2,x,0,1)y =-1/2-2*c+1/2*exp(2)+1/3*c^2编写一个出M文件：function y=new(c)y=-1/2-2*c+1/2*exp(2)+1/3*c^2;>> x=fminsearch('new',0)x =3.00007.编写M文件：function [c,ce]=f2(x);ce=[];c=[x(1)+x(2);x(1)*x(2)-x(1)-x(2)+1.5;-10-x(1)*x(2)];>> f=@(x)exp(x(1))*(4*x(1)^2+2*x(2)^2+4*x(1)*x(2)+2*x(2)+1); >> A=[];B=[];Aeq=[];Beq=[];xm=[-10;-10];xM=[10;10];>> x0=(xm+xM)/2;>> ff=optimset;ff.TolX=1e-10;ff.TolFun=1e-20;>> x=fmincon(f,x0,A,B,Aeq,Beq,xm,xM,@f2,ff)Maximum number of function evaluations exceeded;increase OPTIONS.MaxFunEvals.x =0.41950.4195>> i=1;x=x0;>> while (1)[x,a,b]=fmincon('f',x,A,B,Aeq,Beq,xm,xM,'f2',ff);if b>0,break;endi=i+1;end>> x,ix =1.1825-1.7398i =58书上所描述的ipslv_mex下载地址已经失效了，其他网站上也没有这个函数的下载地址，所以这个题目没有找到该函数，运行失败。

matlab部分实验题答案

这些答案不一定正确，大家可以参考参考，还有部分没完成的，希望有人能快点做出来。

实验一1、（1）>> z1=(2*sin(85*pi/180))/(1+exp(2))z1 =0.2375（2）>> x=[2,1+2i;-0.45,5]x =2.0000 1.0000 + 2.0000i-0.4500 5.0000>> z2=1/2*log(1+sqrt(1+x^2))z2 =0.5738 - 0.0333i 0.7952 + 0.2117i0.2869 + 0.4861i 0.9005 - 0.0073i2、>> A=[12,34,-4;34,7,87;3,65,7]A =12 34 -434 7 873 65 7>> B=[1,3,-1;2,0,3;3,-2,7]B =1 3 -12 0 33 -2 7>> I=eye(3)I =1 0 00 1 00 0 1>> A+6*Bans =18 52 -1046 7 10521 53 49>> A-B+Ians =12 31 -332 8 840 67 1>> A*Bans =68 44 62309 -72 596154 -5 241>> A.*Bans =12 102 468 0 2619 -130 49>> A^3ans =37226 233824 48604247370 149188 60076678688 454142 118820>> A.^3ans =1728 39304 -6439304 343 65850327 274625 343 >> A/Bans =16.4000 -13.6000 7.600035.8000 -76.2000 50.200067.0000 -134.0000 68.0000>> B\Aans =109.4000 -131.2000 322.8000-53.0000 85.0000 -171.0000-61.6000 89.8000 -186.2000>> [A,B]ans =12 34 -4 1 3 -134 7 87 2 0 33 65 7 3 -2 7 >> [A([1,3],:);B^2]ans =12 34 -43 65 74 5 111 0 1920 -5 40>>3、>> A=[1,2,3,4,5;6,7,8,9,10;11,12,13,14,15;16,17,18,19,20;21,22,23,24,25]A =1 2 3 4 56 7 8 9 1011 12 13 14 1516 17 18 19 2021 22 23 24 25>> B=[3,0,16;17,-6,9;0,23,-4;9,7,0;4,13,11]B =3 0 1617 -6 90 23 -49 7 04 13 11>> C=A*BC =93 150 77258 335 237423 520 397588 705 557753 890 717>> D=C(3:5,2:3)D =520 397705 557890 717实验二2、（1）>> syms xs=(x*(exp(sin(x))+1)-2*(exp(tan(x))-1))/(sin(x)^3) Lsk=limit(s,x,0)s =(x*(exp(sin(x)) + 1) - 2*exp(tan(x)) + 2)/sin(x)^3 Lsk =-1/2（2）>> syms a t x>> A=[a^x,t^3;t*cos(x),log(x)]A =[ a^x, t^3][ t*cos(x), log(x)]>> df=diff(A)dfdt2=diff(A,t,2)dfdxdt=diff(diff(A,x),t)df =[ a^x*log(a), 0][ -t*sin(x), 1/x]dfdt2 =[ 0, 6*t][ 0, 0]dfdxdt =[ 0, 0][ -sin(x), 0]>>实验三1、（3）>> a=-3.0:0.1:3.0z3=exp(0.3*a).*sin(a+0.3)a =Columns 1 through 8-3.0000 -2.9000 -2.8000 -2.7000 -2.6000 -2.5000 -2.4000 -2.3000Columns 9 through 16-2.2000 -2.1000 -2.0000 -1.9000 -1.8000 -1.7000 -1.6000 -1.5000Columns 17 through 24-1.4000 -1.3000 -1.2000 -1.1000 -1.0000 -0.9000 -0.8000 -0.7000Columns 25 through 32-0.6000 -0.5000 -0.4000 -0.3000 -0.2000 -0.1000 0 0.1000Columns 33 through 400.2000 0.3000 0.4000 0.5000 0.6000 0.7000 0.8000 0.9000Columns 41 through 481.0000 1.1000 1.2000 1.3000 1.4000 1.5000 1.6000 1.7000Columns 49 through 561.8000 1.90002.0000 2.1000 2.2000 2.3000 2.40002.5000Columns 57 through 612.6000 2.7000 2.8000 2.90003.0000z3 =Columns 1 through 8-0.1738 -0.2160 -0.2584 -0.3005 -0.3418 -0.3819 -0.4202 -0.4561Columns 9 through 16-0.4891 -0.5187 -0.5442 -0.5653 -0.5813 -0.5918 -0.5962 -0.5943Columns 17 through 24-0.5856 -0.5697 -0.5465 -0.5157 -0.4772 -0.4310 -0.3771 -0.3157Columns 25 through 32-0.2468 -0.1710 -0.0885 0.0000 0.0940 0.1928 0.2955 0.4013Columns 33 through 400.5091 0.6178 0.7264 0.8334 0.9378 1.0381 1.13291.2209Columns 41 through 481.3007 1.3707 1.4297 1.4764 1.5093 1.5273 1.5293 1.5142Columns 49 through 561.4813 1.4296 1.3588 1.2683 1.1579 1.0278 0.8780 0.7092Columns 57 through 610.5219 0.3172 0.0963 -0.1393 -0.3880>>（4）>> syms tt=0:0.5:2.5if t>=0t<1z4=t.^2;elseif t>=1t<2z4=t.^2-1;elseif t>=2t<3z4=t.^2-2.*t+1;endt =0 0.5000 1.0000 1.5000 2.0000 2.5000 ans =1 1 0 0 0 0>>4（1）>> m=100:999;n=find(mod(m,21)==0);length(n)ans =43（2）>> M=100+magic(5)M =117 124 101 108 115123 105 107 114 116104 106 113 120 122110 112 119 121 103111 118 125 102 109实验四1、>> x=rand(1,30000); mu=mean(x)sig=std(x)[max_num,weizhi1]=max(x) [min_num,weizhi2]=min(x)y=length(find(x>0.5));p=y/30000mu =0.5020sig =0.2893max_num =1.0000weizhi1 =731min_num =1.2354e-004weizhi2 =9617p =0.5017>>2、>> t=45+50*rand(100,5);P=fix(t);[x,l]=max(P)[y,k]=min(P)mu=mean(P)sig=std(P)s=sum(P,2)[X,m]=max(s)[Y,n]=min(s)[zcj,xsxh]=sort(s)x =94 94 94 92 94l =12 25 6 17 42y =45 45 45 45 45k =1 24 18 80 46mu =68.1300 70.4700 69.1900 67.1900 70.6800 sig =14.7290 14.5806 15.2532 13.8285 13.2702 s =326 342 338 376 375 333 394 339 317 359 338 380 302 379 369 391 378 342 366 363 315 348 383 303 335 313 334 302 296 370 319 350 329 322 365 399 326 391 318 328 335 374 305352 293 363 380 348 336 353 364 342 381 369 349 285 398 344 379 373 359 324 356 332 327 294 311 319 361 357 379 353 366 318 351 327 330 390 329 329 292 348 360 323 297 349335371323372358343363336393332337354 X =399 m =36 Y =285 n =57 zcj =285292293294296297302303 305 311 313 315 317 318 318 319 319 322 323 323 324 326 326 327 327 328 329 329 329 330 332 332 333 334 335 335 335 336 336 337 338 338 339 342 342 342 343 344 345 347348 348 349 349 350 351 352 353 353 354 356 357 358 359 359 360 361 363 363 363 364 365 366 366 369 369 370 371 372 373 374 375 376 378 379 379 379 380 380 381 383 390 391393394398399 xsxh =578246672986132824436826219397531693485916313766774033808178659862741 89 50 96 99 3 11 8 2 18 53 94 59 88 44 22 49 83 56 87 32 76 45 51 73 100 64 71 93 10 62 84 70 20 47 95 52 35 19 74 15 55 309261425417146072124854237916389775836>>3、>> A=randn(10,5)mu=mean(A)sig=std(A)m=max(A)n=min(A)p=sum(A,2)sum(p)A =-0.3316 -1.9682 -0.9379 0.0635 -0.19361.2900 0.8745 -0.3664 0.3067 -0.3796-0.3743 1.2308 -0.9529 1.2654 -0.0922 -0.8671 -0.3518 0.1797 0.9860 1.26620.7588 0.5268 0.1264 -1.2862 -0.0425-1.9617 1.0806 0.2758 1.0919 -2.9548 -0.3597 -0.3459 1.0738 1.0266 -0.44910.1221 -0.1111 0.4171 -0.9018 0.8893-1.5787 -0.1213 0.4899 0.8433 -0.5266-1.5737 1.2627 -1.3792 -1.2064 -0.3800 mu =-0.4876 0.2077 -0.1074 0.2189 -0.2863 sig =1.0449 1.0018 0.7746 1.0040 1.1116 m =1.2900 1.2627 1.0738 1.2654 1.2662 n =-1.9617 -1.9682 -1.3792 -1.2862 -2.9548 p =-3.36781.72511.07681.21300.0832-2.46820.94570.4156-0.8935-3.2766ans =-4.5466>>4、>> x=0:15*pi/180:pi/2;>> sin(x)ans =0 0.2588 0.5000 0.7071 0.8660 0.9659 1.0000>> tan(x)ans =1.0e+016 *0 0.0000 0.0000 0.0000 0.0000 0.0000 1.6331>> format long>> interp1(x,sin(x),'spline')ans =Columns 1 through 4-0.261799387799149 -0.194040720240549 -0.130899693899575 -0.076679265375884Columns 5 through 7-0.035074467269872 -0.008920597817284 0>> interp1(x,tan(x),'spline')ans =1.0e+032 *Columns 1 through 4-0.000000000000000 -0.000000000000000 -0.000000000000000 -0.000000000000000Columns 5 through 70.000000000000000 0.000000000000000 7.2536888214463725、>> N=[1 4 9 16 25 36 49 64 81 100]N =1 4 9 16 25 36 49 64 81 100>> n=sqrt(N)n =1 2 3 4 5 6 7 8 9 10>> format long>> interp1(N,n,'cubic')ans =1 4 9 16 25 36 49 64 81 100>>6（1）>> syms x>> y=(sin(x))^2+(cos(x))^2;>> dy=diff(y);>> x=[pi/6,pi/4,pi/3,pi/2];>> eval(dy)ans =（2）>> syms x>> y=sqrt(1+x^2);>> dy=diff(y);>> x=1x =1>> eval(dy)ans =0.7071 >> x=2x =2>> eval(dy) ans =0.8944 >> x=3x =3>> eval(dy) ans =0.9487 >>实验五1、>> x1=-2:0.1:2;y1=exp(x1);x2=0.1:0.1:5;y2=log(x2);plot(x1,y1,'r',x2,y2,'g');title('二维图');legend('y=exp(x)','y=logx');xlabel('X轴数据');ylabel('Y轴数据'); grid on;>>3、>> t=-pi:pi/100:pi;x=t.*cos(3*t);y=t.*sin(t).*sin(t);plot(x,y);title(date);legend(strvcat('x=tcos(3t)','y=tsin2t')); xlabel('T轴数据');ylabel('X,Y轴数据'); >>。

(完整版)MATLAB)课后实验答案[1]

实验一 MATLAB 运算基础1. 先求下列表达式的值，然后显示MATLAB 工作空间的使用情况并保存全部变量。

(1) 0122sin 851z e =+(2) 21ln(2z x =，其中2120.455i x +⎡⎤=⎢⎥-⎣⎦ (3) 0.30.330.3sin(0.3)ln , 3.0, 2.9,,2.9,3.022a a e e a z a a --+=++=--L (4) 2242011122123t t z t t t t t ⎧≤<⎪=-≤<⎨⎪-+≤<⎩，其中t =0:0.5:2.5 解：4. 完成下列操作：(1) 求[100,999]之间能被21整除的数的个数。

(2) 建立一个字符串向量，删除其中的大写字母。

解：(1) 结果：(2). 建立一个字符串向量例如：ch='ABC123d4e56Fg9';则要求结果是：实验二 MATLAB 矩阵分析与处理1. 设有分块矩阵33322322E R A O S ⨯⨯⨯⨯⎡⎤=⎢⎥⎣⎦，其中E 、R 、O 、S 分别为单位矩阵、随机矩阵、零矩阵和对角阵，试通过数值计算验证22E R RS A O S +⎡⎤=⎢⎥⎣⎦。

解: M 文件如下；5. 下面是一个线性方程组：1231112340.951110.673450.52111456x x x ⎡⎤⎢⎥⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎢⎥⎢⎥⎣⎦(1) 求方程的解。

(2) 将方程右边向量元素b 3改为0.53再求解，并比较b 3的变化和解的相对变化。

(3) 计算系数矩阵A 的条件数并分析结论。

解： M 文件如下： 123d4e56g9实验三选择结构程序设计1. 求分段函数的值。

2226035605231x x x x y x x x x x x x ⎧+-<≠-⎪=-+≤<≠≠⎨⎪--⎩且且及其他用if 语句实现，分别输出x=-5.0,-3.0,1.0,2.0,2.5,3.0,5.0时的y 值。

MATLAB数学实验课后答案

数学实验MATLAB参考答案（重要部分）P20,ex1(5) 等于[exp(1),exp(2);exp(3),exp(4)](7) 3=1*3, 8=2*4(8) a为各列最小值，b为最小值所在的行号(10) 1>=4,false, 2>=3,false, 3>=2, ture, 4>=1,ture(11) 答案表明：编址第2元素满足不等式(30>=20)和编址第4元素满足不等式(40>=10)(12) 答案表明：编址第2行第1列元素满足不等式(30>=20)和编址第2行第2列元素满足不等式(40>=10)P20, ex2(1)a, b, c的值尽管都是1，但数据类型分别为数值，字符，逻辑，注意a与c相等，但他们不等于b(2)double(fun)输出的分别是字符a,b,s,(,x,)的ASCII码P20,ex3>> r=2;p=0.5;n=12;>> T=log(r)/n/log(1+0.01*p)T =11.5813P20,ex4>> x=-2:0.05:2;f=x.^4-2.^x;>> [fmin,min_index]=min(f)fmin =-1.3907 %最小值min_index =54 %最小值点编址>> x(min_index)ans =0.6500 %最小值点>> [f1,x1_index]=min(abs(f)) %求近似根--绝对值最小的点f1 =0.0328x1_index =24>> x(x1_index)ans =-0.8500>> x(x1_index)=[];f=x.^4-2.^x; %删去绝对值最小的点以求函数绝对值次小的点>> [f2,x2_index]=min(abs(f)) %求另一近似根--函数绝对值次小的点f2 =0.0630x2_index =65>> x(x2_index)ans =1.2500P20,ex5>> z=magic(10)z =92 99 1 8 15 67 74 51 58 4098 80 7 14 16 73 55 57 64 414 81 88 20 22 54 56 63 70 4785 87 19 21 3 60 62 69 71 2886 93 25 2 9 61 68 75 52 3417 24 76 83 90 42 49 26 33 6523 5 82 89 91 48 30 32 39 6679 6 13 95 97 29 31 38 45 7210 12 94 96 78 35 37 44 46 5311 18 100 77 84 36 43 50 27 59>> sum(z)ans =505 505 505 505 505 505 505 505 505 505 >> sum(diag(z))ans =505>> z(:,2)/sqrt(3)ans =57.157746.188046.765450.229553.693613.85642.88683.46416.928210.3923>> z(8,:)=z(8,:)+z(3,:)z =92 99 1 8 15 67 74 51 58 40 98 80 7 14 16 73 55 57 64 41 4 81 88 20 22 54 56 63 70 4785 87 19 21 3 60 62 69 71 2886 93 25 2 9 61 68 75 52 34 17 24 76 83 90 42 49 26 33 6523 5 82 89 91 48 30 32 39 6683 87 101 115 119 83 87 101 115 11910 12 94 96 78 35 37 44 46 5311 18 100 77 84 36 43 50 27 59P 40 ex1先在编辑器窗口写下列M函数，保存为eg2_1.m function [xbar,s]=ex2_1(x)n=length(x);xbar=sum(x)/n;s=sqrt((sum(x.^2)-n*xbar^2)/(n-1));例如>>x=[81 70 65 51 76 66 90 87 61 77];>>[xbar,s]=ex2_1(x)xbar =72.4000s =12.1124P 40 ex2s=log(1);n=0;while s<=100n=n+1;s=s+log(1+n);endm=n计算结果m=37P 40 ex3clear;F(1)=1;F(2)=1;k=2;x=0;e=1e-8; a=(1+sqrt(5))/2;while abs(x-a)>ek=k+1;F(k)=F(k-1)+F(k-2); x=F(k)/F(k-1); enda,x,k计算至k=21可满足精度P 40 ex4clear;tic;s=0;for i=1:1000000s=s+sqrt(3)/2^i;ends,toctic;s=0;i=1;while i<=1000000s=s+sqrt(3)/2^i;i=i+1;ends,toctic;s=0;i=1:1000000;s=sqrt(3)*sum(1./2.^i);s,tocP 40 ex5t=0:24;c=[15 14 14 14 14 15 16 18 20 22 23 25 28 ...31 32 31 29 27 25 24 22 20 18 17 16];plot(t,c)P 40 ex6(1)clear;fplot('x^2*sin(x^2-x-2)',[-2,2])x=-2:0.1:2;y=x.^2.*sin(x.^2-x-2);plot(x,y)y=inline('x^2*sin(x^2-x-2)');fplot(y,[-2 2]) (2)参数方法t=linspace(0,2*pi,100);x=2*cos(t);y=3*sin(t); plot(x,y)(3)x=-3:0.1:3;y=x;[x,y]=meshgrid(x,y);z=x.^2+y.^2;surf(x,y,z)(4)x=-3:0.1:3;y=-3:0.1:13;[x,y]=meshgrid(x,y);z=x.^4+3*x.^2+y.^2-2*x-2*y-2*x.^2.*y+6;surf(x,y,z)(5)t=0:0.01:2*pi;x=sin(t);y=cos(t);z=cos(2*t);plot3(x,y,z)(6)theta=linspace(0,2*pi,50);fai=linspace(0,pi/2,20); [theta,fai]=meshgrid(theta,fai);x=2*sin(fai).*cos(theta);y=2*sin(fai).*sin(theta);z=2*cos(fai);surf(x,y,z)(7)x=linspace(0,pi,100);y1=sin(x);y2=sin(x).*sin(10*x);y3=-sin(x);plot(x,y1,x,y2,x,y3)page41, ex7x=-1.5:0.05:1.5;y=1.1*(x>1.1)+x.*(x<=1.1).*(x>=-1.1)-1.1*(x<-1.1);plot(x,y)page41,ex8分别使用which trapz, type trapz, dir C:\MATLAB7\toolbox\matlab\datafun\page41,ex9clear;close;x=-2:0.1:2;y=x;[x,y]=meshgrid(x,y);a=0.5457;b=0.7575;p=a*exp(-0.75*y.^2-3.75*x.^2-1.5*x).*(x+y>1);p=p+b*exp(-y.^2-6*x.^2).*(x+y>-1).*(x+y<=1);p=p+a*exp(-0.75*y.^2-3.75*x.^2+1.5*x).*(x+y<=-1);mesh(x,y,p)page41, ex10lookfor lyapunovhelp lyap>> A=[1 2 3;4 5 6;7 8 0];C=[2 -5 -22;-5 -24 -56;-22 -56 -16]; >> X=lyap(A,C)X =1.0000 -1.0000 -0.0000-1.0000 2.0000 1.0000-0.0000 1.0000 7.0000Chapter 3%Exercise 1>> a=[1,2,3];b=[2,4,3];a./b,a.\b,a/b,a\bans =0.5000 0.5000 1.0000ans =2 2 1ans =0.6552 %一元方程组x[2,4,3]=[1,2,3]的近似解ans =0 0 00 0 00.6667 1.3333 1.0000%矩阵方程[1,2,3][x11,x12,x13;x21,x22,x23;x31,x32,x33]=[2,4,3]的特解Exercise 2(1)>> A=[4 1 -1;3 2 -6;1 -5 3];b=[9;-2;1];>> rank(A), rank([A,b]) %[A,b]为增广矩阵ans =3ans =3 %可见方程组唯一解>> x=A\bx =2.38301.48942.0213Exercise 2(2)>> A=[4 -3 3;3 2 -6;1 -5 3];b=[-1;-2;1]; >> rank(A), rank([A,b])ans =3ans =3 %可见方程组唯一解>> x=A\bx =-0.4706-0.2941Exercise 2(3)>> A=[4 1;3 2;1 -5];b=[1;1;1];>> rank(A), rank([A,b])ans =2ans =3 %可见方程组无解>> x=A\bx =0.3311-0.1219 %最小二乘近似解Exercise 2(4)>> a=[2,1,-1,1;1,2,1,-1;1,1,2,1];b=[1 2 3]';%注意b的写法>> rank(a),rank([a,b])ans =3ans =3 %rank(a)==rank([a,b])<4说明有无穷多解>> a\bans =110 %一个特解Exercise 3>> a=[2,1,-1,1;1,2,1,-1;1,1,2,1];b=[1,2,3]'; >> x=null(a),x0=a\bx =-0.62550.6255-0.20850.4170x0 =11%通解kx+x0Exercise 4>> x0=[0.2 0.8]';a=[0.99 0.05;0.01 0.95]; >> x1=a*x, x2=a^2*x, x10=a^10*x >> x=x0;for i=1:1000,x=a*x;end,xx =0.83330.1667>> x0=[0.8 0.2]';>> x=x0;for i=1:1000,x=a*x;end,xx =0.83330.1667>> [v,e]=eig(a)v =0.9806 -0.70710.1961 0.7071e =1.0000 00 0.9400>> v(:,1)./xans =1.17671.1767 %成比例，说明x是最大特征值对应的特征向量Exercise 5%用到公式(3.11)(3.12)>> B=[6,2,1;2.25,1,0.2;3,0.2,1.8];x=[25 5 20]';>> C=B/diag(x)C =0.2400 0.4000 0.05000.0900 0.2000 0.01000.1200 0.0400 0.0900>> A=eye(3,3)-CA =0.7600 -0.4000 -0.0500-0.0900 0.8000 -0.0100-0.1200 -0.0400 0.9100>> D=[17 17 17]';x=A\Dx =37.569625.786224.7690%Exercise 6(1)>> a=[4 1 -1;3 2 -6;1 -5 3];det(a),inv(a),[v,d]=eig(a) ans =-94ans =0.2553 -0.0213 0.04260.1596 -0.1383 -0.22340.1809 -0.2234 -0.0532v =0.0185 -0.9009 -0.3066-0.7693 -0.1240 -0.7248-0.6386 -0.4158 0.6170d =-3.0527 0 00 3.6760 00 0 8.3766%Exercise 6(2)>> a=[1 1 -1;0 2 -1;-1 2 0];det(a),inv(a),[v,d]=eig(a) ans =1ans =2.0000 -2.0000 1.00001.0000 -1.0000 1.00002.0000 -3.0000 2.0000v =-0.5773 0.5774 + 0.0000i 0.5774 - 0.0000i -0.5773 0.5774 0.5774-0.5774 0.5773 - 0.0000i 0.5773 + 0.0000id =1.0000 0 00 1.0000 + 0.0000i 00 0 1.0000 - 0.0000i%Exercise 6(3)>> A=[5 7 6 5;7 10 8 7;6 8 10 9;5 7 9 10]A =5 76 57 10 8 76 8 10 95 7 9 10>> det(A),inv(A), [v,d]=eig(A)ans =1ans =68.0000 -41.0000 -17.0000 10.0000 -41.0000 25.0000 10.0000 -6.0000 -17.0000 10.0000 5.0000 -3.0000 10.0000 -6.0000 -3.0000 2.0000v =0.8304 0.0933 0.3963 0.3803-0.5016 -0.3017 0.6149 0.5286-0.2086 0.7603 -0.2716 0.55200.1237 -0.5676 -0.6254 0.5209d =0.0102 0 0 00 0.8431 0 00 0 3.8581 00 0 0 30.2887%Exercise 6(4)、(以n=5为例)%关键是矩阵的定义%方法一（三个for）n=5;for i=1:n, a(i,i)=5;endfor i=1:(n-1),a(i,i+1)=6;endfor i=1:(n-1),a(i+1,i)=1;enda%方法二（一个for）n=5;a=zeros(n,n);a(1,1:2)=[5 6];for i=2:(n-1),a(i,[i-1,i,i+1])=[1 5 6];enda(n,[n-1 n])=[1 5];a%方法三（不用for）n=5;a=diag(5*ones(n,1));b=diag(6*ones(n-1,1));c=diag(ones(n-1,1));a=a+[zeros(n-1,1),b;zeros(1,n)]+[zeros(1,n);c,zeros(n-1,1)] %下列计算>> det(a)ans =665>> inv(a)ans =0.3173 -0.5865 1.0286 -1.6241 1.9489-0.0977 0.4887 -0.8571 1.3534 -1.62410.0286 -0.1429 0.5429 -0.8571 1.0286 -0.0075 0.0376 -0.1429 0.4887 -0.5865 0.0015 -0.0075 0.0286 -0.0977 0.3173 >> [v,d]=eig(a)v =-0.7843 -0.7843 -0.9237 0.9860 -0.9237 0.5546 -0.5546 -0.3771 -0.0000 0.3771 -0.2614 -0.2614 0.0000 -0.1643 0.0000 0.0924 -0.0924 0.0628 -0.0000 -0.0628 -0.0218 -0.0218 0.0257 0.0274 0.0257d =0.7574 0 0 0 00 9.2426 0 0 00 0 7.4495 0 00 0 0 5.0000 00 0 0 0 2.5505%Exercise 7(1)>> a=[4 1 -1;3 2 -6;1 -5 3];[v,d]=eig(a) v =0.0185 -0.9009 -0.3066-0.7693 -0.1240 -0.7248-0.6386 -0.4158 0.6170d =-3.0527 0 00 3.6760 00 0 8.3766>> det(v)ans =-0.9255 %v行列式正常, 特征向量线性相关，可对角化>> inv(v)*a*v %验算ans =-3.0527 0.0000 -0.00000.0000 3.6760 -0.0000-0.0000 -0.0000 8.3766>> [v2,d2]=jordan(a) %也可用jordanv2 =0.0798 0.0076 0.91270.1886 -0.3141 0.1256-0.1605 -0.2607 0.4213 %特征向量不同d2 =8.3766 0 00 -3.0527 - 0.0000i 00 0 3.6760 + 0.0000i>> v2\a*v2ans =8.3766 0 0.00000.0000 -3.0527 0.00000.0000 0.0000 3.6760>> v(:,1)./v2(:,2) %对应相同特征值的特征向量成比例ans =2.44912.44912.4491%Exercise 7(2)>> a=[1 1 -1;0 2 -1;-1 2 0];[v,d]=eig(a)v =-0.5773 0.5774 + 0.0000i 0.5774 - 0.0000i-0.5773 0.5774 0.5774-0.5774 0.5773 - 0.0000i 0.5773 + 0.0000id =1.0000 0 00 1.0000 + 0.0000i 00 0 1.0000 - 0.0000i>> det(v)ans =-5.0566e-028 -5.1918e-017i %v的行列式接近0, 特征向量线性相关，不可对角化>> [v,d]=jordan(a)v =1 0 11 0 01 -1 0d =1 1 00 1 10 0 1 %jordan标准形不是对角的，所以不可对角化%Exercise 7(3)>> A=[5 7 6 5;7 10 8 7;6 8 10 9;5 7 9 10]A =5 76 57 10 8 76 8 10 95 7 9 10>> [v,d]=eig(A)v =0.8304 0.0933 0.3963 0.3803-0.5016 -0.3017 0.6149 0.5286-0.2086 0.7603 -0.2716 0.55200.1237 -0.5676 -0.6254 0.5209d =0.0102 0 0 00 0.8431 0 00 0 3.8581 00 0 0 30.2887>> inv(v)*A*vans =0.0102 0.0000 -0.0000 0.00000.0000 0.8431 -0.0000 -0.0000-0.0000 0.0000 3.8581 -0.0000-0.0000 -0.0000 0 30.2887%本题用jordan不行, 原因未知%Exercise 7(4)参考6(4)和7(1), 略%Exercise 8 只有(3)对称, 且特征值全部大于零, 所以是正定矩阵. %Exercise 9(1)>> a=[4 -3 1 3;2 -1 3 5;1 -1 -1 -1;3 -2 3 4;7 -6 -7 0]>> rank(a)ans =3>> rank(a(1:3,:))ans =2>> rank(a([1 2 4],:)) %1,2,4行为最大无关组ans =3>> b=a([1 2 4],:)';c=a([3 5],:)';>> b\c %线性表示的系数ans =0.5000 5.0000-0.5000 1.00000 -5.0000%Exercise 10>> a=[1 -2 2;-2 -2 4;2 4 -2]>> [v,d]=eig(a)v =0.3333 0.9339 -0.12930.6667 -0.3304 -0.6681-0.6667 0.1365 -0.7327d =-7.0000 0 00 2.0000 00 0 2.0000>> v'*vans =1.0000 0.0000 0.00000.0000 1.0000 00.0000 0 1.0000 %v确实是正交矩阵%Exercise 11%设经过6个电阻的电流分别为i1, ..., i6. 列方程组如下%20-2i1=a; 5-3i2=c; a-3i3=c; a-4i4=b; c-5i5=b; b-3i6=0; %i1=i3+i4;i5=i2+i3;i6=i4+i5;%计算如下>> A=[1 0 0 2 0 0 0 0 0;0 0 1 0 3 0 0 0 0;1 0 -1 0 0 -3 0 0 0;1 -1 0 0 0 0 -4 0 0;0 -1 1 0 0 0 0 -5 0;0 1 0 0 0 0 0 0 -3;0 0 0 1 0 -1 -1 0 0;0 0 0 0 -1 -1 0 1 0;0 0 0 0 0 0 -1 -1 1];>>b=[20 5 0 0 0 0 0 0 0]'; A\b ans =13.34536.44018.54203.3274-1.18071.60111.72630.42042.1467>> A=[1 2 3;4 5 6;7 8 0];>> left=sum(eig(A)), right=sum(trace(A))left =6.0000right =6>> left=prod(eig(A)), right=det(A) %原题有错, (-1)^n应删去left =27.0000right =27>> fA=(A-p(1)*eye(3,3))*(A-p(2)*eye(3,3))*(A-p(3)*eye(3,3)) fA =1.0e-012 *0.0853 0.1421 0.02840.1421 0.1421 0-0.0568 -0.1137 0.1705>> norm(fA) %f(A)范数接近0ans =2.9536e-013roots([1 1 1])%Exercise 1(2)roots([3 0 -4 0 2 -1])%Exercise 1(3)p=zeros(1,24);p([1 17 18 22])=[5 -6 8 -5];roots(p)%Exercise 1(4)p1=[2 3];p2=conv(p1, p1);p3=conv(p1, p2);p3(end)=p3(end)-4; %原p3最后一个分量-4roots(p3)%Exercise 2fun=inline('x*log(sqrt(x^2-1)+x)-sqrt(x^2-1)-0.5*x'); fzero(fun,2)】%Exercise 3fun=inline('x^4-2^x');fplot(fun,[-2 2]);grid on;fzero(fun,-1),fzero(fun,1),fminbnd(fun,0.5,1.5)%Exercise 4fun=inline('x*sin(1/x)','x');fplot(fun, [-0.1 0.1]);x=zeros(1,10);for i=1:10, x(i)=fzero(fun,(i-0.5)*0.01);end;x=[x,-x]%Exercise 5fun=inline('[9*x(1)^2+36*x(2)^2+4*x(3)^2-36;x(1)^2-2*x(2)^2-20*x(3);1 6*x(1)-x(1)^3-2*x(2)^2-16*x(3)^2]','x');[a,b,c]=fsolve(fun,[0 0 0])%Exercise 6fun=@(x)[x(1)-0.7*sin(x(1))-0.2*cos(x(2)),x(2)-0.7*cos(x(1))+0.2*sin(x(2))]; [a,b,c]=fsolve(fun,[0.5 0.5])%Exercise 7clear; close; t=0:pi/100:2*pi;x1=2+sqrt(5)*cos(t); y1=3-2*x1+sqrt(5)*sin(t);x2=3+sqrt(2)*cos(t); y2=6*sin(t);plot(x1,y1,x2,y2); grid on; %作图发现4个解的大致位置，然后分别求解y1=fsolve('[(x(1)-2)^2+(x(2)-3+2*x(1))^2-5,2*(x(1)-3)^2+(x(2)/3)^2-4]',[ 1.5,2])y2=fsolve('[(x(1)-2)^2+(x(2)-3+2*x(1))^2-5,2*(x(1)-3)^2+(x(2)/3)^2-4]',[ 1.8,-2])y3=fsolve('[(x(1)-2)^2+(x(2)-3+2*x(1))^2-5,2*(x(1)-3)^2+(x(2)/3)^2-4]',[ 3.5,-5])y4=fsolve('[(x(1)-2)^2+(x(2)-3+2*x(1))^2-5,2*(x(1)-3)^2+(x(2)/3)^2-4]',[ 4,-4])%Exercise 8(1)clear;fun=inline('x.^2.*sin(x.^2-x-2)');fplot(fun,[-2 2]);grid on; %作图观察x(1)=-2;x(3)=fminbnd(fun,-1,-0.5);x(5)=fminbnd(fun,1,2);fun2=inline('-x.^2.*sin(x.^2-x-2)');x(2)=fminbnd(fun2,-2,-1);x(4)=fminbnd(fun2,-0.5,0.5);x(6)=2feval(fun,x)%答案: 以上x(1)(3)(5)是局部极小，x(2)(4)(6)是局部极大，从最后一句知道x(1)全局最小，x(2)最大。

Matlab数学实验一2015(标准答案版)

实验一 MATLAB软件应用复习含具体答案

数学实验(MATLAB)课后习题答案

MATLAB全部实验及答案

MATLAB数学实验答案（全）

（完整版）MATLAB）课后实验答案[1]

MATLAB实验及答案详解

Matlab实验及答案

重庆大学数学实验一 matlab的基本应用 参考答案

MATLAB实验一：参考--答案

MATLAB上机实验1答案

Matlab实验第一次实验答案

Matlab实验一答案

MATLAB全部实验及答案

Matlab实验及答案-推荐下载

东北大学MATLAB实验答案

matlab部分实验题答案

(完整版)MATLAB)课后实验答案[1]

MATLAB数学实验课后答案

重庆大学数学实验一 matlab的基本应用参考答案