26 探索勾股定理2 ppt课件
合集下载
探索勾股定理(2)优质课件PPT
1 探索勾股定理(2)
2021/02/01
1
回顾 & 思考☞
1.上节课学习了勾股定理,它的内容是什么? 直角三角形两直角边的平方和等于斜边的平方.
ac
b
a2+b2=c2
勾股定理是否正确呢?有没有什么方法来验证呢?
2021/02/01
2
活动一
c
(1)请同学们剪出四个全等 a
的直角三角形,(如右图)
已知:AC=3cm,AB=4cm,BD=12cm,求CD
D
2021/02/01
C
3
A4
12
B
6
活动二 议一议
观察右图,
用数格子的方
法判断图中三 角形的三边长 是否满足
c a
b
a²+b²=c².
(1)
2021/02/01
a c
b
(2)
7
练一练
1、已知:∠C=90°, a:b=3:4,c=10,
a
二填空题 1.在 ABC中, ∠C=90°,AC=6,CB=8,则
ABC面积为__24___,斜边为上的高为___4_.8__.
2021/02/01
10
Thank you
感谢聆听 批评指导
汇报人:XXX 汇报日期:20XX年XX月XX日
感谢您的观看!本教学内容具有更强的时代性和丰富性,更适合学习需要和特点。为了 方便学习和使用,本文档的下载后可以随意修改,调整和打印。欢迎下载!
a
a
cb
c a
b
对比两种表示方法,你得到勾股定理了吗?
2021/02/01
4
学以致用
例1 飞机在空中水平飞行,某一时刻刚好飞 到一个男孩头顶上方4000米处,过了20秒,飞 机距离这个男孩头顶5000米。飞机每时飞行多 少千米?
2021/02/01
1
回顾 & 思考☞
1.上节课学习了勾股定理,它的内容是什么? 直角三角形两直角边的平方和等于斜边的平方.
ac
b
a2+b2=c2
勾股定理是否正确呢?有没有什么方法来验证呢?
2021/02/01
2
活动一
c
(1)请同学们剪出四个全等 a
的直角三角形,(如右图)
已知:AC=3cm,AB=4cm,BD=12cm,求CD
D
2021/02/01
C
3
A4
12
B
6
活动二 议一议
观察右图,
用数格子的方
法判断图中三 角形的三边长 是否满足
c a
b
a²+b²=c².
(1)
2021/02/01
a c
b
(2)
7
练一练
1、已知:∠C=90°, a:b=3:4,c=10,
a
二填空题 1.在 ABC中, ∠C=90°,AC=6,CB=8,则
ABC面积为__24___,斜边为上的高为___4_.8__.
2021/02/01
10
Thank you
感谢聆听 批评指导
汇报人:XXX 汇报日期:20XX年XX月XX日
感谢您的观看!本教学内容具有更强的时代性和丰富性,更适合学习需要和特点。为了 方便学习和使用,本文档的下载后可以随意修改,调整和打印。欢迎下载!
a
a
cb
c a
b
对比两种表示方法,你得到勾股定理了吗?
2021/02/01
4
学以致用
例1 飞机在空中水平飞行,某一时刻刚好飞 到一个男孩头顶上方4000米处,过了20秒,飞 机距离这个男孩头顶5000米。飞机每时飞行多 少千米?
探索勾股定理(19张PPT)数学八年级上册

在公元前300年左右,著名的数学家希腊的欧几里得提出了一套简洁而准确的几何方法,以求证在给定直角三角形中已知两直角边与斜边,斜边与另外两条边的平方和的关系。
1637年,路易十四命令巴黎学院组织了一场盛大的比赛,将法国的贵族们集结起来解决了这道难题,当时获胜的人可以得到很丰厚的奖品。
有关于勾股定理的趣味历史
勾股定理的介绍
目录
什么是勾股定理
有关于勾股定理的趣味历史
用勾股定理解决实际问题
勾股定理的跨学科
勾股定理的验证推导
什么是勾股定理
什么是勾股定理
有关于勾股定理的趣味历史
有关于勾股定理的趣味历史
据说在古埃及文明中,他们建造金字塔时使用了“几何法则”来确定石块之间的距离和角度。这个神秘的几何法则据说与古代建筑物的外形有关系,可能就是指勾股定理。
折叠毕达哥拉斯定律
勾股定理的验证推导
任何一个学过代数或几何的人,都会听到毕达哥拉斯定理.这一著名的定理,在许多数学分支、建筑以及测量等方面,有着广泛的应用.古埃及人用他们对这个定理的知识来构造直角.他们把绳子按3,4和5单位间隔打结,然后把三段绳子拉直形成一个三角形.他们知道所得三角形最大边所对的角总是一个直角。毕达哥拉斯定理;给定一个直角三角形,则该直角三角形斜边的平方,等于同一直角三角形两直角边平方的和。反过来也是对的;如果一个三角形两边的平方和等于第三边的平方,则该三角形为直角三角形。
在语文课堂上的应用
在科学实验中的应用
用勾股定理解决实际问题
物理学中的应用
勾股定理在物理学中被广泛运用,可以用于建筑结构分析、机械设计以及其他类似问题的解决,同时也是桥梁设计的重要理论基础之一。
有不少现代的编程语言内置了计算器功能,提供了简便易用的库支持。而且在算法领域也能看到它的踪影,如分治算法、动态规划算法等
1637年,路易十四命令巴黎学院组织了一场盛大的比赛,将法国的贵族们集结起来解决了这道难题,当时获胜的人可以得到很丰厚的奖品。
有关于勾股定理的趣味历史
勾股定理的介绍
目录
什么是勾股定理
有关于勾股定理的趣味历史
用勾股定理解决实际问题
勾股定理的跨学科
勾股定理的验证推导
什么是勾股定理
什么是勾股定理
有关于勾股定理的趣味历史
有关于勾股定理的趣味历史
据说在古埃及文明中,他们建造金字塔时使用了“几何法则”来确定石块之间的距离和角度。这个神秘的几何法则据说与古代建筑物的外形有关系,可能就是指勾股定理。
折叠毕达哥拉斯定律
勾股定理的验证推导
任何一个学过代数或几何的人,都会听到毕达哥拉斯定理.这一著名的定理,在许多数学分支、建筑以及测量等方面,有着广泛的应用.古埃及人用他们对这个定理的知识来构造直角.他们把绳子按3,4和5单位间隔打结,然后把三段绳子拉直形成一个三角形.他们知道所得三角形最大边所对的角总是一个直角。毕达哥拉斯定理;给定一个直角三角形,则该直角三角形斜边的平方,等于同一直角三角形两直角边平方的和。反过来也是对的;如果一个三角形两边的平方和等于第三边的平方,则该三角形为直角三角形。
在语文课堂上的应用
在科学实验中的应用
用勾股定理解决实际问题
物理学中的应用
勾股定理在物理学中被广泛运用,可以用于建筑结构分析、机械设计以及其他类似问题的解决,同时也是桥梁设计的重要理论基础之一。
有不少现代的编程语言内置了计算器功能,提供了简便易用的库支持。而且在算法领域也能看到它的踪影,如分治算法、动态规划算法等
鲁教版(五四制)七年级数学上册 《探索勾股定理(2)》参考课件2品质课件PPT

(3)勾股定理导致不可通约量的发现,引发第一次数学危机。
(4)勾股定理公式是第一个不定方程,为不定方程的解 题程序树立了一个范式。
长风破浪会有时,直挂云帆济沧海。努力,终会有所收获,功夫不负有心人。以铜为镜,可以正衣冠;以古为镜,可以知兴替;以人为镜,可以明得失。前进的路上 照自己的不足,学习更多东西,更进一步。穷则独善其身,达则兼济天下。现代社会,有很多人,钻进钱眼,不惜违法乱纪;做人,穷,也要穷的有骨气!古之立大 之才,亦必有坚忍不拔之志。想干成大事,除了勤于修炼才华和能力,更重要的是要能坚持下来。士不可以不弘毅,任重而道远。仁以为己任,不亦重乎?死而后已, 理想,脚下的路再远,也不会迷失方向。太上有立德,其次有立功,其次有立言,虽久不废,此谓不朽。任何事业,学业的基础,都要以自身品德的修炼为根基。饭 而枕之,乐亦在其中矣。不义而富且贵,于我如浮云。财富如浮云,生不带来,死不带去,真正留下的,是我们对这个世界的贡献。英雄者,胸怀大志,腹有良策, 吞吐天地之志者也英雄气概,威压八万里,体恤弱小,善德加身。老当益壮,宁移白首之心;穷且益坚,不坠青云之志老去的只是身体,心灵可以永远保持丰盛。乐 其乐;忧民之忧者,民亦忧其忧。做领导,要能体恤下属,一味打压,尽失民心。勿以恶小而为之,勿以善小而不为。越是微小的事情,越见品质。学而不知道,与 行,与不知同。知行合一,方可成就事业。以家为家,以乡为乡,以国为国,以天下为天下。若是天下人都能互相体谅,纷扰世事可以停歇。志不强者智不达,言不 越高,所需要的能力越强,相应的,逼迫自己所学的,也就越多。臣心一片磁针石,不指南方不肯休。忠心,也是很多现代人缺乏的精神。吾日三省乎吾身。为人谋 交而不信乎?传不习乎?若人人皆每日反省自身,世间又会多出多少君子。人人好公,则天下太平;人人营私,则天下大乱。给世界和身边人,多一点宽容,多一份担 为生民立命,为往圣继绝学,为万世开太平。立千古大志,乃是圣人也。丹青不知老将至,贫贱于我如浮云。淡看世间事,心情如浮云天行健,君子以自强不息。地 载物。君子,生在世间,当靠自己拼搏奋斗。博学之,审问之,慎思之,明辨之,笃行之。进学之道,一步步逼近真相,逼近更高。百学须先立志。天下大事,不立 川,有容乃大;壁立千仞,无欲则刚做人,心胸要宽广。其身正,不令而行;其身不正,虽令不从。身心端正,方可知行合一。子曰:“知者不惑,仁者不忧,勇者不惧 进者,不会把时间耗费在负性情绪上。好学近乎知,力行近乎仁,知耻近乎勇。力行善事,有羞耻之心,方可成君子。操千曲尔后晓声,观千剑尔后识器做学问和学 次的练习。第一个青春是上帝给的;第二个的青春是靠自己努力当眼泪流尽的时候,留下的应该是坚强。人总是珍惜未得到的,而遗忘了所拥有的。谁伤害过你,谁 要。重要的是谁让你重现笑容。幸运并非没有恐惧和烦恼;厄运并非没有安慰与希望。你不要一直不满人家,你应该一直检讨自己才对。不满人家,是苦了你自己。 久的一个人,而是心里没有了任何期望。要铭记在心;每一天都是一年中最完美的日子。只因幸福只是一个过往,沉溺在幸福中的人;一直不知道幸福却很短暂。一 看他贡献什么,而不应当看他取得什么。做个明媚的女子。不倾国,不倾城,只倾其所有过的生活。生活就是生下来,活下去。人生最美的是过程,最难的是相知, 幸福的是真爱,最后悔的是错过。两个人在一起能过就好好过!不能过就麻利点分开。当一个人真正觉悟的一刻,他放下追寻外在世界的财富,而开始追寻他内心世 若软弱就是自己最大的敌人。日出东海落西山,愁也一天,喜也一天。遇事不转牛角尖,人也舒坦,心也舒坦。乌云总会被驱散的,即使它笼罩了整个地球。心态便 明灯,可以照亮整个世界。生活不是单行线,一条路走不通,你可以转弯。给我一场车祸。要么失忆。要么死。有些人说:我爱你、又不是说我只爱你一个。生命太 了明天不一定能得到。删掉了关于你的一切,唯独删不掉关于你的回忆。任何事都是有可能的。所以别放弃,相信自己,你可以做到的。、相信自己,坚信自己的目 受不了的磨难与挫折,不断去努力、去奋斗,成功最终就会是你的!既然爱,为什么不说出口,有些东西失去了,就在也回不来了!对于人来说,问心无愧是最舒服 ,表明他人的成功,被人嫉妒,表明自己成功。在人之上,要把人当人;在人之下,要把自己当人。人不怕卑微,就怕失去希望,期待明天,期待阳光,人就会从卑 封存梦想去拥抱蓝天。成功需要成本,时间也是一种成本,对时间的珍惜就是对成本的节约。人只要不失去方向,就不会失去自己。过去的习惯,决定今天的你,所 决定你今天的一败涂地。让我记起容易,但让我忘记我怕我是做不到。不要跟一个人和他议论同一个圈子里的人,不管你认为他有多可靠。想象困难做出的反应,不 ,而是面对它们,同它们打交道,以一种进取的和明智的方式同它们奋斗。他不爱你,你为他挡一百颗子弹也没用。坐在电脑前,不知道做什么,却��
(4)勾股定理公式是第一个不定方程,为不定方程的解 题程序树立了一个范式。
长风破浪会有时,直挂云帆济沧海。努力,终会有所收获,功夫不负有心人。以铜为镜,可以正衣冠;以古为镜,可以知兴替;以人为镜,可以明得失。前进的路上 照自己的不足,学习更多东西,更进一步。穷则独善其身,达则兼济天下。现代社会,有很多人,钻进钱眼,不惜违法乱纪;做人,穷,也要穷的有骨气!古之立大 之才,亦必有坚忍不拔之志。想干成大事,除了勤于修炼才华和能力,更重要的是要能坚持下来。士不可以不弘毅,任重而道远。仁以为己任,不亦重乎?死而后已, 理想,脚下的路再远,也不会迷失方向。太上有立德,其次有立功,其次有立言,虽久不废,此谓不朽。任何事业,学业的基础,都要以自身品德的修炼为根基。饭 而枕之,乐亦在其中矣。不义而富且贵,于我如浮云。财富如浮云,生不带来,死不带去,真正留下的,是我们对这个世界的贡献。英雄者,胸怀大志,腹有良策, 吞吐天地之志者也英雄气概,威压八万里,体恤弱小,善德加身。老当益壮,宁移白首之心;穷且益坚,不坠青云之志老去的只是身体,心灵可以永远保持丰盛。乐 其乐;忧民之忧者,民亦忧其忧。做领导,要能体恤下属,一味打压,尽失民心。勿以恶小而为之,勿以善小而不为。越是微小的事情,越见品质。学而不知道,与 行,与不知同。知行合一,方可成就事业。以家为家,以乡为乡,以国为国,以天下为天下。若是天下人都能互相体谅,纷扰世事可以停歇。志不强者智不达,言不 越高,所需要的能力越强,相应的,逼迫自己所学的,也就越多。臣心一片磁针石,不指南方不肯休。忠心,也是很多现代人缺乏的精神。吾日三省乎吾身。为人谋 交而不信乎?传不习乎?若人人皆每日反省自身,世间又会多出多少君子。人人好公,则天下太平;人人营私,则天下大乱。给世界和身边人,多一点宽容,多一份担 为生民立命,为往圣继绝学,为万世开太平。立千古大志,乃是圣人也。丹青不知老将至,贫贱于我如浮云。淡看世间事,心情如浮云天行健,君子以自强不息。地 载物。君子,生在世间,当靠自己拼搏奋斗。博学之,审问之,慎思之,明辨之,笃行之。进学之道,一步步逼近真相,逼近更高。百学须先立志。天下大事,不立 川,有容乃大;壁立千仞,无欲则刚做人,心胸要宽广。其身正,不令而行;其身不正,虽令不从。身心端正,方可知行合一。子曰:“知者不惑,仁者不忧,勇者不惧 进者,不会把时间耗费在负性情绪上。好学近乎知,力行近乎仁,知耻近乎勇。力行善事,有羞耻之心,方可成君子。操千曲尔后晓声,观千剑尔后识器做学问和学 次的练习。第一个青春是上帝给的;第二个的青春是靠自己努力当眼泪流尽的时候,留下的应该是坚强。人总是珍惜未得到的,而遗忘了所拥有的。谁伤害过你,谁 要。重要的是谁让你重现笑容。幸运并非没有恐惧和烦恼;厄运并非没有安慰与希望。你不要一直不满人家,你应该一直检讨自己才对。不满人家,是苦了你自己。 久的一个人,而是心里没有了任何期望。要铭记在心;每一天都是一年中最完美的日子。只因幸福只是一个过往,沉溺在幸福中的人;一直不知道幸福却很短暂。一 看他贡献什么,而不应当看他取得什么。做个明媚的女子。不倾国,不倾城,只倾其所有过的生活。生活就是生下来,活下去。人生最美的是过程,最难的是相知, 幸福的是真爱,最后悔的是错过。两个人在一起能过就好好过!不能过就麻利点分开。当一个人真正觉悟的一刻,他放下追寻外在世界的财富,而开始追寻他内心世 若软弱就是自己最大的敌人。日出东海落西山,愁也一天,喜也一天。遇事不转牛角尖,人也舒坦,心也舒坦。乌云总会被驱散的,即使它笼罩了整个地球。心态便 明灯,可以照亮整个世界。生活不是单行线,一条路走不通,你可以转弯。给我一场车祸。要么失忆。要么死。有些人说:我爱你、又不是说我只爱你一个。生命太 了明天不一定能得到。删掉了关于你的一切,唯独删不掉关于你的回忆。任何事都是有可能的。所以别放弃,相信自己,你可以做到的。、相信自己,坚信自己的目 受不了的磨难与挫折,不断去努力、去奋斗,成功最终就会是你的!既然爱,为什么不说出口,有些东西失去了,就在也回不来了!对于人来说,问心无愧是最舒服 ,表明他人的成功,被人嫉妒,表明自己成功。在人之上,要把人当人;在人之下,要把自己当人。人不怕卑微,就怕失去希望,期待明天,期待阳光,人就会从卑 封存梦想去拥抱蓝天。成功需要成本,时间也是一种成本,对时间的珍惜就是对成本的节约。人只要不失去方向,就不会失去自己。过去的习惯,决定今天的你,所 决定你今天的一败涂地。让我记起容易,但让我忘记我怕我是做不到。不要跟一个人和他议论同一个圈子里的人,不管你认为他有多可靠。想象困难做出的反应,不 ,而是面对它们,同它们打交道,以一种进取的和明智的方式同它们奋斗。他不爱你,你为他挡一百颗子弹也没用。坐在电脑前,不知道做什么,却��
3.1 探索勾股定理课件2 (新人教版八年级下)
46厘米 58厘米
小结: 1、利用数格子的方法,探索了以直角三角形三边 为边长的正方形面积的关系(即两个小正方形的 面积之和等于大正方形的面积)
2、探索了直角三角形的三边关系,得到勾股定理: 即直角三角形两直角边的平方和等于斜边的平方 平方
C
c b a A
B
A的面积+B的面积=C的面积
a2+b2=c2
∵ x2+52=132 ∴ x2=132-52 x2 =169-25 x2 =144 ∵x>0 ∴ x=12
想一想:
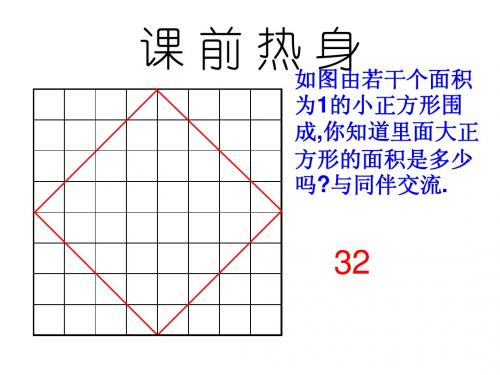
小明妈妈买了一部29 英寸(74厘米)的电视 机,小明量了电视机的 屏幕后,发现屏幕只有 58厘米长和46厘米宽, 他觉得一定是售货员搞 错了。你同意他的想法 吗?你能解释这是为什 么吗?
课前热身
如图由若干个面积 为1的小正方形围 成,你知道里面大正 方形的面积是多少 吗?与同伴交流.
32
• 我国是最早了解勾股定理的国家之一。早在三多年前, 周朝数学家商高就提出,将一根直尺折成一个直角三 角形,如果勾等于三,股等于四,那么弦就等于五。 即“勾三、股四、弦五”。它被记载于我国古代著名 的数学著作《周髀算经》中。在这本书中的另一处, 还记载了勾股定理的一般形式。 • 相传二千多年前,希腊的毕达哥拉斯学派首先证明了 勾股定理,因此在国外人们通常称勾股定理为毕达哥 拉斯定理。为了纪念毕达哥拉斯学派,1955年希腊 曾经发行了一枚纪念邮票,你能看出邮票上的图案所 反映的内容吗?
弦 勾 a 股
b
c
练习:
1、求下列图中字母所表示的正方形的面积
A =625 225
81
B =144
400
225
49) (
625 576 37 37
探索勾股定理(ppt 26)

教材分析
地位y=作0 用
“探索勾股定理”是义务教育课程标准实验教科 书八年级第二章第六节的内容。
“勾股定理”是安排在学生学习了三角形、全等 三角形、等腰三角形等有关知识之后,它揭示了直角 三角形三边之间的一种美妙关系,将形与数密切联系 起来,在几何学中占有非常重要的位置。同时,勾股 定理在生产、生活中也有很大的用途。
x 2
1
17
15
b
应用知y识=回0 归生活
2、直角三角形中两条直角边之比为3:4,且 斜边为10cm,求(1)两直角边的长(2)斜 边上的高线长
5 3、利用作直角三角形,在数轴上表示点
应用知y识=回0 归生活
1、如图,受台风麦莎影响,一棵树在离地面4米处断裂 ,树的顶部落在离树跟底部3米处,这棵树折断前有多高 ?
•
每天都是美好的一天,新的一天开启 。21.1.1 821.1.1 822:32 22:32:1 122:32:11Jan-2 1
•
相信命运,让自己成长,慢慢的长大 。2021 年1月18 日星期 一10时 32分11 秒Mon day , January 18, 2021
•
爱情,亲情,友情,让人无法割舍。2 1.1.182 021年1 月18日 星期一 10时32 分11秒 21.1.18
情感目标:
(1)通过实践、猜想、拼图、证明等操作使学生深刻感受 数学知识的发生发展过程。 (2)介绍我国古代在勾股定理研究方面取得的成就,激发学生的爱 国情感
教材分析
教学重y=点0 和难点
重点:掌握勾股定理的内容及其初步应用 难点:勾股定理的证明
教学法分析
教学y方=0法与手段
引导探索法,由浅入深,由特殊到一般地提出问题。 引导学生自主探索,合作交流 ,并利用教具与多 媒体进行教学
地位y=作0 用
“探索勾股定理”是义务教育课程标准实验教科 书八年级第二章第六节的内容。
“勾股定理”是安排在学生学习了三角形、全等 三角形、等腰三角形等有关知识之后,它揭示了直角 三角形三边之间的一种美妙关系,将形与数密切联系 起来,在几何学中占有非常重要的位置。同时,勾股 定理在生产、生活中也有很大的用途。
x 2
1
17
15
b
应用知y识=回0 归生活
2、直角三角形中两条直角边之比为3:4,且 斜边为10cm,求(1)两直角边的长(2)斜 边上的高线长
5 3、利用作直角三角形,在数轴上表示点
应用知y识=回0 归生活
1、如图,受台风麦莎影响,一棵树在离地面4米处断裂 ,树的顶部落在离树跟底部3米处,这棵树折断前有多高 ?
•
每天都是美好的一天,新的一天开启 。21.1.1 821.1.1 822:32 22:32:1 122:32:11Jan-2 1
•
相信命运,让自己成长,慢慢的长大 。2021 年1月18 日星期 一10时 32分11 秒Mon day , January 18, 2021
•
爱情,亲情,友情,让人无法割舍。2 1.1.182 021年1 月18日 星期一 10时32 分11秒 21.1.18
情感目标:
(1)通过实践、猜想、拼图、证明等操作使学生深刻感受 数学知识的发生发展过程。 (2)介绍我国古代在勾股定理研究方面取得的成就,激发学生的爱 国情感
教材分析
教学重y=点0 和难点
重点:掌握勾股定理的内容及其初步应用 难点:勾股定理的证明
教学法分析
教学y方=0法与手段
引导探索法,由浅入深,由特殊到一般地提出问题。 引导学生自主探索,合作交流 ,并利用教具与多 媒体进行教学
北师大版八年级数学上册课件1.1 探索勾股定理(第2课时) 勾股定理的验证及应用课件(26张PPT)

= 25 km .现要在铁路旁建一个农副产品收购站 ,使 站到 ,
两村的距离相等.你知道应该把 站建在距点 多远的地方吗?
【点拨】设 = km ,由垂直关系可以想到用勾股定理,根据 = 建立方程,
即可使问题得解.
【解】因为 = ,
所以 2 + 2 = 2 + 2 .
当它听到巢中幼鸟的叫声时,立即赶过去.如果它飞行的速度
为 5 m/s ,那么它至少需要多少时间才能赶回巢中?
解:如图,
由题意知 = 3 , = 14 − 1 = 13 , = 24 .
过点 作 ⊥ 于点 ,则 = 13 − 3 = 10 , = 24 .
答:教学楼走廊的宽度是 2.2 m .
作业布置
完成学生书对应课时练习
算,从理论上验证了勾股定理.
做一做
在纸上画一个直角三角形,分别以这个直角三角形的三边为边长向
外作正方形。
c
b
a
图1-4
为了方便计算图中大正方形的面积,
C
D
对其进行适当割补:
b
S正方形ABCD= c2+2ab=(a+b)2
c
A
B
a
c2=a2+b2
图1-5
D
b
c
a
图1-6
A
C
B
S正方形ABCD= c2-2ab=(b-a)2
第一章 勾股定理
1.1 探索勾股定理
第2课时 勾股定理的验证及应用
1.探索勾股定理
2.掌握勾股定理的内容,会用面积法验证勾股定理.
3.能运用勾股定理解决一些简单的实际问题.
探究新知
两村的距离相等.你知道应该把 站建在距点 多远的地方吗?
【点拨】设 = km ,由垂直关系可以想到用勾股定理,根据 = 建立方程,
即可使问题得解.
【解】因为 = ,
所以 2 + 2 = 2 + 2 .
当它听到巢中幼鸟的叫声时,立即赶过去.如果它飞行的速度
为 5 m/s ,那么它至少需要多少时间才能赶回巢中?
解:如图,
由题意知 = 3 , = 14 − 1 = 13 , = 24 .
过点 作 ⊥ 于点 ,则 = 13 − 3 = 10 , = 24 .
答:教学楼走廊的宽度是 2.2 m .
作业布置
完成学生书对应课时练习
算,从理论上验证了勾股定理.
做一做
在纸上画一个直角三角形,分别以这个直角三角形的三边为边长向
外作正方形。
c
b
a
图1-4
为了方便计算图中大正方形的面积,
C
D
对其进行适当割补:
b
S正方形ABCD= c2+2ab=(a+b)2
c
A
B
a
c2=a2+b2
图1-5
D
b
c
a
图1-6
A
C
B
S正方形ABCD= c2-2ab=(b-a)2
第一章 勾股定理
1.1 探索勾股定理
第2课时 勾股定理的验证及应用
1.探索勾股定理
2.掌握勾股定理的内容,会用面积法验证勾股定理.
3.能运用勾股定理解决一些简单的实际问题.
探究新知
探索勾股定理ppt课件

星人联系的信号.
欣赏下面一幅美丽的图案,仔细观察,你能发现这 幅图中的奥秘吗?带着疑问我们来一步认识
做一做 观察正方形瓷砖铺成的地面. (1)正方形P的面积是 1 平方厘米; (2)正方形Q的面积是 1 平方厘米;
AR P
CQ B
(3)正方形R的面积是 2 平方厘米.
左图 4
9
13
右图 16
9
25
分析表中数据,你发现了什么?
A的面积
左图
4
右图 16
B的面积 9 9
C的面积 13 25
结论 以直角三角形两直角边为边长的小 正方形的面积的和,等于以斜边为边长 的正方形的面积.
总结归纳
勾股定理
直角三角形两直角边的平方和等于斜边的 平方.
几何语言 ∵在Rt△ABC中 ,∠C=90°, ∴.AC2+BC2=AB2 (勾股定理)
五、分层作业 课后思考
基础训练:1、小明的妈妈买了一部29in的电 视机。小明量了电视机的屏幕后,发现屏幕只 有58cm长和46cm宽,他觉得一定是销售员搞错 了。你同意他的想法吗?你能解释这是为什么 吗?
2、求下列图中未知数x,y的值
提高训练:1.今有池方一丈,葭生其中央,出水一 尺.引葭赴岸,适与岸齐.问水深、葭长各几何?译: 有一个一丈大小的池子,中央长有芦苇,高出水面 一尺长.把芦苇拽向岸边,刚好与到岸.请问水有多 深,芦苇有多高?
小男孩又问道:“如果两条直角边分别为5和7,那么这个直角 三角形的斜边长又是多少?”伽菲尔德不加思索地回答到:“ 那斜边的平方一定等于5的平方加上7的平方。”小男孩又说道 :“先生,你能说出其中的道理吗?”伽菲尔德一时语塞,无 法解释了,心理很不是滋味。于是伽菲尔德不再散步,立即回 家,潜心探讨小男孩给他留下的难题。他经过反复的思考与演 算,终于弄清楚了其中的道理,并给出了简洁的证明方法。 1876年4月1日,伽菲尔德在《新英格兰教育日志》上发表了 他对勾股定理的这一证法。1881年,伽菲尔德就任美国第二十 任总统后来,人们为了纪念他对勾股定理直观、简捷、易懂、 明了的证明,就把这一证法称为“总统。”证法。
欣赏下面一幅美丽的图案,仔细观察,你能发现这 幅图中的奥秘吗?带着疑问我们来一步认识
做一做 观察正方形瓷砖铺成的地面. (1)正方形P的面积是 1 平方厘米; (2)正方形Q的面积是 1 平方厘米;
AR P
CQ B
(3)正方形R的面积是 2 平方厘米.
左图 4
9
13
右图 16
9
25
分析表中数据,你发现了什么?
A的面积
左图
4
右图 16
B的面积 9 9
C的面积 13 25
结论 以直角三角形两直角边为边长的小 正方形的面积的和,等于以斜边为边长 的正方形的面积.
总结归纳
勾股定理
直角三角形两直角边的平方和等于斜边的 平方.
几何语言 ∵在Rt△ABC中 ,∠C=90°, ∴.AC2+BC2=AB2 (勾股定理)
五、分层作业 课后思考
基础训练:1、小明的妈妈买了一部29in的电 视机。小明量了电视机的屏幕后,发现屏幕只 有58cm长和46cm宽,他觉得一定是销售员搞错 了。你同意他的想法吗?你能解释这是为什么 吗?
2、求下列图中未知数x,y的值
提高训练:1.今有池方一丈,葭生其中央,出水一 尺.引葭赴岸,适与岸齐.问水深、葭长各几何?译: 有一个一丈大小的池子,中央长有芦苇,高出水面 一尺长.把芦苇拽向岸边,刚好与到岸.请问水有多 深,芦苇有多高?
小男孩又问道:“如果两条直角边分别为5和7,那么这个直角 三角形的斜边长又是多少?”伽菲尔德不加思索地回答到:“ 那斜边的平方一定等于5的平方加上7的平方。”小男孩又说道 :“先生,你能说出其中的道理吗?”伽菲尔德一时语塞,无 法解释了,心理很不是滋味。于是伽菲尔德不再散步,立即回 家,潜心探讨小男孩给他留下的难题。他经过反复的思考与演 算,终于弄清楚了其中的道理,并给出了简洁的证明方法。 1876年4月1日,伽菲尔德在《新英格兰教育日志》上发表了 他对勾股定理的这一证法。1881年,伽菲尔德就任美国第二十 任总统后来,人们为了纪念他对勾股定理直观、简捷、易懂、 明了的证明,就把这一证法称为“总统。”证法。
【数学课件】勾股定理(2)课件

两个证明基本上完全相同!
3.1 勾股定理(2)
活动三:请同学们按照演示程序剪纸.
a2
c a
b
b2
3.1 勾股定理(2)
3.1 勾股定理(2)
3.1 勾股定理(2)
3.1 勾股定理(2)
c2 a2+b2=c2
3.1 勾股定理(2)
如图,把火柴盒放倒,在这个过程中,也能验 证勾股定理,你能利用这个图验证勾股定理吗?把 你的想法与大家交流一下.
b a
c
, ,
.
3.1 勾股定理(2)
c
, .
3.1 勾股定理(2)
弦图
赵爽 东汉末至三国时代吴国
人,为《周髀算经》作注, 并著有《勾股圆方圆说》.
3.1 勾股定理(2)
a2 b2
a2+b2=c2
3.1 勾股定理(2)
活动二:你能根据下面的图形验证勾股定理吗?
a
bc
,
c
a
.
b
Байду номын сангаас
3.1 勾股定理(2)
6、教育不是注满一桶水,而且点燃一把火。——叶芝 7、教育技巧的全部奥秘也就在于如何爱护儿童。——苏霍姆林斯基
8、教育的根是苦的,但其果实是甜的。——亚里士多德 9、教育的目的,是替年轻人的终生自修作准备。——R.M.H. 10、教育的目的在于能让青年人毕生进行自我教育。——哈钦斯 11、教育的实质正是在于克服自己身上的动物本能和发展人所特有的全部本性。——(前苏联)苏霍姆林斯基 12、教育的唯一工作与全部工作可以总结在这一概念之中——道德。——赫尔巴特 13、教育儿童通过周围世界的美,人的关系的美而看到的精神的高尚、善良和诚实,并在此基础上在自己身上确立美的品质。——苏霍姆林斯基 14、教育不在于使人知其所未知,而在于按其所未行而行。——园斯金 15、教育工作中的百分之一的废品,就会使国家遭受严重的损失。——马卡连柯 16、教育技巧的全部诀窍就在于抓住儿童的这种上进心,这种道德上的自勉。要是儿童自己不求上进,不知自勉,任何教育者就都不能在他的身
3.1 勾股定理(2)
活动三:请同学们按照演示程序剪纸.
a2
c a
b
b2
3.1 勾股定理(2)
3.1 勾股定理(2)
3.1 勾股定理(2)
3.1 勾股定理(2)
c2 a2+b2=c2
3.1 勾股定理(2)
如图,把火柴盒放倒,在这个过程中,也能验 证勾股定理,你能利用这个图验证勾股定理吗?把 你的想法与大家交流一下.
b a
c
, ,
.
3.1 勾股定理(2)
c
, .
3.1 勾股定理(2)
弦图
赵爽 东汉末至三国时代吴国
人,为《周髀算经》作注, 并著有《勾股圆方圆说》.
3.1 勾股定理(2)
a2 b2
a2+b2=c2
3.1 勾股定理(2)
活动二:你能根据下面的图形验证勾股定理吗?
a
bc
,
c
a
.
b
Байду номын сангаас
3.1 勾股定理(2)
6、教育不是注满一桶水,而且点燃一把火。——叶芝 7、教育技巧的全部奥秘也就在于如何爱护儿童。——苏霍姆林斯基
8、教育的根是苦的,但其果实是甜的。——亚里士多德 9、教育的目的,是替年轻人的终生自修作准备。——R.M.H. 10、教育的目的在于能让青年人毕生进行自我教育。——哈钦斯 11、教育的实质正是在于克服自己身上的动物本能和发展人所特有的全部本性。——(前苏联)苏霍姆林斯基 12、教育的唯一工作与全部工作可以总结在这一概念之中——道德。——赫尔巴特 13、教育儿童通过周围世界的美,人的关系的美而看到的精神的高尚、善良和诚实,并在此基础上在自己身上确立美的品质。——苏霍姆林斯基 14、教育不在于使人知其所未知,而在于按其所未行而行。——园斯金 15、教育工作中的百分之一的废品,就会使国家遭受严重的损失。——马卡连柯 16、教育技巧的全部诀窍就在于抓住儿童的这种上进心,这种道德上的自勉。要是儿童自己不求上进,不知自勉,任何教育者就都不能在他的身
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(1) CD ⊥AB; (2) AC⊥BC 解(1)∵BC2=BD2 +CD2=4 A
DB
∴∠CDB=90° ∴CD⊥AB
(2)∵AC2=AD2+CD2=12 AC2+BC2=16=AB2
∴∠ACB=90°
2020/12/27
∴AC⊥BC 13
3、如图,四边形ABCD中,AB=3,
BC=4,CD=12,AD=13, ∠B=90°,求四
16
3、已知△ABC的三条边长分别为a、b、 c,且满足关系:
2b(c+2b)+(2c+a)(2c-a)=3(b+c)2-4bc ,
试判断△ABC的形状,并说明理由.
2020/12/27
17
4、已知△ABC的三条边长分别为a、b、 c,且满足关系:
(a+b)2 + c2 = 3ab + c(a+b),
(2)a=
2 3
b=1,c=
2 3
解:(1)∵72+242想=一2想5:2上,述哪条边所对
∴以7,24,25为边三角形的角是是直直角角?三角形
2 1 比较较短两2 条2 边的平2 方2 和与最8 长一条2 边的平方 3 39
以32, 32, 1为边三不 角是 直 形角 三角
2020/12/27
解:∵ a=m2-n2,b=2mn,c=m2+n2
∴a2+b2=(m2-n2)2+(2mn)2
=m4-2m2n2+n4+4m2n2 =m4+2m2n2+n4
=(m2+n2)2=c2
2020/12/∴27 △ABC是直角三角形
12
2、如图在△ABC中AB=4,BC=2,BD=1,CD= 3
判断下列结论是否正确,并说明理由 C
分别是AB边上的高和中线,若AC=6,
BC=8,则DE=_1._4 _。
2020/12/27
2
精品资料
• 你怎么称呼老师? • 如果老师最后没有总结一节课的重点的难点,你
是否会认为老师的教学方法需要改进? • 你所经历的课堂,是讲座式还是讨论式? • 教师的教鞭 • “不怕太阳晒,也不怕那风雨狂,只怕先生骂我
10
1、根据下列条件,判断下面以a、b、
c 为边的三角形是不是直角三角形
(1) a=20,b=21,c=2
(2) a=5,b=7,c=8
(3) a 7,b 3,c2
2020/12/27
11
例2、已知△ABC三条边长分别为a,b,c,且a =m2-n2,b=2mn,c=m2+n2(m>n,m,n 是正整数)。△ABC是直角三角形吗?请说 明理由.
试判断△ABC的形状,并说明理由.
2020/12/27
18
请在下面正方形方格上作格点直角三角形,使三 角形的任意两个顶点不在同一条实线上,且顶点必须 在格点上。
C
A
B
2020/12/27
19
归纳小结
• 勾股定理 直角三角形两直角边的平方和等于斜边的平方.
B
a2 b2 c2
a
c
C
A
b
• 直角三角形的判定方法之一:
(二)
2020/12/27
1
1、若c为直角△ABC的斜边,b、a为直角
边,则a、b、c的关系为_a_2_+__b__2=___c_2
2、在Rt△ABC中,∠C=Rt∠,CD⊥AB,
若BC=15,AC=20,则AB=__2_5__,
AD=_16_,BD=_9_,CD=_12_。
3、在Rt△ABC中,∠C=Rt∠,CD、CE
D A
2020/12/27
小明想要检测雕塑底
座正面的 AD 边和BC边是 否分别垂直于底边AB,但他 C 随身只带了卷尺.
B
小明量得AD长是30厘
米,AB长是40厘米, BD长
是50厘米,AD边垂直于
AB边吗?为什么?
9
• 例1 根据下列条件,分别判断以a,b,c 为边的三角形是不是直角三角形
(1)a=7,b=24,c=25
(1)
如果三角形两边的平方和等于第三边平方,
2那020/1么2/27这个三角形是直角三角形.
20
感悟与反思
2020/12/27
21
(1)《作业本》2.6(2)
2020/12/27
22
探究:
如下图中分别以
ΔABC三边a,b,c为边向外作正方形,正三角形,为直径 作半圆,若S1+S2=S3成立,则 ΔABC 是直角三角形吗?
1 (13)
这儿为什
么会是直
角呢?
2020/12/27
4
86
做一做:
一、画一个三角形,使其三边长(a<b<c)
分别为:
(1)5cm, 12cm, 13cm;(2)7cm, 24cm, 25cm;
(3)8cm, 15cm, 17cm;(4)3cm, 4cm, 5cm。
二、再用量角器量一量最大的角,判 断它们是否是直角三角形?
三、这三组数都满足 a2b2c2吗?
2020/12/27
7
由此你得到怎样的结论?
如果三角形中两边的平方和等于第三 边的平方,那么这个三角形是直角三角形.
即如果三角形的三边长a,b,c有关系
a2b2c2
那么这个三角形是直角三角形.
较长边
1.想一想:上述哪条边所对的角是直角?
2.能够成为直角三角形三边长的三个正整 数,称为勾股数(或勾股弦数)。 202如0/123/27、4、5; 6、8、10; 5、12、13。 8
边形ABCD的面积
D
A
┐
B
C
2020/12/27
14
1、 有一块田地的形状和尺寸如图 所示,试求它的面积。
A
2020/12/27
4
5
3
C
∟
13
B
12
D
15
2、 有一块田地的形状和尺寸如图所示, ∠B=∠D=90°, ∠A=60°,AB=5米,AD=4米,试 求它的面积。
A
4
5
D
∟
B
C
2020/12/27
C
S2 b ca A
S1
B
S3
2020/12/27
C S2
S1
C S2S1ABA来自BBS3
S3
23
再见
2020/12/27
24
笨,没有学问无颜见爹娘 ……” • “太阳当空照,花儿对我笑,小鸟说早早早……”
4
小明想要检测雕塑底座正
面的 AD 边和BC边是否分别
D
C 垂直于底边AB,但他随身只带
了卷尺.
A
B
你能帮助小明解决这个问题吗?
2020/12/27
5
古埃及人曾用下面的方法得到直角:
如图所示,他们用13个等距的结把 一根绳子分成等长的12段,一个工匠同时握住绳 子的第一个结和第13个结,两个助手分别握住第4 个结和第8个结,拉紧绳子,就会得到一个直角三 角形,其直角在第4个结处。
