云南省德宏州梁河县一中高中数学《3.1.1 两角差的余弦公式》教学设计 湘教版必修4
3.1《两角差的余弦公式》教学设计

3.1.1 两角差的余弦公式 (名师:郑莹莹)一、教学目标 (一)核心素养掌握用向量方法建立两角差的余弦公式. 在探究公式的过程中,逐步培养学生学会分析问题、解决问题的能力,培养学生学会合作交流的能力. (二)学习目标1.通过探索完成两角差余弦公式的推导2.通过公式的简单应用,使学生初步理解公式的结构及其功能,并为建立其他和(差)角公式打好基础. (三)学习重点通过探索得到两角差的余弦公式 (四)学习难点探索过程的组织和适当引导,这里不仅有学习积极性的问题,还有探索过程必用的基础知识是否已经具备的问题,运用已学知识和方法的能力问题等等. 二、教学设计 (一)课前设计 1.预习任务 已知2cos 45=,3cos30=,由此我们能否得到()cos15cos 4530?=-=是不是等于cos 45cos30-呢?如果不是,那cos15?=o2.预习自测(1)下列式子中正确的个数是( )①cos(α-β)=cos α-cos β;②cos(α-β)=cos αcos β-sin αsin β; ③cos(π2-α)=cos α;④cos(π2+α)=cos α. A .0 B .1C .2D .3 答案:A .解析:【知识点】两角差的余弦公式 【解题过程】①②③④都错点拨:每个都配凑成标准两角差的余弦公式型. (2)计算12sin 60°+32cos 60°=________.答案:32 解析:【知识点】特殊角的三角函数值,两角差的余弦公式 【解题过程】原式=sin 30°sin 60°+cos 30°cos 60° =cos(60°-30°)=cos 30°=32.点拨:先将常值换成三角函数型,在结合公式.(3)设α∈⎝ ⎛⎭⎪⎫0,π2,若sin α=35,则2cos ⎝ ⎛⎭⎪⎫α-π4=( )A.75 B.15 C .-75 D .-15 答案:A .解析:【知识点】两角差公式的展开形式【解题过程】∵α∈⎝ ⎛⎭⎪⎫0,π2,sin α=35,∴cos α=45. ∴2cos ⎝ ⎛⎭⎪⎫α-π4=2⎝ ⎛⎭⎪⎫cos αcos π4+sin αsin π4=cos α+sin α=45+35=75.点拨:先求出需要的三角函数值,再套用公式.(二)课堂设计 1.知识回顾(1)三角函数的定义 (2)两个向量的数量积公式 2.问题探究 探究一 ●活动1在预习任务中我们提出的cos15?=o ,同学们发现它并不是直接将cos 45-cos30︒o.下面我们一起来探究一下两角差的余弦公式()cos ?αβ-=在第一章三角函数的学习当中我们知道,在设角α的终边与单位圆的交点为p ,cos α等于角α与单位圆交点的横坐标,也可以用角α的余弦线来表示,大家思考:怎样构造角β和角αβ-?(注意:要与它们的正弦线、余弦线联系起来.) 【设计意图】通过已经学习过的三角函数线的基本定义,运用数形结合的思想,和学生一起探索出两角差的几何位置. ●活动2我们在第二章学习用向量的知识解决相关的几何问题,两角差余弦公式我们能否用向量的知识来证明?提示:1、结合图形,明确应该选择哪几个向量,它们是怎样表示的? 2、怎样利用向量的数量积的概念的计算公式得到探索结果? 在证明公式之前先引导学生结合三角函数知识写出点A 、点B 的坐标.证明:在平面直角坐标系xOy 内作单位圆O ,以Ox 为 始边作角αβ、,其中,且[]0,αβ∈、πβα≥,它们的终边与单位圆O 的交点分别为A 、B ,则(cos ,sin ),(cos ,sin )OA OB ααββ==由向量数量积的坐标表示,有:βαβαββααsin sin cos cos )sin ,(cos )sin ,(cos +=∙=∙由[]π,0,∈βα,且βα≥知[]πβα,0∈-,那么向量OA 的夹角就是βα-,由数量积的定义,有cos()cos()OA OB OA OB αβαβ∙=-=-于是βαβαβαsin sin cos cos )cos(+=- (1) 由于我们前面的推导均是在[]0,αβ∈、π,且βα≥的条件下进行的,因此(1)式还不具备一般性.事实上,只要[]πβα,0∈-,βα-所表示的就是向量,OA OB 的夹角.(这一点可以结合图形作出说明.)但是,若[]πβα,0∉-,(1)式是否依然成立呢? 当[]πβα,0∉-时,设与的夹角为θ,则cos cos OA OB OA OB θθ∙==βαβαsin sin cos cos +=另一方面,θβπα++=k 2,于是,,2Z k k ∈+=-θπβα所以θβαcos )cos(=-也有βαβαβαsin sin cos cos )cos(+=-【设计意图】在探究公式的过程中,教材不要求学生做到一步到位.首先对角选择较为特殊的范围来进行探究,能让学生从整体上感知本节课所要探究的途径与目的,让大部分学生都参与到探究中来,避免部分学生一开始就感觉到困难,提不起向下探究的兴趣. 探究二 ●活动①对任意的()cos cos cos sin sin αβαβαβαβ-=+、 ,注:1.公式中两边的符号正好相反(一正一负);2.式子右边同名三角函数相乘再加减,且余弦在前正弦在后;3.式子中α、β是任意的.【设计意图】和学生一起记忆新公式,并强调如何能准确熟练的记住. 探究三 ●活动1例1利用差角余弦公式求︒15cos 【知识点】两角差的余弦公式 【解题过程】方法一:cos15cos(4530)cos 45cos30sin 45sin 30︒=︒-︒=︒︒+︒︒=方法二:cos15cos(6045)cos 60cos 45sin 60sin 45︒=︒-︒=︒︒+︒︒=【思路点拨】先找到与15°相关的特殊角,而它的配凑有几种不同形式,都可以尝试用公式计算..同类型训练题:如何求︒75sin ?解析:【知识点】两角差的余弦,诱导公式. 【数学思想】类比【解题过程】sin 75cos15︒=︒=点拨:把没有学过的形式向已经学习过的转化,当然这个题同时也提出了两角和正弦公式.例2化简求值︒︒+︒︒20sin 80sin 20cos 80cos 1)(︒+︒15sin 2315cos 212)(【知识点】两角差的余弦公式的逆用【解题过程】︒︒+︒︒20sin 80sin 20cos 80cos 1)(2160cos )2080cos(=︒=︒-︒=(2)1=cos60sin 602︒=︒所以原式cos60cos15sin 60sin15cos(6015)︒︒+︒︒=︒-︒=点拨:根据结构形式,把公式灵活应用,逆用公式,能将特殊值转化成角的三角函数值形式.答案:(1)12(2同类型训练题:化简求值(1)cos cos(15)sin sin(15)x x x x +︒++︒(2)cos32cos77sin 32cos167︒︒-︒︒答案:(1(2解析:【知识点】两角差的余弦公式的逆用 【解题过程】cos cos(15)sin sin(15)cos(15)cos15x x x x x x +︒++︒=+︒-=︒(1)cos32cos77sin 32cos13cos32cos77sin 32sin 77=cos45︒︒+︒︒=︒︒+︒︒︒(2) 点拨:根据结构形式,把公式灵活应用,逆用公式,能将特殊值转化成角的三角函数值形式. ●活动2例345sin ,(,),cos ,cos()5213πααπββαβ=∈=--已知是第三象限角,求的值 答案:3365-解析:【知识点】同角三角函数关系,两角差的余弦公式 【解题过程】由⎪⎭⎫⎝⎛∈=ππαα,2,54sin ,得53sin 1cos 2-=--=αα又由ββ,135cos -=是第三象限角,得12sin 13β==-所以βαβαβαsin sin cos cos )cos(+=-所以原式=354123351351365⎛⎫⎛⎫⎛⎫-⨯-+⨯-=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭点拨:先把公式中需要的单角的正弦和余弦值都求出来,此时要注意正负号的象限问题. 再套用两角差的余弦公式就可以了. 同类型训练题:已知αβ、都是锐角,1411)cos(,71cos -=+=βαα,求 βcos 的值.答案:1cos 2β=解析:【知识点】两角差的余弦公式,两角和的余弦公式,同角三角函数的关系 【数学思想】类比归纳【解题过程】法一:由1cos ,0,72παα⎛⎫=∈ ⎪⎝⎭,得sin α=又由11cos()cos(())cos cos sin sin()=-14αβαβαβαβ+=--=+-所以111cos sin 714ββ⨯=-,同时22cos +sin 1ββ=联立得 1cos 2β=法二:由题知2παβπ⎛⎫+∈ ⎪⎝⎭,,所以sin()sin αβα+== 1cos cos[()]cos()cos sin()sin =2βαβααβααβα∴=+-=+++点拨:此题是对公式的活用,由学生讨论解决.此题一般有两种方法可以求解.一种方法是把)cos(βα+分解,此公式还没推导,但部分学生可能会把βα+看作βα)(--,然后用两角差的余弦公式分解,再结合同角三角函数的基本关系求解.这种方法虽然较繁,但却让学生在无意当中发现了两角和的余弦公式.另一种方法是把β看做两角差,即αβαβ-+=)(,这种方法显然计算要简单得多.通过不同方法的讲解,鼓励学生从不同的角度思考问题,并指引学生在考试中选择较为简便的方法解题.【设计意图】此题理解公式的基础练习,解此题需要思考使用公式前应作出的必要准备,要作出这些必要的准备,需要运用到同角三角函数的知识.解题时必须强调解决三角变换问题的基本要求:思维的有序性和表述的条理性. 3.课堂总结知识梳理(1)了解两角差的余弦公式的推导过程;(2)熟练记忆公式和逆用形式; (3)能利用公式进行简单的化简和求值.重难点归纳(1)了解两角差的余弦公式的推导过程;(2)对公式的简单应用. (三)课后作业基础型 自主突破1.设(0,)2απ∈,若3sin 5α=,)4απ+=( )A.15B.75C.75-D.15-答案:A解析:【知识点】两角差的余弦公式【解题过程】∵(0,)2απ∈,3sin 5α=,∴4cos 5α=,原式cos cos -+sin sin -44ααππ⎤⎥⎦()()=431cos sin 555αα-=-= 点拨:应用公式展开,将对应的函数值代入 2.sin110sin 40cos 40cos 70+等于( )A.12-C.1 2D.答案:B解析:【知识点】两角差的余弦公式的逆用,诱导公式【解题过程】原式cos40cos70sin40sin(18070)=+-cos40cos70sin40sin70 =+=3 cos(4070)cos(30)-=-=点拨:先统一角的形式,使其与两角差的余弦公式形式一致,再用公式化简. 3.1sin10-的值是( )A.1B.2C.4D.14答案:C解析:【知识点】两角差的余弦公式,诱导公式【解题过程】()()()()()32cos10sin102cos103sin10=2cos60cos10sin60sin10=1cos80cos10sin80sin1022cos6010=41cos80102⎫-⎪-⎝⎡⎤-+-⎣⎦+--=-原式点拨:先将特殊值化为具体三角函数,再将公式结构配凑成标准型4.sin1212ππ-的值是( )B.D.-12答案:B解析:【知识点】特殊角的三角函数值,两角差的余弦公式【解题过程】原式=12sin 12212⎫ππ--⎪⎪⎭=2cos 2cos 1264πππ⎛⎫-+=-= ⎪⎝⎭ 点拨:先将常数配凑成特殊角的三角函数值,并让整体符合两角差的余弦公式,再化简.5.已知3sin 5α=-,α是第四象限角,则sin 4πα⎛⎫- ⎪⎝⎭=____________.解析:【知识点】同角三角函数关系,两角差的余弦公式,诱导公式【解题过程】由3sin 5α=-,α是第四象限角,得4cos 5α===,于是有sin cos()cos cos sin sin 4444ππππαααα⎛⎫-=+=- ⎪⎝⎭4355⎛⎫=-- ⎪⎝⎭ 点拨:先求出需要的三角函数值,将正弦化成余弦形式,再结合两角差的余弦公式.能培养将未知的转化成已经学习过的知识的迁移能力. 6.不满足sin αsin β=22-cos αcos β的一组α,β值是( ) A .α=π2,β=π4 B .α=2π3,β=5π12C .α=2π3,β=π12D .α=π4,β=π2答案:C解析:【知识点】两角差的余弦公式【解题过程】因为sin αsin β=22-cos αcos β,所以cos(α-β)=22,经检验C中的α,β不满足点拨:应用公式展开注意逆用.能力型 师生共研7.已知锐角αβ、满足4cos 5α=,1tan(=3αβ--),求cos β.解析:【知识点】同角的三角函数值的关系,两角差的余弦公式【解题过程】αQ 为锐角,且4cos 5α=,得3sin 5α= 40,0,cos 225ππαβα<<<<=Q ∴22ππαβ-<-<又∵1tan(3αβ-=-) ∴cos()αβ-= 从而sin()tan()cos()αβαβαβ-=--=43cos cos[()]cos cos()+sin sin()(55βααβααβααβ=--=--=+⨯点拨:先求出单角的三角函数值,关键是能将所求角β利用已知的两个整体角αβα-、表示,在求角的时候注意角所在的象限及符号.8.若α为锐角,且cos α=255,则cos ⎝ ⎛⎭⎪⎫π4-α=________.答案:31010解析:【知识点】两角差的余弦公式【解题过程】由α为锐角,且cos α=255,可得sin α=55.于是cos ⎝ ⎛⎭⎪⎫π4-α=cos π4cos α+sin αsin π4=22×255+22×55=31010 点拨:应用公式展开注意逆用.探究型 多维突破9.已知sin sin sin 0,cos cos cos 0.αβγαβγ++=++=(1)求cos()αβ-的值;(2)若[0,3αβγ4π∈]、、,求sin()αβγ++的值. 答案:sin()sin 2αβγ++=π=0解析:【知识点】同角三角函数的关系,两角差的余弦公式【解题过程】(1)sin sin sin ,cos cos cos ,αβγαβγ+=-+=-22(sin sin )(cos cos )1,αβαβ+++=22cos()1,αβ+-=∴1cos()2αβ-=-. (2)由(1)同理得11cos(),cos()22βγαγ-=--=-, ∵[0,3αβγ4π∈]、、,由对称性,不防设03αβγ4π≥>>≥, 则03αβ4π<-<,03βγ4π<-<,03αγ4π<-≤, 又由(1)知3αβ2π-=,3βγ2π-=,3αγ4π-=,若0γ>,则33αγ4π4π=+>矛盾! ∴0γ=,有3β2π=,3α4π=, ∴sin()sin 2αβγ++=π=0.点拨:本着消元的思想,消掉γ进一步配凑出αβ-的整体角的余弦.利用对称思想构造已知角的表示形式,进一步推出矛盾.10.若cos(α-β)=55,cos 2α=1010,并且α、β均为锐角,且α<β,则α+β的值为( )A.π6B.π4C.3π4D.5π6答案:C解析:【知识点】两角差的余弦公式,配角【解题过程】∵0<α<β<π2,∴-π2<α-β<0,0<2α<π,∴由cos(α-β)=55,得sin (α-β)=-255,由cos 2α=1010,得sin 2α=31010.∴cos(α+β)=()cos 2ααβ--⎡⎤⎣⎦=cos 2αcos(α-β)+sin 2αsin(α-β)=1010×55+31010×⎝⎛⎭⎪⎫-255=-22. 又α+β∈(0,π),∴α+β=3π4.点拨:公式形式牢记,利用已知角配凑α+β自助餐 1.cos 110°cos 20°+sin 110°sin 20°= ( )A.122C.0答案:C解析:【知识点】两角差的余弦公式【解题过程】cos(11020)cos900︒-︒=︒=点拨:公式形式牢记,逆用. 2.2cos10sin 20cos 20-的值是( )C.1D.12答案:A解析:【知识点】两角差的余弦公式【解题过程】2cos10sin 20cos 20-2cos 3020sin 20=cos 20--o o o o () 点拨:角的拆分,要尽量统一角的形式结合特殊角三角函数值.3.已知A 、B 均为钝角,sin A =sin B =则A +B 的值为( ) A.74π B.54π4D.4π答案:A解析:【知识点】两角差的余弦公式,两角和的余弦公式.【解题过程】,,cos 22A B A B ππ<<π<<π∴==cos()cos cos sin sin =(A B A B A B +=-=724A B A B ππ<+<π∴+= 点拨:将两角和的余弦配成[]cos cos cos sin sin A B A B A B -=-(-)由此题也就推导出了两角和的余弦公式4.函数22sincos()336x x y π=++的图象中相邻两对称轴的距离是________. 答案:32π 解析:【知识点】两角差的余弦公式,三角函数图形性质.【解题过程】22222sincos cos sin sin cos cos sin sin 336363636x x x x x y ππππ=+-=+ 22cos(),3362/3x T ππ=-==π,相邻两对称轴的距离是周期的一半 点拨:先将函数式化简,要先用到两角和的余弦公式,学生可以通过上面的问题总结出公式,或者也可以将“和”转化为“差”在理解.再逆用两角差的公式收拢.5.若,22sin sin =+βα则cos cos αβ+的取值范围.答案:cos cos αβ≤+≤ 解析:【知识点】同角的三角函数关系,两角差的余弦公式【解题过程】令cos cos t αβ+=,则2221(sin sin )(cos cos ),2t αβαβ+++=+ 221322cos(),2cos()22t t αβαβ+-=+-=-2231722,,222t t t -≤-≤-≤≤≤≤点拨:整体换元的思想,利用同角三角函数的关系,构造两角差的余弦公式,结合函数思想将cos()αβ-表示成t 的函数,通过值域求出t 的范围.6.已知α,β∈[3π4,π],sin ()α+β=-35,sin (β-π4)=1213,则cos (α+π4)=________.答案:-5665解析:【知识点】同角的三角函数关系,两角差的余弦公式【解题过程】∵α,β∈[3π4,π].∴α+β∈[3π2,2π],β-π4∈[π2,3π4],又sin(α+β)=-35,sin (β-π4)=1213,∴cos(α+β)=1-sin 2(α+β)=45,cos (β-π4)=-1-sin 2(β-π4)=-513.∴cos (α+π4)=cos[(α+β)-(β-π4)]=cos(α+β)cos (β-π4)+sin(α+β)sin (β-π4)=45×(-513 )+(-35 )×1213=-5665. 点拨:整体换元的思想,利用同角三角函数的关系,构造两角差的余弦公式.。
3.1.1两角差的余弦公式(教、优秀教案)

3.1.1 两角差地余弦公式
一、教材分析 《两角差地余弦公式》 是人教 A 版高中数学必修 4 第三章 《三角恒等变换》 第一节 《两
角和与差地正弦、余弦和正切公式》第一节课地内容
.本节主要给出了两角差地余弦公式地
推导,要引导学生主动参与,独立思索,自己得出相应地结论
.b5E2RGbCAP
三、解答题、
6.已知 sin
2,
3
, 3 cos 3 ,
2
4
0, ,求 cos( 2
) 地值 .
版权申明
本文部分内容,包括文字、图片、以及设计等在网上搜集整理 . 版权为个人所有
This article includes some parts, including text, pictures,
9 / 11
最后要提醒学生注意,公式推导地前提条件:
、、
都是锐角,且
2. 向量法:
问:①结合图形,明确应选哪几个向量,它们怎么表示?
② 怎样利用向量数量积地概念和计算公式得到结果
.
③ 对探索地过程进一步严谨性地思考和处理,从而得到合理地科学结论
.
设计意图: 让学生经历利用向量知识解决一个数学问题地过程,
体会向量方法解决数学
设计意图: 由给出地背景素材, 使学生感受数学源于生活,又应用于生活, 唤起学生解
决问题地兴趣, 和抛出新知识引起学生地疑惑,在兴趣和疑惑中,
激发学生地求知欲, 引导
学习方向 .5PCzVD7HxA
(二)、研探新知
1 / 11
个人收集整理 仅供参考学习
1. 三角函数线法: 问: ①怎样作出角
、、
地终边 .
3.1.1 两角差的余弦公式 教案

3.1.1 两角差的余弦公式一、教学目标1.引导学生建立两角差的余弦公式。
通过公式的简单应用,使学生初步理解公式的结构及其功能,并为建立其他和差公式打好基础。
2.在探究公式的过程中,逐步培养学生学会分析问题、解决问题的能力,培养学生学会合作交流的能力。
二、教学重点难点重点:两角差余弦公式的探索和简单应用。
难点:探索过程的组织和引导。
三、学情分析之前学习了三角函数的性质,以及平面向量的运算和应用,在此基础上,要考虑如何利用任意角α、β,的正弦余弦值来表示cos(α-β),牢固的掌握这个公式,并会灵活运用公式进行下一节内容的学习。
四、教学方法1.自主性学习法:通过自学掌握两角差的余弦公式。
2.探究式学习法:通过分析、探索、掌握两角差的余弦公式的过程。
3.反馈练习法:以练习来检验知识的应用情况,找出未掌握的内容及其存在的差距。
五、设计思路本节课利用向量的数量积运算的定义来推导两角差的余弦公式,在学习两角差的余弦公式时,应从特例入手,归纳、提炼、拓展到一般的两角差的余弦公式,从单位圆上的三角函数和向量两种不同的途径探索、推导公式。
六、教学过程(一)新课导入某城市的电视发射塔建在市郊的一座小山上.如图所示,小山高BC约为30米,在地平面上有一点A,测得A、C两点间距离约为60米,从A观测电视发射塔的视角(∠CAD)约为45°,∠CAB=15°.求这座电视发射塔的高度。
对于30°,45°,60°等特殊角的三角函数值可以直接写出,利用诱导公式还可进一步求出150°,210°,315°等角的三角函数值。
我们希望再引进一些公式,能够求更多的非特殊角的三角函数值,同时也为三角恒等变换提供理论依据。
若,αβ为两个任意角, 则Cos()Cos Cos αβαβ-=-成立吗? 令60,30αβ=︒=︒,显然Cos(6030)Cos60Cos30︒-︒≠︒-︒154530,Cos15Cos(4530)︒=︒-︒∴︒=︒-︒Q 。
3.1.1《两角差的余弦公式》教学设计

3.1.1《两角差的余弦公式》教学设计本节课中心任务是通过已知的平面向量和三角函数的知识,探索推导出两角差的余弦公式。
并通过简单的运用,使学生初步理解公式的由来、结构、功能及其运用,分一课时完成。
三角恒等变换处于三角函数与数学变换的结合点和交汇点上,两角差的余弦公式是《三角恒等变换》这一章的基础和出发点,是前面所学三角函数知识的继续与发展,是培养学生推理能力和运算能力的重要素材。
所以,从知识的结构和内容上看都具有承上启下的作用。
二、教学实录1.教学目标掌握用向量方法建立两角差的余弦公式。
通过简单运用,使学生初步理解公式的结构及其功能,为建立其他和(差)公式打好基础。
2.教学重、难点(1)教学重点:通过探索得到两角差的余弦公式。
(2)教学难点:探索过程的组织和适当引导,这里不仅有学习积极性的问题,还有探索过程必用的基础知识是否已经具备的问题,运用已学知识和方法的能力问题,等等。
3.学法与教学用具(1)学法:启发式教学。
(2)教学用具:多媒体。
导入:我们在初中时就知道cos45°=,cos30°=,由此我们能否得到cos15°=cos(45°-30°)=?大家可以猜想,是不是等于cos45°-cos30°呢?根据我们在第一章所学的知识可知我们的猜想是错误的!下面我们就一起探讨两角差的余弦公式cos(a-β)=?探讨过程:在第一章三角函数的学习当中我们知道,在设角a的终边与单位圆的交点为P1,cosa等于角a与单位圆交点的横坐标,也可以用角a的余弦线来表示,大家思考:怎样构造角β和角a-β?(注意:要与它们的正弦线、余弦线联系起来。
)展示多媒体动画课件,通过正、余弦线及它们之间的几何关系探索cos(a-β)与cosa、cosβ、sina、sinβ之间的关系,由此得到cos(a-β)=cosacosβ+sinasinβ,认识两角差余弦公式的结构。
高中数学《两角差的余弦公式》教案和教案说明

3.1.1 两角差的余弦公式教学分析本节首先引导学生对cos(α-β)的结果进行探究,让学生充分发挥想象力,进行猜想,给出所有可能的结果,然后再去验证其真假.这也展示了数学知识的发生、发展的具体过程,最后提出了两种推导证明“两角差的余弦公式”的方案.方案一,利用单位圆上的三角函数线进行探索、推导,让学生动手画图,构造出α-β角,利用学过的三角函数知识探索存在一定的难度,教师要作恰当的引导.方案二,利用向量知识探索两角差的余弦公式时,要注意推导的层次性:①在回顾求角的余弦有哪些方法时,联系向量知识,体会向量方法的作用;②结合有关图形,完成运用向量方法推导公式的必要准备;③探索过程不应追求一步到位,应先不去理会其中的细节,抓住主要问题及其线索进行探索,然后再反思,予以完善;④补充完善的过程,既要运用分类讨论的思想,又要用到诱导公式.本节是数学公式的教学,教师要遵循公式教学的规律,应注意以下几方面:①要使学生了解公式的由来;②使学生认识公式的结构特征,加以记忆;③使学生掌握公式的推导和证明;④通过例子使学生熟悉公式的应用,灵活运用公式进行解答有关问题.三维目标1.通过让学生探索、猜想、发现并推导“两角差的余弦公式”,了解单角与复角的三角函数之间的内在联系,并通过强化题目的训练,加深对两角差的余弦公式的理解,培养学生的运算能力及逻辑推理能力,提高学生的数学素质.2.通过两角差的余弦公式的运用,会进行简单的求值、化简、证明,体会化归思想在数学当中的运用,使学生进一步掌握联系的观点,自觉地利用联系变化的观点来分析问题,提高学生分析问题、解决问题的能力.3.通过本节的学习,使学生体会探究的乐趣,认识到世间万物的联系与转化,养成用辩证与联系的观点看问题.创设问题情境,激发学生分析、探求的学习态度,强化学生的参与意识,从而培养学生分析问题、解决问题的能力和代换、演绎、数形结合等数学思想方法.重点难点教学重点:通过探究得到两角差的余弦公式.教学难点:探索过程的组织和适当引导.课时安排1课时教学过程导入新课思路2.(复习导入)我们在初中时就知道cos45°=22,cos30°=23,由此我们能否得到cos15°=cos(45°-30°)=?这里是不是等于cos45°-cos30°呢?教师可让学生验证,经过验证可知,我们的猜想是错误的.那么究竟是个什么关系呢?cos(α-β)等于什么呢?这时学生急于知道答案,由此展开新课:我们就一起来探讨“两角差的余弦公式”.这是全章公式的基础.推进新课新知探究提出问题①请学生猜想cos(α-β)=?②利用前面学过的单位圆上的三角函数线,如何用α、β的三角函数来表示cos(α-β)呢? ③利用向量的知识,又能如何推导发现cos(α-β)=?④细心观察C (α-β)公式的结构,它有哪些特征?其中α、β角的取值范围如何?⑤如何正用、逆用、灵活运用C (α-β)公式进行求值计算?活动:问题①,出示问题后,教师让学生充分发挥想象能力尝试一下,大胆猜想,有的同学可能就首先想到cos(α-β)=cosα-cosβ的结论,此时教师适当的点拨,然后让学生由特殊角来验证它的正确性.如α=60°,β=30°,则cos(α-β)=cos30°=23,而cosα-cosβ=cos60°-cos30°=231-,这一反例足以说明cos(α-β)≠cosα-cosβ. 0060,30,αβ==如让学生明白,要想说明猜想正确,需进行严格证明,而要想说明猜想错误,只需一个反例即可.问题②,既然cos(α-β)≠cosα-cosβ,那么cos(α-β)究竟等于什么呢?由于这里涉及的是三角函数的问题,是α-β这个角的余弦问题,我们能否利用单位圆上的三角函数线来探究呢?图1如图1,设角α的终边与单位圆的交点为P 1,∠POP 1=β,则∠POx=α-β.过点P 作PM 垂直于x 轴,垂足为M,那么OM 就是角α-β的余弦线,即OM=cos(α-β),这里就是要用角α、β的正弦线、余弦线来表示OM.过点P 作PA 垂直于OP 1,垂足为A,过点A 作AB 垂直于x 轴,垂足为B,过点P 作PC 垂直于AB,垂足为C.那么,OA 表示cosβ,AP 表示sinβ,并且∠PAC=∠P 1Ox=α.于是,OM=OB+BM=OB+CP=OAcosa+APsina =cosβcosα+sinβsinα,所以,cos(α-β)=cosαcosβ+sinα sinβ.教师引导学生进一步思考,以上的推理过程中,角α、β、α-β是有条件限制的,即α、β、α-β均为锐角,且α>β,如果要说明此结果是否对任意角α、β都成立,还要做不少推广工作,并且这项推广工作的过程比较繁琐,由同学们课后动手试一试.图2问题③,教师引导学生,可否利用刚学过的向量知识来探究这个问题呢?如图2,在平面直角坐标系xOy 内作单位圆O,以Ox 为始边作角α、β,它们的终边与单位圆O 的交点分别为A 、B,则=(cosα,sinα),=(cosβ,sinβ),∠AOB =α-β.由向量数量积的定义有OA ·OB =|OA ||OB |·cos(α-β)=cos(α-β), 由向量数量积的坐标表示有·=(cosα,sinα)(cosβ,sinβ)=cosαcosβ+sinαsinβ, 于是,cos(α-β)=cosαcosβ+sinαsinβ.我们发现,运用向量工具进行探究推导,过程相当简洁,但在向量数量积的概念中,角α-β必须符合条件0≤α-β≤π,以上结论才正确,由于α、β都是任意角,α-β也是任意角,因此就是研究当α-β是任意角时,以上公式是否正确的问题.当α-β是任意角时,由诱导公式,总可以找到一个角θ∈[0,2π),使cosθ=cos(α-β),若θ∈[0,π],则OA ·OB =cosθ=cos(α-β).若θ∈[π,2π],则2π-θ∈[0,π],且OA ·OB =cos(2π-θ)=cosθ=cos(α-β). 由此可知,对于任意角α、β都有此公式给出了任意角α、β的正弦、余弦值与其差角α-β的余弦值之间的关系,称为差角的余弦公式,简记为C (α-β).有了公式C (α-β)以后,我们只要知道cosα、cosβ、sinα、sinβ的值,就可以求得cos(α-β)的值了.问题④,教师引导学生细心观察公式C (α-β)的结构特征,让学生自己发现公式左边是“两角差的余弦”,右边是“这两角的余弦积与正弦积的和”,可让学生结合推导过程及结构特征进行记忆,特别是运算符号,左“-”右“+”.或让学生进行简单填空,如:cos(A-B)=__________,cos(θ-φ)= __________等.因此,只要知道了sinα、cosα、sinβ、cosβ的值就可以求得cos(α-β)的值了. 问题⑤,对于公式的正用是比较容易的,关键在于“拆角”的技巧,而公式的逆用则需要学生的逆向思维的灵活性,特别是变形应用,这就需要学生具有较强的观察能力和熟练的运算技巧.如cos75°cos45°+sin75°sin45°=cos(75°-45°)=cos30°=23, cosα=cos [(α+β)-β]=cos(α+β)cosβ+sin(α+β)sinβ.讨论结果:①—⑤略.应用示例思路1例1 利用差角余弦公式求cos15°的值.活动:先让学生自己探究,对有困难的学生教师可点拨学生思考题目中的角15°,它可以拆分为哪些特殊角的差,如15°=45°-30°或者15°=60°-45°,从而就可以直接套用公式C (α-β)计算求值.教师不要包办,充分让学生自己独立完成,在学生的具体操作下,体会公式的结构,公式的用法以及把未知转化为已知的数学思想方法.对于很快就完成的同学,教师鼓励其换个角度继续探究.解:方法一:cos15°=cos(45°-30°)=cos45°cos30°+sin45°sin30° =.42621222322+=⨯+⨯ 方法二:cos15°=cos(60°-45°)=cos60°cos45°+sin60°sin45° =21×.426232222+=⨯+ 点评:本题是指定方法求cos15°的值,属于套用公式型的,这样可以使学生把注意力集中到使用公式求值上.但是仍然需要学生将这个非特殊角拆分成两个特殊角的差的形式,灵活运用公式求值.本例也说明了差角余弦公式也适用于形式上不是差角,但可以拆分成两角差的情形.至于如何拆分,让学生在应用中仔细体会.变式训练1.不查表求sin75°,sin15°的值解:sin75°=cos15°=cos(45°-30°)=cos45°cos30°+sin45°sin30° =.42621322322+=⨯+⨯ sin15°= 15cos 12-=2)426(1+-=.426162628-=⨯- 点评:本题是例题的变式,比例题有一定的难度,但学生只要细心分析,利用相关的诱导公式,不难得到上面的解答方法.2.不查表求值:cos110°cos20°+sin110°sin20°.解:原式=cos(110°-20°)=cos90°=0.点评:此题学生一看就有似曾相识而又无从下手的感觉,需要教师加以引导,让学生细心观察,再结合公式C (α-β)的右边的特征,逆用公式便可得到cos(110°-20°).这就是公式逆用的典例,从而培养了学生思维的灵活性.例2 已知sinα=54,α∈(2π,π),cosβ=135-,β是第三象限角,求cos (α-β)的值. 活动:教师引导学生观察题目的结构特征,联想到刚刚推导的余弦公式,学生不难发现,欲求cos(α-β)的值,必先知道sinα、cosα、sinβ、cosβ的值,然后利用公式C (α-β)即可求解.从已知条件看,还少cosα与sinβ的值,根据诱导公式不难求出,但是这里必须让学生注意利用同角的平方和关系式时,角α、β所在的象限,准确判断它们的三角函数值的符号.本例可由学生自己独立完成.解:由sinα=54,α∈(2π,π),得 cosα=.53)54(1sin 122-=--=--a又由cosβ=135-,β是第三象限角,得 sinβ=.1312)135(1cos 122-=---=--β 所以cos(α-β)=cosαcosβ+sinαsinβ =.6533)1312(54)135()53(-=-⨯+-⨯- 点评:本题是直接运用公式C (α-β)求值的基础练习,但必须思考使用公式前应作出的必要准备.特别是运用同角三角函数平方关系式求值时,一定要弄清角的范围,准确判断三角函数值的符号.教师可提醒学生注意这点,养成良好的学习习惯.变式训练已知sinα=54,α∈(0,π),cosβ=135-,β是第三象限角,求cos(α-β)的值.解:①当α∈[2π,π)时,且sinα=54,得cosα=53)54(1sin 122-=--=--a , 又由cosβ=135-,β是第三象限角,得 s inβ=22)135(1cos 1---=--β=1312-. 所以cos(α-β)=cosαcosβ+sinαsinβ =.6533)1312(54)135()53(-=-⨯+-⨯-. ②当α∈(0,2π)时,且sinα=54,得 cosα=53)54(1sin 122=-=-a , 又由cosβ=135-,β是第三象限角,得 sinβ=.1312)135(1cos 122-=---=--β 所以cos(α-β)=cosαcosβ+sinαsinβ =.6563)1312(54)135(53-=-⨯+-⨯ 点评:本题与例2的显著的不同点就是角α的范围不同.由于α∈(0,π),这样cosα的符号可正、可负,需讨论,教师引导学生运用分类讨论的思想,对角α进行分类讨论,从而培养学生思维的严密性和逻辑的条理性.教师强调分类时要不重不漏.课堂小结1.先由学生自己思考、回顾公式的推导过程,观察公式的特征,特别要注意公式既可正用、逆用,还可变用及掌握变角和拆角的思想方法解决问题.然后教师引导学生围绕以下知识点小结:(1)怎么联系有关知识进行新知识的探究?(2)利用差角余弦公式方面:对公式结构和功能的认识;三角变换的特点.2.教师画龙点睛:本节课要理解并掌握两角差的余弦公式及其推导,要正确熟练地运用公式进行解题,在解题时要注意分析三角函数名称、角的关系,准确判断三角函数值的符号.多对题目进行一题多解,从中比较最佳解决问题的途径,以达到优化解题过程,规范解题步骤,领悟变换思路,强化数学思想方法之目的.作业1、 课本习题3.1 A 组2、3、4任选两题;2、 (选做题)课本习题3.1 B 组第4题.教案说明:1.本节课是典型的公式教学模式,因此本节课的设计流程为“实际问题→猜想→探索推导→记忆→应用”.它充分展示了公式教学中以学生为主体,进行主动探索数学知识发生、发展的过程.同时充分发挥教师的主导作用,引导学生利用旧知识推导、证明新知识,并学会记忆公式的方法,灵活运用公式解决实际问题,从而培养学生独立探索数学知识的能力,增强学生的应用意识,激发学生学习的积极性.2.纵观本教案的设计,学生发现推导出公式C(α-β)后就是应用,同时如何训练公式的正用、逆用、变形用也是本节的重点难点.而学生从探究活动过程中学会了怎样去发现数学规律,又发现了怎样逆用公式及活用公式,那才是深层的,那才是我们中学数学教育的最终目的.3.教学矛盾的主要方面是学生的学,学是中心,会学是目的,根据高中三角函数的推理特点,本节主要是教给学生“研究问题、猜想探索公式、验证特殊情形、推导公式、学习应用”的探索创新式学习方法.这样做增强了学生的参与意识,教给了学生发现规律、探索推导,获取新知的途径,让学生真正尝到探索的喜悦,真正成为教学的主体.学生体会到数学的美,产生一种成功感,从而提高了学习数学的兴趣.。
云南省德宏州梁河县一中高中数学《3.1.1 两角差的余弦公式》学案 湘教版必修4

云南省德宏州梁河县一中高一数学《3.1.1 两角差的余弦公式》学案湘教版必修4一、学习目标(1)掌握两角差的余弦公式; 思考题:()cos αβ-= (2)两角差的余弦公式的简单应用; 思考题:0cos165= . 二、问题与例题问题1:()cos αβ-与任意角,αβ的正弦、余弦值之间有什么关系呢?问题2:()cos αβ-会等于cos cos αβ-吗?例题1:你能利用差角余弦公式求0cos15的值吗?例题2:已知4sin 5α= ,,2παπ⎛⎫∈ ⎪⎝⎭,5cos 13β=-,β是第三象限角,求()cos αβ-问题3:联系公式和本题的条件,要计算()cos αβ-,应作哪些准备? 问题4:我们学习了两角差的余弦公式,你能归纳一下本节主要的知识点吗?三、目标检测1、cos()2πα-= 2、()cos 2πα-=3、已知3cos 5α=-,(,)2παπ∈,求cos 4πα⎛⎫- ⎪⎝⎭的值。
4、已知15sin 17θ=,θ是第三象限角,求cos 3πθ⎛⎫- ⎪⎝⎭的值。
配餐作业一、基础题(A 组)1、0000cos75cos15sin 75sin15+等于 ( )[A 、12B 22C 32D 、1 2、5cos 5α=,则cos()4πα-的值为 ( ) A 310 B 、10 C 25 D 310或103、2cos 3πα⎛⎫- ⎪⎝⎭等于 ( )A 、cos ααB 、cos ααC 、1cos 22αα- D 、1cos 22αα+4、()()()()000026cos 19sin 26sin 19αααα+-++-的值为 ( )A 、2B 、2-C 、2D 、2-二、巩固题(B 组)5、已知α、β均为锐角,并且3sin 5α=,()5cos 13αβ+=,求cos β的值。
6、已知3tan 4α=-,2παπ,求cos 4πα⎛⎫- ⎪⎝⎭。
三、提高题(C 组)7、已知23sin ,,32πααπ⎛⎫=∈ ⎪⎝⎭,3cos 4β= ,3,22πβπ⎛⎫∈ ⎪⎝⎭,求()cos βα-的值。
3.1.1两角差的余弦公式教学设计
1.3.1 差角的余弦公式教学设计
一、学习目标:
知识与技能:1、至少会用一种方法证明差角的余弦公式;
2、记忆公式;
3、公式的正用、逆用、拆角;
过程与方法:1、利用单位圆中正弦线、余弦线证明代数几何问题的数学思考方法;
2、多种角度思考问题,多种方法证明公式;
情感态度价值观:1、热爱数学,发现数学的奥妙。
二、重点难点:
重点:公式的记忆、正用、逆用、构造角;
难点:差角余弦公式的证明。
2、猜想cos15°=?
1、当α、β与α-β均为锐角时,在单位圆中已知α与β,
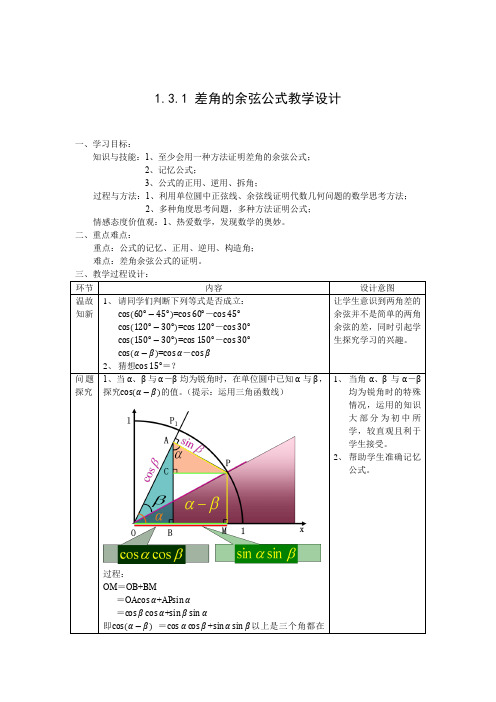
探究cos(α−β)的值。
(提示:运用三角函数线)
过程:
OM=OB+BM
=OA cosα+AP sinα
=cosβcosα+sinβsinα
即cos(α−β)=cosαcosβ+sinαsinβ以上是三个角都在。
高中数学_3.1.1两角差的余弦公式教学设计学情分析教材分析课后反思

2.2.1 直线与平面平行的判定定理教学目标1.知识与技能理解两角差的余弦公式的推导过程;掌握两角差的余弦公式的初步应用。
2.过程与方法通过提出问题,揭示知识背景,引发学生学习兴趣,并经历用向量的数量积推导出两角差的余弦公式的过程,进一步体会向量方法的作用。
3.情感态度与价值观体会探索的乐趣,认识到世间万物的联系与转化,养成用辩证与联系的观点看问题。
创设问题情景,激发学生分析、探求的学习态度,强化学生的参与意识,从而培养学生分析问题、解决问题的能力和数形结合、转化、向量等数学思想方法。
教学重点:掌握两角差的余弦公式及其初步应用。
教学难点:正确使用两角差的余弦公式求值,并能根据具体的问题灵活的使用拆角、变角等方法。
教学方法:(1)自主性学习方法;(2)探究式学习方法;(3)反馈练习法;教学用具:电脑、实物投影仪。
教学过程设计:学情分析基于前两章所学内容:三角函数和平面向量,学生已经积累并掌握的差角余弦公式推导所需要的基础知识,这为公式推导过程的顺利开展奠定的基础。
但是我所教授的学生普遍基础较差,大部分学生对于知识的应用能力还有待提高。
我设计教案时,根据学生的情况,循序渐进。
通过带领学生探索问题——回顾旧知——应用知识解决问题的过程,帮助学生理解并掌握差角余弦公式的推导及其使用公式解决简单问题。
在设计变式时选择了比较简单的题,符合学情。
效果分析通过本节课的学习,学生基本达成了学习目标,多数同学理解差角余弦公式的推导过程,会用差角余弦公式解决简单的化简、求值问题,会正向、逆向使用差角余弦公式,部分同学能当堂针对具体的问题结合之前学习的诱导公式,以及拆角、变角技巧解决较难的题目。
通过例一的学习,掌握了如何应用差角余弦公式求值,结合练习题再次加强的对公式的记忆及正确使用。
当然课堂训练里设计的题目由于用到之前的知识,所以个别同学做起来有点吃力;在例二的学习中,掌握了如何使用条件里给的角所在象限这一条件求所需三角函数值。
教学设计1:3.1.1 两角差的余弦公式

必修四第3章 三角恒等变形 3.1.1 两角差的余弦公式教学目的:知识目标:掌握应用两角差的余弦公式求三角函数值 能用所学知识解决有关综合问题能力目标:让学生经历类比方法学习向量及其几何表示的过程,体验对比理解向量基本概念的简易性,从而养成科学的学习方法。
情感目标:通过本节课的学习,渗透数形结合的思想;树立运动变化观点,学会运用运动变化的观点认识事物;通过学生的亲身实践,引发学生学习兴趣;创设问题情境,激发学生分析、探求的学习态度;让学生感受图形的对称美、运动美,培养学生对美的追求。
教学重点:应用两角差的余弦公式求三角函数值 教学难点:应用两角差的余弦公式求三角函数值 教学过程: 一、复习准备:上节课我们学习了两角差的余弦公式cos(α–β)=cosαcos β+ sinαsinβ(黑板板书)。
这节课我们将学习一下如何应用两角差的余弦公式求三角函数值 例一: 用两角差的余弦公式证明问题(1)cos (π—β)=-cos β (2)cos (2π—β)=cos β证明(1) cos(π—β) = cosπ·cosβ+sinπ·sin β=-1·cosβ +0·sinβ=-cosβ 左边=右边 所以cos(π—β)=-cosβ得证证明(2) cos(2π—β) = cos2π·cosβ + sin 2π·sinβ=1·cosβ + 0·sinβ=cosβ 左边=右边 所以cos(2π—β)=cosβ得证 前面我们都是用抽象的角度,现用具体角度. 例二: 用两角差余弦公式求cos15°.解法一:cos15° =cos(45°—30°)=cos45°·cos30°+sin45°·sin30°12⨯+解法二: cos15°= cos(60°—45°)= cos60°·cos45°+sin60°·sin45° (分成17°-2°是否可行?) 练习:证明: cos(α+β)= cosα·cos β-sinα·sinβ思考 : 能否参考两角差的余弦公式进行推导? 我们的新课改提倡“减负”,从数学的角度,减负就是---“加正”,所以 α+β=α- (- β)证明:∵ cos (α+β)= cos [α-(- β)]=cosα·cos( -β) +sin α ·sin(-β)= cosα·cosβ-sinα·sin β ∴cos(α+β)=cosα·cosβ-sinα·sinβ 课后作业1、利用和、差角余弦公式求cos 75、cos15的值. 解:分析:把75、15构造成两个特殊角的和、差.()231cos 75cos 4530cos 45cos30sin 45sin 3022224=+=-=⨯-=()231cos15cos 4530cos 45cos30sin 45sin 3022224=-=+=⨯+=点评:把一个具体角构造成两个角的和、差形式,有很多种构造方法,例如:()cos15cos 6045=-,要学会灵活运用.2、已知4sin 5α=,5,,cos ,213παπββ⎛⎫∈=- ⎪⎝⎭是第三象限角,求()cos αβ-的值.解:因为,2παπ⎛⎫∈ ⎪⎝⎭,4sin 5α=由此得3cos 5α===-又因为5cos ,13ββ=-是第三象限角,所以12sin 13β===-所以3541233cos()cos cos sin sin 51351365αβαβαβ⎛⎫⎛⎫⎛⎫-=+=-⨯-+⨯-=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭点评:注意角α、β的象限,也就是符号问题.3、利用和、差角余弦公式求、的值.解:6cos 75cos(4530)cos 45cos 30sin 45sin 304-=+=-=6cos 15cos(4530)cos 45cos 30sin 45sin 304+=-=+=点评:把一个具体角构造成两个角的和、差形式,有很多种构造方法,例如:cos 15cos(6045)=-,要学会灵活运用.4、已知4sin 5α=,(,)2παπ∈5,cos 13β=-是第三象限角, 求cos()αβ-的值. 解:因为(,)2παπ∈,4sin 5α=由此得3cos5α==- 又因为5cos 13β=-,β是第三象限角,所以12sin 13β==- 所以33cos()cos cos sin sin 65αβαβαβ-=+=-课后小结:cos(α–β)=cosαcos β+ sinαsinβ板书设计:cos 75cos15。
高中数学_3.1.1 两角差的余弦公式教学设计学情分析教材分析课后反思

3.1.1 两角差的余弦公式教学设计一教学目标知识与能力:理解用向量方法推导两角差的余弦公式并能够初步运用。
过程与方法:在两角差的余弦公式的推导过程中,进一步体会向量方法的作用,分类讨论思想、化归思想的运用。
情感与态度:通过主动参与、独立探索、激发学习兴趣,形成探究、证明、应用的科学学习方式。
二教学重点难点重点:两角差的余弦公式的推导与运用难点:两角差的余弦公式的推导过程的组织与适当引导三教学方法1 通过教师设问引导,学生自主探究,小组合作、交流与讨论,培养学生的自学能力和分析解决问题的能力。
2通过探究、启发、当堂训练的教学程序,采用启发式讲解、互动式讨论的授课方式,借助多媒体辅助教学,达到增加课堂效率的目的,营造生动活泼的课堂教学。
四教学流程五 教学情境设计问题设计意图 师生活动(一) 复习回顾 导入新课点坐标为???由三角函数的定义知,为轴的垂线,垂足作过点点的终边与单位圆交于已知角P MP OM M x P P ==, ,.1α?则,其夹角为已知单位向量=•==b a y x b y x a θ),,(),,(.22211???=-=-=-)2cos()cos()2cos(.3βπβπβπ?)cos(22=-βααπππ,则任意角换成、、思考:若将接近学生认知水平地提出问题,切合本节课的主题。
教师板书课题,学生思考回答,培养学生温故知新的习惯,引导学生思考两角差的余弦如何表示。
(二)分析问题你认为公式会是βαβαcos cos )cos(-=-吗?(1)使学生明确常犯的直觉性错误为什么是错误的。
(2)统一对探究目标中“恒等”要求的认识让学生自己动脑,动手验证,从而认识要探索的公式在“恒等”方面要求的意义。
(三)解决问题(三角函数线法) 怎样联系单位圆上的三角函数线来探 索公式?(1)加强新旧知识的联系性。
(2)使学生从直观角度加强对差角公式结构形式的认识。
让学生亲身经历探索的过程: (1)怎样作出角βαβα-,,的终边;(2)怎样作出角βα-的余弦线(OM)以及角βα,的正弦线、余弦线;(3)怎样利用几何直观寻求OM 的表达式。
3.1.1两角差的余弦公式(教学设计)

3.1.1两角差的余弦公式(教学设计)[教学目标]1、知识与能力:(1) 掌握两角差的余弦公式的推导。
(2)掌握两角差的余弦公式的应用。
并能利用该公式进行简单的证明与计算.2、过程与方法:(1). 经历用向量的数量积推导两角差的余弦公式的过程,进一步体会向量方法的作用.(2).体会“由一般到特殊”的思维过程.3、情感、态度与价值观:通过积极参与数学学习和问题解决的活动,逐步增强批判思维,养成一丝不苟的作风和锲而不舍的精神.[教学重点]两角差的余弦公式的应用。
[教学难点]用向量的数量积推导两角差的余弦公式的过程。
一、 复习回顾1. 任意角三角函数的定义sin ,cos ,tan ,cot yxy xr r x y αααα====2. 同角三角比的关系22tan cot 1sin cos tan ,cot ;cos sin sin cos 1αααααααααα⋅===+=二、师生互动,新课讲解1. 探究:()cos αβαβ-如何用任意角、的正弦、余弦来表示?猜测()cos cos cos αβαβ-=-.()()30cos60cos30c cos cos cos os 60αβαβαβ︒-︒≠︒-︒-=-,因此显对任意角、,然不成立.2. 利用向量探究在平面直角坐标系xOy 内作单位圆O ,以Ox 为始边作角α、β,它们的终边与单位圆O 的交点分别为A 、B . ()()()()()()()cos ,sin cos ,sin .cos cos .cos ,sin cos ,sin cos cos sin sin cos cos cos sin sin .OA OB OA OB OA OB OA OB ααββαβαβααββαβαβαβαβαβ==⋅=⋅-=-⋅=⋅=+-=+ ,由向量数量积的定义,有由向量数量积的坐标表示,有于是则思考:以上推导是否有不严谨之处?若有,请作出补充.[)()[)()[)(]()()()()0,2cos cos .0,cos cos ,20,cos cos cos .cos cos cos sin sin ..OA OB OA OB C αβαβθπθαβθπθαβθπππθππθθαβαβαβαβαβ--∈=-∈==-∈∈===--=+ 当是任意角时,由诱导公式,总可以找到一个角,使若,则;若,则2-,且2-于是,对于任意角、都有简记作3.利用单位圆中的三角函数线探讨两角差的余弦公式(课本P125)在第一章三角函数的学习当中我们知道,在设角α的终边与单位圆的交点为1P ,cos α等于角α与单位圆交点的横坐标,也可以用角α的余弦线来表示,大家思考:怎样构造角β和角αβ-?(注意:要与它们的正弦线、余弦线联系起来.)展示多媒体动画课件,通过正、余弦线及它们之间的几何关系探索()cos αβ-与cos α、cos β、sin α、sin β之间的关系,由此得到cos()cos cos sin sin αβαβαβ-=+,认识两角差余弦公式的结构.思考:我们在第二章学习用向量的知识解决相关的几何问题,两角差余弦公式我们能否用向量的知识来证明? 提示:1)、结合图形,明确应该选择哪几个向量,它们是怎样表示的?2)、怎样利用向量的数量积的概念的计算公式得到探索结果?展示多媒体课件比较用几何知识和向量知识解决问题的不同之处,体会向量方法的作用与便利之处.4.两角差的余弦公式cos()cos cos sin sin αβαβαβ-=+三、公式运用例1、(课本P126例1)利用差角余弦公式求cos15的值. 解:()1cos15cos 4530cos 45cos30sin 45sin302=-=+== 点评:把一个具体角构造成两个角的差形式,有很多种构造方法,例如:()cos15cos 6045=- ,要学会灵活运用. 变式训练1:求cos 105°+sin 195°的值.解析:cos 105°+sin 195°=cos 105°+sin(90°+105°)=cos 105°+cos 105°=2cos 105°=2cos(135°-30°)=2(cos 135°cos 30°+sin 135°sin 30°)=2-62()4sin 5,,cos ,cos .21,53ππββαααβ⎛⎫∈=-- ⎪⎝=⎭是第三象限角课本例已,求知的值例2(P1272)()43sin ,,cos ,525512cos sin 1313cos cos cos sin sin 3541251351333.65πααπαβββαβαβαβ⎛⎫=∈=- ⎪⎝⎭=-=--=+⎛⎫⎛⎫⎛⎫=-⨯-+⨯- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭=-由,得又由,是第三象限角,得,所以解:变式训练2:已知sin θ=45,θ∈(0,π2),求cos(2π3-θ).解析:由sin θ=45,且θ∈(0,π2),得cos θ=35, ∴cos(2π3-θ)=cos 2π3·cos θ+sin 2π3·sin θ=-12×35+32×45=43-310.13cos cos()0,252cos .παα+β<αβ<β例3 已知=,=-,, 求变式训练3:已知sin ⎝⎛⎭⎫α+π4=45,且π4<α<3π4,求cos α的值.【解析】 ∵sin ⎝⎛⎭⎫α+π4=45,且π4<α<3π4,∴π2<α+π4<π,∴cos ⎝⎛⎭⎫α+π4=-1-⎝⎛⎭⎫452=-35.∴cos α=cos ⎣⎡⎦⎤⎝⎛⎭⎫α+π4-π4=cos ⎝⎛⎭⎫α+π4cos π4+sin ⎝⎛⎭⎫α+π4sin π4=-35×22+45×22=210.【互动探究】 在本例中,若把α的范围改为:“54π<α<74π”,其他条件不变,又如何求cos α的值?【解析】 ∵sin ⎝⎛⎭⎫α+π4=45且5π4<α<74π.∴32π<α+π4<2π.∴cos ⎝⎛⎭⎫α+π4=1-sin 2⎝⎛⎭⎫α+π4=1-⎝⎛⎭⎫452=35.∴cos α=cos ⎣⎡⎦⎤⎝⎛⎭⎫α+π4-π4=cos ⎝⎛⎭⎫α+π4·cos π4+sin ⎝⎛⎭⎫α+π4·sin π4=35×22+45×22=7210.课堂练习(课本P127练习NO :1;2;3;4)三、课堂小结,巩固反思:1. 利用向量方法探究推导两角差的余弦公式;2. ()():cos cos cos sin sin .C αβαβαβαβ--=+四、课时必记:1、公式记忆:()():cos cos cos sin sin .C αβαβαβαβ--=+五、【课时作业】一、选择题1.化简cos(45°-α)cos(α+15°)-sin(45°-α)sin(α+15°)的结果为( )A.12 B.-12C.32 D.-32答案 A解析 原式=cos(α-45°)cos(α+15°)+sin(α-45°)sin(α+15°)=cos [(α-45°)-(α+15°)]=cos(-60°)=12.2.若sin αsin β=1,则cos(α-β)的值为( )A.0B.1C.±1D.-1答案 B 解析 由sin αsin β=1,得cos αcos β=0,cos(α-β)=cos αcos β+sin αsin β=1.3.已知点P (1,2)是角α终边上一点,则cos(π6-α)等于( )A 3+66 B.3-66C.-3+66 D.6-36答案 Acos ⎝⎛⎭⎫π6-α=cos π6cos α+sin π6sin α =32×33+12×63=3+66.4.已知cos ⎝⎛⎭⎫θ+π6=513,0<θ<π3,则cos θ等于( )A.53+1226 B.12-5313C.5+12326 D.5+5313答案 A解析 ∵θ∈⎝⎛⎭⎫0,π3,∴θ+π6∈⎝⎛⎭⎫π6,π2,∴sin ⎝⎛⎭⎫θ+π6= 1-cos 2⎝⎛⎭⎫θ+π6=1213.cos θ=cos ⎣⎡⎦⎤⎝⎛⎭⎫θ+π6-π6=cos ⎝⎛⎭⎫θ+π6cos π6+sin ⎝⎛⎭⎫θ+π6sin π6=513×32+1213×12=53+1226.5.若12sin x +32cos x =cos(x +φ),则φ的一个可能值为( )A.-π6B.-π3 C.π6 D.π3答案 A 解析 12sin x +32cos x =cos x cos π6+sin x sin π6=cos ⎝⎛⎭⎫x -π6,故φ的一个可能值为-π6.6.若x ∈[0,π],sin x 3sin 2x 3=cos x 3cos 2x3,则x 的值是( )A.π6B.π4C.π3D.π2答案 D解析 由已知得,cos x 3cos 2x 3-sin x 3sin 2x3=cos x =0.∵x ∈[0,π],∴x =π2.7.已知点A (cos 80°,sin 80°),B (cos 20°,sin 20°),则|AB →|等于( )A.12B.22C.32D.1 答案 D解析 |AB →|=(cos 80°-cos 20°)2+(sin 80°-sin 20°)2=2-2(cos 80°cos 20°+sin 80°sin 20°)=2-2cos 60°= 2-2×12=1. 二、填空题8.已知cos(α-β)cos α+sin(α-β)sin α=m ,且β为第三象限角,则sin β=________.答案 -1-m 2解析 cos (α-β)cos α+sin (α-β)sin α=cos [(α-β)-α]=m .即cos β=m ,∵β为第三象限角,∴sin β=-1-cos 2β=-1-m 2.9.设A ,B 为锐角△ABC 的两个内角,向量a =(2cos A ,2sin A ),b =(3cos B,3sin B ).若a ,b 的夹角的弧度数为π3,则A -B =________ .答案 ±π3 解析 cos π3=a ·b |a |·|b |=6(cos A cos B +sin A sin B )2×3=cos A cos B +sin A sin B =cos(A -B ).又-π2<A -B <π2, ∴A -B =±π3. 10.如图,在平面直角坐标系中,锐角α,β的终边分别与单位圆交于A ,B 两点,如果点A 的纵坐标为35,点B 的横坐标为513,则cos (α-β)=________.答案 5665解析 由三角函数的定义可得,sin α=35,cos β=513,∴cos α=1-(35)2=45,sin β=1213.cos (α-β)=cos αcos β+sin αsin β=45×513+35×1213=5665.三、解答题::11、(课本P137习题3.1 A 组 NO :2)12、(课本P137习题3.1 A 组 NO :3)13、(课本P137习题3.1 A 组 NO :4)参考答案:。
高中数学四 3.1. 1 两角差的余弦公式 【教案】

必修四第三章 3。
1。
1 两角差的余弦公式【教学目标】
1.知识与技能:
通过两角差的余弦公式的探究及简单应用,使学生初步理解公式的结构及其功能。
并为建立其他和(差)角公式打好基础。
2。
过程与方法:
通过利用同角三角函数变换及向量推导两角差的余弦公式,让学生体会利用联系的观点来分析问题,提高学生分析问题、解决问题的能力。
3。
情感态度价值观:
使学生经历数学知识的发现、创造的过程。
体验成功探索新知的乐趣,获得对数学应用价值的认识,激发学生提出问题的意识、努力分析问题、解决问题的激情。
【重点难点】
1.教学重点:两角和与差的余弦公式的理解与灵活运用.
2。
教学难点:两角和与差的余弦公式的推导。
【教学策略与方法】
1。
教学方法:合作探究、启发诱导,学生动手尝试相结合.
2。
教具准备:多媒体【教学过程】
() =-或
cos4530
()
=-
cos15cos6045
3sin 5cos αβ==)54(cos(⨯-=-∴α课堂练习:。
高中数学_3.1.1两角差的余弦公式教学设计学情分析教材分析课后反思

《两角差的余弦公式》教学设计277200课型:新授课一、学情分析(1)授课对象:高一年级的学生(2)学情分析:学生的数学表达能力和逻辑推理能力正处于高度发展阶段,有主动探索新知识的意识,对新知识充满探求的渴望。
在学习本课前,学生已学习了任意角三角函数的概念、平面向量的坐标表示及向量数量积的坐标表示,这为他们探究两角差的余弦公式建立了良好的知识基础。
二、教学内容分析这节内容是教材必修4的第三章《三角恒等变换》第一节,是高考的重要考点,历年高考必考内容。
教材在学生掌握了任意角的三角函数的概念、向量的坐标表示以及向量数量积的坐标表示的基础上,进一步研究用单角的三角函数表示的两角和与差的三角函数.“两角差的余弦公式”在教科书中采用了一种易于教学的推导方法,即先借助于单位圆中的三角函数线,推出α,β,α-β均为锐角时成立.对于α,β为任意角的情况,教材运用向量的知识进行了探究.同时,补充了用向量的方法推导过程中的不严谨之处,这样,两角差的余弦公式便具有了一般性。
三、教学模式、教学支持条件教学模式:诱导—学习---讨论---练习---评价教学支持条件:由于本节内容在公式的证明过程中要用到图形,而多媒体能直观、快捷地展示图形和内空的生成,故在讲授的过程中借助多媒体手段是一个不错的选择。
四、教学目标1、知识目标通过两角差的余弦公式的探究,让学生在初步理解公式的结构及其功能的基础上记忆公式,并用之解决简单的数学问题,为后面推导其他和(差)角公式打好基础。
2、能力目标通过利用同角三角函数变换及向量推导两角差的余弦公式,让学生体会利用联系的观点来分析问题,解决问题,提高学生逻辑推理能力和合作学习能力3、情感目标使学生经历数学知识的发现、创造的过程,体验成功探索新知的乐趣,获得对数学应用价值的认识,激发学生提出问题的意识以及努力分析问题、解决问题的激情。
五、教学重点、难点重点:通过探索得到两角差的余弦公式。
难点:探索过程的组织和适当引导。
云南省德宏州梁河县第一中学高中数学 3.1.1 两角差的余弦公式学案2 新人教版必修4

p αo y x 云南省德宏州梁河县第一中学高中数学 3.1.1 两角差的余弦公式学案2 新人教版必修4 一、学习目标1. 知道公式的由来;2. 知道公式的结构特征,并加以记忆;3. 能运用公式解答有关问题。
【重点、难点】重点:公式的推导和证明 难点:灵活运用公式解答有关问题【学习方法】合作探究、讨论、归纳二、前置作业(一)复习准备1.三角函数的定义:设α是任意角,它的终边与单位圆交于点P(x,y),那么: y =, x =,tan α=2.诱导公式:奇变偶不变,符号看象限。
如:cos(2) k πα+=, cos(90) o α-=, cos() α-=, sin() α-=3.向量的数量积:b a •= (模长形式) b a •= (坐标形式)(二)知识点学习【问题提出】我们在初中时就知道对于30°,45°,60°等特殊角的三角函数值可以直接写出,利用诱导公式还可进一步求出150°,210°等角的三角函数值. 由此我们能否得到cos15°=cos(45°-30°)=?探究1:利用特殊三角函数值探究两角差的余弦公式【问题1】设α,β为两个任意角, 你能判断cos(α-β)=cos α-cos β恒成立吗?【问题2】我们设想cos(α-β)的值与α,β的三角函数值有一定关系,填写并观察下表中的数据,你)3060cos(οο-ο60cos ο30cos ο60sin ο30sin)60120cos(οο- ο120cos ο60cos ο120sin ο60sin【问题3】一般地,你猜想cos(α-β)等于什么?探究2:利用单位圆上的三角函数线探究两角差的余弦公式【问题1】如图1,设α,β为锐角,且α>β,角α的终边与单位圆的交点为P 1,∠POP 1=β,则∠POx=α-β.过点P作PM垂直于x轴,垂足为M,那么cos(α-β)表示哪条线段长?图1【问题2】如何用线段分别表示sinβ和cosβ?【问题3】过点A作AB垂直于x轴,垂足为B,过点P作PC垂直于AB,垂足为C,为什么αP∠OxPAC==∠?1【问题4】cosαcosβ=OAcosα,它表示哪条线段长?sinαsinβ=PAsinα,它表示哪条线段长?【问题5】利用OM=OB+BM=OB+CP可得什么结论?【问题6】上述推理能说明对任意角α,β,都有cos(α-β)=cosαcosβ+sinαsinβ成立吗?探究3:利用向量的知识探究两角差的余弦公式【问题1】根据cosαcosβ+sinαsinβ的结构特征,你能联想到一个相关计算原理吗?【问题2】如图,设角α,β的终边与单位圆的交点分别为A、B,则向量OA、OB 坐标分别是什么?其数量积是什么?图2【问题3】设向量与的夹角θ,则根据数量积定义,•等于什么?【问题4】由图可知向量OB OA 与的夹角θ与α,β有什么关系?由此你可以得到什么结论?【问题5】公式cos(α-β)=cos αcos β+sin αsin β称为差角的余弦公式,记作βα-C ,该公式有什么特点?如何记忆?(三)例题讲解例1 利用差角余弦公式求cos15°的值.变式:不查表求sin75°的值.(四)目标检测1. cos110°cos20°+sin110°sin20°=2. sinxsin(x+y)+cosxcos(x+y)=3.利用公式βα-C 证明:(1)ααπsin )2cos(=- (2)ααπcos )2cos(=-(五)课堂小结配餐作业A 组题1. 习题3.1A 组1.(1)、(3);2.计算cos 80°cos 20°+sin 80°·sin 20°的值为( ).A.22B.32C.12 D .-22 B 组题1. cos 75°cos 30°+sin 75°sin 30° =2. 利用差角余弦公式求cos165°的值.C 组题不查表计算下列格式的值。
高中数学经典教案3.1.1 两角差的余弦公式

3.1.1 两角差的余弦公式
一、教学目标
●知识与技能:
(1)通过实物引例,探究发现两角差的余弦公式;
(2)理解、记忆两角差的余弦公式,(强调公式中角的任意性,公式的结构特征);
(3)学会灵活运用两角差的余弦公式化简三角函数式及求值。
●过程与方法:
通过主动探究、自主合作、相互交流,从具体事例,借助已学知识探索出数学公式,
使学生充分体会知识的发现过程,并渗透由特殊到一般,由具体到抽象的数学思想方
法。
●情感态度与价值观:
使学生体会数学的理性与严谨,了解数学来源于实际,应用于实际的唯物主义思想,
培养学生对新知识的科学态度,勇于探索和敢于创新的精神。
二、教学重点、难点
重点:两角差的余弦公式的推导及应用(化简、求值)。
难点:公式中角的任意性,学会角的变换,创造运用公式进行变换的条件。
三、教学方法与手段
教学方法:诱思探究教学法
学习方法:自主探究、观察发现、合作交流、归纳总结。
教学手段:多媒体辅助教学
四、教学过程。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
云南省德宏州梁河县一中高一数学《3.1.1 两角差的余弦公式》教学
设计湘教版必修4
一、内容及其解析
二、目标及其解析
目标:(1)掌握两角差的余弦公式,并能用之解决简单的问题。
(2)通过对公式的推导,对学生渗透探究思想、类比思想以及分类讨论思想。
解析: (1)通过两角差的余弦公式的探究及简单应用,使学生初步理解公式的结构及其功
能。
并为建立其他和(差)角公式打好基础。
(2)通过两角差的余弦公式的探究及简单应用,使学生初步理解公式的结构及其功能。
并为建立其他和(差)角公式打好基础。
三、教学问题诊断分析
过去教材曾用余弦定理证明两角差的余弦公式,虽能对学生进行思维训练,但过程繁琐,不易被学生接受。
由于向量工具的引入,新教材选择了两角差的余弦公式作为基础,这样处理使得公式的得出成为一个纯粹的代数运算,大大地降低了思考的难度,也更易于学生接受。
四、教学支持条件分析
为了加强学生对两角差的余弦公式的理解,帮助学生克服在学习过程中可能遇到的障碍,我将采用问题诱思法,探究法,演练结合法,让学生更好的理解两角差的余弦公式的理解。
五、教学过程
(一)教学基本流程
用熟悉的知识通过例题练习加
组织学生自主
(二)教学情景 1.创设情境,引出课题:问题:某城市的电视发射塔建在市郊的一座小山上。
如图所示,小山高BC 约为30米,在地平面上有一点A ,测得A,C 两点间距离约为67米,从A 观测电
视发射塔的视角(∠CAD )约为450,如何求这座电视发射塔的高度呢?问题的关键在求
()0tan 45α+的值,实质能否用,αβ的三角函数值把αβ+与αβ-的三角函数值表示出来,进一步引出课题。
2.猜想探究,发现公式:
问题1:()cos αβ-与任意角,αβ的正弦、余弦值之间有什么关系呢?
问题2:()cos αβ-会等于cos cos αβ-吗?
考察:两组数据(1),36π
π
αβ==,这时()cos ?cos ?cos ?αβαβ==-=(2)
,36π
π
αβ==-,这时()cos ?cos ?cos ?αβαβ==-=
猜想:对任意的角,αβ都有()cos cos cos sin sin αβαβαβ-=⋅+⋅成立。
3.启发联想,证明公式:
(1)探究的前提:该如何画图。
建立直角坐标系,建立单位圆,进而利用三角函数线将角α、β、α-β各自的三角函数值用图形表示出来,以研究它们的联系。
(2)探究的核心:如何在已学知识的基础上构建和论证等式cos (α-β)=cos αcos β+sin αsin β。
(3)探究的完善:公式的推导过程是否有不严谨之处呢?引导学生对上述思维过程进行反思:能否真正体现公式中角度α,β的任意性呢?
4.变式训练,掌握公式
例题1:你能利用差角余弦公式求0cos15的值吗?
变题1:你能求0sin 75的值吗?
变题2:已知4sin ,,52πααπ⎛⎫=∈ ⎪⎝⎭,求cos 4πα⎛⎫- ⎪⎝
⎭的值。
变题3:已知4sin 5α=,求cos 4πα⎛⎫- ⎪⎝
⎭的值。
例题2:已知4sin 5α=
,,2παπ⎛⎫∈ ⎪⎝⎭,5cos 13β=-,β是第三象限角,求()cos αβ-的值。
问题3:联系公式和本题的条件,要计算()cos αβ-,应作哪些准备?
5.目标检测
1、cos()2πα-=
2、()cos 2πα-=
3、已知3
cos 5α=-,(,)2π
απ∈,求cos 4πα⎛⎫
- ⎪⎝⎭的值。
4、已知15sin 17θ=,θ是第三象限角,求cos 3π
θ⎛⎫
- ⎪⎝⎭的值。
6.学生小结,教师评价:
问题4:我们学习了两角差的余弦公式,你能归纳一下本节主要的知识点吗?。
